b) ¿A qué distancia de su base llega el clavadista al agua?

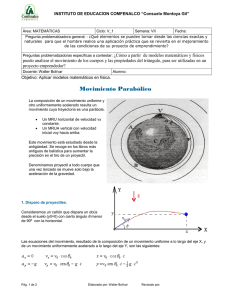
Lanzamiento horizontal: realizado por Guillermo Orozco Henao
en el siguiente enlace practicar el tema modificando las variables, también puedes profundizar
sobre el tema:
http://rsta.pucmm.edu.do/profesor/nestorc/cinematica/bombardeo/bombardeo.htm
http://rsta.pucmm.edu.do/profesor/nestorc/cinematica/parabolico/composicion/composicion.htm
ecuaciones
Vx=Vo
X=Vo.t
Vy=g.t
y=g.t2/2
Vt=√(𝑉𝑥 2 + 𝑉𝑦 2 )
Realizar los ejercicios
1.- Se arroja una piedra en sentido horizontal desde un barranco de 100 m de altura. Choca
contra el piso a 80 m de distancia de la base del barranco. ¿A qué velocidad fue lanzada?
2.- Un tigre salta en dirección horizontal desde una roca de 2 m de altura, con una rapidez de 5.5
m/s. ¿A qué distancia de la base de la roca llegará al suelo?
3.- Un clavadista corre a 1.8 m/s y se arroja horizontalmente desde la orilla de un barranco y llega
al agua 3 s después.
a) ¿Qué altura tenía el barranco?
b) ¿A qué distancia de su base llega el clavadista al agua?
4. Un piloto, volando horizontalmente a 500 m de altura y 1080 km/h, lanza una bomba. Calcular:
a)
¿Cuánto
tarda
en
oír
la
explosión?.
b)
¿A
qué
distancia
se
encontraba
el
objetivo?.
5. Un avión que vuela a 2000 m de altura con una velocidad de 800 km/h suelta una bomba
cuando
se
encuentra
a
5000
m
del
objetivo.
Determinar:
a)
¿A
qué
distancia
del
objetivo
cae
la
bomba?.
b)
¿Cuánto
tarda
la
bomba
en
llegar
al
suelo?.
c)
¿Dónde
esta
el
avión
al
explotar
la
bomba?.
6. Un proyectil es disparado desde un acantilado de 20 m de altura en dirección paralela al río,
éste hace impacto en el agua a 2000 m del lugar del disparo. Determinar:
a)
¿Qué
velocidad
inicial
tenía
el
proyectil?.
b)
¿Cuánto
tardó
en
tocar
el
agua?.
7. Una pelota esta rodando con velocidad constante sobre una mesa de 2 m de altura, a los 0,5 s
de
haberse
caído
de
la
mesa
esta
a
0,2
m
de
ella.
Calcular:
a)
¿Qué
velocidad
traía?.
b)
¿A
qué
distancia
de
la
mesa
estará
al
llegar
al
suelo?.
c)
¿Cuál
era
su
distancia
al
suelo
a
los
0,5
s?.
8. Un avión vuela horizontalmente con velocidad vA = 900 km/h a una altura de 2000 m, suelta
una bomba que debe dar en un barco cuya velocidad es vB = 40 km/h con igual dirección y
sentido.
Determinar:
a)
¿Qué
tiempo
tarda
la
bomba
en
darle
al
barco?.
b)
¿Con
qué
velocidad
llega
la
bomba
al
barco?.
c) ¿Qué distancia recorre el barco desde el lanzamiento hasta el impacto?.
d) ¿Cuál será la distancia horizontal entre el avión y el barco en el instante del lanzamiento?.
e) ¿Cuál será la distancia horizontal entre el avión y el barco en el instante del impacto?.
Movimiento Parabólico: practica y profundiza en el siguiente enlace
http://rsta.pucmm.edu.do/profesor/nestorc/cinematica/parabolico/parabolico.htm
Movimiento parabólico
Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una
parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que
no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme. También es
posible demostrar que puede ser analizado como la composición de dos movimientos rectilíneos,
un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado
vertical.
Ecuaciones
h= Ymax = Vo2.sen2θ
2g
tv = 2. Vo . sen θ
g
Xmax = Vo2 . sen (2θ)
g
Resolver los siguientes problemas:
1. Se lanza un proyectil con una velocidad inicial de 200 m/s, si el alcance es de 700m, hallar
el ángulo, la altura y el tiempo de vuelo
2. Se dispone de un cañón que forma un ángulo de 60° con la horizontal. Si la altura
alcanzada por el proyectil es de 85m, hallar la velocidad, el tiempo y el alcance.
3. Un chico patea una pelota contra un arco con una velocidad inicial de 13 m/s y tarda 2
segundos en su recorrido, hallar el ángulo, la altura y el alcance.
4. Un arquero lanza una flecha con un ángulo de 32°, si el alcance es de 250m, hallar la
velocidad, el tiempo y la altura.
5. Un cañón dispara un proyectil con una velocidad inicial de 100 m/seg, y una inclinación de
30° con respecto al horizonte. Calcular: máximo alcance horizontal. A que altura llega.
Velocidad vertical del proyectil a los 5 seg después del disparo.
6. un proyectil es disparado con un formando un ángulo de 35° con la horizontal. Llega al
suelo a una distancia de 4.000 m del cañón. Calcular: la velocidad inicial del proyectil. El
tiempo de vuelo. La máxima altura.
7. Un futbolista lanza el balón formando un ángulo de 37° con la horizontal y una velocidad
inicial de 48ft/seg. Un segundo jugador se encuentra a una distancia de 100 ft del primero en
la dirección del lanzamiento, comienza a correr hacia la pelota en dicho momento. ¿Con que
velocidad ha de hacerlo para coger el balón antes de que este llegue al suelo?
8. Un mortero dispara un proyectil con un ángulo de 53° por encima del horizontal, y una
velocidad inicial de 60 m/seg. Un tanque avanza directamente hacia el mortero sobre el
terreno horizontal a la velocidad de 3 m/seg. ¿Cuál será la distancia del mortero del tanque
para logar el blanco en el instante en que es disparado el primero?
9. ¿Cuál será la velocidad de un proyectil lanzado verticalmente hacia arriba para alcanzar
una altura de 600 m.? ¿Qué velocidad seria necesaria para alcanzar la misma altura si el
cañón formase un ángulo de 45° con la vertical? Calcúlese el tiempo necesario para alcanzar
el punto más alto en ambas trayectorias. ¿Qué distancia recorrería en dicho tiempo un avión
que volase a la velocidad de 300 Km. /h?
10. Un cañón dispara una bala con una velocidad inicial de 1 Km. /seg y un ángulo de tiro de
45°. ¿Cuál es la duración del vuelo de proyectil? ¿Qué altura máxima alcanza? ¿A que
distancia horizontal llegará?
Responder el siguiente cuestionario:
Pregunta n° 1) En el tiro parabólico ¿qué tipo de movimiento se manifiesta en el eje "x"?.
Pregunta n° 2) En el tiro parabólico ¿qué tipo de movimiento se manifiesta en el eje "y"?.
Pregunta n° 3) ¿En qué posición es nula la velocidad en el eje "y"?.
Se patea un balón que describe una trayectoria parabólica como se aprecia en la figura:
La magnitud de la aceleración en el punto A es a A y la magnitud de la aceleración en el punto
B es aB. Es cierto que
A. aA < aB
B. aA = aB = 0
C. aA > aB
D. aA = aB ≠ 0
18. De los siguientes vectores, el que corresponde a la aceleración del balón en el punto A,
es