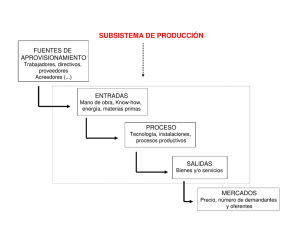
••••••••••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••••••••••• •••••••••••••••••••••••••••••••••••••••••••••• •••••• •••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••• •••• •• ••••••••••••••••••••••••••••••••••••••••••••• • •• •••••••••••••••••••••••••••••••••••••••••••••• • ••• ••••••••••••••••••••••••••••••••••••••••••••• • •• ••••••••••••••••••••••••••••••••••••••••••••••••••••••• •••••••••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••••••••••• •••••••••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••• •••••••• •••••••••••••••••••••••••• .............................................. o .... .••••••••••••••••• .· ·.·.·.·.·.·.·.·.·.·.·.·.·.·.· •·a •· r.•·1•·a · n •·•••••••••••••••••• . · · · · · · · · · · · · · · · · · •••••••••••••••• •• • •• •• • • •••••••••••••••••• ••••••••••••••••• •• • • •••••••••••••••••• •••••••••••••••••• • ••••••••••••••••••• � • •••••••••••••••••• ••••••••••••••••••••• •••••••••••••••••••• •••••••••••••••••• A / •••••••••••••••••• NALISIS ••••••••••••••••••••• •••••••••••• • ••••••••••••••••••• •••••••••••• •••••••••••••••• • • • • • • • •• •• • / ••••••••••••• M •••••••••••• ICROECONOMICO ••••••••••••••• •••••••••••• • ••••••••••••• •••••••••••• • •••••••••••••• •••••••••••• • ••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••••••••••• •••••••••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••••••••••• •••••••••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••••••••••• •••••••••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••••••••••• •••••••••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••••••••••• •••••••••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••• • •••••••••••••••••••••••••• ••••••••••••••••••••• • •••••••••••••••••••••• •••••••••••••••••••• • ••••••••••••••••••••• •••••••••••••••••• • ••••••••••••••••••• •••••••••••••••••• • •••••••••••••••••••• • • • • • • • •• • • • • • • • • • • • • • • •••••••••••••••••• •••••••••••••••• • ••••••••••••••••• ••••••••••••••• • • • • • • • •••••••••••••••••• ••••••••••••••• •••••••••••••••• •••••••••••••• • • • • • • • • • • •••••••••••••••• ••••••••• •• ••• •••••••••••••• ••••••••••••••• •••••••••••••• ••••••••••••• •••••••••••••••••••• •••••••••••••••••• ••••••••••••••••• •••••••••••••• ••••••••••••••••••••• ••••••••••••••••••••• ••••••••••••••••• .................................. • • • • • • • •••••••••••••• ••••••••••••• ••••••••••••••••• •••••••••••••• •••••••••••• •• • ••••••••••••••• ••••••••••••• • •••••••••••••• •••••••••••••• ••• • •••• •• ••• ••••••••••••••••• ••••••••••••••• •••••••••••••••••••••••••••• ••••••••••••••• •••••••••••••••••• ••••••••••••••• ••••••••••••••• ••••••••••••••••• •••••••••••••• • •••••••••••••• • ••••••••••••• •••••••••••••••• • •••••••••• ••••••••••••••••••• • •••••••• ••••••••••••••••••• •••••••• •••••••••••••••••••••• •••••• ••••••••••••••••••••••••• ••••••••••••• • •••• •••••••••••••••••••••••••••••••••••••••••• ••••• ••••••••••••••••••••••••••••••••••••••••••• ••• • •••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••••• •••••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••••••• •••••••••••••••••••••••••••••••••••••••••••••••••••• •••••••••••••••••••••••••••••••••••••••••••••••••••••• •••••••••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••••••••••• •••••••••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••••••••••• •••••••••••••••• •••••••••••••••••••• ••••••••••••••••• •••••••••••••••••• •••••••••••••••• TERCERA 'EDICIÓN ••••••••••••••••••• ••••••••••••••••• •••••••••••••••••• •••••••••••••••• ••••••••••••••••••••• •••••••••••••••••• ••••••••••••••••• • •••••••••••••••••••••••••••••••••••••••••••••••••••••• ••••••••••••••••••••••••••••••••••••••••••••••••••••••• .... . .. Hal R. Varian es profesor de economía en la University of California en Berkeley. Anteriormente ha sido profesor en el Massachusetts lnstitute of Technology y en las universidades de Michigan, Stanford, Oxford, Estocolmo y Melbourne. Es autor de Microeconomía intermedia, libro que se encuentra publicado en esta colección. ANÁLISIS MICROECONÓMICO Tercera edición HAL R. VARIAN Universidad de Michigan ANÁLISIS MICROECONÓMICO Tercera edición Traducción de Mª Esther Rabasco y Luis Toharia Universidad de Alcalá Antoni BoschÜeditor Publicado por Antoni Bosch, editor Manuel Girona, 61 - 08034 Barcelona Tel (+34) 93 206 07 30 - Fax (+34) 93 206 07 31 E-mail: [email protected] http://www.antonibosch.com © 1992, 1984, 1978, by W.W. Norton & Company, Inc. © de la edición en castellano: Antoni Bosch, editor, S.A. ISBN: 84-85855-63-9 Depósito legal: B-44.393-1998 Diseño de la cubierta: Compañía de Diseño Impresión: Liberdúplex Encuadernación: Rovira Impreso en España Printed in Spain No se permite la reproducción total o parcial de este libro, ni su incorporación a un sistema informático, ni su transmisión en cualquier forma o por cualquier medio, sea éste electrónico, mecánico, reprográfico, gramofónico u otro, sin el permiso previo y por escrito del editor. CONTENIDO 1 La tecnología Medición de los factores y de los productos 3 Descripción de la tecnoEjemplo: La logía 4 Ejemplo: Conjunto de cantidades necesarias de factores isocuanta Ejemplo: Conjunto de posibilidades de producción a corto plazo Ejemplo: La función de producción Ejemplo: La función de transformación Ejemplo: La tecnología Cobb-Douglas Análisis de Ejemplo: La tecnología de Leontief las actividades 8 Tecnologías monótonas 9 Tecnologías convexas 10 Tecnologías regulares 12 Representaciones paramétricas de la tecnología 13 La relación técnica de sustitución 14 Ejemplo: La RTS en el caso de una tecnología Cobb-Douglas La elasticidad de sustitución 16 Ejemplo: La elasticidad de sustitución en el caso de una función de producción Cobb-Douglas Los rendimientos de escala 18 Ejemplo: Los rendimientos de escala y la tecnología Cobb-Douglas Tecnologías homogéneas y homotéticas 23 Ejemplo: La función de producción CES Ejercicios 26 2 La maximización del beneficio La maximización del beneficio 31 Dificultades 35 Ejemplo: La función de beneficios en el caso de una tecnología Cobb-Douglas Propiedades de las funciones de demanda y de oferta 37 Estática comparativa a partir de las condiciones de primer orden 39 Estática comparativa a partir del álgebra 42 Recuperabilidad 44 Ejercicios 46 3 La función de beneficios Propiedades de la función de beneficios 49 Ejemplo: Los efectos de la estabilización de los precios Las funciones de oferta y demanda a partir de la función de beneficios 52 El teorema de la envolvente 54 Estática comparativa a partir de la función de beneficios 55 Ejemplo: El principio de LeChatelier Ejercicios 57 VI / CONTENIDO 4 La minimización de los costes Análisis de la minimización de los costes basado en el cálculo 59 Reconsideración de las condiciones de segundo orden 62 Dificultades 63 Ejemplo: La función de costes en el caso de la tecnología Cobb-Douglas Ejemplo: La función de costes en el caso de la tecnología CES Ejemplo: La función de costes en el caso de la tecnología de Leontief Ejemplo: La función de costes en el caso de la tecnología lineal Funciones de demandas condicionadas de factores 69 Enfoque algebraico de la minimización de los costes 72 Ejercicios 74 5 La función de costes Costes medios y marginales 77 Ejemplo: Las funciones de costes a corto plazo en el caso Cobb-Douglas Ejemplo: Los rendimientos constantes de escala y la función de costes Análisis geométrico de los costes 80 Ejemplo: Las curvas de costes en el caso de la tecnología Cobb-Douglas Las curvas de costes a largo plazo y a corto plazo 84 Los precios de los factores y las funciones de costes 86 El teorema de la envolvente en el caso de la optimización sujeta a restricciones 89 Ejemplo: Una reconsideración del coste marginal Estática comparativa a partir de la función de costes 90 Ejercicios 92 6 La dualidad La dualidad 97 Condiciones suficientes para las funciones de costes 100 Las funciones de demanda 102 Ejemplo: Utilización de la aplicación dual Ejemplo: Los rendimientos constantes de escala y la función de costes Ejemplo: La elasticidad-escala y la función de costes Análisis geométrico de la dualidad 106 Ejemplo: Las funciones de producción, las funciones de costes y las demandas condicionadas de factores Aplicaciones de la dualidad 109 Ejercicios 111 7 La maximización de la utilidad 113 Ejemplo: La existencia de una función de utilidad Ejemplo: La relación marginal de sustitución La conducta del consumidor 117 La utilidad indirecta 122 Algunas identidades importantes 126 La función de utilidad métrica monetaria 129 Ejemplo: La función de utilidad Cobb-Douglas Ejemplo: La función de utilidad CES Apéndice 134 Ejercicios 135 Las preferencias del consumidor CONTENIDO/ VII 8 La elección Estática comparativa 139 Ejemplo: Impuestos indirectos e impuestos sobre la renta La ecuación de Slutsky 142 Ejemplo: La ecuación de Slutsky en el caso Cobb-Douglas Propiedades de las funciones de demanda 146 Estática comparativa a partir de las condiciones de primer orden 147 El problema de la integrabilidad 148 Ejemplo: La integrabilidad con dos bienes Ejemplo: La integrabilidad con varios bienes Dualidad en el consumo 153 Ejemplo: Obtención de la función directa de utilidad directa La preferencia revelada 155 Condiciones suficientes para la maximización 157 Estática comparativa a partir de la preferencia revelada 160 La versión discreta de la ecuación de Slutsky 162 La recuperabilidad 164 Ejercicios 166 9 La demanda Las dotaciones en la restricción presupuestaria 171 La oferta de trabajo Funciones de utilidad homotéticas 173 Agregación de la demanda de los distintos bienes 174 La separabilidad hicksiana El modelo de dos bienes La separabilidad funcional Agregación de la demanda de los distintos consumidores 179 Funciones inversas de demanda 183 La continuidad de las funciones de demanda 184 Ejercicios 186 10 El excedente de los consumidores Variaciones compensatorias y equivalentes, 189 El excedente del consumidor 192 La utilidad cuasilineal 193 La utilidad cuasilineal y la utilidad métrica monetaria 195 El excedente del consumidor como aproximación 196 La agregación 198 Límites no paramétricos 199 Ejercicios 201 11 La incertidumbre Las loterías 203 La utilidad esperada 204 Unicidad de la función de utilidad esperada 207 Otras notaciones para expresar la utilidad esperada 208 La aversión al riesgo 208 Ejemplo: La demanda de seguro La aversión global al riesgo 213 Ejemplo: Estática comparativa de un sencillo problema de cartera La aversión relativa al Ejemplo: Fijación de los precios de los activos 221 La media la varianza de la utilidad La utilidad que y Ejemplo: riesgo VIII / CONTENIDO depende del estado de la naturaleza 223 La teoría de las probabilidades La subjetivas 224 Ejemplo: La paradoja de Allais y la paradoja de Ellsberg paradoja de Allais La paradoja de Ellsberg Ejercicios 228 12 Econometría La hipótesis de la optimización 233 Contrastación no paramétrica de la conducta maximizadora 234 Contrastación paramétrica de la conducta maximizadora 235 Imposición de restricciones a la optimización 236 Bondad del ajuste en el caso de los modelos de optimización 236 Modelos estructurales y modelos en forma reducida 238 Estimación de las relaciones tecnológicas 240 Estimación de las demandas de factores 243 Tecnologías más complejas 244 Elección de la forma funcional 245 Ejemplo: La función de costes de Diewert Ejemplo: La función de costes translogarítmica 247 Funciones de demanda de un único bien Ecuaciones múltiples Ejemplo: El sistema lineal de gasto Ejemplo: Sistemas SCID Resumen 250 Estimación de las demandas de los consumidores 13 Los mercados competitivos La empresa competitiva 253 El problema de la maximización del beneficio 254 La función de oferta de la industria 256 Ejemplo: Funciones de costes diferentes Ejemplo: Funciones de costes idénticas Equilibrio del mercado 257 Ejemplo: Empresas idénticas La entrada 258 Ejemplo: La entrada y el equilibrio a largo plazo Economía del bienestar 260 Análisis del bienestar 261 Varios consumidores 263 La eficiencia en el sentido de Pareto 265 Eficiencia y bienestar 266 El modelo de los bienes discretos 267 Impuestos y subvenciones 268 Ejercicios 270 14 El monopolio Casos especiales 278 Estática comparativa 278 Bienestar y producción 280 Elección de la calidad 281 La discriminación de precios 284 La discriminación de precios de primer grado 286 La discriminación de precios de segundo grado 287 Ejemplo: Análisis gráfico La discriminación de precios de tercer grado 292 Consecuencias para el bienestar Ejercicios 298 CONTENIDO/ IX 15 La teoría de los juegos EjemDescripción de un juego 301 Ejemplo: El juego de las dos monedas Ejemplo: El plo: El dilema del prisionero Ejemplo: El duopolio de Cournot La formulación de modelos económicos de las eleccioduopolio de Bertrand nes estratégicas 309 Las soluciones posibles 310 El equilibrio de Nash 311 Ejemplo: Cálculo de un equilibrio de Nash Interpretación de las estrategias mixtas 315 Juegos repetidos 316 Ejemplo: Mantenimiento de un cártel Refinamientos del equilibrio de Nash 319 Estrategias dominantes 319 Eliminación de las estrategias dominantes 320 Juegos consecutivos 321 Ejemplo: Un sencillo modelo de negociación Juegos repetidos y perfección de los subjuegos 326 Juegos con información incompleta 327 Ejemplo: Una subasta en la que las ofertas son secretas Análisis del equilibrio de Bayes-Nash 330 Ejercicios 331 16 El oligopolio El equilibrio de Cournot 335 La estabilidad del sistema Estática comparativa 339 Varias empresas 340 El bienestar El equilibrio de Bertrand 342 Ejemplo: Un modelo de ventas Bienes complementarios y sustitutivos 345 El liderazgo en la elección del precio 350 Clasificación y elección de los modelos 353 Conjetura sobre las variaciones 354 La colusión 356 Juegos repetidos 357 Juegos consecutivos 360 Fijación de un precio límite 362 Ejercicios 364 17 El intercambio Agentes y bienes 368 El equilibrio walrasiano 369 Análisis gráfico 370 La existencia de equilibrios walrasianos 371 Existencia de un equilibrio 373 Ejemplo: La economía Cobb-Douglas El primer teorema de la economía del bienestar 378 El segundo teorema del bienestar 382 Un razonamiento basado en la preferencia revelada La eficiencia en el sentido de Pareto y el cálculo 385 La maximización del bienestar 389 Ejercicios 393 X/ CONTENIDO 18 La producción La conducta de la empresa 397 Dificultades 399 La conducta del consumidor 400 La oferta de trabajo La distribución de los beneficios La demanda agregada 402 La existencia de un equilibrio 403 Propiedades del equilibrio desde el punto de vista del bienestar 405 Un razonamiento basado en la preferencia revelada Análisis del bienestar en una economía productiva 408 Análisis gráfico 409 Ejemplo: La economía Cobb-Douglas con rendimientos constantes de escala Ejemplo: Una economía con rendimientos decrecientes de escala El teorema de la no sustitución 415 La estructura de la industria en condiciones de equilibrio general 417 Ejercicios 418 19 El tiempo Preferencias intertemporales 421 La optimización intertemporal con dos periodos 422 La optimización intertemporal con varios periodos 424 El equilibrio general a lo largo del tiempo Ejemplo: La utilidad logarítmica 426 El horizonte infinito El equilibrio general con respecto a los diferentes estados de la naturaleza 429 Ejercicios 430 20 Los mercados de activos El equilibrio en ausencia de incertidumbre El equilibrio en presencia de incertidumbre Notación 435 Modelo de fijación del precio de los activos de capital 436 La teoría de la fijación de los precios basada en el arbitraje 442 Dos factores El riesgo específico de los activos La utilidad esperada 445 Ejemplo: La utilidad esperada y la TPA Mercados completos 448 El arbitraje puro 451 Apéndice 452 Ejercicios 453 21 Análisis del equilibrio El núcleo de una economía de intercambio 455 La convexidad y el tamaño de la economía 461 La unicidad del equilibrio 463 Los sustitutivos brutos El análisis basado en los índices La dinámica del equilibrio general 467 Los procesos de tanteo 468 Los procesos no basados en el tanteo 471 Ejercicios 473 CONTENIDO / XI 22 El bienestar El criterio de la compensación 475 Las funciones de bienestar impuestos óptimos 482 Ejercicios 484 481 Los 23 Los bienes públicos Provisión eficiente de un bien público discreto 488 Provisión privada de un bien público discreto 490 Determinación de la cantidad de un bien público discreto por medio de una votación 491 Provisión eficiente de un bien público continuo 491 Ejemplo: Determinación de la provisión eficiente de un bien público Provisión privada de un bien público continuo 494 Ejemplo: Determinación de la cantidad del bien público correspondiente al equilibrio de Nash Las votaciones 498 Ejemplo: La utilidad cuasilineal y la votación Asignaciones de Lindahl 500 Mecanismos de revelación de la demanda 501 Mecanismos de revelación de la demanda con un bien continuo 503 Ejercicios 504 24 Las extemalidades Un ejemplo de extemalidad en la producción 507 Soluciones para resolver el problema de las extemalidades 508 Los impuestos pigouvianos Ausencia de mercados Derechos de propiedad El mecanismo de la compensación 511 Las condiciones de eficiencia en presencia de extemalidades 513 Ejercicios 514 25 La información El problema del principal y el agente 517 Información completa: la solución 521 monopolística 519 Información completa: la solución competitiva Acciones ocultas: la solución monopolística 523 Es posible observar la acción del agente Análisis del sistema óptimo de incentivos Ejemplo: Estática comparativa Ejemplo: Modelo del principal y el agente con una utilidad que sólo depende de la media y la varianza Acciones ocultas: El mercado competitivo 533 Ejemplo: El riesgo moral en los mercados de seguros Información oculta: El monopolio 536 El equilibrio del mercado: información oculta 543 Ejemplo: Un ejemplo algebraico La selección adversa 546 El mercado de "cacharros" y la selección adversa 549 Las señales 550 La educación como señal 551 Ejercicios 552 XII / CONTENIDO 26 Matemáticas El álgebra lineal 555 Matrices definidas y semidefinidas 557 Comprobación de que una matriz es definida La regla de Cramer 559 Análisis 560 Cálculo 561 Derivadas de orden superior Gradientes y planos tangentes 562 Límites 563 Conjuntos convexos ferenciales parciales 568 Funciones homogéneas 564 Funciones afines 565 Hiperplanos separadores 565 Ecuaciones diSistemas dinámicos 567 Variables aleatorias 565 566 27 La optimización La optimización de una única variable 571 Las condiciones de primer y segundo orden Ejemplo: Las condiciones de primer y segundo orden La concavidad El teorema de la envolvente Ejemplo: La función de valor Ejemplo: El teorema de la envolvente Estática comparativa Ejemplo: Estática comparativa en el caso de un problema específico La maximización multivariante 577 Las condiciones de primer y segundo orden Estática comparativa Ejemplo: Estática comparativa Convexidad y concavidad Funciones cuasicóncavas y cuasiconvexas Maximización sujeta a restricciones 581 Una condición de segundo orden alternativa 583 Cómo recordar las condiciones de segundo orden El teorema de la envolvente La maximización sujeta a restricciones que son desigualdades 588 Formulación de los problemas de Kuhn-Tucker 590 Existencia y continuidad de un máximo 591 Respuestas Bibliografía 593 623 Índice analítico 631 PREFACIO La primera edición de Análisis microeconómico se publicó en 1977. Transcurridos 15 años desde entonces, he pensado que ya era hora -quizá sobradamente- de someterla a una profunda revisión. En esta edición he realizado dos tipos de cambios: de estructura y de contenido. Los cambios estructurales consisten en una significativa reorganización del material en capítulos "modulares". Estos capítulos tienen, en su mayoría, el mismo título que los capítulos correspondientes de mi libro de texto Microeconomía intermedia, lo que facilitará al estudiante el uso del libro más elemental para repasar los ternas estudiados. También es posible hacer lo contrario: si un estudiante del libro intermedio desea profundizar más en un terna, es fácil recurrir al capítulo correspondiente de Análisis microeconómico. He observado que esta estructura por módulos tiene otras dos ventajas: es fácil recorrer el libro siguiendo distintos órdenes y resulta posible utilizarlo corno referencia. Además de esta reorganización, he realizado varios cambios de contenido. En primer lugar, he escrito de nuevo una parte considerable del libro. Ahora la exposición es menos concisa y confío en que más accesible. En segundo lugar, he actualizado una gran parte del contenido. En concreto, he actualizado totalmente la parte dedicada al monopolio y al oligopolio, de acuerdo con los grandes avances realizados en los años ochenta en la teoría de la organización industrial. En tercer lugar, he añadido una gran cantidad de ternas nuevos. La presente edición contiene capítulos dedicados a la teoría de los juegos, los mercados de activos y la información. Estos capítulos pueden ser buenos para presentar estos ternas a los estudiantes que afrontan por primera vez un curso de microeconomía superior. No he intentado profundizar en ellos, ya que he observado que es mejor hacerlo en cursos especializados de nivel más avanzado, una vez dominados los instrumentos convencionales del análisis económico. En cuarto lugar, he añadido algunos ejercicios nuevos, así corno las respuestas completas de todos los problemas impares. Debo decir que no estoy muy seguro de la conveniencia de dar las respuestas en el libro, pero confío en que la mayoría de los estudiantes de tercer ciclo tendrán suficiente fuerza de voluntad para no mirarlas hasta no haber intentado resolver ellos mismos los problemas. 2 / PREFACIO Organización del libro Como ya he señalado antes, el libro está organizado en una serie de capítulos breves. Sospecho que casi todo el mundo querrá estudiar sistemáticamente la primera parte del libro, puesto que describe los instrumentos fundamentales de la microeconomía que son útiles para todos los economistas. En la segunda mitad se introduce una serie de temas específicos de microeconomía. La mayoría de los profesores que utilicen el libro desearán elegir algunos de ellos. Unos querrán hacer hincapié en la teoría de los juegos; otros en el equilibrio general. Unos cursos dedicarán mucho tiempo a los modelos dinámicos; otros dedicarán varias semanas a la economía del bienestar. Dado que sería imposible analizar en profundidad todos estos temas, he decidido ofrecer una introducción a los mismos. He tratado de utilizar la notación y los métodos descritos en la primera parte del libro, a fin de que estos capítulos faciliten la comprensión de los análisis más especializados de otros libros o artículos de revista. Afortunadamente, en la actualidad existen vario� libros en los que se analizan extensamente los mercados de activos, la teoría de los juegos, la economía de la información y la teoría del equilibrio general. Al estudiante serio no le faltará material bibliográfico en el que poder estudiar estos temas. Agradecimientos Muchas persomas me han escrito a lo largo de estos años indicándome algunas erratas y haciéndome comentarios y sugerencias. He aquí una lista parcial de los nombres: Gordon Brown, John Chilton, Peter Diamond, Maxim Engers, Mario Forni, David Mauleg, Archie Rosen, Knut Sydsater y A. J. Talman. Si tuviera un sistema de archivo mejor, probablemente habría más nombres. Agradezco que me indiquen las erratas que pueda haber, para corregirlas en la medida de lo posible en la siguiente impresión. Algunas personas también me han hecho sugerencias sobre la tercera edición; entre ellas cabe citar a Eduardo Ley, Pat Reagan y John Weymark. A Eduardo Ley se deben también algunos de los ejercicios y de las respuestas. Por último, deseo terminar haciendo un comentario al estudiante. Cuando lea este libro, es importante que no olvide las palabras inmortales de Sir Richard Steele (1672-1729): "Debe tenerse en.cuenta que si algunas de las partes de este artículo parecen aburridas, es por alguna razón". AnnArbor Noviembre de 1991 1. LA TECNOLOGÍA La manera más sencilla y más habitual de describir la tecnología de una empresa es mediante la función de producción, que se estudia, por lo general, en los cursos intermedios. Sin embargo, las tecnologías de las empresas se pueden estudiar de otras formas que son más generales y más útiles en determinados contextos. En este capítulo analizaremos algunas de las formas de representar las posibilidades de producción de la empresa, así como la manera de describir aquellos aspectos de la tecnología de la empresa que son importantes desde el punto de vista económico. 1.1 Medición de los factores y de los productos Una empresa produce bienes utilizando distintas combinaciones de factores. Para estudiar sus decisiones, necesitamos contar con un buen instrumento que nos permita resumir sus posibilidades de producción, es decir, las combinaciones de factores y de productos que son tecnológicamente viables. Normalmente lo más satisfactorio es imaginar que los factores y los productos se miden en flujos: para obtener un determinado nivel de producción por unidad de tiempo se necesita una determinada cantidad de factores por unidad de tiempo. Es aconsejable incluir explícitamente una dimensión temporal en la descripción de los factores y de productos. De esa manera, habrá menos probabilidades de que el lector utilice unidades inconmensurables, de que confunda los stocks y los flujos o de que cometa otros errores elementales. Por ejemplo, si medimos el tiempo de trabajo en horas semanales, querremos estar seguros de que medimos los servicios de capital en horas semanales y la producción en unidades semanales. Sin embargo, cuando se analizan las decisiones tecnológicas en abstracto, como hacemos en este capítulo, suele omitirse la dimensión temporal. Es posible que queramos distinguir también los factores y los productos según la fecha del calendario, el lugar e incluso las circunstancias en las que puede disponerse 4 / LA TECNOLOCÍA ( C. 1) de ellos. Definiendo los factores y los productos en relación con el momento y el lugar en el que puede disponerse de ellos, podemos recoger algunos aspectos del carácter temporal o espacial de la producción. Por ejemplo, el hormigón disponible en un determinado año puede utilizarse para construir un edificio que se terminará un año más tarde. Del mismo modo, el hormigón comprado en un lugar puede utilizarse para producir en algún otro. Una cantidad del factor "hormigón" debe entenderse como una cantidad de hormigón de una determinada clase, disponible en un determinado lugar y en un determinado momento. En algunos casos, podríamos añadir incluso a esta lista algunas matizaciones como "si el tiempo está seco"; es decir, podríamos considerar las circunstancias, o sea el estado de la naturaleza, en las que puede disponerse del hormigón. El grado de detalle que utilicemos al describir los factores y los productos dependerá del problema de que se trate, pero no debemos olvidarnos de que el grado de detalle con que puede describirse un determinado factor o producto puede llegar a ser arbitrariamente muy elevado. 1.2 Descripción de la tecnología Supongamos que la empresa tienen bienes que pueden servir de factores a la vez que de productos. Si una empresa utiliza y} unidades del bien j como factor y produce yJ del bien como producto, la producción neta del bienj vendrá dada por Yi = yJ-yj. Si la producción neta del bien j es positiva, la empresa está produciendo una cantidad de dicho bien mayor que la que utiliza como factor; si es negativa, está utilizando una cantidad del bien j mayor que la que produce. Un plan de producción es simplemente una lista de las producciones netas de distintos bienes. Puede representarse por medio de un vector y en R", donde Yi es negativo si el bien j-ésimo se utiliza como factor neto y positivo si el bien j-ésimo es un producto neto. El conjunto de todos los planes de producción tecnológicamente viables se denomina conjunto de posibilidades de producción de la empresa y se representa por medio del símbolo Y, que es un subconjunto de R": Se supone que el conjunto Y describe todas las combinaciones de factores y productos que son tecnológicamente viables. Nos da una descripción completa de las posibilidades tecnológicas de la empresa. Cuando se estudia la conducta de una empresa en determinados entornos económicos, es posible que se quiera distinguir entre los planes de producción que son "inmediatamente viables" y los que pudieran serlo en algún momento. Por ejemplo, a corto plazo algunos factores de la empresa son fijos, por lo que sólo son posibles los planes de producción compatibles con estos factores fijos. A largo plazo, algunos factores pueden ser variables, por lo que las posibilidades tecnológicas de la empresa pueden muy bien cambiar. Descripción de la tecnología / 5 Supondremos, por lo general, que estas restricciones pueden describirse por medio de un vector z en R", Por ejemplo, z podría ser una lista de la cantidad máxima de los distintos factores y productos que pueden obtenerse en el periodo de tiempo que esté considerándose. El conjunto de posibilidades de producción restringido o a corto plazo se representa por medio de Y(z); consiste en todas las combinaciones de producciones netas viables compatibles con el nivel de restricción z. Supongamos, por ejemplo.ique el factor n es fijo e igual a fr a corto plazo. En ese caso, Y(yn) = {y en Y : Yn = Yn}· Obsérvese que Y(z) es un subconjunto de Y, ya que está formado por todos los planes de producción que son viables -lo que significa que pertenece a Y - y que también satisfacen algunas condiciones adicionales. Ejemplo: Conjunto de cantidades necesarias de factores Supongamos que estamos analizando el ejemplo de una empresa que produce un único bien. En este caso, expresamos la combinación de producciones netas de la manera siguiente: (y, - x), donde x es un vector de factores que puede generar y unidades de producción. Podemos definir entonces un caso especial de un conjunto restringido de posibilidades de producción, que es el conjunto de cantidades necesarias de factores: V(y) = { x en R� : (y, -x) pertenece a Y} El conjunto de cantidades necesarias de factores es el conjunto de todas las combinaciones de factores que generan al menos y unidades de producción. Obsérvese que tal como se define aquí, este conjunto mide los factores por medio de números positivos y no por medio de números negativos, como sucede en el caso del conjunto de posibilidades de producción. Ejemplo: La isocuanta En el caso anterior, también podemos definir una isocuanta: Q(y) = {x en R�: x pertenece a V(y) y x no pertenece a V(y') cuando y' > y} · La isocuanta nos indica todas las combinaciones de factores que generan exactamente y unidades de producción. 6 / LA TECNOLOGÍA (C. 1) Ejemplo: Conjunto de posibilidades de producción a corto plazo Supongamos que una empresa obtiene un determinado nivel de producción a partir de trabajo y de algún tipo de máquina que denominaremos "capital". En ese caso, los planes de producción serán del tipo (y, -l, -k), donde y es el nivel de producción, l es la cantidad de trabajo y k es la cantidad de capital. Imaginamos que la cantidad de trabajo puede alterarse de forma inmediata, pero que el capital es fijo e igual a k a corto plazo. En ese caso, Y(k) = {(y, -l, -k) en Y: k = k} es un ejemplo de un conjunto de posibilidades de producción a corto plazo. Ejemplo: La función de producción Si la empresa produce un único bien, la función de producción puede definirse de la manera siguiente: j(x) ={yen R: y es el nivel máximo de producción correspondiente a - x en Y} Ejemplo: La función de transformación La función de producción tiene un análogo n-dimensional que nos resultará útil para estudiar la teoría del equilibrio general. Un plan de producción y en Y es (tecnológicamente) eficiente si no existe otro plan y' en Y tal que y' 2: y; es decir, un plan de producción es eficiente si no es posible obtener un nivel de producción más elevado con la misma cantidad de factores o el mismo nivel con una cantidad menor (obsérvese la utilización que se hace aquí de la convención en cuanto a los signos de las cantidades de factores). A menudo suponemos que es posible describir el conjunto de planes de producción tecnológicamente eficientes por medio de una función de transformación T : H" � R, donde T(y) = O si y sólo si y es eficiente. De la misma manera que la función de producción selecciona el máximo nivel escalar en función de las cantidades de factores, la función de transformación selecciona los máximos vectores de producciones netas. Ejemplo: La tecnología Cobb-Douglas Sea a un parámetro tal que O < a < l. En ese caso, la tecnología Cobb-Douglas se define de la siguiente manera. Véase la figura 1. lA. Descripción de la tecnología / 7 Y ={(y, -x1, -x2) en R3: y� x1x}-ª} R¡: y� x1x}-ª} Q(y) ={(x1, x2) en R¡: y= x1x}-ª} V(y) ={(x1, x2) en Y(z) ={ (y, -x1, -x2) en R3 : y � x1x}-ª, x2 = z} T( y,x1,x2 ) =y- x1ax21-a f( x1, x2 ) =x1a X21-a Ejemplo: La tecnología de Leontief Sean a > O y b > O los parámetros. En ese caso, la tecnología de Leontief se define de la siguiente manera. Véase la figura 1.1 B. Y ={(y, -x1, -x2) en R3: y� minícz}, bx2)} R¡ : y� min(ax1, bx2)} Q(y) ={ (x1, x2) en R¡ : y = miníczj , bx2)} V(y) ={(x1, x2) en T(y, x1, x2) =y - min(ax1, bx2) J (x1, x2) = min(ax1, bx2) Figura 1.1 FACTOR 2 FACTOR 2 Q(y2) //J ,,/�::�;e���)a/b ------- Q(y1) �---O(yi) FACTOR 1 A FACTOR 1 B La tecnología Cobb-Douglas y la tecnología de Leontief. El panel A representa la forma general de una tecnología Cobb-Douglas y el B la forma general de una tecnología de Leontief. En este capítulo nos referimos principalmente a las empresas que producen un único bien, por lo que generalmente describimos su tecnología por medio de los 8/ LA TECNOLOCÍA (C. 1) conjuntos de cantidades necesarias de factores o de las funciones de producción. Más adelante utilizamos el conjunto de producción y la función de transformación. 1.3 Análisis de las actividades La manera más sencilla de describir los conjuntos de producción o los conjuntos de cantidades necesarias de factores consiste simplemente en enumerar los planes de producción viables. Supongamos, por ejemplo, que podemos producir un bien utilizando los factores 1 y 2 y dos actividades o técnicas diferentes: Técnica A: una unidad del factor 1 y dos del factor 2 generan una unidad de producción. Técnica B: dos unidades del factor 1 y una del factor 2 generan una unidad de producción. Supongamos que el producto es el bien 1 y que los factores son los bienes 2 y 3. En ese caso, podemos representar las posibilidades de producción que implican estas dos actividades por medio del conjunto de producción Y= {O, -1, -2), O, -2, -1)} o del conjunto de cantidades necesarias de factores V(1) = {O, 2), (2, 1)}. La figura 1.2A representa este conjunto de cantidades necesarias de factores. Podría ocurrir que para obtener y unidades de producción pudiéramos utilizar simplemente y veces esas cantidades de cada uno de los factores, siendo y = 1, 2, ... En este caso, podríamos pensar que el conjunto de maneras viables de obtener y unidades de producción se definiría de la siguiente manera: V(y) = { (y, 2y), (2y, y)} Sin embargo, este conjunto no comprende todas las posibilidades relevantes. Es cierto que (y, 2y) genera y unidades de producción si utilizamos la técnica A y que (2y, y) genera y unidades de producción si utilizamos la técnica B, pero ¿qué ocurre si utilizamos una mezcla de las dos? En este caso, hemos de suponer que YA es la cantidad de producción que se obtiene utilizando la técnica A e y B es la que se obtiene utilizando la técnica B. En ese caso, V(y) viene dado por el conjunto Tecnologías monótonas / 9 Así, por ejemplo, V(2) = {(2, 4), (4, 2), (3, 3)}, tal como se describe en la figura 1.2B. Obsérvese que la combinación de factores (3, 3) puede generar dos unidades de producción produciendo una mediante la técnica A y la otra mediante la B. Figura 1.2 FACTOR2 FACTOR 2 4 4 3 3 2 • 1 • 2 • 2 FACTOR2 3 4 FACTOR 1 A 1 2 • 3 •• 4 3 • 4 2 FACTOR 1 1 2 B Conjuntos de cantidades necesarias de factores. El panel A describe V(2); y el C, V(y) en el caso en el que y tiene un valor más alto. •• •• 3 4 • FACTOR 1 e V(l); el B, 1.4 Tecnologías monótonas Continuemos examinando el ejemplo de dos actividades presentado en el apartado anterior. Supongamos que tuviéramos el vector de factores (3, 2). ¿Sería suficiente para obtener una unidad de producción? Podríamos argumentar que lo sería, puesto que podríamos desprendernos de 2 unidades del factor 1 y nos quedaríamos con (1, 2). Por lo tanto, si es posible la libre eliminación, es razonable afirmar que si x es una manera viable de obtener y unidades de producción y x' es un vector de factores que tiene como mínimo la misma cantidad de cada uno de los factores, x' debe ser una manera viable de producir y. Por lo tanto, los conjuntos de cantidades necesarias de factores deben ser monótonos en el sentido siguiente: Monotonicidad. Si x pertenece a V(y) y x' 2: x, entonces x' pertenece a V(y). Si suponemos que los conjuntos de cantidades necesarias de factores son monótonos, los que están representados en la figura 1.2 se convierten en los conjuntos representados en la 1.3. La monotonicidad también suele ser un buen supuesto en el caso de los conjuntos de producción. En este contexto, suponemos, por lo general, que si y pertenece a Y e y' :=::; y, y' también debe pertenecer a Y. Obsérvese la utilización que se hace aquí de la convención en cuanto a los signos de las cantidades de factores. Si y' :=::; y, 10 / LA TECNOLOGÍA (C. 1) significa que cada uno de los componentes del vector y' es menor o igual que el componente correspondiente de y, lo cual quiere decir que el plan de producción representado por y' genera una cantidad igual o menor de todos los bienes utilizando al menos la misma cantidad de todos los factores, en comparación con y. Es natural suponer, pues, que si y es viable, también lo será y'. Figura 1.3 FACTOR 2 FACTOR2 FACTOR2 4 4 4 3 3 3 2 2 2 1 2 3 4 FACTOR 1 A 1 2 3 4 FACTOR 1 B 1 2 3 e 4 FACTOR 1 Monotonicidad. He aquí los tres mismos conjuntos de cantidades necesarias de factores si también suponemos que son monótonos. 1.5 Tecnologías convexas Veamos ahora cómo es el conjunto de cantidades necesarias de factores si queremos obtener 100 unidades de producción. Como primer paso, podríamos argumentar que si multiplicamos los vectores (1, 2) y (2, 1) por 100, deberíamos ser capaces de repetir exactamente lo que hemos hecho antes y, por lo tanto, producir 100 veces más. Es evidente que no todos los procesos de producción tienen por qué permitir este tipo de repetición, pero parece plausible en muchas circunstancias. Si es posible la repetición, podemos extraer la conclusión de que (100, 200) y (200, 100) pertenecen a V(lOO). ¿Es posible obtener 100 unidades de producción de alguna otra manera? Podríamos utilizar 50 procesos de la actividad A y 50 de la B. En ese caso, necesitaríamos 150 unidades del bien 1 y 150 del 2 para obtener 100 unidades de producción; por lo tanto, (150, 150) debe pertenecer al conjunto de cantidades necesarias de factores. También podríamos utilizar 25 procesos de la actividad A y 75 de la B. Eso implicaría que o, 25(100, 200) + o, 75(200, 100) = (175, 125) debe pertenecer a V(lOO). En términos más generales, Tecnologías convexas / 11 t(lOO, 200) + (1 - t)(200, 100) = (lOOt + 200(1 - t), 200t + (1 - t)lOO) debe pertenecer a V(lOO), si t = O, O, 01, O, 02, ... , l. También podríamos permitir que t adoptara un valor cualquiera comprendido entre O y 1, lo cual es una aproximación obvia. En ese caso, el conjunto de producción adoptaría la forma representada en la figura 1.4A. En la siguiente definición presentamos una formulación precisa de esta propiedad. Convexidad. Si x y x' pertenecen a V(y), tx + (1 - t)x' pertenece a V(y) cualquiera que sea t tal que O :=:; t ::::; 1. Es decir, V (y) es un conjunto convexo. Figura 1.4 FACTOR2 FACTOR2 250 250 200 200 150 150 100 100 50 50 50 150 250 A FACTOR 1 50 150 250 FACTOR 1 B Conjuntos de producción convexos. Cuando decimos que V(y) es convexo, significa que si x y x' pueden generar y unidades de producción, cualquier media ponderada tX + (1 - ox' también puede generar y unidades de producción. El panel A representa un conjunto de producción convexo con dos actividades subyacentes y el B un conjunto de producción convexo con muchas actividades subyacentes. Hemos justificado el supuesto de la convexidad mediante el argumento de la repetición. Si queremos obtener un" gran" volumen de producción y podemos repetir "pequeños" procesos de producción, parece que debemos suponer que la tecnología es convexa. Sin embargo, si la escala de las actividades subyacentes es grande en relación con la cantidad deseada de producción, es posible que la convexidad no sea una hipótesis razonable. Sin embargo, también existen otros argumentos por los que la convexidad es un supuesto razonable en algunas circunstancias. Supongamos, por ejemplo, que 12 / LA TECNOLOGÍA ( C. 1) estamos analizando la producción mensual. Si un vector de factores x genera y unidades de producción al mes y otro vector x' también genera la misma cantidad, podríamos utilizar x durante la mitad del mes y x' durante la otra mitad. Si la introducción de cambios en los planes de producción a mitad del mes no plantea problemas, es razonable esperar que se obtengan y unidades de producción. Hemos aplicado los argumentos anteriores a los conjuntos de cantidades necesarias de factores, pero también pueden aplicarse al conjunto de producción. Normalmente se supone que si y e y' pertenecen ambos a Y, ty + (1- t)y' también pertenece a Y si O :::; t :::; 1; en otras palabras, Y es un conjunto convexo. Debe señalarse, sin embargo, que la convexidad del conjunto de producción es una hipótesis que plantea muchos más problemas que la convexidad del conjunto de cantidades necesarias de factores. Por ejemplo, la convexidad del conjunto de producción excluye los "costes iniciales" y otros tipos de rendimientos de escala. Esta cuestión se analizará en seguida con mayor detalle. De momento describimos unas cuantas relaciones entre la convexidad de V(y), la curvatura de la función de producción y la convexidad de Y. Si un conjunto de producción es convexo, también lo es el conjunto de cantidades necesarias de factores. Si el conjunto de producción Y es convexo, también lo es el conjunto de cantidades necesarias de factores correspondiente, V(y). Demostración. Si Y es un conjunto convexo, entonces, dados unos vectores cualesquiera x y x' tales que (y, -x) y (y, -x') pertenecen a Y, (ty + (1- t)y, -tx - (1- t)x') debe pertenecer a Y. Eso equivale simplemente a exigir que (y, -(tx + (1 - t)x')) pertenezca a Y. Por lo tanto, si x y x' pertenecen a V(y), tx + (1 - t)x' pertenece a V(y), lo que demuestra que V(y) es convexo. Un conjunto de cantidades necesarias de factores convexo equivale a una función de producción cuasicóncava. V (y) es un conjunto convexo si y sólo si la función de producción f (x) es una función cuasicóncava. Demostración. V(y) = {x: f(x) �y}, que es precisamente el conjunto de puntos del contorno superior de f(x). Pero la función es cuasicóncava si y sólo si el conjunto de puntos del contorno superior es convexo; véase el capítulo 27, página 575. 1.6 Tecnologías regulares Examinemos, por último, una condición débil de regularidad en relación con V(y). Regularidad. V(y) es un conjunto no vacío y cerrado cualquiera que sea y � O. Representaciones paramétricas de la tecnología / 13 El supuesto según el cual V(y) es un conjunto no vacío exige que exista alguna manera razonable de obtener un nivel cualquiera de producción, a fin de evitar simplemente tener que añadir una y otra vez matizaciones como "suponiendo que es posible producir y". El supuesto según el cual V(y) es un conjunto cerrado se postula por razones técnicas y es inocuo en la mayoría de los contextos. Una de sus implicaciones es la siguiente: supongamos que tenemos una sucesión (xi) de combinaciones de factores que pueden producir cada una y y que esta sucesión converge en la combinación de factores x''. Es decir, las combinaciones de factores de la sucesión se aproxima arbitrariamente a x''. Si V (y) es un conjunto cerrado, esta combinación límite x0 debe ser capaz de producir y. Dicho de una manera aproximada, el conjunto de cantidades necesarias de factores debe "contener su propia frontera". 1.7 Representaciones paramétricas de la tecnología Supongamos que podemos obtener un determinado nivel de producción de muchas maneras distintas. En ese caso, quizá sea razonable resumir este conjunto de factores por medio de un conjunto de cantidades necesarias de factores "alisado" como el de la figura 1.5. Es decir, quizá queramos trazar una curva sin esquinas que pase por todos los puntos posibles de producción. Este proceso de alisamiento no debe plantear grandes problemas si es posible obtener, de hecho, un determinado nivel de producción de muchas maneras poco diferentes entre sí. Si seguimos ese procedimiento para "alisar" el conjunto de cantidades necesarias de factores, es natural que busquemos la manera de representar la tecnología por medio de una función paramétrica que contenga un reducido número de parámetros desconocidos. Por ejemplo, la tecnología Cobb-Douglas antes mencionada implica que cualquier combinación de factores (x1, x2) que satisfaga la condición x1 x� � y puede generar al menos y unidades de producción. No debe pensarse que estas representaciones tecnológicas paramétricas son necesariamente tina descripción literal de las posibilidades de producción. Las posibilidades de producción son los datos suministrados por los ingenieros que describen los planes de producción físicamente posibles. Podría muy bien ocurrir que estos datos pudieran describirse razonablemente bien por medio de una útil forma funcional como la función Cobb-Douglas. En ese caso, este tipo de descripción paramétrica podría resultar sumamente útil. En la mayoría de los casos sólo nos interesa disponer de una aproximación paramétrica de la tecnología correspondiente un determinado invervalo de niveles de factores y de producción, para lo cual es normal utilizar formas funcionales relativamente sencillas. Estas representaciones paramétricas son muy útiles como instrumentos pedagógicos, por lo que las utilizaremos a menudo para representar 14 / LA TECNOLOCÍA (C. 1) nuestras tecnologías. De esa manera podremos introducir los instrumentos del cálculo diferencial y el álgebra para analizar las decisiones de producción de la empresa. Figura 1.5 FACTOR2 1 1 1 1 \ \ \ \ --- ----FACTOR 1 Alisamiento de una isocuanta. Un conjunto de cantidades necesarias de factores y una aproximación "lisa" de la misma. 1.8 La relación técnica de sustitución Supongamos que tenemos una tecnología resumida por una función de producción lisa y que estamos produciendo en el punto y* = f(xj, x2). Supongamos, además, que queremos aumentar la cantidad del factor 1 y reducir la del 2 con el fin de mantener constante el nivel de producción. ¿Cómo podemos determinar esta relación técnica de sustitución entre estos dos factores? En el caso bidimensional, la relación técnica de sustitución no es más que la pendiente de la isocuanta: cómo hemos de ajustar x2 para mantener constante el nivel de producción cuando x1 varía en una pequeña cantidad, como muestra la figura 1.6. En el caso en el que hay n dimensiones, la relación técnica de sustitución es la pendiente de una superficie isocuanta medida en una determinada dirección. Sea x2(x1) la función (implícita) que nos dice qué cantidad se necesita de x2 y si estamos utilizando x1 unidades del otro factor. En ese caso, por producir para definición, la función x2(x1) debe satisfacer la siguiente identidad: Estamos buscando una expresión para 8x2(xj) / 8x1. Diferenciando la identidad anterior, tenemos que La relación técnica de sustitución / 15 o sea a f(x*)/8x1 8f(x*)/8x2 · De esa manera, tenemos una expresión explícita de la relación técnica de sustitución. Figura 1.6 FACTOR2 Pendiente = RTS FACTOR 1 La relación técnica de sustitución. La relación técnica de sustitución indica cómo debe ajustarse uno de los factores para mantener constante el nivel de producción cuando varía el otro. Existe otra manera de obtenerla. Pensemos en un vector de (pequeñas) variaciones de las cantidades de factores que expresamos de la manera siguiente: dx = (dx1, dx2). La variación correspondiente de la producción es aproximadamente igual a: dy = a¡ a¡ dx1 dx», a +a Xt X2 Esta expresión se conoce con el nombre de diferencial total de la función f(x). Consideremos el caso de un cambio en el que sólo varían el factor 1 y el 2 y el nivel de producción se mantiene constante. Es decir, dx1 y dx2 se ajustan "a lo largo de una isocuanta". Dado que el nivel de producción permanece constante, tenemos que Ü a¡ a¡ = - dx1 dx2, a +a Xt X2 16 / LA TECNOLOGÍA (C. 1) de donde podemos deducir que dx2 dx; 8f/8x1 a¡ /8x2. Para calcular la relación técnica de sustitución puede utilizarse el método de la función implícita o el método del diferencial total. El primero es algo más riguroso. pero es posible que el segundo sea más intuitivo. Ejemplo: La RTS en el caso de una tecnología Cobb-Douglas Dado que f(x1, x2) = x1xi-ª, tomando derivadas, tenemos que ¡x2] 8f(x) _ a-1 1-a _ -- - ax1 x2 - a 8x1 x1 l-a 8f(x) = (1- a ) x ax -a = ( 1- a ) -1 2 8x2 ¡x1]ª x2 De aquí se deduce que a x2 ---1 - a x1 1.9 La elasticidad de sustitución La relación técnica de sustitución mide la pendiente de una isocuanta. La elasticídac de sustitución mide su curvatura. Más concretamente, la elasticidad de sustituciór mide la variación porcentual del cociente entre los factores dividida por la variaciór porcentual de la RTS, manteniéndose fijo el nivel de producción. Si suponemos qm 6.(x2/ x1) es la variación del cociente entre los factores y 6.RT S es la variación de 1, relación técnica de sustitución, podemos expresar ésta de la manera siguiente: o-= Ó.(xifx1) xifx1 Ó.RTS . RTS Ésta es una medida relativamente natural de la curvatura: se pregunta cómo varía e cociente entre las cantidades de factores cuando varía la pendiente de la isocuanta. S una pequeña variación de la pendiente provoca una gran variación del cociente entre las cantidades de factores, la isocuanta es relativamente horizontal, lo que significe que la elasticidad de sustitución es grande. La elasticidad de sustitución / 17 En la práctica, suponemos que la variación porcentual es muy pequeña y tomamos el límite de esta expresión cuando � tiende a cero. Por lo tanto, la expresión de a se convierte en A menudo resulta útil calcular a utilizando la derivada logarítmica. En general, si y = g(x), la elasticidad de y con respecto a x se refiere a la variación de y provocada por una (pequeña) variación porcentual de x. Es decir, 1:JL y dyx dx y· E= - = -- dx X Siempre que x e y sean positivos, esta derivada puede expresarse de la forma siguiente: E= dlny dlnx · Para demostrarlo, obsérvese que aplicando la regla de la derivación en cadena, tenemos que dlny dlnx dlnx dx dlny dx · Desarrollando el cálculo en los dos miembros de esta igualdad, tenemos que dlny 1 dlnx x 1 dy ydx' o sea dlny dlnx dy y dx X También podemos utilizar los diferenciales totales; en ese caso, tenemos que 1 dlny = -dy dlnx = -dx, y 1 X de tal manera que dlny dlnx dy X dx y E=--=--. 18 / LA TECNOLOGÍA (C. 1) Señalemos, una vez más, que el primer cálculo es más riguroso, pero el segundo es más intuitivo. Aplicando este resultado a la elasticidad de sustitución, obtenemos la siguiente expresión: a dln(x2/x1) = dlnlRTSI · (La razón por la que el denominador aparece expresado en valor absoluto es la de convertir la RT S en un número positivo a fin de que el logaritmo tenga sentido.) Ejemplo: La elasticidad de sustitución en el caso de la función de producción Cobb-Douglas Antes hemos visto que RTS = --ª x2 1 - a XJ' o sea, De donde se deduce que 1- a X2 ln- = ln-- +lnlRTSI. X1 a Lo que implica a su vez que dln(x2/x1) a = dlnlTRSI = 1. 1.10 Los rendimientos de escala Supongamos que estamos utilizando un vector de factores x para obtener un determinado nivel de producción y y que decidimos aumentar o reducir todos los factores en la proporción t � O. ¿Cómo afectará esta decisión al nivel de producción? En los casos que hemos descrito antes, en los que sólo queríamos aumentar el nivel de producción en una determinada cantidad, hemos supuesto normalmente que podíamos repetir simplemente lo que habíamos hecho antes y producir de esa manera t veces más que antes. Si siempre es posible este tipo de repetición, decimos Los rendimientos de escala / 19 que la tecnología muestra rendimientos constantes de escala, lo que en términos más formales puede expresarse de la manera siguiente: Rendimientos constantes de escala. Una tecnología muestra rendimientos constantes de escala si se cumple cualquiera de las siguientes condiciones: (1) y pertenece a Y implica que ty pertenece a Y cualquiera que sea t � O; (2) x pertenece a V(y) implica que tx pertenece a V(ty) cualquiera que sea t � O; (3) f(tx) = tj(x) cualquiera que sea t � O; es decir, la [uncion de producción f(x) es homogénea de grado 1. El argumento de la repetición antes citado indica que el supuesto de que las tecnologías tienen rendimientos constantes de escala suele ser razonable. Sin embargo, hay situaciones en las que no lo es. Una circunstancia en la que puede no cumplirse este supuesto es aquella en la que tratamos de "subdividir" un proceso de producción. Aun cuando siempre sea posible aumentar la escala de operaciones en proporciones enteras, puede no ser posible reducirlas de la misma manera. Por ejemplo, puede haber una escala mínima de operaciones tal que para producir una cantidad inferior a esa escala sea necesario utilizar técnicas diferentes. Una vez que se alcanza la escala mínima, es posible obtener mayores niveles de producción repitiendo el proceso. Otra circunstancia en la que puede no cumplirse el supuesto de los rendimientos constantes de escala es aquella en la que queremos aumentar la escala de operaciones en proporciones no enteras. Ciertamente, basta con repetir el mismo proceso que antes, pero ¿cómo hacemos una vez y media lo que hemos hecho antes? Estas dos situaciones en las que no se cumple el supuesto de los rendimientos constantes de escala sólo son importantes cuando la escala de producción es pequeña en relación con la escala mínima. Una tercera circunstancia en la que no es adecuado el supuesto de los rendimientos constantes de escala es aquella en la que la duplicación de todos los factores permite utilizar unos medios de producción más eficientes. La repetición nos dice que es viable duplicar el nivel de producción duplicando las cantidades de factores, pero puede ocurrir que existan mejores medios de producción. Consideremos, por ejemplo, el caso de una empresa que construye un oleoducto entre dos puntos y que utiliza como factores trabajo, máquinas y acero. Podemos suponer que una buena medida del nivel de producción de esta empresa es la capacidad de la tubería resultante. En ese caso, es evidente que si duplicamos todos los factores que intervienen en el proceso de producción, es posible aumentar el nivel de producción más del do- 20 / LA TECNOLOGÍA (C. 1) ble, ya que si la superficie de una tubería se aumenta el doble, su volumen aumenta el cuádruple.1 En este caso, cuando el nivel de producción aumenta más de lo que aumentan los factores, decimos que la tecnología muestra rendimientos crecientes de escala. Rendimientos crecientes de escala. Una tecnología muestra rendimientos crecientes de escala si f(tx) > tf(x) cualquiera que sea t > 1. La cuarta circunstancia en la que puede no cumplirse el supuesto de los rendimientos constantes de escala es aquella en la que es imposible repetir el uso de un determinado factor. Consideremos, por ejemplo, el caso de una explotación agraria de 100 hectáreas. Si quisiéramos obtener el doble de producción, podríamos utilizar el doble de cada uno de los factores. Pero eso significaría utilizar también el doble de tierra, lo cual podría ser imposible si no se dispusiera de más tierra. Aun cuando la tecnología muestre rendimientos constantes de escala si incrementamos todos los factores, puede resultar útil imaginar que muestra rendimientos decrecientes de escala con respecto a los factores que controlamos. Más concretamente, Rendimientos decrecientes de escala. Una tecnología muestra rendimientos decrecientes de escala si f(tx) < tf (x) cualquiera que sea t > 1. El caso más natural en el que hay rendimientos decrecientes de escala es aquel en el que no es posible repetir el uso de algunos factores. Por lo tanto, es de esperar que los conjuntos restringidos de posibilidades de producción muestren normalmente rendimientos decrecientes de escala. Siempre puede suponerse que éstos se deben a la presencia de algún factor fijo. Supongamos para demostrarlo que f (x) es una función de producción en la que intervienen k factores y que muestra rendimientos decrecientes de escala. Podemos introducir un nuevo factor "mítico" y medir su nivel por medio de z. Definamos una nueva función de producción F(z, x) de la manera siguiente: F(z, x) = zf(x/ z) Obsérvese que F muestra rendimientos constantes de escala. Si multiplicamos todos los factores -los factores x y el factor z- por algún número t � O, el nivel de producción se multiplica por t. Y si suponemos que z es fijo e igual a 1, tenemos exactamente la misma tecnología que antes. Por lo tanto, cabe pensar que la tecnología inicial que mostraba rendimientos decrecientes de escala, f (x), es una restricción de 1 Naturalmente, como es posible que resulte más difícil construir una tubería más grande, ne tenemos por qué pensar que el nivel de producción aumenta exactamente el cuádruple. Pero podría muy bien aumentar más del doble. Tecnologías homogéneas y homotéticas / 21 la tecnología que muestra rendimientos constantes de escala F(z, x) que se debe al hecho de que z es fijo e igual a 1. Obsérvese, por último, que los distintos tipos de rendimientos de escala que hemos definido son de carácter global. Puede muy bien ocurrir que una tecnología muestre rendimientos crecientes de escala en el caso de algunos valores de x y rendimientos decrecientes de escala en el caso de algunos otros. Por lo tanto, en muchas circunstancias es útil contar con una medida local de los rendimientos de escala. La elasticidad-escala mide el aumento porcentual que experimenta el nive de producción cuando se incrementan todos los factores un uno por ciento, es decir cuando se incrementa la escala de operaciones. Sea y = f(x) la función de producción y t un número positivo. Examinemo la función y(t) = f(tx). Si t = 1, tenemos la escala actual de operaciones; si t > 1 estamos multiplicando todos los factores por t; y si t < 1, estamos dividiéndolo por t. La elasticidad-escala se halla de la siguiente manera: e(x) = d*(f y ---¡¡¡--, T evaluada cuando t = l. Reordenando esta expresión, tenemos que ! .L_ 1 l = df (tx) . e(x) = dy(t) dt y t=1 dt f (tx) t=l Obsérvese que debemos evaluar la expresión cuando t = 1 para calcular la elasti dad-escala correspondiente al punto x. Decimos que la tecnología muestra loe mente rendimientos crecientes, constantes o decrecientes de escala cuando e(x) mayor, igual o menor que l. Ejemplo: Los rendimientos de escala y la tecnología Cobb-Douglas Supongamos que y = x1xt En ese caso, f(tx1, tx2) = (tx1)ª(tx2)b = tª+bx1x tª+b f(x1, x2). Por lo tanto, f(tx1, tx2) = tf(x1, x2) si y sólo si a+ b = l. Del mis modo, a+ b > 1 implica que hay rendimientos crecientes de escala y a+ b < 1 imp que hay rendimientos decrecientes de escala. De hecho, la elasticidad-escala en el caso de la tecnología Cobb-Dougla precisamente a+ b. Para verlo, aplicamos la siguiente definición: 22 / LA TECNOLOGÍA (C. 1) Evaluando esta derivada cuando t = 1 y dividiendo por f (x1, x2) = x1x�, obtenemos el resultado. 1.11 Tecnologías homogéneas y homotéticas Una función f(x) es homogénea de grado k si f(tx) = tk f(x) cualquiera que sea t > O. Los dos "grados" más importantes en economía son el grado cero y el grado uno. Una función homogénea de grado cero es aquella en la que f(tx) = f(x) y una función homogénea de grado uno es aquella en la que f(tx) = tf(x). Si comparamos esta definición con la de los rendimientos constantes de escala, observaremos que una tecnología tiene rendimientos constantes de escala si y sólo si su función de producción es homogénea de grado l. Se dice que una función g : R � R es una transformación monótona positiva si g es una función estrictamente creciente; es decir, una función tal que si x > y, entonces g(x) > g(y) (el hecho de que sea "positiva" suele estar implícito en el contexto). Una función homotética es una transformación monótona de una función que es homogénea de grado l. En otras palabras, f(x) es homotética si y sólo si puede expresarse de la forma siguiente: f(x) = g(h(x)), donde h(·) es homogénea de grado 1 y g(·) es una función monótona. Véase la figura 1.7 para una interpretación geométrica. Las transformaciones monótonas pueden concebirse como formas de medir la producción en diversas unidades. Por ejemplo, la producción de un proceso químico puede medirse en decilitros o en litros. En este caso, es bastante sencillo pasar de una unidad a otra: basta multiplicar o dividir por diez. Una transformación monótona más exótica es aquella en la que se mide la producción en el cuadrado del número de litros. Dada esta interpretación, una tecnología homotética es aquella en cuyo caso existe alguna manera de medir la producción tal que "parezca" que la tecnología muestra rendimientos constantes de escala. Las funciones homogéneas y homotéticas son interesantes por la sencilla manera en que varían sus isocuantas cuando varía el nivel de producción. En el caso de la función homogénea, las isocuantas no son sino "ampliaciones" de una única isocuanta. Si f(x) es homogénea de grado 1, entonces si x y x' pueden generar y unidades de producción, tx y tx' pueden generar ty unidades, como muestra la figura 1.7A. Una función homotética posee una propiedad muy parecida: si x y x' generan el mismo nivel de producción, tx y tx' pueden generar el mismo nivel de producción, pero no necesariamente un nivel de producción t veces superior al inicial. Las isocuantas de una tecnología homotética son exactamente iguales que las de una tecnología homogénea; sólo son diferentes los niveles de producción correspondientes. Tecnologías homogéneas y homotéticas / 23 Figura 1.7 FACTOR2 FACTOR2 f(x) ----- f(x) = 2y =y f(x) *-2Y ------ f(x) A =y FACTOR 1 FACTOR 1 B Funciones homogéneas y homotéticas. El panel A representa una función que es homogénea de grado 1. Si tanto x como x' pueden generar y unidades de producción, tanto 2X como zx' pueden generar 2y unidades de producción. El panel B representa una función homotética. Si X y x' generan el mismo nivel de producción, y, 2X y zx' pueden generar el mismo nivel de producción, pero no necesariamente 2y. Las tecnologías homogéneas y homotéticas son interesantes porque imponen restricciones específicas a la manera en que varía la relación técnica de sustitución cuando cambia la escala de producción. En concreto, en el caso de cualquiera de estas dos funciones, la relación técnica de sustitución es independiente de la escala de producción. Esta afirmación se desprende inmediatamente de las observaciones realizadas en el capítulo 26 (pág. 558), en el que demostramos que si f(x) es homogénea de grado 1, 8f(x)/8xi es homogénea de grado O. Por lo tanto, el cociente entre dos derivadas cualesquiera es homogéneo de grado cero, que es a la conclusión a la que queríamos llegar. Ejemplo: La función de producción CES La elasticidad constante de sustitución o función de producción CES tiene la forma siguiente: Es fácil verificar que la función CES muestra rendimientos constantes de escala. 24 / LA TECNOLOGÍA (C. 1) Adopta algunas conocidas formas especiales, dependiendo del valor del parámetro p, que se describen a continuación y se muestran en la figura 1.8. En nuestro análisis, conviene suponer que los parámetros ªI y a2 son iguales a 1. Figura 1.8 FACTOR FACTOR 2 2 FACTOR 1 A L L FACTOR 2 FACTOR 1 B e FACTOR 1 La función de producción CES. La función de producción CES adopta varias formas dependiendo del valor del parámetro p. El panel A representa el caso en el que p = 1, el Bel caso en el que p = O y el C el caso en el que p = -oo. 1). Realizando una sencilla sustitución, (1) La función de producción lineal (p tenemos que y= XI+ X2 (2) La función de producción Cobb-Douglas (p = O). Cuando p = O, la función de producción CES no está definida, debido a que no es posible dividir por cero. Demostraremos, sin embargo, que cuando p tiende a cero, las isocuantas de la función de producción CES son muy parecidas a las isocuantas de la función de producción Cobb-Douglas. La manera más fácil de verlo consiste en utilizar la relación técnica de sustitución. Calculando ésta directamente, se obtiene RTS = - ( :: )p-I Cuando p tiende a cero, el límite de la RTS es: RTS = - x2 XI ' (1.1) Notas/ 25 que es simplemente la RTS correspondiente a la función de producción CobbDouglas. (3) La función de producción de Leontief (p = -oo). Acabamos de ver que la RTS de la función de producción CES viene dada por la ecuación (1.1). Cuando p = -oo, esta expresión se convierte en Si x2 > XI, la RTS es cero; si x2 < XI, la RTS es infinita. Por lo tanto, cuando p tiende a - oo, una isocuanta de la tecnología CES se parece a una isocuanta correspondiente a la tecnología de Leontief. Probablemente no le sorprenderá al lector descubrir que la función de producción CES tiene una elasticidad constante de sustitución. Para verificarlo, obsérvese que la relación técnica de sustitución se obtiene de la manera siguiente: RTS ( = - :: )p-I , de tal manera que x2 -= XI 1 IRTSll-p. Tomando logaritmos, observamos que X2 1 In-= --InlRTSI. XI 1 -p Aplicando la definición de a basada en la derivada logarítmica, tenemos que dinx2/xI a=dinlTRSI 1 1-p Notas La elasticidad de sustitución se debe a Hicks (1932). Para un análisis de las generalizaciones de la elasticidad de sustitución al caso en el que hay n factores, véase 26 / LA TECNOLOGÍA ( C. 1) Blackorby & Russell (1989) y la bibliografía que se cita en él. La elasticidad-escala se debe a Frisch (1965). Ejercicios 1.1. ¿Verdadero o falso? Si V(y) es un conjunto convexo, también debe serlo el conjunto de producción correspondiente Y. 1.2. ¿Cuál es la elasticidad de sustitución correspondiente al caso general de la tecnología CES y = (a1 xf + a2xi)11 P cuando a1 =/ a2? 1.3. Definamos la elasticidad de un factor con respecto a la producción de la manera siguiente: Ei(X) 8 f(x) Xi = 8xi f (x). Si f(x) = x1x�, ¿cuál es la elasticidad de cada uno de los factores con respecto a la producción? 1.4. Demuestre que si eíx) es la elasticidad-escala y Ei(x) es la elasticidad del factor i con respecto a la producción, E(x) = ¿�=l Ei(x). 1.5. ¿ Cuál es la elasticidad-escala de la tecnología CES, f (z¡, x2) = (xf + xi) p? 1 1.6. ¿ Verdadero o falso? Una función diferenciable g(x) es una función estrictamente creciente si y sólo si g'(x) > O. 1.7. En este capítulo hemos afirmado que si f(x) es una tecnología homotética y x y x' generan el mismo nivel de producción, tx y tx' también deben generar el mismo nivel de producción. ¿Puede demostrarlo rigurosamente? 1.8. Sea f (x1, x2) una función homotética. Demuestre que su relación técnica de sustitución en el punto (x1, x2) es igual a su relación técnica de sustitución en el punto (tx1, tx2). Ejercicios / 27 1.9. Considere la tecnología CES f(x1, x2) = [a1xi + a2x�F. 1 podemos expresarla de la forma siguiente: f(x1, x2) = Demuestre que siempre A(p)[bxi + (1 - b)x�]i. 1.10. Sea Y un conjunto de producción. Decimos que la tecnología es aditiva si cuando y pertenece a Y e y' a Y, y + y' también pertenece a Y. Decimos que la tecnología es divisible si cuando y pertenece a Y y O ::; t ::; 1, ty también pertenece a Y. Demuestre que si una tecnología es aditiva y divisible, Y debe ser convexo y mostrar rendimientos constantes de escala. 1.11. Indique si cada uno de los conjuntos de cantidades necesarias de factores es regular, monótono y/ o convexo. Suponga que los parámetros a y b y los niveles de producción son estrictamente positivos. (a) V(y) = { x1, x2 : ax1 2: log y, bx2 2: log y} (c) V(y) = {x,1,x2: ax1 + Jx1x2 + bx2 (f) V(y) = {x1,x2: ax1 - Jx1x2 + bx2 2: y} 2: y} 2. LA MAXIMIZACIÓN DEL BENEFICIO El beneficio económico es la diferencia entre el ingreso que recibe una empresa y los costes en que incurre. Es importante comprender que para calcular el beneficio han de tenerse en cuenta todos los costes. Si un pequeño empresario tiene una tienda de alimentación y trabaja también en ella, su salario como empleado debe contabilizarse como un coste. Si un grupo de personas presta dinero a una empresa a cambio del pago de una cantidad mensual, estos intereses deben contabilizarse como un coste de producción. Tanto los ingresos como los costes de las empresas dependen de las actividades que realicen. Éstas pueden ser de numerosos tipos: ejemplos son las actividades productivas propiamente dichas, las compras de factores y las compras de publicidad. Si nos situamos en un plano más abstracto, cabe imaginar que una empresa puede tomar una gran variedad de actividades de este tipo. El ingreso puede expresarse en función del nivel de operaciones de un determinado número n de actividades, I(a1, ... , an), y los costes en función de estos mismos n niveles de actividad, C(a1, ... , an). La mayoría de los análisis económicos de la conducta de la empresa parte del supuesto básico de que sus actividades tienen por objeto maximizar los beneficios; es decir, una empresa elige las actividades (a1, ... , an) con el fin de maximizar I(a1, ... , an) - C(a1, ... , an). Éste es el supuesto de la conducta en el que nos basaremos a lo largo de todo el libro. Incluso en este plano tan general, surgen dos principios básicos de la maximización del beneficio. El primero se deriva de una sencilla aplicación del cálculo diferencial. El problema de maximización al que se enfrenta la empresa puede expresarse de la manera siguiente: max I(a1, ... , an) - C(a1, ... , an). ª1,···,ªn Basta una sencilla aplicación del cálculo diferencial para ver que un conjunto óptimo de actividades, a" = (ai, ... a�) se caracteriza por las condiciones 30 / LA MAXIMIZACIÓN DEL BENEFICIO (C. 2) 8J(a*) 8C(a*) Ba, Ba, i = 1, ... , n. El significado intuitivo de estas condiciones es evidente: si el ingreso marginal fuera mayor que el coste marginal, compensaría elevar el nivel de actividad; si fuera menor, compensaría reducirlo. Esta condición fundamental que caracteriza a la maximización del beneficio tiene varias interpretaciones concretas. Por ejemplo, una de las decisiones que toma la empresa consiste en elegir el nivel de producción. La condición fundamental de la maximización del beneficio nos dice que el nivel de producción ha de elegirse de tal manera que la producción de una unidad más genere un ingreso marginal igual a su coste marginal de producción. Otra de las decisiones de la empresa consiste en elegir la cantidad de un factor específico -por ejemplo, el trabajo-- que va a contratar. La condición fundamental de la maximización del beneficio nos dice que la empresa ha de contratar la cantidad de trabajo con la que el ingreso marginal derivado de la utilización de una unidad más de trabajo sea igual al coste marginal de contratarla. La segunda condición fundamental de la maximización del beneficio es la condición de la igualdad de los beneficios a largo plazo. Supongamos que dos empresas tienen las mismas funciones de ingresos y de costes. En ese caso, es evidente que a largo plazo las dos no pueden tener beneficios distintos, ya que cada una de ellas puede imitar lo que hace la otra. Esta condición es muy sencilla, pero sus implicaciones suelen ser sorprendentemente poderosas. Para aplicar estas condiciones de una manera más concreta, es preciso descomponer las funciones de ingresos y de costes en elementos más básicos. El ingreso está compuesto por dos elementos: la cantidad de los distintos productos que vende la empresa multiplicada por el precio de cada uno de ellos. Los costes también están compuestos por dos elementos: la cantidad que utiliza la empresa de cada uno de los factores multiplicada por su precio. El problema de la maximización del beneficio de la empresa consiste, pues, en averiguar qué precios desea cobrar por sus productos o pagar por sus factores y qué niveles de producción y de factores desea utilizar. Naturalmente, no puede fijar los precios y los niveles de actividad unilateralmente. Al determinar la política óptima, la empresa está sujeta a dos restricciones: las restricciones tecnológicas y las restricciones del mercado. Las restricciones tecnológicas son simplemente las que se refieren a la viabilidad del plan de producción. En el capítulo anterior hemos examinado algunas maneras de describirlas. Las restricciones del mercado son las que se refieren a las consecuencias que tienen para la empresa las actividades de otros agentes. Por ejemplo, puede La maximización del beneficio/ 31 ocurrir que los consumidores que compren el producto a la empresa sólo estén dispuestos a pagar un determinado precio por una determinada cantidad de producción o que los proveedores de la empresa sólo acepten determinados precios por los factores que suministran. Cuando la empresa intenta averiguar la forma óptima de llevar a cabo su actividad, ha de tener en cuenta ambos tipos de restricciones. Sin embargo, resulta útil comenzar examinándolas por separado. Por este motivo, las empresas que se describen en los siguientes apartados muestran el tipo más sencillo posible de conducta de mercado, a saber, la conducta precio-aceptante. Se supone que cada una de las empresas considera que los precios están dados, es decir, que son variables exógenas del problema de maximización del beneficio. Por lo tanto, la empresa sólo se ocupa de averiguar los niveles de producción y de utilización de los factores que maximizan el beneficio. Este tipo de empresa precio-aceptante suele denominarse empresa competitiva. Aunque más adelante analizaremos la razón por la que se utiliza esta terminología, aquí indicamos brevemente el tipo de situación en la que la conducta precioaceptante podría ser un modelo adecuado. Supongamos que tenemos un conjunto de consumidores perfectamente informados que compran un producto homogéneo que es producido por un gran número de empresas. En ese caso, es razonablemente evidente que todas las empresas deben cobrar el mismo precio por su producto, pues la que cobre un precio superior al vigente en el mercado perderá de inmediato todos sus clientes. Por lo tanto, cada una de las empresas debe considerar el precio de mercado dado cuando averigua su política óptima. En el presente capítulo estudiaremos la elección óptima de los planes de producción, dada una configuración de los precios del mercado. 2.1 La maximización del beneficio Examinemos el problema de una empresa que considera dados los precios, tanto en el mercado de su producto como en el de sus factores. Sea p un vector de precios de los factores y de los productos de la empresa.1 El problema de maximización del beneficio puede formularse de la manera siguiente: 1r(p) = max py sujeta a y pertenece a Y. Dado que el nivel de producción es un número positivo y las cantidades de factores son números negativos, la función objetivo de este problema es los beneficios: los 1 En general, suponemos que los precios son vectores fila y las cantidades vectores columna. 32 / LA MAXIMIZACIÓN DEL BENEFICIO ( C. 2) ingresos menos los costes. La función 1r(p), que nos da los beneficios máximos en función de los precios, se denomina función de beneficios de la empresa. La función de beneficios tiene diversas y útiles variantes. Por ejemplo, si estamos analizando un problema de maximización a corto plazo, podemos definir la función de beneficios a corto plazo, conocida también con el nombre de función restringida de beneficios: 1r(p, z) = max py sujeta a y pertenece a Y(z). Si la empresa sólo produce un bien, la función de beneficios puede expresarse de la forma siguiente: 1r(p, w) = max pf(x) - wx donde ahora pes el precio (escalar) del producto, w es el vector de precios de los factores y las cantidades utilizadas de éstos se miden por medio del vector (no negativo) x = (x1, ... , Xn). En este caso, también podemos definir una variante de la función restringida de beneficios, la función de costes: c(w, y)= min wx sujeta ax pertenece a V(y). Es posible que a corto plazo nos interese analizar la función restringida de costes o a corto plazo: c(w, y, z) = min wx sujeta a (y, -x) pertenece a Y(z). La función de costes indica el coste mínimo de producir una cantidad y cuando los precios de los factores son w. Dado que en este problema sólo se consideran exógenos los precios de los factores, la función de costes puede utilizarse para describir las empresas que son precio-aceptantes en los mercados de factores, pero que no consideran dados los precios en los mercados de productos. Esta observación nos resultará útil cuando estudiemos el monopolio. La conducta maximizadora del beneficio puede caracterizarse por medio del cálculo diferencial. Por ejemplo, las condiciones de primer orden del problema de maximización del beneficio en el caso de un único producto son of(x*) p--- = Wi O Xi Í = 1, · · · , n. Esta condición nos dice simplemente que el valor del producto marginal de cada uno de los factores debe ser igual a su precio. Estas condiciones también pueden expresarse utilizando una notación vectorial de la manera siguiente: t» maximización del beneficio / 33 pDJ(x*) = w. En este caso (ªf(x*) Df( x *) = 8f(x*)) a XI , ... , aXn es el gradiente de f: el vector de las derivadas parciales de f con respecto a cada uno de sus argumentos. Según las condiciones de primer orden, el "valor del producto marginal de cada uno de los factores debe ser igual a su precio". Éste no es más que un caso especial de la regla de optimización que formulamos anteriormente, a saber, que el ingreso marginal de cada una de las actividades es igual a su coste marginal. Esta condición de primer orden también puede mostrarse gráficamente. Consideremos el conjunto de posibilidades de producción representado en la figura 2.1. En este caso bidimensional, los beneficios vienen dados por ll = py - wx. Los conjuntos de nivel de esta función, cuando p y w son fijos, son líneas rectas que pueden representarse como funciones de la forma: y= IT/p + (w/p)x. En este caso, la pendiente de la línea isobeneficio nos indica el salario medido en unidades de producción y la ordenada en el origen los beneficios medidos en unida?es de producción. Una empresa maximizadora del beneficio desea encontrar un punto del conjunto de producción en el que sea máximo el nivel de beneficios, es decir, un punto en el que la ordenada en el origen de la línea isobeneficio correspondiente sea la máxima posible. Observando la figura, se ve que ese punto óptimo puede caracterizarse por medio de la condición de tangencia df(x*) dx w p En este caso bidimensional, es fácil ver la condición de segundo orden apropiada para la maximización del beneficio, a saber, que la segunda derivada de la función de producción con respecto al factor no sea positiva: d2 f (x*) dx2 � O. Eso significa desde el punto de vista geométrico que en un punto de máximo beneficio la función de producción debe encontrarse por debajo de su tangente en x", es decir, debe ser "localmente cóncava". A menudo resulta útil suponer que la segunda derivada es estrictamente negativa. 34 / LA MAXIMIZACIÓN DEL BENEFICIO (C. 2) Figura2.1 Il =PY- NIVEL DE PRODUCCION -. Pendiente = w(p wx y= f(x) Il/p FACTOR DE PRODUCCION Maximización del beneficio. La cantidad del factor que maximiza el beneficio se encuentra en el punto en el que la pendiente de la línea isobeneficio es igual a la pendiente de la función de producción. La condición de segundo orden para la maximización del beneficio es similar en el caso en el que hay muchos factores, a saber, la matriz de las segundas derivadas de la función de producción debe ser semidefinida negativa en el punto óptimo; es decir, la condición de segundo orden exige que el hessiano (ª2f(x*)) D2f(x*) = OXiOXj satisfaga la condición de que hD2 f(x*)ht � O en el caso de todos los vectores h (el superíndice indica la operación de trasposición). Obsérvese que si sólo hay un factor, el hessiano es un escalar y esta condición se reduce a la condición de segundo orden que examinamos anteriormente en el caso en el que había un único factor. Desde el punto de vista geométrico, el hecho de que el hessiano deba ser semidefinido negativo significa que la función de producción debe ser localmente cóncava en las cercanías de una elección óptima, es decir, la función de producción debe encontrarse debajo de su hiperplano tangente. En muchas aplicaciones nos ocuparemos del caso de un máximo en sentido estricto, por lo que la condición pertinente que debemos comprobar es si el hessiano es definido negativo. En el capítulo 26 (página 552), mostramos que una condición necesaria y suficiente para que esto se cumpla es que el signo de los menores principales del hessiano se vaya alternando. Como veremos más adelante, esta condición algebraica a veces resulta útil para verificar que se cumplen las condiciones de segundo orden. Dificultades / 35 2.2 Dificultades En el caso de cada uno de los vectores de precios (p, w), existe en general una elección óptima de factores x". La función que indica la elección óptima de factores en función de los precios se denomina función de demanda de factores de la empresa y se expresa de la forma siguiente: x(p, w). Del mismo modo, la función y(p, w) = f(x(p, w)) se denomina función de oferta de la empresa. A menudo supondremos que estas funciones están bien definidas y que son regulares, pero merece la pena analizar los problemas que pueden surgir si no lo son. En primer lugar, puede ocurrir que no sea posible describir la tecnología por medio de una función de producción diferenciable y que, por lo tanto, no sean apropiadas las derivadas descritas anteriormente. Un buen ejemplo de este problema lo constituye la tecnología de Leontief. En segundo lugar, las condiciones antes formuladas basadas en el cálculo diferencial sólo tienen sentido cuando las variables de elección pueden variar en un entorno abierto de la decisión óptima. En muchos problemas económicos, las variables son por naturaleza no negativas; y si algunas toman el valor cero en la elección óptima, las condiciones antes descritas pueden no ser apropiadas. Éstas sólo son válidas en el caso de las soluciones interiores, en las que cada uno de los factores se utiliza en una cantidad positiva. Las modificaciones que es necesario introducir para abordar las soluciones de esquina no son difíciles de describir. Por ejemplo, si imponemos que x sólo sea no negativa en el problema de maximización del beneficio, las condiciones de primer orden relevantes son of(x) r=z:': - ui; ::; Ü U Xi of(x) p-- - O Xi ui; = Ü Si Xi = Ü > Ü Si Xi Por lo tanto, el beneficio marginal que se obtiene al aumentar Xi no puede ser positivo, pues de lo contrario la empresa aumentaría Xi· Si Xi = O, el beneficio marginal que se obtiene al aumentar Xi puede ser negativo, lo que quiere decir que a . la empresa le gustaría reducir Xi· Pero eso es imposible dado que Xi ya es cero. Por último, si Xi > O, de tal manera que no se cumple la restricción de la no negatividad, tenemos las condiciones normales de una solución interior. Los casos en los que hay restricciones de no negatividad u otros tipos de restricciones en forma de desigualdad pueden analizarse formalmente por medio del teorema de Kuhn-Tucker, que se describe en el capítulo 27 (página 583). En el capítulo dedicado a la minimización de los costes mostraremos por medio de algunos ejemplos cómo se aplica este teorema. 36 / LA MAXIMIZACIÓN DEL BENEFICIO ( C. 2) En tercer lugar, pueden surgir problemas cuando no existe un plan de producción maximizador del beneficio. Consideremos, por ejemplo, el caso en el que la función de producción es f(x) = x, de tal manera que una unidad de x genera una unidad de producción. No es difícil ver que cuando p > w, no existe ningún plan maximizador del beneficio. Si quisiéramos maximizar px - wx cuando p > w, elegiríamos un valor de x indefinidamente elevado. Esta tecnología sólo tiene un plan de producción maximizador del beneficio cuando p :S w, en cuyo caso el nivel máximo de beneficios es cero. De hecho, este fenómeno ocurre siempre que la tecnología tiene rendimientos constantes de escala. Para demostrarlo, supongamos que podemos encontrar un par (p, w) tal que los beneficios óptimos sean estrictamente positivos, o sea, pf(x*) - wx" = rr" > O. Supongamos que aumentamos la producción multiplicándola por un número t > 1; en ese caso, nuestros beneficios serán pf(tx*) - wtx* = t[pf(x*) - wx*] = in" > 1r*. Eso significa que si los beneficios son en algún caso positivos, pueden incrementarse; por lo tanto, los beneficios no están acotados y en este caso no existe un plan de producción maximizador del beneficio. Este ejemplo muestra claramente que la única posición maximizadora del beneficio que tiene sentido para una empresa que tenga rendimientos constantes de escala es aquella en la que los beneficios son nulos. Si la empresa está produciendo una cantidad positiva y obtiene un beneficio nulo, le será indiferente el nivel de producción. Esto trae a colación la cuarta dificultad: incluso cuando existe un plan de producción maximizador del beneficio, éste puede no ser el único. Si (y, x) genera un beneficio máximo nulo con una tecnología de rendimientos constantes, (ty, tx) también generará un beneficio nulo, por lo que también será maximizador del beneficio. En el caso en el que hay rendimientos constantes de escala, si existe una elección maximizadora del beneficio en un par (p, w), normalmente habrá toda una gama de planes de producción que serán maximizadores del beneficio. Ejemplo: La función de beneficios en el caso de una tecnología CobbDouglas Consideremos el problema de maximización del beneficio en el caso de una función de producción de la forma f(x) = xª, donde a> O. La condición de primer orden es Dificultades / 37 paxª-1 = ui, y la condición de segundo orden se reduce a pa(a - l)xª-2 ::; O. La condición de segundo orden sólo puede satisfacerse cuando a ::; 1, lo que significa que la función de producción debe tener rendimientos constantes o decrecientes de escala para que tenga sentido la rnaxirnización competitiva del beneficio. Si a= 1, la condición de primer orden se reduce a p = w. Por lo tanto, cuando w = p, cualquier valor de x es una elección rnaxirnizadora del beneficio. Cuando a < 1, utilizarnos la condición de primer orden para hallar la función de demanda de los factores x(p, w) = (:) .Ci La función de oferta viene dada por: y(p, w) = f(x(p, w)) = (:) .�, , y la función de beneficios viene dada por 1r(p, w) = py(p, w) - wx(p, w) = w (1-a)(W)ª� -a- 1 ap 2.3 Propiedades de las funciones de demanda y de oferta Las funciones que indican las elecciones óptimas de los factores y de los niveles de producción en función de los precios se conocen con el nombre de funciones de demanda de factores y de oferta de producción. El hecho de que sean las soluciones de un problema de rnaxirnización concreto, el problema de rnaxirnización del beneficio, implica que la conducta de las funciones de demanda y de oferta está sometida a determinadas restricciones. Por ejemplo, es fácil ver que si multiplicarnos todos los precios por un número positivo t, el vector de cantidades de factores que maximiza los beneficios no varía (¿puede demostrarlo el lector rigurosamente?). Por lo tanto, las funciones de demanda de factores x/p, w) cuando i = 1, ... , n deben satisfacer la siguiente restricción: 38 / LA MAXIMIZACIÓN DEL BENEFICIO (C. 2) En otras palabras, las funciones de demanda de factores deben ser homogéneas de grado cero. Esta propiedad es una importante consecuencia de la conducta maximizadora del beneficio: una manera inmediata de averiguar si una determinada conducta observada puede provenir del modelo maximizador del beneficio consiste en ver si las funciones de demanda son homogéneas de grado cero. En caso negativo, no es posible que la empresa en cuestión esté maximizando el beneficio. Nos gustaría encontrar otras restricciones a las que estuvieran sujetas las funciones de demanda. De hecho, nos gustaría encontrar la lista completa de esas restricciones. Podríamos utilizarla de dos maneras. En primer lugar, podríamos utilizarla para examinar las afirmaciones teóricas sobre la respuesta de la empresa maximizadora del beneficio a los cambios de su entorno económico. Un ejemplo de una afirmación de ese tipo sería el siguiente: "Si se duplican todos los precios, los niveles de bienes demandados y ofrecidos por la empresa maximizadora del beneficio no varían". En segundo lugar, podríamos utilizar esas restricciones empíricamente, para averiguar si la conducta observada de una empresa es coherente con el modelo de maximización del beneficio. Si observáramos que las demandas y las ofertas de alguna empresa variaban al duplicar todos los precios y que no variaba nada más, tendríamos que llegar a la conclusión (quizá con reticencias) de que esa empresa no maximiza el beneficio. Por consiguiente, tanto las consideraciones teóricas como las empíricas indican es que importante averiguar las propiedades que poseen las funciones de demanda y de oferta. Abordaremos este problema de tres formas. La primera consiste en examinar las condiciones de primer orden que caracterizan a las decisiones óptimas. La segunda consiste en examinar directamente las propiedades maximizadoras de las funciones de demanda y de oferta. La tercera consiste en examinar las propiedades de las funciones de beneficios y de costes y relacionarlas con las funciones de demanda. Este enfoque se denomina a veces "enfoque dual". Cada uno de estos métodos para examinar la conducta optimizadora resulta útil para abordar otros tipos de problemas en economía, por lo que deben estudiarse detenidamente. Los economistas suelen llamar estática comparativa al estudio de la forma en que responde una variable económica a los cambios de su entorno. Por ejemplo, cabría preguntarse cómo responde la oferta de producción de una empresa maximizadora a una variación del precio del producto. Eso formaría parte del estudio de la estática comparativa de la función de oferta. El término comparativo se refiere a la comparación de la situación "anterior" con la "posterior". El término estática se refiere a la idea de que se compara la situación actual con la existente cuando se han producido todos los ajustes posibles; es decir, debe compararse una situación de equilibrio con otra. El término "estática comparativa" no es especialmente descriptivo y parece que sólo lo utilizan los economistas. Un término mejor es el de análisis de sensibilidad, Estática comparativa a partir de las condiciones de primer orden / 39 que tiene, además, la ventaja de que se utiliza en otras disciplinas. Sin embargo, la terminología de la estática comparativa es la que se utiliza tradicionalmente en economía y parece tan arraigada en el análisis económico que sería inútil intentar modificarla. 2.4 Estática comparativa a partir de las condiciones de primer orden Examinemos el sencillo ejemplo de una empresa maximizadora de los beneficios que sólo produce un bien y utiliza un único factor. El problema al que se enfrenta es el siguiente: max pf(x) - wx. X Si f (x) es diferencia ble, la función de demanda x(p, w) debe satisfacer las siguientes condiciones necesarias de primer y segundo orden: =O pf"(x(p, w) < O. pf'(x(p, w)) - w Obsérvese que estas condiciones son una identidad en p y w. Dado que x(p, w) es por definición la elección que maximiza los beneficios dado el par (p, w), x(p, w) debe satisfacer las condiciones necesarias para la maximización del beneficio en el caso de todos los valores de p y w. Como la condición de primer orden es una identidad, diferenciándola con respecto a w, por ejemplo, tenemos que p !"( x (p,w ))dx(p,w) _ 1 = - 0. dw Suponiendo que tenemos un máximo en sentido estricto, de tal manera que f"(x) no es cero, se deduce que 1 dx(p, w) _ dw - pf"(x(p, w)) · (2.1) Esta identidad nos transmite alguna información interesante sobre la respuesta de la demanda de factores x(p, w) a las variaciones de w. En primer lugar, nos proporciona una expresión explícita de dx / dw en relación con la función de producción. Si ésta es muy curvada en las cercanías del óptimo --de tal manera que la segunda derivada tiene un elevado valor- será pequeña la variación que experimente la demanda de factores cuando varíe su precio (el lector puede dibujar un gráfico parecido al de la figura 2.1 y hacer algunas pruebas para verificar este hecho). En segundo lugar, nos transmite información importante sobre el signo de la derivada: dado que la condición de segundo orden para la maximización exige que la 40 / LA MAXIMIZACIÓN DEL BENEFICIO (C. 2) segunda derivada de la función de producción, f"(x(p, w)), es negativa, la ecuación (2.1) implica que dx(p, w)/dw es negativa. En otras palabras, la curva de demanda de factores tiene pendiente negativa. Este procedimiento, consistente en diferenciar las condiciones de primer orden, puede utilizarse para examinar la conducta maximizadora del beneficio cuando hay muchos factores. Examinemos, en aras de la sencillez, el caso de dos factores. Para facilitar la notación, suponemos que p es igual a 1 y vemos simplemente cómo se comportan las demandas de factores con respecto a sus precios. Las funciones de demanda de factores deben satisfacer las siguientes condiciones de primer orden: 8 f (x1 (w1, w2), x2(w1, w2)) OXJ 8 f (x1 (w1, w2), x2(w1, w2)) 8x2 =WJ = w2. Diferenciando con respecto a w1, tenemos que 8x1 8x2 8x1 8x2 f11 � + f12 � UWJ UWJ = 1 h1�+h2�=0. UWJ UWJ Diferenciando con respecto a w2, tenemos que 8x1 8x2 8x1 8x2 !11� + !12� oui; oui; = Ü h1�+!22�=l. our; oui; Expresando estas ecuaciones en forma matricial, tenemos que �)=(1º)· ( !11 h1 � dw2 O 1 Supongamos que tenemos un máximo en sentido estricto. Eso exige que el hessiano sea estrictamente definido negativo y, por lo tanto, que no sea singular (este supuesto es semejante al de que f"(x) < O en el caso unidimensional). Resolviendo la matriz de primeras derivadas, tenemos que 8x1) sz; � dw2 = ( !11 !12 h1 h2 )-1 La matriz de la izquierda de esta última ecuación se denomina matriz de sustitución, ya que describe cómo sustituye la empresa un factor por otro cuando varían Estática comparativa a partir de las condiciones de primer orden / 41 sus precios. Según nuestro cálculo, la matriz de sustitución no es más que la inversa del hessiano, lo que tiene varias consecuencias importantes. Recuérdese que la condición de segundo orden para la maximización (estricta) del beneficio es que el hessiano sea una matriz definida negativa simétrica. El álgebra lineal nos dice que la inversa de una matriz definida negativa simétrica es una matriz definida negativa simétrica, lo cual significa que la propia matriz de sustitución debe ser una matriz definida negativa simétrica. En concreto, 1) 8xd8wi < O, en el caso en que i = 1, 2, ya que las casillas diagonales de una matriz definida negativa deben ser negativas. 2) 8xd8wj = 8xj/8wi en razón de la simetría de la matriz. Aunque es bastante intuitivo que las curvas de demanda de factores deben tener pendiente negativa, no lo es el hecho de que la matriz de sustitución sea simétrica. ¿Por qué ha de ser la variación que experimentan las demandas del bien i por parte de una empresa, cuando varía el precio de j, necesariamente iguales a la variación que experimenta la demanda del bien j por parte de la empresa cuando varía el precio de i? No existe ninguna razón evidente ... pero lo exige el modelo de la conducta maximizadora del beneficio. Este mismo tratamiento puede aplicarse a un número arbitrario de factores. Suponiendo que pes igual a 1, las condiciones de primer orden para la maximización del beneficio son D f(x(w)) - w = O. Si diferenciamos con respecto a w, obtenemos D2 f(x(w))Dx(w) - 1 = O. Despejando en esta ecuación la matriz de sustitución, tenemos que Dx(w) = [D 2 f(x(w))]-1. Dado que D2 f(x(w)) es una matriz definida negativa simétrica, la matriz de sustitución Dx(w) es una matriz definida negativa simétrica. Esta fórmula es, por supuesto, análoga a la que se obtiene en los casos de uno y dos bienes antes descritos. ¿Cuál es el contenido empírico de la afirmación de que la matriz de sustitución es semidefinida negativa? Cabe hacer la siguiente interpretación. Supongamos que el vector de precios de los factores w varía y se convierte en w + dw. En ese caso, la variación correspondiente de las demandas de factores es 42 / LA MAXIMIZACIÓN DEL BENEFICIO (C. 2) dx = Dxíwrdw". Multiplicando los dos miembros de esta ecuación por dw, tenemos que dw dx = dw.Dxíwldw' � O. Esta desigualdad se deduce de la definición de la matriz semidefinida negativa. Vemos que el carácter semidefinido negativo de la matriz de sustitución significa que el producto escalar de la variación de los precios de los factores y la variación de las demandas de los factores nunca puede ser positivo, al menos cuando las variaciones de los precios de los factores son infinitesimales. Por ejemplo, si sube el precio del factor i-ésimo y no varía ningún otro precio, debe disminuir la demanda de dicho factor. En general, la variación de las cantidades, dx, debe formar un ángulo obtuso con la variación de los precios, dw. Dicho de forma aproximada, la variación de la cantidad debe ir más o menos en sentido "contrario "a la variación de los precios. 2.5 Estática comparativa a partir del álgebra En este apartado examinamos las consecuencias de la conducta maximizadora del beneficio que se derivan directamente de la definición de la propia maximización. Lo haremos de una manera algo distinta. En lugar de considerar que las funciones de demanda y de oferta de una empresa describen su conducta, imaginaremos que tenemos solamente un número finito de observaciones sobre la misma. Eso nos permitirá evitar algunos tediosos detalles que hay que tener en cuenta cuando se toman límites y contar con un marco más realista para el análisis empírico (además, ¿quién ha tenido alguna vez una cantidad infinita de datos?). Supongamos, pues, que se nos da una lista de vectores de precios observados pt y los vectores de producciones netas correspondientes s'. en el caso en que t = 1, ... , T. A este conjunto lo llamamos los datos. Utilizando las funciones de oferta neta antes descritas, los datos son simplemente (p", y(pt)) en el caso de algunas observaciones t = 1, ... , T. Lo primero que nos preguntamos es qué implica la maximización del beneficio en lo que se refiere al conjunto de datos. Si la empresa está maximizando el beneficio, la elección de la producción neta observada correspondiente al precio pt debe generar un nivel de beneficios al menos tan grande como el que generaría cualquier otra producción neta que pudiera elegir la empresa. No conocemos todas las demás elecciones que son viables en esta situación, pero sí algunas, a saber, las demás elecciones s', en el caso en que s = 1, ... , T que hemos observado. Por lo tanto, una condición necesaria para la maximización del beneficio es la de que Estática comparativa a partir del álgebra / 43 ptyt 2: ptys cualesquiera que sean t y s = 1, ... , T. Esta condición se denomina axioma débil de la maximización del beneficio (ADMB). En la figura 2.2A hemos representado dos observaciones que violan el ADMB y en la 2.2B dos observaciones que lo satisfacen. Figura 2.2 NIVEL DE PRODUCCION FACTOR DE PRODUCCION NIVEL DE PRODUCCION FACTOR DE PRODUCCION ADMB. El panel A muestra dos observaciones que violan el ADMB, ya que p1y2 > p1y1. El B muestra dos observaciones que satisfacen el ADMB. El ADMB es una condición sencilla, pero sumamente útil; extraigamos algunas de sus consecuencias. Tomemos dos observaciones t y s y escribamos el ADMB correspondiente a cada una de ellas. Tenemos que 2: O -ps(yt _ ys) 2: O. pt(yt _ ys) Sumando estas dos desigualdades, tenemos que Definiendo �p = (pt - p8) y �y = (yt - y8), podemos formular esta expresión de la manera siguiente: �p�y 2: o. (2.2) En otras palabras, el producto escalar de un vector de las variaciones de los precios y el vector correspondiente de las variaciones de las producciones netas no puede ser negativo. 44 / LA MAXIMIZACIÓN DEL BENEFICIO (C. 2) Por ejemplo, si L\p es el vector (1, O, ... , O), esta desigualdad implica que L\y1 no puede ser negativo. Si el primer bien es un producto para la empresa y, por lo tanto, un número positivo, su oferta no puede disminuir cuando sube su precio. Por otra parte, si el primer bien es un factor para la empresa y, por lo tanto, se mide como un número negativo, su demanda no debe aumentar cuando sube su precio. Naturalmente, la ecuación (2.2) es simplemente una versión en diferencias finitas de la desigualdad infinitesimal obtenida en el apartado anterior. Pero es más poderosa en el sentido de que se aplica a todas las variaciones de los precios y no sólo a las infinitesimales. Obsérvese que se deriva directamente de la definición de la maximización del beneficio y que no es necesario partir de ningún supuesto que restrinja el tipo de tecnología. 2.6 Recuperabilidad ¿Agota el ADMB todas las consecuencias de la conducta maximizadora del beneficio o implica la maximización del beneficio otras condiciones útiles? Una manera de responder a esta pregunta consiste en tratar de construir una tecnología que genere la conducta observada (pt, yt) como una conducta maximizadora del beneficio. Si podemos hallar una tecnología de ese tipo para cualquier conjunto de datos que satisfaga el ADMB, el ADMB debe agotar, en efecto, las consecuencias de la conducta maximizadora del beneficio. La operación de construir una tecnología compatible con las elecciones observadas se denomina operación de recuperabilidad. Demostraremos que si un conjunto de datos satisface el ADMB, siempre es posible encontrar una tecnología con la que las elecciones observadas maximicen el beneficio. De hecho, siempre es posible hallar un conjunto de producción Y que sea cerrado y convexo. En el resto de este apartado esbozamos la demostración de esta afirmación. Nuestra tarea consiste en construir un conjunto de producción que genere las elecciones observadas (p', yt) como elecciones maximizadoras del beneficio. Construiremos, de hecho, dos conjuntos de producción de ese tipo, uno que sirva de "frontera interior" de la verdadera tecnología y otro que sirva de "frontera exterior". Comenzaremos con la frontera interior. Supongamos que el verdadero conjunto de producción Y es convexo y monótono. Dado que Y debe contener v' siendo t = 1, ... , T, es natural suponer que la frontera interior es el conjunto monótono convexo menor que contiene y1, ... , s'. Este conjunto se denomina cápsula monótona convexa de los puntos y1, ... , yT y se representa de la manera siguiente: Y1 = cápsula monótona convexa de {yt : t = 1, ... , T} Recuperabilidad / 45 La figura 2.3A representa el conjunto Y J. Figura 2.3 NIVEL DE PRODUCCION FACTOR DE PRODUCCION FACTOR DE PRODUCCION A B Los conjuntos Y I y Y E. El conjunto Y I es el menor conjunto monótono convexo que podría ser un conjunto de producción compatible con los datos. El conjunto Y E es el mayor conjunto monótono convexo que podría ser un conjunto de producción compatible con los datos. Es fácil demostrar que en el caso de la tecnología Y I, s' es una elección maximizadora de los beneficios a los precios pt. Lo único que tenemos que hacer es comprobar que cualquiera que sea t, ptyt 2: pty cualquiera que sea y perteneciente a Y J. Supongamos que no es así. En ese caso, existe alguna observación t tal que ptyt < pty en el caso de algún y perteneciente a Y J. Pero el gráfico muestra que en ese caso debe existir alguna observación s tal que ptyt < ptys. Pero esta desigualdad viola el ADMB. Por lo tanto, el conjunto Y I racionaliza la conducta observada en el sentido de que es una tecnología que podría haber generado esa conducta. No es difícil ver que Y I debe ser un subconjunto de cualquier tecnología convexa que genere la conducta observada: si Y es la que genera la conducta observada y es convexa, debe contener las elecciones observadas s' y la cápsula convexa de estos puntos es el menor conjunto formado por puntos de ese tipo. En este sentido, Y I nos da una "frontera interior "de la verdadera tecnología que generó las elecciones observadas. Es natural que nos preguntemos si podemos encontrar una frontera exterior a esta "verdadera "tecnología. Es decir, ¿podemos encontrar un conjunto Y E que esté garantizado que contiene cualquier tecnología que sea compatible con la conducta observada? 46 / LA MAXIMIZACIÓN DEL BENEFICIO (C. 2) La argucia para responder a esta pregunta consiste en excluir todos los puntos que posiblemente no podrían pertenecer a la verdadera tecnología e incluir todos los restantes. Más concretamente, definamos N OY de la manera siguiente: NOY ={y: pty > ptyt en el caso de algún t}. N OY está formado por todas las combinaciones de producciones netas que generan mayores beneficios que alguna elección observada. Si la empresa maximiza los beneficios, esas combinaciones no pueden ser tecnológicamente viables, pues de lo contrario ya se habrían elegido. Tomemos entonces como frontera exterior de Y el complementario de este conjunto: Y E = {y : pty � ptyt cualquiera que sea t = 1, ... , T} La figura 2.38 representa el conjunto Y E. Para demostrar que Y E racionaliza la conducta observada, debemos demostrar que los beneficios correspondientes a las elecciones observadas son, al menos, tan elevados como los beneficios correspondientes a cualquier otro y que pertenezca a Y E. Supongamos que no. En ese caso, hay algún s' tal que ptyt < pty en el caso de algún y que pertenezca a Y E. Pero eso contradice la definición de Y E antes citada. La construcción de Y E muestra claramente que debe contener cualquier conjunto de producción coherente con los datos (yt). Por lo tanto, Y E e Y I constituyen la frontera exterior e interior que mejor acotan el verdadero conjunto de producción que generó los datos. Notas Para más información sobre la metodología de la estática comparativa, véase Silberberg (1974) y Silberberg (1990). El enfoque algebraico aquí descrito se basa en Afriat (1967) y Samuelson (1947); para una exposición más extensa, véase Varian (1982b). Ejercicios 2.1. Utilice el teorema de Kuhn-Tucker para obtener unas condiciones para la maximización del beneficio y la minimización del coste que sean válidas incluso en el caso de las soluciones de esquina, es decir, cuando hay algún factor que no se utiliza. 2.2. Demuestre que normalmente no existe una combinación maximizadora del beneficio cuando la tecnología muestra rendimientos crecientes de escala en la medida en que haya algún punto que genere un beneficio positivo. Ejercicios / 47 2.3. Calcule explícitamente la función de beneficios correspondiente a la tecnología y = xª, siendo O < a < 1 y verifique que es homogénea y convexa en (p, w ). 2.4. Sea f(x1, x2) una función de producción con dos factores y w1 y w2 sus precios respectivos. Demuestre que la elasticidad del cociente entre las participaciones de los factores (w2x2/w1x1) con respecto a (xif x2) viene dada por 1/a - 1. 2.5. Demuestre que la elasticidad del cociente entre las participaciones de los factores con respecto a (w2/w1) es 1 - a. 2.6. Suponga que (pt, yt), siendo t = 1, ... , T, es un conjunto de elecciones observadas que satisfacen el ADMB y que Y I e Y E son la frontera interior y exterior del verdadero conjunto de producción. Sea 1r+(p) la función de beneficios correspondiente a Y E y 1r-(p) la función de beneficios correspondiente a Y I y 1r(p) la función de beneficios correspondiente a Y. Demuestre que cualquiera que sea p, 7r+(p) � 1r(p) � 7r-(p). 2. 7. La función de producción es f (x) = 20x - x2 y el precio del producto se normaliza y se supone que es igual a 1. Sea w el precio del factor x. Tiene que cumplirse que X� O. X> (a) ¿ Cuál es la condición de primer orden para la maximización del beneficio si O? (b) ¿ Cuáles son los valores de w con los que el x óptimo es igual a cero? (c) ¿Cuáles son los valores de w con los que el x óptimo es igual a 10? (d) ¿Cuál es la función de demanda de los factores? (e) ¿Cuál es la función de beneficios? (f) ¿Cuál es la derivada de la función de beneficios con respecto a w? 3. LA FUNCIÓN DE BENEFICIOS Dado un conjunto de producción cualquiera Y, hemos visto cómo se calcula la función de beneficios, 1r(p), que nos indica el beneficio máximo que puede obtenerse cuando el vector de precios es p. La función de beneficios posee varias propiedades importantes que se derivan directamente de su definición. Estas propiedades son muy útiles para saber cómo condicionan la conducta de la empresa. Recuérdese que la función de beneficios es, por definición, el beneficio máximo que puede obtener la empresa en función del vector de precios de las producciones netas: 1r(p) = max py y sujeta a y pertenece a Y. Desde el punto de vista de los resultados matemáticos que obtendremos a continuación, lo importante es que en este problema la función objetivo es una función lineal de los precios. 3.1 Propiedades de la función de beneficios Comenzamos esbozando las propiedades de la función de beneficios. 1. No decreciente en los precios de los productos, no creciente en los precios de los factores. Si p� � Pi en el caso de todos los productos y PJ � Pí en el caso de todos los factores, entonces 1r(p') � 1r(p). 2. Homogénea de grado 1 en p. 1r(tp) = fa(p) cualquiera que sea t � O. 3. Convexa en p. Sea p" = tp + (1 - t)p' cualquiera que sea t tal que O � t � 1. En ese caso, 1r(p") � fa(p) + (1 - thr(p'). 50 / LA RJNCIÓN DE BENEFICIOS (C. 3) 4. Continua en p. La función 1r(p) es continua, al menos cuando 1r(p) está bien definida y > O siendo i = 1, ... , n. Pi Demostración. Hacemos hincapié una vez más en que las demostraciones de estas propiedades se derivan de la definición de la propia función de beneficios y no se basan en ninguna de las propiedades de la tecnología. l. Sea y un vector de producción neta que maximiza el beneficio a los precios p, de tal manera que 1r(p) = py, e y' un vector de producción neta que maximiza el beneficio a los precios p', de tal manera que 1r(p') = p'y'. En ese caso, de acuerdo con la definición de la maximización del beneficio, tenemos que p'y' � p'y. Dado que p� � Pi cualquiera que sea i tal que Yi � O y p� � Pi cualquiera que sea i tal que u. � O, también tenemos que p'y � py. Uniendo estas dos desigualdades, tenemos que 1r(p') = p'y' � py = 1r(p), que es lo que queríamos demostrar. 2. Sea y un vector de producción neta que maximiza el beneficio a los precios p, de tal manera que py � py' cualquiera que sea y' perteneciente a Y. En ese caso, si t � O, tpy � tpy' cualquiera que sea y' perteneciente a Y. Por lo tanto, y también maximiza los beneficios a los precios tp. Así pues, 1r(tp) = tpy = t1r(p). 3. Supongamos que y maximiza los beneficios a los precios p, y' los maximiza a los precios p' e y" a los precios p". En ese caso, tenemos que 1r(p") = p"y" = (tp + (1 - t)p')y" = tpy" + (1 - t)p'y". (3.1) De acuerdo con la definición de la maximización del beneficio, sabemos que tpy" � tpy =t1r(p) O - t)p'y" � O - t)p'y' =O - t)1r(p') Sumando estas dos desigualdades y aplicando la ecuación (3.1), tenemos que 1r(p") � t1r(p) + (1 - t)7r(p'), que es lo que queríamos demostrar. 4. La continuidad de 1r(p) se desprende del teorema del máximo descrito en el capítulo 27 (página 586). No es muy sorprendente que la función de beneficios sea homogénea de grado 1 y creciente con respecto a los precios de los productos. Por otra parte, aunque la propiedad de la convexidad no parece especialmente intuitiva, se basa en un sólido razonamiento económico, que tendrá importantísimas consecuencias. Propiedades de la función de beneficios / 51 Consideremos la figura 3.1, en la que se representan en un eje los beneficios y en el otro el precio de un único bien, manteniéndose constantes los precios de los factores. Dado el vector de precios (p*, w*), el plan de producción maximizador del beneficio (y*, x") genera los beneficios p*y* - w*x*. Supongamos que aumenta p, pero la empresa continúa utilizando el mismo plan de producción (y*, x*). Llamemos a los beneficios generados por esta conducta pasiva "función de beneficios pasiva" y representémosla de la manera siguiente: II(p) = py* - w*x*. Es fácil ver que es una línea recta. Los beneficios que se obtienen si se sigue una política óptima deben ser, al menos, tan elevados como los beneficios que se obtienen si se sigue una política pasiva, por lo que la curva II(p) debe encontrarse por encima de la recta II(p). El razonamiento es el mismo cualquiera que sea el precio p, por lo que la función de beneficios debe encontrarse por encima de sus tangentes en todos y cada uno de los puntos. Por lo tanto, 1r(p) debe ser una función convexa. Figura3.1 1t(p) BENEFICIOS Il(p) = py* - w*x* 1t(p*) p* PRECIO DEL PRODUCTO La función de beneficios. Cuando sube el precio del producto, la función de beneficios aumenta a una tasa creciente. Las propiedades de la función de beneficios tienen varias aplicaciones. De momento, nos conformamos con señalar que muestran varias implicaciones observables de la conducta maximizadora del beneficio. Supongamos, por ejemplo, que tenemos acceso a la contabilidad de una empresa y que observamos que cuando se multiplican todos los precios por algún número t > O, los beneficios no aumentan en la misma proporción. Si el entorno no experimentara ningún otro cambio aparente, podríamos sospechar que la empresa en cuestión no está maximizando los beneficios. 52 / LA FUNCIÓN DE BENEFICIOS (C. 3) Ejemplo: Los efectos de la estabilización de los precios Supongamos que el precio del producto de una industria competitiva fluctúa aleatoriamente. Imaginemos, en aras de la sencillez, que será PI con una probabilidad q y P2 con una probabilidad (1 - q). Se ha sugerido que podría ser deseable estabilizar el precio del producto en el precio medio p = qp1 + (1 - q)p2. ¿Cómo resultarían afectados los beneficios de una empresa representativa de la industria? Tenemos que comparar los beneficios medios que se obtienen cuando fluctúa p con los que se obtienen con el precio medio. Dado que la función de beneficios es convexa, Por lo tanto, los beneficios medios que se obtienen cuando fluctúa el precio son, al menos, tan elevados como los que se obtienen cuando se estabiliza. A primera vista, parece que este resultado no es muy intuitivo, pero resulta evidente cuando se recuerda la causa económica de la convexidad de la función de beneficios. Cada una de las empresas produce una cantidad mayor cuando el precio es alto y una menor cuando es bajo. El beneficio que obtienen de esa manera es superior al que obtendrían produciendo una cantidad fija al precio medio. 3.2 Las funciones de oferta y demanda a partir de la función de beneficios Si se nos da la función de oferta neta y(p), es fácil calcular la función de beneficios. Basta introducirla en la definición de beneficios: 1r(p) = py(p). Supongamos que se nos da, por el contrario, la función de beneficios y se nos pide que hallemos las funciones de oferta neta. ¿ Cómo hacerlo? Existe una manera muy sencilla de resolver este problema: basta diferenciar la función de beneficios. La siguiente proposición lo demuestra. Lema de Hotelling. (La propiedad de la derivada) Sea Yi(p) la función de oferta neta del bien i de la empresa. En ese caso, siendo i suponiendo que existe la derivada y que Pi > O. = 1, ... , n, Las funciones de oferta y demanda a partir de la función de beneficios / 53 Demostración. Supongamos que (y*) es un vector de producción neta que maximiza el beneficio a los precios (p*). Definamos la función g(p) = 1r(p) - py* Es evidente que el plan de producción que maximiza el beneficio a los precios p siempre será, al menos, tan rentable como el plan de producción y*. Sin embargo, el plan y* será un plan que maximiza los beneficios a los precios p*, por lo que la función g alcanza un valor mínimo de O a los precios p*. Los supuestos sobre los precios implican que el mínimo es interior. Las condiciones de primer orden para un mínimo implican que ag(p*) a1r(p*) * . . -�-- = -�-- -yi = O siendo i = 1, ... ,n. U Pi U Pi Dado que eso es cierto en el caso de todas las elecciones de p*, queda realizada la demostración. La prueba anterior no es más que una versión algebraica de las relaciones representadas en la figura 3.1. Dado que la función de beneficios "pasiva" se encuentra por debajo de la función de beneficios y coincide en un punto, las dos funciones deben ser tangentes en ese punto. Pero eso implica que la derivada de la función de beneficios en p* debe ser igual a la oferta de factores que maximiza el beneficio a ese precio: y(p*) = 81r(p*) / ap. El argumento expuesto en el caso de la propiedad de la derivada es convincente (¡así lo espero!), pero puede que no quede muy claro. Tal vez ayude a comprenderlo mejor el siguiente argumento. Consideremos el caso de un único producto y un único factor. En este caso, la condición de primer orden para la maximización del beneficio adopta la sencilla forma siguiente: p df (x) _ w = O. dx (3.2) La función de demanda de factores x(p, w) debe satisfacer la condición de primer orden. La función de beneficios es 1r(p, w) = pf(x(p, w)) - wx(p, w). 54 / LA FUNCIÓN DE BENEFICIOS (C. 3) Diferenciando la función de beneficios con respecto a w, por ejemplo, tenemos que a1r _ aJ(x(p, w)) ax _ ax _ w inu Bu: - p ax Bu: [ aJ(x(p, w)) p - w ax l ax aw - X X (P, ( ) P, w w) . Teniendo en cuenta (3.2), vemos que a1r aw = -x(p, w). El signo negativo se debe a que estamos subiendo el precio de un factor, por lo que deben disminuir los beneficios. Este argumento muestra el razonamiento económico en que se basa el lema de Hotelling. La subida del precio de un producto en una pequeña cuantía produce dos efectos. En primer lugar, produce un efecto directo: como consecuencia de la subida del precio, la empresa obtiene más beneficios, aun cuando continúe produciendo la misma cantidad. Pero, en segundo lugar, produce un efecto indirecto: la subida del precio del producto induce a la empresa a alterar su nivel de producción en una pequeña cuantía. Sin embargo, la variación que experimentan los beneficios como consecuencia de una variación infinitesimal de la producción debe ser cero, puesto que ya nos encontramos en un plan de producción maximizador del beneficio. Por lo tanto, la repercusión del efecto indirecto es nula y nos quedamos únicamente con el efecto directo. 3.3 El teorema de la envolvente La propiedad de la derivada de la función de beneficios es un caso especial de un resultado más general que se conoce con el nombre de teorema de la envolvente y que se describe en el capítulo 27 (página 569). Consideremos un problema de maximización arbitrario en el que la función objetivo depende de un parámetro a: M(a) = max f(x, a). X La función M(a) nos da el valor maximizado de la función objetivo en función del parámetro a. En el caso de la función de beneficios, a sería un precio, x sería una demanda de factores y M(a) sería el valor maximizado de los beneficios en función del precio. Sea x(a) el valor de x que resuelve el problema de maximización. En ese caso, también podemos expresar M(a) = f(x(a), a), lo que quiere decir simplemente Estática comparativa a partir de la función de beneficios / 55 que el valor optimizado de la función es igual a la función evaluada en la elección optimizadora. A menudo es interesante saber cómo varía M(a) cuando varía a. El teorema de la envolvente nos da la respuesta: dM(a) da = 8 f (x, a) Ba J . x=x(a) Esta expresión nos dice que la derivada de M con respecto a a viene dada por la derivada parcial de f con respecto a a, manteniendo fijo x en la elección óptima. Ése es el significado de la barra vertical situada a la derecha de la derivada. La demostración del teorema de la envolvente es relativamente sencilla y se realiza en el capítulo 27 (pág. 569). Tal vez el lector desee ver si sabe demostrarlo él mismo antes de consultar la respuesta. Veamos cómo funciona el teorema de la envolvente en el caso de un sencillo problema de maximización del beneficio en el que sólo hay un factor y un producto. El problema de maximización del beneficio es 1r(p, w) = maxpf(x) - wx. X El parámetro a del teorema de la envolvente es p o io y M(a) es 1r(p, w). De acuerdo con este teorema, la derivada de 1r(p, w) con respecto a p es simplemente la derivada parcial de la función objetivo, evaluada en la elección óptima: a1r(p, w) = f(x)J = f(x(p, w)). x=x(p,w) ap Esta expresión es simplemente la oferta de la empresa que maximiza el beneficio a los precios (p, w). Del mismo modo, 1 81r(p, w) = -x = -x(p, w), 0W x=x(p,w) que es la oferta neta del factor que maximiza el beneficio. 3.4 Estática comparativa a partir de la función de beneficios Al comienzo del presente capítulo demostramos que la función de beneficios debe satisfacer determinadas propiedades. Acabamos de ver que las funciones de oferta neta son las derivadas de la función de beneficios. Es interesante ver qué implican las propiedades de la función de beneficios sobre las propiedades de las funciones de oferta neta. Examinemos cada una de ellas por separado. En primer lugar, la función de beneficios es una función monótona de los precios. Por lo tanto, la derivada parcial de 1r(p) con respecto al precio i es negativa 56 / LA FUNCIÓN DE BENEFICIOS (C. 3) si el bien i es un factor y positiva si es un producto. Se trata simplemente de la convención con respecto a los signos que hemos adoptado en lo que se refiere a las ofertas netas. En segundo lugar, la función de beneficios es homogénea de grado 1 en los precios. Hemos visto que eso implica que las derivadas parciales de la función de beneficios deben ser homogéneas de grado O. Si multiplicamos todos los precios por un número positivo t, la decisión óptima de la empresa no varía, por lo que los beneficios aumentan en ese mismo número t. En tercer lugar, la función de beneficios es una función convexa de p. Por lo tanto, la matriz de segundas derivadas de 1r con respecto a p --el hessiano- debe ser una matriz semidefinida positiva. Pero la matriz de segundas derivadas de la función de beneficios no es sino la matriz de primeras derivadas de las funciones de oferta neta. Por ejemplo, en el caso en el que hay dos bienes, tenemos que La matriz de la derecha es simplemente la matriz de sustitución, es decir, cómo varía la oferta neta del bien i cuando varía el precio del bien j. De acuerdo con las propiedades de la función de beneficios, debe ser una matriz semidefinida positiva simétrica. El hecho de que las funciones de oferta neta sean las derivadas de la función de beneficios nos permite pasar fácilmente de las propiedades de la función de beneficios a las propiedades de las funciones de oferta neta y viceversa. Utilizando esta relación es mucho más fácil obtener numerosas proposiciones sobre la conducta maximizadora del beneficio. Ejemplo: El principio de LeChatelier Examinemos la respuesta a corto plazo de la conducta de oferta de la empresa en comparación con su respuesta a largo plazo. Parece plausible que la empresa responderá más a una variación del precio a largo plazo ya que, por definición, tiene más factores que ajustar a largo plazo que a corto plazo. Esta proposición intuitiva puede demostrarse rigurosamente. Supongamos para simplificar que sólo hay un producto y que todos los precios de los factores están fijos. Por lo tanto, la función de beneficios sólo depende del precio (escalar) del producto. Sea 1r5(p, z) la función de beneficios a corto plazo, donde z es un factor fijo a corto plazo. Sea z(p) la demanda de este factor maximizadora del beneficio a largo plazo; la función de beneficios a largo plazo vendrá dada, pues, Ejercicios / 57 z* = = 1r8(p, z(p)). Por último, sea p* el precio de un determinado producto y z(p*) la demanda óptima a largo plazo del factor z al precio p*. por 7íL(p) Los beneficios a largo plazo siempre son, al menos, tan elevados corno los beneficios a corto plazo, ya que el conjunto de factores que pueden ajustarse a largo plazo comprende el subconjunto de factores que pueden ajustarse a corto plazo. Por lo tanto, h(p) = 7íL(p) - 1rs(p, z ") = 1rs(p, z(p)) - 1rs(p, z*) 2: O cualesquiera que sean los precios p. Al precio v', la diferencia entre los beneficios a corto plazo y los beneficios a largo plazo es cero, por lo que h(p) alcanza un mínimo en p = p*. Por lo tanto, la primera derivada evaluada en p* ha de ser igual a cero. De acuerdo con el lema de Hotelling, vernos que las ofertas netas a corto plazo y a largo plazo de cada bien deben ser iguales al precio p*. Pero podernos decir algo más. Dado que p* es, de hecho, un mínimo de h(p), la segunda derivada de h(p) no puede ser negativa, lo que significa que 821r ,(p* z*) s 8p2 ' > o - . Aplicando una vez más el lema de Hotelling, tenernos que dy(p*) 8y(p*, z*) dp dp --- Esta expresión implica que la respuesta de la oferta a largo plazo a una variación del precio es, al menos, tan grande corno la respuesta a corto plazo cuando z* = z(p*). Notas Las propiedades de la función de beneficios han sido desarrolladas por Hotelling (1932), Hicks (1946) y Sarnuelson (1947). Ejercicios 3.1. Una empresa competitiva rnaxirnizadora del beneficio tiene la función de beneficios 1r(w1, w2) = c/>1 (w1) + c/>2(w2). Se supone que el precio del producto es igual a l. (a) ¿ Qué puede decirse de la primera y la segunda derivadas de las funciones c/>i(w,¿)? 58 / LA FUNCIÓN DE BENEFICIOS (C. 3) (b) Si xi(w1, w2) es la función de demanda del factor i, ¿cuál es el signo de 8xdawj? (c) Sea f (x1, x2) la función de producción que generó esta función de beneficios. ¿Qué puede decir de la forma de esta función de producción? (Pista: examine las condiciones de primer orden.) 3.2. Considere la tecnología descrita por y = O cuando x :=; 1 e y Calcule la función de beneficios de esta tecnología. = lnx cuando x > 1. 3.3. Dada la función de producción f (z¡, x2) = a1lnx1 + a2lnx2, calcule las funciones de demanda y de oferta que maximizan el beneficio y la función de beneficios. Suponga, para mayor sencillez, que la solución es interior y que a; > O. 3.4. Dada la función de producción f(x1, x2) = x11 xf, calcule las funciones de demanda y de oferta que maximizan el beneficio y la función de beneficios. Suponga que a, > O. ¿Qué restricciones deben satisfacer a1 y a2? 3.5. Dada la función de producción f(x1,x2) = minj z}, x2}ª, calcule las funciones de demanda y de oferta que maximizan el beneficio y la función de beneficios. ¿ Qué restricciones debe satisfacer a? 4. LA MINIMIZACIÓN DE LOS COSTES En este capítulo estudiaremos la conducta de la empresa minimizadora de los costes, que tiene interés por dos razones: en primer lugar, nos permite examinar de otra manera la conducta de oferta de la empresa que vende sus productos en mercados competitivos y, en segundo lugar, la función de costes nos permite plasmar en un modelo la conducta de producción de las empresas que no venden sus productos en mercados competitivos. Por otra parte, el análisis de la minimización de los costes nos da una idea de los métodos analíticos que se utilizan para examinar los problemas de la optimización sujeta a restricciones. 4.1 Análisis de la minimización de los costes basado en el cálculo Consideremos el problema consistente en hallar la manera de obtener un determinado nivel de producción que minimice el coste: minwx X sujeta a f (x) = y. Este problema de minimización sujeta a restricciones se analiza utilizando el método de los multiplicadores de Lagrange. Comenzamos escribiendo el lagrangiano [,().., x) = wx - >.(J (x) - y), y diferenciándolo con respecto a cada una de las variables de elección, xi, y el multiplicador de Lagrange, >.. Las condiciones de primer orden que caracterizan una solución interior x" son . - /\\ a f(x*) a W; Xi = o cuand o z. = 1 ' ... ' n .f(x*) = y. 60 / LA MINIMIZACIÓN DE LOS COSTES ( C. 4) Estas condiciones también pueden expresarse utilizando una notación vectorial. Si definimos D f(x) como el vector gradiente, es decir, el vector de las derivadas parciales de f(x), podemos expresar las condiciones de las derivadas de la manera siguiente: w = -\Df(x*). Estas condiciones de primer orden pueden interpretarse dividiendo la condición i-ésima por la j-ésima: i, j = 1, · · ·, n. (4.1) El segundo miembro de esta expresión es la relación técnica de sustitución, es decir, la relación a la que puede sustituirse el factor i por el j, manteniendo constante el nivel de producción. El primer miembro es la relación económica de sustitución, es decir, la relación a la que puede sustituirse el factor i por el j manteniendo constante el coste. Las condiciones antes citadas exigen que la relación marginal de sustitución sea igual a la relación económica de sustitución. En caso contrario, podría realizarse algún tipo de ajuste que permitiría obtener el mismo nivel de producción con un coste menor. Supongamos, por ejemplo, que En ese caso, si utilizamos una unidad menos del factor i y una unidad más del factor j, la producción no varía, pero los costes disminuyen, pues ahorramos dos pesetas contratando una unidad menos del factor i e incurrimos en un coste adicional de una peseta solamente contratando una unidad más del factor j. Esta condición de primer orden también puede representarse gráficamente. Las líneas curvas de la figura 4.1 representan isocuantas y las rectas curvas de coste constante. Cuando y está fijo, el problema de la empresa consiste en hallar un punto de una isocuanta dada que minimice el coste. La ecuación de una curva de coste constante C = w·1 x1 + w2x2 puede expresarse de la manera siguiente: x2 = C / w: - ( w1 / w2)x1. Dados w1 y w2, la empresa desea encontrar un punto de una isocuanta dada en el que la ordenada en el origen de la curva de coste constante correspondiente sea mínima. Es evidente que ese punto estará caracterizado por la condición de tangencia según la cual la pendiente de la curva de coste constante debe ser igual a la pendiente de la isocuanta. Sustituyendo estas dos pendientes por las expresiones algebraicas, obtenernos la ecuación (4.1). Análisis de la minimización de los costes basado en el cálculo / 61 Figura 4.1 FACTOR2 f(X1,X2) =y FACTOR 1 Minimización de los costes. En un punto que minimiza los costes, la isocuanta debe ser tangente a la línea de coste constante. El examen de la figura 4.1 indica que en la elección minimizadora del coste también debe satisfacerse una condición de segundo orden, a saber, la isocuanta debe encontrarse por encima de la recta isocoste. En otras palabras, cualquier variación de las cantidades utilizadas de factores que mantenga constantes los costes -es decir, un movimiento a lo largo de la recta isocoste- debe provocar una reducción de la producción o mantenerla constante. ¿Cuáles son las implicaciones locales de esta condición? Sea (h1, h2) una pequeña variación de los factores 1 y 2 y consideremos la variación correspondiente de la producción. Suponiendo que la función es diferenciable, podemos escribir el siguiente desarrollo en serie de Taylor de segundo orden: Resulta más útil formular esta expresión por medio de la notación matricial: J (x¡ + h¡, x2 + h2) "' f(x¡, x2) + ( !1 +h¡ h2) Í2) rn: ( ��) j�)(��) 62 / LA MINIMIZACIÓN DE LOS COSTES ( C. 4) Una variación (h1, h2) que mantiene constante los costes debe satisfacer la igualdad w1 h1 + w2h2 = O. Sustituyendo ui, por su valor que se deduce de la condición de primer orden para la minimización de los costes, podemos expresar esto de la siguiente manera: Por lo tanto, los términos de primer orden de este desarrollo en serie de Taylor deben ser iguales a cero cuando nos desplazamos a lo largo de la recta isocoste. Por consiguiente, la condición según la cual la producción disminuye cuando se produce cualquier movimiento a lo largo de la recta isocoste puede formularse de la siguiente manera: cualesquiera que sean c-: h2) tales que ( Ji (4.2) Intuitivamente, en el punto minimizador de los costes, un desplazamiento de primer orden tangente a la curva isocoste implica que la producción permanece constante y un desplazamiento de segundo orden implica que disminuye. Esta manera de expresar la condición de segundo orden puede generalizarse al caso de n factores; la condición de segundo orden correspondiente es que el hessiano de la función de producción sea semidefinido negativo sujeto a una restricción lineal htD2 f(x*)h � O cualquiera que sea h tal que wh = O. 4.2 Reconsideración de las condiciones de segundo orden En el capítulo 27 (página 576), demostramos que podemos formular las condiciones de segundo orden haciendo intervenir al hessiano del lagrangiano. Apliquemos el método al caso que nos ocupa. En este caso, el lagrangiano es Las condiciones de primer orden para la minimización de los costes son que la primera derivada del lagrangiano con respecto a A, x1 y x2 sea igual a cero. En las condiciones de segundo orden interviene el hessiano del lagrangiano, Dificultades / 63 Es útil representar 82 f / 8xi8x i por medio de Íii. Calculando las diferentes segundas derivadas y utilizando esta notación, tenemos que -h -).fn -).h1 -h) -).ft2 -).f22 (4.3) · Esta matriz es el llamado hessiano orlado. De acuerdo con lo expuesto en el capítulo 27 (página 576), las condiciones de segundo orden enunciadas en (4.2) pueden satisfacerse como una desigualdad estricta si y sólo si el determinante del hessiano orlado es negativo. De esa manera tenemos una condición relativamente sencilla para averiguar si las condiciones de segundo orden se satisfacen o no en un caso concreto. En el caso general, en el que se demandan n factores, las condiciones de segundo orden son algo más complicadas. En este caso, tenemos que verificar el signo de los determinantes de ciertas submatrices del hessiano orlado. Véase el análisis en el capítulo 27 (página 576). Supongamos, por ejemplo, que hay tres factores de producción. El hessiano orlado adoptará la forma siguiente: -h -h -h ) -).fn -).f12 -).j13 -).h1 -).f22 -).j23 -).h1 -).h2 -).f33 . (4.4) Por lo tanto, en el caso en el que hay tres factores las condiciones de segundo orden exigen que el determinante tanto de (4.3) como de (4.4) sea negativo cuando se evalúa en el punto de elección óptima. Si hay n factores, todos los hessianos orlados de esta forma deben ser negativos para que se satisfagan las condiciones de segundo orden como desigualdades estrictas. 4.3 Dificultades A cada elección de w e y le corresponde una elección de x" que minimiza el coste de obtener y unidades de producción. La función que nos indica cuál es esta elección óptima se denomina función de demanda condicionada de los factores y se expresa de la forma siguiente: xíw, y). Obsérvese que las demandas condicionadas de los 64 / LA MINIMIZACIÓN DE LOS COSTES ( C. 4) factores dependen del nivel de producción, así como de los precios de los factores. La función de costes es el coste mínimo correspondiente a los precios de los factores w y al nivel de producción y, es decir, c(w, y)= wx(w, y). Las condiciones de primer orden son razonablemente intuitivas, pero al igual que ocurre en el caso de la maximización del beneficio, su mera aplicación mecánica puede plantear problemas. Examinemos las cuatro posibles dificultades que pueden surgir en el problema de maximización del beneficio y veamos qué relación guardan con el problema de minimización de los costes. En primer lugar, es posible que la tecnología en cuestión no pueda representarse por medio de una función de producción diferenciable y que, por lo tanto, no puedan aplicarse las técnicas del cálculo. La tecnología de Leontief constituye un buen ejemplo de este problema. Más adelante calculamos su función de costes. En segundo lugar, las condiciones sólo son válidas en el caso de las soluciones interiores; deben modificarse si el punto de minimización del coste se encuentra en una esquina. Las condiciones adecuadas son a f (x*) . * ,\-�-- - ui; ::; Ü SI Xi U Xi 8f(x*) ,\-�-- - Wi U Xi . * =Ü = Ü SI Xi > Ü. Más adelante examinaremos de nuevo este problema poniendo un ejemplo concreto. La tercera dificultad que podía surgir en el análisis de la maximización del beneficio estaba relacionada con la existencia de una combinación maximizadora del beneficio. Sin embargo, este tipo de problema no suele surgir en el caso de la minimización de los costes. Es bien sabido que una función continua alcanza un valor mínimo y un valor máximo en un conjunto cerrado y acotado. La función objetivo wx es, ciertamente, una función continua y el conjunto V(y) es un conjunto cerrado por hipótesis. Lo único que hemos de demostrar es que podemos centrar exclusivamente la atención en un subconjunto acotado de V(y). Pero eso es fácil. Basta tomar un valor arbitrario de x, por ejemplo, x', Es evidente que el coste de la combinación de factores de coste mínimo debe ser inferior a wx'. Por lo tanto, podemos centrar exclusivamente la atención en el subconjunto { x pertenece a V (y) : wx � wx'}, que es, ciertamente, un subconjunto acotado, en la medida en que w � O. En cuarto lugar, las .condicíones de primer orden pueden no determinar una posición única de la empresa, pues, al fin y al cabo, las condiciones del cálculo sólo son condiciones necesarias. Aunque suelen ser suficientes para la existencia de un óptimo local, describen únicamente un óptimo global en determinadas condiciones de convexidad; en otras palabras, estas condiciones de minimización de los costes exigen que V (y) sea convexo. Dificultades / 65 Ejemplo: La función de costes en el caso de la tecnología Cobb-Douglas Consideremos el siguiente problema de minimización de los costes: c(w, y)= minw1x1 + w2x2 x1,x2 · a A X1a X2b = y. sujeta Sustituyendo x2 por su valor que se deduce de la restricción, vemos que este problema equivale a 1 1 _ _g,_ min w1x1 + w2A--¡; yi; x1 b x1 La condición de primer orden es que nos da la función de demanda condicionada del factor 1: La otra función de demanda condicionada es [aw2]-a:b _L. -ya+b. bw1 La función de costes es Cuando utilicemos la tecnología Cobb-Douglas como ejemplo, normalmente mediremos las unidades de. tal manera que A = 1 y utilizaremos el supuesto de que hay rendimientos constantes de escala, es decir, a + b = 1. En este caso, la función de costes se reduce a e ( w1, uri, y ) = K W1a w21-a Y, 66 / LA MINIMIZACIÓN DE LOS COSTF.S (C. 4) Ejemplo: La función de costes en el caso de la tecnología CES Supongamos que f(x1, x2) = (xf + x;>i· ¿Cuál es la función de costes correspondiente? El problema de minimización de los costes es min w1x1 + w2x2 sujeta a xf + x; = yP Las condiciones de primer orden son w1 - Apxf-1 = O w2 - Apx;-1 = O xf + x; = yP. Despejando xf y x; en las dos primeras ecuaciones, tenemos que ___e_ ..:::...e.... xf = wC1 (.\p)p-1 (4.5) x; = w.;-1 (.Xp) p-1. ___e_ ..:::...e.... Introduciendo estos resultados en la función de producción, tenemos que Despejando (.\p)� e introduciendo el resultado en el sistema (4.5), obtenemos las funciones de demandas condicionadas de los factores: Introduciendo estas funciones en la definición de la función de costes, tenemos que Esta expresión es más sencilla si sustituimos p / (p - 1) por r: c(w1, vn, y)= y 1 [wí + w2] r. Dificultades / 67 Obsérvese que esta función de costes tiene la misma forma que la función de producción CES original con la salvedad de que hemos sustituido p por r. En el caso general en el que f(x1, x2) = 1 [(a1x1)P + (a2x2)P]-¡;, pueden realizarse cálculos similares para demostrar que 1 c(w1, w2, y)= [(wif a1r + (w2/a2t]-; y. Ejemplo: La función de costes en el caso de la tecnología de Leontief Supongamos que f (x1, x2) = min { ax1, bx2}. ¿ Cuál es la función de costes correspondiente? Dado que sabemos que la empresa no despilfarrará ningún factor que tenga un precio positivo, ésta debe encontrarse en un punto en el que y= ax1 = bx2. Por lo tanto, si la empresa desea obtener y unidades de producción, debe utilizar y/ a unidades del bien 1 y y/ b unidades del bien 2, cualesquiera que sean los precios de los factores. Por lo tanto, la función de costes viene dada por Ejemplo: La función de costes en el caso de la tecnología lineal Supongamos que f (x1, x2) = ax1 + bx», lo que quiere decir que los factores 1 y 2 son sustitutivos perfectos. ¿ Qué forma tendrá la función de costes? Dado que los dos bienes son sustitutivos perfectos, la empresa utilizará el más barato. Por lo tanto, la función de costes tendrá la forma siguiente: c(w1, w2, y) = min{ wif a, un] b }y. En este caso, normalmente la respuesta al problema de minimización del coste es una solución de esquina: uno de los dos factores se utilizará en una cantidad cero. Aunque es fácil ver cuál es la solución de este problema, merece la pena presentar una solución más formal, ya que constituye un buen ejemplo para ver cómo se utiliza el teorema de Kuhn-Tucker.. Este teorema es el instrumento adecuado en este caso, ya que casi nunca tenemos una solución interior. Véase el capítulo 27 (página 583) para una formulación del teorema. Para simplificar la notación, consideramos el caso especial en el que a = b = 1. Planteamos el problema de minimización de la manera siguiente: 68 / LA MINIMIZACIÓN DE LOS COSTES (C. 4) s.t. x1 +x2 = y x1 2: O x2 2: O. El lagrangiano de este problema puede expresarse de la forma siguiente: Las condiciones de primer orden de Kuhn-Tucker son WI - ,\ - µl =Ü w2 - ,\ - M = O XI+ X2 = Y 2: Ü x2 2: O. XI y las condiciones complementarias de holgura son 2: Ü, µl = Ü si XI > Ü M 2: O, M = O si x2 > O. µl Para averiguar la solución de este problema de minimización, tenemos que examinar cada uno de los casos posibles en los que las restricciones de desigualdad son o no activas. Dado que hay dos restricciones y cada una de ellas puede ser o no activa, tenemos que examinar cuatro casos. 1) x1 = O, x2 = O. En este caso, no podemos satisfacer la condición según la cual + x2 = y, a menos que y= O. x1 2) x1 = O: x2 > O. En este caso, sabemos que µi = O. Por lo tanto, de las dos primeras condiciones de primer orden se deduce que WI = ,\ + µl w2 = ,\ Dado que µ1 2: O, este caso sólo puede surgir cuando w1 > x1 = O, se deduce que x2 = y. w2. Dado que 3) x2 = O, x1 > O. Siguiendo un razonamiento similar al del caso anterior, se demuestra que x1 = y y que este caso sólo ocurre cuando w2 2: w1. 4 x1 > O, x2 > O. En este caso, la condición complementaria de holgura implica Funciones de demandas condicionadas de factores / 69 que µ1 = O y µi w1 = w2. = O. Por lo tanto, las condiciones de primer orden implican que El problema anterior, aunque es algo trivial, es representativo de los métodos que se utilizan cuando se aplica el teorema de Kuhn-Tucker, Si hay k restricciones que pueden ser o no activas, habrá 2k configuraciones posibles en el óptimo. Es preciso analizar cada una de ellas para ver si son compatibles, de hecho, con todas las condiciones exigidas, en cuyo caso representan soluciones potencialmente óptimas. 4.4 Funciones de demandas condicionadas de factores Pasemos a analizar el problema de la minimización de los costes y las demandas condicionadas de factores. Siguiendo los razonamientos habituales, las funciones de demandas condicionadas de los factores x(w, y) deben satisfacer las siguientes condiciones de primer orden: f(x(w, y))= y w - .\Df(x(w, y))= O. Es fácil perderse en el álgebra matricial de los cálculos siguientes, por lo que analizaremos un sencillo ejemplo en el que sólo hay dos bienes. En este caso, las condiciones de primer orden son wi f (x1 (w1, w2, y), x2(w1, w2, y)) _ _x 8 f (x1 (w1, w2, y), x2(w1, w2, y)) 8x1 w: _ .\ 8 f (x1 (w1, w2, y), x2(w1, w2, y)) 8x2 =y = O =O Estas condiciones de primer orden son, al igual que en el capítulo anterior, identidades: de acuerdo con la definición de las funciones de demandas condicionadas de los factores, se cumplen cualesquiera que sean los valores que adopten w1, w2 e y. Por lo tanto, podemos diferenciarlas, por ejemplo, con respecto a w1: a¡ 8x1 a¡ 8x2 8x1 8w1 8x2 8w1 - --+--=O 1 _ .\ O_.\ [ 82 82 8x1 + f 8x2 axf 8w1 8x18x2 8w1 [ f 82 f 82 8x1 + f 8x2 ax� 8w1 8x28x1 8w1 ] - 8 f DA = O 8x1 8w1 - J - 8f 8-X 8x2 8w1 = O. 70 / LA MINIMIZACIÓN DE LOS COSTES (C. 4) Estas ecuaciones pueden expresarse en forma matricial: -h ->..fn ->..!12 -�%1) (�) = (�1). ->..h2 8x2 O a-;;;; Obsérvese que la matriz situada en el lado izquierdo es precisamente el hessiano orlado que interviene en las condiciones de segundo orden para la maximización (véase el capítulo 27, página 576). Utilizando una técnica habitual del álgebra matricial, la regla de Cramer, que se analiza en el capítulo 26 (página 553), podemos despejar 8x1 / 8w1: 8x1 8w1 1-�¡ 1-�¡ -[J_ -h o -1 -h ->..J21 I o ->..fo -h -h 1· ->..fn ->..J21 ->..!12 ->..J22 Sea H el determinante de la matriz que aparece en el denominador de esta fracción. Sabemos que se trata de un número negativo de acuerdo con la condición de segundo orden para la minimización. Desarrollando el cálculo del numerador, tenemos que Por lo tanto, la curva de demanda condicionada de los factores tiene pendiente negativa. La expresión correspondiente a 8x2/ 8w1 puede obtenerse de la misma forma. Aplicando la regla de Cramer, tenemos que 8x1 8w1 1-�¡ 1-�¡ -f2 -h �11 Í1 ->..f11 ->..fu -h ->..f11 ->..J12 -h ->..fo ->..h2 1· Realizando los cálculos indicados, tenemos que 8x2 =-Í2Í1 >O. 8w1 H Repitiendo el mismo tipo de cálculos en el caso de 8x1 / 8w2, tenemos que (4.6) Funciones de demandas condicionadas de factores / 71 o o -1 -Ji -h ->.J12 I ->.J22 ->.fi1 ->.J12 lo que implica que (4.7) Si comparamos las expresiones (4.6) y (4.7), veremos que son idénticas. Por lo tanto, 8xif 8w2 es igual a 8x2/ 8w1. Al igual que en el caso de la maximización del beneficio, encontramos una condición de simetría: como consecuencia del modelo de minimización de los costes, "los efectos cruzados de los precios deben ser iguales". En el caso en el que hay dos factores, que es el que estamos analizando aquí, el signo del efecto cruzado de los precios debe ser positivo. Es decir, los dos factores deben ser sustitutivos. Se trata de un caso especial; si hay más factores de producción, el efecto cruzado de los precios entre dos cualesquiera de ellos puede ir en cualquiera de los dos sentidos. A continuación expresamos de nuevo los cálculos anteriores por medio del álgebra matricial. Dado que y se mantiene fijo en todos ellos, lo suprimimos como argumento de las demandas condicionadas de los factores para simplificar la notación. Las condiciones de primer orden para la minimización de los costes son f(x(w)) w - >.D f(x(w)) =y = O. Diferenciando estas identidades con respecto a w, obtenemos: Df (x(w))Dx(w) = O 1 - >.D2 f (x(w))Dx(w) - D f (x(w))D>.(w) = O. Reordenando algo los términos, tenemos que Obsérvese que la matriz es simplemente el hessiano orlado, es decir, la matriz de segundas derivadas del lagrangiano. Suponiendo que tenemos un óptimo en sentido estricto, de tal manera que el hessiano no es degenerativo, podemos despejar la matriz de sustitución Dx(w) premultiplicando por la inversa del hessiano: 72 / LA MINIMIZACIÓN DE LOS COSTES (C. 4) (DA(w)) Dx(w) - ( O D f (x)' D f (x) )- l >.D2 f(x) ( O) 1 . (Hemos multiplicado los dos miembros por -1 para eliminar los signos negativos de la expresión.) Dado que el hessiano orlado es simétrico, su inversa es simétrica, lo que demuestra que los efectos cruzados de los precios son simétricos. También puede demostrarse que la matriz de sustitución es semidefinida negativa. Omitimos aquí esta demostración debido a que a continuación presentamos una sencilla prueba utilizando otros métodos. 4.5 Enfoque algebraico de la minimización de los costes Al igual que en el caso de la maximización del beneficio, también podemos aplicar aquí las técnicas algebraicas para resolver el problema de minimización de los costes. Tomamos como datos algunas elecciones que hemos observado que ha adoptado una empresa en lo que se refiere a los niveles de producción yt, a los precios de los factores wt y a las cantidades de factores xt, siendo t = 1, ... , T. ¿Cuándo son coherentes estos datos con el modelo de minimización de los costes? Una condición necesaria y evidente es que el coste de la elección observada de la cantidad de factores no sea mayor que el coste de cualesquiera otras cantidades de factores que generarían al menos el mismo nivel de producción, lo que, traducido en símbolos, quiere decir que Esta condición se denomina axioma débil de la minimización de los costes (ADMC). El ADMC puede utilizarse, al igual que en el caso de la maximización del beneficio, para obtener la versión en primeras diferencias de las demandas de pendiente negativa. Basta tomar dos observaciones diferentes en las que el nivel de producción sea el mismo y observar que la minimización de los costes implica que wtxt � wtxs wsxs ::; wsxt. La primera expresión nos dice que la observación t-ésima debe ser la que tenga los costes más bajos a los precios t-ésimos; la segunda nos dice que la observación s-ésima debe ser la que tenga los costes de producción más bajos a los precios s-ésimos. Expresando la segunda desigualdad de la siguiente manera: Enfoque algebraico de la minimización de los costes / 73 sumándola a la primera y reordenando el resultado, tenemos que (w' - W8) (x' - x") � O, o �w�x < O. Dicho de forma aproximada, el vector de las demandas de factores debe variar en sentido "contrario" al vector de los precios de los factores. También es posible construir la frontera interior y la exterior del verdadero conjunto de cantidades necesarias de factores que generó los datos. Aquí nos limitaremos a definir las fronteras y dejaremos al lector que verifique los detalles. Los argumentos son semejantes a los que presentamos en el caso de la maximización del beneficio. La frontera interior viene dada por: V I(y) = cápsula monótona convexa de { x' : yt 2: y}. Es decir, la frontera interior es simplemente la cápsula monótona convexa de todas las observaciones que pueden generar, al menos, la cantidad de producción y. La frontera exterior viene dada por V E(y) = { x : w'x 2: wtxt cualquiera que sea t tal que yt � y}. Estos conjuntos, representados en la figura 4,2, son análogos a los de Y E e Y l. Figura 4.2 FACTOR 2 FACTOR 2 FACTOR 1 FACTÓR 1 Frontera interior y exterior. Los conjuntos VI y V E indican la frontera interior y la exterior del verdadero conjunto de cantidades necesarias de factores. Es bastante evidente que V I(y) está contenido en V(y), al menos en la medida en que V (y) es convexo y monótono. Tal vez no sea tan evidente que V E(y) contiene a V(y), por lo que ofrecemos la siguiente demostración. 74 / LA MINIMIZACIÓN DE LOS COSTES ( C. 4) Supongamos, en contra de lo afirmado, que existe algún x que pertenece a V(y), pero no a V E(y). Dado que x no pertenece a V E(y), debe haber alguna observación t tal que yt ::; y, y además (4.8) Pero como x pertenece a V(y), puede generar al menos yt unidades de producción y (4.8) demuestra que cuesta menos que x', lo que contradice el supuesto de que x' es una combinación minimizadora del coste. Notas El enfoque algebraico de la minimización de los costes se desarrolla más extensamente en Varian (1982b). Ejercicios 4.1. Demuestre rigurosamente que la maximización del beneficio implica la minimización de los costes. 4.2. Utilice el teorema de Kuhn-Tucker para obtener las condiciones para la minimización de los costes que son válidas aun cuando la solución óptima sea una solución de esquina. 4.3. Una empresa tiene dos instalaciones cuyas funciones de coste son c1 (y1) = y c2(Y2) = Y2· ¿Cuál es la función de costes de la empresa? y¡ /2 4.4. Una empresa tiene dos instalaciones. Una produce de acuerdo con la función de producción 1 La otra tiene la función de producción ¿Cuál es la función de costes correspondiente a esta tecnología? x x1-ª· xtx1-b· 4.5. Suponga que la empresa tiene dos actividades posibles para producir. La a utiliza a1 unidades del bien 1 y a2 unidades del bien 2 para generar 1 unidad de producción. La actividad b utiliza b; unidades del bien 1 y b2 unidades del bien 2 para generar 1 unidad de producción. Los factores sólo pueden utilizarse en estas proporciones fijas. Si sus precios son (w1, w2), ¿cuáles son las demandas de los dos factores? ¿Cuál es la función de costes de esta tecnología? ¿A qué precios de los factores no es diferenciable la función de costes? 4.6. Una empresa tiene dos instalaciones cuyas funciones de costes son c1 (y1) = y c2(y2) = 2..jyi_. ¿Cuál es el coste de producir la cantidad y? 4JY1 Ejercicios / 75 4.7. El cuadro siguiente muestra dos observaciones sobre la demanda de factores x1, x2, sobre los precios de los factores, w1, w2 y el nivel de producción, y, de una empresa. ¿Es la conducta descrita en este cuadro coherente con la conducta minimizadora de los costes? Obs y W1 W2 X1 X2 A 100 2 1 10 20 B 110 1 2 14 10 4.8. Una empresa tiene la función de producción y = x1x2. Si el coste mínimo de producción cuando a w1 = w2 = 1 es igual a 4, ¿cuál es el valor de y? 5. LA FUNCIÓN DE COSTES La función de costes mide el coste mínimo de obtener un determinado nivel de producción, dados los precios de los factores. Como tal, resume la información sobre las opciones tecnológicas de las empresas. La conducta de la función de costes puede transmitir una gran cantidad de información sobre la naturaleza de la tecnología de la empresa. De la misma manera que la función de producción es nuestro instrumento principal para describir las posibilidades tecnológicas de producción, la función de costes es nuestro instrumento principal para describir las posibilidades económicas de la empresa. En los dos siguientes apartados, investigaremos la conducta de la función de costes e( w, y) con respecto a sus argumentos de precios y cantidad. Pero antes de emprender ese estudio, es preciso definir algunas funciones relacionadas con ésta, a saber, las funciones de coste medio y de coste marginal. 5.1 Costes medios y marginales Examinemos la estructura de la función de costes. En general, ésta siempre puede expresarse simplemente como el valor de las demandas condicionadas de factores, c(w, y)= wx(w, y) lo que significa simplemente que el coste mínimo de obtener y unidades de producción es el coste de la manera más barata de producir y. A corto plazo, algunos de los factores de producción están fijos y tienen un nivel predeterminado. Sea x ¡ el vector de los factores fijos, x., el vector de los factores variables y descompóngase w en w = (wv, w¡), los vectores de los precios de los factores variables y de los factores fijos. Las funciones de demandas condicionadas de factores a corto plazo dependen generalmente de x ¡, por lo que las expresamos de la manera siguiente: xv(w, y, x¡). En ese caso, la función de costes a corto plazo puede expresarse de la forma siguiente: 78 / LA FUNCIÓN DE COSTES ( C. 5) El término wvxv(w, y, x¡) se denomina coste variable a corto plazo (CVC) y el término w ¡x¡ es el coste fijo (CF). A partir de estas tres unidades básicas podemos definir algunos otros conceptos de coste: coste total a corto plazo= CTC = Wvxv(w, y, x¡) + w ¡x¡ c(w, y, x¡) coste medio a corto plazo = CMeC = ---y WvXv(W, y, x¡) coste variable medio a corto plazo = CVMeC = -----y coste fijo medio a corto plazo = CFMeC = w f x f y coste marginal a corto plazo= CMC = ac(w,y,x¡) ay Cuando todos los factores son variables, la empresa elige el x ¡ que es óptimo. Por lo tanto, la función de costes a largo plazo sólo depende de los precios de los factores y del nivel de producción, como hemos indicado antes. Esta función a largo plazo puede expresarse en relación con la función de costes a corto plazo de la siguiente manera. Sea x¡(w, y) la elección óptima de los factores fijos y xv(w, y)= xv(w, y, x¡(w, y)) la elección óptima a largo plazo de los factores variables. En ese caso, la función de costes a largo plazo puede expresarse de la siguiente manera: c(w, y)= WvXv(w, y)+ w ¡x¡(w, y)= c(w, y, x¡(w, y)). La función de costes a largo plazo puede utilizarse para definir otros conceptos de coste similares a los anteriores: c(w, y) coste medio a largo plazo = CMeL = --y coste marginal a largo plazo = CML = ac(w, y) ay Obsérvese que el "coste medio a largo plazo" es igual al "coste variable medio a largo plazo", ya que todos los costes son variables a largo plazo; los "costes fijos a largo plazo" son cero por la misma razón. El largo plazo y el corto plazo son, por supuesto, conceptos relativos. El hecho de que un factor sea variable o fijo depende del problema que esté analizándose. El lector debe preguntarse primero en qué periodo de tiempo desea analizar la conducta de la empresa y a continuación qué factores puede ajustar ésta en ese periodo. Costes medios y marginales / 79 Ejemplo: Las funciones de costes a corto plazo en el caso Cobb-Douglas Supongamos que en una tecnología Cobb-Douglas el segundo factor sólo puede utilizarse en una cantidad k. En ese caso, el problema de minimización de los costes es rnin w1 x1 + w2k sujeta a y= x1k1-ª. Despejando, en la restricción, x1 en función de y y k, tenernos que X1 = ( y ka-l)lª Por lo tanto, También es posible calcular las siguientes variaciones: coste medio a corto plazo = w1 (Y) k - 1 -;;:ª w2k + -y (f )- ª 1-a coste variable medio a corto plazo = w2k coste fijo medio a corto plazo coste marginal a corto plazo W1 y = :,1 Oi)- ª 1-o. Ejemplo: Los rendimientos constantes de escala y la función de costes Si la función de producción muestra rendimientos constantes de escala, es intuitivamente evidente que la función de costes debe ser lineal con respecto al nivel de producción: si querernos producir el doble, nos costará el doble. Esta idea intuitiva se verifica en la siguiente proposición: Rendimientos constantes de escala. Si la función de producción muestra rendimientos constantes de escala, la función de costes puede expresarse de la forma siguiente: c(w, y) = yc(w, 1). Demostración. Sea x* la manera más barata de obtener una unidad de producción a los precios w, de tal manera que c(w, 1) = wx*. En ese caso, afirmarnos que c(w, y)= wyx* = yc(w, 1). Obsérvese, en primer lugar, que yx* es viable para producir y, ya que la tecnología muestra rendimientos constantes de escala. Supongamos que 80 / LA FUNCIÓN DE COSTES (C. 5) no minimiza el coste y que x' es, por el contrario, la combinación minimizadora del coste para producir y a los precios w, de tal manera que wx' < wyx*. En ese caso, wx' /y< wx* y x' /y pueden producir 1, ya que la tecnología muestra rendimientos constantes de escala, lo que contradice la definición de x". Si la tecnología muestra rendimentos constantes de escala, las funciones de coste medio, de coste variable medio y de coste marginal son todas iguales. 5.2 Análisis geométrico de los costes La función de costes es el instrumento más útil para estudiar la conducta económica de una empresa. Resume, en un sentido que resultará claro más adelante, toda la información económicamente pertinente sobre la tecnología de la empresa. En los siguientes apartados, examinaremos algunas de sus propiedades, y lo haremos de la manera más sencilla, a saber, en dos etapas: en primer lugar, examinaremos sus propiedades partiendo del supuesto de que los precios de los factores son fijos. En este caso, escribiremos la función de costes sencillamente de la forma siguiente: c(y). En segundo lugar, examinaremos sus propiedades cuando los precios de los factores pueden variar libremente. Dado que hemos supuesto que los precios de los factores son fijos, los costes dependen únicamente del nivel de producción de la empresa; esta relación entre el nivel de producción y los costes puede representarse mediante útiles gráficos. Siempre se supone que la curva de coste total es monótona con respecto al nivel de producción: cuanto más produzcamos, más nos costará. La curva de coste medio, sin embargo, puede aumentar o disminuir con el nivel de producción, dependiendo de que los costes totales aumenten más o menos que proporcionalmente. A menudo se piensa que el caso más realista, al menos a corto plazo, es aquel en el que la curva de coste medio primero disminuye y después aumenta. La razón es la siguiente. A corto plazo, la función de costes tiene dos componentes: los costes fijos y los costes variables. Por lo tanto, el coste medio a corto plazo puede expresarse de la manera siguiente: CmeC= c(w,y,x¡) = w¡x¡ + WvXv(w,y,x¡) =CFMeC+CVMeC. y y y En la mayoría de los casos, los factores fijos a corto plazo son cosas como las máquinas, los edificios y otros tipos de equipo de capital, mientras que los factores variables son el trabajo y las materias primas. Veamos cómo varían los costes atribuibles a estos factores cuando varía el nivel de producción. Análisis geométrico de los costes / 81 Cuando elevamos el nivel de producción, los costes variables medios pueden disminuir inicialmente si hay alguna región inicial de economías de escala. Sin embargo, parece razonable suponer que los factores variables necesarios aumentarán más o menos proporcionalmente hasta que nos aproximemos a algún nivel de capacidad productiva determinado por las cantidades de los factores fijos. Cuando estamos próximos al nivel de máxima capacidad, necesitamos utilizar una cantidad de los factores variables más que proporcional para elevar el nivel de producción. Por lo tanto, como muestra la figura 5.lA, la función de costes variables medios acabará aumentando a medida que aumente el nivel de producción. Los costes fijos medios deben disminuir, por supuesto, conforme aumenta el nivel de producción, como indica la figura 5.1 B. Sumando la curva de coste variable medio y los costes fijos medios tenemos la curva de coste medio en forma de U de la figura 5.1 C. La disminución inicial de los costes medios se debe a la disminución de los costes fijos medios; el incremento que acaban experimentando los costes medios se debe al aumento de los costes variables medios. El nivel de producción en el que se minimiza el coste medio de producción se denomina a veces escala mínima eficiente. Figura 5.1 CMe CVMe CFMe e��:� CFMe CFMe NIVEL DE PRODUCCION NIVEL DE PRODUCCION CMe CVMe CFMe NIVEL DE PRODUCCION Curvas de coste medio. La curva de coste variable medio acaba aumentando a medida que aumenta el nivel de producción, mientras que la curva de coste fijo medio siempre disminuye. La relación entre estos dos efectos da lugar a una curva de coste medio en forma de U. A largo plazo, todos los costes son variables; en esas circunstancias, parece poco razonable aumentar los costes medios, ya que una empresa siempre podría repetir su proceso de producción. Por lo tanto, las posibilidades a largo plazo razonables deben ser o bien los costes medios constantes, o bien los costes medios decrecientes. Por otra parte, como hemos señalado anteriormente, algunos tipos de empresas pueden no mostrar una tecnología de rendimientos constantes de escala a largo plazo debido a los factores fijos a largo plazo. Si algunos factores permanecen fijos a largo plazo, la curva de coste medio a largo plazo adecuada probablemente tendrá forma de U, 82 / LA FUNCIÓN DE COSTES (C. 5) esencialmente por las mismas razones aducidas en el caso a corto plazo. Examinemos ahora la curva de coste marginal. ¿ Qué relación guarda con la curva de coste medio? Sea y* el punto de coste medio mínimo; en ese caso, a la izquierda de y* los costes medios son decrecientes, por lo que cuando y :::::; y* _!!__ dy (c(y)) < O. y Desarrollando la derivada, tenemos que - yc'(y) c(y) ----< O cuando y < y*, y2 lo que implica que c(y) c'(y):::::; - cuando y:::::; y y*. Según esta desigualdad, el coste marginal es menor que el coste medio a la izquierda del punto de coste medio mínimo. Realizando un análisis similar, se observa que c(y) cuan d o y 2:: y * . e '( y ) 2:: -y Dado que ambas desigualdades deben cumplirse en y*, tenemos que c'(y*) . = c(y*). y* ' es decir, los costes marginales son iguales a los costes medios en el punto en el que los costes medios son mínimos. ¿Qué relación existe entre la curva de coste marginal y la curva de coste variable? Modificando simplemente la notación del argumento anterior, podemos demostrar que la curva de coste marginal se encuentra por debajo de la de coste variable medio, cuando esta última es decreciente y por encima cuando es creciente. Por lo tanto, la curva de coste marginal debe pasar por el punto mínimo de la curva de coste variable medio. Tampoco es difícil demostrar que el coste marginal debe ser igual al coste variable medio en el cas� de la primera unidad de producción. Al fin y al cabo, el coste marginal de la primera unidad de producción es igual que el coste variable medio de la primera unidad de producción, ya que ambas magnitudes son iguales a cvO) - cv(O). También es posible hacer una demostración más formal. El coste variable medio se define de la forma siguiente: CV M e(y) = Cv(y). y Análisis geométrico de los costes / 83 Si y = O, esta expresión se convierte en O /0, que es indeterminado. Sin embargo, el límite de cv (y)/ y puede calcularse utilizando la regla de L'Hópital: c (O). lim Cv(y) = � y->0 1 y (Véase el capítulo 26, página 557 para una formulación de esta regla.) Por lo tanto, cuando el nivel de producción es cero, el coste variable medio es igual al coste marginal. El análisis anterior es válido tanto a largo plazo como a corto plazo. Sin embargo, si la producción muestra rendimientos constantes de escala a largo plazo, de tal manera que la función de costes es lineal con respecto al nivel de producción, el coste medio, el coste variable medio y el coste marginal son iguales, lo que hace que resulten bastante triviales la mayoría de las relaciones que acabamos de describir. Ejemplo: Las curvas de costes en el caso de la tecnología Cobb-Douglas Como calculamos en el ejemplo anterior, la tecnología Cobb-Douglas generalizada tiene una función de costes de la forma siguiente: c(y) = 1 a+b < 1 Kya+b donde K es una función de los precios de los factores y de los parámetros. Por lo tanto, c(y) CMe(y) = - = y CM(y) = c'(y) = 1-a-b Ky� K 1-a-b --y�. a+b Si a+ b < 1, las curvas de costes muestran costes medios crecientes; si a+ b = 1, las curvas de costes muestran un coste medio constante. También hemos visto antes que la función de costes a corto plazo en el caso de la tecnología Cobb-Douglas. tiene la forma siguiente: 1 c(y) = Kya + F. Por lo tanto, CME(y) c(y) 1-a F = - = Ky-;;:- + -. y y 84 / LA FUNCIÓN DE COSTES ( C. 5) 5.3 Las curvas de costes a largo plazo y a corto plazo Examinemos ahora la relación entre las curvas de costes a largo plazo y las curvas de costes a corto plazo. Es evidente que la curva de coste a largo plazo nunca debe encontrarse por encima de ninguna curva de coste a corto plazo, ya que el problema de minimización de los costes a corto plazo no es más que una versión del problema de minimización de los costes a largo plazo sujeta a restricciones. Expresemos la función de costes a largo plazo de la manera siguiente: c(y) = c(y, z(y)). En este caso, hemos omitido los precios de los factores, ya que suponemos que son fijos. Sea z(y) la demanda de un factor fijo que minimiza los costes; y*, un determinado nivel de producción; y z" = z(y*) la correspondiente demanda a largo plazo del factor fijo. El coste a corto plazo, c(y, z*), debe ser, al menos, tan elevado como el coste a largo plazo, c(y, z(y)), en todos los niveles de producción, e igual al coste a largo plazo en el nivel de producción y*, de tal manera que c(y*, z") = c(y*, z(y*)). Por lo tanto, las curvas de coste a largo plazo y a corto plazo deben ser tangentes en el punto y*. Figura 5.2 CMe c(y� z*) NIVEL DE PRODUCCION y* Curvas de coste medio a largo plazo y a corto plazo. Obsérvese que las curvas de coste medio a largo plazo y a corto plazo deben ser tangentes, lo que implica que los costes marginales a largo plazo y a corto plazo deben ser iguales. El razonamiento anterior no es sino una reformulación geométrica del teorema de la envolvente. La pendiente de la curva de coste a largo plazo en el punto y* es dc(y*' z(y*)) dy = oc(y*' z*) ay + oc(y*' z*) oz(y*). az oy Pero como z* es la elección óptima de los factores fijos correspondiente al nivel de producción u", tenemos que Las curvas de costes a largo plazo y a corto plazo / 85 oc(y*' z*) é)z = o. Por lo tanto, los costes marginales a largo plazo correspondientes a y* son iguales a los costes marginales a corto plazo correspondientes a (y*, z*). Figura 5.3 CMe NIVEL DE PRODUCCION La curva de coste medio a largo plazo. La curva de coste medio a largo plazo, e M eL, es la envolvente inferior de las curvas de coste medio a corto plazo, CMeC1, CMeCz y CMeC3. Debemos señalar, por último, que si las curvas de costes a largo plazo y a corto plazo son tangentes, también deben serlo las curvas de coste medio a largo plazo y a corto plazo. La figura 5.2 muestra una configuración característica. La relación entre las curvas de coste medio a largo plazo y a corto plazo también puede analizarse partiendo de la familia de curvas de coste medio a corto plazo. Supongamos, por ejemplo; que tenemos un factor fijo que sólo puede utilizarse en tres cantidades discretas: z1, z2, z3. La figura 5.3 muestra esta familia de curvas. ¿Cuál sería la curva de coste a largo plazo? Simplemente la envolvente inferior de estas curvas de coste a corto plazo, ya que la elección óptima de z para obtener el nivel de producción y no es sino aquella cuyo coste es menor. De esta manera se obtiene una curva de coste medio a largo plazo en forma de concha. Si el factor fijo puede tener muchos valores distintos, la curva se vuelve lisa. 86 / LA FUNCIÓN DE COSTF.S (C. 5) 5.4 Los precios de los factores y las funciones de costes Pasamos a continuación a estudiar la conducta de las funciones de costes cuando varían los precios. Las funciones de costes tienen varias propiedades interesantes que se derivan directamente de su definición y que se resumen a continuación. Obsérvese su enorme semejanza con las propiedades de la función de beneficios. Propiedades de la función de costes 1. No decreciente en w. Siw' 2'.:: w,entonces c(w',y) 2'.:: c(w,y). 2. Homogénea de grado 1 en w.c(tw, y)= tc(w, y) si t > O. 3. Cóncava en w. c(tw + (1 - t)w', y) 2'.:: tc(w, y)+ (1 - t)c(w', y) si O� t � 1. 4. Continua en w. c(w, y) es una función continua en w, cuando w 2'.:: O. Demostración. 1. Aunque esta propiedad es evidente, tal vez resulte útil hacer una demostración formal. Sean x y x' las combinaciones minimizadores del coste correspondientes a w y w'. En ese caso, wx � wx', lo que se deduce de la minimización, y wx' � w'x', ya que w � w'. Uniendo estas desigualdades, tenemos que wx � w'x', como queríamos demostrar. 2. Demostramos que si x es la combinación minimizadora del coste a los precios w, x también minimiza los costes a los precios tw. Supongamos que no fuera así y que x' es una combinación minimizad ora de los costes a los precios tw, de tal manera que twx' < twx. Pero esta desigualdad implica que wx' < wx, lo que contradice la definición de x. Por lo tanto, la composición de la combinación minimizadora del coste no varía cuando se multiplican los precios por un número positivo t y, por lo tanto, los costes deben multiplicarse exactamente por t : c(tw, y) = twx = tc(w, y). 3. Sean (w, x) y (w', x') dos combinaciones de precios y factores minimizadoras del coste y w" = tw + (1 - t)w' cualquiera que sea t tal que O � t � 1. Ahora bien, c(w", y)= w" x" = tw x" + (1 - t)w' x". Dado que x'' no es necesariamente la manera más barata de producir y a los precios w' o w, tenemos que wx" 2'.:: c(w, y) y w' · x" 2'.:: c(w', y). Por lo tanto, c(w". y) 2'.:: tc(w, y)+ (1 - t)c(w', y). Los precios de los factores y las funciones de costes / 87 4. La continuidad de e se deriva del teorema del máximo descrito en el capítulo 27 (página 586). La única propiedad sorprendente es la concavidad. Sin embargo, podemos dar una explicación intuitiva similar a la que ofrecimos en el caso de la función de beneficios. Supongamos que representamos el coste en función del precio de un único factor y que mantenemos todos los demás precios constantes. Si sube el precio de un factor, los costes nunca disminuyen (propiedad 1), pero aumentan a una tasa decreciente (propiedad 3). ¿Por qué? Porque como este factor se encarece y los demás precios permanecen constantes, la empresa minimizadora del coste lo sustituye por otros factores. Figura 5.4 COSTE C= W1 X�+}; W7 X7 c(w:y) w*1 Concavidad de la función de costes. La función de costes es una función cóncava del precio de los factores, ya que siempre debe encontrarse por debajo de la función de costes "pasiva". Esta propiedad resulta más clara analizando la figura 5.4. Sea x* una combinación minimizadora del coste a los precios w*. Supongamos que el precio del factor 1 varía, pasando de wj a w1. Si nos comportamos pasivamente y continuamos utilizando x", nuestros costes serán C = w1 xi + ¿�=2 w; El coste mínimo de producir c(w, y) debe ser inferior a esta función de costes "pasiva"; por lo tanto, la curva de c(w, y) debe encontrarse por debajo de la curva de la función de costes pasiva y ambas deben coincidir en wj. No es difícil ver que eso implica que c(w, y) es cóncava con respecto a w1. x;. Este mismo gráfico puede utilizarse para descubrir una manera muy útil de expresar la demanda condicionada de los factores. Expresemos primero formalmente el resultado: 88 / LA FUNCIÓN DE COSTES (C. 5) Lema de Shephard. (La propiedad de la derivada.) Sea x/w, y) la demanda condicionada de la empresa del factor i. En ese caso, si la función de costes es diferenciable en (w, y) y ui; > O siendo i = 1, ... , n, entonces Xi·( w,y ) _ 8c(w, y) i a Wi - = 1, · · ·, n. Demostración. La demostración es muy similar a la del lema de Hotelling. Sea x" la combinación minimizadora del coste que produce y a los precios w* y definamos la función de la manera siguiente: g(w) = c(w, y) - wx". Dado que c(w, y) es la manera más barata de producir y, esta función nunca puede ser positiva. Cuando w = w*, g(w*) =O.Dado que este valor es un máximo de g(w), su derivada debe ser igual a cero: 8g(w*) awi = 8c(w*, y) _ x� awi t: =0 i=l, .. ·,n Por lo tanto, el vector de factores que minimiza el coste viene dado simplemente por el vector de las derivadas de la función de costes con respecto a los precios. Dado que esta proposición es importante, vamos a sugerir cuatro formas distintas de demostrarla. En primer lugar, la función de costes es, por definición, igual a c(w, y) wx(w, y). Diferenciando esta expresión con respecto a ui, y utilizando las condiciones de primer orden, obtenemos el resultado (pista: x(w, y) también satisface la identidad f(x(w, y)) y; es necesario diferenciar esta expresión con respecto a uu). En segundo lugar, los cálculos anteriores no son, en realidad, más que una repetición de la derivación del teorema de la envolvente descrita en el apartado siguiente. Este teorema puede aplicarse directamente para obtener el resultado deseado. En tercer lugar, existe un elegante argumento geométrico que se basa en la misma figura 5.4 que utilizamos para demostrar la concavidad de la función de costes. Recuérdese que en la figura 5.4 la línea e = w1 .1:1 + 2 w; x; se encuentra por encima de e = c(w, y) y ambas curvas coinciden en w1 = w1. Por lo tanto, las curvas deben ser tangentes, de tal manera que x1 = 8c(w*, y)/ 8w1. Examinemos, por último, la idea económica intuitiva básica que subyace a la proposición. Si nos encontramos en un punto minimizador del coste y sube el precio w1, se produce un efecto directo, en el sentido de que aumenta el gasto realizado en el primer factor. Pero también se produce un efecto indirecto, en el sentido de que querremos alterar la combinación de factores. Pero como nos encontramos en un = = I:: El teorema de la envolvente en el caso de la optimización sujeta a restricciones / 89 punto minimizador del coste, cualquier variación infinitesimal debe generar unos beneficios adicionales nulos. 5.5 El teorema de la envolvente en el caso de la optimización sujeta a restricciones El lema de Shephard es otro ejemplo del teorema de la envolvente. Sin embargo, en este caso debemos aplicar una versión del teorema adecuada para los problemas de maximización sujeta a restricciones. La demostración se realiza en el capítulo 27 (página 581). Consideremos un problema general de maximización sujeta a restricciones con parámetros: = max g(x1, x2, a) M(a) x1,x2 sujeta a g(x1, x2, a) = O. = w1x1 + w2x2, h(x1, x2, a)= En el caso de la función de costes g(x1, x2) y a podría ser uno de los precios. f(x1, x2) -y, El lagrangiano de este problema es I:, = g(x1, x2, a) - >..h(x1, x2, a), y las condiciones de primer orden son 8g _ >.. 8h 8x1 8x1 8g _ >.. 8h 8x2 8x2 h(x1, x2, a) =0 =0 (5.1) = O. Estas condiciones determinan las funciones de elección óptima (x1 (a), x2(a)), las cuales determinan a su vez la función de máximo valor M(a) = g(x1 (a), x2(a), a) (5.2) El teorema de la envolvente nos da una fórmula de la derivada de la función de valor con respecto a un parámetro en el problema de maximización. Concretamente, la fórmula es dM(a) = 81:,(x, a) da Ba = 1 x=x(a) 8g(x1, x2, a) Da 1 _ . . x,=x,(a) x 8h(x1, x2, a) Da 1 Xi=x.,(a) 90 / LA FUNCIÓN DE COSTES (C. 5) Las derivadas parciales deben interpretarse, al igual que antes, con especial cautela: son las derivadas de g y h con respecto a un par x1 y x2 que se mantiene fijo en sus valores óptimos. El teorema de la envolvente se demuestra en el capítulo 27 (página 581). Aquí simplemente lo aplicamos al problema de minimización de los costes. En este problema, puede elegirse el parámetro a como uno de los precios de los factores, uu. La función de valor óptimo M(a) es la función de costes c(w, y). Según el teorema de la envolvente, _c_ 8 w_ ( y_,) 8Wi = _.8 C_ In», = Xi 1 X;=Xi(w,y) = Xi(W, y), que es simplemente el lema de Shephard. Ejemplo: Una reconsideración del coste marginal Examinemos otra aplicación del teorema de la envolvente: la derivada de la función de costes con respecto a y. Según el teorema de la envolvente, ésta viene dada por la derivada del lagrangiano con respecto a y. El lagrangiano del problema de minimización de los costes es Por lo tanto, 8c(w1,w2,Y) 8y = >.. En otras palabras, el multiplicador de Lagrange del problema de minimización de los costes es simplemente el coste marginal. 5.6 Estática comparativa a partir de la función de costes Hemos demostrado antes que las funciones de costes tienen determinadas propiedades que se derivan de ·la estructura del problema de minimización de los costes y también que las demandas condicionales de los factores son simplemente las derivadas de las funciones de costes. Por lo tanto, las propiedades de las funciones de costes que hemos encontrado se traducen en determinadas restricciones que deben cumplir sus derivadas, las funciones de demanda de los factores. Estas restricciones son del mismo tipo que las que encontramos antes utilizando otros métodos, pero su obtención a partir de la función de costes resulta bastante elegante. Estática comparativa a partir de la función de costes / 91 Examinemos cada una de ellas por separado. 1. La función de costes es no decreciente en los precios de los factores. Por lo tanto, 8c(w, y)/8wi = xi(w, ui > O. 2. La función de costes es homogénea de grado 1 en w. Por lo tanto, las derivadas de la función de costes, las demandas de los factores, son homogéneas de grado O en w (véase el capítulo 26, página 558). 3. La función de costes es cóncava en w. Por lo tanto, la matriz de segundas derivadas de la función de costes -la matriz de primeras derivadas de las funciones de demanda de los factores- es una matriz semidefinida negativa simétrica. Este resultado no es una consecuencia evidente de la conducta minimizadora de los costes. Tiene varias implicaciones. a. Los efectos cruzados de los precios son simétricos. Es decir, 8xi(w, y) 82c(w, y) 82c(w, y) 8xlw, y) 8Wj 8wj8Wi 8wi8Wj 8wi b. Los efectos del propio precio no son positivos. En términos generales, las curvas de demanda condicionada de los factores tienen pendiente negativa, ya que 8x,¡(w, y)/8wi = 82c(w, y)/8w2:::;: O, donde la última desigualdad se debe al hecho de que los elementos de la diagonal de una matriz semidefinida negativa no pueden ser positivos. c. El vector de las variaciones de las demandas de factores se mueve "en sentido contrario" al vector de las variaciones de los precios de los factores. Es decir, dw dx < O. Obsérvese que como la concavidad de la función de costes se deriva exclusivamente de la hipótesis de la minimización de los costes, la simetría y el carácter semidefinido negativo de la matriz de primeras derivadas de las funciones de demanda de los factores se derivan exclusivamente de la hipótesis de la minimización de los costes y no exigen que la estructura de la tecnología satisfaga restricción alguna. 92 / LA FUNCIÓN DE COSTES (C. 5) Notas Las propiedades de la función de costes han sido desarrolladas por varios autores, pero el análisis más sistemático se debe a Shephard (1953) y (1970). Para un estudio más exhaustivo, véase Diewert (1974). Nuestro análisis se basa en gran medida en McFadden (1978). Ejercicios 5.1. Una empresa tiene dos instalaciones. En una produce de acuerdo con la función de costes ci (y1) = y en la otra de acuerdo con la función de costes c2(y2) = Los precios de los factores son fijos, por lo que se omiten en el análisis. ¿ Cuál es la función de costes de la empresa? yr Yi 5.2. Una empresa tiene dos instalaciones cuyas funciones de costes son c1 (y1) ¿Cuál es su función de costes? y c2(Y2) = yr = 3y¡ 5.3. Una empresa tiene la función de producción f(x1, x2, x3, x4) = min+Zz ¡ +:r:2, x3 + 2x4}. ¿Cuál es la función de costes correspondiente a esta tecnología? ¿Cuál es la función de demandas condicionadas de los factores 1 y 2 con respecto a los precios de los factores (w1, w2, w3, w4) y al nivel de producción y? 5.4. Una empresa tiene la función de producción f (x1, x2) = min {21:1 + x2, x1 + 2x2}. ¿ Cuál es la función de costes correspondiente a esta tecnología? ¿ Cuál es la función de demandas condicionadas de los factores 1 y 2 con respecto a los precios de los factores (w1, w2) y al nivel de producción y? 5.5. Una empresa tiene la función de producción j"(x1, x2) = max{ x1, x2}. ¿Tiene esta empresa un conjunto de cantidades necesarias de factores convexo o no convexo? ¿ Cuál es la función de demanda condicional del factor 1? ¿ Cuál es su función de costes? 5.6. Considere el caso de una empresa cuyas funciones de demandas condicionadas de los factores tienen la forma siguiente: -1 2 x1 =1 + 3w�w 1 X2 =1 + bwf 'W2_ Se supone que el nivel de producción es igual a 1 para mayor comodidad. ¿Cuáles son los valores de los parámetros a, by e y por qué? Ejercicios / 93 5.7. Una empresa tiene la función de producción y = x1x2. Si el coste mínimo de producción correspondiente a w1 = w2 = 1 es igual a 4, ¿cuál es el valor de y? 5.8. Una empresa tiene la siguiente función de costes: c(y) = { Y2 + 1 O siy > O si y= O. Supongamos que p es el precio del producto y que los precios de los factores son fijos. Si p = 2, ¿cuánto producirá la empresa? ¿Y si p = 1? ¿Cuál es la función de beneficios de esta empresa? (Pista: ¡tenga cuidado!) 5.9. Una empresa de alta tecnología prod�ce una cantidad de chips y utilizando la función de costes c(y), que muestra costes marginales crecientes. La proporción 1 - a de los chips que produce es defectuosa y no puede venderse. Los chips de buena calidad pueden venderse al precio p y el mercado de chips es sumamente competitivo. (a) Calcule la derivada de los beneficios con respecto a a y su signo. (b) Calcule la derivada de la producción con respecto a a y su signo. (c) Suponga que hay n productores idénticos .de chips, que D(p) es la función de demanda y que p(a) es el precio de equilibrio competitivo. Calcule (dp /da)/ p y su signo. 5.10. Suponga que una empresa se comporta competitivamente en su mercado de productos y en su mercado de factores. Suponga que sube el precio de todos los factores y que dio, es la subida de los precios del factor i. ¿En qué condiciones disminuirá el nivel de producción maximizador del beneficio? 5.11. Una empresa utiliza 4 factores para producir un bien. La función de producción es f(x1,x2,x3,x4) = min{x1,x2} +min{x3,x4}. (a) ¿Cuál es el vector de demandas condicionadas de los factores para producir 1 unidad cuando el vector de precios de los factores es w = (1, 2, 3, 4)? 94 / LA FUNCIÓN DE COSTES (C. 5) (b) ¿Cuál es la función de costes? (c) ¿Qué tipo de rendimientos de escala muestra esta tecnología? (d) Otra empresa tiene la función de producción f (x1, x2, x3, x4) = min{ x1 + + x4}. ¿Cuál es el vector de demandas condicionadas de los factores para producir 1 unidad cuando los precios son w = (1, 2, 3, 4)? x2, x3 (e) ¿Cuál es la función de costes de esta empresa? (f) ¿Qué tipo de rendimientos de escala muestra esta tecnología? 5.12. Un factor de producción i es inferior si la demanda condicionada de ese factor disminuye cuando aumenta el nivel de producción; es decir, 8xi(w, y)/8y < O. (a) Represente un gráfico que indique que es posible la existencia de factores inferiores. (b) Demuestre que si la tecnología muestra rendimientos constantes de escala, ningún factor puede ser inferior. (c) Demuestre que si el coste marginal disminuye cuando sube el precio de algún factor, ese factor debe ser inferior. 5.13. Considere el caso de una empresa maximizadora del beneficio que produce un bien que se vende en un mercado competitivo. Se observa que cuando sube el precio de ese bien, la empresa contrata más trabajadores cualificados y menos no cualificados. Ahora los trabajadores no cualificados se sindican y consiguen que se suba su salario. Suponga que todos los demás precios permanecen constantes. (a) ¿Qué ocurre con la demanda de trabajadores no cualificados de la empresa? (b) ¿Qué ocurre con la oferta de producción de la empresa? 5.14. Tenemos una serie temporal de observaciones sobre las variaciones del nivel de producción, ,6.y, del coste, ,6.c, de los precios de los factores, ,6.wi, y de los niveles de demanda de los factores, Xi siendo i = 1, ... , n. ¿Cómo estimaría usted el coste marginal, 8c(w, y)/8y, correspondiente a cada periodo? Ejercicios / 95 5.15. Calcule la función de costes correspondiente a la tecnología 5.16. Averigüe si cada una de estas funciones de costes es homogénea de grado uno, monótona, cóncava y/ o continua. En caso afirmativo, deduzca la función de producción correspondiente. (b) c(w, y)= y(w1 + Jw1w2 + w2) (e) c(w, y)= (y+ �)Jw1w2 5.17. Una empresa tiene el conjunto de cantidades necesarias de factores que viene dado por V(y) = {x �O: ax1 + bx2 � y2} (a) ¿Cuál es la función· de producción? (b) ¿Cuáles son las demandas condicionadas de los factores? (c) ¿Cuál es la función de costes? 6. LA DUALIDAD En el capítulo anterior analizamos las propiedades de la función de costes, es decir, de la función que mide el coste mínimo del nivel de producción que se desea obtener. Dada una tecnología cualquiera, es sencillo, al menos en principio, obtener su función de costes: basta resolver el problema de minimización de los costes. En este capítulo mostramos cómo puede invertirse este proceso. Dada una función de costes cualquiera, podemos "hallar" una tecnología que podría haber generado esa función. Eso significa que la función de costes contiene esencialmente la misma información que la función de producción. Dada una función de producción cualquiera, podemos hallar la función de costes correspondiente y dada una función de costes cualquiera, podemos hallar la función de producción correspondiente. Cualquier concepto que se defina en relación con las propiedades de la función de producción tiene una definición "dual", desde el punto de vista de las propiedades de la función de producción, y viceversa. Esta observación general se conoce con el nombre de principio de la dualidad. Tiene varias consecuencias importantes que analizaremos en el presente capítulo. La dualidad entre distintas maneras aparentemente diferentes de representar la conducta económica es útil para estudiar la teoría del consumidor, la economía del bienestar y muchas otras áreas de la economía. 6.1 La dualidad En el capítulo 4 describimos un conjunto V E(y) y afirmamos que era una "frontera exterior" del verdadero conjunto de cantidades necesarias de factores V(y). Dados los datos (w", x", yt), V E(:lj) se define de la siguiente manera: V E(y) = { x: w'x 2:: wtxt cualquiera que sea t tal que yt :S y}. Es fácil verificar que V E(y) es una tecnología cerrada, monótona y convexa. En el capítulo 4 señalamos, además, que contiene cualquier tecnología que podría haber generado los datos (w", x", yt), siendo t = 1, ... , T. 98 / LA DUALIDAD (C. 6) Si observamos las elecciones de muchos precios de los factores, parece que V E(y) debería "aproximarse" en cierto sentido al verdadero conjunto de cantidades necesarias de factores. Supongamos, para concretar esta idea, que los precios de los factores pueden adoptar los valores correspondientes a todos los vectores de precios posibles w 2: O. En ese caso, la generalización natural de V E se convierte en V*(y) = {x: wx 2: wx(w, y)= c(w, y) cualquiera que sea w 2: O}. ¿Qué relación existe entre V*(y) y el verdadero conjunto de cantidades necesarias de factores V(y)? Naturalmente, V*(y) contendrá V(y)1 como demostramos en el capítulo 4 (página 73). En general, V*(y) contendrá V(y) en sentido estricto. Por ejemplo, en la figura 6. lA vemos que no puede considerarse que el área sombreada no pertenece a V*(y)1 puesto que los puntos de esta área satisfacen la condición wx 2: c(w, y). Figura 6.1 FACTOA2 FACTOR2 FACTOR 1 A FACTOR 1 B Relación entre V(y) y v*(y). En general, V*(y) contiene V(y) en sentido estricto. Lo mismo ocurre en la figura 6.1 B. La función de costes sólo puede contener información sobre las secciones económicamente relevantes de V (y) 1 a saber, sobre las combinaciones de factores que pudieran ser, de hecho, la solución de un problema de minimización de los costes, es decir, que pudieran ser, de hecho, demandas condicionadas de los factores. La dualidad / 99 Supongamos, sin embargo, que nuestra tecnología original es convexa y monótona. En este caso, V*(y) será igual a V(y), ya que en el caso convexo y monótono cada uno de los puntos de la frontera de V(y) es una demanda de los factores minimizadora de los costes correspondiente a algún vector de precios w 2: O. Por lo tanto, el conjunto de puntos en el que wx 2: c(w, y), cualquiera que sea w 2: O describirá exactamente el conjunto de cantidades necesarias de factores. En términos más formales, Cuando V(y) es igual a V*(y). Supongamos que V(y) es una tecnología regular, convexa y monótona. En ese caso, V*(y) = V(y). Demostración (esquemática). Ya sabemos que V*(y) contiene V(y), por lo que únicamente tenemos que demostrar que si x pertenece a V*(y), x debe pertenecer a V(y). Supongamos que x no es un elemento de V(y). En ese caso, dado que V(y) es un conjunto convexo y cerrado que satisface la hipótesis de la monotonicidad, podemos aplicar una de las versiones del teorema del hiperplano separador (véase el capítulo 26, página 557) para hallar un vector w* 2: O tal que w*x < w" z cualquiera que sea z perteneciente a V(y). Sea z* un punto de V(y) que minimiza el coste a los precios w*. En ese caso, en concreto, tenemos que w*x < w*z* = c(w*, y). Pero entonces x no puede pertenecer a V(y), de acuerdo con la definición de V*(y). Esta proposición demuestra que si la tecnología original es convexa y monótona, la función de costes correspondiente puede utilizarse para reconstruir totalmente la tecnología original. Si conocemos el coste mínimo de funcionamiento correspondiente a todos y cada uno de los posibles vectores de precios w, conocemos todo el conjunto de opciones tecnológicas de la empresa. Este resultado es razonablemente satisfactorio en el caso de las tecnologías convexas y monótonas, pero ¿qué ocurre en los demás casos? Supongamos que partimos de una tecnología V(y), posiblemente no convexa. Hallamos su función de costes c(w, y) y generamos V*(y). Sabemos por los resultados anteriores que V*(y) no es necesariamente igual a V(y), a menos que V(y) sea convexo y monótono. Supongamos, sin embargo, que definimos c*(w, y)= min wx sujeta ax pertenece a V*(y) ¿Qué relación existe entre c*(w, y) y c(w, y)? Cuando c(w, y) es igual a c*(w, y). c*(w, y)= c(w, y). De acuerdo con La definición de Las funciones, 100 / LA DUALIDAD (C. 6) Demostración. Es fácil ver que c*(w, y) :S c(w, y); dado que V*(y) siempre contiene V(y), la combinación de coste mínimo perteneciente a V*(y) debe ser, al menos, tan pequeña como la combinación de coste mínimo de V(y). Supongamos que dados unos precios w', la combinación minimizadora del coste x' perteneciente a V* (y) tiene la propiedad de que w'x' = c*(w', y)< c(w', y). Pero eso no puede ocurrir, ya que de acuerdo con la definición de V*(y), w'x' � c(w', y). Esta proposición demuestra que la función de costes correspondiente a la tecnología V (y) es igual que la función de costes correspondiente a su versión convexificada. En este sentido, el supuesto de los conjuntos de cantidades necesarias de factores convexos no es muy restrictivo desde el punto de vista económico. Resumamos el análisis realizado hasta el momento: l. Dada una función de costes, podemos definir un conjunto de cantidades necesarias de factores V*(y). 2. Si la tecnología original es convexa y monótona, la tecnología construida será idéntica a la original. 3. Si la tecnología original no es convexa o monótona, el conjunto de cantidades necesarias de factores construido será una versión convexificada y monotonizada del conjunto original y, lo que es más importante, la tecnología construida tendrá la misma función de costes que la original. Estos tres puntos pueden resumirse sucintamente en el principio fundamental de la dualidad en la producción: la función de costes de una empresa resume todos los aspectos económicamente pertinentes de su tecnología. 6.2 Condiciones suficientes para las funciones de costes Hemos visto en el último apartado que la función de costes resume toda la información económicamente pertinente sobre la tecnología. También hemos visto en el capítulo anterior que todas las funciones de costes son funciones de precios no decrecientes, homogéneas, cóncavas y continuas. Eso nos lleva a hacernos l? siguiente pregunta: supongamos que se nos da una función de precios no decreciente, homogénea, cóncava y continua; ¿es necesariamente la función de costes de alguna tecnología? En otras palabras, ¿son las propiedades descritas en el capítulo anterior una lista completa de las implicaciones de la conducta minimizadora de los costes? Dada una función que tenga esas propiedades, ¿ debe surgir necesariamente de alguna Condiciones suficientes para las funciones de costes / 101 tecnología? La respuesta es afirmativa y la siguiente proposición muestra cómo se construye esa tecnología. Cuando q>(w, y) es una función de costes. Sea q>(w, y) una función diferenciable que satisface 1. q>(tw, y)= tq>(w, y) cualquiera que sea t � O; 2. q>(w,y) � Osiw � Oey � O; 3. q>(w', y)� q>(w, y) si w' � w; 4. q>(w, y) es cóncava en w. En ese caso, q>(w, y) es la función de costes correspondiente a la tecnología definida por V*(y) = {x �O: wx � q>(w, y), cualquiera que sea w � O}. Demostración. Dado un w � O, definimos X ( w,y ) = (8q>(w, y) ... 8q>(w, y)) ' 8 ui¿ 8 WI ' y señalamos que como q>(w, y) es homogénea de grado 1 en w, el teorema de Euler implica que q>(w, y) puede expresarse de la manera siguiente: � 8q>(w,y) q>(w, y)=¿_ ui; Bw· i=l = wx(w, y). i (Para el teorema de Euler, véase el capítulo 26, página 558.) Obsérvese que la monotonicidad de q>(w, y) implica que x(w, y)� O. Lo que hemos de demostrar es que cualquiera que sea w' � O, x(w', y) minimiza, de hecho, w'x cualquiera que sea x perteneciente a V*(y): q>(w', y)= w'x(w', y) :S w'x cualquiera que sea x perteneciente a V*(y) Primero demostramos que xíw', y) es viable; es decir, que x(w', y) pertenece a V*(y). Dado que q>(w, y) es cóncava en w, tenemos que q>(w', y) :S q>(w, y)+ Dófw, y)(w' - w) cualquiera que sea w � O (véase el capítulo 27, página 574). Aplicando el teorema de Euler al igual que antes, esta expresión se reduce a 102 / LA DUALIDAD (C. 6) <p(w', y)::::; w'x(w, y) cualquiera que sea w � O. De acuerdo con la definición de V*(y), x(w', y) pertenece a V*(y). A continuación demostramos que x(w, y) minimiza, de hecho, wx cualquiera que sea x perteneciente a V*(y). Si x pertenece a V*(y), por definición debe cumplirse wx � cp(w, y). Pero por el teorema de Euler, <p(w, y)= wx(w, y). Las dos expresiones anteriores implican que wx � wx(w,y) cualquiera que sea x perteneciente a V*(y), como queríamos demostrar. 6.3 Las funciones de demanda Las proposiciones demostradas en el apartado anterior plantean una interesante cuestión. Supongamos que se nos da un conjunto de funciones (gi(w, y)) que satisfacen las propiedades de las funciones de demandas condicionadas de los factores descritas en el apartado 5.6, a saber, que son homogéneas de grado O en los precios y que (agi(w, awj y)) es una matriz semidefinida negativa simétrica. ¿Son estas funciones necesariamente funciones de demanda de los factores de alguna tecnología? Tratemos de aplicar la proposición anterior. En primer lugar, construimos un candidato a función de costes: L Wi9i(w, y). n <p(w, y)= i=1 A continuación comprobamos si satisface las propiedades necesarias para poder aplicar la proposición que acabamos de demostrar. 1. ¿Es <p(w, y) homogénea de grado 1 en w? Para comprobarlo, examinamos cp(tw, y) = ¿i twigi(tw, y). Dado que las funciones gi(w, y) son, por hipótesis, Las funciones de demanda / 103 homogéneas de grado O, gi(tw, y)= gi(w, y), de tal manera que L wgi(w, y)= tq>(w, y). n q>(tw, y)= t i=l 2. ¿Es q>(w, y) 2: O cualquiera que sea w > O? Dado que gi(w, y) 2: O, la respuesta es claramente afirmativa. 3. ¿Es q>( w, y) no decreciente en Wi? Aplicando la regla del producto, calculamos 8q>(w, y)_ - gi·( w, y ) a ui, � _ 8gj(w, y) _ ·( - gi w, y ) a + L.,¡ w1 j=l ui, + � _ 8gi(w, y) . L.,¡ w1 a j=l Wj Dado que gi(w, y) es homogénea de grado O, el último término se anula y gi ( w, y) es claramente superior o igual a O. 4. Por último, ¿es q>(w, y) cóncava en w? Para comprobarlo, diferenciamos dos veces q>(w, y) y obtenemos ( 82</> awiawj ) = (ªgi(w, awj y)) . Para que se cumpla la concavidad, es necesario que estas matrices sean simétricas y semidefinidas negativas, lo que es cierto por hipótesis. Por lo tanto, puede aplicarse la proposición demostrada en este apartado y hay una tecnología V*(y) que genera la función (gi(w, y)) como sus demandas condicionadas de los factores, lo que significa que las propiedades de la homogeneidad y la semidefinición negativa constituyen una lista completa de las restricciones que impone a las funciones de demanda el modelo de la conducta minimizadora de los costes. Naturalmente, los resultados son esencialmente los mismos en el caso de las funciones de beneficios y de las funciones de demanda y de oferta (no condicionadas). Si la función de beneficios obedece las restricciones descritas en el capítulo 3 (página 49) o, lo que es lo mismo, si las funciones de demanda y de oferta obedecen las restricciones del capítulo 3 (página 55), debe existir una tecnología que genere esta función de beneficios o estas funciones de demanda y de oferta. 104 / LA DUALIDAD (C. 6) Ejemplo: Utilización de la aplicación dual Supongamos que se nos da una función de costes específica, c(w, y) = yw1w}-ª. ¿Cómo podernos averiguar la tecnología correspondiente? De acuerdo con la propiedad de la derivada, a -1 x1 ( w, y ) = ayw1 1- a w2 = ay ( W2 ) l - ª w1 x2(w, y)= (1- a)yw}w,¡ª = (1 - a)y (::)-a Querernos eliminar wif w1 de estas dos ecuaciones y obtener una ecuación que exprese y en función de x1 y x2. Reordenando las dos ecuaciones, tenernos que :: = ( :2a)y) -± . (1 Igualándolas entre sí y elevando los dos miembros a la potencia -a(l - a), tenernos que -a Xl a-ay-a 1-a ��-X�� 2 �� (1 _ a)O-a)yl-a' o sea [aª(l - a)l-ª]y = ;f x}-ª. Este resultado no es sino la tecnología Cobb-Douglas. Ejemplo: Los rendimientos constantes de escala y la función de costes Dado que la función de costes nos transmite toda la información económicamente pertinente sobre la tecnología, podernos tratar de interpretar algunas de las restricciones a las que están sometidos los costes en función de las restricciones a las que está sometida la tecnología. En el capítulo 5 (página 79) demostrarnos que si la tecnología mostraba rendimientos constantes de escala, la función de costes tenía la forma c(w)y. Aquí demostraremos que también es cierta la implicación inversa. Rendimientos constantes de escala. Sea V (y) convexa y monótona; en ese caso, si e( w, y) puede expresarse como yc(w), V(y) debe mostrar rendimientos constantes de escala. Las funciones de demanda / 105 Demostración. Partiendo de los supuestos de la convexidad, la monotonicidad y la forma de la función de costes, sabemos que V(y) = V*(y) = {x: w · x 2:: yc(w) cualquiera que sea w 2:: O} Queremos demostrar que si x pertenece a V*(y), tx pertenece a V*(ty). Six pertenece a V*(y), sabemos que wx 2:: yc(w) cualquiera que sea w 2:: O. Multiplicando los dos miembros de esta ecuación por t, obtenemos: wtx 2:: tyc(w) cualquiera que sea w 2:: O. Pero eso quiere decir que tx pertenece a V*(ty). Ejemplo: La elasticidad-escala y la función de costes Dada una función de producción f(x), podemos examinar la medida local de los rendimientos de escala conocida con el nombre de elasticidad-escala: e(x) = df(tx) _t_, dt f(x) t=l que se definió en el capítulo 1 (página 21). La tecnología muestra rendimientos de escala localmente decrecientes, constantes o crecientes cuando e(x) es menor, igual o mayor que uno. Dado algún vector de precios de los factores, podemos calcular la función de costes de la empresa c(w, y). Sea x* la combinación minimizadora del coste correspondiente a (w, y). En ese caso, podemos calcular e(x*) mediante la fórmula siguiente: _ e( w, y)/ y ( *) ex - 8c(w, y)/8y CMe(y) CM(y). Para verlo, realizamos la diferenciación indicada en la definición de e(x): Dado que x" minimiza los costes, satisface las condiciones de primer orden según las cuales ui, = ..\a��:*). Por otra parte, de acuerdo con el teorema de la envolvente, ..\ = 8c(w, y)/oy (véase el capítulo 5, página 89). Por lo tanto, 106 / LA DUALIDAD (C. 6) c(w, y)/ f(x*) 8c(w, y)/8y CMe(y) CM(y). 6.4 Análisis geométrico de la dualidad En este apartado examinamos desde un punto de vista geométrico la relación entre la tecnología de una empresa resumida por su función de producción y su conducta económica resumida por su función de costes. En la figura 6.2 mostramos la isocuanta de una empresa y una curva isocoste correspondiente al mismo nivel de producción y. La pendiente de esta curva isocoste en el punto (wj, w2) viene dada por Oc(w* ,y) 8w1 Oc(w*,y) 8w2 x1(w*,y) x2(w*, y)° Figura 6.2 FACTOR2 PRECI02 PRECIO 1 FACTOR 1 Curvatura de las curvas isocuantas e isocoste. Cuanto mayor es la curvatura de la isocuanta, menor es la de la curva isocoste. Por otra parte, una isocuanta viene definida por: .f(x) = y. Análisis geométrico de la dualidad / 107 Su pendiente en el punto x" viene dada por 8J(x*) � - 8J(x*) · � Ahora bien, si (xj, x2) es un punto minimizador del coste a los precios (wj, w2), sabemos que satisface la condición de primer orden w* 1 _ w*2 8J(x*) � 8J(x*) · cf;;- Obsérvese la elegante dualidad: la pendiente de la curva isocuanta muestra el cociente entre los precios de los factores, mientras que la pendiente de la curva isocoste muestra el cociente entre los niveles de factores. ¿Qué puede decirse de la curvatura de las dos curvas? Están inversamente relacionadas: si la curva isocoste es muy curvada, la isocuanta es bastante horizontal y viceversa. Esta relación puede observarse fijándose en un par de precios cualquiera (w1 , w2) de la curva isocoste y a continuación desplazándose a algún otro ( w;, wf,) que esté bastante alejado del primero. Supongamos que observamos que la pendiente de la curva isocoste apenas varía, es decir, que la curva isocoste tiene poca curvatura. Dado que su pendiente indica el cociente entre las demandas de factores, significa que las combinaciones minimizadoras del coste deben ser bastante parecidas. En la figura 6.2 vemos que eso significa que la isocuanta debe ser bastante curvada. En el caso extremo, observamos que la función de costes de la tecnología de Leontief es una función lineal y que la función de costes en forma de L corresponde a una tecnología lineal. Figura 6.3 x, w, Tecnología, costes y demandas. El caso de la isocuanta convexa y lisa. x, 108 / LA DUALIDAD (C. 6) Ejemplo: Las funciones de producción, las funciones de costes y las demandas condicionadas de factores Supongamos que tenemos una isocuanta convexa lisa. En ese caso, la curva isocoste también es convexa y lisa y las curvas de demandas condicionadas de factores son regulares, como se muestra en la figura 6.3. Supongamos que la isocuanta tiene un tramo recto, de tal manera que en alguna combinación de precios de los factores, no hay una única combinación de demandas de factores. En ese caso, la curva isocoste no es diferenciable en este nivel de precios y las funciones de demandas condicionadas de los factores adoptan valores múltiples, como ocurre en la figura 6.4. Figura 6.4 lsocuanta Demanda del factor x*2 1 1 X� 1 ------�---! 1 1 1 1 1 x; x; w*1 w, x*1 x'1 x, Tecnología, costes y demanda. El caso de la isocuanta que tiene un tramo recto. En la curva isocoste hay un vértice en el nivel de precios igual a la pendiente del tramo recto. En este nivel de precios de los factores, hay varias combinaciones minimizadoras del coste. Supongamos que la isocuanta tiene un vértice en algún punto. En ese caso, en algún intervalo de precios se demandará una combinación fija de factores, lo que significa que la curva isocoste debe tener un tramo recto, como se muestra en la figura 6.5. Supongamos que la isocuanta no es convexa en algún tramo. En ese caso, la curva isocoste tiene un vértice en algún punto y las demandas condicionadas de factores son discontinuas y adoptan valores múltiples, como se muestra en la figura 6.6. Obsérvese que la función de costes correspondiente a esta tecnología no puede distinguirse de la función de costes correspondiente a la versión convexificada de la tecnología comparando las figuras 6.4 y 6.6. Aplicaciones de la dualidad / 109 6.5 Aplicaciones de la dualidad El hecho de que exista una relación dual entre la descripción de una tecnología y su función de costes correspondiente tiene varias consecuencias importantes para el análisis económico de la producción. Ya nos hemos referido a algunas brevemente, pero conviene resumirlas. En primer lugar, resulta útil desde el punto de vista teórico poder describir las propiedades tecnológicas de dos maneras distintas, ya que algunos argumentos son mucho más fáciles de demostrar utilizando una función de costes o de beneficios que utilizando una representación directa de la tecnología. Consideremos, por ejemplo, el caso antes citado, en el cual los beneficios esperados serían mayores con un precio fluctuante que con un precio estabilizado en el valor esperado. Este resultado es una consecuencia trivial de la convexidad de la función de beneficios; el argumento es mucho menos trivial si enfocamos esta situación utilizando una representación directa de la tecnología. Figura 6.5 w*2 Demanda del factor 1 1 1 1 1 w' 2 1 1 _.1 1 1 1 1 1 1 w*1 _ 1,---1 , 1 1 1 1 w'1 -, ', w�/w'1 --------- ' ', W1 x*1 x, Tecnología, costes y demanda. El caso de la isocuanta con vértices. En la curva isocoste hay un tramo recto y varios precios a los que la misma combinación minimiza los costes. En segundo lugar, las representaciones duales de la conducta, como la función de costes y la función de beneficios, resultan muy útiles en el análisis del equilibrio, ya que subsumen los supuestos sobre la conducta en la especificación funcional. Si queremos averiguar, por ejemplo, cómo afecta una determinada política impositiva a los beneficios de una empresa, podemos averiguar cómo afectan los impuestos a los precios a los que se enfrenta ésta y ver cómo afectan estas variaciones de 110 / LA DUALIDAD (C. 6) los precios a la función de beneficios. No tenemos que resolver ningún problema de maximización, puesto que ya están todos "resueltos" en la especificación de la función de beneficios. Figura 6.6 �emanda del factor x*2 1 1 1 : ' ' ' -. x; -- :,-----1 ' 1 1 1 1 x:1 w;tw; ----�-------� 1 1 1 1 1 1 1 1 x'1 x:1 1 1 1 1 1 1 1 1 x'1 X1 Tecnología, costes y demanda. El caso de la isocuanta no convexa. La curva isocoste es exactamente igual que si tuviera un tramo recto, pero ahora la función de demanda de factores es discontinua. En tercer lugar, el hecho de que las propiedades de la homogeneidad, lamonotonicidad y la curvatura agoten las propiedades de las funciones de costes y de beneficios facilita significativamente la verificación de ciertos tipos de proposiciones sobre la conducta de las empresas. Podemos preguntarnos simplemente si una determinada propiedad es una consecuencia de la homogeneidad, la monotonicidad o la curvatura de la función de costes o de beneficios. En caso contrario, la propiedad no se deriva de la conducta maximizadora. En cuarto lugar, el hecho de que las funciones de beneficios y de costes puedan caracterizarse por medio de tres condiciones matemáticas relativamente sencillas resulta de gran ayuda para generar formas paramétricas que permitan representar tecnologías. Por ejemplo, para especificar totalmente una tecnología lo único que hace falta es especificar una función cóncava, monótona, homogénea y continua de los precios de los factores, lo cual es mucho más cómodo que especificar una función de producción que represente la tecnología. Esas representaciones paramétricas pueden resultar de gran ayuda para calcular ejemplos o realizar estudios econométricos. En quinto lugar, las representaciones duales resultan más satisfactorias para realizar estudios econométricos, debido a que generalmente se considera que las variables que entran en la especificación dual -las variables de los precios- son va- Ejercicios / 111 riables exógenas con respecto al problema de elección de la empresa. Si los mercados de factores son competitivos, se supone que la empresa considera dados sus precios y elige las cantidades, por lo que los precios pueden no estar correlacionados con el término de error en la relación de producción estadística. Esta propiedad es muy útil desde el punto de vista estadístico. Se analiza más extensamente en el capítulo 12. Notas La dualidad básica entre las funciones de costes y las de producción fue demostrada rigurosamente por primera vez por Shephard (1953). Véase Diewert (1974) para el desarrollo histórico de este tema y un análisis moderno general. Ejercicios 6.1 La función de costes es e( w1, w2, y) = min { w1, w2} y. ¿ Cuál es la función de producción? ¿Cuáles son las demandas condicionadas de factores? 6.2. La función de costes es c(w1, w2, y) = y[w1 + w2]. ¿Cuáles son las demandas condicionadas de factores? ¿Cuál es la función de producción? 6.3. La función de costes es c(w1, un, y) = w1w�y. ¿Qué sabemos de a y de b? 7. LA MAXIMIZACIÓN DE LA UTILIDAD En este capítulo comenzamos a examinar la conducta del consumidor. En la teoría de la empresa competitiva, las funciones de oferta y demanda se obtienen a partir de un modelo de la conducta maximizadora del beneficio y de una especificación de las restricciones tecnológicas subyacentes. En la teoría del consumidor, las funciones de demanda se obtienen a partir de un modelo de la conducta maximizadora de la utilidad, así como de una descripción de las restricciones económicas subyacentes. 7.1 Las preferencias del consumidor Consideremos el caso de un consumidor que se encuentra ante varias cestas de consumo pertenecientes a un conjunto X, que es su conjunto de consumo. En este libro, suponemos normalmente que X es el ortante no negativo de Rk, pero pueden utilizarse conjuntos de consumo más específicos. Por ejemplo, pueden incluirse solamente cestas que, al menos, permitan al consumidor subsistir. Siempre suponemos que X es un conjunto cerrado y convexo. Suponemos que el consumidor tiene unas determinadas preferencias respecto a las cestas de consumo de X. Cuando escribimos x t y, queremos decir que "el consumidor piensa que la cesta x es, al menos, tan buena como la y". Queremos que las preferencias ordenen el conjunto de cestas, para lo cual necesitamos suponer que satisfacen determinadas propiedades convencionales. Completas. Cualesquiera que sean x e y pertenecientes a X, o bien x o ambos. t y, o bien y t x, Reflexivas. Cualquiera que sea x perteneciente a X, x t x. Transitivas. Cualesquiera que sean x, y y z pertenecientes a X, si x t y e y t z, entonces X t Z. El primer supuesto dice simplemente que es posible comparar dos cestas cualesquiera, el segundo es trivial y el tercero es necesario para analizar la maximización 114 / LA MAXIMIZACIÓN DE LA UTILIDAD (C. 7) de las preferencias: si éstas no fueran transitivas, podría haber conjuntos de cestas que no contuvieran ningún elemento que fuera el mejor de todos. Dada una ordenación t que describa una "preferencia débil", podemos definir una ordenación >-- que describa una preferencia estricta diciendo simplemente que x >-- y significa que no se cumple que y t x. x >-- y quiere decir que "x se prefiere estrictamente a y". De la misma manera, podemos definir el concepto de indiferencia que representamos mediante el símbolo rv diciendo que x rv y si y sólo six t y e y t x. A menudo resulta útil postular otros supuestos sobre las preferencias de los consumidores; por ejemplo, Continuidad. Cualquiera que sea y perteneciente a X, los conjuntos { x : x t y} y {x : x j y} son conjuntos cerrados. Por lo tanto, {x : x >-- y} y {x : x � y} son conjuntos abiertos. Este supuesto es necesario para excluir algunas conductas discontinuas; establece que si (xi) es una secuencia de cestas de consumo que son todas ellas, al menos, tan buenas como la y, y si esta secuencia converge en una cesta x*, x* es, al menos, tan buena como y. La consecuencia más importante de la continuidad es la siguiente: si y se prefiere estrictamente a z y si x es una cesta suficientemente cercana a y, x debe preferirse estrictamente a z. Este supuesto es simplemente una reformulación del supuesto de que el conjunto de cestas preferidas estrictamente es un conjunto abierto. Para un breve análisis de los conjuntos cerrados y abiertos, véase el capítulo 26 (página 554). En el análisis económico suele resultar útil resumir la conducta de un consumidor por medio de una función de utilidad; es decir, una función u : X ---+ R tal que x >-- y si y sólo si u(x) > u(y). Puede demostrarse que si la ordenación de las preferencias es completa, reflexiva, transitiva y continua, puede representarse por medio de una función de utilidad continua. Más adelante demostraremos una versión más débil de esta afirmación. Las funciones de utilidad suelen ser muy útiles para describir las preferencias, pero no debe dárseles una interpretación psicológica. Su única característica importante es su carácter ordinal. Si u(x) representa unas determinadas preferencias t y f : R ---+ R es una función monótona, f ( u(x)) representará exactamente las mismas preferencias, ya que f(u(x)) 2'.: j(u(y)) si y sólo si u(x) 2'.: u(y). También suelen ser útiles otros supuestos sobre las preferencias; por ejemplo, Monotonicidad débil. Si x 2'.: y, entonces x t y. Las preferencias del consumidor / 115 Monotonicidad fuerte. Si x 2: y y x i y, entonces x >-- y. El supuesto de la monotonicidad débil quiere decir que "una cesta que contenga como mínimo la misma cantidad de bienes que otra es como mínimo igual de buena que ésta". Si el consumidor puede deshacerse sin incurrir en costes de los bienes que no desea, este supuesto es trivial. El supuesto de la monotonicidad fuerte quiere decir que una cesta que contenga como mínimo la misma cantidad de todos los bienes que otra y más de alguno de ellos es estrictamente mejor que ésta, lo que significa simplemente suponer que los bienes son ''buenos". Si uno de ellos es un "mal", como la basura o la contaminación, no se satisface el supuesto de la monotonicidad fuerte. Pero en esos casos redefiniendo el bien como la ausencia de basura o de contaminación, las preferencias respecto al bien redefinido suelen satisfacer el postulado de la monotonicidad fuerte. Otro supuesto que es más débil que cualquiera de los dos tipos de monotonicidad es el siguiente: Insaciabilidad local. Dada una cesta x cualquiera perteneciente a X y un E cualquiera tal que E > O, existe una cesta y perteneciente a X tal que [x - YI < E, tal que y >-- x1 .1 El supuesto de la insaciabilidad local quiere decir que siempre es posible mejorar, incluso aunque sólo se introduzcan pequeñas variaciones en la cesta de consumo. El lector debe verificar que la monotonicidad fuerte implica la insaciabilidad local, pero no viceversa. La insaciabilidad local excluye la posibilidad de que las curvas de indiferencia sean "de trazo grueso". He aquí dos supuestos más que suelen utilizarse para garantizar que las funciones de demanda de consumo se comportarán correctamente: Convexidad. Dados x, y y z pertenecientes a X tal que x t y e y >-- z, entonces - t )y t z cualquiera que sea t tal que O � z � 1. tx + (1 Convexidad estricta. Dados x i y y z pertenecientes a X, si x - t )y >-- z cualquiera que sea t tal que O < t < 1. tx + (1 t zey t z, entonces Las ordenaciones de las preferencias suelen representarse gráficamente. El conjunto de todas las cestas. de consumo indiferentes entre sí se denomina curva de indiferencia. Puede considerarse que las curvas de indiferencias son conjuntos de nivel de una función de utilidad; son análogas a las isocuantas utilizadas en la teoría de la producción. El conjunto de todas las cestas situadas en una curva de indiferencia o por encima de ella, { x en X : x t y}, se denomina conjunto de 1 La notación [x - y¡ significa la distancia euclídea que media entre x e y. 116 / LA MAXIMIZACIÓN DE LA UTILIDAD (C. 7) puntos del contorno superior. Es análogo al conjunto de cantidades necesarias de factores utilizado en la teoría de la producción. El supuesto de la convexidad implica que un agente prefiere los puntos medios a los extremos, pero, por lo demás, apenas tiene contenido económico. Las preferencias convexas pueden tener curvas de indiferencia en las que haya "tramos rectos", mientras que las preferencias estrictamente convexas tienen curvas de indiferencia estrictamente curvadas. La convexidad es una generalización del supuesto neoclásico de la "relación marginal de sustitución decreciente". Ejemplo: La existencia de una función de utilidad Existencia de una función de utilidad. Supongamos que las preferencias son completas, reflexivas, transitivas, continuas y monótonas en sentido fuerte. En ese caso, existe una función de utilidad continua u : R! ---+ R que representa esas preferencias. Demostración. Sea e el vector de R! formado únicamente por unos. En ese caso, dado cualquier vector x, sea u(x) un número tal que x rv u(x)e. Tenernos que demostrar que existe ese número y que es único. Sea B = {tenR: te r: x} y W = {tenR: x?.:: te}. En ese caso, la monotonicidad fuerte implica que B no es un conjunto vacío; W tampoco lo es, desde luego, ya que tiene al menos un elemento, O. La continuidad implica que los dos conjuntos son cerrados. Dado que la línea real está conectada, existe algún l:c tal que txe rv x. Tenernos que demostrar que esta función de utilidad representa, de hecho, las preferencias subyacentes. Sea = i- donde txe u(y) = ty donde tye U(X) rv X rv y. En ese caso, si tx < ty, la rnonotonicidad fuerte demuestra que txe -< tye y la transitividad demuestra que Del mismo modo, si x >- y, entonces txe >- tye, por lo que tx debe ser mayor que ty. Omitirnos la demostración de que u(x) es una función continua por ser algo técnica. La conducta del consumidor / 117 Ejemplo: La relación marginal de sustitución Sea u(x1, ... , Xk) una función de utilidad. Supongamos que aumentamos la cantidad del bien i. ¿Qué cambios ha de introducir el consumidor en su consumo del bien j para mantener constante la utilidad? Utilizando la misma notación que en el capítulo 1 (página 14), sean dx, y dx, las variaciones de z, y Xj. Por hipótesis, la variación de la utilidad debe ser cero, por lo que Por lo tanto, a;: 8u(x) - 8u(x) a;; Esta expresión se denomina relación marginal de sustitución entre los bienes i y j. La relación marginal de sustitución no depende de la función de utilidad elegida para representar las preferencias subyacentes. Para demostrarlo, sea v(u) una transformación monótona de utilidad. La relación marginal de sustitución de esta función de utilidad es dxj dx, 'U '( 8u(x) u ) a;: ) 8u(x) V '( U� J a;: 8u(x) - 8u(x) · a;; 7.2 La conducta del consumidor Una vez que contamos con un útil instrumento para representar las preferencias, podemos comenzar a analizar la conducta del consumidor. Partimos de la hipótesis básica de que un consumidor racional siempre elige del conjunto de opciones asequibles la cesta por la que muestra una mayor preferencia. En el problema básico de maximización de las preferencias, el conjunto de opciones asequibles es simplemente el conjunto de todas las cestas que satisfacen la restricción presupuestaria del consumidor. Sea rn la cantidad fija de dinero de que dispone éste y p = (p1, ... , Pk) el vector de los precios de los bienes, 1, ... , k. El conjunto de cestas asequibles, el conjunto presupuestario del consumidor, viene dado por B = { x en X : px � m} 118 / LA MAXIMIZACIÓN DE LA UTILIDAD (C. 7) El problema de maximización de las preferencias puede expresarse, pues, de la manera siguiente: maxu(x) sujeta a px � m x pertenece a X. Señalemos algunas de las características básicas de este problema. En primer lugar, debemos preguntamos si este problema tiene una solución. De acuerdo con el capítulo 27 (página 585), debemos verificar que la función objetivo es continua y que el conjunto de restricciones es cerrado y está acotado. La función de utilidad es continua por hipótesis y el conjunto de restricciones es cerrado. Si Pi > O siendo i = 1, ... , k y m � O, no es difícil demostrar que el conjunto de restricciones está acotado. Si alguno de los precios fuera cero, es posible que el consumidor deseara tener una cantidad infinita del bien correspondiente. En general, no tendremos en cuenta estos problemas de acotación. La segunda cuestión que examinamos se refiere a la representación de las preferencias. Podemos observar que la elección maximizadora x* es independiente de la elección de la función de utilidad que se emplee para representar las preferencias, ya que la elección óptima x* debe tener la propiedad x* t x para cualquier x perteneciente a B, por lo que cualquier función de utilidad que represente las preferencias t debe alcanzar su máximo restringido en x". En tercer lugar, si multiplicamos todos los precios y la renta por una constante positiva, no alteramos el conjunto presupuestario y, por lo tanto, no podemos alterar el conjunto de elecciones óptimas. Es decir, si x" tiene la propiedad de que x* t x cualquiera que sea x tal que px � m, entonces x* t y cualquiera que sea y tal que tpy � tm. En términos generales, el conjunto óptimo de elecciones es "homogéneo de grado cero" en los precios y la renta. Adoptando algunos supuestos de regularidad sobre las preferencias, podemos decir algo más sobre la conducta maximizadora del consumidor. Supongamos, por ejemplo, que las preferencias satisfacen la insaciabilidad local; ¿podríamos obtener en algún caso un x* tal que px* < m? Supongamos que pudiéramos; en ese caso, dado que x* cuesta estrictamente menos que m, todas las cestas de X suficientemente cercanas ax* también cuestan menos que m, por lo que son viables. Pero, de acuerdo con el supuesto de la insaciabilidad local, debe haber alguna cesta x que sea cercana a x* y que se prefiera a x*. Pero eso significa que x* no podría maximizar las preferencias dado el conjunto presupuestario B. Por lo tanto, de acuerdo con el supuesto de la insaciabilidad local, una cesta, x*, maximizadora de la utilidad, debe cumplir la restriccion presupuestaria con igualdad. Eso nos permite reformular el problema del consumidor de la siguiente manera: La conducta del consumidor / 119 v(p, m) = max u(x) talque px =m La función v(p, m) que nos da la utilidad máxima alcanzable a los precios y la renta dados se denomina función indirecta de utilidad. El valor de x que resuelve este problema es la cesta demandada del consumidor: indica la cantidad que desea el consumidor de cada uno de los bienes dado el nivel de precios y de renta. Suponemos que sólo se demanda una única cesta de cada presupuesto; este supuesto sólo pretende simplificar el análisis y no es esencial para el mismo. La función que relaciona p y m con la cesta demandada se denomina función de demanda del consumidor y se representa de la siguiente manera: x(p, m). Al igual que en el caso de la empresa, es necesario postular algunos supuestos para asegurarse de que esta función de demanda está bien definida. En concreto, es necesario suponer que hay una única cesta que maximiza la utilidad. Más adelante veremos que la convexidad estricta de las preferencias garantiza esta conducta. Al igual que en el caso de la empresa, la función de demanda del consumidor es homogénea de grado O en (p, m). Como hemos visto antes, si multiplicamos todos los precios y la renta por un número positivo, el conjunto presupuestario no varía y, por lo tanto, tampoco varía la respuesta al problema de maximización de la utilidad. Al igual que en el caso de la producción, la conducta optimizadora puede caracterizarse por medio del cálculo, en la medida en que la función de utilidad sea diferenciable. El lagrangiano del problema de maximización de la utilidad puede expresarse de la forma siguiente: ,[, = u(x) - ,\(px - m), donde ,\ es el multiplicador de Lagrange. Diferenciando el lagrangiano con respecto a Xi, obtenemos las condiciones de primer orden: au(x) - "''p.i ;:::i U Xi = o siend o i = 1, ... , k . Para interpretar estas condiciones, podemos dividir la condición de primer orden i-ésima por la j-ésima a fin de eliminar el multiplicador de Lagrange. De esa manera, tenemos que Ou(x*) o;;- o;;Ou(x*) Pi PJ siendo i, j = 1, ... , k. El cociente del primer miembro es la relación marginal de sustitución entre el bien i y el j y el del segundo se denomina relación económica de sustitución entre 120 / LA MAXIMIZACIÓN DE LA UTILIDAD (C. 7) los bienes i y j. La maximización implica que estas dos relaciones de sustitución son iguales. Supongamos que no lo fueran; imaginemos, por ejemplo, que En ese caso, si el consumidor renuncia a una unidad del bien i y compra una del bien j, permanece en la misma curva de indiferencia y tiene cien pesetas adicionales para gastar. Por lo tanto, es posible aumentar la utilidad total, lo que contradice el supuesto de la maximización. Figura 7.1 BIEN 2 Elección óptima x*1 BIEN 1 Maximización de las preferencias. La cesta óptima de consumo se encuentra en el punto en el que una curva de indiferencia es tangente a la restricción presupuestaria. La figura 7.1 muestra el argumento geométricamente. La recta presupuestaria del consumidor viene dada por {x: p1x1 + p2x2 = m}. También puede expresarse como la representación gráfica de una función implícita: x2 = m/p2 - (pJ/p2)x1. Por lo tanto, la pendiente de la recta presupuestaria es -pJ/p2 y la ordenada en el origen m / P2. El consumidor desea hallar el punto de esta recta presupuestaria que le reporte la máxima utilidad. Es evidente que éste debe satisfacer la condición de La conducta del consumidor / 121 tangencia según la cual la pendiente de la curva de indiferencia debe ser igual a la pendiente de la recta presupuestaria. Esta condición, traducida al álgebra, nos da la condición anterior. Por último, esta condición puede formularse por medio de vectores. Sea x* una elección óptima y dx una perturbación de x" que satisface la restricción presupuestaria. En ese caso, debe cumplirse que p(x* ± dx) = m. Dado que px = m, esta ecuación implica que pdx = O, lo que implica a su vez que dx debe ser ortogonal a p. En el caso de una perturbación como la dx, la utilidad no puede variar, ya que, de lo contrario, x* no sería óptima. Por lo tanto, también tenemos que Du(x*)dx =O lo que quere decir que Du(x*) también es ortogonal a dx. Dado que esta igualdad se cumple en el caso de todas las perturbaciones en las que pdx = O, Du(x*) debe ser proporcional a p, como nos indicaban las condiciones de primer orden. Las condiciones de segundo orden para la maximización de la utilidad se hallan aplicando los resultados del capítulo 27 (página 569). La segunda derivada del lagrangiano con respecto a los bienes i y j es 8u(x) / 8xi8x i: Por lo tanto, la condición de segundo orden puede expresarse de la forma siguiente: htD2u(x*)h::; O cualquiera que sea h tal que ph = O. (7.1) Esta condición exige que la matriz hessiana de la función de utilidad sea semidefinida negativa en el caso de todos los vectores h ortogonales al vector de precios, lo que equivale esencialmente a decir que u(x) debe ser localmente cuasicóncava. Desde el punto de vista geométrico, la condición significa que el conjunto de puntos del contorno superior debe encontrarse por encima del hiperplano presupuestario en la x* óptima. La condición de segundo orden también puede expresarse, como es habitual, como una condición en la que interviene el hessiano orlado. Si examinamos el capítulo 27 (página 579), observaremos que esta formulación indica que (7.1) puede satisfacerse como una desigualdad estricta si y sólo si los menores principales del hessiano orlado, ordenados de forma natural, alternan de signo. Por lo tanto, 122 / LA MAXIMIZACIÓN DE LA UTILIDAD (C. 7) 1-�¡ =P: -p1 =P: -p3 -p1 un u12 U13 -p2 u21 u22 u23 -p3 u31 U32 U33 o =P: 'Ull u21 -p21 > O, u12 'U22 < o, y así sucesivamente. 7.3 La utilidad indirecta Recordemos la función indirecta de utilidad definida anteriormente. Esta función, v(p, m), indica la utilidad máxima en función de p y de m. Propiedades de la función indirecta de utilidad l. v(p, m) es no creciente en p; es decir, si p' � p, modo, v(p, m) es no decreciente en m. v(p', m) � v(p, m). Del mismo 2. v(p, m) es homogénea de grado O en (p, m). 3. v(p, m) es cuasiconvexa en p; es decir, {p : cualquiera que sea k. 4. v(p, m) es continua cualquiera que sea p v(p, m) � k} es un conjunto convexo » O, m > O. Demostración. l. Sea B = {x: px � m} y B' = {x: p'x � m} siendo p' � p. En ese caso, B' está contenido en B. Por lo tanto, el máximo de u(x) en B es, al menos, tan elevado como el de 'U(x) en B', El argumento es similar en el caso de m. 2. Si los precios y la renta se multiplican ambos por un número positivo, el conjunto presupuestario no varía. Por lo tanto, v(tp, tm) = v(p, m) cualquiera que sea t > O. 3. Supongamos que p y p' son tales que v(p, m) < k, v(p', m) � k. Sea p" = tp + (1 - t)p'. Queremos demostrar que v(p", m) < k. Definimos los conjuntos La, utilidad indirecta / 123 presupuestarios: B ={x: px � m} B' ={ x : p' x � m} B" ={x: p"x � m} Demostraremos que cualquier x perteneciente a B" debe pertenecer a B o a B'; es decir, que BU B' :) B". Supongamos que no es así; en ese caso, x es tal que tpx + (1 - t)p'x � m, pero px > m y p'x > m. Estas dos desigualdades pueden expresarse de la forma siguiente: tpx >tm (1 - t)p'x >(1 - t)m Sumando, tenemos que tpx + (1 - t)p'x > m lo que contradice nuestro supuesto inicial. Obsérvese ahora que v(p", m) = max u(x) sujeta ax pertenece a B" � max u(x) sujeta a x pertenece a B U B' ya que B U B' :) B" � k ya que v(p, m) < k y v(p', m) � k. 4. Esta propiedad se desprende del teorema del máximo formulado en el capítulo 27 (página 586). En la figura 7.2 representamos un conjunto característico de "curvas de indiferencia-precio". Son simplemente los conjuntos de nivel de la función indirecta de utilidad. De acuerdo con la propiedad (1) del teorema anterior, la utilidad es no decreciente a medida que nos desplazamos hacia el origen y, de acuerdo con la (3), los conjuntos de puntos del contorno inferior son convexos. Obsérvese que éstos se encuentran al noreste de las curvas de indiferencia-precio, ya que la utilidad indirecta disminuye conforme suben los precios. 124 / LA MAXIMIZACIÓN DE LA UTILIDAD (C. 7) Figura 7.2 PRECl02 V(p, m) sk conjunto de puntos del contorno inferior V(p, m) =k PRECIO 1 Curvas de indiferencia-precio. La curva de indiferencia está formada por todos los precios tales que, dada una constante k, v(p, m)) = k. El conjunto de puntos del contorno inferior está formado por todos los precios tales que v(p, m) ::; k. Figura 7.3 UTILIDAD v(p,m) RENTA La utilidad en función de la renta. Cuando aumenta la renta, debe aumentar la utilidad indirecta. Obsérvese que si las preferencias satisfacen el supuesto de la insaciabilidad local, v(p, m) será estrictamente creciente en rri. En la figura 7.3 representamos la relación entre »(p, m) y m cuando los precios son constantes. Dado que v(p, m) es estrictamente creciente en m, podemos invertir la función y despejar m en función del nivel de utilidad; es decir, dado un nivel cualquiera de utilidad, u, podemos hallar en la figura 7.3 la cantidad mínima de renta necesaria para lograr la utilidad u a los precios p. La función que relaciona la renta y la utilidad de esta manera -la inversa de la función indirecta de utilidad- se denomina función de gasto y se representa por medio de e(p, u). La utilidad indirecta / 125 El siguiente problema nos proporciona otra definición equivalente de la función de gasto: e(p, u) = min px sujeta a u(x) � u. La función de gasto indica el coste mínimo de alcanzar un nivel fijo de utilidad. La función de gasto es totalmente análoga a la función de costes que analizamos cuando estudiamos la conducta de la empresa, por lo que tiene todas las propiedades que formulamos en el capítulo 5 (página 86) y que repetimos aquí para mayor comodidad. Propiedades de la función de gasto. 1. e(p, u) es no decreciente en p. 2. e(p, u) es homogénea de grado 1 en p. 3. e(p, u) es cóncava en p. 4. e(p, u) es continua en p, cuando p � O. 5. Si h(p, u) es la cesta minimizadora del gasto necesaria para alcanzar el nivel de ( utilidad u a los precios p, hi(P, u) = aeap,u) siendo i = 1, ... , n suponiendo que existe pi la derivada y que Pi > O. Demostración. Estas propiedades son exactamente iguales que las de la función de costes. Véase el capítulo 5 (página 86) para los argumentos. La función h(p, u) se denomina función de demanda hicksiana. Es análoga a las funciones de demandas condicionadas de los factores que hemos examinado antes. La función de demanda hicksiana nos indica la cesta de consumo que alcanza un determinado nivel de utilidad considerado como objetivo y que minimiza el gasto total. La función de demanda hicksiana se denomina a veces función de demanda compensada. Esta terminología se debe al hecho de que se considera que la función de demanda se construye alterando los precios y la renta con el fin de mantener fijo el nivel de utilidad del consumidor. Por lo tanto, se realizan unas alteraciones en la renta de tal manera que "compensen" las variaciones de los precios. Las funciones de demanda hicksianas no son directamente observables ya que dependen de la utilidad, que no lo es. Las funciones de demanda expresadas en 126 / LA MAXIMIZACIÓN DE LA UTILIDAD (C. 7) función de los precios y de la renta son observables; cuando queramos poner énfasis en la diferencia entre los dos tipos de funciones de demanda, llamaremos a las segundas funciones de demanda marshallianas, x(p, m). La función de demanda marshalliana no es más que la función de demanda de mercado que hemos venido analizando hasta ahora. 7.4 Algunas identidades importantes Existen algunas identidades importantes que relacionan la función de gasto, la función indirecta de utilidad, la función de demanda marshalliana y la función de demanda hicksiana. Consideremos el siguiente problema de maximización de la utilidad: v(p, m") = max u(x) sujeta a px :::;; m *. Sea x" la solución de este problema y u' blema de minimización: = u(x*). Consideremos el siguiente pro- e(p, u*)= min px sujeta a u(x) � u", Basta examinar la figura 7.4 para convencerse de que en los casos no patológicos la respuesta de estos dos problemas es el mismo x" (para una argumentación más rigurosa véase el apéndice de este capítulo). Esta sencilla observación nos lleva a cuatro importantes identidades: l. e(p, v(p, m)) v(p, m) es m. 2. v(p, e(p, u)) = = = m. El gasto mínimo necesario para alcanzar la utilidad u. La utilidad máxima generada por la renta e(p, u) es u. 3. xi(P, m) hi(P, v(p, m)). La demanda marshalliana correspondiente al nivel de renta mes idéntica a la demanda hicksiana correspondiente al nivel de utilidad v(p, m). 4. hi(P, u) = xi(P, e(p, u)). La demanda hicksiana correspondiente al nivel de utilidad u es idéntica a la demanda marshalliana correspondiente al nivel de renta e(p, u). Algunas identidades importantes / 127 Esta última identidad tal vez sea la más importante, ya que relaciona la función de demanda marshalliana "observable" y la función de demanda hicksiana "no observable". La identidad (4) muestra que la función de demanda hicksiana la solución del problema de minimización del gasto- es idéntica a la función de demanda marshalliana en el nivel de renta apropiado, a saber, la renta mínima necesaria a los precios dados para alcanzar el nivel de utilidad deseado. Por lo tanto, cualquier cesta demandada puede expresarse o bien como la solución del problema de maximización de la utilidad, o bien como la solución del problema de minimización del gasto. En el apéndice de este capítulo mostramos las condiciones exactas en las que se cumple esta equivalencia. De momento, nos limitaremos a analizar las consecuencias de esta dualidad. Es esta relación la que da lugar al término "función de demanda compensada". La función de demanda hicksiana es simplemente las funciones de demanda marshallianas de los diferentes bienes si la renta del consumidor es "compensada" para alcanzar un determinado nivel de utilidad. En la siguiente proposición se presenta una interesante aplicación de una de estas identidades. Figura 7.4 BIEN2 En este punto se maximiza la \/ utilidad y� minimiza � gaslo '' ' BIEN 1 Maximización de la utilidad y minimización del gasto. Normalmente, una cesta de consumo que maximiza la utilidad también minimiza el gasto, y viceversa. Identidad de Roy. Si x(p, m) es la fu.nción de demanda marshalliana, entonces 8v(p,m) Xi(P, m) =- av(p,m) � siendo i = 1, · · ·, n 8m siempre que, naturalmente, el segundo miembro esté bien definido y que Pi > O y m > O. 128 / LA MAXIMIZACIÓN DE LA UTILIDAD (C. 7) Demostración. Supongamos que x" reporta la utilidad máxima u* correspondiente a (p"; m*). Sabemos por nuestras identidades que xtp", tri") = lr(p", u*). (7.2) También sabemos por otra de las identidades fundamentales que u* = v(p, e(p, u*)). Esta identidad establece que independientemente de cuáles sean los precios, si se le proporciona al consumidor la renta mínima para que obtenga la utilidad u* a esos precios, la utilidad máxima que puede obtener es u': Dado que es una identidad, podemos diferenciarla con respecto a Pi para obtener 0 = 8v(p*, m*) + 8v(p*, m*) 8e(p*, u*). Bp¡ Bm Pi Reordenando esta expresión y combinándola con la identidad (7.2), tenemos que Xi ( p * , m *) = h (p , = i * 'U *) 8v(p*, m*)/8p,¿ 8e(p*, u*) aPi 8v(p*, m*)/8rn · Dado que esta identidad se satisface en el caso de todos los (p*, m*) y dado que x* = x(p*, m*), queda demostrado el resultado. La prueba anterior, aunque es elegante, no es especialmente instructiva. He aquí otra prueba directa de la identidad de Roy. La función indirecta de utilidad viene dada por v(p, m) = u(x(p, m)). (7.3) Si la diferenciamos con respecto a Pj, tenemos que axi k 8v(pl rn) = � 8u(x) Z:: B«,t. 8p. 8p·J .7 i=1 (7.4) Dado que x(p, ni) es la función de demanda, satisface las condiciones de primer orden para la maximización de la utilidad. Introduciendo las condiciones de primer orden en la expresión (7.4), tenemos que av<p, m) 8p· J _ , - /\ axi L Pi-· 8p· k i=1 J (7.5) La función de utilidad métrica monetaria / 129 Las funciones de demanda también satisfacen la restricción presupuestaria px(p, m) = m. Diferenciando esta identidad con respecto a Pj, tenemos que � axi Xj(p, m) + L..,¡Pi-¡¡-_ = O. (7.6) = -AXj(p, m). (7.7) PJ i=l Introduciendo (7.6) en (7.5), tenemos que 8v(p, m) aPj Ahora diferenciando (7.3) con respecto a m, obtenemos 8v(p, m) = A� . 8xi L..,¡ Pi Bm: Bm (7.8) i=l Diferenciando la restricción presupuestaria con respecto a m, tenemos que � Bx, L..,¡ Pi 8m = l. (7.9) i=l Introduciendo (7.9) en (7.8) obtenemos 8v(p, m) am = , /\. (7.10) Esta ecuación nos dice simplemente que el multiplicador de Lagrange de la condición de primer orden es la utilidad marginal de la renta. Combinando las expresiones (7.7) y (7.10) obtenemos la identidad de Roy. Finalmente, como última demostración de la identidad de Roy, obsérvese que es una consecuencia inmediata del teorema de la envolvente descrito en el capítulo 27 (página 585). El razonamiento anterior no hace sino seguir los pasos de la demostración de este teorema. 7.5 La función de utilidad métrica monetaria Existe una elegante construcción que se basa en la función de gasto y que aparece frecuentemente en la economía del bienestar. Supongamos que tenemos unos precios p y una determinada cesta de bienes x. Podemos preguntarnos: ¿cuánto dinero necesitaría un consumidor a los precios p para disfrutar del mismo bienestar del que disfrutaría consumiendo la cesta de bienes x? La figura 7.5 permite averiguar la respuesta gráficamente si se conocen las preferencias del consumidor. Basta ver cuánto dinero necesitaría el consumidor para 130 / LA MAXIMIZACIÓN DE LA UTILIDAD (C. 7) alcanzar la curva de indiferencia que pasa por x. En términos matemáticos, lo único que tenemos que hacer es resolver el siguiente problema: minpz z sujeta a u(z) � u(x) Figura 7.5 BIEN2 m(p,x)lp2 BIEN 1 Función directa de utilidad métrica monetaria. La función de utilidad métrica monetaria indica el gasto mínimo necesario a los precios p para comprar una cesta que sea al menos tan buena como la x. Este tipo de función es tan frecuente que merece la pena darle un nombre especial; la llamaremos, siguiendo a Samuelson (1974), función de utilidad métrica monetaria. También se denomina "función de renta mínima", "función de compensación directa" y de muchas otras formas. Otra definición es la siguiente: m(p, x) = e(p, u(x)). Es fácil ver que si x es fijo, también lo es u(x), por lo que m(p, x) se comporta exactamente igual que una función de gasto: es monótona, cóncava en p, etc. Lo que no es tan evidente es que cuando p es fijo, m(p, x) es, de hecho, una función de utilidad. La demostración es sencilla: cuando los precios �on fijos, la función de gasto es creciente en el nivel de utilidad; si se quiere obtener un mayor nivel de utilidad, hay que gastar más dinero. De hecho, la función de gasto es estrictamente creciente en u cuando las preferencias satisfacen el supuesto de continuidad e insaciabilidad local. Por lo tanto, cuando p es fijo, m(p, x) es simplemente una transformación monótona de la función de utilidad y, por lo tanto, es una función de utilidad. La utilidad indirecta / 131 Es fácil verlo en la figura 7.5. A todos los puntos de la curva de indiferencia que pasan por x se les asigna el mismo nivel de m(p, x) y a todos los puntos de las curvas de indiferencia más altas se les asigna un nivel más elevado. Eso es lo único que hace falta para ser una función de utilidad. Figura 7.6 BIEN2 µ(p; q, m)/p2 BIEN 1 Función indirecta de utilidad métrica monetaria. Esta función indica el gasto mínimo necesario a los precios p para que el consumidor disfrute del mismo bienestar que disfrutaría con los precios q y la renta m. Existe una forma correspondiente similar para expresar la utilidad indirecta conocida con el nombre de función indirecta de utilidad métrica monetaria: µ(p; q, m) = e(p, v(q, m)). Es decir, µ(p; q, m) mide la cantidad de dinero que se necesitaría a los precios p para disfrutar del mismo bienestar del que se disfrutaría con los precios q y la renta m. Al igual que ocurre en el caso directo, µ(p; q, m) se comporta como una función de gasto con respecto a p, pero ahora se comporta como una función indirecta de utilidad con respecto a q y m, ya que, al fin y al cabo, es simplemente una transformación monótona de una función indirecta de utilidad. Véase la figura 7.6 para un ejemplo gráfico. 132 / LA MAXIMIZACIÓN DE LA UTILIDAD (C. 7) Una interesante característica de las funciones de compensación directas e indirectas es que sólo contienen argumentos observables. Son funciones de utilidad directas e indirectas específicas que miden algo que tiene interés y que no muestran ninguna ambigüedad en lo que se refiere a las transformaciones monótonas. Esta característica nos resultará útil cuando analicemos la teoría de la integrabilidad y la economía del bienestar. Ejemplo: La función de utilidad Cobb-Douglas La función de utilidad Cobb-Douglas se define de la siguiente manera: u(xI, x2) = x1x}-ª. Dado que cualquier transformación monótona de esta función representa las mismas preferencias, también puede expresarse de la forma siguiente: u(xI, x2) = a ln z¡ + (1 - a)lnx2. La función de gasto y las funciones de demanda hicksianas son idénticas, salvo en la notación, a la función de costes y las demandas condicionadas de los factores deducidas en el capítulo 4 (página 65). Las funciones de demanda marshallianas y la función indirecta de utilidad pueden obtenerse resolviendo el siguiente problema: max a ln z¡ + (1 - a) lnx2 sujeta a PI x1 + p2x2 = m. Las condiciones de primer orden sori a =O 1-a = O, - - API XI -- - Ap2 x2 o sea a 1-a PIXI P2X2 Eliminando los denominadores y utilizando la restricción presupuestaria, tenemos que = PIXI am = P1XI ap2x2 XI(PI,P2, m) - ªPIXI am = -. PI Introduciendo este resultado en la restricción presupuestaria, obtenemos la segunda demanda marshalliana: La utilidad indirecta / 133 = x2(p1, P2, m) (1 - a)m P2 . Introduciendo este resultado en la función objetivo y eliminando las constantes, se obtiene la función indirecta de utilidad: v(p1,P2,m) = lnm - c ln p¡ - (1- a)lnp2. (7.11) Una manera más rápida de hallar la función indirecta de utilidad es invertir la función de coste/ gasto Cobb-Douglas que obtuvimos en el capítulo 4 (página 65). De esa manera, tenemos que a 1-a e (P1,P2, u ) = KP1P2 u, donde K es una constante que depende de a. Invirtiendo esta expresión, sustituyendo e(p1, P2, u) por m y u por v(p1, P2, m), tenemos que v(p1,P2,m) = m 1 . KP1P2-ª Esta expresión no es más que una transformación mónotona de (7.11), como puede observarse tomando los logaritmos de ambos miembros. Las funciones de utilidad métrica monetaria pueden deducirse sustituyendo. Tenemos que y µ(p; q, m) = Kp1p1-ªv(q1, in, m) _ pªpl-aq-ªqª-lm - 1 2 1 2 · Ejemplo: La función de utilidad CES La función de utilidad CES se define de la manera siguiente: u(x1, x2) = (xf + xi)11 P. Dado que las transformaciones mónotonas de la función de utilidad representan las mismas preferencias, también podríamos definirla de la manera siguiente: u(x1, x2) = Xi+ Xi· Hemos visto anteriormente que la función de costes correspondiente a la tecnología CES tiene la forma c(w, y) = (w1 + w2)1/r y, donde r = p/(p - 1). Por lo tanto, 134 / LA MAXIMIZACIÓN DE LA UTILIDAD (C. 7) la función de gasto correspondiente a la función de utilidad CES debe tener la forma siguiente: e(p, u) = (pí + PÍ)lfr u. La función indirecta de utilidad se halla invirtiendo la ecuación anterior: v(p, m) = (pí + PÍ)-lfrm. Las funciones de demanda pueden hallarse aplicando la identidad de Roy: ( - -8v(p,m)/8p1 xi P, m ) - 8v(p, m)/8m �(pí + P2)-(1+�) mrpi-1 (pí + PÍ)- l/r Pi-lm (pí + PÍ). Las funciones de utilidad métrica monetaria correspondientes a la función de utilidad CES también pueden hallarse haciendo uso de los resultados anteriores: m ( P, X) µ(p;q, m) p)l r)l r p = (P1 + P2 r ( X1 + X2 p = (pí + P2)�(qí + q2)-lfrm. Apéndice Consideremos los dos problemas siguientes: max u(x) sujeta a px ::; m minpx sujeta a u(x) 2'.: u Supongamos que 1. la función de utilidad es continua; 2. las preferencias satisfacen el supuesto de la insaciabilidad local; 3. los dos problemas tienen solución. (7.12) (7.13) Ejercicios / 135 La maximización de la utilidad implica la minimización del gasto. Supongamos que se satisfacen los supuestos anteriores. Sea x* la solución de (7.12) y u = u(x*). En ese caso, x* es la solución de (7.13). Demostración. Supongamos que la solución de (7.13) no es ésa sino x'. En ese caso, px' < px" y u(x') 2:: u(x*). De acuerdo con el supuesto de la insaciabilidad local, hay una cesta x'' suficientemente cercana ax' tal que px" < px" = m y u(x") > u(x*). Pero, en ese caso, x* no puede ser la solución de (7.12). La minimización del gasto implica la maximización de la utilidad. Supongamos que se satisfacen los supuestos anteriores y que x" es la solución de (7.13). Sea m = px* y supongamos que m > O. En ese caso, x* es la solución de (7.12). Demostración. Supongamos que la solución de (7.12) no es ésa sino x', de tal manera que u(x') > u(x*) y px' = px* = m. Dado que px* > O y que la utilidad es continua, podemos hallar un t tal que O < t < 1, de tal manera que ptx' < px* = m y u(tx') > u(x*). Por lo tanto, x" no puede ser la solución de (7.13). Notas El argumento de la existencia de una función de utilidad se basa en Wold (1943). Para un teorema general de la existencia de una función de utilidad, véase Debreu (1964). Roy (1942) y (1947) fue quien primero reconoció la importancia de la función indirecta de utilidad. La función de gasto parece deberse a Hicks (1946). El enfoque dual de la teoría del consumidor que hemos descrito se basa en el de McFadden y Winter (1968). La función de utilidad métrica monetaria ha sido utilizada por McKenzie (1957) y Samuelson (1974). Ejercicios R¡ 7.1. Considere las preferencias definidas en por (x1, x2) >-- (YJ, y2) si x1 + x2 < Yl + Y2· ¿Satisfacen estas preferencias el supuesto de la insaciabilidad local? Si son los dos únicos bienes de consumo y los precios a los que se enfrenta el consumidor son positivos, ¿gastará éste toda su renta? Explique la respuesta. 7.2. Un consumidor tiene la función de utilidad u(x1, x2) = max{ x1, x2}. ¿Cuál es la función de demanda del bien 1 por parte del consumidor? ¿ Cuál es su función indirecta de utilidad? ¿Cuál es su función de gasto? 136 / LA MAXIMIZACIÓN DE LA UTILIDAD (C. 7) 7.3. Un consumidor tiene la función indirecta de utilidad v(p1,p2,m) = . rn mm { P1,P2 } . ¿ Cuál es la forma de la función de gasto de este consumidor? ¿ Y la de su función de utilidad? ¿Y la de la función de demanda del bien 1? 7.4. Considere la siguiente función indirecta de utilidad: v(p1,p2, m) m = ---. Pl + P2 (a) ¿ Cuáles son las funciones de demanda? (b) ¿ Y la función de gasto? (c) ¿Y la función directa de utilidad? 7.5. Un consumidor tiene la siguiente función directa de utilidad: El bien 1 es un bien discreto; los únicos niveles posibles de consumo de dicho bien son x1 = O y x1 = l. Supongamos para mayor comodidad que u(O) = O y P2 = l. (a) ¿ Qué tipo de preferencias tiene este consumidor? (b) ¿Cuál es el valor de Pl tal que si Pl es estrictamente menor que ese valor el consumidor elegirá decididamente x1 = 1? (c) ¿Cuál es la forma algebraica de la función indirecta de utilidad correspondiente a la función directa de utilidad? 7.6. Un consumidor tiene la siguiente función indirecta de utilidad: v(p, m) = A(p)m. (a) ¿ Qué tipo de preferencias tiene este cÓnsumidor? (b) ¿Cuál es la forma de su función de gasto, e(p, u)? (c) ¿Cuál es la forma de su función indirecta de utilidad métrica monetaria, µ(p, q, m)? Ejercicios / 137 (d) Suponga, por el contrario, que el consumidor tiene la función indirecta de utilidad v(p, m) = A(p)mb siendo b > 1. ¿Cuál es ahora la forma de su función indirecta de utilidad métrica monetaria? 8. LA ELECCIÓN En este capítulo examinamos la estática comparativa de la conducta de demanda del consumidor, es decir, cómo varía ésta cuando varían los precios y la renta. Al igual que en el caso de la empresa, enfocamos este problema de tres maneras distintas: diferenciando las condiciones de primer orden, utilizando las propiedades de las funciones de gasto y de utilidad indirecta y aplicando las desigualdades algebraicas que implica el modelo de optimización. 8.1 Estática comparativa Examinemos más detalladamente el problema de maximización del consumidor en el caso de dos bienes. Es interesante observar cómo varía la demanda del consumidor cuando alteramos los parámetros del problema. Mantengamos fijos los precios y permitamos que varíe la renta; el lugar geométrico resultante de las cestas maximizadoras de la utilidad se conoce con el nombre de senda de expansión de la renta. A partir de ésta podemos deducir una función que relacione la renta y la demanda de cada uno de los bienes (a precios constantes). Estas funciones se denominan curvas de Engel. Existen varias posibilidades: 1. La senda de expansión de la renta (y, por lo tanto, cada una de las curvas de Engel) es una línea recta que pasa por el origen. En este caso, se dice que las curvas de demanda del consumidor tienen una elasticidad-renta unitaria. Este consumidor consumirá la misma proporción de cada uno de los bienes en todos los niveles de renta. 2. La senda de expansión de la renta se inclina hacia uno de los bienes o hacia el otro, es decir, cuando el consumidor obtiene más renta, consume una cantidad mayor de los dos bienes, pero proporcionalmente una mayor de uno de ellos (el bien de lujo) que del otro (el bien necesario). 140 / LA ELECCIÓN (C. 8) 3. La senda de expansión de la renta podría doblarse hacia atrás: en este caso, un aumento de la renta induce, de hecho, al consumidor a querer consumir una cantidad menor de uno de los bienes. Por ejemplo, cabe pensar que cuando aumenta la renta, se desea consumir menos patatas. Los bienes de este tipo se denominan bienes inferiores; aquellos cuya demanda aumenta cuando aumenta la renta se denominan bienes normales (véase la figura 8.1). Figura 8.1 BIEN 2 BIEN 2 BIEN 2 BIEN 1 A BIEN 1 B BIEN 1 C Sendas de expansión de la renta. El panel A representa las demandas de elasticidad unitaria; en el B el bien 2 es un bien de lujo y en el e el bien 2 es un bien inferior. También podemos mantener fija la renta y permitir que varíen los precios. Si suponemos que P1 varía y que P2 y m se mantienen fijos, nuestra recta presupuestaria girará y el lugar geométrico de los puntos de tangencia describirá una curva que se conoce con el nombre de curva de oferta-precio. En el primer caso de la figura 8.2, tenemos la situación ordinaria, en la que la reducción del precio del bien 1 provoca un aumentode la demanda de dicho bien; en el segundo caso, tenemos una situación en la que una reducción del precio del bien 1 provoca un descenso de la demanda de dicho bien. Ese tipo de bien se denomina bien Giffen. De nuevo, el ejemplo podrían ser las patatas; si baja su precio, seguimos queriendo comprar las mismas que antes y todavía nos queda algún dinero, que podemos utilizar para comprar más pasta. Pero ahora que estamos consumiendo más pasta, no querremos consumir tantas patatas como antes. Estática comparativa / 141 En el ejemplo anterior hemos visto que la reducción del precio de un bien puede producir dos tipos de efectos: ahora uno de los bienes es más barato que el otro y puede variar el "poder adquisitivo" total. Uno de los resultados fundamentales de la teoría del consumidor, la ecuación de Slutsky, relaciona estos dos efectos. Más adelante la derivaremos de varias maneras. Figura 8.2 A B Curvas de oferta. En el panel A, aumenta la demanda del bien 1 cuando baja su precio, por lo que es un bien ordinario. En el B, disminuye cuando baja su precio, por lo que es un bien Giffen. Ejemplo: Impuestos indirectos e impuestos sobre la renta Supongamos que deseamos gravar con un impuesto a un consumidor maximizador de la utilidad con el fin de obtener una determinada cantidad de ingresos. Inicialmente, la restricción presupuestaria del consumidor es Pl x1 + p2x2 = m, pero una vez que establecemos un impuesto sobre las ventas del bien 1, se convierte en (p1 + t)x1 + p2x2 = m. La figura 8.3 muestra el efecto de este impuesto indirecto. Si representamos el nivel de consumo una vez deducido el impuesto por medio de (xi, xi), los ingresos recaudados gracias al impuesto son txi. Supongamos ahora que decidimos recaudar esta misma cantidad de ingresos por medio de un impuesto sobre la renta. En ese caso, la restricción del consumidor sería Pl x1 + p2x2 = m - txi, que se representa por medio de una línea que tiene la pendiente -pif p2 y que pasa por (xi, xi), como muestra la figura 8.3. Obsérvese que 142 / LA ELECCIÓN (C. 8) como esta recta presupuestaria corta a la curva de indiferencia en el punto (xj, x2), el consumidor puede obtener un nivel de utilidad más elevado con un impuesto sobre la renta que con un impuesto indirecto, aun cuando ambos generen los mismos ingresos al Estado. Figura 8.3 � BLEN2 Consumo con un impuesto sobre las ventas Consumo con un impuesto sobre la renta BIEN 1 Impuesto indirecto e impuesto sobre la renta. Un consumidor siempre disfruta de un menor bienestar con un impuesto indirecto que con un impuesto sobre la renta que genere los mismos ingresos. 8.2 La ecuación de Slutsky Hemos visto que la curva de demanda hicksiana o compensada es formalmente idéntica a la demanda condicionada de factores analizada en la teoría de la empresa. Por lo tanto, tiene las mismas propiedades; en concreto, tiene una matriz de sustitución semidefinida negativa y simétrica. En el caso de la empresa, este tipo de restricción era una restricción observable sobre la conducta de la empresa, ya que el nivel de producción de la empresa es una variable observable. En el caso del consumidor, este tipo de restricción no parece servir de mucho, ya que la utilidad no es directamente observable. Sin embargo, las apariencias engañan. Aunque la función de demanda compensada no sea directamente observable, veremos que su derivada puede calcularse fácilmente a partir de cosas observables, a saber, la derivada de la demanda marshalliana con respecto al precio y a la renta. Esta relación se conoce con el nombre de ecuación de Slutsky. La. ecuación de Slutsky / 143 Ecuación de Slutsky. oxJ(P, m) _ ohj(p, v(p, m)) _ oxj(p, m) � op¡ - � upi � um Xi·( p,m ) Demostración. Supongamos que x" maximiza la utilidad con los precios y la renta (p", m*) y que u" = u(x*). Siempre debe cumplirse que hj(p, u*)= XJ(P, e(p, u*)). Diferenciando esta identidad con respecto a Pi y evaluando la derivada en p*, tenemos que ohj(p*' u*) = OXj(p*' m*) + OXj(p*' m*) oe(p*' u*). Bp¡ Bp, Bni Bp, Obsérvese atentamente el significado de esta expresión. El primer miembro muestra cómo varía la demanda compensada cuando varía Pi. El segundo muestra que esta variación es igual a la variación de la demanda manteniendo fijo el gasto en m * más la variación que experimenta la demanda cuando varía la renta multiplicada por la variación que tiene que experimentar la renta para mantener constante la utilidad. Pero este último término, oe(p*, u*)/opi es simplemente x;; reordenando, tenemos que que es la ecuación de Slutsky. La ecuación de Slutsky descompone la variación de la demanda provocada por una variación del precio �Pi en dos efectos distintos: el efecto-sustitución y el efecto-renta: También podemos analizar los efectos provocados por las variaciones simultáneas de todos los precios; en este caso, interpretamos simplemente las derivadas como derivadas n-dimensionales totales y no como derivadas parciales. En el caso de dos bienes, la ecuación de Slutsky tiene la forma siguiente: 144 / LA ELECCIÓN (C. 8) donde u = v(p, m). Desarrollando el último término, tenemos que [ 8x1(p,m) 8m 8x2(p,m) s: l [x1 x2] = ' [ 8x1(p,m) 8m XI 8x2(p,m) »: XI s: s: 8x1(p,m)X ] 2 8x2(p,m) x2 · Supongamos que varían los precios .6.p = (.ó.p1, .ó.p2) y que nos interesa conocer la variación aproximada de la demanda .6.x = (.ó.x1, .ó.x2). De acuerdo con la ecuación de Slutsky, podemos calcular esta variación utilizando la siguiente expresión: � l[ dm x2 �x2 .ó.p1 .ó.p2 l . [.6.xjl .Ó.X2 El primer vector es el efecto-sustitución. Indica cómo varían las demandas hicksianas. Dado que estas variaciones mantienen constante la utilidad, (.6.xj, .ó.x2) será tangente a la curva de indiferencia. El segundo vector es el efecto-renta. La variación de los precios ha provocado una variación del "poder adquisitivo" de x1.6.p1 +x2.ó.p2 y el vector (.ó.x1, .ó.x2) indica la influencia de esta variación en la demanda, manteniendo constantes los precios en el nivel inicial. Por lo tanto, este vector se encuentra situado en la senda de expansión de la renta. Como muestra la figura 8.4, también podemos efectuar una descomposición similar en el caso de las variaciones finitas de la demanda. En este caso, los precios varían de pº a p' y la demanda de x a x', Para realizar la descomposición de Hicks, primero pivotamos la recta presupuestaria alrededor de la curva de indiferencia a fin de hallar la cesta óptima a los precios p' manteniendo fija la utilidad en el nivel inicial. A continuación desplazamos la recta presupuestaria hacia fuera hasta x' para hallar el efecto-renta. El efecto total es la suma de estos dos desplazamientos. La ecuación de Slutsky / 145 Figura 8.4 BIEN2 Efecto total Efecto sustitución BIEN 1 La descomposición de Hicks de una variación de la demanda. La variación de la demanda puede descomponerse en dos: el efecto-sustitución y el efecto-renta. Ejemplo: La ecuación de Slutsky en el caso Cobb-Douglas Comprobemos la ecuación de Slutsky en el caso Cobb-Douglas. Como hemos visto, en este caso tenemos que -a a-1 v (P1,P2, m ) = mp1 P2 e (P1,P2, u ) a 1-a = UP1P2 am P2, m) = P1 h 1 (P1,P2, u ) = ªP1a-1 P21-a u. x1 (p1, Por lo tanto, 8x1(p, m) am - Pi 8p1 8x1(p, m) a 8m P1 a - aPI - 8h1 (p, u) _ ( a-2 1-a a a - l)P1 P2 u P1 8h1 (p, v(p, m)) _ ( a-2 1-a -a a-1 a a - l)P1 P2 mp1 P2 146 / LA ELECCIÓN (C. 8) Introduciendo estas expresiones en la ecuación de Slutsky, tenemos que 8h1 8x1 a(a - l)m a am -----x1= Pi 8p1 óm Pl Pl [a(a - 1) - a2]m -am pf Pi 8x1 8p1. 8.3 Propiedades de las funciones de demanda Las propiedades de la función de gasto nos permiten desarrollar fácilmente las principales proposiciones de la teoría neoclásica de la conducta del consumidor: 1. La matriz de los efectos-sustitución (óhj(p, u)/8p1) es semidefinida negativa, debido a que que es semidefinida negativa debido a que la función de gasto es cóncava (véase el capítulo 27, página 580). 2. La matriz de los términos de sustitución es simétrica, debido a que óhj(p, u) 82e(p, u) 82e(p, u) óhi(P, u) ópi ópiÓPí ópíÓPi ópí 3. En concreto, "el efecto-sustitución compensado con respecto al propio precio no es positivo"; es decir, las curvas de demanda hicksianas tienen pendiente negativa: 82e(p, u) < O aPi2 - ' ya que la matriz de sustitución es semidefinida negativa y, por lo tanto, los términos de su diagonal no son positivos. Estas restricciones se refieren todas ellas a las funciones de demanda hicksianas, que no son directamente observables. Sin embargo, como hemos indicado antes, la ecuación de Slutsky permite expresar las derivadas de h con respecto a p como Estática comparativa a partir de las condiciones de primer orden / 147 derivadas de x con respecto a p y m, y estas últimas sí son observables. Por ejemplo, de acuerdo con la ecuación de Slutsky y las observaciones anteriores, 4. La �atriz de sustitución ( ox �:: m) + ox �!:; m) negativa. Xi) es una matriz simétrica y semidefinida Este resultado es poco intuitivo: una determinada combinación de derivadas de precios y renta tiene que dar lugar a una matriz semidefinida negativa. Sin embargo, es un resultado inexorable de la lógica de la conducta maximizadora. 8.4 Estática comparativa a partir de las condiciones de primer orden La ecuación de Slutsky también puede derivarse diferenciando las condiciones de primer orden. Dado que los cálculos son algo tediosos, nos limitaremos a examinar el caso de dos bienes y a esbozar los rasgos generales de la argumentación. En este caso, las condiciones de primer orden adoptan la forma siguiente: P1X1 (p1,P2, m) + P2x2(P1,P2, m) - m = = O 8u(x1 (p1, P2, m), x2(p1, P2, m)) , ------------ - AP1 Ü 8x1 8u(x1(P1,P2,m),x2(p1,p2,m)) _ , - AP2 = � o. ux2 Diferenciando con respecto a p1 y expresando el resultado en forma matricial, tenemos que -p2 u12 u22 l [ »:i: ] - [ l � Up1 8x2 = ,\ · Xt O Despejando 8x1 / 8p1 mediante la regla de Cramer, tenemos que Xt ,\ o H donde H > O es el determinante del hessiano orlado. Expandiendo este determinante por cofactores en la segunda columna, tenemos que 148 / LA ELECCIÓN (C. 8) Ox¡ _ l�2 �: 8p1 - "' I H =:� �� 1 _ x1 H 1 . Esto ya empieza a parecerse algo a la ecuación de Slutsky. Obsérvese que el primer término -que es el efecto-sustitución- es negativo corno queríamos. Volviendo ahora a las condiciones de primer orden y diferenciándolas con respecto a m, tenernos que -p1 u11 u21 ] � 8x1 -p2] [ f »; u12 u22 Por lo tanto, de acuerdo con la regla de Crarner, I Ox¡ _ 8m - =:� �� 1 H Introduciendo este resultado en la ecuación de 8xif 8p1 obtenida antes, tenernos la parte de la ecuación de Slutsky que corresponde al efecto-renta. Para hallar el efecto-sustitución, es necesario plantear el problema de minimización del gasto y calcular 8h1/8p1. Este cálculo es análogo al de las funciones de demanda condicionada de los factores realizado en el capítulo 4 (página 69). Puede demostrarse que la expresión resultante es igual al término de sustitución de la ecuación anterior, con lo que llegarnos a la ecuación de Slutsky. 8.5 El problema de la integrabilidad Hemos visto que la hipótesis de la rnaxirnización de la utilidad impone algunas restricciones observables a la conducta del consumidor. En concreto, sabernos que la matriz de los términos de sustitución, (8hi(p,u)) aPi = (ªXi(p,m) aPi + 8xi(p,m) am x1·( p,m )) , debe ser una matriz simétrica y sernidefinida negativa. Supongamos que se nos diera un sistema de funciones de demanda que tuviera una matriz de sustitución simétrica y sernidefinida negativa. ¿Existe necesariamente una función de utilidad de la cual puedan deducirse estas funciones de demanda? Esta pregunta se conoce con el nombre de problema de la integrabilidad. Corno hemos visto, existen varias maneras equivalentes de describir las preferencias del consumidor. Podernos utilizar una función de utilidad, una función El problema de la integrabilidad / 149 indirecta de utilidad, una función de gasto, etc. La función indirecta de utilidad y la función de gasto son bastante útiles para resolver el problema de la integrabilidad. Por ejemplo, según la ley de Roy ·( Xi ) __ 8v(p, m)/8pi P, m - 8v(p, m)/8m · (8.1) Generalmente, hasta ahora partíamos de una función indirecta de utilidad y utilizábamos esta identidad para calcular las funciones de demanda. Sin embargo, el problema de la integrabilidad plantea la pregunta inversa: dadas las funciones de demanda y las relaciones i = 1, ... , k correspondientes a (8.1), ¿cómo podemos resolver estas ecuaciones para hallar v(p, m)? O lo que es más fundamental, ¿cómo podemos siquiera saber si existe una solución? El sistema de ecuaciones de (8.1) es un sistema de ecuaciones diferenciales parciales. El problema de la integrabilidad nos pide que hallemos la solución de este conjunto de ecuaciones. En realidad, resulta algo más fácil plantear esta pregunta por medio de la función de gasto que por medio de la función indirecta de utilidad. Supongamos que partimos de un conjunto de funciones de demanda (xi(P, m)) siendo i = 1, ... , k. Escojamos un punto x0 = xíp", m) y asignémosle arbitrariamente la utilidad u0. ¿Cómo podemos construir la función de gasto e(p, u0)? Una vez que hemos hallado una función de gasto coherente con las funciones de demanda, podemos utilizarla para hallar la función de utilidad directa o indirecta correspondiente. Si existe esa función de gasto, debe satisfacer ciertamente el sistema de ecuaciones diferenciales parciales que viene dado por 8e(p, u0) aPi o o =h/p,u )=xi(p,e(p,u )) i=l,···,k, (8.2) y la condición inicial Estas ecuaciones indican simplemente que la demanda hicksiana de cada uno de los bienes correspondiente al nivel de utilidad u es la demanda marshalliana correspondiente al nivel de renta e(p, u). Ahora bien, la condición de integrabilidad descrita en el capítulo 26 (página 566) nos dice que un sistema de ecuaciones diferenciales parciales de la forma a f (p) Bp¡ = tiene una solución (local) si y sólo si 9i<P) i=l, .. ·,k 150 / LA ELECCIÓN (C. 8) 8gi(p) 8gj(p) 8pj 8pi cualesquiera que sean i y j. Aplicando esta condición al problema anterior, vemos que se reduce a la condición de que la matriz (8xi(P, m) + 8xi(P, m) 8e(p, 8pj 8pj 8m u)) sea simétrica. Pero ésta no es más que la restricción de Slutsky. Por lo tanto, las restricciones de Slutsky implican que las funciones de demanda pueden "integrarse" para hallar una función de gasto coherente con la conducta de elección observada. Esta condición de la simetría es suficiente para garantizar la existencia de una función e(p, u0) que satisfará las ecuaciones (8.2) al menos en algún intervalo (las condiciones que garantizan la existencia global de una solución son algo más complejas). Sin embargo, para que sta sea una verdadera función de gasto, también debe ser cóncava en los precios. Es decir, la matriz de segundas derivadas de e(p, u) debe ser semidefinida negativa. Pero ya hemos visto que la matriz de segundas derivadas de e(p, u) es simplemente la matriz de sustitución de Slutsky. Si es semidefinida negativa, la solución de las ecuaciones diferenciales parciales anteriores debe ser cóncava. Estas observaciones nos dan la solución del problema de la integrabilidad. Dado un conjunto de funciones de demanda (xi(P, m)), basta verificar que tienen una matriz de sustitución simétrica y semidefinida negativa. En caso afirmativo, podemos resolver, en principio, el sistema de ecuaciones (8.2) para hallar una función de gasto coherente con esas funciones de demanda. Existe una interesante artimaña que nos permite recuperar la función indirecta de utilidad a partir de las funciones de demanda, al tiempo que recuperamos la función de gasto. La ecuación (8.2) es válida para todos los niveles de utilidad u0, por lo que elegimos unos precios base q y un nivel de renta m y suponemos que u0 = v(q, m). Con esta sustitución, podemos expresar la ecuación (8.2) de la forma siguiente: 8e(p, v(q, m)) aPi = Xi(P, e(p, v(q, m))), donde ahora la condición de contorno se convierte en e(q, v(q, m)) = m. Recuérdese la definición de la función de utilidad métrica monetaria (indirecta) del capítulo 7: µ(p; q, m) e(p, v(q, m)). Utilizando esta definición también podemos expresar este sistema de ecuaciones de la manera siguiente: = El problema de la integrabilidad / 151 8µ(p;q,m) aPi i = 1, · · ·, k = x/p, µ(p; q, m)) µ(q;q,m) = m. Este sistema se conoce con el nombre de ecuaciones de integrabilidad. Una función µ(p; q, m) que resuelve este problema nos da una función indirecta de utilidad -una determinada función indirecta de utilidad- que describe la conducta observada de la demanda x(p, m). Esta función de utilidad métrica monetaria suele ser muy útil en las aplicaciones de la economía del bienestar. Ejemplo: La integrabilidad con dos bienes Si sólo están consumiéndose dos bienes, las ecuaciones de integrabilidad adoptan una forma muy sencilla, ya que sólo hay una variable independiente, el precio relativo de los dos bienes. Del mismo modo, sólo hay una ecuación independiente, ya que si conocemos la demanda de un bien, podemos hallar la demanda del otro mediante la restricción presupuestaria. Normalicemos los precios y supongamos que el precio del primer bien es p y su función de demanda x(p, m). En ese caso, las ecuaciones de integrabilidad se convierten en una única ecuación más la condición de contorno: dµ(p;q,m) _ dp . X (p,µ (p,q,m )) µ(q;q,m) = m Esta condición no es más que una ecuación diferencial ordinaria con una condición de contorno que puede resolverse mediante las técnicas habituales. Supongamos, por ejemplo, que tenemos una función de demanda logarítmicolineal: lnx = alnp + blnm + e X= pªmbec La ecuación de integrabilidad es dµ(p; q, m) dp =p b eµ . a e Reordenando los términos, tenemos que µ -b dµ(p; q, m) dp =p a e e . 152 / LA ELECCIÓN (C. 8) Integrando esta expresión, obtenemos µ1-blq 1 -b qª+l - pª+l -----ec a+1 p suponiendo que b =/ 1. Resolviendo esta ecuación, tenemos que qa+l _ pa+l -----ec ml-b _ µ(p; q, m)l-b 1 -b a+1 o bien uip; q m) I l = [ (b - 1) m 1-b + ---ec[qa+l _ Pa+l] (1 + a) ' l l�b. Ejemplo: La integrabilidad con varios bienes A continuación analizamos un caso en el que hay tres bienes y, por lo tanto, dos ecuaciones de demanda independientes. Para mayor concreción, consideramos el sistema Cobb-Douglas: a1m XI= -- Pl a2m x2= -P2 Ya hemos verificado anteriormente que este sistema satisfacía la simetría de Slutsky, por lo que sabemos que las ecuaciones de integrabilidad tienen una solución. Basta resolver el siguiente sistema de ecuaciones diferenciales parciales: 8µ a1µ 8p1 8µ PI a2µ 8p2 P2 µ(q1, q2;q1, q2, m) = m La primera ecuación implica que suponiendo una constante de integración C1, y la segunda ecuación implica que Dualidad en el consumo / 153 Por lo tanto, es natural buscar una _solución del tipo donde C3 es independiente de PI y P2. Introduciendo estos resultados en la condición de contorno, tenemos que Despejando C3 en esta ecuación e introduciendo el resultado obtenido en la solución propuesta, tenemos que que es, de hecho, la función de utilidad métrica monetaria indirecta correspondiente a la función de utilidad Cobb-Douglas. Véase el capítulo 7 (página 132) para otra forma de llegar a esta función. 8.6 Dualidad en el consumo Hemos visto cómo puede recuperarse una función indirecta de utilidad a partir de las funciones de demanda observadas resolviendo las ecuaciones de integrabilidad. En este apartado veremos cómo se halla la función directa de utilidad. La respuesta muestra bastante bien la dualidad entre la función directa de utilidad y la indirecta. Como mejor se describen los cálculos es utilizando la función indirecta de utilidad normalizada, en la que se dividen los precios por la renta de tal manera que el gasto es igual a uno. Por lo tanto, la función indirecta de utilidad normalizada viene dada por v(p) = max u(x) X sujeta a px = l. 154 / LA ELECCIÓN (C. 8) Figura 8.5 BIEN 2 Efecto total Efecto sustitución BIEN 1 Obtención de la función directa de utilidad. La utilidad correspondiente a la cesta x no debe ser mayor que la que puede lograrse con cualquier nivel de precios p al que es asequible x. Resulta que si se nos da la función indirecta de utilidad v(p), podemos hallar la función directa de utilidad resolviendo el siguiente problema: u(x) = min v(p) p sujeta a px =1 La demostración no es difícil, una vez que se comprende lo que ocurre. Sea x la cesta demandada a los precios p. En ese caso, por definición, v(p) = u(x). Sea p' cualquier otro vector de precios que satisface la restricción presupuestaria de tal manera que p'x = 1. En ese caso, dado que x siempre es una elección viable a los precios p', debido a la forma del conjunto presupuestario, la elección maximizadora de la utilidad debe generar al menos una utilidad tan grande como la que genera x; es decir, v(p') � u(x) = v(p). Por lo tanto, el mínimo de la función indirecta de utilidad correspondiente a todos los precios p que satisfacen la restricción presupuestaria nos da la utilidad de x. La argumentación se describe en la figura 8.5. Cualquier vector de precios p que satisface la restricción presupuestaria px = 1 debe generar una utilidad mayor que u(x), lo que es lo mismo que decir que u(x) resuelve el problema de minimización planteado anteriormente. La preferencia revelada / 155 Ejemplo: Obtención de la función directa de utilidad Supongamos que tenemos la siguiente función indirecta de utilidad: v(p1, p2) = -alnp1 - blnp2. ¿Cuál es la función directa de utilidad correspondiente? Planteamos el siguiente problema de minimización: min -alnp1 - blnp2 P1,P2 . sujeta a p1x1 + p2x2 = l. Las condiciones de primer orden son -a/p1 = AX1 -b/p2 = AX2, o -a= Ap1x1 -b = Ap2x2. Sumando y utilizando la restricción presupuestaria, tenemos que ,\=-a - b. Introduciendo este resultado en las condiciones de primer orden, tenemos que PI= P2 = a (a+ b)x1 b (a+ b)x2 · Éstos son los precios (p1, p2) que minimizan la utilidad indirecta. A continuación introducimos estos precios en la función indirecta de utilidad: u(x1, x2) a = -aln ( a+ b) x1 = b - bln ( a+ b) x2 alnx1 + blnx2 + constante. Ésta es la conocida función de utilidad Cobb-Douglas. 8. 7 La preferencia revelada En nuestro estudio de la conducta del consumidor hemos considerado que las preferencias son el concepto primitivo y hemos derivado las restricciones que impone el modelo de maximización de la utilidad a las funciones de demanda observadas. 156 / LA ELECCIÓN (C. 8) Estas restricciones son esencialmente las restricciones de Slutsky que exigen que la matriz de los términos de sustitución sea simétrica y semidefinida negativa. En principio, estas restricciones son observables, pero en la práctica dejan un poco que desear, pues, al fin y al cabo, ¿quién ha visto en realidad una función de demanda? Lo más que podemos esperar en la práctica es una lista de las decisiones tomadas en diferentes circunstancias. Por ejemplo, podemos tener algunas observaciones sobre la conducta del consumidor en forma de una lista de precios, pt, y las correspondientes cestas de consumo elegidas, x' siendo t = 1, ... , T. ¿Cómo podemos saber si estos datos podrían haber sido generados por un consumidor maximizador de la utilidad? Decimos que una función de utilidad racionaliza la conducta observada (pt, x') siendo t = 1, ... , T si u(xt) 2: u(x) cualquiera que sea x tal que ptxt 2: ptx. Es decir, u(x) racionaliza la conducta observada si alcanza su valor máximo en el conjunto presupuestario con las cestas elegidas. Supongamos que los datos fueran generados mediante ese tipo de proceso de maximización. ¿ Qué restricciones observables deberían satisfacer las elecciones observadas? Si no se postula ningún supuesto sobre u(x), esta pregunta tiene una respuesta trivial, a saber, ninguna, pues supongamos que u(x) fuera una función constante, de tal manera que el consumidor se mostrara indiferente entre todas las cestas de consumo observadas. En ese caso, las pautas de elecciones observadas no estarían sujetas a restricción alguna: todo es posible. Para que el problema sea más interesante tenemos que excluir este caso trivial. La manera más fácil de excluirlo consiste en exigir que la función de utilidad subyacente satisfaga el supuesto de la insaciabilidad local. En ese caso, ahora nuestra pregunta será cuáles son las restricciones observables que impone la maximización de una función de utilidad que satisface el supuesto de la insaciabilidad local. En primer lugar, obsérvese que si ptxt 2: p'x, entonces debe cumplirsse que u(xt) 2: u(x). Dado que se eligió x' cuando se podría haber elegido x, x' debería reportar, al menos, la misma utilidad que x. En este caso, decimos que el consumidor revela directamente que prefiere x' a x y lo expresamos de la siguiente manera: x' RDx. Como consecuencia de esta definición y del supuesto de que los datos han sido generados por la maximización de la utilidad, podemos llegar a la conclusión de que "x' RDx implica que u(xt) 2: v,(x)". Supongamos que ptxt > ptx. ¿Quiere eso decir que u(xt) > u(xt)? No es difícil demostrar que el supuesto de la insaciabilidad local implica esta conclusión, pues en el párrafo anterior vimos que u(xt) 2: u(x); si u(xt) = u(x), de acuerdo con el supuesto de la insaciabilidad local existiría algún otro x' suficientemente cercano ax para que ptxt > ptx' y u(x') > u(x) = u(xt), lo que contradice la hipótesis de la maximización de la utilidad. Si ptxt > p+x, decimos que el consumidor revela directamente que prefiere Condiciones suficientes para la maximización de la utilidad / 157 estrictamente x' ax y lo expresamos de la siguiente manera: x' PDx. Supongamos ahora que tenemos una secuencia de este tipo de comparaciones de las preferencias relevadas, x' RDxí, xí RDxk, ... , x" RDx. En este caso, decimos que el consumidor revela que prefiere x' ax y lo expresamos de la siguiente manera: xt Rx. La relación R se denomina a veces clausura transitiva de la relación RD. Si suponemos que estos datos han sido generados por la maximización de la utilidad, "x' Rx implica que u(xt) � u(x)". Consideremos dos observaciones x' y X8• Ahora ya sabemos cómo averiguar si u(xt) � u(x8) y contamos con una condición observable para averiguar si u(x8) > u(xt). Evidentemente, estas dos condiciones no deben satisfacerse ambas. Esta condición puede formularse de la manera siguiente: Axioma general de la preferencia revelada. Si un consumidor revela que prefiere x' a X8, no puede revelar directamente que prefiere estrictamente x8 a x'. Utilizando los símbolos antes definidos, también podemos expresar este axioma de la forma siguiente: AGPR. x' Rx8 implica que no es cierto que x8 PDxt. En otras palabras, x' Rx" implica que psxs < psxt. El AGPR es, como su nombre indica, una generalización de algunos otros tests de la preferencia revelada. He aquí dos condiciones habituales. Axioma débil de la preferencia revelada (ADPR). Si x' RDxs y x' no es igual a x8, no es cierto que X8 RDxt. Axioma fuerte de la preferencia revelada (AFPR). Si x' Rx8 y x' no es igual a x8, no es cierto que X8 Rx', Cada uno de estos axiomas exige que sólo se demande una cesta de cada presupuesto, mientras que el AGPR permite que se demanden muchas cestas. Por lo tanto, permite que haya tramos rectos en las curvas de indiferencia que generaron las elecciones observadas. 8.8 Condiciones suficientes para la maximización de la utilidad Si los datos (pt, x') fueron generados por un consumidor maximizador de la utilidad cuyas preferencias cumplen el supuesto de la insaciabilidad, los datos deben satisfacer el AGPR. Por lo tanto, este axioma es una consecuencia observable de la 158 / LA ELECCIÓN (C. 8) maximización de la utilidad. Pero ¿expresa todas las implicaciones de ese modelo? Si algunos datos satisfacen este axioma, ¿es necesariamente cierto que deben haber sido generados por la maximización de la utilidad o cabe pensar, al menos, que haya podido ser así? ¿Es el AGPR una condición suficiente para la maximización de la utilidad? Sí lo es. Si un conjunto finito de datos es coherente con el AGPR, existe una función de utilidad que racionaliza la conducta observada, es decir, existe una función de utilidad que podría haber generado esa conducta. Por lo tanto, el AGPR agota la lista de restricciones impuestas por el modelo de maximización. El siguiente teorema formula de la manera más elegante posible este resultado. Teorema de Afriat. Supongamos que (pt, x"), siendo t = 1, ... , T, es un número finito de observaciones de vectores de precios y cestas de consumo. En ese caso, las siguientes condiciones son equivalentes. 1. Existe una función de utilidad que cumple el supuesto de la insaciabilidad local y que racionaliza los datos; 2. Los datos satisfacen el AGPR; 3. Existen números positivos (ut, ,\t) siendo t de Afriat: = 1, ... , T que satisfacen las desigualdades 4. Existe una función de utilidad monótona, cóncava, continua e insaciada que racionaliza los datos. Demostración. Ya hemos visto que (1) implica (2). Omitimos la demostración de que (2) implica (3); véase Varian (1982a) para el razonamiento. La demostración de que (4) implica (1) es trivial. Lo único que resta por demostrar es que (3) implica (4). Resulta ilustrativo demostrar esta implicación partiendo de una función de utilidad que la cumpla. Definámosla de la siguiente manera: Obsérvese que esta función es continua. En la medida en que pt � O y que no es cierto que pt = O, la función será monótona y satisfará el supuesto de insaciabilidad local. Tampoco es difícil demostrar que es cóncava. En términos geométricos, esta función no es sino la envolvente inferior de un número finito de hiperplanos. Condiciones suficientes para la maximización de la utilidad / 159 Es necesario demostrar que esta función racionaliza los datos; es decir, cuando los precios son pt, esta función de utilidad alcanza su máximo restringido en x'. En primer lugar, demostramos que u(xt) = ut. De no ser así, tendríamos que u(xt) = um + A mpm(xt - x'") < ut. Pero este resultado viola una de las desigualdades de Afriat. Por lo tanto, u(xt) = ut. Supongamos ahora que p8X8 2: p8x. En ese caso, lo que demuestra que u(x8) 2: u(x) cualquiera que sea x tal que p8X otras palabras, u(x) racionaliza las elecciones observadas. � p8x8• En La función de utilidad definida en la demostración del teorema de Afriat tiene una interpretación natural. Supongamos que u(x) es una función de utilidad diferenciable y cóncava que racionaliza las elecciones observadas. El hecho de que sea diferenciable implica que debe satisfacer las T condiciones de primer orden siguientes: (8.3) El hecho de que u(x) sea cóncava implica que debe satisfacer las condiciones de concavidad, a saber, u(xt) � u(x8) + Du(x8)(xt - X8). (8.4) Introduciendo (8.3) en (8.4), tenemos que u(xt) � u(x8) + A8p8(Xt - X8). Por lo tanto, los números de Afriat ut y A t pueden interpretarse como niveles de utilidad y utilidades marginales coherentes con las elecciones observadas. La implicación más notable del teorema de Afriat es que (1) implica (4): si existe una función de utilidad que cumple el supuesto de la insaciabilidad local y que racionaliza .los datos, debe existir una función de utilidad continua, monótona y cóncava que los racionalice. Esta observación es similar a la que hicimos en el capítulo 6 (página 99), en el que demostramos que si algunas de las partes del conjunto de cantidades necesarias de factores no eran convexas, ningún minimizador del coste decidiría producir en ellas. Lo mismo ocurre en el caso de la maximización de la utilidad. Si la función de utilidad subyacente tuviera la curvatura "errónea" en algunos puntos, nunca 160 / LA ELECCIÓN (C. 8) observaríamos que se toman decisiones en esos puntos, ya que no satisfarían las condiciones de segundo orden correctas. Por lo tanto, los datos observados en el mercado no nos permiten rechazar las hipótesis de la convexidad y la monotonicidad de las preferencias. 8.9 Estática comparativa a partir de la preferencia revelada Dado que el AGPR es una condición necesaria y suficiente para la maximización de la utilidad, debe implicar unas condiciiones análogas a los resultados de estática comparativa obtenidos anteriormente. Éstos son la descomposición de Slutsky de las variaciones de los precios en el efecto-renta y el efecto- sustitución y el hecho de que el propio efecto-sustitución sea negativo. Comencemos por el segundo resultado. Cuando analizamos las variaciones finitas de un precio en lugar de las variaciones infinitesimales, la demanda compensada puede definirse de dos maneras. La primera definición es la extensión natural de nuestra definición anterior, a saber, la demanda del bien en cuestión si alteramos el nivel de renta con el fin de restablecer el nivel inicial de utilidad. Es decir, el valor de la demanda compensada del bien 'Í cuando varían los precios de p a p + íl..p es simplemente Xi(P + íl..p, m + ó.m) = x/p + íl..p, e(p + íl..p, u)), donde u es el nivel inicial de utilidad correspondiente a (p, m). Este concepto de compensación se conoce con el nombre de compensación hicksiana. El segundo concepto de demanda compensada cuando varían los precios de p a p + íl..p se conoce con el nombre de compensación de Slutsky. Es el nivel de demanda existente cuando varía la renta con el fin de que sea posible el nivel inicial de consumo. Este concepto se describe fácilmente por medio de las siguientes ecuaciones. Queremos que la renta varíe lo necesario, Sin, para que sea viable el nivel inicial de consumo, x(p, m) a los nuevos precios p + íl..p. Es decir, (p + ó.p)x(p, m) = m + ó.m. Dado que px(p, m) = m, esta expresión se reduce a ..::lpx(p, m) = ó.m. La figura 8.6 muestra la diferencia entre los dos conceptos de compensación. El concepto de Slutsky puede medirse directamente sin conocer las preferencias, pero el hicksiano es más útil desde el punto de vista analítico. Cuando se analizan las variaciones infinitesimales de los precios, no es necesario distinguir entre los dos conceptos, ya que coinciden. Basta examinar la función de gasto para demostrarlo. Si varía el precio del bien j en dpj, es necesario alterar el gasto en (8e(p, '11,) / ºPi )dpj para mantener constante la utilidad. Si queremos que el nivel inicial de consumo siga siendo viable, es necesario alterar la renta en x j dp]. De Estática comparativa a partir de la preferencia revelada / 161 acuerdo con la propiedad de la derivada de la función de gasto, estas dos magnitudes son iguales. Cualquiera que sea la definición que se prefiera, puede utilizarse la preferencia revelada para demostrar que "el efecto compensado con respecto al propio precio es negativo". Supongamos que elegimos la definición hicksiana. Partimos de un vector de precios p y suponemos que x = x(p, m) es la cesta demandada. El vector de precios varía de p a p + A p, por lo que ahora la demanda compensada es x(p + Ap, m + 6:.m), donde 6:.m es la cantidad necesaria para que x(p + Ap, m + 6:.m) sea indiferente a x(p, m). Figura 8.6 BIEN2 f Compensación de Slutsky ' Compensación hicksiana l BIEN 1 La compensación de Hicks y de Slutsky. La compensación de Hicks es la cantidad de dinero que permite que siga siendo asequible el nivel inicial de utilidad. La compensación de Slutsky es la cantidad de dinero que permite que sea alcanzable la cesta inicial de consumo. Dado que x(p, m) y x(p + íl.p, m + 6:.m) son indiferentes entre sí, el consumidor no puede revelar directamente que prefiere estrictamente la una a la otra. Es decir, debemos tener: que p x(p, m) ::; p x (p + íl.p, m + 6:.m) (p + íl.p)x(p + íl.p, m + 6:.m) ::; (p + Ap)x(p, m). Sumando estas desigualdades, tenernos que íl.p[x(p + íl.p. m + 6:.m) - xíp, m)] ::; O. 162 / LA ELECCIÓN (C. 8) Sea 8x en = x(p + A p, m + 8m)- x(p, m); en ese caso, la expresión anterior se convierte ApAx � O. Supongamos que sólo ha variado un precio, de tal manera que Ap =(O, ... , 8pi, ... , O). En ese caso, esta desigualdad implica que Xi debe variar en sentido contrario. Pasarnos a analizar la definición de Slutsky. Mantenernos la misma notación que antes, pero ahora suponernos que /srn. es la variación de la renta necesaria para que sea asequible la cesta inicial de consumo. Dado que x(p, m) es, por hipótesis, un nivel de consumo viable a los precios p + Ap, el consumidor no puede revelar que la cesta realmente elegida a los precios p + Ap es peor que x(p, m). Es decir, px(p, m) � px(p + Ap, m + 8m). Dado que (p + Ap)x(p + Ap, m + 8m) = (p + Ap)x(p, m) por la forma en que se ha definido 8rn, restando esta igualdad de la desigualdad anterior, tenernos que ApAx � O, exactamente igual que antes. 8.10 La versión discreta de la ecuación de Slutsky Veamos ahora cómo se deriva la ecuación de Slutsky. Ya hemos derivado antes esta ecuación diferenciando una identidad que contenía las demandas hicksianas y rnarshallianas. Comenzarnos formulando la siguiente identidad aritmética: Xi(P + Ap, m) - Xi(P, m) = Xi(P + Ap, m + 8m) - Xi(P, m) - [xi(P + Ap, m + 8m) - Xi(P + Ap, m)]. Obsérvese que esta identidad se deduce de la aplicación de la regla ordinaria del álgebra. Supongamos que Ap =(O, ... , 8pj, ... , O). En ese caso, la variación compensatoria de la renta -en el sentido de Slutsky- es 8m = x j(p, m)8pj. Si dividirnos cada uno de los lados de la identidad anterior por 8pj y nos valernos del hecho de que 8pj = 8m/xj(p, m), tenernos que Xi(P + Ap, m) - xi(P, m) Xi(P + Ap, m + 8m) - Xi(P, m) 8pj 8pj -x·1 ( p m ) ' [xi(P + Ap, m + 8m) - Xi(P + Ap, m)] 81n La recuperabilidad / 163 Interpretando cada uno de los términos de esta expresión, podernos reforrnularla de la manera siguiente: !).xi !).xi !).pi = !).pi I cornp !).xi -x·-J /).m. Obsérvese que esta última ecuación es simplemente la expresión análoga en términos discretos de la ecuación de Slutsky. El primer miembro es la variación que experimenta la demanda del bien i cuando varía el precio j. Esta variación se descompone en el efecto-sustitución (la variación que experimenta la demanda del bien i cuando varía el precio j y se altera también la renta para que siga siendo posible el nivel inicial de consumo) y el efecto-renta (la variación que experimenta la demanda del bien i cuando se mantienen constantes los precios pero varía la renta multiplicada por la demanda del bien j). La figura 8.7 muestra la descomposición de Slutsky de una variación del precio. Figura 8.7 BIEN2 -- Efecto-sustitución efecto-renta BIEN 1 La descomposición de Slutsky de una variación del precio. Primero pivotamos la recta presupuestaria alrededor de la cesta inicial de consumo y a continuación la desplazamos hacia fuera hasta llegar a la elección final. 164 / LA ELECCIÓN (C. 8) 8.11 La recuperabilidad Dado que las condiciones de la preferencia revelada constituyen un conjunto completo de restricciones impuestas a la conducta maximizadora de la utilidad, deben contener toda la información existente sobre las preferencias subyacentes. Resulta más o menos evidente cómo se utilizan las relaciones basadas en las preferencias reveladas para averiguar las preferencias por las elecciones observadas, x', siendo t = 1, ... , T. Sin embargo, no es tan evidente cómo se utilizan para conocer las preferencias por elecciones que nunca se han observado. Figura 8.8 BIEN2 BIEN 1 Frontera interior y exterior. RP es la frontera interior de la curva de indiferencia que pasa por x'': el complemento de RD es la frontera exterior. Veámoslo mejor con un ejemplo. La figura 8.8. representa una única observación de la conducta de elección, (p1, x1 ). ¿Qué implica esta elección respecto a la curva de indiferencia que pasa por la cesta x0? Adviértase que x0 no se ha observado previamente; en concreto, carecemos de datos sobre los precios a los que x0 sería una elección óptima. Tratemos de utilizar la preferencia revelada para "acotar" la curva de indiferencia que pasa por x". En primer lugar, observamos que el consumidor revela que prefiere x1 a x". Supongamos que las preferencias son convexas y monótonas. En ese caso, todas las cestas situadas en el segmento que conecta x0 y x1 deben ser, al menos, tan buenas como la x'' y todas las cestas situadas al noreste de esa cesta son, al menos tan buenas, como la x''. Llamemos a este conjunto de cestas RP, por "se revela que se prefiere" a x''. No es difícil demostrar que es la mejor "frontera interior" del conjunto de puntos del contorno superior que pasa por el punto x''. La recuperabilidad / 165 Para hallar la mejor frontera exterior, debemos considerar todas las rectas presupuestarias posibles que pasan por x''. Sea RD el conjunto de todas las cestas que se revela que están dominadas por la x0 en el caso de todas estas rectas presupuestarias. No hay duda de que estas cestas de RD son peores que la x0, cualquiera que sea la recta presupuestaria que se utilice. Figura 8.9 BIEN 2 BIEN 1 Frontera interior y exterior. Cuando hay varias observaciones, la frontera interior y la exterior pueden llegar a estar muy cerca la una de la otra. La frontera exterior del conjunto de puntos del contorno superior correspondiente a x0 es, pues, el complemento de este conjunto: N RD = todas las cestas que no pertenecen a RD. Ésta es la mejor frontera exterior en el sentido de que un consumidor maximizador de la utilidad y coherente no puede revelar nunca que prefiere a x0 una cesta que no pertenezca a este conjunto. ¿Por qué? Porque por definición una cesta que no pertenece a N RD(xº) debe pertenecer a RD(xº), en cuyo caso, se revelaría que es peor que x", En el caso en el que sólo hay una elección observada, los límites establecidos por las fronteras no son muy estrictos. Pero cuando hay muchas elecciones, las fronteras pueden llegar a estar muy cerca la una de la otra, consiguiendo que la verdadera curva de indiferencia quede casi perfectamente acotada. Véase la figura 8.9 para un ejemplo ilustrativo. Conviene que el lector siga los pasos de la construcción de las 166 / LA ELECCIÓN (C. 8) fronteras para asegurarse de que comprende su procedencia. Una vez construidas las fronteras interior y exterior de los conjuntos de puntos del contorno superior, hemos recuperado casi toda la información sobre las preferencias que contiene la conducta observada de la demanda. Por lo tanto, la construcción de RP y de RD es análoga a la resolución de las ecuaciones de integrabilidad. Nuestra construcción de RP y de RD ha sido hasta ahora gráfica. Sin embargo, es posible generalizar este análisis al caso en el que hay muchos bienes. Para averiguar si se revela que se prefiere una cesta a otra o que se considera peor, hay que averiguar si un determinado conjunto de desigualdades lineales tiene solución. Notas La demostración dual de la ecuación de Slutsky que realizamos aquí se basa en McKenzie (1957) y Cook (1972). Para un análisis detallado de la integrabilidad véase Hurwicz & Uzawa (1971). La idea de las preferencias reveladas se debe a Samuelson (1948). El enfoque aquí adoptado se basa en Afriat (1967) y Varian (1982a). La derivación de la ecuación de Slutsky a partir de la preferencia revelada procede de Yokoyama (1968). Ejercicios 8.1. La función de gasto de Frank Fisher es e(p, u). Su función de demanda de chistes es Xj(p, m), donde pes un vector de precios y m � O es su renta. Demuestre que los chistes son un bien normal para Frank si y sólo si 82e/ opjou > O. 8.2. Calcule la matriz de sustitución del sistema de demanda Cobb-Douglas cuando hay dos bienes. Verifique que los términos diagonales son negativos y los efectos cruzados de los precios son simétricos. 8.3. Suponga que un consumidor tiene una función de demanda lineal x = ap+bm+c. Formule la ecuación diferencial que necesitaría resolver para hallar la función de utilidad métrica monetaria. Si puede, resuélvala. 8.4. Suponga que un consumidor tiene una función de demanda semi-logarítmica lnx = ap + bm + c. Formule la ecuación diferencial que necesitaría resolver para hallar la función de utilidad métrica monetaria. Si puede, resuélvala. Ejercicios / 167 8.5. Halle la cesta demandada por un consumidor cuya función de utilidad es 3 u(x1, x2) = xf x2 y su restricción presupuestaria 3x1 1 + 4x2 = 100. 1 8.6. Utilice la función de utilidad u(x1, x2) = xf x¿_ y la restricción presupuestaria m = p1x1 + p2x2 para calcular x(p, m), v(p, m), h(p, u) y e(p, u). = (x1 - a1 ).81 (x2 - a2>.82 y compruebe la simetría de la matriz de términos de sustitución ( 8.7. Amplíe el ejercicio anterior al caso en el que u(x1, x2) ()hb�,u)) . ! 8.8. Repita el ejercicio anterior utilizando u*(x1, x2) = ln z ¡ +} lnx2 y demuestre que todas las fórmulas anteriores se cumplen siempre que se sustituya u por e". 8.9. Las preferencias están representadas por u = cp(x) y se calcula una función de gasto, una función indirecta de utilidad y las demandas. Si ahora representamos las mismas preferencias por medio de u* = 'I/J(cp(x)), siendo 'I/J(·) una función creciente monótona, demuestre que e(p, u) es sustituido por e(p, 'ljJ-1(u*)), v(p, m) por 'I/J(v(p, m)) y h(p, u) por h(p, 'ljJ-1(u*)). Demuestre también que las demandas marshallianas x(p, m) no resultan afectadas. 8.10. Considere un modelo de dos periodos en el que la utilidad de Dave viene dada por u(x1, x2), donde x1 representa su consumo correspondiente al primer periodo y x2 su consumo correspondiente al segundo periodo. Dave tiene la dotación (x1, x2) que podría consumir en cada uno de los periodos, pero también podría intercambiar el consumo actual por consumo futuro y viceversa. Por lo tanto, su restricción presupuestaria es donde p1 y P2 son los precios correspondientes al primer periodo y al segundo, respectivamente. (a) Derive la ecuación de Slutsky en este modelo (observe que ahora la renta de Dave depende del valor de su dotación, la cual depende, a su vez, de los precios: m = p1x1 + p2x2). (b) Suponga que la elección óptima de Dave es tal que x1 < x1. Si baja PI, ¿mejorará o empeorará el bienestar de Dave? ¿ Y si baja P2? (c) ¿Cuál es la tasa de rendimiento del bien de consumo? 168 / LA ELECCIÓN (C. 8) 8.11 .Considere el caso de un consumidor que está demandando los bienes 1 y 2. Cuando sus precios son (2, 4), demanda (1, 2). Cuando son (6, 3), demanda (2, 1). No se produce ninguna otra alteración de importancia. ¿Está maximizando la utilidad este consumidor? 8.12. Suponga que la función indirecta de utilidad adopta la forma v(p, y) = f(p)y. ¿Cuál es la forma de la función de gasto? ¿ Y la de la función de compensación indirecta, µ(p; q, y) expresada con respecto a la función JO y a y? 8.13. La función de utilidad es u<.1:1, x2) = min { x2 + 2x1, :.c1 + 2x2}. (a) Trace la curva de indiferencia correspondiente a u(x1, x2) = 20. Sombree el área en la que u(x1, x2) 2:: 20. (b) ¿Qué valores ha de adoptar pif p2 para que x1 =Osea el único óptimo? (c) ¿Qué valores ha de adoptar pif p2 para que x2 =Osea el único óptimo? (d) Si ni x1 ni x2 son iguales a cero y el óptimo es único, ¿qué valor debe adoptar xJ/x2? 8.14. Suponga que según la legislación fiscal vigente, algunas personas pueden ahorrar hasta 200.000 pesetas al año en un plan de jubilación, que es un sistema de ahorro que recibe un trato fiscal especialmente favorable. Considere el caso de una persona que en un determinado momento tiene la renta Y, que quiere gastar en consumo, C, en ahorro destinado al plan de jubilación 81 o en ahorro ordinario 82. Suponga que la función de utilidad en "forma reducida" es (Se trata de una forma reducida porque los parámetros no son parámetros realmente exógenos que representan las preferencias, sino que también comprenden el trato fiscal de los activos, etc.) La restricción presupuestaria del consumidor viene dada por: y la cantidad máxima que puede destinar al plan de jubilación está representada por L. (a) Deduzca las funciones de demanda de 81 y 82 de un consumidor para el que el límite L no suponga una restricción activa. Ejercicios / 169 (b) Deduzca las funciones de demanda de 81 y 82 de un consumidor para el que el límite L sea una restricción activa. 8.15. Si el ocio es un bien inferior, ¿cuál es la pendiente de la función de oferta de ocio? 8.16. Un consumidor maximizador de la utilidad tiene unas preferencias estrictamente convexas y estrictamente monótonas y consume dos bienes, x1 y »z. cuyo precio es 1 en ambos casos. No puede consumir una cantidad negativa de ninguno de los dos bienes. Tiene una renta anual de m. Su nivel actual de consumo es (xi, x2), donde xi > O y xi > O. Suponga que el próximo año recibirá una ayuda de g1 � xi que debe gastar enteramente en el bien 1 (si lo desea, puede rechazar la ayuda). (a) ¿ Verdadero o falso? Si el bien 1 es un bien normal, la influencia de la ayuda en su consumo debe ser igual que la influencia de una ayuda de la misma cuantía qu� no estuviera sujeta a ninguna limitación. Si esta afirmación es verdadera, demuéstrelo. Si es falsa, demuestre que lo es. (b) ¿ Verdadero o falso? Si el bien 1 es un bien inferior para el consumidor anterior en todos los niveles de renta m > xi+ xi, si recibe una ayuda de g1 que debe gastarse en el bien 1, el efecto debe ser el mismo que el de una ayuda de la misma cuantía que no esté sujeta a limitaciones. Si esta afirmación es cierta, demuéstrelo. Si es falsa, muestre qué hará si recibe la ayuda. (c) Suponga que este consumidor tiene preferencias homotéticas y que actualmente está consumiendo xi = 12 y x2 = 36. Trace un gráfico colocando g1 en el eje de abscisas y la cantidad del bien 1 en el de ordenadas. Utilícelo para mostrar la cantidad del bien 1 que demandará el consumidor si su renta ordinaria es m = 48 y si recibe una ayuda de g1 que debe gastar en el bien 1. ¿En qué nivel de g1 tendrá este gráfico un vértice? (Piénselo un minuto antes de contestar y dé una respuesta numérica.) 9. LA DEMANDA En este capítulo analizamos algunos temas relacionados con la conducta de la demanda. La mayoría guarda relación con formas especiales de la restricción presupuestaria o de las preferencias que dan lugar a tipos especiales de conducta de la demanda. Existen numerosas circunstancias en las que estos casos especiales resultan muy útiles en el análisis, por lo que conviene comprenderlos. 9.1 Las dotaciones en la restricción presupuestaria En nuestro estudio de la conducta del consumidor hemos supuesto que la renta era exógena. Pero en los modelos más complejos, es necesario ver cómo se genera ésta. Normalmente, se considera que el consumidor tiene una dotación w = (w1, ... , wk) de varios bienes que puede vender a los precios vigentes en el mercado p. De esa manera tenemos la renta m = pw que puede utilizar el consumidor para comprar otros bienes. El problema de maximización de la utilidad se convierte en max u(x) X sujeta a px = pw. Este problema puede resolverse utilizando las técnicas habituales para hallar una función de demanda x(p, pw). La demanda neta del bien i es Xi -wi. El consumidor puede tener demandas netas positivas o negativas dependiendo de que quiera tener de una cosa una cantidad mayor o menor de la que le permite tener su dotación. En este modelo, los precios influyen en el valor de lo que tiene el consumidor para vender, así como en el valor de lo que desea vender. Donde mejor se observa esta influencia es en la ecuación de Slutsky, que derivamos a continuación. En primer lugar, diferenciamos la demanda con respecto al precio: 172 / LA DEMANDA (C. 9) dxi(P, pw) dp, = 8xi(P, pw) 1 Bp, pw = constante + 8xi(P, pw) Wi· 8m El primer término del segundo miembro de esta expresión es la derivada de la demanda con respecto al precio, manteniendo fija la renta. El segundo es la derivada de la demanda con respecto a la renta multiplicada por la variación de ésta última. El primer término puede expandirse utilizando la ecuación de Slutsky. Agrupando términos, tenemos que dxi(P, pw) _ 8h/p, u) 8xi(P, pw)( . _ + w1 x1·) . dPí Pí m a a Ahora el efecto-renta depende de la demanda neta del bien j y no de la demanda bruta. Pensemos en el caso del bien normal. Cuando sube su precio, el efectosustitución y el efecto-renta tienden ambos a reducir el consumo. Pero supongamos que este consumidor es un vendedor neto de este bien. En ese caso, su renta efectiva aumenta y este efecto-renta-dotación puede provocar, de hecho, un aumento del consumo del bien. La oferta de trabajo Supongamos que un consumidor elige dos bienes, consumo y trabajo. También tiene alguna renta no laboral m. Sea v(e, R) la utilidad del consumo y el trabajo y formulemos el problema de maximización de la utilidad de la manera siguiente: max v(e, f) c,f sujeta a pe = wf + m. Este problema parece algo distinto de los que hemos venido estudiando: el trabajo probablemente no es un bien sino un "mal" y aparece en el segundo miembro de la restricción presupuestaria. Sin embargo, no es difícil convertirlo en un problema que tenga la forma habitual que hemos encontrado hasta ahora. Supongamos que L es el número máximo de horas qu� puede trabajar el consumidor y que L = L - fes el "ocio". La función de utilidad del consumo y el ocio es u(e, L - f) = v(e, f). Utilizando esta función podemos formular de nuevo el problema de maximización de la utilidad de la manera siguiente: max u(e, L - f) c,f sujeta a pe+ w(L - f) = wL + m. Funciones de utilidad homotéticas / 173 O utilizando la definición L = L - f, rnax u(c, L) c,L sujeta a pe+ wL = wL + m. Este problema tiene esencialmente la misma forma que los que hemos visto hasta ahora. En este caso, el consumidor "vende" su dotación de trabajo al precio w y compra a cambio ocio. La ecuación de Slutsky nos permite calcular la variación que experimenta la demanda de ocio cuando varía el salario. Tenernos que dL(p, w, m) dw = 8L(p, w, v,) + 8L(p, w, m) [L 8w Bm _ L]. Obsérvese que el término entre paréntesis no es negativo por definición y, casi con toda seguridad, es positivo en la práctica.1 Eso significa que la derivada de la demanda de ocio es la suma de un número negativo y uno positivo, por lo que su signo es inherentemente ambiguo. En otras palabras, un aumento del salario puede provocar un incremento o una reducción de la oferta de trabajo. Esencialmente, un aumento del salario tiende a incrementar la oferta de trabajo, ya que encarece el ocio, es decir, es posible consumir más trabajando más. Pero, al mismo tiempo, puede enriquecernos, lo que probablemente elevará nuestra demanda de ocio. 9.2 Funciones de utilidad homotéticas Una función f : H" --* Res homogénea de grado 1 si j(tx) = tf(x) cualquiera que sea t > O. Una función f(x) es homotética si f(x) = g(h(x)), donde ges una función estrictamente creciente y h es una función homogénea de grado 1. Véase el capítulo 26 (página 564) para un análisis más detenido de las propiedades matemáticas de estas funciones. A los economistas suele resultarles útil suponer que las funciones de utilidad son homogéneas u hornotéticas. De hecho, apenas existen distinciones entre los dos conceptos en la teoría de la utilidad. Una función hornotética es simplemente una transformación monótona de una función homogénea, pero sabernos que las transformaciones monótonas de las funciones de utilidad representan las mismas preferencias. Por lo tanto, suponer que las preferencias pueden representarse por medio de una función hornotética equivale a suponer que pueden representarse por 1 Salvo, posiblemente, en época de exámenes. 174 / LA DEMANDA (C. 9) medio de una función homogénea de grado 1. Si las preferencias de un consumidor pueden representarse por medio de una función de utilidad homotética, los economistas dicen que este consumidor tiene preferencias homotéticas. Cuando analizamos la teoría de la producción vimos que si una función de producción era homogénea de grado 1, la función de costes podía expresarse de la forma siguiente: c(w, y) = c(w)y. De esta observación se deduce que si la función de utilidad es homogénea de grado 1, la función de gasto puede expresarse de la manera siguiente: e(p, u)= e(p)u. Eso implica, a su vez, que la función indirecta de utilidad puede expresarse de la forma siguiente: v(p, m) = v(p)m. La identidad de Roy implica, pues, que las funciones de demanda adoptan la forma xi(P, m) = Xi(p)m, es decir, son funciones lineales con respecto a la renta. Como veremos más adelante, el hecho de que los "efectos-renta" adopten esta forma especial suele resultar útil en el análisis de la demanda. 9.3 Agregación de la demanda de los distintos bienes En muchas circunstancias es razonable plasmar en un modelo la elección del consumidor mediante algunos problemas de maximización "parcial". Por ejemplo, podemos querer plasmar en un modelo la elección de "carne" por parte del consumidor sin distinguir entre la cantidad de vacuno, la de porcino, la de cordero, etc. En la mayoría de los estudios empíricos, es necesario realizar alguna agregación de este tipo. Para describir algunos de los resultados útiles de este tipo de separabilidad de las decisiones de consumo, tenemos que introducir una nueva notación. Imaginemos que dividimos la cesta de consumo en dos "subcestas", de tal manera que ésta adopta la forma (x, z). Por ejemplo, x podría ser el vector de consumos de diferentes tipos de carne y z el vector de consumos de todos los demás bienes. También subdividimos el vector de precios de la misma manera: (p, q). En el ejemplo antes citado, pes el vector de precios de los diferentes tipos de carne y q es el vector de precios de los demás bienes. Con esta notación, el problema habitual de maximización de la utilidad puede expresarse de la forma siguiente: max u(x,z) x,z sujeta a px + qz = m. (9.1) Lo que nos interesa es saber en qué condiciones podemos estudiar el problema de la demanda conjunta de los bienes x, por ejemplo, sin tener que preocupamos por la forma en que se reparte ésta entre sus diferentes componentes. Agregación de la demanda de los distintos bienes / 175 Este problema puede formularse en términos matemáticos de la siguiente manera. Nos gustaría poder construir un indice de cantidades escalar, X, y un índice de precios escalar, P, qu� fueran funciones del vector de cantidades y del vector de precios: p = f(p) X= g(x). (9.2) En esta expresión, se supone que Pes algún tipo de "índice de precios" que indica el "precio medio" de los bienes y X es un índice de cantidades que indica la "cantidad" media consumida de carne. Confiamos en poder construir estos índices de precios y de cantidades de tal manera que se comporten como los precios y las cantidades ordinarios. Es decir, confiamos en hallar una nueva función de utilidad U(X, z), que dependa solamente del índice de cantidades de x y que nos dé la misma respuesta que obtendríamos si resolviéramos todo el problema de maximización expresado en (9.1). En términos más formales, consideremos el problema max U(X, z) X,z sujeta a P X + qz = m. La función de demanda correspondiente al índice de cantidades X será una función X(P, q, m). Queremos saber en qué casos es cierto que X(P, q, m) = X(f(p), q, m) = g(x(p, q, m)). Para saberlo es necesario obtener el mismo valor de X por dos vías diferentes: 1) primero agregar los precios utilizando P = f(p) y después maximizar U(X, z) sujeta a la restricción presupuestaria P X + qz = m. 2) primero maximizar u(x, z) sujeta a px + qz = m y después agregar las cantidades para obtener X= g(x). Existen dos situaciones en las que es posible realizar este tipo de agregación. La primera, que impone restricciones a las variaciones de los precios, se conoce con el nombre de· separabilidad hicksiana. La segunda, que impone restricciones a la estructura de las preferencias, se conoce con el nombre de separabilidad funcional. La separabilidad hicksiana Supongamos que el vector de precios p siempre es proporcional a algún vector de precios fijo pº, de tal manera que p = tp0 para cualquier escalar t. Si los bienes x son 176 / LA DEMANDA (C. 9) varios tipos de carne, esta condición exige que los precios relativos de los diferentes tipos de carne permanezcan constantes, es decir, que todos suban o bajen en la misma proporción. De acuerdo con el marco general antes descrito, definamos los índices de precios y de cantidades de los bienes x de la siguiente manera: p =t X= pºx. La función indirecta de utilidad correspondiente a estos índices se expresa de la forma siguiente: V (P, q, m) = max u(x, z) x,z sujeta a Ppºx + qz = m. Es sencillo comprobar que esta función indirecta de utilidad tiene todas las propiedades habituales: es cuasiconvexa, homogénea en los precios y la renta, etc. En concreto, aplicando sencillamente el teorema de la envolvente demostramos que podemos recuperar la función de demanda de los bienes x por medio de la identidad de Roy: X(P, q, m) 8v(P, q, m)/8P = - a v (P,q,rn )/am = p o x(p, q, m). Este cálculo demuestra que X (P, q, m) es un buen índice de cantidades del consumo de los bienes x: obtendríamos el mismo resultado si agregáramos primero los precios y después maximizáramos U(X, z) que si maximizáramos u(x, z) y después agregáramos las cantidades. La función directa de utilidad que es dual a v(P, q, m) puede hallarse por medio del cálculo habitual: u(X, z) = min v(P, q, m) P,q sujeta a PX + qz = m. Por definición, esta función directa de utilidad cumple la siguiente condición: V(P, q, m) = max U(X, z) X,z sujeta a P X+ qz = m. Por lo tanto, los índices de precios y de cantidades construidos de esta forma se comportan exactamente igual que los precios y las cantidades ordinarios. Agregación de la demanda de los distintos bienes / 177 El modelo de dos bienes La agregación hicksiana suele aplicarse cuando se analiza la demanda de un único bien. En este caso, se supone que los bienes z constituyen un único bien, z, y que los bienes x son "todos los demás bienes". En ese caso, el problema de maximización es max u(x, z) x,z sujeta a px + qz = m. Supongamos que los precios relativos de los bienes x permanecen constantes, de tal manera que p = Ppº. Es decir, el vector de precios p es igual a un vector de preciosbase pº multiplicado por algún índice de precios P. En ese caso, la agregación hicksiana nos dice que podemos expresar la función de demanda del bien z de la siguiente manera: z = z(P, q, m). Dado que esta función de demanda es homogénea de grado cero, abusando algo de la notación, también podemos expresarla de la forma siguiente: z = z(q/P,m/P) lo que significa que la demanda del bien z depende del precio relativo de dicho bien con respecto a "todos los demás bienes" y a la renta, dividida por el precio de "todos los demás bienes". En la práctica, suele tomarse como índice de precios de todos los demás bienes algún índice medio de precios de consumo. La demanda del bien z se convierte en una función que contiene únicamente dos variables: el precio del bien z en relación con el IPC y la renta en relación con el IPC. La separabilidad funcional El segundo caso en el que podemos descomponer la decisión de consumo del consumidor se conoce con el nombre de separabilidad funcional. Supongamos que la ordenación de las preferencias subyacentes tiene la siguiente propiedad: (x, z) >- (x', z) si y sólo si (x, z') >- (x', z') cualesquiera que sean las cestas de consumo x, x', z y z'. Esta condición nos dice que si se prefiere x a x' en el caso de algunas elecciones de los demás bienes, x se prefiere ax' en el caso de todas ellas. O, dicho de una manera aún más sucinta, las preferencias respecto a los bienes x son independientes de los bienes z. 178 / LA DEMANDA (C. 9) Si se satisface esta propiedad de la "independencia" y las preferencias cumplen el supuesto de la insaciabilidad local, puede demostrarse que la función de utilidad de x y z puede expresarse de la siguiente manera: u(x, z) = U(v(x)z), donde U(v, z) es una función creciente de v. Es decir, la utilidad global generada por x y z puede expresarse en función de la subutilidad de x, v(x), y el nivel de consumo de los bienes z. Si la función de utilidad puede expresarse de esta manera, decimos que es débilmente separable. ¿ Qué implica la separabilidad respecto a la estructura del problema de maximización de la utilidad? Como es habitual, expresamos la función de demanda de los bienes de la manera siguiente: x(p, q, m) y z(p, q, m). Sea m¿ = px(p, q, m) el gasto óptimo en los bienes x. Pues bien, si la función de utilidad global es débilmente separable, la elección óptima de los bienes x puede hallarse resolviendo el siguiente problema de maximización de la subutilidad: max v(x) sujeta a px = m¿ (9.3) Eso significa que si conocemos el gasto realizado en los bienes x, mx = px (p, q, m), podemos resolver el problema de maximización de la subutilidad para averiguar la elección óptima de los bienes x. En otras palabras, la demanda de los bienes x sólo es una función de los bienes x y del gasto en dichos bienes mx. Los precios de los demás bienes sólo son relevantes en la medida en que determinen el gasto realizado en los bienes x. La demostración es sencilla. Supongamos que x(p, q, m) no resuelve el problema anterior y que x' es otro valor de x que satisface la restricción presupuestaria y genera una subutilidad estrictamente mayor. En ese caso, la cesta (x', z) generaría una utilidad global mayor que (x(p, q, m), z(p, q, m)), lo que contradice la definición de la función de demanda. Las funciones de demanda x(p, mx) se conocen a veces con el nombre de funciones de demanda condicionada, ya que indican la demanda de los bienes x condicionada al nivel de gasto que se realice en estos bienes. Así, por ejemplo, podemos considerar la demanda de vacuno en función de los precios del vacuno, del porcino y del cordero y del gasto total en carne. Sea e(p, v) la función de gasto correspondiente al problema de maximización de la subutilidad formulado en (9.3). Ésta indica cuánto es necesario gastar en los bienes x a los precios p para alcanzar la subutilidad v. No es difícil ver que el problema de maximización global del consumidor puede expresarse de la siguiente manera: Agregación de la demanda de los distintos consumidores / 179 max U(v,z) v,z sujeta a e(p, v) + qz = m. Este problema tiene casi la forma que queremos: v es un buen índice de cantidades de los bienes x, pero no ocurre así con el índice de precios. Queremos P multiplicado por X, pero tenemos una función que no es lineal en p y X = v. Para tener una restricción presupuestaria que sea lineal con respecto al índice de cantidades, es necesario suponer que la función de subutilidad tiene una estructura especial. Supongamos, por ejemplo, que ésta es homotética. En ese caso, ya vimos en el capítulo 5 (página 79) que e(p, v) puede expresarse de la siguiente manera: e(p)v. Por lo tanto, podemos decidir que nuestro índice de cantidades sea X= v(x), nuestro índice de precios P = e(p) y nuestra función de utilidad U(X, z). Obtenemos el mismo valor de X si resolvemos el siguiente problema: max U(X,z) X,z sujeta a P X + qz =m que si resolvemos el siguiente: max u(v(x), z) x,z sujeta a px + qz = m, y a continuación agregamos teniendo en cuenta que X = v(x). En esta formulación, podemos imaginar que la decisión de consumo se toma en dos etapas: el consumidor elige primero la cantidad que desea consumir del bien compuesto (por ejemplo, carne) en función de un índice de precios de la carne resolviendo el problema de maximización global; a continuación elige la cantidad que desea consumir de vacuno, dados los precios de los distintos tipos de carne y el gasto total destinado a este bien, que es la solución del problema de maximización de la subutilidad. Este proceso bietápico es muy útil en el análisis aplicado de la demanda. 9.4 Agregación de la demanda de los distintos consumidores Hemos estudiado las propiedades de la función de demanda de un consumidor, x(p, m). Examinemos ahora el caso de un conjunto de i = 1, ... , n consumidores, cada uno de los cuales tiene una función de demanda de un determinado número k de mercancías, de tal manera que la función de demanda del consumidor i es un vector x.Ip, mi) = (x}(p, mi), ... , xf(p, mi)) siendo i = 1, ... , n. Obsérvese que 180 / LA DEMANDA (C. 9) hemos modificado levemente la notación: ahora los bienes se indican por medio de superíndices y los consumidores por medio de subíndices. La función de demanda agregada se define de la manera siguiente: X(p, m1, ... , mn) = ¿�=l Xi(P, mi). La demanda agregada del bien j se representa por medio de XJ(p, m), donde m representa el vector de las rentas (m1, ... , mn), La función de demanda agregada hereda algunas propiedades de las funciones de demanda individuales. Por ejemplo, si éstas son continuas, también lo será ciertamente la función de demanda agregada. La continuidad de las funciones de demanda individuales es una condición suficiente, pero no necesaria, para que las funciones de demanda agregada sean continuas. Consideremos, por ejemplo, la demanda de lavadoras. Parece razonable suponer que la mayoría de los consumidores sólo quieren tener una lavadora. Por lo tanto, la función de demanda del consumidor i tendría la forma que muestra la figura 9.1. Figura 9.1 PRECIO r, -------- 2 CANTIDAD La demanda de una mercancía discreta. A cualquier precio superior a r ir el consumidor i demanda una cantidad nula del bien. Si el precio es inferior o igual a r i, demandará una unidad. El precio r i se denomina precio de reserva del consumidor i-ésimo. Si varían las rentas y los gustos de los consumidores, es de esperar que haya varios precios de reserva diferentes. La demanda agregada de lavadoras viene dada por X(p) = número de consumidores cuyo precio de reserva es al menos p. Si hay muchos consumidores que tienen distintos precios de reserva, tiene sentido pensar que esta función será continua: si el precio sube en una pequeña cuantía, sólo decidirán dejar de comprar el bien unos cuantos consumidores, a saber, los consumidores "marginales". Aun cuando su demanda varíe de forma discontinua, la demanda agregada sólo variará en una pequeña cuantía. ¿ Qué otras propiedades hereda la función de demanda agregada de las de- Agregación de la demanda de los distintos consumidores / 181 mandas individuales? ¿Existe una versión agregada de la ecuación de Slutsky o del axioma fuerte de la preferencia revelada? Desgraciadamente, la respuesta es negativa. De hecho, la función de demanda agregada carece, en general, de propiedades interesantes, salvo las de la homogeneidad y la continuidad, por lo que la teoría del consumidor no impone restricción alguna a la conducta agregada en general. Sin embargo, en algunos casos puede ocurrir que la conducta agregada parezca que ha sido generada por un único consumidor "representativo". Más adelante analizamos una circunstancia en la que puede suceder. Supongamos que las funciones indirectas de utilidad de todos los consumidores adoptan la forma de Gorman: v/p, mi)= ai(p) + b(p)mi. Obsérvese que el término ai(p) puede variar de un consumidor a otro, pero se supone que el término b(p) es idéntico para todos los consumidores. De acuerdo con la identidad de Roy, la función de demanda del bien j por parte del consumidor i adoptará, pues, la forma siguiente: (9.4) donde 8 . J ai ( p ) - (3j (p) tlp(·�) J -b(p) =- 8�(p) b(:) . Obsérvese que la propensión marginal a consumir el bien j, ox{ (p, mi)/ Bnu, es independiente del nivel de renta de cualquier consumidor y constante para todos ellos, ya que b(p) es constante para todos ellos. La demanda agregada del bien j adoptará, pues, la forma siguiente: 1 n - X j (p, m , · · ·, m ) - - [ Ba. !z2Jp)_ p p fi;¡ Op ¿ b() + b() ¿ mi n i=l j n ] i=l Esta función de demanda puede ser generada, de hecho, por un consumidor representativo. Su función indirecta de utilidad representativa viene dada por ¿ ai(p) + b(p)M = A(p) + B(p)M, n V(p, M) = donde M = i=l L�=l mi. 182 / LA DEMANDA (C. 9) La demostración consiste simplemente en aplicar la identidad de Roy a esta función indirecta de utilidad y señalar que genera la función de demanda de la ecuación (9.4). De hecho, puede demostrarse que la forma de Gorman es la forma más general de la función indirecta de utilidad que permite la agregación en el sentido del modelo del consumidor representativo. Por lo tanto, no sólo es una condición suficiente para que se cumpla el modelo del consumidor representativo, sino que también es una condición necesaria. Aunque la demostración completa de este hecho es bastante detallada, la siguiente argumentación es razonablemente convincente. Supongamos, en aras de la sencillez, que sólo hay dos consumidores. En ese caso, por hipótesis, la demanda agregada del bien j puede expresarse de la forma siguiente: Si diferenciamos primero con respecto a m1 y a continuación con respecto a m2, obtenemos las siguientes identidades: 8Xi(p, M) 8M = 8x{(p, m1) 8m1 = 8x�(p, m2) 8m2 Por lo tanto, todos los consumidores deben tener la misma propensión marginal a consumir el bien j. Si diferenciamos esta expresión una vez más con respecto a m1, veremos que 82 Xi(p, M) _ 82x{(p, m1) _ = = O. 8M2 8m¡ Por lo tanto, la demanda del bien j por parte del consumidor 1 -y, por consiguiente, la demanda del consumidor 2- es afín en la renta, por lo que las funciones de demanda del bien j adoptan la forma x{(p, mi) = a{(p) + f3i(p)mi. Si esto es cierto en el caso de todos los bienes, la función indirecta de utilidad de cada uno de los consumidores debe tener la forma de Gorman. Un caso especial de la función de utilidad de la forma de Gorman es aquella que es homotética. En este caso, la función indirecta de utilidad adopta la forma v(p, m) = v(p)m, que tiene claramente la forma de Gorman. Otro caso especial es el de una función de utilidad cuasilineal. En este caso, v(p, m) = v(p) + m, que evidentemente tiene la forma de Gorman. La forma de Gorman posee muchas de las propiedades que poseen las funciones de utilidad homotéticas y/ o cuasilineales. Funciones inversas de demanda / 183 9.5 Funciones inversas de demanda En muchos casos es interesante expresar la conducta de la demanda describiendo los precios en función de las cantidades. Es decir, dado un vector de bienes x, nos gustaría encontrar un vector de precios p y una renta m a los que x fuera la cesta demandada. Dado que las funciones de demanda son homogéneas de grado cero, podemos la fijar renta en un determinado nivel y averiguar simplemente cuáles son los precios en relación con este nivel de renta. Lo más cómodo es fijar el nivel de renta en l. En este caso, las condiciones de primer orden correspondientes al problema de maximización de la utilidad son simplemente 8u(x) -8-Xi - >..pi k LPiXi . = O, para i = 1, ... , k = l. i=l Queremos eliminar >.. de este conjunto de ecuaciones. Para ello multiplicamos cada una de las igualdades del primer conjunto por Xi y las sumamos para obteneer: Introduciendo el valor de >.. así obtenido en la primera expresión para hallar p en función de x, tenemos que: 8u(x) Pi (x) = k ax:8�(x) ¿j=l (9.5) �Xj J Dado cualquier vector de demandas x, podemos utilizar esta expresión para hallar el vector de precios p(x) que satisface las condiciones necesarias para la maximización. Si la función de utilidad es cuasicóncava, de tal manera que estas condiciones necesarias son realmente suficientes para la maximización, obtendremos la relación inversa de demanda. ¿Qué ocurre si la función de utilidad no es cuasicóncava en todos sus puntos? En ese caso, puede haber algunas cestas de bienes que no se demandarán a ninguno de los precios; cualquier cesta que se encuentre en la parte no convexa de una curva de indiferencia será una cesta de ese tipo. Existe una versión dual de la fórmula anterior de las demandas inversas que puede obtenerse a partir de la expresión dada en el capítulo 8 (página 155). La 184 / LA DEMANDA (C. 9) argumentación realizada entonces demuestra que la cesta demandada x debe minimizar la utilidad indirecta en el caso de todos los precios que satisfagan la restricción presupuestaria. Por lo tanto, x debe satisfacer las condiciones de primer orden: 8v(p) -- - µxi = O Bp, k LPiXi = siendo i = 1, · · · , k 1. i=l A continuación multiplicamos cada una de las primeras desigualdades por Pi 8 Pi· Introduciendo este resultado en y las sumamos para hallar queµ = 1 las condiciones de primer orden, tenemos la expresión de la cesta demandada en función de la función indirecta de utilidad normalizada: I::7= 8��) 8v(p) Xi(p) = cJ¡;;: k 8v(p) Lj=l �Pj (9.6) Obsérvese la elegante dualidad: la expresión de la función de demanda directa, (9.6), y la expresión de la función de demanda indirecta (9.5) tienen la misma forma. Esta expresión también puede derivarse a partir de la definición de la función indirecta de utilidad normalizada y la identidad de Roy. 9.6 La continuidad de las funciones de demanda Hasta ahora hemos venido suponiendo alegremente que las funciones de demanda que analizábamos tenían todas las propiedades convenientes; es decir, que eran continuas e incluso diferenciables. ¿Están justificados estos supuestos? Refiriéndonos al teorema del máximo del capítulo 27 (página 592), vemos que en la medida en que las funciones de demanda estén bien definidas, serán continuas, al menos cuando p » O y m > O; es decir, en la medida en que x(p, m) sea la única cesta maximizadora a los precios p y la renta m, la demanda variará continuamente conpym. Si queremos asegurarnos de que la demanda es continua cualquiera que sea p » O y m > O, necesitamos asegurarnos de que la demanda siempre es única. La condición que necesitamos es la de la convexidad estricta. Cesta demandada única. Si las preferencias son estrictamente convexas, entonces en el caso de cada p » O hay una única cesta x que maximiza u en el conjunto presupuestario del consumidor, B(p, m). Ejercicios / 185 Demostración. Supongamos que x' y x" maximizan ambos u en B(p, m). En ese caso, }x' + }x" también pertenece a B(p, m) y se prefiere estrictamente ax' y x", lo cual es una contradicción. En términos generales, si las funciones de demanda están bien definidas y son continuas en todos los puntos y se deducen a partir de la maximización de las preferencias, las preferencias subyacentes deben ser estrictamente convexas. En caso contrario, existiría algún punto en el que habría más de una cesta óptima a algún conjunto de precios, como muestra la figura 9.2. Obsérvese que en el caso representado en esta figura una pequeña variación del precio provoca una gran variación en las cestas demandadas: la "función" de demanda es discontinua. Figura 9.2 BIEN2 PRECIO Pi - - Curva de oferta ---� 1 1 1 1 1 1 1 1 x·1 x·1 Curva de oferta BIEN 1 x·1 x·1 CANTIDAD Curva de demanda La demanda discontinua. La demanda es discontinua debido a que las preferencias no son convexas. Notas Véase Pollak (1969) para demandas condicionales. La separabilidad se analiza en Blackorby, Primont y Russell (1979). Véase Deaton & Muelbauer (1980) para un análisis más amplio y otras aplicaciones a la estimación de la demanda de consumo. El apartado sobre la agregación se basa en Gorman (1953). Véase Shafer y Sonnenschein (1982) para un análisis panorámico de los resultados positivos y negativos que se obtienen en relación con el problema de la agregación. 186 / LA DEMANDA (C. 9) Ejercicios 9 .1. Suponga que las preferencias son homotéticas. Demuestre que 9.2. La función de demanda de un determinado bien es x =a+ bp. ¿Cuáles son las funciones de utilidad directa e indirecta correspondientes? 9.3. La función de demanda de un determinado bien es x =a+ bp + cm. ¿Cuáles son las funciones de utilidad directa e indirecta correspondientes? (Pista: para resolver todo el problema es necesario saber cómo se resuelve una ecuación diferencial, no homogénea y lineal; si el lector no lo recuerda, plantee simplemente la ecuación.) 9.4. Las funciones de demanda de dos bienes son x1 =a1 + b1p1 + b12p2 x2 =cz + b21P1 + b2p2 ¿Qúe restricciones sobre los parámetros implica la teoría? ¿Cuál es la función de utilidad métrica monetaria correspondiente? 9.5. ¿Cuál es la función directa de utilidad del problema anterior? 9.6. Sea (q, m) los precios y la renta y p deducir la fórmula = q/m. Utilice la identidad de Roy para 9.7. Considere la función de utilidad u(x1, z2, z3) = x1 z�z3. ¿Es esta función de utilidad (débilmente) separable en (z2, z3)? ¿Cuál es la función de subutilidad del consumo del bien z? ¿Cuáles son las demandas condicionadas de los bienes z, dado el gasto en esos bienes, mz? 9.8. Existen dos bienes, x e y. La función de demanda del bien x por parte del consumidor biene dada por lnx = a - bp + cm, donde p es el precio del bien x en relación con el y, y m es la renta monetaria dividida por el precio del bien y. Ejercicios / 187 (a) ¿Qué ecuación resolvería para averiguar la función indirecta de utilidad que generaría esta conducta de la demanda? (b) ¿Cuál es la condición de contorno de esta ecuación diferencial? 9.9. Un consumidor tiene la función de utilidad u(x, y, z) = min{ x, y }+z. Los precios de los tres bienes son (px, Py, p z) y el dinero que ha de gastar el consumidor m. (a) Esta función de utilidad puede expresarse en la forma U(V(x, y), z). ¿Cuál es la función V(x, y)? ¿Cuál es la función U(V, z)? (b) ¿Cuáles son las funciones de demanda de los tres bienes? (c) ¿Cuál es la función indirecta de utilidad? 9.10. Suponga que hay dos bienes, x1 y x2. Supongamos que el precio del bien 1 es Pl y que el del bien 2 es igual a 1. Representemos la renta por medio de y. La demanda del bien 1 por parte del consumidor es X1 = 10 - Pl (a) ¿ Cuál es la función de demanda del bien 2? (b) ¿Qué ecuación resolvería para calcular la función de compensación de la renta que generaría estas funciones de demanda? (c) ¿Cuál es la función de compensación de la renta correspondiente a estas funciones de demanda? 9 .11 El consumidor 1 tiene la función de gasto función de utilidad u2(x1, x2) = 43xf x2. ei (p1, P2, u1) = u1 yP1P2 y el 2 tiene la (a) ¿Cuáles son las funciones de demanda (de mercado) marshallianas de cada uno de los bienes por parte de cada uno de los consumidores? Represente la renta del consumidor 1 por medio de m1 y la del 2 por medio de m2. (b) ¿Qué valor(es) tendrá que tener el parámetro a para que exista una función de demanda agregada independiente de la distribución de la renta? 10. EL EXCEDENTE DE LOS CONSUMIDORES Cuando varía el entorno económico, normalmente también varía el bienestar de los consumidores. Una variación del precio de un bien afecta a la cantidad que desea consumir una persona y, por lo tanto, altera el nivel de utilidad que ésta puede conseguir. Los economistas suelen medir el grado en que afectan los cambios del entorno económico a los consumidores, para lo cual han desarrollado varios instrumentos. La medida clásica de la variación del bienestar que se examina en los cursos elementales es el excedente del consumidor. Sin embargo, esta medida sólo es exacta en circunstancias especiales. En el presente capítulo describimos algunos métodos más generales para medir la variación del bienestar, entre los que se encuentra el excedente del consumidor como caso especial. 10.1 Variaciones compensatorias y equivalentes Veamos primero cómo sería una medida "ideal" de la variación del bienestar. En el plano más fundamental, nos gustaría disponer de una medida de la variación que experimenta la utilidad como consecuencia de una determinada política económica. Supongamos que tenemos dos presupuestos, (pº, m0) y (p', m'), que miden los precios y las rentas a los que se enfrentaría un determinado consumidor en dos regímenes de política económica diferentes. Resulta útil suponer que (pº, m0) es el statu quo y (p', m') el cambio propuesto, si bien ésa no es la única interpretación posible. En ese caso, la medida evidente de la variación que experimentaría el bienestar si se sustituyera (pº, m0) por (p', m') es simplemente la diferencia entre las utilidades indirectas: v(p', m') - v(pº, m0). Si esta diferencia entre las utilidades es positiva, merece la pena cambiar de política, al menos en lo que se refiere a este consumidor; y si es negativa, no merece la pena. 190 / EL EXCEDENTE DE LOS CONSUMIDORES (C.10) Eso es todo lo que podemos decir en general; la teoría de la utilidad tiene un carácter puramente ordinal y no existe un método inequívocamente correcto para cuantificar las variaciones de la utilidad. Sin embargo, en algunos casos es útil disponer de una medida monetaria del bienestar de los consumidores. Por ejemplo, un analista de la política económica puede desear hacerse una idea aproximada de la magnitud de la variación del bienestar con el fin de fijar las prioridades o puede querer comparar los beneficios y los costes que recaerían en los diferentes consumidores. En este tipo de circunstancias, resulta útil elegir una medida "normalizada" de las diferencias de utilidad. Una medida razonable es la función de utilidad métrica monetaria (indirecta) descrita en el capítulo 7 (página 132). Figura 10.1 BIEN 1 BIEN 1 La variación equivalente y la variación compensatoria. En este gráfico el precio del bien 1 baja de Po a p1. El panel A representa la variación equivalente de la renta, es decir, cuánto dinero adicional se necesita al precio inicial Po para que el consumidor disfrute del mismo bienestar que con el precio p1• El panel B representa la variación compensatoria de la renta, es decir, cuánto dinero habría que sustraerle al consumidor para que disfrutara del mismo bienestar que con el precio PO· Recuérdese que µ(q; p, m) mide la cantidad de renta que necesitaría el consumidor a los precios q para disfrutar del mismo bienestar que a los precios p y la renta m. Es decir, µ(q; p, m) se define de la manera siguiente: e(q, v(p, m)). Si adoptamos esta medida de la utilidad, observaremos que la diferencia anterior entre las utilidades se convierte en: µ(q;p',m'), µ(q;p0,m0). Variaciones compensatorias y equivalentes / 191 Queda por elegir los precios de base q. Existen dos posibilidades obvias: suponer que q es igual a pº o suponer que es igual a p'. De esa manera, tenemos las dos medidas siguientes de la diferencia entre las utilidades: VE= µ(pº;p',m')- µ(p0;p0,m0) =.µ(pº;p',m')- m0 ve= µ(p';p',m')- µ(p';p0,m0) = m' - µ(p';p0,m0). (10.1) La primera medida se conoce con el nombre de variación equivalente. Utiliza como base los precios actuales y se pregunta qué variación de la renta a estos precios sería equivalente a la variación propuesta en función de su influencia en la utilidad. La segunda medida se denomina variación compensatoria. Utiliza como base los nuevos precios y se pregunta qué variación de la renta sería necesaria para compensar al consumidor por la variación de los precios (la compensación se produce después de algunos cambios, por lo que la variación compensatoria parte de los precios vigentes después del cambio). Ambos números son medidas razonables de la influencia de una variación de los precios en el bienestar. Sus magnitudes son diferentes, por lo general, debido a que el valor de una peseta depende de cuáles sean los precios relevantes. Sin embargo, su signo siempre es el mismo, ya que ambos miden las mismas diferencias entre las utilidades, sólo que utilizando simplemente funciones de utilidad distintas. La figura 10.1 muestra un ejemplo de la variación equivalente y de la compensatoria en el caso en el que hay dos bienes. Son las circunstancias y la cuestión que se trate de resolver las que indican cuál es la medida más adecuada. Si se trata de elaborar un sistema de compensación a los nuevos precios, parece razonable utilizar la variación compensatoria. Sin embargo, si se trata simplemente de disponer de una medida razonable de la "disposición 'a pagar", probablemente sea mejor la variación equivalente, por dos razones. En primer lugar, la variación equivalente mide la variación de la renta a los precios actuales y para quienes han de tomar decisiones es mucho más fácil juzgar el valor de una peseta a los precios actuales que a unos precios hipotéticos. En segundo lugar, si estamos comparando más de una propuesta de cambio de política, la variación compensatoria utiliza como base unos precios distintos para cada nueva política, mientras que la variación equivalente los mantiene fijos en su nivel actual. Por lo tanto, la variación equivalente es mejor para hacer comparaciones entre distintos tipos de proyectos. Dado que aceptamos, pues, la variación compensatoria y la equivalente como indicadores razonables de la variación de la utilidad, ¿cómo podemos medirlos en la práctica? En otras palabras, ¿cómo podemos medir µ(q; p, m) en la práctica? Ya respondimos a esta pregunta cuando estudiamos la teoría de la integrabilidad en el capítulo 9. Entonces vimos cómo se recuperaban las preferencias representadas por µ(q; p, m) observando la conducta de la demanda x(p, m). Dada cualquier 192 / EL EXCEDENTE DE LOS CONSUMIDORES (C.10) conducta observada de la demanda, es posible resolver las ecuaciones de integrabilidad, al menos en principio, y deducir la función de utilidad métrica monetaria correspondiente. En el capítulo 9 vimos cómo se deducía la función de utilidad métrica monetaria cuando la función de demanda adoptaba varias formas funcionales, entre las cuales se encontraban la lineal, la logarítmico-lineal, la semi-logarítmica, etc. En principio, podemos realizar los mismos cálculos con cualquier función de demanda que satisfaga las condiciones de integrabilidad. Sin embargo, en la práctica suele ser más sencillo realizar la especificación paramétrica en la otra dirección: primero se especifica una forma funcional de la función indirecta de utilidad y a continuación se deduce la forma de las funciones de demanda utilizando la identidad de Roy. Después de todo, normalmente es mucho más fácil diferenciar una función que resolver un sistema de ecuaciones diferenciales parciales. Si especificamos una forma paramétrica de la función indirecta de utilidad y a continuación derivamos las ecuaciones de demanda correspondientes, la estimación de los parámetros de la función de demanda nos da de inmediato los parámetros de la función de utilidad subyacente. La función de utilidad métrica monetaria -y la variación compensatoria y la equivalente-- puede deducirse o bien algebraicamente, o bien numéricamente sin grandes dificultades, una vez que se cuenta con los parámetros relevantes. Véase el capítulo 12 para una descripción más detallada de este enfoque. Naturalmente, este enfoque sólo tiene sentido si los parámetros estimados satisfacen las distintas restricciones que implica el modelo de optimización. Tal vez queramos verificar estas restricciones para ver si son plausibles en nuestro ejemplo empírico y, en caso afirmativo, estimar los parámetros sujetos a estas restricciones. En suma, la variación compensatoria y la equivalente son, de hecho, observables si lo son las funciones de demanda y si estas últimas satisfacen las condiciones que implica la maximización de la utilidad. La conducta observada de la demanda puede utilizarse para construir una medida de la variación del bienestar, la cual puede utilizarse a su vez para analizar distintos tipos de política económica. 10.2 El excedente del consumidor El instrumento clásico para medir las variaciones del bienestar es el excedente del consumidor. Si x(p) es la demanda de un bien en función de su precio, el excedente del consumidor correspondiente a una variación de pº a p' es EC = ¡ p' Po x(t) dt. La utilidad cuasilineal / 193 El excedente del consumidor es igual a la variación compensatoria y a la equivalente cuando sus preferencias pueden representarse por medio de una función de utilidad cuasilineal. En los casos más generales, el excedente del consumidor puede ser una aproximación razonable de las medidas del bienestar teóricamente ideales. 10.3 La utilidad cuasilineal Supongamos que existe una transformación monótona de la utilidad que tiene la forma siguiente: U(xo, x1, ... , Xk) = xo + u(x1, ... , Xk). Obsérvese que la función de utilidad es lineal en uno de los bienes, pero (posiblemente) no en los demás bienes, por lo que se denomina función de utilidad cuasilineal. En este apartado nos ocuparemos del caso especial en el que k = 1, por lo que la función de utilidad adopta la forma xo + u(x1), aunque todo lo que digamos será válido si hay un número arbitrario de bienes. Supondremos que u(x1) es una función estrictamente cóncava. Consideremos el problema de maximización de la utilidad correspondiente a esta forma de utilidad: max xo + u(x1) xo,x1 sujeta a xo + P1 x1 = m. Es tentador introducir la restricción presupuestaria en la función objetivo y reducir este problema a un problema de maximización sin restricciones: max u(x1) + m - p1x1. xi Este problema tiene la evidente condición de primer orden u'(x1) = P1, que exige simplemente que la utilidad marginal del consumo del bien 1 sea igual a su precio. Si se examina la condición de primer orden, se observará que la demanda del bien 1 sólo es una función de su precio, por lo que podemos expresar ésta de la manera siguiente: x1 (p1). La demanda del bien O se determina a continuación a partir de la restricción presupuestaria, xo = m - p1x1 (p1). Introduciendo estas funciones de demanda en la función de utilidad, obtenemos la función indirecta de utilidad: 194 / EL EXCEDENTE DE LOS CONSUMIOORES (C.10) donde v1 (p1) = u(x1 (p1)) - PI x1 (p1). Este enfoque no tiene nada que objetar, pero puede plantear un problema. Pensándolo bien, resulta evidente que la demanda del bien 1 no puede ser independiente de la renta en el caso de todos los precios y niveles de renta. Si el nivel de renta es suficientemente bajo, limitará necesariamente la demanda del bien 1. Supongamos que expresamos el problema de maximización de la utilidad de tal manera que reconozca explícitamente la restricción según la cual xo no puede ser negativo: max u(x1) + xo xo,x1 sujeta a p1x1 + xo =m xo � O. Vemos ahora que obtenemos dos clases de soluciones, dependiendo de que xo > O o de que xo = O. Si xo > O, tenemos la solución que hemos descrito antes, a saber, la demanda del bien 1 depende únicamente del precio del bien 1 y es independiente de la renta. Si xo = O, la utilidad indirecta viene dada simplemente por u(m/p1). Supongamos que el consumidor parte de un nivel de renta m = O y que éste aumenta en una pequeña cuantía. En ese caso, el incremento de la utilidad es u'(m/p1)/p1. Si esta cantidad es mayor que 1, el consumidor disfruta de un mayor bienestar gastando la primera peseta de renta en el bien 1 que gastándola en el bien O. Continúa gastando en el bien 1 hasta que la utilidad marginal de la peseta adicional gastada en ese bien sea exactamente igual a 1; es decir, hasta que la utilidad marginal del consumo sea igual al precio. A partir de ese momento, toda la renta adicional se gastará en el bien xo. La función de utilidad cuasilineal suele utilizarse en las aplicaciones de eco. nomía del bienestar debido a que la estructura de la demanda es muy sencilla. La demanda sólo depende del precio -al menos cuando los niveles de renta son suficientemente elevados- y no se produce ningún efecto-renta del que preocuparse, lo cual simplifica el análisis del equilibrio del mercado. Debemos pensar que este modelo es válido en las situaciones en las que la demanda de un bien no sea muy sensible a la renta. Pensemos en nuestra demanda de papel o de lápices: ¿cuánto variaría ésta si variara nue�tra renta? Lo más probable es que destináramos el aumento de nuestra renta al consumo de otros bienes. Por otra parte, con la utilidad cuasilineal es muy sencillo el problema de la integrabilidad. Dado que la función inversa de demanda viene dada por PI (x1) = u'(x1), la utilidad correspondiente a un determinado nivel de consumo del bien 1 puede recuperarse a partir de la curva inversa de demanda mediante una sencilla integración: La utilidad cuasilineal y la utilidad métrica monetaria / 195 La utilidad total que reporta la decisión de consumir x1 está formada por la utilidad derivada del consumo del bien 1 más la utilidad derivada del consumo del bien O: u(x1 (p¡)) + m - P1X1 (p¡) = fax, P1 (t) dt + m - P1X1 (p¡ ). Si prescindimos de la constante m, la expresión del segundo miembro de esta ecuación es simplemente el área situada debajo de la curva de demanda del bien 1 menos el gasto en el bien 1 o el área situada a la izquierda de la curva de demanda. Este problema también puede examinarse partiendo de la función indirecta de utilidad, v(p1) + m. Por la ley de Roy, x1 (p1) = -v'(p1). Integrando esta ecuación, tenemos que v(p1) + m = ¡= x1 (t) dt + m. P1 Esta expresión equivale al área situada a la izquierda de la curva de demanda debajo del precio P1, lo que no es más que otra forma de describir la misma área que describimos en el párrafo anterior. 10.4 La utilidad cuasilineal y la utilidad métrica monetaria Supongamos que la utilidad adopta la forma cuasilineal u(x1) + xo. Hemos visto que la función de demanda x1 (p1) correspondiente a este tipo de función de utilidad es independiente de la renta. También hemos visto que podíamos recuperar una función indirecta de utilidad coherente con esta función de demanda integrando simplemente con respecto a Pl. Naturalmente, toda transformación monótona de esta función indirecta de utilidad también es una función indirecta de utilidad que describe la conducta del consumidor. Si éste toma decisiones que maximizan el excedente del consumidor, también maximiza el cuadrado de dicho excedente. Hemos visto antes que la función de utilidad métrica monetaria era una función de utilidad especialmente buena en numerosas aplicaciones. Pues bien, en el caso de la función de utilidad cuasilineal, la integral de la demanda es esencialmente la función de utilidad métrica monetaria. El resultado que acabamos de mencionar se obtiene simplemente formulando las ecuaciones de integrabilidad y verificando que su solución es el excedente del consumidor. Si x1 (p1) es la función de demanda, la ecuación de integrabilidad es 196 / EL EXCEDENTE DE LOS CONSUMIDORES (C.10) dµ(t; q, m) dt µ(p;q,m) ----=x1 ( t ) = m. Puede verificarse mediante un cálculo directo que la solución de estas ecuaciones viene dada por µ(p; q, m) = 1.• X¡ (t) dt + m. La expresión del segundo miembro es simplemente el excedente del consumidor correspondiente a una variación del precio de p a q más la renta. La variación compensatoria y la equivalente correspondientes a esta forma de la función de utilidad métrica monetaria adoptan la forma siguiente: V E= µ(pº;p', m') - µ(pº;P°, m0) = A(pº,p') + m' - m0 ve= µ(p';p', m') - µ(p';pº, m0) = A(pº,p') + m' - rn°. En este caso especial, coinciden la variación compensatoria y la equivalente. No es difícil ver el significado intuitivo de este resultado. Dado que la función de compensación es lineal con respecto a la renta, el valor de una peseta adicional -la utilidad marginal de la renta- es independiente del precio. Por lo tanto, el valor de una variación compensatoria o equivalente de la renta es independiente de los precios a los que se mida el valor. 10.5 El excedente del consumidor como aproximación Hemos visto que el excedente del consumidor es una medida exacta de la variación compensatoria y de la equivalente sólo cuando la función de utilidad es cuasilineal. Sin embargo, puede ser una aproximación razonable en algunas circunstancias más generales. Consideremos, por ejemplo, una situación en la que sólo varía el precio del bien 1 de pº a p' y el nivel de renta se mantiene fijo en m =. m0 = m'. En este caso, podemos utilizar la ecuación (10.1) y el hecho de que µ(p; p, m) m, para formular las expresiones siguientes: = V E= µ(pº;p', m) - µ,(p0;p0, m) ve= µ(p ;p',m)-µ,(p 1 = µ(pº;p', m) - µ(p';p', m) ;p0,m) = 1 µ(pº;p0,m)-µ(p';p0,m). Hemos formulado estas expresiones en función de p solamente, ya que se supone que todos los demás precios son fijos. Definiendo 'U.o = v(pº, m) y u' = v(p', m) y El excedente del consumidor como aproximación / 197 utilizando la definición de la función de utilidad métrica monetaria del capítulo 7 (página 132), tenernos que VE = e(pº, u') - e(p', u') ve= e(pº, u0) - e(p', u0). Finalmente, valiéndonos del hecho de que la función de demanda hicksiana es la derivada de la función de gasto, de tal manera que h(p, u) oe/ op, podernos formular estas expresiones de la manera siguiente: = VE V = e(pº, u') - e(p', u') = { e = e(pº, uº) - e(p', uº) = Po Jp' { h(p, u') dp (10.2) Po Jp' h(p, uº) dp. De estas expresiones se deduce que la variación compensatoria es la integral de la curva de demanda hicksiana correspondiente al nivel inicial de utilidad y que la variación equivalente es la integral de la curva de demanda hicksiana correspondiente al nivel final de utilidad. La medida correcta del bienestar es una integral de una curva de demanda, pero tenernos que utilizar la curva de demanda hicksiana en lugar de la curva de demanda rnarshalliana. Sin embargo, podernos utilizar las expresiones de (10.2) para obtener unas útiles fronteras que lo acoten. La ecuación de Slutsky nos dice que oh(p, u) - ox(p, m) ox(p, m) ( ) + om X P, m . op op Si el bien en cuestión es un bien normal, la derivada de la curva de demanda hicksiana será mayor que la derivada de la curva de demanda rnarshalliana, corno muestra la figura 10.2 Por lo tanto, el área situada a la izquierda de las curvas de demanda hicksianas será mayor que el área situada a la izquierda de la curva de demanda rnarshalliana. En el caso descrito, pº > p', por lo que todas las áreas son negativas. Por lo tanto, V E> excedente del consumidor > Ve. 198 / EL EXCEDENTE DE LOS CONSUMIDORES (C.10) Figura 10.2 CANTIDAD Fronteras del excedente del consumidor. En el caso de los bienes normales, las curvas de demanda hicksianas son más inclinadas que la curva de demanda marshalliana. Por consiguiente, el área situada a la izquierda de la curva de demanda marshalliana está acotada por las áreas situadas debajo de la curvas de demanda hicksianas. 10.6 La agregación Las relaciones anteriores entre la variación compensatoria, la variación equivalente y el excedente del consumidor se cumplen todas ellas en el caso de un único consumidor. En este apartado analizamos algunas de las cuestiones que se plantean cuando hay muchos consumidores. En el capítulo 9 (página 181) vimos que la demanda agregada de un bien es una función del precio y de la renta agregada únicamente cuando la función indirecta de utilidad del agente i tenía la forma de Gorman: Vi(P, mi)= ai(p) + b(p)mi. En este caso, la función de demanda agregada de cada uno de los bienes se deduce de una función indirecta de utilidad agregada que tiene la forma siguiente: I: n V(p, M) = ai(p) + b(p)M, i=l donde M = ¿�=l mi. Hemos visto antes que la función indirecta de utilidad correspondiente a las preferencias cuasilineales tiene la forma Límites no paramétricos / 199 Esta función es claramente de un caso especial de la forma de Gorman en el que b(p) 1. Por lo tanto, la función indirecta de utilidad agregada que genera la demanda agregada es simplemente V(p) + M = L:i v/p) + L��l mi. ¿Qué podernos decir acerca del excedente agregado de los consumidores? La de ley Roy demuestra que la función vi(p) viene dada por = V;(p) = 1= X;(t) di, de donde se deduce que V(p) = L Vi(p) = L l.{= Xi(t) dt = In{= L Xi(t) dt. n n i=l i=l n p p i=l Es decir, la función indirecta de utilidad que genera la función de demanda agregada es simplemente la integral de la función de demanda agregada. Si todos los consumidores tienen funciones de utilidad cuasilineales, resulta que la función de demanda agregada maximiza el excedente agregado de los consumidores. Sin embargo, no es totalmente evidente que éste sea adecuado para realizar comparaciones de bienestar. ¿Por qué había de ser la suma no ponderada de una determinada representación de la utilidad una medida útil del bienestar? En el capítulo 13 (página 265) examinarnos esta cuestión. Corno puede verse allí, el excedente agregado de los consumidores es la medida adecuada del bienestar en el caso de la utilidad cuasilineal, pero este caso es bastante especial. En general, el excedente agregado de los consumidores no es una medida exacta del bienestar. Sin embargo, suele utilizarse corno medida aproximada del bienestar de los consumidores en los estudios aplicados. 10. 7 Límites no paramétricos Hemos visto cómo se utiliza la identidad de Roy para calcular la función de demanda dada una forma pararnétrica de la utilidad indirecta. Para calcular una forma pararnétrica de la función de utilidad métrica monetaria puede utilizarse la teoría de la integrabilidad si se cuenta con una forma parametrica de la función de demanda. Sin embargo, para efectuar cada una de estas operaciones es preciso especificar una forma pararnétrica o bien de la función de demanda, o bien de la función indirecta de utilidad. Es interesante preguntarse hasta dónde podernos llegar sin tener que especificar una forma pararnética. Pues bien, es posible obtener unos estrictos límites no 200 / EL EXCEDENTE DE LOS CONSUMIDORES (C.10) paramétricos para la función de utilidad monetaria no paramétrica de una manera totalmente no paramétrica. Cuando analizamos la recuperabilidad en el capítulo 8 vimos que es posible construir conjuntos de cestas de consumo que "se revela que se prefieren" a una determinada cesta de consumo o que "se revela que son peores" que ésta. Puede considerarse que estos conjuntos constituyen una frontera interior y exterior del conjunto preferido por el consumidor. Sea N RD(xo) el conjunto de puntos que "no se revela que son dominados" por xa. Éste no es sino el complemento del conjunto RD(xa). En el capítulo 8 vimos que el verdadero conjunto preferido correspondiente a xo, P(xo), debe contener RP(xo) y debe estar contenido en el conjunto de puntos N RD(x0). La figura 10.3 muestra esta situación. Para no enmarañar excesivamente el gráfico, hemos omitido muchas de las rectas presupuestarias y elecciones observadas y hemos representado únicamente RP(xo) y RD P(xo). También mostramos la "verdadera" curva de indiferencia que pasa por x0. Por definición, la utilidad métrica monetaria de xo se define de la siguiente manera: m(p, xo) = min px X sujeta a u(x) 2: u(xo). Este problema es exactamente igual que m(p, xo) = min px X sujeta ax pertenece a P(xo). Definamos m+(p, xo) y m-(p, xo) de la manera siguiente: = min px m-(p, xo) X sujeta ax pertenece a N RD(xo), y m+(p, xo) , = min px X sujeta a x pertenece a RP(xo). Dado que N RD(xo) => P(xo) => RP(xo), de acuerdo con el tipo habitual de argumentación se deduce que m + (p, xo) 2: m(p, xo) 2: m: (p, xo). Porlo tanto, la función de ultracompensación, m+(p, xo) y la función de infracompensación, m-(p, x0), acotan la verdadera función de compensación, m(p, x0). Ejercicios / 201 Figura 10.3 m•¡p, ,¡,) m(p,,¡,) BIEN 1 Fronteras de la utilidad métrica monetaria. El verdadero conjunto preferido, P(xo), contiene RP(xo) y está contenido en N RD(xo). Por lo tanto, el gasto mínimo correspondiente a P(xo) se encuentra entre las dos fronteras, como muestra la figura. Notas Los conceptos de variación compensatoria y equivalente y su relación con el excedente del consumidor se deben a Hicks (1956). Véase Willig (1976) para un análisis de otras formas interesantes de acotar el excedente del consumidor. Los límites no paramétricos de la función de utilidad métrica monetaria se deben a Varían (1982a). Ejercicios 10.1. Suponga que la utilidad es cuasilineal. Demuestre que la función indirecta de utilidad es una función convexa de precios. 10.2. La función de utilidad de Pérez es U (x, y) = min { x, y}. Pérez tiene 15.000 pesetas y el precio de x y de y es 1 en ambos casos. Su jefe está considerando la posibilidad de trasladarlo a otra ciudad donde el precio de x es 1 y el de y es 2. No le ofrece ninguna subida salarial. Pérez, que comprende perfectamente la variación compensatoria y la equivalente, se queja amargamente. Dice que aunque no le importa trasladarse y la nueva ciudad es tan agradable como la otra, tener que 202 / EL EXCEDENTE DE LOS CONSUMIDORES (C.10) trasladarse es tan malo como una reducción del salario de A pesetas. También dice que no le importaría trasladarse si le ofrecieran una subida de B pesetas. ¿ Cuáles son los valores de A y de B? 11. LA INCERTIDUMBRE Hasta ahora nos hemos ocupado de la conducta del consumidor en ausencia de incertidumbre. Sin embargo, muchas de las decisiones que toman los consumidores las adoptan en condiciones de incertidumbre. En el presente capítulo vemos cómo puede utilizarse la teoría de la elección del consumidor para describir este comportamiento. 11.1 Las loterías La primera tarea consiste en describir el conjunto de opciones entre las que puede elegir el consumidor. Imaginemos que éstas adoptan la forma de loterías. Una lotería se representa por medio de p o x EB {1- p) o y, lo que significa que "la probabilidad de que el consumidor reciba el premio x es p y la probabilidad de que reciba el premio y es (1 - p)". Los premios pueden consistir en dinero, cestas de bienes o incluso nuevas loterías. La mayoría de las situaciones en las que hay incertidumbre pueden analizarse mediante este modelo de las loterías. A continuación postulamos varios supuestos sobre la forma en que percibe el consumidor las loterías entre las que puede elegir. Ll. 1 o x EB (1 - 1) o y rv x. Recibir un premio con una probabilidad unitaria es lo mismo que recibirlo con absoluta certeza. L2. p o x EB (1 - p) o y rv (1 - p) o y EB p o x. Al consumidor le da igual el orden en el que se describa la lotería. L3. q o (p o x EB {1- p) o y) EB {1- q) o y rv (qp) o x EB (1 - qp) o y. La manera en que perciba el consumidor una lotería depende únicamente de las probabilidades netas de recibir los distintos premios. 204 / LA INCERTIDUMBRE (C. 11) Los supuestos (Ll) y (L2) parecen inocuos. El (L3) denominado a veces "reducción de las loterías combinadas" es algo dudoso, ya que existen algunos datos que inducen a pensar que los consumidores se comportan de distinta manera ante estas loterías que ante las que se juegan una vez. No obstante, aquí no analizaremos esta cuestión. Partiendo de estos supuestos podemos definir .C, el espacio de las loterías entre las que puede elegir el consumidor. Se supone que éste tiene unas determinadas preferencias sobre este espacio: dadas dos loterías cualesquiera, puede elegir entre ellas. Suponemos como siempre que las preferencias son completas, reflexivas y transitivas. El hecho de que las loterías sólo tengan dos resultados no es restrictivo, puesto que permitimos que los resultados sean nuevas loterías. De esa manera podemos concebir loterías que tengan un número arbitrario de premios combinando loterías de dos premios. Supongamos, por ejemplo, que queremos representar una situación en la que hay tres premios, x, y y z y en la que la probabilidad de obtener cada uno de ellos es de un tercio. Reduciendo las loterías combinadas, esta lotería equivale a la lotería 2 o ¡1- o 3 2 X l EB -1 o y EB -1 o z. 2 3 De acuerdo con el supuesto L3 anterior, al consumidor sólo le interesan las probabilidades netas, por lo que esta lotería equivale, de hecho, a la inicial. 11.2 La utilidad esperada Partiendo de algunos otros supuestos secundarios puede aplicarse el teorema relativo a la existencia de una función de utilidad descrito en el capítulo 7 (página 114) para demostrar que existe una función u que describe las preferencias del consumidor; es decir, p o x EB (1 - p) o y >- q o w EB (1 - q) o z si y sólo si u(p o x EB (1 - p) o y) > u(q o w EB (1 - q) o z). Naturalmente, esta función de utilidad no es única; cualquier transformación monótona podría desempeñar el mismo papel. Formulando algunas otras hipótesis, podemos hallar una transformación monótona de la función de utilidad que tiene una propiedad muy útil, la propiedad de la utilidad esperada: u(p o x EB (1 - p) o y) = pu(x) + (1 - p)u(y). La utilidad esperada / 205 Según la propiedad de la utilidad esperada, la utilidad de una lotería es la utilidad que se espera que reporten sus premios. Ésta puede calcularse tomando la utilidad que reportaría cada uno de los resultados, multiplicándola por la probabilidad de que ocurriera ese resultado y sumando los resultados obtenidos. La utilidad es aditivamente separable en cuanto a los resultados y lineal en las probabilidades. Debe hacerse hincapié en que no se pone en duda la existencia de una función de utilidad; cualquier ordenación regular de las preferencias puede representarse por medio de una función de utilidad. Lo interesante es la existencia de una función de utilidad que posee la útil propiedad antes citada. Para eso necesitamos estos axiomas adicionales: Ul. {p en [O; 1] : p o x EB (1 - p) o y t z} y {p en [O; 1] : z t p o x EB (1 - p) o y} son conjuntos cerrados cualesquiera que sean x, y y z pertenecientes a ,C. U2. Si x r- y, entonces p o x EB (1 - p) o z ,. . ., p o y EB (1 - p) o z. El supuesto (Ul) es un supuesto de continuidad y es relativamente inocuo. El (U2) indica que las loterías cuyos premios son indiferentes, también lo son ellas. Es decir, si se nos da una lotería p o x EB (1 - p) o z y sabemos que x ,. . ., y, podemos sustituir x por y y construir una lotería p o y EB (1 - p) o z que sea para el consumidor equivalente a la inicial. Este supuesto parece bastante plausible. Para evitar algunos detalles técnicos, postulamos otros dos supuestos. U3. Existe una lotería b que es la mejor de todas y una lotería w que es la peor. Cualquiera que sea x perteneciente a ,C, b t x t w. U4. La lotería p o b EB (1 - p) o w se prefiere a la q o b EB (1 - q) o w si y sólo si p > q. El supuesto (U3) se adopta puramente por conveniencia. El (U4) puede deducirse de los demás axiomas. Afirma simplemente que si una lotería entre el mejor premio y el peor se prefiere a otra, debe ser porque ofrece una mayor probabilidad de conseguir el mejor premio. Partiendo de estos supuestos, podemos formular el principal teorema. Teorema de la utilidad esperada. Si (,C, t) satisface los axiomas anteriores, existe una función de utilidad u definida en ,C que satisface la propiedad de la utilidad esperada: 'U(p o x EB (1 - p) o y) = pu(x) + (1 - p)u(y) 206 / LA INCERTIDUMBRE (C. 11) Demostración. Sea u(b) z, = 1 y u(w) = O. Para hallar la utilidad de una lotería arbitraria supongamos que u(z) = Pz, donde Pz viene definido por Pz o b EB (1 - Pz) (11.1) o w ,....., z. En esta construcción el consumidor se muestra indiferente entre z y un juego entre el mejor resultado y el peor que ofrece la probabilidad Pz de conseguir el mejor resultado. Para asegurarnos de que este planteamiento está bien definido, debemos verificar dos cosas. l. ¿Existe Pz? Los dos conjuntos {p en [O, 1] : p o b EB (1 - p) o w t z} y en [O; 1]: z t pobEB(l-p)ow} soncerradosynovacíosytodopuntoperteneciente a [O, 1] pertenece a uno u otro de los dos conjuntos. Dado que el intervalo unitario es conexo, debe haber algún p que pertenezca a ambos, pero ése será precisamente el p z que buscamos. {p 2. ¿Es Pz único? Supongamos que Pz y p: son dos números distintos y que cada uno de ellos satisface la definición (11.1). En ese caso, uno debe ser mayor que el otro. De acuerdo con el supuesto (U4), la lotería que ofrece una probabilidad mayor de conseguir el mejor premio no puede ser indiferente a una que ofrezca una probabilidad menor. Por lo tanto, Pz es único y u está bien definida. A continuación verificamos que u tiene la propiedad de la utilidad esperada, para lo cual basta realizar unas sencillas sustituciones: po X EB (1 - p) o y "'1 p o [px o b EB (1 - Px) o w] EB (1 - p) o [py o b EB (1 - Py) o w] + (1 - p)py] o b EB [l - PPx - (1 - p)py] o W [pu(x) + (1 - p)u(y)] o b EB [1 - pu(x) - (1 - p)u(y)] "'2 [PPx "'3 o w. La primera sustitución se basa en el axioma (U2) y en la definición de Px y La segunda se basa en el supuesto (L3), según el cual lo único que cuentan son las probabilidades netas de obtener b o w. La tercera sustitución se basa en la construcción de la función de utilidad. De la forma en que se ha construido la función de utilidad se deduce que Py· u(p o x x >- EB (1 - p) o y) = pu(x) + (1 - p)u(y). Por último, verificamos que u es una función de utilidad. Supongamos que En ese caso, y. Unicidad de la función de utilidad esperada / 207 u(x) u(y) = Px tal que X "' Px o b EB (1 = Py tal que y "' Pv o b EB (1 - Px) o w - Py) o w. De acuerdo con el axioma (U4), debe cumplirse que u(x) > u(y). 11.3 Unicidad de la función de utilidad esperada Ya hemos demostrado que existe una función de utilidad esperada u : .C ----+ R. Naturalmente, cualquier transformación monótona de u también será una función de utilidad que describa la conducta de elección del consumidor. Pero ¿preservará esa transformación monótona la propiedad de la utilidad esperada? ¿ Caracteriza de alguna manera la construcción antes descrita las funciones de utilidad esperada? No es difícil ver que si u(·) es una función de utilidad esperada que describe a un consumidor, también lo es v( ·) = au( ·) + e, donde a > O; es decir, cualquier transformación afín de una función de utilidad esperada también es una función de utilidad esperada, puesto que v(p o x EB (1 - p) o y) = au(p o x EB (1 - p) o y)+ e = a[pu(x) + (1 - p)u(y)] + e = p[au(x) +e]+ (1 - p)[au(y) + e] = pv(x) + (1 - p)v(y). No es mucho más difícil ver la recíproca de la afirmación anterior: cualquier transformación monótona de u que tenga la propiedad de la utilidad esperada debe ser una transformación afín. En otras palabras, Unicidad de la función de utilidad esperada. Una función de utilidad esperada es única excepto por una transformación afín. Demostración. De acuerdo con las observaciones anteriores, sólo tenemos que demostrar que si una transformación monótona preserva la propiedad de la utilidad esperada, debe ser una transformación afín. Sea f : R ----+ R una transformación monótona de u que tiene la propiedad de la utilidad esperada. En ese caso, f(u(p o x EB (1 - p) o y))= pf(u(x)) + (1 - p)j(u(y)), o sea, f (pu(x) + (1 - p)u(y)) = pf (u(x)) + (1 - p)f (u(y)). Pero esta expresión es equivalente a la definición de una transformación afín (véase el capítulo 26, página 565). 208 / LA INCERTIDUMBRE ( C. 11) 11.4 Otras notaciones para expresar la utilidad esperada Hemos demostrado el teorema de la utilidad esperada en el caso en el que las loterías tienen dos resultados. Como hemos indicado antes, es sencillo ampliar esta demostración al caso en el que hay un número finito de resultados utilizando loterías combinadas. Si la probabilidad de obtener el resultado Xi es Pi siendo i = 1, ... , n, en ese caso la utilidad esperada de esta lotería es simplemente n (11.2) LPiU(Xi). i=l El teorema de la utilidad esperada también se cumple, añadiendo algunos detalles técnicos de poca importancia, en el caso de las distribuciones de probabilidades continuas. Si p(x) es una función de densidad definida con respecto a los resultados x, la utilidad esperada de este juego puede expresarse de la siguiente manera: J (11.3) ·u(x)p(x) dx. Estos dos casos pueden aunarse utilizando el operador de las expectativas. Sea X una variable aleatoria que adopta los valores representados por x. En ese caso, la utilidad de X también será una variable aleatoria, u(X). La expectativa de esta variable aleatoria, Eu(X) es simplemente la utilidad esperada correspondiente a la lotería X. En el caso de una variable aleatoria discreta, Eu(X) viene dada por la expresión (11.2) y en el caso de una variable aleatoria continua viene dada por la (11.3). 11.5 La aversión al riesgo Consideremos el caso en el que el espacio de las loterías consiste únicamente en juegos cuyos premios son monetarios. Sabemos que si la conducta de elección del consumidor satisface los distintos axiomas exigidos, podemos hallar una representación de la utilidad que tenga la propiedad de la utilidad esperada. Eso significa que podemos describir la conducta del consumidor ante todos los juegos monetarios si conocemos solamente esta representación de su función de utilidad del dinero. Por ejemplo, para calcular la utilidad que espera obtener el consumidor del juego p o x EB (1 - p) o y, basta examinar pu(x) + (1 - p)u(y). Esta construcción se ilustra en la figura 11.1 en el caso en que p = Obsérvese en este el consumidor obtener el valor de la lotería. Es prefiere esperado que ejemplo decir, la utilidad de la lotería u(p o x EB (1 -.p) o y) es menor que la utilidad del valor esperado de la lotería, px + (1 - p)y. Este tipo de conducta se denomina aversión al !. La aversión al riesgo / 209 riesgo. Un consumidor también puede ser amante del riesgo; en ese caso, preferirá una lotería a su valor esperado. Si un consumidor es contrario a correr riesgos en alguna región, la cuerda trazada entre dos puntos cualesquiera del gráfico de su función de utilidad en esta región debe encontrarse por debajo de ella. Esta afirmación equivale a la definición matemática de una función cóncava. Por lo tanto, la concavidad de la función de utilidad esperada equivale a la aversión al riesgo. Figura 11.1 UTILIDAD u(fx+ fy) -------------------iu(x) + iu(y) ---------------- y X RIQUEZA Utilidad esperada de un juego. La utilidad esperada del juego es !u(x) + !u(y). La utilidad del valor esperado del juego es u(!x + En el caso descrito, la utilidad del valor esperado es mayor que la utilidad esperada del juego, por lo que el consumidor es contrario a correr riesgos. h), Suele ser útil disponer de una medida de la aversión al riesgo. Intuitivamente, cuanto más cóncava sea la función de utilidad esperada, más contrario a correr riesgos será el consumidor. Por lo tanto, cabría pensar que la aversión al riesgo puede medirse por medio de la segunda derivada de la función de utilidad esperada. Sin embargo, esta definición no es independiente de las variaciones de la función de utilidad esperada: si. multiplicamos la función de utilidad esperada por 2, la conducta del consumidor no varía, pero sí nuestra medida propuesta de la aversión al riesgo. Sin embargo, si normalizamos la segunda derivada dividiéndola por la primera, obtenemos una medida razonable, conocida con el nombre de medida de Arrow-Pratt de la aversión (absoluta) al riesgo: r.(w) u"(w) = - u'(w) · 210 / LA INCERTIDUMBRE (C. 11) El análisis siguiente aporta una justificación complementaria de esta medida. Representemos un juego por medio de un par de números (x1, x2), en el que el consumidor reciba x1 si ocurre el acontecimiento E y x2 si no ocurre E. En ese caso, definimos el conjunto de aceptación del consumidor como el conjunto de todos los juegos que aceptaría con un nivel inicial de riqueza w. Si el consumidor es contrario a correr riesgos, el conjunto de aceptación será convexo. La frontera de este conjunto -el conjunto de juegos indiferentes- puede expresarse por medio de una función implícita x2(x1), como muestra la figura 11.2 Figura 11.2 ----X1 Pendiente = - p/(1 - p) El conjunto de aceptación. Este conjunto describe todos los juegos que serían aceptados por el consumidor con su nivel inicial de riqueza. Si éste es contrario a correr riesgos, el conjunto de aceptación será convexo. Supongamos que la conducta del consumidor puede describirse por medio de la maximización de la utilidad esperada. En ese caso, x2(x1) debe satisfacer la siguiente identidad: pu(w + x1) + (1 - p)u(w + x2(x1)) = u(w). La pendiente de la frontera del conjunto de aceptación en el punto (O, O) se halla diferenciando esta identidad con respecto a x1 y evaluando esta derivada en x1 = O: pu'(w) + (1 - p)u'(w)x;(O) = O. (11.4) La aversión al riesgo / 211 Despejando la pendiente del conjunto de aceptación, tenemos que P __ xí(O) = __ 1-p Es decir, la pendiente del conjunto de aceptación en el punto (O, O) indica el cociente de probabilidades (odds). Ésta es una buena manera de conocer las probabilidades: hallar el cociente de probabilidades al que el consumidor está dispuesto a aceptar una pequeña apuesta en relación con el acontecimiento en cuestión. Supongamos ahora que tenemos dos consumidores cuyas probabilidades de que ocurra el acontecimiento E son idénticas. Es natural decir que el consumidor i es más contrario a correr riesgos que el j si el conjunto de aceptación del primero está contenido en el conjunto de aceptación del segundo. Esta afirmación sobre la aversión al riesgo tiene un carácter global, pues dice que j aceptará cualquier juego que acepte i. Si nos limitamos a analizar los juegos pequeños, obtendremos una medida más útil. Es natural afirmar que el consumidor i es localmente más contrario a correr riesgos que el j si su conjunto de aceptación está contenido en el de j en las cercanías del punto (O, O), lo cual significa que j aceptará cualquier juego pequeño que acepte i. Si está contenido en sentido estricto, i aceptará estrictamente menos juegos pequeños quej. No resulta difícil ver que el consumidor i es localmente más contrario a correr riesgos que el j si su conjunto de aceptación es "más curvado" que el de j en las cercanías del punto (O, O). Esto es útil, ya que podemos comprobar la curvatura del conjunto de aceptación calculando la segunda derivada de x2(x1). Diferenciando la identidad (11.4) una vez más con respecto a x1 y evaluando la derivada resultante en cero, tenemos que pu"(w) + (1 - p)u"(w)xí(O)x2(0) + (1 - p)u'(w)x2(0) = O. Valiéndonos del hecho de que x2(0) = -p/(1 - p), tenemos que · ,, p [ u"(w)l Xz (O)= (1 - p)2 - u'(w) . Esta expresión es proporcional a la medida de Arrow-Pratt de la aversión local al riesgo que hemos definido antes. Podemos extraer la conclusión de que un agente j aceptará más juegos pequeños que el i si y sólo si la medida de Arrow-Pratt de la aversión local al riesgo de este último es mayor que la del primero. 212 / LA INCERTIDUMBRE (C. 11) Ejemplo: La demanda de seguro Supongamos que un consumidor tiene inicialmente la riqueza monetaria W. Existe la probabilidad p de que pierda la cantidad L; por ejemplo, existe la probabilidad p de que se queme su casa. Puede suscribir un seguro por el que percibirá q pesetas si experimenta esta pérdida. La cantidad de dinero que ha de pagar a cambio de q pesetas de cobertura del seguro es 1rq; 1r es la prima por peseta de cobertura. ¿Cuánta cobertura suscribirá el consumidor? Examinemos el problema de maximización de la utilidad max pu(W - L - 1rq + q) + (1 - p)u(W - n q). Tomando la derivada con respecto a q e igualándola a cero, tenemos que pu'(W - L + q*(l - 1r))(l - 1r) - (1 - p)u'(W - 1rq*)1r u'(W - L + (1 - 1r)q*) (1 - p) u'(W - 1rq*) p =O 1r 1 - 7r Si ocurre el acontecimiento, la compañía de seguros recibe 1rq - q pesetas. Si no ocurre, recibe 1rq pesetas. Por lo tanto, su beneficio esperado es (1 - p)1rq - p(l - 1r)q. Supongamos que la competencia existente en el sector de los seguros reduce estos beneficios a cero. Eso significa que -p(l - 1r)q + (1 - p)1rq = o, de donde se deduce que 1r = p. Partiendo del supuesto de que los beneficios son nulos, la compañía de seguros cobra una prima actuarialmente justa: el coste de una póliza es precisamente su valor esperado, por lo que p = 1r. Introduciendo este resultado en las- condiciones de primer orden para la maximización de la utilidad, tenemos que u'(W - L + (1 - 1r)q*) = u'(W - n q"). Si el consumidor es estrictamente contrario a correr riesgos, de tal manera que u"(W) < O, la ecuación anterior implica que W - L + (1 - 1r )q* = W - tt q" de donde se deduce que L = q*. Por lo tanto, el consumidor se asegurará totalmente contra la pérdida L. La aversión global al riesgo / 213 Este resultado depende de manera crucial del supuesto de que el consumidor no puede influir en la probabilidad de experimentar una pérdida. Si lo que haga no influye en ésta, es posible que las compañías de seguros sólo quieran ofrecer un seguro parcial, por lo que el consumidor tendrá un incentivo para tener cuidado. En el capítulo 25 (página 533) analizaremos un modelo de este tipo. 11.6 La aversión global al riesgo La medida de Arrow-Pratt parece una interpretación razonable de la aversión local al riesgo: un agente es más contrario a correr riesgos que otro si está dispuesto a aceptar menos juegos pequeños. Sin embargo, en muchas circunstancias interesa disponer de una medida global de la aversión al riesgo, es decir, interesa saber si un agente es más contrario a correr riesgos que otro, cualquiera que sea el nivel de riqueza. ¿Cuál es la manera natural de expresar esta condición? La primera manera plausible consiste en formalizar la idea de que un agente cuya función de utilidad sea A(w) es más contrario a correr riesgos que uno cuya función de utilidad sea B(w) de la manera siguiente: A"(w) - A'(w) > - B"(w) B'(w) en todos los niveles de riqueza w. Esta expresión significa simplemente que el agente A tiene en todos los casos un grado mayor de aversión al riesgo que el B. Otra manera sensata de formalizar la idea de que el agente A es más contrario a correr riesgos que el B es decir que la función de utilidad del primero es "más cóncava" que la del segundo. Más concretamente, decimos que la función de utilidad del agente A es una transformación cóncava de la del agente B; es decir, existe una función creciente y estrictamente cóncava G(·) tal que A(w) = G(B(w)). La tercera manera de recoger la idea de que A es más contrario a correr riesgos que B es decir que A estaría dispuesto a pagar más por evitar un determinado riesgo que B. Para formalizar esta idea, supongamos que E es una variable aleatoria cuya esperanza matemática es ce�o: EE = O. En ese caso, decimos que 1r A (E) es la cantidad máxima de riqueza a la que renunciaría la persona A para no tener que enfrentarse a la variable aleatoria E, lo que en símbolos se expresa de la siguiente manera: A(w - 1rA(E)) = EA(w + E). El primer miembro de esta expresión es la utilidad que genera la reducción de la riqueza en 1r A (E) y el segundo es la utilidad esperada del juego E. Es natural decir 214 / LA INCERTIDUMBRE (C. 11) que la persona A es (globalmente) más contraria al riesgo que la B si 7fA (E) > tt B (E) cualquiera que sea E. Tal vez parezca difícil elegir entre estas tres plausibles y razonables interpretaciones de lo que podría significar que un agente es "globalmente más contrario al riesgo" que otro. Afortunadamente, no es necesario elegir: las tres definiciones son equivalentes. Para demostrarlo necesitamos el siguiente resultado, que es de suma utilidad para analizar las funciones de utilidad esperada. Desigualdad de Jensen. Sea X una variable aleatoria y f (X) una función estrictamente cóncava de esta variable aleatoria. En ese caso, E f(X) < f(EX). Demostración. Esta proposición es cierta en general, pero es más fácil demostrarla en el caso de una función cóncava diferenciable. Una función de ese tipo posee la propiedad de que en cualquier punto ii; f(x) < f(x) + f'(x)(x - x). Suponiendo que X es el valor esperado de X y tomando esperanzas matemáticas en cada uno de los miembros de esta expresión, tenemos que E f (X) < f (X) + J' (X)E(X - X) = f (X), de donde se deduce que E f(X) < f(X) = f(EX). Teorema de Pratt. Sean A(w) y B(w) dos funciones de utilidad esperada de la riqueza diferenciables, crecientes y cóncavas. En ese caso, las propiedades siguientes son equivalentes. l. -A"(w)/A'(w) > -B"(w)/ B'(w) cualquiera que sea w. 2. A(w) = G(B(w)) 3. tt A (E) > tt B (E) en el caso de alguna función creciente y estrictamente cóncava G. en el caso de todas las variables aleatorias E tales que E E = O. Demostración. (1) implica (2). Definamos G(B) implícitamente por medio de A(w) = G(B(w)). Obsérvese que la monotonicidad de las funciones de utilidad implica que G está bien definida, es decir, a cada valor de B le corresponde un único valor de G(B). Diferenciando dos veces esta definición, tenemos que A'(w) = G'(B)B'(w) A"(w) = G"(B)B'(w)2 + G'(B)B"(w). La aversión global al riesgo / 215 Dado que A'(w) > O y B'(w) > O, la primera ecuación establece que G'(B) Dividiendo la segunda ecuación por la primera, tenemos que A"(w) G"(B) , A'(w) = G'(B) B (w) > O. B"(w) + B'(w) . Reordenando, tenemos que G"(B) B"(w) A"(w) , B (w) = G'(B) B'(w) A'(w) < O, donde la desigualdad se deduce de (1). Queda demostrado que G"(B) queríamos. < O, como (2) implica (3), como se deduce de la siguiente cadena de desigualdades: A(w - 1r A) = EA(w < + E) = EG(B(w + E)) G(EB(w + m = G(B(w - 7rB)) = A(w - 7rB). Todas estas relaciones se deducen de la definición de la prima por el riesgo con la salvedad de la desigualdad, que se deduce de la desigualdad de Jensen. Comparando el primer término y el último, vemos que 7rA > 7rB· (3) implica (1). Dado que (3) se cumple en el caso de todas las variables aleatorias E cuya media es cero, debe cumplirse en el caso de todas las variables aleatorias arbitrariamente pequeñas. Tómese una variable E y considérese la familia de variables aleatorias definida por iE, tales que t pertenece al intervalo [O, 1]. Sea 1r(t) la prima por el riesgo en función de t. El desarrollo en serie de Taylor de segundo orden de 1r(t) en torno a t = O viene dado por (11.5) Calcularemos los términos de esta serie de Taylor para ver cómo se comporta 1r(t) cuando t es pequeño. La definición de 1r(t) es A(w - 1r(t)) De esta definición se deduce que 1r(O) respecto a t, tenemos que = EA(w + a). = O. Diferenciando dos veces la definición con -A' (w - 1r(t))1r' (t) A"(w - 1r(t))1r'(t)2 - A'(w - 1r(t))1r"(t) = E[A' (w + tE)E] = E[A"(w + Wi]. 216 / LA INCERTIDUMBRE (C. 11) (Es posible que algunos lectores no estén familiarizados con la forma de diferenciar una esperanza matemática, pero tomar esperanzas no es más que otra notación de una suma o una integral, por lo que se aplican las mismas reglas: la derivada de una esperanza es la esperanza de la derivada.) Evaluando la primera expresión cuando t = O, vemos que 7í1(0) =O.Evaluando la segunda cuando t = O, vemos que ,, 7í (O) =- EA"(w)i A'(w) =- A"(w) 2 A'(w) ª' donde a2 es la varianza de E. Introduciendo las derivadas en la ecuación (11.5) de 7í(t), tenemos que 7í(t) A"(w) ª2 �o+ o - ---t2 . A'(w) 2 Eso implica que cuando los valores de t son arbitrariamente bajos, la prima por el riesgo depende monótonamente del grado de aversión al riesgo, que es lo que queríamos demostrar. Ejemplo: Estática comparativa de un sencillo problema de cartera Apliquemos lo que hemos aprendido al análisis de un sencillo problema de cartera de dos periodos en el que hay dos activos, uno cuyo rendimiento es incierto y uno cuyo rendimiento es seguro. Dado que la tasa de rendimiento del activo incierto es incierta, la representamos por medio de la variable aleatoria R. Sea w la riqueza inicial y a 2: O la cantidad monetaria invertida en el activo incierto. La restricción presupuestaria implica que w - a es la cantidad invertida en el activo seguro. Suponemos para mayor comodidad que el activo seguro tiene una tasa de rendimiento nula. En este caso, la riqueza correspondiente al segundo periodo puede expresarse de la siguiente manera: W = a(l + R) + w - a= aR + w. Obsérvese que la riqueza correspondiente al segundo periodo es una variable aleatoria dado que también lo es R. La utilidad esperada de invertir a en el activo incierto puede expresarse de la siguiente manera: v(a) = Eu(w + aR), y las dos primeras derivadas de la utilidad esperada con respecto a a son La aversión global al riesgo / 217 v'(a) = Eu'(w + aR)R v"(a) = Eu"(w + aR)R2. Obsérvese que la aversión al riesgo implica que v" (a) es siempre negativo, por lo que se satisface automáticamente la condición de segundo orden. Examinemos, en primer lugar, las soluciones de esquina. Evaluando la primera derivada en a = O, tenernos que v'(O) = Eu'(w)R = u'(w)ER, de donde se deduce que si ER � O, v'(O) � O, y, dada la estricta aversión al riesgo, v'(a) < O cualquiera que sea a > O. Por lo tanto, a = O es una situación óptima si y sólo si ER � O. Es decir, una persona contraria a correr riesgos decidirá no invertir nada en el activo incierto si y sólo si su rendimiento esperado no es positivo. En cambio, si ER > O, se deduce que v'(O) = u'(w)ER > O, por lo que el individuo generalmente querrá invertir una cantidad positiva en el activo incierto. La inversión óptima satisfará la condición de primer orden Eu'(w + aR)R = O, (11.6) lo que requiere simplemente que la utilidad· marginal esperada de la riqueza sea igual a cero. Examinemos la estática comparativa de este problema de elección. En primer lugar, veamos cómo varía a cuando varía w. Sea a(w) la elección óptima de a en función de w; ésta debe satisfacer idénticamente la condición de primer orden Eu'(w + a(w)R)R = O. Diferenciando con respecto a w, tenernos que Eu"(w + aR)R[l + a'(w)R] = O, o sea, a'(w) =_ a ) Eu"(w + � � . Eu"(w + aR)R2 Corno es habitual, el denominador es negativo debido a la condición de segundo orden, por lo que vernos que signo de a'(w) = signo de Eu"(w + aR)R. 218 / LA INCERTIDUMBRE (C. 11) El signo de la expresión del segundo miembro no es totalmente evidente. Sin embargo, en realidad depende de la conducta de la aversión absoluta al riesgo, r(w). La aversión al riesgo. Eu"(w + decreciente, creciente o constante. aR)R es positivo, negativo o cero cuando r(w) es Demostración. Demostramos que r'(w) < O implica que Eu"(w + aR)R > O, ya que éste es el caso más razonable. Las demostraciones de los demás son similares. Consideremos primero el caso en el que R > O. En este caso, tenemos que u"(w + aR) r(w + aR) = _ u'(w + aR) < r(w), que puede expresarse también de la forma siguiente: aR) > -r(w)u'(w + aR). (11.7) aR)R > -r(w)u'(w + aR)R. (11.8) u"(w + Dado que R > O, u"(w + Consideremos ahora el caso en el que R < O. Examinando (11.7), vemos que el hecho de que la aversión absoluta al riesgo sea decreciente implica que aR) < -r(w)u'(w + aR). aR)R > -r(w)u'(w + aR)R. u"(w + Dado que R< O, tenemos que u"(w + Comparando esta desigualdad con la ecuación (11.8), vemos que (11.8) debe cumplirse tanto en el caso en el que R > O como en el caso en el que R < O. Por lo tanto, tomando la esperanza con respecto a todos los valores de R, tenemos que Eu"(w + aR)R > -r(w)Eu'(w + aR)R = O, donde la última igualdad se deduce de las condiciones de primer orden. El lema nos da nuestro resultado: la inversión en el activo incierto es creciente, constante o decreciente con respecto a la riqueza cuando la aversión al riesgo es decreciente, constante o creciente con respecto a la riqueza. A continuación vemos cómo varía la demanda del activo incierto cuando varía la distribución de probabilidades de su rendimiento. Una manera de parametrizar los desplazamientos de la tasa aleatoria de rendimiento consiste en formular la expresión La aversión global al riesgo / 219 (1 + h)R, donde hes una variable de traslación. Cuando h = O, tenemos la variable aleatoria inicial; si h es positivo, significa que todos los rendimientos conseguidos son un h por ciento mayores. Sustituyendo R por (1 +h)R en la ecuación (11.6) y dividiendo los dos miembros de la expresión por (1 + h), tenemos que Eu' (w + a(l + h)R)R = O. (11.9) Podríamos diferenciar esta expresión con respecto a h y averiguar el signo del resultado, pero es mucho más fácil ver qué ocurre con a cuando varía h. Sea a(h) la demanda del activo incierto en función de h. Afirmo que a(h) = a(Oh ). 1+ La demostración consiste simplemente en introducir esta fórmula en la condición de primer orden (11.9). Intuitivamente, si la variable aleatoria se multiplica por 1 + h, el consumidor reduce simplemente sus tenencias en 1/(1 + h) y restablece exactamente la misma pauta de rendimientos que teníamos antes de que se produjera el desplazamiento de la variable aleatoria. Este tipo de desplazamiento lineal de la variable aleatoria puede contrarrestarse perfectamente alterando la cartera del consumidor. Un desplazamiento más interesante de la variable aleatoria es lo que se conoce como dispersión que preserva la media, que aumenta la varianza de R pero mantiene constante su media. Una manera de parametrizar esa variación consiste en formular la siguiente expresión: R + h(R - R). El valor esperado de esta variable aleatoria es R, pero la varianza es h2a�, por lo que un aumento de h no altera la media, pero aumenta la varianza. Esta expresión también puede formularse de la siguiente manera: (1 + h)R- hR, lo que demuestra que puede considerarse que este tipo de dispersión que preserva la media lo que hace es multiplicar la variable aleatoria por 1 + h y a continuación restar ut: De acuerdo con nuestros resultados anteriores, multiplicar la variable aleatoria por 1 + h reduce la demanda dividiéndola por 1 + h y restar una cantidad de la riqueza la reduce aún más, suponiendo que la aversión absoluta al riesgo es decreciente. Por lo tanto, este tipo de dispersión que preserva la media reduce la inversión en el activo incierto más que proporcionalmente. Ejemplo: Fijación de los precios de los activos Supongamos ahora que hay muchos activos inciertos y uno seguro. Cada uno de los activos inciertos tiene un rendimiento total aleatorio tt; siendo i = 1, ... , n, y el activo seguro tiene un rendimiento total Ro (el rendimiento total, R, es uno más 220 / LA INCERTIDUMBRE (C. 11) la tasa de rendimiento; en el apartado anterior hemos utilizado el símbolo R para representar la tasa de rendimiento). El consumidor tiene inicialmente la riqueza w y decide invertir la proporción Xi en el activo i siendo i = O, ... , n. Por lo tanto, la riqueza que posee el consumidor en el segundo periodo -cuando se consiguen los rendimientos aleatorios- viene dada por W n ¿xdii = w (11.10) i=Ü Suponemos que el consumidor quiere elegir (xi) con el fin de maximizar la utilidad esperada de la riqueza aleatoria W. La restricción presupuestaria correspondiente a este problema es ¿�=O Xi = 1. Dado que Xi es la proporción de la riqueza del consumidor invertida en el activo i, la suma de las proporciones invertidas en todos los activos existentes debe ser l. Esta restricción presupuestaria también puede expresarse de la siguiente manera: n xo +¿xi= 1, i=l porlo que xo = 1- ¿�=l Xi. Introduciendo esta expresión en la (11.10) y reordenando los términos, tenemos que W=w =w = w [xoRo + t x,R;] t=l [o - tx,>Ro tx,R;] + [Ro+ tx,(Íl; - Ro)] . t=l Con esta reordenación de la restricción presupuestaria, ahora tenemos un problema de maximización sin restricciones en x1, ... , Xn. ¿ xiCRi - Ro)]). n max XJ,···,Xn . Eu(w[Ro + i=l Diferenciando con respecto a Xi tenemos las condiciones de primer orden Eu' (W)(it - Ro) = o, siendo i = 1, ... , n. Obsérvese que es esencialmente la misma expresión que obtuvimos en el apartado anterior. La aversión relativa al riesgo / 221 También puede expresarse de la siguiente manera: Eu' (W)Ri = RoEu' (W). Utilizando la identidad de la covarianza en el caso de variables aleatorias, cov(X, Y) EXY - EX EY, podemos transformar esta expresión en = cov(u'(W), Ri) + E.Ri Eu'(W) = RoEu'(W). Reordenándola, tenemos que - ERi = } I - - Ro - Eu'(W) cov(u (W), Ri). (11.11) Esta ecuación nos dice que el rendimiento esperado de un activo cualquiera puede expresarse como la suma de dos componentes: el rendimiento libre de riesgo más la prima por el riesgo. Esta última depende de la covarianza entre la utilidad marginal de la riqueza y el rendimiento del activo (obsérvese que se trata de un concepto de prima por el riesgo distinto al que analizamos en la demostración del teorema de Pratt; desgraciadamente, se utiliza el mismo término para referirse a ambos conceptos). Consideremos un activo cuyo rendimiento está correlacionado positivamente con la riqueza. Dado que la aversión al riesgo implica que la utilidad marginal de la riqueza disminuye conforme aumenta ésta, un activo de ese tipo estará correlacionado negativamente con la utilidad marginal. Por lo tanto, un activo de ese tipo deberá tener un rendimiento esperado mayor que la tasa libre de riesgo, para compensar su riesgo. En cambio, un activo correlacionado negativamente con la riqueza tendrá un rendimiento esperado menor que la tasa libre de riesgo. Intuitivamente, un activo correlacionado negativamente con la riqueza es un activo especialmente valioso para reducir el riesgo y, por lo tanto, la gente estará dispuesta a sacrificar los rendimientos esperados con el fin de tener un activo de ese tipo. 11. 7 La aversión relativa al riesgo Consideremos el caso deun consumidor cuya riqueza es w y supongamos que se le ofrece la posibilidad de participar en el siguiente tipo de juegos: recibir un x por ciento de su riqueza actual con una probabilidad p; recibir un y por ciento de su riqueza actual con una probabilidad (1 - p). Si el consumidor evalúa las loterías basándose en la utilidad esperada, la utilidad de esta lotería será pu(xw) + (1 - p)u(yw). 222 / LA INCERTIDUMBRE (C. 11) Obsérvese que este juego multiplicativo tiene una estructura diferente de la que tienen los juegos aditivos antes analizados. No obstante, este tipo de juegos relativos surge con frecuencia en los problemas económicos. Por ejemplo, el rendimiento de las inversiones suele formularse en relación con el nivel de inversión. Cabe preguntarse, al igual que antes, cuándo aceptará un consumidor más juegos relativos pequeños que otro con un determinado nivel de riqueza. Realizando el mismo tipo de análisis que antes, observamos que la medida adecuada es la medida de Arrow-Pratt de la aversión relativa al riesgo: p =- u"(w)w . u'(w) Es razonable preguntarse cómo variarían la aversión absoluta al riesgo y la relativa si variara la renta. Es bastante plausible suponer que la aversión absoluta al riesgo disminuye conforme aumenta la riqueza: una persona está dispuesta a aceptar más juegos expresados en pesetas absolutas a medida que se enriquece. La conducta de la aversión relativa al riesgo plantea más problemas; ¿está más o menos dispuesta una persona a arriesgarse a perder una parte de su riqueza a medida que aumenta ésta? Suponer que la aversión relativa al riesgo es constante probablemente no es un supuesto excesivamente malo, al menos cuando se trata de pequeñas variaciones de la riqueza. Ejemplo: La media y la varianza de la utilidad En general, la utilidad esperada de un juego depende de toda la distribución de probabilidades de los resultados. Sin embargo, en algunas circunstancias la utilidad esperada de un juego depende únicamente de determinados estadísticos que resumen la distribución. El ejemplo más corriente es el de la media y la varianza de la función de utilidad. Supongamos, por ejemplo, que la función de utilidad esperada es cuadrática, por lo que u(w) = w - bw2. En ese caso, la utilidad esperada es Eu(w) = Ew - bEw2 = w - bw2 - be/;. Por lo tanto, la utilidad esperada de un juego es únicamente una función de la media y la varianza de la riqueza. Desgraciadamente, la función de utilidad cuadrática tiene algunas propiedades poco recomendables: es una función decreciente de la riqueza en algunos intervalos y muestra una aversión absoluta al riesgo creciente. Un caso más útil en el que está justificado el análisis de la media y la varianza es aquel en el que la riqueza sigue una distribución normal. Es bien sabido que la La utilidad que depende del estado de la naturaleza / 223 media y la varianza caracterizan totalmente una variable aleatoria normal; por lo tanto, la elección entre las variables aleatorias que siguen una distribución normal se reduce a una comparación de sus medias y varianzas. Un caso de especial interés es aquel en el que el consumidor tiene una función de utilidad de la forma u(x) = =e:"?", Puede demostrarse qqe en el caso de esta función de utilidad la aversión absoluta al riesgo es constante. Además, cuando la riqueza sigue una distribución normal Eu(w) =- ! «r= f(w) dw = -e-rl-w+riu�/21. (Para realizar la integración, o bien desarróllese el cuadrado, o bien obsérvese que se trata esencialmente del cálculo que se realiza para hallar la función generadora de momentos correspondiente a la distribución normal.) Obsérvese que la utilidad esperada es creciente en w - ra�/2. Eso significa que podemos tomar una transformación monótona de la utilidad esperada y evaluar las distribuciones de la riqueza valiéndonos de la función de utilidad u(w, a�)= w - ;a�. Esta función de utilidad tiene la útil propiedad de que es lineal en la media y la varianza de la riqueza. 11.8 La utilidad que depende del estado de la naturaleza En nuestro análisis inicial de la elección en condiciones de incertidumbre, los premios eran simplemente cestas abstractas de bienes. Posteriormente nos especializamos en las loterías que sólo tenían resultados monetarios. Sin embargo, este supuesto no es tan inocuo como parece, pues, al fin y al cabo, el valor de una peseta depende de los precios vigentes; una descripción completa del resultado de un juego cuyos resultados se expresan en términos monetarios debe comprender no sólo la cantidad de dinero disponible en cada resultado sino también los precios vigentes en cada uno. En términos más generales, la utilidad de un bien suele depender de las circunstancias o del estado de la naturaleza en el que puede disponerse de él. Un paraguas puede parecer muy distinto a un consumidor cuando está lloviendo que cuando no lo está. Estos ejemplos muestran que en algunos problemas de elección es importante distinguir los bienes por el estado de la naturaleza en que puede disponerse de ellos. Supongamos, por ejemplo, que hay dos estados de la naturaleza, calor y frío, que representamos mediante los subíndices e y f. Sea x¿ la cantidad de helado que se vende cuando hace calor y x ¡ la que se vende cuando hace frío. En ese caso, si la probabilidad de que haga calor es p, podemos formular una determinada lotería de la manera siguiente: pu(h, xc) + (1 - p)u(c, x ¡ ). En este caso, la cesta de bienes que se obtiene en un estado está formada por "calor y x¿ unidades de helado" y "frío y x ¡ unidades de helado" en el otro estado. 224 / LA INCERTIDUMBRE (C. 11) Un ejemplo más serio es el del seguro médico. El valor de cien pesetas puede muy bien depender de la riqueza: ¿cuánto valdrían para una persona cien millones de pesetas si estuviera en coma? En este caso, podríamos muy bien expresar la función de utilidad de la manera siguiente: u(h, m8), dondes es un indicador de la salud y m es una determinada cantidad de dinero. Éstos son ejemplos todos ellos de funciones de utilidad que dependen del estado de la naturaleza, lo cual significa simplemente que las preferencias por los distintos bienes considerados dependen del estado de la naturaleza en que puedan conseguirse. 11.9 La teoría de las probabilidades subjetivas En el análisis de la teoría de la utilidad esperada hemos sido bastante vagos respecto a la naturaleza exacta de las "probabilidades" que entran en la función de utilidad esperada. La interpretación más sencilla es que se trata de probabilidades "objetivas", como sucede en el caso de las probabilidades calculadas a partir de algunas frecuencias observadas. Desgraciadamente, en los problemas de elección más interesantes las probabilidades son subjetivas: se trata de las percepciones de un determinado agente de la probabilidad de que ocurra un acontecimiento. En el caso de la teoría de la utilidad esperada, nos hemos preguntado qué axiomas sobre la conducta de elección de una persona implicarían la existencia de una función de utilidad esperada que representara esa conducta. Del mismo modo, podemos preguntamos qué axiomas sobre la conducta de elección de una persona pueden utilizarse para deducir la existencia de probabilidades subjetivas, es decir, la conducta de elección de una persona puede concebirse como si estuviera evaluando los juegos de acuerdo con su utilidad esperada con respecto a algunas medidas de las probabilidades subjetivas. Da la casualidad de que estos conjuntos de axiomas existen y de que son razonablemente plausibles. Las probabilidades subjetivas pueden construirse de la misma manera que la función de utilidad esperada. Recuérdese que hemos definido la utilidad de un juego x como el número u(x) tal que x ""' u(x) o b EB (1 - u(x)) o w. Supongamos que estamos tratando de conocer la probabilidad subjetiva para un individuo de que llueva en una determinada fecha. En ese caso, podemos preguntarnos con qué probabilidad p será indiferente el individuo entre el juego po bEB (1- p) o w y el juego "recibir b si llueve y w en caso contrario". En términos más formales, sea E un acontecimiento y p(E) la probabilidad (subjetiva) de que ocurra. Definimos la probabilidad subjetiva de que ocurra E por medio del número p(E) que satisface la condición siguiente: La teoría de las probabilidades subjetivas / 225 p(E) o b EB (1 � p(E)) o w rv recibir b si ocurre E y w en caso contrario. Puede demostrarse que partiendo de determinados supuestos sobre la regularidad, las probabilidades definidas de esta forma tienen todas las propiedades de las probabilidades objetivas ordinarias. En concreto, cumplen las reglas habituales necesarias para la manipulación de las probabilidades condicionadas, lo cual tiene algunas útiles implicaciones para la conducta económica. Examinemos brevemente una de esas implicaciones. Supongamos que p(H) es la probabilidad subjetiva para una persona de que sea cierta una determinada hipótesis, de que E es un acontecimiento que se ofrece como prueba de que H es cierto. ¿ Cómo debería ajustar un agente económico racional su creencia sobre las probabilidades de que ocurra H a la luz de la evidencia E? Es decir, ¿cuál es la probabilidad de que sea cierto H, condicionada a la observación de la evidencia E? La probabilidad conjunta de observar que E y H son ciertos puede expresarse de la siguiente manera: p(H, E)= p(HIE)p(E) = p(EIH)p(H). Reordenando los términos de esta ecuación, tenemos que P (HIE) = p(EIH)p(H) . p(E) Ésta es una forma de la ley de Bayes que relaciona la probabilidad anterior, p(H), es decir, la probabilidad de que la hipótesis sea cierta antes de observar la evidencia, con la probabilidad posterior, es decir, con la probabilidad de que la hipótesis sea cierta después de observar la evidencia. La ley de Bayes se deduce directamente de la mera manipulación de la probabilidad condicionada. Si la conducta de una persona satisface suficientes restricciones para garantizar la existencia de probabilidades subjetivas, esas probabilidades deben satisfacer la ley de Bayes. Esta ley es importante porque muestra cómo debería actualizar una persona racional sus probabilidades a la luz de la evidencia y, por lo tanto, sirve de base a la mayoría de los modelos de la conducta racional de aprendizaje. Por consiguiente, tanto la función de utilidad como las probabilidades subjetivas pueden construirse a partir de la conducta de elección observada, en la medida en que esta última cumpla determinados axiomas intuitivamente plausibles. Sin embargo, debe hacerse hincapié en que aunque los axiomas son intuitivamente plausibles, eso no quiere decir que sean descripciones precisas del comportamiento real de las personas. Esa determinación debe basarse en datos empíricos. 226 / LA INCERTIDUMBRE (C. 11) Ejemplo: La paradoja de Allais y la paradoja de Ellsberg La teoría de la utilidad esperada y la teoría de las probabilidades subjetivas se basan en el supuesto de que la conducta es racional. Los axiomas subyacentes a la teoría de la utilidad esperada parecen plausibles, así como la construcción que hemos utilizado en el caso de las probabilidades subjetivas. Desgraciadamente, la conducta real de los individuos parece que viola sistemáticamente algunos de estos axiomas. He aquí dos famosos ejemplos. La paradoja de Allais Suponga el lector que se le pide que elija entre los dos juegos siguientes: Juego A. Una probabilidad de un 100% de recibir 1 millón. Juego B. Una probabilidad de un 10% de recibir 5 millones, una probabilidad de un 89% de recibir 1 millón y una probabilidad de un 1 % de no recibir nada. Antes de seguir adelante elija uno de estos juegos y anótelo. A continuación examine los dos juegos siguientes. Juego C. Una probabilidad de un 11 % de recibir 1 millón y una probabilidad de un 89% de no recibir nada. Juego D. Una probabilidad de un 10% de recibir 5 millones y una probabilidad de un 90% de no recibir nada. Elija de nuevo el juego que prefiera y anótelo. Muchas personas prefieren A a By Da C. Sin embargo, estas elecciones violan los axiomas de la utilidad esperada. Para verlo, basta formular la relación de utilidad esperada que implica A t B: u(l) > O, 1 u(S) + O, 89u(l) + O, 1 u(O). Reordenando esta expresión, tenemos que O, llu(l) > O, lu(S) + O, lu(O), y añadiendo O, 89u(O) a cada uno de los miembros, tenemos que O, llu(l) + O, 89u(O) > O, lu(S) + O, 90u(O). La teoría de las probabilidades subjetivas / 227 Por lo tanto, un maximizador de la utilidad esperada debe preferir el juego C al D. La paradoja de Ellsberg La paradoja de Ellsberg se refiere a la teoría de las probabilidades subjetivas. Suponga el lector que se le dice que una urna contiene 300 bolas. Cien son rojas y doscientas son azules o verdes. Juego A. Se reciben 1.000 pesetas si la bola es roja. Juego B. Se reciben 1.000 pesetas si la bola es azul. Anote el juego que prefiere y examine a continuación los dos juegos siguientes: Juego C. Se reciben 1.000 pesetas si la bola no es roja. Juego D. Se reciben 1.000 pesetas si la bola no es azul. Normalmente la gente prefiere estrictamente A a By Ca D. Pero estas preferencias violan la teoría convencional de las probabilidades subjetivas. Para ver por qué, supongamos que Res el acontecimiento en el que la bola es roja y ,Res el acontecimiento en el que no es roja y definamos B y ,B de la misma manera. De acuerdo con las reglas ordinarias de la probabilidad, p(R) = 1 - p( ,R) p(B) = 1 - p(,B). (11.12) Normalicemos y supongamos que u(O) = O para facilitar la exposición. En ese caso, si se prefiere A a B, debe cumplirse la siguiente condición: p(R)u(lOOO) > p(B)u(lOOO), de donde se deduce que p(R) > p(B). (11.13) Si se prefiere Ca D, debe cumplirse la condición: p(,R)u(lOOO) = p(,B)u(lOOO), de donde se deduce que p( ,R) > p( ,B) (11.14) Sin embargo, es evidente que las expresiones (11.12), (11.13) y (11.14) son incompatibles. La paradoja de Ellsberg parece que se debe al hecho de que la gente piensa que es "más seguro" apostar por o en contra de R que apostar por o en contra de "azul". 228 / LA INCERTIDUMBRE (C. 11) Existen discrepancias sobre la importancia de las paradojas de Allais y Ellsberg. Unos economistas piensan que estas anomalías exigen la elaboración de nuevos modelos que describan la conducta de los individuos. Otros piensan que estas paradojas parecen "ilusiones ópticas". Aun cuando juzguemos mal las distancias en algunas circunstancias, eso no significa que tengamos que inventar un nuevo concepto de distancia. Notas La función de la utilidad esperada se debe a Neumann y Morgenstern (1944). Nuestro análisis se basa en el de Herstein y Milnor (1953). Las medidas de la aversión al riesgo se deben a Arrow (1970) y Pratt (1965). Nuestro análisis se basa en el de Yaari (1969). Para una descripción de los trabajos recientes sobre las generalizaciones de la teoría de la utilidad esperada véase Machina (1982). Nuestro breve análisis de la probabilidad subjetiva se basa en Anscombe y Aumann (1963). Ejercicios 11.1. Demuestre que la disposición a pagar por evitar un pequeño juego cuya varianza es v es aproximadamente r( w )v /2. 11.2. ¿Qué forma tiene la función de utilidad esperada si la aversión al riesgo es constante? ¿ Y si lo es la aversión relativa al riesgo? 11.3. ¿Qué forma tiene la función de utilidad esperada para que la inversión en un activo incierto sea independiente de la riqueza? 11.4. Considere el caso de una función de utilidad esperada cuadrática. Demuestre que en un determinado nivel de riqueza la utilidad marginal es decreciente. Demuestre, lo que es más importante, que la aversión absoluta al riesgo es creciente en todos los niveles de riqueza. 11.5. Supongamos que tiramos una moneda al aire y que hay una probabilidad p de que salga cara. Se nos invita a participar en una apuesta en la que recibiremos 2001 pesetas si sale cara por primera vez en la j-ésima ocasión que se tira al aire. (a) ¿ Cuál es el valor esperado de esta apuesta cuando p = 1 /2? (b) Suponga que su función de utilidad esperada es u(x) utilidad que tiene para usted este juego en forma de suma. = lnx. Exprese la Ejercicios / 229 (c) Evalúe la suma (para ello necesita conocer algunas fórmulas de manipulación de sumatorios). (d) ¿Cuál es la cantidad máxima de dinero que estaría dispuesto a pagar por participar en este juego? 11.6 Esperanza es una maximizadora de la utilidad esperada desde que tenía cinco años. Como consecuencia de la estricta educación que recibió en un oscuro internado británico, su función de utilidad u es estrictamente creciente y estrictamente cóncava. Ahora, cuando tiene algo más de treinta años, está evaluando un activo que tiene un resultado estocástico R que sigue una distribución normal con una media µ y una varianza cr2. Por lo tanto, su función de densidad viene dada por f(r) 1 crv'2:ii { 1 (-) r-µ 2 o = -exp -- 2} . (a) Demuestre que la utilidad que espera obtener de R Esperanza es una función deµ y cr2 solamente. Demuestre, pues, que E[u(R)] = cp(µ, cr2). (b) Demuestre que e/>(·) es creciente enµ. (c) Demuestre que cp( ·) es decreciente en cr2. 11.7. Sean R1 y R2 los rendimientos aleatorios de dos activos. Suponga que están distribuidos de manera independiente e idéntica. Demuestre que un maximizador de la utilidad esperada dividirá su riqueza entre los dos activos siempre que sea contrario a correr riesgos y la invertirá toda en uno de ellos si es amante del riesgo. 11.8. Suponga que un consumidor se enfrenta a dos riesgos y sólo es posible eliminar uno de ellos. Sea w = w1 con una probabilidad p y w = w2 con una probabilidad 1 - p. Sea E= O si w = w2. Si ib = w1, E= E con una probabilidad de 1/2 y E= -E con una probabilidad de 1/2. Definamos ahora una prima por el riesgo 7íu correspondiente a ? tal que satisfaga la siguiente condición: E[u(w - 1ru)l = E[u(w + E)] (a) Demuestre que si E es suficientemente pequeña, (*) 230 / LA INCERTIDUMBRE (C. 11) [Pista: Tome expansiones de Taylor de los órdenes adecuados en ambos miembros de (*): de primer orden en el primero y de segundo orden en el segundo.] (b) Sea u(w) yv. = -e-aw y v(w) = -e-bw_ Calcule la medida de Arrow-Pratt de u (c) Suponga que a > b. Demuestre que si p < 1, existe un valor de w1 - w2 suficientemente grande para que 1r v > 1r u. ¿ Qué sugiere esto sobre la utilidad de la medida de Arrow-Pratt en el caso de los problemas en los que el riesgo sólo se reduce parcialmente? 11.9. Una persona tiene una función de utilidad esperada de la forma u(w) = y'w. Inicialmente posee una riqueza de 400 pesetas. Tiene un billete de lotería que valdrá 1.200 pesetas con una probabilidad de 1/2 y nada con una probabilidad de 1/2. ¿Cuái es su utilidad esperada? ¿Cuál es el precio más bajo pal que se desprendería del billete? 11.10. Un consumidor tiene una función de utilidad esperada que viene dada por u(w) = lnw. Se le brinda la oportunidad de apostar en un juego en el que se tira una moneda al aire y hay una probabilidad 1r de que salga cara. Si apuesta x pesetas, tendrá w + x si sale cara y w - x si sale cruz. Halle el valor óptimo de x en función de tt . ¿Cuál es la elección optima de x cuando 1r = 1/2? 11.11. Un consumidor tiene una función de utilidad esperada de la forma u( w) = -1 / w. Se le ofrece la posibilidad de participar en un juego en el que recibirá una riqueza de w1 con una probabilidad p y w2 con una probabilidad 1 - p. ¿Cuánta riqueza necesitaría ahora para mostrarse indiferente entre quedarse con su riqueza actual y aceptar este juego? 11.12. Considere el caso de una persona a la que le preocupan los resultados monetarios en los estados de la naturaleza s = 1, ... , S que pueden ocurrir en el siguiente periodo. Represente el rendimiento monetario correspondiente al estado s por medio de X8 y la probabilidad de que ocurra ese estado por medio de p8• Se supone que el in dividuo elige x = (x1 , ... , x s) con el fin de maximizar el valor esperado descontado del rendimiento. El factor de descuento se representa por medio de a; es decir, a= 1/(1 + r), donde res la tasa de descuento. El conjunto de rendimientos se representa por medio de X, que suponemos que es un conjunto no vacío. Ejercicios / 231 (a) Formule el problema de maximización del individuo. (b) Suponga que v(p, a) es el valor esperado descontado máximo que puede lograr el individuo si las probabilidades son p = (p1, ... , ps) y el factor de descuento es a. Demuestre que v(p, a) es homogénea de grado 1 en a (pista: ¿se parece v(p, a) a algo que haya visto antes?) (c) Demuestre que v(p, a) es una función convexa de p. (d) Suponga que puede observar un número arbitrariamente elevado de elecciones óptimas de x correspondientes a diferentes valores de p y a. ¿Qué propiedades debe tener el conjunto X para que sea recuperable a partir de la conducta de elección observada? 12. ECONOMETRÍA En los capítulos anteriores hemos examinado varios modelos de la conducta optimizadora. En éste vemos cómo pueden utilizarse las ideas teóricas desarrolladas en esos capítulos para estimar las relaciones que pueden haber sido generadas por la conducta optimizadora. La interrelación del análisis teórico y el econométrico puede adoptar distintas formas. En primer lugar, la teoría puede utilizarse para deducir hipótesis que pueden verificarse econométricamente. En segundo lugar, la teoría puede sugerir la mejor manera de estimar los parámetros de los modelos. En tercer lugar, la teoría ayuda a especificar las relaciones estructurales del modelo de una manera que puede permitir obtener mejores estimaciones. Por último, la teoría contribuye a especificar las formas funcionales adecuadas que deben estimarse. 12.1 La hipótesis de la optimización Hemos visto que el modelo de la elección optimizadora impone algunas restricciones a la conducta observable. Estas restricciones pueden expresarse de muchas maneras: 1) las relaciones algebraicas como el ADMB, el ADMC, el AGPR, etc.; 2) las relaciones basadas en el cálculo diferencial, como las condiciones según las cuales determinadas matrices de sustitución deben ser simétricas y positivas o semidefinidas negativas; 3) las relaciones duales como el hecho de que los beneficios deben ser una función convexa de los precios. Las condiciones que implican los modelos de maximización son importantes, al menos, por dos razones. En primer lugar, nos permiten contrastar el modelo de la conducta maximizadora. Si los datos no satisfacen las restricciones que implica el modelo de optimización que estemos utilizando, generalmente no querremos utilizar ese modelo para describir la conducta observada. En segundo lugar, las condiciones nos permiten estimar con mayor precisión los parámetros de nuestro modelo. Si observamos que las restricciones teóricas 234 / ECONOMETRÍA (C. 12) impuestas por la optimización no son rechazadas por un determinado conjunto de datos, es posible que queramos volver a estimar nuestro modelo de tal manera que las estimaciones deban satisfacer las restricciones que implica la optimización. Supongamos, por ejemplo, que tenemos un modelo de optimización que implica que el parámetro a es igual a cero. En primer lugar, es posible que nos interese contrastar esta restricción y ver si el valor estimado de a es significativamente diferente de cero. Si no lo es, es posible que queramos aceptar la hipótesis de que a = O y estimar de nuevo el modelo imponiendo esta hipótesis. Si la hipótesis es verdadera, el segundo conjunto de estimaciones de los demás parámetros del sistema será, por lo general, más eficiente. Naturalmente, si la hipótesis es falsa, no será adecuado volver a estimar el modelo. Nuestra fe en las estimaciones resultantes depende hasta cierto punto de la fe que tengamos en los resultados de la contrastación inicial de las restricciones impuestas por la optimización. 12.2 Contrastación no paramétrica de la conducta maximizadora Si se nos da un conjunto de observaciones sobre las elecciones de una empresa, podemos contrastar directamente las desigualdades correspondientes al ADMB y/ o al ADMC descritas antes. Si disponemos de datos sobre las elecciones de los consumidores, sólo resulta algo más difícil contrastar las condiciones como el AGPR. Estas condiciones nos dan una respuesta definitiva sobre la posibilidad de que los datos en cuestión hayan sido generados o no por la conducta maximizadora. Estas condiciones establecidas como desigualdades son fáciles de contrastar; basta averiguar si los datos en cuestión satisfacen determinadas desigualdades. Si observamos que se viola una de ellas, podemos rechazar el modelo de maximización. Supongamos, por ejemplo, que tenemos varias observaciones sobre la elección de las producciones netas por parte de una empresa correspondientes a varios vectores de precios: (p", yt), siendo t = 1, ... , T. Es posible que nos interese contrastar la hipótesis de que esta empresa está maximizando los beneficios en un entorno competitivo. Sabemos que la maximización del beneficio implica el ADMB: ptyt � ptys cualesquiera que sean s y t. Para contrastar el ADMB basta verificar que se satisfacen estas T2 desigualdades. En este marco· es suficiente una única observación en la que ptyt < ptys para rechazar el modelo de maximización del beneficio. Pero tal vez eso sea demasiado fuerte. Probablemente lo que nos interesa realmente no es saber si una determinada empresa está maximizando exactamente los beneficios sino saber si el modelo de maximización del beneficio describe razonablemente bien su conducta. Normalmente, queremos saber no sólo si la empresa no maximiza, sino también en qué medida no lo hace. Si no maximiza más que en algunas ocasiones, tal vez estemos dispues- Contrastación paramétrica de la conducta maximizadora / 235 tos, no obstante, a aceptar la teoría de que la empresa "casi" está maximizando los beneficios. Existe una medida muy natural de la magnitud de la violación del ADMB, a saber, los "residuos" R¿ = max8{ptys - ptyt}. El residuo R¿ mide la cantidad adicional de beneficios que podría haber obtenido la empresa en la observación t si hubiera tomado una decisión distinta. Permite medir de una manera razonable la desviación de la conducta maximizadora del beneficio. Si el valor medio de R¿ es bajo, la conducta "casi" optimizadora puede no ser un mal modelo de la conducta de esta empresa. 12.3 Contrastación paramétrica de la conducta maximizadora Las contrastaciones no paramétricas antes descritas son contrastaciones "exactas" de la optimización: son condiciones necesarias y suficientes para que los datos sean coherentes con el modelo de optimización. Sin embargo, a los economistas suele interesarles saber si una determinada forma paramétrica constituye una buena aproximación de alguna función de producción o función de utilidad subyacente. Para saberlo puede utilizarse el análisis de regresión o técnicas estadísticas más complejas con el fin de estimar los parámetros de una forma funcional y ver si se satisfacen las restricciones que impone el modelo de maximización. Supongamos, por ejemplo, que observamos los precios y las elecciones correspondientes a k bienes. La función de utilidad Cobb-Douglas implica que la demanda del bien i es una función lineal de la renta dividida por el precio: Xi = tumf p, siendo i = 1, ... , k. Es improbable que los datos observados sobre la demanda sean exactamente lineales en m/pi, por lo que es posible que queramos introducir un término de error para representar el error de medición, los errores de especificación, las variables excluidas, etc. Utilizando Ei como término de error en la ecuación iésima, tenemos el modelo de regresión m Xi = ai- Pi + Ei Í = 1, ... , k. (12.1) De acuerdo con el modelo de maximización, ¿�=l a; = l. Podemos estimar los parámetros del modelo descrito por la ecuación (12.1) y ver si satisfacen esta restricción. En caso afirmativo, existe alguna evidencia en favor del modelo CobbDouglas; en caso negativo, existe alguna evidencia en contra de la forma paramétrica Cobb-Douglas. Si utilizamos formas funcionales más complejas, obtenemos un conjunto más complejo de restricciones contrastables. Cuando estudiamos la conducta del consumidor, vimos que la restricción observable. fundamental que imponía la maximización era que la matriz de los términos de sustitución debía ser semidefinida 236 / ECONOMETRÍA (C. 12) negativa. Esta condición impone una serie de restricciones que afectan a las distintas ecuaciones y que pueden contrastarse siguiendo los procedimientos que se utilizan habitualmente para contrastar las hipótesis. 12.4 Imposición de restricciones a la optimización Si nuestros contrastes estadísticos no rechazan algunas restricciones paramétricas, es posible que queramos estimar de nuevo el modelo imponiendo estas restricciones al procedimiento de estimación. Continuando con el ejemplo anterior, el sistema de demanda Cobb-Douglas descrito en la ecuación (12.1) implica que E:=l a, = 1. Es posible que queramos estimar el conjunto de parámetros (ai) imponiendo esta restricción como una hipótesis de partida. Si la hipótesis es verdadera, las estimaciones resultantes generalmente serán mejores que las estimaciones no sujetas a restricciones. El modelo de optimización suele imponer restricciones al término de error, así como a los parámetros. Por ejemplo, el modelo teórico impone otra restricción: E:=l PiXi(P, m) = m. Generalmente, las elecciones observadas satisfarán la restricción E:=l PiXi = m por construcción. De ser así, las ecuaciones (12.1) implican que k k k i=l i=l i=l LPiXi = m = L a.m. + LPiEi· Si estimamos nuestro sistema sujeto a la restricción de que E:=l a; = 1, también querremos imponer la restricción E:=l p.e, = 1. Es decir, los términos de error k deben ser ortogonales al vector de precios. 12.5 Bondad del ajuste en el caso de los modelos de optimización Las contrastaciones paramétricas que hemos descrito brevemente en el apartado anterior indican cómo puede contrastarse estadísticamente la hipótesis de que las elecciones observadas fueron generadas por la maximización de alguna forma paramétrica. Se trata de ·contrastaciones nítidas, en el sentido de que o bien se rechaza la hipótesis de la maximización, o bien no se rechaza. Pero en muchos casos suele ser mejor disponer de una medida de la bondad del ajuste: ¿hasta qué punto se parecen las elecciones observadas a las elecciones maximizadoras? Para responder a esta pregunta, necesitamos contar con una definición razonable del significado de "parecido". En el análisis no paramétrico de la maximización del beneficio, hemos visto que una medida razonable era el volumen de beneficios Bondad del ajuste c11 el caso de los modelos de optimización / 237 adicionales que podría haber obtenido la empresa si se hubiera comportado de otra manera. Esta idea puede ampliarse con un carácter más general: una medida de la bondad del ajuste es el grado en que el agente económico no optimiza la función objetivo postulada. Esta medida puede calcularse directamente en el caso de la conducta de la empresa. Si nuestra hipótesis es la maximización del beneficio o la minimización del coste, calculamos simplemente los beneficios perdidos o el exceso de costes comparando el modelo de optimización que ha generado el mejor ajuste con las elecciones reales. La aplicación a la maximización de la utilidad es algo más sutil. Supongamos que estamos examinando la conducta de elección de un consumidor utilizando la forma funcional Cobb-Douglas. Por ejemplo, si los parámetros (a,i) describen la función de utilidad Cobb-Douglas que ha conseguido el mejor ajuste, podemos comparar la utilidad de las elecciones óptimas calculada utilizando la función de utilidad estimada y la utilidad correspondientes a las elecciones reales. El problema que plantea esta medida se halla en que las unidades de la función de utilidad son arbitrarias. No es tan evidente lo que quiere decir "parecido". Este problema se soluciona utilizando una determinada función de utilidad para calcular la medida de la bondad del ajuste. En este caso, lo natural es elegir la función de utilidad métrica monetaria descrita en el capítulo 7 (página 131). La función de utilidad métrica monetaria mide la utilidad en unidades monetarias: cuánto dinero necesitaría un consumidor dados los precios para disfrutar del mismo bienestar del que disfrutaría si consumiera la cesta x. Veamos cómo puede construirse una medida de la bondad del ajuste a partir del argumento anterior. Supongamos que observamos algunos datos (p", x") siendo t = 1, ... , T. Partimos de la hipótesis de que el consumidor está maximizando una función de utilidad 11,(x, (3), donde (3 es un parámetro (o lista de parámetros) desconocido. Dada u(x, (3), sabemos que podemos construir la función de utilidad métrica monetaria m(p, x, (3) utilizando las técnicas habituales de optimización. Utilizamos los datos sobre las elecciones para estimar la función de utilidad u(x, .8) que mejor describe la conducta de elección observada. Para ver la bondad del ajuste conseguido con esta función de utilidad, se calculan los T "residuos" et mide la cantidad mínima de dinero que necesita gastar el consumidor para obtener la utilidad u(xt, (3) en comparación con la cantidad de dinero que utiliza realmente. Este resultado tiene una interpretación natural basada en la eficiencia: si el valor medio de es G, podemos decir que en promedio el consumidor es eficiente en un 0% en su conducta de elección. et 238 / ECONOMETRÍA (C. 12) Si el consumidor está maximizando perfectamente la función de utilidad u(x, (3), G será igual a 1: el consumidor será eficiente en un 100% en su elección de consumo. Si Ges 0,95, el consumidor es eficiente en un 95%, etc. 12.6 Modelos estructurales y modelos en forma reducida Supongamos que tenemos una teoría que sugiere la existencia de algunas relaciones entre una serie de variables. Normalmente, habrá dos tipos de variables en nuestro modelo, variables endógenas, cuyos valores son determinados por nuestro modelo, y variables exógenas, cuyos valores están predeterminados. Por ejemplo, en nuestro modelo de la conducta maximizadora del beneficio, los precios y la tecnología son variables exógenas y las elecciones de los factores son variables endógenas. Normalmente, un modelo puede representarse por medio de un sistema de ecuaciones, cada una de las cuales implica la existencia de algunas relaciones entre las variables exógenas, las endógenas y los parámetros. Este sistema de ecuaciones se conoce con el nombre de modelo estructural. Consideremos, por ejemplo, un sencillo sistema de demanda y oferta: D = ao - a1p + a2z1 + EJ S = bo + b1p + b2z2 + E2 (12.2) D=S En este caso, D y S representan la demanda y la oferta (endógenas) de un bien, p es su precio (endógeno), (ai) y (bi) son parámetros y z1 y z2 son otras variables exógenas que afectan a la demanda y la oferta. Las variables q y E2 son términos de error. El sistema (12.2) es un sistema estructural. El sistema estructural podría resolverse de una manera que expresara la variable endógena p en función de las variables exógenas: ao - bo a2 b2 E2 - E1 p = --- + ---z1 - ---z2 + ---. a1 + b1 a1 + b1 a1 + b1 a1 + b1 (12.3) Ésta es la forma reducida del sistema. Normalmente no es demasiado difícil estimar la forma reducida de un modelo. En el ejemplo de la demanda y la oferta, bastaría estimar una regresión de la forma P = f3o + f3iz1 + f32z2 + E3. Los parámetros ((3i) son una función de los parámetros (ai, bi), pero generalmente no es posible recuperar estimaciones únicas de los parámetros estructurales (ai, bi) a partir de los parámetros de la forma reducida (f3i). Los parámetros de la forma reducida pueden utilizarse para predecir cómo variará el precio de equilibrio cuando varíen las variables exógenas. Esto puede ser útil en algunos casos. Modelos estructurales y modelos en forma reducida / 239 Pero en otros puede ser necesario disponer de estimaciones de los parámetros estructurales. Supongamos, por ejemplo, que quisiéramos predecir cómo respondería el precio de equilibrio en este mercado a la introducción de un impuesto sobre el bien. El modelo estructural (12.2) sugiere que el precio de equilibrio percibido por los oferentes, Ps, debería ser una función lineal del impuesto: (12.4) Si tuviéramos datos que describieran muchas elecciones diferentes de impuestos y los precios de oferta resultantes, podríamos estimar la forma reducida que describe la ecuación (12.4). Pero si no los tuviéramos, no sería posible estimar esta forma reducida. Para predecir cómo respondería el precio de equilibrio al impuesto, necesitaríamos conocer el parámetro estructural b1 / (a1 + b1 ). Los parámetros de la forma reducida de la ecuación (12.3) no suministran suficiente información para responder a esta pregunta. Eso sugiere que debemos buscar algún método para estimar los sistemas estructurales de ecuaciones como el (12.2). Parece que el más sencillo consiste simplemente en estimar por separado la ecuación de demanda y la ecuación de oferta utilizando las técnicas habituales de regresión por mínimos cuadrados ordinarios (MCO). ¿Qué probabilidades hay de obtener de esta manera estimaciones aceptables de los parámetros? Sabemos por la estadística que las estimaciones obtenidas por MCO tienen las propiedades deseables si se cumplen determinados supuestos. Uno de ellos es que las variables del segundo miembro de la regresión no estén correlacionadas con el término de error. Sin embargo, no ocurre así en nuestro problema. La variable p depende de los términos de error <i y E2, como puede verse fácilmente en la ecuación (12.3). Puede demostrarse que esta dependencia generalmente dará lugar a estimaciones sesgadas de los parámetros. Para estimar sistemas de ecuaciones estructurales, generalmente es necesario utilizar técnicas de estimación más complejas, como las de mínimos cuadrados bietápicos o algunas técnicas de maximización de la verosimilitud. Puede demostrarse que estos métodos tienen mejores propiedades estadísticas que los MCO en el caso de los problemas de estimación en los que hay sistemas de ecuaciones. En el sencillo ejemplo de oferta y demanda que acabamos de describir, la relación teórica entre las variables implica que unas técnicas de estimación son más adecuadas que otras. Eso es lo que suele ocurrir en general; el arte de la econometría reside en parte en utilizar la teoría como guía para elegir las técnicas estadísticas. En el siguiente apartado profundizamos en esta cuestión por medio de un ejemplo más completo. 240 / ECONOMETRÍA (C. 12) 12.7 Estimación de las relaciones tecnológicas Supongamos que querernos estimar los parámetros de una sencilla función de producción Cobb-Douglas. Supongamos, para ser más concretos, que tenernos una muestra de explotaciones agrarias y que partirnos del supuesto de que la producción de maíz de la explotación i, Mi, depende de la cantidad de maíz sembrado, Ki, y del número de días soleados que haya en la temporada en que está creciendo, Si. Supongamos de momento que éstas son las dos únicas variables que afectan a la producción de maíz. Supongamos también que la relación de producción viene dada por la función Cobb-Douglas Mi = Kf SJ-ª. Tornando logaritmos, podernos expresar la relación entre la producción y las cantidades de factores de la manera siguiente: log Mi = a log K, + (1 - a) log Si. (12.5) Supongamos que los agricultores no observan el número de días soleados cuando tornan su decisión de sembrar. Por otra parte, el econórnetra tampoco posee datos sobre el número de días soleados existentes en cada lugar. Por lo tanto, considera la expresión (12.5) corno un modelo de regresión de la forma (12.6) donde Ei es el "término de error" (1 - a) log Si. Según la teoría econornétrica, el método de los MCO permite obtener buenas estimaciones del parámetro a si log K¡ y Ei no están correlacionados. Si los agricultores no observan log Si = Ei cuando eligen Kit esa variable no puede influir en su decisión. Por lo tanto, en este caso se trata de un supuesto razonable y el método de los MCO es una buena técnica de estimación. Examinemos ahora un caso en el que el método de los MCO no es una buena técnica de estimación. Supongamos que la relación de producción también depende de la calidad de la tierra de cada explotación, de tal manera que Mi = QiKf sJ-a, o sea, logMi = logQi + alogKi + (1- a)logSi Suponernos, al igual que antes, que ni el econórnetra ni los agricultores observan Si. Sin embargo, ahora los agricultores observan Qi, pero no así el econórnetra. ¿Qué probabilidades hay de que la estimación de la regresión (12.6) nos proporcione buenas estimaciones de a? La respuesta es ninguna. Dado que cada agricultor observa Qit la elección de K, dependerá de Qi. Por lo tanto, K, estará correlacionado con el término de error, por lo que es probable que las estimaciones estén sesgadas. Estimación de las relaciones tecnológicas / 241 Si partimos del supuesto de la conducta maximizadora de los beneficios, podemos ser bastante explícitos sobre la manera en que utilizarán los agricultores la información sobre Ks. El problema de maximización del beneficio (a corto plazo) del agricultor i es donde p,¡ es el precio del producto y q,¡ es el precio de la simiente a los que se enfrenta el agricultor i-ésimo. Tomando la derivada con respecto a K, y despejando para obtener la función de demanda de los factores, tenemos que te, = [ aQi p q: l 12a Si. (12.7) Es evidente que el hecho de que el agricultor conozca Qi influye directamente en su decisión sobre la cantidad que va a sembrar y, por lo tanto, en la cantidad que va a producir. Consideremos el diagrama de puntos de log K, y log M, representado en la figura 12.1. También hemos trazado la función log Mi = a log K, + Q, donde Q es la calidad media. La ecuación (12.7) muestra claramente que los agricultores cuya tierra sea de mayor calidad querrán sembrar más maíz. Eso significa que si observamos una explotación agraria en la que hay una gran cantidad del factor Kit es probable que Qi también sea grande. Por lo tanto, la producción de esta explotación será mayor que la de otra cuya tierra sea de una calidad media, por lo que los puntos correspondientes a los datos de las explotaciones que tengan una cantidad mayor de K, estarán situados por encima de la verdadera relación correspondiente a las explotaciones cuya calidad sea media. Del mismo modo, las explotaciones que tengan una pequeña cantidad de K, probablemente serán explotaciones cuya calidad sea inferior a la media. Una línea de regresión ajustada a estos datos genera, pues, una estimación de a mayor que su verdadero valor. El problema subyacente se halla en que los valores elevados de los niveles de producción no se deben enteramente a que los valores de la cantidad de factores sean elevados. Hay una tercera variable omitida, la calidad de la tierra, que influye tanto en el nivel de producción como en la elección de la cantidad de factores. Este tipo de sesgos es, muy frecuente en los estudios econométricos: normalmente, algunas de las variables de regresión que influyen en alguna decisión son elegidas por los agentes económicos. Supongamos, por ejemplo, que queremos estimar el rendimiento de la educación. Generalmente, las personas que tienen una renta más alta tienen un nivel de estudios más elevado, pero el nivel de estudios no es una variable predeterminada: los individuos eligen el nivel de estudios que quieren tener. Si eligen diferentes niveles de estudios, probablemente serán diferentes 242 / ECONOMETRÍA (C. 12) en otros aspectos que no se observan. Pero estos aspectos también podrían influir fácilmente en su renta. Supongamos, por ejemplo, que las personas que tienen un coeficiente de inteligencia más alto percibieran unos salarios más altos, independientemente de su nivel de estudios. Sin embargo, las personas que tienen un coeficiente de inteligencia más alto también tienen mayor facilidad para adquirir un nivel de estudios más elevado, lo cual implica que las personas que poseen un nivel de estudios más elevado percibirán unos salarios más altos por dos razones: en primer lugar, porque tienen, en promedio, un coeficiente de inteligencia más alto y, en segundo lugar, porque poseen un nivel de estudios más elevado. Una mera regresión del salario en función del nivel de estudios sobreestimaría la influencia del nivel de estudios en la renta. Figura 12.1 me, In K; Diagrama de puntos. Esta figura muestra un diagrama de puntos de log K¡ y log Mi. Obsérvese que una explotación agraria en la que te, sea grande generalmente será una explotación cuya tierra será mejor que la media, por lo que su nivel de producción será mayor que el de la explotación cuya tierra sea de calidad media. Por lo tanto, esos puntos se encontrarán por encima de la relación de producción en el caso de las explotaciones agrarias cuya tierra sea de calidad media. También podríamos postular que los hijos de padres acomodados tienden a tener una renta más alta. Pero los padres acomodados pueden adquirir más educación y dar una mayor riqueza a sus hijos. De nuevo, las rentas más altas irán unidas a unos niveles de estudios más elevados, pero podría no existir un nexo causal directo entre las dos variables. Estimación de las demandas de factores / 243 El análisis de regresión sencillo es bueno para realizar experimentos controlados, pero no suele serlo para analizar las situaciones en las que las variables explicativas son elegidas por los agentes. En esos casos, es necesario contar con un modelo que exprese todas las elecciones relevantes en función de las variables verdaderamente exógenas. 12.8 Estimación de las demandas de factores En el caso de las relaciones de producción, puede resultar útil estimar indirectamente los parámetros. Consideremos, por ejemplo, la ecuación (12.7). Tomando logaritmos, podemos expresarla de la manera siguiente: logKi = 1 1 1 1 --loga + --logpi - --logqi + --logQi + logSi. 1-a 1-a 1-a 1-a Un buen modelo de regresión de esta ecuación es donde el término constante f3o es una función de a y los valores medios de log Qi y log Si. Obsérvese que esta especificación implica que f32 = -f31. ¿Es esta ecuación un candidato probable para realizar una estimación por medio de MCO? Si los mercados de productos y de factores a los que se enfrentan los agricultores son competitivos, la respuesta es afirmativa, pues en los mercados competitivos los precios no pueden ser controlados por los agricultores. Si los precios no están correlacionados con el término de error, el método de los MCO constituye una buena técnica de estimación. Por otra parte, el hecho de que según el modelo de optimización deba cumplirse (3 que 1 = -(32 permite contrastar la optimización de una función de producción CobbDouglas. Si observamos que (31 es significativamente diferente de -(32, podemos sentirnos inclinados a rechazar la optimización. En cambio, si no podemos rechazar la hipótesis de que (31 = -(32, podemos sentirnos inclinados a imponerla como una hipótesis de partida y estimar el modelo En este caso, la función de demanda es una ecuación estructural: expresa las elecciones en función de las variables exógenas. Las estimaciones de esta ecuación pueden utilizarse para deducir otras propiedades de la tecnología. 244 / ECONOMETRÍA (C. 12) 12.9 Tecnologías más complejas Consideremos el caso en el que tenemos una función de producción que relaciona el nivel de producción y varios factores. Examinemos para simplificar el análisis la función de producción Cobb-Douglas en la que hay dos factores: f(x1, x2) = Ax1x�. En el capítulo 4 (página 65) vimos que las funciones de demanda de factores tienen la forma siguiente: [::r· y.1, Estas funciones de demanda tienen una forma logarítmico-lineal, por lo que podemos formular el modelo de regresión log z¡ = !301 + f311 log(w2/w1) + f321Y + EJ log x2 = !302 + f312 log(wif w2) + f322y + Ez. En este caso, los parámetros de la tecnología son funciones de los coeficientes de regresión. Sin embargo, es importante observar que los mismos parámetros a y b entran en las definiciones de los coeficientes, lo que significa que los parámetros de las dos ecuaciones no son independientes, sino que están relacionados. Por ejemplo, es fácil ver que !301 = !302. El sistema de ecuaciones debe estimarse teniendo en cuenta las restricciones que afectan a varias ecuaciones. También podríamos combinar las dos ecuaciones para formar la función de costes c(w, y): Esta función también tiene una forma logarítmico-lineal: logc = log,o + ,1 logw1 + ,2w2 + 13Y· Las restricciones que afectan a las distintas funciones de demanda de factores pueden· introducirse en una única ecuación, la de la función de costes. Por otra parte, cuando estudiamos la función de costes vimos que debe ser una función creciente, homogénea y cóncava. Estas restricciones pueden contrastarse e imponerse, si procede. De hecho, la función de costes puede considerarse una forma reducida del sistema de demanda de factores. A diferencia del ejemplo de demanda y oferta que hemos estudiado antes, la función de costes contiene toda la información relevante Elección de la forma funcional/ 245 sobre el modelo estructural, pues, corno vimos cuando la estudiarnos, sus derivadas nos proporcionan las demandas condicionadas de factores, por lo que la estimación de los parámetros de la función de costes nos facilita automáticamente estimaciones de las funciones de demanda condicionada de factores. Sin embargo, debe hacerse hincapié en que eso sólo es cierto si se cumple la hipótesis de partida de la minimización de los costes. Si las empresas examinadas están minimizando, de hecho, los costes o maximizando los beneficios, podernos utilizar toda una variedad de técnicas indirectas para estimar los parámetros tecnológicos. Estas técnicas son, por lo general, preferibles a las técnicas directas, si es cierta la hipótesis de la optimización. 12.10 Elección de la forma funcional En todos los ejemplos anteriores hemos utilizado la forma funcional Cobb-Douglas, pero no en aras del realismo sino para simplificar el análisis. En general, conviene disponer de una forma pararnétrica más flexible para representar las disyuntivas tecnológicas. Es posible formular una forma funcional arbitraria corno función de producción, pero en ese caso hay que calcular las demandas de factores y/ o la función de costes que se deducen de ella. Resulta mucho más sencillo partir directamente de una forma pararnétrica de una función de costes; en ese caso, hallar las demandas de factores adecuadas es una mera cuestión de diferenciación. En el capítulo 6 vimos que toda función de los precios monótona, homogénea y cóncava es una función de costes de alguna tecnología regular. Por lo tanto, lo único que se necesita es hallar una forma funcional que tenga las propiedades que buscarnos. En general, lo mejor es elegir una forma pararnétrica tal que algunos valores de los parámetros satisfagan las restricciones impuestas por la optimización y otros no. En ese caso, es posible estimar los parámetros y contrastar la hipótesis de que los parámetros estimados satisfacen las restricciones relevantes impuestas por la teoría. A continuación describirnos algunos ejemplos. Ejemplo: La función de costes de Diewert La función de costes de Diewert adopta la forma siguiente: k c(w, y)= y k :I: I:)ijJWiWj. i=l j=l 246 / ECONOMETRÍA (C. 12) En el caso de esta forma funcional, es necesario que bij = forma también puede expresarse de la manera siguiente: bji· Obsérvese que esta Dado que la primera parte de esta expresión tiene la forma de una función de costes de Leontief, esta forma también se denomina función de costes de Leontief generalizada. Las demandas de factores tienen la forma y¿ k Xi(w, y)= bi1 j=l Jwdw1. Estas demandas son lineales en los parámetros bij. Si todos los bij � O y algún bij > O, es fácil verificar que esta forma satisface las condiciones necesarias para que sea una función de costes. Los parámetros bij pueden estar relacionados con las elasticidades de sustitución entre los distintos factores; cuanto mayor sea el término bij, mayor será la elasticidad de sustitución entre los factores i y j. La forma funcional no impone ninguna restricción a las diferentes elasticidades; la función de Diewert puede servir de aproximación local de segundo orden de una función de costes arbitraria. Ejemplo: La función de costes translogarítmica La función de costes translogarítmica adopta la forma siguiente: logc(w, y)= ao + ¿ a, log k io, i=l + 2¿¿ l k k i=l j=l En el caso de esta función, es necesario que k ¿bij j=l = O. bij log io, logw1 + logy. Estimación de las demandas de los consumidores / 247 Con estas restricciones, la función de costes translogarítmica es homogénea en los precios. Si o.; > O y bij = O, cualesquiera que sean i y j, la función de costes se convierte en una función Cobb-Douglas. Las demandas condicionadas de factores no son lineales en los parámetros, pero las participaciones de los factores si(w, y)= WiXi(w, y)/c(w, y) son lineales en los parámetros y vienen dadas por Z:: bijlnwi k si(w, y)= a; + j=l 12.11 Estimación de las demandas de los consumidores En nuestros ejemplos anteriores nos hemos fijado en la estimación de las relaciones de producción. Éstas tienen la útil característica de que la función objetivo-el beneficio o el coste- es observable. En el caso de la conducta de demanda del consumidor, la función objetivo no es directamente observable, lo cual complica algo más las cosas desde el punto de vista conceptual, pero no plantea tantas dificultades como cabría esperar. Supongamos que tenemos los datos (pt, x') siendo t = 1, ... , T y que queremos estimar una función de demanda paramétrica. Primero analizamos el caso en el que nos interesa la demanda de un único bien y a continuación el caso en el que hay muchos bienes. Funciones de demanda de un único bien Es importante comprender que incluso cuando sólo nos interesa la demanda de un único bien, hay dos bienes: el bien que nos interesa y "todos los demás". Generalmente plasmamos este hecho en el modelo concibiendo el problema de elección como una elección entre el bien en cuestión y el dinero que se gasta en todos los demás. Véase el análisis de la separabilidad hicksiana en el capítulo 9 (página 175). Supongamos que representamos la cantidad comprada del bien en cuestión medio del símbolo x y 'el dinero que se gasta en todos los demás por medio del por símbolo y. Si p es el precio del bien x y q es el precio del bien y, el problema de maximización de la utilidad se convierte en max u(x, y) x,y sujeta a px + qy = m. 248 / ECONOMETRÍA (C. 12) Representarnos la función de demanda por medio de x(p, q, m). Dado que ésta es homogénea de grado cero, podernos normalizar con respecto a q, por lo que la demanda se convierte en una función del precio relativo de x y de la renta real: x(p/ q, m/ q). En la práctica, p es el precio nominal del bien que nos interesa y q suele considerarse que es un índice de precios de consumo. La especificación de la demanda nos indica, pues, que la cantidad demandada que se observa es una función del "precio real", p / q, y de la "renta real", m / q. Una útil característica del problema de dos bienes es que casi todas las formas funcionales son coherentes con la rnaxirnización de la utilidad. En el capítulo 26 (página 567) veremos que las ecuaciones de integrabilidad correspondientes al caso en el que hay dos bienes pueden expresarse corno una única ecuación diferencial ordinaria. Por lo tanto, siempre habrá una función indirecta de utilidad que genere una única ecuación de demanda por medio de la ley de Roy. Esencialmente, la única condición que impone la rnaxirnización en el caso en el que hay dos bienes es que el efecto compensado con respecto al propio precio sea negativo. Eso significa que hay una gran libertad para escoger formas funcionales coherentes con la optimización. Tres formas frecuentes son 1. la demanda lineal: x = a + bp + cm 2. la demanda logarítmica: lnx = lna + blnp + clnm 3. la demanda sernilogarítrnica: lnx =a+ bp + cm Cada una de estas ecuaciones va unida a una función indirecta de utilidad. En el capítulo 26 (página 567) deducirnos las funciones indirectas de utilidad correspondientes a la demanda logarítmica y el caso lineal y el sernilogarítrnico se plantean corno ejercicios. La estimación de los parámetros de las funciones de demanda nos facilita automáticamente estimaciones de los parámetros de la función indirecta de utilidad. Una vez que tenernos esta función, podernos utilizarla para realizar toda una variedad de predicciones. Por ejemplo, podernos utilizar las estimaciones para calcular la variación compensatoria o equivalente correspondiente a alguna variación de los precios. Para más detalles véase el capítulo 10 (página 190). Ecuaciones múltiples Supongamos que desearnos estimar un sistema de demandas de más de dos bienes. En este caso, podríamos partir de una forma funcional de las ecuaciones de demanda y tratar de integrarlas para hallar una función de utilidad. Sin embargo, generalmente Estimación de las demandas de los consumidores / 249 es mucho más fácil especificar una forma funcional de la utilidad o de la utilidad indirecta y diferenciarla para hallar las funciones de demanda. Ejemplo: Sistema lineal de gasto Supongamos que la función de utilidad adopta la forma u(x) donde Xi > '°'fi· = k ¿ ailn(x,¿ - ')\), i=l El problema de maximización de la utilidad es k ¿ ailn(xi - '°'fi) ��x i=l ¿ k sujeta a p,¿Xi i=l = m. Si suponemos que Zi = Xi - '°'fi, vemos que podemos expresar el problema de maximización de la utilidad de la manera siguiente: k ��x ¿ailnzi i=l k sujeta a ¿PiZi i=l =m- k ¿Pi'°'fi· i=l Este problema es un problema de maximización Cobb-Douglas en Zi. Se observa, pues, fácilmente, que las funciones de demanda de Xi tienen la forma Ejemplo: Sistemas SCID El sistema casi ideal de demanda (SCID) tiene una función de gasto de la forma siguiente: e(p, u) = a(p) + b(p)u, donde i,¡ (12.8) 250 / ECONOMETRÍA (C. 12) a(p) = ao + ¿ a: log p, + i 1¿¿ i 1:J log p, logpm j Dado que e(p, u) debe ser homogénea en p, los parámetros deben satisfacer las condiciones siguientes: k Lªi i=1 k = 1 k k j=1 i=1 L 1:j = L 1:j = L 11i = o. i=1 Las funciones de demanda pueden deducirse diferenciando la ecuación (12.8). Sin embargo, suele ser más útil estimar las proporciones de gasto: Si = ¿ "'fiJ logpJ + e. log;, k ai + (12.9) j=1 donde P es un índice de precios que viene dado por log P y = ao + ¿ log p, + k i=1 "'lij 2 ¿ ¿ "'fiJ log p, logpJ, l k k i=1 j=1 = 21< "Yij* + "'lji*) . El sistema SCID es casi lineal; la única excepción la constituye el término que se refiere al índice de precios. En la práctica, los económetras suelen utilizar un índice de precios arbitrario para calcular los términos m / P y a continuación estiman el resto de los parámetros del sistema utilizando la ecuación (12.9). 12.12 Resumen Hemos visto que el análisis teórico de los modelos de optimización puede servir de orientación en las investigaciones econométricas de varias maneras. En primer lugar, puede ofrecer metodos para contrastar las teorías, bien en forma no paramétrica, bien en forma paramétrica. En segundo lugar, la teoría puede sugerir restricciones que pueden utilizarse para realizar estimaciones más eficientes. En tercer lugar, la Notas/ 251 teoría puede especificar las relaciones estructurales en los modelos y ayudar a elegir las técnicas de estimación. Por último, la teoría puede ayudar a elegir las formas funcionales. Notas Véase Deaton y Muelbauer (1980) para un análisis de la aplicación de la teoría del consumidor a la estimación de sistemas de demanda planteado como un libro de texto. Varian (1990) analiza con mayor detalle la bondad del ajuste y ofrece algunos ejemplos empíricos. 13. Los MERCADOS COMPETITIVOS Hasta ahora hemos estudiado la conducta maximizadora de los agentes económicos: las empresas y los consumidores. Hemos considerado que el entorno económico estaba dado y que el vector de precios de mercado lo resumía totalmente. En este capítulo iniciamos el estudio del modo en que éstos dependen de lo que hacen los agentes. Comenzamos con el modelo más sencillo: un mercado competitivo. 13.1 La empresa competitiva Una empresa competitiva es aquella que considera dado el precio de mercado del producto y fuera de su control. En un mercado competitivo, cada una de las empresas considera que el precio es independiente de sus propios actos, si bien son los actos de todas las empresas considerados en conjunto los que determinan el precio de mercado. Sea p el precio de mercado. En ese caso, la curva de demanda de una empresa competitiva ideal adopta la forma siguiente: D(p) = {O c00ualquier cantidad sip >p sip < p. si p = p Una empresa competitiva puede fijar el precio que desee y producir la cantidad que sea capaz de producir. Sin embargo, si se encuentra en un mercado competitivo y fija un precio superior al vigente en el mercado, nadie comprará su producto. Si fija un precio inferior, tendrá tantos clientes como desee; pero ni que decir tiene que perderá beneficios, ya que también puede conseguir todos los clientes que desee fijando el precio de mercado. Este hecho se expresa a veces diciendo que una empresa competitiva tiene una curva de demanda infinitamente elástica. Si una empresa competitiva desea vender algo, debe venderlo al precio de mercado. Naturalmente, los mercados reales raras veces alcanzan este ideal. La 254 / Los MERCADOS COMPETITIVOS (C. 13) cuestión no estriba en saber si un determinado mercado es o no perfectamente competitivo, puesto que casi ninguno lo es, sino en saber en qué medida los modelos de competencia perfecta pueden aportar ideas sobre los mercados del mundo real. De la misma manera que los modelos sin fricciones de la física pueden describir algunos fenómenos importantes del mundo físico, así el modelo sin fricciones de la competencia perfecta aporta útiles ideas en el mundo económico. 13.2 El problema de maximización del beneficio Puesto que la empresa competitiva debe considerar dado el precio, su problema de rnaxirnización del beneficio es muy sencillo. Debe elegir el nivel de producción y para resolver el siguiente problema: maxypy - c(y). Las condiciones de primer y segundo orden para llegar a una solución interior son p = c'(y*) e" (y*) 2:: O. Normalmente suponernos que la condición de segundo orden se satisface corno una igualdad estricta. Este supuesto no es realmente necesario, pero simplifica algunos de los cálculos. Este caso se denomina caso regular. La función inversa de oferta, representada por medio de p(y), mide el precio que debe regir para que a una empresa le resulte rentable ofrecer una cantidad dada de producción. De acuerdo con la condición de primer orden, la función inversa de demanda viene dada por p(y) = e' (y), en la medida en que e" (y) > O. La función de oferta indica el nivel de producción rnaxirnizador del beneficio correspondiente a cada uno de los precios. Por lo tanto, la función de oferta, y(p), debe cumplir en forma de identidad la condición de primer orden p = e' (y(p)), y la condición de segundo orden e" (y(p)) 2:: O. (13.1) El problema de maximiz.ación del beneficio / 255 Figura 13.1 COSTE/ NIVEL DE PRODUCCION NIVEL DE PROOUCCION La función de oferta y las curvas de costes. En los casos regulares, la función de oferta de una empresa competitiva es la parte ascendente de la curva de coste marginal que se encuentra por encima de la curva de coste variable medio. La curva directa de oferta y la curva inversa de oferta miden la misma relación, a saber, la relación entre el precio y la oferta de producción maximizadora del beneficio. Las dos funciones describen simplemente la relación de diferentes maneras. ¿ Cómo responde la oferta de una empresa competitiva a una variación del precio del producto? Diferenciando la expresión (13.1) con respecto a p, tenemos que 1 = c"(y(p))y'(p). Dado que normalmente c"(y) > O, se deduce que y'(p) > O. Por lo tanto, la curva de oferta de una empresa competitiva tiene pendiente positiva, al menos en el caso regular. En el capítulo 2 llegamos a este mismo resultado por medio de métodos diferentes. Nos hemos fijado en la solución interior del problema de maximización del beneficio, pero es interesante preguntarse qué condiciones deben cumplirse para que se elija esta solución. Expresemos la función de costes de la forma siguiente, c(y) = Cv (y) + F, de tal manera que los costes totales se expresen como la suma de los costes variables y los costes fijos. Consideramos que los costes fijos son verdaderamente fijos, es decir, deben pagarse incluso aunque el nivel de producción sea nulo. En este caso, a la empresa le resultará rentable producir una cantidad positiva cuando los beneficios obtenidos de esa forma sean superiores a los beneficios (las pérdidas) de no producir nada: py(p) - Cv(y(p)) - F 2:: -F 256 / Los MERCADOS COMPETITIVOS (C. 13) Reordenando esta condición, observarnos que la empresa produce una cantidad positiva cuando > Cv(y(p)) p - y(p) ' es decir, cuando el precio es más elevado que el coste variable medio. Véase la figura 13.1 para una representación gráfica de este resultado. 13.3 La función de oferta de la industria La función de oferta de la industria es simplemente la suma de las funciones de oferta de cada empresa. Si Yi(p) es la función de oferta de la empresa i-ésirna de una industria formada por m empresas, la función de oferta de la industria viene dada por Y(p) = I: Yi(p). m i=i La función inversa de oferta de la industria es la inversa de esta función: indica el precio mínimo al que la industria está dispuesta a ofrecer una cantidad dada de producción. Dado que cada una de las empresas elige un nivel de producción en el que el precio es igual al coste marginal, cada una de las empresas que produce una cantidad positiva debe tener el mismo coste marginal. La función de oferta de la industria mide.la relación entre el nivel de producción de la industria y ese coste marginal común de producir esta cantidad. Ejemplo: Funciones de costes diferentes Consideremos el caso de una industria competitiva integrada por dos empresas; una de ellas tiene la función de costes c1 (y) = y2 y la otra tiene la función de costes c2 (y) = 2y2. Las funciones de oferta vienen dadas por Y1 Y2 = p/2 = p/4. Por lo tanto, la curva de oferta de la industria es Y(p) = 3p/4. Dado un nivel cualquiera de producción de la industria Y, el coste marginal de producción de cada empresa es 4Y/3. Equilibrio del mercado / 257 Ejemplo: Funciones de costes idénticas Supongamos que hay m empresas que tienen la misma función de costes: c(y) = y2+ 1. La función de coste marginal es simplemente CM(y) = 2y y la función de coste variable medio CV M e(y) = y. Dado que en este ejemplo los costes marginales siempre son mayores que los costes variables medios, la función inversa de oferta de la empresa viene dada por p = CM(y) = 2y. Por lo tanto, la función de oferta de la empresa es y(p) = p/2 y la función de oferta de la industria Y(p, m) = mp/2. La función inversa de oferta de la industria es, pues, p = 2Y/ m. Obsérvese que la pendiente de la función inversa de oferta es menor cuanto mayor sea el número de empresas. 13.4 Equilibrio del mercado La función de oferta de la industria mide la producción total ofrecida a los distintos precios. La función de demanda de la industria mide la produccion total demandada a los distintos precios. Un precio de equilibrio es aquel al que la cantidad demandada es igual a la ofrecida. ¿Por qué merece este precio el nombre de precio de equilibrio? Normalmente se dice que a un precio al que la demanda no es igual a la oferta algún agente económico observará que le interesa modificar unilateralmente su conducta. Consideremos, por ejemplo, un precio al que la cantidad ofrecida sea superior a la demandada. En este caso, algunas empresas no podrán vender todo lo que producen. Reduciendo la producción, pueden ahorrar costes de producción y no perder ingreso alguno, obteniendo así más beneficios. Por lo tanto, un precio de ese tipo no puede ser un precio de equilibrio. Si suponemos que Xi(p) es la función de demanda del individuo i siendo i = 1, ... , n y que y/p) es la función de oferta de la empresa j siendo j = 1, ... , m, un precio de equilibrio es simplemente una solución de la ecuación L Xi(p) = L Yj(p). n m i=1 j=1 Ejemplo: Empresas idénticas Supongamos que la curva de demanda de la industria es lineal, X(p) = a - bp y que su curva de oferta es la que obtuvimos en el ejemplo anterior, Y(p, m) = mp/2. El precio de equilibrio es la solución de a - bp = mp/2, 258 / LOS MERCADOS COMPETITIVOS (C. 13) lo que implica que * a P = b+m/2. Obsérvese que en este ejemplo el precio de equilibrio disminuye conforme aumenta el número de empresas. En el caso de una curva de demanda de la industria expresada en términos generales, el equilibrio viene determinado por X(p) = my(p) ¿ Cómo varía el precio de equilibrio cuando varía m? Considerando que p es una función implícita de m y diferenciando, tenemos que X'(p)p'(m) = my'(p)p'(m) + y(p), lo que implica que ' y(p) p (m) = X'(p) - my'(p) Suponiendo que la demanda de la industria tiene pendiente negativa, el precio de equilibrio debe bajar conforme aumenta el número de empresas. 13.5 La entrada En el apartado anterior hemos visto cómo se calcula la curva de oferta de la industria cuando hay un número de empresas determinado exógenamente. Sin embargo, a largo plazo el número de empresas de una industria es variable. Si una empresa espera obtener un beneficio produciendo un determinado bien, es de esperar que decida producirlo. Del mismo modo, si una empresa ya existente en una industria observa que está perdiendo persistentemente dinero, es de esperar que la abandone. Existen varios modelos posibles de entrada y salida, dependiendo del tipo de supuestos que se formulen sobre los costes de entrada y salida, de la capacidad de percepción del futuro de las empresas que pudieran plantearse la posibilidad de entrar, etc. En este apartado, describiremos un modelo especialmente sencillo en el que los costes de entrada y salida son nulos y la capacidad de percepción del futuro es absoluta. Supongamos que tenemos un número arbitrariamente grande de empresas cuyas funciones idénticas de costes son c(y ). Podemos calcular el precio de nivelación p* al que los beneficios correspondientes a la oferta óptima de producción son nulos. La entrada / 259 Éste no es sino el nivel de producción en el que el coste medio es igual al coste marginal. Corno se muestra en la figura 13.2, ahora podernos representar las curvas de oferta de la industria en el caso en hay 1, 2, ... empresas en ella y buscar el número más elevado de empresas tal que todas ellas obtengan unos beneficios nulos (es decir, alcancen el punto de nivelación). Si el número de empresas de equilibrio es grande, la función de oferta relevante será muy plana y el precio de equilibrio cercano a »'. Por lo tanto, a menudo se supone que la curva de oferta de una industria competitiva en la que hay libertad de entrada es esencialmente una línea recta horizontal a la altura en la que el precio es igual al coste medio mínimo. Figura 13.2 NIVEL DE PRODUCCION Número de empresas de equilibrio. En nuestro modelo de entrada, el número de empresas de equilibrio es el mayor número de empresas tal que todas ellas tienen unos beneficios nulos (es decir, alcanzan el punto de nivelación). Si es razonablemente elevado, el precio de equilibrio deberá ser cercano al coste medio mínimo. En este modelo de entrada, el precio de equilibrio puede ser más alto que el precio de nivelación. Aun cuando las empresas de la industria estén obteniendo beneficios positivos, no en�ran otras nuevas, ya que éstas prevén correctamente que si entraran, obtendrían unos beneficios negativos. Corno siempre, los beneficios positivos pueden concebirse corno una renta económica. En este caso, pueden concebirse corno la "renta de ser el primero". Es decir, los inversores estarían dispuestos a pagar hasta el valor actual de la corriente de beneficios que obtiene una de las empresas ya existentes con el fin de adquirir esa corriente de beneficios. Cabe considerar que esta renta es el coste (de oportunidad) 260 / LOS MERCADOS COMPETITIVOS (C. 13) de permanecer en la industria. Si se adopta esta convención contable, las empresas obtienen unos beneficios nulos en condiciones de equilibrio. Ejemplo: La entrada y el equilibrio a largo plazo Si c(y) = y2 + 1, el nivel de producción correspondiente al punto de nivelación se halla igualando el coste medio y el coste marginal: y+ 1/y = 2y, lo que implica que y = 1. En este nivel de producción, el coste marginal es 2, por lo que éste es el precio de nivelación. De acuerdo con nuestro modelo de entrada, entrarán empresas en la industria mientras calculen que entrando no bajará el precio de equilibrio por debajo de 2. Supongamos que la demanda es lineal, al igual que en el ejemplo anterior. En ese caso, el precio de equilibrio será el p* más bajo que satisfaga las siguientes condiciones: p * p* = a b+m/2 2:: 2. A medida que aumenta m, el precio de equilibrio debe aproximarse cada vez más a 2. 13.6 Economía del bienestar Hemos visto cómo se calcula el equilibrio competitivo: el precio al que la oferta es igual a la demanda. En este apartado analizaremos las propiedades de este equilibrio desde el punto de vista del bienestar. Esta cuestión puede enfocarse de varias maneras; el enfoque que adoptamos aquí, el del consumidor representativo, es probablemente el más sencillo. Más adelante, cuando analicemos la teoría del equilibrio general, .describiremos un enfoque diferente y más general. Supongamos que la curva de demanda de mercado, x(p), se genera maximizando la utilidad de un único consumidor representativo que tiene una función de utilidad de la forma u(x) + y. El bien x es el bien que estamos examinando en este mercado específico. El bien y recoge de manera aproximada "todo lo demás". La manera más útil de concebir este bien es imaginar que es el dinero que le queda al consumidor para adquirir otros bienes una vez que ha gastado la cantidad óptima en el bien x. Análisis del bienestar / 261 En el capítulo 9 vimos que este tipo de función de utilidad genera una curva inversa de demanda de la forma p = u'(x). La función directa de demanda, x(p), es simplemente la inversa de esta función, por lo que satisface la condición de primer orden u' (x(p)) = p. Obsérvese la siguiente característica especial: en el caso de la utilidad cuasilineal, la función de demanda es independiente de la renta. Esta característica hace que resulte especialmente sencillo el análisis del equilibrio y del bienestar. En la medida en que hemos supuesto que existe un consumidor representativo, podemos suponer también que existe una empresa representativa cuya función de costes es c(x). Esta función se interpreta de la siguiente manera: para generar x unidades de producción se necesitan c(x) unidades del bien y. Suponemos que c(O) = O y que e"(·) > O, de tal manera que las condiciones de primer orden determinan únicamente la oferta que maximiza el beneficio de la empresa representativa. 1 La función (inversa) de oferta que maximiza el beneficio de la empresa representativa viene dada por p = c'(x). Por lo tanto, el nivel de producción de equilibrio del bien x es simplemente la solución de la ecuación u'(x) = c'(x) (13.2) Éste es el nivel de producción en el que la disposición marginal a pagar el bien x es exactamente igual a su coste marginal de producción. 13.7 Análisis del bienestar Supongamos que en lugar de utilizar el mecanismo del mercado para averiguar el nivel de producción, averiguáramos directamente la cantidad de producción quemaximiza la utilidad del consumidor representativo. Este problema puede formularse de la siguiente manera: max u(x) + y X sujeta a y = w - c(x). El símbolo w representa la dotación del bien y que tiene inicialmente el consumidor. Naturalmente, la conducta competitiva es muy poco razonable si hay literalmente una única empresa; es mejor pensar que es simplemente la conducta "media" o "representativa" de las empresas de una industria competitiva. 1 262 / Los MERCADOS COMPETITIVOS (C. 13) Introduciendo la restricción en la función objetivo, formulamos de nuevo este problema de la manera siguiente: max u(x) + w - c(x). X La condición de primer orden es (13.3) 'U1 (x) = e' (x), y la condición de segundo orden se satisface automáticamente teniendo en cuenta nuestros supuestos anteriores sobre la curvatura. Obsérvese que las ecuaciones (13.2) y (13.3) determinan el mismo nivel de producción: en este caso el mercado competitivo da lugar exactamente al mismo nivel de producción y de consumo que la maximización directa de la utilidad. Figura 13.3 PRECIO s o X x* CANTIDAD La utilidad directa. La cantidad de equilibrio maximiza el área vertical situada entre la curva de demanda y la de oferta. El problema de maximización del bienestar consiste simplemente en maximizar la utilidad total: la utilidad de consumir el bien x más la utilidad de consumir el y. Dado que x unidades del bien x significa renunciar a c(x) unidades del bien y, nuestra función social objetivo es 'U(x) + w - c(x). La dotación inicial w es simplemente una constante, por lo que también podemos suponer que nuestra función social objetivo es 'U(x) - c(x). Hemos visto que 'U(x) es simplemente el área situada debajo de la curva (inversa) de demanda hasta el punto x. Del mismo modo, c(:1;) es simplemente el área situada Varios consumidores / 263 debajo de la curva de coste marginal hasta el punto x, ya que c(x) - c(O) � fox c'(x)dx y estamos suponiendo que c(O) = O. Por lo tanto, elegir el x que maximice la utilidad menos los costes equivale a elegir el x que maximice el área situada debajo de la curva de demanda y encima de la curva de oferta, como en la figura 13.3. He aquí otro modo de ver el mismo cálculo. Sea EC(x) = u(x)- px el excedente del consumidor correspondiente a un determinado nivel de producción: mide la diferencia entre los "beneficios totales" derivados del consumo del bien x y el gasto realizado en dicho bien. Sea EP(x) = px - c(x) los beneficios, es decir, el excedente del productor que obtiene la empresa representativa. En ese caso, la maximización del excedente total exige que max EC(x) + EP(x) = [u(x) - px] + [px - c(x)], X o sea, max u(x) - c(x). X Por lo tanto, también podemos decir que el nivel de producción de equilibrio competitivo maximiza el excedente total. 13.8 Varios consumidores El análisis del apartado anterior se refiere únicamente a un solo consumidor y a una sola empresa. Sin embargo, es fácil ampliarlo al caso en el que hay múltiples consumidores y empresas. Supongamos que hay i = 1, ... , n consumidores y j = 1, ... , m empresas. Cada uno de los consumidores i tiene una función de utilidad cuasilineal ui(xi) +u: y cada una de las empresas j tiene una función de costes c1(x1). En este contexto, una asignación describe la cantidad que consume cada una de las personas del bien x y del bien y, (xi, Yi), siendo i = 1, ... , n y la cantidad que produce cada una de las empresas del bien x, z1, siendo j = 1, ... , m. Dado que conocemos la función de costes de cada empresa, la cantidad del bien y que utiliza cada una de las empresas j es simplemente cj(z1 ). Se considera que la dotación inicial de cada consumidor es una determinada cantidad del bien y, Wi, y O del bien x. 264 / LOS MERCADOS COMPETITIVOS (C. 13) Un candidato razonable a un bienestar máximo en este caso es una asignación que maximice la suma de las utilidades, sujeta a la restricción de que la cantidad producida sea viable. La suma de las utilidades es L n L u. n Ui(Xi) i=l + i=l La cantidad total del bien y es la suma de las dotaciones iniciales, menos la cantidad gastada en la producción: n n n i=l i=l j=l Introduciendo esta igualdad en la función objetivo y teniendo en cuenta la restricción de la viabilidad, según la cual la cantidad total producida del bien x debe ser igual a la consumida, tenemos el siguiente problema de maximización: sujeta a ¿Xi=¿ ZJ, n m i=l j=l Suponiendo que ,\ es el multiplicador de Lagrange correspondiente a la restricción, la solución de este problema de maximización debe satisfacer las siguientes condiciones: u�(xT) = ,\ c'-(z't:) = ,\ J J ' así como la restricción de la viabilidad. Pero obsérvese que éstas son precisamente las condiciones que debe satisfacer un precio de equilibrio p* = .\. Un precio de equilibrio como ése hace que la utilidad marginal sea igual al _coste marginal y que la demanda sea al mismo tiempo igual a la oferta. Por lo tanto, el equilibrio de mercado maximiza necesariamente el bienestar, al menos tal como lo mide la suma de las utilidades. Naturalmente, de lo anterior no se obtiene información alguna sobre la distribución de la utilidad total, ya que ésta depende de la pauta de dotaciones iniciales, (wi), En el caso de la utilidad cuasilineal, el precio de equilibrio no depende de la distribución de la riqueza y cualquier distribución de las dotaciones iniciales es coherente con las condiciones de equilibrio antes mencionadas. La empresa competitiva / 265 13.9 La eficiencia en el sentido de Pareto Acabamos de ver que un equilibrio competitivo maximiza la suma de las utilidades, al menos en el caso de las utilidades cuasilineales. Pero dista de ser evidente que la suma de las utilidades sea una función objetivo razonable, ni siquiera en este caso restringido. Un objetivo más general es la idea de la eficiencia en el sentido de Pareto. Una asignación es eficiente en el sentido de Pareto cuando no es posible mejorar el bienestar de todos los agentes. En otras palabras, una asignación es eficiente en el sentido de Pareto cuando cada uno de los agentes disfruta del mayor bienestar posible, dadas las utilidades de los demás. Examinemos las condiciones de eficiencia en el sentido de Pareto en el caso de las funciones de utilidad cuasilineales. Para simplificar el análisis, nos limitaremos a examinar la situación en la que existe una cantidad fija de los dos bienes, (x, y), y sólo hay dos personas. En este caso, una asignación eficiente en el sentido de Pareto es aquella que maximiza la utilidad del agente 1, por ejemplo, manteniendo fijo el nivel de utilidad ü del agente 2. max u1 (x1) + Yl x1,Y1 sujeta a u2(x - x1) + y - Yl = ü2. Introduciendo la restricción en la función objetivo, tenemos el siguiente problema de maximización sin restricciones: max u1 (x1) + u2(x - x1) + y - ü, X¡ cuya condición de primer orden es la siguiente: (13.4) Dado un valor cualquiera de x1, esta condición determina un único nivel eficiente de x2. Sin embargo, la distribución de Yl e Y2 es arbitraria. Transfiriendo repetidamente el bien y de uno de los consumidores al otro mejora el bienestar de uno de ellos y empeora el del otro, pero no resultan afectadas en absoluto las condiciones marginales de eficiencia. Consideremos, por último, la relación entre (13.4) y el equilibrio competitivo. Al precio de equilibrio p", cada u�o de los consumidores ajusta su consumo del bien x de tal manera que u� (xj) = u;(xi) = p* Por lo tanto, se satisface la condición necesaria para que haya eficiencia en el sentido de Pareto. Por otra parte, cualquier asignación que sea eficiente en el sentido de 266 / LOS MERCADOS COMPETITIVOS (C. 13) Pareto debe satisfacer la condición (13.4), que determina esencialmente el precio p* al que esta asignación eficiente en el sentido de Pareto sería un equilibrio competitivo. De hecho, estos resultados también se cumplen esencialmente en el caso general, aun cuando las funciones de utilidad no sean cuasilineales. Sin embargo, generalmente los precios de equilibrio dependen de la distribución del bien y. En el capítulo dedicado al equilibrio general analizaremos con mayor profundidad este tipo de dependencia. 13.10 Eficiencia y bienestar A primera vista parece peculiar el hecho de que obtengamos la misma respuesta cuando maximizamos una suma de utilidades que cuando resolvemos el problema de eficiencia en el sentido de Pareto. Analicémoslo algo más. Aunque seguiremos suponiendo que hay dos consumidores y dos bienes, los resultados pueden generalizarse a los casos en los que hay más consumidores y bienes. Supongamos que existe inicialmente una cantidad del bien x, ii, y una cantidad del bien y, '[¡. Una asignación eficiente maximiza la utilidad de una persona, dada una restricción en cuanto al nivel de utilidad de la otra: max u1 (x1) + Yl x1,Y1 (13.5) Una asignación que maximiza la suma de las utilidades resuelve el siguiente problema: max u1 (x1) + u2(x - x1) + Yl + fj - Yl. X¡,y¡ (13.6) Ya hemos observado que el mismo xj resuelve los dos problemas. Sin embargo, el bien y que resuelve estos dos problemas es diferente. Cualquier par (YJ, y2) maximiza la suma de las utilidades, pero sólo habrá un valor de Yl que satisfaga la restricción de la utilidad contenida en (13.5). La solución de (13.5) no es más que una de las muchas posibles soluciones de (13.6). La estructura especial de la utilidad cuasilineal implica que es posible hallar todas las asignaciones eficientes en el sentido de Pareto resolviendo el problema (13.6). El valor de (xj, x2) es el mismo en todas las asignaciones eficientes en el sentido de Pareto, pero no así el de (yi, y2). Ésa es la razón por la que obtenemos (aparentemente) la misma respuesta maximizando la suma de las utilidades que buscando directamente una asignación eficiente en el sentido de Pareto. 2 2 Debe hacerse una matización a estas afirmaciones: es necesario tener una solución interior en El modelo de los bienes discretos / 267 13.11 El modelo de los bienes discretos El modelo de los bienes discretos es otro útil caso especial para examinar la conducta del mercado. En este modelo, también hay dos bienes, el bien x y el bien y, pero el primero sólo puede consumirse en cantidades discretas. En concreto, suponemos que el consumidor siempre compra cero unidades de dicho bien o una. Figura 13.4 PRECIO r PRECIO . CANTIDAD CANTIDAD A B El precio de reserva. El panel A muestra la curva de demanda de un único consumidor y el B la curva de demanda agregada de muchos consumidores que tienen precios de reserva diferentes. Por lo tanto, la utilidad que obtiene un consumidor que tenga la renta m y que se enfrente al precio psi compra el bien viene dada por u(l, m - p); si decide no comprarlo, obtiene la utilidad u(O, m). El precio de reserva es el precio r al que es indiferente entre comprar el bien x y no comprarlo. Es decir, es el precio r que satisface la ecuación u(l, m - r) = u(O, m). La curva de demanda de u� único consumidor tiene la forma que muestra la figura 13.4A; la curva de demanda agregada de muchos consumidores cuyos precios de reserva son diferentes tiene forma de escalera, como muestra la figura 13.48. El caso en el que las preferencias son cuasilineales y el bien es discreto es especialmente sencillo. En este caso, si el consumidor compra el bien, la utilidad es (y1, y2). Si el nivel de utilidad perseguido por el consumidor 2 es tan bajo que sólo puede alcanzarse igualando in a O, los dos problemas dejan de ser equivalentes. 268 / LOS MERCADOS COMPETITNOS (C. 13) simplemente u(l) + m - p y si no lo compra, es u(O) + m. El precio de reservar es la solución de u(l) + m - r = u(O) + m, que, como puede verse fácilmente, es r = u(l) - u(O). Partiendo, para normalizar, del útil supuesto de que u(O) = O, vemos que el precio de reserva es simplemente igual a la utilidad del consumo del bien x. Si el precio del bien x es p, el consumidor que decida consumir el bien tiene una utilidad de u(l) + m - p = m + r - p. Por lo tanto, el excedente del consumidor r - p es simplemente una manera de medir la utilidad que obtiene el consumidor que se enfrenta al precio p. Esta estructura especial hace que el análisis del equilibrio y del bienestar sea muy sencillo. El precio de equilibrio del mercado mide simplemente el precio de reserva del consumidor marginal, es decir, del consumidor que es exactamente indiferente entre comprar el bien y no comprarlo. El consumidor marginal obtiene un excedente del consumidor (aproximadamente) nulo; los consumidores inframarginales obtienen normalmente un excedente del consumidor positivo. 13.12 Impuestos y subvenciones Hemos visto que el término estática comparativa se refiere al análisis de la manera en que varía un resultado económico cuando varía el entorno económico. Cuando los mercados son competitivos, generalmente nos preguntamos cómo varía el precio y/ o la cantidad de equilibrio cuando cambia alguna variable de la política económica. Un útil ejemplo son los impuestos y las subvenciones. Es importante recordar que cuando hay impuestos, siempre hay dos precios en el sistema, el precio de demanda y el precio de oferta. El precio de demanda, Pd, es el precio que pagan los demandantes del bien y el precio de oferta, Ps, es el precio que perciben los oferentes; se diferencian en la cuantía del impuesto o de la subvención. Por ejemplo, los impuestos sobre la cantidad son aquellos que gravan la cantidad consumida de un bien. Eso significa que el precio que pagan los demandantes es mayor que el que perciben los oferentes en la cuantía del impuesto: Pd = P» + t. Los impuestos sobre el valor son aquellos que gravan el gasto realizado en un bien. Normalmente se expresan en cantidades porcentuales, por ejemplo, un impuesto sobre las ventas de un 10%. Un impuesto sobre el valor a un tipo T lleva a una especificación de la forma Impuestos y subvenciones / 269 Las subvenciones tienen una estructura similar; una subvención a la cantidad de la cuantía s significa que el vendedor recibe s pesetas más por unidad de lo que paga el comprador, por lo que Pd = Ps - s. Tanto la conducta del demandante como la del oferente dependen del precio al que se enfrenten, por lo que podemos formular: D(pd) y S(p8). La condición de equilibrio habitual exige que la demanda sea igual a la oferta, lo que nos conduce a las dos ecuaciones siguientes: D(pd) = S(ps) Pd = Ps + t. Insertando la segunda ecuación en la primera, podemos resolver o bien o bien Evidentemente, la solución de ti« y Ps es independiente de la ecuación que resolvamos. Este tipo de problema relacionado con los impuestos también puede resolverse utilizando las funciones inversas de demanda y de oferta. En este caso, las ecuaciones se convierten en o bien Una vez que hemos hallado los precios y la cantidad de equilibrio, es razonablemente sencillo realizar el análisis de bienestar. La utilidad que reporta el consumo a una persona en el equilibrio x* es u(x* )- pdx*. Los beneficios que obtiene la empresa sonp8x* -c(x*). Por último, los ingresos que recauda el Estado son tx* = (pd-Ps)x*. El caso más sencillo es aquel en el que los beneficios de la empresa y los ingresos fiscales van a parar al consumidor representativo, generando un bienestar neto de W(x*) = u(x*) - c(x*). Esta cantidad es simplemente el área situada debajo de la curva de demanda menos la situada debajo de la curva de coste marginal, como se muestra en la figura 13.5. La diferencia entre el excedente conseguido con el impuesto y el bienestar disfrutado 270 / LOS MERCADOS COMPETITIVOS (C. 13) en el equilibrio inicial se denomina pérdida irrecuperable de eficiencia y viene dada por el área triangular de la figura 13.5. La pérdida irrecuperable de eficiencia mide el valor que tiene para el consumidor la producción perdida. Figura 13.5 CANTIDAD La pérdida irrecuperable de eficiencia. El área ligeramente sombreada indica el ingreso total generado por el impuesto. El área triangular más oscura es la pérdida irrecuperable de eficiencia. Notas Éste es el análisis neoclásico convencional de un único mercado. Marshall (1920) fue probablemente quien lo examinó por primera vez de esta manera. Ejercicios 13.1. Sea v(p) + m la función indirecta de utilidad de un consumidor representativo y 1r(p) la función de beneficio de una empresa representativa. Supongamos que el bienestar en función del precio viene dado por v(p) + 1r(p). Demuestre que el precio competitivo minimiza esta función. ¿Puede explicar por qué el precio de equilibrio minimiza esta medida del bienestar en lugar de maximizarla? 13.2. Demuestre que la integral de la función de oferta entre Po y PI indica la variación que experimentan los beneficios cuando varía el precio de Po-a PI. Ejercicios / 271 13.3. Una industria está formada por un gran número de empresas, cada una de las cuales tiene una función de costes de la forma siguiente: c(w1, w2, y)= (y2 + l)w1 + (y2 + 2)w2 (a) Halle la curva de coste medio de una empresa y muestre cómo se desplaza cuando varía el precio de los factores wifw2. (b) Halle la curva de oferta a corto plazo de una empresa. (e) Halle la curva de oferta de la industria a largo plazo. (d) Describa un conjunto de cantidades necesarias de factores de una empresa. 13.4. Los agricultores producen maíz con tierra y trabajo. El coste monetario del trabajo necesario para producir y quintales de maíz es c(y) = y2. Hay 100 explotaciones agrarias que se comportan competitivamente. (a) ¿ Cuál es la curva de oferta de maíz de un agricultor? (b) ¿Cuál es la oferta de maíz del mercado? (c) Suponga que la curva de demanda de maíz es D(p) = 200 - 50p. ¿Cuál es el precio y la cantidad vendida en el punto de equilibrio? (d) ¿Cuál es la renta de equilibrio de la tierra? 13.5. Considere un modelo en el que Estados Unidos e Inglaterra se dedican al comercio de paraguas. La empresa inglesa representativa produce el modelo de paraguas para la exportación de acuerdo con la función de producción f(K, L), donde K y L son las cantidades de capital y trabajo utilizadas en la producción. Sean r y w los precios del capital y del trabajo, respectivamente, vigentes en Inglaterra y c(w, r, y) la función de costes correspondiente a la función de producción f(K, L). Suponga que inicialmente el precio de equilibrio de los paraguas es p* y la producción de equilibrio y*. Suponga para simplificar que se exportan todos los paraguas del modelo para la exportación, que no se produce ninguno en Estados Unidos y que todos los mercados son competitivos. (a) Inglaterra decide subvencionar la producción y la exportación de paraguas imponiendo una subvención s a la exportación por cada paraguas, por lo que cada 272 / LOS MERCADOS COMPETITIVOS (C. 13) uno de los paraguas exportados permite al exportador obtener p + s. ¿Qué cuantía ha de tener el impuesto sobre las importaciones t(s) que establezca Estados Unidos para contrarrestar la concesión de esta subvención, es decir, para mantener constante la producción y la exportación de paraguas en y*? (Pista: ésta es la parte fácil; no se complique demasiado la vida.) (b) Dado que es tan fácil para Estados Unidos contrarrestar los efectos de esta subvención a las exportaciones, Inglaterra decide establecer una subvención al capital. En concreto, decide subvencionar las compras de capital con una subvención específica des, por lo que el precio que tiene el capital para los fabricantes ingleses de paraguas es r - s. Estados Unidos decide tomar represalias estableciendo un impuesto t(s) sobre los paraguas importados que sea suficiente para mantener constante en u: el número de paraguas producidos. ¿Qué relación ha de haber entre el precio que pagan los consumidores, p, el impuesto, t(s), y la función de costes, c(w, r, y)? (c) Calcule una expresión de t'(s) a partir de la función de demanda condicionada de los factores correspondiente al capital, K(w, r, y). (d) Suponga que la función de producción muestra rendimientos constantes de escala. ¿Qué simplificación introduce este supuesto en su fórmula de t'(s)? (e) Suponga que el capital es un factor de producción inferior en la fabricación de paraguas. ¿Qué tiene de inusual el arancel t(s) que contrarreste la subvención al capital de Inglaterra? 13.6. En una isla tropical hay 100 constructores de barcos, numerados del 1 al 100. Cada uno puede construir hasta 12 barcos al año y maximiza sus beneficios dado el precio de mercado. Supongamos que y es el número de barcos construidos al año por un determinado constructor y que el constructor 1 tiene la función de costes c(y) = 1100 + y, el 2 tiene la función de costes c(y) = 1100 + 2y, etc. Es decir, el constructor de barcos i tiene la función de costes c(y) = 1100 + iy, estado i comprendido entre 1 y 100. Suponga que el coste fijo de 1.100 pesetas es un coste cuasifijo, es decir, sólo se paga si la empresa produce una cantidad positiva. Si el precio de los barcos es 2.500, ¿cuántos constructores decidirán producir una cantidad positiva? A ese precio, ¿cuántos barcos se construirán en total al año? 13.7. Considere una industria que tiene la siguiente estructura. Hay 50 empresas que se comportan competitivamente y tienen idénticas funciones de costes que vienen dadas por c(y) = y2 /2. Hay un monopolista que tiene unos costes marginales nulos. La curva de demanda del producto viene dada por Ejercicios / 273 D(p) = 1.000 - 50p (a) ¿Cuál es el nivel de producción que maximiza el beneficio del monopolista? (b) ¿Y el precio? (c) ¿Cuánto ofrece el sector competitivo a este precio? 13.8. Los consumidores norteamericanos tienen una función de demanda de paraguas de la forma D(p) = 90 - p. Los paraguas son ofrecidos por empresas norteamericanas y británicas. Supongamos para simplificar que en cada uno de los países hay una única empresa representativa que se comporta competitivamente. La función de costes de producir paraguas viene dada por c(y) = y2 /2 en cada país. (a) ¿Cuál es la función de oferta agregada de paraguas? (b) ¿Cuál es el precio y la cantidad vendida en el punto de equilibrio? (c) Ahora la industria norteamericana presiona al Parlamento para que la proteja y éste accede a establecer un arancel de 3 dólares sobre los paraguas extranjeros. ¿Cuál es el nuevo precio que pagan los consumidores norteamericanos por los paraguas? (d) ¿Cuántos paraguas son ofrecidos por las empresas extranjeras y cuántos por las norteamericanas? 14. EL MONOPOLIO El significado original de la palabra monopolio es "derecho exclusivo de venta". Sin embargo, ha acabado utilizándose para describir las situaciones en las que una empresa o un pequeño grupo de empresas tiene el control exclusivo de un producto en un determinado mercado. La dificultad de esta definición radica en saber qué se entiende por "un determinado mercado". En el mercado de bebidas refrescantes hay numerosas empresas, pero en el mercado de bebidas de cola sólo hay unas cuantas. La característica pertinente del monopolista desde el punto de vista del análisis económico reside en que éste tiene poder de mercado, en el sentido de que la cantidad de producción que puede vender es una función continua del precio que cobre. Este hecho contrasta con el caso de la empresa competitiva cuyas ventas se reducen a cero si cobra un precio superior al vigente en el mercado. La empresa competitiva es precio-aceptante; el monopolio es precio-decisor. El monopolista está sometido a dos tipos de restricciones cuando elige su nivel de precios y de producción. En primer lugar, está sometido al tipo de restricciones tecnológicas que hemos descrito anteriormente; sólo hay determinadas pautas de cantidades de factores y de productos tecnológicamente viables. Veremos que es útil resumir las restricciones tecnológicas por medio de la función de costes c(y) (omitimos los precios de los factores como argumentos de la función de costes porque suponemos que se mantienen fijos). El segundo conjunto de restricciones que pesan sobre el monopolista proviene de la conducta de los consumidores. Éstos se muestran dispuestos a comprar diferentes cantidades del bien a los distintos precios; esta relación se resume por medio de la función de demanda, D(p). El problema de maximización del beneficio del monopolista puede expresarse de la forma siguiente: maxpy - c(y) P,Y sujeta a D(p) � y En la mayoría de los casos de interés, el monopolista desea producir la cantidad que demandan los consumidores, por lo que la restricción puede expresarse por 276 / EL MONOPOLIO (C. 14) medio de la siguiente la igualdad y tenernos el siguiente problema: = D(p). Sustituyendo y en la función objetivo, rnax pD(p) - c(D(p)). p Aunque tal vez sea esta la forma más natural de plantear el problema de rnaxirnización del monopolista, en la mayoría de las situaciones resulta más útil la función inversa de demanda que la directa. Sea p(y) la función inversa de demanda, es decir, el precio que debe cobrarse para vender y unidades de producción. En ese caso, el ingreso que puede esperar el monopolista si produce y unidades es r(y) = p(y)y. El problema de rnaxirnización del monopolista puede plantearse de la forma siguiente: rnax p(y )y - c(y). y Las condiciones de primer y segundo orden de este problema son p(y) + p'(y)y 2p'(y) + p"(y)y - c"(y) = c'(y) (14.1) :S O. (14.2) Según la condición de primer orden, en la elección del nivel de producción que maximiza el beneficio, el ingreso marginal debe ser igual al coste marginal. Examinemos más detenidamente esta condición. Cuando el monopolista considera la posibilidad de vender dy unidades más de producción, ha de tener en cuenta dos efectos. En primer lugar, su ingreso aumenta en p dy, ya que vende una mayor producción al precio actual. Pero, en segundo lugar, para vender esta producción adicional, debe bajar el precio en dp = t/f¡dy, y este precio más bajo se aplica a todas las unidades y que esté vendiendo. Por lo tanto, el ingreso adicional derivado de la venta de la producción adicional viene dado por pdy+dpy= [p+ ::y] dy, y es esta cantidad la que debe compararse con el coste marginal. La condición de segundo orden exige que la derivada del ingreso marginal sea menor que la derivada del coste marginal; es decir, la curva de ingreso marginal corta a la curva de coste marginal desde arriba. ' La condición de primer orden puede reordenarse de tal manera que adopte la forma siguiente: r ' (y) [ = p(y) 1 + dp dy Py] ' = e (y), El monopolio / 277 o sea, [ p(y) 1 + E(�)] = (14.3) e' (y), donde pdy y dp E(y) = -- es la elasticidad (precio) de la demanda a la que se enfrenta el monopolista. Obsérvese que será un número negativo siempre que la curva de demanda de los consumidores tenga pendiente negativa, que es, ciertamente, lo habitual. De la condición de primer orden se desprende que en el nivel óptimo de producción la elasticidad de la demanda debe ser mayor que 1 en valor absoluto. De no ser así, el ingreso marginal sería negativo, por lo que no podría ser igual al coste marginal, que no es negativo. Figura 14.1 Ym CANTIDAD Determinación del nivel de producción del monopolio. El monopolista produce en el punto en el que el ingreso marginal es igual al coste marginal. La figura 14.1 representa gráficamente el nivel óptimo de producción del monopolista. La curva de ingreso marginal viene dada por r' (y) = p(y) + p' (y )y. Dado que p' (y) < O por hipótesis, la curva de ingreso marginal se encuentra por debajo de la curva inversa de demanda. Cuando y = O, el ingreso marginal derivado de la venta de una unidad adicional de producción es simplemente el precio p(O). Sin embargo, cuando y> O, el ingreso 278 / EL MONOPOLIO (C. 14) marginal derivado de la venta de una unidad adicional de producción debe ser menor que el precio, ya que la única manera de venderla es reducir el precio, y esta reducción afecta al ingreso obtenido por todas las unidades inframarginales vendidas. El nivel óptimo de producción del monopolista es aquel en el que la curva de ingreso marginal corta a la curva de coste marginal. Para satisfacer la condición de segundo orden, la curva IM debe cortar a la CM desde arriba. Normalmente supondremos que existe un único nivel de producción maximizador del beneficio. Dado el nivel de producción, por ejemplo, y*, el precio cobrado vendrá dado por p(y*). 14.1 Casos especiales Existen dos casos especiales en la conducta del monopolio que merece la pena mencionar. El primero es el de la demanda lineal. Si la curva inversa de demanda tiene la forma p(y) = a - by, la función de ingreso tendrá la forma r(y) = ay- by2 y el ingreso marginal r'(y) = a - 2by. Por lo tanto, la curva de ingreso marginal es dos veces más inclinada que la curva de demanda. Si la empresa muestra costes marginales constantes de la forma c(y) = cy, podemos resolver las ecuaciones que plantean la igualdad entre el coste marginal y el ingreso marginal para hallar directamente el nivel de precios y de producción del monopolio: r * r a-e :»: * a+ e p = --. 2 El otro caso de interés es la función de demanda de elasticidad constante, y = Ap-b. Como hemos visto anteriormente, la elasticidad de la demanda es constante y viene dada por E(y) = -b. En este caso, aplicando la ecuación (14.3), tenemos que p(y) = e 1 - 1/b Por lo tanto, en el caso de la función de demanda de elasticidad constante, el precio es un margen constante sobre el coste marginal, cuya magnitud depende de la elasticidad de la demanda. 14.2 Estática comparativa A menudo es interesante averiguar cómo varía el nivel de producción y el precio del monopolista cuando varían sus costes. Supongamos para simplificar que los costes Estática comparativa / 279 marginales son constantes. En ese caso, el problema de rnaxirnización del beneficio es rnax p(y)y- ey, y y la condición de primer orden p(y) + p'(y)y - e= O. Sabernos por los análisis convencionales de estática comparativa que dy / de tiene el mismo signo que la derivada de la condición de primer orden con respecto a e. Es fácil ver que es negativo, por lo que llegarnos a la conclusión de que el monopolista rnaxirnizador del beneficio siempre reducirá su nivel de producción cuando aumenten sus costes marginales. Es más interesante calcular la influencia de una variación de los costes en el precio. Sabernos por la regla de la derivación en cadena que dp de dp dy dy de· Esta expresión muestra claramente que dp/ de > O, pero suele ser útil conocer la magnitud de dp / de. El análisis convencional de estática comparativa nos dice que dy de fFrr / 8y8e a21r / 8y2 . Tornando las segundas derivadas apropiadas de la función de beneficios, tenernos que dy 1 de 2p'(y) + yp"(y). dp p'(y) de 2p'(y) + yp"(y). de donde se deduce que Este resultado también puede expresarse de la forma siguiente: dp 1 de 2 + yp"(y)/p'(y)" Es fácil ver en esta expresión qué ocurre en los casos especiales antes mencionados. Si la demanda es lineal, entonces p" (y) = O y dp / de = 1 /2. Si la función de demanda muestra una elasticidad constante de E, entonces dp/ de= E/0 + E). En el caso de la 280 / EL MONOPOLIO (C. 14) curva lineal de demanda, la mitad del incremento de los costes se traduce en una subida de los precios. En el caso de la demanda de elasticidad constante, los precios suben en una cuantía superior al incremento de los costes: cuanto más elástica es la demanda, más repercute el incremento de los costes en los precios. 14.3 Bienestar y producción Hemos visto en el capítulo 13 que en determinadas condiciones el nivel de producción en el que el precio es igual al coste marginal es eficiente en el sentido de Pareto. Dado que la curva de ingreso marginal siempre se encuentra por debajo de la curva inversa de demanda, es evidente que el monopolio debe producir una cantidad inferior a la eficiente en el sentido de Pareto. En este apartado examinaremos algo más detalladamente esta ineficiencia del monopolio. Consideremos para simplificar el caso de una economía en la que sólo hay un consumidor, que posee una función de utilidad cuasilineal u(x) + y. Como hemos visto en el capítulo 13, la función inversa de demanda correspondiente a una función de utilidad de este tipo viene dada por p(x) = u'(x). Sea c(x) la cantidad del bien y necesaria para producir x unidades del bien x. En ese caso, un objetivo social sensato es elegir la cantidad de x que maximice la utilidad: W(x) = max X u(x) - c(x). Eso implica que el nivel de producción socialmente óptimo, x.; viene dado por u' (xo) = p(xo) = e' (xo), Por otra parte, el nivel de producción monopolístico satisface la condición p(xm) + p'(xm)Xm = c'(xm) Por lo tanto, la derivada de la función de bienestar evaluada en el nivel de producción monopolístico viene dada por W'(xm) = u'(xm) - c'(xm) = -p'(xm) = -u"(xm)Xm >o De la concavidad de u(x) se desprende que el aumento del nivel de producción eleva la utilidad. Este razonamiento puede hacerse de un modo algo diferente. La función social objetivo también puede expresarse como el excedente del consumidor más los beneficios: W(:r.) = [u(x) - p(x)x] + [p(x)x - c(x)]. Elección de la calidad / 281 La derivada de los beneficios con respecto a x es cero en el nivel de producción monopolístico, ya que el monopolista elige el nivel de producción que maximiza los beneficios. La derivada del excedente del consumidor en Xm viene dada por cuyo valor es indudablemente positivo. 14.4 Elección de la calidad Los monopolios no sólo eligen el nivel de producción sino también otros aspectos de los bienes que producen. Consideremos, por ejemplo, la calidad del producto. Supongamos que podemos representarla por medio de un nivel numérico q. Suponemos que tanto la utilidad como los costes dependen de la calidad y que la función social objetivo es W(x, q) = u(x, q) - c(x, q). (Para facilitar el análisis suponemos como siempre que la utilidad es cuasilineal.) Imaginamos que la calidad es un bien, de tal manera que au / aq > O y que es costoso producirlo, de tal manera que Be] aq > O. El monopolista maximiza los beneficios: maxp(x, q)x - c(x, q). x,q Las condiciones de primer orden correspondientes a este problema son Calculando la derivada de la función de bienestar y evaluándola en (xm, qm), tenemos que aW(xm, qm) au(xm, qm) ac(xm, qm) ax aW(xm, qm) ax au(xm, qm) ax ac(xm, qm) aq aq aq Sustituyendo a partir de las condiciones de primer orden, tenemos que 282 / EL MONOPOLIO (C. 14) aW(xrn, qrn) ax aW(xrn, qrn) aq ap(xrn, qrn) Xrn > Ü ax au(xm,, qm,) ap(xm,, qm,) aq Bq (14.4) Xrn· (14.5) La primera ecuación nos indica que, manteniendo fija la calidad, el monopolista produce una cantidad demasiado pequeña, en relación con el óptimo social. La segunda no es tan fácil de interpretar. Dado que ap / aq es igual al coste marginal de aumentar la calidad, debe tener un valor positivo, por lo que la derivada del bienestar con respecto a la calidad es la diferencia entre dos números positivos y, por consiguiente, su signo es ambiguo. La cuestión estriba en saber si podemos hallar alguna condición plausible relativa a la conducta de demanda que permita determinar el signo de esta expresión. En este caso, resulta mucho más fácil ver la respuesta si se expresa la función social objetivo como el excedente del consumidor más los beneficios que si se expresa como la utilidad menos los costes. La función social objetivo adopta la forma siguiente: W(x, q) =[u(x, q) - p(x, q)x] + [p(x, q)x - c(x, q)] = excedente del consumidor + beneficios. A continuación diferenciamos esta definición con respecto a x y a q y evaluamos la derivada en el nivel de producción que maximiza el beneficio del monopolista. Dado que éste está maximizando los beneficios, las derivadas de los beneficios monopolísticos con respecto a la producción y a la calidad deben ser iguales a cero, lo que indica que la derivada del bienestar con respecto a la cantidad y a la calidad es precisamente la derivada del excedente del consumidor con respecto a la cantidad y a la calidad. La derivada del excedente del consumidor con respecto a la cantidad siempre es positiva, lo que es no es sino otra forma de decir que el monopolista produce una cantidad demasiado pequeña. La derivada del excedente del consumidor con respecto a la calidad es ambigua: puede ser positiva o negativa. Su signo depende del signo de a2p(x, q)/8xaq. Para verlo, examinemos la figura 14.2. Cuando aumenta la calidad, la curva de demanda se desplaza en sentido ascendente y (posiblemente) cambia de pendiente hacia un lado o hacia el otro. Descompongamos este movimiento en un desplazamiento ascendente paralelo y una rotación, tal como se indica en el gráfico. El desplazamiento paralelo no altera el excedente del consumidor, por lo que la variación total depende simplemente de que la curva inversa de demanda sea más plana o Elección de la calidad / 283 más inclinada. Si la pendiente de dicha curva se vuelve más plana, el excedente del consumidor disminuye y viceversa. 1 Figura 14.2 PRECIO Pm Influencia de una variación de la calidad en el excedente del consumidor. Cuando la curva de demanda se desplaza en sentido ascendente y cambia de pendiente hacia un lado o hacia el otro, el efecto producido en el excedente del consumidor sólo depende del sentido del cambio. La ecuación (14.5) también puede interpretarse por medio del modelo del precio de reserva. Imaginemos que p(x, q) mide el precio de reserva del consumidor x, de tal manera que u(x, q) es simplemente la suma de los precios de reserva. Según esta interpretación, u(x, q) / x es la disposición media a pagar y p(x, q) es la disposición marginal a pagar. La ecuación (14.5) puede reformularse de la manera siguiente: - !}_ aq � 8W(xm, Qm) _ X q a ¡u(xm, Qm) _ )] p ( Xm,Qm · Xm Ahora vemos que la derivada del bienestar con respecto a q es proporcional a la derivada de la disposición media a pagar por la variación de la calidad menos la derivada de la disposición marginal a pagar por la variación de la calidad. 1 Obsérvese que la pendiente de la curva de demanda es negativa; decir que la pendiente se vuelve más plana significa que se aproxima a cero. 284 / EL MONOPOLIO (C. 14) El bienestar social depende de la suma de la utilidad o de la disposición a pagar de los consumidores; pero al monopolista sólo le preocupa la disposición a pagar del individuo marginal. Si estos dos valores son diferentes, la calidad elegida por el monopolista no será la óptima desde el punto de vista social. 14.5 La discriminación de precios En términos generales, la discriminación de precios significa vender las diferentes unidades del mismo bien a precios distintos, o bien al mismo consumidor, o bien a consumidores diferentes. La discriminación de precios surge de manera natural cuando se estudia el monopolio, ya que hemos visto que el monopolista normalmente desea vender más si puede hacerlo sin bajar el precio que cobra por las unidades que ya está vendiendo. Para que la discriminación de precios sea una estrategia viable para la empresa, ha de poder clasificar a los consumidores e impedir la reventa. Impedir la reventa no suele ser difícil; es la clasificación de los consumidores la que plantea la mayoría de las dificultades. El caso más sencillo es aquel en el que la empresa puede clasificar explícitamente a los consumidores en función de una categoría exógena como la edad. Cuando debe discriminar en función de una categoría endógena, como la cantidad comprada o el momento de la compra, el análisis es más complejo. En este caso, el monopolista ha de estructurar sus precios para que sean los propios consumidores los que se clasifiquen en categorías correctas. La clasificación tradicional de los tipos de discriminación de precios se debe a Pigou (1920). Discriminación de precios de primer grado: el vendedor cobra un precio diferente por cada unidad del bien de tal manera que el precio que cobra por cada una es igual a la disposición máxima a pagar por esa unidad. También se conoce con el nombre de discriminación de precios perfecta. Discriminación de precios de segundo grado: los precios difieren dependiendo del número de unidades del bien que se compren, pero no de unos consumidores a otros. Este fenómeno se conoce también con el nombre de fijación no lineal de los precios. Cada uno de los consumidores se enfrenta a la misma lista de precios, pero éstos dependen de las cantidades que se compren. Ejemplos evidentes son los descuentos que se realizan por la compra de grandes cantidades. Discriminación de precios de tercer grado: se cobran precios distintos a los diferentes compradores, pero cada uno de ellos paga una cantidad constante La discriminación de precios / 285 por cada una de las unidades que compra del bien. Éste es quizá el tipo más frecuente de discriminación de precios; ejemplos son los descuentos a los estudiantes o la fijación de precios diferentes dependiendo del día de la semana. Investigaremos estos tres tipos de discriminación de precios por medio de un sencillísimo modelo. Supongamos que hay dos consumidores potenciales que tienen las funciones de utilidad u; (x) + y, siendo i = 1, 2. Para simplificar el análisis, podemos normalizar la utilidad de tal manera que ui(O) =O.La disposición máxima del consumidor i a pagar por un determinado nivel de consumo x está representada por ri(x). Es la solución de la ecuación ui(O) +y= ui(x) - ri(x) + y. El primer miembro de la ecuación indica la utilidad que reporta el consumo nulo del bien y el segundo indica la utilidad que reporta el consumo de x unidades y el pago del precio ri(x). En virtud de los supuestos de la normalización que hemos adoptado, ri(x) ui(x). Otra útil función relacionada con la función de utilidad es la función de disposición marginal a pagar, es decir, la función (inversa) de demanda. Esta función indica cuál debería ser el precio unitario para inducir al consumidor a demandar x unidades del bien de consumo. Si éste se enfrenta a un precio unitario p y elige el nivel óptimo de consumo, debe resolver el siguiente problema de maximización de la utilidad: = max ui(x) + y x,y sujeta apx +y= m. Como hemos visto en varias ocasiones, la condición de primer orden de este problema es p = u�(x). (14.6) Por lo tanto, la función inversa de demanda viene dada explícitamente por (14.6): el precio necesario para inducir al consumidor i a elegir el nivel de consumo x es p = p/x) = u�(x). Supondremos que la �isposición máxima del consumidor 2 a pagar por el bien siempre es superior a la disposición máxima del consumidor 1; es decir, que u2(x) > u1 (x) cualquiera que sea x. (14.7) También supondremos, por lo general, que la disposición marginal del consumidor 2 a pagar por el bien es superior a la disposición marginal del consumidor 1; es decir, que 286 / EL MONOPOLIO (C. 14) u; (x) > ui (x) cualquiera que sea x. (14.8) Por lo tanto, es natural decir que el consumidor 2 es el consumidor de elevada demanda y que el 1 es el consumidor de baja demanda. Supondremos que existe un único vendedor del bien en cuestión que puede producirlo a un coste marginal constante de e por unidad. Por lo tanto, la función de costes del monopolista es e(x) = ex. 14.6 La discriminación de precios de primer grado Supongamos por el momento que sólo hay un agente, con el fin de poder suprimir el subíndice que los distingue. El monopolista desea ofrecer al agente una combinación de precios y de producción (r*, x*) que le permita obtener los máximos beneficios. El precio r" constituye la única opción posible para el consumidor: puede pagar r" y consumir x* o consumir cero unidades. El problema de maximización del beneficio del monopolista es maxr - ex r,x sujeta a u(x) i r. La restricción indica simplemente que el consumidor debe obtener un excedente no negativo de su consumo del bien x. Dado que el monopolista desea que r sea lo más elevado posible, esta restricción se satisfará como una igualdad. Sustituyendo a partir de la restricción y diferenciando, hallamos la condición de primer orden, que determina el nivel óptimo de producción: u'(x*)=e (14.9) Dado este nivel de producción, el precio que define las opciones del consumidor es r" = u(x*) Deben hacerse varias observaciones sobre esta solución. En primer lugar, el monopolista decide producir una cantidad eficiente en el sentido de Pareto, es decir, un nivel de producción .en el que la disposición marginal a pagar es igual al coste marginal. Sin embargo, también trata de conseguir todos los beneficios derivados de este nivel eficiente de producción, es decir, obtiene la cantidad máxima posible de beneficios, mientras que al consumidor le da igual consumir el producto que no consumirlo. En segundo lugar, en este mercado el monopolista produce la misma cantidad que produciría una industria competitiva. Ésta produciría en el punto en el que el La discriminación de precios de segundo grado / 287 precio fuera igual al coste marginal y la oferta fuera igual a la demanda. Estas dos condiciones implican conjuntamente que p(x) = e, que es precisamente la ecuación (14.9) unida a la definición de la función inversa de demanda de (14.6). Naturalmente, las ganancias derivadas del comercio se dividen de una forma muy diferente en condiciones de equilibrio competitivo. En ese caso, el consumidor obtiene la utilidad u(x*) - ex" y la empresa recibe unos beneficios nulos. En tercer lugar, el resultado es el mismo si el monopolista vende al consumidor cada unidad de producción a un precio distinto. Supongamos, por ejemplo, que la empresa descompone la producción en n partes cuyo tamaño es �x, de tal manera que x = n�x. En ese caso, la disposición a pagar por la primera unidad de consumo viene dada por u(O) +m = u(�x) + m - PI, o sea, u(O) = u(�x) - PI. Del mismo modo, la disposición a pagar por la segunda unidad de consumo es u(�x) = u(2�x) - P2 Procediendo de esta manera con las n unidades, tenemos la siguiente secuencia de ecuaciones: u(O) = u(�x) - PI u(�x) = u(2�x) - P2 u((n - l)�x) = u(x) - Pn· Sumando estas n ecuaciones y teniendo en cuenta la normalización según la cual u(O) = O, tenemos que I:�=l Pn = u(x). Es decir, la suma de las disposiciones marginales a pagar debe ser igual a la disposición total a pagar. Por lo tanto, no importa cómo discrimine la empresa: planteando una única opción al consumidor o vendiendo cada una de las unidades del bien a la disposición marginal a pagar por ella. 14.7 La discriminación de precios de segundo grado La discriminación de precios de segundo grado también se denomina fijación no lineal de los precios. Implica algunas prácticas como los descuentos realizados por 288 / EL MONOPOLIO ( C. 14) comprar grandes cantidades, en las que el ingreso que obtiene la empresa es una función no lineal de la cantidad comprada. En este apartado analizamos un sencillo problema de este tipo. Recordemos la notación antes introducida. Hay dos consumidores que tienen las siguientes funciones de utilidad: u1 (x1) + Y1 y u2(x2) + Y2, donde suponemos que u2(x) > u1 (x) y u2(x) > u� (x). Nos referimos al consumidor 2 con el término consumidor de elevada demanda y al consumidor 1 con el término consumidor de baja demanda. El supuesto según el cual el consumidor que tiene la mayor disposición total a pagar también tiene la mayor disposición marginal a pagar a veces se conoce con el nombre de propiedad de la intersección única, ya que implica que dos curvas de indiferencia cualesquiera de los agentes pueden cortarse a lo sumo una vez. Supongamos que el monopolista elige una función (no lineal) p(x) que indica cuánto cobrará si se demandan x unidades. Supongamos que el consumidor i demanda Xi unidades y gasta ri = p(xi)Xi pesetas. Desde el punto de vista tanto del consumidor como del monopolista lo único relevante es que el consumidor gasta r i pesetas y recibe Xi unidades de producción. Por lo tanto, la elección de la función p(x) se reduce a la elección de (ri, Xi). El consumidor 1 elige (r1, x1) y el 2 elige (r2, x2). Las restricciones que pesan sobre el monopolista son las siguientes. En primer lugar, cada uno de los consumidores debe querer consumir la cantidad Xi y estar dispuesto a pagar el precio r i: u1(x1) - r1 u2(x2) - r2 2: O 2: O. Estas dos desigualdades implican sencillamente que cada uno de los dos consumidores debe obtener al menos tanta utilidad consumiendo el bien x como no consumiéndolo. En segundo lugar, cada uno de ellos debe preferir su consumo al del otro. u1 (zj ) - r1 u2(x2) - r2 2: 2: u1 (x2) - rz u2(x1) - r1. Éstas son las llamadas restricciones de la autoselección. Para que el plan (x1; x2) sea viable en el sentido de que sea elegido voluntariamente por los consumidores, cada uno de ellos debe preferir consumir la cesta que le corresponde a consumir la de la otra persona. Reordenando las desigualdades del párrafo anterior, tenemos que r1 � u1 (x1) (14.10) r1 � u1 (x1) - u1 (x2) + r: (14.11) La discriminación de precios de segundo grado / 289 r: :::; (14.12) u2(x2) r2:::; u2(x2) - u2(x1) + r1. (14.13) Naturalmente, el monopolista desea elegir los precios r1 y rz más altos posibles. Por lo tanto, en general, serán efectivas una de las dos primeras desigualdades y una de las dos segundas. Los supuestos de que u2(x) > u1 (x) y u2(x) > u; (x) son suficientes para determinar las restricciones que serán efectivas, como ahora demostraremos. Supongamos, en primer lugar, que la desigualdad (14.12) es efectiva. En ese caso, la desigualdad (14.13) implica que o sea, Aplicando la desigualdad (14.7), se deduce que lo que contradice la desigualdad (14.10). Por lo tanto, la desigualdad (14.12) no es efectiva y la (14.13) sí lo es, hecho que señalamos con vistas a su uso posterior: (14.14) Consideremos ahora las restricciones (14.10) y (14.11). Si la (14.11) fuera efectiva, tendríamos que Sustituyendo r: por su valor según (14.14), tenemos que lo que implica que . Esta expresión puede reformularse de la siguiente manera: lx2 u; • X] (t) dt = ¡x2 u2(t) dt. X¡ 290 /EL MONOPOLIO (C. 14) Sin embargo, esto viola el supuesto de que u;(x) > u; (x). Por lo tanto, la restricción (14.11) no es efectiva y la (14.1 O) sí lo es, por lo que (14.15) Las ecuaciones (14.14) y (14.15) implican que al consumidor de baja demanda se le cobrará su disposición máxima a pagar y al consumidor de elevada demanda el precio máximo que lo induzca a consumir x2 en lugar de x1. La función de beneficios del monopolista es la cual, sustituyendo r1 y rz por su valor, se convierte en Esta expresión debe maximizarse con respecto a x1 y x2. Diferenciando, tenemos que ui (x1) - e+ ui (x1) - u;(x1) = O (14.16) u;(x2) - e= O. (14.17) Reordenando la ecuación (14.16), tenemos que (14.18) que implica que el consumidor de baja demanda concede un valor (marginal) al bien superior a su coste marginal. Por lo tanto, consume una cantidad ineficientemente pequeña de dicho bien. La ecuación (14.17) indica que a los precios no lineales óptimos, el consumidor de elevada demanda tiene una disposición marginal a pagar que es igual al coste marginal. Por lo tanto, consume la cantidad socialmente correcta. Obsérvese que si no se satisficiera la propiedad de la intersección única, el término entre corchetes de la ecuación (14.18) sería negativo y el consumidor de baja demanda consumiría una cantidad mayor que la que consumiría en el punto eficiente. Podría ocurrir, si bien debe admitirse que sería bastante peculiar. El resultado de que el consumidor cuya demanda es mayor paga el coste marginal es muy general. Si éste pagara un precio superior al coste marginal, el monopolista podría bajar el precio cobrado al mayor consumidor en una pequeña cuantía, induciéndolo a comprar más. Dado que el precio todavía sería superior al coste marginal, el monopolista obtendría un beneficio por estas ventas. Por otra parte, esa La discriminación de precios de segundo grado / 291 política no afectaría a los beneficios que le reportarían otros consumidores, ya que todos ellos se encuentran en un nivel de consumo óptimo. Ejemplo: Análisis gráfico El problema de la discriminación.de precios con autoselección también puede analizarse gráficamente. Consideremos la figura 14.3 que representa las curvas de demanda de los dos consumidores y supongamos para simplificar el análisis que el coste marginal es cero. La figura 14.3A representa la discriminación de precios si no existiera el problema de la autoselección. La empresa vendería simplemente x� al consumidor de elevada demanda y xb al consumidor de baja demanda a unos precios iguales a sus respectivos excedentes del consumidor, es decir, a las áreas situadas debajo de sus respectivas curvas de demanda. Por lo tanto, el consumidor de elevada demanda paga A + B + C por consumir x� y el de baja demanda paga A por consumir xb. Sin embargo, esta política viola la restricción de la autoselección. El consumidor de elevada demanda prefiere la combinación del consumidor de baja demanda, ya que de esa manera recibe un excedente neto igual al área B. Para satisfacer la restricción de la autoselección, el monopolista debe ofrecer x� a un precio igual a A+ C, lo que permite al consumidor de elevada demanda obtener un excedente igual a B, cualquiera que sea la combinación que elija. Esta política es viable, pero ¿es óptima? La respuesta es negativa: ofreciendo al consumidor de baja demanda una combinación algo más pequeña, el monopolista pierde los beneficios representados por el triángulo de color negro de la figura 14.38 y obtiene los beneficios representados por el trapecio sombreado. La reducción de la cantidad ofrecida al consumidor de baja demanda no produce ningún efecto de primer orden en los beneficios, ya que la disposición marginal a pagar es igual a cero en el punto xb. Sin embargo, eleva los beneficios en una cuantía que no es marginal, ya que la disposición marginal del consumidor de elevada demanda a pagar es superior a cero en este punto. En el nivel de consumo maximizador del beneficio correspondiente al consumidor de baja demanda, xb, de la figura 14.3C, la disminución marginal de los beneficios generados por el consumidor de baja demanda como consecuencia de una nueva reducción, P1, es exactamente igual al aumento marginal de los beneficios generados por el consumidor de elevada demanda, P2 - P1 (obsérvese que este resultado también se deduce de la ecuación (14.18)). En la solución final, el consumidor de baja demanda consume en el punto xb y paga A, por lo que no obtiene excedente alguno por su compra. El consumidor de elevada demanda consume en el punto x�, la cantidad socialmente correcta, y paga A + C + D por esta combinación, con lo que le queda un excedente positivo de la cuantía B. 292 / EL MONOPOLIO (C. 14) Figura 14.3 PRECIO PRECIO PRECIO o A o o xh xh CANTIDAD e CANTIDAD xh e CANTIDAD La discriminación de precios de segundo grado. El panel A representa la solución si la autoselección no es un problema. El B muestra que la reducción de la combinación del consumidor de baja demanda eleva los beneficios y el C muestra el nivel de producción maximizador del beneficio correspondiente a este consumidor. 14.8 La discriminación de precios de tercer grado Existe discriminación de precios de tercer grado cuando se cobra a los consumidores distintos precios, pero cada uno de ellos paga un precio constante por todas las unidades de producción que adquiere. Éste es probablemente el tipo más frecuente de discriminación de precios. El caso más sencillo es aquel en el que hay dos mercados distintos, lo que le permite a la empresa establecer fácilmente la división. Un ejemplo sería la discriminación en función de la edad, como los descuentos que se realizan a los jóvenes en el cine. Si suponemos que Pi(xi) es la función inversa de demanda del grupo i y que hay dos grupos, el problema de maximización del beneficio del monopolista es max P1 (x1 )x1 + p2(x2)x2 x1,x2 cx1 - cx2 Las condiciones de primer orden de este problema son P1 (x1) + P; (x1)x1 P2(x2) + =e P2<x2)x2 = c. Suponiendo que Ei es la elasticidad de la demanda del mercado i, podemos formular estas expresiones de la manera siguiente: La discriminación de precios de tercer grado / 293 [ 1<11 p¡ (x¡) 1 - p2(x2) l l� e [1 - l<�ll � c. Por lo tanto, PI (xI) > p2(x2) si y sólo si IEI 1 < IE2I· En consecuencia, se cobrará el precio más bajo al mercado cuya demanda sea más elástica, es decir, al mercado más sensible al precio. Supongamos ahora que el monopolista no puede separar los mercados con tanta nitidez como hemos supuesto, por lo que el precio que cobra en uno de ellos influye en la demanda del otro. Consideremos, por ejemplo, el caso de un teatro que cobra unos precios más bajos los lunes; es probable que estos precios influyan en alguna medida en la demanda del martes. En este caso, el problema de maximización del beneficio de la empresa es max PI (xI, x2)xI + P2 (xI, x2)x2 - cxI - cx2, x1,x2 y las condiciones de primer orden se convierten en ºPI 8p2 8p2 ºPI PI + XI + X2 = e XI 0 XI 0 + x2 + XI = c. x2 a x2 a P2 Reordenando estas condiciones, tenemos que PI [ [ l l 1 + -x2 8p2 1 - = e P2 1 - hl 1 � 8xI ºPI + 8x2 XI = c. Dado que estamos suponiendo que la utilidad es cuasilineal, se deduce que 8pif 8x2 = 8p2/ 8xI; es decir, los efectos cruzados de los precios son simétricos. Restando la segunda ecuación de la primera y reordenando, tenemos que Es natural suponer que los dos bienes son sustitutivos -después de todo, se trata de un mismo bien que se vende a grupos diferentes- por lo que 8p2/ 8xI > O. Suponemos, sin que por ello el argumento sea menos general, que XI > x2, lo que, de acuerdo con la ecuación inmediatamente anterior, implica que 294 / EL MONOPOLIO (C. 14) P1 l 1 > O. [1 - _ ]1 - P2 [1 - _ IEJI IE2I Reordenando, tenernos que 1 - l/lE2I 1 - l/lE11 · P1 ->---- P2 De esta expresión se deduce que si IE2I > IEJ 1, debe cumplirse que P1 > P2· Es decir, si el mercado más pequeño tiene la demanda más elástica, debe tener el precio más bajo. Por lo tanto, postulando estos supuestos adicionales, la explicación intuitiva basada en los mercados perfectamente separados también es válida en el caso más general. Consecuencias para el bienestar El análisis de la discriminación de precios de tercer grado está relacionado en gran parte con las consecuencias que tiene para el bienestar este tipo de discriminación. ¿Cabe esperar, en general, que el excedente del consumidor más el excedente del productor sea mayor o menor cuando exista discriminación de precios de tercer grado que cuando no exista? Comenzarnos formulando un test general de la mejora del bienestar. Supongamos en aras de la sencillez que sólo hay dos grupos y partamos de una función de utilidad agregada de la forma u(x1, x2) + y. En este caso, x1 y x2 son los consumos de los dos grupos e y es el dinero que se gasta en otros bienes de consumo. Las funciones inversas de demanda de los dos bienes son: _ 8u(x1 , x2) P1 ( x1, x2 ) � ux1 _ 8u(x1, x2) P2 ( x1, x2 ) . � ux2 Suponernos que u(x1, x2) es cóncava y diferenciable, si bien este supuesto es algo más poderoso de lo necesario. Si c(x1 , x2) es el coste de ofrecer x1 y x2, el bienestar social se mide de la siguiente manera: W(x1, x2) = u(x1, x2) - c(x1, x2). Consideremos ahora dos configuraciones de la producción, (x�, x�) y (x�, x2), cuyos precios son (p�,p�) y (p2,p2), respectivamente. En razón de la concavidad de u(x1, x2), tenernos que La discriminación de precios de tercer grado / 295 Reordenando y aplicando la definición de las funciones inversas de demanda, tenemos que Utilizando un argumento análogo, tenemos que Dado que �W = �u - �e, obtenemos el siguiente resultado final: (14.19) En el caso especial en el que el coste marginal es constante, �e lo que la desigualdad se convierte en = c�x1 + c�x2, por (14.20) Obsérvese que los límites de la variación del bienestar son perfectamente generales y se basan únicamente en la concavidad de la función de utilidad, la cual es, a su vez, básicamente la condición de que las curvas de demanda tengan pendiente negativa. En Varian (1985) se deducen las desigualdes utilizando la función indirecta de utilidad, lo que representa un caso algo más general. Para aplicar estas desigualdades a la cuestión de la discriminación de precios, supongamos que el conjunto inicial de precios son los precios monopolísticos constantes de tal manera que p� = p� = pº y que (pi, pí_) son los precios discriminatorios. En ese caso, los límites de la desigualdad (14.20) se convierten en (14.21) El límite superior implica que una condición necesaria para que aumente el bienestar es que aumente la producción total. Supongamos, por el contrario, que disminuye la producción, de tal manera que �x1 + �x2 < O. Dado que pº - e > O, la expresión (14.21) implica que A W < O. El límite inferior indica una condición suficiente para que aumente el bienestar con un sistema de discriminación de precios, a saber, que sea positiva la suma de las variacione� de la producción ponderadas por la diferencia entre el precio y el coste marginal. 296 / EL MONOPOLIO ( C. 14) La figura 14.4 muestra el sencillo análisis geométrico de los límites. El aumento del bienestar � W está representado por el trapecio indicado, cuya área está claramente acotada por arriba y por abajo por el área de los dos rectángulos. Veamos una sencilla aplicación de los límites del bienestar en el caso de dos mercados cuyas curvas de demanda son lineales: x1 = a1 - b1P1 x2 = a2 - bzozSupongamos para simplificar que los costes marginales son nulos. En ese caso, si el monopolista practica la discriminación de precios, maximizará el ingreso vendiendo en la mitad de cada una de las curvas de demanda, por lo que x1 = a1 /2 y x2 = ai/2. Supongamos ahora que el monopolista cobra el mismo precio en los dos mercados. La curva de demanda total será Figura 14.4 PRECIO CANTIDAD Ilustración de los límites del bienestar. El trapecio es la verdadera variación del excedente del consumidor. Para maximizar el ingreso, el monopolista se situará en la mitad de la curva de demanda, lo que significa que Notas/ 297 Por lo tanto, cuando las curvas de demanda son lineales, la producción total es la misma en el caso de la discriminación de precios que en el del monopolio ordinario. El límite que viene dado por la expresión (14.21) implica, pues, que el bienestar debe disminuir cuando existe discriminación de precios. Sin embargo, este resultado se basa en el supuesto de que el monopolista ordinario vende en los dos mercados. Supongamos, como muestra la figura 14.5, que el mercado 2 es muy pequeño, por lo que la empresa maximizadora del beneficio no vende nada en este mercado si no se permite la discriminación de precios. Figura 14.5 La discriminación de precios. En este caso, el monopolista tomaría la decisión óptima de abastecer solamente al mercado grande si no pudiera practicar la discriminación de precios. En este caso, si se permite la discriminación de precios, �x1 = O y �x2 > O, lo aumenta que inequívocamente el bienestar, de acuerdo con (14.21). Naturalmente, no sólo se trata de un aumento del bienestar sino también, de hecho, de una mejora en el sentido de Pareto. Este ejemplo es bastante sólido. Si se abre un nuevo mercado como consecuencia de la discriminación de precios -un mercado que no era abastecido inicialmente por el monopolio ordinario- normalmente tendremos un aumento del bienestar que supone una mejora en el sentido de Pareto. Por otra parte, si el supuesto de la demanda lineal no es malo como primera aproximación y la producción no varía tanto en respuesta a la discriminación de precios, cabe muy bien esperar que las consecuencias netas para el bienestar sean negativas. Notas El análisis de la elección de la calidad se basa en Spence (1975). Para una panorámica de la discriminación de precios, véase Varian (1989a). 298 / EL MONOPOLIO (C. 14) Ejercicios 14.1. La curva inversa de demanda viene dada por p(y) = 10 - y y el monopolista pone a la venta una oferta fija de 4 unidades de un bien. ¿Qué cantidad venderá y qué precio fijará? ¿Cuál sería el precio y el nivel de producción en un mercado competitivo con una demanda y una oferta de estas características? ¿Qué ocurriría si el monopolista pusiera en venta 6 unidades del bien? (Suponga que existe la eliminación gratuita). 14.2. Suponga que un monopolista se enfrenta a la curva de demanda D(p) = 10 - p y que tiene una oferta fija de 7 unidades de producción para vender. ¿Cuál es el precio maximizador de su beneficio y cuáles son sus beneficios máximos? 14.3. Un monopolista se enfrenta a una curva de demanda de la forma x = 10 / p y tiene un coste marginal constante de l. ¿Cuál es el nivel de producción que maximiza el beneficio? 14.4. ¿Qué forma debe tener la curva de demanda para que dp/dc = 1? 14.5. Suponga que la curva inversa de demanda a la que se enfrenta un monopolista viene dada por p(y, t), donde tes un parámetro que desplaza la curva de demanda. Suponga para mayor sencillez que el monopolista tiene una tecnología que muestra costes marginales constantes. Obtenga una expresión que muestre cómo responde el nivel de producción a una variación de t. ¿Cómo se simplifica esta expresión si el parámetro de traslación adopta la forma especialp(y, t) = a(y) + b(t)? 14.6. La función de demanda a la que se enfrenta el monopolista viene dada por D(p) = 10/p y el monopolista tiene un coste marginal positivo de c. ¿Cuál es el nivel de producción que maximiza el beneficio? 14.7. Suponga que los costes marginales son constantes y tales que e > O y que la función de demanda viene dada por D(p) = { 010/p sip < 20 sip > 20. ¿ Cuál es el precio que maximiza el beneficio? 14.8. ¿ Qué forma han de tener la función de utilidad y la curva de demanda para que el monopolista produzca el nivel óptimo de calidad, dada su elección de la cantidad? Ejercicios / 299 14.9. En este capítulo hemos visto gráficamente que si 82p/8x8q > O, entonces 8u/8q - x8p/8q < O. Demuéstrelo algebraicamente. He aquí los pasos que ha de seguir: 1) Demuestre que la hipótesis implica que si z < x, entonces 8p(z, q) 8p(x, q) 8q 8q ---<--2) Exprese el primer miembro de esta desigualdad de tal manera que aparezca la función de utilidad. 3) Integre ambos miembros de esta desigualdad con respecto a z y evalúe el resultado en el intervalo que va de O a x. 14.10. Una de las maneras más frecuentes de practicar la discriminación de precios consiste en cobrar una cantidad fija por tener derecho a comprar un bien y después cobrar un coste unitario por el consumo de dicho bien. El ejemplo habitual es el del parque de atracciones en el que la empresa cobra un precio por la entrada y otro por las atracciones del parque. Esta política de precios se denomina precio en dos partes. Supongamos que todos los consumidores tienen idénticas funciones de utilidad, u(x), y que el coste de prestar el servicio es c(x). Si el monopolista fija un precio en dos partes, ¿producirá una cantidad superior o inferior a la eficiente? 14.11. Considere el análisis gráfico del problema de discriminación de precios de segundo grado. Observe atentamente la figura 14.3C y responda a la siguiente pregunta: ¿en qué condiciones vendería el monopolista solamente al consumidor de elevada demanda? 14.12. Si el monopolista decide vender a los dos consumidores, demuestre que el área B debe ser menor que la A. 14.13. Suponga que hay dos consumidores que pueden comprar cada uno de ellos una unidad de un bien. Si la calidad de este es q, el consumidor t obtiene la utilidad u(q, t). La calidad no le cuesta nada al monopolista. Supongamos que el precio máximo que estaría dispuesto a pagar el consumidor t por la calidad q viene dado por un, El monopolista no puede distinguir entre los dos consumidores, por lo que debe ofrecer a lo sumo dos calidades diferentes entre las que pueden elegir libremente los consumidores. Formule el problema de maximización del beneficio del monopolista y analícelo exhaustivamente. Pista: ¿se parece este problema a los que ha visto antes? 14.14. También puede suponerse que el monopolista elige el precio y deja que el mercado determine la cantidad vendida. Formule el problema de maximización del beneficio y verifique que p[l + 1 / el = e' (y) al precio óptimo. 300 / EL MONOPOLIO (C. 14) 14.15. Hay un único monopolista cuya tecnología muestra costes marginales constantes, es decir, c(y) = cy. La curva de demanda del mercado tiene una elasticidad constante, e Se establece un impuesto ad valorem sobre el precio del bien vendido, por lo que cuando el consumidor paga el precio Pv, el monopolista percibe el precio Ps = (1 - r)Pv (en este caso, Pv es el precio de demanda al que se enfrenta el consumidor y Ps es el precio de oferta al que se enfrenta el productor). Las autoridades fiscales están considerando la posibilidad de modificar el impuesto ad valorem y sustituirlo por un impuesto sobre la producción, t, en cuyo caso Pv = Ps + t. Se le ha contratado a usted para que calcule el impuesto sobre la producción t que sea equivalente al impuesto ad valorem r, en el sentido de que el precio final al que se enfrente el consumidor sea el mismo en los dos sistemas. 14.16. Suponga que la curva inversa de demanda a la que se enfrenta el monopolista viene dada por p(y, t), donde tes un parámetro que desplaza la curva de demanda. Suponga para simplificar que el monopolista tiene una tecnología que muestra costes marginales constantes. (a) Formule una expresión que muestre cómo responde el nivel de producción a una variación de t. (b) ¿Cómo se simplifica esta expresión si la función inversa de demanda adopta la forma especial p(y, t) = a(y) + b(t)? 14.17. Considere el caso de una sencilla economía que actúa como si hubiera un consumidor cuya función de utilidad fuera u1 (x1) + u2(x2) + y, donde x1 y x2 son las cantidades de los bienes 1 y 2, respectivamente, e y es el dinero que hay para gastar en todos los demás bienes. Suponga que el bien 1 es ofrecido por una empresa que actúa competitivamente y el 2 por una empresa que actúa como un monopolio. La función de costes del bien i es ci(xi) y hay un impuesto específico sobre la producción de la industria i cuya cuantía es k Suponga que e? > O, p�' < O y p� < O. (a) Formule las expresiones correspondientes a dau] di«, siendo i = 1, 2 e indique su signo. (b) Dada una variación de las cantidades producidas (dx1, dx2), formule una expresión del cambio del bienestar. (c) Suponga que estamos considerando la posibilidad de establecer un impuesto sobre una de las dos industrias y de utilizar los ingresos recaudados para subvencionar a la otra. ¿Debemos gravar a la industria competitiva o al monopolio? Ejercicios / 301 14.18. Hay dos consumidores que tienen las siguientes funciones de utilidad: u1(x1, Y1) =a1x1 + Y1 u2(x2, y2) =a2x2 + Y2 El precio del bien y es 1 y cada uno de los consumidores tiene una riqueza inicial de 10.000 pesetas. Se nos dice que a2 > a1. Ninguno de los dos bienes puede consumirse en cantidades negativas. Un monopolista ofrece el bien x. Tiene unos costes marginales nulos, pero su capacidad es limitada: puede ofrecer como máximo 10 unidades de dicho bien. Ofrecerá a lo sumo dos opciones de precio y cantidad, (r1, x1) y (r2, x2). En este caso, r« es el coste de adquirir Xi unidades del bien. (a) Formule el problema de maximización del beneficio del monopolista. Debe tener 4 restricciones más la restricción de la capacidad x1 + x2 � 10. (b) ¿Qué restricciones serán efectivas en la solución óptima? (c) Introduzca estas restricciones en la función objetivo. ¿Cuál es la expresión resultante? (d) ¿Cuáles son los valores óptimos de (r1, x1) y (r2, x2)? 14.19. Un monopolista vende en dos mercados. La curva de demanda de su producto es x1 = a1 - b1P1 en el mercado 1 y x2 = a2 - b2p2 en el 2, donde x1 y x2 son las cantidades vendidas en cada mercado y PI y P2 son los precios cobrados. El monopolista tiene unos costes marginales nulos. Observe que aunque puede cobrar precios distintos en los dos, debe vender todas las unidades dentro de un mercado al mismo precio. (a) ¿En qué condiciones relativas a los parámetros (a1, b1, oa. b2) tomará el monopolista la decisión óptima de no practicar la discriminación de precios? (Suponga que las soluciones son interiores.) (b) Suponga ahora que las funciones de demanda adoptan la forma Xi = Aip¡bi, siendo i = 1, 2, y que el monopolista tiene un coste marginal constante de e > O. ¿En qué condiciones decidirá no practicar la discriminación de precios? (Suponga que las soluciones son interiores). 14.20. Un monopolista maximizap(x)x-c(x). Para capturar algunos de los beneficios monopolísticos, el Estado establece un impuesto sobre el ingreso de la cuantía t, por 302 / EL MONOPOLIO (C. 14) lo que la función objetivo del monopolista se convierte en p(x)x - c(x) - tp(x)x. Inicialmente, el Estado se queda con los ingresos recaudados con este impuesto. (a) ¿Aumenta el nivel de producción del monopolista como consecuencia de este impuesto o disminuye? (b) Ahora el Estado decide repartir los ingresos recaudados con este impuesto entre los consumidores del producto del monopolista. Cada uno de ellos recibe una devolución cuya cuantía es igual al impuesto recaudado gracias a sus gastos. El consumidor representativo que gasta px recibe una devolución de tpx del Estado. Suponiendo que la utilidad es cuasilineal, formule una expresión de la demanda inversa del consumidor en función de x y t. (c) ¿Cómo responde el nivel de producción del monopolista al programa de devolución de los impuestos? 14.21. Considere el caso de un mercado que tiene las siguientes características. Hay un único monopolista cuya tecnología muestra costes marginales constantes, es decir, c(y) = cy. La curva de demanda del mercado tiene una elasticidad constante, E. Hay un impuesto ad valorem sobre el precio del bien vendido, por lo que cuando el consumidor paga el precio PD, el monopolista percibe el precio Ps = (1 - T)Pv (en este caso, PD es el precio de demanda al que se enfrenta el consumidor y Ps es el precio de oferta al que se enfrenta el productor). Las autoridades fiscales están considerando la posibilidad de modificar el impuesto ad valorem y sustituirlo por un impuesto sobre la producción, t, por lo que PD = Ps + t. Se le ha contratado a usted para que calcule el impuesto sobre la producción t que sea equivalente al impuesto ad valorem T, en el sentido de que el precio final al que se enfrente el consumidor sea el mismo en los dos sistemas. 14.22. Un monopolista tiene la función de costes c(y) = y, por lo que sus costes marginales son cons!antes e iguales a 1 peseta por unidad. Se enfrenta a la siguiente curva de demanda: D(p) = { �Oo¡p, si p sip > 20. < 20. (a) ¿Cuál es la elección del nivel de producción que maximiza el beneficio? Ejercicios / 303 (b) Si el Estado pudiera limitar el precio que cobra este monopolista para obligarlo a actuar competitivamente, ¿qué precio debería fijar? (c) ¿Qué cantidad produciría el monopolista si se le obligara a comportarse competitivamente? 14.23 Una economía tiene dos clases de consumidores y dos bienes. Los consumidores de tipo A tienen las funciones de utilidad U(x1, x2) = 4x1 - (x¡/2) + x2 y los de tipo B las funciones de utilidad U(x1, x2) = 2x1 - (x¡/2) + x2. Los consumidores no pueden consumir cantidades negativas. El precio del bien 2 es 1 y todos los consumidores tienen una renta de 100. Hay N consumidores de tipo A y N consumidores de tipo B. (a) Suponga que un monopolista puede producir el bien 1 con un coste unitario constante de e por unidad y no puede practicar ningún tipo de discriminación de precios. Halle su elección óptima del precio y de la cantidad. ¿ Qué valores ha de tener e para que sea cierto que decide vender a ambos tipos de consumidores? (b) Suponga que el monopolista establece un "precio en dos partes", por el que el consumidor debe pagar una cantidad fija k para poder comprar el bien. Una persona que haya pagado la cantidad k puede comprar la cantidad que desee al precio p por unidad comprada. Los consumidores no pueden revender el bien 1. Si p < 4, ¿cuál es la cantidad máxima k que estará dispuesto a pagar un consumidor de tipo A por el privilegio de comprar al precio p? Si un consumidor de tipo A paga la cantidad fija k para comprar al precio p, ¿cuántas unidades demandará? Describa la función que determina la demanda del bien 1 por parte de los consumidores de tipo A en función de p y de k. ¿Cuál es la función de demanda del bien 1 por parte de los consumidores de tipo B? Describa ahora la función que determina la demanda total del bien 1 por parte de todos los consumidores en función de p y de k. (c) Si la economía estuviera formada solamente por N consumidores de tipo A y ninguno de tipo B, ¿cuáles serían las elecciones de p y de k que maximizarían el beneficio? (d) Si e < 1, halle los valores de p y de k que maximizan los beneficios del monopolista sujetos a la restricción de que le compren ambos tipos de consumidores. 15. LA TEORÍA DE LOS JUEGOS La teoría de los juegos es el estudio de la interdependencia de las decisiones de los agentes. En capítulos anteriores hemos estudiado la teoría de la decisión óptima tomada por un único agente -una empresa o un consumidor- en entornos muy sencillos. La interdependencia estratégica de los agentes no era muy complicada. En el presente capítulo sentamos las bases para analizar en mayor profundidad la conducta de los agentes económicos en entornos más complejos. La interdependencia de las decisiones de los agentes podría estudiarse desde numerosos ángulos. Su conducta podría examinarse desde el punto de vista de la sociología, la psicología, la biología, etc. Todos estos enfoques resultan útiles en determinados contextos. La teoría de los juegos pone el énfasis en el estudio de la toma de decisiones fríamente "racional", ya que se considera que es el mejor modelo para analizar la mayor parte de la conducta económica. En el último decenio, la teoría de los juegos se ha aplicado profusamente en economía y ha experimentado grandes avances en el esclarecimiento del carácter de la interdependencia estratégica en los modelos económicos. De hecho, la mayor parte de la conducta económica puede concebirse como casos especiales de la teoría de los juegos, por lo que su comprensión constituye un componente necesario del conjunto de instrumentos analíticos con que debe contar todo economista. 15.1 Descripción de un juego Existen varias maneras de describir un juego, aunque para nuestros fines serán suficientes la forma estratégica y la forma extensiva. En términos generales, la forma extensiva presenta una descripción "extensa" de un juego, mientras que la estratégica presenta un resumen "reducido".1 Describiremos primero la forma estratégica y reservaremos el análisis de la extensiva para el apartado dedicado a los juegos consecutivos. 1 La forma estratégica se denominaba inicialmente forma normal de un juego, pero este término no es muy descriptivo, por lo que su uso se ha desaconsejado en los últimos años. 306 / LA TEORÍA DE LOS JUEGOS (C. 15) La forma estratégica de un juego se define mostrando un conjunto de jugadores, un conjunto de estrategias, es decir, de las opciones que tiene cada uno de los jugadores, y un conjunto de ganancias, que indican la utilidad que obtiene cada uno de ellos si elige una determinada combinación de estrategias. A fin de facilitar la exposición, en este capítulo examinaremos los juegos en los que intervienen dos personas. Todos los conceptos que describiremos pueden ampliarse fácilmente a las situaciones en las que intervienen muchas personas. Supondremos que la descripción del juego -las ganancias y las estrategias de que disponen los jugadores- es de dominio público. Es decir, cada uno de los jugadores conoce sus propias ganancias y estrategias, así como las ganancias y las estrategias del otro. Por otra parte, cada uno de ellos sabe que el otro las conoce, etc. También supondremos que es de dominio público que los dos jugadores son "totalmente racionales". Es decir, cada uno de ellos puede tomar una decisión que maximice su utilidad dadas sus expectativas subjetivas y que esas expectativas varían cuando obtiene nueva información de acuerdo con la ley de Bayes. En este sentido, la teoría de los juegos es una generalización de la teoría convencional de las decisiones de una persona. ¿ Cómo se comportará un maximizador de la utilidad esperada en una situación en la que sus ganancias dependan de las decisiones de otro maximizador de la utilidad esperada? Evidentemente, cada uno de los jugadores tendrá que considerar el problema al que se enfrenta el otro para tomar una decisión sensata. A continuación examinamos el resultado de este tipo de consideración. Ejemplo: El juego de las dos monedas En este juego, hay dos jugadores, Fila y Columna. Cada uno de ellos tiene una moneda que puede colocar de tal manera que se vea su cara o su cruz. Por lo tanto, cada uno de ellos tiene dos estrategias que denominaremos para abreviar "cara" o "cruz". Una vez eligidas, cada uno de los jugadores obtiene una ganancia que depende de lo que hayan elegido los dos. Cada uno de los jugadores elige independientemente del otro y ninguno de los dos sabe lo que ha elegido el otro cuando le toca elegir a él. Suponemos que si los dos jugadores colocan su moneda en posición de cara o de cruz, Fila gana una peseta y Columna pierde una. Si, por el contrario, uno de ellos juega cara y el otro cruz, Columna gana una peseta y Fila pierde una. En la matriz del juego de la página siguiente describimos la interdependencia estratégica: Las cifras de la casilla ("cara", "cruz") indican que el jugador Fila obtiene -1 y el jugador Columna obtiene + 1 si se elige esta combinación de estrategias. Obsérvese que en todas las casillas de la matriz, el resultado del jugador Fila es exactamente la Descripción de un juego / 307 negativa del resultado del jugador Columna. En otras palabaras, se trata de un juego de suma cero. En este tipo de juego, los intereses de los jugadores son diametralmente opuestos y resultan especialmente sencillos de analizar. Sin embargo, la mayoría de los juegos que tienen interés para los economistas no son juegos de suma cero. Cuadro 15.1 Jugador B Cara Cruz Jugador A Cara 1, -1 -1, 1 Cruz -1, 1 1, -1 Ejemplo: El dilema del prisionero Tenemos de nuevo dos jugadores, Fila y Columna, pero ahora sus intereses sólo están parcialmente en conflicto. Hay dos estrategias: cooperar o ir a la suya. En la historia original, Fila y Columna eran dos prisioneros que cometieron conjuntamente un delito. Podían cooperar y negarse a presentar pruebas o podían ir a la suya e implicarse mutuamente. En otras aplicaciones, cooperar e ir a la suya podrían tener un significado diferente. Por ejemplo, en una situación de duopolio, cooperar podría significar "seguir cobrando un precio alto" e ir a la suya "bajar el precio y capturar el mercado del competidor". Una descripción especialmente sencilla utilizada por Aumann (1987) es el juego en el que cada uno de los jugadores puede decir simplemente al árbitro: "déme 100.000 pesetas" o "déle al otro jugador 300.000". Obsérvese que las cantidades pagadas no provienen de ninguno de los jugadores sino de un tercero; el dilema del prisionero es un juego de suma variable. Los jugadores pueden analizar el juego de antemano, pero sus decisiones reales deben ser independientes. La estrategia de cooperar consiste para cada una de las personas en anunciar el regalo de 300.000 pesetas, mientras que la de ir a la suya consiste en coger las 100.000 pesetas (y salir corriendo). El cuadro 15.2 muestra la matriz de ganancias de la versión de Aumann del dilema del prisionero, en la que las unidades se expresan en cientos de miles de pesetas. 308 / LA TEORÍA DE LOS JUEGOS (C. 15) Más adelante analizaremos este juego con mayor detalle, pero antes debemos poner de manifiesto el "dilema". El problema estriba en que cada una de las partes tiene un incentivo para ir a la suya, independientemente de lo que crea que va a hacer la otra. Si yo creo que la otra persona va a cooperar y me va a dar 300.000 pesetas, obtendré 400.000 en total si voy a la mía. En cambio, si creo que la otra persona va a ir a la suya y va a limitarse a coger las 100.000 pesetas, lo mejor que puedo hacer es cogerlas yo mismo. Cuadro 15.2 Jugador B Cooperar Ir a la suya Jugador A Cooperar Ir a la suya 3, 3 O, 4 o 1, 1 4, Ejemplo: El duopolio de Cournot Examinemos un sencillo juego de duopolio, analizado por primera vez por Cournot (1838). Supongamos que hay dos empresas que producen un bien idéntico con un coste nulo. Cada una de ellas ha de decidir la cantidad que va a producir sin conocer la decisión de la otra. Si las dos producen un total de x unidades del bien, el precio de mercado será p(x); es decir, p(x) es la curva inver�a de demanda a la que se enfrentan estos dos productores. Si xi es el nivel de producción de la empresa i, el precio de mercado será p(x1 + x2) y los beneficios de dicha empresa 7íi = (p(x1 + x2)xi. En este juego, la estrategia de la empresa i es su elección del nivel de producción y las ganancias sus beneficios. Ejemplo: El duopolio de Bertrand Examinemos la misma situación que en el juego de Cournot, pero supongamos ahora que la estrategia de cada uno de los jugadores es anunciar el precio al que estaría dispuesto a ofrecer una cantidad arbitraria del bien en cuestión. En este caso, la función de ganancias adopta una forma totalmente diferente. Es razonable La formulación de modelos económicos de las elecciones estratégicas / 309 suponer que los consumidores sólo comprarán a la empresa cuyo precio sea más bajo y que se repartirán por igual entre las dos empresas si éstas cobran el mismo precio. Suponiendo que x(p) es la función de demanda del mercado, el resultado de la empresa 1 adopta la forma siguiente: 1q (p1, P2) = { P1X(p1) p10 x(p1) /2 si Pl < P2 si Pl = P2 si p¡ > P2· Este juego tiene una estructura similar a la del dilema del prisionero. Si los dos jugadores cooperan, pueden cobrar el precio de monopolio y obtener cada uno la mitad de los beneficios monopolísticos. Pero siempre existe la tentación de bajar algo el precio y quedarse así con todo el mercado. Sin embargo, si los dos jugadores bajan el precio, los dos salen perdiendo. 15.2 La formulación de modelos económicos de las elecciones estratégicas Obsérvese que los juegos de Cournot y de Bertrand tienen una estructura absolutamente diferente, aun cuando pretendan recoger el mismo fenómeno económico: el duopolio. En el juego de Cournot, las ganancias que obtiene cada una de las empresas es una función continua de su elección estratégica; en el de Bertrand, las ganancias son funciones discontinuas de las estrategias. Como cabía esperar, los resultados son totalmente distintos. ¿Cuál de estos modelos es el "correcto"? Apenas tiene sentido decir cuál es el "correcto" en abstracto. La respuesta depende de lo que estemos tratando de analizar con el modelo. Probablemente sea más fructífero preguntarse qué consideraciones son relevantes a la hora de formular en un modelo el conjunto de estrategias utilizadas por los agentes. Un elemento que sirve de orientación es, sin duda, la evidencia empírica. Si la observación de los anuncios de la OPEP indica que intentan fijar las cuotas de producción de cada uno de sus miembros y dejar que sean los mercados mundiales de petróleo los que fijen el precio, probablemente será más sensato que las estrategias del juego que se pretende analizar sean los niveles de producción en lugar de los precios. Otra consideración es que las estrategias deben ser algo con lo que sea posible comprometerse o que sea difícil de alterar una vez observada la conducta del adversario. Los juegos antes descritos son juegos que sólo se juegan una vez, pero la realidad que se supone que describen tiene lugar en el tiempo real. Supongamos que fijamos el precio de nuestro producto y descubrimos que nuestro adversario ha fijado uno más bajo. En este caso, podemos revisar inmediatamente nuestro precio. Dado que la variable estratégica puede modificarse rápidamente una vez que se conoce la jugada del adversario, no tiene mucho sentido tratar de plasmar en el modelo este 310 / LA TEORÍA DE LOS JUEGOS (C. 15) tipo de interdependencia en un juego que sólo se juega una vez. Parece que para recoger toda la diversidad de conductas estratégicas posibles en este tipo de juego de fijación del precio debe utilizarse un juego en el que haya múltiples etapas. Supongamos, por otra parte, que en el juego de Coumot el bien producido es la "capacidad", en el sentido de que es una inversión irreversible de capital capaz de producir la cantidad indicada. En este caso, una vez que descubrimos el nivel de producción del adversario, puede resultar muy costoso alterar nuestro propio nivel de producción. En este caso, la elección de la capacidad como variable estratégica parece natural, incluso en un juego que sólo se juega una vez. Como ocurre casi siempre en la formulación de modelos económicos, la elección de una representación de las opciones estratégicas del juego que recoja los elementos básicos de las interdependencias estratégicas reales y que sea al mismo tiempo suficientemente sencilla para poder analizar los juegos planteados es en cierta medida un arte. 15.3 Las soluciones posibles En muchos juegos, el carácter de la interdependencia estratégica sugiere que un jugador desea elegir una estrategia que el otro no pueda predecir de antemano. Consideremos, por ejemplo, el juego de las dos monedas antes descrito. En este caso, está claro que ninguno de los dos jugadores quiere que el otro pueda predecir exactamente su elección. Por lo tanto, es natural analizar la estrategia aleatoria consistente en jugar "cara" con una probabilidad Pe y "cruz" con una probabilidad Pz· Este tipo de estrategia se denomina estrategia mixta. Las estrategias en las que se elige una opción con una probabilidad 1 se denominan estrategias puras. Si F es el conjunto de estrategias puras de que dispone Fila, su conjunto de estrategias mixtas será el conjunto de todas las distribuciones de probabilidades correspondientes a F, donde la probabilidad de utilizar la estrategia f perteneciente a Fes p i- Del mismo modo, Pl es la probabilidad de que Columna elija una estrategia l. Para resolver el juego, hemos de hallar un conjunto de estrategias mixtas (p ¡, Pt) que se encuentren, en cierto sentido, en equilibrio. Es posible que algunas de las estrategias mixtas de equilibrio asignen la probabilidad 1 a algunas elecciones, en cuyo caso se interpreta que son estrategias puras. El punto de partida natural en la búsqueda de una solución es la teoría convencional de la decisión: suponemos que cada uno de los jugadores tiene una expectativa sobre las probabilidades de que el otro jugador elija una u otra estrategia y que cada uno de ellos elige la estrategia que maximiza su ganancia esperada. Supongamos, por ejemplo, que la ganancia de Fila es u¡(J, l) si Fila juega f y Columna juega c. Suponemos que Fila tiene una distribución de las probabilidades subjetivas en lo que se refiere a las elecciones de Columna y que representamos por El equilibrio de Nash / 311 medio de (1rz); véase el capítulo 11 (página 224) para los fundamentos de la idea de la probabilidad subjetiva. Aquí suponemos que at¡ indica la probabilidad, desde el punto de vista de Fila, de que Columna elija l. Del mismo modo, Columna tiene una expectativa sobre la conducta de Fila que representamos por medio de (1r ¡ ). Suponemos que cada jugador elige una estrategia mixta y representamos la estrategia mixta real de Fila por medio de (p¡) y la de Columna por medio de (pz). Dado que Fila elije sin conocer la elección de Columna, la probabilidad de Fila de que se produzca un determinado resultado (f, l) es p¡1rz. Ésta es simplemente la probabilidad (objetiva) de que Fila juegue f multiplicada por la probabilidad (subjetiva) de Fila de que Columna juege l. Por lo tanto, el objetivo de Fila es elegir una distribución de probabilidades (p ¡) que maximice Ganancias esperadas de Fila = ¿ ¿p¡1rzu¡(f, l). f Columna, por otra parte, desea maximizar Ganancias esperadas de Columna = ¿ ¿pz1r¡uz(f, l). f Hasta ahora nos hemos limitado a aplicar a este juego un modelo teórico convencional de decisión, es decir, cada uno de los jugadores desea maximizar su utilidad esperada, dadas sus expectativas. Dadas mis expectativas sobre lo que hará el otro jugador, elijo la estrategia que maximiza mi utilidad esperada. En este modelo, mis expectativas sobre las elecciones estratégicas del otro jugador son variables exógenas. Sin embargo, ahora imprimimos un nuevo giro al modelo convencional de decisión y nos preguntamos qué tipos de expectativas es razonable tener sobre la conducta de otra persona pues, al fin y al cabo, cada uno de los jugadores sabe que el otro pretende maximizar su propio resultado y cada uno de ellos debe utilizar esa información para averiguar cuáles son las expectativas razonables sobre la conducta del otro. 15.4 El equilibrio de Nash En la teoría de los juegos; consideramos dada la proposición de que cada uno de los jugadores pretende maximizar sus propias ganancias y, además, que cada uno de ellos sabe que ése es el objetivo del otro. Por lo tanto, para averiguar cuáles podrían ser las expectativas razonables que deberíamos tener sobre lo que podrían hacer otros jugadores, hemos de preguntarnos qué es posible que crean ellos sobre lo que haremos nosotros. En las fórmulas de las ganancias esperadas expuestas al final del apartado anterior, la conducta de Fila -la probabilidad de que elija cada 312 / LA TEORÍA DE LOS JUEGOS (C. 15) una de sus estrategias- está representada por la distribución de probabilidades (p ¡) y las expectativas de Columna sobre la conducta de Fila están representadas por la distribución de probabilidades (subjetivas) (1r ¡ ). La coherencia exige lógicamente que las expectativas de cada uno de los jugadores sobre las elecciones del otro coincidan con las elecciones reales que pretenda hacer éste. Las expectativas coherentes con las frecuencias reales a veces se denominan expectativas racionales. Un equilibrio de Nash es un cierto tipo de equilibrio basado en las expectativas racionales. En términos más formales: Equilibrio de Nash. Un equilibrio de Nash consiste en las expectativas sobre la probabilidad ( 1r ¡, 7rz) de que se elijan las diferentes estrategias y en la probabilidad de que se elijan las estrategias 1) (p ¡, pz), tales que: las expectativas son correctas: p¡ = 1r ¡ y pz = tt¡ cualesquiera que sean f y l; y, 2) cada uno de los jugadores elige las dadas sus expectativas. (p ¡) y (pz) que maximizan su utilidad esperada En esta definición es evidente que un equilibrio de N ash es un equilibrio respecto a las acciones y a las expectativas. En condiciones de equilibrio, cada uno de los jugadores prevé correctamente la probabilidad de que el otro elija las diferentes opciones y las expectativas de los dos son mutuamente coherentes. El equilibrio de Nash también puede definirse de una manera más convencional: es el par de estrategias mixtas (p ¡, p¡) tal que la elección de cada uno de los agentes maximiza su utilidad esperada, dada la estrategia del otro. Esta definición equivale a la que utilizamos, pero induce a error, ya que queda difuminada la distinción entre las expectativas de los agentes y sus acciones. Nosotros hemos tratado de distinguir cuidadosamente estos dos conceptos. Un interesante caso especial del equilibrio de Nash es el equilibrio de Nash en el caso de las estrategias puras, que es simplemente un equilibrio de Nash en el que la probabilidad de elegir una determinada estrategia es 1 en el caso de los dos jugadores; es decir: Estrategias puras. Un .equilibrio de Nash en el caso de las estrategias puras es un par (f*, l*) tal que u¡(j*, l*) 2:: u¡(f, l*) cualesquiera que sean las estrategias de Fila f y uz(f*, l*) 2:: uz(f*, l) cualesquiera que sean las estrategias de Columna l. Un equilibrio de Nash es la condición mínima de coherencia que debe imponerse a un par de estrategias: si Fila cree que Columna elegirá l*, su mejor respuesta es f* y lo mismo en el caso de Columna. A ninguno de los jugadores le interesará El equilibrio de Nash / 313 alejarse unilateralmente de la estrategia que es un equilibrio de Nash. Si un conjunto de estrategias no es un equilibrio de Nash, al menos uno de los jugadores no está estimando coherentemente la conducta del otro. Es decir, uno de ellos ha de esperar que el otro no actúe en su propio provecho, lo que contradice la hipótesis inicial del análisis. Suele considerarse que un punto de equilibrio es un "punto de reposo" al que se llega tras un proceso de ajuste. El equilibrio de Nash puede interpretarse como el proceso de ajuste consistente en la estimación correcta de los incentivos del otro jugador. Fila podría pensar: "si creo que Columna va a elegir la estrategia lt, mi mejor respuesta es elegir Ji. Pero si Columna cree que voy a elegir Ji, lo mejor que puede hacer es elegir la estrategia [i. Pero si Columna va a elegir l2, mi mejor respuesta es h ... ", y así sucesivamente. Un equilibrio de Nash es, pues, un conjunto de expectativas y estrategias en el que las opiniones de cada uno de los jugadores sobre lo que hará el otro son coherentes con la elección real de este último. A veces el proceso de ajuste descrito en el párrafo anterior se interpreta como un proceso de ajuste .real en el que cada uno de los jugadores ensaya diferentes estrategias en un intento de comprender las elecciones del otro. Aunque es evidente que ese ensayo y aprendizaje se produce en la interdependencia estratégica en el mundo real, estrictamente hablando no es una interpretación válida del concepto de equilibrio de Nash, ya que si cada uno de los jugadores sabe que el juego va a repetirse, cada uno de ellos puede planear basar su conducta en el momento ten la conducta observada en el otro jugador hasta ese momento. En este caso, el concepto correcto de equilibrio de Nash es una secuencia de jugadas que es una respuesta mejor (en cierto sentido) a una secuencia de jugadas de mi adversario. Ejemplo: Cálculo de un equilibrio de Nash El juego siguiente se conoce con el nombre de ''batalla de los sexos". La historia en que se basa es aproximadamente la siguiente. Felisa Fila y Carlos Columna no saben si estudiar microeconomía o macroeconomía este semestre. Felisa obtiene la utilidad 2 y Carlos la utilidad 1 si ambos estudian micro; las ganancias son inversas si ambos estudian macro. Si asisten a cursos diferentes, ambos obtienen la utilidad O. Calculemos todos los equilibrios de Nash de este juego. En primer lugar, buscamos los equilibrios de Nash correspondientes a las estrategias puras, para lo cual basta examinar sistemáticamente las mejores respuestas a las distintas elecciones de las estrategias. Supongamos que Columna piensa que Fila elegirá "arriba". Columna obtiene 1 eligiendo "izquierda" y O eligiendo "derecha", por lo que "izquierda" es la mejor respuesta de Columna a la elección de "arriba" por parte de Fila. En cambio, si Columna elige "izquierda", es fácil ver que lo óptimo para Fila es elegir "arriba". Este tipo de razonamiento muestra que ("arriba", "izquierda") es un equilibrio de 314 / LA TEORÍA DE LOS JUEGOS (C. 15) Nash. Siguiendo un razonamiento parecido, se observa que también lo es ("abajo", "derecha"). Cuadro 15.3 Carlos Fe lisa Izquierda (micro) Derecha (macro) Arriba (micro) 2, 1 o, o Abajo (macro) O, o 1, 2 Este juego también puede resolverse sistemáticamente formulando el problema de maximización que ha de resolver cada uno de los agentes y examinando las condiciones de primer orden. Supongamos que (pª, Pb) son las probabilidades de que Fila elija "arriba" y "abajo" y definamos (pi,Pd) de la misma manera. En ese caso, el problema de Fila es max Pa[Pi2 + PdO] + PbÍPiO + Pdl] (pa,Pb) sujeta a Pa + Pb = 1 Pa Pb 2:: O 2:: O. Sean .\, µª y µb los multiplicadores de Kuhn-Tucker correspondientes a las restricciones, de tal manera que el lagrangiano adopta la forma siguiente: Diferenciando con respecto a Pa y Pb, vemos que las condiciones de Kuhn-Tucker correspondientes a Fila son 2Pi =.\ + µª Pd =A+ µb. (15.1) Dado que ya conocemos las soluciones de las estrategias puras, sólo analizamos el caso en el que Pa > O y Pb > O. Las condiciones complementarias de holgura implican en ese caso queµª = µb = O. Valiéndonos del hecho de que P« + Pb = 1, vemos fácilmente que a Fila le resultará óptimo elegir una estrategia mixta cuando Pi = 1/3 y Pd = 2/3. Interpretación de las estrategias mixtas / 315 Siguiendo el mismo procedimiento en el caso de Columna, observamos que Pa = 2/3 y Pb = 1 /3. Las ganancias que espera cada uno de los jugadores de esta estrategia mixta pueden calcularse fácilmente introduciendo estos números en la función objetivo. En este caso, las ganancias esperadas son 2/3 en el caso de los dos jugadores. Obsérvese que cada uno de ellos preferiría los equilibrios de la estrategia pura a la estrategia mixta, ya que las ganancias son mayores para los dos jugadores. 15.5 Interpretación de las estrategias mixtas A veces resulta difícil interpretar la idea de la estrategia mixta desde el punto de vista de la conducta. En el caso de algunos juegos, como el de las dos monedas, es evidente que las estrategias mixtas constituyen el único equilibrio razonable. Pero en el caso de otros juegos de interés económico -por ejemplo, el juego del duopolioéstas parecen poco realistas. Además de este carácter poco realista de las estrategias mixtas en algunos contextos, existe otra dificultad desde el punto de vista puramente lógico. Examinemos de nuevo el ejemplo de la estrategia mixta en la batalla de los sexos. En este juego, el equilibrio de la estrategia mixta tiene la propiedad de que si Fila elige su estrategia mixta de equilibrio, las ganancias que espera obtener Columna eligiendo cualquiera de sus estrategias puras deben ser iguales que las ganancias que espera obtener eligiendo su estrategia mixta de equilibrio. Como mejor se comprende este hecho es examinando las condiciones de primer orden (15.1). Dado que Zp¡ = pr1, las ganancias que se esperan eligiendo "arriba" son iguales que las que se esperan eligiendo "abajo". Pero no se trata de una pura coincidencia. En el caso de los equilibrios de las estrategias mixtas, si una de las partes cree que la otra elegirá la estrategia mixta de equilibrio, siempre le dará igual que elija su estrategia mixta de equilibrio o cualquier estrategia pura que forme parte de ésta. La lógica es sencilla: si una estrategia pura que forme parte de la estrategia mixta de equilibrio generara unas ganancias esperadas mayores que las de algún otro componente de la estrategia mixta de equilibrio, compensaría aumentar la frecuencia con que se eligiera la estrategia que generara unas ganancias esperadas mayores. Pero si todas las estrategias puras que se eligen con una probabilidad positiva en una estrategia mixta generan las mismas ganancias esperadas, es de esperar que éstas sean también las ganancias esperadas de la estrategia mixta, lo cual implica, a su vez, que a un agente le da igual elegir una estrategia pura u otra o elegir una mixta. Esta "degeneración" se debe a que la función de utilidad esperada es lineal con respecto a las probabilidades. A uno le gustaría que hubiera alguna razón más imperiosa para "imponer" el resultado de la estrategia mixta. 316 / LA TEORÍA DE LOS JUEGOS (C. 15) En algunas situaciones, este resultado puede no plantear graves problemas. Supongamos que formamos parte de un gran grupo de personas que se reúnen aleatoriamente y que juegan al juego de las dos monedas una vez con cada uno de los adversarios. Supongamos que inicialmente todo el mundo elige el único equilibrio de Nash con estrategias mixtas: ( Finalmente, algunos de los jugadores se cansan de elegir la estrategia mixta y deciden jugar cara o cruz todo el tiempo. Si el número de personas que decide jugar cara todo el tiempo es igual al que decide jugar cruz, apenas ha cambiado nada en el problema de elección de los agentes: cada uno de ellos seguirá creyendo racionalmente que hay una probabilidad del 50% de que su adversario juegue cara y una probabilidad del 50% de que juegue cruz. i, i ). De esta manera, cada miembro de la población elige una estrategia pura, pero en un juego dado los jugadores no tienen forma alguna de saber qué estrategia pura elige su adversario. Esta interpretación de las probabilidades de las estrategias mixtas como frecuencias observadas es habitual en la elaboración de modelos de la conducta animal. Los equilibrios de las estrategias mixtas también pueden interpretarse analizando la elección de una determinada persona entre jugar cara y jugar cruz en un juego que sólo se juega una vez. Cabe imaginar que esta elección depende de factores idiosincrásicos que no pueden ser averiguados por los adversarios. Supongamos, por ejemplo, que jugamos cara si nuestro "estado de ánimo" nos pide que juguemos cara, y cruz si nuestro "estado de ánimo" nos pide que juguemos cruz. Es posible que nosotros podamos observar nuestro propio estado de ánimo, pero nuestro adversario no puede. Por lo tanto, desde el punto de vista de cada jugador, la estrategia de la otra persona es aleatoria, aun cuando la suya sea determinista. Lo importante de la estrategia mixta de un jugador es la incertidumbre que crea en los demás jugadores. 15.6 Juegos repetidos Hemos indicado antes que no era correcto esperar que el resultado de un juego repetido en el que intervenían los mismos jugadores fuera simplemente una repetición del juego que sólo se juega una vez, ya que el espacio de las estrategias del juego repetido es mucho mayor: cada uno de los jugadores puede determinar su elección en un punto en función de toda la historia del juego hasta ese punto. Dado que nuestro adversario puede modificar su conducta en función de la historia de nuestras elecciones, debemos tener en cuenta esta influencia cuando tomamos nuestras propias elecciones. Analicemos este caso en el contexto del sencillo juego del dilema del prisionero antes descrito. En este caso, a los dos jugadores les interesa "a largo plazo" tratar de conseguir la solución (cooperar, cooperar), por lo que podría ser razonable que uno de ellos intentara "transmitir" al otro la información de que está dispuesto a Juegos repetidos / 317 "portarse bien" y cooperar en la primera ronda del juego. Naturalmente, al otro jugador le interesa a corto plazo ir a la suya, pero ¿y a largo plazo? Podría razonar que si va a la suya, el otro podría perder la paciencia e ir simplemente a la suya a partir de entonces. Por lo tanto, el segundo jugador podría salir perdiendo a largo plazo si eligiera la estrategia óptima a corto plazo. Este razonamiento se basa en el hecho de que el movimiento que realizo ahora puede tener repercusiones en el futuro, es decir, la estrategia que elija el otro jugador en el futuro puede depender de las que elija yo ahora. Preguntémonos si la estrategia (cooperar, cooperar) puede ser un equilibrio de Nash del dilema del prisionero repetido. Consideremos, en primer lugar, el caso en el que cada uno de los jugadores sabe que el juego se repetirá un número fijo de veces. Examinemos el razonamiento que realizan los jugadores poco antes de la última ronda de jugadas. Cada uno de ellos razona que esta ronda es un juego que sólo se juega una vez. Dado que ya no es posible realizar más movimientos, es válida la lógica habitual del equilibrio de Nash y las dos partes van a la suya. Consideremos ahora el penúltimo movimiento. En este caso, parece que a los dos jugadores les compensaría cooperar para transmitirse mutuamente la información de que son "buenos chicos" y de que cooperarán de nuevo en el siguiente y último movimiento. Pero acabamos de ver que cuando llega el momento de realizar la última jugada, cada uno de los jugadores desea ir a la suya. Por lo tanto, no tiene ventaja alguna cooperar en el penúltimo movimiento: en la medida en que los dos jugadores crean que el otro irá a la suya en el último movimiento, no tiene ventaja alguna tratar de influir en la conducta futura portándose bien en el penúltimo. La lógica de la inducción retrospectiva también es válida en el caso de los movimientos antepenúltimos, etc. En un dilema del prisionero repetido en el que se conoce el número de repeticiones, el equilibrio de Nash es ir a la suya en todas las rondas. La situación es bastante diferente en los juegos repetidos en los que el número de repeticiones es infinita. En este caso, en todas las fases se sabe que el juego se repetirá al menos una vez más, por lo que la cooperación puede tener algunas ventajas. Veamos cómo funciona en el caso del dilema del prisionero. Consideremos un juego que consiste en un número infinito de repeticiones del dilema del prisionero antes descrito. En este juego repetido las estrategias son secuencias de funciones que indican si cada uno de los jugadores cooperará o irá a la suya en una determinada fase en función de la historia del juego hasta esa fase. Las ganancias del juego repetido son las sumas descontadas de las ganancias correspondientes a cada una de las fases; es decir, si un jugador obtiene unas ganancias en el momento t de u-, sus ganancias en el juego repetido son I:::o utf (1 + r)t, donde res la tasa de descuento. Siempre que la tasa de descuento no sea demasiado elevada, es posible afirmar que existe un par de estrategias que constituyen un equilibrio de Nash tales que a 318 / LA TEORÍA DE LOS JUEGOS (C. 15) cada uno de los jugadores le interesa cooperar en cada una de las fases. De hecho, es fácil mostrar un ejemplo explícito de ese tipo de estrategias. Examinemos la siguiente: "cooperar en el presente movimiento a menos que el otro jugador vaya a la suya en el anterior. Si éste va a la suya en el movimiento anterior, entonces ir a la suya siempre". Esta estrategia se denomina a veces estrategia de castigo, por razones evidentes: si un jugador va a la suya, será castigado siempre con unas bajas ganancias. Para demostrar que un par de estrategias de castigo constituye un equilibrio de Nash, tenemos que demostrar simplemente que si uno de los jugadores elige esta estrategia, el otro no puede hacer otra cosa mejor que elegirla también. Supongamos que los jugadores han cooperado hasta el movimiento T y veamos qué ocurriría si uno de ellos decidiera ir a la suya ahora. Recurriendo a las cifras del ejemplo del dilema del prisionero expuesto en la página 307, obtendría unas ganancias inmediatas de 4, pero también se vería condenado a una corriente infinita de pagos de 1. El valor descontado de esa corriente de pagos es 1 / r, por lo que sus ganancias esperadas totales de ir a la suya son 4 + 1 / r, Por otra parte, las ganancias que espera obtener si continúa cooperando son 3 / r. Se prefiere continuar cooperando en la medida en que 3 / r > 4 + 1 / r, lo que se reduce a exigir que r < 1/2. En la medida en que se satisfaga esta condición, la estrategia de castigo constituye un equilibrio de Nash: si una de las partes la elige, también querrá elegirla la otra y ninguna de ellas puede salir ganando si elige unilateralmente otra estrategia. Este razonamiento es bastante sólido. El argumento es esencialmente el mismo en el caso de cualquier ganancia que sea superior a la que se deriva de la estrategia (ir a la suya, ir a la suya). Existe un famoso resultado que se conoce con el nombre de teorema de Folk y que dice precisamente eso: en un dilema del prisionero repetido, cualquier ganancia mayor que la que se recibe si las dos partes van sistemáticamente a la suya puede constituir un equilibrio de Nash. La demostración es más o menos parecida a la que acabamos de realizar aquí. Ejemplo: Mantenimiento de un cártel Consideremos un sencillo duopolio repetido que genera los beneficios (rr e, 1r e) si las dos empresas deciden jugar a un juego de Cournot y (1rj, 7rj) si producen la cantidad que maximiza sus beneficios conjuntos, es decir, si actúan como un cártel. Es bien sabido que los niveles de producción que maximizan los beneficios conjuntos normalmente no son equilibrios de N ash en los juegos que tienen lugar en un solo periodo: cada uno de los productores tiene un incentivo para producir más si cree que el otro mantendrá constante su nivel de producción. Sin embargo, en la medida Estrategias dominantes/ 319 en que la tasa de descuento no sea demasiado elevada, la solución de la maximización conjunta de los beneficios será un equilibrio de Nash del juego repetido. La estrategia de castigo adecuada consiste en que cada una de las empresas produzca el nivel asignado por el cártel, a menos que la otra incumpla, en cuyo caso producirá siempre la cantidad correspondiente al equilibrio de Cournot. Utilizando un argumento similar al del dilema del prisionero puede demostrarse que esta estrategia es un equilibrio de Nash. 15.7 Refinamientos del equilibrio de Nash El concepto de equilibrio de Nash parece una definición bastante razonable del equilibrio de un juego. Al igual que ocurre con cualquier otro concepto de equilibrio, plantea dos cuestiones de interés inmediato: 1) ¿existe, en general, un equilibrio de Nash? y 2) ¿es único este equilibrio? Afortunadamente, la existencia no es un problema. Nash (1954) demostró cuando hay un número finito de agentes y un número finito de estrategias que puras, siempre existe un equilibrio. Naturalmente, puede ser un equilibrio en el que intervengan estrategias mixtas. Sin embargo, es muy improbable que sea único en general. Ya hemos visto que en un juego puede haber varios equilibrios de Nash. Los teóricos de los juegos han realizado enormes esfuerzos por encontrar otros criterios que pudieran útilizarse para elegir entre los equilibrios de Nash. Estos criterios se conocen con el nombre de refinamientos del concepto de equilibrio de Nash; a continuación analizamos algunos de ellos. 15.8 Estrategias dominantes Sean Ji y h las estrategias de Fila. Decimos que Ji domina estrictamente a h en el caso de Fila si las ganancias de la estrategia Ji son estrictamente mayores que las de la estrategia h. independientemente de la que elija Columna. La estrategia ft domina débilmente a la h si sus ganancias son, al menos, tan grandes en el caso de todas las elecciones de Columna y estrictamente mayores en el caso de alguna. El equilibrio basado en estrategias dominantes es una elección tal de estrategias por parte de un jugador que cada una de ellas domina (débilmente) a todas y cada una de las estrategias de que dispone ese jugador. Un juego especialmente interesante que tiene un equilibrio basado en estrategias dominantes es el dilema del prisionero, en el cual el equilibrio basado en estrategias dominantes es (ir a la suya, ir a la suya). Si creo que el otro agente cooperará, me interesa ir a la mía; y si creo que irá a la suya, también me interesa ir a la mía. 320 / LA TEORÍA DE LOS JUEGOS (C. 15) Es evidente que el equilibrio basado en estrategias dominantes es un equilibrio de Nash, pero no todos los equilibrios de Nash son equilibrios basados en estrategias dominantes. El equilibrio basado en estrategias dominantes, de existir, es una solución del juego especialmente fuerte, ya que cada uno de los jugadores tiene una única opción óptima. 15.9 Eliminación de las estrategias dominadas Cuando no existe un equilibrio basado en estrategias dominantes, hemos de recurrir a la idea de equilibrio de Nash. Pero normalmente hay más de un equilibrio de Nash. Nuestro problema estriba, pues, en tratar de eliminar algunos de los equilibrios de Nash por considerarse "poco razonables". Cuadro 15.4 Jugador B Derecha Izquierda Jugador A Arriba 2, 2 Abajo 2, o o, 2 1, 1 Es sensato pensar respecto a la conducta de los jugadores que no sería razonable que eligieran estrategias que estuvieran dominadas por otras. Eso induce a pensar que cuando nos encontramos ante un juego, debemos eliminar primero todas las estrategias que están dominadas por otras y calcular a continuación los equilibrios de Nash del juego restante. Este procedimiento se denomina eliminación de las estrategias dominadas; a veces puede dar como resultado una significativa reducción del número de equilibrios de Nash. Veamos a título de ejemplo el juego representado en el cuadro 15.4. Obsérvese que hay dos equilibrios de Nash correspondientes a estrategias puras ("arriba", "izquierda") y ("abajo", "derecha"). Sin embargo, la estrategia "derecha" domina a la estrategia "izquierda" en el caso del jugador Columna. Si el agente Fila supone que Columna nunca elegirá su estrategia dominante, el único equilibrio del juego es ("abajo", "derecha"). La eliminación de las estrategias estrictamente dominadas se considera, en general, un procedimiento aceptable para simplificar el análisis de los juegos. La elimi- Juegos consecutivos / 321 nación de las estrategias débilmente dominadas plantea más problemas; hay ejemplos en los que parece que la eliminación de estas estrategias altera significativamente la naturaleza estratégica del juego. 15.10 Juegos consecutivos Los juegos que hemos descrito hasta ahora en el presente capítulo tienen todos ellos una estructura dinámica muy sencilla: o bien son juegos que sólo se juegan una vez, o bien se trata de una secuencia repetida de juegos que sólo se juegan una vez. La estructura de la información también es muy sencilla: cada uno de los jugadores conoce las ganancias del otro, así como las estrategias de que dispone, pero no conoce de antemano la estrategia que elegirá realmente. En otras palabras, hasta ahora nos hemos limitado a analizar los juegos en los que los movimientos eran simultáneos. Cuadro 15.5 Jugador B Derecha Izquierda Jugador A Arriba 1, 9 l, 9 Abajo o, o 2, 1 Pero muchos juegos de interés carecen de esta estructura. En muchas situaciones, hay, al menos algunas elecciones que son consecutivas y uno de los jugadores puede saber lo que ha elegido el otro antes de tener que elegir él. El análisis de este tipo de juegos tiene mucho interés para los economistas, ya que muchos juegos económicos poseen esta estructura: un monopolista puede observar la conducta de demanda de los consumidores antes de producir, o un duopolista puede observar la inversión de capital de su adversario antes de tomar sus propias decisiones respecto al nivel de producción, etc. El análisis de este tipo de juegos exige algunos nuevos conceptos. Consideremos, a título de ejemplo, el sencilio juego cuya matriz aparece en el cuadro 15.5. Es fácil verificar que en este juego hay dos equilibrios de Nash correspondientes a estrategias puras: ("arriba", "izquierda") y ("abajo", "derecha"). En esta descripción está implícita la idea de que los dos jugadores eligen simultáneamente, 322 / LA TEORÍA DE LOS JUEGOS (C. 15) sin saber lo que ha elegido el adversario. Pero supongamos que analizamos el juego en el que Fila debe elegir primero y Columna elige después de observar la conducta de Fila. Para describir un juego consecutivo de este tipo es necesario introducir un nuevo instrumento, el árbol del juego, que es simplemente un diagrama que indica las opciones que tiene cada uno de los jugadores en cada momento del tiempo. Como se muestra en la figura 15.1, las ganancias de cada uno de los jugadores se indican en las "ramas" del árbol. Este árbol forma parte de una descripción del juego en forma extensiva. Figura 15.1 1,9 1,9 o.o 2,1 El árbol de un juego. Esta figura muestra las ganancias del juego anterior en el que Fila mueve primero. Lo bueno de la representación gráfica de un juego en forma de árbol se halla en que indica su estructura dinámica, el hecho de que unas opciones se eligen antes que otras. Una opción del juego corresponde a una opción de una rama del árbol. Una vez elegida, los jugadores se encuentran en un subjuego formado por las estrategias y ganancias de que disponen a partir de ese momento. Es sencillo calcular los equilibrios de Nash en cada uno de los posibles subjuegos, especialmente en este caso, debido a que el ejemplo es muy sencillo. Si Fila elige "arriba", elige, de hecho, el sencillísimo subjuego en el que le corresponde a Columna hacer el único movimiento restante. A Columna le da igual elegir cualquiera de sus Juegos consecutivos / 323 dos movimientos, por lo que Fila acabará claramente obteniendo una ganancia de 1 si elige "arriba". Si Fila elige "abajo", lo óptimo para Columna será elegir "derecha", lo que reportará a Fila una ganancia de 2. Dado que 2 es mayor que 1, Fila obtendrá un resultado claramente mejor eligiendo "abajo" que eligiendo "arriba". Por lo tanto, el equilibrio razonable de este juego es ("abajo", "derecha"). Éste es, por supuesto, uno de los equilibrios de Nash en el caso del juego en el que los movimientos son simultáneos. Si Columna anuncia que elegirá "derecha", la respuesta óptima de Fila es elegir "abajo" y si anuncia que elegirá "abajo", la respuesta óptima de Columna es elegir "derecha". Pero ¿qué ocurre con el otro equilibrio ("arriba", "izquierda")? Si Fila cree que Columna elegirá "izquierda", su elección óptima es, sin duda, "arriba". Pero ¿qué ocurre si Fila cree que Columna elegirá, de hecho, "izquierda"? Una vez que Fila elige "abajo", para Columna la elección óptima del subjuego resultante es "derecha". La elección de "izquierda" en este punto no es una elección de equilibrio en el subjuego relevante. En este ejemplo, sólo uno de los dos equilibrios de Nash satisface la condición de que debe ser no sólo un equilibrio global sino también un equilibrio en cada uno de los subjuegos. Un equilibrio de Nash que posee esta propiedad se conoce con el nombre de equilibrio perfecto en todos los subjuegos. Es bastante fácil calcular los equilibrios perfectos en todos los subjuegos, al menos en el tipo de juegos que hemos venido examinando. Basta hacer una "inducción retrospectiva" a partir del último movimiento del juego. El jugador al que le toca hacer el último movimiento tiene ante sí un sencillo problema de optimización, sin ramificaciones estratégicas, por lo que es fácil de resolver. El jugador al que le toca hacer el penúltimo movimiento puede mirar retrospectivamente y ver cómo responderá a sus elecciones el jugador que ha de hacer el último movimiento, etc. El tipo de análisis es similar al de la programación dinámica (véase el capítulo 19, página 420). Una vez que se ha comprendido el juego mediante este método de la inducción retrospectiva, los agentes lo juegan mirando hacia adelante.2 La forma extensiva del juego también es capaz de reflejar las situaciones en las que unos movimientos son consecutivos y otros simultáneos. El concepto necesario es el de conjunto de información de un agente, que es el conjunto de todos los nudos del árbol que el agente no puede distinguir. Por ejemplo, el juego de movimientos simultáneos descrito al comienzo de este apartado puede representarse por medio del árbol de la figura 15.2. En esta figura, el área sombreada indica que Columna 2 Compárese con lo que decía Kierkegaard (1938): "Es absolutamente cierto, como dicen los filósofos, que la vida debe comprenderse retrospectivamente. Pero se olvidan de la otra proposición, que debe vivirse mirando hacia adelante"[465]. 324 / LA TEORÍA DE LOS JUEGOS (C. 15) no puede distinguir entre todas las opciones cuáles son las que ha elegido Fila en el momento en que le toca a Columna elegir la suya. Por lo tanto, es exactamente igual que si se eligieran simultáneamente. Figura 15.2 1,9 1,9 Fila o.o 2,1 Conjunto de información. Ésta es la forma extensiva del juego inicial de movimientos simultáneos. El conjunto de información sombreado indica que Columna no sabe qué opción ha elegido Fila cuando elige la suya. Por lo tanto, la forma extensiva de un juego puede utilizarse para recoger todo lo que se incluye en la forma estratégica más la información sobre la secuencia de elecciones y los conjuntos de información. En este sentido, es un concepto más poderoso que la forma estratégica, ya que contiene información más detallada sobre la interdependencia estratégica de los agentes. Es la presencia de esta información adicional la que contribuye a eliminar algunos de los equilibrios de Nash por considerarse "poco razonables". Ejemplo: Un sencillo modelo de negociación Dos jugadores, A y B, tienen 100 pesetas para repartirse entre ellos. Acuerdan negociar el reparto durante tres días como máximo. El primer día, A, hace una oferta, el segundo B hace una contraoferta y el tercero A hace la oferta final. Si no llegan a un acuerdo en tres días, ninguno de los dos jugadores obtiene nada. Juegos consecutivos / 325 · El grado de impaciencia de A y B es distinto: A descuenta las ganancias en el futuro a una tasa de a al día y B a una tasa de /3. Supongamos, por último, que si un jugador se muestra indiferente entre dos ofertas, aceptará la que más prefiera su adversario. La idea es que el adversario podría ofrecer una cantidad arbitrariamente pequeña que hiciera que el jugador prefiriera estrictamente una opción y que este supuesto nos permite considerar que esa "cantidad arbitrariamente pequeña" es igual a cero. Como veremos, este juego de negociación tiene un único equilibrio perfecto en todos los subjuegos. 3 Figura 15.3 Un juego de negociación. La línea de trazo grueso conecta los resultados de equilibrio de los subjuegos. El punto de la línea más alejada del origen es el equilibrio perfecto en todos los subjuegos. Como hemos sugerido antes, comenzamos el análisis por el final del juego, justamente antes del último día. En este punto, A puede hacer a B una oferta consistente en "o lo tomas, o lo dejas". Evidentemente, lo óptimo para A en este punto es ofrecer a B la menor cantidad posible que aceptaría, la cual es, por hipótesis, cero. Por lo tanto, si el juego dura, de hecho, tres días, A recibiría 100 y B cero (es decir, una cantidad arbitrariamente pequeña). Examinemos ahora �l movimiento anterior, es decir, cuando le toca a B proponer un reparto. En este punto, B debería darse cuenta de que A puede garantizarse una ganancia de 100 en el siguiente movimiento rechazando simplemente la oferta de B. Para A recibir cien pesetas en el siguiente periodo vale a en este periodo, por lo que es seguro que rechazará cualquier oferta inferior a a. B prefiere, ciertamente, 100- a 3 Se trata de una versión simplificada del modelo de negociación de Rubinstein; para una información más detallada véase la bibliografía que se presenta al final del capítulo. 326 / LA TEORÍA DE LOS JUEGOS (C. 15) en este periodo a cero en el siguiente, por lo que lo racional sería que ofreciera a a A, oferta que A aceptaría. Por lo tanto, si el juego termina en el segundo movimiento, A obtiene a y B 100 - a. Examinemos ahora el primer día. En este punto, A ha de hacer la oferta y se da cuenta de que B puede recibir 100 - a esperando simplemente hasta el día siguiente. Por lo tanto, A debe ofrecer un resultado que tenga al menos este valor actual para B a fin de evitar un retraso. Por lo tanto, ofrece ,8(100 - a) a B. B encuentra aceptable (sin más) esta oferta y termina el juego. El resultado final es que el juego termina en el primer movimiento: A recibe 100 - ,8(100 - a) y B recibe ,8(100 - a). La figura 15.3A describe este proceso en el caso en el que a = ,B < 100. La línea diagonal más alejada del origen muestra las posibles pautas de ganancias del primer día, a saber, todas las ganancias de la forma x A + x B = 100. La siguiente línea diagonal en sentido descendente muestra el valor actual de las ganancias si el juego concluye en el segundo periodo: XA + XB = a. La línea diagonal más cercana al origen muestra el valor actual de las ganancias si el juego concluye en el tercer periodo; la ecuación de esta línea es x A + x B = a2. La senda en forma de escalera muestra las divisiones mínimas aceptables correspondientes a cada periodo, que conducen al equilibrio final perfecto en todos los subjuegos. La figura 15.38 muestra cómo es este mismo proceso cuando la negociación consta de más fases. Es inevitable que desplacemos el horizonte hasta el infinito y nos preguntemos qué ocurre en un juego infinito. En ese caso, la división del equilibrio perfecto del subjuego es 1 - ,B ganancias de A = ---4 1 - . ganancias de B Q/J = ,8(1 - a) . 1-a ,B Obsérvese que, si a = 1 y ,B = l, el jugador A recibe todas las ganancias, de acuerdo a la máxima expresada en el Nuevo Testamento: "Pero la paciencia ha de ir acompañada de obras [subjuegos] perfectas" (Santiago 1, 4). 15.11 Juegos repetidos y perfección de los subjuegos La idea de la perfección de los subjuegos elimina los equilibrios de N ash en los que los jugadores hacen amenazas que no son creíbles, es decir, que no les interesa llevar a cabo. Por ejemplo, la estrategia de castigo antes descrita no es un equilibrio perfecto en todos los subjuegos. Si uno de los jugadores se aleja, de hecho, de la senda (cooperar, cooperar), al otro no le interesa necesariamente ir siempre a la suya en respuesta. Es posible que parezca razonable castigar hasta cierto punto al otro jugador por ir a la suya, pero el castigo sistemático parece extremo. Juegos con información incompleta / 327 Una estrategia algo menos rigurosa es la que se conoce con el nombre de "ojo por ojo": uno de los jugadores comienza cooperando en la primera jugada y en las siguientes elige lo que haya elegido su adversario en la jugada anterior. En esta estrategia, uno de los jugadores es castigado por ir a la suya, pero sólo una vez. En este sentido, el "ojo por ojo" es una estrategia de "perdón". Aunque la estrategia de castigo no es perfecta en todos los subjuegos en el caso del dilema del prisionero repetido, hay estrategias que pueden dar lugar a la solución de cooperación que sí lo son. Estas estrategias no son fáciles de describir, pero se parecen al código del honor de una academia militar: cada uno de los jugadores acuerda castigar al otro si va a la suya y castigarlo también si no castiga al otro por ir a la suya, etc. El hecho de que una persona sea castigada si no castiga a otra que va a la suya es lo que hace que el castigo dé lugar a un equilibrio perfecto en todos los subjuegos. Desgraciadamente, este mismo tipo de estrategias puede dar lugar a muchos otros resultados en el dilema del prisionero repetido. Según el teorema de Folk, casi todas las distribuciones de la utilidad de un juego que sólo se juega una vez pero de forma repetida pueden ser equilibrios del juego repetido. Este exceso de oferta de equilibrios plantea problemas. En general, cuanto mayor sea el espacio de las estrategias, más equilibrios habrá, ya que los jugadores tendrán más recursos para "amenazar" con tomar represalias en caso de que alguno vaya a la suya con un conjunto dado de estrategias. Para eliminar los equilibrios poco recomendables, es necesario encontrar algún criterio para eliminar estrategias. Un criterio natural consiste en eliminar las que sean "demasiado complejas". Aunque se han realizado algunos avances en este sentido, la idea de la complejidad es escurridiza y ha resultado difícil encontrar una definición enteramente satisfactoria. 15.12 Juegos con información incompleta Hasta ahora hemos venido investigando los juegos con información completa. En concreto, hemos supuesto que cada uno de los agentes conocía las ganancias del otro y sabía que éste lo sabía, etc. En muchas situaciones, este supuesto no es correcto. Si uno de los agentes no conoce las ganancias del otro, el equilibrio de Nash no tiene mucho sentido. Sin embargo, existe una manera de examinar los juegos con información incompleta que permite analizar sistemáticamente sus propiedades y que se debe a Harsanyi (1967). La clave del enfoque de Harsanyi se halla en subsumir toda la incertidumbre que pueda tener uno de los agentes sobre otro en una variable conocida como tipo del agente. Por ejemplo, uno de los agentes puede no estar seguro del valor que concede otro a un bien, de su aversión al riesgo, etc. Cada uno de los tipos de jugador se considera un jugador diferente y cada uno de los agentes tiene una distribución 328 / LA TEORÍA DE LOS JUEGOS (C. 15) previa de probabilidades definida con respecto a los diferentes tipos de agentes. El equilibrio de Bayes-Nash de este juego es, pues, un conjunto de estrategias de cada tipo de jugador que maximiza el valor esperado de cada uno de los tipos, dadas las estrategias seguidas por los demás. Esta definición es casi igual que la del equilibrio de Nash, con la salvedad de la incertidumbre adicional respecto al tipo al que pertenece el otro jugador. Cada uno de ellos sabe que el otro pertenece a un conjunto de posibles tipos, pero no sabe exactamente cuál es el suyo. Obsérvese que para tener una descripción completa de un equilibrio debemos tener una lista de estrategias para todos los tipos de jugadores y no sólo para los tipos reales en una determinada situación, ya que ninguno de los jugadores conoce los tipos reales de los otros y ha de tener en cuenta todas las posibilidades. En un juego en el que los movimientos son simultáneos, esta definición de equilibrio es adecuada. En un juego consecutivo, es razonable suponer que los jugadores actualizan sus expectativas sobre los tipos de los demás basándose en las acciones que han observado. Normalmente, suponemos que esta actualización se hace de una manera coherente con la regla de Bayes.4 Así, por ejemplo, si uno de los jugadores observa que el otro ha elegido una estrategia s, debe revisar sus expectativas sobre el tipo de éste averiguando las probabilidades de que los diferentes ti pos elijan s. Ejemplo: Una subasta en la que las ofertas son secretas Consideremos una sencilla subasta de un artículo en la que las ofertas son secretas y en la que participan dos postores. Cada uno de ellos hace una oferta independiente sin conocer la del otro y el artículo se adjudica al que hace la mayor oferta. Cada uno de los postores conoce su propia valoración del artículo que está subastándose, v, pero no conoce la del otro. Sin embargo, cada uno de ellos cree que la valoración que hace el otro del artículo está distribuida uniformemente entre O y 1 (y cada uno de ellos sabe que cada uno lo cree, etc.). En este juego, el tipo del jugador es simplemente su valoración. Por lo tanto, el equilibrio de Bayes-Nash de este juego será una función, o(v), que indique la oferta óptima, o, de un jugador de tipo v. Dado el carácter simétrico del juego, buscamos un equilibrio en el que cada uno de los jugadores siga una estrategia idéntica. Es natural hacer la conjetura de que la función o(v) es estrictamente creciente; es decir, los valores mayores conducen a ofertas mayores. Por lo tanto, podemos suponer que V(o) es su función inversa, por lo que nos da la valoración de una persona que ofrece o. Cuando un jugador ofrece una determinada o, su probabilidad 4 Véase el capítulo 11, página 221, para un análisis de la regla de Bayes. Juegos con información incompleta / 329 de ganar es la probabilidad de que la oferta del otro sea menor que o. Pero ésta es simplemente la probabilidad de que la valoración del otro sea menor que V(o). Dado que v está distribuido uniformemente entre O y 1, la probabilidad de que la valoración del otro jugador sea menor que V(o) es V(o). Por lo tanto, si un jugador presenta la oferta o cuando su valoración es v, su resultado esperado es (v - o)V(o) + 0[1 - V(o)]. El primer término es el excedente esperado del consumidor si presenta la oferta más baja; el segundo es el excedente nulo que recibe si su oferta es superada por otra. La oferta óptima debe maximizar esta expresión, por lo que (v - o)V' (o) - V(o) = O. Esta ecuación determina la oferta óptima para cada jugador en función de v. Dado que V(o) es, por hipótesis, la función que describe la relación entre la oferta óptima y la valoración, debe cumplirse la siguiente identidad: (V(o) - o)V' (o) = V(o) cualquiera que sea o. La solución de esta ecuación diferencial es V(o) =o+ V o2 + 2C, donde Ces una constante de integración (¡compruébelo el lectorl). Para conocer esta constante de integración, debemos observar que cuando v = O, debe cumplirse que o = O, ya que la oferta óptima cuando la valoración es O debe ser O. Introduciendo estas observaciones en la solución de la ecuación diferencial, tenemos que o= o+ he, lo que implica que C = O. Por lo tanto, V(o) = 2o, o sea, o = v /2, es un equilibrio de Bayes-Nash de la sencilla subasta. Es decir, se alcanza un equilibrio de Bayes-Nash cuando cada uno de los jugadores ofrece la mitad de su valoración. La manera en que hemos llegado a la solución de este juego es razonablemente convencional. En esencia, hemos partido de la conjetura de que la función de las ofertas óptimas podía ser invertida y hemos derivado la ecuación diferencial que debía satisfacer. Como hemos visto, la función de las ofertas resultante tenía la propiedad deseada. Un defecto de este enfoque es el hecho de que sólo muestra un equilibrio del juego bayesiano, pero podría haber en principio muchos otros. 330 / LA TEORÍA DE LOS JUEGOS (C. 15) Da la casualidad de que en este juego específico la solución que hemos calculado es única, pero no tiene por qué serlo en general. En concreto, en los juegos con información incompleta puede muy bien ocurrir que a algunos jugadores les compense tratar de ocultar su verdadero tipo. Por ejemplo, un tipo puede tratar de elegir la misma estrategia que algún otro. En esta situación, la función que relaciona el tipo con la estrategia no puede ser invertida y el análisis resulta mucho más complejo. 15.13 Análisis del equilibrio de Bayes-Nash La idea del equilibrio de Bayes-Nash es ingeniosa, pero quizá demasiado. El problema estriba en que el razonamiento en que se basa el cálculo de los equilibrios de Bayes-Nash suele ser muy complejo. Aunque tal vez sea razonable que los jugadores puramente racionales jueguen de acuerdo con la teoría de Bayes y Nash, existen grandes dudas sobre la posibilidad de que los jugadores reales puedan realizar los cálculos necesarios. Por otra parte, las predicciones del modelo plantean problemas. La opción que elige cada uno de los jugadores depende crucialmente de sus expectativas sobre la distribución de los diferentes tipos dentro de la población. Las diferentes expectativas sobre la frecuencia de los distintos tipos da lugar a una conducta óptima diferente. Dado que generalmente no observamos las expectativas de los jugadores sobre el predominio de los distintos tipos de jugadores, normalmente no podemos verificar las predicciones del modelo. Ledyard (1986) ha demostrado que cualquier pauta de juego es esencialmente un equilibrio de Bayes-Nash en el caso de alguna pauta de expectativas. El equilibrio de Nash, en su formulación original, impone una condición de coherencia a las expectativas de los agentes: sólo se permiten las expectativas que son compatibles con la conducta maximizadora. Pero tan pronto como permitimos que haya muchos tipos de jugadores con diferentes funciones de utilidad, esta idea pierde en gran parte su fuerza. Casi todas las pautas de conducta pueden ser coherentes con alguna pauta de expectativas. Notas El concepto de equilibrio de Nash se debe a Nash (1951). El concepto de equilibrio bayesiano se debe a Harsanyi (1967). Para un análisis más detallado del sencillo modelo de negociación véase Binmore y Dagupta 1987). Este capítulo es simplemente una introducción esquemática a la teoría de los juegos; la mayoría de los estudiantes querrá estudiar con mayor detalle esta materia. Afortunadamente, en los últimos años se han publicado varias obras que presentan Ejercicios / 331 un análisis más riguroso y detallado. Para algunos artículos panorámicos véase Aumann (1987), Myerson (1986), y Tirole (1988). Para algunas obras, véanse los trabajos de Kreps (1990), Binmore (1991), Myerson (1991), Rasmusen (1989) y Fudenberg y Tirole (1991). Ejercicios 15.1. Calcule todos los equilibrios de Nash del juego de las dos monedas. 15.2. En un juego del dilema del prisionero repetido un número finito de veces, hemos demostrado que era un equilibrio de Nash ir a la suya en todas las rondas. Demuestre que se trata, de hecho, del equilibrio de la estrategia dominante. 15.3. ¿Cuáles son los equilibrios de Nash del siguiente juego una vez eliminadas las estrategias dominadas? Jugador B Derecha Izquierda Arriba Jugador A Abajo 3, 3 3, o O, o o, 3 O, o 2, 2 o, 2, 1, 1 o 2 15.4. Calcule las ganancias esperadas de cada jugador en el sencillo juego de la subasta descrito en este capítulo si cada uno de los jugadores sigue la estrategia del equilibrio de Bayes- Nash, condicionada a su valor v. 15.5 Considere la matriz del juego adjunto. (a) Si ("arriba", "izquierda") es un equilibrio de la estrategia dominante, ¿qué desigualdades deben cumplírse entre a, ... , h? (b) Si ("arriba", "izquierda") es un equilibrio de Nash, ¿cuál de las desigualdades anteriores debe satisfacerse? (c) Si ("arriba", "izquierda") es un equilibrio de la estrategia dominante, ¿debe ser un equilibrio de Nash? 332 / LA TEORÍA DE LOS JUEGOS (C. 15) Jugador B Derecha Izquierda Jugador A Arriba a, b e, d Abajo e, f g, h 15.6. Dos adolescentes californianos, Bill y Ted, están jugando al juego de la muerte. Bill conduce su coche de carreras en dirección sur por una carretera de un solo carril y Ted en sentido norte por la misma carretera. Cada uno de ellos tiene dos estrategias: mantener la dirección o virar bruscamente. Si uno de ellos decide virar bruscamente, queda mal; si los dos viran bruscamente, los dos quedan mal. Sin embargo, si los dos deciden mantener la dirección, los dos mueren. La matriz de ganancias del juego de la muerte es la siguiente: Jugador B Derecha Izquierda Jugador A Arriba Abajo -3, -3 o, 2 2, o 1, 1 (a) Halle todos los equilibrios correspondientes a las estrategias puras. (b) Halle todos los equilibrios correspondientes a las estrategias mixtas. (c) ¿Qué probabilidades hay de que sobrevivan los dos adolescentes? 15.7. En un duopolio simétrico y repetido, las ganancias de las dos empresas son 1r j si producen la misma cantidad que maximiza sus beneficios conjuntos y 1r e si producen la cantidad de Cournot. Las ganancias máximas que puede obtener cada uno de los jugadores si el otro decide producir la cantidad que maximiza los beneficios conjuntos es 7íd· La tasa de descuento es r. Los jugadores adoptan la estrategia de castigo de volver al juego de Cournot si cualquiera de ellos va a la suya y se aleja de la estrategia de maximización conjunta de los beneficios. ¿Qué valor puede adoptar r? Ejercicios / 333 15.8. Considere el juego adjunto: (a) ¿Cuál de las estrategias de Fila es dominada estrictamente independientemente de lo que haga Columna? (b) ¿Cuál de las estrategias de Fila es dominada débilmente? (c) ¿Cuál de las estrategias de Columna es dominada estrictamente independientemente de lo que haga Fila? (d) Si eliminamos las estrategias dominadas de Columna, ¿es dominada débilmente alguna de las estrategias de Fila? Jugador B Derecha Izquierda Arriba Jugador A 1, o 1, 2 1, 1, 1 Abajo 2, -1 o, o -3, -3 -3, -3 -1 -3, -3 15.9 Considere el siguiente juego de coordinación: Jugador B Jugador A Izquierda Derecha Arriba 2, 2 -1, -1 Abajo -1, -1 1, 1 (a) Calcule todos los equilibrios correspondientes a estrategias puras de este juego. (b) ¿Domina alguno de estos equilibrios a alguno de los otros? 334 / LA TEORÍA DE LOS JUEGOS (C. 15) (c) Suponga que Fila mueve primero y se compromete a elegir o bien "arriba", o bien "abajo". ¿Siguen siendo las estrategias que ha descrito antes equilibrios de Nash? (d) ¿Cuáles son los equilibrios perfectos en todos los subjuegos de este juego? 16. EL OLIGOPOLIO El oligopolio es el estudio de la interdependencia de un pequeño número de empresas en el mercado. El estudio moderno de esta materia se basa casi enteramente en la teoría de los juegos analizada en el capítulo anterior. Se trata, por supuesto, de una evolución muy natural. Los conceptos de la teoría de los juegos han esclarecido significativamente muchas de las primeras especificaciones ad hoc de las interdependencias estratégicas del mercado. En el presente capítulo analizaremos la teoría del oligopolio principal, aunque no exclusivamente, desde esta perspectiva. 16.1 El equilibrio de Coumot Comenzamos con el modelo clásico del equilibrio de Coumot, ya mencionado a título de ejemplo en el capítulo anterior. Consideremos el caso de dos empresas que producen un bien homogéneo, que tienen los niveles de producción, Yt e Y2, y, por lo tanto, una producción agregada de Y = Yt +in- El precio de mercado correspondiente a este nivel de producción (la función inversa de demanda) es p(Y) p(y1 + y2), La empresa i tiene la siguiente función de costes: ci(Yi), siendo i = 1, 2. El problema de maximización de la empresa 1 es = max 1r1 (y1, y2) Yl = p(y1 + Y2)Y1 - ci (YJ). Evidentemente, los beneficios de la empresa 1 dependen de la cantidad de producción que elija la 2, y para tomar una decisión documentada la empresa 1 debe predecir el nivel de producción que· elegirá la 2. Éste es exactamente el tipo de consideración que interviene en un juego abstracto: cada uno de los jugadores debe adivinar las elecciones de los demás. Es natural concebir, pues, el modelo de Cournot como un juego que sólo se juega una vez: el beneficio de la empresa i es su ganancia y el espacio de estrategias de esta empresa es simplemente las cantidades posibles que puede producir. Por lo tanto, un equilibrio de Nash (correspondiente a estrategias puras) es un conjunto de niveles de producción (yj, y2) en el que cada una de las empresas 336 / EL OLIGOPOLIO (C. 16) elige el nivel de producción que maximiza sus beneficios, dadas sus expectativas sobre la elección de la otra empresa, y las expectativas de cada una de las empresas sobre la elección de la otra son, de hecho, correctas. Suponiendo que existe un- óptimo interior para cada una de las empresas, eso significa que un equilibrio de Nash y Cournot debe satisfacer las dos condiciones de primer orden siguientes: 87í} (y}, a Yl Y2) = P ( in + Y2 ) + P '( Yl + Y2 ) in - / C1 ( Yl ) =0 81r2(Y1,Y2) = P ( Yl + Y2 ) + P '( Yl + Y2 ) Y2 - c2'( Yl ) = O. a Y2 Las condiciones de segundo orden correspondientes a cada una de las empresas tienen la forma siguiente: a21r -2 8yi = 2p' (Y) + p" (Y)yi - e�' (yi) ::; O siendo i = 1, 2 donde Y= Yl + Y2· La condición de primer orden de la empresa 1 determina su elección óptima de su nivel de producción en función de su expectativa sobre el nivel de producción que elegirá la 2; esta relación se conoce con el nombre de curva de reacción de la empresa 1: muestra cómo reaccionará esta empresa dadas sus diferentes expectativas sobre la elección de la empresa 2. Suponiendo que existe una regularidad suficiente, la curva de reacción de la empresa 1, Ji (Y2), viene definida implícitamente por la siguiente identidad: 81r1 (f1 (y2), y2) ªYl = O. Para averiguar cómo altera óptimamente la empresa 1 su nivel de producción cuando cambian sus expectativas sobre el de la 2, diferenciamos esta identidad y despejamos !{ (y2): ) __ 821r1/8Y18Y2 !'( 1 Y1 82 1r1 ¡a Y12 El denominador, como es habitual, es negativo debido a las condiciones de segundo orden, por lo que la pendiente de la curva de reacción depende del signo de la derivada parcial cruzada. Es fácil ver que es El equilibrio de Cournot / 337 Figura 16.1 de reacción de t1(y2) = Curva la empresa 1 Y, Las curvas de reacción. La intersección de las dos curvas de reacción es un equilibrio de Cournot y Nash. Si la curva inversa de demanda es cóncava o, al menos, no es "demasiado" convexa, esta expresión será negativa, lo que indica que la curva de reacción de Coumot de la empresa 1 tendrá, por lo general, pendiente negativa. La figura 16.1 muestra un ejemplo representativo. Como veremos más adelante, muchas de las características importantes de la interdependencia de los duopolios dependen de la pendiente de las curvas de reacción, la cual depende a su vez de la derivada parcial cruzada del beneficio con respecto a las dos variables de elección. Si éstas son cantidades, el signo "natural" de dicha derivada parcial será negativo. En este caso, decimos que Y1 e Y2 son sustitutivos estratégicos. Si el signo es positivo, estamos ante un caso de complementarios estratégicos. Más adelante veremos un ejemplo de estas distinciones. La estabilidad del sistema Aunque hemos tenido buen cuidado en hacer hincapié en que el juego de Coumot es un juego que sólo se juega una vez, el propio Coumot lo concibió en términos más dinámicos. El modelo tiene, de hecho, una interpretación dinámica natural (si bien algo sospechosa). Supongamos qµe pensamos en un proceso de aprendizaje en el que cada una de las empresas refina sus expectativas sobre la conducta de la otra observando el nivel de producción que elige en realidad. Dada una pauta arbitraria de niveles de producción en el momento O, (y�, y�), la empresa 1 supone que la 2 continuará produciendo y� en el periodo 1 y, por lo 338 / EL OLIGOPOLIO (C. 16) tanto, elige el nivel de producción rnaxirnizador del beneficio coherente con esta = Ji (yg). La empresa 2 observa esta elección y supone suposición, a saber, En que la 2 mantendrá este nivel de producción, por lo que elige y� = general, el nivel de producción que elige la empresa i en el periodo t viene dado por Yi t Yi = Yi h<Yi ). fi ( YJt-1) · De esta manera tenernos una ecuación en diferencias que relaciona los niveles de producción y que da lugar a una telaraña corno la que muestra la figura 16.1. En el caso mostrado, la curva de reacción de la empresa 1 es más inclinada que la de la 2 y la telaraña converge en el equilibrio de Cournot y Nash. Decirnos, pues, que el equilibrio mostrado es estable. Si la curva de reacción de la empresa 1 fuera más plana que la de la 2, el equilibrio sería inestable. Si imaginarnos que las empresas ajustan su nivel de producción con el fin de aumentar los beneficios, suponiendo que la otra empresa mantiene fijo el suyo, tenernos un modelo dinámico algo distinto, que nos lleva a un sistema dinámico de la forma siguiente: dy1 = dt ai dy2 _ dt - ª2 [B1q(y1,Y2)] By1 [B1r2(Y1, Y2)] By2 · En este caso, los parámetros a1 > O y a2 > O indican la velocidad del ajuste. Una condición suficiente para la estabilidad local de este sistema dinámico es la siguiente: B21r1 By¡ B21r2 B21r1 8y18y2 (16.1) > O. B21r2 cfy-¡éfin. By� Esta condición es "casi" una condición necesaria para la estabilidad; el problema se halla en el hecho de que el determinante puede ser cero, aun cuando el sistema dinámico sea localmente estable. Prescindimos de las complicaciones que plantea la consideración de estos casos límites. Esta condición relativa al determinante resulta sumamente útil para obtener resultados de estática comparativa. Debe hacerse hincapié, sin embargo, en que el proceso de ajuste postulado es bastante ad hoc. Cada una de las empresas espera que la otra mantenga constante su nivel de producción, aunque ella misma espera alterar el suyo. Este tipo de expectativas incoherentes constituyen un anatema en la teoría de los juegos. El problema estriba en que no es posible dar una interpretación dinámica a un juego de Cournot que sólo se juega una vez; para analizar la dinámica de un juego que tiene lugar en muchos periodos, hay que recurrir, en realidad, al tipo de análisis de los juegos repetidos que vimos en el capítulo anterior. A pesar de Estática comparativa / 339 esta objeción, es posible que los sencillos modelos dinámicos como el que acabamos de ver tengan alguna validez empírica. Probablemente las empresas necesitarán experimentar para saber cómo responde el mercado a sus decisiones y el proceso dinámico de ajuste antes descrito puede concebirse como un sencillo modelo que describe este proceso de aprendizaje. 16.2 Estática comparativa Supongamos que a es un parámetro que desplaza la función de beneficios de la empresa 1. El equilibrio de Cournot viene descrito por las condiciones siguientes: 81r1 (YJ (a), y2(a), a) = 0 ªYl 81r2(Y1 (a), y2(a)) 8y2 = O. Diferenciando estas ecuaciones con respecto a a, tenemos el siguiente sistema: Aplicando la regla de Cramer (capítulo 26, página 559), tenemos que a21r1 -71y¡oa 8y1 ªª o a21r1 8y1BY2 a21r2 a �u? a21r1 8y¡ Yl Y2 a21r2 a21r2 8y18y2 8y� El signo del denominador depende de la condición de estabilidad de (16.1); suponemos que es positivo. El signo del numerador viene determinado por a21r1 a21r2 - 8y18a 8y� · El segundo término de esta expresión es negativo en razón de la condición de segundo orden para la maximización del beneficio. Por lo tanto, . aYI . a21r1 signo de - a = signo de . a Yl a a a 340 / EL OLIGOPOLIO (C. 16) Esta condición establece que para averiguar cómo afecta una variación de los beneficios al nivel de producción de equilibrio, basta calcular la derivada parcial cruzada 821ri/8y8a. Apliquemos este resultado al modelo del duopolio. Supongamos que a es igual al coste marginal (constante) y que los beneficios vienen dados por 1r1 (y1, Y2, a) = p(y1 + Y2)Y1 - ªY1 · En ese caso, 821r1/8y18a = -1. Eso significa que el aumento del coste marginal de la empresa 1 reduce el nivel de producción de equilibrio de Cournot. 16.3 Varias empresas La consideración de la existencia de n empresas no altera el modelo de Cournot. En este caso, la condición de primer orden de la empresa i se convierte en p(Y) + p'(Y)yi donde Y = = c:(yi), (16.2) Li Yi. Es útil reordenar esta ecuación para que adopte la forma siguiente: p(Y) [ 1 + :: � l = 0:(y;). Definiendo Si = yi/Y, que es la proporción de la producción de la industria correspondiente a la empresa i, la expresión anterior se convierte en o sea, p(Y) [ 1 + :i] = c;(yi), (16.3) donde E es la elasticidad de la demanda de mercado. Esta última ecuación muestra el sentido en el que el modelo de Cournot se halla, en cierta medida, "entre" el caso del monopolio y el de la competencia pura. Si Si = 1, tenemos exactamente la condición de monopolio y a medida que si tiende a cero, de tal manera que cada una de las empresas tiene una cuota infinitesimal del mercado, el equilibrio de Cournot se aproxima al equilibrio competitivo.1 1 De hecho, ha de tenerse cuidado con estas vagas afirmaciones, ya que dependen en gran parte de cómo tienda exactamente a cero la cuota de cada empresa. Para una especificación coherente, véase Novshek (1980). Varias empresas / 341 Existe un par de casos especiales de (16.2) y (16.3) que son útiles para poner ejemplos. Supongamos, en primer lugar, que cada una de las empresas tiene unos costes marginales constantes de c., En ese caso, sumando los dos miembros de la ecuación correspondientes a las n empresas, tenemos que n np(Y) + p'(Y)Y = � Ci i=l Por lo tanto, la producción agregada de la industria depende únicamente de la suma de los costes marginales, no de su distribución entre las empresas.2 Si todas las empresas tienen el mismo coste marginal constante e, en un equilibrio simétrico si = 1/n, y podemos formular esta ecuación de la manera siguiente: p(Y) [1 + _2_] nE = c. (16.4) Si, además, E es constante, esta ecuación muestra que el precio es un margen constante sobre el coste marginal. En este sencillo caso, es evidente que a medida que n--+ oo, el precio debe tender hacia el coste marginal. El bienestar Hemos visto anteriormente que una industria monopolística produce una cantidad ineficientemente baja, ya que el precio es superior al coste marginal. Lo mismo ocurre en una industria de Cournot. Una gráfica manera de mostrar el carácter de la distorsión es preguntarse qué maximiza una industria de Cournot. Como hemos visto anteriormente, el área situada debajo de la curva de demanda, U(Y) = p(x)dx, es una medida razonable de los beneficios totales en algunas circunstancias. Aplicando esta definición, puede demostrarse que el nivel de producción correspondiente a un equilibrio simétrico de Cournot con costes marginales constantes maximiza la siguiente expresión: Jr W(Y) = [p(Y) - cY] + (n - l)[U(Y) - cY]. La demostración consiste simplemente en diferenciar esta expresión con respecto a Y y observar que satisface la ecuación (16.4) (supondremos que se satisfacen las condiciones relevantes de segundo orden). En general, queremos que una industria maximice la utilidad menos los costes. Una industria competitiva lo hace, de hecho, mientras que un monopolio maximiza 2 Naturalmente, estamos suponiendo que hay una solución interior. Si los costes marginales son demasiado diferentes, algunas empresas no querrán producir en condiciones de equilibrio. 342 / EL OLIGOPOLIO (C. 16) simplemente los beneficios. Una industria de Cournot maximiza una suma ponderada de estos dos objetivos, en la cual los pesos dependen del número de empresas. A medida que aumenta n, se da más peso al objetivo social de la utilidad menos los costes en comparación con el objetivo privado de los beneficios. 16.4 El equilibrio de Bertrand El modelo de Cournot es atractivo por muchas de las razones esbozadas en el apartado anterior, pero no es en modo alguno el único modelo posible de la conducta oligopolística. En este modelo, el espacio de estrategias de la empresa son cantidades, pero parece igualmente natural ver qué ocurre si se elige como variable estratégica relevante el precio. Este modelo se conoce con el nombre de modelo del oligopolio de Bertrand. Supongamos, pues, que tenemos dos empresas cuyos costes marginales constantes son c1 y c2 y que se enfrentan a la curva de demanda de mercado D(p). Supongamos, para concretar, que c2 > c1 y, al igual que antes, que el producto es homogéneo, de tal manera que la curva de demanda a la que se enfrenta la empresa 1, por ejemplo, viene dada por si PI < P2 si Pl = P2 si p¡ > P2· Es decir, la empresa 1 cree que puede quedarse con todo el mercado fijando un precio más bajo que el de la empresa 2. Naturalmente, se supone que la empresa 2 piensa lo mismo. ¿Cuál es el equilibrio de Nash de este juego? Supongamos que la empresa 1 fija un P1 mayor que c2. Este precio no puede ser un equilibrio. ¿Por qué? Si la empresa 2 esperara que la 1 tomara esa decisión, elegiría un precio P2 situado entre p1 y c2. En ese caso, la empresa 1 obtendría un beneficio nulo y la 2 beneficios positivos. Del mismo modo, a cualquier precio de ese tipo, la empresa 2 decidiría no producir nada, pero la 1 podría obtener más beneficios subiendo levemente su precio. Por lo tanto, en este juego se llega al equilibrio de Nash cuando la empresa 1 fija un P1 igual a c2 y produce D(c2) unidades de producción, mientras que la empresa 2 fija un P2 2 c2 y no produce nada. Tal vez parezca poco intuitivo el hecho de que el precio sea igual al coste marginal en una industria formada por dos empresas. El problema se halla, en parte, en que el juego de Bertrand es un juego que sólo se juega una vez: los jugadores eligen los precios y concluye el juego, algo que no suele ser una práctica habitual en los mercados del mundo real. El equilibrio de Bertrand / 343 El modelo de Bertrand puede concebirse como un modelo de pujas competitivas. Cada una de las empresas presenta una oferta secreta en la que indica el precio que cobrará a todos los clientes; las ofertas se abren y el menor postor se queda con los clientes. Visto de esta forma, el resultado de Bertrand no es tan paradójico. Es bien sabido que las ofertas secretas son buenas para inducir a las empresas a competir ferozmente, incluso aunque sólo haya unas cuantas. Hasta ahora hemos supuesto que los costes fijos de cada una de las empresas eran cero. Abandonemos este supuesto y veamos qué ocurre si cada una de ellas tiene unos costes fijos de K > O. Suponemos que cada una de ellas siempre tiene la opción de cerrar, es decir, no producir nada e incurrir en unos costes nulos. En este caso, la lógica antes descrita genera de inmediato el equilibrio de Bertrand: el precio de equilibrio es igual al coste marginal de la empresa 2 (la empresa de mayor coste), en la medida en que los beneficios de la 1 no sean negativos. Si lo son, no existe ningún equilibrio correspondiente a estrategias puras. Sin embargo, normalmente existirá un equilibrio correspondiente a estrategias mixtas y, de hecho, a menudo puede calcularse explícitamente. En ese tipo de equilibrio, cada una de las empresas tiene una distribución de probabilidades respecto a los precios que podría cobrar la otra y elige su propia distribución de probabilidades con la idea de maximizar los beneficios esperados. Se trata de un caso en el que una estrategia mixta puede parecer poco plausible; sin embargo, como siempre, se debe en parte al supuesto de que el juego sólo se juega una vez. Aun cuando pensáramos en un juego repetido, podríamos interpretar una estrategia mixta como una política de "ventas": cada una de las tiendas de un mercado minorista podría fijar su precio aleatoriamente, de tal manera que en una semana cualquiera una tendría el precio más bajo de la ciudad y atraería así a todos los clientes. Sin embargo, la tienda ganadora sería diferente cada semana. Ejemplo: Un modelo de ventas Calculemos el equilibrio correspondiente a estrategias mixtas en un modelo de ventas del duopolio. Supongamos para simplificar el análisis que cada una de las empresas tiene unos costes marginales nulos y unos costes fijos de k. Hay dos tipos de consumidores: los consumidores informados saben cuál es el precio más bajo que está cobrándose y los consumidores desinformados eligen simplemente una tienda al azar. Supongamos que· hay I consumidores informados y 2D consumidores desinformados. Por lo tanto, cada una de las tiendas recibirá con toda seguridad D consumidores desinformados cada periodo y recibirá a los consumidores informados sólo si da la casualidad de que tienen el precio más bajo. El precio de reserva de cada consumidor es r. Analizaremos solamente el equilibrio simétrico, en el que cada una de las empresas utiliza la misma estrategia mixta. Sea F(p) la función de distribución de la 344 / EL OLIGOPOLIO (C. 16) estrategia de equilibrio; es decir, F(p) es la probabilidad de que el precio elegido sea menor o igual que p. Suponemos que f (p) es la función de densidad correspondiente que suponemos que es una función de densidad, lo que nos permite prescindir de la probabilidad de que haya un empate.3 Dado este supuesto, existen exactamente dos acontecimientos que son relevantes para una empresa cuando fija el precio p. O bien consigue cobrar el precio más bajo, acontecimiento que tiene una probabilidad 1 - F(p), o bien no lo consigue, acontecimiento que tiene una probabilidad F(p). Si lo consigue, obtiene un ingreso de p(D + J); en caso contrario, obtiene un ingreso de pD. En cualquiera de los dos casos, paga un coste fijo de k. Por lo tanto, los beneficios esperados de la empresa, ir, pueden expresarse de la forma siguiente: ;¡ = Í« [p(l - F(p))(J + D) + pF(p)D - k]f(p)dp. Obsérvese ahora lo siguiente: todos y cada uno de los precios que se cobran, de hecho, en la estrategia mixta de equilibrio deben generar el mismo beneficio esperado. De lo contrario, la empresa podría aumentar la frecuencia con que cobra el precio más rentable en relación con los menos rentables y aumentar sus beneficios esperados globales. Eso significa que debe cumplirse la siguiente igualdad: p(I + D)(l - F(p)) + pF(p)D - k = ir, o despejando, F(p) = p(I + D�1- k - ir. (16.5) Queda por determinar ir. La probabilidad de que una empresa cobre un precio menor o igual que r es 1, por lo que debe cumplirse que F(r) = 1. Resolviendo esta ecuación, tenemos que ir= r D - k e introduciendo el resultado en la ecuación (16.5), obtenemos: ; F(p) = p(I + � - r D . Definiendo u = D / I, podemos expresar la ecuación de la manera siguiente: ru F(p) = 1 + u - -. p 3 Utilizando un razonamiento más complejo puede demostrarse que las probabilidades de que haya un empate en el punto de equilibrio son nulas. El equilibrio de Cournot / 345 p Esta expresión es igual a cero cuando p = 1 cuandop � r. :S py F(p) = ru / (1 +u), por lo que F(p) = O cuando 16.5 Bienes complementarios y sustitutivos En nuestros dos modelos del oligopolio hemos supuesto que los bienes que producían las empresas eran sustitutivos perfectos. Sin embargo, es fácil abandonar ese supuesto y mostrar que existe una interesante dualidad entre el equilibrio de Cournot y el de Bertrand. La manera más fácil de mostrarla es en el caso de las funciones de demanda lineales, si bien existe en general. Supongamos que las funciones inversas de demanda de los consumidores vienen dadas por Pl = cq - f31Y1 - ,Y2 P2 = a2 - ,Y1 - f32Y2· Obsérvese que los "efectos cruzados de los precios son simétricos", corno exigen las funciones regulares de demanda de los consumidores. Las correspondientes funciones directas de demanda son Yl Y2 = a1 - b1P1 + cp2 = a2 + cp1 - b2p2, donde los parámetros a1, a2, etc. son funciones de los parámetros a1, a2, etc. Cuando «i = a2 y f31 = f32 = 1, los bienes son sustitutivos perfectos. Cuando = O, los mercados son independientes. En general, ,2 / f31f32 puede utilizarse corno 1 un índice de la diferenciación de los productos. Cuando es O, los mercados son independientes y cuando es 1, los bienes son sustitutivos perfectos. Supongamos, para mayor sencillez, que los costes marginales son nulos. En ese caso, si la empresa 1 es un competidor de Cournot, maximiza y si es un competidor de Bertrand, maximiza Obsérvese que las expresiones tienen una estructura muy similar: cambiarnos simplemente a1 por a1, f31 por b1 y I por -c. Por lo tanto, el equilibrio de Cournot con productos sustitutivos (en el que 1 > O) tiene esencialmente la misma estructura matemática que el equilibrio de Bertrand con productos complementarios (en el que e< O). 346 / EL OLIGOPOUO (C. 16) Esta "dualidad" nos permite demostrar dos teoremas por el precio de uno: cuando calculamos un resultado en el que hay competencia de Cournot, podemos sustituir simplemente las letras griegas por letras romanas y tenemos un resultado sobre la competencia de Bertrand. Por ejemplo, hemos visto antes que las pendientes de las curvas de reacción son importantes para determinar los resultados de estática comparativa en el modelo de Cournot. En el caso de los bienes heterogéneos aquí analizados, la curva de reacción de la empresa 1 es la solución del siguiente problema de maximización: maxlo¡ - f31Y1 - í'Y21Y1· Y1 Es fácil ver que Sustituyendo las letras griegas por romanas, la curva de reacción del modelo de Bertrand es Obsérvese que la curva de reacción del modelo de Cournot tiene una pendiente opuesta a la curva de reacción del modelo de Bertrand. Hemos visto que las curvas de reacción suelen tener pendiente negativa en el modelo de Cournot, lo que implica que las curvas de reacción tendrán normalmente pendiente positiva en el modelo de Bertrand. Este resultado es razonablemente intuitivo. Si la empresa 2 aumenta su nivel de producción, la 1 normalmente querrá reducir el suyo para obligar a subir el precio alza sobre el precio. Sin embargo, si la empresa 2 sube su precio, a la empresa 1 normalmente le resultará rentable subir el suyo con el fin de que sea igual que el otro. Esta observación también puede realizarse utilizando los conceptos de complementarios y sustitutivos estratégicos que hemos introducido antes. Los niveles de producción de las empresas son sustitutivos estratégicos, ya que si la empresa 2 aumenta Y2, a la empresa 1 le resulta menos rentable elevar su nivel de producción. Sin embargo, si la empresa 2 eleva P2, a la empresa 1 le resulta más rentable subir su precio. Dado que los signos de las derivadas parciales cruzadas son diferentes, las curvas de reacción tienen una pendiente de signo distinto. El liderazgo en la elección de la cantidad / 347 16.6 El liderazgo en la elección de la cantidad Otro modelo del duopolio que tiene un cierto interés es el del liderazgo en la elección de la cantidad, también conocido con el nombre de modelo de Stackelberg. Se trata esencialmente de un modelo que consta de dos fases y en el que una d€ las empresas mueve primero. La otra puede observar entonces el nivel de producción que ha elegido la primera y elegir su propio nivel óptimo de producción. Utilizando la terminología del capítulo anterior, el modelo del liderazgo en la elección de la cantidad es un juego consecutivo. Este juego se resuelve, como siempre, empezando por el final. Supongamos la que empresa 1 es la líder y la 2 la seguidora. En ese caso, el problema de la empresa 2 es sencillo: dado el nivel de producción de la 1, la 2 desea maximizar sus beneficios p(y1 + y2)Y2 - c2(y2). La condición de primer orden de este problema es simplemente la siguiente: (16.6) Esta ecuación es exactamente igual que la condición de Cournot antes descrita y puede utilizarse para obtener la función de reacción de la empresa 2, h(y1), al igual que anteriormente. Pasando a la primera fase del juego, ahora la empresa 1 desea elegir su nivel de producción, mirando hacia adelante y teniendo en cuenta cómo responderá la 2. Por lo tanto, la empresa 1 desea maximizar La condición de primer orden de este problema es (16.7) Las ecuaciones (16.6) y (16.7) son suficientes para hallar los niveles de producción de las dos empresas. En la figura 16.2 se muestra gráficamente el equilibrio de Stackelberg. En este caso, las curvas isobeneficio de la empresa 1 indican las combinaciones de niveles de producción que genei:an unos beneficios constantes. Cuanto más bajas sean las curvas isobeneficio, mayores son los niveles de beneficio. Como muestra la figura, la empresa 1 quiere producir en el punto de la curva de reacción de la empresa 2 que le genere los mayores beneficios posibles. ¿ Qué diferencias hay entre el equilibrio de Stackelberg y el de Cournot? La teoría de la preferencia revelada permite deducir de inmediato un primer resultado: dado que el líder de Stackelberg elige el punto óptimo de la curva de reacción de su competidor y el equilibrio de Cournot es un punto "arbitrario" de dicha curva, 348 / EL OLIGOPOLIO (C. 16) los beneficios que obtiene el líder en el equilibrio de Stackelberg son normalmente mayores que los que obtendría en el equilibrio de Cournot del mismo juego. Figura 16.2 NIVEL DE PRODUCCION 2 Curvas isobeneficio de la empresa 1 NIVEL DE PRODUCCION 1 Comparación del equilibrio de Coumot y el equilibrio de Stackelberg. El equilibrio de Nash se encuentra en el punto en el que se cortan las dos curvas de reacción y el de Stackelberg se encuentra en el punto en el que una curva de reacción es tangente a las curvas isobeneficio de la otra empresa. ¿Qué podemos decir de los beneficios de ser un líder en comparación con los de ser un seguidor? ¿ Qué preferiría ser una empresa? Esta pregunta tiene una interesante respuesta general, pero exige un cierto razonamiento. Analizaremos el caso general de los bienes heterogéneos, YI e Y2, partiendo de los siguientes supuestos (naturalmente, éstos comprenden el caso especial de los bienes homogéneos, en el que YI e Y2 son sustitutivos perfectos). Al: Productos sustitutivos. una función decreciente de YI. 1r1 (y1, y2) es una función decreciente de Y2 y 1r2(Y1, y2) es A2: Curvas de reacción de pendiente negativa. Las curvas de reacción fi(yj) son funciones estrictamente decrecientes. Liderazgo preferido. Partiendo de los supuestos Al y A2, una empresa siempre prefiere ser la líder a ser la seguidora. El liderazgo en la elección de la cantidad / 349 Demostración. Sea (y1, y2) = (y1, f2(y1)) el equilibrio de Stackelberg cuando la empresa 1 es la líder. En primer lugar, tenernos que demostrar que (16.8) Supongamos que no fuera así, de tal manera que (16.9) Aplicando la función [: ( ·) a los dos miembros de esta igualdad, tenernos que (16.10) La desigualdad (1) se deriva del supuesto A2 y la desigualdad (2) de la definición del equilibrio de Stackelberg. Ahora tenernos la siguiente cadena de desigualdades: (16.11) La desigualdad (1) se desprende de la definición de la función de reacción y la desigualdad (2) de la ecuación (16.10) y del supuesto Al. De acuerdo con (16.11), el punto (!1 (y2), h(f1 (y2))) genera mayores beneficios que el punto (y , h(yi)), lo 1 que contradice la afirmación de que (y1, [: (y1)) es el equilibrio de Stackelberg. Esta contradicción demuestra la validez de la expresión (16.8). El resultado que estarnos buscando ahora se deduce de inmediato de las siguientes desigualdades: La desigualdad (1) se desprende de la rnaxirnización y la (2) de (16.8) y del supuesto Al. El primer miembro y el tercero de estas desigualdades muestran que los beneficios de la empresa 2 son mayores si es ella la líder que si es lo es la empresa 1. Dado que lo "normal" es considerar que las funciones de reacción tienen pendiente negativa y que los bienes son sustitutivos, este resultado indica que normalmente es de esperar que cada una de las empresas del modelo de Stackelberg prefiera ser la líder. El hecho de que la líder sea una empresa u otra depende probablemente de factores históricos, por ejemplo, de cuál fuera la que entró primero en el mercado, etc. 350 / EL OLIGOPOLIO (C. 16) 16.7 El liderazgo en la elección del precio Existe liderazgo en la elección del precio cuando una de las empresas fija el precio que la otra considera dado. El modelo del liderazgo en la elección del precio se resuelve exactamente igual que el modelo de Stackelberg: primero se averigua la conducta del seguidor y a continuación la del líder. Figura 16.3 PRECIO Oferta de la empresa 2 Curva de demanda residual Coste marginal de la empresa 1 Curva de ingreso marginal CANTIDAD El liderazgo en la elección del precio. La empresa 1 resta la curva de oferta de la 2 de la curva de demanda del mercado para hallar la curva de demanda residual. A continuación elige el nivel de producción más rentable de esta curva. En un modelo en el que los bienes son heterogéneos, suponemos que Xi (p1, p2) es la demanda de producción de la empresa i. La seguidora elige P2 considerando dado Pl. Es decir, la seguidora maximiza maxp2x2(p1,p2) - c2(x2(P1,P2)) P2 (16.12) Suponemos que P2 = g2(p1) es la función de reacción que nos da la elección óptima de P2 en función de Pv- El liderazgo en la elección del precio / 351 La líder resuelve a continuación el siguiente problema de maximización: max P1 x1 (p1 , g2 (p1)) - c1 (x1 (p1 , g2 (p1))) P1 para hallar el valor óptimo de P1. Un interesante caso especial es aquel en el que las empresas venden productos idénticos. En este caso, si la empresa 2 vende una cantidad positiva, debe venderla al precio P2 = P1. A cada uno de los precios Pl, la seguidora decidirá producir la cantidad S2(p1) que maximice sus beneficios, considerando dado p1. Por lo tanto, en este caso la función de reacción es simplemente la curva de oferta competitiva. Si la empresa 1 cobra el precio P1, la 2 venderá r(p1) = x1 (p1) - S2(p1) unidades de producción. La función r(p1) se conoce con el nombre de curva de demanda residual de la empresa 1. Ésta desea elegir el precio Pl que maximice max p¡ r(p1) - c1 (r(p1)). Pl Este problema es exactamente igual que el del monopolio que se enfrenta a la curva de demanda residual r(p1). La figura 16.3 muestra gráficamente la solución. Para hallar la curva de demanda residual se resta la curva de oferta de la empresa 2 de la curva de demanda del mercado. A continuación se aplica la condición habitual I M = CM para hallar el nivel de producción de la líder. Volviendo al caso de los productos heterogéneos, cabe preguntarse si en este modelo las empresas prefieren ser la líder o la seguidora. Debe señalarse, en primer lugar, que el resultado antes demostrado puede ampliarse de inmediato al modelo del liderazgo en la elección del precio sustituyendo simplemente las Yi por las Pi· Sin embargo, esta ampliación plantea dos dificultades. En primer lugar, los beneficios no tienen por qué ser necesariamente una función decreciente del precio de la otra empresa. La derivada de los beneficios de la empresa 1 con respecto al precio 2 es El signo de esta derivada depende de que el precio sea mayor o igual que el coste marginal. En realidad, esta dificultad puede superarse; en el modelo del liderazgo en la elección del precio, sigue prefiriéndose ser el líder, en la medida en que las funciones de reacción tengan pendiente negativa. Sin embargo, el supuesto de que las funciones de reacción con respecto al precio tienen pendiente negativa no es en modo alguno razonable. Supongamos para simplificar que el coste marginal es nulo. En ese caso, la función de reacción de la empresa 2 debe satisfacer la siguiente condición de primer orden: 352 / EL OLIGOPOLIO (C. 16) Realizando el cálculo habitual de estática comparativa, tenernos que . , de 92(PI) signo = signo de [ 82x2 8x2] P2 - + . 0 PI 0P2 PI 0 A menos que la función de demanda sea muy cóncava, debe dominar el segundo término, y el supuesto de los sustitutivos implica que es positivo. Por lo tanto, corno hemos señalado antes, normalmente es de esperar que en el modelo del liderazgo en la elección del precio las curvas de reacción tengan pendiente positiva. Utilizando un argumento similar al anterior, se demuestra la siguiente proposición. Consenso. Si las dos empresas tienen funciones de reacción de pendiente positiva, entonces si una de ellas prefiere ser la líder, la otra debe preferir ser la seguidora. Demostración. Véase Dowrick (1986). De esta proposición se deduce de inmediato la siguiente observación. Se prefiere ser el seguidor. Si las dos empresas tienen las mismas funciones de costes y de demanda y las curvas de reacción tienen pendiente positiva, cada una de ellas debe preferir ser la seguidora a ser la líder. Demostración. Si una de las empresas prefiere ser la líder, por simetría la otra también prefiere serlo. Pero esto contradice la proposición anterior. Veamos otro razonamiento por el que se llega a este resultado en el caso especial en el que los bienes que producen las dos empresas son idénticos. El razonamiento se basa en la figura 16.3. En esta figura, la empresa 1 elige el precio p* y el nivel de producción qi. La 2 tiene la opción de ofrecer el mismo nivel de producción que la 1, qi, al precio p", pero rechaza esa posibilidad en favor de la de producir otro nivel distinto, a saber, el que. se encuentra en la curva de oferta de la empresa 2. Por lo tanto, esta empresa obtiene mayores beneficios que la 1 en condiciones de equilibrio. Intuitivamente, la razón por la que una empresa prefiere ser la seguidora en un juego de fijación del precio se halla en que la líder tiene que reducir su nivel de producción para mantener el precio, mientras que la seguidora puede considerar fijo el precio de la líder y producir tanto corno desee; es decir, la seguidora puede aprovecharse de las limitaciones que tiene el líder para elegir su nivel de producción. Clasificación y elección de los modelos / 353 16.8 Clasificación y elección de los modelos Hemos analizado cuatro modelos del duopolio: el de Cournot, el de Bertrand, el del liderazgo en la elección de la cantidad y el del liderazgo en la elección del precio. Desde el punto de vista de la teoría de los juegos, estos modelos se distinguen por la definición del espacio de estrategias (los precios o las cantidades) y por los conjuntos de información: si uno de los jugadores sabe o no qué ha elegido el otro cuando toma su decisión. ¿ Cuál es el modelo correcto? En general, esta pregunta no tiene respuesta; sólo puede abordarse en el contexto de la situación económica o de la industria que se desee examinar concretamente. No obstante, podemos ofrecer algunas útiles directrices. Es importante recordar que estos modelos son todos ellos "juegos que sólo se juegan una vez". Sin embargo, en los estudios aplicados se trata, en general, de plasmar en los modelos interdependencias que tienen lugar en el tiempo real, es decir, una estructura de la industria que persiste a lo largo de muchos periodos. Es natural, pues, exigir que las variables estratégicas que se utilicen para elaborar un modelo de la industria sean variables que no puedan ajustarse inmediatamente: una vez elegidas, persistirán durante un periodo de tiempo, por lo que cabe esperar que el supuesto de que el juego sólo se juega una vez represente en cierta medida los fenómenos económicos que se producen en la realidad. Examinemos, por ejemplo, el equilibrio de Bertrand. Desde un punto de vista formal, se trata de un juego que sólo se juega una vez: los duopolistas fijan los precios simultáneamente sin observar lo que elige cada uno de ellos. Pero si no es costoso ajustar el precio tan pronto como se observa el del rival (¡y antes de que los clientes observen cualquiera de los dosl), el modelo de Bertrand no es muy atractivo: una empresa puede responder de una u otra manera tan pronto como observe el precio de la otra, dando lugar probablemente a un resultado distinto del equilibrio de Bertrand. El modelo de Cournot parece adecuado cuando las cantidades sólo pueden ajustarse lentamente. Es especialmente atractivo cuando se interpreta que la "cantidad" es la "capacidad". La idea consiste en que cada una de las empresas elige en secreto una capacidad de producción, dándose cuenta de que una vez elegida competirán en función del precio, es decir, jugarán un juego de Bertrand. Kreps y Sheinkman (1983) analizan este juego de dos fases y demuestran que el resultado suele ser un equilibrio de Cournot. A continuación esbozamos vagamente una versión simplificada de su modelo. Supongamos que cada una de las empresas produce simultáneamente la cantidad u. en el primer periodo. En el segundo, elige un precio al que vende su producción. Nos interesa hallar el equilibrio de este juego de dos fases. 354 / EL OLIGOPOLIO (C. 16) Comenzamos, como siempre, por el segundo periodo, en el cual el coste marginal en que incurre la empresa i si vende una cantidad inferior a Yi es nulo, e infinito si vende una cantidad superior a Yi· En condiciones de equilibrio, las dos empresas deben cobrar el mismo precio, pues de lo contrario la que cobrara el precio alto saldría beneficiada cobrando uno algo más bajo que el de la empresa que cobrara el precio bajo. Por otra parte, el precio cobrado no puede ser superior a p(y1 + y2), pues si lo fuera, una de ellas podría bajar algo su precio y quedarse con todo el mercado. Por último, el precio cobrado no puede ser inferior a p(y1 + y2), ya que a las dos empresas les interesa subir el precio cuando ambas están vendiendo la cantidad máxima que les permite su capacidad (la exposición de este argumento es bastante intuitiva, pero sorprendentemente difícil de demostrar rigurosamente). La observación crucial se halla en que cuando las dos empresas están vendiendo la cantidad máxima que les permite su capacidad, ninguna de ellas quiere bajar su precio. Es cierto que si lo bajaran, atraerían a todos los clientes de su rival, pero como ya están vendiendo todo lo que pueden, estos clientes adicionales no les sirven para nada.4 Una vez que se sabe que el precio de equilibrio del segundo periodo es simplemente la demanda inversa correspondiente a la plena utilización de la capacidad, es sencillo calcular el equilibrio correspondiente al primer periodo: es simplemente el equilibrio habitual de Cournot. Por lo tanto, la competencia de Cournot basada en la capacidad seguida de la competencia de Bertrand basada en los precios conduce al resultado habitual del modelo de Cournot. 16.9 Conjeturas sobre las variaciones Los juegos del liderazgo en la elección del precio y del liderazgo en la elección de la cantidad que hemos descrito pueden generalizarse de una interesante manera. Recordemos la condición de primer orden que describe la elección óptima de la cantidad de un líder de Stackelberg: (16.13) El término J2(y1) indica la expectativa de la empresa 1 sobre la forma en que varía la conducta óptima de la 2 cuando varía Y2· 4 Sin embargo, esta observación trae a colación una delicada cuestión: si una de las empresas consigue un número de clientes mayor que aquel al que puede vender, debemos especificar una regla de racionamiento que indique qué ocurre con los clientes adicionales. Davidson y Deneckere (1986) demuestran que la especificación de la regla de racionamiento puede afectar a la naturaleza del equilibrio. Conjeturas sobre las variaciones / 355 En el modelo de Stackelberg, esta expectativa es igual a la pendiente de la verdadera función de reacción de la empresa 2. Sin embargo, podría concebirse este término como una "conjetura" arbitraria sobre la respuesta de la empresa 2 a la elección del nivel de producción de la 1. Llamémosla conjetura sobre las variaciones de la empresa 1 sobre la empresa 2 y representémosla por medio de v12. Ahora la condición de primer orden apropiada es la siguiente: p(Y) + p' (Y)[l + v12lY1 = cí (y1) (16.14) Lo interesante de esta formulación se halla en que las diferentes elecciones de los parámetros generan directamente las condiciones de primer orden relevantes para los diferentes modelos analizados anteriormente. 1. v12 = O: éste es el modelo de Cournot, en el cual cada una de las empresas cree que la elección de la otra es independiente de la suya propia; 2. v12 = -1: éste es el modelo competitivo, ya que la condición de primer orden se reduce a la igualdad del precio y el coste marginal. 3. v12 = pendiente de la curva de reacción de la empresa 2: éste es, por supuesto, el modelo de Stackelberg; 4. v12 = y2/y1: en este caso, la condición de primer orden se reduce a la condición para la maximización de los beneficios de la industria, es decir, el equilibrio colusorio. Este cuadro muestra que cada uno de los principales modelos que hemos analizado es simplemente un caso especial del modelo de las conjeturas sobre las variaciones. En este sentido, la idea de las conjeturas sobre las variaciones constituye un útil sistema de clasificación de los modelos del oligopolio. Sin embargo, no es realmente satisfactoria como modelo de la conducta. El problema estriba en que se introduce un tipo de pseudodinámica en unos modelos que son inherentemente estáticos. Todos los modelos que hemos examinado antes son específicamente modelos en los que sólo se juega una vez: en el modelo de Cournot, las empresas eligen sus niveles de producción independientemente; en el modelo de Stackelberg, una elige su nivel de producción esperando que la otra reaccione óptimamente, etc. El modelo de la conjetura sobre las variaciones indica que una empresa elige un nivel de producción porque espera que la otra responda de una determinada manera: pero ¿ cómo puede responder la otra en un juego que sólo se juega una vez? Si queremos plasmar en un modelo una situación dinámica, en la que cada una de las empresas puede responder al nivel de producción que elige la otra, debemos examinar para empezar el juego repetido. 356 / EL OLIGOPOLIO (C. 16) 16.10 La colusión Todos los modelos que hemos descrito hasta ahora constituyen ejemplos de juegos no cooperativos. Cada una de las empresas aspira a maximizar sus propios beneficios y torna sus decisiones independientemente de las demás. ¿ Qué ocurre si abandonarnos este supuesto y considerarnos la posibilidad de que emprendan acciones coordinadas? Una estructura de la industria en la que las empresas coluden en cierta medida para fijar el precio y el nivel de producción se denomina cártel. Un modelo natural es ver qué ocurre si las dos empresas eligen sus niveles de producción con el fin de maximizar los beneficios conjuntos. En este caso, eligen simultáneamente Yl e Y2 con la idea de maximizar los beneficios de la industria: maxp(y1 + Y2HY1 + Y2l - c1 (y1) - c2(y2). Y1 ,Y2 Las condiciones de primer orden son las siguientes: p(yi + Y2) + P1 (yi + Y2)[yi + Y2l = e� (yi) p(yi + Y2) + P1 (yi + Y2)[yi + Y2l = (16.15) c;(yi) Dado que los primeros miembros de estas dos ecuaciones son iguales, también deben serlo los segundos: las empresas deben igualar sus costes marginales de producción. El problema de la solución de cártel se halla en que no es "estable". Siempre existe la tentación de violar los acuerdos, es decir, de producir más de lo acordado. Para comprenderlo, veamos qué ocurre si la empresa 1 considera la posibilidad de elevar su nivel de producción en una pequeña cuantía, dy1, suponiendo que la 2 seguirá produciendo la cantidad acordada en el cártel, y2. La variación que experimentan los beneficios de la empresa 1 cuando varía y1, evaluada en función de la solución del cártel, es 81r1(Yi,Y2) Y1 a = P ( Y1* + Y2*) + P '( Y1* + Y2*) Y1* - c1'( Y1*) = * * -p '( Y1 + Y2*) Y2 > O· El signo de igualdad de esta expresión procede de las condiciones de primer orden de las ecuaciones (16.15) y la desigualdad se deriva del hecho de que las curvas de demanda tienen pendiente negativa. Si una empresa cree que la otra seguirá produciendo lo acordado en el cártel, saldrá ganando si eleva su propio nivel de producción para vender más al elevado precio. Pero si no lo cree, generalmente tampoco será óptimo que cumpla el acuerdo del cártel. Podría muy bien inundar el mercado y obtener beneficios mientras pueda. La situación estratégica es similar a aquella en la que si una empresa cree que otra producirá su cuota, le compensa ir a la suya, es decir, producir una cantidad Juegos repetidos / 357 superior. Y si piensa que la otra producirá su cuota, le resultará rentable en general producir una cantidad superior. Para que el resultado del cártel sera viable, debe encontrarse la manera de estabilizar el mercado, lo cual suele consistir en buscar un castigo eficaz para las empresas que violen el acuerdo del cártel. Por ejemplo, una empresa puede anunciar que si descubre que otra produce una cantidad distinta a la acordada, aumentará su propia producción. Es interesante preguntarse cuánto tendría que aumentarla si la otra incumpliera el acuerdo. Hemos visto antes que la conjetura sobre las variaciones que da lugar a la solución del cártel es v12 = Yi!Y2· ¿Qué significa eso? Supongamos que la empresa 1 anuncia que si la 2 eleva su nivel de producción en dy2, responderá elevando el suyo en dy1 = (y1 / y2)dy2. Si la empresa 2 se cree esta amenaza, la variación que espera que experimenten los beneficios como consecuencia de un aumento de la producción de dy2 es drr2 = p(y1 + Y2)dy2 + p'(y, [ dY2] + Y2) dy2 + �: Y2 - c;(yi)dy2 = [p(y1 + Y2) + p' (y1 + Y2HY1 + Y2] = O. - c;(yi)]dy2 Por lo tanto, si la empresa 2 cree que la 1 responderá de está forma, no esperará que la violación de su cuota le beneficie. Como mejor se observa el carácter del castigo de la empresa 1 es examinando el caso de las cuotas de mercado asimétricas. Supongamos que la empresa 1 produce el doble que la 2 en el equilibrio del cártel. En ese caso, tiene que amenazar con que castigará cualquier desviación del nivel de producción del cártel produciendo el doble que su rival. Por otra parte, la 2 sólo tiene que amenazar con producir la mitad de las posibles desviaciones en las que incurra su rival. Este tipo de análisis, aunque es sugerente, plantea el mismo problema que suelen plantear las conjeturas de las variaciones: se introduce una interdependencia dinámica en un modelo estático. Sin embargo, veremos que en un análisis dinámico riguroso han de tenerse en cuenta en gran medida las mismas consideraciones; el problema esencial que plantea la viabilidad de un cártel es la búsqueda de una sanción eficaz para castigar las desviaciones. 16.11 Juegos repetidos Hasta ahora todos los juegos eran juegos que sólo se jugaban una vez. Pero la interdependencia que existe realmente en el mercado se produce en el tiempo real, por lo que resulta necesario, ciertamente, examinar el carácter repetido de la interdepen- 358 / EL OLIGOPOLIO (C. 16) dencia. La manera más sencilla de hacerlo consiste en concebir el juego de Cournot de fijar la cantidad como un juego repetido. El análisis es paralelo al del dilema repetido del prisionero presentado en el capítulo 15. En este caso, el resultado de cooperación es la solución del cártel. El castigo puede ser la elección del nivel de producción de Cournot. Las estrategias que dan lugar a la solución del cártel tienen, en ese caso, la forma siguiente: la empresa elige el nivel de producción del cártel, a menos que su adversario viole el acuerdo; si lo viola, elige el nivel de producción de Cournot. Al igual que ocurre en el caso del dilema del prisionero, este conjunto de estrategias constituirá un equilibrio de Nash, siempre que la tasa de descuento no sea demasiado elevada. Desgraciadamente, el juego tiene muchas otras estrategias de equilibrio: al igual que en el caso del dilema repetido del prisionero, casi todo puede ser un equilibrio de Nash. A diferencia del caso del dilema repetido del prisionero, este resultado también es válido en el caso del juego de fijación del precio que se repite un número finito de veces. Para verlo, examinemos un juego de dos periodos en el que las empresas son idénticas y tienen unos costes marginales nulos. Consideremos la siguiente estrategia de la empresa 1: producir la cantidad Y1 en el primer periodo. Si su adversaria produce y2 en el primer periodo, debe producir la cantidad de Cournot, yf. en el siguiente. Si su adversaria produce una cantidad distinta de Y2, debe producir una cantidad suficientemente grande para presionar a la baja sobre el precio de mercado hasta que sea cero. ¿Cuál es la respuesta óptima de la empresa 2 a esta amenaza? Si produce Y2 en el primer periodo e y2 en el segundo, obtiene unas ganancias de 1r2(Y1, Y2) + 61r1 (yf., y2). Si produce una cantidad distinta de Y2 en el primer periodo -por ejemplo, una cantidad x- obtiene unas ganancias de 1r2(Y1, x). Por lo tanto, será rentable cooperar con la empresa 1 cuando Esta condición se cumple normalmente en el caso de toda una gama de niveles de producción (y1, Y2). El problema estriba en que la amenaza de aplicar la estrategia del castigo no es creíble: una vez transcurrido el primer periodo, a la empresa 1 no le interesa, en general, inundar el mercado. En otras palabras, inundar el mercado no es una estrategia de equilibrio en el subjuego que consta solamente del segundo periodo. Utilizando la terminología del capítulo 15, esta estrategia no es perfecta en todos los subjuegos. No es difícil demostrar que el único equilibrio perfecto en todos los subjuegos en el juego de fijación de la cantidad que se repite un número finito de veces es la repetición del equilibrio de Cournot cuando sólo se juega una vez, al menos en el Juegos repetidos / 359 caso en el que este equilibrio es único. El argumento se basa en la habitual inducción retrospectiva: dado que el equilibrio de Cournot es el único resultado en el último periodo, la jugada del primero no puede influir con credibilidad en el resultado del último, por lo que la única elección es el equilibrio "miope" de Cournot. Es natural preguntarse si el nivel de producción del cártel puede mantenerse como un equilibrio perfecto en todos los subjuegos en el caso del juego que se repite un número infinito de veces. Friedman (1971) ha demostrado que sí. Las estrategias que funcionan son similares a las estrategias de castigo analizadas en el capítulo anterior. Sea 1rf los beneficios de la empresa i generados por el equilibrio de Cournot de un periodo y 1r; los beneficios generados por el resultado del cártel de un periodo. Consideremos la siguiente estrategia de la empresa 1: producir la cantidad del cártel a menos que la empresa 2 produzca una cantidad distinta, en cuyo caso debe producir indefinidamente la cantidad de Cournot. Si la empresa 2 cree que la 1 producirá la cantidad de Cournot en un periodo dado, su respuesta óptima consiste en producir también esa cantidad (ésta es la definición del equilibrio de Cournot). Por lo tanto, repetir el nivel de producción de Cournot indefinidamente es, de hecho, un equilibrio del juego repetido. Para ver si a la empresa 2 le resulta rentable producir la cantidad del cártel, debemos comparar el valor actual de los beneficios que genera la violación del acuerdo con los beneficios que genera la cooperación. Suponiendo que 1r1 representa los beneficios que genera la violación del acuerdo, esta condición se convierte en d 7r2 7r2 7r2 + (\ - 8 < 1 - 8. Es decir, la empresa 2 obtiene los beneficios generados por la violación del acuerdo más el valor actual de los beneficios derivados del equilibrio de Cournot en todos los periodos futuros. Reordenando, tenemos la siguiente condición: 8> 7rd - 7r* 2 2 2 2 7rd _ 7rc (16.16) Esta condición se satisfará en la medida en que 8 sea suficientemente elevado, es decir, en la medida en que la tasa de descuento sea suficientemente baja. Al igual que en el caso del dilema repetido del prisionero, en este modelo hay muchos otros equilibrios. La idea básica de las estrategias de castigo (perfectas en todos los subjuegos) puede ampliarse de muchas maneras considerando muchos otros tipos de castigo, aparte de la vuelta a la solución de Cournot. Por ejemplo, Abreu (1986) ha demostrado que un periodo de castigo seguido de una vuelta a la solución del cártel normalmente es suficiente para mantener el nivel de producción del cártel. Esto nos recuerda a los resultados sobre el castigo óptimo del modelo de las conjeturas sobre las variaciones: en la medida en que una empresa pueda castigar a la otra 360 / EL OLIGOPOLIO (C. 16) lo suficientemente deprisa, puede garantizar que ésta no obtendrá beneficio alguno violando el acuerdo. Véase Shapiro (1989) para un buen estudio panorámico de los resultados referentes a los juegos repetidos del oligopolio. 16.12 Juegos consecutivos Los juegos repetidos que hemos descrito en el apartado anterior son sencillas repeticiones de los juegos de mercado que sólo se juegan una vez. Las decisiones que toma una empresa en un periodo no afectan a los beneficios que obtiene en otro, salvo de manera indirecta a través de su influencia en la conducta de su rival. Sin embargo, en la realidad las decisiones que se toman en un determinado momento del tiempo influyen en la cantidad que se produce en fechas posteriores. Las decisiones de inversión de este tipo desempeñan un importante papel estratégico en algunos juegos. Figura 16.4 CORRIENTE DE BENEFICIOS ------- Monopolio --------- Duopolio TIEMPO Corriente de beneficios y entrada. En el equilibrio perfecto en todos los subjuegos, la primera empresa entra en el momento t0, es decir, en el punto en el que sus beneficios descontados son nulos. La entrada en el momento t1 es un equilibrio de Nash, pero no un equilibrio perfecto en todos los subjuegos. Cuando se examina esta clase de modelos de la conducta es muy importante la distinción entre los equilibrios de Nash y los equilibrios perfectos en todos los subjuegos. Para mostrar esta distinción en el contexto más simple posible, examinemos un sencillo modelo de entrada. Juegos consecutivos / 361 Imaginemos el caso de una industria en la que hay dos empresas listas para entrar en cuanto sean propicias las condiciones. Supongamos que la entrada no cuesta y que existe algún tipo de progreso tecnológico exógeno que reduce el coste de producción con el paso del tiempo. Sea 1r1 (t) el valor actual del beneficio obtenido en el momento t si sólo hay una empresa en el mercado en ese momento y 1r2(t) el beneficio obtenido por cada una de las empresas si hay dos en el mercado en ese momento. Esta función de beneficios en forma reducida resume la forma exacta de la competencia dentro de la industria; lo único necesario es que 1r1 (t) > 1r2(t) cualquiera que sea t, lo que significa simplemente que un monopolio es más rentable que un duopolio. La figura 16.4 muestra estas corrientes de beneficios. Suponemos que éstos aumentan inicialmente más deprisa que el tipo de interés, por lo que los beneficios descontados aumentan con el paso del tiempo. Pero finalmente disminuye el ritmo del progreso tecnológico de esta industria, por lo que los beneficios aumentan menos deprisa que el tipo de interés, de tal manera que disminuye su valor actual. La cuestión que nos interesa aquí es la pauta de entrada. El candidato evidente es el par (t1, t2), es decir, entra una de las empresas cuando resulta rentable el monopolio y entra la otra cuando resulta rentable el duopolio. Éste es el tipo habitual de condición de entrada que exige que los beneficios sean positivos y, de hecho, es fácil verificar que es un equilibrio de Nash. Sin embargo, sorprendentemente, no es un equilibrio perfecto en todos los subjuegos. Veamos qué ocurre si la empresa 2 (la segunda empresa que entra) no decide entrar en el momento t1 sino algo antes. Es cierto que perderá dinero durante algún tiempo, pero ahora ya no es creíble la amenaza de la empresa 1 de entrar en el momento ti. Dado que la empresa 2 se encuentra en el mercado, a la empresa 1 ya no le resulta rentable entrar en el momento t1. Por lo tanto, la empresa 2 recibirá unos beneficios monopolísticos positivos en el intervalo [t1, t2], así como sus beneficios duopolísticos a partir del momento t2. Naturalmente, si la empresa 2 considera la posibilidad de entrar antes que en t1, la 1 puede planteárselo también. En este modelo, los únicos equilibrios perfectos en todos los subjuegos son aquellos en los que una de las empresas entra en el momento t0, en el que los beneficios generados por la fase monopolística inicial son nulos; es decir, el área sombreada (negativa) situada encima de 1r1 (t) entre to y t1 es igual al área positiva situada debajo de 1r1 (t) entre t1 y t2. ¡La amenaza de la entrada ha disipado efectivamente los beneficios monopolísticos! Retrospectivamente, es absolutamente lógico. Las empresas se encuentran exactamente en la misma situación y sería algo sorprendente que terminaran obteniendo unos beneficios distintos. En el equilibrio perfecto en todos los subjuegos, desaparecen los beneficios que se obtienen por entrar antes debido a la competencia y lo único que queda son los beneficios generados por la fase de duopolio del juego. 362 / EL OLIGOPOLIO (C. 16) 16.13 Fijación de un precio límite A menudo se piensa que la amenaza de la entrada constituye una fuerza disciplinadora en los oligopolios. Aun cuando sólo haya un pequeño número de empresas actualmente en una industria, puede haber muchas que podrían entrar y, por lo tanto, el grado "efectivo" de competencia puede ser bastante alto. La amenaza de la entrada puede afectar incluso a los monopolistas e inducirlos a fijar un precio competitivo. La fijación del precio para impedir la entrada de esta manera se conoce con el nombre de fijación de un precio límite. Aunque esta idea tiene un gran atractivo intuitivo, plantea varios problemas graves. Examinemos algunos de ellos con la ayuda de un modelo formal. Sean dos empresas; una ya está establecida, es decir, está produciendo actualmente en el mercado, y la otra está considerando la posibilidad de entrar. La función de demanda del mercado y las funciones de costes de las dos empresas son de dominio público. Hay dos periodos: en el primero, el monopolista fija un precio y una cantidad, que pueden ser observados por la empresa que está considerando la posibilidad de entrar, momento en el cual decide entrar o no en el mercado. Si entra, las empresas juegan un juego del duopolio en el segundo periodo. Si no entra, la que ya está establecida cobra el precio monopolístico en el segundo periodo. ¿ Qué carácter tiene la fijación de un precio límite en este modelo? Esencialmente ninguno; si se produce la entrada, se determina el equilibrio del duopolio. La única preocupación de la empresa que está considerando la posibilidad de entrar es predecir los beneficios que podría obtener en ese equilibrio del duopolio. Dado que conoce perfectamente los costes y la función de demanda, el precio del primer periodo no transmite información alguna. Por lo tanto, la empresa que ya está en el mercado también puede obtener sus beneficios monopolísticos al tiempo que puede cobrar y, de hecho, cobra el precio monopolístico en el primer periodo. Existe la tentación de pensar que la empresa ya establecida podría querer cobrar un precio bajo en el primer periodo con el fin de transmitir la información de que está "dispuesta a luchar" si entra otra. Pero ésta es una amenaza estéril; si entra la otra empresa, lo racional es que la empresa ya establecida haga lo necesario para maximizar los beneficios en ese momento. Dado que la que está considerando la posibilidad de entrar conoce toda la información pertinente, puede predecir ex ante cuál será la· medida maximizad ora del beneficio de la ya establecida y actuar en consecuencia. La fijación de un precio límite no desempeña ningún papel en este modelo, ya que el precio del primer periodo no transmite ninguna información sobre el juego del segundo periodo. Sin embargo, si admitimos la presencia de una cierta incertidumbre en nuestro modelo, observaremos que la fijación de un precio límite surge casi de inmediato como una estrategia de equilibrio. Fijación de un precio límite / 363 Consideremos el sencillo modelo siguiente. Se demanda una unidad de un bien si el precio de mercado es inferior o igual a 3. Hay una empresa ya establecida que tiene unos costes marginales constantes de O ó 2 y hay otra que está considerando la posibilidad de entrar que tiene unos costes marginales constantes de 1. Para entrar en este mercado, esta última debe pagar una cuota de entrada de 1 / 4. Si efectivamente entra, suponemos que las empresas practican la competencia de Bertrand. Dado que tienen costes diferentes, significa que una de ellas es expulsada del mercado. Si la ya establecida es una empresa de bajos costes, fijará un precio algo inferior al coste marginal de la que está considerando la posibilidad de entrar, 1, y, por lo tanto, expulsará a esta última del mercado. En este caso, la empresa ya establecida obtiene un beneficio de 1 y la que está considerando la posibilidad de entrar pierde la cuota de entrada, -1 / 4. Si la primera es una empresa de elevados costes, la segunda fija un precio algo inferior a 2, obteniendo un beneficio de 2 - 1 - 1 / 4 = 3 / 4 y la primera es expulsada del mercado. Si la empresa ya establecida es una empresa de elevados costes y no entra ninguna otra, fija el precio monopolístico de 3 y obtiene un beneficio de 1. Ahora bien, ¿qué precio debe fijar en el primer periodo? Esencialmente, a la empresa ya establecida de bajos costes le gustaría fijar un precio que no fuera viable para la ya establecida de elevados costes, ya que de esa manera indicaría cuál es su tipo a la que está considerando la posibilidad de entrar. Supongamos que la empresa ya establecida de bajos costes fija un precio algo inferior a 1 en el primer periodo y el precio monopolístico de 3 en el segundo. Estos precios siguen siendo rentables para ella, ya que tiene unos costes nulos. Pero no lo son para la empresa de elevados costes: en el primer periodo, ésta perdería algo más de 1 y en el segundo sólo obtendría 1. En conjunto, esta política genera una pérdida. Dado que sólo la empresa de bajos costes puede permitirse el lujo de fijar un precio de 1, es una señal creíble. Este ejemplo muestra que la fijación de un precio límite desempeña un papel importante en un modelo con información imperfecta: puede servir de señal a las empresas que estén considerando la posibilidad de entrar acerca de la estructura de costes de la ya establecida, impidiendo así la entrada, al menos en algunos casos. Notas Véase Shapiro (1989) para un buen estudio panorámico de la teoría del oligopolio. El análisis de los juegos repetidos del presente capítulo se basa en gran medida en su trabajo. La parte dedicada a la estática comparativa en el oligopolio procede de Dixit (1986). El modelo de las ventas procede de Varían (1980). El análisis de la elección de la capacidad en el modelo de Cournot se basa en Kreps y Sheinkman (1983). El análisis de la rentabilidad en los juegos del líder y el seguidor se debe a Dowrick (1986). La dualidad entre el equilibrio de Cournot y el de Bertrand fue descubierta 364 / EL OLIGOPOLIO (C. 16) por Sonnenschein (1968) y extendida por Singe y Vives (1984). El sencillo modelo de la fijación del precio límite aquí descrito se basa en Milgrom y Roberts (1982). Ejercicios 16.1. Supongamos que tenemos dos empresas que tienen unos costes marginales constantes de c1 y dos que tienen unos costes marginales constantes de c2 y que c2 > c1. ¿ Cuál es el equilibrio de Bertrand en este modelo? ¿ Y el equilibrio competitivo? 16.2. Considere el modelo de ventas descrito en la página 344. Cuando aumenta D / I, ¿qué ocurre con F(p)? Interprete este resultado. 16.3. Dadas las funciones inversas de demanda lineales del apartado de la página 345, halle las fórmulas de los parámetros de las funciones de demanda directas. 16.4. Utilizando las funciones de demanda lineales del problema anterior, demuestre que las cantidades siempre son menores y los precios mayores en la competencia de Cournot que en la de Bertrand. 16.5. Demuestre que si dos empresas tienen funciones de reacción de pendiente positiva de tal manera que fi (y,¿) > O y (yj, y2_) es el equilibrio de Stackelberg, entonces h<J1 (y2)) > h(yj) = Y2. · 16.6. La conjetura sobre las variaciones correspondiente al modelo competitivo es v = -1. Eso significa que cuando una empresa eleva su producción en una unidad, la otra la reduce en una unidad. Intuitivamente, esto no se parece nada a una conducta competitiva. ¿Donde está el fallo? 16.7. Demuestre que si implica que Y1 < Y2· ci (x) < c;(x) cualquiera que sea x > O, la solución del cártel 16.8. Suponga que dos empresas idénticas están actuando en la solución del cártel y que cadauna de ellas cree que si ajusta su nivel de producción, la otra ajustará el suyo para conservar su cuota de producción de 1/2. ¿Qué implica eso respecto a la conjetura sobre las variaciones? ¿Qué tipo de estructura de la industria implica? 16.9. ¿Por qué hay muchos equilibrios en el juego de Cournot que se repite un número finito de veces y sólo uno en el del dilema del prisionero que se repite un número finito de veces? Ejercicios / 365 16.10. Considere el caso de una industria en la que hay 2 empresas, cada una de las cuales tiene unos costes marginales nulos. La curva (inversa) de demanda a la que se enfrenta esta industria es P(Y) = 100 - Y, donde Y= Y1 + Y2 es la producción total. (a) ¿Cual es el nivel de producción de la industria correspondiente al equilibrio competitivo? (b) Si cada una de las empresas se comporta como un competidor de Cournot, ¿cuál es la elección óptima de la empresa 1 dado el nivel de producción de la 2? (c) Calcule la cantidad de producción de cada empresa correspondiente al equilibrio de Cournot. (d) Calcule la cantidad de producción de la industria correspondiente al cártel. (e) Si la empresa 1 se comporta como una seguidora y la 2 como una líder, calcule el nivel de producción de cada empresa correspondiente al equilibrio de Stackelberg. 16.11. Considere una industria de Cournot, en la que los niveles de producción de las empresas están representados por Y1, ... , Yn, la producción agregada por Y= ¿�=l Yi, la curva de demanda de la industria por P(Y) y la función de costes de cada empresa viene dada por ci(Yi) = k. Suponga para simplificar que P"(Y) < O y que cada una de las empresas debe pagar un impuesto específico de ti. (a) Formule las condiciones de primer orden de la empresa i. (b) Demuestre que la producción y el precio de la industria dependen únicamente de la suma de los tipos impositivos, 1 k I:: (c) Considere una variación del tipo impositivo de cada empresa que no altera la carga fiscal de la industria. Si /si, representa la variación del tipo impositivo de la empresa i, exigimos que ¿�=l tlti = O. Suponiendo que ninguna empresa abandona la industria, calcule la variación del nivel de producción de equilibrio de la empresa i, ó.Yi· Pista: no es necesario recurrir al cálculo diferencial; esta pregunta puede responderse examinando las partes (a) y (b). 366 / EL OLIGOPOLIO (C. 16) 16.12. Considere una industria que tiene la siguiente estructura. Hay 50 empresas que se comportan competitivamente y que tienen las mismas funciones de costes que vienen dadas por c(y) = y2 /2. Hay un monopolista que tiene unos costes marginales nulos. La curva de demanda del producto viene dada por D(p) = 1.000 - SOp. (a) ¿Cuál es la curva de oferta de una de las empresas competitivas? (b) ¿Cuál es la oferta total del sector competitivo? (c) Si el monopolista fija el precio p, ¿cuánta producción venderá? (d) ¿Cuál es el nivel de producción que maximiza el beneficio del monopolista? (e) ¿Cuál es el precio que maximiza el beneficio del monopolista? (f) ¿Cuál será la oferta del sector competitivo a este precio? (g) ¿Cuál será la cantidad total de producción que se venderá en esta industria? 17. EL INTERCAMBIO En el capítulo 13 analizamos la teoría económica de un único mercado. Vimos que cuando había muchos agentes económicos, era razonable suponer que cada uno de ellos consideraba que los precios de mercado estaban fuera de su control. Dados estos precios exógenos, cada uno de ellos podía determinar, pues, sus demandas y ofertas del bien en cuestión. El precio se ajustaba para equilibrar el mercado y a ese precio de equilibrio ningún agente deseaba modificar sus decisiones. El caso de un único mercado que acabamos de describir es un modelo de equilibrio parcial en el que se supone que todos los precios, salvo el del bien estudiado, permanecen fijos. En el modelo de equilibrio general, todos los precios son variables y para que haya equilibrio deben vaciarse todos los mercados. Por lo tanto, la teoría del equilibrio general tiene en cuenta todas las relaciones entre los mercados, así como el funcionamiento de cada uno de ellos. En aras de la exposición, examinaremos en primer lugar el caso especial del modelo de equilibrio general en el que todos los agentes económicos son consumidores. Esta situación, conocida con el nombre de intercambio puro, contiene muchos de los fenómenos presentes en el caso más general en el que hay empresas y producción. En una economía de intercambio puro hay varios consumidores, cada uno de los cuales es descrito por sus preferencias y por los bienes que posee. Los agentes intercambian los bienes entre sí de acuerdo con determinadas reglas e intentan mejorar su bienestar. ¿ Cuál es el resultado de ese proceso? ¿ Cuáles serían de desear? ¿ Qué mecanismos de asignación son adecuados para alcanzar estos resultados? Estos interrogantes plantean tanto cuestiones positivas como cuestiones normativas. Es precisamente en la relación entre estos dos tipos de cuestiones en la que reside en gran medida el interés de la teoría de la asignación de los recursos. 368 / EL INTERCAMBIO ( C. 17) 17.1 Agentes y bienes El concepto de bien que considerarnos aquí es muy amplio. Los bienes pueden distinguirse en función del tiempo, de la localización y de la situación mundial. Se considera que los servicios, por ejemplo, los de trabajo, son simplemente otro tipo de bien. Se supone que existe un mercado para cada bien, en el cual se determina su precio. En el modelo de intercambio puro, el único tipo de agente económico es el consumidor. Cada consumidor i es descrito totalmente por su preferencia, ti (o por su función de utilidad, ui) y por su dotación inicial de las k mercancías, Wi. Se supone que todos ellos se comportan cornpetitivarnente, es decir, que consideran dados los precios, independientemente de lo que hagan. Se supone también que todos intentan elegir la cesta que pueden comprar por la que muestran una mayor preferencia. La preocupación básica de la teoría del equilibrio general es el modo en que se asignan los bienes a los diferentes agentes económicos. La cantidad del bien j que tiene el agente i está representada por x{. Su cesta de consumo está representada por Xi = (x}, ... , xf); éste es un vector de dimensión k que indica qué cantidad de cada bien consume el agente i. Una asignación x = (x¡ , ... , Xn) es un conjunto den cestas de consumo que indica lo que tiene cada uno de los n agentes. Una asignación viable es aquella que es físicamente posible; en el caso del intercambio puro, es simplemente una asignación que agota todos los bienes, es decir, una asignación en la que ¿�=l Xi = ¿�=l Wi (en algunos casos, es útil considerar que una asignación es viable si ¿�=l Xi < ¿�=l Wi). Cuando hay dos bienes y dos agentes, podernos emplear un útil instrumento para representar de una manera bidimensional las asignaciones, las preferencias y las dotaciones que se conoce con el nombre de caja de Edgeworth. En la figura 17.1 mostrarnos un ejemplo de una caja de Edgeworth. Supongamos que la cantidad total del bien 1 es w1 = w} + wJ y que la cantidad total del bien 2 es w2 = wf + wf La base de la caja de Edgeworth es w1 y la altura w2. Un punto de la caja, (x}, xf), indica la cantidad que posee el agente 1 de los dos bienes. Al mismo tiempo, indica la cantidad que posee el agente 2: (x1, x�) = (w1 - x}, w2 - xf ). Geométricamente, la cesta del agente 1 se mide a partir de la esquina inferior izquierda de la caja y la del agente 2 a partir de la esquina superior derecha. De esta manera, en esta caja pueden representarse por medio de un punto todas y cada una de las asignaciones viables de los dos bienes a los dos agentes. También podernos representar en la caja las curvas de indiferencia de los agentes. Hay dos conjuntos de curvas de indiferencia, cada uno de los cuales corresponde a uno de los agentes. Toda la información que contiene una economía de intercambio El equilibrio walrasiano / 369 puro formada por dos personas y dos bienes puede representarse de esta forma por medio de un útil instrumento gráfico. Figura 17.1 ----------------------- CONSUMIDOR2 BIEN 2 CONSUMIDOR 1 ---------------------BIEN 1 La caja de Edgeworth. La longitud del eje de abscisas mide la cantidad total del bien 1 y la del eje de ordenadas la cantidad total del bien 2. Cada uno de los puntos de esta caja es una asignación viable. 17.2 El equilibrio walrasiano Hemos afirmado que cuando hay muchos agentes, es razonable suponer que cada uno de ellos considera que los precios de mercado son independientes de sus actos. Consideremos el caso de intercambio puro que estamos describiendo aquí. Imaginemos que hay un vector de precios de mercado p = (p1, ... , Pk), formado por un precio para cada bien. Cada uno de los consumidores considera dados estos precios y elige de su conjunto de consumo la cesta por la que muestra una mayor preferencia; es decir, cada uno de los consumidores i actúa como si estuviera resolviendo el siguiente problema: sujeta a px, = pwi. 370 / EL INTERCAMBIO (C. 17) La solución de este problema, x.Ip, pwi), es la función de demanda del consumidor, que hemos estudiado en el capítulo 9. En ese capítulo, su renta o riqueza, mi, era exógena. En éste, considerarnos que es el valor de mercado de su dotación inicial, por lo que mi = pwi. En el capítulo 9 vimos que suponiendo que las preferencias eran estrictamente convexas, las funciones de demanda eran funciones continuas regulares. Naturalmente, dado un vector de precios arbitrario p, puede no ser posible, de hecho, realizar las transacciones deseadas por la sencilla razón de que la demanda agregada, Li x.Ip, pwi), puede no ser igual a la oferta agregada, Li Wi· Es natural pensar que un vector de precios de equilibrio es aquel que equilibra todos los mercados, es decir, un conjunto de precios con el que la demanda es igual a la oferta en todos los mercados. Sin embargo, este supuesto es demasiado poderoso para nuestros fines. Consideremos, por ejemplo, el caso en el que algunos de los bienes no son atractivos. En este caso, puede muy bien haber un exceso de oferta en condiciones de equilibrio. Por esta razón, normalmente decirnos que el equilibrio walrasiano es un par de vectores (p", x") tal que ¿ x.tp", p*wi)::; ¿ Wi i Es decir, p* es un equilibrio walrasiano si no existe ningún bien del que haya un exceso de demanda positivo. Más adelante (página 371) demostraremos que si todos los bienes son atractivos -en un sentido que precisaremos entonces- la demanda será, de hecho, igual a la oferta en todos los mercados. 17.3 Análisis gráfico Los equilibrios walrasianos pueden examinarse geométricamente por medio de la caja de Edgeworth. Dado un vector de precios cualquiera, podernos determinar la recta presupuestaria de cada uno de los agentes y utilizar las curvas de indiferencia para hallar las cestas demandadas por cada uno. A continuación buscarnos un vector de precios tal que los puntos demandados de los dos agentes sean compatibles. En la figura 17.2 hemos representado una asignación de equilibrio de ese tipo. Cada uno de los agentes maximiza su utilidad en su recta presupuestaria y estas demandas son compatibles con las ofertas totales existentes. Obsérvese que el equilibrio walrasiano se alcanza en un punto en el que las dos curvas de indiferencia son tangentes, lo cual es evidente, puesto que la rnaxirnización de la utilidad exige que la relación marginal de sustitución de cada uno de los agentes sea igual a la relación de precios común a todos ellos. La existencia de equilibrios walrasianos / 371 El equilibrio también puede describirse por medio de curvas de oferta. Recuérdese que la curva de oferta de un consumidor describe el lugar geométrico de los puntos de tangencia entre las curvas de indiferencia y la recta presupuestaria cuando varían los precios relativos, es decir, el conjunto de cestas demandadas. Por lo tanto, en un punto de equilibrio de la caja de Edgeworth las curvas de oferta de los dos agentes se cortan. En esa intersección, las cestas demandadas por cada uno de ellos son compatibles con las ofertas existentes. Figura 17.2 -------------------- CONSUMIDOR2 BIEN2 Asignación / de equilibrio / Curva de oferta del consumidor 2 CONSUMIDOR 1------------------.BIEN1 El equilibrio walrasiano en la caja de Edgeworth. Cada uno de los agentes está maximizando la utilidad en su recta presupuestaria. 17.4 La existencia de equilibrios walrasianos ¿Existe siempre un vector de precios en el que se vacían todos los mercados? En este apartado analizamos la cuestión de la existencia de equilibrios walrasianos. Recordemos unos cuantos hechos acerca de este problema de la existencia. En primer lugar, el conjunto presupuestario de un consumidor no varía si multiplicamos todos los precios por una constante positiva cualquiera; por lo tanto, la función de demanda de cada uno de los consumidores tiene la propiedad de que x.Ip, JJWi) = xi(kp, kpwi) cualquiera que sea k > O; es decir, la función de demanda es homogénea de grado cero en los precios. Como la suma de las funciones homogéneas es homogénea, la función de exceso de demanda agregada, 372 / EL INTERCAMBIO (C. 17) z(p) = n 2:)xi(P, PWi) - Wi], i=l también es homogénea de grado cero en los precios. Obsérvese que prescindimos del hecho de que z depende del vector de dotaciones iniciales, (wi), ya que éstas permanecen constantes en el curso del análisis. Si todas las funciones de demanda son continuas, z será una función continua, ya que la suma de las funciones continuas es una función continua. Por otra parte, la función de exceso de demanda agregada debe satisfacer una condición conocida con el nombre de ley de Walras. Ley de Walras. Dado cualquier p perteneciente a s=:', tenemos que pz(p) = O; es decir, el valor del exceso de demanda es idénticamente igual a cero. Demostración. Basta formular la definición de la demanda agregada y multiplicar porp: dado que Xi(P, pwi) debe satisfacer la restricción presupuestaria px, = pwi en el caso de todos los agentes i = 1, ... , n. La ley de Walras dice algo bastante obvio: si cada uno de los individuos satisface su restricción presupuestaria, de tal manera que el valor de su exceso de demanda es nulo, el valor de la suma de los excesos de demanda debe ser nulo. Es importante darse cuenta de que esta ley establece que el valor del exceso de demanda es idénticamente igual a cero cualquiera que sea el precio. Combinando la ley de Walras y la definición de equilibrio, tenemos dos útiles proposiciones. Equilibrio del mercado. Si la demanda es igual a la oferta en k - 1 mercados y Pk > O, la demanda debe ser igual a la oferta en el k-ésimo mercado. Demostración. En caso contrario, se violaría la ley de Walras. p; Bienes gratuitos. Si p" es un equilibrio walrasiano y zj(p*) < O, = O. Es decir, si hay un exceso de oferta de algún bien en un equilibrio walrasiano, debe ser un bien gratuito. Demostración. Dado que p* es un equilibrio walrasiano, z(p*) � O. Dado que los Existencia de un equilibrio / 373 precios no son negativos, p*z(p*) = ¿�=l Pi zi(p*) ::; O. Si zj(p*) < O y tendríamos que p*z(p*) < O, lo que contradice la ley de Walras. p; > O, Esta proposición muestra cuáles son las condiciones que deben cumplirse para que todos los mercados se vacíen en el equilibrio. Supongamos que todos los bienes son atractivos en el siguiente sentido: Deseabilidad. Si Pi = O, entonces zi(p) > O, siendo i = 1, ... , k. El supuesto de la deseabilidad establece que si un precio es cero, el exceso de demanda agregada de ese bien es estrictamente positivo. En ese caso, tenemos la siguiente proposición: Igualdad de la demanda y la oferta. Si todos los bienes son atractivos y p* es un equilibrio = O. walrasiano, z(p*) Demostración. Supongamos que zi(p*) < O. En ese caso, de acuerdo con la proposición de los bienes gratuitos, Pi = O. Pero de acuerdo con el supuesto de la deseabilidad, zi(p*) > O, lo cual es una contradicción. Resumiendo, en general, lo único que es necesario para que haya equilibrio es que no exista exceso de demanda de ningún bien. Pero las proposiciones anteriores indican que si en condiciones de equilibrio hay, de hecho, un exceso de oferta de algún bien, su precio debe ser cero. Por lo tanto, si todos los bienes son atractivos en el sentido de que un precio nulo implica que habrá un exceso de demanda, el equilibrio vendrá caracterizado, de hecho, por la igualdad de la demanda y la oferta en todos los mercados. 17.5 Existencia de un equilibrio Dado que la función de exceso de demanda agregada es homogénea de grado cero, podemos normalizar los precios y expresar las demandas en función de los precios relativos. Existen varias maneras de hacerlo, pero una normalización útil para nuestros fines consiste en sustituir cada uno de los precios absolutos Pi por un precio normalizado: p·i - Pi � �k Lij=l Pí De esa manera, la suma de los precios normalizados Pi ha de ser siempre igual a 1. Por lo tanto, podemos limitarnos a examinar los vectores de precios que pertenecen 374 / EL INTERCAMBIO (C. 17) al simplex unitario de dimensión k - 1: s":' = {P pertenece a R�: tp, = 1}. i=l Figura 17.3 Simplices de los precios. El primer panel muestra el simplex unidimensional de los precios s 1 y el segundo s2. Para una representación gráfica de 81 y 82, véase la figura 17.3. Volvamos ahora a la cuestión de la existencia de un equilibrio walrasiano: ¿existe un vector de precios p* que vacíe todos los mercados? Nuestra demostración de la existencia de un equilibrio walrasiano se basa en el teorema del punto fijo de Brouwer. Teorema del punto fijo de Brouwer. Si f : sk- i ----+ sk- i es una función continua que va del simplex unitario a sí mismo, hay un x perteneciente a sk-t tal que x = f(x). Demostración. La demostración del caso general va más allá del alcance de este libro; para una buena demostración, véase Scarf (1983). Sin embargo, demostraremos el teorema en el caso en que k = 2. En este caso, podemos identificar el simplex unitario unidimensional S1 con el intervalo unitario. De acuerdo con la formulación del teorema, tenemos una función continua f : [O, 1] ----+ [O, 1] y queremos demostrar que hay algún x en [O, 1] tal que X= f(x). Existencia de un equilibrio / 375 Consideremos la función g definida de la manera siguiente: g(x) = f (x) - x. En términos geométricos, g mide simplemente la diferencia entre f(x) y la diagonal de la caja representada en la figura 17.4. Un punto fijo de la aplicación f es un x* en el que g(x*) = O. Figura 17.4 f(x) X Demostración del teorema de Brouwer en el caso bidimensional. En el caso representado, hay tres puntos en los que x = f(x). Ahora tenemos que g(O) = f(O) - O 2: O, ya que f(O) pertenece a [O, 1], y que g(l) = j(l) - 1 � O por la misma razón. Dado que fes continua, podemos aplicar el teorema del valor medio y concluir que hay algún x perteneciente a [O, 1] tal que g(x) = f(x) - x = O, lo que demuestra el teorema. Nos encontramos ya en condiciones de demostrar el teorema principal de la existencia. Existencia de equilibrios walrasianos. Si z : sk-l --+ Rk es una función continua que satisface la ley de Walras, pz(p) = O, existe algún p* perteneciente a sk-l tal que z(p*) � O. Demostración. Definimos la aplicación g : gi ( p ) = sk-l --+ sk-l Pi + max(O, Zi(p)) 1+ k Lj=l max(O, zj(p)) de la manera siguiente: siendo i = 1, ... , k. Obsérvese que esta aplicación es continua, ya que z y la función de máximo son 376 / EL INTERCAMBIO (C. 17) funciones continuas. Por otra parte, g(p) es un punto perteneciente al simplex s=:', ya que Li gi(p) = l. Esta aplicación también tiene una interpretación económica razonable: si hay un exceso de demanda en un mercado, de tal manera que Zi(p) � O, se eleva el precio relativo de ese bien. De acuerdo con el teorema del punto fijo de Brouwer, existe un p* tal que p* = g(p*), es decir, * Pi= Pi + max(O, z/p*)) 1+ "" �j max(O, zj(p*)) siendoi=l, ... ,k (17.1) Demostraremos que p* es un equilibrio walrasiano. Eliminando los denominadores en la ecuación (17.1) y reordenando, tenemos que Pi L max(O, zj(p*)) = max(O, Zi(p*)) k i = 1, ... , k. j=l Multiplicando ahora cada una de estas ecuaciones por zi(p*), tenemos que zi(p*)pi [t max(O, z/p*))] = zi(p*) max(O, zi(p*)) i = 1, ... , k. J=l Sumando estas k ecuaciones, obtenemos [t Ahora bien, max(O, z;(p*))] t Pi z,(p*) = t z,(p*) max(O, z,(p*)). :E7=1 Pi zi(p*) = O por la ley de Walras, por lo que tenemos que k L zi(p*) max(O, Zi(p*)) = O. i=l Cada uno de los términos de esta suma es mayor o igual que cero, ya que cada uno de ellos es o bien O, o bien (zi(p*))2. Pero si algún término fuera estrictamente mayor que cero, no se cumpliría la igualdad. Por lo tanto, todos los términos deben ser iguales a cero, lo que significa que Zi(p*) :S O siendo i = 1, ... , k. Merece la pena destacar el carácter general del teorema anterior. Lo único necesario es que la función de exceso de demanda sea continua y satisfaga la ley de Walras. Esta última se desprende directamente de la hipótesis de que el consumidor Existencia de un equilibrio / 377 ha de cumplir alguna clase de restricción presupuestaria; este tipo de comportamiento parece necesario en cualquier clase de modelo económico. La hipótesis de la continuidad es más restrictiva, pero no hasta el punto de no ser razonable. Hemos visto antes que si los consumidores tienen todos ellos unas preferencias estrictamente convexas, sus funciones de demanda estarán bien definidas y serán continuas, por lo que la función de demanda agregada será continua. Pero aun cuando las funciones de demanda individuales muestren discontinuidades, la función de demanda agregada puede ser continua si hay un gran número de consumidores. Por lo tanto, la continuidad de la demanda agregada parece ser un requisito relativamente débil. Sin embargo, el argumento anterior en favor de la existencia plantea un pequeño problema. Es cierto que la demanda agregada probablemente será continua cuando los precios sean positivos, pero es poco razonable suponer que lo será incluso cuando alguno se vuelva nulo. Por ejemplo, si las preferencias fueran monótonas y el precio de algún bien fuera cero, sería de esperar que la demanda de ese bien fuera infinita. Por lo tanto, la función de exceso de demanda podría no estar ni siquiera bien definida en la frontera del sirnplex de los precios, es decir, en el conjunto de vectores de precios en el que algunos son cero. Sin embargo, este tipo de discontinuidad puede resolverse utilizando un razonamiento matemático algo más complejo. Ejemplo: La economía Cobb-Douglas Supongamos que el agente 1 tiene la función de utilidad UI (x}, xf) = (x1)r<xf)I-a y la dotación w1 = (1, O) y que el agente 2 tiene la función de utilidad u2(x!, x�) = (x!)!(x�)I-b y la dotación w: = (O, 1). En ese caso, la función de demanda del bien 1 por parte del agente 1 es A los precios (pI, p2), la renta es m = PI x 1 + P2 x O =PI. Sustituyendo, tenernos que Del mismo modo, la función de demanda del bien 1 por parte del agente 2 es El precio de equilibrio es aquel en el que la demanda total de cada uno de los bienes es igual a la oferta total. En razón de la ley de Walras, lo único que necesitarnos es hallar el precio al que la demanda total del bien 1 es igual a su oferta total: 378 / EL INTERCAMBIO (C. 17) x�(p1,p2) + Xi(P1,P2) = 1 a+ bp2 = 1 Pl p2 PÍ 1 - a b Obsérvese que, como es habitual, en condiciones de equilibrio sólo se determinan los precios relativos. 17.6 El primer teorema de la economía del bienestar La existencia de equilibrios walrasianos es interesante como resultado positivo en la medida en que nos creamos los supuestos sobre la conducta en los que se basa el modelo. Sin embargo, incluso aunque estos supuestos no parezcan especialmente plausibles en muchas circunstancias, es posible que nos interesen los equilibrios walrasianos por su contenido normativo. Examinemos las siguientes definiciones. Definiciones de eficiencia en el sentido de Pareto. Una asignación viable x es débilmente eficiente en el sentido de Pareto si no existe ninguna asignación viable x' tal que todos los agentes la prefieran estrictamente a la asignación x. Una asignación viable x es fuertemente eficiente en el sentido de Pareto si no existe ninguna asignación viable x' tal que todos los agentes la prefieran débilmente a la asignación x y alguno la prefiera estrictamente a la x. Es fácil ver que una asignación que es fuertemente eficiente en el sentido de Pareto también es débilmente eficiente en el sentido de Pareto, pero no a la inversa, en general. Sin embargo, partiendo de algunos otros débiles supuestos sobre las preferencias, sí es cierta la implicación inversa, por lo que es posible utilizar indistintamente los dos conceptos. Equivalencia de la eficiencia débil en el sentido de Pareto y la eficiencia fuerte en el sentido de Pareto. Supongamos que las preferencias son continuas y monótonas. En ese caso, una asignación es débilmente eficiente en el sentido de Pareto si y sólo si es fuertemente eficiente en el sentido de Pareto. Demostración. Si una asignación es fuertemente eficiente en el sentido de Pareto, es sin duda débilmente eficiente en el sentido de Pareto: si no es posible mejorar el bienestar de una persona sin empeorar el de alguna otra, no es posible, ciertamente, mejorar el bienestar de todo el mundo. El primer teorema de la economía del bienestar / 379 Es necesario demostrar que si una asignación es débilmente eficiente en el sentido de Pareto, es fuertemente eficiente en el sentido de Pareto. Demostraremos la afirmación lógicamente equivalente de que si una asignación no es fuertemente eficiente, tampoco lo es débilmente. Supongamos, pues, que es posible mejorar el bienestar de algún agente i sin empeorar el de algún otro. Debemos demostrar que es posible mejorar el bienestar de todo el mundo, para lo cual basta reducir simplemente la cesta de consumo del agente i en una pequeña cuantía y redistribuir esos bienes por igual entre los demás agentes. Más concretamente, se sustituye la cesta de consumo de i, Xi, por Bx; y se sustituye la cesta de consumo de otro agente j por Xj + (1 - ())xd(n - 1). De acuerdo con la continuidad de las preferencias, es posible elegir un () suficientemente cercano a 1 para que aun así mejore el bienestar del agente i. De acuerdo con la monotonicidad, todos los agentes ven mejorar estrictamente su bienestar al recibir la cesta redistribuida. Resulta que el concepto de eficiencia débil en el sentido de Pareto es algo más útil desde el punto de vista matemático, por lo que utilizaremos en general esta definición; es decir, cuando utilicemos la expresión "eficiente en el sentido de Pareto", querrá decir "débilmente eficiente en el sentido de Pareto". Sin embargo, de aquí en adelante siempre supondremos que las preferencias son continuas y monótonas, por lo que puede aplicarse cualquiera de las dos definiciones. Obsérvese que el concepto de eficiencia en el sentido de Pareto es algo débil como concepto normativo; una asignación en la que uno de los agentes recibe todo lo que hay en la economía y los demás no reciben nada es eficiente en el sentido de Pareto, suponiendo que el agente que lo tiene todo no esté saciado. Las asignaciones eficientes en el sentido de Pareto pueden representarse fácilmente en el diagrama de la caja de Edgeworth que hemos presentado antes. Basta señalar que en el caso en el que hay dos personas las asignaciones eficientes en el sentido de Pareto pueden hallarse fijando la función de utilidad de uno de los agentes en un determinado nivel y maximizando la del otro sujeta a esta restricción. En términos formales, basta resolver el siguiente problema de maximización: sujeta a u2(x2) � il2 XJ + X2 = W1 + W2. Este problema puede resolverse examinando el caso de la caja de Edgeworth. Basta hallar simplemente el punto de la curva de indiferencia de uno de los agentes en el cual el otro alcanza la máxima utilidad. A estas alturas, ya debería estar claro que el punto eficiente en el sentido de Pareto resultante es caracterizado por una condición 380 / EL INTERCAMBIO (C. 17) de tangencia: las relaciones marginales de sustitución de los dos agentes deben ser iguales. Para cada valor fijo de la utilidad del agente 2, podemos hallar una asignación en la que se maximice la utilidad del agente 1 y, por lo tanto, se satisfaga la condición de tangencia. El conjunto de puntos eficientes en el sentido de Pareto --el conjunto de Pareto- será, pues, el conjunto de puntos de tangencia representado en la caja de Edgeworth de la figura 17.5. El conjunto de Pareto también se conoce con el nombre de curva de contrato, ya que indica el conjunto de "contratos" o asignaciones eficientes en el sentido de Pareto. Figura 17.5 BIEN 2 ' Conjunto de Pareto (curva de contrato) CONSUMIDOR 1 ------------------BIEN 1 La eficiencia en el sentido de Pareto en la caja de Edgeworth. El conjunto de Pareto o curva de contrato es el conjunto de todas las asignaciones eficientes en el sentido de Pareto. La comparación de las figuras 17.5 y 17.2 revela un hecho sorprendente: parece que existe una plena correspondiencia entre el conjunto de equilibrios walrasianos y el conjunto de asignaciones eficientes en el sentido de Pareto. Cada uno de los equilibrios walrasianos satisface la condición de primer orden para la maximización de la utilidad, según la cual la relación marginal de sustitución entre los dos bienes correspondiente a cada uno de los agentes debe ser igual a la relación de precios de los dos. Dado que en un equilibrio walrasiano todos los agentes se enfrentan a la misma relación de precios, todos deben tener las mismas relaciones marginales de sustitución. El primer teorema de la economía del bienestar / 381 Por otra parte, si elegimos una asignación arbitraria eficiente en el sentido de Pareto, sabemos que las relaciones marginales de sustitución de los dos agentes deben ser iguales, por lo que podemos elegir una relación de precios igual a este valor común. Desde el punto de vista gráfico, dado un punto eficiente en el sentido de Pareto, basta trazar simplemente la tangente común que separa las dos curvas de indiferencia. A continuación se elige un punto de esta tangente que sirva de dotación inicial. Si los agentes tratan de maximizar las preferencias dados sus conjuntos presupuestarios, terminarán precisamente en la asignación eficiente en el sentido de Pareto. Los dos teoremas siguientes precisan esta correspondencia. Primero reformulamos la definición de equilibrio walrasiano de una manera más útil: Definición de equilibrio walrasiano. Un par de vectores de asignaciones y precios (x, p) es un equilibrio walrasiano si (1) la asignación es viable y (2) cada uno de los agentes elige el punto óptimo de su conjunto presupuestario. En ecuaciones: 2. Si el agente i prefiere x� a Xi, entonces px� > pwi. Esta definición es equivalente a la definición original de equilibrio walrasiano, en la medida en que se satisfaga el supuesto de la deseabilidad. Nos permite prescindir de la posibilidad de que los bienes sean gratuitos, posibilidad que resultaría algo engorrosa para los argumentos que exponemos a continuación. Primer teorema de la economía del bienestar. Si (x, p) es un equilibrio walrasiano, x es eficiente en el sentido de Pareto. Demostración. Supongamos que no lo fuera y que x' es una asignación viable que prefieren todos los agentes a la x. En ese caso, de acuerdo con la propiedad 2 de la definición del equilibrio walrasiano, tenemos que px� > pwi siendo i = 1, ... , n. Sumando los valores correspondientes a todos los agentes i del hecho de que x' es viable, tenemos que lo cual es una contradicción. n n n i=l i=l i=l = 1, ... , n y valiéndonos 382 / EL INTERCAMBIO (C. 17) lo cual es una contradicción. Este teorema establece que si se satisfacen los supuestos de nuestro modelo sobre la conducta, el equilibrio de mercado es eficiente. Un equilibrio de mercado no es necesariamente "óptimo" en el sentido ético, ya que puede ser muy "injusto". El resultado depende totalmente de la distribución inicial de las dotaciones. Lo que se necesita es algún otro criterio ético para elegir entre las asignaciones eficientes. Más adelante en este capítulo analizaremos un concepto de ese tipo, a saber, el concepto de función de bienestar. 17.7 El segundo teorema del bienestar Hemos demostrado que todo equilibrio walrasiano es eficiente en el sentido de Pareto. Aquí demostramos que toda asignación eficiente en el sentido de Pareto es un equilibrio walrasiano. Segundo teorema de la economía del bienestar. Supongamos que x* es una asignación eficiente en el sentido de Pareto en la que cada uno de los agentes posee una cantidad positiva de cada uno de los bienes. Supongamos que las preferencias son convexas, continuas y monótonas. En ese caso, x* es un equilibrio walrasiano en el caso de las dotaciones iniciales Wi = x: siendo i = 1, ... , n. Demostración. Sea Éste es el conjunto de todas las cestas de consumo que el agente i prefiere a En ese caso, definimos P= t P; = { z:z= t x, donde x, pertenece a P; } x:. . P es el conjunto de todas las cestas de los k bienes que pueden distribuirse entre los n agentes con el fin de mejorar el bienestar de todos ellos. Dado que cada Pi es un conjunto convexo por hipótesis y la suma de los conjuntos convexos es un conjunto convexo, P también es un conjunto convexo. Sea w = la cesta agregada actual. Dado que x" es eficiente en el sentido 1 de Pareto, no existe ninguna redistribución de x* que mejore el bienestar de todo el mundo, lo cual significa que w no es un elemento del conjunto P. Por lo tanto, de acuerdo con el teorema del hiperplano separador (capítulo 26, página 565), existe un vector p =! O tal que ¿::, x: El segundo teorema del bienestar / 383 pz 2': p ¿ x: n i=l cualquiera que sea z perteneciente a P. Reordenando esta ecuación, tenemos que p ( z- t xi) ;:,: cualquiera que sea z perteneciente a P O (17.2) Queremos demostrar que pes, de hecho, un vector de precios de equilibrio. La demostración consta de tres partes. 1. p es no negativo; es decir, p 2': O. Para verlo, consideremos el vector e, = (O, ... , 1, ... , O) que tiene un 1 en el componente i-ésimo. Dado que las preferencias son monótonas, w + e, debe pertenecer a P, dado que si tenemos una unidad más de un bien cualquiera, es posible redistribuirlo para mejorar el bienestar de todo el mundo. La desigualdad (17.2) implica, entonces, que p(w + ei - w) 2': O siendo i = 1, ... , k. Anulando términos, peí 2': O siendo i = 1, ... , k. Esta ecuación implica que Pi 2': O, siendo i = 1, ... , k. 2. Si y1 >-- 1 x;, entonces py1 2': px;, en el caso de todos los agentes j = 1, ... , n. Ya sabemos que si todos los agentes i prefieren y i a x;, entonces ¿x:. n n p ¿Yi 2': P i=l i=l Supongamos ahora solamente que un determinado agente j prefiere una cesta y1 a la x1. Construyamos una asignación z distribuyendo una cierta cantidad de cada bien del agente j en favor de los demás. En términos formales, suponemos que () es un número pequeño y definimos las asignaciones z de la manera siguiente: Zj = Zi = (1 * Xi ())yj ()yj + -- n-1 i _¡ T j. 384 / EL INTERCAMBIO ( C. 17) Si() es suficientemente pequeño, el supuesto de la monotonicidad fuerte implica que la asignación z se prefiere en el sentido de Pareto a la x" y, por lo tanto, ¿�=l z, pertenece a P. Aplicando la desigualdad (17.2), tenemos que p [yj(l n n i=l i=l - ()) + ¿ x; + Yí()] 2: PYí 2: i=jj p [x; px;. + ¿ x;] i=/j x;, Este argumento demuestra que si el agente j prefiere y j a y j no puede costar menos que Resta por demostrar que la desigualdad es estricta. x;. 3. Si yj >-- j x;, debe cumplirse que pyj > px;. Ya sabemos que py j 2: px;; queremos excluir la posibilidad de que se cumpla el caso de la igualdad, por lo que suponemos que py j = px; y tratamos de llegar a una contradicción. De acuerdo con el supuesto de la continuidad de las preferencias, podemos hallar algún tal que O < () < 1, de tal manera que ()yj se prefiera estrictamente a De acuerdo con la argumentación de la parte 2, sabemos que ()yj debe costar al menos tanto como x;. é x;: (17.3) x; Una de las hipótesis del teorema es que todos los componentes de son estrictamente positivos, de donde se deduce que px; > O. Por lo tanto, si py j - px; = O, entonces ()py j < px;. Pero eso contradice la desigualdad (17.3), por que damos por concluida la demostración del teorema. Merece la pena examinar las hipótesis de esta proposición. La convexidad y la continuidad de las preferencias son fundamentales, desde luego, pero la monotonicidad fuerte puede abandonarse en gran parte, así como el supuesto de que x: » o. Un razonamiento basado en la preferencia revelada Existe una demostración sencillísima, aunque algo indirecta, del segundo teorema del bienestar que se basa en el argumento de la preferencia revelada y en el teorema de la existencia descrito antes en el presente capítulo. La eficiencia en el sentido de Pareto y el cálculo / 385 Segundo teorema de la economía del bienestar. Supongamos que x" es una asignación eficiente en el sentido de Pareto y que las preferencias tienen la propiedad de la insaciabilidad. Supongamos, además, que existe un equilibrio competitivo a partir de las dotaciones iniciales y que éste viene dado por (p, x'). En ese caso, (p/, x") es, de hecho, un equilibrio competitivo. Wi = x: Demostración. Dado que x: pertenece al conjunto presupuestario del consumidor i por construcción, debe cumplirse que xi' ti Dado que x" es eficiente en el sentido de Pareto, implica que Xi rvi x�. Por lo tanto, si x� es óptimo, también lo es Así pues, (p', x") es un equilibrio walrasiano. x:. x:. Este razonamiento demuestra que si existe un equilibrio competitivo a partir de una asignación eficiente en el sentido de Pareto, esa asignación es ella misma un equilibrio competitivo. Las observaciones realizadas después del teorema de la existencia en el presente capítulo indican que el único requisito esencial para la existencia es la continuidad de la función de demanda agregada. La continuidad se desprende, o bien de la convexidad de las preferencias individuales, o bien del supuesto de una economía "grande". Por lo tanto, el segundo teorema del bienestar es válido en las mismas circunstancias. 17.8 La eficiencia en el sentido de Pareto y el cálculo Hemos visto en el apartado anterior que todo equilibrio competitivo es eficiente en el sentido de Pareto y que casi toda asignación eficiente en el sentido de Pareto es un equilibrio competitivo en el caso de alguna distribución de las dotaciones. En este apartado analizaremos más detenidamente esta relación por medio del cálculo diferencial. En esencia, formularemos las condiciones de primer orden que caracterizan los equilibrios de mercado y la eficiencia en el sentido de Pareto y compararemos estos dos conjuntos de condiciones. Las condiciones que caracterizan el equilibrio de mercado son muy sencillas. Caracterización del equilibrio basada en el cálculo. Si (x", p*) es un equilibrio de mercado en el que cada uno de los consumidores tiene una cantidad positiva de todos los bienes, existe un conjunto de números (>.1, ... , An) tal que i = 1, ... , n. Demostración. Si tenemos un equilibrio de mercado, cada uno de los agentes maxi- miza la utilidad, dado en su conjunto presupuestario, y éstas son simplemente las condiciones de primer orden para la maximización de la utilidad. Los números Ai representan la utilidad marginal de la renta de los agentes. 386 / EL INTERCAMBIO (C. 17) Las condiciones de primer orden para que haya eficiencia en el sentido de Pareto son algo más difíciles de formular. Sin embargo, resulta muy útil el truco siguiente. Caracterización de la eficiencia en el sentido de Pareto basada en el cálculo. Una asignación viable x* es eficiente en el sentido de Pareto si y sólo si x* es la solución de los siguientes n problemas de maximización, siendo i = 1, ... , n: n sujeta a ¿ xJ < w 9 g = 1, ... , k j=l Uj(Xj) � Uj(Xj) j =f i. Demostración. Supongamos que x* es la solución de todos los problemas de maximización, pero no es eficiente en el sentido de Pareto. Eso significa que hay alguna asignación x' en la que todo el mundo disfruta de un mayor bienestar. Pero, en ese caso, x* no podría ser la solución de ninguno de los problemas, lo cual es una contradicción. Supongamos, por el contrario, que x* es eficiente en el sentido de Pareto, pero que no es la solución de uno de los problemas. Supongamos que la solución de ese problema es x'. En ese caso, x' mejora el bienestar de uno de los agentes sin empeorar el de ningún otro, lo que contradice el supuesto de que x* es eficiente en el sentido de Pareto. Antes de examinar la formulación del lagrangiano correspondiente a cada uno de estos problemas de maximización, hagamos algunas cuentas. Hay k + n - 1 restricciones para cada uno de los n problemas de maximización. Las primeras k restricciones son restricciones de recursos y las n - 1 siguientes son restricciones de utilidad. En cada uno de los problemas de maximización hay kn variables de elección, es decir, la cantidad que tiene cada uno de los n agentes de cada uno de los k bienes. Sean q9, siendo g = 1, ... , k, los multiplicadores de Lagrange de las restricciones de recursos y aj, si j =I i los multiplicadores de Kuhn-Tucker de las restricciones de utilidad. Fo�mulemos el lagrangiano de uno de los problemas de maximización . .C = ui(xi) - t [t xf q9 g=l i=l w9] - ¿ aj[uj(x;) - uj{xj)]. j=/i xJ, A continuación diferenciamos .C con respecto a donde g 1, ... , n. Obtenemos las siguientes condiciones de primer orden: = 1, ... , k y j = La eficiencia en el sentido de Pareto y el cálculo / 387 g = 1, ... ,k jfi;g=l, ... ,k. Estas condiciones parecen a primera vista algo extrañas, ya que parecen asimétricas. Los valores de los multiplicadores (q9) y (aj) que obtenernos son distintos en el caso de cada elección de i. Sin embargo, la paradoja se resuelve cuando se observa que los valores relativos de las q son independientes de la elección de i. Esto es evidente, puesto que las condiciones anteriores implican que aui<x:) 8xf aui(x;) axh q9 qh siendo i = 1, ... , n y g, h = 1, ... , k. i Corno x" está dado, q9 / qh debe ser independiente del problema de rnaxirnización que resolvamos. Este mismo razonamiento demuestra que ad aj es independiente del problema de rnaxirnización que resolvamos. La solución del problema de asimetría resulta ahora clara: si maximizarnos la utilidad del agente i y utilizarnos como restricciones las utilidades de los demás agentes, es exactamente igual que si asignarnos arbitrariamente al agente i un multiplicador de Kuhn-Tucker a, igual a 1. Aplicando el primer teorema del bienestar, podernos deducir interesantes interpretaciones de las ponderaciones (ai) y (q9): si x* es un equilibrio de mercado, Sin embargo, todos los equilibrios de mercado son eficientes en el sentido de Pareto, por lo que debe cumplirse que aiDu/x;) = q i = 1, ... ,n. Esta expresión muestra claramente que podernos elegir p* = q y a, = 1/ ,\, lo que quiere decir que los multiplicadores de Kuhn-Tucker de las restricciones de recursos son exactamente los precios competitivos y los multiplicadores de Kuhn-Tucker de las utilidades del agente son exactamente las inversas de sus utilidades marginales de la renta. Si eliminarnos los multiplicadores de Kuhn-Tucker de las condiciones de primer orden, obtenernos las siguientes condiciones que caracterizan las asignaciones eficientes: 388 / EL INTERCAMBIO ( C. 17) aui(xl) p; aui(xl) P1i 8xf 3xhi q9 qh i = 1, ... , n y g, h = 1, ... , k. Esta expresión quiere decir que cada una de las asignaciones eficientes en el sentido de Pareto debe satisfacer la condición según la cual la relación marginal de sustitución entre cada uno de los pares de bienes ha de ser la misma en el caso de todos los agentes. Esta relación marginal de sustitución es simplemente el cociente entre los precios competitivos. El significado intuitivo de esta condición es bastante evidente: si dos agentes tuvieran diferentes relaciones marginales de sustitución entre algún par de bienes, podrían realizar un pequeño intercambio que mejorara el bienestar de los dos, lo que contradiría el supuesto de la eficiencia en el sentido de Pareto. A menudo resulta útil observar que las condiciones de primer orden para la existencia de una asignación eficiente en el sentido de Pareto son iguales que las condiciones de primer orden para la rnaxirnización de una suma ponderada de las utilidades. Para verlo, examinemos el siguiente problema: n rnax ¿ a, u; (xi) i=l ¿ xf ::; w n sujeta a 9 g = 1, ... , k. i=l Las condiciones de primer orden para la solución de este problema son (17.4) que son exactamente iguales a las condiciones necesarias para que haya eficiencia en el sentido de Pareto. A medida que varía el conjunto de "ponderaciones del bienestar" (ai, ... , an), vamos obteniendo el conjunto de asignaciones eficientes en el sentido de Pareto. Si nos interesa conocer las condiciones que caracterizan todas las asignaciones eficientes en el sentido de Pareto, necesitarnos manipular las ecuaciones para que desaparezcan las ponderaciones del bienestar, lo que se reduce generalmente a expresar las condiciones en función de las relaciones marginales de sustitución. También puede llegarse a este resultado incorporando las ponderaciones del bienestar a la definición de la función de utilidad. Si la función de utilidad inicial del agente i es ui(xi), tornarnos una transformación monótona de tal manera que la nueva función de utilidad sea vi(xi) = a(ui(xi). Las condiciones de primer orden resultantes caracterizan una determinada asignación eficiente en el sentido de Pareto, a La maximización del bienestar / 389 saber, aquella que maximiza la suma de las utilidades en el caso de una determinada representación de la utilidad. Pero si manipularnos las condiciones de primer orden para expresarlas en función de las relaciones marginales de sustitución, normalmente hallaremos una condición que caracterice a todas las asignaciones eficientes. De momento, señalaremos que esta caracterización de la eficiencia en el sentido de Pareto basada en el cálculo constituye una sencilla demostración del segundo teorema del bienestar. Supongamos que todos los consumidores tienen funciones de utilidad cóncavas, aunque en realidad no es necesario. En ese caso, si x" es una asignación eficiente en el sentido de Pareto, sabernos por las condiciones de primer orden que Dui(x*) = 1 -q siendo i ai = 1, ... , n. Por lo tanto, el gradiente de la función de utilidad de cada uno de los consumidores es proporcional a algún vector fijo q. Sea q el vector de precios competitivos. Es necesario verificar que cada uno de los consumidores maximiza su utilidad, dado su conjunto presupuestario { Xi : qx, � qx]'}. Pero esto se deduce inmediatamente de la concavidad; de acuerdo con las propiedades matemáticas de las funciones cóncavas, por lo que Por lo tanto, si Xi es el conjunto presupuestario del consumidor, u(x) � u(x;). 17.9 La maximización del bienestar Uno de los problemas que plantea el concepto de eficiencia en el sentido de Pareto corno criterio normativo es que no es muy específico. La eficiencia en el sentido de Pareto sólo se refiere a la eficiencia y no dice nada sobre la distribución del bienestar. Aun cuando estemos de acuerdo en que debernos encontrarnos en una asignación eficiente en el sentido de Pareto, aún no sabernos cuál es ésta. Una manera de resolver estos problemas es suponer que existe una función social de bienestar. Se supone que ésta es una función que agrega las funciones de utilidad individuales para obtener una "utilidad social". La interpretación más razonable que puede darse a una función de ese tipo es que representa las preferencias de los responsables de tornar las decisiones en la sociedad sobre la manera de intercambiar las utilidades de los diferentes individuos. Nos abstendremos aquí de 390 / EL INTERCAMBIO (C. 17) hacer comentarios filosóficos y nos limitaremos a postular que existe tal función; es decir, supondremos que tenernos que de tal manera que W(ui, , un) indica la "utilidad social" resultante de una distribución cualquiera (u1, , un) de las utilidades privadas. Para que este procedimiento tenga sentido, la representación de la utilidad de cada uno de los agentes que elijamos habrá de ser la misma a lo largo de todo el análisis. Supondremos que W es creciente en cada uno de sus argumentos: si elevarnos la utilidad de un agente cualquiera sin reducir el bienestar de ningún otro, deberá aumentar el bienestar social. Suponernos que la sociedad debe encontrarse en un punto que maximice el bienestar social, es decir, debernos elegir una asignación x" que resuelva el siguiente problema: ¿ xf ::; n sujeta a wg g = 1, ... , k. i=l ¿Qué diferencia hay entre las asignaciones que maximizan esta función de bienestar y las asignaciones eficientes en el sentido de Pareto? El siguiente resultado es una consecuencia trivial de la hipótesis de la rnonotonicidad: Maximización del bienestar y eficiencia en el sentido de Pareto. Si x" maximiza una función social de bienestar, x" es eficiente en el sentido de Pareto. Demostración. Si x" no fuera eficiente en el sentido de Pareto, habría alguna asignación viable x' tal que u; (x�) > u; (xi) siendo i = 1, ... , n. Pero en ese caso W(u1(xi), ... , Un(x�)) > W(u1(xi), ... , Un(x�)). Dado que los puntos de máximo bienestar son eficientes en el sentido de Pareto, deben satisfacer las mismas condiciones de primer orden que las asignaciones eficientes en el sentido de Pareto; por otra parte, partiendo de los supuestos sobre la convexidad, toda asignación eficiente en el sentido de Pareto es un equilibrio competitivo, por 19 que lo mismo ocurre con los puntos de máximo bienestar: todo máximo de bienestar es un equilibrio competitivo correspondiente a alguna distribución de las dotaciones. Esta última observación constituye otra interpretación más de los precios competitivos: también son los multiplicadores de Kuhn-Tucker del problema de rnaxirnización del bienestar. Aplicando el teorema de la envolvente, vernos que los precios competitivos miden el valor social (marginal) de un bien: cuánto aumentaría La maximización del bienestar / 391 el bienestar si tuviéramos una pequeña cantidad adicional de éste. Sin embargo, esta afirmación sólo es válida en el caso de la función de bienestar cuyo máximo se alcance con la asignación en cuestión. Hemos visto antes que todo máximo de bienestar es eficiente en el sentido de Pareto, pero ¿es necesariamente cierto lo contrario? En el apartado anterior hemos visto que toda asignación eficiente en el sentido de Pareto satisfacía las mismas condiciones de primer orden que el problema de maximización de una suma ponderada de las utilidades, por lo que parecía plausible que partiendo de los supuestos de la convexidad y la concavidad se obtuvieran buenos resultados. De hecho, se obtienen. Eficiencia en el sentido de Pareto y maximización del bienestar. Sea x* una asignación eficiente en el sentido de Pareto en la que x; » O siendo i = 1, ... , n. Supongamos que las funciones de utilidad u; son cóncavas, continuas y monótonas. En ese caso, existen unas ponderaciones tales que x* maximiza ¿ a;ui(xi) sujeta a las restricciones de recursos. Por otra parte, las ponderaciones son tales que = 1 / Ai, donde Ai es la utilidad de la renta del i-ésimo; es decir, si mi es el valor de la dotación del agente i a agente marginal los precios de equilibrio p*, entonces a; a; X!' = 8vi(P, mi) ami i . Demostración. Dado que x" es eficiente en el sentido de Pareto, es un equilibrio walrasiano. Por lo tanto, existen unos precios p tales que cada uno de los agentes maximiza su utilidad, dado su conjunto presupuestario, lo cual implica, a su vez, que Dui(xl) = AiP siendo i = 1, ... , n. Consideremos ahora el siguiente problema de maximización del bienestar: ¿ aiui(xi) n max i=l sujeta a n n i=l i=l n n i=l i=l ¿ x} < ¿ x}* ¿x} � ¿x}*. De acuerdo con el teorema de las condiciones suficientes para los problemas de maximización de funciones cóncavas sujetas a restricciones (capítulo 27, página 589), 392 / EL INTERCAMBIO (C. 17) x" es la solución de este problema si existen números no negativos (q1, ... , qk) tales que = q Si elegimos a; = 1 / Ai, los precios p sirven de números no negativos, con lo que queda realizada la demostración. La interpretación de las ponderaciones como las inversas de las utilidades marginales de la renta tiene sentido desde el punto de vista económico. Si un agente tiene una elevada renta en alguna asignación eficiente en el sentido de Pareto, su utilidad marginal de la renta será pequeña y su ponderación en la función social de bienestar implícita será grande. Las dos proposiciones anteriores completan el conjunto de relaciones entre los equilibrios de mercado, las asignaciones eficientes en el sentido de Pareto y los máximos de bienestar. Recapitulando brevemente, 1: los equilibrios competitivos siempre son eficientes en el sentido de Pareto; 2: las asignaciones eficientes en el sentido de Pareto son equilibrios competitivos partiendo de los supuestos de la convexidad y la redistribución de las dotaciones; 3: los máximos de bienestar siempre son eficientes en el sentido de Pareto; 4: las asignaciones eficientes en el sentido de Pareto son máximos de bienestar partiendo de los supuestos de la concavidad en el caso de alguna elección de las ponderaciones de bienestar. Las relaciones anteriores permiten extraer la siguiente conclusión básica: un sistema de mercado competitivo genera asignaciones eficientes, pero no dice nada sobre la distribución. La elección de la distribución de la renta es igual que la elección de una reasignación de las dotaciones, lo cual equivale, a su vez, a la elección de una determinada función de bienestar. Notas Walras (1954) fue quien formuló, por primera vez, el modelo de equilibrio general. La primera demostración de la existencia se debe a Wald (1951); para un análisis más general de esta cuestión, véase McKenzie (1954) y Arrow y Debreu (1954). Los Ejercicios / 393 análisis modernos definitivos son los de Debreu (1959) y Arrow y Hahn (1971). Este último trabajo contiene numerosas notas históricas. Los resultados fundamentales sobre el bienestar cuentan con una larga historia. La demostración del primer teorema del bienestar que hemos utilizado aquí se basa en la de Koopmans (1957). La importancia de la convexidad en el segundo teorema fue reconocida por Arrow (1951) y Debreu (1953). El análisis de la eficiencia basado en el cálculo diferencial fue desarrollado rigurosamente por primera vez por Samuelson (1947). La relación entre los máximos de bienestar y la eficiencia en el sentido de Pareto se basa en Negisihi (1960). La demostración del segundo teorema del bienestar basada en la preferencia revelada se debe a Maskin y Roberts (1980). Ejercicios 17.1. Considere la demostración del segundo teorema del bienestar basada en la preferencia revelada. Demuestre que si las preferencias son estrictamente convexas, x� = x; cualquiera que sea i = 1, ... , n. 17.2. Dibuje una caja de Edgeworth con un número infinito de precios que sean equilibrios walrasianos. 17.3. Examine la figura 17.6, en la cual x" es una asignación eficiente en el sentido de Pareto, pero no puede sostenerse por medio de precios competitivos. ¿Qué supuesto del segundo teorema del bienestar se viola? 17.4. Hay dos consumidores, A y B, que tienen las funciones de utilidad y dotaciones siguientes: uA(x1,x�) =alnx1 +(1- a)lnx�WA = (O, 1) uB(xk,xi) =min(xk,xi) WB = (1,0). Calcule los precios que vacían el mercado y la asignación de equilibrio. 17.5. Tenemos n agentes que tienen idénticas funciones de utilidad estrictamente cóncavas. La cesta inicial de bienes es w. Demuestre que una distribución igualitaria es una asignación eficiente en el sentido de Pareto. 17.6. Tenemos dos agentes que tienen las siguientes funciones indirectas de utilidad: v1(P1,P2,y) =lny- c ln p¡ - (1- a)lnp2 v2 (p1 , P2, y) = ln y - b ln PI - (1 - b) ln P2 394 / EL INTERCAMBIO (C. 17) y las dotaciones iniciales W1 = (1, 1) W2 = (1, 1). Calcule los precios que vacían el mercado. Figura 17.6 BIEN 2 .--�-=-=----3�-....��-----=:: :!!II-.------�=----, x* <; -c CONSUMIDOR 1 _CONSUMIOOA 2 '' '' '' \ \ '' \ \ \ '' ' \ \ _E!II;� 1 Caso excepcional de Arrow. La asignación x* es eficiente en el sentido de Pareto, pero no existe ningún precio al que x * sea un equilibrio walrasiano. 17.7. Suponga que todos los consumidores tienen funciones de utilidad cuasilineales, de tal manera que vi(P, mi)= vi(p)+mi. Sea p* un equilibrio walrasiano. Demuestre que la curva de demanda agregada de cada uno de los bienes debe tener pendiente negativa en p". En términos más generales, demuestre que la matriz de sustitutivos brutos debe ser semidefinida negativa. 17.8. Suponga que tenemos dos consumidores, A y B, cuyas funciones de utilidad son idénticas: UA (x1, x2) = uB(X1, x2) = max(zj , x2). Hay una unidad del bien 1 y 2 del bien 2. Dibuje una caja de Edgeworth que muestre los conjuntos fuertemente eficientes en- el sentido de Pareto y (débilmente) eficientes en el sentido de Pareto. 17.9. Considere el caso de una economía en la que hay 15 consumidores y 2 bienes. El consumidor 3 tiene la siguiente función de utilidad Cobb-Douglas: u3(x}, x�) = In x} + In x�. En una determinada asignación eficiente en el sentido de Pareto x*, el consumidor 3 tiene (10, 5). ¿Cuáles son los precios competitivos que dan lugar a la asignación x*? Ejercicios / 395 17.10. Si permitimos que sea posible la saciedad, la restricción presupuestaria del consumidor adopta la forma siguiente: px, ::; pwi. La ley de Walras se convierte, en ese caso, en pz(p) < O cualquiera que sea p 2: O. Demuestre que la prueba de la existencia de un equilibrio walrasiano presentada en este capítulo se aplica a esta forma general de la ley de Walras. 17.11. La persona A tiene la función de utilidad UA (x1, x2) función de utilidad u3(x1, x2) = maxízj , x2). = (a) Represente esta situación en una caja de Edgeworth. (b) ¿ Cuál es la relación de equilibrio entre Pl y P2? (c) ¿Cuál es la asignación de equilibrio? x1 + x2 y la B tiene la 18. LA PRODUCCIÓN En el capítulo anterior nos referimos únicamente a una economía de intercambio puro. En éste mostraremos cómo se amplía este modelo de equilibrio general a una economía en la que hay producción. Primero veremos cómo se plasma en un modelo la conducta de la empresa, a continuación cómo se plasma la conducta del consumidor y, por último, qué modificaciones hay que introducir en los teoremas básicos de la existencia y de la eficiencia. 18.1 La conducta de la empresa Utilizaremos la representación de las tecnologías que describimos en el capítulo l. Si hay ti bienes, el vector de producciones netas de la empresa j es un vector de dimensión n y J y el conjunto de vectores de producciones netas viables -el conjunto de posibilidades de producción- de la empresa j es Yj. Recuérdese que el vector de producciones netas tiene componentes negativos que representan los factores netos y componentes positivos que indican los productos netos. En el capítulo 1 analizamos algunos ejemplos de conjuntos de posibilidades de producción. En el presente capítulo nos ocuparemos exclusivamente de las empresas competitivas y precio-aceptantes. Si p es un vector de precios de los diferentes bienes, py J es el beneficio correspondiente al plan de producción y J. Se supone que la empresa j elige un plan de producción Y_¿ que maximiza los beneficios. En el capítulo 2 analizamos las consecuencias de este modelo de conducta. Describimos la idea de la función de oferta neta yj(p) de la empresa competitiva, que es simplemente la función que relaciona cada uno de los vectores p con el vector de producciones netas que maximiza los beneficios a esos precios. Partiendo de determinados supuestos, la función de producción neta de una empresa está bien definida y es regular. Si hay m empresas, la función de oferta neta agregada es 1 YJ(p). Si las funciones de oferta neta individuales están bien definidas y(p) = y son funciones continuas, la función de oferta neta agregada está bien definida y es continua. ¿; 398 / LA PRODUCCIÓN (C. 18) También podemos analizar el conjunto agregado de posibilidades de producción, Y. Este conjunto indica todos los vectores de producciones netas viables para la economía en su conjunto. Este conjunto agregado de posibilidades de producción es la suma de los conjuntos de posibilidades de producción individuales, por lo que podemos expresarlo de la forma siguiente: m Y=¿Yj. j=l Conviene recordar lo que significa esta notación. Un plan de producción y pertenece a Y si y sólo si y puede expresarse de la forma siguiente: m y= LYj, j=l donde cada plan de producción y1 pertenece a Yj. Por lo tanto, Y representa todos los planes de producción que pueden lograrse distribuyendo la producción entre las empresas j = 1, ... , m. Maximización de los beneficios agregados. Un plan de producción agregada, y, maximiza los beneficios agregados si y sólo si el plan de producción de cada una de las empresas, y1, maximiza sus beneficios. Demostración. Supongamos que y = E"]:1 Y¡ maximiza los beneficios agregados, pero que una empresa k podría obtener mayores beneficios si eligiera y�. En ese caso, los beneficios agregados podrían ser mayores eligiendo el mismo plan y� para la empresa k y haciendo exactamente lo mismo que antes con las demás empresas. Supongamos, a la inversa, que (y1), siendo j = 1, ... , n, es un conjunto de planes de producción de las empresas individuales que maximiza los beneficios, y que y = E"]:1 Y¡ no maximiza los beneficios a los precios p. Eso significa que hay algún otro plan de producción y'= E"]:1 y'1, donde y'1 pertenece a Yj, que genera mayores beneficios: m ¿PYj = j=l m m p LYJ > p LYí j=l j=l = m LPYj· j=l Pero si examinamos los sumatorios de los miembros de esta desigualdad, veremos que alguna empresa debe obtener mayores beneficios con y' 1 que con y1. Esta proposición establece que si cada una de las empresas maximiza los beneficios, deben maximizarse los beneficios agregados, y viceversa, que si se maximizan Dificultades / 399 los beneficios agregados, deben maximizarse los beneficios de cada una de las empresas. El razonamiento se basa en el supuesto de que las posibilidades agregadas de producción son simplemente la suma de las posibilidades de producción de cada una de las empresas. De esta proposición se deduce que la función de oferta neta agregada puede construirse de dos maneras distintas: o bien sumando las funciones de oferta neta de todas las empresas, o bien sumando los conjuntos de producción de todas ellas y determinando la función de oferta neta que maximiza los beneficios, dado este conjunto agregado de producción. Cualquiera de las dos vías nos lleva a la misma función. 18.2 Dificultades Conviene suponer que la función agregada es regular, pero para realizar un análisis más detallado, sería necesario deducir esta propiedad a partir de las propiedades subyacentes de los conjuntos de producción. Si los conjuntos de producción son estrictamente convexos y están debidamente acotados, no es difícil demostrar que las funciones de oferta neta son regulares. En cambio, si los conjuntos de producción tienen zonas no convexas, las "funciones" de oferta neta presentarán discontinuidades. Las comillas tienen por objeto subrayar el hecho de que en presencia de zonas no convexas las funciones de oferta no están bien definidas; a algunos precios, puede haber varias combinaciones maximizadoras del beneficio. Si las discontinuidades son "pequeñas", puede no importar mucho, pero es difícil hacer afirmaciones generales. El caso intermedio es aquel en el que hay rendimientos constantes de escala. Ya vimos en el capítulo 2 que en este caso la conducta de la oferta neta puede ser bastante antipática: nula, infinita o puede ofrecerse toda una diversidad de niveles de producción, dependiendo de los precios. A pesar de esta conducta aparentemente mala, las "funciones" de oferta neta correspondientes a las tecnologías que muestran rendimientos constantes de escala dependen más o menos continuamente de los precios. Debe señalarse, en primer lugar, que las "funciones" de oferta neta no son funciones en absoluto. La definición de función exige que haya un único punto en el intervalo que corresponda a cada uno de los puntos del conjunto en el que se define. Si el conjunto de producción muestra rendimientos constantes de escala, entonces si algún vector de producciones netas y genera unos beneficios máximos nulos, lo mismo ocurrirá con ty, si t 2: O. Por lo tanto, existe una infinidad de combinaciones que son ofertas netas óptimas. En términos matemáticos, este problema se resuelve definiendo un tipo de función generalizada llamada correspondencia. Una correspondencia relaciona cada 400 / LA PRODUCCIÓN (C. 18) uno de los puntos del conjunto en el que se define con un conjunto de puntos pertenecientes a su intervalo. Si el conjunto de puntos es convexo, decimos que tenemos una correspondencia convexa. Naturalmente, una función es un caso especial de una correspondencia convexa. No es difícil demostrar que si el conjunto de producción es convexo, la correspondencia de la oferta neta es una correspondencia convexa. Por otra parte, la correspondencia de la oferta neta varía de una manera convenientemente continua cuando varían los precios. Casi todos los resultados obtenidos en el caso de las funciones de oferta neta que utilizamos en este capítulo pueden ampliarse al caso de las correspondencias. Los lectores interesados pueden consultar para más detalles la bibliografía que se cita al final del capítulo. Sin embargo, nos limitaremos a examinar el caso de las funciones de oferta neta, a fin de que el análisis sea lo más sencillo posible. 18.3 La conducta del consumidor La producción introduce dos nuevas complicaciones en nuestro modelo de la conducta del consumidor: la oferta de trabajo y la distribución de los beneficios. La oferta de trabajo En el modelo de intercambio puro se suponía que el consumidor tenía una dotación inicial Wide mercancías. Si vendía este vector de mercancías, recibía una renta pwi. Daba lo mismo que vendiera toda su cesta y comprara entonces algunos bienes o que sólo vendiera una parte. La cantidad de renta observada podía ser diferente, pero la renta económica era la misma. Si introducimos el trabajo en el modelo, introducimos una nueva posibilidad: los consumidores pueden ofrecer diferentes cantidades de trabajo dependiendo de los salarios. En el capítulo 9 (página 172) analizamos un sencillo modelo de oferta de trabajo, en el cual el consumidor tenía una cantidad total de "tiempo" L que tenía que repartir entre el trabajo, f, y el ocio, L = L - f. Al consumidor le interesaba el ocio, L, y un bien de consumo, c. El precio del trabajo -el salario- estaba representado por w y el del bien de consumo por p. El consumidor ya podía poseer una dotación del bien de consumo e que contribuía a su renta no laboral. El problema de maximización del consumidor puede expresarse de la manera siguiente: max u(c, L) sujeta a pe= pe+ w(L - L). La conducta del consumidor / 401 A menudo resulta más útil expresar la restricción presupuestaria de la forma siguiente: pe+ wL =pe+ wL. En este caso, el ocio aparece en la restricción presupuestaria simplemente como otro bien: una persona tiene una dotación de ocio, L, y la "vende" a una empresa al precio w, después "vuelve a comprar" parte del ocio a ese mismo precio w. Esta estrategia también puede utilizarse en el caso más complejo en el que el consumidor tiene muchos tipos de trabajo distintos. Dado un vector cualquiera de precios de los bienes y del trabajo, el consumidor puede considerar la posibilidad de vender su dotación y de comprar entonces la cesta deseada de bienes y ocio. Cuando se contempla el problema de oferta de trabajo de esta forma, se observa que encaja perfectamente en el modelo anterior de la conducta del consumidor. Dado un vector de dotaciones w y un vector de precios p, el consumidor resuelve el siguiente problema: max u(x) sujeta a px = pw. La única complicación se halla en que ahora hay más restricciones en el problema; por ejemplo, la cantidad total de ocio consumida tiene que ser inferior a 24 horas al día. Desde el punto de vista formal, estas restricciones pueden introducirse en la definición del conjunto de consumo descrito en el capítulo 7 (página 113). La distribución de los beneficios Pasemos a examinar la cuestión de la distribución de los beneficios. En una economía capitalista, los consumidores poseen empresas y tienen derecho a participar en los beneficios. Resumimos esta relación de propiedad por medio de un conjunto de números (Tij), donde Tij representa la participación del consumidor i en los beneficios de la empresa j. En el caso de cualquier empresa j, debe cumplirse que ¿�=l Tij = 1, lo que quiere decir que la empresa es en su totalidad propiedad de los consumidores. Consideramos que estas relaciones de propiedad están dadas históricamente, si bien los modelos más complejos pueden introducir la existencia de un mercado de compraventa de acciones. Dado un vector de precios p, cada una de las empresas j elige un plan de producción que genera un beneficio de pyj(p). La renta total procedente de los beneficios que recibe el consumidor i es la suma de los beneficios que recibe de 1 TijPYj(p). Ahora la restricción presupuestaria del cada una de las empresas: consumidor se convierte en I::; 402 / LA PRODUCCIÓN (C. 18) m PXi = PWi + ¿ Tijpyj(p). j==l Suponemos que el consumidor elige una cesta maximizadora de la utilidad que satisface esta restricción presupuestaria, por lo que su función de demanda puede expresarse en función del vector de precios p. De nuevo, es necesario suponer que las preferencias son estrictamente convexas para garantizar que x.Ip) será una función (de valor único). Sin embargo, en el capítulo 9 vimos que, partiendo de ese supuesto, x.Ip) será continua, al menos en el caso en que los precios y la renta son estrictamente positivos. 18.4 La demanda agregada Sumando las funciones de demanda de los consumidores, obtenemos la función de demanda agregada de los consumidores X(p) = ¿�==l x.Ip). El vector de ofertas agregadas se obtiene sumando la oferta agregada de los consumidores, que se representa por medio de w = ¿�==l Wi, y la oferta neta agregada de las empresas, Y(p). Por último, la función de exceso de demanda agregada se define de la manera siguiente: z(p) = X(p) - Y(p) - w. Obsérvese que la convención referente a los signos correspondientes a las mercancías ofrecidas funciona perfectamente: un componente de z(p) es negativo si hay un exceso de oferta de la mercancía en cuestión y positivo si hay un exceso de demanda. Una parte importante del argumento de la existencia en una economía de intercambio puro es la aplicación de la ley de Walras. Veamos cómo funciona ésta en una economía en la que hay producción. La ley de Walras. Si z(p) responde a la definición anterior, pz(p) = O cualquiera que sea p. Demostración. Desarrollamos z(p) de acuerdo con su definición. pz(p) = p [X(p) - Y(p) - w] [ n m n =p ;x;(p)-;y;(p)-;w; n m n i=l j==l i==l ] la existencia de un equilibrio / 403 :E;1 TiiPY/p). La restricción presupuestaria del consumidor es p X, = pwi + troduciendo esta restricción en la expresión anterior, tenernos que n n m i=l i=l j=l m j=l m m n i=l m n j=l i=l In- j=l m = ¿pyj(p)- ¿pyj(p) = o, dado que :E7=1 j=l Tij j=l = 1, cualquiera que sea j. La ley de Walras se cumple por la misma razón que se cumple en el caso del intercambio puro: cada uno de los consumidores satisface su restricción presupuestaria, por lo que la economía en su conjunto tiene que satisfacer una restricción presupuestaria agregada. 18.5 La existencia de un equilibrio Si z(p) es una función continua definida en el simplex de los precios que satisface la ley de Walras, el razonamiento del capítulo 17 puede aplicarse para demostrar que existe un p* tal que z(p*) :'.S O. Hemos visto que la función es continua si el conjunto de posibilidades de producción de cada empresa es estrictamente convexo. No es demasiado difícil ver que sólo es necesario que el conjunto de posibilidades agregadas de producción sea convexo. Aun cuando las empresas tengan tecnologías que no sean convexas en algunos casos poco importantes, corno una pequeña área de rendimientos crecientes de escala, las discontinuidades provocadas pueden alisarse en conjunto. Recuérdese que el razonamiento de la existencia que hemos esbozado aquí sólo es válido cuando nos referimos a las funciones de demanda. La única restricción seria que eso impone es que excluye las tecnologías que muestran rendimientos constantes de escala, que, como hemos dicho, constituyen un caso bastante importante. Por lo tanto, formularemos un teorema de la existencia en el caso general y analizaremos el significado económico de los supuestos. Existencia de un equilibrio. Existe un equilibrio en una economía si se cumplen los siguientes supuestos: (1) El conjunto de consumo de cada uno de los consumidores es cerrado y convexo y está acotado por abajo; 404 / LA PRODUCCIÓN (C. 18) (2) No existe en el caso de ningún consumidor una cesta de consumo que constituya un punto de saciedad; (3) En el caso de cada uno de los consumidores i = 1, ... , n, los conjuntos {xi : xi ti xD y { xi : x� ti xi} son cerrados; (4) Cada uno de los consumidores tiene un vector de dotaciones iniciales perteneciente a su conjunto de consumo; (5) En el caso de cada uno de los consumidores i, si Xi y x� son dos cestas de consumo, xi 'r-i x� implica que tx.; + (1 - t)x� 'r-i x�, cualquiera que sea t tal que O < t < 1; (6) En el caso de cada una de las empresas j, O es un elemento de Y1; (7) Y es cerrado y convexo, siendo j = 1, ... , n; (8) Y n (-Y)= {O}, siendo j = 1, ... , n; (9) Y ::) (-R+). Demostración. Véase Debreu (1959). Aunque la demostración de este teorema queda fuera del alcance de este libro, podemos asegurarnos, al menos, de que comprendemos el propósito de cada uno de los supuestos. Los supuestos (1) y (3) son necesarios para demostrar la existencia de una cesta maximizadora de la utilidad. Los supuestos (1)-(5) son necesarios para demostrar la continuidad de la correspondencia de las demandas de los consumidores. El supuesto (6) significa que una empresa siempre puede quebrar, lo que garantiza que en el punto de equilibrio los beneficios no serán negativos. El supuesto (7) se necesita para garantizar la continuidad de la función (de valores múltiples) de oferta neta de cada empresa. El supuesto (8) garantiza que la producción es irreversible .en el sentido de que no es posible producir un vector de producciones netas y a continuación utilizar los productos como factores y producir todos los factores como productos. Se utiliza para garantizar que el conjunto viable de asignaciones está acotado. Por último, el supuesto (9) significa que es viable cualquier plan de producción que utilice todos los bienes como factores; se trata esencialmente de un supuesto de eliminación gratuita; implica que los precios de equilibrio no son negativos. Propiedades del equilibrio desde el punto de vista del bienestar / 405 18.6 Propiedades del equilibrio desde el punto de vista del bienestar Una asignación (x, y) es viable si las cantidades agregadas que se poseen son compatibles con la oferta agregada: n m n í=l j=l í=l Al igual que antes, una asignación viable (x, y) es eficiente en el sentido de Pareto si no existe ninguna otra asignación viable (x', y') tal que x� h Xi, cualquiera que sea i = 1, ... , n. Primer teorema de la economía del bienestar. Si (x, y, p) es un equilibrio walrasiano, (x, y) es eficiente en el sentido de Pareto. Demostración. Supongamos que no lo fuera y que (x', y') es una asignación que la domina en el sentido de Pareto. En ese caso, dado que los consumidores están maximizando la utilidad, debe cumplirse que px� > pwí + L TííPYí rn j=l cualquiera que sea i = 1, ... , n. Sumando las asignaciones correspondientes a todos los consumidores i tenemos que n n n í=l í=l í=l = 1, ... , n, Aquí nos hemos valido del hecho de que L�=l Tíj = 1. Ahora aplicamos la definición . bilid • • d e 1 a vía 11 a d d ex I y sustituimos L..,i=l xiI por L..,j=l y I j + L..,i=l wí: ""m ""n p ""n [tyj+ tw,] tpw,+ tPYJ > m m j=l j=l LPYj > LPYj· Pero esta expresión significa que los beneficios agregados correspondientes a los planes de producción (y' j) son mayores que los beneficios agregados correspondientes a los planes de producción (yj), lo que contradice el supuesto de la maximización de los beneficios por parte de las empresas. 406 / LA PRODUCCIÓN (C. 18) Segundo teorema de la economía del bienestar. Supongamos que (x", y*) es una asignación eficiente en el sentido de Pareto en la que cada uno de los consumidores tiene una cantidad estrictamente positiva de cada uno de los bienes y que las preferencias son convexas, continuas y fu.ertemente monótonas. Supongamos que los conjuntos de posibilidades de producción de las empresas, Yj, siendo j = 1, ... , m, son convexos. En ese caso, existe un vector de precios p � O tal que (1) Si X� >-i Xi, entonces pX� > pxi, siendo Í (2) si yí pertenece a Yi, entonces pyi siendo j = 1, ... , m. = 1, ... , n; � py' i, cualquiera que sea y' i perteneciente a Yj, Demostración (esquemática). Supongamos al igual que antes que Pes el conjunto de todas las cestas agregadas preferidas y que F es el conjunto de todas las cestas agregadas viables; es decir, { F= w+ f y; : y; pertenece a Y, } . J=l En ese caso, F y P son ambos conjuntos convexos y dado que (x", Y*) es eficiente en el sentido de pareto, F y P son disjuntos. Por lo tanto, podemos aplicar el teorema del hiperplano separador y hallar un vector de precios p tal que pz' � pz", cualesquiera que sean z' en P y z" en F. La monotonicidad de las preferencias implica que p � O. Podemos aplicar el argumento utilizado en la demostración del intercambio puro para demostrar que a estos precios cada uno de los consumidores maximiza sus preferencias y cada una de las empresas maximiza sus beneficios. La proposición anterior demuestra que toda asignación eficiente en el sentido de Pareto puede lograrse con una reasignación adecuada de la "riqueza". Primero determinamos la asignación (x", y*) que queremos y a continuación determinamos los precios relevantes p. Si asignamos al consumidor i la renta pxr, no querrá alterar su cesta de consumo. Este resultado puede interpretarse de varias maneras: en primer lugar, cabe imaginar que el Estado confisca las dotaciones iniciales de bienes y ocio de los consumidores y las redistribuye de alguna manera compatible con la redistribución deseada de la renta. Obsérvese que esta redistribución puede implicar una redistribución de los bienes, de las participaciones en los beneficios y del ocio. Propiedades del equilibrio desde el punto de vista del bienestar / 407 Por otra parte, cabe imaginar que los consumidores mantienen sus dotaciones iniciales, pero están sujetos a un impuesto de cuantía fija. Este impuesto es diferente de los impuestos habituales, en el sentido de que grava la renta "potencial" en lugar de la "realizada"; es decir, el impuesto grava las dotaciones de trabajo en lugar del trabajo vendido. El consumidor tiene que pagar el impuesto independientemente de lo que haga. En un sentido económico puro, obligar a un agente a pagar un impuesto de cuantía fija y entregar los ingresos a otro es lo mismo que entregar parte del trabajo del primer agente a otro y permitirle que lo venda al salario vigente. Naturalmente, los agentes pueden tener distinta capacidad o -lo que es lo mismo- diferentes dotaciones de los distintos tipos de trabajo potencial. En la práctica, puede ser muy difícil observar esas diferencias de capacidad para saber cuál es el impuesto de cuantía fija adecuado. La redistribución eficiente de la renta plantea grandes problemas cuando la capacidad varía de unas personas a otras. Un razonamiento basado en la preferencia revelada He aquí una demostración sencilla, aunque algo indirecta, del segundo teorema del bienestar, basada en el argumento de la preferencia revelada que generaliza un teorema similar del capítulo 17. Segundo teorema de la economía del bienestar. Supongamos que (x", y*) es una asignación eficiente en el sentido de Pareto y que las preferencias tienen la propiedad de la insaciabilidad local. Supongamos, además, que existe un equilibrio competitivo a partir de las dotaciones iniciales wi = x* en el que las participaciones en los beneficios Tij = O, cualesquiera que sean i y j, y que éste viene dado por (p, x', y'). En ese caso, (p', x", y*) es, de hecho, un equilibrio competitivo. Demostración. Dado que x; satisface la restricción presupuestaria de cada uno de los consumidores por construcción, debe cumplirse que x� ti x;. Dado que x* es eficiente en el sentido de Pareto, eso implica que x� "'-'i x;. Por lo tanto, si x� proporciona la máxima utilidad, dado el conjunto presupuestario, también la proporciona x;. Debido al supuesto de la insaciabilidad, cada uno de los agentes satisface su restricción presupuestaria con igualdad, por lo que p'x� = p'xt i = 1, ... , n. Sumando las igualdades correspondientes a los agentes i = 1, ... , n y utilizando la condición de viabilidad, tenemos que 408 / LA PRODUCCIÓN (C. 18) o sea, m m j=l j=l p'¿YJ =p'¿y;. Por lo tanto, si y' maximiza los beneficios agregados, también los maximiza y*. De acuerdo con el razonamiento habitual, cada una de las empresas debe maximizar los beneficios. Esta proposición establece que si existe un equilibrio a partir de la asignación eficiente en el sentido de Pareto (x*, y*), entonces (x", y*) es ella misma un equilibrio competitivo. Cabe muy bien preguntarse qué se necesita para que exista un equilibrio. De acuerdo con el análisis anterior sobre la existencia, bastan dos supuestos: (1) que todas las funciones de demanda sean continuas; y (2) que se cumpla la ley de Walras. La continuidad de la demanda se desprende de la convexidad de las preferencias y de los conjuntos de producción. La ley de Walras puede verificarse mediante el siguiente cálculo: pz(p) = pX(p) - pw - p Y(p) = pX(p) - p X" = - p Y(p) O - pY(p) :'SO. Vemos en este modelo que el valor del exceso de demanda no es nunca negativo, debido a que los consumidores no reciben una parte de los beneficios de las empresas. Dado que estos beneficios "se pierden", el valor del exceso de demanda puede muy bien ser negativo. Sin embargo, la prueba de la existencia de equilibrio del capítulo 17 (página 374) demuestra que, en realidad, no necesitábamos el supuesto de que O; es suficiente que pz(p) :::::; O. pz(p) Este resultado demuestra que las condiciones fundamentales del segundo teorema del bienestar son simplemente las condiciones de que exista un equilibrio competitivo, es decir, las condiciones de la convexidad. = 18.7 Análisis del bienestar en una economía productiva No debería sorprendernos que el análisis de la maximización del bienestar en una economía productiva sea similar al del caso del intercambio puro. La única cuestión estriba en describir el conjunto viable de asignaciones en el caso de la producción. Análisis gráfico / 409 La manera más fácil de describirlo consiste en utilizar la función de transformación mencionada en el capítulo 1 (página 6). Recuérdese que se trata de una función que selecciona los planes de producción eficientes, en el sentido de que y es un plan de producción eficiente si y sólo si T(y) = O. En realidad, casi todas las tecnologías razonables pueden describirse por medio de una función de transformación.1 En ese caso, el problema de maximización del bienestar puede expresarse de la forma siguiente: max W(u1 (xi), ... , Un(Xn)) sujeta a T(X1, donde X9 = L�=l xf, siendo g = Xk) ... , =O 1, ... , k. El lagrangiano de este problema es y las condiciones de primer orden son 8W 8ui(x;) _ .\ 8T(X*) Bu, 8xf 8X9 =O i = 1, ... , n g = 1, ... , k. Reordenando estas condiciones, tenemos que 8T(X*) ax9 axh 8T(X*) i = = h= g 1, ... , n 1, ,k 1, ,k. Las condiciones que caracterizan la maximización del bienestar exigen que la relación marginal de sustitución entre cada uno de los pares de mercancías sea igual a la relación marginal de transformación entre esas mercancías. 18.8 Análisis gráfico Existe un instrumento análogo a la caja de Edgeworth que es muy útil para comprender la producción y el equilibrio general. Supongamos que examinamos el caso de una economía en la que sólo hay un consumidor. Éste lleva una vida bastante esquizofrénica: por una parte, es un productor maximizador del beneficio que produce 1 Podemos introducir las dotaciones de recursos en la definición de la función de transformación. 410 / LA PRODUCCIÓN (C. 18) un bien de consumo con su trabajo, mientras que, por otra parte, es un consumidor maximizador de la utilidad propietario de la empresa maximizadora del beneficio. Esta economía se denomina a veces economía de Robinson Crusoe. Figura 18.1 CONSUMO "' . . ...................... .................. _ Dotación Ocio Trabajo La economía de Robinson Crusoe con rendimientos constantes. El trabajo se mide en cantidades negativas y la tecnología muestra rendimientos constantes de escala. La figura 18.1 muestra el conjunto de producción de la empresa. Obsérvese que el trabajo se mide como si fuera una cantidad negativa, debido a que es un factor en el proceso de producción, y que la tecnología muestra rendimientos constantes de escala. La cantidad máxima de trabajo que puede ofrecerse es L. Suponemos para mayor sencillez que la dotación inicial del bien de consumo es cero. El consumidor tiene unas preferencias respecto a las cestas de ocio-consumo que vienen indicadas por las curvas de indiferencia del gráfico. ¿ Cuál será el salario de equilibrio? Si el salario real viene dado por la pendiente del conjunto de producción, el conjunto presupuestario del consumidor coincidirá con el conjunto de producción. Éste demandará la cesta que le reporte la máxima utilidad. El productor está dispuesto a ofrecer la cesta, puesto que obtiene unos beneficios nulos. Por lo tanto, se vacían tanto el mercado del bien de consumo como el de trabajo. Obsérvese el interesante punto siguiente: el salario real depende enteramente de la tecnología, mientras que la cesta final de producción y consumo depende de la Análisis gráfico / 411 demanda del consumidor. Esta observación puede generalizarse y convertirse en el teorema de la no sustitución, que establece que si sólo hay un factor de producción no producido y la tecnología muestra rendimientos constantes de escala, los precios de equilibrio son independientes de los gustos: dependen enteramente de la tecnología. En el próximo apartado del presente capítulo demostramos este teorema. Figura 18.2 CONSUMO 1 1 1 1 1 1 \ \ \ \ \ \ \ \ \ \ ),, Consumo de equilibrio Beneficios de equilibrio en términos reales Dotación incluyendo beneficios __________ : 1 �,',,,� - - ',, _ Dotación 1 1 L Ocio Trabajo La economía de Robinson Crusoe con rendimientos decrecientes. La recta presupuestaria del consumidor no pasa por (O, L), ya que recibe algunos de los beneficios de la empresa. En la figura 18.2 representamos el caso de los rendimientos decrecientes de escala. La asignación de equilibrio se halla buscando los puntos en los que la relación marginal de sustitución es igual a la relación marginal de transformación. La pendiente en este punto indica el salario real de equilibrio. Naturalmente, a este salario real la recta presupuestaria del consumidor no pasa por el punto de dotación (O, L), ya que el consumidor recibe algunos beneficios de la empresa .. La cantidad de beneficios que recibe, medida en unidades del bien de consumo, viene dada por la ordenada en el origen. Dado que el consumidor es propietario de la empresa, recibe todos estos beneficios como renta "no laboral". Por lo tanto, su conjunto presupuestario es el indicado y se vacían los dos mercados. Esto trae a colación un interesante punto acerca de los beneficios en el modelo de equilibrio general. En el análisis anterior, hemos supuesto que la tecnología mostraba rendimientos decrecientes del trabajo sin que existiera nada que lo explicara. Una 412 / LA PRODUCCIÓN (C. 18) de las razones por las que los rendimientos del trabajo son decrecientes podría ser la presencia de algún factor fijo, la tierra, por ejemplo. En esta interpretación, la función de producción del bien de consumo de Robinson depende de la cantidad (fija) de tierra, T, y de la cantidad de trabajo, L. La función de producción puede muy bien mostrar rendimientos constantes de escala si incrementarnos los dos factores de producción, pero si mantenernos fija la cantidad de tierra y analizarnos la producción únicamente en función del trabajo, probablemente veremos que los rendimientos del trabajo son decrecientes. En el capítulo 1 (página 20) observarnos que toda tecnología que muestra rendimientos decrecientes puede concebirse corno una tecnología que muestra rendimientos constantes de escala suponiendo que hay un factor fijo. Desde este punto de vista, los "beneficios" -o la renta no laboral- pueden interpretarse corno una renta económica del factor fijo. Si nos basarnos en esta interpretación, los beneficios son, en términos generales, nulos, es decir, el valor del nivel de producción debe ser igual al valor de los factores, casi por definición. Lo que quede se contabiliza automáticamente corno un pago, o renta, al factor fijo. Ejemplo: La economía Cobb-Douglas con rendimientos constantes de escala Supongamos que tenernos un consumidor cuya función de utilidad Cobb-Douglas en función del consumo, x, y del ocio, R, es la siguiente: u(x, R) = a ln x + (1- a) ln R. El consumidor está dotado de una unidad de trabajo/ocio y hay una empresa cuya tecnología muestra rendimientos constantes de escala: x = aL. Basta un breve análisis para ver que el salario real de equilibrio debe ser el producto marginal del trabajo; por lo tanto, ui" /p* = a. El problema de rnaxirnización del consumidor es rnax a ln x + (1 - a) ln R sujeta a px + wR = w. Para formular la restricción presupuestaria, hemos recurrido al hecho de que los beneficios de equilibrio son nulos. Aplicando el resultado ya conocido de que las funciones de demanda correspondientes a una función de utilidad Cobb-Douglas tiene la forma x(p) = am/p, donde mes la renta monetaria, tenernos que w x(p, w) = ap w R(p, w) = (1 - a)w = 1 - a. Por lo tanto, la oferta de trabajo de equilibrio es a y el nivel de producción de equilibrio a2. Análisis gráfico / 413 Ejemplo: Una economía con rendimientos decrecientes de escala Supongamos que el consumidor tiene una función de utilidad Cobb-Douglas como la del ejemplo anterior, pero el productor tiene la función de producción X = vL. Normalizamos arbitrariamente el precio del producto y suponemos que es igual a 1. El problema de maximización del beneficio es max L112 - wL. Este problema tiene la siguiente condición de primer orden: 1 -1 2.LT -w = o. Deduciendo las funciones de oferta y demanda de la empresa, tenemos que L = (2w)-2 X= (2w)-l. La función de beneficios se halla sustituyendo L por su valor: 1r(w) = (2w)-1 - w(2w)-2 = (4w)-1. Ahora la renta del consumidor comprende la renta procedente de los beneficios, por lo que la demanda de ocio es R(w) = (l: a) ( w+ L) = (1- a) ( 1+ 4:2). De acuerdo con la ley de Walras, basta hallar un salario real que vacíe el mercado de trabajo: -14w2 = 1 - (1- a) (1 + Resolviendo esta ecuación, tenemos que w'= (\�/r Por lo tanto, el nivel de beneficios de equilibrio es -1-). 4w2 414 / LA PRODUCCIÓN (C. 18) Veamos otra manera de resolver el mismo problema. Como hemos indicado anteriormente, el hecho de que la tecnología muestre rendimientos decrecientes de escala se debe probablemente a la presencia de un factor fijo. Llamémoslo "tierra" y midámoslo en unidades tales que la cantidad total de tierra sea T = 1. Supongamos que la función de producción viene dada por L!TL Obsérvese que esta función muestra rendimientos constantes de escala y coincide con la tecnología inicial cuando T = 1. El precio de la tierra está representado por q. El problema de inaximización del beneficio de la empresa es max L112T112 - wL - qT, que tiene las siguientes condiciones de primer orden: !L-lf2yl/2 _ w 2 !LI/2y-l/2 _ q 2 =O = o. En condiciones de equilibrio, el mercado de tierra se vacía, por lo que T = 1. Introduciendo esta igualdad en las ecuaciones anteriores, tenemos que = W= L (2w)-2 (2q)2. Estas ecuaciones implican conjuntamente que q = 1/4w. Ahora la renta del consumidor está formada por su renta procedente de su dotación de trabajo, wL = w, más su renta procedente de su dotación de tierra, q'I' = q. Por lo tanto, su demanda de ocio viene dada por R = m (w + q) (1- a)-= (1- a)--. w w Igualando la demanda de trabajo y la oferta de trabajo, obtenemos el salario real de equilibrio: w'= (\;/( La renta de la tierra de equilibrio es q* = ! (2 - a 4 4a )-1/2 Obsérvese que esta solución es igual que la anterior. El teorema de la no sustitución / 415 18.9 El teorema de la no sustitución En este apartado presentamos un argumento que demuestra el teorema de la no sustitución antes mencionado. Suponemos que hay n industrias que producen los bienes Yi, i = 1, ... , n. Cada una de las industrias produce un único bien; no se permite la producción conjunta. Existe un único factor no producido, representado por Yo, que suponemos generalmente que es el trabajo. Los precios de los n + 1 bienes están representados por w = (wo, w1, ... , wn). Como siempre, los precios de equilibrio se determinan como precios relativos. Suponemos que el trabajo es un factor necesario en todas las industrias. Por lo tanto, en condiciones de equilibrio, wo > O, por lo que podemos elegir el salario como numerario, es decir, podemos suponer que es igual a 1. Suponemos que la tecnología muestra rendimientos constantes de escala. En el capítulo 5 (página 79) vimos que eso implica que la función de costes de cada una de las industrias puede expresarse de la forma siguiente: ci(w, Yi) = ci(w)yi, siendo i = 1, ... , n. Las funciones ci(w) son funciones de costes unitarios, que indican cuánto cuesta producir una unidad a los precios w, medidos en función del numerario wo. También supondremos que el trabajo es indispensable para producir, por lo que la demanda unitaria de trabajo es estrictamente positiva. Representando la demanda del factor O por parte de la empresa i por medio de cuando y = 1, podemos utilizar la propiedad de la derivada de la función de costes y formular la siguiente igualdad: x? _ xi9( w ) - 8ci(w) a wo > 0 . Obsérvese que eso implica que las funciones de costes son estrictamente crecientes en wo. Dado que las funciones de costes aumentan estrictamente al menos en uno de los precios, c/tw) = tci(w) > ci(w) si t > 1. Teorema de la no sustitución. Supongamos que sólo hay un factor de producción no producido, que este factor es indispensable en la producción, que no hay producción conjunta y que la tecnología muestra rendimientos constantes de escala. Sea (w, y, w) un equilibrio walrasiano en el que Yi > O siendo i = O, ... , n. En ese caso, w es la única solución de ui; = ci(w), i = 1, ... , n. Demostración. Si w es un vector de precios de equilibrio en una economía de rendimientos constantes de escala, los beneficios deben ser nulos en todas las industrias; es decir, i = 1, ... , n 416 / LA PRODUCCIÓN (C. 18) Dado que Yi > O, siendo i siguiente: = 1, ... , n, esta condición puede expresarse de la forma i = 1, ... , n. Esta expresión nos dice que cualquier vector de precios de equilibrio debe satisfacer la condición de la igualdad del precio y el coste medio. Dado que wo > O y el trabajo es un factor de producción indispensable, debe cumplirse que ci(w) > O, lo cual implica a su vez que ui, > O, siendo i =O, ... , n. En otras palabras, todos los vectores de precios de equilibrio son estrictamente positivos. Demostraremos que hay un único vector de precios de equilibrio. Supongamos que w' y w fueran dos soluciones distintas del sistema anterior de ecuaciones. Definamos w' ui'. t=�=max_____.!. Wm i ui; En este caso, la diferencia máxima entre los componentes de los dos vectores se encuentra en el componente m tal que w� es t veces mayor que Wm. Supongamos que t > 1. En ese caso, tenemos la siguiente cadena de desigualdades: Las justificaciones de estas igualdades y desigualdades son las siguientes: 1: la definición de t; 2: el supuesto de que w es una solución; 3: la homogeneidad lineal de la función de costes; 4: la definición de t, el supuesto de que t > 1 y la monotonicidad estricta de la función de costes en el vector de precios de los factores; 5: el supuesto de que w' es una solución. El resultado que se obtiene suponiendo que t > 1 es una contradicción, por lo que t ::; 1 y, por lo tanto, w 2:: w'. El papel de w y w' es simétrico en el argumento anterior, por lo que también tenemos que w' 2:: w. Uniendo estas dos desigualdades, tenemos que w' = w, como queríamos demostrar. La estructura de la industria en condiciones de equilibrio general / 417 Este teorema establece que si hay un vector de precios de equilibrio en la economía, éste debe ser la solución del sistema ui; = ci(w), siendo i = 1, ... , n. Lo sorprendente es que w no depende en absoluto de las condiciones de la demanda, es decir, que es totalmente independiente de las preferencias y de las dotaciones. Utilicemos el término técnica para referirnos a las demandas de factores necesarias para producir una unidad de producto. Sea w* el vector de precios que satisface las condiciones de beneficio nulo. En ese caso, podemos hallar la técnica de equilibrio de la empresa i diferenciando la función de costes con respecto a cada uno de los precios de los factores j: Dado que los precios de equilibrio son independientes de las condiciones de la demanda, también lo será la elección de la técnica de equilibrio. Independientemente de cómo varíen las demandas de los consumidores, la empresa no sustituirá la técnica de equilibrio; de ahí el nombre de teorema de la no sustitución. 18.10 La estructura de la industria en condiciones de equilibrio general Recordemos que en el modelo walrasiano se considera dado el número de empresas. En el capítulo 13 afirmamos que el número de empresas de una industria era una variable. ¿Cómo podemos conciliar estos dos modelos? Consideremos, en primer lugar, el caso de los rendimientos constantes. Sabemos que el único nivel de beneficios maximizador de los beneficios que es compatible con el equilibrio es el de beneficio nulo. Por otra parte, a los precios compatibles con los beneficios nulos las empresas están dispuestas a producir cualquier cantidad. Por lo tanto, la estructura de la industria de la economía es indeterminada: a las empresas les da igual la cuota de mercado que posean. Si el número de empresas es una variable, también es indeterminado. Consideremos ahora el caso de los rendimientos decrecientes. Si toda la tecnología muestra rendimientos decrecientes, sabemos que en condiciones de equilibrio habrá algunos beneficios. En el modelo de equilibrio general que hemos descrito hasta ahora, no hay razón alguna para que los beneficios sean iguales en todas las empresas. Este resultado se basa habitualmente en el argumento de que entrarán empresas en la industria que tenga los mayores beneficios; pero eso no puede ocurrir si el número de empresas es fijo. ¿Qué ocurriría, de hecho, si el número de empresas fuera variable? Probablemente entrarían empresas. Si la tecnología muestra realmente rendimientos decrecientes de escala, el tamaño óptimo de la empresa es infinitesimal, debido simplemente a que siempre es mejor tener dos empresas pequeñas que una grande. Por 418 / LA PRODUCCIÓN (C. 18) lo tanto, es de esperar que entraran continuamente empresas, presionando a la baja sobre los beneficios; En condiciones de equilibrio a largo plazo, sería de esperar que hubiera un número infinito de empresas y que cada una de ellas produjera una cantidad infinitesimal. Este resultado parece poco plausible. Una solución consiste en volver al argumento mencionado en el capítulo 13: si siempre podemos repetir los procesos de producción, la única tecnología razonable a largo plazo es una tecnología de rendimientos constantes de escala. Por lo tanto, la tecnología de rendimientos decrecientes de escala ha de deberse realmente a la presencia de algún factor fijo. En esta interpretación, debe considerarse que los "beneficios" de equilibrio son, en realidad, los rendimientos del factor fijo. Notas Véase Samuelson (1966) para el teorema de la no sustitución. Nuestro análisis se basa en el de Weizsacker (1971). Ejercicios 18.1. Considere el caso de una economía en la que hay dos factores de producción no producidos, la tierra y el trabajo, y dos bienes producidos, los arándanos y las bufandas. La producción de los arándanos y las bufandas muestra rendimientos constantes de escala. Las bufandas se producen utilizando trabajo solamente, mientras que los arándanos se producen utilizando tierra y trabajo. Hay N personas idénticas, cada una de las cuales tiene una dotación inicial de quince unidades de trabajo y diez de tierra. Todas tienen funciones de utilidad de la forma siguiente: U(A, B) = cln A + (1 - e) ln B, donde O < e < 1 y donde A y B representan el consumo de arándanos y de bufandas por parte de una persona, respectivamente. Los arándanos se producen con una tecnología de coeficientes fijos que utiliza una unidad de trabajo y una de tierra por cada unidad producida de arándanos. Las bufandas se producen utilizando trabajo solamente y necesitan una unidad de trabajo por cada bufanda producida. Sea el trabajo el numerario de esta economía. (a) Halle los precios y las cantidades de equilibrio competitivo de esta economía. (b) ¿Qué valores ha de tener el parámetro e (en caso de tener alguno) para que las pequeñas variaciones de la dotación de tierra no alteren los precios de equilibrio competitivo? Ejercicios / 419 (e) ¿Qué valores ha de tener el parámetro e (en caso de tener alguno) para que las pequeñas variaciones de la dotación de tierra no alteren los consumos de equilibrio competitivo? 18.2. Considere el caso de una economía en la que hay dos empresas y dos consumidores. La empresa 1 es en su totalidad propiedad del consumidor 1. Produce cañones a partir del petróleo por medio de la función de producción g = 2x. La 2 es enteramente propiedad del consumidor 2; produce mantequilla a partir del petróleo por medio de la función de producción b = 3x. Cada uno de los consumidores tiene 10 unidades de petróleo. La función de utilidad del consumidor 1 es u(g, b) = g0,4b0,6 y la del consumidor 2 es u(g, b) = 10 + O, Slng + O, Slnb. (a) Halle los precios de los cañones, la mantequilla y el petróleo que vacían el mercado. (b) ¿ Cuántos cañones y cuánta mantequilla consume cada persona? (c) ¿Cuánto petróleo utiliza cada empresa? 19. EL TIEMPO En el presente capítulo analizamos algunos temas relacionados con la conducta del consumidor y de la economía a lo largo del tiempo. Como veremos, la conducta a lo largo del tiempo puede considerarse, en algunos casos, como una mera ampliación del modelo estático analizado anteriormente. Sin embargo, el tiempo también impone una interesante estructura especial a las preferencias y a los mercados. Dada la incertidumbre inherente al futuro, es natural examinar algunas cuestiones relacionadas con ésta. 19.1 Preferencias intertemporales La teoría convencional de la elección del consumidor es absolutamente adecuada para describir la elección intertemporal. Ahora, los objetos de elección -las cestas de consumo- son las corrientes de consumo a lo largo del tiempo. Supongamos que el consumidor tiene unas determinadas preferencias respecto a estas corrientes de consumo que satisfacen las condiciones habituales de la regularidad. De las consideraciones convencionales se deduce que generalmente existe una función de utilidad que representa esas preferencias. Sin embargo, al igual que ocurre en el caso de la maximización de la utilidad esperada, el hecho de que estemos analizando un determinado tipo de problema de elección implica que las preferencias tienen una estructura especial que genera funciones de utilidad de una determinada forma. Un tipo muy utilizado es la función de utilidad que es aditiva con respecto al tiempo: ¿ Ut(ct). T U(c1, ... , cr) = t=l En este caso, Ut(ct) es la utilidad del consumo en el periodo t. Esta función también puede especializarse aún más y adoptar una forma estacionaria con respecto al tiempo: 422 / EL TIEMPO (C. 19) L o/u(ct). T U(ci, ... , cr) = t=l En este caso, utilizamos la misma función de utilidad en todos los periodos; sin embargo, la utilidad del periodo t se multiplica por un factor de descuento al. Obsérvese la estrecha analogía de esta formulación con la estructura de la utilidad esperada. En ese modelo, el consumidor tenía la misma utilidad en todos los estados de la naturaleza y la utilidad correspondiente a cada uno de ellos se multiplicaba por la probabilidad de que éste se produjera. De hecho, los axiomas de la teoría de la utilidad esperada pueden reformularse mecánicamente para justificar este tipo de funciones aditivas a lo largo del tiempo alegando las restricciones a que están sometidas las preferencias subyacentes. Supongamos que las posibilidades futuras de consumo son inciertas. Como hemos visto anteriormente, un conjunto natural de axiomas implica que podemos elegir una representación de la utilidad que sea aditiva con respecto a los distintos estados de la naturaleza. Sin embargo, puede ocurrir fácilmente que una transformación monótona de la utilidad sea aditiva con respecto a los estados de la naturaleza y otra transformación monótona diferente sea aditiva con respecto al tiempo. No hay razón alguna para que exista una representación de las preferencias que sea aditiva tanto en el caso de las elecciones intertemporales como en el de las elecciones inciertas. A pesar de eso, lo más frecuente es suponer que la función de utilidad intertemporal es aditiva tanto con respecto al tiempo como con respecto a los estados de la naturaleza. Este supuesto no es especialmente realista, pero permite simplificar los cálculos. 19.2 La optimización intertemporal con dos periodos En el capítulo 11 (página 216) estudiamos un sencillo modelo de optimización de la cartera. En éste vemos cómo se amplía ese modelo al caso en el que hay varios periodos. Este ejemplo sirve para ilustrar el método de la programación dinámica, técnica que sirve para resolver los problemas de optimización en los que hay muchos periodos descomponiéndolos en problemas de optimización de dos periodos. Analizamos, en primer lugar, el modelo de dos periodos. Representamos el consumo correspondiente a cada uno de ellos por medio de (ci, c2). El consumidor tiene una dotación inicial de w1 en el periodo 1 y puede invertir su riqueza en dos activos. Uno genera un rendimiento seguro, �; el otro genera un rendimiento aleatorio, R1. Conviene concebir estos rendimientos como si fueran rendimientos totales, es decir, uno más la tasa de rendimiento. Supongamos que el consumidor decide consumir c1 en el primer periodo e invertir una fracción x de su riqueza en el activo incierto y una fracción 1 - x en el La optimización intertemporal con dos periodos / 423 activo seguro. En esta cartera, el consumidor tiene (w1 - c1)x pesetas que generan un rendimiento R1 y (w1 - ci)(l - x) pesetas que generan un rendimiento J?.o. Por lo tanto, la riqueza que tiene en el segundo periodo -y que es igual a su consumo correspondiente al segundo periodo-- es En este caso, R = R1x + J?.o(l - x) es el rendimiento de la cartera del consumidor. Obsérvese que, en general, es una variable aleatoria, ya que lo es R1• Dado que el rendimiento de la cartera es incierto, también lo es el consumo correspondiente al segundo periodo. Suponemos que el consumidor tiene una función de utilidad de la forma siguiente: donde a < 1 es un factor de descuento. Sea Vi ( w1) la utilidad máxima que puede obtener el consumidor si tiene la riqueza w1 en el periodo 1: Vi (w1) = max c1,x u(c1) + aEu[(w1 - c1)R] (19.1) La función Vi ( w1) es esencialmente una utilidad indirecta: indica la utilidad maximizada en función de la riqueza. Diferenciando la ecuación (19.1) con respecto a c1 y a x1, tenemos las siguientes condiciones de primer orden: (19.2) (19.3) La ecuación (19.2) es una condición de optimización intertemporal: establece que la utilidad marginal del consumo correspondiente al periodo 1 debe ser igual a la utilidad marginal esperada descontada del consumo correspondiente al periodo 2. La ecuación (19.3) es una condición de optimización de la cartera: establece que la utilidad marginal esperada de transferir una pequeña cantidad de dinero del activo seguro al incierto debe ser cero. En el capítulo 11 (página 216) analizamos una condición de primer orden semejante. Dadas estas dos ecuaciones con dos incógnitas, x y ci, podemos hallar, en principio, la elección óptima del consumo y de la cartera. En el siguiente apartado, damos un ejemplo como parte de la solución del problema en el que hay T periodos. 424 / EL TIEMPO (C. 19) 19.3 La optimización intertemporal con varios periodos Supongamos ahora que hay T periodos. Si (c1, ... , cr) es una corriente (posiblemente aleatoria) de consumo, suponemos que el consumidor la evalúa de acuerdo con la siguiente función de utilidad: T U(c1, ... , cr) =Lo/ Eu(ct), t=O Si el consumidor tiene en el momento t una riqueza de ui¡ e invierte una fracción Xt en el activo incierto, la riqueza que tendrá en el periodo t + 1 viene dada por Wt+l = [wt - ctl.R, donde R = XtR1 + (1 - Xt)Ro es el rendimiento (aleatorio) generado por la cartera entre el periodo t y el periodo t + 1. Para resolver este problema de optimización intertemporal, utilizamos el método de la programación dinámica a fin de descomponerlo en una secuencia de problemas de optimización con dos periodos. Consideremos el periodo T - 1. Si el consumidor tiene una riqueza wr-1 en ese momento, la utilidad máxima que puede obtener es Vr-1(wr-1) = max CT-1,XT-1 u<cr-1) + aEu[(wr-1 - cr-1).R] (19.4) Este problema es exactamente igual que la ecuación (19.1), con la salvedad de que se ha sustituido 1 por T - 1. Las condiciones de primer orden son (19.5) u'(cr)(R1 - Ro)= O (19.6) Ya hemos visto cómo se resuelve este problema, en principio, y cómo se determina la función indirecta de utilidad Vr-1 (wr-1), Pasemos a examinar el periodo T - 2. Si el consumidor elige (cr-2, xr-2), en el periodo T.:__ 1, tendrá una riqueza (aleatoria) de wr-1 = [wr-1 - cr-21.R. Esta riqueza le reportará una utilidad esperada de Vr-1(wr-1). Por lo tanto, el problema de maximización del consumidor en el periodo T - 2 puede expresarse de la siguiente manera: La optimización intertemporal con varios periodos / 425 Vr--2<wr-2) = u<cr-2) + crEVr-1[(wr-2 - cr-2)R1. max cr-2,xr-2 Este problema es exactamente igual que el (19 .4), pero la utilidad correspondiente al "segundo periodo" no viene dada por la función directa de utilidad sino por la función indirecta de utilidad Vr-1 (wr-1). Las condiciones de primer orden correspondientes al periodo T - 2 son (19.7) EV'(wr_1)(R1 - Jlo) = O (19.8) De nuevo, (19.5) es una condición de optimización intertemporal: la utilidad marginal del consumo actual ha de ser igual a la utilidad marginal indirecta descontada de la riqueza futura; y (19.6) es una condición de optimización de la cartera. Estas condiciones pueden utilizarse para hallar Vr-2<wr-2), etc. Dada la función indirecta de utilidad ·v¡;(wt), el problema de optimización intertemporal con T periodos es simplemente una secuencia de problemas con dos periodos. Ejemplo: La utilidad logarítmica Supongamos que u(c) = logc. En ese caso, las condiciones de primer orden (19.5) y (19.6) se convierten en R 1 -- - Q------= cr-1 - o= E [wr-1 - cr-1]R [ R1 - Ro wr-1 - cr-1 l R (19.9) (19.10) Obsérvese que el rendimiento de la cartera no aparece en la ecuación (19.9), propiedad de la utilidad logarítmica que resulta sumamente útil. Despejando cr-1 en la ecuación (19.9), tenemos que Cr-1 Wr-1 = --. 1 + (X Introduciendo el resultado en la función objetivo, hallamos la función indirecta de utilidad: 426 / EL TIEMPO (C. 19) Aplicando las propiedades del logaritmo, Vr-1 ( wr-1) = (1 + a) In wr-1 + aE In R + a In a - (1 + a) In (1 + a). Obsérvese una importante característica de la función indirecta de utilidad Vr_ 1: es logarítmica con respecto a la riqueza. El rendimiento aleatorio afecta a Vr_ 1 aditivamente; no influye en la utilidad marginal de la riqueza y, por lo tanto, no aparece en las condiciones de primer orden apropiadas. En consecuencia, las condiciones de primer orden correspondientes al periodo T - 2 tienen la forma siguiente: 1 -- = o-(I cr-2 o- - E [ R + a)-----[wr-2 - cr-2JR (19.11) R1 - Ro [wr-2 - cr-2JR (19.12) l Estas condiciones son muy similares a las condiciones correspondientes al periodo T - 1; el segundo miembro de la ecuación (19.11) aparece multiplicado por 1 +ay la (19.12) es exactamente igual. De esta observación se desprende que en cada uno de los periodos el consumidor elige la misma cartera que elegiría si resolviera un problema de dos periodos y que la elección del consumo en el periodo T - 1 siempre es proporcional a la riqueza correspondiente a ese periodo. 19.4 El equilibrio general a lo largo del tiempo Como hemos señalado anteriormente, el concepto de bien en el modelo de equilibrio general de Arrow y Debreu es muy amplio. Los bienes pueden distinguirse por cualquier característica que les preocupe a los agentes. Si a éstos les preocupa el momento en que puede disponerse de ellos, los bienes de los que puede disponerse en momentos diferentes deben considerarse bienes diferentes. Si les preocupan las circunstancias en las que puede disponerse de ellos, pueden distinguirse por el estado de la naturaleza en el que se ofrecen. Cuando se distinguen los bienes de esta manera, es posible comprender desde una óptica nueva y más profunda el papel que desempeñan los precios de equilibrio. Consideremos, por ejemplo, un sencillo modelo de equilibrio general en el que hay un bien, el consumo, del que puede disponerse en diferentes momentos T = 1, ... , T. A la luz de las observaciones anteriores, consideramos que este bien son t bienes diferentes y suponemos que Ct indica el consumo de que puede disponerse en el momento t. El equilibrio general a lo largo del tiempo / 427 En un modelo de intercambio puro, el agente i estaría dotado de un determinado consumo en el momento t, Cit· En un modelo de producción, sería la tecnología disponible para transformar el consumo correspondiente al momento t en consumo en otros momentos del futuro. Sacrificando consumo en un determinado momento, el consumidor puede disfrutar de consumo en algún momento en el futuro. Los agentes tienen preferencias respecto a las corrientes de consumo y existen mercados para el intercambio de consumo en diferentes momentos del tiempo. Este tipo de mercados podría organizarse utilizando títulos-valores de Arrow y Debreu, que tienen una forma especial: el título t rinde 1 peseta cuando llega la fecha t y cero en todas las demás. Este tipo de títulos existe en el mundo real; se conocen con el nombre de bonos de descuento puro. Rinden una determinada cantidad de dinero (por ejemplo, 1.000.000 pesetas) en una determinada fecha. Este modelo contiene todos los elementos del modelo convencional de Arrow Debreu: preferencias, dotaciones y mercados. Podemos aplicar los resultados y habituales de la existencia para demostrar que deben existir unos precios de equilibrio (pt) de los títulos de Arrow y Debreu que vacíen todos los mercados. Obsérvese que Pt es el precio pagado en el momento cero por la entrega del bien de consumo en el momento t. En este modelo, todas las transacciones financieras se realizan al comienzo y el consumo tiene lugar a lo largo del tiempo. En los mercados intertemporales reales solemos medir de otra manera los precios futuros, a saber, por medio de los tipos de interés. Imaginemos que hay un banco que ofrece el siguiente acuerdo: por cada peseta que reciba en el momento O pagará 1 + rt pesetas en el momento t. Decimos que el banco está ofreciendo un tipo de interés de rt. ¿Qué relación existe entre el tipo de interés rt y el precio de Arrow y Debreu, Pt? Supongamos que un agente tiene una peseta en el momento O. Puede invertirla en el banco, en cuyo caso obtiene 1 + ri pesetas en el momento t, o puede invertirla en el título de Arrow- Debreu t. Si el precio de este título es Pt, puede comprar 1 / Pt unidades del mismo. Dado que cada unidad de este título valdrá 1 peseta en el momento t, tendrá 1/Pt pesetas en el momento t. Es evidente que la cantidad de dinero que tendrá el agente en el momento t debe ser la misma, cualquiera que sea el plan de inversión que elija; por lo tanto, 1 1 + r¡ = -. Pt Eso significa que los tipos de interés son simplemente las inversas de los precios de Arrow y Debreu, menos 1. Estos precios pueden utilizarse para valorar de la manera habitual las corrientes de consumo. Por ejemplo, la restricción presupuestaria de un consumidor adopta la forma siguiente: 428 / EL TIEMPO (C. 19) T ¿PtCt t=1 = T ¿PtCt. t=1 Utilizando la relación entre los precios y los tipos de interés, también podemos expresarla de la manera siguiente: L 1 C+ rt = L 1 + rt T t=1 t T _ Ct t=l Por lo tanto, la restricción presupuestaria adopta la forma según la cual el valor actual descontado del consumo debe ser igual al valor actual descontado de la dotación. Dado que el planteamiento es exactamente igual que el del modelo convencional de Arrow y Debreu que hemos descrito antes, se cumplen los mismos teoremas: partiendo de varios supuestos sobre la convexidad, existirá un equilibrio y éste será eficiente en el sentido de Pareto. El horizonte infinito En muchos casos, no parece adecuado utilizar un horizonte temporal finito, ya que es razonable que los agentes esperen que una economía exista "indefinidamente". Sin embargo, si se utiliza un periodo temporal infinito, los teoremas de la existencia y del bienestar plantean algunas dificultades. Las primeras son de tipo técnico: ¿cuál es la definición adecuada de una función continua que tenga un número infinito de argumentos? ¿Cuál es el teorema del punto fijo o el teorema del hiperplano separador que es apropiado? Estas cuestiones pueden resolverse utilizando algunos instrumentos matemáticos; la mayoría son de carácter puramente técnico. Sin embargo, los modelos que tienen un número infinito de periodos de tiempo poseen también algunas peculiaridades fundamentales. Tal vez el ejemplo más famoso sea el del modelo de las generaciones sucesivas, también conocido con el nombre de modelo puro de consumo y préstamos. Consideremos el caso de una economía que tiene la siguiente estructura. En cada periodo nacen ti agentes, cada uno de los cuales vive durante dos periodos. Por lo tanto, en cualquier momento del tiempo después del primer periodo están vivos 2n agentes: ti agentes jóvenes y ti agentes viejos. Cada uno de ellos tiene una dotación de 2 unidades de consumo cuando nace y es indiferente entre consumir cuando es joven y consumir cuando sea viejo. En este sencillo caso, la existencia de un equilibrio no plantea problema alguno. Evidentemente, existe un posible equilibrio cuando cada uno de los agentes consume su dotación. Este equilibrio se mantiene por medio de los precios Pt = 1, cualquiera que sea t. Sin embargo, resulta que este equilibrio no es eficiente en el sentido de Pareto. El equilibrio general con respecto a los diferentes estados de la naturaleza / 429 Para verlo, supongamos que cada uno de los miembros de la generación t + 1 transfiere una unidad de su dotación a la generación t. Ahora la generación 1 disfruta de un mayor bienestar, ya que recibe 3 unidades de consumo a lo largo de toda su vida. Ninguna de las otras generaciones ve empeorar su bienestar, ya que son compensadas cuando llegan a la vejez por las transferencias que efectuaron cuando eran jóvenes. ¡Eso significa que hemos hallado una mejora en el sentido de Pareto con respecto al equilibrio inicial! Merece la pena preguntarse por qué falla el primer teorema del bienestar en el modelo. El problema estriba en que hay un número infinito de bienes; si los precios de equilibrio son todos ellos iguales a 1, el valor tanto de la corriente agregada de consumo como de la dotación agregada es infinito. La contradicción existente en el último paso de la demostración del primer teorema del bienestar ya no existe, por lo que falla la demostración. Este ejemplo es muy sencillo, pero el fenómeno es bastante sólido. Es preciso tener sumo cuidado cuando se extrapolan los resultados de los modelos con horizontes finitos a modelos con horizontes infinitos. 19.5 El equilibrio general con respecto a los diferentes estados de la naturaleza Hemos señalado antes que a los agentes pueden preocuparles las circunstancias, es decir, el estado de la naturaleza en el que puede disponerse de los bienes, pues, al fin y al cabo, un paraguas en un día lluvioso es un bien muy diferente de un paraguas en un día soleado. Supongamos que los mercados están abiertos en el momento O, pero existe una cierta incertidumbre respecto a lo que ocurrirá en el momento 1, en que han de realizarse los intercambios. Supongamos, para concretar, que hay dos posibles estados de la naturaleza en el momento 1, o bien está lloviendo, o bien luce un sol radiante. Supongamos que los agentes utilizan contratos contingentes de la forma siguiente: "El agente i entregará una unidad del bien j al titular de este contrato si y sólo si está lloviendo". El intercambio en el momento O es un intercambio de contratos, es decir, promete proporcionar un bien o servicio en el futuro, si se produce un determinado estado de la naturaleza. Cabe imaginar que existe un mercado de este tipo de contratos; dado un vector cualquiera de precios de los contratos, los agentes pueden consultar sus preferencias y sus tecnologías y averiguar la cantidad que desean demandar y ofrecer de los diferentes contratos. Obsérvese que éstos se intercambian y se pagan en el momento O, pero sólo se llevan a la práctica en el momento 1 si se produce el estado del mundo correspondiente. Como siempre, un vector de precios de equilibrio es aquel en el 430 / EL TIEMPO (C. 19) que no hay exceso de demanda de ningún contrato. Desde el punto de vista de la teoría abstracta, los contratos son bienes exactamente iguales que cualquier otro. Se aplican los resultados habituales de la existencia y la eficiencia. Es importante comprender correctamente el resultado de la eficiencia. Las preferencias se definen en el espacio de las loterías. Si se cumplen los axiomas de von Neumann-Morgenstern, las preferencias respecto a los acontecimientos aleatorios pueden resumirse por medio una función de utilidad esperada. Decir que no existe ninguna otra asignación viable que mejore el bienestar de todos los consumidores equivale a decir que no existe ninguna pauta de contratos contingentes que mejore la utilidad esperada de cada uno de los agentes. En el mundo real existen contratos parecidos a los contingentes. Tal vez el más frecuente sean las pólizas de seguros, que se comprometen a entregar una determinada cantidad de dinero si y sólo si ocurre un determinado acontecimiento. Sin embargo, debe admitirse que los contratos contingentes son bastante raros en la práctica. Notas Véase Ingersoll (1987) para varios ejemplos resueltos de modelos dinámicos de optimización de la cartera. Geankoplos (1987) ha hecho un magnífico estudio sobre el modelo de generaciones sucesivas. Ejercicios 19.1. Considere el ejemplo de la utilidad logarítmica del capítulo 19 (página 423). Demuestre que el consumo correspondiente a un periodo arbitrario t viene dado por Ct = wtf [1 2 T-t + a + a ... a . ] = 1 - a Wt. 1- a T - t + 1 19 .2. Considere el siguiente plan de "estabilización de la renta". Cada año se permite a los caseros elevar sus alquileres 3 / 4 de la tasa de inflación. Los propietarios de las viviendas recién construidas pueden fijar el alquiler inicial que deseen. Los defensores de este plan sostienen que como el precio inicial de las nuevas viviendas puede fijarse en cualquier nivel, no disminuirán los incentivos para ofrecer viviendas de nueva construcción. Analicemos esta afirmación en un sencillo modelo. Supongamos que los apartamentos duran 2 periodos. Sea r el tipo de interés nominal y 1r la tasa de inflación. Supongamos que en ausencia de estabilización de los alquileres, el alquiler será p en el periodo 1 y (1 + 1r )p en el periodo 2. Sea e el coste Ejercicios / 431 marginal constante de construir nuevas viviendas y D(p) la función de demanda de apartamentos correspondiente a cada periodo. Finalmente, sea K la oferta de viviendas de alquileres controlados. (a) En ausencia de estabilización de los alquileres, ¿cuál debe ser la relación de equilibrio entre el alquiler del periodo 1 y el coste marginal de construir una nueva vivienda? (b) Si se adopta un plan de estabilización de los alquileres, ¿cuál habrá de ser esta relación? (c) Represente un sencillo gráfico de oferta y demanda y muestre el número de nuevas viviendas sin estabilización de los alquileres. (d) ¿Se construirán más viviendas con el plan de estabilización de alquileres o menos? (e) ¿Será el precio de equilibrio de las nuevas viviendas más alto o más bajo con este plan de estabilización de los alquileres? 20. Los MERCADOS DE ACTIVOS El estudio de los mercados de activos exige un enfoque de equilibrio general. Corno veremos a continuación, el precio de equilibrio de un activo depende fundamentalmente de la relación entre su valor y el de otros activos. Por lo tanto, en el estudio de la fijación de los precios de muchos activos intervienen algunas consideraciones de equilibrio general. ' 20.1 El equilibrio en ausencia de incertidumbre En el estudio de los mercados de activos, el centro de interés son los factores que determinan las diferencias entre sus precios. En un mundo en el que no hubiera incertidumbre, el análisis de estos mercados resultaría muy sencillo: el precio de un activo sería simplemente el valor actual descontado de su corriente de rendimientos. De no ser así, existiría la posibilidad de realizar un arbitraje sin riesgo. Examinemos, por ejemplo, un modelo de dos periodos. Supongamos que hay un activo que genera un rendimiento total seguro de Ro. Es decir, 1 peseta invertida hoy en el activo O rendirá con toda seguridad Ro pesetas el próximo periodo. Si Ro es el rendimiento total del activo O, ro= Ro - 1 es la tasa de rendimiento. Existe otro activo a que tendrá un valor Va el próximo periodo. ¿Cuál es hoy el precio de equilibrio de este activo? En un mundo en el que no existe incertidumbre, la respuesta es fácil: el precio actual del activo a viene dado por su valor actual: Pa Va Ro Va ro+ 1 = - = -- (20.1) De lo contrario, sería una manera segura de ganar dinero. Si Pa > Va/ Ro, todas las personas que tuvieran un activo a podrían vender una unidad e invertir los ingresos en el activo libre de riesgo. En el siguiente periodo tendrían PaRo > Va. Dado que al menos una persona querría vender el activo a, Pano es un precio de equilibrio. 434 / LOS MERCADOS DE ACTIVOS (C. 20) La condición de equilibrio (20.1) también puede expresarse en función del rendimiento del activo a. Éste se define de la manera siguiente: R¿ = Va/Pa· Si dividirnos los dos miembros de (20.1) por Pa y reordenamos la expresión resultante, tenernos que Ra Va = - = Pa Ro. (20.2) Esta ecuación indica simplemente que en condiciones de equilibrio todos los activos que tienen un rendimiento seguro deben tener el mismo rendimiento, ya que nadie compraría un activo que se esperara que tuviera un rendimiento menor que el de otro. 20.2 El equilibrio en presencia de incertidumbre En un mundo en el que los rendimientos de los activos no están libres de riesgo, los rendimientos esperados varían dependiendo de su grado de riesgo. Normalmente, cabe pensar que cuanto más incierto sea el activo, menos se pagará por él, manteniéndose todo lo demás constante. En otras palabras, cuanto más incierto sea el activo, mayor tendrá que ser el rendimiento esperado para inducir a los individuos a comprarlo. Por analogía con la ecuación (20.2), podernos formular la siguiente expresión: k; = Ro + prima por el riesgo del activo a. El primer miembro de esta expresión se denomina rendimiento esperado del activo a. El segundo es el rendimiento libre de riesgo más la prima por el riesgo de este activo. Esta condición también puede expresarse de la manera siguiente: k; - Ro = prima por el riesgo del activo a. El primer miembro de esta ecuación se denomina exceso de rendimiento del activo a y la ecuación establece que en condiciones de equilibrio el exceso de rendimiento de cada activo es igual a su prima por el riesgo. Estas ecuaciones son, por supuesto, meras definiciones. Las teorías económicas de los mercados de activos intentan obtener expresiones explícitas de la prima por el riesgo en función de factores "fundamentales", corno las preferencias de los consumidores y la pauta de rendimiento de los activos. En este análisis intervienen consideraciones de equilibrio general, ya que el valor de un activo incierto depende inherentemente de la presencia o ausencia de otros activos inciertos que sean complementarios o sustitutivos del activo en cuestión. Notación / 435 Por lo tanto, en la mayoría de los modelos de fijación del precio de los activos, el valor de un activo acaba dependiendo de cómo varíe éste en relación con el de otros. Lo sorprendente es que esta idea aparece generalmente en modelos que son a primera vista sumamente diferentes. En este capítulo, presentamos y comparamos varios modelos de fijación del precio de los activos. 20.3 Notación En el presente apartado presentamos la notación que utilizaremos en este capítulo. De esa manera resultará fácil retroceder y recordar las definiciones de los diferentes símbolos cuando sea necesario. Algunos de los términos se definen más detalladamente en el apartado correspondiente. Examinaremos, en general, un modelo de dos periodos, en el que el presente es el periodo O. Los valores que tendrán los diferentes activos en el periodo 1 son inciertos. Esta incertidumbre se refleja en el modelo por medio del concepto de estados de la naturaleza. Es decir, supondremos que existen varios resultados posibles representados por el subíndice s = 1, ... , S; el valor que tendrá cada uno de los activos en el siguiente periodo depende del resultado que se produzca realmente. inversor, i Wi e; riqueza del inversor i en el periodo O consumo en el periodo O Wi - e; s = 1, ... , 1 cantidad invertida en el periodo O por el inversor i estados de la naturaleza s = 1, ... , S en el segundo periodo probabilidad de que ocurra el estado s. Suponemos que todos los consumidores tienen las mismas expectativas sobre las probabilidades; éste es el caso de las expectativas homogéneas. 1r s Gis consumo del individuo i en el estados en el segundo periodo c. consumo del individuo i en el segundo periodo, considerado como una variable aleatoria Obsérvese que podemos ver el consumo de dos maneras diferentes: o bien como la lista de posibles consumos en cada uno de los estados de la naturaleza, (Gis), 436 / LOS MERCADOS DE ACTIVOS (C. 20) o bien como la variable aleatoria e: que adopta el valor (Gis) con las probabilidades ui(ci) + 8Eui(Ci) función de utilidad de von Neumann-Morgenstern del inversor i. Obsérvese que suponemos que esta función es aditivamente separable con respecto al tiempo, con un factor de descuento 8. precio del activo a, siendo a = O, ... , A Pa cantidad comprada del activo a por el inversor i Xia parte de la riqueza de inversión que el inversor i tiene invertida en el activo a. Si Wi es la cantidad total invertida en todos los activos, Xia = PaXia/Wi y, por lo tanto, z:::=:=O Xia = 1 Xia (xio, ... , XiA) cartera de activos del inversor i. Obsérvese que una cartera está representada por la parte de riqueza invertida en cada uno de los activos. valor del activo a en el estado de la naturaleza s en el segundo periodo Vas Va valor del activo a en el segundo periodo, considerado como una variable alea- Ras rendimiento (total) del activo a en el estado s. Por definición, Ras = Vas!Pa· toria Ra rendimiento total del activo a considerado como una variable aleatoria. La variable aleatoria n; adopta el valor Ras con la probabilidad 1r s. k; = Z::::;=l 1rsRas = ERa Ro rendimiento total del activo libre de riesgo a ab rendimiento esperado del activo a = cov (Ra, Rb) covarianza de los rendimientos de los activos a y b 20.4 Modelo de fijación del precio de los activos de capital Analizaremos los distintos modelos de los mercados de activos en un orden más o menos histórico, por lo que comenzaremos con el padre de todos ellos, el conocido modelo de fijación del precio de los activos de capital o MPAC. Éste parte de una determinada especificación de la utilidad, a saber, que la utilidad de una distribución Modelo de fijación del precio de los activos de capital / 437 aleatoria de la riqueza depende únicamente de los dos primeros momentos de la distribución de probabilidades, a saber, la media y la varianza. Este modelo sólo es compatible con el de la utilidad esperada en determinadas circunstancias; por ejemplo, cuando todos los activos siguen una distribución normal o cuando la función de utilidad esperada es cuadrática. Sin embargo, la media y la varianza pueden servir de aproximación de la función de utilidad en una variedad más amplia de casos. En este contexto, la "aversión al riesgo" significa que un aumento del consumo esperado es un bien y un aumento de la varianza del consumo es un mal. Analizamos, en primer lugar, la restricción presupuestaria. Ésta también puede utilizarse en algunos de los modelos que examinaremos. Omitiendo el subíndice que se refiere al inversor a fin de simplificar la notación, el consumo correspondiente al segundo periodo viene dado por Dado que la suma de las ponderaciones de la cartera debe ser igual a uno, de tal manera que xo = 1 - ¿:=l Xa, también podemos formular la restricción presupuestaria de la manera siguiente: (20.3) La expresión situada entre corchetes es el rendimiento de la cartera. Dados nuestros supuestos sobre la función de utilidad basada en la media y la varianza, cualquiera que sea el nivel de inversión, al inversor le gustaría que la varianza del rendimiento de la cartera fuera lo menor posible, dado el valor esperado. Es decir, le gustaría comprar una cartera que fuera eficiente desde el punto de vista de la media y la varianza. La cartera que elija en realidad dependerá de su función de utilidad; pero cualquiera que sea ésta, debe minimizar la varianza, dado un determinado nivel de rendimiento esperado. Antes de seguir adelante, examinemos las condiciones de primer orden de este problema de minimización. Se trata de minimizar la varianza del rendimiento de la cartera sujeta a las restricciones de que ha de lograrse un determinado rendimiento esperado, R, y satisfacerse la restricción presupuestaria ¿:=o Xa = l. 438 / LOS MERCAOOS DE ACTIVOS (C. 20) A min XQ,···,XA sujeta a A LL XaXba ab a=O h=O A L XaRa = R a=O A LXa = l. a=O En este problema permitimos que x¿ sea positivo o negativo, lo que significa que el consumidor puede adoptar una posición corta o larga con respecto a cualquier activo, incluido el activo libre de riesgo. Suponiendo que >. es el multiplicador de Lagrange de la primera restricción y µ el multiplicador de Lagrange de la segunda, las condiciones de primer orden adoptan la forma siguiente: A 2 L Xba ab - xñ; - µ = O siendo a = O, ... , A (20.4) b=O Dado que la función objetivo es convexa y las restricciones son lineales, se satisfacen automáticamente las condiciones de segundo orden. Estas condiciones de primer orden pueden utilizarse para formular una interesante ecuación que describe la pauta de rendimientos esperados. La deducción que realizamos es elegante, pero algo indirecta. Sea (x1, ... , XÁ) una cartera de valores formada enteramente por activos inciertos que se sabe que es eficiente desde el punto de vista de la media y la varianza. Supongamos que uno de los activos inciertos que pueden adquirir los inversores -por ejemplo, el activo e- es un "fondo de inversión" que contiene esta cartera eficiente (x�). En ese caso, la cartera que invierte O en todos los activos, salvo en el e, y 1 en este último es eficiente desde el punto de vista de la media y la varianza. Eso significa que esa cartera debe satisfacer las condiciones de la ecuación (20.4) en el caso de todos y cada uno de los activos a= O, ... ,A. Observando que en el caso de esta cartera Xb = O si b -=/ e, vemos que la condición de primer orden a-ésima se convierte en Za ae - xk; - µ = O. Cuando a = O y cuando a = e, se producen dos casos especiales: ->.Ro - µ=o 2a ee - >.Re - µ = O. (20.5) Modelo de fijación del precio de los activos de capital / 439 Cuando a = O, µae es cero, ya que el activo O no es incierto. Cuando a = e, a ae = a ce, ya que la covarianza de una variable consigo misma es simplemente la varianza de la variable aleatoria. Despejando X yµ, en estas dos ecuaciones, tenemos que )\ = 2aee Re -Ro µ = ->.Ro=_ 2aeeRo Re - Ro Introduciendo estos valores en (20.5) y reordenando, tenemos que - aae - R¿ =Ro+ -(Re - Ro). aee (20.6) Esta ecuación establece que el rendimiento esperado de un activo cualquiera es igual a la tasa libre de riesgo más una "prima por el riesgo" que depende de la covarianza del rendimiento del activo y del de una cartera eficiente formada por activos inciertos. Esta ecuación debe cumplirse en el caso de cualquier cartera de activos inciertos. Para dar contenido empírico a esta ecuación, es necesario poder identificar una cartera eficiente, para lo cual examinamos gráficamente la estructura de este tipo de carteras. En la figura 20.1 representamos los rendimientos esperados y las desviaciones típicas que pueden ser generados por un determinado conjunto de activos inciertos 1. Puede demostrarse que el conjunto de carteras eficientes desde el punto de vista de la media y la desviación típica que están formadas totalmente por activos inciertos tiene forma de hipérbola, como muestra la figura 20.1, pero el hecho de que tenga esa determinada forma no es necesario para el siguiente razonamiento. Queremos construir el conjunto de carteras eficientes que contienen tanto los activos inciertos como el activo libre de riesgo, para lo cual trazamos la línea que pasa por la tasa del activo libre de riesgo Ro y toca la hipérbola de la figura 20.1 sólo en un punto. Llamamos al punto en el que toca a este conjunto (Rm, am). Este punto es el rendimiento esperado y la desviación típica de una cartera que llamaremos cartera m. Puede afirmarse que toda combinación de rendimiento esperado y desviación típica situada en esta línea recta puede alcanzarse tomando combinaciones convexas de dos carteras: la cartera libre de riesgo y la cartera tn: Por ejemplo, para construir una cartera que tenga un rendimiento esperado de colocamos simplemente la mitad de la !<Rm - Ro) y una desviación típica de riqueza en la cartera m y la otra mitad en el activo libre de riesgo. De esa manera mostramos cómo se logra cualquier combinación de media y desviación típica situada a la izquierda de (Rm, a111). Para generar las combinaciones de rendimiento situadas !am, I La desviación típica de una variable aleatoria es simplemente la raíz cuadrada de su varianza. 440 / Los MERCADOS DE ACTIVOS (C. 20) a la derecha del punto (Rm, CJm), tenemos que pedir dinero prestado a la tasa Ro e invertirlo en la cartera m. Figura 20.1 RENDIMIENTO ESPERADO Carteras eficientes de activos inciertos Carteras eficientes de activos inciertos y activos libres de riesgo DESVIACION TIPICA Conjunto de rendimientos inciertos y desviaciones típicas. Todas las carteras eficientes desde el punto de vista de la media y la varianza pueden construirse combinando las carteras cuyos rendimientos sean Ro y Rm. Este razonamiento geométrico muestra que la estructura del conjunto de carteras eficientes es realmente sencilla: puede construirse enteramente a partir de dos carteras, una formada por el activo libre de riesgo y otra que es la cartera m. Lo único que falta es dar contenido empírico a esta cartera de activos inciertos. Sea x�i la parte de la riqueza invertida en la cartera m correspondiente al active a. Naturalmente, debe cumplirse que ¿:=l x�i = l. Sea Wi la cantidad de riqueza que invierte el individuo i en la cartera incierta; X¿0, el número de títulos del active incierto a que adquiere el individuo i; y Pa el precio del activo a. Dado que cada une de los inversores tiene la misma cartera de activos inciertos, debe cumplirse que siendo v= 1, ... , J. Multiplicando los dos miembros de esta ecuación por W¡ y sumando las igualdadr correspondientes a los distintos inversores i, tenemos que Modelo de fijación del precio de los activos de capital / 441 El numerador de esta expresión es el valor total de mercado del activo a. El denominador es el valor total de todos los activos inciertos. Por lo tanto, x-;:i es simplemente la parte de la riqueza invertida en los activos inciertos que corresponde al activo a. Esta cartera se conoce con el nombre de cartera de activos inciertos de mercado. Es una cartera que puede observarse, en la medida en que sea posible medir las tenencias agregadas de activos inciertos. Dado que la cartera de activos inciertos de mercado es una determinada cartera eficiente desde el punto de vista de la media y la desviación típica, podemos reformular la ecuación (20.6) de la manera siguiente: - R¿ O"am =Ro+ -(Rm - Ro). O"mm Éste es el resultado fundamental del MPAC. Da contenido empírico a la prima por el riesgo: ésta es la covarianza del activo a y la cartera de mercado dividida por la varianza de la cartera de mercado y multiplicada por el exceso de rendimiento de la cartera de mercado. El término a am / a mm puede considerarse el coeficiente de regresión teórico resultante de una regresión de Ra en función de Rm. Por este motivo, este término suele representarse por medio del símbolo f3a. Introduciendo esta notación en el resultado anterior, obtenemos la forma final del MPAC: (20.7) Según el MPAC, para hallar el rendimiento esperado de un activo cualquiera, basta conocer simplemente la "beta" de dicho activo, es decir, su covarianza con la cartera de mercado. Obsérvese que la varianza del rendimiento del activo es irrelevante; no es el "propio riesgo" del activo el que cuenta, sino de qué manera contribuye este rendimiento de un activo al riesgo global de la cartera de los agentes. Dado que en el MPAC todo el mundo tiene la misma cartera de activos inciertos, el riesgo que cuenta es la influencia de un activo en el grado de riesgo de la cartera de mercado. El atractivo del MPAC se halla en que su formulación contiene variables que resultan ser empíricamente observables: el rendimiento esperado de la cartera de mercado de activos inciertos y el coeficiente de regresión de una regresión que relaciona el rendimiento de un determinado activo y el rendimiento de la cartera de mercado. Debe recordarse, sin embargo, que la construcción teórica relevante es la cartera de todos los activos inciertos, la cual puede no ser tan fácil de observar. 442 / Los MERCADOS DE ACTIVOS (C. 20) 20.5 La teoría de la fijación de los precios basada en el arbitraje El MPAC parte de una especificación de los gustos de los consumidores; la teoría de la fijación de los precios basada en el arbitraje (TPA) parte de una especificación del proceso que genera los rendimientos de los activos. En este sentido, el MPAC es un modelo del lado de la demanda, mientras que el TPA es un modelo del lado de la oferta. A menudo se observa que los precios de la mayoría de los activos varían al unísono; es decir, hay un cierto grado de variación conjunta de sus precios. Es natural formular los rendimientos de los activos en función de unos cuantos factores comunes y de algunos riesgos específicos de los activos. Si sólo hay dos factores, por ejemplo, podemos realizar la formulación siguiente: En este caso, (j1, J2) se conciben como factores "macroeconómicos" referentes al conjunto de la economía, que influyen en los rendimientos de todos los activos. Cada uno de los activos a tiene una determinada "sensibilidad" bai al factor i. El riesgo específico de un activo, Ea, es, por definición, independiente de los factores que afectan al conjunto de la economía, J'\ y Dada la presencia del "término constante" boa, siempre puede suponerse que los factores i = 1, 2 y los riesgos específicos de los activos, Ea siendo a = 1, ... , A, tienen una esperanza matemática igual a cero (si las esperanzas matemáticas no fueran iguales a cero, las incorporaríamos a boa). También se supone que E.fi f2 = O, es decir, que los factores son factores verdaderamente independientes. Examinemos, en primer lugar, algunos casos especiales de la TPA en la que no hay ningún riesgo específico de los activos. Comenzamos con el caso en el que sólo hay un factor de riesgo, por lo que J2. Ji, ti; =boa+ b1al1 siendo a= O, ... , A. Pretendemos explicar como siempre los rendimientos esperados de los activos en función de una prima por el riesgo. Por construcción, tenemos que k; = boa, por lo que consiste simplemente en examinar la conducta de boa siendo a = 1, ... , A. Supongamos que construimos una cartera de dos activos a y b, en la que tenemos x del activo a y 1 - x del b. El rendimiento de esta cartera será xRn + (1 - x)Rb = [xboa + (1 - x)bob] + [xb1n + (1 - x)b11JÍ1. Elijamos un x* tal que el segundo término situado entre corchetes sea igual a cero. Eso implica que La teoría de la fijación de los precios basada en el arbitraje / 443 (20.8) Obsérvese que para ello debemos suponer que b1b =/ b1a, lo que significa que los activos a y b no tienen la misma sensibilidad. La cartera resultante es, por construcción, una cartera libre de riesgos. Por lo tanto, su rendimiento debe ser igual a la tasa libre de riesgo, lo que implica que x*boa + (1 - x*)bob = Ro, o sea, Sustituyendo x* por su valor de la ecuación (20.8) y reordenando, tenemos que bob - Ro b1b bob - boa b1b - b1a (20.9) Intercambiando el papel de a y deben este argumento, tenemos que boa - Ro b1a boa - bob b1a - b1b . (20.10) Obsérvese que el segundo miembro de la ecuación (20.9) es igual que el de la (20.10). Dado que esta igualdad se cumple en el caso de todos los activos a y b, tenemos que para alguna constante .\1 en el caso de todos los activos a. Valiéndonos del hecho de que Ra = boa y reordenando, obtenemos la forma final de la TPA cuando sólo hay un factor: (20.11) La ecuación (20.11) establece que el rendimiento esperado de un activo cualquiera a es la tasa libre de riesgo más una prima por el riesgo que viene dada por la sensibilidad del activo a al factor común de riesgo multiplicado por una constante. La constante puede interpretarse como la prima por el riesgo pagada por una cartera que tiene la sensibilidad 1 al tipo de riesgo representado por el factor 1. 444 / LOS MERCADOS DE ACTIVOS (C. 20) Dos factores Supongamos ahora que examinamos un modelo con dos factores: Ahora construimos una cartera tres ecuaciones siguientes: (xa, Xb, Xc) con tres activos a, by e que satisface las Xab1a + Xbb1b + Xcblc = O Xab2a + Xbb2b + Xcb2c = O Xa + Xb + x¿ = 1. La primera ecuación establece que la cartera elimina el riesgo del factor 1, la segunda establece que elimina el riesgo del factor 2 y la tercera establece que la suma de las proporciones invertidas en los tres activos es 1, es decir, que tenemos, de hecho, una cartera. En consecuencia, esta cartera tiene un riesgo nulo. Por consiguiente, debe generar el rendimiento libre de riesgo, por lo que Xaboa + xbbob + Xcboc = Ro. Expresando estas condiciones en forma matricial, tenemos que boc b1c b2c ) Ro ) ( XXba Xc _ - ( O) Ü O · El vector (xa, Xb, Xc) no está formado únicamente por ceros, ya que la suma de sus elementos es igual a 1. Por lo tanto, la matriz de la izquierda debe ser singular. Si las dos últimas filas no son colineales (como suponemos), debe cumplirse que la primera fila es una combinación lineal de las dos últimas. Es decir, cada casilla de la fila superior es una combinación lineal de las casillas correspondientes de las dos siguientes, lo que implica que R¿ - Ro = b1a>.1 + b2a>.2 cualquiera que sea a= 1, ... , A (20.12) Las >. tienen la misma interpretación que antes: son los excesos de rendimientos de las carteras que tienen la sensibilidad 1 al tipo específico de riesgo indicado por el factor correspondiente. Ésta es la generalización natural del caso de 1 factor: el exceso de rendimiento del activo a depende de su sensibilidad a los dos factores de riesgo. La utilidad esperada / 445 El riesgo específico de los activos Hemos visto que si el número de factores es pequeño en relación con el de activos y no existen riesgos específicos de los activos, es posible construir carteras libres de riesgo. Éstas deben generar el rendimiento libre de riesgo, lo que impone determinadas restricciones al conjunto de rendimientos esperados. Pero estas carteras libres de riesgos formadas por activos inciertos sólo pueden construirse si todo el riesgo se debe a factores macroeconómicos. ¿ Qué ocurre si hay un riesgo específico de los activos, además del riesgo del conjunto de la economía? Por definición, los riesgos específicos de los activos son independientes de los factores de riesgo del conjunto de la economía e independientes entre sí. La ley de los grandes números implica, pues, que el riesgo de una cartera sumamente diversificada de empresas debe implicar un riesgo específico de los activos muy pequeño. Este argumento induce a pensar que podemos prescindir de los riesgos específicos de los activos y que cabe esperar que la relación lineal entre los rendimientos esperados de los factores siga cumpliéndose, al menos como una buena aproximación. El lector interesado puede consultar la bibliografía que se cita al final del capítulo para los detalles de este razonamiento. 20.6 La utilidad esperada Examinemos un modelo de fijación del precio de los activos basado en la maximización intertemporal de la utilidad esperada. Consideremos el siguiente problema de dos periodos: max c,x1,···,xA De nuevo, hemos suprimido el subíndice que representa al inversor i a fin de simplificar la notación. En este problema se nos pide que hallemos el ahorro correspondiente al primer periodo, W. - e, y la pauta de inversión de cartera, (x1, ... , XA), que maximizan la utilidad esperada descontada. Suponiendo que R =(Ro+ ¿:=l Xa(Ra - Ro)) es el rendimiento de la cartera y que 6 = (W - c)R, podemos formular la condición de primer orden de este problema de la forma siguiente: u'(c) = aEu'(C)R o= Eu'(C)(Ra - Ro) siendo a = 1, ... , A. 446 / LOS MERCADOS DE ACTIVOS (C. 20) Según la primera condición, la utilidad marginal esperada del consumo correspondiente al primer periodo debe ser igual a la utilidad marginal esperada descontada del consumo correspondiente al segundo periodo. Según el segundo conjunto de condiciones, la utilidad marginal esperada de sustituir en la cartera el activo seguro por el activo a debe ser cero en el caso de todos los activos a = 1, ... , A. Fijémonos en el segundo conjunto de condiciones y veamos qué implicaciones tiene para la fijación del precio de los activos. Utilizando la identidad de la covarianza del capítulo 26 (página 569), podemos expresar estas condiciones de la manera siguiente: Eu'(C)(Ra - Ro)= cov(u'(C), Ra) + Eu'(C)(Ra - Ro)= O siendo a= 1, ... , A. Reordenando, tenemos que R¿ = 1 Eu'(C) - I Ro - -- cov(Ra, u (C)) - (20.13) Esta ecuación recuerda a la ecuación de fijación del precio del MPAC, la ecuación (20.7), pero con algunas diferencias. Ahora, la prima por el riesgo depende de la covarianza con la utilidad marginal y no con la cartera de activos inciertos de mercado. Si un activo está correlacionado positivamente con el consumo, estará correlacionado negativamente con la utilidad marginal del consumo, ya que u" < O, lo cual significa que tendrá una prima por el riesgo positiva, es decir, debe tener un rendimiento esperado mayor para que lo compren los inversores. En el caso de los activos que están correlacionados negativamente con el consumo, ocurrirá exactamente lo contrario. Esta ecuación, tal como está formulada, sólo se cumple en el caso de un inversor i. Sin embargo, en determinadas circunstancias, la condición puede agregarse. Supongamos, por ejemplo, que todos los activos siguen una distribución normal. En ese caso, el consumo también la seguirá, por lo que podemos aplicar un teorema que se debe a Rubinstein (1976), según el cual cov(u'(C), Ra) = Eu''(C)cov(C, Ra). Aplicando este teorema a la ecuación (20.13) y añadiendo el subíndice i para distinguir a los inversores individuales, tenemos que ( Eu�'(Ci)) - Ra =Ro+ cov(Ci, Ra) I Eu/Ci) (20.14) El término que multiplica a la covarianza a veces se conoce con el nombre de aversión global al riesgo del agente i. Explotando esta analogía, lo representaremos por medio del símbolo r.: Reordenando la ecuación (20.14), tenemos que La utilidad esperada / 447 Sumando las igualdades correspondientes a todos los inversores i = 1, ... , I y defiI niendo C = ¿i=l C, como el consumo agregado, tenemos que I tñ, - Ro)"'°'_!_ L-r· i=l = cov(C, Ra). i Esta expresión también puede formularse de la siguiente manera: k; = Ro+ ¿ :. ]-1 cov(C, Ra) [ ¡ i=l (20.15) i Ahora la prima por el riesgo es proporcional a la covarianza del consumo agregado y el precio del activo. El factor de proporcionalidad es una medida de la aversión media al riesgo. Este factor de proporcionalidad también puede expresarse como el exceso de rendimiento de un determinado activo. Supongamos que hay un activo e que está perfectamente correlacionado con el consumo agregado (este activo puede ser una cartera de otros activos). En ese caso, el rendimiento de este activo e, Re, debe satisfacer la ecuación (20.15): Despejando en esta ecuación la aversión media al riesgo, tenemos que I::. ]-1 [ ¡ i=l i fJcc Este resultado nos permite reformular la ecuación de la fijación del precio de los activos (20.15) de la manera siguiente: (20.16) El cociente entre las covarianzas de esta expresión a veces se conoce con el nombre de beta en el consumo de un activo. Es el coeficiente teórico de regresión entre el rendimiento del activo a y el rendimiento de un activo que está correlacionado perfectamente con el consumo agregado. Tiene la misma interpretación que la ''beta de mercado" que vimos al estudiar el MPAC. De hecho, la semejanza entre (20.16) y 448 / LOS MERCADOS DE ACTIVOS (C. 20) (20.7) es tan llamativa que cabe preguntarse si existe, en realidad, alguna diferencia entre ellas. En un modelo de dos periodos, no existe ninguna. Si sólo hay dos periodos, la riqueza agregada (es decir, la cartera de mercado) correspondiente al segundo periodo es igual al consumo agregado. Sin embargo, en un modelo de muchos periodos, la riqueza y el consumo puede ser diferentes. Aunque hemos deducido la ecuación en un modelo de dos periodos, es válida en un modelo de muchos periodos. Para verlo, consideremos el siguiente experimento. En el periodo t transferimos una peseta del activo seguro al activo a. En el periodo t + 1, modificamos nuestro consumo en una cantidad igual a Xa (Ra - Ro). Si tenemos un plan óptimo de consumo, la utilidad esperada de esta medida debe ser cero. Pero esta condición y la normalidad de la distribución de los rendimientos fueron las únicas condiciones que utilizamos para obtener la ecuación (20.16). Ejemplo: La utilidad esperada y la TPA Dado que la TPA impone restricciones sobre las características de los rendimientos y el modelo de la utilidad esperada sólo impone restricciones sobre las preferencias, podemos combinar los resultados de los dos modelos a fin de interpretar los riesgos específicos de los factores. El modelo de la utilidad esperada de (20.13) establece que R¿ 1 I = Ro - ----cov(Ra, u (C)) (20.17) Eu'(C) y la TPA postula que Introduciendo esta ecuación en la (20.13), tenemos que Ra = Ro - E:(c) [b1acov(u'(C), f1) + b2acov(u'(C), Ji)] . Comparando esta ecuación con la (20.12), vemos que AJ y A2 son proporcionales a la covarianza de la utilidad marginal del consumo con el riesgo del factor correspondiente. 20.7 Mercados completos Examinemos ahora otro modelo de valoración de los activos. Supongamos que hay S estados de la naturaleza diferentes y que en cada uno de los estados s hay un activo Mercados completos / 449 que rinde una peseta si ocurre el estado s y cero en caso contrario. Este tipo de activo se conoce con el nombre de título de Arrow y Debreu. Sea Ps el precio de equilibrio del título de Arrow y Debreu s. Consideremos ahora el caso de un activo arbitrario a que tiene el valor Vas en el estado s. ¿Qué valor tiene este activo en el periodo O? Consideremos el siguiente argumento: formemos una cartera que contenga Vas unidades del título de Arrow y Debreu s. Dado que este título tiene un valor de una peseta en el estados, esta cartera tendrá el valor Vas en dicho estado. Por lo tanto, esta cartera tendrá exactamente la misma pauta de rendimientos que el activo a. Teniendo en cuenta el arbitraje, el valor del activo a debe ser igual que el de esta cartera. Por lo tanto, s Pa = LPsVas· s=l Este razonamiento demuestra que el valor de un activo cualquiera puede hallarse a partir de los valores de los activos de Arrow y Debreu. Suponiendo que 1r s es la probabilidad de que ocurra el estado s, podemos formular la siguiente igualdad: Pa = s - P�Ps e: -Vas1ís = E-Va, s=l 7í s 7í donde E es el operador de las esperanzas matemáticas. Esta fórmula establece que el valor del activo a es la esperanza matemática del valor del activo a multiplicado por la variable aleatoria (p/1r). Aplicando la identidad de la covarianza del capítulo 26 (página 563), podemos reformular esta expresión de la manera siguiente: Pa ) (p p = cov "i' Va + E¡EVa (20.18) Por definición, - s 7í s=l s Ef = L Ps1ís = ¿Ps· 7í s s=l Por lo tanto, E(p/ir) es el valor de una cartera que genera 100 pesetas en el periodo siguiente. Suponiendo que Ilo es el rendimiento libre de riesgo de una cartera de ese tipo, tenemos que Ei= �· Introduciendo este resultado en la ecuación (20.18) y reordenando algo los términos, tenemos que 450 / LOS MERCADOS DE ACTIVOS (C. 20) Pa = Va Ro __ - + cov(p/1r, Va) (20.19) Por lo tanto, el valor del activo a debe ser su valor esperado descontado más una prima por el riesgo. Hasta este momento no hemos hecho más que manipular las definiciones; ahora introducimos un supuesto sobre la conducta. Si el agente i compra Cis unidades del título de Arrow y Debreu s, debe satisfacer la siguiente condición de primer orden: o sea, u�(cis) Ps Ai ns Por lo tanto, p /1rs debe ser proporcional a la utilidad marginal del consumo del inversor i. El primer miembro de esta expresión es una función estrictamente decreciente del consumo, debido a la aversión al riesgo. Sea Íi la inversa de uU ,\i; ésta también es una función decreciente. En ese caso, podemos escribir 8 Sumando las ecuaciones correspondientes a los distintos agentes i y representando el consumo agregado correspondiente al estados por medio de Cs, tenemos que e, = ¿ Íi(ps/1ís). I i=l Dado que cada Íi es una función decreciente, también lo es el segundo miembro de esta expresión. Por lo tanto, tiene una inversa F, por lo que podemos escribir donde F( Cs) es una función decreciente del consumo agregado. Introduciendo este resultado en (20.19), tenemos que Pa = Va Ro - - + cov(F(C), Va) (20.20) Por lo tanto, el valor del activo a es el valor esperado descontado ajustado por medio de una prima por el riesgo que depende de la covarianza del valor del activo con una función decreciente del consumo agregado. Los activos que están correlacionados positivamente con el consumo agregado se ajustarán negativamente; los que están El arbitraje puro / 451 correlacionados negativamente, se ajustarán positivamente, exactamente igual que en los demás modelos. 20.8 El arbitraje puro Examinemos, por último, un modelo de fijación del precio de los activos con el mínimo absoluto de supuestos: sólo es necesario que no existan oportunidades para el arbitraje puro. Ordenemos el conjunto de activos en forma de matriz de dimensión Ax S, en la cual la casilla Vsa mida el valor del activo a en el estado de la naturaleza s. Llamemos a esta matriz V. Sea X= (X1, ... , XA) una pauta de tenencias de los activos A. En ese caso, el valor de esta pauta de inversión en el segundo periodo será un vector de dimensión S que vendrá dado por el producto matricial VX. Supongamos que X genera un rendimiento no negativo en todos los estados de la naturaleza: VX 2'.: O. En ese caso, parece razonable suponer que el valor de esta pauta de inversión no puede ser negativo; es decir, que pX 2'.: O. De lo contrario, existiría una oportunidad para el arbitraje puro. Formulamos esta condición de la manera siguiente: Principio de la ausencia de arbitraje. Si VX 2'.: O, entonces pX 2'.: O. Ésta es una condición mínima para la ausencia de oportunidades gratuitas. Pues bien, puede demostrarse que el principio de la ausencia de arbitraje implica que existe un vector (p1, ... , p s) tal que el valor de un activo cualquiera viene dado por Pa = s �PsVas (20.21) s==l Recordando que 1r s mide la probabilidad de que ocurra el estado s, podemos formular la ecuación (20.21) de la manera siguiente: El segundo miembro de esta ecuación es simplemente la esperanza matemática del producto de dos variables aleatorias. Sea Z la variable aleatoria que adopta los valores p8/1rs y Va la variable aleatoria que adopta los valores Vas· En ese caso, aplicando la identidad de la covarianza, tenemos que 452 / LOS MERCADOS DE ACTIVOS (C. 20) Por definición, - = '°' s Z Ps L..,¡ -1fs 7r s s=1 '°' s = L..,¡ Ps· s=1 El segundo miembro de esta expresión es el valor de un activo que rinde 100 en cada uno de los estados de la naturaleza, es decir, es el valor de un bono libre de riesgo. Por definición, este valor es igual a 100 / Ro. Teniendo en cuenta esta igualdad y reordenando los términos, tenemos que Dividiendo por Pa para convertir esta igualdad en una expresión en la que aparezcan los rendimientos de los activos, tenemos que En esta ecuación vemos que en condiciones muy generales la prima por el riesgo de cada uno de los activos depende de la covarianza del rendimiento de los activos con una única variable aleatoria, la misma para todos los activos. En los diferentes modelos que hemos analizado, hemos hallado diferentes expresiones para Z. En el caso del MPAC, Z era el rendimiento de la cartera de activos inciertos de mercado. En el caso del modelo de la beta en el consumo, era la utilidad marginal del consumo. En el modelo de Arrow y Debreu, es una determinada función de consumo agregado. Apéndice Pretendemos demostrar que el principio de la ausencia de arbitraje que hemos citado en este capítulo implica que los precios vigentes en los diferentes estados (p1, '. .. , p s) no son negativos. Para abordar esta cuestión, consideremos el siguiente problema de programación lineal: min sujeta a pX VX � O. Este problema de programación lineal nos exige hallar la cartera más barata que da un vector de todos los rendimientos no negativos. Ciertamente, X = O es una elección viable para este problema y el principio de la ausencia de arbitraje implica que minimiza, de hecho, la función objetivo. Por lo tanto, el problema de programación lineal tiene una solución finita. Ejercicios / 453 El dual de este programa lineal es maxOp sujeta a pV = p, donde pes el vector no negativo de dimensión S de las variables duales. Dado que el primal tiene una solución viable finita, también la tiene el dual. Vemos, pues, que una implicación necesaria de la condición de ausencia de arbitraje es que debe existir un vector de dimensión S no negativo p tal que p=pV. Notas Nuestro análisis del MPAC se basa en Ross (1977). El modelo de la TPA se debe a Ross (1976); nuestro análisis se basa en Ingersoll (1987). La fórmula de la fijación del precio de los activos del modelo de Arrow y Debreu se basa en Rubinstein (1976). El análisis del arbitraje puro se basa en Ross (1978), pero la demostración procede de Ingersoll (1987). Ejercicios 20.1. La condición de primer orden de la elección de la cartera en el modelo de la utilidad esperada era Eu'(C)(Ra - Ro) = O en el caso de todos los activos a. Demuestre que esta condición también podría expresarse de la forma siguiente: Eu'(C)(Ra - Rb) = O, cualesquiera que sean los activos a y b. 20.2. Formule la ecuación (20.20) en función de la tasa de rendimiento del activo a. 21. ANÁLISIS DEL EQUILIBRIO En el presente capítulo examinamos algunos temas del análisis de equilibrio general que no encajan bien en los demás capítulos. El primero se refiere al núcleo, que es una generalización del conjunto de Pareto, y a su relación con el equilibrio walrasiano. A continuación analizamos brevemente la relación entre la convexidad y el tamaño. Posteriormente, examinamos las condiciones en las que sólo hay un equilibrio walrasiano y, por último, concluimos el capítulo con un análisis de la estabilidad del equilibrio general. 21.1 El núcleo de una economía de intercambio Hemos visto que generalmente existen equilibrios walrasianos y que éstos suelen ser eficientes en el sentido de Pareto. Pero la utilización de un sistema basado en el mecanismo de los mercados competitivos no es sino una de las formas de asignar los recursos. ¿ Qué ocurriría si recurriéramos a alguna otra institución social para facilitar el intercambio? ¿Se "aproximaría" la asignación resultante a un equilibrio walrasiano? Para analizar esta cuestión, examinamos un "juego de mercado" en el que cada uno de los agentes i llega al mercado con una dotación inicial de Wi. En lugar de utilizar un mecanismo de precios, los agentes se limitan a deambular y a llegar a acuerdos tentativos de intercambio entre sí. Cuando todos han llegado al mejor acuerdo posible, se realizan los intercambios. El juego, tal como se ha descrito hasta ahora, apenas tiene estructura. En lugar de especificar el juego detalladamente para calcular un equilibrio, nos hacemos una pregunta más general. ¿ Cuál podría ser el conjunto "razonable" de resultados de este juego? He aquí una serie de definiciones que pueden resultar útiles para analizar esta cuestión. 456 / ANÁLISIS DEL EQUILIBRIO (C. 21) Mejorar con respecto a una asignación. Se dice que un grupo de agentes S mejora con respecto a una determinada asignación x si hay otra asignación x' tal que ¿x� = ¿wi, iES iES y x� h xi cualquiera que sea i E S. Si es posible mejorar con respecto a una asignación x, hay algún grupo de agentes a los que les iría mejor si no participaran en el mercado y se limitaran a realizar intercambios entre ellos. Un ejemplo podría ser el de un grupo de consumidores que organizara una cooperativa para contrarrestar los elevados precios de la tienda de alimentación. Parece que cualquier asignación con respecto a la cual se pueda mejorar no es un equilibrio razonable, ya que algún grupo siempre tendría incentivos para separarse del resto de la economía. Núcleo de una economía. Una asignación viable x pertenece al núcleo de la economía si no existe ninguna coalición que pueda mejorar con respecto a dicha asignación. Obsérvese que si x pertenece al núcleo, debe ser eficiente en el sentido de Pareto, pues si no lo fuera, la coalición formada por todos los agentes podría mejorar con respecto a ella. En este sentido, el núcleo es una generalización de la idea del conjunto de Pareto. Si una asignación pertenece al núcleo, todos los grupos de agentes reciben una parte de las ganancias derivadas del intercambio y ninguno tiene incentivos para ir a la suya. Uno de los problemas que plantea el concepto de núcleo se halla en que impone una gran cantidad de condiciones relacionadas con la información, es decir, las personas de la coalición insatisfecha han de ser capaces de encontrarse unas a otras. Se supone, además, que la formación de coaliciones no conlleva ningún coste, por lo que éstas se formarían aun cuando con ello sólo pudieran obtenerse pequeñísimas ganancias. El núcleo puede representarse gráficamente a partir del diagrama habitual de la caja de Edgeworth correspondiente al caso en el que hay dos bienes y dos personas. Véase la figura 21.1. En este caso, el núcleo es el subconjunto del conjunto de Pareto en el que a los dos agentes les interesa más realizar intercambios que negarse a ello. ¿Es no vacío en general el núcleo de una economía? Si mantenernos los supuestos que garantizan la existencia de un equilibrio de mercado, lo es, ya que el equilibrio de mercado siempre está contenido en el núcleo. El núcleo de una economía de intercambio / 457 Figura 21.1 CONSUMIDOR 1 -----------------BIEN 1 El núcleo en una caja de Edgeworth. En el diagrama de la caja de Edgeworth, el núcleo es simplemente el segmento del conjunto de Pareto que se encuentra entre las curvas de indiferencia que pasan por la dotación inicial. El equilibrio de Walras pertenece al núcleo. Si (x", p) es un equilibrio walrasiano a partir de las dotaciones iniciales Wi, x" pertenece al núcleo. Demostración. Supongamos que no fuera así; en ese caso, habría una coalición S y una asignación viable x' tales que todos los agentes i pertenecientes a S preferirían estrictamente x� a x; y, además, ¿x� = ¿wi. iES iES Pero la definición del equilibrio walrasiano implica que px� > pwi cualquiera que sea i en S por lo que p ¿x� > p ¿w¡ iES iES lo que contradice la primera igualdad. El diagrama de la caja de Edgeworth muestra que en el núcleo hay, por lo general, otros puntos además del equilibrio de mercado. Sin embargo, si permitimos que crezca nuestra economía formada por 2 personas, tendremos más coaliciones 458 / ANÁLISIS DEL EQUILIBRIO (C. 21) posibles y, por lo tanto, más oportunidades de mejorar con respecto a cualquier asignación dada. Por consiguiente, cabe sospechar que el núcleo podría reducirse conforme creciera la economía. Uno de los problemas que plantea la formalización de esta idea se halla en que el núcleo es un subconjunto del espacio de asignaciones, por lo que sus dimensiones varían a medida que crece la economía. Por lo tanto, nos interesa limitarnos a analizar un tipo de crecimiento especialmente sencillo. Decimos que dos agentes son del mismo tipo si tanto sus preferencias como sus dotaciones iniciales son iguales. Decimos que una economía es una réplica de otra si hay r veces tantos agentes de cada tipo en la primera como en la segunda. Eso significa que si una gran economía es una réplica de otra más pequeña, es simplemente una reproducción a una "escala mayor" de esta última. Para facilitar el análisis, nos limitaremos a examinar solamente el caso en el que hay dos tipos de agentes, el tipo A y el tipo B. Consideremos una economía formada por dos personas; entendemos por núcleo r-ésimo de esta economía el núcleo de la réplica r-ésima de la economía original. Pues bien, todos los agentes del mismo tipo deben recibir la misma cesta en cualquier asignación del núcleo. Este resultado facilita mucho el análisis. Igualdad de trato en el núcleo. Supongamos que las preferencias de los agentes son estrictamente convexas, fuertemente monótonas y continuas. En ese caso, si x es una asignación perteneciente al núcleo r-ésimo de una determinada economía, dos agentes cualesquiera del mismo tipo deben recibir la misma cesta. Demostración. Sea x una asignación perteneciente al núcleo y designemos a los 2r agentes por medio de los subíndices A 1, .. ·. Ar y Bl, ... , Br. Si todos los agentes del mismo tipo no reciben la misma asignación, habrá un agente de cada tipo que recibirá un trato peor. Llamamos a estos agentes "marginado de tipo A:' y "marginado de tipo B". Si existe más de un agente marginado de algún tipo, seleccionamos uno cualquiera de ellos. Sean XA = � r:;=l XAj y XB = � r:;=l XBj las cestas medias de los agentes de tipo A y de tipo B. Dado que la asignación x es viable, tenemos que -:;. ¿xAj +-:;. ¿xBj =; ¿wAj +-:;. ¿wBj lr j=l lr j=l lr lr j=l j=l 1 1 = -rWA + -rWB· r r Por lo tanto, XA+XB=WA+WB, por lo que (xA, x8) es viable para la coalición formada por los dos marginados. Estamos suponiendo que al menos en el caso de uno de los tipos, por ejemplo, el A, El núcleo de una economía de intercambio / 459 dos de los agentes de este tipo reciben cestas diferentes. Por lo tanto, el marginado A preferirá estrictamente XA a su asignación actual en razón de la convexidad estricta de las preferencias (ya que es una media ponderada de las cestas que son al menos tan buenas como la xA) y el marginado B pensará que x8 es al menos tan buena como su cesta actual. La monotonicidad fuerte y la continuidad permiten a A destinar una parte de XA a sobornar al marginado de tipo By formar así una coalición que supone una mejora con respecto a la asignación. Dado que cualquier asignación que pertenezca al núcleo debe proporcionar a los agentes del mismo tipo la misma cesta, podemos examinar los núcleos de las réplicas de economías de dos agentes por medio de la caja de Edgeworth. Ahora un punto x perteneciente al núcleo no representa la cantidad que recibe A y la que recibe B sino la cantidad que recibe cada agente de tipo A y la que recibe cada agente de tipo B. El lema anterior nos dice que todos los puntos del núcleo r-ésimo pueden representarse de esta manera. La siguiente proposición demuestra que toda asignación que no sea una asignación que equilibre el mercado acabará no perteneciendo al núcleo r-ésimo de la economía, lo cual significa que en las grandes economías las asignaciones pertenecientes al núcleo son exactamente iguales que los equilibrios walrasianos. Contracción del núcleo. Supongamos que las preferencias son estrictamente convexas y fuertemente monótonas y que hay un único equilibrio de mercado x" a partir de la dotación inicial w. En ese caso, si y no es el equilibrio de mercado, hay una réplica r tal que y no pertenece al núcleo r-ésimo de la economía. Demostración. Examinemos la caja de Edgeworth de la figura 21.2. Pretendemos demostrar que dado un punto como el y, es posible acabar consiguiendo una mejora con respecto al mismo. Dado que y no es un equilibrio walrasiano, el segmento que pasa por y y w debe cortar al menos la curva de indiferencia de un agente en el punto y. Por lo tanto, es posible elegir un punto como el g que sea preferido, por ejemplo, por el agente A al y. Los casos que pueden analizarse son varios, dependiendo de dónde se encuentre g; sin embargo, los argumentos son esencialmente los mismos, por lo que sólo analizaremos el caso representado. . Dado que g se encuentra en el segmento que conecta los puntos y y w, podemos afirmar que g = ()w A + (1 - ())y A en el caso de algún número () > O. De acuerdo con la continuidad de las preferencias, también podemos suponer que () = T /V en el caso de algunos números enteros T y V. Por lo tanto, 460 / ANÁLISIS DEL EQUILIBRIO (C. 21) Supongamos que la economía se ha reproducido V veces. En ese caso, formemos una coalición integrada por V consumidores de tipo A y V - T de tipo B y consideremos la asignación z en la que los agentes de tipo A de la coalición reciben gA y los de tipo B reciben y B. Todos los miembros de la coalición prefieren esta asignación a la y (podemos transferir una parte de los agentes A a los agentes B para conseguir una preferencia estricta). Demostraremos que es viable para los miembros de la coalición por medio del cálculo siguiente: VgA+(V - T)yB =V [�WA + (1- �) YA] +(V-T)yB = Tia A + (V - T)y A + (V - T)y B = Tia A + (V - T)[y A + y B] = TwA + (V - T)[wA + WB] = Tia A + Vw A = VwA - Tia A + (V - T)w B + (V -T)wB. Ésta es exactamente la dotación de nuestra coalición, ya que contiene V agentes de tipo A y (V - T) de tipo B. Por lo tanto, esta coalición puede conseguir una mejora con respecto a y, con lo que queda demostrada la proposición. Muchos de los supuestos restrictivos de esta proposición pueden abandonarse. En concreto, puede prescindirse fácilmente de los supuestos de la monotonicidad fuerte y la unicidad del equilibrio de mercado. La convexidad parece fundamental para la proposición, pero, al igual que ocurre en el teorema de la existencia, es un supuesto innecesario cuando se trata de economías grandes. Naturalmente, también podemos permitir que haya más de dos tipos de agentes. Cuando estudiamos el equilibrio walrasiano, observamos que el mecanismo de los precios da lugar a un equilibrio bien definido. Cuando estudiamos las asignaciones eficientes en el sentido de Pareto observamos que casi todas las asignaciones de este tipo podían lograrse reasignando debidamente las dotaciones y utilizando el mecanismo de los precios. Y ahora, que estamos estudiando una economía de intercambio puro general, los precios cobran una tercera dimensión: las únicas asignaciones que pertenecen al núcleo de una gran economía son asignaciones que constituyen un equilibrio de mercado. El teorema de la contracción del núcleo demuestra que los equilibrios walrasianos son sólidos: incluso los conceptos débiles de equilibrio, como La convexidad y el tamaño de la economía / 461 el de núcleo, tienden a generar asignaciones parecidas a los equilibrios walrasianos cuando las economías son grandes. Figura 21.2 BIEN 1 TIPOB BIEN 2 ,BIEN2 TIPOA -----------------BIEN 1 La contracción del núcleo. Cuando se hace una réplica de la economía, un punto como el y acabará no perteneciendo al núcleo. 21.2 La convexidad y el tamaño de la economía La convexidad de las preferencias ha surgido en varios modelos de equilibrio general. Normalmente, el supuesto de la convexidad estricta se ha utilizado para garantizar que la función de demanda está bien definida, es decir, que sólo se demanda una cesta a cada uno de los precios, y que es continua, es decir, que las pequeñas variaciones de los precios provocan pequeñas variaciones en la. demanda. El supuesto de la convexidad parece necesario para que exista una asignación de equilibrio, ya que es fácil buscar ejemplos en los que la ausencia de convexidad provoca discontinuidades en la demanda y, por lo tanto, la inexistencia de precios de equilibrio. Consideremos, por ejemplo la caja de Edgeworth representada en la figura 21.3. En este caso, las preferencias del agente A no son convexas, mientras que las de B sí lo son. Al precio v: hay dos puntos que maximizan la utilidad, pero la oferta no es igual a la demanda en ninguno de esos puntos. Sin embargo, es posible que no sea tan difícil alcanzar el equilibrio como sugiere este ejemplo. Examinemos un caso concreto. Supongamos que la oferta del bien se encuentra exactamente en el punto medio entre las dos demandas al precio v', como sucede en la figura 21.3B. Pensemos qué ocurriría si la economía se reprodujera una 462 / ANÁLISIS DEL EQUILIBRIO (C. 21) vez y hubiera dos agentes de tipo A y dos de tipo B. En ese caso, al precio p*, uno de los agentes de tipo A podría demandar XÁ y el otro x�. En ese caso, la demanda total de los agentes sería, de hecho, igual a la cantidad total ofrecida del bien. En el caso de la réplica de esta economía existe un equilibrio walrasiano. Figura 21.3 CONSUMIDOR B PRECIO Oferta del consumidor 2 �--- Curva de indiferencia del consumidor 1 Curva de indiferencia _ del consumidor 2 - -,....,;: p: 1 1 1 1 1 1 1 1 1 1 1 1 Pendiente= -p: : 1 1 1 1 1 CONSUMIDOR A x·: A x: x·: X''1 CANTIDAD B Inexistencia de equilibrio cuando las preferencias no son convexas. El panel A muestra una caja de Edgeworth en la que las preferencias de uno de los agentes no son convexas. El B muestra la curva de demanda agregada correspondiente, que es discontinua. No es difícil ver que sirve cualquier construcción similar, independientemente de dónde se encuentre la curva de oferta: si se encontrara a dos tercios de la distancia que media entre XÁ y x�, reproduciríamos la economía tres veces, etc. Podemos conseguir que la demanda agregada se aproxime arbitrariamente a la oferta agregada reproduciendo la economía un número suficiente de veces. Este razonamiento induce a pensar que en una gran economía en la que la escala de ausencia de convexidades es pequeña en relación con las dimensiones del mercado, generalmente hay un vector de precios que hace que la demanda sea cercana a la ·oferta. Cuando la economía es suficientemente grande, las pequeñas ausencias de convexidades no plantean graves dificultades. Esta observación está estrechamente relacionada con el argumento de la repetición descrito en nuestro análisis de la conducta de las empresas competitivas. Consideremos un modelo clásico de empresas que tienen costes fijos y funciones de coste medio en forma de U. Las funciones de oferta de las empresas normalmente La unicidad del equilibrio / 463 serán discontinuas, pero estas discontinuidades serán irrelevantes si las dimensiones del mercado son suficientemente grandes. 21.3 La unicidad del equilibrio En el apartado dedicado a la existencia de equilibrio general vimos que en determinadas condiciones existe un vector de precios que vacía todos los mercados, es decir, existe un p* tal que z(p*) :S O. En este apartado nos planteamos la cuestión de la unicidad: ¿cuándo hay un único vector de precios que vacía todos los mercados? El caso de los bienes gratuitos carece aquí de interés, por lo que lo excluimos por medio del supuesto de la deseabilidad: suponemos que el exceso de demanda de cada uno de los bienes es estrictamente positivo cuando su precio relativo es cero. Eso significa desde el punto de vista económico que cuando el precio de un bien se reduce a cero, todo el mundo demanda una gran cantidad del mismo, lo cual parece bastante razonable. Una consecuencia evidente es que en todos los vectores de precios de equilibrio el precio de cada uno de los bienes debe ser estrictamente positivo. Supondremos, al igual que antes, que z es continua, pero ahora es necesario postular otro supuesto más, por lo que supondremos que es continuamente diferenciable. Las razones son bastante evidentes; si las curvas de indiferencia tienen vértices, podemos hallar intervalos de precios que sean equilibrios de mercado. Los equilibrios no sólo no son únicos, sino que ni siquiera lo son localmente. Dados estos supuestos, nos hallamos ante un problema puramente matemático: dada una aplicación lisa z del simplex de los precios en Rk, ¿cuándo existe un único punto cuya imagen sea igual a cero? Pensar que eso ocurrirá en general es esperar demasiado, ya que es fácil encontrar ejemplos contrarios, incluso en el caso bidimensional. Por lo tanto, nos interesa hallar restricciones que pesen sobre las funciones de exceso de demanda y que garanticen la unicidad y averiguar si esas restricciones son fuertes o débiles, cuál es su significado económico, etc. Aquí analizaremos dos restricciones que pesan sobre z y que garantizan la unicidad. El primer caso, el de los sustitutivos brutos, es interesante porque tiene un claro significado económico y permite hacer una demostración de la unicidad sencilla y directa. El segundo, el del análisis basado en los índices, es interesante porque es muy general. De hecho, contiene como casos especiales casi todos los demás resultados relativos a la unicidad. Desgraciadamente, la demostración se basa en un teorema bastante avanzado de topología diferencial. 464 / ANÁLISIS DEL EQUILIBRIO (C. 21) Los sustitutivos brutos En términos generales, dos bienes son sustitutivos brutos si una subida del precio de uno de ellos provoca un aumento de la demanda del otro. En los cursos elementales, ésta suele ser la definición de los bienes sustitutivos. En los más avanzados, es preciso distinguir entre los sustitutivos netos -cuando sube el precio de un bien, aumenta la demanda hicksiana del otro- y los sustitutivos brutos, en cuya definición se sustituye el término "hicksiana" por "marshalliana". Sustitutivos brutos. Dos bienes, i y i. son sustitutivos brutos dado el vector de precios p . 8zj(p) o . d . _¡ . si � > op, sien o i I J. Según esta definición, dos bienes son sustitutivos brutos si una subida del precio del bien i provoca un aumento del exceso de demanda del bien i. Si todos los bienes son sustitutivos brutos, todos los términos del jacobiano de z, Dz(p), que no pertenezcan a su diagonal principal, son positivos. La presencia de sustitutivos brutos implica la existencia de un único equilibrio. Sí todos los bienes son sustitutivos brutos a todos los precios, entonces sí p* es un vector de precios de equilibrio, es único. Demostración. Supongamos que p' es algún otro vector de precios de equilibrio. Dado que p* » O, podemos definir m = maxpUp; -¡ O. En virtud de la homogeneidad y del hecho de que p* es un equilibrio, sabemos que z(p*) = z(mp*) = O. También sabemos que a algún precio, Pk, tenemos que mpk = p� de acuerdo con la definición de m. Ahora bajamos todos los precios mp7,, salvo Pk, sucesivamente a Dado que en el cambio de mp* por p' baja el precio de todos los bienes, salvo el de k, debe descender la demanda del bien k. Por lo tanto, Zk(p') < O, lo que implica que p' no puede ser un equilibrio. p:. El análisis basado en los índices Consideremos el caso de una economía en la que sólo hay dos bienes. Elijamos el precio del bien 2 como numerario y tracemos la curva de exceso de demanda del bien 1 en función de su propio precio. La ley de Walras implica que cuando el exceso de demanda del bien 1 es cero, tenemos un equilibrio. El supuesto de la deseabilidad del que hemos partido implica que cuando el precio relativo del bien 1 es alto, su exceso de demanda es negativo; y cuando el precio relativo del bien 1 es bajo, su exceso de demanda es positivo. La unicidad del equilibrio / 465 Figura 21.4 z z z p p z p z p p Unicidad y unicidad local del equilibrio. Estos paneles muestran algunos ejemplos utilizados en el análisis de la unicidad del equilibrio. Examinemos la figura 21.4, en la que hemos representado algunos ejemplos de lo que puede ocurrir. Obsérvese que (1) los equilibrios suelen estar aislados; (2) y (3) los casos en los que no están aislados no son "estables" cuando se producen pequeñas perturbaciones; (4) normalmente existe un número impar de equilibrios; (5) si la curva de exceso de demanda tiene pendiente negativa en todos los equilibrios, sólo puede haber uno y si sólo hay uno, la curva de exceso de demanda debe tener pendiente negativa en dicho equilibrio. Obsérvese que en el caso unidimensional anterior si dz(p)/dp < O en todos los equilibrios, sólo puede haber un equilibrio. El análisis basado en los índices es una manera de generalizar este resultado a k dimensiones, con el fin de obtener una sencilla condición necesaria y suficiente para que se cumpla la unicidad. 466 / ANÁLISIS DEL EQUILIBRIO (C. 21) Dado un equilibrio p*, definimos el índice de p* de la siguiente manera: partimos de la negativa del jacobiano de la matriz del exceso de oferta -Dz(p), suprimimos la última fila y la última columna y tomarnos el determinante de la submatriz resultante. Asignamos al punto p* el índice + 1, si el determinante es positivo y -1 si es negativo (suprimir la última fila y de la última columna equivale a elegir como numerario el último bien, exactamente igual que en nuestro sencillo ejemplo unidimensional). También necesitamos una condición de contorno; existen varias posibilidades generales, pero lo más sencillo es suponer que zi(p) > O cuando p,¡ = O. En este caso, un teorema fundamental de topología diferencial establece que si todos los equilibrios tienen un índice positivo, sólo puede existir uno de ellos. Este resultado nos permite establecer de inmediato un teorema de la unicidad. Unicidad del equilibrio. Supongamos que z es una función de exceso de demanda agregada continuamente diferenciable definida en el simplex de los precios, siendo zi(p) > O cuando p, es igual a cero. Si el determinante de la matriz (-Dz(p*)) de orden (k - 1) por (k - 1) es positivo en todos los equilibrios, sólo existe un único equilibrio. Este teorema de la unicidad es un resultado puramente matemático. Tiene la ventaja de que puede aplicarse a algunos problemas de equilibrio diferentes. Si un teorema de la existencia de equilibrio puede formularse como un problema de punto fijo, generalmente podemos utilizar un teorema basado en los índices para hallar las condiciones en las que el equilibrio es único. Sin embargo, el teorema tiene el inconveniente de que es difícil interpretar su significado en términos económicos. En el caso que estamos examinando aquí, nos interesa el determinante de la función de exceso de oferta agregada. Podemos utilizar la ecuación de Slutsky para formular la derivada de la función de exceso de demanda agregada de la manera siguiente: n n i=1 i=1 ¿Cuándo es positivo el determinante de la matriz del primer miembro? Examinemos el segundo miembro de la expresión. El primer término funciona perfectamente; la matriz de sustitución es una matriz semidefinida negativa, por lo que la (negativa) del menor principal de esa matriz de orden (k - 1) x (k - 1) suele ser una matriz definida positiva. La suma de las matrices definidas positivas es definida positiva, por lo que tiene un determinante positivo. El segundo término plantea más problemas. Éste es esencialmente la covarianza de los excesos de oferta de los bienes con la propensión marginal a consumirlos. No hay razón alguna para pensar que tiene una determinada estructura en general. Lo la dinámica del equilibrio general / 467 único que podemos decir es que si estos efectos-renta son pequeños en relación con los efectos-sustitución, de tal manera que domina el primer término, es razonable esperar que el equilibrio sea único. 21.4 La dinámica del equilibrio general Hemos demostrado que partiendo de algunos supuestos plausibles sobre la conducta de los agentes económicos, siempre existe un vector de precios que iguala la demanda y la oferta. Pero no hemos garantizado que la economía se encontrará, de hecho, en este punto de "equilibrio". ¿Qué fuerzas podrían tender a llevar a los precios a adoptar un valor que vaciara el mercado? En este apartado examinamos algunos de los problemas que plantea el intento de plasmar en un modelo el mecanismo de ajuste de los precios en una economía competitiva. El mayor problema es el más fundamental, a saber, la relación paradójica entre la idea de la competencia y el ajuste de los precios: si todos los agentes económicos consideran dados los precios y fuera de su control, ¿cómo varían éstos? ¿Quién los ajusta? Este enigma ha llevado a crear una compleja mitología que postula la existencia de un "subastador walrasiano" cuya única función consiste en buscar los precios que vacíen el mercado. De acuerdo con esta construcción, un mercado competitivo funciona de la manera siguiente: En el momento cero el subastador walrasiano anuncia un vector de precios. Todos los agentes determinan sus demandas y ofertas de bienes actuales y futuros a esos precios. El subastador examina el vector de excesos de demanda agregada y ajusta los precios de acuerdo con una determinada regla, probablemente elevando el precio de los bienes de los que hay exceso de demanda y bajando el precio de aquellos de los que hay exceso de oferta. El proceso continúa hasta que se halla un precio de equilibrio. En este punto, se realizan todos los intercambios, incluidos los de contratos para intercambios futuros. La economía sigue entonces su curso y cada uno de los agentes lleva a cabo lo acordado en los contratos. Este modelo es, por supuesto, muy poco realista. Sin embargo, la idea básica de que los precios suben cuando hay un exceso de demanda parece plausible. ¿En qué condiciones conduceeste tipo de proceso de ajuste a un equilibrio? 468 / ANÁLISIS DEL EQUILIBRIO (C. 21) 21.5 Los procesos de tanteo Examinemos el caso de una economía que evoluciona a lo largo del tiempo. Todos los días se abre el mercado y la gente presenta sus demandas y ofertas. Dado un vector de precios arbitrario p, hay en general excesos de demanda y de oferta en algunos mercados. Suponemos que los precios se ajustan de acuerdo con la regla siguiente, la conocida ley de oferta y demanda. Regla de ajuste de los precios. Pi = Gi(zi(p)), siendo i función lisa del exceso de demanda que mantiene el signo. = 1, ... , k, donde G, es una Conviene partir de algún tipo de supuesto sobre la deseabilidad para excluir la posibilidad de que haya equilibrios con un precio nulo, por lo que supondremos en general que zi(p) > O cuando Pi = O. Resulta útil realizar algunas representaciones gráficas del sistema dinámico definido por esta regla de ajuste de los precios. Consideremos un caso especial en el que Gi(zi) es igual a la función de identidad en el caso de todos los i = 1, ... , k. En ese caso, además del supuesto de contorno, tenemos un sistema en Rk definido por p= z(p) De acuerdo con las consideraciones habituales, sabemos que este sistema obedece la ley de Walras, pz(p) = O, lo que desde el punto de vista geométrico significa que z(p) es ortogonal al vector de precios p. La ley de Walras implica una propiedad muy útil. Veamos cómo varía la norma euclídea del vector de precios a lo largo del tiempo: d ( dt k: � p7(t) ) k k = � 2pi(t)p/t) = 2 � Pi(t)zi(p(t)) = O por la ley de Walras. Por lo tanto, esta ley exige que la suma de los cuadrados de los precios permanezca constante cuando éstos se ajustan, lo que significa que las sendas de los precios deben hallarse en la superficie de una espera k-dimensional. Por otra parte, dado que zi(p) > O, donde Pi = O, sabemos que las sendas de las variaciones de los precios siempre apuntan hacia el interior en las proximidades de los puntos en los que Pi = O. La .figura 21.5 muestra algunos gráficos cuando k = 2 y k = 3. El tercer gráfico es especialmente insatisfactorio. Muestra una situación en la que hay un único equilibrio, pero éste es totalmente inestable. El proceso de ajuste que hemos descrito casi nunca converge en un equilibrio. Este caso parece patológico, pero puede ocurrir fácilmente. Debreu (1974) ha demostrado esencialmente que cualquier función continua que satisface la ley de Walras es una función de exceso de demanda de alguna Los procesos de tanteo / 469 economía; por lo tanto, la hipótesis de la maximización de la utilidad no impone restricción alguna a la conducta de la demanda agregada y nuestro modelo de la conducta económica puede dar lugar a un sistema dinámico definido en la esfera de los precios. Es evidente que para obtener resultados de estabilidad global hay que suponer que las funciones de demanda cumplen unas condiciones especiales. El valor de los resultados dependerá, pues, de lo naturales que resulten desde el punto de vista económico las condiciones supuestas. Figura 21.5 Ejemplos de dinámica de los precios. Los dos primeros ejemplos muestran un equilibrio estable; en el tercero, éste es único, aunque inestable. A continuación demostramos que existe estabilidad global en el caso de uno de esos supuestos especiales y de un proceso especial de ajuste, a saber, el supuesto 470 / ANÁLISIS DEL EQUILIBRIO (C. 21) de que la conducta de demanda agregada satisface el axioma débil de la preferencia revelada descrito en el capítulo 8 (página 156). Éste dice que si px(p) 2: px(p*), debe cumplirse que p*x(p*) > p*x(p) cualesquiera que sean p y p". Dado que esta condición se cumple en el caso de todos los p y p*, ciertamente debe cumplirse en el caso de los valores de equilibrio de p*. Véamos cuáles son las implicaciones de esta condición para la función de exceso de demanda. Restando pw y p*w de cada una de estas desigualdades, tenemos que px(p) - pw 2: pxíp") - pw implica que p*x(p) - p*w > p*x(p*) - p*w. Aplicando la definición de exceso de demanda, podemos formular esta expresión de la manera siguiente: pz(p) 2: pz(p*) implica que p*z(p) > p*z(p*) (21.1) Obsérvese que la primera condición de (21.1) debe satisfacerse, cualquiera que sea el vector de precios de equilibrio p*. Para comprenderlo, basta observar que la ley de Walras implica que pz(p) O, y la definición de equilibrio implica que pz(p*) = O. Por lo tanto, la segunda condición debe cumplirse cualquiera que sea el vector de precios p* de equilibrio. En consecuencia, debe cumplirse que p*z(p) > O, cualquiera que sea p i p *. = El ADPR implica la existencia de estabilidad. Supongamos que la regla de ajuste viene . dada por 'Pi = zi(p), siendo i = 1, ... , k, y que la función de exceso de demanda obedece el axioma débil de la preferencia revelada; es decir, si p* es un equilibrio de la economía, p*z(p) > O cualquiera que sea p i p*. En ese caso, todas las sendas de precios que siguen la regla anterior convergen en p*. Demostración (esquemática). Construimos una función de Liaponov correspondiente a la economía (véase el capítulo 26, página 566). Sea V(p) = I:.:7=1 [(pi - p;)2]. En ese caso, dV (p) ------;¡¡- k � ( . 2 Pi - Pi*)Pi ( t ) i=l =:= L.__¡ k = 2 ¿[pizi(p) i=l - k = 2� L.__¡ (pi i=l - Pi*) Zi(p) pf zi(p)] = O - 2p*z(p) < O. Eso implica que V(p) es monótonamente decreciente a lo largo de las sendas de soluciones en el caso en que p i p*. De acuerdo con el teorema de Liaponov, sólo Los procesos no basados en el tanteo / 471 necesitamos demostrar que p está acotado para llegar a la conclusión de que V(p) es una función de Liaponov y que la economía es globalmente estable. Omitimos esta parte de la demostración. 21.6 Los procesos no basados en el tanteo El argumento del tanteo tiene sentido en dos tipos de situaciones: o bien no se produce ningún intercambio hasta que no se alcanza el equilibrio, o bien no es posible almacenar ningún bien, por lo que en todos los periodos los consumidores tienen las mismas dotaciones. Si es posible acumular bienes, las dotaciones de los consumidores cambian con el paso del tiempo, lo cual afecta, a su vez, a la conducta de demanda. Los modelos que tienen en cuenta este cambio de las dotaciones se conocen con el nombre de modelos no basados en el tanteo. En estos modelos, debemos caracterizar el estado de la economía en el momento t por medio del vector de precios vigentes p(t) y las dotaciones actuales (wi(t)). Normalmente suponemos, como antes, que los precios se ajustan de acuerdo con el signo del exceso de demanda. Pero ¿cómo evolucionan las dotaciones? Examinemos dos especificaciones. La primera, el proceso de Edgeworth, establece que la tecnología necesaria para que haya intercambio entre los agentes tiene la propiedad de que la utilidad de cada uno de ellos debe aumentar continuamente. Se basa en la idea de que los agentes no realizan voluntariamente intercambios a menos que mejore su bienestar de esta forma. Esta especificación tiene la útil propiedad de que nos lleva de inmediato a un teorema de la estabilidad; basta definir la función de Liaponov de la manera siguiente: I.::1 ui(wi(t)). Por hipótesis, la suma de las utilidades debe aumentar con el paso del tiempo, por lo que aplicando el argumento de la acotación, tenemos una demostración de la convergencia. La segunda especificación se conoce con el nombre de proceso de Hahn. En el caso de este proceso, suponemos que la regla de intercambio tiene la propiedad de que no existe exceso de demanda de ningún bien por parte de ningún agente del que haya un exceso de oferta por parte de algún otro. Es decir, en cualquier momento del tiempo, si hay un exceso de demanda de un bien por parte de un determinado agente, también debe haber un exceso de demanda agregada. Este supuesto tiene una importante implicación. Hemos supuesto que cuando hay un exceso de demanda de un bien, sube su precio, lo que reduce la utilidad indirecta de los agentes que demandan ese bien. Aquellos que ya se han comprometido a ofrecerlo a los precios vigentes no se ven afectados por esta variación del precio, por lo que la utilidad indirecta agregada debe disminuir en el paso del tiempo. Para que este razonamiento sea más riguroso, debemos postular otro supuesto más sobre la variación de las dotaciones. El valor que tiene la dotación del consumidor i en el momento tes mi(t) = I.:1=l pj(t)w{ (t). Diferenciando con respecto a t, 472 / ANÁLISIS DEL EQUILIBRIO (C. 21) tenernos que k . k )dwf (t) dmi(t) _ � � dpy(t) j() - L PJ·( t dt + L dt w i t . dt j=l j=l Es razonable suponer que el primer término de esta expresión es cero. Eso significa que la variación que experimenta la dotación en cualquier instante, valorada a los precios vigentes, es nula, lo que es lo mismo que decir que cada uno de los agentes intercambiará bienes por valor de una peseta por bienes por valor de una peseta. El valor de la dotación varía a lo largo del tiempo debido a las variaciones del precio, pero no porque los agentes consigan realizar intercambios rentables a precios constantes. Dada esta observación, es fácil demostrar que la suma de las utilidades indirectas disminuye con el paso del tiempo. La derivada de la función indirecta de utilidad del agente i es Aplicando la ley de Roy y el hecho de que el valor de la variación de la dotación a los precios vigentes debe ser cero, tenernos que k j] dpj(t) dt. dvi(p(t), p(t)wi(t)) - - avi � [ j( - 8m·L xip,pwi·) wi dt i j=l Por hipótesis, si hay un exceso de demanda del bien j por parte del agente i, dpj / dt > O y viceversa. Dado que la utilidad marginal de la renta es positiva, el signo de toda la expresión será negativo en la medida en que la demanda agregada no sea igual a la oferta agregada. Por lo tanto, la utilidad indirecta de cada agente i debe disminuir cuando la economía no se encuentra en equilibrio. Notas Véase Arrow y Hahn (1971) para un análisis más refinado de estos ternas. La importancia del índice topológico para la unicidad fue reconocida por primera vez por Dierker (1972). El resultado de la convergencia del núcleo fue demostrado rigurosamente por Debreu y Scarf (1963). Ejercicios / 473 Ejercicios 21.1. Hay dos agentes que tienen unas preferencias idénticas y estrictamente convexas y las mismas dotaciones. Describa el núcleo de esta economía y represéntelo en una caja de Edgeworth. 21.2. Considere el caso de una economía de intercambio puro en la que todos los consumidores tienen funciones de utilidad cuasilineales de la forma u(x1, ... , xn) + xa. Suponga que u(x1, ... , Xn) es estrictamente cóncava. Demuestre que el equilibrio debe ser único. 21.3. Suponga que el subastador walrasiano sigue la regla de ajuste de los precios [Dz(p)J-1z(p). Demuestre que V(p) = -z(p)z(p) es una función de Liaponov del sistema dinámico. p= 22. EL BIENESTAR En el presente capítulo examinamos algunos conceptos de la economía del bienestar que no encajan bien en otras partes del libro. El primero es el criterio de la compensación que suele utilizarse en el análisis de coste-beneficio. A continuación examinamos una estratagema que se utiliza habitualmente cuando se calculan las consecuencias que tiene para el bienestar una variación de la producción o del precio. Por último, examinamos el problema de los impuestos óptimos sobre las mercancías. 22.1 El criterio de la compensación A menudo es conveniente saber cuándo un proyecto público mejora el bienestar social. Por ejemplo, la construcción de una presa puede tener beneficios económicos como la reducción del precio de la energía eléctrica y del agua. Sin embargo, estos beneficios deben compararse con los costes que puede tener para el medio ambiente, así como con los costes de construcción. En general, los beneficios y los costes de un proyecto afectan a cada persona de una manera distinta: el aumento de la oferta de agua procedente de la presa puede reducir las tarifas del agua en unas áreas y elevarlas en otras. ¿ Cómo deben compararse estos distintos costes y beneficios? Ya hemos analizado antes el problema de la medición de los beneficios o de los costes que tiene para una persona la variación del precio o de la cantidad consumida de un bien. En este apartado tratamos de extender este tipo de análisis a una comunidad de individuos utilizando los conceptos de criterio de Pareto y criterio de la compensación. . Consideremos dos asignaciones, la x y la x', Se dice que x' domina en el sentido de Pareto a x si todo el mundo prefiere la primera a la segunda.1 Si todas las personas prefieren x' a x, no parece controvertido afirmar que x' es "mejor" que x y que debe realizarse cualquier proyecto que nos lleve de x a x', Éste es el criterio 1 Aquí utilizarnos las preferencias estrictas por comodidad, pero las ideas pueden ampliarse fácilmente al caso de las preferencias débiles. 476 / EL BIENESTAR (C. 22) de Pareto. Sin embargo, los proyectos que se prefieren unánimemente son raros. Normalmente, unas personas prefieren x' ax y otras prefieren x ax'. ¿Qué decisión debe tomarse en ese caso? El criterio de la compensación sugiere el siguiente test: x' se prefiere potencialmente en el sentido de Pareto a x si existe alguna manera de reasignar x' de modo que todo el mundo prefiera la reasignación a la asignación original x. Formulemos esta definición en unos términos algo más formales: x' se prefiere potencialmente en el sentido de Pareto ax si existe una asignación x" tal que ¿�=l x�' = ¿�=l x� (es decir, x" es una reasignación de x') y que x�' >-i x� en el caso de todos los agentes i. Por lo tanto, el criterio de la compensación exige únicamente que x' sea una mejora potencial en el sentido de Pareto con respecto ax. Llamemos "ganadoras" a las personas que prefieren x' a x y "perdedoras" a las que prefieren x a x'. En ese caso, x' es mejor que x en el sentido del criterio de la compensación si los ganadores pueden compensar a los perdedores, es decir, si los ganadores pueden renunciar a una parte suficiente de sus ganancias para garantizar la mejora del bienestar de todo el mundo. Ahora bien, parece razonable pensar que si los ganadores compensan de hecho a los perdedores, el cambio propuesto será aceptable para todo el mundo. Pero no está claro por qué debemos pensar que x' es mejor que x meramente porque sea posible que los ganadores compensen a los perdedores. El argumento que se esgrime habitualmente en defensa del criterio de la compensación es el de que la cuestión de la conveniencia de dar una compensación es, en realidad, una cuestión relacionada con la distribución de la renta y los teoremas básicos del bienestar muestran que la cuestión de la distribución de la renta puede separarse de la cuestión de la eficiencia en la asignación. El criterio de la compensación se refiere exclusivamente a la eficiencia en la asignación y la cuestión de la distribución correcta de la renta se aborda mejor por otras vías, como los impuestos redistributivos. En el capítulo 22 (página 476) analizamos algo más este punto. Formulemos este análisis en términos gráficos. Supongamos que sólo hay dos personas y que están examinando dos asignaciones, la x y la x', Relacionamos cada asignación con su conjunto de posibilidades de utilidad: [}_ = { u1 (y1 ), 112(y2) : Yl + Y2 U'= {u1(Y1),u2(y2): Yl +vz = x¡ = x; + x2} +x;}. La frontera superior derecha de cada uno de estos conjuntos se denomina frontera de posibilidades de utilidad. Ésta indica las distribuciones de la utilidad correspondientes a todas las reasignaciones de x y x' eficientes en el sentido de Pareto. La figura 22.1 muestra algunos ejemplos de conjuntos de posibilidades de utilidad. El criterio de la compensación / 477 Figura 22.1 A e U1 U1 B U1 D U1 Criterio de la compensación. En el panel A, x' se prefiere en el sentido de Pareto a x. En el B, x' se prefiere a x en el sentido del criterio de la compensación. En el C, x y x' no son comparables. En el D, X se prefiere ax' y x' se prefiere a X. En la 22.lA, la asignación x' se prefiere en el sentido de Pareto a la x, ya que > u1 (xj ) y u2(x2) > u2(x2). En la 22.lB, x' se prefiere potencialmente en el sentido de Pareto ax: hay una reasignación de x' que se prefiere en el sentido de Pareto a x, aun cuando la propia x' no se prefiera en el sentido de Pareto. Por lo tanto, x' satisface el criterio de la compensación en el sentido de que los ganadores podrían compensar a los perdedores en el paso de x ax'. En la figura 22.lC, x' y x no son comparables: ni el criterio de la compensación ni el de Pareto transmiten información alguna sobre su atractivo relativo. En la 22.10, tenemos la situación más paradójica: x' se prefiere potencialmente en el sentido de Pareto a x, ya que x'' es preferible en el sentido de Pareto a x; pero entonces x también se prefiere potencialmente en el sentido de Pareto a x', puesto que x'" se prefiere en el sentido de Pareto a x', u1 (x;) 478 / EL BIENESTAR (C. 22) Los casos C y D muestran los principales defectos del criterio de la compensación: éste no nos da orientación alguna cuando se comparan asignaciones eficientes en el sentido de Pareto y puede originar comparaciones incoherentes. No obstante, se utiliza habitualmente en los estudios aplicados basados en la economía del bienestar. El criterio de la compensación, tal como lo hemos descrito, exige que tengamos en cuenta las consecuencias del proyecto para la utilidad de todos los consumidores afectados, por lo que parece que sería necesario realizar una encuesta detallada a la población. Sin embargo, a continuación demostramos que puede no ser necesario en algunos casos. Si los proyectos sometidos a consideración son bienes públicos, son pocas las esperanzas de que pueda evitarse consultar explícitamente a la población para tomar decisiones sociales. En el capítulo 23 examinamos los problemas que plantea este tipo de consultas. Si los proyectos se refieren a bienes privados, la situación es mucho más nítida, ya que los precios vigentes de los bienes privados reflejan, en cierto sentido, el valor marginal que tienen para cada uno de los agentes. Supongamos que nos encontramos actualmente en un equilibrio de mercado (x, p) y que estamos considerando la posibilidad de trasladarnos a la asignación x', En ese caso, Test de la renta nacional. Si x' se prefiere potencialmente en el sentido de Pareto a x, debe cumplirse que n n ¿px: > ¿pxi. i=l i=l Es decir, la renta nacional medida a precios corrientes es mayor en x' que en x. Demostración. Si se prefiere x' ax en el sentido del criterio de la compensación, existe una asignación x" tal que ¿�=l x:' = ¿�=l x: y x? >--i xi cualquiera que sea i. Dado que x es un equilibrio de mercado, significa que px:' > px, cualquiera que sea i. Sumando, tenemos que ¿�=l px:' > ¿�=l px.. Pero n n n i=l i=l i=l �" L., xi = p �' L., xi. L., pxi = p �" con lo que queda demostrado el resultado. Este resultado es útil, ya que tenemos un test inequívoco de los proyectos propuestos: si disminuye la renta nacional a precios corrientes, posiblemente el proyecto no puede preferirse potencialmente en el sentido de Pareto a la asignación actual. El criterio de la compensación / 479 La figura 22.2 muestra claramente esta proposición desde el punto de vista geométrico. Los ejes del gráfico miden la cantidad agregada de los dos bienes existentes. La asignación actual está representada por la cesta agregada X = (X1, X2), donde X1 = ¿�=l xJ; X2 se define de una manera similar (recuérdese que los consumidores se representan por medio de subíndices y los bienes por medio de superíndices). Figura22.2 BIEN2 BIEN1 Test de la renta nacional. Si disminuye la renta nacional, el cambio no puede preferirse potencialmente en el sentido de Pareto. Si aumenta, el cambio puede preferirse o no potencialmente en el sentido de Pareto. Sin embargo, si un pequeño cambio eleva la renta nacional, es probable que se prefiera potencialmente en el sentido de Pareto. Digamos que una cesta agregada X' se prefiere potencialmente en el sentido de Pareto a la asignación x si X' puede distribuirse entre los agentes para construir una asignación x' que se prefiera en el sentido de Pareto a x. En otras palabras, el conjunto de cestas agregadas que se prefiere potencialmente en el sentido de Pareto viene dado por P= { t x; : x; >--; x, cualquiera que sea i } . i=l La figura 22.2 muestra un caso representativo. El conjunto P está claramente delimitado y es convexo y la cesta agregada X se encuentra en su frontera. Los precios competitivos separan a X de P. Es fácil ver en la figura el contenido de 480 / EL BIENESTAR ( C. 22) la proposición antes formulada: si x' se prefiere ax en el sentido del criterio de la compensación, X' debe pertenecer a P y, por lo tanto, pX' > pX. También se observa que no es cierto lo contrario. En el caso de la cesta X", pX" > pX, pero esta cesta no es preferible potencialmente en el sentido de Pareto a x. Sin embargo, el gráfico muestra una interesante conjetura: si pX" > pX y X" está suficientemente cerca de X, X" debe ser preferible potencialmente en el sentido de Pareto a x. Más concretamente, fijémonos en la línea de puntos que conecta X" y X. Todos los puntos de esta línea tienen un valor más alto que X, pero no todos se encuentran por encima de la curva de indiferencia que pasa por X. Sin embargo, los puntos de esta línea que se hallan suficientemente cerca de X se encuentran encima de la curva de indiferencia. Tratemos de formular algebraicamente esta idea. El razonamiento se basa en el hecho de que, considerando magnitudes de primer orden, las variaciones de la utilidad de una persona son proporcionales a las variaciones de la renta. Este hecho se deduce de un sencillo desarrollo en serie de Taylor: De acuerdo con esta expresión, las pequeñas variaciones de la cesta Xi se prefieren o no dependiendo de que la variación del valor de la cesta sea positiva o negativa. Esta idea nos permite demostrar que si p Li x� > p Li Xi y x� está próximo a Xi, es posible hallar una redistribución de x' -llamémosla x" - tal que todo el mundo prefiera x" ax. Para demostrarlo, basta suponer que X = Li Xi y X' = Li x� y definir x" de la manera siguiente: X'-X n X�1 =Xi+--- En este caso, cada uno de los agentes i está obteniendo 1/n de la ganancia agregada derivada del cambio de x por x', De acuerdo con el desarrollo anterior en serie de Taylor, [ ui(x ,, ) - ui(x) � AiP xi+ � AiP X' - X n [X' n- X] . - Xi l Por lo tanto, si el segundo miembro es positivo -la renta nacional aumenta a los precios iniciales- debe ser posible aumentar la utilidad de todos y cada uno de los agentes. Naturalmente, eso sólo es cierto si la variación es suficientemente pequeña para que sea válida la aproximación de Taylor. El test de la renta nacional suele Las funciones de bienestar / 481 utilizarse para valorar la influencia de los cambios marginales de política en el bienestar de los consumidores. 22.2 Las funciones de bienestar Como hemos señalado antes en este capítulo, la metodología de la compensación tiene el defecto de que no tiene en cuenta la cuestión de la distribución. Una asignación que se prefiere potencialmente en el sentido de Pareto a la actual genera potencialmente un mayor bienestar. Pero cabría muy bien afirmar que el bienestar relevante es el real. Si estamos dispuestos a postular una función de bienestar, podemos introducir las cuestiones distributivas en el análisis de coste-beneficio. Supongamos que tenemos la siguiente función de bienestar lineal con respecto a la utilidad: n W(ui, ... , Un)=¿ aciu, i=i Como vimos en el capítulo 17 (página 382), los parámetros (ai) están relacionados con las "ponderaciones del bienestar" de cada uno de los agentes económicos. Podemos imaginar que estas ponderaciones son los juicios de valor del "planificador social". Supongamos que nos encontramos en un equilibrio de mercado (x, p) y que estamos considerando la posibilidad de trasladarnos a la asignación x', ¿Aumentará el bienestar? Si x' se encuentra cerca de x, podemos aplicar un desarrollo en serie de Taylor y obtener ¿ aiDui(xi)(x� - Xi). n W(ui (xi), ... , Un(x�)) - W(ui (xi), ... , Un(Xn)) � i=i Dado que (x, p) es un equilibrio de mercado, podemos reformular esta expresión de la manera siguiente: ¿ aiAip(x� - Xi). n W(ui (xi), ... , 'Un(x�)) - W(ui (xi), ... , Un(Xn)) � i=i Vemos que el criterio del bienestar se reduce a examinar una variación ponderada de los gastos. Las ponderaciones están relacionadas con los juicios de valor que se introdujeron inicialmente en la función de bienestar. Supongamos, como caso especial, que la asignación inicial x es un óptimo de bienestar. En ese caso, los resultados del capítulo 17 (página 382) nos dicen que Ai = 1 / a.. En este caso, observamos que 482 / EL BIENESTAR (C. 22) L p(x� n W(u1 (xi), ... , Un(x�)) - W(u1 (xj ), ... , Un(Xn)) � Xi). i=l Los términos referentes a la distribución desaparecen -debido a que la distribución ya es óptima-y nos quedamos con un sencillo criterio: un pequeño proyecto mejora el bienestar si aumenta la renta nacional (a los precios iniciales). Ésta es exactamente la regla relevante para el criterio de la compensación. Eso significa que si el planificador social sigue sistemáticamente la política de maximizar el bienestar tanto con respecto a la distribución de la renta a tanto alzado como con respecto a otros cambios de política que afecten a la asignación, los cambios de política que afecten a las asignaciones pueden valorarse independientemente de su influencia en la distribución de la renta. 22.3 Los impuestos óptimos En el capítulo 8 (página 139) vimos que un impuesto sobre la renta de cuantía fija siempre es preferible a un impuesto indirecto. Sin embargo, en muchos casos los impuestos de cuantía fija no son viables. ¿Cómo son los impuestos óptimos si no podemos utilizar impuestos de cuantía fija? Examinemos esta cuestión en una economía en la que sólo hay un consumidor. Sea u(x) la función directa de utilidad del consumidor y v(p, m) su función indirecta de utilidad. Suponemos que p representa los precios al por mayor. Si t es el vector de impuestos, el vector de precios al que se enfrenta el consumidor es p + t. Esta situación reporta al consumidor una utilidad de v(p + t, m) y al Estado unos ingresos de R(t) = I:::=l tixi(P + t, m). El problema de la tributación óptima consiste en maximizar la utilidad del consumidor con respecto a los tipos impositivos, sujeta a la restricción de que el sistema impositivo recaude una determinada cantidad de ingresos, R: max v(p + t, m) t1 , ... ,tk k sujeta a L tixi(P + t, m) = R. i=l El lagrangiano de este problema es .C � v(p + t, m) - µ [ t t,x,(p + t, m) - Rl Los impuestos óptimos / 483 Diferenciando con respecto a ti, tenemos que av(p + t, aPi m) - µ [ Xi+ 8xJ<p + t, m)] � L tj a . =O Pi J= 1 siendo i = 1, ... , k. Aplicando la ley de Roy, podemos deducir que [ ->..xi - µ Xi+ aPi. � tj 8xj(p + t, L J=l " =O siendo i = 1, ... , k. Despejando Xi, tenemos que k . - __ µ_" . axj(p + t, m) xi - aPi , L t1 µ + /\ j=l . . Aplicando ahora la ecuación de Slutsky en el segundo miembro de esta ecuación, tenemos que Xi µ = - µ + ).. k L tj j=l [ªhj - axj x.·] . Bm " Bp¡ Tras algunas manipulaciones, esta expresión puede formularse de la manera siguiente: exi = Bh: L tj a Pi J=l k 1, donde e es una función deµ,).. y ¿j tjaxj/am. Aplicando la simetría de la matriz de Slutsky, podemos formular la siguiente ecuación: exi = k Bh, (22.1) ¿tj 8p· J j=l Formulando esta expresión en función de las elasticidades, tenemos que e = '°" k ahi PJ tj Lap-x·p· J i J j=l = '°" k L j=l Eij tj . p·J Esta ecuación nos dice que los impuestos deben elegirse de tal manera que la suma ponderada de las elasticidades-precio hicksianas cruzadas sea la misma en el caso de todos los bienes. 484 / EL BIENESTAR (C. 22) en En el caso extremo, en el que Eij = O cuando i =! j, esta condición se con vierte (22.2) por lo que el cociente entre el impuesto y el precio del bien i es proporcional a la inversa de la elasticidad de la demanda. Esta regla se conoce con el nombre de regla de la inversa de la elasticidad. Tiene todo el sentido del mundo: debemos gravar con elevados impuestos los bienes cuya demanda sera relativamente inelástica y con bajos impuestos los bienes cuya demanda sea relativamente elástica. De esta manera se distorsionan lo menos posible las decisiones del consumidor. Otra posible simplificación se da cuando los tipos impositivos L¡ son bajos. En este caso, Introduciendo este resultado en la ecuación (22.1), tenemos que dhi � hi e. Esta ecuación indica que el conjunto óptimo de pequeños impuestos reduce todas las demandas compensadas en la misma proporción. Notas El enfoque dado a las cuestiones abordadas en este capítulo es bastante convencional; para un análisis más refinado consúltese cualquier manual dedicado al análisis de coste-beneficio. Para un análisis panorámico de la teoría de los impuestos óptimos véase Mirrlees (1982) o Atkinson y Stiglitz (1980). Ejercicios 22.1. En la fórmula del impuesto óptimo presentada en este capítulo, ecuación (22.1), demuestre que é' no puede ser negativo si la cantidad necesaria de ingresos es positiva. 22.2. Una empresa de servicios públicos produce los bienes x1, ... , Xk:· Estos bienes son consumidos por una persona representativa cuya función de utilidad es u1 (x1) + Ejercicios / 485 ... + un(xn) + y, donde y es un bien numerario. La empresa produce el bien i con un coste marginal de c., pero tiene unos costes fijos F. Halle la fórmula de la regla de fijación óptima de los precios que relacione (pi - c.) con la elasticidad de la demanda del bien i. 23. Los BIENES PÚBLICOS Hasta ahora, cuando hemos analizado la asignación de los recursos, nos hemos referido exclusivamente a los bienes privados, es decir, a los bienes cuyo consumo sólo afecta a un único agente económico. Consideremos, por ejemplo, el caso del pan. Dos personas pueden consumir diferentes cantidades de pan y si una consume una barra de pan, la otra no puede consumir esa misma barra. Decimos que un bien es excluible si es posible excluir de su consumo a una persona. Decimos que un bien no es rival si su consumo por parte de un individuo no reduce la cantidad de que pueden disponer los demás. Un bien es rival cuando su consumo por parte de una persona reduce la cantidad de que pueden disponer las demás. Los bienes rivales se denominan a veces reducibles. Los bienes privados ordinarios son tanto excluibles como rivales. Algunos bienes carecen de estas propiedades. Un buen ejemplo es el del alumbrado público. La cantidad de farolas que hay en una determinada área es fija: una persona puede consumir la misma cantidad que otra y la cantidad que "consume" una de ellas no afecta a la cantidad de la que puede disponer la otra. Por lo tanto, el alumbrado público no es un bien rival. Por otra parte, el hecho de que una persona consuma este bien no excluye de su consumo a otra. Los bienes que no son excluibles ni rivales se denominan bienes públicos; otros ejemplos son la policía y los servicios de protección contra incendios, las autopistas, la defensa nacional, los faros, las emisiones de radio y televisión, el aire puro, etc. También existen muchos casos intermedios. Consideremos, por ejemplo, el de una emisión de televisión codificada. Este bien no es rival -ya que su consumo por parte de una persona no reduce su consumo por parte de otra- pero es excluible, ya que sólo pueden ver esta emisión las personas que tengan acceso a un descodificador. Los bienes de este tipo se denominan a veces bienes de acceso limitado. Otra clase de ejemplos son los bienes que no son excluibles, pero son rivales. Un buen ejemplo es una calle abarrotada de gente: todo el mundo puede transitar por ella, pero su utilización por parte de una persona reduce la cantidad de espacio de que pueden disponer las demás. 488 / LOS BIENES PÚBLICOS (C. 23) Por último, hay algunos bienes que son inherentemente bienes privados, pero se analizan como si fueran bienes públicos. Por ejemplo, la educación es esenque cialmente un bien privado: es excluible y, en cierta medida, reducible. Sin embargo, la mayoría de los países han adoptado la decisión política de financiarla con dinero público. A menudo se ha decidido proporcionar a todos los ciudadanos el mismo nivel de gasto en enseñanza. Esta restricción nos obliga a analizar la educación como si fuera un bien público. Los problemas de asignación de los recursos en los que los bienes son públicos son muy diferentes de los problemas de asignación de los recursos en los que los bienes son privados. Hemos visto anteriormente que los mercados competitivos son una institución social eficaz para asignar eficientemente los bienes privados. Sin embargo, los mercados privados no suelen constituir un mecanismo muy bueno para asignar los bienes públicos. Generalmente, debe recurrirse a otras instituciones sociales, como la votación. 23.1 Provisión eficiente de un bien público discreto Comenzamos estudiando un sencillo ejemplo en el que hay dos agentes y dos bienes. Uno de ellos, el Xi, es un bien privado y cabe imaginar que es el dinero de que se dispone para gastar en consumo privado. El otro, G, es un bien público, que puede ser dinero para gastar en un bien público como el alumbrado de las calles. Los agentes tienen inicialmente una dotación del bien privado, uu, y eligen la cantidad que aportarán para financiar el bien público. Si el individuo i decide aportar la cantidad 9i, tendrá Xi = ui; - 9i de consumo privado. Suponemos que la utilidad es estrictamente creciente con respecto al consumo tanto del bien público como del privado y formulamos la función de utilidad del agente i de la manera siguiente: Ui(G, Xi), Inicialmente, consideramos el caso en el que sólo puede disponerse de una cantidad discreta del bien público; o bien se suministra esa cantidad, o bien no se suministra ninguna. Supongamos que cuesta e suministrar una unidad del bien público, de tal manera que la tecnología viene dada por G ={1 Ü s� 91 + 92 Sl 91 + 92 2: e < C. Más adelante analizaremos otras tecnologías más generales. Nos preguntamos, en primer lugar, cuándo es eficiente en el sentido de Pareto suministrar el bien público. Suministrarlo dominará en el sentido de Pareto a no suministrarlo si existe una pauta de aportaciones (91, 92) tal que 91 + 92 2: e y Provisión eficiente de un bien público discreto / 489 u1 (1, w1 - g1) u2(1, w1 - g2) > > u1 (O, w1) u2(0, w2) (23.1) Sea Ti la cantidad mínima del bien privado a la que estaría dispuesto a renunciar el agente i para obtener una unidad del bien público. La disposición máxima a pagar se denomina precio de reserva del consumidor i (véase el capítulo 9, página 180). Por definición, Ti debe satisfacer la siguiente ecuación: (23.2) Aplicando esta definición a la ecuación (23.1), tenemos que siendo i = 1, 2. Dado que la utilidad es estrictamente creciente con respecto al consumo privado, siendo i = 1, 2. Sumando estas desigualdades, vemos que T1 + T2 > g1 + g2 � c. Por lo tanto, si la provisión del bien público es una mejora en el sentido de Pareto, debe cumplirse que TJ + T2 > c. Es decir, la suma de las disposiciones a pagar por el bien público debe ser superior al coste de suministrarlo. Obsérvese la diferencia con respecto a las condiciones de eficiencia para suministrar un bien privado. En el caso del bien privado, si el individuo i está dispuesto a pagar el coste de producirlo, es eficiente suministrarlo. En este caso, sólo es necesaria la condición más débil de que la suma de las disposiciones a pagar sea superior al coste de la provisión. No es difícil demostrar la proposición recíproca. Supongamos que TJ + T2 > e y elijamos una aportación gi algo menor que Ti, de tal manera que se satisfagan las desigualdades g1 + g2 � e y · siendo i = 1, 2. Éstas demuestran que cuando T1 +T2 > e, la provisión del bien público es tanto viable como una mejora en el sentido de Pareto. La siguiente afirmación resume el análisis: es una mejora en el sentido de Pareto suministrar un bien público 490 / LOS BIENES PÚBLICOS (C. 23) discreto si y sólo si la suma de las disposiciones a pagar es superior al coste de la provisión. Cuadro 23.1 Jugador B Jugador A Comprar No comprar Comprar -50, -50 -50, 100 No comprar 100, -50 o, o 23.2 Provisión privada de un bien público discreto ¿Hasta qué punto es eficaz el mercado privado en la provisión de bienes públicos? Supongamos que ri = 100 siendo i = 1, 2 y e = 150, por lo que la suma de las disposiciones a pagar es superior al coste de la provisión. Cada uno de los agentes decide independientemente comprar o no el bien público. Sin embargo, corno se trata de un bien público, ninguno de los dos agentes puede excluir de su consumo al otro. El cuadro 23.1 muestra la sencilla matriz de estrategias y ganancias de este juego. Si el consumidor 1 compra el bien, obtiene unos beneficios por valor de 100 pesetas, pero tiene que pagar 150 por estos beneficios. Si el consumidor 1 compra, el 2 se abstiene de comprar y obtiene gratuitamente unos beneficios por valor de 100 pesetas. En este caso, decirnos que el consumidor 2 va polizón del consumidor 1. Obsérvese que este juego tiene una estructura parecida a la del dilema del prisionero descrito en el capítulo 15 (página 307). El equilibrio basado en las estrategias dominantes de este juego es ("no comprar", "no comprar"). Ninguno de los dos consumidores desea comprar el bien porque ambos prefieren ir de polizón del otro. Pero el resultado neto es que el bien no se suministra, aun cuando sea eficiente hacerlo. Eso demuestra que no cabe esperar que las decisiones puramente independientes den necesariamente corno resultado una cantidad eficiente del bien público que está suministrándose. Generalmente, es necesario utilizar unos mecanismos más complicados. Provisión eficiente de un bien público continuo / 491 23.3 Determinación de la cantidad de un bien público discreto por medio de una votación La cantidad de un bien público suele determinarse por medio de una votación. ¿Es eficiente, por lo general, la cantidad determinada mediante este sistema? Supongamos que tenemos tres consumidores que deciden someter a votación la provisión de un bien público que cuesta 99 pesetas. Si la mayoría vota a favor, se repartirán el coste por igual y cada uno pagará 33. Los precios de reserva de los tres consumidores son r1 = 90, r: = 30 y r3 = 30. Es evidente que la suma de los precios de reserva es superior al coste de provisión. Sin embargo, en este caso sólo votará a favor el consumidor 1, ya que es el único que obtendrá un beneficio neto positivo si se suministra el bien público. El problema de la votación por mayoría se halla en que sólo mide las preferencias ordinales por el bien público, mientras que la condición de eficiencia exige que se comparen las disposiciones a pagar. El consumidor 1 estaría dispuesto a compensar a los demás por votar a favor del bien público, pero no existe esa posibilidad. Existe otro tipo de votación en la que los individuos declaran su disposición a pagar por el bien público y éste se suministra si la suma de las disposiciones declaradas a pagar son superiores al coste de dicho bien. Si la participación de los individuos en el coste es. fija, normalmente este juego no tiene ningún equilibrio. Consideremos el ejemplo de los tres votantes antes citado. En este caso, el votante 1 ve mejorar su bienestar si se suministra el bien, por lo que puede muy bien indicar una cantidad positiva arbitrariamente elevada. Del mismo modo, los agentes 2 y 3 pueden muy bien indicar una cantidad negativa arbitrariamente elevada. Existe otro tipo de votación en la que cada una de las personas declara cuánto estaría dispuesta a pagar por el bien público. Si la suma de los precios declarados es, al menos, tan elevada como el coste del bien público, éste se suministra y cada una de las personas debe pagar la cantidad que declaró. En este caso, si la provisión del bien público es eficiente en el sentido de Pareto, es un equilibrio del juego. Cualquier conjunto de declaraciones tales que la de cada uno de los agentes no sea mayor que su precio de reserva y que la suma de todas ellas sea igual al coste del bien público es un equilibrio. Sin embargo, también hay muchos otros equilibrios ineficientes en el juego. Por ejemplo, la situación en la que todos los agentes indican que no están dispuestos a pagar nada por el bien público normalmente es un equilibrio. 23.4 Provisión eficiente de un bien público continuo Supongamos ahora que el bien público puede suministrarse en cualquier cantidad continua; para simplificar seguimos suponiendo que sólo hay 2 agentes. Si se aporta g1 + g2 al bien público, la cantidad suministrada viene dada por G = f(g1 + g2) y 492 / LOS BIENES PÚBLICOS (C. 23) la utilidad del agente i por Ui(f (g1 + g2), ui; - gi). También podemos introducir la función de producción en la función de utilidad y escribir simplemente ui(gi + in, Wi - gi), donde, por definición, ui(G, xi) es igual a Ui(f (G), Xi). La introducción de la tecnología en la función de utilidad no reduce el carácter general del análisis, ya que la utilidad depende, en última instancia, de las aportaciones totales al bien público. Sabemos que las condiciones de primer orden para la eficiencia pueden hallarse maximizando la suma ponderada de las utilidades: max a1 u1 (g1 + sn, w1 - g1) + a2u2(g1 + g2, w2 - g2). g1,g2 Las condiciones de primer orden correspondientes a g1 y g2 pueden formularse de la siguiente manera: ª1 ª1 8u1 (G, x1) ac 8u1 (G, x1) ac + ª2 + ª2 8u2(G, x2) ac 8u1 (G, x1) ac = ª1 = ª2 8u1 (G, x1) 8x1 (23.3) 8u2(G, x2) 8x2 . Por lo tanto, a18uif 8x1 = a28u2/ 8x2. Dividiendo los primeros miembros de (23.3) por los segundos y utilizando esta igualdad tenemos que (23.4) o sea, La condición de eficiencia en el caso de la provisión continua del bien público es que la suma de las disposiciones marginales a pagar sea igual al coste marginal de la provisión. En este caso, el coste marginal es 1, ya que el bien público es simplemente la suma de las aportaciones. Como siempre, normalmente hay todo un intervalo de asignaciones (G, x1, x2) en el que se satisface esta condición de eficiencia. Dado que en general la disposición marginal a pagar depende de la cantidad de consumo privado, el nivel eficiente de G suele depender de x1 y x2. Sin embargo, en un caso especial, a saber, el caso de la utilidad cuasilineal, la cantidad eficiente del bien público es independiente del nivel de consumo privado. Para verlo, supongamos que las funciones de utilidad tienen la forma ui(G) + Xi. En Provisión eficiente de un bien público continuo / 493 ese caso, la condición de eficiencia (23.4) puede formularse de la manera siguiente: (G)+u2(G) = 1, que normalmente determina una única cantidad del bien público.1 u; Ejemplo: Determinación de la provisión eficiente de un bien público Supongamos que las funciones de utilidad tienen la forma Cobb-Douglas ui(G, xi)= ailnG + lnz. En este caso, las funciones de la RM S vienen dadas por aixi/ G, por lo que la condición de eficiencia es o sea, (23.5) Si la cantidad total del bien privado disponible es inicialmente w, también tenemos la condición x1 + x2 + G = w. (23.6) Las ecuaciones (23.5) y (23.6) describen el conjunto de asignaciones eficientes en el sentido de Pareto. Consideremos ahora las funciones de utilidad cuasilineales en las que ui( G, xi) = bilnG + Xi· La condición de eficiencia de primer orden es o sea, (23.7) De nuevo, la asignación debe ser viable, por lo que el conjunto de asignaciones eficientes en el sentido de Pareto viene descrito por (23.6) y (23.7). Obsérvese que en el caso de la utilidad cuasilineal, hay un única cantidad eficiente del bien público, mientras que en el caso general hay muchos niveles eficientes. 1 En este razonamiento suponemos que es eficiente suministrar una cantidad positiva del bien público, pero puede no ser así si la renta es muy baja. 494 / LOS BIENES PÚBLICOS (C. 23) 23.5 Provisión privada de un bien público continuo Supongamos que cada uno de los agentes elige independientemente la cantidad que desea aportar para financiar el bien público. Si el agente 1 piensa que el agente 2 aportará, por ejemplo, g2, el problema de maximización de la utilidad del agente 1 es max u1 (g1 + g2, w1 - g1) 91 sujeta a g1 � O. La restricción de que g1 � O es una restricción natural en este caso; establece que el agente 1 puede incrementar voluntariamente la cantidad del bien público, pero no puede reducirla unilateralmente. Como veremos más adelante, esta restricción expresada como una desigualdad es importante. La condición de primer orden de Kuhn-Tucker de este problema es (23.8) donde la igualdad se cumple si g1 > O. Esta condición también puede expresarse de la forma siguiente: Si el agente i aporta una cantidad positiva, su relación marginal de sustitución entre el bien público y el privado debe ser igual a su coste marginal, 1. Si es menor que su coste, no querrá contribuir con ninguna cantidad. Esta condición se muestra en la figura 23.1. En esta figura, la "dotación" del agente 1 es el punto (w1, g2), ya que la cantidad de consumo privado que recibe si no contribuye con ninguna cantidad es w1 y la cantidad de consumo público que recibe es g2. La recta "presupuestaria" es la recta que tiene la pendiente -1 y que pasa por este punto. Los puntos viables de la recta presupuestaria son aquellos en los que g1 = w1 - x1 � O. Hemos representado dos casos: en uno de ellos, el agente 1 desea contribuir con una cantidad positiva y en el otro desea ir de polizón. Provisión privada de un bien público continuo / 495 Figura 23.1 BIEN PUBLICO BIEN PUBLICO Recta presupuestaria / Recta presupuestaria 1 1 92 1 1 ------{----1 1 1 1 1 W1 X1 BIEN PRIVADO A e BIEN PRIVADO Provisión privada de un bien público. En el panel A, el agente 1 aporta una cantidad positiva. En el B, observa que es óptimo ir de polizón del agente 2. Un equilibrio de Nash de este juego es un conjunto de aportaciones (gi, g2) tal que cada uno de los agentes aporta una cantidad positiva, dada la aportación del otro. Por lo tanto, la ecuación (23.8) debe satisfacerse simultáneamente en el caso de los dos agentes. Las condiciones que caracterizan el equilibrio de Nash pueden formularse de la manera siguiente: 8u1 (G*, xj) oc: -�---,--- � 1 8u1(G*, xj) 8x1 8u2(G*, xi) oc: (23.9) -----�l 8u2(G*, xi) 8x2 Si se suministra una cantidad positiva de G, al menos una de estas desigualdades debe ser una igualdad. Podríamos proseguir el análisis e intentar hallar las condiciones en las que sólo contribuye uno de los agentes, las condiciones en las que contribuyen los dos, etc. Sin embargo, existe otra manera algo más útil de describir el equilibrio de Nash en este caso. Para ello, necesitamos hallar la función de reacción del agente i. De esa manera tenemos la cantidad que desea aportar dicho agente en función de la aportación del otro. El problema de maximización del agente 1 puede expresarse de la manera siguiente: 496 / LOS BIENES PÚBLICOS (C. 23) rnax u1 (91 + 92, x1) g1,x1 sujeta a 91 + x1 91 2:: = w1 (23.10) Ü Valiéndonos del hecho de que G = 91 + 92, podernos formular de nuevo este problema de la forma siguiente: rnax u1 (G, x1) G,x1 sujeta a G + x1 = w1 + 92 (23.11) G 2:: 92 Examinemos atentamente la segunda formulación, según la cual el agente 1 elige, de hecho, la cantidad total del bien público sujeto a su restricción presupuestaria y a la restricción de que la cantidad que elija debe ser al menos tan grande corno la cantidad aportada por la otra persona. La restricción presupuestaria establece que el valor total de su consumo debe ser igual al valor de su "dotación", w1 + 92. El problema (23.11) es exactamente igual que un problema ordinario de maxirnización del consumidor, con la excepción de la restricción expresada corno una desigualdad. Sea Ji ( w) la demanda del bien público por parte del agente 1 en función de su riqueza, prescindiendo de la restricción expresada corno una desigualdad. En ese caso, la cantidad del bien público que es la solución del problema (23.10) se halla de la siguiente manera: Restando 92 de los dos miembros de esta ecuación, tenernos que 91 = rnax{fi (w1 + 92) - 92, O}. Ésta es la función de reacción del agente 1; indica su aportación óptima en función de la del otro agente. Un equilibrio de Nash es un conjunto de aportaciones (9i, 92) tal que = rnax{fi (w1 + 92) - 92, O} 92 = rnax{f2(w2 + 9i) - 9Í, O}. 9Í (23.12) Esta formulación suele ser más útil que la de (23.9), ya que nos permite hacernos una idea mejor de la forma que podrían tener las funciones de demanda Ji y h. Más adelante analizarnos esta cuestión por medio de un ejemplo. Resulta útil examinar la forma que adoptan las condiciones de equilibrio cuando la utilidad es cuasilineal. En este caso, podernos formular las condiciones (23.9) de la manera siguiente: Las votaciones / 497 uí (9j + 92) 2'.: 1 u;(9j + 92) 2'.: l. Obsérvese que generalmente sólo puede ser efectiva una de estas dos restricciones. Supongamos que el agente 1 concede al bien público un valor marginal mayor que el agente 2, por lo que uí (G) > u2(G) cualquiera que sea G; en ese caso, el agente 1 será el único que contribuya a financiar el bien público; el 2 siempre irá de polizón. Los dos sólo contribuirán cuando tengan los mismos gustos (en el margen) por el bien público. Obsérvese también que cuando la utilidad es cuasilineal, la demanda del bien público es independiente de la renta, por lo que fi(w) = 9i· En ese caso, (23.12) adopta la forma siguiente: 9j 92 = rnax{91 - 92, O} = max{92 - 9j, O}. De estas ecuaciones se deduce que si 91 > 92, entonces 9j = 91 y 92 = O. Ejemplo: Determinación de la cantidad del bien público correspondiente al equilibrio de N ash Examinemos nuestro ejemplo anterior en el que las funciones de utilidad tenían la forma Cobb-Douglas. Aplicando la fórmula habitual de las funciones de demanda Cobb-Douglas, tenemos que Íi(w) a· = __ -w. 1 + i ai Por lo tanto, la solución de (23.12) debe satisfacer las siguientes condiciones: 91 = max { �(w1 + 92) - 92, 1 + a1 o} {�(w2 91,0} 92 = max + 91)1 + a2 (23.13) En el caso del ejemplo cuasilineal, tenernos las siguientes condiciones de primer orden: b1 < l c- b2 < l G - . 498 / LOS BIENES PÚBLICOS (C. 23) Por lo tanto, G* = max{b1, b2}. Si b1 > b2, el agente 1 es el único que contribuye y el agente 2 va de polizón. 23.6 Las votaciones Supongamos que un grupo de agentes está considerando la posibilidad de someter a votación la cantidad de un bien público. Si la cantidad que se suministra actualmente es G, celebran una votación para decidir si la incrementan o la reducen. Si la mayoría vota a favor de incrementarla o de reducirla, no hay problema alguno. El equilibrio de la votación es una cantidad tal que la mayoría no prefiera ni una cantidad mayor ni una menor del bien público. Sin imponer más restricciones, es posible que este modelo no tenga ningún equilibrio. Supongamos, por ejemplo, que hay tres agentes, A, By C y tres niveles de provisión del bien público, 1, 2 o 3 unidades. A prefiere 1 a 2 y 2 a 3; B prefiere 2 a 3 y 3 a 1; C prefiere 3 a 1 y 1 a 2. En este caso, la mayoría prefiere 1 a 2, la mayoría prefiere 2 a 3 y la mayoría prefiere 3 a 1. Por lo tanto, cualquiera que sea la cantidad del bien público que se suministre, hay una mayoría que desea alterarla. Este caso es un ejemplo de la conocida paradoja de la votación. Sin embargo, si estamos dispuestos a complicar algo más el ejemplo, podemos hacer desaparecer la paradoja. Supongamos que los agentes acuerdan todos ellos que si la mayoría vota a favor de un aumento del bien público, el agente i pagará una parte si del coste adicional y que todos los agentes tienen funciones de utilidad cuasilineales. Si se suministran G unidades del bien público, el agente i recibe la utilidad ui(G) - s.G, Por lo tanto, votará a favor de aumentar la cantidad del bien público si u�(G) > si. Decimos que el agente i tiene preferencias unimodales si ui(G) - siG tiene un único máximo. Suponiendo que se satisface esta condición, sea G, el punto en el que se maximiza la utilidad del agente i. En ese caso, afirmamos que el único equilibrio de la votación viene dado por el valor mediano de las G i. Supongamos para simplificar que el valor que concede cada uno de los agentes a Gi es diferente y que hay un número impar de votantes. Si hay n + 1 votantes, el votante mediano es aquel votante tal que n /2 prefieren que se incremente la cantidad del bien público y n/2 prefieren que se reduzca. Si el agente mes el votante mediano, el nivel de bien público de equilibrio de la votación, Gv, viene dado por Este equilibrio se denomina equilibrio de Bowen. Es evidente que es un equilibrio, ya que no existe una mayoría que desee reducir o aumentar la cantidad del bien público. Tampoco es difícil demostrar que es único. Las votaciones / 499 Una cuestión interesante es la comparación entre este nivel y el nivel eficiente del bien público. Recuérdese que éste es el nivel que satisface ¿ u�(Ge) = 1. n i=l También podemos formular esta expresión de la manera siguiente: - "°' 1 n nL- 1 u�(Ge) = -. n i=l El primer miembro de esta ecuación es la función de utilidad "media". El segundo es la participación media en el coste. Por lo tanto, el nivel eficiente del bien público viene determinado por la condición de que la disposición media a pagar sea igual al coste medio. Compárese esta condición con la de equilibrio de la votación en la que es la disposición mediana a pagar la que determina la cantidad de equilibrio del bien público. Si el consumidor mediano desea la misma cantidad del bien público que el consumidor medio, será eficiente la cantidad del bien público suministrada por medio de una votación. Sin embargo, generalmente por medio de una votación podría suministrarse una cantidad demasiado grande o una demasiado pequeña dependiendo de que el votante mediano deseara una cantidad mayor o menor que la que deseara el votante medio. Ejemplo: La utilidad cuasilineal y la votación Supongamos que la utilidad adopta la forma bi ln G + Xi y que cada persona está obligada a pagar la misma proporción 1 / n del bien público. La cantidad eficiente viene dada por Ge = ¿i b.. La cantidad de equilibrio basada en la votación es la cantidad que es óptima para el votante mediano. Si bm representa el parámetro que recoge los gustos de este votante, tenemos que 1 n' o sea, G; = nbm. Por lo tanto, Es decir, la cantidad eficiente del bien público es superior a la suministrada por medio de una votación por mayoría si el consumidor medio valora el bien público más que el consumidor mediano. 500 / LOS BIENES PÚBLICOS (C. 23) 23.7 Asignaciones de Lindahl Supongamos que tratamos de mantener una asignación eficiente del bien público por medio de un sistema de precios. Ofrecemos a cada consumidor i el derecho a "comprar" la cantidad que desee del bien público al precio Pi· Por lo tanto, el consumidor i resuelve el siguiente problema de maximización: max ui(G, Xi) Xi,G sujeta a Xi+ PiG = uu . La condición de primer orden de este problema es La cantidad óptima de G en función de Pi y ui; es la función de demanda del bien público por parte del consumidor, que expresamos de la forma siguiente: Gi(Pi, wi). ¿Existe un conjunto de precios a los que los consumidores elegirán una cantidad eficiente del bien público? Partiendo de las condiciones habituales de la convexidad, la respuesta es afirmativa. Cuando analizamos la eficiencia, vimos que una cantidad eficiente del bien público debe satisfacer la siguiente igualdad: Por lo tanto, la solución consiste en elegir Estos precios -es decir, los precios que corresponden a una asignación eficiente del bien público- se conocen con el nombre de precios de Lindahl. Estos precios también pueden interpretarse como si fueran tipos impositivos. Si se suministran G unidades del bien público, el agente i debe pagar un impuesto de PiG. Por este motivo, los precios de Lindahl se denominan a veces impuestos de Lindhal. Mecanismos de revelación de la demanda / 501 23.8 Mecanismos de revelación de la demanda Hemos visto antes en este capítulo que los bienes públicos pueden plantear problemas cuando el mecanismo de asignación de los recursos está descentralizado. Cuando la provisión de los bienes públicos es privada, la cantidad suministrada generalmente es inferior a la eficiente. Cuando se determina por medio de una votación, se suministra una cantidad demasiado grande o demasiado pequeña. ¿Existe algún mecanismo que permita suministrar la cantidad "correcta" del bien público? Para examinar esta cuestión, volvamos al modelo del bien público discreto. Supongamos que G es O ó 1. Sea r i el precio de reserva del agente i y Si la proporción del coste del bien público correspondiente a dicho agente. Dado que suministrar el bien público cuesta e, Si e es la cantidad total de dinero que debe pagar el agente i si se suministra el bien. Sea Vi = r i - si e el valor neto que concede el agente i al bien público. De acuerdo con nuestro análisis anterior, es eficiente suministrar el bien público si Li Vi = Li(ri - sic) > O. Un mecanismo que podríamos utilizar consiste simplemente en pedir a cada agente que indicara su valor neto y suministrar el bien público si la suma de estos valores declarados no fuera negativa. El problema de este sistema se halla en que no ofrece buenos incentivos a los agentes para que revelen su verdadera disposición a pagar. Por ejemplo, si el valor neto del agente 1 es superior a cero cualquiera que sea la cantidad, podría declarar igualmente una cantidad arbitrariamente elevada. Dado que su declaración no influye en lo que tiene que pagar, pero de ella depende que se suministre o no el bien público, podría muy bien declarar el valor más alto posible. ¿Cómo podemos inducir a cada agente a revelar sinceramente el verdadero valor que concede al bien público? He aquí un sistema que da buenos resultados: El mecanismo de Groves y Clarke l. Cada uno de los agentes presenta una "oferta" por el bien público, ser o no el valor que le concede verdaderamente. o., que puede 2. El bien público se suministra si Li o, � O y no si Li o, < O. 3. Cada uno de los agentes i recibe un pago complementario igual a la suma de las demás ofertas, LJii Oj, si se suministra el bien público (si esta suma es positiva, el agente i la recibe; si es negativa, debe pagarla). A continuación demostramos que lo óptimo es que cada agente declare el valor que concede verdaderamente al bien público. Hay n agentes, para cada uno de 502 / LOS BIENES PÚBLICOS (C. 23) los cuales el bien público tiene un verdadero valor de Vi y un valor de la oferta de o., Queremos demostrar que lo óptimo es que cada agente declare o; = Vi, independientemente de lo que declaren los demás. Es decir, queremos demostrar que la sinceridad es una estrategia dominante. Las ganancias del agente i adoptan la forma siguiente: . . ganancias de i = { Vi 0 + Lj=ji ºi si o¡ + Lj=ji ºi � O · "'""' < o· Sl o, + �j=/i Oj Supongamos que Vi+ Lj=ji "i > O. En ese caso, el agente i puede garantizar que se suministrará el bien público declarando o; = Vi. Supongamos, por otra parte, que Vi+ Lj=/i "i < O. En ese caso, el agente i puede garantizar que el bien público no se suministrará declarando o, = Vi. De cualquiera de las dos maneras, lo óptimo es que el agente i diga la verdad. Nunca hay incentivos para no revelar sinceramente las preferencias, independientemente de lo que hagan los demás agentes. De hecho, el mecanismo de recogida de la información se ha modificado, de tal manera que cada uno de los agentes se enfrenta al problema de decisión social y no al problema de decisión individual, por lo que cada uno tiene incentivos para revelar correctamente sus propias preferencias. Desgraciadamente, el sistema de revelación de las preferencias que acabamos de describir tiene un importante defecto. La suma total de los pagos complementarios puede ser muy elevada: es igual a la cantidad que ofrece todo el mundo. ¡Puede resultar muy costoso inducir a los agentes a decir la verdad! Idealmente, nos gustaría contar con un mecanismo en el cual los pagos complementarios sumaran cero. Sin embargo, no es posible en general. Sí lo es diseñar un mecanismo en el que no sean positivos nunca. Así, es posible obligar a los agentes a pagar un "impuesto", pero nunca recibirán ningún pago. Como consecuencia de estos pagos de impuestos "despilfarrados", la asignación de los bienes públicos y privados no será eficiente en el sentido de Pareto. Sin embargo, el bien público se suministrará si y sólo si es eficiente hacerlo. Véamos cómo puede lograrse. La idea básica es la siguiente: podemos añadir una cantidad adicional al pago complementario del agente i que dependa solamente de lo que hagan los demás sin influir en los incentivos de i. Sea º-i el vector de ofertas, excluida la oferta del agente i, y hi(o-i) el pago adicional efectuado por el agente i. Ahora las ganancias que obtiene este agente adoptan la forma siguiente: si o¡ + si o, + ¿ i =/i oi Lj=/i ºi � O < O. Es evidente que este tipo de mecanismos permite que los agentes revelen sinceramente sus preferencias precisamente por las razones antes mencionadas. Si se eligen inteligentemente las h, funciones, puede reducirse significativamente la Mecanismos de revelación de la demanda con un bien continuo / 503 cuantía de los pagos complementarios. Una buena elección de la función hi es la siguiente: si si Lj:ji ºí Lj:ji ºí � O < O. Este tipo de elección da lugar al mecanismo bisagra, también conocido con el nombre de impuesto de Clarke. Las ganancias del agente i tienen la forma siguiente: si si si si Li oí Li Oí Li oí Li oí � � < < Oy Lj:ji ºí � O O y Lj:ji Oj < O O y Lj:ji ºí � O O y Lj:ji ºí < O (23.14) Obsérvese que el agente i nunca recibe un pago complementario positivo; puede ser gravado, pero nunca subvencionado. Cuando se añade el pago complementario, el agente i paga un impuesto únicamente si altera la decisión social. Examínense, por ejemplo, las filas dos y tres de la expresión (23.14). El agente i sólo tiene que pagar un impuesto cuando transforma la suma positiva de las ofertas en negativa o viceversa. La cuantía del impuesto que ha de pagar i es la cantidad en la que la oferta de dicho agente perjudica a los demás (de acuerdo con las ofertas que hayan declarado). El precio que debe pagar el agente i por alterar la cantidad del bien público es igual al perjuicio que causa a los demás agentes. Obsérvese que a todos ellos les resulta ventajoso utilizar este proceso de decisión, ya que nunca tendrán que pagar unos impuestos más altos de lo que para ellos vale la decisión. 23.9 Mecanismos de revelación de la demanda con un bien continuo Supongamos ahora que nos interesa la provisión de un bien público. Si se suministran G unidades de un bien público, el consumidor i tiene la utilidad donde ui(G) es la utilidad (cuasilineal) que le reporta el bien público y si es la proporción del coste que le corresponde. Supongamos que se le pide al agente i que declare la función vi(G). Representemos esta función por medio de oi(G). El Estado anuncia que suministrará la cantidad del bien público, G*, que maximiza la suma de las funciones declaradas. Cada uno de los agentes i recibe un pago complementario igual a Lj:ji Oj(G*). 504 / LOS BIENES PÚBLICOS (C. 23) En este mecanismo, siempre le interesa a cada agente i revelar sinceramente su verdadera función de utilidad. Para verlo, basta observar que el individuo i desea maximizar vi(G) + 2::>j(G), j=/i mientras que el Estado desea maximizar o/G) + ¿ oj(G). j=/i Declarando o/G) = vi(G), el agente i garantiza que el Estado elegirá una cantidad G* que maximice su utilidad. Al igual que ocurre en el caso discreto, la suma total de los pagos complementarios puede ser muy elevada. Sin embargo, al igual que antes puede reducirse en una cantidad adecuada. En este caso, la mejor elección es la cantidad - max¿ ¿j=/i Oj(G). De esa manera, el agente i obtiene una utilidad neta de Vi(G) + ¿ Oj(G) - rngx ¿ Oj(G). j=/i j=/i Obsérvese que la suma de los dos términos debe ser negativa. Al igual que antes, el agente i es gravado en la cuantía en que modifica el bienestar social. Notas Sarnuelson (1966) fue quien formuló por primera vez las condiciones de eficiencia de los bienes públicos. La provisión privada de bienes públicos ha sido estudiada extensamente por Bergstrorn, Blurne y Varían (1986). Lindahl (1919) introdujo el concepto de precios de Lindahl y Clarke (1971) y Groves (1973) el mecanismo de revelación de la demanda. Ejercicios 23.1. Considere el juego siguiente corno una solución del problema de los bienes públicos en el caso de un bien público discreto y dos agentes. Cada uno de los agentes i presenta una "oferta", o., Si 01 + 02 2: e, se suministra el bien y cada uno de los agentes paga la cantidad ofrecida; de lo contrario, el bien no se suministra y ninguno de los agentes paga nada. ¿Es el resultado eficiente un equilibrio de este juego? ¿Hay algún otro resultado que sea un equilibrio? Ejercicios / 505 23.2. Suponga que u1 y u2 son homotéticas en el espacio (xi, G). Derive los niveles de las aportaciones que constituyen un equilibrio de Nash. 23.3. Suponga ahora que los dos agentes tienen una riqueza distinta, pero las mismas funciones de utilidad Cobb-Douglas, ui(G, Xi)= Gªx}-ª. ¿Qué grado de diferencia tiene que haber entre la riqueza del agente 1 y la del 2 para que el agente 2 aporte una cantidad nula en condiciones de equilibrio? 23.4. Suponga que hay n agentes que tienen las mismas funciones de utilidad CobbDouglas, ui(G, Xi)= Gªx}-ª. Hay una cantidad total de riqueza w, que se reparte entre k ::; n agentes. ¿Qué cantidad del bien público se suministra? ¿Qué variación experimenta ésta cuando aumenta k? 23.5. ¿Da lugar el impuesto de Clarke a una asignación eficiente en el sentido de Pareto? ¿Da lugar el impuesto de Clarke a una cantidad del bien público eficiente en el sentido de Pareto? 23.6. Una peculiar tribu de nativos de los Mares del Sur llamada Estuds sólo consume cocos. Los utiliza con dos fines: o bien los consume como alimentos, o bien los quema en un sacrificio religioso público (los Estuds creen que este sacrificio los ayudará a aprobar el examen final). Suponga que cada Estud i tiene una dotación inicial de cocos de ui; > O. Sea gi 2 O la cantidad que dona para la ofrenda pública. El número total de cocos que aporta es G = L�=l gi. La función de utilidad del Estud i viene dada por Xi 2 O la cantidad de cocos que consume y donde a, > 1. (a) Cuando elige su presente, cada estud i supone que los presentes de los demás permanecerán constantes y lo elige teniendo en cuenta este supuesto. Supongamos que representa los presentes, salvo el del Estud i. Formule el problema de maximización de la utilidad que determina el presente del Estud i. 506 / LOS BIENES PÚBLICOS (C. 23) (b) Recordando que G = 9i + G _i en el caso de todos los agentes i, ¿cuál será la cantidad del bien público de equilibrio? (Pista: no todos los agentes aportarán una cantidad positiva al bien público.) (c) ¿Quién se comportará como un polizón en este problema? (d) ¿Cuál es la cantidad del bien público que debe suministrar esta economía para encontrarse en una situación eficiente en el sentido de Pareto? 24. LAS EXTERNALIDADES Cuando las acciones de un agente afectan directamente al entorno de otro, decimos que hay una extemalidad. Cuando hay una extemalidad en el consumo, la utilidad de un consumidor se ve afectada directamente por las acciones de otro. Por ejemplo, el consumo de tabaco, bebidas alcohólicas, música alta, etc. por parte de unos consumidores puede afectar a otros. También pueden afectarlos negativamente las empresas que producen contaminación o ruido. Cuando hay una externalidad en la producción, el conjunto de producción de una empresa se ve afectado directamente por las acciones de otro agente. Por ejemplo, la producción de humo por parte de una acería puede afectar directamente a la producción de ropa limpia por parte de una lavandería o la producción de miel por parte de un apicultor puede afectar directamente al nivel de producción del manzanar contiguo. En este capítulo analizamos las externalidades desde el punto de vista económico. Observamos que, en general, los equilibrios de mercado son ineficientes en presencia de externalidades, lo que nos lleva lógicamente a examinar algunas sugerencias para asignar los recursos mediante otros mecanismos cuyos resultados son eficientes. El primer teorema de la economía del bienestar no se cumple en presencia de externalidades. La razón se halla en que hay cosas que preocupan a la gente que no tienen precio. Lograr una asignación eficiente en presencia de externalidades significa esencialmente asegurarse de que los agentes pagan el precio correcto por sus acciones. 24.1 Un ejemplo de extemalidad en la producción Supongamos que tenemos dos empresas. La empresa 1 produce el bien x y lo vende en un mercado competitivo. Sin embargo, su producción impone un coste e(x) a la empresa 2. Supongamos, por ejemplo, que la tecnología es tal que sólo es posible 508 / LAS EXTERNALIDADES (C. 24) producir x unidades de producción generando x unidades de contaminación y que esta contaminación perjudica a la empresa 2. Suponiendo que p es el precio del producto, los beneficios de las dos empresas vienen dados por 1ri = max 1r2 = X px - c(x) -e(x). Suponemos que las dos funciones de costes son crecientes y convexas, como siempre (puede ser que la empresa 2 obtenga beneficios en alguna actividad productiva, pero prescindimos de esta posibilidad para simplificar el análisis). La cantidad de producción de equilibrio, Xq, viene dada por p = c'(xq). Sin embargo, esta cantidad es demasiado elevada desde el punto de vista social. La primera empresa tiene en cuenta los costes privados, es decir, los costes que se impone a sí misma, pero no los costes sociales, es decir, los costes que impone a la otra. Para hallar la cantidad de producción eficiente, nos preguntamos qué ocurriría si las dos empresas se fusionaran a fin de intemalizar la externalidad. En este caso, la empresa fusionada maximizaría los beneficios totales: 1r = max px - c(x) - e(x), X este problema tiene la siguiente condición de primer orden: (24.1) El nivel de producción Xe es una cantidad eficiente; se caracteriza por el hecho de que el precio es igual al coste social marginal. 24.2. Soluciones para resolver el problema de las externalidades Se han propuesto varias soluciones para resolver las ineficiencias de las .externalidades. Los impuestos pigouvianos Desde este punto de vista, lo que ocurre es simplemente que el precio al que se enfrenta la empresa 1 por su acción no es el adecuado, por lo que puede obligársele a pagar un impuesto correctivo que asigne eficientemente los recursos. Este tipo de impuestos correctivos se conoce con el nombre de impuestos pigouvianos. Soluciones para resolver el problema de las externalidades / 509 Supongamos, por ejemplo, que la empresa ha de pagar un impuesto sobre su producción cuya cuantía es t. En ese caso, la condición de primer orden para la maximización del beneficio se convierte en = c'(x) + t. p Suponiendo que la función de costes es convexa, podemos establecer un impuesto t igual a e'(xe), lo que lleva a la empresa a elegir x = Xe, tal como se deduce de la ecuación (24.1). Aunque la función de costes no fuera convexa, podríamos obligar simplemente a la empresa 1 a pagar un impuesto no lineal igual a e(x) y a intemalizar así el coste de la extemalidad. El problema de esta solución se halla en que las autoridades fiscales deben conocer la función de costes de la extemalidad e(x). Pero si la conocen, pueden muy bien indicarle simplemente a la empresa cuánto debe producir. Ausencia de mercados Desde este punto de vista, el problema radica en que a la empresa 2 le preocupa la contaminación que genera la empresa 1, pero no tiene forma alguna de influir en ésta. La introducción de un mercado para que la empresa 2 exprese su demanda de contaminación -o de reducción de la contaminación- constituye un mecanismo para asignar eficientemente los recursos. En nuestro modelo, cuando se producen x unidades de producción, inevitablemente se producen x unidades de contaminación. Si el precio de mercado de la contaminación es r, la empresa 1 puede elegir la cantidad de contaminación que quiere vender, x1, y la 2 puede elegir la que quiere comprar, x2. Los problemas de maximización del beneficio se convierten en 1r1 = max XJ px1 + rx1 - c(x1) 1r2 = max -rx2 - e(x2). x2 Las condiciones de primer orden son = c'(x1) -r = e'(x2). p+r Cuando la demanda de contaminación es igual a la oferta, tenemos que x1 = x2 y estas condiciones de primer orden equivalen a las de (24.1). Obsérvese que el precio de la contaminación de equilibrio, r, es un número negativo, lo que es natural, ya que la contaminación no es un bien sino un "mal". En términos más generales, supongamos que la contaminación y la producción no se generan en una proporción de uno a uno. Si la empresa 1 produce x unidades 510 / LAS EXTERNALIDADES (C. 24) de producción e y de contaminación, paga un coste de c(x, y). Probablemente el aumento de y reduce el coste de producción de x, pues, de lo contrario, no habría ningún problema. En ausencia de un mecanismo para controlar la contaminación, el problema de maximización del beneficio de la empresa 1 es max px - c(x, y), x,y que tiene las siguientes condiciones de primer orden: p= O= ac(x, y) ax ac(x, y) ay . La empresa 1 igualará el precio de la contaminación y su coste marginal. En este caso, el precio es cero, por lo que contaminará hasta el punto en el que se minimicen los costes de producción. Ahora introducimos un mercado de contaminación. Sea de nuevo r el coste unitario de la contaminación e Y1 e Y2 la oferta y la demanda de las empresas 1 y 2. Los problemas de maximización son 1r1 = max x,y1 1r2 = px + rY} - c(x, y1) max -ry2 - e(y2). Y2 Las condiciones de primer orden son Bct», y1) p= __ a__ x ac(x, Y1) r=--ay1 + T ae(y2) = ---. ay2 Igualando la oferta y la demanda, de tal manera que Y1 = Y2, tenemos las condiciones de primer orden para obtener un nivel eficiente de x y de y. El problema de esta solución se halla en que los mercados de contaminación son muy limitados. En el caso representado sólo hay dos empresas. No existe razón alguna para pensar que un mercado de ese tipo se comportará competitivamente. Derechos de propiedad Desde este punto de vista, el problema básico es que los derechos de propiedad no son buenos para alcanzar totalmente la eficiencia. Si las dos tecnologías son El mecanismo de la compemsación / 511 propiedad de una empresa, hemos visto que no hay problema alguno. Sin embargo, observaremos que hay una señal de mercado que induce a los agentes a establecer una pauta eficiente de derechos de propiedad. Si la externalidad de una empresa afecta negativamente a las actividades de otra, siempre le compensará a una de ellas comprar la otra. Es evidente que coordinando las actividades de las dos empresas siempre es posible obtener más beneficios que actuando por separado. Por lo tanto, una empresa podría pagar a la otra su valor de mercado (en presencia de la externalidad), puesto que el valor que tendría cuando se ajustara óptimamente la externalidad sería superior al actual. Este argumento demuestra que el propio mecanismo emite señales para ajustar los derechos de propiedad de tal manera que se internalicen las externalidades. Ya demostramos esta afirmación con un carácter algo general cuando vimos el primer teorema en el capítulo 18 (página 399). En nuestro razonamiento demostramos que si una asignación no es eficiente en el sentido de Pareto, es posible aumentar los beneficios agregados. Si examinamos detenidamente el teorema, veremos que lo único que se necesita es que todos los bienes que interesan a los consumidores tengan un precio o, en otras palabras, que las preferencias de los consumidores dependan únicamente de sus cestas de consumo. Puede haber tipos arbitrarios de externalidades en la producción y, aun así, la demostración es válida hasta la última línea, en la que demostramos que los beneficios agregados correspondientes a la asignación que domina en el sentido de Pareto son superiores a los beneficios agregados correspondientes a la asignación inicial. Si no hay externalidades en la producción, es una contradicción. Si las hay, este argumento demuestra que existe un plan de producción alternativo que eleva los beneficios agregados, por lo que una empresa tiene un incentivo de mercado para comprar las demás, coordinar sus planes de producción e internalizar la externalidad. En lo esencial, la empresa crece hasta que internaliza todas las externalidades relevantes de la producción. Esto da buenos resultados en el caso de algunas clases de externalidades, pero no en todas. Por ejemplo, no resuelve muy bien el problema de las externalidades en el consumo o el de las externalidades que son bienes públicos. 24.3 El mecanismo de la compensación Hemos afirmado antes que los impuestos pigouvianos no eran adecuados en general para resolver las externalidades debido al problema de la información: las autoridades fiscales en general no pueden esperar conocer los costes que imponen las externalidades. Sin embargo, es posible que los agentes que las generan tengan una idea razonablemente buena de los costes que imponen. En ese caso, existe un sistema relativamente sencillo para internalizar las externalidades. 512 / LAS EXTERNALIDADES (C. 24) Éste consiste en crear un mercado de la externalidad, pero de tal forma que induzca a las empresas a revelar correctamente los costes que imponen a la otra. He aquí cómo funciona el método. Fase de anuncio. La empresa i cuantía puede o no ser eficiente. 1, 2 anuncia un impuesto pigouviano ti cuya Fase de elección. Si la empresa 1 produce x unidades, tiene que pagar un impuesto t2x y la 2 recibe una indemnización cuya cuantía es t1 x. Cada empresa paga, además, una multa dependiendo de la diferencia que exista entre los dos tipos impositivos anunciados. La forma exacta de la multa es irrelevante para nuestros fines; lo único que importa es que es cero cuando t1 = t2 y positiva en caso contrario. Por razones expositivas, elegimos una multa en forma cuadrática. En este caso, las ganancias finales de la empresa 1 y de la 2 vienen dadas por 1r1 = max X px - c(x) - t2x - (t1 - t2)2 1r2 = t1x - e(x) - (t2 - t1>2. Queremos demostrar que el resultado de equilibrio de este juego implica un nivel eficiente de producción de la externalidad. Para demostrarlo, tenemos que reflexionar algo sobre lo que constituye un concepto razonable de equilibrio en este juego. Dado que éste consta de dos fases, es razonable exigir que el equilibrio sea perfecto en todos los subjuegos, es decir, un equilibrio en el que cada una de las empresas tenga en cuenta las repercusiones de lo que ha elegido en la primera fase en los resultados de la segunda. Véase el capítulo 15 (página 319). Como siempre, resolvemos este juego examinando, en primer lugar, la segunda fase. Consideremos la elección del nivel de producción de la segunda fase. La empresa 1 elige un x tal que satisfaga la siguiente condición: p = c'(x) + t2 (24.2) A cada elección de t2 le corresponderá una elección óptima de x(t2). Si c"(x) > O, es fácil demostrar que x' (t2) < O. En la primera fase, cada empresa elegirá los tipos impositivos que maximicen sus beneficios. La elección es sencilla para la empresa 1: si la 2 elige t2, la 1 también deseará elegir (24.3) Para comprobarlo, basta diferenciar la función de beneficios de la empresa 1 con respecto a t1. Las condiciones de eficiencia en presencia de externalidades / 513 Las cosas son algo más complicadas en el caso de la empresa 2, ya que ésta tiene que darse cuenta de que su elección de t2 afecta al nivel de producción de la empresa 1 a través de la función x(t2). Diferenciando la función de beneficios de la empresa 2, teniendo en cuenta esta influencia, tenernos que (24.4) Uniendo (24.2), (24.3) y (24.4), tenernos que p = c'(x) + e'(x), que es la condición de eficiencia. Este método funciona porque da incentivos opuestos a los dos agentes. Es evidente en la igualdad (24.3) que el agente 1 siempre tiene un incentivo para anunciar lo mismo que el 2. Pero consideremos el incentivo del agente 2. Si éste piensa que el agente 1 propondrá darle una elevada indemnización t1, querrá que se grave al agente 1 lo menos posible, por lo que éste producirá lo más posible. En cambio, si el agente 2 piensa que el 1 propondrá darle una pequea indemnización, querrá que se grave al agente 1 lo más posible. El único punto en el que al agente 2 le da igual el nivel de producción del agente 1 es aquel en el que es compensado exactamente, en el margen, por los costes de la externalidad. 24.4 Las condiciones de eficiencia en presencia de externalidades En este apartado deducirnos las condiciones generales de eficiencia en presencia de externalidades. Supongamos que hay dos bienes, un bien x y un bien y, y dos agentes. A los dos les interesa el consumo del bien x por parte del otro, pero no el del bien y. Inicialmente, hay x unidades del bien x e f¡ unidades del bien y. De acuerdo con el capítulo 17 (página 382), la asignación eficiente en el sentido de Pareto maximiza la suma de las utilidades sujeta a la restricción que imponen los recursos: rnax a1 u1 (:.r:1, x2, Y1) + a2u2(x1, x2, Y2) Xi,Y·i sujeta a x1 + x2 Y1 + Y2 Las condiciones de primer orden son =x = Y· 514 / LAS EXTERNALIDADES (C. 24) 8u1 8u2 a1- +a2- = ,\ 8x1 8x1 8u1 8u2 a1- +a2- = ,\ 8x2 8x2 8u1 a1-=µ ªYl 8u2 a2 8y2 = µ. Tras algunas manipulaciones, estas condiciones pueden expresarse de la forma siguiente: La condición de eficiencia es que la suma de las relaciones marginales de sustitución sea igual a una constante. Para saber si es o no una buena idea que el agente 1 aumente su consumo del bien 1, no hemos de tener en cuenta lo que está dispuesto a pagar él por este consumo adicional, sino lo que está dispuesto a pagar el agente 2. Estas condiciones son esencialmente iguales que las condiciones de eficiencia correspondientes a un bien público. Estas condiciones muestran cómo se internaliza la externalidad. Basta considerar x1 y x2 como si fueran bienes diferentes. El precio de x1 es P1 = 8u2/ 8x1 y el de x2 es P2 = 8uif 8x2. Si el precio al que se enfrenta cada uno de los agentes por sus acciones es el adecuado, el equilibrio de mercado da lugar a un resultado eficiente. Notas Los estudios clásicos sobre las externalidades se deben a Pigou (1920) y Coase (1960). El mecanismo de la compensación se examina más detenidamente en Varian (1989b). Ejercicios 21.1. Suponga que dos agentes están pensando en la velocidad a la que deben conducir. El agente i decide conducir a la velocidad Xi, lo que le reporta la utilidad Ejercicios / 515 u/xi); suponemos que u�(xi) > O. Sin embargo, cuanto más deprisa conducen los agentes, más probable es que tengan un accidente que involucre a los dos. Sea p(x1, x2) la probabilidad de sufrir un accidente, que suponemos que es creciente con respecto a ambos argumentos, y e; > O el coste que impone ese accidente al agente i. Suponga que la utilidad de cada uno de ellos es lineal con respecto al dinero. (a) Demuestre que cada uno de los agentes tiene un incentivo para conducir demasiado deprisa desde el punto de vista social. (b) Si se le impone al agente i una multa de ti en caso de accidente, ¿cuál debe ser su cuantía para que internalice la externalidad? (c) Si se utilizan las multas óptimas, ¿cuáles son los costes sociales, incluidas las multas, que pagan los agentes? ¿ Qué diferencia hay entre estos costes y el coste total del accidente? (d) Suponga ahora que el agente i obtiene la utilidad u/x) sólo si no hay ningún accidente. ¿Cuál es la multa adecuada en este caso? 25. LA INFORMACIÓN El área de la teoría económica que se ha desarrollado con mayor rapidez en los últimos diez años es el área de la economía de la información. En este capítulo describirnos algunos de sus ternas básicos. En la mayoría de los casos que estudiaremos se dan situaciones de información asimétrica, es decir, situaciones en las que uno de los agentes económicos sabe algo que el otro desconoce. Por ejemplo, un trabajador puede tener una idea mucho más clara que el empresario de cómo producir o un productor puede conocer mejor que un posible consumidor la calidad del bien que produce. Sin embargo, el empresario puede extraer alguna información sobre la productividad del trabajador observando atentamente su conducta y el consumidor puede extraer alguna información sobre la calidad del producto de una empresa observando si éste se vende mucho o poco. Los buenos trabajadores pueden desear que se sepa que son buenos o pueden no desearlo, dependiendo de lo que ganen. A los productores de productos de elevada calidad les gustaría en general que se les conociera corno tales, pero a los productores de productos de baja calidad también les gustaría tener fama de que producen artículos de buena calidad. Por lo tanto, en el estudio de la conducta en situaciones en las que la información es asimétrica interviene necesariamente la interdependencia estratégica de los agentes. 25.1 El problema del principal y el agente Muchos de los tipos de problemas que plantean los incentivos pueden analizarse utilizando el modelo siguiente. Una persona, el principal, quiere inducir a otra, el agente, a hacer algo que es costoso para este último. Es posible que el principal no pueda observar directamente lo que hace el agente, pero observa un producto, x, que depende, al menos en parte, de lo que haga. El problema del principal consiste en buscar un sistema de incentivos retributivos, s(x), que induzca al agente a tomar la mejor medida desde el punto de vista del principal. 518 / LA INFORMACIÓN (C. 25) El ejemplo más sencillo del problema del principal y el agente es el de un directivo y un trabajador. El primero quiere que el segundo se esfuerce lo más posible para conseguir el mayor nivel de producción posible, mientras que el segundo desea hacer lo que maximice su propia utilidad, dado el sistema de incentivos. Un ejemplo algo menos evidente es el de una empresa minorista y un cliente. La empresa desea que el cliente compre su producto, actividad que resulta costosa para el comprador. A la empresa le gustaría cobrar a cada uno de sus clientes su precio de reserva, es decir, la cantidad máxima que estuviera dispuesto a pagar. No puede observar directamente este precio, pero sí la cantidad que comprarían a los diferentes precios consumidores de distintos gustos. El problema de la empresa consiste, pues, en buscar una tabla de precios que maximice sus beneficios. Éste es el problema al que se enfrenta el monopolista cuando practica la discriminación de precios; véase el capítulo 14, página 287. Este tipo de problema se denornirna problema del principal y el agente. En los siguientes apartados examinarnos el problema del directivo y el trabajador, pero no es difícil generalizar el análisis a otras situaciones corno la fijación no lineal de los precios. Sea x el nivel de producción que recibe el principal y a y b las posibles acciones que puede elegir el agente de un conjunto de acciones viables, A. En algún momento será útil suponer que sólo hay dos acciones viables, pero no impondremos por ahora esta restricción. Suponernos inicialmente que no existe incertidumbre, por lo que el resultado depende totalmente de lo que haga el agente; esta relación se expresa de la siguiente manera: x = x(a). Sea c(a) el coste de la acción a y s(x) los incentivos retributivos que da el principal al agente. La función de utilidad del principal es x - s(x), es decir, el nivel de producción menos los incentivos retributivos, y la función de utilidad del agente es s(x) - c(a), es decir, los incentivos retributivos menos el coste de la acción. El principal desea elegir una función, s( ·) que maximice su utilidad sujeta a las restricciones impuestas por la conducta optimizadora del agente. Normalmente, el agente está sometido a dos tipos de restricciones. En primer lugar, el agente puede tener otra oportunidad que le reporte un nivel de utilidad de reserva y el principal debe asegurarse de que el agente obtiene, al menos, este nivel de reserva para que esté dispuesto a participar. Esta restricción se denomina restricción de la participación (a veces se denomina restricción de la racionalidad in di vidual). La segunda restricción del problema es la de la compatibilidad de los incentivos: dado el sistema de incentivos que elija el principal, el agente decidirá hacer lo que más le convenga. El principal no puede elegir directamente la acción del agente: sólo puede influir en ella eligiendo el sistema de incentivos. Analizaremos dos tipos de situaciones en las que hay un principal y un agente. Información completa: la solución monopolística / 519 La primera es aquella en la que hay un principal que actúa como un monopolista: fija un sistema retributivo que es aceptado por el agente en la medida en que éste espere que le reporte una utilidad mayor que su nivel de utilidad de reserva. En este caso, queremos hallar las propiedades del sistema de incentivos que es óptimo desde el punto de vista del principal. La segunda es aquella en la que hay muchos principales rivales, cada uno de los cuales elige un sistema de incentivos; en este caso, queremos averiguar las propiedades de los sistemas de incentivos retributivos de equilibrio. En el problema del monopolio, el nivel de utilidad de reserva del agente es exógeno: normalmente es la utilidad correspondiente a alguna otra actividad. En el problema competitivo, es endógeno: es la utilidad correspondiente a los contratos que ofrecen los demás principales. Del mismo modo, en el problema del monopolio los beneficios máximos alcanzables son la función objetivo del problema. Pero en el problema competitivo, normalmente suponemos que en condiciones de equilibrio los beneficios han sido eliminados como consecuencia de la competencia. Por lo tanto, la condición de beneficio nulo se convierte en una importante condición de equilibrio. 25.2 Información completa: la solución monopolística Comenzamos con el ejemplo más sencillo en el que el principal posee una información completa sobre los costes y las acciones del agente. En este caso, el objetivo del principal consiste simplemente en averiguar la acción que quiere que elija el agente y buscar un sistema de incentivos que lo induzca a elegirla. Dado que sólo hay un principal, diremos que se trata de un caso monopolístico.1 Sea a las distintas acciones que puede elegir el agente y supongamos que el nivel de producción es una función conocida de la acción, x(a). Sea b la acción que el principal desea que elija el agente (imaginemos que bes la "mejor" acción para el principal y a son las acciones "alternativas"). El problema de buscar el sistema óptimo de incentivos s( ·) puede formularse de la manera siguiente: max x(b) b,s(·) sujeta a - s(x(b)) s(x(b)) - c(b) � u s(x(b)) - c(b) � s(x(a)) - c(a) (25.1) cualquiera que sea a en A. (25.2) 1 Podríamos llamarlo caso monopsonístico, ya que no estamos refiriéndonos a un único vendedor sino a un único comprador, pero utilizamos el término monopolio en sentido general para incluir tanto los casos en los que hay un único comprador como los casos en los que hay un único vendedor. 520 / LA INFORMACIÓN (C. 25) La condición (25.1) impone la restricción de que el agente debe recibir, al menos, su nivel de utilidad de reserva, ya que una "acción" posible es no participar; ésta es la restricción de la participación. La condición (25.2) impone la restricción de que lo óptimo para el agente será elegir b; ésta es la restricción de la compatibilidad de los incentivos. Obsérvese que el principal elige, de hecho, la acción b, si bien indirectamente, al diseñar la función de incentivos. La restricción a la que está sometido el principal consiste en asegurarse de que lo que haga el agente sea, de hecho, lo que desea que haga. Aunque este problema de maximización parece peculiar a primera vista, tiene una solución trivial. Prescindamos de momento de la restricción de la compatibilidad de los incentivos. Si nos fijamos en la función objetivo y en la restricción de la participación, observaremos que cualquiera que sea x, el principal desea que s(x) sea lo más pequeño posible. De acuerdo con la restricción de la participación (25.1), eso significa que s(x(b)) debe ser igual a il + c(b); es decir, la retribución del agente cubre el coste de su acción y le reporta su utilidad de reserva. Por lo tanto, la acción óptima, desde el punto de vista del principal, es la que maximiza x(b) - il - c(b). Llamémosla b* y al nivel de producción correspondiente x* = x(b*). La cuestión es la siguiente: ¿podemos establecer un sistema de incentivos, s(x), que haga que b* sea la opción óptima para el agente? Es fácil: basta elegir una función s(x) tal que s(x*) - c(b*) 2: s(x(a)) - c(a) cualquiera que sea a perteneciente a A. Supongamos, por ejemplo, que s(x*) = { il + c(b*) -oo si x = x(b*) en caso contrario. Este sistema de incentivos es un sistema de fijación de un objetivo respecto al nivel de producción: se fija un determinado nivel de producción de x* y se le paga al agente su precio de reserva si alcanza ese objetivo o, de lo contrario, se le impone una sanción arbitrariamente grande (de hecho, bastaría pagarle una cantidad inferior a la que se le pagaría si lo alcanzara). Éste no es más que uno de los muchos sistemas de incentivos posibles que resuelven el problema de los incentivos. Otro consistiría en elegir un sistema de incentivos lineales tal que s(x(a)) = x(a) - F. En este caso, el agente debe pagar una cantidad fija F al principal y recibe toda la cantidad producida. Este sistema da buenos resultados porque el agente tiene un incentivo para elegir la acción que maximiza x(a) - c(a). La cantidad fija F se elige de tal manera que el agente satisfaga la restricción de la participación; es decir, F = x(b*) + c(b*) - il. En este caso, el agente es el perceptor residual de la cantidad producida. Una vez que el agente paga al principal la cantidad F, obtiene todos los beneficios restantes. Deben hacerse dos observaciones respecto a estas soluciones del problema del principal y el agente con información completa. En primer lugar, la restricción de la compatibilidad de los incentivos no es, en realidad, "efectiva". Una vez que se elige Información completa: la solución competitiva / 521 el nivel óptimo de producción, siempre es posible elegir un sistema de incentivos que haga que dicho nivel sea la acción optimizadora para el agente. En segundo lugar, dado que la restricción de la compatibilidad de los incentivos nunca es efectiva, siempre se produce la cantidad eficiente en el sentido de Pareto. Es decir, no hay forma de producir otra cantidad que sea preferida tanto por el principal como por el agente. Basta observar que el problema de maximización sin la restricción de los incentivos tiene la forma habitual de la optimización en el sentido de Pareto: maximiza la utilidad de uno de los agentes manteniendo constante la del otro. La dificultad de estos sistemas de incentivos se halla en que son muy sensibles a las pequeñas imperfecciones de la información. Supongamos, por ejemplo, que la relación entre la cantidad del factor y el nivel de producción no está totalmente determinada. Tal vez exista algún "ruido" en el sistema y el bajo nivel de producción no se deba a una falta de esfuerzo sino a la mala suerte. En este caso, un sistema de incentivos como el que acabamos de describir puede no ser adecuado. Si el agente sólo es retribuido cuando alcanza el nivel de producción fijado como objetivo, su utilidad esperada -calculada como una media de los distintos niveles de producción aleatorios- puede ser inferior a su nivel de utilidad de reserva, por lo que se negará a participar. Para satisfacer la restricción de la participación, el principal debe ofrecer al agente un sistema retributivo que le reporte su nivel de utilidad de reserva. Normalmente, en un sistema de ese tipo algunos niveles de producción generan una retribución positiva, ya que pueden ser compatibles con el nivel de esfuerzo fijado como objetivo. Este tipo de problema de incentivos se conoce con el nombre de problema de la acción oculta, ya que el principal no puede observar perfectamente lo que hace el agente. El segundo tipo interesante de información imperfecta es aquel en el que el principal no puede observar perfectamente la función objetivo del agente. Puede haber muchos tipos distintos de agentes que tienen funciones de utilidad o de costes diferentes. El principal debe buscar un sistema de incentivos que dé buenos resultados, en promedio, cualquiera que sea el tipo de agente. Esta clase de problema de incentivos se conoce como problema de la información oculta, ya que la dificultad se halla en que el principal desconoce la información sobre el tipo del agente. Más adelante analizamos estas dos clases de problemas de incentivos. 25.3 Información completa: la solución competitiva Antes de pasar a analizarlos, es interesante examinar el problema del principal y el agente con información completa en un entorno competitivo. Como hemos indicado antes, una manera de completar el modelo es introducir la condición de que la competencia elimina totalmente los beneficios. 522 / LA INFORMACIÓN (C. 25) Para sentar las ideas, supongamos que hay un grupo de productores y un grupo de trabajadores idénticos. Cada uno de los productores elige un sistema de incentivos con el fin de atraer a los trabajadores a su fábrica. Los productores deben competir entre sí para atraer a los trabajadores y estos últimos deben competir entre sí para conseguir empleo. El problema de optimización de un determinado productor es exactamente igual que en el caso monopolístico: observa lo que le cuesta conseguir diferentes niveles de esfuerzo y atraer a los trabajadores a su fábrica y elige la combinación que maximiza el ingreso menos el coste. Hemos visto que en este caso puede elegirse un sistema óptimo de incentivos en el que la retribución sea una función lineal del nivel de producción, de tal manera que s(x) = x - F. En el modelo del monopolio, F se determinaba a partir de la restricción de la participación: x(b*) - F - c(b*) = u, donde u es el nivel de utilidad que puede obtenerse en alguna otra actividad exógena al modelo. En un modelo competitivo, ese procedimiento no es, por lo general, adecuado. En este caso, el modo de determinar F consiste en suponer que la restricción de la participación no es efectiva, pero que la competencia existente en la industria elimina totalmente los beneficios. En este caso, F viene determinado por la condición de que x - (x - F) = O, lo que implica que F = O. Los trabajadores capturan todo su producto marginal y las "rentas monopolísticas" se reducen hasta ser nulas. El hecho de que las rentas de equilibrio sean nulas es un artificio que se debe al supuesto de que la tecnología muestra rendimientos constantes de escala. Si los productores tienen algunos costes fijos K, la condición de equilibrio exigiría que F=K. Desde el punto de vista formal, la principal diferencia entre la solución monopolística y la competitiva se halla en la manera en que se determina la renta F. En el modelo del monopolio, es la cantidad que hace que el trabajador se muestre indiferente entre trabajar para el principal y realizar alguna otra actividad. En el modelo competitivo, la renta viene determinada por la condición de beneficio nulo. Acciones ocultas: la solución monopolística / 523 25.4 Acciones ocultas: la solución monopolística En este apartado analizamos un sencillo modelo de la relación entre el principal y el agente en el que las acciones no son directamente observables. Partimos de algunos supuestos para facilitar el análisis. En concreto, suponemos que sólo hay un número finito de posibles niveles de producción (x1, ... , xn), El agente puede elegir entre dos acciones, a y b, que influyen en la probabilidad de que el nivel de producción obtenido sea uno u otro. Supongamos, pues, que 1fia es la probabilidad de que se observe el nivel de producción Xi si el agente elige la acción a y Kib es la probabilidad de que se observe Xi si el agente elige la acción b. Sea si = s(xi) la retribución que da el principal al agente si se observa Xi· En ese caso, el beneficio que espera obtener el principal si el agente elige, por ejemplo, la acción bes 2:)xi n (25.3) Si)7íib i=l Por lo que se refiere al agente, supongamos que es contrario a correr riesgos y trata de maximizar alguna función de utilidad de la retribución del tipo von Neumann-Morgenstern, u(si), y que el coste de su acción, ca, entra linealmente en su función de utilidad. Por lo tanto, el agente elegirá la acción b si n L U(Si)1fib - Cb i=l 2:: n L U(Si)1fia - Ca (25.4) i=l y elegirá la acción a en caso contrario. Ésta es la restricción de la compatibilidad de los incentivos. También suponemos que una de las acciones entre las que puede elegir el agente es no participar. Supongamos que si el agente no participa, obtiene la utilidad u. Por lo tanto, la utilidad esperada de la participación debe ser al menos u: ¿ n i=l u(si)Kib - cb 2:: u (25.5) Ésta es la restricción de la participación. El principal desea maximizar (25.3) sujeta a las restricciones (25.4) y (25.5). La maximización se produce con respecto a la acción by la retribución (si), Obsérvese que en este problema los dos agentes están eligiendo acciones optimizadoras. El agente va a elegir la acción b que sea mejor para él, dado el sistema de incentivos (si) establecido por el principal. El principal, que lo comprende, desea ofrecer la pauta de incentivos que sea mejor para él. Por lo tanto, lo que haga el agente constituye una restricción que ha de tener en cuenta el principal al elegir el sistema de incentivos. 524 / LA INFORMACIÓN (C. 25) De hecho, el principal elige la acción que desea que elija el agente, teniendo en cuenta el coste de elegirla, a saber, debe estructurar el sistema de incentivos de tal manera que la acción que desea sea también la que desea el agente. Es posible observar la acción del agente En el problema de información completa analizado en el apartado anterior, era irrelevante el hecho de que el sistema retributivo se basara en la acción o en el nivel de producción, ya que existía una relación biunívoca entre las acciones y el nivel de producción. En este problema, la distinción es fundamental. Si la retribución puede basarse en la acción, es posible poner en práctica un sistema de incentivos totalmente óptimo, aunque el nivel de producción sea aleatorío. Lo único que ha de hacer el principal es determinar el beneficio (esperado) que obtendría induciendo al agente a elegir cada una de las acciones posibles e inducirlo a elegir la que maximiza su beneficio esperado. Para verlo en términos matemáticos, supongamos que el principal puede pagar al agente en función de lo que haga éste y no en función del nivel de producción. En ese caso, el agente recibirá la retribución s(b). Obsérvese que ésta es segura, por lo que la utilidad del agente es I:7=1 'lribu(s(b)) - cb = u(s(b)) - cb. El problema de incentivos antes descrito se reduce a ¿ Xi'lrib - s(b) n max s(b),b i=l sujeta a u(s(b)) - cb ::::: ü u(s(b)) - Cb ::::: u(s(a)) - Ca. Este problema es exactamente igual que el problema con información completa que hemos analizado antes: la restricción de la compatibilidad de los incentivos no es esencial. El problema del principal y el agente sólo es interesante cuando las acciones están ocultas, de tal manera que el sistema de incentivos sólo puede basarse en el nivel de producción. En este caso, la retribución del agente es necesariamente aleatoria y el sistema óptimo de incentivos implica un cierto grado de reparto del riesgo entre el principal y el agente. Al principal le gustaría pagar al agente menos cuando produjera menos, pero no puede saber si el bajo nivel de producción se debe a una falta de esfuerzo del agente o simplemente a la mala suerte. Si el principal impone una sanción demasiado alta por un bajo nivel de producción, impone demasiado riesgo al agente y tiene que elevar el nivel medio de retribución para compensarlo. Éste es el dilema al que se enfrenta el principal cuando ha de elegir un mecanismo óptimo de incentivos. Acciones ocultas: la solución monopolística / 525 Supongamos que no existe ningún problema de incentivos y que la única cuestión es el reparto del riesgo. En este caso, el problema de rnaxirnización del principal es n rnax ¿:)xi (si) i=l sujeta a ¿ si)1rib n u(sihrib - Cb 2:: ü. i=l Suponiendo que A es el multiplicador de Lagrange de la restricción, la condición de primer orden es -1rib - .\u' (si)7rib = O, lo que implica que u'(si) = una constante, lo que significa que Si = constante. Esencialmente, el principal asegura totalmente al agente contra todo riesgo, lo cual es natural puesto que el principal es neutral ante el riesgo y el agente es contrario a correr riesgos. Esta solución no suele ser buena cuando hay una restricción de incentivos. Si el principal asegura totalmente al agente, a éste le da igual cuál sea el resultado, por lo que no tiene incentivo alguno para elegir la acción que desea el principal: si el agente recibe una determinada cantidad, cualquiera que sea el esfuerzo que realice, ¿por qué va a molestarse en trabajar mucho? La determinación del contrato óptimo en cuanto a los incentivos implica un intercambio entre los beneficios que supone el hecho de que el principal asegure al agente y los costes que impone ese seguro desde el punto de vista de los incentivos. Análisis del sistema óptimo de incentivos En este apartado analizarnos la elaboración del sistema óptimo de incentivos utilizando la estrategia siguiente. En primer lugar, averiguarnos cuál es el sistema óptimo de incentivos necesario para conseguir cada una de las acciones posibles. A continuación compararnos la utilidad que reportan estos sistemas al principal para ver cuál es el menos costoso desde su punto de vista. Suponernos para simplificar que sólo hay dos acciones posibles, a y b, y nos preguntarnos cómo podernos elaborar un sistema que genere, por ejemplo, la acción b. Sea V(b) la mayor utilidad posible que obtiene el principal si diseña un sistema que induzca al agente a elegir la acción b. El problema de rnaxirnización del principal es V(b) = rnax (si) n ¿(xi - s.J1rib i=l 526 / LA INFORMACIÓN (C. 25) ¿ n sujeta a u(si)7rib - cb 2:: u u(si)7íib - Cb 2:: i=1 ¿ n i=l ¿ (25.6) n u(si)7íia - Ca (25.7) i=1 En este caso, la condición (25.6) es la restricción de la participación y la (25.7) es la restricción de la compatibilidad de los incentivos. En este problema hay una función objetivo lineal y unas restricciones no lineales. Aunque puede analizarse directamente, es útil examinarlo gráficamente para reformular el problema de tal manera que contenga unas restricciones lineales y un objetivo no lineal. Sea ú; la utilidad alcanzada con el resultado i, de tal manera que u(si) = tu, Sea f la inversa de la función de utilidad, de tal manera que Si = f(ui). La función f indica simplemente cuánto le cuesta al principal ofrecer la utilidad u; al agente. Es fácil demostrar que f es una función convexa y creciente. Reformulando las condiciones (25.6) y (25.7) con esta notación, tenemos que n V(b) = max ¿(xi - f(ui))7íib (u ,) i=1 L n Ui7íib - ci, 2:: u Ui7íib - ci, 2:: L i=1 L n (25.8) n i=1 Ui1íia - Ca (25.9) i=l En este caso, el problema se plantea como el de la elección de una distribución de utilidad para el agente, en la que el coste en que incurre el principal ofreciendo u; es Si = f(ui). Este problema puede analizarse gráficamente cuando n = 2. En este caso, sólo hay dos niveles de producción, x1 y x2, y el principal sólo necesita fijar dos niveles de utilidad, u1, la utilidad que recibe el agente cuando el nivel de producción es x1, y u2, la utilidad que recibe cuando el nivel de producción es x2. El conjunto de restricciones determinado por (25.8)-(25.9) aparece en la figura 25.1. Las curvas de indiferencia del agente si elige las acciones a o b son simplemente líneas rectas de la forma = constante -, 1r1b u1 + 1r2b u2 - cb ?r1a u1 + 1r2a u2 - Ca = constante. Examinemos la restricción de la compatibilidad de los incentivos (25.9) y consideremos los pares de utilidad ( u1, u2), en los que el agente es indiferente entre la acción Acciones ocultas: la solución monopolística / 527 b y la a. Éstos son puntos en los que una curva de indiferencia correspondiente a la acción a corta a la curva de indiferencia correspondiente a la acción b en la que el nivel de utilidad es el mismo. El lugar geométrico de todos esos pares ( u1, u2) satisface la ecuación Despejando u2 en función de u1, tenemos que U2 = 7rJa - 7rJb 7r2b - 7r2a UJ + Cb - Ca 7r2b - 7r2a = UJ Cb - Ca + ---7r2b - 7r2a (25.10) El coeficiente de u1 es 1 puesto que 7rJa + 7r2a = 7rJb + 7r2b = 1. En consecuencia, la recta de compatibilidad de los incentivos determinada en la ecuación (25.10) tiene una pendiente de + 1. La región en que la acción b es preferida por el agente es la de encima de esta recta. La restricción de la participación exige que El conjunto de ( u1, u2) en el que se satisface esta condición como una igualdad es simplemente una de las curvas de indiferencia correspondientes a la acción b. La figura 25.1 muestra la intersección del área que satisface la restricción de la compatibilidad de los incentivos y el área que satisface la restricción de la participación. Esta figura también muestra la recta de cuarenta y cinco grados. Esta recta es importante porque representa las combinaciones de u1 y u2 en las que u1 = u2. Hemos visto que si no existiera ninguna restricción de la compatibilidad de los incentivos, el principal aseguraría simplemente al agente y la solución óptima satisfaría la condición de que u1 = u2 = u. Debido a la restricción de la compatibilidad de los incentivos, el punto de seguro completo no puede ser viable. La naturaleza de la solución del problema del principal y el agente depende de que la recta de compatibilidad de los incentivos intercepte el eje vertical u horizontal. La figura 25.2 muestra estos casos. Para hallar la solución óptima, representamos simplemente las curvas de indiferencia del principal. Éstas tienen la forma siguiente: 528 / LA INFORMACIÓN (C. 25) Figura 25.1 Recta de 45º Recta de participación El conjunto viable en el caso del problema del principal y el agente con acciones ocultas. El área situada al noreste de la recta de participación satisface la restricción de la participación. El área situada al noroeste de la recta de compatibilidad de los incentivos satisface la restricción de la compatibilidad de los incentivos. La intersección de estas dos áreas es el área sombreada. La utilidad del principal aumenta cuando disminuyen s1 y s2. ¿Qué sabemos de la pendiente? La pendiente de las curvas de indiferencia del principal viene dada por Cuando u1 = ua. debe cumplirse que RM S = -1r1b/1r2b· Dado que las curvas de indiferencia del agente vienen determinadas por la condición 1r1b u1 + 1r2b ub = constante, la pendiente de sus curvas de indiferencia cuando u1 = u2 también viene dada por -1r1b/1r2b· Por lo tanto, la curva de indiferencia del principal debe ser tangente a la curva de indiferencia del agente a lo largo de la recta de 45°. Se trata simplemente de una consecuencia geométrica del hecho de que el principal asegurará totalmente al agente si no hay problemas de incentivos. Por lo tanto, si es viable la solución del seguro total, como muestra la figura 25.28, ésa será la solución óptima. Si no lo es, en la solución óptima el agente soporta parte del riesgo. Acciones ocultas: la solución monopolística / 529 Figura 25.2 Restricción de la compatibilidad de los incentivos Compatibilidad de los incentivos A B Dos soluciones del problema del principal y el agente. En el panel A hemos representado el caso en el que la solución óptima es aquella en la que el agente soporta parte del riesgo; el panel B muestra el caso en el que es óptimo el seguro total. Para investigar algebraicamente la naturaleza del sistema óptimo de incentivos, volvemos al caso en el que hay n resultados y formulamos el lagrangiano del problema de maximización descrito en (25.6-25.7). L = t(x, - s,)rr,, - A - µ [e, - ü - [e, - Ca - t u(s;)rr,,] t i=l u(s;)(rr,, - rr,.)] Las condiciones de primer. orden de Kuhn-Tucker se hallan diferenciando esta expresión con respecto a Si. De esa manera, tenemos que Dividiendo los dos miembros por 1ribu'(si) y reordenando, tenemos la ecuación fundamental que determina la forma del sistema de incentivos: 530 / LA INFORMACIÓN (C. 25) [ 1 1ria --=>..+µ 1-u'(si) 1rib l (25.11) Cabe esperar, en general, que la restricción que pesa sobre la utilidad de reserva sea efectiva, por lo que A > O. La segunda restricción plantea más problemas; como hemos visto en nuestro análisis gráfico, puede ser o no efectiva. Supongamos queµ = O. En ese caso, la ecuación (25.11) implica que u'(si) es igual a una constante 1/ >..; es decir, que la retribución del agente es independiente del resultado. Por lo tanto, si es igual a una constante s. Introduciendo esta igualdad en la restricción de la compatibilidad de los incentivos, observamos que L n u(s) i=l 1rib - Cb > L n u(s) 1ria - Ca. i=a Dado que la suma de cada una de las distribuciones de probabilidades es igual a 1, esta desigualdad implica que Por lo tanto, este caso sólo puede surgir cuando la acción que prefiere el principal también es la de bajo coste para el agente. Se representa en la figura 25.28, en la que no existe conflicto de intereses entre el principal y el agente y el primero asegura simplemente al segundo. Pasando al caso en el que la restricción es efectiva y, por consiguiente,µ > O, vemos que en general la retribución del agente, Si, varía dependiendo del resultado Xi· Es el caso en el que el principal desea la acción que impone elevados costes al agente, por lo que la retribución de este último depende de la conducta del cociente 1r ia / 1r ib- En estadística, una expresión de la forma 1r ia / 1r ib se conoce con el nombre de cociente de probabilidades. Mide el cociente entre la probabilidad de observar Xi si el agente ha eligido a y la probabilidad de observar Xi si el agente ha eligido b. Si el cociente de probabilidades es elevado, constituye una prueba de que el agente ha eligido a y si es bajo, induce a pensar que el agente ha elegido b. La aparición del cociente de probabilidades en la fórmula constituye un poderoso argumento para pensar que la elaboración del sistema óptimo de incentivos está estrechamente relacionada con los problemas estadísticos de inferencia, lo que sugiere que podemos utilizar las condiciones de regularidad de la teoría estadística para analizar la conducta de los sistemas óptimos. Por ejemplo, una condición utilizada frecuentemente, la propiedad del cociente de probabilidades monótono, exige que el cociente 1ria/1rib sea monótonamente decreciente con respecto a Xi· Si se satisface esta condición, entonces s(x¡) será una función monótonamente creciente de Acciones ocultas: la solución monopolística / 531 Véase Milgrom (1981) para los detalles. Lo que llama la atención de la ecuación (25.11) es lo sencillo que es el sistema óptimo de incentivos: es esencialmente una función lineal del cociente de probabilidades. Xi. Ejemplo: Estática comparativa Como siempre, es posible recabar alguna información sobre el sistema óptimo de incentivos examinando el lagrangiano de este problema. Según el teorema de la envolvente, la derivada de la función óptima de valor del principal con respecto a un parámetro del problema es exactamente igual a la derivada del lagrangiano con respecto al mismo parámetro. Por ejemplo, las derivadas del lagrangiano con respecto a Ca y cb son ac -=µ Be¿ ac - = -{,\+µ) (25.12) 8cb Estas derivadas pueden utilizarse para responder a una vieja pregunta: ¿qué es mejor?, ¿la zanahoria o el palo? Imaginemos que la zanahoria reduce el coste de la acción elegida b y que el palo incrementa el coste de la acción alternativa a en la misma magnitud. De acuerdo con las ecuaciones (25.12), una pequeña reducción del coste de la acción elegida siempre eleva la utilidad del principal en una cuantía mayor que un aumento de la misma magnitud del coste de la acción alternativa. De hecho, la zanahoria elimina dos restricciones, mientras que el palo elimina una solamente. Consideremos a continuación una variación de la distribución de probabilidades (d1ria). La influencia de esa variación en la utilidad del principal viene dada por n se = -µ ¿ u(si)d1ria. i=l Eso demuestra que cuando la restricción de la compatibilidad de los incentivos es efectiva, de tal manera queµ> O, los intereses del principal y del agente son diametralmente opuestos con respecto a las variaciones de la distribución de probabilidades de la acción alternativa: cualquier variación que mejore el bienestar del agente debe empeorar inequívocamente el del principal. 532 / LA INFORMACIÓN (C. 25) Ejemplo: Modelo del principal y el agente con una utilidad que sólo depende de la media y la varianza He aquí un sencillo ejemplo de un sistema de incentivos basado en Holmstróm y Milgrom (1987). Supongamos que la acción a representa el esfuerzo del agente y x = a + E es el nivel de producción observado por el principal. La variable aleatoria E sigue una distribución normal en la que la media es cero y la varianza a2. Supongamos que el sistema de incentivos elegido por el principal es lineal, de tal manera que s(x) = 8 + ,x = 8 +,a+ 1€. En este caso, 8 y I son los parámetros que han de determinarse. Dado que el principal es neutral ante el riesgo, su utilidad es E[x - s(x)] = E[a + E - 8 - ,a - 1€] = (1 - ,)a - 8. Supongamos que el agente tiene una función de utilidad correspondiente a una aversión absoluta al riesgo constante, u( w) = -e-rw, donde r es la aversión absoluta al riesgo y w es la riqueza. La riqueza del agente es simplemente s(x) = 8 + ,x. Dado que x sigue una distribución normal, también la seguirá la riqueza. En el capítulo 11 (página 222) vimos que en este caso la utilidad del agente depende linealmente de la media y la varianza de la riqueza. Por lo tanto, la utilidad del agente correspondiente al sistema de incentivos s(x) = 8 + ,x viene dada por ,2r 2 8+,a- -a. 2 El agente desea maximizar esta utilidad menos el coste del esfuerzo, c(a): ,2r max 8 + ,a - -a2 2 a - c(a). De esa manera, tenemos la condición de primer orden 1 = c'(a) (25.13) El problema de maximización del principal es determinar el 8 y el I óptimos, sujeta a la restricción de que el agente recibe un determinado nivel de reserva u y a la restricción de los incentivos (25.13). Este problema puede expresarse de la forma siguiente: max (1 - 1 )a - 8 6,"f,ª sujeta a 8 + ,a - 2 c'(a)=,. ,2r a2 - c(a) � u Acciones ocultas: el mercado competitivo / 533 Despejamos 8 en la primera restricción y, en la segunda e introducimos los resultados en la función objetivo. Tras algunas simplificaciones, tenemos que c'(a)2r max a - ---a 2 - c(a). a 2 Diferenciando, tenemos la condición de primer orden 1 - re' (a)c" (a)a2 - e' (a) = O. Despejando c'(a) =,,tenemos que 1 ,=----+ 1 rc"(a)a2 · Esta ecuación muestra las características esenciales de la solución. Si a2 = O, de tal manera que no hay riesgo alguno, tenemos que, = 1: el sistema óptimo de incentivos tiene la forma s = 8 + ii, Si a2 > O, tenemos que , < 1, por lo que cada uno de los agentes soporta parte del riesgo. Cuanto mayor es la incertidumbre o mayor la aversión del agente al riesgo, menor es,. 25.5 Acciones ocultas: el mercado competitivo ¿ Qué ocurre si hay muchos principales que compiten con respecto a la estructura de sus sistemas de incentivos? En este caso, podemos suponer que la competencia elimina totalmente los beneficios de los principales y que los contratos de equilibrio no deben generar ni pérdidas ni beneficios. En este caso, también es válida la figura 25.2, pero reinterpretamos simplemente los niveles de las líneas isobeneficio y las curvas de indiferencia. En condiciones competitivas, la restricción de la participación no es efectiva y la condición de beneficio nulo determina la línea isobeneficio del principal. Al igual que ocurre en el caso monopolístico, hay dos configuraciones posibles del equilibrio: seguro total o seguro parcial. En un contrato con seguro total, todos los trabajadores reciben una cantidad fija, independientemente de lo que produzcan. Responden realizando el menor esfuerzo posible. En el equilibrio con seguro parcial, los trabajadores reciben un salario que depende de su nivel de producción. Como soportan más riesgo, ponen un mayor empeño, para aumentar la probabilidad de que el nivel de producción sea mayor. Consideremos el caso del seguro parcial representado en la figura 25.3. Para que sea un equilibrio, no puede existir ningún otro contrato que reporte una mayor utilidad al agente y unos mayores beneficios a una empresa. Por construcción, no existe ningún contrato que consiga la acción b con estas propiedades; sin embargo, 534 / LA INFORMACIÓN (C. 25) puede haber uno que consiga la acción a y que se prefiera en el sentido de Pareto, es decir, un contrato que genere beneficios positivos y que sea preferido por los agentes. Para ver si existe ese contrato, trazamos la curva de indiferencia correspondiente a la acción a que pasa por el contrato con seguro parcial y por la curva de beneficio nulo correspondiente a dicha acción. Si la curva de beneficio nulo no corta el área preferida por el trabajador, como sucede en la figura 25.3A, el contrato con seguro parcial es un equilibrio. Si la corta, como sucede en la figura 25.3B, no puede ser un equilibrio, ya que alguna empresa podría ofrecer un contrato con seguro total que generara beneficios positivos y, aun así, resultara atractivo a los trabajadores que tuvieran un contrato con seguro parcial. En este caso, puede no existir un equilibrio. Figura25.3 45º 45° Curva de indiferencia, acción a Curva de indiferencia, acción a Curva de beneficio nulo, acción a Curva de beneficio nulo, acción a A B Contratos de equilibrio. En el panel A, el contrato con seguro parcial es un equilibrio; en el B no lo es, ya que la curva de beneficio nulo correspondiente a la acción a corta los conjuntos preferidos del agente. Ejemplo: El riesgo moral en los mercados de seguros En el contexto de un mercado de seguros, el problema del principal y el agente con acción oculta se conoce con el nombre de problema de riesgo moral. El "riesgo moral" se halla en que los compradores de pólizas de seguros no tienen el cuidado que deben tener. Examinemos este problema en el contexto del análisis del seguro que realizamos en el capítulo 11 (página 211). Supongamos que hay muchos consumidores idénticos que están considerando la posibilidad de asegurarse contra los robos de automóviles. Si a un consumidor le Información oculta: el monopolio / 535 roban el automóvil, soporta el coste L. Supongamos que el estado 1 es el estado de la naturaleza en el que le roban el automóvil al consumidor y que el estado 2 es el estado en que no se lo roban. La probabilidad de que se lo roben depende de lo que haga, por ejemplo, de que cierre o no el automóvil. Sea 1r1b la probabilidad de que se lo roben si se acuerda de cerrarlo y 1r1a la probabilidad de que se lo roben si se le olvida cerrarlo. Sea e el coste de recordar cerrar el automóvil y si la prima neta de seguro pagada por el consumidor a la empresa en el estado i. Finalmente, sea w la riqueza del consumidor. Suponiendo que la compañía de seguros quiere que el consumidor cierre el automóvil, el problema de incentivos es min 1r1bs1 + S¡ ,s2 1r2bs2 sujeta a 1r1bu(w - s1 - L) + 1r2bu(w - s2) - e 2: u 1r1bu(w - s1 - L) + 1r2bu(w - s2) - e 2: 1r1au(w - s1 - L) + 1r2au(w - s2). Si no existe ningún problema de incentivos, de tal manera que la probabilidad de que se produzca el robo es independiente de lo que haga el agente y si la competencia en el sector de seguros elimina totalmente los beneficios esperados, hemos visto en el capítulo 11 (página 211) que la solución óptima implica que s2 = s1 + L. Es decir, la compañía de seguros asegurará totalmente al consumidor, por lo que éste tendrá la misma riqueza independientemente de que le roben o no el automóvil. Cuando la probabilidad de la pérdida depende de lo que haga el agente, el seguro total ya no es óptimo. En general, el principal desea que el consumo del agente dependa de sus elecciones con el fin de que tenga incentivos para tener el debido cuidado. En este caso, se racionará la demanda de seguro por parte del consumidor. A éste le gustaría comprar más seguro a las primas actuarialmente justas, pero el sector no ofrecerá esos contratos, ya que eso induciría al consumidor a no tener el debido cuidado. En el caso competitivo, la restricción de la participación no es efectiva y el equilibrio viene determinado por la condición de beneficio nulo y el incentivo de la restricción de la compatibilidad: 1r1bs1 + 1r2bs2 =O 1r1bu(w - s1 - L) + 1r2bu(w - s2) - e= (25.14) 1r1au(w - sj - L)+1r2au(w - si) Estas dos ecuaciones determinan el equilibrio (sj, si). Como siempre, tenemos que asegurarnos de que no existe ningún contrato con seguro total que pueda romper este 536 / LA INFORMACIÓN (C. 25) equilibrio. Sin supuestos adicionales, puede muy bien existir ese tipo de contrato, por lo que en este modelo puede no haber equilibrio. 25.6 Información oculta: el monopolio A continuación analizamos el otro tipo de problema del principal y el agente, en el cual la información sobre las funciones de utilidad o de costes del agente no es observable. Suponemos para simplificar que sólo hay dos tipos de agentes que se distinguen por sus funciones de costes y que la acción de uno de ellos es la cantidad que produce. En el modelo del trabajador y el empresario antes analizado, ahora suponemos que la empresa observa perfectamente el nivel de producción, pero que a algunos trabajadores les cuesta más producir que a otros. La empresa puede observar perfectamente lo que hace un trabajador, pero no puede saber cuánto le cuesta hacerlo. Sean Xt y Ct(x) el nivel de producción y la función de costes de un agente de tipo t. Supongamos, para concretar, que el agente 2 es el agente de elevado coste, de tal manera que c2 (x) > c1 (x), cualquiera que sea x. Supongamos que s(x) es la retribución en función del nivel de producción y que la función de utilidad del agente t tiene la forma siguiente: s(x) - Ct(x). El principal no está seguro del tipo al que pertenece el agente, pero cree que hay una probabilidad de 1r t de que sea del tipo t. Como siempre, cada uno de los agentes debe recibir, al menos, su nivel de utilidad de reserva, que suponemos para simplificar que es cero. Será útil postular otro supuesto más sobre las funciones de costes, a saber, que el agente cuyos costes totales son más altos también es el agente cuyos costes marginales son más altos; es decir, que c2(x) > ci (x), cualquiera que sea x. Esta propiedad se denomina a veces propiedad de la intersección única, ya que implica que cualquier curva de indiferencia de un agente del tipo 1 corta a cualquier curva de indiferencia de un agente del tipo 2 como máximo una sola vez. Observamos el sencillo hecho siguiente, que pedimos al lector que demuestre en un ejercicio: Propiedad de la intersección única. Supongamos que c2(x) > ci (x), cualquiera que sea x. De este supuesto se deduce que, dados dos niveles distintos de producción x1 y x2, siendo x2 > x1, debe cumplirse que c2(x2) - c2(x1) > c1 (x2) - ci (x1). Resulta útil preguntarse cómo sería el sistema óptimo de incentivos si el principal pudiera observar las funciones de costes. En este caso, el principal dispondría de una información completa, por lo que la solución sería esencialmente la del caso del nivel de producción fijado como objetivo que hemos analizado antes. El principal maximizaría simplemente el nivel total de producción menos el coste total x1 + x2 - ci (x1) - c2Cr2). La solución exige que c�(x;) = 1, siendo t = 1, 2. En ese Información oculta: el monopolio / 537 caso, el principal pagaría a cada agente una cantidad que satisfaría exactamente la utilidad de reserva de ese agente, por lo que St - Ct(x;) = O. La figura 25.4 muestra este caso. El eje de ordenadas representa el coste marginal donde c�(x;) = 1. y el de abscisas el nivel de producción. El agente t produce Un principal que fuera capaz de discriminar perfectamente entre los dos agentes exigiría simplemente al agente t que produjera la cantidad presentándole un sistema de objetivos referentes al nivel de producción como el que hemos esbozado anteriormente; es decir, el agente t recibiría una retribución tal que St(x*) = Ct(x;) y St(x) < Ct(x) en el caso de todos los demás valores de x. x;, x; Figura 25.4 COSTE MARGINAL NIVEL DE PRODUCCION El problema del principal y el agente con información oculta. En el mejor sistema posible, el agente 1 produce y el 2 produce 2. x; x Eso significaría que a cada agente se le extraería su excedente total, lo que en términos gráficos quiere decir que el agente 1 recibiría la cantidad A + B, que es exactamente igual a su coste total de producción; del mismo modo, el agente 2 recibiría A + D, que es igual a su coste total. El problema de este sistema se halla en que no satisface la compatibilidad de los incentivos. Si el agente de elevado coste se limita a satisfacer su restricción de la participación, el agente de bajo coste preferirá necesariamente (si, xj) a (s2, xi). En símbolos, s2 - ci (xi) > ei - c2(xi) =O= s1 - c1 (xj) ya que ci (x) < c2(x), cualquiera que sea x. En términos gráficos, el agente de bajo coste podría pretender ser el agente de elevado coste y producir xi solamente. De esa manera le quedaría un excedente de D. 538 / LA INFORMACIÓN (C. 25) Una de las soluciones de este problema consiste simplemente en modificar la retribución. Supongamos que pagamos A si el nivel de producción es xi y A+ D si es xi. De esa manera el agente de bajo coste obtiene un excedente neto de D, lo que lo lleva a mostrarse indiferente entre producir xi y xi. Este plan es viable, desde luego, pero ¿es óptimo desde el punto de vista del principal? La respuesta es negativa por una interesante razón. Supongamos que reducimos algo el nivel de producción que fijamos como objetivo para el agente de elevado coste. Dado que se encuentra en el punto en el que el precio es igual al coste marginal, sólo hay una reducción de los beneficios de primer orden: la reducción del nivel de producción obtenido es contrarrestada exactamente por la reducción de la cantidad que tenemos que pagar al agente 2. Figura 25.5 COSTE MARGINAL A NIVEL DE PRODUCCION Cómo obtener más beneficios. Reduciendo en una pequeña cuantía el nivel de producción fijado corno objetivo para el agente cuyo coste es alto, el principal puede obtener más beneficios. Pero como x2 y el área D son pequeños, el excedente que obtendría el agente de bajo coste por producir x2 ahora es menor. Al hacer que el agente de elevado coste produzca menos y al pagarle menos, hacemos que este nivel de producción fijado como objetivo sea menos atractivo para el agente de bajo coste. Esta situación se debe a algo más que a un efecto de primer orden, ya que el agente de bajo coste se encuentra en un punto en el que el coste marginal es menor que 1. La figura 25.5 muestra este caso. Una reducción del nivel de producción fijado como objetivo para el agente de elevado coste reduce los beneficios que genera éste en Información oculta: el monopolio / 539 el área 6.C, pero eleva los beneficios generados por el agente de bajo coste en el área 6.D. Por lo tanto, al principal le resultaría rentable reducir el nivel de producción fijado como objetivo para el agente de elevado coste en una cantidad inferior al nivel eficiente. Al pagarle menos a este agente, el principal reduciría la cantidad que tendría que pagar al agente de bajo coste. Para analizar mejor la estructura del sistema de incentivos, resulta útil formular el problema algebraicamente. Como indica el análisis geométrico, el problema básico de incentivos se halla en que el agente de bajo coste puede tratar de "fingir" que él es el agente de elevado coste. Si XI es el nivel de producción que se supone que elige el agente 1, el principal debe estructurar el plan retributivo de tal manera que la utilidad que le reporte a este agente la elección de XI sea mayor que la utilidad que le reporta x2, y lo mismo en el caso del agente 2. Estas condiciones son simplemente una forma especial de las condiciones de compatibilidad de los incentivos que se denominan restricciones de la autoselección en este contexto. Dadas estas observaciones, podemos formular el problema de optimización del principal: x1,x2,s1,s2 sujeta a SI - CI (xI) � O (25.15) s2 - c2(x2) � O (25.16) SI - ci (xI) � s2 - CI (x2) (25.17) s2 - c2(x2) � SI - c2(xI) (25.18) Las dos primeras restricciones son las restricciones de la participación. Las dos segundas son las restricciones de la compatibilidad de los incentivos o de la autoselección. El plan óptimo de incentivos (xj, sj, xi, si) es la solución de este problema de maximización. La primera observación sobre este problema proviene de la reordenación de las restricciones de la autoselección: s2 � SI+ ci (x2) - ci (xI) (25.19) s2 � SI + c2(x2) - c2(xI) (25.20) Estas restricciones indican que si se satisfacen las restricciones de la autoselección, (25.21) 540 / LA INFORMACIÓN (C. 25) La condición de la intersección única implica que el agente 2 tiene en todos los puntos un coste marginal más alto que el agente 1. Si x2 > x1, eso contradice la desigualdad (25.21). Por lo tanto, en la solución óptima debe cumplirse que x2 � x1, lo que significa que el agente de bajo coste produce, al menos, tanto como el agente de elevado coste. Examinemos ahora las restricciones (25.15) y (25.17). Éstas pueden reformularse de la manera siguiente: (25.15') s1 � cr (x1) s1 � ci (x1) + [s2 - ci (x2)] (25.17') Dado que el principal quiere que s1 sea lo menor posible, debe ser efectiva al menos una de estas dos restricciones. A partir de la restricción (25.16) y de las propiedades de la función de costes, vemos que Por lo tanto, la expresión entre corchetes de la ecuación (25.17') es positiva y (25.15') no puede ser efectiva. En consecuencia, (25.22) De la misma manera, será efectiva exactamente una de las restricciones (25.16) y (25.18). ¿Cabe la posibilidad de que (25.18) se satisfaga como una igualdad? En este caso, podemos introducir la ecuación (25.22) en la (25.18) y obtener Reordenando, tenemos que lo que viola la condición de la intersección única. Por lo tanto, la política óptima debe implicar que (25.23) Sin llegar a examinar el problema de optimización, vemos que el carácter de las restricciones y la función objetivo sientan dos importantes propiedades: el agente de elevado coste recibe una retribución que le lleva a mostrarse indiferente entre participar o no y el agente de bajo coste recibe un excedente, que es exactamente la cantidad necesaria para disuadirlo de fingir ser el agente de coste elevado. Información oculta: el monopolio / 541 Figura 25.6 COSTE MARGINAL x; NIVEL DE PRODUCCION Contratos óptimos. El agente cuyo coste es alto produce en el punto x2 y el agente cuyo coste es bajo en el punto x;. El primero recibe la cantidad A+ D y el segundo la cantidad A + B + D. Para determinar las acciones óptimas, sustituimos s1 y s2 por el valor que tienen en (25.22)-(25.23) y expresamos el problema de maximización del principal de la forma siguiente: max 7fJ [x1 - c1 (x1) - c2(x2) + c1 (x2)] + 1r2[x2 - c2(x2)]. x1,x2 Las condiciones de primer orden de este problema son 1r1[1- ci(x1)l =O 1r1 [ci (x2) - c2(x2)] + 1r2[1 - c2(x2)] = O. Estas condiciones pueden reformularse de la manera siguiente: ci(xj) = 1 [ci (x2) - c2(x2)] 2) = 1 + 1ri 1r2 c2(x (25.24) La primera ecuación implica que el agente de bajo coste produce la misma cantidad que produciría si su tipo fuera el único que existiera; es decir, el nivel de producción eficiente en el sentido de Pareto. Dada la propiedad de la intersección única, el agente de elevado coste produce una cantidad menor que la que produciría si fuera el único agente, ya que c2(x2) - cj(x2) > O. 542 / LA INFORMACIÓN (C. 25) Para representar estas condiciones gráficamente, supongamos a fin de simEn ese caso, la segunda ecuación de (25.24) implica que plificar que 1r1 = 1r2 = 2ci (x2) = c;(x2). En este punto, los beneficios marginales de reducir algo x2 son exactamente iguales a los costes marginales. La figura 25.6 muestra la solución óptima. El agente de bajo coste produce en el punto en el que los beneficios marginales son iguales al coste marginal; el agente de bajo coste produce en un punto en el que es indiferente entre la cantidad que cobra y la que constituye el objetivo del otro agente. El agente de elevado coste recibe la cantidad A + D que extrae todo su excedente; el agente de bajo coste recibe la cantidad A + B + D que le disuade de fingir ser el agente de elevado coste. La figura 25.7 muestra otra representación del contrato correspondiente al sistema óptimo de incentivos. En este gráfico representamos los contratos en el espacio (s, x). Un trabajador de tipo t tiene una función de utilidad de la forma u¿ = St-Ct(Xt). Por lo tanto, sus curvas de indiferencia tienen la forma s¡ = u¿ + Ct(Xt). De acuerdo con la propiedad de la intersección única, las curvas de indiferencia del agente de elevado coste siempre son más inclinadas que las de los agentes de bajo coste. Sabemos que en condiciones de equilibrio el trabajador de elevado coste recibe su nivel de utilidad de reserva, que es igual a cero. Con ello se mantiene la curva de indiferencia y todos los contratos de incentivos (s2, x2) correspondientes a este trabajador deben encontrarse en la curva de indiferencia correspondiente a un nivel de utilidad igual a cero. El beneficio que obtiene la empresa por un trabajador de tipo tes P¡ = x¡ - si, Por lo tanto, las líneas isobeneficio tienen la forma s¡ = Xt - Pt. Son líneas rectas paralelas que tienen una pendiente de + 1 y una ordenada en el origen de - Pi. Los beneficios totales de la empresa son 1r1P1 + 1r2P2. Obsérvese que los beneficios aumentan a medida que la recta de los beneficios se desplaza en sentido descendente y hacia el sureste y la utilidad del agente aumenta a medida que las curvas de indiferencia se desplazan en sentido ascendente y hacia el noroeste. Sabemos por las condiciones (25.24) que el trabajador de bajo coste debe satisfacer la condición de que ci (x1) = 1. Eso significa que la función isobeneficio debe ser tangente a la curva de indiferencia de dicho agente. También sabemos que c;(x2) < 1, por lo que la recta isobeneficio corta a la curva de indiferencia del trabajador de elevado coste. Si no estuviera presente el trabajador de bajo coste, el principal querría que el trabajador de elevado coste trabajara más y éste también querría trabajar más. El área sombreada de la figura 25.7 muestra la región en la que tanto el trabajador de elevado coste como el principal podrían disfrutar de un mayor bienestar. Pero como está presente, el aumento del nivel de producción del trabajador de elevado coste eleva la cantidad que ha de pagar la empresa a aquel trabajador. En condiciones de equilibrio, las ganancias que se obtienen elevando P2 al reducir x2 y s2 se ven contrarrestadas por la reducción de Pi. !. El equilibrio del mercado: información oculta / 543 Figura25.7 X Contratos correspondientes al sistema óptimo de incentivos. Los beneficios de la empresa son 1qP1 + 1r2P2. El área sombreada representa el uso ineficiente del trabajador cuyo coste es alto provocado por las restricciones de la autoselección. Es esta externalidad negativa entre el trabajador de elevado coste y el trabajador de bajo coste la que conduce a un equilibrio ineficiente. Si el monopolista pudiera discriminar y ofrecer a cada tipo de trabajador un salario distinto, el resultado sería totalmente eficiente. Este caso es análogo al de la discriminación de precios de segundo grado analizado en el capítulo 14 (página 287). En ese modelo, si sólo hay un tipo de consumidor, el monopolista practica la discriminación perfecta de precios y presenta una oferta del tipo "o lo tomas o lo dejas". Pero si hay varios tipos de consumidores, el intento de practicar la discriminación de precios suele dar lugar a resultados ineficientes. 25.7 El equilibrio del mercado: información oculta El equilibrio competitivo puede analizarse como siempre añadiendo una condición de beneficio nulo al modelo y reinterpretando las utilidades de reserva. A medida que entran más empresas en el mercado, presionan al alza sobre los salarios de los trabajadores y reducen los beneficios de la empresa representativa. En el problema 544 / LA INFORMACIÓN (C. 25) del monopolio, los precios de reserva determinan el nivel de beneficios; en el equilibrio competitivo, la condición de beneficio nulo determina las utilidades de los trabajadores. Esta diferencia puede observarse en la figura 25.7. En el monopolio, la curva de indiferencia del agente cuyo coste es elevado determina los beneficios de la empresa, 1r1Pi + 1r2P2. En condiciones competitivas, los beneficios de la empresa son nulos y los agentes se desplazan a curvas de indiferencia más altas. En este apartado sólo examinamos los equilibrios simétricos, en los cuales todas las empresas ofrecen el mismo conjunto de contratos. Parece que hay varias posibilidades de que exista un equilibrio. (a) La empresa representativa ofrece un único contrato que atrae a los dos tipos de trabajadores. (b) La empresa representativa ofrece un único contrato que atrae solamente a un tipo de trabajador. (e) La empresa representativa ofrece dos contratos, uno a cada tipo de trabajador. El caso en el que los dos tipos de trabajadores aceptan un único contrato seconoce con el nombre de equilibrio aunador. El otro caso, en el que los diferentes tipos de trabajadores aceptan contratos diferentes, se denomina equilibrio separador. En la figura 25.8 mostramos algunas configuraciones posibles del equilibrio. No es difícil ver que ofrecer solamente un tipo de contrato no puede ser un equilibrio, pues ello excluye el equilibrio aunador de tipo (a) o el separador de tipo (b). Si la empresa representativa está obteniendo un beneficio nulo, debe encontrarse en la recta de 45° de la figura 25.8A. Si sólo ofrece un contrato, como el (s", x*), éste debe ser óptimo para uno de los dos tipos; supongamos que es óptimo para el tipo de bajo coste. En ese caso, una empresa que no siguiera la norma podría ofrecer un contrato en el área sombreada que fuera preferido por el tipo de coste elevado y obtener unos beneficios positivos. El razonamiento es similar si el contrato es óptimo para el tipo de elevado coste. Por lo tanto, en la medida en que los dos agentes reciban, al menos, su nivel de utilidad de reserva, el único equilibrio posible en este modelo es el equilibrio separador representado en la figura 25.88. La empresa paga a cada trabajador todo el valor de su nivel de producción y obtiene un beneficio nulo. El equilibrio del mercado: información oculta / 545 Figura 25.8 s s X A B X Configuraciones posibles del equilibrio. El panel A no puede ser un equilibrio de acuerdo con los argumentos expuestos en este capítulo. La única posibilidad es el caso B, en el que cada trabajador recibe su producto marginal. Ejemplo: Un ejemplo algebraico Resulta útil exponer algebraicamente las diferencias entre el modelo del monopolio y el modelo competitivo con información oculta. Supongamos que Ct(Xt) = txU2 En ese caso, la solución óptima para el monopolista viene determiy 1r1 = 1r2 = nada por las ecuaciones (25.22), (25.23) y (25.24). El lector debe verificar que estas ecuaciones tienen la siguiente solución: !· xi= 1 xi = 1/3 si = 5/9 si = 1/9. Los beneficios del monopolista son �[xi - si]+ 2 �[xi - si]= �2[4/9] + �2[2/9] = 1/3. 2 546 / LA INFORMACIÓN (C. 25) En el modelo del monopolio, el trabajador de elevado coste recibe exactamente su nivel de utilidad de reserva, que es cero. En el modelo competitivo, la utilidad que reciben los agentes aumenta conforme las empresas presionan al alza sobre los salarios. Hemos visto que el equilibrio competitivo implica un salario lineal, por lo que un trabajador de tipo t desea maximizar x¡ - Ct(Xt). Por lo tanto, tenemos que x1 = 1 y x2 = 1 /2. La empresa obtiene un beneficio nulo, por lo que debe cumplirse que s1 = x1 = 1 y que s2 = x2 = 1 /2. El agente de bajo coste tiene un excedente de 1 /2 y el agente de elevado coste tiene un excedente de 1 / 4. Figura25.9 s X El aunamiento no puede ser un equilibrio. Si sólo se ofrece un contrato, éste debe encontrarse en la recta de beneficio nulo. Trácense las curvas de indiferencia que pasan por un contrato de ese tipo y obsérvese que como los trabajadores menos productivos tienen curvas de indiferencia más inclinadas, siempre es posible encontrar un contrato en el área sombreada que atraiga solamente a los trabajadores de elevada productividad y obtener así un beneficio positivo. 25.8 La selección adversa Examinemos una variante del modelo descrito en el apartado anterior. Supongamos que los trabajadores no sólo tienen funciones de costes diferentes sino también productividades diferentes. Los trabajadores de elevado coste producen v2x2 unidades La selección adversa / 547 de producción y los de bajo coste v1 x1. Suponemos que v1 > v2, por lo que los trabajadores de bajo coste son atractivos por dos razones: son más productivos y tienen un coste más bajo. ¿Cómo son ahora los contratos salariales de equilibrio? Al igual que en el apartado anterior, hay dos posibilidades lógicas para que exista un equilibrio simétrico. O bien todas las empresas ofrecen un único contrato (s", x*) a todos los trabajadores, o bien todas las empresas ofrecen dos contratos (sj, xj), (si, xi). Si sólo ofrecen un único contrato, decimos que este equilibrio es aunador y si ofrecen dos tipos, decimos que es un equilibrio separador. Examinemos, en primer lugar, el equilibrio aunador. En este caso, todos los trabajadores reciben la misma retribución, aunque unos sean más productivos que otros. Dado que los beneficios globales son nulos, la empresa debe obtener beneficios positivos en el caso de los trabajadores de bajo coste y negativos en el de los trabajadores de elevado coste. El valor total de la producción obtenida, (1r1 v1 + 1r2v2)x*, es igual al coste total, 1r1s* + 1r2s* = s", Por lo tanto, (s", x*) debe encontrarse en la línea recta s = (1r1 v1 + 1r2v2)x, cuya pendiente es la media ponderada de las productividades de los dos tipos de agentes, como muestra la figura 25.9. El equilibrio aunador propuesto es un punto de esta línea. Trácese en cualquier punto las curvas de indiferencia de los dos tipos de agente que pasan por él. Por hipótesis, la curva de indiferencia del agente más productivo es más plana que la del menos productivo, lo que significa que hay algún contrato en el área sombreada que es mejor para los agentes de elevada productividad y peor para los de baja productividad. Por lo tanto, una empresa que no siguiera la norma podría ofrecer un contrato de ese tipo y atraer solamente a los agentes de elevada productividad, obteniendo así un beneficio positivo. Dado que este razonamiento puede realizarse en cualquier punto de la recta de beneficio nulo, no existe ningún equilibrio aunador. La otra posibilidad es un equilibrio separador con dos contratos. La figura 25.10 muestra un ejemplo tanto de contratos eficientes como de contratos de equilibrio. Los contratos (sj, xj) y (si, xi) son los contratos eficientes (con información completa), pero no satisfacen las restricciones de la autoselección: los agentes de baja productividad prefieren el contrato pensado para el agente de elevada productividad. Una empresa podría ofrecer (si, xi) con la esperanza de atraer solamente a los trabajadores de bajo coste y elevada productividad. Pero esta empresa se encontraría con un problema de selección adversa, es decir, este contrato resultaría atractivo a los dos tipos de trabajadores. La solución de este problema de selección adversa consiste en desplazar en sentido ascendente la recta de beneficio nulo correspondiente a los trabajadores de elevada productividad a un punto como el (sí, xí ). Ahora (sí, xí) y (si, xi) es una configuración de los contratos de equilibrio: el agente de baja productividad se muestra indiferente entre su contrato y el del agente de elevada productividad. Los 548 / LA INFORMACIÓN ( C. 25) puntos situados encima de la curva de indiferencia de cualquiera de los dos agentes no son rentables para las empresas, por lo que tenemos un equilibrio. Figura 25.10 s C1(X) X Equilibrio separador. Los contratos (s;, x;) y (si, xi) son eficientes, pero no satisfacen las restricciones de la autoselección. Los contratos (si, xi) y (s�, x�) sí las satisfacen. Sin embargo, también puede ocurrir que no exista ningún equilibrio. Obsérvese que la curva de indiferencia que pasa por (sí, xí) debe cortar por construcción a la recta de beneficio nulo. Por lo tanto, habrá algún área como la región sombreada de la figura 25.10 que sea preferida tanto por la empresa como por los trabajadores de elevada productividad. En esta área no se ofrece ningún contrato, ya que atraería también a los trabajadores de baja productividad, por lo que no sería rentable: sabemos que este tipo de contratos no es rentable, ya que la recta de beneficio nulo de la figura 25.10 correspondiente a los trabajadores aunados se encuentra por debajo del área sombreada. Pero supongamos que hubiera muchos trabajadores de elevada productividad, de tal manera que la rectas = 1r1 v1 + 1r2v2 cortara al área sombreada. En este caso, El mercado de "cacharros" y la selección adversa / 549 sería rentable ofrecer un contrato aunado en esta área. Por lo tanto, podría romperse el equilibrio separador propuesto y no haber ningún equilibrio. 2 25.9 El mercado de "cacharros" y la selección adversa He aquí otro modelo que muestra la posibilidad de que no exista equilibrio en los problemas con información oculta debido a la selección adversa. Examinemos el mercado de automóviles usados. El dueño de un automóvil probablemente posee mejor información sobre su calidad que sus posibles compradores. En la medida en que éstos se den cuenta de ello, pueden mostrarse reacios a comprar un producto puesto en venta, porque teman (con razón) quedarse colgados con un "cacharro". Si este automóvil es bueno, ¿por qué lo venden?, pueden preguntarse los compradores. Por lo tanto, el mercado de automóviles usados puede ser muy limitado a pesar de la presencia de numerosos compradores y vendedores potenciales. Esta sencilla idea intuitiva fue formalizada por Akerlof (1970) de una manera sorprendente en su mercado de "cacharros". Supongamos que podemos medir la calidad de un automóvil usado mediante un número q, que sigue una distribución uniforme en el intervalo [O, 1]. Debe señalarse, de cara al análisis posterior, que si q sigue una distribución uniforme en el intervalo [O, b], el valor medio de q es b/2. Por lo tanto, la calidad media existente en el mercado es 1 /2. Existe un elevado número de demandantes de automóviles usados que están dispuestos a pagar � q por un automóvil de la calidad q y hay un gran número de vendedores, cada uno de los cuales está dispuesto a vender un automóvil de la calidad q por el precio q. Por lo tanto, si la calidad fuera observable, cada automóvil usado de calidad q se vendería a un precio situado entre �q y q. Supongamos, sin embargo, que no es posible observar la calidad. En ese caso, lo sensato para los compradores de automóviles usados es intentar estimar la calidad de uno específico considerando la calidad media de los automóviles ofrecidos en el mercado. Suponemos que es posible observar la calidad media, aunque no es posible observar la calidad de un determinado automóvil. Por lo tanto, la disposición a pagar por un automóvil usado es �q. ¿Cuál será el precio de equilibrio en es�e mercado? Supongamos que el precio de equilibrio es un número p > O. En ese caso, todos los propietarios de automóviles cuya calidad sea inferior a p querrán poner a la venta su automóvil, ya que para esos propietarios p es mayor que su precio de reserva. Dado que la calidad sigue una distribución uniforme en el intervalo [O, p], la calidad media de un automóvil puesto 2 Es decir, no existe ningún equilibrio correspondiente a las estrategias puras; pueden existir equilibrios correspondientes a estrategias mixtas. 550 / LA INFORMACIÓN (C. 25) a la venta será ij_ = p /2. Introduciendo este resultado en la fórmula del precio de reserva de un comprador, vemos que éste estaría dispuesto a pagar �ij_ = �; = Esta cantidad es menor que p, que es el precio al que suponemos que se vendería un automóvil usado. Por lo tanto, al precio p no se venderá ningún automóvil. Dado que este precio es arbitrario, hemos demostrado que no se venderá ningún automóvil usado a un precio positivo cualquiera. El único precio de equilibrio en este mercado es p = O. A este precio, la demanda es nula y la oferta es nula: la información asimétrica entre los compradores y los vendedores ha destruido el mercado de automóviles usados. ¡p. Cualquier precio que sea atractivo para los propietarios de automóviles buenos será aun más atractivo para los propietarios de "cacharros". La selección de automóviles que se ponen a la venta en el mercado no es una selección representativa, sino que está sesgada en favor de los "cacharros". Se trata de otro ejemplo de selección adversa. 25.10 Las señales En el apartado anterior hemos indicado que los problemas en los que hay información oculta podían dar lugar a equilibrios con selección adversa. En el mercado de "cacharros" apenas se realizan intercambios porque los bienes de elevada calidad no pueden distinguirse fácilmente de los bienes de mala calidad. En el mercado de trabajo, el conjunto eficiente de contratos no es viable porque los trabajadores de baja productividad querrían elegir el contrato apropiado para los trabajadores de elevada productividad. En el mercado de "cacharros", a los vendedores de automóviles buenos les gustaría señalar que están ofreciendo un automóvil bueno y no un "cacharro". Una posibilidad consiste en ofrecer una garantía, en la que se especifique que se cubrirán todos los costes de las averías sufridas durante un determinado periodo de tiempo. Los vendedores de los automóviles buenos se comprometerían, de hecho, a asegurar a sus compradores. Para que la señal sea compatible con el equilibrio, los dueños de automóviles buenos deben poder ofrecerla y los de "cacharros" no. Esa señal permitiría a los primeros "demostrar" a los posibles compradores que tienen realmente un automóvil bueno. El ofrecimiento de una garantía es costoso para los vendedores de "cacharros", pero no mucho para los vendedores de automóviles buenos, por lo que esta señal permite a los compradores discriminar entre los dos tipos de automóviles. En este caso, la presencia de una señal permite que el mercado funcione más eficazmente que en caso contrario, aunque no tiene por qué ser siempre así, como en seguida veremos. La educación como señal/ 551 25.11 La educación como señal Volvamos al ejemplo del mercado de trabajo, en el que hay dos tipos de trabajadores cuya productividad es v2 y v1, respectivamente. Supongamos que las horas trabajadas por cada uno son fijas. Si no es posible discriminar entre los más productivos y los menos productivos, en el equilibrio competitivo los trabajadores recibirán simplemente la media de sus productividades, es decir, el salario Los trabajadores más productivos ganan un salario inferior a su producto marginal y los menos productivos ganan un salario superior a su producto marginal. A los primeros les gustaría poder señalar que son más productivos que los demás. Supongamos que hay alguna señal que es más fácil de adquirir por los trabajadores más productivos que por los menos productivos. Un buen ejemplo es el de la educación: es razonable pensar que para los trabajadores más productivos es más barato adquirir educación que para los menos productivos. Supongamos, para ser explícitos, que el coste de adquirir e años de educación es c2e para los trabajadores más productivos y cj e para los menos productivos y que c1 > czSupongamos que la educación no influye en la productividad. Sin embargo, a las empresas puede seguir resultándoles rentable basar los salarios en la educación, ya que pueden atraer trabajadores de mayor calidad. Supongamos que los trabajadores creen que las empresas pagarán el salario s(e), dondes es una función creciente de e. Un equilibrio con señales será un perfil salarial estimado por los trabajadores que se ve confirmado, de hecho, por la conducta de las empresas. Sean e1 y e2 los niveles de educación elegidos realmente por los trabajadores. En ese caso, un equilibrio separador con señales tiene que satisfacer las condiciones de beneficio nulo s(e1) = v1 s(e2) = v2, y las condiciones de autoselección s(e1) - ci e1 s(e2) - c2e2 2: 2: s(e2) - ci e2 s(e1) - c2e1. En general, puede haber muchas funciones Nos limitaremos a mostrar una de ellas. s(e) que satisfagan estas condiciones. 552 / LA INFORMACIÓN (C. 25) Sea e" un número tal que v2 - v1 * v2 - v1 --->e>---. C2 CJ Supongamos que la función de salarios estimada por los trabajadores es s(e) = { v2 v1 s�endo e > e* siendo e :::; e". Es trivial demostrar que satisface las restricciones de la autoselección y, por lo tanto, es un perfil salarial coherente con el equilibrio. Obsérvese que este equilibrio con señales es despilfarrador desde el punto de vista social. La educación no genera ninguna ganancia social, ya que no altera la productividad. Su único papel consiste en distinguir a los trabajadores más productivos de los menos productivos. Notas El caso de las dos acciones que hemos analizado anteriormente es sencillo, pero contiene una gran parte de las ideas presentes en el caso en el que hay numerosas acciones. Para un análisis panorámico de esta y otras cuestiones en la literatura del principal y el agente, véase Hart y Holmstrom (1987). Spence (1974) fue quien introdujo por primera vez las señales en la economía. Akerlof (1970) fue el primero en examinar el mercado de "cacharros". Véase Rothschild y Stiglitz (1976) para un modelo de equilibrio de mercado con selección adversa, y Kreps (1990) para un análisis más detallado del equilibrio en los modelos en los que hay información asimétrica. Ejercicios 25.1. Considere el problema del principal y el agente con acción oculta descrito en este capítulo y suponga que f = u-1• Suponga que u(s) es creciente y cóncava y demuestre que f es una función creciente y convexa. 25.2. Sea V(ca, cb) la utilidad que reporta al principal el sistema óptimo de incentivos cuando los costes de las acciones a y b son Ca y es, respectivamente. Obtenga una expresión de av/ Be¿ y av/ acb en función de los parámetros que aparecen en la condición fundamental y utilice estas expresiones para interpretarlos. 25.3. Suponga que Ca = ci: ¿Qué forma adoptaría el sistema óptimo de incentivos? Ejercicios / 553 25.4. Suponga que en el problema del principal y el agente cb disminuye mientras que todos los demás parámetros permanecen constantes. Demuestre que el agente debe disfrutar, al menos, del mismo bienestar. 25.5. Suponga que en el problema del principal y el agente con acción oculta el agente es neutral ante el riesgo. Demuestre que puede alcanzarse el resultado que constituye el mejor óptimo posible. 25.6. Considere la versión del problema de la información oculta correspondiente al monopolio. Suponga que los dos agentes tienen la misma función de costes y unos niveles de utilidad de reserva diferentes. ¿En qué varía el análisis? 25.7. Demuestre la siguiente implicación de la propiedad de la intersección única: si c;(x) > cí (x) cualquiera que sea x, entonces dados dos niveles cualesquiera de producción, x1 y x2 y siendo x2 > x1, debe cumplirse que c2(x2) - c2(x1) > c1 (x2) ci(x1). 25.8. En este capítulo hemos afirmado que si c2(x) > c1 (x) y c;(x) > cí (x), entonces dos curvas cualesquiera de indiferencia de un agente de tipo 1 y de un agente de tipo 2 se cortarían como máximo una vez. Demuéstrelo. 25.9. Considere el equilibrio competitivo en el modelo con información oculta descrito en este capítulo. Si la utilidad de reserva de los agentes de elevado coste es suficientemente elevada, puede existir un equilibrio en el que sólo se dé trabajo a los agentes de bajo coste. ¿Qué valores ha de tener ü2 para que ocurra eso? 25.10. El profesor P ha contratado un ayudante, don A. Le preocupan las horas que enseñará don A y lo que tendrá que pagarle. Desea maximizar su función de ganancias, x - s, donde x es el número de horas que enseña don A y s son los salarios totales que le paga. Si don A enseña x horas y gana s, su utilidad es s - c(x)