FORMULAS - CONTEO DE FIGURAS

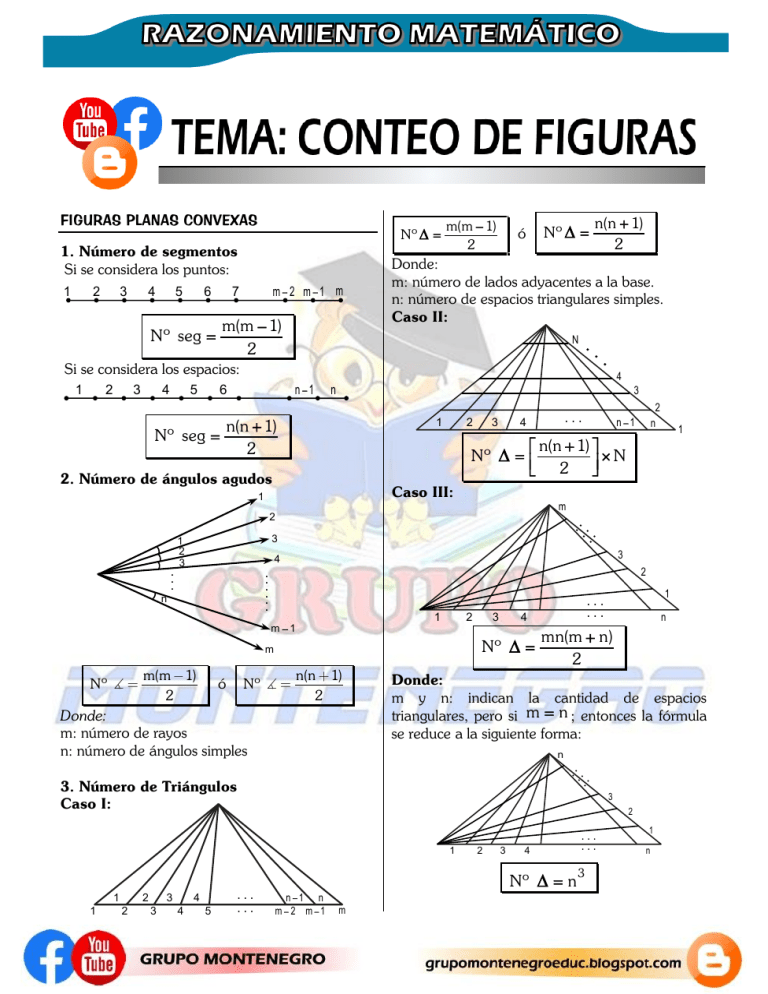
FIGURAS PLANAS CONVEXAS
Nº ∆ =
1. Número de segmentos
Si se considera los puntos:
1
4
3
2
5
Nº seg =
m− 2 m−1 m
7
6
m(m − 1)
2
m(m − 1)
2
ó
Nº ∆ =
Donde:
m: número de lados adyacentes a la base.
n: número de espacios triangulares simples.
Caso II:
N
..
.
Si se considera los espacios:
1
3
2
5
4
6
n−1
1
2
Caso III:
1
m
2
n
3
ó
Nº  
2
1
Nº ∆ =
n(n  1)
2
1
2
3
4
4
5
1
n
mn(m + n)
2
Donde:
m y n: indican la cantidad de espacios
triangulares, pero si m = n ; entonces la fórmula
se reduce a la siguiente forma:
n
. .. .
..
3
2
1
3
..
...
...
4
3
3. Número de Triángulos
Caso I:
2
. .. .
2
Donde:
m: número de rayos
n: número de ángulos simples
1
...
...
1
3
m−1
m(m  1)
2
2
n
n−1
4
..
..
..
m
Nº  
...
4
3
3
 n(n + 1) 
=
×N
Nº ∆ 
 2 
2. Número de ángulos agudos
..
.
4
n
n(n + 1)
Nº seg =
2
1
2
3
n(n + 1)
2
n−1 n
m− 2 m−1
2
3
4
Nº ∆ = n
m
...
...
3
1
n
Caso IV:
n
n−1
n
n−1
.
.
.
..
.
 n(n  1)  m(m  1)
Nº
2
5. Número de Cuadrados
1
Nº ∆ =
n
n(n + 1)(n + 2)
3
Nº


..
. n
Caso I:
3
1
2
2
3
1
Nº ∆ =
n(n + 1)(n + 2)
6
1 2
Caso I:
1
3
4 . .. n
Nº
=
n(n + 1)
2
2
2
1
2
3
..
.
3
Nº= n(n + 1)
4
.
.
.
n
n−1
n
Nº
7. Número de sectores circulares
 n(n  1)
2
Caso I:
Caso II:
2
3
4
..
.
4 . .. n
Caso II:
4. Número de Cuadriláteros
n−1
n
n(n  1)(2n  1)
6
6. Número de Triángulos Rectángulos
Caso IV:
1
2
3
..
.
4 . .. n
4
..
.
1
1
3
3
2
2
2
2
3
3
2
3
4
...
m
1
2
3
.
.
.
n
Nº sect. =
n(n + 1)
2
Caso II
3
1
Nº octog. =
1
2
. ..
. .
.
4
2
n
10. Número de letras superpuestas
3
n=3
.
.
.
2
n(n + 1)
×N
2
1
2
n=3
8. Número de trapecios
.
.
.
3
2
4=m
(n + 1)(n + 2)
2
m(m + 1)
Nº =
2
1
Nº =
n−1
n
Nº sect. =
4=m
1
n
Nº=
sect.
n(n + 1)
2
11. Número de semicírculos
n(n + 1)
2
9. Número de polígonos
(exágonos, octógonos, etc.)
Caso I:
3
superpuestos:
4=D
2
1
1
2
4
n ... 3 2 1
1
2 3 ... n
3
n(n + 1)
Nº exag. =
2
Nº semicir = 2D
3
Caso II:
2
n
.
.
.
3
2
1
1
2
3
..
.
n
4
1 ... 2 3 4 = C
1
2
D=4
3
Nº semicir = 2CD
12. Número de triángulos formados por las
diagonales de un polígono regular
CONTEO DE FIGURAS GEOMÉTRICAS EN EL
ESPACIO
1. Número de cubos
5=n
4
3
n(n − 3)
D=
2
Nº=
∆ D(D + 2)
n=5
13. Número de segmentos entre rectas
secantes
1
2
3
...
4
3
2
1 1
2
3
4
5=n
 n(n + 1) 
Nº cubos = 
 2 
n
1
4
2
2
2. Número de Paralelepípedos
2
3
4
4=p
3
3
2
2
n=6 5 4
3 2 1 1
n
Nº seg. = n(n + 1)(n + 2)
14. Número de triángulos de la forma
siguiente:
..
3. Número de Pirámides
n
6=p
4
3
n(n + 1)(n + 2)
6
5
m=4
2
1
Nº ∆ =
m
n(n + 1) m(m + 1) p(p + 1)
×
×
Nº paralelepipedos =
2
2
2
.
....
.
.
...
.
..
4
3
3
2
1
2
2
Nº pirám=
3
n=4 1
[ nm + (n − 1)(m − 1) + (n − 2)(m − 2) + ...] p
01. ¿Cuántos triángulos y cuadrados hay en las
siguientes figuras?
a) 11 y 8
d) 13 y 13
b) 12 y 8
e) 11 y 12
c) 13 y 9
02. ¿Cuantos triángulos hay en a figura?
a) 12
d) 16
b) 5
e) 9
05. ¿Cuántos triángulos hay en?
a) 10
d) 16
b) 12
e) 14
c) 13
06. ¿Cuántos segmentos hay en a figura?
c) 10
03. ¿Cuántos triángulos hay en la figura?
a) 24
d) 18
b) 26
e) 27
c) 21
07. El número de ángulos agudos es:
a) 18
d) 37
b) 28
e) 41
c) 35
04. ¿Cuántos triángulos tienen al menos un “*”?
A) 9
d) 8
b) 10
e) 12
a) 10
d) 16
b) 12
e) 14
c) 13
08. En la siguiente figura. ¿Cuántos triángulos
hay?
c) 7
a) 46
b) 56
c) 78
09. ¿Cuántos triángulos tienen por lo menos un
(*)?
13. Calcular el número de cuadriláteros.
a) 316
d) 315
a) 10
d) 16
b) 12
e) 14
c) 13
b) 320
e) 318
c) 310
14. ¿Cuántos cuadriláteros hay en?
10. ¿Cuántos sectores circulares hay en?
a) 45
d) 51
b) 49
e) 42
c) 50
11. El número de triángulos en a figura es:
a) 256
d) 190
b) 310
e) 118
c) 210
15. Hallar el número total de cuadriláteros en la
figura adjunta.
a) 44
d) 48
b) 40
e) 36
c) 16
12. ¿Cuántos cuadriláteros hay como máximo en
la figura?
a) 72
d) 82
b) 78
e) 86
c) 80
a) 1740
d) 1780
b) 1830
e) 1870
c) 1810
16. ¿Cuántos cuadrados hay en la figura adjunta?
a) 100
d) 125
b) 93
e) 64
c) 81
17. ¿Cuántos cuadrados hay en la figura?
a) 60
d) 74
b) 68
e) 70
c) 72
18. ¿Cuántos cuadrados hay en total en?
a) 320
d) 152
b) 132
e) 201
c) 121
21. ¿Cuántos triángulos hay en?
a) 24
d) 21
b) 19
e) 22
c) 20
22. ¿Cuántos triángulos hay en?
a) 30
d) 165
b) 90
e) 225
c) 75
23. Calcular el número total de triángulos.
a) 391
d) 803
b) 894
e) 791
c) 409
19. Hallar el máximo número de triángulos en a
figura:
a) 1520
d) 1840
a) 24
d) 21
b) 19
e) 22
c) 20
b) 1540
e) 2100
c) 1270
24. ¿Cuántos cuadriláteros hay en?
20. ¿Cuántos cuadriláteros que por lo menos
tengan un asterisco hay en al figura?
a) 92
d) 218
b) 168
e) 351
c) 350