vigasProntuarioERM

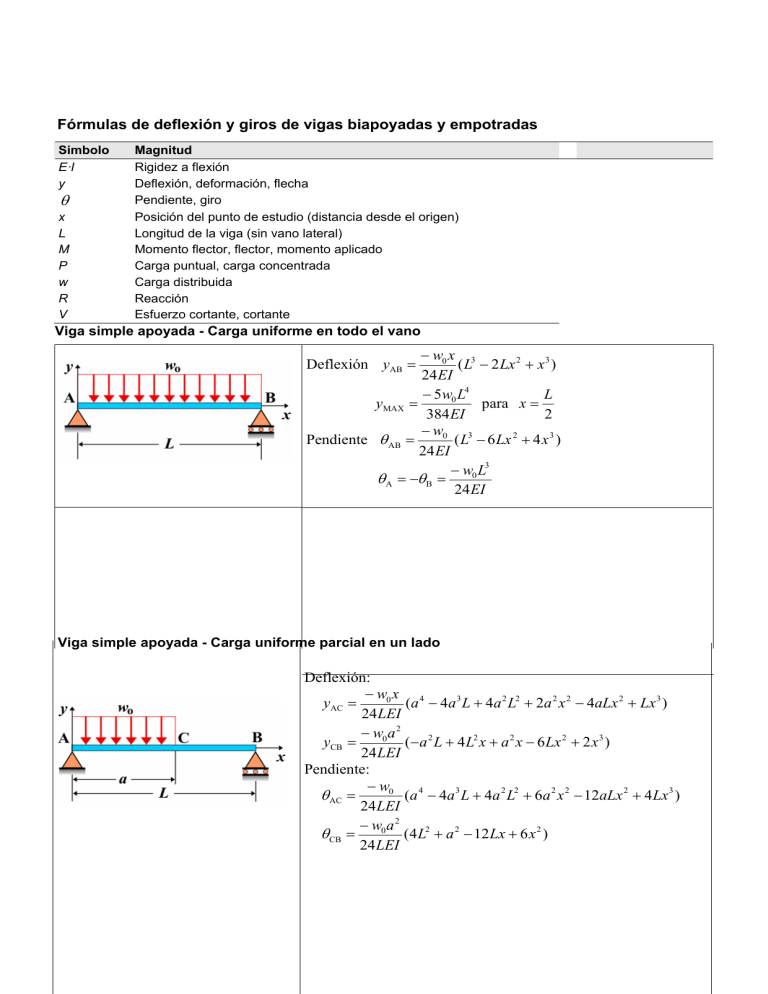
Fórmulas de deflexión y giros de vigas biapoyadas y empotradas
Simbolo
E·I
y
θ
x
L
M
P
w
R
V
Magnitud
Rigidez a flexión
Deflexión, deformación, flecha
Pendiente, giro
Posición del punto de estudio (distancia desde el origen)
Longitud de la viga (sin vano lateral)
Momento flector, flector, momento aplicado
Carga puntual, carga concentrada
Carga distribuida
Reacción
Esfuerzo cortante, cortante
Viga simple apoyada - Carga uniforme en todo el vano
− w0 x 3
( L − 2 Lx 2 + x 3 )
24 EI
− 5w0 L4
L
para x =
yMAX =
384 EI
2
− w0 3
Pendiente θ AB =
( L − 6 Lx 2 + 4 x 3 )
24 EI
− w0 L3
θ A = −θ B =
24 EI
Deflexión yAB =
Viga simple apoyada - Carga uniforme parcial en un lado
Deflexión:
− w0 x 4
yAC =
(a − 4a 3 L + 4a 2 L2 + 2a 2 x 2 − 4aLx 2 + Lx 3 )
24 LEI
− w0 a 2
(−a 2 L + 4L2 x + a 2 x − 6Lx 2 + 2x3 )
yCB =
24 LEI
Pendiente:
− w0
θ AC =
(a 4 − 4a 3 L + 4a 2 L2 + 6a 2 x 2 − 12aLx 2 + 4Lx 3 )
24 LEI
− w0 a 2
θ CB =
(4 L2 + a 2 − 12 Lx + 6x 2 )
24 LEI
Viga simple apoyada - Carga puntual en cualquier punto
Deflexión
− Pbx 2
(L − b2 − x 2 )
6 LEI
− Pa( L − x) 2
=
L − a 2 − (L − x) 2
6 LEI
yAC =
yCB
[
]
Pendiente:
− Pb 2
Pa 2
θ AC =
( L − b 2 − 3x 2 ) θ CB =
L − a 2 − 3( L − x) 2
6 LEI
6 LEI
2
2
− Pb(L − b )
Pa
θA =
θB =
( L2 − a 2 )
6 LEI
6 LEI
[
]
Viga simple apoyada - Carga uniforme parcial
RA x 3
R x3
w
+ αx
yCD = A − 0 ( x − a) 4 + αx
6EI 24 EI
6 EI
3
β ( L − x)
R (L − x)
+
yDB = B
6 EI
L
2
RA x
RA x 2
w
Pendiente: θ AC =
θ CD =
− 0 ( x − a )3 + α
+α
2 EI 6 EI
2 EI
2
β
− RB (L − x)
θ DB =
−
2 EI
L
Deflexión yAC =
Siendo:
w b3 L − 6EIβ − 3RBc 2 L − 3RA L(a + b) 2
α= 0
6 LEI
3
4
4w ab + 3w0b − 8RA (a + b)3 −12 RBc 2 L + 8RBc 3
β= 0
24 EI
Viga simple apoyada - Carga uniformemente creciente en todo el vano
− w0 x
(7L4 −10 L2 x 2 + 3x 4 )
360 LEI
w0 L4
para x = 0,5193L
yMAX = −0,00652
EI
− w0
Pendiente θ AB =
(7L4 − 30 L2 x 2 + 15x 4 )
360 LEI
− 7 w0 L3
w0 L3
θA =
θB =
45 EI
360 EI
Deflexión
y AB =
Viga simple apoyada - Momento antihorario en el lado derecho
− M0x 2
(L − x 2 )
6 LEI
− M0 2
Pendiente θ AB =
( L − 3x 2 )
6 LEI
M L
− M0L
θA =
θB = 0
6 EI
3EI
Deflexión
y AB =
Viga simple apoyada - Momento antihorario en el lado izquierdo
M0x
(2 L2 − 3Lx + x 2 )
6 LEI
⎛3− 3 ⎞
M L2
⎟L
y MAX = 0
para x = ⎜⎜
⎟
9 3EI
⎝ 3 ⎠
M0
Pendiente θ AB =
(2 L2 − 6 Lx + 3 x 2 )
6 LEI
− M 0L
M L
θA = 0
θB =
3EI
6 EI
Deflexión
y AB =
Viga simple apoyada - Momento antihorario en cualquier punto
− M0x 2
( L − 3b 2 − x 2 )
6 LEI
M 0 ( L − x) 2
( L − 3a 2 − ( L − x) 2 )
yCB =
6 LEI
− M0 2
Pendiente θ AC =
( L − 3b 2 − 3x 2 )
6 LEI
M0
θ CB =
(− L2 + 3a 2 + 3( L − x) 2 )
6 LEI
− M0 2
M0
θA =
( L − 3b 2 )
θB =
(− L2 + 3a 2 )
6 LEI
6 LEI
Deflexión
y AC =
Viga en voladizo - Carga uniforme en todo el vano
Deflexión
Pendiente
− w0 4
( x − 4 Lx 3 + 6 L2 x 2 )
24 EI
− w0 L4
para x = L
y MAX = y B =
8 EI
− w0 L3
− w0 3
2
2
θ AB =
(x − 3Lx + 3L x) θ B =
6 EI
6 EI
y AB =
Viga en voladizo - Carga uniforme parcial en el lado empotrado
− w0
(6a 2 x 2 − 4ax 3 + x 4 )
24 EI
− w0 a 3
(4 x − a)
yCB =
24 EI
− w0 a 3
(4 L − a)
y MAX = y B =
24 EI
− w0
(3a 2 x − 3ax 2 + x 3 )
Pendiente θ AC =
6 EI
− w0 a 3
θ CB = θ C = θ B =
6 EI
Deflexión
yAC =
Viga en voladizo - Carga uniforme parcial en el lado libre
− w0 bx 2
(3L + 3a − 2 x)
12 EI
− w0 4
( x − 4 Lx 3 + 6 L2 x 2 − 4a 3 x + a 4 )
yCB =
24 EI
− w0bx
Pendiente θ AC =
( L + a − x)
2 EI
− w0 3
θ CB =
( x − 3Lx 2 + 3L2 x − a 3 )
6 EI
− w0 3
θB =
(L − a3 )
6 EI
Deflexión y AC =
Viga en voladizo - Carga uniforme parcial
− w0bx 2
Deflexión y AC =
(6a + 3b − 2 x)
12 EI
− w0 4
( x − 4(a + b) x 3 + 6(a + b) 2 x 2 − 4a 3 x + a 4 )
yCD =
24 EI
− w0
(4 x[(a + b) 3 − a 3 ] − (a + b) 4 + a 4 )
y DB =
24 EI
− w0 bx
Pendiente θ AC =
( 2a + b − x )
2 EI
− w0 3
θ CD =
( x − 3(a + b) x 2 + 3(a + b) 2 x − a 3 )
6 EI
− w0
θ DB =
((a + b) 3 − a 3 )
6 EI
Viga en voladizo - Carga uniformemente creciente hacia el lado libre en todo el vano
Deflexión
Pendiente
− w0 x 2
(20 L3 − 10 L2 x + x 3 )
120 LEI
− 11w0 L4
para x = L
y MAX =
120 EI
− w0 x
θ AB =
(8L3 − 6 L2 x + x 3 )
24 LEI
− w0 L3
θB =
8EI
y AB =
Viga en voladizo - Carga uniformemente creciente hacia el lado empotrado en todo el vano
Deflexión
Pendiente
− w0 x 2
(10 L3 − 10 L2 x + 5 Lx 2 − x 3 )
120 LEI
w0 L4
para x=L
yMAX =
30 EI
− w0 x
θ AB =
(4 L3 − 6 L2 x + 4 Lx 2 − x 3 )
24 LEI
− w0 L3
θB =
24 EI
y AB =
Viga en voladizo - Carga puntual en el extremo libre
Deflexión
Pendiente
−P
(3Lx 2 − x 3 )
6 EI
− PL3
y MAX = y B =
3EI
−P
θ AB =
(2 Lx − x 2 )
2 EI
− PL2
θ MAX = θ B =
2 EI
yAB =
Viga en voladizo - Carga puntual en cualquier punto
Deflexión
Pendiente
−P
− Pa 2
(3ax 2 − x 3 ) yCB =
(3x − a)
6 EI
6 EI
− Pa 2
y MAX = y B =
(3L − a)
6 EI
−P
− Pa 2
2
θ AC =
(2ax − x ) θ CB = θ C = θ B =
2 EI
EI
y AC =
Viga en voladizo - Momento horario en el extremo libre
Deflexión
Pendiente
− M 0 x2
y AB =
2 EI
− M 0 L2
y MAX =
2 EI
− M0x
θ AB =
EI
para x = L
Viga en voladizo - Momento horario en cualquier punto
Deflexión
Pendiente
− M 0a
− M 0 x2
yCB =
(2 x − a)
y AC =
2 EI
2 EI
− M 0a
y MAX =
(2 L − a) para x = L
2 EI
− M0x
− M 0a
θ AC =
θ CB = θ C = θ B =
EI
EI
Viga con vano lateral - Carga uniforme en todo el vano
− w0 x 4
( L − 2 L2 x 2 + Lx 3 − 2a 2 L2 + 2a 2 x 2 )
24 LEI
− w0 x1
2
3
(4a 2 L − L3 + 6a 2 x1 − 4ax1 + x1 )
y BC =
24 EI
− w0
Pendiente θ AB =
( L4 − 6 L2 x 2 + 4 Lx 3 − 2a 2 L2 + 6a 2 x 2 )
24 LEI
− w0
2
3
θ BC =
(4a 2 L − L3 + 12a 2 x1 − 12ax1 + 4 x1 )
24 EI
Deflexión
y AB =
Viga con vano lateral - Carga uniforme sobre el saliente
w0 a 2 x 2
(L − x 2 )
12 LEI
− w0 x1
2
3
y BC =
(4a 2 L + 6a 2 x1 − 4ax1 + x1 )
24 EI
w a2 2
( L − 3x 2 )
Pendiente θ AB = 0
12 LEI
− w0 2
2
3
θ BC =
(a L + 3a 2 x1 − 3ax1 + x1 )
6 EI
Deflexión y AB =
Siendo x1 = x − L
Viga con vano lateral - Carga puntual en el extremo saliente
− Px1
Pax 2
2
( L − x 2 ) y BC =
(2aL + 3ax1 − x1 )
6 EI
6 LEI
−P
Pa
2
( L2 − 3x 2 ) θ BC =
(2aL + 6ax1 − 3 x1 )
=
6 LEI
6 EI
Deflexión y AB =
Pendiente θ AB
Siendo x1 = x − L
Viga con vano lateral - Carga puntual entre los apoyos
− Pbx 2
(L − b2 − x2 )
6 LEI
− Pa( L − x)
yCB =
(2 Lx − a 2 − x 2 )
6 LEI
Pabx1
y BD =
( L + a)
6 LEI
− Pb 2
Pendiente θ AC =
( L − b 2 − 3x 2 )
6 LEI
− Pa
Pab( L + a)
θ CB =
(2 L2 − 6 Lx + a 2 + 3 x 2 ) θ BD =
6 LEI
6 LEI
Deflexión y AC =
Siendo x1 = x − L