TALLER 50.Dilatación térmica

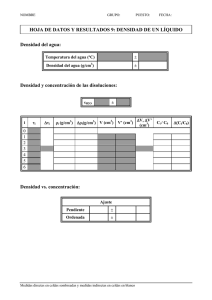
TALLER 50
4º Problemas:
a. Una varilla de cobre tiene una longitud de 1.2 m a una temperatura ambiente de 18 ºC.
¿Cuál será su longitud a 84 ºC?

L  Lo 1  t   1.2 m 1  14  10 6 º C   66 º C
1

L = 1.2011088 m
b. La longitud de un puente de hierro es 34 m a la temperatura ambiente de 18 ºC. Calcular
la diferencia entre sus longitudes en un día de invierno cuya temperatura es –6 ºC y un
día de verano cuya temperatura es 40 ºC.
L 1  Lo 1  t 1 
L 2  Lo 1  t 2 
L 2  L1  Lo 1  t 2   Lo 1  t 1   Lo 1  t 2  1  t 1   Lo t 2  t 1 


L  Lo t 2  t 1   34  12  10 6 22  24 
L  0.018768m
c. Calcular la longitud dilatada por una varilla de aluminio de 42 cm de longitud cuando su
temperatura se eleva de 45 ºC a 10 ºC.
L  Lo 1  t   Lo  Lo t


L  Lo  Lo t  42  24  10 6 35 
L  0.03528cm
d. Un disco de acero tiene un radio de 20 cm a 10 ºC. Calcular su área a 85 ºC.
 
A  Ao1  2t    20 2 1  2  12  10 6  75

A = 1 258.9 cm2
e. Una esfera de vidrio pirex tiene un radio de 5 cm a 5 ºC. Calcular el volumen a 68 ºC.
V  Vo1  3t  
V = 523.92 cm3
 

4
 5 3 1  3  3.2  10 6  63
3
f. Un frasco de vidrio cuyo volumen es 1 000 cm3 a 0 ºC se llena completamente de
mercurio a esta temperatura. Cuando frasco y mercurio se calientan a 100 ºC se
derraman 15.2 cm3 de líquido. Si el coeficiente de dilatación cúbica del mercurio es
0.000182 ºC–1. Calcula el coeficiente de dilatación volumétrico del vidrio.
Para el mercurio:
V  Vo1  3t   1000 1  3  182  10 6  100   1054 .6 cm3
Para el frasco:
V  Vo1  3t   1000 1  3  100   1000  300000 
El volumen que se derrama es:
V  VHg  V fco
15 .2  1054 .6  1000  300 000 
15.2  1054.6  1000  300 000
300000  1054.6  1000  15.2
300 000  9.4
39.4
300000
  1.313  10 4 º C 1

g. Calcular la longitud que tendrá a 60 ºC una varilla de hierro cuya longitud a 10 ºC es 30
cm.

L  Lo 1  t   30 1  12  10 6  50

L = 30.018 cm
h. Una platina de acero tiene un diámetro de 8 500 cm a 10 ºC. ¿A qué temperatura será su
diámetro igual a 8 508 cm?
A  Ao1  2t   Ao  2AoT
A  Ao  2Aot f  t i 
A  Ao
 t f  ti
2Ao
r 2  ro2
 r 2  ro2
r 2  ro2
A  Ao
tf 
 ti 

t


t

 ti
i
i
2Ao
2ro2 
2ro2 
2ro2 

tf 
42542  42502
 10
2 42502 12  106

tf = 88.47 ºC



i.
Un puente de acero tiene a 0 ºC una longitud de 40 m. La temperatura sufre una
variación semestral desde –20 ºC a 4 º C. ¿Cuál es la diferencia entre las longitudes de
este puente a las dos temperaturas extremas?

 Lo 1  t   40 1  12  10

L 1  Lo 1  t   40 1  12  10 6  20   39 .9904 m
L2
6

 4  40 .00192 m
L  L2  L1  40 .00192  39 .9904
L  0.01152m  11.52mm
j.
Para medir un terreno que se halla a 30 ºC se utiliza una cinta de acero cuya indicación
correcta es a 0 ºC. ¿A qué error de medida de la longitud dará origen la dilatación de la
cinta?
L  Lo 1  t   Lo  Lo t


L  Lo  Lo t  Lo 12  10 6 30 
L  0.00036  error de medida