Fisica 1 DGB

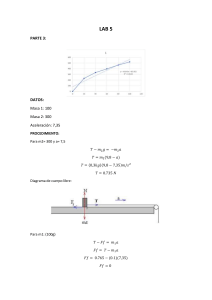
FÍSICA 1
Esta caricatura es la interpretación del artista Dundo acerca de la física. Con ella comenzamos aplicando uno de
los objetivos del enfoque por competencias: la sensibilidad al arte, de manera tal que puedas establecer, desde la
primera página, una relación creativa entre tú y el significado de esta materia.
FÍSICA 1
Díaz Velázquez, Jorge
Física, 1 / Jorge Díaz Velázquez; ilustraciones Diego Cabrera.
-- Tercera edición. -- México: ST Editorial: ST Distribución, 2013.
176 páginas: ilustraciones; 28 cm. -- (Colección bachillerato)
Bibliografía: página 176
En la cubierta: Desarrolla competencias
Incluye Guía para el maestro
ISBN 978 607 508 141 0
ISBN 978 607 508 142 7 (e-book)
1. Física – Estudio y enseñanza (Superior). 2. Física – Problemas,
ejercicios, etc. 3. Física – Manuales de laboratorio. I. Cabrera,
Diego, ilustrador. II. título. III. Serie.
530.0711 -scdd21
Biblioteca Nacional de México
ST Distribución, S.A. de C.V.
Miembro de la Cámara Nacional de la Industria Editorial, registro número 3342.
© Derechos reservados 2013
Primera edición: Estado de México, mayo de 2010
Segunda edición: México, DF, junio de 2012
Tercera edición: México, DF, agosto de 2013
© 2013, Jorge Díaz Velázquez
ISBN: 978 607 508 141 0
ISBN e-book: 978 607 508 142 7
Presidente: Alonso Trejos
Director general: Joaquín Trejos
Publisher: Giorgos Katsavavakis
Coordinadora editorial: Marina Rodríguez
Edición: Alfredo López
Asistente editorial: Daniel Rendón
Director de arte: Miguel Cabrera
Diseñadora: Milagro Trejos
Portada: Monfa
Ilustraciones: Diego Cabrera
Asistentes de producción: Diana Flores y Alicia Pedral
Fotografías: Stockxchange, archivo ST Editorial
Prohibida la reproducción total o parcial de este libro
en cualquier medio sin permiso escrito de la editorial.
Impreso en México. Printed in Mexico.
muestras
digitales
POR EL AMBIENTE
issuu.com/steditorial
También
encuéntranos en:
PRESENTACIÓN
Este libro tiene como propósito que el alumno desarrolle y fortalezca sus
competencias en el campo de las ciencias experimentales para lograr la
construcción de su propio conocimiento; de esta forma se constituye en
una herramienta de aprendizaje en donde se presentan los conceptos
partiendo de las situaciones cotidianas que se han experimentado, o bien
que se pueden realizar reflexionando en forma crítica sobre lo que sucede a nuestro alrededor. Sus contenidos están basados en el programa
de Física 1 correspondiente a la Reforma Integral de la Educación Media
Superior (RIEMS) planteada por la Dirección General de Bachillerato (DGB).
El diseño de contenidos, al igual que en el programa, tiene un enfoque
por competencias, con la intención de que el estudiante se desarrolle
integralmente en todos los ámbitos de su vida: personal, escolar, social
y laboral.
Física 1 se ha diseñado con un lenguaje sencillo que invita a la lectura, y evita el uso de términos demasiado técnicos que compliquen y
desalienten el autoaprendizaje. Cada bloque presenta una evaluación
diagnóstica que permite a los estudiantes saber tanto el nivel de conocimiento que han adquirido, como las habilidades que han desarrollado en
forma previa; presenta ejemplos resueltos y actividades complementarias
que les permiten entender de una mejor manera los fenómenos que se
relacionan con el tema que se estudia; además, contiene lecturas que los
invitan a la reflexión o a la discusión sobre temas de su interés, y como
complemento ofrece prácticas de laboratorio sencillas que los estudiantes pueden realizar en casa.
La estructura general consta de cuatro bloques, en el primero se
abordan los temas relacionados con el desarrollo histórico de la física, el
método científico, las magnitudes físicas y su importancia en la experimentación, qué sistemas de unidades se emplean, cómo se manejan las
cifras y los posibles errores en el proceso de medición, finalmente se inicia al alumno en el proceso de pensamiento abstracto con la presentación
de una herramienta indispensable para comprender el comportamiento de
diversas variables, los vectores. El segundo bloque presenta los temas
relacionados con las formas básicas de movimiento de un cuerpo a partir
del análisis del movimiento en una dimensión –¿qué es?, ¿cómo se describe? Después nos adentramos al movimiento en dos dimensiones tal
como sucede en un tiro parabólico o en un movimiento circular. El tercer
bloque nos muestra la validez de un conjunto de principios que son la
base para el diseño y construcción de un sinfín de dispositivos y sistemas.
En el cuarto bloque se revisa la importancia de la energía en todo proceso o actividad humana y las implicaciones que tiene, pues es sabido por
todos que su uso adecuado nos llevará a etapas de progreso armónico
entre la sociedad y la naturaleza. Iniciemos pues una fascinante aventura
en el mundo de la física.
De antemano, se agradece cualquier comentario o sugerencia por
parte de los lectores que sirva para mejorar esta obra; se pueden enviar al
autor a la siguiente dirección electrónica: [email protected]
No, la física no es abstracta, es divertida porque
nos permite crear sistemas que resultan de la
observación de la naturaleza y la consecuente
experimentación para que se obtenga un
beneficio directo para el ser humano, quizá el
razonamiento y la construcción de modelos sea
abstracta para cualquier principiante. Aprende
y disfruta.
CONTENIDO
Secciones del libro
Reconoce tus competencias
6
7
Bloque 1
Reconoces el lenguaje técnico básico de la física
Para comenzar...
11
Reto
13
Tema 1: Método científico
Métodos de la investigación científica
15
17
Tema 2: Magnitudes físicas y su medición
19
Tema 3: Notación científica
Transformación de unidades de un sistema a otro
22
23
Tema 4: Instrumentos de medición
Tipos de errores en las mediciones
26
27
Tema 5: Vectores
Características
Suma
Descomposición y composición rectangular de vectores
por métodos gráficos y analíticos
31
32
33
Evaluación sumativa
44
33
Bloque 2
Identificas diferencias entre distintos tipos de movimiento
Para comenzar...
51
Reto
53
Tema 1: Nociones básicas sobre movimiento
Sistemas de referencia absoluto y relativo
55
58
Tema 2: Movimiento en una dimensión
Movimiento rectilíneo uniforme
Movimiento rectilíneo uniformemente acelerado
61
61
62
Tema 3: Movimiento en dos dimensiones
Tiro parabólico: horizontal y oblicuo
Movimiento circular: uniforme y uniformemente acelerado
73
73
78
Evaluación sumativa
90
Bloque 3
Comprendes el movimiento de los cuerpos a partir
de las leyes de dínámica Newton
Para comenzar...
95
Reto
97
Tema 1: Leyes de la dinámica
Antecedentes históricos del estudio del movimiento mecánico
Tipos de fuerzas y las tres leyes de dinámica de Newton
99
99
101
Tema 2: Ley de la gravitación universal
115
Tema 3: Leyes de Kepler
Leyes de Kepler
119
120
Evaluación sumativa
124
Bloque 4
SECCIÓN FINAL
Relacionas el trabajo con la energía
Prácticas de laboratorio
Evaluación final
Para terminar. Autoevalúa tus competencias
Fuentes consultadas
Para comenzar...
129
Reto
131
Tema 1: Trabajo
La expresión matemática y unidades de medición del trabajo
133
136
Tema 2: Energía cinética y energía potencial
Energía cinética
Energía potencial
141
143
146
Tema 3: Ley de la conservación de la energía mecánica
152
Tema 4: Potencia
157
Evaluación sumativa
162
166
171
175
176
SECCIONES DEL LIBRO
Los libros de la Colección Bachillerato de ST Editorial apegados a los programas de estudios del Sistema Avanzado de Bachillerato y Educación
Superior (SABES), se distinguen por brindar una estructura didáctica apegada al enfoque didáctico por competencias. Contienen, al inicio de cada
bloque, las competencias y las evidencias que se señalan en los programas de estudios de las diferentes asignaturas, así como la secuencia de
cada bloque, introducción y mapa conceptual. También ofrecen diferentes
tipos de actividades y evaluaciones, así como secciones complementarias
que facilitan el proceso de enseñanza-aprendizaje.
INICIO
Reconoce tus
competencias
Se enlistan las once competencias
genéricas y las competencias
disciplinares respectivas. Se
acompañan de siglas para que sea
posible identificar en cuáles
actividades del libro se
desarrollarán.
Secuencia de los
bloques
Se incluyen todos los bloques del
libro y se destaca gráficamente
el que se estudiará.
ACTIVIDADES Y
EVALUACIONES
Reto
Actividad en donde se plantea una
situación problemática que invita
al alumno a estudiar el bloque.
Actividad de apertura
Al comienzo del tema, se incluye
una actividad motivadora pensada
para que el alumno reflexione y se
interese en el estudio de cada
tema.
COMPLEMENTARIAS
Ilustraciones,
infográficos
Refuerzan y abordan los
contenidos de manera creativa y
explicativa, como una estrategia
visual y efectiva para el proceso
de aprendizaje.
Glosario
Se incluye la definición de
términos de difícil comprensión
que aparecen en cada página.
Retrato
Introducción al bloque
y mapa conceptual
Actividades
individuales y grupales
Se incluye información relevante
sobre algunos de los personajes
clave en el desarrollo de los temas
de cada materia.
Se incluyen un texto introductorio
con una breve explicación de lo que
se estudiará y un mapa conceptual
con los temas más importantes del
bloque.
Con estas se pretende que el
estudiante desarrolle sus
competencias de forma integral.
El mundo que te rodea.
En la web
Evaluaciones
Incluye evaluación diagnóstica que
identifica los conocimientos
y habilidades que el estudiante posee
antes de iniciar el estudio del bloque
(Para comenzar...), y aquellos que
adquirió al finalizar el estudio del
bloque (evaluación sumativa).
También se evalúan los aprendizajes
obtenidos durante el curso
(Evaluación final).
Información complementaria
y de reflexión que vincula los
conocimientos que el estudiante
va construyendo con el entorno
inmediato.
Lecturas
Se incluyen lecturas cuyas
temáticas refuerzan los
contenidos desarrollados en cada
uno de los bloques.
RECONOCE TUS COMPETENCIAS
Las competencias son capacidades que una persona
desarrolla en forma gradual durante el proceso educativo, que incluyen conocimientos, habilidades, actitudes
y valores, en forma integrada, para dar satisfacción a las
necesidades individuales, académicas, laborales y profesionales. Existen principalmente tres tipos de competencias: genéricas, disciplinares y laborales.
Las competencias genéricas le permiten al individuo comprender el mundo, aprender a vivir en él. Estas
competencias son aplicables a todas las áreas del conocimiento, y por lo tanto a todas las asignaturas.
G
Por su parte, las competencias disciplinares engloban
los requerimientos básicos –conocimientos, habilidades,
destrezas y actitudes– que se necesitan en cada campo
disciplinar, para que los estudiantes los apliquen en diferentes contextos y situaciones de su vida.
Estas competencias se podrán entretejer más adelante con las competencias laborales, para conformar un
todo armónico que le da pleno sentido al proceso educativo, de tal manera que los estudiantes adquieran las
destrezas y capacidades necesarias para desenvolverse
en el mundo actual.
D
COMPETENCIAS
GENÉRICAS
COMPETENCIAS DISCIPLINARES
del campo de ciencias experimentales
1 Se conoce y valora a sí mismo y aborda problemas y
1 Establece la interrelación entre la ciencia, la tecnología, la sociedad y el
2
2 Fundamenta opiniones sobre los impactos de la ciencia y la tecnología en
retos teniendo en cuenta los objetivos que persigue.
Es sensible al arte y participa en la apreciación e interpretación de sus expresiones en distintos géneros.
3 Elige y practica estilos de vida saludables.
ambiente en contextos históricos y sociales específicos.
su vida cotidiana, asumiendo consideraciones éticas.
3 Identifica problemas, formula preguntas de carácter científico y plantea
las hipótesis necesarias para responderlas.
4 Escucha, interpreta y emite mensajes pertinentes en
distintos contextos mediante la utilización de medios,
códigos y herramientas apropiados.
4 Obtiene, registra y sistematiza la información para responder a preguntas de carácter científico, consultando fuentes relevantes y realizando
experimentos pertinentes.
5 Desarrolla innovaciones y propone soluciones a problemas a partir de métodos establecidos.
5 Contrasta los resultados obtenidos en una investigación o experimento
con hipótesis previas y comunica sus conclusiones.
6 Sustenta una postura personal sobre temas de interés y
relevancia general, considerando otros puntos de vista
de manera crítica y reflexiva.
7 Aprende por iniciativa e interés propio a lo largo de la
vida.
8 Participa y colabora de manera efectiva en equipos
6 Valora las preconcepciones personales o comunes sobre diversos fenómenos naturales a partir de evidencias científicas.
7
Hace explícitas las nociones científicas que sustentan los procesos para
la solución de problemas cotidianos.
8
Explica el funcionamiento de máquinas de uso común a partir de nociones
científicas.
9
Diseña modelos o prototipos para resolver problemas, satisfacer necesidades o demostrar principios científicos.
diversos.
9 Participa con una conciencia cívica y ética en la vida de
su comunidad, región, México y el mundo.
10 Mantiene una actitud respetuosa hacia la interculturalidad y la diversidad de creencias, valores, ideas y
prácticas sociales.
11 Contribuye al desarrollo sustentable de manera crítica,
con acciones responsables.
10 Relaciona las expresiones simbólicas de un fenómeno de la naturaleza y
los rasgos observables a simple vista o mediante instrumentos o modelos
científicos.
11 Analiza las leyes generales que rigen el funcionamiento del medio físico y
valora las acciones humanas de impacto ambiental.
12 Decide sobre el cuidado de su salud a partir del conocimiento de su cuer-
po, sus procesos vitales y el entorno al que pertenece.
Ubica estas competencias
genéricas en cada actividad,
grupal e individual, así:
COMPETENCIAS
GENÉRICAS
4
6
Estas son competencias disciplinares y disciplinares
extendidas. Ubícalas en cada actividad, grupal e
individual, así:
8
COMPETENCIAS
DISCIPLINARES
2
5
8
Desempeños del estudiante
Bloque 1
Reconoces el lenguaje
técnico básico de la física
a. Identifica la importancia de los métodos de investigación y su
relevancia en el desarrollo de la ciencia como la solución de
problemas cotidianos.
b. Reconoce y comprende el uso de las magnitudes físicas y su
medición como herramientas en la actividad científica de su entorno.
c. Interpreta el uso de la notación científica y de los prefijos
como una herramienta de uso que le permita representar
números enteros y decimales.
d. Identifica las características y propiedades de los vectores
que le permitan su manejo en la solución de problemas
cotidianos.
Estos desempeños pueden identificarse en cada una de
las actividades del bloque, de la siguiente manera:
DESEMPEÑOS DEL
ESTUDIANTE
a
b
c
d
Bloque 1
Bloque 2
Bloque 3
Reconoces el
lenguaje técnico
básico de la física
Identificas
diferencias entre
distintos tipos
de movimiento
Comprendes el movimiento
de los cuerpos a partir de
las leyes de dinámica
de Newton
Objetos de aprendizaje
•฀ Método científico
•฀ Magnitudes físicas y su medición
•฀ Notación científica
•฀ Instrumentos de medición
•฀ Vectores
Bloque 4
Relacionas el trabajo
con la energía
Introducción
Desde el inicio de los tiempos, el ser humano ha
buscado respuesta a la ininidad de fenómenos
que lo rodean y aunque inicialmente encontró
explicaciones en diversas religiones y en lo
sobrenatural, su inquietud constante lo llevó
a la búsqueda de métodos para reproducir lo
que ocurre a su alrededor. De esta forma, el
conocimiento humano se mantiene en constante
evolución y perfeccionamiento, lo que trae como
consecuencia el desarrollo cientíico y de sus
aplicaciones en la industria y en todas las esferas
de la sociedad.
En este primer bloque comenzaremos el estudio
de la física y abordaremos su contribución a nuestro
desarrollo como especie humana; conoceremos
los principales métodos y procedimientos que se
emplean para estudiar y comprender el universo
que nos rodea. El estudio de este bloque te
permitirá capacitarte para abordar el análisis
riguroso de la física, ya que te proporcionará la
habilidad necesaria para comprender, modelar y
resolver problemas relacionados con las magnitudes
fundamentales que se emplean en esta ciencia, así
como la interpretación de cantidades escalares
o vectoriales, al aplicar el método cientíico en
el análisis de diversas situaciones de nuestra vida
cotidiana que se relacionan con la física. De este
modo podrás desarrollar una actitud e interés de
carácter cientíico en la investigación de cualquier
evento que ocurra a tu alrededor. Observa el
siguiente mapa conceptual con los contenidos del
presente bloque.
Conocimiento científico
y magnitudes físicas
se conforman por
emplean
método
científico
campos de estudio
de la física
comprueba en
forma objetiva el
conocimiento
cada disciplina
incide en diversos
aspectos de nuestra
vida diaria
magnitudes
físicas
se dividen según su
origen
naturaleza
en
en
por ejemplo
define el problema
a resolver
plantea hipótesis
de trabajo
soluciona problemas
y elabora reporte final
fundamentales
escalares
derivadas
vectoriales
su aplicación práctica es
determinante en el desarrollo
de la ciencia y de la tecnología
10
st-editorial.com
Para comenzar...
Para que puedas comprender los temas de este bloque, es necesario
que rescates las competencias (conocimientos, habilidades, actitudes y valores) que ya has
adquirido a lo largo de tu vida. Haz tu mejor esfuerzo para responder y detecta aquellos
aspectos que no conoces o dominas para enfocar tu estudio.
I. Escribe en el paréntesis la letra que corresponda a la respuesta correcta.
1.(
) La física estudia:
a. la naturaleza y las transformaciones de la energía.
b. la vida, su origen, su evolución y sus propiedades.
c. la estructura, las propiedades y la transformación de los seres vivos.
d. las cantidades, las fuerzas y sus relaciones.
2.(
) Tres de las etapas del método científico son:
a. observación, hipótesis y muestreo.
b. comparación, problema y conclusiones.
c. restricciones, hipótesis y levantamiento de datos.
d. observación, restricciones y muestreo.
3.(
) Los sistemas de unidades sirven para:
a. uniformar los procesos de medición.
b. medir sin cometer errores.
c. efectuar operaciones de equivalencia.
d. realizar transacciones comerciales.
4.(
) Algunos instrumentos de medición son tan precisos que:
a. sólo el ser humano comete errores por no saber manejarlos.
b. su vida útil es muy corta.
c. deben emplearse con poco cuidado.
d. nunca fallan.
5.(
) Los vectores son:
a. segmentos de recta dirigidos.
b. lechas que representan cantidades.
c. fuerzas asociadas a diversos fenómenos.
d. escalas numéricas para especificar valores.
II. Resuelve los siguientes problemas en tu cuaderno.
1. Efectúa las conversiones que se indican.
a. 5 cm a m.
b. 18 pul a cm.
c. 56 pul2 a m2.
d. 8 l a m3.
e. 5 J a cal.
st-editorial.com
11
2. El registro de la estatura respectiva de los ocho alumnos que constituyen el equipo de baloncesto
de la escuela secundaria “El caracol” es el siguiente: 1.72, 1.76, 1.80, 1.65, 1.79, 1.73, 1.80 y 1.67 m.
Determina la estatura promedio que requieren los aspirantes a formar parte de este equipo.
3. Un árbol proyecta una sombra de 5 m sobre una superficie plana. Calcula su altura considerando
que un observador se coloca al final de tal sombra y al mirar a la punta del árbol determina que
hay un ángulo de 80° entre la dirección de su vista y la punta del árbol. Asume que la estatura del
observador no es importante al compararse con la altura del árbol en cuestión.
4. Calcula la longitud del lado desconocido en el triángulo que se presenta a continuación. ¿Cuánto
miden los ángulos internos?
c = 19 cm
a
b = 12 cm
III. ¿Qué objetos tecnológicos de tu entorno crees que tienen relación con la física?
12
st-editorial.com
RECONOCES EL LENGUAJE TÉCNICO
BÁSICO DE LA FÍSICA
Reto (problema)
El avance de la tecnología es una consecuencia de la puesta en práctica de los avances
que día a día se presentan en las diferentes ramas de la ciencia. Por ejemplo, ¿qué hay
a tu alrededor? Un refrigerador con conexión a Internet, una memoria con capacidad
para almacenar millones de datos en un espacio de menos de 1 cm2, medios de transporte más eficientes en todos los aspectos, telas que permiten confeccionar ropa que
brinda mayor comodidad, alimentos con mayor valor nutrimental, nuevos sistemas de
alumbrado, etc.
I. En equipos de 4 integrantes, analicen cada uno de los siguientes puntos y respondan
en su cuaderno.
1. A partir de la manera más apropiada de resolver un problema en beneficio de la
sociedad, contesten lo siguiente.
a. ¿Qué diferencias y similitudes existen entre resolver un ejercicio que les dejan
como tarea en la escuela y desarrollar un nuevo producto que satisfaga una necesidad social?
b. ¿Es diferente el procedimiento cuando se trata de desarrollar una nueva teoría científica?, ¿por qué?
c. Representen gráficamente la relación entre ciencia, tecnología y los dispositivos
que satisfacen las necesidades de la sociedad.
2. A partir de la relación entre la geometría y funcionalidad de un prototipo de la innovación técnica, contesten lo siguiente.
a. ¿Qué consideraciones harían para que una estufa consuma menos gas (o electricidad) y ocupe el menor espacio posible?
b. ¿Qué dimensiones son fundamentales tomar en cuenta para el desarrollo de su
propuesta?
c. ¿Emplearían los mismos instrumentos de medición para la fabricación de una nueva estufa que los requeridos para vender telas o medir la estatura de los pacientes
de un médico?
d. ¿Todos los procesos de medición son universales?
3. A partir de la forma en que se manejan las cifras que se emplean en el desarrollo de
una actividad productiva o cotidiana para formar un “lenguaje común” para todos,
contesten lo siguiente.
a. ¿De qué manera podemos medir cantidades microscópicas?, ¿cómo las expresamos?
b. ¿Es correcto hacer la referencia de una distancia como una longitud de cientos de
miles de brazadas?, ¿por qué?
c. La micromecánica y la nanotecnología aportan avances sorprendentes cada día y
las variables que involucran son diminutas, ¿cuáles son sus magnitudes?
d. ¿De qué orden serían las magnitudes que se manejarían en una mega ciencia?
4. Según la naturaleza de las variables y parámetros que se consideran para realizar
actividades recreativas o cotidianas, contesten lo siguiente.
a. ¿Cuál es la diferencia entre masa y peso?, ¿de qué les sirve en su vida saberlo?
b. Te lanzas al vacío en paracaídas, ¿qué variables físicas intervienen?, ¿cómo podrías
controlarlas?, ¿qué factores intervienen para que evites una caída que sea fatal?
II. Preparen una presentación al grupo acerca de las conclusiones a que llegan sobre
cada punto.
st-editorial.com
13
Coevaluación
En la siguiente lista de cotejo se presentan una serie de aspectos para que evalúes el desempeño de uno de
tus compañeros durante la realización del reto.
Aspecto
Siempre
Algunas veces
Nunca
Participó activamente en la discusión.
Respetó las ideas de los compañeros y buscó un consenso.
Propuso ideas para estructurar la presentación al grupo.
Trabajó con limpieza y orden.
Cumplió con los acuerdos y normas de trabajo establecidos.
Autoevaluación
Con esta rúbrica evalúa tu desempeño durante el reto. Cada indicador tiene un valor en puntos, que deberás
sumar para determinar tu nivel de desempeño inical.
Aspectos a evaluar
Indicadores de desempeño
4 puntos
3 puntos
2 puntos
1 punto
Métodos de
investigación
y su relevancia
en el desarrollo
de la ciencia
como la solución
de problemas
cotidianos.
Identifiqué la
importancia de
todos los métodos
de investigación
y su relevancia
en el desarrollo
de la ciencia
como la solución
de problemas
cotidianos.
Identifiqué la
mayoría de los
métodos de
investigación
y su relevancia
en el desarrollo
de la ciencia
como la solución
de problemas
cotidianos.
Identifiqué
vagamente los
métodos de
investigación y
su relevancia en
el desarrollo de
la ciencia como
la solución de
problemas cotidianos.
No identifiqué
la importancia
de los métodos
de investigación
ni su relevancia
en el desarrollo
de la ciencia
como la solución
de problemas
cotidianos.
Uso de las
magnitudes físicas
y su medición
como herramientas
de uso en la
actividad científica
de su entorno.
Reconocí y
comprendí el uso de
todas las magnitudes
físicas y su medición
como herramientas
de uso en la
actividad científica
de mi entorno.
Reconocí y
comprendí el
uso de algunas
magnitudes físicas
y su medición
como herramientas
de uso en la
actividad científica
de mi entorno.
Reconocí y comprendí
vagamente el uso
de las magnitudes
físicas y su medición
como herramientas
de uso en la actividad
científica de mi
entorno.
No reconocí ni
comprendí el uso
de las magnitudes
físicas, tampoco
su medición como
herramientas de
uso en la actividad
científica de mi
entorno.
Uso de la notación
científica y de los
prefijos como una
herramienta de
uso que permite
representar
números enteros y
decimales.
Interpreté el uso
de la notación
científica y de los
prefijos como una
herramienta de uso
que me permite
representar números
enteros y decimales.
Interpreté vagamente
el uso de la notación
científica y de los
prefijos como una
herramienta de uso
que me permite
representar números
enteros y decimales.
No interpreté el
uso de la notación
científica ni de los
prefijos como una
herramienta de uso
que me permite
representar
números enteros
y decimales.
Características
y propiedades
de los vectores
que permitan
su manejo y
aplicación en
la solución
de problemas
cotidianos.
Identifiqué todas
las características
y propiedades de
los vectores que
me permiten su
manejo y aplicación
en la solución
de problemas
cotidianos.
Interpreté
parcialmente el
uso de la notación
científica y de los
prefijos como una
herramienta de uso
que me permite
representar
números enteros
y decimales.
Identifiqué algunas
características
y propiedades
de los vectores
que me permiten
su manejo y
aplicación en
la solución
de problemas
cotidianos.
Identifiqué
vagamente las
características
y propiedades de
los vectores que
me permiten su
manejo y aplicación
en la solución de
problemas cotidianos.
No identifiqué
las características
ni propiedades
de los vectores
que me permiten
su manejo y
aplicación en
la solución
de problemas
cotidianos.
Valoración
Excelente: 15 a 16 puntos. Bueno: 11 a 14 puntos.
14
Suficiente: 7 a 10 puntos.
Mi puntaje
Mi total
Insuficiente: 4 a 6 puntos.
st-editorial.com
Tema 1
Tema 2
Tema 3
Tema 4
Método
científico
Magnitudes físicas
y su medición
Notación
científica
Instrumentos
de medición
Continúa
En forma accidental, un investigador consigue que una mezcla de dos sustancias sólidas y un
líquido formen un material de tipo arcilloso que ofrece buenas propiedades para la construcción
de viviendas a bajo costo, sin embargo, no tiene la manera de reclamar los derechos del “invento”
pues le ha sido difícil repetir el “accidente”, cuando ha intentado repetir la mezcla, los resultados
son siempre diferentes y no encuentra en dónde está la falla. ¿Cómo le ayudarías a resolver esta
situación? ¿De qué manera tendría que trabajar el investigador para obtener un resultado óptimo
que sea único y le permita mostrar su desarrollo?
La palabra física proviene del griego physiké, que
signiica “naturaleza de las cosas que se mueven
por sí mismas”. Antes se aceptaba un concepto
rígido de la física: “el estudio de las propiedades
de los cuerpos y las leyes que rigen su comportamiento”; actualmente, la física es la ciencia que
estudia las propiedades de la materia y la energía,
la relación que existe entre ambas, sus transfor-
maciones y cómo se vinculan con el espacio y el
tiempo. La física nos explica, por ejemplo, cómo
y por qué se mueven los cuerpos, cómo la energía se transforma en calor o en trabajo y que la
materia ocupa un lugar en el espacio por sus características de masa, peso y volumen. La física se
sustenta en métodos con rigor cientíico, los cuales se han consolidado a través de la historia del
Materia. Todo lo que ocupa un lugar en el espacio.
Peso. Fuerza con que la Tierra atrae a los cuerpos por la acción del campo gravitacional.
st-editorial.com
Glosario
15
BLOQUE 1
conocimiento y el desarollo tecnológico y cientíico. A través de este despliegue, la física se ha dividido
en diversas áreas de investigación. En este bloque nos interesaremos únicamente de la física clasíca, de
la que se derivan las disciplinas que se presentan en el siguiente infográico:
Infográfico 1 Disciplinas de la física clásica
Acústica
Estudia los fenómenos relacionados con
la producción, transmisión y recepción del
sonido. Los investigadores plantean que la
comunicación acústica de los murciélagos es la
más rica existente en los mamíferos, después de
la de los humanos.
Electromagnetismo
Se dedica al estudio de los fenómenos
eléctricos y su interrelación con los fenómenos
magnéticos. En la actualidad, existe un tren
capaz de trasladarse a una velocidad de 518 km/h
utilizando la levitación magnética, que es uno de
los principios del magnetismo: la repulsión entre
polos iguales.
Termodinámica
Estudia las propiedades térmicas de los
cuerpos y su capacidad para transformar el
calor y la energía en trabajo. El origen de esta
disciplina fue sin lugar a dudas, la curiosidad
que despertó el movimiento producido por la
energía del vapor de agua.
Hidráulica
Investiga el comportamiento de los luidos en
reposo y en movimiento. Desde hace más de
un siglo, se aprovecha la energía hidráulica para
generar electricidad, y de hecho ésta fue una de las
primeras formas que se emplearon para producirla.
La polémica represa Tres Gargantas, (185 metros
de alto y 2 300 de largo) en China, obligó el
traslado de más de un millón de personas que vivían
donde se creó un lago artificial de 660 km para
alimentar las turbinas que producirán electricidad.
Óptica
Se ocupa de las propiedades de los cuerpos
luminosos y de la luz en sí. Por ejemplo, la física
moderna proveyó las herramientas teóricas para
explicar cómo se inició el universo.
Mecánica
Analiza el movimiento y las causas que lo originan;
se divide, a su vez, en cinemática
–que analiza el movimiento por sí mismo– y
en dinámica –que investiga las causas del
movimiento– , un caso particular de la dinámica
es la estática, que estudia las condiciones de
equilibrio ya sea en reposo o en movimiento a
velocidad constante de un cuerpo. La investigación
16
en los campos de las vibraciones, de la estabilidad,
de la resistencia de estructuras y máquinas, de los
cohetes y naves espaciales, el control automático,
la fabricación de motores, circulación de luidos,
de los aparatos y maquinaria eléctrica, y del
comportamiento molecular, atómico y subatómico
dependen en gran parte de los principios
fundamentales de la mecánica.
st-editorial.com
RECONOCES EL LENGUAJE TÉCNICO
BÁSICO DE LA FÍSICA
Actividad individual
COMPETENCIAS
GENÉRICAS
4 7
COMPETENCIA
DISCIPLINAR
4
DESEMPEÑO
DEL ESTUDIANTE
a
Investiga en qué consiste la física moderna y las ramas que la constituyen; posteriormente, realiza una comparación con la física contemporánea.
Métodos de la
investigación científica
¿Qué es la ciencia? ¿Cómo se “hace” la ciencia?
Para el ilósofo griego Aristóteles (384-322 a. C.),
el conocimiento humano se fundamenta en la
experiencia y se adquiere por medio de los sentidos, por lo que la explicación de los fenómenos está en su propia esencia y manifestación;
éste es el principio aristotélico de la investigación cientíica.
En cambio, la lógica formal estudia las relaciones entre diferentes propuestas sin importar
su contenido. En consecuencia, se asume que
la ciencia es un conocimiento razonado, sobre
todo por la gran contribución que la tecnología le ha brindado y por cuestionar creencias y
tradiciones.
La estructura de la lógica como conjunto se ha
desarrollado en forma metódica y sistemática, de
tal manera que es veriicable y nos permite predecir en cierta medida el comportamiento de la
naturaleza por medio de leyes.
¿Por qué el conocimiento cientíico es un
conjunto de métodos? Si un método es el procedimiento ordenado para alcanzar un objetivo,
entonces un método científico es la manera ordenada de buscar la verdad en determinado campo
disciplinario.
Por lo general, encontrarás que toda actividad
cientíica consta de dos etapas: el planteamiento
de principios o hipótesis y su demostración para
obtener conclusiones.
Habrás notado que hablamos de un método
cientíico y no de “el método cientíico”, ya que
un investigador puede seguir diversas metodologías para un in especíico. Entre los métodos
más utilizados por los cientíicos se encuentran
los deinitorios, los clasiicatorios, los estadísticos, los deductivos por hipótesis y los que emplean la medición.
Uno de los pensadores más destacados en
métodos de investigación fue el inglés Francis
FIGURA 1
La aplicación del método científico implica la relación entre
cálculos matemáticos y observación de la naturaleza.
Bacon (1561-1626), quien aseguraba que no es
suiciente la experiencia brindada por nuestros
sentidos ni la razón: debemos evitar los dogmas,
la única forma de descubrir los secretos de la naturaleza es mediante la experimentación. No es suiciente realizar un experimento; debemos repetirlo y
registrar los datos que obtengamos para conseguir
una conclusión satisfactoria.
Para el físico y matemático italiano Galileo
Galilei (1564-1642), el mejor método consistía en la demostración rigurosa por medio de
modelos matemáticos, pues se aplican a postulados comprobables por la experiencia. Si
se trabaja de manera objetiva y meticulosa, la
probabilidad de errores es mínima porque se
usa un modelo matemático: no hay verdades a
medias, se cumple el postulado y es cierto o no
se cumple y es falso.
Ley. Conclusión general sobre la relación constante entre las causas (o antecedentes) y los efectos (o consecuencias) en los fenómenos
de la naturaleza.
Hipótesis. Suposición que se hace para explicar un fenómeno y que resulta fundamental en el método científico.
st-editorial.com
Glosario
17
BLOQUE 1
Infográfico 2 Método científico en física
1
Motivo de la investigación
2
Definición del problema
3
A partir de la observación previa
de un fenómeno se establece un
supuesto para proceder a delinear
el proyecto de investigación.
Se debe delimitar concretamente el
fenómeno bajo estudio, para definir
y entender con claridad cuáles son
las metas por alcanzar.
Planteamiento
de restricciones
Se demarcan los datos o parámetros
que intervienen en el problema por
solucionar, tomando en cuenta los
resultados y avances científicos que
se tengan en el momento de realizar
la investigación. Esto evitará que se
desvíe el curso del trabajo.
4
Planteamiento de la(s)
hipótesis de trabajo
A partir de los datos se formulan
una o varias hipótesis; se predice
el comportamiento del fenómeno
como guía para verificar por qué
ocurre un evento de acuerdo a un
campo específico de estudio.
5
Sistematización del
conocimiento y solución
Toda la información se ordena en
una secuencia lógica para modelar
el fenómeno y reproducirlo bajo
condiciones controladas; así se
obtiene una solución dentro del
marco teórico de la hipótesis.
6
18
Levantamiento de datos
Se elabora una síntesis o reporte
del caso de estudio donde se indique
la metodología de experimentación
y la estadística obtenida de los
resultados; además, se deben
presentar posibles soluciones,
conclusiones y recomendaciones
para desarrollar el producto teórico
o tecnológico.
El matemático y ilósofo francés René Descartes (1596-1650)
airmaba que el método en la ciencia es un conjunto de reglas
fáciles de seguir; si se es cuidadoso, no habrá equivocación y
lo falso no se tomará por cierto, y viceversa. De esta manera,
se podrá adquirir todo el conocimiento posible. Las etapas del
método de Descartes son las siguientes:
• No aceptar como cierta una evidencia si antes no se comprueba.
• Dividir cada problema en tantas partes como sea posible para
resolverlo más fácilmente.
• Colocar por orden de diicultad el conocimiento: se inicia
con lo más sencillo y se termina con lo más complejo.
• Enumerar en forma general y completa todos los elementos
con los que se cuenta para no omitir ningún dato.
En el siglo xix, el pensador de mayor impacto fue el inglés
John Stuart Mill (1806-1873). Desde su punto de vista, hay cinco
métodos para trabajar tanto en las ciencias sociales como en las
ciencias naturales:
Método de la concordancia. Estudia casos diferentes para establecer en qué puntos concuerdan. Si hay una circunstancia común,
ésta debe ser la causa o el efecto del fenómeno bajo estudio.
Método de la diferencia. Toma fenómenos que presentan circunstancias comunes, pero si diieren en un solo hecho, éste constituye
la causa de que ocurra o no tal fenómeno
Método de la concordancia y de la diferencia. Retoma al mismo
tiempo los dos anteriores.
Método de las variaciones concomitantes. Establece relaciones
entre dos fenómenos, los cuales podrían ser efectos de una
misma causa.
Método de los residuos. Analiza por qué la presencia de un
dato particular no puede ser eliminada mediante la experimentación.
Como podrás observar, en todos los casos el propósito especíico
es validar el conocimiento mediante experimentos y modelos. Las
aportaciones de los ilósofos y cientíicos que hemos mencionado
revolucionaron la manera de crear el conocimiento en su época.
En las ciencias naturales como la física, se emplean los métodos
estadístico y deductivo por hipótesis, y por ello consideramos
que un método cientíico apropiado para esta ciencia es el que
releja el infográico 2.
Actividad individual
COMPETENCIA
GENÉRICA
4
COMPETENCIAS
DISCIPLINARES
1 2
3
DESEMPEÑO
DEL ESTUDIANTE
a
Elabora una lista en tu cuaderno de diversos problemas ambientales que se presenten en tu comunidad, región o país y que puedan
ser estudiados y resueltos con la aplicación de un método de la investigación científica. Elije uno de ellos y elabora una hipótesis del
porqué consideras que existe ese problema. Investiga acerca de si
ya hay alguna institución que se esté haciendo cargo de resolver la
situación y cómo. Presenta tus resultados al docente.
st-editorial.com
Tema 2
Tema 3
Tema 4
Tema 5
Magnitudes físicas
y su medición
Notación
científica
Instrumentos
de medición
Vectores
Relexiona acerca de lo siguiente: una parte importante en el desarrollo de una
investigación es la experimentación (como parte de la solución práctica a un
problema), y en ella se reproduce un fenómeno a partir de controlar en forma
adecuada las variables que intervienen. ¿Cómo consideras que pueden controlar
las variables y registrar los datos que se obtengan? ¿Cómo piensas que se pueden
poner de acuerdo los cientíicos en comunicar sus resultados, de manera que la
comunidad cientíica mundial pueda entenderlos?
Magnitudes físicas
y su medición
En la física toda magnitud es susceptible de ser
medida; es decir, de ser comparada con respecto
a un valor de referencia tomado como patrón. Por
tanto, la física requiere del uso de un sistema de
medición para poder evaluar todos los parámetros y especiicar mediante valores numéricos si
se cumple o no con nuestras expectativas. En general, cualquier sistema de unidades se establece
partiendo de unidades que reconoce como fundamentales porque sirven como patrón y deinen un
sistema de medición que es reconocido o aceptado
por la comunidad cientíica, tienen un carácter
único y permiten que a partir de ellas se obtengan
unidades para expresar diferentes variables físicas
que son conocidas como derivadas, que resultan
de la combinación de las unidades fundamentales
st-editorial.com
y nos permiten medir eventos tan dispares como
la velocidad o la intensidad de corriente eléctrica.
Sistema CGS o cegesimal. Fue uno de los primeros sistemas. Es un sistema absoluto en
el que las unidades fundamentales son el
centímetro, el gramo y el segundo, y aunque fue
ampliamente utilizado es completamente obsoleto. Sin embargo, no es de extrañar que encuentres
dispositivos para medir fuerza que se denominan
dinamómetros aunque su escala nos indique valores de fuerza en el sistema internacional de unidades y no precisamente dinas, que son las unidades
(derivadas) de fuerza en tal sistema.
Sistema inglés de unidades. Es un sistema gravitacional,
las unidades fundamentales son el pie, la libra y el segundo, su origen corresponde a los países del Reino Unido,
pero se difundió ampliamente en los Estados Unidos y en la mayoría de los países de habla inglesa, y
19
BLOQUE 1
aunque reciben una denominación común, tienen algunas variaciones en cuanto al valor numérico que se les asigna. En los
Estados Unidos se le reconoce como sistema fps –foot (pie),
pound (libra), second (segundo)– o usc (United States Customary) y su uso se ha limitado a la transición que implica el
cambio al Sistema Internacional de Unidades (si). El sistema inglés ha caído en desuso porque la economía mundial ha impuesto un “lenguaje común”, y los sistemas de
unidades son un componente importante de tal lenguaje.
Observa que en muchos países en vías de desarrollo es común que aún encontremos equipos, maquinaria y dispositivos que contienen componentes cuyas especiicaciones
corresponden a estos sistemas.
En 1875 se estableció en Francia el Buró Internacional
de Pesos y Medidas (bipm) con el propósito de normar
los patrones de medición existentes, ya que algunas mediciones todavía se realizaban conforme a costumbres y
usanzas de cada país o región, de tal manera que no existía
uniformidad en muchos aspectos. Por ejemplo, en las actividades relacionadas con la construcción y el comercio
una unidad de medida recibía el mismo nombre, pero no
equivalía precisamente a la misma cantidad en las diferentes regiones que mantenían relaciones comerciales.
A través de diversas conferencias se llegaron a acuerdos
de carácter internacional y se deinieron las unidades fundamentales del Sistema Internacional de Unidades (si), el cual
fue adoptado en 1960 por el gremio de físicos para presentar
los resultados de sus investigaciones. Se estimaba que en el
año 2000 su empleo sería universal pero no ha sucedido así,
quizá pasarán todavía algunos años para que en todos los
ámbitos de nuestra vida se emplee este sistema, el cual tiene un carácter absoluto. A diferencia de otros sistemas, sus
unidades fundamentales son siete (cuadro 1).
CUADRO 1. MAGNITUDES FUNDAMENTALES DEL SI
Magnitud
Nombre
Símbolo
Longitud (l)
metro
m
Masa (m)
kilogramo
kg
Tiempo (t)
segundo
s
Temperatura
kelvin
K
termodinámica (T)
Corriente eléctrica (i)
ampere
A
Intensidad luminosa (I)
candela
cd
Cantidad de sustancia (n)
mol
mol
En el cuadro 2 podrás apreciar que el si tiene además
como unidades complementarias, las que corresponden
a la medición de ángulos.
CUADRO 2. UNIDADES DE MEDICIÓN DE ÁNGULOS
Magnitud complemento
Nombre
Símbolo
Ángulo plano (q)
radián
rad
Ángulo sólido (W)
estereorradián
sr
20
FIGURA 2
Durante el feudalismo no existía un sistema único de medición de unidades;
por eso, con la llegada del capitalismo, se requirió la creación de un sistema internacional.
Cada una de las unidades mencionadas en los cuadros
anteriores se deine de la manera siguiente:
Metro. Es una longitud igual a 1 650 763.73 longitudes de
onda en el vacío de la radiación que corresponde a la transición entre dos niveles de un átomo de criptón.
Kilogramo. Es la masa de un prototipo de platino irradiado, aprobado en la Conferencia General de Pesos y
Medidas de 1889 y se conserva en el pabellón de Breteuil en Sèvres, Francia.
Segundo. Es la duración de 9 192 631 770 ciclos de la radiación asociada a la transición entre dos niveles de un átomo de cesio.
Grado kelvin. Corresponde a la escala termodinámica de la
temperatura absoluta en la que la temperatura del punto
triple del agua es de 273.15 grados
Ampère. Es la intensidad de una corriente constante que al
circular a través de dos conductores paralelos, rectilíneos de
longitud ininita y sección transversal circular despreciable,
produce una fuerza de 2×10-7 N por cada metro de longitud de los conductores cuando éstos se colocan en el vacío
a una distancia de un metro entre ellos.
Candela. Es la intensidad luminosa en una dirección determinada por una abertura perpendicular a esta dirección y
cuya área es de 1/60 centímetro cuadrado y que radia como
un cuerpo negro (radiador integral) a la temperatura de
solidiicación de platino.
Mol. Es la cantidad de partículas elementales en un sistema
cualquiera y, es igual al número de átomos existentes en 12
gramos de carbono 12.
Radián. Es el ángulo plano que tiene su vértice en el centro de
un círculo y que intercepta sobre la circunferencia de tal círculo
un arco de longitud igual al radio del círculo.
Estereorradián. Es un ángulo sólido cuyo vértice se encuentra en el centro de una esfera y que corta en la supericie de tal esfera un área igual a la de un cuadrado
cuyos lados son iguales al radio de la esfera.
st-editorial.com
RECONOCES EL LENGUAJE TÉCNICO
BÁSICO DE LA FÍSICA
Actividad grupal
COMPETENCIAS
GENÉRICAS
4 8
4 10
COMPETENCIAS
DISCIPLINARES
DESEMPEÑOS
DEL ESTUDIANTE
b
c
I. Reúnanse en equipos y en un cuadro comparativo indiquen el uso en diferentes disciplinas como la biología, la astronomía, la física, la química, entre otras, de cada uno de los prefijos enlistados en el siguiente
cuadro de unidades derivadas de uso común. ¿Qué unidades son de uso común en varias disciplinas?
Unidad
derivada
Superficie
Volumen
Masa
Tiempo
Nombre
de la unidad
Símbolo del múltiplo
o submúltiplo
metro cuadrado
m2
metro cúbico
m3
decímetro cúbico
dm3 = 10-3 m3
centímetro cúbico
cm3 = 10-6 m3
milímetro cúbico
mm3 = 10-9 m3
hectolitro
hL = 100 L
Unidad
derivada
Frecuencia
Densidad o masa
volumétrica
terahertz
THz = 1012 Hz
megahertz
MHz = 106 Hz
kilohertz
kHz = 103 Hz
hertz
Hz
kilogramo por metro
cúbico
gramo por
centímetro cúbico
kg/m3
g/cm3 = 10-3 kg/m3
decalitro
daL = 10 L
newton
N
L = 1 dm3
meganewton
MN = 106 N
decilitro
dL = 0.1 L = 100 cm3
kilonewton
kN = 103 N
centilitro
cL = 0.01 L = 10 cm3
decanewton
daN = 10 N
mililitro
mL = 0.001 L = 1 cm
milinewton
mN = 10-3 N
tonelada
t = 1 000 kg
newton-metro
N·m
quintal
q = 100 kg
joule
J
gramo
g = 10-3 kg
megajoule
MJ = 106 J
miligramo
mg = 10-3 g = 10-6 kg
kilojoule
kJ = 103 J
microgramo
µg = 10-6 g = 10-9 kg
kilowatt-hora
kWh = 3.6 MJ
día
d = 86 400 s
watt-hora
Wh = 3.6 kJ
hora
h = 3 600 s
caloría
cal = 4.1855 J
minuto
min = 60 s
watt
W
milisegundo
ms = 10-3 s
megawatt
MW = 106 W
microsegundo
µs = 10-6 s
kilowatt
kW = 103 W
nanosegundo
ns = 10-9 s
miliwatt
mW = 10-3 W
kilómetro por hora
km/h = m/s
microwatt
µW = 10-6 W
metro por segundo
m/s
pascal
Pa
centímetro por
segundo
cm/s = 10-2 m/s
hectobar o
decanewton por
milímetro cuadrado
hbar o daN/mm2 =
107 Pa
nudo
n = 1 mi/h = 0.514 m/s Esfuerzo y presión
megapascal
MPa = 106 Pa
m/s2
bar
bar = 105 Pa
cm/s2 = 10-2 m/s2
kilopascal
kPa = 103 Pa
rad/s o rd/s
milipascal
mPa = 10-3 Pa
metro por segundo
cuadrado
centímetro por
segundo cuadrado
radián por segundo
Velocidad angular
Símbolo del múltiplo
o submúltiplo
litro
Fuerza
3
Momento o par
Energía, trabajo y
cantidad de calor
Potencia
Velocidad
Aceleración
Nombre
de la unidad
revolución por segundo rps o r/s = 2p rad/s
revolución por minuto rpm o r/min = rad/s
II. Guarden su cuadro comparativo en el portafolio de evidencias.
st-editorial.com
21
Tema 3
Tema 4
Tema 5
Notación
científica
Instrumentos
de medición
Vectores
¿Cómo representarían en cifra numérica la distancia en kilómetros que hay de la Tierra a
la Luna?, ¿cómo lo harían para indicar cuánto mide una bacteria intenstinal? Relexionen
acerca del empleo de unidades de medida que sean útiles y prácticas para brindar datos
manejables para la práctica cientíica y comenten sus conclusiones en la clase.
CUADRO 3. MÚLTIPLOS
Prefijo de
Símbolo
la unidad
1024 = 1 000 000 000 000 000 000 000 000 iotaI
1021 = 1 000 000 000 000 000 000 000 zetaZ
1018 = 1 000 000 000 000 000 000
exaE
15
10 = 1 000 000 000 000 000
petaP
1012 = 1 000 000 000 000
teraT
109 = 1 000 000 000
gigaG
106 = 1 000 000
megaM
103 = 1 000
kilok
102 = 100
hectoh
101 = 10
decada
Factor para multiplicar la unidad
22
Dado que en la ciencia se utilizan cantidades que pueden ir de
lo microscópico, como el tamaño de un electrón, a lo macroscópico,
como la cantidad de estrellas en el universo, es común que se facilite
la lectura de datos y mediciones empleando la notación cientíica, la
cual se basa en el uso de potencias de base 10 y de los múltiplos y submúltiplos de una unidad. En los primeros se presenta una sucesión que
aumenta en 103 cada vez, mientras que en los submúltiplos la sucesión
se reduce en 10-3. Se deinen de este modo los preijos que aparecen en
los cuadros 3 y 4 de la siguiente página.
Para usar cualquier cantidad se debe tener en cuenta lo siguiente:
• Separar los números grandes en grupos de tres antes del punto decimal, con un pequeño espacio entre ellos. Además, para los submúltiplos se requiere colocar un cero antes del punto decimal.
• Los nombres de las unidades son comunes y se escriben siempre
con minúscula, aunque se trate del nombre de un cientíico; en este
caso sólo el símbolo se escribe en mayúscula.
• En las unidades compuestas, los símbolos se combinan con un
punto (·) para el producto y con una diagonal (/) para el cociente.
Nunca se emplea más de una diagonal.
• Cuando el símbolo del múltiplo o submúltiplo de una unidad involucra
un exponente, éste se relaciona con toda la unidad representada; por
ejemplo, cuando escribimos mm2 se reiere a (mm)2.
• Se pueden emplear exponentes negativos.
st-editorial.com
RECONOCES EL LENGUAJE TÉCNICO
BÁSICO DE LA FÍSICA
• Los preijos no se combinan, no es correcto que se registre, por ejemplo, un valor de tiempo de 1 Mµs (un megamicrosegundo) ya que
esto es 1 × 106 × 10-6 = 1 s.
• Los ángulos planos siempre se expresan en radianes (rad) y se emplea adicionalmente el símbolo de grados (°).
• Como prefijo compuesto, el kilogramo se usa sólo en el denominador de una expresión. O sea, no es correcto expresar metros
sobre miligramos (m/mg); lo correcto es megametro sobre kilogramo (Mm/kg).
• Los símbolos nunca se pluralizan.
Actividad grupal
COMPETENCIAS
GENÉRICAS
4 5 8
COMPETENCIAS
DISCIPLINARES
4 10
DESEMPEÑO
DEL ESTUDIANTE
c
CUADRO 4. SUBMÚLTIPLOS
10-1 = 0.1
10-2 = 0.01
10-3 = 0.001
10-6 = 0.000 001
10-9 = 0.000 000 001
10-12 = 0.000 000 000 001
10-15 = 0.000 000 000 000 001
Prefijo de
la unidad Símbolo
decid
centic
milim
microm
nanon
picop
fentof
10-18 = 0.000 000 000 000 000 001
ato-
Factor para multiplicar la unidad
10-21 = 0.000 000 000 000 000 000 001 zepto10-24 = 0.000 000 000 000 000 000 000 001 iocto-
a
z
i
Reúnete con dos compañeros para llevar a cabo las actividades. Trabajen en su
cuaderno.
I. Dadas las siguientes cantidades, exprésenlas en notación científica e indiquen
cuál es el prefijo a emplear para denotar una unidad asociada, tal como muestra
a continuación:
15897000000
En primer término agrupamos considerando tres cifras: 15 897 000 000, y en base
a esto podemos establecer que el exponente a emplear es nueve, pues tenemos
tres grupos de tres cifras, es decir, la cifra se expresa como:
15.897 × 109, y el prefijo más adecuado es el asociado a tal exponente: giga, (G).
Resuelvan:
1. 0.0000016789
2. 3875/0.100096
3. 318760540032×9403456
4. 323538/835323
5. 0.00000000000123415/53421
6. 9864532/1232425178992781262
7. 7612354×14598765432
II. Investiguen las siguientes magnitudes y exprésenlas en notación científica.
1. Longitud:
a. Un año luz.
b. Distancia media Tierra-Luna. c. Un lápiz nuevo.
2. Masa:
a. Júpiter.
b. Sol.
c. Átomo de hidrógeno.
3. Tiempo:
a. Edad de la Tierra.
b. Oscilaciones de onda en el vacío, de la radiación emitida en la transición entre
dos niveles de un átomo de criptón.
III. Realicen un cuadro comparativo que muestre la diferencia entre las unidades
Cigüeñal
fundamentales y las unidades derivadas del sistema inglés y del internacional.
IV. Anexen al portafolio de evidencias la actividad desarrollada.
Transformación de unidades de un sistema a otro
Existe una estrecha relación entre los sistemas de unidades. Por eso es posible realizar
conversiones y establecer equivalencias de las diversas variables de la física. En el cuadro
5 de la siguiente página se muestran los factores de conversión entre el sistema inglés
(fps) y el Sistema Internacional de Unidades (si).
Después del cuadro se presentan ejemplos de ejercicios de transformación de
unidades entre el fps y el si que incluyen el empleo de unidades derivadas [Ej.
1, 2 y 3]. Cada uno te ayudará a reforzar los conceptos estudiados; además, la
solución presenta una secuencia de análisis aplicable a la física y a otras ciencias.
Debes tomar en cuenta que no siempre se puede seguir la misma secuencia, ya
que cada rama tiene sus particularidades especíicas.
st-editorial.com
Pistones
FIGURA 3
En los motores de vehículos, los gases en
combustión provocan una presión en los cilindros que empuja los pistones con determinada
fuerza, que es transmitida hacia el cigüeñal y
lo hacen girar debido al torque originado.
23
BLOQUE 1
En la web
Para conocer más acerca de este tema
visita st-editorial.com/enlaweb/fisica1
y consulta el link número 01
CUADRO 5. CONVERSIÓN DE UNIDADES DEL FPS AL SI
FPS
Magnitud
Multiplica por
SI
pulgada (in)
Longitud
Masa
2.54 × 10-2
pie (ft)
3.048 × 10-1
metro (m)
milla (mi)
1.6093 × 103
milla náutica (mi)
1.852 × 103
libra masa (lbm)
4.5359 × 10-1
slug (lb-sec2/ft)
kilogramo (kg)
ton (2 000 lbm)
Fuerza
Área
Volumen
9.0718 × 102
libra (lb)
4.4482
newton (N)
kip (1 000 lb)
pulgada2 (in2)
4.4482 × 103
6.4516 × 10-4
metro2 (m2)
pie2 (ft2)
pulgada3 (in3)
9.2903 × 10-2
1.6387 × 10-5
metro3 (m3)
pie3 (ft3)
2.8317 × 10-2
pie/segundo (ft/s)
Velocidad
3.048 × 10-1
metro/segundo (m/s)
milla/hora (mi/h)
nudo (milla náutica/h)
kilómetro/hora (km/h)
pulgada/segundo2 (in/s2)
pie/segundo (ft/s )
libra masa/pulgada3 (lbm/in3)
2
2
Densidad o masa
volumétrica
libra masa/pie (lbm/ft )
Momento de una
fuerza
libra-pie (lbft)
3
3
libra-pulgada (lbin)
metro/segundo2 (m/s2)
kilogramo/metro3
(kg/m3)
newton-metro (N · m)
unidad térmica británica (BTU)
Trabajo y energía
joule (J)
pie-libra (ft-lb)
pie-libre/minuto (ft-lb/min)
caballo de potencia (hp = 550 ft-lb/s)
2.54 × 10-2
3.048 × 10-1
2.7680 × 104
16.018
0.11298
1.3558
1.3558
3.60 × 106
2.2597 × 10-2
watt (W)
745.70
atmósfera (14.7 lb/in )
1.0133 × 105
2
Presión y esfuerzo libra/pulgada2 (psi)
1.6093
1.0551 × 103
kilowatt-hora (kW-h)
Potencia
4.4704 × 10-1
5.1444 × 10-1
milla/hora (mi/h)
Aceleración
14.594
newton/metro
(N/m2 o Pa)
libra/pie2
2
6.8948 × 103
47.880
Ejemplo 1
Para apretar los pernos de una estructura es necesario aplicar un torque de 70 lb–in.
¿A cuánto se debe ajustar la herramienta si se encuentra calibrada en N · m?
Solución
a. ¿Con qué datos contamos?
• Torque: 70 lb–in.
• Incógnita: equivalente del torque en unidades del SI.
b. ¿Qué vamos a hacer?
Convertir el dato del valor del torque de un sistema de unidades a otro para poder
ajustar la herramienta.
24
st-editorial.com
RECONOCES EL LENGUAJE TÉCNICO
BÁSICO DE LA FÍSICA
c. ¿Cómo lo vamos a hacer?
Aplicamos el factor de conversión correspondiente y buscamos la variable de torque o momento de
una fuerza; para este caso debemos multiplicar por
0.11298 para obtener el torque en N · m.
Ejemplo 3
d. Operaciones.
Solución
M = 70 lb–in #
¿Cuál es el volumen en litros de un tanque de almacenamiento que se puede aproximar a un cilindro de
3.25 ft de radio y 10.5 ft de altura?
a. ¿Con qué datos contamos?
• Radio del cilindro: 3.25 ft.
• Altura: 10.5 ft.
0.11298 N.m
= 7.9086 N.m
1 lb–in
e. Resultado.
La herramienta se debe ajustar a 7.909 N · m.
b. ¿Qué vamos a hacer?
Transformar el volumen del recipiente de unidades del SI
a litros.
Ejemplo 2
¿Cuál es la potencia en watts que genera el motor de
un auto cuya especificación señala 150 hp?
Solución
a. ¿Con qué datos contamos?
• Potencia: 150 hp.
c. ¿Cómo lo vamos a hacer?
Convertimos los datos a metros y calculamos el
volumen. Debemos recordar que para un cilindro,
V = πr2h. Una vez que se tenga el volumen en m3,
calculamos los litros.
d. Operaciones.
b. ¿Qué vamos a hacer?
Convertir el valor de potencia del FPS al SI.
c. ¿Cómo lo vamos a hacer?
Aplicamos el factor de conversión que según nuestro cuadro es de 745.7.
d. Operaciones.
P = 150 hp #
745.7 W.
= 111 855 W
1 hp
r = 3.25 ft #
0.3048 m
= 0.991 m
1 ft
h = 10.5 ft #
0.3048 m
= 3.20 m
1 ft
V = p × (0.991)3 × 3.20 = 9.87 m3
e. Comprobación y resultado.
En el cuadro de múltiplos y submúltiplos, 1 L equivale a 1 dm3. Éste es equivalente a la milésima parte de 1 m3. Entonces la capacidad del tanque es de
9 870 L.
e. Resultado.
La especificación de potencia en el SI es 112 kW.
Actividad individual
COMPETENCIAS
GENÉRICAS
4
5
7
COMPETENCIA
DISCIPLINAR
7 10
DESEMPEÑO
DEL ESTUDIANTE
b
c
Resuelve en tu cuaderno los problemas siguientes; para ello debes consultar el cuadro 5. Si empleas la calculadora, recuerda que debes ajustarla al modo científico (SCI) o de ingeniería (ENG) para
obtener directamente las cantidades en notación científica. Puedes anotar aquí las respuestas.
1. Para el desarrollo del prototipo de un auto eléctrico, un grupo de estudiantes consiguió un panel
de instrumentos que marca la velocidad en millas por hora en un rango de 0 a 40 con incrementos
de 5. ¿A cuánto equivale cada división en kilómetros por hora?
2. Cuando un carguero se encuentra a 12 km de un puerto empieza una tormenta que lo obliga a reducir su velocidad de 30 a 5 nudos. ¿Cuál es la velocidad en metros por segundo para tal condición? ¿Llegará en menos de una hora a un lugar seguro que está a 1 km de distancia del puerto?
3. Una chef prepara un asado especial de cordero y sigue una receta de su abuela, que indica las
cantidades de algunos ingredientes en libras masa (lbm): cordero, 120; ajo, 1/4; cebolla, 20; sal,
3; hierbas finas, 1/2; tomate, 15; y arándanos, 3/4. Determina estas cantidades en kilogramos o
en gramos.
4. Una motocicleta tiene una cilindrada de 1 L. ¿A cuánto corresponde este valor en centímetros
cúbicos?
5. La grúa de un barco tiene un rótulo que indica que el peso máximo que puede soportar es de 10 000 kip.
¿A cuántos newtons se refiere el rótulo? ¿Cuánto es este valor en masa?
st-editorial.com
25
Tema 4
Tema 5
Instrumentos
de medición
Vectores
Considera el caso de dos competencias de atletismo, una en tu escuela y otra
de carácter mundial, supongamos, los 100 m planos. ¿Qué diferencia puede
haber? ¿Qué tipo de reloj emplearán los jueces? ¿En dónde se requiere mayor
rigurosidad para la medición del tiempo?
Un instrumento de medición puede ser tan simple como una regla graduada o tan complejo
como el sensor de la presión del aire en la llanta de un auto. Actualmente existen dos tipos de
indicadores:
Indicadores analógicos. Muestran el valor de la
medición mediante una aguja o un indicador luminoso que se desplaza en una escala numerada.
Cuando la manecilla o guía se ubica en una posición intermedia se establece el valor en forma
aproximada, de tal manera que es determinante
la habilidad de la persona que realiza la medición
para poder expresar el valor con la mayor precisión posible.
Indicadores digitales. Proporcionan los valores de
la magnitud en números decimales, según la escala
seleccionada. Aunque esto evita una lectura
aproximada, podrían presentarse lecturas erróneas
o incluso ocurrir desperfectos en los instrumentos.
26
Es común que algunas de las cualidades de
los instrumentos de medición te puedan llegar a
confundir; sin embargo, debes evitarlo tendiendo
presente los siguiente: un instrumento es exacto
cuando se realiza una medición y se obtiene con
él, el valor real de la magnitud física; hablamos
de la precisión de un instrumento cuando con él
puedes realizar una medición y se presenta una
variación mínima con respecto al valor real, y
airmaremos que tiene una sensibilidad especíica
cuando el instrumento es capaz de medir valores
muy pequeños.
En actividades de investigación, en la industria y
en el comercio, se emplean diversos equipos e instrumentos de medición que deben ser calibrados
en forma periódica, ya que es la única forma en que
pueden asegurar la calidad dimensional de los procesos, productos y/o servicios que ofrecen. El proceso
de calibración consiste en comparar los instrumentos
st-editorial.com
RECONOCES EL LENGUAJE TÉCNICO
BÁSICO DE LA FÍSICA
FIGURA 4
En casi todos los aviones y controles de vuelos de los aeropuertos se utilizan instrumentos muy sofisticados de
medición con indicadores digitales.
de medición contra patrones previamente certiicados por un organismo reconocido a
nivel nacional para asegurar que cumplen con la precisión requerida y con ello, que las diferentes mediciones que se realizan sean repetibles y se tenga certeza sobre los valores que
se obtienen. Recuerda: para cada actividad existe un instrumento de medición adecuado, y
dependiendo de la precisión requerida es como debes seleccionarlo.
Actividad grupal
COMPETENCIAS
GENÉRICAS
4 5 8
COMPETENCIAS
DISCIPLINARES
3 5
7
DESEMPEÑOS
DEL ESTUDIANTE
b
c
En grupos de tres o cuatro estudiantes, realicen lo siguiente.
1. Investiguen cuáles instrumentos son los que sirven para medir cada una de las siguientes magnitudes: energía, masa, peso, volumen, presión y temperatura. Investiguen también cómo funcionan y por qué son importantes estos instrumentos en la
vida cotidiana.
2. Con la ayuda de una cinta métrica midan al menos cinco veces el perímetro de una
botella de agua, registra el dato y posteriormente con un calibrador (pie de rey) midan en igual número de ocasiones el diámetro de la misma botella. Con la ayuda de
una calculadora determinen a partir del perímetro, el diámetro de la botella. Realicen,
en su cuaderno, un cuadro comparativo en el que indiquen los valores obtenidos y
los errores que se tuvieron al tomar las lecturas. ¿Cuál es la precisión de cada instrumento? ¿Cuál es su sensibilidad?
Tipos de errores en las mediciones
El trabajo cotidiano en muchos ámbitos de nuestra vida requiere que midamos
magnitudes. En general, decimos que medir es determinar en forma experimental el
valor de una magnitud física con instrumentos o dispositivos adecuados.
La investigación cientíica y muchos procesos productivos requieren de la medición de magnitudes en diversos fenómenos con métodos diferentes. Dependiendo del
contexto en que nos encontremos y de las herramientas a nuestro alcance podremos
realizar mediciones en forma directa o indirecta.
Métodos directos de medición. Son aquellos que nos permiten tomar una lectura en
forma directa al colocar un instrumento de medición, por ejemplo, cuando vas a una
mercería para comprar un metro de listón, el encargado toma una cinta métrica y
mide la longitud de listón que necesitas para cortarlo y entregártelo. En la elaboración
st-editorial.com
El mundo que te rodea
Por normatividad se realizan inspecciones a cada una de las estaciones de
servicio que venden gasolina y diesel
en nuestro país, debido a que los sistemas electrónicos que se emplean para
surtir tales energéticos son alterados
de tal manera que en algunas no se
venden la cantidad de litros que marca
el indicador de los despachadores.
27
BLOQUE 1
de bebidas gaseosas, en una etapa del proceso un termómetro y un manómetro
miden la temperatura y la presión del gas carbónico que se agrega al líquido y mediante un dispositivo electrónico, se mantienen constantes tales valores.
Métodos indirectos de medición. En otras situaciones se requiere una mayor certeza en
cuanto a las lecturas obtenidas; por ello se dice que se emplean métodos indirectos.
Una magnitud se mide en varias ocasiones para que mediante algunos cálculos se
determine el valor buscado, esto sucede, por ejemplo, en los dispositivos que algunos
autos traen instalados de fábrica para medir la presión del aire en las llantas: los
sensores detectan el volumen de aire, el radio de la llanta y determinan la presión
que existe, cuando los cálculos del procesador del auto establecen un valor de presión
fuera del rango permitido para que el auto ruede con seguridad, emite la señal de
llanta sin aire o “ponchada”.
La exactitud de un instrumento está determinada por su capacidad de aproximación a una magnitud real de medida. En cambio, la precisión es la probabilidad de que se repita un mismo resultado. Es muy difícil que en un proceso de
medición se obtenga un valor absoluto idéntico al de la magnitud física medida;
siempre se presentará un error, que puede ser absoluto o relativo.
Error absoluto. Corresponde a la diferencia entre la medida real de la magnitud (M)
y la medida obtenida en forma experimental (m):
FIGURA 5
Los errores sistemáticos son corregibles y
entre ellos están, por ejemplo, los errores de
calibración de escalas, el atraso o adelanto
de un reloj de acuerdo con un ritmo conocido, etc.
1. ∆e = M – m
Error relativo. Corresponde al cociente entre el error absoluto (∆e) y la magnitud
real de la magnitud (M). Se puede expresar como un porcentaje:
2. er = ∆e/M
Según sus causas, los errores pueden ser sistemáticos o accidentales:
Errores sistemáticos. Tienen causas diversas y, aunque la mayoría de las veces son atri-
buidos a los instrumentos de medición, no siempre son éstos el origen [Ej. 4]. Estos
errores pueden ser de diferentes tipos, entre ellos teórico, instrumental, ambiental y
de legibilidad (igura 5).
• Teórico: este error se asocia al modelo matemático que se emplee en el diseño
o la calibración del instrumento de medición. También puede corresponder al
modelo utilizado para los cálculos intermedios en una medición indirecta.
• Instrumental: corresponde al instrumento de medición y es el fabricante quien
indica cuál es la posibilidad de error máxima del dispositivo.
• Ambiental: ocurre por el cambio del medio en el que se realiza la medición.
Por esta razón, en algunos procesos industriales hay equipos que operan en
habitaciones especiales donde se controlan las condiciones ambientales, como
temperatura, humedad, luz, etc.
• De legibilidad: se produce cuando el valor que se observa queda ubicado entre
dos divisiones de la escala empleada, y la persona debe seleccionar el valor inferior o el superior.
Errores accidentales. Están asociados al proceso de medición indirecta. Se observan
cuando al repetir una medición no se obtiene el mismo valor. Este error se relaciona con las condiciones físicas y anímicas de la persona que toma la lectura o con
las condiciones del entorno en que se realiza [Ej. 5]. La situación se corrige cuando
se realizan varias lecturas por distintos operarios, se hacen los registros y se toma
la media aritmética como el valor medido:
suma de lecturas
3. x = total de lecturas
Cuando ocurre que bajo las mismas circunstancias los diferentes operarios obtienen
la misma lectura, se dice que las mediciones tienen buena precisión.
28
st-editorial.com
RECONOCES EL LENGUAJE TÉCNICO
BÁSICO DE LA FÍSICA
Actividad grupal
COMPETENCIAS
GENÉRICAS
4 8
COMPETENCIAS
DISCIPLINARES
4 8
DESEMPEÑOS
DEL ESTUDIANTE
b
c
En su comunidad o estado, hagan una visita guiada a un laboratorio de física. Realicen un informe donde tomen
en cuenta las características del laboratorio, el tipo de instrumentos con los que cuenta y para qué sirven (mencionen al menos cinco), las investigaciones que se llevan a cabo allí, las medidas de seguridad (o precautorias)
que se toman para trabajar con dispositivos y equipos, etc. Si no tienen la posibilidad de ir, realicen la investigación en la biblioteca o en Internet. Anexen el informe al portafolio de evidencias.
Ejemplo 4
En una inspección sorpresa a una papelería por parte de la
oficina central de protección al consumidor, la inspectora
pide un tubo que contiene rollos de papel para forrar libros,
y encuentra que cada uno de los diez pliegos tiene el mismo
ancho pero las longitudes varían.
Pliego
1
Longitud
86
(cm)
2
3
4
5
6
87
85
87.5 85.5 88
7
8
9
85.5 86.5 84
10
85
El dueño de la papelería afirma que su cinta métrica es la que
falló, pues hizo todos los cortes a 88 cm y cuando muestra
su instrumento de medición, resulta ser un trozo de cuerda.
¿Cuál es el error en cada medición? ¿Es un error accidental o
sistemático? ¿Multarías al dueño?
e. Resultado.
El error es sistemático. Si consideramos el instrumento
de medición, concluimos que el dueño merece una multa,
pues no usó el instrumento correcto.
Ejemplo 5
En una fábrica de tubos de PVC se ha capacitado a los operarios para que verifiquen las dimensiones de cada sección de
tubo que se fabrica en una máquina determinada. Si el producto presenta más de 10% de desviación en alguna de sus
dimensiones, la persona que trabaja en esa máquina debe
efectuar los ajustes necesarios para corregir tal situación.
La máquina de Pedro fabrica un tubo de 10.0 cm de diámetro exterior, 2.0 mm de espesor y 3.00 m de longitud. ¿Qué
ajustes debe realizar Pedro en su máquina si cuenta con los
siguientes datos?
Lectura
Diámetro
exterior (cm)
Espesor (mm)
Longitud (m)
1
10.5
2.0
3.01
Solución
2
10.5
2.5
3.02
a. ¿Con qué datos contamos?
• Longitudes de acuerdo al cuadro.
• Longitud real: 88 cm.
3
10.1
1.8
2.99
4
10.1
2.0
2.97
5
10.0
1.9
3.01
b. ¿Qué vamos a hacer?
Calcular el error absoluto.
Solución
c. ¿Cómo lo vamos a hacer?
Empleamos la ecuación 1, que nos permite determinar el
error absoluto en forma directa para cada uno de los rollos: ∆e = M – m.
a. ¿Con qué datos contamos?
•฀Diámetro฀exterior:฀10.0฀cm.
•฀Espesor:฀2.0฀mm.
•฀Longitud:฀3.00฀m.
•฀Error฀relativo฀permitido:฀10%.
•฀Mediciones฀obtenidas฀según฀el฀cuadro.
d. Operaciones.
Pliego 1: ∆e = M – m = 88 – 86 = 2 cm.
Pliego 2: ∆e = M – m = 88 – 87 = 1 cm...
Al proceder de la misma manera con todos los pliegos, los
errores encontrados son:
b. ¿Qué vamos a hacer?
Determinar el valor asociado a las 5 lecturas y luego calcular el error absoluto.
Pliego
1
2
3
4
5
6
7
8
9
10
c. ¿Cómo lo vamos a hacer?
Primero, aplicamos la ecuación 3, correspondiente a la
media aritmética para calcular la dimensión medida:
suma de lecturas
x = total de lecturas
Error absoluto
∆e en cm
st-editorial.com
2
1
3
0.5
2.5
0
2.5
1.5
4
3
Después, para determinar el error relativo, aplicamos la
ecuación 1: er = ∆e/M
29
BLOQUE 1
•฀Diámetro฀exterior.
d. Operaciones.
Valor medido:
•฀Diámetro฀exterior.
De =
Tf 10.24 – 10.0
= 0.024 = 2.4%
fr = M =
10.0
•฀Espesor.
10.5 + 10.5 + 10.1 + 10
= 10.24 cm
5
Tf
2.22 – 2.0
= 0.11 = 11%
fr = M =
2.0
•฀Espesor.
e=
•฀Longitud.
2.1 + 2.4 + 2.2 + 2.3 + 2.1
= 2.22 mm
5
Tf
3.00 – 3.00
fr = M =
= 0 = 0%
3.00
•฀Longitud.
L=
e. Resultado.
La dimensión que presenta una desviación es el
espesor: 11%. Este es el único ajuste que debe realizar el operario.
3.01 + 3.02 + 2.99 + 2.97 + 3.01
= 3.00 mm
5
Error relativo:
Actividad individual
5
COMPETENCIA
GENÉRICA
COMPETENCIAS
DISCIPLINARES
5 10
DESEMPEÑOS
DEL ESTUDIANTE
b
c
I. Resuelve los siguientes problemas; para ello, repasa el procedimiento seguido en los ejemplos anteriores y
consulta las ecuaciones de la 1 a la 3 (pág. 28).
1. En un experimento se mide la deformación de un resorte cuando se le aplica una fuerza específica. Este
proceso se repite 12 veces incrementando en forma proporcional la magnitud de la fuerza para calcular la
rigidez elástica del resorte (k). Los valores calculados son los siguientes:
Resorte
Rigidez elástica
(k) (N/m)
1
2
25.1
3
23.2
24.8
4
25.3
5
24.7
6
25.2
7
8
24.8
9
24.7
25.3
10
11
12
24.9
25.2
25.1
A partir de estos datos determina el valor de la constante k.
2. Para verificar en forma experimental los errores que se cometen al usar un instrumento de medición, una
profesora de física escoge al azar a 10 de sus estudiantes y les proporciona un lexómetro y una regla de
1 m graduada en centímetros. Cada estudiante mide con ambos instrumentos la rama de un árbol, cuya
longitud real es de 123.7 cm.
Estudiante
Longitud (cm)
usando la regla
Longitud (cm)
usando el flexómetro
1
2
3
4
5
6
7
8
9
10
124
123.5
124
123
123
123.5
124
123
123
124
123.5
123.8
123.8
123.5
123.8
123.9
123.5
123.6
123.5
123.8
Calcula el error absoluto y el error relativo que cometió cada estudiante al tomar la medida de la rama del árbol.
II. Anexa esta actividad al portafolio de evidencias.
30
st-editorial.com
Tema 5
Vectores
¿Qué se utiliza para representar la acción de la fuerza? Ahora, supón que
eres el piloto de un avión: ¿cómo estableces la ruta a seguir en un viaje de un
continente a otro? Además: ¿por qué en el tablero de un auto se puede leer la
rapidez a la que viaja pero no se conoce su dirección precisa? ¿Sabes qué es un
vector y cómo se emplea?
Sabemos que en todo proceso de medición se requiere de un sistema de unidades compuesto por
unidades fundamentales y unidades derivadas.
Las magnitudes –valor numérico cuantitativo referente a alguna propiedad de un cuerpo,
como la longitud o el área– son de dos tipos:
escalares y vectoriales.
Magnitudes escalares. Como su nombre lo indica, requieren sólo de una escala para especiicar su
valor y no están relacionadas con los conceptos de
dirección o sentido. La energía, la masa, el peso, el
volumen, la presión atmosférica y la temperatura, entre otras, son magnitudes escalares. Algunos
ejemplos son: el registro de temperatura en un día
caluroso, de 39°C; la energía que te proporciona
una barra de chocolate, 54 kJ; la longitud del pie
st-editorial.com
de una persona, de 24.5 cm, para los efectos de la
talla del calzado.
Magnitudes vectoriales. Antes de referirnos a las
magnitudes vectoriales es necesario deinir que
un vector es un segmento de recta dirigido en el
espacio, que siempre requiere la especiicación
de un punto de aplicación, una magnitud, una
dirección y un sentido.
Las magnitudes vectoriales requieren de un
vector para quedar completamente especiicadas, y además de expresar la cantidad numérica
es necesario precisar la forma en que está actuando la variable, por lo que hay que indicar la
dirección y el sentido. Por ejemplo, el viento se
desplaza a 15 km/h con dirección sureste; una
persona camina 10 km hacia el norte.
31
BLOQUE 1
T
FIGURA 6
FIGURA 7
El barómetro es un instrumento que se emplea para medir la presión atmosférica, que es una magnitud escalar.
Actividad grupal
COMPETENCIAS
GENÉRICAS
4 8
Cuando una persona se lanza en bungee se crea en el cable una
fuerza de tensión, que es una cantidad vectorial.
COMPETENCIAS
DISCIPLINARES
3 4
DESEMPEÑO
DEL ESTUDIANTE
d
En grupos de tres o cuatro estudiantes realicen las siguientes actividades:
1. Investiguen qué es el peso y qué es la masa de un cuerpo, qué es una fuerza eléctrica y qué es una
resistencia eléctrica. Desarollen, en su cuaderno, un cuadro en el que comparen cada una de estas magnitudes e indiquen cuáles son escalares y cuáles vectoriales, cómo se originan, en qué se asemejan, en
qué difieren y qué tienen en común.
2.Busquen las cantidades vectoriales de mayor uso en la física, ¿cuáles de ellas estudiarán en esta asignatura? Revisen el temario que les proporcionó el profesor al inicio del curso, ¿por qué son importantes? Realicen un reporte y discutan en el aula sobre la importancia de conocer una herramienta analítica de este tipo.
Características
Un vector es un conjunto ordenado de números
reales –o complejos– que deinen una magnitud
y una dirección a la variable física a la que se asocian; su representación gráica se vincula con un
segmento de recta dirigido, que puede ser ubicado
en un plano cartesiano o bien en un espacio de
tres dimensiones.
La nomenclatura o simbología para representar
una cantidad vectorial consiste en la representación
por medio de una letra mayúscula con una lecha
encima ( A ), o una letra mayúscula en negrita (A).
La magnitud se expresa como | A | o como A. En
este tema emplearemos la negrita para indicar
el vector y la cursiva para indicar su magnitud.
Observa en el gráico 1 un vector cualquiera,
donde se distinguen los elementos que lo caracterizan.
Glosario
32
GRÁFICO 1
A
A
Origen
Extremo
q
Origen o punto de aplicación. Es donde inicia la recta que representa a la cantidad vectorial.
Extremo. Punto inal de la recta. Se debe colocar
una punta de lecha en el extremo de la recta.
Magnitud o módulo. Indica la longitud total del
vector. Depende de la distancia entre el origen y
el extremo.
Cantidad vectorial. Cantidad asociada a una variable física que requiere de magnitud y dirección para su descripción.
st-editorial.com
RECONOCES EL LENGUAJE TÉCNICO
BÁSICO DE LA FÍSICA
Dirección. Se mide en sentido de movimiento opuesto al de
las agujas del reloj; se expresa mediante el ángulo q.
Cuando hay dos o más vectores, se recomienda deinir
un sistema de coordenadas rectangulares como referencia,
para representarlos gráicamente, y para hacer el análisis se
toma en cuenta el sentido o la dirección de cada vector. En
el gráico 2 se puede observar que mientras los vectores P y
Q tienen sentido positivo, el vector S tiene sentido negativo,
opuesto al de P.
Suma
Las coordenadas cartesianas permiten describir vectores a
partir de distintos ejes.
• Si es sólo un eje, nos referimos al vector en una recta.
• Si son dos ejes, los vectores se ubican en un plano.
• Si son tres ejes, las magnitudes vectoriales son descritas en
un espacio.
Los sistemas de vectores, según su ubicación en el plano o
dimensión, se pueden clasiicar en:
• Coplanares.
• No coplanares.
• Deslizantes.
• Libres.
• Colineales.
• Concurrentes.
FIGURA 8
La ilustración vectorial utiliza vectores para generar figuras.
GRÁFICO 2
y
P
a
q
S
st-editorial.com
Q
x
GRÁFICO 3
y
P
Descomposición y composición
rectangular de vectores por
métodos gráficos y analíticos
Consideremos ahora un sistema coordenado rectangular de
referencia (scr) en el plano, que tiene dos dimensiones: el eje
horizontal (x) se llama abscisa, el eje vertical (y) se denomina
ordenada y a la intersección de ambos ejes se le conoce como
origen (o).
En el gráico 3 se representa a escala, y a partir del origen,
un vector cuya magnitud es de 5 unidades, con una orientación cualquiera sobre el cuadrante positivo.
Para conocer las componentes del vector, se traza una
línea paralela a cada uno de los ejes, de tal manera que
cada una pase por el extremo del vector (punta de lecha)
(gráico 4).
¿Cuánto valen las componentes del vector en el sistema
de referencia empleado? Para responder, procedemos a medir de acuerdo a la escala. La longitud de los segmentos ox1
y oy1 es de 3.9 unidades para la horizontal y de 3.1 unidades
para la vertical, tal como se muestra en el gráico 5.
En el análisis anterior se pasó por alto la dirección especíica del vector y que éste no se ubica en el origen del sistema de referencia. Aunque estos puntos son importantes, no
complican la descomposición del sistema de vectores.
En la siguiente página puedes ver la clasiicación de los
vectores.
a
P=5u
x
o
GRÁFICO 4
y
P
P=5u
x
o
GRÁFICO 5
y
P
y1
3.1 u
P=5u
o
3.9 u
x1
x
33
BLOQUE 1
Infográfico 3 Clasificación de los vectores
1
2
Vectores coplanares
Todos los elementos se encuentran
en un mismo plano.
Vectores no coplanares
Son los que se encuentran en distintos planos.
El gráfico muestra el vector Z en el eje e3, el cual
no es coplanar con los vectores P, Q y R ya que estos
se hallan en otro plano definido por los ejes e1 y e2.
Es, entonces, un sistema no coplanar.
R
e2
Q
P
R
Q
P
e1
Z
e3
3
Vectores deslizantes
Son las magnitudes que pueden moverse en la misma
dirección o línea de acción cuando se ubican sobre
un cuerpo. Una fuerza que actúa sobre un cuerpo
y lo desplaza en línea recta es un ejemplo de vector
deslizante.
4
Vectores libres
En estos vectores se especifica uno de sus dos
componentes, ya sea el extremo o el origen, sin
importar su ubicación en el espacio.
A
5
Vectores colineales
Este sistema está formado por vectores
que se encuentran ubicados sobre una misma línea
de acción, pero no necesariamente comparten
la misma dirección. Los vectores A, B y C son
colineales entre sí, mientras que D y E, además de
ser colineales entre ellos, son paralelos a los primeros.
6
Vectores concurrentes
Todas las magnitudes que intervienen se ubican sobre
un mismo punto sin importar su dirección.
e2
e2
T
S
C
E
A
B
R
Q
D
e1
P
e1
34
st-editorial.com
RECONOCES EL LENGUAJE TÉCNICO
BÁSICO DE LA FÍSICA
Actividad grupal
COMPETENCIAS
GENÉRICAS
4 5 8
COMPETENCIAS
DISCIPLINARES
1 4 6 10
DESEMPEÑO
DEL ESTUDIANTE
d
I. En equipos de tres integrantes observen detenidamente cada una de las siguientes imágenes.
II. Para cada una de ellas realicen lo siguiente:
1. Identifiquen los vectores actuantes.
2. Represéntenlas en forma gráfica, indicando dirección y punto de aplicación.
3. Señalen los tipos de vectores presentes.
4. Indiquen la magnitud que tienen.
5. Anoten sus conclusiones.
III. Anexen esta actividad a su portafolio de evidencias.
Toma el vector de 5 unidades, coloca el origen en la coordenada
(2, 3) y orienta el vector con una dirección de 30° medida con respecto a la horizontal en la dirección opuesta al giro de las manillas
del reloj (gráico 6).
Para el siguiente caso se trazan dos rectas paralelas a cada uno de
los ejes de coordenadas (gráico 7). La medición con respecto a la
escala resulta en los valores de 4.3 unidades para la horizontal y 2.5
unidades para la vertical.
Se puede obtener el mismo resultado empleando el método
analítico de descomposición rectangular. En éste se emplean las
funciones trigonométricas básicas de seno y coseno para analizar
un vector a partir de sus componentes rectangulares. No es necesario conocer con precisión la ubicación del origen del vector en el
sistema de referencia.
Sea el vector A con una dirección q medida con respecto al eje
x, y una magnitud de A unidades, que se coloca en el origen de un
sistema de referencia x,y (gráico 8).
De acuerdo a la trigonometría, la función coseno de un ángulo proporciona el valor del cateto adyacente del triángulo rectángulo con respecto a la hipotenusa. Es decir, deine la
componente horizontal del vector, cuando el ángulo se mide
respecto a dicho eje. En el gráico 9, la función seno indica el valor del cateto opuesto del triángulo rectángulo con
respecto a la hipotenusa, por lo que determina la magnitud
de la componente vertical. Si la hipotenusa del triángulo formado
es de A unidades, las componentes del vector son:
GRÁFICO 6
y
V
3
30°
(2, 3)
x
o
2
GRÁFICO 7
y
V
5
3
(2, 3)
x
O
GRÁFICO 8
2.5 U
30°
4.3 U
2
6
y
A
A
4. Ax = A cos q
5. Ay = A sen q
st-editorial.com
q
o
x
35
BLOQUE 1
GRÁFICO 9
Observa que si el vector no se coloca en el origen del sistema de
referencia y se respeta su magnitud y dirección, las componentes
toman el mismo valor. En el caso de que el ángulo q se mida con
respecto al eje y, como se ilustra en el gráico 10, el uso correcto de
las funciones trigonométricas nos da los siguientes valores para las
componentes del vector:
y
A
A
Ay
q
o
x
Ax
4 a. Ax = A sen q
5 a. Ay = A cos q.
GRÁFICO 10
Mediante la comparación de estas igualdades con las dos anteriores se determina que el valor de las componentes se puede
obtener al considerar la dirección, ya sea con el eje horizontal o
respecto al eje vertical.
Sólo es necesario invertir el orden de las funciones trigonométricas para que se obtenga la componente respectiva en la horizontal o
en la vertical (cuadro 6).
y
A
CUADRO 6. FUNCIÓN TRIGONOMÉTRICA
A EMPLEAR EN EL CÁLCULO ANALÍTICO DE COMPONENTES
A
Ay
q
o
x
Ax
y
3u
(0,2)
4u
(1,0)
B
x
(5,0)
GRÁFICO 12
y
A
(0,5)
3u
(0,2)
4u
0
36
Horizontal
cos q
sen q
Vertical
sen q
cos q
Composición gráfica y analítica de un vector
en un sistema de referencia rectangular
A
0
Componente en el eje y
Si un vector puede ser descompuesto en sus proyecciones horizontal y vertical, también podemos proceder en forma inversa, pero
antes debemos considerar que la composición involucra leyes para
los métodos gráicos. Vayamos por partes e iniciemos con la composición simple de un vector de acuerdo a las proyecciones horizontal
y vertical.
GRÁFICO 11
(0,5)
Componente en el eje x
Ángulo medido con la
(1,0)
B
x
(5,0)
Sean dos vectores que se dirigen exactamente en la dirección de los
ejes x y y respectivamente del scr. El vector A tiene una magnitud
de 3 unidades y el vector B, 4 unidades; el primer vector se coloca en
el punto (0, 2) y el segundo en el punto (1, 0) (gráico 11).
Se trazan dos líneas paralelas para cada vector, que a la vez son
perpendiculares a los vectores considerados (gráico 12). La distancia que las separa corresponde a su magnitud.
Cada línea horizontal se cruza con una línea vertical. Cada punto
de intersección corresponde al origen y al extremo del vector que se
ha compuesto (gráico 13). Luego se unen mediante una línea recta
para representar el vector composición; su magnitud corresponde a
la longitud de la línea trazada según la escala. La dirección se mide
con un transportador. La magnitud es de 5 unidades y la dirección
de 37° con respecto a la horizontal.
Procedamos a realizar ahora el ejercicio. ¿Cuánto diiere de los
valores numéricos presentados antes? ¿Puedes calcular el error relativo? ¿Cómo puedes obtener un resultado más preciso? Al tratarse
de componentes rectangulares, se recurre a la composición analítica:
el vector composición forma un triángulo rectángulo y entonces, de
acuerdo al teorema de Pitágoras, la magnitud es:
st-editorial.com
RECONOCES EL LENGUAJE TÉCNICO
BÁSICO DE LA FÍSICA
6. Vc = V2cx + V2cy
GRÁFICO 13
Y la dirección del vector se obtiene así:
y
Vc
A
(0,5)
Vc = 5 u
Vcy
7. q = arctan c m
Vcx
3u
37°
(0,2)
B
4u
De las dos fórmulas anteriores se deduce que:
0
x
(1,0)
(5,0)
8. Vcx = Vc cos q
9. Vcy = Vc sen q
GRÁFICO 14
y
El resultado es justamente como ya se había determinado con el
método gráico explicado anteriormente.
B
4u
Composición gráfica y analítica de dos o más
vectores en un sistema de referencia rectangular
¿Cómo se hace el análisis si hay dos o más vectores? ¿Cómo se efectúa
la composición para tener un vector equivalente? Para la composición gráica de dos vectores se emplean la ley del paralelogramo y la
ley del triángulo.
Ley del paralelogramo. Esta ley señala que el vector composición (o
resultante) de un par de vectores se obtiene al formar con ellos un
paralelogramo. La diagonal de tal polígono es el vector buscado.
Sean los vectores A y B, cada uno con la dirección y la magnitud
indicadas en el gráico 14.
Para formar el paralelogramo, se traza una línea paralela a cada uno
de los vectores hasta que se intercepten. Luego se une el origen
con el punto que interseca la línea. La diagonal formada es el vector composición o la resultante para la suma vectorial de A y B. La
magnitud y la dirección se obtienen directamente del gráico. En
este caso es de 10.2 unidades con una dirección q = 32°, medido con
respecto al eje horizontal x (gráico 15).
Cuando se presentan más de dos vectores, como P, Q y R (gráico
16), el trazo se hace considerando dos vectores a la vez. Primero se
componen P y Q juntos. El vector resultante se compone a la vez con
R. La última diagonal que se traza es el vector composición para los
tres vectores considerados (gráico 17).
Ley del triángulo. La ley del triángulo indica que el vector composición para un par de vectores corresponde a la suma vectorial de éstos.
Se obtiene colocando el origen del segundo en el extremo inal del
primero; la línea que une el origen del primer vector con el extremo
inal del segundo vector corresponde a la línea de acción del vector
composición. El gráico 18 ilustra este postulado. Se consideran de
nuevo los vectores A y B; el resultado obtenido es el mismo.
Para dos vectores el procedimiento es similar al de la regla del
paralelogramo: se toman dos vectores y se obtiene un vector resultante. A éste se agrega el siguiente vector y se obtiene una nueva
resultante. Se continúa de esta manera hasta incluir todos los vectores de la composición. Para obtener un resultado con un error
más reducido podemos emplear los métodos de composición analítica en dos formas:
• La construcción gráica para resolver triángulos empleando las relaciones trigonométricas conocidas como ley de senos y ley de cosenos.
• La descomposición en componentes horizontales y verticales
para efectuar la suma vectorial.
st-editorial.com
7u
60°
A
15°
GRÁFICO 15
x
y
C
B
4u
32°
GRÁFICO 16
60°
7u
A
15°
x
y
P
R
45°
Q
30°
115°
x
GRÁFICO 17
y
VC
R
V1
P
Q
x
GRÁFICO 18
y
C
10.2 u
32°
15°
B
4u
7u
60°
A
x
37
BLOQUE 1
Composición geométrica-analítica: ley de senos y ley de cosenos. Considera los vectores A y B con las magnitudes y direcciones indicadas
en el gráico 19. Para obtener una solución más precisa construimos
primero un triángulo siguiendo la ley del mismo nombre, y en lugar de tomar los valores del vector composición en forma directa,
procedemos a aplicar la ley de los cosenos para obtener la magnitud,
y la ley de los senos para obtener la dirección con respecto al vector
de referencia A (gráico 20).
10. c = a2 + b2 ! 2ab cos q
FIGURA 9
Los egipcios realizaron grandes construcciones como las pirámides empleando relaciones analíticas similares a la ley de
senos y ley de cosenos.
Toma en cuenta que en la ecuación aparece el símbolo (±) y en la
sustitución se emplea el signo positivo (+) porque el ángulo es menor que 90°; si el ángulo (o el complemento del ángulo) fuera mayor
que 90 se emplea el signo negativo (–).
11.
GRÁFICO 19
La magnitud buscada es: c = 62 + 32 + 2 # 6 # 3 # cos 25c = 8.81
unidades y la dirección con respecto al vector A es:
y
B
3u
6u
45°
b = sen- 1 b
A
20°
x
GRÁFICO 20
y
γ
c
a b
25°
3sen155c
8.81 l = 8.27c
Si hay más de dos vectores es preferible realizar la composición por
adición de componentes escalares.
Composición analítica por suma de componentes escalares. Recuerda
que la suma es una composición vectorial. Para efectuarla no es
indispensable dibujar los vectores en un sistema coordenado de
referencia [Ej. 6, 7 y 8] .
Analicemos la composición geométrica analítica con los vectores A
y B (gráico 21).
De acuerdo a las reglas de descomposición tenemos:
Vector
a
b
20°
x
Componente horizontal
(eje x)
Componente vertical
(eje y)
A
6 cos 20° = 5.63
6 sen 20° = 2.05
B
3 cos 45° = 2.12
3 sen 45° = 2.12
C=A+B
7.76
4.17
La magnitud del vector resultante es:
GRÁFICO 21
y
c = ^7.76h2 + ^4.17h2 = 8.81 unidades
B
3u
45°
38
sena senb senc
a = b = c
6u
20°
Y la dirección con respecto al eje horizontal x es:
A
4.17
q = arctan b 7.76 l = 28.27c
x
¿Notas alguna diferencia en los resultados? Seguro que sí. ¿Por qué?
Pues porque al emplear la ley de los cosenos y la ley de los senos
hemos calculado la dirección con respecto a uno de los vectores,
mientras que con este método indicamos la dirección con respecto
a uno de los ejes de referencia: el horizontal. El valor del ángulo q
obtenido aquí, corresponde a la suma del ángulo de 20° de la dirección del vector A con el eje x, más el ángulo de 8.27° del vector
composición con respecto al vector A:
st-editorial.com
RECONOCES EL LENGUAJE TÉCNICO
BÁSICO DE LA FÍSICA
q = 20° + ß = 20° + 8.27° = 28.27°.
GRÁFICO 22
y
Es común que la dirección del vector resultante se exprese con respecto a uno de los ejes de referencia, el eje x por regla general.
En la mayoría de las aplicaciones se calculan la magnitud y la dirección
del vector, aunque no siempre se requiere; es suiciente con expresar el
vector en sus componentes rectangulares. Para ello, se emplean los vectores unitarios. Como su nombre lo indica, tienen una magnitud correspondiente a la unidad y su dirección se asocia con cada uno de los ejes de
referencia. Para el eje x se designa i, y para el eje y se denomina j.
La forma vectorial de la resultante es:
c = 7.76i + 4.17j unidades
S
VC
Q
P
x
GRÁFICO 23
y
c = 8.81 unidades a 28.27° respecto a la horizontal (eje x).
Para tres o más vectores, debes seguir el mismo procedimiento y
considerar la colocación de un vector tras otro, respetando su dirección, sumando los dos primeros vectores; el resultado lo sumas al
tercero, la resultante al cuarto y así sucesivamente. Sean los vectores
P, Q, R y S con las características representadas en el gráico 22.
La solución gráica la efectuaremos justo como hemos descrito.
La representación del gráico 23 que hemos realizado se conoce
como polígono vectorial, y como no siempre contamos con todos
los instrumentos para un trazo adecuado y preciso tenemos que la
solución analítica es la siguiente:
Vector
Componente horizontal
(eje x)
R
Q
5u
3u
30°
60°
R
P
45° 2u
30°
x
4u
S
Componente vertical
(eje y)
P
2 cos 30° = 1.73205
2 sen 30° = 1
Q
5 cos 60° = 2.5
5 sen 60° = 4.33012
R
1cos 45° = 0.70710
1 sen 45° = 0.70710
S
4 cos 210° = – 3.46410
4 sen 210° = – 2
VR = P + Q + R + S
1.47505
4.03723
El vector resultante es:
VR = 1.47505i + 4.03723j unidades
Con VR = 4.29826 unidades a 69.9295° respecto a la horizontal (eje x)
Ejemplo 6
Obtén el vector composición en forma gráfica y analítica para cada
uno de los vectores.
Ax = 7 u, Ay = 3.5 u.
Bx = 6 u, By = 5 u.
Vectores unitarios. Todo vector cuya magnitud es la unidad para un sistema de referencia cartesiano (x, y, z); se le designa i para el eje x,
j para el eje y, y k para el eje z.
st-editorial.com
Glosario
39
BLOQUE 1
Solución
a. ¿Con qué datos contamos?
Las componentes horizontal y vertical de cuatro
vectores.
b. ¿Qué vamos a hacer?
Calcular la magnitud y la dirección del vector
composición para cada caso.
c. ¿Cómo lo vamos a hacer?
Graficamos los ejes de referencia y colocamos
el origen de cada componente. Trazamos las perpendiculares a los ejes para obtener el punto de
intersección que define la magnitud del vector
composición. Medimos la longitud y la dirección
en los gráficos 24 y 25.
En la forma analítica aplicamos el teorema de Pitágoras para obtener la magnitud y dirección del
vector resultante (ecuaciones 6 y 7).
En este ejemplo habrás notado que la solución analítica muestra componentes negativas en el segundo
caso. ¿Qué significa el signo? El signo señala que
el ángulo se mide con respecto a la horizontal en
el sentido del movimiento de las manillas del reloj. Además, toma en cuenta que la diferencia entre
el método gráfico y el método analítico es mínima
cuando somos lo suficientemente hábiles para dibujar los vectores.
Ejemplo 7
Un vector actúa sobre el punto Q (1,1) de un sistema coordenado de referencia y su magnitud es de
3.5 unidades; asimismo, la componente horizontal
es de 2.2 unidades. Determina la dirección y la magnitud de la componente vertical.
Solución
d. Gráficos y operaciones.
La composición analítica nos indica que:
A=
7 2 + 3.5 2 = 7.82 u
a. ¿Con qué datos contamos?
•El฀origen฀del฀vector฀se฀ubica฀en฀Q (1,1).
• La magnitud es de 3.5 unidades.
• La componente horizontal tiene una magnitud
de 2.2 unidades.
Y la dirección es:
b. ¿Qué vamos a hacer?
Buscar la dirección del vector y su componente
vertical.
3.5
i = arctan a 7 k = 26.56c
GRÁFICO 24
y
A
7.7 u
Ay = 3.5 u
q = 27°
x
Ax = 7 u
GRÁFICO 25
y
Bx = -6 u
x
q = 40°
7.9 u
By = -5 u
c. ¿Cómo lo vamos a hacer?
Para la solución gráfica trazamos a partir del
origen (punto Q) la componente horizontal.
Luego, en el extremo de ésta dibujamos una
línea perpendicular, paralela al eje coordenado. En el origen colocamos el vector de 3.5
unidades de magnitud; trazamos la línea que
lo representa de manera que intercepte a la
perpendicular trazada anteriormente. De este
modo obtenemos la dirección y la magnitud de
la componente vertical.
La solución analítica requiere la función coseno
para determinar la dirección y así calcularemos la
magnitud de la componente vertical (gráfico 26).
d. Gráficos y operaciones.
GRÁFICO 26
y
La composición analítica nos indica que:
B=
^- 6h2 + ^- 5h2
Vy = 2.7 u
= 7.81 u
Y la dirección es:
3.5
i = arctan a 7 k = 26.56c
40
3.5 u
52°
Q
Vx = 2.2 u
x
st-editorial.com
RECONOCES EL LENGUAJE TÉCNICO
BÁSICO DE LA FÍSICA
magnitud y la dirección del vector resultante
(gráfico 28).
Al medir la longitud de la línea que intercepta a los
vectores conocidos, la componente vertical tiene una
magnitud de 2.7 unidades y una dirección de 52°.
GRÁFICO 27
Para la solución analítica partimos de la ecuación
8 para despejar la dirección:
cosi =
vx
2.2
k = 51.06c
& i = arcos a
v
3.5
30 u
28 u
35°
y la componente vertical es:
vy = 3.5 sen 51.05° = 2.722 u.
20°
27 u
10°
25 u
e. Resultado.
La respuesta analítica es q = 51° y v y = 2.72
unidades.
GRÁFICO 28
Ejemplo 8
28 u
v = 23 u
20°
Encuentra la resultante en forma gráfica para el sistema de vectores del gráfico 27.
30 u
92°
25 u
35°
Solución
27 u
a. ¿Con qué datos contamos?
Se muestran en el gráfico 27.
b. ¿Qué vamos a hacer?
Determinar la resultante para los cuatro vectores.
d. Resultado.
La resultante tiene una magnitud de 23 unidades
y una dirección de 92° con respecto a la horizontal medida en el sentido de giro opuesto al de las
manillas del reloj.
c. ¿Cómo lo vamos a hacer?
Para realizar la solución gráfica formamos un
polígono vectorial y medimos directamente la
Actividad grupal
10°
COMPETENCIAS
GENÉRICAS
4 6 8
COMPETENCIAS
DISCIPLINARES
3 6
DESEMPEÑO
DEL ESTUDIANTE
d
I. Las características básicas de un vector son origen, magnitud, dirección y sentido.
Reunidos en equipos realicen lo siguiente en su cuaderno:
1. Consideren los vectores P y Q con una magnitud cualquiera no mayor a 5 unidades y
una dirección que los ubica en el primer cuadrante de un sistema de referencia x, y.
2. Tomen un vector S de 3 unidades de magnitud con una dirección de 210°, y efectúen
la suma de los vectores en forma analítica.
3. Notarán que en la adición de componentes no agregamos signo alguno, resulta suficiente respetar la dirección que se marca para obtener un signo negativo en el resultado parcial: no hay ninguna necesidad de hablar de un “sentido”, ya que la dirección
te indica la orientación completa del vector y la ubicación de su línea de acción respecto a una referencia.
4. ¿Es correcta la última afirmación? Discutan en el grupo y elaboren conclusiones sobre la necesidad de definir un vector con magnitud, dirección y sentido.
II. Anexen esta actividad al portafolio de evidencias.
st-editorial.com
41
BLOQUE 1
Actividad individual
COMPETENCIAS
GENÉRICAS
1
5
COMPETENCIA
DISCIPLINAR
7
DESEMPEÑO
DEL ESTUDIANTE
d
I. Otra herramienta de cálculo para vectores y escalares son los tensores. Investiga sobre sus características y cuáles son las aplicaciones prácticas del cálculo tensorial en
la física. ¿Tiene relación con los sistemas de coordenadas? Realiza en hojas blancas,
un informe de tu investigación e ilustra con ejemplos.
II. Resuelve en tu cuaderno los siguientes problemas.
1. Verifica el resultado del ejemplo 9 trazando un polígono que tenga un orden diferente
al que hemos sugerido. Comprueba el resultado en forma analítica con la suma de
componentes rectangulares para cada vector.
2. Determina las componentes rectangulares de un vector cuya magnitud es de 35 cm y
que tiene una dirección de 65° con respecto al eje vertical de un sistema coordenado
de referencia.
3. Determina la magnitud y la dirección para cada uno de los siguientes vectores y represéntalos gráficamente. ¿Qué tienen en común?
Vector
Componente
horizontal (m)
Componente
vertical (m)
A
–8
12
B
9
6
C
4
–6
4. Realiza la composición gráfica de los tres vectores del ejercicio anterior ¿Cuáles son
la magnitud y la dirección de la resultante?
5. Emplea las leyes del paralelogramo, de senos y de cosenos para realizar la composición gráfica y analítica de los vectores P y Q. El primero tiene una magnitud de 12.5 cm
y su dirección es de 45° medido con respecto a la horizontal en el sentido de giro de
las agujas del reloj. La magnitud del segundo vector es de 17.5 cm y su dirección es de
235° medido en la misma forma que el primero.
6. Determina en forma gráfica la resultante de los siguientes vectores. Verifica analíticamente el resultado.
42
Dirección (°) con
respecto al eje x
Vector
Magnitud (cm)
A
6.75
15
B
8.5
270
C
12.25
125
D
5.15
150
E
2.5
290
F
9.35
45
st-editorial.com
RECONOCES EL LENGUAJE TÉCNICO
BÁSICO DE LA FÍSICA
Lee
LosLos
sesenta…
sesenta...
Corre el año 2060, la humanidad ha sido
derrotada por ella misma, la naturaleza
no se adaptó en tan pocas décadas a
los cambios del medio ambiente. La
tecnología desarrollada por los grandes
científicos de las últimos años brinda
toda clase de comodidades, es suficiente con ingresar a la Red para trabajar
desde la comodidad de la sala de tu
casa; cuando necesitas realizar alguna
actividad extraordinaria fuera de tu
domicilio, subes al transbordador personal, defines los vectores de posición
de tu ruta y listo; no hay calles, avenidas o carreteras, todo eso desapareció
hace 40 años.
Cuando cumples con tus actividades, preparas tu retorno avisando desde tu centro
de comunicaciones personal al centro de
menaje de tu casa, que ajuste la temperatura de las habitaciones, ilumine en
forma tenue la sala, el garage y la tina,
para que se prepare en forma automática un baño de burbujas relajantes para
tu arribo. La merienda estará lista en el
centro de alimentos de la cocina, si no
quieres salir es suficiente con solicitar
el envío a casa de todo lo necesario
para disfrutar de la estancia en el propio
domicilio, ¡maravilloso!
Si no fuera por las restricciones… y
esos pequeños detalles que en ocasiones tornan la vida incomoda, ¡ah!
el siglo pasado… sí, el tiempo se fue
como el agua que se desperdició y que
ahora se fabrica: ya no hay fuentes
naturales, se agotaron o se contaminaron, los vectores epidemiológicos más
terribles han provocado el deceso de
millones de seres vivos, no hay especies vegetales, los alimentos de este
tipo son simples preparados químicos,
los animales caseros desaparecieron
como tales, en su lugar hay pequeños
robots, y se deben usar vestimentas
especiales para salir de las casas que
se encuentran aisladas. Para todo hay
protocolos, se debe esperar un tiempo razonable antes de abandonar los
transportes; para entrar a edificios de
tramites gubernamentales o las instalaciones fabriles se debe cumplir con
la identificación positiva y la desinfección corporal, quién diría que en
los espacios subterráneos se crearía
una infraestructura industrial en donde
se realizan actividades antes inimaginables, desde la cría de aves, peces y
ganado para consumo “humano”, hasta
bebidas, ropa, robots, etc. Algunos afortunados ya pueden caminar en la nueva
atmósfera sin la molesta indumentaria, se dice que son los humanos del
nuevo milenio, aunque en realidad son
el resultado de un experimento genético
exitoso. El ser humano ha mutado lo
suficiente para respirar el aire que ahora
es un compuesto de gases venosos para
nosotros, los del último eslabón, tengo
97 años y ya no puedo correr aunque
todavía camino y me gusta mostrar a los
jóvenes de hoy las imágenes de las playas, los bosques, las grandes ciudades
amuralladas que fueron derruidas por el
cambio climático, -70° C de noviembre
a marzo o bien 80° C de abril a octubre
sin valores intermedios, y algunos temporales ocasionales que descomponen
la tierra por lo tóxico de la “lluvia”, en
fin, qué tiempos, si los físicos hubieran
desarrollado métodos seguros para crear
tecnología sin acabar con la naturaleza y
el ser humano hubiera dedicado un poco
de su tiempo a cuidar de sí mismo… Si
Dios existiera…
Jorge Díaz
De manera individual, responde las siguientes preguntas.
1. ¿Cómo imaginas el mundo en el futuro?
2. ¿Qué acciones has realizado para preservar de la naturaleza?
3. ¿La ciencia y la tecnología avanzan cuidando de la naturaleza y del ser humano? Justifica tu respuesta.
4. ¿Es un atentado a la vida experimentar con seres humanos para mutarlos genéticamente?, ¿por qué?
5. ¿Consideras que el ser humano requiere de un apoyo divino para progresar? Justifica tu respuesta.
st-editorial.com
43
Evaluación sumativa
Heteroevaluación
I. Pide a tu profesor que aplique la siguiente rúbrica, con el fin de que pueda registrar tus avances. Cómo
verás es la misma que respondiste en el reto; ahora servirá para medir cuál fue tu desempeño durante el
estudio de este bloque.
Indicadores de desempeño
Aspectos a evaluar
4 puntos
3 puntos
2 puntos
Identifiqué
vagamente los
métodos de
investigación
y su relevancia
en el desarrollo
de la ciencia
como la solución
de problemas
cotidianos.
Reconocí
y comprendí
vagamente el uso
de las magnitudes
físicas y su
medición como
herramientas de
uso en la actividad
científica de mi
entorno.
Interpreté
Interpreté
Uso de la notación Interpreté el uso
vagamente el uso
parcialmente el
científica y de los de la notación
uso de la notación de la notación
prefijos como una científica y de
científica y de
científica y de los
los prefijos como
herramienta de
prefijos como una los prefijos como
una herramienta
uso que permite
herramienta de uso una herramienta
de uso que me
representar
de uso que
números enteros y permite representar que me permite
me permite
representar
números enteros
decimales.
representar
números enteros
y decimales.
números enteros
y decimales.
y decimales.
Identifiqué algunas Identifiqué
Identifiqué todas
Características
vagamente las
características
las características
y propiedades
características
y propiedades de
y propiedades de
de los vectores
y propiedades de
los vectores que
los vectores que
que permitan su
los vectores que
me permiten su
me permiten su
manejo
me permiten su
manejo y aplicación manejo
y aplicación
manejo
y aplicación
en la solución
en la solución
y aplicación
en la solución
de problemas
de problemas
en la solución
de problemas
cotidianos.
cotidianos.
de problemas
cotidianos.
cotidianos.
Identifiqué la
importancia de
todos los métodos
de investigación
y su relevancia
en el desarrollo
de la ciencia
como la solución
de problemas
cotidianos.
Reconocí
Uso de las
magnitudes físicas y comprendí el
uso de todas las
y su medición
como herramientas magnitudes físicas
y su medición como
de uso en la
actividad científica herramientas de
uso en la actividad
de su entorno.
científica de mi
entorno.
Métodos de
investigación
y su relevancia
en el desarrollo
de la ciencia
como la solución
de problemas
cotidianos.
Identifiqué la
mayoría de los
métodos de
investigación
y su relevancia
en el desarrollo
de la ciencia
como la solución
de problemas
cotidianos.
Reconocí
y comprendí el
uso de algunas
magnitudes físicas
y su medición
como herramientas
de uso en la
actividad científica
de mi entorno.
Mi
puntaje
1 punto
No identifiqué
la importancia
de los métodos de
investigación ni
su relevancia en el
desarrollo de la ciencia
como la solución de
problemas cotidianos.
No reconocí ni
comprendí el uso de
las magnitudes físicas,
tampoco su medición
como herramientas
de uso en la actividad
científica de mi entorno.
No interpreté el uso de
la notación científica ni
de los prefijos como una
herramienta de uso que
me permite representar
números enteros
y decimales.
No identifiqué las
características ni
propiedades de los
vectores que me
permiten su manejo
y aplicación en la
solución de problemas
cotidianos.
Valoración
Excelente: 15 a 16 puntos.
Bueno: 11 a 14 puntos.
Suficiente: 7 a 10 puntos.
Mi total
Insuficiente: 4 a 6 puntos.
II. Ha llegado el momento de que entregues a tu profesor todos los productos de las actividades que
realizaste durante este bloque y que guardaste en tu portafolio de evidencias, ya que con esto podrá
evaluarte.
44
st-editorial.com
ANALIZA LOS PROCESOS DE CREACIÓNY
CONFORMACIÓN DE MÉXICO COMO NACIÓN
Autoevaluación
I. Relaciona las columnas; después regresa al bloque para verificar que tus respuestas sean correctas y
modifica aquellas que no lo sean.
1. ( ) Causa de que ocurran los errores sistemáticos.
a. Arquímedes
2. ( ) Prefijo empleado para designar la millonésima parte de b. Vectoriales
la unidad.
c. Unidades derivadas
3. ( ) Científico griego que sistematizó los conocimientos de d. Mega
e. La persona que mide elige el valor a reportar
la física de su tiempo.
f. Unidades fundamentales
4. ( ) Algunas variables de la física se pueden expresar em- g. Las condiciones anímicas de quién mide no
pleando estas cantidades.
son adecuadas
h. Micro
5. ( ) Un sistema de medición se establece a partir de…
i. Escalares
j. Aristóteles
II. Lee el siguiente texto y en tu cuaderno contesta las preguntas posteriores.
El cáncer en México se ha convertido en un problema de salud pública; es la segunda causa de muerte
después de los padecimientos del corazón, pero actualmente el adecuado proceso de investigación
desarrollado por científicos, médicos y empresas farmacéuticas ha reducido el tiempo empleado para
la creación de medicamentos y vacunas de nueva generación.
1. ¿Cuál es la situación en los países desarrollados?
2. ¿Por qué se ha reducido el tiempo para el desarrollo de nuevas vacunas?
3. ¿En qué otras áreas se han producido beneficios por el empleo adecuado de los métodos de investigación? Menciona diez.
III. Realiza las siguientes actividades en tu cuaderno.
1. Una bacteria es un organismo vivo que puede producir diferentes tipos de afecciones, dependiendo de su forma se le asigna un nombre específico, mientras que su tamaño se encuentra entre 0.2 y
15 µm, así encontramos bacilos, cocos, etc. Investiga lo siguiente:
a. Existen organismos más pequeños, ¿qué dimensiones tienen?
b. ¿Cuántas veces es mayor un elefante a un bacilo?
c. ¿Qué cantidad de bacterias se requiere para producir difteria?
2. Dibuja un poste de luz inclinado a 45 grados del suelo y responde lo siguiente:
a. ¿En dónde y por qué colocarías un cable que permita al poste mantenerse en posición vertical?
b. Indica las características del vector fuerza que se presenta en tal cable para que cumpla con la función indicada.
c. ¿En dónde has observado el empleo de cables o cuerdas que producen una fuerza que permite el
equilibrio de un objeto?
3. En una fábrica de tornillos recibieron un pedido especial, el cliente desea que se fabrique un millón de
tornillos cuyo paso sea de 1/16 de pulgada con una longitud de pulgada y media; el jefe de producción
consciente de que todos los productos sólo se fabrican empleando el sistema internacional de unidades,
indica al gerente de ventas que no cuenta con los aditamentos necesarios para fabricar el producto solicitado por lo que no es posible cumplir con el pedido, el gerente no desea escapar el pedido y ordena a los
operarios que se trabaje adaptando “las medidas” al SI. Una semana después de entregado el producto el
cliente lo devuelve a la empresa indicando que no cumplen con lo solicitado pues sólo tienen menos de
1.4 pul de longitud y 0.05 pul de paso.
Elabora un reporte que indique, entre otras cosas, lo siguiente:
a. ¿Qué valores (expresados en mm) tomaron los operarios como factores de conversión?
st-editorial.com
45
b. ¿Cuáles son las equivalencias correctas?
c. ¿Cuál fue el error?
d. ¿Qué se tenía que hacer?
e. ¿Qué tipo de instrumentos se deben emplear?
f. ¿Cómo se debe solucionar el problema?
IV. Para reducir el daño a la salud, provocado por el tránsito vehicular en zonas con un alto índice de
población se decide colocar barreras acústicas que aíslen el ruido y restringir el tránsito de vehículos
las 24 horas del día. Después de las medidas tomadas la gente protesta y realiza manifestaciones
que provocan conflictos viales en toda la ciudad.
Analiza la situación y siguiendo un método de investigación define:
1. Problema y restricciones.
2. Hipótesis de trabajo.
3. Propuestas de solución.
4. Selección de solución.
46
st-editorial.com
5. Forma de poner en práctica la solución.
V. En un accidente aéreo se dictamina que el piloto es el responsable pues no respetó los vectores de
aproximación a la pista asignada; ¿es correcto afirmar que tales vectores no existen? Argumenta tu
respuesta en no más de 10 líneas.
VI. Responde, en tu cuaderno, cada una de las siguientes preguntas.
1. ¿Qué tan importante es para ti el estudio de la física?
2. ¿Este bloque te ha aportado conocimientos que emplearás en otros campos?
3. ¿Se te dificultó el estudio del tema de vectores?
4. ¿En qué situaciones de tu vida diaria aplicas o ves relejados los conocimientos que has adquirido?
5. ¿Te consideras apto para estudiar por tu cuenta temas afines a los vistos en este bloque?
VII. Contesta la siguiente lista de cotejo para que reconozcas cuáles fueron tus actitudes durante este
bloque.
Aspecto
Siempre
Algunas
veces
Nunca
Me integré al trabajo en equipo.
Realicé comentarios acertados de acuerdo con el tema.
Mostré una actitud de respeto y compañerismo.
Participé en todas las actividades.
st-editorial.com
47
Desempeños del estudiante
Bloque 2
Identificas diferencias
entre distintos tipos
de movimiento
a. Define conceptos básicos relacionados con
el movimiento.
b. Identifica las características del movimiento
de los cuerpos en una y dos dimensiones.
c. Reconoce y describe, en base a sus
características, diferencias entre cada tipo
de movimiento.
Estos desempeños pueden identificarse en cada una de
las actividades del bloque, de la siguiente manera:
DESEMPEÑOS DEL
ESTUDIANTE
a
b
c
Bloque 1
Bloque 2
Bloque 3
Reconoces el
lenguaje técnico
básico de la física
Identificas
diferencias entre
distintos tipos
de movimiento
Comprendes el movimiento
de los cuerpos a partir de
las leyes de dinámica
de Newton
Objetos de aprendizaje
•฀ Nociones básicas sobre movimiento
•฀ Movimiento en una dimensión
•฀ Movimiento en dos dimensiones
Bloque 4
Relacionas el trabajo
con la energía
Introducción
Después de concluir un largo y arduo día, decides
que la mejor manera de reponer la energía perdida
es el reposo. Pero, ¿sabías que aun al dormir tu
cuerpo se mueve? Sí, tus pulmones ayudan a
oxigenar el cuerpo, tu corazón trabaja y la sangre
circula, tu estómago hace que la digestión sea
continua… ¡Hasta la más pequeña célula de tu
organismo se mueve! Desde lo más pequeño hasta
lo más grande, nada está en reposo absoluto: la
Tierra se encuentra en movimiento continuo y
por eso hay día, noche y cuatro estaciones. En esta
unidad estudiarás el movimiento en una y dos
dimensiones; analizarás conceptos como distancia,
aceleración, caída libre, movimiento circular y tiro
parabólico, además de sus aplicaciones prácticas
en la vida cotidiana. A continuación verás un
mapa conceptual con los conceptos más relevantes
de este bloque.
Movimiento
lo estudia la
está presente en
cualquier
dinámica
cuerpo
que se divide en
ya sea
cinemática
50
cinética
partícula
puede efectuarse en
una
dimensión
dos
dimensiones
puede ser
cuerpo
rígido
uniforme
(horizontal)
uniforme
acelerado
(horizontal o
vertical)
puede ser
parabólico
circular uniforme
circular uniforme
acelerado
st-editorial.com
Para comenzar...
Para que puedas comprender los temas de este bloque, es necesario
que rescates las competencias (conocimientos, habilidades, actitudes y valores) que ya
has adquirido a lo largo de tu vida. Haz tu mejor esfuerzo para responder y detecta aquellos
aspectos que no conoces o dominas para enfocar tu estudio.
I. Escribe en el paréntesis la letra que corresponda a la respuesta correcta.
1.(
) ¿Qué es el movimiento?
a. Un cambio de posición con respecto al espacio.
b. Un cambio de posición que sucede en un tiempo específico.
c. Un desplazamiento en una dirección específica.
d. La manifestación molecular de un cuerpo.
2.(
) ¿Qué diferencia hay entre rapidez y velocidad?
a. Ninguna, porque se refieren al mismo fenómeno.
b. La primera es una magnitud escalar y la segunda es un vector.
c. La rapidez sí depende del tiempo, la velocidad no.
d. Las opciones b y c son correctas.
3.(
) Los sistemas de referencia del movimiento de un cuerpo sirven para:
a. medir la velocidad de un cuerpo.
b. ubicar un objeto en movimiento.
c. medir la cantidad de movimiento.
d. realizar operaciones de composición vectorial.
4.(
) El movimiento se puede clasificar en:
a. rectilíneo y curvilíneo.
b. uniforme y variable.
c. acelerado y uniforme.
d. libre y parabólico.
5.(
) La caída libre de un objeto es un movimiento:
a. con velocidad constante.
b. con aceleración constante.
c. con aceleración variable.
d. rectilíneo con velocidad variable.
II. Resuelve los siguientes problemas en tu cuaderno.
1. Mientras un niño juega en un parque se da cuenta de que hay un vendedor de helados en una esquina. Entonces camina 20 m hacia el norte, gira hacia el este y recorre 5 m; finalmente recorre 6 m hacia el norte y llega hasta donde está el vendedor.
Determina la distancia recorrida por el niño y la magnitud del desplazamiento total.
2. Un auto viaja de una ciudad a otra y recorre 72 km en 45 min. ¿Con qué rapidez se
realizó el viaje?
3. ¿En qué medida un autobús aumenta su rapidez si sufre un cambio de 3 km/h cada 2 s?
4. Determina el tiempo que tarda una pelota en subir y bajar cuando se lanza verticalmente con una velocidad de 5 m/s.
5. Calcula la velocidad tangencial de una avioneta que describe una trayectoria circular con una velocidad angular de 3 rad/s y un radio de 40 m.
st-editorial.com
51
BLOQUE 2
III. Lee el siguiente texto, reflexiona e investiga.
Julio Verne realizó estudios de leyes en París y por su afición al arte escribió libretos de óperas y obras de teatro. Se dice que
su pasión por la lectura lo condujo a leer diversos textos de geología, ingeniería y astronomía, por lo que con facilidad podía
documentar sus fantásticas aventuras, prediciendo con asombrosa exactitud muchos de los logros científicos del siglo XX. En sus
novelas habla de cohetes espaciales, submarinos, helicópteros, aire acondicionado, misiles dirigidos e imágenes en movimiento,
todo ello situado en una época en la que se consideraban estos inventos como mera fantasía, razón por la que es considerado
como el creador de la ciencia ficción.
1. ¿Qué sistemas de transporte son considerados hoy en día como un sueño a transformarse en realidad en las próximas décadas?
2. ¿Cómo afecta al medio ambiente el movimiento de un cuerpo a alta velocidad?
52
st-editorial.com
Reto (problema)
El movimiento siempre ha representado un reto para el ser humano. Por ejemplo, los retos que imponen las diversas disciplinas deportivas son cada día mayores, incluso se innova en tecnología para
nuevos materiales para uniformes y accesorios que hacen posible alcanzar nuevas metas, por ejemplo,
en cada estilo de la natación se perfeccionan las técnicas, y tanto en el salto de altura como en el salto
con pértiga se requiere de cierta habilidad para superar el listón, y así en diversas disciplinas, en cada
uno de los deportes que hemos mencionado se coordinan los músculos del cuerpo para conseguir que
el deportista logre un determinado movimiento.
Reúnete con dos compañeros para analizar las cuestiones siguientes; en cada una intercambien el rol
de líder y discutan sobre lo solicitado respondiendo los incisos a manera de conclusión.
1. Del concepto general de movimiento y su importancia en el deporte:
a. ¿El movimiento es sólo un cambio de posición?
b. ¿Por qué es importante estudiar el movimiento de un cuerpo?
c. ¿Qué existe en común entre una vuelta de una carrera de Fórmula 1 y una competencia de 400
metros planos?
d. ¿Cuáles son las variables fundamentales en el atletismo?
e. ¿Qué deporte implica que no se realice ningún tipo de movimiento?
2. De los diferentes tipos de movimiento y cómo se pueden agrupar:
a. Un bateador pega un hit y corre hacia la primera base; un corredor de atletismo escucha el disparo
y se “lanza” para ganar la prueba de los 60 m planos bajo techo. ¿Qué trayectoria siguió cada uno?
b. En otros escenarios, un nadador se prepara para competir en 50 m de estilo libre, mientras que
otro se concentra para la prueba de salto de altura, ¿difiere la trayectoria seguida con respecto a
los casos del inciso anterior?
c. ¿Qué caracteriza al efecto de "chanle" en el fútbol, o un saque “bombeado” en el voleibol? ¿Cuál
es la diferencia respecto a los otros movimientos?
d. ¿Qué variables inluyen en el movimiento de una pelota, ya sea en un tiro de fútbol o un pase
largo en fútbol americano?
e. ¿Cómo clasificas el movimiento?
3. De nuestras actividades cotidianas y el movimiento:
a. ¿Qué tipo de movimiento es el que realizas con mayor frecuencia? ¿Qué características tiene? ¿Lo
realizas tú o empleas algún medio para que se efectúe?
b. ¿Qué movimiento realizan las aves al viajar de rama en rama?
c. Si pones una lavadora a funcionar, ¿qué movimiento realizan las aspas? ¿Cómo se comportan el
agua y la ropa?
d. Observa el movimiento de un carrusel, ¿qué movimiento tienen los caballos?
e. Un manipulador industrial puede realizar un movimiento similar al de nuestras manos, ¿de qué
tipo es este movimiento?
st-editorial.com
53
Coevaluación
En la siguiente lista de cotejo se presentan una serie de aspectos para que evalúes el desempeño de uno
de tus compañeros durante la realización del reto.
Aspecto
Siempre
Algunas
veces
Nunca
Participó activamente en la discusión.
Respetó las ideas de los compañeros y buscó un consenso.
Propuso ideas para estructurar la presentación al grupo.
Trabajó con limpieza y orden.
Cumplió con los acuerdos y normas de trabajo establecidos.
Autoevaluación
Evalúa tu desempeño durante la realización del reto. Para ello marca la siguiente rúbrica según corresponda. Posteriormente, verifica la escala de valoración.
Indicadores de desempeño
Aspectos a evaluar
4 puntos
3 puntos
2 puntos
1 punto
Conceptos básicos
relacionados
con el movimiento.
Definí plenamente
conceptos básicos
relacionados
con el movimiento.
Definí la mayoría de
conceptos básicos
relacionados
con el movimiento.
Definí vagamente
conceptos básicos
relacionados
con el movimiento.
No definí
conceptos básicos
relacionados
con el movimiento.
Características
del movimiento de
los cuerpos en una
y dos dimensiones.
Identifiqué todas las
características del
movimiento de
los cuerpos en una
y dos dimensiones.
Identifiqué la
mayoría de las
características del
movimiento de
los cuerpos en una
y dos dimensiones.
Identifiqué
algunas de las
características del
movimiento de
los cuerpos en una
y dos dimensiones.
No identifiqué las
características del
movimiento de
los cuerpos en una
y dos dimensiones.
Características
y diferencias
entre cada tipo
de movimiento.
Reconocí y describí,
con base en sus
características,
todas las diferencias
entre cada tipo
de movimiento.
Reconocí y
describí, con
base en sus
características,
la mayoría de
diferencias entre
cada tipo de
movimiento.
Reconocí y
describí, con
base en sus
características,
algunas diferencias
entre cada tipo
de movimiento.
No reconocí ni
describí, con
base en sus
características,
diferencias entre
cada tipo
de movimiento.
Valoración
Excelente: 11 a 12 puntos.
54
Bueno: 8 a 10 puntos.
Suficiente: 5 a 7 puntos.
Mi puntaje
Mi total
Insuficiente: 3 a 4 puntos.
st-editorial.com
Tema 1
Tema 2
Tema 3
Nociones básicas
sobre movimiento
Movimiento en
una dimensión
Movimiento en
dos dimensiones
Imagina que te encuentras en el tercer carril de una alberca que tiene 8 carriles,
practicando para una competencia en estilo libre de natación. Cada competidor
debe nadar en su carril una distancia de 50 m en cada ocasión para completar
100 m, ¿qué trayectoria sigues?
Si en alguna ocasión, cuando eras pequeño, viste
un tren de juguete, debes recordar que éste circulaba sobre rieles ensamblados en forma de círculo
que deinían su trayectoria en un plano, ¿no es
así?; pero en el caso de una competencia de natación, asumimos que el recorrido corresponde
al de una línea recta, pues un desvío implica un
mayor tiempo y esto te dejaría fuera de los primeros lugares; por lo que existe una gran diferencia.
Cuando es factible realizar el análisis del movimiento empleando sólo una de las coordenadas
de un sistema de referencia, se dice que el movimiento tiene una dimensión, como el de un atleta
que recorre 100 m sin obstáculos en 10 s. Para
todo movimiento en el que se ven involucrados
los dos ejes de un sistema de referencia, al igual
que el tren de juguete, se dice que el movimiento
es bidimensional o de dos dimensiones.
De estudios anteriores debes recordar que la dinámica es la parte de la física que se encarga del análisis
del movimiento de los cuerpos y todo lo que ello implica, y para facilitar su estudio se divide en cinemática
y cinética. La cinemática se encarga de la geometría
del movimiento, que es lo que ahora nos ocupa.
¿Qué es el movimiento?, ¿cómo lo deinimos?
Imagina la siguiente situación. Supón que un día cualquiera visitas en auto a un amigo que vive a 22 km de
tu casa. Ya de camino en el auto, te detienes ante
un semáforo con luz roja, hasta que, después de
unos minutos, aparece la verde. Avanzas de nuevo
y después de recorrer algunas cuadras te detiene otro semáforo; esto se repite hasta que por in
llegas a tu destino. ¿Qué ha ocurrido? Pues te has
desplazado en cierta dirección, has recorrido cierta
distancia con cambios de velocidad y aceleración, lo
cual puede representarse gráicamente.
Velocidad. Desplazamiento de un cuerpo en la unidad de tiempo. A diferencia de la rapidez, la velocidad es una cantidad vectorial.
st-editorial.com
Glosario
55
BLOQUE 2
El mundo que te rodea
El estudio del movimiento en tres dimensiones es más complejo. Aunque se podría pensar que sólo es cuestión
de agregar un eje coordenado más, esto no es así. Por ello resulta fundamental tener en cuenta esta complejidad para el diseño de aplicaciones robóticas y el desarrollo de autómatas.
Vuelta a la izquierda 3 km
Vuelta a la izquierda 3 km
Destino
Vuelta a la derecha 1 km
Vuelta a la izquierda 5 km
Vuelta a la derecha 4 km
Vuelta a la izquierda 1 km
Vuelta a la derecha 2 km
3 km al norte
Origen
FIGURA 1
Representación gráfica del desplazamiento de un móvil.
Al observar la igura 1, te percatarás que hemos señalado el punto de partida del auto como
origen, el cual corresponde a la posición, que no
es otra cosa que la ubicación precisa de un cuerpo en un marco de referencia ijo o móvil; el movimiento es el cambio de posición en el tiempo
de un cuerpo con respecto a la referencia previamente deinida, de tal manera que el tiempo lo
concebimos como una sucesión de eventos. Las
dos características del movimiento son la distancia y el desplazamiento. Los 22 km constituyen
la cantidad escalar que nos indica la distancia
que recorriste para alcanzar el objetivo.
Si no fuera porque el sentido del tráico en las
calles te limita, habrías hecho el recorrido con menos cantidad de vueltas. Para efectuar el recorrido
seguiste en cada tramo una dirección especíica.
El desplazamiento es una cantidad vectorial porque requiere de magnitud, dirección y sentido.
La distancia total recorrida (22 km) es mayor que la magnitud del vector desplazamiento
resultante (11.4 km). Observa el gráfico 1. El
vector S corresponde al desplazamiento total. Si
se aplica el teorema de Pitágoras su magnitud
es de 11.4 km y su dirección es de 105.25° con
respecto al eje horizontal x.
GRÁFICO 1
y
H= 3 i km
F= 3 i km
G= 1 i km
S= A +B + C + D+ E + F + G + H
S= 3 i + 11 j
C= 2 j km
E= 5 j km
D= 4 i km
B= 1 i km
A= 3 j km
Origen
x
Si al regresar directamente a tu casa, sigues
el mismo camino pero en sentido inverso, al inal habrás recorrido una distancia de 44 km y
el desplazamiento total será 0 pues has regresado
56
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
al mismo punto de partida. Es un vector que resulta de la suma de
todos los vectores de desplazamiento parciales.
Otras dos características del movimiento son la rapidez y la velocidad. Erróneamente, ambas son usadas en forma indistinta.
Rapidez (v). Es una cantidad escalar; es un cambio de posición en
una fracción de tiempo. No afecta la dirección o el sentido de movimiento: sólo se recorre una distancia en un determinado tiempo.
P
v
Q
Dx x f – x i
= t –t
1. v =
f
i
Dt
Donde:
v = rapidez expresada en m/s
∆x = distancia neta recorrida entre los puntos inal (xf) e inicial (xi)
expresada en m.
∆t = lapso transcurrido para recorrer la distancia total expresado en s.
Velocidad (v). Es una cantidad vectorial; es el cambio del vector
desplazamiento con respecto al tiempo. Su fórmula se escribe de la
siguiente manera:
FIGURA 2
Cuando un avión hace maniobras para aterrizar, la trayectoria
curvilínea determina el vector velocidad. En la figura se muestra cómo cambia la dirección del vector velocidad para los puntos P y Q, aunque la maniobra sea ejecutada con una rapidez
constante.
s
2. v = t
Esta expresión se lee así:
v = vector velocidad expresado en m/s.
s = vector desplazamiento.
t = lapso en el que se mide el cambio del vector desplazamiento.
La dirección del vector de velocidad es la misma que la del vector
desplazamiento, y en trayectorias rectas pasa desapercibido. Esta situación es más visible en las trayectorias curvas.
La aceleración es una cantidad vectorial que corresponde al cambio del vector velocidad con respecto al tiempo.
v
3. a = t
Donde:
a = vector aceleración expresado en m/s2.
v = vector velocidad.
t = lapso en el que cambia el vector velocidad.
La dirección de la aceleración depende directamente del vector
velocidad, ya que este puede cambiar en magnitud y/o en dirección.
Retrato
Christian Huygens. Nació en 1629 y murió en 1695. Físico holandés, desarrolló en 1678 la teoría del
movimiento ondulatorio de la luz, movimiento mucho más complejo que las formas estudiadas hasta aquí.
Mediante esta teoría él explicó las características de la reflexión y la refracción, las cuales expuso en su
famoso Tratado de la luz. Su propuesta cayó en el olvido, al ser sustituida por la imagen y el prestigio
alcanzados por Newton.
Vector desplazamiento. Indica el cambio de posición de un punto desde su ubicación inicial hasta la final; generalmente es diferente a la
distancia real recorrida.
st-editorial.com
Glosario
57
BLOQUE 2
Sistemas de referencia
absoluto y relativo
Los sistemas de referencia describen el movimiento o la ubicación de un cuerpo con
respecto a otro. Entre ellos, el más común para analizar el movimiento es el Sistema de
Coordenadas Cartesianas o Rectangulares (scr). Según el caso, se emplea un sistema de
carácter absoluto o uno relativo, sin que ello implique que uno sea mejor que otro.
Sistema de referencia absoluto. Describe la posición y el comportamiento de varios objetos al mismo tiempo, y es universalmente aceptado. Por ejemplo, la torre
de control de un aeropuerto recibe la señal de identificación de varios aviones
y tomando como origen al propio aeropuerto ubica a todos los aviones en un
espacio aéreo determinado.
Sistema de referencia relativo. En este caso el punto de referencia está en movimiento, al
igual que el objeto. Por ejemplo, el piloto de un avión que se encuentra en el aire y trata de
ubicar la posición de otro avión en su espacio aéreo. La posición de cada avión será relativa
porque dependerá de la ubicación de la otra aeronave, como se observa en el gráico 2.
GRÁFICO 2
y
( x2, y2 )
( x1, y1 )
( x3, y3 )
( x4, y4 )
x
Las ecuaciones generales asociadas al estudio de la cinemática empleando sistemas
de referencia relativos son las siguientes [Ejs. 1, 2 y 3]:
Para la posición:
4. sA/B = sA - sB [m]
Donde:
sA/B = posición relativa (o aparente) del cuerpo A observado desde el cuerpo B.
sA = posición del cuerpo A.
sB = posición del cuerpo B.
Para la velocidad:
5. vA/B = vA-vB [m/s]
Donde:
vA/B = velocidad relativa (o aparente) del cuerpo A observado desde el cuerpo B.
vA = velocidad del cuerpo A.
vB = velocidad del cuerpo B.
La aceleración se calcula así:
6. aA/B = aA - aB
[m/s2]
Donde:
aA/B = aceleración relativa (o aparente) del cuerpo A observado desde el cuerpo B.
aA = aceleración del cuerpo A.
aB = aceleración del cuerpo B.
58
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
Ejemplo 1
Para ir de excursión al bosque, Laura se reunirá con
sus amigos en el Valle de los Osos. Cuando llega al
campamento de base para registrarse, se percata de
que no lleva mapa, pero sí una brújula. Los paramédicos le indican los peligros del bosque y le dicen
que debe viajar 6 km al noroeste, después subir 4
km en dirección norte y regresar 2 km al sureste para
esquivar un risco peligroso. Así podrá llegar al valle
que busca. Determinemos el desplazamiento total y
la distancia recorrida por esta inquieta exploradora.
Solución
a. ¿Con qué datos contamos?
Recorrido:
• 6 km NO.
• 4 km N.
• 2 km SE.
b. ¿Qué vamos a hacer?
Tomamos cada valor numérico para calcular desplazamiento, distancia y posición final.
c. ¿Cómo lo vamos a hacer?
Identificamos cada dato numérico como vector.
Efectuamos las operaciones correspondientes
valiéndonos de un polígono vectorial.
d. Operaciones.
Para el desplazamiento de la excursionista
(gráfico 3):
B
A
-45°
C
Al iniciar un viaje por autobús de México a Acapulco,
el conductor anuncia que el tiempo estimado para
el recorrido será de 6.0 h, debido a las intensas lluvias en algunos tramos de la carretera. Estimemos
la rapidez del autobús considerando que la distancia
entre ambas ciudades es de 465 km.
Solución
E (x)
b. ¿Qué vamos a hacer?
Calcular la rapidez del autobús considerando los
datos de distancia y tiempo.
S (-y)
Trazamos un SRC en el que el origen coincide con la
ubicación del sitio de registro. Dibujamos los vectores considerando que 1 cm equivale a 2 km y obtenemos el vector resultante de desplazamiento D.
Vector A = 6 km a 135° con respecto al eje horizontal (x), que correspondería al este.
Vector B = 4 km a 90° con respecto al eje horizontal.
Vector C = 2 km a -45° con respecto al eje horizontal.
Medimos directamente en el dibujo de acuerdo a
nuestra escala. D tiene una magnitud de 7.3 km y
su dirección q es de 66° con respecto a la horizontal medidos a partir del oeste.
st-editorial.com
Ejemplo 2
D
135°
O (-x)
e. Resultado.
El vector desplazamiento es D y tiene una magnitud de 7.3 km a 66° del eje que señala al oeste;
además, la distancia recorrida es de 12 km.
Verifica la precisión de este resultado empleando
cualquier método analítico de los que tratamos
en la primera unidad de este texto. ¿No te ha
sucedido que en algunas ocasiones debes recorrer una gran distancia debido a todos los
recovecos que hay en un lugar que deseas visitar? La ubicación final del grupo de amigos
se registra mediante el vector desplazamiento;
éste se toma como referencia inicial por parte
de los equipos de rescate cuando se reporta un
accidente.
a. ¿Cón qué datos contamos?
• Tiempo: t = 6.0 h.
• Distancia: d = 465 km.
• Incógnita: rapidez del autobús.
N (y)
GRÁFICO 3
Para la distancia:
Efectuamos la suma escalar de la magnitud de
cada desplazamiento:
d = 6 + 4 + 2 = 12 km
c. ¿Cómo lo vamos a hacer?
Sustituimos directamente en la ecuación 1 los
datos proporcionados.
d. Operaciones.
v=
465
6 = 77.5 km/h
e. Resultado.
La rapidez será de 77.5 km/h.
Observa que este resultado es un promedio, ya
que se menciona que llueve y se hace un estimado del tiempo que se empleará; no hay certeza en cuanto a la manera en que se recorrerá el
trayecto.
59
BLOQUE 2
Ejemplo 3
El autobús en que te trasladas de la Ciudad de México al parque industrial Lerma viaja a 80 km/h a partir
de la caseta de cobro de la autopista hasta el entronque con el paseo Tollocan, donde se ve obligado a
reducir la velocidad hasta 55 km/h en 8 s. Determinemos el cambio de velocidad con respecto al tiempo.
a. ¿Con qué datos contamos?
• Velocidad inicial: vo = 80 km/h.
• Velocidad final: vf = 55 km/h.
• Tiempo: t = 8.0 s.
km
1h
1000 m
vo = 80 h # 3600 s # 1 km = 22.222 m/s
Sustitución numérica:
a=
b. ¿Qué vamos a hacer?
Calculamos la desaceleración que sufre el autobús en forma repentina.
c. ¿Cómo lo vamos a hacer?
Empleamos la ecuación 3 en forma escalar, ya
que se desconoce cualquier dato acerca de la
COMPETENCIAS
GENÉRICAS
d. Operaciones.
Transformación de unidades.
km
1h
1000 m
vf = 55 h # 3600 s # 1 km = 15.278 m/s
Solución
Actividad grupal
dirección del vector velocidad. La sustitución
numérica requiere que primero hagamos el
cambio de unidades.
4 5 8
15.278 – 22.222
= - 0.868 m/s2
8
e. Resultado.
El autobús se desacelera a razón de 0.87 m/s2; observa que el signo menos de la operación numérica
tiene el significado físico de la reducción de velocidad, los factores del numerador tienen el orden que
escribimos porque estamos evaluando el cambio
entre una condición final y una condición inicial.
COMPETENCIAS
DISCIPLINARES
3 7
DESEMPEÑO
DEL ESTUDIANTE
a
Reúnete con dos compañeros y resuelvan en sus cuadernos los ejercicios de esta sección. Primero, definan los conceptos involucrados y repasen los ejemplos y las ecuaciones del 1 al 6. Después, tengan a la
mano un juego de geometría y una calculadora. Cuando sea necesario, dibujen los vectores de desplazamiento, velocidad y aceleración, no lo hagan a mano alzada, deben realizar los trazos a escala y verificar
los resultados en forma analítica.
1. Un repartidor de pizza arma su itinerario para el último viaje de reparto de su turno de tal manera que
después de la última entrega irá directamente a su casa, donde guarda la moto. Primero debe viajar 45 m
al norte, después realiza otra entrega viajando al este 300 m, y finalmente entrega su último pedido
viajando 70 m al sur. A partir de aquí recorre 50 m al oeste para llegar a su casa. Determina la distancia
total recorrida y la magnitud del desplazamiento total. Supón ahora que puede hacer las entregas sin
restricción de la dirección a seguir. ¿Pueden sugerir un recorrido diferente que sea más conveniente?
2. Calculen la rapidez de un motociclista que recorre una distancia de 375 m en un tiempo de 8.0 s. ¿Qué
aceleración debe aplicar a la moto para que su velocidad se incremente en un 30% en 2.0 s?
3. Un corredor de 100 m planos desea lograr tal recorrido en 8.0 s. ¿Cuál es la rapidez que debe tener?
¿Pueden estimar a cuánto ascenderá su aceleración?
4. Un aficionado a las aves se sienta sobre unas rocas a observar un cóndor que vuela hacia el oeste a 12.0 m/s
respecto al viento, mientras que éste sopla hacia el norte a 15.0 m/s. ¿Cuál es la rapidez del ave con
respecto al aficionado?
5. Un avión de pasajeros vuela en dirección noreste a una velocidad de 500 km/h cuando el piloto capta
en su radar que se acerca una nave no identificada desde el sur a una velocidad de 750 km/h. Calculen
la velocidad aparente entre la nave sin identificación con respecto al avión.
60
st-editorial.com
Tema 2
Tema 3
Movimiento en
una dimensión
Movimiento en
dos dimensiones
El tren suburbano es una solución de transporte que se promociona como
rápida y eiciente, una condición necesaria para que el tiempo de recorrido sea
mínimo es que la trayectoria que presente tenga ciertas características… Realiza
un recorrido en el tren, ¿cómo es la trayectoria?, ¿cómo se mueve el tren?, ¿qué
otro medio de transporte presenta un movimiento similar?
Ya conoces las características básicas del movimiento y la forma en que se divide para su estudio,
pasemos ahora a detallarlo.
Movimiento rectilíneo uniforme
Este tipo de movimiento es el más simple porque se considera que el móvil se caracteriza por
no presentar un cambio de velocidad en un lapso
especíico, lo cual signiica que no hay aceleración ya que el objeto bajo estudio incrementa la
distancia que recorre, empleando siempre el mismo tiempo.
Aquí el cuerpo sólo se desplaza en una dirección
y el desplazamiento coincide con la distancia o
espacio recorrido, cuando no existe cambio de
sentido durante del movimiento. Si representamos el movimiento dentro de un sistema de
st-editorial.com
coordenadas, se tomará el eje x cuando el movimiento sea horizontal y el eje y cuando sea vertical. El auto del gráico 4 tiene una rapidez v en
el instante de referencia to = 0; después le lleva un
tiempo t, recorrer la distancia d y siempre ocurre
de esta manera.
La ecuación escalar de la que nos valdremos es
la siguiente:
d
7. v = t
Donde:
v = velocidad (o rapidez) del cuerpo.
d = distancia recorrida (el incremento es constante, no cambia en el tiempo).
t = tiempo que toma al móvil recorrer la distancia d (se mantiene constante).
61
BLOQUE 2
GRÁFICO 4
t
t=0
t
v
d
A
C
d
D
9. vm =
d
3 000 m
Observa que la ecuación es similar a la de rapidez y es
importante señalar que es común que en este tipo de análisis se hable en forma indistinta de rapidez o velocidad, ya
que por tratarse de una trayectoria rectilínea el vector no
cambia de dirección y su magnitud es constante, de tal manera que se puede considerar que el movimiento siempre
coincide con el eje horizontal (x) de un sistema coordenado de referencia.
Si analizas el gráico 5, verás que el corredor se desplaza
sobre una supericie plana de tal manera que su dirección
siempre coincide con el eje x.
GRÁFICO 5
y
x
Podemos observar el movimiento a velocidad constante en casi todos los medios de transporte cuando “alcanzan
ruta”; por ejemplo, cuando un autobús que ha salido de una
terminal llega a una autopista, el chofer mantiene la velocidad en 90 km/h, ya que los dispositivos de seguridad no
permiten que sea mayor y en situaciones de emergencia los
sensores permiten una rápida reducción de la velocidad. El
propósito de mantener la velocidad constante es reducir
el consumo de combustible, cumplir con el tiempo de viaje, y
evitar los retrasos que puedan ser molestos para los pasajeros.
No estamos considerando las curvas de la carretera porque
éstas no siguen precisamente una línea recta. Observa
que iniciamos esta explicación señalando que el movimiento
es a velocidad constante, no hicimos mención a la trayectoria;
por ello, para estimar la velocidad en una situación como la
señalada, donde por la trayectoria se requiere modiicar
la rapidez, se emplea el concepto de velocidad promedio,
cuya expresión algebraica es la siguiente:
62
d f – d0
t
Donde:
vm = velocidad promedio.
df = distancia al inal del recorrido.
do = distancia al inicio del recorrido.
t = lapso empleado para el recorrido.
O bien:
d
B
d
8. vm =
v
v
v f + v0
2
Donde:
vm = velocidad promedio.
vf = velocidad al inal del recorrido.
vo = velocidad con la que se inicia el recorrido.
Por ejemplo, si en un recorrido de 90 km se emplean
2h, diremos que la velocidad promedio fue de 45 km/h;
pero si conocemos que se inició el recorrido con una velocidad de 30 km/h y se inalizó con una velocidad de
50 km/h, la velocidad promedio es entonces de 40 km/h.
Movimiento rectilíneo
uniformemente acelerado
Aunque en el caso del movimiento rectilíneo uniformemente acelerado la trayectoria también es rectilínea, se
observa que el móvil puede incrementar o reducir su velocidad en forma uniforme, ya que el vector de aceleración se
mantiene constante tanto en magnitud como en dirección,
siempre que sucede así se dice que el movimiento es uniformemente acelerado.
Las ecuaciones escalares que emplearemos las podemos
obtener a partir de las ecuaciones 1, 2, 3, 7, 8 y 9 bajo algunas
consideraciones. Empecemos por recordar que en la ecuación 3 el vector v representa el cambio de velocidad en un
lapso t; de esta forma tenemos:
10. a =
v f – vo
t
De lo anterior se deduce que la velocidad que alcanza un
móvil con aceleración constante después de transcurrido
un tiempo t es:
11. vf = vo + at
Donde:
vf = velocidad inal del móvil.
vo = velocidad inicial del móvil.
a = aceleración del móvil.
t = tiempo en el que se mide el cambio de velocidad.
Consideremos ahora el comportamiento bajo la condición de la velocidad promedio:
12. vm =
d f – do v f + vo
=
t
2
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
Al despejar en esta igualdad la velocidad inal, tenemos:
2^d f – doh
vf =
– vo
t
Al sustituir en la ecuación 11 obtenemos la igualdad:
2^d f – doh
– vo = vo + at
t
De donde se obtiene una ecuación que nos permite calcular la
distancia (o posición) que alcanza un móvil que viaja con aceleración constante:
at2
13. d f = do + vo t + 2
Donde:
df = distancia (o posición) inal del objeto.
do = distancia (o posición) inicial del objeto.
vo = velocidad inicial del móvil.
a = aceleración del móvil.
t = tiempo en el que ocurre el cambio de posición.
FIGURA 3
En las carreras de autos se pueden observar los movimientos
rectilíneos uniforme y uniformemente acelerado e incluso hay
tramos de la pista en la que se describe un movimiento circular.
Para obtener una expresión que relacione la velocidad con la aceleración y la distancia recorrida, despejamos de la ecuación 12 el
tiempo transcurrido:
2^d f – doh
t = v +v
f
o
Sustituyendo este valor de tiempo en la ecuación 11:
2^d f – doh
v f = vo + a = v + v G
f
o
(vf – vo) ⋅ (vf + vo) = 2a (df – do)
Lo anterior inalmente nos conduce a:
14. v f = v2o + 2a ^d f – doh
Donde:
vf = velocidad inal del objeto.
vo = velocidad inicial del objeto.
a = aceleración del objeto.
df = distancia (o posición) inal del objeto.
do = distancia (o posición) inicial del objeto.
En las ecuaciones anteriores debes tener presente que al hablar de
un cambio de velocidad no necesariamente estamos haciendo referencia a un incremento como el que ocurre cuando un auto aumenta
la velocidad en una carretera para rebasar a otro. Se puede dar el caso
de una reducción como la de un corredor de atletismo, que disminuye su velocidad para detenerse después de cruzar la meta. En este
tipo de situaciones se airma que el móvil ha sufrido una desaceleración y para su manejo algebraico se incluye un signo menos a su valor
numérico; este signo se asocia al comportamiento físico del sistema:
la aceleración actúa en una dirección opuesta a la del movimiento
[Ejs. 4, 5, 6 y 7].
st-editorial.com
63
BLOQUE 2
Ejemplo 4
Ejemplo 6
En un viaje de Cuernavaca a la Ciudad de México, el conductor del auto toma la curva conocida como “La Pera” con una
velocidad de 60.0 km/h y cuando llega al parador Tres Marías
se percata de que su velocidad es de 85.0 km/h. ¿De cuánto
es la magnitud de la velocidad promedio?
En las pruebas para el desarrollo del prototipo de un miniauto eléctrico se registraron los siguientes datos sobre su
recorrido en un piso empedrado.
a. ¿Con qué datos contamos?
• Velocidad inicial: vi = 60 km/h.
• Velocidad final: vf = 85 km/h.
b. ¿Qué vamos a hacer?
Calculamos la magnitud de la velocidad promedio del
auto.
c. ¿Cómo lo vamos a hacer?
Dado que se conocen los valores inicial y final de la velocidad del auto empleamos la ecuación 9 para sustituir
directamente los datos.
d. Operaciones.
vm =
vf + vi
85.0 + 60.0
km/h
2 =
2
e. Resultado.
La velocidad promedio de acuerdo a los registros del conductor del auto es de 72.5 km/h.
Ejemplo 5
Determinemos la magnitud de la velocidad que debe mantener en forma uniforme un nadador para recorrer 200 m en
18.0 s durante una competencia para atletas superdotados.
Solución
a. ¿Con qué datos contamos?
• Tiempo: t = 18.0 s.
• Distancia a recorrer: 200 m.
• Incógnita: velocidad constante del nadador.
b. ¿Qué vamos a hacer?
Calculamos la velocidad con la que nada un atleta.
c. ¿Cómo lo vamos a hacer?
Sustituimos directamente en la ecuación 7 los datos de
distancia y tiempo.
d. Operaciones.
200
v = 18 = 11.1 m/s
e. Resultado.
La velocidad es constante e igual a 11.1 m/s.
64
0
10 12.5 15 17.5 20 22.5 25 27.5 30 32.5 35
0
10
15
20
25
30
35
40
45
50
55
60
Realicemos el gráfico de distancia contra tiempo y determinemos el tipo de movimiento del auto y sus características.
Solución
a. ¿Con qué datos contamos?
Los que se muestran en el cuadro anterior.
b. ¿Qué vamos a hacer?
Calculamos las variables de velocidad, aceleración, etc., a
partir del gráfico de distancia contra tiempo.
c. ¿Cómo lo vamos a hacer?
Realizamos la gráfica tomando pares de puntos (t, d). El primer valor corresponde al eje x y el segundo al eje y. La interpretación de la gráfica nos permite identificar el movimiento.
De acuerdo a los datos y al gráfico 6, podemos observar
que los dos primeros registros indican que el prototipo se
acelera en forma continua y cuando alcanza una velocidad
específica, la mantiene constante hasta el final de la prueba, cuando ha recorrido 60 m. Concluimos que el movimiento es uniformemente acelerado en su primera etapa
y uniforme en la segunda.
GRÁFICO 6
y
Distancia (m)
Solución
Tiempo (t [s])
Distancia
recorrida (d [m])
70
60
50
40
30
20
10
0
x
0 10
12.5
15
17.5
20
22.5
25
27.5
30
32.5
Tiempo (s)
d. Operaciones.
Las operaciones se dividen en dos etapas.
•฀฀Etapa฀de฀movimiento฀uniforme:฀en฀esta฀etapa฀del฀movimiento se observa que por cada 2.5 s existe un incremento constante en la distancia recorrida, que es igual a 5 m.
Al sustituir en la ecuación 7 tenemos:
d
5
v = t = 2.5 = 2 m/s
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
•฀฀Etapa฀de฀movimiento฀uniformemente฀acelerado:฀puesto฀
que se conocen la distancia recorrida, la velocidad inicial (la que parte del reposo), y la velocidad final (a los
10 s), calculamos la aceleración que impulsa al prototipo
valiéndonos de la ecuación 10 o de la ecuación 14. Tomemos esta última y sustituyamos los datos:
2
a=
2
v f – v0
2 ^df – d0h
=
22 – 02
2 ^10 – 0h
= 0.2 m/s2
Comprobamos con la ecuación 10, que reproduce el valor calculado previamente.
vf = vo + at = 0 + 0.2 (10) = 2 m/s
e. Resultado.
El auto inicia con una aceleración constante de 0.2 m/s2
que mantiene durante 10 s. Luego mantiene una velocidad
constante de 2 m/s, que alcanza al concluir la etapa anterior (movimiento uniformemente acelerado).
c. ¿Cómo lo vamos a hacer?
Como se tienen todas las características del movimiento
acelerado, primero analizamos esta etapa y luego escribimos la ecuación de distancia total y calculamos el tiempo
total, para determinar la distancia recorrida por sección
del trayecto. Para ello ajustamos previamente las unidades de los datos proporcionados.
d. Operaciones.
Para este caso tenemos que:
km
1h
1000 m
v1 = 100 h $ 3600 s $ 1 km = 27.778 m/s
km
1h
1000 m
v3 = 60 h $ 3600 s $ 1 km = 16.667 m/s
Estos datos nos permiten calcular la desaceleración en el
segundo tramo del recorrido, y entonces, de acuerdo a la
ecuación 11:
Ejemplo 7
En el recorrido de una distancia de 3.0 km un automovilista
parte del sitio A con una velocidad de 100 km/h y la mantiene
constante hasta que al llegar al sitio B se ve obligado a frenar
durante 4.0 s para reducir la velocidad hasta 60 km/h en el sitio C; desde este punto continúa a velocidad constante hasta
llegar a su destino en D (gráfico 7). Calculemos la distancia
recorrida en cada sección del trayecto y el tiempo total de
recorrido, suponiendo que el tiempo empleado de A a B es
igual al que necesitó para ir de C a D.
GRÁFICO 7
A
B
d1
C
d2
D
d3
3 000 m
Solución
a. ¿Con qué datos contamos?
• Distancia total: d = 3 000 m.
• Velocidad inicial del auto: v1 = 100 km/h (constante).
• Velocidad final del auto: v3 = 60.0 km/h (constante).
• Tiempo de recorrido de B a C: tfreno = 4.00 s.
• Tiempo de recorrido de A a B y de C a D: t.
• Incógnitas: distancia recorrida en cada etapa del movimiento y tiempo total de recorrido.
b. ¿Qué vamos a hacer?
Calculamos la distancia que se requiere para cada tramo
del trayecto considerando que la primera etapa y la última se realizan a velocidad constante y requieren el mismo
st-editorial.com
tiempo, mientras que en la parte intermedia existe un
movimiento desacelerado porque el auto frena.
a=
vf – vo 16.667 – 27.778
=
= - 2.78 m/s2
t
4
Con el valor de desaceleración obtenido, calculamos la
distancia requerida para el frenado (d2):
2
- 2.78 ^ 4 h
at 2
d2 = do + vo t + 2 = 0 + 27.778 ^ 4 h +
= 88.9 m
2
Ahora, procedemos al análisis del movimiento uniforme
y el cálculo del tiempo total de recorrido. La ecuación 7
nos permite escribir:
d1 = v1t y d2 = v2t
Se cumple:
d = d1 + d2 + d3
3 000 = 27.8 t + 88.9 + 16.7 t
Y por esta razón:
t = 65.5 s.
El tiempo total es entonces:
tT = 2 (65.5) + 4.00 = 135 s.
Y la distancia en cada tramo del recorrido es:
d1 = 27.8 (65.4) = 1 819 m.
d2 = 89 m.
d3 = 16.7 (65.4) = 1 092 m.
e. Resultado.
La distancia recorrida en cada sección del trayecto es de
1 819 m, 89 m y 1 092 m, respectivamente, y el tiempo
empleado es 135 s. Por lo general, encontramos un comportamiento de este tipo en los automovilistas que circulan
en los llamados ejes viales de la Ciudad de México,
donde no hay una distancia de separación específica
entre los semáforos, ni una clara señalización sobre el
límite de velocidad.
65
BLOQUE 2
Actividad individual
COMPETENCIAS
GENÉRICAS
4
5
3
COMPETENCIAS
DISCIPLINARES
7 10
DESEMPEÑO
DEL ESTUDIANTE
b
I. En los ejercicios siguientes se te presentan problemas de movimiento uniforme y de movimiento uniformemente acelerado. Elabora tu propio formulario con las ecuaciones de la 7 a la 14, prepara tu calculadora y
dibuja en la medida de lo posible cada una de las situaciones que se te plantean, para que identifiques con
claridad qué es lo que ocurre en cada uno de los problemas, considerando todas las variables e incógnitas que
intervienen.
1. Calcula la distancia recorrida por un corredor de fondo en su entrenamiento matutino durante un lapso
de 42 min, a sabiendas de que ha mantenido una velocidad constante e igual a 20 km/h.
2. Determina la aceleración que debe proporcionar el dispositivo lanzador a un avión en la pista de un
portaaviones para que la velocidad de despegue con respecto al portaviones sea de 300 km/h en 80 m.
3. La gráfica siguiente muestra el registro de la distancia que recorre un objeto a partir del reposo. Determina la velocidad y la aceleración del mismo para cualquier instante.
Distancia (m)
y
45
30
15
0
x
0
5
10
15
20
25
30
Tiempo (s)
4. Calcula la aceleración que debe suministrar el motor a un automóvil deportivo para que su velocidad
sea de 100 km/h en 7.2 s a partir del reposo. ¿Qué distancia recorre en ese lapso?
66
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
5. En la validación de capacidad de frenado de un auto se realizan diversos ensayos. Con una velocidad de
80 km/h, el automóvil recorre 30 m antes del alto total, siempre aplicando la misma fuerza de frenado
para producir una desaceleración constante. Determina la distancia que requiere para detenerse a una
velocidad de 40 km/h y 120 km/h considerando que la desaceleración producida al auto por los frenos
es siempre igual.
6. Un automovilista que viaja en una autopista con una velocidad constante de 90 km/h observa que la luz
roja de un cruce de ferrocarril empieza a parpadear y entonces inicia el frenado. El auto se halla a 60 m
del cruce, el tren viaja con una velocidad constante de 80 km/h y se encuentra a 50 m del cruce. ¿Por
qué debe frenar el automovilista?
7. En una situación de emergencia, un avión debe aterrizar en una pista corta de 500 m de longitud. Calcula el lapso del recorrido sobre la pista y la aceleración de frenado del aparato mecánico para reducir
la velocidad de 300 km/h cuando toca tierra a 0 km/h al llegar al final de la pista.
8. Un tren que inicialmente viaja a lo largo de una vía recta con una rapidez de 40 km/h desacelera a una razón
constante de 1.0 m/s2 durante 5.0 s, y durante los 3.0 s siguientes la desaceleración constante es ad. Determina la magnitud de esta desaceleración para que el tren se detenga por completo en el lapso de 8.0 s.
II. Anexa esta actividad a tu portafolio de evidencias.
st-editorial.com
67
BLOQUE 2
Caída libre y tiro vertical
y
x
Movimiento
FIGURA 4
La caída libre es un movimiento uniformemente acelerado influenciado por el campo gravitacional.
Analicemos ahora otro movimiento cuya trayectoria es rectilínea. A
diferencia del caso anterior la dirección coincide por completo con
el eje vertical (y) de un sistema coordenado de referencia. Debido
a que el movimiento se realiza sobre el eje vertical, es fácil observar
que se puede llevar a cabo hacia arriba o hacia abajo. En el primer
caso se denomina tiro vertical, y en el segundo, caída libre. En ambos se trata de un movimiento uniformemente acelerado porque
está inluenciado por la acción del campo gravitacional cuya constante de aceleración para ines prácticos es g = 9.81 m/s2, y actúa en
forma radial hacia el centro de la Tierra.
Caída libre. Se denomina así al movimiento en el que un objeto
cae por su propio peso. Por ejemplo, toma el borrador del pizarrón
y una goma para lápiz, colócalos frente a tus ojos y déjalos caer
al piso. ¿Qué sucede?, ¿cuál tocó primero el piso? Ambos llegaron al
mismo tiempo. ¿La vista te engaña? Escucha atentamente y trata de
distinguir el ruido de cada uno al caer. Repite esta experiencia con
una pelota de golf y con una canica. ¿Qué sucedió ahora? No hay
diferencia apreciable, ambos tocaron el piso al mismo tiempo.
Sube a un árbol o a algún lugar alto y seguro. Repite el experimento con la canica y una hoja de papel. Observarás que la canica llega
“más rápido” al piso. ¿Qué pasó? Cuando realizas el experimento con
objetos de forma geométrica semejante no hay diferencia apreciable,
pero cuando se trata de objetos de forma desigual y en condiciones
ambientales distintas es posible que puedas llegar a observar una gran
diferencia. Los objetos de forma esférica son los que se comportan
siempre en forma semejante, independientemente de cómo los dejes
caer y de cómo se alteren las condiciones ambientales en las que realizas el experimento, la manera en que se presenta la caída es similar
a la de los objetos que se dejan caer en el vacío donde hay ausencia de
cualquier agente externo, como una corriente de aire o una fuerza
de fricción que afecte el movimiento.
Lo anterior se toma como referencia y se supone que la forma, el
tamaño y la masa del objeto son importantes cuando se analiza la
caída de un objeto desde una altura muy grande, ya que son múltiples los factores que se deben tomar en cuenta para un análisis
preciso. En este curso consideramos un comportamiento de tipo
ideal, por lo que las ecuaciones son las asociadas al movimiento
uniformemente acelerado con las modiicaciones pertinentes al
nombre de las variables y a la ubicación del origen del sistema de
referencia. Veamos:
• Velocidad con la que choca un objeto contra el piso en caída
libre.
15. vf = vo - gt
Donde:
vf = velocidad con la que el móvil toca el piso.
vo = velocidad inicial del móvil.
g = constante de aceleración del campo gravitacional.
t = lapso en el que se mide el cambio de velocidad.
• Distancia que recorre de acuerdo al tiempo y la velocidad promedio.
16. d = b
68
v f + vo
lt
2
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
Donde:
d = distancia recorrida en la caída.
vf = velocidad al inal del recorrido.
vo = velocidad con la que se inicia el recorrido.
t = lapso que toma al objeto caer.
• Distancia que recorre cuando se conoce el tiempo y la velocidad
inicial de caída.
gt2
17. d = vo t – 2
Donde:
d = distancia recorrida en la caída.
vo = velocidad con la que se inicia el recorrido.
g = constante de aceleración del campo gravitacional.
t = lapso que toma al objeto caer.
• Velocidad con la que un objeto toca el piso como una función de
la aceleración y la distancia recorrida.
18. v f = v2o – 2g ^ y f – yoh
Donde:
vf = velocidad inal del objeto.
vo = velocidad inicial del objeto.
g = constante de aceleración del campo gravitacional.
d = distancia recorrida (diferencia de alturas).
Tiro vertical. Es todo movimiento en el que un objeto es lanzado en
dirección vertical contra el sentido de acción del campo gravitacional. Quizá lo has visto, por ejemplo, cuando lanzan un arnés hacia
la estructura de un puente y mediante un dispositivo simple una
persona se eleva para realizar actividades de mantenimiento.
El interés básico en el estudio de este movimiento reside en la descripción de sus características, ya que es fácil observar que la velocidad del objeto disminuye conforme va elevándose, de tal manera
que cuando alcanza su altura máxima, la velocidad es cero, para luego
incrementarse en la medida que desciende hasta llegar al punto de
lanzamiento con la misma velocidad con la que se realizó el disparo.
Además, el tiempo que le toma subir es igual al que requiere para
descender porque se mueve con una aceleración constante e igual a la
que ejerce el campo gravitatorio, de tal manera que el movimiento es
uniformemente acelerado [Ejs. 8 y 9 ].
Las ecuaciones que modelan este movimiento las podemos obtener
fácilmente partiendo de la ecuación 15.
vf = vo - gt
Debido a que la velocidad al inal del recorrido es nula se airma
que:
0 = vo - gt
Entonces, el tiempo (t) de ascenso es:
v
19. t = go
st-editorial.com
FIGURA 5
Al lanzar un arnés hacia arriba se está realizando un tiro vertical.
69
BLOQUE 2
Debido a que el descenso se sujeta a la misma aceleración, el tiempo es igual y
entonces el tiempo total del recorrido (tr) es:
2v
20. t r = 2t = g o
Al sustituir el valor del tiempo de ascenso en la ecuación 17, obtenemos la altura
máxima que alcanza un objeto cuando es disparado verticalmente con una velocidad
inicial vo.
gt2
h = vo t – 2
g v 2
v
h = vo b go l – 2 b go l
v2
21. hmáx = 2 go
Ejemplo 8
Ejemplo 9
Antonio se sube a un trampolín y deja caer una pelota
sobre la alberca. El juguete toca el agua 0.85 s después de
que el joven la dejó caer. Determinemos la altura desde la que
se cayó la pelota y la velocidad con la que choca contra la
alberca.
Pedro, el vecino de uno de los pisos superiores, le pide
a Juan que le preste unas pinzas, y éste, para ahorrarse
tiempo, le dice que se las hará llegar por la ventana. Juan
lanza las pinzas hacia arriba en forma vertical con una velocidad de 17.5 m/s y Pedro las atrapa a 6 m por encima
de donde Juan las lanzó. Calculemos la velocidad que llevaban las pinzas cuando Pedro las atrapó y el tiempo que
duró el trayecto.
Solución
a. ¿Con qué datos contamos?
• Velocidad inicial: vo = 0 m/s.
• Tiempo: t = 0.85 s.
• Incógnitas: velocidad con la que la golpea el agua y altura desde la que se dejó caer.
b. ¿Qué vamos a hacer?
Determinar la velocidad final de la pelota y la altura desde
la que se dejó caer.
c. ¿Cómo lo vamos a hacer?
Calculamos las variables indicadas considerando que se
trata de la caída libre de un cuerpo.
d. Operaciones.
De acuerdo a la ecuación 17, tenemos que la altura que
recorre la pelota es:
Solución
a. ¿Con qué datos contamos?
• Velocidad inicial: vo = 17.5 m/s.
• Distancia: d = 6.00 m.
• Incógnitas: velocidad con la que se atrapa las pinzas (vf),
y tiempo del recorrido (t).
b. ¿Qué vamos a hacer?
Determinar la velocidad final de las pinzas y el tiempo del
trayecto vertical.
c. ¿Cómo lo vamos a hacer?
Calculando las variables indicadas a partir de las ecuaciones del movimiento uniforme acelerado en el movimiento
vertical.
2
d = 0#2–
9.81 ^0.85h
= - 3.54 m
2
Y la velocidad con la que choca contra el agua es:
v = vo – gt = 0 – 9.81 ^0.85h = - 8.33 m/s.
e. Resultado.
La velocidad de la pelota es 8.33 m/s hacia abajo. Esto nos
lo indica el signo negativo ya que el punto inicial del movimiento se encuentra por encima del nivel de la alberca;
la altura desde la cual se dejó caer la pelota es 3.54 m.
70
d. Operaciones.
La ecuación general de la altura recorrida por un objeto
en movimiento vertical ascendente nos permite calcular el
tiempo. En principio, tenemos:
6.00 = 17.5 t –
9.81 t 2
2
Lo cual nos conduce a la ecuación cuadrática siguiente:
-4.90 t 2 + 17.5 t - 6 = 0
La solución de esta ecuación es:
t1 = 0.384 s.
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
t2 = 3.184 s.
La velocidad que llevan las pinzas en el momento en que
Pedro las atrapa es:
v = vo – gt = 17.5 - 9.81 (0.384) = 13.731 m/s
e. Resultado.
La velocidad de las pinzas es de 13.7 m/s, y Pedro las atrapa
en forma “instantánea” ¿Por qué? La respuesta es sencilla: en un tiro vertical el objeto sube y baja, por lo que
hay dos instantes de tiempo para cada posición, uno para
el ascenso y otro para el descenso. Al suponer que Pedro
atrapó las pinzas cuando viajaban hacia arriba, el tiempo
es el menor, 0.384 s aunque esto no significa que también
pudiera ocurrir que las atrape cuando regresaban, en tal
caso el tiempo sería 3.184 s.
Solución
a. ¿Con qué datos contamos?
• Tiempo del recorrido: tr = 5.00 s.
• Incógnitas: altura del edificio (h).
b. ¿Qué vamos a hacer?
Calcular la altura del edificio a partir del dato del tiempo.
c. ¿Cómo lo vamos a hacer?
Con el dato del tiempo podemos calcular la velocidad inicial del lanzamiento, y con esto determinamos la altura
máxima que alcanza la piedra.
d. Operaciones.
tr g
5.00 # 9.81
= 24.5 m/s
vo = 2 =
2
Ejemplo 10
La altura máxima que alcanza la piedra desde el punto de
lanzamiento es:
Para medir la altura de un edificio se les ocurre a un par
de amigos hacer lo siguiente: Arturo lanzará una piedra y
Roberto tomará el tiempo que ésta tarda en subir y bajar.
Repiten el experimento varias veces hasta que por fin quedan satisfechos, pues la piedra, en tres ocasiones, alcanzó
la parte superior del edificio y regresó en 5.00 s. ¿Cuál es la
altura del edificio?
Actividad grupal
COMPETENCIAS
GENÉRICAS
4
5
8
COMPETENCIAS
DISCIPLINARES
2
^24.5h
v o2
hmáx = 2 g = 2 # 9.81 = 30.7 m
e. Resultado.
Si consideramos que no se conoce la posición exacta desde la cual se lanza la piedra, podemos concluir que de manera aproximada, el edificio tiene una altura de 32 m.
3
7 10 11
DESEMPEÑOS
DEL ESTUDIANTE
b
c
Reúnete con dos compañeros para resolver los problemas que se presentan; todos corresponden exclusivamente al tema de caída libre y tiro vertical. Aunque ambos son movimientos uniformemente acelerados,
les sugerimos dibujar lo que está ocurriendo en cada situación para que sepan cuál de las fórmulas deben
emplear. Las fórmulas con las que trabajarán en esta sección son de la 15 a la 21.
1. Un niño entrena béisbol y para distraerse lanza la pelota hacia arriba con una velocidad de 15.0 m/s. ¿Cuánto
tiempo tardará en alcanzar un punto situado a 10.0 m del piso en el trayecto de caída?
2. Se lanza un prototipo de misil verticalmente hacia arriba con una velocidad inicial de 240.0 m/s. Calcula la altura máxima que alcanzará y el tiempo que le llevará regresar al suelo desde el momento del disparo. Desprecia
cualquier efecto de fricción o de desviación de la trayectoria del misil por la acción de algún otro agente.
st-editorial.com
71
BLOQUE 2
3. A una niña que se encuentra en un globo aerostático observando el paisaje se le caen de repente sus
gafas; el globo se encuentra fijo a una altura de 300 m. Determina el tiempo que tardan las gafas en
tocar el suelo.
4. Una muchacha está en la orilla de un mirador y lanza una pelota en dirección vertical hacia arriba. La
velocidad inicial de la pelota es de 15.0 m/s y la profundidad del barranco que da al mirador es de 40.0 m.
Determina la distancia total que recorre la pelota desde el sitio en que es lanzada hasta el punto en que
golpea el fondo del barranco.
5. Un helicóptero deja caer una carga de provisiones desde una altura de 25 m con una velocidad inicial
de 2.0 m/s. Calcula el tiempo que tarda la carga en llegar al suelo y la velocidad con la que choca.
¿Qué sucede cuando dejas caer una canica? ¿Qué pasará si cambias la canica por una pelota de
esponja? ¿Qué tipo de movimiento es el que sigue la pelota? Habrás observado que inició como una
caída libre y después cambió por completo, porque en cada rebote de la pelota se modiicaba un tanto la
trayectoria, de tal manera que es necesario que empleemos un plano cartesiano con los ejes coordenados
x y y colocados adecuadamente para describir la geometría del movimiento. Éste es el objeto de estudio
del movimiento bidimensional o en un plano.
72
st-editorial.com
Tema 2
Movimiento en
dos dimensiones
En los parques de diversiones hay numerosos juegos en los que el propósito es que
los usuarios desciendan con malestares diversos como vértigo, sudoración, etc.,
pues en eso consiste lo “divertido” del mismo; ¿has hecho un viaje en un juego de
tal tipo?, ¿bajo qué condiciones ocurre el movimiento?, ¿es un movimiento simple
o es el resultado de una combinación de trayectorias?
El movimiento de los cuerpos en dos dimensiones o también llamados movimientos curvilíneos,
pueden ser tratados como una composición de
dos movimientos rectilíneos: uno horizontal y
otro vertical. Enseguida los estudiaremos.
GRÁFICO 8
y
Movimiento acelerado
(-g)
Tiro parabólico:
horizontal y oblicuo
Recibe la denominación de tiro parabólico todo
movimiento que describe una parábola en su trayectoria y que puede ser analizado en dos dimensiones, ejemplo de ello es el disparo de una bala
por medio de un cañón, el luir del agua desde
una abertura en lo alto de un recipiente, etc. Este
movimiento en sí es el resultado de la combinación de los movimientos rectilíneos que ya hemos
estudiado: el uniforme y el uniformemente acelerado. En el gráico 8 podrás observar cómo una
pelota es lanzada por un jugador de golf.
st-editorial.com
Altura máxima
Movimiento uniforme
x
Distancia recorrida
El movimiento en el eje vertical se encuentra sujeto a la acción de la aceleración del campo
gravitacional mientras que en el eje horizontal la
pelota viaja a velocidad constante, ¿cuál es la altura máxima que alcanza la pelota?, ¿qué distancia
recorrerá sobre la horizontal?, ¿en cuánto tiempo
la pelota alcanza el objetivo? Para conocer estos
73
BLOQUE 2
En la web
Para conocer más acerca de este tema
visita la página web st-editorial.com/
enlaweb/fisica1 y consulta el link
número 02
valores no sólo debemos saber los tipos
de movimiento, también requerimos de
dos datos básicos que no se muestran en
la igura y que son indispensables:
• La velocidad con la que viaja inicialmente el objeto.
• El ángulo con que sale disparado.
Tiro oblicuo. Cuando el ángulo es mayor
a 0° y menor a 90°. Ver gráico 8 [Ej. 11
y 13].
Tiro horizontal. Cuando el disparo o lanzamiento se realiza a 0° exactamente
[Ej. 12].
Las ecuaciones que te presentamos a
continuación son generales y las puedes
aplicar en forma indistinta, sólo es necesario que recuerdes cuál es la diferencia
entre uno y otro tipo de tiro.
Consideremos entonces que la velocidad inicial del lanzamiento es vo y que
forma un ángulo q con la horizontal.
Para el movimiento horizontal a velocidad constante tenemos:
• Velocidad del proyectil (m/s).
22. vx = vocosq
• Distancia que recorre el proyectil (m).
23. x = (vocosq)t
En el movimiento vertical la aceleración es constante e igual a g, de tal manera que se veriica:
• Velocidad inicial del proyectil (m/s).
24. (vo)y = (vosenq)
• Velocidad inal del proyectil (m/s).
25. vy = vosenq - gt
O bien cuando existe una diferencia
de alturas:
26. v y = ^vo seni h2 – 2 g ^ y f – yoh [m/s]
• Recorrido vertical (m).
gt2
27. h = ^vo seni h t – 2
Para este conjunto de ecuaciones debes tener presente que es posible conocer
74
en cualquier instante de tiempo la magnitud (v) y dirección (b) de la velocidad,
es suiciente recordar que el teorema de
Pitágoras nos permite obtener la magnitud de un vector cuyas componentes son
conocidas:
v = v2x + v2y
vy
b = arctan b v l
x
Y que de acuerdo a la ecuación 23 podemos calcular el tiempo (s) de recorrido
para cualquier distancia horizontal como:
28. t =
x
vo cos i
La sustitución de esta ecuación en la
expresión 17 nos permite obtener la ecuación de la altura vertical (m) expresada en
la forma general de la ecuación de una
parábola:
gx2
29. h = ^tan i h x –
2^vo cos i h2
De acuerdo a la ecuación 21 la altura
máxima (m) en el tiro es:
^vo seni h2
30. hmax =
2g
¿Y cómo determinas la distancia máxima? Recordarás que en el tiro vertical el
tiempo total de recorrido es:
2v
tr = g o
Entonces, al sustituir la componente
vertical de velocidad inicial tenemos que
en este caso el tiempo de recorrido (s) es:
31. tr =
2 vo seni
g
Con esta expresión del tiempo total
podemos entonces retomar la ecuación
de distancia horizontal recorrida (x), y la
sustitución y reducción de términos nos
conduce a la ecuación que nos permite
calcular la distancia máxima recorrida
(m) a partir de los datos básicos, velocidad inicial y dirección con la que efectuó
el lanzamiento:
32. L =
v2o sen2i
g
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
Ejemplo 11
El jardinero central de un equipo de béisbol atrapa
la pelota momentos después de que un oponente
la golpea con el bate y rápidamente la lanza hacia el jugador de tercera base con un ángulo de
25° respecto a la horizontal y una velocidad de 20
m/s. Considerando que la posición a la que hizo el
lanzamiento se encuentra a 45 m y el jugador que
espera la pelota la recibirá a la misma altura del
lanzamiento, determinemos si su lanzamiento es
apropiado o no.
Solución
a. ¿Con que datos contamos?
• Ángulo del lanzamiento, q = 25°.
• Velocidad inicial, vo = 20 m/s.
• Distancia entre el lanzador y el receptor, x = 45 m.
• Incógnitas: alcance del lanzamiento, L.
b. ¿Qué vamos a hacer?
Calcular si el lanzamiento tiene el alcance suficiente
o no para que el receptor de tercera base atrape la
pelota.
c. ¿Cómo lo vamos a hacer?
Con los datos analizamos el lanzamiento como un
tiro parabólico y sustituimos directamente en la
ecuación 32:
d. Operaciones.
L=
v o2 sen2i
20 2 sen50c
=
= 31.235 m
g
9.81
e. Resultado.
El alcance del lanzamiento es de 31.235 m por
lo que entonces no es factible que el jugador
de tercera base atrape a la pelota, el impulso
necesario para lanzar la pelota no es suficiente
ya que caerá aproximadamente 14 m antes del
blanco previsto.
Ejemplo 12
El puente suspendido que atraviesa un río se cayó
en la última tormenta y los habitantes de una de las
orillas quieren ayudar a los damnificados de la otra,
arrojándoles medicamentos y alimentos en pequeños
paquetes, con un dispositivo que los lanza horizontalmente. Si los lanzamientos se hacen a 3.5 m por
encima de la orilla que se inundó, determinemos la
velocidad que deben procurar los benefactores al momento de arrojar los paquetes para que se alcancen a
librar los 24 m de ancho que tiene el río.
st-editorial.com
Solución
a. ¿Con qué datos contamos?
• Ángulo del lanzamiento, q = 0°.
• Altura del sitio de lanzamiento, y = 3.5 m.
• Separación entre objetivo y lugar de disparo, x = 24 m.
• Incógnitas: velocidad de cada paquete al ser lanzado, vo.
b. ¿Qué vamos a hacer?
Calcular la velocidad con que deben lanzarse los
paquetes para que atraviesen el río.
c. ¿Cómo lo vamos a hacer?
Con los datos analizamos el lanzamiento como un
tiro horizontal, de tal manera que tomamos el movimiento horizontal y el vertical.
d. Operaciones.
La ecuación 23 nos indica que el recorrido horizontal es:
x = (vocosq)t
Y la sustitución de datos nos lleva a:
24 = vot
De acuerdo a los datos, la distancia vertical a la que
caerán los paquetes es de 3.5 m, entonces para el
movimiento vertical tomamos la ecuación 27 y sustituimos datos:
-3.5 = ^vo sen0ch t –
9.81 t 2
2
De donde se tiene finalmente que el tiempo del recorrido es:
t=
2#7
9.81 = 1.194 s
Así, podemos concluir entonces, que la velocidad
inicial debe ser:
vo = 24/1.194 = 20.090 m/s.
e. Resultado.
La velocidad de lanzamiento debe ser de 20.09 m/s.
Observa que en la sustitución de la altura se tomó
el dato como negativo porque el origen del sistema
de referencia siempre se coloca en el sitio de lanzamiento o disparo y el “blanco” se encuentra por
debajo de tal origen.
Ejemplo 13
Se coloca un mortero a 6 km de la cima de una colina
y se ajusta a 45° para que cualquier proyectil que se
lance pueda librar el pico de tal colina. Calculemos la
magnitud de la velocidad inicial y la altura de la colina
sobre el nivel del mar en el entendido de que el mortero se encuentra a 250 m sobre el nivel del mar.
75
BLOQUE 2
d. Operaciones.
Sabemos que en un tiro vertical la velocidad es nula en la
parte más alta de la trayectoria, entonces, de acuerdo a la
ecuación 25:
0 = vosenq - gt
` t=
v0 sen q
g
vo
Que es el tiempo necesario para que el proyectil alcance
la cima y la libre, al sustituir este valor de tiempo en la
ecuación de desplazamiento en el recorrido horizontal tenemos entonces que:
q
Nivel del mar
FIGURA 6
Observa que los datos del ejemplo 13 aparecen aquí representados.
x = (vocosq)t =
Solución
v o2 cos
sen
g
La velocidad inicial es entonces:
a. ¿Con qué datos contamos?
• Ángulo del lanzamiento, q = 45°.
• Altura del sitio de lanzamiento, yo = 250 m.
• Separación entre el pico de la colina y lugar de disparo,
x = 6 000 m.
• Incógnitas: velocidad del misil al ser lanzado, vo y altura
del pico sobre el nivel del mar, h.
vo =
t=
4
5
=
6000 # 9.81
cos45c sen45c = 343.103 m/s
343.103 sen45c
= 24.731 s
9.81
Con estos datos sustituimos en la ecuación 27 y obtenemos la altura total de la colina:
h = 250 + ^343.103 sen45ch # 24.731 –
c. ¿Cómo lo vamos a hacer?
Debemos primero determinar el tiempo que requiere
cada misil para alcanzar la altura de la colina y librarla.
Con los datos analizamos el lanzamiento tomando el
movimiento horizontal y el vertical
COMPETENCIAS
GENÉRICAS
xg
sen
Con un tiempo de recorrido de:
b. ¿Qué vamos a hacer?
Calcular la velocidad con que se lanza cada misil y la altura de la colina.
Actividad individual
cos
9.81 # 24.731 2
= 3250 m
2
e. Resultado.
La velocidad de lanzamiento debe ser de 343.103 m/s, mientras que la altura de la colina es de 3 250 m sobre el nivel del
mar. Observa que en este caso la altura dato se adiciona para
calcular el total que se solicita.
7
COMPETENCIAS
DISCIPLINARES
3
7 10
DESEMPEÑOS
DEL ESTUDIANTE
b
c
I. Para que puedas resolver con más facilidad estos ejercicios, te recomendamos consultar las ecuaciones
de la 22 a la 32, correspondientes al tiro parabólico. No olvides realizar los dibujos o diagramas necesarios para visualizar lo que sucede. Evita los errores en la consideración de la altura a la que se realiza
un disparo.
1. En una práctica de fútbol americano, el mariscal de campo lanza un pase en donde el balón sigue una
trayectoria que forma un ángulo de 45° con respecto a la horizontal y con una velocidad vo. En el mismo
instante, un receptor que se encuentra a 6 m de distancia empieza a correr con una velocidad constante
de 3 m/s hacia el fondo del campo. Determina la velocidad con que se lanzó la pelota y la distancia recorrida por el corredor, si el receptor atrapa la pelota a la misma altura a la que fue lanzada.
76
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
2. Desde lo alto de un acantilado de 140 m de altura se lanza un proyectil horizontalmente con una velocidad de 60 m/s. Determina el tiempo necesario para que se impacte en el blanco que se ubica en el piso
del acantilado. Si el blanco se encuentra a 300 m del pie del acantilado, ¿hubo error en el lanzamiento?
3. El personal de limpieza de una compañía de servicios deja una manguera tendida en el piso y accidentalmente alguien abre la llave del agua. Debido a la presión y el caudal, el agua sale disparada hacia
arriba con un ángulo de 40° con respecto a la horizontal y una velocidad de 10 m/s, ¿A qué altura golpeará una pared a 6 m de distancia sobre la que algunos clientes hacen fila?
4. El piloto de un avión debe arrojar una caja con medicinas y alimentos en una zona montañosa afectada
por un sismo, y hacer que caiga en un blanco marcado en tierra. El avión vuela horizontalmente con una
velocidad de 193 km/h y a una altura de 152 m por encima del suelo.¿Qué ángulo con la horizontal debe
formar la visual al blanco en el instante del lanzamiento?
II. Anexa esta actividad a tu portafolio de evidencias.
st-editorial.com
77
BLOQUE 2
Movimiento circular: uniforme
y uniformemente acelerado
Consideremos ahora un movimiento en dos dimensiones que no resulta de la combinación de un movimiento rectilíneo uniforme y uno uniformemente acelerado: el
movimiento circular.
Se dice que existe un movimiento circular cuando el cuerpo bajo análisis describe una
trayectoria circular en su recorrido y al igual que en el movimiento rectilíneo se puede presentar un movimiento uniforme o un movimiento uniformemente acelerado. Es
común emplear el término de rotación para describir este tipo de movimiento debido
a que en ambos casos el cuerpo o algunos de sus elementos describen una trayectoria
circular, pero no son sinónimos. Observa el siguiente infográico.
Infográfico 1 Movimiento circular: uniforme y uniformemente acelerado
Resulta muy común que las personas utilicen como
sinónimos movimiento circular y rotación para
nombrar la idea de dar vueltas. Sin embargo, ten
presente que hablamos de rotación cuando existe un
eje fijo alrededor del cual ocurre tal comportamiento
cinemático como es el caso de una rueda o una hélice.
Algunas maniobras aéreas de los pilotos ayudan a ejemplificar cada tipo de movimiento.
Movimiento circular uniforme
Un avión de propaganda que describe
círculos mientras realiza sus anuncios tiene
movimiento circular.
Dos aviones en un espectáculo aéreo se
encuentran de frente en el aire; ambos cambian su trayectoria de recta a circular, y en
algunos casos forman espirales.
Movimiento circular
uniformemente acelerado
Dos o más aviones se acomodan en una formación circular, conocida como “Luftberry”,
en la que uno está detrás del otro; aumentan
la velocidad pero sin chocar entre ellos y sin
modificar las distancias, la aceleración de
cada avión es la misma y aparenta viajar con
movimiento uniforme.
78
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
Retomemos el ejemplo del avión al que hacíamos referencia en el infográico y
ubiquemos uno en un sistema de referencia x, y en donde el origen se coloca precisamente en el centro de la trayectoria descrita (gráico 9)
GRÁFICO 9
y
A
r
x
o
La ubicación de nuestro móvil la realizamos empleando un vector de posición
r, cuya magnitud es igual a la del círculo que describe. En este punto surge nuestra
primera pregunta: ¿Cómo se efectúa el recorrido? Inicialmente se observa un desplazamiento angular (q), que corresponde al arco de circunferencia que recorre el avión
(o cualquier objeto) al pasar del punto A al punto B (gráico 10).
GRÁFICO 10
y
B
A
r
q
o
r
x
El desplazamiento angular se expresa en radianes de acuerdo al Sistema Internacional de Unidades, aunque también es común que se empleen los grados sexagesimales:
un círculo contiene 360° o 2p radianes.
Si ahora asumimos que en el punto A el tiempo de referencia es to y que al llegar
al punto B el cronómetro nos indica un tiempo t1, tenemos entonces que el cambio
de posición angular con respecto al tiempo se deine como la velocidad angular (ω)
del cuerpo:
i –i
i
33. ~ = t B – t A = t
1
o
Donde:
ω = velocidad angular expresada rad/s.
q = qB – qA = desplazamiento angular expresado en radianes.
t = t1 – to = lapso de tiempo en segundos que transcurre para el cambio de la posición A, a la posición B.
st-editorial.com
79
BLOQUE 2
Es importante enfatizar dos aspectos: el primero es que en muchas situaciones de
la vida práctica se emplea como unidad de la velocidad angular las revoluciones por
minuto (rev/min o rpm), y el segundo, que la ecuación 33 es análoga a la ecuación 7,
sólo cambian las variables pues en lugar de ser “lineales” ahora son de tipo “angular”.
Al igual que en el movimiento rectilíneo tenemos que cuando se sabe de una variación
entre la velocidad inicial y la inal, es posible calcular el promedio de la velocidad. En
este caso tenemos:
34. ~m =
~ f + ~i
2
Donde:
ωf = velocidad angular inal.
ωi = velocidad angular inicial.
Consideremos ahora que debido a las condiciones del viento, el avión continúa
describiendo una trayectoria circular, pero que reduce e incrementa su velocidad lineal
en forma secuencial. Esto trae como consecuencia un cambio en la velocidad angular
con la que está efectuando su recorrido. El cambio de velocidad angular con respecto
al tiempo se le denomina aceleración angular, y se representa:
~ –~
~
35. a = t B – t A = t
1
o
Donde:
a = aceleración angular expresada en rad/s2.
ω = ωB – ωA = velocidad angular.
t = t1 – to = lapso de tiempo en segundos que transcurre para el cambio de velocidad.
¿Cómo relacionamos el movimiento lineal con el angular? Para ello recurrimos a
las ecuaciones 7 y 33, ¿Cuál es la variable en común? El tiempo t, despejemos de ambas
ecuaciones esta variable e igualémoslas:
d
i
t=v =~
La velocidad lineal del objeto de acuerdo al movimiento curvilíneo que sigue, conocida como velocidad tangencial es, entonces:
v=
d
~
i
Y al recordar que la longitud de un arco de circunferencia se deine como d = r q,
(gráico 11), se concluye que:
36. v = r ω
Donde:
v = velocidad tangencial del objeto expresada en m/s.
r = radio de la trayectoria circular, en m.
ω = velocidad angular con la que el objeto describe la trayectoria, en rad/s.
Glosario
80
Velocidad tangencial. Velocidad de un cuerpo que se mueve con movimiento circular y que es tangente a la trayectoria que se describe.
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
GRÁFICO 11
d = rq
q
r
La velocidad tangencial siempre mantiene la misma dirección (su nombre nos
lo indica), pero su magnitud puede cambiar con el tiempo. Por lo tanto, el vector
aceleración puede tener un cambio tanto en magnitud como en dirección. Tomemos
dos puntos muy cercanos entre sí en una trayectoria circular, tanto que su separación
no es apreciable a simple vista, en los que se presenta un cambio instantáneo de
velocidad. El gráico 12 ilustra este caso.
GRÁFICO 12
y
v
v
vB
q
vB
vA
x
vA
Los puntos A y B
casi coinciden
El vector de la diferencia de velocidad es:
v = vB - vA
El cambio respecto al tiempo de este vector (en magnitud y dirección) corresponde
a la aceleración lineal del móvil (a) en la trayectoria curva:
a = aB - aA
Al proyectar el vector a sobre la línea de acción de vA y la perpendicular a este vector obtenemos el gráico 13.
GRÁFICO 13
a sen q
a
q
a cos q
st-editorial.com
81
BLOQUE 2
El cambio en magnitud de la aceleración en
la dirección de la velocidad es acosq, mientras
que la proyección perpendicular a la línea de acción del vector velocidad nos muestra el cambio
de dirección del vector velocidad, y su magnitud
es asenq. A la primera componente se le denomina aceleración tangencial y su magnitud es
at = acosq
Sustituyendo a = v/t y considerando que para
ángulos muy pequeños cosq ≈ 1 se concluye que:
v r~
at = t = t
Y puesto que al cambio de velocidad angular
con respecto al tiempo se le denomina aceleración
angular (a) se concluye que:
37. at = r a
Donde:
at = aceleración tangencial del objeto expresada
en m/seg2.
r = radio de la trayectoria circular, en m.
a = aceleración angular con la que el objeto
describe la trayectoria, en rad/s2.
La segunda componente de aceleración nos
muestra el cambio en la dirección de la aceleración
total y se denomina aceleración normal o centrípeta
en este caso consideramos que senq ≈ q para ángulos muy pequeños y entonces al sustituir como en
el caso anterior tenemos:
vi
an = t
Por la deinición de velocidad angular se concluye entonces:
38. an = vω = r ω2
Donde:
an = aceleración normal (o centrípeta) del objeto expresada en m/s2.
r = radio de la trayectoria circular, en m.
v = velocidad tangencial del cuerpo, en m/s.
ω = velocidad angular con la que el objeto describe la trayectoria, en rad/s.
Entonces la magnitud de la aceleración lineal es:
39. a = a2n + a2t
Los ejemplos siguientes te muestran la forma
en que debes emplear las ecuaciones de la 33 a la
39, que hemos obtenido en el análisis de problemas de movimiento circular [Ejs. 14, 15 y 16].
Ejemplo 14
Una rueda esmeriladora gira a 300 rev/min y disminuye su velocidad a 100 rev/min en
12 segundos. Calculemos el número de revoluciones en el tiempo indicado y la desaceleración angular que sufre.
Solución
a. ¿Con qué datos contamos?
• Velocidad angular inicial, ωo = 300 rev/min.
• Velocidad angular final, ωf = 100 rev/min.
• Tiempo en que se reduce la velocidad angular, t = 12 s.
• Incógnitas: numero de revoluciones que gira la rueda para reducir la velocidad y
desaceleración angular que sufre.
b. ¿Qué vamos a hacer?
Calcular desplazamiento angular neto y desaceleración angular de la rueda de esmeril.
c. ¿Cómo lo vamos a hacer?
Dado que sólo conocemos los valores inicial y final de velocidad angular, así como el
tiempo que ocurre esto aplicaremos nuestras definiciones en forma directa.
Glosario
82
Aceleración normal o centrípeta. Aceleración que sufre un cuerpo en movimiento circular uniforme por el cambio de dirección del
vector velocidad; esta aceleración se dirige hacia el centro de la trayectoria que describe el cuerpo.
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
d. Operaciones.
Antes que nada debemos ajustar unidades para la velocidad angular:
rev 2r rad 1 min
~ f = 300 min 1 rev 60 s = 31.416 rad/s
rev 2r rad 1 min
~ o = 100 min 1 rev 60 s = 10.472 rad/s
De la ecuación 33 tenemos que en general, el desplazamiento angular neto es:
d. Operaciones:
Sabemos que la longitud de arco se define como:
d = rq ∴ q = d/r = 6/0.6 = 10 rad
Conocemos que la velocidad tangencial se calcula mediante v = rω, pero ω = q/t, de donde se concluye que:
v = rq/t ∴ t = rq/v
Sustituyendo.
t = 0.6(10)/0.55 = 10.909 s
qf – qo = q = ωt
e. Resultado.
En un tiempo de 10.909 s se desenredan los 6 m de cordel
de tal manera que el carrete da 1.59 revoluciones.
De acuerdo a los datos, la velocidad angular a considerar
es la promedio, es decir:
Ejemplo 16
~m =
31.416 + 10.472
= 20.944 rad/s
2
Entonces, el desplazamiento angular neto es:
q = 20.944(12) = 251.328 rad o 40 revoluciones
Y la aceleración angular:
a=
10.472 – 31.416
= - 1.745 rad/s2
12
Para apagar el incendio de un bosque, un avión viaja a lo
largo de una trayectoria circular que tiene un radio de 32 m.
Determinemos la magnitud de la aceleración del avión si en
un momento dado su aceleración tangencial es de 6 m/s2,
mientras que su velocidad es de 25 m/s.
Solución
e. Resultado.
La desaceleración angular es de 1.745 rad/s2 y se requieren de 40 revoluciones para reducir la velocidad angular
de 300 rpm a 100 rpm.
a. ¿Con qué datos contamos?
• Radio de la trayectoria, r = 32 m.
• Aceleración tangencial, at = 6 m/s2.
• Velocidad tangencial, v = 25 m/s.
• Incógnitas: magnitud de la aceleración del avión.
Ejemplo 15
b. ¿Qué vamos a hacer?
Calcular la aceleración total del avión.
En un proceso de hilado el cordel de un carrete de 60 cm de
radio se jala con una rapidez de 55 cm/s. Determinemos el
tiempo y el número de vueltas que da el carrete para que se
desenreden 6 m del cordel. Supongamos que la variación
del radio no es apreciable.
c. ¿Cómo lo vamos a hacer?
Calcularemos la aceleración centrípeta y luego determinaremos la aceleración total.
Solución
a. ¿Con qué datos contamos?
• Radio del carrete, r = 0.6 m.
• Velocidad tangencial, v = 0.55 m/s.
• Longitud de cordel desenredada, l = 6 m.
• Incógnitas: número de revoluciones del carrete y tiempo
que le toma desenredar 6 m.
b. ¿Qué vamos a hacer?
Calcular desplazamiento angular neto y tiempo para que
esto ocurra.
c. ¿Cómo lo vamos a hacer?
Primero tomamos la definición de longitud de arco y calculamos el desplazamiento angular, después determinamos
la velocidad angular y calculamos el tiempo.
st-editorial.com
d. Operaciones.
Sabemos que la aceleración centrípeta se define como
an = rω2, y dado que también se cumple que ω = v/r, podemos definir:
v2
25 2
an = r = 32 = 19.531
La aceleración total tiene una magnitud de:
a=
a n2 + a t2 =
^19.531h2 + ^ 6 h2
= 20.432
e. Resultado.
La aceleración total del avión es de 20.432 m/s2 y de
acuerdo a los resultados, la componente centrípeta es
mayor a la tangencial, de tal manera que la dirección de
este vector es muy próxima al radio de la trayectoria.
83
BLOQUE 2
Actividad grupal
COMPETENCIAS
GENÉRICAS
1 4 5 8
COMPETENCIAS
DISCIPLINARES
3 6 7 10
DESEMPEÑOS
DEL ESTUDIANTE
b
c
I. Reúnete con dos compañeros para resolver los ejercicios de esta sección. Además de
su calculadora, requieren consultar las ecuaciones de la 33 a la 39, correspondientes a
los conceptos generales del movimiento circular. Si lo consideran necesario, dibujen
en sus cuadernos los diagramas que representan el movimiento que ocurre en cada
problema.
1. El prototipo de un nuevo auto se prueba en una pista circular cuyo radio es de 350 m.
La velocidad en la cual se realiza un ensayo se mantiene constante de modo tal que
el acelerómetro registra una aceleración normal de 1.5 m/s2. Determina la rapidez a la
cual está viajando el automóvil.
FIGURA 7
Cuando la avioneta se mueve a velocidad constante describiendo una trayectoria circular, se origina la aceleración normal o centrípeta.
2. Un globo meteorológico se ubica a una altura de 13 km. Encuentra la rapidez con la
describe una trayectoria circular considerando que es afectado por una aceleración
centrípeta de 7.63 m/s2.
3. Una rueda tiene una velocidad angular inicial en el sentido de giro de las agujas del
reloj de 9 rad/s y una aceleración angular constante de 4 rad/s2. ¿Cuántas vueltas
debe dar para que alcance una velocidad angular de 18 rad/s? ¿Qué tiempo le toma?
4. La rueda de un esmeril gira a 48 rad/s cuando se corta el suministro de energía
eléctrica. Si el tiempo necesario para que la tina se detenga es de 8 s, determina la
desaceleración angular constante del sistema y el número total de vueltas que realiza
la tina para detenerse.
84
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
5. Un auto viaja en una pista circular y en determinado instante su aceleración es de
7.5 m/s2 con una dirección de 50°, como se ilustra en el gráfico y una velocidad de
120 km/h. Determina el radio de la pista y la aceleración tangencial del auto.
II. Anexen esta actividad a su portafolio de evidencias.
Movimiento circular uniforme. Se denomina movimiento circular uniforme a aquél
en que el objeto recorre arcos de circunferencia iguales en lapsos iguales, de tal
manera que la velocidad angular permanece constante [Ej, 17, 18 y 19]. Existen
algunas variables que son útiles cuando se asocia este tipo de movimiento a
otros fenómenos:
• El tiempo que le toma a un cuerpo recorrer toda la trayectoria circular (360° o 2p rad)
se le denomina periodo (T) y su unidad de medida es el segundo (s).
• Al número de veces que el cuerpo cubre completamente la trayectoria circular en la
unidad de tiempo se le denomina frecuencia (f ) y su unidad de medida es ciclos/s
(s-1) o hertz (Hz).
1
40. f = T
La sustitución de la frecuencia en la deinición de velocidad angular nos lleva a obtener ecuaciones alternas para los movimientos lineal y angular:
i
~ = T = if
Y si consideramos que el arco recorrido en el tiempo T es 2p rad tenemos que en
general:
41. ω = 2pf
Y entonces la velocidad tangencial (m/s):
42. v = 2prf
st-editorial.com
85
BLOQUE 2
Movimiento circular uniformemente acelerado. Este
tipo de movimiento ocurre –en forma similar al
movimiento lineal– cuando la velocidad angular
del objeto que describe una trayectoria circular
cambia en el tiempo, incrementándose o reduciéndose de tal manera que la aceleración angular
es constante.
Se considera que la aceleración angular promedio
es, en este caso, la relación entre la diferencia de
velocidad angular inal y velocidad angular inicial,
en un lapso especíico:
43. a =
~ – ~o
t
Se establece que en general:
44. ω = ωo + at
Si se toma en cuenta que el desplazamiento angular
es el producto de la velocidad angular por el tiempo
(ecuación 33) y sustituimos la ecuación de velocidad
angular promedio, se tiene que el desplazamiento angular en este tipo de movimiento es:
at 2
45. i f = io + ~ot + 2
Donde:
qf = ángulo (o posición angular) inal del objeto
expresaso en rad.
qo = ángulo (o posición angular) inicial del objeto.
ωo = velocidad angular inicial del móvil.
a = aceleración angular del móvil.
t = tiempo en el que ocurre el cambio de posición
angular.
Se tiene que la velocidad angular inal, como una
función del cambio de posición angular y de la
aceleración angular, es:
46. ~ f =
~2o + 2a^i f – ioh
Ejemplo 17
Un ventilador funciona a una velocidad angular constante de 150 rad/s. Calculemos la
frecuencia de la rotación y la velocidad tangencial de cualquier punto situado en el borde
de las aspas, a una distancia de 15 cm.
Solución
a. ¿Con qué datos contamos?
• Velocidad angular ω = 150 rad/s.
• Radio de la trayectoria, r = 0.15 m.
• Incógnitas: frecuencia del movimiento y velocidad tangencial en el borde de las aspas.
b. ¿Qué vamos a hacer?
Calcular la frecuencia y la velocidad tangencial de las aspas.
c. ¿Cómo lo vamos a hacer?
Partimos de la consideración de que el movimiento es a velocidad angular constante
y aplicamos directamente las ecuaciones.
d. Operaciones.
Al considerar que ω = 2pf, la sustitución directa del dato nos conduce a:
f = 150/2p = 23.873 Hz.
Por lo que entonces la velocidad tangencial del borde de las aspas es:
v = 2p(0.15)23.873 = 22.5 m/s2.
e. Resultado.
La frecuencia del movimiento circular es de 23.873 Hz y la velocidad tangencial del
borde de las aspas es de 22.5 m/s.
86
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
Ejemplo 18
Una rueda tiene una velocidad angular inicial de 10 rad/s
en sentido horario y una aceleración angular constante
de 3 rad/s2. Determinemos el número de revoluciones que debe ejecutar para alcanzar una velocidad
angular de 25 rad/s en sentido horario. ¿Cuánto
tiempo se requiere?
Solución
a. ¿Con qué datos contamos?
• Velocidad angular inicial, ωo = 10 rad/s.
• Velocidad angular final, ωf = 25 rad/s.
• Aceleración angular, a = 3 rad/s2 (constante).
• Incógnitas: tiempo y número de revoluciones
necesarias para que la rueda alcance la velocidad angular de 25 rad/s.
b. ¿Qué vamos a hacer?
Calcular el tiempo y las revoluciones que da la
rueda en un movimiento angular uniformemente
acelerado.
c. ¿Cómo lo vamos a hacer?
Aplicamos directamente las ecuaciones del movimiento angular uniformemente acelerado.
d. Operaciones.
La velocidad angular se puede expresar como
una función de la aceleración angular y del desplazamiento angular (ecuación 46), así podemos
entonces sustituir los datos y despejar el valor
del desplazamiento angular:
(25)2 = (10)2 + 2(3)(q – qo)
De esta ecuación tenemos:
q = 525/6 = 87.5 rad
Para el cálculo del tiempo empleamos la ecuación 44, donde también sustituimos en forma directa los datos:
25 = 10 + 3 (t - to), lo cual nos conduce a
t = 15/3 = 5 s
e. Resultado.
El número de revoluciones que ejecuta la rueda para aumentar su velocidad de 10 rad/s a
25 rad/s es de 13.92 durante un lapso de
5 segundos.
Ejemplo 19
El volante de una troqueladora tiene una velocidad angular que se incrementa en forma uniforme desde 5 rad/s hasta 20 rad/s en 90 s. Si el
st-editorial.com
diámetro del volante es de 61 cm, determinemos
la magnitud de la aceleración normal y de la aceleración tangencial de un punto cualquiera del
borde del volante en el instante en que t = 90 s,
así como la distancia que tal punto viaja en el lapso de tiempo indicado.
Solución
a. ¿Con qué datos contamos?
• Velocidad angular inicial, ωo = 5 rad/s.
• Velocidad angular final, ωf = 20 rad/s.
• Lapso de tiempo, t - to = 90 s.
• Radio del volante, r = 0.305 m.
• Incógnitas: Aceleración normal y aceleración
tangencial, distancia que recorre un punto del
borde del volante.
b. ¿Qué vamos a hacer?
Calcular numéricamente las magnitudes de aceleración normal, aceleración tangencial y distancia recorrida por un punto del borde del volante.
c. ¿Cómo lo vamos a hacer?
Calculamos la aceleración normal con los datos
que tenemos y después resolvemos el movimiento angular para determinar la aceleración
angular, y con ésta, la aceleración tangencial. A
continuación evaluamos el desplazamiento neto
para calcular la distancia recorrida.
d. Operaciones.
Para la aceleración normal tenemos:
an = r ω2 = 0.305(20)2 = 122 m/s2
Para la aceleración tangencial se tiene que la
ecuación 44 nos indica:
20 = 5 + a (90) \ a = 0.167 rad/s2
Por lo que:
at = r a = 0.305(0.167) = 0.051 m/s2
El desplazamiento angular recorrido, de acuerdo
a la ecuación 46, es:
(20)2 = (5)2 + 2(0.167)(q – qo)
De esta ecuación tenemos:
q = 375/0.333 = 1125 rad
Por lo que la distancia recorrida es:
d = r q = 0.305(1125) = 343.13 m
e. Resultado.
La aceleración tangencial es de 0.051 m/s2; la aceleración normal, 122 m/s2; y la distancia total recorrida
por un punto cualquiera del borde, 343.13 m. La
aceleración normal se toma como referencia en
el diseño dinámico de este tipo de elementos, ya
que la fuerza que deben transmitir debe ser muy
grande con el menor consumo de energía.
87
BLOQUE 2
Actividad individual
COMPETENCIAS
GENÉRICAS
1
4
5
COMPETENCIAS
DISCIPLINARES
3
6 7 10
DESEMPEÑOS
DEL ESTUDIANTE
b
c
Para realizar los siguientes ejercicios, consulta las ecuaciones de la 40 a la 46 y repasa los ejemplos para
que puedas identificar el tipo de movimiento que se te presenta en cada uno de los ejercicios siguientes.
De ser necesario, realiza en tu cuaderno los dibujos o diagramas que creas convenientes para resolver los
problemas propuestos.
1. Una rueda tiene una velocidad angular inicial en el sentido de las agujas del reloj de 10 rad/s, y 12 s
después su velocidad es de 10 rad/s, en sentido opuesto. ¿Cuál es el valor de la aceleración?, ¿cuántas
vueltas dio en total?
2. La velocidad angular de una piedra de esmerilar se incrementa uniformemente desde 3 rpm en t = 0
hasta 10 rpm en t = 4 s, para que se puedan realizar las operaciones de acabado superficial. Calcula la
magnitud de la velocidad y de la aceleración de un punto de desbaste en la superficie exterior de la
piedra, cuyo radio es de 80 cm.
3. La tina de una secadora trabajaba a 50 rad/s cuando hubo un corte de energía eléctrica, y se conoce que
le toma 15 segundos regresar al reposo. Calcula la desaceleración angular que se produce y el número
de vueltas que giró la tina antes de detenerse por completo.
4. Un disco gira inicialmente a una velocidad angular de 8 rad/s cuando se sujeta a una aceleración angular constante de 6 rad/s2. Determina la magnitud de la velocidad y de las componentes normal y
tangencial de la aceleración de un punto situado a 30 cm del centro de giro en el instante en que t = 3 s.
5. El dibujo muestra un arreglo simple para elevar pesos pequeños. La polea es operada por un motor que la mueve con una velocidad angular de 6 rad/s y le aplica una aceleración angular constante de 3 rad/s2.
Determina la magnitud de la velocidad y aceleración del bloque B cuando t = 2 s.
Radio de la
polea 15 cm
B
88
st-editorial.com
IDENTIFICAS DIFERENCIAS ENTRE
DISTINTOS TIPOS DE MOVIMIENTOS
Lee
La sesenta…
velocidad de la vida (Fragmento)
Los
Vivimos en un mundo cada vez más
apresurado, y por nuestra lucha contra
el reloj, nos rodeamos de dispositivos
encargados de medir nuestro andar, y
pretendemos ganar segundos aumentando nuestra velocidad.
Cuando se desarrolló la rueda, el mundo
se transformó, se aceleró la vida de los
seres humanos hasta llegar a los niveles que hoy conocemos, al menos sobre
la superficie terrestre. Con los avances
científicos y tecnológicos, la humanidad
ha sido capaz de conseguir velocidades
difíciles de imaginar, gracias al uso de
máquinas e implementos tecnológicos;
hasta este momento, la máxima velocidad
alcanzada es la de la nave X-43A, que es
siete veces mayor que la del sonido (331
m/s); así que esta nave vuela a 2 317 m/s.
Un ser humano normal camina a una
velocidad promedio de 3 km/h. Hasta
el momento de publicarse este artículo,
el hombre más veloz sobre la faz de la
Tierra era el jamaiquino Asafa Powell,
quien batió el récord del mundo de los
100 m planos en un tiempo de 9.77 s;
tal hazaña la logró durante una reunión
atlética en el estadio olímpico de Atenas. Dicho de otra manera: Powell corre
a unos 97 km/h, pero, claro, sólo durante
un trayecto de 100 m.
Entre los animales de tierra firme, el
que alcanza la mayor velocidad es
el guepardo o chita, capaz de correr a
120 km/h, pero sólo en distancias cortas. Si se trata de mantener velocidad,
encontramos a la gacela de Mongolia, que puede mantenerse corriendo a
100 km/h durante mucho tiempo. Existen otros corredores terrestres como
la liebre de las planicies americanas,
los caballos pura sangre, las cebras,
el avestruz, el zorro de los desiertos,
el canguro, el león africano, el gato
doméstico, los elefantes, entre otros.
En el agua, el animal más veloz es el
pez aguja, capaz de nadar a 100 km/h,
pero enfrenta una situación parecida
a la del guepardo, ya que solamente
puede mantener esa velocidad por poco
tiempo. También en el medio acuático
encontramos un pez volador del género
Exocoetus, que nada a unos 80 km/h;
no obstante, al salir del agua para capturar insectos y otros organismos que
flotan en el aire, puede alcanzar en el
momento del despegue velocidades de
hasta 600 km/h.
El aire es, sin duda, el ambiente donde se
registran las velocidades más altas, y la
mayor de ellas es la del halcón peregrino,
que alcanza 300 km/h en el vuelo en
picada para capturar sus presas. Entre los
voladores más veloces se encuentra también un insecto, el tábano, que alcanza la
velocidad de 145 km/h, seguido de la libélula australiana, que llega a los 90 km/h.
No obstante las velocidades alcanzadas
por los seres vivos mencionados anteriormente, nada es comparable con la
del planeta Tierra, sobre la superficie
del cual nos movemos, que recorre unos
2 000 km/h diariamente cuando rota,
dando origen así al día y la noche. Esta
velocidad se registra en el ecuador, o
paralelo cero, que es el de mayor longitud. Y como si fuera poco, realiza su
movimiento de traslación a una velocidad promedio de ¡108 000 km/h!
Existen infinidad de datos que podríamos
citar en materia de velocidad, como la
de determinadas reacciones químicas,
ciertos fenómenos físicos o algunas funciones biológicas, pero lo que hemos
referido hasta aquí nos ofrece un pequeño
atisbo de la velocidad con la que se desarrolla la vida en nuestro planeta.
Fuente: Heriberto G. Contreras Garibay. “La velocidad de la vida”. Revista de
divulgación científica y tecnológica de la Universidad Veracruzana.
En:http://bit.ly/11lhoxz
I. Realiza un reporte con base en las siguientes preguntas:
1. ¿Es posible que un ser humano alcance 97 km/h o más sin usar ningún aditamento tecnológico?
2. ¿Cómo entrena un corredor?
3. ¿Quién es el poseedor del nuevo récord de los 100 m planos?
4. ¿Qué dispositivos han sido desarrollados para evaluar el rendimiento de un deportista?
II. Discute con tus compañeros sobre los límites del ser humano en cuanto a esfuerzo físico.
st-editorial.com
89
Evaluación sumativa
Heteroevaluación
I. Pide a tu profesor que aplique la siguiente rúbrica con el fin de que pueda registrar tus avances. Como
verás es la misma que respondiste en el reto; ahora servirá para medir cuál fue tu desempeño durante el
estudio de este bloque.
Indicadores de desempeño
Aspectos a evaluar
4 puntos
3 puntos
2 puntos
1 punto
Conceptos básicos
relacionados
con el movimiento.
Definí plenamente
conceptos básicos
relacionados
con el movimiento.
Definí la mayoría de
conceptos básicos
relacionados
con el movimiento.
Definí vagamente
conceptos básicos
relacionados
con el movimiento.
No definí
conceptos básicos
relacionados
con el movimiento.
Características
del movimiento de
los cuerpos en una
y dos dimensiones.
Identifiqué todas
las características
del movimiento
de los cuerpos
en una y dos
dimensiones.
Identifiqué la
mayoría de las
características
del movimiento de
los cuerpos en una
y dos dimensiones.
Identifiqué
algunas de las
características del
movimiento de
los cuerpos en una
y dos dimensiones.
No identifiqué las
características del
movimiento de
los cuerpos en una
y dos dimensiones.
Características
y diferencias
entre cada tipo
de movimiento.
Reconocí y describí,
con base en sus
características,
todas las diferencias
entre cada tipo
de movimiento.
Reconocí y
describí, con
base en sus
características,
la mayoría de
diferencias entre
cada tipo de
movimiento.
Reconocí y
describí, con
base en sus
características,
algunas diferencias
entre cada tipo
de movimiento.
No reconocí
ni describí,
con base en sus
características,
diferencias entre
cada tipo
de movimiento.
Valoración
Excelente: 11 a 12 puntos.
Bueno: 8 a 10 puntos.
Mi puntaje
Mi total
Suficiente: 5 a 7 puntos.
Insuficiente: 3 a 4 puntos.
II. Ha llegado el momento de que entregues a tu profesor todos los productos de las actividades que realizaste durante este bloque y que guardaste en tu portafolio de evidencias, ya que con esto podrá evaluarte.
Autoevaluación
I. Relaciona las columnas; posteriormente, regresa al bloque para verificar que tus respuestas sean correctas y modifica aquellas que no lo sean.
1. ( ) La aceleración tangencial tiene su origen en...
2. ( ) La aceleración normal es el resultado de...
3. ( ) El cambio de posición representa...
4. ( ) El cambio de velocidad de un cuerpo
en la unidad de tiempo es...
5. (
) El movimiento circular se confunde
a menudo con...
a. la aceleración normal.
b. el desplazamiento de la partícula.
c. la rotación.
d. la aceleración de un cuerpo.
e. la velocidad tangencial.
f. la traslación curvilínea.
g. el cambio de velocidad respecto al tiempo.
h. el cambio en la magnitud y dirección del
vector velocidad.
i. el desplazamiento de un cuerpo.
II. Resuelve en tu cuaderno los siguientes ejercicios.
1. Un hombre sale de la ciudad en su auto por un negocio. Al pasar la primera caseta de peaje el hombre acelera y lentamente aumenta la velocidad desde el reposo hasta alcanzar 40 km/hr, después de
recorrer 5 km frena pisando a fondo el pedal y el auto llega al reposo recorriendo una distancia
de 18 m continúa a una razón de 3.6 m/s cada segundo por 40 m, reduciendo después a 2.4 m/s cada
segundo para alcanzar la velocidad de 100 km/h. No se percata de una curva y frena a fondo, el auto
presenta un “jalón” y casi se sale de la pista. A partir de los datos anteriores indica lo siguiente:
90
st-editorial.com
a. ¿Qué tipo de movimiento presenta el auto en cada etapa del recorrido?
b. ¿Cuáles son los parámetros más importantes del comportamiento cinemático del auto?
c. ¿Por qué cambia el comportamiento del auto en curva?
2. Un joven se sube a la rueda de la fortuna de 42 m de diámetro, con todas sus canastillas completas. Esta
rueda inicia su movimiento, el joven abordo nota que, primero la canastilla iba lento, luego muy rápido sin
cambiar de velocidad y luego oscilaba. La duración de todo el recorrido fue de sólo 5 minutos incluyendo
1 minuto de tiempo de registro, como el que le tomó al juego detenerse…
a. ¿Qué tipos de movimiento se presentaron?
b. ¿Qué velocidad tangencial tiene cada canastilla si la velocidad con la que gira la rueda al llegar al
máximo es de 60 rpm?, ¿qué valor tiene la aceleración?
c. ¿Qué ocurre a una canastilla si se desprende en lo alto?, ¿qué tipos de movimiento presentaría?
3. Un automovilista viaja por una carretera secundaria a 90 km/h y antes de una curva observa un aviso
de “Límite de velocidad 60 km/h radar en operación”; sorprendido reduce su velocidad lentamente durante 2 km, hasta alcanzar 60 km/h. Diez segundos después lo detiene la policía federal por no respetar
el límite de velocidad.
a. ¿Por cuánto tiempo viajó a una velocidad diferente a la permitida?
b. ¿Qué tipo de movimiento se realizó?
c. ¿Se violó el reglamento de tránsito?
4. En la feria de la localidad se ha descompuesto el carrusel y llaman a un electricista para que lo repare; este
debe cambiar los controles dañados por un sistema nuevo que permita el movimiento en forma automática,
un inicio lento y un final todavía más suave para que los niños no se mareen. La velocidad del carrusel está
limitada a 5 rpm, el número de vueltas a dar es 25 y la aceleración angular no debe ser mayor que 1 rad/s.
Determina cómo debe ajustar el sistema de control el electricista para tener el tiempo más apropiado en cada
servicio. Toma en cuenta que el consumo de energía eléctrica tiene un costo específico.
III. Reflexiona y responde en tu cuaderno a cada una de las preguntas:
1. ¿Qué aplicación práctica encuentras al estudio del movimiento de los cuerpos?
2. ¿Este bloque te ha aportado conocimientos que te pueden ser útiles en otros campos?
3. ¿Se te dificulta el estudio del movimiento en dos dimensiones?
4. ¿En qué situaciones de tu vida diaria aplicas o ves relejados los conocimientos que has adquirido?
5. ¿Te consideras apto para estudiar por tu cuenta estos temas si se te presentan con un mayor grado de
abstracción matemática?
IV. Contesta la siguiente lista de cotejo para que reconozcas cuáles fueron tus actitudes durante este bloque.
Aspecto
Siempre
Algunas veces
Nunca
Me integré al trabajo en equipo.
Realicé comentarios acertados de acuerdo con el tema.
Mostré una actitud de respeto y compañerismo.
Participé en todas las actividades.
st-editorial.com
91
Unidad
Desempeños
de competencia
del estudiante
Bloque
Bloque23
Nombre
Comprendes
del bloque
el movimiento de
los cuerpos a partir de las leyes
de dinámica de Newton
a. Identifila
cainfl
en los
diferentes
tipos
de movimiento
Reconocerás
uencia
de los
factores
que las fuerzas
que intervienen en el movimiento
interviene
de los cuerpos.
b. Aplica las leyes de la dinámica de Newton,
en la solución y explicación del movimiento de los cuerpos,
observables en su entorno inmediato.
c. Utiliza la ley de la gravitación universal para entender el
comportamiento de los cuerpos
bajo la acción de fuerzas gravitatorias.
d. Explica el movimiento de los planetas en el Sistema Solar
utilizando las leyes de Kepler.
Estos desempeños pueden identificarse en cada una de las actividades
del bloque, de la siguiente manera:
DESEMPEÑOS DEL
ESTUDIANTE
a
b
c
d
Bloque
Bloque
1 1
Bloque
Bloque 2 1
Bloque 2 Bloque 3
Reconoces el
lenguaje
técnico
En el blok1
se elimina
básico
la física
estede
espacio
Identificas
diferencias
entre
Nombre
del bloque
distintos tipos
destacado
de movimiento
Comprendes el movimiento
debloque
los cuerpos a partirNombre
de
Nombre del
del bloque
las leyes de dinámica
de Newton
Bloque 3
Competencias
Habilidades a desarrollar
a. •
Distinguirás los
•฀ Leyes de la dinámica
b.
•฀ Ley c.
de la gravitación universal
•฀ Leyes
d. de Kepler
e.
f.
g.
h.
i.
j.
k.
l.
m.
COMPRENDES EL MOVIMIENTO DE LOS CUERPOS
A PARTIR DE LAS LEYES DE DINÁMICA DE NEWTON
Actitudes y valores
n. •
Asumirás un papel d
Bloque
4
Bloque
4
Bloque 5
Bloque 6
Bloque 7
Relacionas el trabajo
con la
energíadel bloque
Nombre
Nombre del bloque
Nombre del bloque
Nombre del bloque
st-editorial.com
Continúa...
93
Introducción
En los bloques anteriores ya hemos estudiado
las características generales del comportamiento
de los cuerpos cuando éstos se encuentran en
movimiento. Además, ya podemos determinar
variables como posición, distancia, velocidad,
aceleración y tiempo en una o dos dimensiones.
Ahora nos corresponde estudiar las leyes del
movimiento de Isaac Newton y su utilidad
práctica.
A continuación encontrarás un mapa
conceptual con los temas más relevantes del
presente bloque.
Leyes de la física
dos de las más importantes son
94
leyes de
Newton
leyes de
Kepler
como
como
primera
ley
segunda
ley
tercera
ley
primera
ley
segunda
ley
tercera
ley
estudia la
relaciona la
estudia la
estudia las
relaciona las
relaciona el
inercia
masa y la
aceleración
relación
causaefecto
órbitas
áreas y el
tiempo
periodo con
la distancia
st-editorial.com
Para comenzar...
Para que puedas comprender los temas de este bloque, es necesario
que rescates las competencias (conocimientos, habilidades, actitudes y valores) que ya
has adquirido a lo largo de tu vida. Haz tu mejor esfuerzo para responder y detecta aquellos
aspectos que no conoces o dominas para enfocar tu estudio.
I. Escribe en el paréntesis la letra correspondiente a la respuesta correcta.
1. (
) ¿Qué es la dinámica?
a. Es la parte de la física que estudia lo relativo al movimiento de un cuerpo.
b. Es el área que se dedica al estudio de fuerzas en reposo.
c. Es la parte de la mecánica que estudia las causas del movimiento y sus consecuencias.
d. Es el estudio de las relaciones entre trabajo, energía y fuerza en el movimiento
de los cuerpos.
2. (
) ¿Qué diferencia existe entre peso y masa?
a. Ninguna porque se refieren al mismo fenómeno.
b. El primero es una cantidad escalar y la segunda es un vector.
c. El primero es el efecto del campo gravitacional en un cuerpo y la segunda corresponde a la cantidad de materia de éste.
d. El primero depende de la densidad de la sustancia y la segunda es la sustancia.
3. (
) La fuerza de fricción…
a. se opone al movimiento.
b. transforma la energía en movimiento.
c. es perpendicular a las superficies en contacto.
d. realiza un trabajo positivo sobre las superficies en contacto.
4. (
) Las leyes de Newton…
a. son la base de la mecánica moderna.
b. relacionan el efecto de las fuerzas que interactúan con cuerpos y su movimiento.
c. permiten calcular las propiedades de inercia y masa de un cuerpo.
d. son cinco y constituyen el fundamento de la dinámica.
5. (
) Las leyes de Kepler...
a. definen la cantidad de energía de un sistema.
b. relacionan masa y aceleración para describir la trayectoria de un planeta.
c. nos permiten definir el trabajo que realiza un cuerpo.
d. formulan el movimiento general de un planeta.
II. Resuelve los siguientes problemas.
1. Una caja de madera con su contenido totalizan una masa de 75 kg y se coloca sobre una
superficie horizontal. Calcula el coeficiente de fricción entre la caja y la superficie, si se
aplica a la caja una fuerza de 125 N paralela a la superficie y observamos que no se desliza.
st-editorial.com
95
BLOQUE 3
2. La fuerza que transmite el tren motriz a un auto de 1 650 kg cuando arranca desde el reposo en un semáforo es de 4.95 kN. Calcula la velocidad que adquiere al
cabo de 8 s.
3. Un astronauta de 80 kg viaja en una cápsula espacial sujeto a una aceleración de
30 m/s2. ¿Cuál es su peso aparente?
4. Cuando se aplica una fuerza de 250 N a un objeto en reposo le produce una
aceleración de 6.35 m/s2. ¿Cuál es la masa del objeto? ¿Qué velocidad tiene en el
segundo 8 a partir del momento en que se aplicó la fuerza?
5. Determina la velocidad con la que se lanza verticalmente una piedra de 127 g si
la altura que alcanza desde el punto de lanzamiento es de 6 m.
III. Lee el siguiente texto, reflexiona y contesta en tu cuaderno las preguntas que
vienen posteriormente.
La carrera espacial ha permitido un desarrollo continuo de la tecnología dando paso a nuevos materiales
para objetos tan diferentes como ropa o material
quirúrgico. Lógicamente la puesta en órbita de satélites y otras naves espaciales incluye la creación de
sofisticados sistemas de control y telecomunicacio-
nes que guardadas las distancias nos permiten hoy
en día conocer en forma instantánea qué sucede en
otro lugar, conocemos de guerras, colapsos bursátiles, etc., gracias a una tecnología que además ha
contribuido al desarrollo de armas que se activan sin
la intervención directa del ser humano…
1. ¿Cuáles de los dispositivos que utilizas en casa se desarrollaron durante la época de la
“carrera espacial”?
2. ¿Qué inluye en un científico o en un desarrollador de tecnología para crear armas, sin que considere el daño real que puede provocar a la sociedad?
3. ¿Consideras que de continuar desarrollándose, la “carrera espacial” podría tener algún
tipo de impacto ambiental?
96
st-editorial.com
COMPRENDES EL MOVIMIENTO DE LOS CUERPOS
A PARTIR DE LAS LEYES DE DINÁMICA DE NEWTON
Reto (problema)
I. Reúnete con tres compañeros y reflexionen acerca de los siguiente:
El movimiento de un cuerpo es parte de nuestro paisaje cotidiano, por ejemplo, retomen mentalmente
el recorrido que hacen de la escuela a sus casas, ¿qué hay a tu alrededor? Autos, personas, algunos animales y diversos equipos o dispositivos que presentan diferentes movimientos, etc. ¿Pueden enumerar
cada uno de estos movimientos? Revivan ahora la situación y observen atentamente qué movimiento
se realiza y cómo se realiza, ¿cuál es su origen?, ¿por qué existe tal movimiento?
II. Comenten sobre cada una de las situaciones siguientes y anoten sus conclusiones en su cuaderno
para presentarlas al grupo.
1. Del movimiento:
a. ¿Qué tipos de movimiento observan?
b. ¿Qué hay de común en su origen?
c. ¿Qué interviene para transformar el movimiento?
d. ¿Consideran que se presentan pérdidas de energía?
2. De los agentes que dan origen al movimiento:
a. ¿Qué tipo de fuerzas actúan en los cuerpos?
b. ¿Cuáles dan origen al movimiento?
c. ¿Cuáles lo impiden?
d. ¿Qué tipos de fuerzas son consecuencia del movimiento?
3. Del movimiento y su relación con la fuerza:
a. ¿De qué manera podemos medir la fuerza creada por el movimiento de un cuerpo?
b. ¿Es suficiente para modificar las características del movimiento?
c. La fuerza producida, ¿puede funcionar como fuente de energía propia del cuerpo?
d. ¿De qué manera se evita o reduce la acción de la fuerzas de fricción?
4. Del comportamiento general de los cuerpos en movimiento tanto dentro como fuera del campo
gravitacional:
a. ¿Qué tipo de fuerza actúa para que nos mantengamos sobre la superficie terrestre?
b. ¿Por qué un cuerpo que se aproxima a la superficie terrestre no siempre puede alejarse de la misma?
c. ¿Qué trayectoria sigue un cuerpo en órbita alrededor de la Tierra? ¿Por qué?
d. ¿El movimiento de los cuerpos sobre la superficie terrestre se ve afectado por el movimiento de
la tierra alrededor del sol?
Coevaluación
En la siguiente lista de cotejo se presentan una serie de aspectos para que evalúes el desempeño de
uno de tus compañeros durante la realización del reto.
Aspecto
Siempre
Algunas veces
Nunca
Participó activamente en la discusión.
Expresó su opinión bajo consideraciones teóricas.
Su participación fue incluyente y ordenada.
Respetó las ideas de los compañeros y buscó un consenso.
Trabajó con limpieza y orden.
st-editorial.com
97
Autoevaluación
Averigua cuál fue tu desempeño durante la realización del reto. Para ello marca la siguiente rúbrica según corresponda. Cada indicador tiene un valor en puntos que deberás sumar para determinar tu nivel de desempeño inicial.
Indicadores de desempeño
Aspectos a evaluar
4 puntos
3 puntos
2 puntos
1 punto
Mi puntaje
Fuerzas que
intervienen en
el movimiento
de los cuerpos
en los diferentes
tipos de
movimiento.
Identifiqué
plenamente
en los diferentes
tipos de movimiento
las fuerzas que
intervienen en
el movimiento
de los cuerpos.
Identifiqué en los
diferentes tipos de
movimiento algunas
de las fuerzas que
intervienen en
el movimiento
de los cuerpos.
Identifiqué
vagamente en los
diferentes tipos
de movimiento
las fuerzas que
intervienen en
el movimiento
de los cuerpos.
No identifiqué
en los diferentes
tipos de
movimiento
las fuerzas que
intervienen en
el movimiento
de los cuerpos.
Leyes de la
dinámica de
Newton en
la solución y
explicación del
movimiento
de los cuerpos
observables en el
entorno inmediato.
Siempre apliqué las
leyes de la dinámica
de Newton en la
solución y explicación
del movimiento
de los cuerpos
observables en mi
entorno inmediato.
En ocasiones
apliqué las leyes
de la dinámica
de Newton en la
solución
y explicación
del movimiento
de los cuerpos
observables en mi
entorno inmediato.
Rara vez apliqué
las leyes de
la dinámica
de Newton en
la solución y
explicación del
movimiento
de los cuerpos
observables en mi
entorno inmediato.
Nunca apliqué
las leyes de
la dinámica
de Newton en
la solución y
explicación del
movimiento
de los cuerpos
observables en mi
entorno inmediato.
Ley de la
gravitación
universal para
entender el
comportamiento
de los cuerpos bajo
la acción de fuerzas
gravitatorias.
Siempre utilicé la
ley de la gravitación
universal para
entender el
comportamiento
de los cuerpos bajo
la acción de fuerzas
gravitatorias.
En ocasiones
utilicé la ley de
la gravitación
universal para
entender el
comportamiento
de los cuerpos bajo
la acción de fuerzas
gravitatorias.
Rara vez utilicé la
ley de la gravitación
universal para
entender el
comportamiento
de los cuerpos bajo
la acción de fuerzas
gravitatorias.
Nunca utilicé la ley
de la gravitación
universal para
entender el
comportamiento
de los cuerpos bajo
la acción de fuerzas
gravitatorias.
Movimiento de
los planetas en
el Sistema Solar
utilizando las leyes
de Kepler.
Siempre expliqué
el movimiento
de los planetas
en el Sistema Solar
utilizando las leyes
de Kepler.
En ocasiones
expliqué el
movimiento
de los planetas
en el Sistema Solar
utilizando las leyes
de Kepler.
Rara vez expliqué
el movimiento
de los planetas
en el Sistema Solar
utilizando las leyes
de Kepler.
Nunca expliqué
el movimiento
de los planetas
en el Sistema Solar
utilizando las leyes
de Kepler.
Valoración
Excelente: 15 a 16 puntos.
98
Bueno: 11 a 14 puntos.
Suficiente: 7 a 10 puntos.
Mi total
Insuficiente: 4 a 6 puntos.
st-editorial.com
Tema 1
Tema 2
Tema 3
Leyes de
la dinámica
Ley de la
gravitación universal
Leyes de Kepler
La inquietud del ser humano es, sin duda, la causa de sus grandes logros y de sus
no menos difíciles problemas sociales. La creciente demanda de mercancías y la
forma de trasladarlas en forma rápida y segura lo llevó a investigar intensamente
cómo producir y modiicar el movimiento de objetos, y aunque la naturaleza
produce por sí misma diversos tipos de movimiento, el ser humano tuvo que
adaptarlos y recrearlos para su beneicio… ¿Imaginas un mundo sin movilidad?
Antecedentes históricos del
estudio del movimiento mecánico
El estudio del movimiento se remonta a épocas
remotas, y los primeros registros corresponden a los tratados de Aristóteles (384-322 a. C.)
quien en su obra φυσικóς (Física), además de
enunciar una noción de movimiento que implicaba
cambios de posición y de tipo en el estado –físico
o químico– del cuerpo, también airmaba que la
velocidad de caída de un cuerpo es proporcional
a su peso, y el movimiento en sí es común a todos los
componentes del universo, por lo que el centro del
universo es la Tierra y los demás cuerpos celestes
se mueven de manera continua siguiendo trayectorias concéntricas. Posteriormente, surgieron
diversas corrientes de pensamiento y aunque muchos cientíicos realizaron grandes aportaciones,
st-editorial.com
en realidad fueron Galileo Galilei (1564-1642)
y Johannes Kepler (1571-1630) quienes comenzaron la revolución en el campo de la física.
Galileo formuló el principio de la inercia y estableció el principio de la caída libre de los cuerpos,
deiniendo en lo general las leyes que relacionan la
fuerza con el movimiento, y no se limitó solamente a establecer hechos, sino que todo su trabajo lo
fundamentó en experimentos, deinió los modelos matemáticos correspondientes y estableció sus
conclusiones por medio del método cientíico. Su
trabajo es la base para las aportaciones de otros
cientíicos ilustres como Isaac Newton (1642-1727)
y Albert Einstein (1879-1955); curiosamente el año
que murió Galileo nació Newton, matemático y
físico inglés a quien se atribuye el estudio formal
del movimiento.
99
BLOQUE 3
FIGURA 1
Newton descubrió que el espectro
de color que se observa cuando la luz
blanca atraviesa un prisma, era inherente a la luz y no provenía del prisma,
como antes se pensaba.
Desde los 25 años de edad, Newton empezó a mostrar su talento y realizó trabajos sobre las aplicaciones del cálculo diferencial e integral (que él llamaba operación
inversa) para determinar el máximo y el mínimo de una función, el área bajo una
curva, las longitudes de curvas, etc. Hacia el año 1666 ya había presentado sus investigaciones sobre mecánica celeste, que tenían como elemento primordial la teoría de la
gravitación universal, y en 1687 publicó un compendio sobre sus resultados, cuyo título
es Philosophiae naturalis principia mathematica. Los Principia, como abreviadamente
se nombran estos trabajos, muestran un análisis completo del movimiento de los proyectiles, la caída libre de los cuerpos y el movimiento de éstos en diferentes medios, y
presentan los principios fundamentales, conocidos como leyes de Newton.
Si bien es cierto que el trabajo de Newton no fue totalmente original, porque sus
estudios los basó en las investigaciones de Galileo Galilei y Robert Hooke entre otros,
sus aportes al conocimiento se mantienen vigentes y continúan siendo la base de la
llamada mecánica clásica. Comencemos el estudio de las leyes que enunció Newton
como base para entender por qué y cómo un cuerpo se mueve cuando un agente externo actúa sobre él.
Newton deinió un método racional y experimental para su labor cientíica y airmó:
• Primero: se deben considerar sólo las causas necesarias para explicar un fenómeno.
• Segundo: se deben relacionar los efectos que sean similares entre sí.
• Tercero: se debe extender el conocimiento sobre las propiedades de un cuerpo a
todos los cuerpos semejantes con los que se puede experimentar.
• Cuarto: se tiene que considerar que cualquier proposición obtenida por inducción
al observar un fenómeno es válida hasta que se presente un fenómeno que contradiga la proposición o limite su validez.
Actividad grupal
COMPETENCIAS
GENÉRICAS
4 6 7 8
COMPETENCIAS
DISCIPLINARES
1 2 3 4
DESEMPEÑO
DEL ESTUDIANTE
a
Organicen al grupo en equipos y desarrollen las siguientes actividades.
1. Lean el siguiente párrafo.
El entorno social, económico y político ha sido
determinante para el desarrollo de la ciencia y la
tecnología. Hoy en día, los países que gozan de
“buena salud” en estos aspectos se encuentran
a la vanguardia y son líderes a nivel mundial;
sin embargo, algunos otros destacan específicamente en campos que no corresponden en forma
precisa al desarrollo que presentan, ya que no
tienen condiciones sociales o económicas estables. ¿Qué ha sucedido a lo largo del tiempo en
las sociedades en las que se han desenvuelto los
grandes pensadores? ¿Quiénes y cómo gobernaban? ¿Qué avances existían en otros campos de
la ciencia y la técnica?
2. Realicen una investigación en diversos medios, definan los hechos más significativos
y que respondan a todo lo anterior para las épocas de la Antigüedad griega, del Imperio Romano, del Renacimiento y de la Revolución Industrial.
3. Presenten en hojas de papel bond o kraft, una línea del tiempo en la que se muestren
los avances y las aportaciones reales de Aristóteles, Arquímedes, Galileo, Newton,
Copérnico, Kepler, Ptolomeo, Pascal, Joule y Watt entre otros, donde marquen adicionalmente los sucesos históricos más sobresalientes. Además, investiguen lo que
cada uno de ellos pensaba acerca del movimiento.
4. ¿Creen que en la región o comunidad donde viven existen las condicione sociales
y económicas necasarias para el desarrollo de la ciencia? Debatan en torno a este
punto.
En la web
Para conocer más acerca de este
tema visita st-editorial.com/enlaweb/
fisica1 y consulta los siguientes links:
Teoría del campo gravitatorio, 03
La manzana de Newton, 04
100
st-editorial.com
COMPRENDES EL MOVIMIENTO DE LOS CUERPOS
A PARTIR DE LAS LEYES DE DINÁMICA DE NEWTON
Tipos de fuerzas y las tres leyes
de dinámica de Newton
En la mayoría de nuestros actos están presentes diversos tipos de
fuerza; por ejemplo, cuando caminamos, dormimos, trabajamos, o nos
trasladamos de un lugar a otro en auto o en algún medio de transporte. En todas estas actividades siempre está presente una fuerza.
Formalmente se deine como fuerza una cantidad vectorial capaz de
modiicar el estado en que se encuentra un sólido, por la interacción
física entre dos o más cuerpos.
La fuerza es un vector porque siempre existe un punto de aplicación especíico, posee una magnitud y actúa con una dirección que
permite deinir algunas características en cuanto al efecto que produce. La unidad que se emplea para expresar su magnitud es el newton
(N) en honor del cientíico que estudió sus efectos en el movimiento
de los cuerpos.
Al considerar que la fuerza está presente en todas las actividades
de nuestra vida diaria, es necesario que tengamos en cuenta que se
pueden dividir en fuerzas supericiales y fuerzas del cuerpo.
Fuerzas superficiales. Se establecen por el contacto directo entre dos
o más cuerpos; se maniiestan o actúan sobre la supericie de los sólidos y es común que se les considere fuerzas de acción y reacción.
Por ejemplo, si golpeamos con el pie un balón de fútbol, el golpe lo
impulsa en una dirección especíica que es la misma de la fuerza que
el pie ejerce en el momento del contacto. La fuerza sobre el pie es la
de reacción que ocurre y aunque su sentido es opuesto, su magnitud es
exactamente igual a la de la fuerza actuante sobre el balón.
Fuerzas del cuerpo. Se caracterizan por actuar a distancia, y su origen está
relacionado con las propiedades del sólido, ya que dependen directamente de un campo que puede ser de origen gravitacional, magnético o eléctrico, o bien se pueden manifestar a nivel atómico.
Las fuerzas asociadas a las propiedades magnéticas o eléctricas
del cuerpo también se maniiestan como una atracción o una repulsión entre los sólidos que intervienen, ya que puede tratarse de
simples cargas eléctricas o bien de imanes que se atraen o repelen
por el tipo de carga o polo que poseen, positivo o negativo, sin entrar
en contacto directo. Observa el infográico 1.
Las fuerzas generadas a nivel atómico se conocen como fuerzas
nucleares y su efecto es permitir que las moléculas se mantengan
unidas entre sí.
Cuando hablamos de fuerzas cuyo origen se atribuye al campo
gravitacional estamos asociando a la masa el efecto que ejerce el
campo gravitacional, que no es más que una atracción hacia el origen (centro) del campo (que en nuestro caso y en el de todos los
objetos y seres que nos rodean es el centro de la Tierra). Esta fuerza
se conoce como peso y su magnitud se obtiene con el producto de la
masa y la aceleración del campo gravitacional.
FIGURA 2
Al golpear el balón con el pie se ejerce una fuerza superficial.
Infográfico 1 Fuerzas del cuerpo
En las propiedades eléctricas o magnéticas de
los cuerpos se manifiestan las denominadas
fuerzas del cuerpo.
1
Las cargas eléctricas de diferente signo
se atraen.
Fe
2
3
Las cargas eléctricas del mismo signo
se rechazan.
Fe
Fe
Fe
Fe
Los polos de signos opuestos se atraen.
N
S
1. P = mg
Donde:
P = peso, expresado en N.
m = masa, expresada en kg.
g = aceleración producida por el campo gravitacional = 9.81 m/s2.
st-editorial.com
4
Los polos de signos iguales se repelen.
N
N
101
BLOQUE 3
FIGURA 3
En ausencia de un campo gravitacional, como ocurre con los
astronautas en el espacio, no existe una fuerza de atracción
hacia un punto específico.
Fuerzas de fricción
FIGURA 4
Fuerza de fricción al frenar un auto: cuando se aplican los
frenos se producen fuerzas opuestas entre las llantas –fuerza
de fricción, que actúa en un sentido– y el pavimento –fuerza que
actúa en sentido opuesto–.
102
Peso y masa son dos conceptos y magnitudes físicas diferentes.
El peso depende de la aceleración del campo gravitacional, pero es
común que confundamos o usemos en forma indistinta los términos peso y masa. Por ejemplo, airmamos que estamos excedidos
de peso cuando lo observamos en la báscula, cuando realmente
deberíamos hacer referencia a la cantidad de masa acumulada en
nuestro cuerpo, que ha modiicado su volumen.
En el interior de una nave espacial no existe un campo gravitacional y aunque el astronauta tiene su propia masa, carece
de peso; pero si se encuentra, por ejemplo, en la supericie lunar,
como la aceleración del campo gravitacional es menor que la de
la Tierra, se reduce la fuerza de atracción y la “ligereza” del cuerpo humano permite que sea más fácil la realización de algunas
actividades.
La masa es la magnitud que cuantiica la cantidad de materia
de un cuerpo y su unidad de medida en el si es el kilogramo (kg).
Hagamos ahora un poco de memoria. ¿Qué sucede cuando
viajamos en auto y cambia la luz del semáforo? Si el auto parte
del reposo observamos que se requiere acelere para que el coche
empiece a moverse; y si el auto llega a un alto, entonces el conductor pisa el pedal de freno y el vehículo reduce la marcha hasta
detenerse completamente.
En ambos casos intervienen varias fuerzas, pero sólo una de
ellas es de nuestro interés, por el momento. Para que el auto inicie
el movimiento debe vencer la fuerza de oposición que ejerce el
pavimento sobre los neumáticos, y para que se detenga de nuevo,
el pavimento y los frenos deben ejercer una fuerza que se opone
al movimiento. La fuerza que se opone al movimiento se denomina fuerza de fricción, y se presenta siempre que existen dos o
más cuerpos con un movimiento relativo entre sí; es paralela a las
supericies en contacto, sobre una supericie actúa en un sentido, y
en la supericie contigua actúa en el sentido opuesto.
La fuerza de fricción se opone al movimiento pero no siempre
lo impide, por ello se clasiica como fuerza de fricción estática y
fuerza de fricción dinámica.
Fuerza de fricción estática. Se identiica comúnmente como la fuerza que impide el movimiento entre dos supericies en contacto
que se hallan en reposo.
Fuerza de fricción dinámica. Se presenta cuando existe un movimiento relativo a la velocidad constante entre dos supericies.
La fuerza de fricción dinámica es siempre menor que la estática,
y en ambos casos su magnitud se asocia a las condiciones de rugosidad o estado de acabado supericial de los cuerpos en contacto.
Una vez conocida la manera en que actúa la fuerza de fricción,
es necesario señalar que su magnitud tiene un valor que se puede
determinar por medio de la expresión:
2. Fs = msN
Donde:
µs = coeiciente de fricción estático.
N = fuerza normal, perpendicular a las supericies en contacto.
st-editorial.com
COMPRENDES EL MOVIMIENTO DE LOS CUERPOS
A PARTIR DE LAS LEYES DE DINÁMICA DE NEWTON
La expresión anterior sólo describe el valor máximo o límite de
CUADRO 1. COEFICIENTES DE FRICCIÓN
la fuerza de fricción estática, pero no un valor inferior; por tanto,
Valores típicos de m
Superficies en contacto
se aplica a casos en los que se sepa con certeza que el movimiento
Estático Dinámico
es inminente.
Acero sobre acero en seco
0.6
0.4
Una vez que se ha iniciado el movimiento, nos hallamos en conAcero sobre acero con lubricación
0.1
0.05
diciones de fricción cinética o dinámica. Esta fuerza también es
Teflón sobre acero
0.04
0.04
proporcional a la fuerza normal:
3. Fd= mdN
Donde:
µd = coeiciente de fricción dinámico.
El coeiciente de fricción dinámico es siempre menor al coeiciente de fricción estático y por lo general, la dirección de la fuerza
resultante que actúa sobre las supericies en contacto está dada, para
el caso de la fuerza de fricción estática, por:
Acero sobre metal blando en seco
Acero sobre metal blando con
lubricación
Latón sobre acero en seco
Material de frenos sobre fundición
de hierro
Neumáticos sobre pavimento liso y seco
Cable sobre polea de hierro en seco
Cuerda de cáñamo sobre metal
Metal sobre hielo
0.4
0.1
0.3
0.07
0.5
0.4
0.4
0.3
0.9
0.2
0.3
--
0.8
0.15
0.2
0.02
4. tanφs = ms
Siendo φ s, el ángulo de fricción estático y cuando el movimiento es inminente este ángulo recibe el nombre de ángulo
de reposo.
Al producirse el deslizamiento, el ángulo toma un valor máximo
deinido por:
5. tanφd = md
Siendo φd, el ángulo de fricción dinámico.
En el cuadro 1 se proporcionan algunos valores típicos de coeicientes de fricción obtenidos en condiciones normales de trabajo,
los verdaderos coeicientes corresponden a situaciones especíicas
asociadas a la geometría exacta de las supericies en contacto. Se
considera válida una variación del 25% o más respecto a estos valores en cualquier aplicación por las condiciones de limpieza, acabado
de la supericie, presión entre las supericies en contacto, lubricación, velocidad, etc.
En la mecánica nos encontramos con tres tipos de problemas de
fricción por deslizamiento.
Tipo I. Hay que buscar la condición de movimiento inminente. En el
enunciado del problema debe quedar claro que se emplea el coeiciente de fricción estático para los cálculos [Ej.1].
Tipo II. No se precisa que hay movimiento inminente y por ello la
fuerza de fricción puede ser menor incluso que la dada por la expresión que incluye a msN. Se procede a evaluar el equilibrio del sistema
y se determina la magnitud de la fuerza de fricción; una vez que se
conoce la magnitud de la fuerza F, se considera lo siguiente [Ej. 2].
Si F < Fs = msN, la fuerza de fricción es soportada por las supericies
en contacto y el cuerpo se halla en reposo.
Si F > Fs = msN, hay movimiento y la fuerza de fricción que soportan
las supericies en contacto es la dinámica.
Tipo III. Hay movimiento relativo a velocidad constante entre las supericies de contacto y se debe evaluar la magnitud de la fuerza de
fricción considerando md [Ej. 3].
st-editorial.com
103
BLOQUE 3
Ejemplo 1
La fuerza máxima de fricción estática que soporta la
superficie es:
Fs = msN = 0.5(981) = 490.5 N
Un contenedor de 100 kg se encuentra inmóvil y se le aplica una fuerza de 400 N. Calculemos la magnitud y la dirección de la fuerza de fricción que ejerce la superficie sobre
el contenedor.
mS = 0.5
md = 0.4
F
Solución
a. ¿Con qué datos contamos?
• Masa del contenedor: m = 100 kg.
• Fuerza aplicada: F = 400 N.
• Coeficiente de fricción estático: ms = 0.5
• Coeficiente de fricción dinámico: md = 0.4
• Incógnita: magnitud y dirección de la fuerza de fricción, Ff.
b. ¿Qué vamos a hacer?
Efectuar una suma de fuerzas para determinar la fuerza de
rozamiento.
c. ¿Cómo lo vamos a hacer?
Puesto que el contenedor se encuentra inmóvil, suponemos
que permanece en reposo a pesar de la acción de la fuerza
actuante de 400 N y hacemos la suma de fuerzas igual a cero.
Si no se cumple al final con el valor máximo de fuerza de fricción estática, entonces quiere decir que el contenedor está
en movimiento.
e. Resultado.
Como esta fuerza es mayor que la requerida para
el equilibrio, la suposición que hicimos de que el
contenedor permanece en reposo y se encuentra
en equilibrio es correcta y por lo tanto la fuerza de
fricción es 400 N hacia la derecha.
Ejemplo 2
En un experimento se coloca un prisma de acero de 450 g
cerca del borde de una mesa, y en uno de sus lados se
ata un cordel unido a un contrapeso cuya masa es idéntica a la masa del prisma y se hace pasar por una polea.
Determinemos si el prisma se mueve o no, por la acción
del contrapeso, considerando que el coeficiente de fricción estático entre la mesa y el prisma es de 0.9, sin que
exista rozamiento entre el cordel y la polea.
Solución
a. ¿Con qué datos contamos?
• Masa del prisma: m = 0.45 kg.
• Masa del contrapeso: mo = 0.45 kg.
• Coeficiente de fricción estático: ms = 0.9.
• Incógnita: magnitud de la fuerza de fricción para determinar si hay movimiento o no.
d. Operaciones.
Aplicamos la suma de fuerzas igual a cero para que el contenedor se encuentre en reposo.
+
+
-
/ Fx = 0 : Ff – F = 0 ∴ Ff = F = 400 N
/ Fy = 0 : mg – N = 0 ∴ N = mg = 100 (9.81) = 981 N
mg
b. ¿Qué vamos a hacer?
Calculamos la fuerza que actúa sobre el prisma y la
fuerza de fricción estática.
c. ¿Cómo lo vamos a hacer?
Aplicamos una suma de fuerzas. Cuando el prisma
está en reposo, las fuerzas lo equilibran.
Ff
F
N
104
d. Operaciones.
Dibujamos en primer lugar el diagrama de un cuerpo
libre. En este caso tomamos el dibujo del contrapeso
st-editorial.com
COMPRENDES EL MOVIMIENTO DE LOS CUERPOS
A PARTIR DE LAS LEYES DE DINÁMICA DE NEWTON
• Coeficiente de fricción dinámico: md = 0.12.
• Incógnita: magnitud de la fuerza mínima que se requiere
aplicar.
como referencia para la dirección del movimiento, de modo
que si se mueve el prisma, lo hará hacia la izquierda.
b. ¿Qué vamos a hacer?
Calculamos la fuerza que contrarrestará la fuerza estática de fricción para que exista movimiento a velocidad
constante.
T
mg
T
Ff
mog
Fuerza del contrapeso
N
Fuerzas en el prisma
Considerando que sólo el contrapeso tiene fuerzas que actúan en la vertical y que no hay movimiento, tenemos:
+
-
/ Fy = 0 : T – mog = 0 ∴ T = mog = 0.45(9.81) = 4.415 N
Aplicando la suma de fuerzas igual a cero para el prisma:
+
-
c. ¿Cómo lo vamos a hacer?
Aplicamos una suma de fuerzas; la resultante debe ser nula
pues el movimiento es a velocidad constante.
d. Operaciones.
Para facilitar el proceso de solución realizamos el diagrama de un cuerpo libre; ahí aislamos el bloque y
marcamos todas las fuerzas actuantes para visualizar
su efecto y facilitar la escritura de las ecuaciones. Debido a que se desconoce la dirección del movimiento,
suponemos que el bloque se desliza sobre la horizontal
hacia la derecha.
/ Fy = 0 : mg – N = 0 ∴ N = mg = 0.45(9.81) = 4.415 N
+
mg
/ Fx = 0 : Ff – T = 0 ∴ T = Ff = 4.415 N
La fuerza de fricción máxima que soporta el sistema, de
acuerdo a nuestra teoría, es:
P
Ff
Fs = msN = 0.9(4.415) = 3.973 N
e. Resultado.
La fuerza máxima de fricción (Fs) es inferior a la fuerza que
ejerce el contrapeso (T), por lo que el prisma se desliza
sobre la superficie.
Ejemplo 3
Un bloque de madera de 90 kg se coloca sobre una superficie horizontal de tal manera que el coeficiente de fricción
dinámico es de 0.12. Calculemos la fuerza mínima que se
debe aplicar al bloque para que se deslice en la superficie
a velocidad constante.
Solución
N
Aplicamos la suma de fuerzas igual a cero para que el bloque
se mueva a velocidad constante:
+
- / Fy = 0 :
= 882.9 N
+
mg
–
N
=
0
∴
N
=
mg
=
90(9,81)
/ Fx = 0 : P – Ff = 0 ∴ Ff = P = md N = 0.12(882.9) = 105.95 N
e. Resultado.
La fuerza que se debe aplicar para que el bloque se
deslice a velocidad constante sobre la superficie debe
tener una magnitud mínima de 106 N; un valor inferior
al calculado no producirá movimiento.
a. ¿Con qué datos contamos?
• Masa del bloque: m = 90 kg.
st-editorial.com
105
BLOQUE 3
Actividad individual
COMPETENCIAS
GENÉRICAS
4
5 7
COMPETENCIAS
DISCIPLINARES
3
4 10
DESEMPEÑO
DEL ESTUDIANTE
a
I. Para resolver estos ejercicios es necesario que prepares tu calculadora y consultes las ecuaciones y
el cuadro de coeficientes de fricción. Antes de comenzar, repasa los ejemplos resueltos para que aprendas
a auxiliarte con el trazo de los diagramas.
1. Para mover a velocidad constante un bloque de hielo de 20 kg, un estibador lo jala con una fuerza de
49.5 N y en un ángulo de 60° respecto a la vertical. Determina el coeficiente de fricción entre el hielo y
la superficie.
2. Determina la fuerza que debe actuar sobre una caja de 100 N colocada sobre un plano inclinado a 36.87°
para que no resbale hacia abajo del plano. Considera que el coeficiente de fricción estático es de 0.35 y
que la fuerza a aplicar es paralela a la superficie del plano.
3. El viejo escritorio del abuelo tiene un peso de 40 kg y se apoya sobre un piso de mosaico de tal manera
que el coeficiente de fricción estático entre las superficies en contacto es de 0.25. Si para hacer limpieza
te piden que lo muevas, determina la magnitud de la fuerza más pequeña que debes aplicar para que el
escritorio se mueva considerando que:
a. Aplicas la fuerza sobre el borde en forma horizontal.
b. Aplicas la fuerza sobre el borde con un ángulo de 30° respecto a la horizontal. Responde, además, cómo
haces menos esfuerzo, si jalando o empujando el escritorio.
4. Una caja de 35 kg se coloca sobre un plano inclinado a 20°. Si el coeficiente de fricción entre la caja
y el plano es de 0.35, determina la magnitud de la fuerza normal, y si la caja se desliza o no sobre la
superficie.
II. Anexa esta actividad a tu portafolio de evidencias.
106
st-editorial.com
COMPRENDES EL MOVIMIENTO DE LOS CUERPOS
A PARTIR DE LAS LEYES DE DINÁMICA DE NEWTON
Ley de la inercia
Para explicar la primera ley de Newton o ley de la inercia, analicemos de nuevo
el caso del auto que inicia el proceso de alto total aplicando los frenos. Si el
conductor ha sido lo suicientemente cuidadoso, no ocurre nada excepcional;
si, por el contrario, tuvo alguna distracción y se vio obligado a colocar con fuerza el pie sobre el pedal de freno, todos experimentarán un movimiento brusco
hacia el frente. En este caso, una niña o niño pequeño puede salir lanzado hacia el frente y lastimarse, en el caso de que no tenga puesto ningún dispositivo
de seguridad.
¿Qué ocurre cuando este auto, en lugar de frenar, arranca intempestivamente? Las personas que estén dentro experimentarán una fuerza que los empuja
en sentido inverso al de la fuerza que se ejerce para mover o detener el auto;
una lesión común en caso de frenar muy rápido es la torcedura del cuello.
La fuerza a la que hemos hecho mención se asocia invariablemente a la
primera de las tres leyes sobre el movimiento de Newton o ley de la inercia,
que es la propiedad que le permite a todo cuerpo oponerse al movimiento. A
inales del siglo xvii, después de revisar los trabajos de Galileo, Newton tomó
en cuenta esta propiedad al dar a conocer los resultados de su observación y
experimentación. El enunciado es:
Si la resultante de todas las fuerzas que actúa sobre un sólido es cero, éste se mantendrá en su
estado de reposo o movimiento a velocidad constante en una línea recta mientras no se ejerza una
fuerza desequilibrante que modifique tal estado.
Ley de la fuerza y aceleración
La segunda ley de Newton o ley de la fuerza y aceleración es reconocida en
la mecánica como la base de uno de los tres métodos para efectuar el análisis
del comportamiento de un sólido cuando por la acción de diversos agentes
externos se anima de un movimiento especíico. Esta ley establece la relación
entre la masa, la aceleración y la fuerza actuante o resultante en el cuerpo.
Aunque Newton la estableció en términos del impulso asociado a la cantidad
de movimiento de los cuerpos, nosotros la formulamos considerando que
la masa es constante en todo momento y que el cambio de velocidad en el
tiempo se traduce en la aceleración de los cuerpos. El enunciado es:
Si la fuerza resultante que actúa en un sólido no es cero, éste tendrá una aceleración proporcional
a la magnitud de la resultante en la misma dirección.
La expresión matemática asociada a esta ley es:
6. F = ma
Donde:
F = fuerza resultante aplicada, en N.
m = masa del sólido bajo estudio, en kg.
a = aceleración del sólido, en m/s2.
Esta ecuación nos permite observar con mayor claridad que la masa es una
medida cuantitativa de la inercia [Ej. 4]. El efecto que perciben los pasajeros
FIGURA 5
Una etapa de las pruebas que se realizan en Europa para certificar el nivel de
seguridad en un auto: la fuerza del impacto
proyecta a los maniquíes contra el tablero
del auto.
Dispositivo de seguridad. El cinturón y la bolsa de aire (airbag) son mecanismos de seguridad que se incluyeron en la fabricación de
automóviles. Son los elementos que mayor seguridad pasiva aportan a los usuarios en caso de accidente.
st-editorial.com
Glosario
107
BLOQUE 3
de un vehículo cuando éste arranca o frena bruscamente está asociado directamente
a su masa y su aceleración [Ejs. 5 y 6]. Ésta es la razón por la que se puede sufrir una
lesión de consecuencias graves o no, ya que para la misma fuerza, la aceleración de
cada cuerpo cambia de acuerdo a su masa.
Ejemplo 4
Retrato
Jean le Rond d’Alembert. Este matemático, filósofo y enciclopedista francés (1717-1783), estableció el principio
de composición para el movimiento y
afirmó que al usarlo en conjunto con
el principio del equilibrio y la fuerza
de inercia se puede resolver cualquier
tipo de movimiento para un cuerpo, ya
que son principios diferentes que se
complementan: F – ma = 0.
Dos estibadores empujan un contenedor y lo mueven con una aceleración uniforme.
Determinemos el peso del contenedor considerando que el administrador del almacén los observó, y mediante un dispositivo determinó que existe una aceleración
uniforme del contenedor de 7.25 m/s2; además, según sus registros, la fuerza neta
aplicada es de 1 842 N.
Solución
a. ¿Con qué datos contamos?
• Fuerza aplicada sobre el contenedor: F = 1 842 N.
• Aceleración del contenedor: a = 7.25 m/s2.
• Incógnita: peso del contenedor.
b. ¿Qué vamos a hacer?
Calculamos el peso del contenedor con los datos de fuerza aplicada y aceleración
producida.
c. ¿Cómo lo vamos a hacer?
Aplicamos la segunda ley de Newton en forma directa para determinar la masa y el
peso del contenedor.
d. Operaciones.
Imaginemos la situación y representémosla mediante un diagrama de causa y efecto
para determinar la masa y el peso del contenedor.
mg
P
=
N
ma
∑F = ma
A diferencia de lo que ocurre en los problemas de fricción, donde existe un cuerpo
en reposo o en movimiento a velocidad constante, en este caso es necesario realizar
diagramas para observar más fácilmente la aplicación de la segunda ley de Newton.
En la imagen de la izquierda se muestran todas las fuerzas actuantes; en la de la derecha, el efecto producido.
Para el movimiento horizontal tenemos:
108
st-editorial.com
COMPRENDES EL MOVIMIENTO DE LOS CUERPOS
A PARTIR DE LAS LEYES DE DINÁMICA DE NEWTON
+
P
1842
/ Fx = ma: P = ma ` m =
a = 7.25 = 254.068 kg
d. Operaciones.
•฀฀Análisis฀del฀movimiento
Considerando que:
Y de acuerdo a la definición de peso, tenemos para el contenedor:
a=
W = mg = 254.068(9.81) = 2 492.417 N.
Debido a que el movimiento ocurre sobre la superficie horizontal, para las fuerzas verticales se cumple con el equilibrio:
+
.
/Fy
= 0 : mg – N = 0 ∴ N = mg = 2 492.417 N
e. Resultado.
El peso del contenedor es de 2 492.417 N. Las fuerzas verticales no intervienen en el movimiento generado, y no
se considera la fuerza de fricción entre el contenedor y la
superficie.
v – v0
0 – 25
=
= - 5 m/s
t
5
Se puede apreciar que nuestro procedimiento es correcto porque el signo menos (-) obtenido nos señala que la
furgoneta se desacelera en forma uniforme.
•฀฀Análisis฀de฀las฀fuerzas฀actuantes
En el gráfico 2 observa que la fuerza de fricción (Ff) produce una fuerza de inercia en la misma dirección (ma).
GRÁFICO 2
=
Ff
Ejemplo 5
Una furgoneta con una masa de 1 250 kg viaja a 90 km/h en un
camino plano y recto,y se ve obligada a reducir su velocidad en
forma uniforme para llegar al reposo en un cruce de ferrocarril.
Observemos el gráfico 1 y calculemos la magnitud de la fuerza
de frenado si el chofer presiona el pedal de freno durante 5 s.
ma
∑Ff = ma
De acuerdo al diagrama de causa y efecto, para el movimiento horizontal se cumple:
+
/Fx = max : Ff = ma ∴ Ff = 1 250(5) = 6 250 N
e. Resultado.
La fuerza de frenado es de 6 250 N y actúa sobre las cuatro
ruedas del auto de manera uniforme en sentido opuesto
al movimiento.
GRÁFICO 1
90 km/h
Ejemplo 6
masa = 1 250 kg
Solución
a. ¿Con qué datos contamos?
• Masa de la furgoneta: m = 1 250 kg.
• Velocidad inicial del vehículo: vo = 90 km/h = 25 m/s.
• Velocidad final del vehículo: v = 0.
• Tiempo requerido: t = 5 s.
• Incógnita: fuerza de frenado.
b. ¿Qué vamos a hacer?
Calculamos la desaceleración del auto para aplicar la segunda ley de Newton y determinar la fuerza de frenado
aplicada.
c. ¿Cómo lo vamos a hacer?
Primero aplicamos la ecuación del movimiento uniformemente acelerado y después aplicamos la segunda ley de
Newton para el movimiento horizontal.
st-editorial.com
En una construcción se elevan botes con grava a un tercer
piso empleando un malacate cuyo cable tiene una tensión
de 1 146 N. Determinemos la aceleración con la que suben
los botes y el tiempo que le toma a cada uno recorrer los
11 m que representan los tres pisos, considerando que la
masa total del bote con grava es de 75 kg.
Solución
a. ¿Con qué datos contamos?
•฀Masa฀de฀los฀botes:฀m = 75 kg.
•฀Velocidad฀inicial฀de฀cada฀bote:฀vo = 0.
•฀Tensión฀en฀el฀cable:฀T = 1 146 N.
•฀Distancia฀recorrida฀por฀los฀botes:฀y = 11 m.
•฀฀I ncógnita:฀aceleración฀y฀tiempo฀necesarios฀para฀que฀
los botes suban tres pisos.
b. ¿Qué vamos a hacer?
Calculamos la aceleración de cada bote para aplicar las
ecuaciones de movimiento y determinar el tiempo.
109
BLOQUE 3
c. ¿Cómo lo vamos a hacer?
Aplicamos la segunda ley de Newton y después calculamos la velocidad con la
que llegan los botes a la parte superior. Con este dato determinamos el tiempo
mediante la ecuación respectiva, aplicándola al movimiento sobre el eje vertical.
d. Operaciones.
GRÁFICO 3
T
ma
=
∑Fy = ma
mg
En el gráfico 3 observamos que las fuerzas sólo actúan en la vertical, que corresponde a la dirección del movimiento. Entonces ocurre lo siguiente:
•฀Análisis฀de฀fuerzas฀actuantes.
+
/ Fy = may: T – mg = may
∴ ay = (1 146 -75 × 9.81) / 75 = 5.47 m/s2
•฀Análisis฀del฀movimiento.
De acuerdo a la ecuación de la cinemática:
v=
v 0 + 2a ^y – y0h =
2
2 # 5.47 # 11 = 10.97 m/s 2
El tiempo es, entonces, t =
v – v0 10.97
= 5.47 = 2 s
a
e. Resultado.
El tiempo requerido para que suba cada uno de los botes es de 2 s.
Ley de la acción y reacción
En las situaciones antes analizadas se ha enfatizado que las fuerzas que actúan
sobre un sólido cualquiera son determinantes en la producción o modiicación
de un estado. Siempre que se aplica una fuerza sobre un sólido, éste producirá
una fuerza de contacto opuesta sobre el agente que le aplica la fuerza original, y
ésta es precisamente la esencia de la tercera ley formulada por Newton [Ej. 7].
El enunciado es:
A cada fuerza de acción le corresponde una fuerza de reacción de igual magnitud y sentido opuesto.
110
st-editorial.com
COMPRENDES EL MOVIMIENTO DE LOS CUERPOS
A PARTIR DE LAS LEYES DE DINÁMICA DE NEWTON
La ecuación que representa esta ley es la siguiente:
7. Fa/b = -Fb/a
Donde:
Fa/b = fuerza del agente a aplicada sobre el sólido b.
Fb/a = fuerza del sólido b actuando sobre el agente a.
El signo menos se emplea por convención para denotar que la fuerza es de
reacción y tiene igual magnitud pero sentido opuesto al de la fuerza actuante
en estudio.
Al estudiar la fuerza de fricción, analizamos una situación que nos conduce directamente a la tercera ley de Newton; hicimos notar que la fuerza de
fricción se presenta por el contacto directo entre dos objetos y que al analizar por separado tales objetos observamos que existe una fuerza de acción y
otra de reacción [Ej.8]. Aunque en sistemas interconectados, estas fuerzas
permiten establecer el equilibrio de todo el conjunto al anularse su efecto
por pares, las fuerzas de acción y reacción por sí mismas no se equilibran si
estudiamos los componentes de un sistema complejo por separado.
Ejemplo 7
Al entrar una persona en un elevador encuentra una báscula y se sube a ella. Cuando
cierra la puerta, la tensión en el sistema de cables de elevación es de 8 200 N durante
los primeros 3 s de movimiento. Calculemos la lectura de la balanza en ese lapso
de tiempo y la velocidad adquirida por el elevador considerando que la masa de la
persona es de 75 kg y sumada a la del elevador y la báscula da un total de 700 kg.
Solución
a. ¿Con qué datos contamos?
•฀Masa฀de฀la฀persona:฀mo = 75 kg.
•฀Masa฀total:฀m = 700 kg.
•฀Tensión฀en฀el฀cable:฀T = 8 200 N.
•฀Tiempo฀en฀el฀que฀se฀evalúa฀el฀movimiento:฀t = 3 s.
•฀฀Incógnita:฀lectura฀de฀la฀balanza฀y฀velocidad฀adquirida฀por฀el฀elevador฀cuando฀
han transcurrido 3 s.
b. ¿Qué vamos a hacer?
Calculamos la aceleración del sistema, la masa que registra la báscula y la velocidad del elevador.
c. ¿Cómo lo vamos a hacer?
Aplicamos la segunda ley de Newton al sistema y después a la persona para
determinar la masa del registro; al final, empleamos la ecuación para el movimiento sobre el eje vertical.
d. Operaciones.
•฀Análisis฀grái฀co฀de฀fuerzas฀para฀el฀sistema.
st-editorial.com
111
BLOQUE 3
Las fuerzas sólo actúan en la vertical (que corresponde a la
dirección del movimiento) y entonces:
+
-/Fy = may: T – mg = may,
∴ ay = (8200 - 700 × 9.81)/700 = 1.904 m/s2.
20% restante, calculemos la fuerza de frenado en cada una
de las ruedas delanteras y en cada una de las traseras, si se
conoce que el auto desacelera en forma uniforme y que su
masa es de 1 200 kg.
Solución
T
=
a. ¿Con qué datos contamos?
•฀Velocidad฀inicial:฀vo = 90 km/h = 25 m/s.
•฀Velocidad฀i฀nal:฀v = 0.
•฀Distancia฀recorrida:฀s – so = 40 m.
•฀Masa฀del฀auto:฀m = 1200 kg.
•฀Fuerza฀en฀ruedas฀delanteras:฀Fd = 80% Ff.
•฀Fuerza฀en฀ruedas฀traseras:฀Ft = 20% Ff.
•฀฀Incógnita:฀ fuerza฀ de฀ frenado฀ en฀ cada฀ una฀ de฀ las฀ cuatro฀
ruedas.
ma
mg
∑F = ma
•฀฀Análisis฀de฀fuerzas฀para฀la฀persona฀sobre฀la฀báscula:฀
+
-/Fy = may: Fb – mg = may,
∴ Fb = m (ay + g) = 75(1.904 +9.81) = 878.571 N.
mg
ma
=
Fb
∑F = ma
b. ¿Qué vamos a hacer?
Calculamos la fuerza neta de frenado en cada una de las
ruedas del auto de acuerdo al porcentaje señalado.
c. ¿Cómo lo vamos a hacer?
Calculamos en primer término la aceleración del sistema;
con este dato aplicamos la segunda ley de Newton y determinamos la fuerza de fricción.
d. Operaciones.
•฀Análisis฀del฀movimiento.
De acuerdo a los datos del enunciado, tenemos:
2
a=
Establecida ya la fuerza de reacción de la báscula sobre la
persona, y aplicando la tercera ley de Newton, tenemos que
la acción sobre la báscula es un peso igual a Fb, de tal manera que la masa que registra en ese instante es:
m = Fb /g = 878.571/9.81 = 89.56 kg
•฀Análisis฀del฀movimiento.
De acuerdo a las ecuaciones, para el movimiento uniformemente acelerado tenemos:
v = vo + at = 0 + 1.904(3) = 5.713 m/s
e. Resultado.
La báscula registra una masa de 89.56 kg que no es la
masa de la persona, porque ésta se halla en un sistema
no inercial.
La velocidad del elevador es de 5.713 m/s que corresponde, aproximadamente, a 20 km/h.
Ejemplo 8
En una prueba de frenado un auto con tracción delantera
reduce su velocidad de 90 km/h al alto total en 40 m. Considerando que las ruedas delanteras tienen una capacidad de
frenado del 80% del total y que las ruedas traseras ejercen el
112
v 2 – v0
2 ^s – s0h
=
0 – 25 2
2 ^40h
= - 7.813 m/s 2
•฀Análisis฀de฀las฀fuerzas.
Ahora aplicamos la segunda ley basándonos en el siguiente esquema, el cual sólo señala las fuerzas que
intervienen directamente en el cálculo, que en este
caso son horizontales y opuestas a la dirección del movimiento. Observemos el gráfico 4.
GRÁFICO 4
=
ma
Fx
∑Fx = ma
De acuerdo al diagrama:
+
/ Fx = ma : F = ma , ∴ F = 1200(7.813) = 9375 N
x
f
x
f
Considerando que se tienen dos ruedas al frente y dos atrás,
así como los porcentajes de repartición de frenado, se concluye que:
Fd = 0.8Ff /2 = 0.8(9375)/2 = 3750 N
Ft = 0.2Ff /2 = 0.2(9375)/2 = 937.5 N
st-editorial.com
COMPRENDES EL MOVIMIENTO DE LOS CUERPOS
A PARTIR DE LAS LEYES DE DINÁMICA DE NEWTON
e. Resultado.
La fuerza de fricción en cada una de las ruedas delanteras es de 3 750 N, y en cada una de las traseras es de 937.5 N. Observa que no incluimos en el
diagrama el peso y la normal porque estos valores
no intervienen en el movimiento horizontal pues
se equilibran en la vertical; además, el signo negativo en el cálculo cinemático nos indica que se
Actividad individual
COMPETENCIAS
GENÉRICAS
1
4 5
7
trata de una desaceleración y no lo incluimos en
la ecuación de la segunda ley de Newton porque
hemos señalado que el sentido positivo queda
establecido por la dirección de la desaceleración.
¿Podemos también determinar el coeficiente de
fricción entre las ruedas y la superficie en la que
se realiza la prueba de frenado? Claro que sí, determinamos la normal y finalizamos el cálculo.
COMPETENCIAS
DISCIPLINARES
3
7 10
DESEMPEÑOS
DEL ESTUDIANTE
a
b
I. Los siguientes problemas están relacionados con las leyes de Newton. Prepara tu calculadora y dibuja,
en la medida de lo posible, cada una de las situaciones que se te plantean para que identifiques con claridad lo que está sucediendo en cada uno de los problemas. Estudia previamente los ejemplos resueltos y
consulta las ecuaciones 6 y 7 de este tema.
1. Se coloca un bloque de 45 kg sobre una superficie horizontal y se le aplica una fuerza paralela a la superficie de 125 N. Determina la velocidad que alcanza 5 s después de aplicada la fuerza y la distancia
recorrida hasta ese instante.
2. Calcula la fuerza que debe actuar sobre un auto de 1 400 kg para que su velocidad aumente de 20 km/h
a 50 km/h en un tiempo de 3 s. Considera que la fricción es despreciable. Analiza y responde cómo se
produce tal fuerza.
3. Un embalaje con carga tiene una masa total de 250 kg. Calcula la magnitud de la fuerza con la que se
debe jalar para obtener una aceleración constante de 2.5 m/s2 si se conoce que el cable del malacate del
tractor que lo moverá forma un ángulo de 30° con la horizontal y que el coeficiente de fricción entre el
embalaje y la superficie es de 0.4.
st-editorial.com
113
BLOQUE 3
4. Un auto y su conductor tienen una masa total de 1 475 kg y frena de 80 km/h a 20 km/h en 6 s. Calcula
la fuerza de frenado que el piso ejerce sobre las cuatro ruedas del auto y el coeficiente de fricción
correspondiente.
5. Determina la aceleración con la que se pueden elevar las tarimas con costales de azúcar en un almacén
considerando que el cable del malacate ejerce una fuerza constante de 12 500 N, que cada tarima contiene 20 costales de 50 kg cada uno y que la masa de la tarima es de 125 kg. ¿Cuánto tiempo requiere
cada tarima para subir a una altura de 25 m con respecto al nivel del piso?
II. Anexa esta actividad a tu portafolio de evidencias.
114
st-editorial.com
COMPRENDES EL MOVIMIENTO DE LOS CUERPOS
A PARTIR DE LAS LEYES DE DINÁMICA DE NEWTON
Tema 2
Tema 3
Ley de la
gravitación universal
Leyes de Kepler
Reflexiona... ¿Has visto algún documental o película donde se muestre un viaje
espacial y los astronautas flotando en el interior de su nave o moviéndose en la
Luna mediante saltos? Te proponemos que investigues por qué ocurre esto y que
veas la película Apollo XIII (1995), del cineasta estadounidense Ron Howard.
¿Qué ocurriría si no existiera el campo gravitacional? ¿Qué pasaría si se cambia la intensidad de la
aceleración de la gravedad? Las interrogantes anteriores le surgieron a Newton mientras trabajaba en
la dinámica de los cuerpos a partir de las investigaciones de Galileo Galilei y otros notables estudiosos
del movimiento de los cuerpos celestes. Newton estableció que si un objeto era atraído hacia el centro
de la Tierra, entonces debía existir un comportamiento similar entre todos los objetos en el universo.
De esta manera y considerando las teorías del astrónomo polaco Nicolás Copérnico (1473-1543) y
el alemán Johannes Kepler (1571-1630), además de
sus propias observaciones acerca de la caída libre
de un objeto, enunció la siguiente ley:
Dos cuerpos de masas diferentes M y m se atraen mutuamente
con una fuerza que inversamente proporcional al cuadrado de
la distancia que las separa
st-editorial.com
Mm
8. F = G r2
Siendo:
G = constante de gravitación universal cuyo valor numérico es 6.67 × 10-11 Nm2/kg2.
M = masa del cuerpo de mayor tamaño expresado en kilogramos.
m = masa del cuerpo de menor tamaño expresado en kilogramos.
r = distancia que separa a los cuerpos en cuestión expresada en metros.
Atendiendo a la tercera ley de Newton, es indispensable tener presente que la fuerza actuante
tiene igual magnitud y sentido opuesto para
cada cuerpo [Ejs. 8, 9 y 11]. Si consideramos que
la fuerza de atracción gravitacional que ejerce la
Tierra sobre un cuerpo es su peso [Ej. 10], al sustituir éste en la ecuación anterior obtenemos:
115
BLOQUE 3
mg = G
m\m
r2
Lo cual nos conduce a la expresión:
9. g = G
El mundo que te rodea
En la vida diaria, las leyes del movimiento establecidas por Newton constituyen aún en la actualidad, el fundamento para el estudio de las causas
de los cambios en el movimiento. Los
trabajos de Newton sobre la atracción
gravitacional no se pueden reducir a la
simple observación de una manzana
cayendo de la rama de un árbol. Sus
investigaciones y resultados fueron
muy profundos, y lo llevaron a establecer, además, la teoría del movimiento
de las mareas por efecto de la acción
de la Luna, así como la teoría de los
equinoccios.
m\
r2t
Donde:
m’ = masa de la Tierra.
rt = distancia entre el cuerpo y el centro de la Tierra.
Podemos calcular un valor aproximado para la aceleración de la gravedad según
la altura con respecto al nivel del mar a la que se encuentre el cuerpo en estudio. Esta
expresión no incluye el efecto de la rotación terrestre ni considera que la Tierra no es
exactamente una esfera; es por ello que para ines prácticos, en todos los problemas
en los que se realizan mediciones sobre la supericie de la Tierra, se considera como
válido el valor 9.81 m/s2 para la aceleración del campo gravitacional.
Ejemplo 9
Dos masas puntuales de 8 kg y 12 kg respectivamente se hallan separadas por una distancia de 1 m. Determinemos la fuerza de atracción gravitacional entre ellas. ¿Se pueden
comparar con el peso?
Solución
a. ¿Con qué datos contamos?
•฀Masa฀de฀la฀mayor฀partícula:฀M = 12 kg.
•฀Masa฀de฀la฀menor฀partícula:฀m = 8 kg.
•฀Distancia฀entre฀las฀partículas:฀r = 1 m.
•฀฀Incógnita:฀ fuerza฀ de฀ atracción฀ gravitacional฀ y฀ relación฀ entre฀ fuerza฀ y฀ peso฀ de฀ las฀
partículas.
b. ¿Qué vamos a hacer?
Calculamos la fuerza de atracción y el peso de cada partícula.
c. ¿Cómo lo vamos a hacer?
Aplicamos directamente la ley de la gravitación universal y multiplicamos la masa por
la aceleración producida por el campo gravitacional.
d. Operaciones.
De acuerdo a la ecuación 8:
F = 6.67 # 10 -11 a
8 # 12
k = 6.4 # 10 -9 N
12
El peso para cada masa es:
W1 = 8(9.81) = 78.48 N
W2 = 12(9.81) = 117.72 N
Glosario
116
Gravedad. Campo de fuerza de la Tierra cuya acción se mide por el peso; en general se considera que la aceleración que produce tiene
un valor promedio de 9.81 m/s2 en la superficie terrestre.
st-editorial.com
COMPRENDES EL MOVIMIENTO DE LOS CUERPOS
A PARTIR DE LAS LEYES DE DINÁMICA DE NEWTON
e. Resultado.
La fuerza de atracción es de 6.4 x 10-9 N. Al compararla con el peso de cada masa, resulta que en ambos
casos el peso es una fuerza creada en el campo gravitacional, que es infinitamente superior en magnitud, más de 10 000 millones de veces.
Ejemplo 11
Determinemos la fuerza de atracción gravitacional
que ejerce el Sol sobre un astronauta de 80 kg que se
halla sobre la superficie lunar. ¿Cuál es la magnitud
de la fuerza que ejerce la Luna sobre esta persona?
Ejemplo 10
Determinemos el peso de una astronauta que forma parte de la tripulación de una misión espacial.
La masa de esta persona es de 90 kg y se encuentra
en una nave espacial en órbita a 250 km de la superficie de la Tierra.
Solución
a. ¿Con qué datos contamos?
•฀Masa฀de฀la฀astronauta:฀m = 90 kg.
•฀Masa฀de฀la฀Tierra:฀M = 5.976 × 1024 kg.
•฀฀Distancia฀ entre฀ las฀ partículas:฀ r = radio de la
Tierra + radio de la órbita = 6 371 000 + 250 000
= 6 621 000 m.
•฀฀Incógnita:฀fuerza฀de฀atracción฀gravitacional฀que฀
es equivalente, en este caso, al peso.
b. ¿Qué vamos a hacer?
Calcular la fuerza de atracción.
c. ¿Cómo lo vamos a hacer?
Aplicamos directamente la ley de la gravitación
universal.
d. Operaciones.
De acuerdo a la ecuación 8, para la órbita:
W = 6.67 # 10 -11 b
es menor. En este caso, de acuerdo a la ecuación 9,
toma un valor de 9.09 m/s2 en la órbita.
90 # 5.976 # 10 24
l = 818.34 N
6621000 2
e. Resultado.
El peso de la astronauta en esta órbita es de
818.34 N, alrededor de 7% menos que sobre la superficie terrestre. El resultado nos indica claramente que en la medida que el objeto se aleja del centro
de la Tierra, la aceleración del campo gravitacional
COMPETENCIAS
GENÉRICAS
a. ¿Con qué datos contamos?
•฀Masa฀del฀astronauta:฀80฀kg.
•฀Masa฀del฀Sol:฀Ms = 1.99 × 1030 kg.
•฀Masa฀de฀la฀Luna:฀M = 7.35 × 1022 kg.
•฀฀Distancia฀ entre฀ el฀ Sol฀ y฀ la฀ supericie฀ lunar:฀
rs = 1.49215 × 1011 m.
•฀฀Distancia฀ entre฀ el฀ astronauta฀ y฀ el฀ centro฀ de฀ la฀
Luna: r = 1.738 × 106 m.
•฀฀Incógnita:฀fuerza฀de฀atracción฀que฀ejerce฀el฀Sol฀
sobre el astronauta y fuerza de atracción gravitacional de la Luna sobre el astronauta.
b. ¿Qué vamos a hacer?
En ambos casos calculamos la fuerza de atracción.
c. ¿Cómo lo vamos a hacer?
Aplicamos directamente la ley de la gravitación
universal para cada uno de los casos presentados.
d. Operaciones.
•฀Fuerza฀del฀Sol฀sobre฀el฀astronauta:
F = 6.67 # 10 -11 e
4
5 7
80 # 1.99 # 10 30
61.49215 # 1011@ 2
o = 0.477 N
•฀Fuerza฀de฀la฀Luna฀sobre฀el฀astronauta:
F = 6.67 # 10 -11 e
Sobre la superficie terrestre:
W = 90(9.81) = 882.9 N
Actividad individual
Solución
80 # 7.35 # 10 22
61.738 # 100@ 2
o = 129.84 N
e. Resultado.
La fuerza del Sol sobre el astronauta es de 0.477 N,
mientras que la de la Luna sobre la misma persona
es de 129.84 N, más de 250 veces superior. Debemos tener en cuenta que la distancia es determinante para la magnitud de la fuerza ejercida.
COMPETENCIAS
DISCIPLINARES
3 10
DESEMPEÑO
DEL ESTUDIANTE
c
I. En los ejercicios de la página siguiente se presentan exclusivamente problemas de la ley de gravitación
universal. Consulta las ecuaciones 8 y 9, y realiza previamente en tu cuaderno los ejemplos resueltos hasta
aquí, para que puedas solucionar con facilidad cada uno de los ejercicios propuestos a continuación.
st-editorial.com
117
BLOQUE 3
1. Determina la distancia con respecto al centro de la Tierra y de la Luna en la que una masa puntual experimentará la misma fuerza de atracción. Asume que la masa se puede colocar justo en una línea recta imaginaria que
une el centro del planeta y su satélite.
2. Experimentalmente se ha encontrado que la fuerza de atracción gravitacional entre un cuerpo de 70 kg y
otro de masa desconocida es de 3.5 × 10-10 N. Calcula la magnitud de la masa desconocida considerando
que la distancia que separa a los cuerpos es de 29.75 m.
3. Dos masas puntuales de 4.5 kg y 6.75 kg se atraen con una fuerza de 2.025 × 10-5 kg. Calcula la distancia
que las separa.
4. Una persona de 80 kg se coloca al lado de una mujer de 58 kg de tal manera que la distancia que las
separa es de 5 cm. Determina la fuerza de atracción gravitacional entre ambas.
II. Anexa esta actividad a tu portafolio de evidencias.
118
st-editorial.com
Tema 3
Leyes de Kepler
Durante la noche sales a realizar una caminata y te sorprendes al ver el cielo
cubierto de estrellas, y al observarlas con atención te percatas de su movimiento,
pero… ¿realmente se mueven o la que se encuentra en movimiento es la Tierra?
Una estrella fugaz ilumina el cielo y parece viajar a gran velocidad, la miras y se
pierde en el horizonte después de unos segundos. ¿Cayó por la atracción de la
Tierra o más bien la catapultó hacia el espacio exterior? ¿Cómo se comportan
los cuerpos celestes?
Si miramos hacia atrás en el tiempo, encontraremos que algunos fenómenos celestes, como los
eclipses, inquietaban y atemorizaban a los seres
humanos, llevándolos a buscar explicaciones diversas y aunque algunos le atribuían las causas a
dioses o deidades, no todas eran de carácter religioso. Por ejemplo, el astrónomo, matemático y
geógrafo del siglo ii de la era cristiana, Ptolomeo,
en sus primeros escritos formuló la teoría geocéntrica, donde planteaba que la Tierra, inmóvil, era
el centro del universo y todos los planetas y las
estrellas se movían a su alrededor, que los eclipses se sucedían según determinadas normas y las
estrellas tenían un cierto brillo que les permitía
catalogarse. Pasarían más de mil años para que el
gran astrónomo Nicolás Copérnico modiicara por
st-editorial.com
completo la visión de la sociedad con su teoría heliocéntrica, en la que estableció que la Tierra giraba
sobre sí misma una vez al día y que una vez al año
daba una vuelta completa alrededor del Sol. Con
su tratado sobre el comportamiento de los cuerpos
celestes sentó las bases de la astronomía moderna
–parte de la física que fue fundada formalmente
por Johannes Kepler–, enunció las leyes que rigen
el comportamiento de los cuerpos celestes, y describió la manera en que la refracción de la luz en
la atmósfera inluye en la observación del espacio;
pero fue Newton quien desarrolló los telescopios
con espejos parabólicos que, por relexión de la luz,
permiten una mejor observación, y además, quien
complementó el trabajo de Kepler con la ley de la
gravitación universal que ya hemos estudiado.
119
BLOQUE 3
11
10
Leyes de Kepler
9
12
8
julio
1
7
enero
2
6
3
4
5
FIGURA 6
Trayectoria aproximada de la Tierra en su movimiento alrededor
del Sol.
Las leyes enunciadas por Kepler fueron tres:
Primera ley. Los planetas se mueven en órbitas elípticas siendo el
Sol uno de los focos de la elipse descrita. Se conoce también como
la ley de las órbitas.
Segunda ley. La línea recta imaginaria que une el centro del Sol con
el centro de cualquier planeta barre áreas iguales en tiempos iguales.
Si observas la igura, puedes concluir que la velocidad de traslación
de la Tierra diiere en su movimiento alrededor del Sol, ya que al ser
iguales las áreas recorridas en el mes de enero y en el mes de julio se
sigue que la Tierra se desplaza más rápido en el primer mes que en el
séptimo lo cual explica adicionalmente por qué en ciertos periodos la
luz del Sol incide por más horas en su supericie que en otros.
Tercera ley. El cuadrado del periodo orbital de los planetas es proporcional al cubo de las distancias medias al Sol. El periodo (T) de
un planeta o satélite es el tiempo que requiere para efectuar un viaje
completo en su órbita.
Vuelo espacial
Hace 70 años se soñaba con viajar en una nave tripulada al espacio
exterior, hoy en día es común escuchar de actividades en el espacio tales
como la instalación de una estación orbital experimental o la puesta en
órbita de un nuevo satélite de comunicaciones. Para que una nave tripulada viaje al espacio exterior se requieren ciertas condiciones, la parte
inicial del vuelo corresponde a un ascenso vertical en la que después del
despegue la nave acelera de tal manera que la fuerza resultante neta, de
acuerdo a las leyes de Newton, corresponde a la masa de la nave por la
aceleración que adquiere por el impulso de los motores.
Al llegar a cierta altura termina el vuelo propulsado y se inicia la
etapa de vuelo no propulsado, si la velocidad de la cápsula espacial es
la apropiada podrá orbitar alrededor de la Tierra; si no es así pueden
suceder dos cosas: si la velocidad es menor que la requerida, la cápsula sigue una trayectoria parabólica y cae a la supericie terrestre;
pero si la velocidad es mayor, la trayectoria será elíptica y entonces
escapará por completo del campo gravitacional de la Tierra.
De acuerdo a la ley de la gravitación universal de Newton, la fuerza
que ejerce la Tierra sobre un objeto de masa m es proporcional al cuadrado de la distancia que los separa, pero de acuerdo a su segunda ley
tal fuerza es proporcional a la aceleración adquirida a; de esta forma
se establece que la aceleración de un objeto hacia la Tierra es inversamente proporcional al cuadrado de la distancia desde el centro de la
Tierra. El manejo algebraico de las ecuaciones 6, 8 y 9 nos permiten
deinir entonces que la aceleración que adquiere un satélite hacia el
centro de la Tierra [Ej.12] cuando se encuentra en órbita es:
10. a = g
FIGURA 7
En todo momento se cumplen las leyes de Newton al inicio de un
vuelo espacial.
120
r2t
r2
Con r t = radio de la Tierra y r = distancia entre el objeto en órbita y el centro de la Tierra.
Al recordar que en el movimiento circular uniformemente acelerado (Bloque 2, ecuación 38) establecimos que la aceleración centrípeta o
normal es la que en una trayectoria curvilínea tiene una dirección y un
sentido dirigido al centro del radio de curvatura, entonces tenemos que:
r2
v
v2
a = v~ = v a r k = r = g 2r
r
st-editorial.com
COMPRENDES EL MOVIMIENTO DE LOS CUERPOS
A PARTIR DE LAS LEYES DE DINÁMICA DE NEWTON
Por lo que la velocidad con la que el satélite se mantiene en órbita [Ejs. 13 y 14] es:
r2
g rt
11. v =
Para casos en que la órbita se establece muy próxima a la Tierra tenemos que:
12. v =
grt
Si para que un satélite escape al campo gravitacional de la Tierra se requiere que su velocidad sea
mayor a un 40% de la requerida para ponerlo en órbita, tenemos entonces que la velocidad de escape
se puede evaluar con:
13. ve = 2grt
Ejemplo 12
Un cohete se lanza verticalmente y el astronauta
que va en la cápsula orbital experimenta un peso
aparente 6 veces mayor a su peso normal. Determinemos la aceleración de la nave y el empuje del
sistema propulsor, considerando que la masa de
la nave es de 25 000 kg y que el astronauta tiene
una masa de 80 kg. ¿Cuánto cambia la aceleración
cuando la cápsula se encuentra en órbita a una altura de 1 200 km de la superficie terrestre?
Solución
a. ¿Con qué datos contamos?
•฀Masa฀del฀astronauta:฀80฀kg.
•฀Masa฀del฀cohete:฀25฀000฀kg.
•฀฀Peso฀aparente฀del฀astronauta:฀6฀veces฀mayor฀a฀
su peso.
•฀฀Altura฀ de฀ la฀ órbita:฀ 1200฀ km฀ por฀ encima฀ de฀ la฀
superficie terrestre.
•฀฀Incógnita:฀ Aceleración฀ y฀ empuje฀ del฀ cohete฀ en฀
el movimiento vertical así como la diferencia de
aceleración cuando la cápsula ya se encuentra a
1200 km de la superficie.
b. ¿Qué vamos a hacer?
En primer lugar, calcular la aceleración con la que
se lanza la nave y la fuerza de empuje de los motores para después determinar la aceleración a
la cual se sujeta la nave cuando se encuentra en
órbita a 1 200 km de la superficie terrestre.
c. ¿Cómo lo vamos a hacer?
Aplicamos la segunda ley de Newton, pues tenemos
que el peso aparente del astronauta corresponde al
peso propio más la fuerza inercial que se ejerce.
d. Operaciones.
wap = mg + ma
Pero: wap = 6mg
st-editorial.com
Entonces: 6mg = mg + ma ∴ a = 5 g = 49.05 m/s2
El empuje es simplemente: F = 5mtg = 1230174 N
Mientras que al alcanzar los 1 200 km, la aceleración es:
a = 9.81
6371000 2
= 6.95 m/s 2
7571000 2
e. Resultado.
La aceleración que adquiere la nave es alta,
cinco veces la del campo gravitacional. pues requiere vencer no sólo su propio peso, también
debe pasar de un estado de reposo a uno de movimiento continuo en donde debe impulsar una
gran masa y cuando la nave se encuentra a una
altura considerable, el efecto del campo gravitacional se ha reducido al grado de que la aceleración que experimenta la nave a los 1 200 km es
de aproximadamente el 60% del valor la aceleración de la gravedad.
Ejemplo 13
Una nave se encuentra en una órbita circular
alrededor de la Tierra a una altura de 321 km, y
se activan los propulsores para incrementar en
forma instantánea su velocidad y permitir que
escape al campo gravitacional, determinemos
el incremento de velocidad requerido para tal
maniobra.
Solución
a. ¿Con qué datos contamos?
•฀฀Altura฀de฀la฀órbita:฀321฀km฀por฀encima฀de฀la฀superficie terrestre.
•฀Radio฀de฀la฀Tierra:฀6฀371฀km.
•฀฀Incógnita:฀Incremento฀de฀velocidad฀para฀que฀la฀
nave salga del campo gravitacional.
121
BLOQUE 3
b. ¿Qué vamos a hacer?
Calcular el incremento de la velocidad para que
la nave salga del campo gravitacional.
c. ¿Cómo lo vamos a hacer?
En primer término, procedemos a determinar
la velocidad con la que se traslada la nave en
su órbita de 321 km, (ecuación 11) para después
hallar la velocidad de escape (ecuación 13) y
calcular con ambos resultados, el incremento
correspondiente.
d. Operaciones.
La velocidad de la nave a 321 km de altura es:
v=
9.81 #
6371000 2
= 7713.7 m/s = 7.71 km/s
6692000 2
Ejemplo 14
Determinemos la velocidad con la que se debe lanzar
una sonda meteorológica de 50 kg para que se mantenga en órbita a 800 km de la superficie terrestre.
Solución
a. ¿Con qué datos contamos?
•฀Masa฀de฀la฀sonda:฀50฀kg.
•฀Radio฀de฀la฀Tierra,฀rt = 6 371 000 m.
•฀฀Radio฀ de฀ la฀ órbita,฀ r = 6 371 000 + 800 000 =
7 171 000 m.
•฀Incógnita:฀Velocidad฀de฀la฀sonda฀en฀órbita.
b. ¿Qué vamos a hacer?
Calcular la velocidad de lanzamiento de una sonda meteorológica para que se mantenga en una
órbita de 800 km sobre la superficie terrestre.
Y la velocidad de escape es:
ve =
2 # 9.81 # 6371000 = 11180.3 m/s = 11.18 km/s
e. Resultado.
De donde tenemos que el incremento debe
ser de 3.47 km/s. La nave debe incrementar su
velocidad en un 45% o más para alcanzar la velocidad requerida para que salga del campo
gravitacional. Es importante tener presente que
el impulso proporcionado debe estar ligado a la
trayectoria para que efectivamente sea lanzada
al espacio y no se produzca su retorno a la superficie terrestre.
Actividad individual
COMPETENCIAS
GENÉRICAS
1
4 5
c. ¿Cómo lo vamos a hacer?
A partir de la sustitución directa de los datos en
la ecuación 11.
d. Operaciones.
v=
9.81 #
6371000 2
= 7451.65 m/s
7171000 2
e. Resultado.
La velocidad requerida es de 7.5 km/s, valor que
corresponde a un 66% de la velocidad de escape,
la cual asciende a 11.18 km/s.
COMPETENCIAS
DISCIPLINARES
3 10
DESEMPEÑO
DEL ESTUDIANTE
d
En estos ejercicios se presentan exclusivamente problemas relacionados con el movimiento orbital de cuerpos. Consulta las ecuaciones 10 –13, y realiza previamente los ejemplos resueltos hasta aquí, para que puedas solucionar con facilidad cada uno de los ejercicios propuestos a continuación. Trabaja en tu cuaderno.
1. Calcula la velocidad con la que debe viajar un transbordador espacial para liberar un sistema telescópico en una órbita circular a 590 km de la superficie terrestre.
2. Determina la velocidad de un satélite que sigue una órbita circular a 80 km de la superficie de Mercurio.
3. Un satélite de telecomunicaciones se encuentra en una órbita circular a una distancia equivalente a la
mitad del radio de la Tierra, los expertos han establecido que operará con menor perturbación en una
órbita equivalente a 2.5 veces el radio de la Tierra ¿Cuánto se debe incrementar su velocidad?
4. Determina la velocidad de un satélite que se encuentra en órbita a 1 800 km de la superficie terrestre y
su periodo de revolución en minutos.
122
st-editorial.com
COMPRENDES EL MOVIMIENTO DE LOS CUERPOS
A PARTIR DE LAS LEYES DE DINÁMICA DE NEWTON
Lee
Los
sesenta…
Entre
la Luna y la Tierra
El 21 de julio de 1969 se concretó el viaje
del ser humano a la Luna como parte
de un programa de desarrollo espacial
con el que se pretendía que Estados
Unidos se pusiera a la vanguardia con
respecto a la ex Unión Soviética, que ya
había logrado en 1957 poner en órbita el
satélite Sputnik. A más de 50 años del
evento encontramos una gran cantidad
de documentales, reportes y crónicas,
que en algunos casos dejan un tanto lo
científico de lado y afirman que nunca
se logró el descenso en la Luna, sino
que se necesitaba de un gran despliegue mediático para recrear la idea de
una nación poderosa, líder del mundo
occidental y con un modelo económico
superior al de cualquier otra nación con
diferente orientación política.
Actualmente, existe un programa
internacional por medio del cual desde
el año 2000 hay una estación espacial
en una órbita de aproximadamente
300 km de la superficie terrestre, con
una tripulación permanente que realiza
diversos experimentos. Aunque se han
colocado con éxito sondas espaciales
en Marte (de 38 lanzamientos sólo 6
han logrado el aterrizaje), no ha sido
posible desarrollar la tecnología necesaria para que un humano coloque su
huella en suelo marciano.
Se afirma que la NASA estará lista
en las dos próximas décadas para
que una nave tripulada pueda recabar
información y realizar experimentos
en la superficie del llamado planeta
rojo, sin embargo, algunos escépticos
consideran que solamente se realizará
otra gran campaña mediática, pues el
costo es excesivo tanto en materiales
como en los sistemas telemáticos a
desarrollar.
Se estima que hacia mediados del 2014,
la sensación de ingravidez estará al
alcance de las primeras 200 personas
que hayan pagado alrededor de 152 000
euros. Una empresa pondrá en vuelo
suborbital un avión con seis pasajeros a
bordo, en un viaje que durará alrededor
de 90 minutos y se realizará a una velocidad de 1 470 km/h y 110 kilómetros de
altura, menos de los 400 a los que orbita
la estación espacial internacional y una
mínima altura si se compara con los
360 00 kilómetros que alcanzan algunos
satélites.
Fuente: Jorge Díaz. Con datos de:
Avion Revue Internacional, no. 120. Febrero de 2010.
http://bit.ly/16e4hSg
http://bit.ly/7hA9uC
http://1.usa.gov/1YXivJ
http://bit.ly/tU7DLm
http://mun.do/gCAyqa
http://mun.do/10OWUCK
I. Reunidos en parejas, investigen en la biblioteca, la hemeroteca e Internet:
1. ¿Qué factores políticos y económicos prevalecían en la etapa de la llamada “carrera espacial”?
2. ¿Por qué no se incluye a los países en desarrollo en los programas espaciales?
3. ¿Qué piensas sobre los viajes a la Luna?, ¿son un mito o una realidad?
4. Julio Verne imaginaba que era sencillo colocar una nave en órbita, ¿consideras que es factible la vida
del ser humano en una atmósfera distinta a la terrestre?
II. Elaboren un reporte y presenten al grupo sus conclusiones.
st-editorial.com
123
BLOQUE 3
Evaluación sumativa
Heteroevaluación
I. Pide a tu profesor que aplique la siguiente rúbrica con el fin de que pueda registrar tus avances. Como
verás es la misma que respondiste en el reto; ahora servirá para medir cuál fue tu desempeño durante el
estudio de este bloque.
Indicadores de desempeño
Aspectos a evaluar
4 puntos
3 puntos
2 puntos
1 punto
Mi puntaje
Fuerzas que
intervienen en
el movimiento
de los cuerpos
en los diferentes
tipos de
movimiento.
Identifiqué plenamente
en los diferentes
tipos de movimiento
las fuerzas que
intervienen en el
movimiento
de los cuerpos.
Identifiqué en los
diferentes tipos de
movimiento algunas
de las fuerzas que
intervienen en el
movimiento de los
cuerpos.
Identifiqué vagamente
en los diferentes
tipos de movimiento
las fuerzas que
intervienen en
el movimiento
de los cuerpos.
No identifiqué
en los diferentes
tipos de movimiento
las fuerzas que
intervienen en
el movimiento
de los cuerpos.
Leyes de la
dinámica de Newton
en la solución
y explicación del
movimiento de los
cuerpos observables
en el entorno
inmediato.
Siempre apliqué las
leyes de la dinámica
de Newton en la
solución y explicación
del movimiento
de los cuerpos
observables en mi
entorno inmediato.
En ocasiones apliqué
las leyes de la dinámica
de Newton en la
solución y explicación
del movimiento
de los cuerpos
observables en mi
entorno inmediato.
Rara vez apliqué las
leyes de la dinámica
de Newton en la
solución y explicación
del movimiento
de los cuerpos
observables en mi
entorno inmediato.
Nunca apliqué las
leyes de la dinámica
de Newton en la
solución y explicación
del movimiento de los
cuerpos observables
en mi entorno
inmediato.
Ley de la gravitación
universal para
entender el
comportamiento
de los cuerpos bajo
la acción de fuerzas
gravitatorias.
Siempre utilicé la
ley de la gravitación
universal para
entender el
comportamiento
de los cuerpos bajo
la acción de fuerzas
gravitatorias.
En ocasiones utilicé la
ley de la gravitación
universal para entender
el comportamiento
de los cuerpos bajo
la acción de fuerzas
gravitatorias.
Rara vez utilicé la
ley de la gravitación
universal para
entender el
comportamiento de
los cuerpos bajo la
acción de fuerzas
gravitatorias.
Nunca utilicé la ley
de la gravitación
universal para
entender el
comportamiento
de los cuerpos bajo
la acción de fuerzas
gravitatorias.
Movimiento de
los planetas en
el Sistema Solar
utilizando las leyes
de Kepler.
Siempre expliqué
el movimiento
de los planetas
en el Sistema Solar
utilizando las leyes
de Kepler.
En ocasiones expliqué
el movimiento
de los planetas
en el Sistema Solar
utilizando las leyes
de Kepler.
Rara vez expliqué
el movimiento
de los planetas
en el Sistema Solar
utilizando las leyes
de Kepler.
Nunca expliqué
el movimiento
de los planetas
en el Sistema Solar
utilizando las leyes
de Kepler.
Valoración
Excelente: 15 a 16 puntos.
Bueno: 11 a 14 puntos.
Suficiente: 7 a 10 puntos.
Mi total
Insuficiente: 4 a 6 puntos.
II. Ha llegado el momento de que entregues a tu profesor todos los productos de las actividades que realizaste durante este bloque y que guardaste en tu portafolio de evidencias, ya que con esto podrá evaluarte.
Autoevaluación
I. Relaciona las columnas; posteriormente, regresa al bloque para verificar que tus respuestas sean correctas y modifica aquellas que no lo sean.
1. (
2. (
3. (
4. (
5. (
124
) Al agente capaz de modificar el estado de reposo de
un cuerpo se le llama…
) En el momento en que frena un auto reduce su velocidad por la acción de…
) Cuando un martillo golpea un clavo se presentan
fuerzas iguales y opuestas…
) El campo gravitacional nos permite caminar sin lotar debido a que origina el…
) La tercera ley de Kepler se puede expresar como…
a. peso.
b. x µ a/e.
c. de acuerdo a la ley de gravitación
universal.
d. fuerza.
e. inercia.
f. la fuerza de fricción dinámica.
g. T2 µ R3
h. de acuerdo a la 3ª ley de Newton.
i. la fuerza de fricción estática.
st-editorial.com
COMPRENDES EL MOVIMIENTO DE LOS CUERPOS
A PARTIR DE LAS LEYES DE DINÁMICA DE NEWTON
II. Realiza en tu cuaderno lo que se te pide.
1. Lee el siguiente texto:
Los organizadores de Vancouver 2010 estaban preocupados por la escasez de nieve, la economía y el
dopaje, pero antes de empezar les llegó lo peor. Los Juegos Olímpicos de Invierno ya estarían marcados por la tragedia. El georgiano Nodar Kumaritashvili se mató al salirse de la pista de luge durante los
entrenamientos. Perdió el control del trineo en el que los deportistas van tumbados boca arriba, en una
posición un tanto forzada, y se estrelló contra uno de los postes metálicos no protegidos del circuito de
Whistler, considerado el más rápido del mundo. En esos momentos iba a una velocidad cercana a los 145
kilómetros por hora…
Fuente: http://bit.ly/1bRWqLl
2. En el luge, la pista de hielo para el descenso tiene secciones rectas y secciones curvas. A partir de los
datos anteriores, responde:
a. ¿Qué tipos de movimiento provoca la fuerza de impulso que produce el piloto con sus manos?
b. ¿Cuáles son las fuerzas que se generan durante el descenso en cada tipo de sección?
c. ¿Por qué cambian las fuerzas del trineo en cada curva?
d. ¿Cómo afecta el campo gravitacional?
e. ¿Consideras factible que las zonas con nieve presenten susceptibilidad a la atracción lunar tal como
ocurre con las mareas por el movimiento planetario?, ¿por qué?
3. Nuestro planeta se encuentra en un viaje continuo por el espacio, presenta ciertos movimientos que
nos pasan desapercibidos pero que definitivamente inluyen en nuestro día a día y en la disponibilidad
de nuestros recursos; atendiendo a la trayectoria es como podemos sentir la necesidad de abrigo, de
refrescarnos o bien se puede dar el caso de que por una sequía un alimento sea escaso y su precio se
eleve o que ocurra exactamente lo contrario. A partir de esto, responde:
a. ¿Qué trayectoria sigue la Tierra?
b. ¿Cuáles son los movimientos que se presentan?
c. ¿Qué fuerzas lo producen?
d. ¿Qué leyes se cumplen?
4. Determina el coeficiente de fricción entre una superficie de concreto y una caja de madera cuya masa
total, incluyendo su contenido, es de 75 kg. Sobre la caja actúa una fuerza neta de 320 N, paralela a la
superficie, produciendo un movimiento a velocidad constante.
5. Un contenedor de madera de 2 500 N se coloca sobre un ascensor que lo lleva de la planta baja de un
almacén a un tercer piso con una aceleración de 0.5 m/s2. Calcula la fuerza de reacción del piso del
ascensor sobre el contenedor cuando sube. ¿Qué sucede si en vez de subir el ascensor baja?
6. Calcula la distancia requerida para que un objeto de 80 kg sea atraído por otro de 45 kg con una fuerza
de 0.1 N.
7. Determina la velocidad que requiere un satélite artificial para mantener un vuelo orbital bajo una trayectoria circular a una altura sobre la superficie terrestre del 10% del radio de la Tierra.
III. Reflexiona y responde, en tu cuaderno, a cada una de las preguntas:
1. ¿Para qué disciplinas consideras fundamental el estudio de la ley de la gravitación y las leyes de Kepler?
2. ¿Se te dificulta el estudio del movimiento de un cuerpo provocado por fuerzas diversas?
3. ¿En qué situaciones de tu vida a futuro como profesionista crees que emplearás los conocimientos que
has adquirido?
IV. Contesta la siguiente lista de cotejo para que reconozcas cuáles fueron tus actitudes durante este bloque.
Aspecto
Siempre
Algunas veces
Nunca
Me integré al trabajo en equipo.
Realicé comentarios acertados de acuerdo con el tema.
Mostré una actitud de respeto y compañerismo.
Participé en cada actividad.
st-editorial.com
125
Desempeños del estudiante
Bloque 4
Relacionas el trabajo
con la energía
a. Define el concepto de trabajo en física, realizado por
o sobre un cuerpo como un cambio en la posición o la
deformación del mismo por efecto de una fuerza.
b. Relaciona los cambios de la energía cinética y potencial
que posee un cuerpo con el trabajo en física.
c. Utiliza la ley de la conservación de la energía mecánica
en la explicación de fenómenos naturales de su entorno
social, ambiental y cultural.
d. Aplica en situaciones de la vida cotidiana, el concepto de
potencia como la rapidez con la que se consume energía.
Estos desempeños pueden identificarse en cada una de las actividades
del bloque, de la siguiente manera:
DESEMPEÑOS DEL
a b c d
ESTUDIANTE
Bloque 1
Bloque 2
Bloque 3
Reconoces el
lenguaje técnico
básico de la física
Identificas
diferencias entre
distintos tipos
de movimiento
Comprendes el movimiento
de los cuerpos a partir de
las leyes de dinámica
de Newton
Objetos de aprendizaje
•฀ Trabajo
•฀ Energía cinética y energía potencial
•฀ Ley de la conservación de la energía mecánica
•฀ Potencia
Bloque 4
Relacionas el trabajo
con la energía
Introducción
En el bloque anterior estudiamos la relación
entre fuerza, masa y aceleración de un sistema
cualquiera, así como sus implicaciones en cuanto
al comportamiento general de un cuerpo. Ahora
nos corresponde analizar otros aspectos de la
física que también son comunes en nuestra
vida diaria, y que completan el estudio de la
dinámica de un cuerpo, como son el trabajo,
la energía mecánica y la potencia, los cuales se
interrelacionan con los mencionados al inicio y
hacen factible el desarrollo de un sinnúmero de
equipos y sistemas que en un futuro no lejano nos
brindarán mayores comodidades. Estos temas se
resumen en el siguiente mapa conceptual.
Dinámica
de un cuerpo
se estudia por
trabajo
energía
potencia
se define como
se define como
se define como
un producto
escalar de
vectores
el agente
que permite
producir trabajo
el trabajo
realizado por un
sistema en el
tiempo
se manifiesta como
se manifiesta como
se manifiesta como
fuerza necesaria
para desplazar
un cuerpo
energía cinética
y energía
potencial
consumo
de energía
mecánica o
eléctrica
el cambio de energía sin
realizar trabajo es el
principio de
conservación de
la energía
128
st-editorial.com
Para comenzar...
Para que puedas comprender los temas de este bloque, es necesario
que rescates las competencias (conocimientos, habilidades, actitudes y valores) que ya has
adquirido a lo largo de tu vida. Haz tu mejor esfuerzo para responder y detecta aquellos
aspectos que no conoces o dominas para enfocar tu estudio.
I. Selecciona la respuesta correcta.
1.(
) ¿Qué es el trabajo?
a. Es la parte de la física que estudia lo relacionado con la acción de una fuerza
sobre un cuerpo y el desplazamiento que sufre.
b. Es toda actividad por la que se percibe un salario.
c. Es una medida de la energía que disipa un cuerpo.
d. Es una cantidad escalar que relaciona el desplazamiento de un cuerpo con la
fuerza que produce tal desplazamiento.
2.(
) ¿Qué diferencia existe entre trabajo y energía?
a. Ninguna porque se refieren al mismo fenómeno.
b. El primero mide el desplazamiento de un cuerpo producido por una fuerza y la
segunda, el cambio de velocidad o posición del cuerpo.
c. El primero depende de la gravedad y la segunda, de la masa del cuerpo.
d. El primero es una cantidad escalar y la segunda es un vector.
3.(
) La potencia…
a. es el medio que transforma la energía en movimiento.
b. mide el consumo de energía de una máquina.
c. mide la capacidad para realizar trabajo en la unidad de tiempo.
d. realiza un trabajo que se opone al movimiento.
4.(
) El principio de trabajo y energía…
a. señala que el trabajo realizado por las fuerzas que actúan en un cuerpo equivale al cambio de energía mecánica.
b. relaciona el efecto de las fuerzas que interactúan con cuerpos y su movimiento.
c. permite definir las propiedades elásticas de un cuerpo.
d. fue postulado por Newton.
5.(
) La conservación de la energía…
a. establece que el movimiento de un cuerpo es perpetuo a menos que intervengan fuerzas disipadoras.
b.es un principio que permite calcular la aceleración de un cuerpo.
c. establece que la energía permanece inalterable cambiando de cinética a potencial y viceversa.
d. es un principio que permite definir la cantidad de energía de un sistema.
II. Resuelve los siguientes problemas.
1. Una caja de madera con su contenido totalizan una masa de 75 kg y se coloca sobre
una superficie horizontal. Para moverla se le aplica horizontalmente una fuerza de
75 N. ¿Cuál es la magnitud del trabajo realizado?
st-editorial.com
129
BLOQUE 4
2. ¿Cuál es la energía potencial de una persona de 70 kg de masa que salta entre las rocas de un acantilado desde una altura de 2 m para llegar a la parte alta de un risco de 3.5 m de altura?
3. ¿En qué cantidad cambia la energía cinética de un auto cuando modifica su velocidad de 30 km/h
a 50 km/h?
4. ¿Cuál es el trabajo realizado por un camión de volteo de 5 000 kg de masa cuando reduce su velocidad de 60 km/h a 30 km/h?
5. Calcula la potencia requerida para desplazar un vehículo de 1 200 kg de masa a una velocidad de
60 km/h en el entendido de que el motor proporciona a las ruedas una fuerza de tracción de 3 000 N.
III. Lee el siguiente texto y responde en tu cuaderno las preguntas que se plantean posteriormente.
A inicios del siglo pasado la industria
del automóvil inició un proceso de evolución y desarrollo, la idea inicial era
crear un dispositivo que trasladara con
seguridad personas y mercancías. La
competencia por dominar el naciente
mercado fue dura y al final los sistemas
térmicos se impusieron a los eléctricos,
que no podían ser empleados para
trasladar pesos muy grandes, ya que
los requerimientos de potencia y par (o
torque) fueron perfeccionados en forma
rápida en los motores de combustión
interna que funcionan con gasolina y
diesel –combustibles abundantes y
económicos en ese tiempo–, logrando
cubrir un amplio rango de necesidades.
En sus inicios, los motores consumían
demasiado combustible y emitían una
gran cantidad de agentes contaminantes; aunque hoy en día el consumo de
energéticos es menor, la emisión de
contaminantes no lo es del todo y en
algunas partes del mundo existe una
cierta tendencia a emplear sistemas
eléctricos e híbridos, situaciones que
a simple vista, más que una solución
a los problemas energéticos y climáticos, más bien parecen una estrategia
comercial, pues las grandes empresas
no han descontinuado la fabricación de
motores de alta potencia (500 o más
hp) y gran consumo de combustibles de
origen fósil, con la consiguiente contaminación atmosférica.
1. ¿Son adecuadas las medidas que se han tomado en tu ciudad para reducir el uso de automóviles de
gran potencia, elevado consumo de combustible y alto nivel de emisión de contaminantes?
2. ¿Cómo justifican las empresas del área automotriz el desarrollo de tecnologías que no son amigables
con el medio ambiente y el uso racional de combustibles?
130
st-editorial.com
Reto (problema)
Todos trabajamos, lo hacemos de muy diversas maneras y por muchas razones diferentes. ¿Has observado cómo funciona la licuadora en la cocina? ¿Realiza trabajo? ¿Qué elementos intervienen cuando
tú efectúas un trabajo y cuáles cuando lo hace la licuadora? ¿Hay algo en común entre personas y
máquinas cuando realizan trabajo? Con base en esta relexión, hagamos un análisis grupal. Reúnete
con tres compañeros y comenten acerca de los siguientes aspectos, anotando en su cuaderno las conclusiones a cada punto:
1. Del concepto general de trabajo en la física y su importancia en la dinámica:
a. ¿Es suficiente con que un cuerpo se mueva para que realice trabajo?
b. ¿De qué manera un cuerpo en movimiento puede realizar trabajo sobre otro que se encuentra en
reposo?
c. ¿El trabajo es una manifestación de la energía de un cuerpo?
d. ¿Qué tipo de fuerzas intervienen al efectuar trabajo?
e. ¿Hay cambios de energía asociados al trabajo?
2. De la manera en que un sistema puede aprovechar la energía y realizar trabajo:
a. ¿Que tipos de energía se emplean en la dinámica?
b. ¿Puede una transformarse en la otra?
c. ¿Por qué es común que se manifiesten como trabajo?
d. ¿Es infinita la cantidad de energía de un cuerpo?
e. ¿Qué variables intervienen para que se manifieste en diferentes formas?
3. De nuestras actividades cotidianas y el cambio de energía y trabajo:
a. ¿Cómo es un viaje en tren? ¿Qué sucede si lo realizas en un auto? ¿En cuál se requiere un mayor
consumo de energía?
b. ¿Qué variables intervienen para que se mueva con facilidad un medio de transporte de gran tamaño?
c. ¿Puede una máquina o un equipo de reducidas dimensiones efectuar el mismo trabajo que uno
de gran tamaño?
d. Si la energía se conserva, ¿puede una transformación de la misma contribuir a elevar la eficiencia
de un sistema?
e. ¿De qué manera se pueden aprovechar las pérdidas de energía en un sistema?
4. Del concepto de potencia y su inluencia en nuestras actividades diarias:
a. En una feria automovilística se exhibe un auto deportivo y un tractor agrícola, ambos con la
misma especificación de potencia. ¿cuál es la diferencia entre uno y otro?
b. ¿Puede un cuerpo en movimiento circular presentar la misma potencia que uno que se mueve en
movimiento lineal?
c. ¿Por qué una máquina no produce la potencia que se indica en su tabla de especificaciones?
d. ¿Puede un equipo producir un valor alto de potencia con un bajo consumo de energía?
e. ¿De qué manera aprovechas la potencia de los equipos y máquinas que te rodean en tu quehacer
cotidiano?
Coevaluación
En la siguiente lista de cotejo se presentan una serie de aspectos para que evalúes el desempeño de
uno de tus compañeros durante la realización del reto.
Aspecto
Siempre
Algunas veces
Nunca
Participó activamente en cada una de las actividades.
Expresó su opinión bajo consideraciones teóricas.
Su participación fue incluyente y ordenada.
Respetó las ideas de los compañeros y buscó un consenso.
Trabajó con limpieza y orden.
st-editorial.com
131
Autoevaluación
Con esta rúbrica evalúa tu desempeño en el reto.
Indicadores de desempeño
Aspectos a evaluar
4 puntos
3 puntos
2 puntos
1 punto
Concepto de trabajo
en física, realizado
por o sobre un cuerpo
como un cambio
en la posición o la
deformación del
mismo por efecto
de una fuerza.
Definí plenamente el
concepto de trabajo
en física, realizado
por o sobre un cuerpo
como un cambio en
la posición o la
deformación del
mismo por efecto
de una fuerza.
Definí bien el
concepto de
trabajo en física,
realizado por o
sobre un cuerpo
como un cambio
en la posición o la
deformación del
mismo por efecto
de una fuerza.
Definí vagamente el
concepto de trabajo
en física, realizado
por o sobre un
cuerpo como un
cambio en
la posición o la
deformación del
mismo por efecto
de una fuerza.
No definí el
concepto de
trabajo en física,
realizado por o
sobre un cuerpo
como un cambio
en la posición o la
deformación del
mismo por efecto
de una fuerza.
Cambios de la energía
cinética y potencial
que posee un cuerpo
con el trabajo
en física.
Relacioné plenamente
los cambios de la
energía cinética y
potencial que posee
un cuerpo con el
trabajo
en física.
Relacioné bien
los cambios de la
energía cinética y
potencial que posee
un cuerpo con el
trabajo
en física.
Relacioné vagamente
los cambios de la
energía cinética y
potencial que posee
un cuerpo con el
trabajo en física.
No relacioné los
cambios de la
energía cinética
y potencial que
posee un cuerpo
con el trabajo
en física.
Ley de la
conservación de la
energía mecánica
en la explicación de
fenómenos naturales
del entorno social,
ambiental y cultural.
Utilicé plenamente
la ley de la
conservación de la
energía mecánica
en la explicación de
fenómenos naturales
de mi entorno social,
ambiental y cultural.
Utilicé bien la ley
de la conservación
de la energía
mecánica en
la explicación
de fenómenos
naturales de mi
entorno social,
ambiental y
cultural.
Utilicé vagamente
la ley de la
conservación de la
energía mecánica
en la explicación de
fenómenos naturales
de mi entorno social,
ambiental y cultural.
No utilicé la ley
de la conservación
de la energía
mecánica en
la explicación
de fenómenos
naturales de mi
entorno social,
ambiental y
cultural.
Concepto de
potencia como la
rapidez con la que se
consume energía en
situaciones de la
vida cotidiana.
Siempre apliqué en
situaciones de la vida
cotidiana, el concepto
de potencia como la
rapidez con la que se
consume energía.
En ocasiones
apliqué en
situaciones de la
vida cotidiana,
el concepto de
potencia como
la rapidez con la
que se consume
energía.
Casi nunca apliqué en
situaciones de la vida
cotidiana, el concepto
de potencia como la
rapidez con la que se
consume energía.
Nunca apliqué en
situaciones de la
vida cotidiana,
el concepto de
potencia como
la rapidez con la
que se consume
energía.
Valoración
Excelente: 15 a 16 puntos.
puntos.
132
Bueno: 11 a 14 puntos.
Suficiente: 7 a 10 puntos.
Mi puntaje
Mi total
Insuficiente: 4 a 6
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
Tema 1
Tema 2
Tema 3
Tema 4
Trabajo
Energía cinética y
energía potencial
Ley de la conservación
de la energía mecánica
Potencia
Relexiona… ¿Cómo funciona un elevador?, ¿qué sistemas se ocupan para elevar
las redes en un barco pesquero?, ¿por qué se mantiene en vuelo un avión? En todas
estas actividades se realiza trabajo, ya sea por medio de dispositivos o por
medio de la mano de los humanos; ¿qué sucedería a nuestro alrededor si no fuera
posible que se realizara trabajo?
¿Qué ocurre cuando te piden en casa que muevas el
refrigerador porque hay debajo un objeto pequeño?
Primero aplicarás una fuerza que se traduce en un
movimiento con aceleración constante, después vencerás la fuerza de fricción y lo desplazarás una cierta
distancia, y por último, una vez que hayas localizado
y recuperado el objeto, regresarás el refrigerador a su
sitio original. ¡Es mucho trabajo!, ¿no crees?
En física, el término trabajo tiene una connotación muy diferente a la que usamos en nuestra
vida diaria, donde es común emplearlo en forma
indistinta, ya que además de asociar el término a
toda actividad que brinda un beneicio económico,
st-editorial.com
también nos referimos al esfuerzo físico o mental que nos conduce a alcanzar una meta, como
puede ser un primer lugar en atletismo, en matemáticas, etc.
Veamos el caso siguiente: una joven pasea por
el parque en bicicleta, ¿qué fuerzas se presentan
en tal sistema? Si hacemos un recuento de las
fuerzas actuantes podemos observar que se tiene
el peso de la joven y las fuerzas de reacción del
piso sobre la bicicleta, es decir, las fuerzas normales, ¿se realiza trabajo?, claro que sí, ¿cómo?, ¿por
qué? Veamos el gráico 1 de la página siguiente la
acción de las fuerzas que hemos señalado.
133
BLOQUE 4
GRÁFICO 1
Peso
FIGURA 1
El trabajo realizado sobre la pelota es justo lo que nos permite
observar cómo se desplaza siguiendo una trayectoria paralela
a la superficie.
Normal
Normal
Tanto el peso, como las fuerzas normales, no intervienen en el
movimiento, anulan su efecto por la tercera ley de Newton y esto
permite el movimiento sobre la supericie venciendo la fuerza de
fricción que actúa entre las llantas y la calzada; la acción sobre los
pedales por parte de la joven se traduce en movimiento, la fuerza
alterna que se aplica mueve la cadena y ésta a su vez impulsa a la
rueda motriz trasera y provee el impulso necesario, es decir, la fuerza que se ejerce en los pedales produce el trabajo requerido para el
movimiento, y esta fuerza es variable en magnitud y dirección, y su
resultante es la que obliga al objeto a desplazarse una cierta distancia en forma paralela a la supericie.
Imagina ahora a un grupo de niños que juegan al fútbol, cuando
uno de ellos golpea la pelota y la hace rodar observamos que la fuerza aplicada es constante y paralela a la supericie.
En el campo de la mecánica se designa como trabajo (W) la capacidad que tiene un cuerpo para moverse una cierta distancia, en
el instante en que se le aplica una fuerza paralela a la trayectoria del
movimiento generado.
Hay dos cosas importantes a considerar, los agentes –fuerza y
desplazamiento– que intervienen son vectores:
• La fuerza es un vector que se caracteriza por tener magnitud,
dirección y sentido.
• El desplazamiento es también un vector cuya magnitud corresponde a la distancia y su dirección queda deinida precisamente
por la de la fuerza actuante.
En matemáticas se deinen dos tipos de producto entre vectores:
Producto “cruz”. Al multiplicarse dos vectores el resultado es un vec-
tor cuya dirección es perpendicular al plano que deinen los primeros
vectores.
Producto “punto” o producto escalar. Al multiplicar dos vectores se
obtiene como resultado una cantidad escalar, siendo una condición
propia de este producto el que se multiplican sólo las cantidades
en magnitud bajo una proyección ortogonal que corresponde a una
dirección especiica. El trabajo (W) es una cantidad escalar que resulta de realizar el producto escalar del vector fuerza con el vector
desplazamiento.
134
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
Actividad grupal
COMPETENCIAS
GENÉRICAS
4 6 8
COMPETENCIAS
DISCIPLINARES
3 4 6 8
DESEMPEÑO
DEL ESTUDIANTE
a
Para cada una de las ilustraciones que se muestran mencionen:
1. ¿Cuáles son las fuerzas actuantes?
2. ¿Cuál es la fuerza resultante o neta que produce trabajo?
3. Señala el desplazamiento.
a. Máquina revolvedora de concreto.
b. Portaaviones en ejercicios de práctica.
c. Batidora industrial en la preparación de pan.
d. Ferrocarril en un viaje cualquiera.
e. Equipo para cimentaciones.
st-editorial.com
135
BLOQUE 4
La expresión matemática y
unidades de medición del trabajo
Pensemos ahora en una situación muy importante, el trabajo no posee dirección, pero ¿le podemos
asignar un sentido? Estrictamente hablando, no, pero
sí podemos hablar de un trabajo positivo o negativo;
pensemos, por ejemplo, en una piedra que cae verticalmente, la fuerza que actúa sobre ella es su peso y
se dirige al centro de la Tierra, así pues el sentido del
movimiento corresponde directamente al de la fuerza aplicada, sin embargo, en condiciones normales
actúan fuerzas de fricción sobre la piedra que impiden el movimiento y retardan en cierta forma
la caída, estas fuerzas se oponen al movimiento y
también realizan un trabajo que es imperceptible a
nuestra vista. Siempre se considera que el trabajo es
positivo cuando la fuerza aplicada actúa en el mismo
sentido del movimiento que produce [Ejs. 2 y 3];
si por el contrario, la fuerza actuante es opuesta al
movimiento que sigue el cuerpo y no es lo suicientemente grande en magnitud para impedir el desplazamiento en forma instantánea, se considera que el
trabajo realizado es negativo.
Otro punto a considerar es que la fuerza resultante no necesariamente es constante en magnitud
aunque sí en dirección, tal es el caso de los sistemas empleados en el proceso de estampado de
lámina, donde la prensa inicia la transformación
con una fuerza que se incrementa, se mantiene
constante y luego se reduce, para estas situaciones
el cálculo del trabajo se puede realizar mediante
integración numérica o bien a través del análisis
del graico fuerza-desplazamiento que proporciona una aproximación aceptable.
El gráico 2 nos muestra la variación de fuerza con
el desplazamiento que sufre un objeto, el trabajo total corresponde al área bajo la curva, que para efectos
prácticos se puede descomponer en áreas geométricas sencillas cuya suma nos dará el total [Ej. 4].
En general se puede hacer una descomposición en cualquier cantidad de “áreas”; sin embargo, es recomendable considerar el menor
número posible para simpliicar el cálculo, en el
Pasemos ahora al análisis del modelo que nos permite establecer la ecuación general del trabajo, observa
el esquema de la página siguiente, donde una fuerza
(F) que actúa en una dirección cualquiera se aplica a
un contenedor. Podrás observar que debido a la acción de la fuerza el contenedor se mueve una cierta
distancia (d); de acuerdo con la deinición general de
trabajo, al sistema de referencia empleado y a la deinición de producto escalar se establece que:
1. W = Fxd
Donde:
W = trabajo, expresado en joule ( J).
Fx = vector de fuerza paralela a la trayectoria
del objeto bajo estudio expresada en newton (N).
d = vector de desplazamiento cuya magnitud es
la distancia recorrida por el objeto expresada en
metros (m).
Si consideramos que la magnitud de la componente paralela a la trayectoria del movimiento
es la expresión Fx = Fcosq, entonces se tiene que
en forma escalar es:
2. W = (Fcosq)d
Siendo q el ángulo que forma la fuerza neta
(resultante o total) con la trayectoria del objeto
bajo estudio [Ej. 1].
Debemos tener presente que para expresar la
unidad del trabajo en el sistema internacional de
unidades empleamos el joule ( J), porque la unidad
compuesta (Nm) se emplea para expresar el momento (par o torque) producido por una fuerza, que
es una cantidad vectorial; mientras que el trabajo es
una cantidad escalar –que se asocia a la energía como
veremos más adelante– y no posee dirección. En el
obsoleto sistema de unidades cgs (centímetro, gramo,
segundo) se emplea el ergio como unidad de trabajo.
y
F
q
x
d
Glosario
136
Obsoleto. Anticuado, inadecuado a las circunstancias actuales.
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
GRÁFICO 3
GRÁFICO 2
F (N)
F
A2
A1
A3
d
Trabajo
d (m)
Trabajo
gráico 3 se puede apreciar que consideramos tres “áreas”. Observa que señalamos dos triángulos y
un rectángulo, y el trabajo total será simplemente:
n
3. W = A1 + A2 + A3 +… + An = / A i
i=1
Aunque sabemos que el área se expresa en unidades de longitud al cuadrado, para este análisis se
considera que la base se expresa en metros y la altura de cada sección en newton, de allí que la unidad
de trabajo sea el joule.
mg
Ejemplo 1
Se coloca un bloque de 20 kg sobre un plano inclinado a 15° y se le proporciona una velocidad inicial vo.
Calculemos el trabajo que desarrollan las fuerzas
actuantes para que el bloque pueda descender
20 m sobre la superficie del plano, si consideramos
que el coeficiente de fricción entre el bloque y el
plano es de 0.2.
Solución
a. ¿Con qué datos contamos?
• Masa del bloque, m = 20 kg.
• Inclinación de la superficie, q = 15°.
• Distancia recorrida, d = 20 m.
• Coeficiente de fricción, md = 0.2.
• Incógnita: Trabajo desarrollado por el bloque al
descender por el plano inclinado.
b. ¿Qué vamos a hacer?
Calcular el trabajo que realiza el bloque.
15°
movim
mdN
iento
15°
N
Al aplicar la suma de fuerzas verticales (perpendiculares al plano) observamos que se encuentran
en equilibrio y entonces tenemos que la normal es
igual a la proyección del peso en la perpendicular:
+3
ΣF = 0: N – mgcosq = 0
∴ N = 20 × 9.81cos15° = 189.515 N
Las fuerzas que actúan paralelas al plano nos llevan
a obtener la fuerza neta (o resultante)
+ 4 ΣF = F : mgsenq – m N = F
t
t
d
∴ Ft = 20 × 9.81sen15° - 0.2 × 189.515 = 12.877 N 4
c. ¿Cómo lo vamos a hacer?
Para determinar el trabajo calculamos la fuerza
neta paralela a la superficie del movimiento y
después aplicamos la ecuación de trabajo.
d. Operaciones.
Las fuerzas que actúan en el bloque son el peso
(mg), la normal (N) y la fuerza de fricción (mdN ).
st-editorial.com
El trabajo realizado es entonces:
W = Fd = 12.877 × 20 = 257.547 J
e. Resultado.
El trabajo realizado por la fuerza resultante sobre el
bloque al descender en el plano es de 257.547 J.
137
BLOQUE 4
Ejemplo 2
Un auto descompuesto de 1 600 kg de masa se empuja sobre una rampa metálica para que descienda
1.5 m hasta el sitio en que será reparado, considerando que la fricción entre el auto y la rampa es nula, y
que basta un empujón insignificante para que ruede
el auto sobre la rampa, calcula el trabajo realizado.
c. ¿Cómo lo vamos a hacer?
Aplicamos la ecuación de trabajo en el entendido de que la única fuerza que actúa (o interviene
en el proceso) para realizar trabajo es el peso.
d. Operaciones.
Trabajo realizado por el peso:
W = -mgh = -60(9.81) × 2.9 = -1706.94 J
Solución
a. ¿Con qué datos contamos?
• Masa, m = 1 600 kg.
• Distancia recorrida con respecto al nivel del
piso, h = 1.5 m.
• Incógnita: Trabajo desarrollado.
b. ¿Qué vamos a hacer?
Calcular el trabajo que realiza el peso para llevar
el auto de una posición alta a una inferior.
c. ¿Cómo lo vamos a hacer?
Aplicamos la ecuación de trabajo en el entendido de que la única fuerza que actúa (o interviene)
para realizar trabajo es el peso (fuerza vertical).
d. Operaciones.
Trabajo realizado por el peso:
W = Fd = mgh = 1600(9.81) × 1.5 = 23 544 J
e. Resultado.
El trabajo realizado es de 23.54 kJ, el trabajo es
positivo porque el peso actúa en la misma dirección del movimiento, observa que no se considera
ninguna fuerza de fricción, ni la acción necesaria
para que llegue a su posición sin que choque o
algo similar.
Ejemplo 3
Un joven de 60 kg sube de la planta baja al primer
piso de su casa empleando las escaleras. Determinemos el trabajo realizado si consideramos que le
toman 6 segundos subir los 2.9 m de altura.
Solución
a. ¿Con qué datos contamos?
• Masa, m = 60 kg.
• Tiempo, t = 6 s.
• Distancia recorrida, h = 2.9 m.
• Incógnita: Trabajo desarrollado para subir las
escaleras.
b. ¿Qué vamos a hacer?
Sustituir los datos en la ecuación de trabajo
(ecuación 1).
138
e. Resultado.
El trabajo realizado es de 1 706.94 J, en este caso
el signo negativo nos indica que la fuerza actúa
en sentido opuesto al del movimiento y se realiza trabajo en contra del campo gravitacional (la
aceleración de la gravedad apunta hacia el centro de la Tierra). Observa que no es importante la
trayectoria que sigue el joven, ya que el trabajo
se evalúa considerando las fuerzas que actúan
en forma paralela al movimiento del cuerpo.
Ejemplo 4
En una gran construcción se colocan pilotes de cimentación aplicando una fuerza cíclica y variable
directamente sobre éstos, calculemos el trabajo
realizado sobre cada pilote considerando que la variación de la fuerza aplicada y la distancia recorrida
es la que se indica en el gráfico 4.
Solución
a. ¿Con qué datos contamos?
• F = 0 a 5 000 N.
• Distancia recorrida, d1 = 0.35 m, d2 = 0.35 m.
• Incógnita: trabajo desarrollado para encajar los
pilotes en la tierra.
b. ¿Qué vamos a hacer?
Calcular el trabajo desarrollado por la máquina
para colocar cada pilote de cimentación.
GRÁFICO 4
F (N)
5 000
d (m)
0,35
0,7
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
c. ¿Cómo lo vamos a hacer?
Consideramos que el trabajo corresponde al área
total bajo la curva representada, que muestra la
manera en que se aplica en forma repetida la
fuerza de 5 000 N, por lo que procedemos a emplear la ecuación 3.
d. Operaciones.
W = A1 + A 2 + A3
Observamos que tenemos tres áreas formadas
por un triángulo y un rectángulo, ambos de la
misma altura e igual base:
Ai =
FIGURA 2
Ingenieros y arquitectos deben poseer los conocimientos de
física necesarios para que su trabajo sea útil y eficiente.
b#h
2 +b#h
w = 39
0.35 # 5000
+ 0.35 # 5000C = 7875 Nm
2
e. Resultado.
El trabajo realizado es de 7.875 kJ; observa
que la distancia que se entierra el pilote es de
2.1 m.
Actividad individual
COMPETENCIAS
GENÉRICAS
4
5 7
COMPETENCIAS
DISCIPLINARES
3
7 10
DESEMPEÑO
DEL ESTUDIANTE
a
I. Para resolver estos ejercicios es necesario que tengas presentes las ecuaciones 1, 2 y 3, y prepares tu
calculadora. Antes de comenzar, repasa los ejemplos resueltos para que aprendas a auxiliarte con el trazo
de los diagramas.
1. Un contenedor de 120 kg es arrastrado por un cable que forma un ángulo de 40° con la horizontal y
ejerce una fuerza de 1 800 N durante un trayecto horizontal recto de 5 m. Determina el trabajo realizado
por las fuerzas actuantes considerando que el rozamiento es prácticamente nulo.
2. Un auto se descompone cuando viaja sobre una pendiente de 20°, y se detiene después de recorrer
12 m. Calcula el trabajo realizado por la fuerza resultante considerando que la masa del auto es de
1 200 kg y que el coeficiente de fricción entre el auto y el pavimento es de 0.3. ¿Cuál es la magnitud de
la fuerza que debe aplicar el conductor para evitar que el auto se mueva sobre la pendiente?
st-editorial.com
139
BLOQUE 4
3. Un niño deja caer una pelota de 380 g desde la ventana del segundo piso de su casa. Calcula el trabajo
realizado por el peso al descender la pelota 8 metros.
4. Calcula la magnitud de la fuerza paralela a la superficie de deslizamiento que se debe aplicar a un bloque de
mármol de 100 kg para que suba por un plano inclinado a 30° y recorra 5 m con una velocidad constante,
en el entendido de que el trabajo realizado sea de 3 kJ. Considera que la fuerza de fricción es despreciable.
5. Se emplea una prensa para embutir cacerolas aplicando una fuerza tal como muestra el grafico siguiente,
calcula el trabajo desarrollado para la fabricación de cada cacerola.
F (N)
350
200
d (m)
0,02
0,04
0,07
II. Anexa esta actividad a tu portafolio de evidencias.
140
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
Tema 2
Tema 3
Tema 4
Energía cinética y
energía potencial
Ley de la conservación
de la energía mecánica
Potencia
¿Has escuchado a algún político importante cuando declara que actuará
con energía para abatir la pobreza?, ¿has prestado atención cuando en algún
comercial de radio o de televisión se airma que determinado cereal te
proporciona la energía suiciente para iniciar un nuevo día?, ¿qué te están
ofreciendo?, ¿a qué se reieren?
Al igual que ocurre con el concepto de trabajo, el
término energía se emplea de manera indistinta,
como puedes apreciar en las preguntas iniciales del tema. Allí se habla en lenguaje igurado
y se reiere, primero, al uso adecuado del poder
para conseguir el bienestar común, y después a la
energía como el agente capaz de suministrar los
elementos mínimos requeridos para que tu organismo pueda realizar cualquier tipo de actividad y
te mantengas saludable: síntesis de proteínas y de
st-editorial.com
vitaminas, procesos biológicos en general. Además, hacemos referencia a la energía cuando se
trata de obtener calor para transformar materias
primas, de corriente eléctrica para iluminarnos en
la oscuridad y vivir con ciertas comodidades, etc.
En física se da el nombre de energía a la medida
de la capacidad que tiene todo sistema material
para realizar trabajo. En el infográico 1 de la siguiente página te presentamos una clasiicación
general de las formas de energía más empleadas.
141
BLOQUE 4
Infográfico 1 Formas de energía
Las formas de energía siguientes son objeto de estudio
en numerosos campos y disciplinas. En nuestro curso
estudiaremos específicamente la energía mecánica.
1
2
3
4
142
Energía solar
Es el resultado de la radiación
electromagnética del Sol, alrededor
del 40% del total llega a la Tierra y
contribuye a que tengamos otras
formas de energía.
Energía atómica o nuclear
Está contenida en el núcleo de los
átomos, particularmente de materiales
radioactivos, los cuales después de un
proceso de fisión o de fusión liberan la
energía en forma de calor y radiación.
Energía eléctrica
Se produce por medio de diversos
procesos, como el electromagnético y
el hidráulico, entre otros, sin embargo,
todos tienen un resultado común:
los electrones luyen en un material
conductor.
Energía eólica
Esta forma de energía está contenida
en el viento y se empleaba para mover
barcos; hoy en día se ocupa en algunos
lugares en donde se aprovecha para
crear electricidad por medio de los
generadores eólicos, que son similares
en su aspecto físico a los antiguos
molinos. Su uso es todavía limitado por
lo difícil que es asegurar que el lujo del
viento sea constante.
5
6
7
8
9
Energía hidráulica
Está contenida en el agua y se
aprovecha cuando ésta luye en
embalses de ríos o incluso con el ir y
venir de las olas, para que por medio
de diversos dispositivos y maquinaria
se cree energía eléctrica.
Energía química
Las diversas reacciones que se
presentan entre los diversos
compuestos químicos genera energía
que se manifiesta en forma de calor;
la ingesta de alimentos proporciona
los componentes a diversos procesos
bioquímicos para que el cuerpo humano
adquiera calorías, vitaminas y proteínas.
Energía térmica
Es la energía calorífica contenida en la
combustión de las máquinas térmicas
que emplean combustibles de origen
fósil como la hulla y el diesel, entre
otros.
Energía radiante
Se designa con este nombre
a la energía de cualquier tipo
de radiación electromagnética:
rayos gama, rayos X, ultravioleta,
infrarrojos e incluso los rayos
luminosos.
Energía mecánica
Está contenida en todos los cuerpos
y se manifiesta de acuerdo al
comportamiento cinemático de éstos,
de tal manera que la energía mecánica
total de un cuerpo es la suma de
su energía cinética y de su energía
potencial.
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
Energía cinética
La energía cinética de un cuerpo (Ec) representa
el trabajo total que debe realizarse sobre ese cuerpo para que adquiera una determinada velocidad
de magnitud v a partir del reposo. Es una cantidad
escalar siempre positiva, independientemente de
la dirección y el sentido de la velocidad. Al igual
que el trabajo, su unidad es el joule en el si, mientras que en el cgs, se emplea el ergio, la ecuación
que nos permite calcular este tipo de energía es:
Observa:
5. Ec = ½mvf2 – ½mvi2
Y puesto que la energía es la capacidad para
realizar trabajo, podemos escribir entonces:
1
1
Wi " f = 2 mv2f – 2 mvi2
Reordenando:
4. Ec = ½mv2 [ J]
Donde:
m = masa del sistema expresada en kg.
V = magnitud de la velocidad en m/s asumiendo un instante de tiempo cualquiera [Ej. 5].
Para determinar el valor de la energía cuando
existe un cambio de velocidad [Ej. 6], resulta suiciente restar al valor inal el valor inicial.
1
1
6. 2 mvi2 + Wi " f = 2 mv2f
La ecuación 6 nos indica que la energía cinética
que adquiere un objeto corresponde a la energía
cinética que inicialmente tenía más el trabajo que
se realiza para que alcance el estado de movimiento inal a partir del inicial [Ej. 7].
Ejemplo 5
Ejemplo 6
Un auto con masa de 1 350 kg parte del reposo con movimiento uniforme acelerado hasta alcanzar una velocidad
de 60 km/h. Determinemos la energía cinética del auto en
cuestión.
Calculemos la energía cinética de un automóvil compacto de 1 200 kg que viaja a 120 km/h. ¿Cuánto cambia la
energía, si el conductor reduce la velocidad de 120 km/h
a 80 km/h?
Solución
Solución
a. ¿Con qué datos contamos?
•฀Masa฀del฀auto:฀m = 1 350 kg.
•฀Velocidad฀inicial฀del฀auto:฀vo = 0.
•฀Velocidad฀inal฀del฀auto:฀v = 60 km/h = 16.667 m/s.
•฀Incógnita:฀energía฀cinética฀del฀auto.
a. ¿Con qué datos contamos?
•฀Masa:฀m = 1 200 kg.
•฀฀Velocidad฀del฀auto:฀
v = 120 km/h = 33.333 m/s y 80 km/h = 22.222 m/s
•฀฀Incógnita:฀energía฀cinética฀del฀auto฀cuando฀parte฀del฀reposo y cuando reduce su velocidad.
b. ¿Qué vamos a hacer?
Calcular la energía cinética del auto.
c. ¿Cómo lo vamos a hacer?
Sustituimos los datos en la ecuación 4 en forma directa.
d. Operaciones.
Debemos recordar que el auto parte del reposo. La energía cinética es:
1
Ec = 2 ^1350h # 16.667 2 = 187500
e. Resultado.
La energía cinética del auto cuando parte del reposo y alcanza una velocidad de 60 km/h es de 187.5 kJ. Observa en los
cálculos que los datos de la cinemática no son necesarios.
st-editorial.com
b. ¿Qué vamos a hacer?
Calcular la energía cinética del auto considerando que el
movimiento se inicia desde el reposo en el primer caso y
que posteriormente hay una reducción de velocidad de
120 a 80 km/h.
c. ¿Cómo lo vamos a hacer?
Tomamos directamente las ecuaciones 4 y 5 sustituimos
los datos.
d. Operaciones.
•฀Energía฀cinética฀del฀auto฀a฀partir฀del฀reposo.
1
1
Ec = 2 mv 2 = 2 ^1200h # 33.333 2 = 666 666.667 J
143
BLOQUE 4
•฀฀Energía฀cinética฀del฀auto฀cuando฀se฀reduce฀la฀velocidad.
1
1
1
2
2
Ec = 2 mv f – 2 mvi = 2 ^1 200h # 22.222 2 – 33.333 2 =
Calcular la velocidad final del bloque después que se le
da una velocidad inicial y se hace descender por un plano
inclinado.
= - 370 370.370 J
e. Resultado.
La energía cinética del auto al viajar a la velocidad de 120 km/h
es 666.67 kJ, mientras que cuando se reduce a 80 km/h a
partir de la velocidad de 120 km/h, la energía es 370.37 kJ.
Esta energía es equivalente al trabajo que está desarrollando el motor del auto para desplazarse con los cambios de
velocidad señalados; en el segundo caso el signo menos
nos indica en qué cantidad se reduce la energía que suministra el motor al sistema, y en un momento determinado
nos permite establecer la potencia que se requiere para
mover todo el conjunto.
Ejemplo 7
Un bloque de 45 kg es lanzado hacia abajo sobre un plano
inclinado a 15° con una velocidad de 6 m/s. Calculemos la
velocidad que adquiere al recorrer 7 m sobre el plano inclinado si se considera que el coeficiente de fricción entre el
plano y el bloque es de 0.4.
c. ¿Cómo lo vamos a hacer?
Tomamos la ecuación 6 y sustituimos los datos, considerando que el bloque realiza un trabajo que se conjuga con
la energía cinética inicial para que descienda por el plano.
d. Operaciones.
La energía cinética final del auto la obtenemos al despejar el
término correspondiente de la expresión:
1
1
2
2
2 mv f = 2 mv i + W i ! f
El trabajo para llevar el bloque de la posición inicial a la
posición final corresponde al producto de la fuerza neta
aplicada฀por฀la฀distancia฀recorrida.฀Veriica,฀con฀la฀ayuda฀
de un diagrama, que la fuerza resultante en el bloque es:
F = mg (senq – mdcosq)
De esta forma el trabajo es:
W = 45 × 9.81 (sen15° - 0.4cos15°) × 7 = -394.152 J.
Y la energía cinética inicial es:
Eci = ½ × (45 × 62) = 810 J
Solución
a. ¿Con qué datos contamos?
•฀Masa:฀m = 45 kg.
•฀Inclinación฀del฀plano:฀q = 15°.
•฀Velocidad฀inicial฀del฀bloque:฀v = 6 m/s.
•฀Distancia฀que฀recorre฀el฀bloque:฀d = 7 m.
•฀Coeiciente฀de฀fricción:฀md = 0.4.
•฀฀Incógnita:฀velocidad฀que฀alcanza฀el฀bloque฀en฀el฀instante฀
en que ha recorrido 7 m.
b. ¿Qué vamos a hacer?
Por lo que entonces la velocidad final será:
vf =
2 1
2
a
k
m 2 mvi + Wi " f =
2
h
45 ^810 – 394.152 = 4.299 m/s
e. Resultado.
La energía cinética del bloque al descender 7 m sobre el
plano inclinado es de 4.3 m/s, y es importante observar
que el trabajo realizado corresponde a una pérdida de
energía que se traduce en calor por la fricción existente
entre el bloque y la superficie sobre la que desliza.
FIGURA 3
Los atletas obtienen la energía que requieren al transformar los alimentos de una dieta balanceada. La energía que emplean durante la competencia es, en parte,
cinética (cambia la velocidad) y, en parte, potencial (se elevan por encima de las vallas).
144
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
Actividad individual
COMPETENCIAS
GENÉRICAS
4
5 7
COMPETENCIAS
DISCIPLINARES
3
7 10
DESEMPEÑO
DEL ESTUDIANTE
b
Los ejercicios siguientes corresponden al cálculo de la energía cinética de un sistema y la relación que
guarda con el trabajo desarrollado por éste. Es necesario que consultes las ecuaciones 4, 5 y 6 desarrolladas anteriormente en este tema. No olvides repasar los ejemplos para que, de ser necesario, traces los
diagramas correspondientes.
1. En un camino vecinal, un tractor se descompone y su operario solamente lo puede detener cuando choca con
un pajar. Calcula la energía cinética del tractor si en el momento del impacto viaja a 30 km/h y su masa es de
800 kg. ¿A cuánto asciende el trabajo realizado por el pajar sobre el tractor?
2. Calcula la energía cinética de un auto con una masa de 1 200 kg que viaja a 80 km/h y compárala con la
de una furgoneta de 1 590 kg que se mueve a 50 km/h.
3. Encargan a un estibador que acomode un contenedor de 160 kg de masa en un almacén; como no hay
quien lo ayude, él decide empujarlo por el piso una distancia de 30 m hasta que queda acomodado en el
sitio indicado. Si la fuerza de fricción es de 600 N y la velocidad con la que llega al sitio de almacenaje a
partir del reposo es de 6 m/s, determina la magnitud de la fuerza que debe aplicar para mover el contenedor. ¿Qué pasa si no aplica la fuerza en forma paralela a la superficie?
4. En un experimento se deja caer desde el reposo y a una altura de 1.15 m, una esfera de acero de
200 g. Si justo antes de impactar con el piso se mide su velocidad y registra 4.73 m/s, determina en
forma teórica la altura desde la que se dejó caer la esfera. ¿A qué atribuyes la diferencia?
5. Para mejorar el diseño de las defensas de un auto con masa de 1 390 kg, se hace una prueba en la que
se consigue detenerlo al hacerlo chocar con una barra de contención a una velocidad de 20 km/h y con
un desplazamiento de 18 cm, sin que se presenten daños considerables en la defensa del auto. ¿Cuál
es la magnitud de la fuerza que soporta la defensa?
st-editorial.com
145
BLOQUE 4
Energía potencial
A diferencia de la energía cinética, donde se analiza el movimiento de un cuerpo
con una velocidad especíica, ahora estudiaremos el cambio de posición que puede
sufrir el cuerpo por la acción de una fuerza, dando origen a la energía potencial, la
cual se considera como gravitacional o elástica en la mecánica clásica. Observemos
en el infográico 2 el caso de una montaña rusa, donde obligatoriamente se deben
tomar en cuenta la aplicación de leyes físicas, como las relacionadas con trabajo,
energía cinética y energía potencial.
Infográfico 2 Energía cinética y potencial. Aplicaciones en la vida
Un paseo en montaña rusa es una experiencia inolvidable; hace palpitar nuestro
corazón y nos provoca risas incontenibles. Los creadores de estos aparatos buscan
nuevos y atemorizantes diseños, donde obligadamente deben tomar en cuenta la
aplicación de leyes físicas, como las relacionadas con trabajo, energía cinética y
energía potencial.
P
C
El viaje comienza
cuando una
cadena movida
con un motor
(o cualquier
otro dispositivo
mecánico) ejerce
una fuerza sobre
el coche y lo
levanta hasta la
primera cima, que
debe ser la más
alta del recorrido.
P
2
P
ENERGÍA
CINÉTICA
Energía de
un cuerpo en
movimiento;
se mide como
el trabajo y
depende de la
masa del cuerpo
que se mueve y
de su velocidad.
C
Una vez que el coche
llegó a la cima la
gravedad se hace cargo
del resto.
El coche que está en
esa posición posee una
gran cantidad de energía
potencial.
Peso del coche: 100 kg
Altura máxima: 20 m
C
ENERGÍA
POTENCIAL
No se manifiesta por
un movimiento y la
poseen los cuerpos
según su posición
u otras condiciones.
Esta energía
producirá trabajo
si previamente
se transforma.
Peso del coche: 100 kg
Velocidad:฀6฀m/s
P
C
El coche va tomando aceleración
en la medida en que pierde altura.
Por lo tanto, su energía potencial
original (dada por la altura que
tomó) se transforma en energía
cinética (que se hace evidente por
su alta velocidad).
1
3
P
4
C
Cuando el coche comienza
a descender por la primera
vertical pierde gran parte
de esa energía potencial de
acuerdo con su pérdida de
altura. Conforme desciende,
gana energía cinética.
Conforme el viaje sigue, el coche continuamente pierde y gana
altura y velocidad, es decir, gana y pierde energía cinética
y potencial. Existe correspondencia entre la pérdida de una
energía y el aumento de la otra: cada vez que gana altura
(energía potencial) pierde velocidad (energía cinética), y viceversa. Cada pérdida de altura corresponde a una ganancia de
velocidad como energía potencial.
146
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
Ahora, consideremos el movimiento de una masa puntual
que se desplaza sobre una trayectoria cualquiera cerca de la
supericie terrestre, de tal manera que sólo actúa el peso.
Cuando se graica la fuerza contra el valor de deformación, obtenemos un diagrama como el que se muestra en
el gráico 5.
GRÁFICO 5
trayectoria
y
kx
F
0
mg
Para este cuerpo se deine la energía potencial gravitacional (Epg) como el trabajo que se realiza contra el campo
gravitacional para elevar el cuerpo por encima de un plano
de referencia arbitrario donde la energía es cero, y al igual
que la energía cinética se expresa en joule ( J).
x1
x2
x
La energía potencial es el área bajo la recta que se ha
trazado (A = ½ b × h). Si la medimos a partir de la longitud
original del resorte (deformación cero) hasta un valor inicial xi tenemos:
Epe = 12 7^x i – 0h # ^kx i hA
En general:
7. Epg = mgh
1
8. Ep e = 2 kx2
trayectoria
Epg =mgh
Donde:
k = constante de rigidez elástica expresada en N/m.
x = deformación del resorte expresada en m.
h
Epg= 0
mg
Si, por el contrario, se evalúa el trabajo que realiza el
campo gravitacional sobre la masa, entonces W = -mgh, de
donde se deduce que el trabajo del peso es igual y opuesto
a la energía potencial.
Observa que la energía potencial [Ej. 8] de una masa
sólo depende del cambio de altura h y no de la trayectoria
que sigue, debido a que el campo gravitacional tiene el carácter de conservativo.
Pasemos ahora al análisis de la segunda forma de energía
potencial más empleada en la mecánica, la energía potencial elástica (Epe), que corresponde al trabajo que se realiza
sobre un resorte para deformarlo [Ej. 9]. Esta energía se
puede recuperar en forma del trabajo que realiza el resorte
sobre un cuerpo al que se une en el extremo móvil durante
la restauración del resorte a su longitud original. Para evaluar la energía potencial elástica debemos considerar que la
fuerza efectiva de un resorte es:
F = kx
Donde:
k = constante de rigidez elástica.
x = deformación que sufre el resorte.
st-editorial.com
Si deseamos medir la energía potencial entre una deformación inal xf cualquiera y la deformación inicial xi,
debemos calcular el área de cada triángulo y restarlo para
obtener el cambio de energía potencial:
1
9. TEpe = 2 k^x2f – xi2h
Donde:
xf = deformación inal del resorte.
xi = deformación inicial del resorte.
¿Qué signo se asocia a la energía potencial? Se considera
positiva cuando se toma un solo valor de deformación como
en la ecuación 8, pues el valor de deformación se eleva al cuadrado, si tienes un cambio de energía como en la ecuación 9,
es suiciente con que consideres qué está sucediendo cuando
se deforma el resorte, si la deformación aumenta desde la
posición inicial a la posición inal, la variación de energía
potencial también es positiva (valor inal menos valor inicial); por el contrario, la energía potencial es negativa si la
deformación disminuye por presentarse una compresión del
elemento elástico.
Si consideramos que la energía mecánica total es la suma
de las energías cinética y potencial, tenemos entonces que
la expresión que relaciona el trabajo con la energía cinética
(ecuación 6) puede expresarse como:
10. 12 mvi2 + mghi + 12 kx2i + Wi " f = 12 mv2f + mgh f + 12 kx2f
147
BLOQUE 4
Esta ecuación nos señala que la energía mecánica inicial más el trabajo para llevar a un cuerpo de
una posición inicial a una inal es igual a la energía mecánica inal [Ej. 11 y 12] y debemos tener
presente que al momento de aplicarla no se debe
incluir el trabajo que realizan los pesos y las fuerzas
elásticas, ya que se introducen en la ecuación como
formas de energía potencial.
b. ¿Qué vamos a hacer?
Calcular la energía potencial de la defensa en el
momento del impacto.
Ejemplo 8
d. Operaciones.
La energía potencial elástica es:
Epk = ½kx2 = ½ × 180 000 × 0.112 = 1 089 J
Calculemos la energía potencial contenida en una
cascada de agua de 26 m de altura considerando que
la cantidad de masa en movimiento es de 70 000 kg.
c. ¿Cómo lo vamos a hacer?
En este caso procedemos a sustituir los datos en
la ecuación de energía potencial elástica en forma directa (ecuación 8).
e. Resultado.
La energía potencial elástica de la defensa del
auto es de 1.09 kJ.
Solución
a. ¿Con qué datos contamos?
•฀Masa฀del฀agua,฀m = 70 000 kg.
•฀Altura฀de฀la฀caída฀de฀agua,฀h = 26 m.
•฀Incógnita:฀energía฀potencial฀de฀la฀cascada.
b. ¿Qué vamos a hacer?
Calcular la energía potencial que está contenida
en la cascada.
Ejemplo 10
En un experimento se lanza verticalmente hacia arriba
una pelota de 100 gr y se determina que alcanza una
altura de 62 m. Determinemos la energía potencial de
la pelota. ¿Con qué velocidad se lanzó la pelota?
Solución
c. ¿Cómo lo vamos a hacer?
Sustituimos los datos directamente en la ecuación
de energía potencial gravitacional (ecuación 7) ya
que no se hace referencia en el enunciado a componente elástico alguno.
a. ¿Con qué datos contamos?
•฀Masa฀de฀la฀pelota:฀m = 0.1 kg.
•฀Altura฀que฀alcanza฀la฀pelota:฀h = 62 m.
•฀฀Incógnita:฀energía฀potencial฀de฀la฀pelota,฀velocidad del lanzamiento.
d. Operaciones.
La energía potencial es:
Epg = mgh = 70000 × 9.81 × 26 = 17 854 200 J
b. ¿Qué vamos a hacer?
Calcular la energía potencial de una pelota que es
lanzada hacia arriba en forma vertical y la velocidad que se requiere para que alcance una altura
específica.
e. Resultado.
La energía potencial gravitacional almacenada
en la cascada de agua es de 17.854 × 106 J.
Ejemplo 9
Calculemos la energía potencial de la defensa de
un auto de 1 180 kg cuando al realizar una maniobra de estacionamiento golpea una pared, los componentes elásticos de 180 kN/m de rigidez elástica
se comprimen 11 cm.
c. ¿Cómo lo vamos a hacer?
Sustituimos los datos en la ecuación 7 y posteriormente aplicamos la ecuación de trabajo y energía en
el entendido de que la energía potencial corresponde al trabajo que realiza la pelota contra el campo
gravitacional para elevarse una altura de 62 m.
d. Operaciones.
La energía potencial de la pelota es:
Epg = mgh = 0.1 x 9.81 x 62 = 60.822 J
Solución
a. ¿Con qué datos contamos?
•฀Masa฀del฀auto,฀m = 1 180 kg.
•฀Rigidez฀elástica฀de฀la฀defensa,฀k = 180 000 N/m.
•฀Deformación,฀x = 0.11 m.
•฀฀Incógnita:฀energía฀potencial฀de฀la฀defensa฀del฀auto.
148
Como esta energía corresponde al trabajo realizado contra el campo gravitacional porque la pelota
se ha elevado por arriba de una referencia en la
que se considera que la energía es cero tenemos:
1
1
2
2
Wi " f = 2 mv f – 2 mvi
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
Al sustituir los datos consideramos que la velocidad final de la pelota es nula cuando llega a
la altura máxima y el trabajo es negativo (movimiento contrario al sentido en que actúa el peso)
se tiene entonces:
– 60.822 = 0 –
1
2 ^0.1h
#
v2
De esta forma la velocidad que se requiere para
el lanzamiento es:
v=
2 # 60.822
= 34.88 m/s
0.1
e. Resultado.
La energía de la pelota es de 60.822 J mientras
que la velocidad requerida para que alcance la
altura de 62 m es de 34.88 m/s, valor que es común en los lanzamientos de los juegos de béisbol profesional.
•฀฀El฀auto฀empieza฀a฀descender฀cuando฀se฀bloquean฀
las ruedas, en tal posición la energía potencial
gravitacional es nula.
•฀฀Al฀inal฀del฀recorrido฀de฀15฀m฀el฀auto฀se฀detiene, por tanto carece de energía cinética en tal
situación.
•฀No฀hay฀energía฀potencial฀elástica.
•฀฀La฀única฀fuerza฀que฀produce฀trabajo฀es฀la฀de฀fricción฀
pues se considera que al auto almacena energía
potencial gravitacional por el cambio de posición.
1
2
2 mv i + 0 + 0 + W i " f = 0 + mghf + 0
El trabajo que realiza la fuerza de fricción se opone al movimiento y es:
Wi→f = -(mmgcosq)d
Ejemplo 11
Un auto desciende por una pendiente de 3° con una
rapidez de 50 km/h cuando se bloquean las llantas
y el auto se desliza 15 m antes de detenerse. Determinemos el coeficiente de fricción entre las llantas
y el pavimento.
De esta forma, al sustituir datos se establece:
0.5 × m (13.899)2 – (mm × 9.81cos3°)15 = -m × 9.81
× 15sen3°
96.4506m – 146.9483mm = -7.7012m
Ecuación que nos conduce a:
Solución
a. ¿Con qué datos contamos?
•฀Ángulo฀de฀la฀pendiente,฀q = 3°.
•฀฀Velocidad฀inicial฀del฀auto,฀vo = 50 km/h =13.889
m/s.
•฀Distancia฀recorrida฀por฀el฀auto,฀d = 15 m.
•฀฀Incógnita:฀coeiciente฀de฀fricción฀entre฀las฀llantas y el pavimento.
b. ¿Qué vamos a hacer?
Calcular el valor del coeficiente de fricción en el
sistema.
c. ¿Cómo lo vamos a hacer?
Calculamos con los datos la energía del auto y
el trabajo realizado por la fuerza de fricción, para
determinar el coeficiente de fricción m.
d. Operaciones.
La ecuación 10 nos indica que:
1
1 2
1
1 2
2
2
2 mvi + mghi + 2 kxi + W i " f = 2 mv f + mghf + 2 kx f
Para aplicar esta expresión debemos tener en
cuenta que:
m = 0.708
e. Resultado.
El coeficiente de fricción cinético entre las llantas y
el pavimento es de 0.7; observemos que tal como
se señala en el texto no se toma el trabajo realizado
por el peso, pues se incluye como energía potencial gravitacional, además de que no es necesario
conocer la masa del auto.
Ejemplo 12
Un vehículo todo terreno de 1 950 kg viaja a 70 km/h
cuando su conductor se ve obligado a frenar para evitar embestir un hato de ganado que se atraviesa en
el camino más o menos a una distancia de 25 m, si
por lo intempestivo de la acción, el vehículo derrapa
de tal manera que se genera una fuerza de fricción
entre el camino y las ruedas del vehículo de 12.5 kN,
determinemos la distancia que requiere el vehículo
para detenerse sin problema alguno.
Solución
a. ¿Con qué datos contamos?
•฀Masa฀del฀vehículo,฀m = 1 950 kg.
st-editorial.com
149
BLOQUE 4
•฀Velocidad฀inicial,฀vo = 70 km/h = 19.444 m/s.
•฀฀Distancia฀aproximada฀entre฀el฀ganado฀y฀el฀vehículo,฀
x = 25 m.
•฀Fuerza฀de฀fricción,฀F = 12.5 kN.
•฀Incógnita:฀distancia฀que฀derrapa฀el฀vehículo.
La energía cinética inicial es:
1
2
Eci = 2 mv i = ½(1950 ×19.4442) = 368617.4 J
El trabajo que realiza la fuerza de fricción sobre
el auto es:
b. ¿Qué vamos a hacer?
Calcular cuál es la distancia que recorre el vehículo cuando derrapa sobre la superficie.
W = -Fd = -12500d
Dado que la energía cinética final es nula porque
el auto se detiene se cumple que:
c. ¿Cómo lo vamos a hacer?
Aplicamos la ecuación 10 ya que con los datos
podemos calcular directamente la energía cinética del auto y el trabajo realizado por la fuerza
resultante que actúa en la dirección del movimiento del vehículo para determinar la distancia recorrida.
d. Operaciones.
La ecuación general de trabajo y energía nos
indica:
1
2
2 mv i + 0 + 0 + W i " f = 0 + 0 + 0
Actividad individual
COMPETENCIAS
GENÉRICAS
4
5 7
368617.4 – 12500d = 0
De donde se establece que la distancia recorrida es:
d = 29.489 m
e. Resultado.
El auto deslizará 29.5 m antes de detenerse, lo
cual implica que si el ganado no avanza para
cruzar antes el camino, el riesgo de un accidente
grave es muy alto.
COMPETENCIAS
DISCIPLINARES
3
7 10
DESEMPEÑO
DEL ESTUDIANTE
b
I. Los ejercicios siguientes corresponden al cálculo de la energía potencial de un sistema y la relación que
guarda con el trabajo desarrollado por éste y su energía cinética. Es necesario que consultes las ecuaciones de la 7 a la 10 desarrolladas anteriormente en este tema. No olvides repasar los ejemplos para que, de
ser necesario, traces los diagramas correspondientes.
1. Determina la energía potencial de un bombero de 80 kg que para rescatar a una persona sube por una
escalera inclinada a 80° desde el piso hasta una altura de 9 m. ¿Cuál es el trabajo que realiza cuando
desciende al piso cargando a una anciana de 60 kg?
2. Un automóvil mal estacionado en una pendiente empieza a moverse hacia abajo hasta llegar a la parte
plana de una avenida, si la masa del auto es de 1 380 kg y la distancia que recorre sobre el plano inclinado a 18° es de 12 m, determina la velocidad con la que llega al final del recorrido considerando que
la fuerza de fricción entre las llantas y el pavimento es de 2 750 N.
150
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
3. Para probar el prototipo de un dispositivo de lanzamiento de misiles submarinos se coloca un misil de
10 kg en el riel horizontal de lanzamiento comprimiendo el disparador 2 cm, si la rigidez elástica de este
sistema es de 500 N/m, calcula la velocidad que alcanza el misil cuando se ha alejado 4 cm del disparador, asumiendo que el coeficiente de rozamiento en el sistema es de 0.2 y es equivalente al que existe
entre el torpedo y el agua de mar.
4. Un resorte de 90 cm de longitud y 250 N/m de rigidez elástica se coloca sobre el techo y cuidadosamente
se le agrega un contrapeso de 15 kg. Cuando se suelta a partir del reposo, el movimiento del sistema
es de vaivén vertical. ¿Cuál es la longitud total del resorte cuando la masa se encuentra en la posición
más baja?
5. Calcula la velocidad y la aceleración normal que tiene la lenteja de un péndulo de 0.2 kg cuando se libera
desde la posición horizontal como muestra la figura y llega a la posición q = 60°.
r = 60 cm
m
q
II. Anexa esta actividad a tu portafolio de evidencias.
st-editorial.com
151
Tema 3
Tema 4
Ley de la conservación
de la energía mecánica
Potencia
¿Has viajado en una lancha sobre el mar?, ¿qué diferencia has percibido con
respecto a un viaje en lancha sobre un río fangoso? Si no lo has hecho, imagina
las condiciones de navegación, en ambos casos, el día es soleado y la nave tiene
el mismo tipo de motor. ¿En qué medio viajará más rápido?, ¿qué es lo que
afecta el movimiento de la lancha?
A nuestro alrededor observamos día a día un sinfín
de actividades que requieren del suministro de energía y en algunos casos tal suministro es continuo,
¿por qué esta situación? La energía se transforma en
trabajo y éste a su vez, mediante diferentes procesos,
métodos y procedimientos, se convierte en un objeto
especíico, como pan, transporte, ropa, vivienda, etc.
¿Qué hay detrás de la transformación?, ¿qué sucede
con la energía? Es un hecho que los equipos, máquinas y transportes que ha desarrollado el ser humano
están lejos de la perfección y su eiciencia está aún
distante del cien por ciento, pues sufren pérdidas de
energía por diversas causas y ello implica que necesariamente se suministre energía en forma regular,
ya que no existen equipos de movimiento continuo
en los que baste un pequeño impulso para que se
152
genere por sí misma la energía necesaria para mantener las condiciones de operación continua.
La relación entre el trabajo y la energía mecánica
total es importante, pues la aplicación directa de esta
ecuación, en el caso ideal en que sólo actúan fuerzas
conservadoras como el peso y la fuerza de un resorte,
nos permite establecer que el trabajo es nulo, lo cual
nos lleva a una conclusión muy importante
1
1
1
1
11. 2 mvi2 + mghi + 2 kxi2 = 2 mv2f + mgh f + 2 kx2f
En ausencia de fuerzas de carácter conservativo la energía se
mantiene constante.
El enunciado anterior es el principio de conservación de la energía [Ejs. 13, 14 y 15], y aunque quizás
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
hayas observado que un trompo después de cierto tiempo de girar
se detiene, esto no sucede porque perdió su energía, en realidad ésta
se transformó en calor por la fricción del juguete con la supericie y
fue esta misma fuerza de fricción la que hizo que se detuviera; cuando
lo animas de nuevo con la cuerda, la energía que está almacenada lo
hace girar.
Al considerar que cualquier máquina no está exenta de las pérdidas de energía por la acción de diversos agentes es factible deinir
la eficiencia mecánica (em), como la relación entre el trabajo realizado por una máquina y el trabajo realizado sobre esa máquina
en el mismo lapso de tiempo, en el supuesto de que en el interior de dicha máquina no se acumula ninguna forma de energía
[Ej. 16]. La eiciencia siempre es menor a la unidad (o al 100%, es
una fracción adimensional) porque toda máquina funciona con pérdidas por fricción o desgaste; la energía que se pierde se transforma
en calor, que a su vez es disipado por diversos agentes.
La ecuación general para el cálculo de la eiciencia mecánica es:
W
12. em = W
FIGURA 4
Un trompo gira hasta que la fuerza de fricción provoca que se
detenga; un ejemplo industrial de esta misma fuerza es la que
se presenta en el volante de una troqueladora.
s
Donde:
W = trabajo que realiza la máquina, expresado en J.
Ws = trabajo suministrado a la máquina para que funcione,
expresado en J.
La fricción es una fuerza de carácter disipador, la encontramos a nuestro alrededor y está presente bajo diferentes formas,
en un motor eléctrico la encuentras como corrientes parásitas,
es decir como una corriente que produce pérdidas que afectan
el movimiento del sistema; en los motores térmicos se requieren
lubricantes que permiten la movilidad de las piezas metálicas y
cerámicas a altas velocidades, el calor generado por la combustión
y la fricción se reduce por medio del lubricante y del sistema de
refrigeración.
En el caso del viaje en lancha que mencionamos sucede que
el agua y todos los líquidos en general tienen una propiedad denominada viscosidad, la cual genera una fuerza que se opone al
movimiento de cualquier objeto en el luido y del luido en ciertos
conductos, esto tiene ventajas y desventajas, que son de nuestro
interés inmediato. La pérdida de energía que se genera reduce la
cantidad de trabajo que se puede producir y da lugar a otros requerimientos, tales requerimientos son comunes en gran cantidad
de equipos, máquinas y sistemas electromecánicos, las fuerzas de
fricción evitan que se conserve la energía, así que es necesario un
mayor consumo de energía y se genera calor, por lo que se requiere
de sistemas refrigerantes o de absorción de altas temperaturas y de
sistemas lubricantes que ayuden a incrementar la eiciencia inal.
El mundo que te rodea
La tribología es la ciencia y técnica que estudia la interacción entre las superficies en movimiento y los problemas relacionados con ellos: desgaste, fricción, adhesión y lubricación. La tribología humana se encarga del
estudio de estos tres fenómenos en las articulaciones del cuerpo humano, principalmente la cadera y la rodilla.
Para que nos hagamos una idea de lo importante que son las soluciones a problemas tribológicos, por ejemplo,
en los automóviles, en los que existen más de 2 000 contactos tribológicos, las mejoras tribológicas pueden
suponer un ahorro de energía de 18.6%.
st-editorial.com
153
BLOQUE 4
Ejemplo 13
Para simular el comportamiento de la defensa de un auto se
lanza un bloque de 15 kg sobre una superficie horizontal lisa
contra la maqueta de la defensa, cuya rigidez elástica es de
2 200 N/m. Calculemos la velocidad del bloque una vez que
ha comprimido 18 cm al prototipo considerando que inicialmente la velocidad del bloque era de 10 km/h
Solución
a. ¿Con qué datos contamos?
•฀Masa฀del฀bloque,฀m = 15 kg.
•฀Rigidez฀elástica,฀k = 2 200 N/m.
•฀Deformación฀de฀la฀defensa,฀xf = 0.18 m.
•฀฀Velocidad฀inicial฀del฀bloque,฀vo = 10 km/h = 2.778 m/s.
•฀Incógnita:฀velocidad฀inal฀del฀bloque.
b. ¿Qué vamos a hacer?
Calcular la velocidad que alcanza el bloque al comprimir
18 cm la defensa.
c. ¿Cómo lo vamos a hacer?
Empleamos la ecuación de conservación de la energía.
d. Operaciones.
Para este caso la ecuación de conservación de la energía es:
1
1 2 1
1 2
2
2
2 mv i + 2 kx i = 2 mv f + 2 kx f
Porque no se consideran fuerzas que realicen trabajo, incluyendo las de tipo disipador como la fricción, ni se tiene
energía potencial gravitacional (el movimiento de la masa es
sobre la horizontal) y como inicialmente no hay compresión
en la defensa:
1
1
1 2
2
2
2 mvi + 0 = 2 mv f + 2 kx f
De esta forma, al sustituir datos se establece:
0.5 × 15(2.778)2 = 0.5 × 15v2 + 0.5(2200 × 0.182)
Y las operaciones nos llevan a:
22.2303 = 7.5v2 ∴v = 1.72 m/s
e. Resultado.
La velocidad final del bloque es de 6.2 km/h. (Observa que
las unidades son diferentes) ¿Qué sucede con la velocidad
final si se aumenta la velocidad inicial y se mantiene la misma deformación?
Ejemplo 14
En un día lluvioso un auto empieza a subir por una colina a
una velocidad de 90 km/h cuando repentinamente se detiene el motor, ¿qué altura alcanzará respecto a la superficie
plana del inicio de la colina al momento de detenerse por
completo?, ¿qué cantidad de energía se pierde si el piso
está seco y por la fricción sólo se alcanzan dos terceras partes de la altura calculada anteriormente?
154
Solución
a. ¿Con qué datos contamos?
•฀฀Velocidad฀inicial฀del฀auto,฀vo = 90 km/h = 25 m/s al iniciar
el ascenso en una colina.
•฀฀Incógnita:฀altura฀que฀alcanza,฀pues฀el฀motor฀se฀detiene.
b. ¿Qué vamos a hacer?
Calcular la altura que sube el auto sobre la colina respecto
al plano en el que inició el recorrido.
c. ¿Cómo lo vamos a hacer?
Empleamos la ecuación de conservación de la energía.
d. Operaciones.
Para este caso la ecuación de conservación de la energía es:
1
1
2
2
2 mv i + mghi = 2 mv f + mghf
Porque no se considera la energía potencial elástica del
sistema, ahora bien, como inicialmente no hay energía potencial gravitacional y al final la energía cinética es nula:
1
2
2 mv i + 0 = 0 + mghf
De esta forma, al sustituir datos se establece:
0.5 × m(25)2 = m(9.81 × h)
Y las operaciones nos llevan a:
312.5 = 9.81h ∴h = 31.86 m
Si las fuerzas de fricción provocan que la altura sólo sea
de dos terceras partes de la altura anterior, tenemos que
la pérdida de energía del sistema será equivalente a un
tercio de la energía con la que inició el recorrido.
e. Resultado.
La altura alcanzada es de 31.86 m en condiciones en las
que se considera que las fuerzas disipadoras son despreciables, de no ser así la pérdida de energía puede ser
considerable, al grado de que la altura alcanzada sea de
sólo unos metros.
Ejemplo 15
En las maniobras de un cambio de vías, una locomotora
de 12 000 kg que viaja a 12.5 km/h choca contra una guarnición rígida móvil, saliendo rebotada con una velocidad
de 12 km/h, determina la deformación del parachoques de
la locomotora considerando que su rigidez elástica es de
360 kN/m. Si la guarnición absorbe el impacto desplazándose una distancia de 7.5 cm, ¿cuál es la magnitud de la fuerza
disipadora actuante?
Solución
a. ¿Con qué datos contamos?
•฀Masa฀de฀la฀locomotora,฀m = 12 000 kg.
•฀฀Velocidad฀inicial฀de฀la฀locomotora,฀vi = 12.5 km/h = 3.472 m/s.
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
•฀฀Velocidad฀inal฀de฀la฀locomotora,฀vf = 12 km/h = 3.333 m/s.
•฀Rigidez฀elástica,฀k = 360000 N/m.
•฀Desplazamiento฀de฀la฀guarnición,฀xg = 0.075 m.
•฀฀Incógnita:฀deformación฀del฀parachoques฀de฀la฀locomotora฀y฀magnitud฀de฀la฀fuerza฀disipadora.
b. ¿Qué vamos a hacer?
Calcular la deformación del parachoques y la fuerza disipadora.
c. ¿Cómo lo vamos a hacer?
Empleamos la ecuación de conservación de la energía y la expresión de trabajo y energía.
d. Operaciones.
Para este caso la ecuación de conservación de la energía es:
1
1
1 2
2
2
2 mv i = 2 mv f + 2 kx f
Al sustituir datos tenemos:
0.5 × 12 000(3.472)2 = 0.5 × 12000(3.333)2 + 0.5 × (360 000xf2)
Y las operaciones nos llevan a:
5 671.29 = 180 000x2 ∴x = 0.177 m
Para el cálculo de la fuerza disipadora consideramos que la energía de la locomotora al momento del
impacto es equivalente al trabajo desarrollado al desplazar la guarnición.
1
2
2 mv i = Fd
La sustitución de datos nos da como resultado:
F = 888 888.88 N
e. Resultado.
La deformación del parachoques es de 17.7 cm mientras que la fuerza equivalente al impacto de 888.9 kN.
¿Qué material además del concreto se emplea en este tipo de sistemas?
Actividad grupal
COMPETENCIAS
GENÉRICAS
4 5 7
8
COMPETENCIAS
DISCIPLINARES
3 7 10
DESEMPEÑO
DEL ESTUDIANTE
c
A partir de la determinación de la energía que se conserva en un sistema y sus posibles pérdidas,
reunidos en equipos, resuelvan en su cuaderno lo siguiente y, antes de dar solución a cada problema,
consulten las ecuaciones 11 y 12 desarrolladas anteriormente en este tema, y repasen los ejemplos para
que hagan los diagramas correspondientes y todas las consideraciones necesarias.
1. Calculen la altura que alcanza y el ángulo que forma con la vertical una lenteja de 50 g que se ata a
una cuerda de un metro de longitud, se coloca verticalmente en un techo y estando en tal posición,
se le proporciona una velocidad de 2.4 m/s.
2. Para probar la capacidad de absorción de energía de un empaque elástico, se rellena un contenedor
con una capa uniforme de éste y se deja caer a partir del reposo desde una altura de 1 m una caja
con material frágil de 25 kg. Determinen la velocidad justo al momento de golpear el empaque, considerando que éste se deforma 18 mm sin provocar el rebote de la caja.
3. Para atravesar un pequeño río de 2.5 m de ancho plagado de pirañas, tres excursionistas deciden
pasar una cuerda alrededor de una rama y balancearse como péndulo simple, al primer intento uno
de los chicos hace pasar la cuerda alrededor de la rama de tal manera que la distancia para el cruce
se reduce en medio metro, si el peso de cada uno de ellos es de 70 kg, 90 kg y 78 kg respectivamente
y la rama se encuentra a 5 metros con respecto al plano en el que deben impulsarse de tal manera
que pueden coger la cuerda a 1.5 m de altura, determinen qué condición se debe cumplir para que
logren su objetivo.
st-editorial.com
155
BLOQUE 4
4. Determinen la eficiencia de un malacate que consume una potencia de 1 kW para elevar una carga
de 60 kg a una velocidad de 1.5 m/s. ¿Cuál es par que suministra si el tambor que arrolla el cable
tiene un radio 12.5 cm?
5.Determinen el trabajo desarrollado por una bomba de 1/3 hp que en su placa de datos indica que
opera a 3 600 rpm y tiene una eficiencia de 88%.
Lee
El movimiento perpetuo
La búsqueda de la eterna juventud, la piedra filosofal y una máquina de movimiento perpetuo han atrapado la atención del
ser humano desde los tiempos más remotos, cada una de ellas ha tenido fabulosas
teorías y experimentos que a la fecha
siguen siendo un sueño. El caso que nos
ocupa es el de la máquina perfecta, imagina que puedes construir un dispositivo
que, desprovisto de cualquier fuente de
energía, sea capaz de producir en forma
permanente un movimiento de rotación
por el simple hecho de generar su propia
energía, almacenarla y transformarla o
transmitirla a otros equipos, ¡genial!
Entre los dispositivos más antiguos
se tienen las ruedas desbalanceadas
creadas por físicos hindúes entre los
siglos VII y XII; en Occidente los franceses y los ingleses basaron su diseño
en el tornillo de Arquímedes creando
diversos tornillos de recirculación de
agua, pero en todos los casos hay una
falla, violan los principios de la física,
hay quienes apuestan a desafiar la
naturaleza para conseguir la gloria
de demostrar que el frío fluye hacia
el calor generando energía y los más
recientes avances a nivel microscópico
han permitido formular nuevas teorías
acerca del origen de la vida.
La inquietud del ser humano parece
no tener fin y encontramos en la Red
una gran cantidad de individuos que
presentan videos y reportes donde
muestran sus diseños, encontramos
que algunos han cometido errores conceptuales y otros simplemente han
montado trucos, entre los más destacables podemos ver una aplicación que
emplea el principio de conservación
de la energía. Bajo la premisa de que
la energía se preserva y se cambia de
forma en la industria del automóvil,
tenemos que algunos automóviles de
lujo ya incluyen un dispositivo que
recupera la energía que se disipa al
momento de frenar y se transforma
en otro tipo de energía aumentando
la eficiencia del sistema y reduciendo
el consumo de combustible; un buen
desarrollo tecnológico, ¿no crees?
Jorge Díaz
En equipos de tres integrantes realicen una investigación en la biblioteca, en la hemeroteca y en Internet
para contestar las siguientes preguntas:
1. ¿Será factible la creación de la máquina perfecta?, ¿por qué?
2. ¿Qué tipos de energía se involucran en los modernos sistemas de frenado?
3. ¿Cuál de los desarrollos que actualmente se muestran en Internet consideran que es el más acertado?,
¿por qué?
156
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
Tema 4
Potencia
¿Por qué un sedán de lujo tiene un motor de mayor capacidad que un miniauto
urbano?, ¿por qué un tractor no es más rápido que una retroexcavadora?
Es normal escuchar que un auto deportivo es más veloz que cualquier otro
por su potencia, e incluso se ha llegado mencionar en algunos eventos deportivos
que un atleta posee mayor fuerza y potencia y es la razón por la que es un ganador;
sin embargo, ¿a qué nos referimos en la física cuando hablamos de potencia?
Iniciemos el tema respondiendo a las preguntas
anteriores: los autos y los llamados equipos pesados
fueron diseñados para realizar funciones diferentes
y especíicas, si entramos en detalles encontramos
que los autos se emplean para transportar personas
y objetos personales, mientras que vehículos como
el tractor se utilizan para remover tierra y piedras.
Están diseñados considerando la fuerza que se requiere para desplazar tanto la masa que los conforma, como la masa que han de transportar o mover
y para que cumplan con tal objetivo, se considera
como factor de diseño el trabajo que deben realizar
y el tiempo que deben emplear para ello. Esta característica se denomina potencia.
En términos generales, se deine la potencia
mecánica (P) como la capacidad de un sistema
para realizar trabajo en la unidad de tiempo. Su
modelo matemático es el siguiente:
W
13. P = t
Potencia. Rapidez con la que un sistema puede realizar trabajo o consumir energía.
st-editorial.com
Glosario
157
BLOQUE 4
Retrato
James Watt. Científico escocés, primero en concebir y construir una máquina de vapor. Observó que las máquinas
desaprovechaban gran cantidad de vapor, y en consecuencia, una alta proporción de calor latente, susceptible de
ser transformado en trabajo mecánico. Diseñó en 1766 un modelo de condensador separado del cilindro, que permitió lograr un mayor aprovechamiento del vapor, y mejorar de este modo el rendimiento económico de la máquina.
Este avance contribuyó de forma determinante en el avance de la Revolución Industrial.
Donde:
W = trabajo, expresado en J.
t = tiempo expresado en s. [Ej. 16].
En el si se considera el watt como la unidad de potencia mecánica en lugar de la
combinación J/s, en honor de James Watt (1736-1819).
En las especiicaciones de los autos, sobre todo europeos, es común hoy en día
que se emplee el hp o el cv (cheval à vapeur) para indicar la potencia. En el cuadro
de la página 39 de este libro se indican los equivalentes de ambas unidades en el si.
Considerando que el trabajo es el desplazamiento de un sólido por la aplicación de
una fuerza, entonces al sustituir en la ecuación de potencia:
FIGURA 5
Entre las labores propias de un tractor
está la de arrastrar un remolque por
toda clase de terrenos y en cualquier
condición, por lo que el motor del tractor suministra gran potencia y no una
excesiva velocidad.
P=
F#d
t
Y como en el movimiento uniforme la velocidad se calcula mediante esta ecuación:
d
v= t
Entonces podemos concluir que:
14. P = Fv
La ecuación 15 es útil para determinar la potencia cuando el objeto ha vencido las fuerzas que se oponen al movimiento y se mueve a velocidad constante; por ello sólo se requiere
conocer la magnitud de la fuerza neta aplicada y la magnitud de la velocidad con la que
se mueve el objeto, ya que su dirección es la misma que la de la fuerza actuante [Ej. 17].
Al realizar la analogía entre el movimiento lineal y el angular observamos que es factible deinir el término de potencia en un sistema en movimiento circular uniforme como:
15. P = Mω
En la web
Para conocer más acerca del trabajo,
la potencia y la energía, visita la página st-editorial.com/enlaweb/fisica1 y
consulta el link número 05
Glosario
158
En donde el momento M, se expresa en Nm y la velocidad angular ω en rad/s, esta
expresión es de uso común para especiicar la potencia en equipos rotatorios como
motores eléctricos, bombas para agua, etc. [Ej. 18].
Si consideramos que la potencia es la rapidez con la que se realiza trabajo, la eiciencia se puede expresar como:
P final
16. em = P
consumida
hp. Horse power. Unidad del sistema inglés empleada comercialmente para medir la potencia de un sistema electromecánico.
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
Ejemplo 16
la componente vertical de la fuerza con que la
mamá tira del carro y entonces la resultante es:
Una joven madre jala el auto de pedales en el que
juega su hijo. Calculemos la potencia desarrollada
si el pequeño auto de juguete viaja a una velocidad
constante de 1.2 m/s considerando que la masa total del conjunto es de 45 kg y la fuerza que aplica
la señora es de 140 N con una dirección de 40° con
respecto a la horizontal. El coeficiente de fricción
entre el auto y el suelo es de 0.3 y la distancia total
del recorrido, de 18 m.
Solución
a. ¿Con qué datos contamos?
•฀Velocidad฀del฀carrito,฀v = 1.2 m/s.
•฀Masa,฀m = 45 kg.
•฀฀Fuerza฀aplicada,฀F = 140 N a 40° con la
horizontal.
•฀Coei฀ciente฀de฀fricción,฀md = 0.3.
•฀Distancia฀recorrida,฀d = 30 m.
•฀฀Incógnita:฀trabajo฀desarrollado฀y฀potencia฀
requerida para mover el auto de pedales.
b. ¿Qué vamos a hacer?
Calcular la potencia que se requiere para mover
el carro de pedales.
+ ¬ ΣF = F : Fcosq – m (mg – Fsenq) = F
t
t
d
Ft = 140cos40° – 0.3(45 × 9.81 – 140sen40°) = 1.808 N
El trabajo realizado es entonces:
W = F × d = 1.808 × 18 = 32.549 J
Considerando la distancia recorrida y la velocidad:
d
t = v = 18/1.2 = 15 s
Y la potencia es:
W
P = t = 32.549/15 = 2.17 W
e. Resultado.
La potencia suministrada al sistema es de
2.17 W. Para este problema debemos tener en
cuenta que primero obtuvimos la fuerza que produce el movimiento paralelo a la superficie para
facilitar el cálculo final en donde determinamos
el tiempo en el que realiza trabajo.
Ejemplo 17
c. ¿Cómo lo vamos a hacer?
Para determinar la potencia primero calcularemos el trabajo obteniendo la fuerza neta
aplicada, que es paralela a la superficie del
movimiento en el recorrido de 18 m, después
aplicamos la ecuación de velocidad constante
para determinar el tiempo y así sustituir en la
ecuación 14. Observemos el gráfico 6.
Calculemos la potencia requerida para trasladar una
carretilla con materiales de construcción al descender por un tablón de 4 m de longitud inclinado a 20°.
La carretilla la empuja un trabajador a una velocidad
constante de 1 m/s con una fuerza de 300 N paralela
a la superficie. Considera que la masa de la carretilla
es de 120 kg y que el coeficiente de fricción es de 0.4.
d. Operaciones.
Solución
GRÁFICO 6
mg
F
q
mN
N
Al considerar que las fuerzas están en equilibrio
en la vertical y no intervienen en el movimiento
(son perpendiculares a la superficie), se tiene que
la normal es igual al peso en magnitud menos
st-editorial.com
a. ¿Con qué datos contamos?
•฀Distancia฀recorrida,฀d = 4 m.
•฀Inclinación฀de฀la฀superi฀cie,฀q = 20°.
•฀Velocidad,฀v = 1 m/s.
•฀Fuerza฀aplicada฀a฀la฀carretilla,฀F = 300 N.
•฀Masa฀de฀la฀carretilla,฀m = 120 kg.
•฀Coei฀ciente฀de฀fricción,฀md = 0.4.
•฀฀Incógnita:฀potencia฀necesaria฀para฀bajar฀la฀
carretilla por el tablón.
b. ¿Qué vamos a hacer?
Calcular la potencia a partir de la fuerza actuante
y la velocidad.
c. ¿Cómo lo vamos a hacer?
Nos auxiliamos con un diagrama y calculamos
la fuerza neta en el sistema para determinar la
potencia a partir de la ecuación 15.
159
BLOQUE 4
Ejemplo 18
d. Operaciones.
Las fuerzas que actúan en la carretilla son:
Determina la velocidad de operación de una bomba
de agua de 0.5 hp que proporciona un par de 1.2 Nm.
F
20°
mg
Solución
movimiento
a. ¿Con qué datos contamos?
•฀Potencia฀de฀la฀bomba,฀P = 0.5 hp = 372.85 W.
•฀Par฀que฀proporciona,฀M = 1.2 Nm.
•฀Incógnita:฀velocidad฀de฀operación฀de฀la฀bomba.
mdN
20°
b. ¿Qué vamos a hacer?
Calcular la velocidad de operación de la bomba
de agua en rpm.
N
De nueva cuenta hacemos la suma de fuerzas
verticales y tenemos que la normal es igual al
peso en magnitud:
+ 3 ΣF = 0: N – mgcosq = 0 ∴ N = mgcosq
Por lo que la fuerza neta es:
+ 4 ΣF = F : F + mgsenq – m N = F ∴ F = F + mgsenq
d
t
t
t
– md mgcosq
c. ¿Cómo lo vamos a hacer?
Sustituimos los datos directamente en la ecuación
de potencia para sistemas en rotación (ecuación 16)
y despejamos el valor de la velocidad angular en
rad/s, después convertimos a rpm.
d. Operaciones.
La potencia es:
P = Mω
Ft = 300 + 120 × 9.81(sen20° – 0.2cos20°) = 481.385 N
372.85 = 1.2ω
De esta forma la potencia es:
P = F × v = 481.385 × 1 = 481.385 W
∴ ω = 310.708 rad/s = 2 967 rpm
e. Resultado.
La potencia suministrada es de 481.39 W que es
aproximadamente 1/2 hp.
Actividad individual
COMPETENCIAS
GENÉRICAS
4
5 7
e. Resultado.
La velocidad de operación de la bomba es de
2 967 rpm, sin que consideremos pérdidas por
calor o fricción en sus diferentes componentes.
COMPETENCIAS
DISCIPLINARES
3
7 10
DESEMPEÑOS
DEL ESTUDIANTE
b
d
I. Los ejercicios siguientes corresponden al cálculo de la potencia de un sistema y la posible relación que
guarda con el trabajo y la energía de éste. Es necesario que consultes las ecuaciones 13, 14, 15 y 16
desarrolladas anteriormente en este tema. No olvides repasar los ejemplos para que, de ser necesario,
traces los diagramas correspondientes.
1. Un contenedor de 120 kg es arrastrado por un cable que forma un ángulo de 40° con la horizontal y ejerce una fuerza de 1 800 N durante un trayecto horizontal recto de 5 m. Determina el trabajo realizado por
las fuerzas actuantes y la potencia del malacate que jala del contenedor si consideramos que lo arrastra
con una velocidad constante de 40 cm/s y que el rozamiento es prácticamente nulo.
160
st-editorial.com
RELACIONAS EL TRABAJO
CON LA ENERGÍA
2. ¿Qué sucede en el ejercicio anterior si el coeficiente de fricción toma un valor 0.5?
¿Qué ocurre con la potencia en el motor del malacate que arrastra el contenedor?
3. Calcula la potencia que suministra el motor de un montacargas para elevar desde el
piso hasta una altura de 80 cm una tarima con tambos de aceite que totalizan una
masa de 480 kg, con una velocidad constante de 0.6 m/s, para así trasladarla de un
almacén a un camión de distribución.
4. Calcula el trabajo que realiza una fuerza de 180 N que un jugador de hockey sobre
hielo proporciona al disco de 200 g para que éste recorra una distancia de 4 m a la
meta en 0.5 s. Considera que el coeficiente de fricción entre el hielo y el disco es de
0.04 y que la fuerza actúa en forma paralela a la superficie de deslizamiento. ¿Cuál es
la magnitud de la potencia suministrada?
5. Determina la magnitud del momento producido por el eje de una bomba de agua si
consideramos que la potencia efectiva es de 0.75 hp operando a una velocidad de
3 600 rpm. ¿Cuál es la magnitud de la fuerza tangencial generada en el rodete considerando que el eje del rotor tiene un diámetro de 19 mm?
II. Anexa esta actividad a tu portafolio de evidencias.
st-editorial.com
161
Evaluación sumativa
Heteroevaluación
I. Pide a tu profesor que aplique la siguiente rúbrica, con el fin de que pueda registrar tus avances. Como
verás es la misma que respondiste en el reto; ahora servirá para medir cuál fue tu desempeño durante el
estudio de este bloque.
Indicadores de desempeño
Aspectos a evaluar
4 puntos
3 puntos
2 puntos
1 punto
Concepto de
trabajo en física,
realizado por o
sobre un cuerpo
como un cambio
en la posición o la
deformación del
mismo por efecto
de una fuerza.
Definí plenamente el
concepto de trabajo
en física, realizado
por o sobre un cuerpo
como un cambio en
la posición o la
deformación del
mismo por efecto
de una fuerza.
Definí bien el
concepto de trabajo
en física, realizado
por o sobre un cuerpo
como un cambio
en la posición o la
deformación del
mismo por efecto de
una fuerza.
Definí vagamente el
concepto de trabajo
en física, realizado
por o sobre un cuerpo
como un cambio en
la posición o la
deformación del
mismo por efecto
de una fuerza.
No definí el concepto
de trabajo en física,
realizado por o sobre
un cuerpo como un
cambio en la posición
o la deformación del
mismo por efecto
de una fuerza.
Cambios de la
energía cinética y
potencial que posee
un cuerpo con el
trabajo
en física.
Relacioné plenamente
los cambios de la
energía cinética y
potencial que posee
un cuerpo con el
trabajo
en física.
Relacioné bien los
cambios de la energía
cinética y potencial
que posee un cuerpo
con el trabajo
en física.
Relacioné vagamente
los cambios de la
energía cinética y
potencial que posee
un cuerpo con el
trabajo
en física.
No relacioné los
cambios de la energía
cinética y potencial
que posee un cuerpo
con el trabajo
en física.
Ley de la
conservación de la
energía mecánica
en la explicación
de fenómenos
naturales del
entorno social,
ambiental y cultural.
Utilicé plenamente
la ley de la
conservación de la
energía mecánica
en la explicación de
fenómenos naturales
de mi entorno social,
ambiental y cultural.
Utilicé bien la ley
de la conservación de
la energía mecánica
en la explicación de
fenómenos naturales
de mi entorno social,
ambiental y cultural.
Utilicé vagamente
la ley de la
conservación de la
energía mecánica
en la explicación de
fenómenos naturales
de mi entorno social,
ambiental y cultural.
No utilicé la ley
de la conservación de
la energía mecánica
en la explicación de
fenómenos naturales
de mi entorno social,
ambiental y cultural.
Concepto de
potencia como la
rapidez con la que
se consume energía
en situaciones de la
vida cotidiana.
Siempre apliqué en
situaciones de la vida
cotidiana, el concepto
de potencia como la
rapidez con la que se
consume energía.
En ocasiones apliqué
en situaciones de
la vida cotidiana, el
concepto de potencia
como la rapidez con
la que se consume
energía.
Casi nunca apliqué en
situaciones de la vida
cotidiana, el concepto
de potencia como la
rapidez con la que se
consume energía.
Nunca apliqué en
situaciones de la vida
cotidiana, el concepto
de potencia como
la rapidez con la que
se consume energía.
Valoración
Excelente: 15 a 16 puntos.
Bueno: 11 a 14 puntos.
Suficiente: 7 a 10 puntos.
Mi puntaje
Mi total
Insuficiente: 4 a 6 puntos.
II. Ha llegado el momento de que entregues a tu profesor todos los productos de las actividades que realizaste durante este bloque y que guardaste en tu portafolio de evidencias, ya que con esto podrá evaluarte.
Autoevaluación
I. Realiza en tu cuaderno lo que se te pide.
1. En un recipiente de forma cúbica se confina un gas cuyas moléculas se pueden mover libremente chocando contra las paredes; debido a tales choques, las moléculas cambian de dirección y velocidad. En
un momento dado una de las paredes se convierte en un émbolo y se desplaza. A partir de este suceso
realiza lo siguiente:
a. Describe lo que ocurre en el sistema.
b. Identifica qué fuerzas se presentan.
c. Formula un modelo básico del trabajo realizado.
d. ¿Qué tipo de energía se presenta?
162
st-editorial.com
2. Es común que a nuestra mente venga la imagen de un equipo o máquina que se detiene cuando falla el
suministro de energía eléctrica, ¿es posible que se conserve la energía en una máquina y se transforme
para producir la potencia que se requiere en ciertas operaciones de carácter productivo? Indica al menos dos sistemas mecánicos que cumplan con la condición de ser agentes que almacenan energía y la
transforman para producir potencia.
3. Calcula el trabajo realizado por un sistema elevador que transporta desperdicios en un edificio de 16
pisos considerando que la altura total de cada piso es de 3.6 m y que la masa transportada del piso
12 al 1 es de 1 760 kg, incluyendo la masa del equipo transportador.
4. El sistema de frenos de un auto de 1 360 kg falla cuando se encuentra estacionado sobre una pendiente y
empieza a descender lentamente porque una fuerza total de fricción de 1 000 N se opone al movimiento.
Determina la velocidad que alcanza cuando ha descendido una altura de 8 m recorriendo 24 m a lo largo
de la pendiente.
5. En el juego del tiro al blanco de una feria, un joven dispara contra un muñeco de madera de tal manera
que un solo balín de 1.8 g penetra en el muñeco 6 cm y se detiene por completo. Determina la magnitud de la fuerza disipadora de energía considerando que al momento del impacto el balín tiene una
velocidad de 20 m/s.
6. Emplea el principio de conservación de la energía para calcular la velocidad de cada contrapeso para el
instante en que el de 12 kg ha ascendido 20 cm. La masa de la polea y la fricción son despreciables.
7. Calcula la potencia (en hp) necesaria en un sistema de bombeo de agua potable para que la eleve a 90
m desde el cuarto de bombas hasta lo alto de una colina en la que se encuentra un pequeño poblado,
a una razón de 1 m3/s. La eficiencia del sistema es de 74% por las pérdidas de energía en equipos y
tuberías.
II. Relaciona las columnas; posteriormente, regresa al bloque para verificar tus respuestas y modifica
aquellas que no sean correctas.
1. ( ) La energía es…
a. mayor deformación.
2. ( ) La fuerza de fricción es capaz de…
b. retardar el movimiento de un cuerpo.
3. ( ) Cuando la energía mecánica total no con- c. almacenar la energía.
d. una fuerza impulsora.
sidera pérdida alguna se habla de…
4. ( ) Para una misma cantidad de energía potencial e. la conservación de la energía.
f. el agente capaz de producir trabajo.
tenemos que a mayor rigidez elástica…
g. menor deformación.
5. ( ) Cuando el trabajo involucra a las fuerzas h. el trabajo total del sistema.
elásticas y potenciales es igual a…
i. realizar trabajo.
6. ( ) La potencia mide la capacidad para…
j. disipar la energía.
III. Reflexiona y responde en tu cuaderno a cada una de las preguntas:
1. ¿Consideras que es importante el estudio de la relación entre trabajo y energía?, ¿ por qué?
2. ¿Crees posible que se pueda construir una máquina que no presente perdidas de energía en su funcionamiento?
3. ¿Se te dificulta el estudio de los cambios de energía en resortes?
4. ¿En qué situaciones de tu vida a futuro como profesionista consideras que emplearás los conocimientos que has adquirido?
5. ¿Te consideras apto para estudiar por tu cuenta estos y otros temas que sean afines?
IV. En la siguiente lista de cotejo se presentan una serie de aspectos para que evalúes el desempeño de uno
de tus compañeros durante la realización del reto.
Aspecto
Siempre
Algunas veces
Nunca
Me integré al trabajo en equipo.
Realicé comentarios acertados de acuerdo con el tema.
Escuché a mis compañeros y al profesor con atención y respeto.
Participé en todas las actividades.
st-editorial.com
163
SECCIÓN FINAL
Sección
final
164
st-editorial.com
IDENTIFICA A LA QUÍMICA COMO
UNA HERRAMIENTA PARA LA VIDA
st-editorial.com
PRÁCTICAS DE LABORATORIO
166
EVALUACIÓN FINAL
171
PARA TERMINAR.
AUTOEVALÚA TUS COMPETENCIAS
175
FUENTES CONSULTADAS
176
165
PRÁCTICAS DE LABORATORIO
Práctica de laboratorio 1
Medición y errores
Una actividad fundamental de cualquier economía es la metrología, campo de aplicación de la física que define los patrones de medición y las pautas a seguir para garantizar que todo
proceso productivo cumpla con normas, estándares y demás
lineamientos que puedan asegurar una calidad específica.
d
Objetivo
Observar errores en una medición.
Materiales
• Dos ligas planas de 5 mm de ancho
• Platillo de 25 gr
• Una pesa de 25 gr
• Pesas pequeñas de masas diferentes y desconocidas
• Soporte universal
• Regla metálica de 30 cm
• Marcador de punto fino
• Una báscula electrónica
Problema
¿Cómo nos percatamos de errores en una medición?
Procedimiento
Construye una balanza de resorte con las ligas tal como
muestra la figura, antes de colocar el platillo, determina la
longitud de las ligas.
3. Procede a determinar cada peso desconocido con ayuda
de la relación k, la ley de Hooke indica que la constante
k permanece invariable mientras la liga no pierda sus
propiedades.
4. Elabora una tabla con tus resultados anotando en una
columna el valor que se mide en la báscula electrónica.
Cuestionario
1. ¿Coincide el peso de la báscula con el peso que calculaste?
2. ¿Determina el error en cada caso?, ¿a qué lo atribuyes?
3. ¿Qué principios se usan actualmente para diseñar instrumentos de medición?
4. ¿Qué puedes concluir?
Práctica de laboratorio 2
Tiro horizontal
Aunque el estudio del movimiento de un proyectil ha sido ampliamente utilizado con fines bélicos, el tiro horizontal es muy
útil en labores de ayuda en situaciones de urgencia para suministrar víveres y medicamentos en comunidades aisladas.
Objetivo
Construir un sistema de tiro horizontal y comparar resultados teóricos y prácticos en un disparo.
Materiales
1. Coloca una pesa de 25 gr, con este arreglo determina la
relación:
p
k= d
Donde:
d = deformación (longitud final – longitud inicial) que se
produce en la liga por la acción del peso.
p = peso conocido, que este caso corresponde al del platillo y la pesa de 25 gr, es decir 50 gr.
2. Procede a colocar cada una de las pesas cuya masa es
desconocida y en cada caso mide la deformación que sufren las ligas.
166
• Una tira de madera lisa de 12 mm de espesor, 4 cm de
ancho y 80 cm de largo
• Una base de madera cuadrada de 25 cm de lado y 12 mm
de espesor
• Una ménsula
• 80 cm de tubo lexible para instalaciones eléctricas de
½ pulgada de diámetro
• Un balín
• Abrazaderas de plástico
• Un cronometro
• Una navaja
Problema
¿Cómo construir un sencillo sistema de disparo a escala?
st-editorial.com
Procedimiento
1. Pega la ménsula a la tira de madera a 40 cm de un extremo, de tal manera que la curva quede por arriba de la
horizontal. Pega la tira de madera a la base.
2. Coloca la manguera en la tira, siguiendo la trayectoria
curva de la ménsula, fíjala con las abrazaderas de plástico cuidando de que la manguera no se aplaste en los
sitios de contacto.
3. Realiza diferentes cortes en la manguera para que puedas colocar el balín y soltarlo desde diferentes alturas.
• Soporte universal
• Regla metálica de 30 cm
• Marcador de punto fino
Problema
¿Cómo podemos darnos una idea de su ubicación en forma
aproximada?
Procedimiento
1. Dibuja diversas figuras irregulares en el papel cascarón y
recórtalas con el cúter. Ten cuidado, apóyate en una superficie adecuada y haz los cortes despacio para evitar accidentes. Aunque te sugerimos algunas formas, tu profesor
te puede ayudar a determinar cuáles debes dibujar y cortar.
2. En cada una selecciona tres puntos en los cuales harás
un pequeño orificio.
3. Selecciona una de las formas geométricas, coloca el hilo
4. Coloca el balín para cada una de las alturas que definas
y toma el tiempo que tarda en tocar la superficie a partir
del momento en que sale disparado.
5. Registra la distancia a la que cae el balín.
Cuestionario
1 Calcula la velocidad inicial del lanzamiento considerando que conoces la altura desde la cual cae el balín en
caída libre.
2. Calcula los valores teóricos del alcance y de la velocidad
del balín justo al momento del impacto.
3. ¿A qué atribuyes la diferencia? ¿Qué factores inluyen?
4. ¿Qué puedes concluir?
en uno de los orificios y ata la figura en el soporte universal dejando que caiga unos 6 cm, el hilo sobrante ponlo
al frente de la figura de tal manera que puedas obtener la
línea de acción de la fuerza de gravedad.
4. Marca en los bordes de la figura la trayectoria de la línea
de acción. Retira la figura y con ayuda de la regla dibuja
la línea de acción para el primer punto de sujeción.
5. Ata ahora el hilo en los otros puntos y repite el procedimiento hasta obtener las tres líneas de acción. La intersección de tales líneas ocurre en un punto: el centro de masa.
6. Repite con las otras figuras o cuerpos que hayas seleccionado junto con tu profesor el procedimiento para obtener
el centro de masa. Conserva las figuras para otra actividad.
Cuestionario
1. ¿En todos los casos el centro de masa se ubica en el cuerpo?
2. ¿Hubo casos en los que no coincidía el punto de intersección de las tres líneas?, ¿a qué lo atribuyes?
Práctica de laboratorio 3
3. ¿Qué puedes concluir?
El conocimiento del centro de masa de un cuerpo es importante porque esto permite diseñar equipos, máquinas y
sistemas más eficientes como es el caso de autos, grúas,
lavadoras, etc.
Práctica de laboratorio 4
Centro de masa
Objetivo
Determinar el centro de masa de un cuerpo.
Materiales
• Papel cascarón
• Cúter
• Hilo
st-editorial.com
Cálculo experimental de la
aceleración de la gravedad
Te proponemos realizar un sencillo experimento que te permitirá calcular el valor numérico de la aceleración de la gravedad
en tu localidad, la expresión que ocupamos corresponde al
resultado que obtuvo Galileo Galilei cuando estudiaba el comportamiento de un péndulo.
Objetivo
Calcular el valor numérico de la aceleración de la gravedad
en tu localidad.
167
PRÁCTICAS DE LABORATORIO
Materiales
2. ¿Qué error puedes calcular asumiendo que el valor
• Una pelota de golf vieja
• Un metro de hilo cáñamo
• Una armella
• Un soporte universal
• Un cronómetro
• Papel ilustración (38 cm x 26 cm)
g = 9.8095 m/s2 es un promedio aceptado a nivel mundial
para fines prácticos?
3. Determina con la ley de atracción universal de Newton la
aceleración de la gravedad en tu localidad. ¿A qué atribuyes la variación?
4. ¿Qué puedes concluir?
Problema
Práctica de laboratorio 5
¿Cómo podemos conocer el comportamiento de un péndulo?
Procedimiento
1. Inserta la armella en la pelota de tal manera que puedas
unirla a la cuerda.
2. Ata la cuerda al soporte universal de forma tal que la
longitud efectiva del péndulo sea de 32 cm.
3. Coloca el arreglo de tal manera que la cartulina ilustración quede como fondo para el experimento, marca una
línea vertical de referencia y un ángulo de 35°.
4. Desplaza el péndulo a la referencia de 35° y suéltalo con
cuidado para que el movimiento se dé en un solo plano.
Simultáneamente toma el tiempo que se requiere para
que realice 20 oscilaciones completas.
Segunda ley de Newton:
masa y aceleración
El cálculo de la aceleración de un sólido es importante porque nos ayuda a establecer la fuerza que puede producir y
a determinar su comportamiento cinemático, así como sus
posibles aplicaciones.
Objetivo
Cálcular la aceleración de un sólido.
Materiales
• Bloque de acero pulido de 250 gr con un armella al centro
de uno de los costados
• Pesas de diferente gramaje: 50 gr, 100 gr y 250 gr.
• Un vidrio de 20 cm × 30 cm
• Una polea y cordón
• Cronómetro
• Una regla de 30 cm
• Marcador de punto fino
Problema
¿Cuál será su comportamiento cinemático y sus posibles
aplicaciones?
L = 35 cm
Procedimiento
1. Prepara en tu mesa de trabajo un arreglo de la siguiente forma:
vidrio
pesa
5. Repite el experimento en cuatro ocasiones más.
Cuestionario
1. ¿Cuál es el valor de la aceleración de la gravedad? Para
calcularlo divide cada uno de los valores de tiempo obtenido entre 20. Utiliza la expresión:
4r 2 l
g= 2
t
Donde:
l = 32 cm.
t = tiempo obtenido al dividir entre 20 el valor registrado
para 20 oscilaciones.
Registra los valores experimentales obtenidos y calcula
el valor promedio.
168
2. Coloca un peso igual al peso del bloque y observa cómo
se comporta el sistema.
3. Coloca un peso mayor en 50 gr al peso del bloque y toma
el tiempo requerido para que el bloque de acero recorra
20 cm sobre el vidrio (marca previamente los puntos inicial y final del recorrido sobre el vidrio).
4. Incrementa el peso de 50 en 50 gr hasta que la pesa tenga
el doble del valor del bloque y en cada caso registra el
tiempo para el recorrido.
5. ¡Precaución! Hemos usado una superficie de vidrio y un
bloque de acero para que las superficies se deslicen fácilmente, realiza tu experimento con el mayor cuidado para
evitar accidentes.
st-editorial.com
Cuestionario
1. De acuerdo con la velocidad y la distancia recorrida, ¿cuál
es la aceleración del bloque? Realiza los cálculos necesarios.
2. Verifica la magnitud de la velocidad obtenida con el tiempo
registrado y la aceleración obtenida en el punto anterior.
3. Elabora una tabla donde muestres todos los valores, tanto registrados como calculados.
4. ¿Qué tanto afecta el hecho de que ignoremos la fricción?
5. ¿Qué puedes concluir de los valores de aceleración?
Práctica de laboratorio 6
Fuerza de fricción
Todos los cuerpos presentan características de rugosidad,
aunque a simple vista no lo notemos y nuestro tacto no lo
perciba, los acabados de las superficies fabricadas por el
ser humano no son perfectos y al deslizar un cuerpo sobre
otro se presenta una fuerza que se opone al movimiento,
transformando la energía mecánica en calor, el cual se genera por la fricción.
Objetivo
8. Toma el otro prisma y registra los valores que obtienes
para la mezclilla, el vidrio, etc.
Cuestionario
1. Calcula el coeficiente de fricción empleando las leyes de
Newton y evaluando directamente la tangente del ángulo
que mediste.
2. Registra en una tabla los resultados que obtuviste.
3. ¿Qué diferencia existe entre los valores obtenidos por las
ecuaciones de movimiento y con la tangente del ángulo
medido?, ¿a qué lo atribuyes?
4. ¿Cómo determinas el otro coefeciente?
5. ¿Qué puedes concluir?
Práctica de laboratorio 7
Trabajo y energía
Parte 1. Centro de masa
Objetivo
Calcular el coeficiente de fricción.
Determinar el trabajo realizado por cada figura geométrica y
la velocidad del centro de masa.
Materiales
Materiales
• Dos tablas perfectamente lisas de 12 mm de espesor y
12 cm de ancho por 25 cm de largo, unidas en un extremo
por un par de bisagras
• Dos prismas de madera de 3 cm por lado en la base y 7 cm
de longitud
• Papel lija de cuatro grados: gruesa, mediana, fina y extrafina
• Un trozo de mezclilla, un trozo de cartoncillo, un vidrio de
3 cm de ancho por 7 de longitud
• Pegamento blanco
• Un transportador
• Una balanza
Problema
¿Qué coeficiente de fricción se obtiene: el estático o el
dinámico?
Procedimiento
1. Pega un trozo de cada tipo de lija en los costados de uno
de los prismas.
2. Pega en el otro prisma el vidrio, el cartoncillo y la mezclilla, en el lado libre del prisma sólo aplica una capa de
pegamento y deja que se seque.
3. Obtén con la balanza la masa de cada prisma y calcula
su peso.
4. Sujeta firmemente una de las tablas a la mesa de trabajo
y fija el transportador en el costado de la tabla en el extremo en que se halla la bisagra.
5. Coloca el prisma con el lado de lija gruesa haciendo contacto con la superficie de la tabla y muévela lentamente
hacia arriba.
6. Registra el ángulo en el que se inicia el movimiento del
prisma.
7. Repite para los otros costados del prisma.
st-editorial.com
• Figuras geométricas de la práctica de laboratorio 3
• Una báscula electrónica
• Alfiler
• Papel cascarón
• Cronómetro
Problema
¿Cuál es la velocidad del centro de masa?
Procedimiento
1. Utiliza las figuras geométricas de la práctica de laboratorio 3.
2. Pesa cada una de ellas y anota el valor correspondiente.
3. Coloca una de ellas sobre un papel cascarón que se encuentre en posición vertical, emplea un alfiler y ubica la
figura de tal manera que el centro de masa se ubique por
arriba del alfiler a 90° con respecto a la horizontal.
4. Impulsa la figura en sentido horario y déjala caer, toma el
tiempo para que el centro de masa se ubique por debajo
del alfiler.
5. Repite el procedimiento con las otras figuras.
Cuestionario
1. ¿Cuál es el trabajo realizado por cada figura geométrica:
W = mgh?
2. ¿Cuál es, según el principio de trabajo y energía, la velocidad del centro de masa al pasar por debajo del alfiler.
3. De acuerdo con los valores de tiempo, distancia y aceleración de la gravedad, determina la velocidad del centro
de masa.
4. ¿Qué puedes concluir?
169
PRÁCTICAS DE LABORATORIO
Parte 2. Segunda ley de Newton:
masa y aceleración
Problema
Objetivo
Procedimiento
Calcular la velocidad de un sólido sin recurrir al cálculo de la
aceleración con la segunda ley de Newton.
¿Por qué el calor produce este efecto?
1. Corta un rehilete de 9 cm de diámetro como se muestra
en la figura:
Materiales
• Material empleado en la práctica 5
Problema
¿Cómo determinas la velocidad de un cuerpo sin conocer
su aceleración?
Procedimiento
Repite el experimento del bloque de acero.
Cuestionario
2. Coloca el alambre rodeando el foco de 60 W, de tal
manera que sobresalga en forma perpendicular una
sección de 2 cm de altura.
3. Coloca el foco en el socket y el rehilete sobre el foco.
1. Con la relación de conservación de la energía, determina
la velocidad del bloque de acero cuando llega a los 20 cm.
2. Calcula la potencia desarrollada por el bloque.
3. ¿Qué puedes concluir?
Práctica de laboratorio 8
Energía
La energía se encuentra a nuestro alrededor y se manifiesta
en diferentes formas, en ocasiones, nuestras actividades cotidianas nos llevan a ignorar que estamos rodeados por ella.
Objetivo
Demostar que la energía se manifista de formas diferentes.
Material necesario
• Un socket con conexión a una toma de corriente eléctrica
• Un foco de 60 watts, uno de 100 watts y uno ahorrador de
energía de luz blanca
• Un trozo de alambre de 15 cm de longitud aproximadamente
• Una hoja de papel tamaño carta
170
4. Conecta a la energía eléctrica.
5. Espera de 5 a 10 minutos y observa, toma nota.
6. Repite con los otros dos focos.
Cuestionario
1. ¿En qué foco se inició el movimiento en el menor tiempo?
2. Identifica los tipos de energía presentes.
3. ¿En qué otras situaciones de nuestra vida cotidiana hay
transformaciones de energía que nos hacen pensar que
siempre se cumple la ley de conservación de la energía?
4. ¿Qué hace que no se cumple tal ley al cien por ciento en
este experimento?
st-editorial.com
EVALUACIÓN FINAL
Dado que al concluir el curso de Física 1 tienes un nuevo conocimiento en relación con las áreas básicas de
la física, te sugerimos que resuelvas el siguiente cuestionario y los ejercicios propuestos. Toma en cuenta
los siguientes puntos:
• No hay un estricto orden respecto de los temas tratados porque necesitas evaluar tu aprendizaje.
• Las preguntas no sólo se refieren a aspectos teóricos, también se relacionan con la manera en que aplicas en forma “práctica” tus conocimientos.
I. Responde el siguiente cuestionario.
1. ¿Qué enuncia la ley de la gravitación universal?
2. ¿Qué es una hipótesis?
3. ¿Qué es la energía? Cita algunas formas en las que se puede presentar la energía.
4. ¿Cuál es la diferencia entre observar y experimentar?
5. ¿Qué caracteriza a los sistemas de unidades absolutos?
6. ¿Por qué la hoja de un árbol y una piedra no caen con la misma velocidad en la presencia del viento?
7. ¿Cuál es la primera ley de Newton?, escríbela.
8. ¿Cuál es la diferencia fundamental entre la masa y el peso de los cuerpos?
9. ¿Cuáles son las formas básicas de energía potencial?
10. ¿Qué estudia la dinámica?
11. ¿Qué emplea un físico como herramienta para el desarrollo de una investigación?
12. ¿Qué es fricción estática?
13. ¿Qué se requiere para que un cuerpo viaje con aceleración constante?
st-editorial.com
171
EVALUACIÓN FINAL
14. ¿Cuándo se dice que una máquina es más potente que otra?
15. ¿Qué trabajo realiza el peso de un cuerpo que se mueve horizontalmente?
16. ¿De qué manera se puede reducir la fricción?
17. ¿Por qué se afirma que Galileo es el padre de la física experimental?
18. ¿De qué manera contribuye la física a la satisfacción de las necesidades del ser humano?
19. ¿Cuál es la diferencia entre distancia y desplazamiento?
20. ¿Por qué se presenta la aceleración centrípeta?
21. ¿Qué es un fenómeno?
22. ¿Qué es una unidad fundamental?
23. ¿Qué tipos de energía se presentan en un péndulo en movimiento?
24. ¿En qué casos el trabajo se transforma en energía calorífica?
25. ¿Qué ocurre con la fuerza que se necesita aplicar a un cuerpo para que no resbale por un plano inclinado conforme éste aumenta su pendiente?
26. ¿Cómo son entre sí el trabajo invertido y el trabajo producido por una máquina?
27. ¿De cuántas maneras se puede lanzar un misil para que alcance el mismo objetivo?
28. ¿De qué manera puede cambiar la magnitud de la velocidad tangencial de un objeto en movimiento
circular sin cambiar la dirección?
172
st-editorial.com
29. ¿Qué es un sistema coordenado de referencia?
30. ¿Qué es una cifra significativa?
31. ¿Qué tipo de trabajo se realiza cuando un cuerpo acelera por la acción de una fuerza exterior?
32. ¿De qué manera podrías calcular la masa de la Tierra?
33. ¿Qué tipo de energía se almacena en un resorte?
34. ¿Qué mide la báscula cuando acudes a una tienda y pides cierta cantidad de alimento?
35. ¿Qué tipos de errores se presentan en una medición?
II. Realiza en tu cuaderno de notas los ejercicios que se proponen a continuación; después coteja tus respuestas
con tu libro.
1. ¿A qué altura sobre el nivel de la superficie terrestre la aceleración de la gravedad es igual a la mitad
del valor promedio aceptado mundialmente?
2. Determina la fuerza que ejerce un martillo de 2 kg sobre los clavos cuando un carpintero construye
3.
4.
5.
6.
7.
8.
una silla, si la velocidad con la que golpea cada clavo es de 2 m/s y la distancia que se introduce cada
clavo en la madera es de 19 mm.
Las ciudades de Novorita y Granate se unen por medio de una nueva autopista que es completamente recta y ha reducido a 300 km la distancia que las separa. En la prueba de un nuevo modelo de
camioneta, una sale de Novorita al mediodía exactamente (12:00 h) hacia Granate con una velocidad
de 75 km/h, y otra camioneta sale de Granate, al mismo tiempo, con rumbo a Novorita, y con una
velocidad de 55 km/h. ¿A qué hora se cruzarán ambas camionetas? ¿Qué distancia hay de Granate al
punto de cruce?
Determina el peso máximo que puede elevar un polipasto si la potencia máxima que desarrolla en
condiciones normales de operación es de 25 kW y la velocidad con la que se iza la carga es constante
e igual a 9 m/s. ¿Es posible aumentar el peso reduciendo la velocidad sin riesgo de falla?
Si la fuerza que requiere un auto con una masa de 1 200 kg para moverse durante los primeros 100 m
de su recorrido es de 4 500 N, determina el trabajo desarrollado y la potencia empleada considerando
que utiliza una velocidad constante en un tiempo promedio de 14 s.
Determina en forma gráfica la resultante de un vector de 120 u de magnitud que forma un ángulo de 30°
con la horizontal y que se suma a otro vector de 100 u de magnitud que forma un ángulo de 270° con la
horizontal. Ambos ángulos se miden en sentido contrario al movimiento de las agujas del reloj.
A un refugio de ladrones en una colina se lanza un proyectil desde la base con una velocidad de 50 m/s
y un ángulo de 50° respecto a la inclinación de la colina, cuya pendiente es de 20° medida en relación
con la horizontal. ¿Cuál es el alcance del proyectil?
Determina la velocidad con la que inicialmente se lanza una pelota en un tiro vertical si el registro de
tiempo indica que regresa al mismo lugar de lanzamiento 4 s después.
st-editorial.com
173
EVALUACIÓN FINAL
9. Realiza en forma analítica las operaciones vectoriales siguientes: 2A + B – C y F + B − 3C = 0, siendo
los vectores A = 2i + 3j, B = -2i – 4j y C = 2i – 6j.
10. Determina la energía almacenada en el resorte de una báscula que se emplea para pesar 1 kg de mandarina, si se asume que la rigidez elástica del resorte es de 25 N/m.
11. Una barcaza lanza un proyectil sobre el nivel del mar a un ángulo de 30° con la horizontal y con una
rapidez de 90 km/h. Determina la distancia a la que caerá, el tiempo que le tomará alcanzar el objetivo
y la altura máxima sobre el nivel del mar que adquiere en su trayectoria de vuelo.
12. Si todo el trabajo se transforma en calor y no hay pérdidas de energía, ¿qué cantidad de calor se produce cuando un cuerpo de 90 kg cae desde una altura de 10 m y choca contra el suelo?
13. En unas vacaciones observas que 100 m atrás del autobús en que viajas, una patrulla circula a 120 km/h, mientras que la rapidez del autobús está limitada a 60 mph. ¿Cuál es la velocidad de la patrulla con respecto al autobús? Si la velocidad de ambos vehículos es constante, ¿qué tiempo le toma a la patrulla alcanzar al autobús?
14. Un satélite viaja alrededor de la Tierra en una trayectoria circular con una velocidad de 17 500 km/h.
Si la aceleración gravitacional en su trayectoria es de 3 m/s2, determina el radio de la trayectoria y la
altitud en la que se encuentra cuando pasa por un punto en el que el radio terrestre es de 6 375 km.
15. Calcula la velocidad media que emplea un autobús en viajar del Salado a Buenaventura si el recorrido
de 187 km lo efectúa en 2 h y 25 min.
16. Se aplica una fuerza de 120 N a un miniauto de juguete de 45 kg de tal manera que forma un ángulo
de 20° con la superficie horizontal por la que circula. Determina el tiempo necesario para que alcance
una velocidad de 7.2 m/s a partir del reposo.
17. Determina el desplazamiento de una alpinista que para alcanzar el pico de una montaña nevada
asciende 39 km en dirección norte, gira hacia el este y avanza 3 km para evitar una falla geológica,
asciende de nuevo 60 km en dirección noroeste, y de nuevo gira hacia el norte para avanzar 4 km y
llegar a la cima. ¿Cuál es la distancia recorrida? ¿Qué tiempo le llevará llegar a la cima si su rapidez
promedio es de 3 km/h debido al clima, y descansa 8 h por cada 8 h de recorrido?
18. Una rueda de esmeril trabaja a 500 rpm cuando se corta el suministro de energía eléctrica. Determina
el número de vueltas que gira hasta detenerse por completo considerando que desacelera a razón
de 8 rad/s2 y que el operador no ejerce ninguna fuerza para reducir la marcha de la herramienta.
¿Cuánto tiempo se requiere para el alto total?
19. Determina el tiempo que se requiere para que un malacate eleve una carga de 1 000 kg a una altura
de 12 m, considerando que la potencia del conjunto de tracción del malacate es de 30 kW.
20. Una muchacha que está aprendiendo a manejar viaja a una velocidad de 20 km/h y observa que un
semáforo a 150 m de donde ella se encuentra cambia de verde a rojo. La luz roja dura en el semáforo 30 s. Determina si la muchacha requiere acelerar o viajar a velocidad constante para pasar sin
detenerse en el semáforo.
III. Relaciona las columnas.
1. ( ) Unidad de potencia en el sistema inglés.
2. ( ) Efecto que produce una fuerza cuando actúa a lo largo de una distancia.
3. ( ) Proposición que puede ser demostrada.
4. ( ) Medida de cómo funciona una máquina.
5. ( ) Explicación de un fenómeno por lo que se conoce a través de la
experimentación.
6. (
7. (
8. (
9. (
10. (
11. (
12. (
) Conclusión general sobre la relación entre causa y efecto.
) Comparar una magnitud con la unidad patrón.
) Magnitud de la velocidad.
) Rapidez con la que se realiza trabajo.
) Capacidad de un sistema para realizar trabajo.
) Fuerza que se opone al movimiento.
) Propiedad de los cuerpos que se manifiesta como la oposición al cambio
13. (
14. (
) Aceleración que apunta hacia el centro de curvatura.
) Ubicación específica de un cuerpo en un sistema de referencia.
a. Rapidez.
b. Centrípeta.
c. Eficiencia.
d. Fricción.
e. Caballo de fuerza.
f. Posición.
g. Potencia.
h. Ley.
i. Inercia.
j. Energía.
k. Trabajo.
l. Medir.
m. Teorema.
n. Teoría.
de estado de reposo o movimiento.
174
st-editorial.com
PARA TERMINAR. AUTOEVALÚA TUS COMPETENCIAS
Ahora que has terminado este curso, es conveniente que hagas un alto para reflexionar sobre las competencias
genéricas que has adquirido. En el siguiente cuadro, señala el nivel que consideres que has logrado en cada
aspecto. Contesta con honestidad.
SIEMPRE FRECUENTEMENTE POCO
CASI NUNCA
NUNCA
1
Te conoces, te valoras y abordas los problemas
y retos a partir de objetivos.
2
Eres sensible al arte y lo aprecias e interpretas
en todas sus expresiones.
3
Eliges y practicas estilos de vida saludables.
4
Escuchas, interpretas y emites mensajes pertinentes en distintos
contextos, mediante la utilización de herramientas y medios apropiados.
5
Desarrollas innovaciones y propones soluciones
a problemas a partir de un método seleccionado.
6
Mantienes una postura personal sobre temas de interés y
consideras otros puntos de vista de manera crítica y reflexiva.
7
Aprendes por iniciativa e interés propio a lo largo de la vida.
8
Participas y colaboras de manera efectiva en trabajos de equipo.
9
Participas con una conciencia cívica y ética en la vida
de tu comunidad, la región, México y el mundo.
10
Mantienes una actitud respetuosa hacia la diversidad de culturas,
creencias, valores, ideas y prácticas sociales de otras personas.
11
Contribuyes al desarrollo sustentable del medio ambiente,
de manera crítica y con acciones responsables.
st-editorial.com
175
FUENTES CONSULTADAS
Libros
Alonso, M. y E. J. Finn. Física. Vol. 1. México: Fondo Educativo Interamericano, 1970.
Bureau International des poids et mesures. Le Système international d’unités (si). 8e
édition. París: Organisation intergouvernementale de la Convention du Mètre,
2006.
R. Chappert y R. Picand. La mécanique par les problèmes. Fascículos 2 y 3. París: Les
Éditions Foucher, 1985.
Cohen, M. y E. Nagel. Introducción a la lógica y al método cientíico. Vols. 1 y 2. Buenos
Aires: Amorrortu Editores, 1968.
Giancoli, D. C. Física, principios con aplicaciones. 4ª ed. México: Prentice Hall, 1999.
Gié, H. y J. P. Sarmant. Mecánique. París: Technique et Documentation (Lavoisier), 1984.
Gieck, K. Manual de fórmulas técnicas. 75ª ed. México: Alfaomega Grupo Editor, 2003.
Hewitt, P. G. Física conceptual. 9ª ed. México: Pearson Educación, 2004.
Serway, R. A. y J. S. Faughn. Fundamentos de física. Vol. 1. México: homson, 2004.
Tippens, P. E. Física, conceptos y aplicaciones. 6ª ed. México: Mc Graw-Hill, 2001.
Páginas web
Axxón. http://axxon.com.ar
AstroMía. www.astromia.com/
Automovilonline. www.automovilonline.com.mx
Arrakis. www.arrakis.es
Ciencia Popular. www.cienciapopular.com
Escuela Politécnica Superior, España. www.ii.uam.es
Foro Por tierra, mar y aire. www.portierramaryaire.com
Investigación y desarrollo. www.invdes.com.mx
Organización de Estados Iberoamericanos para la Educación, la Ciencia y la Cultura.
www.oei.es
Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura.
www.unesco.org
Revista electrónica La ciencia y el hombre, de la Universidad Veracruzana.
www.uv.mx/cienciahombre/
Sólo Mantenimiento. www.solomantenimiento.com
unam, revista ¿Cómo ves? www.comoves.unam.mx
176
st-editorial.com