Pruebas de normalidad

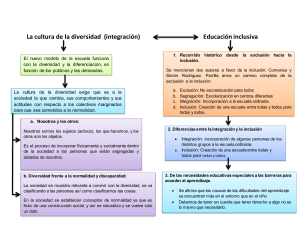
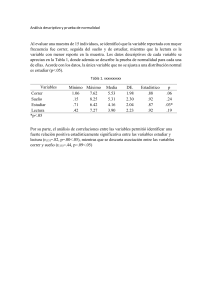
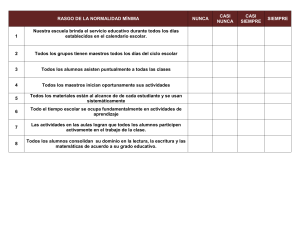
Universidad de Carabobo. Figueredo L., Francisco J. Pruebas de Normalidad.
1
Pruebas de Normalidad
Figueredo L., Francisco J.
Universidad de Carabobo

Resumen—El presente artículo presenta la importancia de
conocer la distribución de la población a la cual se ajustan los
datos, en especial si esa distribución es normal, debido a que
esta última es una condición generalmente exigida por las
pruebas paramétricas usadas en la estadística; entre las pruebas
no paramétricas se encuentran las pruebas de normalidad, que
son usadas para contrastar si se puede decir que los datos
provienen o no de una población normal, se realizó una revisión
de diferentes textos y se llegó a la conclusión que entre las
pruebas de normalidad más usadas están las que se presentan a
continuación, haciendo resaltar que cada prueba se puede usar
en diferentes situaciones, como por ejemplo si los parámetros
con los cuales se quiere ajustar son dados o pueden ser
estimados, así como el tamaño de la muestra es importante e
influye en la potencia de las diferentes pruebas.
Índice de Términos—Estadística
Normalidad, Prueba de hipótesis, Muestra.
no paramétrica,
I. INTRODUCCIÓN
Este documento presenta seis diferentes pruebas de
normalidad con la intención de dar a conocer el
procedimiento que se debe aplicar al momento de
querer realizar este tipo de contraste, estas pruebas se
muestran con el procedimiento propuesto por
Montgomery (2006) y por Maneiro y Mejías (2010)
donde proponen 8 pasos para realizar un contraste de
hipótesis, también se muestran las condiciones que
se deben cumplir para realizar cada una de estas
pruebas con el fin de que el analista utilice la prueba
correspondiente en la situación que lo amerite.
El artículo presenta como primera parte la
importancia de conocer la distribución de la
población donde provienen los datos para la
estadística paramétrica, en especial cuando esta
distribución es normal, una vez establecida dicha
necesidad se explican los ocho pasos propuestos para
las pruebas de hipótesis, por último se explican las
diferentes pruebas de normalidad: histogramas,
prueba de Duncan, prueba de χ2, prueba de Lilliefors
y Van Soest, Anderson-Darling y por último la
prueba de Shapiro-Wilk; después de estas
explicaciones se presentan las conclusiones y las
referencias utilizadas para la realización del artículo.
II. ESTADÍSTICA PARAMÉTRICA
La estadística paramétrica se puede definir como
aquella cuyos métodos permiten hacer inferencias
acerca de parámetros poblacionales de las
distribuciones, por lo tanto, la distribución aleatoria
a la cual se ajusta la población de la cual se extraen
los datos es conocida. Este tipo de estadística es
preferida por los analistas ya que, las distribuciones
son específicas, se pueden confirmar los supuestos
distribucionales y generalmente son más potentes
que las pruebas realizadas con estadística no
paramétrica.
La mayor parte de los procedimientos de prueba de
hipótesis e intervalos de confianza se basan en la
hipótesis de que se trabaja con muestras aleatorias
tomadas de poblaciones normales [1]. Esto hace que
sea necesario conocer si dichos datos provienen o no
de una población normal.
III. LA DISTRIBUCIÓN NORMAL
Este modelo es muy usado en el análisis
económico y comercial para definir el
comportamiento de los procesos; y en el ámbito de
confiabilidad se utiliza para calcular la confiabilidad
donde el equipo se encuentra en situaciones de
desgaste.
Esta distribución puede obtenerse al considerar el
modelo básico de una variable aleatoria binomial
cuando el número de ensayos se vuelve cada vez más
grande, este enfoque fue el originalmente usado por
De Moivre en 1733 [1], luego fue Karl Friedrich
Gauss (1777-1855), quien derivó su ecuación a partir
Seminario Doctoral “Análisis estadístico de datos en Ingeniería” DII-5013 VLC 2017
Universidad de Carabobo. Figueredo L., Francisco J. Pruebas de Normalidad.
de un estudio de errores en mediciones repetidas de
la misma cantidad [2].
La importancia de la distribución normal se
extiende más allá de proporcionar aproximaciones a
las probabilidades binomiales. Por ejemplo, puede
demostrarse que cada vez que un experimento
aleatorio está formado por una serie de ensayos
independientes, donde cada uno da como resultado
un valor observado de la variable aleatoria en
particular, entonces la variable aleatoria representa el
resultado promedio (o total) en n ensayos, tiende
hacia una distribución con función de densidad de
probabilidad similar a la de una distribución normal.
Dicha función es:
1
𝑓 𝑥
𝑒
1
√2𝜋𝜎
∞ 𝜇 ∞𝑦𝜎 0
Cuando la ecuación (1) se cumple, entonces se dice
que la distribución es una normal con 𝐸 𝑥
𝜇𝑦𝑉 𝑥
𝜎 y dicha distribución se grafica como
se muestra en la figura 1.
Figura 1. Curva normal
IV. PRUEBAS DE NORMALIDAD
Una vez identificada la importancia de la
distribución normal, se hace necesario saber si los
datos que se están usando provienen de una
distribución normal. Para esto existen las llamadas
pruebas de normalidad que pueden hacer salir de
dudas a los investigadores que necesiten saber dicha
información.
Entre las pruebas más usadas se destacan a) los
histogramas, b) Duncan (prueba de asimetría y
curtosis), c) la prueba de χ2, d) Lilliefors y Van Soest
(Kolmogorof-Smirnov), e) Anderson-Darling y, f)
2
Shapiro-Wilk, entre otras.
Para explicar cada una de estas pruebas se
procederá a usar los ocho pasos para realizar una
prueba de hipótesis propuesta por Montgomery [1] y
por Maneiro y Mejías [3], los cuales son: 1)
identificar el parámetro de interés, del contexto del
problema, 2) establecer la hipótesis nula H0, 3)
establecer la hipótesis alternativa H1 apropiada, 4)
seleccionar un nivel de significación α, 5) determinar
el estadístico de prueba, 6) Establecer la regla de
decisión, 7) calcular los valores muestrales
necesarios, 8) tomar la decisión de rechazo o no de
la hipótesis nula y analizar la decisión en función del
problema.
A continuación, se presentan cada una de las
pruebas de normalidad mencionadas anteriormente:
a. Histogramas: es una representación gráfica
de los resultados como una distribución de
frecuencias [4]. Esta es la primera
aproximación para conocer si los datos
provienen o no de una población normal y
también es la menos potente de las pruebas
mencionadas en este artículo, por lo tanto, si
no se pasa esta prueba no vale la pena
comparar con otra de las pruebas.
A continuación, se plantea la prueba con el
procedimiento propuesto:
1. El interés es la distribución de la
población donde fueron extraídos los
datos
2. H0: Los datos pueden modelarse por
una distribución normal, con media y
varianza estimadas a partir de la
media y la varianza muestral para
datos agrupados
3. H1: Los datos no pueden modelarse
por una distribución normal
4. Para esta prueba no se usa el nivel de
significación
5. El estadístico tiene que ver con las
frecuencias de las clases (ver figura 2)
6. Se rechaza H0 si las barras no forman
una campana
7. Para realizar los cálculos primero se
debe determinar el número de clases,
este se determina a través de la
ecuación 𝑁 1 3,3 log 𝑛 (2),
Seminario Doctoral “Análisis estadístico de datos en Ingeniería” DII-5013 VLC 2017
Universidad de Carabobo. Figueredo L., Francisco J. Pruebas de Normalidad.
donde N es el número de intervalos de
clases y n es el total de datos que se
tienen, también este puede ser
obtenido por una tabla que se
encuentra en la mayoría de los libros
de estadística (ver tabla I), la
determinación del número de clases
es importante, ya que este puede
hacer que la conclusión cambie si no
se grafica con el número correcto.
Como segundo paso se procede a
ubicar el máximo valor y el mínimo
valor de la muestra y se construye la
tabla de distribución de frecuencias,
después se procede a trazar un eje
horizontal con una escala que
contenga los valores iniciales y
finales de cada clase, los números de
clase o los puntos medio de cada
clase, como tercer paso se traza un eje
vertical, con una escala que contenga
el mayor valor de las frecuencias de
todas las clases y por último se
dibujan las barras.
8. Se procede a dar las conclusiones
correspondientes
3
Tabla I. Número recomendado de clases
Tamaño de la muestra
Número de clases
2048-4095
12
4096-8190
13
Fuente. Maneiro y Mejías (2010)
b. Duncan (Asimetría y Curtosis): esta prueba
se basa en el supuesto de que la distribución
normal tiene un coeficiente de asimetría y
uno de curtosis constante e igual a 0, es decir
si no se puede demostrar que esto es falso
entonces se asume como normal. A
continuación, los pasos:
1. El interés es la distribución de la
población donde fueron extraídos los
datos
2. H0: Los datos pueden modelarse por
una distribución normal, con media y
varianza estimadas a partir de la
media y la varianza muestral para
datos no agrupados, a su vez tiene dos
hipótesis nulas que son la asimetría es
igual a 0 y la curtosis es igual a 0
3. H1: Los datos no pueden modelarse
por una distribución normal
4. Para esta prueba los niveles de
significación comúnmente tabulados
son de 0,01 y 0,05
5. Los estadísticos de prueba son: para
el sesgo 𝑎
para
∑
Figura 2. Histograma de frecuencia
Tabla I. Número recomendado de clases
Tamaño de la muestra
Número de clases
16-31
5
32-63
6
64-127
7
128-255
8
256-511
9
512-1023
10
1024-2047
11
el
∑
(3),
apuntamiento
3
y
𝑎
(4)
6. Se rechaza H0 si |𝑎 | 𝑉𝐶𝐴∝ ó si
𝑉𝐶𝐶∝ 𝑎
𝑉𝐶𝐶∝
7. Se
realizan
los
cálculos
correspondientes para 𝑎 y 𝑎
8. Se procede a dar las conclusiones
correspondientes
c. Prueba de χ2: esta prueba realmente se usa
para ajustar a cualquier tipo de distribución,
y se recomienda cuando se tienen más de 100
datos en al menos cinco intervalos [3], para
poder aplicar esta prueba se deben agrupar
los datos en una tabla de distribución de
frecuencias. A continuación, los pasos para
realizar esta prueba
Seminario Doctoral “Análisis estadístico de datos en Ingeniería” DII-5013 VLC 2017
Universidad de Carabobo. Figueredo L., Francisco J. Pruebas de Normalidad.
1. El interés es la distribución de la
población donde fueron extraídos los
datos
2. H0: Los datos pueden modelarse por
una distribución normal, con media y
varianza conocidas o estimadas a
partir de la media y la varianza
muestral para datos agrupados
3. H1: Los datos no pueden modelarse
por una distribución normal
4. El nivel de significación más usado
para ingeniería es 0,05; sin embargo,
en la tabla de frecuencia acumulada
de χ2 se consiguen diferentes niveles
de confianza para la prueba.
5. χ
∑
(5), donde k es
el número de intervalos de clase, 𝑓
representa a las frecuencias absolutas
de las clases y 𝑒 representa a las
frecuencias teóricas de cada clase, se
debe prestar especial atención en que
𝑓 5, en caso contrario se debe
fusionar esta clase con la clase
superior o inferior para cumplir esta
regla
6. Se rechaza H0 si 𝑋
𝑋∝;
,
donde r es el número de parámetros
estimados, para el caso de la normal
son dos parámetros
7. Para los cálculos se debe calcular 𝑝
como la probabilidad de ocurrencia
según la distribución normal del
intervalo de clase y luego se calcula
𝑒
𝑛∗𝑝
(6), para luego realizar
el cálculo del estadístico
8. Se procede a dar las conclusiones
correspondientes
d. Lilliefors y Van Soest: esta prueba
corresponde a una adaptación de la prueba de
Kolmogorof-Smirnov, solo que para
normalidad se usan las tablas propuestas por
los primeros, esta prueba se basa en la
distribución probabilidad acumulada que
dibuja la muestra y la compara con la teórica
que arroja la distribución (en este caso la
normal). A continuación, los pasos para
4
realizar esta prueba:
1. El interés es la distribución de la
población donde fueron extraídos los
datos
2. H0: Los datos pueden modelarse por
una distribución normal, con media y
varianza estimadas a partir de la
media y la varianza muestral
3. H2: Los datos no pueden modelarse
por una distribución normal
4. Para esta prueba los niveles de
significación comúnmente tabulados
son de 0,01 y 0,05
5. 𝐷
𝑀á𝑥 𝑎 ; 𝑎
(7)
6. Se rechaza H0 si 𝐷
𝐷 ;∝
7. Para efectuar los cálculos, primero se
ordenan los datos de menor a mayor y
se calcula el porcentaje de
observaciones que son menores o
iguales a cada uno de los datos
(H(xi)), después se calcula la
probabilidad teórica de que una
observación sea igual o menor a cada
valor muestral, entonces se calcula la
máxima desviación absoluta entre la
distribución
acumulada
de
frecuencias relativas para la muestra
y la distribución teórica 𝑎
|
𝑀á𝑥|𝐹 𝑋
𝐻 𝑋
(8)
y
𝑎
𝑀á𝑥 𝐹 𝑋 𝐻 𝑋
(9),
para así calcular el estadístico 𝐷
8. Se procede a dar las conclusiones
correspondientes
e. Anderson-Darling: es uno de los más
poderosos estadísticos para detectar
desviaciones de la normalidad, aunque la
prueba puede usarse para probar si una
muestra de datos proviene de una
distribución específica [3], ya que, se basa en
la comparación de la simetría de la
distribución normal. Esta prueba es válida
con muestras pequeñas, se recomienda para n
≤ 25. A continuación, los pasos para realizar
esta prueba:
1. El interés es la distribución de la
población donde fueron extraídos los
datos
Seminario Doctoral “Análisis estadístico de datos en Ingeniería” DII-5013 VLC 2017
Universidad de Carabobo. Figueredo L., Francisco J. Pruebas de Normalidad.
2. H0: Los datos pueden modelarse por
una distribución normal, con media y
varianza dados
3. H1: Los datos no pueden modelarse
por una distribución normal
4. Para esta prueba los niveles de
significación comúnmente tabulados
son de 0,01 y 0,05
5. 𝐴
𝑛 𝑆 (10), si la muestra es
pequeña el estadístico necesita una
corrección 𝐴
𝐴
1
,
4. Para esta prueba los niveles de
significación comúnmente tabulados
son de 0,01 y 0,05
5. 𝑊
(13)
𝑊 ,∝
6. Se rechaza H0 si 𝑊
7. Primero se debe buscar en la tabla de
la prueba los coeficientes 𝑎 , , el
número de 𝑎 que se obtienen es
equivalente a la mitad de la muestra
n,
luego
se
calcula
𝑏
∑ 𝑎, 𝑋
𝑋
(14), el
valor de k será el valor entero de 𝑛⁄2
y los datos deben ser ordenados de
forma ascendente, por último, se
calcula el estadístico de prueba
8. Se procede a dar las conclusiones
correspondientes
,
(11)
6. Se rechaza H0 si 𝐴
𝐴∝
7. Para esta prueba primero debe
𝐿𝑛𝐹 𝑋
calcularse 𝑆 ∑
𝐿𝑛 1 𝐹 𝑋
(12),
por
último, se calcula el estadístico de
prueba y si es necesario se hace la
corrección para muestras pequeñas
8. Se procede a dar las conclusiones
correspondientes
f. Shapiro-Wilk: Esta prueba propuesta por
Samuel Shapiro y Martin Wilk en 1965,
calcula un estadístico W que contrasta si una
muestra aleatoria viene específicamente de
una distribución normal. [3]. Cabe destacar
que mientras más pequeño es el estadístico es
prueba de las desviaciones de normalidad de
la muestra, es decir, esta prueba se contrasta
al contrario de las otras pruebas, a medida
que el valor del estadístico sea más pequeño,
existe mayor probabilidad de rechazar la
hipótesis de normalidad. Esta prueba se
recomienda para muestras que van entre dos
datos y 2000 datos (2 ≤ n ≤ 2000). A
continuación, los pasos para realizar esta
prueba:
1. El interés es la distribución de la
población donde fueron extraídos los
datos
2. H0: Los datos pueden modelarse por
una distribución normal, con media y
varianza dados o estimadas con la
media y la varianza muestral
3. H1: Los datos no pueden modelarse
por una distribución normal
5
V. CONCLUSIONES



Las pruebas de normalidad son pruebas
realizadas a partir de estadística no
paramétrica, por lo tanto, se basan en
contrastes con las acumuladas teóricas, en la
simetría o incluso en el apuntamiento que
caracteriza a la distribución normal.
Como toda prueba de hipótesis al no
rechazar la hipótesis de normalidad, esto no
significa que los datos provengan de una
población normal, solo significa que no
existe evidencia para afirmar lo contrario, en
estos casos se debe tener cuidado con este
tipo de afirmaciones, donde el analista
pudiera suponer que la hipótesis de
normalidad es cierta.
Cada una de las diferentes pruebas de
normalidad tiene unas condiciones que
deben ser cumplidas para poder usarlas,
como, por ejemplo, la prueba de ShapiroWilk es recomendada para muestras
pequeñas y medianas (entre dos y 2000
datos), pero la prueba de χ2 se recomienda
para muestras mayores a 100 datos o para la
prueba de Anderson-Darling se debe realizar
una corrección al estadístico si la muestra es
menor a 25 datos.
Seminario Doctoral “Análisis estadístico de datos en Ingeniería” DII-5013 VLC 2017
Universidad de Carabobo. Figueredo L., Francisco J. Pruebas de Normalidad.


Los parámetros utilizados para realizar el
contraste también son importantes para la
aplicación de cada prueba, como la prueba
de Duncan, la de χ2 y la de Lilliefors y Van
Soest, los parámetros son estimados con la
media y la varianza muestrales, pero la
prueba de Anderson-Darling y la de ShapiroWilk se aplican con parámetros dados.
La mayoría de las pruebas tienen como
condición de rechazo de la hipótesis de
normalidad que el estadístico sea mayor que
el valor crítico, sin embargo, se debe tener
especial cuidado con este criterio, ya que, la
prueba de Shapiro-Wilk este criterio cambia,
y es que el estadístico sea menor al valor
crítico, esto lleva a pensar que existen otras
pruebas donde esta condición también sea
similar y por esta razón el analista no puede
descuidar este aspecto al aplicar una de las
pruebas.
REFERENCIAS
[1] Montgomery, D. y Runger, G. (1996). “Probabilidad y
estadística aplicadas a la ingeniería”. México: McGrawHill
[2] Mendenhall, W.; Beaver, R. y Beaver, B. (2010).
“Introducción a la probabilidad y estadística”. (13°
edición). México: Cenage.
[3] Maneiro, M. y Mejías, A. (2010). “Estadística para
Ingeniería: una herramienta para la gestión de la calidad”.
Venezuela: Universidad de Carabobo.
[4] Walpole, R.; Myers, R.; Myers, S. y Ye, K. (2012).
“Probabilidad y estadística para ingeniería y ciencias” (9°
edición). México: Pearson.
Francisco José Figueredo Lugo
Ingeniero Industrial y especialista en Docencia para la
Educación Superior de la Universidad de Carabobo, doctorando
del programa de Doctorado en Ingeniería, Área: Industrial de la
Universidad de Carabobo, profesor agregado del departamento
de Investigación de Operaciones de la Facultad de Ingeniería de
la Universidad de Carabobo.
Seminario Doctoral “Análisis estadístico de datos en Ingeniería” DII-5013 VLC 2017
6