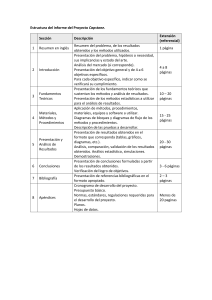
Formulario Análisis Estructural: Teorema de Áreas y Momentos
Anuncio
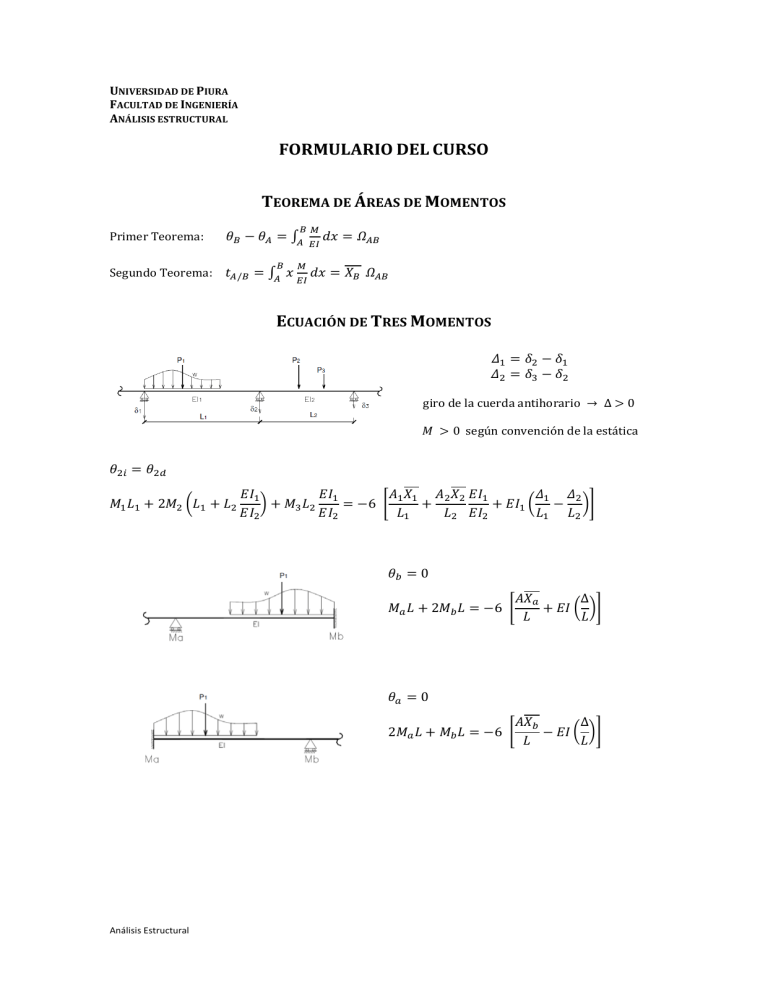
UNIVERSIDAD DE PIURA FACULTAD DE INGENIERÍA ANÁLISIS ESTRUCTURAL FORMULARIO DEL CURSO TEOREMA DE ÁREAS DE MOMENTOS Primer Teorema: 𝐵𝐵 𝑀𝑀 𝜃𝜃𝐵𝐵 − 𝜃𝜃𝐴𝐴 = ∫𝐴𝐴 𝐵𝐵 Segundo Teorema: 𝑡𝑡𝐴𝐴/𝐵𝐵 = ∫𝐴𝐴 𝑥𝑥 𝑀𝑀 𝐸𝐸𝐸𝐸 𝐸𝐸𝐸𝐸 𝑑𝑑𝑑𝑑 = 𝛺𝛺𝐴𝐴𝐴𝐴 𝑑𝑑𝑑𝑑 = 𝑋𝑋𝐵𝐵 𝛺𝛺𝐴𝐴𝐴𝐴 ECUACIÓN DE TRES MOMENTOS 𝛥𝛥1 = 𝛿𝛿2 − 𝛿𝛿1 𝛥𝛥2 = 𝛿𝛿3 − 𝛿𝛿2 giro de la cuerda antihorario → ∆ > 0 𝜃𝜃2𝑖𝑖 = 𝜃𝜃2𝑑𝑑 𝑀𝑀1 𝐿𝐿1 + 2𝑀𝑀2 �𝐿𝐿1 + 𝐿𝐿2 𝑀𝑀 > 0 según convención de la estática 𝐸𝐸𝐼𝐼1 𝐸𝐸𝐼𝐼1 𝐴𝐴1 𝑋𝑋1 𝐴𝐴2 𝑋𝑋2 𝐸𝐸𝐼𝐼1 𝛥𝛥1 𝛥𝛥2 � + 𝑀𝑀3 𝐿𝐿2 = −6 � + + 𝐸𝐸𝐼𝐼1 � − �� 𝐸𝐸𝐼𝐼2 𝐸𝐸𝐼𝐼2 𝐿𝐿1 𝐿𝐿2 𝐸𝐸𝐼𝐼2 𝐿𝐿1 𝐿𝐿2 𝜃𝜃𝑏𝑏 = 0 𝑀𝑀𝑎𝑎 𝐿𝐿 + 2𝑀𝑀𝑏𝑏 𝐿𝐿 = −6 � 𝜃𝜃𝑎𝑎 = 0 2𝑀𝑀𝑎𝑎 𝐿𝐿 + 𝑀𝑀𝑏𝑏 𝐿𝐿 = −6 � Análisis Estructural 𝐴𝐴𝑋𝑋𝑎𝑎 ∆ + 𝐸𝐸𝐸𝐸 � �� 𝐿𝐿 𝐿𝐿 𝐴𝐴𝑋𝑋𝑏𝑏 ∆ − 𝐸𝐸𝐸𝐸 � �� 𝐿𝐿 𝐿𝐿 ÁREAS Y CENTROS DE GRAVEDAD a) Parábola de grado n: X2 A2 h kx A1 𝐴𝐴1 = 𝑏𝑏ℎ 𝑛𝑛 + 1 𝑋𝑋1 = 𝑏𝑏 𝑛𝑛 + 2 𝑛𝑛 = 2 → n X1 ; 𝐴𝐴2 = ; 𝑋𝑋2 = 𝐴𝐴1 = 𝑛𝑛 = 2 → 𝑋𝑋1 = b 𝑏𝑏 4 𝑏𝑏ℎ 3 ; 𝑛𝑛𝑛𝑛ℎ 𝑛𝑛 + 1 ; 𝐴𝐴2 = (𝑛𝑛 + 3)𝑏𝑏 2(𝑛𝑛 + 2) 𝑋𝑋2 = 2𝑏𝑏ℎ 3 5𝑏𝑏 8 b) Triángulo: L a b 𝐴𝐴 = h X1 Análisis Estructural X2 𝐿𝐿ℎ 2 ; 𝑋𝑋1 = 𝐿𝐿 + 𝑎𝑎 3 ; 𝑋𝑋2 = 𝐿𝐿 + 𝑏𝑏 3 DIAGRAMAS DE MOMENTO Análisis Estructural DIAGRAMAS DE MOMENTO Análisis Estructural Mm 𝑑𝑥 L 𝐸𝐼 ∫ TABLA PARA EVALUAR * Efecto Real Efecto Virtual ** * 𝐿 𝐿 𝑀1 (2𝑀3 + 𝑀4 ) + 𝑀2 (𝑀3 + 2𝑀4 ) 6 6 𝐿 𝑏 𝐿 𝑎 (1 + ) 𝑀1 𝑀3 + (1 + ) 𝑀1 𝑀4 6 𝐿 6 𝐿 𝐿 𝑑 𝐿 𝑐 (1 + ) 𝑀1 𝑀3 + (1 + ) 𝑀2 𝑀3 6 𝐿 6 𝐿 (𝑎 − 𝑐)2 𝐿 𝑀 𝑀 [1 − ] 3 1 3 2𝑎𝑑 𝐿 (𝑀 + 𝑀2 )𝑀3 3 1 𝐿 𝑎𝑏 (1 + 2 ) 𝑀1 𝑀3 3 𝐿 𝐿 (𝑀 + 3𝑀2 )𝑀3 12 1 𝐿 𝑎 𝑎2 (1 + + 2 ) 𝑀1 𝑀3 12 𝐿 𝐿 NOTA * Se pueden establecer diagramas adicionales, tomando en cuenta: a b Si a = b Si a = 0 Si b = 0 ** Cuide los signos: si alguno de los momentos presentados se ubica en el lado opuesto del diagrama, considerarlo en las fórmulas con el signo contrario. MOMENTOS DEBIDO A GIRO Y DESPLAZAMIENTO RELATIVO Análisis Estructural MOMENTOS DE EMPOTRAMIENTO Análisis Estructural