INTRODUCCIÓN.
La Geometría Analítica fue decisiva para el desarrollo del Cálculo Diferencial e
Integral, que constituyó una auténtica revolución en el pensamiento matemático. La
aparición del Cálculo, significa hacer referencia a Newton y a Leibniz, a la creación
de una de las herramientas matemáticas más potentes y al nacimiento de un nuevo
paradigma científico: la Naturaleza puede ser explicada a partir de ecuaciones
diferenciales. Esto conlleva a la consideración continua y dinámica de las relaciones
funcionales, en contra de la consideración discreta y estática imperante hasta el
momento.
Se introducen las variables y se comienzan a utilizar expresiones de relaciones
entre variables por medio de ecuaciones. Surgen así muchos ejemplos de
funciones, aunque aún no se distinguen las variables dependiente e independiente
en una ecuación. Es de hacer notar que los objetos de estudio del Cálculo
desarrollado por Newton y Leibniz no fueron las funciones, sino las curvas. Se
intentaban solucionar problemas referidos a longitudes, áreas y tangentes
relacionadas a curvas, como así también encontrar la velocidad de puntos
moviéndose a través de curvas.
Leibniz (1646 - 1716) fue el primer matemático en utilizar la palabra función en 1692,
(Struik, 1969). Usó esta palabra para referirse a cualquier cantidad que varía de un
punto a otro de una curva, tal como la longitud de la tangente, de la normal, de la
subtangente y de la ordenada. Por ejemplo, Leibniz afirmaba que “una tangente es
una función de una curva” (Iacobacci, 1965). También introdujo las palabras:
constante, variable, coordenadas y parámetro en términos de un segmento de
constante arbitrario o cantidad. Clasificó a las curvas en: “algebraicas”, las
representadas por una ecuación de cierto grado y “transcendentes”, las
representadas por una ecuación de grado infinito o indefinido. Es de hacer notar
que Leibniz no utilizaba el concepto de función como lo entendemos en la actualidad
ya que, para él, una curva estaba formada por un número infinito de tramos rectos
infinitamente pequeños.
CLASIFICACIÓN DE LAS FUNCIONES
Existen diferentes tipos de funciones, las cuales nos permiten realizar un estudio más profundo
de éstas y tener una idea de su comportamiento.
POLINÓMICAS: Son aquellas formadas por un
polinomio
Ejemplo: 𝒀 = 𝑿𝟑 + 𝟓𝑿𝟐 − 𝟐𝑿 − 𝟐𝟒
RACIONALES: Son aquellas que se forman por un
cociente de dos polinomios con la condición de que el
divisor no sea igual a cero
ALGEBRAICAS
Ejemplo:
𝟑𝑿
𝒀 = 𝑿−𝟐
Cuando X ≠ 2
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
1
IRRACIONALES: Son aquellas en las que un
polinomio se encuentra dentro de un radical
Ejemplo: 𝒀 = √𝟐𝟓 − 𝑿𝟐 Cuando 25 – X2 ≥ 0
TRIGONOMÉTRICAS: Son aquellas que se obtienen
de una comparación por cociente de los lados de un
triángulo rectángulo y son función de un ángulo (Seno,
Coseno, Tangente, Cotangente, Secante y Cosecante)
Ejemplo: Y = Sen (2X – 5)
FUNCIONES
TRASCENDENTES
EXPONENCIALES: Son aquellas en las que el
exponente está formado por una variable
Ejemplo: Y
= 2X+3
LOGARÍTMICAS: Son la inversa de las funciones
exponenciales y pueden estar formadas con logaritmos
de diferente base.
Ejemplo: Y = log2 (X + 3) Y = log (3X + 2)
En 1665, Newton utilizó la palabra fluent para representar cualquier relación entre
variables. Además, introdujo la noción de diferencial, designada por la palabra
momento, el cual es producido por una cantidad variable llamada genita, en una
aproximación al concepto de función.
Newton y Leibniz contribuyeron decisivamente al desarrollo del concepto de función,
introduciendo el desarrollo de función en una serie de potencias. En esta época la
idea de función era muy restringida, pues se reducía a funciones analíticas,
abarcando inicialmente las que se podían expresar mediante una ecuación
algebraica y poco después, las desarrollables en serie de potencias.
Euler (1707 - 1783) continúa el camino para precisar la noción de función
comenzando a definir nociones iniciales como son: constante y cantidad variable y,
en 1755, define función como una expresión analítica:
"la función de una cantidad variable es una expresión analítica
compuesta de cualquier manera a partir de esa cantidad variable
y de números o cantidades constantes”. (Ruthing, 1984)
Los matemáticos desde Euler hasta Cauchy, pasando por Fourier, parecían estar
de acuerdo con la naturaleza “arbitraria” de las funciones, pero en la práctica ellos
pensaban en las funciones como expresiones analíticas o curvas. Dirichlet fue el
primero en considerar la noción de función como una “correspondencia arbitraria”.
Y restringió explícitamente a un intervalo, el dominio de una función.
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
2
No puede dejar de mencionarse que Fourier utilizaba en sus trabajos unos
razonamientos matemáticos que serían claramente inaceptables en nuestra época.
Fue Dirichlet (1805 - 1859), quien se dedicó a la tarea de convertir el trabajo de
Fourier en un trabajo matemáticamente aceptable, encontrando que el resultado de
Fourier, que afirmaba que toda función podía ser representada por una expansión
en series, era falso. En 1829 Dirichlet estableció las condiciones suficientes para
que tal representación sea posible y definió función de la siguiente forma:
“y es una función de la variable x, definida en el intervalo a<x<b,
si para todo valor de la variable x en ese intervalo, le corresponde un valor
determinado de la variable y. Además, es irrelevante como se establece esa
correspondencia.”
Dentro de una Función existen dos datos de relevancia para poder desarrollar a las
mismas, en la función los factores que intervienen son: Datos Constantes y Datos
Variables.
Los primeros son aquellos que como su nombre lo menciona son Constantes, esto
es, cuando tiene un valor fijo o determinado y este jamás cambia. Estos, se
representan con las letras iniciales del abecedario: a, b, c, d, e, . . .
Los segundos son elementos que pueden cambiar su valor con forme el
comportamiento de la Función, estos son llamados Variables, pueden ser
representados por las últimas letras del abecedario: X, Y, Z.
La Función, además de contener datos Constantes y Variables, esta puede ser
representada mediante conjuntos, entre los cueles, el primer conjunto será el de la
Variable Independiente, esta a su vez, se conocerá como la entrada de datos a
una función, recuerda que se conoce como una variable independiente aquella
cuyo valor no depende de otro valor o variable. La variable independiente en una
función se suele representar por “X”, esta se encuentra representa en el eje de
abscisas dentro del plano cartesiano.
Variable
Independiente “X”
Caja de Función
Mientras que el segundo conjunto se conocerá como la salida de datos de la
función, está salida puede estar conformada por aquella o aquellas Variables
Dependientes, cuyos valores dependerán dela entrada y proceso llevado a cabo
dentro de la caja de función, la variable dependiente de una función se suele
representar por “Y”, de igual forma esta también puede ser reconocida como “f(x)”,
la cual se puede leer como la “Función respecto de X” o lo que es lo mismo
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
3
“función que depende de los valores otorgados a X”, dicha variable se encuentra
representa en el eje ordenadas, dentro del plano cartesiano.
Variable
Independiente “X”
Variable Dependiente
“Y” o “f(x)”
Caja de Función
Nota: Observa la siguiente imagen en la cual podrás recordar como se representan
las abscisas y ordenas dentro del plano cartesiano.
Recuerda que las Funciones pueden ser de forma Explícitas e Implícitas, esto es:
Son Implícitas todas aquellas funciones, que cuando el valor de la salida “Y” o, dicho
de otra forma, la variable independiente se encuentra mezclada entre la función
(junto a la variable dependiente), esta se puede expresar como:
Ejemplo: 3X – Y + 2 = 0, es una Función Implícita
Se consideran función Explícita, a toda aquella función que ya se encuentra
igualada a algo, esto es, cuando la variable independiente se encuentra despejada
y esta se encuentra en función de la variable dependiente.
Ejemplo: Y = 3X + 2 es una Función Explícita
Tanto la Función Implícita como la Función Explicita, se encuentra relacionadas
entre, gracias al teorema de la función implícita.
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
4
Introducción a las Funciones.
¿Qué es una Función Matemática? Una función matemática (también llamada
simplemente función) es la relación que hay entre una magnitud y otra, cuando
el valor de la primera depende de la segunda.
Por ejemplo, si decimos que el valor de la temperatura del día depende de la hora
a la que la consultemos, estaremos sin saberlo estableciendo entre ambas cosas
una función. Ambas magnitudes son variables, pero se distinguen entre:
Variable dependiente. Es la que depende del valor de la otra
magnitud. En el caso del ejemplo, es la temperatura.
Variable independiente. Es la que define la variable
dependiente. En el caso del ejemplo es la hora.
De esta manera, toda función matemática consiste en la relación entre un elemento
de un grupo A y otro elemento de un grupo B, siempre que se vinculen de manera
única y exclusiva. Por lo tanto, dicha función puede expresarse en términos
algebraicos, empleando signos de la siguiente manera:
f: A → B
a → f(a)
En donde A representa el dominio de la función (f), el conjunto de elementos de
partida, mientras que B es el codominio de la función, o sea, el conjunto de llegada.
Por f(a) se denota la relación entre un objeto arbitrario a perteneciente al dominio A,
y el único objeto de B que le corresponde (su imagen).
Estas funciones matemáticas también pueden representarse como ecuaciones,
acudiendo a variables y signos aritméticos para expresar la relación existente entre
las magnitudes. Dichas ecuaciones, a su vez, podrán resolverse, despejando sus
incógnitas, o bien ser graficadas geométricamente.( https://concepto.de/funcionmatematica/#ixzz82kMhuAQf).
Tipos de Funciones Matemáticas.
Las funciones matemáticas pueden clasificarse de acuerdo al tipo de
correspondencia que se da entre los elementos del dominio A y los de B, teniendo
así lo siguiente:
Función inyectiva. Cualquier función será inyectiva si elementos
distintos del dominio A se corresponden con elementos distintos
del B, es decir, que ningún elemento del dominio se corresponde
con la misma imagen de otro.
Función sobreyectiva. Similarmente, hablaremos de una función
sobreyectiva (o subyectiva) cuando a cada elemento del
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
5
dominio A le corresponde una imagen en el B, incluso si ello implica
compartir imágenes.
Función biyectiva. Ocurre cuando una función es inyectiva y
sobreyectiva a la vez, es decir, cuando a cada elemento de A le
corresponde un único elemento de B, y no quedan en el codominio
imágenes sin asociar, o sea, no hay elementos en B que no
correspondan a uno en A.(https://concepto.de/funcion-matematica/#ixzz82kPXJ2Qo).
En
una función matemática es una relación que se establece entre dos
conjuntos, a través de la cual a cada elemento del primer conjunto se le asigna
un único elemento del segundo conjunto o ninguno. Al conjunto inicial o
conjunto de partida también se lo llama dominio; al conjunto final o conjunto de
llegada, en tanto, se lo puede denominar codominio (rango).
Por lo tanto, dados un conjunto A y un conjunto B, una función es la asociación
que se produce cuando a cada elemento del conjunto A (el dominio) se la asigna
un único elemento del conjunto B (el codominio).
Al elemento genérico del dominio se lo conoce como variable independiente; al
elemento genérico del codominio, como variable dependiente. Esto quiere decir
que, en el marco de la función matemática, los elementos del codominio dependen
de los elementos del dominio (https://definicion.de/funcion-matematica/).
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
6
(https://www.lifeder.com/evaluacion-funciones/)
Concepto de Funciones (Dominio, Rango e Imagen)
Intervalos y Notaciones de Intervalos
Antes de comenzar con el concepto de Dominio y Rango, primero estudiaremos
los intervalos y sus diversas formas de representación. Los intervalos son
conjuntos de números reales. Corresponden geométricamente a rectas, semirrecta
y segmentos de recta. De la misma manera que los conjuntos, es posible aplicarles
las operaciones de unión, intersección y complementación.
Estos conjuntos aparecen con frecuencia en el estudio de las propiedades de los
números reales y por tanto también cuando se estudian funciones reales o cálculo
diferencial e integral. Permiten manejar con más comodidad conjuntos infinitos. Para
las definiciones siguientes estaremos suponiendo que a, b ∈ ℝ, con a < b.
Intervalos Acotados
Un intervalo abierto es un conjunto definido como: (a , b) = {x ∈ ℝ | a < x < b },
observa que de esta definición se desprende que a ∉ (a , b) y b ∉ (a , b), entonces,
este intervalo contiene a todos los números reales que están entre a y b pero
sin a ni b. Geométricamente, este conjunto en la recta real, se ve como un segmento
de recta sin los extremos (que se colocan como círculos vacíos en los puntos
correspondientes).
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
7
Un intervalo abierto es aquel que no incluye sus puntos finales: por ejemplo,
{x|–3<x<1}
Para escribir este intervalo en notación intervalo, utilice paréntesis: (-3, 1)
(https://www.varsitytutors.com/hotmath/hotmath_help/spanish/topics/intervalnotation#:~:text=La%20notaci%C3%B3n%20intervalo%20es%20una,%7C%20%E2%80%93%203%20x%201%7D.&text=U
n%20intervalo%20abierto%20es%20aquel,%7C%20%E2%80%93%203%20x%201%7D.).
Un intervalo cerrado es un conjunto definido como: [a , b] = { x ∈ ℝ | a ≤ x ≤b },
observa que para este caso a ∈ [a , b] y b ∈ [a , b], es decir, el intervalo contiene
a a, b y a todos los números reales que están entre ellos. Geométricamente, este
conjunto en la recta real, se ve como un segmento de recta incluyendo sus extremos
(que se colocan como círculos llenos en los puntos correspondientes).
Un intervalo cerrado es aquel que incluye sus puntos finales: por ejemplo, el
conjunto { x | – 3 ≤ x ≤ 1 }
Para escribir este intervalo en notación intervalo, usamos corchetes cerrados: [-3, 1]
Intervalos semi abiertos, es un intervalo que incluye solamente a un extremo. En
este caso, cerrado por la izquierda, abierto por la derecha.
[a , b) = { x ∈ ℝ | a ≤ x < b}
También puede tener intervalos que son mitad abiertos y mitad cerrados:
[-2, 4)
Ahora, definamos el intervalo semi abierto que es abierto por la izquierda y cerrado
por la derecha.
(a , b] = { x ∈ ℝ | a< x ≤ b}
Como puedes observar, en la notación de
intervalos
los
paréntesis
indican
una desigualdad estricta, geométricamente se
especifica el punto no incluido con un círculo
vacío; mientras que los corchetes definen
una desigualdad débil que sí incluye al punto
(a, b]
Video de apoyo para el tema de intervalos
(https://es.khanacademy.org/math/eb-4semestre-bachilleratonme/x5828d8a71717b83a:caracteristicas-deuna-funcion/x5828d8a71717b83a:dominio-yrango/v/introduction-to-interval-notation).
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
8
extremo
y
geométricamente
se
dibuja
con
un
círculo
lleno
(http://uapas2.bunam.unam.mx/matematicas/notacion_intervalos/).
Dominio y Rango.
Dominio: Es el conjunto en el que la función está definida, es decir, en el que puede
tomar sus valores y realizar las operaciones que se indican en dicha relación;
gráficamente está representado en el eje de las X o eje de las abscisas.
Dominio “X”
Dicho de otra forma, el dominio de una función es el conjunto de todas las entradas,
sobre las que la función tiene salidas definidas, por ejemplo:
2
𝑓 (𝑥 ) = 𝑥
Sea la
Para este caso, lo que se encontraría dentro de la caja llamada función sería el
termino
2
, y las entradas a está, todos los valores que pudiera tomar “x”, visto de
𝑥
una forma gráfica, sería de la siguiente manera, para este caso consideraremos una
entrada de x=3, el cual al desarrollar la función no otorgaría lo siguiente:
Dominio x=3
2
𝑓 (𝑥 ) =
𝑥
f(3)=
2
3
Una vez realizada dicha función podemos determinar que, el dominio puede tomar
cualquier valor perteneciente a los números reales con excepción del cero, siendo
su notación matemática de la siguiente forma:
Dominio : { x ∈ ℝ | x ≠ 0}
Rango o Contradominio: Es el conjunto de todos los resultados que obtenemos al
realizar operaciones con los elementos del dominio o imágenes de la función y se
representa gráficamente en el eje de la Y o eje de las ordenadas, a estas salidas
las conoceremos como Rango.
Dominio x=3
2
𝑓 (𝑥 ) =
𝑥
f(3)=
2
Rango
3
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
9
Video de apoyo para el tema de Dominio y Rango: https://es.khanacademy.org/math/eb-4-
semestre-bachillerato-nme/x5828d8a71717b83a:caracteristicas-de-unafuncion/x5828d8a71717b83a:dominio-y-rango/v/domain-of-a-function-intro
El dominio de una función la podemos encontrar de diferentes formas, para ello
vamos conocer dos de los diversos métodos para poder encontrar el dominio y
rango de estas.
Dominio de Funciones Polinomiales
En una función polinomial, cualquier número que se sustituyan en “x” permite
encontrar el valor de “y”, de ahí que el Dominio de estas funciones son todos los
Números Reales. No importa si “x” está elevada a una potencia, multiplicada por
una constante o ésta esté sumada algebraicamente. Para ello utilizaremos el
método de la tabulación:
Ejemplo 1: Encontrar el dominio de la función 𝑦
= 2𝑥 + 3
Dominio
Rango
𝑥
𝑦 = 𝑓(𝑥)
-∞
-∞
-2
-1
0
1
2
-1
1
3
5
7
∞
∞
Ejemplo 2: Determinar el Dominio de la siguiente función 𝒚 = 𝒙𝟑 − 𝟐𝒙𝟐 − 𝟏𝟗 + 𝟐𝟎
Dominio
Rango
𝑥
𝑦 = 𝑓(𝑥)
-∞
-2
-1
0
1
2
∞
Video de apoyo:
https://www.youtube.com/watc
h?v=P_uEbqLNfZ0&t=67s
Como se trata de una Función Polinomial y por tanto para cualquier valor que se le
asigne a la variable independiente “x”, ya sea positivo o negativo, obtendremos el
valor de la variable dependiente “y”, por lo tanto, el Dominio de la función de “x”, tal
que “x” pertenece a los Números Reales (∴ 𝐷 𝑑𝑒 𝑙𝑎 𝑓(𝑥) ⋮ 𝑥𝜖ℝ).
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
10
Una manera de encontrar el Dominio y Rango de un Función es observando las
características de su gráfica. Para graficar la Función, se pueden utilizar diferentes
aplicaciones. Se propone utilizar la aplicación “Desmos”. (Para saber cómo usar
Desmos ir al Anexo A).
Dominio de Funciones Racionales
En las funciones racionales, el denominador deber ser distinto de cero, para poder
efectuar las operaciones. Descartando él o los valores que podrían producir cero en
el denominador, fácilmente se puede conocer el domino de las Funciones.
Ejemplo 1: Determinar el Dominio de la siguiente función:
5
𝑦=
𝑥−2
Como procedimiento, el denominador se iguala a cero y se resuelve
X–2=0
X=2
Nos damos cuenta que el valor de X no puede ser igual a 2, por lo que concluimos
que el Domino de la función son todos los números reales, menos el 2.
Dominio: Todos los números reales menos el 2
a.) R – {2}
Video de apoyo:
b.) – ∞ < X < 2, 2 < X < ∞
https://www.youtube.com/watch?v=umWSSxZNJaQ
c.) (– ∞, 2], [2, ∞)
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
11
Ejemplo 2: Determinar el Dominio de la Función
10
𝑦= 2
𝑥 − 16
El denominador se iguala a 0 y se resuelve
X2 – 16 = 0,
por factorización algebraica
(X + 4) (X – 4) = 0,
se igualan las raíces a cero
X + 4 = 0, y X – 4 = 0
Se despeja cada una de la “x”
X1 = – 4,
X2 = 4
Dominio: Todos los Números Reales, menos el – 4 y el + 4
a.) R – {– 4 y 4}
b.) – ∞ < X – 4, – 4 < X < 4, 4 < X < ∞
c.) (– ∞, – 4], [– 4, 4], [4, ∞)
Ejemplo 3: Determinar el Dominio de la Función:
5
𝑦= 2
𝑥 + 3𝑥 − 4
El denominador se iguala a cero y se resuelve
X2 + 3X – 4=0
(X + 4) (X – 1) = 0
X1 = – 4 y X2 = 1
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
12
Dominio: Todos los Números Reales, menos el – 4 y el + 1
a.) R – {– 4 y 1}
b.) – ∞ < X < – 4, – 4 < X < 1, 1 < X < ∞
c.) (– ∞, – 4], [– 4, 1], [1, ∞)
Dominio de Funciones Irracionales
En las funciones irracionales el valor del radicando debe ser mayor o igual a 0, para
poder efectuar la operación. Por lo que se deben encontrar los valores de X que
cumplan esta condición.
𝑦 = √𝑎 − 𝑥
Ejemplo 1: Determinar el Dominio de la Función
𝑦 = √16 − 𝑥
16 – X ≥ 0
– X ≥ – 16
– (– X ≥ – 16)
X ≤ 16)
Al cambiar el signo, se invierte la desigualdad
X ≤ 16
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
13
Dominio: Todos los Números Reales menores que 16, incluyéndolo
De otra manera, (– ∞ a 16]
Video de apoyo:
https://www.youtube.com/watch?v=4DIk2WiVv44
Ejemplo 2: Encontrar el dominio de la función
𝑦 = √25 − 𝑥 2
Se trata de una Función Irracional, por tanto, los valores del radicando están
limitados, de tal forma que, al sustituir el valor de X, el radicando no sea un
número negativo.
25 – X2 ≥ 0
(5 + X) (5 – X) ≥ 0
5 + X ≥ 0,
X≥–5
5–X≥0
– (– X ≥ – 5) ∴ X ≤ 5
Dominio: Todos los números reales entre – 5 y + 5, incluyéndolos
De [– 5 a 5], incluyéndolos.
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
14
NOTA: Como la Y es positiva, en la gráfica solo se observa la parte donde Y +, si a la función
se le escribe el signo –, la gráfica resultante estaría en la parte de abajo
Ejemplo 3: Encontrar el dominio de la función
Se trata de una Función Irracional, por tanto, los valores del radicando están
limitados, de tal forma que, al sustituir el valor de X, el radicando no sea un
número negativo.
X2 – 36 ≥ 0
X2 ≥ √36
X≥6
Si el valor de X es +
X≥6
Si el valor de X es –
–X≥6
– (–X ≥ 6)
X≤–6
Dominio: Todos los números reales menos los comprendidos entre – 6 a + 6.
Todos los números reales de (– ∞ – 6] y de [6 a ∞) incluyendo el – 6 y el 6.
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
15
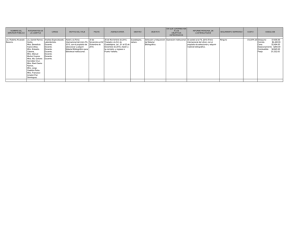
Actividad 1: Encuentra el Dominio y Rango de las Funciones:
Nombre:
ACTIVIDAD 1
Obtención del Dominio de Funciones
Grado y Grupo
8
𝑥−4
1. ) 𝑦 = 𝑥 2 + 5𝑥 − 50
2. ) 𝑦 =
20
3. ) 𝑦 =
2𝑥 − 10
𝑥 2 + 6𝑥
4. )𝑦 = 2
𝑥 − 36
5. )𝑦 =
3𝑥 − 6
𝑥 2 + 3𝑥 − 10
7. )𝑦 = 5𝑥 3 − 3𝑥 2 + 2𝑥 − 4
𝑥 2 + 5𝑥
9. )𝑦 = 2
𝑥 − 25
6. )𝑦 = √𝑥 2 − 100
8. )𝑦 =
6
𝑥 2 − 𝑥 − 12
10. )𝑦 = √64 − 𝑥 2
Documento elaborado por: Mtro. José Cruz Gómez Michel, Mtro. Anuar Zepeda Gómez
16