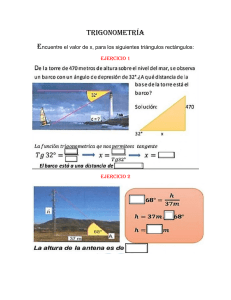
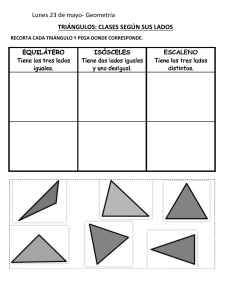
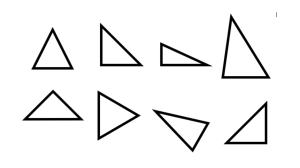MATEMÁTICA 8º Básico GEOMETRÍA Triángulos ¿Qué es un triángulo? Desde pequeños hemos observado y entendido el mundo a partir de sus formas. El estudio de la geometría ha permitido que no nos quedemos sólo en la observación, sino también en la replicación de este mundo, es decir, en su imitación por construcción. En esta oportunidad, centraremos nuestra atención en los triángulos, polígonos que se han utilizado a lo largo de la historia para crear y construir algunas de las maravillas presentes hasta nuestros días. De esta manera, el objetivo de estas páginas es que amplíes tus conocimientos en relación a esta figura y también puedas identificar cuál es su importancia y utilidad en la vida diaria. Actividad: Instrucciones: Observa con atención las imágenes que aparecen a continuación y responde las preguntas que se plantean por cada una de ellas Imagen 1: Imagen 1: ¿Cuál es la utilidad de los triángulos que aparecen en la imagen? ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ Triángulos Imagen 2 Imagen 2: ¿Qué conocimientos sobre triángulos son necesarios para la construcción de este puente de tallarines? _____________________________________________________ _____________________________________________________ _____________________________________________________ _____________________________________________________ _____________________________________________________ Imagen 3: Imagen 3: ¿Qué conclusión podrías señalar de la imagen? ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ Triángulos Red conceptual A continuación encontrarás una red conceptual que pretende explicar de manera sintética a los triángulos TRIANGULOS DESIGUALDAD TRIANGULAR CLASIFICACION ELEMENTOS Medida de lados Medida de ángulos Teorema de Pitágoras Instrucciones: A partir de la red conceptual, responde las siguientes preguntas: 1. ¿Qué aprenderás en esta unidad? ____________________________________________________________ ____________________________________________________________ 2. ¿Por qué el teorema de Pitágoras se relaciona con la clasificación de los triángulos según la medida de sus ángulos? ____________________________________________________________ ____________________________________________________________ ____________________________________________________________ Triángulos ¿Qué es un triangulo? Como ya lo señalamos en un inicio, los triángulos son los polígonos más sencillos y simples de construir. Las principales características que ya debes conocer de ellos están ser el polígono con el menor número de lados, contar con 3 vértices y tres ángulos que le dan su nombre geométrico, no poseer diagonales, que sus ángulos interiores sumen 180 grados, y que los exteriores sumen 360 grados (esto ultimo como característica de todos los polígonos) y que solo los hay convexos. Dentro de sus variadas utilizaciones, los encontramos presentes en la construcción de la pirámides de Egipto, en la torre de pisa, en los soportes de las montañas rusas, etc. Su inclusión en tan variadas actividades se debe, entre otras cosas, a que a partir de los triángulos se puede construir cualquier otro polígono convexo, facilitando el cálculo de área y de ángulos de estos. Teniendo presente las características mas elementales de los triángulos, es que podemos fijar como objetivo que conozcas a fondo sus particularidades y algunos de los teoremas asociados a el. De esta manera se abordara: a) La desigualdad triangular (condición necesaria para la construcción de Triángulos) b) Clasificación de triángulos c) Elementos secundarios de los triángulos d) Teorema de Pitágoras y su reciproco a) Desigualdad triangular Cuando hablamos de desigualdad triangular nos referimos a dos magnitudes que no son iguales (no tienen la misma medida), sino que siempre una es > o < (mayor o menor) que la otra. Este concepto es aplicable a los triángulos pues existe una condición o cláusula que se debe cumplir para poder trazar o construir triángulos que señala lo siguiente: En todo triangulo la suma de las medidas de dos de sus lados es siempre mayor que la medida del tercer lado. Es decir, si a, b y c son las medidas de un triangulo, entonces: Triángulos b A a+b>c a+c>b c+b>a c B C a Si la suma de los lados de un triangulo es un igual o menor que el tercer lado este triangulo no se puede construir. Por ejemplo, un triangulo de lado 3cm, 5 cm. y 2 cm. no podría construirse porque no se cumpla la desigualdad triangular. 3cm + 5 cm > 2 cm 3 cm + 2 cm = 5cm 5 cm + 2 cm > 3 cm b) Clasificación de triángulos Como ya sabrás, los triángulos pueden clasificarse según la medida de sus lados y de sus ángulos b.1) Clasificación según la medida de sus lados: los triángulos pueden clasificarse en equilátero, isósceles y escaleno. b.1.1) Equilátero: sus tres lados tienen igual medida b.1.2) Isósceles: dos de sus lados tienen igual medida b.1.3) Escaleno: sus tres lados tienen distintas medidas Equilátero Isósceles Escaleno Triángulos b.2) Clasificación según la medida de sus ángulos: los triángulos pueden clasificarse en acutángulo, obtusángulo y rectángulo b.2.1) Acutángulo: sus tres ángulos son agudos (menor de 90 grados) b.2.2) Obtusángulo: uno de sus ángulos es obtuso (mayor de 90 grados y menor de 180 grados) b.2.3) Rectángulo: uno de sus ángulos es recto (mide 90 grados). Este tipo de triangulo tiene nombres particulares para sus lados. Aquellos que son adyacentes al ángulo recto se llaman catetos y aquel lado que se encuentra opuesto al ángulo recto se llama hipotenusa (siempre es el lado de mayor medida). De esta manera, un triangulo rectángulo tiene dos catetos y una hipotenusa. Rectángulo Obtusángulo Acutángulo Conocer estas características nos permite obviar ciertas explicaciones para su construcción y análisis. c) Elementos secundarios de los triángulos En un triangulo podemos distinguir entre elementos primarios y secundarios c.1) Elementos primarios: son los que poseen todos los polígonos, como vértices, lados, ángulos interiores, ángulos exteriores y diagonales (recordemos que los triángulos no tienen diagonales) c.2) Elementos secundarios: son aquellos elementos que son característicos de los triángulos como alturas, bisectrices, simetrales y transversales de gravedad. Triángulos c.2.1) Alturas: son los segmentos determinados por las rectas trazadas desde cada vértice del triangulo cortando al lado opuesto, o a una prolongación de este, en ángulo recto. Las tres alturas, o prolongaciones de estas, coinciden en un punto llamado ortocentro (H). c.2.2) Bisectrices: corresponden a cada una de las rectas que dividen a los ángulos interiores del triangulo en dos ángulos de igual medida. Las tres bisectrices se cortan en un punto llamado incentro (I), punto que además es el centro de una circunferencia inscrita en el triangulo. c.2.3) Simetrales: corresponden a rectas perpendiculares a cada lado del triangulo que pasan por el punto medio de estos. El punto de intersección de las simetrales se denomina circuncentro (C), y se encuentra a igual distancia de cada uno de los vértices del triángulo, dando origen a una circunferencia circunscrita al triangulo. Triángulos c.2.4) Transversales de gravedad: corresponden a las rectas que unen cada vértice con el punto medio del lado opuesto. El punto de intersección de las transversales de gravedad se denomina baricentro o centro de gravedad (G). Es importante destacar que dependiendo de las características del triángulo (si es isósceles, acutángulo, etc.) dependerá a su vez la construcción de cada elemento secundario y de la ubicación del punto de intersección de estos. d) Teorema de Pitágoras y su reciproco El teorema de Pitágoras ha sido utilizado a lo largo de la historia para la construcción de monumentos y templos, como es el caso de los egipcios y sus pirámides, extendiendo su uso a otros campos como la astronomía. Este teorema se aplica en un triangulo rectángulo, relacionando las medidas de sus catetos con el de su hipotenusa. Señala lo siguiente: “En un triangulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los catetos” Hipotenusa c Es decir, c2 = a2 + b2 Cateto 2 b a Cateto 1 Triángulos Por ejemplo, en el triangulo ABC, rectángulo en C, tenemos que: a = 3cm b = 4cm A c = 5cm b C c a B Aplicando el teorema, podemos verificar que: a2 + b2 = c2 32 + 4 2 = 5 2 9 + 16 = 5 2 25 = 5 2 Lo cual es cierto, pues 52 es 25, verificándose el teorema para este triangulo. A su vez, existe el teorema recíproco de Pitágoras que establece que si los lados de un triangulo cumplen con la relación c2 = a2 + b2, entonces dicho triangulo es rectángulo. De modo que solo sabiendo las medidas de un triangulo, podemos determinar si es o no rectángulo, para ello debes considerar siempre, antes de aplicar el reciproco de Pitágoras, que la hipotenusa corresponde al lado de mayor medida y los lados restantes corresponden a los catetos. Ya abordados los saberes necesarios para utilizar este nuevo contenido, se presentara un esquema con todo lo abordado hasta ahora, para luego aplicar los conocimientos adquiridos. Triángulos Red conceptual de síntesis TRIANGULOS DESIGUALDAD TRIANGULAR ELEMENTOS CLASIFICACION MEDIDA DE LOS LADOS PRIMARIOS EQUILATERO VERTICES ISOSCLES LADOS ESCALENO ANGULOS INTERIORES MEDIDA DE LOS ANGULOS SUMAN 180 GRADOS ANGULOS EXTERIORES ACUTANGULO OBTUSANGULO RECTANGULO SUMAN 360 GRADOS SECUNDARIOS TEOREMA DE PITAGORAS Y SU RECIPROCO ALTURA ORTOCENTRO BISECTRIZ INCENTRO SIMETRALES CIRCUNCENTRO TRANSVERSALES DE GRAVEDAD BARICENTRO Triángulos Actividades A continuación encontrarás una serie de actividades que te permitirán aplicar los conceptos aprendidos en la guía frente a distintos tipos de ejercicios. Actividad 1. Completa la tabla, determinando si es posible construir un triangulo dadas las siguientes medidas (aplica la definición de desigualdad triangular) y en el caso de ser posible, señala el nombre del triangulo de acuerdo a su clasificación a partir de la medida de sus lados. medidas a) 7 cm., 7 cm. y 5 cm. Es o no es posible Nombre del triangulo b) 8 cm., 3 cm. y 4 cm. c) 5 cm., 5 cm. y 5 cm. d) 6 cm., 3 cm. y 3 cm. Actividad 2. Responde las siguientes preguntas, considerando las características de los triángulos señalados. a) ¿Por qué un triangulo equilátero es siempre acutángulo? ………………………………………………………………………………………………… ………………………………………………………………………………………………… ………………………………………………………………………………………………… ………………………………………………………………………………………………… b) ¿Por qué un triangulo obtusángulo no puede ser equilátero? ………………………………………………………………………………………………… ………………………………………………………………………………………………… ………………………………………………………………………………………………… ………………………………………………………………………………………………… Triángulos c) En un libro se afirma que un triangulo de lados 6cm, 8 cm. y 10 cm. es rectángulo, Explica por que esa afirmación es correcta y compruébalo. ………………………………………………………………………………………………… ………………………………………………………………………………………………… ………………………………………………………………………………………………… ………………………………………………………………………………………………… Actividad 3. Relaciona los conceptos que aparecen en el recuadro con las definiciones que aparecen a continuación. ALTURA – CATETO – BISECTRIZ – BARICENTRO – SIMETRAL – ANGULOS INTERIORES DE UN TRIANGULO – ORTOCENTRO – HIPOTENUSA – CIRCUNCENTRO – TRANSVERSAL DE GRAVEDAD – INCENTRO – ANGULOS EXTERIORES DE UN TRIANGULO a) segmento que va desde el vértice de un triangulo cortando al lado opuesto en 90 grados. ………………………………………. b) lado opuesto al ángulo recto en un triangulo rectángulo. …………………………….. c) punto en que se intersecan las transversales de un triangulo. …………………………. d) ángulos que juntos suman 180 grados. ………………………………………………... e) es el elemento secundario del triangulo que origina una circulo inscrito en el. ………………………………………………………………………………………… f) rectas perpendiculares y que pasan por el punto medio de los lados de un triangulo. …………………………………………………………………………………. Triángulos Actividad 4: Considerando lo aprendido en la guía, vuelve a observar con atención algunas de las imágenes que se presentaron al inicio y responde las preguntas. Imagen 2 Imagen 2: ¿Qué tipo de triángulos y que características tendrán para ser incluidos en esta contracción? ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ Imagen 2: Imagen 2: Explica el teorema de Pitágoras a partir de la imagen. ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ ______________________ ______________________
