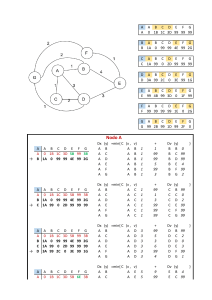
INSTRUCCIONES ARMADURAS EN UN PLANO Objetivo: Comprender y analizar cómo actúan diferentes tipos de masas sobres las vigas de una armadura en dos dimensiones. Materiales: 1 Computadora con software PASCO CAPSTONE. 1 850 Universal Interface. 1 Cable USB para 850 Universal Interface. 1 Advanced Structures Set ME-6992B 4 Load Cell PS-2200. 1 PASPORT Load Cell Amplifier PS-2198 1 Kit de masas y ganchos INTRODUCCION: Una armadura es una estructura compuesta de elementos esbeltos unidos entre sí en sus puntos extremos, dichos elementos pueden ser usados en construcciones. Las armaduras planas se usan con frecuencia para soportar techos y puentes, por lo tanto, es importante conocer las masas que van a actuar sobre ellas y poder analizar si dichos elementos se encuentran en tensión o compresión, para así poder determinar los materiales apropiados para su construcción. En este experimento se pretende comprobar cómo actúan dichas fuerzas sobre las vigas y así mismo en base a los resultados obtenidos de forma experimental, comprobar con cálculos teóricos a partir de método de nodos el cual se basa en el hecho de toda armadura se encuentra en equilibrio, entonces cada uno de sus nodos también lo está. Por lo tanto, si se realiza el diagrama de cuerpo libre de cada nodo, se pueden utilizar las ecuaciones de equilibrio de fuerzas y de esta forma determinar las magnitudes de las fuerzas de dichos elementos que actúan sobre cada nodo. Con apoyo del software PASCO CAPSTONE y el material adecuado para la realización de la práctica, se obtendrán valores experimentales a partir de graficas en tiempo real, dichas graficas mostraran las fuerzas a las cuales se están sometiendo las vigas y de esta forma poder comparar de una forma óptima los resultados teóricos obtenidos. FUNDAMENTO TEÓRICO: Como se menciona anteriormente, es necesario realizar el diagrama de cuerpo libre de cada nodo y de esta forma emplear las fórmulas de equilibrio. Como los elementos de una armadura plana son elementos rectos de dos fuerzas que se encuentran en el mismo plano, cada nodo se encuentra a un sistema de fuerzas coplanar y concurrente. Por lo tanto, solo es necesario satisfacer: ∑ 𝐹𝑥 = 0 𝑦 ∑ 𝐹𝑦 = 0 Esto nos asegura que la armadura se encuentra en equilibrio. Para comprender un poco mejor como actúan las fuerzas en los pasadores, es necesario analizar la siguiente armadura. En la imagen anterior podemos observar que a la armadura se le aplica una fuerza horizontal de 500N, a partir de esto podemos comenzar a analizar cómo actúa dicha fuerza en el pasador B. Se observar que en el pasador actúan tres fuerzas, las cuales corresponden a los 500N aplicados, y las fuerzas ejercidas en las vigas AB y BC, el siguiente diagrama de cuerpo libre indica como actúan dichas fuerzas con respecto al perno. Se observa que la 𝐹𝐵𝐴 se encuentra “jalando” por lo tanto la viga BA se encuentra en un estado de tensión, mientras que la 𝐹𝐵𝐶 esta “empujando” lo cual significa que la viga BC se encuentra en compresión. Cuando se usa el método de los nodos, siempre se debe comenzar en un nodo que tenga por lo menos una fuerza conocida y cuando mucho dos fuerzas desconocidas. Al aplicar las ecuaciones de equilibrio, el sentido correcto de una fuerza de elemento desconocida puede determinarse con uno de dos posibles métodos, los cuales se mencionan a continuación: • El sentido correcto de la dirección de una fuerza desconocida de un elemento puede determinarse, en muchos casos, “por inspección”, lo cual quiere decir que el sentido de la fuerza desconocida de un elemento puede suponerse; luego, después de aplicar las ecuaciones de equilibrio, el sentido supuesto puede verificarse a partir de los resultados numéricos. Una respuesta positiva indica que el sentido es correcto, mientras que una respuesta negativa indica que el sentido mostrado en el diagrama de cuerpo libre se debe invertir. • Suponga siempre que las fuerzas desconocidas en los elementos que actúan en el diagrama de cuerpo libre del nodo están en tensión; es decir, las fuerzas “jalan” el pasador. Si se hace así, entonces la solución numérica de las ecuaciones de equilibrio dará escalares positivos para elementos en tensión y escalares negativos para elementos en compresión. Una vez que se encuentre la fuerza desconocida de un elemento, aplique su magnitud y su sentido correctos (T o C) en los subsecuentes diagramas de cuerpo libre de los nodos. PRECAUCIONES DE SEGURIDAD Y EXPLORACIÓN: • • • • • • • • Usar bata de laboratorio y guantes(opcional) para evitar accidentes. Analizar la armadura y verificar que no hace falta tornillos en cada una de las uniones. Revisar que todas las vigas se encuentran en buen estado, así mismo si alguna se encuentra fracturada o rota, reportarla inmediatamente al encargado de laboratorio. Comprobar que las Load Cell no se encuentran dañadas, así mimos el cable de conexiones. Tener un buen manejo del Load Cell Amplifier y así mismo identificar la forma correcta de conectar las Load Cell en las entradas. Manipular con demasiada precaución la Interface Universal 850 ya que es un equipo muy delicado. Se deberá verificar que tanto el cable USB para la Interface Universal 850 así como su cargador estén en buenas condiciones de uso. Verificar si el equipo de cómputo a utilizar contiene el software PASCO CAPSTONE en caso contrario se deberá solicitar al encargado su instalación. CONSTRUCCIÓN DEL PROTOTIPO: Paso 1: El encargado del laboratorio proporcionara la armadura correspondiente a la práctica: Imagen 1 Paso 2: Una vez teniendo la armadura, es necesario identificar los números de las Load Cell para poder realizar las conexiones correspondientes al Load Cell Amplifier. Imagen 2 Paso 3: Ya que se identificaron los números de las Load Cell, es necesario realizar la conexión correspondiente en la Load Cell Amplifier. Es necesario observar el tipo de conexiones con las que cuenta, ya que si se conecta de una forma errónea se pude dañar el equipo. Imagen 3 Paso 4: Conectar a la alimentación de corriente alterna y así mismo encender la 850 Universal Interface. Imagen 5 Imagen 6 Paso 5: Conectar la 850 Universal Interface a CPU, donde se cuenta con el software PASCO CAPSTONE. Imagen 7 Paso 6: Para el siguiente paso, se conectará la Load Cell Amplifier en la 850 Universal Interface y así mismo también hay que identificar el sentido de la conexión para evitar accidentes y daños al equipo. Imagen 8 Paso 7: Una vez encendida la computadora, entrar al programa , el cual nos llevara a la siguiente ventana, la cual es la interfaz principal para el desarrollo de la práctica. Imagen 9 Paso 8: Posteriormente dar click en “Abrir experimento”. Imagen 10 y elegir “Armaduras” Imagen 11 Paso 9: Si la Load Cell Amplifier está conectada correctamente, el botón Registrar aparecerá en rojo . Imagen 12 Se da click en la opción Registrar y el software comenzar a registrar datos los cuales se mostrarán en la gráfica y dar clic en stop para detener el registro Imagen 13 Podemos observar que las graficas presentan ruido y así mismo diferentes valores, sin embargo, es necesario establecer en 0 cada una de ellas para una mejor obtención de resultados. Paso 10: Presionar el botón TARE en la Load Cell Amplifier, para poder calibrar cada uno de los sensores y así tener valores más precisos. Imagen 14 Una vez presionado el botón, podemos observar un cambio en la gráfica, el cual se observa en la siguiente imagen: Imagen 15 Sin embargo, aun presentan un poco de ruido, ya que los sensores son muy sensibles y registran movimientos con fuerza mínima. Paso 11: Una vez calibrados los sensores, procedemos a colocar diferentes masas en la armadura, para poder observar las fuerzas aplicadas en las vigas. Las masas deberán estar colocadas justo en el medio en la viga de conexión entre ambas armaduras, para poder obtener un valor preciso. Nota: Es necesario NO manipular con demasiada fuerza la armadura, ya que los sensores pueden marcar lecturas erróneas. Evitar que las masas se encuentren en movimiento de oscilación y se mantengan en una posición estática. Imagen 16 Paso 12: Una vez colocadas las masas, volveremos al software para poder registrar la fuerza correspondiente que registra cada una de las vigas. Nota: Evitar recargarse sobre la mesa de trabajo, ya que se genera una aceleración y por lo tanto un movimiento en la armadura, la cual afectara el resultado. Imagen 17 Paso 13: Ya que tenemos la gráfica, es necesario escalar para poder ver cómo actúa la fuerza respecto del tiempo, en cada una de las gráficas se encuentra el botón para escalar los datos y tener una mejor visualización. Imagen 18 Paso 14: Para obtener valores precisos, las gráficas también contienen un botón para obtener el promedio de los valores obtenidos, presionar desplegable, porque nos brinda varias opciones. en el menú Imagen 19 Es necesario seleccionar “media” ya que es nuestro valor de interés. Ya seleccionado, presionaremos ahora el botón con el símbolo, y arrojara el valor correspondiente a la media. Imagen 20 Paso 15: Ya obtenidos los valores de la media, podemos observar que el valor en la fuerza 1 y 2, corresponden a vigas paralelas, por lo tanto, están bajo una fuerza similar así mismo sucede con las fuerzas 3 y 4. Debido a esto y para tener un valor mas aproximado, obtendremos el promedio de ambas fuerzas y así determinaremos la fuerza resultante a las que están sometidas. Fuerza 1 Fuerza 2 Promedio Viga 1 -1.63 -1.58 -1.605 Viga 2 -1.30 -1.38 -1.34 Una vez obtenidos los datos, podemos comparar con los valores obtenidos analíticamente. EVIDENCIAS DEL EXPERIMENTO Hoja de Respuestas del Estudiante Nombre: Contreras Peñaloza Maximiliano Fecha: 29 de noviembre de 2022 1) Pruebas: Realizar una prueba con diferentes masas en los nodos de la armadura, así como se expresa en el siguiente diagrama. 280g B A D A C A A A E 150g A partir de los resultados obtenidos analíticamente, realizar las comparaciones correspondientes con los valores prácticos y así mismo anotar sus conclusiones Tabla de Resultados Fuerza 1 Fuerza 2 Promedio Viga 1 -0.88N -0.76N -0.82N Viga 2 -0.53N -0.32N -0.42N 2) Análisis: En base a los resultados obtenidos en las pruebas, contesta las siguientes preguntas. Si intercambiamos de lugar las masas establecidas, ¿Obtendríamos los mismos valores en las celdas de carga? ¿Y Por qué? Se determino que si, ya que se puede fundamentar con la ley de equilibrio, ya que esta nos supone que la suma de todas las fuerzas debe ser cero, así como los momentos, entonces si serian los mismos valores al intercambiar los pesos ¿Qué pasaría si cambiamos de dirección las fuerzas aplicadas?, ¿Los valores serian negativos o positivos? Los valores que tendríamos serian de signo negativo, ya que se altera la dirección en donde estarían apuntando las fuerzas, si bien se llegaran a hacer los cálculos con esta variación, se obtendrán resultados negativos con lo cual se ve afectado como se comporta la fuerza en cada punto. 3) Vocabulario: Usa los recursos disponibles para encontrar la definición de los siguientes términos y/o conceptos. Masa: Es una magnitud física y propiedad general de la materia1 que expresa la inercia o resistencia al cambio de movimiento de un cuerpo. De manera más precisa es la propiedad de un cuerpo que determina la aceleración de este, cuando este se encuentra bajo la influencia de una fuerza dada. Tensión: Si la fuerza es ejercida por una cuerda, un hilo, una cadena o un cable, la llamamos tensión. Compresión: es la acción y efecto de comprimir. Este verbo refiere a estrechar, apretar, oprimir o reducir a menor volumen. Momento: El momento de una fuerza respecto a un punto o respecto a un eje es una medida de la tendencia de la fuerza a hacer girar el cuerpo alrededor del punto o del eje. Nodo: Es un punto a lo largo de una onda estacionaria donde la onda tiene una amplitud mínima. Por ejemplo, en una cuerda de guitarra que vibra, los extremos de la cuerda son nodos. Conclusiones: Como se pudo ver en la práctica, resulta interesante poder ver como se aplican cálculos físicos en ejemplos bien estructurados, cabe mencionar que se deben tener algunos conocimientos bien estructurados para lograr entender como es la interacción de las fuerzas en alguna estructura, así como el que pasaría si se llega a tener x alteración dentro de la práctica. Solución analítica del problema: 280g B A D A C A A A E 150g Se necesita distribuir correctamente el peso sobre las armaduras: 280𝑔 150g 𝑚1 = = 140g ; 𝑚2 = = 75g 2 2 Posteriormente obtenemos los valores de las fuerzas aplicadas, ya que se encuentran como masas. 𝐹1 = 140g = 0.140Kg = 0.140Kg ( 𝐹2 = 75g = 0.075Kg = 0.075Kg ( 9.81N ) = 1.373N 1 Kg 9.81N ) = 0.736N 1 Kg En base a el diagrama de cuerpo libre podemos determinar dos fuerzas de interés y así mismo establecer las fórmulas de equilibrio. 1.373𝑁 B A 𝐴𝑦 A A D A C A E 𝐸𝑦 0.736𝑁 Por lo tanto, empleando las ecuaciones de equilibrio obtenemos lo siguiente: ∑ 𝐹𝑥 = 0 ∑ 𝐹𝑦 = 𝐴𝑦 + 𝐸𝑦 − 1.373N − 0.736N = 0 Se obtiene el momento con respecto al nodo A, esto para poder obtener las fuerzas que están actuando verticalmente a la armadura ya sea en el nodo A o E. ⟲ + 𝑀𝐴 = −1.373N(0.12m) − 0.736N(0.24m) + 𝐸𝑦 (0.48m) = 0 Despejando 𝐸𝑦 , obtenemos lo siguiente: 𝐸𝑦 = 1.373N(0.12m) + 0.736N(0.24m) (0.48m) 𝐸𝑦 = 0.71125 N Conociendo la fuerza del nodo 𝐸, podemos sustituir el valor y obtener el de 𝐴, obtenemos lo siguiente: 𝐴𝑦 + 𝐸𝑦 − 0.736N − 1.373N = 0 𝐴𝑦 = −0.71125 N + 0.736N + 1.373N = 1.397N ANALISIS DEL NODO A Nodo A: FUERZAS VERTICALES ∑ 𝐹𝑦 = 𝐴𝑦 − 𝐹𝐴𝐵 (𝑆𝑒𝑛 45°) = 0 𝐴𝑦 𝐹𝐴𝐵 𝐹𝐴𝐵 = 1.397 N = 1.976 N 𝑆𝑒𝑛 45° FUERZAS HORIZONTALES 𝐹𝐴𝐶 ∑ 𝐹𝑥 = 𝐹𝐴𝐶 − 𝐹𝐴𝐵 (𝐶𝑜𝑠 45°) = 0 𝐹𝐴𝐶 = 1.976N (𝐶𝑜𝑠 45°) = 1.397 N ANALISIS DEL NODO B Nodo B: FUERZAS VERTICALES ∑ 𝐹𝑦 = −1.373 N + 𝐹𝐴𝐵 (𝑆𝑒𝑛 45°) − 𝐹𝐵𝐶 (𝑆𝑒𝑛 45°) = 0 𝐹𝐵𝐷 𝐹𝐴𝐵 𝐹𝐵𝐶 Se obtiene lo siguiente: −1.373N + 1.976𝑁 (𝑆𝑒𝑛 45°) − 𝐹𝐵𝐶 (𝑆𝑒𝑛 45°) = 0 𝐹𝐵𝐶 = 1.4715 N −1.373 N + 1.976N (𝑆𝑒𝑛 45°) = 0.0343N 𝑆𝑒𝑛 45° FUERZAS HORIZONTALES ∑ 𝐹𝑥 = −𝐹𝐵𝐷 + 𝐹𝐴𝐵 (𝐶𝑜𝑠 45°) + 𝐹𝐵𝐶 (𝐶𝑜𝑠 45°) = 0 Conociendo los valores de 𝐹𝐴𝐵 , 𝐹𝐵𝐶 , obtenemos lo siguiente: −𝐹𝐵𝐷 + 1.976𝑁 (𝐶𝑜𝑠 45°) + 0.0343𝑁 (𝐶𝑜𝑠 45°) = 0 𝐹𝐵𝐶 = 1.976N (𝐶𝑜𝑠 45°) + 0.0343𝑁 (𝐶𝑜𝑠 45°) = 1.9620 N Nodo C: 𝐹𝐵𝐶 𝐹𝐶𝐷 En este nodo solos nos interesa la fuerza sobre 𝐹𝐶𝐷 , quedando de la siguiente forma: ∑ 𝐹𝑦 = −0.736N + 𝐹𝐵𝐶 (𝑆𝑒𝑛 45°) − 𝐹𝐶𝐷 (𝑆𝑒𝑛 45°) = 0 Sustituimos el valor de 𝐹𝐵𝐶 : 1.2262 N −0.736N + 1.962 N(𝑆𝑒𝑛 45°) + 𝐹𝐶𝐷 (𝑆𝑒𝑛 45°) = 0 𝐹𝐶𝐷 = 0.736 N − 1.962N(𝑆𝑒𝑛 45°) 𝑆𝑒𝑛 45° = 0.9211 N