COMPLETE DETAILED SOLUTIONS TO THE PROBLEMS FOR SECTIONS 12.9 AND 12.10 HERE :
https : // www.researchgate.net / publication / 328 927 036
_RESENNIE _ZADAC _PO _KINEMATIKE _ 129 _I _ 1210
http://libreria-universitaria.blogspot.com
SECCIÓN 12.9 Análisis del movimiento absoluto dependiente de dos partículas • 77
12.9 Análisis del movimiento absoluto dependiente de dos partículas
En algunos tipos de problemas el movimiento de una partrcula depen·
derá del movimiento correspondiente de otra partícula, Esta dependencia ocurre comúnmente si las partículas están interconectadas por cuerdas
inextensibles que se encuentren enrolladas alrededor de poleas.. Por ejemplo, el movimiento del bloque A hacia abajo a lo largo del plano inclinado en la figura 12-36 causará un movimiento correspondiente del bloque
B hacia arriba en el aIro plano inclinado. Podemos mostrar esto matemáticamente especificando primero la ubicación de los bloques usando
las coordenadas de posición SA YS8. Adviena que cada uno de los ejes
coordenados es (1) rcferenciado desde un punto fijo (O) o Iínca fija tie
referencia (dnlllm). (2) medido a lo largo de cada plano inclinado en la
dirección del movimiento del bloque A y del bloque B, y (3) tiene sentido positivo de e a A y de D el B. Si la longitud lotal de la cuerda es Ir.
las coordenadas de posición están relacionadas por la ecuaciÓn
SA
+ leo + S8
=
DalllJl1
/'
dS,l
dSfl
tillo 1:. \(,
lr
o
dt
dr
El signo negativo indica que cuando el bloque A tiene velocidad hacia
abajo. esto es, en la direcciÓn de la SA positiva. genera una velocidad
correspondiente hacia arriba del bloque B, es decir. B se mueve en la
dirección S8 negativu.
De manera similar. la diferenciación con respecto al tiempo de las ve·
locidades resulta en la relación entre las aceleraciones. es decir,
(l1l =
~(lA
Un ejemplo más complicado que implica movimiento depe_ndiente de
dos bloques se muestra en la figura 12-37a. En este caso. la posición del
bloque A está especificada mediante SA< Y la posición del extremo de la
cuerda del cual el bloque B está suspendido es definida por ss. Aquí
hemos elegido ejes coordenados que son (1) referidos a puntos fijos o
datums. (2) medidos en la dirección del movimiento de cada bloque. y
(3) positivos hacia la derecha (S,I) Ypositivos hacia abajo (ss). Durante
el movimiento, los segmentos azules de la cuerda que aparece en la figura l2-37a permanecen cvnstaflfes. Si I representa la longitud total de
cuerda menos estos segmentos, entonces las coordenadas de posición
pueden ser relacionadas mediante la ecuación
2l· S + 11 +
SA
Dalllm
= I
Como I y h son constantes durante el movimiento, las dos derivadas con
respecto al tiempo son
Por consiguiente. cuando 8 se mueve hacia abajo (+$8), A se mueve hacia la izquierda (-SA) con dos veces el movimiento.
Datum
"y
Aquí Ico es la longitud de la cuerda que pasa sobre el arco CD. Tomando la derivada con respecto al tiempo de esta expresión. y observando que leo Y Ir permanecen cOllsrmues, mientras que SA Y s8 miden
las longitudes de los segmentos cambiantes de la cue rda, tenemos
-+-~O
~
(.,
fi~
IZ· ,17
http://libreria-universitaria.blogspot.com
18
• CApiTULO 12 Cinemát ica d e u na particu la
DUlum
Este ejemplo también puede resolverse definiendo la posición de l
bloque 8 desde el ce ntro de la polea del {onda ( un punto rijo). figura
12+37b . En este caso
2(11 - ss) + h + SA = I
La diferenciación con respecto al tiempo resulta en
2'vs =
'.
VII
2aB = aA
Aquí los signos son lns mismos. ¿Po r qué'l
h
PROCEDIMIENTO DE ·~NALlSIS
lb)
El método anterior de relaciooar el movimiento dependiente de una
partfcula con el movimiento dc otra puede ser efectuadQ usando escalares algcbraicos o coordenadas de posición siempre que cada partícula se mueva a lo largo de una trayectoria rectilínea. Cuando es
este el caso. sólo cambiarán las magnitudes de la velocidad y la acc+
leración de las parlfcula~ no sus líneas de dirección. El sig'uiente
procedimiento es requerido.
;c
,
n df la m .rdl riada di pmid(J
• Establezca coordenadas de posición que tengan su origen en un
punto fijo o datum.
• Las coordenadas están dirigidas a lo largo de la trayectoria del movimiento y se extienden hacia un punto que tiene el mismo movimiento que cada una de las partículas.
• No es necesario que el origen sea el mismo para cada una de las
coordenadas: sin embargo, es importtmte que cada eje coordenado seleccionado esté dirigido a lo largo de la lruyectoriu del 1110vimimto de la partícula.
• Usando geomet.rfa o trigonometrfa. relacione las coordenadas con
la longitud total de la cuerda,lr, o con esa porción de cuerda. 1,
que excluye los segmentos que no cambian de longitud cuando
las partículas se mueven - tales como segmentos de arco enrollados sobre las poleas.
• Si un problema implica un sistema de dos O más cuerdas enrolladas
alrededor de poleas., entonces la posición de un punto sobre una
cuerda debe ser relacionada con la posición de un punto sobre
otra cuerda usando el procedimiento aOlenor. Se escriben ecuaciones separadas para una longitud fija de cada cuerda del sistema
y lbs posiciones de las dos panfculas son entonces relacionadas mediante esas ecuaciones (vea los ejemplos 12.22 y 12.23).
)(".
En este polQ peJro lero, el mo\'imieT\lo del
bhx lue "¡aje ro depende del movimie nto
del cable conectado al malHcatc que 10 ope·
ra , Es importan te poder re lacionar CS05 mo,
vimie ntos para determinar los requisitos de
potencia del malacate y la ruena en el cable
ocasionada por el movimit nto IlceJerado.
di
t"
'\fH!I
al r;I!."p-r.
• Dos derivadas sucesivas con respecto al tiempo de las ecuaciones de
la COOrdenada de posición dan las ecuaciones de velocidad y aceleración requeridas que relacionan los movimientos de las panfculas.
• En estas ecuaciones., Jos signos de los términos serán consistentes
con aquellos que especifiquen los sentidos positivo y negalivo de
las coordenadas de posición.
http://libreria-universitaria.blogspot.com
SECCION 12.9 Análisis del movimiento absoluto dependiente de dos partlculas
Detenninc la rapidez del bloque A que se ilustra en la figura 12-38 si
el bloque B tiene una rapidez hacia arriba de 6 pies js.
e.
.
O.mm
D
"
'.
I
16
I
pte5lS
'-.h ·c\ór
Fc'Uacj¡ ,', d /u ;·/nl#'
r p ir
Hay una cuerda en este sis,tema con segmentos que están cambiando de longitud. Se usarán las
coordenadas de posición s" y S8 ya que cada una es medida desde un
punto fijo (C (lO) Yse extiende a lo largo de cada trayectoria del 1n0l'imiellfQ de cada bloque. En particular, sn está dirigida al punto E
puesto que e l movimiento de B y E es el mismo _
Los segmentos azules de la cuerda most rada en la figura 12-38 permanecen con longitud constan te y no tienen que ser considerados
cuando los bloques se mueven. La longitud restante de la cuerda. /,
también es constante y está relacionada con las cambiantes coordenadas de posición SA Y \8 mediante la ecuación
l'
10
Tomando la derivada con respec-
a
al tiempo obtenemos
de modo que cuando
VB
= - 6 pics j s (hacia arriba).
VA
= 18 piesj s!
R~p.
19
http://libreria-universitaria.blogspot.com
80
•
CAPITULO 12 Cinemática de una partícula
Determine la rapidez del bloque A que se ilustra en la figura 12·39 si
el bloque B tiene una rapidez hacia arriba de 6 pies/ s.
Como se muestra. las po-sicioncs de los bloques A y 8 son ddinidas usando coordenadas s'"
y 58- Ya que el sistema tiene dos cuerdas que cambian de longitud.
será necesario usar una tercera l."OOrdenada. se. para relacionar SA con
58- En otras palabras. la longitud de una de las cuerdas puede ser
expresada en términos de 5,11 y Se. Y la longitud de la otra cuerda puede ser expresada en términos de $8 y Se.
Los segmentos en azul de las cuerdas mostradas en la figura l2-39
no tienen que ser considerados en el análisis. ¿Por qué,1 Para las longitudes restantes de cuerda, digamos 1I y 12 • tenemos
SA
+
2se = I I
58
+
(sn -
sd
= 12
Al eliminar Se resulta una ecuación que define las posiciones de ambos bloques, es decir,
SA + lbs = 212 + 11
tiempO da
." ...
La derivada COn respecto al
VA
+
4V8
=
O
de manera que cuando va = - 6 pies/ s (hacia arriba),
v.tl.
= +24 pies/ s = 24 pies/ s
!
Rj {/J
http://libreria-universitaria.blogspot.com
SECClON 12.9 Análisis del movimiento absoluto dependiente de dos partkulas
Determine la rapidez con que se eleva el bloque 8 mostrado en la figura 12-40 si el extremo de la cuerda en A es jalado hacia abajo con
rapidez de 2 D1 :s.
D~L
;~l
',
O,..m
"I
.
'í.tJ;
?{
8
s
La posición de A está definida mediante SAo Y la posición del bloque B es especificada por 58
ya que el punto E sobre la polea tendrá el mismo 11101'imie1lfQ que el
bloque. Ambas coordenadas son medidas desde un datum horizontal
que pasa por el pilsador fijo en la polca D. Como el sistema consta
de dos cuerdas. las coordenadas s" y Sil no pueden relacionarse directamente, En vez de ello. estableciendo una tercera coordenada
de posición. Se . podemos expresar la longi tud de una de las cuerdas
en ténninos de S8 Ys e . Y la long.itud de la otra cuerda cn ténninos de
SA.58
y Se·
Excluyendo los segmentos que apílrecen en azul 11 y /2 (junto con
el gancho y las dimensiones del eslabón) pueden ser expresadas como
se + S8 = I I
se) + ( SI:I - se) +
(SA -
SR
= I~
Eliminando se resulla
SA
+ 45.0
= 12
+ 2/ 1
Tal como se requiere. esta ecuación relaciona la posición ,)'8 del bloque B con la posición SA del punto A .
,
1
La derivada con respecto al
tiempo da
VA
dc modo que cuando
VA ""
V8
+ 4V8
""
O
2 mi s (hacia abajo).
= - 0.5
mi s = 0.5 mi s
t
• 81
http://libreria-universitaria.blogspot.com
82
• CA.- 1rUlO 12 Cinemática de una partlcu!a
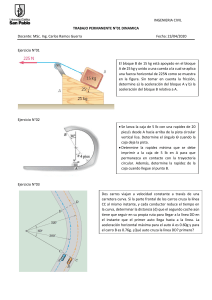
Un hombre ubicado en A está levantando una caja fuerte S, como se
mueSlra en la figura 1241. caminando hacia la derecha con velocidad
constante vA. = 0.5 mIs. Determine la velocidad y la aceleración de la
caja fuerte cuando alcanza la elevación localizada en E. La cuerda tiene 30 m de longitud y pasa sobre una pequeña polca en D.
Sillución
{
la ( e ,rl .1, p"
Este problema es d~cre nte
a los ejemplos previos ya que el segmento de cuerda DA cambia tanlO
en dirección como en magnitud. Sin embargo. los eXlremos de la cuerda. que definen las posiciones de S y A . son especificados por medio de
-'..!', ." las coordenadas.r y y medidas desde un punto fijo y dirigidas a lo faro
go de las rrayeclorias del movimielllo de los extremos de la cuerda.
Las coordenadas x y y pueden estar relacionadas ya que la cuerda
tiene una longitud fija I = 30 m, que en todo momento es igual a la
longitud del segmcmo DA más CD. Usando el teorcma dc Pitágoras
para determinar IDA' tenemos IDA = V( 15}2 + .~: y leo = 15 - y.
Por consigujente.
1 = IDA+ lcD
30 = V (15)' + ...' + (J5 - y )
)' = V 225 + x l
15
-
(1)
l'
J, 'on r
J/",}
Tomando la derivada con respecto al tiempo y usando la regla de la cadena, donde Vs = dy / dl Y ·VA
= d'x I di . resulta
v.\ =
[1
dy
--¡; =
2x
2 V 225 +
JdX
X2
-;¡;
(2)
En y = 10 m, x es determinada a panir de la ecuación 1. esto es. x =
20 m. Por consiguiente. a partir de la ecuació n 2 con VA = 0.5 mIs.
Vs
=
V
20
225 + (20)'
(0.5 ) = 0.4
mi'
= 400 mm/s1
La aceleración es determinada tomando la derivada con respecto
al tiempo de la ecuación 2. Como
dVA l dt = O. y tenemos
a - d_'y _ [ -x(dx/d' ) Jxv
S -
dr -
(225
+ x 2)3/2
+[
A
1
V225 + x 2
En x = 20 m, con
as
J(_dX)v
di
VA
A
= 0.5
+[
VA
es constan te, entonces
l
V225 + .r1
Jx_dV
A _
QA
-;:;;;2=;
25",
v:.T,¡;;
ti! - (225 + x 2)3(2
mi s, la aceleración es
225(0.5 m/s) '
_
, _
,
+ (20 m)'J'" - 0.00360 mis - 3.60 mm/s 1
= [225
Advierta que la velocidad constante en A causa que el otro extremo
e de la cuerda tenga una aceleración, ya que VA causa que el segmento DA cambie su dirección así como su longitud.
http://libreria-universitaria.blogspot.com
SKClÓN 12.10 Análisis del movimiento relativo de dos partlculas usando ejes en traslación
• 83
12.10 Análisis del movimiento relativo de dos partículas usando ejes
en traslación
En lodo este capílUlo el movimiento absolut o de una par.trcula ha sido
determinado usando un solo marco de referencia fijo para las mediciones. Sin embargo, ha)' muchos casos en donde la trayectoria dd movimiento para una partícula es complicada y puede ser factible anaLizar el
movimiento en partes usando dos O más marcos de referencia. Por ejemplo. el movimiento de una partícula localiznda en la punta de la hélice
de un avión. en vuelo. es más fácilmente descrita si se observa primero
el mo\'imiento del avión desde una reFerencia fija y luego se superpone
(vectorialmentc) el movimiento circular de la partícula medido desde
una referencia ubicada en el avión. Cualquier tipo de coordenadas (rectangulares. ciJíndricas. ele.) pueden elegirse para descri bir esos dos movimientos diferentes.
Para el análisis, en esta sección sólo ser¡ín considerados marcos de rejerencill en traslación. El análisis del movimiento relativo de panículas
usando marcos de referencia en rotación será tratado en las secciones
16.8 y 2004. ya que tal análisis depende del conocimiento previo de la cinemática de los segmentos de línea.
Posición . Considere las partfculas A y 8 que se mueven a 10 Imgo de las
trayeclorias arbilrarias aa y bb. respectivamente. como se muestra en la figura 12-42a. La p05idón absolllla de cada partfcula r A Yr8 es medida desde el origen com ún O del marco de referencia fijo .\".)'.z. El origen de un
segundo marco de referencia x '.),'.:¡;:' está unido a. y se mueve con, la partfeula A.A los ejes de este marco sólo les es permitido frtlsladarsecon respecto al marco fijo. La posición relaril'Q de "8 con respecto a A" es
designada mediante un ¡·eelor tle posición relariva r R ti. Usando la suma
vecloriaL los tres vectores moslrados en la fi gura 12-42(1 pueden ser relacionados mediante la ecuación·
(12-33)
'"
I l . U-··U
Veloci d a d . Una ecuación que relaciona las \'elocidades de las partfeu·
·Ias puede ser obte nida tomando la derivada con respecto al tiempo de la
ecuación 12·33.es decir,
(12-34)
Aquí. "R = dra / dl y l 'A = drA/ dr se re rieren a \'e/oeidades absolllfus. ya
que éstas son observadas desde el marco rijo. mientras que la ¡·e/ocidad
relativa " S .A = tira tI / d, es observada desde el marco en traslación. Es
'Una manera fácil d~ recordar la e5trUCIUra de \!!ola ecuaciÓn. 'J de otrM ~lIC10ncs si·
milares. es considerando la ··cancelación~ del subíndice A entre los d..,s tfrminos. es
decir. T/l - T~ - TI! >l '
http://libreria-universitaria.blogspot.com
84
•
CAP[TUlO 12 Cinemática de una partkula
l b)
importante advertir que como los ejes x ', y'. z' se trasladan, las (:om·
ponentes de r8 A. 110 cambiarán de dirección, y por tanto la derivada
con respecto al tiempo de las componentes de este vector tendrán que
dar cuenta sólo del cambio de la magnitud de este vector. La ecuación
L2-34 establece, por consiguienlc, que la velocidad de 8 es iguaJ a la velocidad de A más (veclorialmenle) la vclocidad relativa dc "8 con respecto a A : ' medida por el observador en (rm,ladón fijo en la rderencia
x'. y'. ;:'. íigunl 12-42b,
Aceleración . La derivada con respecto al tiempo de la ecuación 12-34
resulta en una relación veclorial similar enlre las aceleraciOnes (lb:wllllu y
relllliw/ de las partículas A )' B ,
( 12-35)
"1
Aquí. al:l A. es la aceleración de B vista por el ob!.crvador localizado en
A y tra!.lndándosc con cl marco dc referencia x'. y', l. ' . La suma vcctorial se muestra en la figura 12-42c.
DE ANÁLISIS
Al aplicar la ecuación de posición relativa. rH = f A + r8 A. primero cs necesario especificar las ubicaciones de los ejes fijos x,y, t , y
de los ejes en traslación .r.)". ¡'.
Usualmente. el origen A de los ejes en traslación se ubica en un
punto que tiene una posición conocida. 'A. figura 12-42a.
• Una representación gráfica de la suma vectoria l r lj = f A + rs A
puede ser mostrada. y lanto las ca ntidades conocidas como las
desconocidas pueden señalarse en el croquis.
• Como la suma vectorial forma un triángulo. puede haber cuando
mucho do_~ incógllita" representadas por las magnitudes y/ o las
direcciones de las cantidades vectoriales.
Estas incógnitas pueden encontrarse gráfica me me usando lri·
gonomelría (Ic)' de los senos. ley de los cosenos). o resolviendo
cada uno de los tres vcclOres r lJ, r" Y ' S IA en componentes rcc·
tangulares o cartesianas, generando así un conjunto de ecuaciones escalares.
Al volar mur cerca uno de otro, los pilo tos
de I.'S1OS a\ione~ a cho rro deben ser consd e nlc5 de sus posiciones y \'t:!ocidades re 13ti\'3) en todo momento para c\-itar una
colisión.
• Las ecuaciones de movimiento relativo " 8 = "A + " l:IJA Y 1118 =
DA + a8 A son aplicadas de la misma manera que antes, excepto
que en este caso el origen O de los ejes fijos x. y, ¡ no tiene que
ser especificado. figuras 12-42b y 12·42c.
http://libreria-universitaria.blogspot.com
S[WÓN 12.10 Análisis del movimiento relativo de dos partlculas usando ejes en traslación
Un tren, viajando con rapidez constante de 60 mi/h, cruza sobre un
camino como se muestra en la figura 12-430. Si el automóvil A viaja
a 45 mi/b a lo largo del camino. determine la magnitud y la dirección
de la velocidad relativa delIren epn respecto al automóvil.
Solución I
\ntili.\I!> 1't'C oria/. La velocidad relativa ~T¡A es medida desde los
ejes en traslación x', y' unillos al automóvil. figura 12-43a. Esta velocidad se determina a partir de VT = VA + vTIA· Como Vr y ~ A. son
conocidas U/1II0 en magnitud como en dirección, las incógnitas resultan ser las componentes x y y de vrlA. Usando los ejes x, y en la
figura 12-430 y un análisis vectorial cartesiano, tenemos
+
~T
=
VA
60i
=
(45oos45<> j
vTI A
+ 45 sen 45'" j ) + vT/ A
R, "
' ·TIA. = {28.2i - 31.8j} mi/b
La magnitud de 'tIT/A es en tonces
"T,,, ~ V(28.2)'
+ (-3l.8)' ~
42.5 mi/h
<,
A parti.r de la dirección de cada componente. figura 12-43b.la dirección de v TIA definida desde el eje.Y es
lan8 =
("T,,,),.
("T/A).
,,---~--.:.:;.¡
28.2
9 ~ 48.5° '<'
28.2 milh
,
3l.8
=-f'
Advierta que la suma veclorial mostrada en la figura 12-43b indica el
sentido correcto de VTiA.. Esta figura anticipa la .respuesta y puede ser
usada para verificarla.
] 1.8·'"~,ilh
o-----3I ' "'
.>uludof 11
\fUi/i.· ~ ·al·!r.
Las componenles desconocidas de 'ti r IA lambién
(b)
pueden ser determinadas aplicando un análisis escalar. Supondremos que esas componentes actúan en las direcciones x y y positivas.
Enlonces.
Resolviendo cada vector en sus componen les x y)' resulta
(±')
60 ~ 4S cos 4So + ("T,,,), + O
O ~ 4S sen 45° + O + ("T,,,>,
Al resolver las ecuaciones, obtenemos los resultados previos,
( + 1)
!lr= 60 milh
(.)
('!.T/A).: = 28.2 mi/h = 28.2 mi(h (1)~'A), = -31.8 mi/b = 31.8 mi/h!
..
J
• 85
http://libreria-universitaria.blogspot.com
86
•
CApITULO 12 Cinemática de una partícula
EJEMPt.~: 12.~
El avión A mostrado en la figura 12-440 vuela a lo largo de una trayectoria recta , mientras que el avión B 10 hace por una trayectoria
circular con radio de curvatura
= 400 km. Detcnnine la velocidad
y la aceleración de 8 medidas por el piloto de A .
"8
,
y'
toro- L.
700kmlh¡
t •
"
•
100 knv1l 2
1 .,. , 400 km
-----'
")
..-
Solucion
1 '¡t"ruJ",t Los ejes x. y estón localizados en un punto (jjo arbitrario. Como el movimientQ relativo al avión A va a se r detenninado. el
marco de referencia x', y' de traslació" está unido a él. figura 12-44a.
Aplicando la ecuación de la velocidad relativa en forma escalar. ya
que los vectores de velocidad de ambos aviones son paralelos en el
instante mostrado, tenemos
(+ 1)
Vs
=
600 =
VB,A
+ V8{A
700 + V8,A
tiA
= - 100 kmj h = 100 km/ h
!
Resp
La suma vectorial se muestra en la figura 12-44b,
(b)
·\(da, .{.". El avión B tiene componentes tangencial y nonnal de
aceleración. ya que está volando por una rrayectoria clln·a. A partir
de la ecuación 12-20, la magnitud de la componente normal es
(600 km/ h)'
400 km
,
= 900 km/ h
Aplicando la ecuación de aceleración relativa. tenemos
aB = aA
900i - IOOj = 50j
+
a/jIA
+ aBtA
Así.
" RJA =
'o)
f J. U-+&
{900 - 150j} km/h'
A partir de la figura t2-44c, la magnitud y la dirección de aH /A son.
por tanto,
aB ....
~
= 912 km/ h-
8
150
= tan- 1 900
= 9.46
0
~
~-
Advierta que la solución a este problema es posible usando un marco de referencia en traslación, ya que el piloto en el avión A está "trasladándose". Sin embargo, la observación del avión A con respecto al
piloto del avión 8. debe ser obtenida usando un conjunto de ejes en
rotación unidos al avión B. (Por supuesto. esto supone que el piloto
de 8 está fijo en el marco en rotación. de modo que no gira sus ojos
para seguir el movimiento de A.) El análisis de este caso se proporciona en el ejemplo 16.21 .
http://libreria-universitaria.blogspot.com
SECOÓN 12.10 Análisis del movimiento relativo de dos partlculas usando ejes en t raslación
En el instante mostrado en la figura 12-45 los automóviles A y B están viajando con rapidez de 18 y 12 mIs, respectivamente. También
en este instante. A tiene una disminución en rapidez de 2 m/ s2, y B
tiene un incremento en rapidez de 3 m/s2. Detemline la velocidad y ~~~~~
la aceleración de B con respecto a A .
~
Solución
li:lociducL Los ejes fijos x, y son establecidos en un puntO sobre el
suelo y los ejes en lraslat.'lÓn X'ty' están unidos al automóvil A, ¡¡gura 12-45a. ¿Por qué? La velocidad relativa es determinada mediante
v8 = "A + v8 /A' ¿Cuáles son las dos incógnitas? Usando un análisiS
vectOrial cartesiano, tenemos
VB
= "A
+ "B/A
60'
(-18cos600¡ - 18 sen 6O j)
D
- 12j
=
"8 ·A
= {9i + 3.588j}
-.l
+ " 81t l
(.,
mis
Entonces.
V8A ~ V(9)'
L,
+ (3.588)' ~ 9.69 mi s
Rnp
Observando que " S/A tiene componentes + i y + j , figura 12-45b, su
dirección es
(VBf A)y
tanO =
3.588
= - - -
9
(V8/A}...
9 mis
0= 21.71) .d.
\c-dt ncián. El automóvil B tiene componentes tangencial y normal de aceleración. ¿Por qué? La magnitud de la componente
normal es
({IR )" =
v1
P=
(12 m/ sf
2
100 m = 1.440 m/s
(b)
2.440 mls 2
•
Aplicando la ecuación para la aceleración relativa obtenemos
118
=
a ",
+ a BiA
(-1.44Oi - 3j ).:: (2cos60"i T 2 sen 6O j )
" 81A ~ {-2.44Q; - 4.732j) mis'
Q
Aquí aIJI"" tiene componentes
- j
+ aRJA
~ V(2.440 )' + (4.732 )' ~ 5.32 mis'
tanq.. =
~ ~
4.132 mls1
y - j oEntonces, a panir de la fi+
gura 12-45c,
a81A
•••,'L_ _ _;-'
( aB/ A)Y
(aRI..dx
4.732
=--
2.440
62.7' ".
¿Es posible obtener la aceleración relativa de aAIB usando este método? Refiérase al comentario formulado al flnal del ejemplo 12.26.
ro'
•
87
http://libreria-universitaria.blogspot.com
88
CApiTULO 12 Cinemática de una partícula
PROBLEMAS
12·171 Si el extremo del cable !>ituado en A ei> jalado
hacia abajo con rapidez de 2 mIs. determine la rapidc7
con que se eleva el bloque B.
1!· I1!1' Dctenninc elliempo necesario para que la caro
ga situada en B alcance una rapidez de 8 mI s. panlendo
del reposo. si el cable es jalndo hacia el motor con una
aceleración de 0.2 m /~l _
1° ., I.' - ''',!
·11· ln. Si el extremo del cable simado en A es jalado
hacia abajo con rapidez de 2 mi s. determine la rapidcz
con que se IC\'anla el bloque B.
Pnb.l_ - I~
1)·
Detennine el dcsphl7.amiento dellfOnoo SI el camión colocado en e jala el cable 4 pies hacia la derecha.
I
P.,h ':>¡ -
L P4. Detemllne la rapide7. constante con que el ca·
ble ubicado en A debe ser jalado por el motor para ele·
var la carga localizada en 8 15 pies en 5 segundos.
t'.
1:'I-1II1. 1!- 174
1..- 1 ,
·1'T7. Ln caja está siendo le\'antada por el plano inclinado usando el motor M y el arreglo dc cuerda y polca
mostrado. Determine la rapide7 con que la cuerda debe
ser jalada por el motor para mover la caja hacia arriba
por el plano con una rapidez C()nstante de 4 pies/ s.
P,.,b 11- I T'I
http://libreria-universitaria.blogspot.com
PROBLEMAS
89
\11·IMI . S. el bloque A se está moviendo hncia abajo con
rapidez de;4 pies/ s micnlras e se mueve hacia arrib~ a 2
1~. I7t1.
JtU!l1
DClcnnine el desplazamIento del bloque sltua8 si A es jalado hacia abajo 4 pies.
pies / s. determine la rapidez del bloque 8.
J~· 1)j2. S, el bloque A se está mOl'lendo hae.ia abajo a
6 pies/s mlcnU8S el bloque e ~e mueve hacia ahajo a 18
pies / s, determine la velocidad relativa del bloque B con
rcspeclO a C.
l. _1 't'
11-179.
El cable locali2ado en 8
e~
jalado hacia abajo a
<1 pies /s, y está desacelerando a 2 pjes i s~. Determine la
velocidad) la aceleración del bloque A en este Instante.
12·11(11. El arreglo de polcas mostrado está diseñado
para levantar materialcl\. Si BC pemwllct:e fijo mientras
el émbolo P es empujado haCIa abajo con rapidez de
pies/ s.. dctcnnine la rapidez de la carga en A.
p,
I~-
11iI11ll1_
Si el extremo del cable localizado en A está siendo jalado con rapide .. de 2 mI s. determine la rapidez con
que se clc\a d bloque E_
Pr"b_ 1.1-1 ,
<1
,~-ll _ Si el bloque A del sistema de poleas se está
moviendo hacia abajo con raplde .. de ... ples/ S nuentras
el bloque e se está moviendo hacia arriba a 2 pies :s. determine la rapide/: del bloque 8 .
l
•
I"ruh. U- 1!lI
http://libreria-universitaria.blogspot.com
90
CAPiTULO 12 Cinemát ica de una particula
12·IH5. La grua se uso para izar la carga. Si los motO.res
colocados en A y 8 están jalando el cable con rapide,., de
2 y " pies/ s. re!opeclivamentc. de termine la rapidez de la
carga.
2~~A
B
U.1R8. El rodillo colocado en A se mueve hacill arriba con \c\ocidad V,4 "" 3 pIes/ s y tiene aceleración OA =
4 pics /s~ cuando SA ::: ~ pies. Determi ne la velocidad y la
aceleración del bloque B en eslC ins tante.
~5
¡'mI. \. - 111
11·110111. El cilindro e está siendo le\antado usando el
sistema de cable y poleas mostrado. Si el punlO A sobre
e.1 cable es jalado hacia cl tambor con rapIdez de 2 m/ s..
determine la rapidez del cilindro.
P, .h. L'--IIUI
12-1"'11. LII caja e I!slá siendo elc>'lIda al mO\'ersc d rodillo colocado en A hacia abajo con rapide7 constante de
1,',4 = 2 mi s a lo largo de In guía. Determine la velocidad
y la aceleración de la caja en el instante s ... 1 ffi. Cuando el rodillo está en B. 13 caja desca nsa sobre el suelo,
Desprecie el tamaño de la polea en los cálculos. Sugerl'IIcia: Relacione las coordenadas XL }' XII usando la geome·
tría del problema, luego tome las primera y segunda de- l
rivadas con respecto al tiempo.
- -- 'm __
,....
o
1:·
12. lIn. El mO\'imiento del collar instalado en A es controlado por un mOlor situado en B de mancra lal que
cuando el collar eSlá en s.\ =- 3 pies. se mueve hacia amba a 2 pies /s y desacele ra a 1 pie / s!. Determine la velocidad y la acele ración del cable al ser jalado dent ro del
mo tor B en este instan te.
r-- -4 PIC"S---j
I
L
12 -1'10. La nifla ubicada en e está de pie cerca del borde del mueUe y jala la cuerda honzomulmeme con rapidez constan te de 6 pies /s. Determine qué lan rápido se
acerca el bote al muelle en el Instante en que la longitud
de la cuerda 1\8 es de 50 pies..
"
B
•
~ -- " ----,
"' .. h. 12-187
PfUh. 11-1,"'
•
http://libreria-universitaria.blogspot.com
PRoeUMAS
."
U-tIH. El hombre jala al niño hacia la rama e del árbol caminando hacia atrás. Si él panc del reposo cuando
x" ." O Yse mueve hacia Atrás con aceleración constante
01'1 "" 0.2 m/r. determine la rapidez del niño en el instnnte .\'8 = 4 m. Desprecie el tamaño de la rama. Cuando x" ,.. 0.Y8 = 8 m. de manera que A y B coinciden. es
decir. la cuerda es de 16 m de longItud.
91
1l-IQ4. El rnm'imicnta vc,:rtical de la carga es produci·
do por el movimiento del pistón ubicada en A sobre el
braza. Detennine la distancia que el pistón o palea en e
debe moveTSC haeia la i7quierda para elevar la carga 2
pLes. El eable está unido en B. pasa sobre la polea en C.
luego por D./:... F. de nuevo alrededor de E. '!I queda unida en G .
Pr...... 12- 1'11
"n.I>, 11· 194
U·11J). Los collare'i A \' 8 están conectados a la cuero
d"a-qú'e pasiI !;Obre la peq~c-ña polcn en C. Cuando A está ubicado en D. 8 está 2'" pies 11 la izqUIerda de D. Si A
se mueve con rapidez constante de 2 pies/ s hacia la derecha, determine la rapidez de B cuando A está 4 pies a
la derecha de D.
12-1Q5. La arcnll cile del reposo 0.5 m verticalmente
sobre un canalón. Si entonces se desliza can velocidad
tic'" 2 m Is par el canalón. determine la velocidad relativa de la arena justo al caer sobre el canalón en el
punta A con respeclo a la arena que se desliza hacia aha·
jo por el canalón. Éste forma un ángulo de 40 con la
horizontal .
Q
1',.
1.
I"~
1!· I~:t. Si el bloque B se está moqcndo bacia abajo con
velOCidad va y tiene aceleración os- determine la velocidad y la aceleración del bloque A cn ténninos de los parámetros mostrados.
- -',,---
"rlob. 11- 1'
Prub.
U ·· IIJ~
http://libreria-universitaria.blogspot.com
92
CAPITULO 12 Cinematica de una particula
12·19(•. D~ aviones JI y B están volando a In misma
ahurn. Si sus velocidades son VA ::: 600 km / h y VB - 500
km / h de manera tal que el ángulo entre sus cunos en linca recta es 8 .; 75", determine la velocidad del uvi6n B
con respecto al avión A.
11·:WU. Dos a\IOIlCS A y B están volando uno aliado
del Olru con rapidez con~tante de 900 km / h. MlmlCniendo esta rapidez. el i!\'ión J\ comienza a Ylajar por una
Irayecloria espiral,;o (l~OOO) km. donde 8 eSlá en radianes. mientras que el avión B continúa volando en línti!
re<:ta. Determine la rapIdez del avión A con n.. s~cto 01
avión B cuando r =' 750 km.
~A
8
d
/
/
P",h. I!- J'Ill
11·1'17. En el instante mostrado. los aUlo móviles A y B
están viajando con rapidcL de 30 y 20 mi / h. re~pectiva.
mente. Si B cstá incrementando su rapide7 en 1200 mi f h1.
mientras A mantiene una rapidez constante, determine la
velocidad), la aceleración de B con respecto a A .
p.I'1K.
En el instante mostrado. los automóviles A y
viajando COIl rapidez de 30 y 20 mi / h. r~·spec·
th'amente. Si A está incrementando su rapide7 a -lOO
mif h1. mientras que la rapidez de B esta dismmuyendo
a 80 mi/ hl. determine la velocidad y la aceleración de B
con respecto a A.
R
e~tán
~
t.,: 2f)
I'A" 30
B
B
-,
1'. , I! ·
1:
En el instanle mostrado. el ciclista en A eSI! \"¡ajando a 7 mI s IIlrededor de la curva de la pista mientras
incrementll su rapidez en 0.5 m / s2. El ciclista en B eSlá
viajando 11 R,5 mIs a lo largo de una porción recta de la
pista e incrementa su rapidez enO.7 m/i. Delermine la ve·
locidad relativa y la aceleración rdatha de JI con respecto
a B en eslC inslantc.
lO'
7"
m~~ ,O_.3_'_"___
milh-caA
,
1:: - 1~~.
Dos botes dejan la orilla al mismo tiempo y vinjan en las direcciones mostradas. S¡ 'I)A ::: 20 piesi s y
vB = 15 pies/ s. determine la rapidez del bote A con respecto al bote B. ¿Cuánto tiempo después de dejar la orilla los botes estarán a 800 pies uno de otro?
l.' . .. En el instante mOStrado. los automóviles A y H
están viajando con velocidades de 55 y 40 mi/ h, respeco
ll\·umentc. Si 8 est:! incrementando su rapidez en 1200
mi h2. mientras que A mantiene una rapidez conslantc.
delcrmine la velocidad y la aceleración de B con respec·
to a A. El automóvil B se muc\e por una curva que tiene un radio de curvatura de 0.5 millas.
t'/f" 4{) mllh
I' ,.,h. U-I'N
1',.b.Il-!O!
lA.. SS mu'h
!.
http://libreria-universitaria.blogspot.com
PROBLEMAS
93
\)
_1.2I1J. Los automóviles A y B están viajando alrededor"de la pista circutor. En el instante mostrado. A tiene
una rapidez de 90 pies/ s y la está incrementando a ralón
de 15 pies/ s2, mientras que B tiene rapidez de 105 pies/ s
y la está desacelerando a razón de 25 pies/ s!, Determine
la "docidad relativa y la aceleración relativa del automó-
11·206. Un pasajcro en un automóvil observa que las
gotas de agua forman un ángulo de 30" con la honzont.al
cuando el automóvil viaja hacia delante con rapkkz dc
60 km / h. C8lculc la vclocidlld terminal (constante) \',
de la lluvia ~i se supone que cae verticalmente.
vil A COn respeclO al automóvil B en este instante.
-
"u'" 60 kmlh
ru,b. U - !!II'I
"~robo
11-2117. En un Instante dado, el jugador situado en 11
lanza una pelota e con velocidad de 20 m i s en la dirección mostrada . Determine la rapidez constante con que
el jugador localizado en 8 debe correr para que pueda
recihir la pelota 3 la mi\>ma elevación a la que fue lanzada. Calcule también la velocidad relaliva y la acclcmeión
relativa de la pelota con respecto a B ClI el instante en
que el jugador la recibe. El jugador 8 está a 1.5 m de A
cuando A lanza la pelota .
12- 2113
1.1·111-1, Los dos ciclistas A )' B \'¡aJan con la misma rapidez cons!amc 11. Determine la rapidez de A con respec10 a B si A viajll por la pista circular. mientras que B lo
hace a 10 largo de! diámetro del circulo.
e
Pmh 12-2:1'"
I'rull.
11-111S, Un hombre puede remar un bote a S mI s en
aguas tranquilas. Él qUIere cruzar un rlo de 50 m de
ancho pam llegar al punto a, 50 m aguas abajo. Si el rfo
f]uye con velocidad de 2 m/ s.. determine la rapidez del
bote y el tiempo necesario para efectuar el cnlce.
I~ -!"""/
ll·1111\. Un hombre pucdc nadar a " pies/ s en aguas
tranquilas.. É l d<:~ea cruzar d do dc 40 pies de am:ho para llegar al punto B que está 30 pies aguas ubajo. Si el río
fluye con velocidad de 2 pies/ s. determine la rapidez del
hombre y el tiempo que necesita para efectuflr el tTUCt:.
Nota: Micnlrlls está ell el agua él no debe dirigirse hada
B para alcanzar este punto. ¿Por qué'!
30pi~
•
T
B
,',,,t..
I !_!n .~
1/
Pruh. 11- ,!UK
http://libreria-universitaria.blogspot.com
94
•
CAPITULO 12 Ci nemática de una particu[a
PROYECTOS DE DISEÑO
o~
J
eH!).
m .... f'\o Df l'\
ulspo ... nJ\o
SFP\R \DOR
IH C\,\I( "
Las canicas salen dd canalón de producción ti 0.5 pies/ s. Dete rmine el rango para el ángulo O s (J s 30 ' para una ~icióD selecciOnada $ con In cual
~ detl!rmi ne l:t colocación de la loh a con respecto ni extremo del ellnll-
Ión. Pri!scnte un dibujo del dispositivo donde muestre la trayt::cloria seguida por las canien
11\1< 12--11)
REPASO DEL C 'IT' LO
• el" '" tíl/(-" n ,'1;11
'0 la cinemática recti linea se refi ere al movimiento que ocurre a lo largo de una
Unea reCIa, Una coordenada s de posición especifica la ubicación de la partícula sobre la línea, y el dcs·
plazamicnto !ls es el cambio de esta posición.
La velocidad promedio es una cantidad vectorial, definida como el desplazamiento dividido entre el interva lo de tiempo,
v
"....
.lr
.ll
~-
Esto es diferente a la rapidez promedio, la cual es un escalar y es la distancia total viajada dividida en·
lre el tiempo de viaje.
ST
(v$p)prom = Al
El tiempo, la posición. la velocidad instantánea y la ace leración instantánea están relacionados mediante las
ecuaciones diferenciales
v = ds/ dl
o = dvj dl
otls=-v dv
Si se sabe que ht aceleración es constante, e ntonces, por integración de esas ecuaciones se obtiene
-v = 11l + oc'
s = So + Vol + 1 a~tl
v .., ifo + 2a~( s -
So)
tUl
r;,
Si el movimiento es errático. entonces puede ser descrito mediante una g.ráfica_Si
una de estas gráficas está dada, entonces las otras pueden ser establecidas usando las relaciones diferenciales. v = ds / dl, a = dv jtll, o a tI.~ = v tll). Por ejemplo. si se conoce la gráfica V- l, entonces los valores
de la gráfica $- 1 son determinados a partir de as = J'V dt = incrementos de área bajo la gráfica '1)- 1.
Los valores de la gráfica 0 - 1 son determinados a partir de a = d v/ dl = pendiente de la gráfica V- l.
\(ori1,irnln ('1nil¡'rro, r,
Para este caso, el movimiento a lo largo de la trayectoria es resuelto en
movimiento rectilíneo a lo largo de los ejes x, y, ¡:, La ecuación de la trayectoria se usa para re lacionar
el movimiento a lo largo de cada eje.
http://libreria-universitaria.blogspot.com
REPASO DEL CAPfTulO
•
95
• .1101";"';(""0 d~ un proyoctil.
El movimiento de vuelo libre de un proyectil sigue una trayectoria parabólica. Tiene velocidad constante en la dirección horizontal y aceleración constante de g = 9.81 m/ s2 o
32.2 pies/ s1 en la dirección vertical. Dos cualesquiera de las tres ecuaciones para aceleración constante
SOn aplicables en la dirección vertical. 'Y en la dirección horizontal sólo es aplicable .. = "O + (vol/.
\fm·¡",;enlo tlln'ilineo 11, l. Si los ejes normal y tangencial se usan para el análisis, entonces v está siempre en la dirección ( positiva. La aceleración tiene dos componentes. La componente tange ncial. a(> toma
en cuenta el cambio en la magnitud de la velocidad: una disminución de ésta es en la direcci6n ( negativa, y un aumento es en la dirección 1 positiva. La componente nonnal un toma en cuenta e l cambio en la
dirección de la velocidad. Esta componente está siempre en la dirección n positiva.
•
• .u'H'imienw
C'ltn·ilinttl, r. 0, - Si la trayectoria del movimiento es expresada en coordenadas polares,
entonces las componentes de la velocidad y de la acelera.ción pueden ser escritas como
v,
=
r
a,=f - rir
aa = r8 + 2;8
Para aplicar estas ecuaciones. es necesario determinar r, r, r, 0, jj en el instante considerado. Si la traycctoria r = /(8) está dada. entonces debe U.s<lne la regla de la cadena del cálcu lo diferencial para obtener las
derivadas con respecto al tiempo. Una vez que los datos son sustituidos dentro de las ecuaciones, el signo algebraico de los resultados indicará la dirección de las componen tes de v o " a lo largo de cada eje.
UOl';m;f!1 ro flhmllllO depr'l/dü//f( de dlH plU1;cula.~
•
El movimiento dependiente de bloques que están
suspendidos de poleas y cables puede ser relacionado mediante la geomctría del sistema. Esto se hace
estableciendo primero coordenadas de posición, medidas desde un origen fijo a cada bloque de manera
que estén dirigidas a lo largo de la línea de movimiento de los bloques. Usando geometría y/ o trigonometría, las coordenadas son entonces relacionadas con la longitud del cable para famular una ecuación
de coordenadas de posición. La primera derivada con respecto al tiempo de esta ecuación da una relación entre las velocidades de los bloque.s. y una segunda derivada resulta en la relación entre sus aceleraciones.
•
\míli\i\ d~1 mlH' jln;tlltll rrlal;,'u 11\ l/ufo tjn t. trn,luciúlL Si dos partículas A y B experimentan moVimientos independientes, entonces esos movimientos pueden ser relacionados Con sus movimientos
relativos. Usando un conjunto de ejes en traslación unidos a una de las partículas (A). las ecuaciones de
velocidad y aceleración se convierten en
~ B = " )1
+
as =
+ aB A
II A
~ BI"
En movimienlo plano, cada una de estas ecuaciones produce dos ecuaciones escalares. una en x y la otra
en la dirección y. Para enconlrar la solución, los vcclores pueden ser expresados en fama cartesiana o
las componentes escalares en.l" y Y pueden ser escritas direclamentc.
http://libreria-universitaria.blogspot.com
,
El diseno de bandas transpon.adoras para una planta embotelladora requiere conocer
las fuerzas que aQúan sobre ellas y la capacidad para predecir el mOVimiento de las
botellas que transportan
•
•