Manual de Filtracion

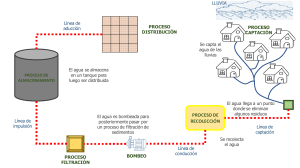
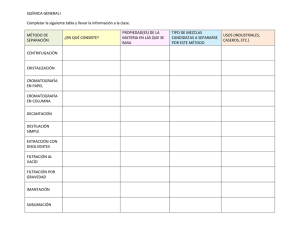
MANUAL DE FILTRACIÓN
&
SEPARACIÓN
Fernando Concha Arcil, Ph.D.
CENTRO DE TECNOLOGÍA MINERAL, CETTEM
TECNOLOGÍA PRODUCTIVA RED CETTEC, FUNDACIÓN CHILE.
UNIVERSIDAD DE CONCEPCIÓN
WWW.MetalurgiaUCN.TK
ÍNDICE
PARTE I. FUNDAMENTOS
1.
INTRODUCCIÓN
1.1 Marco conceptual de los sistemas de separación sólido-líquido.
1.2 Operaciones de separación sólido-líquido en minería.
1.3 Mecanismo de la separación sólido-líquido.
1.4 Selección de técnicas de separación sólido-líquido.
1.5 Equipos utilizados en la separación sólido-líquido.
1.6 Referencias.
2.
TEORÍA DE MEZCLAS
9
2.1 Cinemática.
9
2.2 Cuerpo, configuración y tipos de mezclas 9.
2.3 Deformación y movimiento 11 Balance de masa 13. Balance de masa en
una discontinuidad 16. Ecuación de difusión convectiva 16. Ecuación de
continuidad y condición de salto para mezclas incompresibles 17.
2.4 Dinámica.
18
Balance de momentum lineal 18. Balance de momentum angular 20.
Proceso dinámico 21.
2.5 Referencias.
22
3.
SISTEMAS PARTICULADOS
3.1 Proceso dinámico en un sistema particulado.
Componente fluido 26. Presión de poros 26. Componente sólido 27.
Esfuerzo efectivo del sólido 28. Presión total 29.
3.2 Fuerza de interacción en el equilibrio.
3.3 Discontinuidades.
3.4 Proceso dinámico.
3.5 Referencias.
24
24
SEDIMENTACIÓN DE SISTEMAS PARTICULADOS
4.1 Sedimentación discreta.
Fuerza hidrodinámica sobre una esfera en flujo de Stokes 34. Balance
macroscópico sobre una esfera en flujo de Stokes 34. Fuerza
hidrodinámica sobre una esfera en flujo de Euler 37. Fuerza
hidrodinámica sobre una esfera en flujo de Prandtl 39. Coeficiente de
arrastre para esferas con 0  Re  150.000 42. Velocidad de
sedimentación de una esfera 45. Sedimentación de una suspensión de
33
33
4.
1
1
3
4
6
7
8
30
31
31
32
ii
Manual de Filtración & Separación
esferas 52. Sedimentación de partículas isométricas 57. Sedimentación
de una suspensión de partículas arbitrarias 64.
4.2 Referencias.
5.
6.
7.
TEORÍA DE SEDIMENTACIÓN DE KYNCH
5.1 Conceptos de una suspensión ideal y de un espesador ideal.
5.2 Proceso de Kynch para la sedimentación batch.
Solución por la teoría de características 79. Modos de sedimentación
82.
5.3 Proceso de Kynch para la sedimentación continua.
Espesador ideal continuo: modelación de la alimentación y descarga
88. Proceso de sedimentación continua de Kynch 90. Solución por el
método de características 91. Modos de sedimentación continua 92.
5.4 Estado estacionario y capacidad de un espesador ideal.
5.5 Referencias.
FLUJO EN LECHO POROSO
6.1 Proceso dinámico en un lecho poroso rígido.
Balances locales 104. Ecuación constitutiva de la fuerza resistiva 104.
Ley de Darcy 104. Ley de Forcheimer 104.
6.2 Parámetros geométricos de un lecho poroso rígido.
Ecuaciones de Forcheimer y de Darcy 109. Ecuaciones de Forcheimer
y Darcy en términos de la altura piezométrica 110.
6.3 Modelo capilar de un lecho poroso rígido.
6.4 Proceso dinámico en un lecho poroso rígido.
6.5 Flujo bifásico en un lecho poroso rígido.
Ecuaciones constitutivas de las presiones 116. Ecuaciones
constitutivas de las fuerzas resistivas 118. Precolación en medios
porosos 119. Flujo a presión en medio poroso no-saturado 119.
Saturación residual y saturación efectiva 122.
6.6 Referencias.
70
73
73
76
86
100
102
103
103
105
110
113
114
127
CONSOLIDACIÓN
128
7.1 Proceso dinámico de consolidación.
128
7.2 Teoría de Terzaghi para pequeñas deformaciones.
129
7.3 Ecuación constitutiva de la fuerza hidrodinámica 130. Ecuación
constitutiva del esfuerzo efectivo del sólido 131. Proceso dinámico en
términos de la porosidad 132. Proceso dinámico en términos de la presión
de poros en exceso 132. Solución del problema de valor inicial y de
contorno 133.
7.4 Referencias.
135
ii
ÍNDICE
8.
ESPESAMIENTO
8.1 Introducción.
Desde la Edad de la Piedra al siglo IXX 136. La invención del
espesador Dorr y el diseño de espesadores, 1900 a 1940, 138. El
descubrimiento de las variables de operación de un espesador
continuo, 1940-1950, 140. La era de Kynch, 1950-1970, 141. Teoría
fenomenológica, 1970-1980, 142. Teoría matemática, 1980-2000, 143.
8.2 Equipos.
Espesador convencional, Espesador de alta capacidad y Espesador de
alta densidad 148.
8.3 Teoría de espesamiento.
Proceso dinámico de sedimentación 152. Ecuaciones constitutivas
153. Ecuación de espesamiento 153. Espesamiento batch 155.
Simulación y comparación con datos de la literatura 158.
Espesamiento continuo 161.
8.4 Parámetros de espesamiento.
Parámetros de sedimentación 167. Medición de parámetros de
consolidación 169.
8.5 Capacidad y diseño de espesadores.
Métodos de diseño basados en balances macroscópicos 171: a)
Método de Mishler 171, b) Método de Coe y Clevenger 173. Métodos
de diseño basados en el proceso de sedimentación de Kynch 177, a)
Métodos de diseño basados en el proceso batch de Kynch 178:
Método de Talmage y Fitch 181, Método de Oltman 183; b) Métodos
de diseño basados en el proceso de Kynch continuo 184: Método de
Yoshioka y Hasset 184, Método de Wilhelm y Nadie 186. Métodos de
diseño basados en el modelo fenomenológico 189.
8.6 Estrategias de la operación.
Estado estacionario 195. Concentración de la descarga: efecto del
flujo de alimentación y de la altura del sedimento 196. Dilución de la
alimentación 199. Inventario de material en el espesador 203.
Capacidad máxima 205.Estados estacionarios posibles 206. Efecto del
floculante sobre la capacidad de un espesador 209.
8.7 Investigación, desarrollo y transferencia tecnológica.
Efecto de los floculantes en espesamiento 211. Reología de
sedimentos y descarga de un espesador 212. Efecto de surfactantes y
floculantes hidrófobos en la filtración. Flujo en lecho poroso
compresible 213. Modelación de la alimentación 213. Espesadores de
alta capacidad y alta densidad 214. Optimización de los ciclos de
filtración 215. Optimización de espesadores 215. recuperación de agua
en sistemas de separación sólido-líquido 215. Dinámica y control de
procesos 216.
iii
136
136
144
151
167
171
195
210
iii
iv
9.
Manual de Filtración & Separación
FILTRACIÓN
9.1 Definición, equipos y operación.
Filtración con formación de queque 222. Filtración sin formación de
queque 222. Filtración profunda 223. Variables de operación 224.
9.2 Equipos para la filtración.
Filtros a vacío 226: Filtro de tambor 227, Filtro de discos 227, Filtro
de bandeja 229, Filtro de banda horizontal 230. Equipos de filtración a
presión 230. Filtro prensa de placas verticales 231. Filtro prensa de
discos 240. Filtro de vela 241. Filtros hiperbáricos 242.
9.3 Medios filtrantes.
Telas 243.
9.4 Teoría de filtración.
Formación de queque 248: a) Filtración a presión constante 250, b)
Filtración a volumen constante 257. Secado o soplado del queque.
9.5 Parámetros de filtración.
Medición de los parámetros de filtración 263: a) Porosidad del queque
264; b) permeabilidad del queque y resistencia específica del medio
filtrante 267; Permeabilidad relativa 277.
9.6 Filtros continuos a vacío.
Modelo de un filtro rotatorio 287: a) Formación del queque 288; b)
Cambios de condiciones de operación 290; c) Deshumedecimiento del
queque 291.
9.7 Referencia.
10. FLOCULACIÓN
10.1 Introducción.
Coagulación 302. Floculación 305.
10.2 Floculantes poliméricos.
Propiedades 307. Preparación 309.
10.3 Cinética de la Floculación.
10.4 Hidrodinámica de la floculación.
Floculación en una cañería 312. Floculación en un feedwell 312.
10.5 Referencias.
222
222
226
243
247
262
286
299
301
301
307
310
312
314
PARTE II. APLICACIONES
11. AGREGACIÓN DE PARTÍCULAS EN PROCESAMIENTO DE
MINERALES
11.1 Introducción.
11.2 Agregación en Procesamiento de Minerales.
Floculación 317. Floculantes poliméricos en circuitos de flotación
321.Aglomeración por aceite 326.
315
316
317
iv
ÍNDICE
11.3 Discusión.
11.4 Referencias.
12. TÉCNICAS DE FLOCULACIÓN Y METODOLOGÍAS PARA LA
OPTIMIZACIÓN DE ESPESADORES
12.1 Introducción.
12.2 Caracterización de la floculación.
12.3 Caracterización de suspensiones floculadas.
Medición de la velocidad de sedimentación de flóculos 338.
12.4 Rol de la hidrodinámica en la floculación 339.
12.5 Entendiendo el comportamiento de espesadores.
12.6 Diseño y operación de rastras.
12.7 Conclusiones.
12.8 Agradecimientos.
12.9 Referencias.
13. POLÍMEROS HIDRÓFOBOS DEL TIPO LÁTEX PARA LA
SEPARACIÓN SÓLIDO-LÍQUIDO DE CONCENTRADOS DE
FLOTACIÓN
13.1 Introducción.
13.2 Resultados experimentales.
Efecto de floculantes y aglomerantes hidrófobos sobre la flotación de
molibdenita 350. Efecto de aglomerantes hidrófobos sobre la
floculación de calcopirita y pirita 353. Efecto del látex UBC-1 sobre la
filtración de otros materiales hidrófobos 353.
13.3 Conclusiones.
13.4 Referencias.
14. CFD COMO HERRAMIENTA PARA EL DISEÑO DE
ESPESADORES
14.1 Introducción.
14.2 Modelación matemática.
14.3 Simulación de la alimentación a un espesador.
Dilución de la alimentación 358. Alimentación mediante tobera 361.
Alimentación en feedwell 365.
14.4 Simulación de la inyección de floculantes.
Inyección en tobera de dilución 368. Inyección en feedwell 369.
14.5 Simulación de las rastras.
14.6 Conclusiones.
14.7 Referencias.
15. CONCEPTOS MODERNOS DE FILTROS ROTATORIOS
15.1 Filtro de disco de alto rendimiento “Boozer”.
Características notables del Boozer 377. Datos técnicos 377.
Descripción y funcionamiento de los componentes importantes:
v
328
329
332
333
334
336
342
345
346
346
347
348
349
350
354
354
356
357
357
358
367
371
373
373
375
376
v
vi
Manual de Filtración & Separación
Discos y segmentos 377; Cañerías de colección de filtrado 378;
Tambor central 379. Batea del filtro 380; Cabeza de control 380.
15.2 Operación del filtro de discos Boozer.
Formación del queque 381; Deshumedecimiento del queque 382;
Descarga del queque 382.
16. LAVADO CON FILTRO DE BANDA HORIZONTAL
16.1 Descripción del equipo y sus aplicaciones.
16.2 Estudio de casos.
16.3 Aplicaciones de lavado del queque para remover impurezas.
Mantos de Oro: La Coipa 386. Compañía Minera Escondida: Coloso
387. SQM Salar: Ácido Bórico 388. Compañía Minera Meridian: El
Peñón 388.
16.4 Aplicaciones de lavado de queque para recuperar soluciones.
Mantos de Oro: La Coipa 390; Compañía Minera Escondida: Coloso
390; Compañía Minera Meridian: El Peñón 390.
16.5 Conclusiones.
17. SISTEMAS DE FILTRACIÓN PARA LA DEPOSITACIÓN DE
RELAVES
17.1 Introducción.
Consideraciones en la construcción de un depósito de relave 392.
Comparación de costos 393.
17.2 Determinación del sistema de depositación seca.
Compactación de los relaves 394. Recuperación de agua 395.
Precolación 395.
17.3 Tipo de equipos.
Filtro prensa de doble banda 396. Filtro prensa convencional 397.
Filtro de discos 397. Filtro de bandas 398. Espesador de alta densidad
398.
17.4 Instalaciones existentes.
Mantos Blancos 400. El Indio 401. La Coipa, Can Can y El Peñón
401. ZCCM y Gecamines 403.
18. FILTRACIÓN HI-BAR CON VAPOR APRESIÓN
18.1 Fundamentos de la filtración con vapor a presión.
Filtración convencional con vapor 408. proceso moderno de filtración
con vapor a presión Hi-Bar 408.
18.2 Tecnología de filtración Hi-Bar.
Concepto de la filtración Hi Bar con vapor a presión en la planta 411.
18.3 Beneficios de la filtración Hi Bar con vapor a presión.
18.4 Ensayos en el laboratorio y planta piloto.
Equipos de ensayo de laboratorio 414. Planta piloto Hi Bar 414.
381
383
383
385
386
390
390
392
392
394
396
399
407
408
410
412
414
vi
ÍNDICE
vii
18.5 Aplicaciones de la filtración Hi Bar con vapor a presión.
Desaguado de concentrados en la flotación de carbón 415. Desaguado
de concentrados de minerales de hierro 416. Lavado y secado de un
producto de precipitación química 416.Lavado y secado de yeso en
una planta térmica 417.
18.6 Economía de la filtración Hi Bar con vapor a presión.
18.7 Conclusión.
18.8 Referencias.
19. APÉNDICES
19.1 Apéndice 1 Conversión de medidas de concentración.
19.2 Apéndice 2 Unidades de medida y Dimensiones.
415
418
418
419
420
422
PARTE III. PROVEEDORES
BOKELA
CENTRO DE TRANSFERENCIA DE TECNOLOGÍA MINERAL
(CETTEM)
CIBA ESPECIALIDADES QUÍMICAS CONOSUR SA.
DELKOR
DORR OLIVER
LANZCO
LAROX CHILE LTDA.
vii
PREFACIO
Este libro pretende llenar un vacío existente en la bibliografía de los procesos
extractivos de la industria minera. Temas como la conminución y la flotación han
recibido gran cobertura, en tanto que los procesos de separación sólido-líquido, tales
como el espesamiento y la filtración, han pasado prácticamente inadvertidos.
Pareciera ser que la importancia económica de la reducción de tamaño,
obviamente la etapa más costosa en el procesamiento de un mineral, y la importancia
estratégica de la flotación como proceso de concentración, han relegado la última etapa
del beneficio de un mineral, como es la separación sólido-líquido, a un sitial de menor
relevancia. Es verdad que, cuando el tratamiento de un mineral se desarrolla
normalmente, los ingenieros de proceso tienden a considerar al espesamiento y la
filtración como etapas auxiliares y no fundamentales en la planta. Sin embargo, la
situación cambia cuando surgen problemas en la sedimentación o filtración de
concentrados o relaves, originados la mayor parte de las veces en un cambio en la
composición de la mena tratada, y no es posible recuperar toda el agua necesaria en la
planta o no se logra las humedades especificadas del producto. En ese momento la
separación sólido-líquido cobra una importancia fundamental.
Emergencias como la señalada encuentran al ingeniero débilmente preparado
para enfrentarlas. Puede que se pregunten por qué en la Universidad se dio tan poca
importancia a estas etapas del procesamiento de un mineral; por qué no se les enseñó
estas técnicas en forma más comprehensiva. La verdad es que este “descuido
académico” tiene raíces más profundas. La negligencia en esta área tecnológica de la
enseñanza relacionada al campo minero es generalizada e internacional y proviene de
la poca intensidad y nivel con que se enseña la mecánica y la mecánica de fluidos en
las carreras de ingeniería de minas y metalurgia. Esto ha traído como consecuencia que
la separación sólido-líquido raramente haya sido campo de investigación en estas
disciplinas y que, por lo tanto, los académicos de estas unidades no puedan traspasar a
sus alumnos estos conocimientos desde experiencias propias.
La Universidad de Concepción ha dado un paso fundamental para cambiar esta
situación. Por ya más de 25 años, académicos y alumnos de esta Casa de Estudio,
dirigidos por el autor de este libro, han realizado investigación relevante en el campo
de la separación sólido-líquido aplicado a la minería. Es así como a través de memorias
de título, tesis de postgrado, investigaciones locales e investigaciones cooperativas con
académicos de universidades de otros países, se ha desarrollado una teoría
fenomenológica de la sedimentación que ha permitido poner al campo del
viii
Prefacio
ix
espesamiento industrial en un marco científico y tecnológico adecuado. Marco
fundamental si es que se desea enseñar esta disciplina a estudiantes o ingenieros de
proceso. Tan exitosa ha sido esta labor, que la Sociedad de Ingenieros de Minas de los
Estados Unidos de Norteamérica SME decidió otorgar el premio Antoine Gaudin-1998
al autor del presente libro. Por otra parte, en los últimos cuatro años se ha dedicado
enormes esfuerzos al estudio y experimentación del campo de la filtración con el
objetivo de formular una teoría unificada que englobe los diferentes procesos
involucrados en la separación sólido-líquido. Creemos que se ha logrado.
En este libro, o Manual como lo ha llamado el autor, aún cuando difiere
fundamentalmente de los manuales existentes en el campo de la filtración, se pretende
traspasar el conocimiento acerca del campo de la sedimentación, el espesamiento y la
filtración, logrado durante todos estos años por el Grupo de Sistemas Particulados de
la Universidad de Concepción. Gran parte del material presentado: teoría, formulación
de modelos y resultados, son originales. En el libro se enfatiza los fundamentos
teóricos y las aplicaciones por sobre el conocimiento enciclopédico de equipos y
materiales. En forma consciente se ha mantenido un alto nivel científico, aún cuando
ello no es estrictamente necesario para comprender los procesos y sus aplicaciones.
Estimamos que este enfoque satisfará las expectativas de los diversos grupos que
pudieran tener interés en el libro: estudiantes de ingeniería, estudiantes de postgrado
en ingeniería, ingenieros de procesos de la industria minera, ingenieros consultores y
proveedores de equipos y materiales para la industria minera. Para aquellos
interesados en la teoría, se utiliza un riguroso enfoque fenomenológico basado en la
teoría de mezclas de la mecánica del medio continuo, y, para aquellos interesados en
las aplicaciones, se incluye problemas resueltos en la mayoría de los capítulos que
ilustran el uso de la teoría en el diseño, la operación y la optimización de los procesos
involucrados. Aquellos académicos interesados en la matemática detrás del fenómeno,
pueden satisfacer su inquietud en el reciente libro Sedimentation and Thickening:
Phenomenological Foundation and Mathematical Theory, de los autores, M.C. Bustos,
F. Concha, R. Bürger y E. Tory, publicado en 1999 por Kluwer Academic Publishers,
de Dodrecht, Holanda.
El Manual está dividido en tres partes. La primera, que incluye toda la teoría y
aquellas aplicaciones necesarias para entenderla y aplicarla, ha sido escrita enteramente
por el autor. La segunda parte está formada por una serie de trabajos, solicitados a
diversos especialistas de renombre, que ejemplifican las aplicaciones industriales.
Finalmente la tercera parte entrega información sobre diversas empresas ligadas a la
separación sólido-líquido en la minería chilena.
En el capítulo 1 se entrega el marco conceptual bajo el cual se estudiará los
procesos de separación sólido-líquido. Se menciona las diversas operaciones
involucradas en estos procesos y los mecanismos en que se basan. Se discute
brevemente la selección de técnicas de separación y los equipos utilizados.
El capítulo 2 da una rigurosa, aunque limitada, presentación de la Teoría de
Mezclas. Estimamos que, como los fundamentos de este libro pueden encontrarse en la
mecánica de los sistemas particulados, no hay necesidad de desarrollar la
termodinámica de las mezclas. El capítulo da la estructura mecánica y matemática
x
Manual de Filtración & Separación
necesaria para entender los fundamentos y modelar los procesos de sedimentación y
filtración. Una introducción discute las condiciones que debe cumplir un sistema
multifásico para ser considerado como continuo. Luego se plantea los conceptos de
componente, mezcla y configuración y se presenta las ideas de masa, deformación,
movimiento, cantidad de movimiento y fuerzas para cada uno de los componentes de la
mezcla. Las medidas de deformación, movimiento y velocidad de deformación llevan a
balances macroscópicos y locales de masa y cantidad de movimiento y a las
condiciones de salto. Finalmente, se define un proceso dinámico y la necesidad de
formular ecuaciones constitutivas para definirlo completamente.
En el capítulo 3 se aplican los principios de la Teoría de Mezcla a sistemas
particulados constituidos por suspensiones de sólido finamente dividido en un líquido.
Se comienza definiendo un proceso dinámico para el sistema particulado y las
ecuaciones que éste debe cumplir. Se define la presión de poros, el esfuerzo efectivo
del sólido, la concentración crítica y la fuerza de interacción sólido-fluido y se
completa la teoría estableciendo ecuaciones constitutivas generales para el componente
fluido y para el componente sólido.
La sedimentación de sistemas particulados se trata como un proceso discreto en
el capítulo 4. Se comienza estableciendo las ecuaciones que describen
cuantitativamente la velocidad de sedimentación de una esfera de cualquier tamaño y
naturaleza, para continuar con las suspensiones de esferas y terminar con suspensiones
de partículas de forma arbitraria.
El capítulo 5 describe la sedimentación de sistemas particulados como un medio
continuo. Se establece los conceptos de una suspensión ideal y de un espesador ideal.
La aplicación de la Teoría de Mezclas a suspensiones ideales da como resultado el
proceso de Kynch para la sedimentación batch y continua. Se presenta la solución por
la teoría de características y se define el concepto de Modos de Sedimentación.
Finalmente se establece la ecuación que describe la capacidad de un espesador ideal.
Los sistemas particulados consolidados son tratados en el capítulo 6. Se
comienza estableciendo el proceso dinámico para un lecho poroso rígido. Se analiza las
ecuaciones de Darcy y Forcheimer como ecuaciones constitutivas para la fuerza de
interacción sólido-líquido en el escurrimiento de un fluido por el medio poroso. Se
discute el concepto de permeabilidad y su modelo geométrico. A continuación se
discute el flujo bifásico en un medio poroso rígido y se introduce los conceptos de
capilaridad, saturación y permeabilidades relativas.
Como opuesto al capítulo anterior, en el capítulo 7 se analiza los sistemas
particulados compresibles. Se introduce la teoría de Terzaghi para pequeñas
deformaciones y se establece las ecuaciones constitutivas para la fuerza hidrodinámica
y el esfuerzo efectivo del sólido. El proceso dinámico obtenido se resuelve en términos
de la presión de poros en exceso como función de la porosidad.
En el capítulo 8 se analiza con profundidad el proceso dinámico de
espesamiento. En una extensa introducción se presenta la historia de la sedimentación
desde la Edad de la Piedra hasta hoy, enfatizando las personas e instituciones que han
sido sus protagonistas. A continuación, se muestra los equipos utilizados
Prefacio
xi
industrialmente para el espesamiento. Le sigue un riguroso análisis de la teoría de
espesamiento, desarrollando las ecuaciones que describen el proceso, tanto para el caso
batch como para el continuo. La siguiente sección estudia en detalle los parámetros que
aparecen en las ecuaciones de espesamiento y su determinación experimental. El
capítulo continúa con una descripción cuantitativa de los métodos de diseño de
espesadores dentro del marco de la teoría de espesamiento. Las diversas estrategias de
operación se analizan a continuación y se muestra el efecto de las diversas variables en
el comportamiento de un espesador industrial. Finalmente, se describe los temas de
investigación relevante en el presente.
La filtración es el tema del capítulo 9. Luego de una breve descripción de los
diversos tipos de equipos industriales y de las telas filtrantes, se presenta la teoría de
filtración. Se describe las diversas etapas de un proceso de filtración, analizando
detalladamente cada una de ellas. Se estudia, a continuación, los parámetros de
filtración y su determinación experimental. Finalmente se analiza, por separado, la
modelación y simulación de filtros rotatorios a vacío y filtros a presión.
Terminando la primera parte de este Manual, se presenta la floculación en el
capítulo 10. En secciones sucesivas se introduce los conceptos de coagulación y
floculación, se presenta los reactivos floculantes, se estudia la cinética e hidrodinámica
de la floculación y sus aplicaciones en la operación de espesadores.
La parte II del Manual contiene 8 trabajos por diversos especialistas que
pretende mostrar algunas aplicaciones del espesamiento y la filtración en la industria
minera. El primer trabajo lo presenta el profesor Janusz Laskowski, de la Universidad
de British Columbia en Canadá en el capítulo 11 Agregación de Partículas en
Procesamiento de Minerales, en el que describe los mecanismos de agregación
mediante floculantes poliméricos, látex hidrófobos y aceites emulsificados.
El capítulo 12 muestra un trabajo de los investigadores de CSIRO en Australia:
J. Farrow, P Fawell, R. Johnston, Nguyen, M. Rudman, K. Simic, J. Swift y A. Parker,
Técnicas de Floculación y metodologías para la Optimización de Espesadores. El
trabajo muestra una serie de herramientas y técnicas desarrolladas para abordar los
fenómenos de floculación en espesadores. Se presenta, también, el uso de CFD para
predecir el comportamiento de espesadores bajo diferentes condiciones de operación.
El capítulo 13, escrito por el profesor S. Castro, trata el tema de los Polímeros
Hidrófobos del tipo Látex para la separación sólido-líquido de concentrados de
flotación. Mediante resultados experimentales en el laboratorio se muestra el efecto de
floculantes y aglomerantes hidrófobos sobre la flotación de molibdenita, floculación de
calcopirita y pirita y sobre la filtración de otros materiales hidrófobos.
R. Köck y F. Concha demuestran en el capítulo 14 CFD como Herramienta para
el Diseño de Espesadores, como utilizar CFD para optimizar la adición de floculantes
en tuberías, toberas de inyección y feedwell. Además, se muestra como utilizar esta
herramienta en el diseño de rastras.
xii
Manual de Filtración & Separación
La empresa alemana Bokela presenta en el capítulo 15 Conceptos Modernos de
Filtros Rotatorios, un filtro de discos de nueva tecnología, denominado Boozer, que
presenta grandes ventajas con respecto a los filtros de vacío rotatorios convencionales.
En el capítulo 16 Lavado con Filtro de Banda Horizontal, la empresa Delkor
muestra las aplicaciones de estos filtros en el lavado de queques de filtración. Se
describe equipos y se muestra aplicaciones en diversas empresas mineras chilenas.
En un segundo artículo, Delkor escribe en el capítulo 17 Sistemas de Filtración
para la Depositación de Relaves. Se plantea las consideraciones que se debe tener para
la construcción de un depósito de relaves. Se compara costos de diversas alternativas y
se muestra los equipos que se utiliza. Finalmente se muestra ejemplos en la industria
minera chilena.
Como último artículo invitado, Bokela presenta la Filtración Hi-Bar con vapor a
presión en el capítulo 18. Se expone los fundamentos de la filtración con vapor y las
ventajas de la tecnología hiperbárica con vapor. Se muestra resultados en el laboratorio
y planta piloto y aplicaciones industriales para concentrados de carbón, minerales de
hierro, productos de la precipitación química y lavado y secado de yeso en una planta
térmica.
En la Parte III de este Manual se presenta los perfiles de las siguientes empresas
en forma alfabética: Bokela; Centro de Tecnología Mineral; Ciba Especialidades
Químicas Conosur, Delkor, Lanzco y Larox Chile.
Como ya se dijo en un comienzo, la mayoría del material contenido en este
Manual es original y fue desarrollado por el Grupo de Sistemas Particulados de la
Universidad de Concepción en colaboración con investigadores del Departamento de
Ingeniería Matemática de la Universidad de Concepción y el Instituto de Matemática
Aplicada de la Universidad de Stuttgart en Alemania. Agradecemos sinceramente a
todos aquellos que colaboraron en el desarrollo de la teoría y sus aplicaciones, sin el
trabajo esforzado de los cuales no habría material que presentar.
Especialmente importante fue la participación de los siguientes alumnos, la
mayoría de los cuales son hoy destacados profesionales: E. Almendra, A. Barrientos,
O. Bascur, A. R. Becker, A. Christiansen, H. Droguett, P. Garrido, M. Kunik, F. Melo,
A. Quiero, A. Rojas, V. Soto y R. Valenzuela. La participación de los matemáticos fue
fundamental para avanzar en la solución de los modelos. Se debe mencionar la
colaboración de María Cristina Bustos de la Universidad de Concepción, Wolfgang
Wendland y Raimund Bürger de la Universidad de Stuttgart en Alemania, Kenneth
Karlsen de la Universidad de Bergen en Noruega y Elmer Tory de la Universidad de
Mount Allison en Canadá. A todos ellos nuestros agradecimientos.
El Editor
Centro de Imagen Corporativa
Fundación Chile
Concepción, Febrero de 2001.
CAPÍTULO 1
INTRODUCCIÓN
MARCO CONCEPTUAL PARA LOS SISTEMAS DE SEPARACIÓN SÓLIDOLÍQUIDO
La separación sólido-líquido por métodos mecánicos forma parte de una gran
área de técnicas de separación de fases sólidas, líquidas y gaseosas. Este tipo de
separación aparece en un extenso número de procesos industriales en los diversos
campos de la economía. A ella pertenece la eliminación de agua desde suspensiones en
la industria, la recuperación de agua en procesos de la minería, la purificación de aguas
domiciliarias, la eliminación de polvo, la desgasificación de líquidos y la eliminación
de espumas, entre muchos otros procesos. Es, entonces, pertinente poner los procesos
de separación sólido-líquido dentro del contexto de las operaciones de separación de
fases
Las tablas N°1 y 2 muestran procesos de separación de materiales sólido, líquido
y gaseoso en fase dispersa y continua. Las letras cursivas en negrita corresponden a la
separación sólido-líquido que se analizará en este Manual.
En los procesos de separación sólido-líquido que nos interesan, el componente
líquido siempre se encuentra en fase continua mientras que el componente sólido
puede estar en forma dispersa o continua. En una suspensión que se alimenta a un
espesador, el sólido esta en forma dispersa en la etapa de sedimentación, pero se
considera como fase continua en la etapa de consolidación. En el caso de filtración el
sólido se encuentra disperso en la alimentación al filtro, pero en fase continua una vez
que se formó el queque.
Dentro del contexto de la separación sólido-líquido, denominaremos Sistema
Particulado toda mezcla de materiales en que el sólido esté formado de partículas,
estén éstas en estado disperso o continuo. Cuando las partículas forman una fase
discreta, lo llamamos suspensión o dispersión y cuando están en forma continua, lo
denominamos medio poroso. Asociado a sistemas dispersos estudiaremos la
sedimentación y asociado a medios porosos, la filtración.
En realidad, la clasificación de mezclas de materiales continuos o dispersos no
tiene mayor importancia en la cuantificación de la sedimentación o filtración ya que,
como veremos más adelante en este Manual, toda mezcla de sólidos y fluidos puede ser
considerada una mezcla de materiales continuos si la mezcla se produce a escala
1
2
Manual de Filtración & Separación
Tabla N°1 Mezcla de fases continuas y dispersas y métodos de separación
Fase continua
Fase dispersa
Sólido
Sólido
Líquido
Gas
Sedimentación
Sedimentación
Clarificación
Eliminación de polvo
Filtración
Filtración
Centrifugación
Molienda
Clasificación
Clasificación
Molienda
Flotación
Líquido
Cromatografía
Sedimentación
Sedimentación
Centrifugación
Gas
Degasificación
Flotación
Cromatografía de gases
Degasificación
Tabla N°2 Mezcla de dos fases continuas y su separación
Fase continua
Fase
continua
Sólido
Sólido
Líquido
Gas
Consolidación
Degasificación de
queques de filtración
Expresión
Humectación de
queques de filtración
Líquido
Consolidación
Expresión
Humectación de
queques de filtración
Gas
Degasificación de
queques de filtración
Capítulo 1. Desarrollo Histórico
3
microscópica, o si el volumen de trabajo es mucho mayor que el volumen en que se
realiza la mezcla. Como ejemplo consideremos una mezcla de relaves de cobre en un
espesador. Las partículas de relaves suelen tener tamaños menores a 10-4 m mientras
que el espesador que los contiene posee alturas del orden de 1m y diámetros del orden
de 10 a 102 m. En estos casos podemos suponer que la mezcla se compone de dos fases
continuas, una sólida y una líquida. La fase sólida conserva las principales propiedades
de las partículas sólidas, como su densidad, velocidad de sedimentación y
compresibilidad, pero pierde el concepto de tamaño de partícula.
La estructura microscópica (o de nivel de partícula) es importante al momento
de cuantificar los efectos superficiales entre las fases. Se sabe, por ejemplo, que poros
muy pequeños entre partículas originan fuerzas capilares cuando existen presentes las
tres fases, sólida, líquida y gaseosa.
OPERACIONES DE SEPARACIÓN SÓLIDO-LÍQUIDO EN MINERÍA
La separación de mezclas de sólido-líquido requiere, generalmente, una
secuencia de operaciones como las indicadas en la figura 1.1.
Pretratamiento
Concentración
Separación
Postratamiento
Fig. 1.1 Secuencia de operaciones de separación sólido-líquido.
Cada una de estas etapas puede ser realizada de diversas maneras. El esquema que
sigue muestra algunas formas de llevarlas a cabo:

Quimico


I. Pretratamiento 
 Fisico


 Floculacion

Coagulacion
Crecimiento de cristales


Congelacion

Adicion de ayuda de filtrante

Espesamiento
II. Concentracion 
 Clarificacion
 Tamizaje
III. Separacion Solido-liquido 
 Filtracion
Secado

IV. Postratamiento 
Almacenamiento
Fig. 1.2 Esquema de los procesos de separación sólido-líquido
4
Manual de Filtración & Separación
Mantener un proceso de separación sólido-líquido eficiente requiere considerar
el conjunto de estas operaciones. La economía de la separación sólido-líquido en una
secuencia de etapas con diferentes procesos, como se indica en la figura 1.1, depende,
además de los aspectos individuales de cada etapa, en encontrar los puntos óptimos de
transición entre una etapa y la otra.
MECANISMOS DE LA SEPARACIÓN SÓLIDO-LIQUIDO
La separación de sólido y líquidos de una mezcla se puede realizar mediante
métodos puramente mecánicos y térmicos. La figura 1.3 muestra estos métodos y las
operaciones o procesos a los que da origen.
Las operaciones térmicas de secado y vaporización pueden separar totalmente la
mezcla de sólidos y líquidos, cosa que no logra ninguna de las operaciones mecánicas.
Sin embargo, las operaciones térmicas raramente se utilizan por sí solas en empresas
mineras debido a su alto consumo de energía. Cuando se las utiliza, ellas van
precedidas de las operaciones mecánicas mencionadas y las complementan para
disminuir la humedad residual de la fase sólida. Donde sí se utiliza el secado y la
vaporización es en el laboratorio para la determinación de la concentración de una
suspensión o la humedad de un queque de filtración.
SEPARACIÓN SÓLIDO-LÍQUIDO
OPERACIONES MECÁNICAS
OPERACIONES TÉRMICAS
TAMIZAJE
SECADO
SEDIMENTACIÓN
VAPORIZACIÓN
FILTRACIÓN
Fig. 1.3 Mecanismos de Separación sólido-líquido
Las operaciones mecánicas de separación sólido-líquido se basan en tres
mecanismos, la sedimentación, la consolidación y el flujo en medios porosos.
Se denomina sedimentación al proceso de asentamiento de un material sólido o
líquido desde un fluido, generalmente agua o aire, desde un estado de suspensión. El
proceso se observa en la naturaleza en los procesos geológicos de formación de los
depósitos de rocas y minerales y, mucho más visiblemente, en la sedimentación de
gotas de agua o hielo, denominada lluvia o granizo respectivamente, o en la deposición
de polvo. La figura 1.2 muestra en forma esquemática la sedimentación de esferas
Capítulo 1. Desarrollo Histórico
5
sólidas en un líquido. La eficiencia de la separación depende principalmente de la
magnitud del campo de fuerza de cuerpo aplicada, gravitacional o centrífuga, de la
diferencia de densidades entre las partículas sólida y líquida, del tamaño de las
partículas y de la viscosidad del líquido. La cantidad de líquido de una suspensión que
es capaz de separar la sedimentación es toda aquella que no llena los poros del
sedimento formado. La figura 1.4 muestra un esquema de partículas en sedimentación
gravitatoria. Las formas de aplicar fuerzas de cuerpo, o fuerzas externas, a una
suspensión se muestran en la figura 1.5.
Fig.1.4 Sedimentación de esferas en un líquido
ESPESADOR
GRAVITACIONAL
CLARIFICADOR
SEDIMENTACIÓN
CENTRÍFUGA
CENTRÍFUGA
HIDROCICLÓN
Fig. 1.5 Fuerzas que originan la sedimentación y los equipos asociados.
Cuando el agua retenida en el sedimento es más que la deseada, se debe recurrir a
la filtración. Se denomina filtración al proceso de formar un queque soportado por un
medio filtrante, eliminando líquido denominado filtrado. Cuando todo el líquido de la
suspensión ha pasado por el queque y los poros de éste están llenos de líquido, esto es,
el queque está saturado, la formación de queque ha terminado. Para eliminar más
líquido, se sopla aire a través del queque, él que desplaza al líquido disminuyendo su
humedad. La fuerza impulsora de la filtración es un gradiente de presión. Este
gradiente puede ser la presión hidrostática del líquido a filtrar o un gradiente de presión
exterior impuesto por una bomba. Las variables más importantes en la filtración son la
porosidad y la permeabilidad del queque, esto es la facilidad con que escurre el agua a
través de él. La filtración puede ser ayudada o dificultada por la sedimentación. En
6
Manual de Filtración & Separación
general la suspensión a filtrar se impulsa hacia un recipiente y se hace pasar a través de
un medio poroso denominado medio filtrante. Si el filtro es horizontal, la
sedimentación de las partículas ayudaran a la filtración, en cambio si el filtro es
vertical, las partículas sedimentarán en la dirección perpendicular a la dirección de la
filtración. Las figuras 1.6a y 1.6b muestran estos dos casos.
líquido
sólido
líquido
sólido
Fig. 1.6a Sedimentación y Filtración
en la misma dirección
Fig.1.6b Sedimentación y Filtración en
direcciones perpendiculares.
1.4 SELECCIÓN DE TÉCNICAS DE SEPARACIÓN SÓLIDO-LÍQUIDO
La mayoría de las suspensiones concentradas que resultan de la operación de una
planta de Procesamiento de Minerales, son materiales con comportamiento nonewtoniano, en muchas ocasiones de tipo visco-plásticos, que se caracterizan por tener
memoria. Esto significa, que el comportamiento de una misma suspensión en la misma
operación puede ser diferente si la pulpa ha sido sometida previamente a un pretratamiento o a una operación o proceso previo. En este sentido, por ejemplo, el
espesamiento de una pulpa tiene gran influencia en la posterior filtración. De aquí la
recomendación de optimizar los procesos de separación sólido-líquido en conjunto, en
vez de tratarlos por separado o, en considerar algunos e ignorar otros.
Por otra parte, una misma tarea de separación sólido-líquido puede ser realizada
con secuencias de diferentes combinaciones de equipos, por lo que cualquier estudio
debe considerar estas operaciones en conjunto.
Operar un sistema de separación sólido-líquido requiere conocer los parámetros
más importantes en su comportamiento. Para ello es necesario determinar estos
parámetros en el laboratorio y formular ecuaciones constitutivas del material. Al
realizar estas pruebas, es necesario tener en cuenta las propiedades de memoria que
tienen las pulpas. Las suspensiones sufren lo que se denomina envejecimiento, por lo
Capítulo 1. Desarrollo Histórico
7
que es conveniente realizar los ensayos experimentales directamente en las plantas y, si
se efectúan en equipos continuos, evitar la recirculación del material.
1.5 EQUIPOS UTILIZADOS EN LA SEPARACIÓN SÓLIDO-LÍQUIDO
Las figuras 1.7 y 1.8 muestran los nombres de los principales equipos utilizados
para la separación sólido-líquido en la industria minera, tanto en sedimentación como
en filtración.
SEDIMENTACIÓN
Espesador
Clarificador
Hidrociclón
Centrífuga
Fig. 1.7 Equipos que utilizan la sedimentación como mecanismo
FILTRACIÓN
Gravitacional
Filtro de arena
Vacío
Filtro de tambor
Filtro de discos
Filtro de bandas
Filtro de bandeja
Presión
Filtro prensa vertical
Filtro prensa horizontal
Filtro de vela
Presión y vacío
Filtro hiperbárico
Fig. 1.8 Equipos utilizados en la separación sólido-líquido en minería
8
Manual de Filtración & Separación
1.6 REFERENCIAS
Concha F., Marco conceptual de los Sistemas de Filtración, I Coloquio Nacional de
Avances en los Sistemas de Filtrado de Minerales, Santiago 1995.
Filters and Filtration Handbook, 4th Ed., Elsevier Science, Customer Support Dept.,
P.O.Box 291, 1000AE, Amsterdam, The Netherlands.
Stahl, W., Bott, R. and Anlauf, H., Position of thickening and filtration in the general
scheme of solid liquid separation processes and selection criteria for suitable separation
methods, Seminario Internacional: Técnicas Modernas de Separación Sólido-Fluido en
la Industria Minera, Universidad de Concepción, 1991.
Wakeman, R.J. and Tarleton, E.S., Filtration Equipment Selection, Modelling and
Process Simulation, Elsevier Science Inc., 665 Av. Of the Americas, New York, NY
10010, USA.
CAPÍTULO 2
TEORÍA DE MEZCLAS
Para el estudio de flujo en medios porosos rígidos y deformables y para el
estudio de sedimentación o transporte de suspensiones es conveniente considerar un
cuerpo como compuesto por diversos materiales. Para ello la herramienta más
poderosa es la denominada Teoría de Mezclas. No existe una única Teoría de Mezclas,
sino que varias de ellas, y aquí seguiremos el desarrollo iniciado por Truesdell (1965,
1960, 1984).
La Teoría de Mezcla postula que cada punto del espacio puede ser ocupado
simultáneamente por un número finito de diferentes partículas, una por cada
componente de la mezcla. Es así como la mezcla puede ser representada por la
superposición de n medios continuos, cada uno de los cuales sigue su propio
movimiento con las restricciones impuestas por la interacción entre componentes. Esto
significa que cada componente debe seguir las leyes de conservación de la masa y
momentum modificados para incorporar términos que representen el intercambio de
propiedades entre componentes. Los efectos micro estructurales deben ser
incorporados a través de ecuaciones adicionales denominadas ecuaciones
constitutivas.
Para obtener un tratamiento racional se requiere que las propiedades de las
mezclas resulten como consecuencia de las propiedades de los componentes y que las
mezclas sigan las mismas leyes que son aplicables a los materiales simples.
Tratamientos semejantes o alternativos pueden ser encontrados en muchos
artículos, destacándose las revisiones de Bowen 1976, Atkin and Crain 1976 y
Bedford y Drumheller 1983.
2.1 CINEMÁTICA
2.1.1. Cuerpo, configuración y tipos de mezcla
Denominaremos mezcla a un cuerpo B constituido por n componentes
B  B , con   1, 2,..., n . Los elementos de B se denominan partículas y se
denotan por p  . Cada cuerpo B ocupa una cierta región del espacio euclidiano
tridimensional E, denominada configuración del cuerpo. Los elementos de las
9
Manual de Filtración & Separación
10
configuraciones son puntos del espacio euclidiano cuya posición está dada por el
vector posición r.
La posición de la partícula p   B en el espacio se puede escribir en la forma:
r    ( p ) ,
con   1,2, 3,..., n
(2.1)
Para conocer las propiedades matemáticas de   ver Bowen (1976). La configuración
de la mezcla, esto es, la región del espacio ocupada por la mezcla en el tiempo t, es la
unión de las configuraciones de los componentes:
b g   bB g
 Bt 
n
 1

(2.2)
t
La configuración ( Bt ) tiene un volumen Vm ( t ) denominado volumen material del
cuerpo B en el tiempo t.
A cada cuerpo B , y a cada una de sus configuraciones, se le asigna una
propiedad continua y aditiva m   0 , denominada masa del componente , que
cumple la relación:
 m bB g
n
m ( B) 

(2.3)
t
 1
bg
donde m B es la masa de la mezcla. El concepto continuo de la masa permite definir
la densidad de masa  mediante el proceso de límite:
b g
m  ( Pk )
,
k  V ( P )
m
k
 r, t  lim
con
  1, 2, 3, ..., n
(2.4)
donde Pk 1  Pk son partes de la mezcla que tienen la posición r en común. Esta
densidad de masa recibe el nombre de densidad aparente. La densidad de masa
permite escribir la masa del componente  en la forma:
m  ( Bt ) 
z
 (r, t )dV
(2.5)

Vm ( t )
Si designamos por  la densidad que tendría el componente  si éste fuese el único
b g en la
componente de la configuración ( Bt ) , podemos definir la función  r, t
forma:
  r, t  
  r , t 
  r , t 
, con   1, 2,3,..., n
(2.6)
Capítulo 2 - Teoría de Mezclas
11
Reemplazado esta expresión en la ecuación (2.5) se obtiene:
m   Bt  

Vm (t)
 dV

Vm (t)
  dV
(2.7)
Definamos el elemento de volumen material dV en la forma:
dV   dV
tal que se cumpla:
b g
m  Bt 
(2.8)
z z
 dV 

Vm ( t )
 dV

V ( t )
(2.9)
Al volumen V lo denominaremos volumen parcial del componente  y la función
  r, t  recibe el nombre de fracción volumétrica del componente.
Según la expresión (2.2) el volumen de la mezcla es la suma de los volúmenes
parciales de los componentes, por lo que:
n
   r, t   1

(2.10)
1
Se puede distinguir dos tipos de mezclas, homogéneas y heterogéneas. Mezclas
homogéneas cumplen estrictamente la condición de continuidad del material, porque
la mezcla de los componentes ocurre a escala microscópica. Estas mezclas reciben el
nombre de soluciones. Para mezclas homogéneas  es la concentración del
componente B . En una mezcla heterogénea, la mezcla de los componentes ocurre a
escala macroscópica y, para que ellas puedan ser consideradas continuas, el tamaño
del volumen de integración de las ecuaciones anteriores debe ser mucho mayor que el
nivel de la mezcla. Estas mezclas se conocen con el nombre de multifásicas porque
cada componente puede ser identificado como una fase distinta. En este tipo de
mezclas  r, t es una medida de la estructura local del material y  recibe el
nombre de densidad aparente o densidad a granel.
b g
2.1.2 Deformación y movimiento
Para cada cuerpo B podemos elegir una configuración de referencia   tal
que en esa configuración B sea el único componente de la mezcla (estado puro). La
posición de la partícula p en estas configuraciones se denotará por R  :
R     ( p )
(2.11)
Supondremos que la expresión (2.3) tiene inversa tal que:
1
p    
(R )
(2.12)
Manual de Filtración & Separación
12
Movimiento de la partícula p   B es la secuencia de configuraciones en el tiempo y
queda representada por la expresión:
r    ( p , t ) ,
Reemplazando (2.12) se obtiene:
con   1,2, 3,..., n
b g
r  f R  , t
(2.13)
donde la función f recibe el nombre de función deformación del componente  y
queda expresada por:
1
f     
(2.14)
La función deformación tiene una inversa tal que:
b g
R   f1 r , t
(2.15)
Las componentes cartesianas x i de r y X i de R  reciben el nombre de coordenadas
espaciales y coordenadas materiales de la partícula p   B :
r  xiei
y
R   X i e i
(2.16)
La deformación de cada componente se cuantifica a través del tensor gradiente de la
deformación F definido por:
F 
f
  R r ,
R 
con
det F  0
(2.17)
Asociados al tensor gradiente de la deformación podemos definir todas las otras
medidas de deformación que hemos estudiado para materiales de un sólo componente:
Q  , U  , V , C , B  y G  .
La dilatación de un cuerpo multicomponente, desde su configuración de
referencia a la configuración presente, se puede expresar a través del det F :
J   det F 
dV
dV
(2.18)
donde dV y dV son elementos de volumen material en la configuración actual y
en la configuración de referencia respectivamente.
La velocidad de deformación se cuantifica a través de la velocidad v  y la
aceleración a  , definidos como la primera y segunda derivada material del
movimiento:
Capítulo 2 - Teoría de Mezclas
13
v 
D r

f R  , t   ,
t
Dt
g
  1, 2, 3,..., n
(2.19)
a 
D2 r
2
f
R
,
t
,



Dt 2
t 2
  1, 2, 3,..., n
(2.20)
b
b g
donde la derivada material D  / Dt se calcula siguiendo el movimiento del
componente . Los tensores asociados a las medidas de velocidad de deformación
L , D y W se definen en la forma habitual:
L 
FG 1 btrD gIIJ
H3
K
FG
H
 D 

b g IJK
1
trD I
3
bW g

(2.21)

velocidad de
velocidad de
velocidad de
expansión
cizalle
rotación
donde:
L  v 
(2.22)
c
h
(2.23)
c
h
(2.24)
D 
1
v   ( v  )T
2
W 
1
v  ( v  )T
2
La velocidad de dilatación queda expresada por:
b
J   det F   v 
g
(2.25)
2.1.3 Balance de masa
Admitamos que los componentes de B intercambian masa entre sí y designemos
por g r, t la velocidad de transferencia de masa, por unidad de volumen, al
b g
b g
componente  por todos los otros componentes. Otro nombre para g r, t es
velocidad de crecimiento de la masa del componente  . Entonces, se debe cumplir el
siguiente balance:
 Velocidad de variación de la masa   Velocidad neta de generación de 


del componente  en Vm (t)   del componente  en Vm (t) 

d
dt

Vm (t )
 dV


Vm (t)
g dV
Llevemos ambas integrales a la configuración de referencia para obtener:
(2.26)
Manual de Filtración & Separación
14
z z
z FGH b g IJK
z ed i j
z ed i j
z ed i j
d
dt
 J  dV 
V
g J  dV
V
Introduzcamos la derivada dentro de la primera integral y juntemos los términos dentro
de una sola integral:
V
D
 J   g J  dV  0
Dt
(2.27)
  J    J   g J  dV  0
V
      v  g J  dV  0
V
      v  g dV  0
(2.28)
Vm ( t )
Cuando todos los campos dentro de la integral son continuos podemos hacer uso
del teorema de localización (Gurtin 1981) para obtener:
      v   g
(2.29)
Desarrollando la derivada material y combinando el término convectivo con el
segundo término de (2.29) obtenemos:

    v   g
t
(2.30)
Las expresiones (2.29) y (2.30) corresponden al balance local de masa y se las conoce
como ecuaciones de continuidad del componente .
El balance de masa de la mezcla se obtiene sumando las ecuaciones de
continuidad de todos los componentes:

n
 1

t


t
  v  g
n
n



 1

 1
F  I v  g
GH  JK 

n
n

 1

n
 
 1

(2.31)
 1
Según los postulados iniciales, la mezcla debe seguir las leyes de los materiales puros,
por lo que la expresión (2.31) debe ser equivalente a:
Capítulo 2 - Teoría de Mezclas
15

   v  0
t
de donde se deduce:

n

(2.32)

 1
 b v g
(2.33)
g
(2.34)
n
v 


 1
n
0

 1
Las propiedades así definidas tienen el nombre de densidad de la mezcla  y velocidad
másica de la mezcla v. La ecuación (2.34) muestra que no hay producción neta de
masa en el cuerpo B
Otra forma interesante del balance de masa se obtiene utilizando el teorema de
localización en la ecuación (2.27):
b g
D
 J   g J   0
Dt
Dividiendo ambos términos por  J  y designando la velocidad de crecimiento de la
masa del componente  por unidad de masa de ese mismo componente por
g   g  , podemos escribir:
b g
1 D
 J   g 
 Dt
Integrando en el tiempo se obtiene:
 det F   exp
FG
H
(2.35)
z
t
0
g  (  )d
IJ
K
(2.36)
donde  es la densidad del componente  en la configuración de referencia. Como
hemos supuesto que allí el componente  está puro, denominaremos a esta densidad
la densidad material del componente.
En aquellos casos particulares en que no hay intercambio de masa entre
componentes, la ecuación (2.36) se reduce a:
 det F  
(2.37)
Manual de Filtración & Separación
16
7.1.4 Balance de masa en una discontinuidad
Para cuerpos que presentan discontinuidades, las ecuaciones (2.29) y (2.37) no son
válidas. En estos casos es necesario utilizar la versión especial del Teorema de
Transporte para cuerpos con discontinuidad:
d
dt
z
 dV 
Vm ( t )
z

  dV 
Vm ( t ) t
b g
z
 v  ndS 
Sm ( t )
z
   dS (2.38)
SI ( t )
donde  es una propiedad extensiva cualquiera, [.] indica el salto de una propiedad
en la interface,   v I  e I es la velocidad de desplazamiento de la discontinuidad y
e I es el vector unitario en la dirección del movimiento de la superficie singular.
Reemplazando la expresión (2.38) en el balance macroscópico de masa (2.26) se
obtiene:
z

dV 
Vm ( t ) t
z
 v  ndS 
Sm ( t )
z
  dS 
SI ( t )
z
g dV
Vm ( t )
Tomando el límite de esta expresión cuando los volúmenes en torno a la
discontinuidad tienden a cero resulta:
b
g
 v  e I   
(2.39)
Esta ecuación recibe el nombre de condición de salto para la masas del componente 
o ecuación de Rankin-Hugoniot (Bustos et al 1999).
Las condiciones de salto de la mezcla se obtienen sumando la expresión (2.39)
para todos los componentes:
LM  v e OP  LM  OP
MN b gQP MN PQ
n
n

 

I
 1
 1
y usando los resultados de (2.32) y (2.33) se tiene:
v  e I   
2.1.5 Ecuación de difusión convectiva
En ocasiones es conveniente escribir las ecuaciones de continuidad de cada uno
de los componentes en términos del flujo convectivo de masa. Este es el flujo asociado
al movimiento de la mezcla. Como este movimiento queda descrito por la velocidad
promedio v, el flujo convectivo de masa del componente , en la posición r y el
tiempo t, se define por:
jc   v
Si se suma y resta el flujo convectivo a la ecuación (2.30) resulta:
(2.40)
Capítulo 2 - Teoría de Mezclas
17

    v      ( v   v )  g
t
(2.41)
El primer término del miembro derecho representa la diferencia entre la densidad de
flujo real del componente  y la densidad de flujo convectivo. Esta diferencia recibe el
nombre de flujo difusivo de masa jD y la diferencia de velocidades se denomina
velocidad de difusión:
jD   u
(2.42)
u  v  v
(2.43)
En términos de los flujos convectivo jc y difusivo jD , la ecuación (2.41) puede ser
escrita en la forma:

 jc     jD  g
t
(2.44)
Esta expresión recibe el nombre de ecuación de difusión convectiva. Sumando (2.41)
para todos los valores de  resulta:

t
F  I   F  Iv    F  u I  g
GH  JK GH  JK
GH  JK 
n
n


 1
n


 1
n

 1


 1
Usando resultados previos podemos concluir que:
 j   u
n
n
D
 1


0
(2.45)
 1
2.1.6 Ecuación de continuidad y condición de salto de masa para mezclas de
componentes incompresibles
Algunas mezclas tienen componentes cuyas densidades materiales son
constantes, como por ejemplo una suspensión de partículas sólidas en un líquido. En
estos casos hablamos de mezclas con componentes incompresibles. Debemos estar
conscientes que la mezcla misma puede ser compresible. Usando la definición de
fracción volumétrica, según la ecuación (2.6), la ecuación de continuidad de cada
componente y la condición de salto podemos escribirla en la forma:
 
      v   g 
t
(2.46)

    v   e I       
(2.47)
Manual de Filtración & Separación
18
Como  es constante, podemos dividir estas dos expresiones por su valor y obtener
la ecuación de continuidad y condición de salto para mezclas con componentes
incompresibles:

    v   ĝ  
t
(2.48)

   v   eI       
(2.49)
Sumando para todos los componentes obtenemos:

 n
  n

 n
        v     ĝ   
t  1 
 1
  1




 n

 n

  v   e I      
 1

 1 


Definiendo la velocidad promedio volumétrica q en el forma:
q
n

 v
(2.50)
1
y usando resultados anteriores podemos concluir que:
 n

  q   ĝ   
 1


(2.51)
q 0
(2.52)
2.2 DINÁMICA
2.2.1 Balance de momentum lineal
Cuando se analizan las fuerzas que actúan en cuerpos multicomponentes
debemos agregar a las fuerzas de cuerpo y fuerzas de contacto, presentes en cuerpos de
un solo componente, las fuerzas de interacción entre componentes y las fuerzas que
surgen por el efecto del intercambio de masa entre componentes. Un ejemplo puede
clarificar el sentido de este último tipo de fuerza. Supongamos un cuerpo
multicomponente en movimiento. Si un componente entrega masa a otro componente
lo hará como un flujo asociado a la velocidad de transferencia de masa y a la velocidad
que lleva el componente que entrega la masa.
Aplicando la primera ley de Euler y el principio del esfuerzo de Cauchy a cada
cuerpo B , se obtiene el balance macroscópico de momentum lineal (Concha y
Barrientos 1993a):
Capítulo 2 - Teoría de Mezclas
d
dt
z
 v  dV 
Vm ( t )
z
T  ndS 
Sm ( t )
19
z
bb

g
 m   g v  dV
(2.53)
Vm ( t )
donde T es el tenso esfuerzo en B y se le conoce como el esfuerzo parcial, b es
la fuerza de cuerpo sobre B , m  es la fuerza de interacción entre los componentes,
esto es, la fuerza que todos los otros componentes ejercen sobre B y g es la
velocidad de crecimiento de la masa del componente B por unidad de volumen. El
primer término representa la velocidad de variación del momentum lineal del cuerpo
B , el segundo término es el flujo difusivo de momentum lineal debido a las fuerzas
de contacto y el tercero es la velocidad de crecimiento de momentum lineal debido a
las fuerzas de cuerpo, las fuerzas de interacción y el crecimiento de la masa del
componente B .
El uso de los teoremas de transporte de Reynolds, de GGO (Concha y
Barrientos 1993b) y de localización permiten escribir la forma local del balance de
momentum lineal en las siguientes dos formas equivalentes para regiones del espacio
en que las variables son continuas:

 v     v v    T  b  m   g v
t
b
g b
g
 v     T  b  m 
(2.54)
(2.55)
La primera de estas ecuaciones recibe el nombre de forma de conservación del balance
de momentum lineal.
En discontinuidades, la aplicación del teorema de transporte adecuado da como
resultado la siguiente condición de salto:
b
g
b
g b
 v  v  e I    v  e I  T  e I
g
(2.56)
donde   v I  eI es la velocidad de desplazamiento de la discontinuidad y e I es el
vector unitario normal a la superficie singular apuntando hacia la dirección del
movimiento.
Sumando la ecuación (2.54) para todos los componentes obtenemos:

t
F  v I  F  v v I   T  b b
GH  JK GH 
JK  
n
n

 1


n

 1



n

 1

 m   g v 
g
 1
Introduciendo resultados anteriores y comparando con la ecuación de movimiento de
un material de un solo componente:

   vv    T  b
t
Manual de Filtración & Separación
20
se puede concluir que:
u u
n
T  TI 

(2.57)

 1
T
n
TI 
(2.58)

 1
b
n
b
(2.59)

 1
 bm
n
0

 g v 
g
(2.60)
 1
El término TI recibe el nombre de parte interior del tensor esfuerzo de la mezcla. La
restricción representada por la ecuación (2.60) indica que no se produce crecimiento
neto de momentum lineal y que, por lo tanto, el aumento del momentum lineal de un
componente se hace a expensas de la pérdida de esta propiedad de otro u otros
componentes.
2.2.2 Balance de momentum angular
La aplicación del axioma de momentum angular, también conocido como
segunda ecuación de Euler (Concha y Barrientos 1993c) , y el principio del esfuerzo
de Cauchy a cada uno de los componentes de un mezcla, da como resultado el balance
macroscópico de momentum angular:
d
dt
zd
i
(r  rq )x  v  dV 
Vm ( t )
zd
zd
i
(r  rq )xT  n dS
Sm ( t )

b
gi
(r  rq )x b  m   g v  dV 
Vm ( t )
z
(2.61)
p dV

Vm ( t )
El primer término es la velocidad de variación de momentum angular del componente
B ; el segundo término es el torques debido a las fuerzas de contacto; el tercer
término corresponde al torque debido a las fuerzas de cuerpo, fuerzas de interacción
entre componentes y fuerzas asociadas al crecimiento de masa y el último término
representa el intercambio de momentum angular entre componentes. El término rq se
refiere a la posición del punto Q con respecto al cual se calcula el torque de las
fuerzas.
Cuando las variables son continuas, el balance macroscópico de momentum
angular da origen a la forma local:
Capítulo 2 - Teoría de Mezclas
21
T  TT  P
(2.62)
donde el tensor antisimétrico P tiene como vector axial a p.
Sumando la expresión (2.62) para cada componente resulta:
T  T  P



T



Usando la ecuación (2.58) podemos escribir:
TI  TIT 
P
(2.63)
 
La expresión (2.63) representa el balance de momentum angular local para la mezcla.
De acuerdo a los postulados iniciales, para que esta relación corresponda a la segunda
ley de Cauchy se debe cumplir:


P  0
(2.64)
Se puede concluir, entonces, que la parte interna del tensor esfuerzo parcial es
simétrica:
TI  TIT
(2.65)
En aquellos casos en que no hay intercambio de momentum angular entre
componentes, P  0 , y el esfuerzo parcial es simétrico.
T  TT
(2.66)
El balance de momentum angular en una discontinuidad no da información adicional a
la obtenida del balance de momentum lineal.
7.2.3 Proceso dinámico
Consideremos
una
mezcla
B
formada
por
componentes
B  B
con   1,2,3, ..., n . Sobre B tenemos definidas las siguientes variables de campo:
r  f ( R  , t )
(2.67)
   (r , t )
(2.68)
T  T (r, t )
(2.69)
b  b (r, t )
(2.70)
g  g ( r , t )
(2.71)
m   m  (r , t )
(2.72)
Manual de Filtración & Separación
22
P  P (r , t )
(2.73)
Diremos que estas siete variables constituyen un proceso dinámico si, en las
regiones donde las variables son continuas, cumplen las dos ecuaciones de campo:

    v  g
t
o


  det F    exp 


 v     T  b  m 
con
TI  TIT  P
t
 gˆ
0
  (2.74)

 ( )d  
(2.75)
y en las discontinuidades cumplen:
b g
 v b v e g    b v e g  bT e g
 v  e I   


 

I
 
I
 
(2.76)
(2.77)
I
Se denomina proceso dinámico al conjunto de ecuaciones (2.67) a (2.77),que
cuantifican un modelo fenomenológico. Tenemos siete variables expresadas en
función de la posición r y el tiempo t, y solamente dos ecuaciones de campo. Esto
significa que, para completar la descripción del fenómeno necesitamos cinco
ecuaciones constitutivas que relacionen las variables dinámicas (fuerzas) con las
cinemáticas (movimiento). Estas ecuaciones constitutivas relacionan las siguientes
T , f , b , f , g , f , m  , f y P , f .
variables
b
gb
gb
gb
g b
g
2.3 REFERENCIAS
Atkin, R.J. and Crain, R.E., Continuum theories of mixtures: Basic theory and
historical development, Q. J. Appl. Math., 29, 209-244, 1976.
Bedford, A. and Drumheller, D.S., Theories of inmiscible and structured mixtures, Int.
J. Eng. Sci. 21,(8), 863-960, 1983.
Bowen, R.M., Theory of Mixtures. In Continuum Physics, ed. A.C. Eringen, Vol III,
Academic Press 1976.
Bustos, M.C. and Concha, F., On the construction of Global Weak Solutions in the
Theory of Sedimentation, Mat. Meth. In Appl. Sci., 10, 1988, 248.
Bustos, M.C., Concha, F., Bürger, R. and Tory, E.M., Sedimentation and Thickening,
Phenomenological Foundation and Mathematical Theory, Kluwer Academic Publ.,
Dodrecht, The Netherland, 1999, p. 20.
Concha, F. y Barrientos, A., Mecánica Racional Moderna, Vol. 2, Termomecánica del
Medio Continuo, Dirección de Docencia, Universidad de Concepción, 1993a, 103114.
Concha, F. y Barrientos, A., op cit., 1999b, 66-72.
Concha, F. y Barrientos, A., op cit., 1999c, 105.
Capítulo 2 - Teoría de Mezclas
23
Drew, D.A., Mathematical modeling of two-phase flow, Ann. Review of Fluid
Mechanics 15, 261-91, 1983.
Truesdell, C., Sulle basi de la termomecanica, Rend. Acad. Lincei, 22, 33-88, 1957.
Traducción al inglés en: Rational Mechanics of Materials, Int. Sci. Rev. Ser. 292-305,
Gordon & Breach, New York, 1965.
Truesdell, C. and Toupin, R.A., The classical field theories of mechanics. Handbook
of Physics, Ed. Flügge, Vol III-1, Springer Verlag, New York, 1960.
Truesdell, C., Rational Thermodynamics, Springer Verlag, 2nd. Ed., New York, 1984.
CAPÍTULO 3
SISTEMAS PARTICULADOS
3.1
PROCESO DINÁMICO EN UN SISTEMA PARTICULADO
Consideremos un conjunto de partículas sólidas íntimamente mezcladas con un
fluido bajo las siguientes suposiciones:
(i) Las partículas sólidas son todas pequeñas, con respecto a la vasija que las
contiene, y de la misma densidad, tamaño y forma.
(ii) Las partículas individuales y el fluido son incompresibles.
(iii) No hay transferencia de masa entre el sólido y el fluido.
(iv) La única fuerza de cuerpo es la gravedad.
(v) Las partículas están contenidas en una vasija impermeable y con paredes sin
fricción ante líquidos y sólidos
El movimiento de cada uno de los componentes de la mezcla puede ser descrito
mediante los balances de masa y momentum lineal:
Balance de masa del componente:

        v   g
t
Balance de masa de la mezcla
q  
(3.2)
Balance de momentum lineal:
 v     T  b  m 
(3.3)
Restricción:
 bm
(3.4)
(3.1)
2
g
 1 
2
 1

g
 g v   0
En estas expresiones las variables de campo (r, t), v(r, t) y T(r, t)
representan la fracción volumétrica, la velocidad y los esfuerzos del componente ,
b(r, t) es la fuerza ejercida por el medio ambiente sobre el componente , m(r, t) es
la fuerza de interacción entre componentes y g (r , t ) mide la velocidad con que los
otros componentes entregan masa al componente  por unidad de volumen. El
operador   () representa la divergencia.
24
Capítulo 3. Sistemas Particulados
25
El primer término de la ecuación (3.1) la velocidad de variación de la masa del
componente , el segundo es el flujo de masa del componente  y el tercero
corresponde a la velocidad con que los otros componentes entregan masa al
componente . En la ecuación (3.2) el término de la izquierda representa la variación
espacial de la velocidad volumétrica de la mezcla y el término de la derecha, la
velocidad neta de producción de masa de mezcla por unidad de masa. El primer
término de la ecuación (3.2) es la aceleración del componente , mientras que los
términos de la derecha representan la fuerza total ejercida sobre el componente  (de
contacto, exterior y de interacción). La restricción representada por (3.4) indica que el
intercambio de masa y de fuerzas entre componentes no debe crear una fuerza neta en
la mezcla y que el aumento de momentum de algún componente se compensa con la
pérdida de otros.
En discontinuidades las expresiones (3.1) a (3.3) deben ser reemplazadas por las
condiciones de salto:
      v  e I
(3.5)
   v     v  ( v  e I )  T  e I
(3.6)
en que   vs  e I es la velocidad de desplazamiento de la discontinuidad.
Denominemos   1  s al componente sólido y   2  f al componente fluido.
Como, en virtud de las suposiciones (i) y (ii) la densidad de cada componente es
constante, se puede dividir las tres ecuaciones por este término. Por otra parte, según
(iii) no hay intercambio de masa entre componentes y por (iv) la fuerza de cuerpo es la
gravedad. Finalmente, según (v) el movimiento es uni-dimensional. Entonces, las
ecuaciones (3.1) a (3.3) se reducen a los balances de:
masa del componente sólido

  vs   0
t
masa de la mezcla:
q  0 ,
momentum lineal del fluido:
s v s  Ts  s g  m
momentum lineal sólido:
f (1  ) v f  Tf  f (1  )g  m
con
(3.7)
q  v s  (1  ) v f
(3.8)
(3.9)
(3.10)
donde r es el vector posición, (r,t) es la fracción volumétrica de sólidos y vs(r,t),
vf(r,t), Ts(r,t), Tf(r,t), m, y g son las velocidades, las fuerzas de contacto y de
interacción entre componentes y el vector constante gravitacional g.
En la mayoría de los casos de interés práctico, no hay aceleración en el flujo, o
ésta es muy pequeña comparada con los otros términos de las ecuaciones(3.9) y (3.10).
Además, la fuerza de interacción entre componentes m se puede descomponer en una
fuerza estática, o de equilibrio, me y en una fuerza dinámica md , dependiente del
movimiento. Con esta restricción y definiciones, las ecuaciones (3.9) y (3.10) pueden
ser escritas en la forma:
26
Manual de Filtración & Separación
Balance de momentum lineal del sólido:
0  Ts  s g  m
(3.11)
Balance de momentum lineal del fluido:
0  Tf  f (1  )g  m
(3.12)
3.1.1 Componente Fluido
Para todo tipo de fluido, los esfuerzos pueden ser separados en una parte de
equilibrio y una parte dependiente del movimiento:
Tf   pf (1  )I  TfE
(3.13)
donde pf es la presión parcial, o simplemente la presión, del componente fluido y TfE
es el esfuerzo viscoso del fluido. Reemplazando en la ecuación (3.13) el balance de
momentum lineal del fluido resulta:
p f  TfE  f 1    g  m e  m d
(3.14)
En flujos en sistemas particulados hay dos variables relacionadas con fricción.
Una de ellas es el esfuerzo viscoso TfE que representa la fricción interna dentro del
fluido y la otra la fuerza de interacción m, que corresponde a la fricción entre el fluido
y el sólido. La experiencia demuestra (Marle, 1967; Whitaker, 1967, 1986) que la
fricción fluido-fluido es mucho más pequeña que la fricción sólido-fluido y, por lo
tanto puede ser despreciada en la ecuación (3.14) la que se reduce a:
p f  f (1  )g  m e  m d
(3.15)
Despreciar el término viscoso en la ecuación constitutiva de los esfuerzos
representados por la ecuación (3.13) equivale a considerar el fluido como un fluido
elástico.
3.1.2 Presión de Poros
La presión pf del fluido es una variables definida en superficies que abarca el
componente fluido en su totalidad. Recordar que el componente sólido y el fluido son
medios continuos superpuestos. Por esta razón, la presión del fluido no es mensurable
experimentalmente, ya que solamente parte de la superficie y volumen del lecho
poroso está ocupada por cada componente. La variable experimental asociada al flujo
en lecho poroso es la presión de poros.
En mecánica de fluidos se ha demostrado que, para una mezcla sólido-fluido, la
presión del fluido es continua en superficies permeables, esto es, en superficies que
dejan pasar el fluido pero retienen el sólido. Por esta razón la presión en los poros de
un lecho poroso, que recibe el nombre de presión de poros "p", se puede medir
mediante un manómetro. La figura 3.1 muestra la forma de medir la presión de poros:
Capítulo 3. Sistemas Particulados
27
p  z   f g  h  z 
Manómetro
q
h-L
L-z
L
h-z
h
k
z
q
Fig. 3.1 Medición de la presión de poros.
Procesos que se desarrollan en sistemas particulados generalmente dependen de
la presión en exceso sobre la presión hidrostática, ya que a esta presión de equilibrio el
proceso llega a su fin. Es por ello que se introduce el concepto de presión de poros en
exceso (sobre la hidrostática), o simplemente presión en exceso, "pe", definida por:
pe  z   p  z   f g z (L  z)
(3.16)
3.1.3 Componente Sólido
En general, las propiedades del componente sólido de un medio particulado
dependen fuertemente de la concentración de este componente. Es así como en
sistemas diluidos las partículas tienen mayor libertad de movimiento, mientras que en
medios concentrados, éstas son obstaculizadas en su movimiento por la presencia de
otras partículas. La variable característica que separa estas dos formas de
comportamiento es la concentración crítica c, que se define como aquella
concentración en que las partículas entran en contacto directo unas con otras. A
concentraciones menores de la crítica el medio se denomina suspensión y toda fuerza
de contacto entre partículas se efectúa por intermedio del fluido. A concentraciones
mayores de la crítica el medio recibe el nombre de medio poroso, lecho poroso o
sedimento y los esfuerzos en el sólido puede ser transmitidos de partícula a partícula
directamente. En estos casos se forma una especia de esqueleto que transmite el
esfuerzo en el sólido.
Tomando en consideración estas características, supondremos que el esfuerzo
en el sólido es constante para concentraciones menores que la crítica y se comporta
como un sólido elástico e isotrópico para valores mayores. Por lo tanto, la componente
del esfuerzo Ts puede ser descrito en términos de la presión del sólido ps en la forma
(Bustos et al 1999):
28
Manual de Filtración & Separación
Ts   ps I
con

para   c

ps  
    ps ()  para   c
(3.17)
donde c se denomina concentración crítica. Así, el balance de momentum lineal del
componente sólido se transforma en:
ps  f g  m e  md
(3.18)
3.1.4 Esfuerzo efectivo del sólido
Al igual que en el caso del fluido, la presión en el componente sólido no es una
variable mensurable experimentalmente. Cuando una fuerza compresiva se aplica a un
medio poroso a concentraciones mayores a la crítica, el esfuerzo total es soportado
inmediatamente por el fluido que llena los intersticios entre las partículas aumentando
la presión de los poros. El gradiente de presión establecido en el agua que llena los
poros y el exterior del sedimento, esto es la presión de poros en exceso, inicia el flujo
de agua desde el sedimento hacia fuera de él. Este flujo es acompañado por una
disminución de la presión de poros y un traspaso progresivo del esfuerzo al esqueleto
sólido. Esto, a su vez, produce una deformación del medio poroso, la magnitud de la
cual, depende de la relación constitutiva entre esfuerzo y deformación del material
sólido y cuya velocidad está gobernada por su permeabilidad.
Se denomina consolidación del medio poroso al proceso transiente de traspaso del
esfuerzo aplicado desde el agua que llena los poros lecho poroso al esqueleto sólido
produciendo su asentamiento. La figura mostrada a continuación es un análogo
mecánico de la consolidación.
La figura 3.1 muestra las diversas longitudes que asume un resorte sometido a
determinadas cargas. En la figura inferior cada resorte es sumergido en agua contenida
en un cilindro con un pistón, sin fricción, y una llave.

Figura 1: Inicialmente el sistema está en equilibrio, con la llave abierta y
sin peso.

Figura 2: La llave se cierra y se coloca un peso de 20 kg. Como el agua es
incompresible, la presión en el agua (presión de poros), soporta el peso
total sin producir deformación en el resorte (esqueleto sólido).

Figura 3: La llave se abre y el agua sometida a presión sale como un
chorro con una velocidad controlada por el exceso de presión entre el
interior y el exterior (presión de poros en exceso a la hidrostática) y por la
fricción entre el agua y el tubo de salida.
Capítulo 3. Sistemas Particulados
0 kg
0 kg
29
5 kg
10 kg
15 kg
20 kg
20
0 kg
Peso total
0
20
20
20
20
20
Presión poros
0
20
20
15
10
5
0
Presión sólido
0
0
0
5
10
15
20
Figura
1
2
3
4
5
6
7
Fig. 3.1 Representación mecánica de la consolidación.

Figura 4: A medida que el agua sale, el pistón baja en forma paulatina
comprimiendo al resorte, el que comienza a asumir parte de la presión
externa. Aquí asume 5 kg. y su largo es el correspondiente a la figura
superior sometido a 5 kg. Entretanto el agua tiene una presión de 15 kg.

Figura 5: Sale más agua, el pistón sigue bajando, el resorte asume 10 kg.
y el agua 10 kg.

Figura 6: Sigue saliendo agua, el pistón baja, el resorte asume 15 kg. y el
agua solamente 5 kg.

Figura 7: El agua deja de salir del pistón. Éste ha llegado a la longitud
correspondiente al peso de 20 kg., mientras que el agua no soporta ningún
peso y tiene la presión estática.
El proceso completo, esquematizado por las figuras 1 a 7, ha transferido los 20 kg. de
carga del pistón desde el agua al resorte, esto es, desde la presión de poros al esfuerzo
efectivo del sólido.
3.1.5 Presión total
La presión total pt en un sistema particulado, al igual que en el esquema
mecánico anterior, es la suma de la presión soportada por el fluido mas la presión
soportada por el sólido:
p t  p f  ps  p   e
(3.19)
30
Manual de Filtración & Separación
donde ps y pf son las presiones de los componentes sólido y fluido de la mezcla,
considerados como medios continuos superpuestos ocupando el mismo volumen, y p y
e son la presión de poros y el esfuerzo efectivo del sólido definidos, el primero, sólo
en el fluido contenido en los poros y el segundo sólo en el esqueleto sólido. La
relación entre las variables teóricas y las experimentales se puede obtener al calcular la
fuerza ejercida por el fluido en una superficie de área S:
z
p f dS 
S
z
Sf
zb
g
pdSf  p  sdS
S
(3.20)
donde Sf es el área de una sección del lecho poroso conteniendo solamente fluido, S es
el área total del lecho poroso que incluye el sólido y el fluido y s es la porosidad
superficial. Si se supone que la porosidad superficial s (fracción de la superficie de la
sección del lecho poroso formada por fluido) es igual a la porosidad volumétrica 
(fracción de volumen del lecho poroso formado por fluido)  f    1   , la ecuación
(3.20) se puede escribir en la forma:
z
z
(3.21)
p f  (1   )p
(3.22)
p f dS  p(1   )dS
S
S
de donde resulta:
y, usando la ecuación (3.19) se obtiene:
p s  p   e
(3.23)
Substituyendo las presiones de sólido y fluido por sus equivalentes experimentales
desde las ecuaciones (3.22) y (3.22), los balances locales de momentum lineal (3.18) y
(3.15) se obtiene:
3.2
  p   e  f g  m e  m d
(3.24)
  (1  )p   f (1  )g  m e  md
(3.25)
FUERZA DE INTERACCIÓN EN EL EQUILIBRIO
Consideremos el balance de fuerzas del componente fluido (3.25) en el
equilibrio. En este caso sabemos que la fuerza de interacción dinámica m d  0 y que
b
g
la presión de poros es la presión hidrostática p( z )  f g L  z ) , donde L es la altura
de la columna de agua. Reemplazando en (3.25) resulta:
(1  )f g  p  equilibrio  f (1  )g  m e
m e  p  equilibrio
(3.26)
Capítulo 3. Sistemas Particulados
31
Suponiendo que la forma funcional de esta ecuación es siempre válida, podemos
escribir:
m e  r, t   p
(3.27)
Reemplazando (3.27) en los balances de fuerza (3.25) y (3.24) se obtiene:
p   f g 
md
1 
(3.28)
 e  g 
md
1 
(3.29)
En términos de la presión de poros en exceso pe, la expresión para el fluido se
reduce a:
p e  
md
1 
(3.30)
Combinando (3.29) y (3.30) podemos sustituir (3.29) por:
pe   e  g
3.3
(3.31)
DISCONTINUIDADES
Es bien conocido el hecho que suspensiones desarrollan discontinuidades. Por
esta razón debemos establecer las ecuaciones de salto que reemplazan a las ecuaciones
de campo locales en estas discontinuidades.
3.4
   vs  e I
(3.32)
  v s    vs ( vs  e I )  (pe  f g(L  z)  e )eI 
(3.33)
PROCESO DINÁMICO
Resumiendo los resultados anteriores, se puede decir que el flujo a través de un
sistema particulado puede ser representado por las siguientes variables de campo: la
fracción volumétrica de sólidos (z,t), la velocidad del sólido y del fluido vs(z,t) y
vf(z,t), la presión de poros en exceso pe(z,t), el esfuerzo efectivo del sólido e(z,t) y la
fuerza dinámica de interacción entre el sólido y el fluido md(z,t). Se dice que estas 6
variables de campo constituyen un proceso dinámico si, en las regiones donde las
variables son continuas, cumplen:
1) Las ecuaciones locales de campo:

  v s   0
t
(3.34)
32
Manual de Filtración & Separación
q  0 ,
con
 e  g 
p e  
q  v s  (1  ) v f
md
1 
md
1 
(3.35)
(3.36)
(3.37)
2) En las discontinuidades cumplen las condiciones de salto:
   v s  e I
  v s    vs ( vs  e I )  (pe  f g(L  z)  e )eI 
(3.38)
(3.39)
3) Se debe establecer ecuaciones constitutivas para e y md para describir el
comportamiento del material y completar el conjunto de seis ecuaciones que describen
cuantitativamente el fenómeno:
3.5
m d  m d (, v s , q,)
(3.40)
e  e (, v s , q,)
(3.41)
REFERENCIAS
Atkin, R.J. and Crain, R.E., Continuum theories of mixtures, Basic theory and
historical development, Q. J. Appl. Math., 29, 209-244 (1976).
Bedford, A. And Drumheller, D.S., Theories of immiscible and structured mixtures,
Int. J. Eng. Sci., 21(8), 863-960 (1983).
Bowen, R.M., Theory of Mixtures. In Continuum Physics, ed. A.C. Eringen, Vol. III,
Academic press (1976).
Bustos, M.C., Concha, F., Bürger, R. and Tory, E.M., Sedimentation and Thickening,
Phenomenological Foundation and Mathematical Theory, Kluwer Academic Publ.,
Dodrecht, The Netherland, 1999, 46-47.
Concha, F. y Barrientos, A., Mecánica Racional Moderna. Vol. II Termomecánica del
medio Continuo, Dirección de Docencia, Universidad de Concepción, 1996, 248-266.
Concha, F., Bustos, M.C. and Barrientos, A., Phenomenological Theory of
Sedimentation, in Sedimentation of Small Particles in Viscous Fluids, Ed. E. Tory,
Computational Mechanics Publ., Southampton, 1996, p. 60.
Drew, D.A., Mathematical modeling of two-phase flow, Ann. Review of Fluid
Mechanics, 15, 261-91 (1983).
Truesdell, C., Rational Themodynamics, Springer Verlag, 2nd. Ed., New York, 1984.
CAPÍTULO 4
SEDIMENTACIÓN DE SISTEMAS PARTICULADOS
Se denomina sedimentación el asentamiento de una partícula, o una suspensión
de partículas, en un fluido por efecto de una fuerza externa, que puede ser la gravedad,
una fuerza centrífuga o cualquier otra fuerza de cuerpo. Por muchos años ingenieros e
investigadores del campo de la Tecnología de Partículas han estado buscando una
ecuación simple que relacione la velocidad de sedimentación de suspensiones de
partículas en un fluido con su tamaño, forma y concentración. Un objetivo tan simple
ha requerido un enorme esfuerzo y ha sido solucionado solamente en parte. Desde los
trabajos de Newton (1687) y Stokes (1844) de flujo alrededor de una partícula y las
investigaciones mas recientes de Lapple (1940), Heywood (1962), Brenner (1964),
Batchelor (1967), Zenz (1966), Barnea y Mitzrahi (1973) y muchos otros, hasta los de
Concha y colaboradores (1979-1986), han establecido una teoría heurística, esto es,
basada en principios fundamentales de la mecánica, pero con un mayor o menor grado
de intuición y empirismo. Estos trabajos resuelven primero la sedimentación de una
partícula en un fluido y luego introducen correcciones debido a la interacción entre
partículas, mediante las cuales la sedimentación de una suspensión se ve
dramáticamente disminuida. Este enfoque que usa principios de la mecánica de
partículas ha recibido el nombre de enfoque discreto.
La sedimentación discreta ha sido exitosa para establecer ecuaciones
constitutivas en los procesos de sedimentación, esto es, para establecer las propiedades
de sedimentación de un determinado material particulado en un determinado fluido.
Sin embargo, para analizar un proceso de sedimentación y obtener patrones de
comportamiento que permita predecir capacidades de tratamiento y diseño de equipos,
se ha recurrido a otro enfoque que utiliza la mecánica de medio continuo como base
para analizar el movimiento de suspensiones. Este es el enfoque continuo. En este
capítulo presentaremos y analizaremos el enfoque discreto.
4.1
SEDIMENTACIÓN DISCRETA
La física del proceso de sedimentación más elemental, el asentamiento de una
partícula sólida en un fluido, se conoce desde hace bastante tiempo. La ecuación de
sedimentación de una esfera fue propuesta por Stokes en 1851 y puede considerarse
como el punto de partida de toda discusión de los procesos de sedimentación. Stokes
demostró que la velocidad terminal de una esfera en un fluido es directamente
proporcional a la diferencia de densidades entre el sólido y el fluido, al cuadrado del
33
34
Manual de Filtración & Separación
radio de la esfera, a la fuerza de gravedad e inversamente proporcional a la viscosidad
del fluido. Esta ecuación se basa en un balance de fuerzas sobre la partícula. Sin
embargo, la ecuación obtenida es válida solamente para movimientos muy lentos, ya
que para aquellos más rápidos es necesario desarrollar expresiones más elaboradas. El
problema radica en la fuerza hidrodinámica entre la partícula y el fluido.
Consideremos el flujo incompresible sobre una esfera sólida. Las ecuaciones que
describen este fenómeno son las ecuaciones de continuidad y de Navier-Stokes
(Concha y Barrientos 1993). Desgraciadamente esta última ecuación es no-lineal e
imposible de resolver analíticamente en forma general. Por ello, se ha buscado
mecanismos para resolverla en casos particulares.
Se ha demostrado que el número de Reynolds, Re  f du  , donde , d y u
son la densidad, el diámetro y la velocidad de la partícula y  es la viscosidad del
fluido, expresión adimensional que representa la razón entre las fuerzas convectivas y
difusivas en la ecuación de Navier-Stokes, es un importante parámetro en la
caracterización del flujo. Cuando el número de Reynolds es pequeño, (Re0), como
por ejemplo Re<10-3, las fuerzas convectivas pueden ser despreciadas en la ecuación
de Navier-Stokes, obteniéndose lo que se denomina el flujo de Stokes.
4.1.1 Fuerza hidrodinámica sobre una esfera en flujo de Stokes
Debido a la linealidad de la ecuación diferencial, la velocidad, la presión y la
fuerza hidrodinámica son funciones lineales de la velocidad relativa sólido-fluido. Para
la fuerza hidrodinámica, los parámetros de proporcionalidad dependen del tamaño y
forma de la partícula (6R) y de la viscosidad () del fluido:
FD  6Ru
(4.1)
Es usual escribir la fuerza hidrodinámica en su forma adimensional, conocida como
coeficiente de arrastre:
CD 
FD
1 2 f u 2 R 2
(4.2)
donde f es la densidad del fluido. Reemplazando (4.1) en (4.2) se obtiene el
coeficiente de arrastre de una esfera en régimen de Stokes:
CD 
24
Re
(4.3)
4.1.2 Balance macroscópico sobre una esfera en régimen de Stokes
Supongamos que tenemos una pequeña esfera inmersa en un fluido y suspendida
mediante un hilo. La esfera, de densidad mayor que el fluido, está en equilibrio y el
balance de fuerzas sobre ella debe ser cero. Las fuerzas que actúan son: (1) la fuerza de
Capítulo 4 Sedimentación de Sistemas Particulados
35
gravedad, que atrae la esfera hacia abajo, (2) la fuerza de empuje del fluido, esto es, la
fuerza ejercida por la presión en el fluido que rodea la partícula, que la impulsa hacia
arriba y (3) la fuerza de resistencia del hilo que soporta la partícula. El balance de
fuerzas da:
0  Fhilo  Fgravedad  Fempuje
(4.4)
0  Fhilo0  p Vp g  f Vp g
(4.5)


Fhilo  p  f Vp g  Vp g
(4.6)
Fhilo
Fempuje
Fgravedad
Fig. 4.1 Equilibrio sobre una esfera sumergida en un fluido.
Si en un instante se corta el hilo, se produce un desbalance de las fuerzas y, de
acuerdo a la ley de Newton, la partícula debe acelerar. La aceleración inicial se puede
obtener del nuevo balance de fuerzas en la que ya no existe la resistencia del hilo. La
figura 4.2a muestra este nuevo balance. Una vez que la partícula se pone en
movimiento aparece una nueva fuerza, la fuerza de arrastre entre el sólido y fluido que
se opone al movimiento y que es proporcional a la velocidad relativa entre el sólido y
el fluido, y como este último está inmóvil, es la velocidad que adquiere la partícula.
Fe= fVpg
Fe= fVpg
Fd=-6Ru
Fg=-pVpg
Fig. 4.2a Antes del movimiento.
u(t)
Fg=-pVpg
Fig. 4.2b Inicio de movimiento.
36
Manual de Filtración & Separación
ma (t  0)  Vp g

g
p
a( t  0) 
 Fgravedad  Fempuje  Farrastre
ma(t)
p Vp a(t)  Vp g  6Ru(t)
a(t) 

g
p

9
2p R 2
(4.7)
u(t)
Debido al aumento de la velocidad u con el tiempo, el segundo término de (4.7)
crece mientras el primero permanece constante, llegando un momento en que el
segundo término de (4.7) se hace igual al primero y, por lo tanto la aceleración se
anula. La velocidad a la cual se anula la aceleración se denomina velocidad terminal u
y es una característica de la partícula y del fluido. Despejando u desde (4.7) y
denominándola u resulta:
u 
2 R 2 g 1 d 2g

9 
18 
(4.8)
Esta expresión se conoce como ecuación de Stokes, es válida parra pequeños números
de Reynolds y fue deducida por este investigador en 1851.
Ejemplo 1
Calcular la velocidad terminal de sedimentación de una esfera de cuarzo de
densidad 2.65 g/cm3 y 10m de diámetro en agua a 20 °C.
La viscosidad del agua a 20°C es de 0.01 g/cm-s, entonces, aplicando la ecuación
(4.8) resulta:
u(10) 
1 (2.65  1.00)  (10 10000) 2  981
 9.0  103 cm / s
18
0.01
Dinámica de la sedimentación
La ecuación (4.7) representa la dinámica de la sedimentación gravitacional.
Ordenemos y escribamos explícitamente:
 
u(t)
cuya solución es:
u(t) 
1
18p d
2
u(t) 

g0
p
 18
1 d 2 g 
 1  exp  
2
18  
 pd

t


(4.9)
Capítulo 4 Sedimentación de Sistemas Particulados
37
El término entre paréntesis dentro del exponencial se denomina número de Stokes y el
término que multiplica el paréntesis en término de la derecha es la velocidad de Stokes,
como vimos en (4.8).
Ejemplo 2
Determinar cuanto tiempo necesita una partícula de 10, 50 y 100m para llegar a
la velocidad terminal.
La figura siguiente muestra la evolución de las velocidades de las esfera versus
el tiempo al aplicar la ecuación (4.9). La velocidad terminal para d=100, 50 y 10 m es
de 0.624, 0.216 y 0.0345 cm/s y el tiempo para llegar a estos valores es de 0.0067,
0.017 y 0.0005 segundos, según la ecuación (4.8). Como esto tiempos son muy cortos,
generalmente no se los toma en cuenta y se supone que una partícula llega a su
velocidad terminal instantáneamente.
1.00000
Velocidad en cm/s
d=100 m
d=50 m
0.10000
d=10 m
0.01000
0.0001
0.001
0.01
Tiempo en segundos
Velocidad de sedimentación versus tiempo.
4.1.3 Fuerza hidrodinámica sobre una esfera en flujo de Euler
Cuando el número de Reynolds tiende a infinito (Re), las fuerzas viscosas
desaparecen y la ecuación de Navier-Stokes se transforma en la ecuación de Euler de
flujo invíscido (Gurtin 1981). En este caso la componente tangencial de la velocidad
sobre la superficie de la esfera es una función lineal de la velocidad relativa sólidofluido y la componente radial es nula:
38
Manual de Filtración & Separación
3

u  ()   sen  u y
2

ur  0
(4.10)
pero la presión ya no es lineal y responde a la ecuación de Bernouilli (Batchelor 1967):
p( )  1 2 f u 2  p  1 2 f u 2 =constante
  u 2 
1
p()  p  f u 2  1     
  u  
2


(4.11)
La presión adimensional, o coeficiente de presión sobre la esfera, definida
por: Cp   p( )  p  (1 2) f u 2 queda expresada para el régimen de Euler por:
9
Cp  1  sen 2 
2
(4.12)
La figura 4.3 muestra esta relación en forma gráfica, donde p() y u son la presión y la
velocidad para un ángulo  sobre la superficie de la esfera y p y u corresponde a los
valores de estas variables en el flujo lejos de la esfera.
1.5
Coeficiente de presión Cp
1
0.5
0
0
0.5
1
1.5
2
2.5
3
-0.5
-1
-1.5
Angulo  en radianes
Fig. 4.3 Coeficiente de presión en función de la distancia sobre
la superficie de la esfera en un flujo invíscido (Schlichting
1968, p21).
Para un flujo invíscido estacionario la fuerza de arrastre es cero. Esto se debe a
que, no habiendo viscosidad en el fluido no hay fricción con la partícula y el efecto de
la presión se anula debido a la simetría de la esfera.
Capítulo 4 Sedimentación de Sistemas Particulados
39
4.1.4 Fuerza hidrodinámica sobre una esfera en flujo de Prandtl
Cuando el número de Reynolds tiene valores intermedios, las fuerzas
convectivas tienen el mismo orden de magnitud que las fuerzas viscosas, y el flujo
puede dividirse en dos partes, un flujo invíscido lejano a la partícula y un flujo viscoso
muy cerca de ella donde la viscosidad juega un papel importante. Esta figura forma la
base de la Teoría de Capa Límite (Schlichting 1968).
En el flujo sin viscosidad externo (a la capa límite) se puede aplicar las
ecuaciones de Euler y la distribución de velocidad y presión se puede obtener de la
ecuación de las ecuaciones (4.10) y (4.11). En la capa límite y, debido a la viscosidad,
se establece un importante gradiente de concentración que permite que la condición de
no-deslizamiento del fluido respecto al sólido se cumpla en la superficie de la
partícula.
La pérdida de energía en la capa límite, originada por la disipación viscosa,
retarda el flujo y, en un cierto punto de la superficie de la esfera el flujo cambia de
dirección ayudado por el gradiente de presión adverso que allí existe. Este fenómeno
fuerza al fluido hacia fuera, alejándolo de la superficie de la esfera y produciendo lo
que se conoce como separación de la capa límite. La separación de la capa límite
sobre una esfera ocurre a un ángulo, denominado ángulo de separación, dado por (Lee
and Barrow, 1968):
s  214 Re 0.1
para 24<Re<10.000
(4.13)
El valor del ángulo de separación es de s=155.7 para Re=24 y s=85.2 para
Re=10.000. Para valores del Reynolds excediendo 10.000, el ángulo de separación
disminuye lentamente desde s=85.2 para llegar a 84° y mantenerse en este valor hasta
Re150.000 (Tomotika 1937, Fage 1937, Amai 1938, Cabtree et al 1963).
Debido a la separación de la capa límite, la región de líneas de corriente cerrada
detrás de la esfera contiene un anillo de vórtice que aparece a Re24. La figura 4.4.
muestra una situación similar para el flujo alrededor de un cilindro, donde se aprecia la
separación de la capa límite y la formación de una estela.
El grosor “”de la capa límite se define como la distancia desde la superficie
hasta el lugar en que la velocidad v ha alcanzado el 99% de su valor del flujo externo
invíscido y se ha determinado que es proporcional a Re-0.5. Es así como en el punto de
separación el grosor de la capa límite se puede expresar en la forma:


 01 2
R Re
(4.14)
McDonald (1954) da un valor de 0  9.06 . Taneda (1956) calculó el tamaño
de la región cerrada detrás de la esfera y concluyó que para Re >130 el anillo de
vórtice comienza a oscilar y que a número de Reynolds mayores el fluido rompe la
zona cerrada formando una estela.
40
Manual de Filtración & Separación
La separación de la capa límite previene la recuperación de la presión en la parte
posterior de la esfera, más allá del punto de separación, resultando una distribución
asimétrica, con una mayor presión en el frente que en la región posterior de la esfera.
La figura 4.6 muestra el coeficiente de presión sobre la esfera en un flujo invíscido y
en capa límite. Se observa que después del punto de separación la presión, a números
de Reynolds cercanos a Re150.000, tiene un valor aproximadamente constante,
denominado presión base, igual a p*b  0.4   (Fage 1937, Lighthill 1963, p.108,
Goldstein 1965, pp. 15 y 497, Schlichting 1968, p. 21).
Fig. 4.4 Flujo alrededor de un cilindro a varios números de Reynolds.
Fig.4.5 Tamaño de la zona de vórtices detrás de una esfera a números
de Reynolds intermedios. (Taneda 1956).
Capítulo 4 Sedimentación de Sistemas Particulados
41
1.5
Coeficiente de presión Cp
1
0.5
0
0
0.5
1
1.5
2
2.5
3
-0.5
-1
-1.5
Angulo  en radianes
Fig. 4.6 Coeficiente de presión en función de la distancia sobre la
superficie de la esfera en un flujo invíscido y en capa límite.
La asimetría de la distribución de presión sobre la esfera explica el origen de la
fuerza hidrodinámica de forma, la magnitud de la cual está directamente relacionada
con la posición del punto de separación. Mientras más atrás se encuentre el punto de
separación en la esfera, menor será la fuerza de interacción. Para una esfera sumergida
en un fluido a alto número de Reynolds, el punto de separación se mantiene constante
para un amplio rango de números de Reynolds superiores a 10.000, como ya hemos
visto, y debido a ello, la fuerza de interacción debe permanecer relativamente
constante, excepto cuando el régimen de flujo cambia de laminar a turbulento. Al
mismo tiempo la fuerza de interacción viscosa debido a la fricción dentro de la capa
límite disminuye en proporción al Re 1 2 . De estas consideraciones se puede observar
que a números de Reynolds del orden de 1.000, la fuerza de interacción viscosa ha
disminuido lo suficientemente para que su contribución a la fuerza de interacción total
sea despreciable. Es así como entre Reynolds del orden de 10.000 y 150.000 el
coeficiente de arrastre as aproximadamente constante e igual a C D  0.44 .
Para números de Reynolds mayores a 150.000 el carácter del flujo cambia
tornándose turbulento en el frente de la esfera. El aumento de la energía cinética que la
turbulencia trae, permite que el flujo en la capa límite pueda avanzar mas lejos en la
superficie de la esfera, corriendo el punto de separación a valores cercanos a 110° y
haciendo que la presión base aumente. Estos fenómenos traen como consecuencia una
disminución brusca de la fuerza hidrodinámica, la que a Reynolds mayores aumenta
nuevamente a una mayor velocidad. La figura 4.7 muestra un gráfico de datos
42
Manual de Filtración & Separación
experimentales del coeficiente de arrastre, o fuerza hidrodinámica adimensional,
considerados estándares, versus número de Reynolds. Estos datos muestran el efecto
indicado.
1000.00
Coeficiente de arrastre CD
100.00
10.00
1.00
0.10
0.01
1.E-01
1.E+00
1.E+01
1.E+02
1.E+03
1.E+04
1.E+05
1.E+06
1.E+07
Número de Reynolds Re
Fig. 4.7 Coeficiente de arrastre CD versus número de Reynolds Re,
según datos estándares de Lapple and Shepherd (1940). Ver
también Perry (1963, p. 5.61).
4.1.5 Coeficiente de arrastre para una esfera con 0<Re<150.000
La figura 4.7 muestra cómo varía el coeficiente de arrastre con el número de
Reynolds y confirma que para Re0, C D  Re 1 2 y para Re>>1, C D  0.44 . Con el
objetivo de encontrar una ecuación general que relacione el coeficiente de arrastre y el
número de Reynolds, utilizaremos el concepto de capa límite y recordaremos que, para
una posición determinada en la superficie de la esfera, la presión dentro de la capa
límite es igual a la presión existente inmediatamente fuera de ésta antes del punto de
separación, y es una constante después de este punto. Recordemos también que tanto el
punto de separación como la presión base son constantes.
Consideremos un sistema formado por una esfera de radio R y su capa límite de
espesor  sumergidos en un flujo a alto número de Reynolds Abraham 1970).
Aproximemos por a  R   al radio de este sistema, según se muestra en la figura 4.8
Fuera de la esfera de radio "a", y hasta el punto de separación, el flujo es
invíscido y la distribución del coeficiente de presión está dada por (4.12):
Capítulo 4 Sedimentación de Sistemas Particulados
43
Fig. 4.8 Modelo físico para una esfera en flujo en capa límite.
9
Cp  1  sen 2 
2
Por lo tanto, dentro de la capa límite, y hasta el punto de separación, la distribución de
presión estará dada por:
1
 9

p( )  f u 2  1  sen 2  
2
 2

(4.15)
y más allá del punto del punto de separación esta será:
1
p( )  f u 2 p*b
2
(4.16)
Sobre el sistema de radio "a" en consideración, esfera más capa límite, la fuerza
hidrodinámica se reduce al arrastre de forma debido a la presión, ya que la viscosidad
está confinada dentro del interior de la esfera de radio "a". Por lo tanto la fuerza
hidrodinámica está dada por:
FD 

Sa
p( ) cos dS
(4.17)
El elemento de superficie de la esfera de radio a en coordenadas esféricas es:
dS  a 2sendd
Donde  es la coordenada azimutal. Reemplazando en (4.17) obtenemos:
FD 
2

0
0
 
p( )sen cos dd
(4.18)
44
Manual de Filtración & Separación
Integrando (4.17) en  resulta:
FD  2a 2


0
p( )sen cos d
(4.19)
Como el valor de p es diferente antes y después del punto de separación, dividamos la
integral en dos partes, de 0 a s y de s a :
FD  2a 2 


s
0
p( )send(sen) 


s
p()send(sen) 

Sustituyendo los valores de p() de (4.15) y (4.16) para cada caso e integrando resulta:
9
1
1

FD  a 2f u 2  sen 2 s  sen 4 s  p*b sen 2 s 
16
2
2


(4.20)

Reemplazando a=R+ y definiendo la función f s , p*b en la forma:


1
9
1
f s , p*b  sen 2 s  sen 4 s  p*bsen 2 s
2
16
2
(4.21)
podemos escribir(4.20) en la forma:
2


FD  f u R  1   f s , p*b
R

2

2

(4.22)
En términos del coeficiente de arrastre podemos escribir:


C D  2f s , p*b  1  
R



2
(4.23)
Definiendo el nuevo parámetro C0 en la forma:

C0  2f s , p*b

(4.24)
y reemplazando la razón /R de (4.14), podemos escribir finalmente:
CD 

C0 s , p*b

0 

1  1 2 
Re 

2
(4.25)
Si calculamos el valor de C0 para s=84° y p*b  0.4 , se obtiene f  84, 0.4   0.142
y C0 resulta ser C0  0.284  0.28 . Usando este valor y el valor de 0=9.06,
obtenemos:
9.06 

C D  0.28  1  1 2 
 Re 
2
(4.26)
Capítulo 4 Sedimentación de Sistemas Particulados
45
La expresión (4.26) representa el coeficiente de arrastre para una esfera en régimen de
capa límite. Una comparación de la simulación con esta función y los datos
experimentales estándar se muestra en la figura 4.8.
Los datos experimentales estándar de Lapple and Shepherd (1940) para
partículas esféricas se muestran en la tabla 4.1. y figura 5.7.
4.1.6 Velocidad de sedimentación de una esfera
Hemos visto, que cuando una partícula sedimenta a velocidad terminal se
establece un balance entre las fuerzas de gravedad, fuerzas de empuje y fuerza
hidrodinámica en la forma:
Fgravitacional  Fempuje  Fhidrodinamica  0
por lo tanto:
Fhidrodinamica    Fgravitacional  Fempuje   peso neto de las partículas
FD     p Vp ( g)  f Vp g   Vp g
(4.27)
donde  es la diferencia de densidades entre sólido y fluido. La expresión (4.27)
implica que la fuerza hidrodinámica para partículas en sedimentación se conoce de
antemano y es independiente de la forma de la partícula. Para una partícula esférica
resulta:
4
R 3g
3
(4.28)
FD
4 dg

2
2
3 f u 2
1 2 f u R
(4.29)
FD 
y el coeficiente de arrastre será:
CD 
donde d=2R es el diámetro de la esfera. Como el número de Reynolds está definido
por:
Re 
duf
f
(4.30)
mediante la combinación de éste y el coeficiente de arrastre, se puede definir dos
números adimensionales (Heywood 1962):
 4 f g  3
C D Re 2  
d
 3  2 
f


Re  3 f2  3

u
CD  4 f g 
(4.31)
46
Manual de Filtración & Separación
Tabla 4.1 Coeficiente de arrastre en función del número de Re*
Re
0.1
0.2
0.3
0.5
0.7
1
2
3
5
7
10
20
30
50
70
100
200
300
500
700
1000
2000
3000
5000
7000
10000
20000
30000
50000
70000
100000
200000
300000
500000
700000
1000000
3000000
CD
240.00
120.00
80.00
49.50
36.50
26.50
14.60
10.40
6.90
5.30
4.10
2.55
2.00
1.50
1.27
1.07
0.77
0.65
0.55
0.50
0.46
0.42
0.40
0.39
0.39
0.41
0.45
0.47
0.49
0.50
0.48
0.42
0.20
0.08
0.10
0.13
0.20
CDRe2
2.4
4.8
7.2
12.4
17.9
26.5
58.4
93.6
172.5
259.7
410.0
1.02E+03
1.80E+03
3.75E+03
6.22E+03
1.07E+04
3.08E+04
5.85E+04
1.38E+05
2.45E+05
4.60E+05
1.68E+06
3.60E+06
9.63E+06
1.91E+07
4.05E+07
1.80E+08
4.23E+08
1.23E+09
2.45E+09
4.80E+09
1.68E+10
1.80E+10
2.10E+10
4.90E+10
1.30E+11
1.80E+12
*Lapple and Shepherd 1940.
Re/CD
d*=(CDRe2)1/3 u*=(Re/CD)1/3
4.17E-04
1.34
7.47E-02
1.67E-03
1.69
1.19E-01
3.75E-03
1.93
1.55E-01
1.01E-02
2.31
2.16E-01
1.92E-02
2.62
2.68E-01
3.77E-02
2.98
3.35E-01
1.37E-01
3.88
5.15E-01
2.88E-01
4.54
6.61E-01
7.25E-01
5.57
8.98E-01
1.3
6.38
1.10
2.4
7.43
1.35
7.8
1.01E+01
1.99
15.0
1.22E+01
2.47
33.3
1.55E+01
3.22
55.1
1.84E+01
3.81
93.5
2.20E+01
4.54
259.7
3.13E+01
6.38
461.5
3.88E+01
7.73
909.1
5.16E+01
9.69
1.40E+03
6.26E+01
11.19
2.17E+03
7.72E+01
12.95
4.76E+03
1.19E+02
16.82
7.50E+03
1.53E+02
19.57
1.30E+04
2.13E+02
23.51
1.79E+04
2.67E+02
26.18
2.47E+04
3.43E+02
29.12
4.44E+04
5.65E+02
35.42
6.38E+04
7.51E+02
39.96
1.02E+05
1.07E+03
46.73
1.40E+05
1.35E+03
51.92
2.08E+05
1.69E+03
59.28
4.76E+05
2.56E+03
78.09
1.50E+06
2.62E+03
114.47
5.95E+06
2.76E+03
181.23
7.00E+06
3.66E+03
191.29
7.69E+06
5.07E+03
197.40
1.50E+07
1.22E+04
246.62
Capítulo 4 Sedimentación de Sistemas Particulados
47
1000,00
Coeficiente de arrastre CD
100,00
10,00
1,00
0,10
0,01
0,01
0,1
1
10
100
1000
10000
Número de Reynolds Re
100000 100000 1E+07
0
Fig. 4.9 Coeficiente de arrastre versus número de Reynolds. La
línea continua corresponde a la simulación con la ecuación (4.26)
y los círculos a datos estándar de Lapple y Shepherd (1940).
Concha y Almendra (1979a) definieron los parámetros característicos del sistema
sólido-fluido P y Q:
13
 3 f2 
P

 4 f g 
(4.32)
13
 4 f g 
Q

2
 3 f 
(4.33)
de forma que las ecuaciones (4.31) y se pueden escribir en la forma:
3
d
CD Re     d *3
P
2
(4.34)
3
Re  u 
    u *3
CD  Q 
(4.35)
Las expresiones (4.34) y (4.35) definen un tamaño d* y una velocidad u*
adimensionales, que son características del sistema sólido-fluido. Multiplicando estas
dos ecuaciones podemos verificar que:
48
Manual de Filtración & Separación
Re  d * u *
(4.36)
Reemplazando las expresiones (4.25) y (4.36) en (4.34) obtenemos (Concha y
Almendra 1979a):
2


0
2
  u *d *
d *  C0  1 
12
  u * d * 


3
u * d * 0  u *d *
12

d *3 2
0
C10 2
Resolviendo esta ecuación algebraica de segunda grado obtenemos:
12

1 20  
4
32
 1  1 2 2 d *   1
u* 

4 d *   C 0 0



2
(4.37)
12
 
1
4 0  3 2  
2

d*  C0 u * 1   1  1 2 u *  
  C0
4
 

2
(4.38)
La primera ecuación se conoce con el nombre de ecuación de Concha y Almendra para
una esfera. Estas dos ecuaciones son generales, para esferas sedimentando a cualquier
número de Reynolds. La primera ecuación permite calcular la velocidad de
sedimentación de una partícula de diámetro adimensional d* y la segunda permite
calcular el diámetro adimensional de una partícula que adquiere una velocidad de
sedimentación adimensional de u*.
Para el caso de la esfera, podemos introducir los valores de C0=0.28 y 0=9.06,
para obtener:
u* 

20.52
1  0.0921d *3 2
d*



12

1
d*  0.07u *2 1  1  68.49u *3 2

2
(4.39)

12 2
(4.40)
La figura 4.9 muestra la comparación entre los valores de sedimentación
simulados y los calculados desde los datos experimentales estándar (ver Tabla 4.1).
Capítulo 4 Sedimentación de Sistemas Particulados
49
1,00E+03
Velocidad adimensional u*
1,00E+02
1,00E+01
1,00E+00
1,00E-01
1,00E-02
1,E-01
1,E+00
1,E+01
1,E+02
1,E+03
1,E+04
1,E+05
Diámetro adimensional d*
Fig. 4.9 Velocidad adimensional versus tamaño adimensional para la
sedimentación de esferas según la ecuación (4.39) y comparación con
datos experimentales estándar de Cd versus Re de Lapple and Shepherd
1940.
Ejemplo 3
Para realizar cálculos de sedimentación de partículas esféricas es necesario
conocer los parámetros de tamaño P y velocidad Q, que dependen de las propiedades
del sólido y del fluido. Construya una tabla para estos parámetros en función de la
densidad del sólido. Suponga que la densidad del agua es de 1 g/cm3 y su viscosidad
0.01 g/cm-s.

La definición de P y Q es P  3f2 4f g

13

Q  4 f g 32f

13
. El
resultado se muestra en la tabla de la página siguiente.
Ejemplo 4
Calcular la velocidad de sedimentación de esferas de cuarzo de densidad 2.65 g/cm3 de
los siguientes diámetros: 10 m, 50 m, 100 m, 300 m, 500 m, 1 mm 5 mm y 1 cm
a 20 °C. La ecuación que predice la velocidad de sedimentación es:
u* 

20.52
1  0.0921d *3 2
d*

12

2
1 ,
con
d*  d P y u  Q  u *
50
Manual de Filtración & Separación
Tabla de resultados del ejemplo 3.
s (g/cm3) f (g/cm3) f (g/cms)
1.10
1.15
1.20
1.25
1.30
1.35
1.40
1.45
1.50
1.55
1.60
1.65
1.70
1.75
1.80
1.85
1.90
1.95
2.00
2.05
2.10
2.15
2.20
2.25
2.30
2.35
2.40
2.45
2.50
2.55
2.60
2.65
2.70
2.75
2.80
2.85
2.90
2.95
3.00
3.05
3.10
3.15
3.20
3.25
3.30
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
s (g/cm3) f (g/cm3)
P (cm)
Q (cm/s)
9.1470E-03
7.9906E-03
7.2600E-03
6.7396E-03
6.3422E-03
6.0245E-03
5.7622E-03
5.5404E-03
5.3492E-03
5.1819E-03
5.0338E-03
4.9013E-03
4.7817E-03
4.6730E-03
4.5735E-03
4.4820E-03
4.3974E-03
4.3189E-03
4.2457E-03
4.1772E-03
4.1129E-03
4.0524E-03
3.9953E-03
3.9413E-03
3.8901E-03
3.8415E-03
3.7952E-03
3.7511E-03
3.7089E-03
3.6686E-03
3.6300E-03
3.5929E-03
3.5574E-03
3.5232E-03
3.4902E-03
3.4585E-03
3.4279E-03
3.3983E-03
3.3698E-03
3.3422E-03
3.3154E-03
3.2895E-03
3.2644E-03
3.2400E-03
3.2164E-03
1.0933E+00
1.2515E+00
1.3774E+00
1.4838E+00
1.5767E+00
1.6599E+00
1.7354E+00
1.8049E+00
1.8694E+00
1.9298E+00
1.9866E+00
2.0403E+00
2.0913E+00
2.1400E+00
2.1865E+00
2.2311E+00
2.2741E+00
2.3154E+00
2.3553E+00
2.3940E+00
2.4314E+00
2.4677E+00
2.5029E+00
2.5372E+00
2.5706E+00
2.6032E+00
2.6349E+00
2.6659E+00
2.6962E+00
2.7258E+00
2.7548E+00
2.7832E+00
2.8111E+00
2.8384E+00
2.8651E+00
2.8914E+00
2.9172E+00
2.9426E+00
2.9676E+00
2.9921E+00
3.0162E+00
3.0400E+00
3.0633E+00
3.0864E+00
3.1091E+00
3.35
3.40
3.45
3.50
3.55
3.60
3.65
3.70
3.75
3.80
3.85
3.90
3.95
4.00
4.05
4.10
4.15
4.20
4.25
4.30
4.35
4.40
4.45
4.50
4.55
4.60
4.65
4.70
4.75
4.80
4.85
4.90
4.95
5.00
5.05
5.10
5.15
5.20
5.25
5.30
5.35
5.40
5.45
5.50
5.55
f (g/cms)
P (cm)
Q (cm/s)
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
3.1934E-03
3.1711E-03
3.1494E-03
3.1282E-03
3.1076E-03
3.0876E-03
3.0681E-03
3.0490E-03
3.0304E-03
3.0123E-03
2.9945E-03
2.9772E-03
2.9603E-03
2.9438E-03
2.9276E-03
2.9118E-03
2.8963E-03
2.8811E-03
2.8663E-03
2.8517E-03
2.8375E-03
2.8235E-03
2.8098E-03
2.7963E-03
2.7831E-03
2.7702E-03
2.7575E-03
2.7450E-03
2.7328E-03
2.7207E-03
2.7089E-03
2.6973E-03
2.6858E-03
2.6746E-03
2.6635E-03
2.6527E-03
2.6420E-03
2.6315E-03
2.6211E-03
2.6109E-03
2.6009E-03
2.5910E-03
2.5812E-03
2.5716E-03
2.5622E-03
3.1314E+00
3.1535E+00
3.1752E+00
3.1967E+00
3.2179E+00
3.2388E+00
3.2594E+00
3.2798E+00
3.2999E+00
3.3198E+00
3.3394E+00
3.3588E+00
3.3780E+00
3.3970E+00
3.4158E+00
3.4343E+00
3.4527E+00
3.4709E+00
3.4889E+00
3.5067E+00
3.5243E+00
3.5417E+00
3.5590E+00
3.5761E+00
3.5931E+00
3.6098E+00
3.6265E+00
3.6430E+00
3.6593E+00
3.6755E+00
3.6915E+00
3.7075E+00
3.7232E+00
3.7389E+00
3.7544E+00
3.7698E+00
3.7850E+00
3.8002E+00
3.8152E+00
3.8301E+00
3.8449E+00
3.8596E+00
3.8741E+00
3.8886E+00
3.9029E+00
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Tabla de resultados del ejemplo 4
d (m)
1
10
50
100
300
500
1000
5000
10000
d*
2.7832E-02
2.7832E-01
1.3916E+00
2.7832E+00
8.3497E+00
1.3916E+01
2.7832E+01
1.3916E+02
2.7832E+02
u*oo
3.37E-05
3.35E-03
7.84E-02
2.80E-01
1.55E+00
2.91E+00
5.83E+00
1.90E+01
2.86E+01
uoo (cm/s)
9.4E-05
9.3E-03
2.2E-01
7.8E-01
4.3E+00
8.1E+00
1.6E+01
5.3E+01
8.0E+01
Reoo
9.3798E-07
9.3189E-04
1.0916E-01
7.7900E-01
1.2970E+01
4.0473E+01
1.6214E+02
2.6373E+03
7.9666E+03
Capítulo 4 Sedimentación de Sistemas Particulados
51
Para calcular velocidades de sedimentación a otras temperaturas es necesario
disponer de la densidad y viscosidad del fluido en esas condiciones. El gráfico que
sigue muestra correlaciones de estas variables entre 0 y 100°C (Droguett 2000).
2.50E-04
0.018
0.016
viscosidad agua (g/cm-s)
y = 5E-07x + 0.0002
0.012
2
R = 0.9996
1.50E-04
0.01
0.008
1.00E-04
0.006
0.004
viscosidad aire (g/cm-s)
2.00E-04
0.014
5.00E-05
2
y = 9E-07x - 0.0002x + 0.0156
2
R = 0.9983
0.002
0
0.00E+00
0
10
20
30
40
50
60
70
80
90
100
Temperatura (ºC)
Fig. 4.10 Viscosidades del agua y aire a diversas temperaturas.
1.005
1.40E-03
y = -3E-06x + 0.0013
1.000
2
R = 0.9931
1.20E-03
1.00E-03
3
0.990
densidad aire (g/cm )
3
densidad agua (g/cm )
0.995
0.985
8.00E-04
0.980
6.00E-04
0.975
0.970
4.00E-04
2
y = -4E-06x - 6E-05x + 1.0004
0.965
2
R = 0.9993
2.00E-04
0.960
0.955
0.00E+00
0
10
20
30
40
50
60
70
80
90
100
Temperatura (ºC)
Fig. 4.10 Densidades del agua y aire a diversas temperaturas.
52
Manual de Filtración & Separación
Las correlaciones para las viscosidades con la temperatura T en °C son:
agua  9.0  107 T 2  2.0  10 4 T  1.56  10 2 ( g / cm  s)
(4.41)
aire  5.0  107 T  2.0  10 4 (g / cm  s)
(4.42)
Las correlaciones para las densidades con la temperatura T en °C son:
agua  4.0  10 6 T 2  6.0  10 5 T  1.0004 (g / cm3 )
(4.43)
aire  3.0  106 T  1.3  103 (g / cm3 )
(4.44)
Ejemplo 5
Calcular la velocidad de sedimentación de una esfera de cuarzo de 300 m en
agua a 60 °C.
Considere:
agua  0.982 g / cm3 , agua  6.84  103 g / cms , P  2.796  10 3 , Q  2.4903
d* 
300
 10.730
10000  2.796  103
u *  2.14 y u   2.14  2.4903  5.34 cm s .
4.1.7 Sedimentación de una suspensión de esferas
Cuando una esfera que sedimenta se encuentra rodeada de otras esferas se
produce entorpecimiento en el asentamiento de cada una de ellas. Al trasladarse una
partícula de una posición a otra, puede encontrar ocupado el nuevo lugar y colisionará
con la partícula que lo ocupa desviándose de su trayectoria. Mientras más partículas
existan en la suspensión mayor oportunidad existirá para que se obstaculicen entre
ellas. El resultado es que la velocidad efectiva de sedimentación disminuirá al
aumentar la concentración de la suspensión. Como la obstaculización en la
sedimentación de una partícula depende del volumen del espacio ocupado y no de su
masa, la variable apropiada para describir este fenómeno es la fracción del espacio
ocupada por el sólido, esto es, la fracción volumétrica de sólidos.
Concha y Almendra (1979b) postularon que para una suspensión de partículas
esféricas, todas de la misma densidad y diámetro, la ecuación (4.39) sigue siendo
válida con parámetros P y Q reemplazados por P() y Q(). Para mostrar que se trata
de la suspensión usemos las letras U* y D* en vez de u* y d* de una partícula
individual:
U* 

20.52
1  0.0921D *3 2
D*

12

1
2
(4.45)
Capítulo 4 Sedimentación de Sistemas Particulados
53
donde supondremos que:
D* 
d
P 
U* 
y
u
Q 
(4.46)
Es costumbre considerar las propiedades de una suspensión, tal como la
viscosidad, como el producto de la misma propiedad del fluido y una función de la
concentración. Siguiendo este ejemplo, supongamos que las propiedades P() y Q()
de la suspensión se relacionan con las propiedades del sólido y fluido en la forma:
P     Pf p   
Q     Qf q   
y
(4.47)
Entonces, reemplazando en (4.46) resulta:
D* 
d*
fp 
y
U* 
u*
fq   
(4.48)
Con estas definiciones, la ecuación (4.45) se puede escribir en la forma:
u* 

20.52
f p    f q    1  0.0921f p3 2d *3 2
d*

12

1
2
(4.49)
Esta expresión, conocida con el nombre de ecuación de Concha y Almendra para
suspensiones de esferas, permite calcular la velocidad de sedimentación de partículas
de cualquier tamaño a cualquier concentración. Para ello es necesario conocer los
parámetros fp() y fq().
Expresiones asintóticas para la velocidad
Para valores pequeños del número de Reynolds, Re0, se cumplen las
siguientes expresiones para (4.39) y (4.49):
 1
0.0921d *3 2
32
0.0921d *
f p3 2
 1
Tomando en cuenta estas consideraciones, las ecuaciones (4.39) y (4.49) se reducen a:
2
 0.0921 
2 2
u*  20.52 
 d * f p    fq   
2


2
u*
 0.0921 
 20.52 
d *2

 2 
En esta expresión hemos usado los símbolos u* y u* para indicar la velocidad de una
partícula en un medio infinito y la misma partícula en una suspensión. El cuociente
entre estas dos expresiones resulta ser:
54
Manual de Filtración & Separación
u*
 f p2    f q   
u*
Para Re0
(4.50)
Haciendo una deducción similar para valores altos del número de Reynolds, Re,
para (4.39) y (4.49) se cumple:
 1
0.0921d *3 2
32
0.0921d *
f p3 2
 1
y las ecuaciones (4.39) y (4.49) se reducen a:
u*  20.52x0.0921xd *1 2 f p1 2    f q   
u*  20.52x0.0921xd *1 2
El cuociente entre estas dos expresiones es:
Para Re
u*
 f p1 2    f q   
u*
(4.51)
Formas funcionales para fp() y fq()
Varios autores han presentado ecuaciones para expresar la velocidad de
sedimentación de suspensiones en función de la velocidad de sedimentación de una
partícula en un medio infinito y la concentración. La tabla 4.1 muestra algunas de estas
expresiones.
Tabla 4.2 Expresiones para las velocidades de sedimentación asintóticas
R. y
Zaki
fp()
(1-)-1.51
fq()
(1-)0.64
Concha y Almendra
Massarani
1 3


(1  )(1  0.75 )

2 3 3 4
1.83 
 (1    1.2 ) (1  1.45) 
4
1 3


(1  ) (1  0.75 )

2 3 3
1.83 
 (1    1.2 ) (1  1.45) 

2 3
1 3

 0.087 1  0.751 3 exp  2.37(1  )  


1.83


1

1.45









2 3
1  0.75   0.087 exp  2.37(1  )   
4
1 3
1  1.45 1.83
1 3


La figura 4.10 muestra la velocidad adimensional U* para suspensiones de
esferas de cualquier tamaño y densidad versus el tamaño adimensional D*. Esta curva
es universal.
Capítulo 4 Sedimentación de Sistemas Particulados
55
La figura 4.11 muestra una simulación de la velocidad de sedimentación
adimensional u* de partículas de tamaño adimensional d* para varios valores de la
concentración. Esta figura puede ser usada para analizar el estado de flujo en un lecho
poroso.
Figura 4.10. Velocidad adimensional U* para suspensiones de esferas de
cualquier tamaño y densidad versus el tamaño adimensional D*, junto a datos
experimentales (Concha y Almendra 1979).
Veremos mas adelante que para un medio poroso la velocidad de percolación q está
dada por:
q  vs  (1  )v r
(4.52)
donde q  vs  (1  )vf y v r  vs  vf es la velocidad relativa sólido-fluido. Para un
flujo bifásico esta velocidad de percolación recibe el nombre de velocidad volumétrica.
La figura 4.11 separa el plano en tres regiones, la región de lecho fijo entre el eje
de las abscisas y =0.585, la región de lecho fluidizado entre 0.585>>0 y la región de
transporte hidráulico o neumático entre =0 y el eje de las ordenadas. Wen and Yu
(1966) y Barnea and Mednick (1975) muestran que la velocidad inicial de fluidización
corresponde a una concentración de =0.585.
56
Manual de Filtración & Separación
1.00E+02
=0,3
Velocidad adimensional u*
1.00E+01
=0,2
1.00E+00
=0,4
1.00E-01
=0,1
=0,5
1.00E-02
=0
1.00E-03
=0,585
1.00E-04
0.01
0.1
1
10
100
1000
Diámetro adimensional d*
Fig. 4.11 simulación de la velocidad de sedimentación
adimensional u* de partículas de tamaño adimensional d* para
varios valores de la concentración a 20°C.
Consideremos como un ejemplo que un flujo en un lecho poroso, formado por
partículas esféricas de tamaño adimensional d*=1, el fluido percola a través del lecho a
una velocidad adimensional dada por u* a una temperatura de 20°C. Si la velocidad u*
aumenta su valor, éste se puede calcular de la figura 4.11 trazando una recta vertical en
d*  1 . El fluido percolará a través del lecho fijo hasta que se alcance la velocidad
u*  2.9  104 , momento en el cual el lecho se expandirá. El lecho permanecerá
fluidizado al aumentar la velocidad hasta u*  2  102 y de ahí en adelante las
partículas comenzarán a dejar el lecho al aumentar su velocidad.
Ejemplo 5
Calcular la velocidad de sedimentación de una suspensión de monotamaño de
esferas de 150 m a 15 °C con una concentración de 40% de sólidos en peso.
Los parámetros son:  
40
 0.20
2.65  (100  40)  40
agua  0.9959 ,  agua  0.01280 , P  4.2385  103 , Q  3.0329
f p (0.2)  1.40066 , f q (02)  0.86692
Capítulo 4 Sedimentación de Sistemas Particulados
d* 
150
 3.5390
4.2385  103
u* 
20.52
f p    f q    1  0.0921f p3 2d *3 2
d*

57

12

1
2
u *  0.423 y u  0.423  3.0329  0.128 cm s
Ejemplo 6
Calcular la velocidad de fluidización de una suspensión monotamaño de
partículas de cuarzo de 150 m de diámetro y densidad 2.65 g/cm3 a 15°C y una
concentración de 40% de sólidos en peso. Calcular, además, a que velocidad de
precolación las partículas indicadas comenzarán a ser transportadas.
La velocidad de precolación es q  vs  (1  )v r . Como v r  u , y a la velocidad
de transporte   0 , q(0)   u(0) . Del problema anterior podemos calcular:
q  (1  0.20)  1.28  1.024 cm s
El transporte comenzará cuando la concentración tienda a cero. Como d*  3.539 ,
u *  0.423 y q  u(0)  1.28 cm s
4.1.8 Sedimentación de partículas isométricas
Las partículas no-esféricas tienen un comportamiento diferente a las esféricas
durante la sedimentación. Mientras que las partículas esféricas caen en una trayectoria
vertical, las partículas no-esféricas, vibran rotan y siguen una trayectoria espiral.
Varios autores han estudiado la sedimentación de partículas isométricas, esto es,
partículas con un alto grado de simetría tales como tetraedros, octaedros y
dodecaedros, con tres ejes de simetría mutuamente perpendiculares e iguales. Entre
ellos Wadell (1932, 1934), Pettyjohn and Christiansen (1948) and Christiansen and
Barker (1965). Sus trabajos indican que las partículas isométricas siguen trayectorias
verticales a números de Reynolds pequeños, pero rotan, vibran y tienen trayectorias
helicoidales para números de Reynolds entre 300 y 150.000.
Pettyjohn y Christiansen (1948) demostraron que la velocidad de sedimentación
de partículas isométricas en régimen de Stokes se podía describir mediante la siguiente
expresión:
  
 0.843log 

ue
 0.065 
up
(4.53)
donde ue es la velocidad de sedimentación de una esfera que tiene el mismo volumen
que la partícula (esfera equivalente), entonces:
58
Manual de Filtración & Separación
ue 
d 2e g
18f
(4.54)
en esta expresión de es el diámetro equivalente o diámetro de la esfera equivalente.
Para el rango de números de Reynolds entre 2.000<Re<17.000, estos mismos
autores proponen la siguiente expresión:
ue 
4 d e g
3 f C D
(4.55)
con el coeficiente de arrastre CD dado por:
C D  5.31  4.88
(4.56)
Como hemos dicho, por sobre Re=300, las partículas comienzan a rotar y
oscilar. Para tomar en cuanta este comportamiento, Barker (1951) sugirió introducir
como nueva variable la densidad de la partícula. Él propone la siguiente corrección:
C D  ,     1 18CD   
(4.57)
donde  es el cuociente de densidades entre el sólido y el fluido:    p f . Los datos
de Pettyjohn y Christiansen (1948) y de Barker (1951) se pueden graficar según la
figura 4.12.
Fig. 4.12 Datos de Pettyjohn y Christiansen (1948) y de Barker
(1951) graficados como coeficiente de arrastre versus número de
Reynolds, utilizando como tamaño el diámetro equivalente.
Capítulo 4 Sedimentación de Sistemas Particulados
59
Coeficiente de arrastre y velocidad de sedimentación
Toda la información anterior se puede usar para desarrollar una ecuación que
describa el coeficiente de arrastre y la velocidad de sedimentación de una partícula
isométrica (Concha y Almendra 1979b).
Supongamos que las ecuaciones (4.25) y (4.38) son válidas para partículas
isométricas, con valores de C0 y 0 como funciones de la esfericidad  y del cuociente
de densidades  (Concha y Barrientos 1986):
   ,   
C D  ,    C 0  ,    1  0 1 2 
Re


u*p
2
12
2


1  0  ,    
4
32


1

d
*

1


 1 2  ,    2  ,  

4 d *   C
0
0



(4.58)
2
(4.59)
Donde el número de Reynolds queda definido con el diámetro equivalente.
Supongamos, además, que se cumple:
C 0  ,    C0 f A    f C   
(4.60)
 0  ,    0 f B    f D   
(4.61)
donde C0 y 0 son los parámetros para una esfera.
Hemos ya demostrado, que para una esfera a Re0, la velocidad se puede
aproximar por:
u*e 
d*2
e
C0 02
(4.62)
Del mismo modo para una partícula isométrica tenemos:
u*p 
d*2
e
C 0  ,   02  ,  
(4.63)
Como el diámetro de es el mismo para la esfera y la partícula, reemplazando (4.60) y
(4.61) en (4.63) y haciendo el cuociente entre (4.63) y (4.62) resulta:
Re0
u *e u e

 f A    f B2    f C    f D2   
u*p u p
Por otra parte para Re, se puede comprobar que:
(4.64)
60
Manual de Filtración & Separación
C D  ,  
CD

  ,  
C
0
(4.65)
C0
y reemplazando la expresión
C D  ,  
 f A    fC   
CD
Re,
(4.66)
Para determinar las funciones fA, fB, fC y fD, usaremos las ecuaciones propuestas por
Pettyjohn y Christiansen (4.53) y (4.56) y (4.57) por Barker (1951). De (4.64) y (4.53)
podemos escribir:

f A    f B2    f C    f D2     0.843log

f A    f C     1 1|8
 

0.065 
5.42  4.75
5.42  4.75
(4.67)
(4.68)
De (4.57) y (4.68)se puede concluir que:
fA   
5.42  4.75
0.67
(4.69)
f C     1 18
(4.70)
Como en régimen de Stokes no hay efecto de la densidad, (4.67) implica que:
f D2     f C1      1 18
y
f D      1 36
(4.71)
por lo tanto
 5.42  4.75
 
fB    
0.843log

0.67
0.065 

1 2
(4.72)
Coeficiente de arrastre y velocidad de sedimentación modificados
Introduciendo los valores de fA, fB, fC y fD en la ecuación (4.58) podemos
escribir:




C D , 
0

 C0 1 


fA   fC 

Re  f B )f D   






 

 
2
(4.73)
Capítulo 4 Sedimentación de Sistemas Particulados
61
Definiendo el coeficiente de arrastre modificado CDM y el número de Reynolds
modificado ReM en la forma:
CDM 
C D  ,  
(4.74)
fA   fC 


Re

 f B2    f D2    
ReM  

(4.75)

Si se grafica todos los datos experimentales como CDM versus ReM se obtiene la curva
unificada de la figura 4.13.
Fig. 4.13 Datos experimentales de Pettyjohn y Christiansen (948) y
Barker (1951) graficados como CDM versus ReM par partículas
isométricas.
Un resultado similar se obtiene para la velocidad de sedimentación. Definiendo
el diámetro equivalente adimensional unificado d*eM y la velocidad adimensional
modificada u*M en la forma:
d*eM


d*e  ,  
f A1 2    f B2    f C1 2f D2   

23
(4.76)
62
Manual de Filtración & Separación
u*eM
u*p  ,  

f B   f D  
(4.77)
La curva unificada de u*pM versus d*eM para los datos de Pettyjohn y Christiansen
(1948) y de Christiansen y Barker (1965) se muestra en la figura 4.14.
Fig. 4.14 Curva unificada de u*pM versus d*eM para los datos de
Pettyjohn y Christiansen (1948) y de Barker (1951) se muestra en la
figura 4.14.
Los datos experimentales que se utilizaron para desarrollar las expresiones
anteriores consisten en 419 puntos, incluyendo datos de esferas, cubos, octaedros y
tetraedros y cubren el siguiente rango de parámetros:
0.1 cm
<de<
1.6 cm
1.7 g/cm3
<s<
11.2 g/cm3
0.67
<<
1
<s<
1.43 g/cm3
9x10-3 g/cm-s <<
900 g/cm-s
5x10-3
2x104
3
0.87 g/cm
<Re<
Con los siguientes valores para la esfericidad (Happel and Brenner 1965):
Esfera
=1.000
Octaedro cúbico
=0.906
Capítulo 4 Sedimentación de Sistemas Particulados
63
Octaedro
=0.846
Cubo
=0.806
Tetraedro
=0.670
Ejemplo 7
Calcular la velocidad de sedimentación de un cubo de cuarzo de 1mm de lado,
densidad 2.65 g/cm3 en agua a 25°C.
Por definición la esfericidad es la razón entre la superficie de la esfera
equivalente y la superficie de la partícula. Para un cubo de lado a la superficie y
volumen son Scubo  6a 2 y Vcubo  a 3 . La esfera equivalente tiene el mismo volumen
a3, por lo que su diámetro será:
d e   6V  
13

La esfericidad es:
fA   
  6 
23
6a 2

 6a 3 
a2

13
  6  a
13
13
 
 
6
 0.806
5.42  4.75 5.42  4.75  0.806

 2.3754
5.42  4.75
5.42  4.75
 
 5.42  4.75
 0.843log
fB    

0.065 
 5.42  4.75
 0.67581
1 2
0.806 
 5.42  4.75  0.806

 0.843log

5.42  4.75
0.065 

f  4.0 106  252  6.0  105  25  1.0004  0.9964 (g / cm3 )
 2.65 
f C      1 18  

 0.9964 
1 18
 0.9473
1 36
 2.65 
f D     1 36  

 0.9964 
 1.0274
 0  ,    9.08  f B ( )f D ( )  9.08  0.6758  1.0275  6.305
C 0  ,    0.28  f A ( )f C ( )  0.28  2.3753  0.9471  0.6299
agua  9.0 107  252  2.0 104  25  1.56  102  0.0112 ( g / cm  s)
13
 3 f2 
P

 4 f g 
13


3  0.01122


 4(2.65  0.9964)  0.9964  980.1 
 0.003877
1 2
64
Manual de Filtración & Separación
13
 4 f g 
Q

2
 3 f 
d* 
13
 4  (2.65  0.9964)  0.0112  980.1 


3  0.99642


 2.900
de
0.1

 25.79
P 0.003877
12
2


1  0  ,    
4
*
32


up 
d
*
1
 1   1 2



4 d *   C0  ,    02  ,  



 6.0557 


 25.796 
2
2
2
12



4  25.7962 3
 1 
 1   9.07
(1/ 2)
2 
  0.6299

 6.3050 


u p  Q  u*  2.9  9.07  26.3 cm / s
4.1.9 Sedimentación de una suspensión de partículas arbitrarias
En un estudio realizado por Concha y Christiansen (1986) se realizó
experimentos de fluidización con tres tipos de partículas, caliza (densidad 2.71), cuarzo
(densidad 2.64) y arena de río (densidad 2.70 a 2.79). Los datos experimentales
obtenidos se entregan en la tabla 4.3 y la figura 4.16 muestra el coeficiente de arrastre
para estas partículas en función del número de Reynolds, usando el diámetro
equivalente como medición del tamaño.
CD 
4 d e g
3 f u p2
Concha y Christiansen (1986) extendieron la validez del coeficiente de arrastre y
de la velocidad de sedimentación definidas para una suspensión de esferas, para ser
utilizadas para una suspensión de partículas de forma arbitraria. Para ello, realizaron
experimentos de fluidización con tres tipos de partículas irregulares, mostradas en la
tabla 4.3, y usaron el concepto de esfericidad ya definido para partículas isométricas.
Es así como estas variables pueden ser definidas en la forma:
  , ,    1  0  , ,   
C D  ,  ,    C
0
Re1 2 

2
12
2



1  0  , ,    
4
*
32

u p  , ,   
d
*

1
1   1 2


  C0  , ,    02  , ,  

4
d*



(4.78)
2
(4.79)
Capítulo 4 Sedimentación de Sistemas Particulados
65
Tabla 4.3 Velocidades de fluidización de partículas de forma
arbitraria en agua a 20°C.
de
p
cm
(g/cm3)
Re
up() cm/s
=0.0
=0.1
=0.2
=0.3
=0.4
Caliza
0.0148
2.71
1.87
1.273
0.820
0.490
0.248
-
0.0216
2.71
4.89
2.282
1.517
0.961
0.512
0.244
0.0306
2.71
11.2
3.627
2.523
1.682
0.981
0.496
0.0443
2.71
25.2
5.725
4.159
2.909
1.879
1.056
0.0615
2.71
46.3
7.583
5.835
4.353
2.939
1.853
0.0956
2.71
86.6
10.181
8.045
6.182
4.579
3.056
0.1239
2.71
163
13.285
10.763
8.505
6.512
4.643
0.1859
2.71
324
17.556
14.294
11.631
8.940
6.873
0.2374
2.71
492
20.873
17.210
13.870
10.967
8.779
0.3292
2.71
811
24.802
21.051
17.526
14.238
11.385
0.5060
2.71
1111
27.629
23.672
19.914
16.371
13.570
0.0138
2.64
1.62
1.186
0.708
0.386
0.187
-
0.0207
2.64
4.46
2.171
1.372
0.821
0.411
-
0.0286
2.64
9.48
3.336
2.152
1.319
0.698
0.330
0.0420
2.64
22.1
5.290
3.665
2.432
1.423
0.743
0.0600
2.64
43.1
7.238
5.253
3.672
2.428
1.329
0.0834
2.64
78.8
9.509
7.292
5.428
3.732
2.334
0.1192
2.64
144
12.210
9.791
7.659
5.688
3.865
0.1732
2.64
279
16.213
13.258
10.587
8.204
6.111
0.2373
2.64
457
19.494
16.107
13.088
10.344
7.883
0.3338
2.64
767
23.143
19.594
16.268
13.174
10.327
0.4005
2.64
1031
25.926
22.095
18.477
15.086
11.937
0.0354
2.70
15.0
4.277
3.005
2.025
1.190
0.625
0.0425
2.70
23.1
5.473
3.919
2.698
1.716
0.930
0.0586
2.72
43.5
7.486
5.601
4.050
2.665
1.588
0.0833
2.76
85.6
10.354
7.992
5.984
4.275
2.791
0.1196
2.79
165
13.983
10.930
8.359
6.168
4.342
0.1735
2.79
322
18.712
14.386
10.979
8.605
6.495
0.2344
2.79
5.9
21.874
17.192
13.333
10.636
8.192
0.3287
2.79
848
25.980
20.882
16.807
13.617
10.681
0.4018
2.79
1208
30.277
23.819
19.382
15.741
12.380
Cuarzo
Arena
66
Manual de Filtración & Separación
10000,00
=0.4
Coeficiente de arrastre CD
1000,00
Caliza
Cuarzo
=0.3
Arena
=0.2
100,00
=0.1
=0.0
10,00
1,00
0,10
0,1
1
10
100
1000
10000
Número de Reynolds Re
Fig. 4.16 Coeficiente de arrastre para suspensiones de partículas irregulares
de para partículas de caliza, cuarzo y arena en función del número de
Reynolds, usando el diámetro equivalente como medición del tamaño a
cinco valores de concentración (Concha y Christiansen 1986).
donde  es la esfericidad,  el cuociente de densidades del sólido y el fluido y  la
concentración de sólido. Al igual que en el caso de suspensiones de esferas y de
partículas isométricas, supondremos que las contribuciones de estos parámetros se
puede separar:
  ,  ,    C f    f    f   
C
0
0 A
C
E
(4.80)
 0  , ,    0f B    f D    f F   
(4.81)
y que los valores de fA a fD son los definidos por las expresiones (4.69), (4.72), (4.70) y
(4.71). Concha y Christiansen (1986):
fA   
5.42  4.75
0.67
 
 5.42  4.75
fB    
0.843log

0.67
0.065 

1 2
f C      1 18
f D     1 36
Basados en los datos de la tabla 4.3 encontraron las siguientes expresiones para
las funciones fE y fF:
Capítulo 4 Sedimentación de Sistemas Particulados
  
f E  1  2.2315 

 1  
67
0.89957
(4.82)
1.4191
 1 
f F  1  1.6556 

 1  
(4.83)
Obviamente que los parámetros numéricos de las dos expresiones anteriores son
solamente válidos para las partículas cuyos datos están en la tabla 4.3.
Factor de forma hidrodinámico
Uno de los problemas encontrados para usar estas ecuaciones es que los valores
de la esfericidad geométrica, de terminada para las partículas por cualquier método, no
ha podido ser correlacionado con los valores de la velocidad de fluidización o
sedimentación, como por ejemplo con los valores de la tabla 4.3. Por ello Concha y
Christiansen (1986) definieron una esfericidad hidrodinámica efectiva. Para ello,
usaron las ecuaciones fA a fD, definidas para partículas isométricas, y re-calcularon el
valor de la esfericidad de los datos de la tabla 4.3. Como la forma de estas partículas no
era igual para todo el rango de tamaños, se escribió la esfericidad hidrodinámica como
una función del tamaño de partícula. En el caso de los datos de la tabla 4.3 esa función
fue:
  A0  A1d e  A 2d e2
(4.84)
con los valores de A0, A1 y A2 indicados en la tabla 4.4.
Según los cálculos anteriores, la esfericidad hidrodinámica efectiva de una
partícula de forma arbitraria quedaría definida como: "la esfericidad de una partícula
isométrica que sufre el mismo arrastre (volumen) y tiene la misma velocidad de
sedimentación que la partícula".
Tabla 4.4
Parámetro
Caliza
Cuarzo
Arena
A0
0.81540
0.87806
0.80399
A1
-0.27614
-1.13983
0.04100
A2
-0.03624
1.56763
-0.33082
Error relativo %
1.5
1.2
1.6
Coeficiente de arrastre y velocidad de sedimentación modificados
Se puede obtener una correlación única para el coeficiente de arrastre y la
velocidad de sedimentación de suspensiones de partículas de forma arbitraria,
definiendo un coeficiente de arrastre modificado y una velocidad de sedimentación
modificada:
68
Manual de Filtración & Separación
C DM 
C D  ,  
(4.85)
f A    fC    f E   


Re
Re M   2

2
2
 fB   fD   fF  


d*eM 
u*pM 
f
(4.86)
d*e  ,  
   fC    f E    
13
A
f
f
2
B
23
(4.87)
1 3
(4.88)
   f D2    f E2    
u*p  ,  
2
B
   f D2    f F2    
13
f
A
   fC    f E    
Las figuras 4.17 and 4.18 muestran las correlaciones unificadas para los datos de
la tabla 4.3.
Coeficiente de Arrastre Modificado CDM
1,0E+03
1,0E+02
1,0E+01
1,0E+00
1,0E-01
1,0E-01
1,0E+00
1,0E+01
1,0E+02
1,0E+03
1,0E+04
Número de Reynolds Modificado ReM
Fig. 4.17 Coeficiente de arrastre unificado versus número de
Reynolds modificado para partículas de caliza, cuarzo y arena
(Los mismos datos de la figura 4.16 de Concha y Christiansen
1986)
Ejemplo 8
Calcular la velocidad de fluidización de una suspensión de 35% de sólidos en
peso de partículas de cuarzo de 250 micrones y densidad 2.65 g/cm3 en agua a 25°C.
Del problema 7 tenemos la siguiente información:
Capítulo 4 Sedimentación de Sistemas Particulados
69
Velocidad adimensional u*
100
10
1
0.1
1
10
100
1000
Tamaño adimensional d*
Fig. 4.18 Velocidad de sedimentación unificada versus tamaño
modificado para partículas de caliza, cuarzo y arena. (Concha y
Christiansen 1986)
f  0.9964 g cm3 , s  2.65 g cm3 , f  0.0112 g cms , P  0.003877 , Q  2.900
f A ()  2.3754 , f B ()  0.67581 , f C ()  0.9473 , f D ()  1.0274

0.9964  35
 0.1684
2.65  (100  35)  0.9964  35
 0.1684 
f E  1  2.2315 

 1  0.1684 
0.89957
 1.5305
1.4191
 0.1684 
f F  1  1.6556  0.1684  

 1  0.1684 
 1.0207
 0  , .   9.08  f B ( )f D ( )f F     9.08  0.6758  1.0275  1.0207  6.4357
C 0  ,    0.28  f A ( )f C ( )f E     0.28  2.3753  0.9471  1.5305  0.9641
d* 
d
250  104

 6.448
P 3.877  103
70
Manual de Filtración & Separación
2
12
2



1  0  , ,    
4
*
32
 =
u p  , ,   
d
*

1
1   1 2


  C0  , ,    02  , ,  

4
d*




2 
1  6.4357   

4
6.448
 

1
4   6.4357 
32
 0.96411 2  6.4357 2
12




2

 1  2.44


v r  u  Q  u *p  2.9  2.44  7.076 cm s
La velocidad de fluidización q está dada por:
q  (1  )v r  (1  0.1684)  7.076  5.884 cm s
La dirección del flujo es contraria al de sedimentación de las partículas.
4.2
REFERENCIAS
Abraham, F.F., 1979. Functional dependence of the drag coefficient of a sphere on
Reynolds Number. Phys. Fluid, 13, 2194-2195.
Barnea, E. and Mitzrahi, J., A generalized approach to the fluid dynamics of particulate
systems, 1. General correlation for fluidization and sedimentation in solid multiparticle
systems, Chem. Eng. J., 5, 1973, 171-189.
Barnea, E. And Mednick, R.L., Correlation for minimum fluidization velocity, Trans.
Inst. Chem. Eng., 53, 1975, 278-281.
Batchelor, G.K., An Introduction for Fluid Dynamics, Cambridge University Press,
Cambridge, 1967, 625p.
Concha F., and Almendra, E.R., Settling Velocities of Particulate Systems, 1. Settling
velocities of individual spherical particles. Int. J. Mineral Process., 5, 1979a, 349-367.
Concha F., and Almendra, E.R., Settling Velocities of Particulate Systems, 2. Settling
velocities of suspensions of spherical particles. Int. J. Mineral Process., 6, 1979b, 3141.
Concha F., and Almendra, E.R., Settling Velocities of Particulate Systems, 4. Settling
of no spherical isometric particles. Int. J. Mineral Process., 18, 1986, 297-308.
Concha F., and Almendra, E.R., Settling Velocities of Particulate Systems, 5. Settling
velocities of suspensiones of particles of arbitrary shape. Int. J. Mineral Process., 18,
1986, 309-322.
Concha F. and Barrientos, A., 1986. Settling Velocities of Particulate Systems, 4.
Settling of no spherical isometric particles, Int. J. Mineral Process., 18, 1986, 297-308.
Capítulo 4 Sedimentación de Sistemas Particulados
71
Concha F. and Barrientos, A., Mecánica Racional Moderna, Vol II, Termomecánica
del Medio Continuo, Universidad de Concepción, Dirección de Docencia 1993, 170171.
Fage, A., Experiments on a sphere at critical Reynolds Number, Rep. Mem. Aero. Res.
Counc. London, N°1766, pp. 108, 423.
Ghosal, S.K. and Mukherjea, R.N., Schlupfgeschwindigkeit von Feststoffteilchen in
absatzweise betriebene fest-flüssig Wirbelschichten, Chem. Ing. Tech., 42, 1970, 8185.
Goldstein, S., Editor, Modern Development in Fluid Dynamics, Vol. I and II, Dover,
New York, N.Y., 1965, 702 pp.
Gurtin, M.E., An Introduction to Continuum Mechanics, Academic Press, New York,
1981, 121.
Happel, J. and Brenner, H., Low Reynolds Hydrodynamics, Prentice-Hall, Inc,
Englewood Cliffs N.J., USA, p. 220.
Heywood, H., Uniform and non-uniform motion of particles in fluids. In Proceeding of
the Symposium on the Interaction between Fluid and Particles, Inst. of Chem. Eng.,
London, 1962, pp. 1-8.
Lapple, C.E. and Shepherd, C.B., Calculation of particle trajectories, Ind. Eng. Chem.,
1940, 32, 605.
Lee, K and Barrow, H., Transport process in flow around a sphere with particular
reference to the transfer of mass, Int. Jl. Heat and mass Transfer, 11, 1968, 1020.
Lewis, W.K., Gilliland, E.R. and Bauer, W.C., Characterization of fluidized particles,
Ind. Eng. Chem., 41, 1949, 1104-1117.
Mertes, T.S. and Rhodes, H.B., Liquid-particle behavior: Parts 1 and 2, Chem. Eng.
Progr., 51, 1955, 517-522.
Newton, I., Filosofiae naturalis principia mathematica, London 1687.
Oliver, D.R., The sedimentation of suspensions of closely sized spherical particles,
Chem. Eng. Sci., 15, 1961, 230-242.
Richardson, J.F. and Zaki, W.N., Sedimentation and fluidization: Part I. Trans. Inst.
Chem. Eng., 32, 1954, 35-53.
Rosenhead, L. Editor, Laminar Boundary Layers, Oxford University Press, 1963,
pp.87, 423, 687.
Schlichting, H., Boundary Layer Theory, McGraw-Hill, New York, N.Y., 1968, 747
pp.
Steinour, H.H., Rate of sedimentation. Non-flocculent suspensions of uniform spheres,
Ind. Eng. Chem., 62, 1944, 618-624.Wen, C.Y. and Yu, Y.H., Mechanics of
fluidization, Chem. Eng. Progr. Symposium Sers., 62, 1966, 100-111.
72
Manual de Filtración & Separación
Stokes, G.G., On the theories of internal friction of fluids in motion and of the
equilibrium and motion of elastic solids, Trans. Cambr. Phil. Soc., 8 (9) 1844, 287-319.
Taneda, S., Rep. Res. Inst. Appl. Mech., Kyushu University, 1956, 4, 99.
Tomotika, A.R.A., Reports and Memoranda N°1678, 1936. See also Goldstein 1965,
p.498.
Wilhelm, R.H. and Kwauk, M., Fluidization of solid particles, Chem. Eng. Progr., 44,
1948, 201-218.
CAPÍTULO 5
TEORÍA DE SEDIMENTACIÓN DE KYNCH
___________________________________________________
Tal como se mencionó en el capítulo anterior, para analizar un proceso de
sedimentación y obtener patrones de comportamiento que permitan predecir
capacidades de tratamiento y diseño de equipos, es necesario utilizar el enfoque de la
mecánica del medio continuo. Por ellos, recurriremos a los desarrollos del capítulo de
Teoría de Mezclas para desarrollar la modelación de suspensiones en sedimentación.
La teoría que aquí se presenta se basa en la propuesta por Kynch en 1952 y
desarrollada por Bustos y Concha en 1990 (Concha and Bustos 1991, 1992, Bustos et
al 1999).
5.1
Conceptos de suspensión ideal y espesador ideal.
Consideremos la sedimentación de una mezcla de partículas sólidas y un fluido,
contenidos en una vasija y supongamos que se satisfacen las propiedades para que el
sistema sólido-fluido pueda ser considerado dos medios continuos superpuestos.
Definamos por vs y vf las velocidades del sólido y del fluido respectivamente. Las
suposiciones son:
1.
Todas las partículas sólidas son pequeñas, del mismo tamaño, forma y
densidad.
2.
El sólido y el fluido de la mezcla son incompresibles.
3.
No hay transporte de masa entre componentes.
4.
La velocidad relativa sólido-fluido u  v s  v f en la mezcla es una función
de la concentración de sólidos solamente.
5.
La concentración de las partículas es la misma en toda la sección
transversal de la vasija.
La suposición 1, junto a la 3, permiten establecer una velocidad única para el
componente sólido y la suposición 2 define densidades materiales constantes para cada
componente. La suposición 4, clave en la teoría de Kynch (1952), lleva implícita la
suposición que las fuerzas convectivas son despreciables.
Una mezcla que cumple las propiedades 1 a 4 recibe el nombre de suspensión
ideal (Shannon and Tory 1966, Bustos et al 1990, Concha and Bustos 1992) y puede
73
74
Manual de Filtración & Separación
ser considerada como una superposición de medios continuos con dos componentes
incompresibles.
La suspensión ideal es un modelo de material de mucha utilidad. Tiene una
connotación similar a la de un gas ideal en la termo-mecánica. No existe material real
que sea una suspensión ideal, pero hay muchos materiales que, en casos especiales, se
comportan como una suspensión ideal. La teoría de mezclas permite obtener un
modelo matemático de una suspensión ideal que describe en forma muy aproximada lo
que sucede a una suspensión de pequeñas esferas de vidrio (Shannon and Tory 1966), o
de cualquier otro material que sea incompresible, como por ejemplo las pulpas de
concentrados de cobre sin flocular que siguen bastante de cerca el modelo de una
suspensión ideal.
La concentración  de la suspensión es, en general, una función de las tres
dimensiones del espacio y del tiempo, sin embargo, la suposición 5 permite describir la
sedimentación como un fenómeno uni-dimensional, tal que   z, t  , esto es, que
depende de una coordenada espacial y del tiempo. Esta suposición define el concepto
de un espesador ideal como una vasija sin efecto de paredes (Shannon and Tory 1966,
Bustos et al 1990, Concha and Bustos 1992) y donde la alimentación y descarga se
representan como fuentes y sumideros superficiales.
Hasta el momento todos los trabajos relacionados a la sedimentación, ya sean de
suspensiones ideales o no, utilizan el concepto de espesador ideal. Esto se debe a que
la modelación de la alimentación a un espesador industrial y de su descarga es muy
complicada y que, a pesar de ello, se ha demostrado con herramientas modernas, tales
como la Mecánica de Fluidos Computacional, que la distribución de concentraciones
en estos equipos es sensiblemente unidimensional. (ver figura 5.1).
Fig. 5.1 Distribución de concentración en un espesador industrial de 100 m de
diámetro tratando relaves de cobre. Simulación mediante CFD usando el código
Fluent.
Ecuaciones de campo
La sedimentación de una suspensión ideal en un espesador ideal puede ser descrita
mediante la concentración de la suspensión z, t  , expresada como fracción
75
Capítulo 5 Teoría de Sedimentación
volumétrica de sólidos, y las velocidades de los componentes sólidos v s ( z, t ) y fluido
v f ( z, t ) . Estas variables de campo deben obedecer los balances locales de masa, según
las ecuaciones (2.48):
 
  vs   0
t z


1     (1  )vf   0
t
z
(5.1)
(5.2)
Las expresiones (5.1) y (5.2) reciben el nombre de ecuaciones de continuidad del
componente sólido y del componente fluido respectivamente.
Soluciones para estas ecuaciones de conservación son generalmente
discontinuas. Esto quiere decir, que en la suspensión se pueden formar
discontinuidades y que las ecuaciones (5.1) y (5.2) son válidas solamente en aquellas
regiones donde la concentración es continua. En las discontinuidades, según (2.49), se
debe cumplir:

 vs    (1  )vf 
   (1  )
(5.3)
Estas expresiones se denominan ecuaciones de salto o condiciones de salto.
Sumando las dos expresiones (5.1) y (5.2) se obtiene la ecuación de continuidad
de la mezcla:
q
0
z
(5.4)
q  0
(5.5)
y de (4.7) resulta:
donde q(z,t) es la velocidad promedio volumétrica de la suspensión, definida por:
q  vs  (1  )vf  0
(5.6)
En términos de la velocidad relativa sólido-fluido u  v s  v f , la velocidad
volumétrica puede ser expresada por:
q  vs  (1  )u
(5.7)
La ecuación (5.4)implica que la velocidad volumétrica es una función del tiempo
solamente q  q(t) . Las ecuaciones (5.4) y (5.5) pueden sustituir ventajosamente los
balances de fluido (5.2) y (5.3)
76
Manual de Filtración & Separación
Multiplicando la expresión (5.7) por  y, definiendo las densidades de flujo
f  , t   v s y f b      1    u , podemos escribir la densidad de flujo de sólidos en
la forma:
f  , t   q  f b   
(5.8)
esto es, la densidad de flujo de sólidos total consiste en la suma de una parte lineal q,
correspondiente al movimiento global de la mezcla y una parte no-lineal fb  , que
describe el movimiento relativo local. Cuando se describe la sedimentación en un
espesador ideal cerrado que denominaremos columna de sedimentación, la velocidad
volumétrica es igual a cero, q  0 , ya que no hay alimentación ni salida, por lo que de
(5.8) resulta:
bg
b g bg
f , t  f b 
(5.9)
A esta densidad de flujo la denominaremos densidad de flujo batch.
Usando la definición de f  vs , la ecuación de continuidad del componente
sólido y la condición de salto se pueden escribir en la forma:
 f ( , t )

0
t
z

(5.10)
f

(5.11)
Esta expresión recuerda que, generalmente, las soluciones de un proceso de
sedimentación no son únicas y es necesario disponer de un criterio para elegir la
solución admisible. Más adelante se comprenderá el significado de esta idea. El criterio
mas usado es la condición de entropía de Lax que dice que (Bustos and Concha
1988b):
  

 
f '     ,   f ' 
(5.12)
Cuando la velocidad de desplazamiento de la discontinuidad cumple (5.12)
estrictamente se denomina una onda de choque. Si cualquiera de las igualdades se
satisface, se tiene una discontinuidad de contacto.
5.2
PROCESO DE KYNCH PARA LA SEDIMENTACIÓN BATCH
Cuando una suspensión ideal sedimenta bajo el efecto de la gravedad en una
columna de sedimentación se puede distinguir las siguientes etapas en el proceso.
a)
Antes de comenzar la sedimentación la suspensión se homogeniza por
agitación, de manera que su concentración es constante.
Capítulo 5 Teoría de Sedimentación
77
b)
Cuando la sedimentación comienza, todas las partículas caen a la misma
velocidad, de manera que se forma una interfaz agua-suspensión en la parte
superior de la columna, la que desciende a la misma velocidad que lo hacen
las partículas. Esta etapa se denomina sedimentación dificultada (hindered
settling).
c)
Las partículas que llegan al fondo de la columna se acumulan haciendo que la
concentración aumente rápidamente hasta ocupar toda la superficie
disponible. El material en estas condiciones recibe el nombre de sedimento y
su concentración es . La superficie del sedimento, o interfaz suspensiónsedimento, se mueve hacia arriba a medida que nuevas partículas se le
incorporan.
d)
En un punto determinado de la columna, pero bajo la interface de aguasuspensión, la concentración de la suspensión permanece fija o aumenta con
el tiempo.
e)
Utilizando un instrumento para medir concentraciones, como el de Been and
Sills (1981), se podría seguir el movimiento de una determinada
concentración  en la columna. El movimiento sería necesariamente hacia
arriba a una velocidad denominada velocidad de propagación de la onda de
concentración .
f)
En un determinado instante y a una cierta altura la interfaz agua-suspensión
se encontrará con la interfaz suspensión-sedimento. Las coordenadas de ese
evento se denominan tiempo crítico y altura crítica y ellas definen el punto
crítico en el cual termina la sedimentación.
La figura 5.2 muestra un gráfico de las interfaces agua-suspensión y suspensiónsedimento en función del tiempo. Este gráfico recibe el nombre de curva de
sedimentación.
Fig. 5.2 Curva de sedimentación mostrando las interfaces. (a)
agua-suspensión; (b) suspensión-sedimento; (c) agua-sedimento.
78
Manual de Filtración & Separación
Con base a esta descripción deduciremos un modelo para la sedimentación batch
de una suspensión ideal. Consideremos la sedimentación batch en una columna de
sedimentación que contiene una suspensión con una altura inicial z=L a una
concentración homogénea =0. Para la sedimentación batch se debe agregar dos
suposiciones a las 5 indicadas con anterioridad, lo que totaliza 7:
1.
Todas las partículas sólidas son pequeñas, del mismo tamaño, forma y
densidad.
2.
El sólido y el fluido de la mezcla son incompresibles.
3.
No hay transporte de masa entre componentes.
4.
La velocidad relativa sólido-fluido u  v s  v f en la mezcla es una función
de la concentración de sólidos solamente.
5.
La concentración de las partículas es la misma en toda la sección
transversal de la vasija.
6.
La suspensión tiene una concentración inicial homogénea.
7.
En el fondo de la columna hay un incremento continuo y rápido de
concentración desde la inicial 0 a la final  .
Bajo estas suposiciones son válidas la ecuación de continuidad y condición de salto
siguientes:
 fb (  )

0
t
z

para 0<z<L, t>0
 f b ()
 
(5.13)
(5.14)
La expresión (5.13) es una ecuación hiperbólica cuasi-lineal. Para esta ecuación, las
suposiciones 6 y 7 permiten establecer las condiciones iniciales y de contorno:
b g
b0, t g  
b L, t g  
 z,0   0 para 0  z  L
(5.15)

para t  0
(5.16)
L
para t  0
(5.17)
Las concentraciones  L ,  0 y   son constantes y satisfacen  L  0   0     1 .
Las densidades de flujo batch de las suspensiones ideales cumplen las siguientes
propiedades:
fb (  )  0 para  entre 0 y   , fb ( 0)  f b (   )  0 , fb' ( 0)  0 y fb' (   )  0 (5.18)
79
Capítulo 5 Teoría de Sedimentación
Como
f b   
z

df b    
d
z
 f b'   

, la ecuación (5.13) se puede escribir en la
z
forma:
 '

 f b  
0
t
z
(5.19)
De las expresiones anteriores podemos concluir que la sedimentación de una
suspensión ideal puede ser descrita por la fracción volumétrica de sólidos   z, t  y
depende de la forma funcional de la densidad de flujo de sólidos f b    . Estas dos
funciones constituyen un Proceso de Sedimentación Batch de Kynch (PSK), si en la
región del espacio z-t, con 0  z  L y t  0 donde  es continua, obedecen la
ecuación (5.19), la desigualdad (5.14) en las discontinuidades y las condiciones
iniciales y de contorno (5.15) a (5.17).
5.2.1 Solución por la teoría de características
Escrita en esta forma, la ecuación de la sedimentación batch se puede tratar
como un problema de valor inicial y se resuelve mediante el método de características.
Según Courant and Hilbert (1963), en el dominio (z,t) donde la ecuación (5.19) es
válida, se pueden trazar líneas llamadas características que cumplen las siguientes
condiciones:
dt
dz
d
 '

1 f b   0
(5.20)
donde z y t son las coordenadas de . Entonces la ecuación (5.19) puede ser
reemplazada por:
d  0, y
dz
 f b'   
dt
(5.21)
que indican que la concentración  es constante a lo largo de las características de
pendiente dz dt  f b'    , donde ésta representa la velocidad de propagación de ondas
de concentración constante . Para  constante, f b'    también es constante y, en
estas condiciones, las características son líneas rectas.
Las condiciones de contorno se transforman ahora en condiciones iniciales en la
forma:
0

  z, 0    0

 
para
Lz
para 0  z  L
para
z0
(5.22)
80
Manual de Filtración & Separación
Como las condiciones para z  0 , 0  z  L y z  L son constantes, y las
características que emanan del eje de las ordenadas son paralelas y tienen pendientes
constantes f b'  0  , f b'  0  y f b'    respectivamente (ver figura 5.2). Por otra parte, se
debe notar que f b'  0  , f b'  0  y f b'    son las tangentes en =0, 0 y  a la curva de


densidad de flujo f b    versus ,   0, 0  y  0, *0 son las cuerdas trazadas desde
0 a 0 y de 0 a *0 respectivamente, donde *0 es la concentración del punto de
tangencia a la curva desde 0.
Ejemplo
Considere la sedimentación de una suspensión ideal caracterizada por la curva
de flujo de la figura 5.3. La solución de la ecuación (5.19) se construye trazando las
características que emanan del eje de las ordenadas. Cuando estas características se
cruzan se forma una discontinuidad con velocidad de propagación dada por .
Específicamente para la discontinuidad agua-suspensión se tendrá:
  0, 0  
f b  0   f b  0 
0  0

f b  0 
0
 v s  0 
(5.23)
Las características de pendiente f b'    llenan la base del plano z-t y cortan a las
características de pendiente f b'  0  formando una nueva discontinuidad de pendiente:

   

0 , *0

 
f b *0  f b  0 
(5.24)
*0  0
donde f b *0 , *0 son las coordenadas del punto de tangencia a la curva de flujo, de
   
la cuerda que pasa por el punto f b 0 , 0 .
Entre la característica de pendiente f b'    que sale del origen y la
discontinuidad dada por (5.24), se puede trazar un abanico de características de
pendiente variable que corresponden a las tangentes a la curva de flujo entre las
concentraciones *0 y . Se puede observar que la discontinuidad dada por(5.24) es
una discontinuidad de contacto. El triángulo formado por la onda de choque (5.23) y la
discontinuidad de contacto (5.24) está lleno de características de pendiente f b'  0  .
Finalmente, las características de concentración   0 y *0     se cortan




formando una serie de ondas de choque de pendiente  *0 ,0 a   , *0 .
81
Capítulo 5 Teoría de Sedimentación
Fig. 5.2 Determinación gráfica de los parámetros de
sedimentación de la curva de densidad de flujo de sólidos.
Finalmente la altura final del sedimento se obtiene del siguiente balance
macroscópico: SL0  Sz   , de donde resulta:
z 
0 L

(5.25)
La figura 5.3 muestra la forma de calcular los parámetros en la curva de
densidad de flujo y la curva de sedimentación muestra el plano z-t dividido por tres
discontinuidades entre las cuales las características indican las concentraciones allí
existentes.
Fig. 5.3 Solución por el método de características de un problema de sedimentación.
82
Manual de Filtración & Separación
5.2.2 Modos de Sedimentación
En su trabajo, Kynch (1952) habló de modos de sedimentación, como maneras
en que una suspensión puede sedimentar, pero sin definir claramente el significado de
éstos. El concepto estricto fue dado por Bustos y Concha (1988) y Concha y Bustos
(1991) que definieron Modo de Sedimentación (MS) como los posibles Procesos de
Sedimentación Batch de Kynch (PSK) que una suspensión ideal puede cumplir. Los
modos de sedimentación están enteramente determinados por la ecuación constitutiva
para la densidad de flujo de sólidos y por la concentración inicial de la suspensión y
reflejan la forma como la suspensión pasa de una concentración inicial 0 a la
concentración final . Consideremos las dos regiones de concentración constante 0 y
 bajo la interface agua-suspensión en una columna de sedimentación, (por ejemplo
ver figura 5.3). Mientras para una función de densidad de flujo de sólidos f b    con
un punto de inflexión, existen solamente 3 MS, para una función con dos puntos de
inflexión los MS son 5.
El tipo de MS depende de cómo están separadas las zonas de concentración
constante 0 y :

MS-1 una onda de choque.

MS-2 una discontinuidad de contacto seguida por una onda de rarefacción.

MS-3 una onda de rarefacción.

MS-4 dos discontinuidades de contacto separadas por una onda de
rarefacción.

MS-5 una onda de rarefacción seguida por una discontinuidad de contacto.
En todos los casos, e independiente del tipo de MS, el estado final es un sedimento de
concentración  y altura z   0 L  con una capa de agua sobre él. El tiempo para
llegar a este estado se denomina tiempo crítico y se denota por tc.
a) El Proceso de Sedimentación Batch de Kynch es un MS-1
El PSK es un MS-1 si 0  **
0 (ver figura 5.2). La figura 5.3 muestra la
'
'
solución para MS-1. Como 0  **
0 y f b  0     0 ,    f b    , se forma una
onda de choque z 2  t  de ecuación:
z 2  t     0 ,   t ,
0  t  tc
(5.26)
El tiempo crítico se puede obtener de:
tc 
L
  0 ,      0, 0 
(5.27)
83
Capítulo 5 Teoría de Sedimentación
b) El Proceso de Sedimentación Batch de Kynch es un MS-2
El PSK es un MS-2 si **
  0  a en una curva de flujo con un punto de
   
**
inflexión (ver figura 5.5). Al trazar una tangente desde  f b  0  , 0  a f b **
0 , 0
se forma una discontinuidad de contacto z 2  t  para 0   
*0
, porque 0  **
  0
y *0   . La ecuación de esta discontinuidad es:
 
z 2  t   f b' *0 t , para 0  t  t1
  
(5.28)

donde f b' *0   0 , *0  f b'  0  . Para valores mayores a *0 , de *0     , hay
un aumento continuo de concentración desde *0 a  . (ver figura 5.4). El tiempo t1
,correspondiente al término de la sedimentación a concentración 0 , está dado por:
t1 
L
f b'
(5.29)
     0,  
*0
0
y el tiempo crítico tc:
tc 
0 L
 f b'   
Fig. 5.4 Solución global para un MS-2,
(5.30)
**
  0  a .
c) El Proceso de Sedimentación Batch de Kynch es un MS-3
El PSK es un MS-2 si 0  a en una curva de flujo con un punto de inflexión.
En este caso 0  *0 y hay un aumento continuo de concentración desde 0 a  . Los
tiempos t1 y tc están dados por:
84
Manual de Filtración & Separación
t1 
L
f b'
(5.31)
      0,  
0
0
y el tiempo crítico tc:
tc 
0 L
 f b'   
Fig. 5.5 Solución global para un el caso de un MS-3, con
(5.32)
0  a .
Fig. 5.6 Parámetros de la curva de flujo con dos puntos de
inflexión para el caso de un MS-3, 0  a .
85
Capítulo 5 Teoría de Sedimentación
d) El Proceso de Sedimentación Batch de Kynch es un MS-4
El PSK es un MS-4 si **
  0  a en una curva de flujo con dos puntos de


 
inflexión. (ver figura 5.6). Como *0  *    y  0 , *0  f b' *  f b'  0  , se
forman dos discontinuidades de contacto con las ecuaciones:
 
   t para 0  t  t
z 2  t   f b' *0 t para 0  t  t1
(5.33)
z3  t   f b'
(5.34)
*

c
Desde la concentración 0 habrá un brusco aumento de concentración a *0 , luego un
paulatino aumento a * y nuevamente un brusco aumento desde este valor a  . Los
tiempos t1 y tc , con t1<tc , están dados por:
t1 
tc 
L
f b'
     0,  
*0
(5.35)
0
0 L
 
 f b' *
(5.36)
Fig. 5.7 Curva de flujo con dos puntos de inflexión para el caso de un MS-4,
**
   0  a .
e) El Proceso de Sedimentación Batch de Kynch es un MS-5
El PSK es un MS-5 si a  0  * en una curva de flujo con dos puntos de
inflexión. (ver figura 5.8). En este caso habrá un cambio continuo de concentraciones
86
Manual de Filtración & Separación
desde 0 a * y luego un salto de concentración a  . La discontinuidad de contacto
tiene por ecuación:
 
z3  t   f b' * t , para 0  t  t c
(5.37)
con el tiempo t1<tc están dados por:
t1 
L
f b'
tc 
      0,  
0
(5.38)
0
0 L
 
 f b' *
(5.39)
Fig. 5.8 Curva de flujo con dos puntos de inflexión para el caso de un MS-5,
a  0  * .
5.3 PROCESO DE KYNCH PARA LA SEDIMENTACIÓN CONTINUA
La sedimentación continua se lleva a cabo en un espesador, estanque cilíndrico
con la alimentación de pulpa en un tubo central, conocido como “feedwell”, en la parte
superior y una descarga del sedimento, también central en la parte inferior. Una
estructura metálica soporta las rastras que barren el fondo del estanque para descargar
el sedimento. El agua recuperada en el proceso sale del equipo por un rebalse en toda
la periferia del estanque. La figura 5.9 muestra un esquema de un espesador industrial
continuo.
Desde los trabajos de Coe y Clevenger (1916) se ha establecido que se puede
distinguir cuatro zonas en un espesador continuo.
Capítulo 5 Teoría de Sedimentación
87
Zona I
La zona I corresponde al de agua clara que se recupera y se ubica en la parte superior
del espesador, por encima del feedwell. Esta región recibe el nombre de zona de agua
clara.
Zona II
Debajo del agua clara se forma una región de concentración constante,
denominada “zona de sedimentación constante” (hindered settling zone).
Fig. 5.9 Esquema de un espesador industrial continuo.
En una operación normal, la pulpa que entra a un espesador se diluye, por lo que la
zona II tiene una concentración mucho menor que la concentración de la alimentación.
Este hecho es ignorado muy frecuentemente, especialmente debido a las aseveraciones
de Mishler (1912) y de Coe y Clevenger (1916). Fue Comings (1954) quien descubrió
mediante experimentos en el laboratorio que la concentración de la zona II depende del
flujo de sólidos en la alimentación y es independiente de la concentración de ésta. A
medida que el flujo de alimentación aumenta, aumenta la concentración de la zona II,
pero esta concentración llega a un límite, y flujos mayores no aumentan esta
concentración sino que llevan el sólido en exceso al rebalse. Esto significa que la zona
II tiene un límite de capacidad para aceptar sólido. Coe y Clevenger (1916) llamaron a
este límite la “capacidad de tratamiento de sólido” (solid handling capacity). Veremos
más adelante que esta concentración, que recibe el nombre de concentración
conjugada, se puede determinar con la teoría de Kynch.
Zona III
Bajo la zona de sedimentación constante está la zona III, denominada “zona de
transición”, porque lleva la concentración del espesador desde la concentración
conjugada a la concentración del sedimento. Esta transición puede efectuarse mediante
una onda de choque, mediante una discontinuidad de contacto, mediante una onda de
rarefacción o la combinación de éstas.
88
Manual de Filtración & Separación
Zona IV
Finalmente la zona IV corresponde al “sedimento”. Cuando las partículas que
forman la suspensión están bien dispersas, como por ejemplo en suspensiones ideales,
el sedimento tiene una concentración única y característica del material. Al contrario,
cuando las partículas que forman la suspensión están floculadas, el sedimento sufrirá
compresión y seguirá eliminando agua dependiendo del peso que soporta, por lo que se
forma un gradiente de concentración. En este capítulo se analizará solamente las
suspensiones ideales, dejando para los capítulos 7 y 8 las suspensiones floculadas.
5.3.1 Espesador ideal continuo: modelación de la alimentación y descarga
Tomar en consideración el efecto de la alimentación, movimiento de las rastras y
de la descarga es una complicación innecesaria para la modelación matemática de un
espesador. Se ha demostrado mediante herramientas modernas como la mecánica de
fluidos computacional (CFD) que, independiente del tipo de flujo, axi-simétrico o
tridimensional, que se establece en un espesador, la distribución de concentraciones es
unidimensional en la dirección vertical. La figura 5.1 muestra la distribución de
concentraciones en un espesador de relaves de una planta de flotación de cobre. Estos
resultados permiten simplificar el modelo geométrico de un espesador y justifican usar
el concepto de Espesador Ideal Continuo (EIC) (Concha and Bustos 1992). Como en
un EIC las variables dependen solamente de la coordenada z y el tiempo, es necesario
establecer condiciones en la entrada y la descarga que satisfagan esta condición.
QR
Zona I
QF, F
Zona II
Zona III
Zona IV
QD,D
Fig. 5.10 Espesador Ideal Continuo (RIC).
(1)
Alimentación
La alimentación al espesador se diluye rápidamente y se esparce a toda el área
del equipo. Por ello supondremos que la alimentación entra a través de toda el área del
89
Capítulo 5 Teoría de Sedimentación
espesador y que se diluye instantáneamente. Para el modelo diremos que el EIC es
alimentado mediante una fuente superficial en z  L . Ver figura 5.6. Si Q F  t  es el
caudal o flujo volumétrico, F  t  la concentración y f F  t  la densidad de flujo de
sólidos de la alimentación (flujo volumétrico de sólidos por unidad de tiempo y unidad
de área del espesador) y S es el área del espesador, entonces se cumple que:
fF  t  
Q F  t  F  t 
S
(5.40)
Como ya hemos dicho, el flujo de alimentación que entra al espesador se mezcla y
diluye con el flujo de agua clara producida. Por esta razón la concentración de la
suspensión, inmediatamente bajo la interface agua-suspensión es distinta y menor que
la concentración de la alimentación L (t)    L, t)   F  t  . Sin embargo, la única
fuente de sólidos es la alimentación, por lo que la densidad de flujo de sólidos debe ser
continua en la alimentación:
f k    L, t    f F  t  
 Q F  t  F  t 
S
(5.41)
La densidad de flujo de sólidos en la alimentación puede ser controlada externamente a
través de QF(t) y F(t)
(2)
Descarga
La descarga del EIC se realiza a través de un sumidero superficial. Si Q D  t  es
el caudal o flujo volumétrico, D  t  la concentración y f D  t  la densidad de flujo de
sólidos de la descarga, resulta:
fD  t  
 Q D  t  D  t 
S
(5.42)
El sedimento sale por la descarga en z=0 sin mezclarse con otra fuente, por lo que
allí tanto la densidad de flujo de sólidos f k    0, t   como la concentración   0, t  son
iguales a las del flujo de descarga:
f k    0, t    f D  t  
  0, t   D  t 
 Q D  t  D  t 
S
(5.43)
(5.44)
Si la concentración de la descarga es menor que la de alimentación, se dice que el EIC
se vacía.
90
Manual de Filtración & Separación
(3)
Rebalse
En una operación normal, el rebalse no contiene partículas sólidas. Esto significa
que el sólido está restringido a la zona de sedimentación 0  z  L . Si por cualquier
motivo las partículas sólidas pasan de la suspensión a la zona de agua clara, se dice que
el espesador se rebalsa. El caudal de agua se puede calcular mediante un balance
macroscópico:
Q R  Q F  QD  Q F
D  F
  F
 QD D
D
F
(5.45)
La velocidad volumétrica del agua en la zona I será:
qR  t  
5.3.2
QR  t 
S
(5.46)
Proceso de Sedimentación Continua de Kynch
Con base a esta descripción, deduciremos un modelo para la sedimentación
continua de una suspensión ideal en un Espesador Ideal Continuo (EIC). Consideremos
la sedimentación en un EIC que contiene una suspensión con una concentración inicial
  z, 0   I  z  con 0<z<L, donde I  z  es una función conocida. Las suposiciones
válidas en este caso son (Concha and Bustos 1991):
1.
Todas las partículas sólidas son pequeñas, del mismo tamaño, forma y
densidad.
2.
El sólido y el fluido de la mezcla son incompresibles.
3.
No hay transporte de masa entre componentes.
4.
La velocidad relativa sólido-fluido u  v s  v f en la mezcla es una función
de la concentración de sólidos solamente.
5.
La sedimentación se efectúa en un espesador ideal continuo
6.
La alimentación y la descarga son consideradas como fuente y sumidero
superifical respectivamente.
7.
Inicialmente el EIC tiene una concentación I  z  .
Diremos que la sedimentación continua de una suspensión ideal en un EIC
queda descrita por las variables de campo: concentración de sólido   z, t  y por la
velocidad volumétrica q  z, t  y por la ecuación constitutiva (curva de densidad de
flujo) f k  f k    z, t   . Estas funciones constituyen un Proceso de Sedimentación
Continuo de Kynch (PSCK) si, en las regiones de z-t donde las variables son continuas
cumplen las ecuaciones de campo:
91
Capítulo 5 Teoría de Sedimentación
 ´

 f k  
0
t
z
para 0  z  L , t>0
dq  z, t 
dz
0
(5.47)
(5.48)
y en las discontinuidades satisfacen las condiciones de salto:

 f k ( ) 
 
q  0
(5.49)
(5.50)
y, además, satisfacen las condiciones iniciales:
  z, 0   I  z 
(5.51)
Para una gran mayoría de casos experimentales, la curva de densidad de flujo
f k    es una función con un punto de inflexión. Si a es la concentración en el punto
de inflexión y  es la concentración del sedimento, la función densidad de flujo de
sólidos debe cumplir las siguientes propiedades:

f k  , t   q  t    f b     0 , 0    

f k  0, t   0

f k'  , t   0 , 0    a
(5.53)

f k'  , t   0
(5.54)

f k''  , t   0 , a    
(5.55)
(5.52)
La figura 5.11 muestra la función densidad de flujo de sólidos con un punto de
inflexión.
5.3.4 Solución por el método de características
La solución a la ecuación (5.47) es   constante a lo largo de características
con pendiente dz dt  f k'  , t  dada por:
f k'  , t   q  t   f b'   
(5.56)
De la ecuación (5.48) se sabe que q(t) es independiente de la coordenada z. Para
simplificar la solución, en adelante supondremos que q=constante, por lo que las
características serán líneas rectas, y que la condición inicial consta de dos estados
solamente:
92
Manual de Filtración & Separación
Fig. 5.11 Función densidad de flujo de sólidos con un
punto de inflexión y tres valores de la velocidad
volumétrica q.

I  z    L
 
para c  z
para c  z
(5.57)
El valor de L se puede calcular de las ecuaciones (5.41) y (5.52):
f F  qL  f b  L  t  
5.3.5
(5.58)
Modos de sedimentación continua
En forma similar al caso batch, se denomina Modo de Sedimentación Continuo
(MSC) a los diferentes Procesos de Sedimentación Continuos de Kynch (PSCK). Los
MSC dependen enteramente de la función de densidad de flujo y de la condición
inicial. La figura 5.12 muestra varios parámetros de la curva de densidad de flujo con
un punto de inflexión.
El tipo de MSC depende de cómo están separadas las zonas de concentración
constante 0 y . Para una función de flujo con un punto de inflexión, solamente
existen tres MSC (Concha and Bustos 1991):

MS-1 una onda de choque.

MS-2 una discontinuidad de contacto seguida por una onda de rarefacción.

MS-3 una onda de rarefacción.
93
Capítulo 5 Teoría de Sedimentación
Fig. 5.12 Parámetros de la curva de densidad de flujo con un
punto de inflexión.
El Procesos de Sedimentación Continuos de Kynch es un MSC-1
Tenemos aquí cuatro casos:
1) Si f k'     0 y L  s , se forma una sola onda de choque de ecuación:
z1  t   c    L ,   t , con f k'  L     L ,    f k'   
(5.59)
la solución para el PSCK será un MSC-1 y el espesador se vacía. (Ver figura 5.12 para
definiciones y figura 5.13 para la solución).
Fig. 5.13 Solución global para un MSC-1 con
f b'     0 y L  s .
94
Manual de Filtración & Separación
2) Si f k'     0 y L  s , se forma una sola onda de choque de ecuación:
z1  t   c , con f k'  L     L ,    f k'   
(5.60)
la solución para el PSCK será un MSC-1 y el espesador llega a un estado estacionario
con una descarga de concentración  . (ver figura 5.10 para la solución).
3) Si f k'     0 y L  s  **
 , se forma una sola onda de choque de ecuación igual a
(5.59) pero con   L ,    0 , la solución para el PSCK será un MSC-1 y el
espesador se rebalsa. (Ver figura 5.12 para definiciones y figura 5.14 para la solución).
Fig. 5.14 Solución global para un MSC-1 con
f b'     0 y L  s .
Fig. 5.15 Solución global para un MSC-1 con
f k'     0 y L  s .
95
Capítulo 5 Teoría de Sedimentación
4) Si f k'     0 y L  **
 , se forma una sola onda de choque de ecuación igual a
(5.59) y con   L ,    0 . La solución para el PSCK será un MSC-1 y el espesador
se vacía. (ver figura 5.16 para la solución). El valor de t1 será:
t1  t  
c
   L ,  
(5.61)
Fig. 5.16 Solución global para un MSC-1 con
f k'     0 y L  **
.
El Procesos de Sedimentación Continuos de es un MSC-2
Tenemos aquí también cuatro casos:
1) Si f k'     0 y **
  L  a , se forma una discontinuidad de contacto de ecuación:
 


 
z1  t   c  f k' *L t , con f k'  L    L , *L  f k' *L  0
(5.62)
Hay un cambio brusco de  L a *L y luego un aumento continuo de concentración
hasta  . La concentración de descarga es de  para todo t. Al tiempo t=t1 el EIC se
rebalsa, con t1 dado por (ver figura 5.17):
t1 
Lc
 
f k' *L
(5.63)
96
Manual de Filtración & Separación
Fig. 5.17 Solución global para un MSC-2 con
f k'     0 y **
   L  a .
**
Si f k'     0 y **
   L   M , se forma una discontinuidad de contacto de
2)
ecuación
igual
f k'
L , *L
 L    
a
la
de
(5.62),
ya
que
tenemos
    . Hay un cambio brusco de 
f k'
*L
L
que
M  *L
y
a *L y luego un aumento
continuo de concentración hasta  . La concentración de descarga es de  hasta t2 y
luego decrece continuamente hasta  L entre t 2  t  t1 de manera que el espesador se
vacía. Los tiempos t1 y t2 están dados por (ver figura 5.18a):
t1 


c
L , *L

y
t2 
f k'
c
  

(5.64)

*
*
'
3) Si f k'     0 y L  **
M , se tiene que L  M y  L , L  f k  M   0 , por lo
que el PSCK es un MCS-2, formándose una discontinuidad de contacto horizontal de
ecuación:
z1  t   c y
z2  t  
f k'
c
  
(5.65)
El espesador llega al estado estacionario con dos concentraciones, L y M, (ver figura
5.18c).
4) Si

f k'     0

*
y **
M  L  a  L , se tiene que
 
*
**
M   L  a   L
y
0   L , *L  f k' *L , (ver figura 5.19). Se forma una discontinuidad de contacto de
ecuación igual a la de (5.62). La concentración sufre un cambio brusco de L a *L y
Capítulo 5 Teoría de Sedimentación
Fig. 5.18 Solución global para un MSC-2 con
**
**
f k'     0 y a) **
  L  M , b) D  M ,c) L  M .
*
Fig. 5.19 Solución global para un MSC-2 con **
M  L  a  L .
97
98
Manual de Filtración & Separación
 
luego aumenta continuamente hasta  . Como f k' *L  0 , el EIC se rebalsa en el
tiempo t=t1 de ecuación:
t1 

Lc
 L , *L

(5.66)
El Procesos de Sedimentación Continuos de es un MSC-3
Nuevamente tenemos cuatro casos:
1) Si f k'     0 y a  L   , se tiene f k'  a   f k'  L   f k'     0 , por lo
que la concentración cambia continuamente desde L a  constituyendo un
MSC-3.Para el tiempo t=t1 el EIC se rebalsa (ver figura 5.20a y 5.20b):
t1 
Lc
f k'
 
(5.67)
L
Fig. 5.20 Solución global para un MSC-3 con f k'     0 y a  L   .
2) Si f k'     0 y a  L  M , se tiene que f k'     f k'  M   f k'  L  , por lo que se
formará una onda de rarefacción desde la concentración  L a  constituyendo un
MSC-3. El EIC se rebalsa después del tiempo t  t1 dado por (5.67), (ver figura
5.20c).
Capítulo 5 Teoría de Sedimentación
99
Fig. 5.20 Solución global para un MSC-3 con c) f k'     0 y L  M .
3) Si f k'     0 y L  M , resulta que M     y f k'  L   f k'  M   0  f k'    ,
por lo que se forma un gradiente continuo de concentración entre L a  . La
descarga tiene concentración  hasta t2 y luego disminuye continuamente a M , de
modo que el espesador se vacía, (ver figura 5.20d):
Fig. 5.20 Solución global para un MSC-3 con d) f k' ()  0 y L  M .
4) Si f k'     0 y  M   L , se tiene f k'   M   0  f k'   L   f k'    , (ver figura 5.21),
por lo que se forma un gradiente continuo de concentración entre  L a  . La
solución es un MCS-3 y como f k'     0 , el espesador se vacía en t=t1:
100
Manual de Filtración & Separación
t1 
f k'
c
 L 
t2 
f k'
c
  
(5.68)
Fig. 5.21 Solución global para un MSC-3 con
f k'     0 y a   L   M .
5.4
ESTADO ESTACIONARIO Y CAPACIDAD DE UN ESPESADOR
IDEAL
En el estado estacionario la ecuación (5.47) se reduce a:
df k   
dz
 0 , para 0  z  L
(5.69)
de donde se deduce que la densidad de flujo de sólidos es constante en todo el EIC en
el estado estacionario.
El estudio de los MSC para suspensiones ideales caracterizadas por un punto de
inflexión en la función densidad de flujo de sólidos, permiten observar que existen
solamente dos condiciones para obtener estados estacionarios. La primera se obtiene
para con un MSC-1 para f k'     0 con L  s y D   , ver figura 5.10 y la
segunda con un MSC-2 para f k'     0 con L  **
M y D  M , ver figura 5.14. En
ambos casos se puede escribir las siguientes ecuaciones:
f k     q  f bk    y f k  D   qD
Reemplazando la segunda ecuación en la primera y aplicándola a la concentración L,
tenemos:
f k  L  
f k  D 
D
L  f bk  L 
101
Capítulo 5 Teoría de Sedimentación
f k  L 
L

f k  D 
D

f bk  L 
L
Como en el estado estacionario la densidad de flujo es una constante, f k  L   f k  L 
y f bk  L  L    0, L    I  L   vs  L  , donde  I  L  es la pendiente inicial de
la curva de sedimentación batch de una suspensión ideal de concentración L ,
podemos escribir la expresión anterior:
f F   I  L 
1
(5.70)
 1
1 



 L D 
Como por definición la densidad de flujo de sólidos f F   F sS y el área unitaria
UA  S F , finalmente podemos escribir para la capacidad F S y el área unitaria UA
como:
 1
F
1
1
1 
 s I  L 
y AU 



s  I  L   L D 
S
 1
1 



 L D 
(5.71)
Tal como hemos mencionado, hay dos casos de estados estacionarios dependiendo de
si f k'    es mayor o menor que cero.
Si f k'     0 , L  s y D   , por lo que la expresión (5.71) se transforma en:
 1
F
1
1
1 
 s  I  s 
y AU 
 

s  I  s   s  
S
 1
1 



 s  
(5.72)
Si f k'     0 , L  **
M y D  M , por lo que la expresión (5.71) se transforma en:
 1
F
1
1
1 
 s  I **
y AU 
 ** 

M
**
S
 1
1 
s  I M  M M 
 ** 

 M M 
 
 
(5.73)
En el capítulo 8 tendremos la oportunidad de utilizar esta ecuación y comentar
su aplicabilidad. Aquí solamente mencionaremos que la mayoría de los investigadores
en este campo (Fitch 1996, Shannon and Tory 1996, Hasset 1968, Ecklund and
Jenqvist 1975, Wilhelm and Nadie 1979 y Galvin and Waters 1987) supusieron que la
102
Manual de Filtración & Separación
concentración de la descarga de un espesador ideal era    M , el valor del máximo
local de la curva de flujo. Ellos justificaron este aumento de concentración en la
descarga desde  M a  como un salto de concentración (considerando que solo la
densidad de flujo de sólidos era continua). Al contrario, como hemos visto en este
capítulo, la concentración de descarga, que en el inicio del período transiente de
operación era  , disminuye su valor con el tiempo hasta llegar a  M en el estado
estacionario. Como en los tiempos en que se desarrolló la teoría de Kynch, se suponía
que esta teoría era aplicable a pulpas floculadas, es indudable que la confusión se
produjo porque para una pulpa compresible, efectivamente la concentración aumenta
paulatinamente desde la concentración crítica hasta la de descarga.
La teoría de Kynch, fuera de predecir correctamente el comportamiento de
suspensiones incompresibles, forma parte de una teoría más general, la que sí es válida
para suspensiones compresibles. Además, el ejercicio de construir la solución gráfica
de un proceso de sedimentación de Kynch, permite comprender más fácilmente el
comportamiento y la forma de determinar los parámetros en las pulpas compresibles.
Toda persona que desee comprender la teoría fenomenológica de sedimentación, debe
primero entender la teoría de Kynch.
5.5 REFERENCIAS
Bustos, M.C. and Concha, F., 1988a, On the construction of global weak solutions in
the Kynch theory of sedimentation, Math. Meth. Appl. Sci., 10, 245-264.
Bustos, M.C. and Concha, F., op. cit. 1988b, 248.
Bustos, M.C., Concha, F. and Wendland, W., 1990. Global weak solutions to the
problem of continuous sedimentation of an ideal suspension, Math. Meth. Appl. Sci.,
13, 1-22.
Concha, F. and Bustos, M.C., Settling velocities of particulate systems, 6. Kynch
sedimentation processes: batch settling, Int. Jl. Mineral Process., 32, 1991, 193-212.
Concha, F. and Bustos, M.C., Settling velocities of particulate systems, 7. Kynch
sedimentation processes: continuous thickening, Int. Jl. Mineral Process., 34, 1992, 3351.
Bustos, M.C., Concha, F., Bürger, R. and Tory, E.M., Sedimentation and Thickening:
Phenomenological Foundation and Mathematical Theory, Kluwer Acad. Publ.,
Dodrecht, The Nethelands, 1999, 111-148.
Concha, F. and Bustos, M.C., 1991. Settling velocities of particulate systems, 6. Kynch
sedimentation processes: batch settling, Int. J. Mineral Process., 32, 193-212.
Concha, F. and Bustos, M.C., 1992. Settling velocities of particulate systems, 7. Kynch
sedimentation processes: continuous thickening, Int. J. Mineral Process., 34, 35-51.
Kynch, G.J., 1952. Theory of sedimentation. Trans. Farad. Soc., 48, 166-175.
CAPÍTULO 6
FLUJO EN LECHO POROSO
En 1856 Darcy propuso la primera correlación experimental para el flujo de un
fluido viscoso incompresible a través de un medio poroso formado por partículas
sólidas. Darcy estableció una relación lineal entre el flujo volumétrico por unidad de
área y la caída de presión a través del lecho. Forcheimer (1901) observó que la
correlación de Darcy no es universalmente válida, sino que su aplicabilidad se restringe
a flujos lentos y propuso una extensión de esta relación para flujos mayores. Desde
entonces, las regiones de flujo a bajas velocidades se denominan flujo de Darcy y las
de alta velocidad, flujo de Forcheimer. Además del trabajo de estos dos pioneros del
tema, han contribuido a él Kozeny (1927) y Carman (1937).
La mejor manera de analizar el flujo a través de medios porosos es dividirlo en
dos partes dependiendo de si la matriz de partículas sólidas, a través de la cual escurre
el fluido, es rígida o deformable. En ambos casos el resultado es útil como fundamento
de la industria de procesos, la primera en la filtración y la segunda en el espesamiento.
En este capítulo se desarrollará los fundamentos del flujo en un medio poroso rígido
basándose en la Teoría de Mezclas.
6.1 PROCESO DINÁMICO EN UN LECHO POROSO RÍGIDO
Consideremos un conjunto de partículas sólidas a través del cual escurre un
fluido. Las 5 suposiciones expresadas con anterioridad en el capítulo 3 son válidas:
(i) Las partículas sólidas son todas pequeñas, con respecto a la vasija que las
contiene, y de la misma densidad, tamaño y forma.
(ii) Las partículas individuales y el fluido son incompresibles.
(iii) No hay transferencia de masa entre el sólido y el fluido.
(iv) La única fuerza de cuerpo es la gravedad.
(v) Las partículas están contenidas en una vasija impermeable y con paredes sin
fricción ante líquidos y sólidos
Agreguemos ahora que:
(vi) Las partículas forman un esqueleto sólido rígido e inmóvil.
Una mezcla de partículas y fluido que obedece las restricciones establecidas por
(i) a (vi) se denomina lecho poroso incompresible y puede ser descrito con las
103
104
Manual de Filtración & Separación
ecuaciones derivadas en la sección anterior. Como en este caso el fluido es el único
componente activo, es conveniente usar la porosidad  como variable en vez de la
fracción volumétrica de sólidos :   1   . Por otra parte la velocidad del sólido
vs  0 .
6.1.1
Balances locales
El flujo a través de un lecho poroso rígido puede ser descrito mediante los
balances de masa y momentum lineal para el fluido y mezcla. Del capítulo 3, y
tomando en cuenta las indicaciones anteriores, podemos escribir:
Balance de masa del componente fluido

  v f   0
t
Balance de masa de la mezcla:
q  0 , con
Balance de momentum lineal del fluido: p e  
(6.1)
q  v f y vs  0
md

(6.2)
(6.3)
donde r es el vector posición, (r, t)  1  (r , t)  es la porosidad del lecho, v f (r, t) es
la velocidad del fluido, q(r, t) es la velocidad volumétrica de la mezcla, en esta caso,
la velocidad espacial del fluido, pe (r, t) es la presión de poros en exceso y m d (r, t) es
la fuerza resistiva que el fluido ejerce sobre el sólido.
6.1.2
Ecuación Constitutiva de la fuerza resistiva
Es razonable suponer que la fuerza resistiva, originada por el flujo del fluido a
través del lecho poroso, es una función de la porosidad  y de la velocidad relativa
entre el sólido y el fluido vr:
m d  m d  , v r 
(6.4)
La función más general para md es de la forma:
m d    , v r  v r
donde el coeficiente de resistencia   , v r
(6.5)
 puede ser expandido en serie de Taylor en
la forma:
  , v r    0     1    v r   2    v r  ......
2
6.1.3
(6.6)
Ley de Darcy
Si la velocidad relativa sólido-fluido es pequeña, es posible conservar solamente
el primer término de la expansión en serie del coeficiente de resistencia, dando como
resultado:
Capítulo 6. Flujo en Lecho Poroso
105
m d   0    v r
(6.7)
La expresión (6.7) recibe el nombre de Ley de Darcy y corresponde a una relación
lineal entre la fuerza hidrodinámica y la velocidad relativa entre el fluido y del
esqueleto sólido. Sustituyendo la Ley de Darcy en el balance de momentum lineal del
fluido (6.3) se obtiene:
p e 
 

(6.8)
vr
6.1.4
Ley de Forcheimer
Si la velocidad relativa sólido-fluido adquiere valores mayores, es necesario
utilizar otro término de la expansión en serie del coeficiente de resistencia, entonces:
m d    0     1    v r  v r
(6.9)
Esta es la Ley de Forcheimer. Sustituyendo en el balance de momentum lineal del
fluido obtenemos:
     1   

p e   0

vr  vr

 

(6.10)
Esta ecuación representa el balance de fuerzas en el flujo a través de un lecho poroso a
velocidades mayores.
6.2 PARÁMETROS GEOMÉTRICOS DE UN LECHO POROSO RÍGIDO
Para relacionar los parámetros i con la geometría del lecho poroso, apliquemos
la ecuación (6.10) al caso bien conocido de flujo horizontal en un lecho poroso rígido
de porosidad  constante. Ver figura 6.1, donde q  qk , con q  0 y
p e   pe z  k :
pe=po
pe=pL
q
q
0
k
z
z=L
Fig. 6.1 Medición de parámetros de resistencia en un
lecho poroso rígido homogéneo horizontal.
106
Manual de Filtración & Separación
Como  es constante, de la ecuación (6.1), se deduce que la velocidad del fluido
es constante y la velocidad espacial, o velocidad de percolación, q  v f también es
constante. Por otra parte como v s  0 y v r   v f , el balance de momentum lineal se
puede escribir de (6.10) en la forma:
p e
  ( )  (  ) 
  0 2  1 3 q q
z

 

(6.11)
Integrando esta ecuación con las siguientes condiciones de frontera: pe  z  0   p 0 y
pe  z  L   p L , donde p e  p 0  p L , obtenemos:

pL
p0
      
dp    0 2  1 3 q  q
k 



L
dz
0
     
p L  p0  pe    0 2  1 3 q  qL

 

(6.12)
Dividiendo ambos miembros de (6.12) por qL, resulta:
1 p e  0    1   

 3 q
q L
2

(6.13)
Graficando la ecuación (6.13) con q como abscisa y p e qL como ordenada se
bg
obtiene una línea recta en que el valor de la ordenada para q  0 es  0   2 y la
bg
pendiente de la recta es 1   .
3
7.4E+05
7.3E+05
pe/qL en g/s-cm3
7.2E+05
7.1E+05
7.0E+05
6.9E+05
6.8E+05
6.7E+05
0
10
20
30
40
50
60
Velocidad de percolación q en cm/s
Fig. 6.2 Mediciones de los parámetros geométricos de un lecho poroso rígido
formado por partículas de cuarzo de 28/35 mallas (Massarani 1984).
Capítulo 6. Flujo en Lecho Poroso
107
Se acostumbra a escribir ambos parámetros en términos del coeficiente de
permeabilidad k() y propiedades del fluido. Según Massarani (1984):
bg
0 


2

k
bg
y
bg
bg
bg
1 
c
 f
3

k
(6.14)
donde k es la permeabilidad, medida en Darcy (1 Darcy=10-3 cm2). Con estas
definiciones, los parámetros de la recta en la figura 6.2 son: el valor de la ordenada
bg
para q  0 es  k  y la pendiente de la recta es f c   
k    . Tanto k como c
son funciones de . El orden de magnitud de k() y c() pueden observarse en la tabla
6.1.
Tabla N° 6.1 Orden de magnitud de k() y c (Massarani 1984)

Medio
k () [cm2]
-12
Arenisca de petróleo
0.03
1.0x10
Placa metálica porosa
0.26
1.0x10-7
Concentrado de cobre
0.43
5.0x10
-9
Arena de cuarzo de 28/35 mallas
0.42
1.5x10-6
0.40
-4
Balotines de vidrio de 6mm
4.0x10
c() [-]
3x105
15
1.7
0.49
Con las definiciones (6.14), la ecuación (6.11) se puede escribir en la forma más
conocida:
 
pe
 c() 
q q
 
 f
 k()
z
k() 

(6.15)
Integrando esta expresión se obtiene:
 c

1 pe
q

 f
q L
k 
k 
(6.16)
Para describir la funcionalidad de la permeabilidad k y del parámetro c con la
porosidad se ha propuesta varias ecuaciones, entre ellas las más conocidas son las de
Kozeny (1927) y Carman (1937), de Ergun (1952) y de Massarani (1989) (ver próxima
sección).
Ejemplo 1 (Massarani 1999)
Para un medio poroso constituido por arena de 14/20 mallas en tamaño, de
esfericidad   0.6 , consolidada con Araldit, de longitud L  2.1 cm y una sección
108
Manual de Filtración & Separación
transversal de 16.8 cm2 con una porosidad de =0.37, calcular los parámetros de
permeabilidad k() y c(). Ensayos de flujo a través del medio poroso dieron el
siguiente resultado:
q(cm/s)
6.33
7.47
10.2
12.7
15.2
17.7
20.3
23.9
p (cm Hg)
4.69
6.24
10.4
15.2
21.2
28.0
35.9
48.9
La presión en cm de mercurio debe transformarse a unidades cgs usando la expresión:
p  Hg gh  13.595  980.7  h g cms 2
donde h está en cm de Hg. Con los datos de la tabla siguiente se puede obtener el
gráfico:
q (cm/s)
6.33
7.47
10.18
12.66
15.20
17.73
20.26
23.93
P (cmHg)
4.69
6.24
10.37
15.15
21.07
28.02
35.89
48.90
P g/cms2 P/qL (g/scm3)
6.2530E+04
4.7040E+03
8.3196E+04
5.3035E+03
1.3826E+05
6.4674E+03
2.0199E+05
7.5976E+03
2.8092E+05
8.8007E+03
3.7358E+05
1.0034E+04
4.7851E+05
1.1247E+04
6.5196E+05
1.2974E+04
p/qL g/scm
3
16000
11000
6000
y = 470.57x + 1697.8
2
R = 0.9996
1000
0.00
5.00
10.00
15.00
20.00
Velocidad de percolación q cm/s
Del gráfico podemos escribir:
25.00
30.00
Capítulo 6. Flujo en Lecho Poroso
109
p
 470.57q  1697.8
qL
de donde podemos obtener los parámetros:
k  

0.0118

 6.95  10 6 cm 2
 p qL q 0 1697.8
c   k   
 p q L   1.24
2

6.1.1
Ecuaciones de Forcheimer y de Darcy
Si substituimos los valores de 0 y 1 desde (6.14) en (6.9) y en (6.11) se
obtiene:
md 
  f k()c( ) q
1 

k() 
p e  

q


  f c( ) k() q 
1 
q


k() 

(6.17)
(6.18)
Esta última expresión se denomina ecuación de Forcheimer.
El segundo término de los paréntesis de (6.17) y (6.18) tiene la forma de un
número de Reynolds. Definiendo el número de Reynolds de percolación en la forma:
Re* 
f c() k    q

(6.19)
podemos escribir ambas ecuaciones en la forma:
md 

1  Re* q
k()
p e  

1  Re* q
k()
(6.20)
(6.21)
El número de Reynolds de percolación mide la desviación de la fuerza resistiva de la
ley de Darcy. Efectivamente si Re*<<1, la ecuación (6.20) se transforma en la ley de
Darcy:
md 

q
k()
y (6.21) se reduce a la ecuación de Darcy:
(6.22)
110
Manual de Filtración & Separación
p e  

q
k()
(6.23)
Ejemplo 2
Para los datos del problema 1, definir si el régimen es de Darcy o Forcheimer.
Para decidir debemos calcular el número de Reynolds para los valores extremos
de velocidad:
Re* 
Re* 
f c( ) k    q

f c( ) k    q


1.23  6.84  106  6.33
 1.73
0.0118

1.23  6.84  10 6  23.93
 6.52
0.0118
Como en ambos casos el número de Reynolds es mayor a 1, el régimen es de
Forcheimer.
6.1.2
Ecuaciones de Forcheimer y Darcy en términos de la altura piezométrica
En ocasiones es conveniente expresar las ecuaciones de Darcy o Forcheimer en
términos de la altura piezométrica, en vez de la presión de poros en exceso. Como
pe  f g  h  h 0  , donde f gh 0 es la presión hidrostática, reemplazando en (6.21)
resulta:
h  

1  Re* q
f gk()
Definiendo la conductividad hidráulica K(), medida en cm/s, mediante la expresión:
K(  ) 
f gk(  )

(6.24)
Las ecuaciones de Forcheimer y de Darcy se transforman en:
h  
1
1  Re* q
K()
(6.25)
h  
1
q
K()
(6.26)
6.3 MODELO CAPILAR DE UN LECHO POROSO RÍGIDO
El modelo capilar de un medio poroso rígido, también conocido como modelo
de Blake-Kozeny o Carman-Kozeny, se basa en considerar los poros del lecho como un
Capítulo 6. Flujo en Lecho Poroso
111
conjunto de tubos capilares de sección transversal arbitraria. Se supone que el fluido
sigue la ley de Poiseuille. Para este flujo el gradiente de presión está dado en términos
de la velocidad promedio en los tubos v por:
p e  

v
R 2h
La velocidad promedio en los tubos v corresponde a la velocidad intersticial vf, por lo
que v  q  y la ecuación se transforma en:
p e  

q
R 2h
(6.27)
donde Rh es el radio hidráulico, definido como el área de sólido mojada por el fluido,
dividida por el perímetro del tubo sólido mojado y  es la tortuosidad, un factor
adimensional que depende de la sección transversal del ducto en el atado. Entonces,
para un lecho de partículas:
Rh 
área mojada
L
x
perímetro mojado L

volumen de poros / volumen del lecho
sup erficie de partículas / volumen del lecho








Sp / V Sp (1  ) / V(1  ) (1  )Sp / Vp (1  )S
donde S es la superficie específica por unidad de volumen de lecho. Reemplazando
esta expresión en la ecuación (6.27) obtenemos:
p e  
(1  ) 2  S 2
q
3
de aquí resulta que la permeabilidad queda expresada por:
k( ) 
3
(1  ) 2  S 2
(6.28)
Si las partículas fueran esféricas, entonces la superficie específica quedaría
expresada por S  6 d p y la permeabilidad por:
k( ) 
3d 2p
36(1  )2 
(6.29)
donde dp es el diámetro de la esfera.
Cuando las partículas no son esféricas se puede usar el concepto de esfericidad
. Este se define como la razón entre la superficie de una partícula y la superficie de su
112
Manual de Filtración & Separación
esfera equivalente, esto es, de aquella esfera que tiene el mismo volumen de la
partícula. Entonces:
Por lo tanto:

Se Se Vp Se Ve 6 d e



Sp Sp Ve Sp Vp
S
S
6
d e
(6.30)
donde de es el diámetro equivalente volumétrico, es decir, el diámetro de una esfera
que tiene el mismo volumen que la partícula. En este caso, la permeabilidad resulta ser:
k( ) 
3d 2e  2
36(1  ) 2 
(6.31)
También es posible utilizar el diámetro volumétrico-superficial, o diámetro de
permeabilidad, para describir la superficie específica S de un medio poroso. Según la
definición:

S S
V
 x f (x)dx    1 x  f (x)dx   f (x)dx  

 x f (x)dx   f (x)dx  x 
2
3
S
S
S
V
V
V
1
x12
(6.32)
x12 es el tamaño de permeabilidad ya que, junto a los factores de forma superficial S
y volumétrico V permiten calcular la superficie específica S . Sustituyendo (6.32) en
(6.28) obtenemos (Concha 1973):
k( ) 
2
3x12
(1  ) 2  S  V 
(6.33)
2
Tabla 6.2 Valores del parámetro 
Tipo de conducto

Referencia
Circular
2
Becker (1963)
Elíptico
2.00-2.46
Becker (1963)
1.67
Becker (1963)
5
Coulson y Richardson (1968)
Triangular equilátero
Lecho de partículas con 0.3  0  0.5
Otros modelos propuestos son los de Ergun (1952) y de Massarani (1989) son:
3  d e 
k  
170(1  ) 2
2
Modelo de Ergun para 0.35<<0.45:
(6.34)
Capítulo 6. Flujo en Lecho Poroso
113
c  
Modelo de Ergun para 0.35<<0.45:
0.143
3 2
(6.35)
Modelo de Massarani (1989):
1
c   3 2

0.37
0.01

 k0 
 k 0  
0.13    0.10   
 k 
 k  

0.98
, k 0  106 cm 2 
(6.36)
Ejemplo 3.
Para los datos del ejemplo 1, calcular la permeabilidad mediante los modelos de
Kozeny-Carman, Ergun y Massarani.
El diámetro equivalente correspondiente a la malla promedio x m es
d e  0.986x m (Concha y Aravena 1973). El tamaño de las mallas promedio de la malla
es igual a x m  833  1168  986.4 m , luego d e  0.986  986.4  972.6 m
Kozeny-Carman:
3d 2e  2
(0.37)3  (972.6  104 )2  (0.6)2

 6.53  106 cm 2
k  
36(1  )2 
36  (1  0.37) 2  5
Ergun:
k  
c  
3  d e  
2
150 1   
2

(0.37)3  (972.6  104  0.6) 2
 7.83  106 cm 2
150  (1  0.37) 2
0.143
0.143

 0.635
32

(0.37)3 2
Massarani:
1
c  
(0.37) 3 2
0.37
0.01
 106

 106
 

 0.10 
0.13 

6 
6 
 6.95  10 
 6.95  10  

0.98
 0.744
6.4 PROCESO DINÁMICO EN UN LECHO POROSO RÍGIDO
El escurrimiento estacionario de un fluido newtoniano en un lecho poroso rígido
queda representado por las siguientes variables de campo (r,t), q(r,t) y pe(r,t). Estas
variables constituyen un proceso dinámico si cumplen las siguientes ecuaciones:
(r, t)   0
p e  
y
q (r , t)  q 0

1  Re* q0
k(0 )
(6.37)
(6.38)
114
Manual de Filtración & Separación
donde Re*  f c( 0 ) k( 0 ) q 0  y donde 0, k(0) y c(0) son la porosidad,
permeabilidad y parámetro de resistencia del lecho poroso, mientras que f y  son la
densidad y viscosidad del fluido y pe es la presión de poros en exceso a la hidrostática.
Si el escurrimiento es lento, la ecuación (6.38) se reduce a:
p e  
6.5

q0
k( 0 )
(6.39)
FLUJO BIFÁSICO EN UN LECHO POROSO RÍGIDO
El flujo conjunto de un líquido y un gas en un medio poroso es de gran
importancia en muchos procesos, tales como la filtración, el escurrimiento en suelos y
la recuperación de petróleo. En esta sección analizaremos el escurrimiento de agua y
aire en un medio poroso rígido, tal como se presenta en la fase de deshumidificación o
soplado en el proceso de filtración. Los primeros trabajos en esta línea fueron
presentados en el ámbito del escurrimiento de agua en suelos no-saturados por Raats y
Klute (1968).
Consideremos un lecho poroso rígido por el cual escurre una mezcla de agua y
aire. Las seis suposiciones de la sección 6.1 siguen siendo válidas. La porosidad del
sólido es  y definiremos como "s" la fracción de volumen de poros del sólido que
contiene agua y la denominaremos saturación. Por lo tanto, la fracción de aire
contenida en los poros será (1-s). Entonces, las fracciones de agua y aire contenida en
la mezcla sólido-fluido serán s y (1-s). Al igual que antes, el sólido se considerará
inmóvil y v s  0 .
Los balances locales generales son:
Balance de masa:

   v    0
t
(6.40)
Donde  y v  son la densidad de masa y velocidad del componente  del medio
poroso. Para una mezcla aire líquido podemos escribir:
Para el líquido:    s
Para el aire:
  a (1  s)
Para el sólido:   s (1  )
Con estas definiciones, los balances de masa para los componentes resultan ser:
Para el agua

  s     sv    0
t
(6.41)
Capítulo 6. Flujo en Lecho Poroso
Para el aire:
115

 a (1  s)    a (1  s) v a   0
t
(6.42)
Como el medio poroso es rígido, no hay movimiento del sólido.
Sumando las expresiones (6.41) y (6.42) se obtiene la ecuación de continuidad
de la mezcla de fluidos:

  v   0
t
con  y v definidos por:
    s  a (1  s)
(6.43)
v    q   a q a
(6.44)
q   sv  y q a  (1  s) v a
(6.45)
donde
Balance de momentum lineal:
 v   T  b   m
(6.46)
donde v  , T , b  , y m son la aceleración, los esfuerzos, la fuerza de cuerpo y la
fuerza de interacción para cada componente. Para la mezcla de un líquido y aire en el
medio poroso tenemos:
Para el agua:
 sv   T   sg  m 
(6.47)
Para el aire:
a (1  s) v a  Ta  a (1  s)g  m a
(6.48)
donde m  y m a son las fuerzas de interacción entre componentes.
Consideremos flujos lentos en estado estacionario, tal que los términos de
aceleración sean despreciables. Además, tomaremos en cuente el hecho que la fricción
entre fluidos es mucho menor que aquella de interacción entre éstos y el sólido y, por
ello, despreciaremos los esfuerzos extra del líquido y del aire. Con estas
simplificaciones las ecuaciones de momentum se reducen a:
 p     s g  m 
(6.49)
p a  a (1  s) g  m a
(6.50)
Sumando estas dos expresiones resulta la ecuación tradicional de un fluido, para una
mezcla sólido-fluido:
p  g  m
(6.51)
116
Manual de Filtración & Separación
donde     s  a (1  s) es la densidad de la mezcla de fluidos, m    m   m a  , es
la fuerza que la mezcla de fluidos ejerce sobre el sólido y p  pa  p  es la presión
total.
6.5.1 Ecuaciones constitutivas de las presiones
Las presiones p y pa son variables asociadas a cada componente considerado
como medio continuo que ocupa todo el espacio de la mezcla. Por esta razón ellas no
son variables mensurables experimentalmente. Si denominamos p a la presión de
poros, esto es, la presión del líquido en los poros y pg la presión mensurable del aire,
ambos valores experimentales, se debe cumplir que:
p  sp y
pa  (1  s)pg
(6.52)
Cuando se encuentran en un tubo capilar tres fases, como el caso de un líquido,
que moja al sólido, y un gas, que no lo moja, se genera una fuerza en la frontera de las
tres fases, denominada fuerza capilar, que depende de las tensiones interfaciales de los
tres componentes.
En general, la diferencia de presión entre la fase gaseosa y la fase líquida se
denomina presión capilar y depende de la tensión superficial del líquido y del radio de
curvatura del menisco. La presión capilar está dada por la ecuación de Young-Laplace
(Schubert 1982):
1 1
p c  p g  p   g   
 r1 r2 
(6.53)
donde  g y  son la tensión superficial y la densidad del líquido, respectivamente y
r1 y r2 son los radios de curvatura del menisco.
Como un ejemplo, coloquemos los extremos de cuatro tubos capilares de
diferente diámetro interior en un líquido que moja la superficie del sólido, el líquido se
eleva en los capilares a alturas diferentes, como se indica en la figura 9.20a.
Para un capilar, el radio de curvatura es d/2 y la ecuación (6.53) se reduce a
pc  4  g (1 d)cos  , donde  es el ángulo de contacto. La magnitud de la fuerza
capilar será f c  pc
 d 4  , esto es,
2
f c  d cos  . La altura a la que asciende el
líquido depende del balance entre la fuerza capilar y la fuerza gravitacional, con
f g    d 2 h la magnitud de esta fuerza, resultando en h   g cos    d . Es así
como el líquido sube más alto en los capilares más finos.
Capítulo 6. Flujo en Lecho Poroso
a)
117
b)
Fig. 6.3 Capilaridad: a) Tubos capilares verticales, b) Tubos
capilares horizontales.
Si los tubos capilares se colocan en posición horizontal sumergidos totalmente
en el líquido y se les aplica un gradiente de presión p, el líquido escurrirá por cada
tubo con un flujo volumétrico Q de acuerdo a la ecuación de Poiseuille,
p  8LQ R 4 . Si los tubos llenos de líquido se alzan fuera del líquido y se los
coloca en posición horizontal en una corriente de aire bajo un gradiente de
presión p L , como se indica en la figura 6.3b), se establecerá un balance entre la
fuerza del aire f aire  pd 2 4 L y las fuerzas capilares f capilar  d cos  . Si la fuerza
del aire es mayor que la capilar, el aire desplazará al líquido, como en los tubos 1) a 2),
pero cuando las fuerzas estén equilibradas no habrá escurrimiento, ver tubos 3) y4). El
diámetro del capilar cuando esto ocurre se obtiene d  4L cos  p . Aumentando la
presión, el diámetro del tubo que permanecerá saturado disminuye.
Volviendo ahora a un medio poroso, consideremos el modelo capilar, en el cual
se supone que el medio está constituido por un conjunto muy grande de capilares de
diversos diámetros distribuidos al azar. Si el medio poroso está saturado de un líquido
mojante y sometido a un gradiente de presión, todo el líquido fluirá por los capilares de
acuerdo a su diámetro y a las propiedades del líquido. Si el medio saturado es sometido
ahora a una corriente de aire, el aire desplazará el líquido de los capilares grandes y no
de los más pequeños, dependiendo de la magnitud del gradiente de presión. Cuando se
alcanza el equilibrio, el aire circulará solamente por los capilares grandes, mientras los
más pequeños permanecen saturados de líquido. De esta forma el líquido circulará
tanto por los capilares grandes como por los pequeños. Por los pequeños el líquido
seguirá la ley de Darcy, mientras que por los capilares grandes fluirá en un espacio
anular entre las paredes del tubo y el flujo de aire. Finalmente, por los capilares más
pequeños no habrá flujo y el líquido permanecerá estancado debido a las fuerzas
capilares. Para un gradiente de presión determinado, habrá una cantidad de líquido
mojante retenido en los tubos capilares, que dependerá del gradiente de presión del
aire, del tamaño de los capilares y de la tensión interfacial. Esta cantidad de líquido
constituye la saturación residual designada por s. Para un medio poroso no saturado,
la presión capilar es función de la saturación, además de las variables antes
mencionadas. La figura 6.4 muestra una curva típica de presión capilar versus
saturación.
118
Manual de Filtración & Separación
4.5
4
Presión Capilar pc (bar)
3.5
3
2.5
2
1.5
1
0.5
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Saturación s
Fig. 6.4 Presión capilar versus saturación para un concentrado
de cobre. Los círculos son datos experimentales de un
concentrado de cobre y la línea la ecuación (6.54).
1
 s s
pc  p50   

 1 s 
(6.54)
donde p50 , s y  son constantes. Para detalles ver ecuaciones (6.71) a (6.73).
6.5.2 Ecuaciones constitutivas de las fuerzas resistivas
Es sabido que las fuerzas de interacción entre un sólido y un fluido son mucho
mayores que las fuerzas entre fluidos. Este hecho permite suponer que las ecuaciones
constitutivas para las fuerzas resistivas son función de la porosidad, de la saturación y
de las velocidades relativa entre los componentes fluidos y el sólido. Como el sólido
está inmóvil, la velocidad relativa entre los fluidos y el sólido serán las de los fluidos
mismos. Entonces:
  (,s)  (,s)

m   q  , ,s    0 2  1 3 q   q 

 

(6.55)
  (,s)  (,s)

m a  q a , ,s    0 2  1 3 q a  q a




(6.56)
Reemplazando las expresiones (6.52), (6.55) y (6.56) en las ecuaciones (6.49) y (6.50)
resulta:
  (,s)  (,s)

  sp    sg   0 2  1 3 q   q 




(6.57)
Capítulo 6. Flujo en Lecho Poroso
119
  (,s)  (,s)

  (1  s)pg   a (1  s) g   0 2  1 3 q a  q a

 

(6.58)
Desarrollando (6.57) resulta:
6.5.3 Percolación en medios porosos
La percolación en medios porosos es un proceso lento, por lo que se puede
despreciar el término cuadrático de la velocidad en la ecuación (6.57) de momentum
del líquido. Escribamos la ecuación en la forma:
sp  ps   sg 
 0 (,s)
q
2
(6.59)
La precolación es un fenómeno regido por gravedad en que no existe gradiente de
presión externo. Por ello podemos despreciar el primer término de(6.59) en
comparación con el segundo:
ps   sg 
 0 (,s)
q
2
(6.60)
Despejando la velocidad volumétrica del líquido, tenemos:
q  
1
 3ps   3sg 
 0 (,s)
Definiendo la conductividad hidráulica K(,s) y la difusividad hidráulica D(,s) en la
forma:
K(,s) 
 3sg
 0 (,s)
y
D(,s) 
3 p
 0 (,s)
(6.61)
como g  gk , la velocidad de percolación se puede escribir en la forma:
q   K(,s)k  D(,s)s
(6.62)
Esta ecuación es conocida en la literatura como ecuación de Darcy-Buckingham
(Massarani 1997).
6.5.4 Flujo a presión en medio poroso no-saturado
Cuando el gradiente de presión es más importante que el gradiente de saturación
 p z  s z  y  pg z  s z  , podemos despreciar el gradiente de saturación
de las ecuaciones de momentum lineal (6.57) y (6.58). El resultado es:
  (,s)  (,s)

p    g   0 3  1 4 q   q 
s
 s

(6.63)
120
Manual de Filtración & Separación
  (,s)

 (,s)
p g  a g   30
 41
qa  qa
  (1  s)  (1  s)

(6.64)
Definiendo las permeabilidades relativas k  (,s) y k a (,s) y los parámetros
adimensionales c r (,s) y c ra (,s) , de cada componente en la forma:
k  (,s) 
  k()
 0 (,s)  3s
y k a (,s) 
c  ( ,s) 
k( ) 
0 ( ,s) 4s
y
 a k()
0 (,s) 3 (1  s)
(6.65)
k( ) a
1 ( ,s)  4 (1  s)
(6.66)
ca ( ,s) 
donde k() es la permeabilidad del medio poroso, que depende exclusivamente de la
estructura de éste y es independiente del tipo de fluido y régimen de flujo.
Con estas definiciones podemos escribir:



c (,s)
q  q
p    g  
 
 k()k (s)

k()



(6.67)


a
c (,s)a
qa  qa
p g  
 a
 k()k a (s)

k()


(6.68)
En la ecuación (6.68) hemos tomado en consideración que el gradiente de presión del
aire es mucho mayor que el peso del aire en el lecho.
Si el flujo es lento, esto es si se cumple que i ci (,s) k() q i  1 , para
i  , a , las ecuaciones (6.67) y (6.68) se reducen a:
p    g 
p g  

q
k()k  (,s)
a
qa
k()k a  ,s 
(6.69)
(6.70)
De acuerdo a su definición, la permeabilidad relativa puede ser determinada,
midiendo el flujo del fluido respectivo en un medio no saturado y en uno saturado.
Tobinaga y Freire (1980) dan los resultados que se muestran en la figura 6.5 para la
permeabilidad relativa del agua en el flujo de una mezcla de aire y agua por varios
suelos. Se observa que las permeabilidades relativas medidas resultaron ser
independientes de las propiedades del suelo y se las puede escribir, para todos los casos
estudiados por ellos, en términos de la saturación en la forma:
k   s   1.36  106  exp 13.6s 
Capítulo 6. Flujo en Lecho Poroso
121
Fig. 6.5 Permeabilidad relativa k  del agua en el flujo de una mezcla
de agua y aire en suelos no-saturados. (Tobinaga y Freire 1980).
Ejemplo 4
Experiencias de flujo de agua en un lecho poroso incompresible de área
1.96x10-3 m2, espesor 3.5x10-3 m, porosidad =0.44 dio una permeabilidad de
k()=3.13x10-8 m2. Un soplado posterior a presión de 4 bares y viscosidad de 2.1|x10-5
Pa-s por 60s desplazó una masa da agua, de densidad 1000 kg/m3 y viscosidad 1.2x103
Pa-s. Se pudo correlacionar los volúmenes de agua y aire en el tiempo mediante las
funciones:
Vfiltrado 19.119753  2.4962155  ln(t) (cm 3 )
Q aire

1
(l / h)
0.012528241  0.027846883  (t) 0.5
donde el tiempo está en segundos.
Calcular la permeabilidad relativa del agua y del aire en función del tiempo y ajustar
una función a ambos parámetros.
La ecuaciones para el flujo de agua y aire en el soplado están dadas por (6.67) y
(6.68). Para un determinado tiempo podemos integrar estas ecuaciones para dar:
g
p

q  (t)  
q g (t)

L
k()k  (t)
k()k g (t)
 L    Q  (t) 3.5  10 3 1.2  10 3
2.4962155

k  (t)   

14
6


p
k(
)
S
4
3.1  10 10  1.96  103  t


 
122
Manual de Filtración & Separación

 L   a Q a (t) 3.5  103 2.1  10 5 
1
1


 


k a (t)   

14
6   

0.5






p
k(
)
S
4
3.1
10
3.6
10

0.01253
0.027847
t








El resultado se observa en la figura.
1
4
3
2
kl = 173.52s - 503.15s + 546.05s - 262.65s + 47.22
2
Permeabilidad relativa del agua ka
R = 0.9991
0.5
0
0.5
0.6
0.7
0.8
0.9
1
Saturación s
Permeabilidad relativa del agua
6.5.5
Saturación residual y saturación efectiva
La saturación efectiva se define al sistema bifásico y queda expresada por:
se 
1 s
1  s
(6.71)
donde s es la saturación residual. La saturación efectiva se puede correlacionar con la
presión capilar a través de una ecuación logística:

1  s   pc  
 1  
se 
 
1  s    p50  


1
(6.72)
Donde p50 es el valor de pc para se=0.5 y   2.1972 ln(p 25 p75 ) . Para la saturación
podemos escribir entonces:
 pc p50 

1   pc p50 

s  s   (1  s  ) 
(6.73)
Capítulo 6. Flujo en Lecho Poroso
123
Permeabilidad relativa del aire k a
6.1E-05
5.1E-05
4.1E-05
3.1E-05
2.1E-05
ka = -0.0041s4 + 0.0122s3 - 0.0138s2 + 0.0068s - 0.0012
1.1E-05
R2 = 0.9997
1.0E-06
0.5
0.6
0.7
0.8
0.9
1.0
Saturación s
Permeabilidad relativa del aire.
Ejemplo 5
Durante la etapa de formación del queque, en un proceso de filtración, el agua
retenida en el queque saturado fue de 34.3 cm3. A continuación se aplicó
progresivamente presiones crecientes y se colectó el filtrado recibido. Los resultados se
muestran en la tabla siguiente:
Volumen de filtrado
cm3
0.00
0.50
0.29
0.30
3.67
0.32
6.86
5.71
0.69
Saturación s
1
0.985
0.977
0.968
0.861
0.852
0.652
0.486
0.466
Presión capilar pc
bar
0.0
0.2
0.3
0.4
0.5
0.6
1.0
2.0
4.0
Graficando los datos obtenemos la figura que sigue.
Del gráfico se obtiene s   0.466 . Para calcular los parámetros utilizamos la
ecuación (6.72) para la saturación efectiva se obteniendo la columna 2 de la tabla y el
gráfico que sigue.
124
Manual de Filtración & Separación
4.5
4.0
Presión Capilar pc (bar)
3.5
3.0
2.5
2.0
1.5
1.0
0.5
0.0
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Saturación s
Curva de capilaridad.
1.00
0.90
Saturación (s-sr)/(1-s r)
0.80
0.70
0.60
0.50
0.40
0.30
0.20
0.10
0.00
0.0
1.0
2.0
3.0
4.0
5.0
Presión capilar pc en psi
Modelación de la presión capilar.
Del gráfico se obtiene el valor de p50  0.78 como el valor de pc para s   0.5 y el
valor de  de   2.1972 ln  p 25 p75   2.95 . La línea del gráfico de presión capilar
versus saturación corresponde a la simulación con los parámetros obtenidos.
Capítulo 6. Flujo en Lecho Poroso
p
0.0
0.2
0.3
0.4
0.5
0.6
1.0
2.0
4.0
(s-s)/(1-s)
0
0.0272777
0.0430987
0.0594654
0.2596836
0.2771413
0.6513912
0.9623568
1.0000000
125
Simulación
0
0.0177253
0.0563189
0.1223785
0.2121819
0.3156200
0.6754547
0.9414613
0.9920178
s+(1-s)xa/(1+a)
1.00000000
0.99053472
0.96992573
0.93464988
0.88669485
0.83145895
0.63930719
0.49725967
0.47026248
La saturación residual s se relaciona al balance entre la fuerza de presión y la
fuerza capilar. La variable adimensional que relaciona estas fuerzas es el número de
capilaridad. Este número ha sido definido en diferentes formas. Por ejemplo, de las
definiciones en la sección 6.2.1 de este Manual, se puede obtener el siguiente número
de capilaridad Nc:
Nc  K
d  p 
 cos 
(6.74)
donde K es una constante. La recta de la figura 6.6 muestra la dependencia de la
saturación residual del número de capilaridad, la se puede expresada por (Brown
1955):
s 
1
0.264
Nc
86.3
Fracción de Humedad residual
1
0.1
0.01
1.00E-07 1.00E-06 1.00E-05 1.00E-04 1.00E-03 1.00E-02 1.00E-01
Número de capilaridad Nc
Fig. 6.6 Saturación residual s versus índice de capilaridad Nc
para lechos porosos de gran espesor (Brown 1955).
126
Manual de Filtración & Separación
Los valores pequeños de saturación residual corresponden a medios de alta
porosidad, mientras que los valores altos pertenecen a medios de baja porosidad. En
general podríamos escribir:
s   kN c n
(6.75)
donde k y n se pueden obtener de un gráfico como el de la figura 6.6.
Wakeman (1976) definió el número de capilaridad en la forma:
N cap 
av x 2  p 
1  av 
2
L
donde av es la porosidad promedio del queque, x es el tamaño promedio de las
partículas, p es la presión de poros, L es el espesor del lecho poroso y  es la tensión
superficial del sólido. Con esta definición del número de capilaridad, Wakeman
propones la siguiente correlación para la humedad residual para una variedad de
queques incompresibles:
0.49
s   0.155 1  0.031N cap

(6.76)
Fracción de Humedad residual sr
1.000
0.100
1.00E-05
1.00E-04
1.00E-03
1.00E-02
1.00E-01
Número de capilaridad Ncap
Fig. 6.7 Humedad residual versus número de capilaridad según
Wakeman (1974).
Del gráfico se puede concluir que para números de capilaridad menores que 2.6x10-5
el queque queda completamente saturado y es imposible desplazar agua de él.
Capítulo 6. Flujo en Lecho Poroso
127
6.6 REFERENCIAS
Becker, R., Integration des equations du mouvement d'un fluide visqueux
incompressible, Handbuch der Physik VIII/2, Springer Verlag, 1-384 (1963).
Brown, G.G., Operaciones Básicas de la Ingeniería Química, Ed. Marín, S.A.,
Barcelona, 1955, 232-235.
Concha, F., Operaciones Mecánica, Apuntes de clase, Universidad de Concepción,
1937.
Darcy, H., Les Fontaines Publiques de la Ville de Dijon, Dalmont, París (1856).
Carman, P.C., Trans. Inst. Chem Eng., London, 15, 150 (1937).
Coulson, J.M., Trans. Inst.Chem. Eng., London, 27, 237-253 (1949).
Ergun, S., Fluid flow through packed columns, Chem. Eng. Prog. 48, 89 (1952).
Kozeny, J., Sitzber. Abad. Wiss. Wien, Math. Naturw. Klasse 136 (Abt.Iia), 271
(1927).
Massarani, G., Problemas em sistemas particulados, Ed. Edgard Blucher Ltda, Río de
Janeiro, (1984).
Massarani. G., Aspectos da fluidodinámica em meios porosos, Revista brasileira de
Engenharía, Número Especial, 1989, 96pp.
Schubert, H., Kapillarität in porösen Feststoffsystemen, Springer-Verlag, Berlin, 1982,
55-64.
Wakeman, R.J., 1976. Vacuum deliquoring and residual saturation of incompressible
filtercakes, Int. Jl. Miner. Process. 5, 193-206.
CAPÍTULO 7
CONSOLIDACIÓN
___________________________________________________
Cuando se aplica una carga compresiva sobre un sedimento saturado con agua,
el esfuerzo total es soportado inmediatamente por el agua que llena los intersticios
entre las partículas, llamada presión de poros, aumentando la presión en los poros. El
gradiente de presión que se establece entre esta agua y el agua en el exterior, que se
denomina presión de poros en exceso, inicia un flujo de agua hacia fuera del
sedimento. Este flujo de agua es gobernado por la permeabilidad del medio poroso y va
acompañado de una disminución de la presión de poros. En estas condiciones, para
soportar el esfuerzo aplicado al sedimento, parte de él debe ahora ser soportado por la
estructura del sólido. Esto, a su vez, produce la deformación del sólido, la magnitud de
la cual depende de las propiedades esfuerzo-deformación del sedimento. De acuerdo a
esta descripción, se denomina consolidación al proceso transiente de traspaso del
esfuerzo aplicado desde el agua que llena los poros del sedimento al esqueleto de éste.
El capítulo 3 analiza las fuerzas que intervienen en un proceso en consolidación.
7.1
PROCESO DINÁMICO DE CONSOLIDACIÓN
Consideremos una mezcla de partículas y un fluido con las siguientes
propiedades:
(i)
Las partículas sólidas son todas pequeñas, con respecto a la vasija que las
contiene, y de la misma densidad, tamaño y forma.
(ii)
Las partículas individuales y el fluido son incompresibles.
(iii)
No hay transferencia de masa entre el sólido y el fluido.
(iv)
La única fuerza de cuerpo es la gravedad.
(v)
Las partículas están contenidas en una vasija impermeable y con paredes
sin fricción entre el líquido y el sólido.
(vi)
Las partículas forman un esqueleto sólido compresible y móvil.
Tal mezcla puede ser considerada una superposición de dos medios continuos
interactivos que denominaremos sedimento.
Un sedimento sometido a consolidación es un medio poroso compresible
descrito por las variables de campo: la porosidad (z,t)=(1-), la velocidad del fluido
128
Capítulo 7 Consolidación
129
vf(z,t), la velocidad volumétrica de la mezcla q  z, t   v f  1    v s , la presión de
poros en exceso pe(z,t), el esfuerzo efectivo del sólido e(z,t) y la fuerza dinámica de
interacción entre el sólido y el fluido md(z,t). Se dice que estas 6 variables de campo
constituyen un proceso dinámico si, en la región 0  z  L cumplen (ver capítulo 3):
(1) Las ecuaciones locales de campo:
 
  v f   0 
t z
(7.1)
dq
 0 , donde q  v f  1    v r  v s  v r
dz
(7.2)
pe
m
 d
z

(7.3)
pe e

  1    g z
z
z
(7.4)
(2) las ecuaciones constitutivas:
m d  md  , v f ,q 
(7.5)
e  e  , v f ,q 
(7.6)
(3) las condiciones iniciales y de contorno:
pe  z,0   C,
p e  h, t   0 ,
e  h, t   0 ,
pe
z
0
(7.7)
z 0
donde P es la presión externa aplicada y h es la coordenada de la superficie del
sedimento.
En estas ecuaciones vr es la velocidad relativa sólido-fluido y g la constante de
aceleración de gravedad. Integrando la ecuación (7.4) usando las condiciones iniciales
y de contorno (6.7b) y (6.7c) resulta:
pe  z   e  z   g  1    z    h  z  dz  C
(7.8)
7.1.1 Teoría de Terzaghi para pequeñas deformaciones
En esta sección analizaremos la consolidación causada por fuerzas externas
aplicadas al sedimento de magnitud mucho mayor que el peso de éste. Terzaghi (1943)
fue el primer investigador que formuló una teoría de consolidación. A las suposiciones
(i) a (vi) él agregó:
(vii) El sedimento es isotrópico y está completamente saturado.
(viii) El flujo de agua desde el sedimento sigue las leyes de Darcy.
130
Manual de Filtración & Separación
(ix)
El sedimento sufre solamente pequeñas deformaciones.
(x)
El peso del sedimento es despreciable en comparación con la carga
externa aplicada.
(xi)
La base del sedimento es impermeable y su extensión es muy grande.
Un sedimento que se comporta según las suposiciones (i) a (xi) recibirá el nombre de
sedimento ideal. La figura 7.1 muestra un esquema del problema de Terzaghi.
C
vf
Fig. 7.1 Esquema de un sedimento ideal en
consolidación bajo una fuerza externa.
La suposición (x) permite suponer que el peso del sedimento es despreciable,
por lo que la ecuación (7.8) se reduce a:
p e  z   e  z   C
(7.9)
donde C es la presión externa.
7.1.2 Ecuación constitutiva de la fuerza hidrodinámica.
La suposición (viii) reduce la ecuación constitutiva de la fuerza de interacción a
la función lineal de Darcy. Ver las ecuaciones (6.7) y (6.14a)
md     
2
vr
k 
(7.10)
Sustituyendo esta expresión en el balance de momentum lineal del fluido (7.3),
obtenemos:
pe


vr
z k   
Como no hay flujo hacia fuera del sistema sedimento-agua, q=0 y v r   v f (1  ) .
Reemplazando en la expresión anterior podemos escribir:
v f  
1    k    pe

z
(7.11)
Capítulo 7 Consolidación
131
Usando la ecuación (7.9), podemos sustituir el gradiente de presión por el gradiente de
esfuerzo del sólido:
v f 
1    k    e

z
(7.12)
1    k    de 


d z
7.1.3 Ecuación constitutiva del esfuerzo efectivo del sólido.
El comportamiento de suelos bajo compresión se puede expresar mediante una
relación entre la fracción de huecos "e" y el esfuerzo efectivo del sólido e. La figura
7.2 muestra una ecuación constitutiva típica.
e
e0
e
e0
e
e
Fig. 7.2 Ecuación constitutiva para el esfuerzo en un suelo
sometido a fuerzas externas.
La suposición (ix) supone una función lineal entre la fracción de hueco y el esfuerzo
efectivo de sólidos, tal como se verifica para pequeñas deformaciones de e0 a e en la
figura 7.2. Denominando coeficiente de compresibilidad a la tangente a la curva y
designándola por "av", resulta:
av  
de donde se deduce que:
de
d
con a v  0
eeo
(7.13)
132
Manual de Filtración & Separación
d e
1

de
av
(7.14)
Esta Expresión representa la compresibilidad del medio poroso. Definiendo la fracción
de huecos “e”, como la razón del volumen de huecos al volumen de sólidos en un
medio poroso, podemos establecer que:
e
y

e
y por lo tanto  
1


1

 
 e
de 
1
1   
2
d
(7.15)
(7.16)
Reemplazando (7.16) en (7.14) obtenemos:
d e
1

2
d
a v 1   
(7.17)
7.1.4 Proceso dinámico en términos de la porosidad
Ahora podemos reemplazar (7.17) en la ecuación (7.12) para obtener:
v f  
k 

a v 1     z
(7.18)
Definiendo el coeficiente de consolidación C para pequeñas deformaciones por:
Cv 
k  o 
a v 1   o  
(7.19)
Reemplazando (7.19) en (7.18) y el resultado en la ecuación de continuidad (7.1)
obtenemos la ecuación de consolidación en términos de la porosidad:
    

Cv
t z  z 
7.1.5 Proceso dinámico en términos de la presión de poros en exceso
La expresión (7.17) podemos escribirla en la forma:
d   1    a v de
2
D esta expresión y de (7.9) se puede deducir que:
(7.20)
Capítulo 7 Consolidación
133

p
2
 1    a v e
t
t

pe
2
 1    a v
z
z
(7.21)
Reemplazando estas expresiones en la ecuación de consolidación (7.20) se obtiene
finalmente:
pe
 2 pe
 Cv
t
z 2
(7.22)
Esta ecuación, clásica en mecánica de suelos y denominada ecuación de Terzaghi,
permite obtener la relajación de la presión de poros cuando se somete un suelo a una
carga externa.
7.1.6 Solución del problema de valor inicial y de contorno.
Las condiciones iniciales y de contorno para la presión de poros en exceso son:
pe  z,0   P
(7.23)
pe  h 0 , t   0
(7.24)
pe
z
(7.25)
0
z 0
Esta última condición se obtiene de hacer m d  0, t   0 en la ecuación (7.3).
Para obtener la solución del problema conviene poner la ecuación (7.22) en
forma no dimensional. Definiendo las variables adimensionales: z*  z h , p*e  pe P y
t*  t t 0 , podemos escribir:  t *  t 0 t ,  z *  h z ,  2 z *2  h 2  2 z 2 y
definiendo t 0  h 2 C v , obtenemos al reemplazar en la ecuación y condiciones
iniciales y de contorno:
p*e  2 p*e

t * z *2
(7.26)
p*e  z*,0   1
(7.27)
p*e 1, t *  0
(7.28)
p*e
0
z * z*0
(7.29)
134
Manual de Filtración & Separación
Para resolver este problema se usa le método de separación de variables.
Definiendo p*e  F  z * G  t * , al sustituir en la ecuación diferencia (7.26) resulta:
G" t *
G  t *

F" z *
F  z *
 A 2
donde A es una constante. De aquí se puede establecer las siguientes dos ecuaciones:
F"  z *   A 2 F  z  y G"  t *   A 2G  t *
(7.30)
cuyas respectivas soluciones son:
F  z *  C1 cos Az *  C2senAz *
(7.31)
G  t *  C3 exp   A 2 t *
(7.32)
de modo que la solución de la ecuación (7.26) es:
p*e  z *   C4 cos Az * C5senAz * exp   A 2 t *
(7.33)
donde C 4  C1C3 y C5  C 2C3 .
Aplicando las condiciones de contorno se obtiene finalmente:
   2n  1   2 
 2  1n 
  2n  1  
p  
 cos 
z *  exp   
 t *


 

2
2
n  0  2n  1 








*
e
(7.34)
pe*
t*=0
t*=0.9
Figure 7.3 muestra la solución no-dimensional de la
consolidación según Terzaghi.
Tal como hemos mencionado en varias oportunidades, la consolidación es una
parte esencial de la geomecánica o mecánica de suelos y el desarrollo de este capítulo
sigue los procedimientos de esas disciplinas. Sin embargo, la consolidación también es
parte esencial de la teoría de espesamiento.
Capítulo 7 Consolidación
135
Cuando una suspensión sedimenta, produce en el fondo de la columna de
sedimentación un sedimento que debe soportar el peso del material que sobre él se
deposita. Este peso produce la consolidación del sedimento en forma similar a lo
expuesto en este capítulo. La diferencia estriba en que la carga a que es sometido el
sedimento durante el espesamiento es su propio peso sin tener una cara externa. Esto
hace que las presiones de poro sean mucho menores que en el caso de la geomecánica.
Por otra parte, las deformaciones sufridas por el sedimento en espesamiento no pueden
ser consideradas pequeñas, pues las suspensiones floculadas pueden comprimirse a
varias veces su volumen inicial.
Se puede decir, entonces, que el proceso de consolidación es bastante diferente
en un espesador que en un suelo que sufre una carga. Por esta misma razón el
tratamiento del proceso se realiza en forma diferente. En vez de resolver una ecuación
de difusión en términos de la porosidad o la presión en exceso de poros, se llega una
ecuación de difusión convectiva en términos de la concentración volumétrica del
medio poroso. Este proceso lo analizaremos en detalle en el capítulo 8.
7.2 BIBLIOGRAFÍA
Bowles, J.E., Manual de Laboratorio de Suelos en la Ingeniería Civil, McGraw Hill
Latinoamericana S.A., Bogotá, 1980.
Das, B.M., Principles of Geotechnical Engineering, Thomson Information/Publishing
Group, PWS-Kent Pub. Co., Boston, 1990, 248-253.
Taylor, D.W., Fundamentos de la Mecánica de Suelos, Continental, México, 1969.
Terzaghi, K., Theoretical Soil Mechanics, John Wiley & Sons, New York, 1943.
CAPÍTULO 8
ESPESAMIENTO
8.1 INTRODUCCIÓN
8.1.1
Desde la Edad de la Piedra al siglo IXX
La invención del espesador Dorr en 1905 y su introducción en las plantas
concentradoras de Dakota del Sur en los Estados Unidos de Norteamérica, pueden ser
mencionada como el punto de partida de la era moderna de espesamiento en América.
Por esta razón la historia del espesamiento se puede ligar estrechamente con el devenir
del siglo 20. Pero dejémoslo claro desde el comienzo, el espesamiento no es un
proceso moderno y, por cierto, no fue desarrollado en América.
Cada vez que una mena es beneficiada para obtener un concentrado, se ha
utilizado dos procesos en forma inseparable, la trituración y lavado. Existe evidencia
de beneficio de oro durante la dinastía Egipcia, aproximadamente 2.500 años AC. Las
referencias más antiguas sobre trituración y lavado de oro, es la del geógrafo griego
Agatharchides referido a Egipto 113 AC y la de Ardillon (1897), autor del libro “Las
minas de Laurion en la antigüedad”, en la que describe el proceso usado
extensivamente en las instalaciones griegas entre los años 500 a 300 AC. A. J. Wilson
(1994)describe, la extracción de oro y cobre en el Mediterráneo, desde la caída de las
dinastías egipcias hasta la Edad media y el renacimiento.
Agrícola, en su libro "De re Metallica” describe, in 1556, varios métodos para
lavar oro, plata, estaño y otras menas metálicas. Él describe estanques de
sedimentación usados como clasificadores, como jigs, como espesadores y como
estanques de decantación. Estos aparatos operaban en forma "batch" o semi-continua.
Una descripción típica, extraída de De Re Metallica es la siguiente: “Para
concentrar cobre en Neusohol en los Carpatos, la mena se trituraba, se lavaba y se
hacía pasar por tres estanques agitadores-lavadores. Las partículas finas eran
lavadas a través de harneros en el estanque lleno de agua, donde las partículas finas
pasaban por el tamiz y sedimentaban al fondo del estanque. En un cierto estado de
llenado del estanque con sedimento, se abría la salida del estanque y se permitía que
el agua saliera. Posteriormente el sedimento era removido con palas y llevado a un
segundo y luego a un tercer estanque donde el proceso completo se repetía". El
concentrado de cobre, que sedimentaba en el último estanque se sacaba y fundía".
136
Capítulo 8 Espesamiento
137
Fig.1 Sedimentadores según Agrícola (1556).
El desarrollo del Procesamiento de Minerales desde una actividad primitiva a
una calificada se debe, principalmente, a los Sajones en Saxen, Alemania y a los
"Cornishmen" en Cornwell, Inglaterra, a comienzos del siglo 16. Entre estos dos países
se estableció un fructífero intercambio de tecnología que duró mucho tiempo. Pero fue
en Saxen donde Agrícola escribió su libro De Re Metallica, la primara gran
contribución a la comprensión y desarrollo de la industria minera publicado en 1556 en
138
Manual de Filtración & Separación
Latín y muy luego traducido al alemán e italiano. El libro de Agrícola tuvo un
tremendo impacto, no solamente en la industria minera, sino que en la sociedad en
general y continuó por 300 años siendo un texto para mineros y metalurgistas. Aparte
de su inmenso valor como manual, la mayor influencia de "De Re Metálica" fue en
preparar el terreno para un sistema de educación en minería la que, con varias
modificaciones, fue adoptada mas tarde internacionalmente.
Mientras en Rusia la primera Escuela de Minas se estableció en 1715 en
Protzavodsk, la Academia de Minas de Freiberg, fundada en 1765, fue la más
importante. Veinte años mas tarde se fundó la Escuela de Minas de París, la que no
adquirió importancia sino muchos años después. A pesar de la prolongada e intensa
transferencia tecnológica establecida entre Saxen y Cornwall, los británicos estaban
atrasados en la educación en técnica y, en el siglo 19, no podían ofrecer ninguna
escuela para estudiar esta disciplina. La Royal School of Mines fue fundada en Londres
en 1851 y la Camborn School of Mines, cuyo prospecto fue presentado en 1829,
solamente fue establecida 1859, cuando la producción minera de Cornwall estaba
declinando y los mineros de esa región estaban emigrando en masa a los Estados
Unidos, Australia y Sudafrica.
El descubrimiento de oro en California en 1948 y en Nevada algunos años mas
tarde, sorprendió a los norteamericanos mal preparados para labores mineras, en las
que trabajaban con palas y platos extrayendo oro en la misma forma que lo habían
hecho los egipcios 5.000 años antes. Los únicos mineros profesionales en el continente
Americano en aquella época eran los que venían de Freiberg o de otras escuelas
Europeas. La primera Universidad Norteamericana en establecer la disciplina de minas
y metalurgia fue la de Colombia en Nueva York en 1864. Luego se creó la Colorado
School of Mines en Golden, Colorado en 1874. Hoy día mas de 40 Universidades
ofrecen cursos en Minas y Metalurgia en los Estados Unidos de Norteamérica.
Es evidente de estas referencias que, mediante el uso del lavado y el sorteo, los
egipcios y los griegos en la antigüedad y los alemanes e ingleses, en la Edad Media
usaban el efecto de la diferencia de densidades de los varios componente de una mena
y usaban la sedimentación en procesos que actualmente denominaríamos de
clasificación, sorteo, clarificación y espesamiento. Sin embargo, no hay evidencia que
ellos distinguieran entre estos tres distintos procesos.
8.1.2
La invención del espesador Dorr y el diseño de espesadores, 1900 a 1940
La clasificación, la clarificación y el espesamiento, todos envuelven la
sedimentación de una sustancia sólida particulada en una segunda sustancia líquida,
pero el desarrollo de cada uno de estos procesos ha seguido pasos diferente. Mientras
la clarificación tiene que ver con suspensiones muy diluidas, la clasificación y el
espesamiento deben usar pulpas más concentradas. Tal vez por esta razón, la
clarificación fue el primer proceso susceptible a una modelación matemática. El
trabajo de Hazen (1904) es el primer análisis de los factores que afectan la
sedimentación de partículas sólidas en una suspensión diluida en agua. El trabajo
demuestra que el tiempo no es un factor en el diseño de estanques de sedimentación,
Capítulo 8 Espesamiento
139
sino que las porciones de sólido removidas son proporcionales al área superficial del
estanque, a las propiedades físicas de las partículas y es inversamente proporcional al
flujo volumétrico al estanque. En un comienzo la clasificación utilizaba equipos que
simulaban los estanques de clarificación, agregando dispositivos para la extracción del
sedimento formado en el fondo de los estanques. Por esta razón los primeros modelos
matemáticos de la clasificación se basan en la teoría de Hazen de estanques de
sedimentación. La introducción de los clasificadores hidráulicos, basados en la
sedimentación obstaculizada en campos gravitacionales y, finalmente, la introducción
de la clasificación centrífuga en hidrociclones, separó las teorías, pero el mecanismo de
separación de las partículas sigue siendo la sedimentación obstaculizada debido a una
fuerza de cuerpo.
Es bien sabido que en Procesamiento de Minerales las aplicaciones preceden a la
ciencia. Esto, es por cierto, es verdadero en el caso del espesamiento, en el que el
espesador continuo fue inventado en 1905, mientras que la primera referencia a las
variables que afectan la sedimentación fue hecha en 1908. Como el espesador Dorr fue
inventado para realizar la separación sólido-líquido en el proceso de la cianuración de
oro, la sedimentación de suspensiones conteniendo finas partículas de este metal
apareció como interesante. Varios autores Nichols (1908), Ashley (1909), Forbes
(1912), Mishler (1912, 1917), Clark (1915), Ralston (1916), Free, E.E., (1916) and
Coe and Clevenger (1916) estudiaron el efecto de la concentración de sólidos y del
electrolito, el grado de floculación y la temperatura en el proceso de sedimentación.
La mayor parte de estos estudios introdujo confusión en la comprensión del
fenómeno de asentamiento y fue Mishler (1912), el superintendente de la planta
concentradora de la "Tigre Mining Company" en el desierto de Sonora en Méjico, el
primero de demostrar mediante experimentos que la velocidad de sedimentación de la
pulpa es diferente para suspensiones diluidas que para las concentradas. Mientras la
velocidad de asentamiento de suspensiones diluidas es generalmente independiente de
la altura de la columna de sedimentación, sedimentos densos son gobernados por
diferentes leyes y, en este caso, la velocidad de asentamiento incrementa aumentando
la altura de la columna. Basado en estas observaciones Mishler propuso una ecuación
mediante la cual se podía obtener la capacidad de un espesador industrial basado en
experiencias realizadas en el laboratorio. Él tomaba en consideración solamente las
concentraciones de entrada y salida del equipo industrial.
En 1916 Coe and Clevenger desarrollaron en forma independiente una ecuación
similar a la de Mishler, pero indicaron que no necesariamente la concentración de la
alimentación debía aparecer en la fórmula, sino que aquella concentración de valor
intermedio entre la alimentación y descarga que producía la mínima "capacidad de
tratamiento", acuñando este término que siguió utilizándose de aquí en adelante. Ellos
recomendaron que se encontrara esta concentración mediante ensayos batch de
laboratorio.
Después de estas tres importantes contribuciones de comienzos del siglo 20, la
invención del espesador continuo y los métodos de diseño, la década del 30 fue una de
expansión de esta tecnología. Varios autores (Adamson and Glasson 1925, Egolf and
McCabe 1937 Ward and Kammermeyer 1940, Work and Kohler 1940), trataron de
140
Manual de Filtración & Separación
describir la velocidad de sedimentación de suspensiones mediante la extensión de la
ecuación de Stokes o mediante ecuaciones empíricas pero, en realidad, no se realizó
ninguna contribución importante en esta década. Steward and Roberts dan una muy
buena idea del estado del arte en el campo del espesamiento en esos días en una
revisión realizada en 1933. En ella decían: "La teoría básica es antigua, pero
modificaciones a ella y sus limitaciones sólo han sido parcialmente realizadas. La
compresión de la teoría es especialmente incompleta en el caso de suspensiones
floculadas. Se dispone de métodos de diseño de equipos, pero la innovación y el
invento de nuevas máquinas requieren de la investigación de los interesantes
fenómenos que se observan en la práctica y que medida que nuevos problemas que
aparezcan sean resueltos".
8.1.3
El descubrimiento de las variables de operación de un espesador continuo,
1940-1950
En la década del 40, la Universidad de Illinois se tornó muy activa en
investigación en el campo de espesamiento. Por lo menos 10 tesis fueron realizadas en
este período. Ejemplos de estos trabajos son: "El espesamiento continuo de pulpas
carbonato de calcio; Sedimentación y espesamiento de pulpas; Espesamiento de
pulpas de arcilla; Velocidad limitante en el espesamiento continuo". El mecanismo de
sedimentación continua fue estudiado en el laboratorio para explicar el
comportamiento de espesadores industriales. Comings y colaboradores describieron
sus descubrimientos en un importante trabajo en 1954. Ellos demuestran la existencia
de cuatro zonas en un espesador continuo. Una zona superior de agua clara, una zona
de sedimentación, una zona de compresión y una zona de acción de las rastras. La
conclusión más importante, expresada por primera vez, es que, en un espesador
continuo en el estado estacionario, la concentración de la zona de sedimentación es
constante y depende del flujo y no de la concentración de alimentación. Demostraron
que a bajos flujos de alimentación, los sólidos sedimentan rápidamente a muy pequeña
concentración, independientemente de la concentración de la alimentación. Cuando el
flujo de alimentación se aumenta, también aumenta la concentración de la zona de
sedimentación, llegando a un valor definido cuando se obtiene la mayor capacidad
posible del espesador. Si, en estas circunstancias, se aumenta el flujo de alimentación,
la concentración de la zona de sedimentación permanece constante y el exceso de
sólidos sale por el rebalse. Se verificó que, en la mayoría de los casos, la alimentación
se diluía a una concentración desconocida al entrar al espesador. Otro descubrimiento
fue que, para una mismo flujo de alimentación, la concentración de descarga se podía
controlar aumentando o disminuyendo la altura del sedimento, correspondiendo a un
aumento o disminución del tiempo de residencia del material en el equipo.
Otra contribución de aquella época fue el trabajo de Roberts (1949) quien
postuló la hipótesis empírica de que la velocidad de eliminación de agua de una pulpa
en compresión es, en todo momento, proporcional a la diferencia en la cantidad de
agua presente en ese momento en el sedimento y aquella residual al final del proceso.
Esta proposición se utiliza hoy día como un método de determinar la concentración
crítica de una pulpa.
Capítulo 8 Espesamiento
8.1.4
141
La Era de Kynch, 1950-1970
Desde la invención del espesador Dorr hasta el establecimiento de las variables
que controlan la operación del equipo, el único trabajo cuantitativo fue el método de
diseño de Mishler/Coe y Clevenger. Este método de diseño se basa en un "balance
macroscópico" del sólido y fluido en el espesador. No existía una teoría de
sedimentación que fundamentara el método. En 1952 Kynch, un matemático de la
Universidad de Birmingham en Gran Bretaña, presentó su celebrado trabajo “Una
teoría de sedimentación”. En él propone una teoría cinemática de la sedimentación
basada en la propagación de ondas de concentración en la suspensión. La suspensión es
considerada como un medio continuo y el proceso de sedimentación es representado
por una ecuación diferencial de derivadas parciales hiperbólica de primer orden. Kynch
demuestra que, conociendo la concentración inicial de la suspensión y la densidad de
flujo del sólido, esto es, el producto de la concentración y la velocidad de
sedimentación de suspensiones de diversas concentraciones, se puede obtener una
solución de la ecuación por el método de características, resultando en zonas en que la
concentración varía en forma continua, denominadas ondas de rarefacción y en
discontinuidades denominadas ondas de choque.
El trabajo de Kynch tuvo una tremenda influencia en el desarrollo del
espesamiento en adelante. Cuando Coming se trasladó a la Universidad de Purdue, la
investigación en espesamiento continuó allí por otros 10 años. Tres Tesis de doctorado
fueron realizadas por De Haas, Stroupe and Tory, en las que analizaron la teoría de
Kynch y probaron su validez mediante experimentos con suspensiones de pequeñas
esferas de vidrio, todas del mismo tamaño y densidad, que ellos denominaron
"suspensiones ideales". Sus resultados que demostraban la validez de la teoría de
Kynch para las suspensiones ideales fueron publicados en una serie de artículos
conjuntos entre 1963 y 1966.
La publicación de Kynch también motivó a la industria a explorar la posibilidad
de esta nueva teoría en el diseño de espesadores. Nuevamente la empresa Dorr fue un
paso adelante en sus contribuciones al espesamiento, al desarrollar un método de
diseño de espesadores basado en la teoría de Kynch. Este método, que recibió el
nombre de "método de diseño de Talmage & Fitch" (1955), consistía en realizar un
solo ensayo de sedimentación y, utilizando la teoría de Kynch, deducir el área mínima
necesaria de un espesador para tratar la pulpa en cuestión.
Experiencias realizadas por varios investigadores, entre ellos, Yoshioka y
colaboradores (1957), Hassett (1958, 1961, 1964a, 1964b, 1968), Shannon y
colaboradores (1963), Tory (1965), Shannon and Tory (1965, 1966) y Scott (1968),
demostraron que, mientras la teoría de Kynch era aplicable exactamente a suspensiones
ideales, ese no era el caso para suspensiones floculadas que sufrían compresión.
Yoshioka and Hassett en sus varios trabajos desarrollaron un método de diseño basado
en la curva de densidad de flujo continuo de sólidos.
Una interesante publicación que ha sido pasada por alto en la literatura de
espesamiento es el trabajo de Behn (1957). Este trabajo, por su naturaleza, estaba
142
Manual de Filtración & Separación
adelantado a su tiempo y habría sido bien recibido en los años 70. Behn fue el primer
investigador en relacionar la compresión en el espesamiento con el proceso de
consolidación estudiado en la ingeniería civil con relación al comportamiento de los
suelos. Es interesante indicar que la solución de la ecuación de consolidación de Behn
da como resultado la ecuación formulada empíricamente por Roberts en 1949.
En 1954 Richardson and Zaki proponen una ecuación empírica para describir la
velocidad de sedimentación de una suspensión de cualquier concentración y en 1962
Michaels and Bolgers proponen una generalización de esta expresión.
Un trabajo que fue escrito en 1975, pero que pertenece a la era de Kynch, es la
publicación de Petty en la que extiende la teoría de Kynch a la sedimentación continua
y en la que se propone por primera vez una condición de contorno adecuada en el
fondo del espesador, lo que no es un problema trivial.
Muchos años más tarde Bustos y Concha, en diversos trabajos que indicaremos
mas adelante, formalizaron y completaron la teoría de suspensiones ideales.
8.1.5
Teoría Fenomenológica, 1970-1980
Aún cuando fue Behn quien en 1957 aplicó por primera vez la teoría de
consolidación a la compresión de pulpas compresibles, fue Mompei Shirato y
colaboradores (1970) quienes resolvieron por primera vez la ecuación combinada de
sedimentación-consolidación usando coordenadas materiales y obteniendo curvas de
sedimentación y perfiles de presiones de poro. Si este trabajo hubiese recibido mayor
atención en su tiempo, el desarrollo de una teoría fenomenológica del espesamiento
habría seguido de inmediato. Tomó otros cinco años para que Adorjan (1975, 1976)
presentara una teoría ad-hoc de sedimentación-compresión, dando el primer método
realmente satisfactorio para el diseño de espesadores y para que Smiles (1976a, 1976b)
presentara su enfoque integral. Sin embargo, fue Kos (1975) quien delineó la
sedimentación basado en la teoría de mezclas de Truesdell (1957), seguido por Thacker
y Lavelle (1976), pero quienes le dieron una estructura formal adecuada a la
sedimentación fue un grupo de investigadores brasileños. Más o menos en la misma
época, Dixon (1977a, 1977b, 1978) publicó una serie de trabajos y conclusiones
erróneas.
Una investigación fuerte e importante en sedimentación, y en el campo de los
medios porosos en general, se llevaba a cabo en Brasil en los años 70.
Desgraciadamente ésta raramente fue publicada en revistas internacionales, pero está
bien documentada en revistas y anales de congresos locales. En COPPE, la Escuela de
Graduados de la Universidad federal de Río de Janeiro varios investigadores y
estudiantes graduados estaban involucradas en la aplicación de una herramienta
matemática nueva, la Teoría de Mezclas de la mecánica de medios continuos a los
sistemas particulados. Entre ellos y, para mencionar solamente algunos de ellos se
encontraban G. Massarani, A Silva Telles, R. Sampaio, I. Liu, J. Freire, S. Tobinaga,
L. Kay and J. D’Avila (Telles 1977, D’Avila 1976a,1976b, 1978). Ellos estaban
especialmente interesados en la aplicación en los fundamentos del flujo en lechos
Capítulo 8 Espesamiento
143
poros. Esta teoría dio al espesamiento y a la filtración una estructura científica
rigurosa.
Más o menos en el mismo tiempo, y con estrechos lazos al grupo brasileño,
investigadores de la Universidad de Concepción, en Chile comenzaron a trabajar en la
misma dirección. Sus resultados fueron presentados en las Tesis de Ingeniería de O.
Bascur (1976) y de A.Barrientos (1978), y en el XII Congreso Internacional de
Procesamiento de Minerales en São Paulo, Brazil en 1977 y en la Engineering
Foundation Conference on Particle Technology en New Hampshire, USA, en 1980.
Estos trabajos han continuado hasta la actualidad a través de Tesis de Ingeniería de R.
Becker (1982), A. Quiero (1994) y R. Valenzuela (1994) y de doctorado de P. Garrido
(2000).
8.1.6
Teoría Matemática, 1980-2000
A fines de la década de los 70 y durante los 80, varias publicaciones
demostraron que el modelo fenomenológico del espesamiento, basado en la Teoría de
Mezclas, había sido bien aceptado por la comunidad científica internacional. Entre
ellos se puede citar los trabajos de Concha y Barrientos (1980), Buscall and White
(1987), Azurais y colaboradores (1988), Landman y colaboradores (1988), Bascur
(1989), David and Russel (1989), Kytömaa (1990). A pesar que la teoría de mezclas
hizo un buen trabajo en unificar la sedimentación de suspensiones dispersas con la de
las suspensiones floculadas, una vez que se establecieron las ecuaciones constitutivas
apropiadas y, en esta forma, creó un modelo robusto mediante el cual se podía simular
el asentamiento de cualquier suspensión, el análisis matemático de este modelo no
existía.
Los ingenieros en general estiman que la matemática es una herramienta útil
para resolver problemas específicos, pero muchos de ellos creen que los fundamentos
de la disciplina de Procesamiento de Minerales son puramente físicos y que la
matemática corresponde a una etapa posterior en el desarrollo de la teoría. Cuando ésta
finalmente comienza, puede ser rigurosa pero, establecer la teoría es una tarea extramatemática. Truesdell dijo en 1966 que las características de una buena teoría son que
los conceptos físicos se traducen en matemáticos desde el comienzo y que la
matemática se usa tanto para formular la teoría como para obtener soluciones.
Embebido en las ideas de Truesdell y convencido de que la única forma de
avanzar en el establecimiento de una teoría rigurosa y completa del espesamiento era
interesar a matemáticos en este tema, se inició una fructífera colaboración entre las
Facultades de Ingeniería y de Ciencias Físicas y Matemáticas en la Universidad de
Concepción, la que luego se extendió al Instituto de Matemática de la Universidad de
Stuttgart en Alemania y al Departamento de Matemática y Ciencias de la Computación
de la Universidad de Mount Allison en Sacksville, Canadá. y recientemente al Instituto
de Matemática de la Universidad de Bergen en Noruega Protagonistas de estos trabajos
son M.C. Bustos, A Barrientos y F. Concha de Concepción, W. Wendland, R. Bürger y
M. Kunik de Stuttgart, E.Tory de Sacksville y K. Karlsen de Bergen. El resultado de
esta colaboración de 20 años es: a) La formulación rigurosa y el análisis matemático de
144
Manual de Filtración & Separación
los procesos de sedimentación de suspensiones ideales en columnas de sedimentación
y espesadores ideales, tema del capítulo 5, b) La formulación rigurosa y el análisis
matemático de los procesos de sedimentación de suspensiones floculadas en columnas
de sedimentación y espesadores industriales, tema del presente capítulo, c) La
extensión de la teoría a modelos axi-simétricos, d) El primer modelo de un espesador
de alta capacidad, e) La formulación rigurosa y el análisis matemático de los procesos
de sedimentación de suspensiones poli-dispersas y f) La formulación de ecuaciones
constitutivas para la velocidad de sedimentación de partículas individuales y
suspensiones, tema del capítulo 4. Los temas indicados por c) a e) se analizan en la
sección 8.7 del presente capítulo.
8.2
EQUIPOS.
Los espesadores son equipos típicos que no han cambiado mucho su apariencia
desde la invención del espesador Dorr en 1905. Se han hecho más grandes, se han
construido de diferentes materiales, tales como madera, acero o cemento y se ha
mejorado y modernizado el sistema de tracción de las rastras, pero los elementos
esenciales continúan siendo los mismos. La figura 8.1 muestra el espesador Dorr. Se
puede distinguir el estanque cilíndrico correspondiente al cuerpo del espesador, la
bandeja de alimentación (feedwell), la canaleta de rebalse (overflow launder), las
rastras (rakes)y la abertura de descarga discharge opening), todos ellos elementos
comunes a cualquier espesador.
Fig. 8.1 Espesador Dorr inventado en 1905.
En general el estanque de un espesador es cilíndrico. Las unidades pequeñas, de
menos de 30 metros, se construyen en acero o madera y las unidades mayores, hasta
120 metros de diámetro, en concreto. La base del estanque se construye del mismo
material que el cilindro, excepto en los espesadores grandes, en los cuales algunas
Capítulo 8 Espesamiento
145
veces se usan bases de tierra (Hsia and Reinmiller 1977). La forma de la base es un
cono, destinado a permitir una mejor evacuación del material depositado.
La bandeja de alimentación, o feedwell, es un cilindro concéntrico al estanque y
de pequeño diámetro, cuyo objetivo principal es permitir una buena distribución de la
alimentación al espesador, pero también sirve para mejorar la mezcla de la pulpa y el
floculante y, en muchos casos para diluir la alimentación. El cilindro puede tener bafles
internos y agujeros para la entrada de agua de dilución (Cross 1963). Más sobre este
tema se discutirá en la sección 8.7.
Fig. 8.2 Esquema de un feedwell con dos tubos tangenciales de alimentación y
bafles internos.
Fig. 8.3 Feedwell con dos tubos tangenciales de alimentación.
146
Manual de Filtración & Separación
Las rastras, que pueden tener una gran variedad de formas, principalmente en la
forma de soporte, tiene por objetivo llevar el material depositado en el fondo del
espesador hacia la abertura de descarga. Las rastras giran a velocidades del orden de xx
rpm. Un resultado secundario de las rastras es la formación de canales a su paso por el
material depositado, por los cuales escurre agua, permitiendo un aumento de la
concentración del sedimento. La tracción de las rastras puede ser a través de un motor
central ubicado en la parte superior del eje o periférica, con el motor montado sobre
rieles en el borde del estanque del espesador. En varios modelos de espesadores existen
mecanismos para levantar las rastras cuando el torque en el motor se hace excesivo.
Fig. 8.4 Feedwell de dos entradas y rastra de tracción central.
Fig. 8.5 Rastra de tracción periférica.
Capítulo 8 Espesamiento
147
Fig. 8.6 Mecanismo de tracción periférico para la rastra de la figura 8.2
Fig. 8.7 Esquema de rastras con tirantes alzadores.
Fig. 8.8 Rastras con tirantes alzadores.
Las canaletas de rebalse en la periferia del espesador tiene por objetivo evacuar
el agua recuperada a una velocidad suficientemente baja para evitar el arrastre de
partículas finas. Un flujo de aproximado a 0.1 m3/min de agua por metro lineal de
canaleta es adecuado. La mayoría de las canaletas tienen pequeños vertederos que
permiten controlar mejor el flujo de agua.
148
Manual de Filtración & Separación
Fig 8.9 Canaleta de rebalse típica mostrando los vertederos.
8.1.7
Espesador convencional. Espesador de alta capacidad y espesador de alta
densidad.
Manteniendo la misma forma estructural y los mismos elementos principales, los
espesadores pueden ser de tres tipos. (1) espesadores convencionales, (2) espesadores
de alta densidad y (3) espesadores de alta capacidad. La figura 8.10 muestra el
esquema de estos tres tipos de espesadores.
Alta capacidad
Alta densidad
Convencional
Fig. 8.10 Esquema de espesadores convencionales, de alta densidad y de alta
capacidad.
El espesador convencional se caracteriza porque su bandeja de alimentación se
encuentra en la parte superior del equipo y, al entrar al espesador, el flujo de
alimentación se mezcla con parte del agua recuperada y se diluye a un valor
denominado concentración conjugada. Esta suspensión diluida sedimenta a velocidad
constante formando un manto de altura variable, para transformarse en sedimento en la
parte inferior del equipo. La figura 8.11 muestra un espesador convencional.
Capítulo 8 Espesamiento
149
F
A
A
B
C
C
D
Fig. 8.11 Esquema de un espesador
C:.convencional. A: agua clara;
B: suspensión; C: sedimento.
Fig. 8.12 A: agua clara;
sedimento.
El espesador de alta capacidad tiene como parte distintiva una bandeja de
alimentación muy profunda que descarga el flujo de alimentación bajo el nivel del
sedimento. Al mezclarse la alimentación y sedimento forma una suspensión mayor a la
de la alimentación y mayor o igual que la concentración crítica. Es por esta razón que
en los espesadores de alta capacidad no existe una zona de sedimentación, la que,
como veremos más adelante es la que restringe la capacidad del espesador. Muchas
veces se recicla parte de la descarga del espesador de alta capacidad con el objetivo de
aumentar la concentración de la alimentación antes de producir la mezcla con el
sedimento. El resultado es que, generalmente, estos espesadores tienen mayor
capacidad que los convencionales. Sin embargo, se ha demostrado que los espesadores
de alta capacidad, cuyo tiempo de residencia está en el orden de minutos, en vez de
horas para los convencionales, son intrínsecamente inestables y, por lo tanto, difíciles
de operar y controlar. Las figuras 8.12 y 8.13 muestran esquemas de un espesador de
alta capacidad.
El espesador de alta densidad es un espesador convencional o de alta capacidad,
pero de mucho mayor altura. Esta altura adicional permite obtener una gran presión
sobre el sedimento que descarga del equipo y, por lo tanto, obtener una concentración
de descarga muy grande. En muchos casos, estos espesadores tienen un cono pequeño,
de modo de ayudar a evacuar la descarga. La figura 8.14 muestra un de espesador de
alta densidad.
150
Manual de Filtración & Separación
Fig. 8.13 Esquemas de un espesador de alta capacidad.
Fig. 8.13 Esquema de un Espesador de alta densidad
Capítulo 8 Espesamiento
8.3
151
VARIABLES DE ESPESAMIENTO.
El espesamiento consiste en una secuencia de dos fenómenos, la sedimentación y
la consolidación. Los fenómenos de sedimentación y consolidación tienen
comportamiento físico diferente, por lo que es necesario analizarlos por separado.
Sedimentación
La sedimentación de partículas individuales o suspensiones de partículas fue
analizado en los capítulos 4 y 5. Ella consiste en el asentamiento de unidades, ya sean
partículas individuales o flóculos, debido a la fuerza de gravedad. Al sedimentar las
diversas partículas de una suspensión interaccionan entre si obstaculizando su
trayectoria y disminuyendo la velocidad de asentamiento que tendrían cada partícula
individualmente. Durante la sedimentación las partículas están rodeadas de fluido y la
interacción entre ellas se verifica a través de ese fluido. Como dos partículas no pueden
ocupar el mismo sitio simultáneamente, se dice que la interacción es estérica e
hidrodinámica.
Sedimentación
Consolidación
Fig. 8.13 Modelo físico de la sedimentación y consolidación.
Consolidación
La sedimentación finaliza cuando las partículas individuales, llegan al fondo de
la columna de sedimentación o del espesador y comienzan a descansar unas sobre
otras. Si estas partículas son incompresibles, como sucede por ejemplo con
concentrados de cobre cuando no se usa floculante, el proceso de espesamiento termina
ahí. Sin embargo, si las partículas son compresibles, como es el caso relaves de cobre
floculados, el peso de los flóculos comienza a afectar a los flóculos inferiores
comprimiéndolas y exprimiendo el agua que permanece en el interior de estos. Este
fenómeno de eliminación de agua por compresión se denomina consolidación.
152
Manual de Filtración & Separación
La consolidación es un campo muy importante en la Geotécnica, disciplina que
estudia el comportamiento de la tierra cuando sobre ella se construyen obras tales y
como casas y edificios. En estos casos la fuerza aplicada al material en consolidación
es externa (peso de la obra). Mayores detalles sobre este campo se encuentran en el
capítulo 7. En sedimentación, la situación es diferente, ya que la fuerza que actúa sobre
el sedimento es el peso del material mismo que constituye el sedimento.
La concentración de la suspensión que separa la sedimentación y la
consolidación se denomina concentración crítica y el tiempo cuando ésta comienza se
llama tiempo crítico.
En vista de la descripción anterior, las principales propiedades de un sedimento
son su permeabilidad y su compresibilidad. Se denomina permeabilidad del sedimento
la facilidad con que un fluido puede penetrarlo y atravesarlo. La compresibilidad del
sedimento mide su facilidad de disminuir en volumen cuando se le aplica una fuerza.
Las variables asociadas a estas propiedades son la presión de poros y el esfuerzo
efectivo de sólidos. Mayor información sobre estos conceptos están descritos en el
capítulo 3.
8.3.1 Proceso dinámico de sedimentación
Se puede decir que las propiedades principales de una suspensión en
sedimentación son (1) la resistencia que el fluido opone a la sedimentación de las
partículas, (2) la permeabilidad del sedimento y (3) la compresibilidad del sedimento.
Estas propiedades tienen asociadas las siguientes variables de campo:
Concentración, como fracción volumétrica de sólidos
  z, t 
Densidad de flujo de sólido
f  , t 
Velocidad volumétrica de la suspensión
q(t)
Presión de poros en exceso
pe  z, t 
Esfuerzo efectivo del sólido
e   
Las variables que describen la sedimentación constituyen un proceso dinámico de
sedimentación si, en las regiones donde las variables son continuas, cumplen:
Las ecuaciones locales de campo:
 

v s  0
t z
(8.1)
q
 0 , con q  v s  1    v r
z
(8.2)
b g
Capítulo 8 Espesamiento
153
e
m
 g  d
z
1 
(8.3)
p e e

 g
z
z
(8.4)
En las discontinuidades cumplen las condiciones de salto:
   v s  e I
(8.5)
  vs    v s ( v s  e I )    (pe  f g(L  z)  e )e I 
(8.6)
Se establecen ecuaciones constitutivas para e y md:
m d  m d (, v r )
(8.7)
e  e (, v r )
(8.8)
donde vr es la velocidad relativa sólido-fluido.
8.3.2 Ecuaciones constitutivas
El movimiento de los flóculos a través del fluido involucran fuerzas dinámicas de
interacción que dependen de las variables expresadas en la ecuación (8.7). Como las
partículas son pequeñas, el movimiento es lento y se puede suponer una relación
funcional lineal entre la fuerza hidrodinámica y la velocidad relativa sólido-fluido:
md      v r
(8.9)
Por otra parte, la experiencia ha demostrado que el esfuerzo efectivo del sólido se
puede expresar como una función de la concentración solamente:
e  e   
(8.10)
constante <c
'e     
  c
 0
(8.11)
con la propiedad:
donde 'e     de d .
8.3.3 Ecuación de espesamiento
Reemplazando estas dos últimas expresiones en la ecuación (8.3) resulta:
154
Manual de Filtración & Separación
  
e
vr
 g 
z
1 
Obteniendo vr desde (8.2), podemos escribir:
    vs  q
e
 g 
1  1 
z
Despejando vs y multiplicándolo por  resulta:
2 1    g 
1 e    
vs  q 
 1 

 
 g z 
2
Diferenciando e    con respecto a , podemos escribir:
2 1    g  'e     
1 

  
g z 

2
vs  q 
(8.12)
Definamos el parámetro fbk en la forma:
f bk     
2 1    g
2
  
(8.13)
de modo que la expresión (8.12) se puede escribir en la forma:
 '     
vs  q  f bk     1  e


g z 

(8.14)
Reemplacemos (8.14) en (8.1) y obtendremos:
'
 
  f    e     
  q  f bk        bk

t z
z 
g
z 
(8.15)
Definiendo un coeficiente de dispersión 
en la forma:
0


   f bk    'e   

g

  c

(8.16)
entonces la ecuación diferencial que representa el proceso de espesamiento es:
 
 
 
  q  f bk           
t z
z 
z 
(8.17)
Capítulo 8 Espesamiento
155
La ecuación (8.17) es una ecuación diferencial parabólica degenerada. Recibe este
nombre porque para valores de <c ella se transforma en la ecuación diferencial
hiperbólica:
 
  q  f bk      0
t z
 f k   

0
t
z
(8.18)
donde la función f k    es la función densidad de flujo de sólidos de Kynch. Podemos
reconocer esta ecuación como la ecuación de Kynch (ver ecuaciones (5.47) y (5.56))
para espesamiento continuo. Este resultado es de la más grande importancia, ya que
indica que, para suspensiones floculadas, la ecuación de Kynch sigue siendo válida en
aquellas regiones donde la concentración es menor a la concentración crítica.
8.3.4 Espesamiento batch
Con el objetivo de tener una mejor descripción del proceso de sedimentación batch
de una suspensión floculada, repitamos, y completemos, las etapas del proceso ya
descritas en el capítulo 5.
Cuando una suspensión floculada sedimenta bajo el efecto de la gravedad en una
columna de sedimentación se puede distinguir las siguientes etapas en el proceso.
a) Antes de comenzar la sedimentación la suspensión se homogeneiza por
agitación, de manera que su concentración es constante.
b) Cuando la sedimentación comienza, todas las partículas caen a la misma
velocidad, de manera que se forma una interfaz agua-suspensión en la parte
superior de la columna, la que desciende a la misma velocidad que lo hacen
las partículas. Esta etapa se denomina sedimentación dificultada (hindered
settling).
c) Las partículas que llegan al fondo de la columna y rápidamente ocupan toda la
superficie disponible. En ese momento los nuevos flóculos se acumulan sobre
los anteriores presionándolos y haciendo que su concentración aumente De
ahí en adelante se dice que el sedimento se encuentra en compresión o
consolidación. La superficie del sedimento, o interfaz suspensión-sedimento,
con una concentración igual a la crítica ya que no hay flóculos descansando
sobre ella, se mueve hacia arriba a medida que nuevas partículas se le
incorporan.
d) En un punto determinado de la columna, pero bajo la interface de aguasuspensión, la concentración de la suspensión permanece fija o aumenta con
el tiempo.
e) Utilizando un instrumento para medir concentraciones, como el de Been and
Sills (1981), se podría seguir el movimiento de una determinada
156
Manual de Filtración & Separación
concentración  en la columna. El movimiento sería necesariamente hacia
arriba a una velocidad denominada velocidad de propagación de la onda de
concentración .
f) En un determinado instante y a una cierta altura la interfaz agua-suspensión se
encontrará con la interfaz suspensión-sedimento. Las coordenadas de ese
evento se denominan tiempo crítico y altura crítica y ellas definen el punto
crítico en el cual termina la sedimentación y comienza la consolidación.
g) En un tiempo suficientemente largo, la consolidación termina y
estableciéndose en la columna un gradiente de concentración desde la
concentración crítica hasta la concentración máxima lograda.
La figura 8.14 muestra la curva de sedimentación con las interfaces agua-suspensión y
suspensión-sedimento y curvas de concentración constante en el sedimento.
Fig. 8.14 Curva de sedimentación para un relave de cobre
mostrando las interfaces agua-suspensión, suspensiónsedimento y curvas de concentración constante (Bürger and
Concha 1998).
Para el espesamiento batch la ecuación (8.17) se reduce a:
 f bk     
 

   
t
z
z 
z 
(8.19)
Del comentario a) se deduce la condición inicial y la condición de contorno para z=L y
valores de t mayores a cero. De la ecuación(8.14) cuando se hace vs=0 se deduce la
condición de contorno en la base de la columna:
  z, 0   0 , para 0  z  L
(8.20)
  L, t   0 ,
(8.21)
para t  0
Capítulo 8 Espesamiento
157
f bk        

 0, para 0  t
z z 0
(8.22)
En la sección 8.4 se muestra como determinar los parámetros f bk    y e    .
Las figura 8.15 muestra estos parámetros para una suspensión de carbonato de calcio
floculada y la figura 8.16 muestra f bk    y     para un relave de cobre.
La solución del problema de sedimentación batch con los parámetros de la figura
8.16 se muestran en las figuras 8.14 y 8.16.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
3.500E+05
-5.00E-07
3.000E+05
-1.00E-06
2.500E+05
y = 4.40E+01e2.20E+01x
-1.50E-06
de/d
Densidad de flujo de sólidos m/s
0.00E+00
-2.00E-06
-2.50E-06
2.000E+05
1.500E+05
-3.00E-06
1.000E+05
-3.50E-06
5.000E+04
-4.00E-06
0.000E+00
0.200
-4.50E-06
Fracción volumétrica de sólidos
Función densidad de flujo de sólidos
0.250
0.300
0.350
0.400
0.450
0.500
Fracción volumétrica de sólidos
Esfuerzo efectivo del sólido
Fig 8.15 Parámetros de espesamiento para una suspensión floculada de carbonato
de calcio.
Densidad de flujo de sólidos
Coeficiente de difusión
Fig 8.16 Parámetros de espesamiento para un relave de cobre, Bürger and Concha 1998).
158
Manual de Filtración & Separación
Perfil de concentraciones
Perfil de presiones de poro en exceso
Fig. 8.17 Simulaciones de la sedimentación de un relave de cobre a patir de la
solución de la ecuaciones (8.19) a (8.22), (Bürger and Concha 1998).
8.3.5
Simulación y comparación con datos de la literatura.
El poder de simulación del modelo fenomenológico de sedimentación desarrollado
en esta sección ha sido demostrado por el grupo de investigadores liderado por Concha
(Bürger and Concha 1999, Bürger et al 1999 y Garrido et al 1999). A continuación se
muestran algunos de estos resultados.
Simulación
Experimental
Fig.8.18 Comparación de una simulación con los resultados
experimentales de Been and Sills (1981) para un suelo arcilloso.
Capítulo 8 Espesamiento
a)
159
b)
Fig. 8.19 Simulación y datos experimentales de a) Tiller et al 1980, b)
Bergström 1992.
a) Perfil de concentración
b) Perfil de presiones de poros en exceso
Fig. 8.20 Comparación de la simulación y datos experimentales de Been y Sills (1981)
experiencia N°11, (Garrido et al 2000).
a) Curva de sedimentación
b) Perfil de concentración
para t=22.000 s.
Figura 8.21 Comparación de la simulación y datos experimentales de Holdich and Butt's
(1997), (Garrido et al 2000).
160
Manual de Filtración & Separación
Fig. 8.22 Comparación de simulaciones y datos experimentales de suspensiones
de caolín publicadas por Dreher (1998). a) t=0.052dís, b) t=0.312 días, c) t=0.87
días, d) t=2.13 días, e) 3.91 días y f) 13.27 días (Bürger et al 2000).
Capítulo 8 Espesamiento
161
La comparación de simulaciones de sedimentación batch con datos experimentales
mostrada en las figuras anteriores muestran que el modelo fenomenológico aproxima
bastante bien los resultados experimentales, tanto de curva de sedimentación como de
perfiles de concentración y presión de poros en exceso.
8.3.6
Espesamiento continuo
Para analizar el espesamiento continuo es conveniente estudiar por separado el
estado estacionario del transiente, ya que para el régimen estacionario las ecuaciones
de campo se simplifican significativamente y no es necesario utilizar la ecuación
parabólica degenerada (8.17) que representa el espesamiento en general.
Ecuaciones de campo en el estado estacionario
Las ecuaciones que representan el estado estacionario de un espesador continuo se
las puede deducir eliminando la dependencia del tiempo en las ecuaciones (8.1) a (8.4),
llegando al resultado:
 '     
f
 0, con f  vs  q  f bk     1  e


z
g z 

(8.23)
q
0
z
(8.24)
pe e

 g
z
z
(8.25)
En las discontinuidades cumple la condición de salto:
0
(8.26)
Se observa que en el estado estacionario tanto la densidad de flujo de sólidos f
como la velocidad volumétrica q son constantes a lo largo del espesador y pueden ser
determinados desde las condiciones de contorno. Además, las discontinuidades, si
existen, no se mueven.
Las condiciones de contorno para un espesador ideal ya fueron presentadas en el
capítulo 5, para el caso de sedimentación continua de suspensiones ideales. Para las
suspensiones floculadas estas condiciones son iguales y las reproduciremos a
continuación:
(1) Alimentación
La alimentación al espesador se diluye rápidamente y se esparce a toda el área
del equipo. Por ello supondremos que la alimentación entra a través de toda el área del
espesador y que se diluye instantáneamente. Para el modelo diremos que el EIC es
162
Manual de Filtración & Separación
alimentado mediante una fuente superficial en z=L. Ver figura 8.23. Si Q F  0 es el
caudal o flujo volumétrico, F la concentración y f F la densidad de flujo de sólidos de
la alimentación (flujo volumétrico de sólidos por unidad de tiempo y unidad de área
del espesador) y S es el área del espesador, entonces se cumple que:
fF 
Q F  F
S
El flujo de alimentación entra al espesador se mezcla y diluye con el flujo de
agua clara producida. Por esta razón la concentración de la suspensión, inmediatamente
bajo la interface agua-suspensión es distinta y menor que la concentración de la
alimentación L    L   F . Sin embargo, la única fuente de sólidos es la
alimentación, por lo que la densidad de flujo de sólidos debe ser continua en la
alimentación:
f  L  fF 
Q F F
S
La densidad de flujo de sólidos en la alimentación puede ser controlada externamente a
través de QF y F
(2) Descarga
La descarga del EIC se realiza a través de un sumidero superficial. Si Q D  0 es
el caudal o flujo volumétrico, D la concentración y f D la densidad de flujo de sólidos
de la descarga, resulta:
fD 
Q D  D
S
El sedimento sale por la descarga en z=0 sin mezclarse con otra fuente, por lo
que allí tanto la densidad de flujo de sólidos f    0   como la concentración   0  son
iguales a las del flujo de descarga:
f    0   fD 
Q D D
, con   0   D
S
Si la concentración de la descarga es menor que la de alimentación, se dice que el EIC
se vacía.
La velocidad volumétrica en la descarga es:
qD 
QD
S
por lo que también podemos escribir:
f    0    f D  q D D , con   0   D
Capítulo 8 Espesamiento
163
(3) Rebalse
En una operación normal, el rebalse no contiene partículas sólidas. Esto significa
que el sólido está restringido a la zona de sedimentación 0<z<L. Si por cualquier
motivo las partículas sólidas pasan de la suspensión a la zona de agua clara, se dice que
el espesador se rebalsa. El caudal de agua Q R  0 se puede calcular mediante un
balance macroscópico:
Q R  Q F  QD  Q F
D  F
  F
 QD D
D
F
La velocidad volumétrica del agua en la zona I será:
qR 
QR
S
De estas expresiones se pueden establecer las condiciones de contorno como:
f    L   fF 
Q F F
S
(8.27)
QR
Zona I
QF, F
Zona II
Zona III
Zona IV
QD,D
Fig. 8.23 Espesador Ideal Continuo (EIC). Zona I agua, Zona
II suspensión a concentración constante, Zona II suspensión a
velocidad variable y Zona IV zona de consolidación.
f    0   fD 
Q D D
 q D D , con   0   D
S
(8.28)
La solución en el estado estacionarios será, entonces:
f  z   fF  fD
(8.29)
164
Manual de Filtración & Separación
q(z)  q D 
fF
D
(8.30)
Si la concentración de alimentación es menor que la crítica F  c , al entrar al
espesador la suspensión floculada se diluirá a la concentración   L  para la cual
f    L    f k    L   y, por lo tanto la suspensión floculada a concentraciones menores
a la crítica se comporta exactamente igual a una suspensión ideal y la concentración en
  L  se puede obtener de la ecuación implícita de Kynch (5.58):
q D   L   f bk  L   f F
(8.31)
El espesador tendrá una zona superior (zona II en figura 8.23) con la
concentración constante L . Dependiendo del tipo de Modo de Sedimentación
Continua existirán un gradientes de concentración (zona III en la figura 8.23) o saltos
desde L a la concentración crítica c , que será la parte superior del sedimento. Por
su parte el sedimento tendrá un gradiente de concentraciones (zona IV en figura 8.23)
desde la concentración crítica c en la interfaz suspensión-sedimento y D justo en la
descarga. Este gradiente de concentraciones se puede obtener de la ecuación (8.23) con
f  f F  q D D :
g z
d
 '
 q D   f bk    f F 
dz
e    f bk   
(8.32)
Integrando con la condición de borde   0   D  f F q D se obtiene el perfil de
concentración:
z    


D
'e    f bk   
d
g  q D   f bk     f F 
(8.33)
La figura 8.24 b) muestra tres estados estacionarios calculados mediante la ecuación
(8.33).
Existencia de un estado estacionario
Para que se produzca sedimentación en un espesador, la concentración de la
suspensión debe aumentar hacia abajo, esto es, el gradiente de concentración debe ser
negativo d dz  0 . De la ecuación (8.32) se observa que:
g z
d
 '
 q D   f bk     f F   0
dz
e    f bk   
y como, se debe cumplir que:
q D   f bk     f F
Capítulo 8 Espesamiento
165
Si denominamos función densidad de flujo de sólidos extendida de Kynch a la función
dada por:
f k     q D   f bk    , para L    D
(8.34)
f k     f F , para L    D
(8.35)
La figura 8.24 muestra tres estados estacionarios válidos para un flujo volumétrico
de descarga constante, en los que la recta que representa f=fF está por sobre la curva
f k    entre la concentración crítica y la concentración de descarga.
7
0
0.1
0.2
0.3
0.4
0.5
0.6
6
Densidad de flujo de sólidos m/s
Densidad de flujo de sólidos
0.0E+00
-5.0E-06
-1.0E-05
-1.5E-05
5
4
3
2
1
0
-2.0E-05
0
Fracción volumétrica de sólidos
a) Densidad de flujo de sólidos
0.1
0.2
0.3
0.4
0.5
Fracción volumétrica de sólidos
b) Perfil de concentraciones
Fig. 8.24 Tres estado estacionarios para una velocidad volumétrica q (flujo
volumétrico de descarga por unidad de área) y tres flujos de alimentación fF.
Estas figuras confirman que, en el estado estacionario, se establece una
concentración constante igual a L y un salto desde esta concentración a la
concentración crítica, para luego aumentar gradualmente hasta la concentración de
descarga. La concentración de descarga queda establecida por la intersección de las
rectas f  f F y f  q D  . Se observa, también, que a medida que la recta f  f F se
acerca a la curva f  f k    en la figura a), el nivel de sedimento aumenta en la figura
b)
La figura 8.25 muestra tres estados estacionarios válidos y uno inválido para un
espesador controlado para mantener una concentración de descarga constante.
166
Manual de Filtración & Separación
Densidad de flujo de sólidos en m/s
-2.00E-06 0
0.1
0.2
0.3
0.4
0.5
0.6
-7.00E-06
-1.20E-05
-1.70E-05
-2.20E-05
-2.70E-05
Fracción volumétrica de sólidos
Fig. 8.25 Dos estados estacionarios válidos y uno inválido para tres
flujos volumétricos de descarga y la misma concentración de descarga.
6
5
fF=-2.42E-5 m/s
Altura en m
4
3
2
fF=-1.50E-5 m/s
fF=-1.00E-5 m/s
1
0
0
0.1
0.2
0.3
0.4
Fracción volumétrica de sólidos
Fig. 8.26 Perfil de concentraciones para los estados estacionarios de
la figura 8.25.
Capítulo 8 Espesamiento
8.4
8.4.1
167
PARÁMETROS DE ESPESAMIENTO
Parámetros de sedimentación
La cuantificación de la sedimentación se hace a través de la concentración de la
suspensión, medida como fracción volumétrica de sólidos, y por la densidad de flujo
de sólidos, definida como el producto de la concentración y la velocidad de la
suspensión.
Se realiza pruebas de sedimentación batch a distintas concentraciones, midiendo
la velocidad de asentamiento de la interface agua-suspensión con el tiempo. La tabla
N° 8.1 muestra un ejemplo de datos de suspensiones de carbonato de calcio. Para estos
datos las curvas de sedimentación se muestran en la figura 8.27.
Tabla N° 8.1 Datos de velocidad de sedimentación de carbonato de calcio
FI=0,265
FI=0,044
Altura en m
Tiempo en s
0
1080
1368
1692
1980
2556
3132
6120
9720
15120
22320
36720
51120
65520
79920
94320
108720
123120
137520
151920
166320
-0,0000307
0,103
-3,1621E-06
0,338
0,336
0,335
0,331
0,329
0,326
0,319
0,312
0,301
0,291
0,277
0,274
0,264
0,257
0,252
0,247
0,243
0,238
0,235
0,232
0,230
-0,00000144
0,265
-3,816E-07
0,338
0,292
0,284
0,274
0,265
0,247
0,230
0,172
0,162
0,150
0,139
0,127
0,122
0,118
0,117
0,115
0,115
0,115
0,113
0,113
0,113
FI=0,017
Altura en m
Tiempo en s
0
1080
1332
1620
1908
2520
3096
6120
9720
15120
22320
36720
51120
65520
79920
94320
108720
123120
137520
151920
166320
-0,0000797
0,044
-3,5068E-06
0,338
0,210
0,186
0,162
0,144
0,112
0,096
0,079
0,073
0,064
0,061
0,057
0,056
0,056
0,054
0,054
0,054
0,054
0,054
0,054
0,054
0.35
FI=0,265
0.30
0.25
0.20
0.15
FI=0,103
0.10
FI=0.044
0.05
FI=0,017
0.00
0
50000
100000
150000
200000
Altura en m
Tiempo en s
0
468
720
1008
1908
2520
5508
9108
14508
21708
36108
50508
64908
79308
93708
108108
122508
136908
151308
165708
180108
0,000143
0,017
-0,000002431
0.40
Altura m
Tiempo en s
0
1692
2304
3204
6804
10404
15804
23004
37404
51804
66204
80604
95004
109404
123804
138204
152604
167004
181404
195804
210204
v s=
=
f k=
FI=0,103
Altura en m
250000
Tiempo s
Fig. 8.27 Curva de sedimentación de carbonato de calcio a
diferentes concentraciones
0,338
0,128
0,076
0,051
0,044
0,041
0,037
0,030
0,029
0,029
0,028
0,028
0,027
0,027
0,027
0,026
0,026
0,025
0,025
0,025
0,025
168
Manual de Filtración & Separación
La velocidad inicial de sedimentación de cada concentración aparece en detalle
en las figuras 8.28.
0.150
0.330
FI=0.103
0.100
Serie1
=0.20
0.290
Serie1 =0.017
Altura en metros
Altura en metros
0.310
0.050
0.270
0.250
0.230
y = -1.43E-04x + 1.89E-01
2
R = 9.45E-01
y = -3.07E-05x + 3.26E-01
2
R = 1.00E+00
0.210
0.000
0.190
0
500
1000
1500
0
1000
Tiempo en segundos
2000
3000
4000
Tiempo en segundos
Fig. 8.28 Velocidades iniciales de sedimentación, a) y b).
0.250
0.350
Altura en metros
0.340
0.150
0.100
y = -7.97E-05x + 2.94E-01
2
R = 9.93E-01
0.050
0.330
0.320
y = -1.44E-06x + 3.38E-01
R2 = 9.01E-01
0.310
0.000
0
500
1000
1500
2000
0.300
2500
0
2000
4000
Tiempo en segundos
6000
8000
10000
Tiempo en segundos
Fig. 8.28 Velocidades iniciales de sedimentación, c) y d).
0
1.50E-04
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.00E+00
Densidad de flujo de sólidos m/s
-5.00E-07
1.00E-04
Velocidad*(-1)
Altura en metros
Serie =0.265
1
Serie1 =0.044
0.200
y = 1.72E-04x1.56E+01
R2 = 9.99E-01
5.00E-05
-1.00E-06
-1.50E-06
-2.00E-06
-2.50E-06
-3.00E-06
-3.50E-06
-4.00E-06
0.00E+00
0.6
0.7
0.8
0.9
1
Porosidad
a) Correlación de Richardson y Zaki
1.1
-4.50E-06
Fracción volumétrica de sólidos
b) Curva de densidad de flujo
Fig. 8.29 Parámetros de sedimentación: Velocidad de sedimentación versus
porosidad y densidad de flujo de sólidos versus concentración.
Capítulo 8 Espesamiento
169
Graficando las velocidades iniciales de sedimentación en función de la porosidad se
puede obtener los parámetros de la ecuación de Richardson y Zaki y de la densidad de
flujo de sólidos. Para el ejemplo resulta (Fig. 8.29):
v s ()  1.72 *10 4 (1  )15.6
f k ()  1.72 *10 4 (1  )15.6
8.4.2 Parámetros de consolidación
La consolidación se produce debido al peso que soportan las capas de
sedimento. Por una parte los efectos de la consolidación se observan en la presión en
exceso de poros y por la otra, en el perfil de concentraciones. Por ello, la ecuación
constitutiva del esfuerzo efectivo del sólido se puede calcular midiendo estas dos
variables.
La Tabla N° 2 muestra el perfil de la presión en exceso de poros y el perfil de
concentración en la consolidación de un sedimento de carbonato de calcio.
Tabla N°8.2 Presión de poros en exceso y concentración
Altura m
0.000
0.075
0.110
0.150
0.190
0.250
0.450
0.650
0.850
Presión pe Pa
Concentración 
1775
1773
1750
1700
1640
1500
1000
500
0.000
0.325
0.300
0.275
0.250
0.200
0.150
0.100
0.050
0.000
La figura 8.30 muestran los perfiles de la tabla N° 8.2.
0.9
1
0.7
0.8
0.6
0.7
0.5
0.4
0.3
Tiempo 9000
Tiempos9000 s
0.9
Tiempo 9000 s
Altura en metros
Altura en m
0.8
0.6
0.5
0.4
0.3
0.2
0.2
0.1
y = -56.206x3 + 10.788x2 - 0.5786x + 0.9502
R2 = 0.9947
0.1
0
0
0
500
1000 1500 2000 2500 3000 3500 4000
Presión de poros en exceso en Pa
a) Presión de poros en exceso
0
0.1
0.2
0.3
Fracción volumétrica de sólidos
b) Perfil de concentraciones
Fig. 8.30 Perfiles de presión de poros en exceso y de concentración
0.4
170
Manual de Filtración & Separación
De esta información el gradiente del esfuerzo efectivo de sólidos se obtiene en
la forma:
dpe
 g
      dz
d
dz
'
e
(8.36)
t  constante
El resultado obtenido de la correlación es:
'e     44exp  22 
(8.37)
y, por lo tanto el esfuerzo efectivo de sólidos para este caso será:
e     2exp  22 
(8.38)
Como la expresión (8.36) se basa en la diferenciación gráfica, y ésta no es muy
precisa, es más conveniente obtener otra expresión que no involucre diferenciación.
De:
e
p
  e    z  g
z
z
integrando para un tiempo t constante se obtiene:

e  z 
0
d   
pe  z 
0
d  g     d
z
zc
como e  z c   0 y pe  z c   0 , integrando resulta:
3.500E+05
3.000E+05
2.20E+01x
y = 4.40E+01e
de/d
2.500E+05
2.000E+05
1.500E+05
1.000E+05
5.000E+04
0.000E+00
0.200
0.250
0.300
0.350
0.400
0.450
0.500
Fracción volumétrica de sólidos
Fig. 8.30 Esfuerzo efectivo del sólido en función de la concentración
Capítulo 8 Espesamiento
171
e    z     pe  z   g     d , para t=constante
z
zc
(8.39)
Finalmente si se aplica la expresión (8.39) para un tiempo muy largo, cuando la
consolidación haya terminado, pe  z,    0 y la expresión se reduce a:
e    z    g     d , para t=
z
zc
(8.40)
Talvez el método más cómodo para determinar el esfuerzo efectivo del sólido sea el
basado en la medición del perfil de concentración final de un sedimento y utilizar la
ecuación (8.40). Sin embargo, el método tiene la desventaja de que se debe esperar
hasta que la consolidación termine completamente y la percolación de fluido cese por
completo. Por otra parte, con este método se obtiene una sola curva de e versus  ,
mientras que utilizando la información adicional del perfil de presión de poros se
puede obtener una curva de e versus  para cada tiempo de medición y, por lo
tanto, una mucho mejor estimación de la funcionalidad de e    .
8.5 CAPACIDAD Y DISEÑO DE ESPESADORES
El diseño de un nuevo espesador o la capacidad de un espesador existente se
calcula para el funcionamiento en el estado estacionario. Desde 1912 a la fecha se ha
desarrollado numerosos métodos de diseño de espesadores, los que pueden ser
clasificados dependiendo de los fundamentos utilizados para su desarrollo. Podemos
distinguir métodos basados en balances macroscópicos, en el proceso batch de Kynch,
en el proceso continuo de Kynch y en el método fenomenológico. Cada uno de estos
métodos tiene las limitaciones impuestas por la teoría que le sirvió de base. En esta
sección analizaremos estos métodos de diseño.
8.5.1
Métodos de diseño basados en balances macroscópicos
Los primeros métodos propuestos para calcular la capacidad de un espesador
continuo están basados en un balance macroscópico alrededor del equipo.
a)
Método de Mishler
Consideremos un espesador en el estado estacionario con un flujo másico de
sólidos en la alimentación dado por F [MT-1], una concentración de alimentación de
DF [-] expresada como dilución, esto es, la razón de masa de líquido a masa de sólido,
un flujo másico de descarga D [MT-1], una concentración de descarga de DD [-] y un
flujo másico de rebalse de O [MT-1]. Un balance de sólidos y agua da:
Sólido:
FD
(8.41)
Agua:
FDF = DDD + O
(8.42)
172
Manual de Filtración & Separación
Despejando el flujo másico de agua O y transformándolo en flujo volumétrico QO se
obtiene:
QO 
F  DF  DD 
(8.43)
f
Según Mishler (1912) el caudal de agua QO en un espesador continuo debe ser igual al
producto de la velocidad de agua formada en una columna de sedimentación por su
área S, para una suspensión de la misma concentración que la alimentación. Como la
velocidad de aparición de agua en la columna es igual a la velocidad de descenso de la
interface agua-suspensión, R, la expresión (8.43) se puede escribir en la forma:
S
F  DF  DD 
(8.44)
f R
F DF
O
vs
vs
vs
D DD
Fig. 8.31 Balance macroscópico de masa según
Mishler (1912) y Coe and Clevenger (1916).
Mishler usó las unidades de toneladas cortas/día para F, pies/min para R y lb/pie3 para
f, y escribió la expresión (8.44) en la forma:
S  0.0222
F  DF  DD 
f R
, en pie 2
(8.45)
El método de diseño de Mishler consiste en medir en el laboratorio la velocidad
de asentamiento R  DF  de la interface agua-suspensión en una pulpa de la misma
concentración que la alimentación al espesador y usar la ecuación (8.45).
Este balance tiene implícita la suposición que la concentración en la zona II es la
de la alimentación. Ésta es la falla del método, ya que la concentración de la
suspensión en sedimentación en el espesador no es la de la alimentación, por lo que la
velocidad R estaría mal calculada.
Capítulo 8 Espesamiento
173
Ejemplo 1
Diseñar con el método de Mishler un espesador para procesar 1200 tpd de
carbonato de calcio de densidad 2.5 t/m3 con una concentración de alimentación de
49.3 % de sólidos en peso. Se desea una concentración de descarga de 52.4% de
sólidos en peso. La velocidad de sedimentación del material de alimentación es de –
1.22X10-6 m/s y la densidad del agua es 1 t/m3.
La relación entre dilución y concentración está dada por: D  f (1  ) s  .
AU  
 DF  DD 

f R
(1.0286  0.9158)
 1.0700 m 2 tpd
6
1.22  10  3600  24
S  1.0700  1200  1283.9 m 2
La tabla que sigue muestra los resultados usando el método de Mishler.
b)

Dk
DD
vs
AU
F
S
-
-
-
m/s
m /tpd
tpd
m
0.280
1.0286
0.9158
-1.22E-06
1.070
1200
1283.9
2
2
Método de Coe y Clevenger
Coe y Clevenger (1916) realizan el mismo balance de masa que Mishler, figura
8.31 pero indican que la concentración dentro del espesador no es la de la
alimentación. Ellos argumentan que dentro del espesador hay diferentes
concentraciones y que, en la zona de sedimentación II se establecerá una suspensión de
tal concentración que tenga la mínima velocidad de sedimentación. Todas las otras
concentraciones desaparecerán a medida que se establece el estado estacionario. Es así
como la suspensión de alimentación de concentración DF [-] pasa por diferentes
concentraciones Dk [-] antes de salir del espesador a concentración DD , por lo tanto
el balance de Coe y Clevenger será:
Sólido:
FD
(8.46)
Agua:
FDk = DDD + O
(8.47)
Despejando el flujo másico de agua O y transformándolo en flujo volumétrico QO se
obtiene:
QO 
F  Dk  DD 
f
(8.48)
174
Manual de Filtración & Separación
S
F  Dk  DD 
(8.49)
f R
Como la concentración de la zona II no se conoce de antemano, es necesario realizar
ensayos de sedimentación batch a distintas concentraciones, calcular el área con la
ecuación (8.49) y elegir la máxima área encontrada. Coe y Clevenger usaron las
unidades de lb/pie3 para la densidad del líquido f , pie para la velocidad R y la
capacidad F por área S, resulta en lb/h-pie2. Con estas unidades escribieron:

R  D
F
 min  62.35
D
k
S
Dk - DD


2
 , en lb hora pie

(8.50)
Definiendo el Área Unitaria (AUo) como el recíproco del flujo por unidad de
área, tenemos:

D - DD
AU o  max  0.01604 k
Dk 
R  Dk 


2
 en pie lb / hora

(8.51)
Taggart (1927) y Dalstrohm y Fitch (1985) usaron f  62.4l lb pie 3 , la
velocidad R en pie/h, dando el área unitaria en pie2 por toneladas cortas por día:

D - DD
AUo  max  1.33 k
Dk 
-R  Dk 


2
 en pie ton corta / dia

(8.52)
Ejemplo 2
Diseñar con el método de Coe y Clevenger un espesador para procesar 1200 tpd
de carbonato de calcio. Se desea una concentración de descarga de 52.4% de sólidos en
peso. La tabla 8.1 de este Manual da los resultados de pruebas de sedimentación.
Concentración % sólidos
en peso
Velocidad de
sedimentación vs m/s
49.3
-1.22E-6
47.4
-1.44E-6
22.3
-3.07E-5
10.3
-7.97E-5
4.1
-1.43E-4
La relación entre dilución y concentración P en % de sólidos en peso está dada
por: D  (1  P) P
Capítulo 8 Espesamiento
175

Dk
DD
vs
AU
F
S
-
-
-
m/s
m /tpd
tpd
m
0.280
0.265
0.103
0.044
0.017
1.0286
1.1094
3.4835
8.6909
23.1294
0.9158
0.9158
0.9158
0.9158
0.9158
-1.22E-06
-1.44E-06
-3.07E-06
-7.97E-05
-1.43E-04
1.070
1.556
0.968
1.129
1.798
1200
1200
1200
1200
1200
1283.9
1867.7
1161.6
1354.9
2157.5
AU  D k   
2
 Dk  DD   (23,1294  0.9158)  1.798 m 2
f R  Dk  1.22  10 6  3600  24
2
tpd
De acuerdo al método de Coe y Clevenger, se debe elegir el área mayor encontrada,
que para este caso es S=2157.5 m2.
Con el objetivo de tener una referencia futura expresaremos la capacidad y el
Área Unitaria, según Coe y Clevenger, con las variables utilizadas en el modelo
fenomenológico, s en kg/m3 y I en m/s, y la denominaremos Área Unitaria Básica
AUo :



s I  k  
F
 en TPD m 2
 min  86.4
k 
1
1 
S


k D 


 1
1
1 
2
AU o  max  1.1574 *102


  en m TPD
k 





s I k k
D 

(8.53)
(8.54)
Para Coe y Clevenger (1912) la altura del espesador no tiene importancia si la
descarga tiene una concentración menor que la crítica, excepto para permitir una
amplia profundidad de agua limpia. Por otra parte, cuando la descarga es más
concentrada es necesario disponer en el espesador una capacidad suficiente de
sedimento para que el tiempo de residencia de ésta sea suficiente para permitir llegar a
la concentración de descarga deseada. Para calcular la altura de la zona de compresión
denominemos t* el tiempo para llegar a la concentración de descarga deseada en una
prueba batch. Dividamos el intervalo de tiempo [0,t*] en n intervalos t  t i 1  t1 . La
altura zi de cada intervalo se puede calcular de zi  Vi S con i=1,2,...n, donde Vi es el
volumen de sedimento de densidad promedio i y S es el área de la columna de
sedimentación. El volumen Vi  Ft i i i , donde F es el flujo másico de sólidos al
espesador. Entonces:
176
Manual de Filtración & Separación
Fig. 8.32 Cálculo de la altura de un espesador según
Coe y Clevenger (1914).
zi 
Ft i
, i  1,2..., n
i iS
 1

 AUo


t i

 
  i  i  f  
La altura total será:
z c  i z i
 1 


 AUo 


t i
         , i  1, 2..., n
i
i
i
(8.55)
f
En estas expresiones i  i1  i . A esta altura zc Coe y Clevenger recomiendan
agregarle 0.50 a 1 m para acomodar la alimentación y la zona I de agua clara.
Ejemplo 3
Para los datos del problema 2, calcular la altura del espesador necesaria.
El Área Unitaria encontrada es de AU o  1.80 m 2 tpd para una descarga de 52.4
% de sólidos en peso. En términos de fracción en volumen tenemos:
Capítulo 8 Espesamiento
177
0.350
=0,103
Altura m
0.340
0.330
0.320
0.310
0.300
0
4000
8000
12000
16000
20000
24000
28000
32000
36000
40000
Tiempo s

52.4
 0.297
2.6  (100  52.4)  52.4
Aplicando la ecuación (8.55) obtenemos:
Zi cm
i
0.338
0.331
0.328
0.324
0.319
0.315
0.311
0.308
0.305
0.302
0.300

0.105
0.106
0.107
0.109
0.111
0.112
0.113
0.114
0.115
0.116
ti s
0
4000
8000
12000
16000
20000
24000
28000
32000
36000
39000
Hc (m)=
zi m
0
0.211
0.209
0.206
0.203
0.200
0.197
0.195
0.192
0.190
0.142
1.944
La altura del sedimento debe ser de 1.94 m. Si se le agrega 1.5 m para la alimentación
y agua clara, resulta una altura total del espesador de 3.5 m.
8.5.2
Métodos de diseño basados en el proceso de sedimentación de Kynch
El establecimiento de la teoría de Kynch en 1952 indujo a varios investigadores,
tales como W.P. Talmage, B. Fitch, J.H. Wilhelm, Y. Nadie, H. Oltmann, N.J. Hasset y
N. Yoshioka (Bustos et al 1999) a usar esta teoría como base para el diseño de
178
Manual de Filtración & Separación
espesadores. El método utilizado universalmente hasta entonces era el método de Coe
y Clevenger (1916) y ellos consideraba que requería muchas pruebas de laboratorio y
demasiado tiempo. Se buscaba algún otro método más rápido y la teoría de Kynch daba
esta oportunidad. Para describir los métodos de diseño que surgieron de este grupo de
investigadores, separémoslos en aquellos basados en la sedimentación batch y aquellos
basados en la sedimentación continua. Para estudiar la teoría de Kynch en detalle ver el
capítulo 5.
a)
Métodos de diseño basados en el proceso batch de Kynch
Consideremos una suspensión ideal sometida a sedimentación batch. La teoría de
Kynch dice que la concentración de la suspensión   z, t  se puede predecir desde la
ecuación diferencial hiperbólica en las regiones en donde ella es continua:
 f   

0
t
z
(8.56)
y de la condición de salto:

f
  ,
con        

  ,  

(8.57)
El requisito para obtener la solución es conocer la funcionalidad de f  f    y las
condiciones iniciales y de contorno.
En una curva de sedimentación, como la de la figura 8.33, la tangente a la
interfaz Z/T corresponde a la discontinuidad agua-suspensión y es igual a la velocidad
de sedimentación de la suspensión de concentración :
 I       0,   
f    f  0 
0

f  

 vs    
Z
T
(8.58)
y las rectas que unen el punto (0,0) con los puntos (zk,tk) son las características de
'
pendiente f bk
 k  . La concentración de la suspensión k, correspondiente esta recta
se obtiene del volumen total de sólidos W0 por unidad de área presente en la columna.
Este valor está dado por:
W0  0 L
(8.59)
Durante la sedimentación este volumen de sólidos por unidad de área debe atravesar
una sección de la columna que posee concentración k, esto es la característica de
'
concentración k. Como esta característica se mueve hacia arriba a velocidad f bk
 k  ,
W0 queda dado por:
W0 
  v    f
tk
k
0
s
k
'
bk
 k   dt
Capítulo 8 Espesamiento
179
Fig. 8.33 Curva de sedimentación.
Z z
 k   k
 T tk

 tk

De la figura 8.33 se observa que: Z T   Z  z k  t k , por lo que al reemplazar en la
ecuación anterior se obtiene:
W0  k Z
(8.60)
Combinando las ecuaciones (8.59) y (8.60), resulta que la concentración  k queda
dada por:
 k  0
L
Z
(8.61)
Este análisis se puede repetir para varias tangentes como en la figura 8.34.
De la teoría de Kynch se puede concluir que, conociendo la curva de
sedimentación batch para una suspensión ideal y trazando tangentes a esta curva, se


puede determinar el par  k , v s   k  para 0   k  c . Ver figura 8.34. Conocidos
los valores de la concentración y velocidad de sedimentación, se puede aplicar la
ecuación de Coe y Clevenger (1916).
180
Manual de Filtración & Separación
Fig. 8.34 Método de Kynch para determinar la concentración y velocidad de
sedimentación de una suspensión mediante un solo ensayo batch.
Ejemplo 4
Diseñar con el método de Kynch un espesador para procesar 1200 tpd de
carbonato de calcio, de densidad 2.5 t/m3 con una concentración de alimentación de
49.3% de sólidos en peso. Se desea una concentración de descarga de 52.4% de sólidos
en peso. Se dispone de una curva de sedimentación para la concentración de 10.3% de
sólidos en volumen.
0,4
0,35
10.3% en peso
10.3% en volumen
Altura en m
0,3
0,25
0,2
0,15
0,1
0,05
0
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
Tiempo en s
Trazado de tangentes a la curva de sedimentación según el método de Kynch.
Capítulo 8 Espesamiento
181
De acuerdo a la teoría de Kynch, la altura correspondiente a una concentración
determinada se puede calcular con la ecuación (8.61), de donde resulta:
Zk  L
0
k
Tk
0
k 
m
s


0,338
2850
0,044
0,0440
-1,186E-04
0,7596
1200
911,5
0,300
3500
0,044
0,0496
-8,571E-05
0,9130
1200
1095,6
0,250
4400
0,044
0,0595
-5,682E-05
1,1034
1200
1324,1
0,200
5650
0,044
0,0744
-3,540E-05
1,3314
1200
1597,7
0,150
8500
0,044
0,0991
-1,765E-05
1,7887
1200
2146,4
0,140
10000
0,044
0,1062
-1,400E-05
2,0323
1200
2438,8
Zk
vs
m/s
AU
2
m /tpd
F
S
tpd
m
2
De acuerdo con este método, el área de espesador es de S=2438.8 m2.
Es posible escribir este método en la forma siguiente. Como  I  k   Z T ,
k  0 L Z y D  0 L Z D , reemplazando en la ecuación (8.54), resulta (ver figura
8.35):

T  ZD  
2
AU o  max  1.1574 *102
1 
  en m tpd
Z
L
Z



s 0 

(8.62)
Método de Talmage y Fitch
Talmage y Fitch (1955) se basaron en la figura 8.35 para escribir:
Z Z  ZD

T
tu
(8.63)
donde ZD es la tangente a la curva de sedimentación para la concentración de descarga
D y tu es la intersección de la tangente Z-T con la horizontal trazada desde ZD. La
coordenada ZD se obtiene desde ZD  0 L D .
Reemplazando (8.63) en (8.62) y observando que el máximo de tu es tU , se
obtiene la simple relación:
 t 
t
AUo  max  u   U
Z


L

s 0 L
 s 0 
(8.64)
182
Manual de Filtración & Separación
Fig. 8.35 Construcción de Talmage y Fitch I (1955)
AU o  1.1574 *102
tU
s  0 L
en m 2 tpd
(8.65)
El método de diseño de Talmage y Fitch consiste, entonces, en:
1.
Realizar una prueba de sedimentación con una concentración
"intermedia" (discutiremos más adelante lo que esto
significa).
2.
Dibujar la curva de sedimentación.
3.
Calcular la altura ZD desde ZD  0 L D .
4.
Trazar una línea horizontal desde ZD hasta cortar la curva de
sedimentación. Esta intersección define la coordenada tU.
5.
Usar la expresión AU  t U s0 L para calcular el área
unitaria. Si se usan unidades métricas, utilizar la ecuación
(8.65).
Como el método de Talmage y Fitch está destinado a todo tipo de pulpas,
incompresibles o compresibles, en algunos casos la recta horizontal trazada desde ZD
no corta a la curva de sedimentación. En estos casos Talmage y Fitch recomiendan
trazar la tangente Z-T para la concentración crítica c y obtener tU como intersección
de esta recta con la horizontal trazada desde ZD. Ver figura 8.36.
Capítulo 8 Espesamiento
183
Fig. 8.36 Construcción de Talmage y Fitch II (1955) y
Oltman (Fitch and Stevenson 1976).
Método de Oltman
Con la experiencia, Fitch y Stevenson (1976) encontraron que el área obtenida con
la concentración crítica era muy grande y adoptaron una modificación empírica
propuesta por Oltman, ingeniero de la Dorr Oliver. Sin justificación, Oltman propone
reemplazar la tangente a la curva de sedimentación para la concentración crítica por la
recta trazada desde el punto (L,0) pasando por el punto (zc,tc). Ver figura 8.36.
Tanto el método de Talmage y Fitch II como en el método de Oltman se basan en
el conocimiento de la concentración crítica y en la suposición (errónea) que la pulpa
compresible a la concentración de la descarga cumple la teoría de Kynch.
Ejemplo 4
Diseñar con el método de Talmage y Fitch y el de Oltmann un espesador para
procesar 1200 tpd de carbonato de calcio, de densidad 2.5 t/m3 con una concentración
de alimentación de 49.3% de sólidos en peso. Se desea una concentración de descarga
de 52.4% de sólidos en peso. Se dispone de una curva de sedimentación para la
concentración de 10.3% de sólidos en peso. Se sabe que la concentración crítica es de
alrededor de 42.8% en peso.
Las alturas ZD y Zc son respectivamente: ZD= 0.0486 y Zc=0.0647. De acuerdo a
la teoría de Talmage y Fitch, se puede construir la siguiente figura que sigue.
Como ambos valores quedan por debajo de la curva, no se puede utilizar ni el
método de Talmage y Fitch ni el de Oltmann.
184
Manual de Filtración & Separación
0,4
0,35
10.3% en peso
Altura en m
0,3
0,25
0,2
0,15
0,1
Zc=0,0647
0,05
ZD=0,0486
0
0
1000
2000
3000
4000
5000
6000
7000
8000
9000 10000
Tiempo en s
Construcción de Oltman
b)
Métodos de diseño basados en el proceso de Kynch continuo
En el capítulo 5 se estudió la teoría de Kynch para un proceso de sedimentación
continuo. En la sección 5.2.3 y figuras 5.14a y 5.14c se demuestra que la capacidad de
un espesador ideal tratando una suspensión ideal y su área unitaria están dadas por:
 1
F
1
1
1 
 s  I **
y AU0 
 ** 

M
**
S
 1
1 
s  I M  M M 

 **

 M M 
 
 
(8.66)
donde M y **
M son la concentración del punto máximo de la curva de densidad de
flujo continuo y concentración conjugada respectivamente. La concentración de
descarga es igual a D  M .
Este método implica el conocimiento de la curva de densidad de flujo. Ver figura
5.14 a) y c).
Método de Yoshioka y Hasset
Yoshioka (1957) propuso un método de diseño de espesadores basado en el
conocimiento de la curva de densidad de flujo batch y su relación con la densidad de
flujo continua y con la concentración de descarga (ver capítulo 5, sección 5.2.4):
f k     q  f bk    y f k  D   f F  qD
(8.67)
Capítulo 8 Espesamiento
185
de aquí se puede escribir:
f bk     f F  q
(8.68)
La ecuación (8.68) representa una recta en el gráfico f bk    versus , donde la
pendiente es q y la intersección con el eje de las ordenadas es fF. Según (8.67) la
pendiente q  f F  D . Yoshioka grafica (-fbk) versus . Entonces la ecuación (8.68) se
transforma en:
f bk     f F  q
(8.69)
La figura 8.39 muestra este gráfico.
M
D
Fig. 8.37 Método de diseño de Yoshioka y Hassett.
El método de diseño se puede resumir de la siguiente forma. Para una
concentración de  D  0.4 , trazamos la tangente a la curva de flujo batch partiendo
del punto (0,0.4). Esta recta de pendiente "q" es tangente a la curva en    M , como
hemos visto, y corta al eje de las ordenadas en f D  f F  f bk  D  . Este valor da la
capacidad del espesador.
Ejemplo 5
Diseñar con el método de Yohioka y Hassett un espesador para procesar 1200
tpd de carbonato de calcio, de densidad 2.5 tom3 con una concentración de
alimentación de 49.3% de sólidos en peso. Se desea una concentración de descarga de
52.4% de sólidos en peso. Se dispone de la curva de densidad de flujo del material.
Las concentraciones de alimentación y descarga son:  F  0.280 y  D  0.306 .
186
Manual de Filtración & Separación
Densidad de flujo de sólidosX(-1) m/s
5,00E-06
4,00E-06
3,00E-06
-fF=2,59E-06
2,00E-06
1,00E-06
0,00E+00
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
Fracción volumétrica de sólidos
Construcción de Yoshioka.
La capacidad será S 
F
1200

 2145m 2
6
f F  s  3600  24 2.59  10  2.5  3600  24
Hassett (1958) se dio cuenta de un problema de interpretación en la
concentración de descarga. La figura 8.39 muestra, según la teoría de Kynch, que en el
estado estacionario existirán solamente dos concentraciones en el espesador la
concentración  M y la concentración conjugada **
M . Hassett dice:"...De esta forma, la
teoría predice la ausencia de las concentraciones de alimentación y descarga dentro del
espesador, lo que significa que debe haber un crecimiento abrupto en la concentración
de descarga en el momento de la descarga....". La teoría desarrollada en el capítulo 5
demuestra que el razonamiento de Hassett es erróneo y que el problema estriba en que
las suspensiones que él analizó son compresibles y no cumplen las ecuaciones de
Kynch. La teoría está correcta, pero para suspensiones ideales y no para suspensiones
compresibles.
Método de Wilhelm y Naide
Wilhelm y Nadie (1979) también parten de la sección 5.2.4 del capítulo 5 para
escribir una ecuación similar a la (8.67) para el estado estacionario:
f k     q  f bk     qD
Diferenciando esta expresión con respecto a  para    M , resulta:
q  f bk'  M 
(8.70)
Capítulo 8 Espesamiento
187
'
y reemplazando en la expresión anterior tenemos f bk
 M    f bk     f bk'  M  D ,
la que, aplicada a la concentración   M , da como resultado:
'
f bk
 M  M  f bk  M   f bk'  M  D
(8.71)
Ahora, si suponemos que la velocidad de sedimentación del sólido se puede expresar
en la forma:
v s      a b
(8.72)
la densidad de flujo de sólidos f bk    se puede escribir como f bk     a1 b y su
derivada en   M como:
b
f bk'  M   a(1  b)M
(8.73)
Reemplazando (8.73) en (8.71) y despejando M resulta:
M 
b 1
D
b
(8.74)
Reemplazando ahora M de (8.74) y f bk'  M  de (8.73) en (8.70) resulta:
b
 b 1 
b
q  f bk'  M   a(1  b) 
 D
b


(8.75)
Como en el estado estacionario f F  qD , utilizando (8.75) llegamos al resultado:
1 b
 b 1 
f F  ab(1  b) 

 b 
1D b
(8.76)
y el área unitaria AU0:
1  b 1 
AU0 
s ab  b 
b 1
Db 1
(8.77)
La expresión f bk     a1 b representa a la función densidad de flujo de sólidos
solamente en una pequeña región de concentración, por lo que la curva completa debe
ser representada por una serie de expresiones válidas en esos pequeños tramos. Es así
como se obtendrá una ecuación (8.77) para cada tramo de concentración, como se
observa en la figura 8.40. Wilhelm y Nadie concluyen que se debe tomar el máximo
valor encontrado para (8.77).
188
Manual de Filtración & Separación
Velocidad de sedimentación x(-1) m/s
1,00E+02
1,00E+01
1,00E+00
1,00E-01
1,00E-02
1,00E-03
1,00E-04
0,001
0,01
0,1
1
Porosidad
a) Velocidad de sedimentación
2,00E+00
1,50E+00
2
Area Unitaria AU en m /tpd
AU=1,815
1,00E+00
5,00E-01
0,00E+00
0
0,1
0,2
0,3
0,4
0,5
0,6
Fracción volumétrica de sólidos
b) Área unitaria
Fig. 8.38 Diseño de espesadores según Wilhelm y Nadie (1979).
Ejemplo 6
Diseñar con el método de Wilhelm y Nadie un espesador para procesar 1200 tpd
de carbonato de calcio, de densidad 2.5 t/m3 con una concentración de alimentación de
49.3% de sólidos en peso. Se desea una concentración de descarga de 52.4% de sólidos
en peso. Se dispone de la curva de densidad de flujo del material.
Las concentraciones de alimentación y descarga son: F=0.280 y D=0.306.
Capítulo 8 Espesamiento
189
Velocidad de sedimentación x(-1) m/s
1,00E+02
1,00E+01
-1,16E-01
y = 7,20E+00x
-5,88E-01
y = 1,17E+00x
-1,36E+00
y = 1,25E-01x
1,00E+00
-2,99E+00
y = 3,87E-03x
1,00E-01
y = 1,18E-04x-5,21E+00
1,00E-02
y = 2,02E-06x
-8,58E+00
1,00E-03
y = 2,85E-08x-1,34E+01
1,00E-04
0,001
0,01
0,1
1
Porosidad
Velocidad de sedimentación.
2.50E+03
S=2180 m 2
Area en m
2
2.00E+03
1.50E+03
1.00E+03
5.00E+02
0.00E+00
0
0.1
0.2
0.3
0.4
0.5
0.6
Fracción volumétrica de sólidos
Área Unitaria
El método de Wilhelm y Nadie da un valor de S  2180 m2 para el Área Unitaria.
8.5.3
Métodos de diseño basados en el modelo fenomenológico
En la sección 8.3.6 sobre espesamiento continuo, hemos mostrado que, para que
en un espesador continuo exista un estado estacionario, es necesario que se cumpla la
relación:
190
Manual de Filtración & Separación
f F  q D   f bk    , para L    D
(8.78)
donde fF es la densidad de flujo de sólidos de la alimentación y f k    es la curva de
densidad de flujo de Kynch extendida. Como q  f F D , reemplazando en (8.78) se
cumple para el estado estacionario:
fF 
fF
  f bk    , para L    D
D
Dividiendo por  y ordenando se obtiene:
fF 
f bk    
, para L    D
1 1

 D
(8.79)
Capacidad
Por definición s f F   F S y  I     f bk     , donde F es la capacidad del
espesador como flujo másico de sólido y S es el área del espesador, entonces:
F s I   
, para L    D en unidades ML2 T 1

S 1 1
 D
(8.80)
Área Unitaria
Usando el concepto de área unitaria AU  S F :
AU 
1 1
1
 
s  I      D

2
1
 , para L    D en unidades L TM

(8.81)
Como esta expresión debe ser válida para todo L    D , y f bk     I    y nos
interesa el mayor área unitaria encontrada, podemos escribir:
 1
1 1
AU  max 
 
L D      
D

 s I

 
 
 
1
 1 

    max

  L D  s f bk     D
 
(8.82)
Comparando esta expresión para el área unitaria con (8.54), derivada por Coe y
Clevenger (en nuestra nomenclatura), podemos decir que, la teoría fenomenológica
indica que, el área unitaria para un espesador tiene que ser mayor o igual que el Área
Unitaria Básica de Coe y Clevenger.
AU  AU 0 
F0
(Coe & Clevenger)
S
(8.83)
Capítulo 8 Espesamiento
191
Notar que el área unitaria básica AU0 depende, para cada concentración, de la
concentración de descarga D y de la densidad de flujo de sólidos batch f bk    y es
independiente de la compresibilidad del sedimento.
Denominemos AU0  , D  a la función:
AU0  ; D  
 

 1

s f bk     D

1
(8.84)
La figura 8.41 muestra la función AU0  , D  , para una concentración de
descarga
D  0.3
y
una
función
densidad
de
flujo
de
sólidos
batch
f bk     6.05*10  1    , en m s . Notar que, aunque la función tiene un
máximo local de AU0=18.37 m2s/kg para   0.2107 , el máximo global es de
AU0=55.5 m2s/kg (0.642 m2/TPD) para   L  0.0135 .
4
12.59
Fig. 8.41 Diseño de un espesador según la teoría fenomenológica, con
la función AU0  ; 0.3 .
Altura
Dijimos en los párrafos anteriores, que el Área Unitaria es independiente de la
compresibilidad del sedimento. Esto se refiere al Área Unitaria Básica AU0, ya que la
teoría solamente dice que el Área Unitaria propiamente tal AU debe ser mayor que la
básica. Cuanto mayor, depende de la compresibilidad del sedimento.
De acuerdo a la sección 8.3.6, la altura del sedimento zc se puede calcular en
función de la concentración  para un espesador en el estado estacionario desde:
zc 

c
D
'e    f bk   
d
g z  f F  q D   f bk    
(8.85)
donde D es la concentración de descarga y c la concentración crítica.
La altura total del espesador debe contemplar la altura "zc" para el sedimento, la
altura "h" para la zona de sedimentación y la altura "c" para el agua clara:
192
Manual de Filtración & Separación
H  c  h  zc
(8.86)
Los valores de c y h son arbitrarios. La altura de agua clara varía generalmente entre
0.5 a 1.0 m y, teóricamente, la altura de h debería ser cero, esto es, no se necesita altura
para la sedimentación. Como esta altura incluye la zona de alimentación, conviene
dejar alrededor de 0.5 m para ella.
Adorjan (1975,1976) fue el primer investigador en utilizar el método
fenomenológico para el diseño de espesadores. Aunque su deducción no es la misma
que se hizo en la sección anterior, el resultado es el mismo. Adorjan dice que un
espesador operando en las condiciones límites, esto es cuando en la expresión (8.83) se
utiliza el signo igual, se requiere una altura de sedimento muy grande, por lo que éste
se debe operar a sólo una fracción  del flujo de alimentación. A  lo denominó factor
de carga:

Como F  F0
F
, con 0<  1
F0
AU 
AU 0
 AU0

(8.87)
(8.88)
Adorjan relacionó el factor de carga al factor de seguridad empleado por otros
investigadores. Nosotros preferimos asociar el factor  a la altura adecuada en el
espesador para proveer un rango de capacidades en torno a la nominal.
Ejemplo 7
Usando el modelo fenomenológico, diseñar un espesador para procesar 1200 tpd
de carbonato de calcio, de densidad 2.5 t/m3 con una concentración de alimentación de
49.3% de sólidos en peso. Se desea una concentración de descarga de 52.4% de sólidos
en peso. Se dispone de la curva de densidad de flujo del material.
Las concentraciones de alimentación y descarga son  F  0.280 y  D  0.306 . En
la sección 8.4 de este Manual se determinó los parámetros de espesamiento del
carbonato de calcio, dando como resultado:
f bk ()  1.72  104 (1  )15.6 m s
e     2.0exp  22  Pa
Reemplazando la densidad del sólido, la concentración de descarga y la función
densidad de flujo de sólidos en (8.84) y pasando de m/s a m/d se obtiene:
AU 0  ;  D  
1
 

 1  ; con  L     D
4
15.6 
2.5  3600  24   1.72x10   (1  )  0.306 
Graficando el área unitaria básica AU0 y la densidad de flujo de sólidos de
alimentación fF en función de la concentración  se obtiene:
Capítulo 8 Espesamiento
193
10
9
Area Unitaria Básica m2/tpd
8
7
6
5
4
AU0=1.75 m 2/tpd
2
AU0=1.26m /tpd
3
2
1
L=0.301
0
0
0,1
0,2
0,3
0,4
Fracción volumétrica de sólidos
Área Unitaria Básica versus concentración.
0
0,1
0,2
0,3
0,4
0,00E+00
-1,00E-06
Densidad de flujo de sólidos m/s
fF=-2,65E-6 m/s
-2,00E-06
L=0,0301
-3,00E-06
-4,00E-06
-5,00E-06
-6,00E-06
fF=-3.73E-6 m/s
-7,00E-06
-8,00E-06
Fracción volumétrica de sólidos
Densidad de flujo de sólidos versus concentración.
El máximo valor del Área Unitaria obtenida entre las concentración conjugada y la de
descarga es de 1.75 m2/tpd correspondiente a la fracción volumétrica de sólidos de
  0.25 . A este valor corresponde f F  2.65  106 m / s . El área total de espesador es
de S  1.75  1200  2100 m 2 .
194
Manual de Filtración & Separación
0
0,1
0,2
0,3
0,4
0,5
0,6
0,00E+00
Densidad de flujo de sólidos
q=-8,66E-6 m/s
-1,00E-06
D=0.306
Serie1
Serie5
fF=-2.65E-6
-2,00E-06
-3,00E-06
-4,00E-06
-5,00E-06
Fracción volumétrica de sólidos
Capacidad máxima según el método fenomenológico
6
fF=-2.65E-6 m/s; q=-8.66E-6 m/s
5
Altura en m
4
3
2
1
0
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
Fracción volumétrica de sólidos
Perfil de concentraciones para el espesador diseñado.
Debemos comprobar dos hechos para concluir que el espesador está bien
diseñado. En primer lugar debemos chequear que se puede obtener un estado
estacionario con el espesador diseñado y el flujo y concentración de descarga deseados.
En segundo lugar, debemos establecer si se puede manejar el flujo en un espesador de
6 m de altura, dejando 1 metro para el agua clara y la alimentación.
Las figuras anteriores muestran que el estado estacionario es posible ya que la
densidad de flujo de alimentación está por sobre a la curva de flujo.
Capítulo 8 Espesamiento
195
A continuación se hace una comparación de todos los métodos de diseño
analizados en el Manual.
Resumen de los resultados de los diferentes métodos de diseño
Método de diseño
Área Unitaria Área en m2
Mishler
1.070
1284
Coe y Clevenger
1.798
2158
Kynch
2.032
2439
-
-
Yoshioka y Hasset
1.787
2140
Wilhelm y Nadie
1.815
2180
Fenomenológico básico
1.750
2100
Talmage y Fitch
Es interesante comparar los resultados de los diversos métodos de diseño de
espesadores. Exceptuando el método de Mishler, todos los otros métodos dan valores
de Área Unitaria similares. Sin embargo, no hay que engañarse, ya que los métodos
basados en la teoría de Kynch son muy dependientes del resultado de la prueba
específica con la que se hizo el cálculo. Si este ensayo experimental no fue bien
realizado, o si la concentración de la suspensión con que se hizo la prueba no fue bien
elegida, el resultado va a ser malo. El método de Coe y Clevenger tiene la ventaja de
que son varios los ensayos realizados, de modo que se puede observar la tendencia de
los ensayos individuales y detectar una falla experimental. El método fenomenológico
tiene la ventaja adicional, que los posibles errores experimentales de los ensayos no se
transmiten al diseño, ya que se ajusta la mejor curva de densidad de flujo a los datos
experimentales y con este modelo se realiza el cálculo del Área Unitaria. Con la
posibilidad de calcular la altura del espesador mediante los datos de compresibilidad se
completa este método.
8.6
ESTRATEGIAS DE OPERACIÓN
8.6.1 Estado estacionario
En la sección 8.3 indicamos las condiciones que se deben cumplir para que un
determinado espesador llegue a un estado estacionario, esto es, que la densidad de flujo
de sólido cumpla la condición f k ()  f F para la concentración comprendida entre la
concentración de descarga y la concentración conjugada L    D .
En el estado estacionario se cumple:
f F  qD
(8.89)
196
Manual de Filtración & Separación
donde f F  Q F F S es la densidad de flujo de alimentación, definida como el flujo de
sólidos en la alimentación por unidad de área del espesador y q es la velocidad
volumétrica q  Q D S , definida como el flujo volumétrico de pulpa en la descarga por
unidad de área del espesador.
El perfil de concentración, según la expresión (8.33), queda expresado por:
'e ()f bk ()d
D g q  q  f ()
 D

bk
z()  

(8.90)
8.6.2 Concentración de la descarga: efecto del flujo de alimentación y de la
altura del sedimento
Si suponemos que las condiciones de operación se encuentran dentro de los
límites en los que puede existir un estado estacionario, de (8.89) se puede observar que
la concentración de la descarga depende de las variables fF y q. Si mantenemos
constante la densidad de flujo de alimentación fF, la concentración de descarga se
puede variar manipulando q, esto es, variando el flujo volumétrico de la descarga. En
los espesadores que descargan por gravedad esto se consigue cambiando los anillos de
la descarga y en aquellos que disponen de bombas de velocidad variable, ajustando la
velocidad al valor requerido. La figura 8.39 muestra el rango de concentraciones de
descarga admisibles para un valor determinado de la velocidad volumétrica q.
Si, estando en un estado estacionario con f F  qD , disminuimos q a q1 , habrá
un desbalance entre el sólido que entra y el que sale del espesador. Por ello se
acumulará sólido en el equipo y aumentará el nivel del sedimento. El mayor peso
acumulado hará que la pulpa en el fondo del espesador se comprima más y aumente la
concentración de descarga. Ahora, el nuevo y menor caudal de descarga Q D  q1S
llevará más sólido por lo que éste llegará a igualar a la masa de sólido de alimentación,
estableciéndose un nuevo estado estacionario f F  q1D1 con un mayor nivel de
sedimento y una mayor concentración de descarga.
Si, por el contrario, aumentamos q a un valor q 2 , saldrá más sólido del
espesador del que entra, por lo que el inventario de sólidos disminuirá junto con el
nivel de sedimento. La menor carga de sólidos hará que la concentración de descarga
disminuya hasta llegar al nuevo estado estacionario dado por f F  q 2 D2 con un menor
nivel de sedimento y una menor concentración de descarga.
Un efecto similar tiene el cambio de caudal o concentración de la alimentación
manteniendo el caudal volumétrico de la descarga constante. En ambos casos es
necesario restringir los cambios dentro de aquellos que llevan a un estado estacionario.
Capítulo 8 Espesamiento
197
Fig. 8.42 Rango admisible de concentraciones de descarga para
una velocidad volumétrica determinada igual a q=-1.5x10-5 m/s,
c=0.23, fbk=-6.05x10-4(1-)11.59m/s, (Bürger et al 1999).
Ejemplo 8.
Supongamos que tenemos una pulpa cuyos parámetros de espesamiento son:
f bk ()  6.05  104 (1  )12.59 m / s
y
0

e ()  
2
5.35  exp 17.9  N / m
para   c =0.23
para   c  0.23
Alimentemos un espesador de 60 m de diámetro y 6 m de altura con los
siguientes flujos másicos de sólidos, en tph, de FF=152.5, 178.1 y 203.5 a una
concentración de PF=21.7 % de sólidos en peso. Calcular para los correspondientes
estados estacionarios, la concentración de descarga y sus respectivos nivel de
sedimento, manteniendo el flujo volumétrico de descarga constante en 203.54 m3/h. La
densidad del sólido es de 2.5 t/m3.
FF (tph)  3600  s (ton / m3 )  f F (m / s)  S(m 2 )
Q D (m3 / h)  3600  S(m 2 )  q(m / s)
  f  P /  (s  (100  P)  f  P 
f F  q D
S  D2 4
El nivel del sedimento se obtiene resolviendo la ecuación (8.90):
198
Manual de Filtración & Separación
zc 

0.23
96.123exp 17.9   6.05  104 (1  )11.59 d
1.5  g  qD  q  6.05  104 (1  )11.59 
D
La tabla y figura 8.40 muestran los resultados obtenidos utilizando las ecuaciones
anteriores.
F tph
fF m/s
QD m3/h
q m/s

% sol peso
zc
203.5
178.1
152.7
-8.0E-06
-7.0E-06
6.0E-06
203.54
203.54
203.54
-2.0E-05
-2.0E-05
-2.0E-05
0.40
0.35
0.30
6.3E+01
5.7E+01
5.2E+01
oo
0.93
0.35
En la tabla se muestra los resultados. Con la mayor alimentación el espesador se
rebalsa y sólo se obtiene estados estacionarios con 178.1 y 152.7 tph.
0.0
0.1
0.2
0.3
0.4
0.5
Densidad de flujo de sólidos
0.00E+00
-1.00E-05
-2.00E-05
Fracción volumétrica de sólidos
Fig. 8.43 Efecto del flujo de alimentación en la
concentración de descarga para un mismo valor del flujo
volumétrico de descarga.
Capítulo 8 Espesamiento
199
6
5
Altura en m
4
3
2
1
0
0
0.1
0.2
0.3
0.4
0.5
Fracción volumétrica de sólidos
Perfil de concentraciones para los datos de la figura anterior.
8.6.3
Dilución de la alimentación.
En todo espesador convencional la alimentación se diluye al entrar al espesador,
como hemos demostrado en la sección 8.3.6. Consideremos un espesador alimentado
con un flujo volumétrico QF , una concentración F y un flujo volumétrico de
descarga QD. La densidad de flujo de alimentación será f F  Q F F S y la velocidad
volumétrica q  Q D S . Para obtener un estado estacionario se debe regular QD de
modo que q  f F D , esto es Q D  Sf F D . Si la concentración de alimentación es
menor que la crítica, en la zona de alimentación regirá la ecuación de Kynch para el
espesamiento continuo, entonces para z=L:
qL  f bk  L   f F
(8.91)
Como se puede observar en la figura, la concentración en z=L, denominada
concentración conjugada, no es la de alimentación y tampoco es arbitraria y depende
de la densidad de flujo de alimentación fF y de la velocidad volumétrica q. El valor de
L se obtiene resolviendo la ecuación implícita (8.91).
Ejemplo 9
Consideremos una suspensión de partículas de densidad 2.5 g/cm3 caracterizada
por la siguiente función densidad de flujo batch f bk ()  6.05  104 (1  )12.59 .
Calcular la concentración conjugada L para la operación de un espesador de 60 m de
200
Manual de Filtración & Separación
diámetro alimentado con una pulpa de concentración PF=27.1% de sólidos en peso,
para FF=183 tph y caudal de descarga QD=203.5 m3/h.
0.0
0.1
0.2
0.3
0.4
0.5
0.6
Densidad de flujo de sólidos m/s
0.00E+00
D
-5.00E-06
L
F
-1.00E-05
-1.50E-05
-2.00E-05
Fracción volumétrica de sólidos
Fig. 8.44 Dilución de la alimentación.
6
5
Altura en m
4
3
L=0.01709
2
1
0
0
0.1
0.2
0.3
Fracción volumétrica de sólidos
Fig. 8.45 Dilución de la alimentación.
La ecuación a resolver es:
qL  f bk  L   f F
0.4
Capítulo 8 Espesamiento
201
qL  6.05 104 L (1  L )11.59  f F
fF 
q
 FF
183

 7.2 *106 m / s
3600 * s *S 3600 * 2.5* 2827
Q D
203.5

 2.0 *105 m / s
3600 *S 3600 * 2827
El resultado es: L  0.01709 , esto es: 4.17% de sólidos en peso.
Como en la mayoría de los casos la pulpa que entra a un espesador se diluye,
cabe la pregunta si tuviese alguna ventaja el diluir la pulpa antes de alimentarla al
espesador. Efectivamente podemos indicar dos ventajas. En primer lugar, una pulpa
concentrada que entra a una zona diluida, lo hace como una corriente de densidad, de
modo que su distribución para formar una zona homogénea en el espesador tomará un
cierto tiempo. Esto puede evitarse si la concentración de la alimentación es similar a la
reinante en la zona superior del espesador. En segundo lugar, el floculante se introduce
en la alimentación al espesador, por lo que si la pulpa sufre una dilución, el agua
contenida en ésta se mezclará con agua del espesador, y su contenido de floculante
deberá diluirse nuevamente, lo que podría causar problemas en su distribución.
Por otra lado, la dilución de la alimentación requiere agua, la que generalmente
es escasa en las plantas de procesamiento de minerales y, por lo demás, los espesadores
están destinados a concentrar las suspensiones y no diluirlas. Estas dos necesidades
contrapuestas se solucionan si se introducen mecanismos en la alimentación a
espesadores que permitan una autodilución de la pulpa de entrada. Para ello se utiliza
el agua de rebalse del propio espesador. Los mecanismos más utilizados para diluir la
alimentación se muestran a continuación.
Dilución por Rebalse
Debido a la mayor densidad de la pulpa de la alimentación con respecto al agua,
el nivel del agua de rebalse es siempre mayor que el nivel de la pulpa en el feedwell,
como se indica en la figura.
z11  z 2 2  z33 ,con z3  z1  z 2
z1  (z agua  z 2 )
donde  es la densidad de pulpa. Esto permite derivar parte del agua de rebalse a la
pulpa de alimentación a través de aberturas en el feedwell. La cantidad de agua
traspasada al feedwell será constante e independiente de las condiciones de
alimentación.
202
Manual de Filtración & Separación
Fig. 8.46 Dilución de la alimentación por rebalse del agua de
rebalse, (Folleto Supaflow de Outokumpu Group Co.).
Fig. 8.47 Diseño de ventanas en el feedwell para diluir la
alimentación, (Catálogo Supaflow de Outokumpu Group
Co.).
Dilución por Jet
Cuando se inyecta un flujo a alta velocidad en un flujo estanco, el chorro
succiona agua del medio y lo incorpora a su flujo. La cantidad de agua succionada
Capítulo 8 Espesamiento
203
depende del diámetro del chorro y de su velocidad. Este hecho se aprovecha para diluir
el flujo de alimentación a un espesador, como se muestra en la figura siguiente.
La altura del cajón de alimentación de la pulpa permite regular la velocidad del
chorro y. Por lo tanto, la cantidad de dilución agua succionada. La figura siguiente
muestra la forma de implementar este mecanismo por una empresa manufacturera.
Fig. 8.48 Dilución mediante jet Eductor, (Catálogo Supaflow de
Outokumpu Group C.).
Fig. 8.49 Diseño de un sistema de dilución mediante Jet, E-Duc
(Catálogo EIMCO Process Equipment Co.).
8.6.4
Inventario de material en el espesador
Se denomina inventario del espesador el tonelaje de pulpa almacenado en su
interior. Este inventario consiste en una suspensión de concentración conjugada L y
un sedimento de concentración variable entre c    D . Entonces el inventario está
dado por:
204
Manual de Filtración & Separación


M E  gS  L  z c  L 

c

D

'e ((z))f bk ((z))


f F  q(z)  f bk ((z)) 

(8.92)
Ejemplo 10
Supongamos que tenemos una pulpa cuyos parámetros de espesamiento son:
f bk ()  6.05  104 (1  )12.59 m / s
0
para   c = 0.23

e ()  
5.35  exp 17.9  m / s para   c = 0.23
y
Alimentemos un espesador de 60 m de diámetro y 6 m de altura con un flujo
másico de sólidos, en tph, de FF=178.1 y 152.7 a una concentración de PF=21.7 % de
sólidos en peso, obteniéndose concentraciones de descarga de 57.4 y 61.0 % de sólidos
en peso. La densidad material del sólido es de 2.5 t/m3. Calcular el inventario de
sólidos en el espesador en los dos estados estacionarios indicados y graficar las curvas
de flujo y perfiles de concentración.
FF (tph)  178.1  3600  2.5  f F  2827 f F  7.0  106 m / s
FF (tph)  196.0  3600  2.5  f F  2827 f F  7.7  106 m / s
D  1  57.4 /  (2.5  (100  57.4)  1  57.4   0.350
D  1  61.0 /  (2.5  (100  61.0)  1  61.0   0.390
q
f F 7.0  106 7.7  10 6


 2.0  105 m / s
D
0.350
0.39
zi  L

M E  gS
zi  i 
zi  0
Las concentraciones conjugadas resultan ser L  0.01316 y 0.01476 .
El resultado se muestra en la tabla y figura que sigue:
F tph
fF m/s
QD m3/h
q m/s

zc
Inventario t
178.1
196.0
-7.00E-06
-7.70E-06
203.54
203.54
-2.00E-05
2.00E-05
0.35
0.39
0.93
3.91
2437.4
9175.4
Capítulo 8 Espesamiento
205
0.0
0.1
0.2
0.3
0.4
0.5
0.6
Densidad de flujo de sólidos m/s
0.0E+00
-1.0E-05
-2.0E-05
Fracción volumétrica de sólidos
Densidad de flujo versus concentración
7
6
Altura en m
5
4
3
2
1
0
0
0.1
0.2
0.3
0.4
Fracción volumétrica de sólidos
Perfil de concentraciones
8.6.5
Capacidad máxima
De acuerdo a la sección 8.5.3, el área unitaria básica de un espesador se puede
obtener de la función G  , D  , para L    D , definida en la forma:
G  , D  
 
 m2
 1

s f bk ()  D
 kg s
1
Invirtiendo esta expresión y expresándola en t/h, obtenemos el tonelaje unitario TU:
206
Manual de Filtración & Separación
TU  , D  
3600s f bk ()
tph m 2
 

 1


 D

(8.93)
El tonelaje unitario máximo que puede ser tratado por un espesador se obtiene del
valor mínimo de la función TU  , D  para valores de L    D :
Fmax  S  TU min  , D  ;
L    D
(8.94)
Ejemplo 11
Para los datos de los ejemplos anteriores, determinar la capacidad máxima Fmax ,
en tph, del espesador de 60 m de diámetro para las concentraciones de descarga de 57.4
y 61% de sólidos en peso.
D 
57.4
 0.350
2.5  (100  57.4)  57.4
D 
61.0
 0.385
2.5  (100  61.0)  61.0
TU  ,0.350  
3600  2.5  6.05  104    (1  )12.59
 

 1


 D

tph m 2
Usando esta expresión podemos construir las curvas de la figura 8.41.
La figura 8.41 muestra funciones TU  , D  para L    D , para las
concentraciones de descarga de D  0.35 y D  0.385 , dando un valor único de
0.07 tph/m2. Como el área del espesador es de 2827 m2, el tonelaje máximo capaz de
ser procesado es de 197.9 tph. Sin embargo, del problema anterior observamos que con
196 tph se tiene una altura de 4 metros de sedimento, lo que parece razonable como
máximo.
8.6.6 Estados estacionarios posibles
Hemos visto que la alimentación generalmente se diluye a la concentración
conjugada al entrar al espesador. Por otra parte, un espesador queda muchas veces
limitado por la velocidad de sedimentación de la suspensión existente inmediatamente
bajo el nivel del agua de rebalse, esto es, por la concentración conjugada como se ve en
la figura 8.41. Finalmente, un estado estacionario sólo se obtendrá si la densidad de
flujo de alimentación fF está por sobre la curva de flujo fk().
Capítulo 8 Espesamiento
207
3.00E-01
Tonelaje Unitario TU tph/m2
2.50E-01
2.00E-01
D=0.3.5
1.50E-01
1.00E-01
Tumin=7.0E-2 tph/m 2
5.00E-02
D=0.3.85
L
0.00E+00
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Fracción volumétrica de sólidos
Tonelaje Unitaria TU máximo capaz de ser procesado.
Ejemplo 12
Considere un espesador cuyos parámetros de espesamiento son los dados en el
ejemplo 10. Para una alimentación de concentración 21.7%, y una descarga deseada de
60.5% de sólidos, ambos expresados en peso, establezca cual de los siguientes flujos
de descarga 50.9, 152.6 y 305.2 m3/h resultan en estados estacionarios.
Las concentraciones de alimentación y descarga deben ser expresadas como
fracciones volumétricas mediante la ecuación:   f  P /  (s  (100  P)  f  P  ,
resultando F=0.10 y D=0.38. Las velocidades volumétricas son q=QD/S, dando
q1=5*10-6, q2=1.5*10-5y q3=3*10-5m/s. La figura muestra dos estados estacionarios
posibles y uno cuya densidad de flujo de alimentación es demasiado alto.
Los dos estados estacionarios posibles se obtienen con fF1=-1.90*10-6 y fF2=5.70*10-6 m/s, correspondiente a 48.3 y 145.0 tph de sólidos de alimentación. La
densidad de flujo de fF3=-1.14*10-5 m/s, correspondiente a 289.9 tph, es imposible
porque corta la curva de flujo. La figura 8.43 muestra los perfiles de concentración
para estos tres casos.
208
Manual de Filtración & Separación
0,000
0,00E+00
0,100
0,200
0,300
0,400
0,500
0,700
q1=5E-6
-5,00E-06
Densidad de flujo de sólidos fk
0,600
-1,00E-05
q2=1.5E-5
-1,50E-05
-2,00E-05
q3=3E-5
F=0.1
D=0.38
-2,50E-05
Fracción volumétrica de sólidos
Dos estados estacionarios posibles con q1 y q2 y uno
imposible con q3 .
7
6
Altura m
5
F1=289.9 tph
4
F1=145.0 tph
3
2
1
F1=48.3 tph
0
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Fracción volumétrica de sólidos
Fig. 8.43 Perfiles de concentración para los dos estados estacionarios con
capacidades de 48.3 t/h y 145/t/h y para el tonelaje de 281.9 t/h en que el
espesador se rebalsa.
Capítulo 8 Espesamiento
209
8.6.7 Efecto del floculante sobre la capacidad de un espesador
Consideremos un caso en que se realizan pruebas de sedimentación de caliza, de
densidad =2.5 g/cm3, molida a 58% -200 mallas, con dosis de 3, 4.5, 6, 9 y 12 g/t de
poliacrilamida como floculante y concentraciones de 2.5, 6.0, 11.6 y 30.6 % de sólidos
en peso. Calculando las velocidades iniciales de sedimentación y, mediante ellas, las
densidades de flujo de sólido se obtiene los resultados de la figura (Garrido y Concha
1999.
0
0,1
0,2
0,3
0,00E+00
Densidad de flujo de sólidos m/s
-5,00E-05
0 gr/ton
-1,00E-04
3 gr/ton
4.5 gr/ton
-1,50E-04
12 gr/ton
fbk)=uoo(x)**(1-)
31
6 gr/ton
-2,00E-04
9 gr/ton
-2,50E-04
Fracción volumética de sólidos
Fig. 8.43 Densidad de flujo de sólidos versus fracción volumétrica de
sólidos, representando el efecto de la concentración de sólidos y la
dosificación de floculante sobre mineral de carbonato de calcio, con
u  (x)  9.60 *106 x  1.19 *10 4 x 2  3.76 *103 x  5.73*10 4 , donde x es la dosis
de floculante en g/t de mineral.
Con estas correlaciones se puede estimar la capacidad de un espesador continuo
para obtener una descarga con la concentración 37% de sólidos en peso (=0.190), a
las tres siguientes dosificaciones de floculante 0, 3 y 9 g/t. Para cada uno de ellas la
densidad de flujo de Kynch es f bk  u  (x) *  *(1  )31 .
Dosis gr/t
u m/s
q m/s
fF m/s
F/S tph/m2
0
5.73*10-4
-5.89E-5
1.12E-5
0.101
3
1.43*10-3
-1.12E-4
2.12E-5
0.191
9
-2
-1.80E-5
3.42E-5
0.308
2.10*10
210
Manual de Filtración & Separación
donde F / S  f F  s  3600 en tph/m2. La figura 10 muestra la capacidad máxima de
espesamiento para las tres dosificaciones de floculante, 0, 3 y 9 g/t.
0
0,05
0,1
0,15
0,2
0,25
0,3
0,00E+00
-5,00E-06
fF=1.12E-05
Densidad de flujo de sólidos
-1,00E-05
-1,50E-05
fF=2.12E-05
-2,00E-05
-2,50E-05
-3,00E-05
fF=3.42E-05
-3,50E-05
Serie1 3 gr/ton
-4,00E-05
Serie2 9 gr/ton
-4,50E-05
Serie3 0 gr/ton
-5,00E-05
Fracción volumétrica de sólidos
Fig8.44 Capacidad máxima de espesamiento para una descarga con
=0.190 y dosis de 0, 3 y 9 g/t.
El hecho que un cambio de dosificación de floculante influya en los parámetros
de espesamiento de forma tal que la capacidad del espesador cambie
significativamente, como es el caso mostrado anteriormente, en que la capacidad se
duplico y triplicó al pasar de 0 a 3 y 9 g/t respectivamente, muestra que la adición de
floculante es una variable de suma importancia que no puede ser dejada sin control.
8.7 INVESTIGACIÓN, DESARROLLO Y TRANSFERENCIA
TECNOLÓGICA
Aunque el campo de la separación sólido-líquido ha recibido gran atención en el
último tiempo, con estudios fundamentales en espesamiento, los que han permitido
establecer la dinámica del proceso y con adelantos en el diseño de nuevos equipos de
filtración, especialmente los filtros a presión continuos, éste continua siendo un área
deficitaria en conocimientos y deficitaria en la aplicación de conocimientos bien
establecidos en otros campos de la ciencia. Es así como los fundamentos de la
Capítulo 8 Espesamiento
211
floculación no han sido suficientemente asimilados en el procesamiento de minerales y
la selección de reactivos y su dosificación sigue siendo empírica. El rol de los
reactivos surfactantes y floculantes hidrófobos tampoco ha sido suficientemente
estudiado en su efecto en el deshumedecimiento de queques de filtración. Aspectos
fundamentales del espesamiento como la caracterización reológica del sedimento no
ha recibido la atención necesaria. Esto ha impedido obtener modelos adecuados para el
diseño, operación y control de las rastras. El flujo en lecho poroso compresible y su
aplicación a la filtración a presión necesita estudio. Finalmente, la comprensión de la
operación correcta de un espesador no está completa. Es necesario estudiar y modelar
la alimentación y la descarga y el concepto de un espesador de alta capacidad aún no
ha sido dilucidado. La optimización y control de sistemas de filtración continua y
espesadores continua siendo un problema vigente y la recuperación de agua en las
plantas de procesamiento de mineras es uno de los problemas actuales que se
agudizarán en el futuro. En las siguientes secciones analizaremos estas deficiencias.
8.7.1 Efecto de los floculantes en el espesamiento
El campo de la fisicoquímica nos ha entregado un conocimiento bastante
detallado de la interacción coloidal entre partículas, de la estructura de los agentes
coagulantes y floculantes y de la cinética de floculación. Parte de ello lo hemos
resumido en el Capítulo 10 de este Manual. Sin embargo, la aplicación de estos
reactivos en el proceso de espesamiento no es del todo conocido.
Los ensayos que se realizan normalmente para dosificar floculantes en el
espesamiento determinan la velocidad de sedimentación del sólido a diversas
concentraciones de sólidos y cantidades de floculante. Esto significa que el efecto de
floculantes en la velocidad de sedimentación es bien conocido. A pesar de ello, pienso
que no se ha tomado debida conciencia del efecto de interacción entre concentración de
sólidos y concentración de floculantes. En este sentido hemos indicado que es
necesario construir las curvas de densidad de flujo de sólidos para las distintas dosis de
floculantes y en esta forma conocer el efecto que el floculante tiene en los parámetros
de esta función u  y n de f bk ()  u  (1  ) n . Hasta donde hemos podido
establecer, la dosificación de floculante afecta solamente a u  , pero es posible que no
sea así en todos los casos.
Lo que aún no se ha estudiado es el efecto cuantitativo de la dosificación de
floculantes en las características del sedimento, especialmente en su reología, esto es
en su compresibilidad y en su cizalle. Este conocimiento es fundamental, ya que estas
características del sedimento influyen en la concentración de la descarga y en el torque
de las rastras.
Otro aspecto importante de considerar, es que la adición de floculante se utiliza
como una de las variables de control de un espesador. Es, por lo tanto, fundamental
conocer su acción dinámica.
212
Manual de Filtración & Separación
8.7.2 Reología de sedimentos y descarga de un espesador
Relacionado con el punto anterior está el problema de conocer el
comportamiento reológico de los sedimentos de un espesador. No es frecuente que los
ensayos que se realizan para diseñar un espesador incluyan pruebas de reología de la
suspensión, ni que el control metalúrgico del equipo incluya este tipo de pruebas. Esto
contrasta con el gran cuidado que pone el operador en el control del torque en los
espesadores. Ellos saben que una sobre carga de las rastras puede ser desastrosa y, por
lo tanto, trabajan a valores de torque muy por debajo de los que el sistema motriz del
espesador puede tolerar. Un conocimiento de la reología del sedimentos y un
conocimiento del efecto de esta reología en el torque de las rastras es una información
que sería de gran importancia para el control metalúrgico del proceso de espesamiento.
Hay algunos intentos de establecer relaciones en este campo pero es necesario más
investigación en este campo.
Estos estudios reológicos pueden ser complementados con modelación
fenomenológica del movimiento de las rastras de un espesador y de simulación
mediante Mecánica de Fluidos Computacional (CFD), tal como se mostró en el III
Coloquio de Filtración y Separación realizado en Santiago en 1999 (Köck y Concha
1999) y en el capítulo 14 de este Manual.
8.7.3 Efecto de surfactantes y floculantes hidrófobos en la filtración
Tal como lo hemos indicado en los Capítulos 9 y 11, la filtración se realiza en
etapas secuenciales cuyos fundamentos son diferentes. En primer lugar, las variables
que influyen en la formación del queque no son las mismas que son importantes en la
expresión de éste o en el soplado. Es así como en la última etapa debemos reconocer
que propiedades del sistema sólido-líquido-gas, tales como la saturación, la presión
capilar, la tensión superficial del líquido y el ángulo de contacto trifásico son de
primordial importancia. Es natural entonces, que agentes que varíen estas propiedades
tendrán efecto en la etapa de deshumedecimiento, desaguado o soplado, como se la
suele llamar.
El efecto de surfactantes es reconocido en el campo de la filtración, pero no hay
estudios sistemáticos que muestren cuantitativamente el cambio de las condiciones
superficiales del sólido, de la presión capilar y, en definitiva de la permeabilidad del
queque, como tampoco existen métodos que predigan el efecto de reactivos que
producen beneficio en el deshumedecimiento de queques de filtración (Laskowski
2000). En general, el procedimiento empleado es el de probar reactivos directamente
en la filtración, sin estudiar los mecanismos mediante los cuales el efecto se realiza.
Hay aquí un interesante campo de investigación para establecer métodos eficaces de
probar reactivos para la filtración.
Capítulo 8 Espesamiento
8.7.4
213
Flujo en lecho poroso compresible
Los fundamentos de la filtración que hemos presentado en este Manual están
basados en la teoría de flujo en un medio poroso rígido. Todos sabemos que durante la
filtración el queque sufre deformaciones debido a la compresión, pero también
sabemos que en la mayoría de los casos de filtración este efecto se puede despreciar.
Es así, por ejemplo, que en la filtración a vacío los esfuerzos compresivos a los que
está sometido el queque son pequeños y, por lo tanto, también las deformaciones, las
que pueden ser despreciadas. En la filtración a presión la situación es diferente. Aquí
hay etapas en que el queque puede ser consideradas incompresible y otras en que
definitivamente es compresible. La formación del queque se realiza con un crecimiento
paulatino y sin mucha deformación de éste. También en la etapa de soplado el queque
puede ser considerado incompresible, pero en la etapa de expresión, éste
definitivamente se deforma violentamente.
En este trabajo hemos superado este problema tomando en consideración que la
etapa de expresión es muy corta y que en ella no se elimina una cantidad significativa
de agua, comparada con la etapa de formación del queque, ni es capaz de llegar a las
humedades que se logran con el soplado. Por esta razón, lo que hemos hecho en este
Manual, es considerar el queque como incompresible, tanto para las etapas de
formación del queque como para la etapa de soplado, pero en cada una de estas etapas
la porosidad es diferente. Hemos considerado que lo que hace la etapa de expresión es
reducir la porosidad desde aquella válida en la formación del queque a aquella válida
en el soplado, eliminando, por cierto, la cantidad de agua asociada a esta reducción de
porosidad.
Cuando hay variaciones significativas de porosidad durante la formación del
queque, es posible considerar una porosidad media y variables asociadas a esta
porosidad media.
Un análisis riguroso de la etapa de expresión en la filtración, considerando la
porosidad como variable, ha sido realizado por Shirato (Shitrato et al 1986). Sin
embargo, este enfoque no ha llegado a ser aplicado en la práctica de la filtración por
falta de soluciones numéricas de las ecuaciones que constituyen el modelo. Un
importante paso en el desarrollo de la teoría de filtración con compresión se dio
recientemente con el trabajo de Bürger et al (2000) que presenta una completa solución
de la filtración con sedimentación y expresión mediante simulación numérica.
Por otra parte, actualmente se está utilizando técnicas novedosas para resolver
problemas complejos en flujo en medios porosos. Con métodos como los autómatas
celulares es posible establecer ecuaciones constitutivas que predicen la permeabilidad
variable de un medio cuando está sometido a esfuerzos que cambian su porosidad. Esta
línea de trabajo es muy interesante y novedosa.
8.7.5 Modelación de la alimentación
En la sección sobre operación de espesadores hemos mencionado la importancia
que tiene la manera de alimentar un espesador con relación a la auto dilución, a la
214
Manual de Filtración & Separación
mezcla del floculante y a la dispersión del sólido que trae el flujo de alimentación. El
diseño del feedwell tiene una importancia fundamental en este sentido.
El flujo de alimentación a un espesador, que siempre entra en un ambiente de
una concentración de sólidos diferente, puede ser considerado como una corriente de
densidad que penetra en un fluido de otra densidad y debe dispersarse. Estudios
semejantes son numerosos en el campo de la hidráulica, especialmente relacionados
con la desembocadura de ríos en el mar o de poluyentes en una masa de agua. Esta
analogía no ha sido estudiada en los espesadores y aparece como muy atractivo
realizarla. Para ello es posible utilizar técnicas de CFD (ver capítulos 12 y 14 de este
Manual).
8.7.6 Espesadores de alta capacidad y alta densidad
Los espesadores de alta capacidad tuvieron un auge hace algunos años pero
parece que, en general, no cumplieron con las expectativas puesta en ellos. Se esperaba
un aumento de capacidad de 5 a 10 veces la de un espesador convencional, lo que no
lograron. Por otra parte, estos espesadores han demostrado ser muy difícil de controlar,
por lo que en muchas faenas han sido discontinuados. Con el tiempo, se ha podido
demostrar que lo que se creía era efecto de este tipo de espesadores en el aumento de
capacidad se debía a una mejora sustancial en la forma de adición y en la cantidad de
floculante agregado. Es así como una del empresas que diseñó e impulso originalmente
los espesadores de alta capacidad, ahora denomina con este nombre a espesadores
convencionales que proveen una muy buena acción de floculantes y auto dilución que
han mejorado la capacidad de estos tipos tradicionales de espesadores.
Aquí llamaremos espesadores de alta capacidad, como se vio en la sección de
quipos del capítulo 8, a aquellos equipos que son alimentados por debajo de la capa de
sedimento y que tienen por característica la ausencia de una zona de sedimentación.
Existe solamente un trabajo publicado sobre teoría de espesamiento de alta
capacidad (Concha, Bustos y Barrientos 1995) y es un trabajo preliminar. Es necesario
estudiar con más detalle este tipo de espesadores y establecer sus ventajas y
desventajas en forma cuantitativa. Especialmente es necesario estudiar la dinámica del
proceso ya que, en este caso, el control automático es fundamental.
Los espesadores de alta densidad fueron introducidos en la industria del
aluminio para obtener descargas muy concentradas en forma de pastas. Este ejemplo ha
interesado a la industria del cobre y aparece como muy atractivo estudiar el
comportamiento de estos espesadores para concentrados y relaves con el fin de
recuperar el máximo de agua en las plantas de procesamiento de minerales. Este
requerimiento se hace cada día más necesario. Los espesadores de alta densidad son
espesadores con alimentación convencional, esto es en un feedwell que descarga en un
medio más diluido que la alimentación, pero que tienen una altura mucho mayor que
los espesadores convencionales. La altura de un espesador grande convencional es de
alrededor de 7 metros, mientras que la de un espesador de alta densidad puede ir de 9 a
15 metros. Esta altura, junto con un menor diámetro, un cono más pronunciado para
Capítulo 8 Espesamiento
215
favorecer la descarga y rastras especialmente diseñadas, permite tener un nivel más
alto de sedimento y, por lo tanto, llegar a una mayor concentración de sólidos en la
descarga. Las condiciones de operación y la dinámica de estos equipos no han sido
estudiados para la industria del cobre y es un tema relevante en la actualidad.
8.7.7 Optimización de los ciclos de filtración
En general, la mayoría de las plantas de procesamiento de minerales realizan
optimización de sus procesos y, entre ellos, del proceso de filtración. También existen
empresas proveedoras de equipos que realizan este tipo de trabajo en forma muy
eficiente, tales como los auspiciadores de este proyecto y empresas especialistas en el
tema como Bokela y Cettem. Sin embargo, existe una necesidad de aplicar principios
más rigurosos, tales como los expuestos en este Manual, y técnicas más modernas de
optimización. Para ello es necesario desarrollar un conjunto de actividades y acciones
que permitan demostrar la bondad de este nuevo enfoque.
8.7.8 Optimización de espesadores
La experiencia ha demostrado que hay numerosos espesadores en muchas
empresas mineras nacionales que no operan en forma eficiente y que requieren, para
mejorar su eficiencia, de un estudio de optimización. Este trabajo requiere del estudio
de los parámetros de espesamiento de la pulpa, de la cuantificación de reactivos
floculante y su adición, de la forma de alimentación y dispersión del floculante, de la
autodilución, de la forma de la descarga, de la reología del sedimento y del
funcionamiento de las rastras, de la medición de variables como concentración de
descarga, de presión del fondo, de nivel de sedimento, de turbidez del agua. Con esta
información se puede cuantificar la respuesta dinámica del proceso a perturbaciones y
se puede establecer estrategias de control metalúrgico y control automático.
8.7.9 Recuperación de agua en sistemas de separación sólido-líquido
Cada día se hace más necesaria la recuperación de agua en los procesos de
concentración de minerales y esta acción se torna crítica en aquellas grandes empresas
en que se pretende aumentar en forma significativa la producción y donde el suministro
de agua es limitado. Los procesos de separación sólido-líquido que se utilizan
actualmente para estos fines tienen sus limitaciones, en algunos casos económicas,
como en la filtración que se hace muy costosa para materiales como relaves, o en otros
limitaciones técnicas, como en la descarga de espesadores cuyo material debe ser
transportado por tuberías o canaletas a su destino, sea este los filtros de concentrado o
el depósito de relaves.
Aparece como muy pertinente hoy día un estudio para mejorar la recuperación
de agua de las plantas re-diseñando circuitos de separación sólido-líquido, cambiando
los sistema de transporte y utilizando equipos diferentes a los actuales, como por
ejemplo los espesadores de alta densidad.
216
Manual de Filtración & Separación
8.7.10 Dinámica y control de proceso
La mayor parte de los espesadores tienen, desde su diseño y construcción,
asociados instrumentos de medición de algunas variables y sistemas de control. En la
sección 8.2 de este Manual se ha discutido en detalle este hecho. Sin embargo, estos
sistemas de control no están asociados, o sus puntos de control regulados, por la
dinámica del proceso. En general ellos son ajustados empíricamente. Hace falta
estudios de la dinámica de espesamiento, de la característica de cada material, del
comportamiento de los diversos esquemas de control y de la introducción de nuevos
instrumentos para la medición de variables importantes que actualmente, por falta de
medición, deben ser consideradas perturbaciones.
REFERENCIAS
Adamson, W.H. Jr. and Glasson, P.S., MIT Thesis 1925.
Ardillon, “Les mines du Laurion dans l’antiquité”, 1897.
Adorjan, L.A., A theory of sediment compression, XI IMPC, Caglary, 1975, 1-22.
Adorjan, L.A., Determination of thickener dimensions from sediment compression
and permeability test results, Trans. Inst. Min. Met., Sec C, 85, 1976, 157-163.
Agricola, G., De Metallica, 1556, Translated by H.C. and L.H. Hoover, Dover
Publications Inc., New York, 1950.
Ashley H.E., Theory of the settlement of slimes, mining and Scientific Press, June 12,
1909.
Austin, L.G., Lee, C.H., Concha, F. And Luckie, P.T., Hindered settling and
classification partition curves, Minerals & Metallurgical Processing, November 1992,
161-168.
Bascur, O., A unified solid-liquid separation framework, First Regional Meeting,
American Filtration society, Houston, Texas, October 30-November 1, 1989, 1-11.
Becker, R., Espesamiento continuo: Diseño y Simulación de Espesadores, Memoria de
Titulo, Ingeniería Metalúrgica, Universidad de Concepción, 1982.
Behn, V.C., Settling behavior of waste suspensions, Proceeding of the ASCE, J.
Sanitary Eng. Div., October, 1957, 1423-5 to 1423-20.
Buscall, R. And White, L.R.M The consolidation of concentrated suspensions, J.
Chem. Soc. Faraday Trans. 1, 83, 1987, 873-891.
Bustos, M.C., On the existence and determination of discontinuous solutions to
hyperbolic conservation laws in the theory of sedimentation, Doctoral Thesis, TH
Darmstadt, 1984.
Bustos, M.C. and Concha, F., Simulation of batch sedimentation with compression,
AIChE J., 34(5) 1988, 859-861.
Capítulo 8 Espesamiento
217
Bustos, M.C. and Concha, F., On the construction of global weak solutions in the
Kynch theory of sedimentation, Mathematical Methods in the Applied Sciences, 10,
1988, 245-264.
Bustos M.C., On the existence of a global weak solution for the problem of
sedimentation with compression, J. Mathematical Analysis and Applications, 142(2)
1989, 413-421.
Bustos, M.C. and Paiva, F., Control of continuous sedimentation of ideal suspensions
as an initial and boundary value problem, Mathematical Methods in the Applied
Sciences, 12, 1990, 533-548.
Bustos, M.C., Concha, F. And Wendland, W., Global weak solutions to the problem of
continuous sedimentation of an ideal suspension., Mathematical Methods in the
Applied Sciences, 13, 1990, 1-22.
Bustos, M.C. and Concha, F., Boundary conditions for the continuous sedimentation
of ideal suspensions, AIChE J., 38(7) 1992, 1135-1138.
Bustos, M.C. and Concha, F., Kynch theory of sedimentation. Chapter 2 in
Sedimentation of Small Particles in a Viscous Fluid, Ed. E.M. Tory, Advances in
Fluid Mechanics, Vol 7. Computational Mechanics Publications, Southampton, 1996,
7-49.
Bustos, M.C., Concha, F., Bürger, R and Tory, E., Sedimentation and Thickening;
Phenomenological Foundation and Mathematical Theory., Kluwer Academic
Publisher, Dordrecht, Netherlands, 1999.
Bürger, R. An initial-boundary value problem of quasilinear degenerate parabolic
equation in the theory of sediment with compression, Doctoral Thesis, University of
Stuttgart, 1996.
Bürger, R. And Wendland, W., Existence, uniqueness and stability of generalized
solutions of an initial-boundary value problem for a degenerating quasilinear parabolic
equation, Bericht 97/39, Sonderforscungsbereich 404, Mehrfeldprobleme in der
Kontinuumsmechanik, 1997a, 1-25.
Bürger, R. And Wendland, W., Mathematical problems in sedimentation, Proceedings
of the 3d. Third Summer Conference on Numerical Modelling in Continuum
Mechanics, Prague, Sept 8-11, 1997bb, 1-15.
Bürger, R., Bustos, M.C. and Concha, F., Settling velocities of particulate systems.
Part 9. Phenomenological theory of sedimentation: Numerical Simulation of the
transient behavior of flocculated suspensions in an ideal batch and continuous
thickener, Int. J. Mineral Process., 55, 1999, 267-282.
Bürger, R., Concha F. And Wendland, W., Modelling equations for gravitational
sedimentation-consolidation processes, ZAMM, 00, 1998, 1-18.
Bürger, R. and Concha F., Mathematical model and numerical simulation of the
settling of flocculated suspensions, Int. J. Multiphase Flow, 24, 1998, 1005-1023.
218
Manual de Filtración & Separación
Bürger, R., Concha F. And Tiller, F.M., Applications of the phenomenological theory
to several published experimental cases of sedimentation process, J. Chem Engn.,
80(1-3) 2000, 105-118.
Bürger, R. And Wendland, W., Mathematical model and viscous splitting
approximation for the sedimentation-consolidation processes, 4th Int. Conf. On
Numerical Meth. and Appl., Sofia, Bulgaria, 1998c, 19-23.
Bürger, R. And Wendland W., Entropie-boundary conditions in the theory of
sedimentation with compression, Math. Meth. Appl. Sci., 21, 1998ª, 865-882.
Clark, A., A note on the settling of slimes, Eng. Mining J., 99,(9), 1915, 412.
Comings, E.W., Ind. Eng. Chem., 32,1940, 663.
Comings, E.W., Pruiss, C.E. and DeBord, C., Continuous settling and thickening, Ind.
Eng. Chem., Eng, Design and Process Dev., 46(6)1954, 1164-1172.
Coe, H.S. and Clevenger, G.H., Methods for determining the capacities of slimesettling tanks, Trans. AIME 55, 1916,356-385.
Concha, F. And Bustos, M.C., Theory of sedimentation of flocculated fine particles,
Flocculation, sedimentation and consolidation, B.M. Moudgil and P. Somasundaran,
Eds., New York, 1985, 275-284.
Concha, F., Bustos, M.C. and Barrientos, A., Phenomenological theory of
sedimentation. Chapter 3 in Sedimentation of Small Particles in a Viscous Fluid, Ed.
E.M. Tory, Advances in Fluid Mechanics, Vol 7. Computational Mechanics
Publications, Southampton, 1996, 51-95.
Concha, F. y Bürger, R. Diseño de espesadores, Informe Interno, Laboratorio de
Sistemas Particulados, Universidad de Concepción, 2000.
Concha F., Lee, Ch.H. and Austin, L.G., Settling velocities of particulate systems. Part
8. Batch sedimentation of polydispersed suspensions of spheres, Int. J. Mineral
process., 35, 1992, 159-175.
Concha, F. And Barrientos, A., A critical review of thickener design methods, Kona,
Powder and Particles N° 11, 1993, 79-104.
Concha, F., Barrientos, A. And Bustos, M.C., Phenomenological Model of high
capacity thickening, XXII IMPC, San Francisco, Vol 2., 1995, 75.
Concha, F. And Bürger, R., Wave propagation phenomena in the theory of
sedimentation, In Numerical method for wave propagation phenomena, Eds. E.F.
Toro and J.F. Clarck, Kluwer Academic Publ., Dodrecht, The Netherlands, 1998, 173196.
Cross, H.E., A new approach to the design and operation of thickeners, J. South
African Inst. Min. Met., 63, 1963, 271-298.
Dixon D.C., Momentum-balance aspects of free-settling theory: I. Batch thickening,
Separation Science, 12(2), 1977a, 171-191.
Capítulo 8 Espesamiento
219
Dixon D.C., Momentum-balance aspects of free-settling theory: I. Continuous steadystate thickening, Separation Science, 12(2), 1977b, 193-203.
Dixon D.C., Momentum-balance aspects of free-settling theory: III. Transient
compression resistance, Separation Science, 13(9), 1978, 753-766.
Egolf, C.B. and McCabe, W.L., Trans. AIChE 33, 1937, 620.
Georgius Agricola, 1494-1994, Bergwelten, Edition Glückauf GmbH, Essen, 1994.
Forbes, D.L.H., The settling of mill slimes, Eng. Mining. J., 93, 1912, 411-415.
Free, E.E., Rate of slime settling, Eng. Mining J., 101, 1912, pages 243, 429, 509, 681.
Garrido, P. Y Concha, F., Dosificación de Floculante y su relación a la Operación y
Control de un Espesador Continuo, Anales del III Coloquio de Filtración y
Separación, Santiago, Noviembre 1999.
Garrido, P., Bürger, R. and Concha, Settling velocities of particulate system 11.
Comparison of the phenomenological sedimentation-consolidation model with
published experimental results, Int. Jl. Mineral Process., 60, 2000 (3-4), 213-227.
Nichols, H.G., A method of settling slimes, as applied to their separation from solution
in cyanide treatment, Trans. Inst. Min. Met., London, 17, 1908, 293-329.
Hazen, A., On Sedimentation, Trans. ASCE, paper 980, June 1, 1904, 45-88.
Hassett, N.J., Design and operation of continuous thickeners, The Industrial Chemist,
34, 1958, 116-120; 169-172; 489-494.
Hassett, N.J., Theories of the operation of continuous thickeners, The Industrial
Chemist, January 1961, 25-28.
Hassett, N.J., Mechanism of thickening and thickener design, Trans Inst Min. Met, 74,
1964, 627-656.
Hassett, N.J., Concentrations in a continuous thickener, Industrial Chemist, January,
1964, 29-33.
Hassett, N.J., Thickening in theory and practice, Min. Sci. Eng., 1, 1968, 24-40.
Hsia, E.S. and Reinmiller, F.W., How to design and construct earth bottom thickener,
Min. Eng., 29, 1977, 36-39.
Kammermeyer, K., Settling and thickening of aqueous suspensions, Ind. Eng. Chem.,
33(12)1941, 1484-1491.
Köck, R. y Concha, F., CFD cojo herramienta para el diseño de espesadores, Anales
del III Coloquio de Filtración y Separación, Santiago, Noviembre 1999.
Kynch, G.J., A Theory of sedimentation, Trans. Farady Soc., 48, 1952, 166-176.
Landmann, K.A., White, L.R. and Buscall R., The continuous-flow gravity thickener:
Steady state behavior, AIChE J., 34(2) 1988, 239-252.
220
Manual de Filtración & Separación
Laskowski, J.S. and Castro, S.H., 1999. Aggregation of inherently hydrophobic solids
using hydrophobic agglomerants and flocculants. In J.S. Laskowski (ed.), Polymers in
Mineral Processing-Proc. 3rd. UBC-McGill Int. Symp., 293-310, Met. Soc. of CIM,
Montreal.2000.
Michaels, A.S. and Bolger, J., Settling rates and sedimentation volumes of flocculated
kaolin suspensions, Ind. Eng. Chem. Fund., 1(1), 1962,24-33.
Mishler, R.T., Methods for determining the capacities of slime-thickening tanks, Eng.
Mining J., 1916,
Mishler, R.T., Settling slimes at the Tigre Mill, Eng. Mining J., 94(14), October 5,
1912, 643-646.
Nichols, H.G., Theory of settlement of slimes, Mining and Scientific Press, July 11,
1908, 54-56.
Petty, C.A., Continuous sedimentation of a suspension with a nonconvex flux law,
Chem. Eng. Sci., 30, 1975, 1451-1458.
Quiero, A., Determinación de los parámetros de sedimentación y compresión de una
pulpa industrial, Memoria de Título, Ingeniería Metalúegica, Universidad de
Concepción, 1994.
Ralston, O.C., The control of ore slimes, Eng. Mining J., 101, 1916, pages 763, 890.
Roberts, E.J., Thickening: Art or Science?, Trans. AIME, March 1949, 61-64; Mining
Eng., 1, 1949, 61.
Scott, K.J., Theory of thickening: factors affecting settling rate of solids in flocculated
pulps, Trans. Inst. Min Met, London, 1968, C-85, C-97.
Shannon, P.T., Stroupe E. And Tory E.M., Batch and continuous thickening, Ind. Eng.
Chem., Fundamentals, 2(3)1963 203-211.
Shannon, P.T. and Tory, E.M., Settling of slurries, Ind. Eng. Chem., 57(2)1965, 18-25.
Shannon, P.T. and Tory, E.M., The analysis of continuous thickening, Trans. SME,
235, December 1966, , 375-382.
Smiles, D.E., Sedimentation: Integral behavior, Chem. Eng. Sci., 31, 1976a, 273-275.
Smiles, D.E., Sedimentation and filtration equilibria, Separation Science, 11(1),
1976b, 1-16.
Shirato. M., Analysis of settling of thick slurries due to consolidation, J. Chem. Eng.
Japan, 3(1)1979, 98-104.
Shirato, M., Murase, T. And Iwata M., 1986. Deliquoring by expression. In Progress
in Filtration and Separation 4. Ed. R.J. Wakeman, Elsevier, 181-287.
Talmage, W.P. and Fitch, E.B., Determining thickener unit areas, Ind. Eng. Chem,
Eng. Design and Development, 47(1)1955, 38-41
Capítulo 8 Espesamiento
221
Thacker, W.C. and Lavelle, J.W., Two-phase flow analysis of hindered settling, The
Physics of Fluids, 20,(9), 1977, 1577-1579.
Tory, E.M., Absence of concentration gradients in slurries settling at high Reynolds
Numbers.
Truesdell, C., Sulle basi de la termomecanica, Rend. Acad. Sincei. 22, 1957, 33-88.
Traducción en inglés en Rational Mechanics of Materials, Int. Sci. Rev. Serv., Gordon
&Breach, New York, 1965, 292-305.
Valenzuela, R., Determinación simultánea de las ecuaciones constitutivas para el
esfuerzo efectivo del sólido y la permeabilidad de suspensiones floculadas, Memoria
de Título, Ingeniería Metalúrgica, Universidad de Concepción, 1994
Ward, H.T. and Kammermeyer, K., Sedimentation in the laboratory: Design data from
laboratory experimentation, Ind. Eng. Chem., 32, 1949, 622-626. 1940
Wilson, A.J., The living Rock, Woodhead Pub. Ltd., Cambridge, 1994.
Wilsdorf, H., Kulturgeschichte des Bergbaus. Eine illustrierter Streifzug durch Zeiten
und Kontinente, Verlag Glückauf GmbH, Essen, 1987.
Work, L.T. and Kohler, A.S., Sedimentation of suspensions, Ind. Eng. Chem. 32(10)
1940, 1329-1334.
Yoshioka, N, Hotta, Y., Tanaka, S., Naito, S. and Tsugami, S., Continuous thickening
of homogeneous flocculated slurries, Chem. Eng. Japan, 21, 1957, 66-74.
CAPÍTULO 9
FILTRACIÓN
9.1
DEFINICIÓN, EQUIPOS Y OPERACIÓN
Filtración es el proceso de separación sólido-fluido mediante el cual el sólido es
separado del fluido en una suspensión haciéndolo pasar a través de un lecho poroso,
denominado medio filtrante. El lecho retiene las partículas mientras que el fluido pasa
a través del medio filtrante y recibe el nombre de filtrado.
Para establecer el flujo a través del medio filtrante es necesario aplicar un
gradiente de presión como fuerza impulsora. Existen varias formas para aplicar este
gradiente de presión, por ejemplo: 1) la gravedad, 2) el vacío, 3) una presión, 4) un
vacío y una presión combinados, 5) una fuerza centrífuga y 6) un gradiente de
saturación. La mayor parte de estas formas de aplicar presión da lugar a diferentes
tipos de equipos de filtración, los que se reciben el nombre de filtros.
Se puede distinguir tres clases de filtración: a) la filtración con formación de
queque, b) la filtración sin formación de queque y c) la filtración profunda.
9.1.1 Filtración con formación de queque
La filtración con formación de queque se caracteriza porque el sólido de la
suspensión es retenido en la superficie del medio filtrante como una capa denominada
queque. Esto se produce naturalmente cuando los poros del medio filtrante tienen un
tamaño menor que las partículas. Cuando este no es el caso, es necesario cubrir el
medio filtrante con una delgada capa de material fibroso, denominado ayuda de
filtración, que bloquea el paso de las partículas a través del medio filtrante. En este tipo
de filtración, el flujo de suspensión es perpendicular a la superficie del medio filtrante.
La filtración con formación de queque se utiliza para suspensiones que poseen
más de un 10% de sólidos en volumen y es, sin duda, el proceso de filtración más
importante en la industria minera y en la industria de procesos en general.
9.1.2 Filtración sin formación de queque
Cuando el flujo de la suspensión es paralelo a la superficie del medio filtrante,
éste aún retiene las partículas sólidas. Sin embargo, el flujo de la suspensión produce
una tasa de cizalle muy alto, la que previene la formación de una capa de sólidos
retornándolos a la suspensión. En esta forma el líquido atraviesa el medio filtrante
222
Capítulo 9 Filtración
223
mientras que el sólido permanece en la suspensión aumentando su concentración con el
tiempo. Este tipo de filtración es útil cuando se desea concentrar una suspensión sin
que sea necesario un producto de baja humedad. Aún cuando la filtración sin
formación de queque puede ser utilizada en la separación sólido-líquido, es
principalmente utilizada en la filtración de gases polvorientos.
PULPA
p>p0
QUEQUE
MEDIO FILTRANTE
FILTRADO
p=p0
Fig. 9.1 Filtración con formación de queque
FILTRADO
CONCENTRADO
ALIMENTACION
FILTRADO
Fig. 9.2 Filtración sin formación de queque
9.1.3 Filtración profunda.
Para la filtración de partículas muy finas en suspensiones diluidas se utiliza
comúnmente filtros que tienen medios filtrantes de poros mayores que las partículas
pero de grandes espesores. Las partículas penetran en el interior del medio filtrante y
son capturadas por las fibras o partículas que constituyen el medio filtrante. Este tipo
de filtro pierde su capacidad de filtración después de un cierto tiempo y es necesario
limpiar el medio filtrante eliminando las partículas desde su interior, o sustituir el filtro
224
Manual de Filtración & Separación
por uno nuevo. Dos ejemplos de filtración profunda son los filtros de arena para
piscinas y los filtros de aire en automóviles.
SUSPENSIÓN
Medio Filtrante
FILTRADO
Fig. 9.3 Filtración profunda
Las condiciones en que se realiza una filtración depende de muchos factores,
entre los cuales destacan:
 Las propiedades del fluido, tales como su densidad, viscosidad y corrosividad.
 La naturaleza del sólido, tal como su tamaño, forma y distribución de tamaño.
 Las propiedades de la suspensión, tales como su concentración y
compresibilidad.
 La cantidad de material a tratar.
 El valor del material y si el material valioso es el sólido, el fluido, o ambos.
 Si es necesario lavar el queque.
 Si es importante o no la contaminación del producto.
9.1.4 Variables de Operación
Las principales variables en un proceso de filtración pueden ser separadas en:
variables de entrada, variables de salida, parámetros, perturbaciones y variables
controlables. El esquema indicado en la figura 9.30.
Capítulo 9 Filtración
Granulometría del
sólido
225
PERTURBACIONES
DISEÑO
S
P
Distribución de
tamaño
QF (t)
ENTRADA
S
 F (t)
QP (t)
VARIABLES
SALIDA
S
OPERACIÓN
VARIABLES DE CONTROL
(1- P) (t))
PARAMETROS
t1 ,t2 , t3
Agitación
, K(), (e),
f,  f ,  P  P
Fig. 9.4 Variables en filtración.
Variables de entrada
: Flujo QF(t) y concentración F(t).de entrada de suspensión,
Variables de salida
: Flujo de descarga QP(t) y humedad (1-P)(t).del queque,
Variables de diseño
: Área de filtración S y gradiente de presión P,
Variables de control
: Tiempo de filtración tf, de lavado tl y de secado ts,
magnitud de la agitación.
Parámetros
: Porosidad , permeabilidad k() y compresibilidad e del
queque, densidad f y viscosidad f del filtrado, densidad
P y forma P de las partículas
Perturbaciones
: Granulometría del sólido.
La mayoría de los equipos de filtración, sean continuos o discontinuos, trabajan
en ciclos de formación del queque, lavado, secado y descarga:
 Formación del queque: La magnitud de material depositado en el medio
filtrante depende del gradiente de presión, de la concentración de la suspensión
y del tiempo de succión. En este ciclo hay un flujo continuo de filtrado a través
del medio filtrante y del queque.
 Lavado del queque: La necesidad de lavar el queque depende del objetivo
perseguido por el proceso de filtración. El lavado se efectúa para eliminar
impurezas del queque o para recuperar líquidos valiosos. El lavado del queque
226
Manual de Filtración & Separación
implica calcular la cantidad mínima de agua necesaria para desplazar el líquido
de los poros y el tiempo necesario.
 Secado del queque: Secado del queque es aquella etapa en que el agua
retenida en los poros del queque es desplazada soplando aire o succionado aire
de la atmósfera. Para controlar esta etapa es necesario conocer la cantidad de
agua retenida en el queque. El criterio para seleccionar la humedad residual del
queque es económico, cuando no es una restricción del equipo.
 Descarga del queque: El desprendimiento del queque y su descarga es de gran
importancia para una operación eficiente. En el caso de filtración a vacío la
descarga es muy simple y consiste en raspar las telas y eliminar el producto
por gravedad. En el caso de filtración a presión, o filtración hiperbárica, la
descarga se complica por la necesidad de mantener la presión en la cámara, de
modo que es necesario tener válvulas que permitan presurizar y despresurizar
la zona de descarga en ciclos controlados.
9.2
Equipos para la filtración
Los equipos que utilizan presión en vez de vacío, deben usar mecanismos mucho
más complicados, especialmente para la alimentación y la descarga. Esta ventaja de los
filtros de vacío los ha hecho tradicionalmente muy populares en la industria minera y
en la industria de procesos en general.
La principal desventaja de los filtros a vacío es la obvia limitación en el máximo
gradiente de presión disponible para el proceso, el que depende de la presión
atmosférica local. Como la mayoría de las industrias mineras se encuentran situadas en
montañas a gran altitud, algunas a más de 4.000 metros de altura, el gradiente de
presión disponible es muy pequeño. Esta limitación y los grandes y recientes avances
tecnológicos en mecanismos y sistemas de control, han introducido los filtros a presión
y los han transformado en un producto preferido en la industria minera en la
actualidad.
Una alternativa interesante es la combinación de ambos tipos de filtros, esto es,
los filtros de vacío y los de presión. Si un típico filtro de vacío se introduce en una
cámara presurizada, se pude incrementar el gradiente de presión a los valores
considerados óptimos para la filtración. Estos filtros se denominan filtros hiperbáricos
y combinan la sencillez de construcción y operación de un filtro de vacío con la ventaja
de mayores presiones de los filtros a presión.
9.2.1 Filtros a vacío
Hay cuatro tipos de filtros a vacío: el filtro de tambor, el filtro de discos, el filtro
de bandeja y el filtro de banda horizontal. Mientras los tres primeros son capaces de
producir queques con humedades de hasta 12 a 18% el filtro de bandas logra llegar a
Capítulo 9 Filtración
227
humedades menores, del orden de 8 a 10%. A continuación describiremos brevemente
cada uno de estos equipos.
Filtros de tambor
El filtro de tambor consiste en un tambor rotatorio con su parte inferior
sumergida en la suspensión. La superficie del tambor está cubierta por un medio
filtrante denominado tela filtrante. La suspensión es succionada desde el interior del
tambor, donde se ha generado un vacío. Mientras el filtrado pasa al interior del tambor
y es evacuado a través de tuberías apropiadas, el sólido es retenido en la superficie
cilíndrica formando un queque. A medida que el tambor rota, las secciones de
superficie que estaban sumergidas en la suspensión emergen de ésta, haciendo que aire
sea succionado debido al vacío interior, lo que seca al queque. Durante el giro es
posible lavar el queque rociando agua en su superficie y permitiendo que se seque de la
misma forma anterior. Una vez completado un giro, y antes de entrar nuevamente en la
suspensión, un mecanismo raspa la superficie descargando el queque en una tolva. A
continuación se inicia un nuevo ciclo de filtrado-secado-lavado-secado-descarga.
Fig. 9.5 Filtro de tambor.
Filtros de discos
El filtro de discos consiste en un eje central que soporta un número determinado
de discos, cada uno de los cuales está conectado a un equipo de vacío. Los discos
tienen su parte inferior sumergida en la suspensión, de manera similar al caso del filtro
de tambor. Cada disco está cubierto de una tela filtrante y, al igual que en el filtro de
tambor, trabaja en ciclos de filtrado-secado-lavado-secado y descarga a medida que el
sistema de discos va girando. En los filtros de disco el lavado es más difícil de realizar.
La ventaja de este equipo en comparación al filtro de tambor, es su gran superficie por
unidad de área de piso ocupada, ya que cada disco permite filtrar por ambas caras y se
puede acomodar un número bastante grande de discos en un solo equipo. Otra ventaja
es la forma modular por sectores en que están construidos los discos, lo que permite
mayor facilidad y flexibilidad en el cambio de telas.
228
Manual de Filtración & Separación
Vista del filtro
Detalle de un sector de un disco
Fig. 9.6 Filtro de discos.
Una variante de estos filtros de discos, son los filtros cerámicos. Los filtros
cerámicos en apariencia y funcionamiento son muy similares a los filtros de discos
convencionales. La diferencia estriba en que los sectores que componen los discos son
placas de un material cerámico micro poroso como elemento filtrante, basado en óxido
de aluminio.
Fig. 9.7 Filtro de discos cerámicos.
Capítulo 9 Filtración
229
Existen dos tipos de placas cerámicas disponibles. El primer material posee
poros de 1,5 micrones con un punto de capilaridad de 1,6 bar y el segundo posee poros
de 2,0 micrones con un punto de capilaridad de 1,2 bar. Al sumergirse los discos
dentro de la tina con pulpa, tienen una acción capilar iniciando el proceso de
desaguado sin fuerza externa.
Fig. 9.8 Placa de filtro cerámico.
Los sólidos contenidos en la pulpa se acumulan en la superficie del disco y el
desaguado continúa mientras queda líquido presente. La filtración capilar es un método
de filtración que combina las ventajas del filtro convencional de vacío por su
construcción simple similar y el efecto capilar. Los filtros cerámicos son utilizados
para la filtración de concentrados de cobre y minerales industriales.
Filtros de bandeja
El filtro de bandeja consiste en una serie de bandejas abiertas ubicadas horizontalmente
en un plano que rota alrededor de un eje central vertical. Las bandejas están formadas
por numerosos sectores en forma de trapecio inclinados hacia el eje central que
conectan con una válvula común bajo el centro del equipo. El queque puede ser lavado
mediante chorros de líquido una vez terminada la filtración. Es posible realizar un
lavado co-currente. La descarga del queque se lleva a cabo mediante un tornillo espiral
que lo arrastra hacia el centro, o por volteo de las bandejas. El filtro se adapta muy bien
a materiales granulares a grandes concentraciones. La principal desventaja es que las
bandejas se utilizan solamente por un lado, por lo que el equipo requiere un espacio de
suelo considerable por unidad de producción.
230
Manual de Filtración & Separación
Fig. 9.9 Filtro de bandeja horizontal.
Filtros de banda horizontal
El filtro de banda horizontal semeja una correa transportadora, donde la banda
está formada por una tela filtrante. La mayor ventaja de este filtro es la flexibilidad en
la selección de la longitud de los ciclos de filtración-lavado-secado. En la sección II
tendremos ocasión de analizar este filtro en mayor detalle.
Fig.9.10 Filtro de banda horizontal.
9.2.2 Equipos de filtración a presión
La filtración en equipos tradicionales, tales como filtros rotatorios y filtros de
banda, están siendo menos aceptables en la industria minera y a menudo son
considerados inadecuados debido a su alto contenido de humedad, obligando a hacer
Capítulo 9 Filtración
231
uso de secadores antes de obtener un producto final. Es así como los filtros de presión
son considerados de una tecnología largamente reconocida como un método confiable
y eficiente para lograr más bajas humedades y mejores rendimientos demostrando ser
una solución eficaz para este problema. Los filtros a presión son equipos
inherentemente discontinuos. Al igual que los filtros rotatorios trabajan en ciclos, pero
al contrario de estos, deben detenerse para cargar la suspensión y para descargar el
queque seco.
En La filtración a presión podemos identificar tres tipos de equipos: filtros
prensa de placas verticales, filtros prensa de placas horizontales y filtro prensa de
disco.
Filtro prensa de placas verticales
En los filtros de presión de placas verticales la separación toma lugar en cámaras
formadas entre las superficies de drenaje de placas filtrantes moldeadas que se
mantienen unidas entre sí. Estas placas poseen orificios para la alimentación de la
pulpa y el drenaje líquido filtrado, las placas están fijas entre sí mediante una presión
hidráulica, están montadas verticalmente sobre y entre dos barras laterales o
suspendidas de vigas. Estas barras o vigas están conectadas en un extremo a un cabezal
fijo o alimentador, mientras que por el otro extremo están conectados a un cabezal de
cierre.
Fig. 9.11 Filtro de placas verticales.
Las placas se comprimen entre sí mediante un arreglo de cierre de un pistón
hidráulico en cuyo extremo se encuentra el cabezal móvil que empuja ordenadamente
las placas contra el cabezal fijo, formando así una sola unidad filtrante compuesta por
el grupo de placas de filtración.
232
Manual de Filtración & Separación
Fig. 9.12 Esquema de un filtro-prensa.
El mecanismo de acción de un filtro-prensa se puede describir de la siguiente
forma: El cabezal (G) y el soporte terminal (H) son sostenidos por rieles de las barras
de soporte (I) diseñados especialmente (ver figura 9.9). El pistón hidráulico (D)
empuja las placas de acero (E) contra las placas de polietileno (F) cerrando la prensa
La pulpa es bombeada a las cámaras (A) rodeadas por el medio filtrante (B). Al
bombear, la presión se incrementa forzando al líquido a atravesar la tela, haciendo que
los sólidos se acumulen y formen un queque (C). El filtrado pasa a través de las telas y
es dirigido hacia los canales de las placas y puertos de drenado (J) del cabezal para la
descarga. Este filtrado típicamente contendrá menos de 15 ppm (mg/l) de sólidos en
suspensión. La torta es fácilmente removida haciendo retroceder el pistón neumático,
relajando la presión y separando cada una de las placas, para permitir que el queque
compactado caiga desde la cámara.
La cámara que contiene el queque, está formada de una de las dos formas
siguientes, por dos placas ahuecadas que conforman una cámara o por dos placas
niveladas en el medio con un marco para el queque (similar a un marco de fotografía).
La cara de ambos lados de las placas de filtración poseen una superficie de drenaje en
forma de ranuras o pepitas para permitir que el líquido filtrado drene por detrás de las
telas filtrantes, permitiendo su evacuación a través de ojales situados en las esquinas
inferiores de las cámaras.
Sobre cada una de las dos superficies de la placas están instaladas telas de
filtración. Estas telas están unidas al ojal alimentador fijadas por pernos o difusores
impermeables.
Capítulo 9 Filtración
233
LAVADOR
DE TELAS
SOPORTE
DE TELAS
CABEZA
MOVIBLE
CONDUCTOR DE
CABEZA MÓVIL
CONDUCTOR DEL
SACUDIDOR DE TELA
CONTROL
HIDRÁULICO
SACUDIDOR
MECÁNICO DE
TELAS
ENLACE DE
PLACAS
PLACAS
CILINDROS DE CERRADO HIDRAULICO
CANAL DE DESAGÜE
CONDUCTOR
HIDRÁULICO
Fig. 9.13 Esquema de un filtro de placas verticales.
Las etapas consecutivas del proceso de filtración no comprenden la utilización
de compresión mecánica de la pulpa o queque en las cámaras filtrantes. El proceso
cíclico de la filtración por presión en los filtros de placas verticales consta de las
siguientes fases:

Cerrado: Las placas son comprimidas a alta presión mediante un pistón
hidráulico para evitar fuga de material por entre las placas y sellar las cámaras
filtrantes.

Alimentación: La alimentación de la pulpa se realiza por el ojal alimentador, o
núcleo del cabezal fijo, donde la pulpa de concentrado es bombeada a lo largo
de toda la longitud del filtro hasta llenar las cámaras de filtración. Como la
pulpa fluye bajo presión, las partículas sólidas comienzan a distribuirse entre
ambas caras de la tela filtrante formando una capa inicial de torta de filtro o
pre-revestimiento. Esta capa de pre-revestimiento se transforma en el medio
real de filtración y, a medida que la filtración continúa, el espesor de ésta
aumenta gradualmente hasta que los queques de ambos lados del filtro se tocan
o se unen. El bombeo continúa obteniendo una compresión del queque
formado, el que se detiene una vez que el flujo de líquido es prácticamente
nulo. Es en este punto en que la bomba alimentadora se detiene.

Limpieza: La limpieza del residuo de pulpa que queda retenido en el interior
del núcleo se realiza mediante agua a presión en contracorriente. El agua que
queda retenida en el núcleo se elimina con aire comprimido. Esta etapa dura
alrededor de 45 segundos.

Soplado: Aire a alta presión es introducido a las cámaras lo que genera un
desplazamiento de la humedad retenida en los poros del queque.
234
Manual de Filtración & Separación
ALIMENTACIÓN
DESCARGA
DE FILTRADO
Fig. 9.14 Etapa de alimentación.
DESCARGA DE
FLUIDO
DESPLAZADO
AIRE DE SOPLADO
Fig. 9.15 Etapa de soplado.

Descarga: Una vez terminadas las etapas de filtración y compresión, se abre
las compuertas de la tolva receptora del queque en la parte inferior del filtro.
Las placas del filtro se separan por retracción del pistón al accionar de un
cilindro hidráulico. El queque cae sobre una correa transportadora por simple
gravedad.

Lavado: Antes de comenzar un nuevo ciclo, las compuertas de la tolva
receptora del queque, son automáticamente cerradas para realizar el lavado de
telas con agua y así eliminar las partículas de concentrado adheridas y
mantener limpias las superficies de las placas y telas. Así se evita la posible
colmatación o taponamiento de los poros de las telas y se reduce el desgaste
por abrasión.
Capítulo 9 Filtración
235
PLACAS
TELAS
FILTRANTES
QUEQUE
COMPUERTAS DE
DESCARGA
Fig. 9.16 Etapa de descarga del queque.
La figura 9.14 muestra la fotografía de un filtro prensa de placas verticales.
Fig. 9.17 Filtro prensa de placas verticales.
Filtro prensa de placas horizontales
Recientemente se ha desarrollado un tipo de filtro a presión semi-continuo que
ha encontrado un mercado importante en las empresas mineras. Este sofisticado equipo
combina las dos características más buscadas por la industria minera, una baja
humedad y gran capacidad. La flexibilidad en la capacidad también es importante ya
que los hace convenientes para empresas mineras grandes y pequeñas.
236
Manual de Filtración & Separación
Este tipo de filtro prensa consiste básicamente en una cámara filtrante horizontal
situado dentro de un marco de estructura principal. Por la forma de su diseño, permite
la incorporación de cámaras adicionales montadas unas sobre otras, permitiendo
incrementar el área de filtración sin generar un aumento en el área de piso de la
instalación.
Cada una de estas cámaras de filtración posee sellos inflables en ambos extremos, los
que se dilatan durante la operación para sellar la cámara. Las cámaras se encuentran
fijas a la estructura y no poseen movimiento durante la operación de filtrado.
Cada cámara posee una correa filtrante montada sobre un rodillo impulsor en
cada extremo, operando independientemente de las otras correas que posee el equipo.
Cada rodillo posee un motor hidráulico que acciona la correa durante la operación de
descarga del queque. En la parte superior de cada cámara se encuentra instalado un
diafragma de goma flexible que es utilizado para comprimir la suspensión y el queque,
siendo éste el encargado de formar y reducir la humedad del queque.
Fig. 9.18 Filtro prensa de placas horizontales.
La secuencia operacional para la filtración por presión en placas horizontales, es
como sigue:
Cerrado: Se desarrolla un inflado de los sellos de extremos mediante una presurización
con agua para evitar fugas de las cámaras del filtro.
Capítulo 9 Filtración
237
Fig. 9.19 Cerrado y sellado de las cámaras.

Alimentación: La pulpa es bombeada a presión hacia la cámara del filtro a una
determinada presión. Una vez llena la cámara, la alimentación se corta. La
etapa de alimentación va acompañada de una filtración incipiente, ya que la
presión disminuye a medida que las cámaras se van llenando.
Fig. 9.20 Etapa de alimentación.

Limpieza: En forma opcional se limpia el residuo de pulpa que queda
retenido: La etapa propiamente tal de en el interior del cabezal principal de
alimentación.

Compresión formación del queque comienza con la compresión de la
suspensión mediante un diafragma de goma, utilizando una presión de agua.
Una vez terminado el período de formación del queque, comienza la expresión
que produce una disminución de la porosidad del queque, eliminando una
mayor cantidad de líquido. La alta presión permite el uso de tela de tramado
denso que incrementa la eficiencia de la filtración.
Fig. 9.21 Etapa de formación de queque y expresión por compresión
238
Manual de Filtración & Separación
 Retracción del diafragma: Una vez terminada la expresión con diafragma, se
admite aire que es soplado a través del queque saturado con la finalidad de
desplazar el líquido allí retenido y ayudar a la retracción del diafragma.
Fig. 9.22 Etapa de soplado del queque.

Lavado del queque: La solución de lavado es alimentada por bombeo dentro
de la cámara del filtro formando un volumen parejo sobre el queque. Debido a
que la torta yace plana y sin resquebrajaduras, el agua para el lavado se
distribuye homogéneamente El lavado de queque es completamente opcional y
puede ser utilizada o rechazada mediante una simple reprogramación del PLC.
Fig. 9.23 Etapa de lavado del queque.

Segunda compresión: Se presiona al diafragma nuevamente para forzar la
solución de lavado a pasar a través del queque, desplazando el líquido retenido
en éste casi por completo. Luego de esto, la misma presurización del
diafragma exprime el queque filtrado y lavado para extraer el máximo de
solución de lavado de queque.
Fig. 9.24a Etapa de segunda compresión.
Capítulo 9 Filtración
239
Fig. 9.24b Etapa de segunda compresión.
 Segunda soplado y retracción del diafragma: Después de la segunda
expresión, se sopla el queque con aire comprimido por segunda vez,
retrayendo el diafragma y reduciendo la humedad final del queque. Al
controlar el tiempo de inyección de aire, es posible regular el porcentaje de
humedad final en el queque.
Fig.9.25 Segunda soplado y retracción del diafragma.

Descarga del queque: Los sellos se retraen y se descarga el queque
accionando la correa del filtro después que se ha completado la etapa de
soplado de aire. La puerta desviadora se abre y permite la entrada del queque
al buzón de descarga.
Fig. 9.26 Descarga del queque seco.

Lavado de la correa: Antes de comenzar un nuevo ciclo, se realiza un lavado
a la correa y, durante el movimiento de retroceso de ésta, al interior de la
240
Manual de Filtración & Separación
cámara con la puerta desviatoria cerrada para evitar que caiga líquido junto
con el queque descargado. La correa se detiene regresando a su posición
original y el ciclo se repite automáticamente.
La figura 9.27 muestra un ejemplo de filtro prensa de placa horizontal.
Fig. 9.27 Filtro prensa Larox.
Filtro prensa de discos
El filtro prensa de disco, consiste en una sola cámara, situada sobre una correa
transportadora que, a su ves, es el medio filtrante. Un pistón hidráulico provee la fuerza
para producir la filtración. Las etapas de operación del filtro son las siguientes:
 Alimentación: Con la cámara sellada, la suspensión es bombeado a su interior,
permitiendo el paso del líquido a través del medio filtrante. Éste es recolectado
a través del plato fijo inferior. Las partículas sólidas son retenidas por el
medio.
 Compresión: Cuando ya no es posible la incorporación de más suspensión a la
cámara, ésta es comprimida contra el medio con la ayuda de gas o aire
comprimido, forzando al líquido a pasar a través del sólido conformando un
queque suficientemente seco.
 Descarga del queque: Finalmente, el pistón hidráulico, asciende liberando al
queque seco el cual es transportado por la correa para su posterior tratamiento,
quedando de esta forma disponible para un nuevo proceso.
Capítulo 9 Filtración
Cerrado de las cámaras.
Filtración.
241
Alimentación al filtro.
Descarga del queque.
Fig. 9.28 Esquema de detalle en ciclos de un filtro a presión semi-continuo.
Filtro de vela
Un tipo de filtro que puede ser clasificado como de filtración sin formación de
queque es el filtro de vela. Éste consiste en una serie de tubos de acero perforados
revestidos de una tela filtrante, o tubos de material cerámico poroso. La suspensión se
bombea por la parte exterior de los tubos y el filtrado se colecta en el interior de los
tubos. Estos filtros n0 no utilizados muy frecuentemente en la industria minera, por lo
que no daremos detalles de ellos.
242
Manual de Filtración & Separación
Fig. 9.29 Filtros de vela a presión.
9.2.3 Filtros hiperbáricos
Los filtros de vacío tienen como gradiente de presión limitante 0.8 atmósferas en
las condiciones más favorables, esto es, a nivel del mar. Si son utilizados en zonas muy
altas este gradiente baja drásticamente. Un desarrollo interesante fue realizado en la
Universidad de Karlsruhe en Alemania. En la década del 80 un grupo de investigadores
liderados por el Prof. Dr. Werner Stahl estudiaron y desarrollaron un sistema de
filtración en el cual introdujeron un filtro de vacío dentro de una cámara de
presurizada, aumentando de esta forma el gradiente de presión. En esta forma nació el
filtro hiperbárico.
El equipo consiste en un filtro a vacío, ya sea de disco, tambor o banda, inmerso
en una cámara de presión. Como en todos los filtros a presión, la descarga constituye
un problema. Con este tipo de filtros se puede obtener humedades de 8% y menores.
Fig. 9.30 Filtro hiperbárico.
Capítulo 9 Filtración
9.3
243
MEDIOS FILTRANTES
Un medio filtrante puede ser definido como cualquier material permeable sobre
el cual, o en el cual, son separados los sólidos del fluido durante el proceso de
filtración. Por consiguiente, el principal rol del medio filtrante es provocar una buena
separación entre los componentes de una suspensión con el mínimo consumo de
energía. En orden a realizar una cuidadosa selección de un medio filtrante se deben
tomarse en cuenta muchos factores.
Uno de los primeros estudios de distintos medios filtrantes fue realizado por
Flood (1966), quien clasificó los medios filtrantes como medios de tipo superficie, en
el cual las partículas en suspensión son principalmente retenidas sobre el medio y
medios de tipo profundo, en que las partículas penetran en los poros, donde son
retenidas. Estos últimos medios se usan principalmente para la clarificación de
líquidos.
En los últimos 20 años, Purchas y Hardman (Purchas 1981) han realizaron
estudios de medios filtrantes y los clasifican según la tabla 9.1. El medio filtrante se
caracteriza de acuerdo a diversas propiedades físicas (mecánicas) y químicas. Purchas
identifico 20 propiedades divididas en tres categorías.
a) Propiedades orientadas a la máquina.
(Tabla 9.2).
b) Propiedades orientadas a la aplicación. (Tabla 9.3).
c) Propiedades especificas de filtración. (Tabla 9.4).
9.2.1 Telas
Las telas filtrantes más comunes son hechas de material textil, de fibra natural o
sintética. Existen tres tipos de medios sintéticos usados en la industria de la filtración,
a) Tejido: puede ser de tela cruzada o satín, ya que éste aumenta la resistencia a la
tracción, b) No tejido: consiste en ensamblar varias capas de fibras y c) Compósitos:
Tabla 9.1. Resumen generalizado de medios filtrantes clasificados de acuerdo a su
rigidez (Purchas, 1981)
Principales tipos
Fabricación sólida
Subdivisiones
Pantallas de alambre .
bobinados de alambre.
Anillos apilados.
Hojas metálicas
Perforadas.
Tejido de alambre.
Medios porosos rígidos Cerámicos
Carbón
Plásticos
Cartuchos
Fabricación de laminas
Camas aglutinadas.
Hilo bobinado
Partícula más pequeña retenida (m)
(aprox.)
100
100
5
100
5
<1
10
10
3
2
2
244
Manual de Filtración & Separación
(continuación)
Principales tipos
Hojas plásticas
Membranas
Medios tejidos
Medios no tejidos
Medios holgados
Subdivisiones
Monofilamentos tejidos
Hojas porosas
Poliméricas
Cerámicas
Metálicas
Fibras de hilo
Monofilamentos
Multifilamentos
Hojas de filtro
Papel (celulosa y vidrio)
Polimeros
Fibras
Polvos
Partícula más pequeña retenida (m)
(aprox.)
< 0.1
< 0.1
0.2
5
10
<10
10
5y7
10
1
<1
poliuretanos (polímeros micro porosos regulados) que han dado muy buen resultado.
Básicamente, las características que se debe tener en cuenta son:
1. Condiciones Térmicas y Químicas: En condiciones térmicas y químicas los
polímeros son los medios más adecuado para el medio filtrante. Los más
usados son polipropileno(PP), polietileno (PET) y poliamida (PA).
2. Requerimientos en la Filtración: Los principales requerimientos de la
filtración son: claridad en el filtrado (es decir una alta eficiencia de retención
de partículas finas), rendimiento, contenido de humedad en el queque, efectiva
liberación del queque (de fácil desprendimiento), baja resistencia al paso del
fluido y alta resistencia a la abrasión.
3. Consideraciones con respecto al equipo: Es importante donde se va a usar el
medio filtrante: el tipo de pulpa, volumen del producto, contenido de sólidos
requeridos, así como si es filtración a presión o vacío.
4. Costos: El costo del medio, así como su vida útil es de vital importancia. Este
ítem puede decidir el tipo de medio a utilizar.
Tabla 9.2. Propiedades del medio filtrante orientadas a la máquina (Purchas 1980)
Propiedades orientadas a la máquina: relacionadas con las limitaciones del uso de un
medio filtrante en un tipo especifico de filtro.
Rigidez
Resistencia al estiramiento
Resistencia al cree
Estabilidad en los bordes
Resistencia a la abrasión
Estabilidad a la vibración
Dimensiones compatibles
Habilidad para ser fabricados
Función de sellado
Capítulo 9 Filtración
245
Tabla 9.3. Propiedades específicas de filtración en medios filtrantes (Purchas y Hardman
1980 y 1994)
Propiedades específicas de filtración que determinan la capacidad del medio en un proceso
especifico de filtración.
Partícula más pequeña
retenida.
Eficiencia de retención.
Importante cuando se requiere una remoción de partículas del
100 %. Se debe tener en mente que el tamaño de las
partículas depende de la técnica utilizada para su medición.

Concentracion de particulas en el filtrado
Concentracion de particulas en la suspension a filtrar
Una eficiencia de retención del 100 % corresponde al punto
de corte de la tela (cut–off). La eficiencia de retención
depende de la forma y tamaño de partículas, estructura del
medio, velocidad de alimentación, entre otros.
Resistencia al flujo.
La resistencia al flujo depende de la estructura del medio
filtrante y es a menudo reportado como la medida de
permeabilidad, o resistencia específica, a condiciones
especificas de flujo.
Capacidad ensuciamiento.
Cantidad de sólidos (suciedad) retenida en el medio filtrante
sin exceder una cierta caída de presión a través del filtro.
Tendencia a obturación
Asociada al material que no es removido del medio usando
los procedimientos normales de limpieza, causando un
incremento en la resistencia al flujo de filtrado.
Descarga del queque
Facilidad de remoción del queque del medio filtrante
Tabla 9.4. Propiedades orientadas a la aplicación del medio filtrante (Purchas, 1980)
Aplicación orientadas a las propiedades del medio filtrante. Compatibilidad del medio
filtrante con el ambiente.
Estabilidad química y térmica
Datos técnicos entregados por el fabricante.
Estabilidad biológica
Relacionada a la acumulación y crecimiento biológico en la
superficie de las telas. Fibras naturales son más propensas a
la degradación biológica que las sintéticas.
Estabilidad Dinámica
Derramamiento de fibras y migración de fragmentos de las
telas en el filtrado, característica crítica en algunas
aplicaciones.
Características absorbentes
Absorción de líquido y posterior hinchamiento durante el
proceso de filtración, lo que se traduce en una disminución
de la permeabilidad.
246
Manual de Filtración & Separación
(continuación)
Aplicación orientadas a las propiedades del medio filtrante. Compatibilidad del medio
filtrante con el ambiente.
Mojabilidad
Afecta la presión requerida para iniciar el flujo inicial a
través del medio. Pequeñas cantidades de impureza, alteran
significativamente esta propiedad.
Características de estática
Factor importante para suspensiones de baja conductividad
eléctrica. Aditivos antiestáticos son utilizados para reducir
este efecto.
Disponibilidad
Corresponde a la disposición del medio filtrante como de las
partículas que retuvo después de que se descarte.
Capacidad de reutilización
Muchos medios pueden ser utilizados y re-usados. El
planteamiento para lograr estos son diseñados en el ciclo de
operación de muchos filtros.
Costo
El costo de un medio filtrante puede variar mucho y tiene
que ser evaluado considerando la vida útil del mismo.
Los principales daños que puede sufrir la tela pueden deberse a deformación
estructural, estiramiento, fatiga a la flexión y a daños térmicos y químicos. Los
primeros son el resultado de un mal diseño y a aspectos operacionales, tirón muy fuerte
durante la descarga del queque o tensiones fuertes al inicio del ciclo o de la alta presión
de agua usada en el lavado de la tela. Con respecto a los daños químicos (pH y
corrosividad) y térmicos, estos son subsanados eligiendo una tela adecuada para el
proceso en que va a ser usada. La siguiente tabla muestra las características de distintos
materiales.
Tabla 8.5. Atributos químicos y térmicos de fibras, Hardman 1994)
Resistencia a:
Temperatura Ácidos
Bases
de operación
máxima (ºC)
Polipropileno
910
95


Polietileno
950
85


Poliester (PBT)
1280
100


Poliester (PET)
1380
100


Poliamida 6.6
1140
110


Poliamida 11
1040
100


Poliamida 12
1020
100


PVDC
1700
85


PVDF
1780
100


PTFE
2100
150+


PPS
1370
150+


PVC
1370
80


PEEK
1300
150+


    muy bueno;    bueno;   aceptable;  pobre
Tipo Fibra
Densidad
(kg/m3)
Agentes
oxidantes













Hidrólisis













Capítulo 9 Filtración
247
Cabe señalar que a la tela se le realiza procesos finales de estabilización que
aseguran una estabilidad dimensional y regulación de la permeabilidad. Un ajuste
preciso de su permeabilidad se obtiene a través de tratamientos térmicos llamados
calendering. Comparaciones entre las permeabilidades de diferentes medios filtrantes
pueden ser hechas aplicando la ley de Darcy para datos de flujos versus caída de
presión. Un baño y modificación superficial hace que el queque se desprenda sin
mayor problema de la superficie. Las principales características técnicas de los medios
filtrantes son:















trama
peso/área
Permeabilidad al aire
Permeabilidad al agua
Porosidad
Resistencia a la tensión
fácil descarga del queque
mínima resistencia al flujo
mínima humedad del queque
máxima vida útil de la tela
menor tendencia a la colmatación (obstrucción)
espesor de la tela
resistencia a la temperatura
Resistencia al pH
capacidad de suciedad.
En conclusión, podemos ver que existe una infinidad de medios filtrantes
dependiendo de la aplicación, por lo que la selección de un medio especifico debe
tomar en cuenta muchos factores. Esto hace necesario realizar distintos ensayos de
laboratorio para observar el comportamiento del medio filtrante y así poder evaluar su
comportamiento dependiendo de la aplicación. Entendiendo el importante rol que juega
el medio filtrante en el proceso de filtración, queda claro que una mala elección
acarreara resultados perjudiciales para la filtración, traduciéndose en aumentos de
costos, pérdidas de tiempo y un proceso ineficiente.
9.4
TEORÍA DE FILTRACIÓN
Dependiendo del tipo de material a filtrar y de la magnitud del gradiente de
presión el queque formado durante la filtración puede permanecer rígido o puede
comprimirse. En general, los concentrados de cobre y otros metales, especialmente
cuando no se utiliza floculante en su espesamiento, son materiales incompresibles. Al
contrario, los relaves de flotación son siempre floculados antes de espesar. Por esta
razón son materiales compresibles. Por otra parte, cuando estos relaves son filtrados, lo
que no ocurre frecuentemente, se utiliza filtración a vacío, por lo que el gradiente de
248
Manual de Filtración & Separación
presión aplicado es pequeño y nuevamente el material puede ser considerado
incompresible en esas circunstancias. Es así como en la mayoría de los casos de
filtración en plantas de procesamiento de minerales se puede considerar al queque de
filtración como incompresible y es aplicable la teoría de flujo en un lecho poroso
rígido. En caso contrario, es necesario introducir la consolidación o expresión del
queque.
Consideremos un proceso de filtración con las siguientes restricciones:
i)
Las propiedades de la suspensión, del filtrado y del queque son constantes.
ii)
El queque formado es incompresible.
iii) La superficie de filtración es plana.
iv) La velocidad de percolación del filtrado a través del queque y del medio
filtrante es muy lenta.
La suposición ii) permite considerar el queque como un lecho poroso rígido, lo
que significa que el sólido contenido en el queque no se mueve. La suposición iii)
implica que, en el caso de superficies curvas, como en los tambores rotatorios, el
diámetro del tambor debe ser muy grande comparado con el grosor del queque. La
suposición iv) permite utilizar la ecuación de Darcy como velocidad de percolación.
La filtración, ya sea en filtros continuos o discontinuos, se lleva a cabo en
etapas. Por lo menos se distinguen dos etapas fundamentales en el proceso: a) la
formación de queque, que incluye el bombeo de la suspensión al filtro y la compresión
de la suspensión sobre el medio filtrante (por medio de aire a presión o de un
diafragma o émbolo) hasta el momento en que desaparece la suspensión y el queque se
encuentra totalmente saturado; b) desaguado del queque, que se lleva a cabo
succionando o soplando aire a través del queque y, de esta forma, desplazando el agua
por el aire. Filtraciones más sofisticadas incluyen etapas adicionales tales como: c) la
expresión, que consiste en presionar el queque ya saturado mediante una membrana o
émbolo impermeable eliminando parte del agua por reducción de la porosidad del
queque (estruje). Esta etapa solamente es útil en materiales compresibles. Otra etapa es
d) el lavado del queque, que permite eliminar materiales indeseables o recuperar
materiales valiosos del queque.
9.4.1 Formación del queque.
Formalmente, el proceso de filtración queda descrito por las siguientes variables
de campo (ver capítulo 3): la porosidad del queque (z,t), la velocidad del filtrado
q(z,t) y la presión en exceso a la hidrostática pe(z,t). Estas tres variables constituyen un
proceso de filtración simple si cumplen las siguientes ecuaciones (6.25):
( z, t )   0
(9.1)
q (z, t)  q (t)
(9.2)
Capítulo 9 Filtración
249
p e  

q
k  0 
(9.3)
donde  0 es constante y q es una función del tiempo solamente.
pem
pe
p0
p2
p1
Filtrado
Suspensión
queque
Medio filtrante
z
k
lm
l
Fig. 9.14 Filtración con queque plano, donde
p1  pe  pem  0 y p 2  pem  p0  0 .
Las condiciones de contorno son:
p e (  m )  p 0
(9.4)
p e ((t))  p e
(9.5)
donde p e es el valor de la presión en exceso a la hidrostática en la interfaz entre el
queque y la suspensión z  (t) , y p0 es el valor en la interfaz entre el filtrado y el
medio filtrante z   m
Denominaremos proceso de filtración simple a un proceso de filtración con
queque incompresible. El término simple se refiere a que, en este caso, las ecuaciones
de campo son las más simples que es posible establecer. En la filtración a vacío, el
filtro está parcialmente sumergido en la suspensión que es alimentada al estanque del
filtro mediante una bomba. Se trata de mantener esta suspensión lo más homogénea
posible mediante agitación. Por ello, en este tipo de filtración, el gradiente de presión
aplicado es constante y el flujo de filtrado depende de la resistencia ofrecida por el
medio filtrante más el queque, que crece en espesor con el tiempo. En el caso de la
filtración a presión, la alimentación a filtros se lleva a cabo mediante bombas
centrífugas que impulsan la suspensión. Esto lleva a que el caudal que llega el filtro y
250
Manual de Filtración & Separación
la presión a la que es sometida la suspensión depende de las características de la
bomba. La figura 9.15 muestra curvas características de una bomba centrífuga.
Presión
Flujo
Fig. 9.15 Curvas características de una bomba centrífuga.
Cuando la bomba inicia su acción hay poca resistencia en el filtro por lo que hay
una baja presión y un caudal alto y relativamente constante. Más adelante durante el
proceso la resistencia va aumentando a medida que crece el queque, por lo que
aumenta la presión haciéndose asintótica un determinado valor máximo, mientras que
disminuye el caudal según la curva característica. La curva de la figura se puede
aproximar por dos rectas, una horizontal y una vertical. Esto significa que se puede
inicialmente aproximar la alimentación a filtros y el filtrado, como un proceso a
volumen constante de filtrado, seguida de un proceso con presión constante. Por esta
razón es costumbre analizar la filtración en estas dos condiciones, presión constante y
volumen constante.
a)
Filtración a presión constante
Como indicamos en los párrafos anteriores, durante la fase avanzada de la
filtración en equipos en que la suspensión se alimenta al filtro mediante una bomba
centrífuga la presión se mantiene relativamente constante. Analicemos este caso.
Designemos por p0 la presión en z   m , por pem la presión en z  0 y por p e la
presión en z  (t) , con p1  pe  pem  0 y p 2  pem  p0  0 , de modo que:
p e  pe  p0  p1  p 2  0
(9.6)
Capítulo 9 Filtración
251
Cada una de estas caídas de presión es constante y positiva, por lo que integrando la
ecuación (9.3) a través del medio filtrante con q(t)  q(t)k , y q  0 , y
p e   dp e dz  k , se obtiene:

p e k   qk
k

p0
p em
dp e 

0
p0  pem 
p 2 
m

q(t)dz
k

( m )q(t)
km
m
q(t)
km
(9.7)
donde km y  m son la permeabilidad y espesor del medio filtrante respectivamente y
q(t) es el flujo de filtrado por unidad de área (velocidad espacial o velocidad de
precolación). Integrando ahora la ecuación (9.3) a través del queque resulta:

pe
pem
dp e 

pe  p em 
p1 
( t )
0

q(t)dz
k

(t)q(t)
k  0 

(t)q(t)
k  0 
(9.8)
donde k   0  y   t  son la permeabilidad y espesor del queque respectivamente.
Reemplazando las ecuaciones (9.7) y (9.8) en el gradiente total de presión a través del
queque y del medio filtrante (9.6) resulta:

(t) 
p e    m 
 q(t)
 k m k  0  
(9.9)
El caudal de filtrado Q(t) se puede expresar en términos de la velocidad de
percolación q y del volumen de filtrado Vf (t) :
Q(t)  q(t)S 
dVf (t)
dt
(9.10)
donde S es el área de filtración. Reemplazando (9.10) en la ecuación anterior
obtenemos:
252
Manual de Filtración & Separación

(t)  dVf (t)
p eS    m 

k
 m k   0   dt
(9.11)
Tiempo de filtración
Para llegar a una ecuación práctica que relacione el espesor ( t ) , la masa m s ( t )
del queque producido y el volumen de filtrado obtenido Vf ( t ) con el tiempo de
filtración, observemos que el contenido de sólido del queque es igual al contenido de
sólido de la suspensión asociado al filtrado producido en el tiempo t. Por lo tanto:
Fracción volumétrica de sólidos en la suspensión 0 :
0 
volumen del sólido
Volumen de suspensión

volumen delsólido
Volumen de líquido + volumen del sólido
El volumen de líquido es igual al volumen de filtrado producido mas el líquido
retenido en el queque. Entonces, la concentración 0 será:
0 
m   0 , t  s
 Vf (t)  S(t)0   m  0 , t 
(9.12)
s
Por otra parte, la masa del queque es igual al volumen del queque por la densidad del
sólido:
b g b
g
m  0 , t  s 1   0 S
(9.13)
Reemplazando (9.13) en la ecuación anterior y despejando ( t ) o m   0 , t  obtenemos:
(t) 
0
Vf (t)
1  0   0 S
m  0 , t  
0 1   0 
1  0   0
(9.14)
s Vf (t)
(9.15)
Las expresiones (9.14) y (9.15) dan las relaciones entre grosor del queque, masa de
éste y volumen de filtrado.
Reemplacemos ahora la expresión (9.14) en la ecuación (9.11) para dar:
p eS  
F
GH k
m
m

I
JK
0
dVf
Vf ( t )
S(1   0   0 )k  0
dt
b g
(9.16)
Capítulo 9 Filtración
253
La única variable en esta expresión es el volumen de filtrado. Integrando entre 0 y t y
entre 0 y Vf, resulta:
Sp e
d 

0

t

Vf
0
m
d 
km

Vf
0
0
1
d
2S (1  0   0 )k  0 
Sp e
0
1

t  m Vf 
Vf2

km
2S (1  0   0 )k   0 
(9.17)
Espesor del queque
Reemplacemos Vf de (9.14) en (9.17) para dar, después de algunos arreglos:
 2  2k   0 
k  0 
0
m
pe
t0
2
km

1  0  0 
(9.18)
Cuya solución es:
12
2



0
2pe
m 
  m 

(t)  k  0   


t


km 
  k m  k   0  1  0   0  

(9.19)
b g
Usando las relaciones entre ( t ), Vf ( t ) y m  0 , t en esta última ecuación podemos
escribir:
12
2



0
2pe
m 
  m 



m  0 , t   sS 1   0  k   0   
t


km 
  k m  k   0  1  0   0  

1  0   0
Vf (t)  Sk   0 
0
12
2



0
2pe
m 
  m 




t
 


km 
  k m  k   0  1  0   0  

(9.20)
(9.21)
Las expresiones (9.19), (9.20) y (9.21) representan el grosor del queque, su masa y el
volumen de filtrado obtenido por unidad de tiempo de filtración.
Estas expresiones pueden ser simplificadas si se desprecia la resistencia
específica del medio filtrante R m   m k m . Las tres expresiones se reducen a:
F 2 I F 1     IJ ckb gh
V ( t )  SG J G
H K H  K
12
12
f
0
0
0
12
0
p1e 2 t1 2
(9.22)
254
Manual de Filtración & Separación
F 2I
mb , t g   b1   gSG J
H K
F 2 I F  IJ
( t )  G J G
H K H1    K
12
0
s
12
0
p1e 2 t1 2
(9.23)
0
ckb gh
12
0
12
0
0
0
0
12
0
0
12
FG  IJ ckb gh
H1    K
p1e 2 t1 2
(9.24)
Es importante fijarse que cada uno de estos parámetros, volumen de filtrado,
masa del queque y su espesor son directamente proporcionales a la raíz de la presión y
a la raíz del tiempo de filtración.
Las ecuaciones desarrolladas en la sección anterior son válidas para la filtración
en el estado estacionario, esto es una vez que se ha formado el queque. Esto significa
que solamente son válidas para el tiempo final de la formación del queque y son
perfectamente válidas para el lavado del queque. En el período de formación del
queque el flujo de filtrado no es constante. Inicialmente, la filtración es muy rápida
cuando hay muy poco sólido depositado en el medio filtrante. A medida que el queque
empieza a engrosar el flujo de filtrado disminuye. Cuando la cantidad de sólido que se
deposita por unidad de tiempo es pequeña en comparación al espesor del queque, el
flujo de filtrado se hace constante. En ese momento las ecuaciones desarrolladas son
válidas aún cuando sólido siga depositándose en el queque.
3500
3000
2500
2000
1500
1000
Modelo
Da tos experim entales
500
0
0
20
40
60
80
1 00
120
tiem po de fo rmación de que que (s.)
Fig. 9.16 Modelación etapa de formación de queque en la etapa de
prensado en un filtro a presión.
En la figura 9.16 se observa que el volumen de filtrado aumenta inicialmente en forma
proporcional al tiempo y que más tarde esta proporcionalidad disminuye a t1/2. Este
comportamiento se puede demostrar en la siguiente forma. La ecuación de Darcy sigue
siendo válida durante todo el período de filtración, por lo que podemos escribir:

(t) 
pe    m 
 q(t)
k
 m k  0  
(9.25)
Capítulo 9 Filtración
255
Como se ha supuesto que el queque es incompresible, su porosidad permanecerá
constante durante todo el período de formación por lo tanto, las únicas variables en
(9.25) son (t) y q(t) . Recordemos que hemos supuesto que la caída de presión es
constante. Inicialmente el espesor del queque es muy pequeño y su resistencia al flujo
también pequeña. Es así como el flujo de filtrado es máximo y constante al inicio de la
filtración. Supongamos que el espesor del queque es cero, por lo que (9.25) se reduce
a:
pe  
m
q(t)
km
Como q es igual a q  1 S   Vf t  , la ecuación anterior se aproxima a:
pe  
 m Vf
k m St
de donde concluimos que:
Vf 
Spe  m
t
 km
Esto significa que inicialmente el volumen de filtrado es una función lineal del tiempo.
La figura 9.16 confirma este resultado. Se observa que durante los primeros 20
segundos de filtración el volumen aumenta en forma proporcional al tiempo para luego
disminuir esta proporcionalidad a t1/2. La ecuación clásica de la filtración, (9.21),
utilizada para la determinación de parámetros, es válida cuando el queque se ha
formado en su mayor parte de modo que el aumento de espesor es despreciable y el
flujo de filtrado q se hace constante.
La ecuación (9.20) se puede interpretar también como el tiempo necesario para
filtrar una masa ms de sólido:
2
1
2

0
ms
 m    m    2 pe


t  
 

 
 sS 1  0  k  0  k m   k m    k  0  1  0  0 
(9.26)
Ejemplo 1 (Massarani 1978)
Calcular el área necesaria de un filtro prensa para filtrar 10.000 l/h de una
suspensión de 5% en peso de carbonato de calcio de densidad igual a 2.6g/cm3. El
filtro debe operar a 20°C y 40 psi de presión. Ensayos en el laboratorio con una
muestra de la suspensión en un filtro de 500cm2 de área, presión de 40 psi dio un
queque de 3.2 cm de espesor y un filtrado. El % en peso de sólidos en el queque es de
60.2.
Cálculo de los parámetros de filtración:
De (9.17) podemos escribir:
256
Manual de Filtración & Separación
0
  m 1
t
Vf



Vf Spe  k m 2S (1  0   0 )k   0 



La figura que sigue muestra los valores necesarios para calcular Rm y k():
R m  7.1 103  500  (106  40 /14.5) / 0.01  1.06  109 cm 1
0 
5
 0.0198
2.6  (100  5)  5
(de la suspensión)
q 
60.2
 0.368
2.6  (100  60.2)  60.2
(del queque)
 0  1  0.368  0.632
 1   0.01  14.5
k   0    6   
6
 10   500  40  10
0.0198
  1  

10
2


  4.12  10 cm
2
500
1
0.0198
0.632



 
 

0.03
0.025
t/Vf
0.02
0.015
0.01
t/Vf = 1E-06Vf + 0.0071
2
R = 0.9977
0.005
0
0
5000
10000
15000
20000
Vf
Cálculo de las permeabilidades del queque y medio filtrante
Cálculo del área de filtración
De la ecuación (9.25) se puede calcular el área en función del flujo volumétrico
de filtrado a tratar.
Capítulo 9 Filtración
257

(t)  Q
S   m 

k
 m k   0   p e
 103 
 2777 cm3 s
Q  10000  
3 
3.6
10



 2777  14.5 
2
S  0.01  1.06  109  3.2 4.12  109   
  88842 cm
6
40
10



S  8.88 m 2
b)
Filtración a volumen constante
La filtración a volumen constante se lleva a cabo en las etapas iniciales de
equipos en que la pulpa es impulsada al filtro por una bomba centrífuga o durante la
operación con bombas de desplazamiento positivo.. En este caso el flujo volumétrico
de filtrado es constante. La ecuación (9.9) sigue siendo válida, ahora con pe como
variable y q constante:

(t) 
p e (t)    m 
 q
k
 m k  0  

 Q
pe (t)S    m 

 k m k( 0 )  S
donde Q es el flujo volumétrico constante de filtrado. De esta última ecuación se puede
despejar el valor del espesor del queque:
(t) 
Sk( 0 )
 k( )
pe (t)  m 0
Q
km
m s (t) 
Ss 1   0  k( 0 )
Q
pe (t) 
(9.27)
 m s 1   0  k( 0 )
km
(9.28)
Por otra parte el valor del flujo de filtrado se obtiene de datos de la bomba.
Ejemplo 2 (Wakeman y Tarleton 1999)
Se realizó una experiencia en el laboratorio con un filtro de 45 cm2 de área a 70
kPa de presión. La razón de pesos del queque húmedo y seco fue de 1.34. Las
densidades del sólido, filtrado y pulpa de alimentación son respectivamente:
s  2640 kg m3 , f  1000 kg m3 y o  132 kg m3 y la viscosidad del filtrado es
258
Manual de Filtración & Separación
  0.01 poises . La producción de filtrado en el tiempo se muestra en la tabla que
sigue.
Tiempo t en s
Volumen en cm3
Tiempo t en s
Volumen en cm3
0
0
457
285
170
141
527
320
275
200
589
341
340
230
660
370
390
252
Calcule el tiempo necesario para obtener un espesor de queque de 4.5 cm
Fracción volumétrica de la alimentación:
o 
o  f 1320  1000

 0.195
s  f 2640  1000
  4.5 cm
Espesor del queque deseado:
Existe una relación directa entre la masa de sólido depositada en el queque, la
concentración de la suspensión, la porosidad del queque y el volumen de filtrado. De la
ecuación (9.14) podemos escribir:
0
(t)
1

Vf (t) 1  0   0 S
Por lo tanto
(t)
0.195
1

 0.01307
Vf (t) 1  0.195  0.473 202.5
de donde se puede construir la tabla:
t
s
0
V
cm3
0
l
cm
0
170
275
141
200
1.8
2.6
340
230
3.0
390
252
3.3
457
285
3.7
527
589
320
341
4.2
4.5
660
370
4.8
Capítulo 9 Filtración
259
El espesor del queque de 4.5 cm se obtiene en 589 s.
9.4.2 Secado o soplado del queque
Durante el período de formación del queque se elimina la mayor parte del
líquido de la suspensión. Finalizada esta etapa, que se caracteriza porque la superficie
del queque se ve seca, los poros de éste están llenos de líquido, esto es, están saturados.
Este líquido solamente se puede eliminar utilizando secado o soplado y mediante la
expresión, o con la combinación de estos métodos. En la filtración a vacío la etapa de
secado consiste en la succión de aire a través del queque para desplazar el líquido,
mientras que en la filtración a presión el secado se produce mediante el soplado de aire
a través del queque, lo que recibe el nombre de soplado. La expresión es un
procedimiento totalmente diferente, en la que se aplica una presión sobre el queque
mediante una superficie impermeable. Aunque el queque puede ser considerado
incompresible en la etapa de formación, se comprime bajo la alta presión ejercida por
esta superficie, exprimiendo líquido desde su interior. El fenómeno es similar al de
estrujar de una esponja saturada de agua, y su mecanismo es simplemente la reducción
de volumen de los poros por la compresión. Este tipo de mecanismo se analizará por
separado.
Durante la etapa de secado o soplado en una filtración, escurren
simultáneamente dos fluidos a través del queque, el líquido y el aire. En general el
primero moja al sólido. El aire desplaza al líquido pero deja una película de líquido
adyacente al sólido, retenida por fuerzas capilares, que impide el contacto de éste con
el aire. Es así como el aire fluye por los espacios vacíos encontrando un medio poroso
de propiedades diferentes al del medio poroso seco. El líquido modifica el volumen
disponible y la forma de los poros por los que circula el aire.
Se denomina saturación s la fracción del volumen de poros de un queque
ocupada por el líquido. Esto significa que la saturación varía entre 0s1. Si s  0 , el
queque está seco y si s  1 , el queque está lleno de líquido o saturado.
En el cálculo del flujo de aire a través de un queque húmedo, se utiliza la teoría
de flujo bifásico en medios porosos, considerando una permeabilidad modificada para
cada fluido que pasa por el queque. Para el escurrimiento de cada fluido se utiliza una
corrección para la permeabilidad k() basada en la saturación. Se denomina
permeabilidad relativa del fluido al cuociente entre el flujo de fluido en un queque nosaturado y el flujo del mismo fluido en un queque saturado con el mismo fluido bajo el
mismo gradiente de presión:
260
Manual de Filtración & Separación
k  0s  p e
 z k  0 ,s 
k   0 ,s   q  (0 ,s) q  ( 0 ,s  1) 

k   0  pe
k  0 
  z
k  0s  pg
g z k  0 ,s 

k g   0 ,s   q g ( 0 ,s) q g ( 0 ,s  0) 
k  0  pg
k  0 
g z
(9.29)
(9.30)
De esta forma se puede utilizar la ecuación de Darcy para el flujo en queque nosaturado usando los parámetros del caso saturado. Para el escurrimiento del líquido y
gas se tiene:
q (s)  
q g (s)  
k    0 ,s  k   0 

k g   0 ,s  k   0 
g
p e
(9.31)
p g
(9.32)
La permeabilidad relativa debe ser determinada experimentalmente. La figura
9.17 muestra la permeabilidad relativa de un gas y un líquido mojante en un medio
poroso. Si se sopla aire por el medio poros, en un comienzo escurrirá solamente líquido
y luego escurren líquido y gas en conjunto. Cuando la saturación del líquido es inferior
a la saturación residual s  , fluye solamente aire por el queque. El líquido es retenido
en el interior del medio poroso por las fuerzas capilares.
Para utilizar las curvas de permeabilidad relativa, tales como las mostradas en la
figura 9.17, se les debe ajustar función:
k i ( 0 ,s)  f i  s,s  
con i  ,a
(9.33)
donde s es la saturación y s es la saturación residual y el índice i se refiere al fluido
que escurre.
Capítulo 9 Filtración
261
0.6
Permeabilidad relativa kl y ka
0.5
líquido
aire
0.4
0.3
0.2
0.1
0.0
0.5
0.6
0.7
0.8
0.9
1.0
Saturación
Fig. 9.17 Curvas de permeabilidad relativa para el
escurrimiento de agua y aire en un queque de concentrado de
cobre.
Tiempo de soplado
Consideremos la ecuación de soplado (9.31) integrémosla para obtener:

p e 

  Rm 
 q
 
k( 0 )k  ( 0 ,s) 
(9.34)
Durante el período de soplado, el grosor del queque  permanece constante y es
igual a   ms S 1   0  . La cantidad de agua contenida en el queque en cada instante t
es S 0s(t) , donde la saturación es inicialmente igual a 1 y disminuye con el tiempo.
Entonces, el volumen de filtrado obtenido al tiempo t durante el soplado será
Vf (t)  S 0 (1  s(t)) y su derivada q S  dVf dt  S 0 ds dt . Reemplazando en la
expresión anterior obtenemos:

t
0
p e
d  


s
   R
1
0
m



 d
k( 0 )k  ( 0 , ) 
pe

t  R m 1  s  
0
k  0 
d
1
 f   , 
s

(9.35)
0
La ecuación (9.35) da el tiempo necesario para llegar a una saturación s bajo un
gradiente de presión p e . La integral se puede calcular una vez que se conoce la
función k  ( 0 ,s)
262
Manual de Filtración & Separación
Flujo de aire
Como en filtración a presión, el gradiente de presión es mucho mayor al
gradiente de saturación, éste último se puede despreciar (ver sección 6.5.4 de este
Manual), de modo que para calcular el flujo de aire necesario para llegar a una
saturación s se puede integrar (9.32) directamente para obtener:

p e 

  Rm 
 qg
 g 
k( 0 )k g ( 0 ,s) 
de donde el flujo de aire Qg  Sq g resulta ser:
 Sp e 


Qg  
Rm 


  
k(0 )f g (0 ,s) 
 g 
1
(9.36)
donde a y b, n y m son los parámetros que describen la permeabilidad relativa del aire.
En estas ecuaciones Rm y S son un parámetros del equipo, s , k  0  y 0 son
parámetros característicos del medio poroso, f y  son propiedades del fluido y pe
ms y h son parámetros operacionales.
La humedad del queque es la razón de masa de agua a masa total expresado en
porcentaje, por lo que la relación entre humedad h y saturación s es:
h  100
 f  0s
f 0s  s 1  0 
y
s
s 1   0
h
f 0 100  h
(9.37)
Una vez integrada la ecuación (9.36), podemos reemplazar la saturación por la
humedad y disponer de una ecuación del tiempo de soplado necesario para llegar a una
humedad determinada.
9.5
PARÁMETROS DE FILTRACIÓN Y SU MEDICIÓN
En la figura 9.13 hemos esquematizado las diversas variables que influyen en el
proceso de filtración son. Las separamos en: variables de entrada, el flujo y
concentración de la pulpa de alimentación; variables de salida, la capacidad, espesor y
humedad del queque producido; variables de diseño, área y pérdidas de carga en el
equipo; variables de control, presión aplicada, tiempos de formación del queque, de
lavado, prensado y soplado, temperatura, pH, aditivos, agitación de la pulpa;
perturbaciones, tamaño y distribución de tamaño del sólido y parámetros, porosidad,
permeabilidad y compresibilidad del queque, saturación residual.
En la sección anterior hemos desarrollado relaciones entre estas variables en
términos de los parámetros. Para completar la información necesaria para simular el
Capítulo 9 Filtración
263
proceso de filtración es necesario establecer las dependencias de los parámetros de las
propiedades del sólido y del líquido y de las perturbaciones al proceso.
2.5.1 Medición de los parámetros de filtración
Numerosas empresas han desarrollado instrumentos para la medición de los
parámetros de filtración y todos ellos tienen una estructura similar. Aquí describiremos
el instrumento FILTRATEST, diseñado por la firma Bokela, mediante el cual hemos
realizado las medidas que se muestran en los ejemplos de este Manual.
El FILTRATEST es una celda a presión que permite realizar la filtración de
suspensiones por presión positiva de gas desde 0 hasta 10 bar (150 psi), por lo que se
puede simular cualquier proceso de filtración a vacío o presión. El equipo tiene un
área de filtración es de 19.63 cm2 y dispone de una camisa de agua que le permite
trabajar a temperatura controlada. Un conjunto de rotámetros permite medir el flujo de
aire, cuya presión se regula y mide mediante un manómetro digital.
El filtrado es recolectado en una balanza digital cuya señal se envía
directamente a un computador portátil que registra la masa de filtrado en cada instante
de tiempo. Esta característica hace posible un estudio detallado de la fase de
formación del queque, de la fase de soplado (secado) y de la del prensado.
La transportabilidad del equipo hace posible la realización de pruebas de
filtración directamente en la planta, lo que evita cualquier modificación de las
propiedades de la pulpa.
Un software especialmente diseñado para este instrumento permite determinar
exactamente el tiempo de formación del queque, el tiempo de prensado, el tiempo de
soplado, el flujo de aire y el peso del filtrado en el tiempo. El software calcula
automáticamente la resistencia específica del queque y del medio filtrante y las
permeabilidades relativas del agua y del aire de soplado. Las dos figuras que siguen
muestran un esquema del instrumento y sus conexiones a los elementos periféricos.
Fig. 1 Pantalla inicial del software del FILTRATEST.
264
Manual de Filtración & Separación
Flujómetro
Acondicionador de
señales ROTA
Cable Ribbon PR50-50F
Bloque conector CB-50LP
DAQCard-700
Interfase RS-232
Balanza electrónica
Computador Laptop
Fig. 2 Esquema de conexiones del FILTRATEST y periféricos.
a)
Porosidad del queque
La porosidad del queque está determinada principalmente por el tamaño,
distribución de tamaño y disposición de las partículas que forman el empaquetamiento.
Para comprender mejor el efecto de estas variables en la porosidad, tomemos el
ejemplo del empaquetamiento de esferas. La porosidad de un lecho de esferas de un
solo tamaño es independiente del tamaño de las esferas y depende exclusivamente del
tipo de empaquetamiento. En la tabla 9.xx (Wakeman y Tarleton 1999)se muestra
valores calculados para la porosidad con diferentes tipos de empaque.
Empaquetamiento
Cúbico
Orto-rómbico
Tetragonal
Romohedral
Número de coordinación
Porosidad 
3
0.7766
4
0.6599
5
0.5969
6
0.4764
7
0.4388
8
0.3955
9
0.3866
10
0.3019
11
0.2817
12
0.2595
Capítulo 9 Filtración
265
Se puede observar que, dependiendo del empaque, la porosidad puede variar desde
0.26 a 0.78, esto es 3 veces. Porosidades encontradas en queques de filtración son
frecuentemente cercanas a 0.40.
Lechos de esferas con distribución de tamaño pueden tener permeabilidades
aun menores que los monotamaños, ya que las esferas más pequeñas pueden ocupar los
espacios dejados por las esferas mayores. Varios investigadores han propuesto
ecuaciones para calcular la porosidad de lechos con esferas de distintos tamaños
(Concha 1990), sin embargo es preferible la determinación experimental de la
porosidad del queque en cada caso.
La porosidad del queque de un filtro industrial generalmente se determina
sacando una muestra del queque y midiendo el volumen y el peso del queque seco. En
un equipo de laboratorio es posible conocer la porosidad del queque en el momento en
que el queque se ha formado y está totalmente saturado. En ese instante se puede
realizar un balance de agua y atribuir la diferencia entre el volumen de agua contenida
en la suspensión a filtrar y el volumen del filtrado recuperado al agua que está llenando
los poros del queque y que, por lo tanto, mide la porosidad.
Cualquier método que permita determinar el espesor del queque en cada
instante de una filtración, permite calcular la porosidad del queque, ya que el área de
filtración es conocida y la masa de sólido contenida en el queque también es conocida.
Ejemplo 3
Para determinar la porosidad de un queque en un filtro Larox PF, se tomó una
muestra con un tubo cilíndrico de 5 cm de diámetro. El espesor de la muestra era de 35
mm. El peso una vez secado el sólido fue de 147 g y la densidad del sólido 3.87 g/cm3 .
La porosidad del queque es:
147 3.87
  1
 0.45
  52 4  3.5


Ejemplo 4
Durante una prueba de filtración en un equipo de laboratorio se utilizó 138.7 g
de un concentrado de cobre de densidad 4.3 g/cm3 disperso en agua a una
concentración de 72.2% de sólidos en peso. Se estableció el tiempo de formación de
queque, en que desapareció la suspensión y el queque se encontraba totalmente
saturado, en t1=42.7 s. En ese punto el volumen de filtrado recuperado era de 20.6 cm3.
Calcular la porosidad del queque.

Vfq
Vsq  Vfq

 (100  72.2)
72.2)  138.7   20.60
 0.50
 (100  72.2) 72.2)  138.7   20.60  138.7 *100 72.2
Para queques compresibles, por ejemplo para relaves floculados, la porosidad
del queque es una función de la presión aplicada. Esta relación se da mediante una
ecuación constitutiva, obtenida desde información experimental. Las principales
266
Manual de Filtración & Separación
relaciones propuestas son del tipo potencial o exponencial, de las cuales se da tres
ejemplos:
  1  ps
(9.38)
1
p

  1    s  1


(9.39)
  1   ln ps
(9.40)
Ejemplo 5
Un relave de flotación fue filtrado en un filtro de banda a vacío (0.75 bares)
obteniéndose un queque de porosidad   0.493 . Se realizó pruebas de filtración en el
laboratorio con el relave para obtener la compresibilidad del queque. Los resultados se
muestran en la tabla. Se desea estimar cual sería la porosidad del queque del mismo
material si se filtra en un filtro hiperbárico a 3 bares de sobre-presión y en un filtro
Larox PF a 6 bares de presión.
Los datos de compresibilidad del relave se grafican en la figura que sigue y
permiten proponer la siguiente ecuación constitutiva para la compresibilidad del
queque
  0.484p 0.0611
La simulación con esta ecuación da:
(3.75)  0.484(3.75) 0.0611  0.446
(6)  0.484(6) 0.0611
 0.434
presión de sólido (bar)
Altura del queque (cm.)
0.8
2.90
1.0
1.5
2.87
2.81
2.0
2.77
2.7
2.73
3.0
2.71
3.5
2.70
4.0
2.68
4.7
2.66
5.0
2.63
5.5
6.0
2.62
2.61
Capítulo 9 Filtración
267
Porosidad
0.50
0.45
= 0.4843p
-0.0611
2
R = 0.9907
0.40
0
1
2
3
4
Presión (bar)
5
6
7
Compresibilidad del queque.
b)
Permeabilidad del queque y Resistencia Específica del Medio Filtrante
El medio filtrante es un componente esencial en los equipos de filtración. Es un
medio poroso heterogéneo, con poros de diferentes tamaños y geometría, cuya
estructura puede causar grandes variaciones en la forma en que se depositan las
partículas y grandes variaciones en la distribución del flujo de líquido en la superficie.
Una tela de filtración, no sólo debe retener las partículas sólidas y producir un filtrado
limpio, sino que debe resistir todas las solicitaciones que le imponga el equipo. Por
ello, a las propiedades de resistencia específica se debe agregar la de resistencia
mecánica.
Determinación experimental
Para determinar la permeabilidad k    del queque y la resistencia específica del
medio poroso R m , escribamos la ecuación (9.16) en la forma:
t
R 

0
 m  2
Vf (t)
Vf (t) Spe 2S pe 1  0  0  k  0 
(9.41)
donde R m   m k m ,  m y km son el espesor y la permeabilidad del medio filtrante,
información que en general no se conoce.
268
Manual de Filtración & Separación
Graficando t Vf (t) versus Vf (t) , se puede calcular la resistencia especifica del
medio filtrante R m y la permeabilidad del queque k  0  . Si b=tg es la pendiente de
la recta obtenida y a es su intersección con el eje de las ordenadas, los parámetros
serán:
0
p S
1

Rm  a  e
(9.42)
k  0    2

b 2S pe 1  0   0
Ejemplo 6 (Wakeman y Tarleton 1999)
Se realizó una experiencia en el laboratorio con un filtro de 45 cm2 de área a 70
kPa de presión. La razón de pesos del queque húmedo y seco fue de 1.34. Las
densidades del sólido, filtrado y pulpa de alimentación son respectivamente:
s  2640 kg m3 , f  1000 kg m3 y o  132kg m3 y la viscosidad del filtrado es
  0.01 poises . La producción de filtrado en el tiempo se muestra en la tabla que
sigue.
Fig. 3 Determinación de las resistencias específicas del medio
filtrante y del queque.
Tiempo t en s Volumen en cm3 Tiempo t en s Volumen en cm3
0
0
457
285
170
141
527
320
275
200
589
341
340
230
660
370
390
252
Calcule las resistencias específicas del medio filtrante y del queque.
Fracción volumétrica de la alimentación:
o 
Razón masa del queque húmedo y seco
% sólido en peso del queque:
X
o  f 1320  1000

 0.195
s  f 2640  1000
ms  mf
 1.34
ms
ms
1

 0.746
ms  m f 1.34
Capítulo 9 Filtración
269
Fracción de sólidos en peso del queque:
f X
0.746


 0.527
s 1  X   f X 2.64  (1  0.746)  0.746
  1    1  0.527  0.473
Porosidad del queque:
Graficando t/V versus V se obtiene la figura que sigue, de la cual resultan los
parámetros:
t/V en s/cm
3
2.0
1.0
t/V = 0.0025V + 0.8895
2
R = 0.9831
a=0.8895
b=0.0025
0.0
0.0
100.0
200.0
300.0
400.0
3
Volumen cm
Cálculo de las permeabilidades del queque y medio filtrante.
Resistencia específica del medio filtrante:
Rm  a 
k  
pS
7.0  105  45
 0.88946 
 2.80  109 cm 1

0.01
0
1 
1
0.01
0.195

 8.44  1010 cm 2
2
2
5
b 2S p 1  0   0.00246 2  45  7  10 1  0.194  0.473
Resistencia específica del queque:


0.784

 5.33  109 cm 1
k    8.44  1010
270
Manual de Filtración & Separación
Ejemplo 7
Determinar la resistencia específica del medio filtrante y la permeabilidad del
queque que se espera para la filtración de un concentrado de cobre en un filtro Larox
PF. Se conoce los siguientes datos:
Parámetros
Filtro Larox PF
3
Densidad del sólido, g/cm
3.87
3
Densidad del filtrado, g/cm
1.0
Concentración de pulpa de alimentación, % de sólidos en peso
78.0
Viscosidad del filtrado, kg/m-s
0.0012
Tamaño de partículas
Análisis granulométrico
Temperatura de la pulpa, °C
20
pH de la pulpa
9.1
Presión en formación de queque, bar
2
Presión de soplado, bar
4
Espesor del queque, mm
3.6
Tamaño de la malla
Tamaño promedio x
Masa retenida
m
g
35/48
365
2.32
0.024
48/65
252
0.77
0.008
65/100
178
1.87
0.019
100/150
126
7.75
0.079
150/200
89
16.22
0.165
200/270
63
27.15
0.277
270/400
45
23.73
0.242
-400
31
18.27
0.186
98.15
1.000
SUMA
f3(x)
Se realizó un ensayo de laboratorio en el equipo FILTRATEST (ver más
adelante en esta sección) con un área de filtración de 19.63 cm2. La muestra de 156.78
g de sólido en una pulpa de 78 % de sólidos en peso se colocó en el equipo y se filtró a
2 bares por 39.76 segundos. Se determinó el volumen de filtrado obtenido en el tiempo.
Esta información se muestra en el gráfico que sigue.
Capítulo 9 Filtración
271
Datos de la experiencia de laboratorio
Espesor del queque, mm
36
Peso del queque húmedo, g
168.28
Peso del queque seco, g
156.78
Tiempo de formación del queque t1, s
Área del FILTRATEST cm
39.76
2
19.63
14
3
Volumen filtrado (cm )
12
10
8
6
4
V=-0.078517+(112.29+11.617*t)
2
0.5
2
R =0.992
0
0
10
20
30
40
50
tiempo de formación de queque t en (s.)
Volumen de filtrado versus tiempo para los datos del ejemplo 4.
Agua final en queque:
168.28  156.78  11.50 g
Humedad final:
h final  100  11.50 11.50  156.78   6.83%
Porosidad del queque:
 1
Saturación en t1:
s 1
Agua en queque en t1:
0.43  19.63  3.6  30.16 g
Humedad en t1
h t1  100  0.43  1  19.63  6.3  17.92%
Agua total:
201.48  156.78  44.70 g
Agua en filtrado en t1:
44.70  30.16  14.54 .g
Agua final en filtrado:
44.70  11.50  33.20 .g
156.78
3.87
19.63  3.6
 0.43
272
Manual de Filtración & Separación
Concentración alimentación:
0  77.81/(3.87  (100  77.81)  77.81)  0.48
Si se grafica los datos experimentales de volumen de filtrado versus tiempo en la
forma t/Vf versus Vf, se obtiene el gráfico que sigue.
6
4
3
t/Vf (s/cm )
5
3
2
y = 0.031x + 2.3536
1
y = 0.0861x + 1.8243
2
R = 0.0885
2
R =1
0
0
2
4
6
8
10
12
14
3
Volumen filtrado (cm )
t/Vf versus Vf para los datos experimentales.
Del gráfico se puede observar que la dispersión de datos no permite obtener una buena
correlación (línea punteada) entre las variables, cuyo coeficiente de regresión es sólo
R2=0.0885. Esta dispersión se debe a que las pequeñas variaciones de los datos
originales se amplían al ser presentados en la forma de este gráfico. Para solucionar el
problema conviene obtener una correlación de los datos originales y construir el
segundo gráfico con la correlación obtenida.
En el gráfico Vf versus tiempo se incluye la correlación obtenida, que da un
coeficiente de regresión de R2=0.992. En la figura de t/Vf versus Vf también se
muestra la simulación (línea llena) construida con la correlación de la figura anterior.
Los valores de a y tg son : a 1.8243 (s / cm6 )
y
b  tg  0.0861(s / cm3 )
Usando las expresiones (9.42) se obtiene los siguientes parámetros para la experiencia
en el FILTRATEST:
Rm  a 
k  0  
peS
2  105  19.63
 1.8243 
 5.97  108 cm 1

0.012
0
1

 2
tg 2S pe 1  0  
Capítulo 9 Filtración

273
1
0.012
0.42
 4.32  109 cm 2
2
5
0.0861 2  (19.63)  2  10 1  0.48  0.43
Efecto del tamaño de partículas
La ecuación de Kozeny-Carman para la permeabilidad de un medio poroso se
presentó en la ecuación (6.33):
k  0  
3d e2 2
36 1   
2
Esta ecuación permite observar que la permeabilidad de un queque de filtración
depende directamente de las características de las partículas que lo forman a través de
dos parámetros, el tamaño promedio de las partículas de (diámetro equivalente) y su
forma (esfericidad ), e indirectamente a través del parámetro  y la porosidad. Ésta
última depende, como ya hemos visto, del tamaño, distribución de tamaño y
disposición de las partículas que forman el empaquetamiento. La principal variable de
operación que influye en la permeabilidad es la presión a través de la porosidad.
Ejemplo 8
Para los datos del ejemplo 7, predecir la permeabilidad de un queque de
filtración de un filtro Larox PF trabajando a 6 bares con la ecuación de KozenyCarman, incluyendo el efecto de la presión sobre la porosidad.
A 4 bares de presión la porosidad del queque fue de   0.43 . Como el
concentrado de cobre es prácticamente incompresible, podemos suponer que a 2 y 6
bares la porosidad será la misma. Supondremos una esfericidad de   0.7 para el
concentrado de cobre.
El análisis granulométrico del concentrado se muestra en la tabla de la página
siguiente.
El diámetro equivalente es (Concha et al 1973):
d e  0.69  x12  0.69  54.18  37.39 m
Según Coulson y Richardson (1968),   5 , entonces:
k  0  
3d e2  2
36 1   
2

 0.433  (37.39  104 )2 (0.5)2
36  5  (1  0.43)2
El cálculo da un valor bastante aproximado al experimental.
El tamaño promedio volumétrico-superficial es:
x12  1 1.85E  2  54.18 m
 4.75  109 cm 2
274
Manual de Filtración & Separación
Tamaño de Tamaño promedio
la malla
x m
f3(x)
xf3(x)
f3(x)/x
g
35/48
365
2.32
0.024
8.89
6.67E-5
48/65
252
0.77
0.008
1.98
3.11E-5
65/100
178
1.87
0.019
3.39
1.07E4
100/150
126
7.75
0.079
9.95
6.27E-4
150/200
89
16.22
0.165
14.71
1.86E-3
200/270
63
27.15
0.277
17.43
4.39E-3
270/400
45
23.73
0.242
10.88
5.37E-3
-400
31
18.27
0.186
5.77
6.00E-3
98.15
1.000
72.99
1.85E-2
SUMA
c)
Masa retenida
Saturación residual y curva de capilaridad
La presión de entrada y saturación residual son dos parámetros importantes para
la determinación de las condiciones de operación de un filtro industrial. Se denomina
presión de entrada la mínima presión necesaria para comenzar a desaguar un queque
saturado. Su importancia es que da una cota inferior para la presión de soplado. La
saturación residual es aquella que no disminuye al aumentar la presión. Este parámetro
da una cota superior para la presión de soplado y una cota inferior para la humedad
posible de obtener.
Ejemplo 9.
Calcular la presión de entrada y la saturación residual para los siguientes datos
de un concentrado de cobre de densidad s  3.87 g / cm3 .
pe
Vf filtrado V líquido en queque Porosidad Saturación
0.00
16.47
26.3
0.43
1.00
0.20
17.07
25.7
0.43
0.98
0.40
22.84
19.9
0.43
0.76
0.45
24.32
18.5
0.43
0.70
0.47
26.17
16.6
0.43
0.63
0.50
27.09
15.7
0.43
0.60
Capítulo 9 Filtración
275
(continuación)
pe
Vf filtrado V líquido en queque Porosidad Saturación
0.55
27.79
15.0
0.43
0.57
0.60
28.39
14.4
0.43
0.55
0.65
28.56
14.2
0.43
0.54
0.70
28.57
14.2
0.43
0.54
0.80
28.57
14.2
0.43
0.53
0.90
28.86
13.9
0.43
0.53
1.00
28.89
13.9
0.43
0.51
1.50
29.32
13.5
0.43
0.50
2.00
29.58
13.2
0.43
0.50
2.50
28.58
13.2
0.43
0.50
3.00
29.58
13.2
0.43
0.50
Los datos de la tabla se pueden graficar como se muestra en la figura siguiente.
De la figura que sigue se desprende que los valores de la presión de entrada y
saturación residual son:
pentrada  0.37 bares
s
 0.39
De la curva de capilaridad se observa que basta con soplar a 2 bares para eliminar el
agua del queque hasta llegar a una saturación de 0.39. Como la porosidad del queque
es de   0.43 , la humedad mínima final del queque se puede calcular con la ecuación
(9.38):
h  100
f s
1  0.43  0.39
 100
 7.07 %
f s  s 1   
1  0.43  0.39  3.87  (1  0.43)
La saturación residual depende de varios factores, principalmente de la
porosidad del queque y de su espesor, del tamaño promedio de las partículas, de la
caída de presión a través del queque y de la tensión superficial del filtrado.
Correlación para la saturación residual
Según Wakeman, ver Capítulo 6 ecuaciones (6.74) y (6.75), la saturación
residual se puede calcular en términos del número de capilaridad mediante las
siguientes ecuaciones:
276
Manual de Filtración & Separación
3.50
Presión de soplado, bares
3.00
2.50
2.00
1.50
1.00
0.50
0.00
0.30
0.40
0.50
0.60
0.70
0.80
0.90
1.00
1.10
Saturación, s
Curva de capilaridad para los datos del ejemplo 6.
0.49
s   0.155 1  0.031N cap

N cap 
2
3av x12
pe
1  av 
2

donde N cap es el número de capilaridad,  av y  son la porosidad promedio y el
espesor del queque, x12 es el tamaño promedio volumétrico-superficial de las
partículas, pe es la caída de presión a través del queque y  es la tensión superficial
del líquido.
Ejemplo 11
Determinar la saturación residual para el queque del ejemplo 10. La información
necesaria es:
2
av  0.43 , x12  54.18 m , p  2  106 dinas cm , L  3.6 cm y   72 dinas cm
N cap 
2
3av x12
p
1  av 
2
L
(0.43)3   54.18  104   2  106
2

1  0.43
2
 3.6  72
 0.0544
0.49
s   0.155 1  0.031  N cap
  0.155 1  0.031 (0.055)0.49   0.175
Capítulo 9 Filtración
277
El valor obtenido mediante la correlación de Wakeman es aproximadamente la mitad
del experimental de s   0.39 .
Permeabilidad relativa
Definimos con anterioridad la permeabilidad relativa en el tiempo t como la
razón entre la permeabilidad del agua y del aire para ese tiempo y la permeabilidad del
queque saturado. Esta última es una propiedad del medio poroso exclusivamente.
Para calcular las permeabilidades relativas del agua y del aire durante la etapa de
soplado, es necesario conocer los flujos de agua y aire en función del tiempo durante
esta etapa.
Ejemplo 12
Se desea determinar las permeabilidades relativas del líquido y el aire en un
proceso de filtración de concentrados de cobre. Para ello se realizó experiencias en el
FILTRATEST con una pulpa de alrededor de 73% de sólidos en peso. Las condiciones
experimentales fueron: p  6 bares , área del filtro S  6.55 cm 2 , temperatura 20 °C,
viscosidad del líquido   0.01 g cm  s , viscosidad del aire   0.000187 g cm  s ,
densidad del concentrado s  4.50 g cm3 . Después de terminada la filtración, el
queque húmedo se peso dentro de un envase dando 50.98 g y se procedió a secarlo. El
queque seco con el envase pesó 47.68 g y el envase solo 4.41 g.
La formación del queque tuvo una duración de 37 segundos liberando 5.79 g de
agua. Luego se procedió a exprimir al queque durante 38 segundos a 7.5 bares
eliminando 4.56 g de filtrado. Finalmente se sopló aire a 6 bares durante121 segundos
eliminando 1.99 g adicionales de filtrado. La recolección de filtrado se hizo según lo
indicado en la tabla que sigue y la saturación residual se muestra en la curva de
capilaridad.
Etapa
t
t2
t3
s
s
s
0
Formación 36.69
0
Expresión 75.00 38.31
0
120.57
Soplado
195.57
Total
Vftotal
g
0
5.79
10.35
12.34
12.34
Vfformación
g
0
5.79
5.79
Vfprensado
g
0
0
4.56
4.56
Vfsoplado
g
0
0
0
1.99
1.99
Vlíquido en queque
cm3
15.64
9.85
5.29
3.3
El primer paso en el cálculo es realizar el balance de masa:
Soplado:
Volumen de filtrado producido:
Vf soplado  1.99 cm 3
Masa de sólido en queque:
M solido queque  43.27  4.41  47.68 g
278
Manual de Filtración & Separación
Etapa de formación de queque
Vf
t/ Vf tiempo t Vf
Tiempo t s g Vf (sim) cm3
s
g Vf (sim) cm3
2.14
0.01
0.0491
214.000 20.43 3.35
3.4339
4.18
0.25
0.2932
16.720 22.47 3.75
3.7740
6.21
0.68
0.6570
9.132
24.50 4.06
4.0966
8.24
1.14
1.0682
7.228
26.53 4.48
4.4042
10.27
1.56
1.4913
6.583
28.56 4.70
4.6979
12.31
1.93
1.9115
6.378
30.60 4.99
4.9798
14.34
2.34
2.3170
6.128
32.63 5.27
5.2481
16.37
2.65
2.7064
6.177
34.66 5.48
5.5051
18.40
3.00
3.0788
6.133
36.69 5.79
5.7514
t/ Vf
6.099
5.992
6.034
5.922
6.077
6.132
6.192
6.325
6.337
Vsolido  queque  47.68 / 4.5  9.62 cm 3
Volumen de sólido en queque:
Volumen de líquido en queque final: Vliquido queque  50.98  47.68  3.30 cm3
Volumen de líquido en queque saturado antes de soplar:
Vliquido queque  3.3  1.99  5.29 cm3
4.0
Presión capilar bar
3.0
2.0
1.0
soo=0.535
0.0
0.4
0.5
0.6
0.7
0.8
Saturación
Curva de capilaridad
0.9
1.0
1.1
Capítulo 9 Filtración
279
Volumen total de queque:
Vqueque  5.29  9.62  14.91 cm3
Espesor del queque:

Porosidad del queque:

Vqueque
S

14.91
 2.276 cm
6.55
Vliquido  queque
Vqueque

5.29
 0.355
114.91
Líquido total:
Vtotalliquido  Vliq queque final  Vf  finalsoplado  3.30  12.34  15.64 cm3
0 
Concentración pulpa:
Vsolido
9.62

 0.381
Vliq  total  Vsolido 9.62  15.64
Humedad final:
h  100 
M liquido queque
M solido queque  M liquido queque
Saturación final:
s
 100 
Vliq queque
Vliq quequesaturado
3.30
 7.09%
43.27  3.30

3.30
 0.624
5.29
Prensado:
Volumen de sólido en queque:
Vsolido queque  9.62 cm3
Volumen de filtrado en prensado:
Vf  prensado  4.56 cm3
Volumen de líquido en queque después de prensar:
Vliquido queque  5.29 cm3
Volumen total de queque después de prensar:
Vqueque  5.29  9.62  14.91 cm 3
Espesor del queque después de prensar:

Porosidad del queque después de prensar:  
Vqueque
S

14.91
 2.276 cm
6.55
Vliquido queque
Vqueque

5.29
 0.355
5.29  9.62
Formación del queque
Volumen de sólido en queque:
Vsolido queque  9.62 cm3
Volumen de filtrado en formación del queque:
Vf formacion  5.79 cm3
280
Manual de Filtración & Separación
Volumen de líquido en queque saturado:
Vliquido queque  15.64  5.79  9.85 cm3
Volumen queque:
Vqueque  9.62  9.85  19.47 cm 3
Espesor del queque:

Vqueque
S
Porosidad del queque antes del prensado:  

19.47
 2.972 cm
6.55
Vliquido queque
Vqueque

9.85
 0.506
19.47
La tabla que sigue resumen los resultados.
FORMACIÓN
cgs
Densidad s=4.5
Area (cm2)=6.55
p (bar)=6.00E+06
espesor(cm)=2.972
filtrado(Pa-s)=0.01
X0=73.45
SOPLADO
cgs
Densidad s=4.5
Area (cm2)=6.55
p (bar)=6.00E+06
espesor(cm)=2.276
aire(Pa-s)=1.87E-04
X0=73.45
0=0.381
0=0.381
=0.506
Vfiltrado=5.79
Vfiltrado-final=12.34
Vqueque=19.47
Vsólido-queque=9.62
Vlíquido-queque=9.85
Vfiltrado-expresión=4.56
Vtotal-líquido=15.64
Vtotal-suspensión=25.26
Vlíquido-final-queque=3.30
hfinal%=7.09
s=0.335
Msólido=43.27
=0.355
Vfiltrado-form=5.79
Vfiltrado-final=12.34
Vqueque=14.91
Vsólido-queque=9.62
Vlíquido-queque=5.29
Vfiltrado-expresión=4.56
Vtotal-líquido=15.64
Vtotal-suspensión=25.26
Vlíquido-final-queque=3.30
hfinal%=7.09
sfinal=0.624
Msólido=43.27
Permeabilidad del queque
Para calcular la permeabilidad del queque, se procede a modelar el flujo de
filtrado. De la tabla “Etapa de formación de queque” podemos extraer los datos para
obtener la correlación.
Capítulo 9 Filtración
281
7
6
0.5
Volumen de filtrado Vf cm
3
Vf=exp(a+b/t )
5
a=3.265809415
b=-9.18533905
4
3
2
Datos experimentales
Correlación
1
0
0
5
10
15
20
25
30
35
40
Tiempo s
Correlación del volumen de filtrado con el tiempo en la formación del queque.
Del modelo se grafica t/Vf versus Vf resultando en la figura siguiente, de donde se
obtiene los valores de a  4.9604 y b  0.2422 . Con estos valores se calcula la
permeabilidad y la resistencia específica del medio filtrante:
k() 
0

1
1
0.01
0.381
 2 

2
6
b 2S p 1  0   0. 2422  (6.55)  6  10 1  0.381  0.506
 2.69619  1010 cm 2
50
Datos
Serie2
Lineal (Serie2)
45
40
t/Vf s/cm
3
35
30
t/Vf = 0.2422Vf + 4.9604
2
R = 0.9804
25
20
15
10
5
0
0
1
2
3
4
5
6
Volumen de filtrado cm
7
8
9
10
3
Cálculo de las permeabilidades del queque y medio filtrante.
282
Manual de Filtración & Separación
Rm  a 
pS
6  106  6.55
 4.9604 
 1.95  1010 cm 1
0.01

Permeabilidad relativa
Las tres primeras columnas de la tabla que sigue muestra los datos de soplado.
Es necesario modelar el volumen de filtrado y el flujo de aire. La figura siguiente
muestra el flujo de filtrado versus el tiempo.
2.50
Volumen de filtrado en soplado cm3
Datos experimentales
simulación
2.00
1.50
c
Vf=a+bt
2
R =0.990
1.00
a=-0.048167781
0.50
b=0.5437304
c=0.27787257
0.00
0
20
40
60
80
100
120
140
Tiempo de soplado s
Correlación del volumen de filtrado en el soplado.
De esta correlación se puede calcular el flujo de filtrado en el tiempo como la
derivada de la ecuación anterior. Este flujo más el flujo de aire en función del tiempo
se muestran en la tabla y en las figuras siguientes.
Qf=cbt
3
Flujo de filtrado en el soplado cm /s
0.100
(c-1)
b=0.54373044
c=0.27787257
0.050
Simulado
0.000
0
50
100
Tiempo de soplado s
Correlación del flujo de filtrado en el soplado.
150
Capítulo 9 Filtración
283
t2
Vf (soplado)
Vf (sim)
Qaire
Q aire (sim)
Qfiltrado
kel
kea
s
cm3
cm3
cm3/s
cm3/s
cm3/s
cm2
cm2
0
2.04
4.07
6.1
8.13
10.17
12.2
14.23
16.26
18.29
20.33
22.36
24.39
26.42
28.46
30.49
32.52
34.55
36.58
38.62
40.65
42.68
44.71
46.75
48.78
50.81
52.84
54.87
56.91
58.94
60.97
63.0
65.04
67.07
69.1
71.13
73.16
75.2
77.23
79.26
81.29
83.33
85.36
87.39
89.42
91.46
93.49
95.52
97.55
99.58
101.62
103.65
105.68
107.71
109.75
111.78
113.81
115.84
117.87
119.91
120.57
0.00
0.48
0.76
0.83
0.89
0.99
1.04
1.09
1.09
1.14
1.19
1.19
1.26
1.33
1.33
1.38
1.38
1.43
1.43
1.43
1.48
1.48
1.53
1.58
1.67
1.67
1.67
1.66
1.67
1.71
1.71
1.71
1.71
1.76
1.76
1.76
1.76
1.76
1.76
1.76
1.76
1.76
1.80
1.80
1.80
1.85
1.85
1.85
1.85
1.89
1.89
1.90
1.89
1.93
1.94
1.94
1.99
1.99
1.99
1.99
1.99
0.00
0.61
0.75
0.85
0.93
0.99
1.04
1.09
1.13
1.17
1.21
1.24
1.27
1.30
1.33
1.36
1.38
1.41
1.43
1.45
1.47
1.49
1.51
1.53
1.55
1.57
1.59
1.61
1.62
1.64
1.66
1.67
1.69
1.70
1.72
1.73
1.74
1.76
1.77
1.78
1.80
1.81
1.82
1.83
1.85
1.86
1.87
1.88
1.89
1.90
1.92
1.93
1.94
1.95
1.96
1.97
1.98
1.99
2.00
2.01
2.01
0.00
18.67
15.69
14.07
13.42
12.93
12.93
13.03
13.07
13.07
13.10
12.89
13.03
13.00
12.89
13.07
13.07
12.89
12.96
13.10
13.07
13.03
12.89
13.31
13.24
13.31
13.35
13.28
13.35
13.42
13.42
13.35
13.31
13.31
13.38
13.35
13.31
13.35
13.31
13.46
13.35
13.21
13.24
13.35
13.24
13.35
13.62
13.74
13.66
13.66
13.74
13.66
13.78
13.78
13.70
13.62
13.70
13.70
13.82
13.62
13.62
0.00
12.60
12.75
12.84
12.90
12.95
12.99
13.03
13.05
13.08
13.10
13.12
13.14
13.16
13.18
13.19
13.21
13.22
13.23
13.24
13.25
13.26
13.27
13.28
13.29
13.30
13.31
13.32
13.33
13.33
13.34
13.35
13.36
13.36
13.37
13.38
13.38
13.39
13.39
13.40
13.40
13.41
13.41
13.42
13.42
13.43
13.43
13.44
13.44
13.45
13.45
13.46
13.46
13.47
13.47
13.47
13.48
13.48
13.48
13.49
13.49
0.0903
0.0548
0.0409
0.0333
0.0283
0.0248
0.0222
0.0202
0.0185
0.0172
0.0160
0.0150
0.0142
0.0135
0.0128
0.0122
0.0117
0.0112
0.0108
0.0104
0.0100
0.0097
0.0094
0.0091
0.0089
0.0086
0.0084
0.0082
0.0080
0.0078
0.0076
0.0074
0.0072
0.0071
0.0069
0.0068
0.0067
0.0065
0.0064
0.0063
0.0062
0.0061
0.0060
0.0059
0.0058
0.0057
0.0056
0.0055
0.0054
0.0054
0.0053
0.0052
0.0051
0.0051
0.0050
0.0049
0.0049
0.0048
0.0048
0.0047
5.22818E-11
3.17496E-11
2.37047E-11
1.92638E-11
1.63881E-11
1.43699E-11
1.28583E-11
1.16778E-11
1.07266E-11
9.93805E-12
9.27796E-12
8.71364E-12
8.22482E-12
7.79472E-12
7.41639E-12
7.07910E-12
6.77622E-12
6.50252E-12
6.25263E-12
6.02555E-12
5.81719E-12
5.62523E-12
5.44688E-12
5.28223E-12
5.12897E-12
4.98591E-12
4.85201E-12
4.72578E-12
4.60767E-12
4.49637E-12
4.39127E-12
4.29137E-12
4.19717E-12
4.10777E-12
4.02277E-12
3.94185E-12
3.86434E-12
3.79071E-12
3.72035E-12
3.65303E-12
3.58823E-12
3.52640E-12
3.46705E-12
3.41003E-12
3.35494E-12
3.30217E-12
3.25134E-12
3.20234E-12
3.15506E-12
3.10920E-12
3.06510E-12
3.02247E-12
2.98123E-12
2.94111E-12
2.90244E-12
2.86496E-12
2.82862E-12
2.79335E-12
2.75896E-12
2.74804E-12
1.36768E-10
1.38396E-10
1.39350E-10
1.40027E-10
1.40555E-10
1.40983E-10
1.41346E-10
1.41661E-10
1.41938E-10
1.42187E-10
1.42411E-10
1.42616E-10
1.42805E-10
1.42980E-10
1.43142E-10
1.43294E-10
1.43437E-10
1.43571E-10
1.43699E-10
1.43820E-10
1.43935E-10
1.44044E-10
1.44150E-10
1.44250E-10
1.44346E-10
1.44438E-10
1.44527E-10
1.44613E-10
1.44696E-10
1.44775E-10
1.44853E-10
1.44928E-10
1.45000E-10
1.45070E-10
1.45139E-10
1.45205E-10
1.45270E-10
1.45333E-10
1.45394E-10
1.45453E-10
1.45512E-10
1.45568E-10
1.45624E-10
1.45678E-10
1.45731E-10
1.45783E-10
1.45833E-10
1.45883E-10
1.45932E-10
1.45979E-10
1.46026E-10
1.46072E-10
1.46117E-10
1.46161E-10
1.46204E-10
1.46246E-10
1.46288E-10
1.46329E-10
1.46369E-10
1.46382E-10
krl
1.000
0.194
0.118
0.088
0.071
0.061
0.053
0.048
0.043
0.040
0.037
0.034
0.032
0.031
0.029
0.028
0.026
0.025
0.024
0.023
0.022
0.022
0.021
0.020
0.020
0.019
0.018
0.018
0.018
0.017
0.017
0.016
0.016
0.016
0.015
0.015
0.015
0.014
0.014
0.014
0.014
0.013
0.013
0.013
0.013
0.012
0.012
0.012
0.012
0.012
0.012
0.011
0.011
0.011
0.011
0.011
0.011
0.010
0.010
0.010
0.010
kra
0
0.507
0.513
0.517
0.519
0.521
0.523
0.524
0.525
0.526
0.527
0.528
0.529
0.530
0.530
0.531
0.531
0.532
0.532
0.533
0.533
0.534
0.534
0.535
0.535
0.535
0.536
0.536
0.536
0.537
0.537
0.537
0.538
0.538
0.538
0.538
0.539
0.539
0.539
0.539
0.539
0.540
0.540
0.540
0.540
0.541
0.541
0.541
0.541
0.541
0.541
0.542
0.542
0.542
0.542
0.542
0.542
0.543
0.543
0.543
0.543
La permeabilidad efectiva del líquido y del aire se determina de:
      Q  (t) 
k   efect (t)  


 p   S 
     a Q a (t) 
k   efect (t)  


 p   S 
y se muestran en la tabla anterior y la figura siguiente.
sat
Sat reducida
s
(s-soo/(1-soo)
0.909
0.856
0.843
0.832
0.813
0.803
0.794
0.794
0.784
0.775
0.775
0.762
0.749
0.749
0.739
0.739
0.730
0.730
0.730
0.720
0.720
0.711
0.701
0.684
0.684
0.684
0.686
0.684
0.677
0.677
0.677
0.677
0.667
0.667
0.667
0.667
0.667
0.667
0.667
0.667
0.667
0.660
0.660
0.660
0.650
0.650
0.650
0.650
0.643
0.643
0.641
0.643
0.635
0.633
0.633
0.624
0.624
0.624
0.624
0.624
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
0.
805
691
663
638
598
577
557
557
537
516
516
488
459
459
439
439
419
419
419
398
398
378
358
321
321
321
325
321
305
305
305
305
285
285
285
285
285
285
285
285
285
268
268
268
248
248
248
248
232
232
228
232
215
211
211
191
191
191
191
191
284
Manual de Filtración & Separación
20.00
18.00
14.00
3
Flujo de aire cm /s
16.00
12.00
10.00
Qa=a+blnt
8.00
2
R =0.991
a=12.448972
6.00
b=0.21718605
4.00
Datos experimentales
Simulado
2.00
0.00
0
20
40
60
80
100
120
140
Tiempo de soplado s
Correlación del flujo de aire en el soplado.
Permeabilidad del líquido kl y del aire ka cm
2
1.6E-10
1.4E-10
1.2E-10
1.0E-10
8.0E-11
6.0E-11
líquido
aire
4.0E-11
2.0E-11
0.0E+00
0.600
0.650
0.700
0.750
0.800
0.850
0.900
0.950
Saturación s
Permeabilidades efectivas del líquido y del aire.
La saturación se calcula de:
s
Vliquido  total  Vf  total (t)
Vliquido  total  (Vf  formacion  Vf  exp resion )

20.36  Vf  total (t)
20.36  (7.51  6.14)
Capítulo 9 Filtración
285
Finalmente las permeabilidades relativas se obtienen de las siguientes
ecuaciones:
k
k
k    efect
y
k a  a efect
k()
k()
y el resultado se incluye en la misma tabla anterior.
Una vez determinados estos valores, se puede graficar las permeabilidades
relativas en función de la saturación.
La saturación reducida se calcula en términos de la saturación residual
s   0.535 mediante la ecuación:
sr 
s  s
1  s
El resultado se entrega en la tabla anterior. Las funciones que representan a las
permeabilidades relativas se muestran en la figura y ecuaciones siguientes.
k   s r   exp  4.466256  4.4661532  s r2 
k a  sr  
0.55207243  0.55208459  s r
1  0.91554001  s r  0.07642878s 2r
0.6
Permeabilidad relativa kl y ka
0.5
líquido
aire
0.4
0.3
0.2
0.1
0.0
0.5
0.6
0.7
0.8
0.9
Saturación
Permeabilidades relativas del líquido y del aire.
1.0
286
Manual de Filtración & Separación
Permeabilidad reducida del líquido k l y del aire k a
1.0
líquido
aire
correlación líquido
aire
2
ka=(a+csr)/(1+bsr+dsr )
0.9
a=0.55207243
0.8
b=-0.91554001
0.7
c=-0.55208459
d=-0.076422878
0.6
0.5
0.4
2
kl=exp(a+bsr )
0.3
a=-4.466256
0.2
b=4.4661532
0.1
0.0
0.0
0.2
0.4
0.6
0.8
1.0
Saturación residual sr=(s-soo)/(1-soo)
Correlación para las permeabilidades relativas.
9.6
FILTROS CONTINUOS A VACÍO
La filtración a vacío ha sido y sigue siendo un proceso importante en las
empresas mineras y en los inicios y gran parte del siglo XX fue el único proceso
aplicado. En este tipo de filtración, la pulpa es alimentada a un estanque, en el cual se
encuentra sumergido el filtro propiamente tal, por el lado del medio filtrante que se
encuentra a presión atmosférica. El otro lado del medio filtrante está conectado a un
mecanismo que produce vacío y mantiene una diferencia de presión entre ambos lados
del medio filtrante. La diferencia de presión impulsa el filtrado a través de medio
filtrante dejando el sólido adherido al medio filtrante en la forma de un queque. La
diferencia de presión máxima teórica posible en este tipo de filtros es de 1 atmósfera,
sin embargo las pérdidas en el equipo y, principalmente la altura sobre el nivel del mar
a que se encuentre la concentradora restringe este valor severamente, siendo
frecuentemente de 0.6 a 0.8 bares. Es así como la filtración a vacío se lleva a cabo a
caída de presión pequeña y constante, por lo que el queque producido puede ser
considerado incompresible.
Como ya hemos visto, existen varios tipos de filtros a vacío en el mercado,
principalmente los filtros rotatorios, de discos y tambor, los filtros de banda y los
filtros de bandeja. La selección del tipo de filtro para cada operación depende
principalmente del tipo de material a filtrar. Pulpas con partículas gruesas son muy
difíciles de mantener en suspensión por lo que se las trata preferentemente en filtros de
banda, filtros de tambor con alimentación superior y en filtros de bandeja. Pulpas de
materiales finos se filtran principalmente en filtros de discos o de tambor.
Capítulo 9 Filtración
287
Para todos estos tipos de filtro de vacío de que utilizan telas como medio
filtrante una de las componentes importantes del costo es el consumo de aire, con
demandas de potencia de entre 2 a 15 kW/m2 de área de filtración (Henriksson 2000).
Como alternativa al uso de telas filtrantes, algunos filtros de discos utilizan
membranas cerámicas construidas en base a alúmina. La característica de esta cerámica
es su tamaño pequeño y homogéneo de poros, del orden de 2 micrones, que produce
una succión capilar de acuerdo con la ley de Young-Laplace (ver sección 6.5.1 de este
Manual). Esta acción permite al filtrado fluir a través del medio poroso con una
mínima ayuda de vacío e impide el paso de aire. Por esta razón la energía consumida
por estos filtros para mantener el vacío mucho menor, con demandas de potencia de
sólo 0.05 kW/m2 de área filtrante (Henriksson 2000). El principal problema de estos
filtros es el bloqueo del medio poroso cerámico con pequeñas partículas de sólido, los
que deben ser eliminados mediante lixiviación con ácido concentrado.
9.6.1 Modelo de un Filtro Rotatorio
Consideremos un filtro rotatorio a vacío, como por ejemplo un filtro de discos o de
tambor, girando a N revoluciones por minuto. El tiempo tR , en minutos, que dura cada
revolución será t R  1 N . Si I es la fracción de este tiempo correspondiente a la etapa
de formación de queque, el tiempo total de filtración en minutos por cada revolución
del filtro será:
I
N
Tiempo de formación de queque
tF  I  tR 
Tiempo de deshumedecimiento
t D  (1  I)  t R 
T rev
(9.43)
1 I
T / rev
N
(9.44)
Supongamos que el filtro está sumergido en la suspensión hasta una altura h, ver figura
9.16

h
Fig. 9.16 Filtro rotatorio a vacío
288
Manual de Filtración & Separación
La fracción I del tiempo correspondiente a la formación de queque, debe ser igual a la
fracción de superficie de filtración sumergida en la suspensión, esto es:
I
a)

,
360
tF 
 1
360 N
T rev
y
 1

t D  1 

360

N
(9.45)
Formación del queque
La relación entre el volumen de filtrado producido y el tiempo de formación de
queque está dada por la ecuación (9.15):
Vf2 (t f )  2Sk()R m
1  0  
2S2 k()pe 1  0  
Vf (t f ) 
tF  0
0

0
Sustituyendo (9.43) y (9.45) se obtiene, por revolución del filtro:
Vf2 (N)  2Sk    R m
2S2 k    p e 1  0   
1  0  
Vf (N) 
0
0

0
360N
ordenando
S2  Vf (N)N  2S2 k()R m (1  0  )  Vf (N)N  2S2 k() p e 1  0    
0

 


0

0
N2 
S
N
S
360N



2
(1  0  )  Vf (N)N  2k()p e 1  0    N
 Vf (N)N 
0

  2k()R m N


S
S
360
0

0




2
Velocidad de percolación
Es fácil ver que el término (Vf S) N corresponde al volumen de filtrado por
unidad de área producido en N revoluciones del filtro por unidad de tiempo, esto es, la
velocidad de percolación qf.( L3 L2 T ):
q f (t) 
Vf N 3 2
L LT
S
(9.46)
Remplazando en la expresión anterior, se obtiene una ecuación algebraica de segundo
grado para la velocidad de percolación q f (t) en función de la velocidad de rotación
del filtro en el período de formación de queque:
q f2 (t)  2k()R m N
cuya solución es:
(1  0  )
k()Npe 1  0    
q f (N) 
0
0

0
180
(9.47)
Capítulo 9 Filtración
289
12

(1  0  )  2
p e
0
 
-1
q f (t)  Nk()
 R m 
  R m  LT
0
k() (1  0  ) 180N 


(9.48)
Flujo másico
El flujo másico de queque está relacionado con el volumen de filtrado mediante la
ecuación (9.14), por lo que resulta:
m s (t) 
s 0 (1  )
Sq (t)
1  0    f
(9.49)
Reemplazando en (9.48) obtenemos el flujo másico:
12


pe
0
 
-1
2
ms (t)  s (1  )Sk()N  R m 
  R m  MT
k(
)
(1
)
180N






0



(9.50)
Si la resistencia del medio filtrante puede ser despreciada, las ecuaciones (9.48) y
(9.50) se reducen a:
12
 k() p e (1  0  ) N 
q f (t)  


0
180 

LT-1
(9.51)
12
 k()pe
0
N 
ms (t)  s (1  )S 


(1  0  ) 180 

MT-1
(9.52)
Las ecuaciones (9.48) a (9.52) permiten calcular la capacidad de un filtro a vacío
rotatorio, donde k() es la permeabilidad del queque de porosidad , 0 es la fracción
volumétrica de sólidos de la suspensión a filtrar, s es la densidad del sólido,  es la
viscosidad del filtrado, pe es la caída de presión total a través del filtro (medio
filtrante y queque), N es el número de revoluciones por minuto del filtro y  es el
ángulo sustentado por la parte del filtro sumergida en la suspensión.
Es conveniente separar en las ecuaciones (9.51)y (9.52) aquellas variables que
son propiedades del sólido, fluido y suspensión y aquellas que son del queque y las
variables de operación.
12
 1 (1  0  ) 
q(t)  

0


Propiedades de la
suspensión

12

 

N
 p e
180 

Propiedades del
queque
Variables de
operación
 k() 
12
(9.53)
290
Manual de Filtración & Separación
12
 1 0 (1  ) 2 
ms (t) sS 

  (1  0  ) 

 k() 
12
12

N 

 p e

180


(9.54)
Espesor del queque
La relación entre el flujo de sólidos en el queque y el espesor de éste está dada
por la ecuación (9.12), de donde resulta:
(t) 
m s (t f )
s (1  )SN
(9.55)
L rev
Reemplazando en (9.50) y (9.54), dependiendo si se desprecia o no la resistencia del
medio filtrante, obtenemos por revolución:
12


p e
0
 
2
(t)  k()  R m 
  Rm 
k() (1  0  ) 180N 


12
12
1

0
 
12

(t)  
   k()    p e

180N 

  (1  0  ) 
b)
(9.56)
(9.57)
Cambio de condiciones de operación
Consideremos un filtro rotatorio operando en las condiciones ( pe1 , N 1 ) dando
una capacidad y espesor del queque de (ms1 , 1 ) y en las condiciones de operación
( pe 2 , N 2 ) , con espesor del queque de (ms2 ,  2 ) . El espesor del queque por
revolución es:
(N) 
ms
1
s (1  )S N
y por lo tanto:
 2 (N 2 ) m s2 N1

1 (N1 ) m s1 N 2
Si exigimos que en ambas condiciones de operación 1 y 2, los espesores del queque
permanezcan iguales,  1   2 , se desprende que:
m s2 N 2

m s1 N1
Por otra parte, el cuociente de masa producida se puede obtener de (9.54):
(9.58)
Capítulo 9 Filtración
291
12
ms1  pe1N1 


ms2  pe2 N 2 
(9.59)
reemplazando (9.58) en (9.59) da como resultado:
12
m s1  pe1 


m s2  p e2 
(9.60)
Las expresiones (9.58) a (9.60) permiten calcular la capacidad de un filtro rotatorio
ante un cambio de condiciones de operación, conociendo la capacidad anterior.
c)
Deshumedecimiento del queque
El deshumedecimiento del queque se produce por succión de aire desde el
ambiente mediante el sistema de vacío. El tiempo de deshumedecimiento, que
designamos con t D , corresponde a la fracción (1  I) del tiempo t R , y está dado por
(9.45):
 1

t D  1 
T rev

 360  N
La humedad final del queque depende de cantidad de material a tratar en este tiempo y
de la permeabilidad relativa del material a filtrar. El tiempo de deshumedecimiento está
dado por:
  1  0 


 R m 1  s  
1 
 
k  0 
 360  N pe 
d
1

 k  ,  
s

que relaciona la velocidad de rotación con la saturación final.
El flujo de aire durante el deshumedecimiento está dado por:
 Spe
Qg  
 
 g



Rm 



k()k g (,s) 

1
(9.61)
En estas ecuaciones k i ( 0 ,s)  f i  s,s   , con i  ,a son las formas funcionales de las
permeabilidades relativas del líquido y aire.
Ejemplo 13
Un filtro rotatorio, cuya velocidad es de N=0.03 Hz, produce 27 m3/h de
filtrado. A que velocidad debe ser operado el filtro para obtener 54 m3/s, si el filtro
funciona al mismo vacío y se desprecia la resistencia del medio filtrante.
292
Manual de Filtración & Separación
Como la masa de filtrado es proporcional a la masa de sólido en el queque (ver
ecuación (9.15)), y las caídas de presión son iguales, según (9.59) podemos escribir:
12
Q2  N 2 


Q1  N1 
de donde resulta:
Q 
N 2  N1   2 
 Q1 
2
2
 54 
 (0.03  60)     7.2 rpm
 27 
Ejemplo14
Un filtro rotatorio de tambor de 3 m2 de área funciona a una presión interna de
30 kN/m2 y con un 30 % de su superficie sumergida en la suspensión. La presión
atmosférica es de 1.013x105 N/m2. Calcular la capacidad del filtro y la humedad final
del queque cuando el tambor gira a 0.5 rpm. El queque es incompresible y la tela
filtrante tiene una resistencia igual a la de un queque de 1 mm de espesor. Datos:
Ángulo sumergido
  120
Superficie
S  3 m2
Velocidad de rotación
N  0.5 rpm
Porosidad de la torta
  0.400
Permeabilidad de la torta
k()  5  1013 m 2
Densidad del sólido
s  2000 kg m3
Densidad del filtrado
f  1000 kg m3
Viscosidad del filtrado
  103 Ns m 2
Viscosidad del aire
g  1.85  10 5 Ns m 2
Concentración de la suspensión
20% en peso
Espesor del queque
  2.3 cm
Permeabilidad relativa del líquido k   s r   exp  4.466256  4.4661532  s r2 
Permeabilidad relativa del aire
k a  sr  
0.55207243  0.55208459  s r
1  0.91554001  s r  0.07642878s r2
Capítulo 9 Filtración
293
Saturación residual
s   0.535 .
Humedad final
h  18%
Producto
s 1   h
2 1  0.4 18

 0.659
f  100  h 1 0.4 100  18
Saturación final:
s
Saturación residual final:
sr 
s  s 0.659  0.535

 0.266
1  s
1  0.535
Tiempo de una rotación:
tR 
1 60

 120 s
N 0.5
Tiempo de formación del queque
tF 
120
 120  40 s
360
Tiempo de deshumedecimiento:
 120 
t D  1 
  120  80 s
 360 
Tiempos de filtración
Capacidad:
Resistencia del medio filtrante
Rm 
0.1
mm m 2
k()
 1  103   1 

 2  107 cm 1
13  
2 
 5  10   10 
La capacidad del filtro está dada por (9.20):
12
 


2pe
0
2
m  , t   sSN 1    k     R m 
t  Rm 
k    1  0    
 

 733 g s
 63.3 tpd
Espesor del queque
De la ecuación (9.55) tenemos:

ms
733

 2.44 cm
s 1    SN 2  (1  0.4)  3  104  8.33  103
294
Manual de Filtración & Separación
El flujo de filtrado es:
Qf 
m s 1  0   1
 2686.80 cm3 s
1 
s
0
 2.69  103 m3 s
Humedad del queque
La ecuación (9.34) relaciona el flujo de filtrado con la permeabilidad relativa:

p e 

  Rm 
 q
 
k( 0 )k  ( 0 ,s) 
Despejando la permeabilidad relativa del líquido se obtiene:
k   ,s  

 pe  q  R m  k   
2.44
 7.1  105  3  104

 2  107   5  10 9

3
 0.01  2.69  10

 0.632

Como la ecuación constitutiva de la permeabilidad relativa del filtrado está dada por:
k   s r   exp  4.466256  4.4661532  s r2 
Despejando la saturación reducida sr resulta:
 ln k   ,s   (4.466256 
sr  

4.4661532


0.5
 ln(0.632)  4.466256 


4.4661532


0.5
 0.947
La saturación final será:
s  s   s r  (1  s  )  0.535  0.947  (1  0.535)  0.975
y finalmente la humedad es:
h  100
f s
1  0.4  0.975
 100
 24.5 %
1 0.4  0.975  2  (1  0.4)
f s  s 1   
Flujo de aire
La permeabilidad relativa del aire está dada por:
Capítulo 9 Filtración
k a  sr  

295
0.55207243  0.55208459  s r
1  0.91554001  s r  0.07642878s2r
0.55207243  0.55208459  0.947
 0.454
1  0.91554001  0.947  0.07642878  (0.947) 2
El flujo de aire a través del queque está dado por:
1
 Sp e N 


Qg  
 R m 
 
k(
)k
(
,s
)



a
a
r



 3 104  7.1105  8.33  103  
2.44

7

   2 10 

4
9
1.85

10
5

10

0.454


 
3
4
3
 875 cm s  8.75 10 m s
1
 75.6 m3 d
9.7
FILTROS A PRESIÓN
Tal como se indicó en la sección 9.1.5 los filtros a presión funcionan en forma
semi-continua, esto es en etapas, formando un ciclo de filtrado.
La pulpa es alimentada a las cámaras de filtración, espacios cerrados entre la tela
permeable filtrante y un diafragma impermeable, desde un manifold por tantas
mangueras como cámaras del filtro. Tan pronto como se cierran todas las cámaras, se
bombea la pulpa, la que se distribuye uniformemente a través de la superficie
horizontal de la tela en todas las cámaras. Cuando las cámaras se encuentran llenas, se
bombea aire a alta presión detrás de los diafragmas. Esto inicia la filtración a presión
en todas las cámaras. Aun cuando la filtración se inicia simultáneamente con el llenado
de las cámaras, la formación de la torta se prolonga hasta el final de la etapa de
prensado (expresión). Terminada esta etapa, se sopla aire sobre la torta para desplazar
el agua retenida en sus poros. La torta puede ser descargada en ese momento, o puedes
ser lavada, prensada y secada nuevamente. Terminado el proceso, cilindros hidráulicos
abren el conjunto de placas para descargar el queque. En la tabla que sigue se muestra
un ciclo típico de un filtro a presión (Droguett 2000).
En la tabla Se puede observar que los tiempos de cada etapa del ciclo se pueden
dividir entre el tiempo utilizado efectivamente en la filtración, llamado tiempo de
filtración y el tiempo de operación del equipo que no contribuyen a la filtración y que
reciben en nombre de tiempo muerto. En el ejemplo dado, 265 s corresponden al
tiempo de filtración y 249 s al tiempo muerto. Es importante recalcar que cuando se
desea optimizar un filtro a presión, se debe mejorar no solamente el tiempo de
filtración, sino que se debe intentar disminuir el tiempo muerto.
296
Manual de Filtración & Separación
ETAPA
FUNCIÓN
TIEMPO s
1
Cierre de las placas
50
2
Alimentación (llenado de cámaras)
85
3
Lavado del tubo de alimentación.
13
4
Lavado de mangueras de alimentación.
50
5
Prensado (expresión).
80
6
Liberación de aire comprimido
5
7
Abertura y cierre de tubo de desagüe
30
8
Soplado de la torta.
100
9
Drenaje de presión
10
10
Abertura de válvula de alimentación
1
11
Descarga de la torta y lavado de tela
18
12
Lavado de la tela
72
14
Total ciclo
514
Ejemplo 14
Con los datos del ejemplo 12 y para una temperatura de 20 °C, viscosidad del
líquido   0.01 g cms , viscosidad del aire   0.000187 g cm  s , densidad del
líquido de 1.00 g/cm3 y densidad del concentrado s  4.50 g cm3 , calcule la
capacidad del filtro, en tpd para producir un queque con 8.5% de humedad aplicando
una presión de aire de 6 bares para la formación de queque y soplado y de 7.5 bares
para un prensado de 75 segundos, con un queque de espesor igual a 3.0 cm antes de
prensar, en un filtro prensa de banda horizontal con un área de filtración de 144 m2. La
alimentación y formación del queque toma 85 segundos.
Del resultado obtenido en el problema 12 y datos adicionales tenemos:
Etapa de formación del queque:
p e  6  106 N m 2
  3.0 cm
 0  0.520
R m  9.80  109 cm 1
k()  1.55  1010 cm2
S  144 m 2
Capítulo 9 Filtración
297
Etapa de expresión:
p e  7.5  106 N m 2
Reducción de la porosidad de  0  0.520 a
  0.362
Etapa de soplado:
p e  6  106 N m 2
  0.362
Correlación de las permeabilidades relativas reducidas
k   exp  4.466256  4.4661532  s 2r 
ka 
0.55207243  0.55208459  s r
1  0.91554001  s r  0.07642878sr2
s   0.535
Como el volumen del sólido es constante en el queque antes y después del prensado,
podemos escribir:
Vs  V1 (1  1 )  V2 (1   2 )
y como V    S , resulta:
 2  1 
1  1
1  0.520
 3.0 
 2.26 cm
1  2
1  0.362
Tiempo de soplado:
Para la humedad deseada de 8.5%, la saturación es de:
s
s 1   0
h
4.5 1  0.362 8.5

 0.737
1 0.362 100  8.5
f  0 100  h
sr 
s  s  0.737  0.535

 0.4344
1  s
1  0.535
De la expresión (9.35) y la función de permeabilidad relativa del líquido con
a  4.466256 y b  4.4661532 , calculamos el tiempo de soplado para obtener un
8.5% de humedad final en el queque:
298
Manual de Filtración & Separación
ts 
 0
p e
 0

pe


 1  s  
R m 1  s  

k   0  

d

2
s r exp  a  b 

1
1


 1  s    
1
 R m 1  s  

 
k   0    2b exp  a  b2  


0.43
0.01  2.26  0.362 
2.26  (1  0.535) 
 9.80  109  (1  0.737) 

6
6  10
1.55  1010 

2
 exp  4.466256  4.4661532    


2  4.4661532  

0.43
1
 91.7 s
Flujo de aire:
El flujo de aire se calcula con la ecuación (9.36):
 Sp e 


Qg  
Rm 


  g 
k( 0 )f g ( 0 ,s) 


1
1



 Sp e  

  1.24 106 cm3 s  1.24 m3 s

Q gs  
R
  g   m



a  cs r


k(0 ) 
2 


 1  bs r  ds r  

Consumo de aire:
Va  Qa  t 3  1.24  91.7  113.8 m3
Capacidad del filtro:
El tiempo de un ciclo es de:
t  t a lim. formacion  t prensado  t soplado  t muerto
 85  80  92  249  506 s
Esto significa que por cada ciclo de 506 s, se forma queque por sólo 85 s.
Masa por ciclo:
Capítulo 9 Filtración
299
12
12

2 
0
m   0 , t   s 1   0  S   

    1  0   0 
 k  
 2 
 4.5  (1  0.506)  144  104  

 0.01 
12
0
p1e 2 t1 2
0.5
0.5
0.381
0.5


10 0.5
6 0.5

  1.55  10    6  10   85 
 1  0.381  0.506 
 2.356  107 g ciclo
 2.356  107  3600 / 506 t ciclo
 167.6 tph
9.8
REFERENCIAS
Concha, F., Reología de Suspensiones, Monografía, Universidad de Concepción, 1990.
Droguett, M.H., Optimización del Sistema de Filtrado de la Planta Coloso de Minera
Escondida, Memoria de Título para optar al título de Ingeniero Civil Metalúrgico,
Universidad de Concepción, 2000.
Henriksson, B., Focus on Separation in the Mining Industry, Filtration + Separation, 37
(7), 2000, 26-29.
Holdich, R., Simulation of compressible cake filtration, Filtration + Separation, 31,
1996, 825-829.
Massarani, G., Problemas em Sistemas Particulados, COPPE/UFRJ, 1978, 21.
Massarani, G., Fluodinámica em Sistemas Particulados, UFRJ, 1997,
Tiller, F.M., The role of porosity in Filtration. Numerical method for constant rate and
constant pressure filtration based on Kozeny´s law, Chem. Eng. Prog., 49(9), 1953,
467-479.
Tiller, F.M., The role of porosity in Filtration, Part III, Variable-pressure-variable rate
filtration, AIChE J., 6(4), 1958, 170-174.
Tiller, F.M. and Cooper H.R., The role of porosity in Filtration. Part IV. Constant
pressure filtration, AIChE J., 6(4), 1958, 595-601.
Tiller, F.M. and Cooper H.R., The role of porosity in Filtration. Part V. Porosity
variations in filter cakes, AIChE J., 8(4), 1962, 445-449.
Tiller, F.M. and Shirato, M., The role of porosity in Filtration. Part VI. New definition
of filter resistance, AIChE J., 10(1), 1964, 61-67.
Tiller, F.M. and Lu, W., The role of porosity in Filtration. Part VIII, cake nonuniformity in compression-Permeability Cells. AIChE J., 18(3), 1972, 569-572.
300
Manual de Filtración & Separación
Tiller, F.M. and Yeh, C.S., The role of porosity in Filtration. Part XI, Filtration
followed by expression, AIChE J., 33(8), 1987, 1241-1256.
Tiller, F.M. and Hsyung, N.B. and Cong, D.Z., The role of porosity in Filtration. Part
XII, Filtration with Sedimentation, AIChE J., 41(5), 1153-1164.
Wakeman, R.J. and Tarleton, Filtration: Equipment Selection, modeling and process
Simulation, Elsevier Sci., Oxford, 1999, 81-82.
Wakeman, R.J. and Tarleton, E.S., Filtration: Equipment Selection, modeling and
process Simulation, Elsevier Sci., Oxford, 1999a, 23.
CAPÍTULO 10
AGREGACIÓN DE PARTÍCULAS POR FLOCULACIÓN
10.1 INTRODUCCIÓN
El procesamiento de una mena para transformarla en un material valioso, tal
como un concentrado de un mineral metálico o un mineral industrial, implica realizar
una serie de operaciones consecutivas con el objetivo de liberar las especies valiosas de
la mena, concentrarlas, separarlas del agua en que generalmente están suspendidas y
secarlas. El paso más importante, ya sea porque sin él no existe proceso que recupere
los materiales valiosos o porque es el más costoso de todos, es la reducción de tamaño.
Es esencial disminuir el tamaño de las partículas de la mena hasta un punto tal en que
las especies útiles se encuentren separadas del material estéril o ganga. Solamente así
los procesos de concentración o separación podrán funcionar. A medida que las menas
de alta ley se agotan, es necesario beneficiar materiales cada vez más pobres, que
tienen por característica tener una diseminación más fina y, por lo tanto, requieren un
mayor grado de molienda para su liberación. Por otra parte, es sabido que la flotación,
uno de los procesos de concentración más utilizados en la actualidad, es más efectiva
con partículas de un rango de tamaño intermedio. Partículas muy grandes, aunque
estén liberadas, no pueden ser suspendidas por los agitadores de las celdas y las
burbujas no son capaces de llevarlas a la espuma. Por otra parte, las partículas muy
finas, denominadas lamas, perjudican la eficiencia de la flotación por varias razones
que aquí no discutiremos. También es de conocimiento general que el tamaño de las
partículas de una suspensión es una variable importante en los procesos de separación
sólido-líquido, ya que suspensiones muy finas sedimentan y filtran muy lentamente. Se
llega así a una situación en que, por un lado es necesario moler más fino para liberar
las partículas y por el otro, al hacerlo se perjudica el propio proceso de concentración y
las operaciones posteriores.
La solución que se ha encontrado para este problema consiste en moler tan fino
como sea necesario y luego aglomerar las partículas para crear entes mayores que
puedan ser procesadas adecuadamente. Los aglomerantes se utilizan ocasionalmente en
la flotación (ver capítulo 11 de este Manual) pero tienen su mayor aplicación en los
procesos de separación sólido-líquido. Al aglomerarse, las partículas de una suspensión
crecen en tamaño y adquieren una mayor velocidad de sedimentación, esencial para
lograr una buena separación mediante espesamiento. Los aglomerados forman también
queques de filtración más permeables que los de las partículas individuales, acelerando
todo el proceso de filtración. Se puede distinguir tres procesos de agregación que se
utilizan en la industria minera, la coagulación, la floculación y la agregación hidrófoba.
Estos procesos se distinguen por sus mecanismos de agregación.
301
302
Manual de Filtración & Separación
10.1.1 Coagulación
Se denomina coagulación al proceso de agregación de partículas de una
suspensión basado en la reducción de la repulsión ínter partícula, ya sea por
neutralización de la carga superficial o por compresión de la doble capa eléctrica que
rodean a todas las partículas en un electrolito. La figura 10.1 muestra la distribución de
potencial de una partícula en un electrolito.
Fig. 10.1 Distribución de potencial alrededor de una
partícula con carga eléctrica en un electrolito.
La interacción entre partículas en una dispersión se debe a dos tipos de fuerzas.
Una fuerza atractiva de muy corto alcance, denominada fuerza de Van der Waals, y
una fuerza repulsiva, de mucho mayor alcance, debido a la carga eléctrica superficial
que poseen las partículas. Las fuerzas de Van der Waals dan origen a un potencial de
atracción en la partícula dado por la siguiente expresión:
VA  
d1d 2 H
d1  d 2 12h
(10.1)
donde d1 y d2 son los diámetros de las partículas, h es la distancia entre partículas, H es
la constante de Hameker-London (para dos esferas de cuarzo del mismo tamaño es
aproximadamente A10-20).
CAPÍTULO 11 Floculación
303
La estabilidad de los coloides, que les permite no sedimentar en un campo
gravitacional, se puede explicar por esta fuerza electrostática repulsiva que constituye
una verdadera barrera para que las partículas se acerque lo suficiente como para que
actúen las fuerzas atractivas de Van der Waals. El potencial de repulsión electrostática
VE están dados por (Hogg et al 1966 ):
VE 
1  exp  h  
d1d 2  
2
2
 21 2 ln 
  1   2 ln 1  exp  2h   (10.2)
d1  d 2 8 
1

exp

h
  



donde  es la constante dieléctrica del líquido, 1 y 2 son los potenciales superficiales

de las partículas 1 y 2 y  es el largo de Debye dado por:  1  2q 2 z 2 c 0  r kT

12
,
donde q, z y c son la carga, la valencia y la concentración de los iones en solución, 0
es la permitividad del espacio vacío y r es la constante dieléctrica de la solución. Las
figuras 10.2 y 10.3 muestran en forma esquemática el potencial electrostático de una
partícula suspendida en un electrolito.
Fig. 10.2 Esquema de la distribución de iones y
potenciales alrededor de una partícula inmersa en un
electrolito.
Fig. 10.3 Energía potencial de repulsión versus
distancia para dos partículas de una suspensión.
304
Manual de Filtración & Separación
Se sabe que la coagulación de partículas coloidales, con tamaños menores a
0.1m, está dominada por las fuerzas de London-Van der Waals y el movimiento
browniano. Las fuerzas de interacción entre partículas ha sido cuantificada por la teoría
de Derjagin-Landau-Verwey-Overbeek (DLVO). Esta teoría indica que el potencial
resultante de la atracción de Van der Waals VA y repulsión electrostática da como
resultado lo que se muestra en la figura 10.4.
Fig. 10.4 Energía potencial total versus distancia entre
dos partículas mostrando cuatro tipos de interacción: A)
coagulación rápida, B) coagulación secundaria débil, C)
coagulación con barrera de energía y D) dispersión
espontánea.
En el caso A, las partículas no experiencian fuerza repulsiva y caen directamente en el
mínimo primario, el sistema es totalmente inestable y las partículas sufren una
coagulación rápida irreversible. En el caso B, la repulsión produce un potencial
máximo (Vmax) bastante alto lo que previene que las partículas coagulen
espontáneamente, pero permite una coagulación débil en el potencial mínimo
secundario (Vmin). Estos flóculos pueden re-dispersarse con facilidad La curva C
muestra un potencial máximo lo suficientemente alto para prevenir la floculación. La
curva D representa un sistema con fuerzas repulsivas tan grandes que impiden la
floculación en toda circunstancia resultando en un sistema disperso estable. La barrera
Vmax y el mínimo Vmin se pueden disminuir disminuyendo la repulsión electrostática
mediante un aumento de la fuerza iónica de la solución, lo que disminuye el largo -1
de la doble capa eléctrica, o disminuyendo la carga superficial mediante la adición de
contraiones.
En general las partículas minerales suspendidas en agua poseen una carga
superficial negativa por lo que la adición de cationes multivalentes, tales como Al3+,
Fe3+, Fe2+, Ca2+ o Mg2+, las neutralizan y permiten su acercamiento y la actuación de
CAPÍTULO 11 Floculación
305
las fuerzas atractivas y, por lo tanto, su agregación formando coágulos. La condiciones
de coagulación se pueden cuantificar a través del potencial  , que mide la magnitud
del potencial electrostático en la superficie de las partículas (medido, por ejemplo, por
electroforesis). Se denomina potencial  crítico al potencial bajo el cual las partículas
coagulan. Las óptimas condiciones de coagulación se obtendrían en el punto
isoeléctrico (=0). También se ha establecido empíricamente que la concentración
crítica de iones para producir la coagulación es proporcional a z-2, donde z es la
valencia del catión.
Las suspensiones de partículas presentes en las diversas etapas del
procesamiento de un mineral son de un tamaño mucho mayor que aquellas de un
sistema coloidal. El rango de tamaño para lo que se denomina finos o lamas en
procesamiento de minerales es de 1 a 10 m y las fuerza dominantes en tal sistema son
las fuerzas inerciales ocasionadas por la convección forzada de un agitador o bomba y
por la velocidad de sedimentación. Estas condiciones de flujo pueden conferir enorme
energía a las partículas la que les permitiría sobrepasar la barrera de fuerzas repulsivas
entre partículas sin necesidad de neutralizar la carga. Una agitación demasiado violenta
dispersaría las partículas y la coagulación no se produciría. El resultado de estos dos
tipos de coagulación, por neutralización de la carga superficial y aquel que sobrepasa
la barrera de energía por medios hidrodinámicos, es distinto ya que en el primer caso
se obtiene un agregado neutro mientras que en el segundo el agregado tiene carga
eléctrica.
La velocidad de coagulación queda descrita por la teoría de SmoluchowkiMüller (Laskowski y Pugh 1992, Gregory 1986). Designando por N el número de
partículas, Ec la eficiencia de colisión, k la constante de Boltzman y  la viscosidad del
líquido y T su temperatura, se puede escribir:
dn
4 Ec kT
  k c n 2 , donde k c 
dt
3
(10.3)
La eficiencia de colisión, con valores de 0 a 1, depende de la estabilidad del coloide o
suspensión, con el valor de Ec=1 para un sistema completamente estabilizado.
Integrando la ecuación anterior, se obtiene:
n  n0
1
1  n0kct
(10.4)
donde n0 es la concentración inicial de partículas.
10.1.2 Floculación
La agregación de partículas mediante la adsorción de largas cadenas de
polímeros en varias partículas se denomina floculación. De acuerdo a la forma en que
el polímero actúa sobre las partículas se pueden distinguir diferentes formas de
floculación.
306
Manual de Filtración & Separación
La más importante, denominada floculación por puente, se produce por
adsorción de una cantidad muy pequeña de polímero de larga cadena sobre varias
partículas simultáneamente, produciendo puentes de hidrógeno entre el polímero y
iones de oxígeno presentes en la superficie de partículas contiguas en el flóculo. Este
tipo de floculación produce flóculos muy fuertes. A mayores concentraciones que las
necesarias para la floculación, el floculante se adsorbe completamente en una partícula
dejando poca oportunidad para adsorberse en otras partículas y re-estabilizando la
suspensión. Por esta razón, existe una dosificación óptima para los floculantes
poliméricos.
Fig. 10.5 Floculación por puente de hidrógeno. A)
Floculación de varias partículas; b) re-estabilización por
exceso de floculante.
Si dos o más polímeros lineales se adsorben sobre las partículas, se forma una red de
tipo gel con forma de retículo tridimensional. En este caso el proceso de agregación
recibe el nombre de floculación en red. El estricto control en la adición de floculante,
lineales o ramificados, puede producir flóculos muy compactos conocidos como pelets.
A este proceso se le llama floculación en pelet. Estos tres tipos de floculación están
presentes con todo tipo de floculantes, neutros, catiónicos o aniónicos. En el caso de
los neutros, o no-iónicos, es el único mecanismo presente.
La acción de polímeros catiónicos sobre partículas cargadas negativamente es
algo similar al proceso de coagulación, en que la neutralización de las cargas
superficiales predomina por sobre la formación de puentes. Esta agregación recibe el
nombre de floculación electrostática. Este proceso se debe distinguir de la secuencia
de coagulación electrostática de una suspensión seguida por una floculación por
puente.
La industria minera utiliza más frecuentemente los polímeros aniónicos como
floculantes que los catiónicos o los neutros. En este caso la adsorción se produce por
enlaces covalentes o por reacción química en la superficie de las partículas y la
aglomeración recibe el nombre de floculación por enlace de sal.
De todos estas mecanismos de agregación, la floculación por puente es la más
importante. Cuando se desea elegir un floculante para un proceso de agregación, el tipo
de sólido, su carga superficial y los electrolitos presentes en la solución determinarán
el reactivo necesario y el tipo de floculación.
CAPÍTULO 11 Floculación
10.2
307
FLOCULANTES POLIMÉRICOS: PROPIEDADES Y PREPARACIÓN
10.2.1 Propiedades
Los floculante poliméricos son reactivos orgánicos con moléculas de cadena
larga y pesos moleculares de 106 g o más. Pueden ser naturales, como los polisacáridos
almidón, dextrina y agar-agar y coloides proteínicos como la cola animal, caseina,
gelatina y alginatos, o sintéticos basados en materiales acrílicos provenientes de
derivados del petróleo, tales como las poliacrilamidas de alto peso molecular. La
ventaja de los floculantes sintéticos es que su estructura molecular, en términos de su
contenido químico como peso molecular y su grado de hidrólisis, o ionocidad, pueden
ser diseñada a voluntad de acuerdo a las necesidades encontradas en la industria. Como
son producidos a partir de materias primas químicas, su calidad es más consistente que
la de floculantes naturales. Además, pueden ser diseñados de pesos moleculares mucho
mayores que los encontrados en la naturaleza, lo que les da una ventaja técnica y
económica.
En la figura 10.6 se muestra la estructura de tres tipos de floculantes poliméricos
basados en poliacrilamidas.
Fig. 10.6 Diversos tipos de floculantes
derivados de la poliacrilamida.
La figura 1) muestra la poliacrilamida pura que exhibe propiedades neutras en
solución. La figura 2) muestra co-polímeros de acrilamida con grupos acrilatos, que le
dan carácter aniónico al floculante. El número de estos grupos le da el grado de
anionicidad al reactivo. La figura 3) también muestra co-polímeros, pero esta vez de
carga positiva. La acción de estos floculantes depende de su ionicidad. Los polímeros
en general accionan formando puentes de hidrógeno, como ya hemos visto, pero los
polímeros iónicos reaccionan, además, por interacción electrostática. Por esta razón la
elección del floculante adecuado para una cierta tarea dependerá del potencial y de la
carga superficial de las partículas sólidas como de las condiciones fisicoquímicas de la
308
Manual de Filtración & Separación
solución que la afectan, tales como el pH y la fuerza iónica. Otros ejemplos de
polímeros sintéticos son:
 No-iónicos:
óxido de polietileno; polivinil alcohol.
 Aniónicos:
poliestireno-sulfonato de sodio
 Catiónico:
poietilenamina; cloruro de dialidimetil-amonio.
La tabla 10.1 muestra floculantes poliméricos del tipo de la figura 10.6, sus
propiedades y sus aplicaciones en diversas industrias. Los pesos moleculares de estos
polímeros van de 6 a 20 millones
Tabla 10.1 Tipo de floculantes poliméricos basados en poliacrilamida (Stockhausen 2000)
Tipo de polímero Neutros
Aplicaciones
Aniónicos
leve
<30%
Agua Potable
Agua Industrial
Minería: Carbón/Mineral
Agua de Lavado
Concentrados de Flotación
Relaves de Flotación
Licores de Lixiviación
Suspensiones de bio-tecn.
Industria Química
Salmueras Ácidas
Salmueras Alcalinas
Pigmentos Inorgánicos
Pigmentos Orgánicos
Procesamiento de Metales
Industria del Papel
Industrial/Municipal:Aguas
Sanitarias
Lodos frescos
Lodos digeridos
Lodos sobrantes
Catiónicos
medio fuerte
50%
>75%
leve
<30%
medio fuerte
50%
>75%
CAPÍTULO 11 Floculación
309
Las características más importantes de los floculantes poliméricos son su peso
molecular, la naturaleza de su grupo funcional, especialmente en el caso de grupos
iónicos, la densidad de carga. La densidad de carga depende del número de grupos
ionizables y el grado de ionización. La carga queda determinada en el proceso de
síntesis del reactivo y el grado de ionización depende de la naturaleza del grupo iónico
y de las condiciones de la solución. Grupos fuertemente ionizados, tales como los
sulfonatos o las aminas cuaternarias, están totalmente cargados en la mayoría de los
casos. Grupos débilmente ionizados, tales como carboxilos y aminas terciarias, son
afectados por el pH de la solución. Polímeros aniónicos con grupos carboxílicos no se
cargan totalmente hasta que el pH se lleva a valores mayores de 6. En soluciones más
ácidas el grado de ionización se reduce. Polímeros catiónicos, basados en grupos de
aminas terciarias, muestran una carga reducida cuando el pH es mayor que 8.
Cuando partículas cargadas negativamente entran en contacto con polímeros noiónicos o aniónicos, no hay floculación a menos que se agregue cationes, como pro
ejemplo Ca2+. Este ión promueve la adsorción del polímero sobre la superficie de la
partícula al unirse simultáneamente con los grupos aniónicos del polímero y con los
sitios negativos de la superficie del mineral. Un ejemplo de este efecto se encuentra en
la floculación de caolín con polímeros aniónicos. El caolín no es floculado en
soluciones de NaCl, pero flocula al modo de puente en presencia de una pequeña
cantidad (1-2 mM) de iones Ca2+. Existe una densidad de carga eléctrica óptima de los
poli electrólitos para la floculación por puente. Por ejemplo, la floculación de
suspensiones con poliacrilamida mejora a medida que el peso molecular del polímero
aumenta y existe un valor óptimo de hidrólisis de alrededor de 30%. Un aumento de la
hidrólisis produce la repulsión mutua de diversos segmentos del polímero con el efecto
que la cadena hidrocarbonada se endereza expandiéndose. Simultáneamente, el
aumento de ionicidad disminuye la adsorción del polímero sobre las partículas
negativas. El valor óptimo de hidrólisis es el mejor compromiso entre estas dos
tendencias.
Los polímeros que tienen carga opuesta a las partículas se adsorben fuertemente
debido a la atracción iónica. En estos casos las cadenas de poli-electrolitos adquieren
una configuración plana sobre la superficie de las partículas reduciendo
considerablemente las posibilidades de una adsorción por puente. Los polímeros
catiónicos se utilizan ampliamente para la floculación de partículas negativas y la
neutralización de la carga explica totalmente el mecanismo de floculación. La
condición óptima de floculación, en este caso, corresponde a la neutralización de las
cargas. Un exceso de floculante puede re-estabilizar la suspensión dándole una carga
positiva a las partículas. Los mejores floculantes para esta tarea son polímeros con la
mayor carga eléctrica, siendo su peso molecular un factor secundario.
10.2.2 Preparación
Las empresas proveedoras de floculantes ofrecen estos productos en diversas
formas, frecuentemente como gránulos, emulsiones o soluciones acuosas. Como los
floculantes son utilizados normalmente en soluciones muy diluidas, es conveniente
310
Manual de Filtración & Separación
preparar una solución madre con una concentración entre 0.5 y 1% de floculante en
peso. Para su uso esta solución se diluye nuevamente a valores de 0.01 a 0.1% en peso
según sea necesario.
Cuando se prepara una solución madre a partir de floculante en forma granulada,
es importante que cada gránulo individual sea mojado con agua de manera evite la
formación de grumos que se disuelven muy lentamente. Para preparar solución al 0.5%
echar 497.5 ml de agua destilada en un matraz. Agitando intensamente agregar 2.5g de
floculante granulado lentamente, gránulo por gránulo, de modo que sean succionados
por el vórtice del formado por la agitación. Terminado este proceso, disminuir la
agitación lentamente hasta que no se produzca turbulencia, pero que las partículas
permanezcan en suspensión. Después de algunos minutos, los gránulos comienzan a
hincharse y la solución se torna viscosa y luego de 60 minutos de agitación debiera
haber una solución homogénea. La solución madre lista puede ser guardada en una
botella cerrada y utilizada por aproximadamente 2 meses.
La solución madre se prepara en forma similar para floculantes en forma de
emulsión. En este caso, el líquido se adiciona lentamente al agua agitada en forma de
un hilo fino. La volumen de líquido se calcula con la densidad de la emulsión. Si no se
dispone de otra información usar la densidad de 1 g/cm3. En este caso se debe agitar la
mezcla por al menos 20 minutos.
Floculante provistos en forma de solución acuosa se los puede diluir
directamente a la concentración deseada vertiéndolos en agua destilada mientras se los
agita suavemente. El tiempo de mezcla necesario es sólo de algunos minutos.
10.3 CINÉTICA DE LA FLOCULACIÓN
La velocidad a la que se produce la floculación está gobernada principalmente
por la velocidad de colisión de las partículas, pero también por la fracción de superficie
cubierta por el floculante. Cuando la colisión de partículas se produce por agitación
mecánica o hidrodinámica, la floculación se dice ortocinética. De acuerdo con Healy y
La Mer (1966) y Gregory (1986), en la floculación ortocinética los flóculos se forman
a una velocidad dada por:
dn
  k( )k  Ec ,  ,d  n 2
dt
donde
k()  (1  ) y k  E c ,  ,d  
(10.5)
16
E c  d 3
3
(10.6)
donde  es la cobertura de superficie por floculante, d es el diámetro del flóculo y k es
un parámetro que depende de la eficiencia de colisión Ec, la velocidad de cizalle  y
del tamaño de partícula d. Esta expresión indica que la óptima cobertura de floculante
es de =0.5, por lo tanto k  1 4 para la dosificación óptima de floculante. Si
logramos establecer las condiciones en que se produzca una cobertura óptima de
floculante, la cinética de floculación en estas condiciones se puede escribir en la forma:
CAPÍTULO 11 Floculación
311
dn
4
   d 3Ec n 2
dt
3
(10.7)
Para valores constantes de  , d y Ec , integrando (10.7) se puede obtener la el número
de partículas restantes en el tiempo t:
n
n0
1   4n 0  E c d 3 3 t
(10.8)
Utilizando la relación entre el número de partículas restantes n y concentración de estas
partículas de la suspensión como fracción volumétrica de sólidos, tenemos
  4 3 d 3n y reemplazando en la ecuación anterior se obtiene

0
1   0  E c   t
(10.9)
Definamos el grado de floculación mediante la expresión:
 
G f  100  0

 0 
G f  100
entonces
(10.10)
0  E c t
  0  E c t
(10.11)
Suponiendo que la eficiencia de floculación es del 100%, el grado de floculación
depende solamente de la velocidad de cizalle. La figura que sigue muestra el grado de
floculación en el tiempo para varias velocidades de cizalle.
100,0
90,0
=100 s-1
Grado de Floculación %
80,0
70,0
=50 s
-1
60,0
50,0
=10 s-1
40,0
30,0
20,0
=1 s-1
10,0
0,0
0
5
10
15
20
25
30
Tiempo en segundos
Grado de floculación en el tiempo para varias velocidades
de cizalle.
312
Manual de Filtración & Separación
Se puede observar que la intensidad de agitación del fluido, cuantificado a través de la
velocidad de cizalle influye fuertemente en el tiempo necesario para obtener una buena
floculación. Por ejemplo se necesita 5 y 10 segundos para obtener una floculación del
95% con velocidades de cizalle de 100 y 50 s-1, mientras que con velocidades menores
de 10 s-1no se logra más que un 84% en .
10.4 HIDRODINÁMICA DE LA FLOCULACIÓN
Los parámetros  y Ec dependen de las condiciones hidrodinámicas en que
efectúa la floculación. El valor de la eficiencia de colisión Ec depende de las
condiciones de estabilidad de la suspensión a flocular. Una suspensión totalmente
desestabilizada tiene un Ec=1. Este es el caso de la mayoría de las suspensiones de
minerales, ya que tienen un tamaño mucho mayor que el coloidal. Para un caso
particular el valor de Ec solamente se puede establecer empíricamente. La velocidad de
cizalle se puede establecer de la hidrodinámica del problema. Como ejemplo veremos
los casos de floculación en una cañería y en un estanque agitado.
10.4.1 Floculación en una cañería
En un tubo circular, donde Q es el caudal y D es el diámetro de la cañería,
ambos en unidades homogéneas, la velocidad de cizalle promedio se puede aproximar
por:
 
Q
D3
(10.12)
Por ejemplo, una tubería de 12” con una velocidad de 2 m/s, la velocidad de cizalle es
de   0.14 0.33  5 s 1 .
10.4.2 Floculación en un feedwell
Köck y Concha (1999) presentaron la modelación de un feedwell característico
mediante CFD, usando el código Fluent. En el trabajo se determinó que la velocidad de
cizalle promedio en el aparato es muy pequeña, del orden de 1s-1.
Ejemplo 1.
Calcular el grado de floculación en función del tiempo para un espesador con
una alimentación de Q=2450 m3/h a una concentración de 25% de sólidos en peso.
Suponga que la eficiencia de floculación es de Ec=85% y que la velocidad de cizalle es
de   1, 20, 50 s 1 .
CAPÍTULO 11 Floculación
313
El flujo es: Q  2450 / 3600  0.681 m3 s y la concentración volumétrica de
sólidos es: 0  25  2.5 * (100  25)  25   0.118 . La ecuación a resolver es:
G f  100
0  E c t
0.130 *  * 0.85 * t
 100

  0 E c t
  0.130 *  * 0.85 * t
100.0
90.0
=50 s-1
Grado de floculación en %
80.0
=20 s-1
70.0
=10 s-1
60.0
50.0
40.0
30.0
20.0
=1 s-1
10.0
0.0
0
10
20
30
40
50
60
Tiempo en segundos
Grado de floculación versus tiempo para una eficiencia de
floculación de 85% y diversos valores de la velocidad de cizalle.
En el ejemplo se observa la importancia de la agitación en el grado de
floculación. La tabla muestra los resultados
Grado de floculación en %
Tiempo s
 =50 s
 =20 s-1
 =10 s-1
 =1 s-1
0
0
0
0
0
5
89.8
80.5
63.8
15.0
10
94.6
89.2
77.9
26.0
15
96.3
92.5
84.1
34.4
20
97.3
94.3
87.6
41.3
50
99.0
97.6
90.4
67.4
-1
314
Manual de Filtración & Separación
Mientras con una buena agitación de   20 s 1 a   50 s 1 se llega a valores sobre
90% de floculación en menos de 15 segundos, agitaciones de   1 s 1 a   10 s 1
logran grados de floculación de sólo 38 a 86% para el mismo tiempo.
10.5 REFERENCIAS
La Mer, V.K. and Healy, T.W., 1963. Adsorption-Flocculation reactions of
macromolecules at the solid-liquid interface, Rev. Par. Appl. Chem., 13, 112.
Gregory, J., Flocculation, 1986. In Progress in Filtration and Separation 4., R.J.
Wakeman (ed.), Elsevier, pp. 83-90.
Hogg, R., Healy T.W. and Fuerstenau, D.W., 1966. Trans. Faraday Soc., 62, 1638.
Laskowski, J.S and Pugh, R.J., 1992. Dispersion stability and dispersing agents. In
Colloid Chemistry in Mineral Processing, Ed. J.S. Laskowski and J. Ralston, Elsevier,
New York, 115-171.
Gregory, J., 1986. Flocculation. In Progress in Filtration and Separation 4., Ed. R.J.
Wakeman, Elsevier, New York, 55-99.
Stockhausen Degussa-Hüls Group, 2000. Auxiliaries for the Mining Industries,
Business Unit for Water Treatment catalog.
La Mer, V.K., 1966. Disc. Faraday Soc., 42, 248.
CAPÍTULO 11
AGREGACIÓN DE PARTÍCULAS EN
PROCESAMIENTO DE MINERALES
Janusz S. Laskowski
University of British Columbia
Vancouver, B.C., Canada.
RESUMEN
Debido a la fineza con que generalmente se debe moler para obtener la
liberación de las especies mineralógicas útiles en el procesamiento de un mineral, se
dificulta tanto el proceso de concentración como los procesos de separación sólidolíquido. Por esta razón en la mayoría de los casos se debe recurrir a la agregación de
las partículas, lo que se consigue mediante el uso de floculantes. Estos son productos
macromoleculares formados por polímeros iónicos de cadena larga y son utilizados
comúnmente en el espesamiento y filtración de relaves del proceso de flotación.
Debido a su naturaleza iónica, estos floculantes producen flóculos hidrofílicos que son
incompatibles con la flotación. Por ello, cuando es necesario la agregación en los
circuitos de flotación, sólo se puede incorporar aglomerantes que produzcan flóculos
hidrofóbicos. Por esta misma razón, para la separación sólido-líquido de concentrados
de flotación, es conveniente utilizar floculantes hidrófobos.
315
316
Manual de Filtración & Separación
11.1 INTRODUCCION
La separación de especies valiosas del material desechable en las rocas
solamente se puede realizar si los granos de minerales se encuentran como partículas
discretas liberadas. A medida que la ley de las menas disminuye, las especies minerales
se encuentran cada vez más finamente diseminadas en la roca. La liberación se obtiene
mediante reducción de tamaño en circuitos de trituración y molienda.
Desgraciadamente es imposible obtener una liberación total sin producir una gran
cantidad de material fino indeseable. Los resultados de la separación dependen
fuertemente del tamaño de las partículas y, como en todos los procesos de separación,
existe un rango de tamaño óptimo para la concentración. Las recuperaciones de
materiales muy finos y muy gruesos, que están fuera de este rango óptimo, son bajas.
Por lo tanto para lograr una recuperación global satisfactoria es necesario controlar
cuidadosamente el tamaño de las partículas procesadas.
Las operaciones unitarias en el procesamiento de partículas finas se pueden
dividir en conminución, concentración, desaguado y clarificación. Ver figura 1.
Mena
Agua reciclada
conminución
separación
clarificación
Agregación selectiva
desaguado
Agregación no selectiva
Fig. 1 Diagrama de flujo simplificado de una planta de procesamiento
de minerales
La reducción de tamaño es necesaria para liberar las especies valiosas y la separación
es fuertemente dependiente del grado de liberación. Sin embargo, la separación se
empeora y la separación sólido-líquido (espesamiento y filtración) se hace más difícil
cuando las partículas son muy finas. En estos casos la agregación de partículas puede
CAPÍTULO 11. Agregación en Procesamiento de Minerales
317
ser beneficiosa para ambos procesos. La figura 1 muestra la relación de los procesos de
agregación de partículas con las operaciones. Mientras la agregación selectiva se lleva
a cabo en la operación de separación, en que las propiedades finales de los agregados
son de primordial importancia, como es el caso de la flotación, la agregación noselectiva se realiza en el circuito de desaguado y las propiedades de los agregados son
de menor importancia. Queda en evidencia, entonces, que la diferencia entre estos dos
procesos de agregación es la selectividad. En el primer caso se desea un agregado
selectivo que involucre solamente a las especies valiosas, mientras que para la
separación sólido-líquido, mientras menos selectivos son los agregados mejor.
11.2 AGREGACIÓN EN PROCESAMIENTO DE MINERALES
Existen muchos métodos para aumentar el tamaño de partículas sólidas (Capes
& Darcovich 1997). En el caso de la separación sólido-líquido el método más utilizado
es la floculación (bridging) con reactivos poliméricos, los que son solubles en agua y,
por lo tanto, son hidrofílicos. Por otra parte, las partículas sólidas también pueden ser
agregadas por un segundo líquido, inmiscible en el agua, presente en el proceso. Este
tipo de agregación se denomina aglomeración por aceite y consiste en que un aceite
hidrocarbonado se utiliza para aglomerar partículas hidrófobas suspendidas en agua
(Capes 1989, Laskowski 1992) dando por resultado un aglomerado hidrófobo. Existe
un nuevo material aglomerante de tipo latex, denominado floculante hidrófobo, que
actúan en forma intermedia entre los floculantes y la aglomeración por aceite. Las
partículas de latex son hidrofóbicas y operan en forma similar al aceite aglomerante.
La tabla 1 muestra una clasificación del fenómeno de agregación como función de la
mojabilidad del sólido y el tipo de aditivo químico (Laskowki & Castro).
11.2.1 Floculación
Es aceptado universalmente que el mecanismo de acción para agregar partículas
pequeñas en suspensión usando polímeros como floculantes es la formación de
puentes. Se considera que la formación de puentes es la consecuencia de la adsorción
de segmentos de las macromoléculas del floculante en la superficie de más de una
partícula, que las liga en flóculos sueltos. La cobertura incompleta de la superficie de
estas partículas asegura que, durante la colisión de estos flóculos con otros, haya
suficiente espacio disponible en las partículas para adsorber segmentos de las cadenas
adsorbidas a otras partículas (Hogg 1984). Es importante notar que la adsorción y
floculación no son procesos separados y secuenciales, sino que ocurren
simultáneamente (Hogg 1999). La adición de diferentes dosificaciones y tipos de
mezcla a que es sometida la suspensión dan como resultado tamaños de flóculos y
velocidades de sedimentación muy diferentes (Keyes & Hogg 1979, Hogg et al 1993).
Kitchner (1972) indicaba que el mérito de los floculantes poliméricos es su
habilidad para producir flóculos más grandes y fuertes que los que se puede obtener
por coagulación. Aún cuando teóricamente los floculante pueden ser aplicados a una
suspensión directamente o después de desestabilizarla por coagulación, se sabe por
318
Manual de Filtración & Separación
experiencia que los floculante no son muy efectivos con suspensiones estables, por lo
que es preferible utilizar previamente coagulantes para desestabilizarlas (Kitchner
1972, Wright & Kitchner 1976).
Tabla 1 Fenómenos de agregación como función de la mojabilidad del sólido y tipo de
aditivo químico
Tipo de aditivo
Mojabilidad del
Propiedades
sólido
resultantes
Crecimiento de tamaño
Latex
hidrófobo
Aceite
emulsificado
Si
No
No
Hidrofílico
-
-
Mecanismo
Adsorciónbridging
-
-
Crecimiento de tamaño
Si
Si
Si
Hidrofílico
-
Hidrofílico
Adsorciónbridging
Hidrófobo
Bridging por
líquido
inmiscible
Crecimiento de tamaño
Si
Si
Si
Mojabilidad del flóculo
Hidrofílico
Hidrófobo
Hidrófobo
Adsorciónbridging
Coagulación
hidrófoba
Bridging por
líquido
inmiscible
Sólido hidrofílico Mojabilidad del flóculo
Sólido levemente Mojabilidad del flóculo
hidrófobo
Mecanismo
Sólido hidrófobo
Floculante
hidrofílico
Mecanismo
El caso más típico de uso de floculantes en procesamiento de minerales es la
separación sólido-líquido (agregación no-selectiva en la figura 1). Generalmente están
presentes partículas muy pequeñas, frecuentemente arcillas como en el caso de colas de
flotación, y floculante de poliacrilamida. Aún cuando las poliacrilamidas se las
presenta como floculantes no-iónicos, la verdad es que la mayoría de las versiones
comerciales de estos productos son poliacrilamidas hidrolizadas (o co-polímeros de la
acrilamida y ácido acrílico). Como resultado, ellas contienen algunos grupos
carboxílicos, los que se cuantifican a través del grado de anionionicidad (100% para
una poliacrilamida totalmente hidrolizada, que corresponde al ácido poliacrílico). Esto
significa que las propiedades de tales floculantes dependen no solamente del peso
molecular sino que también de grado de anionicidad. (Rogers & Poling 1978).
La aplicación de floculante poliméricos en la separación sólido-líquido será
ilustrada a través de los resultados obtenidos por Sworska et al (2000) con relaves de
Syncrude. La figura 2 muestra el efecto de la dosificación de Percol 727 (floculante de
poliacrilamida con 30% de anionicidad) y del pH en la velocidad inicial de
CAPÍTULO 11. Agregación en Procesamiento de Minerales
319
sedimentación de los relaves de Syncrude (en su mayoría minerales de arcilla, tales
como caolinita e ilita).
120
7
100
Percol 727, ppm
isr, m/h
6
5
4
3
2
1
80
60
7
40
8
20
0
0
2
4
6
8
10
12
14
pH
Fig. 2 Efecto de la dosificación de Percol 727 y del pH en la
velocidad inicial de sedimentación de los relaves de Syncrude
(Sworska et al 2000).
La figura 3 muestra la concentración de sólido remanente en suspensión después de
que se completara la sedimentación de la experiencia mostrada en la figura 2.
Comparando ambas figuras revela que la floculación en un medio ácido produce
una buena velocidad de sedimentación y un bajo contenido de sólidos en el líquido
sobrenadante. Se sabe que las suspensiones de arcilla tienden a coagular en soluciones
ácidas y, por lo tanto, la floculación en dichas condiciones es muy buena. De acuerdo
con Hogg (1999), cuando se agrega un floculante a una suspensión estable se obtiene
como resultado una distribución bimodal de partículas-flóculos, con flóculos grandes
junto a partículas sólidos dispersas. Las figuras 2 y 3 muestran que esto sucede en
suspensiones alcalinas en la que las arcillas son estables. Esta situación cambia
radicalmente si se adiciona previamente cationes multivalentes (como pro ejemplo
Mg2+ o Ca2+) para desestabilizar la suspensión. La figura 4 muestra los resultados de
introducir iones magnesio en la suspensión.
320
Manual de Filtración & Separación
120
Solid %
Percol 727, ppm
0.5
0.3
100
0.8
1
1.3
80
1.5
60
1.8
40
2.0
2.3
20
2.5
0
0
2
4
6
8
10
12
14
pH
Fig. 3 Concentración de sólido remanente en suspensión en la
solución sobrenadante después de que se completara la sedimentación
en función de la dosificación de Percol 727 y del pH.
100
isr, m/h
9
90
Mg2+, 0.008 mol/dm3
1
80
3
Percol 727, ppm
70
5
60
7
50
11
40
13
30
20
10
15
0
0
2
4
6
8
10
12
14
pH
Fig. 4 Efecto de la dosificación de Percol 727 y del pH en la
velocidad inicial de sedimentación de los relaves de Syncrude
en presencia de 8x10-3 mol/dm3 de iones Mg2+ (Sworska et al
2000).
Los resultados obtenidos con la adición de Mg2+ no son muy diferentes que
aquellos sin este ión, pero en presencia de Mg2+ las velocidades de sedimentación más
CAPÍTULO 11. Agregación en Procesamiento de Minerales
321
altas se encuentran en el rango alcalino. La figura 5muestra la diferencia más
significativa: la desestabilización del sistema por coagulación en la presencia de
cationes multivalentes produce una buena floculación y, ahora, el dominio de las altas
velocidades de sedimentación coincide con el de las más bajas concentraciones de
sólido en la solución sobrenadante. Esto coincide con las ideas de Wright & Kitchner
(1976) que encontraron que las pulpas de montmorillonita pueden hacerse filtrable con
una combinación de coagulantes (por ejemplo, sales de Mg2+) y un floculante
polimérico con el óxido de polietileno, PEO. Este floculante es muy interesante y
Scheiner et al (Brown & Scheiner 1983, Scheiner & Stanley 1985) desarrollaron un
proceso en el cual producían flóculos con PEO de alto peso molecular, les permitían
agrandarse por medio de agitación y luego los separaban en harneros. Se ha indicado
que estos flóculos no se destruían al ser mojados por una lluvia de agua.
Los floculante más comúnmente utilizados en el espesamiento y filtración son
los de poliacrilamidas. Estos floculante mejoran dramáticamente la velocidad de
filtración pero, como son macromolécula hidrofílicas, ellos no reducen la humedad del
queque. Es natural que la humedad del queque sería menor si los flóculos fueran
hidrófobos. En este contexto, el PEO difiere de las poliacrilamidas.
140
Mg2+, 0.008 mol/dm3
Solid %
1
Percol 727, ppm
120
100
0.5
80
60
0.3
40
20
0
0
2
4
6
8
10
12
14
pH
Fig. 5 Efecto de la dosificación de Percol 727 y del pH en la
concentración de sólidos de la solución sobrenadante después
de completa la sedimentación, en presencia de 8x10-3 mol/dm3
de iones Mg2+ (Sworska eta al 2000).
11.2.2 Floculantes poliméricos en circuitos de flotación
Aún cuando la flotación como proceso queda fuera del ámbito de este Manual, es
interesante mostrar la aplicación de la floculación en la flotación, ya que ella está
íntimamente relacionada a las propiedades superficiales de los flóculos. Para discutir
322
Manual de Filtración & Separación
estas aplicaciones es necesario primero tener información sobre las propiedades
superficiales de los flóculos, las que raramente son estudiadas. Palmes & Laskowski
(1993) realizaron estudios comparativos de floculación con dos tipos de carbón y
diversos floculantes, concluyendo que los resultados de floculación dependían tanto del
tipo de floculante como de las propiedades superficiales del carbón. El análisis de las
dos muestras de carbón bituminoso no revelaron diferencia significativa entre ellas.
Tabla 2 Análisis de dos muestras de carbón bituminoso
Muestra
FD-4
FD-13
Ceniza
8.4
9.4
Contenido de humedad %
0.71
2.84
Contenido de materia volátil %
19.74
22.43
78.3
74.4
dmmf
Carbón fijo FC
,%
Sin embargo, la acidez total de las muestras desmineralizadas fue de 0.04 meq/g
para la muestra FD-4 y 1.22 meq/g para la muestra FD-13 y sus humedades de
equilibrio eran de 0.94% para la primera y 4.59% para la segunda (Laskowski & Yu
2000). Estos ensayos revelaron que la muestra FD-13 estaba oxidada y debiera ser
hidrofílica. Mediciones de ángulo de contacto en muestras pulidas de estos carbones
mostraron que la muestra FD-4 tiene av  80 y rec  50 , mientras que la muestra
FD-13 tiene av  45 y rec  25 (Pawlik et al 1997). Estos resultados confirman que
mientras la muestra de carbón FD-4 es hidrófoba la muestra FD-13 es hidrofílica.
La figura 6 muestra el efecto del floculante Polyacrilamida (PAM), Floculante
semi-hidrófobo (F1029-D), del óxido de polietileno (PEO) y del floculante hidrófobo
(UBC-1) en la floculación de las dos muestras de carbón finamente molidas
(Laskowski & Yu 1998, Laskowski & Yu 2000). El floculante semi-hidrófobo F1029D fue descrito por Attia et al (1987) como un co-polímero de acrilamida (85%),
acrilato de sodio (5%) y 2-etilhexil ester del ácido acrílico (10%).
Los resultados revelan que, mientras los PAM floculan ambas muestras bastante
bien, los floculantes F1029-D y PEO floculan la muestra FD-4 muy eficientemente
pero no son tan eficientes con la muestra FD-13 y el floculante MBC-1 flocula muy
bien la muestra FD-4 pero no flocula absolutamente la muestra FD-13 (el floculante
hidrófobo FR-7A se comporta igual que el UBC-1). De estos resultados se puede
concluir que las propiedades de la superficie de los carbones es importante en la
habilidad de floculantes de agregar las partículas. El floculante hidrofílico PAM no es
selectivo y flocula ambas muestras, pero los floculantes hidrófobosUBC-1 y FR-7A
solamente floculan las partículas hidrófobas. Los floculante F1029-D y PEO se
comportan en forma intermedia. Se puede concluir que los floculantes PAM son útiles
en la separación sólido-líquido, pero en flotación solamente se puede usar los
floculantes hidrófobos tipo latex.
CAPÍTULO 11. Agregación en Procesamiento de Minerales
120
80
Flocculation, %
Flocculation, %
FD-4
FD-4
100
80
60
FD-13
40
PAM
20
60
F-1029D
40
FD-13
20
b
a
0
0
0
100
200
300
400
500
600
700
0
100
PAM Dosage, g/t
300
400
500
600
700
100
80
Flocculation, %
80
Flocculation, %
200
F1029-D Dosage, g/t
100
FD-4
60
PEO
40
20
0
323
FD-13
0
100
200
300
400
PEO Dosage, g/t
600
60
UBC-1
40
20
c
500
FD-4
FD-13
700
0
0
100
200
300
400
d
500
600
700
UBC-1 Dosage, g/t
Fig. 6 Efecto de la dosificación de floculante en la agregación de muestras ultrafinas de
carbones FD-4 y FD-13 con a) PAM, b) con F1029-D, c) con PEO y d) con UBC-1
Los resultados de la figura 6 están en perfecto acuerdo con los resultados
obtenidos con PEO por Rubio y Kitchener. Experimentos de adsorción y floculación de
suspensiones de sílice mostraron que PEO se adsorbe en sílice hidrofóbica (formada
por calentamiento a 500-600°C) y la flocula fuertemente (Rubio & Kitchner 1976). La
buena floculación de minerales inherentemente hidrófobos (tales como talco, grafito y
algunos sulfuros) y minerales hidrófobizados por tratamiento previo (por ejemplo de
malaquita y crisocola con Na2S) llevan al concepto de floculación selectiva basada en
la diferencia de mojabilidad de las partículas sólidas (Rubio & Kitchner 1977, Rubio
1981). Esta acción es obviamente de naturaleza diferente que la floculación selectiva
resultante de la interacción química entre una macromolécula hidrofílica y una
superficie sólida (ejemplo adsorción de almidón sobre hematita) y que llevan a la
formación de flóculos hidrofílicos.
También vale la pena mencionar que los resultados de la figura 6 están en pleno
acuerdo con los de Gochin et al (1985) que informa que PEO flocula muy
eficientemente suspensiones de antracita pero era completamente ineficiente para
flocular suspensiones de antracita oxidada.
En la separación sólido-líquido se requiere que la floculación produzca un
aumento de tamaño de las partículas para aumentar la velocidad de sedimentación y
velocidad de filtración. En la flotación, se requiere que la floculación sea selectiva y
que los flóculos producidos sean suficientemente hidrófobos para ser flotables.
Mientras el primer requerimiento es obvio, el segundo necesita mayor discusión.
324
Manual de Filtración & Separación
Pikkat-Ordynskyi & Ostryi (1972) y Williams & Unlu (1978) informaron que
floculantes comerciales, tales como dextrinas y otros polisacáridos, actúan como
depresores en la flotación de carbón. La figura 7 muestra ángulos de contacto sobre
antracita en presencia de diversos polímeros (Pradip & Fuerstenau 1987).
Gebhard & Fuerstenau (1984) estudiaron la flotación de hematita con dodecil
sulfonato de sodio. La hematita se vuelve hidrófoba y flota muy bien con este reactivo.
Sin embargo la adición de 1-2 ppm de PAM o PAA (ácido poliacrílico) es suficiente
para reducir el ángulo de contacto desde valor iniciales de 80-90° a prácticamente 0°
(ver figura 8). Usando hematita muy fina (80% bajo 2 m) Gebhard & Fuerstenau
(1986) demostraron que, a bajas dosis de PAA (hasta 30 mg/m2 de superficie sólida),
se podía mejorar significativamente la flotación de este material. Laskowski & Castro
(1999) muestran el efecto de floculantes comerciales (Nalco 9809) sobre la flotación
de molibdenita, indicando que ésta se deprime con estos floculantes (ver figura 9).
70
Anthracite
Flocculation, %
60
50
PAM & PAA
40
30
Separan NP10, m.wt. 106
Magnafloc 905N, m.wt. 107
Methocel F 4M, m.wt.90,000
20
10
0
0
300
600
900
1200
1500
1800
PAM Dosage, g/t
Fig. 7 Efecto de (PAM) y (PAA) e hidroxilpropil
celulosa (Methocel) en el ángulo de contacto de
antracita a pH 6.0-6.8 (Pradip & Fuerstenau
1987).
Contact Angle, degrees
100
Hematite
80
10-3 mol/dm3 NaCl
10-3 mol/dm3 SDS
pH 4.1
60
Receding
40
20
Advancing
0
0
1
2
3
4
5
PAM Concentration, mg/dm 3
Fig. 8 Efecto de la concentración de PAM sobre la
mojabilidad de discos comprimidos de hematita,
equilibrada con 10-3 M de dodecilsulfonato de sodio
(Gebhard & Fuerstenau 1984).
CAPÍTULO 11. Agregación en Procesamiento de Minerales
325
100
Mo recovery, %
0
2
5
10
80
60
30
40
20
40
60
Mean particle size, mm
Fig. 9 Efecto del tamaño de partícula y dosificación del
floculante Nalco 9809 en la flotación de molibdenita con
ispX=28 g/t, MIBC=36 g/ton, pH=11. (Laskowski & Castro
1999).
Como todos estos resultados provienen de diferentes fuentes y laboratorios, se puede
concluir que el uso de floculantes comerciales de tipo polielectrolito es nocivo en los
circuitos de flotación. Aunque no existe suficiente evidencia del efecto de floculantes
semi-hidrófobos en la flotación, se puede esperar que ellos no sean tan dramáticos.
Hasta la fecha se ha probado varios aglomerantes hidrófobos, también llamados
floculantes hidrófobos, incluyendo latex de poliestireno (Littlefair & Loqwe 1986),
latex FR-7A (Attia et al 1987) y latex UBC-1 (Laskowski eta al 1995). Estos
aglomerantes se preparan por polimerización-emulsión. Los filmes que se obtienen por
evaporación de los látices FR-7A y del UBC-1 son hidrófobos dando ángulos de
avanzada de av  60 en ambos casos. Las partículas hidrofóbicas de estos
aglomerados están cargadas negativamente en agua (Castro et al 1997, Laskowski &
Castro 1999, Laskowski & Yu 2000).
La figura 6 también muestra los resultados de floculación usando UBC-1 y
demuestran claramente que este reactivo flocula selectivamente las partículas de
carbón hidrófobas. Ensayos posteriores de filtración también corroboraron esta
conclusión (Laskowski & Yu 1998, Laskowski & Yu 2000).
Ensayos de floculación confirman que productos comerciales PAM, tales como
Magnafloc 139 y Nalco 9809, y los floculantes hidrófobos utilizados agregan las
partículas de molibdenita (Laskowski & Castro 1999). Sin embargo, como muestran
los resultados de la figura 9, la flotación de molibdenita fina fue deprimida en
presencia de polielectrolitos, mientras que la adición del floculante hidrófobo UBC-1
mejora la flotación (ver figuras 10 y 11).
La diferencia entre los dos aditivos, PAM y UBC-1, es obvia. Ambos agregan
las partículas de molibdenita. Sin embargo el PAM produce flóculos hidrofílicos que
empeoran la flotación mientras que el UBC-1 da flóculos hidrófobos que la mejoran.
Manual de Filtración & Separación
Mo recovery and grade, %
326
100
%R, 12  m
%G, 8  m
80
60
%G, 12  m
40
%R, 8  m
20
pH=11
0
0
50
100
150
200
250
300
350
Agglomerant dosage, g/l
Mo recovery and grade, %
Fig. 10 Efecto de la dosificación del aglomerante UBC-1
sobre la flotación de partículas finas de molibdenita de 8 a
12 m en tamaño.(Castro et al 1997).
100
%R, with UBC-1
80
%R, no UBC-1
60
%G, with UBC-1
%G, no UBC-1
40
5
6
7
8
9
10
11
12
pH
Fig. 11 Efecto del pH sobre la flotación de partículas finas
de molibdenita de 8 a 12 m en tamaño con y sin latex
UBC-1 a 300 g/t y MIBC=12 g/t (Laskowski & Castro
1999).
11.2.3 Aglomeración por aceite
Otro proceso de agregación que no solamente aumenta el tamaño del sistema
particulado, sino que produce un producto final hidrófobo es la aglomeración con
aceite (ver tabla 1). En este proceso, gotas de aceite se adsorben sobre partículas
hidrófobas. Este conjunto de partícula y gota colisiona con otros conjuntos similares
produciendo agregados de mayor tamaño. Los parámetros de operación más importante
en este proceso son la cantidad de aceite, las características del aceite, la propiedad de
las superficies y la intensidad de la agitación (Capes 1989). Este proceso solamente es
posible si las partículas son suficientemente hidrófobas como para ser mojadas
selectivamente por el aceite cuando se encuentran suspendidas en agua. Laskowski
(1992) indica que en general en flotación se utiliza aceites insolubles en agua: para
CAPÍTULO 11. Agregación en Procesamiento de Minerales
327
20
0
g/t only for hydrophobic agglomeration using UBC-1
200
400
600
800
1000
1200
15
10
UBC-1
Kero-DDA Emulsion
5
Kerosene only
Kero-DDS Emulsion
0
0
5
10
15
20
Oil Dosage, %
25
100
Combustible Recovery, %
Ash Content of Agglomerates, %
mejorar la adhesión de partículas hidrófobas a las burbujas (flotación por emulsión),
para aumentar el tamaño de partículas muy pequeñas (flotación de aglomerados) o para
aumentar el tamaño de las partículas hasta un punto tal que los aglomerados puedan ser
separadas por un harnero (aglomeración por aceite). La figura 12 muestra el efecto del
kerosén, del kerosén emulsificado en presencia de surfactantes aniónicos
(dodecilsulfonato de sodio, DDS) o catiónico (dodecilamina, DDA) y del latex UBC-1
en la aglomeración hidrofóbica de carbón bituminoso ultrafino (menos de 45 m).
Laskowski demostró (Laskowski & Yu 1998, 2000) que la emulsificación del kerosén
mediante una intensa agitación produce gotas de alrededor de 20 m en tamaño,
mientras que la adición de 1% de surfactante reduce el tamaño de gotas a 1.5 a 2 m.
Los productos de aglomeración fueron recuperados en un tamiz de 400 mallas, seguido
por secado. Como lo demuestra la figura 12, la aglomeración por aceite y la agregación
con latex UBC-1 son muy similares.
30
0
g/t only for hydrophobic agglomeration using UBC-1
200
400
600
800
1000
1200
Kero-DDS Emulsion
Kero-DDA Emulsion
98
UBC-1
96
94
Kerosene only
92
90
0
5
10
15
20
25
30
Oil Dosage, %
Fig. 12. Comparación del tratamiento de muestras de carbón FD-4 ultrafinas por
aglomeración con aceite, aglomeración con kerosén emulsificado y aglomeración con
latex UBC-1. La emulsión de Kero-DDA fue preparada emulsificando kerosén con 5.4x104
M de solución acuosa de DDA. Kero-DDS fue preparado emulsificando kerosén con
3.4x10-4 M de solución acuosa de DDS.
La recuperación de material combustible es alta en ambos casos, sin embargo la
dosificación de aceite es mucho mayor que la del floculante hidrófobo. Como está bien
establecido que solamente las partículas muy hidrofóbicas pueden ser aglomeradas con
aceite y que ambos procesos, aglomeración con aceite y floculación hidófoba, dan
resultados similares, la hipótesis de que ambos procesos se basan en los mismos
principios es plausible. Por otra parte, como los dos procesos dan como resultado
aglomerados hidrofóbicos, ambos pueden ser incorporados en circuitos de flotación
para mejorar la recuperación de partículas muy finas.
328
Manual de Filtración & Separación
11.3 DISCUSIÓN
En este trabajo se muestra la existencia de varios grupos de aditivos
aglomerantes caracterizados por propiedades superficiales bien diferentes.
Los polielectrolitos de alto peso molecular por ser adsorbidos por varias partículas a la
vez, produciendo su agregación, son utilizados como floculantes. Como las
macromoléculas adsorbidas son hidrofílicas, el agregado resultante también lo es.
Estos polímeros pueden ser utilizados en flotación a muy bajas concentraciones
siempre que floculen selectivamente las especies valiosas de la mena. La utilización de
PEO, que forma parte de estos floculantes, es aún incierta y debe ser más estudiada.
Las poliacrilamidas han encontrado una aplicación muy diferente en la flotación de
fosfatos. En este proceso, se separa silvita de halita por flotación con aminas primarias
de cadena larga en una solución saturada de salmuera (6 M en KCl y NaCl). Para llevar
adelante el proceso es necesario deslamar previamente la suspensión. En una
aplicación (Cormode 1985, Perucca & Cormode 1999) estas lamas (ilita, anhidrita y
dolomita) son floculadas selectivamente con PAM, para luego removerlas por flotación
con aminas. Los flóculos producidos por PAM son hidrófobos y pueden flotar (Alonso
& Laskowski 1999). Aparentemente la flotabilidad de los flóculos bajo estas
condiciones resultan de las diferencias en solubilidad en electrolitos muy concentrados.
Esto confirma que, en general, el fenómeno de floculación también es determinado por
la interacción entre polímero y solvente (agua). Esto generalmente es ignorado a pesar
que juega un importante papel en muy variadas condiciones de alta fuerza iónica.
Los latex hidrofóbicos se adsorben solamente sobre partículas hidrofóbicas por
el mecanismo de coagulación hidrofóbica. Por ello el proceso es selectivo y los
flóculos resultantes son también hidrófobos.
La aglomeración por aceite emulsificado resulta de la adhesión de gotas de
aceite sobre las partículas hidrófobas suspendidas en agua. Por lo tanto el proceso es
selectivo y los aglomerados son hidrofóbicos.
Como se muestra en la figura 1, los aditivos para la agregación pueden ser
usados en dos operaciones unitarias diferentes de los circuitos de procesamiento de
minerales. Para los circuitos de concentración sólo se puede utilizar la agregación
selectiva. Si el proceso es flotación, los agregados deben ser, además, hidrófobos. Para
estas aplicaciones se puede recomendar tanto la aglomeración de partículas finas con
aceite (flotación-aglomeración) como con floculantes hidrófobos. En la separación
sólido-líquido se utiliza generalmente floculantes hidrofílicos. Esto se justifica
plenamente en el espesamiento y filtración de colas de flotación pero su uso es dudoso
para concentrados de flotación. Los concentrados de flotación son hidrófobos por
naturaleza y, por lo tanto, pueden ser fácilmente aglomerados con aceite o floculantes
hidrófobos. Estos aditivos pueden no solamente mejorar la velocidad de filtración, sino
que pueden reducir la humedad del queque. La práctica de utilizar floculante comunes
(hidrofílicos) en el desaguado de concentrados de flotación, que ya son hidrófobos, no
parece una práctica razonable y debe ser re-examinada.
CAPÍTULO 11. Agregación en Procesamiento de Minerales
329
Finalmente es conveniente recalcar que en las plantas de procesamiento de
minerales se utiliza diferentes tipos de aditivos químicos tales como colectores,
espumante y controladores de pH en flotación y floculantes en el espesamiento y
filtración. Aunque polímeros solubles en agua altamente hidrofílicos utilizados como
floculantes no son incompatibles con la flotación, se debe tomar en cuenta que, estando
la flotación y separación sólido-líquido en el mismo circuito de agua, y con la presente
tendencia a la utilización de altas cantidades de floculantes en el espesamiento, es muy
importante la posibilidad de acumulación de altas concentraciones de floculante en el
agua reciclada. Por esta razón es siempre mejor utilizar aditivos compatibles con el
proceso de flotación cuando ello es posible.
11.4 REFERENCIAS
Alonso, E.A. and Laskowski, J.S., 1999. Selection of polymers used as slime modifiers
in potash ore flotation. In J.S. Laskowski (ed.), Polymers in Mineral Processing-Proc.
3rd. UBC-McGill Int. Symp., 405-420, Met. Soc. of CIM, Montreal.
Attia, Y.A., 1985, Cleaning and desulfurization of coal suspensions by selective
flocculation. In Y.A.Attia (ed.) Processing & Utilization of High Sulfur Coals, 267285. Elsevier, Amsterdam.
Brown, P.M.and Scheiner, B.J., 1983.Dewatering of coal-clay waste slurries from
preparation plants, Us Bureau of Mines RI, N°8824.
Capes, C.E., 1989. Liquid phase agglomeration: process opportunities for economic
and environmental challenges. In K.V. Sastry & M.C. Fuerstenau (eds.) Challenges in
Mineral Processing, 237-252, SME, Littleton.
Castro, S.H., Stocker, R and Laskowski, J.S., 1997. The effect of hydrophobic
agglomerant on the flotation of fine molybdenite particles. In Hoberg and Blottnitz
(eds.) Proc. 20th Int. Mineral Processing Congress, 3, 559-569. GMDB, Aachen.
Cormode, D.A., 1985. Insoluble slimes removal from sylvinite ore by selective
flocculation and flotation. 87th Annual CIM Meeting, CIMM, Vancouver.
Gebhard, J.E. and Fuerstenau D.W., 1984. The effect of preadsorbed polymers on
adsorption of sodium dodecylsulfonate on hematite. In M.J. Rosen (ed.).
Structure/Performance Relationship in Surfactants. 253, 291-310, Amer. Chem. Soc.,
Washington D.C.
Gerbhard, J.E. and Fuerstenau D.W., 1986. Flotation behavior of hematite fines
flocculated with polyacryl acid, Minerals and Metallurgical Processing, 3, 164-170.
Gochin, R.J. Lekili, M and Shergold, H.L., 1985. The mechanism of flocculation of
coal particles by polyethylen oxide, Coal Preparation, 2, 19-34.
Hogg, R., 1984. Collision efficiency factors for polymer flocculation, J. Coll. Interf.
Sci., 102, 232-236.
330
Manual de Filtración & Separación
Hogg, R., 1999. Polymer adsorption and flocculation. In J.S. Laskowski (ed.),
Polymers in Mineral Processing-Proc. 3rd. UBC-McGill Int. Symp., 3-18, Met. Soc. of
CIM, Montreal.
Hogg, R., Bunnual, P. And Suharyono, H., 1993. Chemical and physical variables in
polymer-induced flocculation, Minerals and Metallurgical Processing, 10, 81-85.
Keyes, R.O. and Hogg, R., 1979. Mixing problems in polymer flocculation, AIChE
Symp. Series N° 190, 75, 63-72.
Kitchner, J.A., 1972. Principles of action of polymeric flocculants, Br. Polym. J., 4,
217-229.
Laskowski, J.S., 1992. Oil assisted fine particle processing. In J.S. Laskowski and J.
Ralston (eds.), Colloid Chemistry in Mineral Processing, 361-394, Elesevier,
Amsterdam.
Laskowski, J.S., Yu, Z. And Zhan, Y., 1995. Hydrophobic agglomeration of fine coal.
In J.S. Laskowski and G.W. Poling (eds.), Processing of Hydrophobic Minerals and
Fine Coal-Proc. 1st UBC-McGill Int. Symp. 245-258, Met. Soc. of CIM, Montreal.
Laskowski, J.S. and Yu, Z., 1998. Fine coal particle aggregation in coal preparation
plant circuits. In A.C. Partridge and I.R. Partridge (eds.), Proc. 13th Int. Coal Prep.
Congress, 2, 591-599, Australian Coal Society, Brisbane.
Laskowski, J.S. and Castro, S.H., 1999. Aggregation of inherently hydrophobic solids
using hydrophobic agglomerants and flocculants. In J.S. Laskowski (ed.), Polymers in
Mineral Processing-Proc. 3rd. UBC-McGill Int. Symp., 293-310, Met. Soc. of CIM,
Montreal.
Laskowski, J.S. and Yu, Z., 2000. Oil agglomeration and its effect on beneficiation and
filtration of low rank/oxidized coals. Int. J. Mineral Proc., 17, 187-203.
Littlefair, M.J. and Lowe, N.R.S., 1986. On the selective flocculation using
polystyrene latex, Int. J. Mineral Proc., 17, 187-203.
Palmes, J.R. and Laskowski, J.S., 1993. Effect of the properties of coal surface and
flocculant type on the flocculation of fine coal. Minerals and Metallurgical Processing,
10, 218-222.
Pawlik, M, Laskowski, J.S. and Liu, H., 1997. Effect of humic acid and coal surface
properties on rhelogy of coal-water slurries, Coal Preparation, 18, 129-150.
Perucca, C.F. and Cormode, D.A., 1999. The use of polymers in potash beneficiation at
Agrium potash plant. In J.S. Laskowski (ed.), Polymers in Mineral Processing-Proc.
3rd. UBC-McGill Int. Symp., 393-404, Met. Soc. of CIM, Montreal.
Pikkat-Ordynsky, G.A. and Ostryi, V.A., 1972. Coal Flotation Technology, Izd. Nedra,
Moskow.
Pradip and Fuerstenau, D.W., 1987. The effect of polymer adsoption on the wettability
of coal. In Y.A.Attia (ed.) Flocculation in Biotechnology and Separation Systems, 95106, Elsevier, Amsterdam.
CAPÍTULO 11. Agregación en Procesamiento de Minerales
331
Rogers, D.W. and Poling, G.W., 1978. Composition and performance characteristics of
some commercial polyacrylamide flocculants, CIM Bulletin 71, 152-158.
Rubio, J., 1981. The flocculation properties of polyethylene oxide, Coll. Surf. 3, 79-95.
Rubio, J. And Kitchener, J.A., 1976. The mechanism of adsorption of polyethylene
oxide flocculant on silica, J. Coll. Int. Sci., 57, 132-142.
Rubio, J. And Kitchener, J.A., 1977. New basis for selective flocculation of mineral
slimes, Trans IMM, Sec C 86, 97-100.
Scheiner, B.J. and Stanley, D.A., 1985. Flocculation of fine particles with polyethylene
oxide: A proposed mechanism. Trans. SME/AIME 280, 2115-2117.
Sworska, A. Lakowski, J.S. and Cymerman, G., 2000. Flocculation of the Syncrude
fine tailings. Part I. Effect of pH, polymer dosage and Mg2+ and Ca2+ cations. Int. J.
Mineral Proc., in press.
Williams, K.P. and Unlu, M, 1987. Coal flotation in the presence of polymeric
flocculants, Coal Preparation 4, 109-132.
Wright, H.J.L. and Kitchener, J.A., 1976. The problem of dewatering clay slurries:
Factors controlling filterability, J. Coll. Interf. Sci., 56, 57-63.
CAPÍTULO 12
TECNICAS DE FLOCULACION Y METODOLOGIAS
PARA LA OPTIMIZACION DE ESPESADORES
JB Farrow, PD Fawell, RRM Johnston, TB Nguyen, M
Rudman, K Simic and JD Swift
AJ Parker Cooperative Research Centre for Hydrometallurgy
CSIRO Minerals, Box 90 Bentley, Western Australia 6102.
RESUMEN
El Centro de Investigación Cooperativa A.J. Parker para la Hidrometalurgia ha
desarrollado proyectos de optimización de la tecnología de espesadores desde 1988 a
través de la Asociación Australiana para la Investigación en las Industrias Mineras
(AMAIRA) con el apoyo de 25 empresas australianas y extranjeras. Estos proyectos
han dado como resultado una serie de herramientas de investigación y de técnicas para
abordar los fenómenos de floculación y espesamiento. Estudios en el laboratorio y en
plantas industriales se han concentrado en dilucidar cómo afectan a la floculación, y
por lo tanto al espesamiento, factores claves tales como la intensidad y la duración de
la mezcla de pulpa y floculante y la concentración de sólidos presente. Se desarrolló un
completo modelo de mecánica de fluidos computacional (CFD) para predecir posibles
comportamientos en espesadores industriales bajo diversas condiciones de operación,
con base en estudios de laboratorio de floculación y en el diseño y flujos en el equipo.
La aplicación de este modelo de CFD ha producido beneficios significativos en la
operación de espesadores, llegando en un caso a doblar su capacidad. Esta sección
presenta una revisión de los trabajos realizados en estos proyectos, concentrándose en
las herramientas de investigación desarrolladas, en la naturaleza de la información que
se ha adquirido y en las implicaciones para el comportamiento de los espesadores
industriales. También se presentará brevemente los problemas que se investigan en la
actualidad.
332
CAPÍTULO 12 Técnicas de Floculación
333
12.1 INTRODUCCION
El espesamiento es una de las etapas claves en muchos procesos
hidrometalúrgicos. Es una operación de separación sólido-líquido cuyo principio es
muy simple y consiste en producir el agregamiento de las partículas finas de una
suspensión mediante un floculante aumentando de esta forma su tamaño y permitiendo
que ellas sedimenten bajo el efecto de la gravedad produciendo un licor claro y un
sedimento denso. Tradicionalmente el problema de la floculación se ha enfocado en
forma
ad hoc en la industria minera, buscando el lugar óptimo de adición y realizando
modificaciones al feedwell para lograr una mejor operación.
Para buscar una forma de mejorar el entendimiento de los fenómenos
fundamentales que ocurren en el espesamiento, el Centro Paker inició en 1988 el
proyecto P266 financiado por AMIRA, denominado Mejorando la Tecnología de
Espesadores.
Las primeras etapas de la investigación se enfocaron a desarrollar técnicas de
medición de las propiedades de los flóculos, que se forman en espesadores industriales
bajo diferentes condiciones de operación, y en desarrollar métodos para modificar la
estructura de dichos flóculos para optimizar el comportamiento de los equipos. Un
resultado importante de esta etapa fue la identificación de la influencia dominante que
tiene la agitación, utilizada para mezclar el floculante con la pulpa, en las propiedades
de la suspensión floculada y, por lo tanto, en el comportamiento del espesador. El
prototipo de la cámara de cizalle (shear vessel) desarrollada en este proyecto (Farrow
and Swift 1996) ha resultado ser una importante herramienta de laboratorio para
estudios de floculación.
Etapas siguientes del proyecto se dedicaron a establecer la relación entre las
condiciones de mezcla, utilizada para flocular la alimentación, y comportamientos del
espesador tales como capacidad, concentración de la descarga y consumo de
floculante. Se utilizó estudios de laboratorio junto a trabajo en planta para determinar
el significado de la intensidad de mezcla, tiempo de residencia y otros factores en el
estado de floculación alcanzado con diversas suspensiones de minerales. Al mismo
tiempo, se estudió las condiciones hidrodinámicas en los feedwells mediante CFD,
validando los resultados con mediciones en planta usando trazadores y realizando un
muestreo. Comparando los resultados de la floculación en el laboratorio y en las
plantas industriales, se concluyó que había mucho margen de optimización en las
condiciones de floculación industrial en los feedwells. Un resultado tangible de este
nuevo conocimiento fue la modificación realizada a uno de las empresas
patrocinadoras, en la cual se dobló la capacidad de espesamiento ahorrando la
instalación de un nuevo espesador durante la expansión de la planta (Kahane et al
1997).
Trabajos en la empresa Westralian Sands en Capel, Western Australia,
mostraron el efecto de la floculación en el feedwell tiene en el comportamiento de un
espesador de relaves. Un espesador fue utilizado como control para comparar su
334
Manual de Filtración & Separación
comportamiento con el de otros espesadores de la planta en los que se cambiaron las
condiciones hidrodinámicas de floculación. Estos resultados a escala industrial
confirmaron la gran sensibilidad del espesamiento a las condiciones hidrodinámicas
durante la floculación, pero también demostraron la compleja influencia que tienen la
concentración de la suspensión, el reciclo de líquido, el perfil de intensidad de
agitación y el tiempo de agitación tienen sobre el estado de agregación de la
suspensión.
Actualmente un grupo de químicos, ingenieros de proceso y especialistas en
CFD investigan una serie de nuevos fenómenos de interés. Este trabajo es patrocinado
por 18 empresas mineras y de manufactura de espesadores. Una de las nuevas líneas de
investigación enfatiza el mejoramiento de la habilidad de los modelos CFD para
predecir el comportamiento de espesadores a escala industrial incorporando la
modelación de la formación y ruptura de flóculos a distintas condiciones
hidrodinámicas. Mediciones en una tubería en condiciones turbulentas han permitido
obtener datos de cinética de floculación en un amplio rango de condiciones de
agitación bien caracterizadas. Otra dirección de la investigación es el estudio de la
acción de las rastras. El objetivo, en este caso, es encontrar las mejores estructuras y
configuraciones de las rastras para promover la densificación, aumentar el flujo de
descarga y minimizar el torque. Relacionado con este trabajo de laboratorio, se realiza
visitas a plantas para evaluar el desempeño de nuevos diseños de espesadores, estudios
de consolidación de sedimentos y la medición de la cinética de floculación de
productos de las plantas.
En este trabajo se muestra algunas de las herramientas desarrolladas y aplicadas
al estudio del proceso de floculación y utilizadas para optimizar el comportamiento de
espesadores industriales. Se dará información sobre la naturaleza de estas
herramientas, de la información obtenida mediante su uso y de las implicaciones que
ellas tienen en el desempeño de espesadores industriales.
12.2 CARACTERIZACIÓN DE LA FLOCULACION
A pesar del extensivo uso de floculantes de alto peso molecular en el
procesamiento de minerales, las propiedades físicas de éstos no son bien conocidas. En
particular, poco se sabe de la distribución de su peso molecular, debido a la dificultad
de caracterizar polímeros de cadena larga sensitivos al cizalle. Esta información es
esencial para entender y predecir el comportamiento del floculante. La técnica de
fraccionamiento en campo de flujo (FFF) se ha usado con éxito para determinar la
distribución de peso molecular de floculantes (Hecker et al 1999, 2000). En contraste a
la cromatografía de columna de relleno, la FFF hace uso de un canal abierto de
pequeña área menor a 0.01m2 (limitando el cizalle y reduciendo las pérdidas por
adsorción) por el cual se hace pasar un fluido en flujo laminar. La separación se
obtiene como resultados de la aplicación de un flujo perpendicular cruzado. La
especies más pequeñas son capaces de difundir en contra del flujo cruzado y, por lo
tanto, ocupar líneas de corriente de mayor velocidad del fluido y ser separadas de las
especies mayores. Esta técnica permite realizar separaciones en un amplio rango de
335
CAPÍTULO 12 Técnicas de Floculación
pesos moleculares. La utilización de dispersión de láser en multi-ángulo (MALLS)
como detector permite la determinación directa del peso molecular de cada volumen
eluído. Se ha observado una clara relación entre el peso molecular y el tiempo de
elusión, la que ha demostrado ser independiente del tipo de polímero. La figura 1
muestra mediciones de pesos moleculares de dos polímeros utilizados como
floculantes comerciales. Se puede observar la gran amplitud de pesos moleculares
encontrada en cada producto.
1.5
3
1.0
DRI
Señal
(Volts)
Floculante No.
1
Floculante No.
2
0.5
DRI
2 Señal
(Volts)
1
0
106
107
Mw de MALLS
108
0
Fig. 1 Distribución del peso molecular de dos floculantes comerciales noiónicos medidos por la técnica FFF combinada con MALLS. Muestran la
respuesta del refractómetro.
La elución puede complicarse por la presencia de polímero aglomerado, hecho
encontrado en varias soluciones de poliacrilamida. Estos aglomerados pueden ser
eliminados median un control cuidadoso de la composición de la solución (Hecker et al
2000). Se examinó varios floculante mediante la técnica del FFF, cada uno de ellos
resultando en perfiles de elución diferentes. Esta información se ha utilizado para
explicar porqué floculantes del mismo peso molecular promedio se comportan en
forma tan diferente.
La distribución de peso molecular obtenida por FFF ligada a la caracterización
de agregación descrita anteriormente, dan la base para la predicción del
comportamiento de floculantes a partir de propiedades físicas inherentes de ellos.
336
Manual de Filtración & Separación
12.3 CARACTERIZACIÓN DE SUSPENSIONES FLOCULADAS
La efectividad de la mayoría de los espesadores en la industria minera descansa
en la capacidad de reactivos químicos, floculantes, de agregar las partículas finas de la
suspensión de alimentación formando flóculos. La floculación de una suspensión
produce flóculos de diversos tamaños y densidades y exhibe una gran irregularidad de
forma. Ver figura 2. Estas propiedades tienen un profundo efecto en las propiedades de
desaguado de la suspensión, controlando la velocidad de sedimentación, la
consolidación y la reología del sedimento. La medición de las propiedades de flóculos
en una suspensión es compleja debido a la naturaleza frágil de los flóculos y se debe
cuidar que la técnica de medición no altere su tamaño o estructura.
Alto
Agregado denso
pequeño
Agregado poroso
grande
densidad
Agregado
Bajo
Pequeño
Tamaño agregado
Grande
Fig.2 Esquema del tamaño y densidad de flóculos producido por floculación de
una suspensión mineral antes de espesar
Medición de la distribución de tamaño de flóculos
Se ensayó una serie de métodos de determinación de la distribución de tamaño
de los flóculos, incluyendo métodos estándar tales como dispersión de láser (Malvern,
Mastersizer) y sedimentación (Sedigraph). Ninguno de estos fue exitoso debido a la
fractura de los flóculos dentro del sistema de medición. Más éxito se obtuvo con un
método nuevo denominado Medición de la reflectancia de un foco concentrado
(FNRM), el que permite la caracterización de tamaño in situ de agregados entre 1 y
1000 µm en amplio rango de concentraciones de sólido. El principio en que se basa
esta técnica está esquematizado en la figura 3.
337
CAPÍTULO 12 Técnicas de Floculación
Laser beam
Probe at 45° angle to turbulent,
well-mixed flow
Beam
splitter
Optics
rotating at
a fixed high
velocity
Sapphire
window
Fig. 3 Medición de la distribución de tamaño flóculos mediante la
técnica FNRM.
Se enfoca un rayo láser a través de una ventana de zafiro y se barre a una
velocidad constante sobre las partículas de una suspensión que pasa a lo largo de la
ventana. La duración de la luz reflejada se puede correlacionar a un tamaño (largo de
cuerda) del flóculo. Barriendo varios miles de agregados por segundo, es posible
determinar la distribución de tamaño de los agregados. La técnica de FBRM puede
indicar el grado de floculación bajo diferentes condiciones de dosificación, de mezcla o
de cualquier otra. La figura 4 muestra un ejemplo en que la distribución determinada
por FBRM para flóculos formados con la misma dosificación pero diferentes
condiciones de mezcla se comparan con la distribución de tamaño de las partículas sin
flocular.
16
100 rpm
200 rpm
14
75 rpm
50 rpm
12
10
Cuentas
8
6
Sin flocular
(%)
4
2
0
1
10
100
1000
Largo de cuerda (µm)
Fig. 4 Comparación de la distribución de la distribución de tamaño de las
partículas sin flocular con la distribución de tamaño de flóculos, determinados in
situ, formados con la misma dosificación pero distintas condiciones de agitación en
una cámara de cizalle.
338
Manual de Filtración & Separación
Esta técnica también se usó en forma exitosa en espesadores industriales para la
determinación el grado de floculación en diferentes partes del feedwell. Lo más
importante es que se obtuvo una correlación directa entre la longitud promedio de
cuerdas y la velocidad de sedimentación (Hecker et al 1999b). Es así como la
utilización de la técnica FBRM para determinar las condiciones en que se obtiene
el máximo tamaño promedio de flóculo ofrece una nuevo enfoque para optimizar la
operación de un espesador para una determinado sistema pulpa-floculante.
12.3.1 Medición de la velocidad de sedimentación de flóculos
La claridad del rebalse es un criterio clave en muchas operaciones de
procesamiento de minerales, especialmente en aquellos los procesos de sedimentación
gravitacional que preceden la precipitación (refinerías Bayer), electrodeposición
(refinerías de cobre y de zinc) o extracción por solventes (hidrometalurgia del cobre o
del níquel). El rebalse de espesadores con mucho material sólido puede ser detectado
fácilmente mediante el uso de un sistema de video/magnificación que mide el tamaño y
velocidad de sedimentación de los sólidos bajo condiciones quasi-estáticas (Farrow et
al 1993). Así se puede identificar si el alto contenido de sólidos se debe a (1) una mala
floculación, (2) flotación de los agregados por burbujas, (3) floculante no disperso, ojo
de pez, (partículas que se ven pegadas a un glóbulo de gel), (4) ruptura de flóculos
(evidenciado por la presencia de flóculos pequeños de baja velocidad de
sedimentación) o (5) cortocircuito de la alimentación al rebalse (indicando la presencia
de agregados que sedimentan más rápidamente que el promedio de la velocidad de
ascenso del agua en el espesador). Mediciones indicando este último diagnóstico
fueron hechas en el espesador de una refinería de zinc bajo condiciones normales de
operación. Ver figura 5.
4
Velocidad
de
3
2
sedimentación
individual
(m/h)
1
0
0
20
40
60
80
100
120
140
160
Tamaño (µm)
Fig.5 Distribución de la velocidad de sedimentación con el tamaño individual de
flóculos en el rebalse de un espesador de concentrados de zinc en “condiciones
normales de operación”. La línea horizontal es la velocidad del flujo ascendente de
agua.
CAPÍTULO 12 Técnicas de Floculación
339
Mediciones mostraron más tarde que la causa de la alta presencia de sólidos en
el rebalse era el cortocircuito, ya que la mayoría de las partículas tenían una velocidad
de sedimentación mayor que la del agua en ascenso, en varios casos de hasta 8 veces,
la velocidad de ésta (línea segmentada en la figura 5) La presencia de estos agregados
en el rebalse indican que existen corrientes de cortocircuito de la alimentación al
rebalse con velocidades de hasta ocho veces la del agua. Con CFD se pudo detectar
que la causa del cortocircuito era la gran asimetría de la descarga del feedwell abierto
en el fondo, debido al ángulo de entrada de la cañería de alimentación (Johnston et al
1998) como se ve en la figura 6.
Fig. 6 Flujo estacionario en un espesador mostrando un significativo flujo
radial desde el feedwell hacia el rebalse (cortocircuito hacia el rebalse)
obtenido mediante CFD.
12.4 ROL DE LA HIDRODINÁMICA EN LA FLOCULACION
Como ya se ha mencionado en reiteradas oportunidades en este trabajo, las
condiciones de mezcla utilizadas para poner en contacto el floculante con la pulpa de
alimentación es crítica para lograr una eficiente floculación, y por lo tanto, una
operación adecuada del espesador. En este proyecto se desarrolló la cámara de cizalle
(shear vessel, ver figura 7) para proveer información sobre como afecta las condiciones
de agitación al fenómeno de floculación (Farrow and Swift 1996). El instrumento está
basado en una geometría Couette y se basa en poner en contacto el floculante y la
suspensión en el espacio entre cilindros concéntricos. La intensidad de agitación se
selecciona cambiando la velocidad de giro del cilindro interior. El tiempo de mezcla se
varía cambiando el flujo o cambian el punto en que se agrega el floculante (puerto 1 a
4 en la figura 7). Un ejemplo de la información que se puede obtener con la cámara de
cizalle es la que entrega la figura 8. Los datos muestran que la eficiencia de floculación
(velocidad de sedimentación y turbidez residual) dependen fuertemente de la
intensidad de la mezcla (velocidad de rotación) durante el contacto entre el floculante y
340
Manual de Filtración & Separación
la suspensión. Los diferentes floculantes tienen requerimientos diferentes de intensidad
de mezcla para un comportamiento eficiente debido, sin duda, a las diferentes
Heating
fluid
Thermostat
jacket
Heating
fluid
Stirrer
Variable
drive
Insulated
flocculant
tank
Rotating
inner
cylinder
Port 4
Port 3
Port 2
Port 1
Feed
Heating
fluid
Nephelometer
probe
Heating
fluid
Thermostatted
feed tank
V
By-pass
Analysis
column
V
P
To
waste
Fig. 7 Esquema de una cámara de cizalle para la determinación del
efecto de las condiciones de agitación en el comportamiento de
floculantes.
características de adsorción en la superficie de minerales. La intensidad de la mezcla
durante la floculación es un parámetro muy importante que se debe considerar cuando
se estudia el comportamiento de un espesador industrial (Farrow and Swift 1996).
0.5
Initial
0.4
solids
settling
0.3
flux
Flocculant A
Flocculant B
(t m-2 h-1)
0.2
0.1
0
0
100
200
300
400
Rotation speed (rpm)
Fig. 8a Información entregada por la cámara de cizalle sobre el
comportamiento de floculantes. Velocidad de sedimentación en
función de la intensidad de agitación.
341
CAPÍTULO 12 Técnicas de Floculación
800
Flocculant A
600
Flocculant B
Turbidity
(NTU)
400
200
0
0
100
200
300
400
Rotation speed (rpm)
Fig. 8b Información entregada por la cámara de cizalle sobre el
comportamiento de floculantes. Turbidez en función de la intensidad de
agitación. La turbidez indica presencia de sólidos.
También se desarrolló un reactor de tubo lineal para investigar la cinética
floculación, permitiendo la identificación del tiempo óptimo para de mezcla del
floculante con la alimentación. Con esta técnica, el floculante se introduce en la cañería
por donde fluye la suspensión a una cierta velocidad. El tamaño de los agregados se
mide más adelante mediante FBRM para determinar la velocidad a la que crecen los
agregados y se rompen bajo determinadas condiciones de operación. Un ejemplo del
tipo de información que se obtiene con este método se muestra en la figura 9. Aquí se
muestra la velocidad de cambio del tamaño medio de cuerdas como función del tiempo
de reacción bajo dos condiciones de floculación.
150
Curva a
Largo
Cizalle alto
de cuerda 100
Curva b
promedio
(µm)
Cizalle bajo
50
0
0
10
20
30
40
50
60
Tiempo de reacción (s)
Fig. 9 Velocidad de crecimiento y ruptura de flóculos en un reactor tubular
lineal en condiciones de a) alto cizalle y b) bajo cizalle.
342
Manual de Filtración & Separación
Bajo condiciones de cizalle alto (curva a), el tamaño promedio de los agregados
crece rápidamente desde 30 µm hasta 130 µm en 15 segundos, antes que comience a
dominar la ruptura de flóculos, llevando a una permanente disminución del tamaño. En
las condiciones de bajo cizalle (curva b), el crecimiento del tamaño de agregados es
mucho más lenta, aumentando a 100 µm en 50 segundos sin evidencia de ruptura de
flóculos. Esta diferencia en la velocidad de crecimiento de los flóculos tiene gran
importancia en el comportamiento de los espesadores industriales. Un comportamiento
óptimo sólo se obtendrá si la reacción de floculación se completa (alcanzando los
agregados el tamaño máximo) en el feedwell antes que la suspensión pase al cuerpo del
espesador. Para la floculación sometida a alto cizalle se necesitaría 15 segundos en el
feedwell antes que la suspensión sea descargada al espesador, según la figura 9,
mientras que para una suspensión sometida a bajo cizalle el tiempo necesario es de por
lo menos 50 segundos (para el tipo de floculante, concentración de sólidos y
dosificación correspondiente a la figura 9). Como conclusión se puede decir que un
elemento clave en el diseño de los feedwells es proveer un rango de condiciones
hidrodinámicas y un suficiente tiempo de reacción, desde que se introduce el floculante
hasta el instante en que la pulpa de alimentación es descargada al cuerpo del espesador.
12.5 ENTENDIENDO EL COMPORTAMIENTO DE ESPESADORES
Dentro del proyecto AMIRA para el mejoramiento de la tecnología de
espesamiento se desarrolló un modelo bifásico de CFD para estudiar el
comportamiento de la pulpa en los feedwells (Johnson et al 1996; Kanane etal 1997).
El modelo requiere la entrada de la geometría del feedwell y las condiciones de
operación, tales como, flujos, concentración de sólidos y densidad y viscosidad del
líquido. Se requiere hacer varias simplificaciones tales como, suponer un solo tamaño
y densidad de partícula. Se ha incorporado una ecuación de adsorción de floculante
para describir la interacción partícula-floculante.
Una vez establecido el campo de velocidad, el modelo de CFD entrega la
distribución de velocidad de cizalle, la distribución de concentraciones de sólido y
perfil de adsorción de floculante en el feedwell y en la región del espesador adyacente
a éste. Ejemplos particulares de feedwells se muestra en la figura 10 (distribución de
velocidad de cizalle), figura 11 (distribución de concentración de sólidos) y en la figura
12 (perfil de la concentración de floculante libre). Mediante esta información se puede
realizar diseños o modificaciones del diseño de feedwells tomando en cuenta el
diámetro y el ángulo de entrada de la tubería de alimentación de la pulpa.
343
CAPÍTULO 12 Técnicas de Floculación
Plan view
Feed
entry
Side Elevation
Fig. 10. Predicción con CFD de la distribución de velocidad de cizalle en un
feedwell industrial. El tono más claro representa la mayor velocidad de
cizalle mientras que el más oscuro representa la zona de menor cizalle.
El modelo también es una poderosa herramienta para localizar el punto de
adición de floculante en el feedwell, pero requiere entendimiento del comportamiento
de floculación (figura 8) y de la cinética de floculación (figura 9) para una determinada
combinación de suspensión-floculante.
Un aspecto importante del trabajo de modelación con CFD es la validación a
escala industrial. Esta validación implica comparar las simulaciones con muestreos
realizados en diferentes posiciones del feedwell de espesadores industriales en los que
se ha inyectado trazadores (preferentemente líquidos y sólidos) en el flujo de
alimentación que entra en el feedwell. Se ha encontrado que los resultados del
muestreo confirman las predicciones (Kahane et al 1997).
344
Manual de Filtración & Separación
Fig. 11 Predicción con CFD de la distribución de concentración de sólidos en
cinco planos dentro del feedwell. El tono más claro representa la menor
concentración, mientras que el más oscuro la mayor. En el fondo del
feedwell se observa recirculación de líquido. La alimentación se muestra con
una flecha.
Fig. 12 Predicción con CFD del perfil de adsorción de floculante en cinco
planos dentro del feedwell. El tono más claro representa la mayor
concentración de floculante no adsorbido y el tono más oscuro la
concentración menor de floculante no adsorbido.
CAPÍTULO 12 Técnicas de Floculación
345
La aplicación de estas técnicas de modelación con CFD han dado como
resultado mejoramientos significativos en espesadores industriales. Sin embargo, el
modelo está aún en un estado de desarrollo primario y uno de los objetivos del último
proyecto AMIRA para el mejoramiento de la tecnología de espesamiento es mejorar la
capacidad predictiva del modelo CFD, especialmente incorporando mejor información
cinética de la floculación. Un ejemplo de cómo se utilizó el modelo para mejorar el
comportamiento de espesadores industriales en Worsley Alumina Limited (Collie,
Western Australia) ha sido descrito por Kahane et al (1997). En este trabajo se modelo
con CFD y se realizó estudios de trazadores con iones de litio para dar información de
los patrones de flujo y del comportamiento del floculante en el circuito de lavado en
contracorriente de Worsley. Con base en esta información, se relocalizaron las
adiciones de floculante en el flujo de dilución natural producida en la parte baja del
feedwell. Este cambio resultó en una mucho mejor dilución del floculante antes de la
mezcla con la pulpa de alimentación. Este mejoramiento más el rediseño del feedwell
dobló la capacidad de los espesadores, reduciendo en tres los nuevos espesadores
requeridos para un plan de expansión y, por lo tanto, reduciendo el costo de capital.
12.6 DISEÑO Y OPERACIÓN DE RASTRAS
A pesar que el diseño de las rastras y su operación es un aspecto importante en el
comportamiento de un espesador, ellos han recibido poca atención en la literatura.
Actualmente se lleva a cabo un estudio de los fenómenos básicos involucrados en el
diseño de las rastras. El enfoque contempla pequeños ensayos físicos para
complementar los modelos de CFD. Los ensayos físicos permiten obtener datos
confiables para la validación de los modelos de CFD y proveen, además, información
sobre el flujo alrededor de componentes de las rastras y de las estructuras soportantes
que no se pueden obtener fácilmente con CFD. En los experimentos físicos se utilizó
carbopol como fluido para simular el comportamiento no-newtoniano (generalmente
de tipo shear thinning) de las pulpas minerales. Aspectos reológicos, tales como
tixotropía y compresibilidad, son despreciados en los experimentos, pero pueden ser
modelados en el computador y, de esta forma, extendiendo la validez y utilidad del
modelo may allá de los experimentos simples. Eventualmente, esta información se
utilizará en el diseño e implementación de modelos de CFD de una estructura completa
de rastras paras ser incluidas en el modelo global de espesadores con CFD. Un ejemplo
de la modelación con CFD del flujo alrededor de las rastras de un espesador se muestra
en la figura 13.
346
Manual de Filtración & Separación
Fig.13 Predicción con CFD del fluido moviéndose a lo largo de las
superficies de las paletas de rastras.
12.7 CONCLUSIONES
El apoyo de varias compañías mineras, empresas manufactureras de espesadores
y empresas productoras de reactivos químicos en una serie de proyectos de
investigación para el mejoramiento de la tecnología de espesadores, ha dado como
resultado nuevas herramientas para tratar la floculación y su efecto sobre el
comportamiento de espesadores. Estas herramientas han identificado los factores
claves (tales como la intensidad y duración de la mezcla) que afectan la floculación y,
por lo tanto, la eficiencia del espesador. El desarrollo de un modelo amplio de CFD ha
permitido predecir el comportamiento en escala industrial de un espesador bajo
diversas condiciones de operación, conociendo la geometría, flujos y comportamiento
de la floculación obtenidas en el laboratorio. Los beneficios de esta investigación han
llegado a los patrocinadores con herramientas y técnicas para la identificación de los
mejores lugares para colocar la alimentación de floculante y para evaluar el impacto de
las modificaciones de diseño de los feedwells. Sin embargo, aún es necesario continuar
con la investigación para llegar a disponer de una metodología suficientemente robusta
para resolver el amplio rango de problemas encontrados en los procesos de separación
sólido-líquido en las empresas mineras.
12.8 AGRADECIMIENTOS
Se agradece el financiamiento otorgado por las empresas: Alcoa of Australia,
Baker Process, Bateman Process, BHP, Billiton, Centaur Mining & Exploration, Cytec,
Dorr-Oliver, Hydro Aluminium, Kidd Creek Mines, Meriwa, Mim Holdings, Nabalco,
Nalco Chemicals, North Limited, Pasminco, Queensland Alumina, Queensland Nickel,
CAPÍTULO 12 Técnicas de Floculación
347
Río Tinto, SNF, Supaflo Technologies, Western Mining, Westralian Sands, Worsley
Alumina al proyecto AMIRA Mejoramiento de la Tecnología de Espesadores. Esta
investigación también ha recibido el apoyo financiero del programa de gobierno
Australian Government’s Cooperative Research Centre (CRC), a través del Parker
Centre for Hydrometallurgy, lo que agradece.
12.9 REFERENCIAS
J.B. Farrow and J.D. Swift, Int. J. Min. Process., 46, 1996, 263-275.
R.B. Kahane, P. Schwarz and R.R.M. Johnston, International Conference on
Computational Fluid Dynamics in Minerals and Metals Processing and Power
Generation, 3-5 July, Melbourne, Australia, 1997, p109-117.
R. Hecker, P.D. Fawell, A. Jefferson and J.B. Farrow, J. Chromatogr. A, 837, 1999a,
139-151.
R. Hecker, P.D. Fawell, A. Jefferson and J.B. Farrow, accepted in Chemical Eng. J.,
2000.
J.B. Farrow and L.J. Warren, in B. Dobias (Ed.), Coagulation and Flocculation Theory and Application. Marcel Dekker, New York, Chapter 9, 1993.
R. Hecker, L. Kirwan, P.D. Fawell, J.B. Farrow, J.D. Swift, and A. Jefferson, to be
presented at: The Use of Polymers in Mineral Processing, 3rd UBC-McGill Bi-annual
Symposium on Fundamentals of Mineral Processing, Quebec City, August 22-26,
1999b.
R.R.M. Johnston, P. Schwarz, M. Newman, M. Kershaw, J.B. Farrow, K. Simic and
J.D. Swift, Lead and Zinc Processing Symposium, Calgary, 16-19 August, 1998.
J.B. Farrow and J.D. Swift, 4th International Alumina Quality Workshop, Darwin,
Australia, 2-7 June 1996, p. 355-363.
R.R.M. Johnston, T.V. Nguyen, P. Schwarz and K. Simic, 4th International Alumina
Quality Workshop, Darwin, Australia, 2-7 June, 1996, p. 467-475.
CAPÍTULO 13
POLÍMETROS HIDRÓFOBOS DEL TIPO LÁTEX PARA
LA SEPARACIÓN SÓLIDO-LÍQUIDO DE
CONCENTRADOS DE FLOTACIÓN
S.H. Castro
Departamento de Ingeniería Metalúrgica
Universidad de Concepción.
Fax: 41-243418; [email protected]
RESUMEN
En el presente trabajo se muestran avances con un nuevo tipo de reactivos,
denominados aglomerantes hidrófobos, estos son polímeros del tipo látex que forma
finas dispersiones coloidales hidrófobas en medio acuoso y son capaces de aglomerar
en forma selectiva partículas minerales también de carácter hidrófobo.
Estos reactivos abren un interesante potencial de aplicación en espesadores de
concentrados. Pruebas de aglomeración de molibdenita fina muestran que los
aglomerados resultantes flotan mejor que las partículas sin agregación (unitarias),
contrariamente al efecto producido por polímeros hidrofílicos del tipo poliacrilamidas.
Por otro lado, ensayos de velocidad de filtración y mediciones de humedad del queque
con muestras de carbón intrínsicamente hidrófobo, muestran ventajas en ambas
operaciones. Sobre esta base, se discute conceptualmente la floculación y la
aglomeración hidrófoba y el posible campo de aplicación de estos nuevos reactivos.
348
CAPÍTULO 12. Polímeros hidrófobos tipo Látex
349
13.1 INTRODUCCIÓN
En minería las operaciones de separación sólido / líquido son muy importantes,
principalmente el espesamiento y la filtración. En el espesamiento es frecuente el uso
de aditivos químicos, denominados floculantes, para inducir la agregación de las
partículas finas y, de este modo, aumentar su velocidad de sedimentación.
Para los espesadores de relaves de flotación se emplea normalmente polímeros
del tipo poliacrilamidas de alto peso molecular. Estos reactivos son polímeros
hidrofílicos que se fijan a partículas de ganga mediante enlace de puente de hidrógeno
entre los grupos amidos del floculante (-CONH2) y los grupos silanoles (-SiOH) de la
superficie mineral. Se acepta que el mecanismo de floculación es por puentes, es decir,
un segmento del polímero se adsorbe primero sobre una partícula mineral unitaria, y
los segmentos restantes de la misma cadena lo hacen sobre otras partículas,
completando el mecanismo de puente y estructurando un flóculo. En estos espesadores,
en que el objetivo es recuperar agua y el sólido se descarta hacia el tranque de relave,
la naturaleza hidrofílica/hidrofóbica de los flóculos es intrascendente.
Sin embargo, para espesadores de concentrados, dónde el mineral continúa
procesándose, ya sea en etapas de flotación, filtración o secado, las características de
majamiento de los flóculos pueden ser de gran importancia. El uso de estos floculantes
en espesadores de concentrados de flotación puede presentar algunas
contraindicaciones como, por ejemplo, en el caso de aquellos concentrados que
alimentan una planta de molibdeno, debido a que las poliacrilamidas exhiben efectos
depresantes sobre la molibdenita (Castro and Laskowski, 1997). También es de
conocimiento general de los operadores, que usar floculantes del tipo poliacrilamida en
concentrados que poseen un porcentaje alto de ganga fina (lamas), puede producir el
bloqueo de las telas de los filtros. De aquí surge la ventaja de los aglomerantes
hidrófobos, que se caracterizan por formar flóculos también hidrófobos, a diferencia de
los floculantes convencionales que forman flóculos hidrofílicos.
En los últimos años, ha surgido un nuevo tipo de polímeros, que reciben el
nombre de aglomerantes hidrófobos (Attia, et al. 1987; Laskowski et al., 1995;
Laskowski and Castro, 1999; Vigdergauz et al. 1999). Se trata de polímeros del tipo
látex, es decir, de emulsiones de polímeros de estireno-butadieno en proporciones
variables y sintetizados por el método de polimeración en emulsiones. Es así como se
obtiene una emulsión concentrada, con ayuda de un emulsificante, de un látex con
grados variables de hidrofobicidad y que es fácilmente dosificable por dilución. Por
otra parte, Misra y Smith (1999) han informado la efectiva floculación de minerales y
carbón fino con biopolímeros hidrófobos derivados de microorganismos, como
alternativa a los polímeros hidrófobos sintéticos.
En el presente trabajo se muestra las características de agregación que exhiben
estos polímeros y las ventajas que puede tener el uso de un aglomerante hidrófobo
sobre un floculante convencional en el manejo de la agregación de partículas finas de
minerales hidrófobos, como es el caso de concentrados de flotación. Especial énfasis se
350
Manual de Filtración & Separación
pone en destacar la importancia que las características hidrófilicas/hidrofóbicas de los
flóculos tienen aguas abajo del espesamiento.
13.2 RESULTADOS EXPERIMENTALES
Para conocer las características de agregación del aglomerante hidrófobo y su
influencia en el proceso de flotación y en la separación sólido-líquido, se realizó una
serie de experiencias de floculación, flotación y filtración. El aglomerante hidrófobo
utilizado en las experiencias de laboratorio es una dispersión coloidal de partículas
esféricas, menores de 1 micrón, de un polímero hidrófobo tipo látex sintetizado en los
laboratorios de la Universidad de British Columbia (UBC-1) en, Vancouver, Canadá.
La dispersión acuosa es de color blanco (ver figura 1) y da un ángulo de contacto de
avance de 60 grados medido sobre un film obtenido por evaporación.
a). 10.000x sin MIBC
b). 10.000x. con MIBC (Stocker, 1995)
Fig. 13.1 Foto micrografías al microscopio electrónico del látex UBC-1 en ausencia y
presencia de metil isobutil carbinol como agente dispersante.
En la figura 13.1 se muestra microfotografías de la dispersión del látex
hidrófobo UBC-1 empleado en este trabajo tomadas en el microscopio electrónico (R.
Stocker, 1995). Se aprecia una tendencia de las partículas a la forma esférica y tamaños
del orden de 0.1 micrones.
Mayores detalles sobre los materiales utilizados y las condiciones de las pruebas
de flotación, floculación y filtración son descritos por Castro and Laskowski ( 1997) y
Laskowski and Castro (1999).
CAPÍTULO 12. Polímeros hidrófobos tipo Látex
351
13.2.1 Efecto de floculantes y aglomerantes hidrófobos sobre la flotación de
molibdenita.
En la figura 13.2 se muestra el efecto depresante que tienen floculantes del tipo
poliacrilamida sobre la flotación de molibdenita.
Fig. 13.2 Efecto de un floculante convencional sobre
la flotación de diferentes fracciones de tamaño de
molibdenita Castro and Laskowski (1997).
Este efecto es bien conocido en la práctica industrial, razón por lo cual se evita el uso
de floculantes en los espesadores de concentrado colectivo Cu-Mo que alimentan a las
plantas de molibdenita. Lo mismo ocurre con espesadores intermedios dentro de la
planta de molibdeno. En la actualidad no hay reactivos floculantes alternativos que
sean compatibles con la flotación de molibdenita.
La misma situación puede proyectarse al procesamiento de cualquier otro
mineral con flotabilidad natural, como por ejemplo, el carbón, que en general se
depresan por adsorción de polímeros hidrofílicos.
En la Fig. 13.3 se muestra comparativamente el efecto de un polímero
convencional (Magnafloc E-24) y de un látex hidrófobo (UBC-1) sobre la eficiencia de
floculación de molibdenita fina. Se aprecia que ambos tipos de aditivos son capaces de
agregar las partículas de molibdenita, aumentando su velocidad de sedimentación.
352
Manual de Filtración & Separación
Fig.13.3. Efecto de un floculante y un aglomerante
hidrófobo sobre la floculación de dispersiones de
molibdenita fina, Laskowski and Castro (1999).
En la figura 13.4 se muestra el efecto del UBC-1 sobre la flotación de partículas
finas de molibdenita aglomeradas previamente con este látex. Se puede apreciar que la
fracción bajo 8 micrones mejora su flotación debido al aumento de tamaño por
aglomeración, de lo que se concluye, que los aglomerados resultantes son también
hidrófobos. Esta conducta contrasta con lo observado en la figura 3, donde el aumento
de tamaño se logró con un floculante convencional. De lo anterior se puede concluir
que los floculantes del tipo poliacrilamidas generan flóculos hidrofílicos que depresan
la flotación de molibdenita, mientras que los látex hidrófobos forman aglomerados
hidrófobos que mejoran la flotación de molibdenita fina.
Fig.13.4. Efecto promotor del látex UBC-1 sobre la flotación de
fracciones finas de molibdenita (Castro and Laskowski, 1997).
CAPÍTULO 12. Polímeros hidrófobos tipo Látex
353
13.2.2 Efecto de aglomerantes hidrófobos sobre la floculación de calcopirita y
pirita.
En la figura 13.5 se muestra los resultados publicados por Vidgergauz et al
(1999), sobre el efecto floculante del látex SKS-300X sobre dispersiones de calcopirita
y pirita en presencia y ausencia de xantatos.
Fig. 13.5. Influencia del látex SKS-300X sobre la
floculación de calcopirita y pirita. (Vigdergauz, et al. 1999).
13.2.3 Efecto del látex UBC-1 sobre la filtración de otros materiales hidrófobos.
En las figuras 13.6 y 13.7 se muestra el efecto del aglomerante hidrófobo UBC-1
sobre la velocidad de filtración y humedad de queque de un carbón de características
hidrófobas (Laskowski and Castro, 1999). Con UBC-1 se obtiene una mayor velocidad
de filtración y una reducción en la humedad del queque filtrado. Esto se explica por la
naturaleza hidrofóbica de los aglomerados formados en este caso.
De lo anterior se puede concluir que al aglomerar partículas hidrófobas con un
aglomerante hidrófobo, se consigue no sólo una mayor velocidad de drenaje de agua
durante el filtrado, sino una humectación menor del queque filtrado. Estos fenómenos
son coherentes con los conceptos de agregación e hidrofobicidad conseguidos con los
látex.
354
Manual de Filtración & Separación
Fig. 13.6 Efecto del UBC-1 sobre la
velocidad de filtración de una muestra
hidrofóbica de carbón (Laskowski and
Castro, 1999).
Fig. 13.7 Efecto del UBC-1 sobre la
humedad del queque filtrado para el
mismo carbón mostrado en la Fig.6
(Laskowski and Castro, 1999).
13.3 CONCLUSIONES
1.
Los aglomerantes hidrófobos son específicos, en el sentido de que agregan sólo
partículas hidrofóbicas, a diferencia de los floculantes convencionales que
pueden agregar tanto partículas hidrofílicas como hidrofóbicas.
2.
Las propiedades hidrofílicas/hidrofóbicas de los flóculos no son significativas
para la velocidad de sedimentación, pero sí son muy significativas para las
etapas posteriores al espesamiento, como son la flotación y la filtración. Esto
es especialmente válido cuando se manejan partículas hidrofóbicas, ya sean
naturalmente hidrofóbicas o hidrofobizadas por reactivos colectores.
13.4 REFERENCIAS
Attia, Y.A., Yu, S. and Vecci, S. 1987. Selective Flocculation Cleaning of Upper
Freeport Coal with a Totally Hydrophobic Flocculant., Flocculation and Biotechnology
and Separation Systems (Y. Attia, Ed.), Elsevier, pp.547-564.
Castro, S.H. and Laskowski, J.S. 1997. The Effect of Hydrophilic and Hydrophobic
Polymers on Molybdenite Flotation. Proc. 5th Southern Hemisphere Meeting on
Mineral Technology., Buenos Aires-Argentina, Intemin., pp.117-120.
Castro, S.H., Stocker, R. and Laskowski, J.S. 1997. The Effect of Hydrophobic
Agglomerant on the Flotation of Fine Molybdenite Particles. Proc. XX International
Mineral Processing Congress (H. Hoberg and H. Blottnitz, Eds.) GmdB, Aachen,
Vol.3, pp.559-569.
Laskowski, J.S. and Castro, S.H. 1999. Aggregation of Inherently Hydrophobic Solids
Using Hydrophobic Agglomerants and Flocculants. (Proc. 38th Annual Conference of
Metallurgists of CIM)., Polymers in Mineral Processing (J.S. Laskowski, Ed.), pp.293308.
CAPÍTULO 12. Polímeros hidrófobos tipo Látex
355
Laskowski, J.S., Yu, Z. and Zhan, Y. 1995. Hydrophobic Agglomeration of Fine Coal.
Proc. 1st UBC-McGill Bi-Annual International Symposium. Processing of
Hydrophobic Minerals and Fine Coal (J.S. Laskowski and G. Poling, Eds.)., The
Metallurgical Society of CIM., pp.245-258
Misra, M. and Smith, R.W. 1999. Hydrophobic Biopolymers for Flocculation of
Minerals. (Proc. 38th Annual Conference of Metallurgists of CIM)., Polymers in
Mineral Processing (J.S. Laskowski, Ed.), pp.281-291.
Stocker, R. 1995. Mejoramiento de la Flotabilidad de Molibdenita Fina por Agregación
Hidrofóbica con una Dispersión Coloidal de Latex. Memoria de Título, Departamento
de Ingeniería Metalúrgica, Universidad de Concepción.
Vigdergauz, V.E., Schrader, E.A., Stepanov, S.A., Kuznetsov, V.L. and Antonova,
E.A. 1999. Selective Flocculation of Coal and Sulfide Minerals by the emulsions of
Synthetic Polymers. (Proc. 38th Annual Conference of Metallurgists of CIM).,
Polymers in Mineral Processing (J.S. Laskowski, Ed.), pp.265-279
CAPÍTULO 14
CFD COMO HERRAMIENTA PARA EL DISEÑO DE
ESPESADORES
Rodolfo Köck y Fernando Concha
Laboratorio de Mecánica de Fluidos Computacional &
Experimental, Universidad de Concepción, Casilla 53-C,
Correo 3, Fax: 56-41-230759, E-mail: [email protected]
RESUMEN
Tradicionalmente el diseño de espesadores consiste en el cálculo del área
necesaria para la sedimentación de la pulpa a una determinada concentración de
descarga y la elección de equipos de los muchos ofrecidos por distintos fabricantes. La
aplicación de Mecánica de Fluidos Computacional puede cambiar este panorama, ya
que esta herramienta permite elegir detalles constructivos de la alimentación y
descarga del espesador. Usando la modelación numérica del flujo en un espesador, es
posible determinar los patrones en el equipo y en el los dispositivo de alimentación. La
información obtenida permite elegir el mejor sistema de introducción de floculante y
de dilución de la alimentación. El flujo alrededor de las rastras permite comparar la
resistencia ofrecida por distintos diseños y, finalmente, correlacionar el resultado con
el torque medido. El CFD se presta para el rediseño y la optimización de espesadores.
356
CAPÍTULO 14 CFD como herramienta para el diseño de Espesadores
357
14.1 INTRODUCCIÓN
El diseño de espesadores es un tema bastante antiguo que comienza cuando
Mishler (1912) propuso un método para calcular la capacidad de un espesador
realizando pruebas de laboratorio y, por lo tanto, es el primer ingeniero que relaciona
la sedimentación batch con el espesamiento continuo. Cuatro años más tarde Coe y
Clevenger (1916) proponen su afamado método de diseño de espesadores que se utiliza
hasta el presente con bastante éxito. La formulación de la Teoría de Kynch (1952) para
la sedimentación batch permitió el desarrollo de una serie de métodos de diseño de
espesadores, basados en la realización experimental de un sólo ensayo de
sedimentación y el análisis de la curva de sedimentación obtenida de los datos
experimentales. Es así como se conoce el Método de Kynch (Concha y Barrientos
1993), de Talmage y Fitch (1955) y el método de Oltman (Fitch y Stevenson 1977).
Por otra parte, la teoría de Kynch para un espesador continuo permitió el desarrollo de
métodos de diseño como los de Yoshioka y Hasset (Yoshioka 1957, Hasset 1958).
Finalmente, el desarrollo de la teoría fenomenológica de sedimentación trajo aparejado
el método de diseño de Adorjan (Adorjan 1976, Concha y Barrientos 1993, Bustos et al
1999).
Todos estos métodos de diseño tienen por objetivo calcular el área necesaria de
un espesador para tratar un cierto tonelaje diario de una pulpa determinada. Algunos de
estos métodos permiten el cálculo de la altura del espesador, pero la mayoría solamente
provee el diámetro. Es así como después de calcular las dimensiones del espesador, el
ingeniero debe elegir entre los diversos modelos de espesadores ofrecidos por las
empresas fabricantes.
En los últimos años la herramienta matemática denominada Modelación
Numérica ha permitido simular los patrones de flujo en equipos de proceso, lo que se
ha facilitado con el desarrollo de códigos comerciales, tales como FLUENT, CFX,
FIDAP u otro.
El presente trabajo tiene por objetivo mostrar cómo la Modelación Numérica
permite evaluar la calidad de diseño de un espesador determinado o diseñar detalles de
la alimentación y descarga de un espesador. (ver además el capítulo 12).
14.2 MODELACIÓN MATEMÁTICA
La modelación matemática del flujo en un espesador se basa en la Teoría de
Mezclas de la Mecánica de Medios Continuos (Bustos et al 1999), modelando el flujo
de partículas y el flujo de agua como una mezcla con densidades características
El flujo turbulento en un espesador es modelado mediante las ecuaciones de
continuidad y momentum del componente sólido y líquido. La viscosidad turbulenta se
describe mediante el modelo k-. Este modelo de turbulencia incorpora la producción,
convección, difusión y disipación de energía cinética turbulenta, donde k representa la
358
Manual de Filtración & Separación
energía cinética y  es la razón de disipación. El balance de energía turbulenta está
dado por:
 Velocidad de cambio 
de la energía



 Flujo por 
convección 



 Flujo por 
 difusion 



 Fuente o
sumidero 


Esta relación representa a un sistema de dos ecuaciones diferenciales, una para la
energía cinética y otra para la disipación. A estas ecuaciones es necesario agregar
condiciones iniciales y de contorno. La simulación fue llevada cabo con el programa
FLUENT utilizando el modelo k- para describir el flujo turbulento con mallas no
estructuradas. Las simulaciones fueron realizadas en condición estacionaria. La
trayectoria de una gota o partícula, según sea el caso, se predice por integración del
balance de fuerzas que actúan sobre ella. Este balance de fuerzas es el siguiente:
Variación en la
  Fuerza de
 Fuerza de
 Fuerza de

cantidad de movimiento arrastre   gravedad   aceleració n del fluido

 





La fuerza de arrastre por unidad de masa puede ser expresada en función de la
geometría de la partícula (que a sido supuesta como esférica), de su número de
Reynolds, de la densidad y del coeficiente de arrastre. Este último también se calcula
en función del número de Reynolds y de la forma de la partícula. La fuerza requerida
para acelerar el fluido que rodea a la partícula se determina a partir de la relación de
densidades y diferencia de aceleraciones.
Debido a que el flujo en el interior del espesador es turbulento es posible
predecir las trayectorias de las gotas o partículas utilizando la velocidad media del
fluido o incluir el valor instantáneo de la fluctuación de la velocidad del fluido. Para
predecir la dispersión de las partículas debido a la turbulencia se emplean modelos
estocásticos. Para cada uno de los casos analizados anteriormente y por cada diámetro
de partícula considerado se calcularon 10 trayectorias.
14.3 SIMULACIÓN DE LA ALIMENTACIÓN A UN ESPESADOR
El feedwell de un espesador tiene múltiples objetivos. Entre ellos destacan: (1)
recibir la alimentación y evitar que entre con mucha velocidad al espesador, (2) diluir
la alimentación, (3) producir la mezcla floculante y material sólido a sedimentar y
permitir su floculación.
14.3.1 Dilución de la alimentación
Desde hace mucho tiempo los operadores de espesadores se dieron cuenta que es
conveniente diluir la alimentación antes que ésta entre al espesador. La teoría de
espesamiento permite demostrar que, en la mayoría de los casos, la pulpa de
alimentación a un espesador se diluye espontáneamente al entrar al equipo. La
concentración que se obtiene se denomina concentración conjugada y se la puede
predecir de la teoría.
CAPÍTULO 14 CFD como herramienta para el diseño de Espesadores
359
De acuerdo a la teoría de sedimentación, ver sección 8.3.6 del capítulo 8, la
suspensión en sedimentación en un espesador continuo cumple la ley de Kynch,
mientras que el sedimento muestra efectos de compresión. Por esta razón, la
concentración de la suspensión en sedimentación, inmediatamente bajo la zona de agua
clara, se puede calcular conociendo la densidad de flujo de sólidos de la alimentación y
la función continua de Kynch:
f F  q L  f bk ( L )
donde fF es la densidad de flujo de alimentación, que es conocida, q es el flujo
volumétrico de descarga por unidad de área del espesador, también llamado velocidad
volumétrica, que es constante a lo largo del espesador y también es conocida, L es la
concentración buscada y fbk(L) es la densidad de flujo batch de Kynch. Esta ecuación
se resuelve por L. En forma gráfica, la solución se muestra en la figura 4.
Fig. 14.1 Curva de densidad de flujo de Kynch
indicando  L  0.00983, c  0.23 y D  0.36 .
De la figura 14.1 se desprende que existe una concentración definida de sólidos
L a la cual se diluirá la alimentación a su entrada al espesador. Por lo tanto, es de
interés para la empresa que la pulpa sea inyectada al espesador a una concentración lo
más cercana a L , a fin de acelerar el proceso de dilución y evitar tiempos muertos
innecesarios. Sin embargo, alimentar a esos niveles implica un aumento sustancial en
el volumen de agua empleada, con los subsecuentes aumentos en los costos del
transporte, almacenamiento y tratamiento de las aguas residuales. Por esta razón la
pulpa se alimenta a concentraciones mayores que se designa con F. La solución a este
problema consiste en re-utilizar el agua de rebalse de los espesadores en la dilución de
la pulpa inyectada de manera de bajar el porcentaje de sólidos de F a L.
360
Manual de Filtración & Separación
Existen muchas formas de diluir la alimentación y ellas son generalmente objeto
de patentes. Dos ejemplos se dan en las figuras 14.2 a 14.4. Por su mayor complejidad
tecnológica se analiza el alimentador E-duc de la empresa Eimco.
Fig. 14.2 Sistema de alimentación E-duc de Eimco.
Fig. 14.3 Sistema Supaflo de Outokumpu.
CAPÍTULO 14 CFD como herramienta para el diseño de Espesadores
361
Fig. 14.4 Esquema de dilución del Supaflo.
14.3.2 Alimentación mediante una Tobera
El sistema E-duc de Eimco diluye la alimentación por medio de una tobera
ubicada lo mas alto posible en el espesador, pero siempre bajo la superficie del agua
como se muestra en la figura 14.5.
Q1
Q2
Q2
L
Q3
q
D
Fig. 14.5 Esquema de operación de dilución E-duc.
F
362
Manual de Filtración & Separación
Consideremos un flujo de alimentación de 50% de sólidos en peso. Las
características del problema son:
Flujo de entrada, m3/hr
2450
Diámetro tubería salida, mm
988
Concentración entrada 
0.33
Diámetro tubería entrada, mm
760
Diámetro boquilla entrada, mm
520
Conicidad de boquilla
30º
El problema fue resuelto con FLUENT utilizando un modelo monofásico en
base a agua que indica el volumen de arrastre o dilución. Se consideró el efecto
gravitatorio y la superficie libre fue modelada como pared lisa (slip condition) tal como
se muestra en la figura 6.
pared
pared
Velocidad entrada
Presión salida
pared
pared
presión salida
Figura 14.6. Esquema del modelo 3d de una tobera de dilución.
Los resultados fueron los siguientes:
Flujo másico entrada
Flujo másico de dilución
Flujo másico
diluido
682 kg/s
747 kg/s
1430 kg/s
Para el caso de un fluido bifásico, con una concentración de alimentación de
F=0.33, densidad del sólido de 2.7 y de 2450 m3/hr se tendría:
CAPÍTULO 14 CFD como herramienta para el diseño de Espesadores
363
Concentración final L
Concentración final fracción en peso xL
Reducción en
concentración
0.071
0.17
48 %
La altura de elevación requerida para lograr el mencionado comportamiento de
la tobera se obtiene de la simulación efectuada, al igual que la distribución de
velocidades (ver figuras 14.7 y 14.8), distribución de la fracción de pulpa (figura 14.9),
distribución de la granulometría (figura 14.10) e intensidad de la turbulencia (figura
14.11).
Fig. 14.7. Contornos de presión en tobera de dilución
(cuadrante superior).
Fig. 14.8. Contornos de magnitud de la velocidad en tobera
de dilución (corte vertical).
364
Manual de Filtración & Separación
Fig. 14.9. Distribución de concentraciones en tobera.
Fig. 14.10. Distribución de la granulometría de la pulpa en
interior del ducto de mezcla.
Fig. 14.11. Contornos de intensidad de turbulencia.
CAPÍTULO 14 CFD como herramienta para el diseño de Espesadores
365
14.3.3 Alimentación en feedwell
El feedwell corresponde a la cámara de pre-dilución y homogeneización de la
pulpa de manera de facilitar la dinámica de la sedimentación. Un buen feedwell debe
garantizar una salida pareja y fluida de la pulpa en todas direcciones.
Se ha simulado dos modelos de feedwell corrientes: con un ducto de
alimentación y con dos ductos de acuerdo a lo mostrado en la figura 14.12.
Fig. 14.12 Plano esquemático del feedwell convencional simulado.
Las simulaciones bifásicas fueron desarrolladas para dos tipos de espesador,
contemplando agua y otro fluido miscible con una densidad y viscosidad equivalentes
a la de una pulpa corriente.
En la figuras 14.13 y 14.14 se presentan los patrones de flujo, en base a la
granulometría de la pulpa inyectada, para ambos casos convencionales. Los resultados
de la simulación bifásica de los feedwell se muestran en las figuras 14.15 y 14.16.
Fig. 14.13. Granulometría de la pulpa en feedwell convencional de 1 entrada.
366
Manual de Filtración & Separación
Estas simulaciones permiten caracterizar el flujo de la pulpa y la distribución de
partículas en su interior. Además, es posible verificar si el diseño cumple o no con los
requerimientos de homogeneización de la pulpa, lo que se traducirá en un menor
tiempo de sedimentación a la salida. Recordemos que al igual que en la tobera de predilución, la pulpa debe ser diluida hasta el valor característico de L.
Fig. 14.14. Granulometría de la pulpa en feedwell convencional de 2 entradas.
Fig. 14.15. Fracción volumétrica de la pulpa a la salida de un
feedwell convencional.
CAPÍTULO 14 CFD como herramienta para el diseño de Espesadores
367
Fig. 14.16. Fracción volumétrica de la pulpa a la salida de un
feedwell de alta capacidad.
14.4 SIMULACIÓN DE LA INYECCIÓN DE FLOCULANTES
Uno de los costos significativos asociados al proceso de espesamiento lo
constituye el floculante. Por esta razón es conveniente optimizar su utilización. En este
sentido el punto de adición del floculante a la pulpa es de primordial importancia para
garantizar una buena mezcla con la alimentación. Múltiples son los métodos ofrecidos
en la industria para la inyección de floculantes, pero existen pocos estudios respecto de
su eficiencia. A continuación, a modo de ejemplo, se analiza dos métodos. El primero
corresponde a inyección de floculante en la tobera de dilución y el segundo de
inyección en feedwell, como se muestran en las figuras 14.17 y 14.18.
Fig. 14.17. Inyección en tobera.
Fig. 14.18. Inyección en feedwell.
368
Manual de Filtración & Separación
14.4.1 Inyección en tobera de dilución.
De las figuras anteriores es posible observar que la distribución de tamaños y
concentración de partículas de mineral en la cañería de mezcla no es homogénea. Por
otra parte, existen zonas de mayor y menor turbulencia en la tobera. La inyección en la
tobera debe ser tal que no se pierda floculante al agua que rodea la tobera. Se debe
buscar el aprovechamiento de las zonas de alto cizalle y turbulencia que se forman en
el interior de la cañería de mezcla, dado que en estas zonas el floculante podrá alcanzar
su mejor mezcla. Las inyecciones son simuladas por medio de un fluido de densidad
0.6 g/cm3 ubicadas en lugares arbitrarios de la tobera de acuerdo a la figura 14.19.
Cañería de inyección de
floculante
Ducto de mezcla
65
1
Tobera de alimentación
Puntos de inyección
2
3
4
Fig. 14.19. Ubicaciones posibles para la inyección de floculante en tobera de
dilución.
El recorrido de las partículas será afectado por a las componentes variables de
la velocidad o turbulencia. Se consideró un cálculo estocástico para 10 recorridos
posibles. Los resultados se muestran en las figuras 15 a 20.
Fig. 14.20. Inyección del floculante en el
punto 1.
Fig. 14.21. Inyección del floculante en el
punto 2.
CAPÍTULO 14 CFD como herramienta para el diseño de Espesadores
Fig. 14.22. Inyección del floculante en el
punto 3.
Fig. 14.24. Inyección del floculante en
el 5.
369
Fig. 14.23. Inyección del floculante en el
punto 4.
Fig. 14.25. Inyección del floculante en punto
el punto 6.
Al comparar los casos de inyección en la tobera de dilución se advierte que las
alternativas de inyección 5 y 6 seguidas por la 2 y 3 resultan ser las más beneficiosas
por cuanto permite un mayor grado de contacto entre el floculante y las partículas de
menor tamaño. Las inyecciones 1 y 4 deben ser evitadas en lo posible.
14.4.2 Inyección en feedwell.
Respecto de la inyección de floculante directamente en el feedwell, se puede
observar que las partículas pequeñas tienden a permanecer más tiempo en el interior
sin sedimentar y que éstas se concentran en la zona cercana a la admisión. Luego, la
inyección de floculante debe ser llevada a cabo en esa zona para garantizar la
formación de flóculos a partir del fino y para evitar el arrastre del floculante por el
chorro principal de partículas gruesas.
Al inyectar en el feedwell se busca aprovechar el alto nivel de turbulencia
existente dentro de la cámara para la mezcla del floculante. La posición seleccionada
370
Manual de Filtración & Separación
en la modelación también es arbitraria y se muestra en la figura 14.26. El feedwell
modelado es de una entrada.
Ducto de inyección
de pulpa
1
2
Ducto de inyección
de floculante
Feedwell
Fig.14.26. Posiciones de inyección de floculante al interior del feedwell.
De las figuras 14.13, 14.14 y 14.27 se puede ver claramente que las partículas de
menor tamaño (fino) ocupan rápidamente la zona superior del feedwell sin sedimentar.
Fig. 14.27. Distribución de la granulometría de la pulpa al
interior del feedwell.
De lo anterior se desprende que el floculante inyectado al interior del feedwell debe
subir inmediatamente y atacar las partículas de fino en suspensión. Por otra parte, la
inyección del floculante debe estar ubicado de tal forma de no ser arrastrado por el
chorro principal de pulpa. Un ejemplo es el mostrado en las figuras 23 y 24.
CAPÍTULO 14 CFD como herramienta para el diseño de Espesadores
371
Fig. 14-28. Distribución del floculante inyectado en los puntos 1 y 2.
Fig. 14.29. Distribución del floculante inyectado en el punto 2.
14.5 SIMULACIÓN DE LAS RASTRAS
Las rastras son unas estructuras de acero que se “arrastran” por el fondo del
espesador y que tienen por objeto facilitar el escurrimiento del concentrado hacia el
ducto de salida del espesador. Todas estas estructuras de acero son móviles y posibles
de ser izadas fuera del lecho de concentrado cuando el torque para desplazarlas se
torna excesivo.
372
Manual de Filtración & Separación
press outlet
wall

wall
.
Fig. 14.30 Esquema de rastras de un espesador.
El diseño de estos implementos tiene un gran grado de inseguridad por cuanto
se desconocen los perfiles de presión sobre la estructura para las diferentes condiciones
de operación. Por otra parte, también es desconocido es el grado de interferencia de las
rastras en el proceso de sedimentación al existir posibles flujos secundarios
ascendentes en sus cercanías. Sólo se sabe que la presencia de rastras aumenta la
posible concentración que se puede obtener en la descarga.
La simulación del efecto de las rastras en el fondo del espesador se llevó a cabo
considerando un solo fluido de viscosidad variable en función de la altura. La
velocidad de giro es de 0.5 rpm.
Los resultados obtenidos en la simulación se pueden ver en las figuras 14.31 y
14.32. La simulación del efecto sobre las rastras mostrado en estas figuras permite
visualizar las zonas de máximo cizalle y la distribución de presiones sobre la
estructura. Se pueden llevar a cabo simulaciones para diferentes condiciones de
operación (variaciones en la densidad y viscosidad) para una geometría dada
permitiendo así estimar los requerimientos de potencia del sistema. Por otra parte es
posible estudiar el efecto de esta estructura en el lecho de mineral de manera de
determinar las velocidades máximas de operación que no producen el levantamiento
del mineral sedimentado.
CAPÍTULO 14 CFD como herramienta para el diseño de Espesadores
Fig. 14.31 Contornos de velocidad de
deformación y líneas de flujo de la pulpa.
373
Fig. 14.32. Contornos de presión sobre
la estructura y vectores de velocidad.
14.6 CONCLUSIONES
Las simulaciones llevadas a cabo dejan claramente en manifiesto que es posible
aplicar con éxito la técnica CFD en el área de sedimentación y separación SólidoFluido. Los resultados obtenidos pueden ser aprovechados directamente en la etapa de
diseño del espesador para mejorar su rendimiento, lo que se puede traducir en menores
requerimientos de potencia (rastras), menor tiempo de sedimentación (tobera de
dilución y feedwell) y menores costos de operación derivados del ahorro del floculante
(inyección en tobera y feedwell).
14.7 REFERENCIAS
Adorjan, L.A., Determination of thickener dimensions from sediment compression and
permeability test results, Trans. Inst. Min. Met., London, 85, 1976, C157-163.
Bustos, M.C., Concha, F., Bürger, R. And Tory, E.M., Sedimentation and Thickening:
Phenomenological Foundation and Mathematical Theory, Kluwer Acdemic Publishers,
Dordrecht, Holland, 1999.
Coe, H.S. and Clevenger, G.H., Methods for determining the capacity of slime settling
tanks, Trans. AIME, 55, 1916, 356-385.
Concha, F. and Barrientos, A., A critical review of thickener design methods, KONA
Powder and Particle, 11, 1993, 79-104.
Fitch, E.B. and Stevenson, D.G., Gravity Separation Equipment. In Solid-liquid
separation equipment scale-up, Ed. D.B. Purchas, Uplands Press Ltd., Croydon,
England, 1977.
Fluent Inc. “User’s Guide for Fluent”, Volume 2 Release 4.0, Fluent Incorporated,
1996.
374
Manual de Filtración & Separación
Griebel, M Dornseifer, T. and Neunhoeffer T., Numerical Simulation in Fluid
Dynamics, SIAM monographs on mathematical modeling and computation, 1997.
Hasset, N.J., Design and operation of continuous thickeners, Ind. Chem., 1958, 489494.
Köck, R, y Concha F., CFD como herramienta para el diseño de espesadores, III
Coloquio Nacional de Filtración y Separación, Santiago, 4-5 de Noviembre, 1999, 116.
Mishler, R.T., Settling slimes at the Tigre Mill, Eng. Mining J., 94 1912, (14) 643-646.
Talmage, W.P. and Fitch, E.B., Determining thickening unit area, Ind. Eng. Chem., 47,
1955, 38-41.
Wilhelm, J.H. and Nadie, Y., Sizing and operating thickeners, SME Annual Meeting,
Preprint N°79-30, New Orleans, February 1079, 18-22.
Yoshioka, N., Hotta, Y., Naito, S. And Tsugami, S., Continuous thickening of
homogeneous floculated slurries, Chem. Eng. Japan, 21, 1957, 66-74.
CAPÍTULO 15
CONCEPTOS MODERNOS DE FILTROS ROTATORIOS
Ingenieurgesellschaft für
Mechanische Verfahrenstechnik mbH.
Gottesauer Str. 28, 76131 Karlsruhe, Germany · Tel. +49 721 96456-0,
Fax: -10, e-mail: [email protected]
RESUMEN
Los filtros rotatorios de vacío fueron el tipo de filtros utilizados tradicionalmente
en la industria minera por su simple construcción y su fácil operación. Sin embargo,
desde hace ya algún tiempo y debido su baja eficiencia, ellos han sido sustituidos por
filtros hiperbáricos y filtros a presión. Recientemente, Bokela ha diseñado filtros
rotatorios de discos, tambor y de bandeja de diseño innovativo que pueden cambiar
esta situación. En este trabajo se presenta el detalle de construcción y operación del
filtro de discos Boozer y sus ventajas comparativas.
375
376
Manual de Filtración & Separación
15.1 FILTRO DE DISCO DE ALTO RENDIMIENTO “BOOZER”
Boozer es un Filtro Rotatorio de Discos de Vacío diseñado por Bokela para la
filtración de grandes flujos de materiales en la industria minera del cobre, hierro,
plomo, zinc, níquel, carbón, alúmina y otras). El diseño innovador del Boozer impone
un nuevo estándar para los filtros de discos que le permite mostrar una extraordinaria
eficiencia, gran flexibilidad y una operación confiable y económica.
BOKELA Disc Filter, Type "BOOZER"
Fig. 1 Vista frontal y lateral de Filtro de Discos Boozer.
CAPÍTULO 15 Conceptos Modernos de Filtros Rotatorios
377
15.1.1 Características notables del Boozer
Las excelentes características hidráulicas del Boozer dan como resultado un
filtro de gran capacidad y economía:

Más de un 100% de capacidad comparado con filtros de discos
convencionales.

2 a 4% de menos humedad en el queque.

Para muchas aplicaciones, una capacidad de bomba de vacío similar a la de un
filtro convencional, produce una mayor diferencia de presión a través de la tela
filtrante en un 100%.

Mayor velocidad de rotación. Cuando para los filtros convencionales la
velocidad de rotación es de 3 rpm máxima, para el Boozer llega hasta 5 rpm.

Mayor confiabilidad y flexibilidad operacional. Notable reducción de los
problemas de operación tales como colmatación de la tela de filtración,
descarga incompleta del queque, remoción incompleta del filtrado y rehumedecido del queque de filtración.
15.1.2 Datos Técnicos
El Filtro de Discos Boozer se caracteriza por los siguientes detalles:
ITEM
Número de discos
Área de filtración
Diámetro de los discos
Número de segmentos por disco
Sujeción de los segmentos
Volumen de filtrado retenido en segmentos
Peso de un segmento: estándar/liviano
Cañerías del filtrado
Diseño de la batea
DETALLE
1/2/3
40 / 80 / 120m2
5.5 m
30
Palanca o bayoneta
7.5 l/m2
28 / 18 kg
Gran tamaño con forma trapezoidal (f=2.1 °/)*
Batea común con agitador
o batea individual
Porcentaje de sumergimiento del disco
50%
Velocidad del filtro
Hasta 5 rpm
Descarga del queque
Mediante golpe de aire
(sincronizada exactamente mediante una válvula)
*f=sección de la cañería de filtrado conectada al área de filtración.
15.1.3 Descripción y Funcionamiento de los componentes importantes
a)
Discos y Segmentos
Cada disco tiene un diámetro de 5.6 m y posee 30 segmentos montados en el
tambor central. Los segmentos han sido diseñados para ser extremadamente finos y
livianos. El volumen específico de un segmento es de sólo 7.5 l/m2 de área filtrante,
mientras que un filtro convencional tiene 20 a 40 l/m2. Este pequeño volumen y las
condiciones optimizadas de escurrimiento en los segmentos son un prerrequisito para
378
Manual de Filtración & Separación
una baja pérdida de carga y una descarga de queque efectiva. A pesar del gran tamaño
del segmento, su peso es muy pequeño, 28 kg para el segmento estándar y 18 kg para
el diseño más avanzado. El diseño especial del pie del segmento provee una conexión
estable y segura al barril central, permitiendo un montaje y desmontaje muy rápido de
los segmentos.
Fig. 2 Alternativas de sujeción de los segmentos: palanca y bayoneta.
Fig. 3. Detalle de la sujeción tipo bayoneta.
b)
Cañerías de colección de Filtrado y Tambor Central
Cada segmento del filtro montado sobre el tambor central está conectado a una
cañería de colección de filtrado. Las 30 cañerías de colección de filtrado están
arregladas dentro del tambor central y conectan los segmentos de los filtros a los
sistemas de vacío y de aire comprimido, este último para la descarga del queque.
Dependiendo del número de discos hay 1, 2 o 3 segmentos unidos a una cañería de
colección de filtrado.
En contraste a los filtros convencionales, las cañerías de colección de filtrado del
Boozer no son circulares sino que tienen una sección trapezoidal, lo que resulta en un
mayor diámetro efectivo para el flujo que su similar convencional. El valor
característico del parámetro f (f=razón entre el área de la sección de la cañería de
filtrado y el área de filtración conectada) en el filtro Boozer es de entre f=2.1 a 3%,
mientras que los filtros convencionales tienen valores de entre 0.4 a 0.8%
aproximadamente.
CAPÍTULO 15 Conceptos Modernos de Filtros Rotatorios
c)
379
Tambor Central
El tambor rotatorio central tiene un diámetro de 1100 mm y se encuentra en la
batea del filtro. Dos rodamientos lo soportan, uno de rodillos por el lado del sistema
motriz y uno de deslizamiento por el lado de la cabeza de control. La combinación
especial de materiales en el rodamiento de deslizamiento, el sello especial del
rodamiento y la lubricación permanente de los rodamientos asegura una operación
segura y sin problemas por años.
Fig 4. Tambor central con los huecos para los segmentos.
Fig. 5. Sujeción de los segmentos al tambor central.
Manual de Filtración & Separación
380
d)
Batea del Filtro
La suspensión a filtrar se alimenta a la batea del filtro. El Boozer se manufactura en
dos versiones, con una batea común o con bateas individuales. Para las dos versiones la
sumerjencia de los filtros en la pulpa es del 50%.
Fig. 6. Diseño de la batea del filtro con sus versiones común e individual
En el modelo de batea común, un agitador homogeniza la suspensión evitando la
sedimentación o clasificación de las partículas. La alta diferencia de presión efectiva en
la superficie de la tela del filtro mantiene al sólido en el queque a pesar de la agitación
reinante en la suspensión. El vertedero de la batea está diseñado de manera de evitar
derramamiento de suspensión al piso. La cubierta de los rodamientos del tambor
central y el agitador están situados en la pared vertical de la batea.
Para el diseño de batea individual no se utiliza agitador y la las partículas se
mantienen en suspensión con la agitación producida por el movimiento de rotación del
disco. Cada una de las bateas del Boozer está conectada a un gran rebalse común que
asegura un intercambio fácil de pulpa entre bateas a la altura de emergencia de los
discos. Este diseño asegura que todos los discos funcionen al mismo nivel de pulpa y,
visto de arriba, los filtros de batea individual se ven idénticos a los de batea común. El
rebalse de ambos diseños, de batea individual y común, permite el flujo de toda la
pulpa de alimentación si la válvula de desagüe estuviese cerrada.
e)
Cabeza de Control
La cabeza de control es la conexión entre las cañerías colectoras de filtrado dentro del
tambor central rotatorio y las cañerías estáticas de filtrado que lo llevan al estanque de
filtrado. La cabeza de control asegura que las diversas etapas del filtrado, tales como la
CAPÍTULO 15 Conceptos Modernos de Filtros Rotatorios
381
formación del queque, el deshumedecimiento y la descarga del queque, se realicen
como etapas separadas del proceso. Para ello, la cabeza de control tiene dos placa de
control, una móvil conectada a las cañería colectoras de filtrado que rota alrededor del
eje central y una fija que determina la posición de las diversas etapas del proceso. En
esta forma cada segmento del filtro conecta a las sucesivas etapas del proceso a medida
que el filtro rota.
Fig. 7. Cabeza de control del Boozer.
La cabeza de control está diseñada para separar la mezcla de filtrado y aire que
llega, en un flujo de aire y otro de líquido. Como la pérdida de carga en un flujo
bifásico aire/líquido es aproximadamente 10 veces mayor que aquellas de cada fase
separada, este nuevo diseño reduce significativamente la pérdida de carga en el
sistema. Por otra parte, el diseño impide el paso de filtrado, proveniente de la zona de
formación del queque, a la zona de deshumidificación.
15.1.4 Operación del Filtro de Discos Boozer
Durante una vuelta del filtro de disco, cada segmento pasa por los siguientes
etapas del proceso: formación, deshumidificación y descarga del queque. La duración
de cada una de estas etapas se establece en la placa de control de la cabeza de control,
ajustando las secciones del proceso.
a) Formación del queque: Tan pronto como un segmento está completamente
sumergido en la suspensión, éste es conectado a la bomba de vacío por medio de una
cañería de colección de filtrado y la cabeza de control. En ese momento comienza la
etapa de formación de queque. Las partículas del sólido se depositan en la tela filtrante
mientras que el filtrado es succionado hacia el interior del segmento y fluye hacia el
estanque recibidor de filtrado del área de formación de queque. Como la sumerjencia
es del 50%, la zona de formación de queque es grande, lo que lleva a altas tasas de
382
Manual de Filtración & Separación
producto sólido y de filtrado. El gran número de segmentos asegura la formación de un
queque homogéneo en el disco.
b) Deshumedecimiento del queque: Cuando el segmento emerge fuera de la
suspensión, el queque es secado por el aire succionado de la atmósfera a través del
queque y medio filtrante por el sistema de vacío. El aire y el filtrado fluyen por las
cañerías de colección de filtrado y por la cabeza de control hacia el estanque recibidor
de filtrado de la zona de deshumedecimiento. La homogeneidad del queque permite un
deshumedecimiento uniforme y el gran tamaño de las cañerías produce pequeñas
pérdidas de carga y, por lo tanto, altas diferencias de presión en los segmentos.
c) Descarga del queque: Después de pasar por la zona de deshumedecimiento, el
queque se descarga un poco antes que el segmento se sumerja nuevamente el la
suspensión. Cuando la cañería de colección de filtrado en la cabeza de control se alinea
perfectamente con la abertura de la sección de descarga en la placa de control fija, se
insufla aire comprimido a 0.5 bar por el segmento, inflando la tela filtrante. El queque
se desprende y cae en el chute de descarga. Una válvula de control permite el control
electrónico del momento exacto en el que se debe dar el golpe de aire, en forma de
pulso, para la descarga del queque. Este método contrasta con el tradicional de insuflar
aire a baja presión durante toda la etapa. Después de la descarga del queque el
segmento se sumerge nuevamente en la suspensión reiniciando un nuevo ciclo de
filtración.
Fig. 8 Descarga eficiente del Filtro de Discos Boozer
asegura un 100% de desprendimiento de la tela.
CAPÍTULO 16
LAVADO CON FILTRO DE BANDA HORIZONTAL
C.E. Williams
Delkor (South America) Ltd.
Av. C. Colon 4733
Las Condes, Santiago, Chile
16.1 DESCRIPCIÓN DEL EQUIPO Y SUS APLICACIONES
El filtro de banda es un equipo muy sencillo compuesto por un marco de acero
que soporta un conjunto de rodillos, sobre los cuales gira una banda transportadora de
caucho natural u otro elastómero. La banda transportadora se mueve sobre 2 correas de
desgaste y se suspende sobre un sistema de agua o aire para evitar desgaste por causa
de la fricción. Sobre la banda transportadora está la tela de filtración, que puede ser de
monofilamento o punzando. La superficie de filtración consiste en una zona de
formación de queque seguida por una zona de secado. Si se requiere, pueden existir
varias etapas de lavado y al final del filtro, antes de la descarga del queque, una área de
secado.
Los filtros de banda se fabrican con áreas desde 1m2 hasta 154m2. Dependiendo
de las características del material a filtrar, la estructura puede ser fabricada en varios
materiales de construcción. La banda transportadora puede ser soportada por un
sistema de agua o de aire, dependiendo del tamaño del filtro, de las condiciones
ambientales o del proceso en la planta.
Tal como el diseño del filtro de banda, las aplicaciones de este filtro también
son flexibles. Por ejemplo, el filtro puede ser usado para filtrar relaves con el objetivo
de su depositación en seco, o se puede filtrar materiales para recupera el agua y
permitir un transporte manejable de los sólidos. Además, los filtros de banda son
usados en aplicaciones de lavado donde existen dos distintas razones, por una parte
recuperar soluciones de valor y por la otra remover impurezas del queque.
La empresa pionera en el desarrollo y aplicación de los filtros de banda
horizontales es Delkor, quien posicionó este equipo en el mercado mundial. Desde de
sus primeras aplicaciones en el año 1974, varios cambios y desarrollos han sido
383
384
Manual de Filtración & Separación
efectuados para mejorar su funcionalidad y aumentar su eficiencia. Estos adelantos en
la tecnología le han permitido ofrecer equipos más robustos que los primeros filtros .
La sólida estructura de soporte tiene una duración por sobre los 30 años y las bandas
transportadoras duran alrededor de10 años, siendo solamente la tela y correas de
desgaste los elementos de recambio. En un comienzo, los filtros de banda tenían dos o
tres bandas transportadoras con algunas complicaciones en la coordinación de los
movimientos del conjunto. Esto significaba baja eficiencia y pérdidas de vacío. En la
actualidad se fabrican en una sola banda transportadora de hasta 4.8 m de ancho,
mejorando la capacidad y eficiencia de filtración. Otros cambios como ranuras
inclinadas de la banda, estructura inclinada del filtro, telas desarrolladas especialmente
para Delkor y la adición de correas de desgaste y rieles de sacrificio del sello de vacío
han mejorado el filtro de banda horizontal para hacerlo líder en el mercado. Como
consecuencia de todo este desarrollo, Delkor ha fabricado un filtro de banda de 154
m2, el más grande existente en el mercado internacional. Su éxito como empresa lo
demuestran los más de 20.000m2 de área de filtración instaladas y la construcción de la
planta de filtro de banda más grande del mundo con 26 filtros de 80m2. Ver Figura 1.
Fig. 1 Planta con filtros de banda horizontales más grande del
mundo con 26 filtros de 80 m2 cada uno.
En el campo de la separación sólido-líquido siempre ha existido la necesidad de
lavar el queque para recuperar soluciones de valor o para remover impurezas. Aunque
el filtro de banda horizontal es muy flexible en sus aplicaciones, su propósito original
estaba dirigido a aplicaciones de lavado. El filtro de banda ofrece una eficiencia de
lavado máxima con un uso mínimo de agua. Por ejemplo, logra 60% de mayor
eficiencia de lavado que los espesadores de decantación en contracorriente (CCD), los
que requieren grandes cantidades de agua para lavar por dilución. Con un área de
lavado horizontal plana, que es ideal para este propósito, los filtros de banda también
logran una eficiencia de lavado superior a los filtros de tambor y discos, que tienen
superficies curvadas y verticales respectivamente.
CAPÍTULO 17. Lavado con Filtro de Banda Horizontal
385
100.00
Eficiencia de lavado (%)
80.00
60.00
40.00
20.00
0.00
0.00
0.50
1.00
1.50
2.00
2.50
Cuociente de desplazamiento
CCD
FBH
Fig. 2 Comparación de la eficiencia de lavado de queque en un filtro
de banda horizontal y en espesadores en contracorriente (CCD).
16.2 ESTUDIO DE CASOS
En Chile existen numerosas empresas que utilizan filtros de banda horizontales.
Por ejemplo, Delkor ha concretado más de 40 instalaciones desde 1981. De estas
instalaciones, se ha seleccionado 5 para estudiar aplicaciones de lavado de queque. Las
aplicaciones seleccionadas han sido divididas en dos categorías, aquellas cuyo objetivo
es remover impurezas y aquellas cuyo objetivo es recuperar la solución. Las Tablas 1 y
2 resumen estas 5 aplicaciones.
TABLA 1 Aplicaciones de lavado para remover impurezas
Ubicación
Mantos de Oro: La Coipa
Meridian: El Peñón
Tamaño de
filtros
Proceso
12 de 100 m2 Lavado de relaves de oro para remover cianuro.
3 de 54 m2
2
Lavado de relaves de oro para remover cianuro.
Escondida: Coloso
2 de 63 m
Lavado de concentrado de cobre para remover
cloruro.
SQM Salar: Ácido Bórico
1 de 6 m2
Lavado de sales con agua desmineralizada.
2
2 de 4 m
386
Manual de Filtración & Separación
Tabla 2 Aplicaciones de lavado para recuperar solución
Ubicación
Tamaño de filtros
Mantos de Oro:
12 de 100 m
Recuperación de solución de
oro.
3 de 54 m2
Recuperación de soluciones de
Oro.
1 x 63 m2
Lavado de concentrado de
cobre para recuperar el
amoníaco y recircularlo al
proceso de lixiviación.
La Coipa
Meridian:
El Peñón
Escondida:
Proceso
2
Coloso
16.3 Aplicaciones de lavado de queque para remover impurezas.
16.3.1 Mantos de Oro: La Coipa
En la Compañía Minera Mantos de Oro, Planta La Coipa, existen 12 filtros de
banda horizontal Delkor de 100m2. Cada uno es alimentado con 70-80 tph de relaves
de oro, cuyos queques son sometidos a dos etapas de lavado. El objetivo de la segunda
etapa de lavado es remover el cianuro remanente en los relaves antes de depositarlos.
Fig. 3 Tres de los doce filtros de banda Delkor de La Coipa de 100 m2 cada uno.
CAPÍTULO 17. Lavado con Filtro de Banda Horizontal
387
En este caso, los relaves son lavados con agua industrial y con solución estéril
del proceso Merrill Crowe, con una eficiencia de lavado de 94% y de recuperación de
cianuro de entre 95 y 96%. Los filtros logran reducir la cantidad de cianuro a un nivel
tal que permiten que los relaves sean depositados sin causar efecto ambiental negativo
alguno. En el caso de La Coipa, la cantidad de cianuro recuperado paga los costos de
operación de la planta de filtros.
16.3.2 Compañía Minera Escondida: Coloso
La Compañía Minera Escondida tiene instalados 3 filtros de banda Delkor de 63
m2 en su planta de Coloso, Antofagasta. Dos de estos filtros son utilizados para lavar el
concentrado de cobre y eliminar el cloruro y reactivos de flotación. Aun cuando
actualmente la planta ha dejado de operar, es interesante describir su operación por el
interés que tiene este tipo de aplicación. La figura 4 es una ilustración de esta
instalación.
Fig. 4 Vista de la Planta de filtros de banda Delkor de
Minera Escondida en Coloso.
Cada filtro es alimentado con 30-35 tph de concentrado de cobre. Los filtros
tienen 2 etapas de lavado, en las que el queque es lavado con 20-30 m3/hr de agua
desmineralizada para eliminar las impurezas. Las etapas de lavado se realizan en
contracorriente. El primer lavado se hace con la solución de filtrado que ha sido
reciclada de la segunda etapa y esta última se lleva a cabo con el agua desmineralizada.
Esta aplicación de lavado logra una eficiencia mayor al 99% y el producto final
contiene menos de 20 ppm de cloruro.
388
Manual de Filtración & Separación
16.3.3 SQM Salar: Ácido Bórico
SQM Salar posee 3 filtros de banda Delkor instalados en la planta ácido bórico.
Dos de ellos son de 4m2 y uno de 6m2. En esta aplicación las sales son lavadas para
remover el cloruro. Los filtros tratan 50 toneladas por día de sales que vienen desde un
cristalizador. Los 3 filtros trabajan en serie. El primer filtro es alimentado desde el
cristalizador. Su descarga es re-pulpeada con agua destilada y alimentada al segundo
filtro. La descarga de éste, también es re-pulpeada con agua destilada y es alimento al
tercer filtro. Cada filtro tiene sólo una etapa de lavado con razones de desplazamientos
entre 0.8-1:1. En los primeros 2 filtros, las sales son lavadas con solución de filtrado
re-circulada de la etapa siguiente y el tercer filtro es lavado con agua desmineralizada.
La alimentación a filtración contiene más de 3000ppm de cloruro y, gracias a la alta
eficiencia de lavado de los filtros, el cloruro se reduce a menos de 100ppm. La Figura
5 muestra un esquema de la configuración de los 3 filtros instalados en SMQ Salar.
Fig. 5 Proceso de filtración y lavado en contracorriente con filtros de banda
Delkor en SMQ Salar.
16.3.4 Compañía Minera Meridian: El Peñón
La planta El Peñón de la Compañía Minera Meridian cuenta con 3 filtros de
banda Delkor de 54m2. Cada filtro trata 40 a 50 tph de relaves de oro, aplicando 2
etapas de lavado en co-corriente. Uno de los objetivos de tener 2 etapas de lavado, es
remover el cianuro de los relaves antes de depositarlos para evitar efectos ambientales
negativos. Los filtros alcanzan una eficiencia de recuperación del 95% lo que, junto a
las etapas de lavado en espesadores en contracorriente, da una eficiencia global mayor
a 99%. La figura 6 muestra dos vistas de estos filtros.
CAPÍTULO 17. Lavado con Filtro de Banda Horizontal
Fig. 6 Filtros de banda horizontal Delkor de 54 m2
cada uno en la Planta El Peñón de Minera Meridian.
389
390
Manual de Filtración & Separación
16.4 Aplicaciones de lavado de queque para recuperar soluciones
16.4.1 Mantos de Oro: La Coipa
Los 12 filtros de banda horizontal Delkor de 100m2, mencionados
anteriormente, tienen dos etapas de lavado, de la cual la primera tiene el objetivo de
recuperar el oro en solución de los relaves. La figura 3 es una ilustración de los filtros
instalados en La Coipa. Los relaves de oro pasan primero por una etapa de lavado con
solución estéril. Este sistema esta asociado con tres etapas de lavado CCD, usando
espesadores Delkor de Alta Capacidad. La recuperación total lograda es de 99.5% de
oro y plata en solución.
16.4.2Compañía Minera Escondida: Coloso
Uno de los tres filtros de 63m2 instalados en Coloso, ver figura 4, es utilizado
para recuperar el amoníaco y cobre en la solución residual de lixiviación del
concentrado de cobre, para luego reciclarla al proceso de lixiviación-extracción por
solvente-electro-obtención. El filtro recibe 50-60tph de concentrado de cobre y tiene 2
etapas de lavado. Con una razón de lavado equivalente a la solución que sale con el
queque, se logra una eficiencia de lavado mayor al 95%, recuperando el 98-99.8% del
cobre soluble. El principal beneficio del filtro es que permite una buena recuperación
2
de Cu  NH3 4 con el mínimo uso de agua, lo que significa cero emisión de soluciones,
con un balance de agua que se mantiene en el proceso minimizando la dilución de la
solución PLS enviado a SX.
16.4.3 Compañía Minera Meridian: El Peñón
Cada uno de los tres filtros de banda horizontal Delkor de 54m2 instalados en la
planta El Peñón de la Compañía Minera Meridian, tiene dos etapas de lavado, cuyo
objetivo es recuperar el oro en solución de los relaves. Esta etapa de lavado está
asociada con tres etapas de lavado CCD con espesadores Delkor. La eficiencia de
lavado total es de 99%. En la figura 6 se puede ver la instalación de los filtros en El
Peñón.
16.5 CONCLUSIONES
La principal ventaja que ofrece el filtro de banda horizontal es la alta eficiencia
de lavado con un uso mínimo de solución de lavado.
Los beneficios asociados son:

Produce menor volumen de filtrado

Logra más altas concentraciones de filtrado
CAPÍTULO 17. Lavado con Filtro de Banda Horizontal
391

Reduce los costos de tratamiento de la solución de filtrado.

Alta eficiencia de lavado con sólo un desplazamiento (donde el agua de
lavado entrando es igual al agua contenida en el queque).

Permite un diseño de planta con cero emisiones de solución.
CAPÍTULO 17
SISTEMAS DE FILTRACIÓN PARA LA
DEPOSITACIÓN DE RELAVES
D.N. Minson y C.E. Williams
Delkor (South America) Ltd.
Av. C. Colon 4733
Las Condes, Santiago, Chile
17.1 INTRODUCCIÓN
17.1.1 Consideraciones en la construcción de un Depósito de Relaves
Una parte importante en un proyecto minero es la selección de la mejor forma
de depositar los relaves provenientes de la operación actividad, investigación que debe
ser hecha por un Ingeniero Geotécnico. Esta investigación debe considerar:

La liquefacción del embalse por movimientos sísmicos.

La percolación de las soluciones de descarte a través de fallas geológicas.

Control de la entrada y salida de agua del área del embalse.

Erosión y contaminación de ríos y suelos.

Topografía del área de depositación y restricciones del volumen depositado.

Localización del nivel freático.
Por otra parte, después de la construcción de la planta es necesario considerar todos
los recursos necesarios para monitorear la operación del depósito.
La decisión a favor de una depositación seca de los relaves involucra
inversiones adicionales en equipos, pero tiene ventajas en el largo plazo:

Eliminación del riesgo de liquefacción del embalse.
392
Capítulo 17 Sistemas de Filtración para la Depositación de Relaves

Eliminación de la percolación.

Facilidad de control del escape da agua.

No hay riesgo de pérdida del embalse por erosión.

Se eliminan los costos por murallas de retención.

Se puede depositar mayor cantidad de material en una menor área.
393
17.1.2 Comparación de Costos
Las tablas 1.1 y 1.21 comparan los costos de depósitos de relaves húmedos,
utilizando hidrociclones para la construcción de las paredes, con los de depósitos de
relaves secos. El objetivo de este estudio preliminar es analizar la potencialidad de
cambiar desde un sistema convencional húmedo a un sistema de depósitos seco. No se
incluyó un análisis financiero, pero las estimaciones preliminares demuestran que un
sistema seco puede ser económicamente viable.
Tabla 1. Costos de un depósito de relaves húmedo
ITEM
COSTO EN US$
Costos de capital
Excavación; relleno; drenaje; tuberías; etc.
Total
748.000
Costos de Operación (8 años en total)
Espesamiento
5 US c/ton
Bombeo
40US c/ton
Recuperación de agua
40 US c/ton
Mantención y otros
12 US c/ton
Total
4.250.000
Costo de capital para nuevo depósito (después de 8 años)
COSTO TOTAL PARA 1500 tpd
748.000
5.750.000
393
394
Manual de Filtración & Separación
Tabla 2. Costos de un depósito de relaves seco
ITEM
COSTO EN US$
Costos de capital
Planta de filtros, espesadores, transportadora; etc.
Total
1.452.000
Costos de Operación (8 años en total)
Espesamiento
5 US c/ton
Filtro de banda
50 US c/ton
Transportadoras/camiones
20 US c/ton
Recuperación de agua
4 US c/ton
Mantención y otros
5 US c/ton
Total
2.800.000
Costo de capital para nuevo depósito (después de 8 años)
Depósito tiene vida de 20 años
COSTO TOTAL PARA 1500 tpd
0
4.250.000
17.2 DETERMINACIÓN DEL SISTEMA DE DEPOSITACIÓN SECA
El primer factor a considerar es la motivación del usuario para considerar un
sistema seco. Objetivos tales como el costo del agua, restricciones en el área para el
depósito y las propiedades geofísicas del lugar, guían en la selección del equipo más
económico.
17.2.1 Compactación de los relaves
En aquellos lugares en que existen problemas topográficos, como escape de
agua, o problemas geofísicos, tales como fallas en la base del nivel friático, la
construcción de embalses húmedos puede ser problemática. Productos filtrados
pueden ser compactados a un punto tal que sean impermeables. Esto reduce las
posibilidades de percolación, erosión por agua o liquefacción como resultado de
actividad sísmica.
Los relaves filtrados generalmente mantienen una humedad de entre un 10 a un
15%. Aunque los equipos de filtración para relaves rara vez llegan a este nivel de
humedad, si produce un material que se puede compactar a un nivel de humedad
adecuado de 2 a 10 días. Esto ocurre como resultado de depositación subterránea, la
que ocurre cuando la superficie del depósito está en contacto con la atmósfera. El
Capítulo 17 Sistemas de Filtración para la Depositación de Relaves
395
efecto del sol y del viento, además de la ayuda de maquinarias de movimiento de
tierra, permite que el producto se seque y alcance densidades de compactación.
El material compactado tiene la ventaja adicional que puede ser apilado a
alturas significativas, permitiendo una utilización más eficiente del área del embalse.
La tabla 31 identifica las rutas de proceso alternativas y su efectividad para
producir un material compactado. La inversión de capital se refiere solamente al costo
de equipos y no considera los costos por el área de depositación de los relaves.
Tabla 3. Comparación del costo de equipos versus método de desaguado1
Equipos
% de sólidos
Inversión de capital
Efectividad para la
compactación
en peso
US$
Espesadores
50-60
330.000
No
Espesadores de alta
densidad
65-75
450.000
No
Espesadores de alta
densidad (finos) y Filtros
(gruesos)
70-75
700.000
Depende de la razón
fino/grueso
Filtros de vacío
75-83
900.000
Después de 10 días
Filtros de presión
80-87
2.000.000
Después de 2 días
17.2.2 Recuperación de agua
Los equipos de sedimentación y filtración tienen la ventaja de retornar agua a la
planta inmediatamente. Los embalses también recuperan agua, pero esta agua
almacenada en el área del embalse restringe el volumen disponible para deposición de
los relaves. También hay un costo de energía necesaria para bombear el agua desde el
embalse a la planta. La tabla 4 muestra la reutilización de agua estimada para las
alternativas de desaguado para una planta de flotación1.500 tpd.
17.2.3 Percolación
Los relaves compactados no liberan volúmenes significativos de licor.
Generalmente el licor surge a la superficie del material y se evapora. El licor restante
se mantiene impregnando los sólidos compactados como líquido de saturación. De
esta manera se minimiza la contaminación de aguas subterráneas.
395
396
Manual de Filtración & Separación
Tabla 4. Comparación del uso de agua versus tipo de equipo utilizado1
Equipo
Cantidad de agua utilizada
m3/ton ROM
Inversión de capital
Espesadores
1-1.3
330.000
Húmedo
Espesadores de alta
densidad
0.6
450.000
Húmedo
Espesadores de alta
densidad (finos) y
Filtros (gruesos)
0.4
700.000
Depende de la
razón fino/grueso
Filtros de vacío
0.25
900.000
Seco
Filtros de presión
0.18
2.000.000
Seco
Tipo de relave
US$
Nota: No considera agua recuperada desde el embalse.
17.3 TIPOS DE EQUIPOS
Como una regla práctica, las restricciones de las áreas de embalse requieren que
el producto sea filtrado. Cuando las limitaciones se refieren al agua, una combinación
de espesador-filtro es la más favorable. Las opciones típicas de equipos se muestran a
continuación.
17.3.1 Filtro prensa de doble banda
El filtro prensa de dos bandas tiene, como su nombre lo indica, dos bandas
(telas) que pasan entre rodillos y aplican directamente presión y cizalle sobre la pulpa
retenida como un sándwich entre las dos telas. Este equipo solamente sirve para
pulpas compresibles.
Aunque el equipo ofrece una baja inversión de capital inicial, existen dos altos
costos de operación involucrados. El cizalle ejercido constantemente sobre el
sándwich de pulpa produce desgaste de las fibras de la tela, siendo la vida útil de ésta
de entre 10 y 15 días. Por otra parte, se necesita grandes cantidades de floculante,
hasta 300 g/ton, para generar un sedimento compresible. Las humedades finales son
similares a las obtenidas por un sistema de vacío.
Capítulo 17 Sistemas de Filtración para la Depositación de Relaves
397
Fig. 1. Filtro Prensa de doble banda Delkor, de 2m
de ancho, utilizada para sedimentos compresibles.
17.3.2 Filtro Prensa Convencional
El filtro prensa es conocido principalmente para filtración de productos
químicos o de concentrados. El ciclo de filtrado requiere que las cámaras de presión
sean llenadas y vaciadas. Esto significa que el tiempo dedicado efectivamente a la
filtración es sólo una fracción del ciclo total. Por esta razón, estos filtros tienen una
capacidad relativamente pequeña. Como resultado de esto, los costos de capital y
operacionales por tonelada suelen ser altos, pero la humedad obtenida es baja.
Fig. 2 Filtro de Prensa de cámara de 1500x1500, para
finos de carbón.
17.3.3 Filtro de Discos
Los filtros de discos a vacío son muy conocidos en el ambiente minero. La
experiencia ha demostrado que la capacidad de los filtros de discos es 30 a 60% menor
a la de los filtros de banda. Como resultado, los costos operacionales son mayores, en
tanto que las humedades son similares.
397
398
Manual de Filtración & Separación
17.3.4 Filtro de Bandas
Este filtro utiliza una banda horizontal accionada por una polea. El vacío es
producido a través de aberturas en la banda. Como la capacidad por tonelada es alta, el
equipo ha sido aceptado en general como el más económico para filtrar relaves. Aun
cuando la humedad es similar a la de los filtros de discos, se ha encontrado que los
filtros de banda producen una humedad 1 a 2% menor.
Fig. 3 Filtro de banda horizontal Delkor
17.3.5 Espesador de Alta densidad
El espesador de alta densidad (HD) es similar en su construcción a un
espesador convencional, pero se basa en una mayor altura, mayor tiempo de residencia
y mayor uso de floculante para obtener una mayor recuperación de agua. Aunque este
equipo no produce fácilmente material para compactación, genera una pasta que puede
servir adecuadamente para relleno subterráneo con una mayor recuperación de agua.
El costo de capital y el costo unitario de operación es bajo para este equipo, sin
embargo, las propiedades altamente plásticas de la pasta producida pueden crear
dificultades en el bombeo . Por esta razón se debe utilizar bombas de desplazamiento
positivo, las que requieren una gran inversión (más de 1 millón de dólares) y un alto
costo de operación, lo que, frecuentemente, hacen este procedimiento antieconómico.
La figura 4 muestra un esquema de este equipo y la tabla 5 resume los costos de
capital y de operación. El análisis considera un escenario de 8 años tratando relaves de
una planta de flotación de 1.500 tpd, excluyendo el cálculo de NPV.
Capítulo 17 Sistemas de Filtración para la Depositación de Relaves
399
Fig. 4 Esquema de un Espesador Delkor de Alta
Densidad para rellenado subterráneo.
Tabla 5 Comparación del costo de capital y operacional para diferentes
sistemas de desaguado
Equipo
Humedad
Costo Equipo
Costo Operacional
Costo Total
% en peso
US$
US$/ton
8 años de operación
Filtro Prensa de
doble Banda
20
700.00
1.955
10.900.000
Filtro Prensa
15
2.000.000
0.913
6.800.000
Espesador HD
35
450.000
0.382
2.500.000
Filtro de discos
22
900.000
0.760
4.900.000
Filtro de banda
21
886.000
0.395
2.900.000
En la tabla se muestra que el filtro de banda horizontal es la alternativa más económica
globalmente.
17.4 INSTALACIONES EXISTENTES
Existen varias instalaciones de deposición de relaves que utilizan filtros de
banda para una depositación seca. Entre ellas destacaremos tres instalaciones en Chile,
una en Zambia y una en Zaire. La tabla 6 muestra las plantas que se analizará.
399
400
Manual de Filtración & Separación
Tabla 6 Instalaciones de desaguado de relaves utilizando filtros de banda
Planta
País
Capacidad tpd
Mantos Blancos
Chile
10.000
3 de 100 m2
La Coipa
Chile
18.000
12 de 100 m2
Zambia
50.000
26 de 80 m2
Gecamines
Zaire
7.000
6 de 80 m2
El Peñón
Chile
2.000
3 de 54 m2
ZCCM
N° de filtro y tamaño
17.4.1Mantos Blancos
En Mantos Blancos se ha filtrado los relaves desde el comienzo de los años 80.
En aquel tiempo, el alto costo del agua fresca motivó la necesidad de recuperar agua
adicional.
Fig. 5 Diagrama de flujo del tratamiento de los relaves de
Mantos Blancos.
Los relaves de flotación son clasificados en hidrociclones separando los finos de
los gruesos. Los finos son llevados a un espesador, parte de cuya descarga se junta con
los gruesos del hidrociclón y son filtrados en tres filtros de banda de 100 m2. La otra
parte de la descarga del espesador se bombea al depósito de relaves. La proporción de
finos no filtrados varía de modo de minimizar el costo global de la filtración y del
agua fresca. Originalmente se utilizaba filtros de discos, los que subsecuentemente
fueron reemplazados por filtros de banda.
Otro factor importante que determinó la necesidad de filtrar los relaves, fue la
estabilidad del suelo. El alto contenido de sal en el área de deposición de relaves
significaba que la deposición húmeda podría causar problemas serios de disolución de
las sales e inestabilidad del suelo bajo el embalse.
Capítulo 17 Sistemas de Filtración para la Depositación de Relaves
401
La tabla 7 resume los costos operacionales de Mantos Blancos. Es de interés
observar el costo de operación de 0.35 US$/ton de los filtros. Este cae dentro del rango
indicado en la tabla 5. El costo de espesadores, transporte de pulpa y de mantención
del embalse suma aproximadamente 0.15 US$/ton.
Tabla 7 Resumen de costos de operación en Mantos Blancos2
Operación
Relaves de flotación
Tipo de relaves
Combinación de gruesos y finos del ciclonaje
Queque de filtración
19% de humedad
Costo de operación
0.3 US$/ton ROM
Humedad final del depósito
26% Humedad
Requerimientos de agua de la planta
0.43 m3/ton ROM
El consumo de agua incluye 0.03 m3/ton ROM perdida con el concentrado de flotación
de óxidos.
17.4.2 El Indio3
La Compañía Minera El Indio cambio en 1986 su deposición de relaves desde
deposición húmeda a deposición seca por falta de espacio adecuado. La topografía
requería la construcción de una pared de retención para el embalse con depositación
húmeda con una vida útil de 8 años y un túnel de 5 km para desviar una corriente
subterránea de agua. El Indio escogió la filtración para aumentar la vida útil de este
embalse, en el cual se depositarían relaves hasta una altura de 60 m. La opción por
filtración dio una inversión de capital menor comparada con la construcción de la
nueva pared del embalse húmedo con una vida más corta.
El Indio utilizaba filtros de prensa para producir un material con 19% de
humedad, filtrando 70% de los relaves. El resto se enviaba al antiguo embalse
húmedo. La planta terminó sus operaciones en 1997.
17.4.3 La Coipa, Can Can y El Peñón
En las plantas La Coipa, Can Can y El Peñón se depositan los relaves en
embalses secos para minimizar la percolación de soluciones con cianuro hacia las
aguas subterráneas debido a fallas geológicas. Se pudo haber considerado circuitos de
espesadores en contracorriente para recuperar las soluciones, pero las restricciones
impuestas al embalse húmedo favorecía el uso de filtros de banda, el queque de los
cuales contenía atrapado en su interior menos de 20 ppm de CN.
401
402
Manual de Filtración & Separación
Después del espesamiento, la mayoría las soluciones conteniendo el oro y el
cianuro son lavadas en el queque. Por esta razón, 45% del área de filtración está
dedicado al lavado del queque. Ver figura 6.
Fig. 6 Diagrama de flujo de la operación de la Coipa.
En La Coipa, los relaves se transportan hacia abajo y se desparraman usando un
apilador tripper-car RAHCO. La operación de la planta pretende producir un queque
con una humedad de 21%, el que reduce su humedad a sólo 13% después del método
de apilarlo. Modificaciones a éste método podría reducir aún más la humedad a 11%.
Fig. 7 Tres filtros de banda Delkor de 100 m2 de los
relaves de flotación en La Coipa.
Capítulo 17 Sistemas de Filtración para la Depositación de Relaves
403
La tabla 8 muestra un resumen de la operación. No hay detalles de los costos de
operación, pero es suficiente decir que la recuperación del CN paga por la operación
de los filtros. Se debe recordar que, debido a que parte del filtro está dedicado a lavar,
las ton/área de filtro se ve disminuida.
Tabla 8. Resumen de la operación de relaves en La Coipa4
Operación
Residuo de la lixiviación del oro
Tipo de relaves
Filtración de relaves
Queque de filtración
21% humedad
Costo de operación
Pagado por la recuperación de CN
Requerimiento de agua de la planta
0.27 m3/ton ROM
El consumo de floculante de diseño era de 20 a 30 g/ton ROM. Sin embargo,
éste se ha reducido a 15 g/ton, lo que se puede atribuir a la optimización del diagrama
de flujo y al efecto de alimenta el filtro con sedimento del espesador que ya estaba
floculado.
17.4.4 ZCCM y Gecamines
Las plantas ZCCM y Gecamines, en Zambia y Zaire respectivamente, usan
filtración y lavado, principalmente para recuperar cobre y cobalto después de la
lixiviación de los relaves. Estos son luego depositados. Las soluciones ácidas son
enviadas a Extracción por Solvente.
17.5 ESTUDIO DE CASOS
Delkor participó recientemente de un estudio, junto a una importante compañía
de ingeniería de los Estados Unidos de Norteamérica, para un cliente Norteamericano.
El objetivo del estudio fue buscar un método de incrementar la producción, sin la
necesidad de instalar una nueva infraestructura de captación de agua.
Este estudio se separó en tres fases:5

Fase 1. Trabajo de investigación preliminar sobre relaves rougher/cleaner
para 7 diferentes muestras de mineral. En este trabajo el orden de magnitud
de las cifras que identificaban la capacidad de la planta y los costos de
operación

Fase 2. Ensayos más detallados para verificar velocidades de sedimentación
y tiempos de filtración sobre los relaves. Estos resultados fueron usados para
el diseño de detalle.
403
404
Manual de Filtración & Separación

Fase 3. Trabajo de investigación sobre la separación de grueso/finos, para
identificar una forma de desaguar los relaves a menor costo.
Fases 1 y 2: Diseño del Espesador y Filtro
La base del diseño fue el esquema típico para relaves de flotación de un
espesador seguido por un filtro de banda:
Carga de sólido
: 15 ton/dia-m2
Planta de espesadores
: 2 Espesadores de alta capacidad
Uso de floculante
: 20 g/ton
Densidad de la descarga:
: 53% sólidos en peso (espesadores de alta
densidad hubiesen alcanzado 57-60% de
sólidos en peso).
El diseño de los filtros de banda se basó en los resultados de la investigación de
la fase 2. Sin embargo, los resultados de la fase 1 estaban a un 10% del valor del
diseño final.
Humedad del queque
:
23%
Tamaño de planta de filtros
:
8 filtros de banda horizontal (uno standby)
Uso de floculante
:
40 g/ton
Costo de operación
:
0.203 US$/ton ROM (incluido floculante)
El alto contenido de mica de los relaves relativamente gruesos, produjo
descargas de los espesadores mas densos y queques más secos que los esperados.
El costo del polímero utilizado como floculante puede llegar a ser un 70% del
costo total de depositar el relave en el embalse. Por esta razón se investigó el tipo de
polímero y su dosificación. Discusiones posteriores con proveedores de reactivos
indicaron que una mezcla de coagulantes (para neutralizar el efecto de la mica) y
surfactantes de bajo costo también podía ser considerado.
Fase 3: Trabajo de Separación de gruesos y finos
El diagrama de flujo consideraba la separación de los relaves de flotación
rougher/cleaner en hidrociclones. La descarga del hidrociclón alimentaría el filtro de
banda y el rebalse se enviaría a un espesador de alta capacidad. La descarga de este
espesador podría ser depositado separadamente o puesto "encima" del queque de
filtración en la sección final del filtro de banda.
Capítulo 17 Sistemas de Filtración para la Depositación de Relaves
405
Los ensayos de filtración produjeron un queque con 17.5% de humedad, los que
combinados con los finos provenientes del espesador daban una humedad final de
28% en peso.
Los ensayos depositando los finos del espesador sobre el queque de filtración en
la parte final del filtro de banda produjo una humedad final combinada de 21%.
Como conclusión, estos resultados definieron diagramas de flujo alternativos.
La selección de equipos y costos de operación de éstos se muestran en la tabla 9.
Tabla 9. Comparación
desaguado de relaves
de
alternativas
de
Humedad combinada del relave
25%
28%
21%
Costo de operación US$/ton ROM
0.15
0.07
0.15
17.6 CONCLUSIONES
El uso combinado de hidrociclones, espesadores de alta capacidad y filtros de
banda permite reducir el costo de desaguar relaves de flotación a menos de
US$0.10/ton ROM. Esto produce humedades de relave satisfactorios para aumentar la
capacidad de la planta sin necesidad de abastecimiento adicional de agua.
Si la justificación de la depositación de relaves fuese motivada por restricciones
en el depósito de relaves, se debería producir un relave compactable. Para ello, se
precisaría un producto más seco de 21 a 23% de humedad y el costo de tratamiento
aumentaría a 0.15 a 0.20 US$/ton ROM.
17.7 COMENTARIOS
No es común la depositación de relaves con humedades residuales menores,
principalmente porque ello demanda una inversión adicional de capital al comienzo
del proyecto. Sin embargo, esta inversión puede tener un beneficio a largo plazo en
términos de un mejor control de los recursos hídricos y de la contaminación de las
aguas subterráneas. Además, el mejor uso del área de embalse que produce esta
alternativa, evita los posibles problemas ambientales originados a futuro por
requerimiento de sitios adicionales para la depositación de relaves.
Desde el punto de vista de los equipos, el uso de filtros de banda horizontal para
el desaguado de relaves es la ruta más comúnmente utilizada. La tecnología actual ha
permitido el desarrollo de filtros con una gran área unitaria, hasta 154 m2. Ello ha
permitido tener plantas de gran capacidad, tales como las de ZCCM en Zambia, que
trata 50.000 ton/día de relaves.
405
406
Manual de Filtración & Separación
17.8 REFERENCIAS
[1] Desarrollos Ltda., Ingenieros Consultores E.H Smith, Comunicación privada.
[2] Rosas, O., Empresa Minera Mantos Blancos, comunicación privada.
[3] Desarrollos Ltda, Ingenieros Consultores, Compañía Minera El Indio,
comunicación privada.
[4] G. Bush, Compañía Minera Mantos de Oro, planta la Coipa, comunicación
privada.
[5] C.E. Williams, Informe Final de estudio de Casos, Delkor South America Ltd.,
Octubre de 1998.
CAPÍTULO 18
FILTRACIÓN HI-BAR® CON VAPOR A PRESIÓN
BOKELA Ingenieurgesellschaft für Mechanische Verfahrenstechnik mbH
Gottesauer Str. 28, D-76131 Karlsruhe, Germany.
RESUMEN
La filtración con vapor a presión, o tecnología de filtración Hi-Bar® con vapor,
es el proceso de filtración continua a presión más avanzada existente en el mercado. El
proceso y su concepto han sido desarrollados con base a la gran experiencia en
filtración de la empresa Bokela. La filtración moderna con vapor a presión combina la
física del desaguado mecánico con el proceso de secado térmico. La filtración
hiperbárica con vapor a presión se realiza en filtros rotatorios y da como resultado
mínimas humedades y otros beneficios tales como: menor consumo de gas, una muy
buena utilización de la energía, lavado y eliminación de contenidos solubles mediante
un flujo pistón de condensado. Los fundamentos del proceso, los equipos para el
laboratorio y planta piloto, como el diseño de plantas son descritos en este capítulo con
ejemplos prácticos.
407
408
18.1.
Manual de Filtración & Separación
FUNDAMENTOS DE LA FILTRACIÓN CON VAPOR A PRESIÓN
18.1.1 Filtración convencional con vapor
En trabajos previos de filtración con vapor el objetivo era reducir el contenido
de humedad del queque disminuyendo la viscosidad del filtrado y la fuerza de
interacción sólido-líquido. El contenido de humedad mc de un queque de filtración es
función de varias variables:
mc  f  L , h 2c p, t 2 
donde L es la viscosidad del filtrado, hc es el espesor del queque, p es la caída de
presión a través del queque y t2 es el tiempo de desaguado.
Como la viscosidad disminuye al aumentar la temperatura del líquido, el vapor
se utilizaba como fuente de energía para calentar el líquido. Por esta razón se
instalaban campanas sobre los filtros rotatorios para captar el vapor que se hacía pasar
por los poros del queque. Pero antes que el vapor penetrara en el queque, éste se
desaguaba haciendo pasar aire por lo que los poros del queque quedaban parcialmente
llenos de aire. Esto significa que al introducir vapor, una mezcla de éste y aire pasaban
por el queque, dando por resultado una máxima temperatura en el queque muy por
debajo de la temperatura del vapor.
18.1.2 Proceso moderno de filtración con vapor a presión Hi-Bar®
En contraste a la filtración convencional con vapor, el nuevo proceso de
filtración con vapor a presión usa solamente vapor para eliminar el agua del queque.
En primer lugar, el objetivo de la filtración Hi-Bar® es sobrepasar la presión capilar en
los poros del queque. Para explicar este nuevo proceso, ver figura 1, consideremos la
operación de un filtro rotatorio en el proceso de filtración con vapor a presión. El
queque es formado a la temperatura natural de la pulpa de alimentación es
inmediatamente introducido en una cabina de vapor al emerger de la suspensión. El la
cabina existe una atmósfera de vapor sobrecalentado que produce el fenómeno de
frente condensado y que se puede describir en la siguiente forma [1]:
 El vapor se condensa en la superficie fría del queque y la entalpía de
condensación calienta la superficie del éste hasta que la temperatura alcanza la
de condensación.
 El licor madre y el condensado son forzados a través del queque debido a la
diferencia de presión de filtración. En los poros grandes, que se desaguan más
rápidamente que los poros pequeños, el vapor se condensa y el condensado los
llena completamente. Debido a este efecto, todos los poros susceptibles a ser
desaguados por una diferencia de presión (de acuerdo a su tamaño de poros)
estarán llenos de condensado y por lo tanto se formará un frente de condensado
que es presionado a través del queque hacia el medio filtrante como una capa
homogénea de condensado, esto es como un flujo pistón de condensado. Este
CAPÍTULO 21. Filtración Hi-Bar con vapor a presión
409
fenómeno previene la formación de las ramificaciones denominadas “fingering”
[2]
Fig. 1: Modelo de “frente de condensación”
 Mientras el “frente de condensado” se mueve a través del queque, la mayor parte
del licor madre es reemplazada por condensado, y partes más cercanas al medio
filtrante que aún permanecen frías toman contacto con el vapor se calientan con
el vapor que se condensa. Este mecanismo combina transferencia de masa y
calor entre el queque y el vapor.
 Cuando el frente de condensado llega al medio filtrante se corta el suministro de
vapor antes que éste escape libremente a la atmósfera. En ese momento el
queque ha adquirido la temperatura del vapor y sale da la cabina de vapor.
 En ese momento se sopla aire comprimido a través del queque caliente y predesaguado, obteniéndose un muy efectivo secado térmico. Debido a la energía
almacenada en el queque, gran parte del líquido residual se evapora es removido
por el flujo de aire comprimido.
S. Gerl y W. Stahl [3, 4] han investigado en este campo en años recientes y han
aclarado el mecanismo de la filtración con vapor a presión, que constituye los
fundamentos de la tecnología patentada por BOKELA. Estos estudios experimentales
muestran que la combinación de pre-desaguado logrado por el vapor condensado y el
siguiente secado con el aire comprimido lleva a humedades residuales extremadamente
bajas.
410
Manual de Filtración & Separación
18.2 TECNOLOGÍA DE FILTRACIÓN HI-BAR®
En su versión estándar la filtración Hi-Bar® utiliza aire comprimido para llevar
adelante el proceso. Sin embargo la filtración Hi-Bar® con vapor a presión utiliza vapor
sobresaturado tanto para desaguar el queque como para lavarlo. Este proceso está
protegido por una patente de Bokela.
Los filtros Hi-Bar® de discos o tambor se montan en una vasija presurizada, la
que se llena de aire comprimido. Para la filtración con vapor una cabina de vapor cubre
parcialmente la superficie del filtro, formando un ambiente separado de puro vapor en
la vasija. Diseñados con base en un know-how sobre proceso y equipos, ambas
versiones de filtración Hi-Bar® son caracterizadas por los siguientes detalles:
 Proceso de filtración continua con filtros rotatorios de tambor o discos.
 Todas las partes motrices están instaladas fuera de la vasija a presión.
 Gran diferencia de presión, hasta p = 6 bar
 Tecnología confiable para la descarga del queque.
 Descarga del queque por soplado inverso de aire (este aire comprimido está
disponible para la filtración).
Los tipos de filtros Hi-Bar® (ver Tabla 1) son particularmente adecuados para la
filtración masiva, pero también sirven para la filtración de pequeños flujos de material.
El diseño especial de los aparatos provee características hidráulicas excelentes para
obtener grandes capacidades, remover completamente el filtrado y descargar en la
mejor forma el queque. La filtración Hi-Bar® se ha diseñado especialmente para lograr
filtraciones sofisticadas con requerimientos difíciles, tales como lavado del queque,
extracción de solutos o simplemente evitar la quebradura del queque.
Tabla 1 Tamaño de los filtros de Discos y Tambor para la filtración Hi-Bar®
Filtros de Discos Hi-Bar®
Filtros de Tambor Hi-Bar®
Area de Filtración
Numero de Discos
Area de Filtración
Diámetro del
Tambor
[m²]
[-]
[m²]
[m]
15
1
10
3.0
30
2
20
3.0
45
3
30
3.0
60
4
90
6
120
8
CAPÍTULO 21. Filtración Hi-Bar con vapor a presión
411
18.2.1 Concepto de la filtración Hi-Bar® con vapor a presión en la planta
Para tomar una decisión con respecto al uso de vapor en la filtración Hi-Bar® , se
estudia el comportamiento de la pulpa utilizando aire comprimido. Si estos resultados
no cumplen con los objetivos en cuanto a humedad residual del queque, lavado,
extracción de contaminantes, flujo de gas y quebraduras en el queque, o si el producto
de la filtración debe ser posteriormente secado, se aplica la filtración con vapor.
En la filtración Hi-Bar® con vapor a presión, el desaguado y el lavado del
queque se realiza con vapor sobresaturado. Para este efecto se cubre el área del filtro
rotatorio (disco o tambor) con una cabina
Con este propósito, el área de vapor del filtro rotatorio (disco o tambor) se cubre
y se sella con una cabina de vapor (ver figura 2) que separa la zona de vapor del
interior de la vasija a presión que está llena de aire a presión. De esta manera una
vasija de presión estándar sin un aislamiento térmico costoso cumple todos los
requerimientos y las unidades dentro de la vasija no están expuestas al vapor a alta
temperatura. Generalmente la cabina de vapor cubre el queque desde que éste emerge
de la pulpa hasta que el vapor y escapa libremente del queque y que el queque es
lavado, desaguado y calentado con un mínimo consumo de energía. Esto constituye la
primera etapa del proceso. Después de dejar la cabina de vapor el queque se seca hasta
su humedad final haciendo pasar aire comprimido, lo que constituye la segunda etapa
del proceso.
Fig. 2: Filtro de discos Hi-Bar® con cabinas de vapor
El diseño de la cabina se caracteriza por los siguientes elementos: La cabina está
inmersa en la pulpa y un sistema de control mantiene una presión un poco mayor en la
cabina de vapor que en la cámara de aire, de modo que éste no pueda penetrar a la zona
de vapor. La cabina cubre al queque desde el momento que éste emerge de la
suspensión hasta que el vapor sale libremente del queque. El tamaño de la zona de
vapor puede ser adaptado a los requerimientos de procesos con diferentes materiales.
412
Manual de Filtración & Separación
En caso de ser necesario, la cabina de vapor puede cubrir al queque completamente
hasta el punto de descarga. La cabina de vapor previene las pérdidas de vapor por
condensación en las paredes de la vasija. La condensación de vapor también se
previene en la superficie de la pulpa ya que cada disco (en el caso de filtros de disco)
está equipado con una cabina de vapor individual y separada. Este concepto mantiene
el área de contacto entre el vapor y la pulpa en un mínimo. La superficie de la pulpa es
mantenida en contacto con el aire comprimido para impulsar la formación de queque.
18.3 BENEFICIOS DE LA FILTRACIÓN HI-BAR® CON VAPOR A PRESIÓN
Muy baja humedad residual
La gran diferencia de presión, hasta p=6 bar, proporciona un desaguado intenso
del queque sobrepasando la presión capilar de hasta los poros más pequeños.
Simultáneamente, la menor viscosidad del concentrado y el filtrado,
Fig. 3 Diagrama de flujo para filtración Hi-Bar® con vapor a presión
debido al aumento de temperatura, mejora el desaguado mecánico. Después de que el
vapor atraviesa el queque recalentado, éste se deshumedece haciendo pasar aire
comprimido a través de él. Debido a la alta temperatura que ha adquirido el queque,
este aire permite la evaporación rápida del líquido residual. Una disminución adicional
de humedad por vaporización, llegando prácticamente a cero, se obtiene durante la
descarga debido a la alta temperatura del queque.
CAPÍTULO 21. Filtración Hi-Bar con vapor a presión
413
La filtración Hi-Bar® con vapor a presión utiliza la energía del vapor para un muy
rápido y eficiente secado del queque debido a la gran área de intercambio de masa y
energía dentro del queque. Por otra parte, esta forma de secado del queque es muy
conveniente ya que éste no está expuesto a esfuerzos mecánicos ni térmicos. El
recalentamiento del queque no daña el proceso.
Lavado y extracción
El condensado puro y caliente tiene una gran solubilidad para poluyentes
sólidos o líquidos o para cualquier otro contenido del queque de filtración, por lo que
éstos son extraídos, fundidos, disueltos y eliminados. También se mejora el lavado del
queque debido a que la formación del frente de condensación, que impidiendo la
introducción de aire en el queque, se mueve como un flujo pistón reemplazando el licor
madre completamente en el queque.
Benefits of the Hi-Bar Steam Pressure Filtration
optimal
mechanical
dewatering
washing out
no gas
consumption
extraction
diminishing of
crack building
careful drying
Fig. 4 Beneficios de la filtración Hi-Bar® con vapor a presión
Se evita las quebraduras de queque
La fractura de queques de filtración se produce debido a las fuerzas interfaciales
de tensión especialmente cuando está constituido de partículas utrafinas. Durante la
filtración con vapor se reduce drásticamente la influencia de la tensión superficial ya
que el licor madre (filtrado) es reemplazado por el condensado, ambos con tensiones
superficiales similares. Por esta razón se reduce las quebraduras del queque e, incluso,
se evita como se ha demostrado en muchos casos.
414
Manual de Filtración & Separación
Se evita la emisión de gases
Si se desea evitar la emisión de gases durante la filtración, la zona de vapor se
debe extender hasta la descarga del queque y la filtración se puede llevar a cabo sin
consumo de aire. Es así como la filtración Hi-Bar® con vapor a presión es
especialmente útil para filtración con problemas de evacuación de aire.
18.4 ENSAYOS EN EL LABORATORIO Y PLANTA PILOTO
Para determinar las características de filtración de una suspensión se debe llevar
a cabo ensayos en laboratorio para medir todos los datos necesarios bajo condiciones
ideales. Si estos ensayos son exitosos, las condiciones encontradas se verifican en la
planta bajo condiciones reales de operación con una planta piloto móvil de filtración
Hi-Bar® con vapor a presión.
18.4.1 Equipos de ensayo de Laboratorio
El rango de operaciones de un filtro de planta es simulado en laboratorio con
filtración con aire comprimido y vapor a presión variando lo parámetros relevantes.
Estos ensayos entregan información sobre la capacidad de tratamiento de sólidos tales
como la diferencia de presión óptima, el consumo de aire y/o vapor, el consumo de
agua de lavado, el tiempo de formación del queque, el tiempo de desaguado, el
acondicionamiento de la suspensión y la tela de filtración recomendada.
Los ensayos de filtración con aire comprimido son realizados en el equipo
FILTRATEST. Este es un equipo de laboratorio portátil que consiste en una celda de
filtración, con chaqueta de calentamiento de 20 cm2 de área de filtración y una presión
máxima de trabajo de 10 bar. Para la filtración con vapor a presión se diseñó un equipo
de laboratorio especial con 20 cm2 de área de filtración y presiones máximas de 16 bar
y temperaturas de vapor de 210°C. Ambas unidades son portátiles y están equipadas de
todas las más modernas tecnologías de mediciones existentes, de modo que todos los
datos son registrados electrónicamente. Los datos recogidos permiten calcular la
capacidad del filtro, la humedad del queque, el consumo de gas y vapor de la planta de
filtración Hi-Bar® con vapor a presión.
18.4.2 Planta piloto Hi-Bar®
La planta piloto móvil consiste en un filtro rotatorio Hi-Bar® (de discos o de
tambor, de acuerdo con la demanda del cliente) instalado en una vasija a presión. La
unidad está diseñada tanto para la filtración con aire comprimido como para utilizar
vapor a presión con un máximo de p=6 bar. La plata piloto está equipada con todos
los equipos periféricos tales como recibidor de filtrado, compresores, bombas, unidad
de acondicionamiento de la pulpa y control automático.
CAPÍTULO 21. Filtración Hi-Bar con vapor a presión
415
Los ensayos pilotos se llevan a cabo para verificar los resultados de los ensayos
de laboratorio bajo condiciones reales de operación. En los ensayos pilotos se puede
verificar y optimizar el funcionamiento del proceso y de parámetros tales como
diferencia de presión, velocidad del filtro, disposición de las cabinas de vapor,
comportamiento del medio filtrante, descarga del queque Estos datos proveen
información para un escalamiento eficaz a la tamaño industrial.
18.5 RESULTADOS DE LA FILTRACIÓN HI-BAR® CON VAPOR A
PRESIÓN
La filtración Hi-Bar® con vapor a presión muestra ventajas cuando se desea
bajos niveles de humedad, un secado cuidadoso, un lavado efectivo y la remoción de
contaminantes en el queque. Estas demandas provienen principalmente del mundo
minero, de la industria del carbón y de la industria química, del alimento y del medio
ambiente. En estos mercados la filtración Hi-Bar® con vapor a presión muestra
ventajas supremas, como se verá a continuación en un estudio de casos.
18.5.1 Desaguado de concentrados en la flotación de carbón
Los finos de carbón se procesan tradicionalmente mediante la flotación. El
tamaño de partículas del concentrado está en el rango de 35%- 40% menor a 63µm. El
concentrado se desaguaba por medios mecánicos con filtros a vacío o con filtración
continua a presión. Para tener un producto competitivo, la humedad del queque no
debe sobrepasar el 10%. Como éstas tecnologías tradicionales de separación sólidolíquido no cumplen con el requerimientos de humedad estipulado, el queque debe ser
secado térmicamente para obtener el producto de la calidad deseada. La
implementación de filtración Hi-Bar® con vapor a presión permitió eliminar la etapa de
secado.
Para el concentrado 1 indicado en la tabla 2, el contenido de humedad es
reducido por la filtración a vapor desde 19.5% a 8.5% , lo que significa una reducción
de agua de 149 kg por tonelada de sólidos. Este resultado se obtiene con un consumo
de vapor de 92 kg per tonelada de sólidos, lo que significa que 0.62 kg de vapor son
necesarios para remover 1 kg de agua. Este resultado muestra un rendimiento
energético mucho mayor que el secado térmico. Para el concentrado 2, el contenido de
humedad se reduce desde 18% a 9.5%, y 105 kg de agua son removidos por tonelada
de sólido. El consumo de vapor es de 0.67 kg por kg de agua removida. Este resultado
muestra que con la filtración Hi-Bar® con vapor a presión se logró el objetivo de un
máximo de 10% de humedad en el queque en una sola etapa, evitando el secado
térmico, lo que redujo el costo de energía y de inversión de modo significativo.
416
Manual de Filtración & Separación
Tabla 2 Comparación de resultados de desaguado con filtración a presión y
filtración Hi-Bar® con vapor a presión de dos concentrados de carbón
Desaguado de finos de carbón con filtración Hi-Bar con vapor a presión
Comparación de tecnologías de filtración
Concentrado de carbón 1
Hi-Bar
Presión
Filtro discos
SPF*
Technical data
Concentrado de carbón 2
Presión
Filtro discos
Hi-Bar
SPF*
Area filtrante
(m²)
120
146
120
85
Capacidad de sólido
(t/h)
100
100
70
70
(bar)
2,5
2,5
2
2,5
Contenido de humedadad
Diferencia de presión
(wt-%)
19,5
8,5
18
9,5
agua por 1t de soólidos
(kg/t)
242
93
196
105
Flujo de gas
(m³/h)
4500
1600
3500
2100
(t/h)
0
9,2
0
7
(kg/kg)
-
0,62
-
0,67
Consumo de vapor
vapor / kg agua removida
* SPF = filtration con vapor a presión
18.5.2 Desaguado de concentrados de minerales de hierro
La hematita se beneficia mediante flotación produciendo un concentrado con
una distribución de tamaño de 95% menos a 44µm y 35% menor a 5 µm. El
concentrado es desaguado en filtros rotatorios de discos a vacío con campanas de
vapor, produciendo un material de 12.5% de humedad a 585 kg/m2h. Este producto
debe ser peletizado, pero como la peletización requiere una humedad máxima de 9% ,
debe sufrir un previo secado térmico. Este concentrado tiene tendencia a fracturase
durante la filtración. Para cumplir los objetivos de un aumento de producción de la
planta, se pensaba instalar un filtro adicional con capacidad para 230t/h.
Ensayos de filtración Hi-Bar® con vapor a presión demostraron que se podía
aumentar la capacidad de la planta a 2500kg/m²h (cinco veces la de la filtración a
vacío), disminuir la humedad a 9% y, simultáneamente, eliminar el problema de
fractura del queque mediante esta tecnología. Es así como un solo filtro de 120m²
puede procesar mediante la filtración Hi-Bar® con vapor a presión 300 t/h con el
requerimiento de humedad. Este resultado se obtuvo con un consumo pequeño de aire
de 37.5 m³/m²h y de vapor de 38 kg per tonelada de sólidos con una diferencia de
presión de p=6 bar y un espesor de queque de 7 mm.
18.5.3 Lavado y secado de un producto de precipitación química
Los productos de precipitación de una determinada planta química se separan de
su licor madre mediante centrífugas. Se producen aproximadamente 5 t/h de
precipitado el que es lavado y desaguado en seis centrífugas. El producto de las
CAPÍTULO 21. Filtración Hi-Bar con vapor a presión
417
centrífugas tiene un tamaño de 30% menos 71 m. El objetivo de la planta es obtener
una humedad bajo el 4 % y un buen lavado del queque que dejen en él menos de 100
ppm de licor madre. Los altos costos de mantención, la baja disponibilidad de las
centrífugas y el alto valor de la humedad residual obtenida en la planta decidió el hacer
un estudio en el laboratorio y planta piloto de filtración Hi-Bar® con vapor a presión.
Los ensayos demostraron que la filtración Hi-Bar® con vapor a presión podía
cumplir fácilmente los objetivos señalados. Con un consumo muy económico de vapor
de sólo 90 kg/ton de sólidos, la humedad podría llegar al 2% y el lavado dejaba un
queque con 50 ppm de licor madre. Un filtro Hi-Bar® con vapor a presión de 7 m² de
área es suficiente para una producción de 5 t/h del precipitado que actualmente es
tratado en 6 centrífugas. Debido a que la diferencia de presión que se utiliza en la
vasija del Hi-Bar® es de sólo 1.1 bar el producto es tratado muy suavemente lo que
produce menos quebrazón de cristales de manera tal que después de la filtración sólo el
13% de las partículas tiene un tamaño menor a 71 m.
18.5.4 Lavado y secado de yeso en una planta térmica
En la desulfurización de los gases de una planta térmica se produce 230 t/d de
yeso que es lavado y desaguado en un filtro de tambor a vacío de 18 m2 y luego es
secado térmicamente. La gran cantidad de sólidos finos causa problemas en la
filtración y el contenido de humedad, el contenido de cloruros del queque lavado y el
contenido de sólidos en el filtrado están en el límite superior tolerable.
Resultados mediante filtración Hi-Bar® con vapor a presión mostraron que la
humedad del queque se podía reducir por debajo del valor de la demanda. Con la
misma diferencia de presión de p=3.5 bar de una filtración Estos 100 kg de vapor
desplazan los 300 kg de agua por tonelada de sólidos que entran al secador térmico. La
cantidad de energía requerida en el secador térmico se podía reducir a menos de la
mitad. Adicionalmente se mejoró el lavado del queque resultando en un mejor
producto. Hi-Bar® sin vapor y un consumo de vapor de 100 kg por tonelada de sólidos
la humedad del queque se podía reducir de 34 % (515 kg de agua por 1000 kg de
sólidos).
Table 3 Resultados de la filtración a vacío SPF para yeso
Filtration of FGD-gypsum with the Hi-Bar steam pressure filtration
Comparison of filter technologies
filter area [m²]
pressure difference [bar]
steam consumption [kg/t solids]
moisture content [wt-%]
chloride content in the cake [mg/kg]
filtrate solids [%]
Vacuum Filter
Hi-Bar SPF
18
0,7
11
100
1,5
10
1,5
80
3
50
0,3
418
Manual de Filtración & Separación
18.6 ECONOMÍA DE LA FILTRACIÓN HI-BAR® CON VAPOR A PRESIÓN
La economía de la filtración Hi-Bar® con vapor a presión se puede demostrar
para el caso de la filtración de concentrados de carbón reportada en la sección 4.1. Esta
filtración reduce significativamente los costos debido a que no es necesario recurrir al
secado térmico.
En la tabla 5 se muestra los resultados de la filtración a presión sin vapor pero
con secado térmico y la filtración Hi-Bar® con vapor a presión. Con el uso de vapor se
logró la meta de humedad de 10% para ambos concentrados con un consumo
económico de aire y vapor. Para el concentrado 1, el costo de energía se reduce un
59% de los 1.25 a 0.50 millones de US$ por año. Para el concentrado 2, el costo de
energía se reduce un 59% de los 0.68 a 0.42 millones de US$ por año.
Tabla 5 Comparación del costo de energía para la filtración a presión con y sin
vapor
Factibilidad del desaguado de concentrados de carbón mediante SPF
Comparción de costos de energía en US$
Concentrado de carbón 1
Presión
Hi-Bar
Filtros discos
SPF
Energy costs
Concentrado de carbón 2
Presión
Hi-Bar
Filtros discos
SPF
air compression
(DM/a)
104.000
40.500
69.500
steam production
(DM/a)
0
483.000
0
thermal dryer
(DM/a)
1.163.500
total energy costs
relation of energy costs
(DM/a)
(%)
1.267.500
100%
0
523.500
41%
6.140.000
683.500
100%
50500
367.500
0
168.000
61%
* SPF= Filtración Hi-Bar con vapor a presión
La superioridad económica de la filtración Hi-Bar® con vapor a presión
demostrada con estos datos es evidente aún cuando sólo se toman en cuenta los costos
de energía en la comparación, sin tomar en cuenta los costos de inversión y de
operación del sacado térmico.
18.7 CONCLUSIÓN
La filtración Hi-Bar® con vapor a presión combina un proceso de desaguado
mecánico con un proceso de secado térmico con una alta sinergia que lleva a queques
extremadamente secos, reducciones de aire y vapor significativos y una excelente
extracción de sólidos y lavado del contenido líquido del queque. Estas características
CAPÍTULO 21. Filtración Hi-Bar con vapor a presión
419
hacen de la filtración Hi-Bar® con vapor a presión un proceso muy atractivo para la
industria minera, pero también para la industria química, de alimentos y en la
protección ambiental. Es especialmente atractiva para el procesamiento de grandes
tonelajes, pero también muy adecuada para pequeños tonelajes o filtraciones
sofisticadas con condiciones y restricciones complicadas.
El proceso de filtración Hi-Bar® con vapor a presión puede ser ensayado para
cada material en el nivel de laboratorio y planta piloto en condiciones industriales.
Tanto el equipo de laboratorio como el piloto pueden ser transportados a las empresas
mineras para realizar el trabajo encualquier parte del mundo. Una de las características
destacables de la filtración Hi-Bar® con vapor a presión es la simpleza del diseño en
planta con componentes bien probados que aseguran una operación confiable.
18.8 REFERENCIAS
[1] R. Bott, Th. Langeloh: Steam Pressure Filtration - advanced version of the
continuous pressure filtration (Hi-Bar® Filtration); Aufbereitungs-Technik 37 (1996)
Nr. 4
[2] L. Paterson: Dispersion and fingering in miscible and immiscible fluids within a
porous medium, Powder Technology, 36, 1986
[3] S. Gerl, W. Stahl: Dewatering of coal and ore concentrate filter cakes by steam
pressure filtration; XX International Mineral Processing Congress, 1997, Aachen
[4] S. Gerl, W. Stahl: Improved dewatering of coal by steam pressure filtration; Coal
Preparation, 1996, Vol. 17
CAPÍTULO 19
APÉNDICES
APÉNDICE 1 CONVERSIÓN DE MEDIDAS DE CONCENTRACIÓN
Definiciones:
Densidad del sólido
p
f
   p   f
X


D
Densidad del fluido
diferencia de densidades
Fracción de sólidos en peso
Fracción de sólidos en volumen
Densidad de pulpa
Dilución

  f
p  f

f X
 p 1  X   f X

f
f  p D
X

p
f  
p    f 

1

1 D
420
APÉNDICES
421

p f
p 1  X   f X
 f  

 p f 1  D 
p D  f
D


f 1   
p 
1 X
X
f   p   
 p    f 
422
Manual de Filtración & Separación
APÉNDICE 2 UNIDADES DE MEDIDA Y DIMENSIONES
NOMBRE
SÍMBOLO
Longitud
l
Masa
m
Densidad

Tiempo
t
Velocidad
v
Aceleración
a
Fuerza
F
Presión
p
422
mks
m
1
10-2
0.305
kg
1
10-3
0.454
kg/m3
1
10-3
16.00
s
m/s
1
10-2
0.305
m/s2
1
10-2
0.305
Newton (N)
kg-m/s2
1
10-5
4.444
Pascal (Pa)
N/m2
1
0.1
0.680
1.013x105
1.013x105
105
UNIDAD
cgs
cm
102
1
30.5
g
103
1
454
g/cm3
103
1
16x103
s
cm/s
102
1
30.5
cm/s2
102
1
30.5
dina
g-cm/s2
105
1
4.444x105
2
dina/cm
10
1
6.80
1.013x106
1.013x106
106
DIMENSIÓN
otra
pie
3.28
3.28x10-2
1
lbm
2.205
2.205x10-3
1
lbm/pie3
6.249x10-2
6.249x10-5
1
s
pie/s
3.28
3.28x10-2
1
pie/s2
3.28
3.28x10-2
1
Poundal lbf
32.2xlbm-pie/s2
0.225
2.25x10-6
1
psi
lb f/in2
14.7psi=750 mmHg
1.47psi
1 psi
1Torr=1atm=14.7psi=
=760 mmHg
1 bar=14.5psi
L
M
ML-3
T
LT-1
LT-2
MLT-2
ML-1T-2
APÉNDICES
NOMBRE
423
SÍMBOLO
Torque
Tq
Viscosidad dinámica

Viscosidad
cinemática

mks
N-m
1
10-7
1.355
Pa-s
N-s/m2
1
0.1
4.724x10-4
m2/s
1
10-4
9.295x10-2
UNIDAD
cgs
dina-cm
107
1
1.355x107
Poise
dina-s/cm2
10
1
4.724x10-3
Stokes
cm2/s
104
1
9.295x102
DIMENSIÓN
otra
lb f-pie
0.738
7.38x10-8
1
Poundal-s
lbf-s/pie2
2.1168x10 3
2.1168x10 2
1
ML2T-2
ML-1T-1
L2T-1
pie2/s
10.758
1.0758x10 5
1
APÉNDICE 2
UNIDADES DE MEDIDA Y DIMENSIONES
NOMBRE
SÍMBOLO
Longitud
l
Masa
m
Densidad

Tiempo
t
Velocidad
v
Aceleración
a
Fuerza
F
Presión
p
mks
m
1
10-2
0.305
kg
1
10-3
0.454
kg/m3
1
10-3
16.00
s
m/s
1
10-2
0.305
m/s2
1
10-2
0.305
Newton (N)
kg-m/s2
1
10-5
4.444
Pascal (Pa)
N/m2
1
0.1
0.680
1.013x105
1.013x105
105
UNIDAD
cgs
cm
102
1
30.5
g
103
1
454
g/cm3
103
1
16x103
s
cm/s
102
1
30.5
cm/s2
102
1
30.5
dina
g-cm/s2
105
1
4.444x105
2
dina/cm
10
1
6.80
1.013x106
1.013x106
106
422
DIMENSIÓN
otra
pie
3.28
3.28x10-2
1
lbm
2.205
2.205x10-3
1
lbm/pie3
6.249x10-2
6.249x10-5
1
s
pie/s
3.28
3.28x10-2
1
pie/s2
3.28
3.28x10-2
1
Poundal lbf
32.2xlbm-pie/s2
0.225
2.25x10-6
1
psi
lb f/in2
14.7psi=750 mmHg
1.47psi
1 psi
1Torr=1atm=14.7psi=
=760 mmHg
1 bar=14.5psi
L
M
ML-3
T
LT-1
LT-2
MLT-2
ML-1T-2
Unidades de Medida y Dimensiones
NOMBRE
423
SÍMBOLO
Torque
Tq
Viscosidad dinámica

Viscosidad
cinemática

mks
N-m
1
10-7
1.355
Pa-s
N-s/m2
1
0.1
4.724x10-4
2
m /s
1
10-4
9.295x10-2
UNIDAD
cgs
dina-cm
107
1
1.355x107
Poise
dina-s/cm2
10
1
4.724x10-3
Stokes
cm2/s
104
1
9.295x102
DIMENSIÓN
otra
lb f-pie
0.738
7.38x10-8
1
Poundal-s
lbf-s/pie2
2.1168x10 3
2.1168x10 2
1
ML2T-2
ML-1T-1
L2T-1
2
pie /s
10.758
1.0758x10 5
1