CUARTO BIMESTRE CUARTO FÍSICA

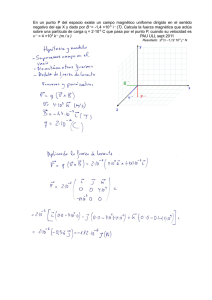
Física
1
Electrostática I
Cuerpo cargado negativamente:
Desde tiempos muy antiguos se conoce la propiedad
que poseen algunos cuerpos de atraer a otros cuerpos
después de ser frotados. Ya tales de mileto (640 –
547 a.c.) hizo experimentos en los que demostró
que el ámbar, después de ser frotado con la piel de
un animal, atraía ciertas semillas. Este fenómeno se
denominó electricidad, y la propiedad que se supone
que adquirían los cuerpos al frotarlos, carga eléctrica.
Un cuerpo se encuentra cargado negativamente si ha
ganado electrones.
Cuerpo con
carga negativa
# e– > #p+
La electrostática es la rama de la física que estudia
los efectos mutuos que se producen entre dos o más
cuerpos en estado de reposo como consecuencia de
su carga eléctrica estudia cargas eléctricas en reposo.
Representación: Q < 0
Cuerpo cargado positivamente:
Un cuerpo se encuentra cargado negativamente si ha
perdido electrones.
Electrización de los cuerpos
El comportamiento eléctrico de los cuerpos está
íntimamente relacionado con la estructura de la
materia. Como se sabe, los cuerpos están formados
por entidades elementales llamadas átomos. En los
átomos existen unas partículas cargadas, llamadas
protones (carga positiva), electrones (carga negativa);
así como también partículas sin carga denominados
neutrones.
Cuerpo con
carga positiva
# e– < #p+
Representación: Q > 0
Cuantificación de la carga
Se define que un cuerpo es eléctricamente neutro
si posee igual cantidad de electrones y protones.
Mientras que un cuerpo se encuentra cargado si ha
perdido o ganado electrones.
Para cuantificar la carga eléctrica de un cuerpo se
utiliza una magnitud física denominada cantidad de
carga eléctrica (Q), cuya unidad en el S.I. es el coulomb
(C), y se calcula mediante la siguiente ecuación:
A continuación se explica básicamente como se
establece el signo de la carga eléctrica de un cuerpo.
Q = ± e–.n
Cuerpo eléctricamente neutro:
Donde las magnitudes y sus respectivas unidades en
el S.I. son:
Un cuerpo es eléctricamente neutro si posee igual
cantidad de electrones y protones.
+: Si el cuerpo pierde electrones
–: si el cuerpo gana electrones
Cuerpo neutro
Q: cantidad de carga eléctrica (C).
# e– = #p+
|e–|: valor absoluto del valor de la carga eléctrica del
electrón (1.6 × 10–19C).
Representación: Q = 0
4.°
año
n: número de electrones ganados o perdidos
3
FÍSICA
1
ELECTROSTÁTICA I
Observación: Una carga eléctrica puede
expresarse en función a ciertas cantidades
equivalentes, por ejemplo:
1mC = 10–3C
1m
mC = 10–6C
1nC = 10–9C
F =
K.Q1.Q2
d2
Donde las magnitudes y sus respectivas unidades en
el S.I. son:
|F|: modulo de la fuerza eléctrica (N).
Leyes de la electrostática
|Q1| y |Q2|: Valores de las cargas eléctricas (C).
Ley cualitativa
K: Constante eléctrica en el vacío ≈ 9 × 109 Nm2/C2.
d: Distancia de separación entre las cargas eléctricas (m).
"Cargas del mismo signo se repelen y cargas de signo
contrario se atraen"
F
Observación: Las fuerzas eléctricas
dependen del medio en el que están
situadas las cargas. No es igual la fuerza
existente entre dos cargas cuando están en
el vacio que cuando están en otro medio
material, como el aceite o el agua.
F
atracción
F
F
repulsión
F
F
Z
repulsión
Ley cualitativa (Ley de Coulomb)
El físico francés Charles Coulomb (1736 – 1806),
utilizando una balanza de torsión, estudio las fuerzas
con las que se atraían o repelían los cuerpos cargados
llegando a determinadas conclusiones, las cuales
fueron resumidas y establecidas en una ley física
denominada ley de coulomb.
La ecuación de ley de coulomb establece que el
modulo de la fuerza (F ) con la que dos cargas (Q1 y Q2)
se atraen o se repelen, es directamente proporcional
al producto de dichas cargas e inversamente
proporcional al cuadrado de la distancia (d) que las
separa.
F
F
Q1
d
Principio de superposición de las fuerzas eléctricas:
Si un cuerpo electrizado interactúa con varias
cargas eléctricas, entonces la fuerza eléctrica resultante que actúa sobre dicho cuerpo es igual a
la suma vectorial de todas fuerzas que le ejercen
cada partícula cargada.
Q1
Q3
Q2
F2
F3
F1
Q2
FR = F1 + F2 + F3
Trabajando en clase
Integral
Resolución:
Aplicando la fórmula:
Q = ± e–.n
Tomando el signo «+» y reemplazando los datos:
1. Determina el número de electrones perdidos en
una carga eléctrica de +32 × 10–19 C.
1
FÍSICA
4
4.°
año
ELECTROSTÁTICA I
Q = +32 × 10–19C y e– = 1,6 × 10–19 C
⇒ 32 × 10–19 = (1,6 × 10–19).n
∴ n = 20
Resolución:
Graficando el enunciado
Q1 = 2m
mC = 2 × 10–6 C
Q2 = 3m
mC = 3 × 10–6 C
d = 3 cm × 10–2 cm
2. Calcula el número de electrones perdidos en una
carga eléctrica de +64 × 10–19 C.
Aplicando la fórmula para calcular el módulo de
la fuerza eléctrica.
3. Si un cuerpo eléctricamente neutro gana 5 × 10
electrones, calcula su carga eléctrica (en C).
20
9
–6
–6
Fe = 9 × 10 × 2 × 10 × 3 × 10
(3 × 10–2)2
4. Indica las cargas correctas: C
Q1 = –8 × 10–19C
Q2 = –5 × 10–19C
Q3 = +12 × 10–19C
∴ Fe = 60 N
9. Dos cargas eléctricas de 7 mC y 3 mC se separan
una distancia de 3 cm. Calcula el módulo de la
fuerza eléctrica (en N) entre las cargas.
UNMSM
10. Dos esferas conductoras idénticas, pequeñas, cuyas cargas son +35 mC y –9 mC se encuentran separados una distancia de 90 cm. ¿Cuál es ahora la
fuerza de interacción (en N) entre ellas?
5. Dos cargas de +4 × 10–6C y –5 × 10–6C se encuentran separadas en una distancia de 3m. ¿Cuál es el
módulo de la fuerza (en N) con que se atraen?
Resolución:
Graficando el enunciado:
Q1 = +4 × 10–6 C
11. Dos partículas puntuales con cargas q1 y q2 se
atraen con una fuerza de magnitud F12. Si la carga q2 se aumenta al triple y también se triplica la
distancia entre ellas, determine la nueva fuerza
electrostática en función de F12.
Q2 = –5 × 10–6 C
d=3m
12. Dos cargas de +4 × 10–3 C y –2 × 10–6 C se encuentran separadas una distancia de 2m. ¿Cuál es el
módulo de la fuerza (en N) con que se atraen?
k|Q1||Q2|
Aplicando la fórmula: Fe =
d2
Reemplazando los datos:
9 × 109 × 4 × 10–6 × 5 × 10–6
Fe =
(3)2
13. Dos cargas de –7 × 10–2 C y –4 × 10–7 C se encuentran separadas una distancia de 3 m. Calcula el
módulo de la fuerza (en N) con que se atraen?
Fe = 2 × 10–2N
14. Se tienen dos cargas eléctricas de +7 × 10–8 C y
–6 × 10–1 C separados una distancia de 9 m. Determina el módulo de la fuerza de interacción en
newton.
6. Se tienen dos cargas eléctricas de +4 × 10–5 C y –3 × 10–5C
separados una distancia de 6 m. Determina el
módulo de la fuerza de interacción (en N) entre
las cargas.
UNI
15. Se tienen tres cargas eléctricas puntuales cuyos
valores son qA = –9 mC; qB = +2 mC; qC = –6 mC
dispuestas como se muestra en la figura, determina el módulo de la fuerza eléctrica resultante (en
N) sobre la carga «C».
7. Dos cargas eléctricas de +5 × 10–5 y –9 × 10–5 C se
separan una distancia de 3cm. Calcula el módulo
de la fuerza eléctrica (en N) entre ellas.
8. Se tienen dos cargas de 2 mC y 3 mC respectivamente y están separadas una distancia de 3 cm.
¿Cuánto vale la fuerza de interacción electrostática (en N) entre ellas?
4.°
año
A
B
3 cm
5
C
6 cm
FÍSICA
1
ELECTROSTÁTICA I
Resolución:
Analizando el gráfico y las fuerzas sobre la carga
«C».
9 mC = 9 × 10–6 C
A
dispuestas como se muestra en la figura, determina el módulo de la fuerza eléctrica resultante (en
N) sobre la carga «q0».
2 mC = 2 × 10–6 C –6 mC = –6 × 10–6 C
FBC
FAC
C
B
q1
Piden el módulo de la fuerza resultante, por vectores:
FR = |FBC – FAC| ... 1
q1
9
–6
–6
⇒ FBC = 9 × 10 × 2 × 10 × 6 × 10 = 30 N
(6 × 10–2)2
FÍSICA
q0
q2
2m
–6
18. Un cuerpo de 20 gramos de masa tiene una carga
Q y reposa sobre una superficie plana horizontal
aislada. Si le acercamos verticalmente desde abajo otro cuerpo con la misma cantidad de carga Q
hasta una distancia de 20cm, el peso del primer
cuerpo se hace cero. Calcula el valor de la carga
Q. (k = 9 × 109 Nm2/C2; g = 10,0 m/S2).
Entonces reemplazando los valores de FBC y FA en
la ecuación 1 se tiene:
FR = |30 – 60|
∴ FR = 30 N
16. Se tienen tres cargas eléctricas puntuales cuyos
valores son q0 = 2 mC, q1 = 50 mC, q2 = –40 mC,
1
2 cm
q3
3m
⇒ FAC = 9 × 10 × 9 × 10 × 6 × 10 = 60 N
(9 × 10–2)2
–6
q2
17. Determina el módulo de la fuerza resultante (en
N) sobre la carga «q3». Si los valores de las cargas
eléctricas son q1 = q2 = q3 = 2 × 10–4 C.
Luego calculando FAB y FAC
9
3 cm
6
4.°
año
2
Electrostática II
Campo eléctrico
Reemplazando la ecuación anterior en la definición
de la intensidad de campo eléctrico:
Teniendo en cuenta la ley de Coulomb, podemos
deducir que toda carga eléctrica genera una fuerza
eléctrica sobre cualquier otra carga colocada en su
proximidad. Por lo tanto, es válido suponer que
a cualquier carga eléctrica se le asocia una región
que permite la interacción (fuerza) con otras cargas
eléctricas.
A la región que rodea una carga eléctrica, se le asocia
un concepto físico denominado campo eléctrico, de
tal manera que el campo eléctrico es toda la región del
espacio en la que dicha carga eléctrica ejerce fuerzas
sobre otras cargas eléctricas.
K.|Q||q|
2
|E | = d
|q|
Se obtiene:
|E | =
Esta última ecuación nos da otra forma de calcular
la intensidad del campo eléctrico, conociendo para
ella el valor de la carga fuente y la distancia sobre el
cual se ubica el punto donde se quiere medir el campo
eléctrico.
E
P
d
Intensidad de campo eléctrico (E ):
Magnitud física vectorial que se utiliza para cuantificar
el campo eléctrico establecido por una carga eléctrica
(Q), también llamada «carga fuente».
F
P
Donde las magnitudes y sus respectivas unidades en
el S.I. son:
|E|: valor de la intensidad de campo eléctrico (N/m).
|Q|: valor de la carga fuente (C).
d: distancia donde se ubica el punto «P».
K: constante eléctrica en el vacío 9 × 109 Nm/C2.
E
Líneas de fuerza y dirección de la intensidad del
campo eléctrico:
Q
Para representar el campo eléctrico se define las líneas
de fuerza, estas líneas salen de la carga fuente si esta
es positiva y entran a la carga fuente si tiene signo
negativo.
El valor de la intensidad de campo eléctrico se calcula
mediante la siguiente ecuación:
|E | = |F |
|q|
|E | = K|Q|
d2
Q
La intensidad de campo eléctrico (E) en un punto
dado se obtiene dividiendo la fuerza (F ) que el campo
ejerce sobre una carga de prueba situada en ese punto
y el valor (+q) de dicha carga de prueba.
F
+q
d
K.|Q|
d2
Unidad en el S.I.
newton/metro (N/m)
Carga Positiva
Carga Negativa
Teniendo en cuenta el valor de F , definido mediante
la siguiente ecuación:
K.|Q1||Q2|
|F | =
d2
4.°
año
7
FÍSICA
2
ELECTROSTÁTICA II
La dirección de la intensidad del campo eléctrico
siempre es tangente a las líneas de fuerza y en su
mismo sentido.
Líneas de fuerza
d
E1
Donde en este caso si se considera el signo de la carga
eléctrica.
Las magnitudes y sus respectivas unidades en el S.I.
son:
V: potencial eléctrico (V).
Q: carga fuente (C).
d: distancia donde se ubica el punto “P”.
K: constante eléctrica en el vacío ≈ 9 × 109 Nm2/C2.
Principio de superposición de las intensidades de
campos eléctricos:
Debido a que la intensidad del campo eléctrico
es una magnitud vectorial. Si se tienen varias
intensidades, la intensidad de campo eléctrico
resultante se calculara aplicando el principio de
superposición.
–q1
Como el potencial eléctrico es una magnitud escalar
(no posee dirección), entonces si se tienen varias
cargas el potencial eléctrico resultante en un punto
«P» determinado, es igual a la suma de los potenciales
eléctricos de cada carga eléctrica.
–q2
E3
E2
E1
Unidad en el S.I.
volt(V)
VP = +K.Q
d
E2
Z
P
Q
Q1
P
P
d1
+q3
VP = V1 + V2 + V3
d2
Ep = E1 + E2 + E3
d3
Q2
Q3
Campo eléctrico uniforme.
Un campo eléctrico es uniforme, si la intensidad del
campo eléctrico es constante. Se representa mediante
líneas de fuerzas paralelas.
E
A
Nota: El valor del potencial eléctrico a una
distancia muy lejana (infinito) de una carga
fuente, se define como cero.
V∞
∞=0
B
Superficie equipotencial:
Una superficie equipotencial es aquella en la que todos
sus puntos tienen igual potencial eléctrico. El mismo
concepto se le asocia a una línea equipotencial.
C
Superficies
equipotenciles
|EA | = |EB | = |EC |
B
Propiedad del campo eléctrico de almacenar energía
eléctrica al ubicar una carga en él.
Para un punto «P» ubicado a cierta distancia de una
carga «Q», el potencial eléctrico se calcula aplicando
la siguiente ecuación:
2
FÍSICA
Q
D
Potencial eléctrico (VP)
A
C
VA = VB
8
VB ≠ VC
VC = VD
4.°
año
ELECTROSTÁTICA II
Las líneas de fuerza de un campo eléctrico, siempre
es perpendicular a sus superficies equipotenciales.
Las características de este trabajo son:
Z El trabajo del campo es independiente de la trayectoria.
Z Para una trayectoria cerrada, el trabajo desarrollado por el campo es nulo.
Z El trabajo efectuado por el campo va a depender
de la carga transportada y de la diferencia de potencial de los puntos de donde parte y llega la carga transportada.
E
S1
S2
S3
Trabajo desarrollado por un agente externo (WA.E.):
Donde la figura:
E: intensidad del campo eléctrico.
S1, S2 y S3: superficies equipotenciales.
Q
q0
B
A
Agente
Externo (A.E.)
Trabajo desarrollado por el campo eléctrico
(WCAMPO)
El trabajo externo será igual al valor del trabajo que
realiza el campo eléctrico pero signo negativo.
Cuando una carga se mueve de un punto a otro en el
interior de un camino eléctrico, el campo desarrolla
un trabajo sobre la carga, este valor se calcula
aplicando la siguiente ecuación:
WCAMPO = –WA.E.
WAA.E.
= q0(VB – VA)
→B
q0
A
Q
B
Nota: Sobre una superficie equipotencial
no se realiza trabajo.
S
WCAMPO
A → B = q0(VA – VB)
Donde las magnitudes y sus respectivas unidades en
el S:I. son:
: cantidad de trabajo realizado por el campo (J).
WCAMPO
A→B
B
q0: carga de prueba (C).
WA → B = 0
A
VA y VB: potenciales eléctricos en los puntos A y B
respectivamente (V).
Trabajando en clase
Integral
Resolución:
Aplicando la fórmula de la intensidad del campo
eléctrico.
E = k|Q|
d2
Reemplazando los datos
9
–8
E = 9 × 10 × 7 × 10
9
∴ E = 70 N/C
1. Determina la intensidad de campo eléctrico (en
N/C) en el punto «P», si el valor de la carga eléctrica Q es –7 × 10–8 C.
3m
Q
4.°
año
P
9
FÍSICA
2
ELECTROSTÁTICA II
2. Calcula la intensidad de campo eléctrico (con
N/C) en el punto «P», si el valor de la carga eléctrica Q es +16 × 10–8 C.
Q
P
Q1
4m
(2)
3. Determina el potencial eléctrico (en kV) de un punto ubicado a 6 m de una carga positiva Q = 2 mC.
2 cm
QB
53°
B
5. Calcula el valor de la intensidad de campo eléctrico
(en N/C) en el punto «M», si los valores de las cargas
eléctricas son: Q1 = + 6 × 10–8 C y Q2 = –8 × 10–8 C.
3m
QB = 6 mC = 6 × 10 C
2m
B
5m
37°
C
VR = VB + VC
9
–6
9
–6
⇒ VR = 9 × 10 × 6 × 10 + 9 × 10 ×(–8 × 10 )
3
4
∴ VR = 0
9. Determina el potencial eléctrico total (en kV) en
el punto «A».
Luego calculando E1 y E2
9
–8
⇒ E1 = 9 × 10 × 6 × 10 = 60 N/C
(3)2
3 mC
5m
9
–8
⇒ E2 = 9 × 10 × 8 × 10 = 180 N/C
(2)2
Reemplazando los valores de E1 y E2 en 1
⇒ ER = 60 + 180
∴ ER = 240N/C
A
37°
+4 mC
10. A 1,0m a la izquierda de una partícula de carga
q1 = 1,0 mC, se encuentra una partícula de carga
q2 = –1,0 mC. Determine el potencial eléctrico, debido a ambas cargas, a 1,0m a la derecha de la partícula de carga q1 (considere k = 9 × 109 Nm2C–2).
6. Determina el valor de la intensidad de campo
eléctrico (en N/C) en el punto «P», si los valores
de la cargas eléctricas son: Q1 = –32 × 10–8 C y
Q2 = +5 × 10–18 C.
FÍSICA
53°
Piden el potencial eléctrico resultante, escalarmente:
Q2 = –8 × 10–8 C
Piden el módulo de la intensidad resultante, vectorialmente
ER = E1 + E2 ... 1
2
QC
C
4m
QC = 8 mC = –8 × 10–6 C
–6
Resolución:
Analizando el gráfico
3m
5m
37°
Analizando el gráfico
A
Q2
M E2
2m
E1
1 cm
A
UNMSM
Q1 = +6 × 10–8 C
A
8. Calcula el potencial eléctrico en (en V) en el vértice «A» del triángulo, si los valores de la cargas
eléctricas son: QB = 6 mC, QC = –8 mC.
9m
3m
2 mC
(1)
8 mC
4. Calcula el valor de la intensidad de campo eléctrico
(en N/C) y el potencial eléctrico (en V) de en el punto «P», si el valor de la carga eléctrica Q es –9 mC.
Q
P
M
3m
7. Determina la intensidad de campo eléctrico resultante en ( N/C) en el punto «A».
2m
Q1
Q2
P
10
4.°
año
ELECTROSTÁTICA II
11. La magnitud del campo eléctrico y el potencial
eléctrico a cierta distancia de una carga puntual
son 3 × 102 N/C y 900 V, respectivamente. Halle la
magnitud de dicha carga. (Considere K = 9 × 109
Nm2C–2)
Q1
Resolución:
Analizando el gráfico:
Q1 = 2 × 10–8 C
Q2 = 18 × 10–8 C
E2 M E1
P
Como el valor del campo eléctrico es cero, se cumple:
E1
∴
14. Calcula el valor de la intensidad de campo eléctrico
(en N/C) y el potencial eléctrico (en V) en el punto
«P», si el valor de la carga eléctrica Q es 81 C.
E2
x = 15 m
16. Dos cargas puntuales Q1 = –50 mC y Q2 = 100 mC
están separadas una distancia de 10cm. El campo
eléctrico en el punto P es cero. ¿A qué distancia,
en cm, de Q1, esta P?
Q1
Q2
P
P
9m
x
UNI
10 cm
17. Dos cargas de igual signo se colocan a lo largo de
una recta con 2 m de separación. La relación de cargas es 4, calcule (en nC) la carga menor si el potencial eléctrico en el punto sobre la recta que se encuentra a igual distancia de las cargas es de 9V.
(k = 9,109 Nm2/C2; 1nC = 10–9C)
15. Determina la distancia «x» en metros, para que la
intensidad de campo eléctrico sea nulo en el punto «M», si los valores de las cargas eléctricas son:
Q1 = +2 × 10–8 C y Q2 = +18 × 10–8 C.
año
=
K.2 × 10 K.18 × 10–8
=
(20 – x)2
x2
–8
13. Determina el potencial eléctrico (en V) de un punto
ubicado a 36 m de una carga positiva Q = 12 mC.
4.°
x
(20 – x)
20 m
2m
Q
x
20 m
12. Calcula la intensidad de campo eléctrico (en N/C)
en el punto «P», si el valor de la carga eléctrica Q
es + 6 × 10–4 C.
Q
Q2
M
11
FÍSICA
2
3
Electrodinámica I
Sentido real de la corriente eléctrica:
La electrodinámica es la parte más importante de la
electricidad que se encarga de estudiar el movimiento
de los portadores de carga y los fenómenos eléctricos
producidos por el traslado de las cargas eléctricas a
través de los conductores.
Las líneas de fuerza están orientados del polo positivo
(+) al polo negativo (–) siendo el electrón la carga
móvil en un conductor solido, este se movería en
sentido contrario a las líneas de fuerza por ser de
carga negativa, esto quiere decir que en un conductor
sólido, las cargas eléctricas (negativas) se mueven
del polo negativo (menor potencial) al polo positivo
(mayor potencial).
→
→
I
E
Conceptos previos
Conductor eléctrico: sustancia que posee un gran
número de electrones libres.
Pila (fuente de voltaje): es un dispositivo eléctrico
que establece, mediante reacciones químicas, una
diferencia de potencial entre sus extremos.
Corriente eléctrica
Sentido convencional de la corriente eléctrica:
La palabra «corriente» significa movimiento,
desplazamiento o circulación de algo. ¿Qué es lo
que puede desplazarse o circular en los conductores
eléctricos?. La respuesta son electrones que se
encuentran «libres» dentro del conductor.
Por razones históricas, convencionalmente asumimos
que son los portadores de carga positiva los que se
movilizan en un conductor.
Por lo tanto, convencionalmente decimos que la
corriente eléctrica va de mayor a menor potencial
eléctrico.
→
→
I
E
Este fenómeno microscópico se puede manifestar en
los conductores bajo la influencia de ciertos factores
entre los cuales no puede faltar una diferencia
de potencial eléctrico, la cual puede establecerse
mediante una batería, pila o alternador.
¿Cómo se establece la corriente eléctrica dentro
de un conductor?
A partir de ahora solo trabajaremos con el sentido
convencional de la corriente eléctrica, a menos que
nos pidan trabajar con el sentido real de la corriente.
Para cuantificar la corriente eléctrica se utiliza una
magnitud física llamada intensidad de corriente
eléctrica.
Para que exista corriente eléctrica dentro de un
conductor, se necesita que exista una diferencia
de potencial entre los extremos del conductor. Por
ejemplo si establecemos un potencial eléctrico
positivo (+) en un extremo y un potencial negativo
(–) en el otro extremo se establecerá una diferencial
de potencial.
–
–
–
3
FÍSICA
Intensidad de corriente eléctrica:
+
+
+
Magnitud física escalar que cuantifica el grado de
corriente eléctrica que circula en un conductor debido
12
4.°
año
ELECTRODINÁMICA I
a su diferencia de potencial entre sus extremos. Su
unidad en el S.I. es el ampere o amperio (A).
en otros casos las trayectorias de los portadores son
desviadas por la presencia de impurezas o vacíos; en
suma, todos estos factores conllevan a la atribución
de una característica fundamental para cada material
y la denominaremos Resistividad eléctrica (ρ).
Si a través de la sección transversal de un conductor
pasa, en un intervalo de tiempo «∆t», una cantidad
de carga «Q» la intensidad de corriente eléctrica se
calculara mediante la siguiente ecuación:
I
∆t
|Q|
Fue poulliet, un físico francés que decidió plantear el
cálculo de la resistencia eléctrica (R) para los metales
sólidos.
Poulliet planteo que la resistencia que ejerce un cuerpo
conductor es directamente proporcional a la longitud
(L) del conductor, e inversamente proporcional a la
sección recta (A) del conductor, siendo el factor de
proporcionalidad la resistividad (ρ).
Sección recta o
Sección trasversal.
Número de
Electrones libres (n)
L
A
I = |Q|
∆t
R = r. L
A
Donde las magnitudes y sus respectivas unidades en
el S.I. son:
Del tema anterior tenemos presente que la cantidad
de carga se calcula mediante la siguiente ecuación:
|Q| = |e–|.n
Resistor:
Se le llama así a todo cuerpo con determinada
resistencia eléctrica. Los símbolos que se utilizan para
identificar a un resistor son:
Reemplazando en la definición de la intensidad de
corriente se tiene:
|e–|.n
I=
∆t
Despejando se obtiene una ecuación que nos relaciona
la intensidad de corriente eléctrica (I) con el número
de electrones (n) que pasan a través de un conductor
en un intervalo de tiempo (∆t):
R
R
Resistor fijo
Resistor variable
(Potenciómetro)
Asociación de resistores
I. ∆t = |e–|.n
Generalmente se tiene un conjunto de resistores
asociados, cada una con su respectiva resistencia
eléctrica, a partir de ese conjunto se requiere obtener
una forma para calcular una resistencia eléctrica
equivalente.
Resistencia eléctrica
Todos sabemos de los beneficios de la corriente
eléctrica y pugnamos por aprovecharla en grandes
cantidades; sin embargo, la naturaleza compleja de la
materia nos impone muchas dificultades, tales como
el movimiento caótico de los electrones libres en los
metales que chocan constantemente con los iones un
tanto estables en la red cristalina incrementándose
así la agitación térmica y evitando un flujo notable;
año
Unidad en el S.I.: ohm, ohmio (Ω)
Donde las magnitudes y sus respectivas unidades en
el S.I. son:
R: resistencia eléctrica (Ω).
L: longitud del conductor (m).
A: área de la sección recta (m2).
ρ: resistividad eléctrica (Ω.m).
I: intensidad de corriente eléctrica (A).
|Q|: cantidad de carga eléctrica (C).
∆t: intervalo de tiempo (s).
4.°
r
Las asociaciones más básicas de resistores son en
serie y paralelo.
A continuación estudiaremos como obtener una
resistencia eléctrica (equivalente) a partir de las dos
asociaciones básicas mencionadas.
13
FÍSICA
3
ELECTRODINÁMICA I
Z
Serie:
R2
R1
a
a
Req
R3
1
1
1
1
=
+
+
Req R1 R2 R3
b
b
Resistencia eléctrica equivalente entre los puntos
«a» y «b».
Req = R1 + R2 + R3
Z
Nota: Si se tiene dos resistencias eléctricas
en paralelo entre dos puntos «A» y «B», la
fórmula práctica para calcular la resistencia
eléctrica equivalente es la siguiente:
Resistencia eléctrica equivalente entre los puntos
«a» y «b» de un conductor.
Paralelo:
R1
R2
a
b
R3
a
R1
Req
RAB =
R2
b
R1 . R2
R1 + R2
Trabajando en clase
Integral
UNMSM
1. A través de un conductor circula una carga de 120 C
durante un minuto; calcula la intensidad de corriente eléctrica (en A)
5. Por un conductor circulan 6,4 A de corriente. Determina el número de electrones que pasa por su
sección recta en 1 min.
Resolución:
Aplicando la fórmula
I.t = |e–|.n
Reemplazando los datos: I = 6,4 A
t = 1 min = 60 s y |e–| = 1,6 × 10–19 C.
⇒ 6,4 × 60 = 1,6 × 10–19 × n
∴ n = 24 × 1020
Resolución:
Aplicando la fórmula:
Q = It
Reemplazando los datos Q = 120 C
t = 1 min = 60 s.
⇒ 120 = I.60
∴ I=2A
2. A través de un conductor circula una carga de 480
C drante unos 2 minutos; calcula la intensidad de
corriente electrica (en A).
6. Si por un conductor eléctrico circula 1,6 A de corriente eléctrica. Calcula el número de electrones
que pasa a través de su sección transversal en 3
min.
3. La intensidad de corriente eléctrica en un conductor es 0,2 A. calcula la cantidad de carga eléctrica (en C) que pasa a través de su sección transversal en cinco minutos.
7. Por un conductor de sección transversal uniforme
circula una corriente de 320 mA. ¿Cuál es el numero de electrones que atraviesan la sección transversal del conductor en 0.1s? (e–=1.6 × 10–19 C)
4. Calcula la resistencia eléctrica (en Ω) de un conductor de 2 m de largo y 4 × 10–6 m2 de sección
trasversal. Considere que la resistividad eléctrica
del conductor es r = 8 × 10–8 m.Ω.
3
FÍSICA
8. Determina la resistencia eléctrica equivalente (en Ω)
entre los puntos c y p, en el caso (a) y (b) respectivamente.
14
4.°
año
ELECTRODINÁMICA I
a)
b)
3Ω
c
12 Ω
4Ω
p
2Ω
1Ω
13. Determina la resistencia eléctrica equivalente (en Ω)
entre los puntos c y p.
p
2Ω
3Ω
Estas resistencias estan en serie.
⇒ Req = 1 + 2 + 3
∴ Req = 6 Ω
p
t
12 Ω
a
UNI
15. Determina la resistencia eléctrica equivalente (en Ω)
entre los puntos c y p.
5Ω
4Ω
c
p
1Ω
4Ω
c
8Ω
5Ω
9Ω
3Ω
20 Ω
3Ω
15
p
p
5Ω
9Ω
20 Ω
⇒
12
Ω
serie
Estos estan en paralelo
⇒ 1 =1+ 1 + 1
Req 5 20 12
e
año
1Ω
serie
7Ω
4.°
20 Ω
Resolución:
11. Calcula la resistencia eléctrica equivalente (en Ω)
entre los puntos c y e.
8Ω
c
p
1Ω
5Ω
7Ω
5Ω
2Ω
p
10. Calcula la resistencia eléctrica equivalente (en Ω)
entre los puntos a y p.
3Ω
p
9Ω
4Ω
p
Estas resistencias están en paralelo.
⇒ 1 = 1 + 1
Req 4 12
∴ Req = 3 Ω
9. Calcula la resistencia eléctrica equivalente (en Ω)
entre los puntos c y p.
4Ω
c
6Ω
9Ω
14. Determina la resistencia eléctrica equivalente (en Ω)
entre los puntos t y p.
12 Ω
4Ω
6Ω
c
c
b)
4Ω
p
3Ω
1Ω
5Ω
20 Ω
p
Resolución:
a)
c
12. Calcula la resistencia eléctrica equivalente (en Ω)
entre los puntos c y p.
c
c
c
∴ Req = 3 Ω
FÍSICA
3
ELECTRODINÁMICA I
16. Determina la resistencia eléctrica equivalente (en Ω)
entre los puntos a y b.
2Ω
4Ω
12 Ω
b)
b
p
2Ω
u
c
6Ω
b)
p
3
FÍSICA
7Ω
6Ω
4Ω
3Ω
8Ω
3Ω
3Ω
18. Determina la resistencia eléctrica equivalente (en Ω)
entre los puntos b y c, en el caso (a) y (b) respectivamente.
a)
4Ω
b
17. Calcula la resistencia eléctrica equivalente (en Ω)
entre los puntos u y p, en el caso (a) y (b) respectivamente.
a)
8Ω
15 Ω
2Ω
a
u
16
b
6Ω
2Ω
6Ω
6Ω
6Ω
c
4.°
año
4
Electrodinámica II
Los ejemplos relaciones con la corriente eléctrica
son variados, yendo desde las grandes corrientes
que constituyen los relámpagos hasta las diminutas
corrientes nerviosas que regulan nuestra actividad
muscular. Pero nostros estamos familiarizados más
con las corrientes eléctricas que circulan en los
conductores solidos (en el alambrado doméstico o
en los artefactos), por los semiconductores (en los
circuitos integrados), por los gases (en las lámparas
fluirescentes), por ciertos líquidos (en las baterías),
e incluso en espacios vacíos (los tubos de imagen de
TV).
Como se estudió en el tema anterior, para que se
produzca una corriente sobre un conductor debe
establecerse una diferencia de potencial, o también
llamado voltaje. Uno de los primeros físicos que
estudio la relación entre intensidad de corriente,
voltaje y resistencia eléctrica fue Georg Simon Ohm
(1787 - 1854); luego de un arduo trabajo concluyo su
estudio enunciando una formula, a la cual luego se le
denomino Ley de Ohm.
V: diferencia de potencial o voltaje (V).
I: intensidad de corriente eléctrica (A).
R: resistencia eléctrica (Ω).
Todo conductor, cuya resistencia eléctrica no cambia,
se denominará óhmico y la gráfica V-I tendrá la
siguiente forma:
V
P
V
V1
O
I
Aplicación práctica de la ley de Ohm
Si tenemos en un circuito varias resistencias y
voltajes, se puede establecer una formula practica
para solucionar este tipo de situaciones.
Para explicar este caso práctico se presenta el siguiente
circuito, en el cual se pide calcular la intensidad de
corriente eléctrica que circula en el circuito.
V1 = 30V R2 = 3Ω V2 = 60V
R3 = 4Ω
1Ω = R1
V3 = 70V
+
Se cumple:
–
V
Luego dibujamos las intensidades de corriente
eléctricas que «salen» de cada voltaje:
V1 = 30V R = 3Ω V2 = 60V
2
V
I
De manera práctica se enuncia la ley de Ohm
mediante la siguiente ecuación:
R=
I3
I1
R3 = 4Ω
1Ω = R1
V = I.R
I2
Donde las magnitudes y sus respectivas unidades en
el S.I. son:
año
I
Tangq
q=R
Se califica así a las conclusiones teórico prácticas
logradas por Georg Simon Ohm en lo referente a la
conductividad uniforme de la mayoría de resistores
metálicos a condiciones ordinarias.
Si se tiene el siguiente circuito:
R
4.°
I1
Además de la gráfica se deduce lo siguiente:
La ley de Ohm
I
q
V3 = 70V
17
FÍSICA
4
ELECTRODINÁMICA II
Luego aplicamos la formula práctica de la ley de Ohm
aplicado a este tipo de circuitos:
Observaciones importantes
Teniendo en cuenta el siguiente gráfico se enuncia
los conceptos de NUDO y MALLA.
A
B
Veq = Ieq . Req
Para obtener la resistencia equivalente (Req) en el
circuito se aplica las formulas ya mencionadas y
practicadas en el capítulo anterior. En este caso se
asume de manera práctica que las resistencias se
encuentran en serie, de tal manera que la resistencia
equivalente se calcula de la siguiente manera:
Req = 1 + 3 + 4 ⇒ Req = 8Ω
Leyes de Kirchhoff
1. Primera ley de Kirchhoff (Ley de los nudos)
La suma de corrientes que entran a un nudo es
igual a la suma de corrientes que salen del nudo.
I I2
Luego reemplazando en la formula práctica de la ley
de Ohm:
40 = Ieq × 8
\ Ieq = 5 A
1
A I
3
Instrumentos de medición eléctricos
1. Amperímetro ( A )
En el nodo «A»:
I3 = I1 + I2
Se emplea para medir la intensidad de corriente
que pasa a través de un conductor o una resistencia. El amperímetro es conectado en serie y por
ello se diseña con la menor resistencia posible.
Cuando se dice que el amperímetro es ideal, se
considera que la resistencia interna es cero.
I
R
A
En general:
nudo
2. Segunda ley de Kirchhoff (Ley de Mallas)
La suma algebraica de las fuerzas electromotrices
(f.em) de una malla cualquiera, es igual a la suma
algebraica de los productos de las intensidades
por las respectivas resistencias.
R1
Se emplea para medir la diferencia de potencial
entre dos bornes del circuito o entre los bornes de
una resistencia.
Se conecta en paralelo y por ello se diseña con la
«mayor» resistencia interna posible.
Un voltímetro se denomina ideal cuando asumimos que su resistencia interna es muy grande,
de tal manera que impide el paso de la corriente
eléctrica a traves de él.
V
ε1
I1
I1
R2
ε2
Suma de las fem = Suma de las (IR)
⇒ ∑ε = ∑IR
Del circuito mostrado, podemos plantearnos la
siguiente ecuación:
I
FÍSICA
∑I entran al = ∑I salen al
nudo
2. Voltímetro ( V )
4
R2
V3
C
D
V1
V2
A. Nudo: Es el punto de unión de 3 o más elementos eléctricos, como por ejemplo del gráfico son los puntos A, B, C y D.
B. Malla: Es un circuito eléctrico cerrado sencillo por ejemplo del gráfico es el circuito formado por los puntos A - B -C - D - A
Para obtener el voltaje equivalente se tiene que
tener en cuenta las direcciones de las corrientes de
cada voltaje; de esta manera aquellos voltajes, cuyas
intensidades de corrientes eléctricas siguen la misma
dirección, se suman y a este resultado se le resta los
voltajes cuyas intensidades van en dirección opuesta.
Del circuito anterior calculamos el voltaje equivalente:
Veq = 30 + 70 – 60 ⇒ Req = 40 V
A
R3
R1
ε1 + ε2 = I1R1 + I2R2
B
18
4.°
año
ELECTRODINÁMICA II
Potencia eléctrica (P)
P = VI = I2R = V
R
2
Es aquella magnitud escalar que mide la rapidez
con que una máquina o dispositivo transforma y/o
consume la energía eléctrica.
R
I
+
Donde las magnitudes y sus respectivas unidades en
el S.I. son:
Z P: potencia eléctrica, se mide en watt (W).
Z V: voltaje (V).
Z I: intensidad de corriente eléctrica (A).
Z R: resistencia eléctrica (Ω).
V
Trabajando en clase
Integral
1. Calcula la intensidad de corriente eléctrica (en A)
que circula en el circuito.
2Ω
4. Determina la resistencia eléctrica «R».
6Ω
6Ω
40 V
Resolución:
Calculando primero la resistencia equivalente.
R
I = 4A + –
32 V
2Ω
Req = 8 Ω
UNMSM
5. Calcula la lectura del voltímetro ideal.
4Ω
6Ω
40 V
Luego aplicando la fórmula
V = I . Req
⇒ 40 = I . 8
\ I = 5A
20 V +
4Ω
I
20 V +
–
1Ω
10 Ω = Req
6Ω V
⇒ V = I . Req
20 = I . 10
⇒ I = 2A
Luego tomando solo al voltímetro
⇒ V = 2 × 6 = 12V
3. Determina la intensidad de corriente eléctrica (en
A) que suministra la batería de 10 V.
año
V
Resolución
Calculando la intensidad de corriente.
30 V
4.°
6Ω
–
2. Calcula la intensidad de corriente eléctrica (en A)
que circula en el circuito.
2Ω
7Ω
6Ω
3Ω
10 V
19
FÍSICA
4
ELECTRODINÁMICA II
6. Calcula la lectura del voltímetro ideal.
3Ω
24 V +
5Ω
–
10. Determina la lectura que marca el amperímetro.
4V
2V
2Ω
V
8V
7. En el circuito mostrado determina la intensidad
de corriente eléctrica que suministra la batería.
10 V
6Ω 6Ω
1Ω
4Ω
1Ω
11. Determina la potencia disipada en el resistor de 8Ω
del circuito mostrado en la figura adjunta. (Despreciar las resistencias internas de las baterías).
4Ω
6Ω
8. Calcula la lectura que marca el amperímetro.
60 V 3 Ω
12 V
+
+
–
–
2Ω
2Ω
12. Calcula la intensidad de corriente eléctrica (en A)
que circula en el circuito.
5Ω
80 V
A
Resolución
Analizando el gráfico.
60 V
90 V
24 V
3Ω
15 Ω
I1
I2
5Ω
40 Ω
6V
2Ω
2Ω
2Ω
6V
8Ω
30 V
5Ω
A
6V
13. Determina el valor de la resistencia eléctrica R si
el amperímetro registra un valor de 6A.
80 V
R
30 V
I3
40 V
90 V
Aplicando la fórmula práctica de la ley de Ohm.
ΣV = Ieq . Req
2Ω
1Ω
90 + 30 – 60 = Ieq . 12
\ Ieq = 5A
20 V
A
14. Calcula la intensidad de corriente eléctrica (en A)
que circula por la resistencia de 9Ω.
4V
13 V
9. Calcula la lectura que marca el amperímetro.
4Ω
75 V
5Ω
5Ω
15 V
A
30 V
4
FÍSICA
169 V
9Ω
2Ω
6Ω
1Ω
4Ω
20
4.°
año
ELECTRODINÁMICA II
UNI
16. Calcula la intensidad de corriente eléctrica (en A)
que circula por la resistencia de 5Ω.
18 V
2Ω
15. En el circuito que se muestra en la figura, determina la intensidad de corriente eléctrica (en A)
que circula a través de la resistencia de 2Ω.
2V
10 V
6V
16 V
4V
7Ω
2Ω
8Ω
Resolución
El método práctico indica que solo se necesita la
malla de la derecha debido a que nos piden la intensidad de corriente en la resistencia de 2Ω.
2V
10 V
7Ω
10 Ω
30 Ω
20 Ω
82,5 V
2V
18. Dos resistencias de 4Ω y 6Ω, se conectan en paralelo y se le aplica una diferencia de potencial de
12 V por medio de una batería. Calcule la potencia, en watts, suministrada por la batería.
I1
4V
2Ω
I2
Aplicamos el caso práctico:
∑V = Ieq . Req
4 – 2 = Ieq . 2
\Ieq = 1A
año
5Ω
17. Calcule la corriente en A, a través de la resistencia
de 20Ω del circuito mostrado en la figura.
2Ω
4V
Luego:
4.°
1Ω
12 V
21
4Ω
6Ω
FÍSICA
4
5
Electromagnetismo I
La lista de aplicaciones tecnológicas importantes
del electromagnetismo es muy amplia. Por ejemplo,
grandes electroimanes se utilizan para transportar
cuerpos pesados, así también a permitido desarrollar
aparatos muy utilizados en nuestra vida diaria tales
como los transformadores, motores, bocinas, las
cintas magnéticas de audio y video, etc.
El objetivo de este capítulo consiste en estudiar la
relación entre la corriente eléctrica y el magnetismo
(específicamente, los campos magnéticos).
Definición y propiedades del campo magnético
MAGNETISMO
Para representar gráficamente el campo magnético
del imán, trazaremos unas líneas denominado líneas
de campo magnético.
Al igual que el campo eléctrico es generado por
una carga eléctrica y a su vez los cuerpos con masa
generan un campo gravitacional; todo iman y toda
carga eléctrica en movimiento o una corriente
eléctrica generan un campo magnético en el espacio
circundante. Para cuantificar el campo magnético en
cada punto, definimos la magnitud física vectorial
inducción magnética B la cual tiene como unidad en
el S.I. el tesla (T).
El fenómeno del magnetismo fue conocido por los
griegos desde el año 800 A.C. Ellos descubrieron que
ciertas piedras, ahora llamadas magnetita (Fe3O4),
atraían piezas de hierro. La leyenda adjudica el
nombre de magnetita en honor al pastor Magnes,
«los clavos de sus zapatos y el casquillo (o punta) de
su bastón quedaron fuertemente sujetos a un campo
magnético cuando se encontraba pastoreando su
rebaño».
En física se dice que un cuerpo posee la propiedad
de magnetismo, cuando atrae (o repele) piezas de
hierro.
A continuación analizaremos los campos magnéticos
para el caso de un imán y conductores lineales.
Para un imán
Acontecimientos históricos
1269: Pierre de Maricourt, enuncia que un imán
posee dos polos, los cuales posteriormente son
denominados polo norte y polo sur.
1600: William Gilbert, utilizando el hecho de que una
aguja magnética (brújula) se orienta en direcciones
preferidas, sugiere que la Tierra es un gran imán
permanente.
El imán atrae al clavo gracias al campo que la rodea y
que es capaz de ejercer acción a distancia.
Para una corriente eléctrica
1750: Jhon Michell, utilizando una balanza de torsión
demostró que los polos magnéticos se ejercen fuerzas
de atracción y repulsión entre sí, y que estas fuerzas
varían con el inverso del cuadrado de la distancia de
separación.
El físico danés Hans Oersted Logro comprobar
experimentalmente que una corriente eléctrica
produce efectos magnéticos. El descubrió de manera
casual que al hacer circular una corriente eléctrica
por un cable conductor, éste lograba desviar la aguja
imantada de una brújula, lo que probaba que el
movimiento de las cargas eléctricas genera alrededor
de éstas un campo magnético.
1819: Hans Oersted, descubrió la relación entre el
magnetismo y la electricidad.
5
FÍSICA
22
4.°
año
ELECTROMAGNETISMO I
I=0
Al observar al conductor de punta, con la corriente
dirigida hacia el observador se notará que las líneas
de campo van en sentido antihorario mientras que si
se observa por el otro extremo se las verá en sentido
horario.
Aguja
I≠0
imantada
¡No pasa nada!
Se puede concluir de la experiencia de Oersted que
toda corriente eléctrica genera un campo magnético
en el espacio circundante.
Para representar el campo magnético asociado al
conductor rectilíneo, Oersted coloco al conductor en
forma perpendicular al plano de la mesa donde coloc
varias agujas imantadas.
I
I
Regla de la mano derecha
Para determinar el sentido de las líneas del campo se
procede a coger el conductor de manera que el debo
pulgar señale el sentido de la corriente, entonces los
dedos restantes cerrarán la mano en el mismo sentido
de las líneas de fuerza.
Norte
Geográfico
Las agujas apuntan
hacia el norte geográfico
(I = 0)
Líneas del
campo
Líneas del
campo
Si el conductor transporta una corriente eléctrica, las
agujas imantadas de desvían:
I
Vista de perfil (2D)
I
B
x xxx
x xxx
x xxx
x xxx
x xxx
Todas las agujas imantadas que se encuentran a
igual distancia del conductor, se orientan formando
«circunferencias concéntricas», cuyo centro se
encuentra a lo largo del conductor.
Graficando las líneas de campo magnético se obtienen
el siguiente gráfico:
Ley de Biot – Savart
Pocas semanas después de conocerse el
descubrimiento de Oersterd, los físicos Jean B. Biot
y Félix Svart investigaron sobre la intensidad de los
campos magnéticos creados por cirrientes eléctricas.
A estos trabajos se sumaron los aportes de André M.
Ampere y Pierre S.Laplace.
Estableceremos las ecuaciones para calcular las
inducciones magnéticas (B ) a una determinada
distancia de conductores lineales por donde circulan
corrientes eléctricas.
I
Líneas de
campo
magnético
B1
R
B2
Vector
Inducción
Magnética
1. Para un segmento conductor rectilíneo
I
a
4.°
año
b
d
Las líneas del campo magnético son circunferencias
concéntricas que se van separando entre sí a medida
que nos alejamos del centro (del conductor).
p
23
FÍSICA
5
ELECTROMAGNETISMO I
3. Para un conductor rectilíneo tipo arco
El módulo de la inducción magnética en el punto
«P» se calcula aplicando la siguiente ecuación:
B=
m0i
4pd
r
(Cosa
a + Cosb
b)
Donde las magnitudes y sus respectivas unidades
en el S.I. son:
B: módulo de la inducción magnética (T)
i: intensidad de corriente eléctrica (A)
d: distancia de separación entre el punto «P» y el
conductor (m)
m0: permeabilidad magnética del espacio libre,
cuyo valor es 4p
p × 10–7 Tm/A
i
q
O
r
El módulo de la inducción magnética en el punto
«O» se calcula aplicando la siguiente ecuación:
B = iqm0
4pr
Donde:
q: ángulo del arco (radianes)
r: radio del arco (m)
2. Para un conductor rectilíneo muy largo
(infinito)
4. Para un conductor circular o espira circular
P
d
O
r
I
El módulo de la inducción magnética en el punto
«O» se calcula aplicando la siguiente ecuación:
El módulo de la inducción magnética en el punto
«P» se calcula aplicando la siguiente ecuación:
B=
I
B=
m0 i
.
2p d
m0 i
.
2 r
Reemplazando en la ecuación el valor de la permeabilidad magnética «m
m0», obtenemos:
Reemplazando en la ecuación el valor de permeabilidad magnética «m
m0», obtenemos:
B = 2p
p × 10–7. i
B = 2 × 10–7. i
r
d
Trabajando en clase
Integral
B = 2 × 10–730/2
∴ B = 3 × 10–6 T
1. C alcula el módulo de la inducción magnética (en
T) a 2 m de un cable rectilíneo muy largo, que
transporta una corriente de 30 A.
Resolución
30A
2. Calcula el módulo de la inducción magnética (en T) a
2 cm de un cable rectilíneo muy largo, que transporta una corriente de 4 A.
2m
3. Determina el módulo de la inducción magnética
(en T) en el centro de una espira circular de un
conductor de radio igual a p cm y por el cual fluye
una corriente y 1 A.
Aplicando la fórmula del conductor rectilíneo
muy largo:
5
FÍSICA
24
4.°
año
ELECTROMAGNETISMO I
4. Determina el módulo de la inducción magnética
(en T) en el punto «P» en cada caso (a) y (b) repectivamente.
25A
Conductor b)
a)
muy largo
6cm
9A
60A
BC = 4p
p.10–5 T
R
P
P
5cm
Aplicando la fórmula del conductor circular:
BC = 2 × 10–7. I
R
Reemplazando los datos I = 60A y BC = 4p
p × 10–5T
⇒ 4p
p × 10–5 = 2p
p × 10–7. 60
UNMSM
5. Calcula a qué distancia (en cm) de un conductor
rectilíneo muy largo; por el cual pasa por la corriente de 50 A, la intensidad de campo magnético es 2.10–4 T.
Resolución:
Graficando el problema:
50A
∴ R = 3 × 10 m
–1
9. ¿Cuál debe ser el tamaño del radio (en m) de una
espira circular para que la inducción magnética
en su centor sea igual a 6,28 × 10–4 T si la corriente eléctrica que circula por ella una intensidad de
300 A?
B = 2 × 10–4 T
10. Determina el módulo de la inducción magnética (en mT) en el punto «A». La intensidad de corriente eléctrica en el conductor es I = 2A.
d=?
Circunferencia
Aplicando la fórmula del conductor rectilíneo
muy largo:
2 × 10–4 = 2 × 10–7 50/d
⇒ d = 5 × 10–2 m
∴ d = 5 cm
A
11. Detemina el módulo de la inducción magnética
(en T) en el punto «P».
Conductor muy
largo
P
i = 6A
37° 20cm
7. Por un alambre rectilíneo infinito circula una determinada corriente eléctrica. Si la magnitud del
campo magnético a 4 cm del alambre es 5 × 10–6 T,
¿cuál es la magnitud del campo magnético a 5 cm
del alambre?
A
12. Calcula el módulo de la inducción magnética (en
T) a 7 m de un cable rectilíneo muy largo, que
transporta una corriente de 14 mA.
8. Una espira circular por el cual fluye una corriente
eléctrica de 60 A, produce una inducción magnética de módulo 4p
p × 10–5 T. Determina la longitud
del radio (en m) de la espira circular.
Resolución
Graficando el problema:
año
R=20cm
I
6. Un alambre rectilíneo muy largo debe producir
una inducción magnética de módulo 2.10–6 T
a 8 × 10–1 m de este alambre. ¿Qué intensidad
de corriente eléctrica (en A) debe pasar por este
alambre?
4.°
R
13. Determina el módulo de la inducción magnética
(en T) en el centro de una espira circular de un
conductor de radio igual a 4p
p cm y por el cual
fluye una corriente y 36 A.
25
FÍSICA
5
ELECTROMAGNETISMO I
14. Determina el módulo de la inducción magnética
(en T) en el punto «P».
Del gráfico se observa que por el método vectorial la inducción magnética resultante se calcula
sumando cada componente:
BR = B1 + B2
P
48A
74°
⇒ BR = 2 × 10–7.
50cm
4
2
+ 2 × 10–7 ×
–2
10×10
10×10–2
⇒ BR = 12 × 10–6 T
∴ BR = 12 m T
16. Determina el módulo de la inducción magnética
(en T) en el punto medio «P» del segmento que une
los conductores rectilíneos de gran longitud, por los
cuales circula corrientes eléctricas. (I = 3A)
UNI
15. Se muestran dos conductores rectilíneos de gran
longitud, por los cuales circulan corrientes eléctricas. Determina el módulo de la inducción
magnética (en mT) en el punto «M», equidistante
de los conductores (I = 2A).
I
2I
P
2I
2mm
M
17. Calcula la inducción magnética (en T) en el punto «O». Considerar que los conductores rectilíneos son muy largos.
10cm
Conductor muy
largo
I
Conductor muy
largo
a
Resolución:
Analizando la gráfica:
4A
B1 B2
x x
M
2I
2A
FÍSICA
3a
9I
18. Calcule la intensidad del campo magnético, en T,
que genera una corriente eléctrica I = 10 A en el
borde de un alambre rectilíneo de radio R = 2 mm.
m0 = permeabilidad del vacío.
m0 = 4p
p × 10–7 Tm/A
10cm 10cm
(1)
(2)
5
P
26
4.°
año
6
Electromagnetismo II
Fuerza magnética sobre un conductor por el
cual circula una corriente eléctrica
Las auroras boreales son un ejemplo del poder de que
tienen las fuerzas magnéticas.
El campo magnético de la tierra ejerce fuerzas sobre
las partículas cargadas radiactivas que provienen del
espacio principalmente del sol, si estas partículas
llegaran a la superficie terrestre no sería posible la vida
en la tierra. La fuerza que se ejercen a estas partículas
el campo magnético terrestre los desvía hacia los
polos, al rozar el gran número de partículas sobre
la atmosfera polar, se desprende luces de diferentes
colores. Estas luces son denominadas auroras.
Cuando un conductor se encuentra dentro de un
campo magnético, cada una de las cargas que el
conduce experimentan fuerzas cuya resultante será
normal al plano que formen el conductor y el campo
magnético. Su sentido viene dado por la regla de la
mano derecha.
Fmag
B
Fuerza magnética sobre una carga móvil
a
I
Debido a que una carga en movimiento genera su
propio campo magnético, al ingresar a otro campo
magnético se produce una interacción entre ellos,
lo cual origina fuerzas de naturaleza magnética,
cuya dirección será normal al plano que forman
la velocidad (V) y el campo (B), y cuando la carga
es positiva, su sentido viene dado por la regla de la
mano derecha.
L
Fmag = BILSena
a
Donde las magnitudes y sus respectivas unidades en
el S.I. son:
Fmag: módulo de la fuerza magnética (N).
B: módulo de la inducción magnética externa (T).
I: intensidad de corriente que circula en el conductor (A).
L: longitud del conductor eléctrico (m).
a: ángulo formado por la velocidad y la inducción
magnética externa.
Fmag
B
q
a
V
Regla de la mano derecha
Fmag = qvBsena
a
Esta es una regla que sirve para determinar la
dirección de la fuerza magnética, tanto en el caso de
una carga móvil y un conductor rectilíneo.
B
Donde las magnitudes y sus respectivas unidades en
el S.I. son:
Fmag: módulo de la fuerza magnética (N).
B: módulo de la inducción magnética externa (T),.
q: cantidad de carga eléctrica (C).
v: módulo de velocidad de la carga móvil (m/s).
a: ángulo formado por la velocidad y la inducción
magnética externa.
4.°
año
F
V
I
27
FÍSICA
6
ELECTROMAGNETISMO II
Inducción electromagnética
f
En esta parte se estudia cómo se genera corriente
eléctrica a partir de un campo magnético variables.
Para ello es necesario definir el concepto de flujo
magnético.
Flujo magnético (f
f): si a través de una superficie
existen líneas de inducción que la atraviesan, se
dice que a través de dicha superficie existe un flujo
magnético. La unidad es en SI del flujo magnético es
el webber (Wb)
a
N
a
a
a
=0
B
A
f = BA
B
Ley de Faraday
A
Cada vez que en un circuito cerrado o conjunto de
N espiras (bobina), se produce una variación de flujo
magnético, aparecerá en el una corriente denominada
corriente inducida, donde la rapidez con que se varia
el flujo nos da la fuerza electromotriz inducida.
f = BACosa
a
Donde además se cumple:
B: módulo de la inducción magnética externa (T)
A: área (m2).
a: ángulo formado por la inducción magnética
externa y el vector normal de la superficie.
Casos especiales:
f|
ε = –N |∆f
∆t
Donde las magnitudes y sus respectivas unidades en
el S.I. son:
B
ε: Fuerza electromotriz o voltaje (V)
N: número de espiras.
A
∆f: variación de flujo magnético (Wb).
∆f
∆t: intervalo de tiempo (S).
Trabajando en clase
Integral
V = 2 × 104 m/s
1. Una partícula cargada con + 5C ingresa a un campo magnético de intensidad 4.10–3 T con una velocidad de módulo 2.104 m/s. Si la velocidad de
la partícula forma un ángulo de 30° con el vector
de inducción magnética, calcula el módulo de la
fuerza magnética (en N) sobre la partícula.
30°
q = + 5C
Aplicando la fórmula para calcular el módulo de
la fuerza magnética.
Resolución:
Graficando el problema:
6
FÍSICA
B = 4 × 10–3 T
FM = |q|.V.B.Sena
a
28
4.°
año
ELECTROMAGNETISMO II
Reemplazando los datos
⇒ FM = 5 × 2 × 104 × 4 × 10–3.Sen30°
∴ FM = 200 N
"a
a" es igual a 90°, debido a que el Bext entra perpendicular a la hoja donde se encuentra el conductor.
⇒ Reemplazando los datos
FM = 50 × (0,2) × 2 × Sen90°
2. Una partícula cargada con –30C ingresa a un
campo magnético de intensidad 4.10–3 T con una
velocidad de módulo 5.104 m/s. si la velocidad de
la partícula forma un ángulo de 37° con el vector
de inducción magnética, calcula el módulo de la
fuerza magnética (en N) sobre la partícula.
∴ FM = 20 N
6. La figura muestra un conductor recto de 3 m de
longitud sobre el cual circula una corriente eléctrica de intensidad l = 8A. Si el campo magnético
externo tiene un módulo de Bext = 4T. Determina
el módulo de la fuerza magnética (en N) sobre el
conductor.
3. Calcula el módulo de la fuerza magnética (en N)
sobre el conductor.
Bext
B
4m
30°
I
Bext = 7T
I = 5A
7. La carga eléctrica «q» de 2 mC ingresa con una
rapidez de V = 100 m/s a un campo magnético de
intensidad Bext = 40 kT. Determina el módulo de
la fuerza magnética sobre la carga. (en kN)
A
4. Determina el módulo de la fuerza magnética (en N).
Bext
Bext = 6T
I = 50A
V
+q
3 cm
37°
8. Determina el módulo de la fuerza magnética (en
N) sobre el conductor.
Bext = 5T
4m
I = 4A
UNMSM
5. La figura muestra un conductor recto de 2 m de
longitud sobre el cual circula una corriente eléctrica de intensidad I = 0.2A. Si el campo magnético externo tiene un módulo de Bext = 50T. Calcula
el módulo de la fuerza magnética (en N) sobre el
conductor.
Bext
3m
Resolución:
Aplicando el método práctico.
I
Resolución:
Aplicando la fórmula del módulo de la fuerza
magnética.
FM = BIL Sena
a
4.°
año
3m
4m
B
L = 5m
Se reemplaza
por este
conductor
I = 4A
29
FÍSICA
6
ELECTROMAGNETISMO II
Luego aplicando la fórmula:
FM = BIL Senxa
a
90°
⇒ FM = 5 × 4 × 5 N
∴ FM = 100 N
4T = B
6 m/s = V
q = 6C
9. En el esquema mostrado la corriente que circula
por el conductor es l = 0.5A y está sometido a la
acción de un campo magnético externo Bext =4T.
Calcula el módulo de la fuerza neta (en N) que
actúa sobre el conductor debido al campo magnético.
Bext
I
13. Calcula el modulo de la fuerza magnética (en N)
sobre el conductor.
I = 10A
B = 10–2T
L = 2m
30°
20 cm
15 cm
I
14. Determina la magnitud de la fuerza magnética
sobre la partícula q.
B = 4T
10. Determina el módulo de la fuerza magnética (en
N) sobre el conductor doblado en forma de semicircunferencia de radio 25cm. Considerar que a
través del conductor circula una coriente eléctrica
de I = 0,5A de intensidad.
150°
q = 2C
V = 12 m/s
Bext = 20T
I
UNI
15. Una bobina de 500 espiras, es sacada en 2s de un
lugar donde el flujo magnético era 31 × 10–2 Wb
a otro donde es 1 × 10–2 Wb. Calcula el voltaje
inducido (en V) en la bobina.
Semicircunferencia
Resolución:
11. Determina el flujo magnético (en Wb) que atraviesa la superficie cuadrada.
∅i = 31.10–2 Wb
Bext = 10T
37°
4m
⇒ N = 500
4m
FÍSICA
∆t = 2s
Luego aplicando la fórmula de la Ley de Faraday
–2
–2
⇒ e = –500 (10 – 31 × 10 )
2
e = 75V
12. Calcula el modulo de la fuerza magnética (en N)
sobre la carga q.
6
∅f = 10–2 Wb
30
4.°
año
ELECTROMAGNETISMO II
16. Una bobina de 300 espiras, es sacada en 3s de un
lugar donde el flujo magnético era 29 × 10–2 Wb
a otro donde es 2 × 10–2 Wb. Determina el voltaje
inducido (en V) en la bobina.
I = 10A intensidad; si el valor de q es 60° y el campo magnético tiene una intensidad de Bext = 10 T.
¿Cuál es la fuerza (en N) que actua sobre dicho
alambre, si: A = 5 cm y CD = 3 cm?
A
17. Se tiene una bobina cerrada compuesta por 20 espiras, la cual se encuentra en una región donde el
flujo magnético que experimenta varía de 180Wb
a 60Wb en 2 segundos. ¿Cuál es el valor medio
del voltaje inducido (en V) en dicha bobina?
C
18. En la figura se muestra un alambre ACD doblado
en C, por la cual circula una corriente eléctrica de
4.°
año
Bext
I
q
I
D
31
FÍSICA
6
7
Física moderna
El descubrimiento de las ondas electromagnéticas
(OEM) permitió el desarrollo de las comunicaciones,
fue Henrich Hertz quien descubrió las ondas
electromagnéticas a finales del siglo XIX, esto
permitió comprobar la teoría de James Clerk Maxwell
(1831 - 1879) el cual predijo que la luz es una onda
electromagnética de energía continua.
También a finales del siglo XIX se descubren
nuevos fenómenos que no se podían explicar por
las teorías clásicas lo cual trajo como consecuencia
la introducción de nuevas ideas y por lo tanto el
desarrollo de nuevas teorías como la teoría cuántica,
la teoría de la relatividad, etc.
La luz con carácter ondulatorio suele ser denominado
ondas electromagnética (OEM), debido a que el
científico James Clerk Maxwell pudo comprobar
teóricamente que la luz está compuesta por los
campos eléctrico y magnético simultáneamente.
La representación de una OEM viajando en el vacío
(o aire) se ilustra a continuación:
y
c
E
B
O
E
B
z
x
Uno de las más importantes teorías establecidas en
el siglo XX fue la teoría cuántica. La teoría cuántica
se inició con el problema del cuerpo negro y cuya
solución fue planteada por Max Planck a inicios del
siglo XX; una de las condiciones que establecía esta
solución era que la luz o radiación electromagnética
(energía) este cuantizada.
Otro de los fenómenos que se logró explicar con
la teoría cuántica fue el Efecto Fotoeléctrico, cuya
solución fue planteda por Albert Einstein y por lo
cual fue acreedor al premio Nobel.
E
B
Donde:
E: Componente eléctrica de la OEM.
B: Componente magnética de la OEM.
En este capítulo se estudiara a la luz y sus diferentes
comportamientos (ondulatorio y corpuscular), así
también se estudiara el efecto fotoeléctrico, debido a
que es una aplicación directa de la Física Cuántica.
Además se cumple para un determinado instante la
siguiente ecuación:
E = cB
Carácter ondulatorio de la luz
Donde las magnitudes y sus respectivas unidades en
el S.I. son:
E: módulo del campo eléctrico (N/C).
B: módulo de la inducción magnética (T).
c = 3 × 108 m/s es la rapidez de la luz.
Para este carácter la luz actúa como un conjunto de
ondas, las cuales se propagan a partir de una fuente
de luz. Algunos fenómenos que se pueden explicar
con este carácter son: la reflexión, la refracción,
interferencia, difracción, polarización, etc.
7
FÍSICA
32
4.°
año
FÍSICA MODERNA
Las ondas electromagnéticas tienen determinadas
características. Podemos representar y definir estas
características a partir del siguiente gráfico de la
componente eléctrica de una OEM.
E(N/C)
A
t
Z
Frecuencia (f): magnitud física que nos cuantifica cuantas ondas se generan por unidad de tiempo. También se define y calcula como la inversa
del periodo. Su unidad en el SI es el Hertz (Hz).
Las ondas electromagnéticas cubren un espectro
(conjunto) extremadamente amplio de longitudes de
onda y frecuencia. Algunos ejemplos de ondas que se
encuentran dentro de este espectro son: las ondas de
radio y televisión, la luz visible, la radiación infrarroja
y ultravioleta, los rayos x y los rayos gamma. A
continuación se muestra el esquema del espectro
electromagnético.
Longitud de
onda A
Periodo
T
De la gráfica se define:
Z La longitud de onda (λ): es la distancia entre dos
crestas (o valles). Su unidad en el SI es el metro (m).
A pesar que las OEM difieren en frecuencia
«f» y longitud de onda «λ», todas las ondas
electromagnéticas se propagan en el vacío con la
misma rapidez, c = 3 × 108 m/s, cumpliéndose además
la siguiente ecuación:
Cada partícula de luz es denominada cuanto o fotón,
un cuanto (o fotón) es la mínima cantidad de energía
en la naturaleza.
La energía de un cuanto (o fotón) de una luz, se
calcula aplicando la siguiente ecuación:
Ef = h.f
c = λ.f
Caracter corpuscular de la luz
Donde las magnitudes y sus respectivas unidades en
el S.I. son:
Ef: energía de un cuanto o fotón (J).
f: frecuencia de la luz (Hz).
h = 6,63 × 10–34 J.s es la constante de Planck.
En este caso la luz actúa
Cuanto
como un conjunto de
corpúsculos o partículas
que se emiten desde
una fuente de luz.
Algunos ejemplos que
pueden ser explicados
con este carácter son: la
radicación de cuerpo negro, el efecto fotoeléctrico,
los niveles de energía en un átomo, etc.
año
Periodo (T): es el tiempo que demora en transitar
una longitud de onda en el espacio (o medio). Su
unidad en el SI es el segundo (s).
Espectro electromagnético
A
4.°
Z
Para calcular la energía de «n» cuantos (o fotones) de
una luz, se aplicara la siguiente ecuación:
Ef = n.h.f
33
FÍSICA
7
FÍSICA MODERNA
Dualidad de la luz y el principio de complementariedad
Ef
Luego de varios acontecimientos y experimentos
se llegó a la conclusión de que la luz (energía) tiene
un carácter dual de Onda y Partícula las cuales son
mutuamente complementarias. Esta conclusión fue
enunciada por Niels Bohr en 1928 en su denominado
Principio de complementariedad. En este principio se
dice que la luz necesita de las dos descripciones (onda
y partícula) para poder entender a la naturaleza, pero
a su vez nunca necesitaremos usar ambas al mismo
tiempo para poder explicar un solo fenómeno.
f0
En este esquema se observa a un fotón, el cual es
absorbido totalmente por un electrón de la placa
metálica. La placa a su vez posee una propiedad
denominada función trabajo (f
f0), la cual representa la
energía mínima para poder extraer a un electrón. Si la
energía del fotón, absorvido por el electrón, es mayor
a la función trabajo, entonces se emitirán electrones
de la placa, a los electrones emitidos Einstein los
llamo fotoelectrones.
Matemáticamente se cumple:
Ef = Ekmax + f0
Aplicando este principio también se puede calcular la
energía de «n» fotones de una luz, teniendo en cuenta
su longitud de onda, mediante la siguiente ecuación:
Ef = n
h.c
λ
Donde las magnitudes y sus respectivas unidades en
el S.I. son:
Ef: energía de un fotón (J).
Ekmax: energía cinética máxima del electrón (J).
f0: función trabajo (J).
Efecto fotoeléctrico
Es aquel fenómeno en el cual, ciertas placas metálicas
emiten electrones cuando se someten a la acción
de luz. El fenómeno se hace más acentuado cuando
las radiaciones son de alta frecuencia (ondas
ultravioletas) y con metales como el cesio, el sodio y
el potasio.
luz
–
–
+
+
+
Si la luz que incide sobre placa no logra emitir
electrones (Ekmax = 0), pero si los logra sacar a la
superficie de la placa, entonces la frecuencia asociada
a esta luz se denomina frecuencia umbral (fumbral), cuyo
valor se calcula mediante las siguientes expresiones:
f
fumbral = 0
h
–
–
+
+
+
placa metálica
La longitud de onda asociada a esta frecuencia umbral
es denominada longitud de onda máxima:
λmáxima = hc
f0
En 1905 Albert Einstein, científico alemán
nacionalizado en EE. UU. propuso basarse en los
estudios de Max Planck (el Cuantum) para poder
explicar dicho fenómeno.
Observación:
Z Las energías y funciones trabajo se suelen expresar en electrón volt (eV), la cual se define:
1 eV ≈ 1,6 × 10–19 J
Einstein llamó al Cuantum de luz: Fotón o partícula
de luz.
Con esto la luz es tratada como si tuviera naturaleza
corpuscular. Al igual que Planck, Einstein planteó su
modelo matemático, el cual fue afinado hasta que al
final obtuvo una ecuación que permitió explicar el
efecto fotoelétrico.
Explicación del efecto fotoeléctrico
A continuación se presenta un esquema práctico del
fenómeno efecto fotoeléctrico:
7
FÍSICA
e– Ekmax
34
Z
La constante de Planck en unidades de eV es:
h ≈ 4,15 × 10–15 eV
Z
Es necesario para solucionar los problemas, las
siguiente equivalencias:
1m
mm = 10–6 m
1nm = 10–9 m
o
1 angstrom ⇒ 1A = 10–10 m
4.°
año
FÍSICA MODERNA
Trabajando en clase
Integral
8. Determina la energía (en J) del fotón de una
OEM cuya frecuencia es 50 MHz. (Considere
h = 6,63 × 10–34 J.s, c = 3 × 108 m/s)
Resolución
Aplicando la fórmula de la energía para fotones
EN = n × h × f
Reemplazamos los datos n = 1, f = 50MHz = 50 × 106
Hz y h = 6,63 × 10–34 J.s.
EN = 1 × (6,63 × 10–34) × (50 × 106)
\ EN ≈ 3,3 × 10–26 J
1. Si la frecuencia de una OEM es 2 × 1014 Hz, calcula su longitud de onda (en m). (Considere
c = 3 × 108 m/s).
Resolución:
Aplicando la fórmula:
C=λ×f
Reemplazando los datos f = 21014 Hz y C = 3 ×
108 m/s
⇒ 3 × 108 = λ × 2 × 1014
\ = 1,5 × 10–6 m
9. Calcula la energía (en J) del fotón de una OEM
cuya longitud de onda es 9nm. (Considere
h = 6,63 × 10–34 J.s, c = 3 × 108 m/s)
2. Calcula la longitud (en m) de una OEM cuya frecuencia es 3 × 1010 Hz. (Considere c = 3 × 108 m/s)
3. Determina la frecuencia (en Hz) de una OEM
que tiene una longitud de onda de 30 m. (Considere c = 3 × 108 m/s)
10. Determine la energía (En J) de 5 fotones de
una luz cuya frecuencia es 8 MHz. (Considere
h = 6,63 × 10–34 J.s
4. En cierto instante una OEM posee una inducción
magnética de modulo 12 × 10–10 T. Si esta se propaga en el vacío calcula el módulo de la intensidad del campo eléctrico (en N/C) en ese instante.
(Considere c = 3 × 108 m/s)
11. Si un láser emite radiación con una longitud de
onda de 1000 nm. ¿Cuántos fotones serán necesarios para alcanzar una energía de 6.21 eV? (Considere h = 4.14 × 10–15 eV.s, c = 2.998 × 108 m/s)
UNMSM
12. Determina la energía (en J) del fotón de una OEM cuya
frecuencia es 5 MHz. (Considere h = 6,63 × 10–34 J.s,
c = 3 × 108 m/s)
5. Calcula frecuencia (en Hz) deo un fotón de rayos
X si su longitud de onda es 50A. (Considere c = 3
× 108 m/s)
Resolución
Aplicando la ecuación del caracter ondulatorio de
la luz
C=λ×f
o
Reemplazando los datos λ = 50A = 50 × 10–10 m
c = 3 × 108 m/s
⇒ 3 × 108 = 50 × 10–10 × f
\ f = 6 × 1016 Hz
13. Calcula la energía (en J) del fotón de una OEM
cuya longitud de onda es 3mm. (Considere
h = 6,63 × 10–34 J.s, c = 3 × 108 m/s).
14. Calcula la frecuencia (en Hz) de un fotón de rayos X si su longitud de onda es 5 nm. (Considere
c = 3 × 108 m/s).
o
UNI
15. Un haz de fotones incide sobre una superficie metálica que tiene una función de trabajo de 6,4 × 10–19 J. Si
cada fotón tiene una energía de 8 × 10–19 J, calcula la energía cinética máxima (en eV) de los fotoelectrones. (Considere 1 eV = 1,6 × 10–19 J).
Resolución
Graficamos el problema
6. La longitud de onda de un fotón de rayos X es 6A
. Determina la frecuencia (en Hz) asociado a este
fotón. (considera c = 3 × 108 m/s)
7. Si se sabe que una onda electromagnética de 40,0
Mhz de frecuencia viaja en el espacio libre, determine el producto de su periodo por su longitud
de onda. (Considere c = 3 × 108 m/s)
4.°
año
35
FÍSICA
7
FÍSICA MODERNA
e
16. Un haz de fotones incide sobre una superficie
metálica que tiene una función de trabajo de
7,2 × 10–19 J. Si cada fotón tiene una energía de
10,4 × 10–19 J, calcula la energía cinética máxima (en eV) de los fotoelectrones. (Considere
1eV = 1,6 × 10–19 J).
Ekmax = ?
–
Ef = 8×10–19 J
f0 = 6,4×10–19 J
17. La función trabajo del potasio es 2eV; si se ilumina sobre una superficie de potasio una luz de
longitud de onda 3 × 10–7 m, ¿cuál es la energía cinética máxima (en eV) de los fotoelectrones emitidos? (Considere h = 4.15 × 10–15 eV.s,
c = 3 × 108 m/s)
Luego aplicando la formula planteada por Albert
Einstein:
Ef = Ekmax + f0
8 × 10–19 = Ekmax + 6,4 × 10–19
⇒ Ekmax = 1,6 × 10–19 J
Luego piden en «eV»
1 eV
⇒ Ekmax = 1,6 × 10–19 J
1,6 × 10–19
\ Ekamx = 1 eV
7
FÍSICA
18. La longitud de onda umbral del efecto fotoeléctrico de la plata es 262 nm, calcule la función trabajo
de la plata en eV (eV = 1.6 × 10–19 J, 1 nm = 10–9 m,
h = 6.62 × 10–34 J.s, c = 3 × 108 m/s).
36
4.°
año