TABLAS DE DERIVADAS

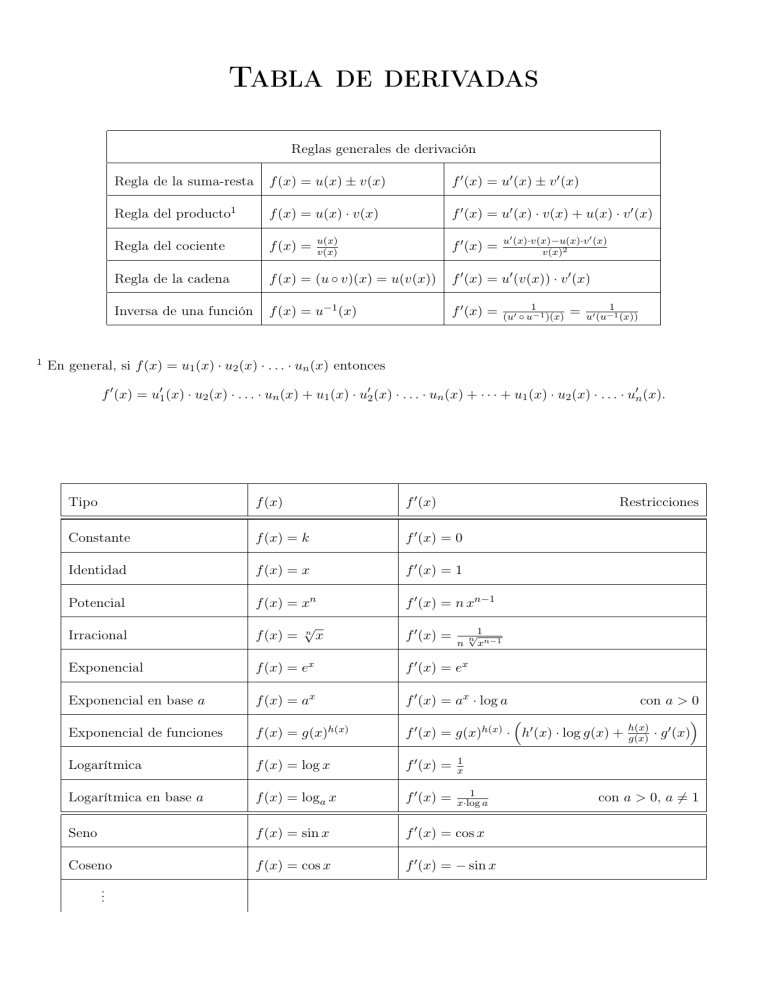
Tabla de derivadas
Reglas generales de derivación
1
Regla de la suma-resta
f (x) = u(x) ± v(x)
f 0 (x) = u0 (x) ± v 0 (x)
Regla del producto1
f (x) = u(x) · v(x)
f 0 (x) = u0 (x) · v(x) + u(x) · v 0 (x)
Regla del cociente
f (x) =
Regla de la cadena
f (x) = (u ◦ v)(x) = u(v(x))
f 0 (x) = u0 (v(x)) · v 0 (x)
Inversa de una función
f (x) = u−1 (x)
f 0 (x) =
u(x)
v(x)
f 0 (x) =
u0 (x)·v(x)−u(x)·v 0 (x)
v(x)2
1
(u0 ◦ u−1 )(x)
=
1
u0 (u−1 (x))
En general, si f (x) = u1 (x) · u2 (x) · . . . · un (x) entonces
f 0 (x) = u01 (x) · u2 (x) · . . . · un (x) + u1 (x) · u02 (x) · . . . · un (x) + · · · + u1 (x) · u2 (x) · . . . · u0n (x).
Tipo
f (x)
f 0 (x)
Constante
f (x) = k
f 0 (x) = 0
Identidad
f (x) = x
f 0 (x) = 1
Potencial
f (x) = xn
f 0 (x) = n xn−1
Irracional
f (x) =
Exponencial
f (x) = ex
f 0 (x) = ex
Exponencial en base a
f (x) = ax
f 0 (x) = ax · log a
Exponencial de funciones
f (x) = g(x)h(x)
con a > 0
0 (x)
f 0 (x) = g(x)h(x) · h0 (x) · log g(x) + h(x)
·
g
g(x)
Logarítmica
f (x) = log x
f 0 (x) =
1
x
Logarítmica en base a
f (x) = loga x
f 0 (x) =
1
x·log a
Seno
f (x) = sin x
f 0 (x) = cos x
Coseno
f (x) = cos x
f 0 (x) = − sin x
√
n
f 0 (x) =
x
..
.
1
Restricciones
n
1
√
n n−1
x
con a > 0, a 6= 1
Tipo
f (x)
f 0 (x)
Tangente
f (x) = tan x
f 0 (x) = 1 + tan2 x =
Cosecante
f (x) = csc x =
1
sin x
f 0 (x) = − csc x · cot x
Secante
f (x) = sec x =
1
cos x
f 0 (x) = sec x · tan x
Cotangente
f (x) = cot x =
1
tan x
f 0 (x) = − csc2 x =
Arco seno
f (x) = arc sin x
f 0 (x) =
√ 1
1−x2
Arco coseno
f (x) = arc cos x
f 0 (x) =
√ −1
1−x2
Arco tangente
f (x) = arc tan x
f 0 (x) =
1
1+x2
Arco cosecante
f (x) = arc csc x
f 0 (x) =
√−1
x x2 −1
Arco secante
f (x) = arc sec x
f 0 (x) =
√1
x x2 −1
Arco cotangente
f (x) = arc cot x
f 0 (x) =
−1
1+x2
Seno hiperbólico
f (x) = sinh x
f 0 (x) = cosh x
Coseno hiperbólico
f (x) = cosh x
f 0 (x) = sinh x
Tangente hiperbólico
f (x) = tanh x
f 0 (x) =
Cosecante hiperbólico
f (x) = csch x =
1
sinh x
f 0 (x) = − csch x · coth x
Secante hiperbólico
f (x) = sech x =
1
cosh x
f 0 (x) = − sech x · tanh x
Cotangente hiperbólico
f (x) = coth x =
1
tanh x
f 0 (x) = − csch2 x =
Arco seno hiperbólico
f (x) = arc sinh x
f 0 (x) =
√ 1
x2 +1
Arco coseno hiperbólico
f (x) = arc cosh x
f 0 (x) =
√ 1
x2 −1
Arco tangente hiperbólico
f (x) = arc tanh x
f 0 (x) =
1
1−x2
Arco cosecante hiperbólico
f (x) = arc csch x
f 0 (x) =
√−1
|x| 1+x2
Arco secante hiperbólico
f (x) = arc sech x
f 0 (x) =
√−1
|x| 1−x2
Arco cotangente hiperbólico
f (x) = arc coth x
f 0 (x) =
−1
x2 −1
Restricciones
1
cos2 x
−1
sin2 x
1
cosh2 x
−1
sinh2 x
Usando la regla de la cadena se obtiene una tabla similar a la anterior para funciones compuestas. Por ejemplo,
Si f (x) = log v(x), entonces f 0 (x) =
2
v 0 (x)
.
v(x)