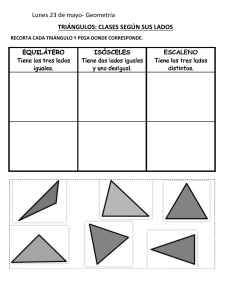
Guía Historia de la geometría La geometría surgió del estudio de los primeros matemáticos de la historia sobre problemas como las medidas de un campo o de un objeto. En el antiguo Egipto surgió una geometría observacional o empírica que provenía de la observación de los objetos. Esta geometría primigenia más adelante fue reformulada y elaborada por los griegos y es la geometría que hoy conocemos. En siglo IV a.C. Pitágoras demostró que las diversas leyes arbitrarias e inconexas de la geometría primitiva, se pueden deducir estableciendo un número de axiomas o postulados. Pitágoras elaboró la teoría del famoso teorema de Pitágoras que afirma que el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto). Axiomas y Teorema Es una proposición que se toma como punto de partida para realizar se toma como punto de partida para realizar la prueba o demostración de preposiciones. Los axiomas se admiten sin que tengan que se probados. Esta se caracteriza de los axiomas evitan la regresión infinita de las pruebas o demostraciones. - La preposición por un punto P exterior a una recta L pasa una y solo una recta paralela. Razonamiento inductivo y deductivo - Inducción Es una forma de razonamiento que va de lo particular a lo general. - Deducción Es el tipo de razonamiento que parte de lo general a lo particular. Segmentos y proporcionalidad - Proporcionalidad Es la circunstancia en la que dos magnitudes mantienen entre sí una razón ociente constante. - Construcción de segmentos Un segmento de una longitud dada se puede construir con ayuda de una regla. Primero marcamos el punto de inicio, luego medimos la distancia o longitud y por últimos marcamos el punto final. Semejanza y congruencia - Semejantes Dos figuras son semejantes si tienen la misma forma sin importar los tamaños entre ellos. - Congruencia En general, las figuras son congruentes si tienen la misma forma y tamaño, aunque su posición u orientación sean distintas. Concepto de ángulo Es la unión de dos rayos o semirrectas que tienen punto en común al cual llamaremos vértice y es el origen de ambos rayos. Tipo de ángulos - Ángulo recto. El ángulo recto es el que mide exactamente 90°. - Ángulo agudo. Los agudos miden entre 0° y 90°. - Ángulo Obtuso: los obtusos son aquellos que mide más de 90° y menos de 180°. - Ángulo llano. Los ángulos llanos miden 180°. - Ángulo completo. El completo mide exactamente 360°. . - Los cóncavos y los convexos son dos clasificaciones de ángulos más generales con respecto a los que ya hemos visto en la sección anterior. - Los convexos son aquellos que miden menos de 180°. Mientras que los cóncavos tienen una amplitud de entre 180° y 360°. - Esto significa que los ángulos convexos pueden ser a la vez obtusos, agudos, y rectos, ya que todos ellos miden menos de 180°. Sistemas de medida de ángulos - Sistema sexagesimal de medida angular Este es el sistema más antiguo de medida de ángulos y fue inventado por los babilonios. En este sistema un ángulo completo o perígono, está dividido en 360 partes iguales y cada parte se llama ángulo sexagesimal. - Si cada minuto sexagesimal lo dividimos en 60 partes iguales la llamaremos segundo sexagesimal. 1/60 = 1 - Así la forma de expresar 43 grados, 18 min y 255 en el sistema sexagesimal sería: 43* 18’ 25’’ Medida Completa En el sistema sexagesimal medida está expresada de forma completa si está escrita en más de una unidad. 73* 15’ 20’’ Medida incompleta En este sistema una medida está incompleta si está escrita en una sola unidad. 73.2556* Tipo de rectas - Rectas paralelas Son dos rectas que pertenecen a un mismo plano, y que no se cortan en un punto son rectas paralelas. - Rectas Perpendiculares Son dos rectas que pertenecen a un mismo plano son perpendiculares si se cortan formando ángulos rectos. - Rectas transversales Una recta transversal o secante corta a cualquier par de rectas el plano en dos puntos. Los ángulos 1, 2, 7 y 8 son ángulos externos. Los ángulos 3, 4, 5 y 6 son ángulos internos. Los pares de ángulos 1 y 7, 2 y 8 son alternos externos. Los pares de ángulos 1 y 5, 2 y 6, 3 y7, 4 y 8 son correspondientes. Los pares de ángulos 4 y 6, 3 y 5 son alternos internos. - Rectas transversales paralelas Los ángulos opuestos por el vértice: 1, 3, 5, 7, 2, 4, 6, 8. Ángulos correspondientes son congruentes: 1, 5, 2, 6, 3, 7, 4, 8. Concepto y tipo de triángulos Un triángulo es la unión de los segmentos que se forman a partir de puntos no colineales. En un triángulo, el ángulo mayor siempre será opuesto al lado más largo. Tipos de triángulos o o Clasificación de triángulos según lados: Triángulo equilátero Triángulo isósceles Triángulo escaleno Clasificación de triángulos según sus ángulos: Triángulo rectángulo Triángulo acutángulo Triángulo obtusángulo Existen tres tipos de triángulos según sus lados que son: Triángulo equilátero: o Tiene sus tres lados iguales, es decir, los tres lados son de la misma longitud. Triángulo isósceles: o Tiene dos lados iguales (de igual longitud) y otro no. Triángulo escaleno: o Tiene los tres lados diferentes, es decir, de distinta longitud. Existen tres tipos de triángulos según sus ángulos que son: Triángulo rectángulo: o Dos de sus lados forman un ángulo recto, o lo que es lo mismo, tiene un ángulo de 90º. Triángulo acutángulo: o Todos sus ángulos son agudos, o lo que es lo mismo, todos sus ángulos miden menos de 90º. Triángulo escaleno: o Dos de sus lados forman un ángulo obtuso, o lo que es lo mismo, tiene un ángulo de más de 90º. Rectas y puntos notables Altura. La altura de un triángulo, respecto de uno de sus lados, se define como la recta perpendicular a dicho lado que pasa por el vértice opuesto. Bisectriz. La bisectriz de un triángulo, correspondiente a uno de sus vértices, se define como la recta que, pasando por dicho vértice, divide al ángulo correspondiente en dos partes iguales. Mediatriz. La mediatriz de un lado de un triángulo se define como la recta perpendicular a dicho lado que pasa por su punto medio. Mediana La mediana de un triángulo, se define como la recta que une dicho vértice del triángulo con el punto medio del lado opuesto.