Resistencia al corte y desplazamiento lateral muros hormigon armado (Rev.3)

UNIVERSIDAD DE LA SERENA
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA EN OBRAS CIVILES
ESTIMACIÓN DE LA CAPACIDAD AL CORTE Y DEL
DESPLAZAMIENTO LATERAL DE MUROS DE HORMIGÓN
ARMADO SOMETIDOS A CARGA CÍCLICA
FELIPE IGNACIO CASTILLO HUERTA
Memoria para optar al título de:
INGENIERO CIVIL
Comisión revisora:
Dr. Ing. Luis Díaz Zamora - Profesor Patrocinante
Dr. Ing. Jaime Campbell Barraza
Ing. Paulo Castillo Calderón
La Serena, 2022
AGRADECIMIENTOS
A todas las personas que he conocido.
A mis amigos, que en cada junta
me han regalado momentos de felicidad, tranquilidad y asombro.
A mis profesores, de la enseñanza básica, media y universitaria,
en especial al profesor guía Luis Díaz Zamora,
quien me apoyó y comprendió durante el desarrollo de esta memoria.
A mis padres Mirtha y Sergio, y hermanos Rodrigo y Sergio, por su apoyo
permanente e incondicional, por el cariño y el sentimiento de calidez familiar.
Al Otis, aunque sus cuatro patas ya no estén en este mundo…
su esencia siempre permanecerá en mi corazón
y en los corazones de quienes lo quisieron.
RESUMEN
En la presente memoria se calcula la resistencia al corte y el desplazamiento lateral de muros
de hormigón armado sometidos a carga cíclica. Para ello, se obtiene la relación momentocurvatura usando las relaciones tensión-deformación del hormigón y el acero, las cuales
incluyen la fase elástica y plástica. Posteriormente, a través de ecuaciones del método por
capacidad, se obtiene la respuesta fuerza-desplazamiento y resistencia al corte del muro. Los
resultados se comparan con los de la campaña experimental de nueve muros de hormigón
armado, demostrando que las ecuaciones teóricas logran estimar con precisión la carga última
y, además, el tipo de falla por corte o flexión.
ABSTRACT
In this report, the shear strength and lateral displacement of reinforced concrete walls
subjected to cyclic loading are calculated. For this, the moment-curvature relationship is
obtained using the stress-strain relationships of concrete and steel, which include the elastic
and plastic phase. Subsequently, through equations of the displacement method, the forcedisplacement response and shear resistance of wall are obtained. The results are compared
with those of the experimental campaign of nine reinforced concrete walls, demonstrating
that the theoretical equations accurately estimate the ultimate load and, in addition, the shear
or bending failure.
TABLA DE CONTENIDOS
1. Introducción.................................................................................................................... 5
1.1
Objetivos ......................................................................................................... 6
1.1.1 Objetivo general ...................................................................................... 6
1.1.2 Objetivos específicos ............................................................................... 6
2. Antecedentes del método de cálculo desarrollado ....................................................... 7
2.1
Curvas constitutivas tensión-deformación de los materiales .......................... 7
2.1.1 Acero ....................................................................................................... 7
2.1.2 Hormigón................................................................................................. 9
2.1.3 Hormigón confinado.............................................................................. 10
2.2
2.3
Cálculo de la relación momento-curvatura ................................................... 12
Cálculo de la relación fuerza-desplazamiento ............................................... 16
2.3.1 Curva de respuesta fuerza-desplazamiento ........................................... 16
2.3.2 Curva de resistencia fuerza-desplazamiento ......................................... 20
2.4
Cálculo del error relativo .............................................................................. 24
3. Resultados de ensayos de muros experimentales ...................................................... 26
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
3.10
3.11
Características del hormigón ......................................................................... 27
Características de las barras de acero ............................................................ 27
Muro R1 ........................................................................................................ 29
Muro R2 ........................................................................................................ 31
Muro B1 ........................................................................................................ 33
Muro B2 ........................................................................................................ 35
Muro B3 ........................................................................................................ 37
Muro B4 ........................................................................................................ 39
Muro B5 ........................................................................................................ 39
Muro B6 ........................................................................................................ 41
Muro F1 ......................................................................................................... 42
4. Análisis de los resultados ............................................................................................. 44
4.1
4.2
Gráficos momento-curvatura......................................................................... 44
Gráficos fuerza-desplazamiento .................................................................... 56
5. Conclusiones ................................................................................................................. 68
6. Referencias .................................................................................................................... 69
Anexo A: Tablas de cálculo momento-curvatura.......................................................... 70
Anexo B: Tablas de cálculo fuerza-desplazamiento ..................................................... 88
5
1. Introducción
Conocer el comportamiento estructural de los muros de hormigón armado es de mucho
interés, dado que constituyen uno de los dos sistemas más utilizados en Chile para resistir las
solicitaciones sísmicas que son muy frecuentes en nuestro país.
El estudio de la norma NCh430.Of2008 (INN, 2008) realizado en el año 2011 y que dio lugar
al Decreto n.⁰ 60 (MINVU, 2011) no efectuó cambios al diseño al corte de este tipo de
elemento estructural, suponiendo, con base en las fallas presentadas, que estas no fueron
debidas al esfuerzo de corte. Estudios actuales de edificios diseñados en la ciudad de Viña
del Mar, indican que el corte pudo ser el causante de la falla de algunos muros (Bartolomé,
Quiun, y Silva, 2011), al concluir que un aumento de la resistencia a flexo-compresión,
produce un aumento en la magnitud del cortante.
La falla de muros por cortante es un tipo de falla frágil caracterizada por la aparición de
grietas diagonales y que puede llegar a producir el pandeo de las barras longitudinales
verticales si el muro no posee estribos de confinamiento. Por esto mismo, este tipo de falla
debe evitarse y se debe diseñar para que ocurra una falla dúctil por flexión.
En este trabajo se pretende utilizar ecuaciones del método por capacidad para estimar la curva
de respuesta fuerza-desplazamiento de un conjunto de muros de hormigón armado ensayados
bajo cargas cíclicas, con el objetivo de determinar la resistencia al corte y el tipo de falla para
luego contrastarlas con los resultados experimentales. Para ello, se desarrollarán gráficos
momento-curvatura de los muros con el programa SAP2000, los cuales se utilizarán en las
ecuaciones del método de capacidad que permitirán elaborar los gráficos fuerzadesplazamiento a través del programa Excel.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
6
1.1 Objetivos
1.1.1 Objetivo general
• Determinar la resistencia al corte y el desplazamiento lateral de muros de hormigón
armado mediante las curvas fuerza-desplazamiento por flexión y corte, obtenidas de
manera teórica.
1.1.2 Objetivos específicos
• Estudiar las ecuaciones de los materiales constituyentes para analizar el
comportamiento estructural de muros de hormigón armado en el rango plástico.
• Recopilar de la bibliografía especializada ensayos de muros de hormigón armado
sometidos a cargas cíclicas, que incluyan los diagramas momento-curvatura
experimentales.
• Desarrollar, utilizando software de ingeniería, modelos para confeccionar diagramas
momento-curvatura teóricos y contrastarlos con los resultados experimentales.
• Determinar las curvas fuerza-desplazamiento a partir de los diagramas momentocurvatura y encontrar el punto de intersección con la resistencia al corte.
• Analizar la bondad del procedimiento al contrastar los valores teóricos de cada muro
con los resultados experimentales.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
7
2. Antecedentes del método de cálculo
desarrollado
2.1 Curvas constitutivas tensión-deformación de los materiales
Las curvas constitutivas tensión-deformación, representan la relación que hay entre la presión
aplicada de manera incremental a un volumen sólido y su respectiva deformación unitaria,
medida en la dirección que se aplica la fuerza, hasta su falla estructural. La sección
transversal de los muros se modela considerando que está asociada a tres curvas: la del acero
de las barras de refuerzo, la del hormigón “normal” y la del hormigón confinado, este último
en el caso de que el muro posea elemento especial de borde.
2.1.1 Acero
La curva constitutiva del acero es la función por partes correspondiente a la Ecuación 2.1
(Montejo y Kowalsky, 2007).
𝐸𝑠 · 𝜀
𝑠𝑖 𝜀 ≤ 𝜀𝑦
𝑓𝑦
𝑠𝑖 𝜀𝑦 < 𝜀 ≤ 𝜀𝑠ℎ
𝑓𝑠 (𝜀) =
𝑚 · (𝜀 − 𝑒𝑠ℎ ) + 2 (𝜀 − 𝜀𝑠ℎ )(60 − 𝑚)
𝑓𝑦 [
+
] 𝑠𝑖 𝜀𝑠ℎ < 𝜀 ≤ 𝜀𝑠𝑢
60(𝜀 − 𝑒𝑠ℎ ) + 2
2(30𝑟 + 1)2
{
(2.1)
Donde:
𝑓𝑦 : Tensión de fluencia.
𝑓𝑢 : Tensión resistente última.
𝐸𝑠 : Módulo elástico del acero.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
8
𝜀𝑠ℎ : Deformación unitaria al comienzo del endurecimiento.
𝜀𝑠𝑢 : Deformación unitaria última.
𝑟 = 𝜀𝑠𝑢 − 𝜀𝑠ℎ
𝑚=
(2.2)
(𝑓𝑢 ⁄𝑓𝑦 )(30𝑟 + 1)2 − 60𝑟 − 1
15𝑟 2
(2.3)
Esta función incluye las tres fases de los aceros utilizados en las barras de refuerzo del
hormigón: a) la fase elástica, una línea recta cuya pendiente es igual al módulo elástico del
material; b) la fase de fluencia, etapa en que el acero se deforma sin aumentar su tensión y se
aprecia en la Figura 2.1 como una línea horizontal; y c) la fase de endurecimiento, que
corresponde a un aumento de las tensiones del acero y por consiguiente un aumento en las
deformaciones. Estas fases se observan en la Figura 2.1.
800
Fluencia
600
Endurecimiento
σ (MPa)
400
Elástica
200
0
-200
-400
-600
-800
-0,125
-0,1
-0,075
-0,05
-0,025
0
0,025
0,05
0,075
0,1
0,125
ε (m/m)
Figura 2.1: Curva tensión-deformación del acero.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
9
2.1.2 Hormigón
La curva constitutiva del hormigón la definen dos funciones. La primera establece la relación
tensión-deformación unitaria del hormigón sometido a cargas de compresión (Ecuación 2.4)
y consiste en una función racional propuesta por Sargin (Molins y Aguado, 2007), pero
modificada para admitir hormigones de hasta 100 MPa. La segunda establece la relación del
hormigón sometido a las cargas de tracción (Ecuación 2.5), que consiste en una función de
magnitud mucho más pequeña que la de compresión (Carreira y Chu, 1986).
𝑓𝑐 (𝜀) = 𝑓𝑐′
𝑓𝑡 (𝜀) = 𝑓𝑡′
𝜀
𝑛 · (𝜀 )
0
𝜀 𝑛𝑘
𝑛 − 1 + (𝜀 )
0
𝜀
𝛽 · (𝜀 )
0
𝜀 𝛽
𝛽 − 1 + (𝜀 )
0
0 ≤ 𝜀 ≤ 𝜀𝑐𝑢𝑐
(2.4)
0 ≤ 𝜀 ≤ 𝜀𝑐𝑢𝑡
(2.5)
Donde:
𝑓𝑐′ : Tensión resistente del hormigón en compresión en probeta cilíndrica estandarizada.
𝜀𝑐𝑢𝑐 : Deformación unitaria última del hormigón en compresión (0,0035).
𝜀𝑐𝑢𝑡 : Deformación unitaria última del hormigón en tracción (0,0002).
𝑛 = 0,8 +
1
𝑘={
0,67 +
𝑓𝑐′
62
𝑓𝑐′
17
(2.6)
𝜀 ≤ 𝜀0
𝜀 > 𝜀0
(2.7)
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
10
𝜀0 =
𝑓𝑐′
𝑛
·
𝐸𝑐 𝑛 − 1
(2.8)
𝐸𝑐 = 3.320√𝑓𝑐′ + 6.900
𝛽=
(2.9)
1
−1
24,82
1 − ( ′ + 0,92)
𝑓𝑐
(2.10)
En la Figura 2.2 se puede observar la magnitud de las curvas de compresión y tracción, siendo
las de tracción de menor magnitud.
5
0
-5
-10
Tracción
Compresión
σ (MPa)
-15
-20
-25
-30
-35
-40
f c'
-45
-50
-0,0040
-0,0035
-0,0030
-0,0025
-0,0020
-0,0015
-0,0010
-0,0005
0,0000
0,0005
ε (m/m)
Figura 2.2: Curva tensión-deformación del hormigón.
2.1.3 Hormigón confinado
Algunos muros se construyen con lo que se denomina “elemento especial de borde”, un
volumen de hormigón que se encuentra confinado por aros o estribos de barras de acero
espaciados muy cerca el uno con el otro, lo que le confiere una resistencia a la compresión
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
11
mucho más alta. La ecuación utilizada para este hormigón especial es la que propuso Mander
(Priestley, Calvi, y Kowalsky, 2007) y corresponde a la Ecuación 2.11.
𝑓𝑐 (𝜀) =
𝑓𝑐𝑐′ · 𝑥 · 𝑟
𝑟 − 1 + 𝑥𝑟
0 ≤ 𝜀 ≤ 𝜀𝑐𝑢𝑐
(2.11)
Donde:
𝑓 ′ 𝑐𝑐 : Resistencia del hormigón a compresión en probeta cilíndrica estandarizada
𝑒𝑐𝑢𝑐 : Deformación unitaria última del hormigón en compresión (0,0035)
𝑒𝑐𝑢𝑡 : Deformación unitaria última del hormigón en tracción (0,0002)
𝑓𝑐𝑐′ = 𝑓𝑐′ (2,254√1 +
7,94𝑓𝑙
𝑓𝑙
−
2
− 1,254)
𝑓𝑐′
𝑓𝑐′
𝜀𝑐
𝜀𝑐𝑐
(2.13)
𝑓𝑐𝑐′
= 0,002 (1 + 5 ( ′ − 1))
𝑓𝑐
(2.14)
𝐸𝑐
𝐸𝑐 − 𝐸𝑠𝑒𝑐
(2.15)
𝑥=
𝜀𝑐𝑐
(2.12)
𝑟=
𝐸𝑐 = 5.000√𝑓𝑐′
𝐸𝑠𝑒𝑐
𝑓𝑐𝑐′
=
𝜀𝑐𝑐
(2.16)
(2.17)
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
12
En la Figura 2.3 se representa la curva de un hormigón G40, cuyo confinamiento le permite
tener aproximadamente un 100% más de resistencia (dependiendo del espaciamiento del
confinamiento), además de deformaciones unitarias mayores que las de un hormigón no
confinado.
10
0
-10
σ (MPa)
-20
-30
-40
-50
-60
-70
-80
-90
-0,09
-0,08
-0,07
-0,06
-0,05
-0,04
-0,03
-0,02
-0,01
0
0,01
ε (m/m)
Figura 2.3: Curva tensión-deformación del hormigón confinado.
2.2 Cálculo de la relación momento-curvatura
El gráfico momento-curvatura entrega información sobre la resistencia última, los estados
límites elásticos y plásticos, y también la rigidez elástica a flexión (EI) de la sección. Es
necesario para determinar la relación fuerza-desplazamiento y su algoritmo de cálculo es el
expuesto a continuación (Priestley, Calvi, y Kowalsky, 2007).
Las hipótesis para la formulación de las ecuaciones son las siguientes:
• El perfil de deformaciones es lineal en todas las etapas de carga (las caras de los cortes
transversales permanecen planas).
• La deformación del hormigón y las barras de acero a una misma distancia del eje
neutro son idénticas.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
13
• Las ecuaciones tensión-deformación de los materiales son conocidas.
• La fuerza axial (si es que la hubiera) se aplica en el centroide de la sección.
La ecuación de equilibrio de fuerzas (Ecuación 2.18) y de equilibrio de momento
(Ecuación 2.19) se deducen de la Figura 2.4:
𝑛
𝑁 = ∫ 𝑓𝑐 (𝑦) · 𝑏(𝑦) 𝑑𝑦 + ∑ 𝑓𝑠(𝑖) · 𝐴𝑠𝑖
(2.18)
𝑖=1
𝑛
𝑀 = ∫ 𝑓𝑐 (𝑦) · 𝑏(𝑦) · 𝑦 · 𝑑𝑦 + ∑ 𝑓𝑠(𝑖) · 𝑦 · 𝐴𝑠𝑖
(2.19)
𝑖=1
Para calcular los puntos de la gráfica se debe proceder de la siguiente manera:
1.
Dividir la sección transversal en láminas paralelas al eje neutro. Determinar el área
del hormigón no confinado, hormigón confinado y acero de refuerzo de cada una de
las láminas.
2.
Seleccionar un valor de deformación para el hormigón en la lámina más comprimida,
partiendo desde el menor valor.
3.
Asumir la ubicación del eje neutro.
4.
Calcular las tensiones del hormigón y del acero en el centro de cada lámina y
determinar sus fuerzas resultantes.
5.
Verificar el equilibrio de fuerzas axiales de la Ecuación 2.18.
6.
Modificar la ubicación del eje neutro asumida en el paso 3 para mejorar la
aproximación en la Ecuación 2.18.
7.
Repetir los pasos 3 al 6 hasta que se cumpla el equilibrio entre las fuerzas externas y
las fuerzas internas.
𝜀
8.
Calcular el momento de acuerdo con la Ecuación 2.19 y la curvatura 𝜑 = 𝑐𝑐.
9.
Incrementar la deformación en la lámina más comprimida (paso 2) y repetir los pasos
del 3 al 8.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
14
Figura 2.4: Deformaciones unitarias y tensiones internas en la sección de hormigón
armado.
10. Continuar incrementando la deformación en la lámina más comprimida hasta alcanzar
la deformación última del hormigón.
El resultado de aplicar el algoritmo anterior es la Figura 2.5, en el que se observan cuatro
estados límite que son de interés:
a)
Agrietamiento del hormigón: En los miembros de hormigón armado este estado límite
marca un cambio significativo en la rigidez. Se produce cuando la tensión de tracción
sobrepasa la resistencia a tracción del hormigón y son las barras longitudinales las
que soportan las fuerzas solicitantes de tracción.
b) Fluencia de las barras de refuerzo: En este estado límite se observa un segundo
cambio significativo en la rigidez de la sección y ocurre cuando las barras
traccionadas alcanzan la tensión de fluencia. Este punto es útil para definir la rigidez
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
15
elástica apropiada en el análisis de sistemas dúctiles usando reglas de histéresis
simplificadas, por ejemplo, una respuesta bilineal.
1200
1100
1000
c) Momento máximo
900
M (kN·m)
800
700
600
d) Curvatura última
b) Fluencia del acero
500
400
300
200
a) Agrietamiento hormigón
100
0
0
0,005 0,01 0,015 0,02 0,025 0,03 0,035 0,04 0,045 0,05 0,055 0,06 0,065 0,07 0,075
φ (1/m)
Figura 2.5: Relación momento-curvatura de la sección de hormigón armado.
c)
Momento máximo: Es el punto de máxima resistencia de la sección, que se alcanza
cuando la deformación unitaria iguala por primera vez a una de las deformaciones
unitarias últimas de las curvas tensión-deformación definidas en la sección 2.1. Un
valor conservador para la deformación última del hormigón a compresión es
𝜀𝑐𝑢 = 0,004.
d) Curvatura última: Luego de alcanzar el momento máximo, la sección se sigue
deformando, pero con una capacidad de carga disminuida. La definición de este punto
es subjetiva, a veces se toma como la ocurrencia de algún evento físico crítico, por
ejemplo, la rotura de las barras de confinamiento. Otra definición común es cuando
la sección disminuye su resistencia en un 20%. Sin embargo, un verdadero estado
límite último es aquel en que el miembro es incapaz de soportar las fuerzas que le son
impuestas.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
16
2.3 Cálculo de la relación fuerza-desplazamiento
2.3.1 Curva de respuesta fuerza-desplazamiento
A medida que las fuerzas y deformaciones comienzan a aumentar, las hipótesis del
comportamiento de los materiales mencionadas con anterioridad se alejan de la precisión y
el cálculo de los desplazamientos utilizando las ecuaciones elásticas no concuerdan con los
datos experimentales. Para solucionar este problema, se utiliza el concepto de “rótula
plástica” de longitud 𝐿𝑃 , sobre la cual la deformación y la curvatura son iguales al valor
máximo de la base del miembro (Priestley, Calvi, & Kowalsky, 2007).
Una parte de la longitud 𝐿𝑃 se encuentra por debajo de la base del miembro, esta recibe el
nombre de 𝐿𝑆𝑃 (ver Figura 2.6) y se calcula como:
𝐿𝑆𝑃 = 0,022 𝑓𝑠 𝑑𝑏𝑙
(2.20)
Donde 𝑓𝑠 es la tensión de las barras de acero longitudinal en MPa (no sobrepasa el valor de
𝑓𝑦 ) y 𝑑𝑏𝑙 el diámetro de estas.
La longitud 𝐿𝑃 se calcula como:
𝐿𝑃 = 𝑘 𝐿𝐶 + 𝐿𝑆𝑃 ≥ 2 𝐿𝑆𝑃
(2.21)
𝑓𝑢
𝑘 = 0,2 ( − 1) ≤ 0,08
𝑓𝑦
(2.22)
Donde:
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
17
Figura 2.6: Significado de 𝐿𝑝 y 𝐿𝑠𝑝 .
En estas ecuaciones 𝐿𝐶 es la longitud desde la sección crítica al punto de contraflexión del
miembro, que para sistemas cantiléver se considerará igual a la altura del muro, es decir,
𝐿𝐶 = 𝐻.
Los desplazamientos en la fisuración del hormigón (∆𝑐𝑟 ), en la fluencia del acero (∆𝑦 ) y
posteriores a la fluencia (∆) causados por el momento flector se determinan con las siguientes
ecuaciones:
𝜙𝑐𝑟 · 𝐻 2
3
(2.23)
𝑀𝑐𝑟
𝐻
(2.24)
𝜙𝑦 · (𝐻 + 𝐿𝑆𝑃 )2
3
(2.25)
∆𝑐𝑟 =
𝐹𝑐𝑟 =
∆𝑦 =
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
18
𝐹𝑦 =
∆= ∆𝑦 ·
𝑀𝑦
𝐻
(2.26)
𝑀
𝑀
+ [𝐿𝑃 · (𝐻 + 𝐿𝑆𝑃 − 0,5𝐿𝑃 )] (𝜙 − 𝜙𝑦 ·
)
𝑀𝑦
𝑀𝑦
𝐹=
𝑀
𝐻
(2.27)
(2.28)
La ductilidad última se define como la relación entre el desplazamiento último (∆𝑢 ) y el
desplazamiento elástico (∆𝑦 ).
𝜇∆ =
∆𝑢
∆𝑦
Cuando los miembros son esbeltos y poseen una relación de
(2.29)
𝑀
𝑉
· 𝐷 > 3, los desplazamientos
por fuerza de corte pueden despreciarse (siendo 𝐷 la profundidad efectiva de la sección
medida en la dirección de la fuerza de corte), en caso contrario; los desplazamientos elásticos
y plásticos debido al cortante se determinan como:
a) Desplazamientos de corte elásticos, previos al agrietamiento de corte: se asume
un comportamiento lineal elástico del desplazamiento lateral previo a la formación
de grietas de corte diagonal, las que ocurren cuando la fuerza 𝐹 alcanza el valor de
resistencia al corte del hormigón 𝑉𝑐 (usando 𝛾 = 0,29 en la Ecuación 2.38). El
desplazamiento correspondiente a este punto se calcula como:
∆𝑠1 =
𝑉𝑐
𝑘𝑠,𝑒𝑓𝑓
(2.30)
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
19
Donde:
𝑘𝑠,𝑒𝑓𝑓 = 𝑘𝑠𝑔 ·
𝑘𝑠𝑔 =
𝐸𝐼𝑒
𝐸𝐼𝑔
(2.31)
𝐺 · 𝐴𝑠
𝐻
(2.32)
𝑀𝑁
𝜙𝑦
(2.33)
𝐸𝐼𝑒 =
El módulo de corte del hormigón puede tomarse como 𝐺 = 0,43𝐸𝑐 y el área de corte
𝐴𝑠 = 0,87𝐴𝑔 , en que 𝐴𝑔 es el área total de la sección transversal.
b) Desplazamientos de corte elásticos, posteriores a las grietas de corte: la rigidez
lateral para los desplazamientos que ocurren después de las grietas diagonales de corte
se basa en el modelo de falla de Paulay. Este considera la flexibilidad al corte de un
modelo puntal-tensor.
∆𝑠2 = ∆𝑠1 +
𝑉𝑁 − 𝑉𝑐
𝑘𝑠,𝑐𝑟
(2.34)
Donde:
𝑘𝑠,𝑐𝑟 =
0,25 𝜌𝑎
·𝐸 𝑏 𝑑
0,25 + 𝑛 · 𝜌𝑎 𝑠 𝑤
(2.35)
𝜌𝑎 es la cuantía de acero de las barras horizontales en la dirección vertical del muro, 𝑏𝑤 el
espesor del muro y 𝑑 la profundidad efectiva de la sección. Se recomienda un valor promedio
de 𝑛 = 10.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
20
c) Fase dúctil: luego de la fluencia del acero, la deformación por corte continuará
aumentando. Experimentos en columnas que no fallan por corte revelan que una
fracción de la deformación total permanece constante en la fase dúctil. Los
desplazamientos por corte son entonces proporcionales a los desplazamientos por
flexión y se determinan como:
∆𝑠 = ∆𝑓 ·
∆𝑠𝑁
∆𝑓𝑁
(2.36)
El desplazamiento total corresponde a la suma de los desplazamientos por corte y flexión,
tanto elásticos como plásticos.
2.3.2 Curva de resistencia fuerza-desplazamiento
La resistencia al corte nominal del hormigón armado esta dado por:
𝑉𝑛 = 𝑉𝑐 + 𝑉𝑠 + 𝑉𝑝
(2.37)
Donde 𝑉𝑐 , 𝑉𝑠 y 𝑉𝑝 son la resistencia al corte del hormigón, armadura transversal y resistencia
provista por la fuerza axial, respectivamente, las cuales se describen a continuación.
a) Resistencia al corte del hormigón: la resistencia al corte proporcionada por el
hormigón está dada por la Ecuación 2.38.
𝑉𝑐 = 𝛼 · 𝛽 · 𝛾√𝑓´𝑐 · (0,8𝐴𝑔 )
(2.38)
Donde:
1≤𝛼 =3−
𝑀
≤ 1,5
𝑉·𝐷
(2.39)
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
21
𝛽 = 0,5 + 20𝜌𝑙 ≤ 1,0
0,25
121
7
𝛾={
−
𝜇
400 400
0,04
(2.40)
𝜇≤3
3 < 𝜇 ≤ 15
(2.41)
𝜇 > 15
𝑀 y 𝑉 son el momento y el corte en la sección crítica, 𝐷 es la profundidad de la sección y
𝜌𝑙 =
𝐴𝑠𝑙
𝐴𝑔
.
En la Ecuación 2.41 el valor de 𝛾 depende de la ductilidad al desplazamiento de la sección.
Miembros existentes
0,35
0,35
0,3
0,3
0,25
0,25
γ (MPa)
γ (MPa)
Miembros nuevos
0,2
0,15
0,2
0,15
0,1
0,1
0,05
0,05
0
0
0
2
4
6
8 10 12 14 16 18 20
0
2
4
6
μ
Uniaxial
8 10 12 14 16 18 20
μ
Biaxial
Uniaxial
Biaxial
Figura 2.7: Valor de 𝛾 para diferentes ductilidades, configuraciones de carga y edad.
La resistencia al corte del hormigón para miembros con momento en las dos direcciones se
degrada más rápido que las secciones con momento solo en una dirección. También, se
distingue una variación del valor de 𝛾 en miembros nuevos y existentes, tal como se observa
en la Figura 2.7.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
22
b) Resistencia al corte provista por la fuerza axial: La fuerza axial de compresión les
confiere a los miembros de hormigón un aumento de su resistencia al corte. Al muro
de la Figura 2.8 se le aplica una fuerza axial 𝑁 y una fuerza de corte 𝑉 en el extremo
superior. En la base existe una zona de compresión de longitud “c” cuya proyección
desde su centro hasta el centroide de la parte superior del muro, genera un ángulo 𝜁
respecto al eje vertical. Entonces, la resistencia al corte 𝑉𝑝 se calcula según la
Ecuación 2.42.
𝑉𝑝 = 0,85 𝑁 · 𝑡𝑎𝑛(𝜁)
(2.42)
c) Resistencia al corte provista por el refuerzo transversal: La contribución del
refuerzo transversal a la resistencia al corte se determina según la Ecuación 2.43.
𝑉𝑠 =
𝐴𝑣 𝑓𝑦ℎ · (𝐷 − 𝑐 − 𝑐0 )
𝑠
(2.43)
Donde 𝐴𝑣 es el área de refuerzo transversal que es atravesado por las gritas de corte, 𝑓𝑦ℎ la
tensión de fluencia de los estribos, D la distancia centro a centro de los estribos, c la distancia
de la fibra más comprimida al eje neutro y 𝑐0 la distancia desde el centro del estribo a la cara
externa del miembro de hormigón. El valor (𝐷 − 𝑐 − 𝑐0 ) puede aproximarse por 0,8 𝑙𝑤
donde 𝑙𝑤 es el largo horizontal del muro.
El resultado de calcular la curva de respuesta descrita en el apartado 2.3.1 y la curva de
resistencia del apartado 2.3.2 es la Figura 2.9. En este se observa la curva de respuesta y dos
posibles casos de resistencia del muro. En el primero, el desplazamiento lateral de 2 cm
corresponde a una fuerza de 107,5 kN (curva de respuesta). En este punto la resistencia al
corte (Resistencia 1) es de 120 kN, se dice entonces que la resistencia es mayor que la
solicitación.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
23
Figura 2.8: Componentes para el cálculo de la resistencia al corte 𝑉𝑝 .
Pero, llegará un momento en el que el incremento de la fuerza F intersecará a la curva
“Resistencia 1” y de allí en adelante la resistencia será inferior a la carga actuante en el muro.
Esta intersección se define como “falla por corte” y significa que, aunque los materiales no
lleguen a su límite de resistencia y deformación, el muro manifestará importantes daños que
le impedirán soportar cargas laterales. Un segundo caso es cuando estas curvas nunca se
intersecan, como lo es el caso de la curva “Resistencia 2”. Aquí el corte máximo queda
limitado por el momento máximo posible desarrollado en la sección transversal, el cual está
sujeto a la resistencia de los materiales utilizados en la construcción.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
24
180
160
140
F (kN)
120
100
80
Falla por
corte
60
Corte máximo
40
20
0
0
2
4
6
8
10
12
Δ (cm)
Respuesta
Resistencia 1
Resistencia 2
Figura 2.9: Curvas de respuesta y resistencia obtenidas con el método desarrollado.
2.4 Cálculo del error relativo
La curva de respuesta fuerza-desplazamiento 𝐹𝑇 (∆) se comparará con la curva experimental
obtenida de ensayos de muros experimentales 𝐹𝐸 (∆) mediante el cálculo del error relativo
entre ellas (Ecuación 2.44).
𝑒(∆) =
|𝐹𝑇 (∆) − 𝐹𝐸 (∆)|
· 100%
𝐹𝐸 (∆)
(2.44)
El resultado de graficar la Ecuación 2.44 será el que se observa en la Figura 2.10, en el cual
existen dos curvas a comparar. Mientras más separadas estén las curvas en un mismo valor
de la abscisa, mayor será el error relativo en ese punto y cuando lleguen a intersecarse, es
decir, 𝐹𝑇 (∆) − 𝐹𝐸 (∆) = 0, el error es del 0% al aplicar la Ecuación 2.44.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
25
600,0
100,0%
90,0%
500,0
80,0%
F (kN)
60,0%
300,0
50,0%
40,0%
200,0
Error (%)
70,0%
400,0
30,0%
20,0%
100,0
10,0%
0,0
0,0000
0,0050
0,0100
0,0150
0,0200
Δ (cm)
0,0250
0,0300
0,0%
0,0350
Figura 2.10: Interpretación de la curva de error relativo 𝑒(∆).
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
26
3. Resultados
de
ensayos
de
muros
experimentales
Los ensayos de muros experimentales que se exponen a continuación provienen de la
publicación “Earthquake resistant structural walls – Test of isolated walls” (Portland Cement
Association, 1976). En esta se describe con detalle la campaña experimental de nueve muros
de hormigón armado denotados como: R1, R2, B1, B2, B3, B4, B5, B6 y F1. La letra indica
la forma de la sección transversal, siendo la “R” una sección rectangular y las letras “B” y
“F” muros con columnas y alas respectivamente en cada uno de sus extremos (ver
Figura 3.1). Todos son de tipo cantiléver y de variadas características geométricas, resistencia
de materiales, disposición de armaduras y patrón de carga. A continuación, se presenta una
descripción de las características necesarias para realizar el análisis fuerza-desplazamiento.
Figura 3.1: Dimensiones de los muros F, B y R respectivamente (medidas en metros).
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
27
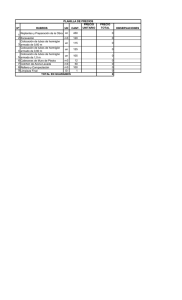
3.1 Características del hormigón
Las propiedades del hormigón utilizado en la construcción de los muros se presentan en la
Tabla 3.1. El módulo elástico y la resistencia a la compresión se obtuvieron a través de
ensayos realizados en los laboratorios de la Asociación de Cemento Portland (Portland
Cement Association, 1976), a probetas cilíndricas de 152 mm de diámetro y 305 mm de alto,
mientras que el módulo de ruptura o resistencia a tracción se obtuvieron del ensayo a flexotracción de vigas de 152 x 152 x 762 mm.
Tabla 3.1: Propiedades mecánicas del hormigón.
Muro
R1
R2
B1
B3
B4
B2
B5
B6
F1
Edad Resistencia compresión Resistencia tracción Módulo elástico
(días)
fc’ (MPa)
fr (MPa)
Ec (GPa)
48
44,7
4,5
27,7
54
46,4
4,4
26,8
55
52,9
5,0
28,1
54
47,2
4,3
27,3
68
45,0
4,6
28,2
47
53,6
4,8
28,9
52
45,3
4,3
27,3
36
42,7
3,6
27,6
68
38,4
4,3
25,4
3.2 Características de las barras de acero
Los muros se armaron con diferentes tamaños de barra. Las barras D3 solamente se usaron
como estribos de “no confinamiento”, las barras de 6 mm se usaron como estribos de
confinamiento y armadura de corte en el centro del muro. Las barras No. 3, No. 4 y No. 6 se
usaron como barras longitudinales de borde. En la Tabla 3.2 se presentan las barras utilizadas
en cada muro y sus propiedades físicas (“εsu” es la deformación unitaria última).
La equivalencia en milímetros de los tamaños de barra de la tabla anterior se presenta en la
Tabla 3.3.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
28
Tabla 3.2: Propiedades físicas de las barras de refuerzo.
Barra Propiedad
fy (MPa)
fu (MPa)
D3
Es (GPa)
εsh
εsu
fy (MPa)
fu (MPa)
6 mm Es (GPa)
εsh
εsu
fy (MPa)
fu (MPa)
No. 3 Es (GPa)
εsh
εsu
fy (MPa)
fu (MPa)
No. 4 Es (GPa)
εsh
εsu
fy (MPa)
fu (MPa)
No. 6 Es (GPa)
εsh
εsu
R1
455,1
496,4
211,0
0,015
0,059
521,9
699,8
216,5
0,015
0,122
511,6
765,3
191,7
0,01
0,098
-
R2
485,4
525,4
195,1
0,015
0,111
535,0
690,9
224,8
0,015
0,124
450,2
708,1
185,5
0,008
0,123
-
B1
473,7
517,8
227,5
0,015
0,11
520,6
695,0
224,1
0,015
0,107
449,5
708,1
195,1
0,008
0,117
-
B2
462,6
513,0
233,0
0,015
0,094
532,3
700,5
221,3
0,015
0,102
410,2
695,0
208,2
0,007
0,133
B3
475,7
529,5
224,1
0,015
0,089
478,5
658,4
209,6
0,015
0,117
437,8
696,4
178,6
0,008
0,109
-
B4
508,8
543,3
195,8
0,015
0,108
504,7
681,2
219,9
0,015
0,126
450,2
706,7
189,6
0,008
0,118
-
B5
477,1
519,9
215,1
0,015
0,101
501,9
671,5
216,5
0,015
0,121
444,0
733,6
203,4
0,007
0,132
B6
477,1
519,9
215,1
0,015
0,101
501,9
671,5
216,5
0,015
0,121
444,0
733,6
203,4
0,007
0,132
F1
480,6
528,1
226,1
0,015
0,103
525,4
704,6
215,8
0,015
0,104
444,7
707,4
193,7
0,008
0,115
-
Tabla 3.3: Tamaños de barras utilizadas en los muros.
Barra Diámetro (mm)
D3
4,95
6 mm
6,35
No. 3
9,52
No. 4
12,7
No. 6
19,05
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
29
3.3 Muro R1
El muro R1 tiene una sección rectangular con un 1,47% de cuantía de acero vertical
(2,83 cm2) en una distancia de 190,5 mm desde cada borde, reforzada con estribos tamaño
D3 a 101,6 mm, tal como se muestra en la Figura 3.3. El ensayo cíclico de carga consistió en
30,5 ciclos (ver Figura 3.2).
La primera grieta de flexión ocurrió en el ciclo n.⁰ 4 cuando la carga era de 53,4 kN. La
primera vez que el acero alcanzó la tensión de fluencia fue en el ciclo n.⁰ 10 cuando la carga
fue de 89,4 kN.
La máxima carga registrada fue de 118,3 kN, la que ocurrió en el ciclo n.⁰ 16 con un
desplazamiento superior de 50,8 mm.
150
100
Fuerza (kN)
50
0
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
-50
-100
-150
Ciclo (n.⁰)
Figura 3.2: Historial de carga del muro R1.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
30
Figura 3.3: Detalle de armadura del muro R1.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
31
3.4 Muro R2
El muro R2 tiene una sección rectangular con un 4,00% de cuantía de acero vertical
(7,60 cm2) en una distancia de 190,5 mm desde cada borde, reforzada con estribos tamaño
D3 cada 101,6 mm y elemento especial de borde en los 1,83 m inferiores de tamaño 6 mm
cada 33,9 mm, tal como se muestra en la Figura 3.5. El ensayo cíclico de carga consistió en
39 ciclos (ver Figura 3.4).
La primera grieta de flexión ocurrió en el ciclo n.⁰ 4 cuando la carga era de 66,7 kN. La
primera vez que el acero alcanzó la tensión de fluencia fue en el ciclo n.⁰ 19 cuando la carga
fue de 164,6 kN.
La máxima carga registrada fue de 216,6 kN, la que ocurrió en el ciclo n.⁰ 34 con un
desplazamiento superior de 127,0 mm.
250
200
150
Fuerza (kN)
100
50
0
-50
0
2
4
6
8
10 12 14 16 18 20 22 24 26 28 30 32 34 36 38
-100
-150
-200
-250
Ciclo (n.⁰)
Figura 3.4: Historial de carga del muro R2.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
32
Figura 3.5: Detalle de armadura del muro R2.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
33
3.5 Muro B1
El muro B1 tiene una sección con columnas rectangulares en sus extremos, tal como se
observa en la Figura 3.7. Posee un 1,11 % de cuantía de acero vertical (10,13 cm2) en cada
columna, reforzada con estribos tamaño D3 cada 203,2 mm. El ensayo cíclico de carga
consistió en 36 ciclos (ver Figura 3.6).
La primera grieta de flexión ocurrió en el ciclo n.⁰ 4 cuando la carga era de 115,7 kN. La
primera vez que el acero alcanzó la tensión de fluencia fue en el ciclo n.⁰ 10 cuando la carga
fue de 200,6 kN.
La máxima carga registrada fue de 271,3 kN, la que ocurrió en el ciclo n.⁰ 28 con un
desplazamiento superior de 101,6 mm.
400
300
Fuerza (kN)
200
100
0
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
36
-100
-200
-300
-400
Ciclo (n.⁰)
Figura 3.6: Historial de carga del muro B1.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
34
Figura 3.7: Detalle de armadura del muro B1.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
35
3.6 Muro B2
El muro B2 tiene una sección con columnas rectangulares en sus extremos con un 3,67 % de
cuantía de acero vertical (34,02 cm2) en cada columna, reforzada con estribos tamaño D3
cada 203,2 mm, tal como se muestra en la Figura 3.9. El ensayo cíclico de carga consistió en
30,5 ciclos (ver Figura 3.8).
La primera grieta de flexión ocurrió en el ciclo n.⁰ 4 cuando la carga era de 133,4 kN. La
primera vez que el acero alcanzó la tensión de fluencia fue en el ciclo n.⁰ 13 cuando la carga
fue de 532,4 kN.
La máxima carga registrada fue de 703,7 kN, la que ocurrió en el ciclo n.⁰ 25 con un
desplazamiento superior de 101,6 mm.
800
600
Fuerza (kN)
400
200
0
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
-200
-400
-600
-800
Ciclo (n.⁰)
Figura 3.8: Historial de carga del muro B2.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
36
Figura 3.9: Detalle de armadura del muro B2.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
37
3.7 Muro B3
El muro B3 es similar al muro B1, con la diferencia de que B3 posee elemento especial de
borde en los 1,83 m inferiores de tamaño 6 mm cada 33,9 mm, tal como se muestra en la
Figura 3.11. El ensayo cíclico de carga consistió en 42 ciclos (ver Figura 3.10).
La primera grieta de flexión ocurrió en el ciclo n.⁰ 4 cuando la carga era de 124,5 kN. La
primera vez que el acero alcanzó la tensión de fluencia fue en el ciclo n.⁰ 10 cuando la carga
fue de 201,0 kN. El comportamiento del muro B3 fue muy similar a los del muro B1 en los
primeros 21 ciclos.
La máxima carga registrada fue de 275,8 kN, la que ocurrió en el ciclo n.⁰ 34 con un
desplazamiento superior de 152,4 mm.
400
300
Fuerza (kN)
200
100
0
0
2
4
6
8
10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42
-100
-200
-300
Ciclo (n.⁰)
Figura 3.10: Historial de carga del muro B3.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
38
Figura 3.11: Detalle de armadura del muro B3 y B4.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
39
3.8 Muro B4
El muro B4 es idéntico al muro B3, por lo que los planos de las armaduras corresponden con
los de la Figura 3.11. La diferencia es que B4 fue ensayado con carga monotónica para
compararlo con B3.
La primera grieta de flexión ocurrió a los 115,6 kN de fuerza. A los 201,5 kN el acero alcanzó
la tensión de fluencia. La máxima carga registrada fue de 334,9 kN asociado a un
desplazamiento lateral de 215,9 mm.
3.9 Muro B5
El muro B5 es similar al muro B2, pero B5 cuenta con elemento especial de borde en los
1,83 m inferiores de tamaño 6 mm cada 33,9 mm, tal como se muestra en la Figura 3.13. El
ensayo cíclico de carga consistió en 30 ciclos (ver Figura 3.12).
La primera grieta de flexión ocurrió en el ciclo n.⁰ 4 cuando la carga era de 133,4 kN. La
primera vez que el acero alcanzó la tensión de fluencia fue en el ciclo n.⁰ 13 cuando la carga
fue de 112,3 kN. La máxima carga registrada fue de 761,9 kN, la que ocurrió en el ciclo
n.⁰ 28 con un desplazamiento superior de 127,0 mm.
Fuerza (kN)
1000
500
0
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
-500
-1000
Ciclo (n.⁰)
Figura 3.12: Historial de carga del muro B5.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
40
Figura 3.13: Detalle de armadura del muro B5 y B6.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
41
3.10 Muro B6
El muro B6 es la reparación del muro B5 y, por lo tanto, la sección transversal es la de la
Figura 3.13. El ensayo cíclico de carga consistió en 30 ciclos (ver Figura 3.14).
La primera grieta de flexión ocurrió en el ciclo n.⁰ 4 cuando la carga era de 133,4 kN. La
primera vez que el acero alcanzó la tensión de fluencia fue en el ciclo n.⁰ 13.
La máxima carga registrada fue de 746,8 kN, la que ocurrió en el ciclo n.⁰ 28 con un
desplazamiento superior de 152,4 mm.
1000
800
600
Fuerza (kN)
400
200
0
-200
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
-400
-600
-800
-1000
Ciclo (n.⁰)
Figura 3.14: Historial de carga del muro B6.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
42
3.11 Muro F1
El muro F1 tiene una sección con alas en sus extremos, tal como se observa en la Figura 3.16.
Posee un 3,89 % de cuantía de acero vertical (35,46 cm2) en cada ala, reforzada con estribos
tamaño 6 mm cada 88,9 mm. El ensayo cíclico de carga consistió en 25 ciclos (ver
Figura 3.15).
La primera grieta de flexión ocurrió en el ciclo n.⁰ 4 cuando la carga era de 173,5 kN. La
primera vez que el acero alcanzó la tensión de fluencia fue en el ciclo n.⁰ 13 cuando la carga
fue de 669,9 kN.
La máxima carga registrada fue de 835,8 kN, la que ocurrió en el ciclo n.⁰ 22 con un
desplazamiento superior de 101,6 mm.
1000
800
600
Fuerza (kN)
400
200
0
-200
0
2
4
6
8
10
12
14
16
18
20
22
24
-400
-600
-800
-1000
Ciclo (n.⁰)
Figura 3.15: Historial de carga del muro F1.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
43
Figura 3.16: Detalle de armadura del muro F1.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
44
4. Análisis de los resultados
4.1 Gráficos momento-curvatura
Los datos de los muros descritos en el Capítulo 3 se ingresaron al programa SAP2000 (CSI,
2022) para desarrollar los gráficos momento-curvatura que se muestran en las páginas
siguientes.
La Figura 4.1 muestra parte del desarrollo del modelo de la sección transversal, en el que se
puede apreciar los diferentes materiales que componen el muro. En este caso, la sección
posee elemento especial de borde destacada en color crema, dentro de las barras
longitudinales formando un núcleo cuadrado en los extremos.
Figura 4.1: Pantalla del editor de secciones, SAP2000.
Una vez ingresadas las curvas de los materiales y la geometría de la sección, se obtiene un
gráfico como el de la Figura 4.2, el cual puede exportarse en tablas que contienen las
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
45
deformaciones unitarias, posición del eje neutro y fuerzas en los materiales para cada punto
momento-curvatura. Estas tablas se adjuntan en el Anexo A: “Tablas de cálculo momentocurvatura”. Desde la Figura 4.3 a la Figura 4.11 se presentan los gráficos momento-curvatura
calculados por SAP2000 y que se contrastan con los gráficos momento-curvatura
experimentales.
Figura 4.2: Diagrama momento-curvatura de la sección transversal.
El valor promedio del error relativo entre los diagramas momento-curvatura teórico y la
envolvente experimental no superan el 14,2% (ver Tabla 4.1), con excepción del muro B6,
que, debido a su reparación, experimentó una pérdida de la rigidez lateral, no así una pérdida
de resistencia (comparar la Figura 4.9 con la Figura 4.10).
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
46
Otro comportamiento observable es el alto valor inicial de la curva de error relativo. Esto
puede deberse a la dificultad de elegir una trayectoria ϕ-M al momento de digitalizar los
gráficos de la publicación de los ensayos de muros experimentales (Portland Cement
Association, 1976). Para valores pequeños de la curvatura las trayectorias se superponen
entre sí para los diferentes ciclos de carga y descarga, haciendo imposible distinguir con
claridad la trayectoria correspondiente a los primeros ciclos.
Tabla 4.1: Error promedio de la curva momento-curvatura.
Muro Error
R1
11,1%
R2
9,2%
B1
7,6%
B2
10,3%
B3
9,7%
B4
14,0%
B5
14,0%
B6
41,9%
F1
14,2%
Otra característica importante es el punto en que la función de error relativo toma el valor
cero, lo que ocurre en la intersección de la curva teórica con la experimental. Los puntos que
son anteriores a la intersección y pertenecen a la curva teórica superan en magnitud al
momento de la curva experimental para los mismos valores de curvatura y después de la
intersección sucede lo contrario. Esto puede explicarse mediante el cambio de las curvas
tensión-deformación de los materiales, las cuales experimentan un desgaste luego de cada
ciclo de carga, que disminuyen su resistencia y el módulo elástico.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.3: Momento-curvatura del muro R1.
47
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.4: Momento-curvatura del muro R2.
48
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.5: Momento-curvatura del muro B1.
49
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.6: Momento-curvatura del muro B2.
50
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.7: Momento-curvatura del muro B3.
51
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.8: Momento-curvatura del muro B4.
52
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.9: Momento-curvatura del muro B5.
53
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.10: Momento-curvatura del muro B6.
54
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.11: Momento-curvatura del muro F1.
55
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
56
4.2 Gráficos fuerza-desplazamiento
El conjunto de puntos momento-curvatura se ingresaron a una tabla de elaboración propia en
el programa Excel, que reproduce la secuencia de cálculo fuerza-desplazamiento descrita en
los apartados 2.3 y 2.4. Las tablas de cálculo se adjuntan en el Anexo B: “Tablas de cálculo
fuerza-desplazamiento” y contienen los puntos representados desde la Figura 4.13 a la 4.21.
De manera análoga a los gráficos momento-curvatura, la función de error relativo devuelve
valores altos cuando los desplazamientos laterales son pequeños y luego se estabilizan y
tienden a mantener un promedio bajo. En general, el muro B4 es el que tiene un mejor ajuste
entre la curva teórica y la experimental (con un error promedio del 11,7%), siendo la
explicación más probable la manera en que se aplicó la fuerza lateral (monotónica, no
cíclica).
La Tabla 4.2 contiene un resumen del análisis de los datos extraídos del cálculo desarrollado
para cada muro. La columna “Entre curvas” corresponde a la suma de los errores relativos
entre la curva teórica y la envolvente experimental dividida por el número total de puntos,
mientras que la columna “En la falla” es el error relativo entre la fuerza máxima experimental
y la fuerza máxima teórica.
Dependiendo de si la curva de resistencia al corte interseca o no a la curva de respuesta
fuerza-desplazamiento, el tipo de falla es por corte o flexión, respectivamente. La última
columna de la Tabla 4.2 contiene esta clasificación. A los muros se les aplicó una fuerza
variable en su extremo superior, generando un corte de igual magnitud a lo largo del muro y
un momento que es igual al producto entre la fuerza y la altura de aplicación. Si la armadura
horizontal de corte es pequeña y el muro falla por corte, se puede esperar la aparición de
grietas diagonales en el centro de la cara del muro. En caso contrario, si el muro presenta
armadura de corte suficiente, es de esperar la aparición de grietas horizontales en los bordes
de la zona inferior del muro, esta falla es de flexión. La Figura 4.12 muestra las fotografías
del muro R1 (izquierda), cuya predicción de falla teórico es de flexión y puede observarse
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
57
que presenta grietas horizontales en los bordes, a diferencia del muro B2 que no se distinguen,
pero sí las grietas diagonales en el centro de la falla por corte. Con excepción del muro B3,
el método teórico logró predecir exactamente el tipo de falla que se produciría en cada muro.
Tabla 4.2: Error relativo (fuerzas) y tipo de falla de los muros analizados.
Muro Entre curvas En la falla
Tipo
R1
24,2%
1,9%
Flexión
R2
12,2%
15,0%
Flexión
B1
12,6%
16,4%
Flexión
B2
13,7%
5,2%
Corte
B3
13,0%
15,2%
Flexión
B4
11,7%
5,9%
Corte
B5
12,5%
2,2%
Corte
B6
42,3%
3,5%
Corte
F1
13,6%
15,5%
Corte
Figura 4.12: Fotografías de los especímenes R1 (falla por flexión) y B2 (falla por corte).
Fuente: (Portland Cement Association, 1976).
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
58
Con respecto al cálculo de los desplazamientos, el muro B4 (ensayado a carga monotónica)
es el que mejor ajuste da al modelo teórico. Para el resto de los muros la estimación podría
mejorarse realizando el cálculo con las curvas tensión-deformación cíclicas.
En la Figura 4.18 (fuerza-desplazamiento del muro B4) se puede observar, por ejemplo, que
la curva de resistencia al corte parte como una recta horizontal desde el punto (0; 513) al
(3,4; 510,8). La deformación unitaria en la fluencia de las barras del muro B4, según la
Tabla 3.2, es de 450,2 / 189.600 = 0,0024 m/m, el cual está asociado a una curvatura de
0,0015 m/m y a un desplazamiento de 1,1 cm (ver Tabla A.6 y Tabla B.11). La ductilidad en
3,4
este punto es de 𝜇 = 1,1 ≈ 3. A partir de este punto, el aumento de la ductilidad produce una
disminución de la resistencia tal como se observa en la Figura 2.7, esta pérdida de resistencia
se detiene cuando la ductilidad alcanza el valor de 15, es decir, cuando el desplazamiento es
de 15 · 1,1 = 16,4 cm. A partir de este punto, la curva de resistencia continúa como una línea
horizontal en la Figura 4.18, que se prolonga hasta el valor de la curvatura última (𝜑𝑢 ).
Nótese en las Figuras 4.13 a 4.21 que no todos los muros desarrollan ductilidades mayores
que 15, por ende, no desarrollan el tramo final horizontal de resistencia al corte, como, por
ejemplo, la Figura 4.13. La resistencia al corte inicial se calcula utilizando la Ecuación 2.37,
con 𝛾 = 0,25, es decir: 𝑉𝑐𝑖 = (1 · 0,649 · 0,25 · √45 · 0,8 · 0,318) + (0,000062 · 504,7 ·
1,905
0,8 · 0,2032) = 0,277 + 0,236 = 0,513 MN. La resistencia al corte final se calcula de
manera similar, pero con 𝛾 = 0,04 (Ecuación 2.37), es decir: 𝑉𝑐𝑓 = (1 · 0,649 · 0,04 · √45 ·
1,905
0,8 · 0,318) + (0,000062 · 504,7 · 0,8 · 0,2032) = 0,044 + 0,236 = 0,280 MN.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.13: Análisis fuerza-desplazamiento del muro R1.
59
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.14: Análisis fuerza-desplazamiento del muro R2.
60
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.15: Análisis fuerza-desplazamiento del muro B1.
61
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.16: Análisis fuerza-desplazamiento del muro B2.
62
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.17: Análisis fuerza-desplazamiento del muro B3.
63
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.18: Análisis fuerza-desplazamiento del muro B4.
64
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.19: Análisis fuerza-desplazamiento del muro B5.
65
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.20: Análisis fuerza-desplazamiento del muro B6.
66
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Figura 4.21: Análisis fuerza-desplazamiento del muro F1.
67
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
68
5. Conclusiones
En esta memoria se han calculado las curvas de respuesta fuerza-desplazamiento y de
resistencia al corte de nueve muros de hormigón armado de distinta sección transversal,
demostrando que la metodología de cálculo puede estimar con relativa exactitud la magnitud
de la fuerza de corte última que resistirá el muro con un error promedio del 9,0%. Además,
logra predecir el tipo de falla (corte o flexión) con una alta precisión.
Los muros R1, R2, B1 y B3 presentaron una falla teórica por flexión, mientras que los muros
B2, B4, B5, B6 y F1 presentaron una falla por cortante. Esto puede deberse al incremento de
inercia de la sección transversal de estos, disminuyendo las tensiones internas en los bordes
para un mismo momento solicitante. El incremento de la resistencia al momento va de la
mano con un incremento de la fuerza horizontal aplicada a los muros, sin embargo, la
armadura transversal no es suficiente para resistir esta fuerza, originando una falla por corte.
Con el objetivo de reducir el riesgo de la falla por corte en elementos de vigas y columnas,
el código de diseño ACI 318-08 obliga a calcular el corte último como el menor valor entre
el cortante máximo obtenido de las combinaciones de carga de diseño que incluyan la carga
sísmica y el cortante asociado con el desarrollo de los momentos nominales del elemento en
cada extremo más el cortante de las cargas gravitacionales mayoradas. Esta indicación no es
obligatoria para el diseño de muros, pero de haberse aplicado, la curva de resistencia nunca
se interceptaría con la curva de respuesta fuerza-desplazamiento, asegurando una falla por
flexión.
Se debe seguir estudiando el mecanismo de resistencia al corte de muros de hormigón armado
en nuestro país con el objetivo de prevenir este tipo peligroso de falla y que se cree ocurrió
en algunos edificios de la ciudad de Viña del Mar durante el sismo del 27 de febrero de 2010
(Bartolomé, Quiun, y Silva, 2011).
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
69
6. Referencias
Bartolomé, S., Quiun, D., y Silva, W. (2011). Comentarios relativos al tipo de falla en los
muros de concreto de edificios chilenos en el sismo del 27 de febrero de 2010. Concreto y
Cemento. Investigación y desarrollo. México.
Carreira, D., y Chu, K. (1986). Stress-Strain Relationship for Reinforced Concrete in
Tension. Technical paper. ACI Journal.
CSI. (2022). Computers and Structures, Inc. SAP2000 v.22. California, Estados Unidos.
INN. (2008). Instituto Nacional de Normalización. Hormigón armado-Requisitos de diseño
y cálculo. Norma Chilena Oficial NCh430of2008. Santiago, Chile.
MINVU. (2011). Ministerio de Vivienda y Urbanismo. Aprueba reglamento que fija los
requisitos de diseño y cálculo para el hormigón Armado y deroga decreto N⁰ 118, de 2010.
Decreto Supremo n.⁰ 60. Diario Oficial de la República de Chile. Santiago, Chile.
Molins, C., y Aguado, A. (2007). Análisis no lineal y comportamiento en servicio y rotura
de secciones construidas evolutivamente sometidas a flexocompresión recta.
Montejo, L., y Kowalsky, M. (2007). CUMBIA Set of codes for the analysis of reinforced
concrete members. Constructed Facilities Laboratory Raleigh, Carolina del Norte, Estados
Unidos.
Portland Cement Association. (1976). Earthquake Resistant Structural Walls - Test of
Isolated Walls. Skokie, Estados Unidos.
Priestley, N., Calvi, M., y Kowalsky, M. (2007). Displacement-Based Seismic Design of
Structures. Instituto Universitario de Estudios Superiores de Pavia, Italia.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
70
Anexos
Anexo A: Tablas de cálculo momento-curvatura
A continuación, desde la Tabla A.1 a A.8 se presentan los cálculos generados por el programa
SAP2000 para hallar la relación momento-curvatura para los distintos muros. Las columnas
corresponden a: la deformación unitaria del hormigón en la fibra extrema en compresión, la
ubicación del eje neutro medido desde la fibra extrema en compresión (en metros), la
deformación unitaria del acero en la fibra más traccionada, la fuerza neta de compresión del
hormigón y el acero (kN), la fuerza neta de tensión del acero (kN) y los valores de momentocurvatura para un determinado estado de equilibrio asociado a las variables anteriores.
Los valores de curvatura y momentos en la fluencia pueden obtenerse interpolando en la
columna “Deformación acero (mm)” los valores de la Tabla 4.2: Propiedades físicas de las
barras de refuerzo.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica – Felipe Castillo Huerta
Tabla A.1: Cálculo de la curvatura y el momento de la sección transversal del muro R1.
Deformación
hormigón (m/m)
0,0000
-0,0001
-0,0002
-0,0004
-0,0006
-0,0007
-0,0008
-0,0010
-0,0011
-0,0012
-0,0014
-0,0016
-0,0017
-0,0019
-0,0021
-0,0023
-0,0025
-0,0028
-0,0031
-0,0035
Eje
neutro
(m)
0,000
0,414
0,614
0,649
0,665
0,701
0,730
0,754
0,772
0,787
0,797
0,806
0,814
0,821
0,826
0,830
0,833
0,834
0,834
0,831
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0000
0,0004
0,0011
0,0020
0,0031
0,0045
0,0062
0,0081
0,0103
0,0128
0,0155
0,0184
0,0216
0,0251
0,0288
0,0328
0,0369
0,0414
0,0460
0,0507
0,0
-20,8
-77,7
-146,2
-220,0
-245,1
-261,4
-271,4
-280,2
-290,2
-303,0
-315,7
-323,0
-332,2
-339,2
-348,2
-354,8
-360,1
-362,3
-362,7
0,0
-7,1
-9,1
-14,0
-20,1
-23,4
-25,7
-27,2
-28,2
-28,9
-31,6
-35,0
-38,2
-41,6
-45,2
-49,3
-53,9
-59,5
-66,3
-72,6
0,0
27,9
85,9
160,3
240,2
268,6
287,2
298,7
308,5
319,6
334,8
350,4
361,2
373,2
385,2
397,3
408,6
419,4
428,7
435,2
0,00000
0,00028
0,00069
0,00124
0,00193
0,00276
0,00373
0,00483
0,00607
0,00745
0,00897
0,01063
0,01242
0,01435
0,01642
0,01863
0,02097
0,02346
0,02608
0,02884
0,00
121,46
144,03
244,21
356,23
381,67
395,49
403,07
409,76
423,66
440,94
458,22
471,67
487,31
499,72
514,02
525,58
536,27
544,73
551,42
71
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla A.2: Cálculo de la curvatura y el momento de la sección transversal del muro R2.
Deformación
hormigón (m/m)
0,0000
-0,0001
-0,0002
-0,0002
-0,0003
-0,0004
-0,0005
-0,0007
-0,0007
-0,0008
-0,0009
-0,0010
-0,0011
-0,0011
-0,0012
-0,0013
-0,0014
-0,0015
-0,0016
-0,0017
-0,0018
-0,0019
Eje
neutro
(m)
0,000
0,141
0,351
0,492
0,536
0,551
0,558
0,574
0,608
0,638
0,663
0,684
0,703
0,718
0,729
0,740
0,749
0,757
0,764
0,770
0,775
0,781
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0000
0,0001
0,0003
0,0007
0,0011
0,0016
0,0021
0,0028
0,0036
0,0044
0,0054
0,0065
0,0077
0,0090
0,0104
0,0118
0,0134
0,0151
0,0168
0,0186
0,0206
0,0226
0,0
-6,2
-33,9
-85,6
-143,6
-212,1
-289,9
-352,1
-368,0
-377,4
-384,1
-389,6
-392,6
-399,0
-410,0
-418,4
-427,6
-437,2
-447,9
-458,0
-466,2
-471,6
0,0
-11,8
-20,1
-25,6
-34,7
-47,1
-62,0
-75,7
-83,7
-90,5
-96,6
-101,9
-106,3
-110,9
-116,2
-120,7
-125,3
-129,9
-134,8
-139,7
-144,1
-147,8
0,0
17,2
53,8
110,8
179,2
259,2
352,0
428,6
450,9
467,8
480,8
491,7
499,0
510,1
526,4
539,2
552,9
567,4
582,7
597,6
609,5
618,6
0,00000
0,00011
0,00026
0,00047
0,00074
0,00105
0,00142
0,00184
0,00231
0,00284
0,00342
0,00405
0,00473
0,00547
0,00626
0,00710
0,00799
0,00894
0,00994
0,01099
0,01210
0,01325
0,00
146,66
176,19
207,99
299,20
420,34
564,38
680,28
706,58
722,84
734,56
743,73
749,92
762,85
784,12
804,37
825,62
847,66
871,22
893,34
911,62
928,30
72
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Deformación
hormigón (m/m)
-0,0021
-0,0022
-0,0023
-0,0025
-0,0027
-0,0029
-0,0032
-0,0035
-0,0038
-0,0040
-0,0043
-0,0045
-0,0048
-0,0050
-0,0053
-0,0056
-0,0059
-0,0063
-0,0066
-0,0069
-0,0072
-0,0075
-0,0079
Eje
neutro
(m)
0,785
0,788
0,791
0,793
0,793
0,792
0,788
0,784
0,783
0,783
0,783
0,783
0,784
0,783
0,783
0,782
0,782
0,782
0,782
0,782
0,782
0,782
0,783
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0248
0,0270
0,0293
0,0316
0,0341
0,0366
0,0391
0,0417
0,0445
0,0474
0,0504
0,0534
0,0566
0,0598
0,0631
0,0665
0,0700
0,0736
0,0773
0,0811
0,0849
0,0889
0,0930
-475,9
-481,4
-484,2
-487,3
-491,7
-495,0
-487,8
-479,6
-478,9
-478,7
-478,3
-478,0
-479,4
-483,2
-486,8
-490,2
-493,4
-496,5
-499,5
-502,4
-505,0
-507,4
-509,7
-151,9
-158,3
-167,0
-173,9
-178,1
-183,2
-193,0
-207,7
-215,1
-222,3
-228,8
-234,3
-238,9
-240,1
-241,2
-242,2
-243,0
-243,8
-244,4
-244,8
-245,2
-245,5
-245,7
628,6
639,4
651,2
661,1
669,7
678,0
680,7
687,3
694,2
700,9
707,0
712,5
717,9
723,0
727,8
732,2
736,3
740,1
743,7
747,1
750,1
752,8
755,3
0,01446
0,01572
0,01704
0,01841
0,01983
0,02130
0,02282
0,02440
0,02603
0,02772
0,02945
0,03124
0,03308
0,03497
0,03692
0,03892
0,04097
0,04307
0,04523
0,04744
0,04970
0,05201
0,05438
944,65
963,70
979,58
992,81
1005,14
1017,59
1024,78
1031,35
1040,59
1050,45
1059,36
1067,22
1075,74
1082,81
1089,34
1095,55
1101,25
1106,57
1111,58
1116,17
1120,30
1123,96
1127,29
73
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Deformación
hormigón (m/m)
-0,0082
-0,0085
-0,0089
-0,0092
-0,0096
Eje
neutro
(m)
0,783
0,783
0,784
0,784
0,784
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0971
0,1014
0,1057
0,1101
0,1146
-511,4
-512,9
-514,3
-515,7
-516,8
-246,1
-246,6
-246,9
-247,1
-247,2
757,5
759,4
761,1
762,6
763,9
0,05680
0,05927
0,06179
0,06437
0,06700
1130,22
1132,94
1135,34
1137,38
1139,09
74
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla A.3: Cálculo de la curvatura y el momento de la sección transversal del muro B1.
Deformación
hormigón (m/m)
0,0000
-0,0001
-0,0002
-0,0003
-0,0004
-0,0005
-0,0006
-0,0007
-0,0008
-0,0009
-0,0010
-0,0012
-0,0013
-0,0014
-0,0016
-0,0017
-0,0018
-0,0020
-0,0021
-0,0023
-0,0025
-0,0026
Eje
neutro
(m)
0,000
0,495
0,654
0,676
0,685
0,718
0,745
0,768
0,786
0,798
0,808
0,816
0,822
0,828
0,833
0,837
0,842
0,846
0,850
0,853
0,855
0,857
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0000
0,0003
0,0009
0,0016
0,0025
0,0036
0,0049
0,0065
0,0083
0,0102
0,0124
0,0147
0,0173
0,0200
0,0230
0,0261
0,0295
0,0330
0,0368
0,0408
0,0449
0,0493
0,0
-52,2
-171,4
-319,9
-491,3
-540,4
-565,2
-587,5
-609,4
-641,2
-679,1
-720,8
-763,5
-804,2
-844,7
-879,8
-899,1
-917,1
-935,4
-953,2
-967,6
-979,7
0,0
-13,7
-16,2
-24,9
-36,9
-43,9
-48,9
-52,4
-55,2
-58,1
-64,1
-71,1
-78,3
-85,7
-93,3
-100,9
-107,4
-114,2
-121,3
-129,0
-137,1
-146,6
0,0
65,8
188,2
345,4
528,9
585,3
614,4
640,0
664,5
699,3
743,2
791,9
842,8
890,4
937,9
980,6
1006,6
1031,7
1056,5
1080,9
1104,1
1125,6
0,00000
0,00022
0,00055
0,00099
0,00153
0,00219
0,00296
0,00384
0,00482
0,00592
0,00712
0,00844
0,00986
0,01140
0,01304
0,01480
0,01666
0,01863
0,02071
0,02291
0,02521
0,02762
0,00
250,18
324,49
557,45
839,91
905,82
928,35
942,10
954,35
986,22
1027,59
1072,53
1119,21
1161,57
1200,31
1239,86
1272,47
1302,04
1331,09
1358,41
1381,44
1402,07
75
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Deformación
hormigón (m/m)
-0,0029
-0,0031
-0,0035
Eje
neutro
(m)
0,858
0,858
0,854
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0538
0,0585
0,0632
-986,7
-990,4
-1000,2
-157,9
-172,5
-174,0
1146,0
1163,3
1173,7
0,03014
0,03277
0,03551
1418,61
1434,17
1444,34
76
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla A.4: Cálculo de la curvatura y el momento de la sección transversal del muro B2.
Deformación
hormigón (m/m)
0,0000
0,0000
-0,0001
-0,0001
-0,0001
-0,0001
-0,0002
-0,0002
-0,0003
-0,0003
-0,0004
-0,0005
-0,0006
-0,0006
-0,0007
-0,0007
-0,0008
-0,0008
-0,0009
-0,0009
-0,0009
-0,0010
Eje
neutro
(m)
0,000
0,200
0,201
0,208
0,292
0,449
0,484
0,502
0,512
0,517
0,521
0,523
0,524
0,534
0,558
0,584
0,606
0,625
0,641
0,656
0,669
0,680
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0000
0,0000
0,0001
0,0001
0,0002
0,0004
0,0006
0,0007
0,0009
0,0011
0,0014
0,0016
0,0019
0,0022
0,0026
0,0030
0,0034
0,0038
0,0043
0,0048
0,0053
0,0059
0,0
-9,0
-21,9
-40,8
-88,9
-194,6
-283,6
-381,3
-488,6
-606,2
-734,6
-874,0
-1023,0
-1137,7
-1173,6
-1182,7
-1191,2
-1199,1
-1205,2
-1212,8
-1218,2
-1224,7
0,0
-12,6
-31,3
-55,8
-74,2
-72,9
-88,4
-108,0
-131,4
-158,1
-187,9
-220,8
-256,9
-286,0
-296,8
-300,9
-304,5
-307,4
-309,3
-311,1
-311,4
-314,8
0,0
21,2
53,2
96,4
162,9
267,8
372,2
489,5
620,1
764,4
922,6
1094,9
1281,0
1423,6
1470,2
1483,4
1495,5
1506,4
1514,4
1522,6
1528,7
1537,9
0,00000
0,00003
0,00007
0,00013
0,00020
0,00029
0,00039
0,00051
0,00064
0,00079
0,00094
0,00112
0,00131
0,00151
0,00173
0,00196
0,00221
0,00247
0,00275
0,00304
0,00334
0,00366
0,00
105,45
263,47
466,67
582,85
526,14
656,29
825,78
1025,25
1251,03
1501,54
1776,05
2072,78
2295,14
2365,58
2386,19
2404,62
2421,24
2434,58
2449,11
2460,14
2471,43
77
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Deformación
hormigón (m/m)
-0,0010
-0,0011
-0,0011
-0,0012
-0,0013
-0,0013
-0,0014
-0,0014
-0,0015
-0,0016
-0,0016
-0,0017
-0,0018
-0,0019
-0,0019
-0,0020
-0,0021
-0,0022
-0,0023
-0,0024
-0,0025
-0,0026
-0,0027
Eje
neutro
(m)
0,691
0,700
0,709
0,716
0,722
0,728
0,733
0,738
0,743
0,747
0,750
0,754
0,757
0,759
0,762
0,764
0,766
0,769
0,770
0,772
0,773
0,773
0,773
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0065
0,0071
0,0077
0,0083
0,0090
0,0097
0,0105
0,0112
0,0120
0,0128
0,0136
0,0145
0,0154
0,0163
0,0172
0,0182
0,0191
0,0201
0,0212
0,0222
0,0233
0,0244
0,0255
-1231,1
-1238,4
-1252,1
-1271,8
-1296,5
-1323,2
-1350,7
-1377,0
-1405,8
-1435,4
-1465,1
-1498,1
-1529,3
-1561,7
-1594,3
-1624,8
-1654,9
-1683,5
-1709,3
-1736,2
-1770,2
-1803,6
-1833,7
-323,8
-332,7
-341,4
-351,0
-362,3
-373,3
-384,4
-395,3
-406,7
-418,4
-430,2
-443,2
-456,0
-470,2
-487,3
-504,5
-522,3
-540,4
-558,6
-573,2
-577,1
-581,9
-587,6
1553,9
1569,8
1593,3
1622,9
1658,9
1696,6
1735,2
1773,6
1813,2
1854,2
1896,5
1939,7
1984,5
2031,1
2081,1
2130,0
2177,1
2223,6
2267,6
2309,3
2348,1
2385,4
2421,2
0,00400
0,00435
0,00471
0,00509
0,00548
0,00589
0,00631
0,00675
0,00720
0,00766
0,00814
0,00864
0,00914
0,00967
0,01020
0,01076
0,01132
0,01191
0,01250
0,01311
0,01374
0,01438
0,01503
2481,90
2493,01
2514,87
2546,80
2589,30
2632,90
2677,61
2721,74
2768,94
2817,15
2865,70
2918,51
2969,72
3022,86
3077,07
3126,53
3173,61
3218,23
3258,55
3296,28
3332,03
3368,83
3404,28
78
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Deformación
hormigón (m/m)
-0,0028
-0,0030
-0,0031
-0,0033
-0,0035
Eje
neutro
(m)
0,772
0,771
0,769
0,767
0,763
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0266
0,0278
0,0289
0,0301
0,0312
-1860,7
-1882,6
-1899,2
-1906,8
-1906,2
-594,3
-602,2
-611,9
-623,0
-636,7
2454,9
2485,8
2510,3
2530,1
2542,4
0,01570
0,01638
0,01708
0,01779
0,01852
3438,86
3471,30
3500,23
3523,07
3543,00
79
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla A.5: Cálculo de la curvatura y el momento de la sección transversal del muro B3.
Deformación
hormigón (m/m)
0,0000
-0,0002
-0,0004
-0,0006
-0,0007
-0,0009
-0,0011
-0,0014
-0,0016
-0,0019
-0,0021
-0,0024
-0,0029
-0,0034
-0,0042
-0,0049
-0,0055
-0,0061
-0,0067
-0,0063
Eje
neutro
(m)
0,000
0,676
0,696
0,748
0,784
0,806
0,819
0,829
0,836
0,843
0,848
0,851
0,851
0,848
0,839
0,837
0,838
0,839
0,839
0,856
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0000
0,0010
0,0025
0,0047
0,0075
0,0109
0,0148
0,0193
0,0243
0,0300
0,0362
0,0430
0,0502
0,0580
0,0660
0,0748
0,0842
0,0942
0,1048
0,1170
0,0
-187,5
-474,2
-545,6
-581,2
-635,4
-703,6
-772,2
-838,6
-882,5
-910,2
-931,8
-941,4
-943,1
-953,9
-969,8
-989,8
-1013,9
-1036,0
-786,6
0,0
-14,5
-32,6
-41,9
-46,6
-52,7
-63,2
-74,7
-87,0
-99,1
-111,4
-126,9
-148,3
-169,5
-169,5
-169,5
-169,5
-169,5
-169,5
-169,5
0,0
201,2
506,9
588,5
628,2
688,3
768,5
845,9
925,5
981,6
1021,7
1058,7
1089,4
1113,3
1121,8
1139,5
1160,7
1183,1
1205,4
955,7
0,00000
0,00063
0,00157
0,00283
0,00439
0,00628
0,00848
0,01099
0,01381
0,01695
0,02040
0,02417
0,02825
0,03264
0,03735
0,04237
0,04771
0,05336
0,05932
0,06560
0,00
336,72
805,22
894,30
915,47
971,39
1048,60
1123,09
1191,35
1250,16
1298,60
1340,09
1372,12
1394,20
1404,65
1417,52
1430,94
1443,80
1452,11
976,03
80
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla A.6: Cálculo de la curvatura y el momento de la sección transversal del muro B4.
Deformación
hormigón (m/m)
0,0000
-0,0002
-0,0004
-0,0006
-0,0008
-0,0010
-0,0012
-0,0015
-0,0018
-0,0020
-0,0023
-0,0027
-0,0033
-0,0041
-0,0048
-0,0054
-0,0060
-0,0067
-0,0074
-0,0069
Eje
neutro
(m)
0,000
0,668
0,692
0,748
0,784
0,805
0,818
0,828
0,835
0,842
0,846
0,848
0,846
0,837
0,833
0,835
0,836
0,836
0,837
0,855
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0000
0,0011
0,0027
0,0051
0,0081
0,0117
0,0160
0,0208
0,0263
0,0324
0,0390
0,0463
0,0541
0,0621
0,0710
0,0806
0,0908
0,1015
0,1129
0,1261
0,0
-212,4
-512,0
-566,8
-603,3
-665,5
-738,4
-806,8
-872,9
-902,9
-925,7
-939,1
-944,0
-956,0
-974,4
-996,2
-1019,0
-1042,7
-1065,8
-808,0
0,0
-17,5
-38,4
-48,0
-53,5
-60,8
-73,2
-86,6
-101,5
-115,1
-131,1
-152,7
-174,3
-174,3
-174,3
-174,3
-174,3
-174,3
-174,3
-174,3
0,0
228,9
550,4
613,4
657,0
726,4
811,2
892,1
974,3
1017,3
1056,9
1091,6
1119,1
1130,3
1147,4
1170,5
1193,2
1216,9
1240,0
981,9
0,00000
0,00068
0,00169
0,00305
0,00474
0,00678
0,00915
0,01186
0,01491
0,01829
0,02202
0,02608
0,03049
0,03523
0,04031
0,04573
0,05149
0,05759
0,06402
0,07080
0,00
378,73
869,50
927,21
948,32
1016,28
1095,17
1168,19
1235,56
1290,18
1335,19
1372,57
1399,58
1412,24
1429,11
1445,43
1459,48
1470,54
1478,65
995,69
81
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla A.7: Cálculo de la curvatura y el momento de la sección transversal del muro B5 y B6.
Deformación
hormigón (m/m)
0,0000
-0,0001
-0,0001
-0,0002
-0,0004
-0,0005
-0,0007
-0,0008
-0,0009
-0,0010
-0,0011
-0,0012
-0,0013
-0,0015
-0,0016
-0,0018
-0,0019
-0,0021
-0,0023
-0,0025
-0,0028
-0,0030
Eje
neutro
(m)
0,000
0,207
0,465
0,508
0,519
0,523
0,533
0,582
0,623
0,654
0,679
0,698
0,712
0,723
0,732
0,739
0,746
0,751
0,755
0,757
0,757
0,755
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0000
0,0001
0,0004
0,0008
0,0012
0,0018
0,0024
0,0032
0,0042
0,0052
0,0064
0,0077
0,0090
0,0105
0,0121
0,0138
0,0156
0,0175
0,0195
0,0216
0,0238
0,0260
0,0
-37,1
-209,6
-410,4
-650,7
-936,8
-1223,9
-1278,0
-1290,2
-1300,9
-1311,3
-1330,0
-1375,3
-1429,7
-1485,0
-1539,0
-1589,3
-1637,9
-1680,7
-1714,2
-1766,4
-1811,8
0,0
-51,3
-71,7
-112,4
-168,0
-236,6
-307,5
-325,1
-331,4
-334,8
-340,9
-362,0
-387,5
-415,8
-445,6
-476,8
-509,1
-544,2
-584,4
-630,7
-646,5
-664,4
0,0
88,3
280,1
522,1
819,3
1174,1
1531,3
1602,4
1621,5
1635,7
1652,1
1691,6
1762,5
1845,3
1930,6
2015,7
2098,1
2182,1
2265,1
2345,2
2412,0
2476,2
0,00000
0,00012
0,00031
0,00055
0,00086
0,00123
0,00166
0,00215
0,00270
0,00331
0,00399
0,00472
0,00552
0,00638
0,00730
0,00828
0,00932
0,01043
0,01159
0,01282
0,01411
0,01546
0,00
432,92
518,78
867,88
1333,86
1900,80
2468,01
2578,41
2609,42
2635,59
2658,32
2694,99
2780,31
2882,58
2989,40
3091,75
3186,09
3280,21
3370,50
3455,23
3528,27
3594,52
82
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Deformación
hormigón (m/m)
-0,0033
-0,0037
-0,0041
-0,0044
-0,0047
-0,0051
-0,0055
-0,0059
-0,0063
-0,0066
-0,0070
-0,0074
-0,0078
-0,0082
-0,0086
-0,0090
-0,0094
-0,0099
-0,0103
-0,0108
-0,0112
-0,0117
-0,0122
Eje
neutro
(m)
0,754
0,751
0,748
0,747
0,748
0,747
0,747
0,747
0,747
0,748
0,749
0,750
0,751
0,752
0,753
0,754
0,755
0,756
0,757
0,758
0,759
0,759
0,760
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0284
0,0308
0,0333
0,0359
0,0387
0,0416
0,0446
0,0476
0,0508
0,0541
0,0576
0,0611
0,0648
0,0685
0,0724
0,0763
0,0804
0,0846
0,0888
0,0932
0,0977
0,1023
0,1070
-1854,1
-1874,7
-1897,1
-1931,7
-1977,8
-2033,6
-2088,7
-2142,3
-2186,2
-2211,8
-2236,1
-2258,0
-2282,3
-2301,7
-2317,8
-2331,3
-2345,8
-2358,9
-2370,1
-2380,3
-2389,0
-2396,9
-2404,2
-684,2
-714,5
-743,8
-766,7
-783,8
-787,0
-790,1
-793,5
-795,3
-793,5
-791,4
-788,9
-784,8
-783,8
-784,8
-785,1
-786,1
-786,8
-787,0
-787,0
-791,7
-796,9
-802,3
2538,6
2588,6
2640,7
2698,8
2761,3
2819,7
2877,6
2934,3
2981,3
3005,4
3027,6
3048,5
3068,0
3086,0
3102,8
3117,9
3131,9
3144,5
3155,8
3166,1
3180,0
3193,4
3206,0
0,01687
0,01834
0,01987
0,02147
0,02313
0,02484
0,02662
0,02846
0,03036
0,03233
0,03435
0,03644
0,03858
0,04079
0,04306
0,04539
0,04779
0,05024
0,05275
0,05533
0,05797
0,06067
0,06343
3658,19
3708,06
3758,62
3812,35
3869,51
3922,59
3973,26
4020,59
4063,15
4101,69
4137,63
4170,17
4202,40
4231,42
4259,00
4282,50
4306,35
4327,81
4346,42
4363,19
4377,78
4390,62
4402,26
83
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Deformación
hormigón (m/m)
-0,0127
-0,0132
-0,0137
-0,0143
-0,0124
Eje
neutro
(m)
0,761
0,761
0,762
0,762
0,794
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,1118
0,1167
0,1217
0,1269
0,1345
-2410,3
-2414,4
-2419,2
-2423,0
-1866,5
-807,8
-813,3
-819,0
-824,8
-799,4
3217,9
3229,1
3239,3
3249,0
2665,1
0,06625
0,06913
0,07208
0,07508
0,07815
4412,15
4419,61
4426,89
4432,50
3011,99
84
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla A.8: Cálculo de la curvatura y el momento de la sección transversal del muro F1.
Deformación
hormigón (m/m)
0,0000
-0,0001
-0,0001
-0,0001
-0,0002
-0,0002
-0,0003
-0,0004
-0,0005
-0,0006
-0,0006
-0,0006
-0,0007
-0,0007
-0,0007
-0,0008
-0,0008
-0,0009
-0,0009
-0,0010
-0,0010
-0,0011
Eje
neutro
(m)
0,000
0,197
0,422
0,546
0,577
0,584
0,590
0,593
0,594
0,631
0,671
0,703
0,728
0,750
0,767
0,782
0,793
0,802
0,809
0,815
0,821
0,826
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0000
0,0001
0,0002
0,0004
0,0007
0,0010
0,0014
0,0018
0,0022
0,0028
0,0035
0,0042
0,0050
0,0058
0,0067
0,0077
0,0087
0,0098
0,0110
0,0122
0,0134
0,0148
0,0
-18,7
-106,6
-244,5
-403,0
-582,3
-793,4
-1034,9
-1302,6
-1377,0
-1387,0
-1395,8
-1402,9
-1407,4
-1411,8
-1414,3
-1435,7
-1470,7
-1507,9
-1546,2
-1582,3
-1614,9
0,0
-33,8
-56,9
-75,7
-107,4
-149,9
-198,7
-254,6
-319,7
-344,3
-353,1
-360,3
-366,1
-370,6
-374,3
-377,2
-384,8
-396,1
-408,3
-420,9
-432,9
-444,2
0,0
53,4
162,2
320,6
509,9
732,3
992,6
1290,0
1622,1
1719,9
1740,0
1755,5
1768,1
1777,4
1785,5
1791,2
1821,0
1868,0
1916,2
1967,0
2015,0
2058,9
0,00000
0,00007
0,00017
0,00030
0,00047
0,00067
0,00090
0,00117
0,00147
0,00180
0,00217
0,00257
0,00300
0,00347
0,00397
0,00450
0,00507
0,00567
0,00631
0,00697
0,00767
0,00841
0,00
334,56
475,81
631,68
933,64
1312,78
1766,20
2288,33
2873,26
3038,00
3061,37
3078,63
3091,15
3099,23
3106,30
3110,88
3158,19
3238,52
3323,99
3412,81
3496,51
3572,34
85
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Deformación
hormigón (m/m)
-0,0011
-0,0012
-0,0012
-0,0013
-0,0014
-0,0014
-0,0015
-0,0016
-0,0016
-0,0017
-0,0018
-0,0018
-0,0019
-0,0020
-0,0021
-0,0022
-0,0023
-0,0023
-0,0024
-0,0025
-0,0026
-0,0027
-0,0029
Eje
neutro
(m)
0,831
0,835
0,838
0,842
0,845
0,847
0,850
0,852
0,854
0,856
0,858
0,859
0,861
0,862
0,864
0,865
0,866
0,867
0,868
0,868
0,869
0,869
0,870
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0162
0,0176
0,0191
0,0207
0,0223
0,0240
0,0258
0,0276
0,0295
0,0314
0,0334
0,0355
0,0376
0,0398
0,0420
0,0443
0,0467
0,0491
0,0516
0,0541
0,0567
0,0594
0,0621
-1649,0
-1682,1
-1710,1
-1737,7
-1766,0
-1790,7
-1815,0
-1838,1
-1858,5
-1878,8
-1896,3
-1912,7
-1928,3
-1942,5
-1956,1
-1966,3
-1974,5
-1979,9
-1983,1
-1983,5
-1981,2
-1975,4
-1967,4
-456,1
-468,2
-479,0
-490,1
-501,9
-513,0
-524,8
-537,0
-548,8
-561,2
-573,3
-585,7
-598,2
-610,0
-623,1
-636,4
-651,0
-666,7
-684,0
-703,0
-723,8
-745,2
-769,0
2104,7
2149,7
2188,2
2227,8
2267,9
2303,8
2340,0
2375,4
2407,5
2440,4
2470,2
2499,4
2527,2
2553,5
2579,1
2602,6
2625,5
2646,5
2666,7
2685,8
2703,8
2720,8
2736,5
0,00917
0,00997
0,01081
0,01168
0,01258
0,01351
0,01448
0,01548
0,01651
0,01758
0,01868
0,01982
0,02098
0,02218
0,02342
0,02469
0,02599
0,02732
0,02869
0,03009
0,03152
0,03299
0,03449
3651,50
3732,44
3802,66
3873,45
3945,98
4010,54
4075,46
4138,89
4196,10
4254,43
4306,93
4358,16
4406,91
4452,10
4496,96
4536,98
4575,71
4610,85
4644,62
4675,78
4705,10
4730,73
4755,15
86
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Deformación
hormigón (m/m)
-0,0030
-0,0031
-0,0032
-0,0034
-0,0037
Eje
neutro
(m)
0,870
0,870
0,870
0,869
0,867
Deformación
acero (m/m)
Compresión
hormigón (kN)
Compresión
acero (kN)
Tensión
acero (kN)
Curvatura
(1/m)
Momento
(kN·m)
0,0649
0,0677
0,0706
0,0735
0,0764
-1955,8
-1941,9
-1932,3
-1928,5
-1891,6
-794,0
-821,4
-842,7
-856,0
-902,0
2750,3
2762,5
2773,9
2784,1
2793,1
0,03603
0,03760
0,03920
0,04083
0,04250
4777,40
4799,04
4817,23
4830,99
4837,24
87
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
88
Anexo B: Tablas de cálculo fuerza-desplazamiento
Las Tablas B.1 a B.18 contienen los resultados de los cálculos fuerza-desplazamiento que
condujeron a los gráficos del apartado 4.2. Para cada muro se presentan dos tablas; la primera
corresponde al cálculo de los desplazamiento por flexión y corte en los rangos elásticos y
plásticos, y la segunda corresponde a los parámetros que dependen de la curvatura para poder
calcular los desplazamientos y la resistencia al corte.
La columna 1 y 2 de la primera tabla de cada muro contienen los valores de curvatura y
momento respectivamente. La columna 3, 4 y 5 contienen los valores del desplazamiento
lateral (en metros) en que la curvatura se encuentra en los intervalos “cero” a curvatura de
fisuración, curvatura de fisuración a curvatura de fluencia y curvatura de fluencia a curvatura
última respectivamente. Las columnas 6, 7 y 8 contienen los desplazamientos por corte
cuando este se encuentra en los intervalos “cero” a resistencia al corte del hormigón (con
𝛾 = 0,29 según la Ecuación 2.35), resistencia al corte del hormigón a corte nominal y corte
nominal al corte último respectivamente. La columna 9 es la suma de los desplazamientos
por corte y por flexión, la columna 10 es la fuerza de corte de la curva de respuesta (FResp),
calculada como el momento dividido por la altura del muro y la columna 11 es la resistencia
al corte (FResi) calculada con los datos de la segunda tabla de cada muro.
En la segunda tabla de cada muro, las columnas 1 y 2 corresponden a la curvatura y momento
respectivamente, las columnas 3, 4 y 5 son las deformaciones unitarias del acero de tracción,
posición del eje neutro a la fibra más comprimida y tensión del acero respectivamente. Las
columnas 6 y 7 son las distancias que definen la ubicación de la rótula plástica según la
Figura 3.2. Las columnas 8 y 9 corresponden a la ductilidad y valor de 𝛾 asociado a dicha
ductilidad. Las columnas 10, 11 y 12 son las resistencias del hormigón, resistencia del acero
y resistencia a compresión respectivamente. La columna 13 es la suma de las resistencias de
las columnas 10, 11 y 12, es decir, la resistencia al corte final.
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a
carga cíclica
Felipe Castillo Huerta
Tabla B.1: Curvas de respuesta y resistencia fuerza-desplazamiento del muro R1.
MC (R1)
Desplazamientos flexión (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu
0,0000
0,0
0,0003
121,5
0,002
0,0007
230,0
0,005
0,0012
290,0
0,009
0,0019
356,2
0,014
0,0028
381,7
0,016
0,0037
395,5
0,019
0,0048
403,1
0,021
0,0061
409,8
0,024
0,0075
423,7
0,027
0,0090
440,9
0,031
0,0106
458,2
0,035
0,0124
471,7
0,039
0,0144
487,3
0,044
0,0164
499,7
0,048
0,0186
514,0
0,053
0,0210
525,6
0,059
0,0235
536,3
0,064
0,0261
544,7
0,070
0,0288
551,4
0,076
Desplazamientos corte (m)
V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,000
0,0
0,0
375,1
0,001
0,3
26,6
375,1
0,001
0,6
50,3
375,1
0,001
1,0
63,4
375,1
0,002
1,6
77,9
375,1
0,002
1,8
83,5
375,1
0,002
2,1
86,5
375,1
0,002
2,3
88,2
375,1
0,002
2,6
89,6
375,1
0,002
2,9
92,7
375,1
0,002
3,3
96,4
375,1
0,002
3,7
100,2
374,8
0,002
4,1
103,2
371,1
0,002
4,6
106,6
367,1
0,002
5,1
109,3
362,9
0,002
5,6
112,4
358,4
0,002
6,1
115,0
353,8
0,003
6,7
117,3
348,9
0,003
7,2
119,1
343,8
0,003
7,8
120,6
338,5
89
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla B.2: Parámetros de cálculo para las curvas fuerza-desplazamiento del muro R1.
φ (1/m) M (kN·m) εst (m/m)
0,0000
0,0
0,0000
0,0003
121,5
0,0004
0,0007
230,0
0,0011
0,0012
290,0
0,0020
0,0019
356,2
0,0031
0,0028
381,7
0,0045
0,0037
395,5
0,0062
0,0048
403,1
0,0081
0,0061
409,8
0,0103
0,0075
423,7
0,0128
0,0090
440,9
0,0155
0,0106
458,2
0,0184
0,0124
471,7
0,0216
0,0144
487,3
0,0251
0,0164
499,7
0,0288
0,0186
514,0
0,0328
0,0210
525,6
0,0369
0,0235
536,3
0,0414
0,0261
544,7
0,0460
0,0288
551,4
0,0507
c
0,000
0,414
0,614
0,649
0,665
0,701
0,730
0,754
0,772
0,787
0,797
0,806
0,814
0,821
0,826
0,830
0,833
0,834
0,834
0,831
fs (kN/m2) LSP (m)
0,0
0,000
71005,7
0,015
203968,8
0,043
375732,0
0,079
511610,0
0,107
511610,0
0,107
511610,0
0,107
511610,0
0,107
511610,0
0,107
511610,0
0,107
511610,0
0,107
511610,0
0,107
511610,0
0,107
511610,0
0,107
511610,0
0,107
511610,0
0,107
511610,0
0,107
511610,0
0,107
511610,0
0,107
511610,0
0,107
LP (m)
0,366
0,381
0,408
0,444
0,473
0,473
0,473
0,473
0,473
0,473
0,473
0,473
0,473
0,473
0,473
0,473
0,473
0,473
0,473
0,473
μ γ (kPa) Vc (kN) Vs (kN) Vp (kN)
0,000 0,25
153,8
221,3
0
0,211 0,25
153,8
221,3
0
0,499 0,25
153,8
221,3
0
0,851 0,25
153,8
221,3
0
1,272 0,25
153,8
221,3
0
1,481 0,25
153,8
221,3
0
1,684 0,25
153,8
221,3
0
1,893 0,25
153,8
221,3
0
2,124 0,25
153,8
221,3
0
2,397 0,25
153,8
221,3
0
2,703 0,25
153,8
221,3
0
3,033 0,25
153,4
221,3
0
3,375 0,24
149,8
221,3
0
3,748 0,24
145,7
221,3
0
4,135 0,23
141,6
221,3
0
4,552 0,22
137,1
221,3
0
4,984 0,22
132,4
221,3
0
5,439 0,21
127,5
221,3
0
5,911 0,20
122,5
221,3
0
6,402 0,19
117,2
221,3
0
90
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
V (kN)
375,1
375,1
375,1
375,1
375,1
375,1
375,1
375,1
375,1
375,1
375,1
374,8
371,1
367,1
362,9
358,4
353,8
348,9
343,8
338,5
Tabla B.3: Curvas de respuesta y resistencia fuerza-desplazamiento del muro R2.
MC (R2)
Desplazamientos flexión (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu
0,0000
0,0
0,0001
146,7
0,001
0,0003
176,2
0,002
0,0005
208,0
0,003
0,0007
299,2
0,005
0,0011
420,3
0,008
0,0014
564,4
0,010
0,0018
680,3
0,013
0,0023
706,6
0,015
0,0028
722,8
0,016
0,0034
734,6
0,017
0,0040
743,7
0,019
0,0047
749,9
0,021
0,0055
762,8
0,022
0,0063
784,1
0,024
0,0071
804,4
0,026
0,0080
825,6
0,029
0,0089
847,7
0,031
0,0099
871,2
0,034
0,0110
893,3
0,036
0,0121
911,6
0,039
0,0133
928,3
0,042
0,0145
944,6
0,044
Desplazamientos corte (m)
V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,000
0,0
0,0
409,5
0,000
0,1
32,1
409,5
0,000
0,2
38,5
409,5
0,000
0,4
45,5
409,5
0,001
0,6
65,4
409,5
0,001
0,9
91,9
409,5
0,001
1,2
123,4
409,5
0,002
1,5
148,8
409,5
0,002
1,6
154,5
409,5
0,002
1,8
158,1
409,5
0,002
1,9
160,7
409,5
0,002
2,1
162,7
409,5
0,002
2,2
164,0
409,5
0,002
2,4
166,9
409,5
0,002
2,6
171,5
409,5
0,002
2,8
175,9
409,5
0,002
3,1
180,6
409,5
0,005
3,6
185,4
409,3
0,005
3,9
190,6
406,2
0,006
4,2
195,4
403,0
0,006
4,5
199,4
399,7
0,007
4,8
203,0
396,3
0,007
5,2
206,6
392,7
91
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
MC (R2)
Desplazamientos flexión (m) Desplazamientos corte (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,0157
963,7
0,047
0,008
5,5
210,8
389,0
0,0170
979,6
0,051
0,008
5,9
214,3
385,1
0,0184
992,8
0,054
0,009
6,2
217,1
381,2
0,0198
1005,1
0,057
0,009
6,6
219,8
377,1
0,0213
1017,6
0,060
0,010
7,0
222,6
372,9
0,0228
1024,8
0,064
0,010
7,4
224,1
368,7
0,0244
1031,3
0,067
0,011
7,8
225,6
364,3
0,0260
1040,6
0,071
0,011
8,2
227,6
359,7
0,0277
1050,5
0,075
0,012
8,7
229,8
354,9
0,0295
1059,4
0,079
0,013
9,1
231,7
350,1
0,0312
1067,2
0,083
0,013
9,6
233,4
345,1
0,0331
1075,7
0,087
0,014
10,1
235,3
340,0
0,0350
1082,8
0,091
0,015
10,6
236,8
334,7
0,0369
1089,3
0,096
0,015
11,1
238,3
329,3
0,0389
1095,6
0,100
0,016
11,6
239,6
323,8
0,0410
1101,2
0,105
0,017
12,1
240,9
318,1
0,0431
1106,6
0,109
0,018
12,7
242,0
312,3
0,0452
1111,6
0,114
0,018
13,2
243,1
306,4
0,0474
1116,2
0,119
0,019
13,8
244,1
300,3
0,0497
1120,3
0,124
0,020
14,4
245,0
294,1
0,0520
1124,0
0,129
0,021
15,0
245,8
287,8
0,0544
1127,3
0,134
0,022
15,6
246,6
281,3
0,0568
1130,2
0,140
0,022
16,2
247,2
274,6
0,0593
1132,9
0,145
0,023
16,8
247,8
267,9
92
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
MC (R2)
Desplazamientos flexión (m) Desplazamientos corte (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,0618
1135,3
0,151
0,024
17,5
248,3
261,0
0,0644
1137,4
0,156
0,025
18,1
248,8
256,1
0,0670
1139,1
0,162
0,026
18,8
249,1
256,1
93
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla B.4: Parámetros de cálculo para las curvas fuerza-desplazamiento del muro R2.
φ (1/m) M (kN·m) εst (m/m)
0,0000
0,0
0,0000
0,0001
146,7
0,0001
0,0003
176,2
0,0003
0,0005
208,0
0,0007
0,0007
299,2
0,0011
0,0011
420,3
0,0016
0,0014
564,4
0,0021
0,0018
680,3
0,0028
0,0023
706,6
0,0036
0,0028
722,8
0,0044
0,0034
734,6
0,0054
0,0040
743,7
0,0065
0,0047
749,9
0,0077
0,0055
762,8
0,0090
0,0063
784,1
0,0104
0,0071
804,4
0,0118
0,0080
825,6
0,0134
0,0089
847,7
0,0151
0,0099
871,2
0,0168
0,0110
893,3
0,0186
0,0121
911,6
0,0206
0,0133
928,3
0,0226
0,0145
944,6
0,0248
0,0157
963,7
0,0270
c
0,000
0,141
0,351
0,492
0,536
0,551
0,558
0,574
0,608
0,638
0,663
0,684
0,703
0,718
0,729
0,740
0,749
0,757
0,764
0,770
0,775
0,781
0,785
0,788
fs (kN/m2) LSP (m)
0,0
0,000
20831,7
0,006
62309,5
0,017
124563,3
0,035
199783,5
0,056
288267,0
0,081
391034,0
0,109
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
LP (m)
0,366
0,372
0,383
0,401
0,422
0,446
0,475
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
μ
γ (kPa) Vc (kN) Vs (kN) Vp (kN)
0,000 0,25
182,6
226,9
0
0,093 0,25
182,6
226,9
0
0,196 0,25
182,6
226,9
0
0,331 0,25
182,6
226,9
0
0,511 0,25
182,6
226,9
0
0,728 0,25
182,6
226,9
0
0,982 0,25
182,6
226,9
0
1,238 0,25
182,6
226,9
0
1,359 0,25
182,6
226,9
0
1,477 0,25
182,6
226,9
0
1,598 0,25
182,6
226,9
0
1,726 0,25
182,6
226,9
0
1,859 0,25
182,6
226,9
0
2,011 0,25
182,6
226,9
0
2,183 0,25
182,6
226,9
0
2,364 0,25
182,6
226,9
0
2,556 0,25
182,6
226,9
0
3,012 0,25
182,4
226,9
0
3,256 0,25
179,3
226,9
0
3,508 0,24
176,1
226,9
0
3,768 0,24
172,8
226,9
0
4,034 0,23
169,4
226,9
0
4,312 0,23
165,8
226,9
0
4,605 0,22
162,1
226,9
0
94
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
V (kN)
409,5
409,5
409,5
409,5
409,5
409,5
409,5
409,5
409,5
409,5
409,5
409,5
409,5
409,5
409,5
409,5
409,5
409,3
406,2
403,0
399,7
396,3
392,7
389,0
φ (1/m) M (kN·m) εst (m/m)
0,0170
979,6
0,0293
0,0184
992,8
0,0316
0,0198 1005,1
0,0341
0,0213 1017,6
0,0366
0,0228 1024,8
0,0391
0,0244 1031,3
0,0417
0,0260 1040,6
0,0445
0,0277 1050,5
0,0474
0,0295 1059,4
0,0504
0,0312 1067,2
0,0534
0,0331 1075,7
0,0566
0,0350 1082,8
0,0598
0,0369 1089,3
0,0631
0,0389 1095,6
0,0665
0,0410 1101,2
0,0700
0,0431 1106,6
0,0736
0,0452 1111,6
0,0773
0,0474 1116,2
0,0811
0,0497 1120,3
0,0849
0,0520 1124,0
0,0889
0,0544 1127,3
0,0930
0,0568 1130,2
0,0971
0,0593 1132,9
0,1014
0,0618 1135,3
0,1057
0,0644 1137,4
0,1101
c
0,791
0,793
0,793
0,792
0,788
0,784
0,783
0,783
0,783
0,783
0,784
0,783
0,783
0,782
0,782
0,782
0,782
0,782
0,782
0,782
0,783
0,783
0,783
0,784
0,784
fs (kN/m2) LSP (m)
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
LP (m)
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
μ
γ (kPa) Vc (kN) Vs (kN) Vp (kN)
4,906 0,22
158,2
226,9
0
5,215 0,21
154,3
226,9
0
5,532 0,21
150,2
226,9
0
5,861 0,20
146,0
226,9
0
6,193 0,19
141,8
226,9
0
6,538 0,19
137,4
226,9
0
6,896 0,18
132,8
226,9
0
7,268 0,18
128,0
226,9
0
7,647 0,17
123,2
226,9
0
8,038 0,16
118,2
226,9
0
8,440 0,15
113,1
226,9
0
8,851 0,15
107,8
226,9
0
9,273 0,14
102,4
226,9
0
9,706 0,13
96,9
226,9
0
10,149 0,12
91,2
226,9
0
10,603 0,12
85,4
226,9
0
11,068 0,11
79,5
226,9
0
11,543 0,10
73,4
226,9
0
12,029 0,09
67,2
226,9
0
12,524 0,08
60,9
226,9
0
13,032 0,07
54,4
226,9
0
13,550 0,07
47,7
226,9
0
14,079 0,06
41,0
226,9
0
14,617 0,05
34,1
226,9
0
15,168 0,04
29,2
226,9
0
95
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
V (kN)
385,1
381,2
377,1
372,9
368,7
364,3
359,7
354,9
350,1
345,1
340,0
334,7
329,3
323,8
318,1
312,3
306,4
300,3
294,1
287,8
281,3
274,6
267,9
261,0
256,1
φ (1/m) M (kN·m) εst (m/m) c fs (kN/m2) LSP (m) LP (m)
μ
γ (kPa) Vc (kN) Vs (kN) Vp (kN) V (kN)
0,0670 1139,1
0,1146 0,784 450200,0
0,126
0,492 15,729 0,04
29,2
226,9
0
256,1
96
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla B.5: Curvas de respuesta y resistencia fuerza-desplazamiento del muro B1.
MC (B1)
Desplazamientos flexión (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu
0,0000
0,0
0,0002
250,2
0,002
0,0005
324,5
0,004
0,0010
557,5
0,007
0,0015
839,9
0,011
0,0022
905,8
0,013
0,0030
928,4
0,015
0,0038
942,1
0,017
0,0048
954,4
0,020
0,0059
986,2
0,022
0,0071
1027,6
0,025
0,0084
1072,5
0,029
0,0099
1119,2
0,032
0,0114
1161,6
0,036
0,0130
1200,3
0,040
0,0148
1239,9
0,044
0,0167
1272,5
0,048
0,0186
1302,0
0,053
0,0207
1331,1
0,058
0,0229
1358,4
0,063
0,0252
1381,4
0,068
0,0276
1402,1
0,074
0,0301
1418,6
0,079
Desplazamientos corte (m)
V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,000
0,0
0,0
521,1
0,001
0,2
54,7
521,1
0,001
0,5
71,0
521,1
0,001
0,9
121,9
521,1
0,002
1,3
183,7
521,1
0,002
1,5
198,1
521,1
0,002
1,7
203,1
521,1
0,002
1,9
206,1
521,1
0,002
2,2
208,7
521,1
0,002
2,4
215,7
521,1
0,002
2,8
224,8
521,1
0,002
3,1
234,6
521,1
0,003
3,5
244,8
514,9
0,003
3,9
254,1
507,1
0,003
4,3
262,5
499,1
0,003
4,7
271,2
490,4
0,003
5,1
278,3
481,5
0,003
5,6
284,8
472,2
0,003
6,1
291,1
462,5
0,003
6,6
297,1
452,2
0,021
8,9
302,2
406,9
0,022
9,6
306,7
392,7
0,024
10,3
310,3
377,9
97
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
MC (B1)
Desplazamientos flexión (m) Desplazamientos corte (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,0328
1434,2
0,085
0,026
11,1
313,7
362,6
0,0355
1444,3
0,091
0,028
11,9
315,9
346,7
98
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla B.6: Parámetros de cálculo para las curvas fuerza-desplazamiento del muro B1.
φ (1/m) M (kN·m) εst (m/m)
0,0000
0,0
0,0000
0,0002
250,2
0,0003
0,0005
324,5
0,0009
0,0010
557,5
0,0016
0,0015
839,9
0,0025
0,0022
905,8
0,0036
0,0030
928,4
0,0049
0,0038
942,1
0,0065
0,0048
954,4
0,0083
0,0059
986,2
0,0102
0,0071 1027,6
0,0124
0,0084 1072,5
0,0147
0,0099 1119,2
0,0173
0,0114 1161,6
0,0200
0,0130 1200,3
0,0230
0,0148 1239,9
0,0261
0,0167 1272,5
0,0295
0,0186 1302,0
0,0330
0,0207 1331,1
0,0368
0,0229 1358,4
0,0408
0,0252 1381,4
0,0449
0,0276 1402,1
0,0493
0,0301 1418,6
0,0538
0,0328 1434,2
0,0585
c
0,000
0,495
0,654
0,676
0,685
0,718
0,745
0,768
0,786
0,798
0,808
0,816
0,822
0,828
0,833
0,837
0,842
0,846
0,850
0,853
0,855
0,857
0,858
0,858
fs (kN/m2) LSP (m)
0,0
0,000
60832,2
0,017
168995,6
0,047
308648,2
0,086
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
449500,0
0,126
LP (m)
0,366
0,383
0,413
0,452
0,491
0,491
0,491
0,491
0,491
0,491
0,491
0,491
0,491
0,491
0,491
0,491
0,491
0,491
0,491
0,491
0,491
0,491
0,491
0,491
μ
γ (kPa) Vc (kN) Vs (kN) Vp (kN)
0,000 0,25
300,3
220,8
0
0,208 0,25
300,3
220,8
0
0,455 0,25
300,3
220,8
0
0,812 0,25
300,3
220,8
0
1,254 0,25
300,3
220,8
0
1,465 0,25
300,3
220,8
0
1,649 0,25
300,3
220,8
0
1,847 0,25
300,3
220,8
0
2,066 0,25
300,3
220,8
0
2,329 0,25
300,3
220,8
0
2,626 0,25
300,3
220,8
0
2,950 0,25
300,3
220,8
0
3,298 0,24
294,1
220,8
0
3,665 0,24
286,4
220,8
0
4,049 0,23
278,3
220,8
0
4,459 0,22
269,6
220,8
0
4,883 0,22
260,8
220,8
0
5,325 0,21
251,4
220,8
0
5,790 0,20
241,7
220,8
0
6,278 0,19
231,4
220,8
0
8,433 0,15
186,1
220,8
0
9,109 0,14
171,9
220,8
0
9,811 0,13
157,1
220,8
0
10,541 0,12
141,8
220,8
0
99
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
V (kN)
521,1
521,1
521,1
521,1
521,1
521,1
521,1
521,1
521,1
521,1
521,1
521,1
514,9
507,1
499,1
490,4
481,5
472,2
462,5
452,2
406,9
392,7
377,9
362,6
φ (1/m) M (kN·m) εst (m/m) c fs (kN/m2) LSP (m) LP (m)
μ
γ (kPa) Vc (kN) Vs (kN) Vp (kN) V (kN)
0,0355 1444,3
0,0632 0,854 449500,0
0,126
0,491 11,295 0,10
125,9
220,8
0
346,7
100
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla B.7: Curvas de respuesta y resistencia fuerza-desplazamiento del muro B2.
MC (B2)
Desplazamientos flexión (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu
0,0000
0,0
0,0000
105,5
0,000
0,0001
263,5
0,001
0,0001
466,7
0,001
0,0002
582,9
0,002
0,0003
526,1
0,002
0,0004
656,3
0,003
0,0005
825,8
0,004
0,0006
1025,3
0,005
0,0008
1251,0
0,006
0,0009
1501,5
0,007
0,0011
1776,0
0,008
0,0013
2072,8
0,010
0,0015
2295,1
0,011
0,0017
2365,6
0,012
0,0020
2386,2
0,012
0,0022
2404,6
0,013
0,0025
2421,2
0,014
0,0027
2434,6
0,015
0,0030
2449,1
0,015
0,0033
2460,1
0,016
0,0037
2471,4
0,017
0,0040
2481,9
0,018
Desplazamientos corte (m)
V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,000
0,0
0,0
794,6
0,000
0,0
23,1
794,6
0,000
0,1
57,6
794,6
0,000
0,1
102,1
794,6
0,000
0,2
127,5
794,6
0,000
0,3
115,1
794,6
0,001
0,3
143,5
794,6
0,001
0,4
180,6
794,6
0,001
0,6
224,2
794,6
0,001
0,7
273,6
794,6
0,001
0,8
328,4
794,6
0,001
1,0
388,5
794,6
0,002
1,1
453,4
794,6
0,002
1,3
502,0
794,6
0,002
1,4
517,4
794,6
0,002
1,5
521,9
794,6
0,002
1,5
525,9
794,6
0,002
1,6
529,6
794,6
0,002
1,7
532,5
794,6
0,002
1,8
535,7
794,6
0,003
1,9
538,1
794,6
0,003
2,0
540,6
794,6
0,003
2,1
542,8
794,6
101
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
MC (B2)
Desplazamientos flexión (m) Desplazamientos corte (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,0043
2493,0
0,019
0,003
2,2
545,3
794,6
0,0047
2514,9
0,020
0,003
2,3
550,1
794,6
0,0051
2546,8
0,021
0,003
2,4
557,0
794,6
0,0055
2589,3
0,022
0,004
2,5
566,3
794,6
0,0059
2632,9
0,023
0,004
2,6
575,9
794,6
0,0063
2677,6
0,024
0,004
2,8
585,7
794,6
0,0067
2721,7
0,025
0,004
2,9
595,3
794,6
0,0072
2768,9
0,026
0,004
3,1
605,6
794,5
0,0077
2817,2
0,028
0,004
3,2
616,2
791,0
0,0081
2865,7
0,029
0,005
3,4
626,8
787,4
0,0086
2918,5
0,030
0,005
3,5
638,3
783,7
0,0091
2969,7
0,032
0,005
3,7
649,5
779,9
0,0097
3022,9
0,033
0,005
3,8
661,2
775,9
0,0102
3077,1
0,035
0,006
4,0
673,0
771,9
0,0108
3126,5
0,036
0,006
4,2
683,8
767,8
0,0113
3173,6
0,038
0,006
4,4
694,1
763,7
0,0119
3218,2
0,039
0,006
4,5
703,9
759,4
0,0125
3258,6
0,041
0,007
4,7
712,7
755,2
0,0131
3296,3
0,042
0,007
4,9
721,0
750,8
0,0137
3332,0
0,044
0,007
5,1
728,8
746,3
0,0144
3368,8
0,046
0,007
5,3
736,8
741,8
0,0150
3404,3
0,047
0,008
5,5
744,6
737,2
0,0157
3438,9
0,049
0,008
5,7
752,2
732,4
0,0164
3471,3
0,051
0,008
5,9
759,3
727,7
102
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
MC (B2)
Desplazamientos flexión (m) Desplazamientos corte (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,0171
3500,2
0,052
0,009
6,1
765,6
722,8
0,0178
3523,1
0,054
0,009
6,3
770,6
717,9
0,0185
3543,0
0,056
0,009
6,5
774,9
712,9
103
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla B.8: Parámetros de cálculo para las curvas fuerza-desplazamiento del muro B2.
φ (1/m) M (kN·m) εst (m/m)
0,0000
0,0
0,0000
0,0000
105,5
0,0000
0,0001
263,5
0,0001
0,0001
466,7
0,0001
0,0002
582,9
0,0002
0,0003
526,1
0,0004
0,0004
656,3
0,0006
0,0005
825,8
0,0007
0,0006 1025,3
0,0009
0,0008 1251,0
0,0011
0,0009 1501,5
0,0014
0,0011 1776,0
0,0016
0,0013 2072,8
0,0019
0,0015 2295,1
0,0022
0,0017 2365,6
0,0026
0,0020 2386,2
0,0030
0,0022 2404,6
0,0034
0,0025 2421,2
0,0038
0,0027 2434,6
0,0043
0,0030 2449,1
0,0048
0,0033 2460,1
0,0053
0,0037 2471,4
0,0059
0,0040 2481,9
0,0065
0,0043 2493,0
0,0071
c
0,000
0,200
0,201
0,208
0,292
0,449
0,484
0,502
0,512
0,517
0,521
0,523
0,524
0,534
0,558
0,584
0,606
0,625
0,641
0,656
0,669
0,680
0,691
0,700
fs (kN/m2) LSP (m)
0,0
0,000
6804,0
0,003
17028,7
0,007
30834,4
0,013
51508,7
0,022
83092,6
0,035
115072,1
0,048
151049,1
0,063
191169,2
0,080
235474,2
0,099
284193,0
0,119
337075,8
0,141
394539,0
0,165
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
LP (m)
0,366
0,369
0,373
0,379
0,387
0,401
0,414
0,429
0,446
0,464
0,485
0,507
0,531
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
μ γ (kPa) Vc (kN) Vs (kN) Vp (kN)
0,000 0,25
343,1
451,5
0
0,030 0,25
343,1
451,5
0
0,075 0,25
343,1
451,5
0
0,134 0,25
343,1
451,5
0
0,197 0,25
343,1
451,5
0
0,256 0,25
343,1
451,5
0
0,342 0,25
343,1
451,5
0
0,441 0,25
343,1
451,5
0
0,553 0,25
343,1
451,5
0
0,678 0,25
343,1
451,5
0
0,816 0,25
343,1
451,5
0
0,963 0,25
343,1
451,5
0
1,122 0,25
343,1
451,5
0
1,268 0,25
343,1
451,5
0
1,354 0,25
343,1
451,5
0
1,425 0,25
343,1
451,5
0
1,500 0,25
343,1
451,5
0
1,578 0,25
343,1
451,5
0
1,659 0,25
343,1
451,5
0
1,744 0,25
343,1
451,5
0
1,832 0,25
343,1
451,5
0
1,924 0,25
343,1
451,5
0
2,020 0,25
343,1
451,5
0
2,120 0,25
343,1
451,5
0
104
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
V (kN)
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
794,6
φ (1/m) M (kN·m) εst (m/m)
0,0047 2514,9
0,0077
0,0051 2546,8
0,0083
0,0055 2589,3
0,0090
0,0059 2632,9
0,0097
0,0063 2677,6
0,0105
0,0067 2721,7
0,0112
0,0072 2768,9
0,0120
0,0077 2817,2
0,0128
0,0081 2865,7
0,0136
0,0086 2918,5
0,0145
0,0091 2969,7
0,0154
0,0097 3022,9
0,0163
0,0102 3077,1
0,0172
0,0108 3126,5
0,0182
0,0113 3173,6
0,0191
0,0119 3218,2
0,0201
0,0125 3258,6
0,0212
0,0131 3296,3
0,0222
0,0137 3332,0
0,0233
0,0144 3368,8
0,0244
0,0150 3404,3
0,0255
0,0157 3438,9
0,0266
0,0164 3471,3
0,0278
0,0171 3500,2
0,0289
0,0178 3523,1
0,0301
c
0,709
0,716
0,722
0,728
0,733
0,738
0,743
0,747
0,750
0,754
0,757
0,759
0,762
0,764
0,766
0,769
0,770
0,772
0,773
0,773
0,773
0,772
0,771
0,769
0,767
fs (kN/m2) LSP (m)
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
410200,0
0,172
LP (m)
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
0,538
μ γ (kPa) Vc (kN) Vs (kN) Vp (kN)
2,228 0,25
343,1
451,5
0
2,343 0,25
343,1
451,5
0
2,467 0,25
343,1
451,5
0
2,595 0,25
343,1
451,5
0
2,727 0,25
343,1
451,5
0
2,863 0,25
343,1
451,5
0
3,005 0,25
343,0
451,5
0
3,150 0,25
339,5
451,5
0
3,300 0,24
335,9
451,5
0
3,456 0,24
332,2
451,5
0
3,614 0,24
328,4
451,5
0
3,778 0,24
324,4
451,5
0
3,944 0,23
320,4
451,5
0
4,117 0,23
316,3
451,5
0
4,288 0,23
312,2
451,5
0
4,467 0,22
307,9
451,5
0
4,644 0,22
303,6
451,5
0
4,825 0,22
299,3
451,5
0
5,011 0,21
294,8
451,5
0
5,201 0,21
290,3
451,5
0
5,393 0,21
285,6
451,5
0
5,590 0,20
280,9
451,5
0
5,788 0,20
276,1
451,5
0
5,991 0,20
271,3
451,5
0
6,195 0,19
266,4
451,5
0
105
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
V (kN)
794,6
794,6
794,6
794,6
794,6
794,6
794,5
791,0
787,4
783,7
779,9
775,9
771,9
767,8
763,7
759,4
755,2
750,8
746,3
741,8
737,2
732,4
727,7
722,8
717,9
φ (1/m) M (kN·m) εst (m/m) c fs (kN/m2) LSP (m) LP (m) μ γ (kPa) Vc (kN) Vs (kN) Vp (kN) V (kN)
0,0185 3543,0
0,0312 0,763 410200,0
0,172
0,538 6,403 0,19
261,4
451,5
0
712,9
106
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla B.9: Curvas de respuesta y resistencia fuerza-desplazamiento del muro B3.
MC (B3)
Desplazamientos flexión (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu
0,0000
0,0
0,0006
336,7
0,004
0,0016
805,2
0,011
0,0028
894,3
0,014
0,0044
915,5
0,017
0,0063
971,4
0,020
0,0085
1048,6
0,025
0,0110
1123,1
0,029
0,0138
1191,4
0,035
0,0170
1250,2
0,040
0,0204
1298,6
0,047
0,0242
1340,1
0,053
0,0283
1372,1
0,060
0,0326
1394,2
0,068
0,0374
1404,7
0,075
0,0424
1417,5
0,084
0,0477
1430,9
0,093
0,0534
1443,8
0,102
0,0593
1452,1
0,112
0,0656
976,0
0,118
Desplazamientos corte (m)
V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,000
0,0
0,0
556,2
0,001
0,5
73,6
556,2
0,002
1,3
176,1
556,2
0,002
1,6
195,6
556,2
0,002
1,9
200,2
556,2
0,002
2,3
212,5
556,2
0,003
2,7
229,4
556,2
0,003
3,2
245,6
554,9
0,003
3,8
260,6
542,2
0,003
4,4
273,4
528,5
0,003
5,0
284,0
513,9
0,003
5,6
293,1
498,2
0,003
6,4
300,1
481,7
0,003
7,1
304,9
464,1
0,003
7,9
307,2
445,7
0,004
8,7
310,0
425,9
0,004
9,6
313,0
404,8
0,004
10,6
315,8
382,4
0,004
11,6
317,6
358,8
0,002
12,1
213,5
348,4
107
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla B.10: Parámetros de cálculo para las curvas fuerza-desplazamiento del muro B3.
φ (1/m) M (kN·m) εst (m/m)
0,0000
0,0
0,0000
0,0006
336,7
0,0010
0,0016
805,2
0,0025
0,0028
894,3
0,0047
0,0044
915,5
0,0075
0,0063
971,4
0,0109
0,0085 1048,6
0,0148
0,0110 1123,1
0,0193
0,0138 1191,4
0,0243
0,0170 1250,2
0,0300
0,0204 1298,6
0,0362
0,0242 1340,1
0,0430
0,0283 1372,1
0,0502
0,0326 1394,2
0,0580
0,0374 1404,7
0,0660
0,0424 1417,5
0,0748
0,0477 1430,9
0,0842
0,0534 1443,8
0,0942
0,0593 1452,1
0,1048
0,0656
976,0
0,1170
c fs (kN/m2) LSP (m)
0,000
0,0
0,000
0,676
179,7
0,000
0,696
455,1
0,000
0,748
845,0
0,000
0,784 1343,1
0,001
0,806 1946,7
0,001
0,819 2643,3
0,001
0,829 3447,0
0,001
0,836 4340,0
0,002
0,843 5358,0
0,002
0,848 6465,3
0,003
0,851 7679,8
0,003
0,851 8965,7
0,004
0,848 10358,8
0,004
0,839 11787,6
0,005
0,837 13359,3
0,006
0,838 15038,1
0,006
0,839 16824,1
0,007
0,839 18717,3
0,008
0,856 20896,2
0,009
LP (m)
0,366
0,366
0,366
0,366
0,366
0,367
0,367
0,367
0,368
0,368
0,368
0,369
0,370
0,370
0,371
0,371
0,372
0,373
0,374
0,375
μ
γ (kPa) Vc (kN) Vs (kN) Vp (kN)
0,000 0,25
353,3
202,9
0
0,494 0,25
353,3
202,9
0
1,226 0,25
353,3
202,9
0
1,526 0,25
353,3
202,9
0
1,791 0,25
353,3
202,9
0
2,147 0,25
353,3
202,9
0
2,577 0,25
353,3
202,9
0
3,053 0,25
352,0
202,9
0
3,568 0,24
339,3
202,9
0
4,123 0,23
325,5
202,9
0
4,713 0,22
310,9
202,9
0
5,346 0,21
295,3
202,9
0
6,016 0,20
278,7
202,9
0
6,725 0,18
261,2
202,9
0
7,471 0,17
242,7
202,9
0
8,271 0,16
222,9
202,9
0
9,125 0,14
201,8
202,9
0
10,031 0,13
179,4
202,9
0
10,984 0,11
155,9
202,9
0
11,404 0,10
145,5
202,9
0
108
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
V (kN)
556,2
556,2
556,2
556,2
556,2
556,2
556,2
554,9
542,2
528,5
513,9
498,2
481,7
464,1
445,7
425,9
404,8
382,4
358,8
348,4
Tabla B.11: Curvas de respuesta y resistencia fuerza-desplazamiento del muro B4.
MC (B4)
Desplazamientos flexión (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu
0,0000
0,0
0,0007
378,7
0,005
0,0017
869,5
0,012
0,0030
927,2
0,016
0,0047
948,3
0,020
0,0068
1016,3
0,025
0,0091
1095,2
0,031
0,0119
1168,2
0,038
0,0149
1235,6
0,045
0,0183
1290,2
0,053
0,0220
1335,2
0,062
0,0261
1372,6
0,071
0,0305
1399,6
0,081
0,0352
1412,2
0,091
0,0403
1429,1
0,102
0,0457
1445,4
0,114
0,0515
1459,5
0,127
0,0576
1470,5
0,141
0,0640
1478,7
0,155
Desplazamientos corte (m)
V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,000
0,0
0,0
513,0
0,001
0,6
82,8
513,0
0,002
1,5
190,2
513,0
0,002
1,8
202,8
513,0
0,002
2,2
207,4
513,0
0,002
2,7
222,3
513,0
0,003
3,4
239,5
510,8
0,003
4,0
255,5
498,5
0,003
4,8
270,2
485,1
0,015
6,8
282,2
449,0
0,018
7,9
292,0
429,1
0,020
9,1
300,2
407,7
0,023
10,4
306,1
384,8
0,026
11,7
308,9
360,5
0,029
13,2
312,6
334,5
0,033
14,7
316,1
306,7
0,037
16,4
319,2
280,3
0,040
18,1
321,6
280,3
0,044
19,9
323,4
280,3
109
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla B.12: Parámetros de cálculo para las curvas fuerza-desplazamiento del muro B4.
φ (1/m) M (kN·m) εst (m/m)
0,0000
0,0
0,0000
0,0007
378,7
0,0011
0,0017
869,5
0,0027
0,0030
927,2
0,0051
0,0047
948,3
0,0081
0,0068 1016,3
0,0117
0,0091 1095,2
0,0160
0,0119 1168,2
0,0208
0,0149 1235,6
0,0263
0,0183 1290,2
0,0324
0,0220 1335,2
0,0390
0,0261 1372,6
0,0463
0,0305 1399,6
0,0541
0,0352 1412,2
0,0621
0,0403 1429,1
0,0710
0,0457 1445,4
0,0806
0,0515 1459,5
0,0908
0,0576 1470,5
0,1015
0,0640 1478,7
0,1129
c
0,000
0,668
0,692
0,748
0,784
0,805
0,818
0,828
0,835
0,842
0,846
0,848
0,846
0,837
0,833
0,835
0,836
0,836
0,837
fs (kN/m2) LSP (m)
0,0
0,000
204957,6
0,057
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
450200,0
0,126
LP (m)
0,366
0,423
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
0,492
μ
γ (kPa) Vc (kN) Vs (kN) Vp (kN)
0,000 0,25
277,0
236,0
0
0,547 0,25
277,0
236,0
0
1,343 0,25
277,0
236,0
0
1,684 0,25
277,0
236,0
0
2,051 0,25
277,0
236,0
0
2,541 0,25
277,0
236,0
0
3,111 0,25
274,8
236,0
0
3,745 0,24
262,5
236,0
0
4,440 0,22
249,1
236,0
0
6,301 0,19
213,0
236,0
0
7,327 0,17
193,1
236,0
0
8,429 0,15
171,7
236,0
0
9,611 0,13
148,8
236,0
0
10,862 0,11
124,6
236,0
0
12,206 0,09
98,5
236,0
0
13,638 0,06
70,7
236,0
0
15,156 0,04
44,3
236,0
0
16,760 0,04
44,3
236,0
0
18,445 0,04
44,3
236,0
0
110
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
V (kN)
513,0
513,0
513,0
513,0
513,0
513,0
510,8
498,5
485,1
449,0
429,1
407,7
384,8
360,5
334,5
306,7
280,3
280,3
280,3
Tabla B.13: Curvas de respuesta y resistencia fuerza-desplazamiento del muro B5.
MC (B5)
Desplazamientos flexión (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu
0,0000
0,0
0,0001
432,9
0,001
0,0003
518,8
0,002
0,0006
867,9
0,004
0,0009
1333,9
0,006
0,0012
1900,8
0,009
0,0017
2468,0
0,012
0,0021
2578,4
0,014
0,0027
2609,4
0,015
0,0033
2635,6
0,017
0,0040
2658,3
0,019
0,0047
2695,0
0,021
0,0055
2780,3
0,023
0,0064
2882,6
0,025
0,0073
2989,4
0,028
0,0083
3091,7
0,031
0,0093
3186,1
0,034
0,0104
3280,2
0,037
0,0116
3370,5
0,040
0,0128
3455,2
0,043
0,0141
3528,3
0,047
0,0155
3594,5
0,050
0,0169
3658,2
0,054
Desplazamientos corte (m)
V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,000
0,0
0,0
833,2
0,000
0,1
94,7
833,2
0,000
0,3
113,5
833,2
0,001
0,5
189,8
833,2
0,001
0,8
291,7
833,2
0,002
1,1
415,7
833,2
0,002
1,4
539,8
833,2
0,002
1,6
564,0
833,2
0,003
1,8
570,7
833,2
0,003
2,0
576,5
833,2
0,003
2,2
581,4
833,2
0,003
2,4
589,5
833,2
0,004
2,7
608,1
833,2
0,004
3,0
630,5
833,2
0,005
3,3
653,8
833,2
0,005
3,6
676,2
828,1
0,006
3,9
696,9
819,6
0,006
4,3
717,5
810,7
0,007
4,7
737,2
801,3
0,007
5,0
755,7
791,6
0,008
5,4
771,7
781,5
0,008
5,9
786,2
771,0
0,009
6,3
800,1
760,2
111
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
MC (B5)
Desplazamientos flexión (m) Desplazamientos corte (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,0183
3708,1
0,058
0,009
6,7
811,0
749,0
0,0199
3758,6
0,062
0,010
7,2
822,1
737,4
0,0215
3812,4
0,066
0,011
7,7
833,8
725,2
0,0231
3869,5
0,070
0,011
8,2
846,3
712,6
0,0248
3922,6
0,075
0,012
8,7
858,0
699,7
0,0266
3973,3
0,079
0,013
9,2
869,0
686,2
0,0285
4020,6
0,084
0,014
9,8
879,4
672,4
0,0304
4063,2
0,089
0,015
10,3
888,7
658,2
0,0323
4101,7
0,094
0,015
10,9
897,1
643,5
0,0344
4137,6
0,099
0,016
11,5
905,0
628,5
0,0364
4170,2
0,104
0,017
12,1
912,1
613,0
0,0386
4202,4
0,110
0,018
12,7
919,2
597,1
0,0408
4231,4
0,115
0,019
13,4
925,5
580,8
0,0431
4259,0
0,121
0,020
14,1
931,5
564,0
0,0454
4282,5
0,127
0,021
14,7
936,7
546,8
0,0478
4306,4
0,133
0,022
15,4
941,9
529,2
0,0502
4327,8
0,139
0,023
16,2
946,6
511,2
0,0528
4346,4
0,145
0,024
16,9
950,7
492,7
0,0553
4363,2
0,152
0,025
17,6
954,3
490,9
0,0580
4377,8
0,158
0,026
18,4
957,5
490,9
0,0607
4390,6
0,165
0,027
19,2
960,3
490,9
0,0634
4402,3
0,172
0,028
20,0
962,9
490,9
0,0663
4412,1
0,179
0,029
20,8
965,0
490,9
0,0691
4419,6
0,186
0,030
21,6
966,7
490,9
112
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
MC (B5)
Desplazamientos flexión (m) Desplazamientos corte (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,0721
4426,9
0,193
0,032
22,5
968,3
490,9
0,0751
4432,5
0,201
0,033
23,3
969,5
490,9
113
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla B.14: Parámetros de cálculo para las curvas fuerza-desplazamiento del muro B5.
φ (1/m) M (kN·m) εst (m/m)
0,0000
0,0
0,0000
0,0001
432,9
0,0001
0,0003
518,8
0,0004
0,0006
867,9
0,0008
0,0009 1333,9
0,0012
0,0012 1900,8
0,0018
0,0017 2468,0
0,0024
0,0021 2578,4
0,0032
0,0027 2609,4
0,0042
0,0033 2635,6
0,0052
0,0040 2658,3
0,0064
0,0047 2695,0
0,0077
0,0055 2780,3
0,0090
0,0064 2882,6
0,0105
0,0073 2989,4
0,0121
0,0083 3091,7
0,0138
0,0093 3186,1
0,0156
0,0104 3280,2
0,0175
0,0116 3370,5
0,0195
0,0128 3455,2
0,0216
0,0141 3528,3
0,0238
0,0155 3594,5
0,0260
0,0169 3658,2
0,0284
0,0183 3708,1
0,0308
c
0,000
0,207
0,465
0,508
0,519
0,523
0,533
0,582
0,623
0,654
0,679
0,698
0,712
0,723
0,732
0,739
0,746
0,751
0,755
0,757
0,757
0,755
0,754
0,751
fs (kN/m2) LSP (m)
0,0
0,000
28292,9
0,012
86851,8
0,036
161133,5
0,068
252622,8
0,106
361848,6
0,152
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
LP (m)
0,366
0,378
0,402
0,433
0,472
0,517
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
μ
γ (kPa) Vc (kN) Vs (kN) Vp (kN)
0,000 0,25
407,5
425,7
0
0,114 0,25
407,5
425,7
0
0,244 0,25
407,5
425,7
0
0,433 0,25
407,5
425,7
0
0,673 0,25
407,5
425,7
0
0,960 0,25
407,5
425,7
0
1,276 0,25
407,5
425,7
0
1,440 0,25
407,5
425,7
0
1,591 0,25
407,5
425,7
0
1,756 0,25
407,5
425,7
0
1,936 0,25
407,5
425,7
0
2,136 0,25
407,5
425,7
0
2,369 0,25
407,5
425,7
0
2,623 0,25
407,5
425,7
0
2,894 0,25
407,5
425,7
0
3,179 0,25
402,4
425,7
0
3,477 0,24
393,9
425,7
0
3,792 0,24
384,9
425,7
0
4,118 0,23
375,6
425,7
0
4,461 0,22
365,8
425,7
0
4,814 0,22
355,8
425,7
0
5,181 0,21
345,3
425,7
0
5,562 0,21
334,4
425,7
0
5,954 0,20
323,3
425,7
0
114
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
V (kN)
833,2
833,2
833,2
833,2
833,2
833,2
833,2
833,2
833,2
833,2
833,2
833,2
833,2
833,2
833,2
828,1
819,6
810,7
801,3
791,6
781,5
771,0
760,2
749,0
φ (1/m) M (kN·m) εst (m/m)
0,0199 3758,6
0,0333
0,0215 3812,4
0,0359
0,0231 3869,5
0,0387
0,0248 3922,6
0,0416
0,0266 3973,3
0,0446
0,0285 4020,6
0,0476
0,0304 4063,2
0,0508
0,0323 4101,7
0,0541
0,0344 4137,6
0,0576
0,0364 4170,2
0,0611
0,0386 4202,4
0,0648
0,0408 4231,4
0,0685
0,0431 4259,0
0,0724
0,0454 4282,5
0,0763
0,0478 4306,4
0,0804
0,0502 4327,8
0,0846
0,0528 4346,4
0,0888
0,0553 4363,2
0,0932
0,0580 4377,8
0,0977
0,0607 4390,6
0,1023
0,0634 4402,3
0,1070
0,0663 4412,1
0,1118
0,0691 4419,6
0,1167
0,0721 4426,9
0,1217
0,0751 4432,5
0,1269
c
0,748
0,747
0,748
0,747
0,747
0,747
0,747
0,748
0,749
0,750
0,751
0,752
0,753
0,754
0,755
0,756
0,757
0,758
0,759
0,759
0,760
0,761
0,761
0,762
0,762
fs (kN/m2) LSP (m)
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
LP (m)
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
μ
γ (kPa) Vc (kN) Vs (kN) Vp (kN)
6,361 0,19
311,6
425,7
0
6,787 0,18
299,5
425,7
0
7,229 0,18
286,9
425,7
0
7,683 0,17
273,9
425,7
0
8,154 0,16
260,5
425,7
0
8,639 0,15
246,7
425,7
0
9,137 0,14
232,4
425,7
0
9,652 0,13
217,8
425,7
0
10,179 0,12
202,7
425,7
0
10,722 0,11
187,2
425,7
0
11,278 0,11
171,4
425,7
0
11,851 0,10
155,0
425,7
0
12,439 0,08
138,3
425,7
0
13,040 0,07
121,1
425,7
0
13,659 0,06
103,4
425,7
0
14,291 0,05
85,4
425,7
0
14,936 0,04
67,0
425,7
0
15,599 0,04
65,2
425,7
0
16,276 0,04
65,2
425,7
0
16,968 0,04
65,2
425,7
0
17,675 0,04
65,2
425,7
0
18,396 0,04
65,2
425,7
0
19,132 0,04
65,2
425,7
0
19,886 0,04
65,2
425,7
0
20,652 0,04
65,2
425,7
0
115
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
V (kN)
737,4
725,2
712,6
699,7
686,2
672,4
658,2
643,5
628,5
613,0
597,1
580,8
564,0
546,8
529,2
511,2
492,7
490,9
490,9
490,9
490,9
490,9
490,9
490,9
490,9
Tabla B.15: Curvas de respuesta y resistencia fuerza-desplazamiento del muro B6.
MC (B6)
Desplazamientos flexión (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu
0,0000
0,0
0,0001
432,9
0,001
0,0003
518,8
0,002
0,0006
867,9
0,004
0,0009
1333,9
0,006
0,0012
1900,8
0,009
0,0017
2468,0
0,012
0,0021
2578,4
0,014
0,0027
2609,4
0,015
0,0033
2635,6
0,017
0,0040
2658,3
0,019
0,0047
2695,0
0,021
0,0055
2780,3
0,023
0,0064
2882,6
0,025
0,0073
2989,4
0,028
0,0083
3091,7
0,031
0,0093
3186,1
0,034
0,0104
3280,2
0,037
0,0116
3370,5
0,040
0,0128
3455,2
0,043
0,0141
3528,3
0,047
0,0155
3594,5
0,050
0,0169
3658,2
0,054
Desplazamientos corte (m)
V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,000
0,0
0,0
821,4
0,000
0,1
94,7
821,4
0,000
0,3
113,5
821,4
0,001
0,5
189,8
821,4
0,001
0,8
291,7
821,4
0,002
1,1
415,7
821,4
0,002
1,4
539,8
821,4
0,002
1,6
564,0
821,4
0,003
1,8
570,7
821,4
0,003
2,0
576,5
821,4
0,003
2,2
581,4
821,4
0,003
2,4
589,5
821,4
0,004
2,7
608,1
821,4
0,004
3,0
630,5
821,4
0,005
3,3
653,8
821,4
0,005
3,6
676,2
816,5
0,006
3,9
696,9
808,2
0,006
4,3
717,5
799,5
0,007
4,7
737,2
790,5
0,007
5,0
755,7
781,0
0,008
5,4
771,7
771,2
0,008
5,9
786,2
761,0
0,009
6,3
800,1
750,5
116
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
MC (B6)
Desplazamientos flexión (m) Desplazamientos corte (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,0183
3708,1
0,058
0,009
6,7
811,0
739,6
0,0199
3758,6
0,062
0,010
7,2
822,1
728,4
0,0215
3812,4
0,066
0,011
7,7
833,8
716,6
0,0231
3869,5
0,070
0,011
8,2
846,3
704,3
0,0248
3922,6
0,075
0,012
8,7
858,0
691,8
0,0266
3973,3
0,079
0,013
9,2
869,0
678,7
0,0285
4020,6
0,084
0,014
9,8
879,4
665,3
0,0304
4063,2
0,089
0,014
10,3
888,7
651,5
0,0323
4101,7
0,094
0,015
10,9
897,1
637,3
0,0344
4137,6
0,099
0,016
11,5
905,0
622,7
0,0364
4170,2
0,104
0,017
12,1
912,1
607,6
0,0386
4202,4
0,110
0,018
12,7
919,2
592,2
0,0408
4231,4
0,115
0,019
13,4
925,5
576,4
0,0431
4259,0
0,121
0,020
14,1
931,5
560,1
0,0454
4282,5
0,127
0,021
14,7
936,7
543,5
0,0478
4306,4
0,133
0,022
15,4
941,9
526,3
0,0502
4327,8
0,139
0,023
16,1
946,6
508,9
0,0528
4346,4
0,145
0,024
16,9
950,7
491,0
0,0553
4363,2
0,152
0,025
17,6
954,3
489,0
0,0580
4377,8
0,158
0,026
18,4
957,5
489,0
0,0607
4390,6
0,165
0,027
19,2
960,3
489,0
0,0634
4402,3
0,172
0,028
20,0
962,9
489,0
0,0663
4412,1
0,179
0,029
20,8
965,0
489,0
0,0691
4419,6
0,186
0,030
21,6
966,7
489,0
117
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
MC (B6)
Desplazamientos flexión (m) Desplazamientos corte (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,0721
4426,9
0,193
0,032
22,5
968,3
489,0
0,0751
4432,5
0,201
0,033
23,3
969,5
489,0
118
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla B.16: Parámetros de cálculo para las curvas fuerza-desplazamiento del muro B6.
φ (1/m) M (kN·m) εst (m/m)
0,0000
0,0
0,0000
0,0001
432,9
0,0001
0,0003
518,8
0,0004
0,0006
867,9
0,0008
0,0009 1333,9
0,0012
0,0012 1900,8
0,0018
0,0017 2468,0
0,0024
0,0021 2578,4
0,0032
0,0027 2609,4
0,0042
0,0033 2635,6
0,0052
0,0040 2658,3
0,0064
0,0047 2695,0
0,0077
0,0055 2780,3
0,0090
0,0064 2882,6
0,0105
0,0073 2989,4
0,0121
0,0083 3091,7
0,0138
0,0093 3186,1
0,0156
0,0104 3280,2
0,0175
0,0116 3370,5
0,0195
0,0128 3455,2
0,0216
0,0141 3528,3
0,0238
0,0155 3594,5
0,0260
0,0169 3658,2
0,0284
0,0183 3708,1
0,0308
c
0,000
0,207
0,465
0,508
0,519
0,523
0,533
0,582
0,623
0,654
0,679
0,698
0,712
0,723
0,732
0,739
0,746
0,751
0,755
0,757
0,757
0,755
0,754
0,751
fs (kN/m2) LSP (m)
0,0
0,000
28292,9
0,012
86851,8
0,036
161133,5
0,068
252622,8
0,106
361848,6
0,152
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
LP (m)
0,366
0,378
0,402
0,433
0,472
0,517
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
μ
γ (kPa) Vc (kN) Vs (kN) Vp (kN)
0,000 0,25
395,6
425,7
0
0,114 0,25
395,6
425,7
0
0,244 0,25
395,6
425,7
0
0,433 0,25
395,6
425,7
0
0,673 0,25
395,6
425,7
0
0,960 0,25
395,6
425,7
0
1,276 0,25
395,6
425,7
0
1,439 0,25
395,6
425,7
0
1,590 0,25
395,6
425,7
0
1,755 0,25
395,6
425,7
0
1,935 0,25
395,6
425,7
0
2,135 0,25
395,6
425,7
0
2,367 0,25
395,6
425,7
0
2,621 0,25
395,6
425,7
0
2,893 0,25
395,6
425,7
0
3,178 0,25
390,7
425,7
0
3,476 0,24
382,5
425,7
0
3,790 0,24
373,8
425,7
0
4,116 0,23
364,7
425,7
0
4,459 0,22
355,2
425,7
0
4,812 0,22
345,5
425,7
0
5,179 0,21
335,3
425,7
0
5,560 0,21
324,8
425,7
0
5,951 0,20
313,9
425,7
0
119
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
V (kN)
821,4
821,4
821,4
821,4
821,4
821,4
821,4
821,4
821,4
821,4
821,4
821,4
821,4
821,4
821,4
816,5
808,2
799,5
790,5
781,0
771,2
761,0
750,5
739,6
φ (1/m) M (kN·m) εst (m/m)
0,0199 3758,6
0,0333
0,0215 3812,4
0,0359
0,0231 3869,5
0,0387
0,0248 3922,6
0,0416
0,0266 3973,3
0,0446
0,0285 4020,6
0,0476
0,0304 4063,2
0,0508
0,0323 4101,7
0,0541
0,0344 4137,6
0,0576
0,0364 4170,2
0,0611
0,0386 4202,4
0,0648
0,0408 4231,4
0,0685
0,0431 4259,0
0,0724
0,0454 4282,5
0,0763
0,0478 4306,4
0,0804
0,0502 4327,8
0,0846
0,0528 4346,4
0,0888
0,0553 4363,2
0,0932
0,0580 4377,8
0,0977
0,0607 4390,6
0,1023
0,0634 4402,3
0,1070
0,0663 4412,1
0,1118
0,0691 4419,6
0,1167
0,0721 4426,9
0,1217
0,0751 4432,5
0,1269
c
0,748
0,747
0,748
0,747
0,747
0,747
0,747
0,748
0,749
0,750
0,751
0,752
0,753
0,754
0,755
0,756
0,757
0,758
0,759
0,759
0,760
0,761
0,761
0,762
0,762
fs (kN/m2) LSP (m)
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
444000,0
0,186
LP (m)
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
0,552
μ
γ (kPa) Vc (kN) Vs (kN) Vp (kN)
6,358 0,19
302,6
425,7
0
6,784 0,18
290,9
425,7
0
7,226 0,18
278,6
425,7
0
7,680 0,17
266,0
425,7
0
8,150 0,16
253,0
425,7
0
8,635 0,15
239,6
425,7
0
9,133 0,14
225,8
425,7
0
9,648 0,13
211,5
425,7
0
10,174 0,12
196,9
425,7
0
10,718 0,11
181,9
425,7
0
11,273 0,11
166,5
425,7
0
11,846 0,10
150,7
425,7
0
12,433 0,08
134,4
425,7
0
13,034 0,07
117,7
425,7
0
13,653 0,06
100,6
425,7
0
14,284 0,05
83,1
425,7
0
14,930 0,04
65,3
425,7
0
15,592 0,04
63,3
425,7
0
16,269 0,04
63,3
425,7
0
16,961 0,04
63,3
425,7
0
17,667 0,04
63,3
425,7
0
18,388 0,04
63,3
425,7
0
19,124 0,04
63,3
425,7
0
19,877 0,04
63,3
425,7
0
20,642 0,04
63,3
425,7
0
120
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
V (kN)
728,4
716,6
704,3
691,8
678,7
665,3
651,5
637,3
622,7
607,6
592,2
576,4
560,1
543,5
526,3
508,9
491,0
489,0
489,0
489,0
489,0
489,0
489,0
489,0
489,0
Tabla B.17: Curvas de respuesta y resistencia fuerza-desplazamiento del muro F1.
MC (F1)
Desplazamientos flexión (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu
0,0000
0,0
0,0001
334,6
0,000
0,0002
475,8
0,001
0,0003
631,7
0,002
0,0005
933,6
0,003
0,0007
1312,8
0,005
0,0009
1766,2
0,007
0,0012
2288,3
0,009
0,0015
2873,3
0,011
0,0018
3038,0
0,012
0,0022
3061,4
0,013
0,0026
3078,6
0,014
0,0030
3091,2
0,015
0,0035
3099,2
0,016
0,0040
3106,3
0,017
0,0045
3110,9
0,018
0,0051
3158,2
0,020
0,0057
3238,5
0,021
0,0063
3324,0
0,023
0,0070
3412,8
0,024
0,0077
3496,5
0,026
Desplazamientos corte (m)
V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,000
0,0
0,0
706,3
0,001
0,1
73,2
706,3
0,001
0,2
104,1
706,3
0,001
0,3
138,2
706,3
0,002
0,5
204,2
706,3
0,002
0,7
287,1
706,3
0,003
0,9
386,3
706,3
0,003
1,2
500,5
706,3
0,004
1,5
628,4
706,3
0,004
1,6
664,5
706,3
0,005
1,8
669,6
706,3
0,005
1,9
673,4
706,3
0,005
2,0
676,1
706,3
0,006
2,2
677,9
706,3
0,006
2,3
679,4
706,3
0,006
2,5
680,4
706,3
0,007
2,6
690,8
706,3
0,007
2,9
708,3
706,3
0,008
3,1
727,0
706,3
0,009
3,3
746,5
706,3
0,009
3,5
764,8
703,5
121
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
MC (F1)
Desplazamientos flexión (m) Desplazamientos corte (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,0084
3572,3
0,028
0,010
3,8
781,4
700,6
0,0092
3651,5
0,030
0,011
4,0
798,7
697,5
0,0100
3732,4
0,032
0,011
4,3
816,4
694,2
0,0108
3802,7
0,034
0,012
4,6
831,7
690,9
0,0117
3873,4
0,036
0,013
4,9
847,2
687,5
0,0126
3946,0
0,038
0,013
5,1
863,1
683,9
0,0135
4010,5
0,040
0,014
5,4
877,2
680,3
0,0145
4075,5
0,043
0,015
5,8
891,4
676,5
0,0155
4138,9
0,045
0,016
6,1
905,3
672,7
0,0165
4196,1
0,047
0,017
6,4
917,8
668,7
0,0176
4254,4
0,050
0,018
6,7
930,5
664,6
0,0187
4306,9
0,052
0,018
7,1
942,0
660,4
0,0198
4358,2
0,055
0,019
7,4
953,2
656,1
0,0210
4406,9
0,058
0,020
7,8
963,9
651,7
0,0222
4452,1
0,060
0,021
8,2
973,8
647,2
0,0234
4497,0
0,063
0,022
8,5
983,6
642,6
0,0247
4537,0
0,066
0,023
8,9
992,3
637,9
0,0260
4575,7
0,069
0,024
9,3
1000,8
633,0
0,0273
4610,9
0,072
0,025
9,7
1008,5
628,1
0,0287
4644,6
0,075
0,027
10,2
1015,9
623,0
0,0301
4675,8
0,078
0,028
10,6
1022,7
617,9
0,0315
4705,1
0,081
0,029
11,0
1029,1
612,6
0,0330
4730,7
0,085
0,030
11,5
1034,7
607,2
0,0345
4755,2
0,088
0,031
11,9
1040,1
601,7
122
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
MC (F1)
Desplazamientos flexión (m) Desplazamientos corte (m)
φ (1/m) M (kN·m) φ≤φcr φcr<φ≤φy φy<φ≤φu V≤Vc Vc<V≤Vy Vy<V≤Vu Δ (cm) FResp (kN) FResi (kN)
0,0360
4777,4
0,091
0,032
12,4
1044,9
596,1
0,0376
4799,0
0,095
0,034
12,8
1049,7
590,4
0,0392
4817,2
0,098
0,035
13,3
1053,6
584,5
0,0408
4831,0
0,102
0,036
13,8
1056,6
578,6
0,0425
4837,2
0,106
0,037
14,3
1058,0
572,6
123
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
Tabla B.18: Parámetros de cálculo para las curvas fuerza-desplazamiento del muro F1.
φ (1/m) M (kN·m) εst (m/m)
0,0000
0,0
0,0000
0,0001
334,6
0,0001
0,0002
475,8
0,0002
0,0003
631,7
0,0004
0,0005
933,6
0,0007
0,0007 1312,8
0,0010
0,0009 1766,2
0,0014
0,0012 2288,3
0,0018
0,0015 2873,3
0,0022
0,0018 3038,0
0,0028
0,0022 3061,4
0,0035
0,0026 3078,6
0,0042
0,0030 3091,2
0,0050
0,0035 3099,2
0,0058
0,0040 3106,3
0,0067
0,0045 3110,9
0,0077
0,0051 3158,2
0,0087
0,0057 3238,5
0,0098
0,0063 3324,0
0,0110
0,0070 3412,8
0,0122
0,0077 3496,5
0,0134
0,0084 3572,3
0,0148
0,0092 3651,5
0,0162
0,0100 3732,4
0,0176
c
0,000
0,197
0,422
0,546
0,577
0,584
0,590
0,593
0,594
0,631
0,671
0,703
0,728
0,750
0,767
0,782
0,793
0,802
0,809
0,815
0,821
0,826
0,831
0,835
fs (kN/m2) LSP (m)
0,0
0,000
14570,1
0,004
43698,7
0,012
85847,8
0,024
136326,1
0,038
195637,0
0,055
265175,3
0,074
344592,3
0,096
433306,9
0,121
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
LP (m)
0,366
0,370
0,378
0,390
0,404
0,420
0,440
0,462
0,487
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
μ
γ (kPa) Vc (kN) Vs (kN) Vp (kN)
0,000 0,25
191,8
514,4
0
0,094 0,25
191,8
514,4
0
0,181 0,25
191,8
514,4
0
0,293 0,25
191,8
514,4
0
0,448 0,25
191,8
514,4
0
0,626 0,25
191,8
514,4
0
0,831 0,25
191,8
514,4
0
1,066 0,25
191,8
514,4
0
1,329 0,25
191,8
514,4
0
1,482 0,25
191,8
514,4
0
1,588 0,25
191,8
514,4
0
1,701 0,25
191,8
514,4
0
1,820 0,25
191,8
514,4
0
1,948 0,25
191,8
514,4
0
2,084 0,25
191,8
514,4
0
2,228 0,25
191,8
514,4
0
2,396 0,25
191,8
514,4
0
2,582 0,25
191,8
514,4
0
2,780 0,25
191,8
514,4
0
2,988 0,25
191,8
514,4
0
3,203 0,25
189,1
514,4
0
3,424 0,24
186,1
514,4
0
3,655 0,24
183,0
514,4
0
3,895 0,23
179,8
514,4
0
124
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
V (kN)
706,3
706,3
706,3
706,3
706,3
706,3
706,3
706,3
706,3
706,3
706,3
706,3
706,3
706,3
706,3
706,3
706,3
706,3
706,3
706,3
703,5
700,6
697,5
694,2
φ (1/m) M (kN·m) εst (m/m)
0,0108 3802,7
0,0191
0,0117 3873,4
0,0207
0,0126 3946,0
0,0223
0,0135 4010,5
0,0240
0,0145 4075,5
0,0258
0,0155 4138,9
0,0276
0,0165 4196,1
0,0295
0,0176 4254,4
0,0314
0,0187 4306,9
0,0334
0,0198 4358,2
0,0355
0,0210 4406,9
0,0376
0,0222 4452,1
0,0398
0,0234 4497,0
0,0420
0,0247 4537,0
0,0443
0,0260 4575,7
0,0467
0,0273 4610,9
0,0491
0,0287 4644,6
0,0516
0,0301 4675,8
0,0541
0,0315 4705,1
0,0567
0,0330 4730,7
0,0594
0,0345 4755,2
0,0621
0,0360 4777,4
0,0649
0,0376 4799,0
0,0677
0,0392 4817,2
0,0706
0,0408 4831,0
0,0735
c
0,838
0,842
0,845
0,847
0,850
0,852
0,854
0,856
0,858
0,859
0,861
0,862
0,864
0,865
0,866
0,867
0,868
0,868
0,869
0,869
0,870
0,870
0,870
0,870
0,869
fs (kN/m2) LSP (m)
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
444700,0
0,124
LP (m)
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
0,490
μ
γ (kPa) Vc (kN) Vs (kN) Vp (kN)
4,142 0,23
176,5
514,4
0
4,398 0,23
173,1
514,4
0
4,662 0,22
169,5
514,4
0
4,932 0,22
165,9
514,4
0
5,213 0,21
162,1
514,4
0
5,501 0,21
158,2
514,4
0
5,795 0,20
154,3
514,4
0
6,101 0,20
150,2
514,4
0
6,412 0,19
146,0
514,4
0
6,734 0,18
141,7
514,4
0
7,060 0,18
137,3
514,4
0
7,395 0,17
132,8
514,4
0
7,742 0,17
128,2
514,4
0
8,094 0,16
123,4
514,4
0
8,455 0,15
118,6
514,4
0
8,822 0,15
113,7
514,4
0
9,199 0,14
108,6
514,4
0
9,584 0,13
103,4
514,4
0
9,975 0,13
98,2
514,4
0
10,377 0,12
92,8
514,4
0
10,786 0,11
87,3
514,4
0
11,205 0,11
81,7
514,4
0
11,632 0,10
75,9
514,4
0
12,065 0,09
70,1
514,4
0
12,506 0,08
64,2
514,4
0
125
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta
V (kN)
690,9
687,5
683,9
680,3
676,5
672,7
668,7
664,6
660,4
656,1
651,7
647,2
642,6
637,9
633,0
628,1
623,0
617,9
612,6
607,2
601,7
596,1
590,4
584,5
578,6
φ (1/m) M (kN·m) εst (m/m) c fs (kN/m2) LSP (m) LP (m)
μ
γ (kPa) Vc (kN) Vs (kN) Vp (kN) V (kN)
0,0425 4837,2
0,0764 0,867 444700,0
0,124
0,490 12,954 0,08
58,2
514,4
0
572,6
126
Estimación de la capacidad al corte y del desplazamiento lateral de muros de hormigón armado sometidos a carga cíclica
Felipe Castillo Huerta