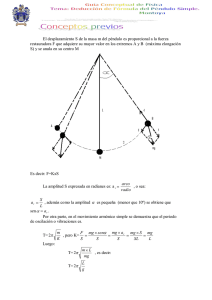
PRÁCTICA: PÉNDULO SIMPLE 1.- OBJETIVOS: Comprobar que el periodo de un péndulo simple es independiente de la masa situada en el extremo del hilo. Obtener experimentalmente la relación T-l (Período-Longitud) Determinar experimentalmente el valor de la aceleración de la gravedad 2.-ATENCIÓN A LOS SIGUIENTES ASPECTOS. 1. La suspensión del hilo ha de ser tal que permita a este oscilar libremente. Así mismo dicha longitud ha de poder variarse. 2. La longitud del péndulo es la distancia entre el punto de suspensión y el centro de la masa suspendida. 3. Cuando medimos magnitudes (l y T) debemos ser meticulosos y precisos ya que la imprecisión condiciona los valores medidos de tal modo que si el error cometido es significativo, el valor de la magnitud que queremos medir quedaría invalidado. 4. Cuando se mida el período de una oscilación hay que procurar que las oscilaciones sean pequeñas y que el péndulo oscile en un plano vertical, sin que efectúe oscilaciones fuera de ese plano. 5. Los intervalos de valor de las medidas de longitud debe decidirlos el alumno de modo que el número de medidas tomadas sea, a ser posible, de 15 o 16. 6. Para cada longitud dada al péndulo, se recomienda tomar 3 medidas del período y calcular su valor medio, que será el utilizado como mejor valor estimado del período correspondiente. 3.- INTRODUCCIÓN TEÓRICA: El péndulo simple está constituido por una masa m, que se puede considerar puntual, unida a uno de los extremos de un hilo inextensible, de longitud “l” y de masa despreciable. Si se suspende la masa del extremo libre del hilo y se separa de la posición vertical de equilibrio un cierto ángulo, tal como se muestra en la figura siguiente, la masa oscilará en torno a la vertical. O θ Dirección normal T Dirección tangencial mg sen θ mg cos θ Posición de equilibrio θ mg Para analizar el movimiento de m, contabilizamos las fuerzas que actúan sobre ella y aplicamos la 2ª ley de Newton. Las fuerzas son su peso y la tensión del hilo y ambas están representadas en la figura anterior. Si descomponemos estas fuerzas en las direcciones intrínsecas, esto es en las direcciones tangencial y normal y aplicamos la 2ª ley de Newton, obtenemos las ecuaciones de movimiento de la masa m, que son: m·g·sen m·aT F T P m·a T m·g·cos m·aN en donde aT y aN son, respectivamente, la aceleración tangencial y la normal. El signo negativo en la primera de las expresiones anteriores se debe a que la componente tangencial del peso tiene sentido opuesto al sentido de la dirección tangencial. Si las oscilaciones son pequeñas, tal como se advierte en la recomendación 4 del apartado anterior, entonces podemos utilizar la siguiente aproximación: sen ; que nos permite expresar la primera de las relaciones anteriores así: m·g· m·aT (1) Teniendo en cuenta ahora la definición de aT y su relación con la aceleración angular, esto es: dv d 2 aT l· l· 2 (2) dt dt podemos escribir la expresión (1) de la manera siguiente: m·l· d 2 d 2 g m · g · · 2 2 dt dt l (3) Si llamamos al factor constante del segundo miembro: g g 2 l l La expresión (3) queda así: d 2 2 · 2 dt (4) Es decir, el movimiento de la masa m tiene lugar de forma que la función que da el valor del ángulo θ, en un instante t cualquiera, esto es: θ = θ(t), debe ser una función que cumpla la ecuación (4). Es decir, θ(t) es una función que al derivarla dos veces se obtiene la misma función multiplicada por una constante. Ahora bien ¿qué funciones son las que al derivarlas se reproducen así mismas, multiplicadas por una constante? Las más sencillas son el seno y el coseno y las exponenciales. Probemos por lo tanto con una función del tipo seno, es decir: (t ) A·sen(t ) (5) En donde la constante A es el valor máximo de θ(t), es decir el valor del ángulo θ en el instante en el que el seno vale 1. Por esta razón, se dice que A es la amplitud del movimiento del péndulo. La función (5) nos da la posición del péndulo en cualquier instante, en cuanto conozcamos A y δ. Ahora bien, por el tipo de movimiento que describe el péndulo, es evidente que la masa m describe un movimiento periódico, es decir; dada su posición y velocidad en un instante cualquiera t, la partícula m volverá a pasar por esa misma posición y con la misma velocidad, al cabo de un cierto tiempo T, que llamamos período del movimiento. Podemos, pues, obtener el valor del período, imponiendo estas dos condiciones: - Que el valor de θ sea el mismo en t y en t +T, esto es: (t ) (t T ) A·sen(t ) A·sen t T sen(t ) sen t T - Que el valor de la velocidad angular sea el mismo en t y en t +T, es decir: d d A··cos(t ) A··cos t T cos(t ) cos t T dt t dt t T Para que el seno y el coseno de dos ángulos sean iguales, los argumentos deben diferir en 2π, esto es: 2 l t T (t ) 2 T 2 T T 2 g (6) La relación matemática (6) es conocida como ley del péndulo. Si elevamos al cuadrado los dos miembros de esta relación, obtenemos: T 2 l 4 2 l c·l T2 g g Esta expresión nos indica que si damos al péndulo distintas longitudes, medimos los períodos correspondientes y construimos una gráfica en la que en abscisas llevemos los valores de l y en ordenadas los de T2, la gráfica resultante debería ser una línea recta de pendiente c, es decir de pendiente: c 4 2 g De cuyo valor podemos obtener el valor de g, una vez que conozcamos el de c. Esta idea es la base de nuestro procedimiento experimental. 4.- OPERACIONES A REALIZAR: 1. Montar los dispositivos de la práctica tal y como aparecen en la figura del guión que se encuentra en el puesto de trabajo del laboratorio, en el caso de que el montaje no esté realizado. 2. Elaborar un cuadro de medidas Ti - li. Para ello, con cada longitud seleccionada, tomamos 3 medidas del período y hacemos su media. Tomaremos este valor como representativo del período correspondiente a esta longitud. ¿Por qué tomamos solamente tres medidas del período? (Leer las notas de Teoría de errores). Se deben tomar 15-16 longitudes diferentes. L (cm) T1 (s) Tabla 1 T1 T1 (s) (s) Valor medio T1 (s) L1 L2 … … … … … … … … … … … … … L16 3. A partir de los valores registrados en el apartado anterior hacer la representación gráfica de T2 en función de l, con Excel, y obtener la línea y la ecuación de regresión correspondiente. 4. Obtener el valor de g a partir de la pendiente de la línea de regresión de la representación de T2 frente a l. 5. Realizando las medidas que estime oportunas demuestre que el periodo de dos péndulos de idéntica longitud es independiente del valor de la masa que coloquemos en su extremo, explicando el proceso que utiliza para ello. 6. Iniciar ahora la oscilación de uno cualquiera de los péndulos, separando su masa de la vertical diferentes distancias crecientes, por ejemplo: - Separando la masa 1 cm de la vertical. Separando la masa 4 cm de la vertical. Separando la masa 7 cm de la vertical. Separando la masa 10 cm de la vertical. Separando la masa 13 cm de la vertical. Separando la masa 16 cm de la vertical. Separando la masa 19 cm de la vertical. Separando la masa 22 cm de la vertical. Separando la masa 25 cm de la vertical. y medir, en cada caso, el período correspondiente. Indique si se puede sacar alguna conclusión de las medidas realizadas. 5.- VIDEO EXPLICATIVO DE LA PRÁCTICA https://youtu.be/LFIYVu_bdkk