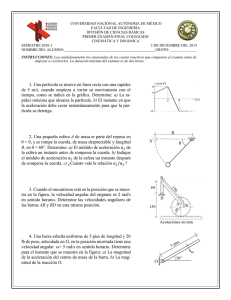
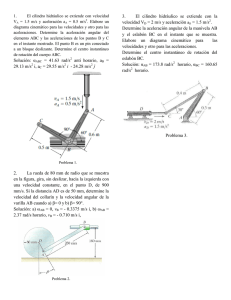
Prof. Dr.-Ing. Jonatan Núñez de la Rosa Departamento de Ingeniería Mecánica [email protected] 2020 Dinámica Taller: Cinemática de Cuerpos Rígidos Problema 1 La unidad de bombeo se compone de la manivela AB, la biela BC, la viga balancín C DE y el tirante F . Si la manivela gira con una velocidad angular de ω = 10 rad s−1 , determine la velocidad angular de la viga balancín y la velocidad del tirante E F G en el instante que se muestra. Problema 2 Si la velocidad angular del eslabón AB es ωAB = 4 rad s−1 en el instante que se muestra, determine la velocidad del bloque corredizo E en este instante. También, identifique el tipo de movimiento de cada uno de los cuatro eslabones. Problema 3 El mecanismo de una mesa de impresión oscilante es propulsado por la manivela AB. Si ésta gira con una velocidad angular de ω = 10 rad s−1 , determine la velocidad del punto C en el instante que se muestra. Problema 4 El sistema de engranes planetarios de una transmisión automática consta de tres engranes planeta A, B y C, montados en un portador D, y acoplados con el engrane sol E y la corona dentada F . Al controlar cuál engrane del sistema planetario gira y cuál recibe la potencia del motor, la transmisión automática puede modificar la velocidad y dirección del automóvil. Si el portador gira con una velocidad angular en sentido contrario al de las manecillas del reloj de ω D = 20 rad s−1 , mientras que la corona dentada lo hace con una velocidad angular en el sentido de las manecillas del reloj de ω F = 10 rad s−1 , determine la velocidad angular de los engranes planeta y el engrane sol. Los radios de los engranes planeta y el engrane sol son de 45 mm y 75 mm, respectivamente. Problema 5 Si la corona dentada D gira en sentido contrario al de las manecillas del reloj con una velocidad angular de ω D = 5 rad s−1 mientras el eslabón AB lo hace en el sentido de las manecillas del reloj con una velocidad angular de ωAB = 10 rad s−1 , determine la velocidad angular del engrane C. Problema 6 Si el bloque corredizo A se mueve a la derecha a vA = 8 ft s−1 , determine la velocidad de los bloques B y C en el instante que se muestra. El elemento C D está conectado por medio de un pasador al elemento ADB. Dinámica Página 1 de 10 Prof. Dr.-Ing. Jonatan Núñez de la Rosa Departamento de Ingeniería Mecánica [email protected] Dinámica Problema 1 Problema 2 Problema 3 Problema 4 Problema 5 Problema 6 Página 2 de 10 Prof. Dr.-Ing. Jonatan Núñez de la Rosa Departamento de Ingeniería Mecánica [email protected] Problema 7 La barra AB tiene el movimiento angular que se muestra. Determine la aceleración del collarín C en este instante. Problema 8 El cilindro hidráulico D se extiende con una velocidad de vB = 4 ft s−1 y una aceleración de aB = 1.5 ft s−2 . Determine la aceleración de A en el instante que se muestra. Problema 9 La manivela AB gira con una velocidad angular de ωAB = 6 rad s−1 y una aceleración angular de αAB = 2 rad s−2 . Determine la aceleración de C y la aceleración angular de BC en el instante que se muestra. Problema 10 El cilindro hidráulico se extiende con la velocidad y aceleración que se indican. Determine la aceleración angular de la manivela AB y el eslabón BC en el instante que se muestra. Problema 11 En un instante dado, el engrane tiene el movimiento angular mostrado. Determine las aceleraciones de los puntos A y B en el eslabón y la aceleración angular de éste en este instante. Problema 12 Determine la aceleración angular del eslabón AB si el eslabón C D tiene la velocidad y desaceleración angulares que se muestran. Dinámica Página 3 de 10 Prof. Dr.-Ing. Jonatan Núñez de la Rosa Departamento de Ingeniería Mecánica [email protected] Dinámica Problema 7 Problema 8 Problema 9 Problema 10 Problema 11 Problema 12 Página 4 de 10 Prof. Dr.-Ing. Jonatan Núñez de la Rosa Departamento de Ingeniería Mecánica [email protected] Problema 13 El engrane A gira en sentido contrario al de las manecillas del reloj con una velocidad angular constante de ωA = 10 rad s−1 , en tanto que el brazo DE lo hace en el sentido de las manecillas del reloj con una velocidad angular de ω DE = 6 rad s−1 y una aceleración α DE = 3 rad s−2 . Determine la aceleración angular del engrane B en el instante que se muestra. Problema 14 Si el extremo A de la barra se mueve con una velocidad constante de vA = 6 m s−1 , determine la velocidad y aceleración angulares de la barra y la aceleración del extremo B en el instante que se muestra. Problema 15 El flotador de punta de ala retráctil se utiliza en un avión habilitado para acuatizar. Determine las aceleraciones angulares αC D , αBD y αAB en el instante que muestra si el gorrón C se desplaza a lo largo del tornillo rotatorio horizontal con una aceleración de aC = 0.5 ft s−2 . En la posición indicada, vC = 0. Además, los puntos A y E están conectados por medio del pasador al ala, y los puntos A y C coinciden en el instante que se muestra. Problema 16 Determine la velocidad y aceleración angulares de la placa C D del mecanismo quebrador de roca en el instante en que AB está horizontal. En este instante θ = 30° y φ = 90°. El eslabón impulsor AB gira con una velocidad angular constante de ωAB = 4 rad s−1 . Problema 17 En el instante que se muestra, la bola B rueda a lo largo de la ranura en el disco con una velocidad de 600 mm s−1 y una aceleración de 150 mm s−2 , ambas medidas con respecto al disco y al alejarse de O. Si en el mismo instante el disco tiene la velocidad y aceleración angulares que se muestran, determine la velocidad y aceleración de la bola en este instante. Problema 18 La bola C se mueve con una velocidad de 3 m s−1 , la cual se incrementa a una razón constante de 1.5 m s−2 , ambas medidas con respecto a la placa circular y dirigidas como se muestra. Al mismo tiempo, la placa gira con la velocidad y aceleración angulares que se indican. Determine la velocidad y aceleración de la bola en este instante. Dinámica Página 5 de 10 Prof. Dr.-Ing. Jonatan Núñez de la Rosa Departamento de Ingeniería Mecánica [email protected] Dinámica Problema 13 Problema 14 Problema 15 Problema 16 Problema 17 Problema 18 Página 6 de 10 Prof. Dr.-Ing. Jonatan Núñez de la Rosa Departamento de Ingeniería Mecánica [email protected] Problema 19 La pluma telescópica de la grúa gira con la velocidad y aceleración angulares que se muestran. Al mismo tiempo, la pluma se extiende con una velocidad constante de 0.5 ft s−1 , medida con respecto a sí misma. Determine las magnitudes de la velocidad y aceleración del punto B en este instante. Problema 20 Cuando θ = 45°, la velocidad angular del eslabón DC es ω DC = 4 rad s−1 y una aceleración angular de α DC = 2 rad s−2 . Determine la velocidad y aceleración angulares de la barra AB en este instante. El collarín en C está conectado a DC por medio de un pasador y se desliza libremente a lo largo de AB. Problema 21 La clavija B fija en la manivela AB se desliza libremente a lo largo de la ranura en el elemento C DE. Si AB gira con el movimiento que se indica, determine la velocidad angular de C DE en el instante que se muestra. Problema 22 En el instante que se muestra la barra AB tiene una velocidad angular ωAB = 4 rad s−1 y una aceleración angular αAB = 2 rad s−2 . Determine la velocidad y aceleración angulares de la barra C D en este instante. El collarín C está conectado a C D por medio de un pasador y se desliza libremente a lo largo de AB. Problema 23 En un instante dado, la barra AB tiene los movimientos angulares que se muestran. Determine la velocidad y aceleración angulares de la barra C D en este instante. Hay un collarín en C. Problema 24 El disco rueda sin deslizarse y en un instante dado su velocidad y aceleración angular es la que se muestra. Determine la velocidad y aceleración angulares del eslabón ranurado BC en este instante. La clavija A está fija al disco. Dinámica Página 7 de 10 Prof. Dr.-Ing. Jonatan Núñez de la Rosa Departamento de Ingeniería Mecánica [email protected] Dinámica Problema 19 Problema 20 Problema 21 Problema 22 Problema 23 Problema 24 Página 8 de 10 Prof. Dr.-Ing. Jonatan Núñez de la Rosa Departamento de Ingeniería Mecánica [email protected] Problema 25 El mecanismo de dos eslabones sirve para amplificar el movimiento angular. El eslabón AB tiene un pasador en B el cual está confinado a moverse en la ranura del eslabón C D. Si en el instante que se muestra, AB (entrada) tiene una velocidad angular de ωAB = 2.5 rad s−1 y una aceleración angular de αAB = 3 rad s−2 , determine la velocidad y aceleración angulares de C D (salida) en este instante. Problema 26 El engrane tiene el movimiento angular que se muestra. Determine la velocidad y aceleración angulares del eslabón ranurado BC en este instante. La clavija A está fija al engrane. Problema 27 La clavija B fija en el engrane se desliza libremente a lo largo de la ranura del eslabón AB. Si el centro O del engrane se mueve con la velocidad y aceleración que se indican, determine la velocidad y aceleración angulares del eslabón en este instante. Problema 28 Un juego mecánico de un parque de diversiones se compone de un brazo rotatorio AB que gira a una aceleración angular constante de αAB = 1 rad s−2 cuando ωAB = 2 rad s−1 en el instante que se muestra. Además, en este instante el carro montado en el extremo del brazo tiene una aceleración angular constante de α0 = −0.6 rad s−2 y una velocidad angular de ω0 = −0.5 rad s−1 , medidas con respecto al brazo. Determine la velocidad y aceleración del pasajero en C en este instante. Problema 29 El mecanismo de «retorno rápido» consta de una manivela AB, un bloque corredizo B y un eslabón ranurado C D. Si la manivela tiene el movimiento angular que se indica, determine el movimiento angular del eslabón ranurado en este instante. Problema 30 El mecanismo de «retorno rápido» consta de la manivela C D y el brazo ranurado AB. Si la manivela gira con la velocidad y aceleración angulares en el instante que se muestra, determine la velocidad y aceleración angulares de AB en este instante. Dinámica Página 9 de 10 Prof. Dr.-Ing. Jonatan Núñez de la Rosa Departamento de Ingeniería Mecánica [email protected] Dinámica Problema 25 Problema 26 Problema 27 Problema 28 Problema 29 Problema 30 Página 10 de 10