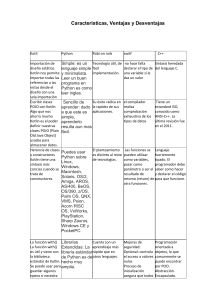
Ejercicios de Python “Todo el mundo en este país debería aprender a programar un ordenador, porque te enseña a pensar”. Steve Jobs. 11/04/16. REGP-Physical-Chemistry Dpt. Programming Python. COMPUTING NUMBERS. Imagina que te llamas Jose Gonźalez Ruiz. Vamos a escribir un encabezado para cada pregunta de la colección de ejercicios Python que debes hacer a partir de tus iniciales: J, G y R. Veamos cómo: print("J*G*R*" * 10) # Esta sentencia multiplica por 10 (o repite 10 veces) todos los caracteres entre comillas: 60 caracteres en total (6*10). Es el marco superior del encabezado. print("Alumno: José González Ruiz. Curso: 4A_ESO") # Ahora imprimes tu nombre y tu curso. print("Trabajo: Python Calculadora-I. Ejercicio: 12.") # Ahora imprimes el título del trabajo (por ejemplo Python Calculadora-I) y el número del ejercicio que vas a resolver (por ejemplo el 5). print("J*G*R*" * 10) # Este es el marco inferior del encabezado. Copia la primera sentencia, porque ambos encabezados son iguales. print() # Imprime una línea en blanco. # Esta es la salida del programa anterior. Es una captura de pantalla de la salida que da Python. Como ves es bastante intuitiva. 0► Escribe tú ahora en Python un encabezado con las iniciales de tu nombre y apellidos como en el ejemplo anterior, pero sin los comentarios que he puesto al lado de cada sentencia y que comienzan por #. Captura la salida y pégala a continuación de la solución en la diapostiva siguiente. Intérprete online de Python: https://www.online-python.com/ REGP-Physical-Chemistry Dpt. Programming Python. Computing Numbers Solución ejerc_ 0: Intérprete online de Python: https://www.online-python.com/ REGP-Physical-Chemistry Dpt. Programming Python. Computing Numbers A partir de ahora empezamos los ejercicios. No olvides escribir el encabezado que has aprendido a hacer en todos y cada uno de los ejercicios que vienen. 1► Escribe las siguientes expresiones matemáticas en el intérprete Python, una línea para cada expresión. Luego corre el código, captura el código , luego captura la salida y pégalas donde se solicita en la solución del ejercicio. Ten en cuenta la prioridad de operaciones que debes conocer de Matemáticas (el primer caso ya está traducido): a) 2 + [3 · (6/2) ] = 2 + (3 * (6/2)) b) (-3)2 d) (4.0)½ + 1 / 2 e) (4/2)5 g) 1.0 / 2.0 / 4 h) 10 / 5·10-3 j) 41/2 k) 10 / 5·10-3 + 1 Solución ejerc_ 1: Captura la pantalla con tu código. REGP-Physical-Chemistry Dpt. Programming Python. c) 6.023 · 1023 ·1.05 f) -32 i) (4/2)5+2 l) 1·10-12 * 5.93·1038 / (1.5·108)2 Computing Numbers Solución ejerc_ 1: ón ejerc_ 1: Captura la pantalla con la salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. Computing Numbers 2► ¿Con qué operador Python averiguas si las siguientes parejas de números son múltiplos y divisores uno de otro? Compruebalo en estos casos: 88700 y 25 88700 y 50 3e10 y 25 Sol_ ejerc_ 2: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. 5348 y 5 Computing Numbers 3► División por 0: ¿Qué sucede si escribimos en el intérprete Python las siguientes operaciones? 12 / 0 34.5 / 0 0/0 Sol_ ejerc_ 3: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. Computing Numbers 4► ¿Según las reglas de potencias de Matemáticas, ¿Cuánto es 00? ¿Qué sucede si escribes esa expresión en Python, cuál es la salida que obtienes? 0** 0 Sol_ ejerc_ 4: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. Computing Numbers 5► En un triángulo rectángulo, un cateto a mide 12 cm y el otro b mide 5 cm. Calcula lo que mide la hipotenusa usando el intérprete Python. Recuerda el Teormea de Pitágoras. a2 + b2 = h2 Sol_ ejerc_ 5: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. Computing Numbers 6► Compré 4 botellas a € 100 cada una y 7 botellas a € 60 cada una. Resuelve con Python: a) ¿Cuántas botellas compré en total? b) ¿Cuánto dinero gasté en total? c) Por término medio, ¿Cuál fue el costo por botella? Sol_ ejerc_ 6: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. Computing Numbers 7► Python diferencia entre mayúsculas y minúsculas. Compruébalo intentando obtener el valor absoluto de -1: abs(-1) Abs(-1) # Ahora obtendrás un mensaje de error. Sol_ ejerc_ 6: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. Computing Numbers 8► Como vimos en clase al hacer potencias, Python trabaja con números enteros de tamaño ilimitado, pero el tamaño de los números float (reales) sí que es limitado, no puede ser tan grande como queramos. Comprobemos: a) Calcula 123.0**456. Escribe el mensaje que devuelve Python. b) Calcula 12**20 (resultado entero porque 12 es entero) y 12.0**20 (resultado float, porque 12.0 es float). Observa las diferencias: print( 12**20) # El entero que obtienes es muy largo (puede ser tan largo como sea necesario). print(12.0**20) # El resultado ahora no es entero. Python “sólo” da unos dígitos y luego una potencia de 10. ¿Cuántos dígitos devuelve Python en el caso de 12**20? ¿Y en el caso de 12.0**20? ¿Cuál es más preciso? c) Calcula ahora 1 / (12**34), ¿Cuántos dígitos devuelve Python? REGP-Physical-Chemistry Dpt. Programming Python. Computing Numbers Sol_ ejerc_ 8: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. VARIABLES in PYTHON. Una variable no es más que el nombre que le damos a una posición de memoria (RAM) donde metemos datos que necesita el programa para correr. El Identificador o nombre que se le puede dar a una variable en Python sólo puede estar formado por letras (mayúsculas o minúsculas sin acento), por dígitos del 1-10 y por el carácter subrayado _. El nombre puede empezar con cualquier carácter permitido de los anteriores, excepto con un número. 1► En este ejercicio y en el siguiente no es necesario el encabezado personal hecho en Python. ¿Son válidos los siguientes nombres de variables? Si no lo son di la razón al lado (un ejemplo ya está hecho). Variable 12horas: Incorrecto; Indice? empieza con un dígito. hora12 from “var” a(b) 21 REGP-Physical-Chemistry Dpt. Programming Python. Variables in Python. área x__x Dos palabras guion-- desviación año import_from una-variable Uno,dos αyΣyΣ x____ ___x___ REGP-Physical-Chemistry Dpt. Programming Python. Variables in Python. 2► Explica a la derecha de cada línea qué hace cada una de las sentencias siguientes y cuál es el valor de x en ese momento (un ejemplo ya está hecho): Qué hace la instrucción: x= 1 # x= x * 10 # El valor anterior que tenía x (1) lo multiplica * 10, y el nuevo valor (10) lo pone de nuevo en x. print(x) # x = x +4 # x = x // x # x = x ** 10 # x = 2*x **2 # x = 2*x **2 # x=x%4 # x=x+1 # REGP-Physical-Chemistry Dpt. Programming Python. Valor actual de x: x= 10 Variables in Python. 3► Utiliza Python para averguar el valor del polinomio P(x)= x4 + x3 + 2x2 – x cuando x= 1, cuando x= 1.1 y cuando x= 1.2. Sugerencia: Asigna a la variable x el valor 1 y luego haz las operaciones indicadas en el polinomio (potencias, sumas, restas). Te muestro el código para x=1; añade tú a este código el código para cuando x= 1.1 y x= 1.2: x= 1 print("El valor de P(x) para x= 1 es:", x**4 + x**3 + 2*x**2 – x ) Sol_ ejerc_ 3: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. Variables in Python. 4► Sea ahora el polinomio P(x)= x4 + x3 + 0.5x2 – x. Hagamos una “tabla” para x= -5, -4, -3, 2, -1, 0, 1, 2, 3, 4, 5. Como ves, es muy fácil hacer una tabla de valores de un P(x) para diferentes valores de x: Sólo hay que cambiar el valor de la variable x y evaluar el P(x) de nuevo con la sentencia print(). Sol_ ejerc_ 4: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. FUNCTIONS in PYTHON. Python incorpora una serie de funciones matemáticas de uso inmediato (built-in functions). Algunas explicadas en clase son round(), int(), float(), abs()…. 1► Pide ayuda a Python: Dile que te diga lo que hace la función abs() por medio de la función help(). Así: help(abs) Haz lo mismo para la función round(). Lee la información que te devuelve Python y contesta: ¿Qué sucede con el resultado que muestra round() si “ndigits” no aparece dentro de ella? Sol_ ejerc_ 1: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. Functions in Python. 2► Utiliza la función round() para redondear los siguientes números: a) 5**(1/2) a 3 dígitos decimales; b) (15 / 7) a 3 dígitos decimales; c) 5**(1/3) a 7 dígitos decimales; d) (15 / 7) a 7 dígitos decimales; pi= 3.1415926536 # Como ves, esta sentencia asigna a pi un valor con 10 decimales. Ahora redondea pi a 4 dígitos pi a 6 dígitos. pi a 9 dígitos. Sol_ ejerc_ 2: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. Functions in Python. 3► Utiliza la función abs() para hallar el valor absoluto de los siguientes números: > 2.15; > (15 / 7); > -2.15 > -2.99999999 Sol_ ejerc_ 3: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. Functions in Python. 4► Utiliza la función int() para convertir en entero los siguientes números float (reales): a) 2.15; c) (15 / 7); e) pi= 3.141592653589793 b) -2.9 d) -2.99999999 f) - pi 5► Ahora utiliza la función float() para convertir en float (real) los siguientes números enteros: a) (15 // 7); c) 3.2e3 b) 15 % 2 d) -14 Sol_ ejerc_ 4-5: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. Functions in Python. 6► Por medio de la función type() puedes saber de qué tipo es un número o, en general, un dato. Copia este código, observa los resultados y pega la pantalla de la salida de resultados. print( type(12)) print( type(12.3) ) print( type(round(12.3)) ) print( type(98//76) ) # Primero se hace la división //, luego Python averigua el tipo (type) y, por último, saca el tipo por pantalla (print). print( type("12") ) # Cuidado! Ahora 12 entre comillas no es un número, es un string como “hola”. print( type("Hola!") ) Sol_ ejerc_ 6: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. Functions in Python. Python también incorpora una serie de funciones matemáticas no disponibles directamente, sino “almacenadas” en un depósito o módulo llamado math. Para poder utilizar estas funciones almacenadas en math, es necesario importarlas. Esto se puede hacer de dos formas: · Podemos importar el módulo math entero, como hemos hecho en clase: import math O bien: from math import * Ahora ya podemos usar todas las funciones y constantes de math: sin(x), cos(x), tan(x), sqrt(x), log(x), pi, e, ... REGP-Physical-Chemistry Dpt. Programming Python. · O bien, podemos importar sólo aquellas funciones y/o constantes que necesitemos en un momento dado: from math import sin, sqrt, pi Ahora ya podemos usar sólo las funciones y constantes que hemos importado: sin(x), sqrt(x) y pi. Nada más ! Functions in Python. 1► Importa el módulo math de cualquiera de las formas vistas antes; luego evalúa las siguientes expresiones en el intérprete Python: a) print( round( (1+ sqrt(5) ) / 2 , 2) ) c) print( round( 2.21123*log(1e3), 3) ) b) print( abs( log(0.1,10) * 25**.5 ) ) d) print( sqrt( 2**log(pi / 3) ) ) Sol_ ejerc_ 6: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. Functions in Python. 2► Por medio de la función sqrt(), calcula la raíz cuadrada de esta lista de números [2, 4, 10, 100, 200, 500, 1000, 2000, 8000, 20000]. Compara estos resultados con los obtenidos haciendo el cálculo por medio de la potencia inversa. Aquí tienes el código: # Calcula la raíz cuadrada de algunos números usando la potencia inversa (1/2): for num in [2, 4, 10, 100, 200, 500, 1000, 2000, 8000, 20000]: print("La raíz de", num, "=", num**(1/2) ) # Calcula la raíz cuadrada de algunos números usando la función sqrt(): for num in [2, 4, 10, 100, 200, 500, 1000, 2000, 8000, 20000]: print("La raíz de", num, "=", sqrt(num) ) ¿Qué método prefieres o cuál te resulta más cómodo para hallar la raíz de 3: Usar la función sqrt(3) o usar la potencia inversa 3 ** (1/2)? ¿Por qué? REGP-Physical-Chemistry Dpt. Programming Python. Functions in Python. Sol_ ejerc_ 2: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. Functions in Python. 3► Por grande que sea un entero N, se puede saber el número de dígitos k que lo forman por medio de la fórmula (escrita en Python): k = 1+ int( log(N,10) ). Como ves, en esta fórmula intervienen la función int() y la función log(). Escribe el código Python necesario para saber cuántos dígitos forman estos números (el primer ejemplo ya está hecho): a) 1000. El código sería: k= 1+int(log(N,10) print(k) # Cuando se ejecuta este código Python devuelve que k= 4, lo cual es correcto. Escribe y ejecuta tú el código para los siguientes números: b) 1e20 c) 2**50 d) 20**200 Sol_ ejerc_ 3: Captura la pantalla con tu código y con la de salida de resultados. REGP-Physical-Chemistry Dpt. Programming Python. REGP-Physical-Chemistry Dpt. Programming Python.