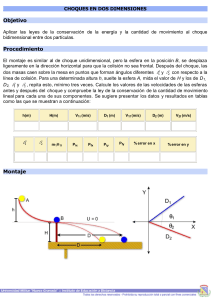
Dinámica de partículas Métodos de energía y momentum 3.2. Método de Energía y Momentum. 3.2.1. Introducción. 3.2.2. Trabajo de una fuerza. 3.2.3. Energía cinética – Principio de trabajo y energía. 3.2.4. Aplicaciones del principio de trabajo y energía. 3.2.5. Potencia y energía. 3.2.6. Energía potencial. 3.2.7. Fuerzas conservativas. 3.2.8. Conservación de la energía. 3.2. Método de Energía y Momentum. 3.2.9. Movimiento debido a una fuerza central conservativa. 3.2.10. Principio de impulso y momentum. 3.2.11. Movimiento de impulsión. 3.2.12. Choque. 3.2.13. Choque central directo. 3.2.14. Choque oblicuo. Trabajo de una fuerza Trabajo de una fuerza constante en movimiento rectilíneo Trabajo de un peso Trabajo de la fuerza ejercida por un resorte Energía cinética de una partícula. Principio de trabajo y energía Potencia y eficiencia Energía Potencial Consideremos ahora un cuerpo unido a un resorte: Fuerzas conservativas Conservación de la energía Cuando una partícula se mueve debido a la acción de fuerzas conservativas, “la suma de la energía cinética y de la energía potencial de la partícula permanece constante”. La suma T+V se llama “energía mecánica total” de la partícula y se simboliza por E. Principio de Impulso y momentum Movimiento de impulsión Choque Choque central directo La relación entre las magnitudes de los impulsos correspondientes, respectivamente, al periodo de restitución y al de deformación se llama coeficiente de restitución y se representa por e Como v´B-v´A representa la velocidad relativa de las dos partíclas después del choque y vA-vB su velocidad relativa antes del choque, la ecuación expresa que la velocidad relativa de las dos partículas después del choque puede obtenerse multiplicando su velocidad relativa antes del choque por el coeficiente de restitución e=0 , choque perfectamente inelástico e=1 , choque perfectamente elástico Es importante observar que en el caso de un choque perfectamente elástico la energía total de las dos partículas como también su momentum total se conservan. Choque central oblicuo 1. Se conserva la componente y del momentum de la partícula A 2. Se conserva la componente y del momentum de la partícula B 3. se conserva la componente x del momentum total de las partículas 4. Se obtiene la componente x de la velocidad relativa de las dos partículas después del choque, multiplicando la componente x de la velocidad relativa antes del choque por el coeficiente de restitución