362014

3/6/2014
1010
A
2020
3030
C
B
4040
D
E
F
6060
5050
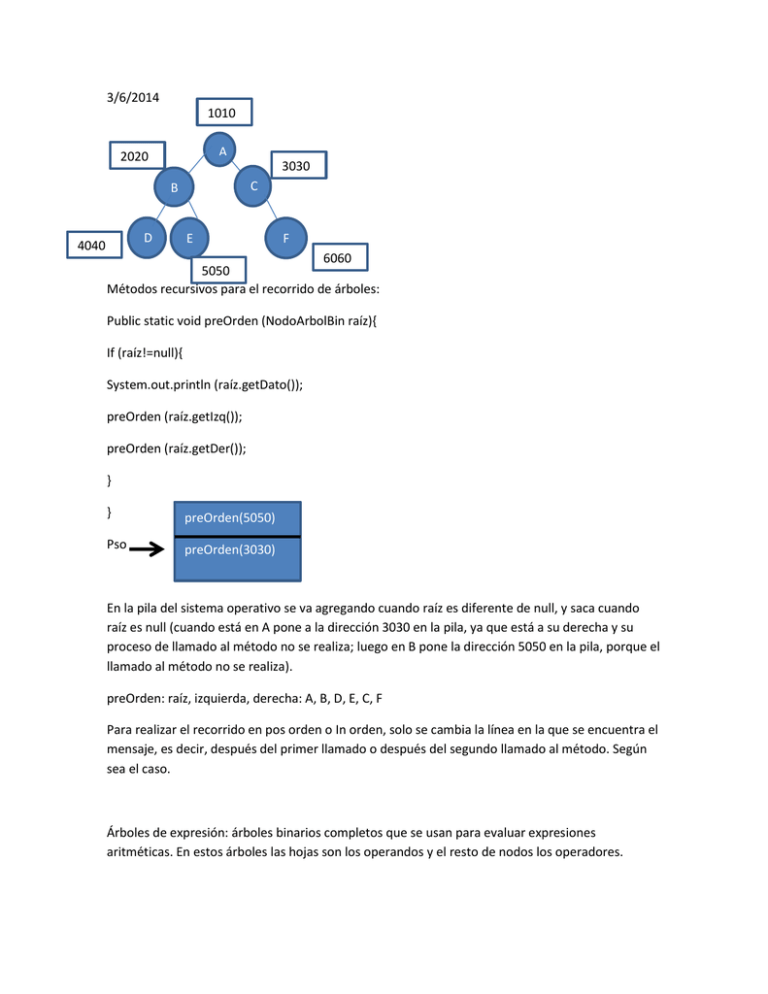
Métodos recursivos para el recorrido de árboles:
Public static void preOrden (NodoArbolBin raíz){
If (raíz!=null){
System.out.println (raíz.getDato());
preOrden (raíz.getIzq());
preOrden (raíz.getDer());
}
}
preOrden(5050)
Pso
preOrden(3030)
En la pila del sistema operativo se va agregando cuando raíz es diferente de null, y saca cuando
raíz es null (cuando está en A pone a la dirección 3030 en la pila, ya que está a su derecha y su
proceso de llamado al método no se realiza; luego en B pone la dirección 5050 en la pila, porque el
llamado al método no se realiza).
preOrden: raíz, izquierda, derecha: A, B, D, E, C, F
Para realizar el recorrido en pos orden o In orden, solo se cambia la línea en la que se encuentra el
mensaje, es decir, después del primer llamado o después del segundo llamado al método. Según
sea el caso.
Árboles de expresión: árboles binarios completos que se usan para evaluar expresiones
aritméticas. En estos árboles las hojas son los operandos y el resto de nodos los operadores.
Expresión aritmética: 1+2*3
a+b*c
Convirtiendo la expresión a posfija: 123*+
Luego se guardan los operandos en una pila:
Se toma el primer operador que se dejó fuera de la pila (*) y se convierte en el nodo padre de los
dos primeros datos que se sacan de la pila; y se van ordenando en el árbol (el primero a la
izquierda y el segundo a la izquierda).
*
b
c
Ahora se guarda el árbol en la pila:
*
p
c
b
a
Siguiendo el proceso para sacar de la pila obtenemos el siguiente árbol que también se guarda en
la pila.
+
p
*
a
b
c
Entonces, para obtener el árbol, basta con decir: a=p.quitar ();
a
+
*
c
b
a
Árboles binarios de búsqueda ABB
v
10 5 24 3 12 33
l
10
a
5
24
3
12
33
10
5
3
24
12
33
En un vector, se agregan los datos tal y como son recibidos; en una lista enlazada, se agregan de
igual manera que en el vector; en cambio, en un árbol ABB se agregan los datos a la izquierda o a
la derecha dependiendo de la comparación con el nodo raíz. Vemos que se agregan los mayores a
la derecha y los menores a la izquierda.
La eficiencia en el proceso de búsqueda está en el menor número de comparaciones hechas.
Entre más grande es el árbol mayor es la eficiencia; si el árbol está lleno y balanceado su eficiencia
aumenta en un 50%, ya que descarta la mitad de los datos.
In orden: 3, 5, 10, 12, 24, 33
4/6/2014
Continuando con los árboles binarios de búsqueda…
-
Permiten el ordenamiento y la eficiencia en el proceso de búsqueda. Mucho mejor que las
estructuras antes vistas.
La salida debe ser ordenada.
1) Inserción
Operaciones
2) Eliminación
1) Para todos los nodos las claves (o datos) en lo posible son únicos, en el subárbol izquierdo
deben ser menores y las del subárbol derecho deben ser mayores. La inserción se hace en
la misma forma en que se consiguen las claves.
Ejemplo: Se quieren insertar en un ABB Los siguientes datos: 7- 3- 10- 5- 2Se hace de la siguiente
manera:
Como la clave 7 es la primera que llega se coloca de inmediato como raíz, y a medida que lleguen
las siguientes se acomodarán teniendo a 7 como referencia.
7
3
5
2
1
10
9
4
3 es menor que 7, así que se acomoda a la izquierda de 7; 10 es mayor que 7, así que se coloca de
su lado derecho; al llegar 9 vemos que es mayor que 7, pero es menor que 10. Así que se coloca en
el subárbol derecho por ser mayor, pero del lado izquierdo de 10 por ser menor a este último; al
llegar 2 sucede algo parecido a lo que sucede con 9, solo que esta vez 2 por ser menor que 7 se
coloca en el subárbol derecho, pero a la izquierda de 3 por ser menor que este último nodo.
2) Hay tres casos para eliminar: 1- Una hoja; 2- Nodo con un subárbol; 3- Nodo con dos
subárboles.
El procedimiento a seguir es el siguiente:
2.1) Solo se suprime.
2.2) Es reemplazado por el descendiente inmediato.
2.3) Es reemplazado por su descendiente más a la izquierda del subárbol derecho, o por el
descendiente más a la derecha del subárbol izquierdo (casi siempre es reemplazado por una hoja).
Ejemplo: Eliminar 7, 4, 1, 10
Vemos que para 7 hay dos posibles candidatos que son 5 y 9, ya que 5 es su descendiente más a la
derecha en el subárbol izquierdo. Y 9 es su descendiente más a la izquierda en el subárbol
derecho.
7
3
10
5
2
9
4
1
Lo remplazamos por 5, así que 4 toma su lugar.
5
3
10
4
2
9
1
Al eliminar 4 se elimina directamente porque es una hoja.
5
3
2
1
10
9
Eliminamos el 1 (también es una hoja):
5
3
10
2
9
Eliminamos el 10 (Es un nodo con un subárbol, así que se reemplaza por el más inmediato):
5
3
9
2
Y así queda nuestro árbol al eliminar los nodos 7, 4, 1 y 10.
Como vemos en el ejemplo anterior, un árbol binario se degenera y pierde su eficiencia. Para
evitar esta tendencia degenerativa, se aplica el criterio de árboles AVL (ideado por los
matemáticos rusos Adelson- Velskii y Landis).
Árboles AVL
Características:
-
Siguen siendo árboles binarios.
Son árboles ABB mejorados, ya que proveen un algoritmo de auto balanceo que evita la
tendencia degenerativa en las operaciones de inserción y eliminación.
Criterios de balanceo por altura
Factor de equilibrio: FE= hsd-hsi.
hsd: Altura del subárbol derecho.
hsi: Altura del subárbol izquierdo.
Para todos los nodos:
Si (FE >-2 y FE <2)
Árbol balanceado.
Sino
Árbol no balanceado.
Fin Si
Casos de rotación (para balancearlo)
Operaciones en AVL
Inserción: Inicialmente es el mismo proceso ABB (menores a la izquierda y mayores a la derecha).
Adicionalmente, se calcula en cada inserción el FE iniciando en la hoja insertada, siguiendo la
rama, hasta llegar a la raíz.
Se pueden presentar los siguientes casos:
1. Llegar a la raíz
2. El FE=0 en algún nodo diferente a la hoja.
3. El FE muestra que hay desbalance; en este caso se reestructura el árbol en un proceso
llamado rotación, que puede ser de los siguientes tipos:
II Izquierda- Izquierda
El nodo insertado se va a la izquierda de dos nodos a la vez.
Insertar: C, B, A
FE= -2
FE= -1
FE= 0
-
C
B
A
Se calcula el FE en la rama correspondiente.
Entonces: Se baja C para para que B quede como raíz.
B
FE= 0
A
FE= 0
C
FE= 0
DD Derecha- Derecha
El nodo insertado se va a la derecha de dos nodos a la vez.
Insertar: A, B, C
-
Se calcula el FE en la rama correspondiente.
Se mueve A hacia abajo para que B quede como raíz.
FE= 2
A
B
FE= 0
B
FE= 1
FE= 0
C
C
A
FE= 0
FE= 0
ID Izquierda- Derecha
El Nodo insertado se va a la izquierda de un Nodo y luego a la derecha del otro.
Insertar: C, A, B
-
Se calcula el FE en la rama correspondiente.
Se mueve C hacia la abajo a la derecha y A hacia abajo a la izquierda para que B quede
como raíz.
FE= -2
A
C
FE= 0
B
FE= 1
FE= 0
B
A
C
FE= 0
FE= 0
DI Derecha- Izquierda
El Nodo insertado se va a la derecha de un Nodo y luego a la izquierda del otro.
Insertar: A, C, B
-
Se calcula el FE en la rama correspondiente.
Se mueve A hacia abajo a la izquierda, y C hacia Abajo a la derecha para dejar a B como
raíz.
FE= 2
A
FE= -1
C
FE= 0
FE= 0
FE= 0
A
B
C
FE= 0
B
Reglas para borrar
Al eliminar se aplica la misma regla ABB, se calcula el FE en la rama donde se elimina el nodo. Si
hay desbalance se aplica la rotación correspondiente.