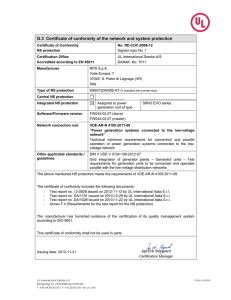
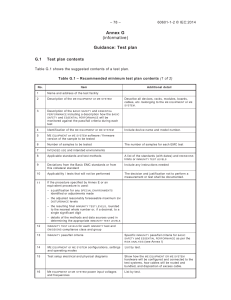
Eurocodes Worked Examples: Structural Design (EN 1990/EN 1991)
Anuncio

Worked Examples IN ACCORDANCE WITH European Standards CEN/TC 250 Structural Eurocodes (EN 1990/EN 1991) Es EUROCODES SPREADSHEETS Structural Design Carlo Sigmund First Edition Ebook Copyright© 2014 http://eurocodespreadsheets.jimdo.com/eurocodes-spreadsheets/ All rights reserved. No part of this work may be reproduced, stored in a retrieval system, or transmitted by any means, electronic, mechanical, photocopying, recording, or otherwise, without prior written permission from the publisher. -----------------------------------------------First Edition: April 2014 Author/Publisher: Sigmund, Carlo <1971-> ISBN n.: 978-1-291-84215-9 ID contenuto: 14612241 Ebook: Worked Examples in accordance with European Standards CEN/TC 250: Structural Eurocodes (EN 1990/EN 1991) -------------------------------The sponsoring editor for this document and the production supervisor was Carlo Sigmund. Electronic mail: [email protected] Although care has been taken to ensure, to the best of our knowledge, that all data and information contained herein are accurate to the extent that they relate to either matters of fact or accepted practice or matters of opinion at the time of publication, The EUROCODES Spreadsheets Structural Design, the author and the reviewers assume no responsibility for any errors in or misinterpretations of such data and/or information or any loss or damage arising from or related to their use. ________________________________________________________ Cover Art from: http://en.wikipedia.org/wiki/File:Beijing_national_stadium.jpg This image was selected as picture of the day on Wikimedia Commons for 3 August 2013. Date: 13 July 2011 - Author: Peter23 This file is licensed under the Creative Commons Attribution 2.5 Generic license The reproduction of this artistic, architectural, or applied artwork, is covered under the Copyright Law of the People's Republic of China Beijing national stadium; Architect: Herzog & de Meuron, ArupSport, China Architectural Design & Research Group ________________________________________________________ Contents Eurocode 0 - EN1990 ......................................................................................... 17 1.1 Foreword .................................................................................................................................................. 17 1.2 National Standards implementing Eurocodes .......................................................................................... 17 1.3 National annex for EN 1990 ..................................................................................................................... 18 1.4 Verification tests....................................................................................................................................... 18 1.5 References [Section 1]............................................................................................................................. 32 Eurocode 1 - EN1991-1-1................................................................................... 33 2.1 Foreword .................................................................................................................................................. 33 2.2 National annex for EN 1991-1-1............................................................................................................... 33 2.3 Distinction between Principles and Application Rules.............................................................................. 33 2.4 Classification of actions............................................................................................................................ 34 2.5 Representation of actions ........................................................................................................................ 35 2.6 Rapresentative values.............................................................................................................................. 36 2.7 Ultimate limit state.................................................................................................................................... 36 2.8 Verification tests....................................................................................................................................... 36 2.9 References [Section 2]............................................................................................................................. 44 Eurocode 1 EN 1991-1-2......................................................................................................... 45 3.1 General .................................................................................................................................................... 45 3.2 Terms relating to thermal actions............................................................................................................. 45 EN 1990, EN 1991 - Eurocodes 0-1 - Worked Examples CONTENTS - page iv 3.3 Structural Fire design procedure ..............................................................................................................47 3.4 Design fire scenario, design fire ...............................................................................................................47 3.5 Temperature Analysis...............................................................................................................................47 3.6 Thermal actions for temperature analysis (Section 3) ..............................................................................48 3.7 Nominal temperature-time curves ............................................................................................................49 3.8 Verification tests .......................................................................................................................................50 3.9 References [Section 3] .............................................................................................................................58 Eurocode 1 EN 1991-1-2 Annex B...............................................................................................................59 4.1 Thermal actions for external members - Simplified calculation method ...................................................59 4.2 Verification tests .......................................................................................................................................65 4.3 References [Section 4] .............................................................................................................................73 Eurocode 1 EN 1991-1-2 Annex C, Annex E ..............................................................................................75 5.1 ANNEX C: Localised fires.........................................................................................................................75 5.2 ANNEX E: fire load densities ....................................................................................................................78 5.3 Verification tests .......................................................................................................................................81 5.4 References [Section 5] .............................................................................................................................87 Eurocode 1 EN 1991-1-2 Annex F, Annex G, Sec. B.5 Annex B................................................................................................89 6.1 ANNEX F: Equivalent time of fire exposure..............................................................................................89 6.2 ANNEX G: configuration factor .................................................................................................................91 6.3 ANNEX B, Section B.5: Overall configuration factors...............................................................................93 EN 1990, EN 1991 - Eurocodes 0-1 - Worked Examples CONTENTS - page v 6.4 Verification tests .......................................................................................................................................93 6.5 Reference [Section 6] ...............................................................................................................................100 Eurocode 1 EN 1991-1-3 .........................................................................................................101 7.1 General .....................................................................................................................................................101 7.2 Classification of actions ............................................................................................................................101 7.3 Design situations ......................................................................................................................................102 7.4 Characteristic values ................................................................................................................................103 7.5 Other representative values .....................................................................................................................103 7.6 Treatment of exceptional snow loads on the ground ................................................................................104 7.7 Snow load on roofs ...................................................................................................................................104 7.8 Roof shape coefficients ............................................................................................................................106 7.9 Local effects .............................................................................................................................................110 7.10 Verification tests .......................................................................................................................................113 7.11 References [Section 7] .............................................................................................................................122 Eurocode 1 EN 1991-1-3: Annex A, Annex B ..............................................................................................123 8.1 Design situations and load arrangements to be used for different locations ............................................123 8.2 Annex B: Snow load shape coefficients for exceptional snow drifts .........................................................124 8.3 Verification tests .......................................................................................................................................128 8.4 References [Section 8] .............................................................................................................................132 Eurocode 1 EN 1991-1-3: Annex C, Annex D ..............................................................................................133 9.1 Annex C: European Ground Snow Load Maps ........................................................................................133 9.2 Annex D: Adjustment of the ground snow load according to return period...............................................134 EN 1990, EN 1991 - Eurocodes 0-1 - Worked Examples CONTENTS - page vi 9.3 Verification tests .......................................................................................................................................135 9.4 References [Section 9] .............................................................................................................................138 Eurocode 1 EN 1991-1-4 [Section 4]......................................................................................141 10.1 General .....................................................................................................................................................141 10.2 Definitions .................................................................................................................................................142 10.3 Design situations ......................................................................................................................................142 10.4 Modelling of wind actions .........................................................................................................................143 10.5 Wind velocity and velocity pressure .........................................................................................................143 10.6 Verification tests .......................................................................................................................................147 10.7 References [Section 10] ...........................................................................................................................152 Eurocode 1 EN 1991-1-4 Section 7 (Page 32 to 37) ...................................................................................153 11.1 Pressure and force coefficients - General ................................................................................................153 11.2 Asymmetric and counteracting pressures and forces...............................................................................154 11.3 Pressure coefficients for buildings ............................................................................................................155 11.4 Vertical walls of rectangular plan buildings...............................................................................................155 11.5 Verification tests .......................................................................................................................................157 11.6 References [Section 11] ...........................................................................................................................160 Eurocode 1 EN 1991-1-4 Section 7 (Page 37 to 39) ...................................................................................161 12.1 Pressure and force coefficients - Flat roofs ..............................................................................................161 12.2 Verification tests .......................................................................................................................................162 12.3 References [Section 12] ...........................................................................................................................164 EN 1990, EN 1991 - Eurocodes 0-1 - Worked Examples CONTENTS - page vii Eurocode 1 EN 1991-1-4 Section 7 (Page 40 to 42) ...................................................................................165 13.1 Pressure and force coefficients - Monopitch roofs ...................................................................................165 13.2 Verification tests .......................................................................................................................................167 13.3 References [Section 13] ...........................................................................................................................170 Eurocode 1 EN 1991-1-4 Section 7 (Page 43 to 46) ...................................................................................171 14.1 Duopitch roofs ..........................................................................................................................................171 14.2 Verification tests .......................................................................................................................................174 14.3 References [Section 14] ...........................................................................................................................177 Eurocode 1 EN 1991-1-4 Section 7 (Page 47 to 48) ...................................................................................179 15.1 Hipped roofs .............................................................................................................................................179 15.2 Verification tests .......................................................................................................................................181 15.3 References [Section 15] ...........................................................................................................................186 Eurocode 1 EN 1991-1-4 Section 7 (Page 48 to 49) ...................................................................................187 16.1 Multispan roofs .........................................................................................................................................187 16.2 Verification tests .......................................................................................................................................188 16.3 References [Section 16] ...........................................................................................................................193 EN 1990, EN 1991 - Eurocodes 0-1 - Worked Examples CONTENTS - page viii Eurocode 1 EN 1991-1-4 Section 7 (Page 50 to 51) ...................................................................................195 17.1 Vaulted roofs and domes..........................................................................................................................195 17.2 Verification tests .......................................................................................................................................196 17.3 References [Section 17] ...........................................................................................................................198 Eurocode 1 EN 1991-1-4 Section 7 (Page 51 to 53) ...................................................................................199 18.1 Internal pressure.......................................................................................................................................199 18.2 Verification tests .......................................................................................................................................201 18.3 References [Section 18] ...........................................................................................................................205 Eurocode 1 EN 1991-1-4 Section 7 (Page 53 to 60) ...................................................................................207 19.1 Pressure on walls or roofs with more than one skin .................................................................................207 19.2 Canopy roofs ............................................................................................................................................208 19.3 Verification tests .......................................................................................................................................210 19.4 References [Section 19] ...........................................................................................................................214 Eurocode 1 EN 1991-1-4 Section 7 (Page 61 to 65) ...................................................................................215 20.1 Free-standing walls, parapets, fences and signboards ............................................................................215 20.2 Shelter factors for walls and fences..........................................................................................................216 20.3 Signboards ...............................................................................................................................................217 20.4 Friction coefficients ...................................................................................................................................218 EN 1990, EN 1991 - Eurocodes 0-1 - Worked Examples CONTENTS - page ix 20.5 Verification tests .......................................................................................................................................219 20.6 References [Section 20] ...........................................................................................................................224 Eurocode 1 EN 1991-1-4 Section 7 (Page 65 to 69) ...................................................................................225 21.1 Structural elements with rectangular sections ..........................................................................................225 21.2 Structural elements with sharp edged section ..........................................................................................227 21.3 Structural elements with regular polygonal section ..................................................................................228 21.4 Verification tests .......................................................................................................................................229 21.5 References [Section 21] ...........................................................................................................................232 Eurocode 1 EN 1991-1-4 Section 7 (Page 69 to 73) ...................................................................................233 22.1 Circular cylinders: external pressure coefficients .....................................................................................233 22.2 Circular cylinders: force coefficients .........................................................................................................235 22.3 Verification tests .......................................................................................................................................237 22.4 References [Section 22] ...........................................................................................................................239 Eurocode 1 EN 1991-1-4 Section 7 (Page 74 to 75) ...................................................................................241 23.1 Circular cylinders: force coefficients for vertical cylinders in a row arrangement .....................................241 23.2 Spheres ....................................................................................................................................................242 23.3 Verification tests .......................................................................................................................................244 23.4 References [Section 23] ...........................................................................................................................246 Eurocode 1 EN 1991-1-4 EN 1990, EN 1991 - Eurocodes 0-1 - Worked Examples CONTENTS - page x Section 7 (Page 76 to 78) ...................................................................................247 24.1 Lattice structures and scaffoldings ...........................................................................................................247 24.2 Verification tests .......................................................................................................................................250 24.3 References [Section 24] ...........................................................................................................................254 Eurocode 1 EN 1991-1-4 Section 7 (Page 78 to 81) ...................................................................................255 25.1 Flags .........................................................................................................................................................255 25.2 Effective slenderness and end-effect factor l............................................................................................................ 256 25.3 Verification tests .......................................................................................................................................258 25.4 References [Section 25] ...........................................................................................................................260 Eurocode 1 EN 1991-1-4 Section 8 (Page 82 to 90) ...................................................................................261 26.1 Wind actions on bridges ...........................................................................................................................261 26.1.1 General..........................................................................................................................................261 26.1.2 Choice of the response calculation procedure ..............................................................................263 26.2 Force coefficients .....................................................................................................................................263 26.2.1 Force coefficients in x-direction (general method) ........................................................................263 26.2.2 Force in x-direction. Simplified Method .........................................................................................265 26.2.3 Wind forces on bridge decks in z-direction....................................................................................266 26.2.4 Wind forces on bridge decks in y-direction....................................................................................267 26.3 Verification tests .......................................................................................................................................267 26.4 References [Section 26] ...........................................................................................................................272 Eurocode 1 EN 1991-1-4 Annex A...............................................................................................................273 EN 1990, EN 1991 - Eurocodes 0-1 - Worked Examples CONTENTS - page xi 27.1 Terrain categories.....................................................................................................................................273 27.2 Transition between roughness categories 0, I, II, III and IV .....................................................................273 27.3 Numerical calculation of orography coefficients .......................................................................................274 27.4 Neighbouring structures ...........................................................................................................................277 27.5 Displacement height .................................................................................................................................278 27.6 Verification tests .......................................................................................................................................279 27.7 References [Section 27] ...........................................................................................................................287 EN 1991-1-4 Annex B...............................................................................................................289 28.1 Procedure 1 for determining the structural factor cscd ................................................................................................. 289 28.2 Number of loads for dynamic response ....................................................................................................292 28.3 Service displacement and accelerations for serviceability assessments of a vertical structure ...............292 28.4 Verification tests .......................................................................................................................................293 28.5 References [Section 28] ...........................................................................................................................298 EN 1991-1-4 Annex C...............................................................................................................299 29.1 Procedure 2 for determining the structural factor cscd ................................................................................................. 299 29.2 Number of loads for dynamic response ....................................................................................................300 29.3 Service displacement and accelerations for serviceability assessments..................................................301 29.4 Verification tests .......................................................................................................................................301 29.5 References [Section 29] ...........................................................................................................................304 EN 1991-1-4 Annex E [from Sec. E.1 to Sec. E.1.5.2.5] ........................................................................305 30.1 Vortex shedding........................................................................................................................................305 30.2 Vortex shedding action .............................................................................................................................308 EN 1990, EN 1991 - Eurocodes 0-1 - Worked Examples CONTENTS - page xii 30.3 Calculation of the cross wind amplitude ...................................................................................................309 30.3.1 Approach 1 for the calculation of the cross wind amplitudes ........................................................309 30.3.2 Correlation length L .......................................................................................................................311 30.3.3 Effective correlation length factor Kw ................................................................................................................... 312 30.3.4 Mode shape factor.........................................................................................................................314 30.4 Verification tests .......................................................................................................................................314 30.5 References [Section 30] ...........................................................................................................................319 EN 1991-1-4 Annex E [from Sec. E.1.5.2.6 to Sec. E.4.3] .....................................................................321 31.1 Calculation of the cross wind amplitude: number of load cycles ..............................................................321 31.2 Vortex resonance of vertical cylinders in a row or grouped arrangement.................................................321 31.3 Approach 2, for the calculation of the cross wind amplitudes...................................................................324 31.4 Galloping ..................................................................................................................................................325 31.4.1 Onset wind velocity .......................................................................................................................325 31.4.2 Classical galloping of coupled cylinders........................................................................................327 31.4.3 Interference galloping of two or more free standing cylinders.......................................................327 31.5 Divergence and Flutter .............................................................................................................................328 31.5.1 Criteria for plate-like structures .....................................................................................................328 31.5.2 Divergency velocity .......................................................................................................................329 31.6 Verification tests .......................................................................................................................................330 31.7 References [Section 31] ...........................................................................................................................334 EN 1991-1-4 Annex F ...............................................................................................................335 32.1 Dynamic characteristics of structures .......................................................................................................335 32.2 Fundamental frequency ............................................................................................................................335 32.3 Fundamental mode shape ........................................................................................................................340 32.4 Equivalent mass .......................................................................................................................................341 EN 1990, EN 1991 - Eurocodes 0-1 - Worked Examples CONTENTS - page xiii 32.5 Logarithmic decrement of damping ..........................................................................................................341 32.6 Verification tests .......................................................................................................................................343 32.7 References [Section 32] ...........................................................................................................................349 Eurocode 1 EN 1991-1-5 Section 5 (Page 17 to 19) ...................................................................................351 33.1 General .....................................................................................................................................................351 33.2 Temperature changes in buildings ...........................................................................................................352 33.3 Verification tests .......................................................................................................................................353 33.4 References [Section 33] ...........................................................................................................................359 Eurocode 1 EN 1991-1-5 Section 6 .............................................................................................................361 34.1 Temperature changes in bridges ..............................................................................................................361 34.1.1 Bridge decks..................................................................................................................................361 34.1.2 Thermal actions.............................................................................................................................361 34.2 Temperature difference components........................................................................................................363 34.2.1 Vertical linear component (Approach 1) ........................................................................................363 34.2.2 Vertical temperature components with non-linear effects (Approach 2)........................................365 34.2.3 Simultaneity of uniform and temperature difference components .................................................366 34.2.4 Bridge Piers: temperature differences...........................................................................................367 34.3 Verification tests .......................................................................................................................................367 34.4 References [Section 34] ...........................................................................................................................373 Eurocode 1 EN 1991-1-5 Annex A, Annex B ..............................................................................................375 35.1 Annex A (Normative): Isotherms of national minimum and maximum shade air temperatures................375 EN 1990, EN 1991 - Eurocodes 0-1 - Worked Examples CONTENTS - page xiv 35.1.1 General..........................................................................................................................................375 35.1.2 Maximum and minimum shade air temperature values with an annual probability of being exceeded p other than 0,02375 35.2 Annex B (Normative): Temperature differences for various surfacing depths ..........................................377 35.3 Verification tests .......................................................................................................................................379 35.4 References [Section 35] ...........................................................................................................................382 Eurocode 1 EN 1991-1-5 Annex D...............................................................................................................383 36.1 Annex D (Informative): Temperature profiles in buildings and other construction works..........................383 36.1.1 General..........................................................................................................................................383 36.2 Verification tests .......................................................................................................................................384 36.3 References [Section 36] ...........................................................................................................................392 Eurocode 1 EN 1991-1-6 .........................................................................................................393 1.1 General .....................................................................................................................................................393 1.2 Design situations and limit states .............................................................................................................394 1.3 Representation of main actions ................................................................................................................395 1.4 Construction loads during the casting of concrete....................................................................................399 1.5 Accidental actions.....................................................................................................................................400 1.6 Seismic actions.........................................................................................................................................400 1.7 Verification tests .......................................................................................................................................400 1.8 References [Section 1] .............................................................................................................................409 1.9 Vba References ........................................................................................................................................410 EN 1990, EN 1991 - Eurocodes 0-1 - Worked Examples CONTENTS - page xv SOFTWARE EC2: Flexure_EC2........................................................................................................411 1.1 General: FlexureRectangularBeamsAndSlabs.xls....................................................................................411 1.2 Layout .......................................................................................................................................................412 1.3 Output - Word document (calculation sheet) ............................................................................................415 1.4 Flexure_EC2 (Beams and slabs) derived formulae ..................................................................................416 1.5 Verification tests .......................................................................................................................................419 1.6 Excel VBa Code (main) ............................................................................................................................422 1.7 References ...............................................................................................................................................427 BiaxialBending(2)_EC2 (Commercial version) ................................................429 1.1 General: BiaxialBending(2).xls .................................................................................................................429 1.2 Output - Word document (calculation sheet) ............................................................................................431 1.3 BiaxialBending(2)_EC2 (“short columns”) derived formulae.....................................................................432 1.4 Verification tests .......................................................................................................................................436 1.5 References ...............................................................................................................................................447 1.6 Further Reading........................................................................................................................................448 Shear_EC2 ..........................................................................................................449 1.1 General: ShearReinforcementBeamSlab.xls ............................................................................................449 1.2 Layout .......................................................................................................................................................450 1.3 Output - Word document (calculation sheet) ............................................................................................453 1.4 Shear_EC2 (Beams and slabs) derived formulae ....................................................................................454 1.5 Verification tests .......................................................................................................................................456 1.6 References ...............................................................................................................................................460 (This page intentionally left blank) Section 1 Eurocode 0 - EN1990 1.1 Foreword E N 1990 “Eurocode: Basis of structural design” is the head document in the Eurocode suite. It describes the basis and general principles for the structural design and verification of buildings and civil engineering works including geotechnical aspects, the principles and requirements for safety and serviceability of structures and guidelines for related aspects of structural reliability in all circumstances in which a structure is required to give adequate performance, including fire and seismic events. Consisting of only one part, it is used with all the other Eurocodes (1 to 9) for design. The Structural Eurocode programme comprises the following standards generally consisting of a number of Parts: • EN 1990 Eurocode 0: Basis of Structural Design • EN 1991 Eurocode 1: Actions on structures • EN 1992 Eurocode 2: Design of concrete structures • EN 1993 Eurocode 3: Design of steel structures • EN 1994 Eurocode 4: Design of composite steel and concrete structures • EN 1995 Eurocode 5: Design of timber structures • EN 1996 Eurocode 6: Design of masonry structures • EN 1997 Eurocode 7: Geotechnical design • EN 1998 Eurocode 8: Design of structures for earthquake resistance • EN 1999 Eurocode 9: Design of aluminium structures. Eurocode standards recognise the responsibility of regulatory authorities in each Member State and have safeguarded their right to determine values related to regulatory safety matters at national level where these continue to vary from State to State. 1.2 National Standards implementing Eurocodes The National Standards implementing Eurocodes will comprise the full text of the Eurocode (including any annexes), as published by CEN, which may be Topic: User’s Manual/Verification tests - EN1990.xls page 17 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 preceded by a National title page and National foreword, and may be followed by a National annex. The National annex may only contain information on those parameters which are left open in the Eurocode for national choice, known as Nationally Determined Parameters, to be used for the design of buildings and civil engineering works to be constructed in the country concerned, i.e.: • values and/or classes where alternatives are given in the Eurocode • values to be used where a symbol only is given in the Eurocode • country specific data (geographical, climatic, etc.), e.g. snow map • the procedure to be used where alternative procedures are given in the Eurocode. It may also contain: • decisions on the application of informative annexes • references to non-contradictory complementary information to assist the user to apply the Eurocode. 1.3 National annex for EN 1990 This standard gives alternative procedures, values and recommendations for classes with notes indicating where national choices may have to be made. Hence the National Standard implementing EN 1990 should have a National annex containing all Nationally Determined Parameters to be used for the design of buildings and civil engineering. 1.4 Verification tests EN1990.XLS. 4.4 MB. Created: 5 January 2013. Last/Rel.-date: 6 March 2013. Sheets: — Splash — Annex A1-B — Annex C — Annex D. EXAMPLE 1-A‐ Target reliability index ‐ test 1 Given: Target reliability index (1 year): 1 = 4 7 (ultimate limit state: see tab. C2‐EN1990). Find the probability of failure P f (see ta. C1‐EN1990) related to and the value of for a different reference period (say 100 years). [Reference sheet: Annex C]‐[Cell‐Range: A1:O1‐A23:O23]. page 18 Topic: User’s Manual/Verification tests - EN1990.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 Solution: In the Level II procedures (see Figure C1‐EN1990 ‐ Overview of reliability methods), an alternative measure of reliability is conventionally defined by the reliability index which is related to the probably of failure P f by: Pf = – where is the cumulative distribution function of the standardised Normal distribution. The general formula for the probability density function of the Normal distribution is: x – 2 exp – -----------------– x – 2 2 2 2 2 e f x = --------------------------------------- = ----------------------------- 2 2 where is the “location parameter” and is the “scale parameter”. The case where = 0 and = 1 is called the Standard Normal distribution. The equation for the standard normal distribution is: xx– ---exp – ---2 2 e f x = ------------------------ = ---------- . 2 2 2 2 The probability of failure P f can be expressed through a performance function g such that a structure is considered to survive if g > 0 and to fail if g < 0: P f = Prob g 0 . If g is Normally distributed, is taken as = g g (where g is the mean value of g, and g is the standard deviation), so that: g – g = 0 and P f = Prob g 0 = Prob g g – g . The cumulative distribution function (CDF) – of a random variable is the probability of its value falling in the interval – ; , as a function of x. The CDF of the standard normal distribution, usually denoted with the capital Greek letter , is the integral: = 4 7 1 f x dx = ---------2 – e x– ---2 2 dx . – END NOTE For = 4 7 = 1 (1 year): 4 7 1 4 7 = ---------2 e x– ---2 2 dx 10 – 6 . – For a reference period of n = 100 years the reliability index n is (see eq. C.3‐EN1990): n = 1 n n = 4 7 100 10 – 6 100 = 10 – 4 n = 3 7 , –1 where n = n is the inverse of the cumulative distribution function. The quantile of the standard normal distribution is the inverse of the cumulative distribution function. example-end Topic: User’s Manual/Verification tests - EN1990.xls page 19 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 EXAMPLE 1-B‐ Approach for calibration of design values (section C7‐EN1990) ‐ test 2 Given: Calculate the design values of action effects E d and resistances R d . Assume a target reliability index equal to = 4 8 . The standard deviations of the action effect and resistance are, respectively: E = 5 0 , R = 5 0 . [Reference sheet: Annex C]‐[Cell‐Range: A27:O27‐A70:O70]. Solution: The design values of action effects E d and resistances R d should be defined such that the probability of having a more unfavourable value is as follows [see (C.6a), (C.6b) EN1990]: P E E d = + E P R R d = – R . substituting E and R into eq. (C.7)‐EN1990, we obtain: 0 16 E R 7 6 . The values of FORM sensivity factors E and R may be taken as – 0 7 and 0 8 , respectively. This gives: – 3 36 1 P E E d = + E = – 0 7 = – 0 7 4 8 = – 3 36 = ---------2 e dx – – 3 84 1 P R R d = – R = – 0 8 = – 0 8 4 8 = – 3 84 = ---------2 x2 – ----2 x– ---2 2 e dx . – Using the given numerical data, we find (leading variable only): P E E d = + E = 3 90 10 –4 –5 P R R d = – R = 6 15 10 . When the action model contains several basic variables, for the accompanying actions the design value is defined by: P E E d = + E 0 4 , from which we obtain: –2 P E E d = + E 0 4 = – 0 28 = – 0 28 4 8 = – 1 344 = 8 95 10 . example-end EXAMPLE 1-C‐ Approach for calibration of design values (section C7‐EN1990) ‐ test 3 Given: Consider the same assumptions in the example above ( = 4 8 ). Assume E = 1 0 , R = 7 0 . Find the design values of action effects E d and resistances R d . [Reference sheet: Annex C]‐[Cell‐Range: A27:O27‐A70:O70]. page 20 Topic: User’s Manual/Verification tests - EN1990.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 Solution: The condition 0 16 E R 7 6 is not satisfied: = 1 0 should be used for the variable with the larger standard deviation, and = 0 4 for the variable with the smaller standard deviation. The value of is negative for unfavourable actions and action effects, and positive for resistances. Using these values of , the design equations become: P E E d = + E = – 0 4 = – 0 4 4 8 = 2 74 10 –2 –7 P R R d = – R = – 1 0 = – 4 8 = 7 93 10 . For the accompanying actions the design value is (smaller standard deviation): –1 P E E d = + E 0 4 = – 0 4 0 4 = – 0 16 4 8 = 2 21 10 . example-end EXAMPLE 1-D‐ Approach for calibration of design values (section C7‐EN1990) ‐ test 4a Given: Derive the design values of variables with a probability equal to 10 – 4 (reliability index around = 3 8 ) using a Gumbel distribution. Assume: E = 30 ; E = 1 0 R = 30 ; R = 7 0 (mean value and standard deviation of the action effect and resistance, respectively). [Reference sheet: Annex C]‐[Cell‐Range: A74:O74‐A140:O140]. Solution: Considering the same assumptions in the example above (condition 0 16 E R 7 6 not satisfied), it is seen that: E –E E E –E R –R R R – R - 0,40 1,52 0,033 9,36 x 10 -1 1,00 - 3,80 0,233 7,23 x 10 -5 Table 1.1 Input data. See previous examples. From table C3‐EN1990 ‐ Design values for various distribution functions, by using the Gumbel distribution with the given numerical data, it follows that: 0 577 0 577 a = -------------- = ---------- = 0 183 ; u = R – --------------- = 30 – --------------- = 26 85 a 0 183 R 6 7 6 577- = 30 – 0------------- = -------- - = 1 283 ; u = – 0------------- 577- = 29 55 . a = ------------E a 1 283 E 6 1 6 Therefore, it is (leading variable action): 1 1 –5 1 X di R = u – --- ln – ln – R = u – --------------- ln – ln 7 235 10 = u – --------------- 2 255 a 0 183 0 183 Topic: User’s Manual/Verification tests - EN1990.xls page 21 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 1 X di R = 26 85 – --------------- 2 255 = 14 5 0 183 1 1 1 –1 X di E = u – --- ln – ln – E = u – --------------- ln – ln 9 357 10 = u + --------------- 2 712 a 1 283 1 283 1 X di R = 29 55 + --------------- 2 712 = 31 7 . 1 283 example-end EXAMPLE 1-E‐ Approach for calibration of design values (section C7‐EN1990) ‐ test 4b Given: Considering the same assumptions in the example above (see tab. 1.1), derive the design values of action effects E d with a probability equal to 10 – 4 using a Normal and a Log‐normal distribution. [Reference sheet: Annex C]‐[Cell‐Range: A74:O74‐A140:O140]. Solution: Remembering that the condition 0 16 E R 7 6 is not satisfied, the design value of action effects for Normal distribution (see tab. C3‐EN1990 ‐ Design values for various distribution functions) becomes: X di E = – = 30 + 0 40 3 8 1 = 31 5 . Having calculated V = E E = 1 30 = 0 033 0 2 , the design value of action effects for Log‐normal distribution becomes: X di E = exp – V = 30 exp 0 40 3 8 0 033 = 30 1 051 = 31 6 . example-end EXAMPLE 1-F‐ 0 factors (section C10‐EN1990) ‐ test 5 Given: Use the expressions in tab. C4‐EN1990 for obtaining the 0 factors in the case of two variable actions. Consider the following assumptions: – reference period T = 50 years – greater of the basic periods (for actions to be combined) T1 = 7 years – reliability index = 3 8 – coefficient of variation V = 0,30 of the accompanying action (for the reference period). [Reference sheet: Annex C]‐[Cell‐Range: A144:O144‐A189:O189]. Solution: page 22 The distribution functions in Table C4 refer to the maxima within the reference period T. These distribution functions are total functions which consider the probability that an action value is zero during certain periods. The theory is based on the calculation of the Topic: User’s Manual/Verification tests - EN1990.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 inverse gamma distributionʹs probability density function of the extreme value of the accompanying action in the reference period. The gamma distribution, like the Log‐normal distribution, is a two‐parameter family of continuous probability distributions. The general formula for the probability density function of the gamma distribution is: –1 x – - – - ----------exp – x---------- f x = ---------------------------------------------------------- ; x ; 0 . where is the shape parameter, is the location parameter, is the scale parameter, and is the “gamma function which” has the formula: = t – 1 –t e dt . 0 The case where = 0 and = 1 is called the “standard gamma distribution”. The equation for the standard gamma distribution reduces to: – 1 –x e -; x 0; 0. f x = x---------------- The gamma distribution can be parameterized in terms of a shape parameter and an inverse scale parameter 1 = , called a rate parameter: 1 g x ; = ------------ x – 1 e – x , With this parameterization, a gamma distribution has mean and variance 2 . As in the log‐normal distribution, x and the parameters and must be positive. The cumulative distribution function is the regularized gamma function: x Fx = PX x = 1 - – 1 –t ----------e t dt . 0 The inverse gamma distributionʹs probability density function is defined over the support x > 0: – – 1 – / x g x ; – 1 = ------------ x e . –1 Therefore, the inverse F x of the cumulative distribution function F x is the quantile of the –1 standard gamma distribution: F x = x . END NOTE Ratio approximated to the nearest integer: N 1 = T T 1 = 50 7 = 7 14 7 . Shape parameter (gamma distribution): k = 2 = 1 V 2 = V –2 = 0 30 –2 = 11 1 = Scale parameter (gamma distribution): Topic: User’s Manual/Verification tests - EN1990.xls page 23 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 = ---------- - = V –2 = 0 30 –2 = 11 1 = --1- = 11 1 –1 = ---- 2 V2 2 From table C4‐EN1990: – 0 7 – 0 7 3 8 – 2 66 = – –1 ------------------------- = – –1 ------------------------------------- = – –1 -------------------------- = 3 3 N1 N1 7 0 4 = 0 4 3 3 = 1 32 = 0 9066 ; 0 4 N1 = 0 9066 7 = 0 5034 0 7 = 0 7 3 8 = 2 66 = 0 9961 ; 0 7 N1 = 0 9961 7 = 0 9730 ; – ln 0 7 = – ln 0 9961 = 0 0039 , – 0 4 = – 0 4 3 3 = – 1 32 = 0 0934 – N 1 – 0 4 = – 7 0 0934 = – 0 6538 exp – N 1 – 0 4 = exp – 0 6538 = 0 5200 0 28 = 0 28 3 8 = 1 06 = 0 8563 ; – ln 0 28 = – ln 0 8563 = 0 1551 Quantiles (for = 11 1 , = 1 11 1 ): –1 N –1 N –1 –1 F S 0 4 1 = F S 0 5034 = 0 9727 , F S 0 7 1 = F S 0 9730 = 1 6546 –1 –1 F S 0 7 = F S 0 9961 = 1 9797 –1 –1 F S exp – N 1 – 0 4 = F S 0 5200 = 0 9850 . Substituting the numerical data listed above into expressions in table C4‐EN1990, we find: a) General expression: –1 N F accompanying F S 0 4 1 9727- = 0 588 . 0 = ----------------------------- = -----------------------------------------------= 0----------------–1 N1 F leading 1 6546 F S 0 7 b) Approximation for very large N 1 : –1 F accompanying F S exp – N 1 – 0 4 0 9850 = ------------------ = 0 497 . 0 = ------------------------------ = --------------------------------------------------------------------–1 1 9797 F leading F S 0 7 c) Normal (approximation): F accompanying 1 + 0 28 – 0 7 ln N 1 V 0 9106 1 + 0 28 3 8 – 0 7 ln 7 0 30 - = --------------------------------------------------------------------------------- = ------------------ = 0 = ------------------------------ = ------------------------------------------------------------1 798 1 + 0 7V 1 + 0 7 3 8 0 30 F leading = 0 506 . d) Gumbel (approximation): F accompanying 1 – 0 78V 0 58 + ln – ln 0 28 + ln N 1 -= 0 = ------------------------------ = -----------------------------------------------------------------------------------------------------------------------1 – 0 78V 0 58 + ln – ln 0 7 F leading 1 – 0 78 0 30 0 58 + ln 0 1551 + ln 7 1 – 0 78 0 30 0 58 – 1 8637 + 1 9459 = ------------------------------------------------------------------------------------------------------------ = --------------------------------------------------------------------------------------------------------- = 1 – 0 78 0 30 0 58 + ln 0 0039 1 – 0 78 0 30 0 58 – 5 5468 0---------------- 8450= = 0 391 . 2 1622 example-end page 24 Topic: User’s Manual/Verification tests - EN1990.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 EXAMPLE 1-G‐ D7.2 Assessment via the characteristic value ‐ test 6 Given: Find the design value of the property X considering already known the ratio d m between the design factor of the conversion factor and the partial factor of the material. Suppose a simple random sample of size n = 30 is drawn from a population having mean and standard deviation (see table below). Suppose the original distribution is normal. n xi n xi 1 19,3 16 17,3 2 19,8 17 19,2 3 20,1 18 22,4 4 20,4 19 16,0 5 20,3 20 15,0 6 19,3 21 15,6 7 18,0 22 18,2 8 17,4 23 17,4 9 21,3 24 19,2 10 19,4 25 16,3 11 20,2 26 15,3 12 20,5 27 14,0 13 21,0 28 13,0 14 22,3 29 15,3 15 18,5 30 16,5 Table 1.2 Sample results (n = 30). Reference Sheet: Annex D. Cell-Range B50:B64 - E50:E64. Find the mean, variance, standard deviation and the coefficient of variation of the sampling distribution. Rounding to the first decimal. [Reference sheet: Annex D]‐[Cell‐Range: A1:O1‐A82:O82]. Solution: Mean of the n = 30 sample results: 19 3 + 19 8 + 20 1 + 20 4 + + 13 0 + 15 3 + 16 5 m X = ------------------------------------------------------------------------------------------------------------------------------------------- = 18 3 . 30 Variance: 1 s x2 = --------------- 19 3 – 18 3 2 + 19 8 – 18 3 2 + 20 1 – 18 3 2 + + 16 5 – 18 3 2 = 6 0 . 30 – 1 Topic: User’s Manual/Verification tests - EN1990.xls page 25 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 6 0 = 2 45 . Standard deviation: s x = Coefficient of variation: sx 45- = 0 13 . V X = -----= 2----------mx 18 3 Values of k n for the 5% characteristic value for n = 30 (see tab. D1‐RN1990): 1 67 V x known kn = 1 73 V x unknown Design value of the property X: Xk n - = -----d m x 1 – k n V x = -----d 18 3 1 – 1 67 0 13 = -----d X d = d ----------m m m m 1 73 14 3 V x known 14 2 V x unknown having considered already known the ratio d m . example-end EXAMPLE 1-H‐ D7.2 Assessment via the characteristic value ‐ test 7 Given: Considering the same sample result in the example above (see tab. 1.2) and supposing the original distribution is Log-normal, find the design value of a property X considering already known the ratio d m . Rounding to the first decimal. [Reference sheet: Annex D]‐[Cell‐Range: A84:O84‐A125:O125]. Solution: Estimated value m y for E : 1 m y = = --n n 1 ln i = --n i=1 n i i=1 1 = ------ ln 19 3 + ln 19 8 + + ln 15 3 + ln 16 5 = 2 897 30 Estimated value s for : sy = s = ln V 2 + 1 V = 0 09 [input: (If V is known from prior knowledge)]. Estimated value s for [(If V is unknown from prior knowledge)]: sy = s = = 1 ----------n–1 n – m i y 2 = i=1 1---- 2 960 – 2 897 2 + 2 986 – 2 897 2 + + 2 602 – 2 897 2 = 0 139 . 29 Values of k n for the 5% characteristic value for n = 30 (see tab. D1‐EN1990): 1 67 V x known kn = 1 73 V x unknown page 26 Topic: User’s Manual/Verification tests - EN1990.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 Design value of the property X: X d = -----d exp m y – k n s y = -----d exp 2 897 – 1 67 0 09 m m 1 73 0 139 15 6 V x known = -----d m 14 2 V x unknown having considered already known the ratio d m . example-end EXAMPLE 1-I‐ D8.2 Standard evaluation procedure (Method (a)) ‐ test 8 Given: Develop a design model leading to the derivation of a resistance function (see section D8.2‐EN1990 ‐ Standard evaluation procedure (Method (a))). Check the validity of this model by means of a statistical interpretation of all available test data (see table below)(1). Verify that a sufficient correlation is achieved between the theoretical values and the test data. [Reference sheet: Annex D]‐[Cell‐Range: A173:O173‐A384:O384]. r ti r ei r ti r ei 10,5 10,9 18,9 18,4 12,6 12,3 19,4 18,9 14,7 14,9 19,7 19,5 14,9 14,2 20,4 20,8 15,1 14,8 20,8 21,0 15,3 14,7 21,4 21,7 15,8 15,2 21,9 22,0 16,1 15,6 22,5 22,8 16,5 15,5 22,9 23,2 16,9 15,0 23,6 23,9 17,2 16,5 23,9 24,1 17,4 16,9 24,7 25,0 17,8 17,5 25,2 25,5 18,1 18,5 25,9 26,2 18,5 18,3 26,4 25,0 Table 1.3 Sample results (n = 30). Reference Sheet: Annex D. Cell-Range A194:B208 - D194:E208. (1) rti theoretical values; rei experimental values from the tests. Topic: User’s Manual/Verification tests - EN1990.xls page 27 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 Solution: For the standard evaluation procedure the following assumptions are made: – the resistance function is a function of a number of independent variables X – a sufficient number of test results is available – all relevant geometrical and material properties are measured – there is no statistical correlation between the variables in the resistance function – all variables follow either a Normal or a log‐normal distribution. Step 1. Develop a design model, say in general: r ti = A i B i C I D I H I L I M I N I Q I T I . Step 2. Compare experimental and theoretical values. The points representing pairs of corresponding values ( r ti ; r ei ) are plotted on a diagram (see data on table 1.3): Figure 1.1 Windows screen image: figure D1-EN1990 (re - rt diagram). As we can see in figure 1.1, all of the points lie on the line = 4 (equation r e = r t ). It means that the resistance function is reasonably exact and complete: a sufficient correlation is achieved between the theoretical values and the test data. Step 3. Estimate the mean value correction factor b. page 28 Topic: User’s Manual/Verification tests - EN1990.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 n r = 10 5 10 9 + 12 6 12 3 + + 26 4 25 0 = 11401 ei r ti i=1 n r = 10 5 2 + 12 6 2 + 14 7 2 + + 25 9 2 + 26 4 2 = 11501 2 ti i=1 n r ei r ti i=1 b = ------------------ = 11401 --------------- = 0 991 . n 11501 r ti2 i=1 Probabilistic model of the resistance r = br t . The mean value of the theoretical resistance function, calculated using the mean values Xm of the basic variables, can be obtained from: r m = br t X m = bg rt X m . Step 4. Estimate the coefficient of variation of the errors. The error term i for each experimental value r ei should be determined from expression (D9‐EN1990): r ei i = -------. br ti From which, using the given numerical data into table 1.3, we find (rounding to three decimal places): r e1 10 9 - = 1 047 ; = ln = ln 1 047 = 0 046 ; 1 = -------- = -------------------------------1 1 br t1 0 991 10 5 r e2 12 3 2 = -------- = --------------------------------- = 0 985 ; 2 = ln 2 = ln 0 985 = – 0 015 ; 0 991 12 6 br t2 r e3 14 9 3 = -------- = --------------------------------- = 1 023 ; 3 = ln 3 = ln 1 023 = 0 023 ; br t3 0 991 14 7 ... r e30 25 0 30 = ---------- = --------------------------------- = 0 956 ; 30 = ln 30 = ln 0 956 = – 0 045 . 0 991 26 4 br t30 Substituting the above numerical data into expressions (D.11), (D.12), (D13), we find: 1 = --n n 1 i = --n i=1 1 s 2 = -----------n–1 n ln = i i=1 n i=1 0 046 – 0 015 + 0 023 + – 0 045 ----------------------------------------------------------------------------------------------- = – 0 005 30 2 0 046 + 0 005 2 + – 0 015 + 0 005 2 + + – 0 045 + 0 005 2 = 0 001 i – = -------------------------------------------------------------------------------------------------------------------------------------------------------------------29 Coefficient of variation V of the i error terms: Topic: User’s Manual/Verification tests - EN1990.xls page 29 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 V = exp s 2 – 1 = exp 0 001 2 – 1 = 0 032 . Step 5. Analyse compatibility. The compatibility of the test population with the assumptions made in the resistance function should be analysed. If the scatter of the r ei ; r ti values is too high to give economical design resistance functions, this scatter may be reduced. To determine which parameters have most influence on the scatter, the test results may be split into subsets with respect to these parameters. When determining the fractile factors k n (see step 7), the k n value for the sub‐sets may be determined on the basis of the total number of the tests in the original series. Step 6. Determine the coefficients of variation V Xi of the basic variables. Consider, for example, the design model for the theoretical resistance r ti as represented by the following relation (bearing resistance for bolts): r ti = 2 5d i t i f ui 2 5 B i C i D i ; ( A i = A = 2 5 = cos t ). The resistance function above covers all relevant basic variables X that affect the resistance at the relevant limit state. The coefficients of variation V Xi will normally need to be determined on the basis of some prior knowledge. Therefore, let us say: 1) coefficient of variation V d = 0 04 of the basic variable of the bolt’s diameter; 2) coefficient of variation V t = 0 05 of the b. v. of the thickness of the connected part; 3) coefficient of variation V fu = 0 07 of the b. v. of the ultimate tensile strength of the materials. Step 7. Determine the characteristic value r t of the resistance. The resistance function for j (= 4) basic variables is a product function of the form: r = br t = b A B C D . Coefficient of variation V r : j V2r = V 2 + 1 V 2 Xi 2 + 1 – 1 = V 2 + 1 V a2 + 1 V d2 + 1 V t2 + 1 V fu + 1 – 1 i=1 having considered V A = 0 for the constant A = 2 5 . Therefore, rounded to two decimal places, we find: V2r = 0 032 2 + 1 0 2 + 1 0 04 2 + 1 0 05 2 + 1 0 07 2 + 1 – 1 = 0 01 V = exp s 2 – 1 = 0 032 n V rt2 = V 2 xi 2 = V a2 + V d2 + V t2 + V fu = 0 + 0 04 2 + 0 05 2 + 0 07 2 = 0 009 . i=1 The number of test is limited (n = 30 < 100). In this case the characteristic resistance r k should be obtained from [see equation (D.17)‐EN1990]: r k = bg rt X m exp – k rt Q rt – k n Q – 0 5Q 2 with: page 30 Topic: User’s Manual/Verification tests - EN1990.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 Q = ln V r2 + 1 = ln 0 01 + 1 = 0 100 Q rt = ln V rt2 + 1 = ln 0 009 + 1 = 0 095 ; rt = Q rt Q = 0 095 0 100 = 0 95 Q = ln V 2 + 1 = ln 0 032 2 + 1 = 0 032 ; = Q Q = 0 032 0 100 = 0 32 . Values of k n for the 5% characteristic value for n = 30 (see tab. D1‐EN1990): k kn 1 64 for n = 1 73 V x unknown Substituting the numerical data into expressions above, we find the characteristic value of the resistance: r k = r m exp – k rt Q rt – k n Q – 0 5Q 2 = = r m exp – 1 64 0 95 0 095 – 1 73 0 32 0 032 – 0 5 0 100 2 = r m exp – 0 171 = = r m exp – 0 171 = r m 0 84 Here the characteristic value r k is represented as being proportional to its mean r m . example-end EXAMPLE 1-J‐D8.3 Standard evaluation procedure (Method (b)) ‐ test 9 Given: Considering the same assumptions in the example above, determine the design value of the resistance by taking account of the deviations of all the variables. [Reference sheet: Annex D]‐[Cell‐Range: A387:O387‐A413:O413]. Solution: In this case the procedure is the same as in D8.2, excepted that step 7 is adapted by replacing the characteristic fractile factor k n by the design fractile factor k d n equal to the product R assessed at 0 8 3 8 = 3 04 as commonly accepted (see Annex C‐EN1990) to obtain the design value r d of the resistance. For the case of a limited number of tests (herein n = 30 < 100) the design value r d should be obtained from: r d = bg rt X m exp – k d rt Q rt – k d n Q – 0 5Q 2 where: k d n is the design fractile factor from table D2 for the case “ V X unknown” k d is the value of k d n for n [ k d = 3 04 ]. The value of k d n for the ULS design value (leading) is 3,44 (see table D2‐EN1990). Therefore, we get: r d = r m exp – k d rt Q rt – k d n Q – 0 5Q 2 = = r m exp – 3 04 0 95 0 095 – 3 44 0 32 0 032 – 0 5 0 100 2 = r m exp – 0 315 = = r m exp – 0 315 = r m 0 73 having represented r d as being proportional to its mean. Topic: User’s Manual/Verification tests - EN1990.xls page 31 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 0 - EN1990 Dividing the characteristic value by the design value we obtain: r m 0 84 r R = ----k = -------------------- 1 15 r m 0 73 rd having estimated V from the test sample under consideration (see data in tab. 1.3). example-end EXAMPLE 1-K‐D8.4 Use additional prior knowledge ‐ test 10 Given: Determine the characteristic value r k of resistance when: – only one further test is carried out. – two or three further tests are carried out. Suppose that the maximum coefficient of variation observed in previous tests is equal to V r = 0 09 . [Reference sheet: Annex D]‐[Cell‐Range: A419:O419‐A438:O438]. Solution: If only one further test is carried out, the characteristic value r k may be determined from the result r e of this test by applying (D.24‐EN1990): r k = r e k = r e 0 9 exp – 2 31V r – 0 5V r2 = r e 0 9 exp – 2 31 0 09 – 0 5 0 09 2 = r e 0 73 where k is a reduction factor applicable in the case of prior knowledge. If two or three further tests are carried out, the characteristic value r k may be determined from the mean value r em of the test results by applying (D.26‐EN1990): r k = r e k = r e exp – 2 0V r – 0 5V r2 = r e exp – 2 0 0 09 – 0 5 0 09 2 = r e 0 83 provided that each extreme (maximum or minimum) value r ee satisfies the condition: r ee – r em 0 10 r em . example-end 1.5 References [Section 1] BS EN 1990 - Eurocode 0: Basis of structural design, 1 July 2002 European Committee for Standardization (2001) Eurocode: Basis of Structural Design, CEN, Brussels, EN 1990 Ferry-Borges, J. and Casteneta, M. (1972) Structural Safety. Laboratorio Nacional de Engenheria Civil, Lisbon. page 32 Topic: User’s Manual/Verification tests - EN1990.xls Section 2 Eurocode 1 - EN1991-1-1 2.1 Foreword T he Eurocode standards provide common structural design rules for everyday use for the design of whole structures and component products of both a traditional and an innovative nature. Unusual forms of construction or design conditions are not specifically covered and additional expert consideration will be required by the designer in such cases. The National Standards implementing Eurocodes will comprise the full text of the Eurocode (including any annexes), as published by CEN, which may be preceded by a National title page and National foreword, and may be followed by a National annex. EN 1991-1-1 gives design guidance and actions for the structural design of buildings and civil engineering works, including the following aspects: — densities of construction materials and stored materials — self-weight of construction elements, and — imposed loads for buildings. EN 1991-1-1 is intended for clients, designers, contractors and public authorities. EN 1991-1-1 is intended to be used with EN 1990, the other Parts of EN 1991 and EN 1992 to EN 1999 for the design of structures. 2.2 National annex for EN 1991-1-1 This standard gives alternative procedures, values and recommendations for classes with notes indicating where National choices have to be made, therefore the National Standard implementing EN 1991-1-1 should have a National Annex containing all Nationally Determined Parameters to be used for the design of buildings and civil engineering works to be constructed in the relevant country. 2.3 Distinction between Principles and Application Rules Depending on the character of the individual clauses, distinction is made in this Part between Principles and Application Rules. The Principles comprise: Topic: User’s Manual/Verification tests - EN1991-1-1.xls page 33 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 2 E UROCODE 1 - EN1991-1-1 — general statements and definitions for which there is no alternative, as well as — requirements and analytical models for which no alternative is permitted unless specifically stated. The Principles are identified by the letter “P” following the paragraph number. The Application Rules are generally recognised rules which comply with the Principles and satisfy their requirements. It is permissible to use alternative design rules different from the Application Rules given in EN 1991-1-1 for works, provided that it is shown that the alternative rules accord with the relevant Principles and are at least equivalent with regard to the structural safety, serviceability and durability which would be expected when using the Eurocodes. 2.4 Classification of actions SELF‐WEIGHT/DEAD LOADING/PERMANENT LOAD. This may be defined as the weight of all permanent construction. It will comprise the forces due to the static weights of all walls, partitions, floors, roofs and finishes, together with any other permanent construction. The self-weight of construction works should be classified as a permanent fixed action, see EN 1990, 1.5.3 and 4.1.1. Where this self-weight can vary in time, it should be taken into account by the upper and lower characteristic values (see EN 1990, 4.1.2). However, in some cases where it is free (e.g. for movable partitions, see 6.3.1.2(8)), it should be treated as an additional imposed load. Self-weight/Dead load/Permanent Load can be calculated from the unit weights given in EN 1991-1-1 “Annex A (informative)”, or from the actual known weight of the materials used if they are of a property type. The Self-weight/Dead load/Permanent load should also include an additional allowance for the weight of the member being designed. Since this cannot be known accurately until the size has been determined, it is necessary initially to estimate the self-weight. IMPOSED LOADS. This is sometimes termed superimposed loading, live loading or super loading, and may be defined as the loading assumed to be produced by the intended occupancy or use of the structure. It can take the form of distributed (UDL - uniformly distributed load), concentrated or impact loads. Imposed loads shall be classified as variable free actions, unless otherwise specified in this standard, see EN 1990, 1.5.3 and 4.1.1.(1) Imposed loads should be taken into account as quasi-static actions (see EN 1990, 1.5.3.13). The load models may include dynamic effects if there is no risk of resonance or other significant dynamic response of the structure, see EN 1992 to EN 1999. When considering forklifts and helicopters, the additional loadings due to masses and inertial forces caused by fluctuating effects should be considered. These effects are taken into account by a dynamic magnification factor which is applied to the static load values, as shown in expression (6.3). (1) For imposed loads on bridges see EN 1991-2. page 34 Topic: User’s Manual/Verification tests - EN1991-1-1.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 2 E UROCODE 1 - EN1991-1-1 DYNAMIC ACTIONS. Actions which cause significant acceleration of the structure or structural members shall be classified as dynamic actions and shall be considered using a dynamic analysis. 2.5 Representation of actions Characteristic values of densities of construction and stored materials should be specified. Mean values should be used as “characteristic values”. Annex A gives mean values for densities and angles of repose for stored materials. The self-weight of the construction works should in most cases, be represented by a single characteristic value and be calculated on the basis of the nominal dimensions and the characteristic values of the densities. When a range is given it is assumed that the mean value will be highly dependent on the source of the material and may be selected considering each individual project. The determination of the characteristic values of self-weight, and of the dimensions and densities shall be in accordance with EN 1990, 4.1.2. For the determination of the imposed loads, floor and roof areas in buildings should be sub-divided into categories according to their use (see Tables 6.1-6.2 EN 1991-1-1). The imposed loads specified in this part are modelled by uniformly distributed loads, line loads or concentrated loads or combinations of these loads. The categories of loaded areas, as specified in Table 6.1, shall be designed by using characteristic values q k (uniformly distributed load) and Q k (concentrated load). Values for q k and Q k are given in Table 6.2. Where a range is given in this table, the value may be set by the National annex. The recommended values, intended for separate application, are underlined. q k is intended for determination of general effects and Q k for local effects. The National annex may define different conditions of use of this Table. For the design of a floor structure within one storey or a roof, the imposed load shall be taken into account as a free action applied at the most unfavourable part of the influence area of the action effects considered. Where the loads on other storeys are relevant, they may be assumed to be distributed uniformly (fixed actions). To ensure a minimum local resistance of the floor structure a separate verification shall be performed with a concentrated load that, unless stated otherwise, shall not be combined with the uniformly distributed loads or other variable actions. Imposed loads from a single category may be reduced according to the areas supported by the appropriate member, by a reduction factor A according to 6.3.1.2(10). In design situations when imposed loads act simultaneously with other variable actions (e.g actions induced by wind, snow, cranes or machinery), the total imposed loads considered in the load case shall be considered as a single action. When the imposed load is considered as an accompanying action, in accordance with EN 1990, only one of the two factors (EN 1990, Table A1.1) and n (6.3.1.2 (11)) shall be applied. The imposed loads to be considered for serviceability limit state verifications should be specified in accordance with the service conditions and the requirements concerning the performance of the structure. For structures susceptible to vibrations, dynamic Topic: User’s Manual/Verification tests - EN1991-1-1.xls page 35 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 2 E UROCODE 1 - EN1991-1-1 models of imposed loads should be considered where relevant. The design procedure is given in EN 1990 clause 5.1.3. 2.6 Rapresentative values For each variable action there are four representative values. The principal representative value is the characteristic value and this can be determined statistically or, where there is insufficient data, a nominal value may be used. The other representative values are combination, frequent and quasi-permanent; these are obtained by applying to the characteristic value the factors 0 , 1 and 2 respectively. A semi-probabilistic method is used to derive the j factors, which vary depending on the type of imposed load. Further information on derivation of the j factors can be found in Appendix C of the Eurocode. 2.7 Ultimate limit state The ultimate limit states are divided into the following categories: — EQU Loss of equilibrium of the structure. — STR Internal failure or excessive deformation of the structure — or structural member. — GEO Failure due to excessive deformation of the ground. — FAT Fatigue failure of the structure or structural members. The Eurocode gives different combinations for each of these ultimate limit states. For the purpose of this publication only the STR ultimate limit state will be considered. 2.8 Verification tests EN1991‐1‐1.XLS. 6.5 MB. Created: 5 January 2013. Last/Rel.-date: 20 March 2013. Sheets: — Splash — CodeSec6 — Annex A — Annex B. EXAMPLE 2-L‐ Reduction factors for imposed loads ‐ test 1 Given: page 36 A five‐storey building is dedicated only or primarily for use as offices. Each deck below the roof is constituted by a reinforced concrete floor slab simply supported on beams, Topic: User’s Manual/Verification tests - EN1991-1-1.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 2 E UROCODE 1 - EN1991-1-1 columns and walls, and has to carry an imposed load (characteristic value) of q k = 5 0 kN m 2 (Category of use: C3). Suppose that the mean influence area supported by a single beam is approximately A = 75 m 2 . Determine both the reduction factors: A for beams (case a: see eq. 6.1‐EN1991‐1‐1) and n (case b: see eq. 6.2‐EN1991‐1‐1) for columns and walls (say, of the first floor). [Reference sheet: CodeSec6]‐[Cell‐Range: A86:O86‐A115:O115]. Solution: From table 6.1 ‐ Categories of use: “C3: Areas without obstacles for moving people, e.g. areas in museums, exhibition rooms, etc. and access areas in public and administration buildings, hotels, hospitals, railway station forecourts.” From table 6.2 ‐ Imposed loads on floors, balconies and stairs in buildings: Category C3: 3 0 q k kN m 2 5 0 ; 4 0 Q k kN 7 0 . Case a. Imposed loads from a single category may be reduced according to the areas supported by the appropriate member (e.g. a beam), by a reduction factor A according to 6.3.1.2(10). Therefore, the reduction factor A is applied to the q k values for imposed loads C3 for floors: A q k q k . Factor according to EN 1990 (see Annex A1, Table A1.1): 0 = 0 7 . Assuming A = 75 m 2 the influence area of the beam, with A 0 = 10 0 m 2 (see NOTE 1‐6.3.1.2) eq. 6.1 becomes: A 5 5 10 m 2 - = 0 63 1 0 . A = --- 0 + ------0 = --- 0 7 + ------------------7 7 A 75 m 2 with the restriction for categories C and D: A 0 6 . Case b. Where imposed loads from several storeys act on columns and/or walls, the total imposed loads may be reduced by a factor n according to 6.3.1.2(11) and 3.3.1(2)P. The area is classified according to table 6.1 into category C. Therefore, in accordance with 6.2.2(2), for columns and/or walls the total imposed loads from n = 4 storey (same category C3: q k = 5 0 kN m 2 ) may be multiplied by the reduction factor: 2 + n – 2 2 + 4 – 2 0 7- = 0 85 , n = --------------------------------0 = -------------------------------------n 4 where n = 4 is the number of storeys (> 2) above the loaded structural elements (in this case, columns and walls of the first floor) from the category C3. In other words: N k tot = q k roof + n n q k A i col = q k roof + 4 0 85q k A i col where A i col is the influence area of the single column/wall of the first floor. example-end EXAMPLE 2-M‐ Imposed loads on floors, balconies and stairs in buildings ‐ test 2a Given: A series of 500 mm deep x 250 mm wide reinforced concrete beams spaced at 4,00 m centres and spanning 6,50 m support a 200 mm thick reinforced concrete slab. If the imposed floor loading is 3 0 kN / m2 and the load induced by the weight of concrete is Topic: User’s Manual/Verification tests - EN1991-1-1.xls page 37 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 2 E UROCODE 1 - EN1991-1-1 Figure 2.2 PreCalculus Excel® form: procedure for a quick pre-calculation. 25 kN / m3 , calculate: 1) the total ULS(1) loading condition for the beams; 2) the beam’s ultimate bending moment and shear. [Reference sheet: CodeSec6]‐[Cell‐Range: A47:O47‐A84:O84]. Solution: From table A1.2(B) ‐ Design values of actions (STR/GEO) (Set B) ‐ EN1990: Gj sup = 1 35 (unfavourable permanent actions); Q 1 = 1 5 (leading variable action). Self‐weight/dead load from 200 mm slab (UDL(2) acting on the beam): 0 20 m 4 00 m 25 kN m 3 = 20 00 kN m . Beam self‐weight (UDL): 0 25 m 0 50 m 25 kN m 3 = 3 125 kN m . Imposed load (UDL beam): 3 0 kN / m2 4 00 m = 12 kN / m . From table A1.2(B) ‐ Design values of actions (STR/GEO) (Set B) ‐ EN1990: Gj sup = 1 35 (unfavourable permanent actions); Q 1 = 1 5 (leading variable action). Hence, the total ULS loading is given by: q d = 1 35 20 00 + 3 125 + 1 5 12 = 49 22 kN / m . Simply supported beam (isolated beams): 1 1 2 2 M Ed = --- q d L = --- 49 22 6 50 = 259 94 kNm 8 8 (1) ULS: Ultimate limit state. (2) UDL: Uniformly distributed load. page 38 Topic: User’s Manual/Verification tests - EN1991-1-1.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 2 E UROCODE 1 - EN1991-1-1 1 1 V Ed = --- q d L = --- 49 22 6 50 = 159 97 kN . 2 2 PreCalculus. (see Figure 2.2) Case a) Characteristic loads (dead + imposed): UDL: q k = 3 125 4 00 + 0 20 25 + 3 00 = 8 78 kN m 2 . Beam’s length: L = 6 50 m . Width floor supported: i = 4 00 m . Partial safety factors for all load (dead and imposed) set equal to 1,45 (approx.). example-end EXAMPLE 2-N‐ Imposed loads on floors, balconies and stairs in buildings ‐ test 2b Given: A simply supported steel beam spans L = 7 m and supports an ultimate central point load of Q d = 170 kN from secondary beams. In addition it carries an ultimate UDL of q d = 1 13 kN / m resulting from its self‐weight. Find ultimate bending moment and shear. [Reference sheet: CodeSec6]‐[Cell‐Range: A47:O47‐A84:O84]. Solution: The maximum ultimate moment and shear are given by, respectively: Figure 2.3 PreCalculus Excel form: procedure for a quick pre-calculation. Topic: User’s Manual/Verification tests - EN1991-1-1.xls page 39 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 2 E UROCODE 1 - EN1991-1-1 Qd L 1 2 2 170 7 1 - + --- q d L = ---------------------- + --- 1 13 7 = 297 5 + 6 92 = 304 42 kNm . M Ed = --------8 8 4 4 Q 1 1 V Ed = ------d + --- q d L = 170 --------- + --- 1 13 7 = 85 + 3 96 = 88 96 kN . 2 2 2 2 PreCalculus (see Figure 2.3). Case a) Characteristic loads (dead + imposed): 13 UDL: q k = 1----------- = 0 84 kN m = 0 84 kN m 2 1 m (self‐weight). Where the width 1 35 floor supported (i [m]) must be set equal to 1 (see Figure 2.3). Point Load: Q k = 170 1 45 = 117 2 kN (imposed loads approximation).We find (see form above): M Ed = 297 4 + 7 46 = 304 86 kNm , V Ed = 84 97 + 4 26 = 89 23 kN . example-end EXAMPLE 2-O‐Imposed loads on floors, balconies and stairs in buildings ‐ test 2c Given: A cantilever steel beam, length L = 1,80 m, supports a total UDL including its self‐weight of q d i = 86 kN (design value). Suppose the lateral torsional buckling resistance moment of the I beam is equal to M buckl = 100 kNm . Check if the beam section is adequate. Figure 2.4 page 40 PreCalculus Excel form: procedure for a quick pre-calculation. Topic: User’s Manual/Verification tests - EN1991-1-1.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 2 E UROCODE 1 - EN1991-1-1 [Reference sheet: CodeSec6]‐[Cell‐Range: A150:O150‐A199:O199]. Solution: The maximum ultimate moment and shear are given by, respectively: 1 1 2 2 M Ed = --- q d i L = --- 86 1 80 = 139 32 kNm ; V Ed = q d L = 86 1 80 = 154 80 kN . 2 2 The beam section is not adequate: M Ed = 139 32 kNm M buckl = 100 kNm . PreCalculus (see Figure 2.4). Cantilever) Characteristic loads (dead + imposed): q k i = 86 kN 1 45 = 59 31 kN (approximation). Length cantilever: L = 1 80 m . Obviously, we find (see form above): M Ed = 139 32 kNm , V Ed = 154 80 kN . example-end EXAMPLE 2-P‐ Areas for storage and industrial activities ‐ Actions induced by forklifts ‐ test 3 Given: A 250 mm thick reinforced concrete floor slab is simply supported on beams and columns. Concrete beams, which are 500 mm deep by 250 mm wide, spanning L = 4,50 m and spaced at 3,50 m centres have to carry an imposed load at least of Q k = 40 kN (axle characteristic load) due to forklifts and transport vehicles on pneumatic tyres (class of forklifts: FL2, see table 6.6‐EN1991‐1‐1). Considering all the imposed loads to be placed at the more unfavourable location, quickly assess the beam’s stresses due to bending moment and shear. [Reference sheet: CodeSec6]‐[Cell‐Range: A150:O150‐A199:O199]. Solution: From table 6.5 ‐ EN1991‐1‐1: Class of Forklift Net weight [kN] Hoisting load [kN] Width of axle a [m] Overall width b [m] Overall length l [m] FL2 31 15 0,95 1,10 3,00 Table 2.4 Dimension of forklift according to class FL2 (from table 6.5-EN 1991-1-1). Dynamic magnification factor = 1 40 (pneumatic tyres). Dynamic characteristic value of the action: Q k dyn = Q k = 1 40 40 kN = 56 kN . Horizontal loads due to acceleration or deceleration of forklifts may be taken as 30% of the vertical axle loads Q k (dynamic factors need not be applied): H k dyn = 0 30 Q k = 0 30 40 kN = 12 kN . From table A.1 ‐ Construction materials‐concrete and mortar (Annex A ‐ EN1991‐1‐1): concrete (normal weight and normal percentage of reinforcing): Topic: User’s Manual/Verification tests - EN1991-1-1.xls page 41 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 2 E UROCODE 1 - EN1991-1-1 Figure 2.5 PreCalculus Excel form: procedure for a quick pre-calculation. = 24 + 1 kN m 3 = 25 kN m 3 . From table A1.2(B) ‐ Design values of actions (STR/GEO) (Set B) ‐ EN1990: Gj sup = 1 35 (unfavourable permanent actions); Q 1 = 1 5 (leading variable action). Substituting the given numerical data, we get: Self-weight/Dead load/Permanent Load (per meter run): – beam: 0 25 m 0 50 m 25 kN m 3 = 3 125 kN m – concrete slab acting on beam: 0 25 m 3 50 m 25 kN m 3 = 21 875 kN m . Imposed loads acting on beam (vertical, per meter run): – load on floor due to storage (say category E1, see table 6.4‐EN1991‐1‐1): q k = 7 5 kN m 2 . Therefore: 7 5 kN m 2 3 50 m = 26 25 kN m . – concentrated load induced by forklift: Q k dyn = Q k = 56 kN . Ultimate design load ( Gj sup x dead + Q 1 x imposed): uniformly distribuited load: q d = 1 35 3 125 + 21 875 + 1 5 26 25 = 73 125 kN m concentrated load: Q d = 1 5 56 kN = 84 kN . Simply supported beam (ULS): 1 1 2 2 M Ed = --- q d L + 0 25Q d L – a = --- 73 125 4 50 + 0 25 84 4 50 – 0 95 = 259 65 kNm 8 8 1 1 V Ed = --- q d L + 0 5Q d = --- 73 125 4 50 + 0 5 84 = 206 53 kN . 2 2 PreCalculus (see Figure 2.5). Characteristic loads (dead + imposed): UDL: q k = 3 125 + 21 875 + 26 25 = 51 25 kN m . Axle load: Q k = 40 kN , beam’s length: L = 4 50 m . Distance tyres (width of axle): a = 0 95 m , dynamic factor: = 1 40 (pneumatic tyres). page 42 Topic: User’s Manual/Verification tests - EN1991-1-1.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 2 E UROCODE 1 - EN1991-1-1 Partial safety factors for all load (dead and imposed) set equal to 1,45 (approx.). example-end EXAMPLE 2-Q‐ Vehicle barriers and parapets for car parks ‐ test 4 Given: Find the horizontal force F (in kN), normal to and uniformly distributed over any length of 1,50 m of a barrier for a car park, required to withstand the impact of a vehicle. [Reference sheet: Annex B]‐[Cell‐Range: A1:O1‐A70:O70]. Solution: Clause B(3)‐EN1991‐1‐1‐Annex B. Suppose: – deformation of the vehicle: c = 100 mm = 100 10 –3 m – deformation of the barrier: b = 0 mm (rigid barrier) – velocity of the vehicle normal to the barrier: v = 4 5 m s – gross mass of the vehicles using the car park: m 2500 kg . (The mass of m = 1500 kg is taken as being more representative of the vehicle population than the extreme value of 2500 kg). The horizontal characteristic force, normal to and uniformly distributed over any length of 1,50 m of a barrier for a car park, is given by: 1 2 --- mv 1500 4 5 2 2 - = 151875 N = 151 88 kN 150 kN (rigid barrier). F k = -------------------- = 0 5 -----------------------------------100 10 –3 c + b From table A1.2(B) ‐ Design values of actions (STR/GEO) (Set B) ‐ EN1990: Q 1 = 1 5 (leading variable action). Hence, the horizontal design force is given by: F d = Q 1 F k = 1 5 151 88 = 227 82 kN . Bumper eight above finish floor level (FFL): h d = 375 mm (design height). Bending moment (design value): M Ed = F d h d = 227 82 0 375 = 85 43 kNm . Clause B(4)‐EN1991‐1‐1‐Annex B. The car park has been designed for vehicles whose gross mass exceeds 2500 kg. Actual mass of the vehicle for which the car park is designed: say m = 3000 kg . Therefore, we get: 1 2 --- mv 3000 4 5 2 2 - = 303750 N = 303 75 kN (rigid barrier). F k = -------------------- = 0 5 -----------------------------------100 10 –3 c + b Design value: F d = Q 1 F k = 1 5 303 75 = 455 63 kN . Bumper eight above finish floor level (FFL): say h ac = 550 mm (actual height). Bending moment (design value): M Ed = F d h ac = 455 63 0 550 = 250 60 kNm . Topic: User’s Manual/Verification tests - EN1991-1-1.xls page 43 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 2 E UROCODE 1 - EN1991-1-1 Clause B(6)‐EN1991‐1‐1‐Annex B. Barriers to access ramps of car parks have to withstand one half of the force determined in B(3) or B(4) acting at a height of 610 mm above the ramp: Design value (ref. clause B(3)): F d = Q 1 0 5 F k = 1 5 0 5 151 88 = 113 91 kN . Bending moment (design value): M Ed = F d h d = 113 91 0 610 = 69 49 kNm . Design value (ref. clause B(4)): F d = Q 1 0 5 F k = 1 5 0 5 303 75 = 227 81 kN . Bending moment (design value): M Ed = F d h d = 227 81 0 610 = 138 96 kNm . Clause B(7)‐EN1991‐1‐1‐Annex B. Opposite the ends of straight ramps intended for downward travel which exceed 20 m in length the barrier has to withstand twice the force determined in B (3) acting at a height of 610 mm above the ramp. Therefore, we get: design value (ref. clause B(3)): F d = Q 1 2 0 F k = 1 5 2 0 151 88 = 455 64 kN . Bending moment (design value): M Ed = F d h d = 455 64 0 610 = 277 94 kNm . example-end 2.9 References [Section 2] BS EN 1991-1-1 Eurocode 1: Actions on structures – Part 1-1: General actions – Densities, self-weight and imposed loads - 29 July 2002. (Incorporating corrigenda December 2004 and March 2009). EN 1991-1-1:2002 - Eurocode 1: Actions on structures - Part 1-1: General actions - Densities, self-weight, imposed loads for buildings CEN/TC 250 - Structural Eurocodes. International Organization for Standardization (1999) Bases for Design of Structures - Notations - General Symbols. ISO, Geneva, ISO 3898. The Concrete Centre. How to Design Concrete Structures using Eurocode 2, 2006. Trevor Draycott, Structural Elements Design Manual, Butterworth Heinemann, 1999. page 44 Topic: User’s Manual/Verification tests - EN1991-1-1.xls Section 3 Eurocode 1 EN 1991-1-2 3.1 General T he methods given in this Part 1-2 of EN 1991 are applicable to buildings, with a fire load related to the building and its occupancy. This Part 1-2 of EN 1991 deals with thermal and mechanical actions on structures exposed to fire. It is intended to be used in conjunction with the fire design Parts of prEN 1992 to prEN 1996 and prEN 1999 which give rules for designing structures for fire resistance. This Part 1-2 of EN 1991 contains thermal actions related to nominal and physically based thermal actions. More data and models for physically based thermal actions are given in annexes. In addition to the general assumptions of EN 1990 the following assumptions apply: — any active and passive fire protection systems taken into account in the design will be adequately maintained — the choice of the relevant design fire scenario is made by appropriate qualified and experienced personnel, or is given by the relevant national regulation. The rules given in EN 1990:2002, 1.4 apply. For the purposes of this European Standard, the terms and definitions given in EN 1990:2002, 1.5 and the following apply. 3.2 Terms relating to thermal actions FIRE COMPARTMENT. Space within a building, extending over one or several floors, which is enclosed by separating elements such that fire spread beyond the compartment is prevented during the relevant fire exposure. FIRE RESISTANCE. Ability of a structure, a part of a structure or a member to fulfil its required functions (load bearing function and/or fire separating function) for a specified load level, for a specified fire exposure and for a specified period of time. EQUIVALENT TIME OF FIRE EXPOSURE. time of exposure to the standard temperature-time curve supposed to have the same heating effect as a real fire in the compartment. Topic: User’s Manual/Verification tests - EN1991-1-2_(a).xls page 45 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 3 E UROCODE 1 EN 1991-1-2 EXTERNAL MEMBER. Structural member located outside the building that may be exposed to fire through openings in the building enclosure. GLOBAL STRUCTURAL ANALYSIS (FOR FIRE). Structural analysis of the entire structure, when either the entire structure, or only a part of it, are exposed to fire. Indirect fire actions are considered throughout the structure. MEMBER. Basic part of a structure (such as beam, column, but also assembly such as stud wall, truss,...) considered as isolated with appropriate boundary and support conditions. DESIGN FIRE SCENARIO. Specific fire scenario on which an analysis will be conducted. EXTERNAL FIRE CURVE. Nominal temperature-time curve intended for the outside of separating external walls which can be exposed to fire from different parts of the facade, i.e. directly from the inside of the respective fire compartment or from a compartment situated below or adjacent to the respective external wall. FIRE LOAD DENSITY. Fire load per unit area related to the floor area q f , or related to the surface area of the total enclosure, including openings, q t . FIRE LOAD. Sum of thermal energies which are released by combustion of all combustible materials in a space (building contents and construction elements). HYDROCARBON FIRE CURVE. Nominal temperature-time curve for representing effects of an hydrocarbon type fire. OPENING FACTOR. Factor representing the amount of ventilation depending on the area of openings in the compartment walls, on the height of these openings and on the total area of the enclosure surfaces. STANDARD TEMPERATURE‐TIME CURVE. Nominal curve defined in prEN 13501-2 for representing a model of a fully developed fire in a compartment. TEMPERATURE‐TIME CURVES. Gas temperature in the environment of member surfaces as a function of time. They may be: — nominal: conventional curves, adopted for classification or verification of fire resistance, e.g. the standard temperature-time curve, external fire curve, hydrocarbon fire curve — parametric: determined on the basis of fire models and the specific physical parameters defining the conditions in the fire compartment. CONVECTIVE HEAT TRANSFER COEFFICIENT. Convective heat flux to the member related to the difference between the bulk temperature of gas bordering the relevant surface of the member and the temperature of that surface. EMISSIVITY. Equal to absorptivity of a surface, i.e. the ratio between the radiative heat absorbed by a given surface and that of a black body surface. FLASH‐OVER. Simultaneous ignition of all the fire loads in a compartment. page 46 Topic: User’s Manual/Verification tests - EN1991-1-2_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 3 E UROCODE 1 EN 1991-1-2 3.3 Structural Fire design procedure A structural fire design analysis should take into account the following steps as relevant: — selection of the relevant design fire scenarios — determination of the corresponding design fires — calculation of temperature evolution within the structural members — calculation of the mechanical behaviour of the structure exposed to fire. Mechanical behaviour of a structure is depending on thermal actions and their thermal effect on material properties and indirect mechanical actions, as well as on the direct effect of mechanical actions. Structural fire design involves applying actions for temperature analysis and actions for mechanical analysis according to this Part and other Parts of EN 1991. Actions on structures from fire exposure are classified as accidental actions, see EN 1990:2002, 6.4.3.3(4). 3.4 Design fire scenario, design fire To identify the accidental design situation, the relevant design fire scenarios and the associated design fires should be determined on the basis of a fire risk assessment. (2) For structures where particular risks of fire arise as a consequence of other accidental actions, this risk should be considered when determining the overall safety concept. Time- and load-dependent structural behaviour prior to the accidental situation needs not be considered, unless (2) applies. For each design fire scenario, a design fire, in a fire compartment, should be estimated according to section 3 of this Part. The design fire should be applied only to one fire compartment of the building at a time, unless otherwise specified in the design fire scenario. (3) For structures, where the national authorities specify structural fire resistance requirements, it may be assumed that the relevant design fire is given by the standard fire, unless specified otherwise. 3.5 Temperature Analysis When performing temperature analysis of a member, the position of the design fire in relation to the member shall be taken into account. For external members, fire exposure through openings in facades and roofs should be considered. (3) For separating external walls fire exposure from inside (from the respective fire compartment) and alternatively from outside (from other fire compartments) should be considered when required. Topic: User’s Manual/Verification tests - EN1991-1-2_(a).xls page 47 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 3 E UROCODE 1 EN 1991-1-2 Depending on the design fire chosen in section 3, the following procedures should be used: — Note with a nominal temperature-time curve, the temperature analysis of the structural members is made for a specified period of time, without any cooling phase; The specified period of time may be given in the national regulations or obtained from annex F following the specifications of the national annex. — Note with a fire model, the temperature analysis of the structural members is made for the full duration of the fire, including the cooling phase. Limited periods of fire resistance may be set in the national annex. 3.6 Thermal actions for temperature analysis (Section 3) Thermal actions are given by the net heat flux h· net W m 2 to the surface of the member. On the fire exposed surfaces the net heat flux h· net should be determined by considering heat transfer by convection and radiation as: · · · h net = h net c + h net r (Eq. 3‐1) where h· net c is the net convective heat flux component and h· net r is the net radiative heat flux component. The net convective heat flux component should be determined by: · h net c W m 2 = c g – m (Eq. 3‐2) where: • c is the coefficient of heat transfer by convection W m 2 K • g is the gas temperature in the vicinity of the fire exposed member [°C] • m is the surface temperature of the member [°C]. On the unexposed side of separating members, the net heat flux h· net should be determined by using equation 3-1, with c = 4 W m 2 K . The coefficient of heat transfer by convection should be taken as c = 9 W m 2 K , when assuming it contains the effects of heat transfer by radiation. The net radiative heat flux component per unit surface area is determined by: · h net r W m 2 = m f r + 273 4 – m + 273 4 (Eq. 3‐3) where: page 48 • is the configuration factor • m is the surface emissivity of the member • f is the emissivity of the fire Topic: User’s Manual/Verification tests - EN1991-1-2_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 3 E UROCODE 1 EN 1991-1-2 –8 • is the Stephan Boltzmann constant 5 67 10 • r is the effective radiation temperature of the fire environment [°C] • m is the surface temperature of the member [°C]. Note W m2K4 Unless given in the material related fire design Parts of prEN 1992 to prEN 1996 and prEN 1999, m = 0 8 may be used. The emissivity of the fire is taken in general as f = 1 0 . Where this Part or the fire design Parts of prEN 1992 to prEN 1996 and prEN 1999 give no specific data, the configuration factor should be taken as = 1 . A lower value may be chosen to take account of so called position and shadow effects. For the calculation of the configuration factor a method is given in annex G. Note In case of fully fire engulfed members, the radiation temperature r may be represented by the gas temperature g around that member. The surface temperature m results from the temperature analysis of the member according to the fire design Parts 1-2 of prEN 1992 to prEN 1996 and prEN 1999, as relevant. Gas temperatures g may be adopted as nominal temperature-time curves according to 3.2, or adopted according to the fire models given in 3.3. Note The use of the nominal temperature‐time curves according to 3.2 or, as an alternative, the use of the natural fire models according to 3.3 may be specified in the national annex. 3.7 Nominal temperature-time curves STANDARD TEMPERATURE‐TIME CURVE. The standard temperature-time curve is given by: g = 20 + 345 log 10 8t + 1 (Eq. 3‐4) where: • g is the gas temperature in the fire compartment [°C] • t is the time [min]. The coefficient of heat transfer by convection is c = 25 W m 2 K . EXTERNAL FIRE CURVE. The external fire curve is given by: g = 20 + 660 1 – 0 687 e –0 32t – 0 313e –3 8t (Eq. 3‐5) where: • g is the gas temperature near the member [°C] • t is the time [min]. Topic: User’s Manual/Verification tests - EN1991-1-2_(a).xls page 49 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 3 E UROCODE 1 EN 1991-1-2 The coefficient of heat transfer by convection is c = 25 W m 2 K . HYDROCARBON CURVE. The hydrocarbon temperature-time curve is given by: g = 20 + 1080 1 – 0 325 e –0 167t – 0 675e –2 5t (Eq. 3‐6) where: • g is the gas temperature in the fire compartment [°C] • t is the time [min]. The coefficient of heat transfer by convection is c = 50 W m 2 K . 3.8 Verification tests EN1991‐1‐2_(A).XLS. 6.4 MB. Created: 3 February 2013. Last/Rel.-date: 3 May 2013. Sheets: — Splash — CodeSec3 — Annex A. NOTE: the code requires a reference to the “OLE Automation” type library EXAMPLE 3-R‐ Section 3.1 ‐ Thermal actions for temperature analysis ‐ test 1 Given: Determine the net heat flux on a fire exposed surface, in case of fully fire engulfed members ( r g around the member). Suppose: c = 4 00 W m 2 K (coefficient of heat transfer by convection); g = 700C (gas temperature in the vicinity of the fire exposed member); m = 70C (surface temperature of the member); = 1 (configuration factor); m = 0 8 (surface emissivity of the member); f = 1 0 (emissivity of the fire); r = 700C (effective radiation temperature of the fire environment). [Reference sheet: CodeSec3]‐[Cell‐Range: A1:O1‐A64:O64]. Solution: The net convective heat flux component is given by: · h net c = c g – m = 4 00 700 – 70 = 2520 W m 2 = 2 52 kW m 2 . The net radiative heat flux component is determined by: 5 67 · - 700 + 273 4 – 70 + 273 4 h net r = m f r + 273 4 – m + 273 4 = 1 0 8 1 ----------10 8 5 6710 11 · h net r = 1 0 8 1 ---------- 8 963 10 11 – 0 138 10 11 = 40 ---------8- = 40000 W m 2 = 40 kW m 2 8 10 10 Therefore, the net heat flux (considering heat transfer by convection and radiation) is given by: · · · h = h +h = 2 52 + 40 = 42 52 kW m 2 . net net c net r Now, considering r g with (say) m = 500C , g = 720C , we get: page 50 Topic: User’s Manual/Verification tests - EN1991-1-2_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 3 E UROCODE 1 EN 1991-1-2 · h net c = c g – m = 4 00 720 – 500 = 880 W m 2 = 0 88 kW m 2 5 67 · - 720 + 273 4 – 500 + 273 4 h net r = m f r + 273 4 – m + 273 4 = 1 0 8 1 ----------10 8 11 5 67 · 11 – 3 570 10 11 = 27 91 10 --------- = 27910 W m 2 = 27 91 kW m 2 h net r = 1 0 8 1 ---------- 9 723 10 10 8 10 8 Figure 3.6 View Plot (from input). See cells Range H63:J65 - Sheet: CodeSec3. Hence, we find: h· net = h· net c + h· net r = 0 88 + 27 91 = 28 79 kW m 2 (see plot above). example-end EXAMPLE 3-S‐ Section 3.2 ‐ Nominal temperature‐time curves ‐ test 2 Given: Determine the standard temperature‐time curve at t = 120 min (time of the exposure), the external fire curve and the hydrocarbon temperature‐time curve at t = 15 min . [Reference sheet: CodeSec3]‐[Cell‐Range: A68:O68‐A190:O190]. Solution: The standard temperature‐time curve is given by (gas temperature in the fire compartment): g = 20 + 345 log 10 8t + 1 . Sobstituting t = 120 min , we get: Topic: User’s Manual/Verification tests - EN1991-1-2_(a).xls page 51 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 3 E UROCODE 1 EN 1991-1-2 g = 20 + 345 log 10 8t + 1 = 20 + 345 log 10 8 120 + 1 = 20 + 345 2 983 = 1049C . Figure 3.7 Standard temperature-time curve. Figure 3.8 External fire curve. The external fire curve is given by (gas temperature near the member): page 52 Topic: User’s Manual/Verification tests - EN1991-1-2_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 3 E UROCODE 1 EN 1991-1-2 g = 20 + 660 1 – 0 687 e –0 32t – 0 313e –3 8t . Sobstituting t = 15 min , we get: g = 20 + 660 1 – 0 687 e –0 32 15 – 0 313e –3 8 15 = 20 + 660 1 – 0 687 e – 4 8 – 0 313e –57 g 20 + 660 1 – 0 687 0 00823 – 0 = 676 3C . We find that: g = 680C = cost for t 40 min approximately. The hydrocarbon temperature‐time curve is given by (gas temperature in the fire compartment): g = 20 + 1080 1 – 0 325 e –0 167t – 0 675e –2 5t . Sobstituting t = 15 min , we get: g = 20 + 1080 1 – 0 325 e –0 167 15 – 0 675e –2 5 15 = 20 + 1080 1 – 0 325 e –2 505 – 0 675e – 37 5 g 20 + 1080 1 – 0 325 e –2 505 – 0 = 20 + 1080 1 – 0 325 0 0817 – 0 = 1071 3C . Figure 3.9 Hydrocarbon curve. We find that: g = 1100C = cost for t 65 min approximately. example-end EXAMPLE 3-T‐ Annex A ‐ Parametric temperature‐time curves ‐ test 3 Given: For internal members of fire compartments, calculate the gas temperature in the compartment using the method given in informative Annex A of EC1 Part 1‐2. The theory assumes that temperature rise is independent of fire load. Topic: User’s Manual/Verification tests - EN1991-1-2_(a).xls page 53 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 3 E UROCODE 1 EN 1991-1-2 The temperature within the compartment is assumed to vary as a simple exponential function of modified time dependent on the variation in the ventilation area and the properties of the compartment linings from this “standard” compartment. Figure 3.10 Plan of fire compartment (height = 3,60 m). [Reference sheet: Annex A]‐[Cell‐Range: A1:O1‐A152:O152]. Solution: Dimension of the compartment: width = 6,50 m; lenght = 15,00 m; heigth = 3,60 m. Dimension of windows: number of windows = 4; width = 2,30 m (mean value); heigth = h eq = 1,70 m (weighted average of window heights on all walls). [kg/m3] c [J/kgK] [W/mK] CEILING 2400 1506 1,50 2400 1506 1 50 = 2328 (a) WALLS 900 1250 0,24 900 1250 0 24 = 519 6 FLOOR 900 1250 0,24 Table 3.5 b = c [J/m2s0,5K] 519 6 Thermal properties of enclosure surfaces. (a). b (thermal absorptivity) with the following limits 100 b 2200 . We assume: ceiling b = 2200 J m 2 s 0 5 K ; walls and floor b = 520 J m 2 s 0 5 K . page 54 Topic: User’s Manual/Verification tests - EN1991-1-2_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 3 E UROCODE 1 EN 1991-1-2 Total area of vertical openings on all walls: A v = 4 2 30 m 1 70 m = 15 64 m 2 . Total area of enclosure (walls, ceiling and floor, including openings): A t = 2 6 50 15 00 + 6 50 + 15 00 3 60 = 349 8 m 2 . Opening factor: h eq 1 70 - - = 15 64 -------------------O = A v ---------= 0 0583 m 1 / 2 At 349 8 with the following limits: 0,02 < O = 0,0583 < 0,20. We find: ceiling A j = 6 50 15 00 = 97 50 m 2 and floor A j = 97 50 m 2 , wall A j = 2 6 50 + 15 00 3 60 – 15 64 = 139 2 m 2 . Hence, we get: bj Aj 97 50 + 520 139 2 + 520 97 5- = 1010 J m 2 s 0 5 K . b = ----------------------- = 2200 ------------------------------------------------------------------------------------------------ At – Av 349 8 – 15 64 with the following limits: 100 < b = 1010 < 2200. Time factor function: O b 2 0 0583 1010 2 = ----------------------------------2- = --------------------------------------------- = 2 802 . 0 04 1160 0 04 1160 2 Design value of the fire load density related to the surface area A f of the floor: q f d = 700 MJ m 2 . Floor area of the fire compartment: A f = 97 5 m 2 . Design value of the fire load density related to the total surface area A t of the enclosure: A 97 5 q t d = q f d -----f = 700 --------------- = 195 11 MJ m 2 . At 349 8 Fire growth rate: say t lim = 20 min 0 333 h (medium fire growth rate). 0 2 10 –3 q t d O = 0 2 10 –3 195 11 0 0583 = 0 67 h . t max = max 0 2 10 –3 q t d O ; 0 333 h = max 0 67 ; 0 333 = 0 67 h . t max t lim the fire is ventilation controlled. The maximum temperature max in the heating phase happens for t * = t *max : t *max = t max = 0 67 2 802 = 1 88 h . Maximum temperature (heating phase): – 0 2t * – 0 204e – 1 7t * – 0 472e – 19t * max = 20 + 1325 1 – 0 324e t *max = 1 88 h max = 20 + 1325 1 – 0 324e – 0 2 1 88 – 0 204e – 1 7 1 88 – 0 472e – 19 1 88 max 20 + 1325 1 – 0 324 0 687 – 0 204 0 041 – 0 = 1039C . Cooling phase t t *max : with t max = 0 67 h t lim = 0 33 h , we get: x = 1 (see eq. A.12). Topic: User’s Manual/Verification tests - EN1991-1-2_(a).xls page 55 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 3 E UROCODE 1 EN 1991-1-2 – 3 q t d – 3 195 11 - 2 802 = 0 669 2 802 = 1 88 h With t ** max = 0 2 10 -------- = 0 2 10 ----------------O 0 0583 – 3 q t d - = 1 88 h 2 h , we get: 0 5 h 0 2 10 ------ O * ** g = max – 250 3 – t ** max t – t max x , g = max – 250 3 – 1 88 t * – 1 88 = 1039 – 250 3 – 1 88 t * – 1 88 . For (say) t = 1 10 h t * = t = 1 10 2 802 = 3 08 h , we find: Figure 3.11 Parametric curve: heating, cooling. g = 1039 – 250 3 – 1 88 t * – 1 88 = 1039 – 250 3 – 1 88 3 08 – 1 88 = 703C . Rounding error: 100 x (703 – 699,7)/699,7 = 0,5%. example-end EXAMPLE 3-U‐‐ Annex A ‐ Parametric temperature‐time curves ‐ test 4 Given: Maintaining the same assumptions in the previous example and assuming q f d = 200 MJ m 2 , calculate the cooling phase. [Reference sheet: Annex A]‐[Cell‐Range: A107:O107‐A152:O152]. page 56 Topic: User’s Manual/Verification tests - EN1991-1-2_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 3 E UROCODE 1 EN 1991-1-2 Solution: We find: A 97 5 q t d = q f d -----f = 200 --------------- = 55 75 MJ m 2 At 349 8 t max = max 0 2 10 –3 q t d O ; 0 333 h = max 0 19 ; 0 333 = 0 333 h Time factor function (A.2b): O lim b 2 0 0167 1010 2 -2 --------------------------------------------- = 0 23 , with lim = --------------------------------- 0 04 1160 0 04 1160 2 0 1 55 75 0 1 q t d - = --------3- ------------------- = 0 0167 . O lim = --------3- ------10 0 333 10 t lim If (O > 0,04 and qt,d < 75 and b < 1160), lim in (A.8) has to be multiplied by k given by: q t d – 75 1160 – b O – 0 04 0583 – 0 04- 55 75 – 75 1160 – 1010 - --------------------- = 1 + 0----------------------------------k = 1 + ---------------------- ------------------ --------------------------- ------------------------------ 0 04 75 1160 0 04 75 1160 k = 1 + 0 4575 – 0 2567 0 1293 = 0 98 . We get: t *max = t max k lim = 0 333 0 98 0 231 0 08 h . Maximum temperature (heating phase): – 0 2t * – 0 204e – 1 7t * – 0 472e – 19t * max = 20 + 1325 1 – 0 324e t *max 0 757 h max = 20 + 1325 1 – 0 324e – 0 2 0 076 – 0 204e – 1 7 0 076 – 0 472e – 19 0 076 max 20 + 1325 1 – 0 324 0 985 – 0 204 0 879 – 0 472 0 236 = 537C , Rounding error: 100 x (537 – 536,1)/536,1 < 0,2%. 0 2- q------ 55 75 0 2- ---------------------t d - = -------t ** 2 802 = 0 536 h . max = -------10 3 O 10 3 0 0583 t max t lim = 0 333 h (the fire is fuel controlled): t lim 0 333 2 802 x = -------------- --------------------------------------- = 1 74 . 0 536 t ** max For 0 5 t ** max 2 : * ** * g = max – 250 3 – t ** max t – t max x = max – 250 3 – 0 536 t – 0 536 1 74 . For (say) t = 0 50 h t * = t = 0 50 2 802 = 1 40 h , we find: g 537 – 250 3 – 0 536 1 40 – 0 536 1 74 = 249C , Rounding error: 100 x (249 – 248,4)/248,4 < 0,25%. example-end Topic: User’s Manual/Verification tests - EN1991-1-2_(a).xls page 57 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 3 E UROCODE 1 EN 1991-1-2 3.9 References [Section 3] BS EN 1991-1-2. Eurocode 1: Actions on structures – Part 1-2: General actions – Actions on structures exposed to fire. 26 November 2002 EN 1991-1-2:2002/AC:2013. Eurocode 1: Actions on structures - Part 1-2: General actions - Actions on structures exposed to fire. CEN Brussels, February 2013. Manual for the design of building structures to Eurocode 1 and Basis of Structural Design - April 2010. © 2010 The Institution of Structural Engineers. page 58 Topic: User’s Manual/Verification tests - EN1991-1-2_(a).xls Section 4 Eurocode 1 EN 1991-1-2 Annex B 4.1 Thermal actions for external members - Simplified calculation method T his method considers steady-state conditions for the various parameters. The method is valid only for fire loads q f d 200 MJ m 2 . This method allows the determination of: — the maximum temperatures of a compartment fire — the size and temperatures of the flame from openings — radiation and convection parameters. CONDITIONS OF USE. When there is more than one window in the relevant fire compartment, the weighted average height of windows h eq , the total area of vertical openings A v and the sum of windows widths are used. When there are windows in only wall 1, the ratio D/W is given by: D W = W2 W1 . (Eq. 4‐7) When there are windows on more than one wall, the ratio D/W has to be obtained as follows: W A v1 , D W = -------2 -------W1 Av (Eq. 4‐8) where: • W 1 is the width of the wall 1, assumed to contain the greatest window area • A v1 is the sum of window areas on wall 1 • W 2 is the width of the wall perpendicular to wall 1 in the fire compartment. When there is a core in the fire compartment, the ratio D/W has to be obtained as follows: Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls page 59 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 4 E UROCODE 1 EN 1991-1-2 A NNEX B W 2 – L c A v1 D W = --------------------------------, W 1 – W c A v (Eq. 4‐9) where: • L c and W c are the length and width of the core • W 1 and W 2 are the length and width of the 'fire compartment • the size of the fire compartment should not exceed 70 m in length, 18 m in width and 5 m in height. (5) All parts of an external wall that do not have the fire resistance (REI) required for the stability of the building should be classified as window areas. The total area of windows in an external wall is: — the total area, according to (5), if it is less than 50% of the area of the relevant external wall of the compartment — firstly the total area and secondly 50% of the area of the relevant external wall of the compartment if, according to (5), the area is more than 50%. These two situations should be considered for calculation. When using 50% of the area of the external wall, the location and geometry of the open surfaces should be chosen so that the most severe case is considered. The flame temperature should be taken as uniform across the width and the thickness of the flame. EFFECT OF WIND ‐ MODE OF VENTILATION, DEFLECTION BY WIND. If there are windows on opposite sides of the fire compartment or if additional air is being fed to the fire from another source (other than windows), the calculation shall be done with forced draught conditions. Otherwise, the calculation is done with no forced draught conditions. Figure 4.12 Deflection of flame by wind (from fig. B.1). Flames from an opening should be assumed to be leaving the fire compartment (see figure below): page 60 — perpendicular to the facade — with a deflection of 45° due to wind effects. Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 4 E UROCODE 1 EN 1991-1-2 A NNEX B Figure 4.13 Flame dimensions, no through draught (from fig. B.2). CHARACTERISTIC OF FIRE AND FLAMES: NO FORCED DRAUGHT. The rate of burning or the rate of heat release is given by [MW]: 0 036 1/2 – --------------h eq A f q f d O Q = min -----------------; 3 15 1 – e A v ------------ F DW . (Eq. 4‐10) The temperature of the fire compartment is given by [°K]: T f = 6000 1 – e – 0 1 O – 0 00286 O 1 – e + T0 . (Eq. 4‐11) The flame height (see Figure B.2) is given by: 2/3 Q L L = max 0 ; h eq 2 37 --------------------------- – 1 A h g v g eq (Eq. 4‐12) where: • • • A v is the total area of vertical openings on all walls A v = A v i i h eq = A v i h i A v is the weighted average of windows on all walls i A t is the total area of enclosure (walls, ceiling and floor, including openings) • q f d is the design fire load density MJ m 2 related to the floor area A f • A f is the floor area of the fire compartment • O = A v h eq A t is the “opening factor” of the fire compartment • F = 1200 s is the free burning duration (in seconds) Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls page 61 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 4 E UROCODE 1 EN 1991-1-2 A NNEX B • D W i the “ratio” (see section B.2 “Conditions of use”) • = A f q f d A v A t • T 0 = 273 K = 20C is the “initial temperature” • g is the internal gas density kg m 3 • g = 9 81 m s 2 . The flame width is the window width (see Figure B.2). The flame depth is 2/3 of the window height: 2/3 heq (see Figure B.2). (6) The horizontal projection of flames: — in case of a wall existing above the window, is given by: L H = h eq 3 if h eq 1 25w t ; L H = 0 3 h eq h eq w t 0 54 if h eq 1 25w t and distance to any other window > 4w t ; L H = 0 454 h eq h eq 2w t 0 54 in other cases, (with w t = sum of window widths on all walls) — in case of a wall not existing above the window, is given by: L H = 0 6 h eq L L h eq 1 / 3 . The flame length along axis is given by: — when L L 0 , L f = L L + h eq 2 if wall exists above window or if h eq 1 25w t ; Lf = L2L + L H – h eq 3 2 + h eq 2 if no wall exists above window or if h eq 1 25w t — when L L = 0 , then L f = 0 . The flame temperature at the window is given by [°K]: 520 - + T0 T w = --------------------------------------------------------L f w t -------------1 – 0 4725 Q (Eq. 4‐13) with L f w t Q 1 . The emissivity of flames at the window may be taken as f = 1 0 . The flame temperature along the axis is given by [°K]: L x w t T z = T w – T 0 1 – 0 4725 --------------+ T0 Q (Eq. 4‐14) with L x w t Q 1 and L x is the axis length from the window to the point where the calculation is made. The emissivity of flames may be taken as: f = 1 – e – 0 3df (Eq. 4‐15) where d f is the flame thickness [m]. The convective heat transfer coefficient is given by [W/m2K]: c = 4 67 1 d eq 0 4 Q A v 0 6 . page 62 (Eq. 4‐16) Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 4 E UROCODE 1 EN 1991-1-2 A NNEX B (13) If an awning or balcony is located at the level of the top of the window on its whole width for the wall above the window and h eq 1 25w t , the height and horizontal projection of the flame should be modified as follows: — the flame height L L given in eq. 4-12 is decreased by W a 1 + 2 — the horizontal projection of the flame given in (6), is increased by W a . Figure 4.14 Deflection of flame by balcony (from fig. B.3). With the same conditions for awning or balcony as mentioned in (13), in the case of no wall above the window or h eq 1 25w t , the height and horizontal projection of the flame should be modified as follows: — the flame height L L given in eq. 4-12 is decreased by W a — the horizontal projection of the flame L H , obtained in (6) with the above mentioned value of L L , is increased by W a . FORCED DRAUGHT. The rate of burning or the rate of heat release is given by [MW]: A f q f d Q = -----------------. F (Eq. 4‐17) The temperature of the fire compartment is given by [°K]:(1) T f = 1200 1 – e – 0 00288 + T 0 . (Eq. 4‐18) (1) There were errors in the equation B.19 of Annex B of the English version of the standard. These have been corrected in the BS EN 1991-1-2:2002. Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls page 63 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 4 E UROCODE 1 EN 1991-1-2 A NNEX B Figure 4.15 Flame dimensions, through or forced draught (from fig. B.4). The flame height (see Figure B.4) is given by: Q L L = 1 366 1 u 0 43 ---------- – h eq A (Eq. 4‐19) v where u m s is the wind speed, moisture content. The horizontal projection of flames is given by: L H = 0 605 u 2 h eq 0 22 L L + h eq . (Eq. 4‐20) The flame width is given by w f = w t + 0 4L H . The flame length along axis is given by L f = L2L + L2H 0 5 . The flame temperature at the window is given by [°K]: 520 T w = --------------------------------------------------------------- + T 0 Lf Av 1 – 0 3325 ------------------ Q (Eq. 4‐21) with L f A v Q 1 . The emissivity of flames at the window may be taken as f = 1 0 . The flame temperature along the axis is given by [°K]: Lx Av T z = T w – T 0 1 – 0 3325 -------------------+ T0 Q (Eq. 4‐22) where L x is the axis length from the window to the point where the calculation is made. The emissivity of flames may be taken as: f = 1 – e – 0 3df page 64 (Eq. 4‐23) Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 4 E UROCODE 1 EN 1991-1-2 A NNEX B Figure 4.16 Deflection of flame by awning (from fig. B.5). where d f is the flame thickness [m]. The convective heat transfer coefficient is given by [W/m2K]: u 0 6 Q c = 9 8 1 d eq 0 4 ------------------ + --------- . 17 5 A v 1 6 (Eq. 4‐24) Regarding the effects of balconies or awnings, see Figure B.5 (below), the flame trajectory, after being deflected horizontally by a balcony or awning, is the same as before, i.e. displaced outwards by the depth of the balcony, but with a flame length L f unchanged. 4.2 Verification tests EN1991‐1‐2_(B).XLS. 6.85 MB. Created: 6 February 2013. Last/Rel.-date: 3 June 2013. Sheets: — Splash — Annex B. EXAMPLE 4-V‐Section B.2 ‐ Conditions of use ‐ test 1 Given: Find the ratio D/W when: Case 1) there are windows in only one wall Case 2) there are windows on more than one wall Case 3) there is a core in the fire compartment. Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls page 65 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 4 E UROCODE 1 EN 1991-1-2 A NNEX B When Case 1) or 2) applies, assume that: – the width W 1 of the wall 1 (assumed to contain the greatest window area) is equal to 0,40 m – the width W 2 of the wall perpendicular to wall 1 in the fire compartment is equal to 0,25 m – the sum A v1 of windows areas on wall 1 is equal to 4,20 m2 – the total area A v of vertical openings on all walls is equal to 6,80 m2. When Case 3) applies, assume that: – the length L c and width W c of the core are equal to 5,00 m and 3,50 m respectively – the length W 1 and the width W 2 of the fire compartment are equal to 6,00 m and 6,50 m respectively. [Reference sheet: Annex B]‐[Cell‐Range: A75:Q75‐CommandButton]. Solution: Case 1). From eq. (B.1): W 25- = 0 625 . D W = -------2 = 0----------W1 0 40 Figure 4.17 PreCalculus Excel® form: procedure for a quick pre-calculation: Case 1). Case 2). From eq. (B.2): W A v1 0 25 4 20 D W = -------2 -------= ------------ ---------------- = 0 386 . W1 Av 0 40 6 80 Case 3). From eq. (B.3): W 2 – L c A v1 6 50 – 5 00 4 20 - = 0 371 . D W = -------------------------------- = -------------------------------------------------- W 1 – W c A v 6 00 – 3 50 6 80 Note page 66 All parts of an external wall that do not have the fire resistance (REI) required for the stability of the building should be classified as window areas. Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 4 E UROCODE 1 EN 1991-1-2 A NNEX B Using the PreCalculus Excel form, for the Case 2) we find: Figure 4.18 PreCalculus Excel form: procedure for a quick pre-calculation: Case 2). Finally, for the case 3), we find: Figure 4.19 PreCalculus Excel form: procedure for a quick pre-calculation: Case 3). Note The size of the fire compartment should not exceed 70 m in length, 18 m in width and 5 m in height. The flame temperature should be taken as uniform across the width and the thickness of the flame. example-end Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls page 67 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 4 E UROCODE 1 EN 1991-1-2 A NNEX B EXAMPLE 4-W‐ Sec. B.4.1, Characteristic of fire and flames: no awning or balcony ‐ test2 Given: Assume that: A f = 30 00 m 2 ; q f d = 500 MJ m 2 (taken from Annex E); h eq = 1 70 m ; A t = 112 00 m 2 ; A v = 6 80 m 2 and D/W = 0,625. Assuming no awning or balcony is located at the level of the top of the windows, find: – the rate of burning – the temperature of the fire compartment – the flame height, width and depth – the horizontal projection of flames – the flame temperature at the window – the flame temperature along the axis – the emissivity of flames – the convective heat transfer coefficient. [Reference sheet: Annex B]‐[Cell‐Range: A59:O59‐A264:O264 and A343:O343‐A502:O502]. Solution: No forced draught. “Opening factor” of the fire compartment: O = A v h eq A t = 6 80 1 70 112 = 0 0792 m 1 / 2 . Rate of burning or rate of heat release (eq. 4‐10): 0 036 1/2 – --------------h eq A f q f d O Q = min -----------------; 3 15 1 – e A v ------------ F DW 0 036 1/2 – ----------------- 30 500 1 70 0 0791 min ------------------- ; 3 15 1 – e 6 80 --------------- 1200 0 625 = min 12 5 ; 12 9 = 12 5 MW . Factor : = A f q f d A v A t = 30 500 6 80 112 543 5 MJ m 2 . Temperature of the fire compartment (eq. 4‐11): T f = 6000 1 – e – 0 1 O T f = 6000 1 – e – 0 1 0 0792 – 0 00286 O 1 – e + T0 – 0 00286 543 5 0 0791 1 – e + 293K T f = 6000 0 7171 0 2812 0 7887 + 273 955K + 293K = 1248K T f = 1248 – 273 = 975C . Internal gas density, say = 0 50 kg m 3 . Flame height (eq. 4‐12): 2/3 Q L L = max 0 ; h eq 2 37 --------------------------- – 1 A h g v g eq 2/3 12 5 L L = max 0 ; 1 70 2 37 ------------------------------------------------------------------------ – 1 = 2 056 m . 6 80 0 50 1 70 9 81 The flame width is the window width: say w t = 1 00 m . Flame depth: 2h eq 3 = 2 1 70 3 = 1 13 m . page 68 Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 4 E UROCODE 1 EN 1991-1-2 A NNEX B Horizontal projection of flames: Case a) ‐ Wall above the window and h eq 1 25w t : if h eq 1 25w t , L H = h eq 3 = 1 70 3 = 0 57 m . If h eq 1 25w t and distance to any other window > 4w t , L H = 0 3h eq h eq w t 0 54 = 0 3 1 70 1 70 1 00 0 54 = 0 68 m . In other cases: L H = 0 454h eq h eq 2w t 0 54 = 0 454 1 70 1 70 2 1 00 0 54 = 0 71 m . Flame length along axis (when L L 0 ): L f L L + 0 5h eq = 2 056 + 0 5 1 70 = 2 91 m . Check: 1 70 2 2 056 + 0 57 2 + ----------------- 9 2 86 m 2 h eq 2 2 1 70 2 L f = L L + L 1 = L L + L H + ------- = 2 056 + 0 68 + ------------------- = 2 94 m 9 9 2 96 m 2 1 70 2 056 + 0 71 2 + -----------------9 Mean value: L f = 2 86 + 2 94 + 2 96 3 = 2 92 m L L + 0 5h eq = 2 91 m (satisfactory). The flame temperature at the window is given by (eq. 4‐13): 520 - + T0 T w = --------------------------------------------------------L f w t -------------1 – 0 4725 Q 520 T w = ---------------------------------------------------------------------- + 293K = 877K = 877 – 273 = 604C . 2-------------------------- 91 1 00- 1 – 0 4725 12 5 with L f w t Q = 2 91 1 00 12 5 = 0 23 1 (case applicable). Case b) ‐ No wall above the window or h eq 1 25w t : L H = 0 6h eq L L h eq 1 / 3 = 0 6 1 70 2 056 1 70 1 / 3 = 1 09 m . L 1 0 5h eq = 0 5 1 70 = 0 85 m . Lf = L2L + L H – h eq 3 2 + 0 5h eq = 2 056 2 + 1 09 – 1 70 3 2 + 0 5 1 70 = 2 97 m . The flame temperature at the window is given by (eq. 4‐13): 520 - + T0 T w = --------------------------------------------------------L f w t 1 – 0 4725 -------------- Q 520 T w = ---------------------------------------------------------------------- + 293K = 879K = 879 – 273 = 606C . 2-------------------------- 97 1 00- 1 – 0 4725 12 5 with L f w t Q = 2 91 1 00 12 5 = 0 23 1 (case applicable). The emissivity of flames at the window may be taken as f = 1 0 . Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls page 69 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 4 E UROCODE 1 EN 1991-1-2 A NNEX B Figure 4.20 Plots eq. (B.15). The flame temperature along the axis is given by (eq. 4‐14): L x w t T z = T w – T 0 1 – 0 4725 --------------+ T0 . Q L x 1 00 For case a: T z = 877 – 293 1 – 0 4725 --------------------+ 293 . 12 5 page 70 Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 4 E UROCODE 1 EN 1991-1-2 A NNEX B For (say) L x = 1 45 m , we get (case a): 1 45 1 00 T z = 877 – 293 1 – 0 4725 ---------------------------- + 293 = 845K = 845 – 273 = 572C . 12 5 L x 1 00 For case b: T z = 877 – 293 1 – 0 4725 --------------------+ 293 . 12 5 For (say) L x = 1 49 m , we get (case b): 1 49 1 00 T z = 879 – 293 1 – 0 4725 ---------------------------- + 293 = 846K = 846 – 273 = 573C . 12 5 Flame thickness (say): d f = 1 00 m , geometrical characteristic of an external structural element (diameter or side): d eq = 0 70 m . Emissivity of flames (eq. 4‐15): f = 1 – e –0 3df = 1 – e –0 3 1 00 = 0 26 . Convective heat transfer coefficient (eq. 4‐16): c = 4 67 1 d eq 0 4 Q A v 0 6 = 4 67 1 0 70 0 4 12 5 6 80 0 6 = 7 8 W m 2 K . Forced draught. Rate of burning or rate of heat release (eq. 4‐17): A f q f d 30 00 500 Q = -----------------= ---------------------------- = 12 50 MW . F 1200 Temperature of the fire compartment (eq. 4‐18): T f = 1200 1 – e – 0 00288 + T 0 = 1200 1 – e – 0 00288 543 5 + 293 = 1242K T f = 1242 – 273 = 969C . Flame height (eq. 4‐19), with wind speed equal to (say) u = 6 00 m s : Q 12 5 L L = 1 366 1 u 0 43 ---------- – h eq = 1 366 1 6 00 0 43 ---------------- – 1 70 = 1 33 m . A 6 80 v The horizontal projection of flames is given by (eq. 4‐20): L H = 0 605 u 2 h eq 0 22 L L + h eq = 0 605 6 00 2 1 70 0 22 1 33 + 1 70 = 3 59 m . The flame width is given by: w f = w t + 0 4L H = 1 00 + 0 4 3 59 = 2 44 m . The flame length along axis is given by: L f = L L2 + L H2 = 1 33 2 + 3 59 2 = 3 83 m . The flame temperature at the window is given by (eq. 4‐21): 520 520 T w = -------------------------------------------------------------- + T 0 = -------------------------------------------------------------------------- + 293 = 1001K A L 3 83 6 80 f v 1 – 0 3325 -------------------------------1 – 0 3325 ------------------- Q 12 5 T w = 1001 – 273 = 728C , with L f A v Q = 3 83 6 80 12 5 = 0 8 1 (case applicable). The emissivity of flames at the window may be taken as f = 1 00 . The flame temperature along the axis is given by (eq. 4‐22): Lx Av T z = T w – T 0 1 – 0 3325 -------------------+ T0 Q Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls page 71 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 4 E UROCODE 1 EN 1991-1-2 A NNEX B Figure 4.21 Plots eq. (B.25). 2 50 6 80 T z = 1001 – 293 1 – 0 3325 -------------------------------- + 293 = 878K = 878 – 273 = 605C , 12 5 with (say) L x = 2 50 m . The convective heat transfer coefficient is given by (eq. 4‐24): Q + -------u - 0 6 c = 9 8 1 d eq 0 4 ----------------- 17 5 A v 1 6 12 5 - + 6---------- 00- 0 6 = 25 4 W m 2 K . c = 9 8 1 0 70 0 4 ------------------------------- 17 5 6 80 1 6 example-end EXAMPLE 4-X‐ Sec. B.4.1, Characteristic of fire and flames: with awning or balcony ‐ test3 Given: Consider the same assumptions in the example above. Find the flame height L L and the horizontal projection L H of the flame if an awning or balcony (with horizontal projection: W a = 0 50 m ) is located at the level of the top of the window on its whole width. [Reference sheet: Annex B]‐[Cell‐Range: A267:O267‐A340:O340]. Solution: Case a), wall above and h eq 1 25w t . The flame height L L given in eq. 4‐12 is decreased by W a 1 + 2 : L*L = L L – W a 1 + 2 = 2 06 – 0 50 1 + 2 = 0 85 m . The horizontal projection of the flame L H given in (6), is increased by W a : page 72 Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 4 E UROCODE 1 EN 1991-1-2 A NNEX B L*H = L H + W a = 0 57 + 0 50 = 1 07 m * L H = L H + W a = 0 68 + 0 50 = 1 18 m * L H = L H + W a = 0 71 + 0 50 = 1 21 m Case b), no wall above or h eq 1 25w t . The flame height L L given in (3) is decreased by W a : L*L = L L – W a = 2 06 – 0 50 = 1 56 m . The horizontal projection of the flame L H given in (6), with the above mentioned value of L*L , is increased by W a : L H = 0 6h eq L L* h eq 1 / 3 * L L = 1 56 m L H = 0 6h eq L*L h eq 1 / 3 = 0 6 1 70 1 56 1 70 1 / 3 = 0 99 m . L*H = W a + L H = 0 50 + 0 99 = 1 49 m . example-end 4.3 References [Section 4] BS EN 1991-1-2. Eurocode 1: Actions on structures – Part 1-2: General actions – Actions on structures exposed to fire. 26 November 2002. EN 1991-1-2:2002/AC:2013. Eurocode 1: Actions on structures - Part 1-2: General actions - Actions on structures exposed to fire. CEN Brussels, February 2013. EN 1991-1-2 (2002) (English): Eurocode 1: Actions on structures - Part 1-2: General actions - Actions on structures exposed to fire [Authority: The European Union Per Regulation 305/2011, Directive 98/34/EC, Directive 2004/18/EC]. European Committee for Standardisation. Topic: User’s Manual/Verification tests - EN1991-1-2_(b).xls page 73 (This page intentionally left blank) Section 5 Eurocode 1 EN 1991-1-2 Annex C, Annex E 5.1 ANNEX C: Localised fires T he thermal action of a localised fire can be assessed by using the expression given in this annex. Differences have to be made regarding the relative height of the flame to the ceiling. The heat flux from a localised fire to a structural element should be calculated with expression (3.1): · · · h net = h net c + h net r = c g – m + m f r + 273 4 – m + 273 4 (Eq. 5‐25) and based on a configuration factor established according to annex G. The flame lengths L f of a localised fire (see Figure C.1) is given by: L f = – 1 02D + 0 0148Q 2 / 5 . (Eq. 5‐26) Figure 5.22 From figure C.1. Topic: User’s Manual/Verification tests - EN1991-1-2_(c).xls page 75 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 5 E UROCODE 1 EN 1991-1-2 A NNEX C, A NNEX E When the flame is not impacting the ceiling of a compartment ( L f H ; see Figure C.1) or in case of fire in open air, the temperature z in the plume along the symmetrical vertical flame axis is given by: z = 20 + 0 25Q c2 / 3 z – z 0 – 5 / 3 900C (Eq. 5‐27) where: • D is the diameter of the fire [m], see Figure C.1 • Q is the rate of heat release [W] of the fire according to E.4 • Q c is the convective part of the rate of heat release [W], with Q c = 0 8Q • z is the height [m] along the flame axis, see Figure C.1 • H is the distance [m] between the fire source and the ceiling, see Figure C.1. The virtual origin z 0 of the axis is given by: z 0 = – 1 02D + 0 00524Q 2 / 5 . (Eq. 5‐28) When the flame is impacting the ceiling ( L f H ; see Figure C.2) the heat flux · h W m 2 received by the fire exposed unit surface area at the level of the ceiling is given by: · h = 100000 if y 0 30 · h = 136300 to 121000y if 0 30 y 1 0 · h = 15000y – 3 7 if y 1 0 (Eq. 5‐29) where: Figure 5.23 From figure C.2. page 76 Topic: User’s Manual/Verification tests - EN1991-1-2_(c).xls S ECTION 5 • • • E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-2 A NNEX C, A NNEX E r + H + zy is a parameter given by: y = -------------------------L h + H + z r is horizontal distance [m] between the vertical axis of the fire and the point along the ceiling where the thermal flux is calculated, see Figure C.2 H is the distance [m] between the fire source and the ceiling, see Figure C.2. L h is the horizontal flame length (see Figure C.2) given by the following relation: L h = 2 9H Q*H 0 33 – H (Eq. 5‐30) Q*H is a non-dimensional rate of heat release given by: Q . Q*H = -------------------------------------6 1 11 10 H 2 5 (Eq. 5‐31) z is the vertical position of the virtual heat source [m] and is given by: z = 2 4D Q*D 2 / 5 – Q *D 2 / 3 when Q*D 1 0 z = 2 4D 1 0 – Q*D 2 / 3 when Q*D 1 0 . (Eq. 5‐32) where: Q . Q *D = -------------------------------------6 1 11 10 D 2 5 The net heat flux h· net received by the fire exposed unit surface area at the level of the ceiling, is given by: · · h net = h – c m – 20 – m f m + 273 4 – 293 4 (Eq. 5‐33) (see expressions 3.2, 3.3). The rules set up to this point are valid if the following conditions are met: the diameter of the fire is limited by D < 10 m; the rate of heat release of the fire is limited by Q < 50 MW. In case of several separate localised fires, expression (C.4, see eq. 5-29) may be used in order to get the different individual heat fluxes h· 1 , h· 2 ,... received by the fire exposed unit surface area at the level of the ceiling. The total heat flux may be taken as: · · · h tot = h 1 + h 2 + 10 5 W m 2 . Topic: User’s Manual/Verification tests - EN1991-1-2_(c).xls (Eq. 5‐34) page 77 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 5 E UROCODE 1 EN 1991-1-2 A NNEX C, A NNEX E 5.2 ANNEX E: fire load densities The fire load density used in calculations should be a design value, either based on measurements or in special cases based on fire resistance requirements given in national regulations. The design value may be determined: — from a national fire load classification of occupancies; and/or — specific for an individual project by performing a fire load survey. The design value of the fire load q f d is defined as: q f d MJ m 2 = q f k m q1 q2 n (Eq. 5‐35) where: • q f k is the characteristic fire load density per unit floor area [MJ/m²] (see f.i. Table E.4) • m is the combustion factor equal to 0,8 • q1 is a factor taking into account the fire activation risk due to the size of the compartment (see Table E.1) • q2 is a factor taking into account the fire activation risk due to the type of occupancy (see Table E.1) Compartment floor area Af [m2] Danger of Fire Activation q1 Danger of Fire Activation q2 25 1,10 0,78 Art gallery, museum, swimming pool 250 1,50 1,00 Offices, residence, hotel, paper industry 2500 1,90 1,22 Manufactory for machinery & engines 5000 2,00 1,44 Chemical laboratory, painting workshop 10000 2,13 1,66 Manufactory of fireworks or paints Table 5.6 • Examples of Occupancies From table E.1 - Factors q1 , q2 . n is a factor taking into account the different active fire fighting measures i (sprinkler, detection, automatic alarm transmission, firemen,…). These active measures are generally imposed for life safety reason (see Table E.2 and clauses (4) and (5)): n = 10 ni . i=1 For the normal fire fighting measures, which should almost always be present, such as the safe access routes, fire fighting devices, and smoke exhaust systems in staircases, the ni values of Table E.2 should be taken as 1,0. However, if page 78 Topic: User’s Manual/Verification tests - EN1991-1-2_(c).xls S ECTION 5 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-2 A NNEX C, A NNEX E these fire fighting measures have not been foreseen, the corresponding ni value should be taken as 1,5. If staircases are put under overpressure in case of fire alarm, the factor n8 of Table E.2 may be taken as 0,9. CHARACTERISTIC FIRE LOAD. It is defined as: Q fi k = M k j H ui i = Q (Eq. 5‐36) fi k j where: • M k j is the amount of combustible material [kg], according to (3) and (4) • H ui is the net calorific value [MJ/kg], see (E.2.4) • i is the optional factor for assessing protected fire loads, see (E.2.3). CHARACTERISTIC FIRE LOAD DENSITY. It is defined as: Q fi k q f k = ---------Af (Eq. 5‐37) where A f is the floor area of the fire compartment or reference space. NET CALORIFIC VALUES. Net calorific values should be determined according to EN ISO 1716:2002. The moisture content of materials may be taken into account as follows: H u = H u0 1 – 0 01u – 0 025u (Eq. 5‐38) where: Material wood • u is the moisture content expressed as percentage of dry weight • H u0 is the net calorific value of dry materials. Hu Material Hu Material Hu 17,5 Alcohols 30 Polyvinylchloride, PVC (plastic) 20 cellulosic materials 20 Fuels 45 Bitumen, asphalt 40 carbon 30 Pure hydrocarbons plastics 40 Leather 20 Paraffin series 50 ABS (plastic) 35 Linoleum 20 Olefin series 45 Polyester (plastic) 30 Rubber tyre 30 Aromatic series 40 Polyisocyanerat and polyurethane (plastics) 25 Table 5.7 Net calorific values H u [MJ/kg] of combustible materials for calculation of fire loads. Topic: User’s Manual/Verification tests - EN1991-1-2_(c).xls page 79 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 5 E UROCODE 1 EN 1991-1-2 A NNEX C, A NNEX E RATE OF HEAT RELEASE Q. The growing phase may be defined by the expression: t 2 Q = 10 6 ---- t (Eq. 5‐39) where: • Q is the rate of heat release [W] • t is the time [s] • t is the time needed to reach a rate of heat release of 1 MW. The parameter t and the maximum rate of heat release RHR f , for different occupancies, are given in Table E.5. These values according to Table E.5 are valid in case of a factor q2 = 1 0 (see table E.1). Fire growth rate t [s] RHRf [kW/m2] Dwelling Medium 300 250 Hospital (room) Medium 300 250 Hotel (room) Medium 300 250 Library Fast 150 500 Office Medium 300 250 Classroom of a school Medium 300 250 Shopping centre Fast 150 250 Theatre (cinema) Fast 150 500 Transport (public space) Slow 600 250 Occupancy Table 5.8 Fire growth rate and RHRf for different occupancies (from Table E.5). For an ultra-fast fire spread, t corresponds to 75 s. The growing phase is limited by an horizontal plateau corresponding to the stationary state and to a value of Q given by RHR f A fi where: — A fi is the maximum area of the fire m 2 which is the fire compartment in case of uniformly distributed fire load but which may be smaller in case of a localised fire — RHR f is the maximum rate of heat release produced by 1 m 2 of fire in case of fuel controlled conditions kW m 2 (see Table E.5). The horizontal plateau is limited by the decay phase which starts when 70% of the total fire load has been consumed. The decay phase may be assumed to be a linear decrease starting when 70% of the fire load has been burnt and completed when the fire load has been completely burnt. If the fire is ventilation controlled, this plateau level has to be reduced following the available oxygen content, either automatically in case of the use of a computer program based on one zone model or by the simplified expression: page 80 Topic: User’s Manual/Verification tests - EN1991-1-2_(c).xls S ECTION 5 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-2 A NNEX C, A NNEX E Q max MW = 0 10 m H u A v h eq (Eq. 5‐40) where: • m = 0 8 is the combustion factor • H u is the net calorific value of wood with H u = 17 5 MJ kg • A v the opening area m 2 • h eq is the mean height of the openings [m]. When the maximum level of the rate of heat release is reduced in case of ventilation controlled condition, the curve of the rate of heat release has to be extended to correspond to the available energy given by the fire load. If the curve is not extended, it is then assumed that there is external burning, which induces a lower gas temperature in the compartment. 5.3 Verification tests EN1991‐1‐2_(C).XLS. 7.20 MB. Created: 12 February 2013. Last/Rel.-date: 12 February 2013. Sheets: — Splash — Annex C — Annex E. EXAMPLE 5-Y‐ Localised fires ‐ test 1 Given: The steel temperature of a beam (IPE550) has to be verified. It is part of an underground car park below a building. The beams of the car park are accomplished without any use of fire protection material. The most severe fire scenario is a burning car in the middle of the beam. Find the net heat flux (vs m @ generic time t ): h· net = h· net Q ; m Q = Qt . Assumptions: diameter of the fire: D = 4,00 m; rate of heat release Q = Q(t) = 5 MW (mean reference value for the calculations @ generic time t ); distance between the fire source and the ceiling (beam): H = 3,10 m; configuration factor = 1 ; surface emissivity of the member: m = 0 70 ; emissivity of the fire: f = 1 0 ; surface temperature(1) (mean value) of the member (beam), say: m = 150C ; coefficient of heat transfer by convection: c = 25 W m 2 K . [Reference sheet: Annex C]‐[Cell‐Range: A1:O1‐A81:O81]. (1) The surface temperature m results from the temperature analysis of the member according to the fire design Parts 1-2 of prEN 1992 to prEN 1992 to prEN 1996 and prEN 1999, as relevant. Topic: User’s Manual/Verification tests - EN1991-1-2_(c).xls page 81 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 5 E UROCODE 1 EN 1991-1-2 A NNEX C, A NNEX E Solution: The natural fire model of a localised fire is used. Flame length: 6 2/5 L f = – 1 02D + 0 0148Q 2 / 5 = – 1 02 4 00 + 0 0148 5 10 = 2 997 m H , the flame is not impacting the ceiling (lower flange of a steel beam). Virtual origin of the axis: 6 2/5 z 0 = – 1 02D + 0 00524Q 2 / 5 = – 1 02 4 00 + 0 00524 5 10 = – 1 57 m . 6 6 Convective part of the rate of heat release: Q c = 0 8Q = 0 8 5 10 = 4 10 W . Height [m] along the flame axis, see Figure C.1 (immediately below the lower flange of the beam): z = 2 98 m . Temperature z in the plume along the symmetrical vertical flame axis: 6 2/3 z = 20 + 0 25Q c2 / 3 z – z 0 – 5 / 3 = 20 + 0 25 4 10 2 98 + 1 57 – 5 / 3 = 524C 900C . The net heat flux (vs m @ generic time t ) is calculated according to Section 3.1 of EN 1991‐1‐2 (the flame is not impacting the beam): · h = – + + 273 4 – + 273 4 , net c z m m f z m 5 67· h net m ; t = 25 524 – m + 1 0 70 1 0 ---------- 524 + 273 4 – m + 273 4 . 10 8 For (say) m = 150C , we get: 5 67 · - 524 + 273 4 – 150 + 273 4 = 24094 W m 2 . h net t = 25 524 – 150 + 1 0 70 1 0 ----------10 8 example-end EXAMPLE 5-Z‐ Localised fires ‐ test 2 Given: Same fire scenario of the first example. The natural fire model of a localised fire is used. Find the net heat flux (vs m @ generic time t ): h· net = h· net Q ; m Q = Qt . Assumptions: diameter of the fire: D = 2,00 m; rate of heat release Q = Q(t) = 5 MW (mean reference value for the calculations @ generic time t ); distance between the fire source and the ceiling (beam): H = 2,70 m; configuration factor = 1 ; surface emissivity of the member: m = 0 70 ; emissivity of the fire: f = 1 0 ; surface temperature (mean value) of the member (beam): m = 650C ; coefficient of heat transfer by convection: c = 25 W m 2 K . [Reference sheet: Annex C]‐[Cell‐Range: A85:O85‐A173:O173]. Solution: Flame length: 6 2/5 L f = – 1 02D + 0 0148Q 2 / 5 = – 1 02 2 00 + 0 0148 5 10 = 5 037 m H , the flame is impacting the ceiling (see Figure C.2). page 82 Topic: User’s Manual/Verification tests - EN1991-1-2_(c).xls S ECTION 5 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-2 A NNEX C, A NNEX E Horizontal distance between the vertical axis of the fire and the point along the ceiling (steel beam) where the thermal flux is calculated, see Figure C.2: z = 0 (assumption). Non‐dimensional rate of heat release: Q 5000000 Q*H = -------------------------------------= -------------------------------------------------- = 0 376 . 6 6 2 5 1 11 10 H 1 11 10 2 70 2 5 Horizontal flame length (see Figure C.2): L h = 2 9H Q *H 0 33 – H = 2 9 2 70 0 376 0 33 – 2 70 = 2 97 m . Vertical position z of the virtual heat source ( Q*D 1 ): 5000000 Q Q*D = -------------------------------------= -------------------------------------------------- = 0 796 1 6 6 2 5 1 11 10 2 00 2 5 1 11 10 D z = 2 4D Q*D 2 / 5 – Q *D 2 / 3 = 2 4 2 00 0 796 2 / 5 – 0 796 2 / 3 = 0 26 m . Parameter: 0 + 2 70 + 0 26 · r + H + z y = --------------------------- = ------------------------------------------------ 0 50 , with 0 30 y 1 : h = 136300 to 121000y . 2 97 + 2 70 + 0 26 L h + H + z Therefore: h· = 136300 W m 2 to 121000 0 50 = 60500 W m 2 . Net heat flux received (vs m @ generic time t ) by the fire exposed unit surface area at the level of the ceiling (steel beam): · · h = h – – 20 – + 273 4 – 293 4 . net c m m f m 5 67· · h net m ; t = h – 25 m – 20 – 1 0 7 1 0 ---------- m + 273 4 – 293 4 . 10 8 For say m = 650C , we get: 5 67· · · h net t = h t – 25 650 – 20 – 1 0 7 1 0 ---------- 650 + 273 4 – 293 4 = h – 44264 W m 2 10 8 · h net t = 136300 to 60500 – 44264 = 92036 to 16236 W m 2 . example-end EXAMPLE 5-AA‐ Fire load densities ‐ test 3 Given: The gas temperature of a fully engulfed fire in an office has to be determined. A natural fire model is chosen for the calculation of the gas temperature. For fires with a flash‐over, the method of the compartment fires can be used. A simple calculation method for a parametric temperature‐time curve is given in Annex A of EN 1991‐1‐2. Find the design value q f d of the fire load density. Assumptions: floor area A f = 135 m 2 ; total area of vertical openings: A v = 27 m 2 . The fire load consisted of 20% plastics, 11% paper and 69% wood, so it consisted mainly of cellulosic material. Therefore the combustion factor is: m = 0 8 . [Reference sheet: Annex E]‐[Cell‐Range: A1:O1‐A169:O169]. Topic: User’s Manual/Verification tests - EN1991-1-2_(c).xls page 83 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 5 E UROCODE 1 EN 1991-1-2 A NNEX C, A NNEX E Solution: For the determination of the fire load density the Annex E of EN 1991‐1‐2 offers a calculation model. The design value of the load density may either be given from a national fire load classification of occupancies and/or specific for an individual project by performing a fire load evaluation. At this example, the second method is chosen. From Table E.1 for compartment floor area up to 250 m 2 : q1 = 1 50 , q2 = 1 00 . From table E.1 and clauses (4) and (5): n1 = n2 = n3 = 1 0 , n4 = 0 73 , n5 = 0 87 , n6 = 1 0 , n7 = 0 78 , n8 = n9 = n10 = 1 0 . Therefore, we get: n = 10 ni = 1 0 1 0 1 0 0 73 0 87 1 0 0 78 1 0 1 0 1 0 = 0 495 . i=1 Amount of combustible material [kg], according to (3) and (4): Material No. Mki [kg] Huoi [MJ/kg] ui [%] i i=1 2000 19,5 9 1,0 i=2 3200 20 5 1,0 i=3 1000 20 5 1,0 Table 5.9 Amount and characteristics of combustible materials. Net calorific values with u = moisture content (% of dry weight): H u1 = H uo1 1 – 0 01u 1 – 0 025u 1 = 19 5 1 – 0 01 9 – 0 025 9 17 5 H u2 = H uo2 1 – 0 01u 2 – 0 025u 2 = 20 1 – 0 01 5 – 0 025 5 18 9 H u3 = H uo3 1 – 0 01u 3 – 0 025u 3 = 20 1 – 0 01 5 – 0 025 5 18 9 Characteristic fire load: Q fi k = M Q fi k = Q k i H ui i = fi k j Q fi k j = 2000 17 5 1 0 + 3200 18 9 1 0 + 1000 18 9 1 0 = 35000 + 60480 + 18900 = 114380 MJ . Actual compartment floor area: A f = 135 m 2 . Characteristic fire load density q f k per unit area: q f k = Q fi k A f = 114380 135 847 MJ m 2 . Design value of the fire load: q f d = q f k m q1 q2 n = 847 0 8 1 50 1 00 0 495 = 503 MJ m 2 . example-end EXAMPLE 5-AB‐ Rate of heat release Q ‐ test 4 Given: page 84 Plot the growing phase of the rate Q of the heat release in case of uniformly distributed fire load. Occupancy: office with a medium fire growth rate and max rate of heat release Topic: User’s Manual/Verification tests - EN1991-1-2_(c).xls S ECTION 5 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-2 A NNEX C, A NNEX E Figure 5.24 Growing phase limited by the horizontal plateau: the fire is fuel controlled. RHR f = 250 kW m 2 (factor q2 = 1 0 ). Maximum area of the fire compartment equal to A fi = 70 m 2 . Opening area A v = 10 m 2 ; mean height of the openings: h eq = 1 80 m . Find the time at which the growing phase is limited by the horizontal plateau corresponding to the stationary state. [Reference sheet: Annex E]‐[Cell‐Range: A174:O174‐A309:O309]. Solution: From Table E.5 (“Fire growth rate and RHRf for different occupancies”): t = 300 s , RHR f = 250 kW m 2 . The growing phase may be defined by the expression: t 2 Q = 10 6 ---- . t Case a): the fire is fuel controlled. The growing phase is limited by an horizontal plateau corresponding to the stationary state and to a value of Q given by: Q max = RHR f A fi = 250 70 = 17500 kW = 17 5 MW . Horizontal plateau starts at (see plot above): 1000 RHR f A fi 1000 250 70- = 1255 s = 21 min . t = t ----------------------------------------------- = 300 ---------------------------------------6 6 10 10 Topic: User’s Manual/Verification tests - EN1991-1-2_(c).xls page 85 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 5 E UROCODE 1 EN 1991-1-2 A NNEX C, A NNEX E Figure 5.25 Growing phase limited by the horizontal plateau: the fire is ventilation controlled. The horizontal plateau is limited by the decay phase which starts when 70% of the total fire load has been consumed. The decay phase may be assumed to be a linear decrease starting when 70% of the fire load has been burnt and completed when the fire load has been completely burnt. Case b): the fire is ventilation controlled. In this case the plateau level has to be reduced following the available oxygen content, either automatically in case of the use of a computer program based on one zone model or by the simplified expression E.6 given in Annex A of EN 1991‐1‐2. At this example, the second method is chosen: Q max MW = 0 10 m H u A v h eq Q max MW = 0 10 0 8 17 5 10 1 80 = 18 78 MW . Horizontal plateau starts at (see plot above): 1000 Q max kW 1000 18780- = 1300 s = 22 min . t = t --------------------------------------------- = 300 ---------------------------------6 6 10 10 When the maximum level of the rate of heat release is reduced in case of ventilation controlled condition, the curve of the rate of heat release has to be extended to correspond to the available energy given by the fire load. If the curve is not extended, it is then page 86 Topic: User’s Manual/Verification tests - EN1991-1-2_(c).xls S ECTION 5 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-2 A NNEX C, A NNEX E assumed that there is external burning, which induces a lower gas temperature in the compartment. example-end 5.4 References [Section 5] BS EN 1991-1-2. Eurocode 1: Actions on structures – Part 1-2: General actions – Actions on structures exposed to fire. 26 November 2002. ECSC Project, Development of design rules for steel structures subjected to natural fires in CLOSED CAR PARKS, CEC agreement 210-AA/211/318/518/620/933, Brussels, June 1996. EN 1991-1-2:2002/AC:2013. Eurocode 1: Actions on structures - Part 1-2: General actions - Actions on structures exposed to fire. CEN Brussels, February 2013. EN 1991-1-2 (2002) (English): Eurocode 1: Actions on structures - Part 1-2: General actions - Actions on structures exposed to fire [Authority: The European Union Per Regulation 305/2011, Directive 98/34/EC, Directive 2004/18/EC]. European Committee for Standardisation. Example to EN 1991 Part 1-2: Compartment fire. PART 5a: Worked examples, 2005. P. Schaumann, T. Trautmann. University of Hannover – Institute for Steel Construction, Hannover, Germany. Topic: User’s Manual/Verification tests - EN1991-1-2_(c).xls page 87 (This page intentionally left blank) Section 6 Eurocode 1 EN 1991-1-2 Annex F, Annex G, Sec. B.5 Annex B 6.1 ANNEX F: Equivalent time of fire exposure T he following approach may be used where the design of members is based on tabulated data or other simplified rules, related to the standard fire exposure. The method given in this annex is material dependent. It is not applicable to composite steel and concrete or timber constructions. The concept of an equivalent period of fire exposure has been used for many years to quantify a real fire exposure (based on physical parameters) with an equivalent period of heating in the standard furnace test. The basic concept relates the maximum temperature in a natural fire to the time taken to reach the same temperature in a standard furnace test. The concept has been derived largely from tests on protected steel members although it has been extended to incorporate reinforced concrete members. If fire load densities are specified without specific consideration of the combustion behaviour (see annex E) then this approach should be limited to fire compartments with mainly cellulosic type fire loads. The equivalent time of standard fire exposure is defined by t e d min : t e d = q f d k b w f k c (Eq. 6‐41) where: • q f d is the design fire load density according to annex E • k b is the conversion factor according to (4) • w f is the ventilation factor according to (5) • k c is the correction factor function of the material composing structural cross-sections and defined in Table F.1. Where no detailed assessment of the thermal properties of the enclosure is made, the conversion factor k b may be taken as: Topic: User’s Manual/Verification tests - EN1991-1-2_(d).xls page 89 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 6 E UROCODE 1 EN 1991-1-2 A NNEX F, A NNEX G, S EC . B.5 A NNEX B k b = 0 07 min m 2 MJ when q f d is given in MJ m 2 . otherwise k b may be related to the thermal property b = according to Table F.2. Cross-section material Correction factor kc Reinforced concrete 1,0 Protected steel 1,0 Not protected steel Table 6.10 c of the enclosure 1,37 x O From Table F.1 - Correction factor k c in order to cover various materials (O is the opening factor defined in Annex A). For determining “b” for multiple layers of material or different materials in walls, floor, ceiling, see annex A (5) and (6). c [J/m2s1/2K] b = kb [min.m2/MJ] b > 2500 0,04 720 < b < 2500 0,055 b < 720 0,07 Table 6.11 From Table F.2 - Conversion factor k b depending on the thermal properties of the enclosure. The ventilation factor w f [-] may be calculated as: 90 0 4 – v 4 6 0 0 3 w f = --------- 0 62 + ------------------------------------- 0 5 H 1 + bv h (Eq. 6‐42) where: • v = A v A f is the area of vertical openings in the facade A v related to the floor area of the compartment A f where the limit 0 025 v 0 25 should be observed • h = A h A f is the area of horizontal openings in the roof A h related to the floor area of the compartment A f • b v = 12 5 1 + 10 v – v2 10 0 • H the height of the fire compartment [m]. It shall be verified that: t e d t fi d where t fi d is the design value of the standard fire resistance of the members, assessed according to the fire Parts of prEN 1992 to prEN 1996 and prEN 1999. page 90 Topic: User’s Manual/Verification tests - EN1991-1-2_(d).xls S ECTION 6 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-2 A NNEX F, A NNEX G, S EC . B.5 A NNEX B 6.2 ANNEX G: configuration factor The configuration factor is defined in EN 1991-1-2 Section 1.5.4.1 and measures the fraction of the total radiative heat leaving a given radiating surface that arrives at a given receiving surface. Its value depends on the size of the radiating surface, on the distance from the radiating surface to the receiving surface and on their relative orientation. EXTERNAL MEMBERS. For the calculation of temperatures in external members, all radiating surfaces may be assumed to be rectangular in shape. They comprise the windows and other openings in fire compartment walls and the equivalent rectangular surfaces of flames, see annex B. In calculating the configuration factor for a given situation, a rectangular envelope should first be drawn around the cross-section of the member receiving the radiative heat transfer, as indicated in Figure G.2 (this accounts for the shadow effect in an approximate way). The value of should then be determined for the mid-point P of each face of this rectangle. f,4 f,2 f,1 f,3 Figure 6.26 From Figure G.2 - Envelope of receiving surfaces. The configuration factor for each receiving surface should be determined as the sum of the contributions from each of the zones on the radiating surface (normally four) that are visible from the point P on the receiving surface, as indicated in Figures G.3 and G.4. These zones should be defined relative to the point X where a horizontal line perpendicular to the receiving surface meets the plane containing the radiating surface. No contribution should be taken from zones that are not visible from the point P. The contribution of each zone should be determined as follows: — receiving surface parallel to radiating surface — receiving surface perpendicular to radiating surface Topic: User’s Manual/Verification tests - EN1991-1-2_(d).xls page 91 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 6 E UROCODE 1 EN 1991-1-2 A NNEX F, A NNEX G, S EC . B.5 A NNEX B — receiving surface in a plane at an angle to the radiating surface. Receiving surface parallel to radiating surface: 1 a b b a - arc tan ------------------------ + ------------------------ = ------ ----------------------- arc tan ------------------------. 2 1 + a 2 0 5 1 + a 2 0 5 1 + b 2 0 5 1 + b 2 0 5 (Eq. 6‐43) Receiving surface perpendicular to radiating surface: 1 a 1 = ------ arc tan a – ------------------------ arc tan ------------------------. 2 1 + b 2 0 5 1 + b 2 0 5 (Eq. 6‐44) Receiving surface in a plane at an angle to the radiating surface: 1 a 1 – b cos = ------ arc tan a – -------------------------------------------------------------------------------------------------- arc tan + 2 1 + b 2 – 2b cos 0 5 1 + b 2 – 2b cos 0 5 1 acos b – cos cos - arc tan ----------------------------------- + arc tan ----------------------------------- . + ------ ---------------------------------- a 2 + sin2 0 5 a 2 + sin2 0 5 2 a 2 + sin2 0 5 (Eq. 6‐45) f,1 f,3 Figure 6.27 From Figures G.3 and G.4 - Receiving surface in a plane parallel (perpendicular) to that of the radiating surface. page 92 Topic: User’s Manual/Verification tests - EN1991-1-2_(d).xls S ECTION 6 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-2 A NNEX F, A NNEX G, S EC . B.5 A NNEX B 6.3 ANNEX B, Section B.5: Overall configuration factors The overall configuration factor of a member for radiative heat transfer from an opening should be determined from: C 1 f 1 + C 2 f 2 d 1 + C 3 f 3 + C 4 f 4 d 2 f = ----------------------------------------------------------------------------------------------------------------- C1 + C2 d1 + C3 + C4 d2 (Eq. 6‐46) where: • f i is the config. factor of member face “i” for that opening, see annex G • d i is the cross-sectional dimension of member face “i” • C i is the protection coefficient of member face “i” as follows: C i = 0 for a protected face; C i = 1 for an unprotected face. The configuration factor f i for a member face from which the opening is not visible should be taken as zero. The overall configuration factor z of a member for radiative heat transfer from a flame should be determined from: C 1 z 1 + C 2 z 2 d 1 + C 3 z 3 + C 4 z 4 d 2 z = ------------------------------------------------------------------------------------------------------------------- C1 + C2 d1 + C3 + C4 d2 (Eq. 6‐47) where z i is the configuration factor of member face “i” for that flame, see annex G. The configuration factors z i of individual member faces for radiative heat transfer from flames may be based on equivalent rectangular flame dimensions. The dimensions and locations of equivalent rectangles representing the front and sides of a flame for this purpose should be determined as given in annex G. For all other purposes, the flame dimensions given in B.4 of this annex should be used. 6.4 Verification tests EN1991‐1‐2_(D).XLS. 6.40 MB. Created: 22 February 2013. Last/Rel.-date: 22 February 2013. Sheets: — Splash — Annex F — Annex G — B.5 (Annex B). EXAMPLE 6-AC‐ Equivalent time of fire exposure ‐ test 1 Given: Suppose a fire compartment with mainly cellulosic type fire loads. The dimensions of the compartment are: width = 7,04 m; length = 17,72 m; height = 3,60 m. The dimensions of windows are: width = 2,20 m; height = 1,60 m; number of windows = 3. Total area of Topic: User’s Manual/Verification tests - EN1991-1-2_(d).xls page 93 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 6 E UROCODE 1 EN 1991-1-2 A NNEX F, A NNEX G, S EC . B.5 A NNEX B horizontal openings on roof A h = 0 m 2 . Total area of enclosure A t = 427 56 m 2 . Design fire load density q f d = 570 MJ m 2 ; Thermal absorptivity b = 1060 J m 2 s 1 / 2 K ; Total area of vertical openings on all walls A v = 10 56 m 2 . Assume a correction factor k c for reinforced concrete or protected steel (EC1 Part 1‐2, table F.1, page 53). Find the equivalent time of standard fire exposure. [Reference sheet: Annex F]‐[Cell‐Range: A1:O1‐A84:O84]. Solution: Correction factor for reinforced concrete or protected steel is: k c = 1 0 (see Table F.1 ‐ “Correction factor k c in order to cover various materials”). Conversion factor (EC1 Part 1‐2, table F.2, page 54): for 720 b 2500 J m 2 s 1 / 2 K is k b = 0 055 min m 2 MJ . Note If no detailed information is available on the thermal properties of the compartment linings or if there are uncertainties about the final construction or changes may be made over the course of the building’s design life then the default value of k b = 0 07 should be used. Actual value assumed for the calculations: k b = 0 07 . Factor v = A v A f = 10 56 124 66 = 0 085 0 025 ; 0 25 . Factor h = A h A f = 0 124 66 = 0 . Factor b v = 12 5 1 + 10 v – v2 = 12 5 1 + 10 0 085 – 0 085 2 = 23 0 10 0 . Ventilation factor (with H = 3 60 m height of the fire compartment): 90 0 4 – v 4 6 0 0 3 w f = --------- 0 62 + ------------------------------------- 0 5 . H 1 + bv h 6 0 0 3 90 0 4 – 0 085 4 w f = ------------ 0 62 + ----------------------------------------------- = 1 76 0 5 . 3 60 1 + 23 0 0 Design fire load density (according to annex E): q f d = 570 MJ m 2 . Equivalent time of standard fire exposure: t e d = q f d k b w f k c = 570 0 07 1 76 1 0 = 70 2 min . example-end EXAMPLE 6-AD‐ Equivalent time of fire exposure ‐ test 1b Given: The previous calculation has assumed a single opening factor corresponding to removal of all glazing within the fire compartment at the onset of flashover. In reality the breaking of glass is a time dependent variable and sensitivity studies should be undertaken to ascertain the effect of only part of the glazing failing during the fire. In this example assume that only half of the openings are available to contribute to the combustion process. Find the equivalent time of standard fire exposure. [Reference sheet: Annex F]‐[Cell‐Range: A1:O1‐A84:O84]. page 94 Topic: User’s Manual/Verification tests - EN1991-1-2_(d).xls S ECTION 6 Solution: E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-2 A NNEX F, A NNEX G, S EC . B.5 A NNEX B Let us assume A v = 0 5 10 56 m 2 = 5 28 m 2 . Therefore: factor v = A v A f = 5 28 124 66 = 0 042 0 025 ; 0 25 . Factor b v = 12 5 1 + 10 v – v2 = 12 5 1 + 10 0 042 – 0 042 2 = 17 8 10 0 . Ventilation factor: 6 0 0 3 90 0 4 – 0 042 4 w f = ------------ 0 62 + ----------------------------------------------- = 2 44 0 5 . 3 60 1 + 23 0 0 Equivalent time of standard fire exposure: t e d = q f d k b w f k c = 570 0 07 2 44 1 0 = 97 4 min . If it is assumed that only half of the openings are available to contribute to the combustion process then the value of time equivalent increases by 38,7%. example-end EXAMPLE 6-AE‐ Configuration factor: external members ‐ test 2 Given: In the following analysis, the radiation is assumed to be produced by (through) a window rectangular in shape (width = 3,00 m x height = 2,00 m). The receiver (target) is a concrete column (cross‐section 300 mm x 1000 mm). Figure 6.28 Size and geometry of the window. A rectangular envelope is drawn around the cross‐section of the column receiving the radiating heat transfer (see Figure 6.26). Topic: User’s Manual/Verification tests - EN1991-1-2_(d).xls page 95 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 6 E UROCODE 1 EN 1991-1-2 A NNEX F, A NNEX G, S EC . B.5 A NNEX B Assume that the entire radiating surface is in a plane parallel to the member face f,1 and part of the radiating surface (rectangles 5 and 6) is perpendicular to the plane of the member face f,3 (see details in figure 6.27). Note that the zones (rectangles) 1‐2‐3‐4 are not visible from the point P (green one) which is on the face f,3 (and symmetrically on the face f,4). For the calculations assume that s // = 100 cm (see details in figure 6.27): Rectangle 1 Rectangle 2 Rectangle 3 Rectangle 4 Rectangle 5 Rectangle 6 w1 = 50 cm w2 = 150 cm w3 = 150 cm w4 = 50 cm w5 = 100 cm w6 = 100 cm h1 = 100 cm h2 = 100 cm h3 = 100 cm h4 = 100 cm h5 = 100 cm h6 = 100 cm Table 6.12 Radiating surfaces: geometry. Find the configuration factor for the member faces f,1; f,3; f,4 (see figure 6.26). Note The member face f,2 is not visible from the point P: no contribution should be taken. [Reference sheet: Annex G]‐[Cell‐Range: A1:O1‐A183:O183]. Solution: The column width is equal to 300 mm. Therefore: s = s // + 0 5b = 100 + 0 5 30 = 115 cm (see figure 6.26). From table 6.12, we get: Rectangle 16 Rectangle 45 w1 = 150 cm w2 = 150 cm h1 = 100 cm h2 = 100 cm Table 6.13 Radiating surfaces 5+6: geometry. Case a): receiving surface f,1 parallel to radiant surface with rectangles 16‐2‐3‐45. Case b): receiving surface f,3 (or f,4) perpendicular to radiant surface with rectangles 5‐6. Ratio Rect. 1 Rect. 2 Rect. 3 Rect. 4 Rect. 5 Rect.6 Rect. 16 Rect. 45 h a = ---s // 100/100 100/100 100/100 100/100 - - 100/100 100/100 wb = --s // 50/100 150/100 150/100 50/100 - - 150/100 150/100 ha = ---s - - - - 100/115 100/115 - - w b = ----s - - - - 100/115 100/115 - - Table 6.14 page 96 Geometrical parameters [-]. Topic: User’s Manual/Verification tests - EN1991-1-2_(d).xls S ECTION 6 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-2 A NNEX F, A NNEX G, S EC . B.5 A NNEX B Case a: f 1 = 2 + 3 + 45 + 16 (receiving surface parallel to radiating surface): 1 b b a a - arc tan ------------------------5 + ------------------------ i = ------ ----------------------- arc tan ------------------------. 0 5 0 0 5 0 5 2 2 2 2 2 1 + a 1 + a 1 + b 1 + b Case b: f 3 = f 4 = 5 + 6 (receiving surface perpendicular to radiating surface): 1 a 1 i = ------ arc tan a – ------------------------ arc tan ------------------------. 2 1 + b 2 0 5 1 + b 2 0 5 Case a, rectangles no. 2‐3‐45‐16: (a = 1,00; b = 1,50) 1 b b a a - arc tan ------------------------5 + ------------------------ i = ------ ----------------------- arc tan ------------------------ 0 5 0 0 5 0 5 2 2 2 2 2 1 + a 1 + a 1 + b 1 + b 1 1 5 1 5 1 1 - arc tan ----------------------------------- i = ------ ------------------------ arc tan ------------------------+ ----------------------------------2 1 + 1 2 0 5 1 + 1 2 0 5 1 + 1 5 2 0 5 1 + 1 5 2 0 5 1 i = ------ 0 707 arc tan 1 061 + 0 832 arc tan 0 555 2 1 i = ------ 0 707 0 815 rad + 0 832 0 507 rad = 0 159 . 2 Therefore: f 1 = 2 + 3 + 45 + 16 = 0 159 + 0 159 + 0 159 + 0 159 = 0 636 1 . Case b, rectangles no. 5‐6: (a = 0,87; b = 0,87) 1 a 1 i = ------ arc tan a – ------------------------ arc tan ------------------------ 0 5 0 5 2 2 2 1 + b 1 + b 1 0 87 1 i = ------ arc tan 0 87 – --------------------------------------5 arc tan --------------------------------------5 0 0 2 2 2 1 + 0 87 1 + 0 87 1 1 i = ------ 0 716 – 0 754 arc tan 0 656 , i = ------ 0 716 – 0 754 0 581 = 0 044 . 2 2 Therefore: f 3 = f 4 = 5 + 6 = 0 044 + 0 044 = 0 088 1 . example-end EXAMPLE 6-AF‐ Configuration factor: external members ‐ test 2b Given: Consider a concrete column (receiving surface with cross‐section 300 mm x 1000 mm) and a vertical radiating surface rectangular in shape (width = 3,00 m x height = 2,00 m). Each receiving surface “i” is in a plane at an angle i to that of the radiating surface. Find the configuration factor f i for each receiving face of the column. No contribution should be Topic: User’s Manual/Verification tests - EN1991-1-2_(d).xls page 97 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 6 E UROCODE 1 EN 1991-1-2 A NNEX F, A NNEX G, S EC . B.5 A NNEX B Figure 6.29 Geometry for the calculations (dimensions are given in millimetres). taken from zone f,4 that is not visible from the radiating surface B’’A’’. Assume: receiving surface f,1, radiating surface (A’A’’) rectangles (2‐3) with (input) w = 79,3 cm, h = 200 cm, s = 65,0 cm. Receiving surface f,2, radiating surface (B’’B’) rectangles (6‐5) with (input) w = 79,3 cm, h = 200 cm, s = 165,0 cm. Receiving surface f,3, radiating surface (B’’C’) rectangles (6‐5‐1‐4‐2*‐3*) with input w = (79,3 + 141,1 + 79,3 ‐ 0,86) cm = 298,84 cm, h = 200 cm, s = 100 cm. See details on the figure above. [Reference sheet: Annex G]‐[Cell‐Range: A1:O1‐A183:O183]. Solution: Receiving surface f,1, radiating surface (A’A’’, input with = 45 ): a = h s = 200 65 = 3 077 , b = w s = 79 3 65 = 1 220 , = 4 . cos = 0 707 ; sin = 0 707 ; 2 cos = 1 414 ; sin 2 = 0 500 . 1 + b 2 – 2b cos 0 5 = 0 874 , a 2 + sin2 0 5 = 3 157 , 1 – b cos = 0 137 , acos = 2 175 , b – cos = 0 513 . 1 a 1 – b cos f 1 = ------ arc tan a – -------------------------------------------------------------------------------------------------- arc tan + 2 1 + b 2 – 2b cos 0 5 1 + b 2 – 2b cos 0 5 1 b – cos - cos acos - . + ------ ---------------------------------- arc tan ----------------------------------+ arc tan ---------------------------------- a 2 + sin2 0 5 a 2 + sin2 0 5 2 a 2 + sin2 0 5 1 2175 0 513 0707 137 3077 f 1 = ------ arc tan 3 077 – 0-------------- arc tan --------------- + --------------- arc tan --------------- + arc tan --------------- 2 3157 3157 3157 0 874 0 874 page 98 Topic: User’s Manual/Verification tests - EN1991-1-2_(d).xls S ECTION 6 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-2 A NNEX F, A NNEX G, S EC . B.5 A NNEX B 1 2175 137 f 1 = ------ 1 257 – 0-------------- 1 294 + --------------- 0 161 + 0 220 . 2 3 157 0 874 1 f 1 = ------ 1 257 – 0 157 1 294 + 0 689 0 161 + 0 220 = 0 209 . 2 Receiving surface f,2, radiating surface (B’’B’, input with = 135 ): a = h s = 200 165 = 1 212 , b = w s = 79 3 165 = 0 481 , = 3 4 . cos = – 0 707 ; sin = 0 707 ; 2 cos = – 1 414 ; sin 2 = 0 500 . 1 + b 2 – 2b cos 0 5 = 1 383 , a 2 + sin2 0 5 = 1 403 , 1 – b cos = 1 340 , acos = – 0 857 , b – cos = 1 188 . We get: 1 f 2 = ------ 0 881 – 0 963 0 720 – 0 611 0 702 – 0 567 = 0 006 . 2 Receiving surface f,3, radiating surface (B’’C’, input with = 45 ): a = h s = 200 100 = 2 000 , b = w s = 298 84 100 = 2 988 , = 4 . cos = 0 707 ; sin = 0 707 ; 2 cos = 1 414 ; sin 2 = 0 500 . 1 + b 2 – 2b cos 0 5 = 2 388 , a 2 + sin2 0 5 = 2 121 , 1 – b cos = – 1 113 , acos = 1 414 , b – cos = 2 281 . We get: 1 f 3 = ------ 1 107 + 0 466 0 697 + 0 677 0 822 + 0 322 = 0 351 . 2 example-end EXAMPLE 6-AG‐ Overall configuration factors ‐ test 3 Given: Find the overall configuration factor f of the concrete column (see example above) for radiative heat transfer from an opening with rectangular shape 300 cm x 200 cm. Assume for each member face “i”: C i = 1 (unprotected face). The configuration factor for the member face f,4 should be taken as zero (see figure 6.29). [Reference sheet: B.5 (Annex B)]‐[Cell‐Range: A1:O1‐A52:O52]. Solution: From the results in the previous example: f 1 = 0 209 ; f 2 = 0 006 ; f 3 = 0 351 ; f 4 = 0 . Cross‐sectional dimension of member (300 mm x 1000 mm): faces f,1‐f,2: d 1 = 30 cm ; faces f,3‐f,4: d 2 = 100 cm . Therefore, from equation: C 1 f 1 + C 2 f 2 d 1 + C 3 f 3 + C 4 f 4 d 2 f = ----------------------------------------------------------------------------------------------------------------- C1 + C2 d1 + C3 + C4 d2 Topic: User’s Manual/Verification tests - EN1991-1-2_(d).xls page 99 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 6 E UROCODE 1 EN 1991-1-2 A NNEX F, A NNEX G, S EC . B.5 A NNEX B we find: 1 0 209 + 1 0 006 30 + 1 0 351 + 1 0 100 = 41 55- = 0 160 1 0 . f = ---------------------------------------------------------------------------------------------------------------------------------------------- 1 + 1 30 + 1 + 1 100 260 example-end 6.5 Reference [Section 6] BS EN 1991-1-2. Eurocode 1: Actions on structures – Part 1-2: General actions – Actions on structures exposed to fire. 26 November 2002. ECSC Project, Development of design rules for steel structures subjected to natural fires in CLOSED CAR PARKS, CEC agreement 210-AA/211/318/518/620/933, Brussels, June 1996. EN 1991-1-2 (2002) (English): Eurocode 1: Actions on structures - Part 1-2: General actions - Actions on structures exposed to fire [Authority: The European Union Per Regulation 305/2011, Directive 98/34/EC, Directive 2004/18/EC]. European Committee for Standardisation. EN 1991-1-2:2002/AC:2013. Eurocode 1: Actions on structures - Part 1-2: General actions - Actions on structures exposed to fire. CEN Brussels, February 2013. Manual for the design of building structures to Eurocode 1 and Basis of Structural Design April 2010. © 2010 The Institution of Structural Engineers. page 100 Topic: User’s Manual/Verification tests - EN1991-1-2_(d).xls Section 7 Eurocode 1 EN 1991-1-3 7.1 General E N 1991-1-3 gives guidance to determine the values of loads due to snow to be used for the structural design of buildings and civil engineering works. This Part does not apply for sites at altitudes above 1500 m, unless otherwise specified. Advice for the treatment of snow loads for altitudes above 1500 m may be found in the National Annex. Annex A gives information on design situations and load arrangements to be used for different locations. Annex B gives shape coefficients to be used for the treatment of exceptional snow drifts. Annex C gives characteristic values of snow load on the ground based on the results of work carried out under a contract specific to this Eurocode, to DGIII/D3 of the European Commission. Annex D gives guidance for adjusting the ground snow loads according to the return period. Annex E gives information on the bulk weight density of snow. The statements and assumptions given in EN 1990:2002, 1.3 apply to EN 1991-1-3. The rules given in EN 1990:2002, 1.4 apply to EN 1991-1-3. In some circumstances tests and proven and/or properly validated numerical methods may be used to obtain snow loads on the construction works. The circumstances are those agreed for an individual project, with the client and the relevant Authority. 7.2 Classification of actions Snow loads shall be classified as variable, fixed actions (see also Section 5.2, EN 1991-1-3), unless otherwise specified in this standard, see EN 1990:2002, 4.1.1 (1)P and 4.1.1 (4). Snow loads covered in this standard should be classified as static actions, see EN 1990:2002, 4.1.1 (4). In accordance with EN 1990:2002, 4.1.1 (2), for the particular condition defined in 1.6.3, exceptional snow loads may be treated as accidental actions depending on geographical locations. In accordance with EN 1990:2002, 4.1.1 (2), for the particular condition defined in 1.6.10, loads due to Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls page 101 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 exceptional snow drifts may be treated as accidental actions, depending on geographical locations. Snow loads are generally classified as variable, fixed actions. However certain drift loads (see Sections 5.4 and 5.6.3(b), EN 1991-1-3) are treated as accidental actions. See also Chapter 2. 7.3 Design situations The relevant snow loads shall be determined for each design situation identified, in accordance with EN 1990:2002, 3.5. For local effects described in Section 6 (EN 1991-1-3) the persistent/transient design situation should be used. The relevant snow loads are to be used for each identified design situation in accordance with Section 2.8.3 and/or Appendix B. Important UNDRIFTED SNOW LOAD ON THE ROOF. Load arrangement which describes the uniformly distributed snow load on the roof, affected only by the shape of the roof, before any redistribution of snow due to other climatic actions. DRIFTED SNOW LOAD ON THE ROOF. Load arrangement which describes the snow load distribution resulting from snow having been moved from one location to another location on a roof, e.g. by the action of the wind. NORMAL CONDITIONS. For locations where exceptional snow falls and exceptional snow drifts are unlikely to occur, the transient/persistent design situation should be used for both the undrifted and the drifted snow load arrangements determined using 5.2(3)P a) and 5.3. EXCEPTIONAL CONDITIONS. For locations where exceptional snow falls may occur but not exceptional snow drifts the following applies: — the transient/persistent design situation should be used for both the undrifted and the drifted snow load arrangements determined using 5.2(3)P a) and 5.3, and — the accidental design situation should be used for both the undrifted and the drifted snow load arrangements determined using 4.3, 5.2(3)P (b) and 5.3. For locations where exceptional snow falls are unlikely to occur but exceptional snow drifts may occur the following applies: — the transient/persistent design situation should be used for both the undrifted and the drifted snow load arrangements determined using 5.2(3)P a) and 5.3, and — the accidental design situation should be used for snow load cases determined using 5.2(3)P c) and Annex B. For locations where both exceptional snow falls and exceptional snow drifts may occur the following applies: page 102 Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 — the transient/persistent design situation should be used for both the undrifted and the drifted snow load arrangements determined using 5.2(3)P a) and 5.3, and — the accidental design situation should be used for both the undrifted and the drifted snow load arrangements determined using 4.3, 5.2(3)P(b), 5.3. — the accidental design situation should be used for the snow load cases determined using 5.2(3)P c) and Annex B. When snow loads are derived using Annex B (as well as the other “accidental” design situations) no partial safety factor is applied to them. This is because they are considered to only occur in extreme cases and are therefore classified as accidental. 7.4 Characteristic values The characteristic value of snow load on the ground s k should be determined in accordance with EN 1990:2002, 4.1.2 (7)P, and the definition for characteristic snow load on the ground is given in Section 5.2 (EN 1991-1-3). The National Annex specifies the characteristic values to be used. To cover unusual local conditions the National Annex may additionally allow the client and the relevant authority to agree upon a different characteristic value from that specified for an individual project. The characteristic ground snow loads s k should be obtained from the maps shown in Annex C (“European Ground Snow Load Maps”) and Table C.1 (“Altitude - Snow Load Relationships”). In special cases where more refined data is needed, the characteristic value of snow load on the ground s k may be refined using an appropriate statistical analysis of long records taken in a well sheltered area near the site. If the designer suspects that there are unusual local conditions that need to be taken into account, then the Meteorological Office should be consulted. Where a more refined characteristic ground snow load value s k is required, the Meteorological Office should be consulted. 7.5 Other representative values According to EN1990:2002, 4.1.3 the other representative values for snow load on the roof are as follows: — combination value: 0 s — frequent value: 1 s — quasi-permanent value: 2 s , where “s” is the snow load over the roof: s = s s k ; C i ; i . The values of i may be set by the National Annex of EN 1990:2002. The recommended values of the coefficients 0 , 1 and 2 for buildings are dependent upon the location of the Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls page 103 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 site being considered and should be taken from EN 1990:2002, Table A1.1 or Table 4.1 below (EN 1991-1-3), in which the information relating to snow loads is identical. Finland, Iceland, Norway, Sweden 0,70 0,50 0,20 Reminder of other CEN member states, for sites located at altitude H > 1000 m above sea level 0,70 0,50 0,20 Reminder of other CEN member states, for sites located at altitude H < 1000 m above sea level 0,50 0,20 0,00 Regions Table 7.15 From Table 4.1 - Recommended values of coefficients i for different locations for building. 7.6 Treatment of exceptional snow loads on the ground For locations where exceptional snow loads on the ground can occur, they may be determined by: s Ad = C esl s k (Eq. 7‐48) where: • s Ad is the design value of exceptional snow load on the ground for the given location • C esl is the coefficient for exceptional snow loads. It may be set by the National Annex. The recommended value for C esl is 2,0 • s k is intended as the upper value of a random variable, for which a given statistical distribution function applies, with the annual probability of exceedence set to 0,02 (i.e. a probability of not being exceeded on the unfavourable side during a “reference period” of 50 years).(1) 7.7 Snow load on roofs NATURE OF THE LOADS. Snow can be deposited on a roof in many different patterns. The properties of a roof or other factors causing different patterns include: — the shape of the roof — its thermal properties — the roughness of its surface — the amount of heat generated under the roof — the proximity of nearby buildings (1) The characteristic ground snow loads s k are given by the National Annex for each CEN country. The snow load on the roof is derived from the snow load on the ground s k , multiplying by appropriate conversion factors (shape, thermal and exposure coefficients). page 104 Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 — the surrounding terrain — the local meteorological climate, in particular its windiness, temperature variations, and likelihood of precipitation (either as rain or as snow). LOAD ARRANGEMENTS. The two primary load arrangements to be taken into account are (see Section 5.2): 1. undrifted snow load on roofs 2. drifted snow load on roofs. The load arrangements should be determined using 5.3; and Annex B, where specified in accordance with 3.3. The loads should be assumed to act vertically and refer to a horizontal projection of the roof area. Specialist advice should be sought where the consecutive melting and freezing of snow together with possible rainfall is likely to occur and block roof drainage. Topography Ce Windswept(a) 0,8 Normal(b) 1,0 Sheltered(c) 1,2 Table 7.16 From Table 5.1 - Recommended values of C e for different topographies. (a). Windswept topography: flat unobstructed areas exposed on all sides without, or little shelter afforded by terrain, higher construction works or trees. (b). Normal topography: areas where there is no significant removal of snow by wind on construction work, because of terrain, other construction works or trees. (c). Sheltered topography: areas in which the construction work being considered is considerably lower than the surrounding terrain or surrounded by high trees and/or surrounded by higher construction works. Snow loads on roofs shall be determined as follows: i. for the persistent/transient design situations: s = i Ce Ci sk ii. for the accidental design situations where exceptional snow load is the accidental action (except for the cases covered in 5.2 (3) P c): s = i C e C i s Ad iii. (Eq. 7‐49) (Eq. 7‐50) for the accidental design situations where exceptional snow drift is the accidental action and where Annex B applies: s = i sk (Eq. 7‐51) where: • i is the snow load shape coefficient (see Section 5.3 and Annex B) • s k is the characteristic value of snow load on the ground Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls page 105 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 • s Ad is the design value of exceptional snow load on the ground for a given location (see eq. 7-48 above). • C e is the exposure coefficient • C t is the thermal coefficient. The exposure coefficient C e should be used for determining the snow load on the roof. The choice for C e should consider the future development around the site. C e should be taken as 1,0 unless otherwise specified for different topographies. The National Annex may give the values of C e for different topographies. The recommended values are given in Table 5.1 above. The thermal coefficient C t should be used to account for the reduction of snow loads on roofs with high thermal transmittance > 1 W m 2 K , in particular for some glass covered roofs, because of melting caused by heat loss. For all other cases: C t = 1 0 . 7.8 Roof shape coefficients This Section gives snow load shape coefficients for undrifted and drifted snow load arrangements for all types of roofs identified in this standard, with the exception of the consideration of exceptional snow drifts defined in Annex B, where its use is allowed. Special consideration should be given to the snow load shape coefficients to be used where the roof has an external geometry which may lead to increases in snow load that are considered significant in comparison with that of a roof with linear profile. ✍ ROOF SNOW LOAD SHAPE COEFFICIENT. Ratio of the snow load on the roof to the undrifted snow load on the ground, without the influence of exposure and thermal effects. MONOPITCH ROOFS. The snow load shape coefficient 1 that should be used for monopitch roofs is given in Table 5.2 and shown in Figure 5.2. Angle of pitch of roof : 0° < < 30° 30° < < 60° > 60° 1 = 0,8 0,8·(60 – )/30 0,0 2 = 0,8 + 0,8·/30 1,6 -- Table 7.17 From Table 5.2 - Snow load shape coefficients. The values given in Table 5.2 above apply when the snow is not prevented from sliding off the roof. Where snow fences or other obstructions exist or where the lower edge of the roof is terminated with a parapet, then the snow load shape coefficient should not be reduced below 0,8. The load for both designer roofs which are the value of 1 page 106 arrangement of Figure 5.2 below should be used the undrifted and drifted load arrangements. The should give special consideration to large flat treated as a monopitch roof with = 0°, where can be = 1,0. Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 1 Figure 7.30 From Figure 5.2 - Snow load shape coefficient - monopitch roof. There is research evidence that for larger roofs (e.g. square or almost square roofs with length about 40 m) the snow layer may be non uniform and the maximum value of the ratio between the roof and the ground snow loads reaches unity. PITCHED ROOFS. The snow load shape coefficients that should be used for pitched roofs are given in Figure 5.3, where 1 is given in Table 5.2. The values given in Table 5.2 apply when snow is not prevented from sliding off the roof. Where snow fences or other obstructions exist or where the lower edge of the roof is terminated with a parapet, then the snow load shape coefficient should not be reduced below 0,8. 1 (1) 1 (2) Case (i) 1 (1) 1 (2) Case (ii) 0 1 (2) 1 (1) 0 1 2 Case (iii) Continental climates: 1 (i) Maritime climates: 0 Figure 7.31 From Figure 5.3 - Snow load shape coefficients - pitched roofs. Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls page 107 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 Case (i) 1 (1) 1 (2) 1 (1) 2 () Case (ii) 1 (1) 1 2 = (1 + 2)/2 1 1 (2) 1 (2) 2 Figure 7.32 From Figure 5.4 - Snow load shape coefficients for multi-span roofs. Important The undrifted load arrangement which should be used is shown in Figure 5.3, case (i). The drifted load arrangements which should be used are shown in Figure 5.3, cases (ii) and (iii), unless otherwise specified for local conditions. Based on local conditions, an alternative drifting load arrangement may be given in the National Annex. MULTI‐SPAN ROOFS. For multi-span roofs the snow load shape coefficients are given in Table 5.2. The undrifted load arrangement which should be used is shown in Figure 5.4 (above), case (i). The drifted load arrangement which should be used is shown in Figure 5.4, case (ii), unless specified for local conditions. Where permitted by the National Annex, Annex B may be used to determine the load case due to drifting. Special consideration should be given to the snow load shape coefficients for the design of multi-span roofs, where one or both sides of the valley have a slope greater than 60°. CYLINDRICAL ROOFS. The snow load shape coefficients that should be used for cylindrical roofs, in absence of snow fences, are given in the following expressions (see also Figure 5.6): — for 60 , 3 = 0 — for 60 , 3 = 0 2 + 10 h b . An upper value of 3 should be specified. The upper value of 3 may be specified in the National Annex. The recommended upper value for 3 is 2,0. Rules for considering the effect of snow fences for snow loads on cylindrical roofs may be given in the National Annex. The undrifted load arrangement which should be page 108 Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 Figure 7.33 From Figure 5.6 - Snow load shape coefficients for cylindrical roof. used is shown in Figure 5.6, case (i). The drifted load arrangement which should be used is shown in Figure 5.6, case (ii), unless specified for local conditions. Based on local conditions an alternative drifting load arrangement may be given in the National Annex. ROOF ABUTTING AND CLOSE TO TALLER CONSTRUCTION WORKS. The snow load shape coefficients that should be used for roofs abutting to taller construction works are given in the following expressions and shown in Figure 5.7: — 1 = 0 8 assuming the lower roof is flat — 2 = s + w where: • s is the snow load shape coefficient due to sliding of snow from the upper roof. For 15 , s = 0 . For 15 , s is determined from an additional load amounting to 50% of the maximum total snow load, on the adjacent slope of the upper roof calculated according to 5.3.3 • w is the snow load shape coefficient due to wind w = b 1 + b 2 2h h s k , where = 2 kN m 3 is the weight density of snow. An upper and a lower value of w should be specified. The range for w may be fixed in the National Annex. The recommended range is 0 8 w 4 • the drift length is determined as follows: l s = 2h . A restriction for l s may be given in the National Annex. The recommended restriction is 5 l s 15 m . Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls page 109 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 Figure 7.34 From Figure 5.7 - Snow load shape coefficients for roofs abutting to taller construction works. If b 2 l s the coefficient LR at the end of the lower roof is determined by interpolation between 1 and 2 truncated at the end of the lower roof (see Figure 5.7, case b). Note The undrifted load arrangement which should be used is shown in Figure 5.7, case (i). The drifted load arrangement which should be used is shown in Figure 5.7, case (ii), unless specified for local conditions. Where permitted by the National Annex, Annex B may be used to determine the load case due to drifting. 7.9 Local effects This section gives forces to be applied for the local verifications of: — drifting at projections and obstructions; — the edge of the roof; — snow fences. The design situations to be considered are persistent/transient. DRIFTING AT PROJECTIONS AND OBSTRUCTIONS. In windy conditions drifting of snow can occur on any roof which has obstructions as these cause areas of aerodynamic shade in which snow accumulates. The snow load shape coefficients and drift lengths for quasi-horizontal roofs should be taken as follows (see Figure 6.1), unless specified for local conditions: 1 = 0 8 , 2 = h s k , where = 2 kN m 3 is the weight density of snow and l s = 2h with the restriction 5 l s 15 m . Where page 110 Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 Figure 7.35 From Figure 6.1 - Snow load shape coefficients at projections and obstructions. permitted by the National Annex, Annex B may be used to determine the load case due to drifting. SNOW OVERHANGING THE EDGE OF A ROOF. The design of those parts of a roof cantilevered out beyond the walls should take account of snow overhanging the edge of the roof, in addition to the load on that part of the roof. The loads due to the overhang may be assumed to act at the edge of the roof and may be calculated as follows: 2 s e = ks ------ (Eq. 7‐52) where: • s e is snow load per metre length due to the overhang (see Figure 6.2) Figure 7.36 From Figure 6.2 - Snow overhanging the edge of a roof (“se” characteristic load). Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls page 111 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 Figure 7.37 Snow loads on snowguards and other obstacles (“Fs” characteristic load). • s is the most onerous undrifted load case appropriate for the roof under consideration (see Section 5.2) • = 3 kN m 3 is the weight density of snow • k is a coefficient to take account of the irregular shape of the snow (the values of k may be given in the National Annex). The recommended way for calculating k is as follows: k = 3-- d k d where d is the depth of the snow layer on the roof in meters. SNOW LOADS ON SNOWGUARDS AND OTHER OBSTACLES. Under certain conditions snow may slide down a pitched or curved roof (see Figure above). The coefficient of friction between the snow and the roof should be assumed to be zero. For this calculation the force F s exerted by a sliding mass of snow, in the direction of slide, per unit length of the building should be taken as: F s = s b sin (Eq. 7‐53) where: page 112 • s is the snow load on the roof relative to the most onerous undrifted load case appropriate for roof area from which snow could slide (see 5.2, 5.3) • b is the width on plan (horizontal) from the guard or obstacle to the next guard or to the ridge • is the pitch of the roof, measured from the horizontal. Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 7.10 Verification tests EN1991‐1‐3_(A).XLS. 6.00 MB. Created: 23 February 2013. Last/Rel.-date: 23 February 2013. Sheets: — Splash — CodeSec4-5 — CodeSec6. EXAMPLE 7-AH‐ Roof shape coefficients: Pitched roofs ‐ test 1 Given: Low wind velocities are sufficient to blow snow accumulations from a roof or to cause a drift of snow which could lead to a local enhancement of the snow load. Roof shape coefficients are needed for an adjustment of the ground snow load to a snow load on the roof taking into account these effects. Assuming a geographical location where exceptional snow falls are unlikely to occur but exceptional snow drifts may occur, find the roof shape coefficients using the data given in tables below for angles of pitch of roof equal to 1 = 30 and 2 = 40 . Angle of pitch of roof : 0° < < 15° 15° < < 30° 30° < < 60° > 60° 0,8 0,8 + 0,4·( – 15)/15 1,2·(60 – )/30 0,0 1 = Table 7.18 Drifted snow load shape coefficient for a duo-pitched roof(a). (a). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design April 2010. © 2010 The Institution of Structural Engineers. Angle of pitch of roof : 0° < < 30° 30° < < 60° > 60° 0,8 0,8·(60 – )/30 0,0 1 = Table 7.19 Undrifted snow load shape coefficient (from Table 5.2, EN 1991-1-3). [Reference sheet: CodeSec4‐5]‐[Cell‐Range: A29:O29‐A63:O63]. Solution: The most unfavourable load situation has to be chosen for the design. The undrifted and drifted load arrangements which should be used are shown in Figure 7.38 below. Using the given numerical data, we get: (Case ii and iii) ‐ Drifted load arrangement (see Table 7.18 above): 1 = 30 , 1 1 = 0 8 + 0 4 1 – 15 15 = 0 8 + 0 4 30 – 15 15 = 1 20 ; 1 1 = 0 . 2 = 40 , 1 2 = 1 2 60 – 2 30 = 1 2 60 – 40 30 = 0 80 ; 1 2 = 0 . (Case i) ‐ Undrifted load arrangement (see Table 7.19 above): 1 = 30 , 1 1 = 0 80 . 2 = 40 , 1 2 = 0 8 60 – 2 30 = 0 8 60 – 40 30 = 0 53 . Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls page 113 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 Figure 7.38 Snow load shape coefficient – pitched roofs. These values lead to the two relevant load cases given in figure 7.39. In fact, from load arrangements in Figure 7.38 we get: Figure 7.39 Snow load shape coefficient and load arrangements for calculations (summary sketch) – pitched roofs. Where snow fences or other obstructions exist or where the lower edge of the roof is terminated with a parapet, then the snow load shape coefficient should not be reduced below 0.8. If this case applies: 1 1 = 0 53 0 80 . example-end EXAMPLE 7-AI‐ Roof shape coefficients: Pitched roofs ‐ test 1b Given: page 114 Let us assume that exist the same assumptions as in the previous example. The characteristic value for the ground snow load on height 100 metres, where the building is located, is equal to (say): s k = 0 85 kN m 2 . The exposure factor is chosen as C e = 1 0 . Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 The thermal coefficient is also set to C t = 1 0 . Find the most unfavourable load situations that have to be chosen for the design. [Reference sheet: CodeSec4‐5]‐[Cell‐Range: A29:O29‐A63:O63]. Solution: For locations where exceptional snow falls are unlikely to occur but exceptional snow drifts may occur the transient/persistent design situation should be used for both the undrifted and the drifted snow load arrangements determined using 5.2(3)P a) and 5.3, and the accidental design situation should be used for snow load cases determined using 5.2(3)P c) and Annex B. Therefore, for persistent/transient design situations (see Section 5.2(3)P a)): s = i C e C i s k = i 1 0 1 0 0 85 kN m 2 = i 0 85 kN m 2 . Figure 7.40 Snow load arrangements for calculations (summary sketch): characteristic value of snow loads. Here the following values of shape coefficients and snow loads on the roof are obtained: (Case ii and iii) ‐ Drifted load arrangement (see Table 7.18 on page 113): 1 = 30 , 1 1 = 1 20 ; s = 1 0 85 = 1 20 0 85 = 1 02 kN m 2 . 2 = 40 , 1 2 = 0 80 ; s = 1 0 85 = 0 80 0 85 = 0 68 kN m 2 . (Case i) ‐ Undrifted load arrangement (see Table 7.19 on page 113): 1 = 30 , 1 1 = 0 80 ; s = 1 0 85 = 0 80 0 85 = 0 68 kN m 2 . 2 = 40 , 1 2 = 0 53 ; s = 1 0 85 = 0 53 0 85 = 0 45 kN m 2 . These values lead to the three relevant load cases given in figure 7.40. example-end EXAMPLE 7-AJ‐ Snow load shape coefficients for multi‐span roofs ‐ test 2 Given: A building with shed roof is given. It is assumed that this building is located in Sweden, snow load zone 2, on a height above mean sea level of 300 m (with s k = 2 85 kN m 2 ). The Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls page 115 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 surroundings of the building represent normal conditions, so that the roof can not be denoted as “wind swept” or “wind sheltered” (see Table 7.16 on page 105). An effective heat insulation is applied on the roof and therefore the thermal coefficient C t = 1 0 has to be used for the calculation. Assumption: 1 = 40 , 2 = 30 . [Reference sheet: CodeSec4‐5]‐[Cell‐Range: A65:O65‐A100:O100]. Solution: For the determination of roof shape coefficients for shed roofs the more unfavourable case of two load cases has to be applied (see also Figure 7.32 on page 108): Figure 7.41 Determination of roof shape coefficients for shed roofs. Figure 7.42 Load arrangements on the roof (summary sketch): characteristic value of snow loads. Partial factor for snow load in isolation (transient/persistent): 1,50. page 116 Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 Snow load on roof (see Section 5.2.(3)P a)): s = i C e C i s k = i 1 0 1 0 2 85 kN m 2 = i 2 85 kN m 2 . Values of shape coefficients and snow loads on the roof: (Case i) ‐ Undrifted load arrangement (see Table 7.19 on page 113): 1 = 30 , 1 1 = 0 80 ; s = 1 2 85 = 0 80 2 85 = 2 28 kN m 2 . 2 = 40 , 1 2 = 0 8 60 – 2 30 = 0 8 60 – 40 30 ; 1 2 = 0 53 ; s = 1 2 85 = 0 53 2 85 = 1 51 kN m 2 . (Case ii) ‐ Drifted load arrangement (see Table 7.17 on page 106): = 0 5 1 + 2 = 0 5 30 + 40 = 35 , 2 = 1 60 ; s = 2 2 85 = 1 60 2 85 = 4 56 kN m 2 . These values lead to the two relevant (characteristic) load cases given in figure 7.42 above. example-end EXAMPLE 7-AK‐ Cylindrical roofs ‐ test 3 Given: Find the snow load shape coefficients and the load arrangements for the case of drifted and undrifted snow that should be used for cylindrical roofs, in absence of snow fences. Assume: b = 7 00 m , h = 1 50 m , l s = 6 00 m (see Figure 7.33 on page 109). The upper value for 3 is 2 0 . [Reference sheet: CodeSec4‐5]‐[Cell‐Range: A103:O103‐A130:O130]. Solution: For 60 , 3 = 0 . For 60 , 3 0 2 + 10 h b = 0 2 + 10 1 50 7 00 = 2 34 2 . Actual value for 3 assumed for the calculations: 3 = 2 00 . Therefore 0 5 3 = 1 00 . Figure 7.44 Load arrangements for the case of drifted and undrifted snow on cylindrical roof (summary sketch). Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls page 117 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 These values lead to the three relevant load cases given in the figure above. In particular, in the right part of the figure is represented a further possible case of arrangement of loads on the roof. example-end EXAMPLE 7-AL‐ Roof abutting and close to taller construction works ‐ test 4 Given: Find the snow load shape coefficients that should be used for roofs abutting to taller construction works. Assume (see Figure 7.34 on page 110): = 18 (upper roof); b 1 = 12 00 m ; h = 3 20 m ; b 2 = 7 50 m . Characteristic value of snow load on the ground: s k = 1 50 kN m 2 , (see Case a on Figure 7.45). [Reference sheet: CodeSec4‐5]‐[Cell‐Range: A182:O182‐A214:O214]. Solution: Assuming the lower roof is flat: 1 = 0 8 . Snow load shape coefficient due to sliding of snow from the upper roof: 0 30 with 1 = 0 80 (see Table 7.17 on page 106) and 15 with s = 0 5 1 = 0 40 . Drift length: l s = 2h = 2 3 20 m = 6 40 m 5 ;15 m (ok). Weight density of snow: = 2 0 kN / m3 . Snow load shape coefficient due to wind: b1 + b2 h 12 00 + 7 50 2 0 3 20 - = -------------------------------------- = 3 05 ----- = ----------------------------------- = 4 27 with w = -------------------sk 2h 2 3 20 1 50 w 0 80 ; 4 00 (ok). Finally, we get (see details on the Figure below): 2 = s + w = 0 40 + 3 05 = 3 45 - , 1 = 0 80 @ l s = 6 40 m b 2 = 7 50 m . example-end EXAMPLE 7-AM‐ Roof abutting and close to taller construction works ‐ test 4b Given: Let assume the same assumptions set out in the previous example but with b 2 = 4 00 m . Find the snow load shape coefficients (see Case b on Figure 7.45). [Reference sheet: CodeSec4‐5]‐[Cell‐Range: A182:O182‐A214:O214]. Solution: In this case, we have: b 2 = 4 00 m l s = 2h = 6 40 m . Therefore, the coefficient at the end of the lower roof is determined by linear interpolation between 1 and 2 truncated at the end of the lower roof. Snow load shape coefficient due to wind: page 118 Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 Figure 7.45 Snow load shape coefficients (summary sketch: example 7-AL and 7-AM). b1 + b2 h 12 00 + 4 00 2 0 3 20 - = -------------------------------------- = 2 50 ----- = ----------------------------------- = 4 27 with w = -------------------sk 2h 2 3 20 1 50 w 0 80 ; 4 00 (ok). We find: 2 = s + w = 0 40 + 2 50 = 2 90 - , 2 – 1 ls – b2 2 90 – 0 80 6 40 – 4 00 - + 0 80 = 1 59 - . LR = --------------------------------------------- + 1 = ------------------------------------------------------------------------ls 6 40 The snow load shape coefficients are shown in figure above for both the latest two examples. example-end EXAMPLE 7-AN‐ Local effects: drifting at projections and obstructions ‐ test 5 Given: Wind‐blown snow on flat roofs that are obstructed by walls/obstructions of taller sections of building causes wind drifts. Assume: drift height = obstruction height = h = 2 00 m ; drift width: l s = 2h = 4 00 m 5 ; 15 m ; distances of the obstruction from the edges of the roof measured on the horizontal axis: b sx = 2 00 m , b dx = 6 00 m . Find the snow load shape coefficients if the characteristic value of snow load on the ground is equal to s k = 1 50 kN / m2 and 2 max = 2 - . [Reference sheet: CodeSec6]‐[Cell‐Range: A1:O1‐A49:O49]. Solution: Actual value for the drift width that we must assume for the calculations: Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls page 119 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 Figure 7.46 Snow load shape coefficients (summary sketch). l s = l s min = 5 0 m . Weight density of snow: = 2 00 kN / m3 with 2 = h s k = 2 00 2 00 1 50 = 2 67 2 max = 2 . Actual value assumed for the calculations: 2 = 2 - . We have (see details on the figure below): Case b): b sx = 2 00 m l s = 4 00 m and Case a): b dx = 6 00 m l s = 4 00 m . Therefore, using the given numerical data, we get: Case b): linear interpolation with b sx = 2 00 m : 2 – 1 l s – b sx 2 00 – 0 80 5 00 – 2 00 - + 0 80 = 1 52 - . LR = ----------------------------------------------- + 1 = ------------------------------------------------------------------------ls 5 00 Case a): 2 = 2 00 - , 1 = 0 80 - . example-end EXAMPLE 7-AO‐ Snow overhanging the edge of a roof ‐ test 6 Given: A building is located at a height above mean sea level of 900 m. Find the characteristic value of the load due to the snow overhang acting at the edge of the roof. Let us assume that the most onerous undrifted load case for the roof under consideration is equal to s = 4 00 kN / m2 . To take account of the irregular shape of the snow assume k = 3 0 irrespective of whether that the actual depth of the snow layer on the roof is d = 0 90 m . [Reference sheet: CodeSec6]‐[Cell‐Range: A54:O54‐A77:O77]. page 120 Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 Solution: Snow load per metre length due to the overhang: 3 4 00 2 ks 2 s e = ------- = -------------------------- = 16 00 kN / m 3 00 having taken the weight density of the snow as 3 00 kN / m3 . Figure 7.47 Snow overhanging the edge of the roof. Partial factor for snow load in isolation (transient/persistent): 1,50. A summary sketch is shown in the figure above. The design situation is to be considered as persistent/transient. Therefore, the design value of the load is: s e d = Q s e = 1 50 16 00 kN / m = 24 00 kN / m . example-end EXAMPLE 7-AP‐ Snow loads on snowguards and other obstacles ‐ test 7 Given: Find the characteristic value of the force F s (per unit length of the building) exerted by a sliding mass of snow with an angle of pitch of roof equal to = 30 . Assume that the horizontal width from the ridge to the guard is equal to b = 4 00 m . The characteristic snow load on the roof, relative to the most onerous undrifted load case, is taken equal to s k = 2 50 kN / m2 . [Reference sheet: CodeSec6]‐[Cell‐Range: A95:O95‐A112:O112]. Solution: In the direction of the slide, we have: F s = s b sin = 2 50 4 00 sin 30 = 5 00 kN / m . F s is to be considered per unit length of the building. The design situation is to be considered as persistent/transient. Therefore, the design value of the load is: F s d = Q F s = 1 50 5 00 kN / m = 7 50 kN / m . Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls page 121 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 7 E UROCODE 1 EN 1991-1-3 Figure 7.49 Snow overhanging the edge of a roof. In the figure above is shown a summary sketch. example-end 7.11 References [Section 7] Derivation of snow load, Technical Guidance Note, TheStructuralEngineer, March 2012. Web resource: www.istructe.org/resources-centre/library. EN 1991-1-3:2003/AC:2009. Eurocode 1: Actions on structures - Part 1-3: General actions - Snow loads. Brussels: CEN/TC 250 - Structural Eurocodes, March 2009. EN 1991-1-3 (2003) (English): Eurocode 1: Actions on structures - Part 1-3: General actions - Snow loads [Authority: The European Union Per Regulation 305/2011, Directive 98/34/EC, Directive 2004/18/EC]. Manual for the design of building structures to Eurocode 1 and Basis of Structural Design April 2010. © 2010 The Institution of Structural Engineers. page 122 Topic: User’s Manual/Verification tests - EN1991-1-3_(a).xls Section 8 Eurocode 1 EN 1991-1-3: Annex A, Annex B 8.1 Design situations and load arrangements to be used for different locations T able A.1 below (from Annex A, normative) summarises four cases A, B1, B2 and B3 (see 3.2, 3.3(1), 3.3(2) and 3.3(3) respectively) identifying the design situations and load arrangements to be used for each individual case. Normal condition Case A Exceptional condition Case B1 Exceptional condition Case B2 Exceptional condition Case B3 No exceptional falls No exceptional drift Exceptional falls No exceptional drift No exceptional falls Exceptional drift Exceptional falls Exceptional drift Reference Sec. 3.2(1) Reference Sec. 3.3(1) Reference Sec. 3.3(2) Reference Sec. 3.3(3) Persistent/transient design situation: [1], [2] Persistent/transient design situation: [1], [2] Persistent/transient design situation: [1], [2] Persistent/transient design situation: [1], [2] [1] Undrifted: i C e C t s k [1] Undrifted: i C e C t s k [1] Undrifted: i C e C t s k [1] Undrifted: i C e C t s k [2] Drifted: i C e C t s k [2] Drifted: i C e C t s k [2] Drifted: i C e C t s k (a) [2] Drifted: i C e C t s k Accidental(b) design situation: [3], [4] Accidental(c) design situation: [3], [4] Accidental(c) design situation: [3], [4] [3] Undrifted: -- [3] Undrifted: i C e C t C esl s k [4] Drifted: i C e C t C esl s k Table 8.20 [3] Drifted: i s k i C e C t C esl s k (d) [4] Drifted: i s k (e) From Table A.1 - Design Situations and load arrangements to be used for different locations. (a). Except for roof shapes in Annex B. (b). Where snow is the accidental action. (c). See table footnote above. (d). For roof shapes in Annex B. (e). For roof shapes in Annex B. Topic: User’s Manual/Verification tests - EN1991-1-3_(b).xls page 123 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 8 E UROCODE 1 EN 1991-1-3: A NNEX A, A NNEX B Exceptional conditions are defined according to the National Annex. For cases B1 and B3 the National Annex may define design situations which apply for the particular local effects described in section 6. 8.2 Annex B: Snow load shape coefficients for exceptional snow drifts This annex (normative) gives snow shape coefficients to determine load arrangements due to exceptional snow drifts for the following types of roofs: a. multi-span roofs b. roofs abutting and close to taller construction works c. roofs where drifting occurs at projections, obstructions and parapets d. for all other load arrangements Section 5 and Section 6 should be used as appropriate. When considering load cases using snow load shape coefficients obtained from this Annex it should be assumed that they are exceptional snow drift loads and that there is no snow elsewhere on the roof. In some circumstances more than one drift load case may be applicable for the same location on a roof in which case they should be treated as alternatives. MULTI‐SPAN ROOFS. The snow load shape coefficient for an exceptional snow drift that should be used for valleys of multi-span roofs is given in Figure B1 and B2(2). The shape coefficient given in figure below is determinated as: 1 = min 2h s k ; 2b 3 l s1 + l s2 ; 5 (Eq. 8‐54) Figure 8.50 From Figure B1 - Shape coefficient and drift lengths for exceptional snow drifts – valleys of multi-span roofs. page 124 Topic: User’s Manual/Verification tests - EN1991-1-3_(b).xls S ECTION 8 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-3: A NNEX A, A NNEX B Figure 8.51 From Figure B2 - Shape coefficients and drift lengths for exceptional snow drifts - Roofs abutting and close to taller structures. where s k is the characteristic value of snow load on the ground and b 3 should be taken as the horizontal dimension of three slopes(1) (see details on Figure 8.50). The drift lengths are determined as follow: l s1 = b 1 l s2 = b 2 (Eq. 8‐55) ROOFS ABUTTING AND CLOSE TO TALLER STRUCTURES. The snow load shape coefficients for exceptional snow drifts that should be used for roofs abutting a taller construction work are given in Figure B2 and Table B1. The snow load case given in Figure B2 is also applicable for roofs close to, but not abutting, taller buildings, with the exception that it is only necessary to consider the load actually on the lower roof, i.e. the load implied between the two buildings can be ignored. The effect of structures close to, but not abutting the lower roof will depend on the roof areas available from which snow can be blown into the drift and the difference in levels. However, as an approximate rule, it is only necessary to consider nearby structures when they are less than 1,50 m away. (1) For roofs of more than two spans with approximately symmetrical and uniform geometry, b3 should be taken as the horizontal dimension of three slopes (i.e. span x 1,5) and this snow load distribution should be considered applicable to every valley, although not necessarily simultaneously. Care should be taken when selecting b3 for roofs with non-uniform geometry, significant differences in ridge height and/or span may act as obstructions to the free movement of snow across the roof and influence the amount of snow theoretically available to form the drift. Topic: User’s Manual/Verification tests - EN1991-1-3_(b).xls page 125 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 8 E UROCODE 1 EN 1991-1-3: A NNEX A, A NNEX B The drift length is the least value of 5h , b 1 or 15 m : l s = min 5h ; b 1 ; 15 m , where Angle of roof pitch i: Shape coefficient 0 15 15 30 30 60 60 1 = 3 3 30 – 15 0 0 2 = 3 3 3 60 – 30 0 Table 8.21 From Table B1 - Shape coefficients for exceptional snow drifts for roofs abutting and close to taller structures. 3 is equal to (see details on Figure 8.51 on page 125): 2h 2 max b 1 ; b 2 -; 8 . 3 = min ------ ; ---------------------------------------------s k min 5h ; b 1 ; 15 m (Eq. 8‐56) ROOFS WHERE DRIFTING OCCURS AT PROJECTIONS AND OBSTRUCTIONS. The snow load shape coefficients for exceptional snow drifts that should be used for roofs where drifting occurs at projections and obstructions, other than parapets, are given in B4(2) and Figure B3 below. Shape coefficients for drifting behind parapets are given in B4(4). Figure 8.52 From Figure B3 - Shape coefficients for exceptional snow drifts for roofs where drifting occurs at projections and obstructions. page 126 Topic: User’s Manual/Verification tests - EN1991-1-3_(b).xls S ECTION 8 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-3: A NNEX A, A NNEX B Figure 8.53 From Figure B4 - Shape coefficients for exceptional snow drifts - roofs where drifting occurs at parapets. If the vertical elevation against which a drift could form is not greater than 1 m 2 , the effect of drifting can be ignored. This clause applies to: — drifting against obstructions not exceeding 1 m in height. — drifting on canopies, projecting not more than 5 m from the face of the building over doors and loading bays, irrespective of the height of the obstruction. — slender obstructions over 1m high but not more than 2 m wide, may be considered as local projections. For this specific case h may be taken as the lesser of the projection height or width perpendicular to the direction of the wind. The shape coefficient given in Figure B3 is determined as the least value of: 1 = min 2h 1 s k ; 5 ; 2 = min 2h 2 s k ; 5 . (Eq. 8‐57) In addition, for door canopies projecting not more than 5 m from the building, 1 should not exceed: Topic: User’s Manual/Verification tests - EN1991-1-3_(b).xls page 127 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 8 E UROCODE 1 EN 1991-1-3: A NNEX A, A NNEX B 2 max b 1 ; b 2 1 max = ---------------------------------------------------------min b 1 ; min 5h ; 5 m (Eq. 8‐58) where the drift length l si is taken as the least value of 5h i or b i (with i = 1 or 2) and h i 1 m : l si = min b i ; min 5h i ; 5 m . (Eq. 8‐59) ROOFS WHERE DRIFTING OCCURS AT PARAPETS. The snow load shape coefficients for exceptional snow drifts that should be used for roofs where drifting occurs at parapets are given in Figure B4 (see Figure 8.53 on page 127). The shape coefficient given in Figure B4 is determined as: 2h 2b 1 = min ------ ; ----------------------------------------------- ; 8 s k min b 1 ; 5h ; 15 m (Eq. 8‐60) with b = max b1 ; b 2 for the case “f” and b = b 1 for the cases “d” and “e” (see Figure 8.53 on page 127). The drift length l s is taken as: l s = min b 1 ; 5h ; 15 m . (Eq. 8‐61) For drifting in a valley behind a parapet at a gable end the snow load at the face of the parapet should be assumed to decrease linearly from its maximum value in the valley to zero at the adjacent ridges, providing the parapet does not project more than 300 mm above the ridge. 8.3 Verification tests EN1991‐1‐3_(B).XLS. 5.95 MB. Created: 04 March 2013. Last/Rel.-date: 04 March 2013. Sheets: — Splash — Annex A — Annex B. EXAMPLE 8-AQ‐ Multi‐span roofs ‐ test 1 Given: A building with shed roof is given. It is assumed that this building is located 1 km south of Inverness city centre and is 90 m above mean sea level (with s k 0 60 kN m 2 ). Calculate the design snow load for an exceptional snow drift with an height of build up snow within the valley of the multi‐span roof equal to h = 1 50 m . Assume: b 1 = 3 00 m and b 2 = 5 00 m . Horizontal dimension of three slopes: b 3 = 13 00 m . (All of the variables mentioned herein are defined in Figure 8.50 on page 124). [Reference sheet: Annex B]‐[Cell‐Range: A20:O20‐A50:O50]. page 128 Topic: User’s Manual/Verification tests - EN1991-1-3_(b).xls S ECTION 8 Solution: E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-3: A NNEX A, A NNEX B Drift lengths: l s1 = b 1 = 3 00 m , l s2 = b 2 = 5 00 m . With the given numerical data, we get: 2b 3 2h 1 50 - = 5 00 - ; ----------------2 13 00 - = 3 25 - . ------ = 2----------------------= ----------------------------l s1 + l s2 sk 0 60 3 00 + 5 00 The shape coefficient is determined as the lowest value from the following (5; 3,25; 5): 1 = min 2h s k ; 2b 3 l s1 + l s2 ; 5 = min 5 00 ; 3 25 ; 5 = 3 25 - . The snow drift (design) load is defined by Clause 5.2(3)Pc) in Eurocode 1‐1‐3 thus: s = 1 s k = 3 25 0 60 = 1 95 kN m 2 . This is considered to be an accidental action as it is classified as an extreme condition. Therefore in Ultimate Limit State (ULS) and Equilibrium (EQU) analyses, no partial factor would be applied to this load. EXAMPLE 8-AR‐ Roofs abutting and close to taller structures ‐ test 2 Given: Find the snow load shape coefficients and design loads for exceptional snow drifts that should be used for roofs abutting a taller building. Figure 8.51 on page 125 explains how the extent of the snowdrift is defined. Assume: s k = 0 60 kN m 2 ; h = 5 00 m ; b 1 = 7 00 m ; b 2 = 12 00 m ; = 18 . [Reference sheet: Annex B]‐[Cell‐Range: A79:O79‐A125:O125]. Solution: Drift length: l s = min 5h ; b 1 ; 15 m = min 5 5 ; 7 00 ; 15 m = 7 00 m . b = max b 1 ; b 2 = max 7 00 ; 12 00 = 12 00 m . 2h 2 max b 1 ; b 2 2 5 00 2 12 00 - ; 8 = min ------------------- ; ---------------------- ; 8 3 = min ------ ; ---------------------------------------------s k min 5h ; b 1 ; 15 m 0 60 7 00 3 = min 16 7 ; 3 43 ; 8 = 3 43 - . From Table B1 with 15 30 : 1 = 3 30 – 15 = 3 30 – 18 15 = 3 43 0 8 = 2 74 - , 2 = 3 = 3 43 - . Therefore, we find: s 1 = 1 s k = 2 74 0 60 = 1 64 kN / m2 s 2 = 2 s k = 3 43 0 60 = 2 06 kN / m2 . Each snow drift load is considered to be an accidental action as it is classified as an extreme condition (see Annex A). Therefore in Ultimate Limit State (ULS) and Equilibrium (EQU) analyses, no partial factor would be applied to this load. example-end EXAMPLE 8-AS‐ Roofs where drifting occurs at projections and obstructions ‐ test 3 Given: Referring to the details shown in the Figure 8.53 on page 127, assume: Case a: h 1 = 1 00 m ; h 2 = 1 00 m ; b 1 = 3 00 m ; b 2 = 7 00 m . Topic: User’s Manual/Verification tests - EN1991-1-3_(b).xls page 129 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 8 E UROCODE 1 EN 1991-1-3: A NNEX A, A NNEX B Case b: h = 3 00 m ; b 1 = 2 00 m ; b 2 = 75 00 m . Case c: h 1 = 1 00 m ; h 2 = 0 80 m ; b 1 = 3 00 m ; b 2 = 6 00 m . Calculate the exceptional snow drift loads for the three cases mentioned above. [Reference sheet: Annex B]‐[Cell‐Range: A146:O146‐A247:O247]. Solution: Drift lengths l si = min b i ; min 5h i ; 5 m : Case a: l s1 = min b 1 ; min 5h 1 ; 5 m = min 3 00 ; min 5 ; 5 m = 3 00 m . l s2 = min b 2 ; min 5h 2 ; 5 m = min 7 00 ; min 5 ; 5 m = 5 00 m . Case b: l s1 = min b 1 ; min 5h ; 5 m = min 2 00 ; min 5 3 ; 5 m = 2 00 m . Case c: l s1 = min b 1 ; min 5h 1 ; 5 m = min 3 00 ; min 15 ; 5 m = 3 00 m . l s2 = min b 2 ; min 5h 2 ; 5 m = min 6 00 ; min 5 0 80 ; 5 m = 4 00 m . Shape coefficients given in figure B3: Case a: 2 = 1 = min 2h 1 s k ; 5 = min 2 1 00 0 60 ; 5 = min 3 33 ; 5 = 3 33 - . Case b: 1 = min 2h 1 s k ; 5 = min 2 3 00 0 60 ; 5 = min 10 ; 5 = 5 00 - with the limit: 2 max b 1 ; b 2 2 75 00 - = 75 00 - (ok). 1 max = ---------------------------------------------------------- = -----------------------------------------min b 1 ; min 5h ; 5 m min 2 00 ; 5 00 Case c: 1 = min 2h 1 s k ; 5 = min 2 1 00 0 60 ; 5 = min 3 33 ; 5 = 3 33 - . 2 = min 2h 2 s k ; 5 = min 2 0 80 0 60 ; 5 = min 2 67 ; 5 = 2 67 - . Exceptional snow drift loads: Case a: 1 s k = 2 s k = 3 33 0 60 = 2 00 kN / m2 . Case b: 1 s k = 5 00 0 60 = 3 00 kN / m2 . Case c: 1 s k = 3 33 0 60 = 2 00 kN / m2 ; 2 s k = 2 67 0 60 = 1 60 kN / m2 . Each snow drift load is considered to be an accidental action as it is classified as an extreme condition (see Annex A). Therefore in Ultimate Limit State (ULS) and Equilibrium (EQU) analyses, no partial factor would be applied to this load. example-end EXAMPLE 8-AT‐ Shape coefficients for exceptional snow drifts ‐ roofs where drifting occurs at parapets or adjacent structures ‐ test 3b Given: page 130 An indoor sports hall is to be constructed adjacent to an existing further education college. It is located 1 km south of Inverness city centre and is 90 m above mean sea level (with s k = 0 60 kN / m2 ). Calculate the characteristic snow load on the roof of the new sports hall. The roof pitch angle to the sports hall is 8°. Topic: User’s Manual/Verification tests - EN1991-1-3_(b).xls S ECTION 8 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-3: A NNEX A, A NNEX B Figure 8.54 Snowdrift load onto the main roof due to the adjacent existing structure: the adjacent building is h = 60 meters high. (Worked example taken from: www.thestructuralengineer.org). [Reference sheet: Annex B]‐[Cell‐Range: A251:O251‐A322:O322]. Solution: Initially, the basic snow load was calculated equal to s k = 0 60 kN / m2 . The shape factor for the overall snow load on the duo‐pitch roof for the new sports hall is then determined and the corresponding snow load is calculated. With (see EN 1991‐1‐3, Table 5.2 ‐ “Snow load shape coefficients”): = 8 1 = 0 8 - the snow load onto sports hall roof is calculated as follow: s = 1 s k = 0 8 0 60 = 0 48 0 5 kN / m2 . Note that this load is a variable static action and therefore would have a partial factor of 1 5 Q k if it were being considered in isolation to other loads. Finally, we consider the snowdrift load onto the main roof due to the adjacent existing structure, which is significantly taller than the sports hall. See Figure 8.53 on page 127 (case f) and figure above. Drift length: l s = min b 1 ; 5h ; 15 m = min 17 50 ; 5 60 ; 15 m = 15 00 m . Shape coefficients given in figure B4: 2h 2 max b 1 ; b 2 120 2 35 00 - ; 8 = min ------------ ; ---------------------- ; 8 = min 200 ; 4 67 ; 8 , 1 = min ------ ; ---------------------------------------------s k min b 1 ; 5h ; 15 m 0 60 15 00 1 = 4 67 - . Therefore, the snow drift load is calculated as follow: Topic: User’s Manual/Verification tests - EN1991-1-3_(b).xls page 131 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 8 E UROCODE 1 EN 1991-1-3: A NNEX A, A NNEX B s = 1 s k = 4 67 0 60 = 2 80 kN / m2 . This load is deemed to be an accidental action and therefore no partial factors are applied to it within ULS and EQU analyses. example-end 8.4 References [Section 8] Derivation of snow load, Technical Guidance Note, TheStructuralEngineer, March 2012. Web resource: www.istructe.org/resources-centre/library. EN 1991-1-3:2003/AC:2009. Eurocode 1: Actions on structures - Part 1-3: General actions - Snow loads. Brussels: CEN/TC 250 - Structural Eurocodes, March 2009. EN 1991-1-3 (2003) (English): Eurocode 1: Actions on structures - Part 1-3: General actions - Snow loads [Authority: The European Union Per Regulation 305/2011, Directive 98/34/EC, Directive 2004/18/EC]. Manual for the design of building structures to Eurocode 1 and Basis of Structural Design April 2010. © 2010 The Institution of Structural Engineers. page 132 Topic: User’s Manual/Verification tests - EN1991-1-3_(b).xls Section 9 Eurocode 1 EN 1991-1-3: Annex C, Annex D 9.1 Annex C: European Ground Snow Load Maps T his Annex presents the European snow maps which are the result of scientific work carried out under contract to DGIII/D-3 of the European Commission, by a specifically formed research Group. The objectives of this Annex, defined in 1.1(5), are: — to help National Competent Authorities to redraft their national maps — to establish harmonised procedures to produce the maps. Figure 9.55 From Figure C.1 - European Climatic regions. Topic: User’s Manual/Verification tests - EN1991-1-3_(c).xls page 133 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 9 E UROCODE 1 EN 1991-1-3: A NNEX C, A NNEX D This will eliminate or reduce the inconsistencies of snow load values in CEN member states and at borderlines between countries. The European snow map developed by the Research Group are divided into 9 different homogeneous climatic regions, as shown in Figures C.1 to C.10. Climatic Region Expression Alpine Region: A 2 s k = 0 642Z + 0 009 1 + --------- 728 Central East: A 2 s k = 0 264Z – 0 002 1 + --------- 256 Greece: A 2 s k = 0 420Z – 0 030 1 + --------- 917 Iberian Peninsula: A 2 s k = 0 190Z – 0 095 1 + --------- 524 Mediterranean Region: A 2 s k = 0 498Z – 0 209 1 + --------- 452 Central West: As k = 0 164Z – 0 082 + -------966 Sweden, Finland: As k = 0 790Z + 0 375 + -------336 UK, Republic of Ireland: Table 9.22 As k = 0 140Z – 0 1 + -------501 From Table C.1 - Altitude - Snow Load Relationships. In each climatic region a given load-altitude correlation formula applies and this is given in Table C.1 above where: • s k is the characteristic snow load on the ground kN m 2 • A is the site altitude above Sea Level [m] • Z is the zone number given on the map (1; 2; 3; 4; 4,5). 9.2 Annex D: Adjustment of the ground snow load according to return period Ground level snow loads for any mean recurrence interval different to that for the characteristic snow load, s k , (which by definition is based on annual probability of exceedence of 0,02) may be adjusted to correspond to characteristic values by application of Sections D(2) to D(4). If the available data show that the annual maximum snow load can be assumed to follow a Gumbel probability distribution, then the relationship between the characteristic value of the snow page 134 Topic: User’s Manual/Verification tests - EN1991-1-3_(c).xls S ECTION 9 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-3: A NNEX C, A NNEX D load on the ground and the snow load on the ground for a mean recurrence interval of n years is given by the formula (D.1):(1) 1 – V ------6- ln – ln 1 – P + 0 57722 n sn ---- = ------------------------------------------------------------------------------------------------- 1 + 2 5923V sk where: • s k is the characteristic snow load on the ground (with a return period of 50 years, in accordance with EN 1990:2002) • s n is the ground snow load with a return period of n years • P n is the annual probability of exceedence (equivalent to approximately 1 n , where n is the corresponding recurrence interval (years)) • V is the coefficient of variation of annual maximum snow load(2). However, expression (D.1) should not be applied for annual probabilities of exceedence greater than 0,2 (i.e. return period less than approximately 5 years). Where permitted by the relevant national Authority expression (D.1) may also be adapted to calculate snow loads on the ground for other probabilities of exceedence. For example for: a. structures where a higher risk of exceedence is deemed acceptable b. structures where greater than normal safety is required. 9.3 Verification tests EN1991‐1‐3_(C).XLS. 8.40 MB. Created: 09 March 2013. Last/Rel.-date: 09 March 2013. Sheets: — Splash — Annex C — Annex D. EXAMPLE 9-AU‐ European Ground Snow Load Maps ‐ test 1 Given: Assuming A = 100 mamsl (meters above mean sea level) and zone number Z = 2 , find the characteristic snow load on the ground s k for all the climatic regions on Table C.1 “Altitude ‐ Snow Load Relationship”. [Reference sheet: Annex C]‐[Cell‐Range: A53:O53‐A100:O100]. (1) Where appropriate another distribution function for the adjustment of return period of ground snow load may be defined by the relevant national Authority. (2) Information on the coefficient of variation may be given by the relevant national Authority. Topic: User’s Manual/Verification tests - EN1991-1-3_(c).xls page 135 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 9 E UROCODE 1 EN 1991-1-3: A NNEX C, A NNEX D Solution: Alpine Region: A 2 s k = 0 642Z + 0 009 1 + --------- 728 100 2 = 0 642 2 + 0 009 1 + --------- 728 = 1 32 kN / m2 . Central East: A 2 100 2 s k = 0 264Z – 0 002 1 + --------- = 0 264 2 – 0 002 1 + --------- = 0 61 kN / m2 . 256 256 Greece: A 2 s k = 0 420Z – 0 030 1 + --------- 917 100 2 = 0 420 2 – 0 030 1 + --------- 917 = 0 82 kN / m2 . 100 2 = 0 190 2 – 0 095 1 + --------- 524 = 0 30 kN / m2 . 100 2 = 0 498 2 – 0 209 1 + --------- 452 = 0 83 kN / m2 . Iberian Peninsula: A 2 s k = 0 190Z – 0 095 1 + --------- 524 Mediterranean Region: A 2 s k = 0 498Z – 0 209 1 + --------- 452 Central West: 100 A s k = 0 164Z – 0 082 + --------- = 0 164 2 – 0 082 + --------- = 0 35 kN / m2 . 966 966 Sweden, Finland: A - = 0 790 2 + 0 375 + 100 s k = 0 790Z + 0 375 + ---------------- = 2 25 kN / m2 . 336 336 UK, Republic of Ireland: A - = 0 140 2 – 0 1 + 100 s k = 0 140Z – 0 1 + ---------------- = 0 38 kN / m2 . 501 501 example-end EXAMPLE 9-AV‐ European Ground Snow Load Maps ‐ test 2 Given: Assuming A = 200 mamsl , Z = 2 , C e = 1 , C t = 1 find for the UK: 1) the characteristic ground snow load s k 2) the design value of exceptional snow load on the ground for locations where exceptional snow loads on the ground can occur 3) the snow load on roofs for the persistent/transient design situations 4) the snow load on roofs for the accidental design situations where exceptional snow load is the accidental action 5) the snow load on roofs for the accidental design situations where exceptional snow drift is the accidental action and where Annex B applies. [Reference sheet: Annex C]‐[Cell‐Range: A102:O102‐A150:O150]. page 136 Topic: User’s Manual/Verification tests - EN1991-1-3_(c).xls S ECTION 9 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-3: A NNEX C, A NNEX D Figure 9.56 Characteristic ground snow load for UK and Republic of Ireland (zone N. 2). Solution: 1) UK, Republic of Ireland: A - = 0 140 2 – 0 1 + 200 s k = 0 140Z – 0 1 + ---------------- = 0 58 kN / m2 . 501 501 2) With a coefficient for exceptional snow loads equal to C esl = 2 : s Ad = C esl s k = 2 0 58 = 1 16 kN / m2 . 3) With C e = 1 , C t = 1 : s = 1 C 2 C t s k = 1 1 1 0 58 = 1 0 58 kN / m2 . 4) With s Ad = 1 16 kN / m2 : s = 1 C e C 1 s Ad = 1 1 16 kN / m2 . 5) s = 1 s k = 1 0 58 kN / m2 . example-end EXAMPLE 9-AW‐ Adjustment of the ground snow load according to return period ‐ test 3 Given: According to Annex D, find the ratio s n s k for a coefficient of variation of annual maximum snow load V = 0 5 and a recurrence interval equal to n = 90 years. [Reference sheet: Annex D]‐[Cell‐Range: A15:O15‐A31:O31]. Topic: User’s Manual/Verification tests - EN1991-1-3_(c).xls page 137 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 9 E UROCODE 1 EN 1991-1-3: A NNEX C, A NNEX D Solution: From eq. D.1 with P n = 1 n = 1 90 0 0111 : 6 1- + 0 57722 1 – V ------6- ln – ln 1 – P + 0 57722 1 – 0 5 ------- ln – ln 1 – ----n 90 sn ---- = ------------------------------------------------------------------------------------------------- = --------------------------------------------------------------------------------------------------------- , 1 + 2 5923V 1 + 2 5923 0 5 sk sn 2 527 ---- = --------------- 1 10 . 2 296 sk Figure 9.57 Ratio sn/sk with V = 0,5 plotted against “n” (years). For a characteristic snow load on the ground equal to s k = 0 58 kN / m2 (return period of 50 years), we get ( n = 90 years): s n = 1 10 s k = 1 10 0 58 = 0 64 kN / m2 . example-end 9.4 References [Section 9] Derivation of snow load, Technical Guidance Note, TheStructuralEngineer, March 2012. Web resource: www.istructe.org/resources-centre/library. page 138 Topic: User’s Manual/Verification tests - EN1991-1-3_(c).xls S ECTION 9 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-3: A NNEX C, A NNEX D EN 1991-1-3:2003/AC:2009. Eurocode 1: Actions on structures - Part 1-3: General actions - Snow loads. Brussels: CEN/TC 250 - Structural Eurocodes, March 2009. EN 1991-1-3:2003. Eurocode 1 - Actions on structures - Part 1-3: General actions - Snow loads. Brussels: CEN/TC 250 - Structural Eurocodes, July 2003 (DAV). EN 1991-1-3 (2003) (English): Eurocode 1: Actions on structures - Part 1-3: General actions - Snow loads [Authority: The European Union Per Regulation 305/2011, Directive 98/34/EC, Directive 2004/18/EC]. Manual for the design of building structures to Eurocode 1 and Basis of Structural Design April 2010. © 2010 The Institution of Structural Engineers. Topic: User’s Manual/Verification tests - EN1991-1-3_(c).xls page 139 (This page intentionally left blank) Section 10 Eurocode 1 EN 1991-1-4 [Section 4] 10.1 General E N 1991-1-4 gives guidance on the determination of natural wind actions for the structural design of building and civil engineering works for each of the loaded areas under consideration. This includes the whole structure or parts of the structure or elements attached to the structure, e. g. components, cladding units and their fixings, safety and noise barriers. This Part is applicable to: — buildings and civil engineering works with heights up to 200 m, see also (11). — bridges having no span greater than 200 m, provided that they satisfy the criteria for dynamic response, see (12) and 8.2. This part is intended to predict characteristic wind actions on land-based structures, their components and appendages. Certain aspects necessary to determine wind actions on a structure are dependent on the location and on the availability and quality of meteorological data, the type of terrain, etc. These need to be provided in the National Annex and Annex A, through National choice by notes in the text as indicated. Default values and methods are given in the main text, where the National Annex does not provide information. Guyed masts and lattice towers are treated in EN 1993-3-1 and lighting columns in EN 40. This part does not give guidance on the following aspects: — torsional vibrations, e.g. tall buildings with a central core — bridge deck vibrations from transverse wind turbulence — wind actions on cable supported bridges — vibrations where more than the fundamental mode needs to be considered. The general assumptions given in EN 1990, 1.3 apply. The rules in EN 1990, 1.4 apply. Load and response information and terrain parameters may be obtained Topic: User’s Manual/Verification tests - EN1991-1-4_(a).xls - EN1991-1-4_(a)_2.xls page 141 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 10 E UROCODE 1 EN 1991-1-4 [S ECTION 4] from appropriate full scale data. The National Annex may give guidance on design assisted by testing and measurements. 10.2 Definitions For the purposes of this European Standard, the definitions given in ISO 2394, ISO 3898 and ISO 8930 and the following apply. Additionally for the purposes of this Standard a basic list of definitions is provided in EN 1990,1.5. FUNDAMENTAL BASIC WIND VELOCITY. The 10 minute mean wind velocity with an annual risk of being exceeded of 0, 02, irrespective of wind direction, at a height of 10 m above flat open country terrain and accounting for altitude effects (if required). BASIC WIND VELOCITY. The fundamental basic wind velocity modified to account for the direction of the wind being considered and the season (if required). MEAN WIND VELOCITY. The basic wind velocity modified to account for the effect of terrain roughness and orography. PRESSURE COEFFICIENT. External pressure coefficients give the effect of the wind on the external surfaces of buildings; internal pressure coefficients give the effect of the wind on the internal surfaces of buildings. FORCE COEFFICIENT. Force coefficients give the overall effect of the wind on a structure, structural element or component as a whole, including friction, if not specifically excluded BACKGROUND RESPONSE FACTOR. The background factor allowing for the lack of full correlation of the pressure on the structure surface RESONANCE RESPONSE FACTOR. The resonance response factor allowing for turbulence in resonance with the vibration mode. 10.3 Design situations The relevant wind actions shall be determined for each design situation identified in accordance with EN 1990, 3.2. In accordance with EN 1990, 3.2 (3)P other actions (such as snow, traffic or ice) which will modify the effects due to wind should be taken into account.(1) In accordance with EN 1990, 3.2 (3)P, the changes to the structure during stages of execution (such as different stages of the form of the structure, dynamic characteristics, etc.), which may modify the effects due to wind, should be taken into account. Fatigue due to the effects of wind actions should be considered for susceptible structures.(2) (1) See also EN 1991-1-3, EN 1991-2 and ISO 12494. (2) The number of load cycles may be obtained from Annex B, C and E. page 142 Topic: User’s Manual/Verification tests - EN1991-1-4_(a).xls - EN1991-1-4_(a)_2.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 10 E UROCODE 1 EN 1991-1-4 [S ECTION 4] 10.4 Modelling of wind actions REPRESENTATIONS OF WIND ACTIONS. The wind action is represented by a simplified set of pressures or forces whose effects are equivalent to the extreme effects of the turbulent wind. CLASSIFICATION OF WIND ACTIONS. Unless otherwise specified, wind actions should be classified as variable fixed actions, see EN 1990, 4.1.1. CHARACTERISTIC VALUES. The wind actions calculated using EN 1991-1-4 are characteristic values (See EN 1990, 4.1.2). They are determined from the basic values of wind velocity or the velocity pressure. In accordance with EN 1990 4.1.2 (7)P the basic values are characteristic values having annual probabilities of exceedence of 0,02, which is equivalent to a mean return period of 50 years.(3) MODELS. The effect of the wind on the structure (i.e. the response of the structure), depends on the size, shape and dynamic properties of the structure. This Part covers dynamic response due to along-wind turbulence in resonance with the along-wind vibrations of a fundamental flexural mode shape with constant sign. RESPONSE OF STRUCTURES. The response of structures should be calculated according to Section 5 from the peak velocity pressure, q p , at the reference height in the undisturbed wind field, the force and pressure coefficients and the structural factor c s c d (see Section 6). q p depends on the wind climate, the terrain roughness and orography, and the reference height q p is equal to the mean velocity pressure plus a contribution from short-term pressure fluctuations. 10.5 Wind velocity and velocity pressure The mean wind velocity v m should be determined from the basic wind velocity v b which depends on the wind climate as described in 4.2, and the height variation of the wind determined from the terrain roughness and orography as described in 4.3. The peak velocity pressure is determined in 4.5. The fluctuating component of the wind is represented by the turbulence intensity defined in 4.4. The National Annex may provide National climatic information from which the mean wind velocity v m , the peak velocity pressure q p and additional values may be directly obtained for the terrain categories considered. BASIC WIND VELOCITY. The basic wind velocity, v b , defined as a function of wind direction and time of year at 10 m above ground for terrain category II,(4) is given by: v b = c dir c season c prob v b 0 (Eq. 10‐62) (3) All coefficients or models, to derive wind actions from basic values, are chosen so that the probability of the calculated wind actions does not exceed the probability of these basic values. (4) See Table 4.1 (EN 1991-1-4), “Terrain categories and terrain parameters”. Topic: User’s Manual/Verification tests - EN1991-1-4_(a).xls - EN1991-1-4_(a)_2.xls page 143 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 10 E UROCODE 1 EN 1991-1-4 [S ECTION 4] where: • c dir c season v b 0 is the basic wind velocity, defined as a function of wind direction and time of year at 10 m above ground of terrain category II • v b 0 is the characteristic 10 minutes mean wind velocity, irrespective of wind direction and time of year, at 10 m above ground level in open country terrain with low vegetation such as grass and isolated obstacles with separations of at least 20 obstacle heights. • c dir is the directional factor • c season is the season factor • c prob is the probability factor:(5) 1 – K ln – ln 1 – p n c prob = ------------------------------------------------------- . 1 – K ln – ln 0 98 (Eq. 10‐63) The 10 minutes mean wind velocity having the probability p for an annual exceedence is determined by multiplying the basic wind velocity c dir c season v b 0 by the probability factor, c prob given by expression above. See also EN 1991-1-6. MEAN WIND. The mean wind velocity v m z at a height z above the terrain depends on the terrain roughness and orography and on the basic wind velocity and should be determined using expression: vm z = cr z c0 z vb (Eq. 10‐64) where: • c r z is the roughness factor • c 0 z is the orography factor, taken as 1 0 unless otherwise specified.(6) The roughness factor, c r z , accounts for the variability of the mean wind velocity at the site of the structure due to: • the height above ground level • the ground roughness of the terrain upwind of the structure in the wind direction considered. The procedure for determining c r z may be given in the National Annex. The recommended procedure for the determination of the roughness factor at height z is based on a logarithmic velocity profile and is given by expressions: c r z = k r ln z z 0 for z min z z max c r z = k r ln z min z 0 = cost for z z min . (Eq. 10‐65) (5) The values for “K” and “n” may be given in the National Annex. The recommended values are 0,2 for “K” and 0,5 for “n”. (6) See Section 4.3.3. page 144 Topic: User’s Manual/Verification tests - EN1991-1-4_(a).xls - EN1991-1-4_(a)_2.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 10 E UROCODE 1 EN 1991-1-4 [S ECTION 4] where: • z 0 is the roughness length • k r is terrain factor depending on the roughness length z 0 [m] calculated using: z 0 0 07 k r = 0 19 ---------- 0 05 • z min is the minimum height defined in Table 4.1 • z max is to be taken as 200 m. Terrain category z0 [m] zmin [m] 0 - Sea or coastal area exposed to the open sea 0,003 1 I - Lakes or flat and horizontal area with negligible vegetation and without obstacles 0,01 1 II - Area with low vegetation such as grass and isolated obstacles (trees, buildings) with separations of at least 20 obstacle heights 0,05 2 III - Area with regular cover of vegetation or buildings or with isolated obstacles with separations of maximum 20 obstacle heights (such as villages, suburban terrain, permanent forest) 0,3 5 IV - Area in which at least 15% of the surface is covered with buildings and their average height exceeds 15 m 1,0 10 Table 10.23 From Table 4.1 - Terrain categories and terrain parameters. The terrain roughness to be used for a given wind direction depends on the ground roughness and the distance with uniform terrain roughness in an angular sector around the wind direction. Small areas (less than 10% of the area under consideration) with deviating roughness may be ignored. WIND TURBOLENCE. The turbulence intensity I v z at height z is defined as the standard deviation of the turbulence divided by the mean wind velocity. The recommended rules for the determination of I v z are given in expressions below: v kl for z min z z max I v z = ------------- = --------------------------------------vm z c 0 z ln z z 0 kl for z z min I v z = ---------------------------------------------c 0 z ln z min z 0 (Eq. 10‐66) where: • k l is the turbulence factor. The value of k l may be given in the National Annex. The recommended value for k l is 1,0 Topic: User’s Manual/Verification tests - EN1991-1-4_(a).xls - EN1991-1-4_(a)_2.xls page 145 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 10 E UROCODE 1 EN 1991-1-4 [S ECTION 4] • c 0 z is the orography factor • z 0 is the roughness length, given in Table 4.1. PEAK VELOCITY PRESSURE. The peak velocity pressure q p z at height z , which includes mean and short-term velocity fluctuations, should be determined. The National Annex may give rules for the determination of q p z . The recommended rule is given in expression: q p z = 1 + 7 I v z 0 5 v m2 z = c e z q b (Eq. 10‐67) where: • = 1 25 kg m 3 is the air density • q b = 0 5 v b2 is the basic velocity pressure • ce z = qp z qb . Figure 10.58From Figure 4.2 - Illustrations of the exposure factor ce(z) for c0=1,0; kI=1,0. page 146 Topic: User’s Manual/Verification tests - EN1991-1-4_(a).xls - EN1991-1-4_(a)_2.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 10 E UROCODE 1 EN 1991-1-4 [S ECTION 4] 10.6 Verification tests EN1991‐1‐4_(A).XLS. 6.32 MB. Created: 12 March 2013. Last/Rel.-date: 12 March 2013. Sheets: — Splash — CodeSec4. EXAMPLE 10-AX‐ Wind velocity and velocity pressure ‐ probability factor ‐ test1 Given: Find the 10 minutes mean wind velocity having the probability p = 0 010 for an annual exceedence. Assume: c dir = 0 85 , c season = 0 98 (temporary buildings erected for less than one year), v b 0 = 30 m s (fundamental value of the basic wind velocity). [Reference sheet: CodeSec4]‐[Cell‐Range: A37:O37‐A67:O67]. Solution: Annual probability of exceedence of p = 0 010 with mean return period: 1 1 N --- = --------------- = 100 years . p 0 010 Basic wind velocity: c dir c season v b 0 = 0 85 0 98 30 = 24 99 m s . Probability factor (with K = 0 2 and n = 0 5 ): 1 – K ln – ln 1 – p n 1 – 0 2 ln – ln 1 – 0 010 0 5 1 920 0 5 c prob = ------------------------------------------------------- = ----------------------------------------------------------------------- = --------------- = 1 04 . 1 780 1 – K ln – ln 0 98 1 – 0 2 ln – ln 0 98 Ten minutes mean wind velocity (having the probability p = 0,010 for an annual exceedence): v b = c dir c season c prob v b 0 = 24 99 c prob = 24 99 1 04 = 25 99 m s . example-end EXAMPLE 10-AY‐ Mean wind ‐ roughness factor ‐ test2 Given: Find the roughness factor for an height above ground level at the site of the structure equal to z = 5 m . Assume a suburban terrain. [Reference sheet: CodeSec4]‐[Cell‐Range: A100:O100‐A182:O182]. Solution: From Table 4.1 (“Terrain categories and terrain parameters”): III: “Area with regular cover of vegetation or buildings or with isolated obstacles with separations of maximum 20 obstacle heights (such as villages, suburban terrain, permanent forest)”. With: z 0 = 0 3 m ; z min = 5 m . For z zmin , we get: Topic: User’s Manual/Verification tests - EN1991-1-4_(a).xls - EN1991-1-4_(a)_2.xls page 147 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 10 E UROCODE 1 EN 1991-1-4 [S ECTION 4] z 0 0 07 0 3 0 07 k r = 0 19 ----------= 0 19 ------------ = 0 215 . 0 05 0 05 Therefore, z = 5 m = z min : c r z = k r ln z min z 0 = 0 215 ln 5 0 3 = 0 61 - . Figure 10.59Graph of the roughness factor against “z”. For (say) z = 9 m with z min z zmax 5 m z 200 m : c r z = k r ln z z 0 = 0 215 ln 9 0 3 = 0 73 [see cell: R139, sheet: CodeSec4]. example-end EXAMPLE 10-AZ‐ Mean wind ‐ flat terrain ‐ test3 Given: Find the mean wind velocity at height z = 5 m above the terrain. Assume: v b = 25 95 m s . [Reference sheet: CodeSec4]‐[Cell‐Range: A256:O256‐A264:O264]. Solution: Flat terrain: orography factor equal to c 0 z = 1 = cost for any “z”. From which, using the results calculated in the previous example, we have: v m z = v m 5 = c r 5 c 0 5 v b 0 61 1 25 95 = 15 8 m s . page 148 Topic: User’s Manual/Verification tests - EN1991-1-4_(a).xls - EN1991-1-4_(a)_2.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 10 E UROCODE 1 EN 1991-1-4 [S ECTION 4] Figure 10.60Turbolence intensity against “z” (Cat. III, c0 = 1; kl = 1). NOTE v b = 25 9515 [see cell: P66, sheet: CodeSec4]. c r 5 = 0 60598 [see cell: T122, sheet: CodeSec4]. Therefore: c r 5 c 0 5 v b = 0 60598 1 25 9515 = 15 72609 [see cell: T258, sheet: CodeSec4]. example-end EXAMPLE 10-BA‐ Wind turbulence ‐ test4 Given: Find the turbulence intensity I v z at height z = 5 m above the terrain. Let assume a turbulence factor k l and an orography factor c 0 z both equal to unity. Terrain cat.: III. [Reference sheet: CodeSec4]‐[Cell‐Range: A282:O282‐A364:O364]. Solution: From Table 4.1 (terrain category III): roughness length: z 0 = 0 30 , z min = 5 m , z max = 200 m . We have (see previous examples): flat terrain c 0 = 1 = cost . For z min z zmax 5 m z 200 m , we find: kl 1 I v z = --------------------------------------= ------------------------------------- = 0 355 0 36 . c 0 z ln z z 0 1 ln 5 0 30 Topic: User’s Manual/Verification tests - EN1991-1-4_(a).xls - EN1991-1-4_(a)_2.xls page 149 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 10 E UROCODE 1 EN 1991-1-4 [S ECTION 4] For (say) z = 17 m , we get: kl 1 I v z = --------------------------------------= ---------------------------------------- = 0 2478 [see cell: R339, sheet: CodeSec4]. c 0 z ln z z 0 1 ln 17 0 30 example-end EXAMPLE 10-BB‐ Peak velocity pressure ‐ test5 Given: Find the peak velocity pressure at height z = 5 m . Use the numerical data given in the previous examples. Assume an air density equal to 1 25 kg m 3 . [Reference sheet: CodeSec4]‐[Cell‐Range: A389:O389‐A458:O458]. Solution: From previous example, we found: v m z = c r z c 0 z v b 15 8 m s . Therefore, with I v 5 = 0 36 , = 1 25 kg m 3 , we get: 1 + 7 I v z 0 5 v m2 z = 1 + 7 0 36 0 5 1 25 15 8 2 10 –3 0 55 kN / m2 , q p z = q p 5 = 0 55 kN / m2 . NOTE v m = 15 7261 [see cell: T258, sheet: CodeSec4]. I v 5 = 0 35544 [see cell: V310, sheet: CodeSec4]. Therefore: 1 + 7 I v z 0 5 v m2 z = 1 + 7 0 35544 0 5 1 25 15 7261 2 = 539 15 N m 2 [see cell: P398, sheet: CodeSec4]. example-end EXAMPLE 10-BC‐ Exposure factor ‐ test6 Given: Find the exposure factor at height z = 5 m . Use the numerical data given in the previous examples ( q p 5 = 539 15 N m 2 = 0 539 kN m 2 ). [Reference sheet: CodeSec4]‐[Cell‐Range: A544:O544‐A548:O548]. Solution: basic velocity pressure: q b = 0 5 v b2 0 5 1 25 26 2 10 –3 = 0 42 kN / m2 . Exposure factor: c e 5 = q p 5 q b = 0 54 0 42 1 28 - . example-end page 150 Topic: User’s Manual/Verification tests - EN1991-1-4_(a).xls - EN1991-1-4_(a)_2.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 10 E UROCODE 1 EN 1991-1-4 [S ECTION 4] EXAMPLE 10-BD‐ Fundamental value of the basic wind velocity, altitude factor (UK NA) ‐ test7 Given: The basic wind velocity, v b , defined as a function of wind direction and time of year at 10 m above ground for terrain category II, called Country terrain in the UK National Annex is given by: v b = c dir c season c prob v b 0 where v b 0 is the fundamental value of the basic wind velocity given by: v b 0 = v b map c alt with v b map which is given in Figure below. Figure 10.61Value of vb,map [m/s]. Figure taken from: Manual for the design of building structures to Eurocode 1 and Basis of Structural Design April 2010. © 2010 The Institution of Structural Engineers. Topic: User’s Manual/Verification tests - EN1991-1-4_(a).xls - EN1991-1-4_(a)_2.xls page 151 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 10 E UROCODE 1 EN 1991-1-4 [S ECTION 4] The altitude factor c alt is given by: c alt = 1 + 0 001 A for z 10 m , c alt = 1 + 0 001 A 10 z 1 / 5 for z 10 m . where A is the altitude of the site in metres above mean sea level and z is either z s as defined in Figure 6.10 (EN 1991‐1‐4) or z e the height of the part above ground as defined in Figure 7.4 (EN 1991‐1‐4). Find the fundamental value of the basic wind velocity around the city of Glasgow ( A 70 mamsl ) assuming an height (say as defined in Figure 6.10) equal to z e = z = 11 m . [Reference sheet: CodeSec4]‐[Linked Cell: I37]. Solution: From Figure 10.61, near the city of Glasgow: v b map = 25 5 m s . For z 10 m , we get: c alt = 1 + 0 001 A 10 z 1 / 5 = 1 + 0 001 70 10 11 1 / 5 = 1 069 . Therefore: v b 0 = v b map c alt = 25 5 1 069 = 27 26 m s . Figure 10.62PreCalculus Excel® form: procedure for a quick pre-calculation. PreCalculus (see Figure 10.62). c alt = 1 068678 , v b 0 = v b map c alt = 25 5 1 068678 27 251 m s . example-end 10.7 References [Section 10] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design, April 2010. © 2010 The Institution of Structural Engineers. page 152 Topic: User’s Manual/Verification tests - EN1991-1-4_(a).xls - EN1991-1-4_(a)_2.xls Section 11 Eurocode 1 EN 1991-1-4 Section 7 (Page 32 to 37) 11.1 Pressure and force coefficients - General T his section should be used to determine the appropriate aerodynamic coefficients for structures. Depending on the structure the appropriate aerodynamic coefficient will be: — internal and external pressure coefficients, see 7.1.1(1) — net pressure coefficients, see 7.1.1(2) — friction coefficients, see 7.1.1(3) — force coefficients, see 7.1.1(4). Pressure coefficients should be determined for: 1. buildings, using 7.2 for both internal and external pressures, and for 2. circular cylinders, using 7.2.9 for the internal pressures and 7.9.1 for the external pressures. Net pressure coefficients should be determined for: 1. canopy roofs, using 7.3 2. free-standing walls, parapets and fences using 7.4. Friction coefficients should be determined for walls and surfaces defined in 5.3 (3) and (4), using 7.5. 1. force coefficients should be determined for: 2. signboards, using 7.4.3 3. structural elements with rectangular cross section, using 7.6 4. structural elements with sharp edged section, using 7.7 5. structural elements with regular polygonal section, using 7.8 6. circular cylinders, using 7.9.2 and 7.9.3 7. spheres, using 7.10 8. lattice structures and scaffoldings, using 7.11 and flags, using 7.12. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_3.xls page 153 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 11 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 32 TO 37) A reduction factor depending on the effective slenderness of the structure may be applied, using 7.13. Note Force coefficients give the overall effect of the wind on a structure, structural element or component as a whole, including friction, if not specifically excluded. 11.2 Asymmetric and counteracting pressures and forces If instantaneous fluctuations of wind over surfaces can give rise to significant asymmetry of loading and the structural form is likely to be sensitive to such loading (e.g. torsion in nominally symmetric single core buildings) then their effect should be taken into account. For free-standing canopies and signboards, 7.3 and 7.4 should be applied. The National Annex may give procedures for other structures. The recommended procedures are: a. for rectangular structures that are susceptible to torsional effects the pressure distribution given in Figure 7.1 should be applied for the representation of the torsional effects due to an inclined wind or due to lack of correlation between wind forces acting at different places on the structure b. for other cases an allowance for asymmetry of loading should be made by completely removing the design wind action from those parts of the structure where its action will produce a beneficial effect. NOTE: Zone E: cpe (UK) = 1,3 x cpe (EC1) Zone D: cpe (UK) = 1,3 x cpe (EC1) Note The recommended procedure in EC1 Part 1‐4 to account for torsion should not be used in the UK: blue pressure distibution (zone E) should be used instead, the shape of the pressure distribution in zone D remains unchanged. Figure 11.63From Figure 7.1 [modified] - Pressure distribution used to take torsional effects into account. page 154 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_3.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 11 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 32 TO 37) If ice or snow alters the geometry of a structure so that it changes the reference area or shape, this should be taken into account. 11.3 Pressure coefficients for buildings The external pressure coefficients are given for loaded areas A of 1 m 2 and 10 m 2 in the tables for the appropriate building configurations as c pe 1 , for local coefficients, and c pe 10 , for overall coefficients, respectively. Values for c pe 1 are intended for the design of small elements and fixings with an area per element of 1 m 2 or less such as cladding elements and roofing elements. Values for c pe 10 may be used for the design of the overall load bearing structure of buildings. The National Annex may give a procedure for calculating external pressure coefficients for loaded areas above 1 m 2 based on external pressure coefficients c pe 1 and c pe 10 . The recommended procedure for loaded areas up to 10 m 2 is given by expression: c pe = c pe 1 – c pe 1 – c pe 10 log A for 1 A m 2 10 (Eq. 11‐68) where A is the loaded area. Note This recommended procedure should not be used in the UK. In the UK the c pe 1 values should be used for all areas < 1 m 2 and the c pe 10 values should be used for all areas > 10 m 2 . The c pe 1 values should be used for small cladding elements and fixings and the c pe 10 values for larger cladding elements and for overall structural loads. c pe values are given for orthogonal wind directions 0°, 90° and where appropriate 180°. These represent the worst case values over the range of wind directions of ±45° about each orthogonal axis. No specific coefficients are given for overhanging or protruding roofs. In these cases the pressure on the top surface of the overhanging roof is determined from the appropriate roof zone and the pressure on the underside is taken as that on the adjacent part of the vertical wall. 11.4 Vertical walls of rectangular plan buildings The external pressure coefficients c pe 10 and c pe 1 for the walls of rectangular plan buildings are defined in Figure 7.5 (“Key for vertical walls”) and the values are given in Table 7.1 (“Recommended values of external pressure coefficients for vertical walls of rectangular plan buildings”). The values of c pe 10 and c pe 1 may be given in the National Annex. The recommended values are given in Table 7.1, depending on the ratio h/d. For intermediate values of h/d, linear interpolation may be applied. The values of Table 7.1 also apply to walls of buildings with inclined roofs, such as duopitch and monopitch roofs. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_3.xls page 155 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 11 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 32 TO 37) Figure 11.64From Figure 7.5 - Key for vertical walls. For buildings with h/d > 5, the total wind loading may be based on the provisions given in 7.6 to 7.8 and 7.9.2. In cases where the wind force on building structures is determined by application of the pressure coefficients c pe on windward and leeward side (zones D and E) of the building simultaneously, the lack of correlation of wind pressures between the windward and leeward side may have to be taken into account. The lack of correlation of wind pressures between the windward and leeward side may be considered as follows. For buildings with h/d > 5 the resulting force is multiplied by 1. For buildings with h/d < 1, the resulting force is multiplied by 0,85. For intermediate values of h/d, linear interpolation may be applied. page 156 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_3.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 11 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 32 TO 37) Zone A B C D E h/d c pe 10 c pe 1 c pe 10 c pe 1 c pe 10 c pe 1 c pe 10 c pe 1 c pe 10 c pe 1 5 – 1,2 – 1,4 – 0,8 – 1,1 – 0,5 – 0,5 + 0,8 + 1,0 – 0,7 – 0,7 1 – 1,2 – 1,4 – 0,8 – 1,1 – 0,5 – 0,5 + 0,8 + 1,0 – 0,5 – 0,5 < 0,25 – 1,2 – 1,4 – 0,8 – 1,1 – 0,5 – 0,5 + 0,8 + 1,0 – 0,3 – 0,3 Table 11.24 From Table 7.1 - Recommended values of external pressure coefficients for vertical walls of rectangular plan buildings. [For intermediate values of h/d, linear interpolation may be applied]. 11.5 Verification tests EN1991‐1‐4_(A)_3.XLS. 6.12 MB. Created: 14 May 2013. Last/Rel.-date: 14 May 2013. Sheets: — Splash — CodeSec7(32to37). EXAMPLE 11-BE‐ External pressure coefficients for building ‐ test1 Given: A 20,0 m x 25,0 m x 8,0 m at eaves, 9,0 m at apex warehouse is to be constructed. Find the external pressure coefficients c pe 10 and c pe 1 for vertical walls (zone A, B, C, D and E as defined in Figure 7.5). Using the recommended procedure given in Figure 7.2, find the external pressure coefficients c pe for all the vertical zone. Assume a rectangular plan building. [Reference sheet: CodeSec7(32to37)]‐[Cell‐Range: A1:O1‐A197:O197]. Solution: We have: d = 20 0 m ; b = 25 0 m (crosswind dimension); h = 9 0 m (at apex) and h min = 8 0 m (at eaves). From Figure 7.5: e = min b ; 2h = min 25 0 ; 2 9 0 = 18 0 m . Elevation for e d applies: e 18 --- = ------ = 3 6 m ; 5 5 4e 18 0 - = 14 4 m ; ------ = 4----------------------5 5 d – e = 20 0 – 18 0 = 2 0 m . Entering Table 7.1 (see Table above) with: h 9 0 --- = ------------ = 0 45 d 20 0 we obtain (linear interpolation between h/d = 1 and h/d < 0,25 rows) for: Zone D Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_3.xls page 157 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 11 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 32 TO 37) Figure 11.65Sheet: “CodeSec7(32to37)” - Geometry Input. c pe 10 – 0 7 0---------------------- 8 – 0 7- = ----------------------------0 45 – 0 25 1 – 0 25 c pe 10 = 0 73 Zone E (with c pe 10 = c pe 1 ) c pe 10 – – 0 3 –-------------------------------------0 5 – – 0 3 - = ------------------------------------0 45 – 0 25 1 – 0 25 c pe 10 = c pe 1 = – 0 35 . Therefore, we get: Zone A B C D E h/d c pe 10 c pe 1 c pe 10 c pe 1 c pe 10 c pe 1 c pe 10 c pe 1 c pe 10 c pe 1 < 0,25 – 1,2 – 1,4 – 0,8 – 1,1 – 0,5 – 0,5 + 0,73 + 1,0 – 0,35 – 0,35 Table 11.25 From Table 7.1 - Recommended values of external pressure coefficients for vertical walls of rectangular plan buildings. [Linear interpolation applied]. Calculations of areas. Zone A (with e < d and consequently e/5 < d/2): h – h min h AB – h min ------------------- = ------------------------e5 0 5 d –8 9 – 8 - h--------------------------------------= AB 3 6 0 5 20 h AB = 8 36 m e h AB + h min --5 8 36 + 8 00 3 60 A A = -------------------------------------- = -------------------------------------------------------- = 29 448 m 2 10 m 2 . 2 2 page 158 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_3.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 11 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 32 TO 37) Zone C (with e < d, it is d – e = 2 m < 0,5d): h – h min h BC – h min ------------------- = -----------------------d–e 0 5 d –8 9 – 8 - h--------------------------------------= BC 2 0 5 20 h BC = 8 20 m h BC + h min d – e 8 20 + 8 00 2 00 - = 16 20 m 2 10 m 2 . - = ------------------------------------------------------A C = -------------------------------------------------2 2 Total area (zones A + B + C): d 20 A A + B + C = h + h min --- = 9 + 8 ------ = 170 m 2 . 2 2 Zone B: A B = 170 – 29 449 – 16 20 = 124 351 m 2 10 m 2 . External pressure coefficients cpe. All the calculated loaded areas are above 10 m2. Therefore c pe = c pe 10 . Zone A B C D E h/d c pe c pe c pe c pe c pe < 0,25 – 1,2 – 0,8 – 0,5 + 0,73 – 0,35 Table 11.26 Calculated values of external pressure coefficients for vertical walls of rectangular plan buildings. [Linear interpolation applied]. As it was plausible to expect all the coefficients of external pressure coincide with the values of c pe 10 . example-end EXAMPLE 11-BF‐ Asymmetric and counteracting pressures and forces ‐ test2 Given: Assume that short term fluctuations of wind gusts over the building’s surfaces can give rise to asymmetric loading. Use the recommended procedure used in the UK to calculate the external pressure coefficient for the zone D and E. Numerical data form previous example. [Reference sheet: CodeSec7(32to37)]‐[Cell‐Range: A216:O216‐A264:O264]. Solution: The recommended procedure in EC1 Part 1‐4 to account for torsion should not be used in the UK, Figure below should be used instead. The zones D and E and the external pressure coefficients are given in Figure 7.5 and in Table 7.1 respectively. According to the provisions of the UK National Annex we have EC1 c peUK = 1 3 c pe (with c pe = c pe 10 ) and pressure distributions of triangular shape (see Figure below). Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_3.xls page 159 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 11 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 32 TO 37) Figure 11.66Pressure distribution used to take torsional effects into account (UK National Annex). Zone E UK c pe = 1 3 – 0 35 – 0 45 Zone D UK c pe = 1 3 0 73 0 95 . example-end 11.6 References [Section 11] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design, April 2010. © 2010 The Institution of Structural Engineers. page 160 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_3.xls Section 12 Eurocode 1 EN 1991-1-4 Section 7 (Page 37 to 39) 12.1 Pressure and force coefficients - Flat roofs F lat roofs are defined as having a slope ( * ) of – 5 * 5 . The roof should be divided into zones as shown in Figure 7.6. The reference height for flat roof and roofs with curved or mansard eaves should be taken as h. The reference height for flat roofs with parapets should be taken as h + h p , see Figure 7.6. Pressure coefficients for each zone are given in Table 7.2. The resulting pressure coefficient on the parapet should be determined using 7.4. Figure 12.67From Figure 7.6 - Key for flat roofs. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_4.xls page 161 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 12 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 37 TO 39) Zone Roof type F Sharp eaves With parapets H I cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 hp/h = 0,025 - 1,8 - 2,5 - 1,2 - 2,0 - 0,7 - 1,2 ± 0,2 ± 0,2 hp/h = 0,05 - 1,6 - 2,2 - 1,1 - 1,8 - 0,7 - 1,2 ± 0,2 ± 0,2 hp/h = 0,10 - 1,2 - 1,8 - 0,8 - 1,4 - 0,7 - 1,2 ± 0,2 ± 0,2 r/h = 0,05 - 1,0 - 1,5 - 1,2 - 1,8 - 0,4 - 0,4 ± 0,2 ± 0,2 r/h = 0,10 - 0,7 - 1,2 - 0,8 - 1,4 - 0,3 - 0,3 ± 0,2 ± 0,2 r/h = 0,20 - 0,5 - 0,8 - 0,5 - 0,8 - 0,3 - 0,3 ± 0,2 ± 0,2 = 30° - 1,0 - 1,5 - 1,0 - 1,5 - 0,3 - 0,3 ± 0,2 ± 0,2 = 45° - 1,2 - 1,8 - 1,3 - 1,9 - 0,4 - 0,4 ± 0,2 ± 0,2 = 60° - 1,3 - 1,9 - 1,3 - 1,9 - 0,5 - 0,5 ± 0,2 ± 0,2 Curved Eaves Mansard Eaves G Table 12.27 From Table 7.2 - External pressure coefficients for flat roofs. For roofs with parapets or curved eaves, linear interpolation may be used for intermediate values of h p h and r h . For roofs with mansard eaves, linear interpolation between = 30°, 45° and = 60° may be used. For > 60° linear interpolation between the values for = 60° and the values for flat roofs with sharp eaves may be used. In Zone I, where positive and negative values are given, both values shall be considered. For the mansard eave itself, the external pressure coefficients are given in Table 7.4a “External pressure coefficients for duopitch roofs: wind direction 0°”, Zone F and G, depending on the pitch angle of the mansard eave. For the curved eave itself, the external pressure coefficients are given by linear interpolation along the curve, between values on the wall and on the roof. 12.2 Verification tests EN1991‐1‐4_(A)_4.XLS. 5.93 MB. Created: 17 May 2013. Last/Rel.-date: 17 May 2013. Sheets: page 162 — Splash — CodeSec7(37to39). Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_4.xls S ECTION 12 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 37 TO 39) EXAMPLE 12-BG‐ External pressure coefficients for flat roofs‐ test1 Given: Let us assume a simple rectangular building with flat roof. The dimensions of the building are: height h = 12 m , width b = 30 m (crosswind dimension) and depth d = 15 m . The pressure coefficients c pe 10 and c pe 1 are given in Table 7.2 for flat roofs. Assume a pitch angle of the mansard eave equal to = 35 . [Reference sheet: CodeSec7(37to39)]‐[Cell‐Range: A1:O1‐A130:O130]. Solution: In the general clause for buildings it can be seen that the wind forces needs to be calculated in four orthogonal wind directions perpendicular to the side walls, because the pressure coefficients represent the most unfavourable values in a range of wind directions. The external pressure coefficients and accompanying reference height can now be determined for the flat roof with: e = min b ; 2h = min 30 ; 2 12 = 24 m . According to Figure 7.6: e- = 24 --e- = 24 ------ = 6 m ; ---------- = 2 4 m ; --e- = 12 m . Therefore, loaded areas: 4 10 2 4 10 e e A F = --- ------ = 6 2 4 = 14 4 m 2 ; 4 10 e e A G = b – 2 --- ------ = 30 – 2 6 2 4 = 43 2 m 2 4 10 e e A H = --- – ----- b = 12 – 2 4 30 = 288 m 2 2 10 e A I = d – --- b = 15 – 12 30 = 90 m 2 . 2 The pressure coefficient is c pe = c pe 10 because each loaded area “A” for the main structure is larger than 10 m 2 . Roof type: 1) sharp eaves See values in Table 7.2 for sharp eaves. Roof type: 2) eaves with parapets Let us assume (say) an height of the parapet equal to h p = 1 5 m . Therefore: h p h = 1 5 12 = 0 125 0 10 (see values in Tables 7.2 for h p h = 0 10 ). Roof type: 3) curved eaves and 4) mansard eaves Let us assume say r = 0 7 m : r h = 0 7 12 0 0583 . Entering Table 7.2, linear interpolation (“curved eaves”) between r/h = 0,05 and r/h = 0,10: c pe 10 – – 0 7 – 1 0 – – 0 7 -------------------------------------- = ---------------------------------------0 10 – 0 0583 0 10 – 0 05 first decimal). Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_4.xls c pe 10 = – 0 95 – 1 0 (number rounded to the page 163 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 12 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 37 TO 39) c pe 10 – – 1 2 – 1 5 – – 1 2 - = ---------------------------------------------------------------------------0 10 – 0 0583 0 10 – 0 05 first decimal). c pe 1 = – 1 45 – 1 5 (number rounded to the Similarly, we obtain: Zone Roof type F G H I cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 Curved Eaves r/h = 0,0583 - 0,950 - 1,450 - 1,133 - 1,733 - 0,383 - 0,383 ± 0,2 ± 0,2 Mansard Eaves = 35° - 1,067 - 1,600 - 1,100 - 1,633 - 0,333 - 0,333 ± 0,2 ± 0,2 Table 12.28 Calculated external pressure coefficients for flat roofs. For the calculation of the recommended procedure given in Figure 7.2, please refer to verification manual enclosed with the Excel file EN1991‐1‐4_(a)_3.xls: the algorithm implemented in the spreadsheet is the same. 12.3 References [Section 12] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design, April 2010. © 2010 The Institution of Structural Engineers. page 164 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_4.xls Section 13 Eurocode 1 EN 1991-1-4 Section 7 (Page 40 to 42) 13.1 Pressure and force coefficients - Monopitch roofs T he roof, including protruding parts, should be divided into zones as shown in Figure 7.7. The reference height z e should be taken equal to h . The pressure coefficients for each zone that should be used are given in Table 7.3a and 7.3.b. Zone for wind direction = 0° Pitch angle [°] F G Zone for wind direction = 180° H F cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 - 1,7 - 2,5 - 1,2 - 2,0 - 0,6 - 1,2 0,00 0,00 0,00 0,00 0,00 0,00 - 0,9 - 2,0 - 0,8 - 1,5 - 0,3 - 0,3 0,2 0,2 0,2 0,2 0,2 0,2 - 0,5 - 1,5 - 0,5 - 1,5 - 0,2 - 0,2 0,7 0,7 0,7 0,7 0,4 0,4 0,00 0,00 0,00 0,00 0,00 0,00 0,7 0,7 0,7 0,7 0,6 0,6 60° 0,7 0,7 0,7 0,7 0,7 75° 0,8 0,8 0,8 0,8 0,8 5° 15° 30° 45° G H cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 - 2,3 - 2,5 - 1,3 - 2,0 - 0,8 - 1,2 - 2,5 - 2,8 - 1,3 - 2,0 - 0,9 - 1,2 - 1,1 - 1,3 - 0,8 - 1,5 - 0,8 - 0,8 - 0,6 - 1,3 - 0,5 - 0,5 - 0,7 - 0,7 0,7 - 0,5 - 1,0 - 0,5 - 0,5 - 0,5 - 0,5 0,8 - 0,5 - 1,0 - 0,5 - 0,5 - 0,5 - 0,5 Table 13.29 From Table 7.3a - External pressure coefficients for monopitch roofs.(a) (a). At = 0° the pressure changes rapidly between positive and negative values around a pitch angle of = +5° to +45°, so both positive and negative values are given. For those roofs, two cases should be considered: one with all positive values, and one with all negative values. No mixing of positive and negative values is allowed on the same face. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_5.xls page 165 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 13 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 40 TO 42) (a) general e = min[b; 2h] = min[b; 2ze] (b) wind direction = 0° and = 180° (c) wind direction = 90° Figure 13.68From Figure 7.7 - Key for monopitch roofs. page 166 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_5.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 40 TO 42) S ECTION 13 Linear interpolation for intermediate pitch angles may be used between values of the same sign. The values equal to 0,00 are given for interpolation purposes. Zone for wind direction = 90° Pitch angle [°] Fup Flow G H I cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 5° - 2,1 - 2,6 - 2,1 - 2,4 - 1,8 - 2,0 - 0,6 - 1,2 - 0,5 - 0,5 15° - 2,4 - 2,9 - 1,6 - 2,4 - 1,9 - 2,5 - 0,8 - 1,2 - 0,7 - 1,2 30° - 2,1 - 2,9 - 1,3 - 2,0 - 1,5 - 2,0 - 1,0 - 1,3 - 0,8 - 1,2 45° - 1,5 - 2,4 - 1,3 - 2,0 - 1,4 - 2,0 - 1,0 - 1,3 - 0,9 - 1,2 60° - 1,2 - 2,0 - 1,2 - 2,0 - 1,2 - 2,0 - 1,0 - 1,3 - 0,7 - 1,2 75° - 1,2 - 2,0 - 1,2 - 2,0 - 1,2 - 2,0 - 1,0 - 1,3 - 0,5 - 0,5 Table 13.30 From Table 7.3b - External pressure coefficients for monopitch roofs. 13.2 Verification tests EN1991‐1‐4_(A)_5.XLS. 5.91 MB. Created: 8 June 2013. Last/Rel.-date: 8 June 2013. Sheets: — Splash — CodeSec7(40to42). EXAMPLE 13-BH‐ External pressure coefficients for monopitch roofs‐ test1 Given: Let us consider the wind pressure on an industrial hall. The main structure consists of a simple rectangular building with monopitch roof. The dimensions of the building are: High eave height 4,5 m, low eave height 3 m, width 15 m and depth 30 m (from low to high eave). It is assumed in this example, that in case of a storm there is no opening in the surface of the hall, so that the internal pressure can be neglected, i.e. c pi = 0 . Find the external pressure coefficients for the roof. [Reference sheet: CodeSec7(40to42)]‐[Cell‐Range: A1:O1‐A129:O129]. Solution: The pitch angle is equal to = 5 7 (slope: 10,0%): 4 5 – 3 15 = 0 1 10% . The reference height above the ground (or above h dis ) is z e = h = 4 5 m . For wind directions = 0 and = 180 the crosswind dimension is then b = 15 m . Linear interpolation from Table 7.3a (“External pressure coefficients for monopitch roofs”): Zone for wind direction = 0° (with all negative values): – 1 7 – – 0 9 = c------------------------------------pe 10 – – 0 9 c pe 10 – 1 64 (zone F) ------------------------------------------15 – 5 7 15 – 5 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_5.xls page 167 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 13 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 40 TO 42) c pe 1 – – 2 0 – 2 5 – – 2 0 = ----------------------------------------------------------------------------15 – 5 7 15 – 5 – 1 2 – – 0 8 = c------------------------------------pe 10 – – 0 8 ------------------------------------------15 – 5 7 15 – 5 c pe 1 – – 1 5 – 2 0 – – 1 5 = ----------------------------------------------------------------------------15 – 5 7 15 – 5 – 0 6 – – 0 3 = c------------------------------------pe 10 – – 0 3 ------------------------------------------15 – 5 7 15 – 5 c pe 1 – – 0 3 – 1 2 – – 0 3 = ----------------------------------------------------------------------------15 – 5 7 15 – 5 c pe 1 – 2 47 (zone F) c pe 10 – 1 17 (zone G) c pe 1 – 1 97 (zone G) c pe 10 – 0 58 (zone H) c pe 1 – 1 14 (zone H). Zone for wind direction = 0° Pitch angle [°] 5° 15° F G Zone for wind direction = 180° H F cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 - 1,7 - 2,5 - 1,2 - 2,0 - 0,6 - 1,2 0,00 0,00 0,00 0,00 0,00 0,00 - 0,9 - 2,0 - 0,8 - 1,5 - 0,3 - 0,3 0,2 0,2 0,2 0,2 0,2 0,2 G H cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 - 2,3 - 2,5 - 1,3 - 2,0 - 0,8 - 1,2 - 2,5 - 2,8 - 1,3 - 2,0 - 0,9 - 1,2 Table 13.31 From Table 7.3a - External pressure coefficients for monopitch roofs.(a) (a). At = 0° the pressure changes rapidly between positive and negative values around a pitch angle of = +5° to +45°, so both positive and negative values are given. For those roofs, two cases should be considered: one with all positive values, and one with all negative values. No mixing of positive and negative values is allowed on the same face. Zone for wind direction = 0° (with all positive values): c pe 10 – 0 2 0 – 0 2 - = ------------------------------- c pe 10 = c pe 1 0 01 (zone F, G, H). -------------------------15 – 5 7 15 – 5 Linear interpolation from Table 7.3a (“External pressure coefficients for monopitch roofs”): Zone for wind direction = 180° – 2 3 – – 2 5 = c------------------------------------pe 10 – – 2 5 ------------------------------------------15 – 5 7 15 – 5 c pe 1 – – 2 8 – 2 5 – – 2 8 = ----------------------------------------------------------------------------15 – 5 7 15 – 5 page 168 c pe 10 – 2 31 (zone F) c pe 1 – 2 52 (zone F) from Table c pe 10 = c pe 1 = – 1 3 (zone G) from Table c pe 10 = c pe 1 = – 2 0 (zone G) Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_5.xls S ECTION 13 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 40 TO 42) – 0 8 – – 0 9 = c------------------------------------pe 10 – – 0 9 ------------------------------------------15 – 5 7 15 – 5 from Table c pe 10 – 0 81 (zone H) c pe 10 = c pe 1 = – 1 2 (zone H) Linear interpolation from Table 7.3b (“External pressure coefficients for monopitch roofs”): Zone for wind direction = 90°: – 2 1 – – 2 4 = c------------------------------------pe 10 – – 2 4 ------------------------------------------15 – 5 7 15 – 5 c pe 1 – – 2 9 – 2 6 – – 2 9 = ----------------------------------------------------------------------------15 – 5 7 15 – 5 – 2 1 – – 1 6 = c------------------------------------pe 10 – – 1 6 ------------------------------------------15 – 5 7 15 – 5 c pe 10 – 2 12 (zone Fsup) c pe 1 – 2 62 (zone Fsup) c pe 10 – 2 07 (zone Flow) from Table c pe 1 = – 2 4 (zone Flow) c pe 10 – – 1 9 – 1 8 – – 1 9 ------------------------------------------- = ------------------------------------15 – 5 7 15 – 5 c pe 1 – – 2 5 – 2 0 – – 2 5 ------------------------------------------- = ----------------------------------15 – 5 7 15 – 5 c pe 10 – – 0 8 – 0 6 – – 0 8 ------------------------------------------- = ------------------------------------15 – 5 7 15 – 5 from Table c pe 10 – 1 81 (zone G) c pe 1 – 2 04 (zone G) c pe 10 – 0 61 (zone H) c pe 10 – 0 51 (zone I) c pe 1 = – 1 2 (zone H) c pe 10 – – 0 7 – 0 5 – – 0 7 ------------------------------------------- = ------------------------------------15 – 5 7 15 – 5 c pe 1 – – 1 2 – 0 5 – – 1 2 ------------------------------------------- = ----------------------------------15 – 5 7 15 – 5 c pe 1 – 0 55 (zone I). Zone for wind direction = 90° Pitch angle [°] Fup Flow G H I cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 5° - 2,1 - 2,6 - 2,1 - 2,4 - 1,8 - 2,0 - 0,6 - 1,2 - 0,5 - 0,5 15° - 2,4 - 2,9 - 1,6 - 2,4 - 1,9 - 2,5 - 0,8 - 1,2 - 0,7 - 1,2 Table 13.32 From Table 7.3b - External pressure coefficients for monopitch roofs. From Figure 7.7 “Key for monopitch roofs”: (b) wind directions = 0° and = 180° (with crosswind dimension b = 15,00 m): e = min b ; 2h = min 15 ;2 4 5 = 9 0 m . Therefore, assuming cos 1 , we get e/4 = 2,25 m and e/10 = 0,90 m with: A(F) = 2,25 x 0,90 = 2,025 m2; A(H) = (30 – 0,90) x 15 = 436,50 m2; A(G) = (15 – 2 x 2,25) x 0,90 = 9,45 m2. We have: 1 < A(F) < 10; A(H) > 10 and 1 < A(G) < 10. Therefore: F and G with c pe = c pe 1 – c pe 1 – c pe 10 log A , H with c pe 10 . Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_5.xls page 169 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 13 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 40 TO 42) (c) wind directions = 90° (with crosswind dimension b = 30,00 m): e = min b ; 2h = min 30 ;2 4 5 = 9 0 m . Therefore, assuming cos 1 , we get e/10 = 0,90 m, 0,4e = 3,60 m and d – e/2 = 15 – 0,5 x 9 = 10,50 m with: A(Fup) = A(Flow) = 0,90 x 2,25 = 2,025 m2; A(G) = (30 – 2,25 x 2) x 0,90 = 25,50 x 0,90 = 22,95 m2, A(H) = (0,4 x 9,00) x 30,00 = 108 m2 and A(I) = (10,50 x 30,00) = 315,00 m2. We have: 1 < A(Fup/low) < 10; A(H) > 10 and A(G) > 10. Therefore: Fup/low with c pe = c pe 1 – c pe 1 – c pe 10 log A , G, H and I with c pe 10 . Finally, we find: Figure 13.69Final report. In particularly for Fup (A = 2,025 m2), we have: c pe = c pe 1 – c pe 1 – c pe 10 log A = – 2 62 – – 2 62 – – 2 12 log 2 025 = – 2 47 . example-end 13.3 References [Section 13] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design, April 2010. © 2010 The Institution of Structural Engineers. page 170 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_5.xls Section 14 Eurocode 1 EN 1991-1-4 Section 7 (Page 43 to 46) 14.1 Duopitch roofs T he roof, including protruding parts, should be divided into zones as shown in Figure 7.8. The reference height z e should be taken equal to h . The pressure coefficients for each zone that should be used are given in Table 7.4a and 7.4.b. Zone for wind direction = 0° Pitch angle [°] F G H I J cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 - 45° - 0,6 - 0,6 - 0,6 - 0,6 - 0,8 - 0,8 - 0,7 - 0,7 - 1,0 - 1,5 - 30° - 1,1 - 2,0 - 0,8 - 1,5 - 0,8 - 0,8 - 0,6 - 0,6 - 0,8 - 1,4 - 15° - 2,5 - 2,8 - 1,3 - 2,0 - 0,9 - 1,2 - 0,5 - 0,5 - 0,7 - 1,2 - 5°(a) - 2,3 - 2,5 - 1,2 - 2,0 - 0,8 - 1,2 0,2(b) 0,2(b) 0,2(b) 0,2(b) - 0,6 - 0,6 - 0,6 - 0,6 - 1,7 - 2,5 - 1,2 - 2,0 - 0,6 - 1,2 0,00 0,00 0,00 0,00 0,00 0,00 - 2,3 - 2,5 - 1,3 - 2,0 - 0,9 - 2,0 - 0,8 - 1,5 - 0,3 - 0,3 - 0,4 - 0,4 - 1,0 - 1,5 0,2 0,2 0,2 0,2 0,2 0,2 0 0 0 0 - 0,5 - 1,5 - 0,5 - 1,5 - 0,2 - 0,2 - 0,4 - 0,4 - 0,5 - 0,5 0,7 0,7 0,7 0,7 0,4 0,4 0 0 0 0 5° 15° 30° Table 14.33 From Table 7.4a - External pressure coefficients for duopitch roofs.(c) (Cont’d) Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_6.xls page 171 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 14 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 43 TO 46) Zone for wind direction = 0° 0 0 0 0 0 0 - 0,2 - 0,2 - 0,3 - 0,3 0,7 0,7 0,7 0,7 0,6 0,6 0 0 0 0 60° 0,7 0,7 0,7 0,7 0,7 0,7 - 0,2 - 0,2 - 0,3 - 0,3 75° 0,8 0,8 0,8 0,8 0,8 0,8 - 0,2 - 0,2 - 0,3 - 0,3 45° Table 14.33 From Table 7.4a - External pressure coefficients for duopitch roofs.(c) (Cont’d) (a). Linear interpolation for intermediate pitch angles of the same sign may be used between values of the same sign. (Do not interpolate between = + 5° and = - 5°, but use the data for flat roofs in 7.2.3). The values equal to 0,0 are given for interpolation purposes. (b). No interpolation between - 15° and - 5° with cpe,10 = cpe,1 = + 0,2. See first part of note (a) above. (c). At = 0° the pressure changes rapidly between positive and negative values on the windward face around a pitch angle of á = - 5° to + 45°, so both positive and negative values are given. For those roofs, four cases should be considered where the largest or smallest values of all areas F, G and H are combined with the largest or smallest values in areas I and J. No mixing of positive and negative values is allowed on the same face. Zone for wind direction = 90° Pitch angle [°] F G H I cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 - 45° - 1,4 - 2,0 - 1,2 - 2,0 - 1,0 - 1,3 - 0,9 - 1,2 - 30° - 1,5 - 2,1 - 1,2 - 2,0 - 1,0 - 1,3 - 0,9 - 1,2 - 15° - 1,9 - 2,5 - 1,2 - 2,0 - 0,8 - 1,2 - 0,8 - 1,2 - 5° - 1,8 - 2,5 - 1,2 - 2,0 - 0,7 - 1,2 - 0,6 - 1,2 5° - 1,6 - 2,2 - 1,3 - 2,0 - 0,7 - 1,2 - 0,6 - 0,6 15° - 1,3 - 2,0 - 1,3 - 2,0 - 0,6 - 1,2 - 0,5 - 0,5 30° - 1,1 - 1,5 - 1,4 - 2,0 - 0,8 - 1,2 - 0,5 - 0,5 45° - 1,1 - 1,5 - 1,4 - 2,0 - 0,9 - 1,2 - 0,5 - 0,5 60° - 1,1 - 1,5 - 1,2 - 2,0 - 0,8 - 1,0 - 0,5 - 0,5 75° - 1,1 - 1,5 - 1,2 - 2,0 - 0,8 - 1,0 - 0,5 - 0,5 Table 14.34 From Table 7.4b - External pressure coefficients for duopitch roofs. page 172 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_6.xls S ECTION 14 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 43 TO 46) (a) general e = min[b; 2h] = min[b; 2ze] (b) wind direction = 0° (c) wind direction = 90° Figure 14.70From Figure 7.8 - Key for duopitch roofs. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_6.xls page 173 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 14 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 43 TO 46) 14.2 Verification tests EN1991‐1‐4_(A)_6.XLS. 5.98 MB. Created: 12 June 2013. Last/Rel.-date: 12 June 2013. Sheets: — Splash — CodeSec7(43to46). EXAMPLE 14-BI‐ External pressure coefficients for duopitch roofs‐ test1 Given: A simple rectangular building with duopitch roof is given. The dimensions of the building are: Ridge height 6,00 m, gutter height 2,00 m, width b = 30,00 m and depth d = 15,00 m. Find the external pressure coefficients for the roof. [Reference sheet: CodeSec7(43to46)]‐[Cell‐Range: A1:O1‐A146:O146]. Solution: The pitch angle is equal to 28 (slope: 53,2%): 6 – 2 0 5 15 0 533 53 3% . The reference height above the ground (or above h dis ) is z e = h = 6 0 m . For wind directions = 0 the crosswind dimension is then b = 30 m . Linear interpolation from Table 7.4a (“External pressure coefficients for monopitch roofs”): Zone for wind direction = 0° Pitch angle [°] 15° 30° F G H I J - 0,9 - 2,0 - 0,8 - 1,5 - 0,3 - 0,3 - 0,4 - 0,4 - 1,0 - 1,5 0,2 0,2 0,2 0,2 0,2 0,2 0 0 0 0 - 0,5 - 1,5 - 0,5 - 1,5 - 0,2 - 0,2 - 0,4 - 0,4 - 0,5 - 0,5 0,7 0,7 0,7 0,7 0,4 0,4 0 0 0 0 Table 14.35 From Table 7.4a - External pressure coefficients for duopitch roofs (all negative value). Zone for wind direction = 0° (with all negative values): c pe 10 – – 0 5 – 0 9 – – 0 5 ------------------------------------------- = ------------------------------------30 – 28 30 – 15 c pe 1 – – 1 5 – 2 0 – – 1 5 ------------------------------------------- = ----------------------------------30 – 28 30 – 15 c pe 10 – – 0 5 – 0 8 – – 0 5 ------------------------------------------- = ------------------------------------30 – 28 30 – 15 from Table page 174 c pe 1 – 1 57 (zone F) c pe 10 – 0 54 (zone G) c pe 1 = c pe 10 – 0 21 (zone H) c pe 1 = – 1 5 (zone G) c pe 10 – – 0 2 ------------------------------------------– 0 3 – – 0 2 = ------------------------------------30 – 28 30 – 15 from Table c pe 10 – 0 55 (zone F) c pe 10 = c pe 1 = – 0 4 (I) Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_6.xls S ECTION 14 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 43 TO 46) c pe 10 – – 0 5 ------------------------------------------– 1 0 – – 0 5 = ------------------------------------30 – 28 30 – 15 c pe 1 – – 0 5 ------------------------------------------– 1 5 – – 0 5 = ----------------------------------30 – 28 30 – 15 c pe 10 – 0 57 (zone J) c pe 1 – 0 63 (zone J). Zone for wind direction = 0° Pitch angle [°] 15° 30° F G H I J - 0,9 - 2,0 - 0,8 - 1,5 - 0,3 - 0,3 - 0,4 - 0,4 - 1,0 - 1,5 0,2 0,2 0,2 0,2 0,2 0,2 0 0 0 0 - 0,5 - 1,5 - 0,5 - 1,5 - 0,2 - 0,2 - 0,4 - 0,4 - 0,5 - 0,5 0,7 0,7 0,7 0,7 0,4 0,4 0 0 0 0 Table 14.36 From Table 7.4a - External pressure coefficients for duopitch roofs (all positive value). Zone for wind direction = 0° (with all positive values): 0 2 – 0 7 - = c-------------------------------pe 10 – 0 7 -------------------------------30 – 28 30 – 15 c pe 10 = c pe 1 = 0 63 (zone F) 0 2 – 0 7 - = c-------------------------------pe 10 – 0 7 -------------------------------30 – 28 30 – 15 c pe 10 = c pe 1 = 0 63 (zone G) 0 2 – 0 4 - = c-------------------------------pe 10 – 0 4 -------------------------------30 – 28 30 – 15 c pe 1 = c pe 10 0 37 (zone H) from Table c pe 10 = c pe 1 = 0 (I) from Table c pe 10 = c pe 1 = 0 (J). Zone for wind direction = 90° Pitch angle [°] F G H I cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 15° - 1,3 - 2,0 - 1,3 - 2,0 - 0,6 - 1,2 - 0,5 - 0,5 30° - 1,1 - 1,5 - 1,4 - 2,0 - 0,8 - 1,2 - 0,5 - 0,5 Table 14.37 From Table 7.4b - External pressure coefficients for duopitch roofs. Zone for wind direction = 90° c pe 10 – – 1 1 – 1 3 – – 1 1 ------------------------------------------- = ------------------------------------30 – 28 30 – 15 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_6.xls c pe 10 – 1 13 (zone F) page 175 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 14 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 43 TO 46) c pe 1 – – 1 5 ------------------------------------------– 2 0 – – 1 5 = ----------------------------------30 – 28 30 – 15 c pe 10 – – 1 4 ------------------------------------------– 1 3 – – 1 4 = ------------------------------------30 – 28 30 – 15 from Table c pe 1 – 1 57 (zone F) c pe 10 – 1 39 (zone G) c pe 10 – 0 77 (zone H) c pe 1 = – 2 0 (zone G) c pe 10 – – 0 8 ------------------------------------------– 0 6 – – 0 8 = ------------------------------------30 – 28 30 – 15 from Table c pe 1 = – 1 2 (zone H) from Table c pe 10 = c pe 1 = – 0 5 (J). From Figure 7.8 “Key for duopitch roofs”: (b) wind directions = 0° (with crosswind dimension b = 30,00 m): e = min b ; 2h = min 30 ;2 6 0 = 12 0 m . Therefore, with cos 0 88295 , we get e/4 = 3,00 m and e/10 = 1,20 m with: A(F) = 3,00 x 1,20/cos = 4,08 m2; A(J) = 1,20 x 30/cos = 40,77 m2; A(G) = (30 – 2 x 3,00) x 1,20/cos = 32,62 m2; A(I) = A(H) = 0,5 x (15 – 2 x 1,20) x 30/cos = 214,06 m2. We have: 1 < A(F) < 10; A(G, H, I, J) > 10. Therefore, we have F with: c pe = c pe 1 – c pe 1 – c pe 10 log A = c pe 1 = 0 63 c pe = c pe 1 – c pe 1 – c pe 10 log A = – 1 57 – – 1 57 – – 0 55 log 4 08 = – 0 95 and G, H, I, J with cpe = cpe,10. (b) wind directions = 90° (with crosswind dimension b = 15,00 m): e = min b ; 2h = min 15 ;2 6 0 = 12 0 m . Therefore, with cos 0 88295 , we get e/4 = 3,00 m, e/10 = 1,20 m, 0,4e = 4,80 m, d – e/2 = (30 – 0,5 x 12) = 24,00 m, b – 2 x (e/4) = 15 – 2 x (12/4) = 9,00 m with: A(F) = 3,00 x 1,20/cos = 4,08 m22; A(G) = (0,5 x 9,00) x 1,20/cos = 6,12 m2; A(H) = 0,5 x 15 x 4,80/cos = 40,77 m2, A(I) = 0,5 x 15,00 x 24,00/cos = 203,86 m2. We have: 1 < A(F, G) < 10; A(H, I) > 10. Therefore, we have F, G with: F: c pe = c pe 1 – c pe 1 – c pe 10 log A = – 1 57 – – 1 57 – – 1 13 log 4 08 = – 1 30 G: c pe = c pe 1 – c pe 1 – c pe 10 log A = – 2 00 – – 2 00 – – 1 39 log 6 12 = – 1 52 and H, I with cpe = cpe,10. Figure 14.71Excel® report. page 176 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_6.xls S ECTION 14 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 43 TO 46) At = 0° the pressure changes rapidly between positive and negative values on the windward face around a pitch angle of = – 5° to + 45°, so both positive and negative values are given. Figure 14.72Excel® report: external pressure coefficients for duopitch roofs (cases to be considered). For those roofs, four cases should be considered where the largest or smallest values of all areas F, G and H are combined with the largest or smallest values in areas I and J. No mixing of positive and negative values is allowed on the same face. example-end 14.3 References [Section 14] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design, April 2010. © 2010 The Institution of Structural Engineers. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_6.xls page 177 (This page intentionally left blank) Section 15 Eurocode 1 EN 1991-1-4 Section 7 (Page 47 to 48) 15.1 Hipped roofs T he roof, including protruding parts, should be divided into zones as shown in Figure 7.9. The reference height z e should be taken equal to h . The pressure coefficients for each zone that should be used are given in Table 7.5. Zone for wind direction = 0° and 90° Pitch angle [°] F G H I J K L cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 - 1,7 - 2,5 - 1,2 - 2,0 - 0,6 - 1,2 - 0,3 - 0,3 - 0,6 - 0,6 - 0,6 - 0,6 - 1,2 - 2,0 0,0 0,0 0,0 0,0 0,0 0,0 - 0,3 - 0,3 - 0,6 - 0,6 - 0,6 - 0,6 - 1,2 - 2,0 - 0,9 - 2,0 - 0,8 - 1,5 - 0,3 - 0,3 - 0,5 - 0,5 - 1,0 - 1,5 - 1,2 - 2,0 - 1,4 - 2,0 0,2 0,2 0,2 0,2 0,2 0,2 - 0,5 - 0,5 - 1,0 - 1,5 - 1,2 - 2,0 - 1,4 - 2,0 - 0,5 - 1,5 - 0,5 - 1,5 - 0,2 - 0,2 - 0,4 - 0,4 - 0,7 - 1,2 - 0,5 - 0,5 - 1,4 - 2,0 0,5 0,5 0,7 0,7 0,4 0,4 - 0,4 - 0,4 - 0,7 - 1,2 - 0,5 - 0,5 - 1,4 - 2,0 0,0 0,0 0,0 0,0 0,0 - 0,3 - 0,3 - 0,6 - 0,6 - 0,3 - 0,3 - 1,3 - 1,3 - 2,0 0,7 0,7 0,7 0,7 0,6 0,6 - 0,3 - 0,3 - 0,6 - 0,6 - 0,3 - 0,3 - 1,3 - 2,0 60° 0,7 0,7 0,7 0,7 0,7 0,7 - 0,3 - 0,3 - 0,6 - 0,6 - 0,3 - 0,3 - 1,2 - 2,0 75° 0,8 0,8 0,8 0,8 0,8 0,8 - 0,3 - 0,3 - 0,6 - 0,6 - 0,3 - 0,3 - 1,2 - 2,0 5° 15° 30° 45° Table 15.38 From Table 7.5 - External pressure coefficients for hipped roofs (Zones F, G, H, I, J, K, L).(a) (a). At = 0° the pressures changes rapidly between positive and negative values on the windward face at pitch angle of = + 5° to + 45°, so both positive and negative values are given. For those roofs, two cases should be considered: one with all positive values, and one with all negative values. No mixing of positive and negative values are allowed. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_7.xls page 179 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 15 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 47 TO 48) Zone for wind direction = 0° and 90° Pitch angle [°] M N cpe,10 cpe,1 cpe,10 cpe,1 5° - 0,6 - 1,2 - 0,4 - 0,4 15° - 0,6 - 1,2 - 0,3 - 0,3 30° - 0,8 - 1,2 - 0,2 - 0,2 45° - 0,8 - 1,2 - 0,2 - 0,2 60° - 0,4 - 0,4 - 0,2 - 0,2 75° - 0,4 - 0,4 - 0,2 - 0,2 Table 15.39 From Table 7.5 - External pressure coefficients for hipped roofs (Zones M, N).(a) (a). At = 0° the pressures changes rapidly between positive and negative values on the windward face at pitch angle of = + 5° to + 45°, so both positive and negative values are given. For those roofs, two cases should be considered: one with all positive values, and one with all negative values. No mixing of positive and negative values are allowed. Linear interpolation for intermediate pitch angles of the same sign may be used between values of the same sign. The values equal to 0,0 are given for interpolation purposes. Figure 15.73From Figure 7.9 - “Key for hipped roofs” (geometry input). page 180 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_7.xls S ECTION 15 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 47 TO 48) Figure 15.74From Figure 7.9 - “Key for hipped roofs” (zones for wind directions). 15.2 Verification tests EN1991‐1‐4_(A)_7.XLS. 6.13 MB. Created: 15 June 2013. Last/Rel.-date: 15 June 2013. Sheets: — Splash — CodeSec7(47to48). EXAMPLE 15-BJ‐ External pressure coefficients for hipped roofs of building ‐ test1 Given: A simple rectangular building with hipped roof is given. The low-rise building walls have an eave height of hmin = 3,00 m, hip roof edges are b = 14,55 m by d = 9,75 m, and the roof pitch is 1:3 ( and 90 of about 18° with h = ze = 4,60 m). Find the pressure coefficients that should be used in design calculations. [Reference sheet: CodeSec7(47to48)]‐[Cell‐Range: A1:O1‐A282:O282]. Solution: Derived measures plan: a = h cot g 90 = h – h min cot g 90 = 4 60 – 3 00 cot g 18 = 4 90 m ; c = 0 5d 2 + a 2 = 0 5 9 75 2 + 4 90 2 = 6 91 m ; f = b – 2a = 14 55 – 2 4 90 = 4 75 m . Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_7.xls page 181 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 15 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 47 TO 48) Measures of angles in plant: a 4 90 1 = arc tan ------------ = arc tan ------------------------- 45 , with 2 = 90 – 1 = 45 . 0 5d 0 5 9 75 Figure 15.75Key for the hipped roof. Case b) e = min b ; 2h = min 14 55 ; 2 4 60 = 9 20 m ; e 4 = 9 20 4 = 2 30 m ; e 10 = 9 20 10 = 0 92 m . Case c) e = min b ; 2h = min 9 75 ; 2 4 60 = 9 20 m ; e 4 = 9 20 4 = 2 30 m ; e 10 = 9 20 10 = 0 92 m . Derived measures plan: [ʺxʺ, ʺmʺ; ʺkʺ; ʺiʺ] Case b) x = e 10 tan 1 = 0 92 1 = 0 92 m ; m = a d – e 10 d = 4 90 9 75 – 0 92 9 75 = 4 44 m ; k = a – m cot g 1 = 4 90 – 4 44 1 = 0 46 m . Case c) x = e 10 tan 2 = 0 92 1 = 0 92 m ; m = 0 5b a 0 4e = 0 5 9 75 4 90 0 4 9 20 = 3 66 m ; page 182 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_7.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 47 TO 48) S ECTION 15 i = a 0 5 b 0 5b – e 10 = 4 90 0 5 9 75 0 5 9 75 – 0 92 = 3 98 m . Areas of the roof Note Calculation and verification control areas on the spreadsheet: see Cell V125 and V161. Areas with cos 0 = cos 90 0 95 : A(F) A(G) A(H) A(I) A(J) A(K) A(L) A(M) A(N) Case b) 1,78 9,63 36,32 38,44 4,27 2,52 4,52 20.61 - Case c) 1,78 4,98 16,58 16,54 8,59 - 4,72 7,09 37,70 Table 15.40 Actual areas [m2]. From Table 7.5 ‐ “External pressure coefficients for hipped roofs of building”, linear interpolation with 0 90 = 18 : Zone for wind direction = 0° and 90° Pitch angle [°] 15° 30° F G H I J K L cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 - 0,9 - 2,0 - 0,8 - 1,5 - 0,3 - 0,3 - 0,5 - 0,5 - 1,0 - 1,5 - 1,2 - 2,0 - 1,4 - 2,0 0,2 0,2 0,2 0,2 0,2 0,2 - 0,5 - 0,5 - 1,0 - 1,5 - 1,2 - 2,0 - 1,4 - 2,0 - 0,5 - 1,5 - 0,5 - 1,5 - 0,2 - 0,2 - 0,4 - 0,4 - 0,7 - 1,2 - 0,5 - 0,5 - 1,4 - 2,0 0,5 0,5 0,7 0,7 0,4 0,4 - 0,4 - 0,4 - 0,7 - 1,2 - 0,5 - 0,5 - 1,4 - 2,0 Table 15.41 From Table 7.5 - External pressure coefficients for hipped roofs (Zones F, G, H, I, J, K, L). Zone for wind direction = 0° and 90° Pitch angle [°] M N cpe,10 cpe,1 cpe,10 cpe,1 15° - 0,6 - 1,2 - 0,3 - 0,3 30° - 0,8 - 1,2 - 0,2 - 0,2 Table 15.42 From Table 7.5 - External pressure coefficients for hipped roofs (Zones M, N). Therefore, we get (maintaining the approximation of 0 90 = 18 ): Zone for wind direction = 0° (negative values for “F”, “G”, “H”): c pe 10 – – 0 5 ------------------------------------------– 0 9 – – 0 5 = ------------------------------------30 – 18 30 – 15 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_7.xls c pe 10 – 0 82 (zone F) page 183 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 15 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 47 TO 48) c pe 1 – – 1 5 ------------------------------------------– 2 0 – – 1 5 = ----------------------------------30 – 18 30 – 15 c pe 10 – – 0 5 ------------------------------------------– 0 8 – – 0 5 = ------------------------------------30 – 18 30 – 15 c pe 1 – 1 90 (zone F) c pe 10 – 0 74 (zone G) c pe 10 – – 0 2 ------------------------------------------– 0 3 – – 0 2 = ------------------------------------30 – 18 30 – 15 c pe 1 = c pe 10 – 0 28 (zone H) c pe 10 – – 0 4 ------------------------------------------– 0 5 – – 0 4 = ------------------------------------30 – 18 30 – 15 c pe 1 = c pe 10 – 0 48 (I) c pe 10 – – 0 7 ------------------------------------------– 1 0 – – 0 7 = ------------------------------------30 – 18 30 – 15 c pe 10 – 0 94 (zone J) c pe 10 – – 1 2 ------------------------------------------– 1 5 – – 1 2 = ------------------------------------30 – 18 30 – 15 c pe 1 = c pe 10 – 1 44 (J) c pe 10 – – 0 5 ------------------------------------------– 1 2 – – 0 5 = ------------------------------------30 – 18 30 – 15 c pe 10 – 1 06 (zone K) c pe 10 – – 0 5 ------------------------------------------– 2 0 – – 0 5 = ------------------------------------30 – 18 30 – 15 c pe 1 = c pe 10 – 1 70 (K) from Table c pe 1 = – 1 5 (zone G) from Table c pe 1 = – 1 40 (zone L) from Table c pe 10 = – 2 00 (zone L) c pe 10 – – 0 8 – 0 6 – – 0 8 ------------------------------------------- = ------------------------------------30 – 18 30 – 15 from Table c pe 10 – 0 64 (zone M) c pe 10 = c pe 1 = – 1 20 (M). Using the same calculation algorithm we obtain: Zone for wind direction = 0° (positive values for “F”, “G”, “H”): Zone for wind direction = 0° Pitch angle [°] 15° 18° 30° F G H I J K L cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 cpe,10 cpe,1 - 0,9 - 2,0 - 0,8 - 1,5 - 0,3 - 0,3 - 0,5 - 0,5 - 1,0 - 1,5 - 1,2 - 2,0 - 1,4 - 2,0 0,2 0,2 0,2 0,2 0,2 0,2 - 0,5 - 0,5 - 1,0 - 1,5 - 1,2 - 2,0 - 1,4 - 2,0 0,26 0,26 0,30 0,30 0,24 0,24 - 0,48 - 0,48 - 0,94 - 1,44 - 1,06 - 1,70 - 1,40 - 2,0 - 0,5 - 1,5 - 0,5 - 1,5 - 0,2 - 0,2 - 0,4 - 0,4 - 0,7 - 1,2 - 0,5 - 0,5 - 1,4 - 2,0 0,5 0,5 0,7 0,7 0,4 0,4 - 0,4 - 0,4 - 0,7 - 1,2 - 0,5 - 0,5 - 1,4 - 2,0 Table 15.43 From Table 7.5 - External pressure coefficients for hipped roofs (Linear interpolation, zones F, G, H, I, J, K, L). page 184 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_7.xls S ECTION 15 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 47 TO 48) Zone for wind direction = 0° Pitch angle [°] M N cpe,10 cpe,1 cpe,10 cpe,1 15° - 0,6 - 1,2 - 0,3 - 0,3 18° - 0,64 - 1,20 - - 30° - 0,8 - 1,2 - 0,2 - 0,2 Table 15.44 From Table 7.5 - External pressure coefficients for hipped roofs (Linear interpolation, zone M). Zone for wind direction = 90° (values for “F”, “G”, “H”): Since 0 = 90 the calculations are identical for both. In particular, for 90 = 18° (case c): Zone for wind direction = 0° Pitch angle [°] M N cpe,10 cpe,1 cpe,10 cpe,1 15° - 0,6 - 1,2 - 0,3 - 0,3 18° - - - 0,28 - 0,28 30° - 0,8 - 1,2 - 0,2 - 0,2 Table 15.45 From Table 7.5 - External pressure coefficients for hipped roofs (Linear interpolation, zone M). Section 7.2.1 (see Figure 7.2) applies for all areas except zones H, I, M (case b with A > 10 m2) and H, I, N (case c with A > 10 m2). Therefore, with c p = c pe 1 – c pe 1 – c pe 10 log A (maintaining the approximation of 0 90 = 18 ) we have: Zone F G H I J K L M Case b(a) 0,26 0,30 0,24 - 0,48 - 1,12 - 1,44 - 1,61 - 0,64 Case b(b) - 1,63 - 0,75 - 0,28 - 0,48 - 1,12 - 1,44 - 1,61 - 0,64 Table 15.46 External pressure coefficients cpe for wind direction = 0°. (a). Zone for wind direction = 0° (positive values for "F", "G", "H") (b). Zone for wind direction = 0° (negative values for "F", "G", "H") Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_7.xls page 185 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 15 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 47 TO 48) Zone F G H I J N L M Case c(a) 0,26 0,30 0,24 - 0,48 - 0,97 - 0,28 - 1,60 - 0,72 Case c(b) - 1,63 - 0,97 - 0,28 - 0,48 - 0,97 - 0,28 - 1,60 - 0,72 Table 15.47 External pressure coefficients cpe for wind direction = 90°. (a). Zone for wind direction = 90° (positive values for "F", "G", "H") (b). Zone for wind direction = 90° (negative values for "F", "G", "H") example-end 15.3 References [Section 15] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design, April 2010. © 2010 The Institution of Structural Engineers. page 186 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_7.xls Section 16 Eurocode 1 EN 1991-1-4 Section 7 (Page 48 to 49) 16.1 Multispan roofs P ressure coefficients for wind directions 0°, 90° and 180° for each span of a multispan roof may be derived from the pressure coefficient for each individual span. Modifying factors for the pressures (local and global) for wind directions 0° and 180° on each span should be derived: — from 7.2.4 for monopitch roofs, modified for their position according to Figure 7.10 a and b — from 7.2.5 for duopitch roofs for < 0 modified for their position according to Figure 7.10 c and d. The zones F/G/H used should be considered only for the upwind face. The zones I and J should be considered for each span of the multispan roof. The reference height z e should be taken as the height of the structure, h, see Figure 7.10. Figure 16.76From Figure 7.10 - Key to multispan roofs [Case a) and b)]. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_8.xls page 187 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 16 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 48 TO 49) = 0° = 180° Figure 16.77From Figure 7.10 - Key to multispan roofs [Case c) and d)]. In configuration b) two cases should be considered depending on the sign of pressure coefficient c pe on the first roof. In configuration c) the first c pe is the c pe of the monopitch roof, the second and all following c pe are the c pe of the troughed duopitch roof. 16.2 Verification tests EN1991‐1‐4_(A)_8.XLS. 6.10 MB. Created: 21 June 2013. Last/Rel.-date: 21 June 2013. Sheets: — Splash — CodeSec7(48to49). EXAMPLE 16-BK‐ External pressure coefficients for multispan roofs‐ test1 Given: page 188 Let us consider the wind pressure on an industrial hall with multispan roofs. The whole construction is built from standardized components (herein called as “blocks”). Each block consists of a simple rectangular building with monopitch roof with a slope near to 11°. The dimensions of the single rectangular building are: High eave height 7,00 m, low eave height 5,10 m, width 10,00 m (from low to Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_8.xls S ECTION 16 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 48 TO 49) high eave) and depth 30,00 m. It is assumed in this example, that in case of a storm there is no opening in the surface of the hall, so that the internal pressure can be neglected, i.e. c pi = 0 . Find the external pressure coefficients for the roof. Neglect the friction forces due to the wind along the area of the roof parallel to the wind. [Reference sheet: CodeSec7(48to49)]‐[Cell‐Range: A1:O1‐A389:O389]. Solution: Note At paragraph 7.2.7 (2) of the Standard it is shown: “(2) The zones F/G/J used should be considered only for the upwind face. The zones H and I should be considered for each span of the multispan roof.” According to the Manual published by the Institution of Structural Engineers (“Manual for the design of building structures to Eurocode 1 and Basis of Structural Design” ‐ April 2010) at paragraph 6.7.2.7 is shown: “The roof zones F, G and H should be considered only for the upwind faces. The zones J and I should be considered for each span of the multispan roof.” The latter information will be applied in the spreadsheet. Below is a sketch of the structure which defines the external pressure coefficients c pe on roofs for zones F, G, H, with a wind on long side.The plan of the building is indicated in the next figure as well. [In this spreadsheet the frictional forces are not considered: see Sec. 5.3 and 7.5]. Figure 16.78Elevation of the building (Zones “F”, “G”, “H” for Case “a” and “b”). Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_8.xls page 189 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 16 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 48 TO 49) Figure 16.79Plan of the building (Zones “Fup”, “Flow”, “G”, “H”, “I” for Case “a” and “b”). Using data for “Monopitch roofs” (reference file: EN1991‐1‐4_(a)_5.xls) with: – Case = 0° and = 180°, input: b = 30,00 m, = 11°, h = ze = 7,00 m, d = 10,00 m. – Case = 90° with b = 10,00 m, = 11°, h = ze = 7,00 m, d = 30,00 m we obtain: Figure 16.80From output file EN1991-1-4_(a)_5.xls. The height of the structure at low eave is (assuming = 11 ): h min = h loweave = h – b tan = 7 00 – 10 00 tan 11 = 5 06 m 5 10 m . Using data of external pressure coefficients for vertical walls of rectangular plan buildings (reference file: EN1991‐1‐4_(a)_3.xls) with: d = 10,00 m, b = 30,00 m, hmin = 5,06 m, h = 7,00 m, we obtain (BLOCK‐1): cpe(D) = 0,76, cpe(E) = – 0,42. page 190 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_8.xls S ECTION 16 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 48 TO 49) From Figure 7.10 “Key to multispan roofs” we have: Block-1 Block-1 Block-2 Block-3 Block-n Block-2 Block-3 Block-n Figure 16.81Case a) and b) from Figure 7.10 [modified]. BLOCK‐1: with = 180° ‐ case a) we have cpe < 0: cpe(F) = – 2,50; cpe(G) = – 1,30; cpe(H) = – 0,86 Vertical roof wall D: cpe(D) = 0,76 BLOCK‐2‐3‐n: with = 180° ‐ case a) we have cpe < 0: c pe H = 0 8 – 0 86 = – 0 69 ; c pe H = 0 6 – 0 86 = – 0 52 . Vertical roof wall D: 0 8c pe D = 0 8 0 76 = 0 61 ; 0 8c pe D = 0 6 0 76 = 0 46 . BLOCK‐1: with = 0° ‐ case b) we have cpe > 0: cpe(F) = 0,12; cpe(G) = 0,12; cpe(H) = 0,12 Vertical roof wall E: cpe(E) = – 0,40 see Case b) on Figure 7.10. BLOCK‐2‐3‐n: with = 0° ‐ case b) we have cpe > 0: cpe = – 0,40. Vertical roof wall D: cpe = – 0,40. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_8.xls page 191 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 16 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 48 TO 49) BLOCK‐1: with = 0° ‐ case b) we have cpe < 0: cpe(F) = – 1,52; cpe(G) = – 0,96; cpe(H) = – 0,42 Vertical roof wall D: cpe(D) = – 0,42 BLOCK‐2‐3‐n: with = 180° ‐ case a) we have cpe < 0: c pe H = 0 8 – 0 42 = – 0 34 ; c pe H = 0 6 – 0 42 = – 0 25 . Figure 16.82Output from spreadsheet. page 192 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_8.xls S ECTION 16 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 48 TO 49) Figure 16.83Output from spreadsheet. The verification for the remaining two cases (“c” and “d”) are omitted for brevity since the algorithm implemented in the spreadsheet is the same. example-end 16.3 References [Section 16] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design, April 2010. © 2010 The Institution of Structural Engineers. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_8.xls page 193 (This page intentionally left blank) Section 17 Eurocode 1 EN 1991-1-4 Section 7 (Page 50 to 51) 17.1 Vaulted roofs and domes T his section applies to circular cylindrical roofs and domes. The values of cpe,10 and cpe,1 to be used for circular cylindrical roofs and domes may be given in the National Annex. The recommended values of cpe,10 are given in Figures 7.11 and 7.12 for different zones. The reference height should be taken as ze = h + f. Figure 17.84From Figure 7.11 - Recommended values of external pressure coefficients cpe,10 for vaulted roofs with rectangular base. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_9.xls page 195 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 17 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 50 TO 51) For Zone A: • for 0 < h/d < 0,5, the coefficient cpe,10 is obtained by linear interpolation • for 0,2 < f/d < 0,3 and h/d > 0,5, two values of cpe,10 have to be considered • the diagram is not applicable for flat roofs. Figure 17.85From Figure 7.12 - Recommended values of external pressure coefficients cpe,10 for domes with circular base. Note: cpe,10 is constant along arcs of circles, intersections of the sphere and of planes perpendicular to the wind; it can be determined as a first approximation by linear interpolation between the values in A, B and C along the arcs of circles parallel to the wind. In the same way the values of cpe,10 in A if 0 < h/d < 1 and in B or C if 0 < h/d < 0,5 can be obtained by linear interpolation in the Figure above. Pressure coefficients for the walls of rectangular buildings with vaulted roofs should be taken from 7.2.2. 17.2 Verification tests EN1991‐1‐4_(A)_9.XLS. 5.91 MB. Created: 1 July 2013. Last/Rel.-date: 1 July 2013. Sheets: page 196 — Splash — CodeSec7(50to51). Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_9.xls S ECTION 17 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 50 TO 51) EXAMPLE 17-BL‐ External pressure coefficients for vaulted roof with rectangular base ‐ test1 Given: Let us consider a vaulted roof with rectangular base. Assume (see Figure 7.11): f = 2 00 m ; h = 5 00 m ; d = 15 00 m . Find the coefficients of external pressure cpe,10 to be used in the design calculations for the zones “A”, “B”, “C”. [Reference sheet: CodeSec7(50to51)]‐[Cell‐Range: A1:O1‐A65:O65]. Solution: We have: f d = 2 00 15 00 = 0 133 ; h d = 5 00 15 00 = 0 333 0 5 . Equation A(h/d = 0): 0 8 f 0 8 c pe 10 = --------- --- = --------- 0 133 = 0 213 . 0 5 d 0 5 Equation A(h/d > 0,5): c pe 10 = – 1 20 . Linear interpolation within the range 0 1 f d 0 2 between equation A(h/d = 0) and A(h/d > 0,5): – 1 20 – 0 213 –-----------------------------------1 20 – 0 213- = c--------------------------------pe 10 – 0 213 c pe 10 = ------------------------------------- 0 333 + 0 213 = – 0 73 . 0 5 – 0 0 333 – 0 0 5 – 0 Equation B(f/d) within the range 0 05 f d 0 5 : c pe 10 = – --f- – 0 7 = – 0 133 – 0 7 = – 0 83 . d Equation C(f/d) within the range 0 05 f d 0 5 : c pe 10 = – 0 40 . Finally, we have: zone A c pe 10 = – 0 73 , zone B c pe 10 = – 0 83 , zone C c pe 10 = – 0 40 . example-end EXAMPLE 17-BM‐ External pressure coefficients for dome with circular base ‐ test2 Given: A dome with circular base is given. Find the pressure coefficients values of cpe,10 in “A”, “B” and “C” along the arcs of circles parallel to the wind (see Figure 7.12). Assume: f = 2 00 m ; h = 4 00 m ; d = 15 00 m . [Reference sheet: CodeSec7(50to51)]‐[Cell‐Range: A66:O66‐A130:O130]. Solution: We have: f d = 2 00 15 00 = 0 133 ; h d = 4 00 15 00 = 0 267 . Zone “A” within the range 0 25 h d 1 , zone “B” and “C” within the range 0 h d 0 5 . Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_9.xls page 197 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 17 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 50 TO 51) Zone A. Linear interpolation between equation A(h/d = 0,25) and A(h/d > 1): Equation A(h/d = 0,25): 0 8 + 1 4 0 8 + 1 4 f c pe 10 = --------------------------- --- – 0 05 – 1 4 = --------------------------- 0 133 – 0 05 – 1 4 = – 0 99 0 5 – 0 05 d 0 5 – 0 05 Equation A(h/d > 1) within the range: 0 1 f d 0 4 – 0 09 1 3 : – 1 4 + 1 65 c pe 10 = ---------------------------------------------------------------- --f- – 0 1 – 1 65 = 0 4 – 0 09 1 3 – 0 1 d – 1 4 + 1 65 = ---------------------------------------------------------------- 0 133 – 0 1 – 1 65 = – 1 61 . 0 4 – 0 09 1 3 – 0 1 Linear interpolation for A(h/d = 0,267): –------------------------------------------1 61 – – 0 99 - = c---------------------------------------pe 10 – – 0 99 0 267 – 0 25 1 – 0 25 c pe 10 = – 1 00 . Equation B(h/d = 0): – 0 6 + 1 2 0 5 – 0 05 c pe 10 = ---------------------------- --f- – 0 5 – 1 2 with: = 1 4 – 0 6 --------------------------- + 0 05 = 0 214 d – 0 5 0 8 + 1 4 – 0 6 + 1 2 c pe 10 = ------------------------------ 0 133 – 0 5 – 1 2 = – 0 43 . 0 214 – 0 5 Equation B(h/d > 0,5) within the range 0 1 h d 0 25 : – 1 2 + 0 8 – 1 2 + 0 8 c pe 10 = ---------------------------- --f- – 0 1 – 0 8 = ---------------------------- 0 133 – 0 1 – 0 8 = – 0 89 . 0 25 – 0 1 d 0 25 – 0 1 Linear interpolation for B(h/d = 0,267): – 0 89 – – 0 43 c pe 10 – – 0 43 -------------------------------------------- = ---------------------------------------0 267 – 0 0 5 – 0 c pe 10 = – 0 68 . Linear interpolation between C(h/d = 0) cpe,10 = 0 and C(h/d > 0,5) cpe,10 = – 0,5: – 0 5 – 0 c pe 10 = ---------------------- 0 267 – 0 + 0 = – 0 27 . 0 5 – 0 Finally we have: zone A c pe 10 = – 1 00 , zone B c pe 10 = – 0 68 , zone C c pe 10 = – 0 27 . example-end 17.3 References [Section 17] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). page 198 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_9.xls Section 18 Eurocode 1 EN 1991-1-4 Section 7 (Page 51 to 53) 18.1 Internal pressure I nternal and external pressures shall be considered to act at the same time. The worst combination of external and internal pressures shall be considered for every combination of possible openings and other leakage paths. The internal pressure coefficient, cpi, depends on the size and distribution of the openings in the building envelope. When in at least two sides of the buildings (facades or roof) the total area of openings in each side is more than 30% of the area of that side, the actions on the structure should not be calculated from the rules given in this section but the rules of 7.3 and 7.4 should instead be used. Note The openings of a building include small openings such as: open windows, ventilators, chimneys, etc. as well as background permeability such as air leakage around doors, windows, services and through the building envelope. The background permeability is typically in the range 0,01% to 0,1% of the face area. Additional information may be given in a National Annex. Where an external opening, such as a door or a window, would be dominant when open but is considered to be closed in the ultimate limit state, during severe windstorms, the condition with the door or window open should be considered as an accidental design situation in accordance with EN 1990.(7) A face of a building should be regarded as dominant when the area of openings at that face is at least twice the area of openings and leakages in the remaining faces of the building considered. This can also be applied to individual internal volumes within the building. (7) Checking of the accidental design situation is important for tall internal walls (with high risk of hazard) when the wall has to carry the full external wind action because of openings in the building envelope. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_10.xls page 199 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 18 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 51 TO 53) For a building with a dominant face the internal pressure should be taken as a fraction of the external pressure at the openings of the dominant face. The values given by Expressions 18-69 and 18-70 should be used. When the area of the openings at the dominant face is twice the area of the openings in the remaining faces, c pi = 0 75 c pe (Eq. 18‐69) When the area of the openings at the dominant face is at least 3 times the area of the openings in the remaining faces, c pi = 0 90 c pe (Eq. 18‐70) where cpe is the value for the external pressure coefficient at the openings in the dominant face. When these openings are located in zones with different values of external pressures an area weighted average value of cpe should be used. When the area of the openings at the dominant face is between 2 and 3 times the area of the openings in the remaining faces linear interpolation for calculating cpi may be used. For buildings without a dominant face, the internal pressure coefficient cpi should be determined from Figure 7.13, and is a function of the ratio of the height and the depth of the building, h/d, and the opening ratio µ for each wind direction , which should be determined from Expression (7.3). Figure 18.86From Figure 7.13 - Internal pressure coefficients for uniformly distributed openings. page 200 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_10.xls S ECTION 18 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 51 TO 53) For each wind direction the opening ratio is given by: area of openings where c pe is negative or 0 0 = ---------------------------------------------------------------------------------------------------------------------- . area of all openings Important (Eq. 18‐71) This applies to facades and roof of buildings with and without internal partitions. The reference height zi for the internal pressures should be equal to the reference height ze for the external pressures (see 5.1(1)P) on the faces which contribute by their openings to the creation of the internal pressure. If there are several openings the largest value of ze should be used to determine zi. Where it is not possible, or not considered justified, to estimate for a particular case then cpi should be taken as the more onerous of + 0,2 and – 0,3. The internal pressure coefficient of open silos and chimneys should be based on Expression: c pi = – 0 60 . (Eq. 18‐72) The internal pressure coefficient of vented tanks with small openings should be based on Expression: c pi = – 0 40 . (Eq. 18‐73) The reference height zi is equal to the height of the structure. 18.2 Verification tests EN1991‐1‐4_(A)_10.XLS. 6.32 MB. Created: 5 July 2013. Last/Rel.-date: 5 July 2013. Sheets: — Splash — CodeSec7(51to53). EXAMPLE 18-BN‐ Internal pressure ‐ Sec. 7.2.9(5) ‐ test1 Given: For the wind direction the plan dimensions of the building are: width 9,75 m (crosswind dimension) and depth 14,55 m. The low-rise building walls have an eave height of hmin = 3,00 m, hip roof edges are b = 14,55 m by d = 9,75 m, and the roof pitch is 1:3 ( and 90 of about 18° with h = ze = 4,60 m). The actual roof area is equal to A roof = 149 3 m 2 (pitch angles around 18°). The friction forces Ffr are neglected. Find the internal pressure coefficient c pi to be used in the design calculations. Assume the following openings areas (see figure below): Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_10.xls page 201 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 18 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 51 TO 53) Figure 18.87Sketch: facades of the building. A(1) = 23,00 m2, A(2) = 0 m2, A(3) = 4,00 m2, A(4) = 2,00 m2, A(5) = 3,00 m2. [Reference sheet: CodeSec7(51to53)]‐[Cell‐Range: A1:O1‐A114:O114]. Solution: Areas of the building facades: AF1 = 14,55 x 3,00 = 43,65 m2 = AF3 AF2 = 9,75 x 3,00 = 29,25 m2 = AF4 AF5 = 149,30 m2 (manual input). Openings areas in other facades: Aj = Aj = Aj = Aj = Aj = page 202 A(2) + A(3) + A(4) + A(5) = 9,00 m2 A(1) + A(3) + A(4) + A(5) = 32,00 m2 A(1) + A(2) + A(4) + A(5) = 28,00 m2 A(1) + A(2) + A(3) + A(5) = 30,00 m2 A(1) + A(2) + A(3) + A(4) = 29,00 m2. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_10.xls S ECTION 18 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 51 TO 53) Ratio: Sec. 7.2.9(5) Facade No. 1: A 1 A j = 23,00/9,00 = 2,56. With 2 2 56 3 . Facade No. 2: A 2 A j = 0,00/32,00 = 0 Facade No. 3: A 3 A j = 4,00/28,00 = 0,14 Facade No. 4: A 4 A j = 2,00/30,00 = 0,07 Facade No. 5: A 5 A j = 3,00/29,00 = 0,10. The facade No. 1 should be regarded as dominant. The area of openings at that facade is more than twice the area of openings and leakages in the remaining facades of the building considered. The area of the openings at the dominant facade is between 2 ( c pi = 0 75 c pe ) and 3 ( c pi = 0 90 c pe ) times the area of the openings in the remaining facades: linear interpolation for calculating cpi may be used. Therefore: c pi – 0 75 c pe 0 90 – 0 75 c pe ---------------------------------------------- = ---------------------------------2 56 – 2 3–2 c pi = 0 83 c pe , where c pe is the value for the external pressure coefficient at the openings in the dominant facade. When these openings are located in zones with different values of external pressures an area weighted average value of c pe should be used. Figure 18.88PreCalculus Excel® form: procedure for a quick pre-calculation. In the facade No. 1 let us assume: zone A ( c pe = – 1 25 ), zone B ( c pe = – 0 80 ), zone C ( c pe = – 0 50 ). Assume a rectangular opening. The dimension are 12,10 by 1,90 meters: A 1 = 23 m 2 . The opening is located through the zone A for 0,90 m, through the zone B and C for 7,36 m and 3,84 m respectively. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_10.xls page 203 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 18 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 51 TO 53) Therefore: Zone A (0,90/12,10 = 0,07 = 7%), zone B (7,36/12,10 = 0,61 = 61%), zone C (3,84/12,10 = 0,32 = 32%). Area weighted average value of c pe : – 1 25 0 07 – 0 80 0 61 – 0 50 0 32 = – 0 74 . c pe = ---------------------------------------------------------------------------------------------------1 Therefore, for the wind direction , the internal pressure is: c pi = 0 83 c pe = 0 83 – 0 74 = – 0 61 . example-end EXAMPLE 18-BO‐ Internal pressure ‐ Sec. 7.2.9(9) ‐ test2 Given: Let us assume the same assumptions in the previous example but “considering” the building without a dominant facade. Find the internal pressure coefficient c pi . [Reference sheet: CodeSec7(51to53)]‐[Cell‐Range: A115:O115‐A173:O173] Solution: For building without a dominant facade, the internal pressure coefficient c pi should be determined from Figure 7.13 for each wind direction . Figure 18.89From Figure 7.13 - Internal pressure coefficients for uniformly distributed openings. page 204 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_10.xls S ECTION 18 Sec. 7.2.9(6) E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 51 TO 53) Opening ratio: area of openings where c pe is negative or 0 0 23 00 + 0 00 + 4 00 + 0 00 + 3 00- = 0 94 = ---------------------------------------------------------------------------------------------------------------------- = --------------------------------------------------------------------------------------23 00 + 0 00 + 4 00 + 2 00 + 3 00 area of all openings For the wind direction the ratio of the height and the depth of the building is: h--- = -------------4 60- = 0 32 . d 14 55 Value between h/d = 0,25 and h/d = 1,0. Linear interpolation used. Equation h/d < 0,25 with 0 90 : c pi = 0 94 = – 0 30 Equation h/d > 1 with 0 95 : c pi – 0 35 –-----------------------------0 5 – 0 35- = ---------------------- – 0 33 0 95 – 0 33 c pi = 0 94 = – 0 49 Linear interpolation for 0,25 < h/d = 0,32 < 1: c pi + 0 30 – 0 49 + 0 30 ---------------------------------- = ----------------------------0 32 – 0 25 1 – 0 25 c pi = – 0 32 . Where it is not possible, or not considered justified, to estimate for a particular case then cpi should be taken as the more onerous of + 0,2 and – 0,3. example-end 18.3 References [Section 18] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design, April 2010. © 2010 The Institution of Structural Engineers. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_10.xls page 205 (This page intentionally left blank) Section 19 Eurocode 1 EN 1991-1-4 Section 7 (Page 53 to 60) 19.1 Pressure on walls or roofs with more than one skin T he wind force is to be calculated separately on each skin. The permeability of a skin is defined as the ratio of the total area of the opening to the total area of the skin. A skin is defined as impermeable if the value is less than 0,1%. If only one skin is permeable, then the wind force on the impermeable skin should be determined from the difference between the internal and the external wind pressure as described in 5.2(3). If more than one skin is permeable then the wind force on each skin depends on: — the relative rigidity of the skins — the external and internal pressures — the distance between the skins — the permeability of the skins — the openings at the extremities of the layer between the skins. As a first approximation the following recommended rules may be applied: — for walls and roofs with an impermeable inside skin and a permeable outside skin with approximately uniformly distributed openings, the wind force on the outside skin may be calculated from cp,net = (2/3)·cpe for overpressure and cp,net = (1/3)·cpe for underpressure. The wind force on the inside skin may be calculated from cp,net = cpe – cpi — for walls and roofs with an impermeable inside skin and an impermeable more rigid, outside skin, the wind force on the outside skin may be calculated from cp,net = cpe – cpi — for walls and roofs with a permeable inside skin with approximately uniformly distributed openings and an impermeable outside skin, the wind force on the outside skin may be calculated from cp,net = cpe – cpi, and the wind force on the inside skin from cp,net = (1/3)·cpi Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_11.xls page 207 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 19 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 53 TO 60) — for walls and roofs with an impermeable outside skin and an impermeable, more rigid inside skin, the wind force on the outside skin may be calculated from cp,net = cpe and the wind force on the inside skin from cp,net = cpe – cpi. If entries of air put the layer of air into communication with faces of the building other than the face on which the wall is situated (Figure 7.14(b)), these rules are not applicable. Figure 19.90 From Figure 7.14 - Corner details for external walls with more than one skin. 19.2 Canopy roofs A canopy roof is defined as the roof of a structure that does not have permanent walls, such as petrol stations, dutch barns, etc. The degree of blockage under a canopy roof is shown in Figure 7.15 (see below). It depends on the blockage , which is the ratio of the area of feasible, actual obstructions under the canopy divided by the cross sectional area under the canopy, both areas being normal to the wind direction. NOTE: = 0 represents an empty canopy, and = 1 represents the canopy fully blocked with contents to the down wind eaves only (this is not a closed building). The overall force coefficients, cf, and net pressure coefficients cp,net, given in Tables 7.6 to 7.8 for = 0 and = 1 take account of the combined effect of wind acting on both the upper and lower surfaces of the canopies for all wind directions. Intermediate values may be found by linear interpolation. page 208 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_11.xls S ECTION 19 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 53 TO 60) Downwind of the position of maximum blockage, cp,net values for = 0 should be used. Figure 19.91 From Figure 7.15 - Airflow over canopy roofs. The overall force coefficient represents the resulting force. The net pressure coefficient represents the maximum local pressure for all wind directions. It should be used in the design of roofing elements and fixings. NOTE: for canopies with double skins, the impermeable skin and its fixings should be calculated with cp,net and the permeable skin and its fixings with (1/3)·cp,net. Friction forces should be considered (see 7.5). The reference height ze should be taken as “h” as shown in Figures 7.16 and 7.17. Figure 19.92 From Figure 7.16 - Location of the centre of force for monopitch canopies. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_11.xls page 209 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 19 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 53 TO 60) Loads on each slope of multibay canopies, as shown in Figure 7.18, are determined by applying the reduction factors cm given in Table 7.8 to the overall force, and net pressure coefficients for isolated duo-pitch canopies. Figure 19.93 From Figure 7.18 - Multibay canopies. 19.3 Verification tests EN1991‐1‐4_(A)_11.XLS. 6.13 MB. Created: 21 July 2013. Last/Rel.-date: 21 July 2013. Sheets: — Splash — CodeSec7(53to54) — CodeSec7(54to60) EXAMPLE 19-BP‐ Pressure on walls or roofs with more than one skin ‐ Sec. 7.2.10 ‐ test1 Given: Let us assume that the extremities of the layer between the skins are closed (see Figure 7.14(b) - “Corner details for external walls with more than one skin”) for a wall (cpe = – 1,2; cpi = 0,8) with an impermeable inside skin and a permeable outside skin with approximately uniformly distributed openings. Find the net pressure coefficients cp,net on the outside and inside skin. [Reference sheet: CodeSec7(53to54)]‐[Cell‐Range: A1:O1‐A102:O102]. Solution: For walls and roofs with an impermeable inside skin and a permeable outside skin with approximately uniformly distributed openings, the wind force on the outside skin may be calculated from cp,net = (2/3)·cpe for overpressure and cp,net = (1/3)·cpe for underpressure. The wind force on the inside skin may be calculated from cp,net = cpe – cpi. Therefore: Outside skin 2 2 c p net = --- c pe = --- – 1 2 = – 0 8 (overpressure), 3 3 1 1 c p net = --- c pe = --- – 1 2 = – 0 4 (underpressure). 3 3 page 210 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_11.xls S ECTION 19 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 53 TO 60) Inside skin c p net = c pe – c pi = – 1 2 – 0 8 = – 2 0 . The National Annex may give values for the wind effects on external walls and roofs with more than one skin. As a first approximation it is recommended that the wind pressure on the most rigid skin may be taken as the difference between the internal and the external pressures. example-end EXAMPLE 19-BQ‐ Canopy roofs ‐ Sec. 7.3 ‐ test2 Given: A monopitch canopy with a roof angle = 8 is given. Find c p net and c f values for a blockage = 0 and = 0 7 . If the length of the surface parallel to the wind is equal to 12,00 m and the crosswind dimension is b = 8,00 evaluate the wind (minimum and maximum) force F w acting on the structure. Assume a peak velocity pressure (see Figure 7.16 with ze = h) equal to q p h = 1500 N m 2 and c s c d = 1 . [Reference sheet: CodeSec7(54to60)]‐[Cell‐Range: A1:O1‐A120:O120]. Solution: Linear interpolation from Table 7.6 with 5 10 : Blockage = 0 : – 1 5 – – 1 1 - = c-----------------------------------p net – – 1 1 ------------------------------------8–5 10 – 5 c p net = – 1 34 (Zone A) – 2 0 – – 1 7 - = c-----------------------------------p net – – 1 7 ------------------------------------8–5 10 – 5 c p net = – 1 88 (Zone B) – 2 1 – – 1 8 - = c-----------------------------------p net – – 1 8 ------------------------------------8–5 10 – 5 c p net = – 1 98 (Zone C) – 0 9 – – 0 7 - = c---------------------------f – – 0 7 ------------------------------------8–5 10 – 5 c f = – 0 82 (overall force coefficient). Blockage = 1 :(8) c p net = – 1 60 (Zone A) c p net = – 2 44 (Zone B) c p net = – 2 62 (Zone C) c f = – 1 40 . Blockage = 0 7 :(9) c p net = – 1 52 (Zone A) c p net = – 2 27 (Zone B) (8) The calculations (linear interpolation) are omitted because the algorithm used in the spreadsheet is the same. (9) See note above. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_11.xls page 211 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 19 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 53 TO 60) c p net = – 2 43 (Zone C) c f – – 0 82 –------------------------------------------1 40 – – 0 82 - = ------------------------------0 7 – 0 1–0 c f = – 1 23 . Dimension “d” (see Figure 7.16): 12 00 - = 12 00- = 12 12 m . d = -------------------------------cos 8 0 990 Distance of the center of the force F w from the windward edge: d 12 12 --- = --------------- = 3 03 m . 4 4 Reference area of the structure or structural element (see Sec. 5.3 “Wind forces”): A ref = d b = 12 12 8 00 = 96 96 m 2 . Peak velocity pressure: q p h = 1500 N m 2 = 1 50 kN m 2 . Wind forces (blockage = 1 ) acting on the structural component (roof)(10) Case 1) Wind (minimum) force acting (upwards) on the structure (roof): F w = c s c d q p z e c f A ref = 1 1 50 – 1 40 96 96 = – 206 6 kN . Case 2) Wind (maximum) force acting (downwards) on the roof (with c f = 0 46 for all ): F w = c s c d q p z e c f A ref = 1 1 50 0 46 96 96 = 66 9 kN . example-end EXAMPLE 19-BR‐ Canopy roofs ‐ Sec. 7.3 ‐ test2b Given: A multibay duopitch canopy with a roof angle = 16 7 (3:10) is given. Using the same assumptions as in the previous example, for each slope find the overall force coefficients and the net pressure coefficients by applying the reduction factors mc given in Table 7.8 to the c p net values given in Table 7.7. Evaluate the wind (minimum) force F w acting on the single pitch of the roof (end bay) for a blockage = 1 . [Reference sheet: CodeSec7(54to60)]‐[Cell‐Range: A136:O136‐A260:O260]. Solution: Linear interpolation from Table 7.6 with 15 20 : Blockage = 0 : cpe,net = – 1,00 (Zone A), cpe,net = – 1,73 (Zone B), cpe,net = – 1,40 (Zone C), cpe,net = – 1,87 (Zone D), cf = – 0,83. Blockage = 1 : cpe,net = – 1,33 (Zone A), cpe,net = – 2,20 (Zone B), cpe,net = – 1,60 (Zone C), cpe,net = – 2,10 (Zone D), cf = – 1,30. Linear interpolation with 0 1 for = 0 30 : cpe,net = – 1,10 (Zone A), cpe,net = – 1,87 (Zone B), cpe,net = – 1,46 (Zone C), cpe,net = – 1,94 (Zone D), cf = – 0,97. (10) Both values for Fw must be used separately in static calculations (two combinations of load). page 212 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_11.xls S ECTION 19 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 53 TO 60) Loads on each slope of multibay canopies, as shown in Figure 7.18, are determined by applying the reduction factors mc given in Table 7.8 to the overall force, and net pressure coefficients for isolated duo‐pitch canopies. mc factors for all Bay Location on maximum (downward), force and pressure coefficients on minimum (upward), force and pressure coefficients 1 End bay 1,0 0,8 2 Second bay 0,9 0,7 3 Third and subsequent bays 0,7 0,7 Table 19.48 From Table 7.8 - Reduction factors mc for multibay canopies. Therefore, we obtain: Figure 19.94 Output from spreadsheet. Minimum wind forces (blockage = 1 ) acting on the structural component (roof) Dimension “d” (see Figure 7.17): d = 12 00 m (see previous example). Distance of the center of the force F w from the windward edge: d 12 00 --- = --------------- = 3 00 m . 4 4 Reference area of the single pitch of the roof (see Sec. 5.3 “Wind forces”): 0 5 d 0 5 12 00 A ref = --------------------- b = --------------------------------- 8 00 = 50 11 m 2 . cos cos 16 7 Peak velocity pressure: q p h = 1500 N m 2 = 1 50 kN m 2 (see previous example). Wind (minimum) force acting (upwards) on the single pitch (with c f = – 1 30 for = 1 and cm = 1 for “End bay”): F w = c s c d q p z e mc c f A ref = 1 1 50 – 1 30 1 50 11 = – 97 71 kN . Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_11.xls page 213 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 19 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 53 TO 60) Wind (maximum) force acting (downwards) on the single pitch (with c f = 0 47 for all and cm = 1 for “End bay”): F w = c s c d q p z e mc c f A ref = 1 1 50 0 47 1 50 11 = 35 33 kN . Both values for Fw must be used separately in static calculations (at least two load combinations for single pitch of the roof). example-end 19.4 References [Section 19] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design, April 2010. © 2010 The Institution of Structural Engineers. page 214 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_11.xls Section 20 Eurocode 1 EN 1991-1-4 Section 7 (Page 61 to 65) 20.1 Free-standing walls, parapets, fences and signboards F or free-standing walls and parapets resulting pressure coefficients cp,net should be specified for the zones A, B, C and D as shown in Figure 7.19. Figure 20.95 From Figure 7.19 [modified] - Key to zones of free-standing walls and parapets. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_12.xls page 215 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 20 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 61 TO 65) The values of the resulting pressure coefficients cp,net for free-standing walls and parapets depend on the solidity ratio . For solid walls the solidity should be taken as 1, and for walls which are 80% solid (i.e. have 20% openings) = 0,8. Porous walls and fences with a solidity ratio 0 8 should be treated as plane lattices in accordance with 7.11. Values of the resulting pressure coefficients cp,net for free-standing walls and parapets may be given in the National Annex. Recommended values are given in Table 7.9 for two different solidity ratio. These recommended values correspond to a direction of oblique wind compared to the wall without return corner (see Figure 7.19) and, in the case of the wall with return corner, to the two opposite directions indicated in Figure 7.19 (modified)(11). The reference area in both cases is the gross area. Linear interpolation may be used for solidity ratio between 0,8 and 1. Solidity = 1 Zone with return corners A B C D lh3 2,3 1,4 1,2 1,2 lh = 5 2,9 1,8 1,4 1,2 l h 10 3,4 2,1 1,7 1,2 2,1 1,8 1,4 1,2 1,2 1,2 1,2 1,2 with return corners of length > h(a) = 0 8 Table 20.49 Recommended pressure coefficients cp,net for free-standing walls and parapets. (a). Linear interpolation may be used for return corner lengths between 0,0 and h. The reference height for free standing walls and fences should be taken as ze = h, see Figure 7.19. The reference height for parapets on buildings should be taken as ze = (h + hp), see Figure 7.6. 20.2 Shelter factors for walls and fences If there are other walls or fences upwind that are equal in height or taller than the wall or fence of height, h, under consideration, then an additional shelter factor can be used with the net pressure coefficients for walls and lattice fences. The value of the shelter factor s depends on the spacing between the walls or fences x, and the solidity , of the upwind (sheltering) wall or fence. Values of s are given in Figure 7.20. The resulting net pressure coefficient on the sheltered wall, cp,net,s, is given by: c p net s = s c p net . (Eq. 20‐74) (11) See “WIND-I” and “WIND-II”. page 216 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_12.xls S ECTION 20 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 61 TO 65) Figure 20.96 From Figure 7.20 - Shelter factor s for walls and fences for -values between 0,8 and 1,0. The shelter factor should not be applied in the end zones within a distance of h measured from the free end of the wall. In addition, no advantage from shelter should be taken on parts of the downwind wall which extend beyond the projected ends of the upwind wall. 20.3 Signboards For signboards separated from the ground by a height zg greater than h/4 (see Figure 7.21) or less than h/4 with b/h < 1, the force coefficients are given by Expression (7.7): c f = 1 80 . (Eq. 20‐75) The resultant force normal to the signboard should be taken to act at the height of the centre of the signboard with a horizontal eccentricity “e”. The value of the horizontal eccentricity e may be given in the National Annex. The recommended value is: e = 0 25 b . (Eq. 20‐76) Signboards separated from the ground by a height zg less than h/4 and with b h 1 should be treated as boundary walls, see 7.4.1. Divergence or stall flutter instabilities should be checked. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_12.xls page 217 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 20 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 61 TO 65) Figure 20.97 From Figure 7.21 - Key for signboards. 20.4 Friction coefficients Friction should be considered for the cases defined in 5.3(3). Friction forces can arise when the wind blows parallel to external surfaces such as walls or roofs. Friction coefficients cfr, for walls and roof surfaces are given in Table 7.10. The Figure 20.98 From Figure 7.22 [modified]- Reference area for friction. page 218 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_12.xls S ECTION 20 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 61 TO 65) reference area Afr is given in Figure 7.22. Friction forces should be applied on the part of the external surfaces parallel to the wind, located beyond a distance from the upwind eaves or corners, equal to the smallest value of 2b or 4h. Surface Friction coefficient cfr Smooth (i.e. steel, smooth concrete) 0,01 Rough (i.e. rough concrete, tar-boards) 0,02 very rough (i.e. ripples, ribs, folds) 0,04 Table 20.50 From Table 7.10 - Frictional coefficients cfr for walls, parapets and roof surfaces. The reference height ze should be taken equal to the structure height above ground or building height “h”, see Figure 7.22. 20.5 Verification tests EN1991‐1‐4_(A)_12.XLS. 6.34 MB. Created: 24 July 2013. Last/Rel.-date: 24 July 2013. Sheets: — Splash — CodeSec7(61to64) — CodeSec7(64to65). EXAMPLE 20-BS‐ Free‐standing walls and parapets ‐ Sec. 7.4.1 ‐ test1 Given: A free standing wall with return corner is given. Height of the free standing wall h = 4,00 m. Length of the free standing wall L = 3,50 m. Solidity ratio = 0 85 . According to Table 7.9, find the recommended pressure coefficients cp,net. [Reference sheet: CodeSec7(61to64)]‐[Cell‐Range: A1:O1‐A78:O78]. Solution: We have: 0,3h = 1,20 m; 2h = 8,00 m; 4h = 16,00 m; L/h = 3,50/4,00 = 0,88 (rounded value). Solidity 0 8 1 with return corners and 0 L h : linear interpolation between 0,0 and h. From Table 7.9: = 0 8 with cp,net = 1,2 (zones A, B, C, D), = 1 with return corners of length > h with cp,net = 2,1 (zone A); 1,8 (zone B); 1,4 (zone C); 1,2 (zone D). Case with L < 2h applies (see Figure 7.18): only the zones A and B. Linear interpolation between 0,0 and h = 4,00 m with = 1 and L = 3,50 m: c p net – 0 2 1 – 0 ------------------ = -------------------3 50 – 0 4–0 c p net = 1 8375 1 84 (zone A with = 1 ) c p net – 0 1 8 – 0 ------------------ = -------------------3 50 – 0 4–0 c p net = 1 575 1 58 (zone B with = 1 ). For zone A linear interpolation between = 0 8 with cp,net = 1,2 and = 1 with cp,net = 1,84: Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_12.xls page 219 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 20 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 61 TO 65) c p net – 1 2 1------------------------- 84 – 1 2- = ----------------------------0 85 – 0 80 1 0 – 0 8 c p net = 1 36 . For zone B linear interp. between = 0 8 with cp,net = 1,2 and = 1 with cp,net = 1,58: c p net – 1 2 1------------------------- 58 – 1 2- = ----------------------------0 85 – 0 80 1 0 – 0 8 c p net = 1 295 1 30 . The reference height for free standing walls should be taken as ze = h = 4,00 m, see Figure 7.19. example-end EXAMPLE 20-BT‐ Shelter factors for walls and fences ‐ Sec. 7.4.2 ‐ test2 Given: A wall upwind taller than the wall of height h = 4,00 m considered in the previous example is given. The solidity of the upwind sheltering wall is equal to 0,9. The spacing between the walls is x < 40,00 m. Find the resulting pressure coefficient cp,net,s on the sheltered wall. [Reference sheet: CodeSec7(61to64)]‐[Cell‐Range: A82:O82‐A144:O144]. Solution: Height of wall under consideration: h = 4,00 m. Therefore: x/h = (40,00)/(4,00) = 10. From Figure 7.20 ‐ “Shelter factor s for walls and fences for ‐values between 0,8 and 1,0”: s = 0 65 for = 1 with x/h = 10; s = 0 45 for = 0 8 with x/h = 10. Figure 20.99From Excel® output. page 220 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_12.xls S ECTION 20 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 61 TO 65) Linear interpolation (sheltering wall with = 0 9 ) for 0 8 1 : s = 0 65 + 0 45 2 = 0 55 . From previous example we have (case with L < 2h applies): cp,net = 1,36 (zone A); 1,30 (zone B). Therefore the resulting net pressure coefficients are: c p net s = s c p net = 0 55 1 36 = 0 75 (zone A); c p net s = s c p net = 0 55 1 30 = 0 72 (zone B). The shelter factors should not be applied in the end zones within a distance of h measured from the free end of the wall. example-end EXAMPLE 20-BU‐ Signboards ‐ Sec. 7.4.3 ‐ test3 Given: A signboard separated from the ground by a height zg = 2,00 m is given. The dimension of the signboard are h = 10,00 m (height), b = 3,00 (width). The peak velocity pressure at the reference height z e = z g + 0 5h = 7 00 m is q p z e = 1 50 kN m 2 . Calculate the shear and bending reaction at the base of the structure. [Reference sheet: CodeSec7(61to64)]‐[Cell‐Range: A149:O149‐A253:O253]. Solution: Reference area: A ref = b h = 3 00 10 00 = 30 00 m 2 . Case 2 applies with: z g h 4 2 00 10 00 4 = 2 50 b h 1 3 00 10 00 = 0 30 1. Therefore, we have c f = 1 80 and e = 0 25b = 0 25 3 00 = 0 75 m . Shear and bending reactions acting at the base of the structure F w = c s c d q p z e c f A ref = c s c d 1 50 1 80 30 00 = c s c d 81 00 kN . M wV = F w e = c s c d 81 00 0 75 = c s c d 60 75 kNm . M wH = F w z e = c s c d 81 00 7 00 = c s c d 567 00 kNm . example-end EXAMPLE 20-BV‐ Friction coefficients ‐ Sec. 7.5 ‐ test4 Given: A simple rectangular building with duopitch roof is given. The dimensions of the building are: ridge height h = ze = 6,00 m, gutter height hmin = 2,00 m, width b = 15,00 m (crosswind dimension) and depth d = 30,00 m. Find the frictional force considering a lack of correlation of wind pressures. [Reference sheet: CodeSec7(64to65)]‐[Cell‐Range: A1:O1‐A128:O128]. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_12.xls page 221 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 20 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 61 TO 65) Solution: Pitch roof angle: h – h min 4 00 ------------------ = tan = ------------ 0 53 28 cos 0 88 . 7 50 0 5b Substituting the given numerical data we obtain: min 2b ; 4h = min 2 15 00 ; 4 6 00 = 24 00 m , d – min 2b ; 4h = 30 00 – 24 00 = 6 00 m , A fr = 2 d – min 2b ; 4h h min + 0 5b cos = 2 6 00 2 00 + 0 5 15 00 0 88 A fr = 126 00 m 2 . With a peak velocity pressure (say) q p z e = 1 50 kN m 2 and a frictional coefficient c fr = 0 02 , we get: F fr = c fr q p z e A fr = 0 02 1 50 126 00 = 3 78 kN , F fr A fr = c fr q p z e = 0 02 1 50 = 0 03 kN m 2 . In the summation of the wind forces acting on building structures, the lack of correlation of wind pressures between the windward and leeward sides may be taken into account. The lack of correlation of wind pressures between the windward and leeward side may be considered as follows. For buildings with h/d > 5 the resulting force is multiplied by 1. For buildings with h/d < 1, the resulting force is multiplied by 0,85. For intermediate values of h/d, linear interpolation may be applied. Building with h d = 6 00 30 00 = 0 20 h d 1 . Therefore, the resulting frictional force should be multiplied by = 0 85 : F fr = 0 85 3 78 = 3 21 kN ; F fr A fr = c fr q p z e = 0 02 1 50 0 85 = 0 0255 kN m 2 . example-end EXAMPLE 20-BW‐ Free‐standing walls and parapets ‐ Wind actions (Sec. 5.3 ‐ Eq. (5.3)) ‐ test5 Given: Using the same data given in the Example 20‐BS, find the wind forces acting on the free‐standing wall. Let us assume the following assumptions: – peak velocity pressure at the reference height z e = h = 4 00 m : q p z e = 600 N m 2 – structural factor (as defined in Sec. 6): c s c d = 1 0 . [Reference sheet: CodeSec7(61to64)]‐[Cell‐Range: A1:O1‐A78:O78]. Solution: From Example 11‐V we have: Case with L 2h (see Figure 7.18). Linear interpolation from Table 7.9 with solidity ratio equal to = 0 85 - : – Zone A: c p net = 1 36 – Zone B: c p net = 1 30 . From Figure 7.19 ‐ “Key to zones of free‐standing walls and parapets” (case L 2h ), we get: page 222 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_12.xls S ECTION 20 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 61 TO 65) Figure 20.100 PreCalculus Excel® form: procedure for a quick pre-calculation. Zone A: 0 3h = 0 3 4 00 = 1 20 m with A ref A = 0 3h 2 = 0 85 0 3 4 00 2 = 4 08 m 2 (rounded value), Zone B: L – 0 3h = 3 50 – 0 3 4 00 = 2 30 m with A ref B = L – 0 3 h h = 0 85 3 50 – 0 3 4 00 4 00 = 7 82 m 2 (rounded value), Shear and bending reactions acting at the base of the structure Zone A F w A = c s c d q p z e c p net A ref A = 1 0 0 60 1 36 4 08 = 3 33 kN . M wA = F w A 0 5h = 3 33 2 00 = 6 66 kNm . Zone B F w B = c s c d q p z e c p net A ref B = 1 0 0 60 1 30 7 82 = 6 10 kN . M wB = F w 0 5h = 6 10 2 00 = 12 20 kNm . example-end Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_12.xls page 223 (This page intentionally left blank) 20.6 References [Section 20] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design, April 2010. © 2010 The Institution of Structural Engineers. Section 21 Eurocode 1 EN 1991-1-4 Section 7 (Page 65 to 69) 21.1 Structural elements with rectangular sections T he force coefficient c f of structural elements of rectangular section with the wind blowing normally to a face should be determined by Expression: c f = c f 0 r (Eq. 21‐77) where: • c f 0 is the force coefficient of rectangular sections with sharp corners and without free-end flow as given by Figure 7.23 (see Figure 21.102 below) • r is the reduction factor for square sections with rounded corners. r depends on Reynolds number, see Note 1 • is the end-effect factor for elements with free-end flow as defined in 7.13. NOTE 1 The values of r may be given in the National Annex. Recommended approximate upper bound values of r are given in Figure 7.24 (see Figure 21.101 below) and are obtained under low-turbulent conditions. These coefficients are assumed to be safe. Sec. 5.3 The wind force F w acting on a structure or a structural component may be determined directly by using Expression (5.3): F w = c s c d c f q p z e A ref (Eq. 21‐78) where: • c s c d is the structural factor as defined in Section 6 • q p z e is the peak velocity pressure (defined in 4.5) at reference height z e (defined in Section 7 or Section 8) • A ref is the reference area and should be determined by Expression (7.10): A ref = l b Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_13.xls (Eq. 21‐79) page 225 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 21 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 65 TO 69) Figure 21.102 From Figure 7.23 - Force coefficients cf,0 of rectangular sections with sharp corners and without free end flow. [Not represented in logarithmic scale]. Figure 21.101 From Figure 7.24 - Reduction factor r for a square cross-section with rounded corners. page 226 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_13.xls S ECTION 21 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 65 TO 69) where: • l is the length of the structural element being considered • b is the length of the surface perpendicular to the wind direction. For plate-like sections (d/b < 0,2) lift forces at certain wind angles of attack may give rise to higher values of cf up to an increase of 25%. 21.2 Structural elements with sharp edged section The force coefficient c f of structural elements with sharp edged section (e.g. elements with cross sections such as those shown in Figure 7.25) should be determined using Expression (7.11): c f = c f 0 (Eq. 21‐80) where: NOTE 2 • c f 0 is the force coefficient. The National Annex may specify c f 0 . For all elements without free-end flow the recommended value is 2,0. This value is based on measurements under low-turbulent conditions. It is assumed to be a safe value • is the end-effect factor (see Sec. 7.13 - EN 1991-1-4). For buildings where h/d > 5, cf may be determined from Expression (7.13). The reference areas (see Figure 7.25 below), should be taken as follows: in x-direction: A ref x = l b in y-direction: A ref y = l d (Eq. 21‐81) where “l” is the length of the structural element being considered. Important In all cases the reference height z e should be taken as equal to the maximum height above ground of the section being considered. Figure 21.104 From Figure 7.25 - Sharp edged structural sections. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_13.xls page 227 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 21 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 65 TO 69) 21.3 Structural elements with regular polygonal section The force coefficient c f of structural elements with regular polygonal section with 5 or more sides should be determined using Expression (7.13): c f = c f 0 (Eq. 21‐82) where: • c f 0 is the force coefficient of structural elements without free-end flow • is the end-effect factor as defined in 7.13. The values of c f 0 may be given in the National Annex. Recommended conservative values based on measurements under low-turbulent conditions are given in Table 7.11 below. Number of sides Section Finish of surface and of corners Reynolds number (Re)(a) cf,0 5 Pentagon All All 1,80 6 Hexagon All All Re 2 4 10 1,45 r b 0 075 Re 3 0 10 5 1,30 surface smooth(b) Re 2 0 10 5 1,30 r b 0 075 Re 7 0 10 5 1,10 All All surface smooth(c) corners rounded 2 0 10 Re 1 2 10 surface smooth(b) 8 10 12 Octagon Decagon All others 16 to 18 surface smooth(c) corners rounded 1,30 5 Dodecagon Hexdecagon to Octadecagon 1,60 5 5 0,90 Re 4 0 10 5 1,30 Re 4 0 10 5 1,10 Re 2 0 10 5 5 see Sec. (7.9)(d) 5 2 0 10 Re 1 2 10 0,70 Table 21.51 From Table 7.11 - Force coefficient cf,0 for regular polygonal sections. (a). Reynolds number with v = vm and vm given in 4.3, Re, is defined in 7.9 (b). r = corner radius, b = diameter of circumscribed circumference, see Figure 7.26 (c). From wind tunnel tests on sectional models with galvanised steel surface and a section with b = 0,3 m and corner radius of 0,06·b. (d). Treat as a circular cylinder (see Section 7.9 - EN 1991-1-4). NOTE For buildings where h/d > 5, cf may be determined from Expression (7.13). The reference area A ref should be obtained from Expression (7.14): page 228 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_13.xls S ECTION 21 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 65 TO 69) Figure 21.105 From Figure 7.26 - Regular polygonal section. A ref = l b (Eq. 21‐83) where: Important • l is the length of the structural element being considered • b is the diameter of circumscribed circumference, see Fig. 7.26. The reference height z e is equal to the maximum height above ground of the section being considered. 21.4 Verification tests EN1991‐1‐4_(A)_13.XLS. 6.10 MB. Created: 01 August 2013. Last/Rel.-date: 01 August 2013. Sheets: — Splash — CodeSec7(65to67) — CodeSec7(67to69). EXAMPLE 21-BX‐ Structural elements with rectangular sections ‐ Sec. 7.6 ‐ test1 Given: Find the force coefficient c f of a structural element of rectangular section with the wind blowing normally to the face. The end‐effect factor for the element with free‐end flow is equal to = 0 9 . The length of the surface perpendicular to the wind direction and along the wind direction are respectively b = 0 35 m , d = 1 00 m . Let us assume: c s c d = 1 1 , q p z e = 1 50 kN / m2 with the reference height z e equal to the maximum height above ground of the section being considered. The influence of Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_13.xls page 229 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 21 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 65 TO 69) neighbouring structures on the wind velocity can be disregarded (see Sec. 4.3.4). Determine the wind force F w acting on the structural element directly by using Expression 5.3 ‐ EN 1991‐1‐4. [Reference sheet: CodeSec7(65to67)]‐[Cell‐Range: A1:O1‐A154:O154]. Solution: Using the given numerical data we find: d b = 1 00 0 35 = 2 86 (rounded value) with 2 0 d b 5 0 . From Figure 7.23 (modified)(12)‐ “Force coefficients cf,0 of rectangular sections with sharp corners and without free end flow”, within the range 2 0 d b 5 0 we have the expression: 0 – 1 651------------------------- 0 – 1 65- = c------------------------f 0 – 1 65 - c f 0 = 1------------------------- 2 86 – 2 0 + 1 65 = 1 46 (rounded value). d b – 2 0 5 0 – 2 0 5 0 – 2 0 Figure 21.106 Force coefficients of rectangular sections (Excel® output). No reduction factor for square section with rounded corners applies for d b : r = 1 . Therefore we find: c f = c f 0 r = 1 46 1 0 9 = 1 31 - . The reference area is A ref = l b = 6 5 0 35 = 2 28 m 2 . The wind force F w acting on the structural element is (Eq. 5.3 ‐ EN 1991‐1‐4): (12) Figure not represented in logarithmic scale. page 230 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_13.xls S ECTION 21 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 65 TO 69) F w = c s c d c f q p z e A ref = 1 10 1 31 1 50 2 28 = 4 93 kN (rounded value). F w A ref = 4 93 2 28 = 2 16 kN / m2 , F w l = 4 93 6 50 = 0 76 kN m . example-end EXAMPLE 21-BY‐ Structural elements with sharp edged section ‐ Sec. 7.7 ‐ test2 Given: Find the force coefficient c f of a structural element with sharp edged section (say a rolled steel section HEA300) and having an end‐effect factor = 1 . Using the same assumptions given in the previous example determine the wind forces F w acting on the structural element along the two perpendicular directions x and y directly by using Expression 5.3 ‐ EN 1991‐1‐4. The reference height z e is taken equal to the maximum height above ground of the section being considered. The influence of neighbouring structures on the wind velocity can be disregarded (see Sec. 4.3.4). [Reference sheet: CodeSec7(67to69)]‐[Cell‐Range: A1:O1‐A76:O76]. Solution: For all elements without free‐end flow the recommended value for c f 0 is 2,0. This value is based on measurements under low‐turbulent conditions. It is assumed to be a safe value. Therefore: c f = c f 0 = 2 0 1 = 2 0 - . The reference areas are (profile HEA300 with depth b = 300 mm and width d = 290 mm , according to Figure 7.25 ‐ “Sharp edged structural sections”): in x-direction: A ref x = l b = 6 50 0 30 = 1 95 m 2 in y-direction: A ref y = l d = 6 50 0 29 = 1 89 m 2 The wind forces F w acting on the structural element are (Eq. 5.3 ‐ EN 1991‐1‐4): Wind force acting in x‐direction (see Fig. 7.25): F w x = c s c d c f q p z e A ref x = 1 10 2 00 1 50 1 95 = 6 44 kN (rounded value). F w x A ref x = 6 44 1 95 = 3 30 kN / m2 , F w x l = 6 44 6 50 = 0 99 kN m . Wind force acting in y‐direction (see Fig. 7.25): F w y = c s c d c f q p z e A ref y = 1 10 2 00 1 50 1 89 = 6 24 kN (rounded value). F w y A ref = 6 24 1 89 = 3 30 kN / m2 , F w y l = 6 24 6 50 = 0 96 kN m . example-end EXAMPLE 21-BZ‐ Structural elements with regular polygonal section ‐ Sec. 7.8 ‐ test2 Given: A vertical structural element (length l = 7 5 m ) with a octagonal cross‐section and a corner radius equal to r = 30 mm is given. The cross‐section (with = 1 ) is Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_13.xls page 231 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 21 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 65 TO 69) circumscribed by a circumference with a radius r = 150 mm . Assume a mean wind velocity (as defined in Sec. 4.3 ‐ EN 1990‐1‐4) equal to v m z e = 25 m s at a reference height z e equal to the maximum height above ground of the section being considered. The influence of neighbouring structures on the wind velocity can be disregarded (see Sec. 4.3.4). [Reference sheet: CodeSec7(67to69)]‐[Cell‐Range: A79:O79‐A160:O160]. Solution: Corner radius with r b = 30 300 = 0 10 - 0 075 - . Reynolds number (as defined in Sec. 7.9, but with v = v m ): b vm ze 5 0 30 m 25 00 m s - = -----------------------------------------------------------Re = ---------------------- = 5 0 10 - . – 6 15 10 m s 2 Entering Table 7.11 (“Force coefficient cf,0 for regular polygonal sections”) with r b 0 075 –5 and 2 Re 10 7 we obtain (from linear interpolation): c f 0 – 1 30 1 10 – 1 30 1 10 – 1 30 -5 c f 0 = -----------------------------5- 5 – 2 105 + 1 30 = 1 18 - . -----------------------------5- = -------------------------Re – 2 10 7 – 2 10 7 – 2 10 The force coefficient is: c f = c f 0 = 1 18 1 = 1 18 - . The reference area of the structural element (as defined in Sec. 7 or 8) is: A ref = l b = 7 50 0 30 = 2 25 m 2 . Therefore, assuming (say) c s c d = 1 1 and q p z e = 1 50 kN / m2 (with the reference height z e equal to the maximum height above ground of the section being considered), the wind force F w acting on the structural element is (Eq. 5.3 ‐ EN 1991‐1‐4): F w = c s c d c f q p z e A ref = 1 10 1 18 1 50 2 25 = 4 38 kN (rounded value). F w A ref = 4 38 2 25 = 1 95 kN / m2 , F w l = 4 38 7 50 = 0 58 kN m . example-end 21.5 References [Section 21] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Guide for the assessment of wind actions and effects on structures. National Research Council of Italy. CNR-DT 207/2008. ROMA – CNR June 11th, 2010. page 232 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_13.xls Section 22 Eurocode 1 EN 1991-1-4 Section 7 (Page 69 to 73) 22.1 Circular cylinders: external pressure coefficients P ressure coefficients of circular sections depend upon the Reynolds numbers “Re” defined by Expression (7.15): b v ze Re = ------------------ (Eq. 22‐84) where: • b is the diameter [m] • is the kinematic viscosity of the air ( = 15 10 • v z e is the peak wind velocity [m/s] defined in Note 2 of Figure 7.27 (see Fig. 22.107 below) at height z e : v ze = 2 qp ze -------------------- –6 m2 s ) (Eq. 22‐85) and q p z (peak velocity pressure [N/m2] at height z = z e ) given in Sec. 4.5 - EN 1991-1-4. The air density is kg m 3 . The reference height ze is equal to the maximum height above ground of the section being considered. “l” is the length of the structural element being considered. The external pressure coefficients c pe of circular cylinders should be determined from Expression (7.16): c pe = c p 0 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_14.xls (Eq. 22‐86) page 233 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 22 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 69 TO 73) Figure 22.107 From Figure 7.27 - Pressure distribution for circular cylinders for different Reynolds number ranges and without end-effects. The above Figure is based on an equivalent roughness ratio k/b less than 5∙10‐4. Typical values of roughness height “k” are given in Table 7.13 (see Table below). Note where: • c p 0 is the external pressure coefficient without free-end flow (see below) • is the end-effect factor (see Expression below). The external pressure coefficient c p 0 is given in Figure 7.27 for various Reynolds numbers as a function of angle . The end-effect factor is given by Expression (7.17): 0 min with: = 1 – min min A with: = + 1 – cos --- ---------------------2 A – min (Eq. 22‐87) A 180 with: = where: • min is the position of the minimum pressure in [°] • A is the position of the flow separation (see Figure 7.27) • is the end-effect factor (as defined in Sec. 7.13 - EN 1991-1-4). The reference area A ref should be determined from Expression (7.18): A ref = l b (Eq. 22‐88) where: page 234 • b is the diameter of the cylindrical cross-section • l is the length of the structural element being considered. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_14.xls S ECTION 22 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 69 TO 73) Typical values for the pressure distribution for circular cylinders are given in Table 7.12: min [°](a) cp0,min [-](b) A [°](c) cp0,h [-](d) 5 85 - 2,2 135 - 0,4 6 80 - 1,9 120 - 0,7 7 75 - 1,5 105 - 0,8 Re [-] 5 10 2 10 1 10 Table 22.52 From Table 7.12 - Typical values for the pressure distribution for circular cylinders for different Reynolds number ranges and without end-effects. (a). min is the position of the minimum pressure in [°] (see Figure 7.27) (b). c p0 min is the value of the minimum pressure coefficient (c). A is the position of the flow separation in [°] (d). c p0 h is the base pressure coefficient. 22.2 Circular cylinders: force coefficients The force coefficient c f for a finite circular cylinder should be determined from Expression (7.19): c f = c f 0 (Eq. 22‐89) where: • c f 0 is the force coefficient of cylinders without free-end flow (see Figure 7.28 below) • is the end-effect factor (see Sec. 7.13 - EN 1991-1-4). The reference area A ref should be obtained by Expression (7.20): A ref = l b (Eq. 22‐90) where: • b is the diameter of the cylindrical cross-section • l is the length of the structural element being considered. The reference height z e is equal to the maximum height above ground of the section being considered. Note SEC. 5.3 For cylinders near a plane surface with a distance ratio zg/b < 1,5 (see Figure 7.29) special advice is necessary. The wind force F w acting on a structure or a structural component may be determined directly by using Expression (5.3): Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_14.xls page 235 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 22 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 69 TO 73) Figure 22.108 From Figure 7.28 [modified] - Force coefficient cf,0 for circular cylinders without free-end flow and for different equivalent roughness k/b. F w = c s c d c f q p z e A ref (Eq. 22‐91) where: • c s c d is the structural factor as defined in Section 6 • c f is the force coefficient • q p z e is the peak velocity pressure at height z e • A ref the reference area (see above). Figure 22.109 From Figure 7.29 - Cylinder near a plane surface. page 236 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_14.xls S ECTION 22 Note E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 69 TO 73) For stranded cables cf,0 is equal to 1,2 for all values of the Reynolds number Re. Values of equivalent surface roughness “k” are given in Table 7.13 below: Equivalent roughness k [mm] Type of surface Equivalent roughness k [mm] glass 0,0015 smooth concrete 0,2 polished metal 0,002 planed wood 0,5 fine paint 0,006 rough concrete 1,0 spray paint 0,02 rough sawn wood 2,0 bright steel 0,05 rust 2,0 cast iron 0,2 brickwork 3,0 galvanised steel 0,2 Type of surface Table 22.53 From Table 7.13 - Equivalent surface roughness k. 22.3 Verification tests EN1991‐1‐4_(A)_14.XLS. 6.03 MB. Created: 16 September 2013. Last/Rel.-date: 16 September 2013. Sheets: — Splash — CodeSec7(69to73). EXAMPLE 22-CA‐ Circular cylinders: external pressure coefficients ‐ Sec. 7.9.1 ‐ test1 Given: Find the external pressure coefficients of a structural element with cylindrical shape. The diameter of the cross‐section is b = 350 mm . Let us assume the following assumptions: – peak velocity pressure @ height z e : q p z e = 1 50 kN / m2 – air density: = 1 226 kg m 3 – end‐effect factor (as defined in Sec. 7.13): = 0 75 . Find also the actual value of the end‐effect value (as given by Expression 7.17) for an angle = 120 (see Figure 7.27 ‐ “Pressure distribution for circular cylinders for different Reynolds number ranges and without end‐effect”). [Reference sheet: CodeSec7(65to67)]‐[Cell‐Range: A1:O1‐A160:O160]. Solution: Peak wind velocity (as defined in Note 2 of Figure 7.27 @ height z e ): v ze = 2 qp ze --------------------- = 2 1500 N m 2 ----------------------------------------= 49 5 m s . 1 226 kg m 3 Reynolds number (as defined in Expression 7.15): Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_14.xls page 237 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 22 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 69 TO 73) b v ze 6 0 35 m 49 5 m s - = --------------------------------------------------------Re = ------------------- = 1 15 10 - . –6 2 15 10 m s From Table 7.12 ‐ “Typical values for the pressure distribution for circular cylinders for different Reynolds number ranges and without end‐effect” (linear interpolation with 5 6 5 10 Re 2 10 ): min – 85 80 – 85 - = -------------------------------------------5 ---------------------------------6 6 5 1 15 10 – 5 10 2 10 – 5 10 min = 82 8 c p0 min + 2 2 – 1 9 + 2 2 - = -------------------------------------------5 ---------------------------------6 6 5 1 15 10 – 5 10 2 10 – 5 10 c p0 min = – 2 07 - A – 135 120 – 135 -5 ---------------------------------- = ------------------------------------------6 6 5 1 15 10 – 5 10 2 10 – 5 10 A = 128 5 c p0 h + 0 4 – 0 7 + 0 4 -5 ---------------------------------- = ------------------------------------------6 6 5 1 15 10 – 5 10 2 10 – 5 10 c p0 h = – 0 53 - . According to figure above and to Expression (7.17), we have the extreme values to be used in design calculations: for 0 30 for min = 82 8 c pe max = c p0 max = + 1 00 1 00 = 1 00 - c pe min = c p0 min = – 2 07 1 00 = – 2 07 - for A = 128 5 180 c pe = c p0 h = – 0 53 0 75 = – 0 40 - (constant). For an angle within the range min A , according to the second equation into Expression (7.17), with = 120 we get: – min = + 1 – cos --- ---------------------2 A – min 120 – 82 8 = 0 75 + 1 – 0 75 cos --- --------------------------------- 2 128 5 – 82 8 = 0 82 - With (say) = 90 we get = 0 99 - . example-end page 238 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_14.xls S ECTION 22 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 69 TO 73) EXAMPLE 22-CB‐ Circular cylinders: force coefficients ‐ Sec. 7.9.2 ‐ test2 Given: A smooth concrete structural element with a circular cross‐section and vertical cylindrical shape is given. The cross‐section (with = 0 75 ) has a circumference with a radius 6 r = 175 mm . Assume a Reynolds number Re = 1 15 10 at a reference height z e equal to the maximum height above ground of the section being considered. Let us assume: c s c d = 1 1 , q p z e = 1 50 kN / m2 with the reference height z e equal to the maximum height above ground of the section being considered. The influence of neighbouring structures on the wind velocity can be disregarded (see Sec. 4.3.4). Determine the wind force F w acting on the structural element directly by using Expression 5.3 ‐ EN 1991‐1‐4. [Reference sheet: CodeSec7(65to67)]‐[Cell‐Range: A1:O1‐A160:O160]. Solution: From Table 7.13 ‐ “Equivalent surface roughness k” for smooth concrete we have: k = 0 2 mm . Therefore, the equivalent roughness ratio k/b: k b = 0 2 mm 2 175 mm = 0 00057 (rounded value with: 10 –4 k b 10 –3 ). The following Expression applies: 0 18 log 10 k b 0 18 log 10 0 00057 c f 0 = 1 2 + ------------------------------------------------------- = 0 81 - . - = 1 2 + ----------------------------------------------------------------------6 1 + 0 4 log Re 10 6 1 + 0 4 log 1 15 10 10 6 The force coefficient is: c f = c f 0 = 0 81 0 75 = 0 61 - (rounded value). The reference area is: A ref = l b = 7 5 m 0 35 m = 2 63 m 2 . Therefore, assuming (say) c s c d = 1 1 and q p z e = 1 50 kN / m2 (with the reference height z e equal to the maximum height above ground of the section being considered), the wind force F w acting on the structural element is (Eq. 5.3 ‐ EN 1991‐1‐4): F w = c s c d c f q p z e A ref = 1 10 0 61 1 50 2 63 = 2 65 kN (rounded value). F w A ref = 2 65 2 63 = 1 00 kN / m2 , F w l = 2 65 7 50 = 0 35 kN m . example-end 22.4 References [Section 22] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Guide for the assessment of wind actions and effects on structures. National Research Council of Italy. CNR-DT 207/2008. ROMA – CNR June 11th, 2010. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_14.xls page 239 (This page intentionally left blank) Section 23 Eurocode 1 EN 1991-1-4 Section 7 (Page 74 to 75) 23.1 Circular cylinders: force coefficients for vertical cylinders in a row arrangement F or vertical circular cylinders in a row arrangement, the force coefficient c f 0 depends on the wind direction related to the row axis and the ratio of distance “a” and the diameter “b” as defined in Table 7.14. The force coefficient, c f , for each cylinder may be obtained by Expression (7.21): c f = c f 0 (Eq. 23‐92) where: • c f 0 is the force coefficient of cylinders without free-end flow, (Sec. 7.9.2) • is the end-effect factor (Sec. 7.13) • is the factor given in Table 7.14 (for the most unfavourable wind direction). a/b a b 3 5 1,15 3 5 a b 30 210 – a b = ----------------------180 a b 30 1,00 Note: a = distance; b = diameter. Table 23.54 From Table 7.14 - Factor for vertical cylinders in a row arrangement [modified]. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_15.xls page 241 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 23 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 74 TO 75) 23.2 Spheres The alongwind force coefficient c f x of spheres should be determined as a function of the Reynolds number Re (see 7.9.1) and the equivalent roughness k b (see Table 7.13). ✍ Pressure coefficients of circular sections depend upon the Reynolds numbers “Re” defined by Expression (7.15): b v ze Re = ------------------ (Eq. 23‐93) where: • b is the diameter [m] • is the kinematic viscosity of the air ( = 15 10 • v z e is the peak wind velocity [m/s] defined in Note 2 of Figure 7.27 at height z e (see Figure 7.30 below): v ze = –6 2 qp ze -------------------- m2 s ) (Eq. 23‐94) and q p z (peak velocity pressure [N/m2] at height z = z e ) given in Sec. 4.5 - EN 1991-1-4. The air density is kg m 3 . The reference height ze for the sphere is equal to the height of center of gravity ''G'' of the sphere from the plane surface (see Figure 7.31 - EN 1991-1-4). The values of c f x may be given in the National Annex. Recommended values based on measurements in low turbulent flow are given in Figure 7.30. Figure 23.110 From Figure 7.31 - Sphere near a plain surface [modified]. page 242 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_15.xls S ECTION 23 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 74 TO 75) Figure 23.111 From Figure 7.30 - Alongwind force coefficient of a sphere. Important Figure 7.30 is based on the Reynolds number given by Eq. 23-93. The values in Figure 7.30 are limited to values z g b 2 , where z g is the distance of the sphere from a plain surface, “b” is the diameter (see Figure 7.31). For z g b 2 the force coefficient c f x is be multiplied by the factor 1,6. The vertical force coefficient c f x of spheres is given by Expression (7.22): for: zg b 2 c f z = 0 60 - for: zg b 2 c f z = 0 (Eq. 23‐95) In both cases the reference area A ref should be obtained by Expression (7.23): b2 A ref = ----- . 4 (Eq. 23‐96) The reference height should be taken as (see Figure 23.110): z e z g + b--2 Important (Eq. 23‐97) where the equal sign must be considered when the ground coincides with the horizontal surface considered. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_15.xls page 243 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 23 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 74 TO 75) 23.3 Verification tests EN1991‐1‐4_(A)_15.XLS. 5.93 MB. Created: 21 September 2013. Last/Rel.-date: 21 September 2013. Sheets: — Splash — CodeSec7(74to75). EXAMPLE 23-CC‐ Force coefficients for vertical cylinders in a row arrangement ‐ Sec. 7.9.3 ‐ test1 Given: Smooth concrete structural elements with a circular cross‐section (diameter b ) and vertical cylindrical shape (length l = 7 50 m ) are given in a row arrangement with a distance a = 3b . The cross‐section of each column (with = 1 00 ) has a circumference of radius r = 175 mm . Assume a force coefficient without free‐end flow (see Sec. 7.9.2 ‐ EN 1991‐1‐4) equal to c f 0 = 0 81 - at a reference height z e equal to the maximum height above ground of the sections being considered. Let us assume: c s c d = 1 1 , q p z e = 1 50 kN / m2 . The influence of neighbouring structures on the wind velocity can be disregarded (see Sec. 4.3.4). Determine the wind force F w acting on the structural element directly by using Expression 5.3 ‐ EN 1991‐1‐4. [Reference sheet: CodeSec7(74to75)]‐[Cell‐Range: A1:O1‐A64:O64]. Solution: From Table 7.14 with a b = 3 3 5 we have = 1 15 - . Substituting the given numerical data into Eq. 23‐92, we get: c f = c f 0 = 0 81 1 00 1 15 = 0 93 - (rounded value). The reference area for each column is: A ref = l b = 7 5 m 0 35 m = 2 63 m 2 . Therefore, assuming c s c d = 1 1 and q p z e = 1 50 kN / m2 (with the reference height z e equal to the maximum height above ground of the sections being considered), the wind force F w acting on each structural element is (Eq. 5.3 ‐ EN 1991‐1‐4): F w = c s c d c f q p z e A ref = 1 10 0 93 1 50 2 63 = 4 03 kN (rounded value). F w A ref = 4 03 2 63 = 1 53 kN / m2 , F w l = 4 03 7 50 = 0 54 kN m . example-end EXAMPLE 23-CD‐ Spheres ‐ Sec. 7.10 ‐ test2 Given: Find the wind forces acting on a sphere made of galvanized steel with a diameter of b = 550 mm . The distance of the sphere from the nearest horizontal plain surface is equal to z g = 150 mm . Let us assume the following assumptions: – air density: = 1 226 kg m 3 – structural factor (as defined in Section 6): c s c d = 1 10 - – peak velocity pressure @ height z e : q p z e = 1 50 kN / m2 . page 244 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_15.xls S ECTION 23 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 74 TO 75) Note: The reference height z e was taken equal to the height of center of gravity ʹʹGʹʹ of the sphere from the ground ( z e z g + b 2 ). [Reference sheet: CodeSec7(74to75)]‐[Cell‐Range: A67:O67‐A195:O195]. Solution: From Table 7.13 ‐ “Equivalent surface roughness k” for galvanized steel we have: k = 0 2 mm . Therefore, the equivalent roughness ratio k/b: k 0 2 mm --- = ------------------------- = 0 000364 (rounded value with: 10 –4 k b 10 –3 ). b 550 mm Peak wind velocity (as defined in Note 2 of Figure 7.27 @ height z e ): v ze = 2 qp ze --------------------- = 2 1500 N m 2 ----------------------------------------= 49 5 m s . 1 226 kg m 3 Reynolds number (as defined in Expression 7.15): b v ze 6 0 55 m 49 5 m s - = --------------------------------------------------------Re = ------------------- = 1 81 10 - . –6 2 15 10 m s From Figure above with linear interpolation we find (rounded value): c f x – 0 3 0 4 – 0 3 = -------------------------------------------------– 3 – 4 k b – 10 –4 10 – 10 c f x – 0 3 0 4 – 0 3 -------------------------= --------------------------------------– 3 – 4 0 000364 – 10 –4 10 – 10 c f x = 0 33 - . We have: z g = 150 mm 0 5 550 mm = 275 mm . Therefore, the force coefficient c f x has to be multiplied by a factor equal to 1,6: c f x = 1 60 0 33 = 0 53 - . Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_15.xls page 245 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 23 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 74 TO 75) The vertical force coefficient c f z of the sphere is given by: c f z = 0 60 - for z g = 150 mm 0 5 550 mm = 275 mm . The reference area in both cases is: b2 0 55 m 2 A ref = ----- = -------------------------- = 0 238 m 2 . 4 4 The wind forces F w acting on the sphere are (Eq. 5.3 ‐ EN 1991‐1‐4): Wind force acting in x‐direction (see Fig. 7.31): F w x = c s c d c f x q p z e A ref = 1 10 0 53 1 50 0 238 = 0 21 kN (rounded value). Wind force acting in z‐direction (see Fig. 7.31): F w z = c s c d c f z q p z e A ref = 1 10 0 60 1 50 0 238 = 0 24 kN (rounded value). example-end 23.4 References [Section 23] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Guide for the assessment of wind actions and effects on structures. National Research Council of Italy. CNR-DT 207/2008. ROMA – CNR June 11th, 2010. page 246 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_15.xls Section 24 Eurocode 1 EN 1991-1-4 Section 7 (Page 76 to 78) 24.1 Lattice structures and scaffoldings T he force coefficient, c f , of lattice structures and scaffoldings with parallel chords should be obtained by Expression (7.25): c f = c f 0 (Eq. 24‐98) where: • c f 0 is the force coefficient of lattice structures and scaffoldings without end-effects. It is given by Figures 7.33 to 7.35 as a function of solidity ratio (Sec. 7.11 Eq. (2)) and Reynolds number Re • Re is the Reynolds number using the average member diameter b i , see Note below • is the end-effect factor (see Sec. 7.13) as a function of the slenderness of the structure, , calculated with “l” and width b = d , see Figure 7.32. Figure 24.112 From Figure 7.32 - Lattice structure or scaffolding. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_16.xls page 247 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 24 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 76 TO 78) Figure 24.113 From Figure 7.33 - Force coefficient cf,0 for a plane lattice structure with angle members as a function of solidity ratio . Figure 24.114 From Figure 7.34 - Force coefficient cf,0 for a spatial lattice structure with angle members as a function of solidity ratio . page 248 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_16.xls S ECTION 24 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 76 TO 78) Figure 24.115 From Figure 7.35 - Force coefficient cf,0 for plane and spatial lattice structure with members of circular cross-section. Note Figure 7.35 is based on the Reynolds number with: v = 2 qp and q p given in EN 1991‐1‐4 ‐ Sec. 4.5. kg m 3 is the density of air. The National Annex may give a reduction factor for scaffolding without air tightness devices and affected by solid building obstruction. A recommended value is given in prEN 12811. The solidity ratio, , is defined by Expression (7.26): = A Ac (Eq. 24‐99) where: Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_16.xls page 249 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 24 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 76 TO 78) • A is the sum of the projected area of the members and gusset plates of the face projected normal to the face: A = b l + A i i i gk (Eq. 24‐100) k • A c is the area enclosed by the boundaries of the face projected normal to the face: A c = d l • l is the length of the lattice • d is the width of the lattice • b i , l i is the width and length of the members “i” (see Figure 7.32), projected normal to the face) • A gk is the area of the k-th gusset plates, projected normal to face. The reference area A ref should be directly determined by Expression: A ref = A n b i l i + N A gk (Eq. 24‐101) where: Important • b i is the average width of the members (projected normal to face) • l i is the average length of the members (projected normal to face) • n and N are the number of member “i” and of gusset plate (projected normal to face) respectively • A gk is the (average) area of the gusset plates, (projected normal to face). The reference height is equal to the maximum height of the element above ground. 24.2 Verification tests EN1991‐1‐4_(A)_16.XLS. 6.19 MB. Created: 24 September 2013. Last/Rel.-date: 24 September 2013. Sheets: — Splash — CodeSec7(76to78). EXAMPLE 24-CE‐ Lattice structures and scaffoldings ‐ Sec. 7.11 ‐ Fig. 7.33 and 7.34 ‐ test1 Given: Find the wind force F w acting on a lattice structure using the Expression (5.3) ‐ EN 1991‐1‐4. Let us assume the following assumptions: – width of the lattice: d = 1000 mm – length of the lattice: l = 16000 mm page 250 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_16.xls S ECTION 24 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 76 TO 78) – average Area gusset plate (projected normal to the face): A gk = 120000 mm 2 – average width of the member ʹʹiʹʹ (projected normal to the face): b i = 80 mm – average length of the member ʹʹiʹʹ (projected normal to the face): l i = 1300 mm – number of member ʹʹiʹʹ (projected normal to the face): n = 48 – cross section of the elements of the structure: not circular – number of gusset plate (projected normal to the face): N = 30 – peak velocity pressure (as defined in Sec. 4.5 ‐ EN 1991‐1‐4): q p z e = 1 50 kN / m2 – air density: = 1 226 kg m 3 – structural factor (as defined in Section 6): c s c d = 1 1 – end‐effect factor for elements with free‐end flow: = 0 90 . [Reference sheet: CodeSec7(76to78)]‐[Cell‐Range: A1:O1‐A205:O205]. Solution: Reference area: A ref = b l + A i i i gk n b i l i + N A gk = 48 80 1300 + 30 120000 k 6 A = A ref 8 59 10 mm 2 = 8 59 m 2 (rounded value). 7 Solidity ratio with A c = d l = 1000 16000 = 1 60 10 mm 2 : 6 7 = A A c = 8 59 10 1 60 10 = 0 537 0 54 - . PLANE LATTICE STRUCTURE. From Figure 7.33 ‐ “Force coefficient cf,0 for a plane lattice structure with angle members as a function of solidity ratio ” with = 0 54 - we have c f 0 = 1 60 - . The force coefficient (Eq. 7.25) is c f = c f 0 = 1 60 0 90 = 1 44 - . Therefore, assuming c s c d = 1 1 and q p z e = 1 50 kN / m2 (with the reference height z e equal to the maximum height above ground of the section being considered), the wind force F w acting on the plane lattice structural element is (Eq. 5.3 ‐ EN 1991‐1‐4): F w = c s c d c f q p z e A ref = 1 10 1 44 1 50 8 59 = 20 41 kN (rounded value). F w A ref = 20 41 8 59 = 2 38 kN / m2 , F w l = 20 41 16 00 = 1 28 kN m . SPATIAL LATTICE STRUCTURE. From Figure 7.34 - “Force coefficient cf,0 for a spatial lattice structure with angle members as a function of solidity ratio ”, assuming the CASE “A”, “B” or “C” (see Figure below) we have c f 0 = 1 68 - . The force coefficient (Eq. 7.25) is c f = c f 0 = 1 68 0 90 = 1 51 - . The wind force F w acting on the spatial lattice structural element is (Eq. 5.3 ‐ EN 1991‐1‐4): (rounded value). 1 51 F w = ------------ 20 41 kN = 21 40 kN (rounded value) with: 1 44 F w A ref = 21 40 8 59 = 2 49 kN / m2 , F w l = 21 40 16 00 = 1 34 kN m . example-end Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_16.xls page 251 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 24 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 76 TO 78) EXAMPLE 24-CF‐ Lattice structures: plane/spatial latice structure ‐ circular cross‐section ‐ Fig. 7.35 ‐ test2 Given: Find the wind force F w acting on a spatial lattice structure of square section with members of circular cross‐section. Let us assume the same geometry assumptions from the previous example. Note. The influence of neighbouring structures on the wind velocity may influence the Reynolds number value with a variation by ±10%. [Reference sheet: CodeSec7(76to78)]‐[Cell‐Range: A207:O207‐A421:O421]. Solution: Peak wind velocity (as defined in Note 2 of Figure 7.27 @ height z e ): v ze = 2 qp ze --------------------- = 2 1500 N m 2 ----------------------------------------= 49 5 m s . 1 226 kg m 3 Reynolds number (as defined in Expression 7.15), using the average member diameter b i = 80 mm : bi v ze 0 08 m 49 5 m s - = 2 64 105 - . - = --------------------------------------------------------Re = ---------------------–6 15 10 m 2 s 7 Solidity ratio with A c = d l = 1000 16000 = 1 60 10 mm 2 : 6 7 = A A c = 8 59 10 1 60 10 = 0 537 0 54 - . Entering Figure 7.35 with 5 Re = 2 64 10 - and 0 5 0 6 we find: c f 0 = 0 87 - (see Figure below): Figure 24.116 From Figure 7.35 - Force coefficient cf,0 for plane and spatial lattice structure with members of circular cross-section [with Re from Eq. (7.15) and 0,5 < < 0,6]. page 252 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_16.xls S ECTION 24 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 76 TO 78) Assigning to the Reynolds number a variation of +10% we obtain: c f 0 = 0 89 - (see Figure below): Figure 24.117 From Figure 7.35 - Force coefficient cf,0 for plane and spatial lattice structure with members of circular cross-section [for 1,10 x Re with Re from Eq. (7.15) and 0,5 < < 0,6] Assigning to the Reynolds number a variation of –10% we obtain: c f 0 = 1 07 - (see Figure below): Figure 24.118 From Figure 7.35 - Force coefficient cf,0 for plane and spatial lattice structure with members of circular cross-section [for 0,90 x Re with Re from Eq. (7.15) and 0,5 < < 0,6] Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_16.xls page 253 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 24 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 76 TO 78) The most unfavourable case for the safety is the second: c f 0 = 1 07 - . The force coefficient (Eq. 7.25) is c f = c f 0 = 1 07 0 90 = 0 96 - . Therefore, assuming c s c d = 1 1 and q p z e = 1 50 kN / m2 (with the reference height z e equal to the maximum height above ground of the section being considered), the wind force F w acting on the plane lattice structural element is (Eq. 5.3 ‐ EN 1991‐1‐4): F w = c s c d c f q p z e A ref = 1 10 0 96 1 50 8 59 = 13 61 kN (rounded value). F w A ref = 13 61 8 59 = 1 58 kN / m2 , F w l = 13 61 16 00 = 0 85 kN m . example-end 24.3 References [Section 24] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Guide for the assessment of wind actions and effects on structures. National Research Council of Italy. CNR-DT 207/2008. ROMA – CNR June 11th, 2010. page 254 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_16.xls Section 25 Eurocode 1 EN 1991-1-4 Section 7 (Page 78 to 81) 25.1 Flags F orce coefficients c f and reference areas A ref for flags are given in Table 7.15 below. The reference height z e is equal to the height of the flag above ground. (case a) case b) Flags Aref hL hL 1 --- h L 2 cf 1 80 - m A ref – 1 25 0 02 + 0 7 ---------f - ------- h h2 m A ref – 1 25 0 02 + 0 7 ---------f - ------- h h2 Table 25.55 From Table 7.15 - Force coefficients cf for flags. Referring to the table 7.15: Note • m f is the mass per unit area of the flag • is the air density (see Sec. 4.5 (1) NOTE 2) • z e is the height of the flag above ground. The equation for free flags includes dynamic forces from the flag flutter effect. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_17.xls page 255 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 25 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 78 TO 81) 25.2 Effective slenderness and end-effect factor Where relevant, the end-effect factor should be determined as a function of slenderness ratio . Note The force coefficients, cf,0, given in 7.6 to 7.12 are based on measurements on structures without free‐end flow away from the ground. The end‐effect factor takes into account the reduced resistance of the structure due to the wind flow around the end (end‐effect). Figure 7.36 and Table 7.16 are based on measurements in low turbulent flow. Values, taking the effect of turbulence into account may be specified in the National Annex. The effective slenderness should be defined depending on the dimensions of the structure and its position. The National Annex may give values for and . Recommended values for are given in Table 7.16 and indicative values for are given in Figure 7.36 for different solidity ratio . The solidity ratio (see Figure 7.37) is given by Eq. (7.28): = A Ac (Eq. 25‐102) where A is the sum of the projected areas of the members, A c is the overall envelope area A c = L b . Figure 25.119 From Figure 7.36- Indicative values of the end-effect factor as a function of solidity ratio versus slenderness . page 256 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_17.xls S ECTION 25 No. E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 78 TO 81) Position of the structure, wind normal to the plane of the page Effective slenderness [-] 1 For polygonal, rectangular and sharp edged sections and lattice structures: L for L > 50 m: = min 1 4 --- ; 70 m b L for L < 15 m: = min 2 0 --- ; 70 m b 2 For circular cylinders: L for L > 50 m: = min 0 7 --- ; 70 m 3 b L for L < 15 m: = min 1 0 --- ; 70 m b Remaining case (No. 4): 4 L for L > 50 m: = max 0 7 --- ; 70 m b L for L < 15 m: = max 1 0 --- ; 70 m b Table 25.56 From Table 7.16 - Recommended values of for cylinders, polygonal sections, rectangular sections, sharp edged structural sections and lattice structures.(a) (a). For intermediate values of “L” linear interpolation should be used. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_17.xls page 257 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 25 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 78 TO 81) Figure 25.120 From Figure 7.37 - Definition of solidity ratio . 25.3 Verification tests EN1991‐1‐4_(A)_17.XLS. 6.09 MB. Created: 28 September 2013. Last/Rel.-date: 28 September 2013. Sheets: — Splash — CodeSec7(78to79) — CodeSec7(80to81). EXAMPLE 25-CG‐ Flags ‐ Sec. 7.12 ‐ test1 Given: Find the wind force F w (13) acting on a (free) rectangular flag using the Expression (5.3) ‐ EN 1991‐1‐4. Let us assume the following assumptions: – length and height of the flag: L = 4 00 m , h = 2 20 m respectively – mass per unit area of the flag: m f = 280 gr m 2 = 0 28 kg m 2 – peak velocity pressure (as defined in Sec. 4.5 ‐ EN 1991‐1‐4): q p z e = 1 50 kN / m2 – air density: = 1 25 kg m 3 – structural factor (as defined in Section 6): c s c d = 1 0 . [Reference sheet: CodeSec7(78to79)]‐[Cell‐Range: A1:O1‐A85:O85]. Solution: From Table 7.15 ‐ “Force coefficients cf for flags” ‐ case a): A ref = h L = 2 20 4 00 = 8 80 m 2 m A ref – 1 25 0 28 8 80 c f = 0 02 + 0 7 ---------f - -------= 0 02 + 0 7 -------------------------------------- -------------------2 h h2 1 25 2 20 2 20 – 1 25 = 0 054 - Therefore, assuming c s c d = 1 0 and q p z e = 1 50 kN / m2 (with the reference height z e equal to the maximum height above ground of the flag), the wind force F w acting on the flag is (Eq. 5.3 ‐ EN 1991‐1‐4): (13) The wind actions calculated using EN 1991-1-4 are characteristic values (See EN 1990, 4.1.2). page 258 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_17.xls S ECTION 25 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 78 TO 81) F w = c s c d c f q p z e A ref = 1 0 0 054 1 50 8 80 = 0 71 kN (rounded value). F w A ref = 0 71 8 80 = 0 08 kN / m2 , F w L = 0 71 4 00 = 0 18 kN m . example-end EXAMPLE 25-CH‐ Effective slenderness and end‐effect factor ‐ Sec. 7.13 ‐ test2 Given: Find the end‐effect factor for a lattice structures. According to figures in Table 7.16 let us assume the following assumptions: – length and height of the lattice structure: L = 18 00 m , h = 0 75 m respectively – distance from the horizontal plain surface (ground): z g = 3 40 m – sum of the projected areas of the lattice members (see Figure 7.37): A = 3 00 m 2 . [Reference sheet: CodeSec7(80to81)]‐[Cell‐Range: A1:O1‐A243:O243]. Solution: From Table 7.16 ‐ “Recommended values of for cylinders, polygonal sections, rectangular sections, sharp edged structural sections and lattice structures”, for polygonal, rectangular and sharp edged sections and lattice structures we have: L 18 00 for L > 50 m: = min 1 4 --- ; 70 m = min 1 4 --------------- ; 70 m = 33 6 - b 0 75 18 00 for L < 15 m: = min 2 0 --------------- ; 70 m = 48 0 - . 0 75 Linear interpolation for 15 L 30 with L = 18 00 m : – 48 0 33 6 – 48 0- = ------------------------------------------------L – 15 50 – 15 33 6 – 48 0 – 48 0 ------------------------------ = --------------------------50 – 15 18 00 – 15 = 46 77 - . Overall envelope area (see Figure 7.37 ‐ “Definition of solidity ratio “: A c = L b = 18 00 0 75 = 13 50 m 2 . Solidity ratio (see Expression (7.28)): = A A c = 3 00 13 50 = 0 22 - (rounded value) within the range 0 1 0 5 and with 10 100 . Linear interpolation between: = 0 07 log + 0 84 = 0 07 log 46 77 + 0 84 = 0 957 for = 0 5 and 10 100 = 0 01 log + 0 98 = 0 01 log 46 77 + 0 98 = 0 997 for = 0 1 and 10 100 Note National Research Council of Italy ‐ Advisory Committee on Technical Recommendations for Construction ‐ Guide for the assessment of wind actions and effects on structures ‐ CNR‐DT 207/2008. ROMA – CNR June 11th, 2010. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_17.xls page 259 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 25 E UROCODE 1 EN 1991-1-4 S ECTION 7 (P AGE 78 TO 81) Figure 25.121 Excel chart (output). Therefore, we get (linear interpolation): – 0 957 0 997 – 0 957 ------------------------------------ = ------------------------- – 0 5 0 1 – 0 5 – 0 957 0---------------------------------- 997 – 0 957= -------------------------0 22 – 0 5 0 1 – 0 5 = 0 98 - . Similarly for = 1 0 we obtain: = 0 87 - . example-end 25.4 References [Section 25] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Guide for the assessment of wind actions and effects on structures. National Research Council of Italy. CNR-DT 207/2008. ROMA – CNR June 11th, 2010. page 260 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_17.xls Section 26 Eurocode 1 EN 1991-1-4 Section 8 (Page 82 to 90) 26.1 Wind actions on bridges 26.1.1 General T his section only applies to bridges of constant depth and with cross-sections as shown in Figure 8.1 consisting of a single deck with one or more spans. Wind actions for other types of bridges (e.g. arch bridges, bridges with suspension cables or cable stayed, roofed bridges, moving bridges and bridges Figure 26.122 From Figure 8.1 - Cross-sections of normal construction decks. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_18.xls page 261 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 26 E UROCODE 1 EN 1991-1-4 S ECTION 8 (P AGE 82 TO 90) with multiple or significantly curved decks) may be defined in the National Annex. The angle of the wind direction to the deck axis in the vertical and horizontal planes may be defined in the National Annex. The wind forces exerted on various parts of a bridge (deck and piers) due to wind blowing in the same direction should be considered as simultaneous if they are unfavourable. Wind actions on bridges produce forces in the x, y and z directions as shown in Figure 8.2, where: — x-direction is the direction parallel to the deck width, perpendicular to the span — y-direction is the direction along the span — z-direction is the direction perpendicular to the deck. Figure 26.123 From Figure 8.2 - DIrections of wind actions on bridges. The forces produced in the x- and y-directions are due to wind blowing in different directions and normally are not simultaneous. The forces produced in the z-direction can result from the wind blowing in a wide range of directions; if they are unfavourable and significant, they should be taken into account as simultaneous with the forces produced in any other direction. Note The notation used for bridges differs from that in 1.7. The following notations (see Figure 8.2 above) are used for bridges: – L length in y‐direction – b width in x‐direction – d depth in z‐direction. The values to be given to “L”, “b” and “d” in various cases are, where relevant, more precisely defined in various clauses. When Sections 5 to 7 are referred to, the notations for “b” and “d” need to be readjusted. page 262 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_18.xls S ECTION 26 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 8 (P AGE 82 TO 90) 26.1.2 Choice of the response calculation procedure For normal road and railway bridge decks of less than L = 40 m span a dynamic response procedure is generally not needed. For the purpose of this categorization, normal bridges may be considered to include bridges constructed in steel, concrete, aluminium or timber, including composite construction, and whose shape of cross sections is generally covered by Figure 8.1. If a dynamic response procedure is not needed, cscd may be taken equal to 1,0. The National Annex may give criteria and procedures. 26.2 Force coefficients 26.2.1 Force coefficients in x-direction (general method) Force coefficients for parapets and gantries on bridges should be determined were relevant. The National Annex may give force coefficients for parapets and gantries on bridges. It is recommended to use Section 7.4. Force coefficients for wind actions on bridge decks in the x-direction are given by: c f x = c fx 0 (Eq. 26‐103) where c fx 0 is the force coefficient without free-end flow (see 7.13). Figure 26.124 From Figure 8.3 - Force coefficient for bridges, cfx,0. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_18.xls page 263 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 26 E UROCODE 1 EN 1991-1-4 S ECTION 8 (P AGE 82 TO 90) A bridge has usually no free-end flow because the flow is deviated only along two sides (over and under the bridge deck). For normal bridges c fx 0 may be taken equal to 1,3. Alternatively, c fx 0 may be taken from Figure 8.3 where some typical cases for determining A ref x (as defined in 8.3.1(4)) and d tot are shown. Where the windward face is inclined to the vertical (see Figure 8.4), the drag coefficient c fx 0 may be reduced by 0,5% per degree of inclination, 1 from the vertical, limited to a maximum reduction of 30%. Figure 26.125 From Figure 8.4 - Bridge with inclined windward face. Note This reduction is not applicable to Fw, defined in 8.3.2, unless otherwise specified in the National Annex. Where a bridge deck is sloped transversely, c fx 0 should be increased by 3% per degree of inclination, but not more than 25%. Reference areas A ref x for load combinations without traffic load should be based on the relevant value of d tot as defined in Figure 8.5 and Table 8.1. However, the total reference area A ref x should not exceed that obtained from considering an equivalent plain (web) beam of the same overall depth, including all projecting parts. Figure 26.126 From Figure 8.5 - Depth dtot to be used for Aref,x. page 264 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_18.xls S ECTION 26 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 8 (P AGE 82 TO 90) Road restraint system on one side on both side Open parapet or open safety barrier d + 0,3 m d + 0,6 m Solid parapet or solid safety barrier d + d1 d + 2d1 d + 0,6 m d + 1,2 m Open parapet and open safety barrier Table 26.57 From Table 8.1 - Depth dtot to be used for Aref,x. Instead of the areas for load combinations without traffic load, the reference areas A ref x for load combinations with traffic load should be taken into account where they are larger: — for road bridges, a height of 2 m from the level of the carriageway, on the most unfavourable length, independently of the location of the vertical traffic loads — for railway bridges, a height of 4 m from the top of the rails, on the total length of the bridge. Note The reference height, ze, may be taken as the distance from the lowest ground level to the centre of the bridge deck structure, disregarding other parts (e.g. parapets) of the reference areas. Wind pressure effects from passing vehicles are outside the scope of this Part. For wind effects induced by passing trains see EN 1991-2. 26.2.2 Force in x-direction. Simplified Method The wind force in the x-direction may be obtained using Expression (8.2 [modified]): 1 F w = c s c d --- v b2 C A ref x 2 (Eq. 26‐104) where: • is the density of air (see Sec. 4.5) • v b is the basic wind speed (see Sec. 4.2(2)) • C is the wind load factor C = c e c f x where c e = c e z e is the exposure factor given in Sec. 4.5 and c f x is given in Sec. 8.3.1(1) • A ref x is the reference area given in Sec. 8.3.1 • c s c d is the structural factor (as defined in Sec. 6).(14) (14) For the purpose of this categorization, normal bridges may be considered to include bridges constructed in steel, concrete, aluminium or timber, including composite construction, and whose shape of cross sections is generally covered by Figure 8.1. If a dynamic response procedure is not needed (L > 40 m), cscd may be taken equal to 1,0. For normal road and railway bridge decks of less than L = 40 m span a dynamic response procedure is generally not needed. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_18.xls page 265 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 26 E UROCODE 1 EN 1991-1-4 S ECTION 8 (P AGE 82 TO 90) Note C‐values may be defined in the National Annex. Recommended values are given in Table 8.2. b/dtot(a) ze < 20 m ze = 50 m < 0,5 6,7 8,3 > 4,0 3,6 4,5 Table 26.58 From Table 8.2 - Recommended values of the force factor C for bridges(b). (a). For intermediate values of d/btot and of ze linear interpolation may be used. (b). This table is based on the following assumptions: – terrain category II according to Table 4.1 – force coefficient cf,x according to Sec. 8.3.1(1) – c0 = 1,0 – k1 = 1,0. 26.2.3 Wind forces on bridge decks in z-direction Force coefficients c f z should be defined for wind action on the bridge decks in the z-direction, both upwards and downwards (lift force coefficients). c f z should not be used to calculate vertical vibrations of the bridge deck. The National Annex may give values for c f z . In the absence of wind tunnel tests the recommended value may be taken equal to ±0,9. This value takes globally into account the influence of a possible transverse slope of the deck, of the slope of terrain and of fluctuations of the angle of the wind direction with the deck due to turbulence. As an alternative c f z may be taken from Figure 8.6. In using it: — the depth d tot may be limited to the depth of the deck structure, disregarding the traffic and any bridge equipment — for flat, horizontal terrain the angle of the wind with the horizontal may be taken as ± 5° due to turbulence. This is also valid for hilly terrain when the bridge deck is at least 30 m above ground. The reference area A ref z is equal to the plan area (see Figure 8.2): A ref z = b L (Eq. 26‐105) No end-effect factor should be taken into account. The reference height z e is the same as for c f x (see Sec. 8.3.1(6)). Therefore, according to Eq. 26-104 we have: 1 F w z = c s c d --- v b2 c e c f z A ref z 2 (Eq. 26‐106) If not otherwise specified the eccentricity of the force in the x-direction may be set to e = b/4. page 266 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_18.xls S ECTION 26 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 8 (P AGE 82 TO 90) Figure 26.127 From Figure 8.6 - Force coefficient cf,z for bridges with transversal slope and wind inclination. 26.2.4 Wind forces on bridge decks in y-direction 1) If necessary, the longitudinal wind forces in y-direction should be taken into account. Note The National Annex may give the values. The recommended values are: – for plated bridges, 25% of the wind forces in x‐direction, – for truss bridges, 50% of the wind forces in x‐direction. 26.3 Verification tests EN1991‐1‐4_(A)_18.XLS. 6.34 MB. Created: 01 October 2013. Last/Rel.-date: 01 October 2013. Sheets: — Splash — CodeSec8. EXAMPLE 26-CI‐ Force coefficients in x‐direction (general method) ‐ Sec. 8.3.1 ‐ test1 Given: Find the force coefficients c f x for wind actions on bridge deck in the x‐direction according to Figure 8.3. Consider the two cases: case a) construction phase, open parapets Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_18.xls page 267 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 26 E UROCODE 1 EN 1991-1-4 S ECTION 8 (P AGE 82 TO 90) (more than 50% open) and open safety barriers; case b) solid parapets, noise barrier, solid safety barriers or traffic. Let us assume the following assumptions (see Figure 8.2 ‐ “Directions of the wind actions on bridges”): – bridge span (considered): L = 30 00 m – width of the deck of the bridge: b = 13 00 m – depth of the deck of the bridge: d = 2 10 m – max height of vehicles/trains along the entire bridge span: d tot = 4 m . [Reference sheet: CodeSec8]‐[Cell‐Range: A1:O1‐A128:O128]. Solution: From Figure 8.3 ‐ “Force coefficient for bridges, cfx,0” we have: Case a): d tot = d = 2 10 m , b d tot = 13 00 2 10 = 6 19 - (rounded value). According to Figure 8.3 we get: c fx 0 = 1 30 - (see figure below). Figure 26.128 Excel® output: case a). Case b): d tot = d + d tot = 2 10 + 4 = 6 10 m , b d tot = 13 00 6 10 = 2 13 - (rounded value). According to Figure 8.3 we get: c fx 0 = 1 89 - (see figure below). The straight line with constant slope (< 0) has the equation: c fx 0 – 2 4 1---------------------- 3 – 2 4- = ----------------------------b d tot – 0 5 4 – 0 5 page 268 1 3 – 2 4 c fx 0 – 2 4 ------------------------ = --------------------------2 13 – 0 5 4 – 0 5 c fx 0 = 1 89 - . Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_18.xls S ECTION 26 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 8 (P AGE 82 TO 90) Figure 26.129 Excel output: case b). For normal bridges c fx 0 may be taken equal to 1,3. Alternatively, c fx 0 may be taken from Figure 8.3 (see input above). example-end EXAMPLE 26-CJ‐ Force in x‐direction ‐ Simplified Method ‐ Sec. 8.3.2 and 8.3.4 ‐ test2 Given: Find the wind forces acting on the deck of a plated bridge in the x,y‐directions for both cases a) and b) (see Figure 8.3 ‐ “Force coefficient for bridges, cfx,0”). Using the numerical data given in the previous example, assume the following additional assumptions: – reference height (distance from the lowest ground level to the centre of the bridge deck structure): z e = 35 m – exposure factor given in Sec. 4.5 (@ height ze): c e = c e z e = 3 73 - – basic wind speed (see Sec. 4.2(2)): v b = 25 m s – density of air: = 1 25 kg m 3 – structural factor (as defined in Section 6): c s c d = 1 00 - – type of traffic load: “railway bridge” Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_18.xls page 269 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 26 E UROCODE 1 EN 1991-1-4 S ECTION 8 (P AGE 82 TO 90) – the bridge deck is sloped transversely. Transverse slope of the deck: 2 = 2 – road restraint system (see Table 8.1): “open parapet and open safety barrier”. [Reference sheet: CodeSec8]‐[Cell‐Range: A138:O138‐A350:O350]. Solution: From Sec. 8.3.1(2) for 2 = 2 we get: 2 3 100 deg 6 100 = 0 06 (6%). Increasing factor for the force coefficient c fx 0 : IF = 1 06 - . From previous example: c fx 0 = 1 30 - . Actual value used for calculations (increase factor applied): c fx 0 = IF 1 30 - = 1 06 1 30 = 1 38 - (rounded value). Case a): Construction phase (see Figure 8.3) From Table 8.1 ‐ “Depth dtot to be used for Aref,x” with “open parapet and open safety barrier” we obtain: d tot = d + 0 6 m = 2 10 + 0 60 = 2 70 m (for road restraint system: on one side) and d tot = d + 1 2 m = 2 10 + 1 20 = 3 30 m (for road restraint system: on both side) with: b d tot = 13 00 2 70 = 4 81 - (for road restraint system: on one side) b d tot = 13 00 3 30 = 3 94 - (for road restraint system: on both side). Road restraint system on one side: A ref x = d tot L = 2 70 30 00 = 81 00 m 2 Road restraint system on both side: A ref x = d tot L = 3 30 30 00 = 99 00 m 2 . From Table 8.2 ‐ “Recommended values of the force factor C for bridges”, linear interpolation with 20 m z e 50 m and b d tot = 4 81 - , b d tot = 3 94 - . Thus, linear interpolation between z e 20 m and z e = 50 m for b d tot 4 0 : C – 3 60 4---------------------------- 50 – 3 60- = --------------------z e – 20 50 – 20 4 50 – 3 60 C – 3 60 ------------------------------ = ---------------------50 – 20 35 – 20 C = 4 05 - . Linear interpolation for b d tot = 3 94 - (within the range 0 5 ; 4 0 ) with: C – 6 70 8---------------------------- 30 – 6 70- = --------------------z e – 20 50 – 20 C – 6 70 4 05 – 7 50 ------------------------------ = -----------------------------b d tot – 0 5 4 0 – 0 5 8 30 – 6 70 C – 6 70 ------------------------------ = ---------------------50 – 20 35 – 20 4---------------------------- 05 – 7 50- -------------------------C – 6 70 = 4 0 – 0 5 3 94 – 0 5 C = 7 50 - . Thus: C = 4 11 - . Case (a): Road restraint system on one side without traffic loads with C = 4 05 - . Case (b): Road restraint system on both side without traffic loads with C = 4 11 - . Instead, using the exposure factor: C = c e z e c f x = 3 73 1 38 = 5 15 - WIND FORCES IN THE X‐DIRECTION (see Figure 8.2) Case (a) with C = 5 15 - , A ref x = 81 00 m 2 : 1 –3 F w = c s c d --- v b2 C A ref x = 1 0 5 1 25 25 00 2 5 15 81 00 10 = 162 95 kN 2 F w L = 162 95 30 00 = 5 43 kN m (rounded values). page 270 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_18.xls S ECTION 26 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-4 S ECTION 8 (P AGE 82 TO 90) Case (b) with C = 5 15 - , A ref x = 99 00 m 2 : 1 –3 F w = c s c d --- v b2 C A ref x = 1 0 5 1 25 25 00 2 5 15 99 00 10 = 199 16 kN 2 F w L = 199 16 30 00 = 6 64 kN m (rounded values). WIND FORCES IN THE Y‐DIRECTION (see Figure 8.2) Case (a) with C = 5 15 - , A ref x = 81 00 m 2 for plated bridge (Fact = 0,25): 1 F w y = 0 25 c s c d --- v b2 C A ref x = 0 25 162 95 kN = 40 74 kN 2 F w y L = 40 74 30 00 = 1 36 kN m (rounded values). Case (b) with C = 5 15 - , A ref x = 99 00 m 2 : 1 –3 F w = c s c d --- v b2 C A ref x = 1 0 5 1 25 25 00 2 5 15 99 00 10 = 199 16 kN 2 F w L = 199 16 30 00 = 6 64 kN m (rounded values). Note Wind forces in the y‐direction for the Case (C) (“bridge carrying lanes of traffic”) are calculated using the same algorithm in the spreadsheet. The calculation is then omitted. EXAMPLE 26-CK‐ Force in z‐direction ‐ Simplified Method ‐ Sec. 8.3.3 ‐ test2b Given: Referring to the data in the previous example, calculate the wind forces on the bridge deck in z‐direction. The force coefficients c f z may be taken from Figure 8.6. In using it, assume the following assumptions: – d tot = 2 10 m (limited to the depth of the deck structure, disregarding the traffic and any bridge equipment) – hilly terrain – bridge superelevation: = 3 (see Figure below): – wind load factor C calculated from exposure factor @ z e : c e z e = 3 73 - – eccentricity of the force in the x‐direction set to e = b 4 = 13 00 4 = 3 25 m . [Reference sheet: CodeSec8]‐[Cell‐Range: A357:O357‐A454:O454]. Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_18.xls page 271 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 26 E UROCODE 1 EN 1991-1-4 S ECTION 8 (P AGE 82 TO 90) Solution: For flat, horizontal terrain the angle of the wind with the horizontal may be taken as ±5° due to turbulence. This is also valid for hilly terrain when the bridge deck is at least 30 m above ground. Therefore (see Figure 8.6 ‐ “Force coefficient cf,z for bridges with transversal slope and wind inclination”), we get: = + = 5 + 3 = 8 with: b d tot = 13 00 2 10 = 6 19 - . From Figure 8.6, linear interpolation between the two straight lines with constant slope (= 0 for = 10 and < 0 for = 6 ): c f z – 0 75 0 90 – 0 75 ------------------------------ = ------------------------b d tot – 0 21 – 0 – 0 75 0---------------------------- 90 – 0 75- c------------------------= f z 6 19 21 – 0 c f z = 0 79 - (for = 6 ), 0 90 – 0 79 c f z – 0 79 ------------------------------ = -------------------------8 – 6 10 – 6 c f z = 0 85 - (for c f z 0 ) Thus: c f z – 0 79 0 90 – 0 79 ------------------------------ = ------------------------ – 6 10 – 6 c f z = – 0 85 - for c f z 0 . WIND FORCES IN THE Z‐DIRECTION (see Figure 8.2) With C = c e z e c f z = 3 73 0 85 = 3 17 - , A ref z = b L = 13 00 30 00 = 390 m 2 : 1 –3 F w z = c s c d --- v b2 C A ref x = 1 0 5 1 25 25 00 2 3 17 390 10 = 482 93 kN 2 F w z L = 482 93 kN 30 00 = 16 10 kN m TORQUE: M w z = F w z e = F w z b 4 = 482 93 kN 13 00 m 4 = 1569 52 kNm T w z = M w z L = 1569 52 kNm 30 00 m = 52 32 kNm m . example-end 26.4 References [Section 26] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Guide for the assessment of wind actions and effects on structures. National Research Council of Italy. CNR-DT 207/2008. ROMA – CNR June 11th, 2010. page 272 Topic: User’s Manual/Verification tests - EN1991-1-4_(a)_18.xls Section 27 Eurocode 1 EN 1991-1-4 Annex A 27.1 Terrain categories I llustrations of the upper roughness of each terrain category are given in Section A.1. The mean wind velocity at a height z above the terrain depends on the terrain roughness and orography and on the basic wind velocity. The terrain category are: — terrain category 0: sea, coastal area exposed to the open sea — terrain category I: lakes or area with negligible vegetation and without obstacles — terrain category II: area with low vegetation such as grass and isolated obstacles (trees, buildings) with separations of at least 20 obstacle heights — terrain category III: area with regular cover of vegetation or buildings or with isolated obstacles with separations of maximum 20 obstacle heights (such as villages, suburban terrain, permanent forest) — terrain category IV: area in which at least 15% of the surface is covered with buildings and their average height exceeds 15 m. 27.2 Transition between roughness categories 0, I, II, III and IV Two recommended procedures are given: — Procedure 1 — Procedure 2. PROCEDURE 1. If the structure is situated near a change of terrain roughness at a distance less than 2 km from the smoother category 0 or less than 1 km from the smoother categories I to III the smoother terrain category in the upwind direction should be used. Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls page 273 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 27 E UROCODE 1 EN 1991-1-4 A NNEX A PROCEDURE 2. Determine the roughness categories for the upstream terrain in the angular sectors to be considered. For every angular sector, determine the distance x from the building to the upstream roughness changes. If the distance x from the building to a terrain with lower roughness length is smaller than the values given in Table A.1, then the lower value for the roughness length should be used for the angular sector considered. If this distance x is larger than the value in Table A.1, the higher value for the roughness length should be used. For intermediate values of height z , linear interpolation may be used. Where no distance x is given in Table A.1 or for heights exceeding 50 m, the smaller roughness length should be used. Small areas (less than 10% of the area under consideration) with deviating roughness may be ignored in both procedures. 27.3 Numerical calculation of orography coefficients At isolated hills and ridges or cliffs and escarpments different wind velocities occur dependent on the upstream slope = H L u in the wind direction, where the height H and the length L u are defined in Figure A. 1. Figure 27.130From Figure A.1 - Illustration of increase of wind velocities over orography. The orography factor, c 0 z = v m v mf accounts for the increase of mean wind speed over isolated hills and escarpments (not undulating and mountainous regions), where: • v m is the mean wind velocity at height z above terrain • v mf is the mean wind velocity above flat terrain. The orography factor is related to the wind velocity at the base of the hill or escarpment. The effects of orography should be taken into account in the following situations: page 274 Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 27 E UROCODE 1 EN 1991-1-4 A NNEX A a. for sites on upwind slopes of hills and ridges: where 0 05 0 3 and x L u 2 b. for sites on downwind slopes of hills and ridges: where 0 3 and x L d 2 where 0 3 and x 1 6H c. for sites on upwind slopes of cliffs and escarpments: where 0 05 0 3 and x L u 2 d. for sites on downwind slopes of cliffs and escarpments: where 0 3 and x 1 5L e where 0 3 and x 5H . The orography factor is defined by: c 0 = 1 for 0 05 (Eq. 27‐107) c 0 = 1 + 2s for 0 05 0 3 (Eq. 27‐108) c 0 = 1 + 0 6s for 0 3 (Eq. 27‐109) where: ✍ • s is the orographic location factor • is the upwind slope H L u in the wind direction • L u is the actual length of the upwind slope in the wind direction • L e is the effective length of the upwind slope: L e = L u for shallow slope 0 05 0 3 , L e = H 0 3 for steep slope 0 3 • L d is the actual length of the downwind slope in the wind direction • H is the effective height of the feature • x is the horizontal distance of the site from the top of the crest • z is the vertical distance from the ground level of the site. The following expressions may be used to compute the value of orographic location factor, s : a) upwind section for all orography (Figures A.2 and A.3): 1. for the range: x z – 1 5 ----- 0 and 0 ----- 2 0 Lu Le (Eq. 27‐110) Bx s = A exp ------- Lu (Eq. 27‐111) take: where: Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls page 275 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 27 E UROCODE 1 EN 1991-1-4 A NNEX A z 4 z 3 z 2 z A = 0 1552 ----- – 0 8575 ----- + 1 8133 ----- – 1 9115 ----- + 1 0124 (Eq. 27‐112) Le Le Le Le and: z 2 z B = 0 3542 ----- – 1 0577 ----- + 2 6456 Le Le 2. (Eq. 27‐113) for the ranges: x z ----- – 1 5 or ----- 2 Le Le (Eq. 27‐114) take s = 0 . b) downwind section for cliffs and escarpments (Figure A.2): 1. for the ranges: x z 0 1 ----- 3 5 and 0 1 ----- 2 0 Le Le (Eq. 27‐115) x 2 x s = A log ----- + B log ----- + C Le Le (Eq. 27‐116) z 3 z 2 z A = – 1 3420 log ----- – 0 8222 log ----- + 0 4609 log ----- – 0 0791 Le Le Le (Eq. 27‐117) z 3 z 2 z B = – 1 0196 log ----- – 0 8910 log ----- + 0 5343 log ----- – 0 1156 Le Le Le (Eq. 27‐118) z 3 z 2 z C = 0 8030 log ----- + 0 4236 log ----- – 0 5738 log ----- + 0 1606 . Le Le Le (Eq. 27‐119) take: where: 2. for the range: x 0 ----- 0 1 Le (Eq. 27‐120) interpolate between values for x L e (with s = A in Eq.27-112) and x L e = 0 1 . 3. page 276 when z L e 0 1 use the values for z L e = 0 1 Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 27 E UROCODE 1 EN 1991-1-4 A NNEX A 4. for the ranges: x L e 3 5 or z L e 2 0 take the value s = 0 . c) downwind section for hills and ridges (Figure A.3): 1. for the ranges: x z 0 ----- 2 0 and 0 ----- 2 0 Ld Le (Eq. 27‐121) Bx s = A exp ------- Ld (Eq. 27‐122) take: where: z 4 z 3 z 2 z A = 0 1552 ----- – 0 8575 ----- + 1 8133 ----- – 1 9115 ----- + 1 0124 (Eq. 27‐123) Le Le Le Le z 2 z B = – 0 3056 ----- + 1 0212 ----- – 1 7637 Le Le 2. (Eq. 27‐124) for the ranges: x z ---- 2 0 or ----- 2 0 take s = 0 . Ld Le (Eq. 27‐125) 27.4 Neighbouring structures If a building is more than twice as high as the average height h ave of the neighbouring structures then, as a first approximation, the design of any of those nearby structures may be based on the peak velocity pressure at height z n above ground. Let r be the radius given by expressions (see Figure below): r = h high if h high 2d l arg e r = 2d l arg e if h high 2d l arg e , then, we have: for x r , z n = 0 5r (Eq. 27‐126) 2h low for r x 2r , z n = 0 5 r – 1 – ------------ x – r r (Eq. 27‐127) for x 2r , z n = h low (Eq. 27‐128) Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls page 277 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 27 E UROCODE 1 EN 1991-1-4 A NNEX A where: • h high is height of the tallest building • d small , d l arg e are the plan dimensions of the tallest building • h ave is the average height of the neighbouring structures • h low is the height of the nearby structure • x is the distance from the tallest building (see x 1 or x 2 on figure below). Figure 27.131From Figure A.4 - Influence of a high rise building, on two different nearby structures (1 and 2) 27.5 Displacement height For buildings in terrain category IV, closely spaced buildings and other obstructions causes the wind to behave as if the ground level was raised to a displacement height, h dis . Hence, the profile of peak velocity pressure over height may be lifted by a height h dis . Figure 27.132Obstruction height and upwind spacing (the figure shows a particular case). page 278 Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 27 E UROCODE 1 EN 1991-1-4 A NNEX A For range: x 2h ave , h dis = min 0 8 h ave ; 0 6h (Eq. 27‐129) for range: 2h ave x 6h ave , h dis = min 1 2 h ave – 0 2 x ; 0 6h (Eq. 27‐130) when x 6h ave take: h dis = 0 . (Eq. 27‐131) Note In the absence of more accurate information the obstruction height may be taken as have = 15 m for terrain category IV. 27.6 Verification tests EN1991‐1‐4_(B).XLS. 6.73 MB. Created: 14 March 2013. Last/Rel.-date: 14 March 2013. Sheets: — Splash — Annex A. EXAMPLE 27-CL‐ Transition between roughness categories 0, I, II, III and IV ‐ test1 Given: The transition between different roughness categories has to be considered for calculations. Roughness categories for the upstream terrain in the angular sector are considered from terrain “Category I” to terrain “Category III” and viceversa. Assume an height above ground equal to z = 9 m and a distance from the building to a terrain with lower roughness length equal to x = 21 km . Find which value for the roughness length should be used. Use the “Procedure 2”. [Reference sheet: Annex A]‐[Cell‐Range: P9:R9‐P10:R10‐CommandButton]. Solution: From Table A.1: Height z I to II I to III 5m 0,50 km 5,00 km 7m 1,00 km 10,00 km 10 m 2,00 km 20,00 km 15 m 5,00 km 20 m 12,00 km 30 m 20,00 km 50 m 50,00 km Table 27.59 From Table A.1 - Distance x. for z = 9 m , entering the third column, we get (linear interpolation): Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls page 279 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 27 E UROCODE 1 EN 1991-1-4 A NNEX A x – 10 0020 00 – 10 00 ---------------------------------------------------------- = z – 7 00 10 – 7 20 00 – 10 00- x---------------------– 10 00----------------------------------= 10 – 7 9 – 7 00 x = 16 67 m . Then, we have: x = 21 km 16 67 m . Thus, the higher value for the roughness length should be used: z 0 = 0 3 m (see Table 4.1, EN 1991-1-4). Figure 27.133PreCalculus Excel® form: procedure for a quick pre-calculation. Figure 27.134PreCalculus Excel form: procedure for a quick pre-calculation. page 280 Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 27 E UROCODE 1 EN 1991-1-4 A NNEX A From terrain category III to category III the standard has not recommended procedures: the smoother terrain category might be applied. example-end EXAMPLE 27-CM‐ Transition between roughness categories 0, I, II, III and IV ‐ test1b Given: Using the same assumptions of the previous example, find the roughness length to be used for calculations for z = 60 m and x = 21 km . Use the “Procedure 2”. [Reference sheet: Annex A]‐[Cell‐Range: P9:R9‐P10:R10‐CommandButton]. Solution: As determined by the Standard (A.2(1)), where no distance x is given in Table A.1 or for heights exceeding 50 m, the smaller roughness length should be used. Figure 27.135PreCalculus Excel form: procedure for a quick pre-calculation. From Table 4.1 (“Terrain categories and terrain parameters“): z 0 = min 0 01 ; 0 3 = 0 01 m . example-end EXAMPLE 27-CN‐ Transition between roughness categories 0, I, II, III and IV ‐ test1c Given: From terrain category II to category III, find the roughness length to be used for z = 25 m and x = 8 km . Use the “Procedure 2”. [Reference sheet: Annex A]‐[Cell‐Range: P9:R9‐P10:R10‐CommandButton]. Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls page 281 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 27 E UROCODE 1 EN 1991-1-4 A NNEX A Solution: For z = 25 m , entering Table A.1, we get (linear interpolation): x = 7 00 + 10 00 2 = 8 50 m . Height z II to III II to IV 5m 0,30 km 2,00 km 7m 0,50 km 3,50 km 10 m 1,00 km 7,00 km 15 m 3,00 km 20,00 km 20 m 7,00 km 30 m 10,00 km 50 m 30,00 km Table 27.60 From Table A.1 - Distance x. Then, we have: x = 8 km 8 50 m . Figure 27.136PreCalculus Excel form: procedure for a quick pre-calculation. Thus, the lower value for the roughness length should be used: z 0 = 0 05 m . example-end EXAMPLE 27-CO‐ Transition between roughness categories 0, I, II, III and IV ‐ test1d Given: page 282 A building is situated near a change of terrain roughness at a distance of x = 2500 m from the smoother terrain category (Category 0). Find the terrain category in the upwind direction to be used for calculations. Use “Procedure 1”. Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 27 E UROCODE 1 EN 1991-1-4 A NNEX A [Reference sheet: Annex A]‐[Cell‐Range: P9:R9‐P10:R10‐CommandButton]. Solution: As determined by the Standard (A.2(1)), if the structure is situated near a change of terrain roughness at a distance less than 2 km from the smoother category 0 the smoother terrain category in the upwind direction should be used. Figure 27.137PreCalculus Excel form: procedure for a quick pre-calculation. We have x = 2500 m 2 km . Therefore, the actual terrain category where the building is situated should be used for calculations. example-end EXAMPLE 27-CP‐ Numerical calculation of orography coefficients ‐ test2 Given: Find the upstream slope, the orography location factor, the orography factor, and the type of slope for a site with: – an actual length of the upwind slope in the wind direction: L u = 250 m – an actual length of the downwind slope in the wind direction: L d = 100 m – a vertical distance from the ground level of the site: z = 10 m – an effective height of the feature: H = 50 m – an horizontal distance of the site from the top of the crest: x = 160 m . [Reference sheet: Annex A]‐[Cell‐Range: A1:N1‐A120:N120]. Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls page 283 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 27 E UROCODE 1 EN 1991-1-4 A NNEX A Solution: Upstream slope in the wind direction: = H L u = 50 250 = 0 20 . From Table A.2 “Values of the effective length Le”: Type of slope ( = H/Lu) Shallow 0 05 0 3 : L e = L u Steep 0 3 : L e = H 0 3 Table 27.61 From Table A.2. orography factor for 0 05 0 3 : c 0 = 1 + 2s . Effective length: L e = L u = 250 m . The orography factor, c o z = v m v mf accounts for the increase of mean wind speed over isolated hills and escarpments (not undulating and mountainous regions). It is related to the wind velocity at the base of the hill or escarpment. The effects of orography should be taken into account in the following situations: a) for sites on upwind slopes of hills and ridges: – where 0 05 0 3 and x = 160 m L u 2 = 125 m [Case Not Applicable] b) for sites on downwind slopes of hills and ridges: – where 0 3 and x = 160 m L d 2 = 50 m [Case Applicable] – where = 0 20 0 30 [Case Not Applicable] and x 1 6H c) for sites on upwind slopes of cliffs and escarpments: – where 0 3 and x L u 2 = 125 m [Case Not Applicable] d) for sites on downwind slopes of cliffs and escarpments: – where 0 3 and x = 160 m 1 5L e = 375 m [Case Applicable] – where 0 3 [Case Not Applicable] and x 5H . a) Upwind section for all orography (see Figures A.2 and A.3): In this case, considering x = – 160 m , for the range – 1 5 x L u 0 and 0 z L e 2 0 , we have: – 1 5 – 160 250 0 and 0 10 250 2 0 . [Case Applicable] Therefore, with z L e = 0 04 , we get: z 4 z 3 z 2 z A = 0 1552 ----- – 0 8575 ----- + 1 8133 ----- – 1 9115 ----- + 1 0124 Le Le Le Le A = 0 1552 0 04 4 – 0 8575 0 04 3 + 1 8133 0 04 2 – 1 9115 0 04 + 1 0124 –7 –7 A = 3 97 10 – 548 8 10 + 0 00290 – 0 07646 + 1 0124 = 0 9388 . z 2 z B = 0 3542 ----- – 1 0577 ----- + 2 6456 = 0 3542 0 04 2 – 1 0577 0 04 + 2 6456 Le Le B = 0 000567 – 0 04231 + 2 6456 = 2 6039 . Therefore, with x L u = – 0 64 , we get: x s = A exp B ----- = 0 9388 exp – 2 6039 0 64 = 0 1773 . Lu b) downwind section for cliffs and escarpments (Figure A.2): In this case, considering x = + 160 m , for the range 0 1 x L e 3 5 and 0 1 z L e 2 0 , we have: 0 1 160 250 3 5 and 0 1 10 250 3 5 . [Case Not Applicable] page 284 Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 27 E UROCODE 1 EN 1991-1-4 A NNEX A Therefore, with z L e = 0 04 , we get: z 3 z 2 z A = – 1 3420 log ----- – 0 8222 log ----- + 0 4609 log ----- – 0 0791 Le Le Le A = – 1 3420 log 0 04 3 – 0 8222 log 0 04 2 + 0 4609 log 0 04 – 0 0791 A = 3 66622 – 1 60677 – 0 64431 – 0 0791 = 1 3360 . z 3 z 2 z B = – 1 0196 log ----- – 0 8910 log ----- + 0 5343 log ----- – 0 1156 Le Le Le B = – 1 0196 log 0 04 3 – 0 8910 log 0 04 2 + 0 5343 log 0 04 – 0 1156 B = 2 78545 – 1 74122 – 0 74692 – 0 1156 = 0 1817 . z 3 z 2 z C = 0 8030 log ----- + 0 4236 log ----- – 0 5738 log ----- + 0 1606 Le Le Le C = 0 8030 log 0 04 3 + 0 4236 log 0 04 2 – 0 5738 log 0 04 + 0 1606 C = – 2 19372 + 0 82781 + 0 80214 + 0 1606 = – 0 4032 . Therefore, with x L e = 160 250 = 0 64 , we get: x 2 x s = A log ----- + B log ----- + C = 1 3360 log 0 64 2 + 0 1817 log 0 64 – 0 4032 Le Le s = 0 05019 – 0 03522 – 0 4032 = – 0 3882 . EXAMPLE 27-CQ‐ Numerical calculation of orography coefficients ‐ test2b Given: Assume that it is valid the case “b) Downwind section for cliffs and escarpments” within the range: 0 x Le 0 1 with x L e = 10 250 = 0 08 and z L e = 10 250 = 0 04 . [Reference sheet: Annex A]‐[Cell‐Range: A127:N127‐A158:N158]. Solution: Referring to the calculations above, we find with x Le = 0 1 : A x L e = A 0 1 = – 0 0202 ; B x L e = B 0 1 = – 0 5213 ; C x L e = C 0 1 = 0 3550 (reference cells: U109; U112 and U115). We get with x L e = 0 1 : x 2 x s = A log ----- + B log ----- + C = – 0 0202 log 0 1 2 – 0 5213 log 0 1 + 0 3550 Le Le s 0 1 = – 0 02 + 0 5213 + 0 3550 = 0 856 . Linear interpolation: 0 9388 – 0 8561 0 1 – 0 08 s x L e = s 0 08 = ----------------------------------------------------------------------------------- + 0 8561 = 0 8726 . 0 1 with x L e = 0 for: z 4 z 3 z 2 z s 0 = A = 0 1552 ----- – 0 8575 ----- + 1 8133 ----- – 1 9115 ----- + 1 0124 = 0 9388 Le Le Le Le Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls page 285 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 27 E UROCODE 1 EN 1991-1-4 A NNEX A (see previous example with z L e = 0 04 ). example-end EXAMPLE 27-CR‐ Numerical calculation of orography coefficients ‐ test2c Given: Find the orography location factor for “c) Downwind section for hills and ridges”. Let us assume the same assumptions in the previous example. [Reference sheet: Annex A]‐[Cell‐Range: A162:N162‐A180:N180]. Solution: In this case, we are in the range: 0 x L d 2 0 and 0 z L e 2 0 . In particular, from the previous examples we have: x L d = 0 20 and z Le = 0 04 with z 4 z 3 z 2 z A = 0 1552 ----- – 0 8575 ----- + 1 8133 ----- – 1 9115 ----- + 1 0124 Le Le Le Le A = 0 1552 0 04 4 – 0 8575 0 04 3 + 1 8133 0 04 2 – 1 9115 0 04 + 1 0124 A = 0 9388 (see example 27‐CP on page 283). z 2 z B = – 0 3056 ----- + 1 0212 ----- – 1 7637 Le Le B = – 0 3056 0 04 2 + 1 0212 0 04 – 1 7637 B = – 0 000489 + 0 040848 – 1 7637 = – 1 7233 . We find: x s = A exp B ----- = 0 9388 exp – 1 7233 0 20 = 0 665 . Ld In this case, the orography factor is given by: c 0 z = 1 + 2s = 1 + 2 0 665 0 20 = 1 266 . example-end EXAMPLE 27-CS‐ Neighbouring structures ‐ test3 Given: Find the height z n = z e above ground at which the peak velocity pressure may be based on for structure influenced by a high rise building. Assume: – height of the tallest building: h high = 60 m – plan dimensions of the tallest building: d l arg e = 20 m ; d small = 15 m – average height of the neighbouring structures: h ave = 20 m – height of the nearby structure: h low = 20 m – distance “x” of the considered structure from the tallest building: x = 10 m . page 286 Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 27 E UROCODE 1 EN 1991-1-4 A NNEX A [Reference sheet: Annex A]‐[Cell‐Range: A254:N254‐A287:N287]. Solution: For h high 2d l arg e = 40 m we have: r = 2d l arg e = 40 m (radius). As determined by the Standard, for x r : z n = 0 5r = 20 m . In this case, increased wind velocities can’t be disregarded: h low 0 5h high . The considered building h low = 20 m is more than twice as high as the average height h ave = 20 m of the neighbouring structures: h high 2h ave then, as a first approximation, the design of any of those nearby structures may be based on the peak velocity pressure calculated at height z n = 20 m . example-end EXAMPLE 27-CT‐ Displacement height ‐ test4 Given: Find the displacement height h dis for: – an average height of the neighbouring structures: h ave = 20 m – an height of the building: h = 35 m – a distance building from nearby structures: x = 45 m . [Reference sheet: Annex A]‐[Cell‐Range: A312:N312‐A328:N328]. Solution: In this case, for the range 2h ave x 6h ave , we get: h dis = min 1 2 h ave – 0 2 x ; 0 6h h dis = min 1 2 20 – 0 2 45 ; 0 6 35 = min 15 ; 21 = 15 m . In the absence of more accurate information the obstruction height may be taken as h ave = 15 m for terrain category IV. example-end 27.7 References [Section 27] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design April 2010. © 2010 The Institution of Structural Engineers. Eurocode Load Combinations for Steel Structures. The British Constructional Steelwork Association Limited. BCSA Publication No. 53/10. December 2010. Topic: User’s Manual/Verification tests - EN1991-1-4_(b).xls page 287 (This page intentionally left blank) Section 28 EN 1991-1-4 Annex B 28.1 Procedure 1 for determining the structural factor cscd T he structural factor c s c d should take into account the effect on wind actions from the non simultaneous occurrence of peak wind pressures on the surface c s together with the effect of the vibrations of the structure due to turbulence c d . The detailed procedure for calculating the structural factor c s c d is given in expression below (Eq. 6.1 – EN 1991-1-4 Section 6.3 “Detailed procedure”). This procedure can only be used if particular conditions given in 6.3.1 (2) apply. 1 + 2k p I v z s B 2 + R 2 c s c d = --------------------------------------------------------------1 + 7 Iv zs (Eq. 28‐1) where: • z s is the reference height for determining the structural factor, see Figure 6.1.(1) • k p is the peak factor defined as the ratio of the maximum value of the fluctuating part of the response to its standard deviation • I v is the turbulence intensity defined in 4.4 (EN 1991-1-4) • B 2 is the background factor, allowing for the lack of full correlation of the pressure on the structure surface • R 2 is the resonance response factor, allowing for turbulence in resonance with the vibration mode. The size factor c s takes into account the reduction effect on the wind action due to the non simultaneity of occurrence of the peak wind pressures on the surface and may be obtained from Expression: 1 + 7 Iv zs B 2 c s = ---------------------------------------1 + 7 Iv zs (Eq. 28‐2) (1) For structures where Figure 6.1 does not apply z s may be set equal to h , the height of the structure. Topic: User’s Manual/Verification tests - EN1991-1-4_(c).xls page 289 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 28 EN 1991-1-4 A NNEX B The dynamic factor c d takes into account the increasing effect from vibrations due to turbulence in resonance with the structure and may be obtained from Expression: 1 + 2k p I v z s B 2 + R 2 c d = ----------------------------------------------------------. 1 + 7 Iv zs B 2 (Eq. 28‐3) The procedure to be used to determine k p , B and R may be given in the National Annex. A recommended procedure is given in Annex B. An alternative procedure is given in Annex C. As an indication to the users the differences in c s c d using Annex C compared to Annex B does not exceed approximately 5%. Figure 28.1 From Figure 6.1 - General shapes of structures covered by the design procedure. WIND TURBULENCE. For heights z 200 m the turbulent length scale L z may be calculated using Expression: z - L z = L t ------- 200 z min L z = L t --------- 200 for z z min (Eq. 28‐4) for z z min with L t = 300 m and z , z min in meters. The exponent is equal to: = 0 67 + 0 05 ln z 0 , where the roughness length z 0 is measured in metres. The wind distribution over frequencies is expressed by the non-dimensional power spectral density function: n S v z n 6 8 f L z n S L z n = -------------------------= -----------------------------------------------------2 v 1 + 10 2 f L z n 5 / 3 page 290 (Eq. 28‐5) Topic: User’s Manual/Verification tests - EN1991-1-4_(c).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 28 EN 1991-1-4 A NNEX B where S v z n is the one-sided variance spectrum, and f L z n = n L z v m z is a non-dimensional frequency determined by the frequency n = n 1 x , the natural frequency of the structure in Hz, by the mean velocity v m z and the turbolence length scale L z . BACKGROUND FACTOR. It may be calculated using Expression: 1 B 2 = --------------------------------------------------0 63 b + h 1 + 0 9 ------------ L zs (Eq. 28‐6) where: • b h is the width and height of the structure, as given in Figure 6.1 • L z s is the turbulent length scale given in B.1(1) at reference height z s as defined in Figure 6.1. The peak factor can be expressed by the following equation: kp = 0 6 2 ln T + ----------------------------2 ln T (Eq. 28‐7) with the limit k p 3 to which corresponds lim = 0 08 Hz . From the expression above, we have: • the up-crossing frequency • T the averaging time for the mean wind velocity, T = 600 seconds. The up-crossing frequency should be obtained from expression: R2 - lim = 0 08 Hz = n 1 x -----------------2 B + R2 (Eq. 28‐8) where n 1 x is the natural frequency of the structure, which may be determined using Annex F. RESONANCE RESPONSE FACTOR. It should be determined using expression: 2 R 2 = ------ S L z s n 1 x R h h R b b 2 (Eq. 28‐9) where: • is the total logarithmic decrement of damping given in F.5 (Annex F) • S L is the non-dimensional power spectral density function • R h R b are the aerodynamic admittance functions for a fundamental mode shape: 1 1 R h = ----- – ---------2 1 – exp – 2 h with R h = 1 for h = 0 h 2 h Topic: User’s Manual/Verification tests - EN1991-1-4_(c).xls (Eq. 28‐10) page 291 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 28 EN 1991-1-4 A NNEX B 1 1 R b = ----- – ---------2 1 – exp – 2 b with R b = 1 for b = 0 b 2 b (Eq. 28‐11) 4 6 h 4 6 b with: h = ---------------- f L z s n 1 x and b = ---------------- f L z s n 1 x . L zs L zs 28.2 Number of loads for dynamic response Figure below shows the number of times N g , that the value S of an effect of the wind is reached or exceeded during a period of 50 years. Figure 28.2 Number of gust loads Ng (= 1000) for an effect S/Sk (= 54%) during a 50 years period. The relationship between S S k and N g is given by expression: S ------- = 0 7 log N g 2 – 17 4 log N g + 100 . Sk (Eq. 28‐12) 28.3 Service displacement and accelerations for serviceability assessments of a vertical structure The maximum along-wind displacement is determined from the equivalent static wind force F w acting on a structure (see EN 1991-1-4, Section 5.3 - “Wind forces”). The standard deviation of the characteristic along-wind acceleration of the structural point at height z should be obtained using Expression: page 292 Topic: User’s Manual/Verification tests - EN1991-1-4_(c).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 28 EN 1991-1-4 A NNEX B c f b I v z s v m2 z s - R K x 1 x z a x z = --------------------------------------------------------m 1 x (Eq. 28‐13) where: • c f is the force coefficient (see Section 7) • is the air density • b is the width of the structure as defined in Figure 6.1 • z s is the reference height as defined in Figure 6.1 • I v z s is the turbulence intensity at height z = z s above ground • v m z s is the mean wind velocity for z = z s • R is the square root of resonant response • K x is the non-dimensional coefficient • m 1 x is the along wind fundamental equivalent mass (see Annex F, Section F.4(1)) • n 1 x is the fundamental frequency of along • 1 x z is the fundamental along wind modal shape.(2) The non dimensional coefficient, K x , is defined by: h z 2 + 1 + 1 ln ----s + 0 5 – 1 z0 0 - ------------------------------------------------------------------------------------------------------K x = ------------------------------------------h z + 1 2 ln ----s z0 v m2 z s 1 x z dz v 2 m z 1 x z dz (Eq. 28‐14) 0 where: • z 0 is the roughness length (see Table 4.1) • is the exponent of the mode shape (see Annex F). The characteristic peak accelerations are obtained by multiplying the standard deviation in Eq. 28-13 by the peak factor in Eq. 28-7 using the natural frequency as upcrossing frequency, i.e. = n 1 x . 28.4 Verification tests EN1991‐1‐4_(C).XLS. 6.32 MB. Created: 02 April 2013. Last/Rel.-date: 02 April 2013. Sheets: — Splash — Annex B. (2) As a first approximation the expressions given in Annex F be used. Topic: User’s Manual/Verification tests - EN1991-1-4_(c).xls page 293 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 28 EN 1991-1-4 A NNEX B EXAMPLE 28-A‐ Procedure 1 for determining the structural factor cscd ‐ test1 Given: Find the turbulent length scale L z and the power spectral density function S L z n at an actual height z act = 30 m above ground level at the site of the structure. Suppose a displacement height h dis = 10 m , a mean wind velocity (mean return period: N = 100 years) equal to v m z act – h dis = 36 4 m s and n 1 x = 0 5 Hz (lower natural frequency of the structure: mode shape 1). Choose terrain category “0”. [Reference sheet: Annex B]‐[Cell‐Range: A1:N1‐A73:N73]. Solution: Entering Table 4.1 (“Terrain categories and terrain parameters”) for terrain category “0”: z 0 = 0 003 m and z min = 1 m . We have: z = z act – h dis = 30 – 10 = 20 m , = 0 67 + 0 05 ln z 0 = 0 67 + 0 05 ln 0 003 = 0 38 For z = 20 m z min = 1 m : z 20 0 38 L z = L t --------- = 300 --------- = 125 m . 200 200 Non‐dimensional frequency: n L z - = 0-------------------- 5 125- = 1 7 - . f L z n = -----------------vm z 36 4 Figure 28.3 Power spectral density function for terrain Category 0 and natural frequency equal to 0,5 Hz. page 294 Topic: User’s Manual/Verification tests - EN1991-1-4_(c).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 28 EN 1991-1-4 A NNEX B Power spectral density function (see plot above): n S v z n 6 8 f L z n 6 8 1 7 S L z n = -------------------------= ------------------------------------------------------ = --------------------------------------------- = 0 09 v2 1 + 10 2 f L z n 5 / 3 1 + 10 2 1 7 5 / 3 for z = z act – h dis = 30 – 10 = 20 m and n = n 1 x = 0 5 Hz . example-end EXAMPLE 28-B‐ Procedure 1 for determining the structural factor cscd ‐ test2 Given: Find the structural factor c s c d as defined in 6.3.1 (see EN 1991‐1‐4 Section 6) for a building with a central core plus peripheral columns and shear bracings. Assume that the structure has a parallelepiped shape and a total logarithmic decrement of dumping (as given in F.5) equal to = 5% . The width and the height of the structure are equal to b = 20 m and h = 60 m respectively. Assume a mean wind velocity (mean return period: N = 50 years, in terrain category “0”) equal to v m z s = 37 4 m s for z s = 0 6h . [Reference sheet: Annex B]‐[Cell‐Range: A77:N77‐A224:N224; A338:N338‐A360:N360]. Solution: We have: z s = 0 6h = 0 6 60 = 36 m with v m z s = 37 4 m s . For z s = 36 m z min = 1 m , we get (with n = n 1 x = 0 5 Hz ): z 36 0 38 L z = L t --------- = 300 --------- = 156 5 m . 200 200 n L zs 5 156 5- = 2 09 - . f L z s n = -------------------= 0--------------------------vm zs 37 4 n S v z s n 6 8 f L z s n 6 8 2 09 S L z s n = --------------------------- = -------------------------------------------------------- = ------------------------------------------------ = 0 08 . v2 1 + 10 2 f L z s n 5 / 3 1 + 10 2 2 09 5 / 3 Background factor: 1 1 - = 0 629 B = - = -------------------------------------------------------B 2 = --------------------------------------------------0 63 0 63 b + h 20 + 60 1 + 0 9 ------------1 + 0 9 ----------------- L zs 156 5 B 2 = 0 793 . Resonance response factor (variables): 4 6 h 4 6 60 h = ---------------- f L z s n 1 x = ------------------- 2 09 = 3 69 L zs 156 5 4 6 b 4 6 20 b = ---------------- f L z s n 1 x = ------------------- 2 09 = 1 23 . L zs 156 5 Aerodynamic admittance functions (for fundamental mode shape 1): 1 1 1 1 R h = ----- – ---------2 1 – exp – 2 h = ------------ – ----------------------2 1 – exp – 2 3 69 = 0 234 3 69 2 3 69 h 2 h 1 1 1 1 R b = ----- – ---------2 1 – exp – 2 b = ------------ – ----------------------2 1 – exp – 2 1 23 = 0 511 . b 2 b 1 23 2 1 23 Topic: User’s Manual/Verification tests - EN1991-1-4_(c).xls page 295 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 28 EN 1991-1-4 A NNEX B Resonance response factor allowing for turbulence in resonance with the considered vibration mode of the structure: 2 2 R 2 = ------ S L z s n 1 x R h h R b b = ------------------- 0 08 0 234 0 511 = 0 944 . 2 2 0 05 Up‐crossing frequency: R 2 - = 0 5 ----------------------------------0 944 - = 0 387 Hz 0 08 Hz . = n 1 x -----------------0 629 + 0 944 B2 + R2 Peak factor (with T = 600 s): T = 0 387 600 = 232 2 . kp = 0 6 2 ln T + ----------------------------= 2 ln T 0 6 2 ln 0 387 600 + -------------------------------------------------- = 3 48 3 . 2 ln 0 387 600 Figure 28.5 Peak factor with natural frequency equal to 0,5 Hz. From Section 6 ‐ EN 1991‐1‐4 assuming (say) I v z s = 0 10 , we get: 1 + 7 Iv zs B 2 1 + 7 0 10 0 793 c s = ---------------------------------------- = ------------------------------------------------ = 0 915 1 + 7 Iv zs 1 + 7 0 10 1 + 2k p I v z s B 2 + R 2 1 + 2 3 48 0 1 0 629 + 0 944 c d = ----------------------------------------------------------= ----------------------------------------------------------------------------------- = 1 204 1 + 7 0 1 0 793 1 + 7 Iv zs B 2 with: c s c d = 0 915 1 204 = 1 102 . From Eq. 6.1 (see Sec. 6.3.1) we find: page 296 Topic: User’s Manual/Verification tests - EN1991-1-4_(c).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 28 EN 1991-1-4 A NNEX B 1 + 2k p I v z s B 2 + R 2 1 + 2 3 48 0 1 0 629 + 0 944 c s c d = --------------------------------------------------------------- = --------------------------------------------------------------------------------------- = 1 102 . 1 + 7 0 1 1 + 7 Iv zs An alternative procedure to be used to determine k p is given in Annex C. example-end EXAMPLE 28-C‐ Number of loads for dynamic response ‐ test3 Given: Find the number of times N g that the value 0 85 S k of an effect of the wind is reached or exceeded during a period of 50 years, where S k is the effect of the wind due to a 50 years return period. [Reference sheet: Annex B]‐[Cell‐Range: A227:N227‐A266:N266]. Solution: From Eq. B.9, with S expressed as a percentage of the value S k , we find: S- = 0 7 log N 2 – 17 4 log N + 100 = 0 7 log 8 2 – 17 4 log 8 + 100 = 85% -----g g Sk for N g = 8 . example-end EXAMPLE 28-D‐ B.4 Service displacement and accelerations for serviceability assessments of a vertical structure ‐ test4 Given: Find the characteristic peak acceleration of the structural point at height z = h = 60 m where h is the height of the building (see same assumptions from previous examples). Assume a force coefficient (see Section 7.6 ‐ Eq. 7.9) equal to c f = 1 3 and an air density = 1 226 kg m 3 . The along wind fundamental equivalent mass (see Annex F, Sec. F.4(1)) 4 was calculated previously equal to m 1 x = 10 kg m . [Reference sheet: Annex B]‐[Cell‐Range: A270:N270‐A333:N333]. Solution: From Annex F, Sec. F.3 (“building with a central core plus peripheral columns or larger columns plus shear bracings”): we find an exponent of the modal shape = 1 . Therefore: 1 z 60 1 x = --- = ------ = 1 . h 60 Non‐dimensional coefficient (see Eq. B.11): z 2 + 1 + 1 ln ----s + 0 5 – 1 z0 K x ------------------------------------------------------------------------------------------------------z + 1 2 ln ----s z0 Topic: User’s Manual/Verification tests - EN1991-1-4_(c).xls page 297 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 28 EN 1991-1-4 A NNEX B 36 2 1 + 1 1 + 1 ln --------------- + 0 5 – 1 0 003 56 36 K x -------------------------------------------------------------------------------------------------------------------- = --------------- = 1 50 . 37 57 36 1 + 1 2 ln --------------- 0 003 Square root of resonant response (see calculations previous examples): R = R2 = 0 944 = 0 972 . Standard deviation a x z of the characteristic along‐wind acceleration of the structural point at height z = h = 60 m : 1 3 1 226 20 0 1 37 4 2 - 0 972 1 50 1 0 = 0 65 . a x z = --------------------------------------------------------------------------10 4 Using the natural frequency n 1 x as up‐crossing frequency, we get the new the peak factor: k p n = 0 6 2 ln n 1 x T + ----------------------------------- = 2 ln n 1 x T 0 6 2 ln 0 5 600 + -------------------------------------------- = 3 56 3 2 ln 0 5 600 The characteristic peak acceleration is obtained by multiplying the standard deviation in (B.10) by the peak factor in B.2(3) using the natural frequency n 1 x as upcrossing frequency : k p n a x z = 3 56 0 65 = 2 31 m s 2 . example-end 28.5 References [Section 28] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design April 2010. © 2010 The Institution of Structural Engineers. Eurocode Load Combinations for Steel Structures. The British Constructional Steelwork Association Limited. BCSA Publication No. 53/10. December 2010. page 298 Topic: User’s Manual/Verification tests - EN1991-1-4_(c).xls Section 29 EN 1991-1-4 Annex C 29.1 Procedure 2 for determining the structural factor cscd T he structural factor c s c d should take into account the effect on wind actions from the non simultaneous occurrence of peak wind pressures on the surface c s together with the effect of the vibrations of the structure due to turbulence c d . The detailed procedure for calculating the structural factor c s c d is given in Equation 6.1 (EN 1991-1-4 Section 6.3 “Detailed procedure”). The procedure to be used to determine k p , B and R may be given in the National Annex. A recommended procedure is given in Annex B. An alternative procedure is given in Annex C. As an indication to the users the differences in c s c d using Annex C compared to Annex B does not exceed approximately 5%. BACKGROUND FACTOR. It may be calculated using Expression: 1 B 2 = -------------------------------------------------------------------------------------------------------------------------2 2 2 h 3 b h b ------------- + ------------- + ------------- ------------- 1 + --- L zs L zs L zs 2 L zs (Eq. 29‐1) Figure 29.1 From Figure 6.1 - General shapes of structures covered by the design procedure. Topic: User’s Manual/Verification tests - EN1991-1-4_(d).xls page 299 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 29 EN 1991-1-4 A NNEX C where: • b h are the width and height of the structure respectively (see Figure 6.1) • L z s is the turbulent length scale given in B.1 (1) at reference height z s defined in Figure 6.1 The resonance response factor should be determined using Expression: 2 R 2 = ------ S L z s n 1 x K s n 1 x 2 (Eq. 29‐2) where: • is the total logarithmic decrement of damping given in Annex F • S L is the wind power spectral density function given in B.1(2) • n 1 x is the natural frequency of the structure, which may be determined using Annex F • K s is the size reduction function given in above: 1 K s n 1 x = ---------------------------------------------------------------------------------------------------------------------------2 2 1 + G y y 2 + G z z 2 + --- G y y G z z (Eq. 29‐3) with: c y b n 1 x c z h n 1 x y = ------------------------- , z = ------------------------vm zs vm zs where c y c z are the decay constants both equal to 11,5 and v m z s is the mean wind velocity at reference height z s (as defind in Figure 6.1). The constants G introduced in equation above depend on the mode shape variation along the horizontal y-axis and vertical z-axis respectively and should be chosen as follow: — for buildings with a uniform horizontal mode shape variation and linear vertical mode shape variation y z = z h with K y = 1 , K z = 3 2 : Gy = 1 2 , Gz = 3 8 — for chimneys with a uniform horizontal mode shape variation and parabolic vertical mode shape variation y z = z 2 h 2 with K y = 1 , K z = 5 3 : G y = 1 2 , G z = 5 18 — for bridges with a sinusoidal horizontal mode shape variation y z = sin y b with K y = 4 , K z = 1 : G y = 4 2 , G z = 1 2 . 29.2 Number of loads for dynamic response See Annex B, Section B.3. page 300 Topic: User’s Manual/Verification tests - EN1991-1-4_(d).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 29 EN 1991-1-4 A NNEX C 29.3 Service displacement and accelerations for serviceability assessments The maximum along-wind displacement is the static displacement determined from the equivalent static wind force defined in 5.3. The standard deviation a x of the characteristic along-wind acceleration of the structural point with coordinates (y,z) is approximately given by Expression: R K y K z y z a x = c f I v z s v m2 z s ----------------------------------------------- ref max (Eq. 29‐4) where: • c f is the force coefficient (see Section 7.6, Eq. 7.9) • is the air density (see Section 4.5) • z s is the reference height, see Figure 6.1 • I v z s is the turbulence intensity at height z s above ground, see 4.4(1) • v m z s is the characteristic mean wind velocity at height z s , see 4.3.1(1) • R is the square root of the resonant response, see C.2(4) • K y K z are the constants given in C.2(6) • ref is the reference mass per unit area (see Annex F, SectionF.5(3)) • y z is the mode shape • max is the mode shape at the point with maximum amplitude The characteristic peak accelerations are obtained by multiplying the standard deviation a x by the peak factor k p (see Annex B, Section in B.2(3)) using the natural frequency as upcrossing frequency, i.e. = n 1 x . 29.4 Verification tests EN1991‐1‐4_(D).XLS. 6.36 MB. Created: 11 April 2013. Last/Rel.-date: 11 April 2013. Sheets: — Splash — Annex C. EXAMPLE 29-A‐ Procedure 2 for determining the structural factor cscd ‐ test1 Given: Assume a multi spam (simply‐supported) bridge carrying two line of traffic. The construction consists of a reinforced concrete slab supported by steel girders with welded cover plate. The longest spam length is equal to b = 40 m and the bridge width is equal to d = 13 m (see Figure 6.1). The reference mass per unit area of the bridge is ref = 2500 kg m 2 according to Annex F, Sec. F.5(3). The height of the piles of the bridge is h 1 = 41 5 meters and the entire height of the bridge (as defined in Figure 6.1) is assumed to be h = 3 meters (deck, security barrier and the vehicles during bridge service Topic: User’s Manual/Verification tests - EN1991-1-4_(d).xls page 301 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 29 EN 1991-1-4 A NNEX C life with traffic). Assuming: c f = c fx 0 = 1 3 (force coefficient), z s = h 1 + 0 5h = 43 m (reference height, as defined in Figure 6.1), v m z s = 37 4 m s (mean wind velocity at height z s above ground), terrain category “0”, find: 1) the characteristic peak acceleration for a natural frequency n 1 x = 1 5 Hz of the bridge (1th mode shape) 2) the structural factor c s c d for the deck of the bridge. [Reference sheet: Annex B]‐[Cell‐Range: A77:N77‐A360:N360]. Solution: 1) Entering Table 4.1 (“Terrain categories and terrain parameters”): z 0 = 0 003 m , z min = 1 m . For z = z s = 43 m z min : 43 0 38 L z s = 300 --------- = 167 4 m , with 200 = 0 67 + 0 05 ln z 0 = 0 67 + 0 05 ln 0 003 = 0 380 . Non‐dimensional frequency: n 1 x L z s 1 5 167 4 f L z s n 1 x = -------------------------- = ---------------------------- = 6 71 - vm zs 37 4 Power spectral density function: n S v z s n 6 8 f L z s n 6 8 6 71 S L z s n = --------------------------- = -------------------------------------------------------- = ------------------------------------------------ = 0 039 0 04 . 1 + 10 2 6 71 5 / 3 v2 1 + 10 2 f L z s n 5 / 3 Background factor: 1 B 2 = -------------------------------------------------------------------------------------------------------------------------2 2 2 3--- -----------h b h b - 1+ + ------------- + ------------- ------------ L zs L zs L zs 2 L zs 1 B 2 = ---------------------------------------------------------------------------------------------------------------------------------- = 0 736 B = 2 2 2 3 3 40 40 3 1 + --- --------------- + --------------- + --------------- --------------- 167 4 167 4 167 4 2 167 4 B 2 = 0 858 . Size reduction factor (variables), with n 1 x = 1 5 Hz : c y b n 1 x c z h n 1 x 11 5 40 1 5 11 5 3 1 5 y = ------------------------- = ------------------------------------ = 18 45 , z = ------------------------= --------------------------------- = 1 38 . vm zs vm zs 37 4 37 4 Type of structure: bridge with a sinusoidal horizontal mode shape variation with y b = 0 5 y z = max = 1 . Therefore, from Table C.1: G y = 4 2 = 0 405 , G z = 0 5 , K y = 4 = 1 273 , K z = 1 . Size reduction function: 1 K s n 1 x = ----------------------------------------------------------------------------------------------------------------------------2 2 1 + G y y 2 + G z z 2 + --- G y y G z z 1 - = 0 109 . K s n 1 x = -----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------2 2 2 2 1 + 0 405 18 45 + 0 5 1 38 + --- 0 405 18 45 0 5 1 38 page 302 Topic: User’s Manual/Verification tests - EN1991-1-4_(d).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 29 EN 1991-1-4 A NNEX C Resonance response factor (with a total logarithmic decrement of dumping equal to 0,05): 2 2 R 2 = ------ S L z s n 1 x K s n 1 x = ------------------- 0 039 0 109 = 0 420 R = 2 2 0 05 R 2 = 0 648 . Up‐crossing frequency: 0 420 R2 - = 1 5 ------------------------------------ = 0 902 Hz 0 08 Hz . = n 1 x -----------------2 0 736 + 0 420 B + R2 Peak factor (with T = 600 s): T = 0 902 600 = 541 4 . kp = 0 6 2 ln T + ----------------------------= 2 ln T 0 6 2 ln 541 4 + ------------------------------------ = 3 72 3 . 2 ln 541 4 Standard deviation of the characteristic along‐wind acceleration of the structural point with coordinates (y; z) = (0,5b; 44,5 m): R K y K z y z , with (say) I v z s = 0 10 : a x = c f I v z s v m2 z s ----------------------------------------------- ref max 0 648 1 273 1 1 a x = 1 3 1 226 0 1 37 4 2 ------------------------------------------------- = 0 073 . 2500 1 Using the natural frequency n 1 x as up‐crossing frequency, we get the new the peak factor: k p n = 0 6 2 ln n 1 x T + ----------------------------------- = 2 ln n 1 x T 0 6 2 ln 1 5 600 + -------------------------------------------- = 3 85 3 . 2 ln 1 5 600 The characteristic peak acceleration is obtained by multiplying the standard deviation in (B.10) by the peak factor in B.2(3) using the natural frequency n 1 x as upcrossing frequency : k p n a x z = 3 85 0 073 = 0 28 m s 2 0 3 m s 2 . 2) From Section 6 ‐ EN 1991‐1‐4 assuming (say) I v z s = 0 10 , we get: 1 + 7 Iv zs B 2 1 + 7 0 10 0 858 c s = ---------------------------------------- = ------------------------------------------------ = 0 94 1 + 7 Iv zs 1 + 7 0 10 1 + 2k p I v z s B 2 + R 2 1 + 2 3 72 0 1 0 736 + 0 420 c d = ----------------------------------------------------------= ----------------------------------------------------------------------------------- = 1 12 2 1 + 7 0 1 0 858 1 + 7 Iv zs B with: c s c d = 0 94 1 12 = 1 05 . From Eq. 6.1 (see Sec. 6.3.1) we find: 1 + 2k p I v z s B 2 + R 2 1 + 2 3 72 0 1 0 736 + 0 420- = 1 06 . c s c d = --------------------------------------------------------------- = -------------------------------------------------------------------------------------1 + 7 Iv zs 1 + 7 0 1 An alternative procedure to be used to determine k p is given in Annex C. example-end Topic: User’s Manual/Verification tests - EN1991-1-4_(d).xls page 303 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 29 EN 1991-1-4 A NNEX C 29.5 References [Section 29] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design April 2010. © 2010 The Institution of Structural Engineers. Eurocode Load Combinations for Steel Structures. The British Constructional Steelwork Association Limited. BCSA Publication No. 53/10. December 2010. page 304 Topic: User’s Manual/Verification tests - EN1991-1-4_(d).xls Section 30 EN 1991-1-4 Annex E [from Sec. E.1 to Sec. E.1.5.2.5] 30.1 Vortex shedding V ortex-shedding occurs when vortices are shed alternately from opposite sides of the structure. This gives rise to a fluctuating load perpendicular to the wind direction. Structural vibrations may occur if the frequency of vortex.shedding is the same as a natural frequency of the structure. This condition occurs when the wind velocity is equal to the critical wind velocity defined in E.1.3.1. Typically, the critical wind velocity is a frequent wind velocity indicating that fatigue, and thereby the number of load cycles, may become relevant. The response induced by vortex shedding is composed of broad-banded response that occurs whether or not the structure is moving, and narrow-banded response originating from motion-induced wind load. CRITERIA FOR VORTEX SHEDDING. The effect of vortex shedding should be investigated when the ratio of the largest to the smallest crosswind dimension of the structure, both taken in the plane perpendicular to the wind, exceeds 6. The effect of vortex shedding need not be investigated when: v crit i 1 25 v m (Eq. 30‐1) where: • v crit i is the critical wind velocity for mode i, as defined in E.1.3.1 • v m is the characteristic 10 minutes mean wind velocity specified in 4.3.1(1) at the cross section where vortex shedding occurs. CRITICAL WIND VELOCITY VCRIT,I. The critical wind velocity for bending vibration mode i is defined as the wind velocity at which the frequency of vortex shedding equals the natural frequency (mode i) of the structure or the structural and is given in expression: b n i y v crit i = --------------St Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls (Eq. 30‐2) page 305 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 30 EN 1991-1-4 A NNEX E [ FROM S EC . E.1 TO S EC . E.1.5.2.5] where: • b is the reference width of the cross-section at which resonant vortex shedding occurs and where the modal deflection is maximum for the structure or structural part considered; for circular cylinders the reference width is the outer diameter • n i y is the natural frequency of the considered flexural mode i of cross-wind vibration; approximations for n1,y are given in F.2 • St is the Strouhal number as defined in E.1.3.2. The critical wind velocity for ovalling vibration mode i of cylindrical shells is defined as the wind velocity at which two times of the frequency of vortex shedding equals a natural frequency of the ovalling mode i of the cylindrical shell and is given in expression: b n i 0 v crit i = --------------2 St (Eq. 30‐3) where: • b is the outer shell diameter • St is the Strouhal number as defined in E.1.3.2 • n i 0 is the natural frequency of the ovalling mode i of the shell. STROUHAL NUMBER ST (SEC. E.1.3.2). The Strouhal number for different cross-section may be taken from table E.1. Figure 30.1 From Figure E.1 - Strouhal number (St) for rectangular cross-section with sharp corners. page 306 Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls S ECTION 30 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN EN 1991-1-4 A NNEX E [ FROM S EC . E.1 TO S EC . E.1.5.2.5] Cross-section St (for all Re numbers) 0,18 from Figure E.1 d/b = 1 0,11 d/b = 1,5 0,10 d/b = 2 10,14 d/b = 1 0,13 d/b = 2 0,08 d/b = 1 0,16 d/b = 2 0,12 d/b = 1,3 0,11 d/b = 2,0 0,07 NOTE: extrapolations for Strouhal numbers as function of d/b are not allowed Table 30.1 From Table E.1 - Strouhal numbers St for different cross-sections. Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls page 307 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 30 EN 1991-1-4 A NNEX E [ FROM S EC . E.1 TO S EC . E.1.5.2.5] SCRUTON NUMBER SC. The susceptibility of vibrations depends on the structural damping and the ratio of structural mass to fluid mass. This is expressed by the Scruton number Sc, which is given in Expression: 2 s m i e Sc = ------------------------ b2 (Eq. 30‐4) where: • s is the structural damping expressed by the logarithmic decrement • is the air density under vortex shedding conditions • m i e is the equivalent mass m e per unit length for mode i (see Annex F, Sec. F.4(1)) • b is the reference width of the cross-section at which resonant vortex shedding occurs. REYNOLDS NUMBER RE. The vortex shedding action on a circular cylinder depends on the Reynolds number Re at the critical wind velocity v crit i . The Reynolds number is given in expression: b v crit i Re v crit i = ------------------ (Eq. 30‐5) where: • b is the outer diameter of the circular cylinder • = 15 10 • v crit i is the critical wind velocity (see Sec. E.1.3.1). –6 m 2 s is the kinematic viscosity of the air 30.2 Vortex shedding action The effect of vibrations induced by vortex shedding should be calculated from the effect of the inertia force per unit length F w s , acting perpendicular to the wind direction at location s on the structure and given in expression: F w s = m s 2 n i y 2 i y s y F max (Eq. 30‐6) where: page 308 • m s is the vibrating mass of the structure per unit length kg m • n i y is the natural frequency of the structure • i y s is the mode shape of the structure normalised to 1 at the point with the maximum displacement • y F max is the maximum displacement over time of the point with i y s equal to 1 (see Sec. E.1.5). Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls S ECTION 30 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN EN 1991-1-4 A NNEX E [ FROM S EC . E.1 TO S EC . E.1.5.2.5] Figure 30.2 From Figure E.2 - Basic value of the lateral force clat,0 versus “Re” for circular cylinders. 30.3 Calculation of the cross wind amplitude Two different approaches for calculating the vortex excited cross-wind amplitudes are given in E.1.5.2 and E.1.5.3. The approach given in E.1.5.2 can be used for various kind of structures and mode shapes. It includes turbulence and roughness effects and it may be used for normal climatic conditions. The approach given in E.1.5.3 may be used to calculate the response for vibrations in the first mode of cantilevered structures with a regular distribution of cross wind dimensions along the main axis of the structure. Typically structures covered are chimneys or masts. It cannot be applied for grouped or in-line arrangements and for coupled cylinders. This approach allows for the consideration of different turbulence intensities, which may differ due to meteorological conditions. For regions where it is likely that it may become very cold and stratified flow conditions may occur (e.g. in coastal areas in Northern Europe), approach E.1.5.3 may be used.v 30.3.1 Approach 1 for the calculation of the cross wind amplitudes CALCULATION OF DISPLACEMENTS. The largest displacement y F max can be calculated using expression: y F max 1 1 = -------2 ------ K K w c lat -------------St Sc b Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls (Eq. 30‐7) page 309 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 30 EN 1991-1-4 A NNEX E [ FROM S EC . E.1 TO S EC . E.1.5.2.5] Cross-section clat,0 From Figure E.2 1,1 d/b = 1 0,8 d/b = 1,5 1,2 d/b = 2 0,3 d/b = 1 1,6 d/b = 2 2,3 d/b = 1 1,4 d/b = 2 1,1 d/b = 1,3 0,8 d/b = 2,0 1,0 NOTE: extrapolation for lateral force coefficients as function of d/b are not allowed. Table 30.2 page 310 From Table E.2 - Basic value of the lateral force coefficient clat,0 for different cross-sections. Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls S ECTION 30 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN EN 1991-1-4 A NNEX E [ FROM S EC . E.1 TO S EC . E.1.5.2.5] where: • St is the Strouhal number given in Table E.1 • Sc is the Scruton number given in E.1.3.3 • K w is the effective correlation length factor (see Sec. E.1.5.2.4) • K is the mode shape factor (see Sec. E.1.5.2.5) • c lat is the lateral force coefficient (see Table E.2). LATERAL FORCE COEFFICIENT CLAT. The basic value c lat 0 of the lateral coefficient is given in Table E.2 above. The lateral force coefficient c lat is given in Table E.3 below. Critical wind velocity ratio clat v crit i ------------ 0 83 v m Lj c lat = c lat 0 v crit i - 1 25 0 83 ----------v m Lj v crit i - c c lat = 3 – 2 4 ---------- v m Lj lat 0 v crit i 1 25 ----------v m Lj c lat = 0 where: c lat 0 is the basic value of c lat as given in Table E.2 and, for circular cylinders, in Figure E.2 v crit i is the critical wind velocity (see Sec. E.1.3.1) v m Lj is the mean wind velocity (see 4.3.1) in the centre of the effective correlation length as defined in Figure E.3”.). Table 30.3 From Table E.3 - Lateral force coefficient clat versus critical wind velocity ratio, vcrit,i/vm,Lj. 30.3.2 Correlation length L The correlation length L j , should be positioned in the range of antinodes. Examples are given in Figure E.3. For guyed masts and continuous multispan bridges special advice is necessary. If more than one correlation length is shown, it is safe to use them simultaneously, and the highest value of c lat should be used. Table 30.4 yF(sj)/b Lj/b < 0,1 6 0,1 to 0,6 4,8 + 12yF(sj)/b > 0,6 12 From Table E.4 - Effective correlation length Lj as a function of vibration amplitude yF(sj). Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls page 311 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 30 EN 1991-1-4 A NNEX E [ FROM S EC . E.1 TO S EC . E.1.5.2.5] Figure 30.3 From figure E.3 - Examples for application of the correlation length Lj (J = 1, 2, 3). 30.3.3 Effective correlation length factor Kw The effective correlation length factor K w is given in expression: n i y s ds j=1 L j K w = -------------------------------------- 0 6 m i y s (Eq. 30‐8) ds j = 1 Lj where: page 312 • i y is the mode shape (see Annex F, Sec. F.3) • L j is the correlation length • l j is the length of the structure between two nodes (see Figure E.3); for cantilevered structures it is equal to the height of the structure Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls S ECTION 30 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN EN 1991-1-4 A NNEX E [ FROM S EC . E.1 TO S EC . E.1.5.2.5] • n is the number of regions where vortex excitation occurs at the same time (see Figure E.3) • m is the number of antinodes of the vibrating structure in the considered mode shape i y • s is the coordinate defined in Table E.5. For some simple structures vibrating in the fundamental cross-wind mode and with the exciting force indicated in Table E.5 the effective correlation length factor K w can be approximated by the expressions given in Table E.5. Structure mode shape Kw i y s K See F.3 with = 2 0 , n = 1, m = 1 3L j b L j b 1 L j b2 --------------- 1 – ----------- + --- ----------- 3 0,13 See Table F.1 with n = 1, m = 1 Lj b cos --- 1 – ----------2 0,10 See Table F.1 with n = 1, m = 1 Lj b 1 Lj b ------------ + --- sin 1 – ---------- 0,11 Modal analysis n = 3, m = 3 n m i y s ds i y s ds j = 1 Lj j = 1 Lj 0,10 NOTE 1: The mode shape i y s is taken from F.3. The parameters n and m are defined in Expression (E.8) and in Figure E.3. NOTE 2: = l b . Table 30.5 From Table E.5 - Correlation factor Kw and mode shape factor K for some simple structures. Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls page 313 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 30 EN 1991-1-4 A NNEX E [ FROM S EC . E.1 TO S EC . E.1.5.2.5] 30.3.4 Mode shape factor The mode shape factor K is given in expression: m i y s ds j = 1 lj K = -----------------------------------------------m 4 (Eq. 30‐9) 2 i y s ds j = 1 lj where: • m is defined in Sec. E.1.5.2.4(1) • i y s is the cross-wind mode shape (see Annex F, Sec. F.3) • l j is the length of the structure between two nodes (see Figure E.3). For some simple structures vibrating in the fundamental cross-wind mode the mode shape factor is given in Table E.5. 30.4 Verification tests EN1991‐1‐4_(E).XLS. 6.64 MB. Created: 15 April 2013. Last/Rel.-date: 15 April 2013. Sheets: — Splash — Annex E_(a). EXAMPLE 30-A‐ Basic parameters for vortex shedding: Strouhal number ‐ test1 Given: Find the Strouhal number for: – a rectangular cross‐section with d b = 10 3 – a “H” cross‐section with d b = 5 4 . Use data given in Table E.1 and apply the linear interpolation. [Reference sheet: Annex E_(a)]‐[Cell‐Range: A1:N1‐A111:N111]. Solution: Rectangular cross‐section with d b 3 33 . From Figure E.1, linear interpolation between the two points A(3; 0,06) and B(3,5; 0,15): St – 0 06- ---------------------St – 0 060---------------------------- 15 – 0 06- = --------------------- db–3 3 33 – 3 3 5 – 3 St = 0 120 , see plot below. “H” cross‐section with d b = 1 25 . page 314 Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls S ECTION 30 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN EN 1991-1-4 A NNEX E [ FROM S EC . E.1 TO S EC . E.1.5.2.5] Figure 30.4 From Figure E.1 - Strouhal number (St) for rectangular cross-sections with sharp corners. Linear interpolation between the two points A(1; 0,11) and B(0,10; 1,5): St – 0 10 St – 0 10 0---------------------------- 11 – 0 10- = ------------------------ --------------------------1 5 – d b 1 5 – 1 25 1 5 – 1 St = 0 105 . Extrapolation for Strouhal numbers as function of d b are not allowed. example-end EXAMPLE 30-B‐ Criteria for vortex shedding: critical wind velocity ‐ test2 Given: Find the critical wind velocity for bending vibration mode i (and the critical wind velocity for ovalling vibration mode i of cylindrical shells) for St = 0 18 - . Assume a natural frequency of the considered flexural mode i (of the ovalling mode i of the shell) equal to 1,5 Hz. The reference width of the cross‐section (the outer shell diameter) is 0 6 m . [Reference sheet: Annex E_(a)]‐[Cell‐Range: A131:N131‐A164:N164]. Solution: The critical wind velocity for bending vibration mode i is defined as the wind velocity at which the frequency of vortex shedding equals the natural frequency (mode i) of the structure or the structural: b n i y 0 6 1 5 = ---------------------- = 5 00 m s . v crit i = --------------St 0 18 Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls page 315 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 30 EN 1991-1-4 A NNEX E [ FROM S EC . E.1 TO S EC . E.1.5.2.5] The critical wind velocity for ovalling vibration mode i of cylindrical shells is defined as the wind velocity at which two times of the frequency of vortex shedding equals a natural frequency of the ovalling mode i of the cylindrical shell: b n i 0 6 1 5- = 2 50 m s v crit i = --------------= 0--------------------2 St 2 0 18 where b is the outer shell diameter and n i 0 is the natural frequency of the ovalling mode i of the shell. example-end EXAMPLE 30-C‐ Basic parameters for vortex shedding: Scruton number ‐ test3 Given: Find the Scruton number and the Reynolds number at the critical wind velocity v crit i for a structural element with an equivalent mass per unit length (mode i) equal to m i e = 3000 kg m and a structural damping s = 5% (expressed by the logarithmic decrement). Assume a reference width of the cross‐section at which resonant vortex shedding occurs equal to b = 0 6 m . [Reference sheet: Annex E_(a)]‐[Cell‐Range: A169:N169‐A209:N209]. Solution: With an air density under vortex shedding conditions equal to = 1 226 kg m 3 , we have: 2 s m i e 2 0 05 3000 - = -----------------------------------2- = 679 72 - . Sc = ------------------------1 226 0 6 b2 Critical velocity (see Sec. E.1.3.1), (see previous example) v crit i = 5 00 m s : b v crit i 6 0 6 5 00 - = -----------------------Re v crit i = ------------------- = 0 2 10 = 200000 - – 6 15 10 with = 15 10 –6 m 2 s (kinematic viscosity of the air). example-end EXAMPLE 30-D‐ Vortex shedding action: effect of vibrations ‐ test4 Given: A structural element of vibrating mass per unit length m s = 1500 kg m has a natural frequency (mode shape i) n i y = 0 5 Hz . The mode shape of the structure (normalised to 1) at the point “s” with the maximum displacement is equal to y F max = 50 mm . Find the inertia force F w s per unit length acting perpendicular to the wind direction at location “s” on the structural element. [Reference sheet: Annex E_(a)]‐[Cell‐Range: A169:N169‐A209:N209]. page 316 Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls S ECTION 30 Solution: E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN EN 1991-1-4 A NNEX E [ FROM S EC . E.1 TO S EC . E.1.5.2.5] Mode shape of the structure normalised to 1 at the point “s” with the maximum displacement (say): i y s = 1 00 . From Eq. (E.6): F w s = m s 2 n i y 2 i y s y F max = 1500 2 0 5 2 1 00 0 05 = 740 N m . example-end EXAMPLE 30-E‐ Calculation of the cross wind amplitude: Approach 1 ‐ test5 Given: Find the largest displacement y F max of the cross wind amplitudes for: St = 0 18 - , Sc = 679 - . Assume an effective correlation length factor (given in E.1.5.2.4) equal to K w = 0 6 - and a Reynolds number Re v crit i = 7000000 - for a circular cross‐section with b = 60 cm . The mode shape factor (given in E.1.5.2.5) is K = 0 13 - . [Reference sheet: Annex E_(a)]‐[Cell‐Range: A235:N235‐A256:N256]. Solution: 6 From Table E.2 and Figure E.2, for circular cross‐section and Re = 7 10 - , we have: c lat 0 – 0 2 0 3 – 0 2 = ---------------------------------------------------------------------------------------------------------------------6 6 6 log Re – log 5 10 log 10 10 – log 5 10 c lat 0 = 0 249 - . Figure 30.5 From Figure E.2 - Basic value of the lateral force coefficient clat,0 versus Reynolds number Re(vcrit,i) for circular cylinders, see E.1.3.4. Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls page 317 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 30 EN 1991-1-4 A NNEX E [ FROM S EC . E.1 TO S EC . E.1.5.2.5] Assuming (say) v crit i v m Lj = 1 0 , from Table E.3 with 0 83 v crit i v m Lj 1 25 , we find: v crit i - c lat 0 = 3 – 2 4 1 0 0 249 = 0 149 - . c lat = 3 – 2 4 ----------v m Lj From Expression (E.7), using the given numerical data, we get: y F max 1 1 1 1 -------------- = -------2 ------ K K w c lat = -------------------2 --------- 0 13 0 6 0 149 = 0 000528 . Sc 679 0 18 St b Therefore: y F max = b 0 000528 = 0 60 0 00051 = 0 00032 m 0 3 mm . example-end EXAMPLE 30-F‐ Calculation of the cross wind amplitude: correlation length ‐ test6 Given: Find the effective correlation length L j = 1 for a vibration amplitude (j = 1) equal to y F s 1 = 5 cm . Assume a width of the structure (length of the surface perpendicular to the wind direction) equal to b = 1 20 m (and then equal to b = 0 40 m ) [Reference sheet: Annex E_(a)]‐[Cell‐Range: A404:N404‐A459:N459]. Solution: We have: y F s 1 b = 0 05 1 2 = 0 0417 . From Table E.4, for y F s 1 b 1 0 , we get: L 1 b = 6 0 . For y F s 1 b = 0 05 0 4 = 0 125 , from Table E.4 for 0 1 y F s 1 b 0 6 , we get: L 1 b = 4 8 + 12 y F s 1 b = 4 8 + 12 0 125 = 6 30 L 1 = b 6 30 = 2 52 m . example-end EXAMPLE 30-G‐ Calculation of the cross wind amplitude: correlation length factor ‐ test7 Given: Find the correlation length factors with n = 1 and m = 1 for the three simple structures in Table E.5. Assume L j b = 6 00 - for b = 1 20 m and L j b = 6 30 - for b = 0 40 m (see previous example). Length of the structure between two nodes (for cantilevered structures it is equal to the height of the structure): l = 20 m . Assume b = 0 4 m for the vertical cantilever beam and b = 1 20 m for the horizontal beams. [Reference sheet: Annex E_(a)]‐[Cell‐Range: A465:N465‐A510:N510]. Solution: Case a) Cantilever, with = l b = 20 0 4 = 50 0 - and L j b = 6 30 : 3L j b L j b 1 L j b2 - + --- -----------K w = --------------- 1 – ---------- 3 3 6 30 6 30 1 6 30 2 = ------------------- 1 – ------------ + --- ------------ 50 3 50 50 = 0 332 . Case b) Simply supported beam spanning l = 20 m , with page 318 Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN EN 1991-1-4 A NNEX E [ FROM S EC . E.1 TO S EC . E.1.5.2.5] S ECTION 30 = l b = 20 1 20 = 16 67 - and L j b = 6 00 : Lj b K w = cos --- 1 – ---------- 2 6 00- = cos --- 1 – -------------2 16 67 = 0 536 0 6 . Case c) Horizontal beam held rigidly at each end spanning l = 20 m , with = l b = 20 1 20 = 16 67 - and L j b = 6 00 : Lj b 1 Lj b - + --- sin 1 – ----------K w = ---------- 6 00 1 6 00 = --------------- + --- sin 1 – --------------- 16 67 16 67 = 0 648 0 6 . Actual value to be used in calculations (see Expression (E.8)): K w = 0 6 - . example-end 30.5 References [Section 30] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design April 2010. © 2010 The Institution of Structural Engineers. Eurocode Load Combinations for Steel Structures. The British Constructional Steelwork Association Limited. BCSA Publication No. 53/10. December 2010. Topic: User’s Manual/Verification tests - EN1991-1-4_(e).xls page 319 (This page intentionally left blank) Section 31 EN 1991-1-4 Annex E [from Sec. E.1.5.2.6 to Sec. E.4.3] 31.1 Calculation of the cross wind amplitude: number of load cycles T he number of load cycles N caused by vortex excited oscillation is given by expression: v crit 2 v crit 2 - exp – -------N = 2T n y 0 ------- v0 v0 (Eq. 31‐1) where: • n y is the natural frequency of cross-wind mode Hz . Approximations for n y are given in Annex F • v crit is the critical wind velocity m s given in E.1.3.1 • v 0 is the 20% of the characteristic mean wind velocity as specified in Sec. 4.3.1(1)(1) • T is the life time in seconds, which is equal to 3 2 10 multiplied by the expected lifetime in years • 0 is the bandwidth factor describing the band of the wind velocities with vortex-induced vibrations.(2) 7 31.2 Vortex resonance of vertical cylinders in a row or grouped arrangement For circular cylinders in a row or grouped arrangement with or without coupling (see Figure E.4) vortex excited vibrations may occur. The maximum deflections of oscillation can be estimated by Expression (E.7) and the calculation procedure (1) v 0 is 2 times the modal value of the Weibull probability distribution assumed for the wind velocity [m/s]. (2) The bandwidth factor 0 is in the range 0 1 0 3 . It may be taken as 0 = 0 3 . Topic: User’s Manual/Verification tests - EN1991-1-4_(f).xls page 321 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 31 EN 1991-1-4 A NNEX E [ FROM S EC . E.1.5.2.6 TO S EC . E.4.3] Figure 31.1 From Figure E.4 - In-line and grouped arrangements of cylinders. given in E.1.5.2 with the modifications given by the following expressions. For in-line, free standing circular cylinders without coupling: a c lat = 1 5 c lat sin gle for 1 --- 10 b a c lat = c lat sin gle for --- 15 b a linear interpolation for 10 --- 15 b (Eq. 31‐2) a a St = 0 1 + 0 085 log --- for 1 --- 9 b b a St = 0 18 for --- 9 . b where: c lat sin gle = c lat as given in Table E.3. For coupled cylinders: a c lat = K iv c lat sin gle for 1 0 --- 3 0 b (Eq. 31‐3) where: • K iv is the interference factor for vortex shedding (Table E.8) • St is the Strouhal number (given in Table E.8) • Sc is the Scruton number (given in Table E.8). For coupled cylinders with a b 3 0 specialist advice is recommended. page 322 Topic: User’s Manual/Verification tests - EN1991-1-4_(f).xls S ECTION 31 Coupled cylinders E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN EN 1991-1-4 A NNEX E [ FROM S EC . E.1.5.2.6 TO S EC . E.4.3] Scruton number Sc (see Eq. E.4) a/b = 1 a/b > 2 a/b < 1,5 a/b > 2,5 Kiv = 1,5 Kiv = 1,5 aG = 1,5 aG = 3,0 Kiv = 4,8 Kiv = 3,0 aG = 6,0 aG = 3,0 Kiv = 4,8 Kiv = 3,0 aG = 1,0 aG = 2,0 Linear interpolation Reciprocal Strouhal numbers of coupled cylinders with in-line and grouped arrangements. NOTE: extrapolation for the factor a G as function of d b are not allowed. Table 31.1 From Table E.8 - Data for estimation of cross-wind response of coupled cylinders at in-line and grouped arrangements. Topic: User’s Manual/Verification tests - EN1991-1-4_(f).xls page 323 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 31 EN 1991-1-4 A NNEX E [ FROM S EC . E.1.5.2.6 TO S EC . E.4.3] 31.3 Approach 2, for the calculation of the cross wind amplitudes The characteristic maximum displacement at the point with the largest movement is given in expression: y max = y k p (Eq. 31‐4) where: • y is the standard deviation of the displacement • k p is the peak factor (see Eq. 31-8 below). The solution of the Eq. 31-4 is given by the following expression: -----y = c 1 + c 12 + c 2 b 2 (Eq. 31‐5) where the constants c 1 and c 2 are given by: a2 Sc - c 1 = ----L- 1 – ---------------2 4 K a (Eq. 31‐6) 2 b2 a C 2 b c 2 = ------------- -----L- ------c4- --m e K a St h (Eq. 31‐7) where: • C c is the aerodynamic constant dependent on the cross-sectional shape, and for a circular cylinder also dependent on the Reynolds number Re as defined in E.1.3.4(1), given in Table E.6. • K a is the aerodynamic damping parameter as given in E.1.5.3(4) • a L is the normalised limiting amplitude giving the deflection of structures with very low damping, given in Table E.6 • St is the Strouhal number given in Table E.1 • is the air density under vortex shedding conditions • m e is the effective mass per unit length, given in F.4(1) • h b are the height and width of structure respectively. For structures with varying width, the width at the point with largest displacements is used. The aerodynamic damping constant K a decreases with increasing turbulence intensity. For a turbulence intensity of 0%, the aerodynamic damping constant may be taken as K a = K a max , which is given in Table E.6. For a circular cylinder and square cross-section the constants C c , K a max and a L are given in Table E.6. The peak factor k p should be determined by the following expression: kp = page 324 Sc 4 2 1 + 1 2 arc tan 0 75 ----------------- 4 K a (Eq. 31‐8) Topic: User’s Manual/Verification tests - EN1991-1-4_(f).xls S ECTION 31 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN EN 1991-1-4 A NNEX E [ FROM S EC . E.1.5.2.6 TO S EC . E.4.3] Constants(a) Circular cylinder Re < 105 Circular cylinder Re = 5 x 105 Circular cylinder Re > 106 Square cross-section Cc 0,02 0,005 0,01 0,04 K a max 2 0,5 1 6 aL 0,4 0,4 0,4 0,4 Table 31.2 From Table E.6 - Constants for determination of the effect of vortex shedding. (a). For circular cylinders the constants Cs and Ka,max are assumed to vary linearly with the logarithm of the Reynolds number for 105 < Re < 5 x 105 and for 5 x 105 < Re < 106, respectively. The number of load cycles may be obtained from E.1.5.2.6 using a bandwidth factor of 0 = 0 15 . 31.4 Galloping 31.4.1 Onset wind velocity Galloping is a self-induced vibration of a flexible structure in cross wind bending mode. Non circular cross sections including L-, I-, U- and T-sections are prone to galloping. Ice may cause a stable cross section to become unstable. Galloping oscillation starts at a special onset wind velocity v CG and normally the amplitudes increase rapidly with increasing wind velocity. The onset wind velocity of galloping, v CG , is given in expression: 2Sc v CG = --------- n 1 y b aG (Eq. 31‐9) where: • Sc is the Scruton number as defined in E.1.3.3(1) • n 1 y is the cross-wind fundamental frequency of the structure(3) • b is the width of the structural element/structure as defined in Table E.7 below • a G is the factor of galloping instability (see Table E.7); if no factor of galloping instability is known, a G = 10 may be used. It should be ensured that: v CG 1 25 v m z (Eq. 31‐10) where v m z is the mean wind velocity as defined in Expression (4.3)(4) and calculated at the height z , where galloping process is expected, likely to be the (3) Approximations of n 1 y are given in Annex F, Sec. F.2. Topic: User’s Manual/Verification tests - EN1991-1-4_(f).xls page 325 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 31 EN 1991-1-4 A NNEX E [ FROM S EC . E.1.5.2.6 TO S EC . E.4.3] Factor of galloping instability aG Cross-section Factor of galloping instability aG Cross-section 1,0 1,0 4 d/b = 2 2 d/b = 2 0,7 d/b = 1,5 1,7 d/b = 2,7 5 d/b = 1 1,2 d/b = 5 7 d/b = 2/3 1 d/b = 3 7,5 d/b = 1/2 0,7 d/b = 3/4 3,2 d/b = 1/3 0,4 d/b = 2 1 NOTE: extrapolation for the factor a G as function of d b are not allowed. Table 31.3 From Table E.7 - Factor of galloping instability aG. (4) See Section 4.3.1. page 326 Topic: User’s Manual/Verification tests - EN1991-1-4_(f).xls S ECTION 31 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN EN 1991-1-4 A NNEX E [ FROM S EC . E.1.5.2.6 TO S EC . E.4.3] point of maximum amplitude of oscillation. If the critical vortex shedding velocity v crit is close to the onset wind velocity of galloping v CG : v CG - 1 5 0 7 -------v crit (Eq. 31‐11) interaction effects between vortex shedding and galloping are likely to occur. In this case specialist advice is recommended. 31.4.2 Classical galloping of coupled cylinders For coupled cylinders (see Figure 31.1) classical galloping may occur. The onset velocity for classical galloping of coupled cylinders, v CG , may be estimated by expression: 2Sc v CG = --------- n 1 y b aG (Eq. 31‐12) where Sc , a G and b are given in Table E.8 and n 1 y is the natural frequency of the bending mode (see Annex F, Sec. F.2). It should be ensured that: v CG 1 25 v m z (Eq. 31‐13) where v m z is the mean wind velocity as defined in Expression (4.3), calculated at the height z , where the galloping excitation is expected, that is likely to be the point of maximum amplitude of oscillation. 31.4.3 Interference galloping of two or more free standing cylinders Interference galloping is a self-excited oscillation which may occur if two or more cylinders are arranged close together without being connected with each other. If the angle of wind attack is in the range of the critical wind direction k and if a b 3 (see Figure E.5), the critical wind velocity, v CIG , may be estimated by: v CIG = 3 5 n 1 y b --a- Sc b ------------a IG (Eq. 31‐14) where: • Sc is the Scruton number as defined in Sec. E.1.3.3(1) • a IG = 3 0 is the combine stability parameter • n 1 y is the fundamental frequency of cross-wind mode.(5) • a is the spacing • b is the diameter. (5) Approximations are given in Annex F, Sec. F.2. Topic: User’s Manual/Verification tests - EN1991-1-4_(f).xls page 327 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 31 EN 1991-1-4 A NNEX E [ FROM S EC . E.1.5.2.6 TO S EC . E.4.3] Figure 31.2 From Figure E.5 - Geometric parameters for interference galloping. Interference galloping can be avoided by coupling the free-standing cylinders. In that case classical galloping may occur (see E.2.3). 31.5 Divergence and Flutter 31.5.1 Criteria for plate-like structures Divergence and flutter are instabilities that occur for flexible plate-like structures, such as signboards or suspension-bridge decks, above a certain threshold or critical wind velocity. The instability is caused by the deflection of the structure modifying the aerodynamics to alter the loading. Divergence and flutter should be avoided. To be prone to either divergence or flutter, the structure satisfies all of the three criteria given below: 1. the structure, or a substantial part of it, has an elongated cross-section (like a flat plate) with b d less than 0,25 (see Figure E.6) 2. the torsional axis is parallel to the plane of the plate and normal to the wind direction, and the centre of torsion is at least d 4 downwind of the windward edge of the plate, where d is the inwind depth of the plate measured normal to the torsional axis. This includes the common cases of torsional centre at geometrical centre, i.e. centrally supported signboard or canopy, and torsional centre at downwind edge, i.e. cantilevered canopy 3. the lowest natural frequency corresponds to a torsional mode, or else the lowest torsional natural frequency is less than 2 times the lowest translational natural frequency. The criteria should be checked in the order given (easiest first) and if any one of the criteria is not met, the structure will not be prone to either divergence or flutter. page 328 Topic: User’s Manual/Verification tests - EN1991-1-4_(f).xls S ECTION 31 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN EN 1991-1-4 A NNEX E [ FROM S EC . E.1.5.2.6 TO S EC . E.4.3] Figure 31.3 From Figure E.6 - Rate of change of aerodynamic moment coefficient, dc M d , with respect to geometric centre “GC” for rectangular section”. 31.5.2 Divergency velocity The critical wind velocity for divergence is given in expression: 1 v div --22k = --------------------------- dc d 2 --------M- d (Eq. 31‐15) where: • k is the torsional stiffness Nm rad • c M is the aerodynamic moment coefficient (see Eq. E.25) • dc M d is the rate of change of aerodynamic moment coefficient with respect to rotation about the torsional centre, is expressed in radians • is the density of the air (see Sec. 4.5) • d is the in wind depth (chord) of the structure (see Figure E.6) • b is the width as defined in Figure E.6. Values of dc M d measured about the geometric centre of various rectangular sections are given in Figure E.6. Topic: User’s Manual/Verification tests - EN1991-1-4_(f).xls page 329 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 31 EN 1991-1-4 A NNEX E [ FROM S EC . E.1.5.2.6 TO S EC . E.4.3] It should be ensured that: v div 2 v m z s (Eq. 31‐16) where v m z s is the mean wind velocity as defined in Eq. (4.3) at height z s (defined in Figure 6.1). 31.6 Verification tests EN1991‐1‐4_(F).XLS. 6.73 MB. Created: 16 April 2013. Last/Rel.-date: 16 April 2013. Sheets: — Splash — Annex E_(b). EXAMPLE 31-A‐ Calculation of the cross wind amplitude: number of load cycles ‐ test1 Given: Find the number of load cycles N caused by vortex excited oscillation for: – a natural frequency of cross-wind mode n y = 4 50 Hz – a critical wind velocity v crit = 5 5 m s – a life time of the structure equal to t = 50 years and – a bandwidth factor 0 = 0 3 . Assume v 0 = 0 20 v m = 5 m s where v m = 25 m s is the characteristic mean wind velocity as specified in 4.3.1(1). [Reference sheet: Annex E_(b)]‐[Cell‐Range: A1:N1‐A25:N25]. Solution: From Eq. (E.10), substituting the given numerical data, we have: v crit 2 v crit 2 7 9 - exp – -------N = 2T n y 0 -------. With T = 3 2 10 50 = 1 6 10 s , we get: v0 v0 5 5 2 5 5 2 9 9 N = 2 1 6 10 4 50 0 3 --------- exp – --------- = 1 5587 10 1 6 billion . 5 0 5 0 It means a load cycles per second equal to: 9 1 5587 10N ---- = --------------------------- 1. 9 T 1 6 10 NOTE The National Annex may specify the minimum value of N . The recommended value is N 10 4 . example-end page 330 Topic: User’s Manual/Verification tests - EN1991-1-4_(f).xls S ECTION 31 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN EN 1991-1-4 A NNEX E [ FROM S EC . E.1.5.2.6 TO S EC . E.4.3] EXAMPLE 31-B‐ Vortex resonance of vertical cylinders in a row or grouped arrangement ‐ test2 Given: Estimate the maximum deflection of oscillation of a (Case a) free standing and (Case b) in‐line/grouped arrangements of cylinders (see Figure E.4) with a b = 1 70 and b = 0 50 m . For c lat sin gle = 0 20 - , assume Sc = 120 - for in‐line, free standing circular cylinders without coupling and Sc = 400 - for “coupled”. The effective correlation length factor K w (given in E.1.5.2.4) is equal to 0,60 and 0,80 respectively for “in‐line” and “coupled”. Similarly, the mode shape factor K is equal (say) to 0,13 and 0,15 respectively. [Reference sheet: Annex E_(b)]‐[Cell‐Range: A29:N29‐A169:N169]. Solution: Case a) In‐line, free standing circular cylinders without coupling: for 1 a b 10 : c lat = 1 5 c lat sin gle = 1 5 0 20 = 0 30 - . for 1 a b 9 : St = 0 1 + 0 085 log a b = 0 1 + 0 085 log 1 70 = 0 120 . Case b) For coupled cylinders (with i = 2‐3‐4): for 1 a b 3 : c lat = K iv c lat sin gle = 3 54 0 20 = 0 71 - , having considered for K iv the linear interpolation between (say) the point A(1; 4,8) and B(2; 3,0) in Table E.8: K iv – 3 0 K iv – 3 0 4 8 – 3 0 4---------------------- 8 – 3 0- = --------------------------------------------- = ---------------------K iv = 3 54 - . 2–ab 1 – 1 70 2–1 2–1 Entering Table E.8 for a b = 1 70 we obtain 1 St = 6 St 0 170 - . Case a): From Eq. (E.7): y F max 1 1 - 0 13 0 60 0 30 0 0135 K K w c lat = ---------------------------------------------------- = ---------------- 0 120 2 120 St 2 Sc b Therefore: y F max = 0 0135 b = 0 0135 0 50 = 0 00677 = 6 7 mm . Case b): y F max 1 1 - 0 15 0 80 0 71 0 0073 K K w c lat = ---------------------------------------------------- = ---------------- 0 170 2 400 St 2 Sc b Therefore: y F max = 0 0135 b = 0 0073 0 50 = 0 0037 = 3 4 mm . example-end EXAMPLE 31-C‐ Approach 2, for the calculation of the cross wind amplitudes‐ test3 Given: Estimate the characteristic maximum displacement at the point with the largest movement of a structure with a circular cylinder shape. Assume: – height of the structure: h = 6 0 m – width of the structure (at the point with largest displacements): b = 0 8 m – air density under vortex shedding conditions: = 1 25 kg m 3 – effective mass per unit length (given in F.4 (1)): m e = 1000 kg m Topic: User’s Manual/Verification tests - EN1991-1-4_(f).xls page 331 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 31 EN 1991-1-4 A NNEX E [ FROM S EC . E.1.5.2.6 TO S EC . E.4.3] – Strouhal number (given in Table E.1): St = 0 180 - – Scruton number (given in E.1.3.3): Sc = 125 - 5 – Reynolds number (at the point with largest displacements): Re = 2 5 10 - . [Reference sheet: Annex E_(b)]‐[Cell‐Range: A172:N172‐A255:N255]. Solution: 5 Entering Table E.6 with Re = 2 5 10 - , for circular cylinders assuming C c and K a max 5 to vary linearly with the logarithm of the Reynolds number for 10 5 Re 5 10 , we get: 5 log 5 10 – log Re - 0 02 – 0 005 = 0 0115 C c = 0 005 + ----------------------------------------------------------5 log 5 10 – log 10 5 5 log 5 10 – log Re - K a = K a max = 0 5 + ---------------------------------------------------------- 2 – 0 5 = 1 1460 . 5 log 5 10 – log 10 5 Therefore, with a L = 0 4 , we have: a2 0 4 2 Sc 125 c 1 = ----L- 1 – ----------------- = ---------------- 1 – ----------------------------- = – 0 614 2 2 4 K a 4 1 1460 2 b2 a C 2 b 1 25 0 8 2 0 4 2 0 0115 2 0 8 - ------------- 1 9 10– 6 . c 2 = ------------- -----L- ------c-4 --- = -------------------------------- ---------------------- ----------------------- 1 1460 0 180 2 6 0 m e K a St h 1000 From the expression: -----y = c 1 + c 12 + c 2 = – 0 614 + – 0 614 2 + 1 9 10– 6 1 55 10– 6 b 2 we find the standard deviation of the displacement: y b = –6 1 55 10 0 00124 y = 0 00124 0 8 = 0 0099 . The peak factor is given by the expression: kp = Sc 4 2 1 + 1 2 arc tan 0 75 ----------------- = 4 K a 4 125 2 1 + 1 2 arc tan 0 75 ----------------------------- 4 1 1460 k p = 4 08 . The characteristic maximum displacement at the point with the largest movement is given in expression: y max = y k p = 0 00099 4 08 = 0 0040 m = 4 mm . example-end EXAMPLE 31-D‐ Galloping: Onset wind velocity ‐ test4 Given: Find the onset wind velocity of galloping for a rectangular cross‐section with b = 0 30 m , d = 0 60 m and for: – a Scruton number as defined in E.1.3.3(1): Sc = 125 - – a cross‐wind fundamental frequency of the structure: n 1 y = 0 5 Hz (see Sec. F.2) – a width of the structure (as defined in Table E.7): b = 0 30 m page 332 Topic: User’s Manual/Verification tests - EN1991-1-4_(f).xls S ECTION 31 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN EN 1991-1-4 A NNEX E [ FROM S EC . E.1.5.2.6 TO S EC . E.4.3] – a critical wind velocity (given in E.1.3.1): v crit = 5 50 m s . [Reference sheet: Annex E_(b)]‐[Cell‐Range: A302:N302‐A399:N399]. Solution: Entering Table E.7 for rectangular cross‐section with d b = 2 0 we find a factor of galloping instability equal to a G = 2 0 - . From Expression (E.18): 2Sc 2 125 v CG = --------- n 1 y b = ---------------- 0 5 0 30 = 18 75 m s . aG 2 0 Assuming (say) a mean wind velocity at the height “z” (where galloping process is expected) equal to v m z = 20 00 m s , we get: v CG 75- = 3 41 [Satisfactory]. -------- = 18 -------------v crit 5 50 If the critical vortex shedding velocity v crit is close to the onset wind velocity of galloping v CG : 0 7 v CG v crit 1 5 specialist advice is recommended. It should be ensured that: v CG 1 25 v m z . Substituting the given numerical data: v CG 1 25 v m z v CG = 18 75 m s 1 25 20 00 = 25 00 m s [Unsatisfactory]. example-end EXAMPLE 31-E‐ Interference galloping of two or more free standing cylinders ‐ test5 Given: A structural element is constructed by arranging close together two cylinders without being connected with each other (spacing a = 0 80 m and diameter b = 0 40 m , see Figure E.5). Assuming that the angle of wind attack is in the range of the critical wind direction k 10 , estimate the critical wind velocity for Sc = 125 - and a IG = 3 0 - . The fundamental frequency of cross‐wind mode is equal to n 1 y = 0 5 Hz . [Reference sheet: Annex E_(b)]‐[Cell‐Range: A486:N486‐A514:N514]. Solution: From Expression (E.23) with a b = 2 00 3 : v CIG = 3 5 n 1 y b -----------------------a b Sc= 3 5 0 5 0 40 a IG 2 0 125--------------------= 6 39 m s . 3 0 Interference galloping can be avoided by coupling the free‐standing cylinders. In that case classical galloping may occur (see E.2.3). example-end EXAMPLE 31-F‐ Divergence and Flutter: critical wind velocity for divergence ‐ test6 Given: A structural element with a rectangular cross‐section d = 0 80 m , b = 0 15 m has a torsional stiffness equal to k = 1000 Nm rad . Find the critical wind velocity for Topic: User’s Manual/Verification tests - EN1991-1-4_(f).xls page 333 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 31 EN 1991-1-4 A NNEX E [ FROM S EC . E.1.5.2.6 TO S EC . E.4.3] divergence for a density of air = 1 25 kg m 3 and for a mean wind velocity (as defined in Expression 4.3) at height z s (defined in Figure 6.1) equal to 20 00 m s . [Reference sheet: Annex E_(b)]‐[Cell‐Range: A555:N555‐A628:N628]. Solution: From Figure E.6 with b d = 0 1875 : dc M b b 2 2 --------- = – 6 3 --- – 0 38 --- + 1 6 = – 6 3 0 1875 – 0 38 0 1875 + 1 6 = 1 307 . d d d From Expression (E.24): 1 --21/2 2k 2 1000 v div = --------------------------- = -----------------------------------------------------= 43 73 m s . 1 25 0 80 2 1 307 dc d 2 --------M- d It should be ensured that: v div 2 v m z s . Substituting the given numerical data into expression above we find: v div = 43 73 m s 2 20 00 m s [Satisfactory]. example-end 31.7 References [Section 31] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design April 2010. © 2010 The Institution of Structural Engineers. Eurocode Load Combinations for Steel Structures. The British Constructional Steelwork Association Limited. BCSA Publication No. 53/10. December 2010. page 334 Topic: User’s Manual/Verification tests - EN1991-1-4_(f).xls Section 32 EN 1991-1-4 Annex F 32.1 Dynamic characteristics of structures c alculation procedures recommended in this section assume that structures possess linear elastic behaviour and classical normal modes. Dynamic structural properties are therefore characterised by: — natural frequencies — modal shapes — equivalent masses — logarithmic decrements of damping. Natural frequencies, modal shapes, equivalent masses and logarithmic decrements of damping should be evaluated, theoretically or experimentally, by applying the methods of structural dynamics. 32.2 Fundamental frequency FLEXURAL FREQUENCY N1. For cantilevers with one mass at the end a simplified expression to calculate the fundamental flexural frequency n 1 of structures is given by expression: 1 g n 1 = ------ ----2 x 1 (Eq. 32‐17) where: • g = 9 81 m s 2 is the acceleration of gravity • x 1 is the maximum displacement due to self weight applied in the vibration direction. The fundamental flexural frequency n 1 of multi-storey buildings with a height larger than 50 m can be estimated using expression: n 1 Hz = 46 -----h Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls (Eq. 32‐18) page 335 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 32 EN 1991-1-4 A NNEX F Figure 32.4 From Figure F.1 - Geometric parameters for chimneys. where h is the height of the structure in meters. Note The same expression may give some guidance for single‐storey buildings and towers. FLEXURAL FREQUENCY N1. The fundamental flexural frequency n 1 , of chimneys can be estimated by expression: 1 b Ws - ------n 1 Hz = ----------2 h eff Wt (Eq. 32‐19) with h eff = h 1 + h 2 3 and where: • b is the top diameter of the chimney • h eff is the effective height of the chimney m , h 1 and h 2 are given in Figure F.1. • W s is the weight of structural parts contributing to the stiffness of the chimney • W t is the total weight of the chimney • 1 is equal to 1000 for steel chimney, and 700 for concrete and masonry chimneys. OVALLING FREQUENCY N1,0. The fundamental (lowest) ovalling frequency n 1 0 of a long cylindrical shell without stiffening rings may be calculated using expression: t3 E n 1 0 = 0 492 -------------------------------------s 1 – 2 b 4 (Eq. 32‐20) where: page 336 • E N m 2 is Young’s modulus (of the structural material) • t m is the shell tickness Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 32 EN 1991-1-4 A NNEX F • is Poisson ratio (of the structural material) • s is the mass of the shell per unit area kg m 2 • b m is the diameter of the shell. VERTICAL BENDING FREQUENCY N1,B. The frequency n 1 B of a plate or box girder bridge may be approximately derived from expression: EI K2 n 1 B = ----------------2- -------b2 L m (Eq. 32‐21) where: • L m is the length of the main span of the bridge • E N m 2 is Young’s modulus (of the plate or girders bridge) • I b m 4 is the second moment of area of the full cross-section of the bridge for vertical bending at mid-span Figure 32.5 From Figure F.2 - Factor K used for the derivation of fundamental bending frequency. Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls page 337 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 32 EN 1991-1-4 A NNEX F • m kg m is the mass per unit length of the full cross-section at midspan (for dead and super-imposed dead loads) • K is a dimensionless factor depending on span arrangement: for single span bridge: • K = if simply supported • K = 3 9 if propped cantilevered • K = 4 7 if fixed end supports in the case of more spans K is obtained from Figure F.2 above. If the value of EI b m at the support exceeds twice the value at mid‐span, or is less than 80% of the mid‐span value, then the eq. 32‐21 should not be used unless very approximate values are sufficient. The fundamental torsional frequency of plate girder bridges is equal to the fundamental bending frequency calculated from eq. 32‐21, provided the average longitudinal bending inertia per unit width is not less than 100 times the average transverse bending inertia per unit length. Note TORSIONAL FREQUENCY. The fundamental torsional frequency of a box girder bridge may be approximately derived from equation: n 1 T = n 1 B P 1 P 2 + P 3 (Eq. 32‐22) with: • 2 P 1 = mb ---------lp r l ------------------2 j j • P2 = • L2 Jj P 3 = ------------------------------------------------2K 2 b 2 I b 1 + b 2 lp Figure 32.6 Cross-section of the bridge at mid-span. page 338 Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 32 EN 1991-1-4 A NNEX F Figure 32.7 Cross-section single box at mid-span. where: • n 1 B is the fundamental bending frequency in Hz • b is the total width of the bridge • m is the mass per unit length defined in F.2(5) • is Poisson’s ratio of girder material • r j is the distance of individual box centre-line from centre-line of bridge • l j kg m 2 m is the second moment of mass per unit length of individual box for vertical bending at mid-span, including an associated effective width of deck • I b m 4 is the second moment of area of the full cross-section of the bridge for vertical bending at mid-span • l p kg m 2 m is the second moment of mass per unit length of the full cross-section of the bridge at mid-span. It is described by equation: md b 2 -+ I p = --------------12 l pj + m j r j2 (Eq. 32‐23) where: • m d is the mass per unit length of the deck only, at mid-span • I pj is the mass moment of inertia (per unit length) of individual box at mid-span • m j is the mass per unit length of individual box only, at mid-span, without associated portion of deck. • J j m 4 is the torsion constant of individual box at mid-span. It is described by expression (F.12): Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls page 339 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 32 EN 1991-1-4 A NNEX F 4A 2 J j = ---------jds ----t (Eq. 32‐24) where: • A j is the enclosed cell area at mid-span (see Figure 32.7 above) • ds t is the integral around box perimeter of the ratio length/thickness for each portion of box wall at mid-span. Note Slight loss of accuracy may occur if the proposed Eq. 32‐24 is applied to multibox bridges whose plan aspect ratio (= span/width) exceeds 6. 32.3 Fundamental mode shape The fundamental flexural mode 1 z of buildings, towers and chimneys cantilevered from the ground may be estimated using expression: z 1 z = --- h (Eq. 32‐25) where: • = 0 6 for slender frame structures with non load-sharing walling or cladding • = 1 0 for buildings with a central core plus peripheral columns or larger columns plus shear bracings Scheme Mode shape 1(s) s sin - l 1--s 1 – cos 2 - 2 l Table 32.4 page 340 From Table F.1 - Fundamental flexural vertical mode shape for simple supported and clamped structures and structural elements. • = 1 5 for slender cantilever buildings and buildings supported by central reinforced concrete cores • = 2 0 for towers and chimneys • = 2 5 for lattice steel towers. Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 32 EN 1991-1-4 A NNEX F The fundamental flexural vertical mode 1 s of bridges may be estimated as shown in Table 32.4 above. 32.4 Equivalent mass The equivalent mass per unit length m e of the fundamental mode is given by: N l m s s ds s s j 1 1 j m m s j m j=1 0 - ---------------------------------------------------------------m e = --------------------------------------l N 2 1 s ds 0 s j (Eq. 32‐26) 12 s j m j=1 where, setting s j + 1 – s j = s j and 0 5 s j + 1 + s j = s j m : • s j is the part number “j” (with j = 1 2 N ) of the structure or the structural element • l = • m s j m is the mean value of the mass per unit length within the interval s j • 12 s j m is the square of the mean value of the mode shape within the interval s j . N s j is the height or span of the structure or the structural element j=1 32.5 Logarithmic decrement of damping The logarithmic decrement of damping ä for fundamental bending mode may be estimated by expression: = a + s + d (Eq. 32‐27) where: • a is the logarithmic decrement of aerodynamic damping for the fundamental mode • s is the logarithmic decrement of structural damping • d is the logarithmic decrement of damping due to special devices (tuned mass dampers, sloshing tanks etc.). In most cases the logarithmic decrement of aerodynamic damping a , for the fundamental bending mode of alongwind vibrations may be estimated by expression 32-28: Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls page 341 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 32 EN 1991-1-4 A NNEX F Structural damping s Structural type reinforced concrete buildings 0,10 steel buildings 0,05 mixed structures concrete + steel 0,08 reinforced concrete towers and chimneys 0,03 unlined welded steel stacks without external thermal insulation 0,012 unlined welded steel stack with external thermal insulation 0,020 steel stack with one liner with external thermal insulation(a) steel stack with two or more liners with external thermal insulation(a) h/b < 18 0,020 20 < h/b < 24 0,040 h/b > 26 0,014 h/b < 18 0,020 20 < h/b < 24 0,040 h/b > 26 0,025 steel stack with internal brick liner 0,070 steel stack with internal gunite 0,030 coupled stacks without liner 0,015 guyed steel stack without liner 0,04 steel bridges + lattice steel towers welded 0,02 high resistance bolts 0,03 ordinary bolts 0,05 composite bridges concrete bridges 0,04 prestressed (no cracks) 0,04 with cracks 0,10 Timber bridges 0,06÷0,12 Bridges, aluminium alloys 0,02 Bridges, glass or fibre reinforced plastic cables 0,04÷0,08 parallel cables 0,006 spiral cables 0,020 Note: The values for timber and plastic composites are indicative only. In cases where aerodynamic effects are found to be significant in the design, more refined figures are needed through specialist advice (agreed if appropriate with the competent Authority). Note 1: For cable supported bridges the values given in Table F.2 need to be factored by 0,75. Table 32.5 page 342 From Table F.2 - Approximate values of logarithmic decrement of structural damping in the fundamental mode, s. Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 32 EN 1991-1-4 A NNEX F (a). For intermediate values of h/b, linear interpolation may be used. cf vm zs cf b vm zs - --------------------------------------- a = ------------------------------2n 1 e 2n 1 m e (Eq. 32‐28) where: • c f is the force coefficient for wind action in the wind direction stated in Section 7 • is the air density (see Sec. 4.5(1)) • b is the width of the structure (as defined in Figure 6.1) • v m z s is the mean wind velocity for z = z s (see Sec. 4.3.1 (1)) • n 1 is the fundamental frequency of along wind vibration of the structure • m e is the equivalent mass per unit length of the fundamental mode. Approximate values of logarithmic decrement of structural damping, s , are given in Table F.2 above. If special dissipative devices are added to the structure, d should be calculated by suitable theoretical or experimental techniques. 32.6 Verification tests EN1991‐1‐4_(G).XLS. 6.22 MB. Created: 30 April 2013. Last/Rel.-date: 30 April 2013. Sheets: — Splash — Annex F. EXAMPLE 32-G‐ Dynamic characteristics of structures: fundamental frequency ‐ test1 Given: Find the fundamental flexural frequency n 1 of a cantilever beam with one mass at the end for a maximum displacement due to self weight applied in the vibration direction equal to x 1 = 5 mm . [Reference sheet: Annex F]‐[Cell‐Range: A1:N1‐A16:N16]. Solution: From Expression (F.1): 1 g 1 9 81 n 1 = ------ ----- = ------ ----------------------= 7 05 Hz 2 x 1 2 5 1000 Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls page 343 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 32 EN 1991-1-4 A NNEX F with x 1 = 5 mm = 0 005 m . example-end EXAMPLE 32-H‐ Dynamic characteristics of structures: fundamental frequency ‐ test1b Given: Find the fundamental flexural frequency n 1 of a multi‐storey building with an height h = 60 m . [Reference sheet: Annex F]‐[Cell‐Range: A19:N19‐A24:N24]. Solution: From Expression (F.2): n 1 Hz = 46 h = 46 60 = 0 77 Hz . example-end EXAMPLE 32-I‐ Dynamic characteristics of structures: fundamental frequency ‐ test1c Given: Find the fundamental flexural frequency n 1 of a masonry chimney whose height is equal to h = 50 m above ground. The chimney, with a truncated cone shape, has an outer diameter ranging from 3,90 meters to 1,90 meters from the base to the top. The total weight of the chimney is W t = 534 tons . [Reference sheet: Annex F]‐[Cell‐Range: A29:N29‐A64:N64]. Solution: From Figure F.1, assuming h 2 = h = 50 m and then h 1 = 0 we get: h eff = h 1 + h 2 3 = 0 + 50 3 = 16 67 m . Assuming 1 = 700 - (masonry chimney) and a weight of structural part, that contributes to the stiffness of the structure, equal to the whole weight of the chimney ( W s = W t ), from Expression (F.3) we get: 1 b Ws 700 1 90- ------- = -----------------------n 1 Hz = ---------- 1 = 4 79 Hz 2 h eff 16 67 2 Wt having considered b = 1 90 m the top outer diameter of the chimney. example-end EXAMPLE 32-J‐ Dynamic characteristics of structures: fundamental frequency ‐ test1d Given: page 344 Find the fundamental ovalling frequency n 1 0 of a long cylindrical steel shell (without stiffening rings) with a diameter b = 1 00 m and a tickness t = 3 mm . Assume for the shell a mass per unit area equal to s = 22 50 kg m 2 . Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 32 EN 1991-1-4 A NNEX F [Reference sheet: Annex F]‐[Cell‐Range: A67:N67‐A84:N84]. Solution: Young’s modulus and Poisson ratio (for steel): 11 E = 210000 MPa = 2 10 10 N m 2 , = 0 25 - . From Expression (F.5): 11 0 003 3 2 10 10 t3 E = 0 492 -------------------------------------------------------------------------------- = 8 07 Hz . n 1 0 = 0 492 -------------------------------------2 4 s 1 – b 22 50 1 – 0 25 2 1 00 4 Expression above gives the lowest natural frequency of the shell. example-end EXAMPLE 32-K‐ Dynamic characteristics of structures: fundamental frequency ‐ test2 Given: Find the fundamental vertical bending frequency n 1 B of a box girder bridge with a length of the main span equal to L = 31 m . Assume a single span simply supported bridge (precast prestressed concrete beams) and a second moment of area of the full cross‐section of the bridge for vertical bending at mid‐span equal to 6 I b = 2 85 m 4 = 3 950000 10 mm 4 . The mass per unit length of the full cross‐section at mid‐span (for dead and super‐imposed dead loads) is equal to m = 13000 kg m . [Reference sheet: Annex F]‐[Cell‐Range: A87:N87‐A144:N144]. Solution: Dimensionless factor K depending on span arrangement (single span bridge: simply supported): K = 3 14 . 10 Young’s modulus of boxes girder bridge: E = 36 GPa = 36000 MPa = 3 60 10 N m 2 . From Expression (F.6): 10 EI K2 2 3 60 10 2 85 = 4 59 Hz n 1 B = ----------------2- -------b- = -----------------------2- --------------------------------------------------2 L 2 31 m 13000 Note: typical bandwidth for 1st few modes (medium beam girder): 0 5 5 7 Hz. example-end EXAMPLE 32-L‐ Dynamic characteristics of structures: fundamental frequency ‐ test3 Given: Using the given numerical data from previous example, find the fundamental torsional frequency of the box girder bridge. The total width of the bridge is b = 13 00 m and the concrete slab thickness is 25 cm. The structure of the bridge is made up of n = 3 precast box beams with prestressed concrete slab. Each box at mid‐span has the following torsional characteristics: – mean thickness for each portion of box wall: t m = 0 19 m Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls page 345 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 32 EN 1991-1-4 A NNEX F – total sum of the lengths of each wall portion of box: s = 4 10 m – enclosed cell area at mid‐span (individual box): A j = 1 80 m 2 For the calculations let us assume: – mass per unit length of the deck only (at mid‐span): m d = 9600 kg m – mass moment of inertia of individual box at mid‐span: I pj = 2000 kg m 2 m – second moment of mass per unit length of individual box for vertical bending at midspan, including an associated effective width of deck: I j = 6000 kg m 2 m – mass per unit length of individual box only, at mid‐span, without associated portion of deck: m j = 2650 kg m n =3 r j2 n = 13 5 m 2 . – mean value of the sum of the squares (rj²): r 2 = j=1 [Reference sheet: Annex F]‐[Cell‐Range: A147:N147‐A236:N236]. Solution: From Expression (F.11), the second moment of mass per unit length of the full cross‐section of the bridge at mid‐span is: md b2 -+ I p = --------------12 n =3 md b2 - + n l pj + m j l pj + m j r j2 = --------------r j2 n 12 j=1 13 -2 + 3 2000 + 2650 13 5 = 248525 kg m 2 m . I p = 9600 ---------------------------12 From Expression (F.12), torsion constant (mean value) of individual box (at mid‐span): 4A j2 4A j2 t m 4A j2 0 19 4 1 80 2 J j = ---------- ---------- = ------------------ = ------------------------------------------------ = 0 60 m 4 s ds s 4 10 ---------tm t J j = 3 0 60 = 1 80 m 4 . From previous example we have: – second moment of area of the full cross‐section of the bridge for vertical bending at 6 mid‐span equal to I b = 2 85 m 4 = 3 950000 10 mm 4 – fundamental vertical bending frequency n 1 B = 4 59 Hz – mass per unit length of the full cross‐section at midspan: m = 13000 kg m . Therefore, from Expressions (F.8), (F.9) and (F.10) we get: 2 13000 13 -2 = 8 84 - P 1 = mb ---------- = -----------------------------------lp 248525 P2 = r l ------------------2 j b2 lp j 3 13 5 6000 = ---------------------------------------= 0 006 - 13 2 248525 L2 Jj 31 2 1 80 - = -------------------------------------------------------------------------- = 0 152 - . P 3 = ------------------------------------------------2 2 2 2 13 2 2 85 1 + 0 2 2K b I b 1 + Finally we obtain: n 1 T = n 1 B P 1 P 2 + P 3 = 4 59 8 84 0 006 + 0 152 = 5 42 Hz . page 346 Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 32 EN 1991-1-4 A NNEX F Plan aspect ratio: span/width = (31 m)/(13 m) = 2,38 < 6 [Satisfactory]. example-end EXAMPLE 32-M‐ Fundamental mode shape ‐ test4 Given: A masonry chimney is 50 meters high (see data from example 32‐I on page 344). The height is discretized in equal parts of 1 meter. For each part, calculate the average height s j m from the ground, the mass per unit length m s j m and the fundamental flexural mode 1 s j m using Expression (F.13) with z = s j m . Find the equivalent mass m e per unit length (see Expression (F.14)). [Reference sheet: Annex F]‐[Cell‐Range: A240:N240‐A393:N393]. Solution: Let us assume: s j = s j + 1 – s j = 1 00 m = cost . Therefore, we have: s j = 1 m with s j m = 0 5 m . Then s j + s j = 2 m with s j m = 1 5 m ; s j + s j + s j = 3 m with s j m = 2 5 m and so on... Using Expression (F.13) with = 2 0 (for towers and chimneys), we have for example: s j + s j + s j + = 15 m , with z = s j m = 14 5 m . Hence, we obtain: Figure 32.8 Calculated values (spreadsheet input). Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls page 347 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 32 EN 1991-1-4 A NNEX F s j m 14 5 z 1 s j m = --- = -------- = ------------ = 0 0841 with 21 s j m = 0 0071 and so on...(see h 50 h 2 2 tables above). The values of the masses per unit length were calculated assuming a density for the masonry equal to 1900 kg per cubic meter (the thickness of the walls of the chimney varies from 1,25 meters at the base to 25 cm at the top). From Tables above, we obtain: N s j 12 s j m = 9 9675 , j=1 N s s j 1 j m m s j m = 49291 7393 . j=1 Therefore, we find: N l m s s ds s s 1 j 1 j m m s j m j=1 49291 7393 0 - ---------------------------------------------------------------- = ------------------------------ 4945 kg m . m e = --------------------------------------l N 9 9675 2 1 s ds s j 12 s j m 0 j=1 Note: for cantilevered structures with a varying mass distribution m e may be approximated by average value of m s over the upper third of the structure. In this case: h 50 --- = ------ = 16 7 m . 3 3 s j h III = h – h--- = 33 3 m we get ( j 33 ): Using data from tables above, for 3 -----------------------------------------------------------------------------------------------------------------------7266 + 6950 + 6638 + + 3281 + 3033 + 2791 me = 4929 53 kg m . 17 ✍ The last calculation remains a good approximation even if the chimney is of truncated conical shape. example-end EXAMPLE 32-N‐ Logarithmic decrement of damping ‐ test5 Given: Find the logarithmic decrement of damping for fundamental bending mode of the masonry chimney analysed in the previous examples. Assume a mean wind velocity (at height z s = 0 6 h ) equal to v m z s = 28 m s . The stack height is 50 meters from the ground. Assume a force coefficient (see Sec. 7) c f round to 1,05. [Reference sheet: Annex F]‐[Cell‐Range: A430:N430‐A464:N464]. Solution: page 348 From Figure 6.1: z s = 0 6 h = 0 6 50 = 30 m (case a: vertical structures). The outer diameter of the chimney at height of 30 meters above the ground is equal (say) to b = 2,70 meters. From previous example (see example 32‐I on page 344), the fundamental frequency of along wind vibration of the structure is n 1 = 4 79 Hz and the equivalent Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 32 EN 1991-1-4 A NNEX F mass m e (see previous example 32‐M) equal to 4945 kg/m. Therefore, the logarithmic decrement of aerodynamic damping (for the fundamental mode) is: cf vm zs cf b vm zs 05 1 25 2 70 28 - = 0 0021 . - ---------------------------------------- = 1-------------------------------------------------------------------- a = ------------------------------2n 1 e 2n 1 m e 2 4 79 4945 From Table F.2 (“Approximate values of logarithmic decrement of structural damping in the fundamental mode, s”), for reinforced concrete towers and chimneys we have: s = 0 030 . From Expression (F.15), finally we find: = a + s + d = 0 002 + 0 + 0 030 = 0 032 - , in this case having considered equal to zero the logarithmic decrement of damping due to special devices. example-end 32.7 References [Section 32] EN 1991-1-4:2005/A1:2010. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, April 2010. EN 1991-1-4:2005. Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions. Brussels: CEN/TC 250 - Structural Eurocodes, March 2005 (DAV). Manual for the design of building structures to Eurocode 1 and Basis of Structural Design April 2010. © 2010 The Institution of Structural Engineers. Eurocode Load Combinations for Steel Structures. The British Constructional Steelwork Association Limited. BCSA Publication No. 53/10. December 2010. DESIGN MANUAL FOR ROADS AND BRIDGES. VOLUME 1. HIGHWAYS STRUCTURES, APPROVAL PROCEDURES AND GENERAL DESIGN. Section 3 General Design. BD 49/01. DESIGN RULES FOR AERODYNAMIC EFFECTS ON BRIDGES. May 2001. Topic: User’s Manual/Verification tests - EN1991-1-4_(g).xls page 349 (This page intentionally left blank) Section 33 Eurocode 1 EN 1991-1-5 Section 5 (Page 17 to 19) 33.1 General T hermal actions shall be classified as variable and indirect actions, see EN 1990:2002, 1.5.3 and 4.1.1. All values of thermal actions given in this Part are characteristic values unless it is stated otherwise. In general thermal variations cause deformations in single structural elements as well as in the overall structure itself. If the structure is hyperstatic, a further consequence of thermal variations is the emergence of coactive stress states. Therefore, the effects of thermal variations may involve aspects of a structure’s functionality as well as its safety. Characteristic values of thermal actions as given in this Part are values with an annual probability of being exceeded of 0,02, unless otherwise stated, e.g. for transient design situations. DESIGN SITUATIONS Thermal actions shall be determined for each relevant design situation identified in accordance with EN 1990. Structures not exposed to daily and seasonal climatic and operational temperature changes may not need to be considered for thermal actions. The elements of loadbearing structures shall be checked to ensure that thermal movement will not cause overstressing of the structure, either by the provision of movement joints or by including the effects in the design. REPRESENTATION OF ACTIONS Daily and seasonal changes in shade air temperature, solar radiation, reradiation, etc., will result in variations of the temperature distribution within individual elements of a structure. The magnitude of the thermal effects will be dependent on local climatic conditions, together with the orientation of the structure, its overall mass, finishes (e.g. cladding in buildings), and in the case of building structures, heating and ventilation regimes and thermal insulation. Topic: User’s Manual/Verification tests - EN1991-1-5_(a).xls page 351 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 33 E UROCODE 1 EN 1991-1-5 S ECTION 5 (P AGE 17 TO 19) 33.2 Temperature changes in buildings Thermal actions on buildings due to climatic and operational temperature changes shall be considered in the design of buildings where there is a possibility of the ultimate or serviceability limit states being exceeded due to thermal movement and/or stresses. DETERMINATION OF TEMPERATURES Thermal actions on buildings due to climatic and operational temperature changes should be determined in accordance with the principles and rules provided in this Section taking into account national (regional) data and experience. The climatic effects shall be determined by considering the variation of shade air temperature and solar radiation. Operational effects (due to heating, technological or industrial processes) shall be considered in accordance with the particular project. The uniform temperature component of a structural element T u is defined as: T u = T – T 0 (Eq. 33‐29) where T is an average temperature of a structural element due to climatic temperatures in winter or summer season and due to operational temperatures. DETERMINATION OF TEMPERATURE PROFILES The temperature T in Eq. 33-29 should be determined as the average temperature of a structural element in winter or summer using a temperature profile. In the case of a sandwich element T is the average temperature of a particular layer. When elements of one layer are considered and when the environmental conditions on both sides are similar, T may be approximately determined as the average of inner and outer environment temperature T in and T out . The temperature of the inner environment, T in should be determined in accordance with Table 5.1. The temperature of the outer environment, T out should be determined in accordance with: — Table 5.2 for parts located above ground level — Table 5.3 for underground parts. The temperatures T out for the summer season as indicated in Table 5.2 are dependent on the surface absorptivity and its orientation: — the maximum is usually reached for surfaces facing the west, south-west or for horizontal surfaces — the minimum (in °C about half of the maximum) for surfaces facing the north. Season Temperature Tin Summer T1 = 20°C(a) Winter T2 = 25°C(a) Table 33.6 From Table 5.1 - Indicative temperatures of inner environment Tin. (a). Values for T1 and T2 may be specified in the National Annex. When no data are available the values T1 = 20°C and T2 = 25°C are recommended. page 352 Topic: User’s Manual/Verification tests - EN1991-1-5_(a).xls S ECTION 33 Season E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-5 S ECTION 5 (P AGE 17 TO 19) Temperature Tout [°C](a) Significant factor Summer Relative absorptivity depending on surface colour 0,5 bright light surface Tmax + T3 0,7 light coloured surface Tmax + T4 0,9 dark surface Tmax + T5 Winter Tmin Table 33.7 From Table 5.2 - Indicative temperatures Tout for buildings above the ground level. (a). Values of the maximum shade air temperature Tmax, minimum shade air temperature Tmin, and solar radiation effects T3, T4, and T5 may be specified in the National Annex. If no data are available for regions between latitudes 45°N and 55°N the values T3 = 0°C, T4 = 2°C, and T5 = 4°C are recommended, for North-East facing elements and T3 = 18°C, T4 = 30°C and T5 = 42°C for South-West or horizontal facing elements. Season Summer Winter Table 33.8 Depth below the ground level Temperature Tout [°C](a) Less than 1 m T6 More then 1 m T7 Less than 1 m T8 More then 1 m T9 From Table 5.3 - Indicative temperatures Tout for underground parts of buildings. (a). Values T6, T7, T8 and T9 may be specified in the National Annex. If no data are available for regions between latitudes 45°N and 55°N the values T6 = 8°C, T7 = 5°C, T8 = - 5°C and T9 = - 3°C are recommended. 33.3 Verification tests EN1991‐1‐5_(A).XLS. 8.31 MB. Created: 15 November 2013. Last/Rel.-date: 15 November 2013. Sheets: — Splash — CodeSec5. EXAMPLE 33-O‐ Temperature changes in buildings ‐ Determination of temperature profiles ‐ test1 Given: Let us analyse a regular steel framework that forms three 5,0 m bays (with an overall plane surface of 15,0 m) and two floors, 3,0 m in height (for a total of 6,0 m), as represented in Figure 33.9 (see below). Topic: User’s Manual/Verification tests - EN1991-1-5_(a).xls page 353 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 33 E UROCODE 1 EN 1991-1-5 S ECTION 5 (P AGE 17 TO 19) Figure 33.9 Example of a steel frame. See “Development of skills facilitating implementation of Eurocodes Handbook 3 - Action effects for buildings”. Leonardo da Vinci Pilot Project CZ/02/B/F/PP-134007. 10/2005 The following structural elements go to make up the framework: — beams (spanning 5,0 m): IPE 300 — columns: HEB 320. Let us consider four different uniform temperature components: 1. Case 1: heating of every structural element (beams and columns) of the structure (summer season) 2. Case 2: cooling of every structural element (beams and columns) of the structure (winter season) 3. Case 3: heating of the external beams and columns 4. Case 4: cooling of the external beam and columns. Find the four thermal (characteristic) load cases upon the steel frame. Assumptions: a. South-West facing elements b. light coloured surfaces. [Reference sheet: CodeSec5]‐[Cell‐Range: A1:O1‐A260:O260]. Solution: From Table 5.1 ‐ “Indicative temperatures of inner environment Tin” we have T 1 = 20C (Summer) and T 2 = 25C (Winter). Let us assume (say): – maximum shade air temperature: T max = 40C – minimum shade air temperature: T min = – 9C . From Table 5.2 ‐ “Indicative temperatures Tout for buildings above the ground level” for light coloured surfaces we have T out = T max + T 4 = 40 + 30 = 70C (Summer) and T out = T min = – 9C (Winter). page 354 Topic: User’s Manual/Verification tests - EN1991-1-5_(a).xls S ECTION 33 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-5 S ECTION 5 (P AGE 17 TO 19) Average temperature of a structural element:(1) T = T in + T out 2 = 20 + 70 2 = 45C (Summer), T = T in + T out 2 = 25 – 9 2 = 8C (Winter). Assuming an initial temperature T 0 = 10C (see Annex A ‐ Sec. A.1(3)), the uniform temperature component of a structural element is (mean value):(2) T u = T – T 0 = 45 – 10 = 35C (Summer), T u = T – T 0 = 8 – 10 = – 2C (Winter). Therefore, above ground level ( h g = 0 ), we get: Single bay Figure 33.10Heating of every structural element (beams and columns) of the structure (summer season). Single bay Figure 33.11Cooling of every structural element (beams and columns) of the structure (winter season). (1) See EN 1991-1-5, Section 5.3(1) - NOTE 2. (2) See EN 1991-1-5, Section5.2(5) - Eq. (5.1). Topic: User’s Manual/Verification tests - EN1991-1-5_(a).xls page 355 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 33 E UROCODE 1 EN 1991-1-5 S ECTION 5 (P AGE 17 TO 19) Single bay Figure 33.13Heating of the external beams and columns. Single bay Figure 33.12Cooling of the external beam and columns. EXAMPLE 33-P ‐ Temperature changes in buildings ‐ Determination of temperature profiles ‐ test1b Given: Assuming the same assumptions from the previous example, find the four thermal (characteristic) load cases upon underground parts of a concrete building (3 meters deep under the ground). [Reference sheet: CodeSec5]‐[Cell‐Range: A261:O261‐A368:O368]. Solution: Zone with h 1 m (zone B): Average temperature of a structural element:(1) T = T in + T out 2 = 20 + 8 2 = 14C (Summer with T 6 = 8C ), page 356 Topic: User’s Manual/Verification tests - EN1991-1-5_(a).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-5 S ECTION 5 (P AGE 17 TO 19) S ECTION 33 T = T in + T out 2 = 25 – 5 2 = 10C (Winter with T 8 = – 5C ). Assuming an initial temperature T 0 = 10C (see Annex A ‐ Sec. A.1(3)), the uniform temperature component of a structural element is (mean value):(1) T u = T – T 0 = 14 – 10 = 4C (Summer), T u = T – T 0 = 10 – 10 = 0C (Winter). Zone with h 1 m (zone A): Average temperature of a structural element:(2) T = T in + T out 2 = 20 + 5 2 = 12 5C (Summer with T 7 = 5C ), T = T in + T out 2 = 25 – 3 2 = 11C (Winter with T 9 = – 3C ). Assuming an initial temperature T 0 = 10C (see Annex A ‐ Sec. A.1(3)), the uniform temperature component of a structural element is (mean value):(3) T u = T – T 0 = 12 5 – 10 = 2 5C (Summer), T u = T – T 0 = 11 – 10 = 1C (Winter). Therefore, above ground level ( h g = 0 ), we get: Single bay Figure 33.14Heating of every structural element (beams and columns) of the structure (summer season). (1) See EN 1991-1-5, Section 5.3(1) - NOTE 2. (1) See EN 1991-1-5, Section5.2(5) - Eq. (5.1). (2) See note 1. (3) See note 2. Topic: User’s Manual/Verification tests - EN1991-1-5_(a).xls page 357 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 33 E UROCODE 1 EN 1991-1-5 S ECTION 5 (P AGE 17 TO 19) Single bay Figure 33.15Cooling of every structural element (beams and columns) of the structure (winter season). Single bay Figure 33.16Heating of the external beams and columns. Single bay Figure 33.17Cooling of the external beam and columns. page 358 Topic: User’s Manual/Verification tests - EN1991-1-5_(a).xls S ECTION 33 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-5 S ECTION 5 (P AGE 17 TO 19) 33.4 References [Section 33] EN 1991-1-5:2003. Eurocode 1: Actions on structures - Part 1-5: General actions - Thermal actions. Brussels: CEN/TC 250 - Structural Eurocodes, November 2003 (DAV). EN 1991-1-5:2003/AC:2009. Eurocode 1: Actions on structures - Part 1-5: General actions - Thermal actions. Brussels: CEN/TC 250 Structural Eurocodes, March 2009. Manual for the design of building structures to Eurocode 1 and Basis of Structural Design April 2010. © 2010 The Institution of Structural Engineers. Development of skills facilitating implementation of Eurocodes - Handbook 3 Action effects for buildings. Leonardo da Vinci Pilot Project CZ/02/B/F/PP-134007. Aachen 10/2005. Topic: User’s Manual/Verification tests - EN1991-1-5_(a).xls page 359 (This page intentionally left blank) Section 34 Eurocode 1 EN 1991-1-5 Section 6 34.1 Temperature changes in bridges 34.1.1 Bridge decks T hree types of bridge superstructures are distinguished in EN 1991-1-5. For the purposes of this Part, bridge decks are grouped as follow: • Type 1. Steel deck: — steel box girder — steel truss or plate girder • Type 2. Composite deck • Type 3. Concrete deck: — concrete slab — concrete beam — concrete box girder. THERMAL ACTIONS Representative values of thermal actions should be assessed by the uniform temperature component (see EN 1991-1-5, Sec. 6.1.3) and the temperature difference components (see EN 1991-1-5, Sec. 6.1.4). The vertical temperature difference component should generally include the non-linear component. Either Approach 1 or Approach 2 should be used. 34.1.2 Thermal actions UNIFORM TEMPERATURE COMPONENT The uniform temperature component depends on the minimum and maximum temperature which a bridge will achieve. This results in a range of uniform temperature changes which, in an unrestrained structure would result in a change in element length. Topic: User’s Manual/Verification tests - EN1991-1-5_(a)_2.xls page 361 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 34 E UROCODE 1 EN 1991-1-5 S ECTION 6 Figure 34.18From Figure 6.1 - Correlation between minimum (maximum) shade air temperature Tmin (Tmax) and minimum (maximum) uniform bridge temperature component Te,min (Te,max). The minimum and maximum uniform (effective) bridge temperatures Te,min (Te,max) can be determined from the relationship given in Fig. 6.1 on the basis of isotherms of shade air temperatures Tmin (Tmax). The characteristic values of minimum and maximum shade air temperatures for a site location may be obtained e.g. from national maps of isotherms. These characteristic values represent shade air temperatures at mean sea level in open country being exceeded by annual extremes with the probability of 0,02. The relationship given in Fig. 6.1 is based on a daily temperature range of 10°C. Such a range may be considered as appropriate for most Member States. The maximum uniform temperature component Te,max and the minimum uniform temperature component Te,min for the three types of bridge decks may be determined from the following relationships based on Figure 6.1: page 362 T e max = T max + 16C T e max = T max + 4C for 30C T max 50C . T e max = T max + 2C (Eq. 34‐30) T e min = T min – 3C T e min = T min + 4C for – 50 C T max 0C . T e min = T min + 8C (Eq. 34‐31) Topic: User’s Manual/Verification tests - EN1991-1-5_(a)_2.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 34 E UROCODE 1 EN 1991-1-5 S ECTION 6 For steel truss and plate girders the maximum values given for Type 1 may be reduced by 3°C. For construction works located in specific climatic regions as in e.g. frost pockets, additional information should be obtained and evaluated. Minimum shade air temperature (Tmin) and maximum shade air temperature (Tmax) for the site shall be derived from isotherms in accordance with 6.1.3.2. The National Annex may specify Te,min and Te,max. Figure 6.1 below gives recommended values. SHADE AIR TEMPERATURE Characteristic values of minimum and maximum shade air temperatures for the site location shall be obtained, e.g. from national maps of isotherms. Information (e.g. maps of isotherms) on minimum and maximum shade air temperatures to be used in a Country may be found in its National Annex. Where an annual probability of being exceeded of 0,02 is deemed inappropriate, the minimum shade air temperatures and the maximum shade air temperatures should be modified in accordance with annex A. RANGE OF UNIFORM BRIDGE TEMPERATURE COMPONENT The values of minimum and maximum uniform bridge temperature components for restraining forces shall be derived from the minimum (Tmin) and maximum (Tmax) shade air temperatures (see 6.1.3.1 (3) and 6.1.3.1 (4)). The initial bridge temperature T0 at the time that the structure is restrained may be taken from annex A for calculating contraction down to the minimum uniform bridge temperature component and expansion up to the maximum uniform bridge temperature component. Thus the characteristic value of the maximum contraction range of the uniform bridge temperature component, T N con should be taken as: T N con = T 0 – T e min (Eq. 34‐32) and the characteristic value of the maximum expansion range of the uniform bridge temperature component, T N exp should be taken as: T N exp = T e max – T 0 . (Eq. 34‐33) 34.2 Temperature difference components 34.2.1 Vertical linear component (Approach 1) For the vertical temperature difference component, two alternative approaches are provided in EN 1991-1-5 which may be nationally selected: (1) linear, or (2) non linear temperature distribution. The models applied in the linear approach are given in Table 6.1 (“Recommended values of linear temperature difference component for different type of bridge decks for road, foot and railway bridges”) for bridges based on a depth of surfacing of 50 mm. For other surfacing thicknesses, the coefficient ksur should Topic: User’s Manual/Verification tests - EN1991-1-5_(a)_2.xls page 363 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 34 E UROCODE 1 EN 1991-1-5 S ECTION 6 be applied (see Table 6.2 - “Recommended values of ksur to account for different surfacing thickness”). Top warmer then bottom TM,heat [°C] Bottom warmer than top TM,cool [°C] Type 1. Steel deck 18 13 Type 2. Composite deck 15 18 - concrete box girder 10 5 - concrete beam 15 8 - concrete slab 15 8 Type of Deck(a) Type 3. Concrete deck: Table 34.9 From Table 6.1 - Recommended values of linear temperature difference component for different type of bridge decks for road, foot and railway bridges. (a). The values given in the table represent upper bound values of the linearly varying temperature difference component for representative sample of bridge geometries. The values given in the table are based on a depth of surfacing of 50 mm for road and railway bridges. For other depths of surfacing these values should be multiplied by the factor ksur. Recommended values for the factor ksur is given in Table 6.2. Road, foot and railway bridges Type 1 Surface Thickness Type 2 Type 3 Top warmer then bottom Bottom warmer then top Top warmer then bottom Bottom warmer then top Top warmer then bottom Bottom warmer then top [mm] ksur ksur ksur ksur ksur ksur unsurfaced 0,7 0,9 0,9 1,0 0,8 1,1 waterproofed(a) 1,6 0,6 1,1 0,9 1,5 1,0 50 1,0 1,0 1,0 1,0 1,0 1,0 100 0,7 1,2 1,0 1,0 0,7 1,0 150 0,7 1,2 1,0 1,0 0,5 1,0 ballast (750 mm) 0,6 1,4 0,8 1,2 0,6 1,0 Table 34.10 From Table 6.2 - Recommended values of ksur to account for different surfacing thickness. (a). These values represent upper bound values for dark colour. page 364 Topic: User’s Manual/Verification tests - EN1991-1-5_(a)_2.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 34 E UROCODE 1 EN 1991-1-5 S ECTION 6 34.2.2 Vertical temperature components with non-linear effects (Approach 2) Values of vertical temperature differences for bridge decks to be used in a Country may be found in its National Annex. Figure 34.20From Figure 6.2a - Temperature differences for bridge decks - Type 1: Steel Decks. Figure 34.19From Figure 6.2b - Temperature differences for bridge decks - Type 2: Composite Decks. Topic: User’s Manual/Verification tests - EN1991-1-5_(a)_2.xls page 365 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 34 E UROCODE 1 EN 1991-1-5 S ECTION 6 Figure 34.21From Figure 6.2c - Temperature differences for bridge decks - Type 3: Concrete Decks. Recommended values are given in Figures 6.2a/6.2b/6.2c and are valid for 40 mm surfacing depths for deck type 1 and 100 mm for deck types 2 and 3. For other depths of surfacing see Annex B. In these figures “heating” refers to conditions such that solar radiation and other effects cause a gain in heat through the top surface of the bridge deck. Conversely, “cooling” refers to conditions such that heat is lost from the top surface of the bridge deck as a result of re-radiation and other effects. 34.2.3 Simultaneity of uniform and temperature difference components In some cases, it may be necessary to take into account both the temperature difference T M heat (or T M cool ) and the maximum range of uniform bridge temperature component T N exp (or T N con ) given as: T M heat + N T N exp T M cool + N T N con (Eq. 34‐34) M T M heat + T N exp M T M cool + T N con (Eq. 34‐35) where the most adverse effect should be chosen. The National annex may specify numerical values of N and M . If no other information is available, the page 366 Topic: User’s Manual/Verification tests - EN1991-1-5_(a)_2.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 34 E UROCODE 1 EN 1991-1-5 S ECTION 6 recommended values (reduction factors) for N and M are: N = 0 35 , M = 0 35 . Where both linear and non-linear vertical temperature differences are used (see 6.1.4.2) T M should be replaced by T which includes T M and T E (see Figures 6.2a/6.2b and 6.2c), where: • T M linear temperature difference component • T E non-linear part of the difference component • T sum of linear temperature difference component and non-linear part of the temperature difference component. 34.2.4 Bridge Piers: temperature differences For concrete piers (hollow or solid), the linear temperature differences between opposite outer faces should be taken into account. The National annex may specify values for linear temperature differences. In the absence of detailed information the recommended value is 5°C. For walls the linear temperature differences between the inner and outer faces should be taken into account. The National annex may specify values for linear temperature differences. In the absence of detailed information the recommended value is 15°C. 34.3 Verification tests EN1991‐1‐5_(A)_2.XLS. 8.31 MB. Created: 20 November 2013. Last/Rel.-date: 20 November 2013. Sheets: — Splash — CodeSec6. EXAMPLE 34-Q‐ Characteristic thermal actions in bridges ‐ Consideration of thermal actions ‐ test1 Given: Determine the maximum uniform temperature component T e max and the minimum uniform temperature component T e min for the three types of bridge decks determined from the relationships based on Figure 6.1. Let us assume that the characteristic values of minimum T min and maximum T max shade air temperatures for a site location (say the city of Birmingham) was obtained e.g. from the UK national maps of isotherms. These characteristic values represent shade air temperatures at mean sea level in open country being exceeded by annual extremes with the probability of 0,02. [Reference sheet: CodeSec6]‐[Cell‐Range: A1:O1‐A86:O86]. Solution: From the UK isotherms maps (see “Manual for the design of building structures to Eurocode 1 and Basis of Structural Design” ‐ The Institution of Structural Engineers Manual for the design of building structures to Eurocode 1. April 2010), we have (near Birmingham): Topic: User’s Manual/Verification tests - EN1991-1-5_(a)_2.xls page 367 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 34 E UROCODE 1 EN 1991-1-5 S ECTION 6 T max = 34C (rounded value for probability p = 0,02) T min = – 18C (rounded value for probability p = 0,02). Therefore, we get: T e max = T max + 16C = 34 + 16 = 50C for 30C T max 50C . T e max = T max + 4C = 34 + 4 = 38C T e max = T max + 2C = 34 + 2 = 36C T e min = T min – 3C = – 18 – 3 = – 21C T e min = T min + 4C = – 18 + 4 = – 14C for – 50 C T max 0C . T e min = T min + 8C = – 18 + 8 = – 10C Figure 34.22Excel® output graph (for Bridge deck Type 1). The algorithm to draw the graph above is the same. We omit the other two cases (Type 2 and Type 3). example-end page 368 Topic: User’s Manual/Verification tests - EN1991-1-5_(a)_2.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 34 E UROCODE 1 EN 1991-1-5 S ECTION 6 EXAMPLE 34-R‐ Characteristic thermal actions in bridges ‐ Uniform temperature component ‐ test2 Given: Assuming the same assumptions from the previous example, find the maximum T ed max and minimum T ed min constant temperature component for the design of bridge bearings (linear behaviour) and expansion joints. Let us assume an initial bridge temperature T 0 = 10C at the time that the structure is restrained (see NOTE in Annex A ‐ Sec. A.1(3)). To take into account the uncertainty of the position of the bearings at the reference temperature (see EN 1993‐2, Annex A “Technical specifications for bearings”, Table A.4 “Numerical values for T0”) let us assume a safety term equal to T 0 = 10C . [Reference sheet: CodeSec6]‐[Cell‐Range: A90:O90‐A169:O169]. Solution: Note. In the following the main contents of a future Annex E to EN 1990, that would substitute the now Annex A to EN 1993‐2 is presented. From Expressions (6.1) and (6.2) we get the characteristic value of the maximum contraction and maximum expansion value of the uniform bridge temperature component respectively (bridge deck Type 1): T N con = T 0 – T e min = 10 – – 21 = 31C T N exp = T e max – T 0 = 50 – 10 = 40C . Note For bearings and expansion joints the National Annex may specify the maximum expansion range of the uniform bridge temperature component, and the maximum contraction range of the uniform bridge temperature component, if no other provisions are required. The recommended values are (TN,exp + 20) °C and (TN,con + 20)C°, respectively. If the temperature at which the bearings and expansion joints, are set is specified, then the recommended values are (TN,exp + 10)°C and (TN,con + 10) °C, respectively. Hence let us assume (say): T N con = 31 + 10 = 41C T N exp = 40 + 10 = 50C . Design values of the temperature difference (see technical publication: “Bridge Design to Eurocodes Worked examples”. Worked examples presented at the Workshop “Bridge Design to Eurocodes”, Vienna, 4‐6 October 2010. Support to the implementation, harmonization and further development of the Eurocodes. Appendix A: Design of steel bridges. Overview of key content of EN 1993 – G. Hanswille, W. Hansen, M. Feldmann, G. Sedlacek): T ed max = T 0 + F T N exp + T 0 = 10 + 1 35 50 + 10 = 87 5C T ed min = T 0 – F T N con – T 0 = 10 – 1 35 51 – 10 = 55 4C . Bearing with linear behaviour (overall design temperature range): T d = T ed max – T ed min = 101 – – 68 9 = 142 9C . example-end Topic: User’s Manual/Verification tests - EN1991-1-5_(a)_2.xls page 369 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 34 E UROCODE 1 EN 1991-1-5 S ECTION 6 EXAMPLE 34-S‐ Characteristic thermal actions in bridges ‐ Temperature difference components ‐ test3 Given: Assuming the same assumptions form the previous examples, find the vertical linear temperature component (Approach 1) for a bridge deck Type 1 with a surface thickness equal to 100 mm. [Reference sheet: CodeSec6]‐[Cell‐Range: A173:O173‐A238:O238]. Solution: Entering Table 6.1 ‐ “Recommended values of linear temperature difference component for different types of bridge decks for road, foot and railway bridges” with steel deck Type 1 we get (for k sur = 1 ): – linear temperature difference component (heating): T M heat = 18C ; – linear temperature difference component (cooling): T M cool = 13C . The values given above represent upper bound values of the linearly varying temperature difference component for representative sample of bridge geometries. The values given in Table 6.1 are based on a depth of surfacing of 50 mm for road and railway bridges. For other depths of surfacing these values should be multiplied by the factor ksur. Recommended values for the factor ksur are given in Table 6.2. For surface thickness equal to 100 mm and for bridge deck Type 1 we have: 0 7 (top warmer than bottom) k sur = 1 2 (bottom warmer then top). Hence we get (for surface thickness equal to 100 mm): T M heat = k sur 18C = 0 7 18 = 12 6C T M cool = k sur 13C = 1 2 13 = 15 6C . Figure 34.23Excel® output graph (for Bridge deck Type 1): characteristic values. page 370 Topic: User’s Manual/Verification tests - EN1991-1-5_(a)_2.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 34 E UROCODE 1 EN 1991-1-5 S ECTION 6 EXAMPLE 34-T‐ Characteristic thermal actions in bridges ‐ Vertical temperature (Approach 2) ‐ test3b Given: Let us consider a bridge deck Type 3 (prestressed precast concrete beam bridge). The height of the precast beam is 36 in = 0.91 m (rounded value). The thickness of the reinforced concrete bridge deck is 25 cm. Assuming a surfacing depth equal to 100 mm find the temperature difference for heating and cooling (see Figure 6.2c). [Reference sheet: CodeSec6]‐[Cell‐Range: A242:O242‐A365:O365]. Solution: Entering Table 6.2c with h = 0 91 + 0 25 = 1 16 m we get: (a) Heating h 1 = 0 3 h = 0 3 1 16 = 0 35 m 0 15 m h 1 = 0 15 m h 2 = 0 3 h = 0 3 1 16 = 0 35 m with 0 10 m h 2 0 25 m h 2 = 0 25 m h 2 = 0 3 h = 0 3 1 16 = 0 35 m 0 10 m + surfacing depth in metres = 0 20 m . For h 0 8 m we have T 1 = 13 0C ; T 2 = 3 0C ; T 3 = 2 5C . (b) Cooling h 1 = h 4 = 0 20 h = 0 20 1 16 = 0 23 m 0 25 m h 1 = h 4 = 0 23 m h 2 = h 3 = 0 20 h = 0 25 1 16 = 0 29 m 0 20 m h 2 = h 3 = 0 29 m . Linear interpolation for T j within the range 1 0 m h 1 5 m with h = 1 16 m : h [m] T1 [°C] T2 [°C] T3 [°C] T4 [°C] 1,0 – 8,0 – 1,5 – 1,5 – 6,3 1,16 T1 T2 T3 T4 1,5 – 8,4 – 0,5 – 1,0 – 6,5 Table 34.11 Values from Figure 6.2c - Temperature differences for bridge decks - Type 3: Concrete decks. T 1 – – 8 0 --------------------------------------– 8 4 – – 8 0 - = -------------------------------1 16 – 1 0 1 5 – 1 0 T 1 = – 8 13C T 2 – – 1 5 --------------------------------------– 0 5 – – 1 5 - = -------------------------------1 16 – 1 0 1 5 – 1 0 T 2 = – 1 18C T 3 – – 1 5 --------------------------------------– 1 0 – – 1 5 - = -------------------------------1 16 – 1 0 1 5 – 1 0 T 3 = – 1 34C T 4 – – 6 3 --------------------------------------– 6 5 – – 6 3 - = -------------------------------1 16 – 1 0 1 5 – 1 0 T 4 = – 6 36C . Rounded to the first decimal place we get: T 1 = – 8 1C ; T 2 = – 1 2C ; T 3 = – 1 3C ; T 4 = – 6 4C . Topic: User’s Manual/Verification tests - EN1991-1-5_(a)_2.xls page 371 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 34 E UROCODE 1 EN 1991-1-5 S ECTION 6 Figure 34.24Excel® output graph (for Bridge deck Type 3c): characteristic values. EXAMPLE 34-U‐ Characteristic thermal actions in bridges ‐ Simultaneity of uniform and temperature difference components ‐ test4 Given: Taking into account both the temperature difference T M heat (or T M cool ) and the maximum range of uniform bridge temperature component T N exp (or T N con ) assuming simultaneity, find the most adverse effect to be chosen as input in the FEM analysis. Refer to the data in Example 34‐S (bridge deck Type 1 with T e min = – 21C , T e max = 50C ). [Reference sheet: CodeSec6]‐[Cell‐Range: A415:O415‐A509:O509]. Solution: From Expressions (6.1) and (6.2) we get the characteristic value of the maximum contraction and maximum expansion value of the uniform bridge temperature component respectively (bridge deck Type 1): T N con = T 0 – T e min = 10 – – 21 = 31C T N exp = T e max – T 0 = 50 – 10 = 40C . From data in Example 34‐S we have: T M heat = 12 6C (expansion); T M cool = 15 6C (contraction). From Expressions (6.3) and (6.4), using the given numerical data, we get respectively: Load – Case 6.3-a: T M heat + N T N exp = 12 6 + 0 35 40 = 12 6 + 14 C Load – Case 6.3-b: T M cool + N T N con = – 15 6 + 0 35 – 31 = – 15 6 + 10 9 C Load – Case 6.4-a: M T M heat + T N exp = 0 75 12 6 + 40 = 9 45 + 40 C Load – Case 6.4-b: M T M cool + T N con = 0 75 – 15 6 + – 31 = – 11 7 – 31 C having assumed N = 0 35 , M = 0 75 for the reduction factors. page 372 Topic: User’s Manual/Verification tests - EN1991-1-5_(a)_2.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 34 E UROCODE 1 EN 1991-1-5 S ECTION 6 Having thus considered four different combinations of load (Case 6.3‐a; Case 6.3‐b; Case 6.4‐a; Case 6.4‐b), we have (see Figure above): Figure 34.25Excel® output graph (for Bridge deck Type 1): characteristic values. 34.4 References [Section 34] EN 1991-1-5:2003. Eurocode 1: Actions on structures - Part 1-5: General actions - Thermal actions. Brussels: CEN/TC 250 - Structural Eurocodes, November 2003 (DAV) EN 1991-1-5:2003/AC:2009. Eurocode 1: Actions on structures - Part 1-5: General actions - Thermal actions. Brussels: CEN/TC 250 Structural Eurocodes, March 2009 Manual for the design of building structures to Eurocode 1 and Basis of Structural Design April 2010. © 2010 The Institution of Structural Engineers Topic: User’s Manual/Verification tests - EN1991-1-5_(a)_2.xls page 373 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 34 E UROCODE 1 EN 1991-1-5 S ECTION 6 JRC Scientific and Technical Reports. Bridge Design to Eurocodes Worked examples. Worked examples presented at the Workshop “Bridge Design to Eurocodes”, Vienna, 4-6 October 2010. Support to the implementation, harmonization and further development of the Eurocodes. Y. Bouassida, E. Bouchon, P. Crespo, P. Croce, L. Davaine, S. Denton, M. Feldmann, R. Frank, G. Hanswille, W. Hensen, B. Kolias, N. Malakatas, G. Mancini, M. Ortega, J. Raoul, G. Sedlacek, G. Tsionis. page 374 Topic: User’s Manual/Verification tests - EN1991-1-5_(a)_2.xls Section 35 Eurocode 1 EN 1991-1-5 Annex A, Annex B 35.1 Annex A (Normative): Isotherms of national minimum and maximum shade air temperatures 35.1.1 General T he values of both annual minimum and annual maximum shade air temperature represent values with an annual probability of being exceeded of 0,02. Thermal actions must be considered to be variable and indirect actions. Regulations furnish characteristic values whose probability of being exceeded is 0,02, which is equivalent to a return period of 50 years. The fundamental quantities on which thermal actions are based are the extreme air temperatures, that is, the maximum and minimum, in the shade at the building site. Such values are furnished by the National Meteorological Institute of each Member State. Eurocode EN 1991-1-5 does not include maps of extreme temperatures. Such task is left up to the National Meteorological Institutes. Indicative maps for some CEN countries were included in the preliminary standard ENV 1991-2-5. The initial temperature T 0 should be taken as the temperature of a structural element at the relevant stage of its restraint (completion). If it is not predictable the average temperature during the construction period should be taken. The value of T 0 may be specified in the National annex or in a particular project. If no information is available T 0 may be taken as 10°C. In case of uncertainty concerning sensitivity of the bridge to T 0 , it is recommended that a lower and upper bound of an interval expected for T 0 are considered. 35.1.2 Maximum and minimum shade air temperature values with an annual probability of being exceeded p other than 0,02 If the value of maximum (or minimum) shade air temperature, T max p ( T min p ), is based on an annual probability of being exceeded p other than 0,02 the ratios may be determinated from the following expressions based on a Generalized Extreme Value (GEV) Distribution (Type I: Gumbel): Topic: User’s Manual/Verification tests - EN1991-1-5_(b).xls page 375 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 35 E UROCODE 1 EN 1991-1-5 A NNEX A, A NNEX B — for maximum ( T max ): T max p --------------- = k 1 – k 2 ln – ln 1 – p T max — (Eq. 35‐36) for minimum ( T min ): T min p -------------- = k 3 + k 4 ln – ln 1 – p , T min (Eq. 35‐37) where T min ( T max ) is the value of minimum (maximum) shade air temperature (at height above sea level h 0 ) with an annual probability of being exceeded of 0,02. The National annex may specify the values of the coefficients k 1 , k 2 , k 3 and k 4 . If no other information is available the following values are recommended: k 1 = 0 781 ; k 2 = 0 056 ; k 3 = 0 393 ; k 4 = – 0 156 . (Eq. 35‐38) Expression 35-37 can only be used if T min is negative. If specific data are available (mean “m” and the standard deviation “”of the type I extreme value distribution) then the following expressions shall be used: — for maximum ( T max ): uc k 1 = --------------------------uc + 3 902 (Eq. 35‐39) k k 2 = -----1- , uc (Eq. 35‐40) u = m – 0 57722 c c = 1 2825 (Eq. 35‐41) with: — for minimum ( T min ): uc k 3 = -------------------------uc – 3 902 (Eq. 35‐42) k k 4 = -----3uc (Eq. 35‐43) u = m + 0 57722 c c = 1 2825 (Eq. 35‐44) with: page 376 Topic: User’s Manual/Verification tests - EN1991-1-5_(b).xls S ECTION 35 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-5 A NNEX A, A NNEX B 35.2 Annex B (Normative): Temperature differences for various surfacing depths Temperature difference profiles given in Figures 6.2a 6.2c are valid for 40 mm surfacing depths for deck type 1 and 100 mm surfacing depths for types 2 and 3. The National annex may give values for other depths. Recommended values are given in the following tables: Table B.1 (for Type 1), B.2 (for Type 2) and B.3 (for Type 3). Surfacing thickness Temperature difference [°C] Heating Cooling T1 T2 T3 T4 T1 unsurfaced 30 16 6 3 8 20 mm 27 15 9 5 6 40 mm 24 14 8 4 6 Table 35.12 From Table B.1 - Recommended values of T for deck Type 1. Depth of slab h = 0,2 m Surface thickness Heating Cooling T1 T1 16,5 5,9 23,0 5,9 50 mm 18,0 4,4 100 mm 13,0 3,5 150 mm 10,5 2,3 200 mm 8,5 1,6 T1 T1 unsurfaced(a) 18,5 9,0 waterproofed 26,5 9,0 50 mm 20,5 6,8 100 mm 16,0 5,0 150 mm 12,5 3,7 200 mm 10,0 2,7 unsurfaced (a) waterproofed h = 0,3 m Temperature difference [°C] Table 35.13 From Table B.2 - Recommended values of T for deck Type 2. Topic: User’s Manual/Verification tests - EN1991-1-5_(b).xls page 377 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 35 E UROCODE 1 EN 1991-1-5 A NNEX A, A NNEX B (a). These values represent upper bound values for dark colour. Depth of slab [m] Surfacing thickness Temperature difference [°C] Heating 0,2 0,4 0,6 (Cont’d) 0,8 Cooling T1 T2 T3 T1 T2 T3 T4 unsurfaced 12,0 5,0 0,1 4,7 1,7 0,0 0,7 waterproofed(a) 19,5 8,5 0,0 4,7 1,7 0,0 0,7 50 mm 13,2 4,9 0,3 3,1 1,0 0,2 1,2 100 mm 8,5 3,5 0,5 2,0 0,5 0,5 1,5 150 mm 5,6 2,5 0,2 1,1 0,3 0,7 1,7 200 mm 3,7 2,0 0,5 0,5 0,2 1,0 1,8 unsurfaced 15,2 4,4 1,2 9,0 3,5 0,4 2,9 waterproofed(a) 23,6 6,5 1,0 9,0 3,5 0,4 2,9 50 mm 17,2 4,6 1,4 6,4 2,3 0,6 3,2 100 mm 12,0 3,0 1,5 4,5 1,4 1,0 3,5 150 mm 8,5 2,0 1,2 3,2 0,9 1,4 3,8 200 mm 6,2 1,3 1,0 2,2 0,5 1,9 4,0 unsurfaced 15,2 4,0 1,4 11,8 4,0 0,9 4,6 waterproofed(a) 23,6 6,0 1,4 11,8 4,0 0,9 4,6 50 mm 17,6 4,0 1,8 8,7 2,7 1,2 4,9 100 mm 13,0 3,0 2,0 6,5 1,8 1,5 5,0 150 mm 9,7 2,2 1,7 4,9 1,1 1,7 5,1 200 mm 7,2 1,5 1,5 3,6 0,6 1,9 5,1 unsurfaced 15,4 4,0 2,0 12,8 3,3 0,9 5,6 waterproofed(a) 23,6 5,0 1,4 12,8 3,3 0,9 5,6 50 mm 17,8 4,0 2,1 9,8 2,4 1,2 5,8 100 mm 13,5 3,0 2,5 7,6 1,7 1,5 6,0 150 mm 10,0 2,5 2,0 5,8 1,3 1,7 6,2 200 mm 7,5 2,1 1,5 4,5 1,0 1,9 6,0 Table 35.14 From Table B.3 - Recommended values of T for deck Type 3. page 378 Topic: User’s Manual/Verification tests - EN1991-1-5_(b).xls S ECTION 35 Depth of slab [m] E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-5 A NNEX A, A NNEX B Surfacing thickness (Cont’d) Temperature difference [°C] unsurfaced 15,4 4,0 2,0 13,4 3,0 0,9 6,4 waterproofed(a) 23,6 5,0 1,4 13,4 3,0 0,9 6,4 50 mm 17,8 4,0 2,1 10,3 2,1 1,2 6,3 100 mm 13,5 3,0 2,5 8,0 1,5 1,5 6,3 150 mm 10,0 2,5 2,0 6,2 1,1 1,7 6,2 200 mm 7,5 2,1 1,5 4,3 0,9 1,9 5,8 unsurfaced 15,4 4,5 2,0 13,7 1,0 0,6 6,7 waterproofed(a) 23,6 5,0 1,4 13,7 1,0 0,6 6,7 50 mm 17,8 4,0 2,1 10,6 0,7 0,8 6,6 100 mm 13,5 3,0 2,5 8,4 0,5 1,0 6,5 150 mm 10,0 2,5 2,0 6,5 0,4 1,1 6,2 200 mm 7,5 2,1 1,5 5,0 0,3 1,2 5,6 T1 T2 T3 T1 T2 T3 T4 1,0 1,5 Heating Cooling Table 35.14 From Table B.3 - Recommended values of T for deck Type 3. (a). These values represent upper bound values for dark colour. 35.3 Verification tests EN1991‐1‐5_(B).XLS. 6.12 MB. Created: 28 November 2013. Last/Rel.-date: 28 November 2013. Sheets: — Splash — AnnexA — AnnexB. EXAMPLE 35-V‐ Isotherms of national minimum and maximum shade air temperatures ‐ test1 Given: The values of maximum and minimum shade air temperature at sea level (h = 0) with an annual probability of being exceeded of 0,02 are given respectively: – T max = 34C (rounded value for probability p = 0,02) – T min = – 18C (rounded value for probability p = 0,02). Topic: User’s Manual/Verification tests - EN1991-1-5_(b).xls page 379 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 35 E UROCODE 1 EN 1991-1-5 A NNEX A, A NNEX B Find the values of maximum and minimum shade air temperatures for an annual probability of being exceeded p equivalent to a return period of 50 years for an height above sea level h = 150 m. [Reference sheet: AnnexA]‐[Cell‐Range: A1:O1‐A23:O23]. Solution: If no information is available the values of shade air temperature may be adjusted for height above sea level by subtracting 0,5°C per 100 m height for minimum shade air temperatures and 1,0°C per 100 m height for maximum shade air temperatures. Therefore, for a return period of T = 50 years p = 1 T = 1 50 = 0 02 we get: – for minimum: – 0 5C – 0 5C T min = h --------------------- = 150 m --------------------- = – 0 75C 100 m 100 m T min p = T min + T min = – 18 + – 0 75 = – 18 75C . – for maximum: – 1 0C – 1 0C T max = h --------------------- = 150 m --------------------- = – 1 50C 100 m 100 m T max p = T max + T max = 34 + – 1 50 = 32 50C . Figure 35.26PreCalculus Excel® form: procedure for a quick pre-calculation. EXAMPLE 35-W‐ Isotherms of national minimum and maximum shade air temperatures ‐ test1b Given: Assuming the same assumptions from the previous example find the values of maximum T max p and minimum T min p shade air temperature based on an annual probability of being exceeded p equivalent to a return period of 90 years for an height above sea level h = 150 m. Let us assume that the mean value “m” and the standard deviation “” of a Generalized Extreme Value (GEV) Distribution (Type I: Gumbel) are respectively: – for maximum temperatures: m T max = 34C ; T max = 3C . page 380 Topic: User’s Manual/Verification tests - EN1991-1-5_(b).xls S ECTION 35 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN E UROCODE 1 EN 1991-1-5 A NNEX A, A NNEX B – for minimum temperatures: m T min = – 7 C ; T min = 3C . Find the ratios T max p T max , T min p T min against the annual probability p of being exceeded within the range [0,005; 0,5]. [Reference sheet: AnnexA]‐[Cell‐Range: A26:O26‐A167:O167]. Solution: From Expressions (A.7) and (A.8): – for maximum temperatures: u = m – 0 57722 c = 34 – 0 57722 0 43 = 32 66C c = 1 2825 = 1 2825 3 = 0 43 – for minimum temperatures: u = m + 0 57722 c = – 7 + 0 57722 0 43 = – 5 65C c = 1 2825 = 1 2825 3 = 0 43 Figure 35.27Excel® output graph (from Figure A.1). It moreover follows that: – for maximum temperatures: uc = 32 66 0 43 = 14 04 - Topic: User’s Manual/Verification tests - EN1991-1-5_(b).xls page 381 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 35 E UROCODE 1 EN 1991-1-5 A NNEX A, A NNEX B k 0 78 uc 14 04 k 1 = --------------------------- = ------------------------------------ = 0 78 - ; k 2 = -----1- = --------------- = 0 06 - uc 14 04 uc + 3 902 14 04 + 3 902 – for minimum temperatures: uc = – 5 65 0 43 = – 2 43 - . k uc - = -----------------------------------------0 38 = – 0 16 - . – 2 43 k 3 = -------------------------= 0 38 - ; k 4 = -----3- = --------------------uc uc – 3 902 – 2 43 – 2 43 – 3 902 Values of maximum and minimum shade air temperature (annual probability of being exceeded p = 0,011) – for maximum (rounded value): T max p --------------- = k 1 – k 2 ln – ln 1 – p = 0 78 – 0 06 ln – ln 1 – 0 011 = 1 0 - T max – for minimum: (rounded value): T min p -------------- = k 3 + k 4 ln – ln 1 – p = 0 38 + – 0 16 ln – ln 1 – 0 011 = 1 1 - T min For the ratios T max p T max , T min p T min against the annual probability p of being exceeded within the range [0,005; 0,5] see Figure 35.27 above. example-end 35.4 References [Section 35] EN 1991-1-5:2003. Eurocode 1: Actions on structures - Part 1-5: General actions - Thermal actions. Brussels: CEN/TC 250 - Structural Eurocodes, November 2003 (DAV) EN 1991-1-5:2003/AC:2009. Eurocode 1: Actions on structures - Part 1-5: General actions - Thermal actions. Brussels: CEN/TC 250 Structural Eurocodes, March 2009 Implementation of Eurocodes - Handbook 3 - Action effects for buildings. Guide to basis of structural reliability and risk engineering related to Eurocodes supplemented by practical examples. LEONARDO DA VINCI PILOT PROJECT CZ/02/B/F/PP-134007. Aachen 10.2005 Thermal Actions. Czech Technical University in Prague, Czech Republic. Milan Holický and Jana Marková. 2013. page 382 Topic: User’s Manual/Verification tests - EN1991-1-5_(b).xls Section 36 Eurocode 1 EN 1991-1-5 Annex D 36.1 Annex D (Informative): Temperature profiles in buildings and other construction works 36.1.1 General T emperature profiles may be determined using the thermal transmission theory. In the case of a simple sandwich element (e.g. slab, wall, shell) under the assumption that local thermal bridges do not exist a temperature T(x) at a distance x from the inner surface of the cross section may be determined assuming steady thermal state as: T in – T out dQ - Rx T x = T in – ------- R x = T in – -------------------------R tot dt (Eq. 36‐45) where: • T in C is the air temperature of the inner environment • T out C is the temperature of the outer environment • R tot C W is the total thermal resistance (of part) of the element (e.g. wall or window) including resistance of both surfaces • R x C W is the thermal resistance at the inner surface and of (part of) the element from the inner surface up to the point “x”. The resistance values R tot and R x may be determined using the coefficient of heat transfer and coefficients of thermal conductivity given in EN ISO 6946 (1996) and EN ISO 13370 (1998): R tot = R in + hi ---- + R i i out hN h1 h2 - + R out = R in + --------------- + --------------- + + ---------------- 1 A1 2 A2 N AN (Eq. 36‐46) where: Topic: User’s Manual/Verification tests - EN1991-1-5_(c).xls page 383 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 36 E UROCODE 1 EN 1991-1-5 A NNEX D • R in C W is the thermal resistance at the inner surface (of part) of the element • R out C W is the thermal resistance at the outer surface (of part) of the element • N is the number of layers between the inner and the outer surfaces • i W m C is the thermal conductivity of the layer-i • h i m is the thickness of the layer-i • A i m 2 is the heat transfer surface considered in the calculations (and part) of the entire actual surface A A i (e.g. wall or window). Hence: hi h1 h2 R x = R in + --------------- + --------------- + + ------------- 1 A1 2 A2 i Ai (Eq. 36‐47) where layers (or part of a layer) from the inner surface up to point “x” are considered only. Note Thermal resistance in buildings: 0,10 to 0,17 [m2 °C/W] (depending on the orientation of the heat flow), and Rout = 0,04 [m2 °C/W] (for all orientations). The thermal conductivity i for concrete (of volume of weight from 21 to 25 kN/m3) varies from 1,16 to 1,71 W/(m°C). 36.2 Verification tests EN1991‐1‐5_(C).XLS. 6.04 MB. Created: 01 December 2013. Last/Rel.-date: 01 December 2013. Sheets: — Splash — AnnexC — AnnexD. EXAMPLE 36-X‐ Temperature distribution within a wall of a building ‐ test1 Given: Find the thermal resistance and the temperature distribution within a wall (see Figure below) assuming one‐dimensional steady‐state heat transfer. Determine the thermal power (heat flow rate dQtot/dt) transmitted through the entire wall. Let us assume the following assumptions: – heat transfer coefficient at the inner surface: hi = 10 W/m2°C – air temperature of the inner environment: T in = 20C – heat transfer coefficient at the outer surface: hout = 25 W/m2°C – air temperature of the outer environment: T out = – 15C page 384 Topic: User’s Manual/Verification tests - EN1991-1-5_(c).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 36 E UROCODE 1 EN 1991-1-5 A NNEX D – thermal conductivity of the layer 1 (gypsum): 1 = 0 17 W m 2 C – thermal conductivity of the layer 2 (glass fibre batt): 2 = 0 045 W m 2 C – thermal conductivity of the layer 3 (plywood): 3 = 0 13 W m 2 C – thermal conductivity of the layer 4 (metal siding): 4 = 0 10 W m 2 C – wall 3 meters high and 5 meters wide (actual surface A = 15 00 m 2 ). See in the picture below for geometric details. [Reference sheet: AnnexA]‐[Cell‐Range: A1:O1‐A191:O191]. Layer4 Layer1 Layer3 Layer2 Figure 36.28A wall assembly. Solution: Taking A j = 1 00 m 2 as heat transfer area to be used in calculations and using the given numerical data we find: 1 1 - = 0 10 C W R in = ---------------= ----------------h in A j 10 1 1 1 R out = ------------------- = ------------------ = 0 04 C W 25 1 h out A j h1 13 10 3 R 1 = --------------- = -------------------------------------- = 0 076 C W 1 A1 0 17 1 00 Topic: User’s Manual/Verification tests - EN1991-1-5_(c).xls page 385 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 36 E UROCODE 1 EN 1991-1-5 A NNEX D h2 95 10 3 R 2 = --------------- = ----------------------------------------- = 2 11 C W 2 A2 0 045 1 00 h3 13 10 3 R 3 = --------------- = -------------------------------------- = 0 10 C W 3 A3 0 13 1 00 h4 13 10 3 - = 0 13 C W . R 4 = --------------- = ------------------------------------4 A4 0 10 1 00 Resistance value (see Eq. D.2): hN h1 h2 - + R out = 0 10 + 0 076 + 2 11 + 0 10 + 0 13 + 0 04 R tot = R in + --------------- + --------------- + + ---------------- 1 A1 2 A2 N AN R tot = 2 56 C W (rounded value). Heat flow rate Heat flow rate dQtot/dt transmitted through the entire wall: T in – T out 20C – – 15C dQ tot - A j A = --------------------------------------------- 1 00 m 2 15 00 m 2 ------------ = -------------------------R 2 56 C W dt tot dQ tot dQ 1 W ------------ = ------- ----- A = 13 67 ------2 15 00 m 2 = 205 W . dt A m dt j Temperatures distribution within the wall Layer 1 (gypsum): dQ T 1 = T in – ------- R in = 20 – 13 67 0 10 = 18 6C dt Layer 2 (glass fibre batt): dQ T 2 = T in – ------- R in + R 1 = 20 – 13 67 0 10 + 0 076 = 17 6C dt Layer 3 (plywood): dQ T 3 = T in – ------- R in + R 1 + R 2 = 20 – 13 67 0 10 + 0 076 + 2 11 = – 11 2C dt Layer 4 (metal siding): dQ T 4 = T out + ------- R out + R 4 = – 15 + 13 67 0 04 + 0 13 = – 12 7C dt Outer surface: dQ T 5 = T out + ------- R out = – 15 + 13 67 0 04 = – 14 5C . dt page 386 Topic: User’s Manual/Verification tests - EN1991-1-5_(c).xls Layer4 Layer2 Layer3 Layer1 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 36 E UROCODE 1 EN 1991-1-5 A NNEX D Figure 36.29Excel® output graph (according to example Figure D.1 in Annex D). Final step. Mark the temperatures at each component edge (interface), and then draw straight lines joining each point to the next. This completes both the arithmetic and graphic representations of the temperature or thermal gradient (see Figure above). example-end EXAMPLE 36-Y‐ Temperature distribution within a wall of a building ‐ test1b Given: A wall 3 meters high and 5 meters wide is made up with long horizontal bricks of size 16 cm x 22 cm (cross section), separated by horizontal layers of mortar (thickness 3 cm). The bricks are covered by two vertical layers of mortar of thickness 2 cm each and finally by an outer insulating material (thickness 3 cm). Find the thermal resistance and the temperature distribution within the wall assuming one‐dimensional steady‐state heat transfer. Let us assume the following assumptions: – heat transfer coefficient at the inner surface: hi = 10 W/m2°C – air temperature of the inner environment: T in = 20C – heat transfer coefficient at the outer surface: hout = 25 W/m2°C Topic: User’s Manual/Verification tests - EN1991-1-5_(c).xls page 387 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 36 E UROCODE 1 EN 1991-1-5 A NNEX D – air temperature of the outer environment: T out = – 10C – thermal conductivity of the layer 1 (insulating material): 1 = 0 026 W m 2 C – thermal conductivity of the layer 2 (mortar): 2 = 0 22 W m 2 C – thermal conductivity of the layer 3 (brick): 3 = 0 72 W m 2 C – thermal conductivity of the layer 4 (mortar): 4 = 0 22 W m 2 C – wall 3 meters high and 5 meters wide (actual surface A = 15 00 m 2 ). See in the picture below for geometric details. [Reference sheet: AnnexA]‐[Cell‐Range: A1:O1‐A191:O191] Solution: Let us consider a wall surface portion Aj (see Figure below) with an height of dj1 + dj2 + dj3 = 0,25 meters for 1 meter deep, since it is representative of the entire wall (thermally). Hence, taking A j = 0 25 m 1 00 m = 0 25 m 2 as heat transfer area to be used in calculations and using the given numerical data we find: 1 1 R in = ---------------= ------------------------------- = 0 4 C W h in A j 10 0 25 Mortar dj1 = 15 mm j1 = 0,22 W/(m °C) ‐ mortar dj2 = 220 mm j2 = 0,72 W/(m °C) ‐ brick dj3 = 15 mm j3 = 0,22 W/(m °C) ‐ mortar hj = 160 mm Figure 36.30Wall with four vertical layers and interior and exterior films. Thermal network also shown. page 388 Topic: User’s Manual/Verification tests - EN1991-1-5_(c).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 36 E UROCODE 1 EN 1991-1-5 A NNEX D 1 - = ------------------------------1 R out = ------------------ = 0 16 C W h out A j 25 0 25 Layer 1 (outer layer): h1 30 10 3 - = 4 61 C W R 1 = --------------- = ---------------------------------------1 A1 0 026 0 25 Layer 2 and Layer 4 (mortar): h2 20 10 3 - = 0 36 C W R 4 = R 2 = --------------- = ------------------------------------2 A2 0 22 0 25 Layer 3 (mortar + brick) ‐ parallel thermal network model: 1 R j = ------------------------------------ with (see Figure 36.30): 1 1 1 ------- + ------- + ------R j1 R j2 R j3 hj 160 R j1 = ----------------- = ---------------------- = 48 48 C W j1 d j1 0 22 15 hj 160 R j2 = ----------------- = ------------------------- = 1 01 C W j2 d j2 0 72 220 hj 160 R j3 = ----------------- = ---------------------- = 48 48 C W . j3 d j3 0 22 15 Therefore, we get (for j = 3): 1 1 R j = ------------------------------------ = ------------------------------------------------------- = 0 97 C W . 1 1 1 1 1 1 ------- + ------- + --------------------- + ------------ + --------------48 48 1 01 48 48 R j1 R j2 R j3 Note For input in TABLE‐2 (see sheet “AnnexD”) we use the equivalent value j,eq: hj 160 j eq = ---------------------------------------------- = ------------------------------------------------------ = 0 66 W m C . R j d j1 + d j2 + d j3 0 97 15 + 220 + 15 Resistance value (see Eq. D.2): R tot = R in + R 1 + R 2 + R j = 3 + R 4 + R out = 0 4 + 4 61 + 0 36 + 0 97 + 0 36 + 0 16 R tot = 6 86 C W (rounded value). Heat flow rate Heat flow rate dQtot/dt transmitted through the entire wall: T in – T out 20C – – 10C dQ tot - A j A = -------------------------------------------- 0 25 m 2 15 00 m 2 ------------ = -------------------------R tot dt 6 86 C W Topic: User’s Manual/Verification tests - EN1991-1-5_(c).xls page 389 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 36 E UROCODE 1 EN 1991-1-5 A NNEX D Figure 36.31PreCalculus Excel® form: procedure for a quick pre-calculation. dQ tot dQ 1 W ------------ = ------------ A = 17 50 ------2 15 00 m 2 = 262 W , dt A j m dt T in – T out 20C – – 10C - = 4 37 W for the surface area A used for - = -------------------------------------------with: dQ ------- = -------------------------j R tot dt 6 86 C W thermal calculations. Temperatures distribution within the wall Layer 1 (outer layer): dQ T 1 = T in – ------- R in = 20 – 4 37 0 40 = 18 3C dt page 390 Topic: User’s Manual/Verification tests - EN1991-1-5_(c).xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 36 E UROCODE 1 EN 1991-1-5 A NNEX D Layer 2 (mortar): dQ T 2 = T in – ------- R in + R 1 = 20 – 4 37 0 40 + 4 61 = – 1 9C dt Layer 3 (mortar + brick ‐ parallel thermal network model): dQ T 3 = T in – ------- R in + R 1 + R 2 = 20 – 4 37 0 40 + 4 61 + 0 36 = – 3 5C dt Layer 4 (mortar): dQ T 4 = T out + ------- R out + R 4 = – 10 + 4 37 0 16 + 0 36 = – 7 7C dt Outer surface: Layer3 Layer4 Layer2 Layer1 dQ T 5 = T out + ------- R out = – 10 + 4 37 0 16 = – 9 3C . dt Figure 36.32Excel® output graph (according to example Figure D.1 in Annex D). This example demonstrates calculation of the thermal resistance and temperature distribution within a wall assuming one‐dimensional steady‐state heat transfer. Note that in some cases different parts of the wall may have different layers (in this case see layer No. 3). To determine a correct wall R‐value in such cases, we need to calculate the correct value through each heat flow path and determine the overall R‐value based on the relative area of each path. Topic: User’s Manual/Verification tests - EN1991-1-5_(c).xls page 391 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 36 E UROCODE 1 EN 1991-1-5 A NNEX D 36.3 References [Section 36] EN 1991-1-5:2003. Eurocode 1: Actions on structures - Part 1-5: General actions - Thermal actions. Brussels: CEN/TC 250 - Structural Eurocodes, November 2003 (DAV) EN 1991-1-5:2003/AC:2009. Eurocode 1: Actions on structures - Part 1-5: General actions - Thermal actions. Brussels: CEN/TC 250 Structural Eurocodes, March 2009 Implementation of Eurocodes - Handbook 3 - Action effects for buildings. Guide to basis of structural reliability and risk engineering related to Eurocodes supplemented by practical examples. LEONARDO DA VINCI PILOT PROJECT CZ/02/B/F/PP-134007. Aachen 10.2005 Thermal Actions. Czech Technical University in Prague, Czech Republic. Milan Holický and Jana Marková. 2013. page 392 Topic: User’s Manual/Verification tests - EN1991-1-5_(c).xls Section 1 Eurocode 1 EN 1991-1-6 1.1 General T his part of EN 1991 provides principles and general rules for the determination of actions which should be taken into account during the execution of buildings and civil engineering works. In EN 1991-1-6, actions during execution are separated, according to their origin and in conformity with EN 1990, in Construction loads and Non construction loads. Actions during execution which include, where appropriate, construction loads and those other than construction loads shall be classified in accordance with EN 1990:2002, 4.1.1. Construction loads (see also Sec. 4.11) should be classified as variable actions ( Q c ). Table 4.1 gives the full description and classification of construction loads: — Personnel and hand tools (variable)(1) (free) — Storage movable items (variable) (free) — Non-permanent equipment (variable) (fixed/free)(2) — Movable heavy machinery and equipment (variable) (free) — Accumulation of waste materials (variable) (free) — Loads from parts of structure in temporary states (variable) (free). Construction loads, which are caused by cranes, equipment, auxiliary construction works/structures may be classified as fixed or free actions depending on the possible position(s) for use. The limits may be defined in the National Annex and for the individual project. In accordance with EN 1990:2002, 1.3(2), control measures may have to be adopted to verify the conformity of the position and moving of construction loads with the design assumptions. (1) Variation in time: variable. (2) Where construction loads are classified as fixed, then tolerances for possible deviations from the theoretical position should be defined. Where construction loads are classified as free, then the limits of the area where they may be moved or positioned should be determined. Topic: User’s Manual/Verification tests - EN1991-1-6.xls page 393 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 1.2 Design situations and limit states DESIGN SITUATIONS. Transient, accidental and seismic design situations shall be identified and taken into account as appropriate for designs for execution. Design situations should be selected as appropriate for the structure as a whole, the structural members, the partially completed structure, and also for auxiliary construction works and equipment. The selected design situations shall take into account the conditions that apply from stage to stage during execution in accordance with EN 1990:2002, 3.2(3)P. The selected design situations shall be in accordance with the execution processes anticipated in the design. Design situations shall take account of any revisions to the execution processes. Any selected transient design situation should be associated with a nominal duration equal to or greater than the anticipated duration of the stage of execution under consideration. The design situations should take into account the likelihood for any corresponding return periods of variable actions (e.g. climatic actions). Note The return periods for the determination of characteristic values of variable actions during execution may be defined in the National Annex or for the individual project. Recommended return periods for climatic actions are given in table 3.1, depending on the nominal duration of the relevant design situation. Duration Return period [years] < 3 days 2(a) < 3 months (but > 3 days) 5(b) < 1 year (but > 3 months) 10 > 1 year 50 Table 1.15 From Figure 3.1 - Recommended return periods for the determination of the characteristic values of climatic actions. (a). A nominal duration of three days, to be chosen for short execution phases, corresponds to the extent in time of reliable meteorological predictions for the location of the site. This choice may be kept for a slightly longer execution phase if appropriate organizational measures are taken. The concept of mean return period is generally not appropriate for short term duration. (b). For a nominal duration of up to three months actions may be determined taking into account appropriate seasonal and shorter term meteorological climatic variations. For example, the flood magnitude of a river depends on the period of the year under consideration. A minimum wind velocity during execution may be defined in the National Annex or for the individual project. The recommended basic value for durations of up to 3 months is 20 m/s in accordance with EN 1991-1-4. Relationships between characteristic values and return period for climatic actions are given in the appropriate parts of EN 1991. page 394 Topic: User’s Manual/Verification tests - EN1991-1-6.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 Note The rules for the combination of snow loads and wind actions with construction loads Qc (see 4.11.1) should be defined. These rules may be defined in the National Annex or for the individual project. Actions due to wind excitation (including aerodynamic effects due to passing vehicles, including trains) that are likely to produce fatigue effects in structural members should be taken into account. Actions due to creep and shrinkage in concrete construction works should be determined on the basis of the expected dates and duration associated with the design situations, where appropriate. ULTIMATE LIMIT STATES. Ultimate limit states shall be verified for all selected transient, accidental and seismic design situations as appropriate during execution in accordance with EN 1990(1). Generally, accidental design situations refer to exceptional conditions applicable to the structure or its exposure, such as impact, local failure and subsequent progressive collapse, fall of structural or non-structural parts, and, in the case of buildings, abnormal concentrations of building equipment and/or building materials, water accumulation on steel roofs, fire, etc. SERVICEABILITY LIMIT STATES. The serviceability limit states for the selected design situations during execution shall be verified, as appropriate, in accordance with EN 1990. Operations during execution which can cause excessive cracking and/or early deflections and which may adversely affect the durability, fitness for use and/or aesthetic appearance in the final stage shall be avoided. Load effects due to shrinkage and temperature should be taken into account in the design and should be minimized by appropriate detailing. The combinations of actions should be established in accordance with EN 1990:2002, 6.5.3 (2). In general, the relevant combinations of actions for transient design situations during execution are: — the characteristic combination — the quasi-permanent combination. 1.3 Representation of main actions Characteristic and other representative values of actions shall be determined in accordance with EN 1990, EN 1991, EN 1997 and EN 1998. Note The representative values of actions during execution may be different from those used in the design of the completed structure. Representative values of construction loads ( Q c ) should be determined taking into account their variations in time. The representative values of actions during execution may be different from those used in the design of the completed structure. (1) See also EN 1991-1-7. Topic: User’s Manual/Verification tests - EN1991-1-6.xls page 395 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 Common actions during execution, specific construction loads and methods for establishing their values are the following: — actions on structural and non-structural members during handling — geotechnical actions — actions due to prestressing — effects of pre-deformations — temperature, shrinkage, hydration effects — wind actions — snow loads — actions caused by water — actions due to atmospheric icing — construction loads. ACTIONS ON STRUCTURAL AND NON‐STRUCTURAL MEMBERS DURING HANDLING. The self-weight of structural and non-structural members during handling should be determined in accordance with EN 1991-1-1. Dynamic or inertia effects of self-weight of structural and non-structural members should be taken into account. GEOTECHNICAL ACTIONS. The characteristic values of geotechnical parameters, soil and earth pressures, and limiting values for movements of foundations shall be determined according to EN 1997. ACTIONS DUE TO PRESTRESSING. Loads on the structure from stressing jacks during the prestressing activities should be classified as variable actions for the design of the anchor region. Prestressing forces during the execution stage should be taken into account as permanent actions. EFFECTS OF PRE‐DEFORMATIONS. The treatment of the effects of pre-deformations shall be in conformity with the relevant design Eurocode (from EN 1992 to EN 1999). The action effects from pre-deformations should be checked against design criteria by measuring forces and deformations during execution. TEMPERATURE, SHRINKAGE, HYDRATION EFFECTS. The effects of temperature, shrinkage and hydration shall be taken into account in each construction phase, as appropriate. For buildings, the actions due to temperature and shrinkage are not generally significant if appropriate detailing has been provided for the persistent design situation. In the case of bridges, for the determination of restraints to temperature effects of friction at bearings, that permit free movements, they should be taken into account on the basis of appropriate representative values.(1) WIND ACTIONS. The need for a dynamic response design procedure for wind actions should be determined for the execution stages, taking into account the degree of completeness and stability of the structure and its various elements. Where a dynamic response procedure is not needed, the characteristic values of static wind forces Q W should be determined according to EN 1991-1-4 for the appropriate return period. (1) See EN 1337. page 396 Topic: User’s Manual/Verification tests - EN1991-1-6.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 The effects of wind induced vibrations such as vortex induced cross wind vibrations, galloping flutter and rainwind should be taken into account, including the potential for fatigue of, for example, slender elements. When determining wind forces, the areas of equipment, falsework and other auxiliary construction works that are loaded should be taken into account. SNOW LOADS. Snow loads shall be determined according to EN 1991-1-3 for the conditions of site and the required return period.(1) ACTIONS CAUSED BY WATER. In general, actions due to water, including ground water, ( Q wa ) should be represented as static pressures and/or hydrodynamic effects, whichever gives the most unfavourable effects. Actions caused by water may be taken into account in combinations as permanent or variable actions. Figure 1.33 From Figure 4.1 - Pressure and force due to currents. The magnitude of the total horizontal force F wa (N) exerted by currents on the vertical surface should be determined by expression 4.1. See also Figure 4.1: 1 2 F wa = --- k wa hbv wa 2 (Eq. 1‐48) where: • v wa is the mean speed (m/s) of the water averaged over the depth “h” • h is the water depth (m), but not including local scour depth • b is the width (m) of the object • wa is the density of water ( kg m 3 ) • k is the shape factor: k = 1 44 for an object of square or rectangular horizontal cross-section, and k = 0 70 for an object of circular horizontal cross-section. (1) For bridges see also Annex A2. Topic: User’s Manual/Verification tests - EN1991-1-6.xls page 397 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 F wa may be used to check the stability of bridge piers and cofferdams, etc. A more refined formulation may be used to determine F wa for the individual project. The effect of scour may be taken into account for the design where relevant. See 3.1(12) and 1.5.2.3 and 1.5.2.4. Where relevant, the possible accumulation of debris should be represented by a force F deb (N) and calculated for a rectangular object (e.g. cofferdam), for example, from: 2 F deb = k deb A deb v wa (Eq. 1‐49) where: • k deb is the debris density ( kg m 3 ) parameter • v wa is the mean speed (m/s) of the water averaged over the depth • A deb is the area ( m 2 ) of obstruction presented by the trapped debris and falsework. Expression above may be adjusted for the individual project, taking account of its specific environmental conditions. The recommended value of k deb is 666 kg m 3 . ACTIONS DUE TO ATMOSPHERIC ICING. The representative values of these actions may be defined in the National Annex or for the individual project. Guidance may be found in EN 1993-3 and in ISO 12494. CONSTRUCTION LOADS. Construction loads ( Q c ) may be represented in the appropriate design situations (see EN 1990), either, as one single variable action, or where appropriate different types of construction loads may be grouped and applied as a single variable action. Single and/or a grouping of construction loads should be considered to act simultaneously with non-construction loads as appropriate. Usually, they are modelled as free actions. Construction loads to be included for consideration are given in Table 4.1 (“Representation of construction loads Qc”). They are the following: page 398 1. Q ca personnel and hand tools (working personnel, staff and visitors with hand tools or other small site equipment) 2. Q cb storage of movable items (building and construction materials, precast elements, equipment) 3. Q cc non-permanent equipment in position for use during execution (formwork panels, scaffolding, falsework, machinery, containers) or during movement (travelling forms, launching girders and nose, counterweights) 4. Q cd movable heavy machinery and equipment (cranes, lifts, vehicles, power installations, jacks, heavy lifting devices and trucks) 5. Q ce accumulation of waste materials (surplus of construction materials or excavated soil, demolition materials) 6. Q cf loads from part of structure in a temporary state or loads from lifting operations. Topic: User’s Manual/Verification tests - EN1991-1-6.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 Construction loads Q c may be represented in the appropriate design situations (see EN 1990), either, as one single variable action, or where relevant by a group of different types of construction loads, which is applied as a single variable action. Single and/or a grouping of construction loads should be considered to act simultaneously with Non construction loads as appropriate. Recommended values of factors for construction loads are given in Annex A1 of this standard for buildings, and in Annex A2 to EN 1990 for bridges. 1.4 Construction loads during the casting of concrete Actions to be taken into account simultaneously during the casting of concrete may include working personnel with small site equipment ( Q ca ), formwork and load-bearing members ( Q cc ) and the weight of fresh concrete (which is one example of Q cf ), as appropriate. For the density of fresh concrete see EN 1991-1-1:2002 Table A.1. Q ca , Q cc and Q cf may be given in the National Annex. Recommended values of actions due to construction loads during casting of concrete ( Q cf ) may be taken from Table 4.2, and for fresh concrete from EN 1991-1-1;2002, Table A.1. Other values may have to be defined, for example, when using self-levelling concrete or precast products. Loads according to (1), (2) and (3), as given in Table 4.2, are intended to be positioned to cause the maximum effects, which may be symmetrical or not. Action Loaded area (1) Outside the working area (2) Inside the working area (3 m) x (3 m) - or the span length if less (3) Actual area Table 1.16 Load [kN/m2] 0,75 (covering Qca) 0,75 < 0,10Qcf < 1,50 (includes Qca and Qcf) Self-weight of the formwork, load-bearing element (Qcc) and the weight of the fresh concrete for the design thickness (Qcf) From Table 4.2 - Recommended characteristic values of actions due to construction loads during casting of concrete. Topic: User’s Manual/Verification tests - EN1991-1-6.xls page 399 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 1.5 Accidental actions Accidental actions such as impact from construction vehicles, cranes, building equipment or materials in transit (e.g. skip of fresh concrete), and/or local failure of final or temporary supports, including dynamic effects, that may result in collapse of load-bearing structural members, shall be taken into account, where relevant. The effects of the accidental actions should be assessed to determine the potential for inducing movement in the structure, and also the extent and effect of any such movement should be determined, with the potential for progressive collapse assessed. 1.6 Seismic actions Seismic actions should be determined according to EN 1998, taking into account the reference period of the considered transient situation. 1.7 Verification tests EN1991‐1‐6.XLS. 12.47 MB. Created: 12 December 2013. Last/Rel.-date: 12 December 2013. Sheets: — Splash — CodeSec2to4 — BridgeDeck. EXAMPLE 1-Z‐ Return period for climatic action during execution ‐ test1 Given: According to Table 3.1 “Recommended return periods for the determination of the characteristic values of climatic actions” find the characteristic value of the snow load on the ground for a nominal duration of 14 days. Let us assume a characteristic snow load on the ground (with a return period of 50 years) s k = 0 60 kN m 2 . Suppose that the available data show that the annual maximum snow load can be assumed to follow a Gumbel probability distribution with a coefficient of variation of annual maximum snow loads equal to 0,3. [Reference sheet: CodeSec2to4]‐[Cell‐Range: A67:O67‐A104:O104]. Solution: Enter Duration column Table 3.1: < 3 months (but > 3 days), with a return period T = 5 years 1 we can find the annual probability of exceedence: p --- = 1--- = 0 20 . T 5 The relationship between the characteristic value of the snow load on the ground and the snow load on the ground for a mean recurrence interval of n years is given by [Annex D of EN 1991-1-3]: page 400 Topic: User’s Manual/Verification tests - EN1991-1-6.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 6 6 1 – 0 3 ------- ln – ln 1 – 0 20 + 0 57722 1 – V ------- ln – ln 1 – p + 0 57722 sn ---- = ------------------------------------------------------------------------------------- = --------------------------------------------------------------------------------------------------- 0 69 1 + 2 5923 0 3 sk 1 + 2 5923V s n = 0 69 0 60 kN m 2 = 0 41 kN m 2 (rounded value). Figure 1.34 Snow loads according to return period (Excel output). Relationships between characteristic values and return period for climatic actions are given in the appropriate Parts of EN 1991. example-end EXAMPLE 1-AA‐ Actions caused by water ‐ test2 Given: Determine the magnitude of the total horizontal force F wa exerted by a river currents on the vertical surface of a bridge pier whose width perpendicularly to the water speed is 4 meters long. Topic: User’s Manual/Verification tests - EN1991-1-6.xls page 401 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 Let us assume a slender pier with a cross‐section of square shape (4 m x 4 m), a water depth h = 4 m (not including local scour depth) and an averaged mean water speed v wa = 0 95 m s . Calculate the force on the slender pier due to a possible accumulation of debris as well. [Reference sheet: CodeSec2to4]‐[Cell‐Range: A275:O275‐A344:O344]. Solution: According to Eurocodes for an object of rectangular horizontal cross‐section the shape factor is equal to 1,44 regardless of the value of the Reynolds number. In this case, with b = L = 4 m the Reynolds number is (@ 1 Atm): v wa L 0 95 m s 4 m - = 2 50 106 - . - = -----------------------------------------------Re = ----------–6 1 52 10 m 2 s –1 According to some scientific publications(1) is: 4 6 k = 2 0 for 2 10 Re 2 50 10 . Therefore: 1 1 2 F wa = --- k wa hbv wa = --- 2 0 1000 4 4 0 95 2 = 14440 N = 14 44 kN . 2 2 F wa b = 14 44 kN 4 m = 3 61 kN m . Assuming (say) A deb = b 1 50 m = 4 1 50 = 6 m 2 we get: 2 F deb = k deb A deb v wa = 666 6 0 95 2 = 3606 4 N = 3 61 kN . example-end EXAMPLE 1-AB‐ Action during execution on bridge slabs ‐ test3 Given: A continuous composite deck of a road bridge is made up of two steel girders with I cross‐section and a concrete slab with total width 12,0 m. The slab depth, with a 2.5% symmetrical superelevation, varies from 0,4 m over the girders to 0,25 m at its free edges and 0,30 m at the central point. The centre‐to‐centre spacing between main girders is 7 m and the slab cantilever either side is 2,5 m long.(2) Find at least two different load cases that could be envisaged in principle to maximize effects on the slab cross sections on the support and on the midspan, respectively. Consider a fresh concrete weight Q cf of about 7 50 kN m 2 in this example. [Reference sheet: BridgeDeck]‐[Cell‐Range: A275:O275‐A344:O344]. Solution: During the casting of the concrete slab, working personnel ( Q ca ), formwork and load‐bearing members ( Q cc ) and weight of the fresh concrete, which is classified as Q cf , should be considered acting simultaneously. (1) “Meccanica dei Fluidi”, Marchi E., Rubatta A. - UTET, 1981. (2) Reference to the design of a three span continuous steel-concrete composite two girders bridge. JRC Scientific and Technical Reports. Bridge Design to Eurocodes Worked examples. Worked examples presented at the Workshop “Bridge Design to Eurocodes”, Vienna, 4-6 October 2010. Support to the implementation, harmonization and further development of the Eurocodes. Editors A. Athanasopoulou, M. Poljansek, A. Pinto G., Tsionis, S. Denton. page 402 Topic: User’s Manual/Verification tests - EN1991-1-6.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 Figure 1.35 Load arrangement maximizing effects on the support cross section of the slab. According to EN 1991‐1‐7 recommendations, during the concrete casting of the deck, in the actual area it can be identified two parts, the working area, which is a square whose side is the minimum between 3,0 m and the span length, and the remaining (outside the working area). The actual area is loaded by the self‐weight of the formwork and load bearing element Q cc and by the weight of the fresh concrete Q cf , the working area by 0 10Q cf , with the restriction 0 75 kN m 2 0 10 Q fc 1 50 kN m 2 , and the area outside the working area by 0 75 kN m 2 , covering Q ca . According to Table 4.1 “Representation of construction loads (Qc)” and figure in Table 4.2 “Recommended characteristic values of actions due to construction loads during casting of concrete” we have (see figure above): (1) Load action (outside working area): Q ca = 1 00 kN m 2 (2) Load action (working area) Topic: User’s Manual/Verification tests - EN1991-1-6.xls page 403 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 Figure 1.36 Load arrangement maximizing effects on the midspan of the slab. Q ca + Q cf = 1 00 + 7 50 = 8 50 kN m 2 (3) Load action (actual area) Q cc + Q cf = 0 50 + 7 50 = 8 00 kN m 2 . From which, using the given numerical data, we get: CASE 1 Support A (SX) ‐ shear forces (characteristic values): V kA SX = 0 for load action (1) V kA SX = – Q ca + Q cf L – d = – 8 50 2 50 = – 21 25 kN m for load action (2) V kA SX = – Q cc + Q cf L – d = – 8 00 2 50 = – 20 00 kN m for load action (3). page 404 Topic: User’s Manual/Verification tests - EN1991-1-6.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 Support A (SX) ‐ Bending moments (characteristic values): M kA = 0 for load action (1) M kA = – 0 5 Q ca + Q cf L – d 2 = – 0 5 8 50 2 50 2 = – 26 56 kNm m for load action (2) M kA = – 0 5 Q cc + Q cf L – d 2 = – 0 5 8 00 2 50 2 = – 25 00 kNm m . CASE 2 Support A (DX) ‐ shear forces (characteristic values): V kA DX = Q ca e = 1 00 2 00 = 2 00 kN m for load action (1). Mid‐span B ‐ Bending moments (characteristic value): M kB = 0 5Q ca e 2 – 0 5Q ca L – d 2 = 0 5 1 00 2 00 2 – 0 5 1 00 2 50 2 = – 1 13 kNm m for load action (1). Support A (DX) ‐ shear forces (characteristic values): V kA DX = 0 5 Q ca + Q cf 3 = 0 5 8 50 3 = 12 75 kN m for load action (2). Mid‐span B ‐ Bending moments (characteristic value): Q ca + Q cf 3 2a – 3 8 50 3 2 7 – 3 - = ---------------------------------------------------------- = 35 06 kNm m M kB = ---------------------------------------------------------8 8 for load action (2). Support A (DX) ‐ shear forces (characteristic values): V kA DX = 0 5 Q cc + Q cf a + 2 L – d – Q cc + Q cf L – d V kA DX = 0 5 8 00 7 00 + 2 2 50 – 8 00 2 50 = 28 00 kN m for load action (3). Mid‐span B ‐ Bending moments (characteristic value): Q cc + Q cf a 2 – 4 L – d 2 8 00 7 00 2 – 4 2 50 2 = 24 00 kNm m - = ------------------------------------------------------------------------M kB = ---------------------------------------------------------------------8 8 for load action (3). Design load (ULS) With all partial safety factors equal to 1,5 the ultimate design loads are the following: CASE 1 (@ support A) shear force: V Ed = 1 50 0 – 20 00 – 21 25 = – 61 88 kN m bending moment: M Ed = 1 50 0 – 25 00 – 26 56 = – 77 34 kNm m . CASE 2 (@ support A) shear force: V Ed = 1 50 2 00 + 28 00 + 12 75 = 64 13 kN m . Bending moment (@ mid‐span): M Ed = 1 50 – 1 13 + 24 00 + 35 06 = 86 90 kNm m . Topic: User’s Manual/Verification tests - EN1991-1-6.xls page 405 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 Note. Loads Q ce due to accumulation of waste materials may vary significantly, and over short time periods, depending on types of materials, climatic conditions, build‐up and clearance rates, and they can also induce possible mass effects on horizontal, inclined and vertical elements (such as walls). example-end EXAMPLE 1-AC‐ Pre‐dimensioning and calculation of the bridge slab transverse reinforcing steel ‐ test4 Given: Let us suppose that the design moment over the main steel girdes and at mid‐span of the slab (between the main steel girders) is equal to approximately 3 times the maximum value calculated during execution phase. The slab depth varies from 0,4 m over the girders to 0,25 m at its free edges and 0,30 m at the central point. Find the main tensile transverse reinforcement, using for the concrete a simplified rectangular stress distribution (EN 1992‐1‐1 Cl. 3.1.7(3)) for grades of concrete up to C50/50. (Concrete class C35/45 and reinforcing bars used are class B high bond bars with a yield strength f yk = 500 MPa . [Reference sheet: BridgeDeck]‐[PreCalculus Excel® form: Cell‐Row: 133 and 241]. Solution: For grades of concrete up to C50/60: f cd = cc f ck c = 0 85f ck 1 5 f yd = f yk s = f yk 1 15 = 0 87f yk . For singly reinforced sections, the design equations can be derived as follows: F c = 0 85f ck 1 5 b 0 8x = 0 4533f ck bx (compression concrete) F st = 0 87f yk A s (main tensile steel reinforcement). Design moment about the centre of the tension force (beam lever arm “z”): M = 0 4533f ck bx z = 0 4533f ck b 2 5 d – z z = 1 1333f ck b zd – z 2 . Figure 1.37 Singly reinforced section: beam lever arm “z”. page 406 Topic: User’s Manual/Verification tests - EN1991-1-6.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 Let K = M bd 2 f ck , therefore 1 1333f ck b zd – z 2 M - = ------------------------------------------------z- – --z- 2 . K = -------------= 1 1333 -d d bd 2 f ck bd 2 f ck Solving the quadratic equation with the limit d 0 8x : z --- = 0 5 1 + 1 – 3 529K , z = 0 5d 1 + 1 – 3 529K . d Note It is considered good practice in the UK to limit “z” to the maximum value 0,95d. This guards against relying on very thin sections of concrete which at the extreme top of a section may be of questionable strength. Taking moments about the centre of the compression force we obtain the area of the main tensile reinforcement: M A s = ------------------------------ (req’ d) 0 87f yk z if K < K’, where K’ is used to limit the depth of the neutral axis to avoid “overreinforcement” (i.e. to ensure that the reinforcement is yelding at failure, thus avoiding brittle failure of the concrete). Conversely, if K > K’ the section should be resized or compression reinforcement is required. Note In line with consideration of good practice outlined above, the Excel form (Bending) allows the free choice of the redistribution ratio with the following recommended values:(1) k1 = 0,44, k2 = 1,25(0,6 + 0,0014/cue) and k5 = 0,7 (class B and C steel reinforcement). For example, to obtain K’ = 0,167 the input requires = 1 (default input value). Design ultimate bending moment due to ultimate loads: M Ed 3 max M kA ;M kB = 3 87 kNm m 260 kNm m . Let us assume an effective depth of tension reinforcement of about: d = 0 85h = 0 85 300 mm = 255 mm (at mid‐span of the slab) d = 0 85h = 0 85 400 mm = 340 mm (section above the main steel girders). At mid‐span: M Ed 260 10 6 = ------------------------------------------- = 0 114 K = 0 167 (singly reinforced section). K = ------------------ 1000 255 2 35 bd 2 f ck Section above the main steel girders: M Ed 260 10 6 = ------------------------------------------- = 0 064 K = 0 167 (singly reinforced section). K = ------------------ 1000 340 2 35 bd 2 f ck (1) EN 1992-1-1 Cl. 5.5(4) - Note. Topic: User’s Manual/Verification tests - EN1991-1-6.xls page 407 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 Figure 1.38 PreCalculus Excel® form: procedure for a quick pre-calculation: @ mid-span. At mid‐span: z = 0 5d 1 + 1 – 3 529K = 0 5 255 1 + 1 – 3 529 0 114 = 226 1 mm 0 95d Section above the main steel girders: z = 0 5d 1 + 1 – 3 529K = 0 5 340 1 + 1 – 3 529 0 064 = 319 8 mm 0 95d . Area of tensile reinforcement At mid‐span: M Ed 260 10 6 A s = -----------------------------= ------------------------------------------------ = 2644 mm 2 m (try H25 @ 170 mm) 0 87f yk z 0 87 500 226 Section above the main steel girders: M Ed 260 10 6 A s = -----------------------------= ------------------------------------------------ = 1869 mm 2 m (try H20 @ 170 mm). 0 87f yk z 0 87 500 320 page 408 Topic: User’s Manual/Verification tests - EN1991-1-6.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 Figure 1.39 PreCalculus Excel® form: procedure for a quick pre-calculation: @ section above the main steel girders. 1.8 References [Section 1] EN 1991-1-6:2005/AC:2013. Eurocode 1 - Actions on structures Part 1-6: General actions - Actions during execution. CEN/TC 250 Structural Eurocodes, February 2013 EN 1991-1-6:2005. Eurocode 1 - Actions on structures Part 1-6: General actions - Actions during execution. June 2005 JRC Scientific and Technical Reports. Bridge Design to Eurocodes Worked examples. Worked examples presented at the Workshop “Bridge Design to Eurocodes”, Vienna, 4-6 October 2010. Support to the implementation, harmonization and further development of the Eurocodes. Editors A. Athanasopoulou, M. Poljansek, A. Pinto G., Tsionis, S. Denton Topic: User’s Manual/Verification tests - EN1991-1-6.xls page 409 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN S ECTION 1 E UROCODE 1 EN 1991-1-6 Worked Examples to Eurocode 2: Volume 1. MPA - The Concrete Centre. 2012 1.9 Vba References MODULE NAME: modPastePicture. Author: STEPHEN BULLEN, Office Automation Ltd - 15 November 1998. http://www.oaltd.co.uk. page 410 Topic: User’s Manual/Verification tests - EN1991-1-6.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 Annex 1 Flexure_EC2 1.1 General: FlexureRectangularBeamsAndSlabs.xls T his sheet allows for the design of a section of solid slab or a rectangular beam section. The spreadsheet calculates the area of longitudinal steel reinforcement in accordance with EN 1992-1-1:2004 Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings. All applied loads and moments should be ultimate and positive, as positive moments induce tension in the bottom reinforcement ( A s ). The user is required to input desired amounts of redistribution to the initial moments according to Cl. 5.5(4) “Linear elastic analysis with limited redistribution”. With respect to cantilevers, the additional tensile force in the longitudinal reinforcement due to shear (input V Ed 0 ) in the design section is calculated from Exp. (6.18) - Cl. 6.2.3(7). With regard the concrete, the minimum strength used is C12/15 (Table 3.1). The spreadsheet allows input for grades of concrete up to C50/60. Input is self explanatory but, in order to facilitate use of this spreadsheet, some degree of automation has been introduced. The rectangular stress block shown in EN 1992-1-1, Figure 3.5 “Rectangular stress distribution” is used. Where more than one horizontal layer of bars are required per section, the user may choose to specify up to 4 separate layers per reinforcement in order to increase section strength. The spreadsheet takes automatic measures to ensure minimum spacing of reinforcement is met (Cl. 8.2(3) “Spacing of bars”). Combo-boxes to the right under “DETAILING” Excel® Form define minimum bar sizes to be used. Combo-box to the right under “PreCalculus” Excel® Form define concrete characteristic compressive strength at 28 days. To ensure proper placing and compaction of concrete around reinforcement, a maximum steel content is also specified and checked. Thus the maximum area of tension reinforcement in a beam (or solid slab) should not exceed 4 per cent of the gross cross-sectional area of the concrete (Cl. 9.2.1.1). No check is performed in order to control cracking of the concrete. Therefore the minimum area of tension reinforcement is checked (Exp. 9.1N, Cl. 9.2.1.1). Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls page 411 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 To avoid sudden failure it is important to ensure that the tension steel reaches its yield stress before the concrete fails in compression. Tests on beams have shown that the steel yields before the concrete crusches when the depth “x” to the NA (neutral axis) depth does not exceed 0 45d (with “d” effective depth of tension reinforcement) and hence that the steel in tension will reach its ultimate stress before the concrete fails in compression. If the value K = M bd 2 f ck for a particular beam or slab was found to be greater then a particular limit K it would indicate that the concrete above the NA was overstressed in compression. Therefore either the beam (or slab) would have to be increased in size, or compressive reinforcement would have to be introduced above the NA to assist the concrete. Compression reinforcement ( A s2 ) is checked and eventually calculated. No check is performed in order to control beam deflection. NOTE for freeware version: in each analysis it has been assumed that the compression steel has yielded so that the steel stress is always equal to 0,87fyk. 1.2 Layout The basic layout for Flexure_EC2 sheet is shown on the following screen dump: Figure 1.40 Sheet “Splash” from Excel® 2003. page 412 Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 PreCalculus Form: Figure 1.41 Input (white blank test boxes) and calculus (blue text boxes). Default value for = 1 (red). Figure 1.42 Input values k1, k2 and k5. Default values (EN 1992-1-1). Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls page 413 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 View Notes Form: Figure 1.43 Example. Required compression and tensile reinforcement. N. Annex Form: DETAILS Form: Figure 1.44 Coloured in blue the necessary inputs. How to remove links to Excel file “FlexureRectangularBeamsAndSlabs.xls”: page 414 Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 1.3 Output - Word document (calculation sheet) Example calculation sheet (output): Figure 1.45 Sample print with compression steel (Word® Office® must be installed on your system). Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls page 415 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 1.4 Flexure_EC2 (Beams and slabs) derived formulae According to EN 1992-1-1 Sec. 3.1.6 “Design compressive and tensile strengths” the rectangular stress block shown in the Figure 1.46 below is used: Figure 1.46 Strain and design forces in a section. As = tensile reinforcement. As2 compression reinforcement. Beam cross-section with height “h” and width “b”. We know from theory of bending that when bending is induced in a rectangular beam the material fibres above the neutral axis are subjected to compressive stresses and those below to tensile stresses. Concrete has excellent qualities for resisting compression. However, its resistance to tension is so poor that it is ignored. Instead, steel reinforcement is introduced to resist tension. For any beam to be adequate in bending, its internal moment of resistance must not be less than the externally applied bending moment. Therefore the design ultimate resistance moment M of a concrete beam (or slab) must be greater than or at least equal to the ultimate bending moment MEd. SINGLY REINFORCED SECTIONS. For grade of concrete up to C50/60:(1) cu = 3 5 1000 , = 1 and = 0 8 (see figure above). The ultimate design strength of concrete and steel are respectively: f cd = cc f ck c = 0 85f ck 1 5 f yd = f yk s = f yk 1 15 = 0 87f yk . For singly reinforced section, the design equation can be derived as follow (see Figure 1.47 below): F c = 0 85f ck 1 5 b 0 8x = 0 453f ck bx F st = 0 87A s f yk Considering moment about the centroid of the tension force: (1) Cm/n means: fck = m [MPa] and fck,cube = n [MPa]. page 416 Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 Figure 1.47 Singly reinforced beam lever arm “z”. M = 0 453f ck bx . With z = d – 0 4 x and x = 2 5 d – z : M = 0 453f ck b2 5 d – z z M = 1 1333f ck b zd – z 2 Let K = M bd 2 f ck , 1 1333f ck b zd – z 2 M K = -------------- = ------------------------------------------------2 bd f ck bd 2 f ck z 2 K = 1 1333 --z- – --- . d d Solving the quadratic equation, for the solution with the limit d > 0,8x: z --- = 0 5 1 + 1 – 3 529K . d Note The spreadsheet check and respect the limit z < 0,95d. The area of reinforcement required ( M = MEd ) is: M Ed A s = --------------------. 0 87f yk z REDISTRIBUTION RATIO According to Cl. 5.5(4) the ratio xu/d is restricted by the amount of redistribution carried out. Where xu is the depth of the NA at ULS after redistribution. For f ck 50 MPa : x k 1 + k 2 -----u k 5 where Class B and Class C reinforcement is used (see Annex C). d Note The values of k1, k2 and k5 for use in a Country may be found in the National Annex. The user may choose to specify which values to be used in the calculation. Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls page 417 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 Assuming for example k1 = 0,4 and k2 = 1: x 0 4 + -----u 0 7 d x for -----u = 0 45 d xu ----- 0 3 d xu ----- – 0 4 and d 0 45 + 0 4 = 0 85 . Assuming x u = 0 45d : M = 0 453f ck bx u z M = 0 453f ck b 0 45d d – 0 4 0 45d M = 0 167f ck bd 2 Therefore (for k1 = 0,4 and k2 = 1): M - = 0 167 (see also Table below): K = -------------f ck bd 2 1 0,95 0,9 0,85 0,8 0,75 0,7 % redistribution 0 5 10 15 20 25 30 0,208 0,195 0,182 0,167 0,153 0,137 0,120 K’ Table 1.17 Limits on K’ with respect to redistribution ratio for k1 = 0,4 and k2 = 1,0. Note - Cl. 5.5(4). COMPRESSION REINFORCEMENT. The majority of beam used in practice are singly reinforced, and these beams can be designed the formula mentioned above. In some cases, compression reinforcement is added in order to: 1. increase section strength (i.e. where K K ) 2. to reduce long term deflection 3. to decrease curvature/deformation at ultimate limit state (ULS). With reference to Figure 1.46, we need to consider an extra compression force: F sc = A s2 s2 where sc is the stress value of the compression steel: 0 < sc < 0,87fyk = fyd. From the proportion of the strain distribution diagram: cu3 s2 --------------- = -------xu xu – d2 s2 0035--------------- = 0----------------xu – d2 xu s2 0 0035 ---------------= ------------------ . xu d2 xu ----- – --------d d d (Eq. 1‐50) 0 87f yk Let s2 lim el = d 2 d lim el for s2 = -----------------: Es x 0 87f yk s2 lim el = -----u 0 0035 – ----------------- 0 0035 . d Es page 418 (Eq. 1‐51) Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 For f yk = 500 MPa , E s = 200000 MPa and x u d = 0 45 : s2 lim el = 0 170 . If 2 = d 2 d s2 lim el , then it is necessary to calculate the strain s2 from the Eq. 1-50: s2 0 0035 --------------- = -----------------x x -----u ----u- – 2 d d s2 x -----u – 2 d = 0 0035 ---------------- . x -----u d (Eq. 1‐52) s2 s2 0 87 f yk Let s2 = -----------------within the range 0 s2 1 with s2 = --------------------------: 0 87f yk Es s2 x -----u – 2 Es d = ----------------- 0 0035 ---------------- . 0 87 f yk x -----u d (Eq. 1‐53) Therefore, for 2 = d 2 d s2 lim el it is 0 s2 1 (compression steel not yielded). For 2 s2 lim el it is s2 = 1 s2 = 0 87f yk (compression steel yielded). The area of tension reinforcement can be considered in two parts: 1. the first part to balance the compressive force above del NA (concrete) 2. the second part to balance the force in the compression steel. When a compression reinforcement is required ( K K ) then: Kf ck bd 2 A s = FIRST PART + SECOND PART = --------------------+ A s2 s2 0 87f yk z where --z- = 0 5 1 + 1 – 3 529K (in this case using K instead of K ). d Note The spreadsheet check and respect the limit z < 0,95d. Taking moments about the centroid of the tension force (see Figure 1.46): M = M + s2 A s2 d – d 2 2 M = Kf ck bd + s2 A s2 d – d 2 Rearranging: K – K f ck bd 2 K – K f ck bd 2 A s2 = ------------------------------------ = ------------------------------------------------------. s2 d – d 2 s2 0 87f yk d – d 2 1.5 Verification tests FLEXURERECTANGULARBEAMSANDSLABS.XLS. 5.09 MB. Created: 16 December 2013. Last/Rel.-date: 16 December 2013. Sheets: — Splash — CREDITS. Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls page 419 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 EXAMPLE 1-AD‐ Pre‐dimensioning of a rectangular section with compression reinforcement ‐ test1 Given: A rectangular concrete beam (width b = 350 mm, height = 300 mm) is required to resist an ultimate moment of MEd = 214 kNm (assuming – 20% moment redistribution: = 0,80). If the beam is compose of grade 35 concrete and high yield (HY) reinforcement, determine the area of the steel required. Solution: According to Figure 1.46 let us assume: d 2 = 46 mm and an effective depth d = 228 mm . Figure 1.48 Cross-section details with d2 = 46 mm and d = 227,5 mm. Ratio of the redistributed moment to the elastic bending moment: = 0 80 k 1 + k 2 x u d for f ck 50 MPa . Let us assume k 1 = 0 4 , k 2 = 1 and k 5 = 0 7 Figure 1.49 Cl. 5.5(4) for grade of concrete up to fck = 50 MPa. page 420 Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 = 0 80 0 4 + 1 0 6 + 0 0014 cu2 x u d k 5 = 0 7 (for reinforcement Class B and C). With cu2 = 0 0035 (for f ck 50 MPa ): x u d = 0 40 for linear elastic analysis with limited redistribution): K = 0 453 1 – 0 4 x u d x u d = 0 152 . COMPRESSIVE STEEL. d 2 = 46 mm < x u = 0 40 228 = 91 mm (satisfactory). 2 = d 2 d = 0 202 . Let Es s2 200000 0 0035 0 0035 s2 = ----------------- ------------------ x u d – 2 = ------------------ ------------------ 0 40 – 0 202 = 0 80 = -----------------0 87f yk x u d 435 0 40 0 87f yk 0 0035 – 0 87f yk E s 0 0035 ------------------ = -------------------------------------------------- s2 lim el xu d 0---------------- 00350 0035 – 435 200000 = ------------------------------------------------------0 40 s2 lim el s2 lim el = 0 151 2 s2 lim el compressed steel not yielded: s2 = s2 0 87f yk = 0 80 0 87 500 = 348 MPa FLEXURAL DESIGN. M Ed 214 10 6 - = 0 336 K = 0 152 (provide compression reinforcement). K = -------------- = ----------------------------------2 350 228 2 35 bd f ck For d > 0,8xu using K instead K : z d = 0 5 1 + 1 – 3 529 K 0 5 = 0 5 1 + 1 – 3 529 0 152 0 5 = 0 840 < 0,95. Beam lever arm: z = 0 840d = 0 84 228 = 192 mm . AREA OF THE COMPRESSION REINFORCEMENT REQUIRED: K – K f ck bd 2 0 336 – 0 152 35 350 228 2 A s2 = ------------------------------------ = ---------------------------------------------------------------------------------- = 1850 mm 2 s2 d – d 2 348 228 – 46 Try 5H22 x 1 layers. Single layer with: H22 @ 65 mm. PERCENTAGE AREA OF THE COMPRESSION REINFORCEMENT PROVIDED: s2 = 100 A s2 bd = 100 1900 350 228 = 2 38 % < 4bh/100 = As,max (satisfactory). AREA OF TENSION REINFORCEMENT REQUIRED: With z = 192 mm 0 95d : Kf ck bd 2 Kf ck bd 2 K – K f ck bd 2 Kf ck bd 2 K – K f ck bd 2 A s = --------------------+ A s2 s2 = --------------------+ ------------------------------------- s2 = --------------------+ ------------------------------------- s2 d – d 2 0 87f yk z 0 87f yk z 0 87f yk z 0 87f yk d – d 2 Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls page 421 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 Figure 1.50 PreCalculus Excel® form: procedure for a quick pre-calculation: using UK Annex of EC2. Kf ck bd 2 K – K f ck bd 2 0 152 35 350 228 2 + 1850 0 80 = 2639 mm 2 A s = --------------------+ ------------------------------------- s2 = ------------------------------------------------------------ s2 d – d 2 0 87f yk z 0 87 500 192 Try 2H25 x 2 layers. Single layer with: H25 @ 128 mm. PERCENTAGE AREA OF THE COMPRESSION REINFORCEMENT PROVIDED: s2 = 100 A s2 bd = 100 1900 350 228 = 3 69 % < 4bh/100 = As,max (satisfactory). 1.6 Excel VBa Code (main) Private Sub Cmb_Calculus_Click() '--------------------------------------------------------Dim fy As Variant Dim b As Variant Dim h As Variant Dim d1 As Variant Dim d2 As Variant Dim Kpr As Variant Dim fck As Variant Dim M1 As Variant page 422 Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 Dim delta As Variant Dim k2 As Variant Dim Dim Dim Dim Dim Alfa2 As Variant sigma2 As Variant xu As Variant Dim Gamma2 As Variant Gamma2Lim As Variant d2max As Variant Dim Mprint As Variant Dim Dim Dim Dim Dim Dim Dim Dim K As Variant z As Variant DeltaM As Variant M As Variant A As Variant NUM As Variant DEN As Variant A2 As Variant Dim Dim Dim Dim T As Double T1 As Double NIRQ As Double NIRQ1 As Double Dim z1 As Variant '--------------------------------------------------------- '--------------------------------------------------------******Check input '--------------------------------------------------------fck = Worksheets("frmB").Range("A16").Value k2 = Worksheets("frmB").Range("G8").Value k1 = Worksheets("frmB").Range("G7").Value h = Worksheets("frmB").Range("M6").Value d1 = Worksheets("frmB").Range("M7").Value d2 = Worksheets("frmB").Range("M8").Value DeltaM = Worksheets("frmB").Range("M9").Value M = 1 * M1 + 1 * DeltaM Mprint = M / (10 ^ 6) Worksheets("frmB").Range("M11").Value = Round(Mprint, 2) TextBox_M = Worksheets("frmB").Range("P11").Value Worksheets("frmB").Range("E11").Value = delta xu = (delta - k1) / k2 Kpr = 0.453 * xu * (1 - 0.4 * xu) 'Kpr = Worksheets("frmB").Range("H14").Value 'TextBox_Kpr = Worksheets("frmB").Range("J14").Value TextBox_Kpr = Round(Kpr, 3) TextBox_h = Worksheets("frmB").Range("M6").Value TextBox_d1 = Worksheets("frmB").Range("M7").Value TextBox_d2 = Worksheets("frmB").Range("M8").Value TextBox_DeltaM = Worksheets("frmB").Range("S9").Value Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls page 423 (This page intentionally left blank) TextBox_k1 = Worksheets("frmB").Range("E7").Value TextBox_k2 = Worksheets("frmB").Range("E8").Value TextBox_k5 = Worksheets("frmB").Range("E9").Value TextBox_VEd = Worksheets("Linked").Range("C59").Value TextBox_cotT = Worksheets("Linked").Range("C60").Value TextBox_Alfa = Worksheets("Linked").Range("C61").Value '--------------------------------------------------------- If ((fy * b * h * d1 * Kpr * M = 0) Or (d2 + d1 >= h) Or (d2 >= xu * (h - d1)) Or (Alfa2 < 0)) Or ((h <= d1) Or (h <= d2)) Then TextBox_Alert = "Please check your input!" TextBox_Alert2 = "Enter values that are consistent and positive." TextBox_K = "[--]" TextBox_z = "[--]" TextBox_A = "[--]" TextBox_A2 = "[--]" TextBox_d2max = "[--]" TextBox_sigma2 = "[--]" Else '--------------------------------------------------------K = M / (b * fck * (h - d1) ^ 2) T = (1 - 3.529 * K) T1 = (1 - 3.529 * Kpr) '--------------------------------------------------------If K <= Kpr Then '--------------------------------------------------------If (1 - 3.529 * K) < 0 Then TextBox_K = "[--]" TextBox_z = "[--]" TextBox_A = "[--]" TextBox_A2 = "[--]" TextBox_d2max = "[--]" TextBox_sigma2 = "[--]" TextBox_Alert = "Please, check your input!" TextBox_Alert2 = "Case Not Applicable: geometry inadequate." Else '--------------------------------------------------------- If 0.5 * (h - d1) * (1 + Sqr(T)) > 0.95 * (h - d1) Then TextBox_Alert = "Note: singly reinforced section with K =< K' = " & Round(Kpr, 3) & "." TextBox_Alert2 = "z limited to a maximum of 0,95d = " & Round(0.95 * (h - d1), 1) & " mm." z = 0.95 * (h - d1) TextBox_z = Round(z, 0) A = M / (0.87 * fy * z) TextBox_A = Round(A, 0) A2 = 0 TextBox_A2 = Round(A2, 0) TextBox_K = Round(K, 3) TextBox_sigma2 = "[--]" TextBox_d2max = Round(xu * (h - d1), 0) & " mm" TextBox_S = "" TextBox_F = "" Else TextBox_Alert = "Note: singly reinforced section with K <= K' = " & Round(Kpr, 3) & "." z = 0.5 * (h - d1) * (1 + Sqr(T)) TextBox_z = Round(z, 0) E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 TextBox_Alert2 = "z (for K = " & Round(K, 3) & ") = " & Round(z, 1) & " mm < 0,95d = " & Round(0.95 * (h - d1), 1) & " mm." A = M / (0.87 * fy * z) TextBox_A = Round(A, 0) A2 = 0 TextBox_A2 = Round(A2, 0) TextBox_K = Round(K, 3) TextBox_sigma2 = "[--]" TextBox_d2max = Round(xu * (h - d1), 0) & " mm" TextBox_S = "" TextBox_F = "" End If Worksheets("Linked").Range("C43").Value = Round((0.5 * (1 + Sqr(T))), 2) 'single Worksheets("Linked").Range("C44").Value = Round((0.5 * (h - d1) * (1 + Sqr(T))), 1) 'single '--------------------------------------------------------End If '--------------------------------------------------------Else '--------------------------------------------------------If (1 - 3.529 * Kpr) < 0 Then TextBox_K = "[--]" TextBox_z = "[--]" TextBox_A = "[--]" TextBox_A2 = "[--]" TextBox_d2max = "[--]" TextBox_sigma2 = "[--]" TextBox_Alert = "Please, check your input!" TextBox_Alert2 = "Case Not Applicable: geometry inadequate." Else '--------------------------------------------------------- Gamma2 = d2 / (h - d1) Gamma2Lim = (xu) * (0.0035 - (0.87 * fy / 200000)) / 0.0035 d2max = xu * (h - d1) TextBox_d2max = Round(d2max, 0) & " mm" If (Gamma2 <= Gamma2Lim) Then Alfa2 = 1 TextBox_F = "(compressed steel yielded: d2/d = " & Round(Gamma2, 3) & " <= (d2/d)lim,el = " & Round(Gamma2Lim, 3) & ")." sigma2 = 0.87 * fy TextBox_sigma2 = Round(sigma2, 0) TextBox_S = "Sigma_s2 = 1,00 x 0.87fyk." Else Alfa2 = (200000 / (0.87 * fy)) * (0.0035 / xu) * (xu - Gamma2) TextBox_F = "(compressed steel not yielded: d2/d = " & Round(Gamma2, 3) & " > (d2/d)lim,el = " & Round(Gamma2Lim, 3) & ")." sigma2 = Alfa2 * 0.87 * fy TextBox_sigma2 = Round(sigma2, 0) TextBox_S = "Sigma_s2 = " & Round(Alfa2, 3) & " x 0.87fyk." End If If 0.5 * (h - d1) * (1 + Sqr(T1)) > 0.95 * (h - d1) Then TextBox_Alert = "Provide compression steel: K > K'. Recalculate for d2 > 0." TextBox_Alert2 = "z (for K' instead of K) limited to a maximum of 0,95d = " & Round(0.95 * (h - d1), 1) & " mm." z = 0.95 * (h - d1) Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls page 425 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 TextBox_z = Round(z, 0) A2 = ((K - Kpr) * fck * b * (h - d1) ^ 2) / (Alfa2 * 0.87 * fy * (h d1 - d2)) TextBox_A2 = Round(A2, 0) A = ((K - Kpr) * fck * b * (h - d1) ^ 2) / (0.87 * fy * (h - d1 - d2)) + (Kpr * fck * b * (h - d1) ^ 2) / (0.87 * fy * z) TextBox_A = Round(A, 0) TextBox_K = Round(K, 3) Else TextBox_Alert = "Provide compression steel: K > K'. Recalculate for d2 > 0." z = 0.5 * (h - d1) * (1 + Sqr(T1)) TextBox_z = Round(z, 0) TextBox_Alert2 = "z (for K' instead of K) = " & Round(z, 1) & " mm < 0,95d = " & Round(0.95 * (h - d1), 1) & " mm." A2 = ((K - Kpr) * fck * b * (h - d1) ^ 2) / (Alfa2 * 0.87 * fy * (h d1 - d2)) TextBox_A2 = Round(A2, 0) A = ((K - Kpr) * fck * b * (h - d1) ^ 2) / (0.87 * fy * (h - d1 - d2)) + (Kpr * fck * b * (h - d1) ^ 2) / (0.87 * fy * z) TextBox_A = Round(A, 0) TextBox_K = Round(K, 3) End If Worksheets("Linked").Range("D43").Value = Round((0.5 * (1 + Sqr(T1))), 2) 'double Worksheets("Linked").Range("D44").Value = Round((0.5 * (h - d1) * (1 + Sqr(T1))), 1) 'double '--------------------------------------------------------End If '--------------------------------------------------------End If '--------------------------------------------------------Worksheets("Linked").Range("C30").Value = b Worksheets("Linked").Range("C31").Value = h Worksheets("Linked").Range("C32").Value = M / (10 ^ 6) Worksheets("Linked").Range("C35").Value = fy Worksheets("Linked").Range("C38").Value = (h - d1) Worksheets("Linked").Range("C39").Value = d2 Worksheets("Linked").Range("C41").Value = Round(K, 3) Worksheets("Linked").Range("C45").Value = Round(A2, 0) Worksheets("Linked").Range("C47").Value = Round(A, 0) ' fine scrittura output '-------------------------------------------------------End If page 426 Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 F LEXURE _EC2 1.7 References BRITISH STANDARDS INSTITUTION. The structural use of concrete – Part 1: Code of practice for design and construction, BS 8110–1:1997 EN 1992-1-1:2004. Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings. Brussels: CEN/TC 250 - Structural Eurocodes, December 2004 (DAV) EN 1992-1-1:2004/AC:2010. Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings. Brussels: CEN/TC 250 Structural Eurocodes, December 2010Reinforced Concrete Design to Eurocode, Bill Mosley, John Bungey and Ray Hulse, Palgrave Macmillan. 7th Edition JRC Scientific and Technical Reports. Bridge Design to Eurocodes Worked examples. Worked examples presented at the Workshop “Bridge Design to Eurocodes”, Vienna, 4-6 October 2010. Support to the implementation, harmonization and further development of the Eurocodes. Editors A. Athanasopoulou, M. Poljansek, A. Pinto G., Tsionis, S. Denton MPA The Concrete Centre. Worked Examples to Eurocode 2: Volume 1. Practical Design to Eurocode 2. 2013 Reinforced Concrete Design to Eurocode, Bill Mosley, John Bungey and Ray Hulse, Palgrave Macmillan. 7th Edition. Topic: User’s Manual/Verification tests - FlexureRectangularBeamsAndSlabs.xls page 427 (This page intentionally left blank) Annex 1 BiaxialBending(2)_EC2 (Commercial version) 1.1 General: BiaxialBending(2).xls T his sheet allows for the design of a column section and checks the area of longitudinal steel reinforcement in accordance with EN 1992-1-1:2004 Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings. The spreadsheet gives two interaction charts for moments M Edx and M Edy against axial load N Ed for rectangular sections of “short columns” with symmetrical or asymmetrical reinforcement arrangements according to Sec. 5.8.9 “Biaxial Bending”, Exp. (5.39) and estimates the approximate moment curvature relationship (elastic and post-peak branch) of columns with concrete strength ranging from fck = 12 MPa to fck = 90 MPa confined with steel (e.g. overlapping hoopsets) with yield strength ranging from 400 to 600 MPa using the model proposed by Kent & Park (1971). In this spreadsheet a simplified stress-strain model is used in order to be easily adapted for hand analysis to enable rapid design checks to be performed. The majority of reinforced concrete columns are subjected to primary stresses caused by flexure, axial force, and shear. Secondary stresses associated with deformations are usually very small in most columns used in practice. These columns are referred to as “short columns”. In this sheet it is assumed that the design moments M Edx and M Edy entered have already been adjusted in order to take into account the 2nd order effect in each direction x-x and y-y. Long columns, columns with small cross-sectional dimensions, and columns with little end restraints may develop secondary stresses associated with column deformations, especially if they are not braced laterally. These columns are referred to as “slender columns”. Consequently, slender columns resist lower axial loads than short columns having the same cross-section. Failure of a slender column is initiated either by the material failure of a section, or instability of the column as a member, depending on the level of slenderness. The latter is known as column buckling. NOTE: no check is performed in order to control column buckling. Topic: User’s Manual/Verification tests - BiaxialBending(2).xls page 429 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) Moments are considered to be about the x-x and y-y axis. All applied loads and moments should be ultimate and positive, as positive moments induce tension in the bottom reinforcement A sx (and A sy ). With asymmetrical arrangements of reinforcement the diagrams indicate that negative moments are theoretically possible. After much consideration, the diagram is considered to be correct but strictly is valid only for load cases where the moments are positive with at least minimum eccentricity. This limit is shown on the graph ( M min = max h 30 ; 20 mm )(1). A reciprocal diagram is generated automatically when top and bottom steels are reversed in the input. With regard the concrete, the minimum strength used is C12/15. The spreadsheet allows input for grades of concrete up to C90/105 (see Table 3.1). Input is self explanatory but, in order to facilitate use of this spreadsheet, some degree of automation has been introduced. The rectangular stress block shown in EN 1992-1-1, Figure 3.5 “Rectangular stress distribution” is used. To ensure proper placing and compaction of concrete around reinforcement, a maximum steel content is also specified and checked. Thus the maximum area of tension reinforcement in a column should not exceed 4 per cent of the gross cross-sectional area of the concrete (Cl. 9.5.2). No check is performed in order to control cracking of the concrete. Therefore the minimum area of tension reinforcement is checked (Exp. 9.12N, Cl. 9.5.2(2)). The coordinates of the points on the failure surface are determined by rotating a plane of linear strain in two dimensions ( N Rd ; M Rd ) on the column section. The linear strain diagram limits the maximum concrete strain, c , at the extremity of the section to 3,5/1000 (EC2 Table 3.1). The formulation is based consistently upon the general principles of ultimate strength design (EC2 6.1). The stress in the steel is given by the product of the steel strain and the steel modulus of elasticity, s = s E s , and is limited to the yield stress of the steel, f yd = constant (EC2 3.2.7). The area associated with each reinforcing bar is assumed to be placed at the actual location of the center of the bar, and the algorithm does not assume any further simplifications with respect to distributing the area of steel over the cross-section of the column. Therefore the spreadsheet can take automatic measures to ensure minimum spacing of reinforcement is met (Cl. 8.2(3) “Spacing of bars”). Note This sheets “MEdx”, “MEdx (u)”, “MEdy” and “MEdy (u)” show workings and are not necessarily intended for printing out other than for checking purposes. The Excel file is linked to a standard report in Word and saves all the data as a new Word file (calculation sheet). NOTE for freeware version: the user may choose to specify only two concrete classes: C20/25 and C25/30. The coefficient cc taking account of long term effects on the compressive strength and of unfavourable effects resulting from the way the load is applied was set equal to 0,85 = constant. Nominal cover to enclosing link was set equal to 25 mm = constant and the diameter of enclosing link was set equal to 8 mm = constant. (1) See EN 1992-1-1: 2004, Cl. 6.1(4). page 430 Topic: User’s Manual/Verification tests - BiaxialBending(2).xls A NNEX 1 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) 1.2 Output - Word document (calculation sheet) Example calculation sheet (output): Figure 1.51 Sample print with compressive steel (Word® Office® must be installed on your system). Topic: User’s Manual/Verification tests - BiaxialBending(2).xls page 431 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) 1.3 BiaxialBending(2)_EC2 (“short columns”) derived formulae According to EN 1992-1-1 Sec. 3.1.6 “Design compressive and tensile strengths” the rectangular stress block shown in the Figure 1.52 below is used: Figure 1.52 Strain and design forces in a section. As = tensile reinforcement. As2 compressive reinforcement. Column cross-section with height “h” and width “b”. The concrete compressive stress block is assumed to be rectangular, with an effective strength of f cd (EC2 3.1.7) and effective height of x , as shown in Figure 1.52, where is taken as: = 1 0 for f ck 50 MPa (Eq. 1‐54) f ck – 50 - for 50 MPa f ck 90 MPa = 1 0 – ---------------------200 (Eq. 1‐55) and is taken as: = 0 8 for f ck 50 MPa (Eq. 1‐56) f ck – 50 - for 50 MPa f ck 90 MPa . = 0 8 – ---------------------400 (Eq. 1‐57) The depth of the equivalent rectangular block is referred to as d c (see figure above), such that: d c = x . (Eq. 1‐58) where x is the depth of the stress block in compressive. page 432 Topic: User’s Manual/Verification tests - BiaxialBending(2).xls A NNEX 1 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) Default values for c , s , cc , E s are provided by the spreadsheet but can be overwritten by the user. The design is based on the nominal cross-section area of the reinforcement and the design values derived from the characteristic values given in Sec. 3.2.2. The following assumption is made for the design stress-strain diagram for reinforcing steel: horizontal top branch without the need to check the strain limit (see case b in Figure 3.8). The behaviour of the steel is identical in tension and compressive, being linear in the elastic range up to the design yield stress f yd = f yk s = 0 87f yk , where f yk is the characteristic yield stress and s = 1 15 is the partial factor of safety. Within the elastic range, the relationship between the stress and strain is: s = Es s (Eq. 1‐59) f yd f yk s so that the design yield strain is yd = ----- = ------------------ at the ultimate limit for Es Es f yk = 500 MPa : f yk s 500 1 15 yd = ------------------ = ----------------------------= 0 00217 . 5 Es 2 0 10 Note It should be noted that EC2 permits the use of an alternative design stress‐strain curve (see case “a” in Figure 3.8) with an inclined top branch and the maximum strain limited to a value which is dependent on the class of reinforcement. However only the more commonly used curve (a) shown in Figure 3.8 will be used in this spreadsheet. BENDING PLUS AXIAL LOAD AT THE ULS. The applied axial force N Ed may be tensile (negative) or compressive (positive). In the analysis that follows, a compressive force is considered. For a tensile force the same basic equations of equilibrium, compatibility of strains, and stress-strain relationships would apply, but it would be necessary to change the sign of the applied load ( N Ed 0 ). The cross-section is subjected at least to a moment M Ed 0 and an axial force N Ed 0 . Let • F c be the compressive force developed in the concrete and acting through the centroid of the stress block • F s2 be the compressive force in the reinforcement A s2 and acting trough its centroid • F s be the tensile (or compressive) force in the reinforcement area A s and acting through its centroid. The applied force N Ed must be balanced by the forces developed within the cross-section, therefore: N Ed = F c + F s2 + F s Topic: User’s Manual/Verification tests - BiaxialBending(2).xls (Eq. 1‐60) page 433 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) In this equation F s will be negative whenever the position of the neutral axis is such that the reinforcement A s is in tension. The design moment M Ed (about say the x-x axis) must be balanced by the moment of resistance of the forces developed within the cross-section. Hence, taking moments about the mid-depth of the gross cross-sectional area of the column: x- + F h--- – d – F h--- – d M Ed = F c h--- – ----s2 2 s 2 2 2 2 (Eq. 1‐61) where d = h – d 1 is the effective depth perpendicular to x-x axis. In this equation – F s 0 5h – d will be positive whenever the reinforcement A s is in tension. When the depth of neutral axis is such that x h then the whole concrete section is subject to uniform compressive stress (limited to the value c3 = 0 002 for a rectangular stress block) and hence the expression above must be rewritten in the following form: M Ed = F s2 h--- – d 2 – F s h--- – d 2 2 (Eq. 1‐62) The relative magnitude of the moment M Ed and the axial load N Ed governs whether the section will fail in tension or in compression. With large effective eccentricity ( e = M Ed N Ed ) a tensile failure is likely, but with a small eccentricity a compressive failure is more likely. The magnitude of the eccentricity affects the position of the neutral axis and hence the strains and stresses in the reinforcement. Let • s2 be the compressive strain in reinforcement A s2 (top) • s be the tensile (or compressive) strain in reinforcement A s (bottom) • yd be the tensile yield strain of steel. For values of x less then h , from linear strain distribution (see Figure 1.52): cu3 s2 ------------- = -------x x – d2 x–d s2 = -------------2- 0 0035 x (Eq. 1‐63) cu3 s ----------- = -------x d–x d–x s = ------------ 0 0035 . x (Eq. 1‐64) and Balanced failure s = yd occurs with yielding of the tension steel A s and crusching of the concrete at the same instant: d d x = x bal = -----------------= --------------------------. yd yd 1 + --------1 + ----------------- cu3 0 0035 page 434 (Eq. 1‐65) Topic: User’s Manual/Verification tests - BiaxialBending(2).xls A NNEX 1 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) For example, substituting the values of yd = 0 00217 for grade 500 steel: x bal = 0 617d (Eq. 1‐66) with s2 = s2E s f yd and s = yd E s = f yd . BIAXIAL BENDING ‐ BRESLER METHOD. Separate design in each principal direction, disregarding biaxial bending, may be made as a first step. Imperfections need to be taken into account only in the direction where they will have the most unfavourable effect. In the absence of an accurate cross section design for biaxial bending, the following simplified criterion may be used: M Edx M Edy -----------+ -----------1 M Rdx M Rdy a a (Eq. 1‐67) where, for the given ultimate axial load N Ed on column: • M Edx is the design bending moment about x-x axis (including a 2nd order moment) and M Rdx is the respective ultimate bending moment • M Edy is the design bending moment about y-y axis (including a 2nd order moment) and M Rdy is the respective ultimate bending moment • “a” is the exponent. In particularly, for rectangular cross-sections: N Ed N Rd 0,1 0,7 1,0 a 1,0 1,5 2,0 Table 1.18 Coefficient “a” against ratio NEd/NRd with linear interpolation for intermediate values. where: N Rd = A c f cd + A s tot f yd (Eq. 1‐68) is the design axial resistance of section. A c (for rectangular section A c = bh ) is the gross area of the concrete section and A s tot is the whole area of longitudinal reinforcement. For N Ed 0 (tensile) the above expression must be rewritten in the following form (concrete tensile neglected): N Rd = 0 – A s tot f yd = – A s tot f yd (Eq. 1‐69) always with N Ed N Rd 0 . Interaction diagrams N Rd ; M Rdx and N Rd ; M Rdy can be constructed for any shape of cross-section which has an axis of symmetry by applying the basic equilibrium and strain compatibility equations with the stress-strain relations. These diagrams can be very useful for design purposes. Topic: User’s Manual/Verification tests - BiaxialBending(2).xls page 435 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) 1.4 Verification tests BIAXIALBENDING(2).XLS. 4.94 MB. Created: 15 January 2014. Last/Rel.-date: 15 January 2014. Sheets: — Splash — BiaxBd; KenT_Park; M_Curv — MEdx; MEdx (u) — MEdy; MEdy (u) — CREDITS. EXAMPLE 1-AE‐ M‐N interaction diagrams for a column with symmetrical cross‐section ‐ test1 Given: Construct the interaction diagrams for the column cross‐section shown in figure below with f ck = 30 MPa and f yk = 500 MPa (Class C). Let us assume N Ed = 700 kN > 0 MEdy MEdx Figure 1.53 Symmetrical column cross-section. (compressive), M Edx = 370 kNm and M Edy = 70 kNm . Maximum size of aggregate d g = 25 mm . Coefficient taking account of long term effects on the compressive strength and of unfavourable effects resulting from the way the load is applied: cc = 1 00 . page 436 Topic: User’s Manual/Verification tests - BiaxialBending(2).xls A NNEX 1 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) Note: in this spreadsheet the moments are always taken about the centre‐line of the concrete section and not about to axis referred to as the “plastic centroid” when A s A s2 . Solution: Ultimate design strength of materials: f ck 0 30 - = 1-----------------f cd = cc ----- = 20 00 MPa (concrete) c 1 50 Stress‐strain design diagram (concrete): 3 5- , = 1---------- 75- , = 1 0 , = 0 80 . grade of concrete C30/37 with cu3 = ----------c3 1000 1000 f yk f yk f yd = ------ = ------------ = 0 87f yk = 0 87 500 = 435 MPa (longitudinal reinforcement). s 1 15 67 5 75 - with ud = 0 9 uk = ------------ . Reinforcement (Class C): uk = ----------1000 1000 Stress‐strain design diagram (steel): horizontal top branch without the need to check the strain limit (design assumption). DETAILING (CL. 8.2(2)). Minimum clear distance between vertical links: b – 2 c nom + link = 400 – 2 30 + 10 = 320 mm Maximum number of horizontal bars ( long = H18): N = 5 (1 layer) Minimum clear distance between adjacent horizontal bars H18: b – 2 c nom + link – N long 320 – 5 18 = --------------------------------- = 57 5 mm = -----------------------------------------------------------------------------------N – 1 4 min = max long ; d g + 5 mm ; 20 mm = max 18 ; 25 + 5 mm ; 20 mm = 30 mm min (satisfactory). Note When the diameter and the number of the longitudinal bars are entered, the spreadsheet for each layer checks that (N – 1)min + Nlong < b – 2(cnom + link). In this particular case: (5 – 1)(30 mm) + 5(18 mm) = 210 mm < 320 mm (satisfactory). AREAS OF REINFORCEMENT ‐ BRESLER METHOD For bending moment about x‐x axis (b = 400 mm, h = 650 mm): Top A s2x = 5H18 = 1272 mm 2 , d 2 = c nom + link + 0 5 long = 30 + 10 + 0 5 18 = 49 mm , Bottom: A sx = 5H18 = 1272 mm 2 , d = h – d 1 = 650 – 49 = 601 mm with d 1 = d 2 . (d = 601 mm effective depth perpendicular to x‐x axis). For bending moment about y‐y axis (b = 650 mm, h = 400 mm): Top A s2y = 3H18 + 2H18 = 1272 mm 2 , d 2 = c nom + link + 0 5 long = 30 + 10 + 0 5 18 = 49 mm , Bottom: A sx = 3H18 + 2H18 = 1272 mm 2 , d = h – d 1 = 400 – 49 = 351 mm with d 1 = d 2 . (d = 351 mm effective depth perpendicular to y‐y axis). Topic: User’s Manual/Verification tests - BiaxialBending(2).xls page 437 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) Figure 1.54 Bresler Method (Model): main longitudinal reinforcement areas. MAIN POINTS ON THE INTERACTION DIAGRAM WITH VARYING DEPTHS OF NEUTRAL AXIS X‐X. Point A: s2 = 0 01 ; = 0 @x = h = 650 mm, x = 0 8 650 = 520 mm , x 650 --- = --------------------- = 1 08 . d 650 – 49 s2 0 01 0 00082 - d 1 = – ------------------- s = – ------------49 = – 0 00082 , ------s- = ----------------------------------- = 0 377 1 s f yd , h – d2 650 – 49 435 200000 yd s = s E s = – 0 00082 200000 = – 164 MPa , s2 = f yd = – 435 MPa with s yd . – 164 1272 – 435 1272 N Rd = s A s + f yd A s2 = ----------------------------------------------------------------------= – 762 kN (tensile) 10 3 1272 276 – 435 1272 276 - = – 95 kNm M Rd = – s A s 0 5h – d 1 + f yd A s2 0 5h – d 2 = 164 -----------------------------------------------------------------------------------------10 6 (MRd < 0 when counter‐clockwise). 67 5- ; x ; A = 0 (conrete tensile neglected): Point B: s = s2 = – ud = –---------------c 1000 – 435 1272 + 1272 N Rd = – f yd A s + A s2 = ---------------------------------------------------------- = – 1107 kN (tensile) 1000 M Rd = – f yd A s 0 5h – d 1 + f yd A s2 0 5h – d 2 = 0 (pure tensile). 67 5 Point C: c = 0 @x = 0; s = – ud = – ------------ with s yd s = – f yd = – 435 MPa . 1000 – ud s2 -------- = ----------d d2 d 67 5 49 s2 = – ud -----2 = – ------------ --------------------- = – 0 0055 . d 1000 650 – 49 s2 0 0055 ---------- = ----------------------------------- = 2 5 1 s2 = – f yd = – 435 MPa . 435 200000 yd page 438 Topic: User’s Manual/Verification tests - BiaxialBending(2).xls A NNEX 1 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) 435 1272 – 435 1272 = – 1107 kN (tensile). N Rd = f yd A s + f yd A s2 = –----------------------------------------------------------------------10 3 M Rd = – s A s 0 5h – d 1 + s2 A s2 0 5h – d 2 = f yd A s – A s2x 0 5h – d 1 = 0 (pure tensile). 67 5 75- . Point D: s = – ud = – ------------ ; c = c3 = 1----------1000 1000 c3 1 75 - d = ------------------------------ 601 = 15 mm < d 2 = 49 mm . x = 0 8 15 = 12 mm , x = --------------------- c3 + ud 1 75 + 67 5 x 15 --- = --------- = 0 025 . d 601 With x d 2 : c3 s2 ------------- = -----x x – d2 x–d 1 75 15 – 49 s2 = c3 -------------2- = ------------ ------------------ = – 0 0040 < 0 (tensile). x 1000 15 s2 0 0040 ---------- = ----------------------------------= 1 8 1 s2 = – f yd and s = – f yd (tensile). yd 435 200000 1 0 20 400 0 8 15 – 435 2 1272 N Rd = f cd bx – f yd A s + A s2 = ---------------------------------------------------------------------------------------------------- = – 1011 kN < 0 1000 (tensile). M Rd = f cd bx 0 5h – 0 5x + s2 A s2 0 5h – d 2 – s A s 0 5h – d 1 (moments > 0 when counter‐clockwise) M Rd = f cd bx 0 5h – 0 5x – f yd A s2 + A s 0 5h – d 1 0 20 400 0 8 15 325 – 7 5 + 435 0- = 30 5 kNm M Rd = 1------------------------------------------------------------------------------------------------------------------10 6 (MRd > 0 when clockwise). 67 5 50 Point E: s = – ud = – ------------ ; c = cu3 = 3-----------. 1000 1000 cu3 3 50 - d = ----------------------------x = ----------------------- 601 = 29 6 mm < d 2 = 49 mm . x = 0 8 29 6 = 24 mm , cu3 + ud 3 50 + 67 5 x--- = -------24- = 0 040 . d 601 With x d 2 : cu3 s2 ------------- = -------x x – d2 x–d 3 50 29 6 – 49 s2 = cu3 -------------2- = ------------ ------------------------ = – 0 0023 < 0 (tensile). x 1000 29 6 s2 0 0023 ---------- = ----------------------------------= 1 05 1 s2 = – f yd and s = – f yd (tensile). yd 435 200000 0 20 400 0 8 29 6 – 435 2 1272 - = – 917 kN < 0 N Rd = f cd bx – f yd A s + A s2 = 1--------------------------------------------------------------------------------------------------------1000 (tensile). Topic: User’s Manual/Verification tests - BiaxialBending(2).xls page 439 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) 0 20 400 0 8 29 6 325 – 7 5 + 435 0- = 60 1 kNm M Rd = 1------------------------------------------------------------------------------------------------------------------------10 6 (MRd > 0 when clockwise). 75 Point F: s = – 0 01 ; c = c3 = 1----------- ; = – f yd . 1000 s c3 d 1 75 x - d = ---------------------------- = -------------------- x = ------------------ 601 = 89 5 mm ; x = 0 8 89 5 = 71 6 mm , c3 + s c3 + s 1 75 + 10 c3 x--- = 89 5- = 0 149 . ----------d 601 s2 c3 ------ = ------------x – d2 x x–d 1 75 89 5 – 49 s2 = c3 -------------2- = ------------ ------------------------ = 0 00079 > 0 (compressive). x 1000 89 5 s2 0 00079 ---------- = ----------------------------------- = 0 363 1 s2 f yd , s2 = s2 E s = 0 00079 200000 = 158 MPa , 435 200000 yd s = – f yd = – 435 MPa with s yd . 1 0 20 400 0 8 89 5 + 1272 158 – 435 - = 220 kN > 0 N Rd = f cd bx – f yd A s + s2 A s2 = -------------------------------------------------------------------------------------------------------------------10 3 (compressive). M Rd = f cd bx 0 5h – 0 5x + s2 A s2 0 5h – d 2 – s A s 0 5h – d 1 (moments > 0 when counter‐clockwise) M Rd = f cd bx 0 5h – 0 5x + s2 A s2 0 5h – d 2 + f yd A s 0 5h – d 1 0 20 400 0 8 89 5 325 – 35 8 + 1272 435 + 158 276 = 374 kNm M Rd = 1----------------------------------------------------------------------------------------------------------------------------------------------------------------------10 6 (MRd > 0 when clockwise). Point G: c = cu3 = 0 0035 ; s = – 0 01 with s = – f yd (tensile). cu3 d 3 5 x - = ---------------------- x = ---------------------- d = --------------------- 601 = 155 8 mm ; ------- c3u + s cu3 + s 3 5 + 10 cu3 x = 0 8 155 8 = 124 6 mm , x--- = 155 8- = 0 259 . -------------d 601 s2 c3 ------ = ------------x – d2 x x–d 3 5 155 8 – 49 s2 = cu3 -------------2- = ------------ --------------------------- = 0 00240 > 0 (compressive). x 1000 155 8 s2 0 00240 ---------- = ----------------------------------- = 1 1 1 s2 = f yd , s = – f yd = – 435 MPa with s yd . 435 200000 yd 0 8 20 400 1 0 155 8 + 1272 0 - = 997 kN > 0 N Rd = f cd bx – f yd A s + f yd A s2 = -------------------------------------------------------------------------------------------------10 3 (compressive). M Rd = f cd bx 0 5h – 0 5x + f yd A s2 0 5h – d 2 + f yd A s 0 5h – d 1 1 0 20 400 0 8 155 8 325 – 62 3 + 1272 435 + 435 276 M Rd = -------------------------------------------------------------------------------------------------------------------------------------------------------------------------= 567 kNm 10 6 page 440 Topic: User’s Manual/Verification tests - BiaxialBending(2).xls A NNEX 1 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) (MRd > 0 when clockwise). Note: from stage at point H to stage at point M the equations are the same as shown at point G. The procedure implemented in the spreadsheet is the same and all these intermediate values of N Rd ; M Rd provide a more accurate curve (interation diagram). Therefore: 3 5- ; = – 0 005 ; Point H: c = cu3 = ----------1000 s N Rd = 1583 kN > 0 (compressive); M Rd = 663 kNm . 3 5 Point I: c = cu3 = ----------- ; = – 0 0025 ; 1000 s N Rd = 2243 kN > 0 (compressive); M Rd = 720 kNm . 3 5- ; = – = – f yd = – 435 = – 0 00217 < 0 (tensile) Point J: c = cu3 = --------------------------------yd 1000 s Es 200000 with s = – f yd (tensile). cu3 d 3 5 x - d = ---------------------------------- = ------------------------- x = ----------------------- 601 = 371 0 mm ; c3u + yd cu3 + yd 3 5 + 2 17 cu3 x = 0 8 371 0 = 296 8 mm , x 371 0 --- = --------------- = 0 617 . d 601 s2 c3 ------ = ------------x – d2 x x–d 3 5 371 – 49 s2 = cu3 -------------2- = ------------ --------------------- = 0 0030 > 0 (compressive). x 1000 371 s2 0 0030 ---------- = ----------------------------------= 1 4 1 s2 = f yd , s = – f yd = – 435 MPa with s yd . yd 435 200000 1 0 20 400 0 8 371 + 1272 0 - = 2374 kN > 0 N Rd = f cd bx – f yd A s + f yd A s2 = -------------------------------------------------------------------------------------------10 3 (compressive). M Rd = f cd bx 0 5h – 0 5x + f yd A s2 0 5h – d 2 + f yd A s 0 5h – d 1 0 20 400 0 8 371 0 325 – 148 4 + 1272 435 + 435 276 = 725 kNm M Rd = 1----------------------------------------------------------------------------------------------------------------------------------------------------------------------------10 6 (MRd > 0 when clockwise). 3 5- ; = – 0 0021 ; Point K: c = cu3 = ----------1000 s N Rd = 2441 kN > 0 (compressive); M Rd = 719 kNm . 3 5 Point L: c = cu3 = ----------- ; = – 0 0012 ; 1000 s N Rd = 3112 kN > 0 (compressive); M Rd = 655 kNm . 3 5 - ; = – 0 0002 ; Point M: c = cu3 = ----------1000 s N Rd = 4140 kN > 0 (compressive); M Rd = 522 kNm . Topic: User’s Manual/Verification tests - BiaxialBending(2).xls page 441 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) 3 5- ; x = h (compressive) with x--- = -------------------650 - = 1 08 . Point N: c = cu3 = ----------1000 d 650 – 49 s2 cu3 --------- = ------------h – d1 h h–d 3 5 650 – 49 s2 = cu3 -------------1- = ------------ --------------------- = 0 00324 > 0 (compressive). h 1000 650 s2 0 00324 -------- = ----------------------------------= 1 5 1 s2 = f yd = 435 MPa > 0 (compressive). yd 435 200000 d1 s2 49 - = 0 00324 --------------------- = 0 00026 > 0 (compressive). ------------- = ----s- s = s2 ------------d1 h – d1 650 – 49 h – d1 0 00026 ------s- = ----------------------------------= 0 12 1 s = s E s = 52 MPa > 0 (compressive). yd 435 200000 1 0 20 400 0 8 650 + 52 + 435 1272 N Rd = f cd bx + s A s + f yd A s2 = ----------------------------------------------------------------------------------------------------------= 4779 kN > 0 10 3 (compressive). M Rd = f cd bx 0 5h – 0 5x + f yd A s2 0 5h – d 2 – s A s 0 5h – d 1 0 20 400 0 8 650 325 – 260 + 1272 435 – 52 276- = 405 kNm M Rd = 1------------------------------------------------------------------------------------------------------------------------------------------------------------10 6 (MRd > 0 when clockwise). Point O: c = s = s2 = c3 = 0 00175 > 0 (compressive). yd = 0 00217 > c = s = s2 = c3 = 0 00175 with: s = s2 = 0 00175 200000 = 350 MPa > 0. 20 400 650 + 2 1272 350 - = 6091 kN . N Rd = f cd bh + f yd A s + f yd A s2 = ------------------------------------------------------------------------------10 3 M Rd = s2 A s2 0 5h – d 2 – s A s 0 5h – d 2 = 0 . ULTIMATE BENDING MOMENT ABOUT AXIS X‐X WITH AXIAL COMPRESSIVE FORCE Compressive force (ULS): N Ed = 700 kN . See stages F ( N Rd = 220 kN ; M Rd = 374 kNm ) and G ( N Rd = 997 kN ; M Rd = 567 kNm ) with 220 N Ed 997 . Linear interpolation for M Rdx : 567 – 374 M Rdx = ------------------------ 700 – 220 + 374 = 493 kNm . 997 – 220 ULTIMATE BENDING MOMENT ABOUT AXIS Y‐Y WITH AXIAL COMPRESSIVE FORCE Using the same procedure implemented on the spreadsheet for b = 560 mm and h = 400 mm, we obtain: M Rdy = 285 kNm (linear interpolation) with N Ed = 700 kN (compressive). page 442 Topic: User’s Manual/Verification tests - BiaxialBending(2).xls A NNEX 1 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) BIAXIAL BENDING ‐ BRESLER METHOD 400 650 20 + 4072 435 = 6971 kN , N Rd = bhf cd + A s tot f yd = ----------------------------------------------------------------------1000 N Ec 700 -------- = ------------ = 0 10 a = 1 00 . 6971 N Rd Therefore: M Edx a M Edy a 370 1 00 70 1 00 -----------+ -----------= --------- + --------= 0 750 + 0 246 = 0 996 1 (satisfactory). M Rdx M Rdy 285 493 example-end EXAMPLE 1-AF‐ Uniaxial behaviour of confined concrete under compression up to the post‐peak branch (moment‐curvature relationship) ‐ test2 Given: Determine the moment‐curvature relation for a reinforced concrete column (see previous example) using the stress‐strain relation by hand computations using the equivalent rectangular stress‐block parameters. Assumptions: – bending moment about x‐x axis – design ultimate axial load on column N Ed = 700 kN 0 (compressive) – concrete C30/37 – longitudinal and transversal reinforcement characteristic strength: f yk = 500 MPa – depth in respect of major axis: h = 650 mm – width in respect of minor axis: b = 400 mm . The lateral dimensions h and b relative to the axes of the rectangular column are shown in Figure 1.53. – centre to centre between ties (longitudinal spacing of the set of ties): s = 100 mm – diameter of the peripheral hoop: link = 10 mm – diameter inner link: link = 10 mm . Dimension of the reduced section (spalling of the concrete cover) measured center‐to‐center of peripheral ties: – reduced depth in respect of major axis: h red = 580 mm – reduced width in respect of minor axis: b red = 330 mm . For the purpose of this verification test only the design of short braced column will be studied. Solution: A stress‐block approach is developed to calculate strength and deformation (see EN 1992‐1‐1 Sec.3.17, Figure 3.5). An analytical stress‐block based moment‐curvature simplified analysis is performed on the concrete structural element for confined concrete (spalling of the concrete cover): Kent & Park model. Topic: User’s Manual/Verification tests - BiaxialBending(2).xls page 443 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) The equations of the most commonly used existing stress‐strain models cannot be easily integrated in order to determine the equivalent rectangular stress‐block parameters for hand analysis and design purposes. Although the stress‐strain models proposed by various researchers have varying levels of sophistication, for the best models it is difficult to check their accuracy. In this spreadsheet a simplified stress‐strain model is used in order to be easily adapted for hand analysis to enable rapid design checks to be performed. Design stress force (along the y‐direction) into the confined concrete core due to the presence of confining reinforcement (1 peripheral hoop + 1 inner link): tr yy 1000 ------------ 2A link + 1A link f yd s 10 3 78 500 1 15 = ------------------------------------------------------------------------- = --------------------------------------------------------------- = 3 1 MPa 330 b red 10 3 having considered link = 10 mm . Characteristic strength confined conrete core (for bending moments obout x‐x axis): f cc = f ck + 4 1 tr yy = 30 + 4 1 3 1 = 42 7 MPa Volumetric ratio of confining hoops to volume of concrete core measured to the outside of the perimeter hoops. In this case equal to: 1000 1000 ------------ A link 3 b red + h red ------------ 78 3 330 + 580 s 100 - = -------------------------------------------------------------------- = 0 0111 . s = -------------------------------------------------------------------------b red h red 10 3 330 580 10 3 f cc MPa 42 7 - = 6197 psi . - = -------------------f cc psi = ------------------------------------------------0 00689 MPa psi 0 00689 Confinement only affected the slope of the post‐peak branch and empirical equations were used to adjust this. Strain corresponding to the stress equal to 50% of the maximum concrete strength for unconfined concrete: 3 + 0 002f cc 3 + 0 002 6197 50u = -----------------------------= ---------------------------------------- = 0 00296 with f c – 1000 6197 – 1000 b red 3 3 330 50h = --- s -------= --- 0 0111 --------- = 0 0151 (for bending moment about x‐x axis). s 4 4 100 The post‐peak branch was assumed to be a straight line whose slope was defined primarily as a function of concrete strength. The expression for the falling branch of the stress‐strain relation is given by: 0 5 0 5 Z m = --------------------------------------------------- = ----------------------------------------------------------------- = 31 13 . 50u + 50h – 0 002 0 00296 + 0 0151 – 0 002 Compressive characteristic strength of confined concrete (simplified parameters for stress‐block): f c res = f cc 1 – Z m cu – 0 002 = f cc 0 75 (design assumption when the postpeak remaining moment capacity of the column reduces to 75% of the maximum moment capacity). Therefore, for f cc = 42 7 MPa we obtain f c res = 32 MPa (characteristic value) for cu = 0 01011 10 1 1000 . page 444 Topic: User’s Manual/Verification tests - BiaxialBending(2).xls A NNEX 1 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) Ultimate design strength of materials (stress‐block semplified model): f ck 0 30- = 20 00 MPa (unconfined concrete with - = 1-----------------f cd = cc ----c max = cu3 ) c 1 50 f c res 0 32- = 21 33 MPa (confined concrete with - = 1-----------------f cd res = cc ---------c max cu3 ) c 1 50 f yk f yk f yd = ----- = ----------- = 0 87f yk = 0 87 500 = 435 MPa (longitudinal and transverse s 1 15 reinforcement). 75 - with = 0 9 = 67 5- . ----------Reinforcement (Class C): uk = ----------ud uk 1000 1000 Stress‐strain design diagram (steel): horizontal top branch without the need to check the strain limit (design assumption). For bending moment about x‐x axis: a) Stress‐strain design diagram (unconfined concrete): 3 5 1 75 grade of concrete C30/37 with cu3 = ----------- , = ------------ , = 1 0 , = 0 80 . 1000 c3 1000 b) Stress‐strain design diagram (confined concrete): 1 1 75 grade of concrete C30/37 with cu3 = 10 ------------ , c3 = ------------ , = 1 0 , = 0 80 1000 1000 (stress‐block design approximate assumptions). The procedure used in the analysis of the column when the postpeak remaining moment capacity of the column reduces to 75% (design assumption) of the maximum moment capacity is similar to the procedure being widely used with unconfined concrete. The stress‐block model will be used for this purpose too. DESIGN BENDING MOMENT ABOUT X‐X AXIS AT MAXIMUM STRENGTH ( f c red ) AND MAXIMUM CONCRETE STRAIN ( cu3 = 10 1 10 3 ) Using the same procedure implemented on the spreadsheet (see previous example) for b = 400 mm and h = 650 mm, we obtain (see details in “MEdx (u)” sheet): M Rdx red = 442 kNm (linear interpolation) with N Ed = 700 kN (compressive). –2 red = 6 254 10 m –1 is the curvature when the concrete strain reaches cu3 = 10 1 10 3 , the strain at peak stress in confined concrete and M Rdx red the corresponding moment. CURVATURE AT THE ONSET OF FIRST YIELDING OF THE LONGITUDINAL BARS Ultimate axial load at balanced stage ( c = cu3 = 3 5 10 3 ; s = – yd ) for unconfined conrete N Rd = 2373 kN N Ed = 700 kN (compressive). Topic: User’s Manual/Verification tests - BiaxialBending(2).xls page 445 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) Therefore, for x = 171 mm (depth to neutral axis for bending moment about x‐x axis) with the assumption: f yd 500 1 15 - = – ----------------------------- = – 0 002174 with s = – f yd = – 435 MPa (tensile) s = – yd = – ----Es 200000 the axial equilibrium is satisfied for: 0 87 30 3 5- with f = f----ck - = 20 MPa c max = ------------ cu3 = ----------cd cc - = 1 00 1 00 ----------c 1000 1 50 1000 0 62 2 174 s2 = ------------ yd = --------------- with s2 = 123 7 MPa (compressive). 1000 1000 In this case, the bending moment and curvature at the onset of first yielding of the longitudinal bars (bottom) are respectively: M x yel = 477 kNm yel = 0 00506 m –1 or yel h ‰ = 3,29 ( h = 650 mm cross‐section depth in respect of major axis). The moment curvature response is determined for each critical points such as yielding of longitudinal reinforcement ( yel ; M x yel ), till the onset of cover spalling ( red ; M Rdx red ) (see figure below). From numerical data of the previous example: M Rdx = 493 kNm with Figure 1.55 Excel® output. page 446 Topic: User’s Manual/Verification tests - BiaxialBending(2).xls A NNEX 1 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) u = 0 02135 (linear interpolation) the unconfined concrete column ductility is = u yel = 0 02135 0 00506 = 4 2 . The ultimate ductility defined as: red 06254- = 12 4 red = -------- = 0------------------- yel 0 00506 where red = curvature when the postpeak remaining moment capacity of the column reduces to 75% of the maximum moment capacity (when the longitudinal reinforcement steel strain reaches the ultimate strain or when the strain in concrete reaches the maximum confined strain cu3 = 10 1 10 3 as calculated above). example-end 1.5 References BRITISH STANDARDS INSTITUTION. The structural use of concrete – Part 1: Code of practice for design and construction, BS 8110–1:1997 EN 1992-1-1:2004. Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings. Brussels: CEN/TC 250 - Structural Eurocodes, December 2004 (DAV) EN 1992-1-1:2004/AC:2010. Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings. Brussels: CEN/TC 250 Structural Eurocodes, December 2010 JRC Scientific and Technical Reports. Bridge Design to Eurocodes Worked examples. Worked examples presented at the Workshop “Bridge Design to Eurocodes”, Vienna, 4-6 October 2010. Support to the implementation, harmonization and further development of the Eurocodes. Editors A. Athanasopoulou, M. Poljansek, A. Pinto G., Tsionis, S. Denton Kent, D.C., and Park, R. (1971). Flexural members with confined concrete. Journal of the Structural Division, Proc. of the American Society of Civil Engineers, 97(ST7), 1969-1990. MPA The Concrete Centre. Worked Examples to Eurocode 2: Volume 1. Practical Design to Eurocode 2. 2013 R. Park, T. Paulay, Reinforced Concrete Structures, Wiley & Sons, London, 1976. Reinforced Concrete Design to Eurocode, Bill Mosley, John Bungey and Ray Hulse, Palgrave Macmillan. 7th Edition. Topic: User’s Manual/Verification tests - BiaxialBending(2).xls page 447 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 B IAXIAL B ENDING (2)_EC2 (C OMMERCIAL VERSION ) 1.6 Further Reading A Thesis by Madhu Karthik Murugesan Reddiar. Submitted to the Office of Graduate Studies of Texas A&M University in partial fulfillment of the requirements for the degree of Master of Science. Stress-strain model of unconfined and confined concrete and stress-block parameters. December 2009. Confinement Reinforcement Design for Reinforced Concrete Columns. P. Paultre, M.ASCE1; and F. Légeron, M.ASCE2. Journal of Structural Engineering © ASCE/May 2008. page 448 Topic: User’s Manual/Verification tests - BiaxialBending(2).xls Annex 1 Shear_EC2 1.1 General: ShearReinforcementBeamSlab.xls T his sheet allows for the design of a section of solid slab or a rectangular beam section. The spreadsheet checks beams or slabs for shear and calculates any shear reinforcement required in accordance with EN 1992-1-1:2004 Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings. The user is required to input desired characteristic strength of the materials, amount of concrete cover to shear reinforcement ( c nom - EN 1992-1-1 Exp. 4.1) and the longitudinal reinforcement ( A sl ) which extends > l bd + d beyond the section considered. All applied load and stress should be ultimate and positive. With regard the concrete, the minimum strength used is C12/15 (Table 3.1). The spreadsheet allows input for grades of concrete up to C50/60. Input is self explanatory but, in order to facilitate use of this spreadsheet, some degree of automation has been introduced. The design of members with shear reinforcement is based on the truss model given in Figure 6.5 (EN 1992-1-1). The angle between the concrete compression strut and the beam axis perpendicular to the shear force is chosen within the range 1,00÷2,50 (Cl. 6.2.3(2) Exp. (6.7N)). Applied shear force ( V Ed ) is compared with three values for the resistance ( V Rd ). V Rd C represents the shear capacity of concrete alone; V Rd max is the shear resistance determined by the capacity of the notional concrete struts; and V Rd s is the capacity of a section with shear reinforcement. Where more than one vertical links are required per section, the user may choose to use inner links alternative or bent-up bars in order to increase section strength. The spreadsheet takes automatic measures to ensure maximum spacing (longitudinal and transversal) of shear reinforcement is met (Cl. 9.2.2 for Beams and Cl. 9.3.2 for Solid slabs). Combo-boxes to the right under “DETAILING” Excel® Form define minimum bar sizes to be used. Combo-box to the right under “PreCalculus” Excel® Form define concrete characteristic compressive strength at 28 days. No check is performed in order to control cracking of the concrete in shear. Therefore the maximum shear force allowed is checked (Exp. 6.5, Cl. 6.2.2(6)). Topic: User’s Manual/Verification tests - ShearReinforcementBeamSlab.xls page 449 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 S HEAR _EC2 The value of shear force, V Ed , used can, provided there is diagonal compression and continuity of tension reinforcement ( A sl ) for at least l bd (design anchorage length), be evaluated at “d” from the face of support (see Figure 6.3). This method presented in EC2 is known as “The Variable Strut Inclination Method”. The use of this method allows the designer to seek out economies in the amount of shear reinforcement provided, but recognising that any economy achieved may be at the expense of having to provide additional curtailment and anchorage length to the tension steel over and above the normally required for resistance to bending. Calculations with axial forces in the cross-section due to loading or prestressing are not carried out in this spreadsheet: N Ed = 0 with cp = 0 . NOTE for freeware version: Enclosing links only available with diameter 8 mm. No inner link. 1.2 Layout The basic layout for Shear_EC2 sheet is shown on the following screen dump: Figure 1.56 Sheet “Splash” from Excel® 2003. page 450 Topic: User’s Manual/Verification tests - ShearReinforcementBeamSlab.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 S HEAR _EC2 DETAILING Form: Figure 1.57 Input (white blank test boxes) and calculus (blue text boxes). Default value for cc = 0,8 (red). Figure 1.58 Report. Topic: User’s Manual/Verification tests - ShearReinforcementBeamSlab.xls page 451 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 S HEAR _EC2 PreCalculus Form: Figure 1.59 Coloured in blue results in output. White text boxes only to change the design values. View Notes... How to remove links to Excel file “ShearReinforcementBeamSlab.xls”: page 452 Topic: User’s Manual/Verification tests - ShearReinforcementBeamSlab.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 S HEAR _EC2 1.3 Output - Word document (calculation sheet) Example calculation sheet (output): Figure 1.60 Sample print with compression steel (Word® Office® must be installed on your system). Topic: User’s Manual/Verification tests - ShearReinforcementBeamSlab.xls page 453 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 S HEAR _EC2 1.4 Shear_EC2 (Beams and slabs) derived formulae The following notation is used in the equations for the shear design: • V Ed the shear force due to the actions at the ultimate limit state occurring at cross-section being considered (see Figure 6.3) • V Rd max = V Rd max cot ; tan is the design value of the maximum shear force which can be sustained by the member, limited by crushing of the compression struts • V Rd s = V Rd s cot ; tan • is the angle between the concrete compression strut and the beam axis perpendicular to the shear force • is the angle between shear reinforcement and the beam axis perpendicular to the shear force • d effective depth of the cross-section • b w width of the web on T, I or L beams • f ywk characteristic yield strength of shear reinforcement • f ywd = f ywk 1 15 = 0 87f ywk design yield of shear reinforcement • A sw is the cross-sectional area of the shear reinforcement • s is the longitudinal spacing of the shear reinforcement bars • f ck characteristic compressive cylinder strength of concrete at 28 days • f cd = cc f ck 1 50 design value of concrete compressive strength • cc is the coefficient taking account of long term effects on the compressive strength and of unfavourable effects resulting from the way the load is applied • cw is a coefficient taking account of the state of the stress in the compression strut • = 1 = 0 6 1 – f ck 250 is a strength reduction factor for concrete cracked in shear. Shear reinforcement is not normally required provided the design ultimate shear force V Ed does not exceed V Rd C : V Rd C = C Rd C k 100 l f ck 1 / 3 b w d (Eq. 1‐70) 1/2 v min b w d = 0 035k 3 / 2 f ck bw d (Eq. 1‐71) but not less than: where: k = 1 + 200 d mm 2 0 and l = A sl b w d 0 02 . Where A sl is the area of tensile reinforcement, which extends > l bd + d beyond the section considered (see EN 1992-1-1, Figure 6.3). page 454 Topic: User’s Manual/Verification tests - ShearReinforcementBeamSlab.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 S HEAR _EC2 When, on the basis of the design shear calculation, no shear reinforcement is required, minimum shear reinforcement should nevertheless be provided according to 9.2.2. Where V Ed exceeds V Rd C shear reinforcement is required. The beam section should be considered inadequate whether at least one of the following two conditions is not met: V Ed 0 5b w df cd (Eq. 1‐72) V Ed V Rd max = V Rd max cot = 1 00 . (Eq. 1‐73) In such case the section should be resized or the materials strength increased. If Eq. 1-72 and 1-73 are met: a. if V Ed V Rd max = V Rd max cot = 2 50 the design value of the shear force which can be sustained by the yielding shear is given by V Rd s = V Rd s cot = 2 50 b. if V Ed V Rd max = V Rd max cot = 2 50 calculate angle , of strut for full shear force at end of beam = 0 5arc sin 2V Ed cw 1 f cd b w z c. if 21 80 45 the design value of shear force is given by V Rd s = V Rd s cot d. if 21 80 the design value of the shear force is given by: V Rd s = V Rd s cot = 2 50 . The shear force applied to the section must be limited so that excessive compressive stresses do not occur in the diagonal compressive struts, leading to compressive failure of the concrete. Thus the maximum design shear force V Rd max is limited by the ultimate crushing strength of the diagonal concrete member in the analogous truss and its vertical component. According to EN 1992-1-1: • for members with vertical shear reinforcement: f cd V Rd max = cw b w z 1 --------------------------------- cot + tan • (Eq. 1‐74) for members with inclined shear reinforcement: cot + tan V Rd max = cw b w z 1 f cd ---------------------------------- 1 + cot2 (Eq. 1‐75) where z = 0 9d is the lever arm due to bending with shear. In the case of “section adequate” with V Ed V Rd C , all shear will be resisted by ( V Rd s ) the provisions of shear reinforcement bars with no direct contribution from the shear capacity of the concrete itself. According to EN 1992-1-1: • for members with vertical shear reinforcement: Topic: User’s Manual/Verification tests - ShearReinforcementBeamSlab.xls page 455 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 S HEAR _EC2 A sw - zf ywd cot V Rd s = -------s • (Eq. 1‐76) for members with inclined shear reinforcement: A sw - zf ywd cot + cot sin V Rd s = -------s (Eq. 1‐77) where z = 0 9d is the lever arm due to bending with shear. For bent-up bars according to the truss model in Figure 6.5 the longitudinal spacing between shear assemblies is given by: z s = --- cot + cot n (Eq. 1‐78) where “n” is the number of shear assemblies along the beam axis. The area of each shear assemblies is A sw . In the case of only one shear assembly (n = 1) the longitudinal spacing to be considered in the shear calculations is given by: s = z cot + cot (Eq. 1‐79) where 45 90 . 1.5 Verification tests SHEARREINFORCEMENTBEAMSLAB.XLS. 5.58 MB. Created: 26 December 2013. Last/Rel.-date: 26 December 2013. Sheets: — Splash — CREDITS. EXAMPLE 1-AG‐ Pre‐dimensioning and checking shear reinforcement ‐ test1 Given: The beam cross‐section in Figure below is given. The characteristic material strengths are C30/35 for the concrete and f ywk = 500 MPa for the steel. Check if the shear reinforcement in the form of vertical link ( 3 = 50 %) and bent‐up bars can support, in shear, the given ultimate load V Ed = 340 kN . Solution: Take an effective depth d = 557 mm 550 mm . The breadth of section b = b w = 350 mm . The nominal cover to links c nom = 25 mm . Level arm z = 0 9d = 495 mm . Design shear stress occurring at cross‐section being considered: v Ed = V Ed b w d = 340 10 3 350 550 = 1 77 MPa . Design materials strengths: concrete f cd = cc f ck 1 50 = 0 85 30 1 50 = 17 00 MPa page 456 Topic: User’s Manual/Verification tests - ShearReinforcementBeamSlab.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 S HEAR _EC2 Figure 1.61 Beam cross-section. f cd = 1 f cd = 0 6 1 – 30 250 17 = 0 528 17 = 8 976 MPa . Steel (shear reinforcement): f ywd = f ywk 1 15 = 500 1 15 = 435 MPa . Area of tensile reinforcement which extends > ( l bd + d ) beyond the section considered: A sl = 600 mm 2 (considered 3H16 at the face of beam support). SHEAR RESISTANCE (WITHOUT SHEAR REINFORCEMENT). Design value for the shear stress resistance: A sl 600 - = 0 0031 0 02 (satisfactory). l = -------- = --------------------------bw d 350 550 200 200 k = 1 + --------- = 1 + --------- = 1 603 2 0 (satisfactory). d 550 C Rd C k 100 l f ck 1 / 3 = 0 12 1 603 100 0 0031 30 1 / 3 = 0 40 MPa 1/2 v min = 0 035k 3 / 2 f ck = 0 035 1 603 3 / 2 30 1 / 2 = 0 39 MPa v Rd C = max 0 40 ; 0 39 = 0 40 MPa . Shear reinforcement required: v Ed = 1 77 v Rd· C = 0 40 MPa . 30 v Ed 0 5f cd = 0 5 0 6 1 – --------- 17 = 4 49 MPa (satisfactory) 250 Topic: User’s Manual/Verification tests - ShearReinforcementBeamSlab.xls page 457 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 S HEAR _EC2 cw b w z 1 f cd 1 350 495 0 528 17 V Rd max = -----------------------------= ---------------------------------------------------------- = 777546 N with: 1 + tan 1 + 1 777546 - = 4 04 MPa v = 1 77 MPa (beam adequate). v Rd max = v Rd max cot = 1 = --------------------------Ed 350 550 DETAILING. Shear reinforcement for beam (stirrups and bent‐up bars) with 3 = 0 5 (see Cl. 9.2.2(4)). Design stress at cross‐section being considered v Ed = V Ed b w d = 1 77 MPa (with 0 5 1 77 = 0 88 MPa @stirrups and 0 88 MPa @bent‐up bars). Chosen cot = 1 00 with 1 00 2 50 (Cl. 6.2.3(2) ‐ Note ‐ Exp. (6.7N)). Stirrups: N = 1 enclosing links with diameter H10, and no inner links. Longitudinal spacing (vertical links): s = 190 mm (chosen). = 90 angle between vertical links and the beam axis). A sw = 2 78 = 157 mm 2 , A sw s = 157 190 = 0 827 mm 2 mm = 827 mm 2 m . Bent‐up bars: 2H16 ( A sw = 402 mm 2 ) bent‐up at an angle from the bottom of the beam = 45 (for 2 times) with a longitudinal spacing given by: z 495 s = --- cot + cot = --------- 1 + 1 = 495 mm . n 2 Maximum longitudinal spacing (vertical links = 90 ): s l max = 0 75d 1 + cot = 0 75 550 1 + 0 = 413 mm . Compression longitudinal reinforcement which is included in the resistance calculation (bending): H20 with s l max = 15 20 mm = 300 mm . min 413 ; 300 = 300 mm s = 190 mm (satisfactory). Transverse vertical spacing: b w – 2c nom – Enclink 350 – 2 25 – 10 s t = ------------------------------------------------ = ----------------------------------------- = 290 mm N innerLink + 1 0+1 where N innerLink is the number of inner links. Minimum shear reinforcement (for sin = 1 ): A sw 0 08 f ck 0 08 30 mm 2 mm 2 ------- b w 1 = ---------------------- 350 1 = 0 306 ----------- = 306 ----------= w min b w sin = --------------------- s min f ywk mm m 500 A sw A sw -------- = 0 827 mm 2 mm -------(satisfactory). s min s SHEAR CAPACITY. Capacity of the concrete section with vertical and inclined shear reinforcement to act as a strut: page 458 Topic: User’s Manual/Verification tests - ShearReinforcementBeamSlab.xls E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 S HEAR _EC2 cw b w z 1 f cd 1 350 495 0 528 17 V Rd max = ---------------------------------- = -------------------------------------------------------------- = 777546 N (vertical links) cot + tan 1 + 1 cw b w z 1 f cd 1 350 495 0 528 17 cot + cot = ------------------------------------------------------------- 1 + 1 = 1555092 N V Rd max = ----------------------------- 1 + cot2 1 + 12 (bent‐up bars). Value used for shear calculations: V Rd max = min 777546 ; 1555092 = 777546 N . SHEAR REINFORCEMENT (VERTICAL LINKS): A sw -------- = 0 827 mm 2 mm s cot = 1 00 , cot + tan = 2 00 . A sw - zf ywd cot = 0 827 495 435 1 00 = 178074 N . V Rd s = -------s min 178074 ; 777546 - = 0 92 Mpa v min V Rd s ; V Rd max b w d = -----------------------------------------------------EdLink = 0 88 MPa 350 550 (satisfactory). SHEAR REINFORCEMENT (BENT‐UP BARS): A sw 2 201 -------- = --------------------- = 0 812 mm 2 mm s 495 cot + cot = 2 00 , sin = sin 45 = 0 71 , 1 + cot2 = 2 00 . A sw - zf ywd cot + cot sin = 0 812 495 435 2 00 0 71 = 248278 N . V Rd s = -------s min 248278 ; 777546 - = 1 29 Mpa v min V Rd s ; V Rd max b w d = -----------------------------------------------------EdLink = 0 88 MPa 350 550 (satisfactory). NOTE. Provide H10 mm diameter enclosing links, (and no inner link) at 190 mm centres. Provide 2H16 bent‐up at = 45 for n = 2 times with a longitudinal spacing s 495 mm . MAXIMUM EFFECTIVE CROSS‐SECTIONAL AREA OF THE SHEAR REINFORCEMENT (COT = 1,00): Stirrups: A sw max f cd 17 - b = 0 5 1 0 528 ------------- 350 = 3 611 mm 2 mm ------------------ 0 5 cw 1 -------s f ywd w 435 Bent‐up bars: A sw max f cd 17 ------------------ 0 5 cw 1 --------------------- b = 0 5 1 0 528 ------------------------------- 350 = 5 086 mm 2 mm . s f ywd sin w 435 0 71 Topic: User’s Manual/Verification tests - ShearReinforcementBeamSlab.xls page 459 E UROCODES S PREADSHEETS S TRUCTURAL D ESIGN A NNEX 1 S HEAR _EC2 1.6 References BRITISH STANDARDS INSTITUTION. The structural use of concrete – Part 1: Code of practice for design and construction, BS 8110–1:1997 EN 1992-1-1:2004. Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings. Brussels: CEN/TC 250 - Structural Eurocodes, December 2004 (DAV) EN 1992-1-1:2004/AC:2010. Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings. Brussels: CEN/TC 250 Structural Eurocodes, December 2010Reinforced Concrete Design to Eurocode, Bill Mosley, John Bungey and Ray Hulse, Palgrave Macmillan. 7th Edition Reinforced Concrete Design to Eurocode, Bill Mosley, John Bungey and Ray Hulse, Palgrave Macmillan. 7th Edition. page 460 Topic: User’s Manual/Verification tests - ShearReinforcementBeamSlab.xls