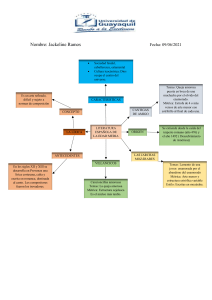
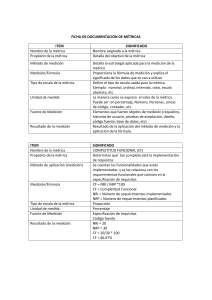
Tarea 1
Análisis Matemático I. Grupo 4206.
Prof. Manuel Falconi Magaña
1. Probar que N tiene una cantidad numerable infinita de subconjuntos ajenos dos a dos e infinitos.
2. Probar que cualquier colección de intervalos en R abiertos, no vacíos y ajenos dos a dos es numerable.
3. Sea X un conjunto finito. En P(X) definimos
d(A, B) = card(A 4 B),
donde A 4 B es la diferencia simétrica, es decir, A 4 B = (A \ B) ∪ (B \ A). Demostrar que d es una
métrica en P(X).
4. Sea X un conjunto no vacío. Si para x, y ∈ X se define
(
d(x, y)
=
1, si x 6= y
0, si x = y
Mostrar que d es una métrica.
5. Sean x, y ∈ R. Definimos
d2 (x, y)
(x − y)2
p
|x − y|
=
d3 (x, y)
= |x2 − y 2 |
d1 (x, y)
=
= |x − 2y|
|x − y|
d5 (x, y) =
1 + |x + y|
d4 (x, y)
Determinar cuáles de las anteriores son métricas.
6. Un conjunto E ⊂ Rn es convexo si
λy + (1 − λ)z ∈ E,
para todo y, z ∈ E y para todo λ ∈ [0, 1]. Demostrar que toda bola
Bε (x0 )
= {x ∈ Rn : d(x, x0 ) < ε}
es un conjunto convexo.
7. Algunos requerimientos de la métrica son redundantes: Sea X un conjunto no vacío, d : X × X −→ [0, ∞)
una función que satisface d(x, y) = 0 si y sólo si x = y, y d(x, y) ≤ d(x, y) + d(y, z) para todo x, y, z ∈ X.
Demostrar que d es una métrica en X, es decir, que satisface d(x, y) ≥ 0 y que d(x, y) = d(y, x).
8. Sea f : [0, ∞) −→ [0, ∞) una función creciente que cumple f (0) = 0, f (x) > 0, si x > 0 y además
f (x + y) ≤ f (x) + f (y) para todo x, y ≥ 0. Demostrar que si d es una métrica en X, entonces f ◦ d es
una métrica en X.
1
9. Demostrar que si d es una métrica en X, entonces
ρ(x, y)
=
σ(x, y)
=
τ (x, y)
=
p
d(x, y),
d(x, y)
,
1 + d(x, y)
mı́n{d(x, y), 1},
también son métricas en X.
10. Dado el conjunto {0, 1}N = {(xn )∞
n=1 : xn ∈ {0, 1}}, demostrar que
d(x, y) =
∞
X
2−n |xn − yn |,
∞
x = (xn )∞
n=1 , y = (yn )n=1 ,
n=1
Define una métrica en {0, 1}N .
11. Verificar que
d(f, g)
máx |f (t) − g(t)|,
=
a≤t≤b
define una métrica en C[a, b] (la colección de todas las funciones continuas, real-valuadas definidas en el
intervalo cerrado [a, b]).
12. Mostrar que
Z
ρ(f, g)
1
|f (t) − g(t)| dt
=
0
Z
σ(f, g)
1
mı́n{|f (t) − g(t)|, 1} dt
=
0
son métricas en C[0, 1].
2