Ascione 2011 Earth-to-air heat exchangers for Italian climates

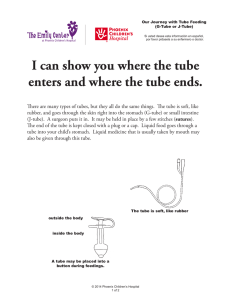
Renewable Energy 36 (2011) 2177e2188
Contents lists available at ScienceDirect
Renewable Energy
journal homepage: www.elsevier.com/locate/renene
Earth-to-air heat exchangers for Italian climates
Fabrizio Ascione a, Laura Bellia b, Francesco Minichiello b, *
a
b
DING, University of Sannio, P. zza Roma 21, 82100 Benevento, Italy
DETEC, University of Naples Federico II, P. le Tecchio 80, 80125 Napoli, Italy
a r t i c l e i n f o
a b s t r a c t
Article history:
Received 15 July 2010
Accepted 12 January 2011
Available online 21 February 2011
The European Energy Efficiency Building Directive 2002/91/CE, as well as other acts and funding
programs, strongly promotes the adoption of passive strategies for buildings, in order to achieve indoor
thermal comfort conditions above all in summer, so reducing or avoiding the use of air conditioning
systems.
In this paper, the energy performances achievable using an earth-to-air heat exchanger for an airconditioned building have been evaluated for both winter and summer. By means of dynamic building
energy performance simulation codes, the energy requirements of the systems have been analysed for
different Italian climates, as a function of the main boundary conditions (such as the typology of soil,
tube material, tube length and depth, velocity of the air crossing the tube, ventilation airflow rates,
control modes). The earth-to-air heat exchanger has shown the highest efficiency for cold climates both
in winter and summer.
The possible coupling of this technology with other passive strategies has been also examined. Then,
a technical-economic analysis has been carried out: this technology is economically acceptable (simple
payback of 5e9 years) only in the cases of easy and cheap moving earth works; moreover, metallic tubes
are not suitable.
Finally, considering in summer a not fully air-conditioned building, only provided with diurnal
ventilation coupled to an earth-to-air heat exchanger plus night-time ventilation, the possible indoor
thermal comfort conditions have been evaluated.
! 2011 Elsevier Ltd. All rights reserved.
Keywords:
Ground cooling
Heat exchanger
Earth-to-air
Energy saving
Building
Dynamic simulation
1. Introduction
An earth-to-air heat exchanger (EAHX) consists in one or more
tubes lied under ground in order to cool (in summer) or pre-heat
(in winter) air to be supplied in a building. This air is often outdoor
air necessary for ventilation, but also useful to partially or totally
handle the building thermal loads. The physical phenomenon is
simple: the ground temperature is commonly higher than the
outdoor air temperature in winter and lower in summer, so it makes
the use of the earth convenient as warm or cold sink, respectively.
Normally, the soil temperature, at a depth of 5e8 m under the
ground level, remains almost constant throughout the year; its
temperature profile as a function of the depth depends on several
factors, such as the physical properties of the soil, the sky covering
and the climate conditions [1].
Givoni [2] identified two macro-groups of earth tubes, those
with open and closed loop; in this paper, the first typology has been
considered. Typical buried tube lengths are 30e60 m, usually posed
* Corresponding author. Tel.: þ39 081 2538665; fax: þ39 081 2390364.
E-mail address: [email protected] (F. Minichiello).
0960-1481/$ e see front matter ! 2011 Elsevier Ltd. All rights reserved.
doi:10.1016/j.renene.2011.01.013
at 2e4 m under ground level. The tubes are located in almost
horizontal position, with a slight inclination to remove possible
condensed water.
A physical model to simulate the EAHX was developed and
validated by Mihalakakou et al. [3,4]. Benkert et al. [5] underlined
the lack of optimisation criteria; moreover, they developed the
computer tool GAEA, based on a physical model and then experimentally validated with good results.
The EAHXs are characterised by high energy saving potential
and require low maintenance. Moreover, Pfafferot [6] underlined
that in winter the re-heating of the air downstream of the EAHX is
however necessary before supplying air in the building, while in
summer indoor comfort conditions are sometimes achievable also
without an active re-cooling.
However, few research investigations [7,8] have been carried out
to evaluate the energy performances of the EAHX as a function of
the main boundary conditions, above all for Italian climates.
Thus, in this paper an extended parametric analysis on EAHXs is
presented, starting from a validated physical-mathematical model.
This investigation has been carried out by using appropriate
dynamic simulation codes, especially Energy Plus [9] and Calculation Soil Temperature [10]; some modelling conditions adopted in
2178
F. Ascione et al. / Renewable Energy 36 (2011) 2177e2188
these codes have been calculated also by means of the above
mentioned GAEA code.
Three different Italian climates (cities of Naples, Rome, Milan)
and an air-conditioned building have been analysed for both winter
and summer. The energy requirements of these systems have been
evaluated as a function of the main boundary conditions (such as
the typology of soil, tube material, tube length and depth, velocity
of the air crossing the tube, ventilation airflow rates, control
modes). Then, the possible coupling of this technology with other
passive strategies has been examined, and a technical-economic
analysis has been performed.
Finally, considering in summer a not fully air-conditioned
building, only provided with diurnal ventilation coupled to an earthto-air heat exchanger plus night-time traditional ventilation, the
possible indoor thermal comfort conditions have been evaluated.
2. Case study and results
2.1. The complex building-system and the used physical model
In Fig. 1, the modelled office building is shown: it is well thermally insulated, with efficient heating and cooling systems. The
main characteristics of the building and systems are reported in
Table 1.
Several authors studied the physical model governing the earthto-air heat exchange: the Krarti’s model [11] is here used. A full
description of the model, as well as the model validation, is reported
in Reference [7], while in the following only the main characteristics
of the model are shown.
The heat transfer mechanisms around the earth tube are quite
complex, so some assumptions have been made:
- the pipe has a uniform internal/external diameter in the axial
direction;
- the soil around the pipe is homogeneous and its thermal
conductivity has a constant value;
- the soil temperature near the pipe is not influenced by the pipe,
so the surface temperature of the pipe is uniform in the axial
direction;
- the convective flow inside the pipe is thermally and hydrodynamically developed.
The annual TMEAN
Equation (1):
SURF
of the soil is calculated by means of the
he ¼ hs $ð1 þ 0:0168$a$f Þ
(2)
hr ¼ hs $ð1 þ 0:0168 $a $RH$f Þ
(3)
So, he and hr represent the convective heat transfer coefficient at
the soil surface, increased taking into account, respectively, the
fraction of evaporation rate (he) and the fraction of evaporation rate
plus the relative humidity of the ambient air (hr).
The phase angle difference between the air and the soil surface
temperature trends, the amplitude of the soil surface temperature
variation (As), and the related phase constant (t0) are then determined. Considering a soil characterised by uniform thermal diffusivity as, the Equation (4) provides the ground temperature as
a function of depth and time.
i
h
TGROUND ðz;tÞ ¼TMEAN SURF &As exp &zðp=365,as Þ1=2
n
io
h
$cos ð2p=365Þ$ t &t0 &ðz=2Þð365=p,as Þ1=2 ð4Þ
The main equations describing the heat exchange between soil,
buried tubes and crossing air are:
Rconv ¼ 1=ð2p$r1 $L$hc Þ
(5)
% &
'( %
(
Rcond&tube ¼ 1= 2p$L$kp $ln ðr1 þ r2 Þ=r1
(6)
Rcond&tube=soil ¼ ½1=ð2p$L$ks Þ'$ln½ðr1 þ r2 þ r3 Þ=ðr1 þ r2 Þ'
(7)
The distance between the tube external surface and the undisturbed soil (r3) is assumed equal to the radius of the tube.
hc ¼ Nu$kair =2$r1
(8)
Ut ¼ 1=Rtot
(9)
Rtot ¼ Rconv þ Rcond&tube þ Rcond&tube=soil
(10)
The heat transfer between the air inside the tube and the soil is
characterised by the following equation:
TMEAN SURF ¼ ð1=he Þ$½hr $TMEAN AIR & 3$DR þ bs $Sm
& 0:0168$hs $f $bð1 & RHÞ'
As regards he and hr, both are related to the convective heat transfer
coefficient at the soil surface, hs, as described in the Equations (2)
and (3), with a ¼ 103 Pa/( C.
(1)
_ a ca ½dTa ðyÞ'
Ut dy½Ta ðyÞ & TGROUND ðz; tÞ' ¼ &m
Fig. 1. The modelled building: volumetric scheme, plan of the ground floor and thermal zones.
(11)
2179
F. Ascione et al. / Renewable Energy 36 (2011) 2177e2188
Table 1
Main characteristics of the modelled office building and systemsa.
Dimensions of the office building and boundary design conditions
Width (NeS direction)
Height
Surface to volume ratio
Tsummer-set-point (no cooling
during no occupancy periods)
Uwindows
Uroof
Cooling efficiency
(fan coils þ water chiller)
Electric energy cost
Type of soil
a
12.8 m
8.0 m (two floors)
0.47 m&1
26 ( C
1.1 W/m2 K
0.17 W/m2 K
hel ) SEER ¼ 0.36 ) 3.00 ¼ 1.08
0.20 €/kWh
heavy and wet clay
Length
Plan area and volume
Ventilation airflow rate
Twinter-set-point
(16 ( C during no occupancy periods)
Uwalls
Ubasement floor
Heating efficiency
(fan coils þ gas condensing boiler)
Natural gas cost
32.30 m
413 m2e3304 m3
21.6 m3/h per person
20 ( C
0.29 W/m2 K
0.29 W/m2 K
hOVERALL ¼ 0.76
0.65 €/Nm3
A hourly scheduling is fixed with reference to occupancy, lighting and other electric equipments installed.
By solving this equation, the temperature of the air leaving the
earth tube and entering the building, Ta (L), is finally obtained as
follows:
- if
Ta ðLÞ ¼ TGROUND ðz; tÞ þ eA
Tam > TGROUND ðz; tÞ
(12)
- if
Tam ¼ TGROUND ðz; tÞ
Ta ðLÞ ¼ TGROUND ðz; tÞ
(13)
temperature variation equal to 9 ( C, mean solar irradiance
equal to 117 W/m2, clayey soil and grassy-moist surface);
- the second one (figure on the right) refers to the values
calculated by the authors using the numerical model of Krarti
[11] and the weather data of Wien.
The results are obviously different when varying the depth, the
considered mid-European city and the kind of soil, but a quite
satisfactory accordance of the model with respect to typical literature data is confirmed.
2.2. EAHX cooling potential: parametric analysis for summer
conditions
- if
Ta ðLÞ ¼ TGROUND ðz; tÞ & eA
Tam < TGROUND ðz; tÞ
(14)
where
A ¼
)
)
_ a ca ln))Tam & TGROUND ðZ; TÞ)) & UL
m
(15)
_ a ca
m
Table 2 describes the main design characteristics of the EAHX
simulated.
Fig. 2 shows a satisfactory accordance between the two
following soil temperature trends, both related to the depth of 1 m:
- the first one (figure on the left, line related to the depth of 1 m)
is relative to the literature values reported in Reference [13],
with reference to a typical mid-European weather (mean
temperature of the ambient air equal to 10 ( C, amplitude of the
Table 2
Earth tube base model: design characteristics.
Whole Office Building
Design volumetric airflow
rate (for each zone)
Design volumetric airflow rate
(for the entire building)
and fan position
Tube depth and length
Tube material and thickness
Tube radius and soil conditions
Buried tube: pressure drop and air speed
Building ducts: pressure drop and air speed
Fan absorbed electrical power
2 x 0.096 m3/s for Zones 1 & 3
2 x 0.144 m3/s for Zones 2 & 4
2 x 0.088 m3/s for Zones Y & X
2361 m3/h ( ¼ 0.66 m3/s) Exhaust fan
Depth ¼ 3.0 m; length ¼ 50 m
(horizontal) + 5 m (vertical)
PVC: k ¼ 0.16 W/(mK);
thickness ¼ 5 mm
165 mm e Heavy and
damp soil
2 Pa/m - 7.7 m/s
2 Pa/m - 4 O 6 m/s
1250 W
In the following, various parameters have been varied; when not
specified, the values are those reported in Table 2.
2.2.1. Influence of the climate and soil composition
The soil typologies reported in Table 3 have been considered.
The results are reported in Fig. 3 (required specific thermal energy
in Fig. 3A, required specific primary energy in Fig. 3B). Compared to
the reference case (without EAHX), the best energy performances
have been obtained for wet and heavy soil and cold winter climates
(Milan) e maximum savings of about 44% in terms of thermal
energy, about 37% for primary energy. In fact, in these climates, the
time constant of the ground at the design depth (3 m) makes the
soil particularly apt as cold sink in summer (the ground is colder
compared to other cities).
Anyway, even the less suitable kind of soil (light and dry) allows
significant savings: in terms of thermal energy, these are about 25%
for Naples, 30% for Rome, 34% for Milan (Fig. 3A).
Note that the high water content of some soil typologies improves
the EAHX performances. As regards the material surrounding the
buried tube, a good contact between soil and tubes has to be ensured,
by means of compacted clay or sand. These kinds of soil are also
suitable for a correct tube installation.
In terms of primary energy requirements (Fig. 3B), all the
savings obtained are minor because of the electric energy required
by the fans.
Heavy and wet clay has been considered in the following analyses.
2.2.2. Influence of the tube material
The thermal conductivity of the tube material appears in the
Equation (6) and therefore in the Equation (9). The obtained results
(Fig. 4) show that concrete, plastic or metallic materials lead to very
similar energy performances. In fact, due to the small thickness of
the tubes (5 mm in the case of PVC, 7 mm for the metallic material,
7 cm for the concrete), the different thermal conductivity values
scarcely influence the heat exchange, if the right depths and lengths
are used.
2180
F. Ascione et al. / Renewable Energy 36 (2011) 2177e2188
Fig. 2. Under ground soil temperature: literature values [13] for mid-European weather and values calculated using the Krarti’s model with reference to Wien weather.
Note that the concrete tubes require a further internal coating to
avoid possible radon infiltrations; furthermore, hygienic conditions
inside the tubes must be assured, for example by using antimicrobial coatings.
2.2.3. Influence of the tube length
The thermal exchange between the ground and the air crossing
the tube increases with the length of the buried tubes (Fig. 5aec).
In Fig. 5d, the specific energy requests for summer cooling are
reported.
It can be inferred that, for all the considered climates, lengths of
about 10 m are unsatisfactory, while significant advantages do not
occur for lengths over 70 m, according to Reference [7]. In this last
case, the further minimal air temperature reduction at the tube
outlet does not compensate the higher energy required by fans
(due to major necessary heads). Thus, for the climates here
considered, lengths of about 50 m are preferable, which optimise
heat exchange and first costs.
With reference to Fig. 5d, compared to the base system without
ground cooling, an EAHX of 50 m allows primary energy savings of
about 12.5 kWh/m2a for Naples (the primary energy required for
the base case is equal to 55.3 kWh/m2a), 14.2 kWh/m2a for Rome
(52.2 kWh/m2a for the base case), 13.0 kWh/m2a for Milan
(41.3 kWh/m2a for the base case).
2.2.4. Influence of the tube depth
The ideal depth of buried tubes is about 8 m under the ground
level. In fact, in this case the time lag is approximately 6 months, so
the ground is characterised by the lowest yearly temperatures in
summer and the highest in winter (Fig. 2B); thus, the thermal
recovery is optimal in both the seasons. The depth of 6e9 m is also
preferable compared to major depths characterised by ground
temperature almost constant during the year.
Fig. 6 shows that the depth of 3 m under the ground level
implies a better thermal exchange compared to the depth of 1 m
(not satisfactory depth), while a further deepness (4 m) allows only
a minimal improvement. Thus, if the excavation costs are low
Table 3
Thermal-physical properties of the considered soil.
Albedo: 0.1 for wet soil, 0.2 for
moderate soil, 0.3 for dry soil
Dry density
kg/m3
Conductivity
W/(m K)
Diffusivity
m2/day
Soil
Heavy clay (15% water)
Heavy clay (5% water)
Light sand (15% water)
Light sand (5% water)
1925
1925
1285
1285
1.4
1.0
1.0
0.9
0.042
0.047
0.047
0.055
O
O
O
O
1.9
1.4
2.1
1.9
O
O
O
O
0.061
0.061
0.093
0.120
(unleashed soils), a deeper tube can be useful, while, in presence of
rock, a depth of 3 m is the best compromise.
In Fig. 6, also a different air velocity inside the tubes has been
considered (high velocity). The reference air velocity into the
buried tubes is 7.7 m/s (Table 2) and this determines a pressure
drop of 2 Pa/m (fan power equal to 1250 W). Raising the air velocity
to 20 m/s, a reduction of the tube costs is achieved, but two
negative effects on performance occur:
the higher pressure drop (19 Pa/m) imposes a major fan power
(2600 W);
the overall heat exchange is reduced due to the minor exchange
surface (a higher velocity, with unvaried flow rate, implies a lower
radius), even if the convective heat transfer coefficient rises with
the air velocity.
Globally, high air velocities are not energy convenient, as clearly
shown in Fig. 6, above all in terms of primary energy.
In order to better understand the results of Fig. 6, with reference
to the comparison between low and high velocity of the air inside
the tube, it can be useful to report the following known concepts.
The fan electric power rises with the required pressure head, as
shown in the Equation (18) reported in the following section. The
pressure head of the fan is evaluated on the basis of the global
pressure loss of the most unfavourable circuit in the total duct layout.
The global pressure losses of an air distribution system are the sum
of the frictional pressure losses and the dynamic pressure losses,
calculated by means of the Equations (16) and (17), respectively.
Dp ¼ l$L$
w2 r
$
2 dh
Dp ¼ z$r $
w2
2
Frictional losses
Dynamic losses
(16)
(17)
So, the pressure losses depend on the terms L (length of the
duct), l (Darcy friction factor), r (air density), dh (hydraulic diameter of the tube), z (dynamic loss coefficient) and the square-value
of the air velocity (w2). Considering the Equations (16)e(18), it can
be obtained that a high air speed, compared to the case of a low one,
induces a higher air-duct global pressure loss, and, therefore,
a major fan-required pressure head and, finally, a higher necessary
fan electric power.
2.2.5. Influence of the fan position and airflow rate
Earth-to-air heat exchangers can use intake fans, exhaust ones
or both, depending on the complexity of the air ducts. The exclusively use of exhaust fans requires a careful sizing of the ventilation
F. Ascione et al. / Renewable Energy 36 (2011) 2177e2188
2181
Fig. 3. Influence of the ground typology on the energy requests for summer cooling.
system, so that the room extraction grilles can guarantee the
correct incoming airflow rates in all the building zones. In this
paper, only two different solutions have been considered: intake
fans and exhaust fans.
In Fig. 7A and B (on the left side), the influence of the fan
position is shown. Considering the same ventilation airflow rate
(i.e. 1 ACH), the energy request for building summer cooling is very
similar in the two cases of intake fan and exhaust fan; when an
intake fan is used, the energy required is higher of only about
0.4 kWh/m2a (in terms of thermal energy), as the increase of the air
temperature due to the crossing of the fan is little (this increase
depends on shape and rotational speed of the fan blades).
In addition, different amounts of ventilation air (2 and 4 ACH)
supplied into the building have been also considered (Fig. 7A and B,
on the right side). Of course, in the considered climates, the
achievable thermal energy savings increase when raising the
airflow rate crossing the EAHX (Fig. 7A), as in summer the under
ground soil temperature is usually lower than the indoor comfort
temperature, independently of climate, ground composition, tube
length, depth and material. Thus, using an earth tube, the increase
of the ventilation air amount determines a reduction of the thermal
energy requests for cooling.
In terms of primary energy, the results are very different. In fact,
the fan electric power grows with the airflow rate, according to
Equation (18):
Fan electric power ¼ðVolumetric flow rate$Pressure headÞ
=hFAN
ð18Þ
Thus, when considering 1 or 2 ACH, the thermal energy requests
are different (Fig. 7A), while the primary energy requirements are
very similar (Fig. 7B). A further growth of the airflow amount
(4 ACH) determines a further reduction of the thermal energy
required (Fig. 7A), but also a significant growth of the primary
energy (Fig. 7B).
Moreover, it can be noted that the primary energy performances
relative to the cases with 1 and 2 ACH are almost equivalent in
summer (Fig. 7B), but not in winter. In fact, in winter, the EAHX
ventilation can be used as pre-heating strategy, because the heat
exchange between the soil and the outdoor air makes the ventilation energetically less disadvantageous (but, anyway, the ventilation remains disadvantageous). Therefore, contrary to what occurs
in summer, in winter any rise of the supplied outdoor air over the
necessary air-change induces an increase of the ventilation thermal
load and of the energy requirements; furthermore, other energy
disadvantages derive from higher fan needs.
2.2.6. Influence of the EAHX control mode
Five different control modes of the EAHX have been considered,
in which the daily working period has been varied (Table 4); all the
results are reported in Fig. 8.
It is clear that, despite higher fan energy requirements, the most
convenient solution is the use of the EAHX during all the diurnal
hours, and it is verified for all the considered climates. Thus, the first
control mode (mode 1, e.g. 15 h/day) represents the best solution,
with a cooling primary energy request (lines in Fig. 8B) equal to:
for Naples, 42.8 kWh/m2a (vs. 55.3 kWh/m2a without the earth
tube, i.e. &23%);
for Rome, 38.0 kWh/m2a (vs. 52.2 kWh/m2a without the earth
tube, i.e. &27%);
for Milan, 28.3 kWh/m2a (vs. 41.3 kWh/m2a without the earth
tube, i.e. &31%).
2.3. EAHX optimisation and coupling to other energy saving
techniques for summer conditions
Considering the results previously presented, the best of the
configurations studied for the earth-to-air heat exchanger is characterised by the following conditions: depth ¼ 3 m, length ¼ 50 m,
Fig. 4. Influence of the buried pipe material on the energy requests for summer cooling.
2182
F. Ascione et al. / Renewable Energy 36 (2011) 2177e2188
Fig. 5. Influence of the tube length on the EAHX outlet air temperature (a, b, c) and on the energy requests for summer cooling (d).
Fig. 6. Influence of the tube depth and air velocity on the energy requests for summer cooling.
2183
F. Ascione et al. / Renewable Energy 36 (2011) 2177e2188
Fig. 7. Influence of the fan position and airflow rate on the energy requests for summer cooling.
material ¼ PVC, ventilation airflow rate ¼ 1 ACH, air speed ¼ 7.7 m/s,
exhaust fan use, control mode 1 (15 h/day).
Up to now, the analysis has been carried out considering only
the EAHX and no other passive techniques for energy saving in
buildings. On the contrary, in this section, the EAHX is coupled to
window shadings (outdoor blinds with horizontal slats) and nighttime ventilation, still with reference to summer conditions. In fact,
as regards ventilation, it is suitable to use both the diurnal ventilation (fresh air supplied into the building) and the night-ventilation (in order to cool the building envelope and activate its mass).
In Fig. 9 the energy requests for summer cooling are reported, in
terms of thermal energy (Fig. 9A) and primary energy requirements
(Fig. 9B). Adopting all the 3 passive techniques for the examined
building, the reduction of the active cooling energy requests becomes
more significant. In terms of thermal energy, the following requirements have been obtained:
for Naples: 33 kWh/m2a (59 kWh/m2a in the base case with
no energy saving technology, i.e. &44%);
for Rome: 28 kWh/m2a (56 kWh/m2a in the base case, i.e. &50%);
for Milan: 17 kWh/m2a (44 kWh/m2a in the base case, i.e. &61%).
It can be noted that the current Italian rule [12] imposes a limit
of 30 kWh/m2a (even if for the residential buildings) to the
thermal needs for summer cooling. By using the 3 passive cooling
solutions, the building respects the legal limit value for Rome
(28 kWh/m2a) and Milan (17 kWh/m2a), but not for Naples
(33 kWh/m2a).
Note that the curve slopes in Fig. 9 seem to show that the
highest energy saving potential is related to the use of the EAXH.
2.4. Energy efficiency ratios for the ventilation system with EAHX in
summer conditions
For the examined cities, the following energy efficiency ratios
have been calculated for summer conditions:
- energy efficiency ratio (EER) at the design conditions e
Equation (19);
- mean summer seasonal energy efficiency ratio (SEER) e
Equation (20).
_
EERDESIGN ¼ m$c$ðT
external&air & TEAHX outlet&air Þ=
Fan electric power ½kWthermal =kWelectric '
ð19Þ
SEER ¼ Qground recovered =Fan seasonal electric request
½kWhthermal =kWhelectric '
ð20Þ
These performance coefficients (the values are reported in Table 5)
have been evaluated both for the total system (“TOTAL” as subscript in
Table 5, i.e. considering the energy required by the fans for the whole
ventilation system) and with reference to the only EAHX (pressure
drops z 1/3 compared to the whole ventilation system).
The highest energy efficiency ratios have been obtained for
Milan, i.e. for the zone with the coldest winter (so, in summer the
ground is colder compared to the other zones). Note that, also
considering the seasonal performance coefficient referred to the
whole ventilation system (SEERTOTAL), values about 10 Whthermal/
Whelectric are about three times higher than those obtainable using
a typical and efficient cooling system for single room (split-system).
It is also noteworthy that the obtained results are coherent with
the evaluations reported in Reference [13].
2.5. Energy saving potential obtainable using the EAHX in winter
conditions
In this section, the EAHX in winter conditions is examined, with
reference to its optimal configuration described at the beginning of
Section 2.3.
In Fig. 10 the temperature of the outdoor air and that of the air at
the EAHX exit have been reported for winter conditions; so, the
EAHX pre-heating potential (proportional to the thermal energy
recovery obtainable in winter) has been evaluated. In moderate
climates (Naples and Rome), the outdoor air is heated of about 4 ( C
Table 4
Analysed control modes for the EAHX (working period and time).
Control mode 1
16/06 O 15/09
(15 h/day)
Control mode 2
16/06 O 15/09
(13 h/day)
Control mode 3
16/06 O 15/09
(11 h/day)
Control mode 4
Control mode 5
16/06 O 15/09
(9 h/day)
16/06 O 30/06
(15 h/day)
01.07 O 31/08
(11 h/day)
01/09 O 15/09
(15 h/day)
2184
F. Ascione et al. / Renewable Energy 36 (2011) 2177e2188
Fig. 8. Influence of the earth tube control modes on the energy requests for summer cooling.
Fig. 9. Energy requests obtained coupling three passive solutions for summer cooling.
through the EAHX, while in Milan the temperature increase is
significantly higher (z10 ( C).
In the case of building without EAHX, the thermal energy for
winter heating is about 6.4 kWh/m2a for Naples, 7.5 kWh/m2a for
Rome and 32.3 kWh/m2a for Milan. Results obtained using an earth
tube for 9 h/day (8.00e13.00 and 15.00e19.00), in the period from
November to March, for 5 days/week, are reported in the following.
Naples: savings of about 1.9 kWh/m2a in terms of thermal
energy and 2.5 kWh/m2a in terms of primary energy. As the fan
primary energy consumption is equal to 4.9 kWh/m2a, the
primary energy balance is negative (&2.4 kWh/m2a), so the use
of the EAHX is not convenient.
Rome: savings of about 2.1 kWh/m2a for thermal energy and
2.8 kWh/m2a for primary energy; the primary energy balance is
negative also in this case (&2.1 kWh/m2a).
Milan: savings of about 5.2 kWh/m2a for thermal energy and
6.9 kWh/m2a for primary energy; the primary energy balance is
positive (þ2.0 kWh/m2a), so the use of the EAHX is suitable also
in winter.
Table 5
Ventilation system and EAHX energy efficiency ratios.
EERtotal
EEREAHX
SEERtotal
SEEREAHX
kWth/kWel
kWth/kWel
kWhth/kWhel
kWhth/kWhel
Naples
Rome
Milan
10.4
25.3
7.5
18.3
10
24.3
8.9
21.8
12.9
31.4
12.4
30.2
Finally, a high efficiency and an energetic convenience of the
EAHX in winter conditions have been obtained only in the case of
cold climates.
2.6. Cost-benefit analysis
The cost-benefit analysis is based on the costs reported in Table 6.
Four different design solutions have been examined, as a function of
the soil type (with the related excavation and refilling costs) and the
EAHX material:
1) PVC tube, unleashed soil (excavation costs: 2.4 €/m3; refilling
costs: 2.0 €/m3);
2) PVC tube, tender rock (excavation costs: 8.1 €/m3; refilling
costs: 2.0 €/m3);
3) PVC tube, hard rock (excavation costs: 32.5 €/m3; manual
refilling costs: 8.0 €/m3);
4) Metallic tube, unleashed soil (excavation costs: 2.4 €/m3;
refilling costs: 2.0 €/m3).
All these solutions (ventilation system with EAHX) have been
compared with a traditional ventilation system without EAHX.
In Table 7, a simple payback analysis is reported. On the basis of
the results reported in Section 2.5, the savings obtainable in winter
conditions have been considered only for Milan.
Table 7 shows that the ground moving represents a relevant cost,
equal or higher compared to the tube, according to Reference [13];
2185
F. Ascione et al. / Renewable Energy 36 (2011) 2177e2188
Fig. 10. EAHX winter pre-heating potential.
Table 6
EAHX costs and moving earth costs (rough estimate).
Excavation costs
Open section
excavation
Unleashed rocks:
sand,
clay, gravel
Tender rock
€/m3 Refilling costs
2.4
Adopting mechanical
devices and using the
material previously
moved off: 2.0 €/m3
8.1
EAHX costsb
plastic,
F ¼ 160 mm
plastic,
F ¼ 315 mm
plastic,
€/m
8.0
28.0
44.0
F ¼ 400 mm
Hard rock
32.5
metallic,
EAHX not suitable. In particular, the use of metallic material does not
guarantee any benefit, as installation costs are much higher, while
thermal performances are only slightly better compared to the
PVC tubes (so, the differences of savings are neglected in Table 7).
This analysis shows again that the highest benefits are obtained
in climates with colder winter (Milan). Moreover, the economic
suitability related to the use of an EAHX is more relevant for new
buildings compared to the case of existing building energy
refurbishment.
52.0
F ¼ 150 mm
Force section excavation
(not considered here)
2.9
Unleashed rocks:
sand,
claya
Tender rock
9.1
Hard rock
a
b
Manually executed
refilling,
using the material
previously
moved off: 8.0 €/m3
52.8
metallic,
F ¼ 315 mm
metallic,
F ¼ 400 mm
170.0
concrete,
F ¼ 300 mm
concrete,
F ¼ 400 mm
34.0
202.0
40.0
Over e 2 m, extra-cost of around 2 €/m3.
Installation: extra-cost of about 20%.
this is not true only for the case 4, as the metallic tube is very
expensive. When the ground allows an easy moving work (cases 1
and 2), the earth tube represents a very suitable improvement of the
ventilation system, with reduced payback periods (5e9 years). On
the contrary, onerous ground moving works (hard rock, case 3) and/
or the use of expensive material (metallic tube, case 4) make the
2.7. Indoor thermal conditions in building provided only with
ventilation and EAHX, in summer conditions
In the previous sections, all the energy evaluations have been
carried out considering a fully air-conditioned building and calculating the active cooling savings achievable in summer by using an
EAHX coupled to the ventilation system.
According to another approach, typical of the middle Europe
climates, in this section the EAHX benefits have been estimated
considering the possible indoor thermal comfort conditions for
a not fully air-conditioned building; the building is provided only
with diurnal ventilation coupled to EAHX, plus nocturnal ventilation: therefore, the indoor temperature varies. The indoor thermal
comfort conditions have been fixed according to the EN Standard
15251 [14], as regards the adaptive thermal comfort criteria
(Equations (21) and (22), Fig. 11 and Table 8). The Equations (21)
and (22) are necessary to define the limits of each thermal environment category:
Table 7
Simple payback analysis for the EAHX.
1
2
3
4
Saving in summer
conditions (€)
Saving in winter
conditions (€)
System
extra-cost (€)
Naples
Rome
Milan
633.9
720.1
659.3
e
e
120.1
3513
Naples
Rome
Milan
633.9
720.1
659.3
e
e
120.1
Naples
Rome
Milan
633.9
720.1
659.3
Naples
Rome
Milan
633.9
720.1
659.3
Payback
(years)
Component costs
%
5.5
4.9
4.5
Solution 1:
Ground moving
Earth tube
50
50
5771
9.1
8.0
7.4
Solution 2:
Ground moving
Earth tube
69
31
e
e
120.1
17809
28.1
24.7
22.8
Solution 3:
Ground moving
Earth tube
90
10
e
e
120.1
12495
19.7
17.4
16.0
Solution 4:
Ground moving
Earth tube
14
86
2186
F. Ascione et al. / Renewable Energy 36 (2011) 2177e2188
Fig. 11. Temperature limits of the thermal environment categories for buildings without active cooling system, in summer (according to adaptive thermal comfort criteria - EN
15251).
upper limit / TINDOOR MAX ¼ 0:33$TOUTDOOR MEAN MONTHLY
þ 18:8 þ X
ð21Þ
lower limit / TINDOOR MIN ¼ 0:33$TOUTDOOR MEAN MONTHLY
þ 18:8 & X
ð22Þ
thermal zone 2: 1st floor, south-exposed;
thermal zone 3: ground floor, north-exposed.
where:
for category I (90% acceptation, 10% dissatisfied), X ¼ 2 ( C;
for category II (80% acceptation, 20% dissatisfied), X ¼ 3 ( C;
for category III (65% acceptation, 35% dissatisfied), X ¼ 4 ( C.
In order to simplify the analysis, the mean monthly outdoor
temperature of July has been considered for the whole summer
season.
Then, the indoor temperatures have been evaluated considering
the building provided only with diurnal ventilation coupled to
EAHX, plus nocturnal ventilation; the evaluation has been carried
Table 8
Temperature limits of the thermal environment categories for buildings without
active cooling system, for three Italian cities and summer conditions (according to
adaptive thermal comfort criteria - EN 15251).
Naples
(mean July T
w 26.7 ( C)
Rome
(mean July T
w 25.7 ( C)
Milan
(mean July T
w 25.1 ( C)
out only for the summer diurnal hours during the working days and
for each thermal zone (note that the room exposure is relevant in
the evaluation of the temperature inside a building not fully airconditioned). Two different thermal zones have been considered
here (the most and the less critical zone as regards the thermal
loads):
Category I
(90% acceptation)
Category II
(80% acceptation)
Category III
(65% acceptation)
25.6e29.6 ( C
24.6e30.6 ( C
23.6e31.6 ( C
25.3e29.3 ( C
24.3e30.3 ( C
23.3e31.3 ( C
25.1e29.1 ( C
24.1e30.1 ( C
23.1e31.1 ( C
The calculated indoor temperatures are reported in Table 9: the
values represent the percentage time fraction in which thermal
comfort conditions are obtained, with reference to the above
specified categories. The following results can be highlighted.
Thermal zone 2: despite the use of passive cooling solutions,
thermal comfort conditions are rarely obtained, above all in the
hottest climate (Naples e time periods between 10% and 23% of
the summer working time). Also in the less critical climate
(Milan), where both the night-time ventilation and the ground
Table 9
Summer indoor thermal conditions in a building provided only with ventilation and
EAHX for three Italian cities, subdivided with respect to the thermal environment
categories reported in EN 15251.
Naples
Rome
Milan
Zone 2 (1st floor, south-exposed)
Category I
Category II
10.0%
13.0%
20.0%
26.1%
27.4%
36.5%
Category III
23.0%
29.9%
42.7%
Naples
Rome
Milan
Zone 3 (ground floor, north-exposed)
Category I
Category II
35.6%
43.3%
50.1%
67.2%
80.3%
88.8%
Category III
49.6%
74.4%
90.0%
F. Ascione et al. / Renewable Energy 36 (2011) 2177e2188
2187
Fig. 12. Frequency and cumulative frequency of the summer indoor temperature values for the thermal zone 3 of an office building in Milan, and thermal environment evaluation
according to EN 15251.
cooling potentials are higher, partial comfort conditions (category III) are obtained only for 43% of the global diurnal working
hours. With reference to Naples and Rome, even if the admitted
indoor temperatures are higher compared to Milan (Fig. 11 and
Table 8), the indoor conditions are worse.
Thermal zone 3: the comfort conditions of category I are only
partially achieved in Naples (36% of summer working time) and
Rome (50%), while more interesting results are obtained for
Milan (80%). Enlarging the admitted indoor temperature range
(categories II and III), the building in Milan shows better
performances (about 90%). Considering the comfort conditions
of category III, minor results are achieved for Rome and Naples
(respectively, 74% and 50%).
The main results for Milan and thermal zone 3 are reported also
in Fig. 12: so, for cold climates such as Milan, the achievable indoor
thermal conditions are good (about 90% of the summer diurnal
time characterised by indoor temperature lower than 30 ( C, as
shown by the cumulative frequency curve).
On the contrary, with reference to Naples and Rome, the indoor
summer temperatures obtainable using EAHX coupled to ventilation aren’t fully satisfactory (Table 9); anyway, the use of the active
cooling can be noticeably reduced.
3. Conclusions
With reference to three localities, representative of the different
Italian climates, the energy performances of a buried earth-to-air
heat exchanger have been evaluated as a function of the main
boundary conditions. In fact, the thermal requirements of a building
can be significantly reduced by means of the pre-handling of the
ventilation air through the heat transfer with the ground.
The following conclusions of the analysis can be drawn as
regards summer conditions:
- the best energy performances have been obtained for wet/
humid soil and for the coldest climates (Milan) e maximum
energy savings of about 44% in terms of thermal energy, about
37% for primary energy;
- the influence of the tube material (usually, PVC, metal or
concrete) on the energy performance is negligible;
- as regards the tube length, values of about 10 m are unsatisfactory. Moreover, a length of nearly 50 m is a good compromise;
in fact, adopting a tube longer than 50 m, the cooling energy
reduction is negligible, while the electric energy requirements
for fans increase significantly;
- about the tube depth, a good compromise between energy
performance and moving earth costs is achieved with a depth
of about 3 m;
- in spite of a minor heat transfer coefficient, low speeds (about
8 m/s) of the airflow inside the tubes are preferable, as the
pressure drops and fan electric energy requirements decrease;
the higher energy costs due to the use of intake fans instead of
exhaust ones are negligible;
- as regards the ventilation airflow rate, 1 or 2 ACH are equivalent
and preferable in terms of total primary energy requirements;
- about the control mode of the EAHX, the best solution consists
in a long use.
In winter, the minimum ventilation airflow rate necessary for an
acceptable indoor air quality is preferable as regards energy
requirements; moreover, the convenience of the EAHX in winter
has been obtained only for cold climates (Milan).
As regards the technical-economic analysis, the use of an EAHX
is suitable (simple payback of 5e9 years) only when the moving
earth works are easy and cheap (for example, this is not true for
hard rock); otherwise, high moving earth costs or expensive tube
materials (metals) induce too long payback values.
Finally, considering in summer a not fully air-conditioned
building, only provided with diurnal ventilation coupled to EAHX
plus night-time ventilation, the possible indoor thermal comfort
conditions have been evaluated for the diurnal hours during the
working days. Only for building zones with low thermal loads and
for the coldest climate (Milan), the achievable results are good (90%
of the hours characterised by indoor temperature lower than 30 ( C
and so by partial thermal comfort conditions). As regards the other
building zones and the other cities (Naples and Rome), worse
indoor thermal conditions have been obtained.
2188
F. Ascione et al. / Renewable Energy 36 (2011) 2177e2188
Nomenclature
a
A
As
b
c
dh
f
hc
hs
k
L
_
m
Nu
Q
R
RH
Rtot
r1
r2
r3
T
Ta(y)
Tam
TGROUND
t
t0
Ut
w
Z
constant (¼103 Pa/( C), Pa ( C&1
area, m2
amplitude of the soil surface temperature variation, ( C
constant (609 Pa), Pa
specific heat, kJ kg&1 K&1
hydraulic diameter of the tube, m
fraction of evaporation rate, kJ
convective heat transfer coefficient at the inner tube
surface, W m&2 K&1
convective heat transfer coefficient at the soil surface,
W m&2 K&1
thermal conductivity, W m&1 K&1
length of the tube or duct, m
mass flow rate of the air crossing the EAHX, kg s&1
number of Nusselt
thermal energy, kJ or kWh
total thermal resistance, K W&1
ambient air relative humidity
global total thermal resistance between the air in the tube
and the soil, K W&1
inner radius of the tube, m
thickness of the tube, m
distance between the tube external surface and the
undisturbed soil, m
temperature( C
air temperature inside the tube at the distance y from the
tube inlet, ( C
ambient air temperature, ( C
(z, t) ground temperature at time t and depth z, ( C
time passed from the begin of the year, days
phase constant of the soil, days
overall heat transfer coefficient, W m&2 K&1
air speed inside the duct, m s&1
depth of the tube section centre with respect to the
ground level, m
Greek letters
as
soil thermal diffusivity, m2 s&1
bs
soil absorption coefficient (¼ 1esoil albedo)
DR
radiation constant (63 W/m2), W m&2
DP
pressure loss, Pa
3
z
l
r
hemispherical emittance of the ground surface
dynamic loss coefficient
Darcy friction factor
air density, kg m&3
Acronyms
EER
energy efficiency ratio at the design conditions
SEER
mean summer seasonal energy efficiency ratio
Subscripts
a
air (in the tube)
air
(outdoor ventilation) air
cond
conduction
conv
convection
p
pipe ¼ tube
s
soil
SURF
(soil) surface
References
[1] Argiriuou A. Ground cooling. In: Santamouris M, Asimakopoulos D, editors.
Passive cooling of buildings; 2001. p. 360e401.
[2] Givoni B. The earth as a cooling source for buildings. In: Givoni B,
editor. Passive and low energy cooling of buildings. J. Wiley & Sons;
1994. p. 191e238.
[3] Mihalakakou G, Santamouris M, Asimakopoulos DN. Modelling the thermal
performance of earth-to air heat exchangers. Solar Energy 1994;53:301e5.
[4] Mihalakakou G. On estimating soil surface temperature profiles. Energy and
Buildings 2002;34:251e9.
[5] Benkert S, Heidt FD, Scholer D. Calculation tool for earth heat exchangers
GAEA. In: Proceeding of building simulation, vol. 2. Prague: Fifth International
IBPSA Conference; 1997.
[6] Pfafferott J. Evaluation of earth-to-air heat exchangers with a standardized
method to calculate energy efficiency. Energy and Buildings 2003;35:971e83.
[7] Lee KH, Strand RK. The cooling and heating potential of an earth tube system
in buildings. Energy and Buildings 2008;40:486e94.
[8] Lee KH, Strand RK. Implementation of an earth tube system into EnergyPlus
program. IBPSA USA SimBuild Publications; 2006.
[9] U.S. Department of Energy. EnergyPlus simulation software, version 2.0.0; 2007.
[10] U.S. Department of Energy. Calculation of soil temperature, auxiliary program
of EnergyPlus; 2007.
[11] Krarti M, Lopez-Alonzo C, Claridge DE, Kreider JF. Analytical model to predict
annual soil surface temperature variation. Journal of Solar Energy Engineering
1995;117:91e9.
[12] Italian Presidential Decree n. 59/2009, Regolamento di attuazione del D.Lgs.
192 sul rendimento energetico in edilizia, 2009.
[13] Pfafferott J, Walker-Hertkorn S, Sanner B. Ground cooling: recent progress. In:
Santamouris M, editor. Advances in passive cooling; 2007. p. 190e227.
[14] Standard EN 15251, Indoor environmental input parameters for design and
assessment of energy performance of buildings addressing indoor air quality,
thermal environment, lighting and acoustics, 2007.