Funciones Matemáticas: Guía de Funciones a Trozos, Trigonométricas, Exponenciales y Logarítmicas
Anuncio

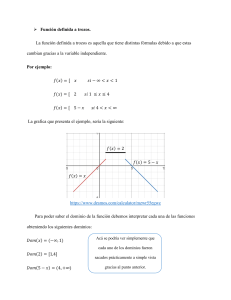
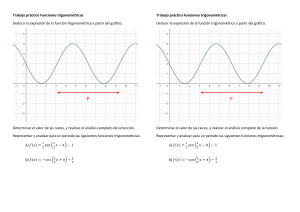
Función definida a trozos. La función definida a trozos es aquella que tiene distintas fórmulas debido a que estas cambian gracias a la variable independiente. Por ejemplo: 𝑓(𝑥) = [ 𝑥 𝑓(𝑥) = [ 2 𝑠𝑖 − ∞ < 𝑥 < 1 𝑠𝑖 1 ≤ 𝑥 ≤ 4 𝑓(𝑥) = [ 5 − 𝑥 𝑠𝑖 4 < 𝑥 < ∞ La grafica que presenta el ejemplo, sería la siguiente: 𝑓(𝑥) = 2 𝑓(𝑥) = 5 − 𝑥 𝑓(𝑥) = 𝑥 https://www.desmos.com/calculator/mzwr55egwc Para poder saber el dominio de la función debemos interpretar cada una de las funciones obteniendo los siguientes dominios: 𝐷𝑜𝑚(𝑥) = (−∞, 1) Acá se podría ver simplemente que cada uno de los dominios fueron 𝐷𝑜𝑚(2) = [1,4] 𝐷𝑜𝑚(5 − 𝑥) = (4, +∞) sacados prácticamente a simple vista gracias al punto anterior. Y para poder determinar el rango de la función debemos fijarnos directamente en la gráfica en la parte de la f(x)=2, está en la recta numérica va del punto 1 hasta el punto 4, siendo el rango entonces 𝑅𝑎𝑛(𝑥) = (1,4). Funciones trigonométricas. Son aquellas relacionadas a las razones trigonométricas de un Angulo, estas se obtienen a partir de los tres lados de un triángulo rectángulo, comparando sus tres lados a, b y c. 𝑠𝑒𝑛: 𝑠𝑒𝑛 = 1 𝛑 𝑐𝑜𝑠𝜃 = cos ( − 𝜃) = 𝑐𝑠𝑐𝜃 2 𝑐𝑜𝑡𝜃 𝑐𝑜𝑠: 𝑐𝑜𝑠 = 1 𝛑 𝑠𝑒𝑛𝜃 = sin ( − 𝜃) = 𝑠𝑒𝑐𝜃 2 𝑡𝑎𝑛𝜃 𝑡𝑎𝑛: 𝑡𝑎𝑛 = 1 𝛑 𝑠𝑒𝑛𝜃 = cot ( − 𝜃) = 𝑐𝑜𝑡𝜃 2 𝑐𝑜𝑠𝜃 Razones trigonométricas. https://www.desmos.com/calculator/eig0yihm3z Funciones trigonométricas inversas. Las funciones trigonométricas inversas son como su nombre lo indica, las funciones inversas de las razones trigonométricas, las cuales son (seno, coseno y tangente). Las razones trigonométricas inversas son las siguientes: Arcoseno. Arcocoseno. Arcotangente. Arcoseno (sen -1): Arcoseno como lo dice su nombre es la función inversa del seno. 𝑠𝑖 𝑎𝑟𝑐𝒔𝒆𝒏𝑥 = 𝛼, 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑠𝑒𝑛𝜶 = 𝑥 𝑎𝑟𝑐𝒔𝒆𝒏(𝑠𝑒𝑛 𝛼) = 𝛼 Ejemplos: 𝑑𝑜𝑚(𝑥) = [−1,1] 𝛑 𝛑 𝑐𝑜𝑑𝑜𝑚𝑖𝑛𝑖𝑜(𝑥) = [− , ] 2 2 Arcocoseno (cos-1 ): Se llama Arcocoseno debido a que es la función inversa del coseno. 𝑠𝑖 𝑎𝑟𝑐𝒄𝒐𝒔𝑥 = 𝛼, 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝑐𝑜𝑠𝜶 = 𝑥 𝑎𝑟𝑐𝒄𝒐𝒔(cos 𝛼) = 𝛼 Ejemplos: 𝑑𝑜𝑚(𝑥) = [−1,1] 𝑐𝑜𝑑𝑜𝑚𝑖𝑛𝑖𝑜(𝑥) = [0, 𝛑] Arcotangente (tan-1) Esta es la función inversa de la tangente. 𝑠𝑖 𝑎𝑟𝑐𝒕𝒂𝒏 𝒙 = 𝛼, 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 tan 𝜶 = 𝑥 𝑎𝑟𝑐𝒕𝒂𝒏(tan 𝛼) = 𝛼 https://www.desmos.com/calculator/ij7d9ge7pj Función exponencial 𝒃 ͯ . Se trata de aquella función en la que la variable independiente x aparece en el punto del exponente, pero aun así sigue teniendo una base constante. Su fórmula es la siguiente: 𝑓(𝑥) = 𝑎 ͯ La única exigencia con la que se cuenta de esta función es que a debe ser un real positivo, 𝑎 > 0 Y diferente de 1, 𝑎 ≠ 1. En caso de Cuando 0 < a < 1, entonces la función exponencial es una función decreciente y cuando a > 1, es una función creciente. 𝑓(𝑥) = 𝑎 ͯ https://www.desmos.com/calculator/7kaur8cbyj 𝐷𝑜𝑚(𝑥): 𝑝𝑎𝑟𝑎 𝑒𝑠𝑡𝑒 𝑒𝑗𝑒𝑚𝑝𝑙𝑜 𝑠𝑒𝑟𝑎𝑛 𝑡𝑜𝑑𝑜𝑠 𝑙𝑜𝑠 ℝ 𝑦 𝑒𝑙 𝑅𝑎𝑛(𝑥): 𝑡𝑜𝑑𝑜𝑠 𝑙𝑜𝑠 ℝ +. Función logarítmica de base 𝒃. Como lo indica su nombre la función está compuesta por un logaritmo, de la siguiente manera: 𝑓(𝑥) = 𝑙𝑜𝑔ₐ(𝑥) A será un ℝ + , 𝑎 > 0, y diferente de 1, 𝑎 ≠ 0. En caso de que 0 < a < 1, entonces la función logarítmica es una función decreciente y cuando a > 1, será una función creciente. 𝑓(𝑥) = 𝑙𝑜𝑔ₐ(𝑥) https://www.desmos.com/calculator/sdqu2ufnrd 𝐷𝑜𝑚(𝑥): 𝑝𝑎𝑟𝑎 𝑒𝑠𝑡𝑒 𝑒𝑗𝑒𝑚𝑝𝑙𝑜 𝑠𝑒𝑟𝑎𝑛 𝑡𝑜𝑑𝑜𝑠 𝑙𝑜𝑠 ℝ + 𝑦 𝑒𝑙 𝑅𝑎𝑛(𝑥): 𝑡𝑜𝑑𝑜𝑠 𝑙𝑜𝑠 ℝ.