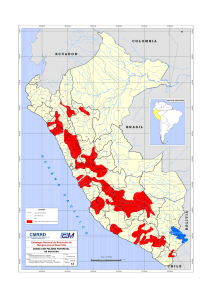
CONFERENCIA PREVENCION DE HUAICOS TEMA AVANCES EN LA PREDICCION DE HUAICOS MEDIANTE MODELOS MUMERICOS Dr. Ing. Samuel Quisca A. CONTENIDO CO O Introducción Proceso de ocurrencia, tránsito y deposición de huaicos Avances y perspectivas en el modelamiento de huaicos Conclusiones 1.0 INTRODUCCION PRINCIPALES PELIGROS NATURALES EN EL PERU Según BID-CEPAL-IDEA (2004) Ocurrencia de inundaciones y huaycos en cuencas del país durante FEN 1997-98 Se muestran las cuencas del país donde ocurrieron inundaciones y flujos de huaycos durante la presencia del fenómeno El Niño 1997-98. Aquí es necesario precisar que la combinación de las inundaciones, flujos hi hiperconcentrados d o huaycos h se producen d en las cuencas media y alta de la costa, siendo más persistente su presencia en las cuencas de la sierra, y en la selva alta. Fuente: Quisca (2006) Zonas propensas a eventos extremos: • Inundaciones • Huaycos • Aluviones • Precipitaciones y lluvias (97/98) Fuente: PREDES PLAN DE GESTION DE RIESGO DE INUNDACIONES Y HUAYCOS PELIGRO VULNERABILIDAD 100% Daños 75% X 50% = Tipo 1 Tipo 2 Tipo 3 25% 0% 0,00 0,50 1,00 1,50 2,00 2,50 Intensidad Intensidad del peligro Funciones de daño de bienes expuestos RIESGO = Daños potenciales x Valor económico MAPAS DE PELIGROS, VULNERABILIDAD Y RIESGO CUENCA PUYANGO TUMBES A NIVEL DE DISTRITOS El BID-IDEA (2005) propone una metodología para medir la vulnerabilidad y el riesgo utilizando í di índices relativos l ti a escala l nacional, i l a fin fi de d facilitar f ilit ell acceso a información i f ió relevante l t para la l toma de decisiones que permita identificar y proponer acciones efectivas de gestión de riesgo, considerando aspectos macroeconómicos, sociales, institucionales y técnicos. CUENCA CHIRA - PIURA A NIVEL DE DISTRITOS 2.0 Proceso de ocurrencia, tránsito y deposición de huaicos Divisoria ((Parte aguas) g ) VERTIENTES Red de Cauces VALLE Río receptor CUENCA Eventos de flujos hiperconcentrados y flujos de huaycos CLASIFICACION DE LOS FLUJOS DE ESCOMBROS (CONT.) Suaréz, J. (2001) muestra una clasificación en función del perfil característico de cada tipo de flujo. Los flujos de detritos ocurren generalmente en canales de gran pendiente y tiene una longitud de recorrido menor que los flujos hiperconcentrados y los flujos de lodo. Alltura con resspecto al pie del flujo o Flujos de detritos Flujos hiperconcentrados Shiramizudani (China) Kamikamihori (Japón) Takahashi-1991 nt rre o aT as Xikon ar 97 g eli 9 a m m )1 (China) ca ia) G a pón as omb L a (J ol (C m2 2 k 4 km .5 3 2 .6 23 .4 33 2 km Flujos de lodos n lia Ju ) n a la o S ue Rí nez e (V ta ua g i a la) o N zue í e R en 2 (V km P ae z 2 Distancia con respecto al pie del flujo bia) (Colom 562 k m2 Experimentos de flujos de huaycos a escala real – The Chemolgam Debris Flow Testing Ground, Ex-URSS (1972–1991) Se realizaron 7 experimentos en la parte alta del río Chemolgan, localizado a 60 km y al Oeste de Alma-Ata, capital de la República de Kazakhstan. Características del mayor flujo de huayco generado: Qmax=430 m3/s, V=11 m/s, Densidad mezcla bifásica = 2400 kg/m3, Rocas transportadas 3 m – 4 m Características del 7mo. Experimento p (Symposium ( y p Soviético-Chino-Japonés, p , 12 Setiembre 1991): Volumen: 40,000 m3 Qmax (agua) : 25 m3/s Qmax (huayco) : 200 -300 300 m3/s Densidad huayco: 2000 – 2200 kg/m3 3.0 AVANCES Y PERSPECTIVAS EN EL MODELAMIENTO NUMERICO DE HUAICOS MODELOS REOLOGICOS • Los p primeros modelo matemáticos para p la caracterización de los flujos j de escombros partieron de la base de la resistencia de los materiales, de acuerdo a la ecuación de Coulomb (Johnson y Rodine, 1984). • Posteriormente se involucraron modelos hidráulicos como los de Bingham y Bagnold, los cuales fueron adaptados al comportamiento de fluidos producto de la mezcla sedimento fino y agua. • Existen 2 enfoques básicos para modelar el comportamiento de los flujos huaycos: – Considerar la masa entera (fluido y sólido) como un “fluido continuo” con p propiedades p particulares. p El modelamiento con este enfoque se aproxima muy bien a los flujos de lodos con material fino. – Se considera el fluido como una mezcla de agua con sedimentos muy finos (arcilla, limos, etc.), y el material grueso por separado. El material t i l grueso se caracteriza t i por la l distribución di t ib ió del d l tamaño t ñ y sus respectivas concentraciones de las partículas sólidas. Bagnold (1954) de experimentos con partículas cizallándose en un cilindro giratorio encontró que el esfuerzo de corte al grano, T (definido como el esfuerzo al corte debido a la transferencia de momentum dentro del fluido intergranular o intersticial) y el efuerzo normal al grano, P (definido como el esfuerzo normal ejercido por el fluido intergranular) en la región de grano inercial (grain-nertial) puede ser expresado como: 2 ⎛ du ⎞ T = ai ρ s (λd ) ⎜ ⎟ senφ d ⎝ dz ⎠ 2 2 ⎛ du ⎞ P = ai ρ s (λd ) ⎜ ⎟ cos φ d d ⎠ ⎝ dz 2 Donde ai es una constante numérica, ρs es la densidad del grano, λ es la concentración lineal (λ (λ=[(Cm/C)^1/3-1]^-1), [(Cm/C) 1/3 1] 1), d es el diámetro del grano y Φd es el ángulo “dinámico” de fricción interna. Cm es la concentración máxima aproximadamente igual a 0.615. Modelo viscoso de Coulomb τ = c + σ n tan φ donde c es la cohesión σn es el esfuerzo normal Φ es el ángulo de fricción interna Johnson (1970) propuso que la resistencia dinámica total es una combinación de resistencia de cedencia, friccionales y resistencias viscosas llamado este el modelo viscoso de Coulomb δu τ = c + σ n tan φ + µ δy donde, µ es la viscosidad y δu/δy es la tasa de deformación. Este es uno de los modelos más antiguos sobre flujos de escombros. escombros Modelo de Bingham y Pseudoplástico Este modelo es muy bien relacionado con el flujo de lodo debido a la presencia de granulometría fina fina. El esfuerzo de cedencia τy y la viscosidad µ son los dos parámetros δu τ =τy + µ δy Este modelo ha sido frecuentemente usado en el pasado en flujos de lodo y flujos hiperconcentrados (O´Brien y Julien, 1985; Fei, 1983). Yano &Daido (1965) usaron el modelo de fluido de Bingham para describir el flujo de lodo. lodo Este modelo es probablemente el más popular en China y en Japón (Chen, 1987). Johnson (1970) uso este modelo para describir el flujo de escombros permanentes en un canal circular. Modelo cuadrático de O’Brien y Julien Presentado por O´Brien y Julien (1985): τ =τy + µ donde ⎛ δu ⎞ δu + C1 ⎜⎜ ⎟⎟ δy ⎝ δy ⎠ 2 τy es el esfuerzo de cedencia µ es la viscosidad dinámica C1 es el parámetro turbulento-dispersivo Este modelo reológico es utilizado por el software FLO-2D. Modelo de fluido Dilatante Basado en experimentos de Bagnold (1954) donde el esfuerzo dispersivo normal se relaciona con el esfuerzo cortante del grano por: 2 ⎛ δu ⎞ ⎟⎟ sin φd δ y ⎝ ⎠ τ g = ai ρ s λf (λ ) D 2 ⎜⎜ donde: ai es una constante determinado de experimentos par el régimen de inercia del grano (ai = 0.042) ρs densidad de las partículas D diámetro de la partícula λ concentración lineal de las partículas f(λ) es una función de λ MODELAMIENTO MATEMATICO DE LOS HUAICOS ECUACIONES PARA ALGUNOS MODELOS NUMÉRICOS HIDRÁULICOS Continuity Momentum ∂Q ∂A + − qL = 0 ∂x ∂t ∂Q ∂(Q 2 / A) ⎛ ∂h ⎞ + + gA⎜ + Sf = 0 ∂t ∂x ⎝ ∂x ⎠ ∂Q ∂( A + Ao ) + − qL = 0 ∂x ∂t ∂Q ∂(Q 2 / A) ⎛ ∂h ⎞ + + gA⎜ + S f + Se ⎟ + L + Wf B = 0 ∂t ∂x ⎝ ∂x ⎠ ∂Q ∂sc ( A + Ao ) + − qL = 0 DAMBRK ∂x ∂t ∂(smQ ) ∂( βQ 2 / A) ⎛ ∂h ⎞ + + gA⎜ + S f + Se + Si ⎟ + L = 0 ∂x ∂t ⎝ ∂x ⎠ ∂Q ∂sc ( A + Ao ) + − qL = 0 ∂x ∂t ∂(smQ ) ∂( βQ 2 / A) ⎛ ∂h ⎞ + + gA⎜ + S f + Se + Si ⎟ + L + Wf B = 0 ∂t ∂x ⎝ ∂x ⎠ Básica DWOPER FLDWAV Donde sc : sinuosidad Ao : Area inactiva sm : sinuosidad β : factor de corrección del momentum Se : efecto de expansión/contracción Si : flujo lodo/escombros L : Flujo de entrada y de salida lateral WfB : efecto del viento CATEGORÍA DE MODELOS MODELO ECUACIONES DE NAVIERSTOKES TEORIA DE FLUJO MULTIFASICOS AUTOMATAS CELULARES FUENTE Modelo unidimensional de flujo no permanente. Puede analizar fluidos del tipo Bingham. http://www.weather.gov/ohd/ hrl/rvrmech/fld_avail.htm DAN-W Es un software geotécnico usado para el análisis de tránsito dinámico en deslizamientos y avalanchas avalanchas. http://www.claraw.com/DANWRunoutAnalysi s.html DBF-1D Es un nuevo modelo de flujo de escombros unidimensional que analiza 2 fases. Predice las velocidades del flujo, tirantes, distancia recorrida y presiones de impacto. http://www.wsl.ch/hazards/db f-1d/dbf-1d-de.ehtml FLO-2D Es un modelo de tránsito dinámico de avenidas en 2 dimensiones, que simula flujo en canales, superficies no confinadas y flujo en calles. Su aplicación es para flujos de avenida, flujos hiperconcentrados y flujos de escombros. http://www.flo-2d.com NWS-FLDWAV TEORIA DE LAS AGUAS POCO PROFUNDAS (SHALLOW WATER) DESCRIPCIÓN Monofásico En desarrollo Multifásico En desarrollo AVAL-1D Es un programa exclusivo para análisis dinámico de avalanchas unidimensional que predice las distancias recorridas velocidades del flujo y presiones de impacto recorridas, impacto. HUAYCO-1D HUAYCO-2D En desarrollo Por desarrollar Por investigar http://www.slf.ch/aval-1d/ MODELOS NUMERICOS EXISTENTES MODELO NUMÉRICO FLO-2D MODELO NUMÉRICO FLO FLO-2D 2D El FLO FLO--2D es un modelo de tránsito de avenidas bidimensional J. O'Brien es creador del software FLOFLO-2D El modelo hidráulico FLO FLO--2D ha sido aprobado por FEMA para estudios de ríos y análisis de avenidas. Las ecuaciones que rigen el modelo son la Ecuación de Continuidad y las Ecuaciones de Cantidad de Movimiento donde: h es la profundidad del flujo; Vx y Vy son las p de la velocidad componentes media, t es el tiempo, g la aceleració aceleraci ón de la gravedad, Sf es la pendiente de fricció fricción; So la pendiente del lecho e i es intensidad i t id d d de lla precipitació precipitaci i it ió ión. MODELO NUMÉRICO DBF-1D M Marc Christen Ch i t (2006) MODELO NUMÉRICO RAMS-2D PROCEDIMIENTO PARA LA CONCEPCION Y DISEÑO DE MEDIDAS ESTRUCTURALES PARA EL CONTROL DE FLUJOS DE HUAYCOS • CONOCIMIENTO DE LA HIDROLOGIA Y DEL PROCESO GEOMORFOLOGICO DE LA CUENCA ORIENTADO DE IDENTIFICAR LAS ZONAS ALIMENTADORAS DE CUENCA, SEDIMENTOS Y SUS VOLUMENES POTENCIALES. • CONOCIMIENTO DE LAS ACCIONES ANTROPICAS Y EL MEDIO AMBIENTE DE LA CUENCA • EVALUACION DE CAMPO DE LOS HUAYCOS OCURRIDOS, DETERMINANDO LAS FUENTES DE MATERIALES SÓLIDOS • COMPRENDER EL MECANISMO O MECANISMOS PREDOMINANTES DE FORMACION Y OCURRENCIA DEL HUAYCO EN LA CUENCA • DEFINIR LA ZONA DE TRANSITO O DEL PROCESO DE DESARROLLO DEL FLUJO DE HUAYCO • CONCEPTUALIZAR EL PROCESO DE FORMACION DEL CONO DE DEYECCION EXISTENTE. Gracias ….