Modelo de Transporte(1)

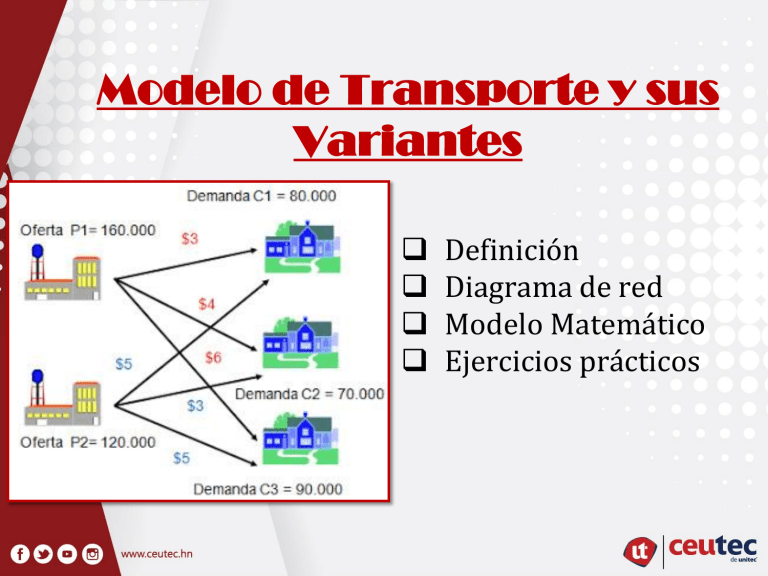
Modelo de Transporte y sus
Variantes




Definición
Diagrama de red
Modelo Matemático
Ejercicios prácticos
¿Qué significa problema de
transporte?
• Supóngase que un fabricante
tiene tres plantas que producen
el mismo producto. Estas plantas
a su vez mandan el producto a
cuatro almacenes. Cada planta
puede mandar productos a todos
los almacenes, pero el costo de
transporte varía con las
diferentes combinaciones. El
problema es determinar la
cantidad que cada planta debe
mandar a cada almacén con el
fin de minimizar el costo total
de transporte.
Modelo general del problema de
transporte
Problema general de transporte
Información necesaria
 Unidades de un bien
 Orígenes (fuentes)
 Destinos ( Plantas o almacenes)
 Recursos en el origen
 Demanda en el destino
 Costos por unidad distribuida
desde el origen al destino
Modelo de Transporte
Objetivo
Los datos del
modelo son:
• El modelo de transporte busca determinar un
plan de transporte de una mercancía de varias
fuentes a varios destinos.
• 1) Nivel de oferta en cada fuente y la cantidad de
demanda en cada destino.
• 2) El costo de transporte unitario de la mercancía a
cada destino.
Modelo de Transporte
Se tienen varios supuestos:
Propiedad de
soluciones
Supuesto de
factibles: un
Supuesto de
costo: el costo de
problema de
requerimientos: distribuir unidades
transporte tiene
de un origen a un
cada origen tiene
soluciones factible
un suministro fijo destino cualquiera
si y sólo si la
de unidades que se es directamente
sumatoria de
deben distribuir
proporcional
recursos en los
por completo entre al número de
orígenes es igual a
los destinos.
unidades
la sumatoria de
distribuidas.
demandas en los
destinos.
Propiedad de
soluciones enteras:
En los casos en los que
tanto los recursos
como las demandas
toman un valor entero,
todas las
variables básicas (asig
nadas), de cualquiera
de las
soluciones básicas fact
ibles (inclusive
la solución optima),
asumen también valor
es enteros.
EJERCICIO 1
• Considere el problema de transporte que se originan
debido a un accidente. Existen tres ambulancias con
distintas capacidades para trasladar heridos hacia cuatro
servicios de urgencia. La tabla siguiente presenta la
capacidad de las ambulancias y los servicios de urgencia
• Los costos generados por el transporte se muestran en la
siguiente tabla.
 DESARROLLO: A) DIAGRAMA DE RED
a) DIAGRAMA DE RED DE TRANSPORTE
DEMANDA
CAPACIDAD/OFERTA
3
A1
X1
X4
X5
7
A2
5
TOTAL  15
Personas
A3
X12
4
SU2
3
X2
X3
X6
X7
X8
X9
SU1
SU3
4
X10
X11
SU4
4
15 Personas
 DESAROLLO : B) MODELO MATEMATICO
b) MODELO MATEMATICO DE TRANSPORTE
 Determinar Función Objetivo que minimice los costos de transporte :
 MIN Z=
2X1+2X2+2X3+1X4+10X5+8X6+5X7+4X8+7X9+6X10+6X11+8X12
 Determinar Restricciones ( Capacidad/oferta ):
 X1+X2+X3+X4 <=3 Ambulancia 1
 X5+X6+X7+X8 <=7 Ambulancia 2
 X9+X10+X11+X12 <=5 Ambulancia 3
 Determinar Restricciones ( Demanda ):
 X1+X5+X9 >= 4 Servicio urgencia 1
 X2+X6+X10>=3 Servicio urgencia 2
 X3+X7+X11>=4 Servicio urgencia 3
 X4+X8+X12>=4 Servicio urgencia 4
 X1-12>=0 Lógica o no negativa
EJERCICIO 2
Distancias recorridas (millas )
$$ Costos de transporte
Plantas
Denver
Miami
Plantas
Denver
Miami
Los
Ángeles
1000
1690
Los Ángeles
(1690*$ 0.08)
=135
Detroit
1250
1350
(1000*$ 0.08
)
= 80
Detroit
(1250*$ 0.08)
=100
(1350*$ 0.08)
=108
New Orleans
(1275*$ 0.08)
=102
(850*$ 0.08)
=68
New
Orleans
1275
850
 DESARROLLO: A) DIAGRAMA DE RED
a) DIAGRAMA DE RED DE TRANSPORTE
CAPACIDAD/OFERTA
DEMANDA
1,000
1,500
1,200
TOTAL 
3,700 PZAS
P1
( Angeles)
P2
( Detroit)
P3
( N.Orlean)
X1
$ 80
X2
$ 135
X3
X4
D1
( Denver)
2,300
D2
1,400
$ 100
$ 108
X5
$ 102
( Miami )
X6
$ 68
3,700 PIEZAS
 DESAROLLO : B) MODELO MATEMATICO
b) MODELO MATEMATICO DE TRANSPORTE

Determinar Función Objetivo que minimice los costos de
transporte :
 MIN Z= 80X1+135X2+100X3+108X4+102X5+68X6

Determinar Restricciones ( Capacidad/oferta ):
 X1+X2<=1000
( Los Ángeles )
 X3+X4<=1500
( Detroit )
 X5+X6<=1200
( New Orleans )

Determinar Restricciones ( Demanda ):
 X1+X3+X5 >=2300 ( Denver )
 X2+X4+X6> =1400 ( Miami )

X1-6>=0 Lógica o no negativa
EJERCICIO 3
Problema de Transporte – Cosmic Computer Company
CCC tiene 3 plantas de embalaje de microcomputadoras en San Francisco, Los
Ángeles y Phoenix. La planta de los Ángeles tiene una capacidad de producción de
2000 unidades. Las plantas de San Francisco y Phoenix pueden producir un
máximo de 1700 unidades al mes. Las computadoras de CCC se venden en cuatro
tiendas detallistas ubicadas en San Diego (vende1,700 unidades) ,Barstow (vende
1000 unidades),Tucson(vende 1,500 unidades) y Dallas (vende1,200 unidades).
El costo de embarque de una microcomputadora desde cada planta hasta las
tiendas es el siguiente:
Plantas
San
Diego
Barstow
Tucson
Dallas
San
Francisco
5
3
2
6
Los
Ángeles
4
7
8
10
Phoenix
6
5
3
8
 Como Gerente usted debe determinar el plan de embarque de menor
costo.
 DESARROLLO: A) DIAGRAMA DE RED
 DESARROLLO : B) MODELO MATEMATICO
• Determinar Función Objetivo
F.O=Minimizar costo de embarques desde todas las plantas a todas las tiendas
(Costo de embarque desde SF) + (Costo de embarque desde LA)+ (Costo de embarque desde P).
Minimizar
(5XSS+3SB+2XST+6XSD)+(4XLS+7XLB+8XLT+10XLD)+(6XPS+5XPB+3XPT+8XPD
• Determinar Restricciones
1. Capacidad
XSS+XSB+XST+XSD < o = 1700 (San Francisco)
XLS+XLB+XLT+XLD < o = 2000 (Los Ángeles)
XPS+XPB+XPT+XPD < o = 1700 (Phoenix)
2. Demanda
XSS+XLS+XPS = 1700 (San Diego)
XSB+XLB+XPB = 1000 (Barstow)
XST+XLT+XPT = 1500 Tucson)
XSD+XLD+XPD = 1200 (Dallas)
Tabla de transporte
• La estructura especial del problema de
transporte permite una representación
compacta del problema utilizando el
formato de tabla de transporte. Este
formato permite modelar muchas
situaciones que no tiene que ver con
bienes de transporte.
Balanceo del modelo de
transporte
• La representación de la tabla de
transporte asume que el modelo esta
balanceado , es decir , que la demanda
total es igual a la oferta total . Si el
modelo esta desbalanceado, podemos
agregar un origen o un destino ficticios
para restaurar el balance
TABLA DE TRANSPORTE STANDARD
DESTINO
COSTO
CANTIDADES A
TRASPORTAR
ORIGEN
DESTINO
O
R
I
G
E
N
PLANTA 1
CIUDAD 1
CIUDAD 2
3
55
7
4
8
100
1
PLANTA 2
2
DEMANDA
100
OFERTAS
100
150
150
6
0
PLANTA 3
CIUDAD 3
50
150
50
50
300
300
Modelo de Transporte
Solución básica factible
A partir de 3 métodos de solución :
1.- Regla de la esquina
noroeste: La
primera elección X1,1, es
decir, se inicia
la asignación por la esquina
noroeste de tabla. Luego
se desplaza a la columna de
la derecha
si todavía quedan recursos
en ese origen. De lo
contrario se mueve
al reglón debajo hasta
realizar todas las
asignaciones.
3.- Método de asignación
de Vogel: Para
cada reglón y columna, se
2.- Método de la ruta
preferente: Se fundamenta calcula su diferencia, que
en la asignación a partir del se define como la
costo mínimo de distribuir diferencia
una unidad. Primero se
aritmética entre el
identifica este costo se
costo unitario más pequeñ
realiza la asignación de
o y el costo menor que le
recursos máxima posible y sigue en ese renglón o
luego se identifica el
columna. En el renglón o
siguiente costo menor.
columna con la mayor
diferencia, se le asigna al
menor costo unitario.
Métodos de solución de modelos de
transporte
1.- Esquina noroeste.
El método se inicia en la celda de la
esquina noroeste
Paso 1. Asigne lo más posible a la
celda seleccionada, y ajuste las
cantidades asociadas de oferta y
demanda.
Paso 2. Tache la columna o fila con
oferta o demanda cero para indicar
que no se hagan más asignaciones en
esa fila o columna.
Ejercicio 1- Esquina Noroeste
SunRay Transport Company transporta granos de tres silos a
cuatro molinos. La oferta (en camiones cargados) y la demanda
(también en camiones cargados) junto con los costos de
transporte por unidad por camión cargado en las diferentes
rutas, se resumen en la Tabla 5.16. Los costos de transporte por
unidad, cij (que se muestran en la esquina de cada casilla) están
en cientos de dólares. El modelo busca el programa de envíos a
un costo mínimo entre los silos y los molinos.
12
7
9
20
SOLUCION – Tabla de transporte
Silos/
Molinos
M1
S1
10
S2
12
S3
4
Demanda
M2
2
5
M3
M4
Oferta
20
11
15=10=0
9
20
25=20=5=0
10
7
5
14
15
16
5
18
10=0
10
5=0
15=5=0
15=0
15=10=0
50/50
F+c-1 < =celdas asignadas
3+4-1< =celdas asignadas
6=6  si se cumple ( formula de solución básica factible )
Costo total  (5 *$10)+(10*$2)+(5*$7)+(15*$9)+(5*$20)+(10*$18)
Costo total  $ 520
Gracias !!!!