TUP 2021
Matemática
Profesora: Lorena Cofre
Sistemas de ecuaciones lineales en el plano
Sabemos que las ecuaciones en el plano representan rectas, los sistemas de
ecuaciones en el plano están formados en general por dos ecuaciones de
rectas. La solución de este sistema de ecuaciones son los puntos que
satisfacen las ecuaciones de ambas rectas de forma simultánea, esto quiere
decir, que son aquellos puntos del plano que pertenecen a ambas rectas,
en caso de existir.
Veamos algunos ejemplos:
Ejemplo de un Sistema Compatible determinado, un solo punto del plano
pertenece a ambas rectas.
{
−𝑦 + 2𝑥 = 3
𝑦 + 4𝑥 = 3
{
𝑦 = 2𝑥 + 3
𝑦 = −4𝑥 + 3
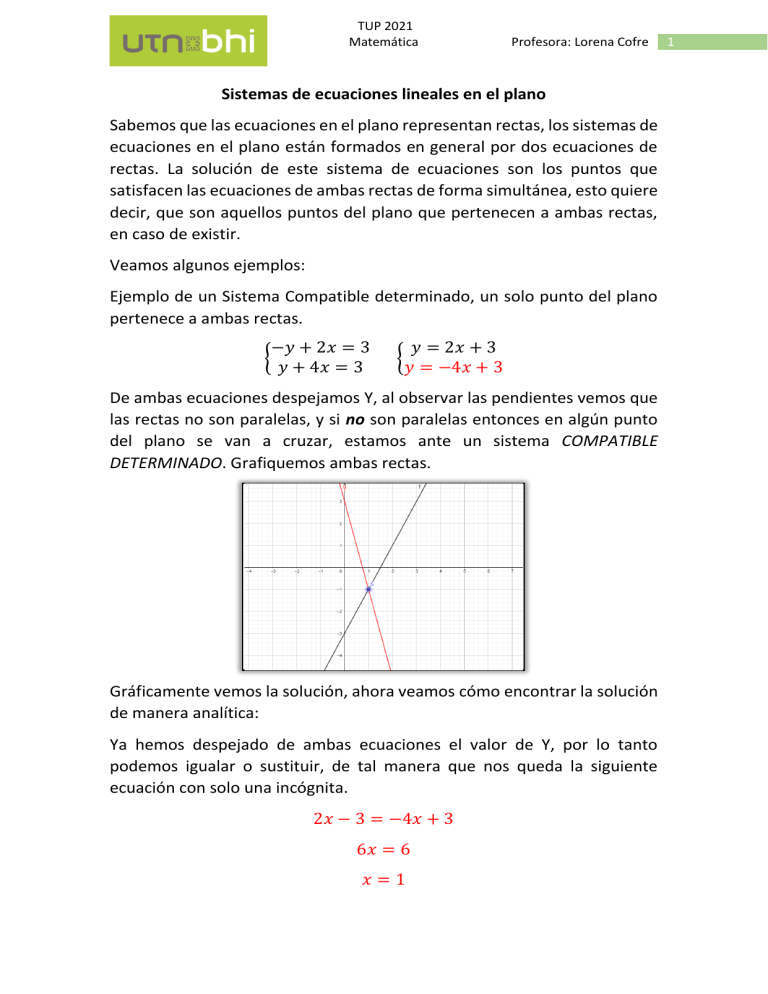
De ambas ecuaciones despejamos Y, al observar las pendientes vemos que
las rectas no son paralelas, y si no son paralelas entonces en algún punto
del plano se van a cruzar, estamos ante un sistema COMPATIBLE
DETERMINADO. Grafiquemos ambas rectas.
Gráficamente vemos la solución, ahora veamos cómo encontrar la solución
de manera analítica:
Ya hemos despejado de ambas ecuaciones el valor de Y, por lo tanto
podemos igualar o sustituir, de tal manera que nos queda la siguiente
ecuación con solo una incógnita.
2𝑥 − 3 = −4𝑥 + 3
6𝑥 = 6
𝑥=1
1
TUP 2021
Matemática
Profesora: Lorena Cofre
Ahora que tenemos el valor de x, lo sustituimos en cualquiera de las dos
ecuaciones de las rectas o en ambas, para verificar que encontramos el
mismo valor de y.
𝑦 = 2 ∗ 1 − 3 = −1
{𝑦 = −4 ∗ 1 + 3 = −1
𝑦 = −1
La solución única de este problema es:
S= (1,-1)
Ejemplo de un Sistema INCOMPATIBLE, NO EXISTEN puntos del plano que
pertenezcan a ambas rectas.
−𝑦 + 2𝑥 = 3
{
𝑦 − 2𝑥 = 3
𝑦 = 2𝑥 − 3
{
𝑦 = 2𝑥 + 3
De ambas ecuaciones despejamos Y, al observar las pendientes vemos que
las rectas son paralelas, y si son paralelas entonces tenemos dos opciones,
es la misma recta o distintas rectas que jamás se cortan. En este caso vemos
que tienen diferente ordenada al origen, por lo tanto son distintas rectas
que al ser paralelas, no tienen ningún punto en común. El sistema es
INCOMPATIBLE. Grafiquemos ambas rectas.
2𝑥 − 3 = 2𝑥 + 3
−3 = 3
𝐴𝐵𝑆𝑈𝑅𝐷𝑂‼ 𝑃𝑂𝑅 𝐿𝑂 𝑇𝐴𝑁𝑇𝑂 𝐸𝑆𝑇𝐸 𝑆𝐼𝑆𝑇𝐸𝑀𝐴 𝑁𝑂 𝑇𝐼𝐸𝑁𝐸 𝑆𝑂𝐿𝑈𝐶𝐼𝑂𝑁𝐸𝑆.
S=ᴓ
2
TUP 2021
Matemática
Profesora: Lorena Cofre
Ejemplo de un Sistema Compatible indeterminado, infinitos puntos del
plano pertenecen a ambas rectas.
{
−𝑦 + 2𝑥 = −3
𝑦 − 2𝑥 = 3
𝑦 = 2𝑥 + 3
{
𝑦 = 2𝑥 + 3
De ambas ecuaciones despejamos Y, al observar las pendientes vemos que
las rectas son paralelas, y es la misma recta ya que tienen la igual ordenada
al origen. Tienen infinitos puntos en común, si graficamos ambas, una está
sobre la otra. El sistema es COMPATIBLE INDETERMINADO. Grafiquemos
ambas rectas.
S= {(x , 2x+3): x ∈ R}
SISTEMAS DE INECUACIONES
Describamos la siguiente región mediante inecuaciones:
3
TUP 2021
Matemática
Profesora: Lorena Cofre
𝟏
𝒚≤− 𝒙+𝟒
𝟒
𝒚 ≤ −𝟑𝒙 + 𝟏𝟓
𝒚≥𝟎
{
𝒙≥𝟎
PROBLEMA:
La fábrica de Hilados y Tejidos "SALAZAR" requiere fabricar dos tejidos de
calidad diferente T y T’; se dispone de 500 Kg de hilo a, 300 Kg de hilo b y
108 Kg de hilo c. Para obtener un metro de T diariamente se necesitan 125
gr de a, 150 gr de b y 72 gr de c; para producir un metro de T’ por día se
necesitan 200 gr de a, 100 gr de b y 27 gr de c.
DETERMINAR LAS VARIABLES
Basándonos en la formulación del problema nuestras variables de decisión
son:
XT: Cantidad de metros diarios de tejido tipo T a fabricar.
XT’: Cantidad de metros diarios de tejido tipo T’ a fabricar.
DETERMINAR LAS RESTRICCIONES DEL PROBLEMA
En este paso determinamos las funciones que limitan el problema, estas
están dadas por capacidad, disponibilidad, proporción, no negatividad
entre otras. De disponibilidad de materia prima:
0,125XT + 0,200XT’ <= 500 (Hilo “a”)
0,150XT + 0,100XT’ <= 300 (Hilo “b”)
0,072XT + 0,027XT’ <= 108 (Hilo “c”)
De no negatividad XT, XT’ >= 0
4
TUP 2021
Matemática
Profesora: Lorena Cofre
5




