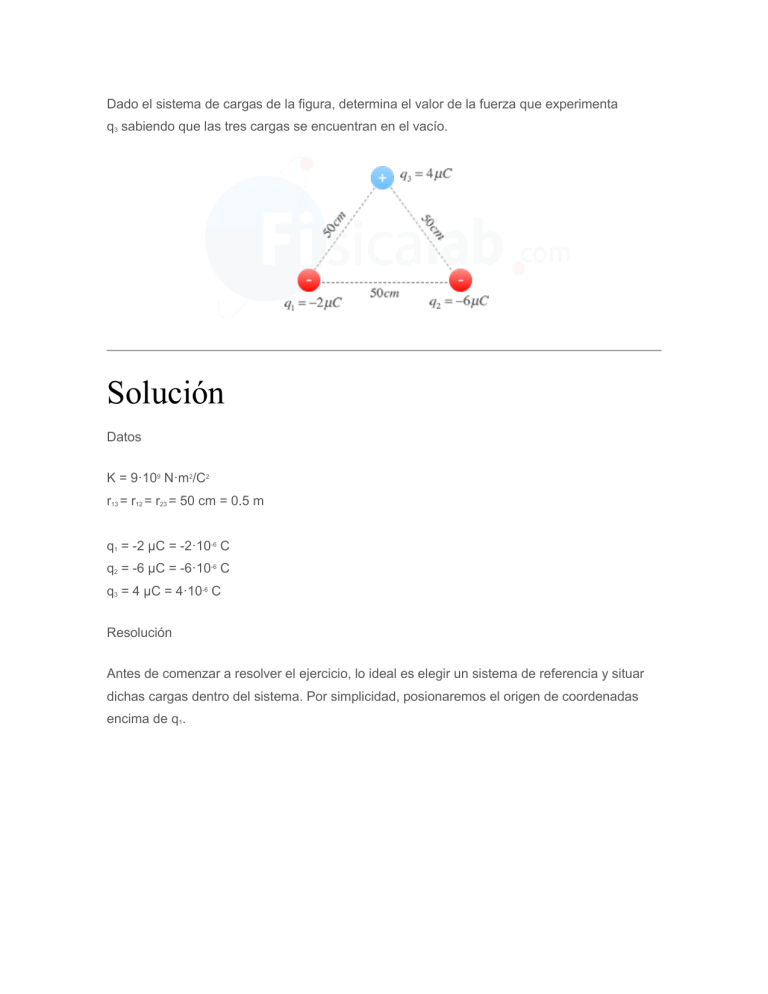
Dado el sistema de cargas de la figura, determina el valor de la fuerza que experimenta q3 sabiendo que las tres cargas se encuentran en el vacío. Solución Datos K = 9·109 N·m2/C2 r13 = r12 = r23 = 50 cm = 0.5 m q1 = -2 µC = -2·10-6 C q2 = -6 µC = -6·10-6 C q3 = 4 µC = 4·10-6 C Resolución Antes de comenzar a resolver el ejercicio, lo ideal es elegir un sistema de referencia y situar dichas cargas dentro del sistema. Por simplicidad, posionaremos el origen de coordenadas encima de q1. Si observamos la figura nos daremos cuenta de que la posición de q1 y q2 es: q1 (0,0) m q2 (0.5,0) m Sin embargo, calcular la posición de q3 no es algo tan trivial. La componente x será la mitad de la distancia entre q1 y q2 (x = 0.25 m) y para calcular la componente y tendremos que hacer uso de la definición de coseno (o alternativamente del teorema de pitágoras) teniendo en cuenta que en un triángulo equilatero todos sus ángulos poseen 60º y que cada triángulo equilatero se puede descomponer en dos triángulos rectángulos. Girando uno de ellos obtenemos: De esta forma para calcular la altura (b) a la que se encuentra la carga q3, basta con aplicar la definición de coseno: cos 30º=b0.5 m⇒b=0.5 m⋅cos 30º ⇒b =0.43 m Por tanto la posición de nuestras cargas es: q1 (0,0) m q2 (0.5,0) m q3 (0.25,0.43) m Aplicando el principio de superposición de fuerzas eléctricas, la fuerza (F3) que actúa sobre q3 será la suma vectorial de: la fuerza que ejerce q1 sobre q3 (F→1,3). Como q1 y q3 tienen distinto signo, F→1,3 será atractiva. la fuerza que ejerce q2 sobre q3 (F→2,3). Como nuevamente q2 y q3 tienen distinto signo, F→2,3 será atractiva. F→3=F→1,3+F→2,3 Estudiando cada fuerza por separado tenemos que: Fuerza F→1,3 F→1,3=K⋅q1⋅q3r1,32⋅u→1,3 De todos los valores que necesitamos para calcular F→1,3, nos falta u→1,3. Sin embargo sabemos que u→1,3 es un vector unitario de r→1,3, por lo que: u→1,3=r→1,3r1,3 Como conocemos la posición de q1 y q3, conocemos los puntos extremo y origen del vector r→1,3. Aplicando el concepto de vector: r→1,3=(q3x−q1x)⋅i→+(q3y−q1y)⋅j→ ⇒r→1,3= (0.25−0)⋅i→+(0.43−0)⋅j→ ⇒r→1,3= 0.2 5⋅i→+0.43⋅j→ De aquí sabemos que: u→1,3=r→1,3r1,3=0.25⋅i→+0.43⋅j→0.5⇒u→1,3=0.5⋅i→+0.86⋅j→ Por tanto: F→1,3=K⋅q1⋅q3r1,32⋅u→1,3 ⇒F→1,3=9⋅109⋅−2⋅10−6⋅4⋅10−60.52⋅(0.5⋅i→+0.85⋅j→) ⇒F →1,3=−0.14⋅i→−0.24⋅j→ N Fuerza F→2,3 Aplicando los mismos pasos que para la fuerza anterior: F→2,3=K⋅q2⋅q3r2,32⋅u→2,3⇒F→2,3=K⋅q2⋅q3r2,32⋅r→2,3r2,3⇒F→2,3=9⋅109⋅−6⋅10−6⋅4⋅10 −60.52⋅(0.25−0.5)⋅i→+(0.43−0)⋅j→0.5⇒F→2,3=0.43⋅i→−0.74⋅j →N Una vez que hemos calculado ambas fuerzas, ya estamos en disposición de calcular la fuerza resultante que ejercen q1 y q2 sobre q3: F→3=F→1,3+F→2,3 ⇒F→3=(−0.14+0.43)⋅i→+(−0.74−0.24)⋅j→ ⇒F→3= 0.29⋅i→−0 .98⋅j→ N Por ultimo, para obtener su valor numérico calcularemos su módulo: F3=√ 0.292+(−0.98)2−−−−−−−−−−−−−−⇒F3 = 1.02 N Dos cargas q1=10 µC y q2=5 µC se encuentran situadas respectivamente en los puntos (0,0) y (3,0) de un sistema de coordenadas en el vacío. Si pasado un instante de tiempo q2 se desplaza hasta la posición (6,0), ¿Cual es el trabajo realizado por la fuerza eléctrica que actúa sobre q2? Solución Datos q1=10 µC q2=5 µC P1 = (0,0) P2A = (3,0) P2B = (6,0) K = 9·109 N·m2/C2 Resolución Para resolver este ejercicio, basta con aplicar la fórmula del trabajo eléctrico realizado por una fuerza eléctrica de un campo eléctrico creado por una carga puntual: W(P2A→P2B) = −K⋅q1⋅q2⋅[1rB−1rA] En este caso conocemos K, q1, q2 aunque desconocemos rA y rB. Sin embargo, podemos calcular dichos vectores de posición: rA−→=(3,0)−(0,0) = (3,0)rB−→=(6,0)−(0,0) = (6,0) y posteriormente su módulo: rA=32+02−−−−−−√=3 mrB=62+02−−−−−−√=6 m Una vez que poseemos todos los datos, podemos calcular el trabajo: W(P2A→P2B) = −K⋅q1⋅q2⋅[1rB−1rA] ⇒W(P2A→P2B) =−9⋅109⋅10⋅10−6⋅5⋅10−6⋅[16−13] ⇒W(P2A→P2B) =0.075 J Disponemos de 3 cargas en el vacio q1 = 7 mC, q2 = -3 mC y q3 = 3 mC situadas respectivamente en los puntos A (-3,0) m, B(0,0) m y C(4,0) m, determinar el campo eléctrico creado en el punto Z (0,3). Solución Datos q1 = 7 mC = 7 · 10-3 C q2 = -3 mC = -3 · 10-3 C q3 = 3 mC = 3 · 10-3 C A (-3,0) B (0,0) C (4,0) Z (0,3) Resolución Para resolver este ejercicio vamos a sumar la intensidad del campo eléctrico (principio de superposición) creado en Z por cada una de las cargas q1, q2 y q3. Recuerda que el campo eléctrico creado por una carga puntual se obtiene por medio de la siguiente expresión: E→=K⋅qr2⋅u→r Con este fin vamos a calcular los vectores r→1,r→2,r→3 que unen respectivamente cada carga con el punto Z: r→1=0−(−3)⋅i→+3−0⋅j→=3⋅ i→+3⋅j→r→2=0−0⋅i→+3−0⋅j→=3⋅j→r→3=0−4⋅i→+3 −0⋅j→=−4⋅i→+3⋅j→ Sus módulos son: r1=32+32−−−−−−√=18−−√mr2=02+32−−−−−−√=3mr3=42+32−−−−−−√=25−−√=5m y sus vectores unitarios: u→r1=318−−√/⋅i→+318−−√/⋅j→u→r2=0/2⋅i→+3/3⋅j→=j→u→r3=−45/⋅i→+35/⋅j→ En este punto vamos a calcular el campo creado independientemente en Z por q1, q2 y q3 y que llamaremos E→1,E→2yE→3 respectivamente: E→1=K⋅q1r12⋅u→r1⇒E→1=9⋅109⋅7⋅10−3(18−−√)2⋅(318−−√/⋅i→+318−−√/⋅j→)⇒E→ 1=2476415.1⋅i→+2476415.1⋅j→N/C E→2=K⋅q2r22⋅u→r2⇒E→2=9⋅109⋅−3⋅10−3(3)2⋅(3⋅j→)⇒E→2=−9⋅106⋅j→N/C E→3=K⋅q3r32⋅u→r3⇒E→3=9⋅109⋅3⋅10−3(5)2⋅(−45/⋅i→+35/⋅j→)⇒E→3=−864000⋅ i →+648000⋅j→N/C Para obtener el campo en Z basta con sumar vectorialmente los 3 campos eléctricos: E→=E→1+E→2+E→3⇒E→=1612415.1⋅i→+3124415.1⋅j→ Un electrón se introduce en un campo eléctrico uniforme perpendicularmente a sus líneas de campo con una velocidad inicial de 2·105 m/s. Si la intensidad del campo eléctrico es 106N/C, determinar: a) La aceleración que sufre el electrón al introducirse en el campo eléctrico. b) La ecuación de la trayectoria que sigue dicho electrón. Solución Datos q = 1.6·10-19 v0 = 2·105 m/s E = 106 N/C m = 9.1·10-31 Kg Resolución Cuestión a) Dado que la líneas de campo son perpendiculares a la velocidad del electrón esto quiere decir que si suponemos que el electrón avanza horizontalmente, sufrirá una fuerza eléctrica vertical. Dado que sufre una fuerza en el eje y, solo dispondrá de aceleración en el eje y (ay). Fe=m⋅ay ⇒ay=Fem⇒ay=q⋅Em⇒ay=−1.6⋅10−19⋅1069.1⋅10−31⇒ay=−1.76⋅1017 m/s2 Cuestión b) Aunque el electrón únicamente adquiere una aceleración vertical (ay), entra en el campo horizontalmente, es decir dispone de una velocidad en el eje x. Esto implica que debemos estudiar su trayectoria en los dos ejes. En el eje x, al no tener aceleración se moverá siguiendo un movimiento rectilíneo uniforme (m.r.u.) y en el eje y unmovimiento rectilíneo uniformemente acelerado (m.r.u.a.). Por tanto, su posición en cada eje: Eje X. x=v0⋅tEje Y. y=1/2⋅ay⋅t2 Despejando el tiempo en la primera ecuación y sustituyéndola en la primera: y=ay⋅x22⋅v02⇒y=−1.76⋅1017⋅x22⋅(2⋅105)2⇒y=−4.4⋅106 x2 Podemos comprobar que el electrón al entrar en el campo describe una parábola. Dado un anillo de radio u, que posee una distribución de carga Q uniforme, determinar el valor del campo creado en cualquier punto del eje del anillo situado a distancia x de su centro. ¿Qué ocurre con el campo en el centro del anillo? ¿Y a una distancia muy grande? Solución Para resolver este ejercicio vamos a dividir el anillo en pequeñas porciones infinitesimales de carga, cada una de las cuales influirá en la creación del campo eléctrico en cualquier punto P situado a lo largo del eje del anillo. La simetría que posee el anillo, hace que solo influyan las componentes x del campo eléctrico (dEx, dEx', ...) ya que las componentes y se anulan (dEy, dEy',...). Por tanto, nos centraremos en calcular la suma de todas las primeras. Para ello, calcularemos el valor de la componente x del campo eléctrico creado por dQ, aplicando la definición de coseno: dEx=dE⋅cos θ Adicionalmente, si consideramos el campo creado por una carga puntual y que según la figura cos Θ = x/r dEx=K⋅dQr2⋅xr Nuevamente, aplicando el teorema de Pitágoras al triángulo que resulta de la figura: d=x2+u2−−−−−−√ Por tanto: dEx=K⋅dQ(x2+u2)2−−−−−−−−√⋅x(x2+u2)⇒dEx=K⋅dQ⋅x(x2+u2)3/2 Partiendo de esta ecuación deseamos calcular el campo creado por cada una de las cargas situadas a lo largo del anillo, por esta razón vamos a darle una vuelta y a expresarla en función de la longitud del anillo: dQ=λ⋅dl Ahora podemos integrar a lo largo de dicah longitud: E=∫2πu0Kλ⋅dl⋅x(x2+u2)3/2 Resolviendo la integral: E=∫2πu0Kλ⋅dl⋅x(x2+u2)3/2⇒E=Kλ⋅x(x2+u2)3/2∫2πu0dl ⇒E=Kλ⋅x(x2+u2)3/2⋅2⋅π⋅u Dado que λ=Q/2·π·u : E=KQ⋅x(x2+u2)3/2 Una vez que conocemos la expresión del campo eléctrico a cualquier distancia x del eje del anillo, vamos a responder a las preguntas que nos solicitan en el ejercicio: En el centro del anillo x = 0, por tanto si sustituimos en la expresión del campo eléctrico obtendremos que E = 0. En un punto situado muy lejos x>>>u obtendremos que E = K· Q / x2, es decir, a una distancia extremadamente grande el anillo se comporta como si se tratase de una carga puntual.