5-CLASE-MAGNITUDES-PROPORCIONALES.

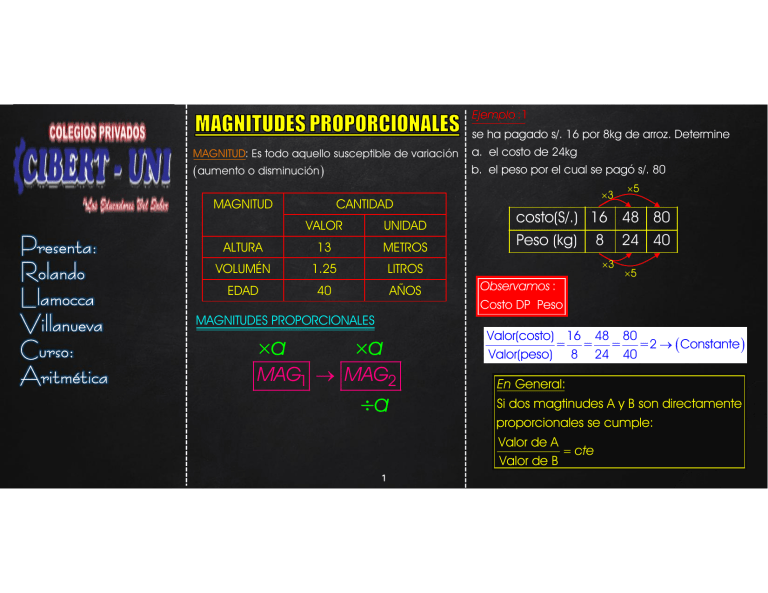
Ejemplo :1
se ha pagado s/. 16 por 8kg de arroz. Determine
MAGNITUD: Es todo aquello susceptible de variación
a. el costo de 24kg
 aumento o disminución 
b. el peso por el cual se pagó s/. 80
MAGNITUD
Presenta:
Rolando
Llamocca
Villanueva
Curso:
Aritmética
CANTIDAD
VALOR
UNIDAD
ALTURA
13
METROS
VOLUMÉN
1.25
LITROS
EDAD
40
AÑOS
3
5
costo(S/.) 16 48 80
Peso (kg)
8
3
Observamos :
Costo DP Peso
24 40
5
MAGNITUDES PROPORCIONALES
a
a
MAG1  MAG2
a
Valor(costo) 16 48 80
= = = =2   Constante 
Valor(peso) 8 24 40
En General:
Si dos magtinudes A y B son directamente
proporcionales se cumple:
Valor de A
 cte
Valor de B
1
Ejemplo : 2
Costo
Un automovil, con una velocidad de 20m/s tarda
30s en recorrer cierta distancia.
a. ¿Qué tiempo tardaría si la velocidad fuera de 60m/s
b. ¿Qué velocidad debería emplearse si tarda 25s?
 40;80 
80
Valor-costo y
 k
valor-peso
x
48
3
 24;48
8
Tiempo(s)
y  xk  f x   kx
Observamos :
Velocidad IP Tiempo
24
6
5
Velocidad(m/s) 20 60 24
 8;16 
16

40
Peso
30 10 25
3

6
5
Valor(velocidad)  Valor(tiempo)
=20  30=60  10=24  25=600   Constante 
Observación: En cada punto de la gráfica
En General:
Si dos magtinudes A y B son inversamente
proporcionales se cumple:
Valor de A  Valor de B  cte
el cociente de cada par de valores
resulta constante
2
Ejemplo : 3
Velocidad
10 costureras (todas de igual rendimiento) pueden confeccionar
400 casacas iguales en 48 días. ¿Cuántas casacas confeccionarían
si solo fueran 8 las costureras y dispondrían de 45 días?
10;60 
60
Valor-Velocidad  valor-tiempo  y  x  k
24
 24;48
Sol :
k
y  x  k  f x  
x
Cos tureras DP trabajo

Cos tureras IP tiempo
Luego con los datos
 30;20 
20
10
25
Esquema-de-Proporcionalidad
cos tureras trabajo tiempo
30 Tiempo
i.
10
400
48
ii.
8
n
45
 costureras    tiempo   cte
 trabajo 
Se trabaja en el esquema
10    48  cte   8   45   n  300
 400 
 n
OBSERVACIÓN :
Cuando se trabaja con más de una magnitud
se tiene una PROPORCIONALIDAD COMPUESTA
Observación: En cada punto de la gráfica
el producto de cada par de valores
resulta constante
3
En gerenal
Sean las magnitudes A,B,C,D y E de las cuales eligimos a la
magnitud A como referencia y la relacionamos con las otras
 A es DP a B   C, D y E constantes 
 A es IP a C   B, D y E constantes 
 A es IP a D   B, C y E constantes 
Se tendrá
Engranajes en contacto
AC D
 cte
BE
DA  # de dientes de A
DB  # de dientes de B
VA  # de vueltas de A
 A es DP a E   B, C y D constantes 
VB  # de vueltas de B
Propiedades:
I. Si:
A DP B  B DP C  A DP C
II. Si:
Se Cumple:
# Dientes IP # Vueltas =k
D A  VA  DB  VB
A DP B  A n DP B n , n  
n
n
A IP B  A IP B , n  
III. Si:
A DP B
A DP C
Engranajes con Eje común
 C es constante 
B es constante 
Se Cumple:
A
 A DP B  C 
k
BC
IV. Si:
A IP B
A IP C
se dan el mismo numero
de vueltas
 C es constante 
B es constante 
 A IP B  C  A  B  C  k
VA  VB
4
L A  # longitud de la bicicleta A
V A  # de vueltas de A
LB  # longitud de la bicicleta B
VB  # de vueltas de B
Se Cumple:
# Longitud IP # Vueltas =k
Precio  Distancia
k
Area
450  75 Precio  150
225  1 Precio  1



1
3
1
3
Precio  675
L A  VA  LB  VA
5
# DA  # VA  # DB  # VB
 a  16   24  a  32   a  24   b
  a  16   24  a  32  a  48
a  32   a  24   b  b  64
24  x  70   45  x  x  80
# VB  80  menor
# VA  150
Piden : a  b  112
4min  80
1min  20  20 RPM
6
Gastos  # horas
k
Invitados
1200  12 Gastos  12  4  1200  12 Gastos  16 



100
100  20
100
80
240  3 Gastos  1

1
1
Gastos : 720
m 16

 m  12
3
4
16  4  8  n  n  8
Piden : m  n  20

Ahorro :1200  720  480
7