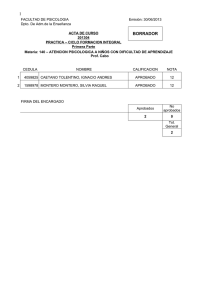
Análisis estadístico con SPSS Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Método de investigación y obtención de dato Transversal Encuestas Cuantitativo Longitudinal Observación Experimentación Panel Sesiones de grupo Cualitativo Entrevistas a profundidad Técnicas proyectivas Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Características: Tipos y escalas Escalas Naturaleza Nominal Distribución frecuencias La moda Representación gráfica Ordinal Distribución frecuencias La moda Cuartiles Representación gráfica Intervalo Tendencia central Dispersión Asimetría Curtosis Representación gráfica Razón Tendencia central Dispersión Asimetría Curtosis Representación gráfica Atributo Característica Discreta Variable Continua Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de datos Descriptivo Medidas de tendencia central Medidas de dispersión Gráficas Inferencial Estimación por intervalos Pruebas de hipótesis Descriptivo Tabulación cruzada Coeficiente de correlación Gráficas Inferencial Diferencia de medidas tend cent Regresión simple ANOVA Descriptivo Análisis factorial Análisis de conglomerados Inferencial Regresión Múltiple ANOVA Univariado Análisis de datos Bivariado Multivariado Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis descriptivo Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala nominal: Análisis de datos El principal análisis de datos cuando nos encontramos con una escala nominal es el uso de estadísticas de frecuencias Analizar → Estadísticas descriptivas → Frecuencias Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala nominal: Análisis de datos En el cuadro de diálogo se indican las variables para las cuales necesitamos la tabla de frecuencias La opción de estadísticas permite diversos análisis estadísticos como: • Valores percentiles • Medidas de dispersión • Medidas de tendencia central • Gráficas de distribución Seleccionamos: Estadísticas Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala nominal: Análisis de datos La moda es la una medida de tendencia central que indica la categoría con mayor número de frecuenciaa y la indicada para la escala nominal… Seleccionamos: Moda → Continuar… Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala nominal: Análisis de datos Una forma relevante de analizar los datos de escala nominal es a través del método gráfico, una forma de generarlo es por medio del cuadro de diálogo de Frecuencias La opción de gráficos permite presentar los resultados en valores porcentuales o frecuencias en: • Gráficas de barras • Gráficas de Pie • Histogramas •Curva normal Seleccionamos: Gráfica Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala nominal: Análisis de datos La gráfica de barras es la de mayor uso y la más recomendada para presentar el análisis de este tipo de variables. El caso del histograma no tiene sentido en el caso de variables en escala nominal. Seleccionamos: Gráfica de barras → Frecuencias → Continuar… Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala nominal: Análisis de datos La tabla de resultados muestra la frecuencia de las categorías y el porcentaje que representan del total Cuando no existen valores perdidos el porcentaje y el porcentaje válido son los mismos Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala nominal: Presentación gráfica La gráfica, que se presenta en la hoja de resultados, requiere en algunas ocasiones formato adicional para una presentación más profesional… Damos doble “Click” sobre el gráfico → Se abrirá automáticamente el editor de gráficos Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala nominal: Presentación gráfica Una forma fácil de ello es a través de los cuadros de diálogo que presenta el programa Damos doble “Click” con el botón derecho sobre el las barras del gráfico→ Mostrar etiquetas de datos Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala nominal: Presentación gráfica La pestaña de “Valor de datos” permite mostrar los valores tanto de frecuencia como de porcentaje.. La ventana de Propiedades permite modificar • Etiquetas y valor de datos • Categorías (fusionar, excluir o cambiar de orden) • Modificar los colores del relleno y del borde de las barras y del texto • Cambiar el tamaño del gráfico Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala nominal: Presentación gráfica Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala ordinal: Análisis de datos Un caso clásico es cuando nos encontramos fuente a variables que expresan opinión. La distribución de frecuencias se realiza igual que en el caso de la escala nominal. En el cuadro de diálogo de Estadísticas podemos seleccionamos: • La Moda • Cuartiles Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala ordinal: Análisis de datos Al igual que en el caso de la escala nominal, la representación gráfica puede ser por diagramas de Pie o diagramas de frecuencias En el cuadro de diálogo Gráficas, seleccionamos: Gráfica de Pie→ Porcentajes → Continuar… Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala ordinal: Análisis de datos Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala ordinal: Presentación gráfica En SPSS 13.0, el gráfico presenta los valores perdidos dentro del gráfico, una solución sencilla a eso, es crear el gráfico directamente… Menú de Análisis En el menú principal seleccionamos: Menú de Gráficas Análisis estadístico con SPSS Gráficas→ Pie→ Resumen para grupos de casos → En la casilla de opciones asegurarse que no está activa la celda “Mostrar grupos definidos por valores perdidos” Ricardo Rojas Montero [email protected] Análisis descriptivo Una Variable Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala intervalo: Análisis de datos Una variable discreta puede adoptar los valores de: 1,2,3,…,n. Para su análisis, en el menú de Análisis, estadísticas descriptivas, frecuencias, en la sección de estadísticas seleccionamos todas aquellas estadísticas que nos son de interés. Seleccionamos: Estadísticas Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala intervalo: Análisis de datos Estadísticas de Distribución… Asímetría: Una medida de asimetría de una distribución. Toma el valor de cero cuando es simétrica; negativo cuando está sesgada a la izquierda, positivo cuando está sesgada a la derecha. Curtosis: Una medida de la extensión del conglomerado de observaciones con respecto a un punto. Toma el valor de cero frente a la distribución normal; positivo frente a una mayor conglomeración y colas largas; negativo frente a observaciones poco conglomeradas y colas cortas Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala intervalo: Análisis de datos Los resultados que arroja el programa se presenta como: Statistics p5_1 N Valid Missing Mean Std. Error of Mean Median Mode Std. Deviation Variance Skewness Std. Error of Skewness Kurtosis Std. Error of Kurtosis Range Minimum Maximum Sum Percentiles 25 50 75 Análisis estadístico con SPSS 185 0 77.02 17.942 5.00 0 244.040 59555.695 3.535 .179 10.683 .355 999 0 999 14249 .00 5.00 30.00 Sesgada a la derecha Muy agrupadas a la media pero los datos se encuentran extendidos Ricardo Rojas Montero [email protected] Escala intervalo: Análisis de datos Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis de datos Una variable continua puede adoptar los valores infinitos entre n y n+1. Las variables continuas tienen la característica de facilitar el estudio descriptivo de normalidad. Rasgos fundamentales f(x) • Perfectamente simétrica, con eje de simetría en la vertical que para por la media (coeficiente de asimetría = 0) • Dominio de la variable X de -∞ a + ∞ • Asintótica al eje de abcisas (f(x)>0) • Mesocúrvica (coeficiente de curtosis=0). x Una distribución de media 0 y D.E. 1 se obtiene al tipificar cualquier variable que siga la distribución normal media Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis de datos Para verificar que una variable analizada tiene una distribución normal, lo más adecuado es: • Tipificar la variable Z= X-m δ • Calcular la media y la desviación estándar de la variable tipificada, y verificar si sus valores son 0 y 1 respectivamente. • Calcular los coeficientes de asimetría y curtosis y comprobar si los valores son 0. Otra forma de hacerlo es trazando sobre el histograma de la variable la curva de la distribución normal y probando que se ajusta. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis de datos La representación gráfica se elige en el cuadro de diálogo Frecuencias: Gráficos. Elegimos la presentación del histograma con la curva de normalidad Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis de datos El histograma de frecuencias, junto con la curva normal se muestran a continuación. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis de datos Otra forma de analizar la normalidad de los datos es a través del análisis descriptivo. En el menú principal seleccionamos: Análisis→ Estadísticas descriptivas→ Descriptivos Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis de datos El análisis descriptivo es una forma fácil de obtener valores tipificados sin tener que generar los valores a través de cálculos complicados. El menú opciones permite estadísticos tales como: •Media •Suma •Dispersión •Desv. Estand. •Mínimo •Máx •Varianza •Rango •Error Estand de la media •Distribución •Asimetría •Curtosis Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis de datos Los valores que obtenemos son: Descriptive Statistics N p9 Valid N (listwise) 86 86 Minimum 3 Maximum 100 Mean 58.29 Std. Deviation 29.415 Los estadísticos descriptivos Los datos tipificados Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis gráfico Un análisis gráfico que nos ayuda a entender el comportamiento de una variale en el tiempo son las gráficas de líneas (secuencia) y los diagramas de caja y brazo…. Para este análisis es importante definir las fechas en SPSS, para ello…. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis gráfico Seleccionamos del Menú: - Gráficos - Secuencias Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis gráfico En el menú de diálogo seleccionamos la variable a graficar…. Y la etiqueta para el eje temporal.. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis gráfico El resultado es una gráfica que nos presenta el comportamiento de la variable en el tiempo…. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis gráfico Sin embargo, la utilización de gráficas de “caja y brazo” permiten conocer el comportamiento estacional y la varianza de la variable de interés. Para ello…. Seleccionamos: - Gráficas - Boxplot En el menú de diálogo: - Simple - Resumen por grupos de casos Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis gráfico Seleccionamos la variable y la categoría…. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis gráfico El nuevo gráfico permite observar el comportamiento de tendencia en el tiempo además de su variabilidad… Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis gráfico Para observar la estacionalidad mensual realizamos el mismo procedimiento pero en esta ocasión con categorías mensuales…. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Escala Razón: Análisis gráfico El gráfico muestra el comportamiento estacional de la variable en el año.. Esto es, En los meses de enero son los de mayor inflación con alta varianza, sin embargo en los meses julio la inflación es la más baja del año… Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Prueba de hipótesis (Media estadística) Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Regla de decisión para prueba de hipótesis en SPSS Una forma sencilla para tomar una decisión de rechazar o aceptar una hipótesis nula en SPSS es simplemente comparando el α con el p-value que el programa proporciona. Si el α > p-value entonces se rechaza la hipótesis nula.. Región de aceptación de H0 α= Nivel de confianza P-value .01 .05 .10 99% 95% 90% .015 No se rechaza H0 con un nivel de confianza del 99% Se rechaza H0 con un nivel de confianza del 95% Análisis estadístico con SPSS .07 Cuanto más pequeño sea el p-value mayor evidencia existe en contra de la H0 No se rechaza H0 con un nivel de confianza del 95% Se rechaza H0 con un nivel de confianza del 90% Ricardo Rojas Montero [email protected] Regla de decisión para prueba de hipótesis en SPSS Rechazar H0 cuando α > p value Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Prueba t La prueba t es una prueba paramétrica usada para determinar si dos medias son significativamente diferentes la una de la otra. Existen tres tipos de pruebas t: • Prueba t de muestra simple. Determina si la media observad es diferente de un valor dado. • Prueba t de independencia. Compara las medias de dos grupos independientes de individuos. • Prueba t pareada. Compara las medias de dos conjuntos de observaciones de los mismos individuos o de pares de individuos. Todas estas pruebas requieren que los datos sean por lo menos de escala de INTERVALO, NORMALMENTE DISTRIUIDAS e IGUAL VARIANZA. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Prueba t La prueba t se utiliza en el análisis de muestreos cuando el número de casos es menos a 30.. Supongamos que obtenemos una muestra de una población normal con media µ y varianza δ… Si x es el promedio de las n observaciones y la varianza será s f(x) Grados de Libertad = ∞ La apariencia de la distribución t es similar a la de la normal estándar, es decir, simétrica y unimodal. Grados de Libertad = 10 Grados de Libertad = 1 media Análisis estadístico con SPSS x Sin embargo la distribución t tiene colas más amplias que la normal. Pero a medida que los grados de libertad aumentan la distribución se asemeja a la normal. Ricardo Rojas Montero [email protected] Prueba t de muestra simple Se afirma que una población tiene una media de 1, para afirma lo anterior se toma una muestra de 25 casos para verificar lo dicho.. H0: mx= m La hipótesis que probaremos es que la media de nuestra muestra es igual a una media que nosotros creemos… En el menú principal: Análisis→ Comparar medias → Prueba T para una media Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Prueba t de muestra simple En el cuadro de diálogo de la prueba T para una media seleccionamos la variable a ser analizada El botón de “Opciones” permite establecer el intervalo de confianza para nuestra prueba El valor de prueba es el valor que afirmamos que es la media poblacional… Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Prueba t de muestra simple En la hoja de resultados de SPSS observamos la solución a la prueba… En este caso se rechaza la Hipótesis nula H0: mx=m Por lo tanto, podemos afirmar que la media poblacional es igual a la media muestral One-Sample Test Test Value = 1 Nicotina t -1.745 df 24 Sig. (2-tailed) .094 Mean Difference -.12360 Regla de rechazo: 95% Confidence Interval of the Difference Lower Upper -.2697 .0225 Con 95% de confianza sabemos que la diferencia entre la media poblacional y la muestral es de -.2697 y 0.225 α > p value Para un nivel de confianza del 95%, rechazamos hipótesis nula si, 0.05 >0.094 No rechazamos lo hipótesis nula Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Prueba t de independencia La prueba de independencia compara el desempeño o evaluación de las unidades de análisis de dos grupos. Esta prueba debe ser utilizada cuando los datos son paramétricos y se obtuvieron por medio de un diseño de grupos independientes. H0: m1 = m2 Es posible para construir las dos poblaciones utilizar tanto un atributo (SI/NO) como una variable (edad: <18 / >=18) Para verificar la hipótesis nula existen dos estadísticos de prueba diferentes de acuerdo a: • Igualdad de varianza • Desigualdad de varianza Por lo tanto, es necesario realizar una prueba de hipótesis sobre la igualdad de las varianza a través de la prueba de Levene Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Prueba t de independencia Para realizar la prueba de independencia sobre la diferencia de las medias seleccionamos.. En el menú principal: Análisis→ Comparar medias → Prueba T para muestras independientes Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Prueba t de independencia SPSS presenta el cuadro de diálogo de prueba T de muestras independientes. A la izquierda del cuadro aparece la lista de variables.. Seleccionamos la variable a comparar, y… Definimos los grupos, esto es, le indicamos al programa cuáles son los valores con los cuales codificamos los grupos a comparar Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Prueba t de independencia No es necesario especificar al programa que realice la prueba de Levene, pues esta se realiza automáticamente y se presenta en el resultado. Si rechazamos la H0 de varianzas iguales, entonces, el p-value para la prueba T será el de “Varianzas iguales no asumidas”… Independent Samples Test Levene's Test for Equality of Variances F p7 Equal variances assumed Equal variances not assumed 1.150 Sig. .285 t-test for Equality of Means t df Sig. (2-tailed) Mean Difference Std. Error Difference 95% Confidence Interval of the Difference Lower Upper .035 183 .972 .110 3.146 -6.098 6.318 .032 106.369 .974 .110 3.397 -6.625 6.845 Regla de rechazo: α > p value Regla de rechazo: α > p value Para un nivel de confianza del 95%, rechazamos hipótesis nula si, 0.05 >.285 Para un nivel de confianza del 95%, rechazamos hipótesis nula si, 0.05 >.972 No rechazamos lo hipótesis nula de varianzas iguales No rechazamos lo hipótesis nula de igualdad de medias de los grupos Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de Varianza Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de varianza Es una de las técnicas más utilizada en los análisis de los datos de diseños experimentales y es una extensión de la prueba T de Stundent para dos muestras… Se utiliza cuando queremos contrastar más de dos medias H0 : m1 = m2=m3= m4=….=mn El procedimiento del ANOVA permite dividir la varianza de la variable dependiente en dos o más componentes, cada uno de los cuales puede ser atribuido a una fuente (variable o factor) identificable. Los modelos que permiten construir el ANOVA se resumen como: Valor Observado = Σ (Efectos atribuibles) + Σ (Efectos no atribuibles o residuales) Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de varianza. Modelos Los modelos del Análisis de Varianza se clasifican de acuerdo a tres criterios: el número de factores, el muestreo de niveles y el tipo de aleatorización. En este caso sólo nos enfocaremos a los modelos por Número de Factores… 1. Factor único de clasificación. Los experimentos que utilizan sólo una variables independiente y una variable dependiente se analizan mediante varianza de un factor o unidireccional (one way). 2. El análisis de Varianza con dos factores de clasificación utilizado para examinar el efecto de dos factores en una variable observada. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de varianza. Factor único El procedimiento de ANOVA de un factor genera un análisis para una variable dependiente cuantitativa respecto a una única variable de factor, la variable independiente. Se utiliza para contrastar la hipótesis de si las medias en varios grupos son iguales. En el menú principal: Análisis→ Comparar medias → ANOVA de un factor Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de varianza. Factor único En el siguiente ejemplo, deseamos conocer si existe una diferencia en la esperanza de vida por regiones económicas, para ello… En el cuadro de diálogo seleccionamos como: Variable dependiente: esperanza de vida Factor: Región Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de varianza. Factor único La hoja de resultados muestra el análisis de ANOVA… Recordemos que la Hipótesis Nula es: ANOVA H0 : m1 = m2=m3= m4=….=mn Average female life expectancy Between Groups Within Groups Total Sum of Squares 7568.810 4501.539 12070.349 df 5 103 108 Mean Square 1513.762 43.704 F 34.636 Sig. .000 Regla de rechazo: α > p value Para un nivel de confianza del 99%, rechazamos hipótesis nula si, 0.01 >.000 Rechazamos lo hipótesis nula de igualdad de medias de los grupos Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de varianza. Factor único Ahora que conocemos que sí existe una diferencia por medio de la variable independiente o factor, el siguiente paso es conocer cuáles son las medias que difieren, para ello… Seleccionamos el botón “Post Hoc de Comparación Múltiple” Bajo supuesto que las varianzas no son iguales, seleccionamos la prueba T2 de Tamanhe que se basa en la t de Student Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de varianza. Factor único Multiple Comparisons Dependent Variable: Average female life expectancy Tamhane (I) Region or economic group OECD East Europe Pacific/Asia Africa Middle East Latn America (J) Region or economic group East Europe Pacific/Asia Africa Middle East Latn America OECD Pacific/Asia Africa Middle East Latn America OECD East Europe Africa Middle East Latn America OECD East Europe Pacific/Asia Middle East Latn America OECD East Europe Pacific/Asia Africa Latn America OECD East Europe Pacific/Asia Africa Middle East Mean Difference (I-J) Std. Error 4.095* .393 12.683* 2.653 25.832* 1.848 8.507* 1.122 8.333* 1.633 -4.095* .393 8.588 2.657 21.737* 1.854 4.412* 1.131 4.238 1.639 -12.683* 2.653 -8.588 2.657 13.149* 3.213 -4.176 2.857 -4.350 3.094 -25.832* 1.848 -21.737* 1.854 -13.149* 3.213 -17.325* 2.131 -17.499* 2.439 -8.507* 1.122 -4.412* 1.131 4.176 2.857 17.325* 2.131 -.174 1.947 -8.333* 1.633 -4.238 1.639 4.350 3.094 17.499* 2.439 .174 1.947 Sig. .000 .003 .000 .000 .001 .000 .073 .000 .015 .228 .003 .073 .005 .925 .940 .000 .000 .005 .000 .000 .000 .015 .925 .000 1.000 .001 .228 .940 .000 1.000 95% Confidence Interval Lower Bound Upper Bound 2.84 5.35 3.61 21.76 19.64 32.03 4.72 12.29 2.95 13.72 -5.35 -2.84 -.50 17.67 15.53 27.94 .61 8.21 -1.16 9.64 -21.76 -3.61 -17.67 .50 2.91 23.39 -13.59 5.23 -14.28 5.58 -32.03 -19.64 -27.94 -15.53 -23.39 -2.91 -24.12 -10.53 -25.13 -9.86 -12.29 -4.72 -8.21 -.61 -5.23 13.59 10.53 24.12 -6.31 5.96 -13.72 -2.95 -9.64 1.16 -5.58 14.28 9.86 25.13 -5.96 6.31 Recordemos que la Hipótesis Nula es: H0 : mi = mj Para cada uno de los casos: Regla de rechazo: α > p value Para un nivel de confianza del 99%, rechazamos hipótesis nula si, 0.01 >p value *. The mean difference is significant at the .05 level. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de varianza. Dos factores El análisis de Varianza con dos factores de clasificación sirve para examinar el efecto de dos factores en una variable observada. Este tipo de diseño presenta varias ventajas: • Estudio de los efectos principales: • Eficiencia. Permite analizar los efectores de varios factores simultáneamente y sus efectos de interacción • Control sobre factores adicionales. Las variables independientes sirven como variables de control. • Estudio del efecto interactivo: • Estudio de la interacción. La inclusión de varios factores en el diseño permite investigar la interacción de los factores, y sus efectos sobre la variable observada. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de varianza. Dos factores Las hipótesis que se ponen a prueba en el Análisis de varianza de dos factores son: Filas: H0: m1= m2 = m3 = … = mf La media de las f poblaciones contempladas en las filas son iguales, es decir, no hay un efecto por el primer factor Columnas: H0: m1= m2 = m3 = … = mc La media de las c poblaciones contempladas en las columnas son iguales, es decir, no hay un efecto por el segundo factor Interacción: H0: todos (mij - mi - mj + m)=0 No hay una diferencia entre las medias de las poblaciones que no pueda ser explicado por el efecto de filas ni por el efecto de columnas Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de varianza. Dos factores Ejemplo. Se desea conocer si existe una diferencia en salarios recibidos al graduarse de la Universidad, se cree que la diferencia de salarios está relacionada con el género y la facultada donde estudiaron los graduados.. Al analizar las medias de la muestra obtenida se obtuvieron los siguientes gráficos: Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de varianza. Dos factores Al analizar el efecto entre colegio y género, parece que existe una diferencia, no sólo por el género y el colegio, sino también por la interacción entre género y facultad del egresado Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de varianza. Dos factores Para comprobar si existe una diferencia de salario por el tipo de facultad y el género del egresado, procedemos a realizar un análisis de ANOVA de dos factores para ello.. En el menú principal: Análisis→ Modelo Lineal General→ Univariado Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de varianza. Dos factores En el cuadro de diálogo seleccionamos las variables a analizar… Variable dependiente: Salarios Variables independientes: Género y Colegio Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de varianza. Dos factores En la hoja de resultados observamos… Tests of Between-Subjects Effects Dependent Variable: Starting Salary Type III Sum Source of Squares Corrected Model 1.033E+010 a Intercept 2.476E+010 college 6701435981 gender 20147204.5 college * gender 381003159 Error 4.303E+010 Total 8.006E+011 Corrected Total 5.336E+010 df 15 1 7 1 7 1084 1100 1099 Mean Square 688932388.8 2.476E+010 957347997.3 20147204.51 54429022.74 39691430.21 F 17.357 623.757 24.120 .508 1.371 a. R Squared = .194 (Adjusted R Squared = .183) Sig. .000 .000 .000 .476 .214 Si existe una diferencia de salarios por tipo de facultad No hay una diferencia significativa por el Género del graduado No hay una diferencia significativa por el Género del graduado y el colegio del que egresó Para cada uno de los casos: Regla de rechazo: α > p value Para un nivel de confianza del 99%, rechazamos hipótesis nula si, 0.01 >p value Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de Tablas de Contingencia Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Tablas de contingencia La tabla de contingencia es una forma de representar N casos clasificados con arreglo a dos criterios. Es una primera forma de observar si existe una diferencia en las categorías de la variable dependiente. Pues a través de ella podemos calcular: 1) La significancia en la asociación y 2) La fortaleza de la asociación Variable independiente e l ba i r a V e t ne i dne pe d ) s e l i m , os er gn I ( 0-10 Hombre Mujer 25% 50% 11-20 100% Análisis estadístico con SPSS 100% 100% Se puede observar que existe una diferencia en el ingreso por la variable de sexo.. El porcentaje en las tablas de contingencia deben establecerse en las columnas o filas donde se encuentra la variable independiente… Ricardo Rojas Montero [email protected] Tablas de contingencia En SPSS, el análisis de tablas de contingencia se solicita seleccionando… En el menú principal: Análisis→ Estadísticas descriptivas→ Tablas de contingencia Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Tablas de contingencia En el cuadro de diálogo de la tabla de contingencia debemos especificar la variable que se presenta en columna y en fila… En el botón de “Celdas” es donde se debe especificar cómo será presentado el porcentaje de nuestra tabla Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Tablas de contingencia En el cuadro de diálogo de la tabla de contingencia debemos especificar la variable que se presenta en columna y en fila… p1 * tipo Crosstabulation % within tipo tipo p1 Total "(1) Muy malo" "(2) Malo" "(3) Regular" "(4) Bueno" "(5) Muy bueno" "Nacional" 1.2% 2.4% 15.9% 51.2% 29.3% 100.0% "Internacional" 1.0% 2.9% 13.6% 48.5% 34.0% 100.0% Total 1.1% 2.7% 14.6% 49.7% 31.9% 100.0% Podemos decir a simple vista que tal vez no existe una diferencia en la evaluación global (P1) por el tipo de empresa… Sin embargo, para ello es necesario sustentarlo con un análisis estadístico Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Tablas de contingencia. Prueba de independencia Para conocer la significancia en la asociación de las variables, el análisis que debe realizarse es la prueba de independencia, esto es, probar que la que no existe asociación entre las columnas y las filas de la tabla. Por Ho: Son independientes El estadístico de prueba para verificar esta hipótesis es el denominado Ji-cuadrada de Pearson, el cual presenta la forma: Σ (FO-FT)2 FT El nivel de confianza está dado por: 1- α La probabilidad de aceptar la hipótesis nula cuando es verdadera. 1- α Región de aceptación Análisis estadístico con SPSS α Para un nivel de confianza del 90%, rechazamos hipótesis nula si, 1-p value > 1-α Región de rechazo Ricardo Rojas Montero [email protected] Tablas de contingencia. Prueba de independencia SPSS permite dos pruebas de independencia que depende de los valores de nuestras variables… Pruebas de independencia • Chi-cuadrada. Cuando tenemos tablas de contingencia con cualquier cantidad de columnas y filas. • Estadística de Cochran’s & Mantel-Haenszel. Prueba de independencia cuando la variable dependiente e independiente son dicotómicas. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Tablas de contingencia El estadístico de Ji-Cuadrado se solicita a través del botón de “Estadísticas”… Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Tablas de contingencia Si el valor del estadístico de prueba pertenece a la región de aceptación, con confianza 1α, se acepta Ho, en caso contrario se rechaza… Chi-Square Tests Pearson C hi-Square Likelihood Ratio Linear-by-Linear Association N of Valid Cases Value .608 a .609 .314 4 4 Asymp. Sig. (2-sided) .962 .962 1 .575 df Para un nivel de confianza del 90%, rechazamos hipótesis nula si, 1-p value > 90% 3.8% >90% 185 a. 4 cells (40.0%) have expected count less than 5. The minimum expected count is .89. Si alguna frecuencia teórica adopta valores muy pequeños el resultado puede alcanzar valores muy elevados y conducir un rechazo o aceptación equívoco. Por lo que… Por lo tanto no podemos rechazar la Ho… Las respuestas de los grupos son independientes de cómo les fue en la feria!!!… es recomendable recodificar la tabla o aumentar el número de casos observados!!! Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Tablas de contingencia Originalmente, la tabla de contingencia se encuentra de la siguiente forma… p1 * p15 Crosstabulation % within p15 "(1) Nada Productiva" p1 Total "(1) Muy malo" "(2) Malo" "(3) Regular" "(4) Bueno" "(5) Muy bueno" 100.0% 100.0% Análisis estadístico con SPSS p15 "(2) Poco "(3) Productiva" Productiva" .9% 10.0% 3.7% 30.0% 18.3% 50.0% 56.9% 10.0% 20.2% 100.0% 100.0% "(4) Muy Productiva" 1.5% 6.2% 36.9% 55.4% 100.0% Total 1.1% 2.7% 14.6% 49.7% 31.9% 100.0% Por lo que es necesario recodificar las variables Ricardo Rojas Montero [email protected] Tablas de contingencia Para recodificar, en el menú principal seleccionamos “Transformar”, “Recodificar” y la opción “En la misma variable” En el cuadro de diálogo de “Recodificar en la misma variable” introducimos la variable a recodificar y el botón “Viejos y nuevos valores” Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Tablas de contingencia SPSS ofrece una manera sencilla de cmabiar los viejos y nuevos valores, así como cambios por rangos y otras opciones Una vez cambiados los valores es necesario cambiar las etiquetas de las variables directamente en la hoja de “Vista de Variables” Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Tabla de contingencia Realizado la recodificación, y volviendo a crear nuestras tablas de contingencia, podemos observar que nuestra conclusión de las variables es diferente.. p1 * p15 Crosstabulation % within p15 p15 p1 Total "(1) Nada /Poco Productiva" "(1) Muy malo/Malo" 36.4% "(3) Bueno/Muy Bueno" 63.6% 100.0% "(2) Productiva/ Muy Productiva" 17.2% 82.8% 100.0% Total 18.4% 81.6% 100.0% Para un nivel de confianza del 90%, rechazamos hipótesis nula si, 1- p value > 1-α 1-(.082) >90% 91.8%>90% Por lo tanto rechazamos Ho… Las respuestas de los grupos NO SON INDEPENDIENTES Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Tabla de contingencia. Pruebas de asociación Conociendo que existe una asociación significativa entre las variables analizadas (en términos técnicos, entre las columnas y las filas). El siguiente paso importante es: analizar la fortaleza de la asociación • Nominal. • Medidas de asociación •Coeficiente de contingencia. •V deCramer. •Medidas de reducción al error (predicción) • Lambda. •Coeficiente de incertidumbre. • Ordinal •Medidas de asociación •Gamma •Tau de Kendall •Medidas de reducción al error (predicción) •D de Sommers • Nominal por intervalo •Eta. Análisis de una variable categórica codificada numéricamente y una variable cuantitativa Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Tablas de contingencia. Lambda Para analizar si estamos realizando un pronóstico incorrecto con respecto a la variable dependiente e independiente utilizamos el estadístico LAMBDA El coeficiente de lambda se calcula a través de la fórmula: λ= P(I1) – P(I2) P(I1) Donde: P(I1) P(I2) Es la probabilidad de realizar un pronóstico incorrecto cuando sólo se considera la información correspondiente a la característica dependiente Es la probabilidad de realizar un pronóstico incorrecto cuando se considera la información adicional correspondiente a otra característica El coeficiente de lambda siempre se mueve de 0 a 1 0<λ<1 λ=0 Significa que la característica independiente no es útil para pronosticar la dependiente λ=1 Significa que la característica independiente es perfecta para realizar el pronóstico Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Tablas de contingencia El análisis de Lambda aparece en el botón de “Estadísticas” del menú de diálogo del análisis de tabla cruzada.. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de Correlación Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de correlación El análisis de correlación tiene por objeto estudiar y cuantificar el grado de ajuste o asociación entre un conjunto de puntos correspondientes a la población o muestra observada Si sólo se considera una variable independiente y= f(x), Se utiliza el análisis de correlación simple En el caso de más de una variable independiente y= f(x,z,w,….) Se utiliza el análisis de correlación Múltiple Para ello podemos realizar correlaciones bivaridas o correlaciones parciales Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de correlación SPSS ofrece tres pruebas para medir la correlación de los datos de acuerdo a tipo de variable analizada.. • Pearson. Cuando las variables son contínuas • Spearman. Cuando utilizamos los rangos de las observaciones o valores en orden que les corresponden • Tau de Kendall. Medida de asociación entre dos atributos sometidos a escala ordinal Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de Fiabilidad Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de fiabilidad El análisis de fiabilidad surge por la necesidad de conocer si un indicador empírico (o un conjunto de ellos) representa adecuadamente un determinado concepto teórico. Es recomendable que cualquier procedimiento o instrumento de medida goce de las propiedades: • Fiabilidad (reliability): Hace referencia al hecho de que un experimento, prueba o procedimiento de medida arroja los mismo resultados al realizar pruebas repetidas • Validez: Es la relación entre el concepto y el indicador La fiabilidades está relacionado con el tema empírico y la validez con el tema teórico. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de fiabilidad Existen diferentes formas de medir la fiabilidad de una escala, pero el Coeficiente Alfa de Cronbach es uno de los más utilizados para este tipo de pruebas El coeficiente de Cronbach mide: Que tan bien un conjunto de preguntas (o variables) miden la construcción de una dimensión potencial. Por ende.. Si los datos tienen una estructura multidimensional el Alfa de Conbach será bajo El alfa de Cronbach no es una prueba estadística… es un coeficiente de fiabilidad Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de fiabilidad El coeficiente Alfa, al interpretarse en términos de correlación, varía de 0 a 1(Si se obtienen valores negativos se ha violado el modelo de fiabilidad) La fórmula que permite calcular el alfa de Cronbach es: K cov / var α = 1+((k-1)cov/var) Donde: K : Número de ítems en la escala cov: Covarianza media entre ítem var: Varianza media de los ítems Si los ítems están tipificados, la fórmula se simplifica a: α= Donde: r: Kr 1+(k-1)r es la correlación media entre ítems Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de fiabilidad Ejemplo analizando la organización de un evento. Se desea conocer cómo evalúan la organización de un evento para ello se realiza una “batería” de preguntas relacionadas con este concepto. En el menú principal seleccionamos: Análisis→ Escala→ Análisis de fiabilidad Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de fiabilidad En el cuadro de diálogo de análisis de fiabilidad, se seleccionan los ítems que desea considerar, y seleccionamos el modelo alfa. En el menú de estadísticas podemos encontrar una mayor interactividad con la prueba, así como una mayor versatilidad de análisis: • Estadísticas descriptivas • Estadísticas de resumen • ANOVA • Estadísticas Inter-ítem Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de fiabilidad Una de las estadísticas más utilizadas en la práctica es la “Escala si el ítem es eliminado”, la cual nos permite mejorar nuestra escala al eliminar o aumentar ítems para medir nuestro concepto Estadísticas adicionales T2 de Hotelling. Genera una prueba con Ho: todos los ítems tienen la misma media Prueba de adicionalidad de Turkey. Ho: No existe una interacción multiplicativa entre los ítems Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de fiabilidad El alfa de Cronbach con los datos actuales se muestra en la tabla de “Estadísiticas de Fiabilidad”, mientras que las posibles alfas se muestran en las “Estadísticas de ítem-total” Reliability Statistics Cronbach's Alpha .824 Cronbach's Alpha Based on Standardized Items .833 Este sería el alfa si no contemplamos la pregunta p14_1 N of Items 13 p14_1 p14_2 p14_3 p14_4 p14_5 p14_6 p14_7 p14_8 p14_9 p14_10 p14_11 p14_12 p14_13 Análisis estadístico con SPSS Item-Total Statistics Scale Mean if Item Deleted 44.83 45.06 45.00 44.81 44.91 45.31 44.95 44.95 44.99 45.42 44.55 44.53 44.99 Scale Variance if Item Deleted 129.513 121.094 128.163 144.212 141.906 140.879 141.497 122.231 120.772 113.256 144.238 145.033 140.663 Corrected Item-Total Correlation .499 .603 .505 .273 .437 .387 .440 .580 .607 .627 .393 .429 .363 Squared Multiple Correlation .580 .640 .332 .286 .436 .402 .392 .816 .827 .556 .337 .434 .239 Cronbach's Alpha if Item Deleted .810 .800 .810 .824 .816 .818 .816 .803 .800 .800 .819 .819 .819 Ricardo Rojas Montero [email protected] Análisis de fiabilidad Si realizamos el ejercicio manualmente, podemos comprobar el resultado anterior: La fórmula que permite calcular el alfa de Cronbach es: K cov / var α = 1+(k-1)cov/var 13 .752 / 2.835 .824 = 1+((13-1).752/2.835 Donde: K : Número de ítems en la escala cov: Covarianza media entre ítem var: Varianza media de los ítems Análisis estadístico con SPSS (13) (.752) (2.835) Ricardo Rojas Montero [email protected] Análisis de Regresión Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Introducción Estudios anteriores han demostrado que incrementos en el contenido de alquitrán y nicotina en un cigarrillo están acompañados de incrementos en el Monóxido de Carbono emitidos* Objetivo: Explicar relación entre el contenido de nicotina, alquitrán y el Monóxido de Carbono. Diseño de Investigación: Transversal utilizando análisis de regresión lineal múltiple por mínimos cuadrados Hipótesis: A mayor cantidad de alquitrán/nicotina que contenga un cigarrillo es más probable que produzca mayores cantidades de Monóxido de Carbono El modelo será generado a partir de una base de datos con información sobre el contenido de alquitrán, de nicotina, de monóxido de carbono producidos en la combustión y el peso de un cigarrillo para 25 marcas de cigarros diferentes. *Fuente: Federal Trade Commision. “Tar”, nicotine and carbon monoxide of the smoke of 1294 varieties of domestic cigarretes for the year 1998 Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Generalidades Se pretende estudiar la relación entre el monóxido de carbono producido en la combustión de un cigarrillo y su contenido en alquitrán y nicotina Modelo Varible Independiente Hipótesis: Varible Dependiente Nicotina Alquitrán Peso Monóxido de Carbono H1: ↑ alquitrán ↑ proba de q de Monóxido de Carbono controlados por Nicotina y Peso H2: ↑ Nicotina ↑ proba de q de Monóxido de Carbono controlados por alquitrán y peso Hipótesis alternativa: H0: No existe relación entre las variables Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis: Procedimiento 1. Análisis exploratorio de los datos. 2. Matriz de correlaciones. 3. Modelo inicial y primer análisis de regresión. 4. Eliminación de variables en el modelo inicial. 5. Repetición de los pasos 3 y 4 hasta obtener un modelo definitivo, cuyas variables tengan todas un valor p menor a 0.05 . 6. Pronósticos efectuados sobre el modelo definitivo. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis: Exploración Moda N.D. Moda N.D. Varianza 32.1 Varianza 0.01 Desv Stand 5.67 Desv Stand 0.09 Moda 1.02 Moda 10.2 Varianza 0.13 Varianza 22.46 Desv Stánd 0.35 Desv. Stand 4.74 Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis: Exploración Gráficamente es posible observar que existe una clara relación entre las diversas variables, exceptuando Monóxido y Peso **Significante al 0.01; * Significante al 0.05 Análisis estadístico con SPSS C. Correlación C. Correlación 0.95** 0.92** C. Correlación C. Correlación 0.97** 0.46* Ricardo Rojas Montero [email protected] Modelo Para nuestro modelo inicial se consideraron todas las variables descritas anteriormente, para el número total de observaciones. Por lo que el modelo es de la forma: Y=β ^ ^ 0 +β ^ ^ X1 + β 1 ^ 2 X2 + β ^ 3 X3 + ε Para este análisis el procedimiento fue por medio de: • Modelo de eliminación hacia atrás. • Tres modelos analizados: • Monoxido = Intercepto + Nicotina + Alquitrán + Peso + Error • Monóxido = Intercepto + Alquitrán + Error • Monóxido = Intercepto + Nicotina + Error Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de Regresión Para desarrollar un análisis de regresión en SPSS… En el menú principal seleccionamos: Análisis→ Regresión→ Lineal Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de Regresión Como variable dependientes seleccionamos aquella que nos interesa explicar y como variables dependiente aquellas que suponemos que explican su comportamiento… Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de Regresión En la opción de estadísticas seleccionamos: Estimación de coeficientes de regresión, Ajuste de modelo, diagnóstico de colinearidad y Prueba de Durbin Watson para análisis de residuales. Estimación de coeficientes de regresión. Muestra los coeficientes de regresión y la prueba de significancia de cada una de las B’s Ajuste de modelo. Proporciona la R2 del modelo, es decir, la varianza total explicada y el análisis de varianza. Diagnóstico de colinearidad. Desarrolla una prueba para analizar si una variable independientes está correlacionada linealmente con otra variable independiente Prueba de Durbin Watson para análisis de residuales. Genera una prueba de correlación serial de los residuales. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de Regresión Un análisis importante en la regresión cuando es utilizada para estimación es analizar que los valores residuales tengan una distribución normal… SPSS permite dos análisis gráficos de los residuales.. El histograma con curva de distribución y Grágica de probabilidad normal… En caso que los residuales no tengan una distribución normal, se debe tener cuidado de utilizar el modelo de regresión para predecir nuevos datos… Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de Regresión El primer resultado importante de analizar en el modelo es el R2 que determina cuanta varianza es explicada por nuestro modelo y el Análisis ANOVA Model Summaryb Model 1 R R Square .958 a .919 Adjusted R Square .911 Std. Error of the Estimate 1.41252 DurbinWatson 2.865 a. Predictors: (Constant), Nicotina, Alquitrán b. Dependent Variable: Monoxido Utilizando Nicotina y Alqauitrán el modelo explica el 91.9% del comportamiento de la producción de Monóxido… Entre mayor sea el valor de la R2 mejor es el modelo… El segundo paso es realizar una prueba de hipótesis para comprobar que almenos una de nuestras estimaciones es diferentes de cero ANOVAb Model 1 Regression Residual Total Sum of Squares 495.255 43.895 539.150 df 2 22 24 a. Predictors: (Constant), Nicotina, Alquitrán b. Dependent Variable: Monoxido Mean Square 247.628 1.995 F 124.110 Sig. .000 a Regla de rechazo: α > p value Para un nivel de confianza rechazamos hipótesis nula si, 0.01 >0.00 del 99%, Rechazamos la hipótesis nula y por lo menos un B es diferente de cero… Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de Regresión Identificado que por lo menos una B es diferente de cero con el análisis ANOVA, el siguiente paso es conocer que B es diferente de cero, para ello, analizamos…. Coefficientsa Model 1 (Constant) Alquitrán Nicotina Unstandardized Coefficients B Std. Error 3.090 .844 .962 .237 -2.646 3.787 Standardized Coefficients Beta 1.151 -.198 t 3.662 4.067 -.699 Sig. .001 .001 .492 Collinearity Statistics Tolerance VIF .046 .046 21.627 21.627 a. Dependent Variable: Monoxido Para cada coeficiente analizamos su hipótesis nula.. Regla de rechazo: H0: B0 = 0 H0: B1 = 0 H0: B2 = 0 En este caso, alquitrán muestra no ser significativo para explicar la producción de monóxido.. Análisis estadístico con SPSS α > p value Para un nivel de confianza rechazamos hipótesis nula si, 0.01 >0.00 del 99%, Rechazamos la hipótesis nula de Bi es diferente de 0 Ricardo Rojas Montero [email protected] Análisis de Regresión Esto sucede porque puede existir un problema de colinearidad de las variables o por que la variable realmente no ayuda a explicar el comportamiento de nuestra variable dependiente, por ello, es necesario realizar un análisis de colinearidad.. a Collinearity Diagnostics Model 1 Dimension 1 2 3 Eigenvalue 2.891 .106 .004 Condition Index 1.000 5.229 28.710 Variance Proportions (Constant) Alquitrán Nicotina .01 .00 .00 .71 .02 .01 .28 .98 .99 a. Dependent Variable: Monoxido En este caso, el 98% de la varianza de alquitrán es explicado por la Nicotina, por lo tanto existe un problema de colinearidad entre estas variables Análisis estadístico con SPSS Existen dos formas de realizar una inspección de colinearidad… Previo al análisis de regresión realizar un análisis de correlación, o Realizar en el análisis de regresión un diagnóstico de colinearidad… En los casos en que el valor de la proporción de la varianza sea muy alta, tenemos presencia de colinearidad Ricardo Rojas Montero [email protected] Análisis de Regresión Otro resultado que muestra SPSS, es el análisis de normalidad de los residuales, el cual utilizamos cuando vamos a utilizar el modelo para generar predicciones… Entre mayor sea el ajuste a una curva normal de los residuales mejor será nuestro modelo para predecir valores Análisis estadístico con SPSS Entre mayor sea el ajuste a línea recta de los residuales mejor será nuestro modelo para predecir valores Ricardo Rojas Montero [email protected] Modelo 1 El análisis del primer modelo (Monoxido = Intercepto + Nicotina + Alquitrán + Peso + Error) muestra que Nicotina y Peso pueden no funcionar para nuestro objetivo. Resultados Resumen del Modelo R .919 D-W 2.860 2 ANOVA Sig. 0.00 Residual 43.89 Regresión 495.25 Total 539.15 Beta P-value Constante 3.202 .365 Alquitrán 0.963 .001 .046 Nicotina -2.632 .507 .046 Peso -.130 .974 .750 Análisis estadístico con SPSS Tolerancia Resumen del Modelo 1. El modelo tiene una excelente bondad. La proporción de variación total en Y explicada por el modelo es del 91.9% 2. No Existe autocorrelación. No debe esperarse que el efecto de un incremento en el alquitran de un cigarrillo incida sobre la producción de otro cigarrillo. Anova 1. Rechazo la hipótesis de β 0=β 1=β 2=β 3=0; por lo que almenos una β es diferente de cero. Coeficientes 1. Sólo alquitran rechaza la hipótesis de β j=0. 2. Esto puede deberse a que alquitrán y nicotina están linealmente relacionados (multicolinealidad). Una variable con poca tolerancia contribuye con poca información al modelo. Peso se elimina Ricardo Rojas Montero Ricardo Rojas Montero [email protected] Modelo 2 Debido a que Nicotina y Alquitrán muestraron una alta correlación es necesario probar las variables por separado (Monoxido = Intercepto + Nicotina + Error) Resultados Resumen del Modelo R2 .857 D-W 2.674 ANOVA Sig. 0.00 Residual 76.89 Regresión 462.25 Total 539.15 Beta P-value Constante 1.665 .107 Nicotina 12.395 .000 Media de residuos Resumen del Modelo 1. La proporción de variación total en Y explicada por el modelo es del 85.7% 2. No Existe autocorrelación. No debe esperarse que el efecto de un incremento en la Nicotina de un cigarrillo incida sobre la producción de otro cigarrillo. Anova 1. Rechazo la hipótesis de β 0=β 1=0; por lo que almenos una β es diferente de cero. Coeficientes 1. Sólo Nicotina rechaza la hipótesis de β j=0. 2. El valor medio de los residuos es cercano a cero por lo que tiene buena bondad de ajuste 5.116E-15 Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Modelo 3 El mejor modelo es el que sólo toma como variable independiente al alquitrán (Monoxido = Intercepto + Alquitrán + Error) Resultados Resumen del Modelo R2 .917 D-W 2.893 ANOVA Sig. 0.00 Residual 44.86 Regresión 494.28 Total 539.15 Beta P-value Constante 2.743 .000 Alquitrán 0.801 .000 Media de residuos 3.730E-15 Análisis estadístico con SPSS Resumen del Modelo 1. La proporción de variación total en Y explicada por el modelo es del 91.7%. Mayor que en el modelo 2. 2. No Existe autocorrelación. No debe esperarse que el efecto de un incremento en el alquitran de un cigarrillo incida sobre la producción de otro cigarrillo. Anova 1. Rechazo la hipótesis de β 0=β 1=0; por lo que almenos una β es diferente de cero. Coeficientes 1. Ambas variables rechazan la hipótesis de β j=0. 2. La media de los residuos es menor que con el modelo 2. Ricardo Rojas Montero [email protected] Modelo 3 (Continuación) Gráfico de probabilidad Normal Análisis estadístico con SPSS valores pronosticados y observados Ricardo Rojas Montero [email protected] Modelo El modelo resultantes se puede escribir de la forma: Monóxido = 2.743 + (0.801)Alquitrán + ε Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Conclusiones • No hubo evidencia suficiente de la existencia de relación entre Monóxido y el peso del cigarrillo. • Alquitrán o nicotina tienen buenas mediadas de bondad para explicar la producción de Monóxido; sin embargo, • El modelo con mejor ajuste fue el que consideraba Alquitrán como variable explicativa. • Sólo 8.3% de la varianza no es explicada por el Alquitrán • La base de monóxido para cualquier cigarro es de 2.7 miligramos • Un incremento unitario de alquitrán provoca un incremento de 0.8 miligramos en el Monóxido Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de Factorial Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial El análisis factorial permite expresar una serie de variables observadas en función de un número menor de factores analizando para ello la correlación entre las variables. Trata de identificar las dimensiones subyacente que determinan la relación entre variables, es decir,…. Los factores comunes Los factores comunes son variables hipotéticas no directamente observadas. Por ejemplo: • Personalidad de marca • Competitividad • Creatividad • Percepción de calidad • Entre otras… Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial Aunque no existe una solución única en el análisis factorial para un conjunto de datos, se deben contemplar dos principios básicos para seleccionar una solución.. • Principio de Parsiomonia • Interpretabilidad Esto es una buena solución es aquella que es: simple e interpretable Debemos seleccionar el menor número de factores posibles y éstos deben tener un significado lógico con base en el tema que estamos analizando. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial Otro uso importante del análisis factorial es la identificación de individuos similares. A diferencia del análisis de cluster, el cual basa la agrupación de unidades de acuerdo a distancia, el análisis factorial… identifica sujetos que demuestran un patrón similar en las variables incluidas en el análisis Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial: Supuestos Tamaño de muestra: • Se debe utilizar el análisis cuando se tenga un tamaño de muestra mayor a 50 observaciones. • Regla general: Mínimo 20 casos por cada variable (nivel óptimo), 10 casos por cada variable (nivel medio) Supuestos: • Normalidad en las datos si es el análisis va a ser utilizado para significancia de los factores • Multicolinearidad: Pues el objetivo del análisis es identificar conjunto de variables interrelacionadas. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial La correlación de las variables se analiza por medio de autocorrelaciones parciales o antiimagen de correlaciones. Cuya diferencia radica en que una prueba muestra los valores negativos de otra Regla: Si existen factores reales en la muestra los valores serán pequeños… si no existen factores reales los valores serán altos. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial: Análisis exploratorio Otra forma de analizar el supuesto de colinearidad, la existencia de factores, es a través de… Prueba de Esfericidad de Bartlett •Es una prueba estadística sobre la presencia de correlación entre variables. •Muestra la probabilidad de que la matriz de correlación tenga correlaciones significantes con al menos una de las variables Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial: Análisis exploratorio Otra medida que cuantifica el grado de intercorrelación entre las variables y la factibilidad de del análisis factorial es la.. Prueba de adecuación de la muestra (KMO) • El rango de la variable va de 0 a 1, 1 cuando cada variable es perfectamente predicha por otra variable y el valor de 0 cuando no existe esta relación. • Un valor de .8 se califica como meritorio; • Entre .8 y .7 medio • Entre .7 y .6 regular • Menor a .6 no adecuado Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial: Generación de factores Una vez identificadas las variables, el siguiente paso es identificar la estructura adyacente en los datos. Para ello… 1. Se debe seleccionar el método de extracción 2. Seleccionar el número de factores adecuado Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial: Común vs. componentes El análisis de componentes se utiliza cuando el objetivo es resumir en mayor medida la información (varianza) en un mínimo de factores para propósito predictivos. Considera la varianza total y deriva los factores que contienen poca proporción de varianza única. El análisis de factores comunes es usado para identificar los actores o dimensiones que reflejan lo que las variables tienen en común. Considera en el análisis la varianza que existe en común en las variables. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial Sea la matriz de observaciones XNxn en la que se expresan los valores de las variables X1, X2, X3…,Xn, con N número de casos… XNxn= X11 X11 X21 X21 X31 X31 X11 X21 X31 X1n X2n X3n XN1 XN1 XN1 XNn El objeto del análisis factorial es expresar cada variable como una combinación lineal de una serie de factores comunes F1, F2,…,Fm (m<n) y un factor único. Para evitar problemas ocasionados por las dimensiones de las diferentes variables es recomendable tipificarlas previo al análisis. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial: Matriz de correlación Una vez tipificadas las variables es posible obtener la matriz de correlaciones. La matriz de correlaciones es una matriz cuadrada y simétrica que contiene los coeficientes de correlación lineal entre las variables observadas. En la diagonal principal de la matriz Rnxn se encuentran las correlaciones=covarianzas de cada variable consigo misma, es decir, las varianzas de las variables observadas. Por ende, la suma de ellas es la varianza total. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial: Extracción de factores Existen diferentes métodos de extracción de factores, pero los más utilizados son el método de componentes principales y el de factorización de ejes principales. Componentes principales. Se trata de obtener unas nuevas variables o componentes como combinación lineal de las variables observadas. Este método transforma un conjunto de variables correlacionadas en un conjunto de variables incorrelacionadas Ejes principales. Es un caso particular del de Componentes Principales. Trata de maximizar una función con n variables cuando las variables están relacionadas a través de un número arbitrario de ecuaciones auxiliares. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial: Rotación de factores Con el fin de lograr una estructura simple que facilite la interpretación de los factores, es necesario realizar la rotación de los factores… Rotación ortogonal. Tiene por objetivo reducir la Matriz Factorial a una estructura simple. • Varimax. Maximiza la varianza de los coeficientes, i.e., maximiza la varianza explicada por cada componente. • Quartimax. Minimiza el número de factores necesarios para explicar una variable • Equimax. Es una combinación del método Varimax y el método quartimax. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial: Interpretación La extracción ortogonal permite representar a los factores mediante ejes perpendiculares. Por lo que si se asocia a cada variable un vector que parta del origen, es posible conseguir una interprtación gráfica de los factores. El coseno del ángulo que determinan los vectores asociados a las variables permite establecer una correlación entre factores.. Cosα = r -1≤ cos α ≤ +1 -1≤ r ≤ +1 Si el ángulo de los dos vectores es 00 Correlación perfecta entre variables (Cos 00= 1) Análisis estadístico con SPSS Si el ángulo de los dos vectores Si el ángulo de los dos vectores es 900 es 1800 No hay Correlación entre variables (Cos 900= 0) Correlación perfecta negativa entre variables (Cos 1800= -1) Ricardo Rojas Montero [email protected] Análisis de factorial. Ejemplo La cultura política de los ciudadanos, por revisión teórica, se sabe que los componentes de la cultura política son tres: 1. Orientación cognoscitiva (creencias y conocimientos sobre el sistema político) 2. Afectiva (sentimientos sobre el sistema político) 3. Evolutiva (compromisos hacia los valores políticos y juicios de desempeño del sistema político) Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial. Ejemplo Para ello se formularon un conjunto de preguntas para medir la cultura política de los ciudadanos.. 2a. En México ¿Quién tiene facultad para aprobar las reformas a la Constitución? 2c. ¿Cuál partido político propone cobrar IVA a medicinas, alimentos y colegiaturas? 2d. En la Cámara de Diputados ¿Qué partido tiene el mayor número de representantes? 2f. ¿Sabe usted cuanto tiempo duran los diputados federales en el cargo? 2g. ¿Cómo se llama el Gobernador de este Estado? 2h. ¿A qué partido pertenece el Gobernador de este Estado? 4a.1 En escala donde 1 es nada y 5 mucho ¿Qué tanto cree usted que los diputados se preocupan por las necesidades de la gente? 4d. ¿Usted confía en el Gobierno Federal? 4e. ¿Usted cree que la corrupción es de los políticos, de los ciudadanos o de ambos? 4h. ¿Considera usted que durante los últimos años ha disminuido las diferencias entre los mexicanos? 4f. ¿Quién cree usted que respeta menos las leyes: los gobernantes, los ciudadanos o ambos? Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial. Ejemplo Se realiza un análisis de fiabilidad para conocer la validez interna de nuestras preguntas…. Reliability Statistics Cronbach's Alpha .783 Item-Total Statistics N of Items 9 ¿Qué tanto cree usted que los diputados se preocupan por las necesidades de la gente? ¿Qué tanto cree usted que los diputados se preocupan por las necesidades de la gente? ¿Usted cree que la corrupción es de los políticos, de los ciudadanos o de ambos? ¿Quién cree usted que respeta menos las leyes: los gobernantes, los ciudadanos o ambos? ¿Considera usted que durante los últimos años ha disminuido las diferencias entre los mexicanos? ¿Cuál partido político propone cobrar IVA a medicinas, alimentos y colegiaturas? En México ¿Quién tiene facultad para aprobar las reformas a la Constitución? En la Cámara de Diputados ¿Qué partido tiene el mayor número de representantes? ¿Sabe usted cuanto tiempo duran los diputados federales en el cargo? Análisis estadístico con SPSS Scale Mean if Item Deleted Scale Variance if Item Deleted Corrected Item-Total Correlation Cronbach's Alpha if Item Deleted 28.34 217.358 .454 .765 30.27 210.486 .459 .763 30.75 227.779 .453 .768 29.66 230.643 .403 .773 28.96 210.844 .464 .763 29.46 192.024 .523 .755 29.50 202.371 .511 .756 28.53 187.456 .546 .751 28.69 204.192 .462 .763 Ricardo Rojas Montero [email protected] Análisis de factorial. Ejemplo Una vez observado la validez interna de nuestro conjunto de preguntas, el siguiente paso es realizar la reducción de variables a variables artificiales, para ello… En el menú principal seleccionamos: Incluimos las variables a analizar Análisis→ Reducción de datos→ Factor Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial. Ejemplo Una vez observado la validez interna de nuestro conjunto de preguntas, el siguiente paso es realizar la reducción de variables a variables artificiales, para ello… En el cuadro de estadísticas descriptivas seleccionamos Solución inicial (muestra el porcentaje de varianza extraída de cada variable En el cuadro de extracción seleccionamos el método a utilizar, en este caso “Componentes principales” Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial. Ejemplo Debemos seleccionar un método de rotación para poder interpretar los resultados.. Si deseamos utilizar los factores para clasificar a los casos de acuerdo a las variables artificiales, seleccionamos “salvar como variables” Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial. Ejemplo Uno de los primeros resultados que debemos observar es la varianza total explicada… Muestra el total de la varianza que está explicada por medio de los componentes o variables artificiales generadas Total Variance Explained Component 1 2 3 4 5 6 7 8 9 Total 3.366 1.241 .857 .706 .687 .624 .595 .513 .411 Initial Eigenvalues % of Variance Cumulative % 37.396 37.396 13.789 51.185 9.526 60.711 7.845 68.556 7.637 76.193 6.933 83.126 6.616 89.741 5.696 95.438 4.562 100.000 Extraction Sums of Squared Loadings Total % of Variance Cumulative % 3.366 37.396 37.396 1.241 13.789 51.185 Rotation Sums of Squared Loadings Total % of Variance Cumulative % 2.416 26.845 26.845 2.191 24.340 51.185 Extraction Method: Principal Component Analysis. La varianza explicada de nuestros doscomponentes es de 51.185% Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial. Ejemplo Para nombrar nuestras variables artificiales, debemos analizar la matriz de componentes rotados, de esta forma, el concepto explicado por la variable artificial se establecerá de acuerdo a las variables de las cuales extraiga la mayor varianza, esto es… a Rotated Component Matrix 1 ¿Sabe usted cuanto tiempo duran los diputados federales en el cargo? ¿Cuál partido político propone cobrar IVA a medicinas, alimentos y colegiaturas? En la Cámara de Diputados ¿Qué partido tiene el mayor número de representantes? En México ¿Quién tiene facultad para aprobar las reformas a la Constitución? ¿Qué tanto cree usted que los diputados se preocupan por las necesidades de la gente? ¿Qué tanto cree usted que los diputados se preocupan por las necesidades de la gente? ¿Usted cree que la corrupción es de los políticos, de los ciudadanos o de ambos? ¿Quién cree usted que respeta menos las leyes: los gobernantes, los ciudadanos o ambos? ¿Considera usted que durante los últimos años ha disminuido las diferencias entre los mexicanos? Component 2 .677 .112 .711 .166 .766 .129 .670 .197 .376 .468 .329 .543 .090 .825 .022 .829 .399 .462 Para el componente 1, estas son las variables a las que “extrae” mayor varianza Para el componente 2, estas son las variables a las que “extrae” mayor varianza Extraction Method: Principal Component Analysis. Rotation Method: Varimax with Kaiser Normalization. a. Rotation converged in 3 iterations. Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial. Ejemplo De esta forma, nosotros podemos nombrar a nuestras variables artificiales, por lo que… Componente 1: Conocimiento político. Componente 2: Creencia sobre el sistema político Análisis estadístico con SPSS Ricardo Rojas Montero [email protected] Análisis de factorial. Ejemplo a) No hay correlación entre P41 y P2f, es decir, el hecho que no conozcan el periodo de duración de los diputados no implica que tengan una apreciación positiva sobre el respeto a la ley a) b) Análisis estadístico con SPSS b) Existe correlación entre P2d y P2f, es decir, el hecho que no conozcan el periodo de duración de los diputados está relacionado también con el desconocimiento de quien tiene mayoria en la cámara Ricardo Rojas Montero [email protected]