Fundamentos de Ciencia de los Materiales (Problemas)
2
Tema 2: Estructura íntima de los materiales
Problemas Resueltos
2.1. Justifique, según la teoría del enlace, el comportamiento anómalo del agua al helarse.
¿Por qué aumenta el volumen después de solidificar?
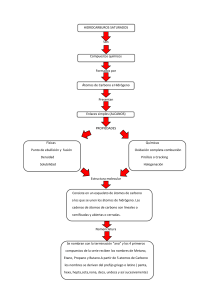
Los puntos de fusión y de ebullición de los hidruros de la familia del oxígeno (H2S, H2Se, H2Te)
aumentan progresivamente con el tamaño molecular. Sin embargo, el agua (H2O) incumple esta regla y
tiene puntos de fusión y de ebullición anormalmente altos. Esto tiene que deberse a que entre sus moléculas intervienen fuerzas más intensas que las que existen en el resto de los hidruros. El enlace producido por estas fuerzas de atracción se denomina puente de hidrógeno. Todas las propiedades singulares del agua tienen su justificación en estos enlaces. El puente de hidrógeno mantiene ligadas entre sí, formando agregados moleculares, gran número de moléculas de agua en la fase líquida. Esto
también sucede en la fase sólida, pero el estado sólido exige, además, un ordenamiento superior que
impone restricciones adicionales, que se traducen en una estructura molecular más abierta. El resultado es que la densidad del sólido es menor que la del líquido (comportamiento anómalo). La siguiente
figura ilustra el principio de actuación del puente de hidrógeno y la estructura cristalina del hielo:
2.2. Dibuje una dirección [ 1 1 0 ] en una celdilla unidad cúbica.
En primer lugar, se dibuja una celdilla unidad adecuada y el
sistema de ejes coordenados. En la figura adjunta la celdilla
unidad es cúbica y el punto O, origen del sistema de coordenadas, está localizado en un vértice del cubo.
Las proyecciones de la dirección [ 1 1 0 ] a lo largo de los
ejes son a, –a y 0·a, respectivamente. Esta dirección viene
definida por un vector que va desde el origen de coordenadas al punto P, que se localiza desplazándose a unidades a
lo largo del eje X, y, desde esta posición, desplazándose –a
unidades en sentido opuesto al eje Y. Este vector no tiene
componente z, ya que la proyección del eje Z es 0.
Quedaría por último trazar un vector paralelo al obtenido y que esté situado en el interior de la
celdilla.
Fundamentos de Ciencia de los Materiales (Problemas)
3
2.3. Haga una lista con los miembros de la familia de direcciones <110> en el sistema cúbico.
Esta familia de direcciones corresponde a todas las direcciones de las caras de celdilla unidad,
y como existen dos diagonales en cada una de las caras, se tienen un total de 12 miembros:
<110> = [110], [ 1 1 0 ], [ 1 10 ], [ 1 1 0 ], [101], [ 10 1 ], [ 1 01 ], [ 1 0 1 ], [011], [ 01 1 ],
[ 0 1 1 ], [ 0 1 1 ]
2.4. Para una celdilla unidad cúbica trace las siguientes direcciones cristalográficas: (a) [101]
(b) [211] (c) [ 10 2 ] (d) [ 3 1 3 ] (e) [ 1 1 1 ] (f) [ 2 12 ] (g) [ 3 1 2 ] (h) [ 301 ]
2.5. Para una celdilla unidad cúbica trace los siguientes planos cristalográficos: (a) ( 10 1 )
(b) ( 2 1 1 ) (c) ( 012 ) (d) ( 3 1 3 ) (e) ( 1 1 1 ) (f) ( 2 12 ) (g) ( 3 1 2 ) (h) ( 301 )
Fundamentos de Ciencia de los Materiales (Problemas)
4
Problemas Propuestos
2.1. Explique por qué los materiales con enlace covalente son, generalmente, menos densos que
los unidos iónica o metálicamente.
2.2. ¿Qué tipo de enlace cabe esperar en cada uno de los siguientes materiales: xenón sólido, fluoruro cálcico (CaF2), telururo de cadmio (CdTe) y wolframio?
Sol: VDW; predominantemente iónico con cierto carácter covalente; predominantemente covalente con cierto carácter iónico; metálico.
2.3. Explique por qué el fluoruro de hidrógeno (HF), que tiene una masa molecular inferior al cloruro de hidrógeno (HCl), presenta una temperatura de ebullición más elevada (19.4 ºC del primero frente a –85 ºC del segundo).
2.4. ¿Cuál es la diferencia entre red cristalina y estructura cristalina?
2.5. Dibuje, en celdillas unidades cúbicas separadas, los siguientes planos y direcciones:
a) (123), [123]
b) ( 1 10 ), [ 1 10 ]
c) Demuestre que los dos planos anteriores contienen la dirección [ 11 1 ]
2.6. Calcule, gráfica y vectorialmente, los índices de Miller de la línea de intersección de un plano
(111) con otro ( 11 1 ) en un cristal cúbico.
Sol: [ 1 10 ] o [ 1 1 0 ]
2.7. Dibuje en una celdilla unidad cúbica, las siguientes direcciones cristalográficas:
A: [ 1 10 ] B: [121] C: [ 0 1 2 ] D: [ 121 ]
5
Fundamentos de Ciencia de los Materiales (Problemas)
Tema 3: La escala atómica de los materiales metálicos
Problemas Resueltos
3.1. (a) Calcule el volumen de la celdilla elemental CCC en función del radio atómico, R.
(b) Demuestre que el factor de empaquetamiento para dicha estructura es 0.74.
a) En la celdilla unidad esquematizada en la figura, cada átomo contacta con el vecino a lo largo de la diagonal de la cara, cuya longitud es 4R. Dado que la celdilla unidad es un cubo, su
volumen es a3, donde a es la longitud de la arista. Del triángulo rectángulo de la cara:
a 2 + a 2 = (4R )
de donde se deduce,
2
a = 2R 2
El volumen Vc de la celdilla unidad valdrá:
(
Vc = a 3 = 2 R 2
)
3
= 16 2 R 3
b) El factor de empaquetamiento se define como la fracción de volumen ocupado, esto es:
f emp =
volumen ocupado
V
=
volumen total celdilla VC
El volumen ocupado y el de toda la celdilla unidad se pueden expresar en función del radio
atómico R. El volumen de cada átomo, supuesto perfectamente esférico, es 4/3πR3, y dado
que existen 4 átomos (8 x1/8 + 6 x1/2 = 4) en cada celdilla unidad CCC, el volumen ocupado
será:
4
16
V = 4 πR 3 = πR 3
3
3
Por tanto, el factor de empaquetamiento atómico valdrá:
f emp =
(16 / 3)πR 3 = 0.74
V
=
VC
16 2 R 3
3.2. Calcule la densidad del cobre y compárela con la densidad experimental, sabiendo que
tiene un radio atómico de 0.128 nm (1.28 Å), una estructura cristalina CCC y masa molar 63.5
g/mol.
La densidad se define como el cociente entre la masa y el volumen ocupado. La estructura
CCC contiene 4 átomos/celdilla. El volumen de la celdilla del cobre valdrá (ver problema anterior):
(
Vc = a 3 = 2 R 2
)
3
(
)
= 16 2 R 3 = 16 2 0.128 ⋅ 10 −9 m = 4.75 ⋅ 10 − 29 m 3 = 4.75 ⋅ 10 − 23 cm 3
3
la densidad puede calcularse, cómodamente, mediante factores de conversión:
D=
4 átomos
1 celdilla
1 mol
63.5 g
⋅
⋅
⋅
= 8.88 g/cm3
celdilla 4.75 ⋅10− 23 cm3 N A átomos 1 mol
6
Fundamentos de Ciencia de los Materiales (Problemas)
El valor experimental tabulado es de 8.94 g/cm3, valor muy próximo al encontrado teóricamente. Tenga bien presente la importancia de lo que hemos realizado: mediante razonamientos basados en entes microscópicos (la celdilla) hemos obtenido una propiedad macroscópica del
material (la densidad). Esto es posible gracias a la naturaleza cristalina del material, por la que
éste puede considerarse obtenido por la repetición de celdillas.
3.3. En la siguiente tabla se dan el radio atómico, la red cristalina, la electronegatividad y la
valencia más común de varios elementos. Para los no-metálicos sólo se ha indicado el
radio atómico. Indicar cuáles de estos elementos pueden formar con el níquel:
a. Una disolución sólida de sustitución con solubilidad total.
b. Una disolución sólida de sustitución con solubilidad parcial.
c. Una disolución sólida de inserción.
Elemento
Ni
C
H
O
Ag
Al
Co
Cr
Fe
Pt
Zn
Radio
Red
Electro- Valencia
atómico (nm) cristalina negatividad
0.1246
CCC
1.8
2+
0.0710
0.0460
0.0600
0.1445
CCC
1.9
1+
0.1431
CCC
1.5
3+
0.1253
HC
1.8
2+
0.1249
CC
1.6
3+
0.1241
CC
1.8
2+
0.1387
CCC
2.2
2+
0.1332
HC
1.6
2+
Para que exista solubilidad sustitutiva completa deben cumplirse los siguientes requisitos:
1) la diferencia entre los radios atómicos del Ni y del otro elemento (|ΔR| en %) tiene que
ser inferior al 15%,
2) las redes cristalinas deben ser las mismas,
3) las electronegatividades deben ser similares, y
4) las valencias deben ser muy parecidas.
En la tabla siguiente se muestran algunos parámetros de interés:
Elemento |ΔR| % Red cristalina
Ni
CCC
C
43
H
63
O
52
Ag
16
CCC
Al
15
CCC
Co
0.6
HC
Cr
0.2
CC
Fe
0.4
CC
Pt
11
CCC
Zn
7
HC
Δ EN Valencia
2+
+ 0.1
- 0.3
0
- 0.2
0
+ 0.4
- 0.2
1+
3+
2+
3+
2+
2+
2+
Fundamentos de Ciencia de los Materiales (Problemas)
7
a) Con los datos que muestra la tabla se ha de concluir que el Pt es el único elemento que satisface todos los requisitos necesarios para formar una solución sólida de sustitución con solubilidad completa. (A temperaturas elevadas también el Co y el Fe los cumplen, porque, a esas
temperaturas, sus redes cristalinas se transforman al tipo CCC, permitiendo la solubilidad completa).
b) La Ag, el Al, el Co, el Cr, el Fe y el Zn forman disoluciones sólidas de solubilidad parcial.
Todos estos metales tienen red CC o HC, y/o la diferencia entre sus radios atómicos y el del Ni
no supera el 15%, y/o tienen una valencia diferente de 2+.
c) El C, el H, y el O forman disoluciones sólidas intersticiales. Estos elementos tienen radios
atómicos significativamente menores que el radio atómico del Ni.
3.4. Calcule la composición en porcentaje en masa de una aleación que contiene 218.0 kg de
Titanio, 14.6 kg de Aluminio y 9.7 kg de Vanadio.
Si llamamos CTi, CAl y CV a las concentraciones de Ti, Al y V en la aleación, tendremos:
CTi =
218.0 kg
⋅ 100 = 89.97 % en masa
(218.0 + 14.6 + 9.7) kg
C Al =
14.6 kg
⋅ 100 = 6.03 % en masa
(218.0 + 14.6 + 9.7) kg
CV =
9.7 kg
⋅ 100 = 4.00 % en masa
(218.0 + 14.6 + 9.7) kg
3.5. El níquel forma una solución sólida sustitucional con el cobre. Calcular el número de
átomos de níquel por centímetro cúbico en una aleación cobre-níquel, que contiene 1.0%
Ni y 99.0% Cu en peso. Las densidades del níquel y del cobre puros son de 8.90 y 8.93
g/cm3, respectivamente.
Los porcentajes expresados significan que de cada 100g de aleación, 1.0 g se deben al Ni y los
99.0 g restantes se deben al Cu. Si expresamos estos valores en moles, obtenemos:
n Ni = 1.0 g ⋅
nCu
1 mol
= 0.017 moles de Ni
58.69 g
1 mol
= 99.0 g ⋅
= 1.56 moles de Cu
63.54 g
La fracción de átomos de Ni puede obtenerse:
f Ni =
N Ni
n Ni
N
0.017
=
⋅ A =
= 0.011 átomos Ni / átomos
N Ni + N Cu (n Ni + nCu ) N A 0.017 + 1.56
Fundamentos de Ciencia de los Materiales (Problemas)
8
Por otro lado, el número de átomos de Cu por unidad de volumen (en un trozo de Cu puro),
vendría dado por:
nCu = 8.93
1 mol N A átomos
g
⋅
⋅
= 8.46 ⋅ 10 22 átomos Cu/cm3
3
1 mol
cm 63.54 g
Dado que la solución sólida es sustitutiva, cada átomo de Ni reemplaza a un único átomo de
Cu, por lo que, admitiendo que el volumen no cambia tras las sustituciones, el número de átomos (en general) por unidad de volumen será igual al valor antes calculado, es decir, n =
8.46·1022 átomos/cm3. Y, por lo tanto, el número de átomos de Ni por unidad de volumen:
n Ni = 0.011
átomos Ni
átomos
⋅ 8.46 ⋅ 10 22
= 9.31 ⋅ 10 20 átomos Ni / cm3.
átomos
cm 3
Problemas Propuestos
3.1. Demuestre para la estructura cristalina cúbica centrada en el cuerpo que la longitud de la arista
a de la celdilla unidad y el radio atómico R están relacionados según a = 4 R / 3 .
3.2. Demuestre que el factor de empaquetamiento atómico para la CC es 0.68.
3.3. Suponiendo un metal de estructura cristalina cúbica simple con los átomos localizados en los
vértices del cubo y tocándose entre sí a lo largo de las aristas del cubo, (a) ¿Cuál es el número
de coordinación para esta estructura cristalina? (b) Calcule el factor de empaquetamiento atómico.
Sol: (a) 6 (b) 0.52
3.4. En la tabla siguiente se muestran la masa atómica, la densidad y el radio atómico de tres hipotéticas aleaciones. Determine para cada una de ellas si su estructura cristalina es CCC, CC o
CS y justifíquelo.
Aleación Masa atómica Densidad Radio atómico
(uma)
(g/cm3)
(nm)
A
43.1
6.4
0.122
B
184.4
12.3
0.146
C
91.6
9.6
0.137
Sol: A es CC, B es CS, C es CC
3.5. Los parámetros reticulares de los metales potasio (CC) y plata (CCC) son, respectivamente,
4.62 Å y 4.08 Å. Calcular: (a) Los radios atómicos del potasio y de la plata, (b) La densidad
atómica superficial (nº de átomos/cm2) del plano atómico más denso de cada uno de los metales.
Sol: (a) R(K) = 2 Å, R(Ag) = 1.44 Å (b) D(K) = 6.67·1014 átomos/cm2, D(Ag) = 1.39·1015 átomos/cm2
Fundamentos de Ciencia de los Materiales (Problemas)
9
3.6. Durante el calentamiento, el hierro puro cambia su estructura cristalina de CC a CCC a 912 ºC.
¿Sufrirá el hierro una expansión o una contracción en este cambio? Dato: A 912 ºC el radio
atómico es de 0.1258 nm y de 0.1291 nm, para el hierro CC y CCC, respectivamente.
Sol: Sufre contracción de un 0.7%
3.7. A la temperatura ambiente el hierro tiene una estructura CC, siendo la longitud de la arista
2.87Å, (a) ¿Cuál es el radio atómico del hierro?, (b) Señale sobre la celdilla elemental, la posición de un intersticio tetraédrico, indicando sus coordenadas precisas.
Sol: (a) 1.24 Å (b) (½ , 1, ¾)
3.8. El radio del átomo de carbono es de 0.77 Å, mientras que el del hierro es de 1.26 Å. A temperaturas inferiores a 912 ºC, el hierro presenta una estructura CC, mientras que a temperaturas
comprendidas entre 912 y 1392 ºC, su estructura es CCC. Una de estas dos estructuras puede
contener en sus huecos, porcentualmente, mucho más carbono que la otra. ¿Qué estructura
disolverá más carbono?
Sol: La estructura CCC.
3.9. Calcular el máximo radio que puede tener un átomo intersticial en un cristal de cobre (CCC),
sin distorsionarlo. La longitud de la arista de la celdilla CCC del cobre es 3.61 Å.
Sol: 0.53 Å
3.10. Sabiendo que la solubilidad máxima del carbono en la ferrita (hierro CC) es de 0.02%, calcule:
(a) cuántas celdillas unitarias existen por átomo de carbono y (b) suponiendo que el carbono se
sitúa en los intersticios octaédricos, qué porcentaje de huecos octaédricos del hierro están
ocupados por el carbono, en estas condiciones. Datos M(Fe) = 55.85, M(C)=12.01
Sol: (a) 537.49 celdillas/átmC (b) 0.03% de huecos octaédricos ocupados
3.11. ¿Puede disminuir la densidad de una solución sólida sustitucional con respecto al valor de la
densidad del elemento base ¿Y si la solución es intersticial?
Sol: (a) Sí, cuando la masa atómica del átomo que sustituye es menor que la del átomo anfitrión, (b) Si el volumen
no cambia apreciablemente, como sucede en la mayoría de las situaciones, la densidad aumentará
3.12. Una solución sólida formada con los elementos A(disolvente) y B(soluto) tiene una composición
del c% en B. Si las densidades de los elementos constituyentes son ρA y ρB, respectivamente.
Calcule la densidad de la solución sólida suponiendo que: a) el mecanismo es sustitucional, b)
el mecanismo es intersticial. Suponga conocidas las masas molares de A y B (MA, MB).
3.13. El Zn forma una disolución sólida de sustitución con el cobre. Calcule el porcentaje en peso (en
masa) de zinc que debe añadirse al cobre para conseguir una aleación que contenga 1.75·1021
átomos de Zn por centímetro cúbico. Las densidades del Zn y del Cu puros son de 7.13 y 8.93
g/cm3, respectivamente. M(Zn) = 65.39 , M(Cu) = 63.54 uma.
Sol: 2.13 % en peso
3.14. Calcule el número de átomos de Zn que hay en 1 m3 de una aleación (solución sólida sustitucional) de cobre-zinc, que contiene un 1.0% Zn y un 99.0% Cu en peso. ¿Qué suposición habría que adoptar? Las densidades del Zn y del Cu puros son de 7.13 y 8.93 g/cm3, respectivamente, las masas atómicas: M(Cu)= 63.55 , M(Zn)= 65.39.
Sol: 8.10·1026 átomos Zn/m3
3.15. a) Calcule la densidad del Fe-CC sabiendo que el parámetro cristalino es a(Fe-CC) = 2.91Å.
b) Calcule la densidad de una solución sólida de Fe y C del 0.02% en peso de C.
Datos: M(Fe) = 55.85; M(C)= 12.01 .
Sol: (a) 7.526 g/cm3 (b) 7.528 g/cm3
Fundamentos de Ciencia de los Materiales (Problemas)
10
Tema 4: La escala atómica de los materiales cerámicos
Problemas Resueltos
4.1 Se sabe que los radios de los iones Fe2+ y O= valen, respectivamente, 0.077 nm y 0.140
nm. ¿Qué estructura cabe esperar para el compuesto FeO?
El compuesto FeO es un compuesto del tipo AX. El cociente entre los radios del catión y del
anión valdrá:
R Fe
0.077 nm
=
= 0.550
RO
0.140 nm
2+
2−
Este valor está comprendido entre 0.414 y 0.732; por consiguiente, el número de coordinación
del ion Fe2+ es 6, y también el del O2–, puesto que existe el mismo número de cationes que de
aniones. La estructura cristalina deberá de ser, por tanto, del tipo NaCl.
4.2 Calcule la densidad teórica del NaCl y compárela con el valor experimental.
Datos: R(Na+) = 0.102 nm, M(Na+) = 22.90 umas, R(Cl–) = 0.181 nm, M(Cl–) = 35.45 umas
El número de unidades-fórmulas de NaCl por celdilla unidad es
igual a 4, porque tanto los iones de sodio como los iones de cloro
forman redes CCC. La masa atómica de una unidad-fórmula se calcula como M(NaCl) = 22.90 + 35.45 = 58.35 umas, por lo que la
masa atómica de una celdilla unidad valdrá 4 x 58.35 = 233.4 umas.
Por otro lado, la celdilla es cúbica y su volumen Vc = a3, siendo a la
arista del cubo unidad. La longitud de la arista de la celdilla ha de
valer (ver figura):
a = 2 RNa + + 2 RCl − = 0.566 nm = 0.566 ⋅10−7 cm
Vc = a 3 = 1.81 ⋅ 10 −22 cm 3
Con todo, la densidad teórica puede ahora calcularse sencillamente:
ρ teórica =
M c 233.4 g
1 mol
1 celdilla
=
⋅
⋅
= 2.14 g / cm 3
− 22
3
3
mol
N
celdillas
a
1.81 ⋅ 10 cm
A
El valor obtenido está muy próximo al valor medido experimentalmente de 2.16 g/cm3
4.3 A un crisol para fundir vidrio de sílice se añade ceniza de sosa (Na2CO3) y piedra caliza
(CaCO3). Por efecto de la temperatura, estos ingredientes se descomponen y producen
sosa (Na2O) y cal (CaO), y liberan dióxido de carbono (CO2). Calcule la masa de ceniza de
sosa y de piedra de caliza que debe añadirse a 56 kg de cuarzo (SiO2) para producir un
vidrio cuya composición en peso sea 78% SiO2, 17% Na2O y 5% CaO.
Datos: M(Na2CO3) = 105.99; M(Na2O) = 61.98; M(CaCO3) = 100.09; M(CaO) = 56.08 umas
Las reacciones de descomposición de las que habla el encunciado son las siguientes:
Fundamentos de Ciencia de los Materiales (Problemas)
11
Na 2 CO3 → Na 2 O + CO2
CaCO3 → CaO + CO2
Si llamamos x a la masa de Na2O e y a la masa de CaO, los porcentajes requeridos implican
que:
y
x
0.17 =
0.05 =
56 + x + y
56 + x + y
Resolviendo este sistema de ecuaciones, se obtiene x = 12.20 kg, y = 3.59 kg.
Podemos ahora calcular las masas de Na2CO3 y CaCO3 teniendo en cuenta que por cada mol
de Na2CO3 descompuesto, se obtiene 1 mol de Na2O y que lo mismo sucede con el CaCO3 y el
CaO. Por tanto:
m( Na 2 CO3 ) = 12.2 kg
M ( Na 2 CO3 )
105.99
= 12.2 kg
= 20.86 kg
M ( Na 2 O)
61.98
M (CaCO3 )
100.09
= 3.59 kg
= 6.41 kg
m(CaCO3 ) = 3.59 kg
56.08
M (CaO )
Problemas Propuestos
4.1. Demuestre que para un número de coordinación 3, el valor mínimo del cociente entre los radios del
catión y del anión es 0.155.
4.2. La estructura cristalina del corindón, encontrada para el Al2O3, consiste en una estructura HC de
iones O2– en la que los iones Al3+ ocupan posiciones octaédricas. (a) ¿Qué fracción de las posiciones octaédricas existentes están ocupadas con iones Al3+? (b) Dibuje dos planos compactos de iones O2– en una secuencia AB e indique las posiciones octaédricas que estarán llenas con los iones
Al3+.
Sol: (a) 2/3
4.3. Un material cerámico, que se compone de un 8% en peso de Cr2O3 y de un 92% de MgO, forma
una solución sólida con una estructura cristalina tipo NaCl donde los iones oxígeno ocupan la totalidad de los nudos propios de una red CCC y los cationes se sitúan en los huecos octaédricos.
(a) ¿Cuál es la razón de iones Mg2+ a iones Cr3+?
(b) ¿Qué fracción de sitios catiónicos queda vacante?
Datos: M(Mg) = 24.31; M(Cr) = 52.00; M(O) = 16.00 umas
Sol: (a) 21.53 (b) 2.2%
4.4. Un material cerámico hipotético de tipo AX tiene una densidad de 2.10 g/cm3 y una celdilla de simetría cúbica, con parámetro de red de 0.57 nm. Las masas molares de los elementos A y X son 28.5
y 30.0 g/mol, respectivamente. ¿Cuál o cuáles de las siguientes estructuras son posibles para dicho material: NaCl, CsCl o ZnS (variedad esfalerita)?
Sol: Son posibles dos estructuras: la del NaCl y la del ZnS
4.5. Una forma cristalina de la sílice (SiO2) tiene una celdilla unidad cúbica. A partir de los resultados de
Difracción de Rayos X, se sabe que la celdilla unidad tiene una arista de longitud 0.700 nm. Si la
densidad medida es de 2.32 g/cm3, ¿cuántos iones Si4+ y O2– hay por celdilla unidad?
Datos: M(Si) = 28.09; M(O) = 16.00
Fundamentos de Ciencia de los Materiales (Problemas)
12
Sol: 8 Si4+ y 16 O2– por celdilla
4.6. Calcule la densidad teórica del diamante sabiendo que la distancia C–C y el ángulo entre enlaces
son 0.154 nm y 109.5º, respectivamente. Compare este valor con el valor experimental de 3.51
g/cm3. M(C) = 12.01 uma.
Sol: 3.54 g/cm3
4.7. El silicio, el Ge y el estaño gris poseen la red cúbica del diamante. Calcule para el silicio (a) la densidad lineal atómica a lo largo de la dirección [111], y (b) la densidad superficial atómica del plano
(111). Dato: R(Si) = 0.117 nm
Sol: (a) 2.14 átomo/nm, (b) 7.91 átomos/nm2
4.8. ¿Qué diferencia existe entre la temperatura de transición vítrea y la temperatura de fusión?
4.9 Un material con enlace atómico predominantemente de naturaleza iónica, ¿es más o menos proclive que un material covalente a formar un sólido no-cristalino tras la solidificación?¿Por qué?
4.10 Realice un dibujo esquemático en dos dimensiones de la disposición atómica en: (i) un cristal
de SiO2, (ii) un vidrio de sílice y (iii) un vidrio de sílice modificado con adiciones de Na2O. ¿Qué diferencias de comportamiento caben esperar durante el proceso de calentamiento hasta la fusión
entre tales materiales?
4.11. El vidrio de sílice pura (SiO2) tiene una densidad de 2.2 g/cm3, mientras que el cuarzo (SiO2 cristalino) tiene una densidad de 2.65 g/cm3. (a) ¿Qué porcentaje de espacio vacío existe en el vidrio de
sílice y en el cuarzo? (b) ¿Por qué es tan bajo el factor de empaquetamiento atómico del vidrio de sílice? Datos: M(Si) = 28.1 umas, M(O) = 16 umas; R(Si) = 0.04 nm, R(O) = 0.14 nm, NA =6.023·1023
Sol: (a) 38.27% en el cuarzo y 48.76% en el vidrio de sílice
4.12 El vidrio ordinario de ventanas, aunque está básicamente constituido por sílice (aproximadamente un 75%) contiene, además, óxidos de sodio (Na2O) y de calcio (CaO). (a) ¿Qué función
desempeñan estos óxidos desde el punto de vista industrial? (b) ¿Cómo influye la adición de estos
óxidos sobre la estructura del vidrio? Justifique la mayor densidad del vidrio ordinario (2.5 g/cm3)
respecto al vidrio de sílice (2.2 g/cm3) (c) ¿Cómo se designan los óxidos de este tipo en la tecnología del vidrio?
Sol:
4.13 Un vidrio contiene un 80% de SiO2 y un 20% de Na2O. ¿Qué fracción de oxígenos queda nocompartida? Datos: M(Si) = 28.09, M(O) = 16.00, M(Na) = 22.99 umas
Sol: 21.48%
Fundamentos de Ciencia de los Materiales (Problemas)
13
Tema 6: La escala atómica de los materiales poliméricos
Problemas Resueltos
6.1. La longitud total L de una molécula polimérica lineal depende de la longitud del enlace
entre átomos de la cadena (d ), del número total de enlaces en la molécula (N) y del ángulo de enlace entre átomos de la cadena (θ ), según la expresión: L = Ndsen(θ / 2) .
Además, la distancia media cabeza-cola (r ) de una serie de moléculas poliméricas es
igual a r = d N . Un polietileno lineal tiene una masa molecular media de 300 000
g/mol; calcule los valores medios de L y r para este material.
Datos: M(H) = 1; M(C)=12.01; Longitud del enlace C-C = 0.154 nm; ángulo del enlace C-C
=109º
Para el polietieleno cada monómero contiene 2 carbonos y 4 hidrógenos. De este modo, la masa molecular de un monómero es
m = 2M C + 4M H = 28.05 g/mol
y, por tanto, el número medio de monómeros que contendrá la cadena dada será de:
M 300000
n=
=
= 10695.2 monómeros
m
28.05
Como en cada monómero existen 2 átomos de carbono, tendremos 2 enlaces C-C por monómero, lo que significa que el número total de enlaces en la molécula (N) es justamente, N = 2 x
10 695.2 = 21 390.4 enlaces. Además, dado que la longitud del enlace C-C es 0.154 nm y el
ángulo de enlace C-C es de 109º, de la ecuación que proporciona el enunciado se obtiene:
⎛ 109º ⎞
⎛θ ⎞
L = Ndsen⎜ ⎟ = 21390.4 ⋅ 0.154 nm ⋅ sen⎜
⎟ = 2681.8 nm
⎝ 2 ⎠
⎝ 2⎠
Finalmente, es posible calcular la distancia media cabeza-cola (r), utilizando la expresión que
facilita el enunciado,
r = d N = 0.154 nm 2390.4 = 22.52 nm
6.2. Indique cuál de los dos polímeros de las parejas siguientes es más cristalino y explique
por qué:
a) Cloruro de polivinilo lineal isotáctico; polipropileno lineal atáctico.
b) Polipropileno lineal y sindiotáctico; cis-isopreno totalmente entrecruzado.
c) Fenol-formladehido en armazón; poliestireno lineal e isotáctico.
d) Politetrafluoroetileno ligeramente ramificado; polietileno lineal.
a) El 1º es más proclive a cristalizar que el 2º por dos razones: 1) el grupo lateral CH3 en el
polipropileno es más voluminoso que el Cl del PVC, y 2) las estructuras isotácticas tienen
más tendencia a la cristalización que las estructuras atácticas, por su mayor ordenación.
b) El 1º es más proclive a cristalizar que el 2º ya que los polímeros lineales son más cristalizables que los entrecruzados (por el impedimento que los entrecruzamientos suponen a la
conveniente reordenación de las cadenas).
Fundamentos de Ciencia de los Materiales (Problemas)
14
c) El 2º es más proclive a la cristalización que el 1º; los polímeros en armazón raramente
cristalizan, mientras que la cristalización para los isotácticos es relativamente sencilla.
d) El 2º es más cristalino que el 1º. Ambas estructuras son relativamente simples, sin embargo, la ramificación, por pequeña que sea, dificulta la cristalización.
Problemas Propuestos
6.1. ¿Qué longitud tendría una molécula de cadena larga de polietileno lineal si se supone que su
masa es de 100 000 umas. Datos: longitud de enlace C-C =1.54 Å; ángulo entre enlaces C-C =
109.5º ; M(H) = 1 uma; M(mero) = 28 umas
Sol: 8985.54 Å
6.2. El polietileno de alta densidad se puede clorar induciendo la sustitución aleatoria de átomos de
hidrógeno por átomos de cloro. (a) Determine la concentración de Cl (en % en masa) que se
debe añadir para que la sustitución alcance el 8% de los átomos de hidrógeno originales, (b)
¿En qué difiere la cloración del polietileno de la del cloruro de polivinilo? Datos: M(C) = 12.01;
M(Cl) = 35.45 ; M(H) = 1.01
Sol: (a) 29.0 % en peso; (b) para el PVC la proporción de sustitución es fija (25%) y probablemente mucho menos
aleatoria.
6.3. Para cada una de las parejas de polímeros que siguen, tras escribir sus fórmulas estructurales,
decida cuál de los dos tiene mayor tendencia a la cristalización, indicando brevemente el motivo de su elección: (a) PVC isotáctico y polipropileno atáctico (b) polipropileno sindiotáctico y
poliisopreno-cis vulcanizado (c) armazón de fenol-formaldehido (termoestable) y copolímero
alternado de poli(estireno-butadieno).
Sol: (a) PVC atáctico (b) Polipropileno sindiotáctico (c) copolímero alternado de poli(estireno-butadieno)
6.4. El polietileno (PE) y el policloruro de vinilo (PVC) pertenecen a la familia de los plásticos vinílicos. (a) Escriba la fórmula estructural del PE y del PVC. (b) Indique de forma razonada, cuál de
los dos plásticos tiene una mayor tendencia a la cristalinidad. (c) ¿Cómo se explica el mayor
punto de fusión del PVC (204ºC) frente al del PE (135ºC).
Sol: (b) El polietileno (c) En el PVC existen fuertes lazos de conexión entre las cadenas poliméricas debido a los
momentos dipolares originados por los átomos de cloro.
15
Fundamentos de Ciencia de los Materiales (Problemas)
Tema 7: Imperfecciones cristalinas
Problemas Resueltos
7.1. Calcule el número de vacantes por metro cúbico en el cobre en equilibrio a 1000 ºC. La
energía de activación para la formación de vacantes es 1.44·10–19 J/átomo, la masa atómica del cobre es de 63.5 g/mol y la densidad 8.4 g/cm3.
Para resolver el problema hay que tener presente que, en equilibrio, el número de vacantes,
NV, en un determinado material, en el que existen N átomos, viene dada por:
⎛ Q ⎞
N V = N exp⎜⎜ − V ⎟⎟
⎝ k BT ⎠
en donde QV es la energía de activación (la energía vibratoria requerida para la formación de
una vacante), T es la temperatura absoluta y kB la constante de Boltzmann (=1.38·10–23
J/átomo). De la expresión anterior se deduce fácilmente la concentración de vacantes, sin más
que dividir entre el volumen del material. La concentración de vacantes (= número de vacantes
por unidad de volumen) vendrá dada por:
⎛ Q
nV = n exp⎜⎜ − V
⎝ k BT
⎞
⎟⎟
⎠
en donde ahora, n representa el número de átomos por unidad de volumen. Este valor puede
calcularse a través de los datos que facilita el problema:
n=
8.4 g 1 mol N A átomos
⋅
⋅
= 7.97 ⋅ 10 22 átomos/cm3
1 mol
cm 3 63.5 g
con lo que ya podemos calcular la concentración de vacantes:
nV = 7.97 ⋅ 10 22
⎞
⎛
1.44 ⋅10 −19 J / átomo
átomos
⎟⎟ = 2.20 ⋅ 1019 vacantes/cm3
⎜
exp
−
3
− 23
⎜
1
.
38
10
/(
)
1273
cm
J
átomo
K
K
⋅
⋅
⋅
⎠
⎝
7.2. La velocidad de difusión del carbono en el hierro α (ferrita) y en el hierro γ (austenita) están dadas por:
Dα = 0.079 cm²/s · e (–18 100 cal/mol)/RT
Dγ = 0.21 cm²/s · e (–33 800 cal/mol)/RT
a) Calcule los dos coeficientes de difusión a 800° y 1000°C (R = 1.98 cal/mol·K).
b) Explique la magnitud de Dα comparada con Dγ en función de la estructura atómica.
c) Explique por qué los tratamientos de carburación del acero se realizan cuando el acero
es austenítico.
a)
Para la T1 = 800 + 273 = 1073 K, sustituyendo en las expresiones de las difusividades,
obtenemos:
Dα = 1.576·10–5 cm2/s
Dγ = 2.587·10–8 cm2/s
16
Fundamentos de Ciencia de los Materiales (Problemas)
Para la T2 = 1000 + 273 = 1273 K, se obtiene
Dα = 6.011·10–5 cm2/s
Dγ = 3.151·10–7 cm2/s
En ambos casos, se comprueba que la difusividad es mayor para la fase α.
b) La fase a es CC, por tanto, no es una estructura de máxima densidad de empaquetamiento. La fase γ es CCC, y sí es de máxima densidad de empaquetamiento. Dado que el
carbono se difunde a través del hierro mediante mecanismos intersticiales, es lógico que le
resulte más fácil difundirse en la fase α, puesto que es la que presenta una mayor proporción de intersticios, es decir, de espacio vacío.
c) En la carburación se introduce carbono en la superficie de la pieza. En principio, a la
luz del razonamiento del apartado anterior, parecería lógico emplear la fase α y no la fase γ
para dicho proceso, pues en la primera, la difusión se realiza más rápidamente. Sin embargo,
la fase γ es capaz de disolver mayor cantidad de carbono, así que se sacrifica la velocidad
en pro de una posible mayor concentración.
7.3. La superficie del acero puede endurecerse mediante carburación (difusión del carbono
en el acero desde un medio rico en carbono). Durante un tratamiento de este tipo a 1000
ºC, hay una caída en la concentración de carbono del 5 al 4% (atómico, referidos al total
de átomos) a una distancia entre 1 y 2 mm de la superficie del acero. Estímese el flujo de
los átomos de carbono en el acero en esa zona próxima a la superficie. (La densidad del
Fe-γ a 1000 ºC es 7.63 g/cm3, su masa atómica es de 55.85 umas, su D0 = 20· 10–6 m2/s y
la energía de activación para la difusión es de 142000 J/mol).
Dado que las distancias de las que habla el problema son relativamente pequeñas, vamos a
aproximar los diferenciales que aparecen en la primera ley de Fick por incrementos.
J ≈ −D
ΔC
Δx
Por tanto, para calcular el valor del flujo nos interesa conocer el valor del cociente (gradiente):
ΔC C 2 − C1
=
x 2 − x1
Δx
Conocemos los valores de x1 = 1 mm y x2 = 2 mm, pero desconocemos los valores absolutos
de las concentraciones respectivas, aunque el enunciado nos proporciona sus valores en relación a la concentración del hierro ( = nº de átomos de Fe / unidad de volumen). Calculemos en
primer lugar dicha concentración:
[Fe] = 7.63
por lo tanto, C1 =
ser:
g N A átomos
⋅
= 8.23 ⋅ 10 22 átomos / cm 3
3
55.85 g
cm
5
4
⋅ [Fe] y C 2 = ⋅ [Fe] , por lo que el gradiente de concentración resulta
95
96
17
Fundamentos de Ciencia de los Materiales (Problemas)
ΔC C 2 − C1 0.011[Fe] 10 mm
=
⋅
= 9.05 ⋅10 21 átomos / cm 4
=
1 mm
1cm
x2 − x1
Δx
El coeficiente de difusividad a la temperatura de 1000 ºC valdrá:
⎞
⎛
⎟
⎜ − 142000 J
6 m
mol
⎟ = 2.98 ⋅ 10 −11 m 2 / s
⎜
D(1273K ) = D0 ⋅ exp(−Q / RT ) = 20 ⋅ 10
exp
⎟
⎜
J
s
⋅ 1273K ⎟
⎜ 8.31
mol K
⎠
⎝
2
y llevando estos resultados a la ecuación de Fick, obtenemos, finalmente:
m2
átomos ⎛ 100 cm ⎞
ΔC
⎟ = 2.70 ⋅ 1015 átomos /(m 2 ⋅ s )
J≈ D
= 2.98 ⋅ 10 −11
⋅ 9.05 ⋅ 10 21
⋅⎜
s
Δx
cm 2 ⎜⎝ 1 m ⎟⎠
2
7.4. ¿Qué tipo de defectos puntuales son posibles en el MgO con Al2O3 como impureza?
¿Cuántos iones Al3+ deben añadirse para formar cada uno de estos defectos?
Por cada ion Al3+ que sustituye al Mg2+ en el MgO, se añade una carga positiva neta. De este
modo, para garantizar la neutralidad eléctrica, esta carga positiva adicional debe ser eliminada
o compensada con una carga negativa. Las cargas negativas pueden ser iones O2– intersticiales, cuya formación no es difícil. Las cargas positivas pueden ser eliminadas mediante la formación de vacantes de Mg2+ (una vacante de Mg por cada dos iones Al3+ añadidos).
7.5 En un sistema cúbico, calcule los índices de la línea de la dislocación de una dislocación
de cuña cuyo vector de Burgers es b = a/2[ 0 1 1 ] y que yace sobre el plano (111).
Los vectores b y n son perpendiculares al vector t., por tanto, los productos escalares b·t y n·t
serán nulos. Así pues, suponiendo que t = [h k l ], se tendrá:
b·t = [0 –½ ½ ]·[ h k l ] = –½ k + ½ l = 0 ⇒ k = l
b·n = [1 1 1]·[ h k l ] = h + k + l = 0
⇒ h + 2k = 0 ⇒ k = –½ h
Luego el vector t = [ h -½ h -½ h ] = [2 11]
Problemas Propuestos
7.1. Calcule la energía de activación para la formación de vacantes en el aluminio, sabiendo que el número de vacantes en equilibrio a 500ºC es de 7.57·1023 m–3. La masa atómica y la densidad (a
500ºC) del aluminio son 26.98 g/mol y 2.62 g/cm3, respectivamente.
Sol: 1.2·10–19 J/átomo
Fundamentos de Ciencia de los Materiales (Problemas)
18
7.2. Para la estructura cristalina CCC, los lugares intersticiales que pueden ocupar los átomos de soluto
están situados en el centro de las aristas de las celdillas unidad. Calcular el radio R de un átomo de
soluto que pueda colocarse en uno de estos lugares, en función del radio del átomo del disolvente.
Sol: 0.41R
7.3. En el proceso de dopado, realizado a 800°C, para la fabricación de un material semiconductor, se
ha difundido fósforo (P) en germanio (Ge). Si en un instante dado la concentración de P en la superficie del germanio es de 50% (en átomos por ciento) y la concentración del dopante a una profundidad de 0.1 mm de la superficie es cero, calcule el flujo de átomos de P entre la superficie y
esa zona, a 800°C. Datos: R = 1.987 cal/(mol·K); Energía de activación = 57 500 cal/mol; D0 = 2
cm²/s.; El germanio tiene estructura cristalina de tipo diamante (CCC con la mitad de los huecos tetraédricos ocupados), siendo a = 0.56·10–9 m.
Sol: 8.82·1016 átomos/(m2s)
7.4. Una lámina de acero de 2.5 mm de espesor está dentro de una atmósfera de nitrógeno a 900ºC y
se ha alcanzado el estado estacionario para la difusión. El coeficiente de difusión del nitrógeno en
acero a esta temperatura es de 1.2·10–10 m2/s y el flujo de difusión es de 1.0·10–7 kg/(m2.s). También se sabe que la concentración de nitrógeno en la cara del acero de mayor presión es de
2kg/m3. ¿A qué distancia de esta superficie, que está a elevada presión, es la concentración de 0.5
kg/m3? Suponga un perfil de concentración lineal.
Sol: 1.8· 10–3 m = 1.8 mm.
7.5. Una de las caras de una lámina de hierro CC (a = 0.287 nm) de 2 mm de espesor se expuso a una
atmósfera gaseosa carburante y la otra cara, a una atmósfera descarburante y todo a 675ºC. Después de alcanzar la condición de estado estacionario, el hierro se enfrió hasta la temperatura ambiente. Se determinaron las concentraciones de carbono en las dos caras y resultaron ser 0.015 y
0.0068% en peso. Calcule el coeficiente de difusión si el flujo difusivo era de 7.36· 10–9 kg/(m2·s).
Exprese las concentraciones en porcentaje en peso, en kilogramos de carbono por metro cúbico de
hierro. Dato: M(Fe) = 55.85 uma.
Sol: CA = 1.18 kgC / m3Fe; CB = 0.535 kgC/m3; D = 2.3· 10–11 m2/s
7.6. Una aleación férrea de Fe-Ni contiene un 8.5 % de Ni (en peso) en el centro de un grano (C) y un
8.8 % de Ni (en peso) en el límite de grano (L). Calcule el flujo de átomos de níquel entre esos dos
puntos (C y L), separados por una distancia de 40 μm, a la temperatura de 1200 ºC.
Datos: Masa atómica (Ni) = 58.71; Masa atómica (Fe) = 55.85; Parámetro reticular de la aleación (CCC) = 0.365 nm; Difusividad del Ni en el Fe a 1200 ºC = 9·10–15 m2/s
Sol: 5.4·1016 átomos/(m2·s)
7.7. Supongamos que existe un hipotético material cerámico que está compuesto por iones A2+ y X2–.
Supongamos que una pequeña fracción de los iones X2– pueden existir como X–. (a) En estas circunstancias, nombre el defecto que podría formarse para mantener la neutralidad eléctrica. (b)
¿Cuántos de estos iones X– se requieren para cada defecto? (c) ¿Cómo expresaría la fórmula química para este material no-estequiométrico?
Sol: (a) Preferentemente vacantes de A2+, pero también intersticiales de X2– (b) 2 iones X– por cada vacante de
A2+ (c) A1–y X
7.8. Para las estructuras cristalinas CCC y CC, el vector de Burgers b se puede expresar como b = a/2
[h k l ], donde a es la longitud de la arista de la celdilla unidad y [ hkl ] es la dirección cristalográfica
de mayor densidad atómica lineal. (a) ¿Cuáles son las representaciones del vector de Burgers en
las estructuras cristalinas CCC, CC y CS. (b) Si la magnitud del vector de Burgers es |b| = a/2
(h2+k2+l2)½ , determine el valor de |b| para el cobre y el hierro. Datos: las longitudesde la celdilla del
Fe(CC) y del Cu (CCC) son, respectivamente, 0.287 y 0.362 nm.
Fundamentos de Ciencia de los Materiales (Problemas)
19
Sol: (a) CCC: b = a/2 <110> , CC: b = a/2 <111> , CS: b = a <100> (b) Para el Cu, 0.256, para el Fe, 0.248 nm
7.9. La estructura cúbica centrada en las caras (CCC), que presentan muchos metales, es una estructura de máxima compacidad.
a. ¿Cómo están empaquetados los planos atómicos en esta estructura?
b. Mencione y dibuje los planos y direcciones de deslizamiento de esta estructura.
Sol: (a) ABCABCABC.... (b) los planos {111}, las diagonales de las caras
7.10 Calcule los índices de la línea de la dislocación de una dislocación de cuña en una red CC, sabiendo que b = a/2[ 1 11 ] y que está en un plano (110). Haga un dibujo de la red CC con indicación
de (i) el plano de deslizamiento, (ii) la posición del vector de Burgers y (iii) la línea de la dislocación.
Sol: [ 1 1 2 ]
7.11 Un sistema de deslizamiento activo en el Mo (CC) es el {112} <111> (Esta notación quiere decir
que la familia de planos {112} son planos de deslizamiento y que la familia de direcciones <111>
son direcciones de desplazamiento, paralelas al vector de Burgers). (a) Calcule los índices de la línea de la dislocación de una dislocación de cuña. (b) Haga un dibujo de la red CC con inidcación
de: i) el plano de deslizamiento, (ii) la posición del vector de Burgers (calcule, previamente, los índices de Miller de este vector, sabiendo que el radio atómico del Mo es de 1.36 Å, (iii) la línea de la
dislocación, (iv) la dirección del vector desplazamiento (movimiento) de la línea de la dislocación,
con indicación de sus índices.
Sol: b = 2R [1 1 1]
3
7.12 Bajo ciertas condiciones, el sistema de deslizamiento (i) {001}<110> es operativo en las estructuras de tipo NaCl, además del sistema de deslizamiento habitual, que es el (ii) {110}< 1 1 0 >. (a)
Haga esquemas ilustrando los procesos de deslizamiento del NaCl, según los sistemas de deslizamiento (i) y (ii), (b) ¿cuántos sistemas de deslizamiento (i) existen?
Sol: (b) 6 sistemas
7.13 Los límites de flexión de ángulo pequeño tienen un ángulo de desorientación menor de 5º. (a)
Calcule el espaciado entre las dislocaciones en un límite de flexión simétrico de 2º, en un cristal de
cobre. La longitud de la arista de la celdilla unidad es 3.61 Å. (b) ¿Cuáles son los índices de Miller
del plano del límite de flexión de ángulo pequeño (= plano bisector)?
Sol: (a) 72.9 Å
(b) {0 1 1}