64375588-TALLER-DE-FLOTACION

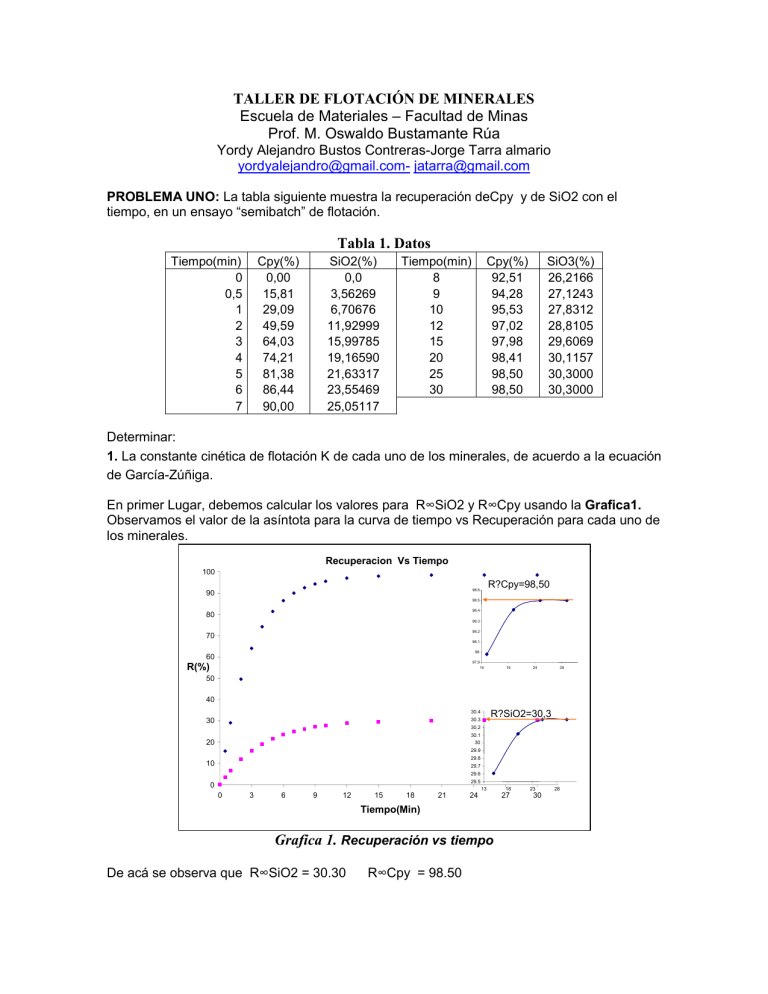
TALLER DE FLOTACIÓN DE MINERALES
Escuela de Materiales – Facultad de Minas
Prof. M. Oswaldo Bustamante Rúa
Yordy Alejandro Bustos Contreras-Jorge Tarra almario
[email protected] [email protected]
PROBLEMA UNO: La tabla siguiente muestra la recuperación deCpy y de SiO2 con el
tiempo, en un ensayo “semibatch” de flotación.
Tabla 1. Datos
Tiempo(min)
0
0,5
1
2
3
4
5
6
7
Cpy(%)
0,00
15,81
29,09
49,59
64,03
74,21
81,38
86,44
90,00
SiO2(%)
0,0
3,56269
6,70676
11,92999
15,99785
19,16590
21,63317
23,55469
25,05117
Tiempo(min)
8
9
10
12
15
20
25
30
Cpy(%)
92,51
94,28
95,53
97,02
97,98
98,41
98,50
98,50
SiO3(%)
26,2166
27,1243
27,8312
28,8105
29,6069
30,1157
30,3000
30,3000
Determinar:
1. La constante cinética de flotación K de cada uno de los minerales, de acuerdo a la ecuación
de García-Zúñiga.
En primer Lugar, debemos calcular los valores para R∞SiO2 y R∞Cpy usando la Grafica1.
Observamos el valor de la asíntota para la curva de tiempo vs Recuperación para cada uno de
los minerales.
Recuperacion Vs Tiempo
100
R?Cpy=98,50
98.6
90
98.5
98.4
80
98.3
98.2
70
98.1
98
60
97.9
14
R(%)
19
24
29
50
40
R?SiO2=30,3
30.4
30.3
30
30.2
30.1
20
30
29.9
29.8
10
29.7
29.6
29.5
0
13
0
3
6
9
12
15
18
21
24
Tiempo(Min)
Grafica 1. Recuperación vs tiempo
De acá se observa que R∞SiO2 = 30.30
R∞Cpy = 98.50
18
27
23
30
28
Luego, linealizando la ecuación de García-Zúñiga como sigue, obtenemos k.
R(t )  R * (1  e  k*t )  Ecuancion
Garcia  Zuñiga
R(t )
 (1  e k*t )
R
R  R(t )

 e  k *t
R
 R  R(t ) 
 Ln 
  k * t
R



 y   m * x  Forma linealizad a

Con los datos de la tabla 1. Y con R∞SiO2 = 30.30 y R∞Cpy = 98.50
Obtenemos la siguiente grafica para cada especie mineral.
1
0
-1
SiO2
-2
-3
-4
-5
-6
Cpy
-7
-8
-9
0
5
10
15
20
25
Tiempo(Min)
Grafica 2.Calculo de K
y = -0.3498x - 0.0007 R2 = 1
Ecuación Linealizada para Cpy
y = -0.2537x + 0.0138 R2 = 0.9999 Ecuación Linealizada para SiO2
Donde la constante cinética de Flotación es la pendiente de la recta, Para Cpy es 0.3498 (t-1),
y para SiO2 es 0.2537 (t-1),
2. Describa el modelo de la cinética de flotación para cada uno de los minerales involucrados.
De acuerdo a la linealización y=mx, observamos además el termino ± b, Este valor nos indica
que nuestro análisis no cruza por cero, y lo llamaremos corrección a tiempo 0.
R Vs Tiempo
100
90
R(t)Cpy=98,50 * ( 1 - Exp ( - 0,3498 * ( t + 0,002))
80
70
60
R(% 50
40
R(t)SiO2=30,30 * ( 1 - Exp ( - 0,2537 * ( t - 0,054)
30
20
Tiempo
Optimo
=15.6
10
0
0
3
6
9
12
15
18
21
24
27
30
Tiempo(Min)
Grafica 3.Modelo Cinético de Flotación.
3. Determine la corrección a tiempo cero del modelo cinético encontrado.
Del punto anterior tenemos que la corrección ha tiempo cero (θ ) viene dada por el intercepto
de la recta con el eje R(%), así tenemos:
Tabla 2.
θCpy
θSiO2
b
-0.0007
0.0138
b/k
-0.002
0.054
4. Determinar el tiempo óptimo de flotación, empleando el criterio de maximizar la diferencia
de recuperación _R entre la ganga (cuarzo) y calcopirita.
t opt
 K Cpy * R Cpy 

Ln 
K SiO 2 * R SiO 2 


K Cpy  K SiO 2
t opt  15.61 Min
PROBLEMA DOS:
Para el caso anterior, se desea diseñar una instalación de 9000 ton/dia de mineral, con un
peso especifico de 2,80.
El porcentaje en peso de sólidos en el circuito “Rougher” es de 35% en peso y se asume que
el tiempo de residencia es el tiempo óptimo calculado en el problema anterior.
Calcule:
1. Flujo másico de sólidos por hora (suponiendo que se trabaja 24 horas al día).
Mineral
Masa Sólido / tiempo
Ton/Dia
9000
Ton/h
375
2. Flujo de agua en el alimento de la batería de flotación
%MSol 
MsOL
MsOL
 MPulpa 
MPulpa
%MSol
MH2O  MPulpa  MsOL
Tabla3.
% sólido
Flujo Másico(Ton/Hora)
Flujo Pulpa(Ton/Hora)
Flujo H2O (Ton/Hora)
35
375
1071.429
696.429
3. Flujo másico y volumétrico de pulpa que alimentaba batería “Rougher”.(Todo esto ha
temperatura ambiente).
MPulpa  MH2O  MsOL
VPulpa  VH2O  VsOL
 Sol 
M Sol
VSol
 H20  1
Ton
m3
Tabla 4.
Densidad Sólido(Ton/m3)
Flujo Másico(Ton/Hora)
Flujo Volumétrico Sólido (m3/h)
Flujo Vol Total (m3/h)
2.8
375
133.93
830.36
Densidad H2O(Ton/m3)
Flujo H2O (Ton/Hora)
Flujo Volumétrico Agua(m3/h)
1
696.43
696.43
4. Calcule el volumen de pulpa que se encuentra en cada instante en la celda, Usando el
concepto del tiempo promedio de residencia y asumiendo que las celdas de flotación se
comportan como tanques perfectamente agitados. (En estado Estacionario)
Tiempo Optimo (Horas)
Flujo Volumétrico Sólido (m3/h)
Volumen Nominal de la celda (m3)
0.2601
133.929
34.844
5. Calcule el numero N de celdas en la batería, si se desea utilizar celdas de120 pie3, 240 pie3
y 1600 pie3. Considere que la capacidad nominal de la celda no es la efectiva, pues la celda
en un instante determinado posee mineral, agua y burbujas. Asuma que las burbujas ocupan
un 25% de la celda. (1 pie3 = 0.02832 m3). NOTA: EL NÚMERO DE CELDAS SE ACONSEJA
SER SIEMPRE PAR.
# Celdas 
Volumen efectivo de la celda (m 3 )
Volumen de celda Deseada (m 3 )
Tabla 5.
Volumen Nominal de la celda (m3)
(Pie3)
% ocupado por espuma
Volumen de espuma en celda(Pie3)
Volumen efectivo de celda (Pie3)
34.84
1230.36
0.25
307.59
922.77
# de celdas de 120 pie3
# de celdas de 240 pie3
# de celdas de 1600 pie3
Par mas
cercano
8
7.69
3.89
0.58
4
1
6. Calcule el flujo de aire a la celda para las condiciones planteadas
SI suponemos que la espuma esta conformada solamente por gas, suponemos que el 25%
del volumen nominal de la celda es Aire, por lo tanto, el flujo de aire por hora de acuerdo con
la tabla 5 será:
VolumenEspuma  VolumenNo min al * %Ocupado por espuma.
Volumen de espuma en la celda(m3)
307.59
7. Grafique la batería con las celdas seleccionadas, Recuerde que debe dividir el tiempo
promedio de residencia entre el total de celdas calculadas, y por lo tanto, puede calcular
aproximadamente la Recuperación de Calcopirita y de ganga en la salida de cada celda.
Como el circuito de flotación en nuestra elección es de 4 Celdas de Capacidad 240 Pie3 está en
corriente directa podemos decir que la recuperación global es la sumatoria de las recuperaciones
parciales de cada celda.
i
1
2
3
4
Tiempo(Min)
3.90
7.80
11.70
15.61
Tabla 6.Recuperacion en cada Celda
%Rglobal Cpy(i) %Rglobal SiO2(i)
73.33
18.89
92.07
26.06
96.86
28.72
98.08
29.71
R1
R2
R3
R4
∑
%R Cpy
73.33
18.74
4.79
1.22
98.08
% R SiO2
18.89
7.17
2.67
0.99
29.71
PROBLEMA TRES
4.1. La figura siguiente muestra un circuito de flotacion en contracorriente.
Demuestre que la recuperacion global del circuito es:
RG 
C 4 t C4
A.t a
R4 
C 4 t C4
C 3 t C3
R3 
C 3 t C3
C 2 t C 2  T4 t 4
R2 
C 2 t C2
C1 t C1  T3 t C3
R1 
C1 t C1
At a  T2 t C 2
En Nodo 2  C1 t C1  T3 t C3  C 2 t C 2  T2 t C 2  Balance de masa para cada Nodo
En Nodo 3  C 2 t C 2  T4 t 4  C 3 t C3  T3 t C3
En Nodo 4  C 3 t C3  C 4 t C 4  T4 t C 4
RG 
R 4 .C 3 t C3
A.t a
R G  R 4 .R 3 .
(C 2 t C 2  T4 t t 4 )
A.t a
T4 t t 4
)
C 2 t C2
 Sumando y Re s tan do T2 t t 2
 T2 t t 2  T2 t t 2 )
C 2 t C 2 .(1 
RG 
R 4 .R 3
.
A.t a .(C 2 t C 2
T4 t t 4
)
C 2 t C2
 Factorizando
T2 t t 2
 T2 t t 2 )(A.t a 
)
C 2 t t 2  T2 t t 2
C 2 t C 2 .(1 
R G  R 4 .R 3 .
(C 2 t C 2
T4 t t 4
)
C 2 t C2
 R 4 .R 3 .
 Re emplazando R 2
T3 t t 3
(C1 t C1  T3 t t 3 )(A.t a 
)
C1 t C1  T3 t t 3
C 2 t C 2 .(1 
RG
T4 t t 4
)
C 2 t C2
 Re solviendo el producto
T3 t t 3
( A.t a 
)
C1 t C1  T3 t t 3
(1 
R G  R 4 .R 3 .R 2
(1 
R G  R 4 .R 3 .R 2
T4 t t 4
T t
).(C1 t C1 .(1  3 t 3 ))
C 2 t C2
C 3 t C3
 Sumando y Re s tan do T2 t t 2
( A.t a  T2 t t 2  T2 t t 2 )
R G  R 4 .R 3 .R 2
(C 2 t C 2  T4 t t 4 ).(C1 t C1  T3 t t 3 )
 Factorizamos
(A.t a )(C 2 t C 2 )
(C 2 t C 2 (1 
R G  R 4 .R 3 .R 2
((1 
R G  R 4 .R 3 .R 2
T4 t t 4
T t
)).(C1 t C1 .(1  3 t 3 ))
C 2 t C2
C 3 t C3
 Factorizamos y cancelamos
(A.t a )(C 2 t C 2 )
T4 t t 4
T t
)).(C1 t C1 .(1  3 t 3 ))
C 2 t C2
C 3 t C3
 Sumando y res tan do T2 t t 2
(A.t a  T2 t t 2  T2 t t 2 )
T4 t t 4
T t
)(1  3 t 3 )
C 2 t C2
C 3 t C3
 R 4 .R 3 .R 2 .
 Re emplazamos R1
T2 t t 2
(A.t a  T2 t t 2 )(1 
)
A.t a  T2 t t 2
C1 t C1 .(1 
RG
T4 t t 4
T t
).(1  3 t 3 )
C 2 t C2
C 3 t C3
 Re solviendo
T2 t t 2
(1 
)
A.t a  T2 t t 2
(1 
R G  R 4 .R 3 .R 2 .R 1
R G  R 4 .R 3 .R 2 .R 1
(C 2 t C 2  T4 t t 4 ).(C1 t C1  T3 t t 3 ).(A.t a  T2 t t 2 )
 factorizando
(A.t a )(C 2 t C 2 )(C1 t C1 )
(C 2 t C 2 )(1 
R G  R 4 .R 3 .R 2 .R 1
R G  R 4 .R 3 .R 2 .R 1 .(1 
 (1 
esta Fraccion
T4 t t 4
T t
T t
).(C1 t C1 )(1  3 t 3 ).(A.t a )(1  2 t 2 )
C 2 t C2
C1 t C1
A.t a
 Simplifica ndo
(A.t a )(C 2 t C 2 )(C1 t C1 )
T4 t t 4
T t
T t
)(1  3 t 3 )(1  2 t 2 )  Si Ti t ti  C i  2 t Ci  2
C 2 t C2
C1 t C1
A.t a
T4 t t 4
T t
T t
)(1  3 t 3 )(1  2 t 2 )  Estos ter min os son despresciables.
C 2 t C2
C1 t C1
A.t a
Por lo que tenemos que la recuperacion Global en un circuito inverso es :
 R G  R 4 .R 3 .R 2 .R 1 
4.2. En el circuito en serie, que se describe a continuacion, demuestre que la recuperacion
global del circuito Rglobal es:
RG 
R1 
C.t C
A.t a
C1 t C1
A.t a
R2 
C 2 t C2
T1 t C1
R3 
C 3 t C3
C n t Cn
R n 
T2 t C 2
Tn 1 t C( n 1)
En Nodo 1  At a  C1 t C1  T1 t t1  Balance de masa para cada Nodo
En Nodo 2  T1 t t1  C 2 t C 2  T2 t t 2
En Nodo 3  T2 t t 2  C 3 t C3  T3 t t 3

En Nodo n  Tn 1 t C( n 1)  C n t Cn  Tn t tn
RG 
C.t C C1 t C1  C 2 t C 2   C n t Cn

A.t a
A.t a
RG 
C.t C C1 t C1 C 2 t C 2
C t


   n cn
A.t a
A.t a
A.t a
A.t a
RG 
R 1 .A.t a

A.t a
R 2 .T1 t C1
R n. Tn t tn

Tt
T1 n t t (1 n )
C1 t C1 (1  1 C1 )
C n t Cn (1 
)
C1 t C1
C n 1 t C( n 1)
Si log ramos T1 n t t (1 n )  C n 1 t C( n 1)
T1 n t t (1 n )
C n t C( n 1)
 Estos ter min os se hacen insignific antes.
 La recuperacion global del circuito directo es :
R G  R 1  R 2    R n.