UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS
(Universidad del Perú, DECANA DE AMÉRICA)
FACULTAD DE INGENIERIA DE SISTEMAS E IFORMATICA
ESCUELA PROFESIONAL DE INGENIERÍA DE SISTEMAS
Curso: Probabilidades y Muestreo
Práctica N°1
Profesora: Gregoria Natividad Ramón Quispe
Semestre 2021-I
PARTE 1
1.
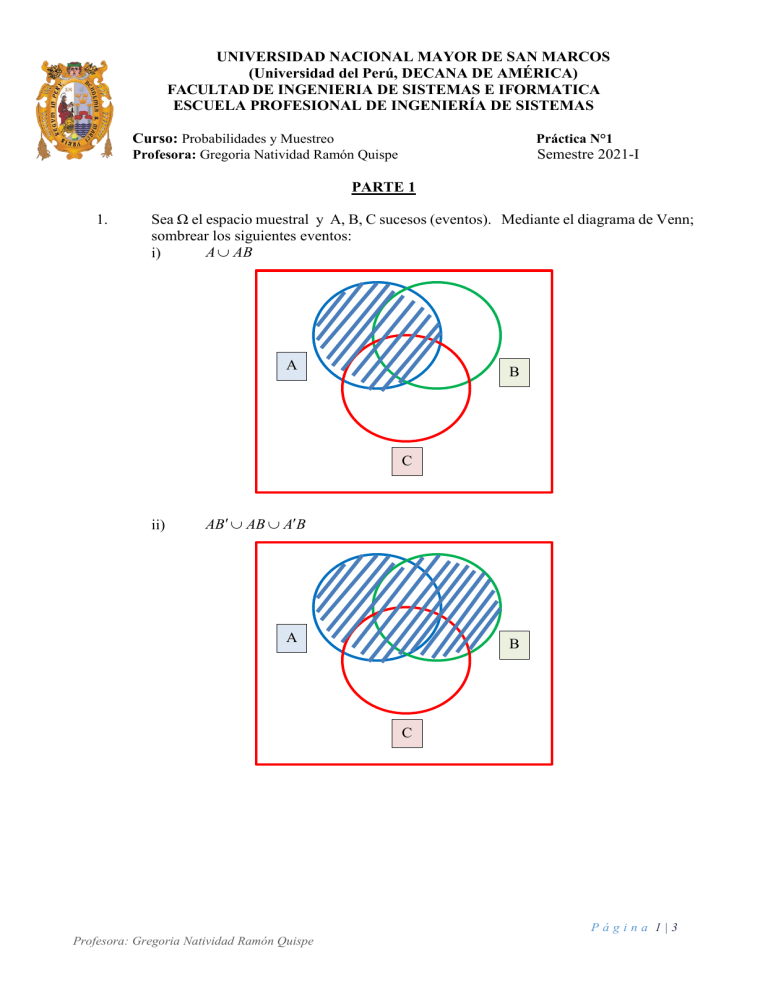
Sea Ω el espacio muestral y A, B, C sucesos (eventos). Mediante el diagrama de Venn;
sombrear los siguientes eventos:
A AB
i)
A
B
C
ii)
AB AB AB
A
B
C
Página 1|3
Profesora: Gregoria Natividad Ramón Quispe
i)
ACB
A
B
C
2.
El diseño de un carburador es tal que la salida de aire puede ser estrecha (E) o abierta
(A) y la tasa de flujo de gas puede ser lenta (L) o rápida (R). Una persona adquiere uno
de estos carburadores y lo pone a funcionar tal y como lo ha recibido sin graduarlo:
i)
Describir el espacio muestral asociado a la observación de las dos características:
salida de aire y flujo de gas
Solución:
Ω = {𝐸𝐿, 𝐸𝑅, 𝐴𝐿, 𝐴𝑅}
ii) Obtener los eventos elementales de:
M la salida de aire no es abierta
S la tasa de flujo de gas es rápida
Solución:
M = {(𝐸, 𝐿); (𝐸, 𝑅)}
S = {(𝐸, 𝑅); (𝐴, 𝑅)}
iii) ¿Qué significado tiene MS, M U S, SM y cuáles son los eventos elementales que le
pertenecen?
Solución:
𝑀𝑆 = 𝑀 ∩ 𝑆: 𝐿𝑎 𝑠𝑎𝑙𝑖𝑑𝑎 𝑑𝑒 𝑎𝑖𝑟𝑒 𝑛𝑜 𝑒𝑠 𝑎𝑏𝑖𝑒𝑟𝑡𝑎 𝑦 𝑙𝑎 𝑡𝑎𝑠𝑎 𝑑𝑒 𝑓𝑙𝑢𝑗𝑜 𝑒𝑠 𝑟á𝑝𝑖𝑑𝑎.
𝑀𝑆 = 𝑀 ∩ 𝑆 = {(𝐸, 𝑅)}
M ∪ S: 𝐿𝑎 𝑠𝑎𝑙𝑖𝑑𝑎 𝑑𝑒 𝑎𝑖𝑟𝑒 𝑛𝑜 𝑒𝑠 𝑎𝑏𝑖𝑒𝑟𝑡𝑎 𝑜 𝑙𝑎 𝑡𝑎𝑠𝑎 𝑑𝑒 𝑓𝑙𝑢𝑗𝑜 𝑒𝑠 𝑟á𝑝𝑖𝑑𝑎.
M ∪ S = {(𝐸, 𝐿); (𝐸, 𝑅); (𝐴, 𝑅)}
𝑆𝑀 = 𝑆 ∩ 𝑀: 𝐿𝑎 𝑠𝑎𝑙𝑖𝑑𝑎 𝑑𝑒 𝑎𝑖𝑟𝑒 𝑛𝑜 𝑒𝑠 𝑎𝑏𝑖𝑒𝑟𝑡𝑎 𝑦 𝑙𝑎 𝑡𝑎𝑠𝑎 𝑑𝑒 𝑓𝑙𝑢𝑗𝑜 𝑒𝑠 𝑟á𝑝𝑖𝑑𝑎.
𝑀𝑆 = 𝑀 ∩ 𝑆 = {(𝐸, 𝑅)}
Página 2|3
Profesora: Gregoria Natividad Ramón Quispe
3.
De una urna que contiene los nombres de 30 trabajadores de una pequeña empresa, se
extrae al azar los nombres de 3 trabajadores. La persona cuyo nombre sea seleccionado
en primer lugar recibe $100, y aquellas cuyos nombres sean extraídos en segundo y tercer
lugar reciben $50 y $25 respectivamente. ¿Cuántos resultados posibles están asociados
con este experimento?
Solución:
Aplicamos el 𝐏𝐫𝐢𝐧𝐜𝐢𝐩𝐢𝐨 𝐝𝐞 𝐥𝐚 𝐌𝐮𝐥𝐭𝐢𝐩𝐥𝐢𝐜𝐚𝐜𝐢ó𝐧
30𝑥29𝑥28 = 24360
4.
Una flota de nueve taxis se ha de distribuir a tres aeropuertos, en forma tal que tres
vayan al aeropuerto A, cinco al aeropuerto B y uno al aeropuerto C. ¿De cuántas formas
diferentes se puede lograr esta distribución?
Solución:
Aplicamos 𝐂𝐨𝐦𝐛𝐢𝐧𝐚𝐜𝐢𝐨𝐧𝐞𝐬.
𝐶39 𝑥𝐶56 𝑥𝐶11 = 84𝑥6𝑥1 = 504
5.
Claudio quiere acceder al celular de su papá y sabe que la clave de acceso consta de
cuatro cifras impares que pueden ser repetidas o no, y si además sabe que la suma de las
cifras que se ubican en los extremos es igual a 10 y la suma de las cifras que ocupan los
dos lugares centrales es 8. ¿Cuántas tentativas como máximo puede realizar Claudio para
tener acceso al celular?
Solución:
Aplicamos el 𝐏𝐫𝐢𝐧𝐜𝐢𝐩𝐢𝐨 𝐝𝐞 𝐥𝐚 𝐌𝐮𝐥𝐭𝐢𝐩𝐥𝐢𝐜𝐚𝐜𝐢ó𝐧
1° 2° 3° 4°
↓ ↓ ↓ ↓
5𝑥1𝑥4𝑥1 = 20
6.
Se lanza una moneda 10 veces. ¿De cuántas maneras diferentes se pueden obtener cinco
caras y cinco sellos?
7.
Sabina debe repartir 10 regalos entre sus tres sobrinos. ¿De cuántas maneras diferentes
puede repartir los regalos si el mayor debe recibir cuatro regalos y los menores tres
regalos cada uno?
Página 3|3
Profesora: Gregoria Natividad Ramón Quispe