Señales y Sistemas. Filtros

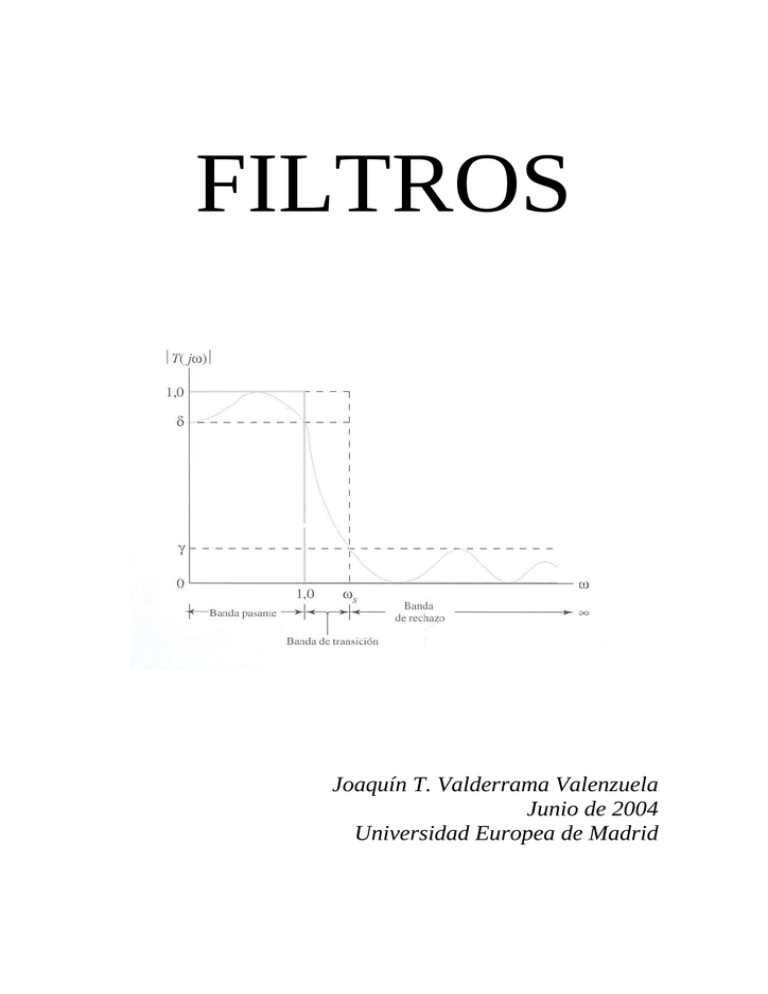
FILTROS
Joaquín T. Valderrama Valenzuela
Junio de 2004
Universidad Europea de Madrid
Señales y sistemas
Joaquín T. Valderrama Valenzuela
Índice
Página
1) Introducción. Filtro Ideal
3
2) Filtro Paso Bajo de orden 1
4
3) Filtro Paso Alto de orden 1
6
4) Filtro Paso Banda
7
5) Filtros Activos de Paso Bajo de
Orden n
8
- Aproximación de Butterworth
9
- Aproximación de Chebyshev
12
6) Sumario
16
7) Bibliografía
17
2
Señales y sistemas
Joaquín T. Valderrama Valenzuela
INTRODUCCIÓN. FILTRO IDEAL
El término filtro se utiliza comúnmente para describir un dispositivo que
discrimina, según algún atributo de los objetos que se aplican a su entrada, aquello que
pasa a su través. Por ejemplo, un filtro de aire permite que el aire que pasa a su través,
evitando que las partículas de polvo presentes en el aire lo atraviesen. Un filtro de aceite
realiza una función similar, con la excepción de que es aceite la sustancia que se permite
que pase a través del filtro mientras que las partículas de suciedad se recogen a la
entrada, evitando que lo atraviesen. En fotografía, un filtro ultravioleta se utiliza a
menudo para evitar que la luz ultravioleta, presente en la luz solar y que no es parte de
la luz visible, afecte a las sustancias de la película.
Podemos ver una señal como una superposición de componentes senoidales que
ocupan una banda de frecuencias. Los filtros separan dicha señal del ruido adicional y
de otras señales, dejando pasar selectivamente las frecuencias deseadas y atenuando las
que no interesan. A veces, el filtro modifica la señal de forma intencionada, dando más
peso o énfasis a ciertas frecuencias frente a otras o cambiando las fases de algunos
componentes de la señal. En esta memoria aprenderemos a especificar los distintos tipos
de filtrado.
Imagen 1
Las características de filtro ideal de la imagen son fundamentales en la teoría de
filtros. Como deja pasar todas las frecuencias menores de un rad/s con ganancia uno, y
elimina todas las frecuencias mayores a un rad/s con ganancia cero, se llama filtro paso
bajo con frecuencia de corte en un rad/s. La banda de frecuencia en que la ganancia es
uno es la banda pasante y la banda en la que la ganancia es cero es la banda de rechazo.
En un filtro ideal, el desplazamiento de fase es cero en todas las frecuencias
En un filtro, la ganancia importante es la relativa, y no la absoluta, por tanto,
cualquier factor de escala que afecte igualmente a todas las frecuencias no afecta en
nada al filtrado. Por ejemplo, un filtro con ganancia − 50 para ω ≤ 1 y 0 para ω > 1 es
equivalente al filtro ideal de paso bajo en cascada con un amplificador con ganancia
− 50 . Si las especificaciones exigen un factor de escala en particular, siempre podremos
añadir un amplificador o divisor de tensión a la salida del filtro.
Desafortunadamente, el filtro ideal paso bajo no puede llegar a realizarse con un
circuito que tenga un número finito de elementos, por ello examinaremos a continuación
un circuito práctico que se le aproxime. Por ejemplo, el filtro paso bajo ideal tiene una
respuesta al impulso
3
Señales y sistemas
Joaquín T. Valderrama Valenzuela
hlp (n) =
sen(ωc ·π ·n)
π ·n
−∞ ≤ n ≤ ∞
Vemos que este filtro no es causal ni absolutamente sumable, por lo que es
inestable. Por tanto, este filtro ideal es físicamente irrealizable. Sin embargo, su
característica de respuesta en frecuencia se puede aproximar mucho con filtros prácticos
y realizables físicamente.
El principio básico subyacente en el método de los polos y ceros es el de
localizar los polos cerca de los puntos de la circunferencia unidad correspondientes a las
frecuencias que desean ser acentuadas, y situar los ceros cerca de aquellos puntos que se
corresponden con frecuencias que desean ser amortiguadas. Además, deben imponerse
las siguientes condiciones:
-
-
Todos los polos deben estar en el interior de la circunferencia unidad para
que el filtro sea estable. Sin embargo, los ceros pueden situarse en cualquier
punto del plano z.
Todos los ceros y polos complejos deben tener su conjugado
correspondiente, de manera que los coeficientes del filtro sean reales.
FILTRO PASO BAJO ORDEN 1
En el diseño de filtros digitales paso bajo, los polos deben situarse cerca de los puntos
de la circunferencia unidad correspondientes a las bajas frecuencias (cerca de ω = 0 ) y
los ceros deben situarse cerca de los puntos de la circunferencia unidad
correspondientes a las altas frecuencias (cerca de ω = π ). Lo contrario es lo necesario
para filtros paso alto.
La siguiente imagen muestra la localización de los polos y ceros de tres filtros
paso alto y tres filtros paso bajo.
Imagen 2
4
Señales y sistemas
Joaquín T. Valderrama Valenzuela
Imagen 3
El circuito anterior muestra un ejemplo de filtro activo en el que un
preamplificador inversor con ganancia menos uno compensa la inversión de señal
ocasionada por la siguiente etapa. En términos de tensiones expresadas en una
transformada de Laplace, la función de transferencia T(s) es
T ( s) =
Vo ( s)
1
=
Vi ( s ) s + 1
que tiene el diagrama de polos y ceros de la imagen anterior, un único polo en el
eje real negativo del plano s. Dado que su denominador es un polinomio de grado uno
en s, T(s) es un filtro de primer orden.
Para hallar la respuesta frecuencial del filtro de primer orden, hacemos s = jω
teniendo, en notación polar, la función de transferencia con valores complejos y las
consiguientes gráficas representativas.
T ( jω ) = T ( jω ) ∠φ (ω ) =
1
ω +1
2
∠ − tan −1 (ω )
Imagen 4
De donde vemos que para ω >> 1 , la ganancia es muy pequeña, siendo
insignificante el desplazamiento de fase para ω <<1.
5
Señales y sistemas
Joaquín T. Valderrama Valenzuela
FILTRO PASO ALTO
A veces queremos utilizar un filtro para dejar pasar altas frecuencias y atenuar
las bajas. Para ello utilizamos filtros paso alto, mostrados en la siguiente figura.
Imagen 5
Transformación RC-CR
Una vez que sabemos diseñar un circuito activo RC para realizar un filtro paso
bajo con una frecuencia de corte de un rad/s siempre podemos encontrar un circuito
activo RC que realce el filtro paso alto con frecuencia de corte de un rad/s. El principio
clave, denominado transformación RC-CR, se describe de la siguiente manera: “Para
transformar un circuito activo RC paso bajo con una frecuencia de un rad/s en un
circuito activo RC paso alto con la misma frecuencia de corte, reemplazaremos cada
resistencia de Ri ohmios por un condensador Ci =1/Ri faradios, y cada condensador Cj
faradios por una resistencia de Rj=1/Cj ohmios. Las ganancias de los elementos activos
no cambian”.
Así pues, al aplicar la transformación RC-CR al circuito anterior, obtenemos el
siguiente circuito.
Imagen 6
s
. Las demás figuras
s +1
muestran el diagrama de polos y ceros con las correspondientes curvas de respuesta
frecuencial obtenidas al sustituir s = jω .
Siendo su función de ganancia de tensión T ( s) =
T ( jω ) =
ω
ω2 +1
φ (ω ) =
π
2
− tan −1 (ω )
6
Señales y sistemas
Joaquín T. Valderrama Valenzuela
Se puede observar que
T (ω ) = 1 y que el desplazamiento de fase se hace
lím
ω
→∞
minúsculo al aumentar la frecuencia.
FILTRO PASO BANDA
Otra clase de filtros son los filtros de paso banda, idealizados en la siguiente
figura.
Imagen 7
La frecuencia de referencia es la frecuencia central uc = 1rad / s . Este filtro deja
pasar todas las frecuencias de una banda pasante definida por frecuencias de corte
superior e inferior, u H y u L , y rechaza las demás. La anchura de la banda pasante es la
anchura de banda B, dada en rad/s por B = u H − u L . La frecuencia central de cualquier
filtro paso banda se define como la media geométrica de las frecuencias de corte, esto
es, uc = 1 = u H u L
Filtro paso banda escalado en frecuencia.
A continuación, consideraremos la forma en que cambia la característica ideal de
la imagen anterior cuando escalamos en frecuencia con un factor de escala no negativo,
α = ωc . La frecuencia central pasa a ser ωc rad / s ; los límites superior e inferior de la
banda pasante cambian a ωH = ωC uH y ωL = ωC uL , respectivamente, como en la
siguiente imagen. Tras el escalado, la media geométrica queda:
ω H ω L = (ωC u H )(ωC u L ) = ωC u H u L = ωC
Imagen 8
7
Señales y sistemas
Joaquín T. Valderrama Valenzuela
Cuando hacemos escalado de frecuencia, el ancho de banda B se modifica
también a un nuevo valor BW, como se puede ver a partir de:
BW = ωH − ωL = ωC (uH − uL ) = ωC B
Como la frecuencia central y el ancho de banda se encuentran escalados en el
mismo factor, su relación e mantiene constante, o invariable con el escalado de
frecuencias. El factor de calida, Q, de un filtro paso banda se define como la relación
entre la frecuencia central y la banda pasante, es decir,
Q=
ωC
BW
=
1
B
FILTROS ACTIVOS DE PASO BAJO DE ORDEN N
A partir de ahora, veremos cómo filtrar de forma tan precisa que no va a poder
realizarse sólo con filtros de primer o de segundo orden. Nos aproximaremos al filtro
ideal tanto como queramos por medio de filtros de órdenes superiores.
En primer lugar, decir que sólo con tres parámetros seremos capaces de definir
especificaciones que controlen las características físicas de la aproximación. La
siguiente imagen muestra la característica paso bajo ideal y los parámetros δ , γ y ωs .
Imagen 9
Utilizamos δ para representar la ganancia de banda de paso mínima y γ para
especificar la máxima de la banda de rechazo. El factor de selectividad ωs define una
banda de transición en la que la función de aproximación pasa de satisfacer la
8
Señales y sistemas
Joaquín T. Valderrama Valenzuela
especificación de la banda pasante a satisfacer a la de la banda de rechazo. Hay muchas
funciones de aproximación, pero nos limitaremos a mencionar las dos más sencillas,
conocidas como la aproximación de Butterworth y de Chebyshev.
Aproximación de Butterworth
La siguiente figura muestra las curvas de respuesta frecuencial de magnitud de
unos cuantos elementos de la familia de filtros de Butterworth.
Imagen 10
Según se sube el orden n, los filtros se aproximan más al ideal. Como todas las
1
curvas tienen ganancia
a una frecuencia de referencia de un rad/s, se suele utilizar
2
1
en estos filtros; sin embargo, otros valores de δ requieren un escalado de
δ=
2
frecuencias especial. Introducimos de forma indirecta T (s ) del filtro de Butterworth ya
que T ( s )T (− s ) es mucho más fácil de describir matemáticamente. Este producto se
escribe como
T ( s )T ( − s ) =
1
1
=
n 2n
1 + ( −1) s
B( s) B(− s)
(Ecuación 1)
… en donde n es el orden del filtro y B (s ) es el polinomio de Butterworth de
orden n. Por definición, los polos de T ( s )T (− s ) son los 2n número complejos s que
hacen cero al denominador, es decir, valores de s que cumplen
s 2 n = −(−1) n
9
Señales y sistemas
Joaquín T. Valderrama Valenzuela
Cuando n es impar, los polos cumplen
o
s 2 n = 1 = 1 e jm360 = 1∠ m 360° , m = 0, 1, 2, 3, ...
Recordando que podemos representar el número “1” bien en notación
exponencial o polar, al tomar la raíz 2n-ésima obtenemos los distintos polos.
s = 1 e m 360° /( 2 n ) = 1 e m180° / n , m = 0, 1, 2, ..., 2n − 1 para n impar
(Ecuación 2)
Imagen 11
Las siguientes imágenes muestran los polos para n = 1 , 2, 3 y 4. En general, para
n impares, los polos caen en el círculo unidad, espaciados uniformemente a intervalos
de 180º/n, con el polo de m = 0 situado en s = +1 . Cuando n es par los polos cumplen
s 2 n = −1 = 1 e180 º + m 360 º , m = 0, 1, 2, K
(Ecuación 3)
… que hace que
s = (1 e180º + m360º )1 /( 2 n ) = 1 e(90º + m180º) / n ,
para m = 0, 1, 2, K, 2 n − 1, n par
Cuando n es par, los 2n polos se sitúan con un espaciado uniforme en el círculo
unidad, pero el primer polo ( m = 0) se sitúan en 90º/n.
10
Señales y sistemas
Joaquín T. Valderrama Valenzuela
Para que nuestros filtros sean estables no deben tener polos en la parte derecha
del plano complejo. Por lo tanto, al tomar el polinomio del denominador de la Ecuación
1 en forma factorizada, hacemos una división del producto en dos polinomios: B (s ) ,
que sólo consiste en los polos de la parte izquierda del plano, y B (− s ) que contiene los
factores restantes. El resultado, B (s ) es el polinomio Butterworth de grado n. La
1
función filtro Butterworth de grado n es la función T ( s ) =
que tiene n polos de la
B( s)
parte izquierda, todos en el círculo unidad.
Aunque B (s ) no se puede expresar de una forma sencilla, sus polos se pueden
calcular fácilmente para cualquier n, utilizando la Ecuación 2, y la Ecuación 3, y a partir
de las raíces de B ( s ) = 0 podemos calcular B (s ) . Es conveniente que al diseñar filtros
prácticos se disponga de resultados tabulados, como la siguiente tabla.
… que muestra B (s ) factorizada en polinomios de primer y segundo orden.
Estas tablas nos ahorrarán el trabajo de calcular los polos de la parte izquierda del plano
y luego combinar los polos configurados en términos de segundo orden. Estas tablas
ahorran trabajo a la hora de calcular los polos de la parte izquierda del plano y luego
combinar los polos configurados en términos de segundo orden.
Una vez que decidimos utilizar un filtro de Butterworth de determinado orden,
por ejemplo, n = 5 , podemos usar la tabla anterior para diseñar un circuito en cascada
de filtros activos que nos dan conjuntamente la respuesta Butterworth deseada, por
ejemplo, para n=5…
T (s) =
1
= T1 ( s )T2 ( s )T3 ( s )
( s + 1)( s + 0.6180 s + 1)( s 2 + 1.6180 s + 1)
2
… donde T1 ( s ) es un filtro de primer orden y T2 ( s ) y T3 ( s) son filtros de
segundo orden. Conocemos de las secciones anteriores la forma de diseñar circuitos que
realizan la función de filtros de primer y segundo orden. Para diseñar filtros de
Butterworth sólo necesitamos aprender a conseguir el orden necesario del filtro a partir
de las especificaciones dadas.
11
Señales y sistemas
Joaquín T. Valderrama Valenzuela
Imagen 12
A partir de la Ecuación 1 obtenemos que la curva de respuesta frecuencial de
magnitud al cuadrado de magnitud al cuadrado del filtro de Butterworth es
T ( jω ) =
1
2
1 + ω 2n
Por lo tanto
T ( jω ) =
1
1 + ω 2n
En donde si nos fijamos, la “imagen 10” representa la ecuación anterior para
valores determinados de n. Para n más altos, los filtros se hacen más complejos y más
caros; sin embargo, vemos que para ω >> 1 , la ganancia tiende a cero.
Aproximación de Chebyshev
La “imagen 13” muestra las respuestas en frecuencia de los tres primeros
miembros de la familia de filtros de Chebyshev. Como en los filtros de Butterworth, el
parámetro n especifica el orden del filtro. Para n > 1 , las características de Chebyshev
no son monótonas en la banda de paso como las funciones Butterworth sino que
muestran un rizado o variación de ganancia. El diseñador debe controlar la ganancia
mínima de la banda pasante, δ , por medio de un parámetro de Chebyshev, ∈ .
Permitiendo los rizados de banda pasante, este filtro consigue una mayor atenuación de
la banda de rechazo que el filtro de Butterworth del mismo orden.
12
Señales y sistemas
Joaquín T. Valderrama Valenzuela
Imagen 13
Diseñar filtros de Chebyshev con el mismo rizado es parecido a diseñar filtros de
Butterworth. Existen tablas que dan funciones T (s ) que describen filtros paso bajo de
una frecuencia de corte de un rad/s para los valores deseados de n y ∈ .
Polinomios de Chebyshev
La función del filtro de Chebyshev T ( jω ) se describe de forma indirecta con el
cuadrado de su función de magnitud
T ( jω ) =
2
1
2
2
1+ ∈ C n (ω )
(Ecuación 4)
… en donde el polinomio de Chebyshev de grado n, Cn (ω ) viene definido por
Cn (ω ) = cos(n cos−1 (ω ))
En este punto no es obvio que Cn (ω ) sea un polinomio, y mucho menos que sea
interesante. A continuación se procederá a explicar ambos puntos.
En primer lugar indicaremos a comprobar que Cn (ω ) cumple la fórmula
recursiva, es decir, que se cumple
Cn + i (ω ) = 2ω Cn (ω ) − Cn −1 (ω )
Esto significa que podemos generar un polinomio de Chebyshev una vez
hallados los dos polinomios consecutivos de un orden inmediatamente inferior.
Afortunadamente, los dos primeros polinomios son obvios. Para n = 0 y n = 1 tenemos:
C0 (ω ) = cos(0 cos−1 (ω )) = 1
y
C1 (ω ) = cos(cos−1 (ω )) = ω
13
Señales y sistemas
Joaquín T. Valderrama Valenzuela
Si seguimos generando polinomios sucesivos de mayor orden tenemos:
C2 (ω ) = 2ω 2 − 1
C3 (ω ) = 2 ω (2 ω 2 − 1) = 4 ω 3 − 3ω
C4 (ω ) = 8ω 4 − 8ω 2 + 1
y así continuamente, mostrando, efectivamente que Cn (ω ) describe un
polinomio en ω de orden n. La siguiente imagen muestra los polinomios para n = 1 , 2 y
3. Olvidando cualquier tipo de obligación de generar más polinomios, miramos los
generados y observamos que los polinomios Cn (ω ) tienen algunas propiedades
notables. Aunque no se presenta ninguna demostración, las siguientes propiedades se
pueden aplicarse a todos los polinomios de Chebyshev.
- Cn (1) = 1 para todos los n
- Cn (−1) = 1 para n pares; Cn (−1) = −1 para n impares
- Todas las raíces de Cn (ω ) = 0 son reales y en el margen ω < 1
- Cn (ω ) → ∞ para ω → ∞
- Cn (ω ) oscila con igual amplitud entre -1 y +1 cuando ω ≤ 1
Imagen 14
Diseño de filtros de Chebyshev
Una vez que hemos definido los polinomios de Chebyshev, examinaremos cómo
se utilizan para aproximarse al filtro paso bajo ideal, utilizando el polinomio de tercer
orden. A partir de la Ecuación 4 la función de transferencia del filtro de Chebyshev es
T ( jω ) =
1
1+ ∈2 Cn (ω )
2
14
Señales y sistemas
Joaquín T. Valderrama Valenzuela
Para diseñar el filtro de Chebyshev con ganancia γ en la frecuencia ωs ,
despejaremos la ecuación anterior de la siguiente manera.
T ( jω ) = γ =
[
1
1+ ∈2 cosh(n cosh −1 ωs )
]
2
Despejando n, obtenemos la ecuación de diseño
[(
)
cosh −1 1 / γ 2 − 1
n=
cosh −1 ω s
0 .5
]
/∈
Conociendo ωs y γ se puede crear el filtro de orden n.
Posición de los polos de Chebyshev.
Aunque no aparezcan las demostraciones, T ( s ) T (− s ) tiene sus 2n polos situados
en una elipse en el plano complejo s, tal y como muestra la imagen. Para la función del
filtro de Chebyshev, T (s ) , sólo seleccionaremos los factores del denominador que
corresponden a los polos de la parte izquierda del plano.
Imagen 15
De donde cada polo se puede calcular mediante las tablas, o si no son adecuadas,
siempre podemos calcular los valores de los polos mediante
⎡1
⎡1
⎛ 2k − 1 π ⎞
⎛ 1 ⎞⎤ ⎛ 2k − 1 π ⎞
−1 ⎛ 1 ⎞ ⎤
sk = σ k + jωk = − senh ⎢ senh −1 ⎜ ⎟⎥ sen⎜
⎟
⎟ + j cosh ⎢ senh ⎜ ⎟⎥ cos⎜
⎝ ∈ ⎠⎦ ⎝ n 2 ⎠
⎝ ∈ ⎠⎦ ⎝ n 2 ⎠
⎣n
⎣n
15
Señales y sistemas
Joaquín T. Valderrama Valenzuela
SUMARIO
Si hacemos un pequeño resumen de lo expuesto en este trabajo, podemos decir,
básicamente, que los filtros procesan los componentes frecuenciales de las señales,
modificando su amplitud relativa, fase o ambas. Todo cambio de ganancia o fase que
sea uniforme en todas las frecuencias no tiene efecto en el proceso de filtrado. Los
principales tipos de filtros son paso bajo, paso alto y paso banda, aunque también se
utilizan otros tipos como los llamados “pasa todo” y “rechazo de banda”. Cada uno de
los cuales, en su forma ideal, tiene una ganancia unidad en frecuencias de bandas
pasante y cero en la de rechazo.
Los filtros no pueden realizarse en sus formas ideales con números o
componentes finitos, por lo que deberemos trabajar con funciones y circuitos que se
aproximen a los filtros ideales. Los filtros paso bajo y paso alto se pueden aproximar
con sencillas funciones de transferencia de primer orden y sus circuitos relacionados.
El escalado de frecuencia, que consiste en cambiar los valores de todos los
condensadores y boninas mediante el mismo factor de escala α , modifica la magnitud y
fase del filtro prototipo a otra frecuencia, que es α veces la frecuencia original, siendo
α positivo y real. La transformación paso bajo a paso alto, p = 1 / s , se aplica a ambas
funciones y a los circuitos de los filtros. Con esta herramienta podemos transformar los
filtros paso bajo RLC en filtros paso alto relacionados y, a la inversa.
Y por último, con las funciones de Butterworth, Chebyshev podemos construir
filtros que se aproximen a filtros ideales incrementando su precisión, a la vez que el
orden del filtro (así como su complejidad y precio). Al utilizar tablas de filtros o
cálculos matemáticos, podemos relacionar los filtros de Butterworth o Chebyshev de
cualquier orden con filtros prototipo que consisten en etapas de filtros activos TC de
primer y segundo orden en cascada o circuitos en escalera.
Y prácticamente, decir que sería prácticamente imposible definir todas las
utilidades de los filtros en la electrónica actual, pero éstos son utilizados básicamente en
telecomunicaciones, donde existe la necesidad de separar (demultiplexar) señales, tales
como datos que han sido multiplexados por división en frecuencia, sin distorsionar estas
señales en el proceso de demultiplexado.
16
Señales y sistemas
Joaquín T. Valderrama Valenzuela
BIBLIOGRAFÍA
- “Tratamiento digital de señales”
o Autores.
ƒ John G. Proakis
ƒ Dimitris G. Manolakis.
o Editorial: Prentice Hall
- “Circuitos Electrónicos”
o Autor: Norbert R. Malik
o Editorial: Prentice Hall
- Apuntes de la asignatura “Análisis de Circuitos”. Curso
2002 – 2003.
- Páginas Web.
o http://www.hemerodigital.unam.mx/ANUIES/ipn/a
vanpers/sep97/vol161/sec_6.html
o http://webdiee.cem.itesm.mx/web/servicios/archivo/
trabajos/comunicaciones/filtros/
17