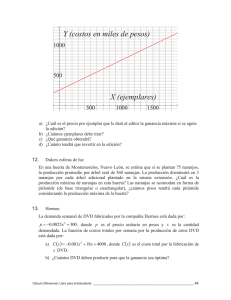
Actividad Sincrónica 14 de marzo de 2022 Estimado estudiante resuelva los siguientes ejercicios en grupos de 10 personas, recordando siempre los 4 pasos básicos para la resolución de modelos de programación lineal simple. EJERCICIO 1 Unos grandes almacenes desean liquidar 200 camisas y 100 pantalones de la temporada anterior. Para ello lanzan, dos ofertas, A y B. La oferta A consiste en un lote de una camisa y un pantalón, que se venden a Bs 30; la oferta B consiste en un lote de tres camisas y un pantalón, que se vende a Bs 50. No se desea ofrecer menos de 20 lotes de la oferta A ni menos de 10 de la B. ¿Cuántos lotes ha de vender de cada tipo para maximizar la ganancia? EJERCICIO 2 Se dispone de 600 g de un determinado fármaco para elaborar pastillas grandes y pequeñas. Las grandes pesan 40 g y las pequeñas 30 g. Se necesitan al menos tres pastillas grandes, y al menos el doble de pequeñas que de las grandes. Cada pastilla grande proporciona un beneficio de Bs2 y la pequeña de Bs1. ¿Cuántas pastillas se han de elaborar de cada clase para que el beneficio sea máximo? EJERCICIO 3 En una granja de pollos se da una dieta, para engordar, con una composición mínima de 15 unidades de una sustancia A y otras 15 de una sustancia B. En el mercado sólo se encuentra dos clases de compuestos: el tipo X con una composición de una unidad de A y 5 de B, y el otro tipo, Y, con una composición de 5 unidades de A y 1 de B. El precio del tipo X es de Bs10 y del tipo Y es de Bs30. ¿Qué cantidades se han de comprar de cada tipo para cubrir las necesidades con un coste mínimo? EJERCICIO 4 Con el comienzo del curso se va a lanzar unas ofertas de material escolar. Unos almacenes quieren ofrecer 600 cuadernos, 500 carpetas y 400 bolígrafos para la oferta, empaquetándolo de dos formas distintas; en el primer bloque pondrá 2 cuadernos, 1 carpeta y 2 bolígrafos; en el segundo, pondrán 3 cuadernos, 1 carpeta y 1 bolígrafo. Los precios de cada paquete serán Bs 6.5 y Bs7, respectivamente. ¿Cuántos paquetes le conviene poner de cada tipo para obtener el máximo beneficio? EJERCICIO 5 Un autobús que hace el recorrido Cali-Buga, ofrece asientos para fumadores al precio de Bs10.000 y a no fumadores al precio de Bs 6.000. Al no fumador se le deja llevar 50 Kg. de peso y al fumador 20 Kg. Si el autobús tiene 90 asientos y admite un equipaje de hasta 3.000 Kg. ¿Cuál ha de ser la oferta de asientos de la compañía para cada tipo de pasajeros, con la finalidad de optimizar el beneficio? Además, debe considerarse que, por políticas de la empresa, deben ofrecerse como mínimo 10 asientos para pasajeros no fumadores. EJERCICIO 6 Un comerciante acude al mercado popular a comprar naranjas con Bs 50.000. Le ofrecen dos tipos de naranjas: las de tipo A a Bs 50 el Kg. y las de tipo B a Bs 80 el Kg. Sabiendo que sólo dispone de su camioneta con espacio para transportar 700 Kg. de naranjas como máximo y que piensa vender el Kg. de naranjas tipo A a Bs 58. y el Kg. de tipo B a Bs 90. plantee un modelo de programación lineal que permita resolver la situación anterior. EJERCICIO 7 Un vendedor de frutas necesita 16 cajas de naranjas, 5 de plátanos y 20 de manzanas. Dos mayoristas están en condiciones de satisfacer sus necesidades, pero solo venden la fruta en contenedores completos. El mayorista A envía en cada contenedor 8 cajas de naranjas, 1 de plátanos y 2 de manzanas. El mayorista B envía en cada contenedor 2 cajas de naranjas, una de plátanos y 7 de manzanas. Sabiendo que el mayorista A se encuentra a 150 Km. de distancia y el mayorista B a 300 Km., calcular cuántos contenedores habrá de comprar a cada mayorista, con el objeto de ahorrar tiempo y dinero, reduciendo al mínimo la distancia. EJERCICIO 8 Un proveedor debe preparar con 5 bebidas de fruta en existencia, al menos 500 galones de un ponche que contenga por lo menos 20% de jugo de naranja, 10% de jugo de toronja y 5% de jugo de arándano. Si los datos del inventario son los que se muestran en la tabla siguiente ¿Qué cantidad de cada bebida deberá emplear el proveedor a fin de obtener la composición requerida a un costo total mínimo? EJERCICIO 9 Un empresario pretende fabricar dos tipos de congeladores denominados A y B. Cada uno de ellos debe pasar por tres operaciones antes de su comercialización: Ensamblaje, pintura y control de calidad. Los congeladores requieren, respectivamente, 2,5 y 3 horas de ensamblaje, 3 y 6 Kg. de esmalte para su pintura y 14 y 10 horas de control de calidad. Los costos totales de fabricación por unidad son, respectivamente, 30 y 28, y los precios de venta 52 y 48, todos ellos en miles de bolivianos. El empresario dispone semanalmente de máximo, 4500 horas para ensamblaje, de máximo 8400 Kg. de esmalte y 20000 horas máximo, para control de calidad. Los estudios de mercado muestran que la demanda semanal de congeladores no supera las 1700 unidades y que, en particular, la de tipo A es de, al menos 600 unidades. EJERCICIO 10 Una empresa de confecciones puede producir 1000 pantalones o 3000 blusas (o una combinación de ambos) diariamente. El departamento de acabado puede trabajar sobre 1500 pantalones o sobre 2000 blusas (o una combinación de ambos) cada día; el departamento de mercadeo requiere que se produzcan diariamente al menos 400 pantalones. Si el beneficio de un pantalón es de $ 4000 y el de una blusa es de $ 3000. ¿Cuántas unidades se deben producir de cada uno para maximizar las utilidades?