
ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Miguel Ángel Gómez García Profesor Titular Javier Fontalvo Alzate Profesor Asociado Wilmar Osorio Viana Profesor ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Miguel Ángel Gómez García Profesor Titular Javier Fontalvo Alzate Profesor Asociado Wilmar Osorio Viana Profesor Manizales, 2012 Miguel Ángel Gómez García Elementos para el análisis y diseño de reactores químicos / Miguel Angel Gómez García, Javier Fontalvo Alzate, Wilmar Osorio Viana. - Manizales: Universidad Nacional de Colombia. Facultad de Ingeniería y Arquitectura, 2012. XII, 333 p.; 140 il.; 24 cm -- (Libro de texto) ISBN: 978-958-761-034-5 Palabras clave: 1. Ingeniería de las reacciones químicas, 2. Reactores químicos, 3. Diseño de reactores, 4. Optimización, 5. Métodos numéricos ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS © Universidad Nacional de Colombia Sede Manizales Facultad de Ingeniería y Arquitectura © Miguel Ángel Gómez García Javier Fontalvo Alzate Wilmar Osorio Viana ISBN: 978-958-761-034-5 El contenido de esta obra corresponde al derecho de expresión de los autores y no compromete el pensamiento institucional de la Universidad Nacional de Colombia, ni genera responsabilidad frente a terceros. El autor asume la responsabilidad por los derechos de autor y conexos contenidos en la obra, así como por la eventual información sensible publicada en ella. Prohibida la reproducción total o parcial por cualquier medio sin la autorización escrita del titular de los derechos patriomoniales. Esta publicación fue autorizada por la Resolución CFIA No. 264 del 12 de abril de 2011 (Acta 014). Coordinación editorial: Dirección de Investigación y Extensión de la Facultad de Ingeniería y Arquitectura Corrección de estilo: Marta Isabel Serna Nieto Diseño de la carátula: E. Sotelo Zúñiga A Izabela y Sofía, colectiva e individualmente, por el amor y la alegría de cada día Miguel Ángel A aquellos que poseen la capacidad de construir y son el futuro, nuestros estudiantes Miguel Ángel, Javier, Wilmar TĆćđĆ ĉĊ ĈĔēęĊēĎĉĔ PRÓLOGO VII 1. CALOR DE REACCIÓN Y FACTIBILIDAD INTRODUCCIÓN 1.1. PARÁMETROS ENERGÉTICOS ASOCIADOS A LAS REACCIONES QUÍMICAS 1.1.1. CALOR DE REACCIÓN 1.1.1.1. 1.1.1.2. 1.1.1.3. EFECTO DE LA TEMPERATURA SOBRE EL CALOR DE REACCIÓN EFECTO DE LA PRESIÓN SOBRE EL CALOR DE REACCIÓN. REACCIONES EN FASE GAS CÁLCULO DE LA ENTALPÍA DE REACCIÓN EMPLEANDO PROPIEDADES MOLARES PARCIALES 1.2. EL CAMBIO EN LA ENERGÍA LIBRE DE GIBBS BIBLIOGRAFÍA 1 2 3 5 6 8 11 15 2. ¿CÓMO APROVECHAR MEJOR LOS BALANCES MOLARES DE UN SISTEMA REACCIONANTE? INTRODUCCIÓN 2.1. BALANCE MOLAR PARA UN SISTEMA CON UNA REACCIÓN INDEPENDIENTE 2.2. BALANCES MOLARES PARA UN SISTEMA CON MÁS DE UNA REACCIÓN INDEPENDIENTE BIBLIOGRAFÍA 17 18 24 28 3. ALGORITMOS PARA EL CÁLCULO DE COMPOSICIONES DE EQUILIBRIO PARA SISTEMAS CON MÚLTIPLES REACCIONES INTRODUCCIÓN 3.1. MÉTODO DE MINIMIZACIÓN DE LA ENERGÍA LIBRE DE GIBBS 3.1.1. ENFOQUE ESTEQUIOMÉTRICO 3.1.2. 3.2 3.1.1.1. ALGORITMO DE CÁLCULO 3.1.2.1. ALGORITMO DE CÁLCULO ENFOQUE NO ESTEQUIOMÉTRICO MÉTODO DE LA CONSTANTE DE EQUILIBRIO 3.2.1. ALGORITMO DE CÁLCULO BIBLIOGRAFÍA 29 29 30 31 35 37 42 43 45 I 4. CINÉTICA PARA EL DISEÑO DE REACTORES QUÍMICOS INTRODUCCIÓN 4.1. CINÉTICA Y TERMODINÁMICA 4.2. LA ECUACIÓN DE VELOCIDAD DE REACCIÓN 4.3. AJUSTE DE DATOS EXPERIMENTALES PARA LA DETERMINACIÓN DE LOS PARÁMETROS DE LA ECUACIÓN DE VELOCIDAD DE REACCIÓN PARA SISTEMAS NO IDEALES 4.3.1. CASO DE ESTUDIO 1: PRODUCCIÓN SIMULTÁNEA DE SULFATO DE POTASIO Y ÁCIDO CLORHÍDRICO. ANÁLISIS CINÉTICO MEDIANTE EL MÉTODO TERMOMÉTRICO 4.3.1.1 4.3.2. MODELO PARA EL MÉTODO TERMOMÉTRICO CASO DE ESTUDIO 2: CINÉTICA DE LA SÍNTESIS EN FASE VAPOR DEL ACETATO DE ETILO BIBLIOGRAFÍA 47 48 49 51 52 53 59 65 5. BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE INTRODUCCIÓN REPRESENTACIÓN GRAFICA DE UNA BATERÍA DE CSTRS EN UN 5.1. DIAGRAMA DE ETAPAS 5.2. OPTIMIZACIÓN DE BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE 5.2.1. 5.2.2. CASO ISOTÉRMICO CASO NO ISOTÉRMICO 5.2.2.1. 5.3 ALGORITMO DE CÁLCULO DISEÑO Y OPTIMIZACIÓN DE UNA BATERÍA DE QUIMIOSTATOS 5.3.1. ESTEQUIOMETRIA DE LA ACCIÓN METABÓLICA DEL MICROORGANISMO 5.3.2. 5.3.3. CINÉTICA DE LA PRODUCCIÓN DE BIOMASA BALANCES DE MATERIA EN EL QUIMIOSTATO 5.3.3.1. ALGORITMO DE SOLUCIÓN PARA PROBLEMAS DE DESEMPEÑO O DIMENSIONAMIENTO DE UN QUIMIOSTATO 5.3.4. 5.3.5. REPRESENTACIÓN ADIMENSIONAL DE LA CINÉTICA DE MONOD CRITERIOS DE OPTIMIZACIÓN DEL TAMAÑO DE UNA BATERÍA DE QUIMIOSTATOS Y ALGORITMO DE SOLUCIÓN BIBLIOGRAFÍA 67 68 73 73 78 78 82 84 85 87 89 94 96 104 6. ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES INTRODUCCIÓN PARÁMETROS PARA EL ANÁLISIS DE SISTEMAS CON MÚLTIPLES 6.1. REACCIONES II 107 109 6.2. DETERMINACIÓN DEL RENDIMIENTO INSTANTÁNEO 115 6.3. 6.4. DISEÑO ÓPTIMO A PARTIR DE DATOS DE RENDIMIENTO REACCIONES PARALELAS: MÁS DE UN PRODUCTO 6.4.1. EFECTO DE LAS VARIABLES DE OPERACIÓN 116 6.5. 6.6. 6.4.1.1. EFECTO DE LA TEMPERATURA 6.4.1.2. 6.4.1.3. 6.4.1.4. 6.4.1.5. EFECTO DE LA PRESIÓN EFECTO DE LA RECIRCULACIÓN DE PRODUCTO EFECTO DEL CATALIZADOR ¿Y EL MEZCLADO? REACCIONES EN SERIE: PRODUCTOS QUE CONTINÚAN REACCIONANDO REACCIONES COMPLEJAS 6.6.1. EFECTO DE LA RELACIÓN DE ALIMENTACIÓN DE LOS REACTIVOS 6.6.2. RENDIMIENTO DEL PRODUCTO 6.6.2.1. RENDIMIENTOS DEL PRODUCTO EN REACTORES TUBULARES 6.6.2.2. ¿Y EL MEZCLADO? BIBLIOGRAFÍA 121 123 123 124 124 124 125 128 131 132 133 134 137 138 7. DIAGRAMAS TRIANGULARES PARA LA SELECCIÓN DE ESQUEMAS DE REACCIÓN ÓPTIMOS INTRODUCCIÓN 7.1. BALANCES MOLARES EN REACTORES IDEALES ISOTÉRMICOS 141 7.2. 144 CONSTRUCCIÓN DEL SIMPLEX CONCENTRACIONAL SIMPLEX CONCENTRACIONAL A PARTIR DE DATOS OBTENIDOS EN 7.2.1. UN REACTOR BATCH 7.2.2. SIMPLEX CONCENTRACIONAL A PARTIR DE DATOS OBTENIDOS EN UN CSTR 7.3. REGLAS GENERALES PARA DETERMINAR EL MEJOR TIPO DE REACTOR BIBLIOGRAFÍA 142 145 147 149 156 8. ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES INTRODUCCIÓN 8.1. ELEMENTOS PARA LA DETERMINACIÓN DE UNA REGIÓN ALCANZABLE 8.1.1. ELECCIÓN DE LOS PROCESOS FUNDAMENTALES 8.1.2. ELECCIÓN DE LAS VARIABLES DE ESTADO 8.1.3. DEFINIR LOS VECTORES DE PROCESO 8.1.4. DETERMINAR LA GEOMETRÍA DE LAS UNIDADES DE PROCESO 8.1.4.1. REACTORES DE FLUJO PISTÓN (PFR) 8.1.4.2. REACTORES CONTINUOS DE TANQUE AGITADO (CSTR) 157 158 158 159 160 160 160 161 III 8.1.5. CONDICIONES NECESARIAS 8.1.5.1. LA REGIÓN INCLUYE TODAS LAS CONDICIONES DE ALIMENTO 163 163 8.1.5.2. NINGÚN VECTOR DE PROCESO SOBRE LOS LÍMITES DE LA AR ESTÁ DIRIGIDO HACIA FUERA DE LA AR 164 8.1.5.3. NINGÚN PUNTO ESTACIONARIO CON MEZCLADO COMO PROCESO EXISTE EN EL ÁREA DE COMPLEMENTO DE LA REGIÓN 8.2. 8.3. 8.4. 8.5. ¿CÓMO CONSTRUIR LA REGIÓN ALCANZABLE? ¿CÓMO INTERPRETAR LAS FRONTERAS COMO DIAGRAMA DE FLUJO DE PROCESO? ¿CÓMO ENCONTRAR EL ÓPTIMO? CASOS DE ESTUDIO 8.5.1. REACCIONES DE TRAMBOUZÉ & PIRET 8.5.2. 8.5.3. 8.5.1.1. 8.5.1.2. SISTEMA A VOLUMEN CONSTANTE SISTEMA A VOLUMEN VARIABLE 8.5.1.3. SISTEMA NO IDEAL DESHIDROGENACIÓN OXIDATIVA DE BUTENO A BUTADIENO SISTEMAS NO ISOTÉRMICOS: OPERACIÓN ADIABÁTICA 8.5.3.1. 166 167 174 176 178 178 178 182 184 188 192 CONSTRUCCIÓN DE LA REGION ALCANZABLE PARA LA OPERACIÓN ADIABÁTICA 193 8.5.3.2. CONSTRUCCIÓN DE LA REGIÓN ALCANZABLE PARA PFTRS ADIABÁTICOS CON ENFRIAMIENTO INTER-ETAPAS 196 8.5.3.3. CONSTRUCCIÓN DE LA REGIÓN ALCANZABLE PARA PFTRS ADIABÁTICOS USANDO COLD SHOOTING PARA ENFRIAMIENTO INTERETAPAS BIBLIOGRAFÍA 200 202 9. DERIVACIÓN DE LOS PERFILES VELOCIDAD - TEMPERATURA - CONVERSIÓN Y DE PROGRESIÓN ÓPTIMA DE TEMPERATURA PARA REACCIONES REVERSIBLES INTRODUCCIÓN 207 9.1. CONSIDERACIONES GENERALES 208 9.2. ECUACIONES PARA LOS PERFILES r-T-XA 209 9.3. IV 9.2.1. REACCIONES DEL TIPO aA ↔ rR 209 9.2.2. REACCIONES DEL TIPO aA + bB ↔ rR 211 9.2.3. REACCIONES DEL TIPO aA + bB ↔ rR + sS 212 9.2.4. REACCIONES DEL TIPO aA ↔ rR + sS 214 ECUACIONES PARA LA PROGRESIÓN ÓPTIMA DE TEMPERATURA (POT) 215 9.4. PERFILES VELOCIDAD-TEMPERATURA-CONVERSIÓN PARA CINÉTICAS COMPLEJAS 9.4.1. 9.4.2 217 OBTENCIÓN DE LAS CURVAS DE ISOVELOCIDAD: MÉTODO DE HOMOTOPÍA MONOPARAMÉTRICA 218 9.4.1.1. 219 ALGORITMO OBTENCIÓN DEL LUGAR GEOMÉTRICO DE LOS PUNTOS DE MÁXIMAS CONVERSIONES: MÉTODO DE LA HOMOTOPÍA MONOPARAMÉTRICA APLICADO A UN PROBLEMA DE OPTIMIZACIÓN 221 9.4.2.1 222 ALGORITMO BIBLIOGRAFÍA 224 10. DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA INTRODUCCIÓN 227 10.1. UN MÉTODO PARA ALCANZAR CONVERSIONES INACCESIBLES 10.1.1. CASO DE ESTUDIO 10.1.2. MODELO 10.1.3. ALGORITMO DE CÁLCULO ANÁLISIS DE LA DINÁMICA DE UNA BATERÍA DE CSTRS 228 10.2.1. ARRANQUE, PERTURBACIÓN Y PARADA A VOLUMEN CONSTANTE 240 10.2.2. IDENTIFICACIÓN Y CARACTERIZACIÓN DIRECTA DE LOS MÚLTIPLES ESTADOS ESTACIONARIOS DE LA BATERÍA 245 10.2. 10.3. 10.4. ARRANQUE DEL CSTR A VOLUMEN VARIABLE CSTRS NO ISOTÉRMICOS Y LA ESTABILIDAD DE SUS ESTADOS ESTACIONARIOS 10.4.1. DETERMINACIÓN Y CARACTERIZACIÓN DIRECTA DE LOS MÚLTIPLES ESTADOS ESTACIONARIOS 10.4.2. DESEMPEÑO DINÁMICO Y VISUALIZACIÓN DE LA ESTABILIDAD BIBLIOGRAFÍA 228 230 232 237 250 256 256 262 267 11. PÉRDIDA DE CARGA EN REACTORES CON FLUJO PISTÓN INTRODUCCIÓN 11.1. CRAQUEO TÉRMICO DE ETANO : DESCRIPCIÓN DEL REACTOR 11.2. MODELO MATEMÁTICO 11.2.1. BALANCE MOLAR 11.2.2. BALANCE DE ENERGÍA TÉRMICA 11.2.3. BALANCE DE ENERGÍA MECÁNICA 271 272 273 273 274 274 V 11.3. RESULTADOS BIBLIOGRAFÍA 276 278 12. REACTORES CON RECIRCULACIÓN: “EL TUBO QUE SE VOLVIÓ TANQUE” INTRODUCCIÓN 12.1. “EL TUBO QUE SE VOLVIÓ TANQUE” BALANCES MOLARES Y DE ENERGÍA EN UN REACTOR CON RE12.2. CIRCULACIÓN. CASO ADIABÁTICO BIBLIOGRAFÍA 279 280 284 286 13. OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS INTRODUCCIÓN 289 13.1. POTENCIAL ECONÓMICO 290 13.2. OPTIMIZACIÓN EN TÉRMINOS DE LAS VARIABLES DE PROCESO 292 13.3. CASOS DE ESTUDIO 294 13.3.1. CASO 1: CONVERSIÓN INTERMEDIA ÓPTIMA EN UN ARREGLO DE DOS REACTORES EN SERIE 294 13.3.2. CASO 2: OPTIMIZACIÓN MULTIVARIABLE PARA UNA BATERÍA DE CSTRs CON RECICLO 297 13.3.3. CASO 3: OPTIMIZACIÓN DE LAS GANANCIAS USANDO UN 13.3.4. 13.3.5. REACTOR BATCH 303 CASO 4: INFLUENCIA DEL CAMBIO DEL PRECIO DEL PRODUCTO EN EL MERCADO SOBRE EL ÓPTIMO ECONÓMICO DE UN REACTOR BATCH 307 CASO 5: DECIDIENDO ENTRE UN ÓPTIMO ECONÓMICO Y UN MENOR RIESGO DE SEGURIDAD EN EL DISEÑO DE UN C STR NO-ISOTÉRMICO 312 BIBLIOGRAFÍA 317 14. PREDICCIÓN, PREVENCIÓN Y EVALUACIÓN DE RIESGOS CON REACCIONES QUÍMICAS INTRODUCCIÓN 319 14.1. CASO I: REACTOR PARA LA POLIMERIZACIÓN DE ÓXIDO DE PROPILENO 320 14.2. CASO II: SISTEMA CON DOS REACCIONES EXOTÉRMICAS A → B → C 326 BIBLIOGRAFÍA VI 332 PėŘđĔČĔ Las tecnologías químicas han constituido uno de los soportes fundamentales para satisfacer algunas necesidades de la sociedad. Los reactores químicos industriales se usan para la fabricación de productos químicos básicos, especializados, combustibles, materiales, fertilizantes, alimentos, medicamentos y cosméticos, entre otros, así como para el control de contaminantes atmosféricos y el tratamiento de aguas. También constituyen herramientas básicas para la investigación en el laboratorio de nuevos procesos químicos y nuevos materiales y productos. Estas unidades de proceso han experimentado un interesante desarrollo tecnológico y hoy por hoy, la ingeniería química dispone de un complejo y especializado conjunto de herramientas para su análisis, diseño, operación y control. Los ingenieros químicos son los únicos profesionales con la formación para el manejo de esas herramientas. La importancia de esta tecnología en diversos sectores industriales y nuestra pasión por su estudio, nos ha motivado a presentar esta obra. El principal propósito de este libro es complementar la literatura disponible para un primer curso sobre la Ingeniería de las Reacciones Químicas (IRQ). Se tratan, de forma detallada, algunos conceptos que se exponen de manera supercial en la literatura. Los temas se han recopilado con el n de fomentar la discusión crítica de los mismos y su solución mediante el uso de herramientas modernas, haciendo especial énfasis en la solución numérica de problemas mediante el uso de paquetes de software. Todos los cálculos incluidos en el texto fueron implementados en MatLab® por los autores. VII Este libro está divido en catorce capítulos. En el primer capítulo se describen los formalismos termodinámicos fundamentales y el cálculo riguroso de la entalpía y la energía libre de reacción, para establecer las condiciones más favorables para la ocurrencia de una reacción. La introducción de variables de progreso de la reacción como la conversión o el grado de avance, facilitan el tratamiento matemático de los problemas de la IRQ al reducir su dimensionalidad. Para aprovechar mejor la información contenida en los balances molares, se presenta en el capítulo dos una metodología general para identicar grácamente la región permisible en la que están contenidas todas las posibles soluciones físicamente realistas del problema de balance de materia. La determinación del estado de equilibrio químico se presenta en el capítulo tres. Se exponen en detalle dos estrategias para resolver el problema de determinar las composiciones de equilibrio a una temperatura, presión y relación de alimento especicadas: el método de la minimización de la energía libre de Gibbs y el método de la constante de equilibrio. La parte básica conceptual se complementa con el cuarto capítulo donde se presentan algunos conceptos claves relativos a la cinética de reacciones. Se incluyen dos ejemplos que tratan sobre la determinación de parámetros cinéticos para sistemas termodinámicamente no ideales. El uso de reactores de tanque agitado y mezcla completa (CSTR de sus siglas en inglés) es de gran importancia a nivel industrial. En el capítulo cinco se trata el problema de optimización de estos sistemas de reactores para reducir a un mínimo el volumen total requerido para el proceso. Se aborda además el tema de los quimiostatos (biorreactores). Los sistemas reaccionantes que se presentan en la práctica industrial comúnmente consisten en múltiples reacciones químicas que ocurren de forma simultánea al interior del reactor, generando junto con el producto deseado, subproductos y residuos. Para el diseño de tales sistemas, es necesario contar con un conjunto de conceptos y herramientas técnicas que permitan el correcto diseño del reactor, teniendo en cuenta consideraciones sobre el rendimiento en la utilización de la materia prima, la conversión y la selectividad en la obtención del producto deseado. En el capítulo seis se presentan los conceptos fundamentales para el análisis de sistemas con reacciones múltiples: en paralelo, en serie, y en esquemas complejos, enfatizando en el análisis de los efectos de las diferentes VIII condiciones de operación sobre el desempeño del reactor. Se presentan dos métodos de análisis para establecer el mejor tipo de reactor(es) y su arreglo, de tal forma que se logre la selectividad y/o rendimiento requerido hacia un producto deseado: i. En el capitulo siete se presenta un método gráco basado en el uso de los balances molares por componente y la representación de los caminos de reacción sobre un simplex concentracional o espacio de concentraciones, metodología propuesta por Trambouzé & Piret (AIChE J., 5–1959–384). El esquema analítico original se implementa numéricamente lo que permite estudiar cualquier tipo de ley de velocidad. Basados en criterios geométricos, este método permite denir el mejor tipo de esquema de reacción para alcanzar, en un sistema dado de reacciones, el máximo rendimiento de un producto deseado. ii. En el capítulo ocho se expone una de las herramientas más sosticadas de análisis y síntesis (diseño) de sistemas con reacciones múltiples que existen en la actualidad: el método de las Regiones Alcanzables (RA). Su generalidad permite la determinación de la zona completa de operación en la que debe encontrarse cualquier posible diseño de un reactor para efectuar el proceso, lo que a su vez proporciona una poderosa herramienta para la síntesis del reactor o sistema de reactores apropiados. La construcción gráca de dicha región alcanzable para un sistema reaccionante con cinéticas conocidas, hace uso de los balances molares y de consideraciones sobre los procesos básicos de mezclado y reacción. En este capítulo se presenta una revisión de los fundamentos de la metodología que incluye la construcción de la región, los criterios necesarios que debe cumplir la región determinada para ser catalogada como RA, y su aplicación a diversos sistemas reaccionantes tanto isotérmicos como noisotérmicos. La representación de perles a velocidad de reacción constante en un diagrama rectangular de conversión contra temperatura, es de gran utilidad para el diseño de diversos tipos de reactores químicos, en especial de aquellos en que ocurren reacciones reversibles exotérmicas. En el capítulo nueve se describen algunos casos básicos generales, para los cuales es posible trazar el diagrama usando expresiones analíticas y algunos casos reales que involucran ecuaciones cinéticas no-lineales donde la solución analítica ya no es posible. Aquí se describen algunas técnicas numéricas y en especial el uso del método de homotopía para el trazado de los diagramas y de sus propiedades características. IX En el capitulo diez se analiza el funcionamiento de reactores de mezcla (CSTR) en estado dinámico, incluyendo protocolo de arranque y parada. De igual importancia resultan las consideraciones sobre las posibles perturbaciones a las que pueda estar expuesto el reactor durante su operación y su respuesta ante ellas. Se incluyen los múltiples estados estables (MSS por sus siglas en inglés) de origen concentracional y/o térmico, la determinación y caracterización de los MSS, un procedimiento de diseño de baterías para alcanzar estados que resultan inaccesibles por su inestabilidad en un solo reactor y el análisis del desempeño dinámico durante el arranque, la parada y las perturbaciones empleando planos de fase. Para involucrar el balance de energía mecánica en el diseño de un reactor, se analiza en el capítulo once la pérdida de carga que se presenta en el craqueo térmico de hidrocarburos, involucrando las pérdidas por la fricción así como por los continuos cambios en el número de moles y en la densidad de la mezcla por la reacción. El reactor tubular con recirculación es reconocido tanto por su valor conceptual para ilustrar el efecto en la operación de las condiciones de mezcla, que van desde el ujo pistón hasta la mezcla completa, así como por su utilidad en sistemas con reacciones autocatalíticas o en las que se requieren bajas conversiones por paso. En el capítulo doce se presenta un análisis del reactor con recirculación y se discute en especial el desempeño del reactor de reciclo no-isotérmico, destacando los efectos que la transferencia de calor puede tener en relación con los efectos del mezclado intermedio proporcionado por el lazo de recirculación. El aspecto de la economía del proceso resulta determinante en la viabilidad tanto técnica como comercial de un determinado proceso productivo, por lo que se requiere una inclusión directa y cuantitativa de las variables económicas en los procedimientos de diseño de las unidades de reacción química. En el capítulo trece se discute, a través de casos de estudio, la forma como los elementos económicos básicos, asociados con las variables de proceso de los reactores químicos, se incorporan en el diseño incluyendo costos de materias primas, valor del producto obtenido y costos de adquisición, operación y mantenimiento. Se discute el concepto de potencial económico del proceso y la forma de establecer funciones de X costos en términos de las variables de proceso. Esto conduce a la formulación de problemas de optimización en los que se busca maximizar el potencial económico o las ganancias y/o minimizar los costos asociados con el reactor. Finalmente, en el capítulo catorce, se presentan dos casos que ilustran el potencial de la IRQ para la evaluación de condiciones de riesgo de accidentes durante la operación de un reactor químico. Este tema debe recibir atención especializada, particularmente durante la etapa de diseño y desarrollo del proceso, donde es más fácil identicarlas y corregirlas antes de la puesta en operación del equipo. Adicionalmente, el diseño mismo puede incorporar consideraciones especiales que aseguren la integridad del equipo y del personal, evitando condiciones de riesgo de explosión o estableciendo protocolos de operación para enfrentarlas en caso de que se presenten. El enfoque de este texto tomó forma después de varios años de trabajo en el curso de IRQ en el Departamento de Ingeniería Química de la Universidad Nacional de Colombia, en Manizales. Queremos reconocer especialmente la participación de algunos estudiantes que han trabajado con nosotros como auxiliares de docencia después de haber aprobado el curso de IRQ. Entre ellos están: Felipe Valencia, Víctor Marulanda, Julián García, Víctor Trejos, Sebastián López, Edgar Iván Rodríguez, Jesús David Coral, Fernando Ramírez, Benjamín Calderón, Harold Ibarra, Jorge Eduar Cardona, Juan Carlos Ojeda, y Noel Gómez; su entusiasmo intelectual le han dado especial sentido a la vida académica. Así mismo, nuestros sinceros reconocimientos a los profesores José Nelson Rojas Grisales, Kevin Giovanny Molina Tirado y Edison Gil Pavas por sus comentarios y propuestas durante el proceso de correcciones; así como al infatigable grupo de edición liderado por el profesor Jorge Galindo. Finalmente, los agradecimientos sinceros a todos los estudiantes miembros de nuestro Grupo de Investigación en Aplicación de Nuevas Tecnologías (GIANT). M. Á. Gómez García J. Fontalvo Alzate W. Osorio Viana Manizales, MMXII XI CAPÍTULO 1 - CALOR DE REACCIÓN Y FACTIBILIDAD 1 CĆđĔė ĉĊ ėĊĆĈĈĎŘē Ğ FĆĈęĎćĎđĎĉĆĉ INTRODUCCIÓN La termodinámica es una de las herramientas más útiles en el análisis y diseño de procesos químicos. Su utilidad se deriva no solamente de la posibilidad de entender el funcionamiento de procesos existentes, su mejoramiento y optimización, sino que, usada apropiadamente, permite predeterminar condiciones de operación y ofrecer una visión más amplia para el diseño de nuevos procesos reactivos. De hecho, son cuatro las preguntas principales que un ingeniero químico debe responder sobre las reacciones químicas: i. ii. iii. iv. ¿Qué tan rápido ocurren? ¿Qué tan lejos pueden llegar? ¿Qué cantidad de calor será liberada o requerida? ¿Qué tan factible es que se produzcan? La primera pregunta la responde la cinética química y se relaciona principalmente con los cambios químicos y los ujos de masa y calor asociados a las reacciones. Las otras tres se pueden resolver mediante consideraciones termodinámicas. Como las reacciones químicas involucran la formación, rompimiento o reordenamiento de enlaces químicos, ellas están acompañadas por cambios energéticos. El cambio entálpico de una reacción proporciona la información necesaria para cualquier análisis del 1 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS sistema en términos de la primera ley de la termodinámica. Adicionalmente, el cambio en la energía libre de Gibbs es útil para denir, desde el punto de vista termodinámico, si un proceso reactivo es factible que se produzca y a qué condiciones. Así mismo, también sirve para determinar cómo el cambio de las variables del proceso puede inuir en la conversión o avance de una reacción reversible. Por estas razones, en este capítulo se presenta el cálculo riguroso de dos parámetros energéticos asociados con la ingeniería de las reacciones químicas: el calor de reacción y la energía libre de Gibbs. En efecto, como la velocidad de reacción depende fuertemente de la temperatura, es fundamental tener en cuenta el calor de reacción para el diseño de reactores químicos. 1.1 PARÁMETROS ENERGÉTICOS ASOCIADOS A LAS REACCIONES QUÍMICAS Para determinar numéricamente los valores del calor de reacción y del cambio en la energía libre de Gibbs es necesario denir inicialmente un estado de referencia. Su elección es arbitraria y se basa principalmente en la facilidad para la experimentación y en su reproducibilidad. Los estados estándar más utilizados se presentan en la Tabla 1.1: Tabla 1.1. Estados estándar o normal para diferentes fases FASE Gas Líquida Sólida ESTADO ESTÁNDAR O NORMAL Gas perfecto con fugacidad unitaria Líquido puro a 1 atmósfera Sólido puro a 1 atmósfera El cálculo involucrará el uso de cantidades estequiométricas de los distintos reactantes y se supondrá que la reacción ocurre isotérmicamente por algún mecanismo o vía y termina con la conversión completa de reactantes a productos (cada uno en su estado estándar). 2 CAPÍTULO 1 - CALOR DE REACCIÓN Y FACTIBILIDAD 1.1.1. CALOR DE REACCIÓN En la inmensa mayoría de las reacciones químicas ocurre generación o absorción de energía. Esta energía puede ser de diferentes formas: lumínica, caloríca, etc. El segundo tipo de energía es el que más interesa a los ingenieros químicos. Esto se debe a que la entalpía absoluta de los productos de una reacción es usualmente diferente a la de los reactivos, aún cuando ambos estén a la misma temperatura. En una reacción exotérmica, la entalpía de los productos es menor que la de los reactantes y se libera calor. En una reacción endotérmica, la entalpía de los productos es mayor que la de los reactantes y el calor es absorbido. Los cambios de entalpía para una reacción en el estado estándar son denotados por el símbolo ΔHoRxn. Como la entalpía es una función de estado, los valores nales de esta variable son independientes del camino o forma en que se de el cambio. Por ejemplo, para calcular a 25°C y 1 atmósfera el cambio entálpico normal (estándar) de reacción o calor normal (estándar) de la reacción: aA( g ) bB( g ) cC( g ) dD( g ) (1.1) es útil interpretar la energía (entalpía) de cada componente como: a gmoles de A como gas perfecto a 1 atm y 25 º C aH Ao b gmoles de B como gas perfecto a 1 atm y 25 º C bH Bo c gmoles de C como gas perfecto a 1 atm y 25 º C cH Co d gmoles de D como gas perfecto a 1 atm y 25 º C dH Do y de la denición de cambio entálpico normal de reacción, el calor de reacción, por gmol de A, en el estado de referencia, es: 1 o o o o o H Rxn ,A cH C dH D aH A bH B a (1.2) Es posible utilizar los valores tabulados para reacciones normales de formación, ΔHof, y de combustión, ΔHoc, en el cálculo del ΔHoRxn de otras transformaciones. Así por ejemplo, el calor de reacción o cambio entálpico normal para la producción de gas de síntesis, a partir de metano y vapor de agua: 3 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS CH 4 (g) H 2O (g) CO (g) 3H 2 (g) (1.3) se calcula mediante la Ley de Hess de combinación de ecuaciones a partir de los calores normales de formación, ΔHof, de los compuestos que intervienen como se muestra a continuación: CH 4( g ) C( s ) 2 H 2( g ) H of 17,889 kcal.gmol 1 H 2O( g ) H of 57, 798 kcal.gmol 1 C( s ) 1 2 1 2 O2( g ) H 2( g ) O2( g ) CO( g ) H of 26, 416 kcal.gmol 1 ¡Al sumar estas tres reacciones, como si fueran ecuaciones algebraicas, se encuentra la reacción buscada y el valor del calor de reacción normal correspondiente! CH 4( g ) H 2O( g ) CO( g ) 3H 2( g ) H of ,298 49, 271 kcal.gmol 1 En términos generales, ΔHoRxn es igual a: o H Rxn i H ofi (1.4) donde vi es el coeciente estequiométrico: su signo es positivo para productos, negativo para reactivos y será igual a cero para cualquier compuesto inerte presente. El ΔHof de un elemento (tal como O2, N2, etc) es igual a cero. La fase de las sustancias que intervienen en una reacción es un aspecto clave que afecta enormemente el valor del calor estándar de reacción. Para ilustrar mejor este concepto se compararán las siguientes ecuaciones termoquímicas: C2 H 6( g ) 2O2( g ) 2CO2( g ) 3H 2O(l ) ΔHoRxn = -372830 cal.(gmol de etano)-1 C2 H 6( g ) 2O2( g ) 2CO2( g ) 3H 2O( g ) ΔHoRxn = -341135 cal.(gmol de etano)-1 La diferencia entre las dos es que la primera produce el agua en la fase líquida y la segunda en fase gaseosa, cuyas entalpías –obviamenteson distintas. En efecto, ellas dieren en el calor de vaporización de las tres 4 CAPÍTULO 1 - CALOR DE REACCIÓN Y FACTIBILIDAD moles de agua formadas, el cual puede determinarse al restar la primera reacción de la segunda. A continuación se presentan los métodos para el cálculo, a partir de sus deniciones, del calor de reacción y el cambio de la energía libre de Gibbs en funcion de la temperatura y la presión. Las propiedades volumétricas de la mezcla reaccionante serán calculadas utilizando la forma general de las ecuaciones cúbicas de estado (luego, su aplicación quedará limitada a la clase de uidos cuyas propiedades pueden ser descritas por tales ecuaciones). La funcionalidad respecto a la temperatura se calculará a partir de los datos de capacidades calorícas, los cuales están para muchas sustancias disponibles en la literatura (Poling et al., 2001). Los métodos de cálculo presentarán explicitamente la forma de manipular esos datos para que sean aplicables a las condiciones especícas a las cuales tiene lugar la reacción bajo estudio. 1.1.1.1. EFECTO DE LA TEMPERATURA SOBRE EL CALOR DE REACCIÓN La capacidad caloríca de un compuesto puro, A, está denida a presión constante como: H A Cp A T P (1.5) Para la reacción (1.1), en donde no hay cambio de fase, el calor de reacción por cada mol de A es: H Rxn , A c H C d H D H A b H B (1.6) T P a T P a T P T P a T P y entonces: H Rxn , A c d b CpC CpD Cp A CpB a a T P a (1.7) 5 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Si se conoce el valor de ΔHoRxn,A a la temperatura To, al integrar la ecuación anterior desde To hasta T se tiene que, para una reacción sin cambio de fase, el calor de reacción a T es igual a: H Rxn , A,1 atm ,T H T | CpdT o Rxn , A To (1.8) To Yaws y Chiang (1988a) correlacionaron la entalpía de formación de gas ideal, en función de la temperatura, mediante una expansión del tipo: ΔHf=A+BT+CT2 para más de 700 compuestos orgánicos (también para el agua y cloruro de hidrógeno). El cálculo del calor de reacción a una temperatura determinada será de especial utilidad en el diseño de reactores para evaluar las condiciones de equilibrio de la reacción y el balance de energía. 1.1.1.2. EFECTO DE LA PRESIÓN SOBRE EL CALOR DE REACCIÓN. REACCIONES EN FASE GAS Al elegir el estado estándar o de referencia de una reacción se asumen valores de temperatura y presión. Para cada componente, tanto los valores de las entalpías de formación, a la temperatura de referencia, como las capacidades calorícas en función de la temperatura, ambos como gas ideal, están disponibles. El efecto de la presión se puede involucrar mediante la inclusión de un término adicional como se presenta en la ecuación (1.9): P H Rxn , P H Rxn,T |Po 1 atm vi T T Po P dP i (1.9) El último término del lado derecho de la ecuación (1.9), el cual corresponde a la entalpía parcial molar residual, puede ser evaluado mediante una ecuación de estado. Para esto, se partirá de la expresión genérica que para las ecuaciones cúbicas de estado proponen Poling et al. (2001): 6 CAPÍTULO 1 - CALOR DE REACCIÓN Y FACTIBILIDAD P RT a 2 b ub wb 2 (1.10) Dado que en la ecuación (1.9) se debe determinar la derivada parcial del volumen con respecto a la temperatura (a presión constante) y las ecuaciones de estado son explícitas respecto a la presión, es conveniente evaluar el término entre corchetes de esa ecuación según: P T dP P RT P d T P T P i T o i P (1.11) Desarrollando la derivada parcial de la ecuación (1.11) se obtiene: (da ) R P dT 2 2 T b ub wb (1.12) Reemplazando la ecuación (1.10) y (1.12) en la ecuación (1.11) e integrando se obtiene que: 1 a 2 Z (u u 2 4 w 2 ) B T da P dT ln RT ( Z 1) 1 1 P RT T P d 2 2 i u 2 4 w b 2 Z (u u 2 4 w ) B T i (1.13) donde B = (Pb/RT)i. Luego, reemplazando esta última ecuación en la ecuación (1.9) se obtiene de manera explícita la corrección por presión del calor de reacción utilizando una ecuación cúbica de estado. Por ejemplo, en el caso de la ecuación de estado de Peng-Robinson, donde u = 2 y w = -1, la expresión para el calor de reacción en función de la temperatura y la presión queda: H Rxn , P H Rxn,T |1 atm i T ( da dT ) a Z (1 2) B ln RT ( Z 1) (1.14) 2 2b Z (1 2) B i La variación del calor de reacción con la temperatura y la presión para la reacción de formación de amoníaco, utilizando la ecuación de Peng-Robinson se presenta en la Figura 1.1. 7 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 1.1. Inuencia de la temperatura y la presión sobre el calor de reacción para la formación de amoníaco (se utilizó la ecuación de estado de Peng-Robinson) En el caso de la reacción de formación de amoníaco se observa la alta dependencia del calor de reacción con las dos variables analizadas: a mayor temperatura, independiente de la presión, la reacción se hace más exotérmica. Esto también es cierto para el caso de una temperatura constante e incrementando la presión. 1.1.1.3. CÁLCULO DE LA ENTALPÍA DE REACCIÓN EMPLEANDO PROPIEDADES MOLARES PARCIALES Aunque es común y generalmente aceptado en las labores de ingeniería realizar los cálculos del calor de reacción empleando expresiones como las dadas por las ecuaciones (1.4), (1.8) y (1.9), basadas en la 8 CAPÍTULO 1 - CALOR DE REACCIÓN Y FACTIBILIDAD utilización de las entalpías de las sustancias puras involucradas, desde un punto de vista termodinámicamente más riguroso, la reacción química ocurre entre los componentes de una mezcla y no entre las sustancias puras. Por esta razón, el cambio entálpico por reacción debería determinarse empleando las entalpías molares parciales de los componentes así: C H rxn i hˆi i 1 (1.4b) donde ĥi es la entalpía molar parcial del componente i en la mezcla reaccionante y es función de la temperatura, la presión y la composición. Esto permite incluir ahora la dependencia del calor de reacción con la composición, pero el cálculo exige que la mezcla esté compuesta por las cantidades estequiométricas de cada uno de los componentes involucrados, de manera tal que el resultado quede referido a una cantidad dada de reactivo consumido (propiedad intensiva). El uso de las entalpías molares parciales permite tener en cuenta los efectos de no idealidad de la mezcla y permite incluir el efecto que el proceso de mezclado de los componentes tiene sobre el efecto entálpico neto debido únicamente a la reacción química. Así pues, emplear las entalpías de los componentes puros para determinar el calor de una reacción química equivale a suponer que la mezcla es ideal (Belore, 2003), caso en el cual la ecuación (1.4b) se reduce a la ecuación (1.4a), ya que la entalpía de mezclado de una solución ideal es cero (Sandler, 2006). Un ejemplo del efecto de la no idealidad de la mezcla reaccionante sobre el calor de reacción se presenta en la Figura 1.1b, para el caso de la síntesis de amoníaco. En ella puede apreciarse que a bajas presiones (p.e., 1 bar), tanto las expresiones convencionales como las rigurosas prácticamente dan lugar al mismo resultado, debido a que a estas condiciones la mezcla se comporta como una solución ideal. Al elevar la presión a 152 bar, aumenta el comportamiento no ideal de la mezcla y surge una notable diferencia entre el cálculo simplicado que sólo considera la inuencia de la temperatura (ecuación 1.8), el cálculo más preciso, que tiene en cuenta la inuencia de la presión (ecuación 1.9), y el cálculo riguroso, en términos de las entalpías molares parciales (Marroquín de la Rosa et al., 2006). 9 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 1.1b. Inuencia de la temperatura, la presión y la no idealidad (entalpías molares parciales) de la mezcla sobre el calor de reacción para la formación de amoníaco (se utilizó la ecuación de estado de Peng-Robinson) Es interesante hacer notar que a tan altas presiones, la mezcla puede empezar a comportarse de forma “ideal” cuando la temperatura sea lo sucientemente alta, tal como lo señala la aproximación de las dos curvas inferiores en el extremo derecho de la Figura 1.1b; mientras que a baja temperatura, despreciar los efectos de no idealidad de la mezcla puede conducir a subestimaciones signicativas del verdadero valor del calor de reacción. Se hace necesario considerar con cuidado si la simplicación al cálculo del calor de reacción es aceptable o no para una reacción química dada y, según el rango de condiciones (presión y temperatura) de interés, denir si se justica el esfuerzo computacional, mucho mayor, de realizar el cálculo riguroso empleando las entalpías molares parciales. 10 CAPÍTULO 1 - CALOR DE REACCIÓN Y FACTIBILIDAD 1.2. EL CAMBIO EN LA ENERGÍA LIBRE DE GIBBS En la mayoría de las reacciones químicas no existe posibilidad de que el sistema haga algún trabajo diferente a un cambio de volumen. En otras palabras, el sistema no está sujeto a ninguna fuerza externa diferente a la presión. Las condiciones de equilibrio son aquellas en las cuales, para cualquier cambio, las fuerzas que lo impiden están balanceadas por aquellas que lo causan y, además, cualquier cambio pequeño que suceda es reversible (proceso cuasi-estático). Cuando una reacción química ocurre a temperatura y presión constantes, la energía libre del sistema disminuye a medida que la reacción evoluciona espontáneamente. Cuando la energía libre ha alcanzado el valor más bajo posible, a una temperatura y presión determinadas, la reacción cesará. Cualquier intento por continuar la reacción en el mismo sentido deberá aplicar alguna fuerza extra al sistema. En la mayoría de las reacciones no existe esa fuerza extra y la reacción se detiene en el punto en que la energía libre alcanza su valor mínimo. En ese instante la composición de la mezcla de reactantes y productos será la composición de equilibrio. Esta es la composición que los ingenieros químicos calculan con el n de establecer el rendimiento máximo posible del proceso (para un tratamiento más detallado sobre la denición de algunos parámetros y conceptos presentados en esta sección revisar, por ejemplo, Sandler, 2006). De forma análoga al cambio entálpico estándar de reacción, existe el cambio en la energía libre de Gibbs estándar, ΔGoRxn, para una reacción. El cambio en la energía libre de Gibbs estándar es la variación correspondiente a la formación de los productos en sus estados estándar a partir de reactantes en sus estados estándar. Así, para la reacción (1.1), el cambio en la energía libre de Gibbs, por mol de A, calculada a partir de las energías libres de formación es: 1 o o o o o GRxn ,A cG fC d G fD aG fA bG fB a (1.15) En general, el cambio en la energía libre de Gibbs estándar referido a un proceso isotérmico en el que ocurre una reacción, empezando con cantidades estequiométricas de reactantes, es diferente de cero y está dado por: 11 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS o GRxn i io (1.16a) donde μº es el potencial químico en el estudio estándar. Ahora, para una reacción química, el criterio básico del equilibrio es que la energía libre de Gibbs asociada con el progreso de la reacción sea cero: GRxn i i 0 (1.16b) Por lo tanto, combinando (1.16a) y (1.16b), se puede decir que: o GRxn ( i i io ) (1.17) Adicionalmente, en términos de la actividad de cada componente, ai, la ecuación (1.17) se puede expresar como: o GRxn RT i ln ai RT ln a i i (1.18) Y, por ejemplo, para la reacción de la ecuación (1.1) se obtiene que: ac ad o GRxn RT ln Ca Db a A aB RT ln K a (1.19) donde Ka, que es la constante de equilibrio, y ΔGoRxn se evaluan a una temperatura T. Del análisis de la ecuación (1.19) se puede concluir facilmente que si el cambio en la energía libre de Gibbs es negativo, la termodinámica para la reacción es favorable. Ahora, si el cambio en la energía libre es altamente positivo, la termodinámica para la reacción no es favorable y ésta solo puede ser posible bajo circunstancias muy especiales (Rase, 1977). Un criterio aproximado para las reacciones químicas es el siguiente (Yaws y Chiang, 1988b): 12 CAPÍTULO 1 - CALOR DE REACCIÓN Y FACTIBILIDAD ∆GRxn < 0 kJoule.gmol-1 Favorable 0 < ∆GRxn < 50 kJoule.gmol-1 Posiblemente favorable ∆GRxn > 50 kJoule.gmol-1 Desfavorable Luego, en general: Ka a i i i o exp(GRxn / RT ) Ka f (T, estado de agregación, vi y estado estándar) (1.20) Debe tenerse especial cuidado con la funcionalidad de Ka para poder diferenciar su signicado físico de su valor numérico, ya que éste servirá más adelante para cuanticar, por ejemplo, el valor de la conversión de una mezcla en equilibrio. Para analizar la inuencia de los cambios de temperatura y presión sobre la energía libre de Gibbs, se partirá de la denición de esta última. La energía libre de Gibbs, en función de la entalpía y la entropía se dene como: G H T S (1.21) Como se estableció anteriormente, la expresión generalizada para calcular el cambio entálpico a T y P es: dH CpdT T dP T P (1.22) De forma similar, la expresión generalizada para la entropía a T y P es: dS Cp dT dP T T P (1.23) 13 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS El primer término de la ecuación anterior tiene en cuenta la dependencia de la entropía con la temperatura. El segundo término representa la entropía residual. Reemplazando las ecuaciones (1.22) y (1.23) en la ecuación (1.21) se obtiene la funcionalidad de la energía libre de Gibbs con la temperatura y la presión: P G G o RT Z 1 Po dP P (1.24) donde Z es el factor de compresibilidad. Utilizando una ecuación de estado cúbica general del tipo presentado en la ecuación (1.10) para evaluar la integral en la ecuación (1.24) se obtiene: 2Z u u 2 4w 12 B dP RTA RT Z 1 RT Z 1 RT ln Z B ln 1 1 2 P Po u 2 4w B 2Z u u 2 4w 2 B P (1.25) Donde A=aP/(RT)2, y B=bP/(RT). Aplicando la ecuación (1.25) a, por ejemplo, el caso de la ecuación de estado de Peng-Robinson, donde u = 2 y w = -1, la expresión para el cambio de la energía libre de Gibbs en función de la temperatura y la presion queda: RTA Z 1 2 B GRxn ,T , P GRxn ,T ,1 atm i RT Z 1 RT ln Z B ln B 8 Z 1 2 B i (1.26) La variación de la energía libre de Gibbs con la temperatura y la presión para la reacción de formación de amoníaco, utilizando la ecuación (1.26), se presenta en la Figura 1.2. De la Figura 1.2 se hace evidente la necesidad que tiene el proceso de formación de amoníaco de operar a altas presiones. Por ejemplo, la temperatura queda restringida a valores inferiores a 800 K cuando la presión del sistema es de 304 bar. 14 CAPÍTULO 1 - CALOR DE REACCIÓN Y FACTIBILIDAD Figura 1.2. Inuencia de la temperatura y la presión sobre la energía libre de Gibbs para la formación de amoníaco (se utilizó la ecuación de estado de Peng-Robinson) BIBLIOGRAFÍA Belore, L.A. (2003): Transport Phenomena for Chemical Reactor Design. New Jersey: John Wiley & Sons. Marroquin de la Rosa, J.O.; Laredo Sánchez, G.C.; Viveros García, T. & Ochoa Tapia, J.A. (2006): “CEoS Aid in Evaluation of Enthalpy of Reaction”. En: Chem. Eng. Proc., 45(7), 559 – 567. Poling, B.E.; Prausnitz, J.M. & O’Connell J.P. (2001): The Properties of Gases and Liquids (5th Ed.). New York: McGraw Hill. 15 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Rase, H.F. (1997): Chemical Reactor Design for Process Plants. Vol I: Principles and Fundamentals. New Jersey: John Wiley & Sons. Sandler, S.I. (2006): Chemical, Biochemical and Thermodynamics. New Jersey: John Wiley & Sons. Engineering Yaws, C.L. & Chiang, P.Y. (1988a): “Enthalpy of Formation for 700 Major Organic Compounds”. En: Chem. Eng., 1(Sep.), 26 – 29. Yaws, C.L. & Chiang, P.Y. (1988b): “Find Favourable Reactions Faster”. En: Hydroc. Proc., 67(11), 81 – 84. 16 CAPÍTULO 2 - ¿CÓMO APROVECHAR MEJOR LOS BALANCES DE UN SISTEMA REACCIONANTE? 2 ¿CŘĒĔ ĆĕėĔěĊĈčĆė ĒĊďĔė đĔĘ ćĆđĆēĈĊĘ ĒĔđĆėĊĘ ĉĊ Ěē ĘĎĘęĊĒĆ ėĊĆĈĈĎĔēĆēęĊ? INTRODUCCIÓN Al analizar un sistema reaccionante es habitual recurrir a diferentes aproximaciones tales como la termodinámica (a partir de energías libres de reacción), la cinética (involucrando velocidades de reacción directas e inversas) y los balances de materia (basados en conversiones o en coordenadas de reacción - grado de avance). Sin embargo, la solución de problemas que involucran múltiples reacciones (tales como los relacionados con la química atmosférica y la combustión) puede ser relativamente compleja debido a la necesidad de calcular diferentes coordenadas de reacción (una para cada reacción independiente), las cuales a su vez pueden diferir en varios ordenes de magnitud. En tal sentido el acotamiento de los valores de estas variables a una región en la cual se encuentre su solución podría presentar enormes ventajas, sobre todo en sistemas que además de involucrar múltiples reacciones químicas, incluyan el reactor donde se llevan a cabo y la planta química como un todo (problemas de optimización). Este capítulo presenta elementos adicionales para un mejor aprovechamiento y entendimiento de los balances molares. Este se ilustra con dos ejemplos que permiten además su solución gráca. 17 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 2.1. BALANCE MOLAR PARA UN SISTEMA CON UNA REACCIÓN INDEPENDIENTE Las cantidades molares que reaccionan en un sistema cerrado pueden ser descritas según la ecuación estequiométrica: 0 1 R1 2 R2 k Rk (2.1) y ellas son función de la coordenada de reacción según la expresión: dni i d (2.2) ni nio i donde nio y vi corresponden al número de moles del componente i en el estado inicial (ξ = 0) y a su coeciente estequiométrico, respectivamente. La coordenada de reacción ( ξ ) está denida según la ecuación: ni nio (2.3) i Luego, las fracciones molares de los diferentes componentes son también función de ξ como lo describen las siguientes expresiones: xi ni k n j j 1 donde: k n j j 1 k n j 1 o j k nio i n j 1 j o j k j n j 1 o j (2.4) (2.5) El término de la sumatoria incluye todos los componentes del sistema, incluso los inertes, y Δν = Σνj corresponde al cambio en el número de moles debido a la reacción química. Adicionalmente, se establece el requisito: nio i 0 18 (2.6) CAPÍTULO 2 - ¿CÓMO APROVECHAR MEJOR LOS BALANCES DE UN SISTEMA REACCIONANTE? que describe el intervalo en el cual la coordenada de reacción varía: [ξmin , ξmax]. Si se analiza detenidamente la ecuación (2.6) es posible concluir que este requisito implica que si la reacción tiene lugar de izquierda a derecha, ξmax está limitado por las cantidades iniciales del reactivo límite; pero si la reacción tiene lugar de derecha a izquierda ξmin está limitado por la cantidad inicial de producto! El siguiente ejemplo muestra la utilidad de las expresiones presentadas. EJEMPLO 2.1. Balances molares en un sistema gaseoso homogéneo. La reacción de formación de amoníaco a partir de nitrógeno e hidrógeno está representada por la ecuación: N 2 3H 2 2 NH 3 Determínese los valores de ξmax y ξmin para los casos que se presentan en la Tabla 2.1, para cada uno de los cuales se han utilizado diferentes cantidades iniciales de las sustancias participantes en la reacción. Tabla 2.1. Condiciones iniciales para cuatro casos del ejemplo 2.1 Número de moles iniciales, nio Sustancia Caso A Caso B Caso C Caso D H2(g) 3,0 3,0 3,0 3,0 N2(g) 1,0 1,0 3,0 10,0 NH3(g) 0,0 1,0 0,0 0,0 Ar(g) 0,0 2,0 0,0 0,0 Los balances molares en función del grado de avance de la reacción se resumen en la Tabla 2.2 (Tabla estequiométrica). 19 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Tabla 2.2. Balance molar o tabla estequiométrica para el ejemplo 2.1 Sustancia H2(g) νi -3 nio(ξ = 0) n1o ni(ξ) xi(ξ) n1o- 3ξ n1o 3 n oj 2 N2(g) -1 n2o n2o- ξ n2o noj 2 NH3(g) +2 n3 n3 + 2ξ n1o 2 n oj 2 n4o n oj 2 Ar(g) 0 o o n4o n4o n n j 0 j 2 El algoritmo para determinar los valores de ξmax y ξmin consiste en los siguientes pasos: • Determinar el reactivo límite: Para todos los cuatro casos, corresponde al hidrógeno. • Determinar para el reactivo límite el valor de la relación nio/ νi. Este valor corresponde al límite máximo de la coordenada de reacción. En este caso ξmax = n1o/ 3. • El valor de ξmin se calcula con base en la cantidad inicial de producto (que no está en exceso, podría denirse como el producto limite). En este caso solo se tiene un producto: NH3, y se obtiene que: ξmin = -n3o/ 2. Entonces, para los cuatro casos propuestos en la Tabla 2.1 se tiene que: 20 CAPÍTULO 2 - ¿CÓMO APROVECHAR MEJOR LOS BALANCES DE UN SISTEMA REACCIONANTE? Tabla 2.3. Intervalo de cambio de la coordenada de reacción Caso A Caso B Caso C Caso D ξmin ξmax 0,00 -0,50 0,00 0,00 1,00 1,00 1,00 1,00 Con base en estos valores es posible determinar la dependencia del número de moles y la fracción molar de cada componente en función del grado de avance, en el intervalo observado en la Tabla 2.3, utilizando las formulas determinadas en la Tabla 2.2 (columnas 4 y 5). Los resultados se presentan en la Figura 2.1 para los cuatro casos. De los resultamos presentados en la Figura 2.1 se puede decir que: • En los casos A y C, la cantidad de gas inerte permanece estable a pesar del aumento de ξ. • En el caso B, la fracción molar del gas inerte aumenta con el incremento de ξ debido a la disminución del número de moles en el sistema. • En general se puede argumentar que el aumento de ξ (transformación de reactivos en productos) origina la disminución de las fracciones molares de los reactivos y el aumento de las fracciones molares de los productos. Sin embargo, en el caso en que se tienen tres moles iniciales de N2 (caso C), su fracción molar no cambia; en el caso de un gran exceso (caso D), la fracción molar aumenta a pesar de que la cantidad de N2 en el sistema disminuye (?). ¡Aparente paradoja! La fracción molar de un componente aumenta simultáneamente con la disminución de su cantidad. Aparentemente existe una grave discrepancia entre el anterior enunciado y lo expresado por el principio de Le Chatelier. Sin embargo, diferentes publicaciones demuestran que este principio no es universalmente válido y que existen varias excepciones. Liu et al. (1996) y Corti y Franses (2003) son dos trabajos que precisan las excepciones al principio de Le Chatelier mediante el estudio de la reacción de síntesis de amoníaco. 21 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 2.1. Representación del balance molar que describe la variación del grado de avance ξ para cada sustancia en cada caso del ejemplo 2.1 22 CAPÍTULO 2 - ¿CÓMO APROVECHAR MEJOR LOS BALANCES DE UN SISTEMA REACCIONANTE? Para tratar de entender este comportamiento “paradójico”, es necesario analizar la dependencia de la fracción molar con el grado de avance xi (ξ). Una forma de hacerlo es derivando la ecuación (2.4) con respecto al grado de avance para obtener que: 0 0 dxi i n j j ni i 2 d n 0j i (2.7) La cual puede reducirse a: dxi i n 0j ni0 2 d n 0j i (2.8) Analizando los términos del numerador y denominador es evidente que es necesario considerar dos tipos de reacciones: Tipo I (Δν ≥ 0): El valor del primer componente del numerador en la ecuación (2.8) es positivo mientras el segundo es negativo. Su diferencia será entonces negativa. En este caso, la fracción molar de la sustancia i disminuye con el aumento de la coordenada de reacción. Como resultado de la transformación de los reactivos en productos es posible observar una disminución de la cantidad de reactivos y su fracción molar. Tipo II (Δν < 0): El signo del numerador cambia dependiendo del componente. En el caso en que el valor de la derivada de la ecuación (2.8) sea igual a 0, del numerador se tiene que: i n0j ni0 0 (2.9) Esta expresión puede ser reorganizada de forma que: i 0 i n caso C. n0j (2.10) Luego, su fracción molar será constante tal como se observó en el 23 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Sin embargo, si el valor de la derivada de la ecuación (2.8) es mayor a 0: i n0j ni0 0 y reorganizando: i 0 i n n0j (2.11) (2.12) El valor de la derivada de la ecuación (2.8) será positivo y, adicional a la transformación del reactivo i en producto, su fracción molar aumentará como se observa en el caso D. Finalmente, en el caso que el valor de la derivada de la ecuación (2.8) es menor a 0: i n0j ni0 0 (2.13) y después de reorganizar: i 0 i n n0j (2.14) es posible observar que el valor de la derivada de la ecuación (2.8) será negativo y su fracción molar disminuirá con la transformación de reactivo en producto. 2.2. BALANCE MOLAR PARA UN SISTEMA CON MÁS DE UNA REACCIÓN INDEPENDIENNTE Considérese ahora un sistema que consiste de “k” componentes y en el cual tienen lugar “q” reacciones independientes que pueden describirse como: k 0 ij Ri i 1 24 j 1, 2, q (2.15) CAPÍTULO 2 - ¿CÓMO APROVECHAR MEJOR LOS BALANCES DE UN SISTEMA REACCIONANTE? donde νij corresponde al coeciente estequiométrico del componente “i” en la reacción “j”. La cantidad del componente “i” en el sistema puede expresarse en función de los grados de avance de las reacciones en las cuales participa mediante la expresión: q ni 1 , , q n ij j 0 i j 1 (2.16) en la cual el término de sumatoria incluye todas las reacciones independientes. De manera análoga a lo expuesto en la sección anterior, la fracción molar de cada elemento en el sistema puede calcularse como: q xi 1 , , q ni0 ij j k j 1 q k i 1 i 1 j 1 ni0 ij j (2.17) Como conclusión, de estas expresiones es posible decir que la cantidad y la fracción molar de cada componente “i” son función del grado de avance de todas las reacciones presentes en el sistema. Los valores extremos de la coordenada de reacción [ξj,min , ξj,max] pueden describirse por la condición: q ni 1 , , q ni0 ij j 0 j 1 (2.18) De acuerdo con esta condición, los valores limites [ξj,min , ξj,max] de una reacción “j” no será un valor numérico (como en el caso los sistemas con una sola reacción). En cambio, ellos estarán relacionados por funciones. Esto se mostrará en el siguiente ejemplo. 25 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS EJEMPLO 2.2. Balances molares en un sistema con dos diferentes reacciones Analícese ahora la formación de H2 y CO mediante la reacción de reformado de metano con vapor de agua en presencia de un catalizador. En este sistema, dos reacciones independientes son posibles: CH 4 H 2O CO 3H 2 (e2.1) CO H 2O CO2 H 2 (e2.2) Determínese el intervalo de cambio de los grados de avance de cada reacción según las condiciones iniciales que se presentan en la Tabla 2.4. Tabla 2.4. Condiciones iniciales para el ejemplo 2.2 Sustancia H2(g) Número de moles iniciales, nio 0,0 CO(g) 0,0 CO2(g) 0,0 H2O(g) 1,0 CH4(g) 1,0 El balance molar para este ejemplo queda como se muestra en la Tabla 2.5. Tabla 2.5. Balance molar o tabla estequiométrica para el ejemplo 2.2 Sustancia H2(g) nio 0,0 vi(e2.1) 3 vi(e2.2) 1 n(ξi) 3ξ1 + ξ2 límites ξ2 ≥ - 3ξ1 CO(g) 0,0 1 -1 ξ1 - ξ2 ξ1 ≤ ξ2 CO2(g) 0,0 0 1 ξ2 ξ2 ≥ 0 H2O(g) 1,0 -1 -1 1 - ξ1 - ξ2 ξ2 ≤ 1 - ξ1 CH4(g) 1,0 -1 0 1 - ξ1 ξ1 ≤ 1 26 CAPÍTULO 2 - ¿CÓMO APROVECHAR MEJOR LOS BALANCES DE UN SISTEMA REACCIONANTE? La condición de la ecuación (2.18) tiene, en este caso, cinco formas diferentes como se presenta en la Tabla 2.5 (columna “límites”). Estas ecuaciones pueden representarse como se muestra en la Figura 2.2. Figura 2.2. Representación de los balances molares que describe la variación de los grados de avance ξj para sustancias en cada caso del ejemplo 2.2 Dentro de la Figura 2.2 se encuentra demarcado el lugar geométrico que contiene los valores de ξ1 y ξ2 que cumplen con las condiciones de la ecuación (2.18) para el ejemplo 2.2. Este corresponde al triángulo de límites A[0,0;0,0]; B[0,5;0,5] y C[1,0;0,0]. Luego, la solución del problema del equilibrio químico aquí planteado se encuentra en esa “región permisible” como lo puede vericar el lector. Así mismo, puede comprobarse fácilmente que un sistema que consta inicialmente solo de CO e H2, la reacción (e2.2) no ocurre. ¿Qué condiciones se requieren para que la reacción (e2.1) no tenga lugar en el sistema reaccionante? ¿Qué condiciones se requieren para que ni la reacción (e2.1) ni la (e2.2) tengan lugar en el sistema reaccionante? 27 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS BIBLIOGRAFÍA Corti, D.S. & Franses, E.I. (2003): “Exceptions to The Le Chatelier Principle”. En: Chem. Eng. Edu., 37(4), 290 - 295. Liu, Z.K.; Ågren, J. & Hillert, M. (1996): “Application of The Le Chatelier Principle on Gas Reactions”. En: Fluid Phase Equilibria, 121(1-2), 167-177. 28 CAPÍTULO 3 - ALGORITMOS PARA EL CÁLCULO DE COMPOSICIONES DE EQUILIBRIO PARA SISTEMAS CON MÚLTIPLES REACCIONES 3 ALGORITMOS PARA EL CÁLCULO DE COMPOSICIONES DE EQUILIBRIO PARA SISTEMAS CON MÚLTIPLES REACCIONES INTRODUCCIÓN El análisis del equilibrio químico de un sistema en el que intervienen múltiples reacciones requiere la solución simultánea de tantas ecuaciones como reacciones linealmente independientes. Estos cálculos, realizados manualmente, pueden resultar tediosos y complejos debido a la no linealidad de las ecuaciones resultantes. En general, para determinar las raíces que satisfacen estas ecuaciones, es necesario utilizar iterativamente algún método numérico con la ayuda de un programa en computador. En esta sección se describen algunas técnicas o algoritmos que pueden emplearse en la solución de este tipo de problemas. Los métodos analizados se presentan en dos grupos: los métodos de minimización de la energía libre de Gibbs y el método de la constante de equilibrio. 3.1. MÉTODO DE MINIMIZACIÓN DE LA ENERGÍA LIBRE DE GIBBS En el equilibrio la energía total de Gibbs del sistema tiene su valor mínimo. La energía libre de Gibbs total de un sistema de N componentes en una sola fase, a presión y temperatura constante, puede escribirse como sigue: 29 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS N Gtot ni i T , P, yi (3.1) i 1 El problema es encontrar los valores del número de moles ni que minimizan a Gtot, para T y P especicadas, los cuales están sujetos a restricciones de los balances de materia. Esto se puede lograr mediante dos enfoques diferentes, cuya aplicación depende de la información inicial con la que se cuente. 3.1.1. ENFOQUE ESTEQUIOMÉTRICO Se puede resolver el problema de determinar las composiciones en el equilibrio de una mezcla reaccionante a una presión y temperatura dadas, minimizando la energía libre de Gibbs total de la mezcla haciendo uso de la estequiometria de las j reacciones (para calcularse como función de los grados de avance (ξj) o conversiones (Xj)). Este valor mínimo puede ser localizado por implementación de una técnica de optimización (localización de puntos jos), como lo es el método de Newton-Gauss. Para ello recuérdese que la energía libre de Gibbs total de un sistema de componentes múltiples está denida por la ecuación (3.1), donde μi, yi, y ni son el potencial químico, la fracción molar y el número de moles del componente i, respectivamente. Las diferentes relaciones entre el potencial químico están dadas por la ecuación: i Gi T , P RT ln ai (3.2) donde ai es la actividad del componente i. Reemplazando (3.2) en (3.1) y recordando como se dene la actividad en un sistema gaseoso se obtiene: N N ˆ T , P, yi Pyi Gtot ni Gi T , P RT ni ln i i T , P P o i 1 i 1 (3.3) La energía libre de Gibbs de componente puro en fase gaseosa se puede escribir como: 30 CAPÍTULO 3 - ALGORITMOS PARA EL CÁLCULO DE COMPOSICIONES DE EQUILIBRIO PARA SISTEMAS CON MÚLTIPLES REACCIONES Gi T , P RT G ofi o P H fi 1 1 Ln RT R T T P (3.4) T T Cp 1 1 dT Ln i (T , P ) CpdT RT T R T T Donde ΔHº y ΔGº son las entalpías y energías libres de formación estándar, y R es la constante universal de los gases. 3.1.1.1. ALGORITMO DE CÁLCULO 1. Gtot de la mezcla 1.1. Usando las propiedades sicoquímicas de las sustancias puras, se emplea la ecuación de estado para calcular los parámetros necesarios, obteniendo los valores de las energías libres de Gibbs de los componentes puros, a la presión y temperatura requerida. 1.2. Realizar una tabla estequiométrica para la reacción en cuestión, empleándola para conocer los números de moles y las correspondientes fracciones molares de cada sustancia en función del grado de avance o la conversión. 1.3. Determinar el intervalo de valores que tomará la variable de progreso y jar un valor en ese intervalo (estimado inicial). Aquí puede ser especialmente útil la metodología desarrollada en el Capítulo 2. Emplear la tabla estequiométrica para calcular el número de moles y las fracciones molares, correspondientes al valor seleccionado. 1.4. Calcular los coecientes de fugacidad, a las fracciones molares calculadas en el paso anterior. Llevar estos resultados a (3.3). 2. Minimización El método de Newton–Gauss, presenta una fórmula de iteración para estimar los puntos jos (máximos o mínimos) de una F(X). 31 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS k 1 k X X F X k F X k En este caso X será la variable de progreso de la reacción y F(X), F’(X), F’’(X) son la energía libre de Gibbs total de la mezcla reaccionante, su primera y segunda derivadas respectivamente. 2.1. Escoja un valor para la variable de progreso de la reacción inicial X0. Con este valor calcule F(X), F’(X) y F’’(X) como se ha descrito en el algoritmo anterior. 2.2. Con la fórmula de iteración, estímese un nuevo valor de la variable de progreso de la reacción X1. 2.3. Fije un valor máximo para el valor de F’(X) y verique si ésta es menor o igual que dicho máximo (conocido como tolerancia). 2.4. Si F’(X) es menor que la tolerancia haga Xequilibrio= X1 y termine el proceso. Si no, haga X0 = X1 y regrese al paso 2.1. EJEMPLO 3.1. Oxidación del dióxido de azufre Determínese la conversión (X) en el equilibrio aplicando el enfoque estequiométrico, en un intervalo de temperatura de 650 - 1200 K y un intervalo de presión de 1 - 80 atm, para una alimentación de 0,092 gmol de SO2, 0,127 gmol de O2 y 0,781 gmol de N2 para la reacción: SO2 1 2 O2 SO3 Solución En las Tablas 3.1 y 3.2 se presentan los balances de materia en función de la conversión y las energías libres de Gibbs y entalpías de formación en el estado estándar respectivamente. 32 CAPÍTULO 3 - ALGORITMOS PARA EL CÁLCULO DE COMPOSICIONES DE EQUILIBRIO PARA SISTEMAS CON MÚLTIPLES REACCIONES Tabla 3.1. Balance molar o tabla estequiométrica en función de la conversión para el ejemplo 3.1 Ec. Sustancia nio (gmol) ni(X) yi(X) 1 2 3 4 SO2(g) O2(g) SO3(g) N2(g) 0,092 0,127 0,0 0,781 n1 = 0,092(1 – X) n2 = 0,092(1,3804 - 0,5X) n3 =0,092(0,0 + X) n4 = 0,781 y1 = n1/nT y2 = n2/nT y3 = n3/nT y4 = n4/nT Totales nTo = 1 nT = 1 – 0,046X Tabla 3.2. Energía libre de Gibbs y entalpía estándar de formación a To = 298,15 K y Po = 1 atm Sustancia SO2 O2 SO3 N2 ∆Gof (J/gmol) -3,004×105 0,000 -3,713×105 0,000 ∆Hof (J/gmol) -2,971×105 0,000 -3,960×105 0,000 Reemplazando los valores de las Tablas 3.1 y 3.2 en las ecuaciones (3.3) y (3.4) para el cálculo de la energía libre de Gibbs de cada uno de los componentes de la mezcla y la energía libre de Gibbs total respectivamente, se obtiene: SO2: O2: 5 3, 004 105 P 2,97110 1 1 Ln RT R P T T G1 T , P RT T T 1 Cp dT 1 Cp1 dT Ln (T , P) 1 RT T 1 R T T 0, 0 P 0, 0 1 1 RT Ln P R T T G2 T , P RT T T 1 Cp dT 1 Cp2 dT Ln (T , P ) 2 RT T 2 R T T 33 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS SO3: N 2: 5 3, 713 105 P 3,960 10 1 1 Ln T T RT R P G3 T , P RT T T 1 Cp dT 1 Cp3 dT Ln (T , P ) 3 RT T 3 R T T 0, 0 P 0, 0 1 1 RT Ln P R T T G4 T , P RT T T 1 Cp dT 1 Cp4 dT Ln (T , P ) 4 RT T 4 R T T ˆ T , P, y1 Py1 Gtot n1G1 n2G2 n3G3 n4G4 RT [n1 ln 1 1 T , P P o ˆ T , P, y2 Py2 ˆ3 T , P, y3 Py3 ˆ4 T , P, y4 Py4 ln ln n n n2 ln 2 ] 2 T , P P o 3 3 T , P P o 4 4 T , P P o De la implementación de los algoritmos 1 y 2 y utilizando la información de la Tabla 3.1, para expresar las fracciones molares en función de la conversión, se obtiene la Figura 3.1. Figura 3.1. Conversión de SO2 en el equilibrio en función de la presión y la temperatura 34 CAPÍTULO 3 - ALGORITMOS PARA EL CÁLCULO DE COMPOSICIONES DE EQUILIBRIO PARA SISTEMAS CON MÚLTIPLES REACCIONES Compare estos resultados con los valores de presión y temperatura utilizados en el proceso industrial, ¿Qué conclusiones se pueden obtener? 3.1.2. ENFOQUE NO ESTEQUIOMÉTRICO Este método utiliza los balances de materia elementales y no los balances por componente, por lo que no es necesario conocer la estequiometría de la reacción o de las reacciones que ocurren en el sistema bajo estudio. Es necesario entonces conocer las composiciones iniciales del sistema, la presión, temperatura y las especies involucradas en las reacciones. La solución a este problema se basa en el método de los multiplicadores indeterminados de Lagrange (Zeleznik y Gordon, 1968). El método de los multiplicadores de Lagrange se basa en que las variables independientes de la función a minimizar se encuentran relacionadas por una o más ecuaciones, las cuales son llamadas las funciones de restricción, que condicionan la búsqueda del mínimo solo en la región de valores de las variables donde simultáneamente satisfacen a la función y a las restricciones. Para encontrar el mínimo de la función, sujeta a las restricciones, se modica ésta (la función modicada equivale a la función original) y se obtiene una nueva función en la cual se emplean las restricciones, de tal manera que el valor de la función no cambie y, por lo tanto, el valor de las variables cumplen con un mínimo; aunque las derivadas de la nueva función modicada sí dieren de las derivadas de la función original. Como ya se denió, la función a minimizar es la ecuación dada en (3.1), y los balances de materia en el sistema reaccionante, que son condiciones que deben cumplirse siempre, se pueden plantear como una restricción (se supone que el sistema es cerrado, por lo tanto la masa total debe permanecer constante y las variaciones de las moles de cada componente, deben corresponder a un cambio químico). Así las restricciones serán los balances elementales (balances por elementos linealmente independientes). De los balances de materia elementales, se puede establecer la composición inicial del sistema: C N eo nio ie (3.5) i 1 35 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS donde Neo, son las moles iniciales del elemento e, nio son las moles iniciales de la sustancia i, y αie, es el coeciente atómico del elemento e en la sustancia i. Esta relación es para los C elementos que intervienen en el sistema. Reorganizando la ecuación (3.5), en cualquier instante debe cumplirse que: C n io i 1 ie N eo 0 (3.6) Las C ecuaciones anteriores son las restricciones a implementar en el método. Para modicar la función original, se incluyen una serie de nuevas variables llamadas los multiplicadores de Lagrange: C k k C F , e e 1 Gtot e ni ie N eo ni i 1 e 1 i 1 (3.7) La función entonces a minimizar es la ecuación (3.7), con las moles de cada sustancia y los multiplicadores de Lagrange, como las variables independientes sobre las cuales se minimiza. El punto mínimo de una función F, debe cumplir dos condiciones: 1- La primera derivada parcial de F con respecto a todas las variables independientes debe ser igual a cero (condición necesaria). 2- La matriz Hessiana (segunda derivada de la función F con respecto a las variables independientes) evaluada en el punto mínimo debe ser positiva denida. Es decir, todos los valores propios deben ser reales positivos mayores que cero (condición necesaria). A nivel conceptual, una reacción química estará en equilibrio estable cuando la energía libre de Gibbs se encuentre en un mínimo global, pero si el mínimo es local, el equilibrio será inestable. Las dos condiciones anteriores no dicen si el mínimo es global o local, por lo que es necesario establecer un método para hallar todos los puntos jos de la función, y así seleccionar el mínimo global. Aplicando la condición (1) de minimización a la función F, se obtienen las siguientes expresiones: 36 CAPÍTULO 3 - ALGORITMOS PARA EL CÁLCULO DE COMPOSICIONES DE EQUILIBRIO PARA SISTEMAS CON MÚLTIPLES REACCIONES C F Gtot e ie 0 i 1,...C ni T , P ,n ji ,e ni T , P ,n ji e 1 F e T , P ,n j ,ve k n i 1 i ie N eo 0 e 1,...k (3.8a) (3.8b) De la ecuación (3.7), se tiene: Gtot i Gio RT ln aˆi n i T , P ,n ji (3.9) De lo anterior, hay (k+C) ecuaciones no lineales simultáneas, con k moles de cada sustancia y C multiplicadores de Lagrange como las variables independientes. El método numérico empleado para solucionar el sistema de ecuaciones resultante puede ser el de Newton-Raphson. 3.1.2.1. ALGORITMO DE CÁLCULO La información necesaria al inicio es: 1. • Todas las especies presentes en el sistema (reactivos, productos e inertes) y su fase. • Condiciones de referencia (presión y temperatura). • Condiciones de presión y temperatura a la cual se realizará el cálculo. • Moles iniciales de cada sustancia. Se estima un valor inicial de las variables independientes del sistema de ecuaciones (k número de moles en el equilibrio y C multiplicadores de Lagrange). Con esto se calculan las fracciones molares de cada sustancia. 37 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 2. Con las moles iniciales de cada sustancia, y los coecientes atómicos de cada elemento (moles del elemento e en el compuesto i), se emplea la ecuación (3.2), para calcular las moles iniciales totales por elemento. 3. Se utiliza la ecuación (3.8b) para plantear C funciones objetivo. 4. Con los modelos termodinámicos adecuados, se computan las k funciones objetivos restantes, mediante el uso de las ecuaciones (3.8a), a la T y P especicadas y las fracciones molares determinadas en el paso 1. 5. Se verica el criterio de convergencia. Si se cumple, el valor de las variables independientes utilizadas en los pasos 3 y 4, es una posible solución al sistema; seguir al paso 8. En caso contrario, seguir al paso siguiente. 6. Mediante el uso de una aproximación numérica, se calcula la matriz Jacobiana del sistema de ecuaciones (3.8a) y (3.8b). 7. Utilizando la fórmula de iteración del método de NewtonRaphson multivariable, se estima un nuevo valor de las variables independientes (k número de moles en el equilibrio y C multiplicadores de Lagrange). Se calculan las fracciones molares y se regresa al paso 3. 8. Se calcula la Hessiana de la función original Gtot, con los valores dados de la solución en (5), y se verica si es positiva denida, en este caso se tiene un mínimo global. En caso contrario, se varía el estimado inicial de las variables independientes aleatoriamente, y se regresa al paso (3). El método de Newton-Raphson multivariable empleado en solucionar sistemas de N ecuaciones no lineales simultáneas, con N variables independientes, como el caso presentado en (3.8a) y (3.8b), se puede formular como: 1 X K X K J 1 X K F X K 38 (3.10) CAPÍTULO 3 - ALGORITMOS PARA EL CÁLCULO DE COMPOSICIONES DE EQUILIBRIO PARA SISTEMAS CON MÚLTIPLES REACCIONES El criterio de convergencia puede ser de diferentes formas, como que la norma de las funciones objetivo o la norma de la diferencia entre iteraciones sucesivas sea menor que una tolerancia, tal como se muestra a continuación: X K 1 X k tol (3.11) EJEMPLO 3.2. Composición de equilibrio para reacciones químicas simultáneas y no especicadas. Dada una mezcla inicial con 1 gmol de CO y 1 gmol de H2, determínese la composición de equilibrio de un sistema que a condiciones nales consta de CO, H2, CO2, CH4 y H2O a 900 K y 1 atmósfera. Solución A partir de las condiciones iniciales es posible establecer que 1 gmol de CO contiene 1 g.átomo de C y otro de O; y 1 gmol de H2 contiene 2 g.átomos de H. Sea A el número de gramos átomo del elemento k presentes en el sistema. Por consiguiente: NCo = 1, NOo = 1 y NHo = 2. Consecuentemente, si αi,k es el número de gramos átomo del elemento k por gramo mol de la sustancia i, se puede establecer que: Tabla 3.3. Número de gramos átomos de cada elemento por g.mol de cada sustancia I αi,C αi,O αi,H CO CO2 CH4 H2 H2O 1 1 1 0 0 1 2 0 0 1 0 0 4 2 2 Luego debe determinarse el valor de la energía libre de Gibbs de cada compuesto a la temperatura y presión del sistema (ΔGof,i a 900 K y 1 atm). A partir de la base de datos reportada en el libro de Poling et al. (2001), 39 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS se obtienen los siguientes valores: para el CO, -45744 cal.gmol-1; para el H2, 0 cal.gmol-1; para el CO2, -94596 cal.gmol-1; para el CH4, -2029 cal.gmol-1 y para el H2O = -47352 cal.gmol-1. De las ecuaciones (3.6) y (3.8a) y la información que se acaba de determinar, se obtiene el sistema a minimizar. Para cada sustancia i, se obtiene una ecuación de la forma: y P 0 i 1,...C G of ,i RT ln i i e ie P o e Luego, las cinco ecuaciones son: Para el CO: 0 -45744 RT ln yCO RT ln CO C O Para el CO2: 0 -94596 RT ln yCO RT ln CO C 2O Para el CH4: 0 2029 RT ln yCH RT ln CH C 4H Para el H2: 2 2 4 4 RT ln yH 2 RT ln H 2 2H 0 0 Para el H2O: -47352 RT ln yH O RT ln H O 2H O 2 2 De aquí se obtienen cinco ecuaciones con ocho incógnitas. Luego, es necesario denir tres ecuaciones adicionales. Estas son los balances de materia para cada elemento, expresados en función de las fracciones molares como lo expresa la ecuación (3.8b): y i i ie N eo / nTo Luego, para cada elemento se obtiene Para el C: yCO yCO2 yH 2O 1/ nTo Para el O: yCO 2 yCO2 yH 2O 1/ nTo 40 CAPÍTULO 3 - ALGORITMOS PARA EL CÁLCULO DE COMPOSICIONES DE EQUILIBRIO PARA SISTEMAS CON MÚLTIPLES REACCIONES Para el H: 4 yCH 4 2 yH 2 2 yH 2O 2 / nTo Se resuelve el sistema de ecuaciones mediante el método detallado anteriormente, teniendo en cuenta que la sumatoria de las fracciones molares debe ser igual a uno. Los valores de la fracciones en el equilibrio obtenidos son: yCO2 = 0,126; yCO = 0,374; yCH 4 = 0,168; yH 2 = 0,29; yH 2O = 0,042 La variación de las fracciones en el equilibrio en función de la temperatura se presenta en la Figura 3.2. Figura 3.2. Composición en el equilibrio de los productos obtenidos para el ejemplo 3.2 en función de la temperatura En el intervalo analizado, la tendencia de las curvas (monótonas crecientes o decrecientes, según el caso) de las fracciones en el equilibrio obtenidas para cada componente indica que el valor límite de los valores de los grados de avance no se ha alcanzado. Este límite podría alcanzarse a temperaturas mayores. ¿Cuál es ese valor límite y a qué temperatura se alcanza? 41 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 3.2. MÉTODO DE LA CONSTANTE DE EQUILIBRIO Desde las primeras etapas en el desarrollo de la historia de los cálculos del equilibrio, se hizo aparente que el sistema de ecuaciones podría solucionarse mediante un método de substituciones sucesivas. Meissner et al. (1969) establecieron el método de “los reactores en serie”, para calcular la composición del equilibrio de un sistema de reacciones múltiples, de manera tal que cada una de las reacciones participantes se analice por separado. El método se basa en el hecho que cualquier sistema de reacciones múltiples, homogéneas o heterogéneas, puede reducirse a una serie de reacciones individuales que ocurren separadamente (esto gracias a la segunda ley de la termodinámica). El método de cálculo de la composición de equilibrio de una reacción simple, a partir de la constante de equilibrio, puede ser extendido para el caso en el que R reacciones independientes ocurren bajo el siguiente esquema. La mezcla reaccionante bajo estudio se introduce al primero de una serie de reactores isotérmicos. Cada uno de los reactores “contiene un catalizador selectivo” el cual permite que solo una de las reacciones del sistema proceda hasta el equilibrio. Se numeran las secuencias de reacción como sigue, en el reactor 1 ocurre la reacción 1, en el 2 la reacción 2, en el 3 la reacción 3, así hasta que en el reactor R ocurre la reacción R (para el primer ciclo). Para el siguiente ciclo de reacción se tiene que, en el reactor R+1 ocurre la reacción 1, en el R + 2 la reacción 2, así hasta que en el reactor 2R ocurre la reacción R. El mismo ciclo de reacciones se repite en los próximos R reactores, y así sucesivamente hasta que todas las relaciones independientes de equilibrio se satisfacen simultáneamente en un intervalo de precisión pre-establecido, teniendo en cuenta que en el reactor j, todas las especies, excepto las que intervienen en la reacción j se consideran como inertes. Entonces para un grupo de R reacciones y N componentes se generaría un sistema de R ecuaciones con R incógnitas; para este caso cada reacción depende de una y solo una incógnita: grado de avance j (ξj) o conversión j (Xj). Se generarán j ecuaciones como la (3.12), las cuales se resuelven sucesivamente una después de la otra: N Fj j K e j (T , P ) a ij T , P, nij j i 1 42 vij (3.12) CAPÍTULO 3 - ALGORITMOS PARA EL CÁLCULO DE COMPOSICIONES DE EQUILIBRIO PARA SISTEMAS CON MÚLTIPLES REACCIONES Esta técnica puede ser de gran utilidad en sistemas de reacciones múltiples que dieren signicativamente en su grado de reversibilidad o cuando al menos una de ellas es prácticamente irreversible. 3.2.1. ALGORITMO DE CÁLCULO 1. Especicar condiciones de operación T, P, y nio; usando las propiedades sicoquímicas de las sustancias puras, se emplea una EOS para calcular los ∆Grxn(T, P) para cada una de las R reacciones, obteniendo con éstos, los valores de las constantes de equilibrio de las R reacciones Kej (T, P) o tomándose de datos experimentales. 2. Realizar una tabla estequiométrica para cada una de las reacciones en cuestión, empleándolas para conocer los números de moles y las correspondientes fracciones molares de cada sustancia en función del grado de avance de la reacción o la conversión. 3. Determinar el intervalo de valores que tomará la variable de progreso en la reacción j, y jar un valor en éste rango (estimado inicial ξjo). 4. Emplear la tabla estequiométrica para calcular el número de moles y las fracciones molares de la reacción j, correspondientes al valor seleccionado. 5. Calcular la actividad de los N componentes en la reacción j (teniendo en cuenta la fase de la reacción), a las fracciones molares calculadas en el paso anterior. Llevar estos resultados a (1), para así calcular Fj(ξj) y Fj’(ξj) . 6. Vericar el valor de Fj(ξj): Si Fj(ξj) es menor que una tolerancia, hacer ξjc = ξjk, y regresar al paso 3 con j = j + 1, y nijo= ni(j-1) (moles iniciales de la reacción j iguales a las moles nales de la reacción j-1) hasta que j > R y así poder ir al paso 7. Si Fj(ξj) no es menor que una tolerancia, estimar un nuevo valor de la variable de reacción por implementación de una técnica de localización de raíces como lo es el método de Newton-Raphson. 43 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS j j k 1 k F j k F ' j k y regresar al paso 3. 7. Calcular la norma del vector ξjc = [ξ1c ξ2c ξ3c… ξRc], donde c el numero del ciclo: Si la norma de ξjk es menor que una tolerancia, hacer ξjeq = Σ(ξjc) para el número total de ciclos y terminar. Si la norma de ξjk no es menor que una tolerancia, hacer j = 1 nijo= niR (moles iniciales del reactor 1 en el nuevo ciclo iguales a las moles nales de la reacción R en el ciclo anterior) y regresar al paso 3. EJEMPLO 3.3. Reacción del sulfuro de hidrógeno con óxido de azufre ¿Cuál es el grado de avance de equilibrio de un sistema que contiene 35% de H2S, 15% de SO2 y 50% de N2 a una temperatura de 1500 K y una presión de 0,8 atm?, las reacciones son las siguientes: 1 2 H2S H2 + 1 2 S2 2H 2 S + SO2 2H 2 0 + Kp (1500 K) = 0,334 3 2 S2 Kp (1500 K) = 30,20 Solución Se realizan los balances de materia por componente y por reacción (asumiendo como en el modelo que la reacción 1 solo se da en el “reactor” 1, con N2 y SO2 actuando como inertes, y la 2 en el 2, con H2O actuando como inerte), y se designan las ξj como las moles de los productos de cada proceso individual. Luego, reemplazando en la ecuación (3.6), se obtienen dos funciones objetivo de la siguiente forma. 1 i 44 F1 K e,1 pH 2 pS22 pH 2 0,334 1 12 1 1 2 0.8 1 2 0,35 1 1 12 1 1 2 CAPÍTULO 3 - ALGORITMOS PARA EL CÁLCULO DE COMPOSICIONES DE EQUILIBRIO PARA SISTEMAS CON MÚLTIPLES REACCIONES 3 ii F2 K e ,2 pH2 2O pS22 pH2 2 S pSO2 2 2 0, 097 3 2 2 0,8 30, 2 2 0,156 2 2 0,15 2 1, 097 12 2 2 3 1 2 2 1 2 Resolviendo para estas ecuaciones, por medio de la implementación del algoritmo anterior con una tolerancia de 1×10-9, y asumiendo una base de cálculo de 1 mol alimentada al “reactor 1”, se obtienen los resultados que se presentan en la Tabla 3.4. Tabla 3.4. Composición saliente de los “reactores” para el ejemplo 3.3 Ciclo Ecuación 1 Moles iniciales i gmoles ii gmoles H 2S H2 S2 SO2 H 2O N2 0,35 0,00 0,00 0,15 0,00 0,50 0,156 0,194 0,097 0,15 0 0,50 0,023 0,194 0,197 0,084 0,133 0,50 Total moles 1,00 1,097 1,131 … … 13 i gmoles ii gmoles … … … … … … 0,0636 0,0548 0,2011 0,0342 0,2316 0,5 0,0636 0,0548 0,2011 0,0342 0,2316 0,5 … 1,085 1,085 Se requiere de 13 ciclos de cálculo de dos “reactores” cada uno, para cumplir con la tolerancia especicada. Según las moles iniciales y las del equilibrio, el grado de avance en el equilibrio de las reacciones 1 y 2 son, respectivamente: ξ1 = 0,0548 y ξ2 = 0,1158. BIBLIOGRAFÍA Meissner, H.P.; Kusik, C.L. & Dalzell, W.H. (1969): “Equilibrium Composition with Multiple Reactions”. En: Ind. Eng. Chem. Fund., 8(4), 659 – 665. Poling, B.E.; Prausnitz, J.M. & O’Connell, J.P. (2001): The Properties of Gases and Liquids (5th Ed.). Ney York: McGraw Hill. Zeleznik, F.J. & Gordon, S. (1968): “Calculation of Complex Chemical Equilibria”. En: Ind. Eng. Chem., 60(6), 27-57. 45 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 46 CAPÍTULO 4 - CINÉTICA PARA EL DISEÑO DE REACTORES QUÍMICOS 4 CĎēĴęĎĈĆ ĕĆėĆ Ċđ ĉĎĘĊŕĔ ĉĊ ėĊĆĈęĔėĊĘ ĖĚŃĒĎĈĔĘ INTRODUCCIÓN La cinética de las reacciones es el estudio de las velocidades de reacción, es decir, es la determinación de cómo la velocidad de producción o desaparición de una sustancia se ve afectada por condiciones de reacción tales como temperatura, presión, catalizador y concentración de los reactantes. Es un intento por formular leyes de naturaleza física y química que correlacionen y expliquen el efecto de las condiciones de proceso sobre la velocidad, pretendiendo extrapolarlas a otras condiciones. El alcance de la cinética es muy amplio, puesto que está relacionado con la velocidad de reacciones en una renería de petróleo, la velocidad de crecimiento de microorganismos en un proceso bioquímico, la velocidad de descomposición de un material radioactivo, o la velocidad de transformación de una reacción orgánica en un equipo a presión. Independiente de la aplicación, los dos factores más importantes a ser considerados son la ley de velocidad y el camino (mecanismo) por medio del cual se da la reacción. Una vez la ley de velocidad de reacción es conocida, es posible determinar el tamaño del reactor necesario para alcanzar determinadas condiciones de operación (v.g., conversión, rendimiento). Sin embargo, el diseño del reactor es mucho más complejo, ya que por lo general se presentan simultáneamente más de una reacción y procesos físicos, tal como la difusión, pueden llegar a ser determinantes (esto es especialmente importante en las reacciones catalíticas y debe ser considerado en el estudio cinético) (Cusack, 1999). 47 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS En este capítulo se discuten inicialmente algunas generalidades de la cinética como medio para obtener una ley de velocidad. Se hace especial énfasis en el efecto de diferentes condiciones de proceso sobre los parámetros y funcionalidad de la ley de velocidad. Finalmente, se presentan dos aplicaciones. 4.1. CINÉTICA Y TERMODINÁMICA Existe una clara relación entre la cinética de las reacciones y la termodinámica. Ambas involucran el efecto que sobre los sistemas reaccionantes tienen la temperatura, la presión y la composición del sistema. Sus diferencias, sin embargo, exceden ampliamente sus similaridades. La termodinámica está relacionada con la composición del sistema después de que este se ha “detenido”, o, en otras palabras, el equilibrio que el sistema logrará en un tiempo innito. La cinética está relacionada con la composición del sistema en cualquier instante mientras se “detiene”. La termodinámica no está relacionada con el tiempo. En cinética, el tiempo es la principal variable. La termodinámica no entrega información de la naturaleza del camino a través del cual se produce la reacción, mientras la cinética estudia ese camino (mecanismo). Considérese por ejemplo que las reacciones: A BC se llevan a cabo en un reactor discontinuo. El producto deseado es B y se requiere saber la cantidad de B que puede obtenerse a unas condiciones dadas. El cálculo de las condiciones de equilibrio, por supuesto, cae en el campo de la termodinámica. Se pueden evaluar las constantes termodinámicas y de ellas encontrar que la mezcla en el equilibrio sólo contiene el 1% de B. De esta información se podría inferir que el proceso no es factible. Ahora, se podría analizar la información cinética obtenida durante el transcurso de la reacción. Esta se presenta esquemáticamente en la Figura 4.1. 48 CAPÍTULO 4 - CINÉTICA PARA EL DISEÑO DE REACTORES QUÍMICOS Figura 4.1. Variación de la concentración con el tiempo para el sistema de reacciones A BC en un reactor discontinuo Si la reacción fuera detenida en el tiempo t1, la concentración de B en la mezcla resultante podría ser lo sucientemente alta para garantizar su recuperación de una forma económica. En este caso el uso de la termodinámica como única herramienta conduciría a una conclusión falsa. 4.2. LA ECUACIÓN DE VELOCIDAD DE REACCIÓN Para poder determinar la cantidad de moles que reaccionan en un proceso químico, debe conocerse la ecuación de velocidad de reacción de la especie en particular. Si esta especie es un reactivo, su rapidez de reacción puede depender de las concentraciones de varias especies, incluyendo la suya propia, y es costumbre hablar de reacciones de orden n, casi siempre entero y no mayor a 3. Cuando se dice que una reacción dada es de orden n con respecto a una especie determinada, por ejemplo A, se quiere dar a entender que es proporcional a la concentración de A, en un momento dado, elevada a la potencia n. Por ejemplo, si se desea formular 49 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS una expresión que establezca la velocidad de descomposición de A en un cierto tipo de reactor, si la cinética es de primer orden con respecto a A, una respuesta común es escribir que: dC A kC A dt (4.1) donde k es la constante de velocidad de primer orden y CA es la concentración de A en el tiempo t. Esta ecuación no es correcta para todos los casos. Sólo lo es cuando el reactor es intermitente y de volumen constante. Luego, para generalizar, la velocidad de reacción debe escribirse como: rA kC A (4.2) la cual se puede utilizar en las ecuaciones de balance de materia y energía, para diferentes tipos de reactores. Es importante denir que el valor numérico de la constante de velocidad depende de cuál de los productos o reactivos se seleccione como la sustancia de referencia con el propósito de denir la velocidad de reacción. Por ejemplo, si la estequiometría de la reacción es: A B 2C (4.3) La relación entre las velocidades de cambio del número de moles en un reactor intermitente será: dN C dN dN 2 A 2 B dt dt dt (4.4) El número de moles de C aumenta dos veces más rápido de lo que disminuye el número de moles de A o de B, y se deduce que una constante de velocidad denida con respecto a la disminución de A (o de B) sólo tendrá la mitad del valor de la otra denida con respecto al incremento de C. Al utilizar constantes de velocidad publicadas en la literatura abierta es esencial tener en cuenta la sustancia de referencia en particular que seleccionaron los autores. 50 CAPÍTULO 4 - CINÉTICA PARA EL DISEÑO DE REACTORES QUÍMICOS En el caso relativo a soluciones o mezclas de gases no ideales, es necesario expresar la velocidad de reacción en función de las actividades de los componentes participantes en la reacción (Froment & Bischoff, 1990). Por ejemplo, para la reacción (4.3) podría ser: rA ka A aB k ' aC2 (4.5) Si se decide expresar la velocidad de reacción en términos de concentraciones en el caso de sistemas no ideales, las constantes de velocidad de reacción tendrían que asumir la desviación de la idealidad del sistema reaccionante y, por lo tanto, deberán ser función de la concentración. Si la ecuación (4.5) se iguala a cero (velocidad neta de reacción igual a cero) debe surgir la expresión para la constante de equilibrio como la relación de las velocidades directa e inversa de reacción. Esta denición rigurosa de constante de equilibrio en función de las actividades sólo se puede obtener si la expresión cinética está expresada en términos de actividad. Sin embargo, el cálculo de esa constante a partir de datos calorimétricos (v.g., cambio entálpico y cambio entrópico por reacción, ver capítulo 1) no permite obtener el mismo valor de la constante de equilibrio cinética. A continuación se analizan dos métodos para el ajuste de datos experimentales para el cálculo de parámetros. Este tema, en general bien tratado para los casos simples en la literatura de ingeniería de las reacciones (por ejemplo los textos de Levenspiel, 1999; Fogler, 2006; Rojas; 2008), se abordará aquí para el caso especíco de dos sistemas no ideales. 4.3. AJUSTE DE DATOS EXPERIMENTALES PARA LA DETERMINACIÓN DE LOS PARÁMETROS DE LA ECUACIÓN DE VELOCIDAD DE REACCIÓN PARA SISTEMAS NO IDEALES Mediante experimentos a escala de laboratorio, es posible obtener datos que posteriormente permiten el ajuste de las constantes de un modelo o ecuación propuesta (Levenspiel, 1999; Fogler, 2006; Rojas; 2008). Los métodos de medición cinética buscan estudiar el cambio de las concentraciones de las especies a lo largo de la reacción, de una forma directa o indirecta. Cuando no es factible medir las concentraciones de forma directa así como 51 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS ante la imposibilidad de utilizar métodos cuantitativos químicos (v. g., titulación, colorimetría, absorción atómica, cromatografía liquida o gaseosa, desplazamiento de gas, etc.) o porque la naturaleza de la reacción lo impide (como en el caso de una velocidad de reacción muy rápida: v. g., el caso de reacciones de combustión), es necesario relacionar la concentración de una o más especies con alguna propiedad física/intensiva del sistema como el pH, la temperatura, conductividad eléctrica, la absorbancia, la turbidez, etc. A continuación se presentan dos casos de estudio que involucran sistemas no ideales: el primero se trata de una reacción en fase líquida, para un sistema iónico. Para seguir el transcurso de la reacción se utiliza el método termométrico, expresando la constante de la ley de velocidad en función de la concentración. En el segundo caso, para una reacción de estericación en fase vapor, se ajusta una ley de velocidad en función de las actividades de las sustancias participantes a los datos experimentales. 4.3.1. CASO DE ESTUDIO 1: PRODUCCIÓN SIMULTÁNEA DE SULFATO DE POTASIO Y ÁCIDO CLORHÍDRICO. ANÁLISIS CINÉTICO MEDIANTE EL MÉTODO TERMOMÉTRICO Los métodos termométricos son comúnmente usados para medir propiedades termodinámicas como el calor latente o el calor de combustión de un compuesto (Shoemaker et al., 1989). La adaptación de este método al cálculo de los parámetros de la ley de velocidad de una reacción se basa en la solución simultánea de los balances de materia y energía en un sistema cerrado (batch) adiabático (Nguyen et al., 2001). Así, los cambios de temperatura se utilizan para relacionar directamente la concentración. Considérese el caso de la reacción exotérmica e irreversible entre cloruro de potasio y ácido sulfúrico, en solución de varios solventes, como se muestra en la ecuación (4.6). Solventes 2 KCl( solución ) H 2 SO4 K 2 SO4( sólido ) 2 HCl( solución ) (4.6) La reacción entre el cloruro de potasio y el ácido sulfúrico en solución, genera productos que se presentan en tres fases: sólida, en 52 CAPÍTULO 4 - CINÉTICA PARA EL DISEÑO DE REACTORES QUÍMICOS solución, y una tercera fase gas, que contiene ácido clorhídrico, que puede estar presente en el líquido dependiendo de la cantidad de agua, solvente, ácido sulfúrico y sales presentes. En solución, tanto el ácido sulfúrico como el cloruro de potasio se disocian en diferentes grados. Esto controla los niveles de conversión y rendimiento del proceso. La intensicación de procesos ha señalado a la cristalización reactiva, en presencia de varios solventes, como una alternativa interesante para este proceso en lugar de la energívora tecnología convencional (López, 2011). El fundamento del modelo del método termométrico para el ajuste de los parámetros cinéticos se presenta a continuación. 4.3.1.1. MODELO PARA EL MÉTODO TERMOMÉTRICO Para un sistema cerrado, en donde no se toman en cuenta los cambios en su energía cinética y potencial, ni presenta interacciones de naturaleza magnética ni eléctrica, el balance de energía está dado por las ecuaciones (4.7) y (4.8) (Fogler, 2006). n Q Ws Fi H i i 1 n entra Fi H i i 1 sale Esistema t (4.7) donde la energía total del sistema, Esistema, contiene al término del cambio de moles de todas las especies Ni, como se muestra en la ecuación (4.8). Esistema n n N E i N i H i PVi i 1 i 1 (4.8) El balance molar para el sistema reactivo tiene la forma: dN i i rV i dt (4.9) Habiendo denido que el sistema no experimenta ningún intercambio energético con el universo en forma de calor o trabajo (se desprecia el cambio energético por agitación, el calor de solución y la evaporación de algún reactante), cambiando los términos de la ecuación (4.7) en función de sus deniciones y acoplándola con el balance molar 53 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS (ecuación 4.9), se obtiene una expresión que predice el cambio de la temperatura con el tiempo en función del calor de la reacción (ΔHrxn) y del calor especíco de las sustancias de la mezcla (Cpi). Esto se muestra en la ecuación (4.10). dT H Rxn T rV i dt Cpi (4.10) i Conociendo la no idealidad termodinámica del sistema reactivo, considérese una ley de velocidad para el proceso propuesto de la forma: rA k T , C A0 C A CB (4.11) donde: A : cloruro de potasio y B : ácido sulfúrico. Las ecuaciones (4.12) y (4.13) muestran la funcionalidad de la constante cinética con la temperatura y la concentración de alimento del cloruro de potasio. E k T , CKCl ,0 Ao exp RT (4.12) Ao kc1 ln C A0 kc 2 (4.13) Como se decidió expresar la velocidad de reacción en términos de concentraciones, la constante de velocidad de reacción asumirá la desviación de la idealidad del sistema reaccionante y, por lo tanto, es función de la concentración. Al incluir la ley de velocidad en la ecuación (4.10), se obtiene la expresión completa: dT H Rxn T k T , C A0 C A CB dt C A0 i Cpi (4.14) En la ecuación (4.14) sus diferentes variables cambiarán en el tiempo. Por esta razón, su utilización en un programa experimental puede 54 CAPÍTULO 4 - CINÉTICA PARA EL DISEÑO DE REACTORES QUÍMICOS ser técnicamente muy dispendiosa. Para nes prácticos, esta expresión se puede simplicar considerando los métodos de velocidad inicial y velocidad máxima (Levenspiel, 1999; Fogler, 2006; Rojas; 2008). Ambos métodos se basan de medir un cambio inicial o máximo en la temperatura, el cual puede relacionarse con las velocidades de reacción inicial y máxima, tal como se muestra en las ecuaciones (4.15) y (4.16). dT rAo f dt 0 (4.15) dT rA, Max f dt Max (4.16) La técnica de velocidad inicial se basa en jar la concentración inicial de uno de los reactivos y variar, en diversos ensayos, la del otro reactivo (Nguyen et al., 2001). En el caso que la concentración del reactivo A sea la que varía inicialmente en cada experiencia, manteniendo la concentración inicial de B constante, la ecuación (4.14) se reescribe, utilizando la funcionalidad mostrada en la ecuación (4.15), como: kt 0 H Rxn T0 CB0 1 dT C A0 dt 0 Cpi (4.17) i La forma linealizada de la ecuación (4.17) se obtiene aplicando logaritmos a ambos lados de esa ecuación obteniendo las ecuaciones (4.18) y (4.19), en donde C1 agrupa todos los términos constantes para una corrida experimental. kt 0 H Rxn T0 CB0 dT 1 log C A0 log log Cpi dt 0 i (4.18) dT log log C1 1 log C A0 dt 0 (4.19) Estas expresiones permiten calcular los coecientes cinéticos mediante el uso de varios incrementos iniciales (velocidades de cambio) 55 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS en la temperatura. De forma análoga, se pueden obtener expresiones que permiten calcular el coeciente cinético β correspondiente al otro reactivo (en este caso B), como se muestra en las ecuaciones (4.20) y (4.21). kt 0 H Rxn T0 C A0 dT 1 log CB 0 log log Cpi dt 0 i (4.20) dT log log C2 1 log CB 0 dt 0 (4.21) En el método de la velocidad máxima el principio es esencialmente el mismo al explicado para la velocidad inicial. Este método supone que el incremento de la temperatura de la reacción entre To y Tf se comporta linealmente. Para justicar esta simplicación, se usa el siguiente procedimiento geométrico: se sabe que antes y después de la reacción en un sistema cerrado adiabático la temperatura no cambia. Entonces, es posible denir dos zonas en el termograma tal como se muestra en la Figura 4.2. Consecutivamente, se traza una línea que pasa por el máximo incremento de la temperatura en la zona de reacción (identicado como un punto rojo en la Figura 4.2) generando dos áreas aproximadamente iguales: una por encima y otra por debajo de ese máximo (teorema del valor medio). Físicamente, la igualdad entre las dos áreas generadas representa una aceleración inicial aproximadamente igual a una desaceleración nal en la velocidad de reacción. Esto se muestra en la ecuación (4.22) junto con la consecuente expresión luego de aplicar el modelo termométrico (ecuación 4.23). dT dT log log dt Max dt 0 (4.22) kt 0 H Rxn T0 CB0 dT log 1 log C A0 (4.23) log dt Cp Max i i 56 CAPÍTULO 4 - CINÉTICA PARA EL DISEÑO DE REACTORES QUÍMICOS Figura 4.2. Esquema gráco del método de velocidad máxima De forma análoga, para la especie B, se pueden hacer las mismas aproximaciones como se muestra en la ecuación (4.24). kt 0 H Rxn T0 C A0 dT 1 log CB 0 (4.24) log log Cpi dt Max i Ahora, si el calor generado por reacción es igual al calor que absorbe la mezcla en un sistema cerrado adiabático, como lo muestra la ecuación (4.25): Tf M sln C p sln dT M A0 H Rxn T0 (4.25) y si el cambio en la capacidad caloríca de la solución por efecto de la temperatura es muy bajo, es posible calcular la relación entre el cambio entálpico de la reacción dividido el Cp de toda la mezcla por cada 57 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS experimento (conociendo las masas totales de la solución y la alimentada del cloruro de potasio) como lo muestra la ecuación (4.26). M sln C p sln T M A0 H Rxn (4.26) Finalmente, los datos experimentales de temperatura en función del tiempo, a varias condiciones iniciales conocidas, se ajustan utilizando un modelo multiparamétrico. En la Figura 4.3 se comparan los datos experimentales junto con el ajuste obtenido. Como se puede ver, la expresión cinética es capaz de predecir el efecto del cambio en la concentración de alimento del cloruro de potasio y del ácido sulfúrico así como el efecto de la temperatura de alimento. a. Concentraciones de alimento de KCl b. Concentraciones de alimento de H2SO4 c. Temperatura de alimento Figura 4.3.Vericación del ajuste del modelo al conjunto de datos experimentales 58 CAPÍTULO 4 - CINÉTICA PARA EL DISEÑO DE REACTORES QUÍMICOS El ajuste multiparamétrico demostró que la ley de velocidad para la producción de ácido clorhídrico y sulfato de potasio se puede considerar como una cinética elemental. 4.3.2. CASO DE ESTUDIO 2: CINÉTICA DE LA SÍNTESIS EN FASE VAPOR DEL ACETATO DE ETILO (BASADO EN EL TRABAJO DE VENKATESWARLU ET AL., 1958) La esterificación catalizada del ácido acético con etanol en fase vapor procede según la siguiente estequiometria: CH3COOH(V) + CH3CH2OH(V) ↔ CH3COOCH2CH3(V) + H2O(V) A(V) + B(V) ↔ R(V) + S(V) (4.27) Varias expresiones cinéticas se pueden proponer para esta reacción siguiendo la metodología del paso controlante, propuesta por LangmuirHinshelwood-Hougen-Watson (Froment & Bischoff, 1990), así: • Reacción superficial controlante: Reacción entre el ácido acético adsorbido y el etanol en fase vapor. a a Ek sr m f (aR ) a A aB R S K A K rA 1 K A a A K B a B K s aS K R a R • Reacción superficial controlante: Reacción entre los dos reactivos adsorbidos. a a Ek sr m f (aR ) a A aB R S K A K B K rA 2 1 K A aA K B aB K s aS K R aR • (4.28) (4.29) Adsorción de ácido acético como etapa controlante: a a Eka m f (aR ) a A R S aB K rA a R aS 1 K A a K K B aB K s aS K R aR B (4.30) 59 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS • Desorción del acetato de etilo como etapa controlante: a a a Eks m f (aR ) A B S K K aR rA a A aB K R aR 1 K A a A K B aB KK s aR • (4.31) Modelo simplicado de Venkateswarlu et al. (1958): a a Ek s m f (aR ) a A R S aB K rA 1 K s as (4.32) Un ingenioso equipo experimental permitió a Venkateswarlu et al. (1958) obtener datos experimentales a diferentes condiciones de reacción. Algunos de esos valores se reportan en la Tabla 4.1. A partir del balance molar en un reactor integral, es posible obtener una expresión para calcular la velocidad de reacción a partir de los datos presentados en la Tabla 4.1. Así, aplicando el balance a un elemento diferencial de volumen en el reactor tubular se tiene que: Fi |ww Fi |w ri W dFi ri dW dFi Fd (4.33) d ri d (W / F ) Por lo tanto, al gracar ξ vs. (W/F) y calcular la pendiente en cada punto se obtiene el valor de –r. Como ejemplo, en la Figura 4.4 se muestran los datos experimentales para T = 246ºC, junto con el ajuste de los valores de velocidad de reacción calculados. 60 CAPÍTULO 4 - CINÉTICA PARA EL DISEÑO DE REACTORES QUÍMICOS Tabla 4.1. Datos para la reacción de estericación a varias temperaturas (Venkateswarlu et al., 1958) Avance *, W/F (g catalizador sobre T (ºC) ξ (mol/gramos alimentagramos alimentados/hora) dos) Composición mol alimento: A:0,4481, B:0,4088, R:0,1431 246 0,0010 0,285 0,0020 0,492 0,0028 0,89 0,0030 0,958 0,0034 1,175 0,0042 1,695 Composición mol alimento: A:0.4373, B:0.4256, R:0.1372 266 0,0010 0,235 0,0020 0,495 0,0024 0,615 0,0030 0,85 0,0040 1,275 0,0050 1,86 Composición mol alimento: A:0,2548, B:0,5722, R:0,1730 286 0,0010 0,285 0,0024 0,8 0,0028 1,133 0,0030 1,29 0,0032 1,43 0,0034 1,595 * calculada como nio ni F 61 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS ξ 0,0010 0,0020 0,0028 0,0030 0,0034 0,0042 -r (mol/gcat.h) 0,0034 0,0031 0,0024 0,0023 0,0019 0,0010 Figura 4.4. Relación entre la conversión y la razón peso catalizador – alimentación para la estericación a 246ºC Para el ajuste de los parámetros de las velocidades de reacción, es necesario contar con un modelo de fugacidad que permita calcular las actividades de las diferentes sustancias participantes en la reacción. Como la reacción se lleva a cabo en fase vapor, la actividad se dene como: ai 62 fi xi Pi o fi xio P o o (4.34) CAPÍTULO 4 - CINÉTICA PARA EL DISEÑO DE REACTORES QUÍMICOS siendo el estado referencia i puro (xi=1); Po = 1bar; φo=1. La fracción molar se puede relacionar con la conversión (denida como en la Tabla 4.1) según la siguiente expresión: x xio vi i (4.35) Se escogió la ecuación de estado de Peng-Robinson-Stryjek-Vera (PRSV) para calcular el coeciente de fugacidad de la siguiente forma (Stryjek & Vera, 1986): P RT a v b v (v b ) b (v b ) (4.36) 2 RT R 2Tc 2 , b 0, 07779 c , k es 1 (1 ) k T donde a 0, 45723 r Pc Pc una constante para cada compuesto como puro: k (0,37889 1, 48971 0,171318 2 0, 01965 3 ) k1 (1 Tr )(0, 7 Tr ) y las reglas de mezclado empleadas: bmix xi bi i amix xi x j (ai a j )0.5 (1 xi kij x j k ji ) i j Los valores para kij y kji utilizados son reportados por Wyczesany (2007). Finalmente, la expresión para el coeciente de fugacidad queda: b bP ln Z 1 ln Z bm RT 2 x j aij Z 1 2 bm P am b j RT ln b P bm 2 2bRT am Z 1 2 m RT (4.37) Las actividades de las sustancias calculadas a cada valor de velocidad de reacción se muestran en la Tabla 4.2. 63 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Tabla 4.2. Coecientes de fugacidad y actividad para cada sustancia -r φA φB φS φR aA aB aS aR 0,0034 0,0031 0,0024 0,0023 0,0019 0,0010 0,9994 1,0006 1,0015 1,0017 1,0021 1,0029 1,0034 1,0042 1,0048 1,0049 1,0052 1,0057 1,0093 1,0077 1,0064 1,0061 1,0055 1,0044 1,0069 1,0063 1,0059 1,0058 1,0056 1,0052 0,4048 0,3563 0,3174 0,3077 0,2882 0,2491 0,3665 0,3176 0,2785 0,2687 0,2490 0,2098 0,0494 0,0987 0,1380 0,1478 0,1674 0,2065 0,1953 0.2445 0,2838 0,2936 0,3132 0,3525 Con base en la información presentada en la Tabla 4.2, y considerando los modelos propuestos (ecuaciones 4.28 a 4.32), se realizó el ajuste de datos sujeto a la minimización de siguiente función objetivo: Sobj = MIN(∑(rexp- rcalc)2). En la Tabla 4.3 se presentan los resultados. Tabla 4.3. Constantes cinéticas y de equilibrio de adsorción para cada ecuación propuesta Ecuación (4.28) (4.29) (4.30) (4.31) (4.32) Eksm (mol/ gcat.h) 0,0409 0,0527 0,1172 0,0716 0,043 KA K KB KS KR Sobj 16,6484 16,9779 4,2884 4,6184 - 2,926 2,386 2,321 2,9668 - 10,001 10,039 10,036 8,1123 - 4,5790 4,9165 5,0209 6,4419 17,73 8,1991 8,1203 7,4688 8,0839 - 1,954×10-4 1,154×10-4 1,146×10-4 1,475×10-4 5×10-4 * -: No fue considerado por ese modelo. Según los valores de la función objetivo, los ajustes obtenidos reproducen satisfactoriamente los datos experimentales. Sin embargo, tal como se presenta en la Tabla 4.3, la ecuación (4.29), que asume la adsorción del ácido acético como la etapa controlante, presenta el menor valor de Sobj. Sin embargo, este hecho no valida el mecanismo de reacción propuesto. En el artículo referencia, Venkateswarlu et al. (1958) simplicaron las ecuaciones de velocidad utilizando algunos argumentos cuestionables. Los resultados aquí presentados indican que los valores de las constantes excluidas por ellos pueden llegar a tener valores signicativos, haciendo inapropiado su exclusión. El procedimiento de ajuste se repitió a diferentes temperaturas con el n de determinar la funcionalidad de los diferentes parámetros ajustados 64 CAPÍTULO 4 - CINÉTICA PARA EL DISEÑO DE REACTORES QUÍMICOS según la expresión de Arrhenius, tal como se muestra en las ecuaciones (4.38) y (4.39). k s A exp Ki Eac RT Aa ( Ea Ed ) exp Ad RT (4.38) (4.39) En la Figura 4.5 se presentan los resultados obtenidos del ajuste. Figura 4.5: Ajuste de los parámetros de la ley de velocidad a la ley de Arrhenius Figura 4.5. Ajuste de los parámetros de la ley de velocidad a la ley de Arrhenius BIBLIOGRAFÍA Cusack, R.W. (1999): “A Fresh Look at Reaction Engineering”. En: Chem. Eng., 106(11), 134 – 146. Fogler, H.S. (2006): Elements of Chemical Reaction Engineering (4th Ed.). New Jersey: Prentice Hall. 65 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Froment, G.F. & Bischoff, K.B. (1990): Chemical Reactor Analysis and Design. New Jersey: John Wiley & Sons. Levenspiel, O. (1999). Chemical Reaction Engineering (3rd Ed.). New Jersey: John Wiley & Sons. López, J.S. (2011): Tesis de Maestría en Ingeniería Química. Universidad Nacional de Colombia, sede Manizales. Nguyen, D.; Fogler, H.S. & Chavadej, S. (2001): “Fused Chemical Reactions. 2. Encapsulation: Application to Remediation of Parafn Plugged Pipelines”. En: Industrial & Engineering Chemistry Research, 40(23), 5058-5065. Rojas Grisales, J.N. (2008): Elementos de Cinética Química. Manizales: Universidad Nacional de Colombia, sede Manizales. Shoemaker, D. & Garland, C. (1989): Experimentos de Físico-Química. Madrid: Mc Graw Hill. Stryjek, R. & Vera, J.H. (1986): “PRSV: An Improved Peng-Robinson Equation of State for Pure Compounds and Mixtures”. En: Can. J. Chem. Eng., 64(2), 323-333. Wyczesany, A. (2007): “Modeling of Simultaneous Chemical and Phase Equilibria in Esterication of Acetic Acid with Ethanol in HighPressure Carbon Dioxide”. En: Ind. Eng. Chem. Res., 46(16), 54375445. Venkateswarlu, C.; Satyanarayana, M. & Narasinga-Rao, M. (1958): “Vapor-Phase Catalytic Esterication of Ethyl Alcohol with Acetic Acid”. En: Ind. Eng. Chem., 50(6), 973 - 978. 66 CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE 5 BĆęĊėŃĆĘ ĉĊ ėĊĆĈęĔėĊĘ ĉĊ ĒĊğĈđĆ ĈĔĒĕđĊęĆ Ċē ĘĊėĎĊ INTRODUCCIÓN El problema del análisis o diseño de un tren o batería de reactores continuos de tanque agitado (CSTRs) puede enfrentarse empleando diversas estrategias. La estrategia más apropiada suele ser aquella más simple que permita una respuesta lo sucientemente conable y precisa. La apropiada denición del problema y de sus admisibles simplicaciones, permite en muchos casos emplear estrategias de solución grafo-numérica fáciles de implementar. Estas proporcionan su solución mediante la representación gráca del problema, permitiendo además el entendimiento de los factores involucrados y su inuencia. En general, los métodos grafo-numéricos consisten en la manipulación de las ecuaciones de diseño (ecuaciones de conservación) y ecuaciones constitutivas de un problema, de tal forma que puedan ser representadas grácamente (por lo general en dos dimensiones). En el caso del diseño de baterías de CSTRs, son bastante conocidas las representaciones grácas (velocidad de reacción contra conversión o concentración) propuestas originalmente por Levenspiel (1999) y ampliamente usadas por otros autores (Smith, 1980; Hill, 1977; Fogler, 2006). Aquí, se presenta una forma alternativa de representación del problema de análisis de una batería de CSTRs en la forma de un diagrama de etapas, con base a lo originalmente propuesto por Aris (1973), análogo a los universalmente co67 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS nocidos diagramas de etapas de equilibrio usados en el diseño de procesos de separación. 5.1. REPRESENTACIÓN GRÁFICA DE UNA BATERÍA DE CSTRS EN UN DIAGRAMA DE ETAPAS Para derivar el modelo del método grafo-numérico, se manipula convenientemente el balance molar del reactor n-ésimo de la batería, tal como sigue: Entra Genera Sale Acumula (5.1) Asumiendo estado estacionario y representando el ujo molar del reactivo límite por FA, la velocidad de reacción por rA y el volumen del reactor por V, se obtiene de la ecuación 5.1 que: FA,n 1 rA,nVn FA,n (5.2) FA,n 1 FA,n rA,nVn (5.3) Empleando la denición de conversión para el reactivo límite de la reacción, siendo FAo el ujo molar de alimento fresco al primer tanque y X la conversión global medida desde el alimento fresco se obtiene fácilmente que: FA,0 1 X n 1 FA,0 1 X n rA,nVn FA,0 X n X n 1 rA,nVn (5.4) (5.5) Ahora, escribiendo . el ujo molar como el producto de la concentración CAo y el caudal Vo, se reescribe la ecuación anterior de tal forma que aparezca el tiempo medio de residencia τ: X n X n 1 rA,n 68 1 Vn C A,0 Vo (5.6) CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE X n 1 Xn n C A,0 r A, n (5.7) La ecuación (5.7) constituye el fundamento del método grafonumérico, pues permite, habiendo especicado el tiempo de residencia, la concentración del alimento y la cinética de la reacción en el reactor n-ésimo, escrita en términos de la correspondiente conversión, una representación de la conversión a la salida del reactor n-1, en función de la conversión a la salida del reactor inmediatamente posterior, n. Para mayor practicidad del método, se supondrá inicialmente que todos los reactores de la batería tienen el mismo tamaño (el mismo tiempo medio de residencia) y que operan a la misma temperatura, con lo cual se podrá representar toda la batería sobre una misma curva o línea de operación, dada por: X n 1 Xn C A,0 r A, n (5.8) Sólo resta especicar la cinética de la reacción y escribirla en términos de la conversión. En el caso de una cinética de primer orden: r kC A,0 1 X n A, n (5.9) Reemplazando en la ecuación (5.8) y reorganizando: X n 1 k 1 k X n (5.10) En este caso se puede apreciar que la representación gráca de Xn-1 contra Xn viene dada por una línea recta de pendiente (1+τk) e intercepto –τk. Al emplear el método para conocer las conversiones intermedias que se alcanzarán en una batería de n reactores con un alimento especicado, se traza el diagrama Xn-1 contra Xn, se ubican el intercepto y el punto (1, 1), y se traza la línea de operación de la batería. Se ubica el punto de alimentación de la batería (generalmente conversión inicial nula) sobre el eje de las ordenadas (Xn-1) y se busca el punto de corte con la línea de operación, el cual señalará en el eje de abscisas (Xn) la conversión de salida del primer reactor X1. Con la ayuda de una línea de 45° sobre el diagrama, se proyecta 69 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS la conversión obtenida sobre el eje de las ordenadas y se repite el proceso tantas veces como sea necesario (n veces si el número de reactores de la batería está especicado o hasta que se alcance una conversión nal deseada, luego de lo cual se determina el número de reactores de la batería dados por el número de escalones formados sobre la gráca). Así pues, se cuenta con un método simple para resolver problemas de desempeño o dimensionamiento (entendido como el número de reactores requeridos, todos de un tamaño igual conocido). También es posible usar el método para resolver problemas de dimensionamiento en los cuales se desee conocer el tamaño de los reactores de la batería dado su número y la conversión nal deseada, pero se requerirá de una iteración gráca, que suele ser tediosa, para lo cual se recomienda resolver el problema numéricamente empleando el conjunto completo de balances y después (si se desea), representar los resultados sobre el diagrama aquí propuesto. Si la cinética es de segundo orden o compleja, la ecuación (5.7) ya no vendrá dada por una línea recta, sino por una curva, pero aplica el mismo procedimiento descrito anteriormente. Si los reactores de la batería han de tener diferentes tamaños u operar a diferentes temperaturas, puede usarse el mismo concepto anterior teniendo en cuenta que deberá trazarse una curva por cada tiempo de residencia o temperatura (es decir, una curva para cada reactor de la batería). EJEMPLO 5.1. Se desea determinar las conversiones intermedias y la conversión nal obtenida en una batería de seis CSTRs en serie de igual tamaño, para la reacción en fase líquida A→B. La concentración del alimento fresco es de 10 mol/L y el tiempo de residencia en cada uno de los reactores es de 5 min. Con propósitos comparativos, se propone analizar las cinéticas de reacción correspondientes a: 1) primer orden, 2) segundo orden, y 3) cinética no-elemental. Los resultados obtenidos se presentan en las Figuras 5.1 a 5.3, respectivamente. 70 CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE Figura 5.1. Diagrama de etapas para una batería de seis CSTRs en serie. Cinética de primer orden –rA = kCA, con k = 0,196 min-1 Figura 5.2. Diagrama de etapas para una batería de seis CSTRs en serie. Cinética de segundo orden –rA = kCA2, con k = 0,196 min-1 71 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 5.3. Diagrama de etapas para una batería de seis CSTRs en serie. Cinética no elemental –rA = kCA/(1+KCA)2, con k = 0,196 min-1 y K = 0,09 L/mol El caso de la cinética de primer orden, Figura 5.1, para el cual la línea de operación de la batería es recta, permite apreciar bien la construcción de las etapas. Lo mismo ocurre en el caso de la cinética no-elemental, Figura 5.3. Sin embargo, en el caso de la cinética de segundo orden, Figura 5.2, la aproximación de la línea de operación (curvada) a la línea auxiliar de 45º a elevadas conversiones, diculta la observación y uso del diagrama (en especial si se hace a mano). En cualquier caso, para alcanzar conversión nal completa se requerirá de una batería de innitas etapas, pues la línea auxiliar y la de operación se interceptan en el extremo superior derecho. Los diferentes resultados ilustran dos cosas: el efecto de la cinética sobre la facilidad de alcanzar una conversión determinada en cada reactor y en la batería de reactores, y cómo entre mayor sea la distancia de la línea de operación a la línea auxiliar, mayor será el grado de conversión entre dos etapas sucesivas. En este segundo caso resulta evidente ahora cómo tal efecto se reduce gradualmente hacia las últimas etapas de la batería en el caso de cinéticas de primer orden o de forma abrupta como en el caso de la cinética de segundo orden. De esta forma se evidencia la inuencia del tipo de cinética sobre el número requerido de reactores de una batería (y su tamaño) para alcanzar una conversión nal deseada. 72 CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE 5.2. OPTIMIZACIÓN DE BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE La optimización es una de las principales herramientas cuantitativas en la toma de decisiones que los ingenieros tienen para afrontar cierto tipo de problemas en las industrias químicas. Tales problemas pueden ir desde la disminución de costos de operación hasta reducir el impacto ambiental causado por una transformación química. En realidad, el diseño óptimo de reactores ha ocupado un lugar privilegiado en la Ingeniería Química y es necesario aprender a generar herramientas que permitan realizar este tipo de evaluaciones. A continuación se presenta la forma de abordar la optimización de un tren de reactores en serie (CSTRs) cuando estos operan de forma isotérmica y de forma no isotérmica, con el n de obtener el volumen óptimo (mínimo) para una conversión nal determinada. Se presenta a continuación un método que sustituye el procedimiento gráco que involucra la maximización de rectángulos propuesto por Levenspiel (1999). 5.2.1. CASO ISOTÉRMICO Considérese un tren de N CSTRs cuya conversión de entrada y salida (con respecto al reactivo límite) son Xo y XN respectivamente. El problema de diseño es encontrar los (N-1) conversiones óptimas intermedias (X1, X2, ... XN-1) que minimizan el tamaño global o total del tren de reactores. Según Levenspiel (1999), la selección óptima de la conversión intermedia Xi es tal que en la gráca de 1/(-rA) vs X, la diagonal del rectángulo sombreado posee la misma pendiente que la tangente a la curva en el punto Xi, como se muestra esquemáticamente en la Figura 5.4. De esta forma, en un tren de varios reactores, para el primer reactor se debe cumplir que: f ( X 2 ) f ( X 1 ) df ( X ) X1 X 0 dX X1 (5.11) 73 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 5.4. Criterio para la determinación del tamaño óptimo de un CSTR Donde f(X)= 1/(-rA) y |X significa “evaluado en X1”. Nótese que la condición involucra para un reactor tres conversiones diferentes. Reorganizando la ecuación (5.11) se obtiene que: 1 w f ( X 2 ) f ( X 1 ) ( X 1 X 0 ) ( X 1 ) 0 tiene: (5.12a) Donde F(X1) = df(X)/dX׀X1. En general, para el i-ésimo reactor se w i ) 0 f ( X i 1 ) f ( X i ) ( X i X i 1 ) ( X i (5.12b) Y para el (N-1)-ésimo reactor: wN 1 74 f ( X N ) f ( X N 1 ) ( X N 1 X N 2 ) ( X N 1 ) 0 (5.12c) CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE La solución simultánea de las N-1 ecuaciones entrega el valor de las N-1 incógnitas (X1,X2, ... XN-1), de donde se puede calcular el tamaño óptimo (V/FAo)i para el i-ésimo reactor a partir del balance molar de la ecuación (5.13): (V/FAo)i = (Xi - Xi-1) f(Xi) (5.13) Para resolver el conjunto de N-1 ecuaciones (5.12b) y (5.12c), que equivale al mismo número reactores, se puede utilizar algún método de mínimos cuadrados para ajuste de parámetros de ecuaciones no lineales (Gauss – Newton y Levenberg – Marquardt). La idea es minimizar la suma de cuadrados de las funciones w. EJEMPLO 5.2. Suponga que la reacción elemental A → R ocurre en una cascada de seis CSTRs isotérmicos. Se alimenta A puro a una concentración de 1 mol/L, y se espera alcanzar una conversión final del 80 %. Para esta reacción la cinética es: -rA = k1CA – k2CR donde k1 = 0,196 min-1, k2 = 2,124×10-3 min-1. En términos de la conversión, X, la ley de velocidad se puede expresar como: -rA = CAo[ k1(1-X) – k2X] A continuación se presentan en la ones obtenidas para los seis reactores en todo de Levenberg-Marquardt (Edgar para llevar a cabo la minimización de (Gómez García & Fontalvo, 2000). Tabla 5.1 las conversiserie, utilizando el mé& Himmelblau, 1989) la suma de cuadrados 75 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Tabla 5.1. Resultados de la optimización de seis CSTR isotérmicos: las cinco conversiones intermedias y volúmenes Reactor 1 2 3 4 5 6 Conversión 0,2392 0,4204 0,5576 0,6616 0,7404 0,8000 Volumen (L) 0,0355 0,0204 0,0117 0,0067 0,0038 0,0022 La representación gráfica de la solución se muestra en la Figura 5.5. Figura 5.5. Gráfica de Levenspiel para seis CSTRs óptimos en serie para la reacción A ↔ R De la Figura 5.5 es evidente a partir de los tamaños relativos los rectángulos que cada reactor tiene un tamaño diferente y que el último de la serie es el más pequeño. EJEMPLO 5.3. La oxidación de CO catalizada sobre platino en un CSTR isotérmico está descrita por una cinética del tipo Langmuir-Hinshelwood: 76 CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE kCco rA (1 KCco ) 2 donde k = 0,196 min-1 y K = 0,01 l/mol. En la Tabla 5.2 se presentan los resultados obtenidos utilizando el método de Levenberg-Marquardt (Edgar & Himmelblau, 1990). Tabla 5.2. Resultados de la optimización de seis CSTRs isotérmicos para la cinética de la oxidación de CO Reactor 1 2 3 4 5 6 Conversión 0,2353 0,4152 0,5528 0,6580 0,7385 0,8000 Volumen (L) 21,6095 15,1480 10,2537 6,5464 3,7383 1,6112 La representación de estos resultados en una gráca de Levenspiel para la determinación de los volúmenes de la cascada de reactores en serie se presenta en la Figura 5.6. Figura 5.6. Arreglo de seis CSTRs en serie para la oxidación de CO 77 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS El método numérico de Levenberg-Marquardt demostró ser bastante robusto para este tipo de cálculos y logró convergencia en todos los casos (cinéticas) analizados. 5.2.2. CASO NO ISOTÉRMICO Con frecuencia las reacciones químicas requieren un intercambio de calor para que se puedan llevar a cabo. El cambio de temperatura que se genera en estos equipos influye directamente en el tamaño del reactor (o tiempo espacial). Para reacciones endotérmicas irreversibles, el tamaño óptimo para el reactor ideal se obtiene al operar el reactor isotérmicamente a la máxima temperatura permisible. Sin embargo, para una reacción exotérmica reversible el tamaño óptimo del reactor se obtiene siguiendo el lugar geométrico de las máximas velocidades de reacción, es decir, la Progresión Óptima de Temperatura (POT) (Fogler, 2006). Para resolver una batería de CSTRs no isotérmicos (en el sentido que cada reactor opera a una temperatura diferente) se debe tener en cuenta la variación de la temperatura. Es decir, cada conversión intermedia tiene su correspondiente temperatura. A continuación se propone un algoritmo de cálculo para obtener la conversión y la temperatura óptima en cada reactor del sistema. 5.2.2.1. ALGORITMO DE CÁLCULO 1. Defina un vector inicial de conversiones intermedias X = (X1, X2, ... XN-1)o. 2. Como la velocidad de reacción es función de la temperatura y f X , T , y como ya se especificó la conversión, es decir rA X, evalúe el vector de temperaturas iniciales T = (T1,T2, ... TN-1)o correspondientes a cada conversión, con la ayuda de un método numérico como el Newton-Gauss o la Sección Dorada 3. Determine los parámetros cinéticos con los valores de temperatura obtenidos en el paso 2. 78 CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE 4. Utilice el método de Levenberg-Marquard para calcular los nuevos valores de conversión X = (X1, X2, ... XN-1)k, teniendo en cuenta que la función objetivo a minimizar es la misma que para el caso isotérmico. 5. Con los nuevos valores de conversión estime nuevos valores de temperatura como en el paso 2. Continué con los pasos 3 y 5. 6. Repita el paso 5 hasta que se cumpla el criterio de convergencia elegido, se recomienda utilizar como criterio de parada que la norma del vector gradiente sea menor que una tolerancia. Una vez se termina el ciclo iterativo, se obtienen las temperaturas y conversiones óptimas de diseño para el tren de reactores. A continuación se presentan dos ejemplos de aplicación. EJEMPLO 5.5. Retómese la reacción del ejemplo 5.2, pero en este caso se va a tener en cuenta la variación de la temperatura en la expresión de la ley de velocidad. De esta forma, para la reacción elemental reversible de primer orden: -rA = k1CA – k2CR donde k1 = exp(17,2 – 11600/RT), k2 = exp(41,9 – 29600/RT) y R = 1,987 cal/molK. Se alimenta A puro a una concentración de 1 mol /L. Los resultados obtenidos se presentan en la Tabla 5.3. Tabla 5.3. Resultados de la optimización de seis CSTRs no isotérmicos. Conversiones y temperaturas intermedias, volúmenes. Reactor 1 2 3 4 5 6 Conversión 0,2802 0,4676 0,5957 0,6859 0,7514 0,8000 Temperatura (K) 366,8376 355,1323 348,0761 342,8885 338,7236 335,2110 Volumen (L) 0,1768 0,6742 1,5779 3,0149 5,1435 8,1544 79 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Estos resultados se presentan en la Figura 5.7 junto con las curvas de isovelocidad y la progresión optima de conversión-temperatura. Figura 5.7. Carta de isovelocidades con los puntos de operación óptimos para seis CSTRs en serie Como era de esperarse, las parejas de datos de concentración y temperatura óptimas coinciden exactamente sobre la curva de progresión óptima. Los resultados obtenidos en los ejemplos 5.2 y 5.4 se comparan en una gráca de Levenspiel para el cálculo de volúmenes en la Figura 5.8. Como se puede observar en la Figura 5.8, el volumen que se obtiene para un reactor cuando no se tiene en cuenta la variación de la temperatura es mucho mayor que cuando se tiene en cuenta los efectos energéticos. Figura 5.8. Comparación entre el volumen de cada CSTR para los casos de operación isotérmica y no isotérmica 80 CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE EJEMPLO 5.5. La velocidad de oxidación de SO2, catalizada sobre pentóxido de vanadio, se basa en el concepto de Hougen – Watson y en la suposición que la reacción entre el SO2 adsorbido y el oxígeno de la fase gas es el paso controlante. La expresión de velocidad es de la forma (Froment & Bischoff, 1990): pSO3 k1 po2 pSO2 1 pSO2 p1/2O2 K p r , K 2 pSO2 K 3 pSO3 ) 2 22.414(1 donde r presenta las unidades kmol SO2/(kg cat.hr), con k1 = exp(12,160-5473/T); k2 = exp(-9,953+8619/T); k3 = exp(-71,745+52596/T); Kp = exp(11300/T-10,68); y pi las presiones parciales de los distintos componentes. Se desea alcanzar una conversión del 80%. La presión a la que ocurre la reacción es de 1 atm y los ujos molares iniciales son los siguientes: FSO2 = 1 kmol/h, FO2 = 1,4 kmol/h, FSO3 = 0 kmol/h, Finertes = 11,4 kmol/h. Tenga en cuenta que en esta reacción hay un cambio neto en el número de moles y por lo tanto no se puede despreciar el parámetro de cambio de volumen. Los resultados obtenidos se presentan en la Tabla 5.4 Tabla 5.4. Resultados de la optimización de seis CSTR no isotérmicos Conversiones y temperaturas intermedias Reactor 1 2 3 4 5 Conversión 0,2778 0,4639 0,5920 0,6833 0,7501 Temperatura (K) 942,49 881,59 846,31 821,01 801,11 6 0,8000 785,74 Volumen (L) 3,0601 11,2533 25,9870 49,2184 83,3427 131,2553 81 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS De manera análoga al ejemplo 5.4, los resultados se representaron sobre un diagrama conversión-temperatura, que incluye como parámetro las curvas a velocidad de reacción constante, como se presenta en la Figura 5.9. Figura 5.9. Carta de Isovelocidades para la oxidación de SO2 Nótese que los valores de las parejas de datos de conversión-temperatura obtenidos tienen correspondencia biunívoca con los valores obtenidos para la POT en este sistema reactivo. Es importante recalcar respecto al método numérico que su convergencia depende fuertemente de los valores de conversión y temperatura inicialmente supuestos para cada uno de los reactores. Los valores obtenidos para el caso isotérmico pueden servir de un muy buen estimativo inicial para el caso no isotérmico. 5.3. DISEÑO Y OPTIMIZACIÓN DE UNA BATERÍA DE QUIMOSTATOS La biotecnología se ocupa de la manipulación de organismos vivientes o sustancias químicas derivadas de ellos para la obtención de productos de valor agregado a escala industrial. En la actualidad la biotecnología constituye una de las áreas de trabajo más importantes de la ingeniería 82 CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE química por sus aplicaciones en una amplia gama de sectores productivos como alimentos, medicamentos, cosméticos, biocombustibles, químicos especializados, e insumos químicos (Doran, 1995; Bailey & Ollis, 1987; Trejos et al., 2009). En relación con los procesos de reacción química, los reactores químicos en donde se realizan fenómenos de transformación bioquímica se denominan reactores bioquímicos o biorreactores, diferenciándose dos tipos básicos de procesos biotecnológicos: i. Los que utilizan microorganismos (levaduras, bacterias, células, denominados en general como biomasa) que transforman una materia prima (denominada sustrato) en un producto de interés. Aquí, la reacción bioquímica ocurre como un proceso autocatalítico en el cual los microorganismos que realizan la transformación química (gracias a su metabolismo) presentan ciclos vitales en los cuales se reproducen y mueren durante el proceso. ii. Los que utilizan catalizadores de origen biológico (altamente especícos y selectivos), llamados enzimas, para realizar la transformación bioquímica del sustrato. En general, los procesos biorreactivos son complejos y presentan características únicas que no se observan en los procesos reactivos convencionales (por ejemplo, permiten la síntesis altamente selectiva de compuestos químicos a STP: ¡condiciones estándar (ambiente) de presión y temperatura!). Aunque a nivel industrial y de laboratorio existen una gran variedad de tipos de bioreactores, el CSTR (denominado tradicionalmente en el área biotecnológica como quimostato) ha sido uno de los más empleados debido a sus características especiales para reacciones en fase líquida, su versatilidad en procesos continuos a gran escala, controlabilidad, facilidad de mantenimiento y limpieza (un aspecto esencial para evitar la contaminación del cultivo de microorganismos). En esta sección se discutirán algunos aspectos elementales del diseño de una batería de quimostatos, complementando los planteamientos presentados por Fogler (2006) y Levenspiel (1999), aplicados especícamente al uso de un microorganismo para la producción de etanol. 83 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 5.3.1. ESTEQUIOMETRÍA DE LA ACCIÓN METABÓLICA DEL MICROORGANISMO El microorganismo consume el sustrato y demás nutrientes presentes en el caldo de cultivo y gracias a su maquinaria celular interna los metaboliza, transformándolos en una gran variedad de sustancias químicas que usa para mantenerse vivo y obtener energía para sus actividades. El producto deseado puede ser una de esas sustancias principales del metabolismo (producto intracelular) o un residuo de la acción metabólica excretado (producto extracelular), el cual debe ser posteriormente separado y puricado, siendo esta una de las etapas más complejas y costosas de todo el proceso. En el caso de la producción de etanol usando la levadura Saccharomyces cerevisiae, el etanol es un residuo extracelular formando por la fermentación anaerobia (en ausencia de oxígeno) de un sustrato constituido por azúcares asimilables como la glucosa o la sacarosa (provenientes a su vez de fuentes como la caña de azúcar, el maíz, o residuos agroindustriales). Debido a que el metabolismo de un microorganismo está constituido por un gran número de reacciones bioquímicas complejas, algunas de las cuales pueden ser desconocidas, no es posible o práctico representar la transformación bioquímica mediante una ecuación estequiométrica simple, razón por la cual se opta por emplear información empírica sobre las proporciones entre sustrato, producto, y biomasa. Dichas proporciones se conocen como coecientes de rendimiento (másicos) y juegan el mismo papel que los conocidos coecientes estequiométricos. Siendo S, C, y P, sustrato, biomasa, y producto respectivamente: Células Sustrato Células producto S yc / s C y p / s P yc / s y p/s masa de nuevas células formadas masa de sustrato consumido para formar células (5.15) masa de producto formado masa de sustrato consumido para formar producto (5.16) y p/c 84 (5.14) masa de producto formado masa de nuevas células formadas (5.17) CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE 5.3.2. CINÉTICA DE LA PRODUCCIÓN DE BIOMASA La velocidad de la reacción bioquímica de los procesos en los cuales se usa un microorganismo depende en general de la temperatura y de las concentraciones de sustrato, biomasa (y en algunos casos del producto). La expresión más usada se denomina cinética de Monod (por el premio Nobel Jacques L. Monod, 1949), la cual expresa la velocidad del crecimiento celular o producción de biomasa y tiene la forma: rg ko max Cc Cs K s Cs Cp k 1 * o Cp (5.18) n (5.19) donde las concentraciones son másicas (y no molares), debido a la dicultad de conocer las fórmulas moleculares para representar la biomasa (las cuales existen pero son aproximadas). La velocidad de crecimiento celular está dada en dimensiones de masa por unidad de volumen y unidad de tiempo. La constante ko tiene en cuenta el posible efecto inhibitorio ocasionado por la presencia del producto (n y Cp* son constantes empíricas especícas de cada sistema reaccionante). Se sabe que en el caso de la fermentación alcohólica, existe inhibición por producto a concentraciones de etanol superiores al 12°GL, ya que a partir de esa concentración resulta venenoso para la misma levadura (también es posible involucrar en la cinética, posibles efectos inhibitorios de la concentración de sustrato y de biomasa). El coeciente cinético μmax se conoce como velocidad especica máxima y posee dimensiones de tiempo inverso; el coeciente cinético Ks tiene dimensiones de concentración másica. Las constantes cinéticas dependen de la temperatura generalmente mediante expresiones del tipo Arrhenius. Sin embargo, debe considerarse que los procesos biotecnológicos generalmente ocurren en intervalos de temperatura alrededor de los 32-37°C, óptimos para la subsistencia de los microorganismos o la estabilidad de las enzimas, las cuales suelen ser compuestos muy termolábiles. 85 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Las células presentan un ciclo vital constituido por fases. Una vez inoculadas en el medio o caldo de cultivo ellas: 1) se adaptan al medio en una fase de latencia en la que no se observa reproducción, 2) se reproducen a una gran velocidad en la llamada fase de crecimiento exponencial, 3) empiezan a morir números signicativos de células a una tasa que iguala el nacimiento de nuevas células, lo que se conoce como fase estacionaria, 4) la tasa de muerte celular sobrepasa la tasa de nacimiento y la concentración de células se empieza a reducir hasta llegar a cero. Durante estas etapas ocurre consumo de sustrato para mantener viva a las células, lo que se conoce como mantenimiento; la velocidad de consumo de sustrato especícamente para mantenimiento viene dada por: rsm mCc (5.20) La constante m se conoce como constante de mantenimiento celular y se dene como: m masa de sustrato consumido para mantenimiento masa actual de células tiempo (5.21) La velocidad de muerte celular natural se puede expresar como: rd kd Cc (5.22) La velocidad de formación del producto dependerá de la fase vital en la que se encuentre operando el cultivo: rp y p / c rg fase de crecimiento exponencial rp y p / s rs neta fase estacionaria (5.23) Por último, deberá considerarse entonces que el sustrato se consume tanto para el mantenimiento, así como para la formación del producto y el crecimiento de biomasa, por lo que la velocidad neta de consumo de sustrato es: rs neta 86 ys / c rg ys / p rp rsm (5.24) CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE 5.3.3. BALANCES DE MATERIA EN EL QUIMOSTATO Un esquema de una planta de producción de etanol en un quimostato se presenta en la Figura 5.10. Figura 5.10. Esquema de un quimostato para una fermentación anaerobia En el caso particular de la fermentación anaerobia de melaza de caña o una solución fermentable proveniente de un residuo agroindustrial, se obtienen como producto principal un licor oscuro, con un porcentaje en etanol no mayor a 12°GL, el cual debe ser posteriormente puricado y dos subproductos importantes: la biomasa y el dióxido de carbono gaseoso, el cual se pude licuar y vender como hielo seco. Para el caso de un quimostato, los balances de materia se desarrollan como de costumbre, solo que en términos de la masa y no de las moles. En el caso general será necesario escribir los balances tanto para el sustrato, como para la biomasa y el producto. A escala industrial, es común que los quimostatos se diseñen para que operen en estado estacionario. Por esta razón los balances pueden expresarse como: Entra Genera Sale 87 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Para el sustrato: VoCso rsV VC s (5.25) el caudal se puede considerar constante y se dene la velocidad espacial como el inverso del tiempo de residencia, la cual recibe el nombre particular de velocidad de dilución, D: Vo 1 V D (5.26) Con lo cual el balance de sustrato toma la forma: D Cso Cs rs (5.27) Considerando que el reactor opera con el cultivo en la fase de crecimiento (para lo cual se prepara un inoculo del microbio en otro recipiente en donde se adapta al ambiente durante la fase de latencia, antes de ser transferido al reactor), la forma completa del balance será: n Cp Cc Cs mCc (5.28) D Cso Cs ys / c ys / p y p / c 1 * max C K C p s s En el caso de las células (biomasa), se tiene en cuenta que generalmente el alimento fresco al reactor no contiene material celular (el cultivo se inocula por un puerto especial del equipo), y que existe una aparición de nuevas células así como su desaparición por muerte, entonces: rgV rdV VC c (5.29) DC rg rd c (5.30) Cp DCc 1 * C p n Cc Cs kd Cc max K C s s (5.31) Para el producto, se tiene en cuenta que el alimento fresco no lo contiene, por lo que: 88 CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE rpV VC p DC p rp Cp DC p y p / c 1 * C p n Cc Cs max K s Cs (5.32) (5.33) (5.34) 5.3.3.1. ALGORITMOS DE SOLUCIÓN PARA PROBLEMAS DE DESEMPEÑO O DIMENSIONAMIENTO DE UN QUIMOSTATO Las variables de diseño en el caso de un quimostato son las concentraciones de salida de sustrato (Cs), biomasa (Cc), y producto (Cp). Los parámetros operativos de interés son la velocidad de dilución (D), la cual es una medida del tamaño del biorreactor, la concentración inicial de sustrato en el alimento fresco (Cso) y la conversión deseada. Todas las constantes del modelo cinético así como los coecientes de rendimiento deberán ser conocidos para poder intentar una solución, para lo cual generalmente se recurre a información publicada en la literatura o se obtiene experimentalmente. Para los problemas de desempeño, en los cuales se desea conocer la conversión (concentraciones de salida) que se pueden alcanzar en un quimostato de tamaño conocido y para un alimento dado: 1. Fijar D y Cso. 2. Resolver las ecuaciones (5.28, 5.31 y 5.34) para Cs, Cc y Cp y calcular la conversión. Para los problemas de dimensionamiento en los cuales se desea establecer el tamaño requerido del quimostato para obtener un grado de conversión determinado a partir de un alimento dado: 1. Fijar Cso y Cs o la conversión. 2. Resolver las ecuaciones (5.28, 5.31 y 5.34) para D, Cc y Cp. 89 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS EJEMPLO 5.6. Condición de lavado en un quimostato y optimización de la productividad Se puede demostrar que simplicando el modelo presentado se obtienen expresiones analíticas explícitas para la concentración de sustrato y biomasa (Fogler, 2006). Asumiendo que la velocidad de muerte celular es despreciable (en la fase de crecimiento exponencial), que no existe inhibición por producto y despreciando también el consumo de sustrato por mantenimiento y formación de producto, se obtiene: Cs Cc DK s max D yc / s Cso K s max Cso D max D Cso K s (5.35) (5.36) En tales condiciones, si la velocidad de dilución es mayor que la velocidad de crecimiento celular, la concentración de células disminuirá hasta que todas las células abandonen el reactor (lo que se denomina lavado). Así pues, dicha condición deberá evitarse, pues el reactor no puede operar si no existe biomasa en su interior, por lo cual se deberá determinar el valor máximo de la tasa de dilución (o el mínimo tiempo de residencia) para que exista lavado, lo cual se logra despejando el valor de la velocidad de dilución para el cual la concentración de biomasa a la salida se hace cero, obteniéndose: Dmax max Cs K s Cs o (5.37) o Por otro lado, también se puede optimizar la productividad de biomasa del biorreactor, denida como el ujo másico de biomasa por unidad de volumen del quimostato. La biomasa es un subproducto importante del proceso, el cual puede usarse como materia prima para la fabricación de alimento para animales por su alto valor nutricional o para compostaje. Aplicando el criterio de la primera derivada a la ecuación que dene la productividad, se encuentra el valor óptimo de la velocidad de dilución que hace máxima la productividad y que ha de ser menor al valor máximo de la dilución que ocasiona el lavado: 90 CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE Pro m c CcVo DCc V V (5.38) DK s DCc Dyc / s Cso max D (5.39) d DCc 0 dD D Dopt Ks Dópt max 1 K s Cso (5.40) (5.41) Se debe considerar que es posible realizar la determinación de la tasa máxima de dilución para lavado así como la tasa de dilución óptima para máxima productividad de biomasa con el modelo completo sin simplicaciones, pero deberá hacerse a través de un método numérico. Se invita al lector a proponer un algoritmo para dicho cálculo. En la Tabla 5.5 se presentan los parámetros y condiciones de simulación para un quimostato para la producción de etanol (Fogler, 2006). Tabla 5.5. Parámetros y condiciones de simulación de un quimostato para la producción de etanol usando levadura Saccharomyces cerevisiae (Fogler, 2006) CS Concentración de sustrato en el alimento CC 250 g / dm3 Concentración celular en el alimento 0 g / dm3 Cp Concentración de producto en el alimento 0 g / dm3 yc/s Coeciente de rendimiento células/sustrato 0,08 g/g yp/s Coeciente de rendimiento producto/sustrato 0,45 g/g yp/c Coeciente de rendimiento producto/células 5,6 g/g Cp Concentración máxima de inhibición 93 g / dm3 n Parámetro de inhibición 0,52 - μmax Coeciente cinético máximo Monod 0,33 1/h KS Coeciente cinético Monod 1,7 g / dm3 O O O * kd Coeciente cinético de muerte celular 0,01 1/h m Parámetro de mantenimiento celular 0,03 gs / gch 91 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 5.11. Concentraciones de sustrato (Cs), biomasa (CC) y producto (CP) en función de la velocidad de dilución durante la producción de etanol en un quimostato. Se muestra el efecto de despreciar la inhibición por producto, la muerte celular y el consumo de sustrato para mantenimiento y formación de producto (modelo simplicado) La Figura 5.11, en la que se presentan las concentraciones de las sustancias predichas con el modelo completo y el simplicado, muestra las importantes y signicativas diferencias que se presentan al despreciar el efecto de la inhibición por producto: en concreto se subestima el consumo de sustrato y se sobreestima la formación de biomasa y producto. 92 CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE Figura 5.12. Productividad de biomasa en función de la velocidad de dilución durante la producción de etanol en un quimostato. Se muestra el efecto de despreciar la inhibición por producto, la muerte celular y el consumo de sustrato para mantenimiento y formación de producto (modelo simplicado) La Figura 5.12 presenta la productividad en función de la tasa de dilución e ilustra de una forma más dramática el efecto de las simplicaciones sobre el diseño del quimostato. Aunque la velocidad de dilución máxima para lavado se predice de forma similar por ambos modelos, la optimización de la dilución que hace máxima la productividad diere signicativamente, al igual que el valor mismo de la productividad máxima, el cual es cerca de cinco veces menor al considerar los efectos de inhibición y consumo de sustrato para mantenimiento y formación de producto y muerte celular. Este ejemplo ilustra la importancia de considerar todos los fenómenos implicados en el proceso reactivo (y de valorar el impacto de las simplicaciones de dicho modelo) para obtener diseños y predicciones lo más ajustadas a la realidad que se observará durante la operación del reactor. 93 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 5.3.4. REPRESENTACIÓN ADIMENSIONAL DE LA CINÉTICA DE MONOD Tal como se ha comprobado, los efectos inhibitorios del producto y el efecto del mantenimiento, la formación del producto, y la velocidad de muerte celular pueden ser factores determinantes en el desempeño de un quimostato. Debido a que conviene tener una representación geométrica simple de las ecuaciones de diseño, presentaremos la forma adimensional de la cinética de Monod, imitando la propuesta de De Gooijer et al. (1996) pero evitando las simplicaciones. Empleando el balance de biomasa y suponiendo que el alimento no contiene células es posible obtener que: D kd Cs K s Cs donde ko max (5.42) Por lo tanto, el balance de sustrato se puede reescribir como: rs k d Cs o Cs (5.43) Según la propuesta de De Gooijer et al. (1996), se denen las siguientes variables adimensionales: rs ko max Cso , rs , K s , Cs kd K s Cso Cso (5.44) en donde es una nueva variable adimensional que considera el efecto de la velocidad de muerte celular. Al reemplazar estas deniciones en el balance de sustrato anterior, y operando algebraicamente, se obtiene: 1 1 1 1 (5.45) Retomando el balance de sustrato original: D Cso Cs rs 94 (5.46) CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE D Cso Cso ko max Cso (5.47) D 1 ko max (5.48) ko max D (5.49) 1 1 Esta última expresión muestra que un quimostato en estado estacionario puede representarse grácamente en un diagrama de (1/ρ) contra (1-α) en donde el tamaño del quimostato (dado como koμmax/D) vendrá representado por un rectángulo de largo (1-α) y alto (1/ρ). La curva de la cinética se representa entonces por la ecuación (5.45), con la forma característica de una cinética autocatalítica con un mínimo del inverso de la velocidad adimensional. También se puede representar la gráca en términos de la conversión, considerando que: Cs Cso 1 X s (5.50) 1 X s (5.51) Reemplazando α en la ecuación (5.45) y operando, se obtiene la ecuación análoga: 1 X s X s 1 X s X s 1 (5.52) la representación geométrica de la ecuación de diseño en términos de la conversión será análoga a la ecuación (5.49): ko max 1 Xs D (5.53) El resultado se puede generalizar fácilmente para una batería de quimostatos en serie (se sugiere al lector realizar el ejercicio de demostración), para obtener la siguiente expresión para el reactor i-ésimo de la batería: 95 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS koi max Di X si 1 X si1 i (5.54) Debe notarse que el término de inhibición ko depende de la concentración de producto en el reactor y que tanto como son variables que dependen de la velocidad neta de consumo de sustrato y por ende no son independientes. También recuérdese que para arribar a esta ecuación de balance adimensional se ha supuesto que el alimento no contiene biomasa. Dado lo anterior, con propósitos de programación, conviene disponer de una ecuación explicita para la velocidad neta de consumo de sustrato adimensional. Reemplazando la denición de en la ecuación (5.52), se obtiene: 1 X s X s 1 X s kd ko max Xs (5.55) 5.3.5. CRITERIO DE OPTIMIZACIÓN DEL TAMAÑO DE UNA BATERÍA DE QUIMOSTATOS Y ALGORITMO DE SOLUCIÓN Aunque la cinética microbiana del tipo Monod presenta una forma peculiar con un mínimo del inverso de la velocidad de reacción en función del avance de la reacción, la representación de la batería sobre el diagrama de diseño se realiza, como en los casos corrientes, empleando la ecuación (5.54). Es de notar que los reactores que se encuentran a la izquierda del mínimo de la curva cinética están representados por áreas que quedan bajo la curva, distinto a lo que ocurre con los reactores que se encuentran a la derecha del mínimo. Sin embargo, al aplicar el criterio geométrico de optimización de la batería, correspondiente con la minimización del área total de los reactores, se demuestra que el criterio de optimización derivado para los casos corrientes es igualmente aplicable a esta situación (donde (1/ρ) viene dado por la ecuación (5.52)): 1 X i1 96 1 d 1 0 X i X i 1 dX X i Xi (5.56) CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE Conviene también recordar que en el caso de una batería de quimiostatos en serie, se puede denir una conversión global medida desde el alimento fresco al primer reactor (como en la ecuación 5.56), y también se puede hablar de la conversión por paso que mide el grado de conversión entre la entrada y la salida de cada reactor en particular. En el caso del iésimo reactor de la batería, ambas están relacionadas por la ecuación: Cso X pasoi 1 _1 Cso _i 1 X global i (5.57) El algoritmo de solución para el problema de optimización de las conversiones intermedias en una batería de N quimostatos isotérmicos en serie, es completamente igual al discutido en relación con los reactores químicos corrientes: se plantean y resuelven N-1 ecuaciones del tipo (5.56) en N-1 variables desconocidas (conversiones intermedias), especicado previamente el ujo y composición del alimento fresco, la conversión nal deseada y el número de biorreactores. Dichas ecuaciones pueden resolverse mediante un método numérico para sistemas de ecuaciones algebraicas simultáneas o por un método numérico de optimización sobre una función objetivo, tal como se ha descrito en la sección 5.2. De una manera más detallada, el algoritmo propuesto implica las siguientes etapas: 1. Fijar todos los parámetros cinéticos y estequiométricos requeridos. 2. Fijar las condiciones del alimento al primer quimiostato, el número de biorreactores de la batería y la conversión nal deseada. 3. Resolver las N-1 ecuaciones de optimización: 3.1. Resolver los tres balances de materia para la velocidad de dilución, la concentración de biomasa y de producto a la salida de cada tanque, mediante un método numérico. Calcular la velocidad neta de consumo de sustrato en cada tanque. Calcular la derivada del inverso de la velocidad de reacción en cada tanque, mediante un método numérico. Computar las N-1 funciones objetivo para la optimización. Resolver las N-1 funciones de optimización mediante un método numérico. 3.2. 3.3. 3.4. 3.5. 97 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 4. Con los resultados obtenidos de las conversiones intermedias óptimas, calcular los valores respectivos de velocidad de dilución (tiempo de residencia), concentración de biomasa y de producto a la salida de cada tanque, como en el paso 3.1. 5. Calcular la productividad de salida de cada tanque. 6. Representar grácamente los resultados obtenidos para la batería óptima en el diagrama de Levenspiel (1999) o de Aris (1973). EJEMPLO 5.7. Optimización del tamaño de una batería de quimostatos para la producción de etanol Como ilustración de las ideas precedentes, se presenta la solución al problema de optimización del tamaño de una batería de tres quimostatos en serie para la producción de etanol que permita lograr una conversión nal de 95%. Se han empleado los mismos parámetros y condiciones de Figura 5.13. Batería de quimostatos para la producción de etanol. Superior: la biomasa es ltrada y separada a la salida de cada tanque. Inferior: la biomasa circula entre los tanques 98 CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE simulación del Ejemplo 5.6., presentados en la Tabla 5.5. Dos situaciones operativas posibles han sido consideradas: una batería en la cual la biomasa es filtrada y separada a la salida de cada tanque, de tal forma que el alimento al subsiguiente reactor no contenga biomasa (Figura 5.13a) y la situación más simple en la cual se deja a la biomasa circular entre los tanques (Figura 5.13b). Los resultados obtenidos se resumen en la Tabla 5.6. Tabla 5.6. Resultados de la optimización del tamaño de una batería de tres quimostatos en serie para la producción de etanol, considerando que la biomasa sea filtrada y separada entre tanques o que circule libremente entre ellos Filtrado de biomasa Parámetro operativo Circulación de biomasaf Bioreactor 1 Bioreactor 2 Bioreactor 3 Bioreactor 1 Bioreactor 2 Bioreactor 3 D (1/h) 0,2871 0,2643 0,1772 0,20148 3,8622 6,7198 Xs (-) 0,2795 0,4689 0,9500 0,87944 0,92476 0,9500 Cs (g/dm3) 180,1246 132,768 12,5 30,1408 18,8088 12,5 Cc (g/dm3) 2,696 1,8213 4,5348 8,3497 8,7785 9,0164 Cp (g/dm3) 15,6237 26,2088 53,0365 49,079 51,6078 53,015 Pro (g/hdm3) 0,77403 0,48137 0,80373 1,68227 33,9041 60,5881 1,6828 1,1554 0,81364 1,68278 >85 >100 0,203 0,194 0,187 0,203 >10 >10 Pro max Dmax pro Pro max (g/hdm3)a (1/h)b 5,087 3,2974 1,8025 - - - Dmax pro (g/h*dm3)c (1/h)d 0,27525 0,25095 0,18878 - - - Dmax lav (1/h)e 0,29788 0,27522 0,21001 - - - Los parámetros cinéticos y estequiométricos, así como las condiciones del alimento fresco se presentan en la Tabla 5.5. a. Productividades máximas por biorreactor. b. Velocidades de dilución para máxima productividad. c. Productividades de salida máximas de sustrato estimadas según el modelo simplificado. d. Velocidades de dilución para máxima productividad de biomasa estimadas según el modelo simplificado. e. Velocidades de dilución máxima para lavado estimadas según el modelo simplificado. f. En este caso no se puede usar el modelo simplificado para estimar condiciones de productividad máxima o de lavado pues existe una concentración finita de biomasa a la entrada. El esquema del proceso en el cual se realiza el filtrado y separación de la biomasa entre tanques implica que, en virtud de que cada reactor opera a condiciones de diferente concentración, los microorganismos en su interior se encuentran adaptados a ese ambiente y dejarlos ingresar al siguiente quimostato originará un estrés por el cambio en su medio de 99 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS cultivo. Se puede especular que tal esquema, si el tiempo de adaptación de la biomasa que ingresa a un biorreactor es mucho menor que el tiempo de residencia en el mismo, podría ser viable. Sin embargo, debido a la alta sensibilidad de estos seres vivos a las condiciones de su entorno, los tiempos de adaptación y fase de latencia suelen ser tales que resulta mejor ltrar la biomasa entre los tanques y reducir así los niveles de estrés de los mismos. La representación del primer caso, gráca de Levenspiel, se muestra en la Figura 5.14, y la gráca de Aris en la Figura 5.15, así como la productividad de biomasa (Figura 5.16) y las concentraciones de salida (Figura 5.17) en función de la velocidad de dilución para cada tanque. Figura 5.14. Inverso de la velocidad de consumo de sustrato adimensional contra la conversión global de sustrato. Las curvas continuas representan la cinética a concentración de producto constante e igual al valor de salida para cada tanque. Las curvas con línea a trazos representan la cinética a concentración de biomasa y producto constantes e iguales a los valores de salida de cada tanque. El tamaño de los reactores viene dado por el área del rectángulo indicado en trazo grueso; el punto de operación de cada quimostato se señala con un círculo 100 CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE Figura 5.15. Conversión global en el reactor n-1 contra conversión global en el reactor n. Las curvas continuas representan las líneas de operación a concentración de producto constante e igual al valor de salida para cada tanque. Las curvas con línea a trazos representan las líneas de operación a concentración de biomasa y producto constantes e iguales a los valores de salida de cada tanque. El cambio entre etapas se muestra en trazo grueso y el punto de operación de cada quimostato se señala con un círculo Al comparar los resultados obtenidos para la optimización del tamaño que se muestran en la Tabla 5.6, surgen algunas consideraciones importantes. Se nota que al ltrar la biomasa, cada tanque efectúa un nivel signicativo de conversión por paso, mientras que al dejar circular la biomasa, el primer reactor efectúa una conversión mucho mayor, mientras que el tercer reactor presenta un nivel muy bajo de conversión por paso. Desde este punto de vista, resulta más conveniente ltrar la biomasa, ya que todas las unidades son más funcionales. Por otro lado, al comparar los tamaños óptimos de la batería en ambos casos, se aprecia claramente que al dejar circular la biomasa entre los tanques, el tamaño de la batería óptimo es menor que el de la batería óptima en la que se ltra la biomasa. Esto se debe a que una mayor concentración de biomasa habita en cada quimostato al dejar que la biomasa circule por la batería (en relación con 101 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 5.16. Productividad de biomasa en función de la velocidad de dilución para cada quimostato a sus condiciones de operación óptimas. Los puntos de operación se señalan con un círculo el caso de ltración), lo que a su vez deriva en una mayor velocidad de producción de biomasa y con ello una mayor velocidad de consumo de sustrato (mayor conversión) y mayor formación de producto, todo lo cual se traduce en un menor tamaño de cada biorreactor. Sin embargo, es de destacar que en el caso simulado, la concentración nal de producto es casi idéntica en ambos casos, prácticamente independiente de que se ltre o no la biomasa. Existe una importante inuencia de la ltración de la biomasa sobre su productividad. Al dejar que la biomasa circule entre los quimostatos, se logra una productividad signicativamente mayor en cada uno de ellos, pues la concentración de biomasa es mayor y el tamaño menor (mayor velocidad de dilución) en relación con el caso en que la biomasa sea ltrada. 102 CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE Figura 5.17. Concentraciones de sustrato, biomasa y producto en función de la velocidad de dilución para cada quimostato a sus condiciones de operación óptimas. Los puntos de operación se señalan con un círculo Desde este punto de vista, el esquema de la batería con circulación de biomasa resulta más atractivo. Por otro lado, la productividad de la batería con ltros muestra que, como se ilustra en la Figura 5.17, las condiciones de mínimo tamaño de la batería no implican que cada biorreactor esté operando a su condición de máxima productividad de biomasa. Por último, considérese que aunque se han eliminado algunas simplicaciones problemáticas, se ha supuesto que el tiempo de adaptación de la biomasa es mucho menor que el tiempo de residencia y que no existen efectos inhibitorios por altas concentraciones de biomasa o sustrato sobre el cultivo. Debido a que siempre se podrán proponer modelos más generales y rigurosos, invitamos al lector a investigar más sobre este apasionante tema. 103 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS BIBLIOGRAFÍA Aris, R. (1973): Análisis de reactores. Madrid: Ed. Alhambra. Bailey, J.E. & Ollis, D.F. (1987): Biochemical Engineering. New York: McGraw-Hill. Doran, P. (1995): Principios de ingeniería de bioprocesos. México: Acribia S.A. D. de Gooijer, C.D.; Bakker, W.A.M.; Beeftink, H.H. & Tramper, J. (1996): “Bioreactors in Series: An Overview of Design Procedures and Practical Applications”. En: Enzyme and Microbial Technology, 18(3), 202-219. Edgar, T.F.; Himmelblau, D.M. (1989): Optimization of Chemical Processes. New York: McGraw Hill. Fogler, H.S. (2006): Elements of Chemical Reaction Engineering (4th Ed.). New Jersey: Prentice Hall. Froment, G. F.; Bischoff, K. B. (1990). Chemical Reactor Analysis and Design. New Jersey: John Wiley & Sons. Gómez García, M.Á. & Fontalvo, J. (2000): “Optimización de reactores CSTR en serie. Caso isotérmico”. En: NOOS, 11(1), 57 – 63. Hill, Ch.G. (1977): An introduction to chemical engineering kinetics and reactor design. New Jersey: John Wiley & Sons. Levenspiel, O. (1999): Chemical Reaction Engineering (3rd Ed.). New Jersey: John Wiley & Sons. Monod, J.L. (1949): “The Growth of Bacterial Cultures”. En: Ann. Rev. Microbiol., 3(Oct.), 371 – 395. 104 CAPÍTULO 5 - BATERÍAS DE REACTORES DE MEZCLA COMPLETA EN SERIE Smith, J.M. (1980): Chemical Engineering Kinetics (3th Ed.). New York: McGraw-Hill. Trejos, V.M.; Fontalvo, J. & Gómez García, M.Á. (2009): “Descripción matemática y análisis de estabilidad de procesos fermentativos”. En: DYNA, 76(158), 111 – 121. 105 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 46 CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES 6 EđĊĒĊēęĔĘ ĕĆėĆ Ċđ ĆēġđĎĘĎĘ ĉĊ ĘĎĘęĊĒĆĘ ĈĔē ėĊĆĈĈĎĔēĊĘ ĒŮđęĎĕđĊĘ INTRODUCCIÓN Prácticamente todos los procesos reactivos industriales involucran reacciones múltiples. Un caso particular es el de la industria de las olenas, uno de los sistemas reaccionantes más grande e importante de los procesos petroquímicos. En efecto, el etileno es hoy, quizás, uno de los compuestos orgánicos con mayor volumen de producción alrededor del mundo (alrededor de 80 x 106 toneladas por año). Actualmente, las olenas son producidas mediante un proceso conocido como crackeo térmico (thermal cracking) en el cual los alcanos reaccionan homogéneamente (se rompen) a temperaturas elevadas. Con etano y n-butano las principales reacciones son: C2 H 6 C2 H 4 H 2 C4 H 10 C4 H 8 H 2 C2 H 6 C2 H 2 2H 2 C4 H 10 C4 H 6 2H 2 C2 H 6 H 2 2C2 H 4 C4 H 10 2C2 H 4 H 2 3C2 H 6 C6 H 6 6 H 2 C4 H 10 C3 H 8 CH 4 C2 H 6 2CS 3H 2 C4 H 10 4CS 5H 2 Estos son solo unos pocos de los muchos productos presentes en estos procesos de reacción. Estas son reacciones homogéneas que involucran la formación de cadenas de radicales libres, las cuales son 107 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS difíciles de controlar para lograr altas selectividades. Las dimensiones típicas de un reactor de crackeo térmico son: 10 m de largo, 7.5 m de alto y 3.6 m de ancho, operan a temperaturas elevadas (650 ºC) y bajas presiones (3 bares), con tiempos de residencia bajos (0.35 - 0.8 segundos) (Froment, 1981). El diseño y análisis de sistemas con reacciones múltiples implica determinar la conguración del reactor que maximice la obtención de productos deseados y minimice la de los indeseados. Sin embargo, los constantes cambios en el ambiente industrial continúan jando las prioridades de la industria química. Estas pueden ser clasicadas bajo los siguientes encabezados: mercado, materias primas, seguridad y control de la contaminación (Blumenberg, 1992). Las variaciones de la economía de mercado y de las materias primas, las uctuaciones a corto y largo plazo de los precios y la disponibilidad, demandan exibilidad y adaptabilidad de los procesos. Adicionalmente, los estándares de seguridad y la normatividad ambiental cada día más exigentes se han convertido en “fuerzas impulsoras” adicionales para el desarrollo de nuevos procesos. Un caso industrial puede ilustrar mejor estos conceptos. Un ejemplo de un proceso dominado por las condiciones del mercado es el caso de la producción de metilaminas. Ellas son producidas a partir de la reacción de metanol con amoniaco, a 350 – 450 °C y 20 bar, en un reactor de lecho fijo empacado con una zeolita (Ullmann, 2008). La formación de mono-, di- y trimetilaminas (MMA, DMA, TMA) procede hasta el equilibrio termodinámico, según el valor de temperatura y de relación nitrógeno/carbono existente. El equilibrio termodinámico favorece la formación de TMA, mientras el mercado requiere preferencialmente DMA. Para mejorar la selectividad de este proceso, las investigaciones recientes se han direccionado hacia la formulación de catalizadores selectivos a la forma y tamaño de los productos (Segawa & Tachibana, 1991). Este concepto se esquematiza en la Figura 6.1. El equilibrio se alcanza dentro de la zeolita. Sin embargo, solo el MMA y el DMA tienen el tamaño y la forma precisa para difundir fuera de los canales del catalizador. Luego, el tamaño de poro de la zeolita constituye una variable adicional para el control de la distribución de productos. 108 CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES Figura 6.1. Esquema de la síntesis de metilaminas sobre catalizadores selectivos a la forma y tamaño de los productos Una característica importante de los sistemas con reacciones múltiples es su sensibilidad a las condiciones de reacción, obteniéndose por ejemplo, amplias diferencias en las distribuciones de los productos de reacción entre operaciones discontinuas y continuas debido a la variación en los tiempos de reacción. En las reacciones múltiples las variables de reacción tales como temperatura, presión, mezclado y el tiempo de residencia afectan la distribución de producto. En la mayoría de los casos, esta distribución es mucho más importante que el volumen del reactor. A continuación se presentan una serie de conceptos y métodos de análisis para sistemas que involucran reacciones múltiples, los cuales servirán como complemento del tratamiento expuesto en los textos clásicos de Ingeniería de las Reacciones Químicas. 6.1. PARÁMETROS PARA EL ANÁLISIS DE SISTEMAS CON MÚLTIPLES REACCIONES En la obtención de productos químicos, la fracción de reactivos que se convierten a productos es con frecuencia uno de los parámetros 109 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS más importantes. Existen tres parámetros que resultan especialmente útiles para el análisis de sistemas con múltiples reacciones: respecto a un reactivo se utiliza la conversión, y respecto a un producto se utiliza la selectividad y/o el rendimiento. Tales conceptos son importantes en la economía de un proceso químico y es igualmente importante tener una interpretación clara de su signicado para su correcta aplicación. Sin embargo, en la literatura existe una gran variedad de terminologías, notaciones y deniciones según el autor (ver por ejemplo Fogler, 2006; Levenspiel, 1999; Missen et al., 1999; Schmidt, 1998). La posibilidad de confusión es evidente. En esta sección se proporcionan deniciones operacionales que presenten valores normalizados entre 0 y 1. La conversión, XA, del reactante A, es la relación entre la cantidad de A que ha reaccionado hasta algún punto (tiempo o posición) y la cantidad de A alimentada al sistema. Es una medida del grado de consumo del reactante. Su denición es exactamente igual, independiente de que el sistema presente una o múltiples reacciones. En este último caso, se debe denir una conversión por cada reacción donde esté involucrado el reactante A, aunque en algunos casos también se puede denir una conversión global (Fogler, 2006). El rendimiento de un producto es una medida de la selectividad de un reactante en algún punto (tiempo o posición) para formar un producto, y por esa razón algunos autores lo denen como selectividad. El rendimiento puede ser menor al 100% debido a varios factores tales como: • Tiempo de reacción insuciente. • Restricciones termodinámicas (equilibrio). • La presencia de reacciones laterales y/o consecutivas. Es por lo general una excepción, en lugar de una regla, que los reactivos solo participen en una sola reacción. Con frecuencia se obtienen coproductos indeseados o el producto deseado continúa reaccionando. En tales instancias es evidente que existirán reacciones deseadas e indeseadas compitiendo. Sin embargo, las velocidades a las que se dan estas transformaciones varían con el cambio en las composiciones que 110 CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES se generan durante la reacción. Un rendimiento del 80% no signica necesariamente que 0,8 moles del producto deseado son obtenidas por cada mol del reactivo base de cálculo durante la reacción: el rendimiento pudo haber sido más alto, algo como 95%, durante la primera parte del proceso para luego disminuir, por ejemplo a un 75%, en las últimas etapas; y el valor nal obtenido será el promedio (alternativamente el rendimiento puede aumentar durante la reacción). La selectividad y/o el rendimiento se pueden representar de dos formas: como el rendimiento “instantáneo o diferencial” (en un punto) y el rendimiento “global o integral” (desde la entrada hasta un punto particular). Para analizar más fácilmente estas deniciones, supóngase un sistema de reacciones de la forma: A B C D + otras reacciones donde C es el producto deseado, D el producto indeseado, A, B son los reactivos, y α, β, χ, y ψ corresponden a los coecientes estequiométricos, negativos para reactivos y positivos para productos. Si A y B se adicionan inicialmente al sistema en proporciones estequiométricas, la denición de rendimiento para C será la misma si se calcula relativa a A o B. Una situación más general es aquella donde uno de los reactivos se adiciona en exceso y el rendimiento de C se debe calcular relativo al reactivo límite. Suponiendo que este último compuesto es A y que en cada instante d(nA) moles de A reaccionan y producen d(nC) moles de C (junto a una cantidad de sustancias indeseadas resultantes de la reacción alterna) el rendimiento instantáneo de C, ϕC/A , puede denirse en función de las moles de A alimentadas inicialmente como: C/ A C nC nC nA 0 0 (6.1) donde C es el valor absoluto del valor de α en la ecuación que involucra C, y nk0 se reere a las cantidades de A y C presentes inicialmente. En términos generales, ϕk/A depende de la concentración de las diferentes k 111 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS especies, así como de la temperatura, y su valor variará con el transcurso de la reacción. La suma de los rendimientos instantáneos es igual a la conversión de A: N k / A k C 1 k nk nk nA nA XA nA nA k C 1 N 0 0 0 0 De esta forma, la definición de ϕk/A estará normalizada de forma que: 0 k / A 1 El rendimiento global Φ’C/A puede ser denido como la relación entre las moles de A que reaccionaron para formar C y las moles de A que han reaccionado: C' / A C ( nC ) C nC nC ( nA )r nA nA (6.2) C ( nC ) ( nA )t (6.3) 0 0 O también como: C / A donde nC son las moles de C formadas durante la reacción, (nA)r son las moles de A que se han transformado hasta un momento determinado, y (nA)t corresponden a las moles totales de A que han ingresado al sistema. La suma de los rendimientos globales de los k componentes diferentes a A será igual a la unidad. Es decir: N k C 1 k' / A nA nA k nk nk 1 nA nA k C 1 n A n A N 0 0 0 0 0 k' / A 1 Luego, a partir de las deniciones de conversión y de rendimiento instantáneo es fácil encontrar la siguiente relación: 112 CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES C' / A X A C / A Las dos deniciones de rendimiento, ecuaciones (6.2) y (6.3), son idénticas si todo A reacciona, pero la ecuación (6.3) es la más apropiada si, al nal de la reacción, permanece algo de reactante sin reaccionar y este no es recuperable. Para una reacción discontinua (batch), o una reacción en continuo donde se puede asumir ujo pistón (reactor tubular ideal, PFR), reorganizando la ecuación (6.1) en forma diferencial e integrando para el tiempo total de reacción, la cantidad total de producto que se forma al nal del proceso es: ( nC ) C ( n A )r d( nA ) ( n A )0 (6.4) Ahora, combinando las ecuaciones (6.2) y (6.4), el rendimiento global para un proceso discontinuo o para un reactor tubular ideal será la integral sobre el rendimiento instantáneo: ' Batch ,PFR 1 ( nA )r ( n A )r d( nA ) (6.5) d( nA ) (6.6) ( n A )0 O alternativamente: Batch ,PFR 1 ( nA )t ( n A )r ( n A )0 Si la misma reacción general se lleva a cabo en una serie de CSTRs, en un período de tiempo determinado, las moles de A que reaccionan en el primero y segundo tanques serán ∆(nA)1, ∆(nA)2. Si los tanques se asumen perfectamente mezclados y en estado estacionario, las ∆(nA)1 moles que reaccionan en el primer tanque generarán, de la ecuación (6.1), un aumento de (χ/αC)ϕ1∆(nA)1 moles de C, donde ϕ1 es el rendimiento instantáneo a las condiciones estacionarias obtenidas en ese equipo. De manera análoga se 113 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS puede calcular para n tanques de un tren de reacción, la cantidad total de producto como: ( nC )nCSTR C n ( n i 1 i ) (6.7) A i Esta ecuación es análoga a la ecuación (6.4). El rendimiento global para el sistema de CSTRs se obtiene de la combinación de (6.7) con las deniciones de las ecuaciones (6.2) o (6.3) así: ' nCSTR 1 ( nA )r n ( n ) i A i ( n A i i 1 (6.8) O: nCSTR 1 ( nA )t n i 1 i ) (6.9) Estas expresiones, análogas a las ecuaciones (6.5) y (6.6), muestran que el rendimiento global en los n CSTRs corresponde a la sumatoria de los rendimientos estacionarios característicos de los diferentes tanques, de acuerdo con la cantidad de reacción que ocurre en cada uno. De esta forma, el concepto de rendimiento instantáneo proporciona la conexión lógica para el rendimiento global que se obtiene en las diferentes etapas del proceso. El uso de concentraciones en lugar de las cantidades molares (nA), (nA)r, etc., resulta, con frecuencia, más conveniente, especialmente en casos donde la expresión para la cinética de reacción es conocida. Asumiendo que el volumen no cambia signicativamente durante el curso de la reacción y que no se adiciona más reactivo después del inicio de la reacción, las ecuaciones (6.5) a (6.9) pueden transformarse a: 114 ' Batch ,PFR 1 C Ao C A f CA f dC C Ao A (6.10) CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES Batch ,PFR ' nCSTR 1 C Ao 1 C Ao C A f nCSTR 1 C Ao CA f dC n ( C i 1 i n ( C i 1 A (6.11) C Ai 1 ) (6.12) C Ao i Ai Ai C Ai 1 ) (6.13) donde CA es la concentración instantánea de A, CAo es la concentración inicial de A (o, en el caso de un tren de CSTRs, corresponde al valor que tiene en el primer tanque a las condiciones de alimentación) y CAf es el valor nal a la salida del proceso. 6.2. DETERMINACIÓN DEL RENDIMIENTO INSTANTÁNEO Con el n de hacer uso práctico de las relaciones denidas en la sección anterior, es necesario conocer la forma como cambia el rendimiento durante el transcurso de la reacción. En casos donde las cinéticas son conocidas, tanto para la obtención del producto deseado como del indeseado, ϕ puede calcularse en función de la composición o del tiempo. Por ejemplo, considérese dos reacciones en fase líquida del siguiente tipo: k1 2 A B X Y k2 A B Z donde X es el producto deseado y Z es el producto indeseado. Supóngase por simplicidad, que B está en exceso con respecto a ambas reacciones y que las velocidades para la formación de X y de Z varían con el cuadrado de la concentración de A y con la primera potencia de A respectivamente, por lo que se obtiene: dnX k '1 C A2 dt dnZ k '2 C A dt (6.14) 115 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS donde los parámetros de velocidad de reacción, k’1 y k’2, incluyen tanto las constantes de velocidad de reacción como la funcionalidad respecto a la concentración de B. De las ecuaciones (6.1) y (6.14) se obtiene que el rendimiento instantáneo es: 2dn dnA 2dnX 2k ' C 1 A 2dnX dnZ 2k '1 C A k '2 X X / A (6.15) Sustituyendo la ecuación (6.15) en las ecuaciones (6.10) a (6.12) se obtiene el rendimiento global analíticamente. 6.3. DISEÑO ÓPTIMO A PARTIR DE DATOS DE RENDIMIENTO Una mezcla reaccionante dada, está completamente determinada mediante parámetros como el avance de la reacción, junto con la temperatura y la presión. Asumiendo que estos dos últimos permanecen constantes, el valor de ϕ puede gracarse en función del parámetro variable (este puede ser el avance de la reacción, la fracción de uno de los reactivos o el tiempo). Aunque este es el método más utilizado, es necesario precisar que este hecho no es general, ya que en procesos en serie (por ejemplo, A → X → Y) las velocidades relativas de las dos reacciones están inuenciadas tanto por la concentración de A como la de X, y el intervalo de concentraciones, que es diferente en un reactor de mezcla, en un reactor discontinuo o en un reactor tubular. Luego, es discutible la utilización del rendimiento fraccional con el propósito de denir el diseño óptimo del reactor. Cualquiera que sea la elección, la gráca resultante se denirá como la curva ϕ (Denbigh, 1961). Una curva típica se representa en la Figura 6.2, donde ϕ se muestra en función de (CA)/(CA)t, la fracción total del reactivo que se ha transformado. Para el caso en que un sistema de reacciones se realice en un reactor discontinuo o en un reactor tubular ideal, la trayectoria de la reacción será de izquierda a derecha como lo muestra el sentido de la echa, y de esta gráca y de las ecuaciones deducidas previamente se dene de inmediato que el rendimiento global será igual al área bajo la curva hasta un valor determinado en el eje de la abscisa que corresponda a la cantidad nal de 116 CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES Figura 6.2. Comparación de los rendimientos discontinuos y CSTR reactante transformado, denido como (CA)r. Por ejemplo, de la ecuación (6.6): Batch ,PFR ( C A )r ( C A )0 d( C A ) ( C A )t el área bajo la curva puede determinarse por algún método de integración numérico o gráco. De esta forma, el conocimiento de la curva ϕ puede ser una herramienta útil en estudios económicos para procesos en reactores discontinuos o reactores tubulares, en relación con la duración de la reacción. Un aspecto importante que se puede involucrar en el diseño óptimo de reactores CSTR es el método de la “maximización de rectángulos” (Levenspiel, 1999; Gómez García & Fontalvo, 2000; Capítulo 5 de este libro). En este caso no será el área bajo la curva ϕ la que determine el rendimiento global sino el área del grupo de rectángulos, de igual número al de tanques de reacción, cada uno de los cuales toca la curva ϕ con su esquina superior, como se muestra en la Figura 6.2. Por ejemplo, aplicando la ecuación (6.9) a un grupo de 3 tanques en serie se obtiene que: 117 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 3,CSTRs 1 ( C A )3 ( C A )1 ( C A )2 2 3 ( C A )t ( C A )t ( C A )t Debido a que ϕ disminuye progresivamente con el aumento en el grado de avance de la reacción, como en la Figura 6.2, la comparación de las áreas obtenidas para el reactor de mezcla y el discontinuo (o el tubular) demuestra que el rendimiento global es considerablemente más pequeño en un reactor de mezcla (CSTR), para las mismas condiciones de operación. Físicamente esto se debe a que la concentración de los reactivos es inevitablemente menor en el CSTR donde, en cada equipo de reacción, la corriente de alimentación se mezcla con el material que ya ha reaccionado. Esto puede ser de gran importancia para explicar por qué aparecen diferencias entre el rendimiento de reacciones a escala industrial, cuando un proceso químico, inicialmente estudiado en el laboratorio (por ejemplo en un equipo discontinuo), es escalado a un CSTR industrial. Existen dos métodos por los cuales el desempeño del CSTR puede ser mejorado para tal situación. El más obvio es el aumento del número de equipos en serie (donde el área de los rectángulos se aproxima cada vez más al área bajo la curva), pero los costos de capital, por lo general, limitan mucho esta posibilidad. El segundo método, para un número jo de tanques, es denir el grado relativo de reacción en cada uno de los equipos con el n de maximizar el área de los rectángulos. Esto se puede lograr mediante: (a) la elección apropiada de los volúmenes relativos de los tanques en serie, o (b) la modicación del suministro de la alimentación, de manera que esta sea dividida entre los tanques. El segundo de estos métodos resulta más útil en casos donde la reacción es tan rápida que la variación de los tamaños relativos de los tanques como medio para controlar el grado avance de la reacción, resulte inconveniente. Las curvas de rendimiento como la de la Figura 6.2 no son únicas. Existen sistemas donde ϕ puede aumentar con el avance de la reacción, o pasar por un máximo o un mínimo. La Figura 6.3 muestra el caso de un máximo donde la variación de ϕ es función de la concentración de el reactivo A. 118 CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES Figura 6.3. Curva de rendimiento con máximo (la concentración del reactivo disminuye de izquierda a derecha) En este caso, el rendimiento global que se obtiene en un CSTR puede, evidentemente, exceder al obtenido en un reactor discontinuo o en un reactor tubular ideal. Lo que se requiere, con el n de maximizar el área de los rectángulos, es utilizar inicialmente un tanque donde se obtengan, en lo posible, las condiciones de reacción, bajo condiciones estacionarias, cercanas a las que presentan el mayor valor de ϕ (un poco a la izquierda de ϕ1 en la Figura 6.3); y utilizando tanques adicionales solo con el propósito de disminuir la concentración del reactivo hasta su valor nal. Para que un grupo de reactores sea óptimo se debe cumplir, para las n relaciones entre las concentraciones de las etapas sucesivas, que (Gómez García & Fontalvo, 2000; Capítulo 5): ( Ci Ci 1 ) d ) 0; 1 i n ( Ci ) ( Ci 1 dCi (6.16) Aunque una expresión de ϕ en función de C se puede obtener fácilmente, la solución analítica de las n ecuaciones diferenciales resultantes de la ecuación (6.16) es generalmente imposible, a excepción de que ϕ sea una función lineal de C. Las ecuaciones que representan el sistema 119 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS permiten la determinación de una solución gráca, de manera que, para valores de Co, Cn y ϕ(Ci) conocidos, se inicia por suponer la concentración en el primer reactor; cualquiera que sea la elección se obtendrá un valor especíco del rendimiento, que corresponde al punto de corte con la curva ϕ(Ci), y para un valor jo de n (número de reactores) se continúa la construcción gráca hasta alcanzar Cn. La Figura 6.4 muestra la forma de utilizar el método gráco: Figura 6.4. Determinación de la concentración Ci, para Co, Cn y ϕ(Ci) conocidos Las variables y el orden para construir la Figura 6.4 corresponden a la siguiente secuencia de 4 pasos: 1. a Ci Ci 1 p d 2. b a dC Ci ( Ci Ci 1 ) d dC Ci 3. c ( Ci ) b ( Ci ) ( Ci Ci 1 ) 4. d c ( Ci ) ( Ci Ci 1 ) 120 d dC Ci d dC Ci ( Ci 1 ) Ci 1 CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES Figura 6.5. Cálculo de ϕ(C3) para un ϕ(C) dado La Figura 6.5 presenta la gráfica completa para tres reactores. Hasta aquí la temperatura y la presión han sido consideradas constantes. En muchas ocasiones, como las reacciones en fase líquida, la variación de la presión tiene efectos mínimos. En cuanto a la temperatura, esta debe considerarse siempre como una variable independiente. Un cambio deliberado y controlado en su valor puede ocasionar efectos benécos sobre el rendimiento de muchas reacciones. 6.4. REACCIONES PARALELAS: MÁS DE UN PRODUCTO Las reacciones paralelas son aquellas en las cuales se forma más de un producto mediante reacciones separadas y donde los productos, una vez formados, no reaccionan de nuevo. Reacciones paralelas típicas pueden describirse así: A R A B R o A S A C S y A R A B S 121 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Se utilizará, inicialmente para este análisis, el más elemental de los tipos de reacciones paralelas, donde el reactivo A se transforma en R y S, como ejemplo para discutir el efecto que el cambio de las variables de proceso pueden tener sobre este tipo de reacciones. Las ecuaciones de velocidad para cada una de las reacciones involucradas son similares a las utilizadas en reacciones simples y, para el sistema a analizar, pueden escribirse de la siguiente manera: dC A k1C An k2C Am dt dCR k1C An dt dCS k2C Am dt (6.17) donde m y n corresponden al orden de reacción. Si las reacciones son del mismo orden (es decir, si n y m son iguales) puede escribirse que: dC A ( k1 k2 )C An dt (6.18) Y si ambas reacciones son de primer orden: C A C AO e ( k1 k2 )t CR CR O CS CS O k1 / ( k1 k2 ) k1 / ( k1 k2 ) ( C AO ( 1 e ( k1 k2 )t )) ( C AO ( 1 e ( k1 k2 )t )) (6.19) Estas ecuaciones son similares a las obtenidas para una reacción de primer orden del tipo A → B excepto que ahora se tienen dos productos. R y S están relacionados por los valores de las constantes de velocidad que aparecen en sus respectivas ecuaciones de formación mediante la siguiente expresión: ( CR CRO ) ( C S C SO ) 122 k1 k2 (6.20) CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES El caso donde cada reacción es de orden diferente requerirá de solución numérica. Este hecho se analizará más adelante. 6.4.1. EFECTO DE LAS VARIABLES DE OPERACIÓN Dos parámetros de reacción están disponibles para la manipulación de la formación del producto deseado y de los coproductos: la concentración y la temperatura. Manipulando la alimentación al reactor y la geometría del mismo son las mejores formas de controlar la concentración, mientras el balance de energía relaciona la capacidad de la planta y del reactor para transferir calor. Generalmente existen reglas para la elección del procedimiento de alimentación, la geometría del reactor y el nivel de temperatura (Fogler, 2006; Levenspiel, 1999; Worstell, 2001). Los efectos de estas y otras variables se analizan a continuación. 6.4.1.1. EFECTO DE LA TEMPERATURA Como las reacciones paralelas corresponden a la suma de dos reacciones simples, el efecto de la temperatura es análogo al de las reacciones simples. Sin embargo, es de anotar que si el valor de una de las constantes de velocidad de reacción aumenta mucho más rápido con la temperatura que el valor de la otra, es decir con el incremento de temperatura k1 >> k2, una temperatura alta aumentará el rendimiento en particular del producto de la reacción 1. Así, si R es el producto deseado, el mejor rendimiento se obtiene al aumentar la temperatura si k1 tiene una funcionalidad mayor con respecto a la temperatura (según Arrhenius, es decir, una mayor energía de activación), o disminuyendo la temperatura de reacción si es k2 el que la tiene. Sin embargo, si la temperatura disminuye drásticamente, la velocidad de cada reacción decaerá considerablemente. Esto traerá como consecuencia que se necesite un reactor de gran tamaño para conservar el valor deseado de conversión, generándose, por lo tanto, un problema económico adicional que debe ser resuelto mediante la solución acoplada de un balance económico (costo del reactor) y del rendimiento del producto. 123 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 6.4.1.2. EFECTO DE LA PRESIÓN El efecto de la presión es muy similar al caso de una reacción simple. Si la reacción es en fase líquida, el único efecto de la presión se presentará sobre la volatilidad de los productos y/o los reactivos. Para las reacciones en fase gas, el efecto de la presión es directamente proporcional a la concentración. Si las reacciones son ambas de primer orden o de igual orden, (n = m), un aumento en la presión aumentará la velocidad de reacción pero no afectará la distribución de producto (si las reacciones son de equilibrio, deben manejarse consideraciones adicionales). Si los órdenes de las reacciones son diferentes, un aumento en la presión favorecerá la reacción de mayor orden y aumentará el rendimiento del reactante formado por tal reacción. 6.4.1.3. EFECTO DE LA RECIRCULACIÓN DE PRODUCTO Si las reacciones son reversibles, la recirculación de R y/o S diluirá los reactivos y disminuirá la velocidad de reacción. Si los órdenes de las reacciones son los mismos para la formación de cada producto, la dilución afectará ambas reacciones en el mismo grado. Para reacciones con diferentes ordenes, la que presente el mayor orden de reacción se verá más inuenciada por la recirculación de los productos. Por lo tanto, para el sistema: k1 A R dCR dt k1C A2 k2 A S dCS dt k2C A (6.21) el rendimiento de S puede incrementarse mediante la recirculación de S y/o R, lo cual disminuye la concentración de A en el alimento al reactor. 6.4.1.4. EFECTO DEL CATALIZADOR Ordinariamente se piensa en el catalizador en términos de la conversión. En el caso de una reacción simple, el efecto que presenta la adición del catalizador será el de acelerar la velocidad de reacción 124 CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES permitiendo utilizar un reactor más pequeño que el que se necesitaría sin catalizador, o el de facilitar las condiciones de operación, como temperatura y presión, para hacerlas menos severas. Una de las principales áreas de investigación en la catálisis es la selectividad, entendida como la habilidad del catalizador para aumentar el rendimiento de uno de los reactivos a expensas del otro (Blumenberg, 1992) y los efectos difusionales deben ser considerados en el análisis (Worstell, 2001). En el caso de reacciones paralelas, el efecto más importante del catalizador es el de aumentar ya sea k1 o k2 dependiendo de cuál sea el producto deseado. Si el producto deseado es R, el catalizador deberá actuar de modo tal que la relación k1 a k2 aumente. En muchas ocasiones esto es más efectivo que el variar las condiciones de temperatura, presión o ciclo de producción. 6.4.1.5. ¿Y EL MEZCLADO? Para reacciones complejas existen dos elementos a considerar. Uno es el efecto del mezclado sobre el volumen del reactor (y el tiempo de residencia) y el otro es el efecto del mezclado sobre la distribución de producto. En el caso de reacciones paralelas del tipo: k1 A R k2 A S la distribución de los productos no depende de la clase de reactor. Esto puede demostrarse fácilmente comparando las ecuaciones obtenidas para un reactor de mezcla con las de un reactor de ujo pistón. Las ecuaciones pueden ser derivadas de la misma manera como se hace para reacciones simples. Así, considerando un balance de materia para un sistema continuo de mezcla completa (CSTR) para reacciones de primer orden, el balance de materia para el componente A está dado por las ecuaciones: vC Ao vC A k1 k2 C AV 0 C Ao C A k1 k2 C A V / v C A C Ao / 1 k1 k2 V / v (6.22) 125 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS O en términos del tiempo de residencia: C A C Ao / 1 k1 k2 (6.23) La ecuación (6.23) es la misma ecuación que se deriva para un reactor de mezcla para una reacción simple, excepto que (k1 + k2) reemplaza a k. Utilizando un balance de materia para las sustancias R y S se encuentra la distribución del producto. Un balance para R genera las siguientes ecuaciones: vCRo vCR k1C AV 0 CR CRo k1C A V / v (6.24) CR CRo k1C A para S: Y, de manera análoga, se puede obtener la ecuación de balance CS CSo k2C A (6.25) Luego, dividiendo las ecuaciones (6.24) y (6.25) se obtiene: k1 / k2 CR CRo / CS CSo (6.26) que es igual a la ecuación que se obtiene de realizar el mismo análisis para un reactor tubular. Luego, se puede concluir que, para reacciones de primer orden en paralelo, la distribución de producto o el rendimiento del producto deseado es independiente de la forma del reactor. Más adelante se mostrará que este no es el caso para reacciones en serie o en serie – paralelo. Si las reacciones para la formación de R y S son de orden diferente, esto no es cierto ni para reacciones en paralelo. 126 CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES Para mostrar la comparación entre los reactores tubulares y los de mezcla completa, se darán los siguientes valores a las constantes de velocidad de reacción: k1 0,35 h 1 y k2 0,13 h 1 asumiendo también que A puro se alimenta al reactor a una concentración de 4 lbmol/ft3. La solución del problema mostrará la variación de la concentración de cada una de las sustancias involucradas en la reacción en función del tiempo de residencia en el reactor (entre cero y seis horas). En la Figura 6.6 se presentan los valores obtenidos para la solución de ambos modelos, con y sin mezcla, con el n de evaluar los efectos del mezclado sobre la conversión. Figura 6.6. Efecto del mezclado en la conversión para reacciones en paralelo Es interesante ver cómo varía la historia de la concentración paso a paso. En ambos casos, el del reactor de mezcla y el del reactor tubular, el rendimiento de R es igual a 0,728 y será independiente del tiempo, y de la conversión o grado de mezclado ya que es igual a: k1 / ( k1 k2 ) 127 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 6.5. REACCIONES EN SERIE: PRODUCTOS QUE CONTINÚAN REACCIONANDO En muchas reacciones, el producto, una vez formado, continúa reaccionando para formar nuevos productos. Esta es una reacción en serie y la forma más simple de expresarla es la siguiente: k1 k2 A R S Una gráca típica de concentración en función del tiempo de residencia para esta reacción se presenta en la Figura 6.7. Figura 6.7. Efecto del mezclado para reacciones en serie Entre los aspectos a destacar de la Figura 6.7 están: 128 • La concentración de R pasa a través de un valor máximo. • Existe un punto de inexión para la curva de concentración de S. CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES Las ecuaciones de velocidad para estas reacciones son las siguientes: dC A k1C An dt dCR k1C An k2CRm dt dCS k2CRm dt (6.27) Para cinéticas de primer orden, de la integración de las ecuaciones (6.27) se obtiene: C A C Ao e k1t CR k1C Ao / ( k2 k1 ) e k t e k t CRo e k t 1 2 2 (6.28) Y la concentración de S que puede ser determinada de un balance de materia (ver nota sección 6.6.2.1 – método de las composiciones intermedias): C Ao C A CR CRo CS CSo (6.29) Realizando un balance para A en un reactor de mezcla completa, donde se lleva a cabo esta reacción en serie, se obtiene: vC Ao vC A k1C AV 0 C Ao C A 1 k1 V / v (6.30) C A C Ao / ( 1 k1 ) Donde τ es el tiempo de residencia para el CSTR. Un balance de materia para R queda: vCRo vCR k1C AV k2 CRV 0 CRo k1C A V / v CR ( 1 k2 V / v ) (6.31) CR CRo k1C A / ( 1 k2 ) 129 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Combinando las ecuaciones (6.30) y (6.31) se obtiene: CR CRo 1 k1 k1C Ao 1 k1 1 k2 (6.32) Si CRo es igual a cero entonces: CR k1C Ao 1 k1 1 k2 (6.33) Una vez conocidos los valores de la concentración de A y R para cualquier valor de tiempo de residencia, los valores de S se pueden determinar de un balance como el de la ecuación (6.29). En la Figura 6.7 se muestran las concentraciones de A, R y S en función del tiempo de residencia para reactores de mezcla y tubulares. En el punto de máxima concentración de R en el euente, la concentración de R es mayor en el reactor tubular que en el de mezcla. En la Figura 6.8 se graca el rendimiento de R en función de la conversión de A para un reactor de mezcla y uno tubular. Se puede observar que para cualquier valor de conversión siempre es mayor el rendimiento para un reactor tubular. Figura 6.8. Comparación del rendimiento obtenido en un reactor de mezcla y un reactor tubular (k2/k1 = 0,37) 130 CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES Un ejemplo de aplicación de este tipo de grácas (rendimiento vs. concentración), fue publicado por Barilli et al. (1970) para el proceso de producción de alkilbencenos lineales, la base para la producción de detergentes biodegradables. El análisis de datos experimentales es bastante interesante y se sugiere al lector revisar esta referencia. 6.6. REACCIONES COMPLEJAS Las reacciones complejas son aquellas que se presentan paralelas con respecto a uno o más reactivos y, al mismo tiempo, en serie con respecto al producto. Un ejemplo de las reacciones complejas es el siguiente: A B R, A R S , A S T , A T U Aquí se tiene una reacción en paralelo con respecto a A y al mismo tiempo reacciones en serie con respecto a B, R, S y T. Las reacciones complejas se encuentran con frecuencia en situaciones industriales, como es el caso donde una molécula se adiciona a algún compuesto para formar una molécula más grande la cual es también reactiva al agente o sustancia que se está agregando. Algunos ejemplos de reacciones en fase líquida de este tipo son: • Cloración de benceno (Mc Mullen, 1948). • Hidrogenación de o-cresol (Schumann et al., 1989) • Hidrogenación de benceno (Döbert & Gaube, 1996). Las ecuaciones diferenciales que representan sistemas de reacciones complejas son difíciles de integrar analíticamente, excepto para ciertos casos especiales. El hecho que A reaccione tanto con el/los otro(s) reactivo(s) tanto como con los productos, hace que la relación entre CA y el tiempo sea más complicada que las obtenidas para reacciones en serie o en paralelo, siendo virtualmente imposible obtener una ecuación integral simple que relacione CA con el tiempo de residencia. El ingeniero químico se ve enfrentado a resolver los siguientes interrogantes respecto de estos sistemas: 131 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS • ¿Qué tipo y qué tamaño de reactor se debe utilizar? • ¿Qué condiciones, temperatura y presión, se deben utilizar? • ¿En qué cantidad, si es del caso, se deben utilizar los reactivos en exceso? • ¿Cuál será la conversión de los reactivos? Todas esas preguntas están relacionadas a la selección y diseño del reactor, y pueden ser resueltas con ayuda de la cinética. 6.6.1. EFECTO DE LA RELACIÓN DE ALIMENTACIÓN DE LOS REACTIVOS Aunque la presencia de dos reactivos hace que la descripción de este tipo de reacciones sea más compleja, el control físico de la reacción sea hace más fácil que para reacciones en serie. Compárense los siguientes sistemas reaccionantes: 1. A R S A B R 2. A R S Supóngase que en ambos casos R es el producto deseado y S es el indeseado. Entonces, el máximo rendimiento de R en ambos casos podría obtenerse operando el reactor de manera que se alcancen bajas conversiones por paso y recircular el A no convertido. Si ese fuera el caso, el límite inferior para la conversión de A por paso sería regulado, en cada caso, solo por aspectos económicos tanto del reactor como de los equipos de recuperación. Sin embargo, debe alcanzarse un rendimiento elevado para cada tipo de reacción. Supóngase que el reactante A es un material que se descompone fácilmente de manera que no puede ser recuperado en un sistema de reciclo. Todo el reactante A, una vez dentro del reactor, reacciona hacia el producto deseado, R, y éste convertido en el producto indeseado, S, o se pierde ya sea en la zona de reacción o en el sistema de recuperación. Si esto es cierto, muy poco se puede hacer para alcanzar un alto rendimiento del producto deseado en el caso de las reacciones en 132 CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES serie. En el caso de las reacciones complejas, un rendimiento elevado de R puede alcanzarse utilizando la relación óptima entre B y A en la alimentación. Así, pueden obtenerse altos rendimientos de R basados en la cantidad de A cargado al reactor para reacciones complejas, asegurando que el reactante B pueda recuperarse y recircularse. Si el costo de B es del mismo orden de magnitud que el de A y, adicionalmente, B no puede recircularse, entonces el mismo problema permanece tanto para la reacción en serie como para la compleja. Afortunadamente, en muchas reacciones comerciales el compuesto B puede recuperarse y recircularse (como en el caso de los alcoholes y óxido de etileno) o tiene un valor bajo (por ejemplo agua y óxido de etileno). 6.6.2. RENDIMIENTO DEL PRODUCTO En la mayoría de los problemas de diseño de reactores industriales, la idea es obtener el mayor rendimiento posible utilizando el reactor más pequeño. Existen muchos casos en los que el rendimiento del producto es mucho más prioritario que el tamaño del reactor. En tal caso, es más importante conocer exactamente como varía el rendimiento para cualquier grado de conversión que el conocimiento del tiempo de residencia. Algunos casos en los cuales la distribución de producto es mucho más importante que el tiempo de residencia son: • Cuando la reacción es extremadamente rápida, tomando lugar en fracciones de segundos. • Cuando los reactivos y los productos son tan costosos que aún para reacciones a pequeña escala la depreciación del reactor tiene un efecto muy pequeño sobre el costo total del producto. • Cuando los costos de los equipos de separación, para tratar las corrientes euentes del reactor, las de recirculación y puricación de productos, tienen órdenes de magnitud mayores que los del mismo reactor. Para estos casos se pueden denir expresiones integrales las cuales representan una descripción completa de la distribución de producto para 133 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS cualquier valor dado de relación de alimentación o grado de conversión para los cuales no se involucra el tiempo de residencia como variable. Eliminando este parámetro se pueden obtener ecuaciones diferenciales que son más simples que las que contienen esa variable de tiempo de residencia. Este tipo de ecuaciones se han desarrollado para reactores de ujo (PFTR y CSTR) y discontinuos. Considérese el siguiente grupo de reacciones elementales las cuales tienen lugar en un sistema homogéneo: k1 A B R k2 A R S Las ecuaciones de velocidad para este sistema son: rA k1C ACB k2C ACR k1C ACB rB rR k1C ACB k2C ACR (6.34) rS k2C ACR Esas cuatro ecuaciones se aplican indistintamente del tipo de reactor en el que tenga lugar la reacción: discontinuos, tubular o de mezcla. 6.6.2.1. RENDIMIENTO DEL PRODUCTO EN REACTORES TUBULARES Para reactores discontinuos y tubulares se puede obtener una ecuación diferencial que relaciona la concentración, por ejemplo del producto deseado, R, con uno de los reactivos, por ejemplo B, dividiendo sus expresiones de aparición o desaparición correspondientes y contenidas dentro del grupo presentado en las ecuaciones (6.35) de manera que se obtiene la ecuación: dCR dCB 134 k1C ACB k2C ACR k1C ACB (6.35) CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES que se reduce a: dCR k2CR 1 dCB k1CB dCR k2CR 1 dCB k1CB (6.36) (6.37) La ecuación (6.37), que es una ecuación diferencial lineal, corresponde a la expresión general: dy dx Py Q Cuya solución se realiza utilizando el factor integrante de la forma: Pdx Pdx Pdx y e e Qdx Ie O en este caso: CR k1 k1 k2 CB ICB (6.38) donde I es el factor o constante de integración determinado de las condiciones iniciales, y κ equivale a la relación k2/k1. Para denir la constante de integración, se sustituyen las condiciones iniciales en la ecuación (6.38) de manera que cuando t = 0, CR = CRo = 0 y CB = CBo, y por lo tanto: 0 1 / ( 1 ) CBo ICBo 1 I 1 / ( 1 ) CBo Por lo tanto, la ecuación (6.38) queda: CR 1 1 1 CB CBo CB 1 1 (6.39) 135 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS La ecuación de rendimiento básica para R sin recirculación es la (6.39). Es aplicable a reactores discontinuos y tubulares y permite determinar la concentración del producto R que corresponde a cualquier concentración del reactante B. Es interesante como con esta ecuación se puede determinar la relación k2/k1 a partir de un mínimo de corridas experimentales, la cual permite calcular el rendimiento para cualquier condición de alimentación (Levenspiel, 1999). Una vez conocida CR en función de CB, se pueden determinar los valores de CA y CS de un balance de materia, es decir: CS CBo CB CR (6.40) C A C Ao CR 2CS (6.41) NOTA: Para sistemas con reacciones únicas es sencillo determinar las relaciones adicionales que existen entre las concentraciones de los diferentes compuestos participantes en la mezcla reaccionante, pero para reacciones complejas no lo es, debido a que una sustancia participa alternativa y/o simultáneamente en más de un proceso de transformación. Para superar esto, es útil usar un procedimiento sistemático en el cual se enumere cada una de las reacciones y se denan, para cada una de ellas, las cantidades iniciales y nales de reactantes involucrados. Para aquellas sustancias que participan en más de una reacción, las cantidades iniciales para una reacción particular es la misma que la cantidad nal de la reacción precedente en la cual participó esta sustancia. Resulta conveniente, entonces, denir con un subíndice la cantidad nal de cualquier sustancia en una reacción con el número de la reacción en que participó. De esta forma se deben escribir todos los balances, entre cantidades iniciales, intermedias y nales. Este método se denomina el de las “composiciones intermedias”. Estos balances luego se combinan y reorganizan de manera que se eliminen las cantidades intermedias, dejando sólo las cantidades iniciales y nales para la reacción completa. Así, para las reacciones que se están analizando se tiene que: Reacción Reacción 1: A+B → R Reacción 2: A+R → S 136 Cantidades iniciales CAo, CBo, CRo CAi, CRi, CSo Cantidades nales CAi, CB, CRi CA, CR, CS CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES Balance para la reacción 1: CAo- CAi = CBo- CB = CRi- CRo Balance para la reacción 2: CAi- CA = CRi- CR = CS- CSo Eliminando algebraicamente las cantidades con subíndice i, se obtiene de los balances de materia que: CRi – CR = CS – CSo; CRi – CR = CS y como CBo – CB = CRi – CRo; CBo – CB = CRi. Luego reemplazando: CS = CRi – CR = CBo – CB – CR que corresponde a la ecuación (6.40). De manera análoga es posible determinar la ecuación (6.41). 6.6.2.2. ¿Y EL MEZCLADO? Para el cálculo del rendimiento del producto deseado en un equipo de mezcla completa, se plantean las ecuaciones de balance, similares a las obtenidas para los reactores discontinuos y tubulares (ecuaciones (6.39) a (6.41)), para el reactor de tanque agitado. Un balance de materia para el reactante B: vCBo vCB Vk1C ACB 0 CBo CB (V / v )k1C ACB (6.42) Para el producto deseado R: vCRo vCR Vk1C ACB Vk2C ACR 0 CR CRo (V / v )C A ( k1CB k2CR ) (6.43) Y para el producto no deseado S: vCSo vCS Vk2C ACR 0 CS CSo (V / v )k2C ACR (6.44) 137 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS De la relación entre los balances para R y B se obtiene: CR CRo ( k1CB k2CR ) CBo CB k1CB CR CRo kC C 1 2 R 1 R CBo CB k1CB CB CR Y entre S y B: (6.45) CRoCB ( CBo CB )CB CB ( CBo CB ) CS CSo k2CR CBo CB k1CB CS CSo k2CR CR CBo CB k1CB CB (6.46) Que son las ecuaciones básicas para un reactor de mezcla completa, las cuales se pueden resolver junto con el balance total presentado en las ecuaciones (6.40) y (6.41). BIBLIOGRAFÍA Barilli, F.; Calcagno, B.; Di Fiore, L. & Ghirga, M. (1970): “Reactor Design for Lineal Alkylbenzenes Plant”. En: Ind. Eng. Chem., 62(6), 62 – 67. Blumenberg, B. (1992): “Chemical Reaction Engineering in Today’s Industrial Environment”. En: Chem. Eng. Sci., 47 (9-11), 2149 – 2162. Denbigh, K.G. (1961): “Instantaneous and Overall Reaction Yields”. En: Chem. Eng. Sci., 14 (1) 25 – 38. 138 CAPÍTULO 6 - ELEMENTOS PARA EL ANÁLISIS DE SISTEMAS CON REACCIONES MÚLTIPLES Döbert, F. & Gaube, J. (1996): “Kinetics and Reaction Engineering of Selective Hydrogenation of Benzene Towards Cyclohexene”. En: Chem. Eng. Sci., 51(11), 2873 – 2877. Fogler, H.S. (2006): Elements of Chemical Reaction Engineering (4th Ed.). New York: Prentice Hall. Froment, G.F. (1981): “Thermal Cracking for Olens Production. Fundamentals and their Application to Industrial Problems”. En: Chem. Eng. Sci., 36 (6), 1271 – 1282. Gómez García, M.A. & Fontalvo, J. (2000): “Optimización de reactores CSTR en serie. Caso isotérmico”. En: NOOS, 11(1), 57 – 63. Levenspiel, O. (1999): Chemical Reaction Engineering (3rd Ed.). New Jersey: John Wiley & Sons. Missen, R.W.; Mims, C.A. & Saville, B.A. (1999). Introduction to Chemical Reaction Engineering and Kinetics. New Jersey: John Wiley & Sons. McMullen, R.B. (1948): “Distribution of Reaction Products in Benzene Chlorination”. En: Chem. Eng. Prog. 44 (3), 183 – 188. Schmidt, L.D. (1998): The Engineering of Chemical Reactions. Oxford: University Press. Schumann, W.K.; Kut, O.M. & Baiker, A. (1989): “Inuence of Reactions Parameters on the Stereoselectivity of the Nickel-Catalyzed Gas-Phase Hydrogenation of O-Cresol. 1. Kinetics and Reaction Pathway”. En: Ind. Eng. Chem. Res., 28 (6), 693 – 697. Segawa, K. & Tachibana, H. (1991): “Higly Selective Methylamine Synthesis Over Modied Mordenite Catalysts”. En: J. Catal., 131(2), 482 – 490. 139 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Wiley Ed. (2008): Ullmann's Encyclopedia of Industrial Chemistry. New Jersey: John Wiley & Sons. Worstell, J.H. (2001): “Don´t Act like a Novice About Reaction Engineering”. En: Chem. Eng. Proc., 97(3), 68 – 72. 140 CAPÍTULO 7 - DIAGRAMAS TRIANGULARES PARA LA SELECCIÓN DE ESQUEMAS DE REACCIÓN ÓPTIMAS 7 DĎĆČėĆĒĆĘ ęėĎĆēČĚđĆėĊĘ ĕĆėĆ đĆ ĘĊđĊĈĈĎŘē ĉĊ ĊĘĖĚĊĒĆĘ ĉĊ ėĊĆĈĈĎŘē ŘĕęĎĒĔĘ INTRODUCCIÓN Frecuentemente los ingenieros químicos se ven enfrentados al problema de escoger el mejor tipo de reactor o arreglo de reactores (esquema de reacción) para un proceso que presenta múltiples reacciones. A pesar de que para el proceso se tengan definidas las condiciones de temperatura, composición de alimentación, peso del catalizador y cinética de la reacción, la selección del esquema de reacción que genere la mejor selectividad y/o rendimiento hacia un producto deseado es una tarea que requiere evaluar diferentes tipos de criterios. En la literatura se proponen análisis basados, entre otros, en la maximización de la selectividad y/o rendimiento de un producto específico (Levenspiel, 1999; Fogler, 2005). En este documento se presentan criterios adicionales siguiendo la metodología propuesta por Trambouzé & Piret (1959). El esquema analítico original se implementa numéricamente, lo que permite estudiar cualquier tipo de ley de velocidad. El método gráfico se basa en la solución, para diferentes tipos de reactores, de los balances molares por componente y la representación de los caminos de reacción sobre un simplex concentracional o espacio de concentraciones. Basados en criterios geométricos, este método permite definir el mejor tipo de esquema de reacción para alcanzar el máximo rendimiento de un producto deseado. Sin embargo, el desempeño que se puede alcanzar dependerá del tipo de reacciones involucradas. 141 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 7.1. BALANCES MOLARES EN REACTORES IDEALES ISOTÉRMICOS Partiendo del balance molar general para la especie A en un sistema reactivo se tiene que (Fogler, 2005): Entra Sale Genera Acumulacion (7.1) V dN FAo FA rA dV A dt 0 (7.2) A partir de la ecuación (7.2) es posible obtener las ecuaciones de diseño para varios tipos de reactores: batch y de flujo continuo (PFTR y CSTR). Estas se encuentran resumidas en la Tabla 7.1. Tabla 7.1. Balances molares en reactores ideales Reactor Diferencial Batch dCi ri dt Integral dN i Nio rV i t Ni Cio Ci ri 0 CSTR PFTR Algebraica dCi ri d dCi Cio r i Ci τ es el tiempo de residencia de los reactivos dentro del reactor. De acuerdo con los balances de la Tabla 7.1, tanto para el reactor PFTR, CSTR y batch, se puede apreciar que la complejidad de su solución dependerá de la ley velocidad de reacción. Conforme al trabajo realizado por Trambouzé & Piret (1959), una forma para seleccionar el mejor esquema de reacción es ubicar sobre un simplex concentracional los datos experimentales de concentración a la salida del reactor, batch y/o CSTR. 142 CAPÍTULO 7 - DIAGRAMAS TRIANGULARES PARA LA SELECCIÓN DE ESQUEMAS DE REACCIÓN ÓPTIMAS En este caso se asumirán como datos experimentales aquellos que arroja la solución de cada uno de los balances de los reactores presentes en la Tabla 7.1. En un sistema de reacciones complejo, donde se conocen todos los reactantes y productos involucrados, así como las leyes de velocidad que los relacionan, la evaluación de la eficiencia del sistema (distribución de productos) se puede analizar mediante tres términos: la conversión (X), el rendimiento (Y) y la selectividad (S). La forma más directa de calcular estos parámetros es por medio de un modelo estequiométrico canónico como lo proponen Missen & Smith (2000). Considérese el reactante A que sufre una serie de transformaciones, entre las cuales se encuentra una reacción para obtener el producto deseado D: A D A DD + otras reacciones La conversión fraccional del reactante A, medida de la cantidad de este reactante consumido, se define como la relación entre las moles de A que reaccionaron y las moles iniciales así: XA FAo FA N NA ; X A Ao FAo N Ao (7.3) de donde 0 XA 1 El rendimiento de un producto es una medida del avance de una reacción hasta algún punto (tiempo o posición) en términos de un producto y un reactivo especificados. Así, el rendimiento del producto D con respecto a un reactivo A es la relación entre la cantidad de D formada y la cantidad teórica que se habría formado si toda la cantidad de A presente inicialmente hubiera reaccionado para formar D; esto es, las moles de A que reaccionaron para formar D por mol inicial de A, tal como se muestra en la ecuación (7.4). 143 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS YD / A A D FD FDo A D N D N Do ; YD / A D D FAo N Ao (7.4) de donde 0 YD / A 1 Respecto al tercer parámetro, la selectividad de un producto D con respecto a un reactivo específico A, es una medida de la cantidad de A que ha reaccionado para formar a D relativa a la cantidad total de A que ha reaccionado; esto es, las moles de A que reaccionaron para formar D por mol de A que reaccionó, tal como en la ecuación (7.5). SD / A A D FD FDo A D N D N Do ; SD / A D FAo FA D N Ao N A (7.5) de donde 0 S D / A 1; 7.2. N SK / A k C 1 A K N K N Ko 1 k N Ao N A CONSTRUCCIÓN DEL SIMPLEX CONCENTRACIONAL La técnica desarrollada por Trambouzé & Piret (1959) permite determinar el mejor tipo de reactor o esquema de reactores para un tipo dado de leyes de velocidad. Para esto se combinan los balances molares y las leyes de velocidad dependiendo del tipo de reactor. El grupo de ecuaciones se resuelve simultáneamente para obtener un diagrama que involucra la composición de todos los componentes implicados. Esta metodología se describe en detalle a continuación para dos tipos de reactores: batch (es de anotar que aunque la solución numérica de los balances para los reactores batch y PFTR es numéricamente análoga, las variables t y τ son conceptualmente diferentes) y CSTR. 144 CAPÍTULO 7 - DIAGRAMAS TRIANGULARES PARA LA SELECCIÓN DE ESQUEMAS DE REACCIÓN ÓPTIMAS 7.2.1. SIMPLEX CONCENTRACIONAL A PARTIR DE DATOS OBTENIDOS EN UN REACTOR BATCH Mediante la representación dentro de un simplex concentracional de los datos de concentración en función del tiempo, obtenidos en un reactor batch, se puede establecer las composiciones de los productos correspondientes a unas condiciones de alimentación dadas. Para ilustrar mejor este concepto se propone el siguiente esquema de reacciones en el cual el producto intermedio B es el deseado: k1 A B k2 B C (7.6) k3 B D La ley de velocidad de cada reacción es elemental, por lo tanto las ecuaciones diferenciales a resolver son las siguientes: dC A k1C A dt (7.7) dCB k1C A k2CB k3CB dt (7.8) dCC k2CB dt (7.9) dCD k2CB dt (7.10) Los valores de las constantes específicas de velocidad de reacción se reportan en la Tabla 7.2 (operación isotérmica). 145 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Tabla 7.2. Parámetros cinéticos del sistema de reacciones Constante específica de velocidad de reacción k1 k2 k3 s-1 0,1 0,02 0,02 Las ecuaciones (7.7) a (7.10) se resolvieron simultáneamente, empleado una técnica numérica del tipo Runge Kutta, a diferentes condiciones de alimento. Los resultados se presentan en un triangulo equilátero, en donde un vértice represente el reactivo puro, otro el componente deseado y el último vértice los demás componentes, como se muestra en la Figura 7.1. De esta forma, se representa la variación de los caminos de concentración, usando diferentes composiciones de alimento, Foj o Noj, y tras conducir la reacción durante un tiempo τ o t, respectivamente. Figura 7.1. Simplex concentracional de los caminos de composición batch o PFTR para cuatro componentes 146 CAPÍTULO 7 - DIAGRAMAS TRIANGULARES PARA LA SELECCIÓN DE ESQUEMAS DE REACCIÓN ÓPTIMAS 7.2.2. SIMPLEX CONCENTRACIONAL A PARTIR DE DATOS OBTENIDOS EN UN CSTR Frecuentemente es de interés, para propósitos de diseño, realizar investigaciones cinéticas en las cuales se utiliza un CSTR. Para analizar este caso, considérese el siguiente sistema de reacciones: k1 A B k2 B C (7.11) Los valores de k1 y k2 están dados en la Tabla 7.2, luego el sistema de ecuaciones a resolver es el siguiente: C Ao C A k1C A 0 (7.12) CBo CB k1C A k2CB 0 (7.13) CCo CC k2CB 0 (7.14) Los caminos de concentración, obtenidos tras la solución simultánea de las ecuaciones (7.12) a (7.14) mediante un método de Newton-Raphson, para diferentes composiciones de alimento, Foj, y diferentes tiempos de residencia, τj, se presentan en la Figura 7.2. En la Figura 7.2, una línea recta que una un punto de composición de alimento, Fo1, y una composición alcanzada a un tiempo de residencia, τj, es tangente a su intersección con la curva de composiciones batch. El desempeño de un sistema de CSTR en serie se analiza en la Figura 7.3. En ella, una línea recta desde un punto de alimentación dado, F01, generará un producto de composiciones P1 correspondiente a un tiempo de residencia, τ1. Si las coordenadas P2 corresponden al producto de salida del segundo CSTR, cuyo alimento es P1, una línea recta que pasa a través de esos puntos indicará el camino de composiciones. Adicionalmente, el mismo valor de composición de producto P2 puede obtenerse si el alimento corresponde al punto F02. El camino de composiciones, para distintos tiempos de residencia, corresponde a la curva F02 - P2. De acuerdo con esto, las posibles composiciones para obtener el producto de composición P2 estarán ubicadas en la línea recta que une los puntos F02 - P1 - P2. 147 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 7.2. Simplex concentracional de los caminos de composición CSTR para tres componentes Figura 7.3. Simplex concentracional de los caminos de composición CSTR. Caso de dos CSTR en serie 148 CAPÍTULO 7 - DIAGRAMAS TRIANGULARES PARA LA SELECCIÓN DE ESQUEMAS DE REACCIÓN ÓPTIMAS 7.3. REGLAS GENERALES PARA DETERMINAR EL MEJOR TIPO DE REACTOR Tres tipos de curvas de concentración pueden obtenerse siguiendo el esquema de cálculo propuesto en la sección 7.2. Estas se presentan en la Figura 7.4. El mejor tipo de esquema de reacción, que permitirá obtener una elevada selectividad y/o rendimiento hacia el producto deseado, se puede determinar del análisis de las curvas de la Figura 7.4. Hallando los extremos de las funciones involucradas en su construcción, utilizando el criterio de las segundas derivadas parciales, es posible determinar los mínimos o máximos absolutos de los caminos de composición. De esta forma, tres reglas se pueden proponer: i. Si las curvas de concentración son convexas hacia el producto deseado (B), el PFTR será el que dé el mejor rendimiento (Figura 7.5a). Es decir, se debe cumplir para cualquier valor de A, B y C que: d 2CB 0 (7.15) dC A 2 ii. Por el contrario, si las curvas que describen el camino de reacción son cóncavas respecto al producto deseado, el reactor que da un mejor rendimiento será un CSTR (Figura 7.5b). Luego, para cualquier valor de concentración de reactivos y productos, la segunda derivada de la concentración del compuesto deseado respecto al reactivo límite tiene que ser mayor que cero: d 2CB 0 dC A 2 (7.16) iii. Adicionalmente, cualquier tipo de reactor generará el mismo valor de conversión si los caminos de concentración son líneas rectas (Figura 7.5c). Es decir, si la segunda derivada de la concentración del compuesto deseado con respecto al reactivo límite es igual a cero. d 2CB 0 (7.17) dC A 2 149 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS En este caso, la selección del mejor reactor debe involucrar otros criterios, tales como considerar la fase en la cual se está llevando a cabo la reacción y así determinar que reactor ofrece una mayor ventaja en cuanto a la operabilidad. a. b. c. Figura 7.4. Posibles formas que adquieren los caminos de composición en el simplex concentracional Si en un mismo simplex de concentración, se cumple la ecuación (7.15) para un determinado rango de concentraciones y la ecuación (16) se cumple para otro, se podría utilizar un sistema de PFTR y CSTR con el fin de optimizar el rendimiento hacia el producto deseado. El punto de cambio entre los reactores será aquel donde se cumpla el criterio de la ecuación (17). 150 CAPÍTULO 7 - DIAGRAMAS TRIANGULARES PARA LA SELECCIÓN DE ESQUEMAS DE REACCIÓN ÓPTIMAS EJEMPLO 7.1. En el siguiente esquema de reacción el producto deseado es el compuesto C y la concentración inicial del reactivo A es de 0,25mol.m-3. Determine el mejor esquema de reactores para alcanzar la máxima concentración de C. k1 A B (7.18) k2 A C k3 A D Los valores de las constantes de reacción se reportan en la Tabla 7.3. Tabla 7.3. Parámetros cinéticos para las reacciones (7.18) k1 , mol.(m3.s) -1 k2 , s-1 k3 , m6.(mol2.s) -1 0,025 0,2 0,4 Solución De la estequiometría del sistema reaccionante, es posible establecer las siguientes relaciones: dC A k1 k2C A k3C A2 dt dCC k2C A dt (7.19) De esta ecuación se establece que los caminos de composición presentan una doble curvatura tal como se muestra en la Figura 7.5. 151 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 7.5. Simplex concentracional de los caminos de composición batch para el sistema de reacciones representado por la ecuación (7.19) Luego, a partir de las ecuaciones (7.17) se obtiene que: k2C A k2 2k3C A k2 k1 k2C A k3C A2 k k C 1 2 A k3C A2 2 (7.20) Los criterios (7.15 – 7.17) muestran que la ecuación (7.20) presenta como límites para la selección del tipo de reactor los siguientes valores: 2CC k 0 cuando C A2 1 2 k3 C A 2CC k 0 cuando C A2 1 2 k3 C A 2CC k 0 cuando C A2 1 2 k3 C A 152 (7.21) CAPÍTULO 7 - DIAGRAMAS TRIANGULARES PARA LA SELECCIÓN DE ESQUEMAS DE REACCIÓN ÓPTIMAS Estos criterios de la ecuación (7.21), según los valores de las constantes específicas de velocidad, definen una concentración límite de CA = 0,25. Es decir, la mejor opción de diseño será aquella que involucra un CSTR, hasta disminuir el valor de concentración de A hasta dicho valor, seguido por un PFTR en serie. Este caso se representa en la Figura 7.6. Figura 7.6. Simplex concentracional de los caminos de composición batch para los cuatro componentes del sistema de reacciones representado por la ecuación (7.18) Los resultados obtenidos para dicho esquema requieren de un tiempo de residencia de 7,5 segundos para el CSTR. Para el reactor tubular se fijó un valor de 5,7 segundos para ese parámetro. Con este esquema se alcanzan conversiones de A próximas al 50%. Como era de esperarse, según los criterios mencionados, el uso de un segundo CSTR en serie, en lugar del PFTR, disminuirá la conversión de A (aproximadamente hasta 45%). En la Figura 7.6 se presentan adicionalmente, con propósitos comparativos, los resultados obtenidos utilizando un PFTR o un CSTR. Si se definen respectivamente los tiempos de residencia en 7 y 27 segundos, 153 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS se obtendría una conversión de A cercana al 40% para el reactor tubular y del 27% para el reactor de mezcla. Dichos valores evidentemente son inferiores a los que proporciona el esquema definido por los criterios (7.15 – 7.17). EJEMPLO 7.2. Considérese el siguiente esquema de reacciones en paralelo o competitivas: k1 A B (7.22) k2 A C La primera reacción de la ecuación (7.22), es de orden n y la segunda reacción es de orden m. En este caso, el producto deseado es el compuesto B. Los parámetros de las constantes específicas y los valores de n y m, se dan en la Tabla 7.4. Tabla 7.4. Parámetros cinéticos y orden de reacción para la ecuación (7.22) k1 , s-1 k2 , m3.(mol.s) -1 0,1 0,1 n m 1 2 Determine cómo se afecta la conversión según el tipo de reactor o del arreglo de reactores que se seleccione. La alimentación consiste de A puro con una concentración de 1 mol.m-3. Solución Se analizan ahora tres alternativas de diseño: (a) un PFTR; (b) un CSTR, el cual puede trabajar a diferentes tiempos de residencia; y (c) un tren de CSTRs en serie. Para obtener el camino de reacción en el PFTR, se resolvieron las ecuaciones de balance correspondientes (ver Tabla 7.1) para todos los compuestos. La integración se realizó hasta un tiempo de residencia de τ = 100 s. Los resultados se muestran en la Figura 7.7. 154 CAPÍTULO 7 - DIAGRAMAS TRIANGULARES PARA LA SELECCIÓN DE ESQUEMAS DE REACCIÓN ÓPTIMAS Figura 7.7. Comparación de los desempeños de varios tipos de reactores para las reacciones de la ecuación (7.22) Como se puede apreciar en la Figura 7.7, caso (a), la forma que asume el camino de concentraciones para el sistema de reacciones en un PFTR es cóncava hacia el producto deseado B. En este reactor, se obtiene un rendimiento hacia el producto deseado cercano al 70%. Según el criterio de la ecuación (7.16), un CSTR debería proporcionar mejores rendimientos que el anterior. De esta forma, si se trabaja con un CSTR, caso (b) en la Figura 7.7, al mismo tiempo de residencia, es posible obtener un rendimiento cercano al 85% hacia el producto deseado. En la misma Figura se presentan los valores obtenidos para otros tiempos de residencia (10 y 20 s). Ahora, si se desea utilizar un tren de 10 CSTRs en serie en el cual el tiempo de residencia total sea de 20 s, se obtiene el comportamiento representado por el caso (c) de la Figura 7.7. Esta curva muestra que a medida que se incrementa el número de CSTRs en serie, la composición de salida del sistema de reactores se aproxima al comportamiento de un PFTR. La Tabla 7.5 muestra un resumen numérico de los resultados presentados en la Figura 7.7. 155 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Tabla 7.5. Comparación de los rendimientos alcanzados a diferentes tiempos de residencia en el PFR y CSTR para el sistema de reacciones (7.22) CA CB Tiempo de residencia, s-1 10 20 30 100 0,2254 0,0734 0,0258 2,22e-7 0,4899 0,6224 0,6677 0,6931 10 20 30 100 0,4142 0,2808 0,2153 0,0854 0,4142 0,5616 0,6458 0,8443 CC XA YD/A SD/A 0,4921 0,6231 0,6679 0,6931 0,6331 0,6718 0,6854 0,6931 0,4142 0,5616 0,6458 0,8443 0,7071 0,7808 0,8229 0,9221 PFTR 0,2847 0,7746 0,3043 0,9266 0,3065 0,9742 0,3069 0,9999 CSTR 0,1716 0,5858 0,1577 0,7192 0,1390 0,7847 0,0713 0,9156 Como se puede ver en la Tabla 7.5, a iguales tiempos de residencia, las conversiones en el PFTR son mayores que para el CSTR. Sin embargo, a altos valores de tiempos de residencia, es posible alcanzar los mayores rendimientos y selectividades hacia el compuesto deseado B en el CSTR. BIBLIOGRAFÍA Fogler, H.S. (2006): Elements of Chemical Reaction Engineering (4th Ed.). New Jersey: Prentice Hall. Levenspiel, O. (1999): Chemical Reaction Engineering (3rd Ed.). New Jersey: John Wiley & Sons. Missen, R.W. & Smith,W.R. (2000): “Yield, Selectivity and All That”. En: Chem. Eng. Educ., 34(4), 320 – 324. Trambouzé, P.J. & Piret, E.L. (1959): “Continuous Stirred Tank Reactors: Design for Maximum Conversion of Raw Material to Desired Product”. En: AIChE J., 5(3) 384 – 390. 156 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES 8 EĘęėĆęĊČĎĆ ĉĊ đĆĘ ėĊČĎĔēĊĘ ĆđĈĆēğĆćđĊĘ ĕĆėĆ đĆ ĘŃēęĊĘĎĘ Ğ ĔĕęĎĒĎğĆĈĎŘē ĉĊ ĘĎĘęĊĒĆĘ ĉĊ ėĊĆĈęĔėĊĘ INTRODUCCIÓN El método de las “regiones alcanzables” (AR, attainable regions, por sus siglas en inglés) consiste en un análisis geométrico sistemático que permite resolver problemas complejos de síntesis y optimización de procesos. Proporciona guías para el análisis cinético de sistemas que involucran múltiples reacciones (selección del mejor arreglo de reactores de flujo en estado estable para optimizar una función dada) así como algunas condiciones (reglas) para comprobar los resultados. Una AR está definida como el espacio de concentraciones que involucra todas las posibles condiciones (intermedias o de salida) que se pueden alcanzar en un sistema de reacciones múltiples, de cinéticas conocidas, que se llevan a cabo en un sistema de reactores de flujo, con una composición de alimento y un flujo dados. El método de análisis de las AR en el espacio concentracional fue propuesto inicialmente por Horn (1964), con los más recientes desarrollos y extensiones propuestos por Glasser et al. (1987, 1994), Hildebrandt et al. (1990), Omtveit et al. (1994), Milne et al. (2004). En síntesis, el problema es el siguiente: dados unas condiciones de alimento y un número de procesos involucrados (mezclado, reacción, calentamiento, enfriamiento, etc.), se desea determinar cuál es la mejor combinación de esos procesos que definirán el esquema o configuración óptima de reactores, así como las condiciones óptimas de reacción. La 157 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS función objetivo es normalmente de naturaleza económica, pero eventualmente puede incluir elementos de seguridad o ambientales. A continuación se presentan, tratando de conservar su singular descripción, algunas de las ideas conceptuales propuestas por Glasser et al. (1987). Estas definen los pasos que deben ser desarrollados con el fin de completar un análisis de “región alcanzable”. El concepto AR será ilustrado con base en uno de los ejemplos desarrollados inicialmente por ellos. El problema consiste en encontrar el mejor esquema de reacción (configuración o arreglo de reactor(es)) que maximiza la cantidad del producto B formado por el siguiente esquema de reacción (cinética de van de Vusse (1964)): k1 k3 B A C k2 k4 2 A D (8.1) Las reacciones 1, 2, y 3 son de primer orden respecto a A, B, y B, respectivamente, mientras la reacción 4 es de segundo orden respecto a A. Las constantes de velocidad a una temperatura particular son: k1 = 0,01 s-1, k2 = 5 s-1, k3 = 10 s-1, y k4 = 100 m3.(kmol.s)-1. Se tiene una concentración de A en la alimentación de 1 kmol.m-3. 8.1. ELEMENTOS PARA LA DETERMINACIÓN DE UNA REGIÓN ALCANZABLE 8.1.1. ELECCIÓN DE LOS PROCESOS FUNDAMENTALES En la síntesis de un sistema reactivo deben considerarse varios fenómenos físicos y/o químicos entre los cuales se incluyen: mezclado, reacción, separación, y transferencia de calor y/o de masa. Estos fenómenos deben ser realizados en reactores o en unidades de operación existentes, aunque también deben considerarse diseños innovadores. En esencia, para los propósitos de este análisis, los únicos procesos que estarían permitidos en el reactor o en el sistema de reactores son el mezclado y la reacción química. 158 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES 8.1.2. ELECCIÓN DE LAS VARIABLES DE ESTADO Es necesario escoger todas las variables requeridas para caracterizar el estado del sistema bajo estudio. La variable temporal debe ser suficiente para describir la dinámica de todos los procesos fundamentales que ocurren dentro del sistema. En el caso de un problema de optimización, se deben incluir todas las variables en una función objetivo (que es la función que se quiere optimizar, la cual puede ser un costo o una condición del producto). Las variables que caracterizan el estado de un sistema se agrupan en forma de vectores, los cuales se definen como vectores característicos. Adicionalmente, las variables deben escogerse de tal forma que obedezcan las leyes de mezclado lineal, es decir deben obedecer la “regla de la palanca para el mezclado” (Apéndice 8.1). Por ejemplo, en el caso de la cinética de van de Vusse (1964) las leyes de velocidad para las tres reacciones involucradas, ecuación (8.1), son respectivamente: rA k1c A k2 cB k4 c A2 rB k1c A k2 cB k3 cB rC k3 cB rD (8.2) k4 2 cA 2 En este caso, cA y cB son suficientes para describir todas las leyes de velocidad. Luego, con las expresiones para rA y rB será suficiente para describir el sistema y sólo cA y cB deben ser incluidas en el vector característico: c c A ,cB (8.3) Si el interés es producir el componente C o minimizar el volumen del reactor, entonces es necesario incluir cC o t en el vector característico, respectivamente, y el sistema deberá resolverse en un espacio tridimensional. Inicialmente, para este método se analizarán sistemas cuyo vector característico está compuesto por dos composiciones (luego el análisis se realizará en el espacio concentracional). Para sistemas que 159 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS requieran de mayores dimensiones, u otras diferentes a la concentración, se propondrán otros métodos adicionales más adelante. 8.1.3. DEFINIR LOS VECTORES DE PROCESO Los vectores del proceso están definidos de tal forma que ellos muestran el cambio instantáneo en el estado del vector característico, c¸ si un proceso fundamental ocurre. Cabe anotar que la dirección del vector es lo importante, pero no su magnitud. Así, el vector de reacción r(c) dará el cambio instantáneo de estado solo si un proceso reactivo ocurre. El cambio de estado por reacción es justo aquel dado por las ecuaciones para un reactor operando a partir de las condiciones iniciales (alimentación al sistema). Por ejemplo, para un PFR, donde ocurre una reacción con densidad constante, el vector de reacción debe dar la dirección de cambio en c si ocurre reacción, esto es: dc r c d (8.4) El vector de mezclado, v(c,c*), da el cambio instantáneo en la dirección del estado c si se agrega material en estado c*. El vector de mezcla (a densidad constante) está dado por: v c,c* c* c (8.5) 8.1.4. DETERMINAR LA GEOMETRÍA DE LAS UNIDADES DE PROCESO 8.1.4.1. REACTORES DE FLUJO PISTÓN (PFR) En general, para cualquier número de componentes y de reacciones, un PFR se describe por: n dFi rji dV j 1 (8.6) En el caso de operación a densidad constante (velocidad de flujo volumétrica constante) se obtiene que: 160 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES dc r c d (8.7) Luego, la interpretación geométrica del PFR es tal que el vector r(c) es tangente a todos los puntos de la trayectoria de concentraciones, esto debido a que el vector de reacción puede ser ubicado en diferentes posiciones dependiendo del tiempo de residencia. Para el caso de estudio (problema de van de Vusse (1964)), el PFR estaría descrito por el siguiente sistema de ecuaciones diferenciales: dc A k1c A k2 cB k4 c A2 d dcB k1c A k2 cB k3 cB d (8.8) Si se desea utilizar la notación vectorial para los balances molares del PFR, es útil valerse de la definición de velocidad de reacción global para representar el lado derecho de los balances, así: dc A rA c A ,cB d dcB rB c A ,cB d (8.9) Luego, la ecuación vectorial sería: d c A ,cB d rA c A ,cB ,rB c A ,cB (8.10) 8.1.4.2. REACTORES CONTINUOS DE TANQUE AGITADO (CSTR) Es posible demostrar para un CSTR que: n Fi Fio rji V j 1 (8.11) 161 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS que: En el caso que la operación sea a densidad constante se obtiene ci cio r c (8.12) Las ecuaciones que describen el CSTR resultan en un grupo de ecuaciones algebraicas que deben ser resueltas simultáneamente para un tiempo espacial dado. Para el problema de van de Vusse, el CSTR está descrito por las ecuaciones algebraicas: 4 c A c Ao rjA k1c A k2 cB k4 c A2 j 1 4 rjB cB cBo k1c A k2 cB k3 cB j 1 (8.13) En notación vectorial, estas ecuaciones se pueden escribir de la misma forma del lado derecho de las ecuaciones del PFR: c A c Ao rA c A ,cB cB cBo rB c A ,cB (8.14a) Para completar la notación vectorial se reescribe la ecuación (8.14a) como: o o rA cA ,cB ,rB cA ,cB c A c A ,cB cB (8.15) Nótese que el vector r(c), que contiene la cinética, es el mismo que para el PFR. La interpretación geométrica de un CSTR es tal que el vector v es co-lineal al vector de reacción escalado (riτ) (compare las ecuaciones (8.5) y (8.15)). Esto es, el vector de reacción es co-lineal con la línea desde el alimento hasta el producto del CSTR. Esto se puede observar más claramente si se reorganiza la ecuación (8.14a) de la siguiente forma: cB cBo rB c A ,cB dcB c A c Ao rA c A ,cB dc A 162 (8.14b) CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Esta es la ecuación de la tangente a la trayectoria del sistema (solución particular al sistema de ecuaciones) en el punto (cA, cB) desde (cA0, cB0). 8.1.5. CONDICIONES NECESARIAS Para que una región sea catalogada como candidata a ser una “región alcanzable” se requiere que la región sea convexa, y que ningún vector de reacción sobre los puntos de la frontera apunten hacia fuera de la región. Esto implica que se deben cumplir las siguientes tres condiciones: 8.1.5.1. LA REGIÓN INCLUYE TODAS LAS CONDICIONES DE ALIMENTO Como diferentes condiciones de alimento al sistema pueden generar diferentes productos, las condiciones fijas de alimento deben ser incluidas dentro de la región, como se muestra en la Figura 8.1. Figura 8.1. Esquema de la primera condición necesaria para la construcción de la AR 163 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 8.1.5.2. NINGÚN VECTOR DE PROCESO SOBRE LOS LÍMITES DE LA AR ESTÁ DIRIGIDO HACIA FUERA DE LA AR Considere de nuevo el espacio concentracional de la Figura 8.1 el cual no satisface esta condición. El vector de reacción, r(c), en un punto c sobre la frontera de la región, apunta hacia fuera. De la sección anterior, se sabe que el vector de reacción es tangente a una trayectoria PFR. Así, si un vector de reacción apunta hacia fuera del punto c, es posible usar ese punto c como un punto de alimento para un PFR, como se muestra en la Figura 8.2. Esto permitirá extender la región o espacio concentracional, lo cual querría decir que anteriormente no se habría definido aún por completo la AR. Figura 8.2. Esquema de la segunda condición necesaria para la construcción de la AR La región a la derecha del punto C es convexa, lo cual no es cierto a la izquierda del mismo punto. Se dice que una región es convexa si al contener dos puntos cualquiera X y Y, contiene todos los puntos del segmento X-Y. La región es cóncava si el segmento que une X y Y pasa a través del complemento de la región. La Figura 8.3 representa esta explicación geométricamente. 164 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Figura 8.3. Esquema de una región convexa y una región cóncava En otras palabras, en una región convexa todos los vectores apuntan hacia adentro de la región, o al menos son tangentes, o cero. Una región cóncava puede transformarse en una convexa agregando un “espacio convexo”. Para explicar mejor esto considérese ahora la siguiente región cóncava donde un vector v, que no es tangente en c, apunta hacia fuera de la región tal como se muestra en la Figura 8.4. Figura 8.4. Esquema del tratamiento para la corrección de concavidad para la construcción de la AR 165 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Se sabe, de la regla de la palanca, que se pueden obtener todos los productos a lo largo de la línea recta que une c con c*, y por lo tanto es posible extender la región a todos los posibles productos. La mayor extensión posible para la región candidata puede obtenerse mediante la selección del vector de mezcla más externo hasta el punto de alimentación tal como se muestra en la Figura 8.5. Figura 8.5. Esquema de la extensión de la AR por mezclado Las coordenadas del punto C son tales que corresponden con el lugar de máxima formación de B relacionada con el consumo de A. En resumen, el espacio de concentración puede extenderse, en este caso, por mezclado. 8.1.5.3. NINGÚN PUNTO ESTACIONARIO CON MEZCLADO COMO PROCESO EXISTE EN EL ÁREA DE COMPLEMENTO DE LA REGIÓN Un punto estacionario es un punto donde el vector resultante del proceso fundamental operando en el punto es un vector cero o nulo. Así, en el caso del sistema con reacción y mezclado un punto estacionario satisface la solución de la ecuación (8.16): 166 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES r c v c,c* 0 (8.16) Para condiciones de mezclado donde a > 0. Sin embargo, la ecuación del CSTR es: r c v c,c* 0 (8.17) Por lo tanto, un punto estacionario con reacción y mezclado como proceso fundamental representa un posible producto del CSTR. Nótese que el mezclado tal como se definió en la sección anterior sólo puede llevarse a cabo en una región convexa. Dado que en este ejemplo sólo ocurren los procesos de reacción y mezclado, esta conclusión puede ser rescrita como la condición: c c* r c (8.18) Ningún vector en el complemento de la región puede ser “retroextendido” desde el punto C (ver Figura 8.5) para intersectar la región candidata. 8.2. ¿CÓMO CONSTRUIR LA REGIÓN ALCANZABLE? La AR se construye utilizando una aproximación de crecimiento. En cada etapa, las condiciones necesarias deben ser comprobadas para determinar posibles extensiones de la región. Es importante notar que cuando se usa la técnica de la AR se está interesado en definir el límite de la misma. Cualquier otro punto interior puede alcanzarse mediante puntos de mezcla desde la frontera de la AR. Sin embargo, algunas veces los puntos interiores pueden ser aceptados como de operación por razones económicas o técnicas. En todo caso, la frontera de la AR incluirá siempre el mejor desempeño. Antes de construir la AR, resulta interesante analizar el problema de las reacciones de van de Vusse (1964) –ecuación (8.1)– con base en las teorías clásicas de la ingeniería de las reacciones químicas (Levenspiel, 1999). Note que, a partir de los valores de las constantes de velocidad, la 167 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS reacción de equilibrio A ↔ B está favorecida hacia la izquierda. Por tal razón solo aparecerá una pequeña cantidad de B. Adicionalmente, debido a la reacción en serie B → C la cantidad de B será aún más pequeña. Debe notarse que la velocidad de reacción de A para producir D es muy alta comparada con la de A para producir B. De estas consideraciones, se puede esperar que una alta conversión de A generará una alta concentración de B. Un CSTR podría ser adecuado, pero éste exigirá un volumen más grande que un PFR. El primer paso para encontrar la AR es determinar las trayectorias del CSTR y del PFR utilizando como punto de partida las condiciones de alimento al sistema, punto O, tal como se muestra en la Figura 8.6 para las reacciones de van de Vusse (1964). Figura 8.6. Trayectorias de concentración del CSTR y del PFR para las reacciones de van de Vusse De la Figura 8.6 se puede concluir que en un PFR se puede obtener una concentración de B mayor que la que se alcanza en un CSTR: se alcanzan conversiones de A de 0,85 y de 0,7, respectivamente. Luego, si se considera solo la teoría de los reactores ideales, la conclusión es que el PFR será el reactor elegido. Ahora la pregunta es: ¿existe la posibilidad de encontrar un mejor sistema de reacción? Para contestar esta pregunta es necesario examinar más en detalle la información de la Figura 8.6. Nótese 168 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES que para ambos sistemas las curvas no son convexas, luego los vectores de mezclado apuntarán hacia fuera de la región y la segunda condición no se satisface. Además la curva del CSTR es más amplia que la del PFR. Luego, se definirá como base de análisis el CSTR. La trayectoria de la reacción en el espacio cA – cB puede encontrarse directamente a partir de las relaciones de selectividad (Wen et al., 2002). Definiendo la selectividad global ϕB como: B cB cBo cAo cA cB B c Ao c A (8.19) Luego, en el espacio concentracional, la representación del comportamiento de selectividad constante corresponde a una línea recta. Así, el punto de cruce entre la línea de selectividad (de pendiente negativa) y la región convexa del CSTR corresponderá al máximo de la selectividad que se alcanzará por reacción y mezclado para esa región. Luego, se debe cumplir la siguiente condición. dB B B dCB 0 dC A C A CB dC A (8.20) Luego, sustituyendo la ecuación (8.19) en la (8.20) se obtiene que: dCB cB dC A c Ao c A (8.21) A partir de la definición de selectividad instantánea, SB, se obtiene que: SB rB rA k C k C k C S B 1 A 2 B 3 B2 k1C A k2CB k4 C A (8.22) 169 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Para que la selectividad instantánea sea máxima, se debe cumplir la misma condición que para la selectividad global, es decir: dS B S B S B dCB 0 dC A C A CB dC A (8.23) Derivando la ecuación (8.22), según la ecuación (8.23), y reemplazando se obtiene: CB C 1 C 2 k4 k4 k1 A 2 A k1 CA C Ao CA k3 C Ao k1 k2 k1 k3 (8.24) k1 La trayectoria de la ecuación (8.24) en el espacio concentración permite entonces determinar el punto P localizado en el lugar de máxima formación de B relacionada con el consumo de A en un CSTR. Esto se muestra en la Figura 8.7. Figura 8.7. Determinación del lugar de máxima selectividad o punto P Las coordenadas del punto P se pueden determinar también a partir de la analogía geométrica que, en ese punto, tendrían la ecuación de la 170 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES curva del CSTR y la de la línea recta OP: es decir, en ese punto P la derivada de CB en función de CA es igual a la pendiente de la línea OP. Las coordenadas del punto P permiten definir la línea OP, extensión de la región alcanzable, tal como se mostró en la Figura 8.5. La cual representa un CSTR con by-pass, tal como se esquematiza a continuación. Esquema 8.1. CSTR con by-pass de alimento En este sistema pueden variarse dos parámetros: i. El tiempo de residencia en el CSTR: este es el caso que se analizó inicialmente y equivale a la forma como varían las concentraciones de los reactantes A y B en la corriente de salida (curva del CSTR en la Figura 8.7); y ii. La fracción de alimento en el by-pass: nótese que en el Esquema 1, la concentración de la corriente de alimento al sistema (corriente 1), la corriente que se alimenta al reactor (corriente 1a), y la corriente de by-pass (corriente 1b) están todas representadas por el mismo punto cA = 1, cB = 0 (punto O, Figura 8.7). El producto representado por la corriente 3, el cual se alcanza mediante el mezclado de la corriente de producto del CSTR (corriente 2) y la corriente de alimento (corriente 1b), cae sobre la línea recta OP, y se puede determinar mediante el uso de la regla de la palanca. Variando la cantidad de alimento que pasa por el by-pass es posible mover la concentración de salida del reactor (corriente 3), desde el punto de alimento (p.e., todo el alimento pasa por el by-pass) hasta el punto en el otro lado de la línea (p.e., sobre la curva del CSTR, que corresponde a que no hay by-pass). La AR extendida se presenta en la Figura 8.8 luego de la corrección de concavidad. 171 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 8.8. Corrección de concavidad de la trayectoria de concentración del CSTR mediante una región de mezclado (línea OP) La región es ahora convexa. Nótese también que el punto P es un punto de operación del CSTR, así que en ese punto el vector de reacción y la línea OP son colineales. Por lo tanto, el vector de reacción en P apuntará hacia fuera de la región. Luego, es posible ampliar la región agregando un PFR empezando desde el punto P tal como se presenta en la Figura 8.9. Esta nueva región es convexa, luego ningún vector de reacción apuntará hacia fuera de la región. Es de esperarse entonces que, si los límites corresponden a la AR, los vectores de reacción apunten tanto hacia la región (a lo largo de la sección de by-pass) o que sean tangentes a la región (a lo largo de la región del PFR). De esta forma se satisfacen todas las tres condiciones de la sección 8.3. Luego, la AR que se determinó corresponde a la región completa. Para comprobar este hecho, considérense un punto cualquiera (A) o (B) que cae sobre la curva del CSTR con by-pass y del CSTR, respectivamente. Cada punto representa el producto obtenido, de concentraciones CAx y CBx, en cada uno de esos reactores. ¿Qué pasaría sí se agrega un PFR en ese punto? Si ya se determinó la AR, las curvas obtenidas deben estar incluidas dentro de ella. Luego de determinar las 172 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Figura 8.9. Construcción de la AR para el problema de van de Vusse Figura 8.10. Comparación de las curvas de concentración a diferentes condiciones de alimento para el problema de van de Vusse 173 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS concentraciones de salida del sistema se obtiene una curva similar a la del PFR, tal como se muestra en la Figura 8.10. Se puede observar que el PFR dibujado desde el punto P alcanza la máxima concentración posible de salida. ¿Qué es lo especial en ese PFR? ¿Qué propiedad tiene la corriente de alimento en este punto? 8.3. ¿CÓMO INTERPRETAR LAS FRONTERAS COMO DIAGRAMA DE FLUJO DE PROCESO? Para determinar el diagrama de flujo necesario para obtener un producto en particular se traza el camino sobre la región alcanzable para alcanzar tales condiciones. Esto permite determinar la secuencia correcta de los procesos fundamentales requeridos para alcanzar un producto especificado. Tomando como base la metodología propuesta por Wen et al. (2002), es posible determinar el lugar geométrico de los puntos de máxima selectividad calculados a diferentes condiciones de alimento contenidas en la AR. Esto permite obtener una primera separatriz de la AR. Este corresponde a la línea EP en la Figura 8.11. Ahora, de manera análoga a lo realizado en la Figura 8.9, desde cualquier punto sobre la línea EP se pueden dibujar trayectorias de PFRs. Los máximos de estas curvas permiten identificar la segunda separatriz de la AR correspondiente al lugar geométrico de los máximos de esas curvas, línea AC en la Figura 8.11. Las separatrices de la Figura 8.11 dividen la AR en tres regiones. La región I se puede denominar la región del CSTR debido a que allí se debe utilizar un CSTR (o un CSTR con by-pass) para alcanzar la máxima selectividad de B. La región II se puede denominar como la región del PFR ya que allí, para el intervalo de posibles condiciones de alimentación analizadas y desde cualquier punto sobre la línea EP, la máxima selectividad B se alcanzará con un PFR. Y finalmente, la región III que podría considerarse como la región inoperable dado que no se obtendría ninguna mejora de la selectividad de B. Finalmente, es posible definir que la forma de establecer el mejor arreglo de reactores para un sistema específico implica la determinación, 174 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Figura 8.11. Tres zonas de la región alcanzable para las reacciones de van de Vusse Figura 8.12. Posibles configuraciones para el sistema de reacciones de van de Vusse 175 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS para el espacio concentracional, de las coordenadas de máxima selectividad del producto deseado (punto P). A partir del punto P, incluir el reactor que permitió expandir la AR de tal forma que se alcance el máximo de selectividad para el producto deseado. La Figura 8.12 muestra las posibles configuraciones de reactores o arreglos de reactores para el problema de van de Vusse. Sobre el diagrama, recuérdese que el punto P se obtiene en un CSTR. Para puntos a la derecha de P se requiere la mezcla de P con el alimento al sistema en el punto O, este es entonces justo un CSTR con by-pass de alimento. Puntos a la izquierda de P se obtienen siguiendo el proceso de reacción desde el punto P, lo cual se logra agregando un PFR. Puede observarse que esos puntos se obtienen a partir de una estructura que comprende un CSTR seguido por un PFR en serie. ¿Qué tipo de configuraciones estarán definidas para las trayectorias con condiciones de alimento (A) o (B) de la Figura 8.10? 8.4. ¿CÓMO ENCONTRAR EL ÓPTIMO? Una vez la AR ha sido construida, es simple definir el óptimo para una función objetivo especificada. El óptimo se encuentra superponiendo una grafica de contornos de la función objetivo en la grafica de la AR. Eso quiere decir que se grafica junto a la AR el lugar geométrico de los puntos que tienen el mismo valor de la función objetivo (Hildebrandt, 2007). Luego se identifica la curva que es tangente a la frontera de la AR. El punto donde la curva de la función objetivo toca la AR corresponde al punto óptimo de operación del sistema. Utilizando los resultados obtenidos para el caso de van de Vusse, si se desea determinar cuál es la máxima producción posible de B, se puede entonces incluir la función objetivo que podría ser por ejemplo la ecuación (8.25): Sobj cB Los resultados se muestran en la Figura 8.13. 176 (8.25) CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Figura 8.13. Ubicación del máximo de concentración de B posible en el sistema de van de Vusse restrigido por la función objetivo Sobj cB Figura 8.14. Ubicación del máximo de concentración de B posible en el sistema de van de Vusse restringido por la función objetivo Sobj 7000cB 5c A2 177 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS como: Se puede definir una función objetivo de beneficio económico tal Sobj 7000cB 5c A2 (8.26) Los resultados se presentan en la siguiente Figura 8.14. Luego es fácil determinar tanto el valor óptimo de la función objetivo así como el diagrama de flujo de proceso requerido para alcanzar este óptimo. ¿Cuáles serían los tiempos de residencia totales para alcanzar los óptimos señalados en las Figuras 8.13 y 8.14? 8.5. CASOS DE ESTUDIO 8.5.1. REACCIONES DE TRAMBOUZÉ & PIRET (1959) ciones: Trambouzé & Piret (1959) analizaron el siguiente sistema de reack1 A B k2 A C (8.27) k3 A D Los valores para las constantes especificas de velocidad de reacción son k1=0,025 mol ( L min) 1 , k2=0,2 min 1 , k3=0,4. La ley de velocidad para la primera reacción es de orden cero, de orden uno y dos para la segunda y tercera reacción respectivamente. La concentración de alimento de A es de 1 mol/L. Se desea determinar la mejor configuración de reactor(es) para maximizar la concentración del producto C. 8.5.1.1. SISTEMA A VOLUMEN CONSTANTE Para construir la curva del CSTR, se tiene el siguiente sistema de ecuaciones a resolver: 178 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES c A0 c A k1 k2 c A k3c A2 (8.28a) cC 0 cC k2 c A (8.28b) Despejando τ se obtiene la siguiente expresión: c A0 c A 2 k1 k2 c A k3c A (8.29) Luego, la trayectoria del CSTR se puede obtener de: i. resolver las ecuaciones (8.28a) y (8.28b); o ii. Generar para el intervalo de valores de cA, un vector de valores de τ, ecuación (8.29), y luego con esos valores obtener los correspondientes para cC (ecuación 8.28b). La trayectoria descrita por el PFR viene dada por la solución del sistema de ecuaciones diferenciales: dc A k1 k2 c A k3c A2 d (8.30b) dcC k2 c A d (8.30b) Para obtener una solución analítica, se separan variables y se integran las ecuaciones (8.30a) y (8.30b) se obtiene: 4 c c A0 A 2k3c A k2 2k3c A0 k2 k2 2 k2 2c A0 k3 cC c k2 2 Ln C0 2 2 k3 (8.31a) (8.31b) La trayectoria del PFR se puede obtener de manera análoga al procedimiento descrito para el CSTR: i. resolviendo las ecuaciones (8.30a) y (8.30b); o ii. Con las ecuaciones (8.31a) y (8.31b). Los resultados de las trayectorias en el espacio de composiciones para el CSTR y el PFR se muestran en la Figura 8.15. 179 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 8.15. Trayectorias de concentración del CSTR y del PFR para las reacciones de Trambouzé & Piret. Se incluyen también la AR y sus zonas Nótese que es posible ampliar la región cóncava, de la curva del CSTR, correspondiente al lugar geométrico de la composición alcanzada por un CSTR con by-pass. Como se explicó anteriormente, para alcanzar esto se traza una línea recta desde el punto de alimento (1,0) hasta el punto de tangencia (P) con la curva del CSTR. Para esto se puede despejar τ de la ecuación (8.28b) y se iguala con la expresión para τ de la ecuación (8.29), despejando de la ecuación resultante cC así: k c c c cC 2 A A0 A 2 k1 k2 c A k3c A (8.32) Se debe cumplir entonces que la línea recta sea tangente a la curva del CSTR, luego su pendiente deberá ser igual a la derivada de la ecuación (8.32): dcC m dc A 180 (8.33) CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Luego, con base en lo expuesto para las ecuaciones (8.14b) y (8.19), la ecuación de la línea recta tangente será: dc cC C c A c A0 cC 0 dc A (8.34) donde c A0 = 1 kmol/m3 , cC 0 = 0. Igualando las ecuaciones (8.32) y (8.34) se determinan las coordenadas del punto P, que en este caso son [0,25; 0,375], ver Figura 8.15. A manera de ilustración, se puede observar que las mismas coordenadas se pueden determinar a partir de la definición de selectividad. Retomando la ecuación (8.22), pero en función de las leyes de velocidad de este caso se obtiene que: SC rC k2 C A rA k1 k2C A k3C A2 Aplicando el criterio de la ecuación (8.23) se obtiene que: CA k1 k3 que en este caso, confirma el valor de CA = 0,25 encontrado de la combinación de las ecuaciones (8.32) y (8.34). Este valor permanece constante para cualquier condición de alimento en el intervalo de concentraciones de A considerado. El lugar geométrico de los valores de máxima selectividad corresponde entonces a la línea recta EP que se indica en la Figura 8.15. Esta línea corresponde entonces a la separatriz de dos regiones del diagrama concentracional: la región I correspondiente al CSTR, y la región II al PFR. El arreglo de reactores se muestra en la Figura 8.16. La composición de producto se logra maximizar agregando un PFR a partir del punto P. La concentración de producto se incrementa en un 14,15 y 15,18 por ciento, respecto al uso de sólo un PFR y un CSTR, respectivamente. 181 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 8.16. Región alcanzable para el problema de Trambouzé & Piret 8.5.1.2. SISTEMA A VOLUMEN VARIABLE Siguiendo la metodología de Fogler (2006), los balances pueden ser modificados de manera que se incluya el cambio de volumen por reacción química. En este caso, el problema de Trambouzé & Piret ha sido modificado, tal como lo sugiere Hildebrandt et al. (1990), de la siguiente forma: k1 A B k2 A 2C k3 A D Los valores de las constantes específicas de velocidad se conservan tal como en el enunciado del ejercicio. En el caso del CSTR los balances quedan: 182 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES 2 FA FA FA0 FA V k1 k2 cTo k3 cTo FT FT (8.35a) FB Vk1 (8.35b) F FC V 2k2 cTo A FT (8.35c) F 2 FD V k3 cTo A FT (8.35d) Para el PFR, el sistema de ecuaciones que representa el sistema reaccionante queda como: 2 FA dFA FA rA k1 k2 cTo k3 cTo dV FT FT (8.36a) dFB rB k1 dV (8.36b) dFC F rC 2k2 cTo A dV FT (8.36c) F dFD rD k3 cTo A dV FT 2 (8.36d) Cabe recordar que: FT FA FC FD FE . Los resultados obtenidos numéricamente, de resolver simultáneamente las ecuaciones (8.35a) a (8.35d) y (8.36a) a (8.36d), se presentan en la Figura 8.17. Todos los puntos sobre la línea AP pueden alcanzarse utilizando un CSTR que tenga la cantidad apropiada de by-pass. La selectividad máxima en todos los casos es de 2,05. 183 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 8.17. Región alcanzable para el problema modificado de Trambouzé & Piret: Modelo a volumen variable 8.5.1.3. SISTEMA NO IDEAL En este caso, la ley de los gases ideales no es aplicable y es necesario considerar el comportamiento no-ideal de los gases involucrados. Existe un gran número de modelos de propiedades termodinámicas no ideales que pueden ser utilizados. En este caso de estudio, se seguirán las condiciones que para este problema propone Zhou & Manousiouthakis (2007). Se propone entonces utilizar una ecuación cúbica de estado para calcular un factor de compresibilidad, Z, que involucre el comportamiento no ideal de todos los gases implicados en el término de concentración de la siguiente forma: C 1 P Z RT (8.37) Esta ecuación es apropiada tanto para sustancias puras como para mezclas. Con fines académicos, se realizará un cambio de nomenclatura de manera que los balances se presentarán en función de las fracciones 184 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES másicas de cada componente. El factor de compresibilidad puede calcularse utilizando la ecuación de Redlich & Kwong (R-K) (Poling et al., 2000): P RT a 2 (1 C ) b (1 C ) b(1 C ) (8.38) donde 1/C es el volumen molar, a y b son las dos constantes, dependientes de las especies, que pueden determinarse a partir de la temperatura critica, la presión critica y la temperatura de operación. Combinando la definición del factor de compresibilidad y la ecuación R-K se obtiene que: aP bPRT b 2 P 2 abP 2 Z3 Z2 Z 0 2 2 3 3 R T R T (8.39) Esta ecuación tiene solución analítica para tres raíces. Si existen múltiples raíces reales, el máximo valor de Z corresponderá a la fase vapor y el valor más pequeño de Z corresponderá a la fase liquida. Para aplicar la ecuación R-K a mezclas, es necesario utilizar reglas de mezclado para promediar las constantes ai y bi de cada componente en la mezcla, por ejemplo de la siguiente manera (Poling et al., 2000): n n a xi x j ( a i a j ) 2 i 1 i1 R 2Tci2.5 a 0, 42748 PciT 0.5 ; n b xi bi (8.40a) RTci2.5 b 0, 08664 Pci (8.40b) ; i 1 donde Tci y Pci son la temperatura critica y la presión critica, respectivamente para los i componentes. Sus valores numéricos se presentan en la Tabla 8.1. Como el factor de compresibilidad de la mezcla es función de todas las composiciones xi y subsecuentemente de todas las fracciones másicas, zi, las velocidades de reacción de los distintos componentes dependerán de todas las zj. 185 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Tabla 8.1. P ropiedades c ríticas s upuestas pa ra l os c ompuestos de l a c inética de Trambouzé & Piret Componente Tc K Pc kPa A B C D 544 538 460 548 5030 4950 3500 5090 Se considerará el sistema de reacciones analizado en el caso 8.5.1.2. Las constantes de velocidad de reacción tienen los mismos valores numéricos utilizados anteriormente. Las reacciones se llevan a cabo en fase gaseosa a una presión de 56 atm y una temperatura de 550 K, se alimenta A puro, el cual tiene un peso molecular, MA, de 40 g/mol. Para expresar los balances en términos de las fracciones másicas se debe tener en cuenta que en el caso que la densidad sea variable, las concentraciones en función de la fracción másica para los componentes A y C se expresan como: C A C0 zA 1 zC ; CC C0 2 zC 1 zC (8.41) donde C0 corresponde a la concentración total inicial. En el caso que se tenga densidad constante, las expresiones de concentración para los mismos componentes se encuentran determinadas por las siguientes ecuaciones: C A C0 z A ; CC 2C0 zC (8.42) Luego los balances para el CSTR quedan de la siguiente forma: 186 2 zA zA k3 C0 z A0 z A M A k1 k2C0 z 1 zC 1 C (8.43a) z M C 2k2C0 A zC zC 0 1 zC (8.44b) CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Y para el PFR: 2 dz A zA zA M A k1 k2C0 k3 C0 d 1 zC 1 zC (8.45a) dzC z M C 2k2C0 A 1 zC d (8.46b) Los resultados obtenidos, tanto para densidad constante como variable, se presentan en la Figura 8.18 de forma comparativa para los casos. Figura 8.18. Región alcanzable para el problema modificado de Trambouzé & Piret: se asumió gas no ideal De la Figura 8.18 se puede observar que, para el caso de gases no ideales, la AR es ligeramente mayor cuando se considera el modelo a densidad constante. Lo anterior se explica del efecto que tiene el cálculo de las fracciones molares (más evidentes en los perfiles). Las fracciones másicas de C en el punto máximo corresponden a 0,4892 y 0,4831 para los modelos a densidad constante y variable, respectivamente. 187 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 8.5.2. DESHIDROGENACIÓN OXIDATIVA DE BUTENO A BUTADIENO ADAPTADO DE MILNE ET AL. (2004A, 2004B) El proceso simplificado para la deshidrogenación oxidativa del buteno fue postulado por Milne et al. (2004a, 2004b) tal como se esquematiza en la Figura 8.19. Figura 8.19. Esquema de reacción para la deshidrogenación oxidativa de buteno a butadieno Se requiere determinar las condiciones de operación necesarias para maximizar el rendimiento a butadieno a partir de una alimentación fija de buteno. Para esto se propone identificar la AR para el sistema buteno – butadieno para un PFR. Las reacciones químicas involucradas, junto a las constantes de velocidad de reacción respectivas, son las siguientes Tellez et al., (1999): Oxidación de buteno 1 k7 C4 H 8 O2 C4 H 6 H 2O 2 1 1 k7 685x10 3 exp 19810 773 T k8 C4 H 8 4O2 4CO 4H 2O 1 1 k8 32,33x10 3 exp 17585 773 T k9 C4 H 8 6O2 4CO2 4H 2O 1 1 k9 115,67 x10 3 exp 12894 773 T 188 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Oxidación de butadieno 7 k10 C4 H 6 O2 4CO 3H 2O 2 C4 H 6 1 1 k10 118,17 x10 3 exp 17633 773 T 11 k11 O2 4CO2 3H 2O 2 1 1 k11 435x10 3 exp 12268 773 T Las leyes de velocidad respectivas son las siguientes: r7 k7 pC4 H8O r8 k8 pC4 H8 O r9 k9 pC4 H8 O r10 k10 pC4 H 6 O r11 k11 pC4 H 6 O donde los parámetros θO y λO corresponden a los sitios de oxidación selectiva y no selectiva, respectivamente, del catalizador. Estos se pueden calcular según las siguientes expresiones (con pi en kPa, y T en K): O O 2k12 pO2 2k12 pO2 k7 pC4 H8 2k13 pO2 2k13 pO2 8k8 12k9 pC4 H8 7 k10 11k11 pC4 H 6 1 1 k12 2995 x103 exp 13772 773 T 1 1 k13 3255 x103 exp 662 773 T Al reactor se alimentan dos corrientes: una con buteno puro, mientras en la otra la presión parcial de oxígeno varía entre 15 y 85 kPa. El sistema trabaja a presión y temperatura constantes en 1 atm y 773 K, 189 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS respectivamente. Si se asume modelo de gas ideal y densidad constante, las ecuaciones de balance para este reactor quedan, en general, como: dpC4 H 8 d´ dpC4 H6 d´ dpO2 d´ r7 r8 r9 RT r7 r10 r11 RT 21 r7 4r8 6r9 72 r10 112 r11 RT La Figura 8.20 presenta los resultados obtenidos. Cuando la presión parcial inicial de oxígeno es de 85 kPa, la reacción procede hasta que todo el oxígeno se consume. Cuando esto ocurre, las concentraciones residuales de buteno y butadieno son 0,0009 y 0,07, respectivamente. A presiones parciales menores que 85 kPa, la reacción se detiene con el consumo total de oxígeno. El máximo rendimiento de butadieno, c.a. 0,51, se alcanza para una presión parcial inicial de oxígeno de 65 kPa. Sin embargo, aún quedan presentes importantes cantidades de buteno y butadieno. Estos resultados se presentan en la Figura 8.21 en función de la presión parcial de oxígeno. Finalmente, la Figura 8.22 muestra la variación de la fracción molar residual de buteno con la presión parcial inicial de oxígeno y el tiempo de residencia en el reactor, evidenciando la rapidez del proceso reactivo a las condiciones bajo estudio. Milne et al. (2004a, 2004b) resolvieron este caso utilizando balances en función de fracciones másicas: ¿qué diferencias se encuentran entre los resultados?; ¿cómo explicar dichas diferencias?; ¿cómo se afectan los resultados si se tuviera en cuenta la perdida de carga en el reactor?; ¿qué resultados se alcanzarán en un CSTR? 190 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Figura 8.20. Perfiles de las fracciones molares de buteno y butadieno a diferentes presiones parciales iniciales de oxígeno, en un PFR Figura 8.21. Tiempos de residencia para el butadieno a diferentes presiones parciales iniciales de oxígeno, en un PFR 191 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 8.22. Tiempos de residencia para el buteno a diferentes presiones parciales iniciales de oxígeno, en un PFR 8.5.3. SISTEMAS NO ISOTÉRMICOS: OPERACIÓN ADIABÁTICA. ADAPTADO DE HILDEBRANDT ET AL. (1990) Este es otro de los casos que se puede analizar por medio de la aproximación geométrica propuesta por el método de las regiones alcanzables. Se seguirá considerando el caso bidimensional. Es decir, se incluirán solo dos variables: concentración y temperatura. Para un sistema que opera adiabáticamente, donde ocurre solo una reacción, se propone examinar a continuación dos casos: a. construir la región alcanzable en el espacio concentración-tiempo; y b. definir la región alcanzable en el caso de utilizar solo reactores de flujo pistón. Considérese la siguiente velocidad de reacción en función de la concentración C: 4000 8000 8 r 5 105 exp C 5 10 exp 1 C T T 192 (8.45) CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Es fácil demostrar que, para un proceso adiabático a presión constante, con calor de reacción y capacidad calorífica constantes, la temperatura del sistema podría variar según la ecuación (8.46): T T0 Tad 1 C (8.46) donde T0 es la temperatura de alimento y Tad es la temperatura adiabática. A manera de ejemplo, se asumirán valores para estas temperaturas de 300 y 200 K, respectivamente. 8.5.3.1. CONSTRUCCIÓN DE LA REGION ALCANZABLE PARA LA OPERACIÓN ADIABÁTICA Resolviendo los balances para el PFR y el CSTR se obtienen las trayectorias mostradas en la Figura 8.23. Figura 8.23. Región alcanzable para diferentes reactores en operación adiabática La curva AGBC representa la trayectoria de un reactor de flujo pistón con alimentación en el punto A. Parte de esta trayectoria es una curva cóncava. Esta concavidad puede ser corregida con una trayectoria 193 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS que incluya la concentración del punto de alimento (A) con la concentración del punto B: es decir, una línea recta AB tangente a la curva AGBC en el punto B. La curva ADEF corresponde a la trayectoria de un CSTR. Nótese que esta curva pasa por los puntos B y D, y además su trayectoria entre esos dos puntos está por debajo de la línea AB. Adicionalmente, el lugar geométrico de los puntos solución del CSTR no es convexo. Es posible entonces dibujar una línea recta entre el punto A y el punto E, la cual permite llenar la concavidad y representa mezclado entre esos dos puntos. Es posible ahora ubicar otro PFR desde el punto E (colineal con la línea AE). Este corresponde a la curva EHC: un PFR con alimentación desde el punto E. Nótese que la trayectoria de los PFR son iguales (aunque desplazadas) desde los puntos G y E, terminando ambas en el mismo punto C. El límite inferior de la región alcanzable está dado por la curva AEHC. En el límite, cuando la concentración tienda a la concentración de equilibrio del sistema, el tiempo de residencia (τ) tenderá a infinito. El otro límite está dado por la línea resultante del mezclado de la composición de alimento con la del equilibrio. En la Figura 8.23 se observa que la concentración C disminuye con el aumento del tiempo de residencia hasta alcanzar un valor cercano a 0,18. A partir de esta concentración, la curva se asintotiza debido a la restricción del equilibrio. En cuanto a la curva del CSTR, el tiempo de residencia aumenta con la disminución de la concentración C hasta aproximadamente 0,85. A partir de este valor, disminuciones adicionales en la concentración requerirán de menores tiempos de residencia pero solo hasta alcanzar el punto E. Si se desea determinar el tiempo de residencia mínimo para una concentración de salida dada, la respuesta se puede determinar sobre la curva AEHC. Cualquier punto por encima de esta curva se puede alcanzar también. Si se desea, por ejemplo, operar a las condiciones señaladas por el punto I en la Figura 8.23, es necesario utilizar un PFR capaz de operar las condiciones de salida indicadas por el punto B pero con by-pass de forma tal que este último fije las condiciones de salida en I. Considérese ahora el caso en el cual una corriente de alimento, equivalente al punto A en la Figura 8.24, que ingresa a un PFR. La trayectoria de concentración vs. tiempo de residencia dentro de ese reactor está dada por la curva AXBC (y que corresponde a la curva AGBC en la Figura 8.23). 194 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Figura 8.24. Región alcanzable para solo reactores tubulares adiabáticos con enfriamiento inter-etapas Si se permite un by-pass y mezclado desde cualquier punto a lo largo de la trayectoria del PFR, se obtiene la región alcanzable para un solo PFR con by-pass cuyos límites están dados por la curva ADBC y la línea vertical desde el punto A. La línea AB de ese límite llena la concavidad de la trayectoria del PFR y BC es parte de la trayectoria del mismo reactor. El tiempo aún se refiere al tiempo de residencia en el sistema, el cual ahora consiste de un PFR y un by-pass. Por ejemplo, se puede mezclar fluido desde el PFR con tiempo de residencia B con alimento dado por el punto A, en una relación tal que se obtenga una composición y tiempo de residencia correspondiente a D. Si ahora se desea utilizar un segundo PFR en serie con el reactor anterior, existen dos puntos que se pueden considerar. Primero, la trayectoria de un PFR adiabático tiene forma fija y en este caso las condiciones iniciales son únicas. Así, la trayectoria del PFR desde el punto de alimento D, por ejemplo, equivale justamente a la trayectoria AXBC desplazada hacia abajo hasta que el punto X sobre la curva AXBC toque el punto D. Además, como la temperatura en el reactor depende solo de la conversión 195 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS para el caso adiabático, la temperatura en el punto D debe ser la misma del punto X. Así, el desplazamiento de una trayectoria siempre cumple la condición (relación) adiabática. Consecuentemente, como las trayectorias de los PFR no se pueden cruzar unas con otras, la trayectoria del segundo PFR debe ser tal que extienda la región alcanzable, en este caso, desde ese punto D ubicado sobre la línea AB (nótese que en ese punto la pendiente de la línea AB es igual a la de la trayectoria del PFR o simplemente 1/r). El resultado anterior ocurre porque la trayectoria del PFR no puede moverse fuera de la región alcanzable de un PFR entre A y D. Como las trayectorias del PFR no pueden cruzar ni tener alimentos entre D y B, la trayectoria del segundo PFR está dada por la curva DJKC. De nuevo, es posible definir mediante mezcla, para cada punto que se alcanza con el sistema de dos reactores, la región alcanzable para dos PFRs; cuyo límite está dado por la línea ALJKC y la línea vertical desde el punto A. El límite ALJKC representa la relación entre los tiempos mínimos de residencia para todas las posibles composiciones de salida del arreglo de dos PFRs adiabáticos en serie. De forma análoga se puede continuar la construcción para más de dos reactores en serie. El tercer reactor operará a lo largo de la curva LMNC, con la región alcanzable limitada por la línea AM y la trayectoria del PFR definida por MNK. Es interesante notar que el cambio en los límites de la región alcanzable entre dos y tres etapas es mucho menor que entre una y dos etapas y cómo el punto de tangencia se desplaza hacia la izquierda. Cada etapa adicional proporcionará cada vez un cambio más pequeño para la región alcanzable hasta que, en el límite, se alcanzará la frontera más baja de toda la región alcanzable: AEHC. Se requerirá de un infinito número de PFRs para alcanzar el punto E. Esta región contendrá todos los posibles arreglos de reactores, inclusive los analizados en la Figura 8.23. 8.5.3.2. CONSTRUCCIÓN DE LA REGIÓN ALCANZABLE PARA PFRS ADIABÁTICOS CON ENFRIAMIENTO INTER-ETAPAS El uso de múltiples PFRs en serie, con intercambiadores de calor inter-etapas, ha probado ser de gran utilidad en el caso de reacciones reversibles en operación adiabática. Un arreglo de este tipo se presenta esquemáticamente en la Figura 8.25. 196 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Figura 8.25. Esquema de un arreglo de PFRs en serie con enfriamiento inter-etapas Los intercambiadores de calor esquematizados en la Figura 8.25 permiten ajustar la temperatura de la corriente de alimento a cada reactor según se requiera o convenga. El objetivo ahora es determinar, a partir de los diagramas de las regiones alcanzables, la mejor configuración de reactores tubulares que minimicen el tiempo total de residencia para una concentración de salida dada. Las trayectorias adiabáticas en flujo pistón para diferentes temperaturas de entrada al sistema se presentan en la Figura 8.26. Nótese que las diferentes trayectorias adiabáticas son convexas y que todas ellas están limitadas por la curva más externa (la trayectoria XYZ) y la línea vertical de coordenadas (1,0). Estos límites corresponden entonces a la región alcanzable. Figura 8.26. Trayectorias para reactores tubulares adiabáticos a diferentes temperaturas de alimento fresco. Curva XYZ: límite de la región alcanzable para el sistema con un reactor tubular adiabático 197 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Considérese inicialmente la necesidad de determinar cuál es la mejor temperatura de alimento para el primer reactor. Si se examinan las trayectorias del PFR con temperaturas de alimento de 320, 325, y 330 K (Figura 8.26), es posible observar que la trayectoria del PFR que tiene como temperatura de alimento 325 cae sobre el límite de la región alcanzable entre los puntos A y B. Para concentraciones menores que A, la trayectoria del PFR con una temperatura de alimento de 320 K requiere menores tiempos de residencia que para el PFR con temperatura de alimento de 325 K. Similarmente, para concentraciones mayores que B, la trayectoria del PFR con temperatura de alimento de 330 K tiene menores tiempos de residencia que la trayectoria del PFR con una temperatura de alimento de 325 K. Así, para operar en el límite de la región alcanzable, la concentración de salida Cs que un PFR puede alcanzar, a una concentración y una temperatura de alimento especificada, C0y T0, respectivamente, con el mínimo tiempo de residencia, debe cumplir la siguiente relación: C C 1 r T 1 dC dC 0 0 R 2 T T 0 T 0 T 0 C0 R C s s Ahora, ¿cómo calcular la mejor temperatura de alimento para la siguiente etapa? Se sabe de antemano que la concentración de salida de la primera etapaestá sobre la región alcanzable como se muestra en la Figura 8.26. La idea es determinar la temperatura de alimento al segundo reactor cuya trayectoria permita extender al máximo los límites de la región alcanzable. La condición para determinar ese límite se define mejor si se plantea el problema en una forma diferente: determinar la trayectoria del PFR que cumple la condición adiabática para el segundo reactor. Como ejemplo de esto, considérese que la trayectoria de la segunda etapa de reacción está dada por la curva ABC en la Figura 8.27. De nuevo, como se mostró en la Figura 8.26, la envolvente de la región alcanzable para el primer reactor corresponde a la curva XYZ. Se debe encontrar la concentración de alimento a la trayectoria ABC del PFR que más extenderá la región alcanzable. Esto es equivalente a encontrar el punto de alimento que moverá la trayectoria del segundo reactor tan abajo como sea posible. 198 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Figura 8.27. Trayectorias para reactores tubulares adiabáticos con enfriamiento interetapas. Curva AD: mejor primer etapa. Curva XYZ: límite de la región alcanzable para el sistema con un reactor tubular adiabático. Curva JKL: límite de la región alcanzable para el sistema con dos reactores tubulares adiabáticos Para hacer esto se puede mover la curva ABC hacia arriba o hacia abajo dentro de la envolvente XYZ y encontrar el punto donde la pendiente de la curva límite de la región alcanzable y de la trayectoria del PFR especificado son iguales. En este punto corresponde al punto D para la trayectoria ABC de la Figura 8.27. Una vez definida la composición de alimento al segundo PFR, se puede repetir el procedimiento anterior para todas las temperaturas de alimento y así determinar la nueva envolvente o límite de la región alcanzable. En este caso, la curva JKL representa el límite de la región alcanzable para un sistema de dos PFRs con intercambiadores de calor inter-etapas (Figura 8.25). Esta construcción se puede continuar sistemáticamente para un mayor número de etapas. 199 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 8.5.3.3. CONSTRUCCIÓN DE LA REGIÓN ALCANZABLE PARA PFRS ADIABÁTICOS USANDO COLD SHOOTING PARA ENFRIAMIENTO INTER-ETAPAS Los objetivos ahora son determinar la región alcanzable cuando se usa alimento fresco para modificar la temperatura de las corrientes interetapas (cold shooting) así como establecer la configuración que minimiza el tiempo de residencia para una concentración de salida determinada usando igualmente cold shooting. En este esquema, el alimento del sistema se calienta antes de ingresar al primer reactor tal como se muestra en la Figura 8.28 para tres reactores. De esta forma es posible variar la temperatura de alimento al primer reactor. Así mismo, con la cantidad de material que pasa por el by-pass es posible modificar el tiempo de residencia y la temperatura de alimento en cada una de las etapas de reacción. Figura 8.28. Esquema de un arreglo de PFRs en serie con alimento fresco para enfriamiento inter-etapas (cold shooting) El primer paso para la construcción de la región alcanzable es idéntico al explicado en la sección 8.5.3.2., y, como se explicó anteriormente, una línea que una los puntos XYZ de la Figura 8.29 será el límite de la región alcanzable para el caso de un PFR (las curvas punteadas y la curva AB corresponden a diferentes trayectorias para diferentes temperaturas de alimento, como se mostró en la Figura 8.26). Para encontrar los límites de la región alcanzable para el segundo reactor, es necesario considerar de nuevo el problema de determinar el mejor punto de alimento para ese reactor. Considérese, por ejemplo, un segundo reactor el cual tiene una temperatura de la corriente de salida sea de 300 K. Para el primer reactor presentado en la Figura 8.26, se pueden mezclar todas las posibles concentraciones de salida con el by-pass (alimento sin calentar, el cual se asume aquí que está a 250 K) en 200 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Figura 8.29. Región alcanzable para reactores tubulares adiabáticos con alimento fresco para enfriamiento inter-etapas (cold shooting) las proporciones apropiadas de tal forma que genere la línea isoentálpica que corresponda a la temperatura de alimento de 300 K. Las líneas isoentálpicas representan puntos posibles de alimentación para la segunda etapa de reacción y se muestran en la Figura 8.29 como las curvas DEF, GHI, y JKL. Para la relación isoentálpica simple utilizada en este ejemplo, ecuación (8.46), las líneas de alimento son simplemente una relación constante entre la longitud de la línea entre el punto de salida y el punto de alimento (A). Para cada línea de alimento, es posible, mover la trayectoria AB, la cual tiene como temperatura de alimento 300 K (ver también Figura 8.23), hacia arriba o hacia abajo hasta encontrar el punto de alimento que genere la segunda trayectoria más baja o la trayectoria que más extiende la región alcanzable, como se mostró anteriormente. Este punto de alimento es siempre el punto donde la trayectoria ABC del PFR es tangente al lugar geométrico del alimento, y que es tangente a la trayectoria del primer reactor. Ahora es necesario establecer si la trayectoria del primer PFR genera la menor segunda trayectoria. En este caso, el lugar geométrico de alimento GHI genera la trayectoria dada. Esto puede repetirse para todas 201 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS las posibles temperaturas de alimento al segundo reactor, con el fin de encontrar el límite de la región alcanzable y así establecer las condiciones óptimas para el segundo reactor. Este método se puede repetir para todas las etapas que se quieran involucrar. BIBLIOGRAFÍA Fogler, H.S. (2006): Elements of Chemical Reaction Engineering (4th Ed.). New Jersey: Prentice Hall. Glasser, D.; Hildebrandt, D. & Crowe, C.M. (1987): “A Geometric Approach to Steady Flow Teactors: The Attainable Region and Optimization in Concentration Space”. En: Ind. Eng. Chem. Res., 26(9), 1803 – 1810. Glasser, D.; Hildebrandt, D. & Godorr, S. (1994): “The Attainable Region for Segregated, Maximum Mixed and other Reactor Models”. En: Ind. Eng. Chem. Res., 33 (5) 1136 – 1144. Hildebrandt, D.; Glasser, D. & Crowe, C.M. (1990): “Geometry of the Attainable Region Generated by Reaction and Mixing with and without Constraints”. En: Ind. Eng. Chem. Res., 29 (1), 49 – 58. Hildebrandt, D. (2007). Comunicación personal. Horn, F. (1964): “Attainable and Non-Attainable Regions in Chemical Reaction Technique”. En: Third European Symposium on “Chemical Reaction Engineering”. New York: Pergamon Press; pp. 1 – 10. Levenspiel, O. (1999): Chemical Reaction Engineering (3rd Ed.). New Jersey: John Wiley & Sons. Milne, D.; Glasser, D.; Hildebrandt, D. & Hausberger, B. (2004a): “Application of the Attainable Region Concept to the Oxidative Dehydrogenation of 1-butene in Inert Porous Membrane Reactors”. En: Ind. Eng. Chem. Res., 43(8), 1827 – 1831. 202 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES Milne, D.; Glasser, D.; Hildebrandt, D. & Hausberger, B. (2004b): “Correction. Application of the Attainable Region Concept to the Oxidative Dehydrogenation of 1-butene in Inert Porous Membrane Reactors”. En: Ind. Eng. Chem. Res., 43(8), 7207 – 7208. Omtveit, T.; Tanskanens, J. & Kristian, M.L. (1994): “Graphical Targeting Procedures for Reactor Systems”. En: Comp. Chem. Eng. 18(1), S113 – S118. Poling, B.E.; Prausnitz, J.M. & O´Connell, J.P. (2000): The Properties of Gases and Liquids (5th Ed.). New York: McGraw Hill. Téllez, C.; Menéndez, M. & Santamaria, J. (1999): “Kinetic Study of the Oxidative Dehydrogenation of Butane on V/MgO Catalysts”. En: J. Catal., 183(2), 210 – 221. Trambouzé, P.J. & Piret, E.L. (1959): “Continuous Stirred Tank Reactors: Design for Maximum Conversion of Raw Material to Desired Product”. En: AIChE J., 5(3) 384 – 390. Van de Vusse, J.G. (1964): “Plug-flow versus Tank Reactors”. En: Chem. Eng. Sci., 19(2), 994. Wen, Z.; Chuanguang, Z.; Zhishan, Z.; Fangyu, H. & Chengyue, L. (2002): “Strategy of an Attainable Region Partition for Reactor Network”. En: Ind. Eng. Chem. Res., 41(2), 190 – 195. Zhou, W. & Manousiouthakis, V.I. (2007): “Variable Density Fluid Rector Network Synthesis – Construction of the Attainable Region through the IDEAS Approach”. En: Chem. Eng. J., 129(2), 91 – 103. 203 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS APÉNDICE 8.1. LA REGLA DE LA PALANCA Considérese un proceso de mezclado. Se tiene una corriente 1 y una corriente 2 que se mezclan para producir la corriente 3 tal como se muestra en la Figura 8.A. Figura 8.A. Representación esquemática de un proceso de mezclado Este proceso de mezclado se puede representar en el diagrama concentracional, como en la Figura 8.B. Figura 8.B. Representación esquemática en el diagrama de concentraciones de un proceso de mezclado Se están mezclando dos corrientes representadas en el diagrama por los puntos 1 y 2. El punto 1 consta de los componentes A y B con concentraciones cA1 y cB1, respectivamente; y el punto 2 con los mismos componentes pero a las concentraciones cA2 y cB2, respectivamente. Las velocidades de flujo volumétricas de 1 y 2 son respectivamente v1 y v2. Se asume que el mezclado ocurre muy rápidamente (instantáneamente) comparado con la velocidad de reacción. De esta forma, mientras se mezclan las corrientes representadas por los puntos 1 y 2 no ocurre reacción química. De esta 204 CAPÍTULO 8 - ESTRATEGIA DE LAS REGIONES ALCANZABLES PARA LA SÍNTESIS Y OPTIMIZACIÓN DE SISTEMAS DE REACTORES forma, es posible escribir los balances molares de cada componente en la corriente 3. Aplicando un balance molar al componente A se obtiene: c A3 Reorganizando se obtiene: c A1v1 c A2 v2 v1 v2 v1 c A2 c A3 v2 c A3 c A1 De forma análoga para el componente B se obtiene: v1 cB 2 cB3 v2 cB3 cB1 Igualando estas dos ecuaciones se obtiene: cA2 cA3 cB 2 cB3 cA3 cA1 cB3 cB1 Finalmente se reorganiza la ecuación anterior para obtener: cB3 cB1 cB 2 cB3 cA3 cA1 cA2 cA3 Y es posible notar de la Figura 8.23 que: tan cB3 cB1 cA3 cA1 tan cB 2 cB3 cA2 cA3 Y que, Por lo tanto: A partir de este resultado se puede concluir que todos los tres puntos son colineales. 205 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 46 CAPÍTULO 9 - DERIVACIÓN DE LOS PERFILES DE VELOCIDAD - TEMPERATURA Y DE PROGRESIÓN ÓPTIMA PARA REACCIONES REVERSIBLES 9 DĊėĎěĆĈĎŘē ĉĊ đĔĘ ĕĊėċĎđĊĘ ěĊđĔĈĎĉĆĉ ęĊĒĕĊėĆęĚėĆ Ğ ĉĊ ĕėĔČėĊĘĎŘē ŘĕęĎĒĆ ĉĊ ęĊĒĕĊėĆęĚėĆ ĕĆėĆ ėĊĆĈĈĎĔēĊĘ ėĊěĊėĘĎćđĊĘ INTRODUCCIÓN Como lo establece Levenspiel (1999), tanto para reacciones endotérmicas como para reacciones irreversibles, el tamaño de reactor óptimo ideal se obtiene de conducirlo isotermicamente a la mayor temperatura posible. Sin embargo, para reacciones exotérmicas reversibles, el tamaño óptimo de reactor se obtiene de seguir el lugar geométrico de los máximos de las curvas a velocidad de reacción constante (frecuentemente denominadas como Progresión Óptima de Temperatura, POT) sobre las cartas de velocidad-temperatura-conversión (r-T-XA). Las cartas r-T-XA permiten la apreciación visual de la naturaleza de los perfiles de velocidad-temperatura-conversión, y por lo tanto de la POT, para un tipo de reacción específica. El tratamiento presentado por Levenspiel (1999) a los casos anteriormente mencionados incluye la solución analítica, algunas veces sustituida por métodos gráficos, el caso de una reacción simple ( A R ). Resulta apropiado tener una base matemática general que permita utilizar los criterios ya establecidos de manera tal que el ingeniero en la práctica disponga de una buena herramienta para cualquier reacción de interés. En este capítulo se proporcionarán: a. Con base a lo propuesto por Omoyele et al. (1989), se presenta inicialmente un tratamiento analítico para la generación de las curvas 207 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS de r-T-XA para los casos más simples que complementan el presentado por Levenspiel (1999). Las relaciones matemáticas analíticas que describen los lugares geométricos de las máximas velocidades para reacciones exotérmicas. b. La preparación de las cartas r-T-XA para la determinación de las regiones de operación para reactores adiabáticos empacados. Adicionalmente, se presentan los algoritmos de cálculo detallados para casos industriales de reacciones con cinéticas complejas. 9.1. CONSIDERACIONES GENERALES La mayoría de las reacciones reversibles de importancia industrial pueden clasificarse en cuatro grupos como se presenta en la Tabla 9.1 (Omoyele et al., 1989). Tabla 9.1. Tipos de reacciones reversibles de importancia industrial Tipo aA ↔ rR aA+bB ↔ rR aA+bB ↔ rR+sS aA ↔ rR+sS Ejemplo Reacciones de polimerización e isomerización Reacciones de oxidación, hidrogenación y halogenación Reacciones de esterificación, saponificación y neutralización Reacciones de descomposición, deshidrogenación y sublimación Si k1 y k2 representan, las constantes de velocidad directa e inversa, respectivamente, para una velocidad de reacción homogénea -rA, es posible definir de manera general que: M N i 1 j 1 rA k 1 C i i k 2 C j j (9.1) donde 208 k1 A1 exp E1 / RT (9.2a) k2 A2 exp E2 / RT (9.2b) CAPÍTULO 9 - DERIVACIÓN DE LOS PERFILES DE VELOCIDAD - TEMPERATURA Y DE PROGRESIÓN ÓPTIMA PARA REACCIONES REVERSIBLES Inicialmente, se asumirán sistemas con densidad constantes. De esta forma la concentración de cualquier especie i, Ci, durante el curso de la reacción estará dado por: C C Ao k k X A k (9.3) Donde Qk = Cko/CAo, nk es el coeficiente estequiométrico del componente k referido al reactivo límite A, y XA la conversión (nomenclatura de Fogler, 2006). 9.2. ECUACIONES PARA LOS PERFILES r-T-XA Se considerará a continuación el desarrollo de las ecuaciones de velocidad-temperatura-conversión para algunos casos simples que tienen solución analítica. Estos permitirán comprender la metodología de cálculo y las diferentes posibilidades que se pueden encontrar en función del tipo de cinética. 9.2.1. REACCIONES DEL TIPO aA ↔ rR como: De la ecuación (9.1), la velocidad de reacción, -rA, puede escribirse r k 1C A 1 k 2 C R1 A (9.4) Donde α1 y b1 son los órdenes de reacción con respecto a las especies A y R, respectivamente. De la ecuación (9.3): C A C Ao 1 X A (9.5a) C C Ao R R X A R (9.5b) Combinando las ecuaciones (9.4) y (9.5a) y (9.5b) se obtiene: 1 k1C Ao1 1 X A 1 k2C Ao R R X A 1 rA 0 (9.6) 209 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Esta es una ecuación de la forma f(XA) = 0. La ecuación (9.6) puede resolverse simultáneamente con las ecuaciones (9.2a) y (9.2b) para producir los datos de temperatura-conversión (T-XA) para un valor especificado de –rA, una vez que los parámetros CAo, ΘR, α1, β1 y υR son conocidos. EJEMPLO 9.1 Considere que la reacción aA↔rR es de primer orden respecto al reactivo y producto: α1 = β1 = 1. La ecuación (9.6) se reduce entonces a: k1C Ao 1 X A k2C Ao R R X A rA 0 Reorganizando esta ecuación se obtiene: XA k1 k2 R rA / C Ao k1 k2 R Se asume que no existe alimentación de producto (ΘR = 0) y que es una reacción reversible unimolecular (υR = 1). Los diferentes parámetros Figura 9.1. Perfiles de velocidad de reacción para una reacción del tipo aA↔rR 210 CAPÍTULO 9 - DERIVACIÓN DE LOS PERFILES DE VELOCIDAD - TEMPERATURA Y DE PROGRESIÓN ÓPTIMA PARA REACCIONES REVERSIBLES cinéticos tienen los siguientes valores: E1 = 11600 cal.gmol-1, E2 = 29600 cal.gmol-1, A1 = exp(17,2), A2 = exp(41,9) y CAo = 1 mol.L-1, y se desea estudiar el intervalo de temperatura entre 260 a 400K. Se obtienen los resultados presentados en la Figura 9.1. 9.2.2. REACCIONES DEL TIPO aA+bB↔rR La velocidad de reacción, -rA, puede escribirse como: rA k1C A1 CB 2 k2CR1 (9.7) C C Ao B B X A B (9.8) donde: Con CA y CR como se presentan en las ecuaciones (9.5a) y (9.5b). Combinando las ecuaciones (9.7), (9.8), (9.5a) y (9.5b) se obtiene: k1C Ao1 2 1 X A 1 B B X A 2 1 k2C Ao R R X A 1 rA 0 (9.9) Ecuación que representa los perfiles r-T-XA para este tipo de ecuación. EJEMPLO 9.2 queda: Supóngase que: α1 = α2 = β1 = 1 y que ΘB = 1; la ecuación (9.9) 2 k1C Ao 1 X A B B X A k2C Ao R R X A rA 0 Que es una expresión cuadrática en XA. Si se hace -υA = -υB = υR = 1, entonces para el caso en que no existe alimentación de producto (ΘR = 0) se obtiene: 211 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS X A1,2 2 2 k2C Ao 2k1C Ao k2C Ao 2k1C Ao 4k1CAo2 k1CAo2 rA 2 1 2 2 2k1C Ao Donde la conversión presenta dos valores posibles (solo uno con significado físico). Retomando los valores del ejemplo 1 y haciendo CAo = 0,1 mol.L-1 se obtienen los resultados que se presentan en la Figura 9.2. Figura 9.2. Perfiles de velocidad de reacción para una reacción del tipo aA+bB↔rR 9.2.3. REACCIONES DEL TIPO aA+bB↔rR+sS En este caso, la expresión de velocidad de reacción, -rA, es: rA k1C A1 CB 2 k2CR1 CS2 (9.10) Donde CA, CB y CR fueron definidos previamente y CS es: C C Ao S S X A S 212 (9.11) CAPÍTULO 9 - DERIVACIÓN DE LOS PERFILES DE VELOCIDAD - TEMPERATURA Y DE PROGRESIÓN ÓPTIMA PARA REACCIONES REVERSIBLES Substituyendo CA, CB, CR y CS en la ecuación (9.10), y después de organizar un poco se obtiene: k1C Ao1 2 1 X A B B X A R R X A S S X A 1 1 2 k2C Ao 2 1 2 rA 0 (9.12) La construcción de la carta r-T-XA para este caso se ilustra a continuación. EJEMPLO 9.3 Con los órdenes cinéticos: α1 = α2 = β1 = β2 = 1, la ecuación (9.12) quedará de forma compacta como: 2 k1 1 X A B B X A k2 R R X A S S X A rA / C Ao 0 Si se asume que -υA = -υB = υS = υR = 1, que se alimentan los reactantes A y B en relación equimolar (ΘB = 1) y que además no existe inicialmente producto (ΘR = ΘS = 0), la solución de la ecuación anterior entrega: X A1,2 2 2k1 4k12 4 k1 k2 k1 rA / C Ao 2 k1 k2 1 2 Observe, sin embargo, que si k1=k2 la ecuación anterior es inaplicable ya que XA se hace infinito. Esta limitación se puede superar fácilmente al manipular la primera ecuación de este ejemplo, para dar X A1,2 1 r / k C A 1 2 Ao 2 Con los mismos parámetros cinéticos utilizados en el ejemplo 9.2, se obtienen los datos r-T-XA que se presentan en la Figura 9.3. 213 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 9.3. Perfiles de velocidad de reacción para una reacción del tipo aA+bB↔rR+sS 9.2.4. REACCIONES DEL TIPO aA↔rR+sS La ecuación de velocidad para esta reacción es: r k1C A1 k2CR1 CS2 A (9.13) Substituyendo CA, CR y CS se obtiene: 1 2 k1C Ao1 1 X A 1 k2C Ao R R X A 1 S S X A 2 rA 0 (9.14) Esta es la ecuación a partir de la cual se pueden obtener los perfiles r-T-XA. Para detallar esto, considérese el ejemplo 9.4. EJEMPLO 9.4 Tomando: α1 = β1 = β2 = 1, la ecuación (9.14) quedará: 2 k1C Ao 1 X A k2C Ao R R X A S S X A rA 0 214 CAPÍTULO 9 - DERIVACIÓN DE LOS PERFILES DE VELOCIDAD - TEMPERATURA Y DE PROGRESIÓN ÓPTIMA PARA REACCIONES REVERSIBLES Suponga de nuevo, como antes, que -υA = υR = υS = 1, que la alimentación contiene A puro y que además no existe inicialmente producto (ΘR = ΘS = 0). La solución de la ecuación anterior entrega: X A1,2 2 k1C Ao k1C Ao 4k2C Ao k1CAo rA 2 1 2 2 2k2C Ao Con los mismos parámetros cinéticos utilizados en ejemplos anteriores, se obtienen la carta r-T-XA que se presenta en la Figura 9.4. Figura 9.4. Perfiles de velocidad de reacción para una reacción del tipo aA ↔ rR+sS 9.3. ECUACIONES PARA LA PROGRESIÓN ÓPTIMA DE TEMPERATURA (POT) Aunque el lugar geométrico de las máximas velocidades (también conocido como la Progresión Óptima de Temperatura, POT), el cual debe seguirse con el fin de obtener el tamaño óptimo de reactor (para una reacción exotérmica), puede determinarse fácilmente sobre las cartas r-T-XA, es más funcional determinar una expresión que nos relacione la temperatura 215 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS óptima, Topt, y la conversión, XA, para cualquier tipo de expresión cinética. De las Figuras 9.1 a la 9.4, es evidente que los perfiles r-T-XA para una reacción exotérmica son unimodales. Como resultado, la temperatura óptima se obtiene de la relación: rA 0 T X (9.15) A Donde el subíndice XA implica que la derivada parcial se lleva a cabo a conversión constante. Así, para la ecuación cinética general presentada en la ecuación (9.1) se obtiene: rA k1 M i k2 N j Ci Cj 0 T j 1 T X A T i 1 Pero: (9.16) Ya que tanto Ci como Cj son solo función de XA (ver ecuación 9.3). k1 A1 E1 exp E1 / RT T RT 2 k2 A2 E2 exp E2 / RT T RT 2 (9.17a) (9.17b) Combinando las ecuaciones (9.16), (9.17a) y (9.17b) se obtiene: A1 E1 exp E1 / RT M i A2 E2 exp E2 / RT N j rA 0 Ci Cj i 1 j 1 (9.18) RT 2 RT 2 T X A A T = Topt. Considérese ahora la solución a la ecuación (9.18) para los cuatro tipos de expresiones de velocidad presentados en la Tabla 9.1. Estas expresiones se encuentran resumidas en la Tabla 9.2. La representación de estas ecuaciones se encuentra incluida en las Figuras 9.1 a 9.4 (lugar geométrico de los puntos que unen los máximos de cada curva de velocidad constante). 216 CAPÍTULO 9 - DERIVACIÓN DE LOS PERFILES DE VELOCIDAD - TEMPERATURA Y DE PROGRESIÓN ÓPTIMA PARA REACCIONES REVERSIBLES Tabla 9.2. Soluciones analíticas a la Progresión Óptima de Temperatura (POT) según el tipo de reacción o de cinética Tipo Ecuación POT Topt aA rR Topt aA bB rR aA bB rR sS aA rR sS 9.4. Topt E2 E1 1 1 A2 E2C Ao R R X A 1 R ln A1 E1 1 X A 1 E2 E1 AEC R R X A 1 R ln 2 2 Ao 1 2 A1 E1 1 X A B B X A 1 1 2 E2 E1 1 1 1 2 A2 E2C Ao R R X A 1 S S X A 2 R ln A1 E1 1 X A 1 B B X A 2 Topt 1 1 1 A E C R ln 2 2 Ao E2 E1 R R X A S S X A A1 E1 1 X A 1 2 1 PERFILES VELOCIDAD-TEMPERATURA-CONVERSIÓN PARA CINÉTICAS COMPLEJAS En la sección anterior se analizaron algunas cinéticas sencillas, las cuales presentan solución analítica. Sin embargo, algunos de los procesos reactivos clásicos más representativos de la capacidad de desarrollo de los ingenieros químicos son catalíticos. Estos están caracterizados por cinéticas complejas cuya solución analítica es prácticamente imposible. De allí la necesidad de definir un método numérico lo suficientemente robusto para que sirva al ingeniero químico en el análisis del tipo de problemas aquí presentados. El método de continuación por homotopía ha demostrado ser una de las herramientas valiosa (Gritton et al., 2001). A continuación, se desarrollará explícitamente este método numérico. Luego se aplicará a la obtención de las cartas r-T-XA para tres procesos clásicos industriales: 217 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS • Síntesis de metanol. • Síntesis de amoníaco. • Oxidación de SO2. 9.4.1. OBTENCIÓN DE LAS CURVAS DE ISOVELOCIDAD: MÉTODO DE HOMOTOPÍA MONOPARAMÉTRICA Cualquier ley de velocidad puede expresarse fácilmente en función de la conversión (con ayuda de la tabla estequiométrica). Es decir, las concentraciones (composiciones molares o presiones parciales) de cada componente se pueden expresar en función de una única variable. Por lo tanto, una ley de velocidad cualquiera puede expresarse como una función de la forma: r r X ,T (9.19) Donde X es la conversión y T es la temperatura. Entonces, existirán múltiples valores de X y T que arrojarán un único valor de r. El objetivo es encontrar las condiciones de X y T que satisfacen tal valor. El procedimiento propuesto es el siguiente: 1. Especificar r y T. 2. Expresar las concentraciones (composiciones o presiones parciales) de cada componente en función de la conversión. 3. Suponer X. 4. Calcular r con la ley de velocidad, evaluada a la T especificada y la X supuesta. 5. Comparar el r calculado y el r especificado. Si son muy similares (tolerancia), terminar. Si no, ir al paso 6. 6. Generar un nuevo valor de X (con cualquier método de convergencia conocido, aunque es recomendable usar el método de Newton) y regresar al paso 4. 218 CAPÍTULO 9 - DERIVACIÓN DE LOS PERFILES DE VELOCIDAD - TEMPERATURA Y DE PROGRESIÓN ÓPTIMA PARA REACCIONES REVERSIBLES El procedimiento anterior trata de resolver un problema que genera una función objetivo F(X,T) de la forma: F X , T r X , T respecificado 0 (9.20) Como X =X(T) o, lo que es matemáticamente lo mismo, T =T(X), diferenciando la ecuación anterior con respecto a T (la elección de este parámetro de continuación se explicará más adelante) se obtiene: F dX F 0 X T dT T X (9.21) Es importante aclarar que el parámetro se escoge según convenga para la solución del problema. Despejando, F dX T dT F X (9.22) X T Entonces, para un valor de velocidad de reacción especificada, el problema de convergencia que inicialmente se tenía se transformó en un problema de integración de la ecuación (9.22). En muchos casos no es posible diferenciar analíticamente la ecuación (9.20) por lo tanto la ecuación anterior es aproximadamente igual a: F X T T F X X (9.23) T Expresando la ecuación anterior en diferencias finitas y despejando, X k 1 F T X F X k X T (9.24) T 9.4.1.1. ALGORITMO Es necesario, para este tipo de homotopía, tener algún conocimiento general del comportamiento de la función a resolver, además de un punto 219 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS inicial donde la función objetivo (ecuación (9.20)) se satisfaga. En este documento se estudiarán reacciones exotérmicas, pero el algoritmo, con algunas breves modificaciones, es completamente aplicable a reacciones endotérmicas. Para reacciones exotérmicas, a elevadas temperaturas, la conversión de equilibrio será muy baja para cualquier valor de la velocidad de reacción. Entonces una zona de fácil convergencia será a valores T altos para un valor cualquiera de r (esta es la razón por la que se escogió T como parámetro). Se utiliza la ecuación (9.20) para hallar X. Este valor de X se obtiene aplicando los seis pasos presentados anteriormente. Después de realizar el procedimiento descrito en el párrafo anterior, se procede a calcular las derivadas parciales que aparecen en las ecuaciones (9.22) y (9.24) numérica o analíticamente, dependiendo de la complejidad del caso. Si estas derivadas se calculan analíticamente, el paso a seguir es la integración de la ecuación (9.22) y así quedará resuelto el problema para el valor de r especificado. Para el caso de la evaluación numérica de las derivadas se debe hacer notar que estas se calculan después de que el problema ha convergido por primera vez. Es decir, están evaluadas a la T y la X que satisfacen la ecuación (9.20). A continuación se debe fijar el ∆T el cual será utilizado en la ecuación (9.24). Se debe tener mucho cuidado al definir el signo de ∆T (aquí interviene también el previo conocimiento del comportamiento de la función). Como se inició el procedimiento desde una T alta, cuya solución es una conversión baja, el ∆T debe ser negativo para cubrir todo el intervalo de conversiones y caer en la zona de altas conversiones (a bajas T). El destino de la ecuación (9.24) es predecir un valor de la conversión, utilizando datos de la convergencia anterior, para un nuevo valor de la temperatura. Este nuevo valor de la temperatura está definido por: 1 T k T k T (9.25) En este punto ya se tiene un nuevo valor predicho de la conversión (ecuación (9.24)) para una nueva temperatura (ecuación (9.25)). Estos datos se utilizarán como estimados iniciales en el método de convergencia 220 CAPÍTULO 9 - DERIVACIÓN DE LOS PERFILES DE VELOCIDAD - TEMPERATURA Y DE PROGRESIÓN ÓPTIMA PARA REACCIONES REVERSIBLES empleado para resolver la ecuación (9.20) utilizando los seis pasos presentados inicialmente. 9.4.2. OBTENCIÓN DEL LUGAR GEOMÉTRICO DE LOS PUNTOS DE MÁXIMAS CONVERSIONES: MÉTODO DE LA HOMOPATÍA MONOPARAMÉTRICA APLICADO A UN PROBLEMA DE OPTIMIZACIÓN El objetivo es obtener los puntos donde se alcance la condición: dX 0 dT rA (9.26) Estos puntos son algo complicados de calcular ya que no se tiene una función explícita a la cual se le pueda realizar el tratamiento respectivo. A continuación se planteará un método para obtener esta curva. Se tenía que: F X , T r X , T respecificado 0 (9.20) Y además que, F dX F 0 X T dT T X (9.21) Pero el objetivo es calcular los puntos donde dX/dT = 0. Por lo tanto, reemplazando en la ecuación anterior, F 0 G X , T T X (9.27) Teniendo presente que T =T(X) y después de diferenciar la ecuación (9.27) se obtiene: G dT G 0 T X dX X T (9.28) 221 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Despejando y aplicando un procedimiento similar al mostrado anteriormente, se puede obtener: G X T k 1 Tk G T T X (9.29) X El objetivo es hallar los valores de T y X que satisfacen la ecuación (9.27) y con ayuda de la ecuación (9.29) se pueden predecir los valores de la temperatura que podrían satisfacer esta ecuación. 9.4.2.1. ALGORITMO 1. Fijar un valor de conversión. 2. Con ayuda de un método de convergencia, obtener la temperatura que satisface la ecuación (9.27). 3. Calcular, con la ecuación (9.29), para un nuevo valor de conversión (Xk+1=Xk+ΔX), la temperatura que servirá como estimado inicial. 4. Para estos nuevos valores de X y T, regresar al paso 2. Como se podrá observar, se obviaron pasos en este algoritmo. Esto es porque solo ha cambiado el planteamiento del problema con respecto al caso anterior de obtención de las curvas de isovelocidad. Es decir, un problema de optimización no es más que un replanteamiento de un problema de obtención de un cero de una función cualquiera en una variable. La información utilizada y los resultados obtenidos para el análisis de tres casos industriales se resumen a continuación en las Figuras 9.5 a 9.7. 222 CAPÍTULO 9 - DERIVACIÓN DE LOS PERFILES DE VELOCIDAD - TEMPERATURA Y DE PROGRESIÓN ÓPTIMA PARA REACCIONES REVERSIBLES Caso 1: Síntesis de metanol (Belore, 2003) pCH3OH -3 -1 r k1 pCO pH2 2 , mol CO.cm .min KP k1 2 104 exp 5000 T , K p exp 26.7 , 10913.9 T Figura 9.5. Perfiles de isovelocidad para la reacción de síntesis de metanol Caso 2: Síntesis de Amoniaco (Froment & Bischoff, 1990) pN p1.5 H r k1 2 2 pNH 3 pNH -1 -1 k2 1.53 , Kmol N2.kgCat .hr pH 2 20800 47400 k1 1.79 2.57 , 104 exp , 1016 exp k2 RT RT R 1.987 , kcal mol·K Figura 9.6. Perfiles de isovelocidad para la reacción de síntesis de amoníaco 223 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Caso 3: Oxidación de SO2 (Froment & Bischoff, 1990) pSO3 k1 pO2 pSO2 1 1 pSO2 pO22 K P r 22.414 1 K 2 pSO2 K 3 pSO3 , , k1 exp 12.160 5473 T 52596 K 3 exp 71.745 , 2 , Kmol SO2.kgCat-1.hr-1 K 2 exp 9.953 8619 , T T K P exp 11300 10.68 , T Figura 9.7. Perfiles velocidad-temperatura-conversión para la reacción de oxidación de SO2 BIBLIOGRAFÍA Belfiore, L.A. (2003): Transport Phenomena for Chemical Reactor Design. New Jersey: John Wiley & Sons. Fogler, H.S. (2006): Elements of Chemical Reaction Engineering (4th Ed.). New Jersey: Prentice Hall. Froment, G.F. & Bischoff, K.B. (1990): Chemical Reactor Analysis and Design. New Jersey: John Wiley & Sons. 224 CAPÍTULO 9 - DERIVACIÓN DE LOS PERFILES DE VELOCIDAD - TEMPERATURA Y DE PROGRESIÓN ÓPTIMA PARA REACCIONES REVERSIBLES Gritton, K.S.; Seader, J.D. & Lin, W.J. (2001): “Global Homotopy Continuation Procedures for Seeking all Roots of a Nonlinear Equation”. En: Comp. Chem. Eng., 25(7-8), 1003 – 1019. Levenspiel, O. (1999): Chemical Reaction Engineering (3rd Ed.). New Jersey: John Wiley & Sons. Omoyele, J.A.; Adesina, A.A. & Udegbunam, E.O. (1989): “Optimal Design of Nonisothermal Reactors”. En: Chem. Eng. Comm., 79(2), 95 – 107. 225 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 46 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA 10 DĎēġĒĎĈĆ Ğ ĒĚđęĎĕđĎĈĎĉĆĉ ĉĊ ĊĘęĆĉĔĘ ĊĘęĆĈĎĔēĆėĎĔĘ Ċē ėĊĆĈęĔėĊĘ ĉĊ ĒĊğĈđĆ ĈĔĒĕđĊęĆ INTRODUCCIÓN Es posible que un CSTR presente múltiples estados estacionarios (MSS por sus siglas en ingles), o múltiples posibles condiciones de operación en estado estable, en virtud de la dependencia no lineal, con la temperatura, del coeciente cinético. Inclusive, es bien conocido que existe la posibilidad que un CSTR isotérmico presente MSS cuando la ley de velocidad de reacción presenta una dependencia altamente no-lineal de las concentraciones. Este fenómeno recibe el nombre de múltiples estados estacionarios concentracionales, y da origen a interesantes problemas de diseño y optimización de baterías de CSTRs. En cualquier caso, siempre es necesario realizar un estudio detallado de cada uno de esos estados estacionarios para determinar si corresponde a un estado estable o inestable, y sus implicaciones en el diseño y operación: procedimientos de arranque y parada, y control ante perturbaciones. En este capítulo se analizan varios casos de los antes mencionados, con un enfoque particular al análisis numérico de la descripción matemática que representa un sistema con uno o varios CSTRs. Se muestra de forma clara la identicación y caracterización directa de los MSS. Inicialmente se presenta una metodología de diseño que permite establecer la forma de alcanzar condiciones especícas de operación. Luego, se presenta un análisis de la dinámica de los CSTR: especícamente las condiciones de 227 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS arranque (con énfasis en el caso a volumen variable), parada, y análisis de respuesta a perturbaciones. Finalmente, se presenta en la última sección, mediante un ejemplo, un análisis dinámico que permite establecer qué tan estable es un estado estacionario. 10.1. UN MÉTODO PARA ALCANZAR CONVERSIONES INACCESIBLES Algunos de los posibles estados estacionarios, aunque apropiados respecto a la respuesta del sistema reactivo, pueden resultar inaccesibles para la operación. Este es el caso que se analizará en este capítulo, ya que surgen procedimientos especiales para el diseño de las baterías y consideraciones especiales sobre la estabilidad de los estados estacionarios. 10.1.1. CASO DE ESTUDIO Un ejemplo de una ley de velocidad de reacción altamente nolineal respecto a la concentración viene dado por la expresión cinética: kC A rA 2 1 KC A (10.1) donde k(s-1) y K (m3/kmol). Este tipo de expresiones cinéticas se encuentra en casos como (Chen & Crynes, 1987): la deshidrogenación catalítica de etileno a etano, la oxidación de CO en exceso de O2 catalizada por platino, la polimerización de estireno, etc. En el caso de cinéticas no lineales como la del tipo Michaelis-Menten o tipo Monod, básicas para procesos bioquímicos, no se reporta la presencia de MSS concentracionales, a menos que se presenten fenómenos de inhibición (un análisis de la estabilidad de procesos fermentativos se encuentra en Trejos et al., 2009). La representación de la ley de velocidad, curva, junto con el balance molar en un CSTR, la línea recta ABGI, se muestra en la Figura 10.1. En la Figura 10.1 se aprecia que la velocidad de reacción posee un valor máximo a una concentración intermedia y que, en virtud de esto, la línea de balance molar del reactor puede cortarla hasta en tres puntos, dependiendo del valor del tiempo de residencia. Los puntos de corte 228 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA Figura 10.1. Representación de la ley de velocidad de reacción contra la concentración de reactante A para la cinética no lineal (10.1) corresponden con los estados estacionarios de operación, que en este caso pueden varias desde 1 hasta 3. En el caso ilustrado, los puntos marcados como B, G, e I son los estados estacionarios. En los casos de los estados estacionarios B e I, si ocurre una perturbación en la concentración de salida del reactor alrededor de esos puntos, las velocidades de consumo de reactivo por reacción y salida de reactivo por convección se contrarrestan, regresando al sistema al punto de operación inicial (esta consideración no es general). Luego, estos estados estacionarios se pueden clasicar como estables. En el caso del estado G, el sistema no puede por si solo contrarrestar el efecto de una perturbación lo que ocasionará que el sistema se desplazará hacia alguno de los otros dos estados estables (B o I), por lo que este estado estacionario se puede clasicar como inestable o metaestable (la caracterización denitiva de los estados estacionarios requiere de un análisis cuantitativo riguroso empleando los valores propios de la matiz característica del modelo dinámico, lo que se presentará más adelante). Ante el propósito de diseñar una batería de reactores que alcance las condiciones del estado inestable (para un solo reactor), se trataría de permitir que sea el último reactor de la batería el que opere a esa condición, buscando que éste sea el correspondiente al caso de un solo estado estacionario, el cual es siempre estable. 229 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 10.1.2. MODELO Del balance molar en estado estacionario en un CSTR y empleando la ley de velocidad (10.1) propuesta se obtiene: 1 C Ao kC CA A 2 1 KC A Deniendo las variables adimensionales de concentración Y, así como el número de Damköhler, Da, como: Y KC A (10.2) Yo KC Ao (10.3) Da k (10.4) El número de Damköhler es el cociente entre la velocidad de reacción de A y la velocidad de transporte convectivo de A, medidos a las condiciones de entrada al reactor (Fogler, 2006). Su importancia radica en que ofrece la posibilidad de comparar el comportamiento de múltiples reactores bajo las más diversas condiciones de operación. Por otro lado, el uso de variables adimensionales permite una generalización completa del análisis de diseño y tiene un no despreciable valor estético en los procesos de modelamiento matemático (Aris, 1975; Dobre & Sanchez-Marcano, 2007). La ecuación puede reorganizarse de la forma: 1 Y Yo Y 2 Da 1 Y (10.5) Operando algebraicamente, el balance molar (10.5) puede escribirse como un polinomio cúbico en la concentración adimensional Y: Y 3 Yo 2 Y 2 2Yo Da 1 Y Yo 0 (10.6) Dados K y CAo, se calcula Yo y al jar un valor para Da, se resuelve el polinomio para Y, con lo que se puede conocer el valor de 230 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA CA. Si el polinomio presente tres raíces diferentes, existirán tres estados estacionarios, mientras que si las raíces son todas iguales, existirá un único estado estacionario. En términos de las concentraciones adimensionales, la conversión fraccional toma la forma: XA Yo Y Yo (10.7) Reemplazando esta denición de conversión en el balance molar (10.5), el número de Damköhler se puede calcular como: Da X A 1 Yo 1 X A 2 (10.8) 1 X A Luego, si el número de Damköhler es conocido y se desea calcular las múltiples conversiones de estado estacionario, se deberá resolver el correspondiente polinomio cúbico: Y X 2Y 2 o 3 A o 2Yo2 X A2 1 2Yo Yo2 Da X A Da 0 (10.9) De la ley de velocidad dada por la ecuación (10.1), se puede calcular la derivada de la velocidad de reacción con respecto a la concentración, como: d rA k 1 KC A 3 dC A 1 KC A (10.10) Al analizar la pendiente de la línea de operación del primer reactor de la batería (línea del balance molar), en el diagrama –rA contra CA, es fácil ver que esta estará dada por: rA C A'' 1 0 C A'' 1 C Ao kC A'' 1 1 KC C '' A1 2 '' A1 C Ao (10.11) '' en donde C A es la concentración del estado estacionario a la salida del primer reactor de la batería. Ahora bien, si la pendiente de la línea de operación es tangente a la curva de velocidad de reacción, en el punto de corte, igualando las ecuaciones (10.10) y (10.11), se obtiene: 1 231 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS (10.12) KC Ao C A'' 1 C Ao 0 (10.13) C A'' 1 1 KC A'' 1 1 KC A'' 1 2 K C A'' 2 1 '' A1 C C '' A1 C Ao KC Ao KC 2 Ao 8 KC Ao 4K (10.14) en donde la ecuación (10.14) es la solución analítica de la ecuación cuadrática (10.13). En el caso del n-ésimo rector de la batería, la ecuación (10.14) se puede generalizar como: C A'' n KC An1 KC An1 2 8 KC An1 4K (10.15) De la misma forma, el tiempo medio de residencia en el reactor n-ésimo es: n C An1 C An 1 KC An 2 kC An (10.16) 10.1.3. ALGORITMO DE CÁLCULO 1. Fijar los valores de: Vo, CAo, k, y XA o concentración nal deseada CAm. 2. Calcular Yo (Ec. 10.3) y el número de Damköhler Da (Ec. 10.8). 3. Calcular las tres raíces del polinomio en Y (Ec. 10.6). 4. Vericar que la conversión deseada sea inalcanzable (diagrama de bifurcación). 5. Asignar a la raíz mayor del polinomio el nombre CA1’. 6. Calcular CA1’’ (Ec. 10.14). 7. Calcular la concentración de salida del primer reactor como C A1 232 C ' A1 C A'' 1 / 2 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA 8. Calcular el número de Damköhler, Da, del segundo reactor usando CA1. 9. Calcular las tres raíces del polinomio en Y (Ec. 10.6) para el segundo reactor. 10a. Si la raíz mayor no está en el intervalo [CA1, CAm], terminar. 10b. Si la raíz mayor está en el intervalo [CA1, CAm]: 11. • Asignar a la raíz mayor del polinomio el nombre CA2’. • Calcular CA2’’ (Ec. 10.15). • Calcular CA2=(C'A2+C"A2)/2 del segundo reactor. Regresar al paso 8 con los resultados para el reactor n-ésimo hasta que se cumpla el criterio de convergencia del paso 10a. EJEMPLO 10.1 Tal como lo proponen Chen & Crynes (1987), supóngase que el ujo volumétrico de alimento es 0,3 m3/s y que su concentración es CAo = 14 kmol/m3. Las constantes de la ley de velocidad son: k = 1 s-1 y K = 1 m3/kmol. La concentración nal deseada es de 2,8 kmol/m3, correspondiente a 80% de conversión. Determine las condiciones de operación para uno o dos reactores. El diagrama XA contra Da, Figura 10.2, permite determinar claramente, para estas condiciones de operación, la zona de múltiples estados estacionarios y la región de conversiones inaccesibles. En este caso, Da = 57,76, por lo que es necesario emplear una batería para alcanzar el 80% de conversión que se desea. ¿Cómo determinar el número de reactores de la batería y su correspondiente tamaño?. Nótese en la Figura 10.2 que ambos reactores operan sobre curvas distintas debido a que poseen condiciones de alimento diferentes. Los puntos de operación respectivos se encuentran unidos con una echa. Para el reactor 1 se 233 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 10.2. Conversión contra número de Damköhler para los dos reactores isotérmicos de la batería señala el intervalo de números de Da para los que se presentan MSS. Los estados estacionarios intermedios, de los tres posibles, son metaestables o inestables. El conjunto de ellos, entre los puntos de encendido y apagado, constituyen la región de conversiones inaccesibles. Obsérvese que el segundo reactor de la batería no posee MSS y que el primer reactor opera en la zona de MSS, pero en un estado estacionario estable. Al implementar el algoritmo de cálculo presentado, se obtienen los resultados presentados en la Figura 10.3, en la que se aprecia que una batería con dos reactores es suciente. Sus características se resumen en la Tabla 10.1. Es de notar que el tiempo de residencia de la batería es mayor que el de un solo reactor que pudiese operar en el estado estacionario inestable, es decir, el procedimiento no implica optimización del volumen. En la Figura 10.3 se muestran las líneas de operación de los reactores: AF y FG. Los segmentos AB y AD determinan las concentraciones en los puntos C y E (pasos 5 y 6 del algoritmo). La concentración en el punto F corresponde a la calculada en el paso 7 y dene la concentración de salida del primer reactor. El punto H muestra la concentración de salida del 234 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA Figura 10.3. Representación gráca de los resultados del proceso de diseño de una batería de dos reactores isotérmicos para alcanzar la conversión correspondiente al punto G Tabla 10.1. Condiciones de operación de una batería de 2 CSTRs isotérmicos en serie para alcanzar una conversión del 80% Parámetro Da CAo (kmol/m3) τ (s) V (m3) CA (kmol/m3) XA (%) Reactor 1 57,76 14,0 63,49 19,04 7,20 48 Reactor 2 22,69 7,2 22,72 6,81 2,8 80 segundo reactor, igual a la deseada. Obsérvese que un solo reactor, dado por la línea ABGI, presenta tres cortes con la curva cinética, correspondientes a tres estados estacionarios con concentraciones de 0,58, 2,8 y 8,62 kmol/m3. El estado G es el estado intermedio inestable. En el caso de la batería, se puede apreciar que la línea de operación del primer reactor presenta tres puntos de corte, pero el reactor opera en un estado estable, mientras que la 235 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS línea de operación del segundo reactor solo presenta un punto de corte, a las condiciones nales deseadas. En la Figura 10.4 se presenta un diagrama que permite identicar las zonas en las que existirá un solo estado estacionario a alta conversión, un solo estado estacionario a baja conversión, y la zona en la que existirán múltiples estados estacionarios, en función del número de Damköhler y la concentración de alimento adimensional, Yo. Para realizarla se evalúa el discriminante de la ecuación cúbica (10.6) y se calculan los dos valores límite de Yo (Yo1 ,Yo2) para un valor dado del número de Damköhler. Existirá multiplicidad concentracional si para un valor dado de Da, Yo1 < Yo < Yo2. Según la Figura 10.4, el área por debajo de Yo1 da lugar a un solo estado estacionario de alta conversión, y el área por encima de Yo2 a un solo estado estacionario de baja conversión. Esta gráca constituye una herramienta valiosa para realizar el proceso de diseño conceptual de un reactor o una batería de CSTRs. Figura 10.4. Regiones de estados estacionarios en un CSTR isotérmico en función del número de Damköhler y la concentración de alimento adimensional Es interesante destacar que el procedimiento descrito para el diseño de la batería está enfocado hacia el dimensionamiento de una batería que 236 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA permita alcanzar una conversión que en un solo reactor constituiría un estado inaccesible o inestable. Sin embargo, surge la pregunta por la multiplicidad de estados estacionarios que pueda presentar la batería misma y la estabilidad o inestabilidad de cada uno de esos estados, lo cual se estudia en la siguiente sección (obsérvese que según los resultados de la Tabla 10.1, el primer reactor de la batería se encuentra en la región de multiplicidad de la Figura 10.4). También es interesante la pregunta en relación con la optimización de la batería en términos de la minimización de su volumen total. Esto es posible y se puede aplicar la fórmula de recurrencia derivada en el Capítulo 5. Los resultados se muestran grácamente en la Figura 10.5. El volumen mínimo total para este sistema es de 15,85 m3. Figura 10.5. Minimización del volumen requerido con dos CSTRs para la cinética del ejemplo 10.1 10.2. ANÁLISIS DE LA DINÁMICA DE UNA BATERÍA DE CSTRS Aunque los reactores se diseñen para trabajar en un estado estacionario, durante su operación es posible que el equipo experimente 237 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS eventos dinámicos importantes que deben ser considerados con sumo cuidado. Al menos dos de estos eventos dinámicos serán inevitables y de hecho, indispensables: el arranque (start up) y la parada (shut down). A diferencia de los equipos electrónicos, los equipos de procesamiento químico presentan procesos dinámicos generalmente complejos (en especial si el sistema presenta MSS), lo que deriva en la necesidad de planear la forma como el equipo ha de ser encendido (o apagado) de tal forma que éste alcance el estado estacionario deseado, evitando al tiempo que la dinámica conduzca al sistema hacia condiciones de operación indeseables, inseguras o peligrosas e incontrolables. Un tercer tipo de fenómeno dinámico que puede experimentar un reactor de régimen permanente se origina en la posibilidad que, durante su operación en estado estacionario, algunos de las condiciones de operación que se suponen constantes, como el caudal o la concentración del alimento o el caudal o la temperatura del uido de servicio, cambien momentáneamente. Esto se conoce como una perturbación. Dicho fenómeno es muy común en la industria debido a fallas, errores, o accidentes y es la razón por la cual los sistemas requieren de sistemas de control automático capaces de detectar esas perturbaciones y reducir su efecto manteniendo los equipos operando en las condiciones deseadas de forma segura. Adicionalmente, cuando se implementan en planta modicaciones en la producción o cambios operativos planeados, los equipos experimentan perturbaciones controladas por medio de las cuales se los conduce a un nuevo estado. Es de recalcar que durante su operación transitoria, la calidad del producto obtenido está fuera de especicaciones (dadas por el estado estacionario deseado), por lo que el material procesado durante los tiempos de arranque y parada o después de una perturbación larga, ha de ser sometido a un procesamiento especial, recirculado, o desechado. Esto sugiere la necesidad que las dinámicas generen respuestas (soluciones) rápidas y seguras, de tal forma que se reduzcan los costos asociados y el riesgo químico (Mizrahi, 2002). La existencia de múltiples estados estacionarios debido a cinéticas no lineales y/o operación no-isotérmica implica, desde el punto de vista de la dinámica, la consideración sobre la estabilidad o inestabilidad de esos estados estacionarios. Aunque es frecuente que se desee operar en un 238 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA estado estacionario que es estable, existen casos en que las consideraciones de producción (ej. calidad del producto) exigen trabajar en un estado estacionario inestable, tal como se ha descrito en la sección precedente. En lo referente a la dinámica frente a perturbaciones en las condiciones de operación, en algunos casos el reactor o reactores de una batería pueden regularse a si mismos (sistemas autorregulados) dependiendo de la magnitud y duración de la perturbación y retornar al estado estacionario inicial después de un cierto tiempo. En otros casos, el reactor requerirá de un sistema de control automático que conduzca al reactor al estado estacionario inicial después de una perturbación (Elnashaie & Garhyan, 2003). En la literatura se ha presentado especial atención al caso de la dinámica de los CSTRs no isotérmicos, en virtud de la existencia de múltiples estados estacionarios térmicos (Perlmutter, 1972; Vleeschhouwer & Fortuin, 1990; Shacham et al., 1994; Bequette, 1998; Fogler, 2006). Sin embargo, el análisis de la dinámica de los CSTRs isotérmicos con múltiples estados estacionarios concentracionales y la dinámica de baterías de CSTR es más especializado (Liou & Chien, 1990; Mjalli & Subramanian, 2008; Belore, 2003). El caso más complejo de las dinámicas de baterías de CSTR’s no-isotérmicos con MSS térmicos y concentracionales no se discute tampoco en los libros de texto básico y las referencias son bastante especializadas (Varma, 1980; Liu et al., 1997; Švandová et al., 2006; Favache & Dochain, 2008). Por último, se quiere destacar que la preocupación por la seguridad y la reducción del riesgo químico en la operación de reactores es un factor prioritario y motivante para el estudio de la dinámica de reactores. Lamentablemente son muchos los accidentes industriales que han implicado la muerte de muchas personas por la explosión de un reactor químico o la fuga de sustancias químicas toxicas liberadas al ambiente, debido al escape de reacciones incontroladas o “runaway reactions” (Chemical Safety Board, US. web site). El ingeniero químico debe siempre considerar que los aspectos técnicos especializados, como lo pueden llegar a ser los estudios de dinámica de reactores, encuentran su razón de ser fundamental en el cuidado del bienestar público, la seguridad del personal y la integridad física y el patrimonio comercial de la planta. 239 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 10.2.1. ARRANQUE, PERTURBACIÓN Y PARADA A VOLUMEN CONSTANTE Considérese el proceso de arranque de la batería ilustrada en la Figura 10.6: que incluye dos CSTRs en serie isotérmicos, en los cuales ocurre una reacción química cuya ley de velocidad viene dada por la ecuación 10.1. Figura 10.6. Batería de 2 CSTRs en serie isotérmicos con MSS El proceso de arranque de un CSTR isotérmico a volumen constante es una situación poco común y poco realista pero permite una primera aproximación para el entendimiento de la dinámica del sistema (Fogler, 2006; Ingham et al., 2007). El modelamiento matemático requiere el planteamiento del balance molar considerando el término de acumulación de material. Considerando el primer reactor: Entra Genera Sale Acumula dN A FAo rAV1 FA1 dt VoC Ao rAV1 240 VoC A1 d V1C A1 dt (10.17) (10.18) CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA Vo C Ao C A1 dC A1 rAV1 V1 dt dC A1 Vo kC A1 C Ao C A1 dt V1 1 KC A1 2 (10.19) (10.20) Por analogía con la ecuación (10.20), para el segundo reactor el balance toma la forma: dC A2 Vo kC A2 C A1 C A2 dt V2 1 KC A2 2 (10.21) Las condiciones iniciales de las ecuaciones diferenciales ordinarias establecen que a tiempo cero, CA1=14 y CA2=0 kmol/m3 (sin embargo, las condiciones iniciales pueden variar según el caso). Después de alcanzar el estado estacionario, se simula una perturbación al caudal de la alimentación a los 2000 s, en la cual el valor cambia súbitamente durante 300 s de 0,3 a 1 m3/s, para luego retornar a su valor original (perturbación tipo escalón). Finalizando la operación, después de operar en el estado estacionario durante 4500 s, se simula la parada de la batería haciendo la concentración del alimento CA1=0 kmol/m3. Los resultados de la simulación, empleando el integrador ode23tb de MatLab®, se presentan en la Figura 10.7. De los resultados de simulación de la Figura 10.7 se aprecia claramente que, después del arranque (a las condiciones iniciales establecidas), la batería alcanza las condiciones de estado estacionario establecidas durante el diseño de la batería (Tabla 10.1). También se aprecia que un solo reactor, que opera a las mismas condiciones de entrada que la batería, no puede llegar al estado estacionario inestable de 2,8 kmol/m3. Él se estabiliza en 8,62 kmol/m3, que corresponde al estado estable de baja conversión. Esto ilustra el por qué del término “conversiones inaccesibles”. Ante la perturbación en el caudal de entrada, cambia el estado de operación de los reactores. Finalizada la perturbación, los reactores regresan espontáneamente a sus estados estacionarios originales. Durante la parada, una vez eliminado el suministro de reactivo, la concentración de salida en los reactores cae a cero rápidamente. 241 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 10.7. Dinámica de la batería de 2 CSTRs durante: el arranque, una perturbación al caudal de alimento, y la parada. R1: primer reactor de la batería, R2: segundo reactor de la batería, Rúnico: un solo reactor a las mismas condiciones de entrada de la batería En la Figura 10.8, se simula otro tipo de perturbación. Después del arranque y de haber alcanzado el estado estacionario, se genera una perturbación tipo escalón a la concentración del alimento durante 300 segundos, pasando súbitamente de su valor original de 14 a 10 kmol/m3, para luego realizar el apagado después de 4500 segundos tal como se describió antes. En la Figura 10.8 se aprecia que frente a una perturbación en la concentración del alimento, la dinámica es completamente distinta a la observada en la Figura 10.7. En este caso el arranque es análogo, pero una vez se efectúa la perturbación que reduce el valor de la concentración de alimento por 300 s, los reactores alcanzan un nuevo estado estacionario diferente al original, lo que sugiere que el estado estacionario original era de naturaleza inestable. En el caso del reactor único, la perturbación mueve al sistema a otro estado estacionario de alta conversión (0,58 kmol/m3) (nótese que el estado estacionario intermedio sigue siendo inaccesible para una 242 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA Figura 10.8. Dinámica de la batería de 2 CSTR’s durante el arranque, una perturbación a l a c oncentración de l a limento y l a pa rada. R 1: pr imer r eactor de l a ba tería, R2: segundo reactor de la batería, Rúnico: un solo reactor a las mismas condiciones de entrada de la batería sola unidad). El reactor 1 de la batería también se desplaza a otro estado estacionario de mayor conversión (97% correspondiente a 0,45 kmol/m3), lo cual se puede conrmar con la ayuda de la Figura 10.2. La dinámica muestra que frente a ciertas perturbaciones el estado estacionario es inestable, y el sistema se mueve hacia otro de alta conversión. Se puede concluir en general que el comportamiento dinámico frente a una perturbación dependerá de: (a) la naturaleza de la variable perturbada, (b) la dirección de la perturbación en relación con el valor estacionario, (c) la intensidad de la perturbación y su duración, (d) así como de las características de estabilidad, inestabilidad, meta estabilidad del estado estacionario, ya que como se ha observado, un estado puede parecer estable frente a una perturbación, pero resultar inestable si esta cambia su dirección, magnitud o duración. Otra herramienta útil para estudiar la dinámica de las baterías de reactores en serie consiste en el llamado plano de fase del sistema 243 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS dinámico. Defínanse las concentraciones adimensionales y normalizadas de cada reactor como: YAº K C A1 / C Ao 1 º YA K C A2 / C Ao (10.22) 2 Representando la variación de una de estas concentraciones adimensionales en función de la otra, para diferentes condiciones iniciales de las ecuaciones (10.20) y (10.21), en el caso de una dinámica de arranque normal a volumen constante, se obtiene la Figura 10.9. Figura 10.9. Plano de fase de la dinámica de una batería isotérmica de dos CSTRs con 3 MSS. Los puntos señalan los estados estacionarios. La línea resaltada es la trayectoria dinámica durante una perturbación a la concentración de entrada, que desplaza al sistema del estado estable superior derecho, pasando por el estado inestable intermedio hasta el estado estable inferior izquierdo. Nótese que el plano está dividido en dos regiones principales a derecha e izquierda del estado estacionario intermedio inestable. Si se arranca el reactor en un punto de la zona derecha, se converge al estado estable superior, si se arranca en la zona izquierda se converge al estado estable inferior 244 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA Este mapa dinámico, completamente general, permite identicar visualmente los puntos estacionarios estables, inestables y meta-estables (análogos a los puntos jos caracterizados como nodos estables, inestables y sillas en los planos de equilibrios de fase). En este mapa se puede observar la trayectoria de la concentración en la batería de dos reactores durante cualquier evento dinámico (incluidas las perturbaciones). Aquí se puede conrmar que la batería posee dos estados estacionarios estables, señalados con círculos, hacia donde convergen los diferentes ramales del plano (uno de ellos fue el punto de diseño de la batería y el otro uno de mayor conversión total identicado mediante este análisis de perturbación). Es posible que operando en un estado estacionario, una perturbación conduzca el sistema hasta el otro estado estacionario de la batería, tal como se probó en la Figura 10.8. Nótese que cada una de las curvas representadas corresponde a una trayectoria del sistema en el arranque (a volumen constante) desde unas condiciones iniciales especícas. Las trayectorias se alejan de los puntos inestables, llegan a los puntos estables y pasan cerca de los puntos silla, sin alcanzarlos. En este plano de fase las trayectorias no deben cortarse entre sí, pues esto implicaría que para unas mismas condiciones iniciales el sistema tiene más de una trayectoria posible. Esto ocurre en sistemas autónomos (aquellos descritos por ecuaciones diferenciales en donde la derivada no es función del tiempo). Sin embargo, si el sistema es no-autónomo (como en el caso de una perturbación), puede visualizarse en el plano de fase una trayectoria que se puede cortar con otras, tal como se muestra en la Figura 10.9 para la trayectoria seguida por el sistema durante la perturbación mostrada en la Figura 10.8. 10.2.2. IDENTIFICACIÓN Y CARACTERIZACIÓN DIRECTA DE LOS MÚLTIPLES ESTADOS ESTACIONARIOS DE LA BATERÍA Es posible identicar y caracterizar matemáticamente cada uno de los estados estacionarios de un sistema sin necesidad de realizar el estudio dinámico completo. Para comprender la forma de hacerlo, considérese el caso de la batería de dos CSTRs ilustrada en la Figura 10.6. Para ella, el modelo de estado estacionario, derivado de las ecuaciones (10.20) y (10.21), viene dado por las siguientes dos ecuaciones: 245 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS F1 C A1 , C A2 F2 C A1 , C A2 1 C 1 C A1 Ao C kC A1 1 KC 2 0 A1 C A2 A1 kC A2 1 KC A2 (10.23) 2 0 Se desea entonces saber, con base en este modelo, si el sistema retornará o no al estado estable después de sufrir una perturbación. Si lo hace, esta solución de estado estable se dene como un estado “asintóticamente” estable. Si no, será un estado inestable. Obviamente, es posible resolver numéricamente las ecuaciones diferenciales no lineales en estado transiente para responder esa pregunta, como se mostró en la sección anterior, pero en ese caso sería entonces necesario analizar caso por caso. El método consiste en linealizar las ecuaciones diferenciales, sin perder en generalidad y evitando ese tedioso procedimiento. Considérese entonces la expansión en series de Taylor de las funciones no lineales F1 y F2, ecuación (10.23), alrededor del estado estacionario de la siguiente forma: F1 F C A1 C A1s 1 C A2 C A2 s C A1 C A2 F2 F C A1 C A1s 2 C A2 C A2 s C A1 C A2 , C A2 F1 C A F1 C A1s , C A2 s 1 , C A2 F2 C A F2 C A1s , C A2 s 1 en donde se pueden denir las variables de desviación, λ1 y λ2, como: 1 2 C C A1 A2 C A1s C A2 s y que representan una medida de qué tan lejos está el sistema del estado estacionario. Es posible derivar esas variables de desviación y comprobar que ellas también cumplen con el modelo en estado transiente (ecuaciones (10.21) y (10.22)). Substituyendo la expansión en series de Taylor para F1 y F2, se obtienen las siguientes ecuaciones lineales aproximadas para las variables de desviación: 246 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA 1 F1 F 1 1 2 t C A1 C A2 2 F2 F 1 2 2 t C A1 C A2 Deniendo la matriz jacobiana, Ja, del sistema F1 y F2 con respecto a CA1 y CA2 se obtiene de forma compacta las ecuaciones lineales de desviación variable como: Ja t (10.24) donde, para el caso bajo estudio, las matriz jacobiana y la evaluación de sus derivadas parciales serán: F1 C A1 Ja F2 C A1 2 1 k 1 KC A1ee 2kKC A1ee 1 KC A1ee 4 1 1 KC A1ee Ja 1 2 F1 C A2 F2 C A2 (10.25) 0 2 k 1 KC 2kKC A2 ee 1 KC A2 ee A2 ee 4 2 1 KC A2 ee 1 Las ecuaciones lineales pueden resolverse analíticamente. Su solución contiene las combinaciones lineales de términos de la forma eλt en los cuales λ corresponde a los valores propios de Ja. En el caso de una matriz de 2x2 se tendrán dos valores propios, los cuales pueden ser reales o complejos. Si son complejos, ellos pueden ser pares de complejos conjugados. Finalmente, la estabilidad de las ecuaciones lineales está determinada por la parte real de los valores propios. Se procede entonces al siguiente procedimiento de análisis (Perlmutter, 1972; Bequette, 1998): 247 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 1. Encontrar las múltiples soluciones del modelo del sistema en estado estacionario. 2. Obtener la matriz jacobiana del modelo del sistema en estado estacionario. 3. Calcular el valor de la matriz jacobiana en cada uno de los estados estacionarios. 4. Calcular los valores propios de la matriz jacobiana en cada estado estacionario. 5. Aplicar los siguientes criterios para caracterizar cada estado estacionario: Siendo Re (λ1) y Re (λ2) la parte real de los dos valores propios de este sistema: Valores propios Carácter del estado estacionario Re 1 0 y Re 2 0 Estable Re 1 0 y Re 2 0 Inestable tipo silla Re 1 0 y Re 2 0 Inestable Re 1 Re 2 0 1 y 2 complejos conjugados Re 1 Re 2 0 1 y 2 complejos conjugados Re 1 Re 2 0 1 y 2 complejos conjugados Espiral estable Espiral inestable Ciclo límte Los resultados obtenidos para el caso bajo estudio se resumen en la Tabla 10.2. En la Figura 10.10, se presenta la ilustración de la batería de dos CSTRs isotérmicos operando según los tres estados estacionarios de la Tabla 10.2. 248 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA Tabla 10.2. Resultados de la identicación y caracterización directa de los múltiples estados estacionarios de la batería de dos CSTRs en serie isotérmicos bajo estudio Estado estacionario A B C Concentraciones de salida (kmol/m3) Reactor Reactor 1 2 0,4469 0,0196 4,3477 0,3018 7,2054 2,7995 Conversión Valores propios Final Caracterización (%) λ1 λ2 99,8 97,8 80,0 -0,9691 -0,3605 -0,0112 -0,1984 0,0061 -0,0045 Estable Silla Estable Figura 10.10. Diagrama velocidad de reacción contra concentración de reactante. Se ilustran las líneas de operación de una batería de dos reactores isotérmicos con tres estados estacionarios posibles Los resultados obtenidos están en concordancia con todo lo observado y analizado durante el estudio dinámico. Se puede concluir que, aunque la batería se diseñó originalmente para alcanzar un estado inestable que resultaba inaccesible usando un solo reactor, la batería con dos reactores presenta a su vez un estado estacionario inestable e inaccesible! 249 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Esto se ha originado debido al procedimiento mismo de diseño, cuya naturaleza es geométrica y gráfica, lo cual deriva en que algún reactor de la batería resulta con una línea de operación que corta tres veces la curva de la cinética, originado un estado intermedio inestable. Este problema en el método de diseño ha sido estudiado por Mjalli & Subramanian (2008) y corregido mediante una técnica de optimización, la cual se invita al lector a revisar. 10.3. ARRANQUE DEL CSTR A VOLUMEN VARIABLE Ya se discutió el desempeño de un CSTR durante su arranque a volumen constante. En la práctica, el volumen de la mezcla reaccionante varía desde el momento en que se pone en funcionamiento el reactor, durante el proceso de llenado, hasta alcanzar las condiciones de estado estacionario; esto mientras ocurre simultáneamente la transformación química. Para modelar esta operación, será necesario considerar el cambio de la masa total contenida en el reactor con el tiempo, lo que está relacionado con las velocidades de flujo de alimentación y descarga del tanque. Suponiendo que el caudal de alimentación se mantiene constante durante la operación, la velocidad de llenado estará determinada por la velocidad de la corriente de salida. Con propósitos ilustrativos, se modelará la velocidad de descarga de una forma simplificada haciendo uso de la ley de Torricelli. por: El balance molar en estado dinámico para el reactor 1 viene dado V1 dC A1 dt C A1 dV1 VoC Ao V1C A1 rAV1 dt (10.26) Dado que el volumen no será constante, al desarrollar el término diferencial se obtiene: V1 dC A1 dC A1 dt 250 dt C A1 dV1 VoC Ao V1C A1 rAV1 dt kC A1 Vo V C Ao 1 C A1 V1 V1 1 KC A1 2 C A1 dV1 V1 dt (10.27) (10.28) CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA Para describir la variación del volumen con el tiempo, se realiza un balance másico global alrededor del reactor: Entra Sale Acumula m o oVo dM 1 dt m 1 1V1 d 1V1 dt (10.29) (10.30) Para muchas reacciones en fase líquida, se puede suponer que la densidad de la mezcla no cambia signicativamente debido a la reacción y al cambio en el número de moles, por lo que se puede considerar constante (una excepción importante la constituirían las reacciones de polimerización, en las que las propiedades de la mezcla reactiva como la densidad y la viscosidad cambian enormemente con el avance de la reacción). Reorganizando la ecuación (10.30) se obtiene: dV1 Vo V1 dt (10.31) Para describir la dependencia del caudal de descarga del reactor con otros parámetros geométricos del mismo, se considerará un balance de energía mecánica simple entre la supercie libre del liquido en la parte superior del tanque y el punto de descarga en la parte inferior. Asumiendo que la energía potencial del uido en la supercie libre se conserva, transformándose en energía cinética a la salida (Ley de Torricelli), se obtiene: mgh 1 2 mV 2 (10.32) donde h es la altura del uido en el tanque y V es la velocidad lineal del uido en la boquilla de descarga: V 2 gh (10.33) El caudal de salida se puede expresar como el producto de la velocidad lineal y el área de la sección transversal de la boquilla de salida As: 251 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS V VAs (10.34) V As 2 gh (10.35) Asumiendo que el tanque es un cilindro perfecto de radio R, el volumen geométrico del uido contenido en él será: Por lo tanto: V1 R 2 h (10.36) 2 gV1 V1 As1 R12 (10.37) V1 As1 2g R1 V1 1 (10.38) 2 1 V1 p1V1 2 (10.39) donde se ha identicado a los términos constantes como un parámetro jo p1. Finalmente el modelo dinámico completo vendrá dado por dos ecuaciones diferenciales para el tanque 1: 1 dV1 Vo p1V1 2 dt dC A1 dt (10.40a) kC A1 Vo V C Ao 1 C A1 V1 V1 1 KC A1 2 C A1 dV1 V1 dt (10.41a) Si se considera una batería de dos reactores en serie, el modelo dinámico para el arranque a volumen variable del segundo tanque vendrá dado por: 1 dV2 V1 p2V2 2 (10.40b) dt dC A2 V1 kC A2 C A2 dV2 V C A1 2 C A2 2 (10.41b) dt V2 V2 V2 dt 1 KC A2 252 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA Empleando la ecuación (10.40a), es posible obtener de antemano el valor del volumen del reactor 1 en estado estacionario (lo mismo puede hacerse para el reactor 2), dado por: V1ee 2 2 Vo 2 g As1 p1 R1Vo (10.42) El tiempo necesario para alcanzar el volumen de estado estacionario (teniendo en cuenta que en dicho caso el ujo volumétrico se hace constante e igual al del alimento a través de toda la batería) se puede calcular por la integración directa de la ecuación (10.40a), para obtener: tvee1 2Vo Vo 2 ln p1 V p V 1 2 1 ee1 o 2 1 Vee 2 p1 1 (10.43) Para realizar la simulación del proceso de arranque será necesario establecer las condiciones de alimentación, así como las condiciones iniciales de concentración y volumen en cada uno de los reactores. En virtud de que se ha realizado previamente un análisis en estado estacionario de la operación de la batería, ya se conocen los valores de estado estacionario de los volúmenes de mezcla reaccionante en cada reactor. Con dicha información y considerando que en estado estacionario el caudal a través de la batería se hace constante e igual al valor de entrada, se puede calcular para cada tanque el valor apropiado de su parámetro de descarga p1, usando la ecuación (10.39). Empleando las mismas condiciones de alimentación descritas en la sección precedente, CAo = 14 kmol/m3 y Vo = 0,3 m3/s, y considerando que los volúmenes de estado estacionario de los reactores 1 y 2 son respectivamente 19,047 y 6,8160 m3, se obtienen los correspondientes valores de los parámetros de descarga: p1 = 0,0687 y p2 = 0,1149 m3/2/s. Las condiciones iniciales más evidentes dictarían que en el tiempo cero ambos tanque se encuentren vacíos, por lo que sus concentraciones de salida serán también nulas (nótese que las ecuaciones diferenciales (10.41) se indeterminan si el volumen es igual a cero, por lo que en la solución numérica se debe de tomar un número muy pequeño). Los resultados se muestran en las Figuras 10.11 y 10.12. 253 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 10.11. Volumen de mezcla reaccionante en los dos CSTRs en serie de una batería isotérmica en función del tiempo para un arranque a volumen variable Figura 10.12. Concentración de salida del reactivo A en los dos CSTRs en serie de una batería isotérmica en función del tiempo para un arranque a volumen variable 254 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA En las Figuras 10.11 y 10.12 se observa que, después de un tiempo de 1000 segundos, los volúmenes alcanzan su valor de estado estacionario y que las concentraciones crecen rápidamente hasta el valor de entrada para luego descender, demorándose un poco más en estabilizarse. En la Figura 10.13 se presenta el plano de fases de la batería con la trayectoria del arranque. Figura 10.13. Plano de fase de la dinámica de una batería isotérmica de dos CSTRs con 3 MSS. Las líneas que cortan el plano de fases representan dos trayectorias de arranque a volumen variable En la Figura 10.13 se aprecia que arrancando el reactor a las condiciones del punto (0.0), la trayectoria que sigue la batería la desplaza sobre el borde inferior y el borde derecho para conducirla al estado estacionario estable superior. Nótese que para este tipo de arranque, no importa en qué zona del plano esté la condición inicial, el sistema tiende a estabilizarse en el estado estable superior (como ejemplo, se presenta la trayectoria del arranque que inicia en las concentraciones adimensionales normalizadas (0,2, 0,6)). Se le propone al lector investigar el desempeño de esta batería cuando experimenta diversos tipos de perturbaciones y concluir sobre el grado de estabilidad de los estados estacionarios (claro está que también sería divertido saber que pasaría sí la batería fuera noisotérmica!). 255 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 10.4. CSTRS NO ISOTÉRMICOS Y LA ESTABILIDAD DE SUS ESTADOS ESTACIONARIOS En el diseño de reactores de tanque agitado y ujo continuo es de crucial importancia determinar todas las soluciones posibles de las ecuaciones de balance de materia y energía, conocidas como múltiples estados estacionarios. La multiplicidad puede originarse inclusive en el caso isotérmico debido a cinéticas no-lineales en la concentración. En el caso de reactores no-isotérmicos, la multiplicidad de estados estacionarios se origina por la no linealidad que presenta el balance molar y de energía acoplados, en virtud de la dependencia exponencial de la constante cinética con la temperatura según la ley de Arrhenius. Adicionalmente, en este tipo de sistemas, el análisis de la estabilidad dinámica de cada uno de los estados estacionarios resulta esencial para la realización de operaciones de arranque, control y procedimientos de parada, así como para el propósito más fundamental de establecer las condiciones de operación apropiadas desde el punto de vista de la producción (p.e., evitar reacciones secundarias indeseadas) y la seguridad (p.e., riesgos de explosión). En esta sección se estudia el desempeño de un CSTR no-isotérmico con intercambio de calor en el que ocurre una reacción exotérmica de primer orden A→B. Las propiedades y parámetros de simulación del sistema, considerados constantes, se han adoptado del trabajo de Shacham et al. (1994) y se presentan en la Tabla 10.3. En primer lugar se determinan y se caracterizan los múltiples estados estacionarios de forma directa, para luego analizar la dinámica y estabilidad de cada uno de ellos, ilustrando la importancia y complementariedad de ambos enfoques. 10.4.1. DETERMINACIÓN Y CARACTERIZACIÓN DIRECTA DE LOS MÚLTIPLES ESTADOS ESTACIONARIOS Las ecuaciones de balance molar, de energía en el reactor y de energía del intercambiador de calor (chaqueta o serpentín), en estado estacionario para el CSTR son, respectivamente: 256 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA (10.44) CpoVo To T HVkC A UA T T j 0 (10.45) Vo C Ao C A VkC A 0 j Cp jV j T j T j UA T T j 0 (10.46) o Tabla 10.3. Parámetros de simulación de un CSTR no-isotérmico Vo Vf Vj V Vc ko E R U A Cp Cpj Tjo To ΔHrxn CAo ρ ρj Caudal de entrada al reactor Caudal de salida del reactor Caudal de refrigerante Volumen del reactor Volumen de la chaqueta Factor cinético preexponencial Energía de activación Constante universal de los gases Coeciente de transferencia de calor Area de transferencia de calor Capacidad caloríca de la mezcla Capacidad caloríca del refrigerante Temperatura de entrada refrigerante Temperatura de entrada alimento Calor de reacción Concentración de A en el alimento Densidad de la mezcla reaccionante Densidad del refrigerante 40 40 49,9 48 3,85 7,08×1010 30000 1,99 150 250 0,75 1 530 530 -30000 0,5 50 62,3 ft3 / h ft3 / h ft3 / h ft3 ft3 h-1 BTU / mol BTU / mol ºR BTU/ h ft2 ºR ft2 BTU / lbml ºR BTU / lbml ºR ºR ºR BTU / mol mol / ft3 lbm / ft3 lbm / ft3 Aunque las ecuaciones de balance de energía (10.45) y (10.46) pueden plantearse de forma intuitiva, resulta conveniente analizar más detenidamente su origen. El primer principio de la termodinámica aplicado a un sistema de ujo establece que: 257 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS n dEˆ n Q W Fi Ei entrada Fi Ei salida dt i 1 i 1 (10.47) en donde Ei representa la energía total especíca del componente i-ésimo puro con ujo molar Fi (nótese la simplicación usando propiedades de sustancias puras y no propiedades molares parciales, lo cual equivale a suponer mezclas ideales con efectos de mezclado despreciables). Q y W son las tasas de transferencia de calor y trabajo, t es el tiempo y Ê es la energía total en el interior del sistema, asociada al material acumulado. Considerando que el sistema se encuentra en estado estacionario, que las energías cinética y potencial son despreciables, por lo que la energía total corresponde a energía interna, y que el trabajo total corresponde al trabajo de ujo más un trabajo de eje (agitador), el cual también es despreciable, se tiene, después de emplear la denición de entalpía, que: n n i 1 i 1 Q Fi H i entrada Fi H i salida 0 (10.48) El término de transferencia de calor puede expresarse en términos del coeciente global de transferencia de calor, U, el área de transferencia de calor, A, y una fuerza guía dada por la diferencia entre la temperatura del reactor y la del medio refrigerante (para un análisis más detallado de este término véase Fogler, 2006): Q UA T T j (10.49) En virtud de que en el intercambiador de calor del reactor (sea este del tipo tanque enchaquetado o con serpentín sumergido) no existe reacción química y no se considerará acumulación de material, al reemplazar la ecuación (10.49) en la (10.48) y considerar que el Cp del uido refrigerante es constante (independiente de la temperatura) se obtiene la ecuación (10.46). En el caso del balance de energía para el reactor, es necesario considerar que, por la ocurrencia de la transformación química, el balance molar en estado estacionario estará dado por: Fio i rAV Fi Fio rV i A 258 (10.50) CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA Reemplazando las ecuaciones (10.49) y (10.50) en (10.48) y considerando que el calor se transere desde el reactor hacia el intercambiador de calor, usando la convención de signos aceptada, se obtiene: n n UA T T j Fio H io Fio i rA V H i 0 (10.51) i 1 n i 1 n UA T T j Fio H io H i rAV i H i 0 i 1 n i 1 UA T T j Fio H io H i rAV H rxn 0 i 1 (10.52) (10.53) Considerando que el Cp de la mezcla reactiva permanece constante y reemplazando la ley de velocidad de reacción en la ecuación (10.53) se obtiene la ecuación (10.45). Determinar los estados estacionarios implica identicar todos los conjuntos de valores (CA, T, Tj) que simultáneamente son solución de las ecuaciones (10.44) a (10.46). Esto puede conseguirse grácamente reorganizando las ecuaciones para establecer, en función de la temperatura, las ecuaciones que representan las tasas de generación y remoción de energía. Los cortes entre estas dos ecuaciones corresponden a las soluciones buscadas. Deniendo unas nuevas variables como: CA Tj VoC Ao Vo Vk T jo T 1 UA Cp j jV j (10.54) (10.55) (10.56) y después de manipular algebraicamente los balances se obtiene: G (T ) HVkC A (10.57) 259 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS R(T ) CpoVo T To UA T T j (10.58) donde G(T) es la tasa de generación de energía en el reactor, debido a la reacción química, y R(T) es la tasa de remoción de energía, debido al cambio entálpico entre las corrientes de entrada y salida y al enfriamiento a través de la chaqueta. Empleando los parámetros presentados en la Tabla 10.3 y resolviendo las ecuaciones (10.57 y 10.58), se obtienen los resultados que se presentan en la Figura 10.14. Figura 10.14. Curvas de remoción y generación de calor para un CSTR. Los puntos de corte representan los estados estacionarios de operación Se pretende entonces establecer cuáles son los valores de temperatura (T) tal que G(T)= R(T), y que corresponden a los estados estacionarios. La determinación numérica precisa de los múltiples estados estacionarios se puede realizar empleando un método de Newton-Raphson sobre la función objetivo univariable: F(T) = G(T) - R(T) = 0. Los resultados obtenidos se presentan en la Tabla 10.4. La caracterización matemática de los estados estacionarios, como estables o inestables, se basa en el valor que toman los valores propios 260 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA Tabla 10.4. Múltiples estados estacionarios Estado estacionario 1. Inferior 2. Intermedio 3. Superior T (ºR) 537,1641 599,9909 651,0596 Tj (ºR) 536,6157 594,6328 641,7920 CA (mol / ft3) 0,4739 0,2451 0,0591 de la matriz del espacio de estado del sistema (o matriz característica) evaluada en dichos puntos. La matriz del espacio de estado es la matriz jacobiana del sistema de las tres ecuaciones en tres variables dado por las ecuaciones (10.44) a (10.46), cuya evaluación se detalla en la sección 10.2.2. En la Tabla 10.5 se presentan los valores propios de dicha matriz cuando ésta se evalúa en cada uno de los puntos estacionarios del sistema (Tabla 10.4). Tabla 10.5. Valores propios de la matriz de espacio de estado Estado estacionario 1. Inferior 2. Intermedio 3. Superior λ1 -0,9757 + 0i -0,5320 + 0i -187,721 + 0i λ2 -1,2667 + 0i -188,0727 + 0i 0,07456+2.754i λ3 Carácter -188,7001 + 0i Estable 3,0496 + 0i Inestable Silla 0,07456 - 2,754i Espiral inestable Puede concluirse sobre la estabilidad del punto estacionario analizando el signo de la parte real de los valores propios y si el valor propio es un complejo, con los criterios establecidos en la sección 10.2.2. Los valores obtenidos muestran que el estado estacionario inferior es estable, mientras que el intermedio y el superior son inestables. Nótese que el punto jo superior, inestable, presenta dinámica oscilatoria ya que tiene dos valores propios complejos conjugados, por lo cual se cataloga como una espiral inestable. Esto es contra intuitivo si se considera el análisis cualitativo que suele hacerse para juzgar sobre la estabilidad usando el diagrama de la Figura 10.14, en la cual se podría concluir que el estado estacionario superior es “estable” pues si la temperatura aumenta por encima del valor estacionario, la velocidad de remoción de energía es mayor que la de generación, lo cual enfriaría el reactor y lo retornaría a su estado inicial; por otro lado, si la temperatura desciende por debajo 261 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS de ese valor “estable”, la velocidad de generación de energía se hace mayor que la de remoción, lo cual elevaría nuevamente la temperatura y la retornaría al estado inicial. Todo esto señala que el estado estacionario es “localmente estable” –estable frente a muy pequeñas perturbaciones– pero no es “globalmente estable” como lo indica el valor propio. Así se demuestra que para juzgar sobre la estabilidad de una condición de operación de un reactor químico no es suciente (y en algunos casos como el actual, inapropiado) basarse sólo en el análisis cualitativo de estado estacionario y que siempre es necesario una caracterización de los estados estacionarios y un análisis detallado de la dinámica del sistema. A continuación se presenta la simulación del modelo dinámico del reactor para unas condiciones iniciales cercanas a los estados estacionarios identicados previamente en la Tabla 10.4, esto es, el comportamiento dinámico después de una pequeña perturbación del estado estacionario. Se estudia la estabilidad dinámica local de cada uno de los tres estados estacionarios, se simulan los planos de fases del reactor y se analiza la estabilidad de los tres estados estacionarios a la luz de la caracterización establecida usando los valores propios de la matriz de espacio de estado del sistema. 10.4.2. DESEMPEÑO DINÁMICO Y VISUALIZACIÓN DE LA ESTABILIDAD Las ecuaciones de balance de materia y energía para el reactor y la chaqueta se presentan en las ecuaciones (10.59) a (10.61), respectivamente. dC A Vo C Ao C A kC A dt V (10.59) HkC A dT Vo UA To T T T j dt V Cp C p V (10.60) dT j V j UA T jo T j T T j dt Vc C p j jVc (10.61) 262 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA No se incluyen los balances de materia globales del reactor y de la chaqueta debido a que se ha supuesto que los caudales son constantes entre la entrada y la salida; es decir, el volumen total de los uidos en el reactor y en la chaqueta permanecen constantes, lo que implica que los resultados obtenidos no son validos para operaciones de llenado o vaciado. La demostración del balance molar en estado transitorio, ecuación (10.59) se ha presentado en la sección 10.2.1. Para la demostración de los balances de energía en estado transitorio considérese el término de acumulación en el balance de energía de la ecuación (10.47): n n N i Ei Eˆ N iU i i 1 i 1 n N H i 1 i i Pi (10.62) en donde Ei es la energía especica de las Ni moles del componente i-ésimo puro en el interior del sistema, se ha considerado sólo energía interna Ui y se ha empleado la denición de entalpía (nótese la simplicación usando propiedades de sustancias puras y no propiedades molares parciales, lo cual equivale a suponer mezclas ideales con efectos de mezclado despreciables). Diferenciando la ecuación (10.62) con respecto al tiempo se obtiene: n dH i n dN i d n dEˆ Ni Hi P N ii dt i 1 dt dt dt i 1 i 1 (10.63) n dH i n dN i d dEˆ Ni Hi PV dt i 1 dt dt dt i 1 (10.64) dEˆ dt n N i 1 i dH i n dN i dV dP Hi P V dt dt dt dt i 1 (10.65a) Dado que se ha supuesto volumen constante, el tercer término de la ecuación (10.65a) se cancela y suponiendo que las variaciones de presión en el interior del reactor son despreciables, por lo que el último término de la ecuación también se cancela, se obtiene que: dEˆ dt n Ni i 1 dH i n dN i Hi dt dt i 1 (10.65b) 263 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Es claro que el balance molar en el reactor permite rescribir el segundo término de la ecuación (10.65b), ya que: dN i Fio rV Fi i dt (10.66) Para la entalpía puede considerarse la definición fundamental: dH i Cpi dT (10.67) Reorganizando y diferenciando con respecto al tiempo se obtiene: dH i dT Cpi dt dt (10.68) Reemplazando las ecuaciones (10.66) y (10.68) en la ecuación (10.65b), se obtiene: dEˆ dT dt dt dEˆ dT dt dt n n N Cp H F i i 1 i n i i 1 n N Cp H F i i 1 dEˆ dT dt dt i i i 1 n (10.69) Fi rAV i H i (10.70) io io n i 1 i i i 1 n N Cp H F i i rA V Fi io i 1 Fi rAV H rxn (10.71) Reemplazando la ecuación (10.71) en la ecuación (10.47) y procediendo con las mismas suposiciones expuestas previamente, se obtiene: dT dt n n N Cp H F i 1 i i i 1 i io n n Fi rAV H rxn UA T T j Fio H io Fi H i i 1 i 1 (10.72) de donde finalmente se obtiene: n dT dt i 1 n NiCpi i 1 264 UA T T j Fio H io H i rAV H rxn (10.73) CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA En las Figuras 10.15 a 10.17 se presentan los resultados obtenidos para la variación de la concentración del reactante A (CA), la temperatura del reactor (T), y la temperatura de salida del refrigerante (Tj) en función del tiempo, tomando como condiciones iniciales valores cercanos a los de estado estacionario. Figura 10.15. Concentración de salida del reactor en función del tiempo Figura 10.16. Temperatura en el reactor en función del tiempo 265 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 10.17. Temperatura en la chaqueta del reactor en función del tiempo Se aprecia que bajo pequeñas perturbaciones, el estado estacionario inferior (1º EE) se autorregula; el estado estacionario intermedio (2º EE) es inestable y se mueve hacia el EE superior. El estado estacionario superior (3º EE) se comporta de forma oscilatoria alrededor del punto estacionario, por lo que en rigor, es imposible alcanzarlo exactamente y, aunque es el punto de mayor conversión, no debe ser el punto de operación. Es de esperar que el desempeño dinámico del sistema dependa de las condiciones iniciales de las variables dependientes así como del valor de los parámetros del modelo, con respecto a los cuales pueden existir diferentes grados de sensibilidad. Para tener una imagen más completa de la dinámica del sistema, se presenta en la Figura 10.18 el plano de fases concentración-temperatura del reactor. En el plano de fases de la Figura 10.18 se observa la trayectoria del sistema a través del tiempo a partir de diferentes condiciones iniciales. Es evidente de la Figura que el estado estacionario inferior es estable pues para diferentes condiciones iniciales el sistema se estabiliza allí. Se observa que ninguna trayectoria llega al estado estacionario intermedio, lo que muestra que es inestable. Es interesante resaltar que ciertas condiciones iniciales llevan el sistema hacia una trayectoria oscilatoria alrededor del estado estacionario superior, como se muestra en la ampliación dentro de 266 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA la Figura 10.18, lo que hace de este punto un estado inestable. En este caso, con las tres variables dependientes del tiempo, realmente se debería de hablar de un “espacio de fases” tridimensional. Figura 10.18. Plano de fases concentración-temperatura del reactor para el CSTR. Los tres estados estacionarios se señalan con círculos. BIBLIOGRAFÍA Aris, R. (1994): Mathematical Modelling Techniques. New York: Dover. Belore, L.A. (2003): Transport Phenomena for Chemical Reactor Design. New Jersey: John Wiley & Sons. Bequette, B.W. (1998): Process Dynamics: Modeling, Analysis and Simulation. New Jersey: Prentice Hall. Chemical Safety Board, CSB, U.S. www.csb.gov. 267 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Chen, C.T. & Crynes, B.L. (1987): “A method for Achieving Inaccessible Conversions by use of Cascade CSTR’s”. En: Chemical Engineering Science, 42(5), 1229-1232. Dobre, T.G.; Sanchez-Marcano, J.G. (2007). Chemical Engineering: Modelling, Simulation and Similitude. New Jersey: John Wiley & Sons. Elnashaie, S.S.E.H. & Garhyan, P. (Eds.) (2003): Conservation Equations and Modeling of Chemical and Biochemical Processes. New York: Marcel Dekker. Favache A. & Dochain, D. (2009): “Thermodynamics and Chemical Systems Stability: The CSTR case study revisited”. En: Journal of Process Control, 19(3), 371-379. Fogler, H.S. (2006): Elements of Chemical Reaction Engineering (4th Ed.). New Jersey: Prentice Hall. Ingham, I.; Dunn, I.J.; Heinzle, E.; Prenosil, J.E. & Snape, J.B. (2007): Chemical Engineering Dynamics: An Introduction to Modelling and Computer Simulation (3th Ed.). New Jersey: John Wiley & Sons. Liou, C.T. & Chien, Y.S. (1990): “Steady-State Multiplicity Caused by Nonideal Mixing in Two Isothermal CSTR’s”. En: AIChE Journal, 36(6), 951-954. Liu, C.I.; Wen, H.J. & Lee, D.J. (1997): “Complex Dynamics Resulting from Coupling Between Oregonators in a Series of Two CSTRs with Recycle”. En: Journal of Physical Chemistry A., 101(2), 170-173. Mizrahi, J. (2002): Developing an Industrial Chemical Process: An Integrated Approach. New York: CRC Press. Mjalli, F.S. & Subramanian, J.N. (2008): “Achieving Stability Under Inaccessible Conversions Using CSTR Cascades”. En: International Journal of Chemical Reactor Engineering, 6 (A77). 268 CAPÍTULO 10 - DINÁMICA Y MULTIPLICIDAD DE ESTADOS ESTACIONARIOS EN REACTORES DE MEZCLA COMPLETA Perlmutter, D.D. (1972): Stability of Chemical Reactors. New Jersey: Prentice Hall. Shacham, M.; Brauner, N. & Cutlip, M. B. (1994): “Exothermic CSTRs: Just How Stable are the Multiple Steady States?” En: Chemical Engineering Education, 28(1), 30-35. Švandová, Z.; Kotora, M.; Markoš, J. & Jelemenský, L. (2006): “Dynamic Behaviour of a CSTR with Reactive Distillation”. En: Chemical Engineering Journal, 119(2-3), 113-120. Trejos, V.M.; Fontalvo, J. & Gómez García, M.Á. (2009): “Descripción matemática y análisis de estabilidad de procesos fermentativos”. En: DYNA, 158(76), 111 – 121. Varma, A. (1980): “On the Number and Stability of Steady States of a Sequence of Continuous-Flow Stirred Tank Reactors”. En: Ind. Eng. Chem. Fundam., 19(19), 316-319. Vleeschhouwer, P.H.M. & Fortuin, J.M.H. (1990): “Theory and Experiments Concerning the Stability of a Reacting System in a CSTR”. En: AIChE J., 36(6), 961-965. 269 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 46 CAPÍTULO 11 - PÉRDIDA DE CARGA EN REACTORES CON FLUJO PISTÓN 11 PĴėĉĎĉĆ ĉĊ ĈĆėČĆ Ċē ėĊĆĈęĔėĊĘ ĈĔē ċđĚďĔ ĕĎĘęŘē INTRODUCCIÓN Para realizar cálculos preliminares de diseño que involucren reactores tubulares, el procedimiento usual es asumir ujo pistón. La presión se involucra solo a través de su inuencia sobre la velocidad de reacción. Para reacciones en fase líquida, la inuencia de las variaciones de la presión es usualmente insignicante pero, para reacciones en fase gas o cuando se encuentran presentes mezclas de gases y líquidos, la caída de presión a través de un segmento dado de reactor se debe tener en cuenta para poder determinar el volumen de reactor requerido para alcanzar una tarea especíca. La caída de presión en sistemas homogéneos se puede calcular a partir de la ecuación de Bernoulli, utilizando las relaciones empíricas apropiadas donde sea necesario estimar el factor de fricción, las longitudes equivalentes para las secciones en “U” u otros aditamentos y las pérdidas asociadas con cambios en el diámetro del tubo. La caída de presión permisible en un reactor tubular debe determinarse con base en los costos de operación. Reactores tubulares son de uso común para el caso de reacciones homogéneas favorecidas por el régimen de ujo pistón y reacciones homogéneas endotérmicas que requieren de altas relaciones supercie de transferencia de calor/volumen (lo cual se logra con tubos de diámetros pequeños). Un ejemplo clásico lo constituye el caso de los reactores utilizados para las reacciones de craqueo térmico. 271 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS A continuación se presenta de forma detallada la deducción de una expresión que permita involucrar, en el diseño de un reactor tubular de ujo pistón, la caída de presión. Este capítulo se basa en el proceso de craqueo térmico de etano tal y como lo propuso Froment (1981). Así, para el caso de un reactor no isotérmico, se mostrará cómo se plantean, se acoplan y se resuelven simultáneamente las ecuaciones de conservación de masa, energía térmica y energía mecánica. 11.1. CRAQUEO TÉRMICO DE ETANO: DESCRIPCIÓN DEL REACTOR El craqueo térmico de hidrocarburos se lleva a cabo en reactores tubulares muy largos que se ubican vertical u horizontalmente en hornos donde se quema gas. Los quemadores se ubican a ambos lados de los tubos. Estos hornos constan de una primera sección, de transferencia de calor por convección, en la cual se alimenta y se precalienta el hidrocarburo y el vapor de agua diluyente y una segunda sección, de transferencia de calor por radiación, en la cual se lleva a cabo la reacción. La longitud del reactor en la sección de radiación es de 95 m. La longitud de las secciones rectas es de 8,85 m, la longitud y el radio de los codos son de 0,55 m y 0,178 m, respectivamente. El diámetro interno del tubo es de 0,108 m. Se alimenta etano a 68,68 kg/(m2.s), con una composición molar de 98,2 % de etano, Tabla 11.1. Reacciones y parámetros cinéticos para el craqueo térmico de etano Froment & Bischoff (1990) Reacción Orden Factor pre-exponencial E, kJ/kmol C2 H 6 C2 H 4 H 2 1 4,65 × 1013, s-1 273020 C2 H 4 H 2 C2 H 6 2 8,75 × 108, m3/(kmol.s) 136870 2C2 H 6 C3 H 8 CH 4 1 3,85 × 1011, s-1 273190 C3 H 6 C2 H 2 CH 4 1 9,81 × 108, m3/(kmol.s) 154580 C2 H 2 CH 4 C3 H 6 2 5,87 × 104, m3/(kmol.s) 29480 C2 H 2 C2 H 4 C4 H 6 2 1,03 × 1012, m3/(kmol.s) 172750 C2 H 4 C2 H 6 C3 H 6 CH 4 2 7,08 × 1013, m3/(kmol.s) 253010 272 CAPÍTULO 11 - PÉRDIDA DE CARGA EN REACTORES CON FLUJO PISTÓN 1 % de C2H4 y 0,8 % de C3H6. Además, se alimenta 0,4 kg de vapor de agua por cada kg de etano. La presión y la temperatura de entrada son de 2,99 atm y 680 ºC, respectivamente. Es de anotar que, en planta, la conversión de etano está restringida aproximadamente al 60% para evitar la formación excesiva de coque (Froment, 1981). El proceso de craqueo térmico de etano se puede representar mediante siete reacciones. Estas, junto con los respectivos parámetros cinéticos, se presentan en la Tabla 11.1. 11.2. MODELO MATEMÁTICO Simular el reactor descrito en la sección anterior requiere de la solución simultánea de los balances molares por componente, junto con el balance de energía y la ecuación de pérdida de carga. Estas se deducen a continuación. 11.2.1. BALANCE MOLAR Para un reactor tubular, el balance molar se puede definir para el elemento diferencial de volumen como (Fogler, 2006): Entra – Sale + Genera por reacción = Acumula Fj Fj z z z R j Ac z 0 (11.1) donde Rj es la velocidad total de reacción del componente j. Dividiendo por ∆z y evaluando el límite cuando ∆z → 0 se obtiene después de reorganizar que: dFj dt2 dt2 R A R r ij i j c j dz 4 4 i (11.2) donde j =1, ..., 8; i = 1, ..., 7; rj es la velocidad de la i-ésima reacción la cual puede expresarse como: 273 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS ri ki C j i ,k con Cj yjP RT (11.3) Fj P j 1 Fj RT (11.4) 9 Las reacciones y los parámetros se encuentran en la Tabla 11.1. 11.2.2. BALANCE DE ENERGÍA TÉRMICA Con base en el elemento diferencial de volumen para un reactor tubular, se obtiene que el balance de energía para el reactor viene dado por (Fogler, 2006): dT dz 1 9 j 1 Fj C p j dt2 q z d t 4 H i Rxn ,i r i (11.5) donde q(z) es el ujo de calor transferido por las paredes del tubo. Froment & Bischoff (1990) denieron, a partir de simulaciones y experimentos independientes de la transferencia de calor en este tipo de reactores, los siguientes valores de ujo de calor: primer tubo: 96 kJ/(m2.s); segundo tubo: 84 kJ/(m2.s), tercer tubo: 80 kJ/(m2.s), cuarto tubo: 71 kJ/(m2.s), quinto tubo: 63 kJ/(m2.s), del sexto al décimo tubos: 59 kJ/(m2.s). 11.2.3. BALANCE DE ENERGÍA MECÁNICA La ecuación de pérdida de carga debe involucrar tanto las pérdidas de carga por fricción en las secciones rectas y en los codos que las une, como también por cambios en la cantidad de movimiento. Partiendo de la ecuación general de energía mecánica (Bird et al., 2006) se tiene: 2 u 2 ˆ 0 g h 1 dP Wˆ Ev 2 1 274 (11.6) CAPÍTULO 11 - PÉRDIDA DE CARGA EN REACTORES CON FLUJO PISTÓN donde Êv representa la velocidad total de conversión irreversible de energía mecánica en energía térmica (calor). Para una conducción larga, recta, de diámetro constante se tiene que: ˆ 1 u2 z f Ev 2 RH (11.7) donde RH es el radio hidráulico y f es el factor de fricción de Fanning. Luego, reorganizando se obtiene que: ˆ 2 f z u2 Ev dt (11.8) Para los codos, la pérdida de energía mecánica se puede evaluar con un término adicional suplementario, factor ζ, según la formulación de Nekrasov (Froment & Bischoff, 1990) así: 90 0,35 0, 051 0,19 0, 7 dt rb donde Λ corresponde al ángulo descrito por el codo (en este caso 180°) y rb es el radio del codo. Asumiendo que Ŵ y Δh son iguales a cero, se obtiene de la forma diferencial de la ecuación (11.6) y reorganizando: f udu 1 dP 2u 2 0 dz d r t b que: (11.9) Sabiendo que uρ=G, reemplazando y reorganizando se obtiene 2f dP 2 du u u dz dz dt rb (11.10) donde α corresponde a un factor de proporcionalidad. Sabiendo que u = (G/Mm)(RT/P), con Mm el peso molecular promedio, y suponiendo gas ideal para el cálculo de la densidad (ρ = P.Mm/RT), reemplazando se obtiene: 275 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 1 2 f F 1 dT d 1 rb T dz dz M m dP M m dt dz 1 P M P G 2 RT m (11.11) Donde 1 d 1 dz M m GAc N j 1 dFj dz El factor de fricción se puede calcular a partir de la ecuación de Colebrook (De Nevers, 2005): 1 1.255 4 log 3.7 d Re f f t con Re (11.12) dt G Para el cálculo de la viscosidad se utilizó el método de Lucas para los componentes puros junto al método de Wilke & Chang para las mezclas (Poling et al., 2000). 11.3. RESULTADOS Se resolvieron simultáneamente las ecuaciones (11.2), (11.5), y (11.11) utilizando un método de Runge Kutta. Los perles de conversión, presión, y temperatura se presentan en la Figura 11.1. De la Figura 11.1 se puede observar como la reacción inicia (conversión 1%) después de aproximadamente 6 m de reactor y la temperatura ha alcanzado los 735 K. Las pérdidas de carga son evidentes. La característica irregular de la curva se debe a la presencia de los codos que unen las secciones rectas de tubería. La misma gura incluye los valores de planta reportados a la salida del reactor por Froment (1981). 276 CAPÍTULO 11 - PÉRDIDA DE CARGA EN REACTORES CON FLUJO PISTÓN Figura 11.1. Perles de conversión, presión y temperatura para el reactor de craqueo térmico de etano (Símbolos abiertos: datos de planta Froment, 1981) Figura 11.2. Distribución de productos en función de la conversión para el craqueo térmico de etano (Símbolos abiertos: datos de planta Froment, 1981) 277 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Los rendimientos para etileno, hidrógeno, y metano calculados y reportados de datos de planta se comparan en la Figura 11.2. BIBLIOGRAFÍA Bird, R.B.; Stewart, W.E. & Lightfoot, E.N. (2006): Transport Phenomena (2nd Ed.). New Jersey: John Wiley & Sons. De Nevers, N. (2005): Fluid Mechanics for Chemical Engineers (3rd Ed.). New York: McGraw Hill. Fogler, H.S. (2006): Elements of Chemical Reaction Engineering (4th Ed.). New Jersey: Prentice Hall. Froment, G.F. (1981): “Thermal Cracking for Olens Production. Fundamentals and their Application to Industrial Problems”. En: Chem. Eng. Sci. 36 (6), 1271 – 1282. Froment, G.F. & Bischoff, K.B. (1990): Chemical Reactor Analysis and Design. New Jersey: John Wiley & Sons. Poling, B.E.; Prausnitz, J.M. & O´Connell, J.P. (2000): The Properties of Gases and Liquids (5th Ed.). New York: McGraw Hill. 278 CAPÍTULO 12 - REACTORES CON RECIRCULACIÓN: "EL TUBO QUE SE VOLVIÓ UN TANQUE" 12 RĊĆĈęĔėĊĘ ĈĔē ėĊĈĎėĈĚđĆĈĎŘē: "Ċđ ęĚćĔ ĖĚĊ ĘĊ ěĔđěĎŘ Ěē ęĆēĖĚĊ" INTRODUCCIÓN Todos los tipos de reactores pueden ser operados ventajosamente utilizando la recirculación de parte de un producto o de una corriente intermedia. Por ejemplo, cuando la recirculación se calienta o se enfría apropiadamente, esta puede servir para moderar los cambios indeseables de temperatura dentro del reactor (Fogler, 2006). Esta función se puede alcanzar haciendo circular parte del uido reaccionante, mediante una bomba, a través de un intercambiador de calor externo. Adicionalmente, las corrientes de salida del reactor pueden también ser procesadas generando cambios de composición antes de su reciclo (Villermaux, 1985). Los reactores con recirculación pueden operarse como reactores por lotes. En el caso de estudios de laboratorio, existen dos tipos de reactores de recirculación: el reactor con recirculación interna (“Reactor Berty”) y el reactor con recirculación externa. Estos reactores utilizan un catalizador sólido el cual es empacado en “canastas” o en lechos, respectivamente. La forma de operación de estos sistemas permite homogenizar las condiciones de reacción. Así por ejemplo, con el aumento en el reciclo en un PFTR, los cambios de temperatura y composición a través del reactor mismo se hacen más pequeños (esta forma de operación se conoce también como reactor diferencial). 279 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS En este capítulo se analizan diferentes esquemas de reacción con recirculación. Inicialmente, con el n de introducir los conceptos básicos, se analizan el caso ampliamente presentado en la literatura: el reactor tubular con recirculación a volumen constante. Seguidamente, se analizan varios esquemas no isotérmicos con recirculación externos, que incluyen el balance de energía. 12.1. “EL TUBO QUE SE VOLVIÓ UN TANQUE” Considérese el caso de un reactor tubular (PFTR) en el cual la corriente de salida es físicamente dividida (no se presenta separación química) y parte es reciclada y mezclada con la corriente de alimento al sistema en un punto justo anterior a la entrada al PFTR, tal como se muestra en la Figura 12.1. Figura 12.1. Esquema de un PFTR con recirculación donde las conversiones X1 a la entrada del reactor y XS a la salida del mismo se miden desde el alimento fresco. La reacción ocurre únicamente en la sección del PFTR y no, por ejemplo, en la corriente de reciclo. A valores intermedios de recirculación, el comportamiento de un reactor tubular con recirculación es intermedio entre un reactor de mezcla completa (CSTR) y un PFTR. Por denición y para todas las sustancias que participan en el sistema, la relación de recirculación R corresponde a la relación entre el ujo de materia que se recircula respecto a la que sale del sistema. Es decir: 280 CAPÍTULO 12 - REACTORES CON RECIRCULACIÓN: "EL TUBO QUE SE VOLVIÓ UN TANQUE" R Fj 3 (12.1) Fjs Tomando como referencia la entrada al sistema presentado en la Figura 12.1, los balances a la entrada y a la salida del ciclo de recirculación se escriben como: Fj 2 Fjs Fj 3 Fjs 1 R F j1 F j 3 F j 0 F j 0 R Fj 2 R 1 (12.2) (12.3) El ujo de materia dentro del reactor es 1+R veces mayor que en el ciclo exterior, de suerte que los ujos de referencia deben ser multiplicados por 1+R: F j1 1 R Fj 0 j F0 X 1 (12.4) Fj 2 1 R Fj 0 j F0 X S (12.5) Fj 0 R Fj 0 j F0 X S 1 R Fj 0 j F0 X 1 (12.6) de donde: Luego es posible obtener que: X1 R X 1 R S (12.7) Siendo la velocidad volumétrica de ujo de referencia igual a υ0(1+R), el balance molar para el reactor tubular con recirculación, queda entonces como: X S V dX C0 rj 0 1 R X1 V C0 1 R 0 XS R XS 1 R (12.8) dX rj (12.9) 281 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS De forma gráca, análoga a como lo propone Levenspiel (1999), el signicado del tiempo de residencia aparece luego de gracar C0 /r en función de X como se muestra en la Figura 12.2. Figura 12.2. Representación gráca de un PFTR con recirculación Si XS = OB y (RXS)/(1+R) = OA, la cantidad τ/(1+R) es la supercie ABDF. Si se traza una recta EC tal que esa supercie es igual a la correspondiente ABCE, se puede observar que el tiempo de residencia no es otro que la supercie del rectángulo OBCG. Si R es pequeño, el comportamiento del reactor se aproxima al de un PFTR simple. Cuando R es grande, el teorema del valor medio permite escribir la ecuación (12.9) de la forma: C0 1 R X S con R 1 XS 1 R rX R XS X XS 1 R Cuando R → ∞, X → XS la ecuación (12.9) se vuelve: 282 (12.10) CAPÍTULO 12 - REACTORES CON RECIRCULACIÓN: "EL TUBO QUE SE VOLVIÓ UN TANQUE" C0 X S rS (12.11) que no es otra que la ecuación característica de un CSTR. Lo anterior se puede observar fácilmente si se analiza el caso isotérmico sin cambio de volumen de la reacción A → productos, cuya ley de velocidad se asume de 1er orden. Así, retomando la ecuación (12.9) y haciendo que X = XA se obtiene que: k 1 exp 1 R XA R k exp 1 R 1 R (12.9b) La Figura 12.3 representa las fracciones residuales (1-XA) en función del número de Damköhler: Da = kCon-1τ, donde n corresponde al orden de reacción, a diferentes valores de R. Figura 12.3. Fracción residual a la salida de un PFTR con recirculación para diferentes valores de R 283 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS De la Figura 12.3 se puede concluir que haciendo variar R entre 0 e innito, se puede obtener un desempeño intermedio entre el PFTR (R = 0) y el CSTR (R = ∞) 12.2. BALANCES DE MASA Y DE ENERGÍA EN UN REACTOR CON RECIRCULACIÓN. CASO ADIABÁTICO Los cambios de temperatura y concentración en un reactor adiabático con recirculación dependerán de la relación de recirculación R. Asúmase para el análisis la nomenclatura que se presenta en la Figura 12.4. Figura 12.4. Esquema de un PFTR adiabático con recirculación Siguiendo la metodología presentada en la sección 12.1, considerando el caso a densidad constante, se puede obtener fácilmente que: C1 C0 RC2 1 R (12.12) Adicionalmente, el cambio en la concentración a través del reactor está relacionado con el cambio en el sistema completo mediante la expresión: C1 C2 C0 RC2 C0 C2 C2 1 R 1 R (12.13) Para el caso a densidad y capacidad caloríca constantes, la temperatura a la entrada del reactor estará expresada por: 284 CAPÍTULO 12 - REACTORES CON RECIRCULACIÓN: "EL TUBO QUE SE VOLVIÓ UN TANQUE" T1 T0 RT2 1 R (12.14) Y el balance de energía adiabático quedará: H Rxn C0 C2 CP 1 R T1 T2 (12.15) de donde se puede obtener que: T1 T2 T0 T2 H Rxn H Rxn C2 C0 C1 C2 1 R CP 1 R CP (12.16) Así, los cambios en concentración y temperatura a través del reactor se pueden hacer tan pequeños como se deseen solo ajustando el valor de la relación de recirculación R. EJEMPLO 12.1. Considérese el caso de la reacción elemental 2A → B que se lleva a cabo en un PFTR adiabático con recirculación. Parte de la corriente de producto se recircula después de ser enfriada hasta 350 K que corresponde a la temperatura de la corriente de alimento fresco. A se alimenta al sistema a una concentración CA0 = 2 M. La constante especíca de velocidad de reacción es k = exp(21-8000/T). Adicionalmente, la temperatura en el reactor depende de la concentración según la expresión T = 350 + 30(CA1 - CA). Razone los siguientes dos casos: a. cuando la concentración de salida es de CA2 = 0,05, determine el valor del tiempo de residencia y la temperatura de salida; b. con el tiempo de residencia correspondiente al caso en que R = 0 y CA2 = 0,05, determine la temperatura de salida y los valores de CA1 y CA2. a. Asumiendo que la conversión global es X2, es posible obtener que: C A1 C A0 RC A 2 2 1 R 1 X 2 1 R 1 R (e.1) y además que: 285 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS C A 2 C A0 1 X 2 2 1 X 2 que: (e.2) Adicionalmente, del balance molar para el PFTR se puede decir C A1 dC A kC A2 CA 2 1 R (e.3) De esta forma, para un valor dado de R y como se conoce CA2, es posible determinar los límites de la integral y resolver simultáneamente la ecuación (e.3) junto con la relación de la concentración y la temperatura. Los resultados se presentan en la Figura 12.5. Figura 12.5. Variación del tiempo de residencia, concentración de entrada al reactor y temperatura de salida para el caso a del ejemplo 12.1 b. Esta parte del ejemplo se deja al lector para su desarrollo y análisis. BIBLIOGRAFÍA Fogler, H.S. (2006): Elements of Chemical Reaction Engineering (4th Ed.). New York: Prentice Hall. 286 CAPÍTULO 12 - REACTORES CON RECIRCULACIÓN: "EL TUBO QUE SE VOLVIÓ UN TANQUE" Levenspiel, O. (1999): Chemical Reaction Engineering (3rd Ed.). New Jersey: John Wiley & Sons. Villermaux, J. (1985): Génie de la Réaction Chimique. Conception et Fonctionnement des Réacteurs. Paris: Lavoisier. 287 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 46 CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS 13 OĕęĎĒĎğĆĈĎŘē ĊĈĔēŘĒĎĈĆ ĕĆėĆ đĆ ĉĊċĎēĎĈĎŘē ĉĊ đĆĘ ĈĔēĉĎĈĎĔēĊĘ ĉĊ ĔĕĊėĆĈĎŘē ĉĊ ėĊĆĈęĔėĊĘ ĖĚŃĒĎĈĔĘ INTRODUCCIÓN El propósito de la actividad industrial en la que se efectúan transformaciones químicas es el de convertir unas materias primas en un producto de valor agregado de la forma más eciente, segura, limpia, y rentable posible. El aspecto de la economía resulta determinante en la viabilidad tanto técnica como comercial de un determinado proceso productivo, por lo que se requiere una inclusión directa y cuantitativa de las variables económicas en los procedimientos de diseño de las unidades de reacción química (Peters & Timmerhaus, 1991; Mizrahi, 2002; Vogel, 2005). En este capítulo se discute, a través de casos de estudio, la forma como los elementos económicos básicos asociados con el diseño de los reactores químicos se incorporan en el proceso de diseño o de modicación de las condiciones de operación de una unidad instalada, incluyendo costos de materias primas, valor del producto obtenido y costos de adquisición, operación y mantenimiento. Se discute el concepto de potencial económico del proceso y la manera de formular funciones de costo en términos de las variables de proceso para diferentes tipos de reactores, lo que conduce a la formulación de problemas de optimización en los que se busca maximizar el potencial económico o las ganancias y/o minimizar los costos asociados con el reactor. 289 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 13.1. POTENCIAL ECONÓMICO El concepto de potencial económico lo propuso Douglas (1985) , en relación con su innovadora técnica para sintetizar un proceso químico y evaluar, metódicamente a lo largo del proceso de diseño, el potencial del proceso para proporcionar una ganancia económica neta. Haciendo uso del potencial económico (también llamado ganancia neta), Douglas logró demostrar como la rentabilidad económica de un proceso varía a medida que su diseño se rena y que es una herramienta efectiva para orientar apropiadamente las decisiones relacionadas con diferentes aspectos del diseño como el número y tipo de equipos a usar, la estructura del proceso y las condiciones de operación. La denición de trabajo será entonces: Potencial económico = ∑ Ganancias - ∑ Costos Potencial económico > 0 Negocio rentable Potencial económico < 0 Potencial económico = 0 Negocio a pérdida Empresa sin ánimo de lucro El concepto de potencial económico puede pues aplicarse a un proceso químico completo o a cada una de sus unidades. El propósito del ingeniero de diseño o del ingeniero de proceso es mantener el potencial económico en el valor más alto posible. Para lograrlo es necesario entender cuáles y cuántos son los elementos que contribuyen a las ganancias y a los costos. La naturaleza de estos elementos puede ser muy variada y compleja. Algunos de los más básicos y relevantes en relación con un reactor químico se listan a continuación: 290 CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS GANANCIAS COSTOS Venta del producto (y subproductos) Costos de capital Recuperación de materia prima no Costos de materias primas convertida Energía co - generada en el proceso Costos de la energía requerida Costos de inversión de los equipos Costos de operación del reactor Costos de mantenimiento y limpieza Costo de la separación del producto Costos de bombeo y recirculación De una manera más formal (Turton et al., 2003), los costos totales de un proceso se clasican en: (1) Costos de capital: referidos a los costos de compra de los equipos, (2) Costos de manufactura: divididos a su vez en costos directos, jos y gastos generales. Los costos directos se relacionan con la materia prima, el tratamiento de los residuos, los servicios, la labor operativa, el mantenimiento y la reparación y el pago por el uso de patentes. Los costos jos se relacionan con los impuestos, la depreciación de los equipos y el costo de operaciones auxiliares. Los gastos generales incluyen los costos de administración, la distribución y venta del producto, así como la investigación y desarrollo que se realicen en la compañía. Un estudio riguroso del potencial económico de una unidad (o proceso) debe considerar no sólo los elementos fundamentales del negocio (el costo de las materias primas y de fabricación y la venta del producto), sino que debe incluir otras importantes variables económicas y comerciales, tales como (Peters & Timmerhaus, 1991; Turton et al., 2003): depreciación de los equipos, impuestos, tasas retributivas, tasas de interés, inación, tasa de cambio del mercado, valor presente neto, valor de la imagen corporativa, costos del tratamiento y eliminación de residuos, tasa interna de retorno, entre otros. 291 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 13.2. OPTIMIZACIÓN EN TÉRMINOS DE LAS VARIABLES DE PROCESO Para ser de utilidad práctica en la evaluación de una unidad o un proceso químico, la función de potencial económico debe formularse matemáticamente en términos de las variables de diseño y de proceso relevantes. Dichas variables deben ser manipulables o controlables por las decisiones o las acciones del ingeniero. Para lograrlo, tanto las ganancias como los costos que se incluyan en la función de potencial económico deben escribirse a su vez como función de dichas variables de proceso. Esto se consigue empleando la información conocida de precios y costos (tabulada, encontrada en manuales, bases de datos o conocida por estudios previos técnicos y/o comerciales del proceso) y combinándola con los balances molares, la estequiometría y las ecuaciones de diseño de las unidades. El propósito es poder manipular el potencial económico a través del valor de una variable de diseño (tamaño del reactor) o de proceso (condiciones de operación). El objetivo nal será encontrar los valores de esas variables que hacen máximo el valor del potencial económico, lo que se conoce como optimización. La optimización es un procedimiento matemático en el cual se busca y determina el valor máximo o mínimo de una función de una o varias variables. Optimizar signica encontrar los valores de las variables independientes de la función, tales que la función toma un valor máximo o mínimo. Si se trata de la función de potencial económico, se busca encontrar un máximo. En ocasiones, se trata con las llamadas funciones de costo (sólo se evalúa el término de costos de la función de PE), en cuyo caso se busca por un mínimo. La optimización se puede realizar matemáticamente aplicando a la función el criterio de la primera y la segunda derivada, o empleando métodos numéricos de optimización directa tales como: método de Newton-Gauss, métodos del gradiente, o algoritmos genéticos (Edgar et al., 2001). En ocasiones, la representación gráca de la función a optimizar permite identicar los puntos óptimos de forma simple y directa, tal y como se muestra en el esquema 1. Por último téngase presente que el ingeniero químico debe operar el proceso para obtener la mayor productividad, con la más alta calidad del 292 CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS producto, al mínimo costo posible (máxima rentabilidad) y con el menor impacto ambiental, todo simultáneamente! Centrarse sólo en los aspectos económicos de la actividad productiva en desmedro de los otros aspectos puede derivar en graves faltas éticas (Martin & Schinzinger, 2005). Esquema 1. Representación de algunas posibles funciones para optimizar el potencial económico 293 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 13.3. CASOS DE ESTUDIO 13.3.1. CASO 1: CONVERSIÓN INTERMEDIA ÓPTIMA EN UN ARREGLO DE DOS REACTORES EN SERIE Se desea realizar una evaluación técnico-económica para determinar cómo procesar la materia prima A para producir la sustancia B, según la estequiometría A→B. La reacción ocurre en fase líquida y se caracteriza por obedecer a una ecuación cinética no elemental dada por –rA = 0,05×CA / (1+ 12×CA)2 [mol / L×s]. Debido a la demanda en el mercado del producto B, la cantidad a producir indica que el proceso debe realizarse en algún tipo de reactor continuo. Se dispone de una corriente de A con un ujo de 5 L / s y una concentración de 0,3 mol / L. Como integrante del grupo de ingeniero(a)s de la compañía, usted ha sido responsabilizado(a) de dar respuesta a la siguiente pregunta: la investigación realizada indica que en otras compañías que producen B han usado un arreglo de dos reactores en serie para disminuir los costos totales del proceso. Si se quisiera lograr una conversión total igual a 88%, usando un PFR seguido de un CSTR, ¿existirá algún valor de la conversión intermedia que permita maximizar la ganancia económica del proceso? La materia prima A tiene un costo de 10 pesos / mol, el producto B tiene un valor de 20 pesos / mol, el costo de operación de los dos reactores se ha estimado en función del volumen total del arreglo como 1×10-3 pesos / L×s. Otros costos asociados a los reactores se han correlacionado en función de la conversión intermedia como (X 2,5 + X - 0,3) pesos / s. Solución El proceso se esquematiza en la Figura 13.1. Realizando los respectivos balances molares en términos de la conversión global (medida desde el alimento al primer reactor), se puede demostrar fácilmente que los volúmenes de ambos reactores serán: 294 CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS Figura 13.1. Esquema de un proceso con un PFR seguido de un CSTR. Se busca la conversión intermedia que hace máximo el potencial económico 1 2 VRPFR 100 ln 720 X 1 648 1 1 X 1 1 X 1 V 1478 1687 X 1 RCSTR (13.1) (13.2) Por lo tanto, el volumen total del arreglo viene dado por la expresión: 1 2 Vtotal 100 ln 720 X 1 648 1 1 X 1 1478 1687 X 1 1 X 1 (13.3) Es momento de formular una función de potencial económico. Debe tenerse presente que el objetivo es obtener una función matemática que exprese como depende el potencial económico de la conversión intermedia. En principio, conviene formular la función en términos descriptivos incluyendo cada uno de los factores económicos que describe el problema: Potencial económico = + Valor del producto - osto C ateria de mima pr - osto C ración de opeeactoresr - tros O stos ga l oceso de pr (13.4a) Debido a que estamos considerando un proceso continuo, podemos hablar del potencial económico por unidad de tiempo o tomar un periodo de tiempo denido para hacer el cálculo. Resulta evidente que la primera opción permite un tratamiento más general del problema. El siguiente paso consiste entonces en expresar la ecuación (13.4) en términos de las variables del problema, lo que no es más que una cuestión de consistencia dimensional básica: 295 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS mol pesos pesos mol pesos PE FB 20 FAo 10 s mol s mol s (13.4b) 3 pesos 2,5 0,3 pesos Vtotal L 110 X1 X1 Ls s Lo que resta en este momento es reemplazar las diferentes variables que aparecen en la ecuación por su equivalente en términos de la variable a optimizar: el ujo de producto será igual al producto del ujo de alimento fresco FAo por la conversión nal X2 y el volumen total viene dado por la ecuación (13.3). Reemplazando todo en el potencial económico se obtiene nalmente: 1 2 0,1 ln PE 0, 648 1 X 1 1 X1 0,967 X 1 X 12,5 X 10,3 9,154 (13.5) Se debe recordar que se desea optimizar el potencial económico, esto es, encontrar el valor de la variable independiente (en este caso X1), que lo hace máximo. Existen varias estrategias para resolver este problema, como la de aplicar el criterio de la primera derivada a la ecuación (13.5). Sin embargo, una Figura 13.2. Ganancia neta contra la conversión intermedia para unas condiciones de alimentación jas y conversión nal deseada de 88%. Existe una ganancia máxima para una conversión a la salida del PFR de 50% 296 CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS solución gráca será suciente en este caso. Se le asignan valores a X1 y se graca la función de potencial económico para estudiar su comportamiento (nótese que existe la restricción X1< X2). El resultado obtenido se muestra en la Figura 13.2, en la cual se aprecia fácilmente que para una conversión intermedia de 50%, se obtiene una ganancia neta máxima de 8,3 pesos/s. Con la conversión intermedia determinada, es posible calcular el tamaño de ambos reactores a través de las ecuaciones (13.1) y (13.2). Nótese también que el resultado no implica que la conversión en el segundo CSTR sea de 38%. 13.3.2. CASO 2: OPTIMIZACIÓN MULTIVARIABLE PARA UNA BATERÍA DE CSTRS CON RECICLO Un grupo de ingenieros químicos encargados del departamento de investigación y desarrollo de una compañía discuten sobre la mejor forma de producir el compuesto P. El proceso corresponde a una reacción auto catalítica elemental en fase líquida con estequiometría A+P→2P. El grupo de ingenieros tiene la misión y el reto de diseñar un proceso innovador. Ya saben que lo común es el uso de un PFR de reciclo, pero desean explorar otras alternativas más económicas y, si es posible, más efectivas. En este momento evalúan la última propuesta de diseño, lograda después de muchas horas de duro trabajo de exploración: el uso de una batería de dos CSTRs en serie, con reciclo sin separación al primero, tal como se muestra en la Figura 13.3 (XA2 y XA4 representan las conversiones globales medidas desde el alimento fresco). Figura 13.3. Arreglo de dos CSTRs con un reciclo al primero para efectuar una reacción autocatalítica 297 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Usted ha sido invitado como ingeniero(a) a participar en la evaluación de este diseño. Se desea optimizar el potencial económico del proceso, con la restricción de que el volumen total de la batería sea mínimo y teniendo en cuenta que el reactivo A que no reacciona en la batería se recupera casi sin costo en otra parte del proceso. Si ambos reactores han de operar a diferentes temperaturas y la relación entre los coecientes cinéticos en el reactor 2 y el 1, k2/k1, es de 2, se requiere determinar: 1. La conversión global nal óptima de la batería 2. La conversión intermedia óptima 3. La conversión por paso óptima en el reactor 1 4. La relación de recirculación óptima (R) 5. Los volúmenes óptimos respectivos de los reactores 6. El valor de la ganancia económica óptima Se cuenta con la siguiente información: Símbolo/ecuación Nombre Flujo molar de A alimento fresco Concentración molar de A alimento fresco Coeciente cinético a la temperatura del reactor 1 Coeciente cinético a la temperatura del reactor 2 Valor Unidades 1 mol / s 0,1 mol / L 1 L / (mol s) 2 L / (mol s) Pp Precio del producto 5 $ / mol PA Precio del reactivo 2 $ / mol FAo C Ao k1 k2 298 0, 03 R 2 R 0,5 Costo de bombear el reciclo $/s 0, 02 X A2 4 1 X A4 X A2 1 X 2 X A A 4 1 X A 4 2 Costo de operar los reactores $ / (s L total) CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS Solución Inicialmente, considérese detenidamente para este problema la ecuación de diseño para el CSTR con reciclo. Después de formular los balances molares correspondientes en el punto de mezcla, el reactor y el punto de separación, se puede concluir que el volumen del reactor 1 viene dado por: VR1 FAo 1 kC 1 X 2 2 Ao (13.6) Pudiéndose concluir que el reciclo (sin separación) NO tiene inuencia sobre el tamaño del reactor de mezcla completa. El volumen del reactor 2 está dado por: VR2 FAo kC 2 Ao X4 X2 X 4 1 X 4 (13.7) Por otro lado, se puede demostrar que la conversión por paso en el CSTR con reciclo está determinada por la misma expresión que en el caso conocido del PFR, lo que permite concluir que el reciclo SI tiene inuencia sobre la conversión por paso en el reactor: Xˆ 12 FA1 FA2 X2 FA1 1 R 1 X 2 (13.8) Posteriormente se debe racionalizar el problema de optimización económica de tal forma que pueda ser formulado en términos matemáticos. Para ello considérense las siguientes apreciaciones: el potencial económico debe ser máximo y el volumen de la batería debe ser mínimo (lo cual puede considerarse como una restricción en el proceso de optimización del potencial económico); el volumen de la batería no depende de R, pero si depende de X2 y X4, mientras que el potencial dependerá de R, X2, X4 (dado que están incluidos los costos de bombear el reciclo y el de operación de los reactores). Entonces, hay que encontrar X2 que minimiza el volumen para un X4 dado (esto es, se tomará la conversión global de salida como variable independiente), lo que elimina una variable del potencial ya que X2 = f(X4) 299 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS (según la minimización del volumen), por lo que el potencial dependerá de R y X4, lo que deja una función en dos variables independientes para aplicar el criterio de optimización (1ª derivada) multivariable! La solución se encuentra, resolviendo dos ecuaciones en dos incógnitas. El volumen total de la batería viene dado por la suma de los volúmenes de ambos reactores: VRtotal FAo X4 X2 1 2 C Ao k1 1 X 2 k2 X 4 1 X 4 (13.9) Aplicando el criterio de la primera derivada con respecto a X2 (para un valor jo de X4), se obtiene el valor mínimo del volumen del arreglo: d VRtotal dX 2 0 en el óptimo (13.10a) (13.10b) k1 1 X 2 k2 X 4 1 X 4 0 2 X 2 ópt k 1 2 X 4 1 X 4 k1 1 2 (13.10c) Debido a que se debe cumplir siempre la restricción física de X1 < X2, se puede concluir de la ecuación (13.10c) que X4 solo puede tomar valores que cumplan la desigualdad X4 > 1 / (K + 1), K = k2/k1. Para alcanzar una determinada conversión global en la batería, se puede analizar si es más conveniente que el segundo reactor opere más frío o más caliente que el primero. Empleando la ecuación (13.10c) se puede ver que el reactor 2 debe operar más caliente (k2>k1) para que el volumen óptimo necesario sea menor: Para X 4 0,9 Si k2 / k1 2, X 2 0,59 Vtotal 410 L Si k2 / k1 1, X 2 0, 70 Vtotal 590 L Si k2 / k1 0,5, X 2 0, 79 Vtotal 710 L Esto también puede apreciarse en la Figura 13.4. 300 CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS Figura 13.4. Conversión global intermedia óptima para un volumen mínimo en función de la conversión de salida en el esquema de dos CSTRs con recirculación. La región sombreada está prohibida El siguiente paso en el análisis del problema es formular la función de potencial económico, primero de forma cualitativa y luego escribiendo los diferentes términos según las variables del proceso: Potencial Económico = + Ganancia por venta del producto + Ganancia por el reactivo recuperado - Costo de reactivo fresco - Costo de operación reactores - Costo de bombeo del reciclo mol P $ mol A $ PE FAo X 4 PP FA 1 X 4 PA s mol P o s mol A mol A $ $ $ FAo PA VRtot L PR PRe s mol A s Ls (13.11a) (13.11b) 301 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Reemplazando los términos correspondientes y operando algebraicamente se obtiene la expresión: PE 3 X 4 2 X 42 0, 03 R 2 R 0,5 (13.11c) La optimización de esta función en dos variables independientes puede hacerse usando el criterio de la primera derivada (vericando posteriormente que el punto crítico encontrado es un máximo). Las condiciones correspondientes son: VR total X 4 R 3 4X4 0 y VR total R X4 0, 03 2 R 1 0 (13.12) Dado que las anteriores ecuaciones están desacopladas, la obtención del punto óptimo es directa y se obtienen como resultados X4 = 75% y R = 0,5. Figura 13.5. Potencial económico en función de la conversión global de salida en el esquema de dos CSTRs con recirculación. La región sombreada esta prohibida 302 CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS Reemplazando estos valores en la ecuación (13.11c) se obtiene un potencial económico máximo de 1,12 $/s. En estas condiciones X4 > 1 / (2 + 1) o X4 > 0,33. El valor de la conversión a la salida del reactor 2 se encuentra empleando la ecuación (13.10c), con lo que se obtiene un valor de 39%. El valor de la conversión por paso correspondiente es, según la ecuación (13.8) de 30%. Finalmente los volúmenes óptimos de los reactores se calculan con las ecuaciones de diseño (13.6) y (13.7) como 164 y 96 litros para el reactor 1 y 2 respectivamente. En las Figuras 13.5 y 13.6 se presentan de forma gráca los resultados obtenidos y la ubicación de los dos reactores en el diagrama básico de diseño. Figura 13.6. Inverso de la velocidad de reacción en función de la conversión global para el esquema de dos CSTRs con recirculación. Las regiones sombreadas representan el tamaño óptimo de los reactores 13.3.3. CASO 3: OPTIMIZACIÓN DE LAS GANANCIAS USANDO UN REACTOR BATCH Se realiza una reunión de los ingenieros de la planta para denir cuál será el mejor camino a seguir respecto a la operación del reactor batch 303 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS donde ocurre la reacción acuosa de segundo orden 2A→ 2B, cuya constante especíca de velocidad es de 1 litro/(mol-h). La concentración inicial del reactante es de 1 mol/litro. Se estableció que el tiempo de carga de reactivos y descarga de productos es igual a 1 hora/batch. El costo de la materia prima fresca es de $100/batch. El valor del producto depende del grado de conversión alcanzado en el reactor y puede decirse que actualmente es de $200XA/batch, donde XA es la conversión fraccional de A. Un primer ingeniero insiste que no hay nada de que preocuparse. Él mismo denió hace algunos años el modo de operación que se ha venido utilizando hasta hoy: al MÁXIMO de producción de B. De esta forma, las ganancias actuales no podrían ser mejores! Por otro lado, un segundo ingeniero argumenta que al ser una reacción irreversible NO es cierto que sea necesario trabajar a la MÁXIMA producción de B, simplemente el proceso debe operar a una alta conversión de A. Sin embargo, el tercer ingeniero los corrige y les argumenta que a esos niveles de conversión “óptimos o no óptimos” parte del reactivo no está siendo utilizado y que éste último podría ser reutilizado en el proceso (lo cual no tendría supuestamente ningún costo adicional). El gerente de la planta airadamente increpa al grupo de ingenieros y les exige, ante la amenaza del despido colectivo, que la conversión de A tiene que ser TOTAL. ¿Cuál de las opciones planteadas genera las mayores ganancias para el proceso? Solución Dado que se proponen varias opciones de proceso, es necesario evaluarlas todas para saber cuál es la mejor en términos de la ganancia económica del proceso. Por otra parte, el proceso se realiza por lotes, luego, entre más se realicen, mayor cantidad de producto se obtendrá. Esto estará denido por el tiempo total de operación: Tiempo total de Tiempo de carga Tiempo de reacción operación por batch y descarga por batch por batch t T (h) t CD (h) t R (h) 304 (13.13) CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS Considerando el balance molar en el reactor, la cinética y la estequiometría en términos de la conversión, se obtiene la siguiente expresión para el tiempo de reacción: tR 1 1 1 kC Ao 1 X (13.14) Reemplazando la ecuación (13.14) en la (13.13), considerando que el tiempo de carga y descarga es de 1 hora, se obtiene al reemplazar los valores numéricos de las constantes y operar: tT 1 horas 1 X batch (13.15) El número total de lotes por día será: h 1 batch batch N 24 24 1 X día tT h día (13.16) La cantidad (en moles) de B producida será, de acuerdo con la estequiometría y el número de lotes procesados: NB = N(NAoX) = N(VRCAoX) = 24VRX(1-X) (13.17) Propuesta del primer ingeniero: se trabajará al máximo de producción de B, esto es, en condiciones en que: dN B 0; dX d 0 24VR X 1 X dX 1 2 X 0 X 0,5 (13.18) (13.19) Debido a que las ganancias netas del proceso se pueden establecer como la resta entre el valor del producto y el costo de la materia prima, entonces: $ G 200 X 100 batch (13.20) 305 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS De la ecuación (13.20) resulta claro que si la conversión es del 50%, las ganancias netas serán nulas. Propuesta del segundo ingeniero: operar a altas conversiones de A, ¿pero cuál? Si se formula una función objetivo para el potencial económico del proceso, teniendo en cuenta el número de lotes procesados por día, se puede proponer que: $ $ batch PE G N día batch día 200 X 100 24 1 X (13.21) Aplicando el criterio de la primera derivada para establecer la conversión que hace máximo el potencial económico, se obtiene: dPE 0; dX 2400 2 1 X 2 X 1 0 (13.22) Es fácil ver que la solución de la ecuación (13.22) es X = 0.75. Reemplazando este valor en la ecuación (13.21) se obtiene una valor máximo de la ganancia neta diaria de $300/día. Propuesta del tercer ingeniero: reutilizar “sin ningún costo” la cantidad de A que no ha reaccionado. Luego, los costos de A serán iguales a 100×X $/batch (equivalentes a descontar del costo del alimento fresco, el costo del A recuperado), lo que a su vez modica el potencial económico según la expresión: $ PE 24 1 X 100 X (13.23) N G 24 1 X 200 X 100 X día Aplicando el criterio de la primera derivada sobre la ecuación (13.23), se obtiene como solución un valor de X = 50% y unas ganancias netas máximas de $600/día. Propuesta del gerente: trabajar a conversión total. Apreciando la ecuación (13.14) se concluye que para lograrlo se requieren tiempos de reacción 306 CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS innitos, lo cual no es viable. También es interesante notar que, independiente de la función de potencial económico, cuando la conversión se hace completa la ganancia neta tiende a cero. Esto se ilustra en la Figura 13.7, en donde se aprecia también la solución gráca de las propuestas, representando el potencial económico contra la conversión según los diferentes escenarios (una herramienta muy convincente para reuniones de trabajo!). Figura 13.7. Potencial económico en función de la conversión de A, para un reactor batch (los tiempos de reacción se calculan con la ecuación 13.14) La propuesta más apropiada consiste en trabajar a una conversión de 50%, recuperando el A no convertido, para aumentar las ganancias netas hasta unos $600/día. 13.3.4. CASO 4: INFLUENCIA DEL CAMBIO DEL PRECIO DEL PRODUCTO EN EL MERCADO SOBRE EL ÓPTIMO ECONÓMICO DE UN REACTOR BATCH Una empresa se encuentra ante un grave dilema debido a la entrada en vigencia del tratado de libre comercio. Hasta el momento, la empresa ha 307 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS estado vendiendo el producto C a un confortable precio de 30 U$/lbmol. Sin embargo, la escala de producción de C en otros países profetiza una caída sustancial del precio en el mercado (hasta 25 U$/lbmol). Por tal razón, a usted ingenier@ y responsable de planta, se le solicita realizar un análisis del proceso reactivo. Este último consiste de una reacción en fase líquida conducida en un reactor batch. La reacción es A+B→C, con una ley de velocidad de reacción que tiene la forma -rA=2,5CA(0,2+CA) lbmol A/(h.ft3). Al reactor, que tiene un volumen de 150 ft3, se le cargan los reactivos A y B a concentraciones de 1,2 y 1,4 lbmol/ft3, respectivamente. Cada uno de los reactivos tiene un costo de 5 U$/lbmol. El esquema del proceso permite recuperar y retornar al proceso el 95% los reactantes no convertidos. El costo de dicha recuperación es de 1,5 U$/lbmol de cada compuesto. Adicionalmente, se sabe que el tiempo necesario para la descarga y preparación del reactor para su operación es de 1,25 h/batch. Sabiendo que las condiciones económicas de la empresa requieren de un benecio económico superior a los 17000 U$/día, se requiere vericar si el precio de venta de 30 U$/lbmol si es en realidad “confortable” como lo aseguran los administradores de la empresa y determinar cuáles serían las condiciones de operación, si existen, que permitirían obtener el benecio económico requerido una vez entrado en rigor el tratado de libre comercio. Solución El primer paso debe ser el desarrollo de una ecuación de diseño del reactor considerado, incorporando los balances molares, la cinética y la estequiometría de la reacción. En este caso, se obtiene la siguiente ecuación para el tiempo de reacción: C 0,8571 0, 2 C A dC A 1 A tR 2 ln 2,5 1,2 C A 0, 2 C A CA (13.24) El tiempo total de operación en un reactor por lotes debe incluir el tiempo de carga, el de reacción, el de descarga y el de limpieza o acondicionamiento para la nueva carga. En este caso, el tiempo total 308 CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS vendrá dado por la suma del tiempo de reacción y del tiempo de descarga y preparación: 0,8571 0, 2 C A h tT 1, 25 2 ln CA batch (13.25) El número de lotes procesados por día vendrá dado por la expresión: N 24 h 1 batch 24 batch día tT h 0,8571 0, 2 C A día 2 ln 1, 25 CA (13.26) El siguiente paso es la formulación conceptual de la función del potencial económico del proceso. En este caso, teniendo en cuenta la información proporcionada en el problema: Potencial económico = + Ganancia por venta del producto C + Ganancia por el reactivo A recuperado + Ganancia por el reactivo B recuperado - Costo de reactivo A fresco - Costo de reactivo B fresco - Costo de recuperación reactivo A - Costo de recuperación reactivo B (13.27a) El paso siguiente es la expresión de cada uno de los términos de la función de potencial económico en términos de las variables del proceso. Debe identicarse la variable independiente fundamental con respecto a la cual se realizará la optimización, que en este caso debe ser el nivel de conversión nal alcanzado. Dado que la conversión nal corresponde a un valor nal de concentración del reactivo límite A, se usará esta última por simplicidad en la expresión de las ecuaciones resultantes (nótese que tampoco se usa el equivalente en tiempo de operación por la misma razón). Empleando la información suministrada y la estequiometría de la reacción, se obtienen las siguientes expresiones como se presenta en la Tabla 13.1. 309 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Tabla 13.1. Variables del caso de estudio 4 Ganancia por venta de C Ganancia por recuperación de A Ganancia por recuperación de B Costo de A fresco Costo de B fresco Costo de recuperación de A Costo de recuperación de A Precio base (US$/lbmol) 30 (antes TLC) 25 (durante TLC) Cantidad (lbmol/batch) 5 nAR=0,95nA nC=(nAo-nA) Valor (US$/batch) 30(nAo-nA) 25(nAo-nA) 5(0,95nA) 5 5 nBR=0,95nB nB=nBo-nAo+nA nAo nBo 1,5 nAR=0,95nA 1,5(0,95nA) 1,5 nBR=0,95nB nB=nBo-nAo+nA 1,5(0,95)(nBonAo+nA) 5 5(0,95nA) 5nAo 5nBo Teniendo en cuenta las concentraciones iniciales y el volumen del reactor, las moles iniciales de A y B son respectivamente 180 y 210 lbmol/batch. Las moles nales de A se pueden escribir en términos de la concentración nal como nA = VRCA = 150CA. De acuerdo con lo anterior, el potencial económico diario del proceso, antes y durante el TLC, vendrá dado por las expresiones (13.27b1) y (13.27b2) respectivamente. El paso nal consiste en analizar como se comporta el potencial económico con respecto a la concentración nal de A, o lo que es equivalente, a la conversión de A. Esto se ilustra en la Figura 13.8. 310 US$ PE día 24 3549, 75 3502,5C A 0,8571 0, 2 C A 2 ln 1, 25 CA (13.27b1) US$ PE día 24 2649, 75 2752,5C A 0,8571 0, 2 C A 2 ln 1, 25 CA (13.27b2) CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS Figura 13.8. Potencial económico antes y durante el TLC en función de la conversión de A para un reactor batch De la observación de la Figura 13.8 pueden concluirse varias cosas interesantes. En primer lugar se nota que operar a conversiones menores al 20% resulta en un potencial económico negativo, es decir, en pérdidas. Por otra parte, dado que se estableció que la compañía debe tener ganancias superiores a los 17000 US$/día, antes del TLC se deberá operar el reactor a una conversión entre el 40 y 97%, y durante el TLC esta ventana de operación se reduce a un intervalo de 52 y el 92%. Debido a la caída del precio del producto durante la aplicación del TLC, la ganancia neta máxima del proceso se reduce desde 31000 US$/día a cerca de 22500 US$/día. Esto indica que, para lograr la máxima rentabilidad en estos momentos de fuerte competencia en el mercado, el reactor deberá operarse a una conversión de 76%, con un tiempo de reacción correspondiente a 45 minutos. 311 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 13.3.5. CASO 5: DECIDIENDO ENTRE UN ÓPTIMO ECONÓMICO Y UN MENOR RIESGO DE SEGURIDAD EN EL DISEÑO DE UN CSTR NO- ISOTÉRMICO Para la fabricación de un compuesto combustible se utiliza la reacción A→B, en fase líquida, usando un reactor CSTR. El coeciente cinético es 1,127 min-1 a 40ºC y 1,421 min-1 a 50ºC. La reacción es altamente exotérmica (- 50 Julios / gramo de A) y el peligro de explosión del reactor aumenta mientras más cercana a 90ºC sea la temperatura de operación, pues tanto el reactivo como el producto son compuestos altamente inamables y volátiles; a 95,5ºC los ingenieros de la compañía han predicho runaway, falla y destrucción total del sistema! En el momento el proceso opera de la siguiente forma: a un reactor de 0,5 m se alimentan 90 kg/min de A puro (MMA = 90 g/mol, ρA = 900 kg/m3, CpA = 4 J/g×K) a To = 40ºC. El reactor opera a 85ºC. Se usa un ujo muy grande de uido refrigerante a Ta = 34ºF en la chaqueta del reactor. El coeciente global de transferencia de calor U se ha estimado como constante e igual a 810 W/m2×K. 3 La rentabilidad de la compañía se ha reducido en los últimos meses por la crisis económica y se desea reducir los costos de operación, los cuales están principalmente dominados por el costo de la materia prima. Estudios previos han establecido que el costo de operación de la planta de producción de B, se puede correlacionar en función del ujo de A alimentado al reactor como: Costo=Y4+Y3-3Y2+11 (Costo en millones de pesos/día) donde: Y=-6,7+0,064FAo (FAo en kg/min) Se requiere determinar la conversión a la cual opera el reactor actualmente, establecer el número de estados estacionarios posibles a las condiciones de operación actuales (y analizar su estabilidad). Desde luego, el objetivo principal es determinar las condiciones óptimas de operación del reactor instalado. 312 CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS Solución En virtud de que la temperatura del alimento es diferente a la temperatura de operación del reactor, se puede concluir que el reactor es no-isotérmico, razón por la cual debemos enfocar nuestros esfuerzos en desarrollar un modelo matemático completo para el equipo que incluya el balance de materia y el balance de energía. Debido a que no se proporciona la expresión para el coeciente cinético en función de la temperatura, el primer paso consistirá en determinar dicha funcionalidad. Para lograrlo, se pueden usar los dos valores reportados del coeciente cinético a dos temperaturas diferentes, teniendo en cuenta que ambos obedecen la ley de Arrhenius. De este análisis se concluye fácilmente que: 1 1 k T 1,127 exp 2345, 7 313,15 T (K) (13.28) y que a la temperatura de operación del reactor (85ºC), k = 2,89 min-1. La combinación directa del balance molar, la cinética y la estequiometría de la reacción en función de la conversión, resultan en la expresión: VR Vo X k 1 X (13.29) donde Vo es el caudal de alimentación al reactor que, empleando el ujo másico y la densidad del alimento, es igual a 0,1 m3/min. Dado que el reactor posee un volumen conocido, podemos emplear la ecuación (13.29) para determinar la conversión actual a la que está operando el reactor: 0,5 m3 2,89 min -1 VR k X 0,93 Vo VR k (13.30) m3 m3 0,1 0,5 2,89 min min Considerando que el calor de reacción y la temperatura del uido de servicio permanecen constantes (y ésta última es menor que la temperatura 313 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS del reactor), se puede establecer el balance de energía por medio de la ecuación: UA T Ta FAo Cp A T To FAo X H rxn 0 (13.31) Debido a que se propone optimizar un reactor ya existente e instalado, el área de transferencia de calor permanece ja y es constante. Con los datos de operación actual puede calcularse con ayuda de la ecuación (13.31) como: kg J kg 3 4 J 90 4 10 85 40K 90 min 0,93 5 10 kg min kg min 3 m2 A J s 810 2 60 85 1,11K m s K 1min (13.32) Para discernir sobre los estados estacionarios de operación, su multiplicidad y su estabilidad, la estrategia más simple en este caso es gracar ambas ecuaciones de balance en un diagrama conversióntemperatura. El número de cortes de ambas curvas representará el número de estados estacionarios posibles. X BM 1 1 VR 1,127 exp 2345, 7 313,15 T 1 1 Vo VR 1,127 exp 2345, 7 313,15 T FA Cp ATo UATa X BE o FAo H rxn UA FAo Cp A T FA H rxn o (13.33) (13.34) En la Figura 13.9 se presenta la solución gráca de las dos ecuaciones anteriores, para el estado actual de operación del reactor, al cual sólo existe un estado estacionario, muy probablemente de naturaleza estable (una caracterización denitiva de la estabilidad requiere del cálculo de los eigenvalores de la matriz de estado como se explica en el capítulo 10). 314 CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS Figura 13.9. Solución gráfica de los balances de materia y energía para un CSTR no-isotérmico Figura 13.10. Costo de operación de una planta con un CSTR no-isotérmico en función del flujo másico de alimentación al reactor 315 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Finalmente, según la información proporcionada, ya se dispone de la función de costos en términos del ujo másico de alimentación al reactor, con lo que nos han ahorrado el trabajo de formularla (esta información puede estar disponible debido a estudios previos del proceso, lo que revela la importancia de mantener un record completo de todos los estudios de diseño, operación, mantenimiento y comerciales de la planta). Así pues, lo más simple es representar grácamente la función de costo y determinar por inspección visual el valor del ujo de alimento que hace mínimo el costo de operación de la planta. Esto se muestra en la Figura 13.10, en la cual se aprecia que existen tres puntos críticos del costo: un valor mínimo global, un mínimo local y un valor máximo. Empleando los ujos másicos de alimentación correspondientes a los dos mínimos de la Figura 13.10, se analiza el desempeño del reactor, empleando la misma metodología propuesta anteriormente (Figura 13.9). Los resultados obtenidos se compendian en la siguiente tabla, en la que se señala cualitativamente el riesgo de explosión, comparando la desviación de la temperatura de operación del reactor con el valor limite establecido de 90ºC. Tabla 13.2. Resumen de los resultados obtenidos en el caso 5 kg FAo min X A % T ºC millones de pesos Costo día Peligro de explosión 90 79 119 93 95 90 85 95 73 8,2 5,8 10 Bajo Alto Muy bajo Como puede apreciarse en la Tabla 13.2 de resultados, cuando el proceso opera en el punto de mínimo costo de operación, la temperatura del reactor excede el valor de seguridad y el riesgo de explosión es inaceptablemente alto. Hemos visto que existe un segundo mínimo costo local y aunque en este punto de operación el riego de explosión es muy bajo, el costo de operación resulta ser superior al actual! La recomendación nal es mantener el proceso en su estado actual de operación, dado que el interés por reducir los costos de operación deriva en un aumento inadmisible en el riesgo de explosión. Esto ilustra el hecho 316 CAPÍTULO 13 - OPTIMIZACIÓN ECONÓMICA PARA LA DEFINICIÓN DE LAS CONDICIONES DE OPERACIÓN DE REACTORES QUÍMICOS de que, aunque la presión por reducir los costos y aumentar las ganancias del proceso constituyen un objetivo permanente y una fuente constante de preocupación para los ingenieros químicos, deben considerarse otros aspectos durante el proceso de optimización de los costos, entre ellos: reducir el riesgo de seguridad para el personal, la comunidad y las instalaciones, mantener la calidad del producto y minimizar el impacto ambiental del proceso. BIBLIOGRAFÍA Edgar, T.F.; Himmelblau, D.M. & Lasdon, L. (2001): Optimization of Chemical Process. New York: McGraw-Hill. Douglas, J.M. (1985): “A Hierarchical Decision Procedure for Process Synthesis”. En: AIChE Journal, 31(3), 353-362. Martin, M.W. & Schinzinger, R. (2005): Ethics in Engineering (4th Ed.). New York: McGraw-Hill. Mizrahi, J. (2002): Developing an Industrial Chemical Process: an Integrated Approach. New York: CRC Press. Peters, M.S. & Timmerhaus, K.D. (1991): Plant Design and Economics for Chemical Engineers. New York: McGraw-Hill. Turton, R.; Bailie, R.C.; Whiting, W.B. & Shaeiwitz, J.A. (2003). Analysis, Synthesis, and Design of Chemical Processes (2nd Ed.). New Jersey: Prentice Hall. Vogel, G.H. (2005): Process Development. From the Initial Idea to the Chemical Production Plant. New Jersey: John Wiley & Sons. 317 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS 46 CAPÍTULO 14 - PREDICCIÓN, PREVENCIÓN Y EVALUACIÓN DE RIESGOS CON REACCIONES QUÍMICAS 14 PėĊĉĎĈĈĎŘē, ĕėĊěĊēĈĎŘē Ğ ĊěĆđĚĆĈĎŘē ĉĊ ėĎĊĘČĔĘ ĈĔē ėĊĆĈĈĎĔēĊĘ ĖĚŃĒĎĈĆĘ INTRODUCCIÓN Predecir y prevenir los riesgos inherentes a la manipulación de reacciones y/o reactores químicos es una parte esencial del aprendizaje de la Ingeniería de las Reacciones Químicas. El número de accidentes ocurridos en la industria de procesos es mayor que lo esperado (Kletz, 1998). Estos pueden ocurrir por diferentes razones: se falla en convencer a los trabajadores de la planta química que ellos deben vigilar los procesos, se falla en enfrentar problemas previos (detectados en auditorias o aquellos que en algunos casos resultan evidentes), o se falla deliberadamente haciéndose el de la vista gorda para evitar conictos o terminar un trabajo rápidamente. En otras palabras, la mayoría de los incidentes son el resultado de malas prácticas ingenieriles. La U.S. Chemical Safety Board presenta en su dirección electrónica varios casos industriales muy bien detallados (ver videos e informes) para el caso de problemas con reactores químicos, entre ellos: el caso de la planta de BP Amoco Polymers, Inc., en Augusta Georgia en 2001; el caso de Synthron en Morganton, NC, en el 2006; el caso de T2 Laboratories, en Jacksonville, FL, en 2007 (Willey et. al); etc. Adicionalmente, se puede consultar el ejemplo basado en un caso real descrito en detalle por Fogler (2006) correspondiente al caso de la “ruptura del reactor de nitroanilina” ocurrido en Sauget, IL, en 1969. 319 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Los benecios relacionados con el diseño de procesos seguros mediante herramientas de software, involucran el hecho de que los modelos matemáticos pueden ser fácil y económicamente modicados para reejar cambios estructurales y operacionales que puedan ocurrir durante el ciclo de vida del proceso reactivo. El ingeniero de proceso puede después introducir y/o evaluar fallas que no pueden ser anticipadas en la etapa de diseño sin mayores dicultades en la programación. En este capítulo se presentan dos ejemplos, basados en los trabajos de Schacham et al. (2000, 2001, y 2003), que permiten comprender la forma como se investigan diferentes condiciones de operación y de riesgo que pueden ocurrir en un reactor químico. 14.1. CASO I: REACTOR PARA LA POLIMERIZACIÓN DE ÓXIDO DE PROPILENO La polimerización de óxido de propileno es un proceso altamente exotérmico, el cual se lleva a cabo a altas presiones. Se requiere que la operación se ejecute a temperatura constante (isotérmico) con el n de prevenir condiciones de run away y que la presión del sistema aumente incontroladamente. Modelos matemáticos para la simulación del reactor donde se lleva a cabo este proceso han incluido inclusive la presencia del disco de ruptura para el alivio de la presión (Ingham et al., 1994). Una descripción esquemática de este tipo de reactor se presenta en la Figura 14.1. Ingham et al. (1994) consideraron la fabricación de un poliol lubricante a través de la reacción (14.1). C4 H 9OH n 1 C3 H 6O C4 H 9 OC3 H 6 n OCH 2CHOHCH 3 calor (14.1) El alcohol catalizado se carga inicialmente al reactor, hasta el “nivel inicial” (Figura 14.1). Luego, se alimenta el óxido al reactor a una velocidad constante hasta que se alcanza el “nivel nal” del batch o carga (Figura 14.1). El exceso del calor de reacción se remueve mediante un intercambiador de calor externo. Consideraciones económicas dictan que el proceso se debe llevar a cabo a la mayor velocidad de reacción posible. La velocidad de reacción es una función de la temperatura, concentración del catalizador y concentración del óxido en fase líquida (la cual es función 320 CAPÍTULO 14 - PREDICCIÓN, PREVENCIÓN Y EVALUACIÓN DE RIESGOS CON REACCIONES QUÍMICAS Figura 14.1. Esquema del reactor para la polimerización de óxido de propileno de la presión). Los límites de temperatura de operación y concentración del catalizador están denidos por consideraciones de degradación térmica y dicultades de puricación. Para maximizar la velocidad de reacción, la presión se debe mantener tan alta como sea posible durante el tiempo total de duración del proceso batch. Los límites de presión y velocidad de reacción están dictados por la resistencia del reactor y la capacidad de remoción de calor. Las ecuaciones del modelo matemático del reactor, del sistema de remoción de calor, del oricio del disco de explosión se presentan en la Tabla 14.1. Bajo condiciones normales de operación, la masa reaccionante es recirculada a través del sistema de intercambio de calor a una velocidad de ujo, Fc, enfriándola a la temperatura T0. Adicionalmente, el disco de ruptura está intacto y la velocidad de descarga de vapor a través de él es de cero. Si por alguna razón, la presión del sistema excede los 8 bar, el disco se rompe iniciándose la descarga de vapor a dos posibles velocidades (dependiendo de las condiciones). El calor latente de vaporización del óxido que se descarga enfría el reactor. Cuando el disco se rompe, la 321 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS alimentación al reactor se detiene por completo. Los resultados del modelo para la variación de la temperatura y la presión, en condiciones normales de operación, para un batch con una duración de 33 horas y 20 minutos se presentan en la Figura 14.2. La temperatura presenta solo cambios moderados durante el transcurso de la reacción. Después de cerca de 13 horas, la temperatura alcanza un máximo de 112 °C. El aumento en la velocidad de reacción asociada con el incremento de la temperatura (y de la presión) reduce la concentración del óxido. Esto, a su vez, genera una reducción en la velocidad de reacción (y la temperatura) hasta que la tendencia se invierte de nuevo, generando un aumento en la temperatura. El cambio de presión presenta una tendencia similar, alcanzó un máximo de 6,35 bar (inferior al valor límite de ruptura del disco: 8 bar). El peso molecular del producto al nal de la reacción es de 2895. Figura 14.2. Cambio de la temperatura y la presión dentro del reactor con el tiempo de reacción, a condiciones normales de operación 322 CAPÍTULO 14 - PREDICCIÓN, PREVENCIÓN Y EVALUACIÓN DE RIESGOS CON REACCIONES QUÍMICAS Tabla 14.1. Ecuaciones del modelo y valores de las variables del Caso I Definición Valor inicial Masa total en el reactor, M, kg Ecuación M(0) = 4400 Masa de óxido en el reactor, Mc, kg Mc(0) = 0 Temperatura en el reactor, TR, °C TR (0) = 80 Masa del óxido que ha reaccionado, X, kg X (0) = 0 V Velocidad de descarga de vapor, V, kg.min-1 V dM F V dt dM c F V r dt dTR H c H v Qg Qr dt M .Cp dX r dt 0,85 K v P TR 273 , cuando P>1,9 0,85 K v P TR 273 1 1 P 2 Velocidad de reacción, r, kg de óxido. min-1 Cambio de entalpía del alimento, Hc,kJ.min-1 Calor latente del vapor de descarga, Hv, kJ.min-1 r k .M c H c F .Cp. T0 TR H v V . Qg r.H R Calor de reacción, Qg, kJ.min-1 Qr Fc .Cp TR T0 Calor removido, Qr, kJ.min -1 P = 1, si P < 1 Presión de vapor del óxido, P, bar 3430 11.7 1, 45e 3 M w C P exp TR 273 Constante de velocidad de reacción, k, 21000 k 9e9 exp 1,987 T 273 R Concentración del óxido, kg.kg-1 C Mc / M Peso molecular del polímero, Mw, kg.mol-1 M w Temperatura de alimento, T0, °C Calor de vaporización del óxido, λ, kJ.kg-1 Capacidad caloríca del alimento, Cp, kJ.kg-1.°C-1 Calor de reacción, HR, kJ.(kg óxido) -1 M 0 X / M 0 / 74 T0 80 670 Cp 3,5 H R 1660 Velocidad de recirculación, Fc, kg.min-1 Fc 3300 Coeciente de descarga, Kv, K v 100 323 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Considérese ahora una situación donde se produce una falla en el sistema de enfriamiento de cinco minutos de duración después de 700 minutos de haber empezado la reacción. Una opción para simular la falla en el sistema de enfriamiento es haciendo que la velocidad de recirculación, Fc, sea cero. Los resultados se presentan en la Figura 14.3. La falla del sistema de enfriamiento genera una aceleración espectacular del aumento de la presión y de la temperatura en el sistema (condiciones de run away). Figura 14.3. Cambio de la temperatura y la presión dentro del reactor con el tiempo de reacción, con cinco minutos de falla del sistema de enfriamiento En la Figura 14.3 se puede observar que la temperatura alcanza un máximo valor de 263 °C aproximadamente 45 minutos después de que se logró restablecer el ujo del uido de servicio a su valor de diseño. La presión alcanza el umbral de 8 bar cinco minutos antes y el disco se rompe. Debido al enfriamiento ocasionado por el calor latente de vaporización del vapor descargado, la disminución en la velocidad de reacción llega a cero y debido a la disminución en la concentración de óxido, la temperatura cae a 80 °C después de 120 minutos de haberse roto el disco. La presión cae a 1 bar instantáneamente. El peso molecular del producto en este caso es de 1325, el cual está por fuera de 324 CAPÍTULO 14 - PREDICCIÓN, PREVENCIÓN Y EVALUACIÓN DE RIESGOS CON REACCIONES QUÍMICAS especicaciones. Así, esta carga en particular se pierde debido a una falla en el sistema de enfriamiento. Existen varias estrategias que pueden utilizarse para prevenir la temperatura de run away y la pérdida de la carga al reactor. Una opción podría ser aumentar la velocidad de recirculación a su máximo, Fc = 5000 kg.min-1, una vez se restablezca el enfriamiento. Los resultados para este caso se presentan en la Figura 14.4. Figura 14.4. Cambio de la temperatura y la presión dentro del reactor con el tiempo de reacción, cuando la velocidad de recirculación se aumenta al máximo, cinco minutos después de fallar el sistema de enfriamiento Se puede observar en la Figura 14.4 que ahora, la máxima temperatura que se alcanza en el sistema es de solo 100,5 °C y que el valor de la presión permanece por debajo del límite de ruptura. Así, este fue un batch exitoso ya que el peso molecular del producto fue de 2566, el cual está sólo un poco por debajo del valor normal, pero dentro de especicaciones. 325 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Sería interesante considerar fallas del sistema de enfriamiento de mayor duración y evaluar sus consecuencias. Así mismo, resulta muy formativo evaluar otro tipo de problemas y soluciones por medio de la herramienta de software diseñada para reproducir este caso de estudio. 4.2. CASO II: SISTEMA CON DOS REACCIONES EXOTÉRMICAS A→B→C Las reacciones exotérmicas A → B → C (esta secuencia de reacciones es típica de procesos de hidrogenación y de nitración) se llevan a cabo en fase líquida en un reactor batch, como se esquematiza en la Figura 14.5. Figura 14.5. Esquema del reactor batch para el Caso II Después de cargar los reactantes al reactor, se alimenta vapor a la chaqueta del mismo con el n de calentar la masa reaccionante hasta la temperatura deseada. Luego, se cambia el uido de servicio por agua de enfriamiento para remover a través de la chaqueta el calor de reacción exotérmico liberado y hacer así que el reactor siga un desempeño temperatura-tiempo predeterminado. El objetivo es maximizar la producción del producto deseado B. Las ecuaciones del modelo matemático del reactor y del sistema de remoción de calor se presentan en la Tabla 14.2a (para detalles adicionales ver páginas 51-62 y 150-157 del libro de 326 CAPÍTULO 14 - PREDICCIÓN, PREVENCIÓN Y EVALUACIÓN DE RIESGOS CON REACCIONES QUÍMICAS Luyben, 1990). Las condiciones presentes en la Tabla 14.2b se consideran como las correspondientes a una operación normal. La reacción tiene una duración de 200 minutos. El reactor está diseñado para soportar hasta 1600 psi, la cual se alcanza cuando la temperatura se aproxima a 500 ºF. Resolviendo el modelo presente se obtienen los resultados que se muestran en la Figura 14.6. Figura 14.6. Variación de la temperatura y la concentración de B con el tiempo de reacción (condiciones normales de operación) A condiciones normales de operación, la máxima concentración del producto deseado es 0,48 lbmol/ft3, lo cual equivale a que el 60% de A se ha convertido en B. La temperatura alcanza un máximo de 211,7 ºF (que se puede considerar bien dentro de la zona de seguridad). La temperatura aumenta progresivamente durante la fase de calentamiento con vapor. Esta alcanza el máximo poco tiempo después de suspender el vapor y empezar a usar el agua de enfriamiento. Después de ese punto, la temperatura en el reactor disminuye gradualmente hasta terminar la reacción. 327 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Tabla 14.2a. Ecuaciones del modelo y valores de las variables del Caso II Definición Valor inicial Ecuación Concentración de A, CA, mol/ft3 CA (0) = 0,8 Concentración de B, CB, mol/ft3 CB (0) = 0 Temperatura en el reactor, T, ºF T (0) = 80 dT dt dC A k1C A dt dCB k1C A k2CB dt H Rxn1k1C A H Rxn 2 k2CB QmV Qm Q j dTm dt mCpmVm Temperatura de las paredes del Tm (0) = 80 reactor, Tm, ºF dT j K c err d sdt /10 , para enfriamiento dt Temperatura en la chaqueta de enTj (0) = 259 Q friamiento/calentamiento, Tj, ºF Fw0 Tinj T j j j , para calentamiento dT j dt Vj Calor transferido a través de las paredes del reactor, Qm, BTU/min Presión del vapor dentro de la chaqueta, Pj, psi Constante de velocidad de reacción, k1, min-1 Constante de velocidad de reacción, k2, min-1 Área de transferencia de calor para enfriamiento, A0, ft2 Velocidad de ujo másico del condensado, wc, lb/min Calor transferido a la chaqueta, Qj, BTU/ min Velocidad de ujo de agua de enfriamiento, Fwo, lb/min Desviación de la densidad del vapor para el control, err Velocidad de ujo másico del vapor, ws, lb/min Variación de la densidad del vapor, ρs(0)=0,0803 ρ s, 328 Qm hi A0 m T Tm / 60 Pj exp 15, 70036 8744, 4 / T j 460 k1 729,5488exp 15000 / 1,99 T 460 k2 6567,587 exp 20000 / 1,99 T 460 A0 V j Aj ,max / V j ,max wc Q j / H vap Qj hos Aj max T j Tm / 60 Q j how A0 Tm T j / 60 Fwo 8.33Cvw wp xw / j err s 18 144 Pj / 1545 T j 460 Tm ws xs Cvs PVAPOR Pj d S ws wc dt V j max CAPÍTULO 14 - PREDICCIÓN, PREVENCIÓN Y EVALUACIÓN DE RIESGOS CON REACCIONES QUÍMICAS Tabla 14.2b. Valores de las constantes para el Caso II Definición Valor Presión de suministro de vapor, PVAPOR, psi 35 Coeciente de transferencia de calor en la chaqueta, hos, con vapor, BTU/(h.ºF.ft3) Coeciente de transferencia de calor en la chaqueta, how, con agua, BTU/(h.ºF.ft3) Calor de condensación del vapor, Hvap, BTU/lb Ganancia del controlador, Kc Coeciente de la válvula de vapor, Cvs Coeciente de la válvula de agua, Cvw Presión del agua, wp, psi Calor de la reacción A → B, H Rxn1 ,BTU/mol Calor de la reacción B → C, H Rxn 2 ,BTU/mol Densidad de la mezcla reactiva, ρ, lb/ft3 Definición Temperatura para el cambio de calentamiento a enfriamiento, ºF Valor 200 1000 Volumen total de la chaqueta, Vjmax, ft3 18,83 400 Coeciente de transferencia de calor, hi, BTU/(h.ºF.ft2) 160 939 7000 112 100 20 -40000 -50000 50 Área de transferencia de calor en la chaqueta, A0m, ft2 Área total de transferencia de calor en la chaqueta, Ajm, ft2 Volumen del reactor, V, ft3 Densidad de la pared metálica, ρm, lb/ft3 Calor especíco de la pared metálica, Cpm, BTU/(lb.ft3) Volumen de la pared metálica, Vm, ft3 Densidad del agua de enfriamiento, ρj, lb/ft3 Temperatura de entrada del agua de enfriamiento, Tinj, ºF 56,5 56,5 42,4 512 0,12 9,42 62,3 80 329 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS La Figura 14.7 presenta el efecto de haber sobrecargado el reactor: se cambió la concentración inicial de A hasta 1,0 lbmol/ft3 (en lugar de 0,8 lbmol/ft3 en operación normal). Figura 14.7. Variación de la temperatura y la concentración de B con el tiempo de reacción cuando la concentración de A se aumenta a 1,0 lbmol/ft3 Nótese en la Figura 14.7 que la temperatura en el reactor siempre aumenta aun después de haber detenido el alimento de vapor. El aumento es gradual inicialmente, pero luego, después de 35 minutos, se alcanza una condición de run away. La temperatura alcanza el umbral límite de 500 ºF después de 42 minutos de reacción. Disminuir el periodo de calentamiento con vapor puede prevenir la temperatura de run away en este caso. La variación de la temperatura y la concentración, cuando se ja la temperatura máxima de calentamiento con vapor en 125 ºF, se presenta en la Figura 14.8. La temperatura continúa aumentando largo tiempo después de que se suspende el calentamiento, alcanzando un máximo de 241 ºF. En este punto, sin embargo, la concentración de A es lo sucientemente baja como para que el sistema de enfriamiento logre controlar el exceso de calor liberado por la reacción previniendo el run away. La concentración nal 330 CAPÍTULO 14 - PREDICCIÓN, PREVENCIÓN Y EVALUACIÓN DE RIESGOS CON REACCIONES QUÍMICAS de B es de 0,637 lbmol/ft3, equivalente a una conversión de A del 63,7%, superando incluso el desempeño a condiciones normales de operación. Figura 14.8. Variación de la temperatura y la concentración de B con el tiempo de reacción cuando la concentración de A se aumenta a 1,0 lbmol/ft3 y el período de calentamiento con vapor disminuye La Figura 14.9 presenta el desempeño del reactor en el caso que exista una falla en el sistema de enfriamiento: se suspende el suministro de agua de enfriamiento dos horas después de haber iniciado la reacción. En la Figura 14.9 se observa que la temperatura, aunque aumenta considerablemente (la temperatura nal es de 278 ºF en lugar del valor normal de 193 ºF), está aún lejos del valor límite de 500° F. La concentración del producto deseado es de 0,495 lbmol/ft3, levemente superior al valor normal esperado. El efecto de las fallas del sistema de enfriamiento depende mucho del momento y su duración. ¿Qué pasaría en el caso que la falla se presente durante la primera hora de la operación batch y esta falla se prolongara por 25 minutos? 331 ELEMENTOS PARA EL ANÁLISIS Y DISEÑO DE REACTORES QUÍMICOS Figura 14.9. Variación de la temperatura y la concentración de B con el tiempo de reacción cuando falla el control y aumenta el período de calentamiento alcanzado una temperatura dentro del reactor de 220 ºF BIBLIOGRAFÍA Fogler, H.S. (2006): Elements of Chemical Reaction Engineering (4th Ed.). New York: Prentice Hall. Ingham, J.; Dunn, I.J.; Heinzle, E. & Prenosil, J.E. (1994): Chemical Engineering Dynamics. Weinheim: VCH. Kletz, T. (1998): What Went Wrong? Case Studies of Process Plant Disasters (4th Ed.). New York: Gulf Professional Publishing. Luyben, W.L. (1990): Process Modeling Simulation and Control for Chemical Engineers (2nd Ed.). New York: McGraw Hill. 332 CAPÍTULO 14 - PREDICCIÓN, PREVENCIÓN Y EVALUACIÓN DE RIESGOS CON REACCIONES QUÍMICAS Shacham, M.; Braumer, N. & Cutlip, M.B. (2000): “Open Architecture Modeling and Simulation in Process Hazard Assessment”. En: Comp. Chem. Eng., 24(2-7), 415 – 421. Shacham, M.; Braumer, N. & Cutlip, M.B. (2001): “Prediction and Prevention of Chemical Reaction Hazards. Learning by Simulation”. En: Chem. Eng. Educ., 35(4), 268 – 273. Shacham, M.; Braumer, N. & Cutlip, M. B. (2003): “Modular and Sequential Construction of Complex Process Models – Applications to Process Hazard Assessment”. En: A. Kraslawski & I. Turunen (Eds.): Proceedings Supplement Volume of the European Symposium on Computer Aided Process Engineering – 13. Lapperanta (Finland): Lappenranta University of Technology; pp. 41 – 52. U.S. Chemical Safety and Hazard Investigation Board. http://www.csb. gov/ Willey, R.J; Fogler, H.S.; Cutlip, M.B. (2011): "The Integration of Process Safety into a Chemical Reaction Engineering Course: Kinetic Modeling of the T2 Incident". En: AIChE J., 30(1), 39-44. 333


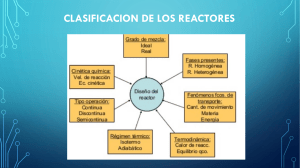
![A↔ B (-rA) = 0.04CA-0.01CR, [=] mol*L](http://s2.studylib.es/store/data/005357341_1-6e8dd554fb791e1c2c9f555a9c29f5b3-300x300.png)




