hipotesis-lineas-de-transmision compressfg es f

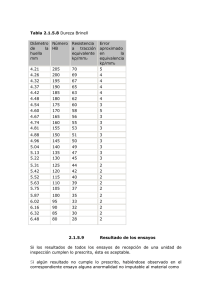
f
Donde:
x  lc * sen
x  4.1* sen20.1
x  1.4..m
x
tan 30 
lc  B
(4.1  B) tan 30  1.4
B  3..m
Calculo Mecánico de conductores:
Reacuerdo al conductor elegido que es el BUNTING, tenemos los siguientes datos:
De Tabla
Alcan
Carga de rotura ó tiro de rotura
15059 Kg
Sección total
646 mm2
Hilos de aluminio
45
Hilos de acero
7
Diámetro completo
33.07 mm
Luego de las tablas de elasticidad finales y coeficientes de dilatación lineal apara
alambres y conductores fuente ALCAN SALES INC Pág. 23.
Tiro de cable
ACSR
Cableado Modulo de elasticidad final Kg/ mm2 Coeficiente de dilatación final
42/7
6000
21.2
45/7
6470
20.9
= 6470 Kg/mm2
Modulo de elasticidad
Coeficiente de dilatación final = 20.9*10-6 ºC-1
1) HIPÓTESIS I:(de esfuerzos dianos EDS)
Se refríe a las condiciones normales de operación de la línea y también a la condición
de instalación de dicha línea.
Datos:
T medida = 10ºC
V viento = 0 Km/s
1
f1
= ¿?
=
¿?
EDS asumido = 18 % tiro de ruptura
Vano medido
Pedo del conductor
= 300 m
= 1.996 Kg/m
Calculo de EDS:
  0.18 *
TR
1
S
15059Kg
 1  0.18 *
646mm2
1  4.196Kg / mm2  esfuerzo..diario  EDS
Calculo de flecha en EDS
f1 
f1 
f1 
a 2 *Wc
8 *To
a 2 *Wc
8 * 1 * S
3002 *1.996
8 * 4.196 * 646
f1  8.28m
2) HIPÓTESIS II:(De Máximos Esfuerzos)
Supone las mayores exigencia mecánicas del conductor, generalmente interviene la
mínima temperatura, formación de hielo si lo hubiera y presión del viento máximo.
T min
=
-20 ºC
V viento
=
90 Km/h
1
=
?
f1
=
?
De la ECE que se basa en los cambios físicos que sufre el conductor producto de los
cambios climáticos.

 W 2 * a2 * E
     W 2a 2 E
  2
1
2
* E T2 T1
 2 2
1 
24 * s 2 * 12
24 * s 2


Donde:
=
Esfuerzo Kg/mm2
a =
Coeficiente de dilatación lineal / ºC
E =
Modulo de elasticidad Kg/mm2
S =
Sección del cable mm2
a =
Vano m
W1 =
W2
T1 T2 =
Peso unitario del conductor Kg/m
Temperaturas

Solución:
A  E T1  T2  
B
W 22a 2 E
24s 2
W 2a 2 E
1
24s 2 12
 
Donde la ecuación general de ECE es:
 3  3  B  0
2
2
  1  
Reemplazamos valores en 



1.9962 * 3002 * 6470




A 20.9 *10 * 6470 20 10
24 * 6462 * 4.1962
A  4.057  13.156  4.196
A  4.9
W 2a 2 E
B 2 2
24s
6
Como no tenemos valores de W2
W vc = presión del viento sobre el conductor
De la figura:
W 2  Wvc2 W 2
2
cond
Wvc  0.0048*Vviento 2
c  2

1000
Donde:
Vv
c
Velocidad del viento
=
90 Km/h
Diámetro del conductor
=
33.07 mm
Diámetro del manguito de hielo
=
10.00 mm
Reemplazamos en la formula anterior
Wvc  0.0048*902
c  2

1000
33.07  2*10
Wvc  0.0048*Vviento 2

1000
Wvc  2.068kg
W 2  Wvc2  W 2
2
cond
W 2  2.068 1.9962
2
2
W2  2.874..kg
Reemplazamos W2 en:
B
B
W 2a2 E
2
24s2
2.8742 *3002 * 6470
24 * 6462
B  480.21
Luego reemplazamos en:
 3  A 3  B  0
2
2
 3  4.9 3  480.21  0
2
2
Re solviendo
 2  6.485...kg / mm2 ... Esfuerzo máximo
Calculamos la flecha
2
f 2 a *Wc
8 * 2 * S
2
f2 ¨ 300 *1.996
8 * 6.485 * 646
f2  5.36..m ............... Flecha mínima
3) HIPÓTESIS III: (de esfuerzo máximo y flecha máxima)
Se refiere a la condición de máximo acercamiento del conductor al terreno.
Condiciones:
Tmax
=
40 ºC
Vviento
=
Nula
De la ecuación de cambio de estado
 3  3  B  0
3
3
Calculo de:
A





 * E * T 3

 

T2

a 2 *W 2*E   
3
2
2 
24 * S * 22

A  20.9 *106 * 647040  20 
3002 * 2.3742 * 6470
24 * 6462 * 5.5892
A  8.113  10.489  5.589
A  13.01
B
B 
a 2 *W32 * E
24 * S 2
3002 *1.9962 * 6470
24 * 6462
B  231.628
Calculo de W3
Pero :
WVC
 0.0048 *Vv 2 *
 c  2

100
Como Vv es nulo
Wvc  0
luego
W3  Wc
Al reemplazar los valores de Ay B
 3  13.01 3  231.63B  0
3
3
resolviendo
 3  3.72kg / mm2 .... Esfuerso..Minimo
Flecha:
2
f3  a *Wc
8 * 3 * S
2
f3  300 *1.996
8 * 3.72 * 646
f3  9.34m.................. Flecha..Maxima
4) HIPÓTESIS IV: (Que Se Da A Temperatura Mínima)
Condiciones:
T min = -20 ºC
Vv
= 0 Km/h
4
= ?
f4
= ?
De la ECE:
 3  A 3  B  0
4
4

A *E * T
4
 T3
 
a2 *W * E
3
2
24 * S * W 32

A  20.9 * 10  6 * 6470 20  40  
A  8.13  16.738  2.716
A  5.91
B 
a 2 * W 42 * E
24 * S 2
Como..Vv  0... W 4 Wc
3002 * 1.9962 * 6470
B 
24 * 6462
B  231.628
Reemplazamos A y B
3
3002 * 1.9962 * 6470 
 3.72
24 * 6462 * 3.722
 3  A 3  B  0
4
4
 3  5.91 3  231.63  0
4
4
Re solviendo
 4  4.677 ... kg / mm2
Flecha
a 2 *Wc
3002 *1.996
f4 

8 * 4 * S 8 * 4.677 * 646
f 4  7.43...m
Calculo Mecánico Para El Cable De Guarda:
Material
= Acero galvanizado
Tipo
= EHS
Sección
= 51.08 mm
Diámetro
= 9.525 mm
Carga de rotura
= 6980 Kg
Peso unitario
= 0.41 kg/m
Modulo elasticidad
= 19000 Kg/mm2
Coeficiente de dilatación = 11.5 * 10-6 ºC
Nº de hilos
= 7
os valores se obtienen de la tabla:
Módulos de elasticidad finales y coeficientes de dilatación lineal para alambres y
conductor.
Tipo de alambre
o conductor
Acero galvanizado
Modulo de Coeficiente de dilatación
Cableado
elasticidad
7
19000
5) HIPÓTESIS I:(de esfuerzos dianos EDS)
Datos:
T medida
V viento
Calculo de EDS:
= 10ºC
= 0 Km/s
1
= ¿?
f1
= ¿?
Lineal * 10-6 ºC
11.5
Calculo de EDS:
  0.18 *
1
  0.18 *
TR
S
6980Kg
1
51.08
1  24.6.Kg / mm2  esfuerzo  diario  EDS
Calculo de flecha en EDS
a 2 *Wc
8 *To
a 2 *Wc
f1 
f1 
8 * 1 * S
f1 
3002 * 0.41
8 * 24.6 * 51.08
f1  3.67m
6) HIPÓTESIS II:(De Máximos Esfuerzos y Flecha Mínima)
T min
=
-20 ºC
V viento
=
90 Km/h
1
=
?
f1
=
?
De la ECE que se basa en los cambios físicos que sufre el conductor producto de los
cambios climáticos.

 W 2 * a2 * E
     W 2a 2 E


 2
1
* E T2 T1
 22 2
2
2
1 
24 * s * 1
24 * s 2


Donde:
=
Solución:

A
Esfuerzo Kg/mm2
a =
Coeficiente de dilatación lineal / ºC
E =
Modulo de elasticidad Kg/mm2
S =
Sección del cable mm2
a =
Vano m
W1cg
=
W2cg
Peso unitario del conductor Kg/m
T1 T2 =
Temperaturas final y inicial
   
E T1 T2
W 2a2 E
   
1
24s 2 12
1
Reemplazamos valores en 
A  11.5 *106 *1900020 10 
A  23.57
W 2a 2 E
B 2 2
24s
Como no tenemos valores de W2
0.412 * 3002 *1900
24 * 51.082 * 24.62
W vc = presión del viento sobre el Cable De guarda
De la figura:
2
2
 Wvc2  W 1cg
W 2cg
Wvc  0.0048 *Vviento
c  2

1000
Donde:
Vv
c
Velocidad del viento
Diámetro del conductor
Diámetro del manguito de hielo
Reemplazamos en la formula anterior
Wvc  0.0048 * 902
9.525  2 *1
1000
Wvc  0.0049..kg
2
2
 Wvc2  W 1cg
W2cg
W 22  0.00492  0.412
W2  0.41...kg
Reemplazamos W2 en:
B
W 2a 2 E
B 
2
24s 2
0.412 * 3002 *19000
24 * 51.082
B  4590.4
Luego reemplazamos en:
 3  A 3  B  0
2
2
 3  (23.57) * 3  4590.4  0
2
2
Re solviendo
 2  29.02...kg / mm2 ... Esfuerzo máximo
Calculamos la flecha
2
f 2 a *Wc
8 * 2 * S
3002 * 0.41
8 * 29.02 * 51.08
f 2  3.11..m ................. Flecha mínima
f 2 ¨
7) HIPÓTESIS III: (de esfuerzo máximo y flecha máxima)
Tmax
=
40 ºC
Vviento
=
0 Km/h
De la ecuación de cambio de estado
 3  A 2  B  0
3
3
Calculo de:
A





  * E * T3

 

T2

a 2 *W 2*E   
3
2 
24 * S 2 * 22

A  11.5 *106 *1900040  20  
3002 * 0.412 *19000
24 * 51.082 * 29.022
A  10.46
a 2 *W 32 * E ............
.......... porque..la..velocidad .es.nula
B
W3cg  W1cg
24 * S 2
3002 * 0.412 *19000
B 
24 * 51.082
B  4590.4
Al reemplazar los valores de Ay B
3
3
 4590.4  0
3cg
 (10) 3cg
resolviendo
 3  20.93...kg / mm2 .... Esfuerso..Minimo
Flecha:
f 3 
a 2 *W 3cg
8 * 3 * S
3002 * 0.41
8 * 20.93 * 51.08
f3  4.31.m .................. Flecha..Maxima
f3 
8) HIPÓTESIS IV:
Condiciones:
T min = -20 ºC
Vv
= 0 Km/h
4
= ?
f4
= ?
De la ECE:
 3  A 3  B  0
4
4
A   * E * T4  T3 
a 2 *W * E

3
24 * S 2 *W 32
A  11.5 *106 *19000 20  40 
3
3002 * 0.412 *19000
 20.93
24 * 51.08 * 20.932
A  23.56
a 2 *W 42 * E
24 * S 2
Como..Vv  0... W 4cg Wcg
3002 * 0.412 *19000
B 
24 * 51.082
B  4590.4
B
Reemplazamos A y B
 3  A 3  B  0
4

3
4cg
4
 23.56 * 34cg  4590.4  0
Re solviendo
 4cg  29 .. kg / mm2
Flecha
a 2 *W
3002 * 0.41
4cg

f 4 
8 * 4 * S 8 * 29 * 51.08
f 4  3.11...m
Calculo Mecánico De Estructuras:
Sección del conductor ACSR BUNTING
Vano
Esfuerzo máximo del conductor
Esfuerzo en máxima temperatura
Velocidad del viento
Peso del conductor BUNTING
Peso del aislador polimérico + ferretería
Disposición de conductores
Peso de cable de guarda
Sección del cable de guarda
Esfuerzo máximo en el cable de guarda
Posición del conductor
Posición del cable de guarda
= 646 mm2
= 300 m
= 6.485 Kg/mm2
3.72 Kg/mm2=esfuerzo
=
mínimo conductor
= 90 Km/h
= 1.996 Kg/m
=
= 3 fases
= 0.41 Kg/m
= 51.08 mm2
= 29.02 Kg/mm2
= 27.84 m
= 30.84
 Calculo de la presión del viento sobre la torre:
P  K *V 2
Pvt  0.007 *V 2
Pvt  0.007 * 902
Pvt  56.7..Kg / m2
 Calculo del presión del viento sobre el conductor:
Pvc  0.00481*V 2
Pvc  0.00481* 902
Pvc  .38.96.Kg / m2
 Calculo de la presión del viento sobre el cable de guarda
Pvcg  .38.96.Kg / m
 Calculo de la presión del viento sobre los aisladores
Pva  0.00962 *V 2
Pva  0.00962 * 902
Pva  .77.92.Kg / m2