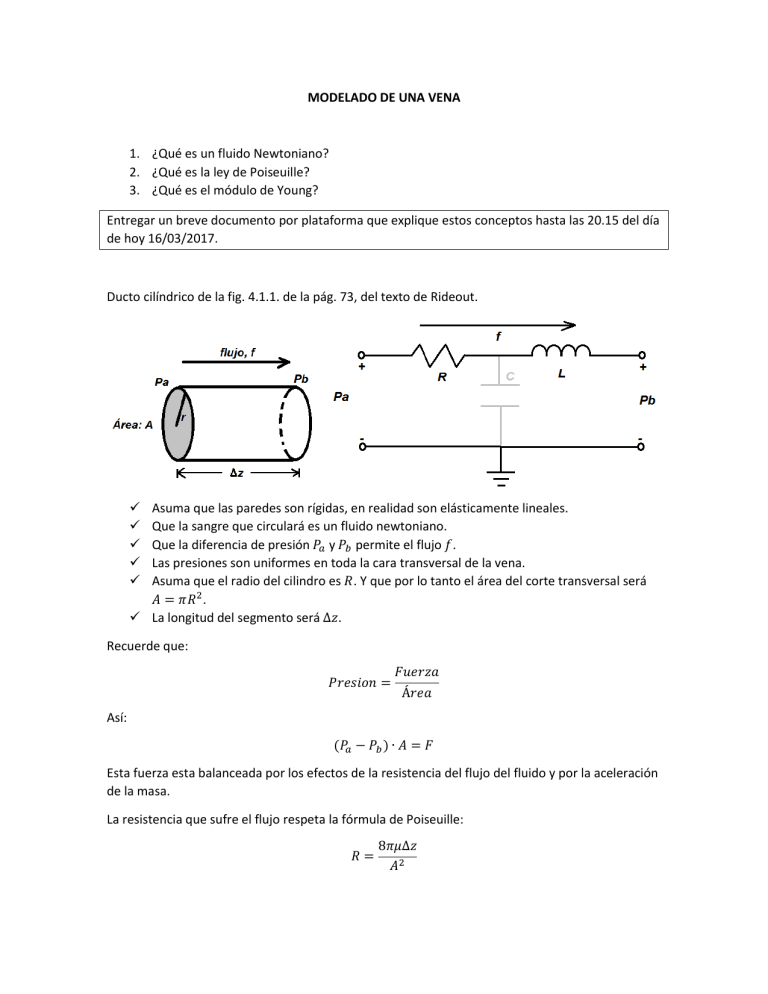
MODELADO DE UNA VENA 1. ¿Qué es un fluido Newtoniano? 2. ¿Qué es la ley de Poiseuille? 3. ¿Qué es el módulo de Young? Entregar un breve documento por plataforma que explique estos conceptos hasta las 20.15 del día de hoy 16/03/2017. Ducto cilíndrico de la fig. 4.1.1. de la pág. 73, del texto de Rideout. Asuma que las paredes son rígidas, en realidad son elásticamente lineales. Que la sangre que circulará es un fluido newtoniano. Que la diferencia de presión 𝑃𝑎 y 𝑃𝑏 permite el flujo 𝑓. Las presiones son uniformes en toda la cara transversal de la vena. Asuma que el radio del cilindro es 𝑅. Y que por lo tanto el área del corte transversal será 𝐴 = 𝜋𝑅 2. La longitud del segmento será Δ𝑧. Recuerde que: 𝑃𝑟𝑒𝑠𝑖𝑜𝑛 = 𝐹𝑢𝑒𝑟𝑧𝑎 Á𝑟𝑒𝑎 Así: (𝑃𝑎 − 𝑃𝑏 ) ∙ 𝐴 = 𝐹 Esta fuerza esta balanceada por los efectos de la resistencia del flujo del fluido y por la aceleración de la masa. La resistencia que sufre el flujo respeta la fórmula de Poiseuille: 𝑅= 8𝜋𝜇Δ𝑧 𝐴2 Asumiendo que el flujo es constante a lo largo del diámetro del tubo, la caída de presión por la resistencia viscosa está dada por: (𝑃𝑎 − 𝑃𝑏 )|𝑣𝑖𝑠 = 𝑓 ∙ 𝑅 Para hallar la caída de presión debido a la aceleración de la masa, se debe considerar la masa en el cilindro: 𝑀 = 𝜌 ∙ 𝐴 ∙ Δ𝑧 Donde 𝜌 es la densidad de la masa. Si se asume que la velocidad del flujo de sangre 𝑣 es uniforme a lo largo del diámetro del tubo, el flujo total estará dado por: 𝑓 =𝑣∙𝐴 Por la segunda ley de Newton: 𝑚∙𝑎 =𝐹 𝑀∙ 𝑑𝑣 𝑑(𝑓/𝐴) = (𝜌 ∙ 𝐴 ∙ Δ𝑧) ∙ 𝑑𝑡 𝑑𝑡 𝑀∙ 𝑑𝑣 𝑑𝑓 = 𝜌 ∙ Δ𝑧 ∙ 𝑑𝑡 𝑑𝑡 Esta fuerza de aceleración debe ser igual a la aceleración producida por la diferencia de presión. Así: 𝐹 = (𝑃𝑎 − 𝑃𝑏 ) ∙ 𝐴 = 𝑀 ∙ 𝑑𝑣 𝑑𝑓 = 𝜌 ∙ Δ𝑧 ∙ 𝑑𝑡 𝑑𝑡 La caída de presión por la aceleración esta dada por: (𝑃𝑎 − 𝑃𝑏)|𝑎𝑐𝑒𝑙 = 𝜌 ∙ Δ𝑧 𝑑𝑓 ∙ 𝐴 𝑑𝑡 Se puede definir un coeficiente de INERTANCIA 𝐿. 𝐿= 𝜌 ∙ Δz 𝐴 Sumando la caída de la presión por la resistencia viscosa y la aceleración tendremos: 𝑃𝑎 − 𝑃𝑏 = 𝑅 ∙ 𝑓 + 𝐿 ∙ 𝑑𝑓 𝑑𝑡 Una corrección del hecho de que la velocidad cerca las paredes es menor, y considerando un cilindro con sección transversal parabólica entrega un valor más aproximado para la inertancia. 𝐿= 9 ∙ 𝜌 ∙ Δz 9 ∙ 𝜌 ∙ Δ𝑧 = 4∙𝐴 4 ∙ 𝜋 ∙ 𝑟2 Además se negó la elasticidad de las venas, esto se puede modelar considerando la “complianza” 𝐶 de una vena cilíndrica de radio 𝑟, longitud Δ𝑧, espesor de la pared ℎ y módulo de elasticidad de Young 𝐸. 𝐶= 3 ∙ 𝜋 ∙ 𝑟 3 ∙ Δ𝑧 2∙𝐸∙ℎ 1 Donde la pared del material es uniforme con una razón de Poisson de 𝜎 = 2. [Continua en Pág. 74.]








