Diseño estructural de vivienda

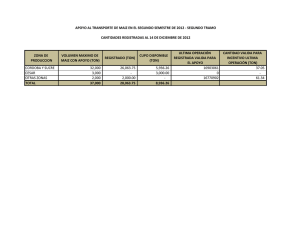
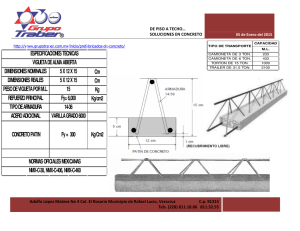
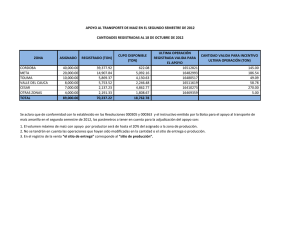
FACULTAD DE INGENIERÍA
DISEÑO ESTRUCTURAL DE UNA VIVIENDA UNIFAMILIAR DE TRES
PISOS UBICADA EN EL DISTRITO VEINTISÉIS DE OCTUBRE
Trabajo de Investigación para optar el Grado de
Bachiller en Ingeniería Civil
Cano Ojeda Yesenia Lizbeth
Correa Arroyo César Omar
Inga Laban Luis David
Santamaría Bocanegra Jhon Jairo
Saucedo Ayosa Juan Jose
Asesor:
Mg. Arturo Martínez Ramírez
Piura, Noviembre de 2021
Resumen
El presente trabajo consiste en el diseño de los elementos estructurales de
una vivienda de 3 pisos más una azotea ubicada en el distrito de 26 de octubre
siguiendo las especificaciones de las Normas Técnicas Peruanas.
Los elementos diseñados en el presente trabajo son columnas, vigas, losas
aligeradas, muros de albañilería, placas de concreto y cimentaciones. Para su diseño,
se tuvieron en cuenta factores como la zona sísmica del lugar, el tipo de suelo, el uso
de la vivienda, las irregularidades, etc. Al estar situada la estructura en una zona
altamente sísmica, se diseñó bajo las consideraciones especiales de diseño
sismorresistente para el caso de columnas, vigas y placas.
El procedimiento de trabajo fue, en primer lugar, definir la configuración
estructural de la vivienda. Luego, se predimensionaron los elementos estructurales
según el criterio de los integrantes y la arquitectura proporcionada. Luego, se
procedió a modelar la estructura en un software matemático para realizar un análisis
sísmico estático y dinámico. La principal herramienta de diseño fue el uso del
software de cálculo estructural ETABS. De este software, además, se obtuvieron las
cargas a las que eran sometidos los elementos estructurales para los distintos casos
de carga. Por último, a partir de los datos proporcionados por el programa se
diseñaron los elementos. El procedimiento de diseño de cada elemento se describe
mediante ejemplos, mientras que para los cálculos se usaron hojas de cálculo de
Excel.
2
Tabla de contenido
Resumen.......................................................................................................................................2
Introducción .................................................................................................................................8
Capítulo 1 Generalidades .............................................................................................................9
1.1.
Arquitectura del edificio ...............................................................................................9
1.2.
Estudio de mecánica de suelos ...................................................................................10
1.3.
Reglamentos, cargas de diseño y materiales empleados .............................................12
Capítulo 2 Estructuración y Predimensionamiento ....................................................................14
2.1.
Estructuración.............................................................................................................14
2.2.
Predimensionamiento de elementos estructurales .......................................................14
2.2.1.
Columnas ............................................................................................................14
2.2.2.
Vigas ..................................................................................................................15
2.2.3.
Losas aligeradas..................................................................................................15
2.2.4.
Muros de corte ....................................................................................................15
Capítulo 3 Simulación estructural en ETABS ............................................................................17
Capítulo 4 Análisis Sísmico .......................................................................................................21
4.1. Análisis ...........................................................................................................................21
4.1.1 Fuerza cortante en la base ..........................................................................................22
4.2. Análisis dinámico ............................................................................................................24
4.2.1 Aceleración espectral.................................................................................................24
4.2.2 Modos de vibración ...................................................................................................25
4.2.3 Derivas ......................................................................................................................26
Capítulo 5 Diseño de Vigas ........................................................................................................28
5.1. Generalidades ..................................................................................................................28
5.2. Diseño por flexión: ..........................................................................................................29
5.3. Comprobación del Diseño por flexión: ............................................................................36
5.4. Diseño por corte: .............................................................................................................38
Capítulo 6 Diseño de losas aligeradas ........................................................................................45
Capítulo 7 Diseño de Columnas .................................................................................................53
7.1. Diseño por capacidad: .....................................................................................................54
Capítulo 8 Diseño de muros de corte ..........................................................................................61
8.1. Predimensionamiento de refuerzo en elementos de borde ...............................................61
8.2. Diseño por flexocompresión:...........................................................................................64
Capítulo 9 Diseño de Muros de albañilería ................................................................................68
9.1. Metodología de diseño según norma E-070.....................................................................68
9.2. Verificación de esfuerzo axial en muro ...........................................................................69
9.3. Verificación del agrietamiento en muro ..........................................................................70
3
9.4. Verificación de la resistencia al corte del edifico ............................................................72
9.5. Diseño de la albañilería confinada ...................................................................................74
9.6. Verificación de la necesidad de colocar refuerzo horizontal en los muros.......................75
9.7. Verificación del agrietamiento diagonal en los pisos superiores .....................................76
9.8. Diseño de las columnas de confinamiento .......................................................................77
9.9. Diseño por compresión ....................................................................................................79
9.10. Diseño por corte fricción ...............................................................................................79
9.11. Determinación del refuerzo vertical de las columnas de confinamiento ........................80
Capítulo 10 Diseño de cimentaciones: .......................................................................................83
10.1. Generalidades: ...............................................................................................................83
10.2. Diseño de zapata aislada ................................................................................................83
10.3. Diseño de zapatas conectadas con viga .........................................................................90
10.4. Diseño de zapata corrida .............................................................................................100
Conclusiones ............................................................................................................................105
Recomendaciones .....................................................................................................................106
Referencias Bibliográficas .......................................................................................................107
4
Lista de Figuras:
Figura 1. Vista en elevación de la edificación. Fuente: AutoCAD .................................................9
Figura 2. Plano en planta del primer piso de la edificación. Fuente: AutoCAD...........................10
Figura 3. Perfil estratigráfico del suelo. Fuente: Estudio de Mecánica de Suelos ......................11
Figura 4. Vista en 3D del modelo de la edifiación. Fuente: ETABS .............................................18
Figura 5. Vista en planta del primer techo de la edificación. Fuente: ETABS ............................19
Figura 6. Vista en elevación del eje 2 de la edificación. Fuente: ETABS ....................................20
Figura 7. Aceleración espectral en el eje X. ...............................................................................25
Figura 8. Aceleración espectral en el eje Y. ...............................................................................25
Figura 9. Momentos debido a la envolvente. ............................................................................30
Figura 10. Sección transversal de la viga en el extremo izquierdo. ...........................................31
Figura 11. Sección transversal de la viga en el centro. ..............................................................33
Figura 12. Sección transversal de la viga en el extremo derecho. .............................................34
Figura 13. Momentos actuantes en la viga. ...............................................................................39
Figura 14. DFC de viga. Fuente: Elaboración propia. .................................................................41
Figura 15. DFC por resistencia. ..................................................................................................41
Figura 16. Aligerado tipo I con tabiquería perpendicular. .........................................................45
Figura 17. Aligerado 2, sin tabiquería en un solo tramo. ...........................................................47
Figura 18. Momentos en aligerado 2. ........................................................................................48
Figura 19. Momentos en volados.. ............................................................................................49
Figura 20. Paño tipo 1 en azotea. ..............................................................................................50
Figura 21. Paño tipo 2 en azotea. ..............................................................................................51
Figura 22. Momentos en paño tipo 3. .......................................................................................51
Figura 23. Columnas de pórticos a diseñar de la estructura. .....................................................54
Figura 24. Diagrama de interacción para las columnas a diseñar. Fuente: American Concrete
Institute. .....................................................................................................................................55
Figura 25. Ubicación aproximada de Kn y Rn en el diagrama de interacción. ...........................56
Figura 26. Valor aproximado de Rn. ..........................................................................................57
Figura 27. DCL de la placa predimensionada. ............................................................................62
Figura 28. Muro PX-1 modelada en ETABS. ...............................................................................64
Figura 29. Diagrama de interacción de la placa PX-1. ................................................................65
Figura 30. Muro PX-2 modelada en ETABS. ...............................................................................66
Figura 31. Diagrama de interacción de la placa PX-2. ................................................................66
Figura 32. Muro con dos paños. Fuente: Apuntes de clases de DAA Udep ..............................78
Figura 33. Cálculo de corte Vu. ..................................................................................................87
Figura 34. Dimensiones de la zapata a calcular. ........................................................................88
Figura 35. Cargas y momentos de columnas y placas. ...............................................................94
5
Lista de Tablas:
Tabla 1. Condición de cimentación. Fuente. Estudio de Mecánica de Suelos. ...........................11
Tabla 2. Parámetros del suelo. Fuente: Estudio de Mecánica de Suelos ....................................12
Tabla 3. Dimensiones de vigas en la estructura..........................................................................15
Tabla 4. Espesor de losas según la Norma E060. ........................................................................15
Tabla 5. Resumen de parámetros sísmicos de la estructura. .....................................................22
Tabla 6. Distribución de las fuerzas en dirección X.....................................................................23
Tabla 7. Distribución de las fuerzas en dirección Y. ....................................................................23
Tabla 8. Desplazamientos máximos permitidos. Fuente: Norma E030......................................24
Tabla 9. Desplazamientos de los entrepisos del edificio en X. ...................................................24
Tabla 10. Desplazamientos de los entrepisos del edificio en Y...................................................24
Tabla 11. Masas participativas de cada modo de vibrar.............................................................26
Tabla 12. Derivas respecto al eje X. ............................................................................................26
Tabla 13. Derivas respecto al eje Y. ............................................................................................27
Tabla 14. Acero mínimo para cada viga. Fuente: Elaboración propia. ........................................29
Tabla 15. Diseño por flexión para vigas ......................................................................................35
Tabla 16. Verificación del diseño por flexión ..............................................................................37
Tabla 17. Diseño por corte para vigas ........................................................................................44
Tabla 18. Cargas axiales en columnas en el primer entrepiso generadas por la envolvente (kg)
...................................................................................................................................................53
Tabla 19. Tipo de diseño de cada elemento ...............................................................................53
Tabla 20. Fuerzas provenientes del análisis en ETABS................................................................55
Tabla 21. Cargas últimas y nominales de la columna. ................................................................55
Tabla 22. Valores Kn y Rn de cada combinación de diseño. .......................................................56
Tabla 23. Resumen de cálculos del diseño de columnas. ...........................................................59
Tabla 24. Refuerzo para columnas. ............................................................................................60
Tabla 25. Dimensiones de las placas. .........................................................................................61
Tabla 26. Cargas en el muro. ......................................................................................................61
Tabla 27. Cargas últimas y nominales. .......................................................................................61
Tabla 28. Puntos que conforman el diagrama de interacción en X. ...........................................64
Tabla 29. Cargas provenientes del análisis en ETBAS. ................................................................65
Tabla 30. Cargas últimas y nominales. .......................................................................................65
Tabla 31. Puntos del diagrama de interacción en X. ...................................................................66
Tabla 32. Parámetros para el cálculo de la resistencia. ..............................................................68
Tabla 33. Metodología de diseño para cada muro. ....................................................................69
Tabla 34. Comprobación del artículo 19.1.b sobre el esfuerzo axial máximo. ...........................70
Tabla 35. Valor de cortante y momento debido a sismo moderado. .........................................71
Tabla 36. Control de fisuración de los muros. ............................................................................72
Tabla 37. Cortante para sismo severo. .......................................................................................73
Tabla 38. Cortante para sismo severo del segundo piso y azotea. .............................................73
Tabla 39. Verificación del comportamiento elástico del edificio. ...............................................74
Tabla 40. Cálculo del factor de amplificación. ............................................................................75
Tabla 41. Fuerza cortante y momento por sismo severo. ..........................................................75
Tabla 42. Verificación del refuerzo horizontal en los muros. .....................................................76
Tabla 43. Verificación del agrietamiento diagonal en los pisos superiores. ...............................77
Tabla 44. Fuerzas internas en columnas de confinamiento. Fuente: Norma Técnica E.070
Albañilería ..................................................................................................................................77
6
Tabla 45. Datos para el cálculo de las fuerzas internas en las columnas de confinamiento. ......78
Tabla 46. Fuerzas internas en las columnas de confinamiento. .................................................78
Tabla 47. Datos para el diseño por compresión. ........................................................................79
Tabla 48. Datos para el diseño por corte fricción. ......................................................................80
Tabla 49. Cálculo de la sección de concreto por compresión y corte fricción. ...........................80
Tabla 50. Datos para el cálculo del refuerzo vertical en las columnas de confinamiento. .........81
Tabla 51. Cálculo del acero para las columnas de confinamiento. .............................................82
Tabla 52. Datos obtenidos del software ETABS sobre la columna C4 .......................................84
Tabla 53. Cargas y momentos de servicio ..................................................................................84
Tabla 54. Área de zapata para todas las combinaciones de servicio ..........................................85
Tabla 55. Verificación de las presiones en el suelo ....................................................................86
Tabla 56. Cargas y momentos de diseño ....................................................................................86
Tabla 57. Calculo de las presiones en el suelo............................................................................87
Tabla 58. Datos obtenidos del ETABS sobre la columna C1 ........................................................91
Tabla 59. Cargas y momentos de servicio ..................................................................................91
Tabla 60. Datos obtenidos del ETABS sobre la placa PX-2 ..........................................................92
Tabla 61. Cargas y momentos de servicio ..................................................................................92
Tabla 62. Área de zapata para todas las combinaciones de servicio ..........................................93
Tabla 63. Área de zapata para todas las combinaciones de servicio ..........................................93
Tabla 64. Cargas, reacciones y momentos de servicio ...............................................................94
Tabla 65. Verificación de presiones en el suelo ..........................................................................95
Tabla 66. Cargas, reacciones y momentos de diseño .................................................................96
Tabla 67. Calculo del qu de diseño .............................................................................................96
Tabla 68. Mu para todas las combinaciones de diseño ..............................................................98
Tabla 69. Datos obtenidos del software ETABS sobre el muro Y1 ............................................100
Tabla 70. Cargas y momentos de servicio ................................................................................100
Tabla 71. Área de zapata para todas las combinaciones de servicio ........................................101
Tabla 72. Verificación de presiones en suelo ...........................................................................102
Tabla 73.Cargas y momentos de diseño ...................................................................................102
Tabla 74. Calculo del qu de diseño ...........................................................................................103
7
Introducción
El diseño estructural de la edificación unifamiliar que se realizará en el
presente trabajo, permitirá tener una vivienda segura y sismorresistente de concreto
armado la cual servirá para evitar fallas parciales o totales de los elementos
estructurales ante un evento sísmico.
Realizar el diseño estructural de la vivienda unifamiliar de acuerdo a las
normativas peruanas es de suma importancia teniendo en cuenta que las
construcciones de viviendas informales, según la Cámara Peruana de la
construcción, CAPECO, representan alrededor del 80% a nivel nacional, es decir, de
cada 10 viviendas que se construyen en el Perú 8 son informales y son vulnerables
ante cualquier evento sísmico de alta intensidad.
Además, el Perú se encuentra ubicado en lo que se conoce como “El cinturón
de fuego del Pacífico”, lo que supone que el país se encuentra en territorio con
constantes movimientos sísmicos, muchos de ellos han sido de regular intensidad
habiendo causado pérdidas materiales y de vidas humanas.
Un sismo de regular intensidad como el que se produjo en Pisco en el año
2007 puso al descubierto los errores que se cometen cuando se construye una
edificación, sobre todo resaltando la informalidad y el poco criterio en que han sido
diseñadas aun cuando existen normas de construcción nacionales.
El diseño estructural de la edificación nos permitirá tener información
valiosa sobre la construcción, esto es, sobre los elementos estructurales: vigas,
columnas; así como el de los cimientos.
Por lo que realizar un diseño estructural de la edificación y construir de
manera segura y con los materiales de construcción adecuadas permitirá proteger a
la edificación y a las personas que vivan en ella, además de predecir el
comportamiento de la estructura cuando se es sometido a diferentes cargas
dinámicas.
8
Capítulo 1
Generalidades
1.1. Arquitectura del edificio
La arquitectura brindada en los planos de la edificación muestra que está destinada a
una vivienda unifamiliar de 3 niveles más azotea. El primer nivel de la edificación está
destinada a locales comerciales y un estacionamiento, mientras que el segundo y tercer
nivel serán destinados a habitaciones; la edificación también cuenta con una azotea.
La altura total de la vivienda es de 10.65m a nivel de techo terminado y de 11.55m
incluyendo un parapeto de 0.90m desde el nivel de techo terminado en la azotea.
Además, se tendrá en cuenta los niveles de piso terminado para saber la altura de cada
nivel tal y como mandan en los planos entregados.
El área total del terreno a construir es de 163 m2, teniendo un área techada de 274.21
m2 y un área libre de 31.9 m2. La geometría de la vivienda es asimétrica e irregular en
ambos sentidos por lo que se considerará esto en el diseño estructural, además presenta
muros altos y muros bajos presentes en la azotea.
Figura 1. Vista en elevación de la edificación.
Fuente: AutoCAD
9
Figura 2. Plano en planta del primer piso de la edificación.
Fuente: AutoCAD
1.2. Estudio de mecánica de suelos
Se ha brindado el estudio de mecánica de suelos del terreno en donde se construirá la
edificación. Los datos obtenidos del EMS serán necesarios para poder realizar el
análisis sísmico de la estructura además de dar información acerca de las propiedades
del suelo, importantes para dimensionar las cimentaciones.
En la fig 3 se muestra el perfil estratigráfico del suelo analizado, caracterizado por la
presencia de arcilla limo arenosa de baja plasticidad.
10
Figura 3. Perfil estratigráfico del suelo.
Fuente: Estudio de Mecánica de Suelos
El terreno es heterogéneo a la profundidad estudiada, encontrándose arcillo limo
arenoso (CM-ML), en donde ese apoyara la cimentación superficial; también se
encontró material de relleno (orgánico y/o basura) el cual de debe ser eliminado en su
totalidad, de ninguna manera de cimentara sobre material orgánico.
No se encontró además nivel freático en la exploración por lo cual, el terreno no
presentará condiciones para una posible licuación, además el suelo no presenta cloruros
ni sulfatos que puedan llegar a perjudicar las cimentaciones.
La tabla 1 muestra las condiciones para las cimentaciones, siendo estas recomendadas
por el EMS pudiéndose verificar y/o modificar de acuerdo a un diseño de
cimentaciones.
Tabla 1. Condición de cimentación.
Fuente. Estudio de Mecánica de Suelos.
Condiciones de la cimentación
Tipo de cimentación
Cimentación
superficial/zapatas aisladas
Profundidad min. de cimentación
Dimensión utilizada (B)
Capacidad portante neta admisible
Factor de seguridad
0.80 m
1.50 m
1.22 kg/m2
3
La tabla 2 representa los parámetros de efectos de sismo necesarios para poder
desarrollar el diseño estructural de la edificación.
11
Tabla 2. Parámetros del suelo.
Fuente: Estudio de Mecánica de Suelos
Parámetros
Tipo de suelo
Periodo de plataforma (Tp)
Periodo de cambio de curvatura
(Tl)
Factor de zona (Z)
Factor de amplificación sísmica
Valor
S1
0.4
2.5
0.45
1
1.3. Reglamentos, cargas de diseño y materiales empleados
Para el análisis y diseño de la edificación se han empleado las normas presentes en el
Reglamento nacional de Edificaciones (RNE).
Norma E 0.20
Para el análisis y diseño de la vivienda, de acuerdo a la norma, la edificación deberá ser
capaz de resistir las cargas que le impongan como consecuencia del uso de la
edificación. Estas cargas actuaran con las combinaciones dadas por esta norma, de
modo que no excedan en las deflexiones ni deformaciones permitidas.
Las cargas que actuaran en las edificaciones son las indicadas en la norma:
Carga muerta: Esta carga comprende, según la norma, el peso propio de los materiales
que conforman los elementos estructurales y los que deberá soportar la edificación
Carga viva: Son aquellas cargas presentes en la edificación dada por su uso y la
ocupación de la misma, estas cargas son temporales, varían de acuerdo a su intensidad y
cambian en cuanto a su ubicación.
Cargas sísmicas: Son las cargas actuantes lateralmente a la edificación, producidas por
la acción de un sismo en ambas direcciones.
Norma E 0.30
Se empleará la norma para especificar las solicitaciones sísmicas y los requisitos
mínimos de configuración, rigidez y resistencia que debe tener una edificación ante la
acción de un sismo.
Norma E 0.50
De acuerda a la norma, se empleará para realizar los estudios de mecánica de suelos con
el fin de conocer y obtener los datos para el diseño de las cimentaciones para de esta
manera asegurar la estabilización de la edificación
Norma E 060
La norma indica los requisitos y exigencias mínimas que se deben realizar para el
análisis, el diseño de los materiales, de los elementos estructurales de concreto armado.
Norma E 070
12
La norma establece los requisitos mínimos para el diseño, los materiales, la
construcción en edificaciones de albañilería estructuradas principalmente por muros
confinados y muros armados.
Marco teórico de diseño
El diseño estructural que se llevará a cabo en la edificación, se hará de acuerdo a las
normas, conceptos de libros y/o tesis. Los conceptos que se abordarán para el
dimensionamiento y el funcionamiento de los elementos estructurales son los
siguientes:
-
Diseño por flexión
Diseño por capacidad
Diseño por corte
Control de deflexiones
Detalles de los refuerzos
13
Capítulo 2
Estructuración y Predimensionamiento
2.1.Estructuración
El primer paso al estructurar el edificio fue definir el tipo de sistema estructural del
mismo. Para ellos, se usó el criterio de densidad de muros en ambas direcciones de la
edificación: presente en la Norma E070:
∑ 𝐿. 𝑡 𝑍. 𝑈. 𝑆. 𝑁
=
𝐴. 𝑝
56
En la dirección X:
9.15𝑥0.13 0.45𝑥1𝑥1𝑥4
≥
99.16
56
0.119 ≥ 0.032 … … … 𝑁𝑜 𝑐𝑢𝑚𝑝𝑙𝑒
En la dirección Y:
27.67𝑥0.13 0.45𝑥1𝑥1𝑥4
≥
99.16
56
0.036 ≥ 0.032 … … … 𝐶𝑢𝑚𝑝𝑙𝑒
Entonces, en la dirección X se usará un sistema a base de elementos de concreto
(pórticos o muros), mientras que en la dirección Y se puede usar un sistema basado en
muros portantes. Por lo tanto, la estructura tendrá 2 configuraciones diferentes.
Debido a que en la dirección X los muros portantes serían insuficientes, fue conveniente
usar muros de corte en algunos muros horizontales con el objetivo de aumentar la
rigidez lateral sin aumentar los efectos torsionales en el caso de un eventual sismo.
Por último, las losas serán unidireccionales en la dirección X, dado que transmitirán las
cargas a los muros portantes.
2.2.Predimensionamiento de elementos estructurales
Se buscó que los elementos estructurales no tengan un gran impacto en la arquitectura,
pero respetando los requerimientos mínimos establecidos en el reglamento. Cabe
destacar que las dimensiones expuestas no son definitivas, sino que irán variando según
lo requiera la edificación.
2.2.1. Columnas
Las dimensiones iniciales de las columnas se estimaron de acuerdo a su función o
posición. Por ejemplo, estas cambiaban de acuerdo a si eran de amarre o pertenecientes
a un pórtico.
Para las columnas de pórticos, se optó por trabajar con una única sección de 30x30cm
para hacer uso de diagramas de interacción estandarizados.
14
2.2.2. Vigas
En el caso de las vigas, se predimensionaron de dos tipos de acuerdo al sistema
estructural al que pertenecían.
Para las vigas en el eje X, pertenecientes a pórticos, el peralte se determinó según las
indicaciones de la Norma E060.
Para vigas simplemente apoyadas:
ℎ=
𝐿
16
Por lo que se calculó el peralte con la mayor dimensión de luz libre en el plano:
ℎ=
420
= 26.25 𝑐𝑚
16
ℎ ≈ 30 𝑐𝑚
Por otra parte, en el caso de las vigas soleras del eje Y, se optó por un peralte de 20 cm
debido a que se apoya sobre un muro portante.
Por último, para los voladizos se optó por usar vigas peraltadas de 40 cm.
El ancho de todas las vigas se predimensionó como 20 cm.
Tabla 3. Dimensiones de vigas en la estructura.
Dimensiones de vigas
Vigas Chatas: 30 cm x 20
cm
Vigas Peraltadas: 20 cm x
40 cm
2.2.3. Losas aligeradas
El espesor de las losas aligeradas se dimensionó utilizando la siguiente tabla,
perteneciente a la Norma E060:
Tabla 4. Espesor de losas según la Norma E060.
Luz (m)
L < 4.0 m
4.0 m < L < 5.5 m
5.0 m < L < 6.0 m
6.0 m < L < 7.5 m
Peralte (cm)
17
20
25
30
De igual forma que con las vigas de los pórticos, la mayor luz libre es 4.20 m, por lo
que se asignó un peralte de losa de 20 cm.
2.2.4. Muros de corte
Para estos elementos, el espesor de los muros de corte se dimensionó a criterio de los
diseñadores al analizar la planta de la edificación, siendo en este caso 30 cm.
15
16
Capítulo 3
Simulación estructural en ETABS
Para el modelado de la estructura se optó por usar el software ETABS. Dentro de las
ventajas que ofrece este programa, está la facilidad para replicar estructura de la
edificación y la información que brinda al realizar la simulación de cargar y sismos, lo
cual ayuda al diseñador a modificar los elementos estructurales hasta que se cumplan las
solicitudes requeridas.
Para el presente trabajo, se definieron los siguientes materiales:
Concreto:
•
Resistencia a la compresión (f’c) = 210 kg/cm2
•
Módulo de elasticidad (Ec)= 219499.64 Kg/m2
•
Módulo de corte (G)= 954.35 kgf/mm2
•
Módulo de Poisson (ν)= 0.15
Acero de refuerzo:
•
Módulo de elasticidad (Es) = 2x10^6 kg/cm2
•
Fluencia del refuerzo (fy) = 4200kg/cm2
Albañilería:
•
Módulo de elasticidad (E) = 500*f’m=500*65 = 32500 kg/cm2
•
Módulo de Poisson = 0.15
Como ya se mencionó, el edificio tiene dos configuraciones, por lo que el edificio fue
simulado en la dirección Y creando muros con el material de albañilería, mientras en
que en la dirección X se simularon los pórticos correspondientes mediante vigas y
columnas.
De igual forma que con los muros, las placas de concreto también fueron modeladas en
algunos de los muros de la dirección X.
Por último, se modelaron las losas correspondientes mediante áreas de espesor casi 0 y
asignándoles su peso propio, para que transmitan estas cargas a los demás elementos de
la edificación.
Las alturas de entrepisos son 2.78m para el primer piso y 2.63m para el resto de niveles,
incluyendo azotea.
Entre otras consideraciones del edificio se tiene:
•
Las combinaciones de cargas son las indicadas en la Norma E030.
17
•
El peso de la edificación también se considera según la Norma E030,
adicionándole el 25% de la carga viva. Esto se simuló en la opción Mass Source
del software.
•
Cada entrepiso se comporta como un diafragma rígido con el objetivo de
integrar todos los elementos como uno al desplazarse cada entrepiso ante la
acción de fuerzas horizontales.
•
Todos los apoyos den la base del edificio se consideran como empotrados.
El modelo resultante del edificio es el siguiente:
Figura 4. Vista en 3D del modelo de la edifiación.
Fuente: ETABS
18
Figura 5. Vista en planta del primer techo de la edificación.
Fuente: ETABS
19
Figura 6. Vista en elevación del eje 2 de la edificación.
Fuente: ETABS
Como se puede observar de la vista en elevación, si bien existen muros que no son
existentes en toda la altura del edificio, se han considerado en los entrepisos
correspondientes ya que estos aportan rigidez en los primeros pisos de la edificación.
20
Capítulo 4
Análisis Sísmico
Se realizará el análisis y diseño estructural según la norma vigente E 030 del
Reglamento Nacional de Edificaciones de una vivienda unifamiliar de 3 niveles más una
azotea. Teniendo en cuenta que la edificación se realizará en la ciudad de Piura, ubicada
en una zona altamente sísmica, se requiere que la estructura del edificio este orientado a
conseguir un buen desempeño ante acciones sísmicas por lo que se busca que la
estructuración cumpla con los requisitos exigidos por la norma.
4.1. Análisis
Considerando las condiciones del suelo, las características de la estructura y su uso, se
han utilizado los siguientes parámetros sísmicos
-
Facto de zona: La edificación se encuentra ubicado en la ciudad de Piura, según
el mapa de la zona sísmica, se encuentra en la zona 4, por lo tanto, Z:0.45
-
Factor U: De acuerdo a la tabla N°5 de la norma, la edificación pertenece a la
categoría de edificaciones comunes: viviendas. Por lo que le corresponde un
factor U=1
-
Factor del suelo S: Se tiene un perfil de suelo S1, con un factor de suelo de S=1,
además de Tp= 0.4 y Tl=2.5
-
Factor de amplificación sísmica C
El factor de amplificación sísmica viene dado por las siguientes expresiones, de
acuerdo al periodo fundamental de vibración
Calculo del periodo fundamental de vibración:
𝑇=
ℎ𝑛
𝐶𝑡
Donde:
ℎ𝑛 = 𝐴𝑙𝑡𝑢𝑟𝑎 𝑡𝑜𝑡𝑎𝑙 𝑑𝑒𝑙 𝑒𝑑𝑖𝑓𝑖𝑐𝑖𝑜 = 10.67𝑚
𝐶𝑡
= 𝐷𝑒 𝑎𝑐𝑢𝑒𝑟𝑑𝑜 𝑎 𝑙𝑎𝑠 𝑐𝑎𝑟𝑎𝑐𝑡𝑒𝑟𝑖𝑠𝑡𝑖𝑐𝑎𝑠 𝑑𝑒 𝑙𝑎 𝑒𝑑𝑖𝑓𝑖𝑐𝑎𝑐𝑖ó𝑛 𝑒𝑛 𝑎𝑛á𝑙𝑖𝑠𝑖𝑠, 𝑠𝑒 𝑐𝑢𝑚𝑝𝑙𝑒 𝑞𝑢𝑒 𝑑𝑒 𝑎𝑐𝑢𝑒𝑟𝑑𝑜 𝑎 𝑙𝑎 𝑛𝑜𝑟𝑚𝑎 𝐶𝑡
= 60
Por lo tanto
𝑇=
10.67
= 0.1778
60
De acuerdo a los valores de Tp y Tl, tenemos que
𝑇 < 𝑇𝑝
Por lo que según el cap. 14 de la norma, C=2.5
21
-
Factor básico de reducción sísmica
Factor definido según el sistema estructural en ambas direcciones.
En la dirección X, se comprobó que las placas de concreto absorbían más del
70% de la cortante de la edificación, por lo que definió como un sistema de
muros estructurales con un valor de reducción de Ro=6.
En la dirección Y, le corresponde un valor de Ro=3 al ser un sistema de
albañilería confinada.
-
Coeficiente de reducción sísmica
𝑅 = 𝑅𝑜 ∗ 𝐼𝑎 ∗ 𝐼𝑝
Se tiene que la estructura es regular en altura, mientras que tiene irregularidad
torsional en planta, por lo que Ia=1 y Ip=0.75.
Por lo tanto:
En la dirección x, R=4.5
En la dirección y, R=2.25
-
Estimación del peso (P)
La edificación se encuentra en la categoría C según la clasificación de la norma
por lo que la estimación del peso se hará con una participación de 25% de la
carga viva. El modelo Etabs nos da el resultado del peso del edificio
𝑃 = 328.07 𝑡𝑜𝑛𝑓
En la siguiente tabla se muestra los parámetros obtenidos:
Tabla 5. Resumen de parámetros sísmicos de la estructura.
Parámetros sísmicos
Z
0.45
U
1
C
2.5
S
1
Rox
6
Roy
3
Iax=Iay
1
Ipx=IpY
0.75
Rx
4.5
Ry
2.25
4.1.1 Fuerza cortante en la base
Para determinar la fuerza cortante actuando será como se indica en la norma:
𝑉=
𝑍∗𝑈∗𝐶∗𝑆
∗𝑃
𝑅
22
En la dirección X:
𝑉=
0.45𝑥1𝑥2.5𝑥1
𝑥328.07 = 61.51 𝑡𝑜𝑛𝑓
6
En la dirección Y:
𝑉=
0.45𝑥1𝑥2.5𝑥1
𝑥 328.07 = 123.03 𝑡𝑜𝑛𝑓
3
Distribución de la fuerza por pisos
La norma nos brinda una formulación para hallar las fuerzas sísmicas en cada piso:
𝐹𝑖 = 𝛼𝑖 ∗ 𝑉
Pi(hi)k
Donde αi = ∑n
j=1 pj (hj )
k
, donde n indica en el número de pisos de la edificación y k tiene
el valor de 1 puesto que T es menor a 0.5
Tabla 6. Distribución de las fuerzas en dirección X.
N° pisos
1
2
3
Pi (tonf)
328.07
328.07
328.07
hi
2.78
2.63
2.63
K Pi*(hi^K)
1
912.03
1
862.82
1
862.82
Pi*hi
912.03
862.82
862.82
2637.68
Alfa
0.346
0.327
0.327
Fi
18.233
17.249
17.249
Alfa
0.346
0.327
0.327
Fi
18.233
17.249
17.249
Tabla 7. Distribución de las fuerzas en dirección Y.
N° pisos
1
2
3
Pi (tonf)
328.07
328.07
328.07
hi
2.78
2.63
2.63
K
1
1
1
Pi*(hi^K)
912.03
862.82
862.82
Pi*hi
912.03
862.82
862.82
2637.68
Para el análisis estático, se analizará la estructura de acuerdo a las cargas aplicadas en el
centro de masa de la estructura.
Se debe comprobar que la estructura en análisis cumpla con los máximos
desplazamientos según en el material predominante en la estructura.
23
De acuerdo a la norma, estos máximos desplazamientos de acuerdo al material son los
siguientes:
Tabla 8. Desplazamientos máximos permitidos.
Fuente: Norma E030.
Material predominante
(∆i/hi)
Concreto armado
Acero
Albañilería
Madera
0.007
0.001
0.005
0.001
Edificios de concreto armada
con muros de ductilidad
limitada
0.005
Para la edificación en análisis se puede observar que en la dirección X predomina
estructuras de concreto armado por lo que la distorsión máxima es de 0.007, mientras
que en la dirección Y se observan muros de albañilería predominante por lo que su
distorsión máxima es de 0.005.
Tabla 9. Desplazamientos de los entrepisos del edificio en X.
Nivel
Base
Techo Primer Nivel
Techo Segundo Nivel
Techo Tercer Nivel
Techo de azotea
Desplazamiento absoluto
m
0.0000
0.0010
0.0029
0.0049
0.0064
Dirección X
ΔX
H entrepiso Deriva elástica Deriva inelástica
ΔX/h o ΔY/h *0.75*6
0.0000
0.0000
0.0000
0.0000
0.0010
2.7800
0.0004
0.0016
0.0019
2.6300
0.0007
0.0032
0.0020
2.6300
0.0007
0.0034
0.0015
2.6300
0.0006
0.0026
cumple?
<0.007
SI
SI
SI
SI
SI
Tabla 10. Desplazamientos de los entrepisos del edificio en Y.
Nivel
Base
Techo Primer Nivel
Techo Segundo Nivel
Techo Tercer Nivel
Techo de azotea
Desplazamiento absoluto
m
0.0000
0.0005
0.0010
0.0013
0.0015
Dirección Y
ΔY
H entrepiso deriv elastica deriva inelastica
ΔX/h o ΔY/h *0.75*3
0.0000
0.0000
0.0000
0.0000
0.0005
2.7800
0.0002
0.0004
0.0005
2.6300
0.0002
0.0004
0.0004
2.6300
0.0001
0.0003
0.0001
2.6300
0.0001
0.0001
cumple?
<0.005
SI
SI
SI
SI
SI
4.2. Análisis dinámico
Este análisis permite conocer el comportamiento de la estructura cuando se sometido a
un movimiento representado por un espectro de respuesta en su base.
4.2.1 Aceleración espectral
Para cada dirección en análisis se ha utilizado un espectro de inelástico de pseudoaceleraciones dado por:
24
𝑆𝑎 =
𝑍𝑥𝑈𝑥𝐶𝑥𝑆
𝑥𝑔
𝑅
Mediante el uso de ETABS, se halla los gráficos de la aceleración espectral
Figura 7. Aceleración espectral en el eje X.
Figura 8. Aceleración espectral en el eje Y.
4.2.2 Modos de vibración
La norma considera que en cada dirección se deben considerar aquellos modos de
vibración, cuyas masas efectivas sean por lo menos el 90% de la masa total, pero se
toma en cuenta por lo menos los 3 primeros modos predominantes en cada dirección en
análisis.
25
Tabla 11. Masas participativas de cada modo de vibrar.
Modo
1
2
3
4
5
6
7
8
9
10
11
12
Periodo (s)
0.201
0.107
0.073
0.06
0.058
0.054
0.05
0.043
0.041
0.039
0.039
0.037
Masa participante
en X
0.6824
0.0688
0.0004
0.0192
0.0419
0.0888
0.0012
0.0008
0.0013
0.0127
0.012
0.000002802
Masa participante
en Y
0.0188
0.124
0.6895
0.0017
0.0001
0.0001
0
0.0008
0.000002534
0.0119
0.004
0.00004506
90.37
97.81
%masa
participante
Se tomará los periodos en donde la participación de masa sea mayor puesto que estos
modos al que corresponden estos modos serán los que describan el comportamiento de
la estructura.
𝑃𝑎𝑟𝑎 𝑙𝑎 𝑑𝑖𝑟𝑒𝑐𝑐𝑖ó𝑛 𝑋 = 0.201𝑠, 0.107𝑠, 0.054𝑠
𝑃𝑎𝑟𝑎 𝑙𝑎 𝑑𝑖𝑟𝑒𝑐𝑐𝑖ó𝑛 𝑌 = 0.201𝑠, 0.107𝑠, 0.073𝑠
4.2.3 Derivas
Para el control de derivas, se ha realizado parecido al obtenido por el control de
distorsiones del análisis estático.
Tabla 12. Derivas respecto al eje X.
Nivel
Base
Pimer piso
Segundo piso
Tercer piso
Azotea
Desplazamiento absoluto
m
0.0000
0.0012
0.0036
0.0062
0.0091
Dirección X
H entrepiso Deriva elástica Deriva inelástica
ΔX/h o ΔY/h *0.75*6
0.0000
0.0000
0.0000
0.0000
0.0012
2.7800
0.0004
0.0020
0.0024
2.6300
0.0009
0.0040
0.0026
2.6300
0.0010
0.0044
0.0030
2.6300
0.0011
0.0051
ΔX
26
cumple?
<0.007
SI
SI
SI
SI
SI
Tabla 13. Derivas respecto al eje Y.
Nivel
base
primer piso
segundo piso
tercer piso
azotea
Desplazamiento absoluto
m
0.0000
0.0004
0.0008
0.0012
0.0024
Dirección Y
H entrepiso deriv elastica deriva inelastica
ΔX/h o ΔY/h *0.75*3
0.0000
0.0000
0.0000
0.0000
0.0004
2.7800
0.0002
0.0003
0.0004
2.6300
0.0002
0.0003
0.0004
2.6300
0.0001
0.0003
0.0012
2.6300
0.0005
0.0010
ΔY
27
cumple?
<0.005
SI
SI
SI
SI
SI
Capítulo 5
Diseño de Vigas
5.1. Generalidades
Para este capítulo se realizarán los procesos de diseño de vigas de concreto armado para
las distintas vigas que se encuentran en la estructura, basándonos en los criterios
estipulados en la Norma E.060.
Debido a que la estructura se encuentra expuesto a cargas de sismo, se consideraran los
siguientes puntos para el diseño de una viga:
Diseño por flexión y verificación por capacidad.
Diseño por corte: obtener DFC por capacidad, amplificación sísmica y
resistencia.
Vigas de la estructura:
En la modelación de la estructura en el software ETABS, se han descrito 2 tipos de
vigas distintas según su peralte:
Vigas Peraltadas 20x40 cm
Vigas Chatas 30x20 cm
Se deberá calcular el área de acero mínimo necesario para los distintos tipos de viga,
para eso se tomará en cuenta los siguientes datos:
𝑓’𝑐 = 210 𝑘𝑔/𝑐𝑚2 ) Resistencia a la compresión del concreto
𝑓𝑦 = 4200 𝑘𝑔/𝑐𝑚2 Resistencia de fluencia del acero
Se procederán a aplicar las ecuaciones para el siguiente ejemplo de viga:
Viga 20x40 cm:
Primero se calcula la Inercia bruta de la viga:
𝑏 = 20 𝑐𝑚
ℎ = 40 𝑐𝑚
𝑦𝑡 =
𝐼𝑔 =
40
= 40 𝑐𝑚
2
20𝑥403
= 10 667 𝑐𝑚4
12
Con el dato de la Inercia bruta se calcula el momento de fisuración (𝑀𝑐𝑟 ):
28
𝑀𝑐𝑟 =
𝑓𝑟. 𝐼𝑔 2√210𝑥10 667
=
= 154 575 𝑘𝑔. 𝑐𝑚
𝑌𝑡
10
Según la Norma Peruana, se exige que el acero mínimo de cualquier sección en
flexión debe garantizar que la resistencia de la sección fisurada sea por lo menos
1,2 veces el momento flector causante del agrietamiento en la sección:
𝑀𝑢 = 1.2𝑀𝑐𝑟 = 1.2𝑥154 575 = 185 490 𝑘𝑔. 𝑐𝑚
Se calcula el Ku para ingresar a las tablas de Diseño en Flexión y obtener la
cuantía (𝜌)
𝑘𝑢 =
𝑀𝑢
185 490
=
= 8.02 𝑘𝑔/𝑐𝑚2
2
𝑏. 𝑑
20𝑥342
𝜌𝑚𝑖𝑛 = 0.218%
As𝑚𝑖𝑛 = ρ𝑚𝑖𝑛 𝑏𝑑 = 0.218%𝑥20𝑥34 = 1.48 𝑐𝑚2
Se aplicará el mismo procedimiento para las vigas chatas 30x20 cm. A continuación, se
muestra la tabla donde se encuentran los datos de las vigas y el acero mínimo necesario
para cada uno:
Tabla 14. Acero mínimo para cada viga. Fuente: Elaboración propia.
UND
b
h
cm
cm
d
cm
yt
Ig=bh³/12
f'c
𝑓𝑟 = 2 𝑓 𝐶
fy
𝑓𝑟𝐼𝑔
𝑀 𝑟=
𝑦𝑡
Mu=1.2Mcr
𝑘𝑢 =
𝑀𝑢
𝑏𝑑 2
pmín
Asmín=pmín*b*d
cm
cm4
kg/cm2
kg/cm2
kg/cm2
Vigas
VCH30x20
VP20x40
30
20
20
40
14
34
11
31
10
20
20000
106667
210
210
29
29
4200
4200
kg.cm
57966
154575
kg.cm
69559
185490
kg/cm2
11.83
8.02
%
cm2
0.325%
1.37
0.218%
1.48
5.2. Diseño por flexión:
El diseño de una viga por flexión se realiza teniendo en cuenta lo estipulado en la norma
E.060. Partiremos de la envolvente del Diagrama Momento Flector, obtenidos del
software ETABS, para calcular el área de acero necesario en las vigas.
29
Se calculará el área de acero necesaria para una viga peraltada de 20x40cm ubicada en
el eje C y entre los ejes 1 y 2. Esta viga se encuentra en el primer piso y está orientada
en la dirección X.
Viga peraltada 20x40 cm:
En la siguiente imagen se muestra la envolvente del DMF de la viga en estudio:
Figura 9. Momentos debido a la envolvente.
A continuación, se calculará el acero negativo y positivo en los extremos y en el centro
de la viga.
Datos de la viga 20x40 cm:
b=20 cm
d(1 capa)=h-6=34 cm
Extremo Izquierdo:
𝑀𝑢 (−) = 730 𝑘𝑔 − 𝑚
𝐾𝑢 = 3.16
𝑘𝑔
𝑐𝑚2
𝜌 = 0.08%
𝐴𝑠 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑑𝑜 =
0.08
𝑥20𝑥34 = 0.57 𝑐𝑚2
100
Se verifica que cumpla con el As min:
0.57 𝑐𝑚2 > 1.48 𝑐𝑚2 … 𝑁𝑂 𝐶𝑈𝑀𝑃𝐿𝐸
𝐴𝑠 = 1.48 𝑐𝑚2
𝑉𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 2 Ø1/2"
𝐴𝑠 𝑐𝑜𝑙𝑜𝑐𝑎𝑑𝑜 = 2.58 𝑐𝑚2
𝑀𝑢 (+) = 86 𝑘𝑔 − 𝑚
30
𝐾𝑢 = 0.37
𝑘𝑔
𝑐𝑚2
𝜌 = 0.01%
𝐴𝑠 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑑𝑜 =
0.01
𝑥20𝑥34 = 0.07 𝑐𝑚2
100
Se verifica que cumpla con el As min:
0.07 𝑐𝑚2 > 1.48 𝑐𝑚2 … 𝑁𝑂 𝐶𝑈𝑀𝑃𝐿𝐸
𝐴𝑠 = 1.48 𝑐𝑚2
𝑉𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 2 Ø1/2"
𝐴𝑠 𝑐𝑜𝑙𝑜𝑐𝑎𝑑𝑜 = 2.58 𝑐𝑚2
En la siguiente imagen se visualiza como queda la sección transversal del
extremo izquierdo de la viga.
Figura 10. Sección transversal de la viga en el extremo izquierdo.
Centro:
𝑀𝑢 (−) = 504 𝑘𝑔 − 𝑚
𝐾𝑢 = 2.18
31
𝑘𝑔
𝑐𝑚2
𝜌 = 0.06%
𝐴𝑠 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑑𝑜 =
0.06
𝑥20𝑥34 = 0.40 𝑐𝑚2
100
Se verifica que cumpla con el As min:
0.40 𝑐𝑚2 > 1.48 𝑐𝑚2 … 𝑁𝑂 𝐶𝑈𝑀𝑃𝐿𝐸
𝐴𝑠 = 1.48 𝑐𝑚2
𝑉𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 2 Ø1/2" Para dar continuidad a los extremos de la viga
𝐴𝑠 𝑐𝑜𝑙𝑜𝑐𝑎𝑑𝑜 = 2.58 𝑐𝑚2
𝑀𝑢 (+) = 975 𝑘𝑔 − 𝑚
𝐾𝑢 = 4.22
𝑘𝑔
𝑐𝑚2
𝜌 = 0.11%
𝐴𝑠 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑑𝑜 =
0.11
𝑥20𝑥34 = 0.77 𝑐𝑚2
100
Se verifica que cumpla con el As min:
0.77 𝑐𝑚2 > 1.48 𝑐𝑚2 … 𝑁𝑂 𝐶𝑈𝑀𝑃𝐿𝐸
𝐴𝑠 = 1.48 𝑐𝑚2
𝑉𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 2 Ø1/2" Para dar continuidad a los extremos de la viga
𝐴𝑠 𝑐𝑜𝑙𝑜𝑐𝑎𝑑𝑜 = 2.58 𝑐𝑚2
En la siguiente imagen se visualiza como queda la sección transversal del centro
de la viga.
32
Figura 11. Sección transversal de la viga en el centro.
Extremo Derecho:
𝑀𝑢 (−) = 189701 𝑘𝑔 − 𝑚
𝐾𝑢 = 8.21
𝑘𝑔
𝑐𝑚2
𝜌 = 0.22%
𝐴𝑠 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑑𝑜 =
0.22
𝑥20𝑥34 = 1.52 𝑐𝑚2
100
Se verifica que cumpla con el As min:
1.52 𝑐𝑚2 > 1.48 𝑐𝑚2 … 𝐶𝑈𝑀𝑃𝐿𝐸
𝐴𝑠 = 1.52 𝑐𝑚2
𝑉𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 2 Ø1/2"
𝐴𝑠 𝑐𝑜𝑙𝑜𝑐𝑎𝑑𝑜 = 2.58 𝑐𝑚2
𝑀𝑢 (+) = 525 𝑘𝑔 − 𝑚
𝐾𝑢 = 2.27
𝑘𝑔
𝑐𝑚2
𝜌 = 0.06%
33
𝐴𝑠 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑑𝑜 =
0.06
𝑥20𝑥34 = 0.41 𝑐𝑚2
100
Se verifica que cumpla con el As min:
0.41 𝑐𝑚2 > 1.48 𝑐𝑚2 … 𝑁𝑂 𝐶𝑈𝑀𝑃𝐿𝐸
𝐴𝑠 = 1.48 𝑐𝑚2
𝑉𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 2 Ø1/2"
𝐴𝑠 𝑐𝑜𝑙𝑜𝑐𝑎𝑑𝑜 = 2.58 𝑐𝑚2
En la siguiente imagen se visualiza como queda la sección transversal del
extremo derecho de la viga.
Figura 12. Sección transversal de la viga en el extremo derecho.
Por lo tanto, la viga quedaría distribuida por 2 varillas de Ø1/2" en la parte superior y 2
varillas de Ø1/2" en la parte inferior.
De igual manera que para esta viga de estudio, se realizó el mismo procedimiento para
el resto de las vigas que componen la estructura del proyecto. A continuación, se
presentarán unas tablas con los cálculos del acero necesario para cada viga:
34
Tabla 15. Diseño por flexión para vigas
Vigas peraltadas del piso 1
Ubicación
Eje en el que Entre que ejes
se encuentra se encuentra
Viga
b (cm)
h (cm)
d (cm)
Mu (kg.m)
Izquierda
Eje C
Entre 1 y 2
VP20x40
20
40
34
Centro
Derecha
Izquierda
Eje E
Entre 2 y 3c
VP20x40
20
40
34
Centro
Derecha
Izquierda
Eje F
Entre 1 y 2
VP20x40
20
40
34
Centro
Derecha
Izquierda
Eje G
Entre 1 y 2
VP20x40
20
40
34
Centro
Derecha
Izquierda
Eje G
Entre 2 y 3c
VP20x40
20
40
34
Centro
Derecha
-730.08
86.26
504.61
975.73
-1897.01
-525.05
-1616
-152
598
1113
-1276
61
-191
-109
399
1025
-1324
737
-1568
121
605
1303
-1784
-236
-1081
394
30
161
-802
751
Ku (Kg/cm2)
p (%)
As (cm2)=pbd
3.16
0.37
2.18
4.22
8.21
2.27
6.99
0.66
2.59
4.81
5.52
0.26
0.83
0.47
1.73
4.43
5.73
3.19
6.78
0.52
2.62
5.64
7.72
1.02
4.68
1.70
0.13
0.70
3.47
3.25
0.08%
0.01%
0.06%
0.11%
0.22%
0.06%
0.19%
0.02%
0.07%
0.13%
0.15%
0.01%
0.02%
0.01%
0.05%
0.12%
0.15%
0.09%
0.18%
0.01%
0.07%
0.15%
0.21%
0.03%
0.13%
0.05%
0.00%
0.02%
0.09%
0.09%
0.57
0.07
0.40
0.77
1.52
0.41
1.29
0.12
0.47
0.88
1.01
0.05
0.15
0.08
0.31
0.81
1.05
0.58
1.25
0.09
0.47
1.03
1.42
0.18
0.85
0.31
0.02
0.13
0.63
0.59
Asmín (cm2)
1.48
1.48
1.48
1.48
1.48
As (cm2)
1.48
1.48
1.48
1.48
1.52
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
1.48
35
As colocado
Distribución
(cm2)
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ3/4"
2 φ3/4"
2 φ3/4"
2 φ3/4"
2 φ3/4"
2 φ3/4"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
2 φ1/2"
5.3. Comprobación del Diseño por flexión:
Se calculará los momentos nominales en los extremos y en el centro de la viga, para
comprobar que cumplan con los requerimientos por capacidad establecidos por la norma
E.060.
Evaluaremos para la viga peraltada de 20x40cm con la cual se estuvo trabajando
anteriormente en el diseño por flexión:
La viga en estudio posee 2 varillas de Ø1/2" en la parte superior y 2 varillas de Ø1/2" en
la parte inferior
Primero, se calcula el área de acero colocado:
𝐴𝑠 𝑐𝑜𝑙𝑜𝑐𝑎𝑑𝑜 (2 Ø1/2") = 2.58 𝑐𝑚2
Se procede a calcular los momentos nominales en los extremos y en el centro:
Para 2 Ø1/2":
𝜌=
2.58
= 0.38%
20𝑥34
𝐾𝑢 = 13.72
𝑘𝑔
𝑐𝑚2
𝑀𝑢 = 13.72𝑥20𝑥342 = 316 736 𝑘𝑔. 𝑐𝑚
𝑀𝑛 (−) =
316 736
= 351 929 𝑘𝑔. 𝑐𝑚
0.9
𝑀𝑛 (+) =
316 736
= 351 929 𝑘𝑔. 𝑐𝑚
0.9
Por lo tanto:
𝑀𝑛 𝑚á𝑥 = 351 929 𝑘𝑔. 𝑐𝑚
En los extremos, se comprueba que 𝑀𝑛 (+) ≥ 𝑀𝑛 (−)/3 ∶
351 929 ≥
351929
3
351 929 ≥ 117 310 … 𝐶𝑈𝑀𝑃𝐿𝐸
A lo largo de toda la viga, se comprueba que 𝑀𝑛 ≥ 𝑀𝑛 𝑚𝑎𝑥/4:
36
351 929 ≥ 87 982 … 𝐶𝑈𝑀𝑃𝐿𝐸
De igual manera que para esta viga de estudio, se realizó el mismo procedimiento para el
resto de las vigas que componen la estructura del proyecto. A continuación, se presentarán
unas tablas con la comprobación del diseño por flexión de cada viga:
Tabla 16. Verificación del diseño por flexión
Vigas peraltadas del piso 1
Ubicación
Eje en el
Entre que
que se
ejes se
Viga
As colocado (cm2)
p (%)
Mn (kg.cm)
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
2.58
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
0.38%
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
351929
Izquierda
Eje C
Entre 1 y 2
VP20x40
Centro
Derecha
Izquierda
Eje E
Entre 2 y 3c
VP20x40
Centro
Derecha
Izquierda
Eje F
Entre 1 y 2
VP20x40
Centro
Derecha
Izquierda
Eje G
Entre 1 y 2
VP20x40
Centro
Derecha
Izquierda
Eje G
Entre 2 y 3c
VP20x40
Centro
Derecha
37
Mn-/3
Mn max/4
117310
Extremos de la viga
Largo de la viga
Mn+>Mn-/3
Mn>Mnmax/4
CUMPLE
87982
CUMPLE
117310
CUMPLE
117310
CUMPLE
87982
CUMPLE
117310
CUMPLE
117310
CUMPLE
87982
CUMPLE
117310
CUMPLE
117310
CUMPLE
87982
CUMPLE
117310
CUMPLE
117310
CUMPLE
87982
117310
CUMPLE
CUMPLE
5.4. Diseño por corte:
En el diseño por corte se calcula los estribos y sus espaciamientos a lo largo de la viga
según las fuerzas cortantes que predominen en la estructura. El Vu debe ser el mayor valor
de:
El obtenido por capacidad de flexión de los extremos de la viga
El obtenido de la amplificación de cargas de sismo
El obtenido por resistencia
Se tomará como ejemplo la viga peralta de 20x40 cm con la cual se trabajó anteriormente
en el diseño por flexión:
Por capacidad de flexión:
𝑏 = 20 𝑐𝑚
𝑑 (1𝑐𝑎𝑝𝑎) = 34 𝑐𝑚
2 𝑏𝑎𝑟𝑟𝑎𝑠 𝑑𝑒 𝑎𝑐𝑒𝑟𝑜 𝑑𝑒 Ø1/2"
𝜌=
2.58
= 0.38%
20𝑥34
𝐾𝑢 = 13.72
𝑘𝑔
𝑐𝑚2
𝑀𝑢 = 13.72𝑥20𝑥342 = 316 736 𝑘𝑔. 𝑐𝑚
𝑀𝑛 =
316 736
= 351 929 𝑘𝑔. 𝑐𝑚
0.9
𝑀𝑛 𝑖𝑧𝑞 (−) = 351 929 𝑘𝑔. 𝑐𝑚
𝑀𝑛 𝑖𝑧𝑞 (+) = 351 929 𝑘𝑔. 𝑐𝑚
𝑀𝑛 𝑐𝑒𝑛𝑡𝑟𝑜 (−) = 351 929 𝑘𝑔. 𝑐𝑚
𝑀𝑛 𝑐𝑒𝑛𝑡𝑟𝑜 (+) = 351 929 𝑘𝑔. 𝑐𝑚
𝑀𝑛 𝑑𝑒𝑟 (−) = 351 929 𝑘𝑔. 𝑐𝑚
𝑀𝑛 𝑑𝑒𝑟 (+) = 351 929 𝑘𝑔. 𝑐𝑚
38
Figura 13. Momentos actuantes en la viga.
Se calculará las cortantes en los apoyos izquierdo y derecho, para esto hay que saber que la
VP 20x40cm, que se está estudiando, tiene una luz libre de 4.35 m.
Caso 1:
Sección izquierda
Cortante obtenida de los momentos:
𝑀𝑛 → 𝑉 𝑖𝑧𝑞𝑢𝑖𝑒𝑟𝑑𝑎 =
351 929 + 351 929
= 1 618 𝑘𝑔
4.35
Cortante obtenida por Wu:
Cargas de gravedad tributarias de la viga:
𝐶𝑀 = 1103
𝐶𝑉 = 240
𝑘𝑔
𝑚
𝑘𝑔
𝑚
Se calcula la carga última:
𝑊𝑢 = 1.25𝑥 (1103 + 240) = 1679
𝑘𝑔
𝑚
Se halla la cortante:
𝑊𝑢 → 𝑉 𝑖𝑧𝑞𝑢𝑖𝑒𝑟𝑑𝑎 =
1679𝑥4.35
= 3651 𝑘𝑔
2
Cortante total:
𝑉 𝑡𝑜𝑡𝑎𝑙 = 1618 + 3651 = 5269 𝑘𝑔
39
Sección derecha
Cortante obtenida de los momentos:
𝑀𝑛 → 𝑉 𝑑𝑒𝑟𝑒𝑐ℎ𝑎 = −
351 929 + 351 929
= −1 618 𝑘𝑔
4.35
Cortante obtenida por Wu:
𝑊𝑢 → 𝑉 𝑑𝑒𝑟𝑒𝑐ℎ𝑎 =
1679𝑥4.35
= 3651 𝑘𝑔
2
Cortante total:
𝑉 𝑡𝑜𝑡𝑎𝑙 = −1618 + 3651 = 2033 𝑘𝑔
Caso 2:
Dado que comparten los mismos momentos, pero en diferentes sentidos las fuerzas
cortantes serán las mismas
Por lo tanto:
Sección izquierda
𝑉 𝑐𝑟í𝑡𝑖𝑐𝑎 = 5269 𝑘𝑔
Sección derecha
𝑉 𝑐𝑟í𝑡𝑖𝑐𝑎 = 5269 𝑘𝑔
En la siguiente figura se muestra el DFC obtenido por capacidad de flexión en los
extremos de la VP 20x40 cm:
40
Figura 14. DFC de viga. Fuente: Elaboración propia.
A continuación, se muestra el DFC por resistencia, obtenido del software ETABS:
Figura 15. DFC por resistencia.
Se comparan los DFC para escoger el Vu. Como se puede observar en los DFC, predomina
el obtenido por capacidad de flexión, por lo tanto:
Sección izquierda
𝑉 𝑐𝑟í𝑡𝑖𝑐𝑎 = 5269 𝑘𝑔
Sección derecha
𝑉 𝑐𝑟í𝑡𝑖𝑐𝑎 = 5269 𝑘𝑔
Con dichas fuerzas cortantes críticas se procederá a realizar el diseño por corte:
𝑏 = 20 𝑐𝑚
𝑑 = 34 𝑐𝑚
𝑉 𝑐𝑟í𝑡𝑖𝑐𝑎 = 5269 𝑘𝑔
Se calcula Vu:
𝑉𝑢 (𝑚𝑒𝑑𝑖𝑑𝑎 𝑎 𝑢𝑛𝑎 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎 d) = 4 699 𝑘𝑔
Se halla Vc:
𝑉𝑐 = 0.53𝑥√210𝑥20𝑥34 = 5 223 𝑘𝑔
Se halla Vn:
41
𝑉𝑛 =
𝑉𝑢 4 699
=
= 5 528 𝑘𝑔
𝜙
0.85
Se cumple que 𝑉𝑐 < 𝑉𝑛, entonces sí se necesitan estribos y se calcula Vs:
𝑉𝑠 = 𝑉𝑛 − 𝑉𝑐 = 305 𝑘𝑔
Suponemos estribos de 3/8”, entonces:
𝐴𝑣 = 1.42 𝑐𝑚2
Se calcula el espaciamiento:
𝑠=
1.42𝑥4200𝑥44
= 664 𝑐𝑚
305
El espaciamiento en la zona confinada con los requerimientos del diseño por capacidad
según la Norma E060 son:
𝑑
4
(𝑚í𝑛 15𝑐𝑚) =
34
4
= 8.5 𝑐𝑚 ≫> 𝑠𝑒 𝑒𝑠𝑐𝑜𝑔𝑒 15 𝑐𝑚
10 𝑑𝑏𝑙 = 10𝑥(𝜙1/2”) = 8𝑥1.27 = 12.7 𝑐𝑚
24 𝑑𝑏𝑒 = 24𝑥(𝜙3/8”) = 24𝑥0.95 = 22.8 𝑐𝑚
30 cm
Se escoge el menor valor de las expresiones anteriores, entonces el espaciamiento en la
zona de confinamiento sería:
𝐸𝑠𝑝𝑎𝑐𝑖𝑎𝑚𝑖𝑒𝑛𝑡𝑜 𝑑𝑒 𝑑𝑖𝑠𝑒ñ𝑜 = 𝑆 𝑑𝑖𝑠𝑒ñ𝑜 = 10 𝑐𝑚
𝐿𝑜𝑛𝑔𝑖𝑡𝑢𝑑 𝑑𝑒 𝑐𝑜𝑛𝑓𝑖𝑛𝑎𝑚𝑖𝑒𝑛𝑡𝑜 = 2ℎ = 0.8 𝑚
Fuera de la zona de confinamiento, se halla el espaciamiento de la misma forma tomando
en cuenta que el Vu a utilizar ahora se encuentra a una distancia de 0.80 m.
Se calcula Vu:
𝑉𝑢 (𝑚𝑒𝑑𝑖𝑑𝑎 𝑎 𝑢𝑛𝑎 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎 0.8 m) = 3926
Se halla Vc:
𝑉𝑐 = 0.53𝑥√210𝑥20𝑥34 = 5 223 𝑘𝑔
Se halla Vn:
42
𝑉𝑛 =
𝑉𝑢
= 4 619 𝑘𝑔
𝜙
No se cumple que 𝑉𝑐 < 𝑉𝑛, por lo cual se utiliza el requerimiento establecido en la
Norma E060:
𝑑
2
=
34
2
= 17 𝑐𝑚
60 𝑐𝑚
Se escoge el menor valor de las expresiones anteriores, entonces el espaciamiento en la
zona de central sería:
𝐸𝑠𝑝𝑎𝑐𝑖𝑎𝑚𝑖𝑒𝑛𝑡𝑜 𝑑𝑒 𝑑𝑖𝑠𝑒ñ𝑜 = 𝑆 𝑑𝑖𝑠𝑒ñ𝑜 = 15 𝑐𝑚
La distribución final de estribos sería [email protected] [email protected].
De igual manera que para esta viga de estudio, se realizó el mismo procedimiento para el
resto de las vigas que componen la estructura del proyecto. A continuación, se presentarán
unas tablas con el diseño por corte de cada viga:
43
Tabla 17. Diseño por corte para vigas
Vigas peraltadas del piso 1
Ubicación
Eje en el
Entre que
que se
ejes se
Viga
Wu (kg/m)
L (m)
Vc (kg)
Vu(d) (kg)
DISEÑO POR CORTE
Zona de confinamiento
Zona central
Sdiseño (cm) Lconfinamiento (m)
Vu (2h)
Sdiseño (cm)
Distribución
Eje C
Entre 1 y 2
VP20x40
1679
4.35
5223
4699
10
0.8
3926
15
φ3/8"
8
@
10
R
@
15
Eje E
Entre 2 y 3c
VP20x40
1679
3.6
5223
4406
10
0.8
3634
15
φ3/8"
8
@
10
R
@
15
Eje F
Entre 1 y 2
VP20x40
1679
4.35
5223
4699
10
0.8
3926
15
φ3/8"
8
@
10
R
@
15
Eje G
Entre 1 y 2
VP20x40
1679
4.35
5223
4699
10
0.8
3926
15
φ3/8"
8
@
10
R
@
15
Eje G
Entre 2 y 3c
VP20x40
1679
3.6
5223
4406
10
0.8
3634
15
φ3/8"
8
@
10
R
@
15
44
Capítulo 6
Diseño de losas aligeradas
Para el diseño de aligerado se tendrá en cuenta la tabiquería existente en los pisos de la
edificación, así como la combinación 1.4CM+1.7CV. Los aligerados serán de sección
típica, de ladrillo de 30x30x15.
Metrado de aligerado
CM
𝑘𝑔
-
𝑃𝑒𝑠𝑜 𝑝𝑟𝑜𝑝𝑖𝑜 = 300 𝑚2 𝑥0.4𝑚 = 120𝑘𝑔/𝑚
-
𝑃𝑖𝑠𝑜 𝑡𝑒𝑟𝑚𝑖𝑛𝑎𝑑𝑜 = 100 𝑚2 𝑥0.4𝑚 = 40𝑘𝑔/𝑚
-
𝐶𝑀𝑡𝑜𝑡𝑎𝑙 = 160 𝑘𝑔/𝑚
-
𝑃𝑖𝑠𝑜 𝑡𝑖𝑝𝑖𝑐𝑜 =
-
𝐴𝑧𝑜𝑡𝑒𝑎 = 100 𝑚2 𝑥 0.4𝑚 = 40 𝑘𝑔/𝑚
-
𝑇𝑎𝑏𝑖𝑞𝑢𝑒𝑟𝑖𝑎 𝑝𝑒𝑟𝑝𝑒𝑛𝑑𝑖𝑐𝑢𝑙𝑎𝑟 = 1800 𝑚2 𝑥0.15𝑥2.425𝑥0.4 = 261.9 𝑘𝑔
𝑘𝑔
CV
300𝑘𝑔
𝑚2
𝑘𝑔
𝑥0.4𝑚 = 120 𝑘𝑔/𝑚
𝑘𝑔
Aligerado tipo 1, con tabiquería perpendicular (entre eje A-C, tramo 1-5)
Para los momentos en los extremos de la vigueta usaremos el método de lo coeficientes,
por lo que se tiene:
𝑊𝑢 = 280 𝑘𝑔/𝑚
𝑀𝑢(−) = 220.76 𝑘𝑔. 𝑚
Figura 16. Aligerado tipo I con tabiquería perpendicular.
Tenemos :
𝐴𝑠𝑚𝑎𝑥 + = 7.5 𝑐𝑚2
𝐴𝑠𝑚𝑖𝑛+ = 0.41 𝑐𝑚2
𝐴𝑠𝑚𝑎𝑥 − = 2.70 𝑐𝑚2
𝐴𝑠𝑚𝑖𝑛− = 1.01 𝑐𝑚2
45
Para momentos positivos
-
𝑀𝑢 = 608.93 𝑘𝑔. 𝑚
𝐾𝑢 = 5.26
𝜌 = 0.14%
𝐴𝑠 = 0.95 𝑐𝑚2 > 𝐴𝑠 min +
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 1/2
-
𝑀𝑢 = 681.84 𝑘𝑔. 𝑚
𝐾𝑢 = 5.89
𝜌 = 0.16%
𝐴𝑠 = 1.08 𝑐𝑚2
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 1/2"
Para momentos negativos
Para los momentos en los extremos
𝑊𝑢 = 280 𝑘𝑔/𝑚
𝑀𝑢(−) = 220.76 𝑘𝑔. 𝑚
-
𝑀𝑢 = 220.76 𝑘𝑔. 𝑚
𝐾𝑢 = 7.64
𝜌 = 0.20%
𝐴𝑠 = 1.56 𝑐𝑚2 < 𝐴𝑠 min −= 1.01 𝑐𝑚2
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 1/2
Distancia hasta donde se requiere momento negativo en los extremos de la viga
𝑑 = 0.108(4.35) = 0.46𝑐𝑚
𝑑 = 0.50 𝑐𝑚
-
𝑀𝑢 = −1201.84 𝑘𝑔. 𝑚
𝐾𝑢 = 41.57
𝜌 = 1.28 %
𝐴𝑠 = 2.18 𝑐𝑚2
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 3/8" + 1 − 1/2"
46
Figura 17. Aligerado 2, sin tabiquería en un solo tramo.
Aligerado 2, sin tabiquería en un solo tramo.
Para los momentos positivos
-
𝑀𝑢 = 999.86 𝑘𝑔. 𝑚
𝐾𝑢 = 8.65
𝜌 = 0.22%
𝐴𝑠 = 1.5 𝑐𝑚2 > 𝐴𝑠 min +
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 3/8" + 1 − 1/2"
Para los momentos negativos en los extremos
Para los momentos en los extremos de la vigueta usaremos el método de los
coeficientes, por lo que se tiene:
𝑊𝑢 = 280 𝑘𝑔/𝑚
𝑀𝑢(−) = 220.76 𝑘𝑔. 𝑚
-
𝑀𝑢(−) = 220.76 𝑘𝑔. 𝑚
𝐾𝑢 = 7.64
𝜌 = 0.20%
𝐴𝑠 = 0.34 𝑐𝑚2 < 𝐴𝑠 min −= 1.01 𝑐𝑚2
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 1/2"
Distancia hasta donde se requiere momento negativo en los extremos de la vigueta
𝑑 = 0.108(4.35) = 0.46𝑐𝑚
47
𝑑 = 0.50 𝑐𝑚
Aligerado 2, sin tabiquería en dos tramos tramo.
Figura 18. Momentos en aligerado 2.
Para momentos positivos
-
𝑀𝑢 = 559.52 𝑘𝑔. 𝑚
𝐾𝑢 = 4.84
𝜌 = 0.12%
𝐴𝑠 = 0.82 𝑐𝑚2 > 𝐴𝑠 min +
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 1/2"
Para momentos negativos
Para los momentos en los extremos de la vigueta usaremos el método de los
coeficientes, por lo que se tiene:
𝑊𝑢 = 280 𝑘𝑔/𝑚
𝑀𝑢(−) = 186.67 𝑘𝑔. 𝑚
-
𝑀𝑢(−) = 186.67 𝑘𝑔. 𝑚
𝐾𝑢 = 6.46
𝜌 = 0.18%
𝐴𝑠 = 0.31 𝑐𝑚2 < 𝐴𝑠 min −= 1 𝑐𝑚2
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 1/2"
Distancia hasta donde se requiere momento negativo en los extremos de la vigueta
𝑑 = 0.108(4) = 0.43𝑐𝑚
𝑑 = 0.50 𝑐𝑚
48
-
𝑀𝑢(−) = 621.28 𝑘𝑔. 𝑚
𝐾𝑢 = 21.49
𝜌 = 0.60%
𝐴𝑠 = 1.02 𝑐𝑚2
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 1/2"
Volados
Para los momentos en los extremos
𝑊𝑢 = 280 𝑘𝑔/𝑚
𝑀𝑢(−) = 220.76 𝑘𝑔. 𝑚
Figura 19. Momentos en volados..
-
𝑀𝑢 = 999.86 𝑘𝑔. 𝑚
𝐾𝑢 = 8.65
𝜌 = 0.23%
𝐴𝑠 = 1.56 𝑐𝑚2 > 𝐴𝑠 min +
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 3/8" + 1 − 1/2"
-
𝑀𝑢(−) = 220.76 𝑘𝑔. 𝑚
𝐾𝑢 = 7.64
𝜌 = 0.20%
𝐴𝑠 = 0.34 𝑐𝑚2 < 𝐴𝑠 min −= 1 𝑐𝑚2
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 1/2"
49
Techo de azotea
Paño tipo 1
Para los momentos en los extremos
𝑊𝑢 = 480 𝑘𝑔/𝑚
𝑀𝑢(−) = 378.45 𝑘𝑔. 𝑚
Figura 20. Paño tipo 1 en azotea.
-
𝑀𝑢 = 766.24 𝑘𝑔. 𝑚
𝐾𝑢 = 6.63
𝜌 = 0.18%
𝐴𝑠 = 1.22 𝑐𝑚2 > 𝐴𝑠 min +
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 1/2"
-
𝑀𝑢(−) = 378.45 𝑘𝑔. 𝑚
𝐾𝑢 = 13.09
𝜌 = 0.36%
𝐴𝑠 = 0.61𝑐𝑚2 < 𝐴𝑠 min −= 1 𝑐𝑚2
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 3/8" + 1 − 8 𝑚𝑚
Paño tipo 2
Para los momentos en los extremos
𝑊𝑢 = 480 𝑘𝑔/𝑚
𝑀𝑢(−) = 64.8 𝑘𝑔. 𝑚
50
Figura 21. Paño tipo 2 en azotea.
-
𝑀𝑢 = 132.84 𝑘𝑔. 𝑚
𝐾𝑢 = 1.15
𝐶𝑜𝑛𝑡𝑟𝑜𝑙𝑎𝑟𝑎 𝑒𝑙 𝐴𝑠𝑚𝑖𝑛 +
𝐴𝑠 = 0.4 𝑐𝑚2
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 3/8"
-
𝑀𝑢(−) = 64.8 𝑘𝑔. 𝑚
𝐾𝑢 = 2.24
𝐶𝑜𝑛𝑡𝑟𝑜𝑙𝑎𝑟á 𝑒𝑙 𝐴𝑠𝑚𝑖𝑛−= 1 𝑐𝑚2
𝐴𝑠 min −= 1 𝑐𝑚2
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 3/8" + 1 − 8 𝑚𝑚
Paño tipo 3
Para los momentos en los extremos
𝑊𝑢 = 480 𝑘𝑔/𝑚
𝑀𝑢(−) = 320 𝑘𝑔. 𝑚
Figura 22. Momentos en paño tipo 3.
-
𝑀𝑢 = 6256.0 𝑘𝑔. 𝑚
𝐾𝑢 = 5.65
51
𝜌 = 0.16%
𝐴𝑠 = 1.1 𝑐𝑚2 > 𝐴𝑠 min +
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 1/2"
-
𝑀𝑢(−) = 320 𝑘𝑔. 𝑚
𝐾𝑢 = 11.03
𝜌 = 0.30 %
𝐴𝑠 = 0.51 𝑐𝑚2 < 𝐴𝑠 min −= 1 𝑐𝑚2
# 𝑣𝑎𝑟𝑖𝑙𝑙𝑎𝑠 = 1 − 3/8" + 1 − 8 𝑚𝑚
52
Capítulo 7
Diseño de Columnas
Para el diseño de las columnas, en primer lugar, se verificó que los mismos se
comporten como elementos sometidos a flexo compresión, caso contrario, se comportan
como vigas y serán diseñados como tal:
Para determinarlo, se hará uso de la siguiente ecuación:
𝑃𝑢 > 0.1𝑓 𝑐 ∗ 𝐴𝑔
Debido a que todas las columnas tienen unas dimensiones de 30 cm x 30 cm, el valor
que ha de ser comparado con Pu es:
𝑃𝑢 > 0.1 ∗ 210 ∗ 30 ∗ 30
𝑃𝑢 > 18900 𝑘𝑔
Para cada columna que no pertenezca a un muro de corte, se tomaron los mayores
valores de carga axial y momento en generados por la envolvente en todos los
entrepisos. Se muestran un cuadro resumen de las cargas axiales generadas por la
envolvente en cada columna, es decir la mayor carga generada por alguna hipótesis de
diseño:
Tabla 18. Cargas axiales en columnas en el primer entrepiso generadas por la envolvente (kg)
Pu (ton)
Ubicación de columna
Eje A
Eje C
Eje E
Eje F
Eje G
Eje 1
-
Entre 1b y 1c
16
22.12 28.07 -
Eje 2
10.46
Eje 3c
11.47
32.04 17.66
18.44 36.86
Eje 4
10.88
22.06
18.87 25.92 -
Se observa que las columnas del eje G soportan una mayor carga axial, lo cual tiene
sentido ya que estas son continuas hasta el techo de la azotea. De la información
arrojada del programa, se determinan qué elementos será diseñados por
flexocompresión o caso contrario, se diseñarán de forma similar a una viga.
Tabla 19. Tipo de diseño de cada elemento
Columnas
Eje A
Eje C
Eje E
Eje F
Eje G
Eje 1
Flexión
Flexocompresión
Entre 1b y 1c
Flexión
Eje 2
Flexión
Flexocompresión
Flexión
Flexión
Flexocompresión
Flexocompresión
Eje 3c
Flexión
Eje 4
Flexocompresión
Flexión
Flexocompresión
Aquellos elementos diseñados a flexocompresión trabajarán con un valor de reducción
φ = 0.7, mientras que aquellos que serán diseñados a flexión, al tener el comportamiento
de una viga, usarán un valor φ = 0.9.
En la siguiente figura se muestra una vista en planta de la estructura con las columnas a
diseñar
53
Figura 23. Columnas de pórticos a diseñar de la estructura.
A continuación, se muestra el proceso de diseño de una columna mediante un ejemplo
de diseño de la columna C8, que se encuentra en la intersección de los ejes G-2. Se
destaca que esta es la columna que presenta mayor carga axial.
7.1. Diseño por capacidad:
Se realizará el diseño por capacidad basado en las consideraciones especiales para
diseño sismorresistente presentes en la Norma E030, debido a que la zona del proyecto
es una zona sísmica.
Como ayuda del diseño, se hará uso de los diagramas de interacción otorgados por la
ACI. Estos diagramas relacionan los máximos valores de compresión y momentos a los
que puede ser sometido el elemento con la cantidad de refuerzo necesario en la
columna.
Estos son dependientes de la resistencia del concreto, el esfuerzo de fluencia del acero y
la relación entre la longitud entre refuerzos longitudinales y el ancho de la columna.
Para las columnas de la estructura, este último valor es:
𝛾=
30 − 12
30
𝛾 = 0.6
Por lo tanto, se usará el siguiente diagrama de interacción:
54
Figura 24. Diagrama de interacción para las columnas a diseñar. Fuente: American Concrete Institute.
Habiendo definido el diagrama a utilizar, se realizará el diseño de la columna C8 en el
primer entrepiso. En el caso de las cargas de sismo, se considera solo las fuerzas en el
eje X, ya que los pórticos a los que pertenecen todas las columnas son diseñados para
resistir las fuerzas en esta dirección y es donde se generarán los mayores momentos,
además que en la dirección Y los muros de albañilería serán quienes absorban las
fuerzas en dicha dirección.
Para dicha columna, los valores de P, M y V son:
Tabla 20. Fuerzas provenientes del análisis en ETABS.
CM
CV
SX
P
V2
M3
tonf
tonf tonf-m
2.2156 0.0518 0.0462
1.7444 -0.0172 -0.016
-0.9646
0.623
1.031
Mientras que las cargas últimas y nominales provenientes de las hipótesis de diseño son:
Tabla 21. Cargas últimas y nominales de la columna.
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Pu
tonf
6.0673
3.9854
5.9146
1.0294
2.9586
Vu
tonf
0.0433
0.6663
-0.5798
0.6696
-0.5764
Mu
tonf-m
0.0375
1.0688
-0.9933
1.0726
-0.9894
55
Pn
tonf
8.6676
5.6934
8.4494
1.4706
4.2266
Vn
tonf
0.0618
0.9518
-0.8282
0.9566
-0.8234
Mn
tonf-m
0.0535
1.5268
-1.4189
1.5323
-1.4135
Los valores de Pu y Mu sirven para calcular los parámetros de Kn y Rn, necesarios para
usar el diagrama de interacción:
𝐾𝑛 =
𝑅𝑛 =
𝑃𝑛
𝑓 𝑐 ∗ 𝐴𝑔
𝑀𝑛
𝑓 𝑐 ∗ 𝐴𝑔 ∗ ℎ
Para cada combinación, estos valores son:
Tabla 22. Valores Kn y Rn de cada combinación de diseño.
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Kn
0.0458603
0.030124
0.044706
0.0077811
0.0223631
Rn
0.000944
0.026927
-0.025025
0.027024
-0.024929
Figura 25. Ubicación aproximada de Kn y Rn en el diagrama de interacción.
Se observa que todos los valores se encuentran dentro del área correspondiente a una
cuantía de refuerzo del 1% (los Rn negativos se toman como absolutos debido a la
simetría de la sección), siendo esta la cuantía mínima en una columna, por lo que se
usará este valor para definir el refuerzo longitudinal.
El área de acero mínima para las dimensiones de la columna es:
56
𝐴𝑠 𝑚í𝑛 =
1
∗ 30 ∗ 30 = 9𝑐𝑚2
100
𝐴𝑠𝑐𝑜𝑙 = 4∅3/4" = 11.36𝑐𝑚2 = 1.26%
Por lo que el refuerzo escogido serán 4 varillas de ¾” de diámetro, las cuales conforman
un área de refuerzo de 11.36 cm2.
Continuando con el diseño por capacidad, se intersecará el valor de Kn y con la línea
correspondiente a la cuantía final (1.26%), de esta forma obteniendo un nuevo valor de
Rn:
Figura 26. Valor aproximado de Rn.
𝑅𝑛 = 0.119
De Rn’, se obtienen los valores del nuevo momento nominal Mn:
𝑀𝑛 = 0.119 ∗ 210 ∗ 303
𝑀𝑛 = 6.74 𝑡𝑜𝑛. 𝑚
Dicho momento nominal se usará para obtener la cortante de diseño, la cual es:
𝑉𝑢 =
𝑀𝑛𝑠 + 𝑀𝑛𝑖
ℎ𝑛
Se considera que el momento es el mismo en ambos extremos de la columna, por lo que
la cortante es:
𝑉𝑢 =
13.49
= 5.23 𝑡𝑜𝑛
2.58
Entonces:
57
𝑉𝑛 =
5.23
= 6.15 𝑡𝑜𝑛
0.85
La resistencia a la cortante del concreto para elementos a compresión es:
𝑉𝑐 = 0.53√210 ∗ 26 ∗ 30 ∗ (1 +
6067.3
)
140 ∗ 30 ∗ 30
𝑉𝑐 = 6.279 𝑡𝑜𝑛
Aparentemente la resistencia a la cortante proporcionada por el concreto es suficiente
para resistir la cortante nominal. Sin embargo, se deben colocar un mínimo de estribos
según las condiciones especiales de diseño sismorresistente.
Se asume un diámetro de estribos de 3/8” y el espaciamiento estará limitado por la
Norma E060. Según la Norma, para sistemas a base de muros estructurales se considera
lo siguiente:
Longitud de zona de confinamiento:
ℎ𝑛
Longitud 𝐿0 ≥ 𝑚á𝑥 ( 6 , 𝐵𝑚á𝑥 , 50𝑐𝑚) − −→ 𝑚á𝑥(43, 30, 50𝑐𝑚)
Espaciamiento de estribos 𝑆0 ≥ 𝑚í𝑛 (8𝐷𝑏𝑙,
𝐵𝑚í𝑛
2
, 10𝑐𝑚) →
𝑚í𝑛(15.28, 15, 10𝑐𝑚)
Longitud de zona central:
Espaciamiento 𝑆 ≤ 𝑚í𝑛 (12 𝐷𝑏𝑙, 25 𝑐𝑚) − −→ 𝑚í𝑛 (22.92, 25𝑐𝑚)
Espaciamiento en los nudos:
S=So (si está totalmente confinado por vigas: S=150mm)
Para nuestra columna en cuestión, los valores son:
𝐿0 = 50𝑐𝑚
𝑆0 = 10 𝑐𝑚
𝑆 = 20 𝑐𝑚
Para el resto de columnas, se repitió el procedimiento, resultando en que la cuantía
mínima de acero fue suficiente para las cargas y momentos actuantes ya que todos los
puntos Kn-Rn se ubicaban dentro del diagrama de interacción. El resumen de cálculos
se presenta en las siguientes tablas:
58
C15
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Pu
tonf
8.2585
1.6481
12.6341
-1.1327
9.8533
Vu
tonf
-0.0363
0.3699
-0.4319
0.3834
-0.4184
Mu
tonf-m
-0.0449
0.7161
-0.7936
0.7315
-0.7781
Pn
tonf
9.1761
1.8313
14.0379
-1.2585
10.9481
Vn
tonf
-0.0404
0.4110
-0.4799
0.4260
-0.4648
Mn
tonf-m
-0.0499
0.7956
-0.8817
0.8128
-0.8646
Kn
0.0486
0.0097
0.0743
-0.0067
0.0579
Rn
-0.0009
0.0140
-0.0156
0.0143
-0.0152
C18
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Pu
tonf
11.1941
8.8228
10.3798
4.8123
6.3693
Vu
tonf
-0.0855
0.5348
-0.6836
0.5622
-0.6562
Mu
tonf-m
-0.0897
0.8670
-1.0235
0.8950
-0.9954
Pn
tonf
12.4379
9.8031
11.5331
5.3470
7.0770
Vn
tonf
-0.0950
0.5943
-0.7595
0.6247
-0.7291
Mn
tonf-m
-0.0996
0.9633
-1.1372
0.9944
-1.1060
Kn
0.0658
0.0519
0.0610
0.0283
0.0374
Rn
-0.0018
0.0170
-0.0201
0.0175
-0.0195
C16
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Pu
tonf
9.2217
4.4559
11.6059
1.5259
8.6759
Vu
tonf
0.1069
0.4948
-0.3140
0.4524
-0.3564
Mu
tonf-m
0.0855
0.8300
-0.6865
0.7945
-0.7219
Pn
tonf
10.2463
4.9510
12.8954
1.6955
9.6399
Vn
tonf
0.1188
0.5498
-0.3489
0.5026
-0.3960
Mn
tonf-m
0.0950
0.9222
-0.7627
0.8827
-0.8021
Kn
0.0542
0.0262
0.0682
0.0090
0.0510
Rn
0.0017
0.0163
-0.0135
0.0156
-0.0141
C20
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Pu
tonf
8.1866
3.4283
10.8759
0.8971
8.3447
Vu
tonf
-0.1347
0.2759
-0.5059
0.3258
-0.4560
Mu
tonf-m
-0.1347
0.6303
-0.8611
0.6790
-0.8124
Pn
tonf
9.0962
3.8093
12.0844
0.9967
9.2719
Vn
tonf
-0.1497
0.3066
-0.5621
0.3620
-0.5066
Mn
tonf-m
-0.1496
0.7004
-0.9568
0.7545
-0.9027
Kn
0.0481
0.0202
0.0639
0.0053
0.0491
Rn
-0.0026
0.0124
-0.0169
0.0133
-0.0159
C14
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Pu
tonf
10.4471
-3.8923
22.0858
-7.2155
18.7625
Vu
tonf
0.1150
0.4740
-0.2818
0.4250
-0.3308
Mu
tonf-m
0.0930
0.8110
-0.6568
0.7695
-0.6984
Pn
tonf
14.9244
-5.5604
31.5511
-10.3079
26.8036
Vn
tonf
0.1643
0.6772
-0.4025
0.6071
-0.4726
Mn
tonf-m
0.1329
1.1586
-0.9383
1.0992
-0.9976
Kn
0.0790
-0.0294
0.1669
-0.0545
0.1418
Rn
0.0023
0.0204
-0.0165
0.0194
-0.0176
C1
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Pu
tonf
22.4003
15.3006
23.1506
7.3147
15.1647
Vu
tonf
-1.3160
-0.6415
-1.6103
-0.1613
-1.1301
Mu
tonf-m
-1.2082
-0.1781
-1.8897
0.2621
-1.4495
Pn
tonf
32.0004
21.8580
33.0723
10.4495
21.6638
Vn
tonf
-1.8800
-0.9164
-2.3004
-0.2304
-1.6144
Mn
tonf-m
-1.7259
-0.2544
-2.6995
0.3744
-2.0708
Kn
0.1693
0.1157
0.1750
0.0553
0.1146
Rn
-0.0304
-0.0045
-0.0476
0.0066
-0.0365
C2
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Pu
tonf
10.9630
-14.0598
32.8963
-17.9407
29.0153
Vu
tonf
0.0114
0.1205
-0.1010
0.1164
-0.1050
Mu
tonf-m
0.0022
0.5155
-0.5123
0.5140
-0.5138
Pn
tonf
15.6615
-20.0854
46.9946
-25.6295
41.4505
Vn
tonf
0.0162
0.1721
-0.1442
0.1662
-0.1500
Mn
tonf-m
0.0031
0.7365
-0.7318
0.7343
-0.7340
Kn
0.0829
-0.1063
0.2486
-0.1356
0.2193
Rn
0.0001
0.0130
-0.0129
0.0130
-0.0129
C3
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Pu
tonf
5.0251
2.5305
5.4003
-0.3316
2.5382
Vu
tonf
-0.5678
-0.0713
-0.9063
0.1267
-0.7083
Mu
tonf-m
-0.5231
0.3663
-1.2671
0.5484
-1.0850
Pn
tonf
5.5835
2.8116
6.0003
-0.3684
2.8202
Vn
tonf
-0.6309
-0.0792
-1.0069
0.1408
-0.7870
Mn
tonf-m
-0.5812
0.4070
-1.4079
0.6093
-1.2055
Kn
0.0295
0.0149
0.0317
-0.0019
0.0149
Rn
-0.0103
0.0072
-0.0248
0.0107
-0.0213
C4
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Pu
tonf
4.9900
0.3320
7.6958
-2.2752
5.0886
Vu
tonf
0.7102
1.0183
0.1955
0.7567
-0.0661
Mu
tonf-m
0.6425
1.3601
-0.2623
1.1231
-0.4994
Pn
tonf
5.5444
0.3689
8.5509
-2.5280
5.6540
Vn
tonf
0.7892
1.1314
0.2172
0.8408
-0.0734
Mn
tonf-m
0.7139
1.5112
-0.2915
1.2478
-0.5548
Kn
0.0293
0.0020
0.0452
-0.0134
0.0299
Rn
0.0126
0.0267
-0.0051
0.0220
-0.0098
C5
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Pu
tonf
5.8411
2.8433
6.5593
-0.2003
3.5157
Vu
tonf
0.2250
0.8349
-0.4484
0.7552
-0.5280
Mu
tonf-m
0.2007
1.2005
-0.8557
1.1292
-0.9270
Pn
tonf
6.4901
3.1592
7.2881
-0.2225
3.9063
Vn
tonf
0.2500
0.9276
-0.4982
0.8391
-0.5867
Mn
tonf-m
0.2230
1.3339
-0.9508
1.2546
-1.0300
Kn
0.0343
0.0167
0.0386
-0.0012
0.0207
Rn
0.0039
0.0235
-0.0168
0.0221
-0.0182
C7
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Pu
tonf
19.0980
11.7303
22.2929
6.8322
17.3948
Vu
tonf
-0.3211
0.1081
-0.6751
0.1983
-0.5849
Mu
tonf-m
-0.2946
0.5598
-1.0798
0.6427
-0.9969
Pn
tonf
27.2828
16.7576
31.8470
9.7602
24.8497
Vn
tonf
-0.4587
0.1544
-0.9644
0.2833
-0.8356
Mn
tonf-m
-0.4208
0.7997
-1.5426
0.9181
-1.4242
Kn
0.1444
0.0887
0.1685
0.0516
0.1315
Rn
-0.0074
0.0141
-0.0272
0.0162
-0.0251
C8
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Pu
tonf
6.0673
3.9854
5.9146
1.0294
2.9586
Vu
tonf
0.0433
0.6663
-0.5798
0.6696
-0.5764
Mu
tonf-m
0.0375
1.0688
-0.9933
1.0726
-0.9894
Pn
tonf
8.6676
5.6934
8.4494
1.4706
4.2266
Vn
tonf
0.0618
0.9518
-0.8282
0.9566
-0.8234
Mn
tonf-m
0.0535
1.5268
-1.4189
1.5323
-1.4135
Kn
0.0459
0.0301
0.0447
0.0078
0.0224
Rn
0.0009
0.0269
-0.0250
0.0270
-0.0249
1.4CM+1.7CV
1.25(CM+CV)+CSX
1.25(CM+CV)-CSX
0.9CM+CSX
0.9CM-CSX
Pu
tonf
18.5885
14.3887
18.1395
8.7169
12.4677
Vu
tonf
0.3224
0.7078
-0.1646
0.5773
-0.2951
Mu
tonf-m
0.2920
1.1065
-0.6145
0.9883
-0.7327
Pn
tonf
26.5549
20.5553
25.9136
12.4527
17.8110
Vn
tonf
0.4605
1.0112
-0.2351
0.8247
-0.4215
Mn
tonf-m
0.4171
1.5807
-0.8779
1.4119
-1.0467
Kn
0.1405
0.1088
0.1371
0.0659
0.0942
Rn
0.0074
0.0279
-0.0155
0.0249
-0.0185
C9
Tabla 23. Resumen de cálculos del diseño de columnas.
59
En todos estos elementos la cuantía necesaria para los momentos y cargas es la mínima
de 1%. Además, se comprobó en el diseño por corte que los espaciamientos en el centro
están siempre limitados por los 20cm que indica la Norma. En consecuencia, el refuerzo
será:
Tabla 24. Refuerzo para columnas.
Refuerzo longitudinal
4φ3/4"
Estribos
3/8” - [email protected], [email protected] , Rsto @ 0.20 cm
60
Capítulo 8
Diseño de muros de corte
A fin de proveer la suficiente rigidez en la estructura en la dirección X se fueron
añadiendo muros de corte de concreto, los cuales serán diseñados según los
lineamientos de la Norma E060.
Los datos correspondientes de compresión axial, fuerza cortante y momentos se
obtuvieron del análisis realizado en ETABS.
Los datos de espesor y largo de las placas se muestran a continuación:
Tabla 25. Dimensiones de las placas.
Placa PX-1:
Espesor: 30 cm
Largo: 150 cm
Placa PX-2
Espesor: 30 cm
Largo: 183 cm
El largo de los muros se determinó según la arquitectura, mientras que el espesor se
dimensionó de 30 cm debido a que el largo de estas placas no es muy grande.
A manera de ejemplo, se mostrará el proceso que se siguió para el diseño de la placa
PX-1, ubicada en el eje F.
Las cargas en dicho muro según el análisis son:
Tabla 26. Cargas en el muro.
Mientras que las fuerzas resultantes de las combinaciones de carga son:
Tabla 27. Cargas últimas y nominales.
1.4CM+1.7CV
1.25(CM+CV)+CS
1.25(CM+CV)-CS
0.9CM+CS
0.9CM-CS
Pu (ton)
Vu (ton)
49.90
-4.10
91.69
-18.89
76.90
-1.57
21.86
-24.53
22.44
-23.94
Mu (ton.m)
Pn (ton)
Vn (ton)
Mn (ton.m)
-2.42
55.44
-1.74
-2.69
64.86
-4.55
24.29
72.07
-69.00
101.88
-27.25
-76.67
65.73
-20.99
24.94
73.03
-68.14
85.45
-26.60
-75.71
8.1. Predimensionamiento de refuerzo en elementos de borde
Como primer paso para el diseño, se procedió a predimensionar la cantidad de refuerzo
longitudinal en los elementos de borde, para lo cual es necesario también determinar la
cantidad de refuerzo necesario en el alma de la placa, cuya cuantía mínima vertical es
0.25%.
Sabiendo esto, asumiendo un espaciamiento entre barras longitudinales de 30cm, se
tiene:
61
𝐴𝑠
≥ 0.25%
30𝑥30
𝐴𝑠 ≥ 2.25𝑐𝑚2 − −→ 𝐴𝑠 = 2∅1/2 "
𝐴𝑠 = 2.58𝑐𝑚2 = 0.29%
Habiendo obtenido el acero en el alma, se realiza un diagrama de cuerpo libre para
obtener el acero en los elementos de borde usando las fuerzas de cada combinación.
Figura 27. DCL de la placa predimensionada.
Donde:
𝑇𝑆1 = 𝑓𝑢𝑒𝑟𝑧𝑎 𝑑𝑒 𝑡𝑟𝑎𝑐𝑐𝑖ó𝑛 𝑑𝑒𝑙 𝑎𝑐𝑒𝑟𝑜 𝑒𝑛 𝑒𝑙 𝑐𝑒𝑛𝑡𝑟𝑜
𝑇𝑆2 = 𝑓𝑢𝑒𝑟𝑧𝑎 𝑑𝑒 𝑡𝑟𝑎𝑐𝑐𝑖ó𝑛 𝑑𝑒𝑙 𝑎𝑐𝑒𝑟𝑜 𝑒𝑛 𝑒𝑙 𝑏𝑜𝑟𝑑𝑒
Del DCL:
𝑇𝑠1 = 0.0029𝑥0.8𝑥150𝑥30𝑥4200 = 43.848𝑘𝑔
𝑇𝑠2 =
𝑀𝑛 − 0.6(𝑇𝑠1𝑥𝑃𝑢)
1.2
Se calculó cuál sería la combinación que requeriría una mayor cuantía en el elemento de
borde, la cual resultó ser la cuarta combinación:
𝑇𝑠2 =
73.03 − 0.6(43.85 − 18.89)
1.2
𝑇𝑠2 = 48.38 𝑡𝑜𝑛
𝐴𝑠 =
48380
= 11.52 𝑐𝑚2 ≥ 1%
4200
𝐴𝑠𝑐𝑜𝑙 = 6∅ 5/8" = 12 𝑐𝑚2 = 1.33%
62
Longitud de elemento de borde
Dicha longitud está limitada como el máximo valor entre:
𝐿𝑏𝑒 ≥ 𝐶 − 0.1𝐿𝑚
𝐿𝑏𝑒 ≥ 𝐶/2
El valor de C se define como la siguiente relación:
𝐶=
0.003
𝜑
Donde el denominador es la curvatura asociada a el mayor momento Mu
correspondiente a la carga Pu que lo produce. Dicho valor de momento se obtiene del
diagrama de interacción Pu vs Mu de la sección.
Tanto el diagrama de interacción como el diagrama Momento vs Curvatura se
obtuvieron simulando la placa en ETABS. La carga Pu que produce el mayor Mu es la
carga de la tercera combinación, siendo su valor 101.88 ton. Según el diagrama de
interacción, el momento encontrado para esta carga son 148 ton.m.
Luego, la curvatura correspondiente a este momento es:
𝜑 = 0.0041
Por lo que el valor de C es:
𝐶 = 0.732 𝑚
Entonces la longitud del elemento de borde será:
𝐿𝑏𝑒 ≥ 𝑚á𝑥 (0.58; 0.37)
𝐿𝑏𝑒 = 0.60𝑚
Se hallará el valor del C límite para saber si es necesario seguir las especificaciones de
la Norma E060 al momento de confinar los elementos de borde.
𝛿𝑢 0.0377
=
= 0.0035 < 0.005
ℎ𝑚
10.67
𝐶𝑙í𝑚 =
𝐿𝑚
1.5
=
= 0.5𝑚
𝛿𝑢
600𝑥0.005
600𝑥 (ℎ𝑚)
𝐶 > 𝐶𝑙í𝑚 − −→ 𝑆𝑒 𝑛𝑒𝑐𝑒𝑠𝑖𝑡𝑎 𝑐𝑜𝑛𝑓𝑖𝑛𝑎𝑟 𝑠𝑒𝑔ú𝑛 𝑙𝑎 𝐸060
Debido a que las longitudes de los elementos de borde ocupan casi toda la longitud del
muro, resulta más conveniente diseñar la placa como si debiera estar confinada en toda
su extensión de manera similar a una columna, con una cuantía vertical mayor al 1%.
𝐴𝑠𝑐𝑜𝑙 > 0.01𝑥30𝑥150 = 45𝑐𝑚2
63
𝐴𝑠𝑐𝑜𝑙 = 16∅3/4" = 45.44 𝑐𝑚2
Las varillas de acero se confinarán con estribos de 3/8”, cuyos espaciamientos seguirán
las especificaciones de la Norma E060.
El acero colocado está separado cada 20cm, por lo que se cumple con la máxima
separación entre ramas especificada.
8.2. Diseño por flexocompresión:
Habiendo definido la sección de la placa, se modela nuevamente la sección para obtener
el diagrama de interacción correspondiente.
Figura 28. Muro PX-1 modelada en ETABS.
Los puntos que conforman el diagrama en la dirección X son:
Tabla 28. Puntos que conforman el diagrama de interacción en X.
64
Figura 29. Diagrama de interacción de la placa PX-1.
Se observa que todos los puntos correspondientes a las cargas últimas están dentro del
diagrama de interacción. El diagrama es simétrico debido a que la sección y la
distribución de acero también lo es. Además, debido a que los muros de albañilería
absorben en casi su totalidad la mayoría de las fuerzas provenientes en la dirección Y,
no será necesario que se analice en esta dirección.
La segunda placa, si bien tiene un poco más de longitud, esta sigue siendo relativamente
corta y absorbe mayor cortante que la placa ya diseñada, por lo que directamente se
propuso realizar un diseño similar, diseñándola como una columna de gran extensión.
Las cargas según el análisis en ETABS y las cargas últimas y nominales son:
Tabla 29. Cargas provenientes del análisis en ETBAS.
P
tonf
26.8808
4.8226
-58.5302
Output Case
Dead
Live
Sismo Din. X
V2
tonf
0.7766
0.1874
23.0925
M3
tonf-m
0.2464
0.1864
72.587
Tabla 30. Cargas últimas y nominales.
1.4CM+1.7CV
1.25(CM+CV)+CS
1.25(CM+CV)-CS
0.9CM+CS
0.9CM-CS
Pu (ton)
Vu (ton)
45.83
-18.90
98.16
-34.34
82.72
Mu (ton.m)
1.41
24.30
-21.89
23.79
-22.39
0.66
73.13
-72.05
72.81
-72.37
Pn (ton)
Vn (ton)
Mn (ton.m)
50.92
1.56
0.74
-21.00
27.00
81.25
109.07
-24.32
-80.05
-38.15
26.43
80.90
91.91
-24.88
-80.41
La cuantía correspondiente para la segunda placa es:
𝐴𝑠𝑐𝑜𝑙 > 0.01𝑥30𝑥183 = 54.9𝑐𝑚2
𝐴𝑠𝑐𝑜𝑙 = 20∅3/4" = 56.8 𝑐𝑚2
65
Figura 30. Muro PX-2 modelada en ETABS.
Luego, del diagrama de interacción arrojado por ETABS:
Tabla 31. Puntos del diagrama de interacción en X.
Pn (ton)
Mn (ton.m)
Pu (ton)
Mn (ton.m) φ
970.8835
0
679.61845
0
970.8835
121.8543
679.61845
85.29801
918.5006
193.0662
642.95042
135.14634
793.2077
247.8464
555.24539
173.49248
657.8589
286.8279
460.50123
200.77953
506.8454
312.2533
354.79178
218.57731
360.2474
310.9436
252.17318
217.66052
212.3646
279.2804
148.65522
195.49628
64.8431
218.4526
45.39017 152.91682
-79.4172
130.8559
-71.47548
117.77031
-239.5218
0
-215.56962
0
0.70
0.70
0.70
0.70
0.70
0.70
0.70
0.70
0.70
0.90
0.90
A continuación, se muestra el diagrama de interacción, así como los pares Pu-Mn.
Figura 31. Diagrama de interacción de la placa PX-2.
66
Se observa que los pares Pu-Mn se ubican dentro del diagrama de interacción provisto,
por lo que la cuantía vertical en la placa es la adecuada.
67
Capítulo 9
Diseño de Muros de albañilería
En este capítulo sobre el diseño de muros de albañilería se seguirán los pasos para
cumplir los requerimientos de la Norma E070. Por lo tanto, según sus requisitos
generales para el diseño de los muros confinados, podremos suponer que los muros son
de sección rectangular de espesor “t” y largo “L”, además para la elección del elemento
de refuerzo cuando los muros se intercepten perpendicularmente se tomara al mayor
brindado por el diseño independiente de los muros, ya sea sección transversal de la
columna como su refuerzo vertical.
Para la obtención de las cargas necesarias para la verificación según la Norma, estas se
han obtenido del programa ETABS, en donde se ha modelado nuestra estructura con los
muros de albañilería, además de las cargas gravitacionales de servicio con o sin
sobrecarga, se han obtenido del capítulo 4 sobre los metrados de carga.
9.1. Metodología de diseño según norma E-070
La norma E-070 presenta dos metodologías para diseñar muros:
Para muros portantes: Si 𝜎𝑚 > 0.01 ∗ 𝑓′𝑚 -----------Articulo 30
Para muros no portantes: Si 𝜎𝑚 ≤ 0.01 ∗ 𝑓′𝑚 -------Articulo 31
Donde:
El esfuerzo axial máximo es igual a,
𝜎𝑚 =
𝑃𝑚
𝐶𝑀 + 𝐶𝑉
=
𝐿∗𝑡
𝐿∗𝑡
f’m es la resistencia a la comprensión de la albañilería del ensayo de pilas
Tabla 32. Parámetros para el cálculo de la resistencia.
f’m
t
65
0.13
68
kg/cm2
m
Tabla 33. Metodología de diseño para cada muro.
Nivel
Pier
Azotea
Azotea
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Y-4
Y-11
Y-3
Y-8
Y-9
Y-10
Y-14
Y-17
X-4
Y-2
Y-6
Y-7
Y-13
Y-16
X-3
Y-1
Y-5
Y-12
Y-15
X-2
Pm=CM+CV
ton
2.18
1.26
12.68
3.19
1.37
1.54
7.56
4.63
0.90
24.53
19.03
3.59
14.71
7.93
1.90
34.74
35.15
21.66
10.26
2.67
L
m
3.05
1.38
10.29
1.38
1.43
1.15
7.15
5.1
0.94
12.25
8.85
1.15
7.15
5.1
0.94
12.25
10.9
7.15
5.1
0.94
t
m
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
σm
f'm
ton/m2 ton/m2
5.50
650
7.03
650
9.48
650
17.81
650
7.38
650
10.29
650
8.14
650
6.98
650
7.37
650
15.40
650
16.54
650
24.01
650
15.83
650
11.97
650
15.55
650
21.81
650
24.81
650
23.30
650
15.48
650
21.88
650
0.01*f'm
ton/m2
6.5
6.5
6.5
6.5
6.5
6.5
6.5
6.5
6.5
6.5
6.5
6.5
6.5
6.5
6.5
6.5
6.5
6.5
6.5
6.5
se diseña
como muro:
no portante
portante
portante
portante
portante
portante
portante
portante
portante
portante
portante
portante
portante
portante
portante
portante
portante
portante
portante
portante
9.2. Verificación de esfuerzo axial en muro
En este articulo contempla el esfuerzo axial máximo que debe cumplir el muro, para
esto es necesario los valores de Pm por muro, con el total de sobrecarga. Siendo dos
valores de resistencias que dependen de la resistencia característica a compresión de la
albañilería, la altura libre y el espesor efectivo del muro.
El esfuerzo axial máximo 𝜎𝑚 producido por la carga de gravedad máxima de servicio
𝑃𝑚 incluyendo el 100% de la sobrecarga será inferior a:
𝑃𝑚
𝜎𝑚 =
≤ 0.2𝑓
𝐿∗𝑡
ℎ 2
[1 − (
) ] ≤ 0.15𝑓′𝑚
𝑚
35 ∗ 𝑡
A continuación, se muestra la tabla comprobando el requisito del artículo 19.1.b sobre
el esfuerzo axial máximo. De no cumplirse la expresión anterior, habrá que mejorar la
calidad de la albañilería, aumentar el espesor del muro, transformar en concreto armado
o ver la manera de reducir la magnitud de la carga axial.
69
Tabla 34. Comprobación del artículo 19.1.b sobre el esfuerzo axial máximo.
Nivel
Azotea
Azotea
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Pier Pm=CM+CV
Y-4
Y-11
Y-3
Y-8
Y-9
Y-10
Y-14
Y-17
X-4
Y-2
Y-6
Y-7
Y-13
Y-16
X-3
Y-1
Y-5
Y-12
Y-15
X-2
ton
2.18
1.26
12.68
3.19
1.37
1.54
7.56
4.63
0.90
24.53
19.03
3.59
14.71
7.93
1.90
34.74
35.15
21.66
10.26
2.67
L
H
t
m
3.05
1.38
10.29
1.38
1.43
1.15
7.15
5.1
0.94
12.25
8.85
1.15
7.15
5.1
0.94
12.25
10.9
7.15
5.1
0.94
m
2.63
2.63
2.63
2.63
2.63
2.63
2.63
2.63
2.63
2.63
2.63
2.63
2.63
2.63
2.63
2.78
2.78
2.78
2.78
2.78
m
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
0.13
σm
f'm
ton/m2 ton/m2
5.50
650
7.03
650
9.48
650
17.81
650
7.38
650
10.29
650
8.14
650
6.98
650
7.37
650
15.40
650
16.54
650
24.01
650
15.83
650
11.97
650
15.55
650
21.81
650
24.81
650
23.30
650
15.48
650
21.88
650
0.2*f'm(1(h/35t)^2)
0.15f'm
ton/m2
86.57
86.57
86.57
86.57
86.57
86.57
86.57
86.57
86.57
86.57
86.57
86.57
86.57
86.57
86.57
81.47
81.47
81.47
81.47
81.47
ton/m2
97.5
97.5
97.5
97.5
97.5
97.5
97.5
97.5
97.5
97.5
97.5
97.5
97.5
97.5
97.5
97.5
97.5
97.5
97.5
97.5
σm≤0.2*f'm(1σm≤0.15*f'm
(h/35t)^2)
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
Al cumplir con el requisito entonces no se cambiará el espesor ni el material de
albañilería.
9.3. Verificación del agrietamiento en muro
Siguiendo con los requisitos brindados por la Norma, se realizará la verificación
mencionado en el artículo 26.1 donde los muros deberán cumplir con un primer control
de fisuración que afrontaran frente a cargas de sismo generados por un sismo moderado,
es decir en este caso se empleara un factor de reducción R=6, con ello se obtendrán los
valores de cortantes Ve y de momentos Me, que nos servirán para verificar si la cortante
producida por este sismo, será menos que el 55% de la resistencia al corte de la albañilería
Vm. Los valores de las cortantes y momentos por sismo moderado son obtenidos
mediante el programa ETABS al cambiar el valor del factor de reducción a R=6. Llevando
estos datos a una tabla obtenemos:
70
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
cumple
Tabla 35. Valor de cortante y momento debido a sismo moderado.
Story
Pier
Ve
ton
Azotea
Y-4
Azotea
Y-11
Tercer Nivel Y-3
Tercer Nivel Y-8
Tercer Nivel Y-9
Tercer Nivel Y-10
Tercer Nivel Y-14
Tercer Nivel Y-17
Tercer Nivel X-4
Segundo Nivel
Y-2
Segundo Nivel
Y-6
Segundo Nivel
Y-7
Segundo Nivel
Y-13
Segundo Nivel
Y-16
Segundo Nivel
X-3
Primer Nivel Y-1
Primer Nivel Y-5
Primer Nivel Y-12
Primer Nivel Y-15
Primer Nivel X-2
2.87
3.26
13.05
0.96
1.34
0.58
8.04
5.25
0.85
17.50
13.27
0.82
10.15
6.52
1.87
20.16
18.38
11.88
7.39
1.68
Me
ton.m
4.11
4.49
26.42
0.97
1.83
0.70
11.65
7.30
1.18
42.19
19.40
1.15
16.85
9.76
2.74
53.87
42.56
25.65
12.07
2.95
Para la verificación es necesario la obtención de la resistencia al agrietamiento diagonal
es decir Vm, la cual se calcula mediante la fórmula para unidades de arcilla y de
concreto:
𝑉𝑚 = 0.5 × 𝑣′𝑚 × 𝛼 × 𝑡 × 𝐿 + 0.23𝑃𝑔
Donde:
α = factor de reducción de la resistencia al corte por esbeltez
1
𝑉𝑒 × 𝐿
≤ 𝛼 =
≤1
3
𝑀𝑒
Ve = Fuerza cortante del muro obtenida del análisis sísmico.
Me = Momento del muro obtenido del análisis sísmico.
Pg= CM+25%CV
Es entonces necesario el valor de Me, para el valor del factor de reducción de resistencia
al corte por efectos de esbeltez, este valor debe estar en el rango de 1/3 y de 1, si el
valor resulta menor o mayor que los límites, se escogerá este valor de limite, siendo
entonces como mínimo 1/3 o máximo 1. Además, se requiere la carga gravitacional con
una sobrecarga reducida (Pg.)
71
Tabla 36. Control de fisuración de los muros.
Story
Pier
Azotea
Azotea
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Y-4
Y-11
Y-3
Y-8
Y-9
Y-10
Y-14
Y-17
X-4
Y-2
Y-6
Y-7
Y-13
Y-16
X-3
Y-1
Y-5
Y-12
Y-15
X-2
L
m
3
1
10
1
1
1
7
5
1
12
9
1
7
5
1
12
11
7
5
1
α
α
2
1
5
1
1
1
5
4
1
5
6
1
4
3
1
5
5
3
3
1
1
1
1
1
1
0.95
1
1
0.67
1
1
0.82
1
1
0.64
1
1
1
1
0.54
Pg
ton
2.19
1.27
12.15
3.09
1.28
1.43
7.20
4.43
0.85
22.86
17.40
3.19
13.64
7.38
1.74
32.16
31.69
19.89
9.42
2.46
V'm
ton/m2
81.00
81.00
81.00
81.00
81.00
81.00
81.00
81.00
81.00
81.00
81.00
81.00
81.00
81.00
81.00
81.00
81.00
81.00
81.00
81.00
Vm
Ve≤0.55*Vm
ton/m2
16.56
no se fisura
7.56
no se fisura
56.97
no se fisura
7.98
no se fisura
7.82
no se fisura
6.11
no se fisura
39.30
no se fisura
27.87
no se fisura
3.53
no se fisura
69.75
no se fisura
50.60
no se fisura
5.69
no se fisura
40.78
no se fisura
28.55
no se fisura
3.56
no se fisura
71.89
no se fisura
64.68
no se fisura
42.22
no se fisura
29.02
no se fisura
3.22
no se fisura
9.4. Verificación de la resistencia al corte del edifico
Finalmente se verificará la resistencia al corte del edificio, expuesto en el artículo
26.4. Con el objeto de proporcional la adecuada resistencia y rigidez a la vivienda, en
todos sus pisos, se debe de cumplir que la resistencia al corte sea mayor que la fuerza
cortante producida por el sismo severo. Es decir, la sumatoria de las resistencias al corte
deberá ser mayor que la fuerza actuante en el entrepiso de la vivienda. Al tener el sismo
severo un factor de reducción de R=3, se multiplico por 2 a todas las cortantes obtenidas
por sismo moderado.
72
Tabla 37. Cortante para sismo severo.
Story
Pier
Azotea
Azotea
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Y-4
Y-11
Y-3
Y-8
Y-9
Y-10
Y-14
Y-17
X-4
Y-2
Y-6
Y-7
Y-13
Y-16
X-3
Y-1
Y-5
Y-12
Y-15
X-2
Ve
ton
2.87
3.26
13.05
0.96
1.34
0.58
8.04
5.25
0.85
17.50
13.27
0.82
10.15
6.52
1.87
20.16
18.38
11.88
7.39
1.68
VE=Ve*2
ton
5.7
6.5
26.1
1.9
2.7
1.2
16.1
10.5
1.7
35.0
26.5
1.6
20.3
13.0
3.7
40.3
36.8
23.8
14.8
3.4
Al pedirnos la fuerza cortante de entrepiso entonces se sumaron por piso y por
dirección, luego se verifico si la suma de Vm por piso y dirección sea mayor que la
fuerza cortante. Cabe recordar que en la dirección X se usaran algunas placas por las
que estas también aportaran un Vm, por lo que, si no cumple, es porque no se ha
considerado el aporte de los muros de concreto. Pero se asumirá que el aporte de las
placas que se realizara en el siguiente capítulo es suficiente para aportar esta resistencia
y rigidez.
Tabla 38. Cortante para sismo severo del segundo piso y azotea.
NIVEL Y DIRECCION ΣVm(ton/m2) VEi (ton) ΣVm≤VEi
Azotea (Y)
24.12021
12.2666 no cumple
Tercer Nivel (Y)
146.0497477
60.161 no cumple
Tercer Nivel (X)
3.529843908
60.161 cumple
Segundo Nivel (Y)
195.3714015
100.236 no cumple
Segundo Nivel (X)
3.564570425
100.236 cumple
Primer Nivel (Y)
207.810077
118.973 no cumple
Primer Nivel (X)
3.222655711
118.973 cumple
Como se predijo los Vm en el primer y segundo piso en la dirección X, no son
suficientes para soportar la carga sísmica de su entrepiso, es por eso por lo que se
usaron algunas placas en esta dirección y son diseñadas en el siguiente capítulo.
73
Por último, en el acápite e de este capítulo, si esta sumatoria de Vm es mayor o igual a 3
veces la cortante por sismo severo en entre piso se considerará que el edificio se
comportará elásticamente. Bajo esta condición entonces se empleará refuerzo mínimo.
Tabla 39. Verificación del comportamiento elástico del edificio.
NIVEL Y DIRECCION ΣVm(ton/m2) VEi (ton) 3*VEi (ton) ΣVm≤3*VEi
Azotea (Y)
24.12021
12.2666
36.7998 cumple
Tercer Nivel (Y)
146.0497477
60.161
180.483 cumple
Tercer Nivel (X)
3.529843908
60.161
180.483 cumple
Segundo Nivel (Y)
195.3714015
100.236
300.708 cumple
Segundo Nivel (X)
3.564570425
100.236
300.708 cumple
Primer Nivel (Y)
207.810077
118.973
356.919 cumple
Primer Nivel (X)
3.222655711
118.973
356.919 cumple
Al no cumplirse con esta condición entonces el edificio no se comportará elásticamente.
9.5. Diseño de la albañilería confinada
Para el diseño se utiliza el artículo 27 de la Norma E070. Para el primer apartado se
verifica que nuestro edificio es menor que 5 pisos o que 15 metros de altura. Además,
en el diseño se contemplará que todos los muros de los entrepisos bajos del edificio
fallaran por fuerza cortante.
Con respecto apartado c es necesario calcular la fuerza cortante y el momento actuante
debido a un sismo severo, se utilizan factores que amplifican las fuerzas obtenidas
anteriormente para un sismo moderado, como se muestra a continuación.
𝑉𝑢𝑖 = 𝑉𝑒𝑖 ×
𝑉𝑚1
𝑉𝑒1
𝑀𝑢𝑖 = 𝑀𝑒𝑖 ×
𝑉𝑚1
𝑉𝑒1
En este caso, se utilizó una hoja de cálculo para obtener los valores ante sismo severo,
aun así, se corroboro que los valores estuvieran cercanos con los que brindaba la
modelación hecha. Del mismo modo hay que recalcar que el factor de amplificación a
considerar deberá ser como mínimo 2 y máximo 3.
2 ≤
𝑉𝑚1
≤3
𝑉𝑒1
74
Tabla 40. Cálculo del factor de amplificación.
EJE Y
EJE X
Vm1
Ve1
207.8
3.22
57.8
1.68
Factor de
Factor de
amplificación amplificacion
3.60
1.92
3
2
Tabla 41. Fuerza cortante y momento por sismo severo.
Story
Pier
Ve
Me
Azotea
Azotea
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Y-4
Y-11
Y-3
Y-8
Y-9
Y-10
Y-14
Y-17
X-4
Y-2
Y-6
Y-7
Y-13
Y-16
X-3
Y-1
Y-5
Y-12
Y-15
X-2
ton
2.87
3.26
13.05
0.96
1.34
0.58
8.04
5.25
0.85
17.50
13.27
0.82
10.15
6.52
1.87
20.16
18.38
11.88
7.39
1.68
ton.m
4.11
4.49
26.42
0.97
1.83
0.70
11.65
7.30
1.18
42.19
19.40
1.15
16.85
9.76
2.74
53.87
42.56
25.65
12.07
2.95
Factor de
amplificacion
3
3
3
3
3
3
3
3
2
3
3
3
3
3
2
3
3
3
3
2
Vu
Mu
ton
8.61
9.79
39.14
2.89
4.02
1.75
24.13
15.76
1.70
52.49
39.82
2.46
30.44
19.55
3.73
60.48
55.13
35.64
22.16
3.36
ton.m
12.32
13.47
79.26
2.92
5.48
2.11
34.95
21.91
2.37
126.58
58.20
3.46
50.55
29.29
5.48
161.62
127.69
76.96
36.22
5.89
9.6. Verificación de la necesidad de colocar refuerzo horizontal en los muros
Para la verificación de la necesidad de colocar refuerzo horizontal en los muros es
necesario comprobar dos condiciones, la primera que indica que todo muro que tenga un
cortante producido por un sismo severo que sea mayor o igual a su resistencia de corte
deberá llevar refuerzo horizontal. Y la segunda condición es que tenga un esfuerzo a
compresión axial mayor o igual a 0.05 fm. También se ha considerado los pisos
superiores, para verificar si alguno requiere un refuerzo horizontal y evitar el
agrietamiento.
La cuantía del acero que será usado para refuerzo horizontal si cumple una de las
condiciones, será mayor o igual que 0.001. Las varillas penetraran las columnas como
mínimo 12.5 cm y terminaran con gancho a 90 grados vertical de 10cm de longitud.
75
Tabla 42. Verificación del refuerzo horizontal en los muros.
Story
Pier
Azotea
Azotea
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Primer Nivel
Y-4
Y-11
Y-3
Y-8
Y-9
Y-10
Y-14
Y-17
X-4
Y-2
Y-6
Y-7
Y-13
Y-16
X-3
Y-1
Y-5
Y-12
Y-15
X-2
Vu
ton
8.61
9.79
39.14
2.89
4.02
1.75
24.13
15.76
1.70
52.49
39.82
2.46
30.44
19.55
3.73
60.48
55.13
35.64
22.16
3.36
Vm
ton/m2
12.32
13.47
79.26
2.92
5.48
2.11
34.95
21.91
2.37
126.58
58.20
3.46
50.55
29.29
5.48
161.62
127.69
76.96
36.22
5.89
σm
f'm 0.05*f'm
ton/m2ton/m2 ton/m2
5.50
650
32.5
7.03
650
32.5
9.48
650
32.5
17.81 650
32.5
7.38
650
32.5
10.29 650
32.5
8.14
650
32.5
6.98
650
32.5
7.37
650
32.5
15.40 650
32.5
16.54 650
32.5
24.01 650
32.5
15.83 650
32.5
11.97 650
32.5
15.55 650
32.5
21.81 650
32.5
24.81 650
32.5
23.30 650
32.5
15.48 650
32.5
21.88 650
32.5
σm>= 0.05*f'm
Vu>= Vm
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
no lleva refuerzo
9.7. Verificación del agrietamiento diagonal en los pisos superiores
Se verificará en cada entrepiso superior que el Vm sea mayor a la fuerza cortante
generado por un sismo severo, si no se cumple esta condición el entrepiso que no
cumpla se agrietara y sus confinamientos deberán ser diseñados para soportar Vm en
forma similar al primer piso.
76
Tabla 43. Verificación del agrietamiento diagonal en los pisos superiores.
Story
Pier
Azotea
Azotea
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Tercer Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Segundo Nivel
Y-4
Y-11
Y-3
Y-8
Y-9
Y-10
Y-14
Y-17
X-4
Y-2
Y-6
Y-7
Y-13
Y-16
X-3
Vu
ton
8.61
9.79
39.14
2.89
4.02
1.75
24.13
15.76
1.70
52.49
39.82
2.46
30.44
19.55
3.73
Vm
ton/m2
12.32
13.47
79.26
2.92
5.48
2.11
34.95
21.91
2.37
126.58
58.20
3.46
50.55
29.29
5.48
Vm>Vu
no hay agrietamiento
no hay agrietamiento
no hay agrietamiento
no hay agrietamiento
no hay agrietamiento
no hay agrietamiento
no hay agrietamiento
no hay agrietamiento
no hay agrietamiento
no hay agrietamiento
no hay agrietamiento
no hay agrietamiento
no hay agrietamiento
no hay agrietamiento
no hay agrietamiento
9.8. Diseño de las columnas de confinamiento
Para el diseño de las columnas es necesario la determinación de la sección de
concreto, será necesario hallar las fuerzas de Compresión y de la fuerza cortante,
adicionalmente también necesitaremos la fuerza por Tracción para el área de acero que
se usará en las columnas. Por eso hallamos inicialmente estas fuerzas, y que debido a que
los muros mantienen una continuidad por columnas internas, se consideraran en paños.
Tabla 44. Fuerzas internas en columnas de confinamiento.
Fuente: Norma Técnica E.070 Albañilería
Donde Nc son los números de columnas de confinamiento. Lm es la longitud del paño
mayor o 0.5 L, lo que sea mayor.
77
Figura 32. Muro con dos paños.
Fuente: Apuntes de clases de DAA Udep
Tabla 45. Datos para el cálculo de las fuerzas internas en las columnas de confinamiento.
Muro
Y-1
Y-5
Y-12
Y-15
X-2
Vm1
Mu1
h
ton/m2
ton.m
m
161.62
161.62
127.69
127.69
76.96
76.96
36.22
36.22
5.89
5.89
2.68
2.68
2.68
2.68
2.68
M
L
F
ton.m
m
ton
-54.95
12.25
-43.41
10.9
-26.17
7.15
-12.31
5.1
-2.00
0.94
Nc
-4.49
-3.98
-3.66
-2.41
-2.13
Lm
m
9
9
3
3
2
6.13
5.45
4.15
4.45
0.94
Pg=25%CV+CM Pt
Pc
ton
ton
ton
32.16
16.08
31.69
15.85
19.89
2.04
11.99
9.42
2.04
6.75
2.46
7.34
8.58
Tabla 46. Fuerzas internas en las columnas de confinamiento.
Muro COLUMNA
Y-1
Y-5
Y-12
Y-15
X-2
Interior
Extrema
Interior
Extrema
Interior
Extrema
Interior
Extrema
Extrema
Vc
ton
8.09
12.13
6.38
9.58
11.17
16.75
7.90
11.85
2.95
T
ton
19.276
-20.567
15.547
-19.830
16.856
-15.650
12.278
-9.169
-10.707
C
ton
-1.60
11.60
0.15
11.86
-2.43
8.33
-2.76
4.34
6.45
Como se puede observar de la tabla algunos valores de tracción resultan negativos, esto
quiere decir que estas columnas no trabajarán a tracción y lo harán a compresión.
Halladas ya las fuerzas internas se procede inicialmente con el cálculo para la sección
de concreto por compresión y corte fricción y así obtener las dimensiones para cada
columna.
78
9.9. Diseño por compresión
Para el diseño por compresión, se calculará el área del núcleo mediante:
𝐶
𝐴𝑛 = 𝐴𝑠 +
∅ − 𝐴𝑠 × 𝑓𝑦
0.85 × 𝛿 × 𝑓′𝑐
Donde:
∅ = 0.75, según se utilice estribos cerrados.
𝛿 = 0.8 o 1, según columnas sin muros transversales y para columnas con muro
confinadas respectivamente.
Para el acero mínimo se usará 4 varillas de 8mm de diámetro.
Tabla 47. Datos para el diseño por compresión.
DATOS PARA EL DISEÑO POR COMPRESION
fy
4200 kg/cm2
f'c
210
kg/cm2
As
2.01 4Ø8mm
Ø
0.75 estribos cerrados
sin muros
0.8
transversales
δ
confinadas por muros
1
tramsversales
9.10. Diseño por corte fricción
Para el diseño por corte fricción la sección transversal de las columnas estará
diseñada mediante la fórmula:
𝐴𝑐𝑓 =
𝑉𝑐
0.2×𝑓 𝑐 ×∅
≥ 𝐴𝑐 ≥ 15𝑡 (𝑐𝑚2 )
Donde:
∅ = 0.85
Debido a las dos posibilidades existentes se escogerá el área mayor obtenida pero
no debe ser menor que 15 veces el espesor de la columna lo que es igual al espesor
efectivo del muro, que en nuestro caso se considera de 13cm.
79
Tabla 48. Datos para el diseño por corte fricción.
DISEÑO POR CORTE FRICCION
Ø
0.85
t
13
15*t
195
20*t
260
Si bien la dimensión mínima es 15t, es preferible usar columnas de confinamiento de
20t o 25t como mínimo para evitar la segregación en el vaciado.
Tabla 49. Cálculo de la sección de concreto por compresión y corte fricción.
MURO
Y-1
Y-5
Y-12
Y-15
X-2
COLUMNA
Interior
Extrema
Interior
Extrema
Interior
C (Kg)
1597
11596
150
11865
2433
Extrema
8331
Interior
2762
Extrema
4340
Extrema
6446
δ
0.8
0.8
0.8
0.8
1
1
0.8
0.8
0.8
1
1
0.8
An (cm2)
-42
51
-56
54
-27
17
21
-31
-17
-13
3
3
Vc (Kgf)
8087
12131
6384
9576
11167
Acf (cm2) Area. Teorica Area>=15*t Area. Selecc dimensiones
227
227
cumple
260
20x13
340
340
cumple
340
25x15
179
179
no cumple
260
20x13
268
268
cumple
268
25x13
313
313
cumple
313
25x13
16751
469
469
cumple
469
20x25
7901
221
221
cumple
260
20x13
11851
332
332
cumple
332
25x15
2945
82
82
no cumple
260
20x13
9.11. Determinación del refuerzo vertical de las columnas de confinamiento
Para la determinación del refuerzo vertical en las columnas de confinamiento, estas se
diseñan para ser capaces de soportar la acción combinada de corte fricción y tracción,
como mínimo se colocarán 4 varillas para formar un núcleo confinado. El esfuerzo es la
suma del refuerzo requerido por corte fricción y el requerido por tracción.
𝐴𝑠𝑓 =
𝑉𝑐
𝑓𝑦 × 𝑢 × ∅
𝐴𝑠𝑡 =
𝑇
𝑓𝑦 × ∅
𝐴𝑠 = 𝐴𝑠𝑓 + 𝐴𝑠𝑡 ≥
0.1 × 𝑓′𝑐 × 𝐴𝑐
𝑓𝑦
Donde:
∅ = 0.85, factor de reducción de resistencia.
u = 1, al tomar que para las juntas se eliminara la lechada del cemento e
intencionalmente serán rugosas.
80
Para el caso del cálculo de los estribos, se usará como mínimo estribos de 6mm 1@5cm,
4@10cm y el resto @25cm. Adicional se le agregaran 2 estribos en la unión solera
columnas y estribos @10cm en el sobrecimiento.
Tabla 50. Datos para el cálculo del refuerzo vertical en las columnas de confinamiento.
DATOS
fy (kg/cm2)
4200
f'c (kg/cm2)
210
µ
1
Ø
Ac (cm2)
As min
0.85
225
2.01
81
Tabla 51. Cálculo del acero para las columnas de confinamiento.
muro
Y-1
Y-5
Y-12
Y-15
X-2
COL.
C (Kgf) Vc (Kgf)
Interior 1597
8087
Extrema 11596 12131
Interior
150
6384
Extrema 11865
9576
Interior 2433
11167
Extrema 8331
16751
Interior 2762
7901
Extrema 4340
11851
Extrema 6445.54 2945.1
T (Kgf)
19276
20567
15547
19830
16856
15650
12278
9169
10707
Asf(cm2) Ast (cm2) As (cm2)
2.27
5.40
7.66
3.40
5.76
9.16
1.79
4.35
6.14
2.68
5.55
8.24
3.13
4.72
7.85
4.69
4.38
9.08
2.21
3.44
5.65
3.32
2.57
5.89
0.82
3.00
3.82
(0.1*F'c*Ac) As>=(0.1*F'c
/Fy
*Ac)/Fy
SE ESCOGE
1.13
cumple 4 Ø 5/8'' (8 cm2)
1.13
cumple 4Ø 1/2'' +2Ø5/8''(9.16cm2)
1.13
cumple 2Ø 5/8''+2Ø1/2''(6.58cm2)
1.13
cumple 4Ø 1/2'' +2Ø5/8''(9.16 cm2)
1.13
cumple 4 Ø 5/8'' (8 cm2)
1.13
cumple 4Ø 1/2'' +2Ø5/8''(9.16cm2)
1.13
cumple 2Ø 1/2''+2Ø5/8''(6.58cm2)
1.13
cumple 2Ø 1/2''+2Ø5/8''(6.58cm2)
1.13
cumple 4Ø 1/2'' (5.16cm2)
82
ESTRIBOS
Ø 6mm [email protected], [email protected], [email protected]
Ø 6mm [email protected], [email protected], [email protected]
Ø 6mm [email protected], [email protected], [email protected]
Ø 6mm [email protected], [email protected], [email protected]
Ø 6mm [email protected], [email protected], [email protected]
Ø 6mm [email protected], [email protected], [email protected]
Ø 6mm [email protected], [email protected], [email protected]
Ø 6mm [email protected], [email protected], [email protected]
Ø 6mm [email protected], [email protected], [email protected]
Capítulo 10
Diseño de cimentaciones:
10.1. Generalidades:
Para este capítulo se realizará los procesos de diseño de cimentaciones en base de la
información obtenida del EMS del lugar donde se construirá la vivienda y de los criterios
estipulados en la Norma E.050 y E.060.
Resumen de las condiciones de cimentación:
•
•
•
•
•
Tipo de cimentación: cimentación superficial / zapatas aisladas
Profundidad de cimentación mínima: 0.80m
Dimensión utilizada B(m): 1.50m
Capacidad portante neta admisible: 1.22 kg/cm2
Factor de seguridad: 3.0
Debido al comportamiento que generan las fuerzas sobre las cimentaciones, se han
determinado los siguientes casos a desarrollar para el diseño:
•
•
•
Zapatas aisladas
Zapatas conectadas con vigas
Zapatas corridas
Se procederá a diseñar todos los casos posibles que se encuentren en la estructura de la
vivienda unifamiliar:
10.2. Diseño de zapata aislada
Para el diseño de una de estas zapatas se tomará como ejemplo la cimentación debajo de la
columna C4, que se ubica en la intercepción de los ejes E y 3c. La columna se encuentra en
el centro de la zapata.
Predimensionamiento:
Se considero una altura de cimentación de 60 cm en caso de que trabajar acero de ¾” para
lo cual se necesita esta dimensión para el anclaje, malla y recubrimiento.
El predimensionamiento de la zapata se obtendrá a partir de la combinación de las cargas
de servicio que afectan a la zapata. A continuación, se muestra una primera tabla donde se
aprecian las cargas obtenidas del software ETABS y una segunda tabla donde se aprecia la
combinación en servicio de las cargas.
83
Tabla 52. Datos obtenidos del software ETABS sobre la columna C4
ETABS
CARGA
P (ton)
Mx (ton.m) My (ton.m)
CM
10.2782
0.2713
-0.0047
CV
1.6445
0.0923
0.0044
CEQX
3.6274
0.8053
-
CEQY
0.6644
-
0.3891
CEQ
Tabla 53. Cargas y momentos de servicio
CARGAS EN SERVICIO
P (ton)
M (ton)
11.42935
0.33591
CM + CVred
0.75(CM+CVred+0.8CSx) 10.7484525 0.7351125
0.75(CM+CVred-0.8CSx) 6.3955725 -0.2312475
13.18012
0.91554
CM+0.8CSx
7.37628
-0.37294
CM-0.8CSx
0.75(CM+CVred+0.8CSy) 8.9706525 0.232245
0.75(CM+CVred-0.8CSy) 8.1733725 -0.234675
10.80972
0.30658
CM+0.8CSy
9.74668
-0.31598
CM-0.8CSy
Se procede a calcular la capacidad portante neta del suelo en condición estática y sísmica.
Condición estática:
𝑞𝑛𝑠 = 𝑞𝑎𝑑𝑚 − 𝛾𝑠 ℎ𝑠 − 𝛾𝑐 ℎ𝑐 − 𝑠/𝑐
𝑞𝑛𝑠 = 12.2 − 1.7 ∗ 0.2 − 2.4 ∗ 0.6 − 0.2
𝑞𝑛𝑠 = 10.22 𝑡𝑜𝑛/𝑚2
Condición sísmica:
𝑞𝑛𝐸𝑄 = 1.33𝑞𝑎𝑑𝑚 − 𝛾𝑠 ℎ𝑠 − 𝛾𝑐 ℎ𝑐 − 𝑠/𝑐
𝑞𝑛𝐸𝑄 = 1.33 ∗ 12.2 − 1.7 ∗ 0.2 − 2.4 ∗ 0.6 − 0.2
𝑞𝑛𝐸𝑄 = 14.25 𝑡𝑜𝑛/𝑚2
84
Se calcula el área de la zapata para todas las combinaciones, aplicando la siguiente
formula:
𝐴𝑧𝑎𝑝 =
𝑃
𝑓𝑞𝑛
f: Considera efectos de flexión de manera preliminar.
Se toma la mayor área de entre las combinaciones que contenga la mayor carga axial y la
que contenga el mayor momento.
Tabla 54. Área de zapata para todas las combinaciones de servicio
CARGAS EN SERVICIO
P (ton)
M (ton)
f
qn (ton/m2)
CM + CVred
0.75(CM+CVred+0.8CSx)
0.75(CM+CVred-0.8CSx)
CM+0.8CSx
CM-0.8CSx
0.75(CM+CVred+0.8CSy)
0.75(CM+CVred-0.8CSy)
CM+0.8CSy
CM-0.8CSy
11.429
10.748
6.396
13.180
7.376
8.971
8.173
10.810
9.747
0.336
0.735
-0.231
0.916
-0.373
0.232
-0.235
0.307
-0.316
0.95
0.85
0.95
0.85
0.9
0.95
0.95
0.95
0.95
10.22
14.25
14.25
14.25
14.25
14.25
14.25
14.25
14.25
Azap (m2)
1.177
0.888
0.473
1.088
0.575
0.663
0.604
0.799
0.720
1.177
Por recomendación del EMS se tomará una dimensión utilizada B de 1.5 metros, que por
ende nos exigiría un largo mínimo de 0.8 metros. Con fines constructivos se utilizará un
largo L de 1.5 metros y de esta manera obtener un volado de igual dimensión en ambas
direcciones. Debido a las dimensiones de la cimentación podemos apreciar que se está
realizando el diseño de una zapata cuadrada.
Lo siguiente es verificar que las presiones en el suelo cumplan con los mínimos y máximos
establecidos. Se utilizará la siguiente fórmula para calcular las presiones:
𝑞=
𝑃
6𝑀
± 2
𝐵𝐿 𝐵𝐿
A continuación, se muestra una tabla con todas las combinaciones de servicio y las
respectivas presiones en el suelo:
85
Tabla 55. Verificación de las presiones en el suelo
q (ton/m2)
Verificación
CARGAS EN SERVICIO
qmax
(ton/m2)
qmín
(ton/m2)
qmax<qn
qmín>0
CM + CVred
0.75(CM+CVred+0.8CSx)
0.75(CM+CVred-0.8CSx)
CM+0.8CSx
CM-0.8CSx
0.75(CM+CVred+0.8CSy)
0.75(CM+CVred-0.8CSy)
CM+0.8CSy
CM-0.8CSy
5.677
6.084
3.254
7.485
3.941
4.400
4.050
5.349
4.894
4.483
3.470
2.431
4.230
2.615
3.574
3.215
4.259
3.770
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
Se comprueba que las presiones cumplen con los valores establecidos. Por lo tanto, las
dimensiones de la zapata obtenidas en el predimensionamiento nos servirán para el diseño
de esta misma.
Diseño Estructural:
Se amplifican las cargas según lo estipulado en la Norma E.060. A continuación, se
muestra una tabla con todas las combinaciones de diseño y sus respectivos valores de
cargas y momentos.
Tabla 56. Cargas y momentos de diseño
CARGAS DE DISEÑO
Pu (ton)
Mu (ton)
1.4CM + 1.7CVred
1.25(CM+CVred)+CSx
1.25(CM+CVred)-CSx
0.9CM+CSx
0.9CM-CSx
1.25(CM+CVred)+CSy
1.25(CM+CVred)-CSy
0.9CM+CSy
0.9CM-CSy
16.346
17.914
10.659
12.878
5.623
14.951
13.622
9.915
8.586
0.490
1.225
-0.385
1.049
-0.561
0.387
-0.391
0.385
-0.393
Luego se calculan los esfuerzos sobre el suelo con la siguiente formula:
𝑞𝑢 =
𝑃𝑢 6𝑀𝑢
±
𝐵𝐿 𝐵𝐿2
86
En la siguiente tabla se observan todas las combinaciones de diseño con sus respectivos
esfuerzos en el suelo:
Tabla 57. Calculo de las presiones en el suelo
qu (ton/m2)
CARGAS DE DISEÑO
q1 (ton/m2) q2 (ton/m2)
1.4CM + 1.7CVred
1.25(CM+CVred)+CSx
1.25(CM+CVred)-CSx
0.9CM+CSx
0.9CM-CSx
1.25(CM+CVred)+CSy
1.25(CM+CVred)-CSy
0.9CM+CSy
0.9CM-CSy
8.136
10.140
5.423
7.589
3.497
7.333
6.750
5.091
4.515
6.395
5.784
4.052
3.858
1.502
5.957
5.359
3.722
3.117
Se toma el mayor valor de qu para el diseño: qu = 10.14 ton/m2
Verificación por corte:
No es practica usual colocar refuerzo por corte en cimentaciones. Se espera que el concreto
resista la demanda de resistencia por corte.
Se procede a calcular la cortante a una distancia “d” de la cara de la columna, como se
muestra en la figura.
Figura 33. Cálculo de corte Vu.
87
Se calcula el Vu, por metro de ancho (𝑏𝑤 = 1𝑚):
𝑉𝑢 = 𝑞𝑢 ∗ (
1.5 − 0.3
− 0.5) ∗ 1𝑚
2
𝑉𝑢 = 1.014 𝑡𝑜𝑛
Se calcula el 𝜙𝑉𝑐 por metro de ancho (𝑏𝑤 = 1𝑚):
𝜙𝑉𝑐 = 0.85 ∗ 0.53 ∗ √𝑓′𝑐 ∗ 𝑑 ∗ 𝑏𝑤
𝜙𝑉𝑐 = 32.642 𝑡𝑜𝑛
Por lo tanto, se verifica que 𝑉𝑢 < 𝜙𝑉𝑐 .
Verificación por punzonamiento:
Se debe verificar que la resistencia al corte de concreto sea menor que:
2
𝑉𝑐 = 0.53 (1 + ) √𝑓𝑐 . 𝑏𝑜 𝑑
𝛽
𝑉𝑐 = 0.27 (
𝑎𝑠 𝑑
+ 2) √𝑓𝑐 . 𝑏𝑜 𝑑
𝑏𝑜
𝑉𝑐 = 1.06√𝑓𝑐 . 𝑏𝑜 𝑑
En donde:
𝑏𝑜 = Perímetro de la sección crítica.
𝛽 = Relación de lado largo a lado corto en la zapata.
𝑎𝑠 = 40 para columnas interiores, 30 para columnas en borde y 20 para columnas en
esquina.
En la siguiente imagen podemos apreciar las dimensiones a calcular para este diseño.
Figura 34. Dimensiones de la zapata a calcular.
88
Se calcula las dimensiones del cuadrilátero 𝑏0 :
En el lado corto tendrá una dimensión de 0.3 m (columna) más 0.5 m (d); en total 0.8
metros.
En el lado largo tendrá una dimensión de 0.3 m (columna) más 0.5 m (d); en total 0.8
metros.
Entonces
𝑏0 = 2 ∗ (0.8 + 0.8) = 3.2
𝛽=
1.5
=1
1.5
𝛼 = 40 (𝑐𝑜𝑙𝑢𝑚𝑛𝑎 𝑖𝑛𝑡𝑒𝑟𝑛𝑎)
Se calcula el valor de la cortante:
𝑉𝑢 = 𝑞𝑢 ∗ (1.5 ∗ 1.5 − 0.8 ∗ 0.8)
𝑉𝑢 = 16.325 𝑡𝑜𝑛
Se escoge el valor de Vc:
2
𝑉𝑐 = 0.53 (1 + ) √210 ∗ 3.2 ∗ 0.5 = 368.661 𝑡𝑜𝑛
1
𝑉𝑐 = 0.27 (
40 ∗ 0.5
+ 2) √210 ∗ 3.2 ∗ 0.5 = 516.473
3.2
𝑉𝑐 = 1.06√210 ∗ 3.2 ∗ 0.5 = 245.774
Se escoge Vc=516.473
Luego, 𝜙𝑉𝑐 = 0.85 ∗ 516.473 = 439.002 𝑡𝑜𝑛
Por lo tanto, se verifica que 𝑉𝑢 < 𝜙𝑉𝑐
Diseño por flexión:
Se obtienen dos momentos últimos en las dos direcciones de la zapata, sin embargo, al
tener el mismo volado en ambas direcciones, el momento es el mismo. Considerar 1 metro
de ancho.
𝑀𝑢 = 10.14
𝑡𝑜𝑛
0.6
∗
1𝑚
∗
0.6𝑚
∗
𝑚 = 1.825 𝑡𝑜𝑛. 𝑚
𝑚2
2
Se calcula el Ku para entrar a la tabla de cuantía.
𝐾𝑢 =
1.825 𝑡𝑜𝑛. 𝑚
= 0.73 𝑘𝑔/𝑐𝑚2
100𝑐𝑚 ∗ 502 𝑐𝑚
Con la cuantía calculada se compara con la cuantía mínima, en caso de no ser mayor se
toma el mínimo.
89
𝜌 = 0.019% < 𝜌𝑚𝑖𝑛𝑖𝑚𝑎 = 0.18% − 𝑆𝑒 𝑢𝑡𝑖𝑙𝑖𝑧𝑎 𝑒𝑙 𝑚í𝑛𝑖𝑚𝑜
Se calcula la cantidad de acero, teniendo en cuenta que el mínimo antes mencionado aplica
también al acero por temperatura de la zapata. Se debe escoger el mayor para continuar el
diseño.
𝐴𝑠 = 0.18% ∗ 100𝑐𝑚 ∗ 50𝑐𝑚 = 9 𝑐𝑚2
𝐴𝑠𝑡𝑒𝑚𝑝 = 0.18% ∗ 100𝑐𝑚 ∗ 60𝑐𝑚 = 10.8 𝑐𝑚2
Se escoge 10.8 𝑐𝑚2 .
Luego se elige la barra de acero adecuada y se calcula la separación.
𝐴𝑐𝑒𝑟𝑜 𝜙3/4"
𝐴𝑟𝑒𝑎 𝑎𝑐𝑒𝑟𝑜 𝜙3/4" = 2.84 𝑐𝑚2
𝑆=
2.84 𝑐𝑚2 ∗ 100𝑐𝑚
= 26. 3 𝑐𝑚
10.8 𝑐𝑚2
𝐷𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛 𝑐𝑜𝑛𝑠𝑡𝑟𝑢𝑐𝑡𝑖𝑣𝑎 𝑦 𝑐𝑜𝑛𝑠𝑒𝑟𝑣𝑎𝑑𝑜𝑟𝑎 = 25𝑐𝑚
En consecuencia, el diseño será barras de 𝜙3/4"cada 25 cm en las dos direcciones.
10.3. Diseño de zapatas conectadas con viga
Para el diseño de estas zapatas se tomará como ejemplo las cimentaciones debajo la
columna C1 y la placa PX-2. La columna C1 se encuentra ubicada en la intercepción del
eje C y 1 y está en el límite de propiedad, mientras que la placa PX-2 se encuentra en el eje
C entre los ejes 2 y 3 y es interna.
Debido a cargas y momentos muy altos producidos en las placas, se ha creído conveniente
usar una viga de cimentación para conectar la cimentación debajo de la placa hacia una
cimentación de una columna con el fin de que las zapatas sean capaces de resistir
momentos y cortes altos sin deformaciones o fisuración importante
Predimensionamiento:
Se considero una altura de cimentación de 60 cm en caso de que trabajar acero de ¾” para
lo cual se necesita esta dimensión para el anclaje, malla y recubrimiento.
El predimensionamiento de las zapatas se obtendrán a partir de la combinación de las
cargas de servicio que afectan a la zapata. A continuación, se muestra una primera tabla
donde se aprecian las cargas obtenidas del software ETABS y una segunda tabla donde se
aprecia la combinación en servicio de las cargas.
90
Para la columna C1:
Tabla 58. Datos obtenidos del ETABS sobre la columna C1
ETABS
CARGA
P (ton)
Mx (ton.m) My (ton.m)
CM
12.4943
-0.6615
0.0042
CV
2.09
-0.1677
0.0041
CEQX
3.8888
0.8486
-
CEQY
1.4726
-
0.3887
CEQ
Tabla 59. Cargas y momentos de servicio
CARGAS EN SERVICIO
P (ton)
M (ton)
CM + CVred
0.75(CM+CVred+0.8CSx)
0.75(CM+CVred-0.8CSx)
CM+0.8CSx
CM-0.8CSx
0.75(CM+CVred+0.8CSy)
0.75(CM+CVred-0.8CSy)
CM+0.8CSy
CM-0.8CSy
13.9573
12.801255
8.134695
15.60534
9.38326
11.351535
9.584415
13.67238
11.31622
0.00707
-0.0750075
-1.0933275
0.01738
-1.34038
0.2385225
-0.2279175
0.31516
-0.30676
91
Para la placa PX-2:
Tabla 60. Datos obtenidos del ETABS sobre la placa PX-2
ETABS
CARGA
P (ton)
Mx (ton.m) My (ton.m)
CM
26.6618
0.0723
0.0805
CV
4.8003
0.1524
0.0355
CEQX
58.1337
71.9392
-
CEQY
3.5962
-
1.6132
CEQ
Tabla 61. Cargas y momentos de servicio
CARGAS EN SERVICIO
P (ton)
M (ton)
CM + CVred
0.75(CM+CVred+0.8CSx)
0.75(CM+CVred-0.8CSx)
CM+0.8CSx
CM-0.8CSx
0.75(CM+CVred+0.8CSy)
0.75(CM+CVred-0.8CSy)
CM+0.8CSy
CM-0.8CSy
30.02201
57.3967275
-12.3637125
73.16876
-19.84516
24.6742275
20.3587875
29.53876
23.78484
0.17898
43.297755
-43.029285
57.62366
-57.47906
1.0469325
-0.8889075
1.37106
-1.21006
92
Capacidad portante neta del suelo en condición estática y sísmica.
𝑞𝑛𝑠 = 10.22 𝑡𝑜𝑛/𝑚2
𝑞𝑛𝐸𝑄 = 14.25 𝑡𝑜𝑛/𝑚2
Se calcula el área de las zapatas para todas las combinaciones, aplicando la siguiente
formula:
𝐴𝑧𝑎𝑝 =
𝑃
𝑓𝑞𝑛
f: Considera efectos de flexión de manera preliminar.
Para la cimentación que se encuentra en el limite de propiedad se le multiplicara el factor
1.2 a la carga P para dar un aproximado del efecto de la excentricidad,
Se toma la mayor área de entre las combinaciones que contenga la mayor carga axial y la
que contenga el mayor momento.
Para la columna C1:
Tabla 62. Área de zapata para todas las combinaciones de servicio
CARGAS EN SERVICIO
P (ton)
M (ton)
f
qn (ton/m2)
CM + CVred
0.75(CM+CVred+0.8CSx)
0.75(CM+CVred-0.8CSx)
CM+0.8CSx
CM-0.8CSx
0.75(CM+CVred+0.8CSy)
0.75(CM+CVred-0.8CSy)
CM+0.8CSy
CM-0.8CSy
13.957
12.801
8.135
15.605
9.383
11.352
9.584
13.672
11.316
0.007
-0.075
-1.093
0.017
-1.340
0.239
-0.228
0.315
-0.307
1
1
0.75
1
0.7
0.95
0.95
0.95
0.95
10.22
14.25
14.25
14.25
14.25
14.25
14.25
14.25
14.25
Azap (m2)
1.639
1.078
0.914
1.315
1.129
1.007
0.850
1.212
1.003
1.639
Para placa PX-2:
Tabla 63. Área de zapata para todas las combinaciones de servicio
CARGAS EN SERVICIO
P (ton)
M (ton)
f
qn (ton/m2)
CM + CVred
0.75(CM+CVred+0.8CSx)
0.75(CM+CVred-0.8CSx)
CM+0.8CSx
CM-0.8CSx
0.75(CM+CVred+0.8CSy)
0.75(CM+CVred-0.8CSy)
CM+0.8CSy
CM-0.8CSy
30.022
57.397
-12.364
73.169
-19.845
24.674
20.359
29.539
23.785
0.179
43.298
-43.029
57.624
-57.479
1.047
-0.889
1.371
-1.210
1
0.75
0.75
0.75
0.75
0.9
0.9
0.9
0.9
10.22
14.25
14.25
14.25
14.25
14.25
14.25
14.25
14.25
93
Azap (m2)
2.938
5.372
1.157
6.848
1.857
1.924
1.588
2.304
1.855
6.848
Por lo tanto, para la columna sus dimensiones serán 1 metro de ancho y 1.7 de largo, con el
objetivo de no tener una excentricidad muy grande en esta cimentación, recordando que la
columna C1 se encuentra en el límite de propiedad.
Mientras que para la placa sus dimensiones serán de 2 metros de ancho y 3.5 de largo para
que tenga un volado parecido en ambas direcciones.
En la siguiente figura se observa cómo están distribuidos los momentos y cargas de la
columna y placa, además de las reacciones en los centros de las zapatas.
Figura 35. Cargas y momentos de columnas y placas.
En la siguiente tabla se muestran las reacciones en los centros de las zapatas para cada
estructura.
Tabla 64. Cargas, reacciones y momentos de servicio
Predimensionamiento
Columna/Placa
C1
PX-2
CARGAS EN SERVICIO
P (ton)
M (ton)
R (ton)
CM + CVred
0.75(CM+CVred+0.8CSx)
0.75(CM+CVred-0.8CSx)
CM+0.8CSx
CM-0.8CSx
0.75(CM+CVred+0.8CSy)
0.75(CM+CVred-0.8CSy)
CM+0.8CSy
CM-0.8CSy
CM + CVred
0.75(CM+CVred+0.8CSx)
0.75(CM+CVred-0.8CSx)
CM+0.8CSx
CM-0.8CSx
0.75(CM+CVred+0.8CSy)
0.75(CM+CVred-0.8CSy)
CM+0.8CSy
CM-0.8CSy
13.957
12.801
8.135
15.605
9.383
11.352
9.584
13.672
11.316
30.022
57.397
-12.364
73.169
-19.845
24.674
20.359
29.539
23.785
0.007
-0.075
-1.093
0.017
-1.340
0.239
-0.228
0.315
-0.307
0.179
43.298
-43.029
57.624
-57.479
1.047
-0.889
1.371
-1.210
14.943
4.671
17.992
4.655
22.417
11.916
10.523
14.323
12.466
29.036
65.527
-22.221
84.119
-32.878
24.110
19.420
28.888
22.635
94
Se calcula el q para cada cimentación aplicando la siguiente formula:
𝑞=
𝑅
𝐴𝑧𝑎𝑝
Luego se verifica que las dimensiones asumidas anteriormente cumplan con el requisito
que q < qn.
En la siguiente tabla se observan los valores del q para cada combinación.
Tabla 65. Verificación de presiones en el suelo
Predimensionamiento
Columna/Placa
C1
PX-2
Verificación de Presiones
q (ton/m2) Verificación
CARGAS EN SERVICIO
CM + CVred
0.75(CM+CVred+0.8CSx)
0.75(CM+CVred-0.8CSx)
CM+0.8CSx
CM-0.8CSx
0.75(CM+CVred+0.8CSy)
0.75(CM+CVred-0.8CSy)
CM+0.8CSy
CM-0.8CSy
CM + CVred
0.75(CM+CVred+0.8CSx)
0.75(CM+CVred-0.8CSx)
CM+0.8CSx
CM-0.8CSx
0.75(CM+CVred+0.8CSy)
0.75(CM+CVred-0.8CSy)
CM+0.8CSy
CM-0.8CSy
qmax<qn
8.790
2.747
10.583
2.738
13.186
7.009
6.190
8.425
7.333
4.289
9.361
3.174
12.017
4.697
3.525
2.908
4.220
3.398
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
Cumplen perfectamente todas las combinaciones que su capacidad de suelo sea menor que
la capacidad portante neta.
Ahora pasaremos al diseño de las zapatas y de la viga de cimentación.
95
Diseño Estructural de zapatas:
Se amplifican las cargas según lo estipulado en la Norma E.060. A continuación, se
muestra una tabla con todas las combinaciones de diseño y sus respectivos valores de
cargas y momento, además de las reacciones en los centros de las cimentaciones.
Tabla 66. Cargas, reacciones y momentos de diseño
DISEÑO ESTRUCTURAL DE ZAPATA
Columna/Placa
C1
PX-2
CARGAS DE DISEÑO
Pu (ton)
Mu (ton)
Ru
1.4CM + 1.7CVred
1.25(CM+CVred)+CSx
1.25(CM+CVred)-CSx
0.9CM+CSx
0.9CM-CSx
1.25(CM+CVred)+CSy
1.25(CM+CVred)-CSy
0.9CM+CSy
0.9CM-CSy
1.4CM + 1.7CVred
1.25(CM+CVred)+CSx
1.25(CM+CVred)-CSx
0.9CM+CSx
0.9CM-CSx
1.25(CM+CVred)+CSy
1.25(CM+CVred)-CSy
0.9CM+CSy
0.9CM-CSy
19.979
21.335
13.558
15.134
7.356
18.919
15.974
12.717
9.772
43.039
95.661
-20.606
82.129
-34.138
41.124
33.931
27.592
20.399
0.011
-0.125
-1.822
0.253
-1.444
0.398
-0.380
0.392
-0.385
0.283
72.163
-71.715
72.004
-71.874
1.745
-1.482
1.686
-1.541
21.385
7.784
29.987
1.081
23.283
19.859
17.538
13.215
10.894
41.633
109.212
-37.035
96.182
-50.065
40.184
32.367
27.094
19.277
Se calcula el qu para cada cimentación aplicando la siguiente formula:
𝑞=
𝑅
𝐴𝑧𝑎𝑝
En la siguiente tabla se observan los valores de qu para cada combinación y además el qu
que se utilizara para el diseño,
Tabla 67. Calculo del qu de diseño
DISEÑO ESTRUCTURAL DE ZAPATA
qu (ton/m2)
Columna/Placa
C1
PX-2
CARGAS DE DISEÑO
Ru/Pu
1.4CM + 1.7CVred
1.25(CM+CVred)+CSx
1.25(CM+CVred)-CSx
0.9CM+CSx
0.9CM-CSx
1.25(CM+CVred)+CSy
1.25(CM+CVred)-CSy
0.9CM+CSy
0.9CM-CSy
1.4CM + 1.7CVred
1.25(CM+CVred)+CSx
1.25(CM+CVred)-CSx
0.9CM+CSx
0.9CM-CSx
1.25(CM+CVred)+CSy
1.25(CM+CVred)-CSy
0.9CM+CSy
0.9CM-CSy
21.3850711
7.78442526
29.9865608
1.08104975
23.2831853
19.8592678
17.537988
13.215473
10.8941933
43.038877
109.212212
37.0349233
96.1819403
50.0651953
41.1237125
33.9313125
27.59182
20.39942
96
qu diseño
(ton/m2)
12.579
4.579
17.639
0.636
13.696
11.682
10.316
7.774
6.408
6.148
15.602
5.291
13.740
7.152
5.875
4.847
3.942
2.914
17.639
15.602
Las zapatas se diseñan como aisladas con reacción uniforme en el suelo. Por lo tanto, se
obviará este proceso ya que es parecido al visto anteriormente y se procederá a colocar el
resultado del diseño de las zapatas:
Para la columna C1:
Cimentación superficial/Zapata conectada con viga
B= 1 m
L= 1,7 m
H= 0,6 m
NFZ: -0,8 m
En la dirección de L se colocan barras de acero de ϕ3/4" @ 25 cm.
En la dirección de B se colocan barras de acero de ϕ3/4" @ 20 cm.
Para la placa PX-2:
Cimentación superficial/Zapata conectada con viga
B= 2 m
L= 3.5 m
H= 0,6 m
NFZ: -0,8 m
En la dirección de L se colocan barras de acero de ϕ3/4" @ 25 cm.
En la dirección de B se colocan barras de acero de ϕ3/4" @ 20 cm.
Diseño estructural de viga de cimentación:
Se diseñará una viga de cimentación ubicada 10 cm por encima del nivel final de
cimentación de las zapatas.
Primero se comienza estimando el valor de H que esta entre la décima y séptima parte de la
distancia entre los centros de la columna y la placa.
𝐻∼
𝑆 𝑆
𝑎
10 7
El valor de S= 5.115 m. por lo tanto, H=0.6 m.
Además, como la viga compartirá la misma dimensión que la columna y la placa tienen en
común, la viga tendrá un B=0.3 m.
97
Diseño por flexión para la viga de cimentación:
Se obtendrá el valor de Mu para todas las combinaciones de sus respectivos DMF’s, y se
escogerá el mayor de todos para el diseño.
Tabla 68. Mu para todas las combinaciones de diseño
Mu (ton.m)
7.003
7.342
2.923
5.550
1.131
7.019
5.211
4.844
3.035
7.342
El valor del Mu para el diseño es 7.342 ton.m
Se calcula el Ku para entrar a la tabla de cuantía.
𝐾𝑢 =
7.342 𝑡𝑜𝑛. 𝑚
= 8.39 𝑘𝑔/𝑐𝑚2
30𝑐𝑚 ∗ 542 𝑐𝑚
Con la cuantía calculada se compara con la cuantía mínima para una viga de 30x60 cm, en
caso de no ser mayor se toma el mínimo.
𝜌 = 0.23% < 𝜌𝑚𝑖𝑛𝑖𝑚𝑎 = 0.19% − 𝑆𝑒 𝑢𝑡𝑖𝑙𝑖𝑧𝑎 𝑒𝑙 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑑𝑜
Se calcula la cantidad de acero:
𝐴𝑠 = 0.23% ∗ 30𝑐𝑚 ∗ 54𝑐𝑚 = 3.70 𝑐𝑚2
Además, en la parte inferior de la viga se corre de 1/3 a ½ del área de acero calculado.
Luego se elige la barra de acero adecuada para la parte superior e inferior de la viga:
As-:
2 𝑏𝑎𝑟𝑟𝑎𝑠 𝑑𝑒 𝑎𝑐𝑒𝑟𝑜 𝜙5/8"
𝐴𝑟𝑒𝑎 2 𝜙5/8" = 4 𝑐𝑚2
As+:
2 𝑏𝑎𝑟𝑟𝑎𝑠 𝑑𝑒 𝑎𝑐𝑒𝑟𝑜 𝜙3/8"
𝐴𝑟𝑒𝑎 2 𝜙3/8" = 1.42 𝑐𝑚2
98
Diseño por corte para la viga de cimentación:
Se obtendrá el valor de Vu para todas las combinaciones de sus respectivos DFC’s, y se
escogerá el mayor de todos para el diseño.
Se obtiene Vu:
𝑉𝑢 = 16.43 𝑡𝑜𝑛
Se halla Vc:
𝑉𝑐 = 0.53𝑥√210𝑥30𝑥54 = 12.44 𝑡𝑜𝑛
Se halla Vn:
𝑉𝑛 =
𝑉𝑢 16.43 𝑡𝑜𝑛
=
= 19.32 𝑡𝑜𝑛
𝜙
0.85
Se cumple que 𝑉𝑐 < 𝑉𝑛, entonces sí se necesitan estribos y se calcula Vs:
𝑉𝑠 = 𝑉𝑛 − 𝑉𝑐 = 6.89 𝑡𝑜𝑛
Suponemos estribos de 3/8”, entonces:
𝐴𝑣 = 1.42 𝑐𝑚2
Se calcula el espaciamiento:
𝑠=
1.42𝑐𝑚2𝑥4200𝑘𝑔/𝑐𝑚2𝑥54𝑐𝑚
= 46.77 𝑐𝑚
6.89 𝑡𝑜𝑛
El espaciamiento en la zona confinada con los requerimientos del diseño por capacidad
según la Norma E060 son:
𝑑
4
(𝑚í𝑛 15𝑐𝑚) =
54
4
= 13.5 𝑐𝑚 ≫> 𝑠𝑒 𝑒𝑠𝑐𝑜𝑔𝑒 15 𝑐𝑚
10 𝑑𝑏𝑙 = 10𝑥(𝜙5/8”) = 10𝑥1.59 = 15.9 𝑐𝑚
24 𝑑𝑏𝑒 = 24𝑥(𝜙3/8”) = 24𝑥0.95 = 22.8 𝑐𝑚
30 cm
Se escoge el menor valor de las expresiones anteriores, entonces el espaciamiento en la
zona de confinamiento sería:
𝐸𝑠𝑝𝑎𝑐𝑖𝑎𝑚𝑖𝑒𝑛𝑡𝑜 𝑑𝑒 𝑑𝑖𝑠𝑒ñ𝑜 = 𝑆 𝑑𝑖𝑠𝑒ñ𝑜 = 15 𝑐𝑚
𝐿𝑜𝑛𝑔𝑖𝑡𝑢𝑑 𝑑𝑒 𝑐𝑜𝑛𝑓𝑖𝑛𝑎𝑚𝑖𝑒𝑛𝑡𝑜 = 2ℎ = 1.2 𝑚
99
Fuera de la zona de confinamiento, se utiliza el espaciamiento máximo:
𝑑
2
=
54
2
= 27 𝑐𝑚
60 𝑐𝑚
Se escoge el menor valor de las expresiones anteriores, entonces el espaciamiento en la
zona de central sería:
𝐸𝑠𝑝𝑎𝑐𝑖𝑎𝑚𝑖𝑒𝑛𝑡𝑜 𝑑𝑒 𝑑𝑖𝑠𝑒ñ𝑜 = 𝑆 𝑑𝑖𝑠𝑒ñ𝑜 = 25 𝑐𝑚
La distribución final de estribos sería [email protected] [email protected] [email protected].
10.4. Diseño de zapata corrida
Para el diseño de una estas zapatas se tomará como ejemplo la cimentación debajo del
muro Y1, que se encuentra en el eje 1 entre los ejes A y G.
Predimensionamiento:
El predimensionamiento de la zapata se obtendrá a partir de la combinación de las cargas
de servicio que afectan a la zapata. A continuación, se muestra una primera tabla donde se
aprecian las cargas obtenidas del software ETABS y una segunda tabla donde se aprecia la
combinación en servicio de las cargas.
Tabla 69. Datos obtenidos del software ETABS sobre el muro Y1
ETABS
CARGA
P (ton)
Mx (ton.m) My (ton.m)
CM
31.3054
-5.3451
0.2453
CV
3.4312
4.6467
0.0746
CEQX
28.9782
39.3865
-
CEQY
1.6091
-
0.0278
CEQ
Tabla 70. Cargas y momentos de servicio
CARGAS EN SERVICIO
P (ton)
M (ton)
CM + CVred
0.75(CM+CVred+0.8CSx)
0.75(CM+CVred-0.8CSx)
CM+0.8CSx
CM-0.8CSx
0.75(CM+CVred+0.8CSy)
0.75(CM+CVred-0.8CSy)
CM+0.8CSy
CM-0.8CSy
33.707
42.667
7.894
54.488
8.123
26.246
24.315
32.593
30.018
0.298
22.063
-25.201
26.164
-36.854
0.240
0.206
0.268
0.223
100
Se procede a calcular la capacidad portante neta del suelo en condición estática y sísmica.
Condición estática:
𝑞𝑛𝑠 = 𝑞𝑎𝑑𝑚 − 𝛾𝑠 ℎ𝑠 − 𝛾𝑐 ℎ𝑐 − 𝑠/𝑐
𝑞𝑛𝑠 = 12.2 − 1.7 ∗ 0.2 − 2.4 ∗ 0.6 − 0.2
𝑞𝑛𝑠 = 10.22 𝑡𝑜𝑛/𝑚2
Condición sísmica:
𝑞𝑛𝐸𝑄 = 1.33𝑞𝑎𝑑𝑚 − 𝛾𝑠 ℎ𝑠 − 𝛾𝑐 ℎ𝑐 − 𝑠/𝑐
𝑞𝑛𝐸𝑄 = 1.33 ∗ 12.2 − 1.7 ∗ 0.2 − 2.4 ∗ 0.6 − 0.2
𝑞𝑛𝐸𝑄 = 14.25 𝑡𝑜𝑛/𝑚2
Se calcula el área de la zapata para todas las combinaciones, aplicando la siguiente
formula:
𝑃
𝑓𝑞𝑛
𝐴𝑧𝑎𝑝 =
f: Considera efectos de flexión de manera preliminar.
Se toma la mayor área de entre las combinaciones que contenga la mayor carga axial y la
que contenga el mayor momento.
Tabla 71. Área de zapata para todas las combinaciones de servicio
CARGAS EN SERVICIO
P (ton)
M (ton)
f
qn (ton/m2)
CM + CVred
0.75(CM+CVred+0.8CSx)
0.75(CM+CVred-0.8CSx)
CM+0.8CSx
CM-0.8CSx
0.75(CM+CVred+0.8CSy)
0.75(CM+CVred-0.8CSy)
CM+0.8CSy
CM-0.8CSy
33.707
42.667
7.894
54.488
8.123
26.246
24.315
32.593
30.018
0.298
22.063
-25.201
26.164
-36.854
0.240
0.206
0.268
0.223
1
0.5
0.5
0.5
0.5
1
1
1
1
10.22
14.25
14.25
14.25
14.25
14.25
14.25
14.25
14.25
Azap (m2)
3.958
7.188
1.330
9.179
1.368
2.211
2.048
2.745
2.529
9.179
La zapata tiene un largo L de 12.4 metros, que por ende nos exigiría un ancho mínimo de
0.8 metros. Por recomendación del EMS se utilizará un valor de B = 1.5 m.
101
Lo siguiente es verificar que las presiones en el suelo sean menores que la capacidad
portante neta:
A continuación, se muestra una tabla con todas las combinaciones de servicio y las
respectivas presiones en el suelo:
Tabla 72. Verificación de presiones en suelo
CARGAS EN SERVICIO
P (ton)
M (ton)
qn (ton/m2)
qmax
(ton/m2)
qmax<qn
CM + CVred
0.75(CM+CVred+0.8CSx)
0.75(CM+CVred-0.8CSx)
CM+0.8CSx
CM-0.8CSx
0.75(CM+CVred+0.8CSy)
0.75(CM+CVred-0.8CSy)
CM+0.8CSy
CM-0.8CSy
33.707
42.667
7.894
54.488
8.123
26.246
24.315
32.593
30.018
0.298
22.063
-25.201
26.164
-36.854
0.240
0.206
0.268
0.223
10.22
14.25
14.25
14.25
14.25
14.25
14.25
14.25
14.25
1.820
2.868
1.080
3.610
1.395
1.417
1.313
1.759
1.620
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
CUMPLE
Se comprueba que las presiones cumplen con los valores establecidos. Por lo tanto, las
dimensiones de la zapata obtenidas en el predimensionamiento nos servirán para el diseño
de esta misma.
Diseño Estructural:
Se amplifican las cargas según lo estipulado en la Norma E.060. A continuación, se
muestra una tabla con todas las combinaciones de diseño y sus respectivos valores de
cargas y momentos.
Tabla 73.Cargas y momentos de diseño
CARGAS DE DISEÑO
Pu (ton)
Mu (ton)
1.4CM + 1.7CVred
1.25(CM+CVred)+CSx
1.25(CM+CVred)-CSx
0.9CM+CSx
0.9CM-CSx
1.25(CM+CVred)+CSy
1.25(CM+CVred)-CSy
0.9CM+CSy
0.9CM-CSy
47.911
71.112
13.156
57.153
-0.803
43.743
40.525
29.784
26.566
0.432
36.771
-42.002
34.576
-44.197
0.400
0.344
0.249
0.193
102
Luego se calculan los esfuerzos sobre el suelo. En la siguiente tabla se observan todas las
combinaciones de diseño con sus respectivos esfuerzos en el suelo:
Tabla 74. Calculo del qu de diseño
CARGAS DE DISEÑO
Pu (ton)
Mu (ton)
q1 (ton/m2)
qu diseño
(ton/m2)
1.4CM + 1.7CVred
1.25(CM+CVred)+CSx
1.25(CM+CVred)-CSx
0.9CM+CSx
0.9CM-CSx
1.25(CM+CVred)+CSy
1.25(CM+CVred)-CSy
0.9CM+CSy
0.9CM-CSy
47.911
71.112
13.156
57.153
-0.803
43.743
40.525
29.784
26.566
0.432
36.771
-42.002
34.576
-44.197
0.400
0.344
0.249
0.193
2.587
4.780
1.800
3.972
1.107
2.362
2.188
1.608
1.433
4.780
Se toma el mayor valor de qu para el diseño: qu = 4.780 ton/m2
Verificación por corte:
Se calcula el Vu, por metro de ancho (𝑏𝑤 = 1𝑚):
𝑉𝑢 = 𝑞𝑢 ∗ ((1.5 − 0.15) − 0.5) ∗ 1𝑚
𝑉𝑢 = 4.06 𝑡𝑜𝑛
Se calcula el 𝜙𝑉𝑐 por metro de ancho (𝑏𝑤 = 1𝑚):
𝜙𝑉𝑐 = 0.85 ∗ 0.53 ∗ √𝑓′𝑐 ∗ 𝑑 ∗ 𝑏𝑤
𝜙𝑉𝑐 = 32.642 𝑡𝑜𝑛
Por lo tanto, se verifica que 𝑉𝑢 < 𝜙𝑉𝑐 .
Diseño por flexión:
Se obtienen los momentos últimos en la dirección corta de la zapata. Considerar 1 metro de
largo
𝑀𝑢 = 4.06
𝑡𝑜𝑛
1.35
∗ 1𝑚 ∗ 1.35𝑚 ∗
𝑚 = 4.36 𝑡𝑜𝑛. 𝑚
2
𝑚
2
Se calcula el Ku para entrar a la tabla de cuantía.
𝐾𝑢 =
4.36 𝑡𝑜𝑛. 𝑚
= 1.74 𝑘𝑔/𝑐𝑚2
100𝑐𝑚 ∗ 502 𝑐𝑚
Con la cuantía calculada se compara con la cuantía mínima, en caso de no ser mayor se
toma el mínimo.
103
𝜌 = 0.046% < 𝜌𝑚𝑖𝑛𝑖𝑚𝑎 = 0.18% − 𝑆𝑒 𝑢𝑡𝑖𝑙𝑖𝑧𝑎 𝑒𝑙 𝑚í𝑛𝑖𝑚𝑜
Se calcula la cantidad de acero, teniendo en cuenta que el mínimo antes mencionado aplica
también al acero por temperatura de la zapata el cual ira colocado en la dirección larga de
la cimentación.
𝐴𝑠 = 0.18% ∗ 100𝑐𝑚 ∗ 50𝑐𝑚 = 9 𝑐𝑚2
𝐴𝑠𝑡𝑒𝑚𝑝 = 0.18% ∗ 100𝑐𝑚 ∗ 60𝑐𝑚 = 10.8 𝑐𝑚2
Para 𝐴𝑠 = 9 𝑐𝑚2 .
𝐴𝑐𝑒𝑟𝑜 𝜙3/4"
𝐴𝑟𝑒𝑎 𝑎𝑐𝑒𝑟𝑜 𝜙3/4" = 2.84 𝑐𝑚2
𝑆=
2.84 𝑐𝑚2 ∗ 100𝑐𝑚
= 31.56 𝑐𝑚
9 𝑐𝑚2
𝐷𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛 𝑐𝑜𝑛𝑠𝑡𝑟𝑢𝑐𝑡𝑖𝑣𝑎 𝑦 𝑐𝑜𝑛𝑠𝑒𝑟𝑣𝑎𝑑𝑜𝑟𝑎 = 30 𝑐𝑚
Para 𝐴𝑠𝑡𝑒𝑚𝑝 = 10.8 𝑐𝑚2 .
𝐴𝑐𝑒𝑟𝑜 𝜙3/4"
𝐴𝑟𝑒𝑎 𝑎𝑐𝑒𝑟𝑜 𝜙3/4" = 2.84 𝑐𝑚2
𝑆=
2.84 𝑐𝑚2 ∗ 100𝑐𝑚
= 26. 3 𝑐𝑚
10.8 𝑐𝑚2
𝐷𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛 𝑐𝑜𝑛𝑠𝑡𝑟𝑢𝑐𝑡𝑖𝑣𝑎 𝑦 𝑐𝑜𝑛𝑠𝑒𝑟𝑣𝑎𝑑𝑜𝑟𝑎 = 25𝑐𝑚
Por fines constructivo se elige un diseño de barras de 𝜙3/4"cada 25 cm en las dos
direcciones
104
Conclusiones
•
Uno de los principales problemas que se tuvo al diseñar la estructura era la falta de
muros portantes en la dirección X en el primero piso, y por consecuencia en los
pisos superiores, cuyos muros sólo eran tabiquería y no aportaban rigidez en dicha
dirección. Por esta razón fue necesario aprovechar los pocos muros en la dirección
X que había haciéndolos placas de concreto o cambiando su espesor mediante
muros de cabeza.
•
Para el diseño de columnas, resultó que la cuantía mínima fue suficiente para
cumplir con todas las cargas y momentos, esto se puede deber a que los muros de
corte soportan gran parte de la carga de la estructura, además de que absorben una
gran cantidad de fuerza cortante.
•
La estructura es irregular en planta debido a que se tiene algunas zonas de gran
rigidez en comparación con otras. Es por ellos que fue importante realizar un
análisis sísmico dinámico.
•
En el diseño de las vigas, se pudo apreciar que la gran mayoría de estas eran
diseñadas con el acero mínimo necesario, esto debido a que al ser una vivienda
unifamiliar la estructura no se somete a cargas muy elevadas. Esto permitió
facilidad al momento de diseñar y además evitar problemas de sobre reforzar la
viga con demasiado acero.
•
Se dio como respuesta estructural, ante las cargas y momentos muy altos
producidos en la base de las placas, unir mediante vigas la cimentación de la placa
con la cimentación de una columna que se encuentre en su mismo eje, para que de
esta manera la cimentación pueda resistir las cargas y momentos altos sin
deformaciones o fisuración importante.
•
El alto valor de la longitud de borde en el diseño de placas se puede deber a que el
largo de las mismas es relativamente corto (ambas son menores a 2m). Estos datos
sugieren que cuanto menor sea la longitud de la placa, esta necesitará un mayor
confinamiento.
•
Si se tienen muros que están conectados de manera perpendicular y que comparten
el elemento vertical de refuerzo; se sabe que se tiene que analizar cada muro (Toda
la sección rectangular) en la dirección del sismo.
•
Si en el análisis independiente que se realiza en cada muro se obtienen valores
distintos de varillas; por ejemplo: 4 Diámetro 1/2" y en la otra dirección nos sale 4
diámetro 3/8" ; se considera el mayor refuerzo del elemento proveniente del diseño
independiente de cada muro; es decir 4 diámetro 1/2".
105
Recomendaciones
•
Para el diseño de las estructuras se ha preferido estandarizar muchos elementos
para un proceso constructivo más factible.
•
En este trabajo no se ha dado la solución de zapatas combinadas, pero sería una
buena respuesta estructural ante las grandes dimensiones de las zapatas aisladas, las
cuales, al no estar muy separadas, terminan interceptándose entre ellas mismas.
•
Se podría proponer como una alternativa económica el variar el diseño de las placas
en los pisos superiores (último piso o últimos dos pisos), como reducir el diámetro
de refuerzo de las placas o proponer un diseño con elementos de borde.
106
Referencias Bibliográficas
•
•
•
•
•
Comité Técnico Especializado RNE (2006). Reglamento Nacional de
Edificaciones E.020 Cargas. SENCICO, Lima.
Ministerio de Vivienda, Construcción y Saneamiento (2018) Norma Técnica
E.030 "Diseño sismorresistente", El Peruano, Lima.
Reglamento Nacional de Edificaciones (2009). Norma E.060 Concreto Armado,
Lima: DIGIGRAF CORP. SA.
Comité Técnico Especializado RNE (2006). Reglamento Nacional de
Edificaciones E.070 Albañilería. SENCICO, Lima.
Otazzi Pasino, Gianfranco (2015). Apuntes del curso Concreto Armado I. 15.a
ed. Lima.
•
Gamero, O.; Nathals, K. y Sipion, D. (2020). Diseño estructural de vivienda
unifamiliar (2 pisos) en la ciudad de Piura con albañilería confinada (Trabajo de
investigación de bachiller en Ingeniería Civil). Universidad de Piura, Facultad
de Ingeniería. Programa Académico de Ingeniería Civil. Piura, Perú
•
Atencia, R.; et al (2021). Diseño de una vivienda unifamiliar de 3 pisos en el
distrito de Pachacamac-Manchay (Trabajo de investigación de bachiller en
Ingeniería Civil). Universidad San Ignacio de Loyola.
•
Ávalos, V. y Fernández, D. (2019). Diseño estructural y comparación
económica de una vivienda unifamiliar en el sistema de albañilería confinada y
acervo liviano en la ciudad de Trujillo (Tesis para optar el título de Ingeniero
Civil). Universidad Privada Antenor Orrego – UPAO
•
Aymara, F.; et al (2020). Propuesta de diseño de una vivienda unifamiliar para
reducir la vulnerabilidad sísmica en el distrito de Lurigancho-Chosica (Trabajo
de investigación de bachiller en Ingeniería Civil). Universidad San Ignacio de
Loyola.
•
Project Management Institute (2017). Guía de los Fundamentos para la
Dirección de Proyectos. Sexta Edición. Newtown Square, Pennsylvania.
•
Redacción RPP (21 de junio de 2021). “El 80% de las viviendas en el Perú son
informales y serían vulnerables ante un terremoto”. Recuperado de:
https://rpp.pe/economia/economia/el-80-de-las-viviendas-en-el-peru-soninformales-y-serian-vulnerables-ante-un-terremoto-noticia-1343757
•
Gonzales, B. (2016). "Propuesta de un modelo estructural y diseño en concreto
armado de un módulo de aulas de una institución educativa aplicado al
prototipo 780 actual de OINFE" (Tesis para optar el título de Ingeniero Civil).
Universidad Particular de Chiclayo.
•
Cardoso, R; Guerrero, L; Valencia, Cristian. Plan de gestión y administración
para la construcción del hospital San Vicente de Paul en el Municipio de
Venadillo departamento del Tolima. (Trabajo de proyecto de grado, del
seminario de grado en gestión de obras civiles, presentado como requisito para
obtener el título de ingenieros civiles). Universidad Cooperativa de Colombia.
107
•
Bazán, Juan. Elaboración del plan de calidad de la obra Shamrock el polo a través
del sistema de gestión de calidad de GYM (Informe técnico por experiencia
profesional calificada para optar el título de ingeniero civil). Universidad Ricardo
Palma.
108