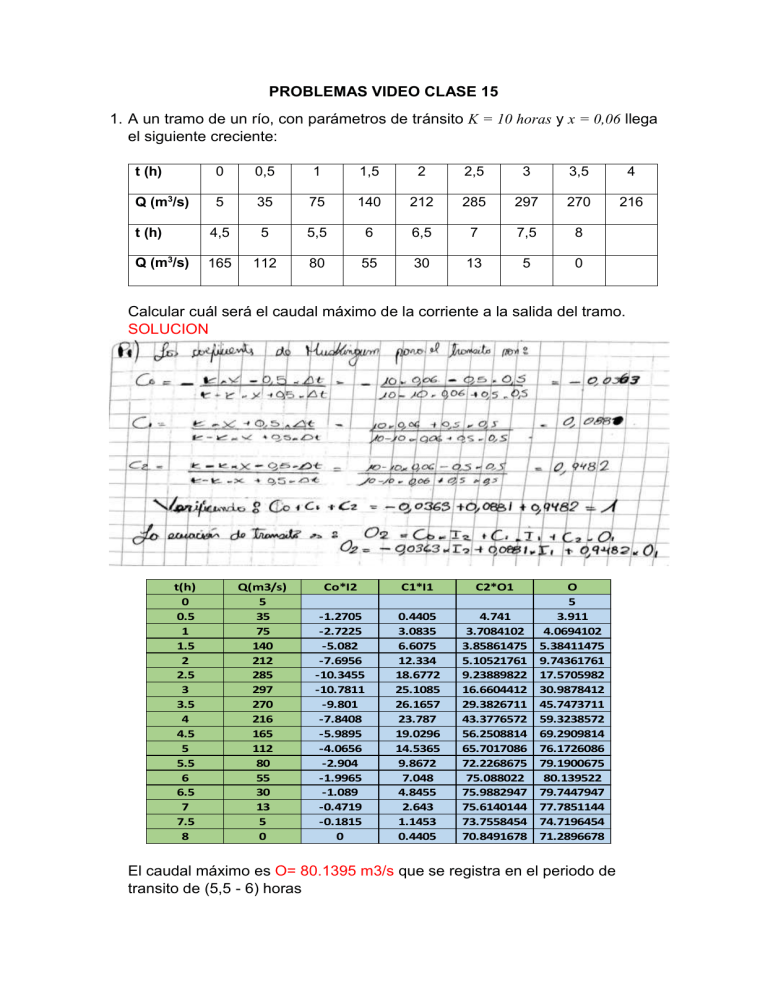
PROBLEMAS VIDEO CLASE 15 1. A un tramo de un río, con parámetros de tránsito K = 10 horas y x = 0,06 llega el siguiente creciente: t (h) 0 0,5 1 1,5 2 2,5 3 3,5 4 Q (m3/s) 5 35 75 140 212 285 297 270 216 t (h) 4,5 5 5,5 6 6,5 7 7,5 8 Q (m3/s) 165 112 80 55 30 13 5 0 Calcular cuál será el caudal máximo de la corriente a la salida del tramo. SOLUCION t(h) 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8 Q(m3/s) 5 35 75 140 212 285 297 270 216 165 112 80 55 30 13 5 0 Co*I2 C1*I1 C2*O1 -1.2705 -2.7225 -5.082 -7.6956 -10.3455 -10.7811 -9.801 -7.8408 -5.9895 -4.0656 -2.904 -1.9965 -1.089 -0.4719 -0.1815 0 0.4405 3.0835 6.6075 12.334 18.6772 25.1085 26.1657 23.787 19.0296 14.5365 9.8672 7.048 4.8455 2.643 1.1453 0.4405 4.741 3.7084102 3.85861475 5.10521761 9.23889822 16.6604412 29.3826711 43.3776572 56.2508814 65.7017086 72.2268675 75.088022 75.9882947 75.6140144 73.7558454 70.8491678 O 5 3.911 4.0694102 5.38411475 9.74361761 17.5705982 30.9878412 45.7473711 59.3238572 69.2909814 76.1726086 79.1900675 80.139522 79.7447947 77.7851144 74.7196454 71.2896678 El caudal máximo es O= 80.1395 m3/s que se registra en el periodo de transito de (5,5 - 6) horas 2. Se tiene dos subcuencas A y B, que confluyen en un punto aguas abajo. En dichas subcuencas se tienen los siguientes eventos de precipitación efectiva: t (h) 2 4 6 8 10 Precipitación en A (mm) 15 Precipitación en B (mm) 9 12 6 10 Hasta el punto de confluencia, los parámetros de Muskingum para ambas cuencas son: Subcuenca A: K = 9 h; x = 0,03 Subcuenca B: K = 7 h; x = 0,04 El hidrograma unitario de media hora de duración para ambas subcuencas es: t (h) Q (m3/s)/mm 0 0 2 5,4 4 93,4 6 8 242,5 121 10 50,7 12 18,9 14 5,2 Determine el hidrograma de escorrentía directa en la confluencia de ambas subcuencas. SOLUCION