
Libro digital de Matemática Básica: (MA420) Línea Ingeniería
Item Type
info:eu-repo/semantics/book
Authors
Alva Cabrera, Rubén Jesús; Arrue Reyes, José; Callo Moscoso,
Luis Alberto; Cárdenas Zavala, Germain Leonardo; Fernández
Quispe, Nedín Esteban; Figueroa Neyra, Walter Antonio; Flores
Osorio, Alejandro Isaías; Medina Martínez, Antonio Marcos;
Mejía Delgado, Elías; Novoa Allagual, Armando Alfredo; Reynaga
Alarcón, Carlos; Ruiz Herrera, Jenniel; Serquén Pisfil, Alejandro;
Sueros Zarate, Jonathan Abrahán; Tiza Domínguez, Mario Saul;
Benturo Balavarca, Juan Carlos; Quinch Flores, Eduardo
Publisher
Universidad Peruana de Ciencias Aplicadas
Rights
info:eu-repo/semantics/openAccess; AttributionNonCommercial-ShareAlike 4.0 International
Download date
22/03/2021 16:41:56
Item License
http://creativecommons.org/licenses/by-nc-sa/4.0/
Link to Item
http://hdl.handle.net/10757/653944
UPC – Departamento de Ciencias - Matemática Básica (MA420)
UNIVERSIDAD PERUANA DE
CIENCIAS APLICADAS
Libro Digital
Matemática Básica (MA420)
Línea Ingeniería
Autores:
Alva Cabrera, Rubén Jesús
Arrue Reyes, José
Benturo Balavarca, Juan Carlos
Callo Moscoso, Luis Alberto
Cárdenas Zavala, Germain Leonardo
Fernández Quispe, Nedín Esteban
Figueroa Neyra, Walter Antonio
Flores Osorio, Alejandro Isaías
Medina Martínez, Antonio Marcos
Mejía Delgado, Elías
Novoa Allagual, Armando Alfredo
Quincho Flores, Eduardo
Reynaga Alarcón, Carlos
Ruiz Herrera, Jenniel
Serquén Pisfil, Alejandro
Sueros Zarate, Jonathan Abrahán
Tiza Domínguez, Mario Saul
Profesores MA420
i
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Índice:
Pág.
Introducción ............................................................................................................................... ix
Plano cartesiano y rectas ............................................................................................................. 1
➢ Motivación ...................................................................................................................................... 2
➢ Distancia y punto medio ................................................................................................................. 3
➢ Pendiente de un segmento de recta ............................................................................................... 3
➢ Ecuación de la recta ........................................................................................................................ 4
➢ Forma punto – pendiente de la recta ............................................................................................. 4
➢ Forma pendiente – intersección con el eje 𝑦.................................................................................. 5
➢ Ecuación general de la recta ........................................................................................................... 5
➢ Recta vertical y horizontal............................................................................................................... 5
➢ Rectas paralelas y perpendiculares ................................................................................................. 6
➢ Practiquemos en clase .................................................................................................................... 6
➢ Respuestas ...................................................................................................................................... 7
➢ Practiquemos más en casa .............................................................................................................. 7
➢ Respuestas ...................................................................................................................................... 8
➢ Ejercicios resueltos en vídeo .......................................................................................................... 8
La circunferencia .......................................................................................................................... 9
➢ Motivación ...................................................................................................................................10
➢ Ecuación de la circunferencia........................................................................................................11
➢ Ejemplos .......................................................................................................................................11
➢ Practiquemos en clase ..................................................................................................................13
➢ Respuestas ....................................................................................................................................14
➢ Practiquemos más en casa ...........................................................................................................14
➢ Respuestas ...................................................................................................................................14
➢ Ejercicios resueltos en vídeo ........................................................................................................15
La parábola ................................................................................................................................ 16
➢ Motivación ....................................................................................................................................17
➢ Definición geométrica de una parábola ........................................................................................18
➢ Parábola con eje focal vertical y vértice en el origen de coordenadas.........................................20
➢ Parábolas trasladadas con eje focal paralelo al eje 𝑦 ...................................................................20
➢ Parábola con eje focal horizontal y vértice en el origen de coordenadas ....................................21
➢ Parábolas trasladadas con eje focal paralelo al eje 𝑥 ...................................................................22
➢ Practiquemos en clase ..................................................................................................................22
➢ Respuestas ...................................................................................................................................23
➢ Practiquemos más en casa ............................................................................................................23
➢ Respuestas ....................................................................................................................................24
➢ Ejercicios resueltos en vídeo ........................................................................................................24
Profesores MA420
ii
UPC – Departamento de Ciencias - Matemática Básica (MA420)
La elipse .................................................................................................................................... 27
➢ Motivación ....................................................................................................................................28
➢ Definición geométrica de una elipse .............................................................................................29
➢ Elipse con centro 𝐶(ℎ; 𝑘) y eje focal paralelo al eje 𝑥 ..................................................................30
➢ Elipse con centro 𝐶(ℎ; 𝑘) y eje focal paralelo al eje 𝑦 ..................................................................31
➢ Practiquemos en clase y respuestas .............................................................................................32
➢ Practiquemos más en casa y respuestas .......................................................................................33
➢ Ejercicios resueltos en vídeo ........................................................................................................34
Resolución de problemas con cónicas ......................................................................................... 36
➢ Practiquemos en clase .................................................................................................................36
➢ Respuestas ....................................................................................................................................37
➢ Practiquemos más en casa ............................................................................................................38
➢ Respuestas ...................................................................................................................................39
➢ Ejercicios resueltos en vídeo ........................................................................................................40
Matrices .................................................................................................................................... 41
➢ Motivación ....................................................................................................................................42
➢ Matrices ........................................................................................................................................42
➢ Orden de una matriz .....................................................................................................................42
➢ Matriz por extensión ....................................................................................................................43
➢ Tipos de matrices ..........................................................................................................................43
➢ Operaciones con matrices.............................................................................................................44
➢ Suma de matrices ..........................................................................................................................44
➢ Multiplicación de una matriz por un escalar.................................................................................44
➢ Multiplicación de matrices ............................................................................................................45
➢ Ejercicios resueltos........................................................................................................................45
➢ Determinantes ..............................................................................................................................48
➢ Practiquemos en clase y respuestas .............................................................................................49
➢ Practiquemos más en casa ...........................................................................................................49
➢ Respuestas ...................................................................................................................................50
➢ Ejercicios resueltos en vídeo ........................................................................................................51
Vectores en 2D .......................................................................................................................... 52
➢ Motivación ....................................................................................................................................53
➢ Vectores en 2D, Magnitud Escalar, Magnitud Vectorial ...............................................................54
➢ Magnitud o longitud de un vector ................................................................................................54
➢ Operaciones algebraicas sobre vectores ......................................................................................54
➢ Dirección de un vector ..................................................................................................................55
➢ Vector en términos de su componente horizontal y vertical .......................................................55
➢ Vector unitario en la dirección de un vector ................................................................................56
➢ Vectores en términos de 𝐢 y 𝐣 .......................................................................................................56
Profesores MA420
iii
UPC – Departamento de Ciencias - Matemática Básica (MA420)
➢
➢
➢
➢
➢
➢
➢
➢
➢
➢
Forma componente de un vector .................................................................................................56
Definición del producto punto ......................................................................................................56
Ángulo entre dos vectores ............................................................................................................56
Vectores ortogonales y paralelos..................................................................................................57
La proyección de un vector sobre otro vector ..............................................................................57
Propiedades de vectores ...............................................................................................................57
Practiquemos en clase ..................................................................................................................57
Respuestas ...................................................................................................................................58
Practiquemos más en casa y respuestas .......................................................................................58
Ejercicios resueltos en vídeo ........................................................................................................59
Vectores en 3D .......................................................................................................................... 60
➢ Sistema tridimensional de coordenadas cartesianas ...................................................................61
➢ Planos coordenados ......................................................................................................................62
➢ Distancia y punto medio de un segmento en 3D .........................................................................62
➢ Vectores en 3D ..............................................................................................................................63
➢ Magnitud o módulo de un vector en 3D .......................................................................................64
➢ Vector unitario ..............................................................................................................................64
➢ Vector unitario en la dirección de un vector ................................................................................65
➢ Vectores unitarios canónicos ........................................................................................................65
➢ Igualdad de vectores .....................................................................................................................65
➢ Operaciones con vectores en 3D ..................................................................................................66
➢ Adición – sustracción ....................................................................................................................66
➢ Producto de un escalar por un vector...........................................................................................66
➢ Producto escalar o punto ..............................................................................................................66
➢ Ángulo entre vectores ...................................................................................................................66
➢ Producto vectorial .........................................................................................................................67
➢ Propiedades del producto vectorial ..............................................................................................68
➢ Respuestas ...................................................................................................................................68
Sistemas de ecuaciones lineales (SEL) ......................................................................................... 70
➢ Motivación ....................................................................................................................................71
➢ Sistemas de ecuaciones lineales (SEL) ..........................................................................................71
➢ Clasificación del sistema de ecuaciones lineales ..........................................................................72
➢ Operaciones elementales de filas (renglones) ..............................................................................73
➢ Forma escalonada por filas de una matriz ....................................................................................73
➢ Practiquemos en clase y respuestas .............................................................................................74
➢ Practiquemos en más casa y respuestas .......................................................................................75
➢ Ejercicios resueltos en vídeo ........................................................................................................76
Funciones: Dominio y rango ....................................................................................................... 78
➢ Motivación ....................................................................................................................................79
Profesores MA420
iv
UPC – Departamento de Ciencias - Matemática Básica (MA420)
➢
➢
➢
➢
➢
➢
➢
➢
Definición de función ....................................................................................................................80
Gráfica de una función ..................................................................................................................81
Criterio de la recta vertical ............................................................................................................81
Dominio y rango de forma geométrica .........................................................................................82
Dominio de forma algebraica ........................................................................................................82
Practiquemos en clase y respuestas .............................................................................................83
Practiquemos en más en casa y respuestas .................................................................................84
Ejercicios resueltos en vídeo ........................................................................................................85
Propiedades de funciones .......................................................................................................... 86
➢ Motivación ...................................................................................................................................87
➢ Propiedades de funciones .............................................................................................................87
➢ Ceros de una función ....................................................................................................................87
➢ Intervalos positivos o negativos de una función ...........................................................................88
➢ Continuidad de una función ..........................................................................................................88
➢ Intervalos de monotonía de una función ......................................................................................91
➢ Extremos de una función ..............................................................................................................91
➢ Máximo absoluto de una función .................................................................................................91
➢ Mínimo absoluto de una función ..................................................................................................92
➢ Máximo relativo o local de una función........................................................................................92
➢ Mínimo relativo o local de una función ........................................................................................93
➢ Practiquemos en clase y respuestas .............................................................................................94
➢ Practiquemos en más casa ............................................................................................................95
➢ Respuestas ...................................................................................................................................96
➢ Ejercicios resueltos en vídeo ........................................................................................................96
Funciones básicas, seccionadas y técnicas de graficación parte I .................................................. 97
➢ Motivación ...................................................................................................................................98
➢ Funciones básicas .........................................................................................................................98
➢ Función constante .........................................................................................................................98
➢ Función identidad .........................................................................................................................99
➢ Función cuadrática ........................................................................................................................99
➢ Función raíz cuadrada ...................................................................................................................99
➢ Función valor absoluto ................................................................................................................100
➢ Función recíproca ........................................................................................................................100
➢ Funciones seccionadas ................................................................................................................101
➢ Definición de función seccionada ...............................................................................................101
➢ Técnicas de graficación ...............................................................................................................101
➢ Traslación Horizontal ..................................................................................................................101
➢ Traslación Vertical .......................................................................................................................102
➢ Practiquemos en clase ................................................................................................................103
➢ Respuestas .................................................................................................................................104
Profesores MA420
v
UPC – Departamento de Ciencias - Matemática Básica (MA420)
➢ Practiquemos más en casa ..........................................................................................................104
➢ Respuestas .................................................................................................................................105
➢ Ejercicios resueltos en vídeo ......................................................................................................106
Técnicas de graficación parte II ................................................................................................. 107
➢ Motivación .................................................................................................................................108
➢ Reflexión respecto al eje 𝑥 .........................................................................................................108
➢ Reflexión respecto al eje 𝑦 ..........................................................................................................109
➢ Alargamientos y compresiones verticales ..................................................................................110
➢ Practiquemos en clase y respuestas ..........................................................................................112
➢ Practiquemos más en casa y respuestas ....................................................................................113
➢ Ejercicios resueltos en vídeo ......................................................................................................114
Función inyectiva e inversa – Operaciones con funciones .......................................................... 116
➢ Motivación .................................................................................................................................117
➢ Función inyectiva o uno a uno ....................................................................................................117
➢ Criterio de la recta horizontal (CRH) ...........................................................................................117
➢ Función inversa ...........................................................................................................................118
➢ Principio de reflexión ..................................................................................................................118
➢ Regla de correspondencia de la función inversa ........................................................................119
➢ Operaciones con funciones (Suma, resta, producto y cociente) ................................................119
➢ Practiquemos en clase ................................................................................................................120
➢ Respuesta ...................................................................................................................................121
➢ Practiquemos más en casa .........................................................................................................122
➢ Respuestas .................................................................................................................................123
➢ Ejercicios resueltos en vídeo ......................................................................................................125
Composición de funciones ........................................................................................................ 126
➢ Motivación .................................................................................................................................127
➢ Composición de funciones ..........................................................................................................127
➢ Practiquemos en clase ................................................................................................................128
➢ Respuestas .................................................................................................................................129
➢ Practiquemos más en casa y respuestas ....................................................................................129
➢ Ejercicios resueltos en vídeo ......................................................................................................130
Función cuadrática y problemas de optimización ...................................................................... 131
➢ Motivación ..................................................................................................................................132
➢ Función cuadrática: Forma normal .............................................................................................132
➢ Valor del máximo o mínimo absoluto de una función cuadrática ..............................................133
➢ Practiquemos en clase ................................................................................................................134
➢ Respuestas .................................................................................................................................135
➢ Practiquemos más en casa ..........................................................................................................135
Profesores MA420
vi
UPC – Departamento de Ciencias - Matemática Básica (MA420)
➢ Respuestas ..................................................................................................................................136
➢ Ejercicios resueltos en vídeo ......................................................................................................137
Ecuaciones exponenciales y logarítmicas – Funciones exponenciales ......................................... 138
➢ Definición de logaritmo ...............................................................................................................139
➢ Leyes de los logaritmos ...............................................................................................................139
➢ Ecuaciones logarítmicas ..............................................................................................................140
➢ Ecuaciones exponenciales ..........................................................................................................141
➢ Motivación sobre función exponencial .......................................................................................142
➢ Definición de función exponencial ..............................................................................................142
➢ Gráfica de funciones exponenciales............................................................................................143
➢ Definición de función exponencial natural ................................................................................143
➢ Practiquemos en clase y respuestas ...........................................................................................145
➢ Practiquemos más en casa .........................................................................................................145
➢ Respuestas .................................................................................................................................146
➢ Ejercicios resueltos en vídeo ......................................................................................................147
Funciones logarítmicas ............................................................................................................. 149
➢ Motivación .................................................................................................................................150
➢ Función logaritmo .......................................................................................................................151
➢ Función logaritmo natural ..........................................................................................................152
➢ Gráficas de funciones logaritmo .................................................................................................152
➢ Practiquemos en clase y respuestas ...........................................................................................153
➢ Practiquemos más en casa y respuestas .....................................................................................154
➢ Ejercicios resueltos en vídeo ......................................................................................................155
Problemas de modelación con funciones exponenciales y logarítmicas ..................................... 157
➢ Practiquemos en clase ................................................................................................................157
➢ Respuestas .................................................................................................................................158
➢ Practiquemos más en casa ......................................................................................................159
➢ Respuestas ..................................................................................................................................160
➢ Ejercicios resueltos en vídeo ......................................................................................................162
Funciones trigonométricas seno, coseno y sus inversas ............................................................. 163
➢ Motivación ..................................................................................................................................164
➢ Circunferencia unitaria................................................................................................................164
➢ La circunferencia unitaria de 16 puntos......................................................................................165
➢ Función seno ...............................................................................................................................165
➢ Características de la función seno...............................................................................................166
➢ Función inversa del seno o función arcoseno .............................................................................166
➢ Función coseno ...........................................................................................................................168
➢ Características de la función coseno ...........................................................................................168
Profesores MA420
vii
UPC – Departamento de Ciencias - Matemática Básica (MA420)
➢
➢
➢
➢
Función inversa del coseno o función arcocoseno .....................................................................169
Practiquemos en clase y respuestas ...........................................................................................170
Practiquemos más en casa y respuestas .....................................................................................170
Ejercicios resueltos en vídeo ......................................................................................................172
Resolución de triángulos rectángulos ..................................................................................... 174
➢ Motivación .................................................................................................................................175
➢ ¿Qué es un ángulo de elevación? ...............................................................................................175
➢ ¿Qué es un ángulo de depresión? ...............................................................................................175
➢ Problemas resueltos ...................................................................................................................175
➢ Ley de senos y cosenos ..............................................................................................................179
➢ Problemas resueltos ...................................................................................................................180
➢ Practiquemos más en casa ..........................................................................................................182
➢ Respuestas ..................................................................................................................................183
Funciones sinusoidales y ecuaciones trigonométricas ............................................................... 184
➢ Motivación ..................................................................................................................................185
➢ Definición de función sinusoidal .................................................................................................186
➢ Definición de ecuación trigonométrica .......................................................................................187
➢ Practiquemos en clase ................................................................................................................189
➢ Respuestas .................................................................................................................................190
➢ Practiquemos más en casa y respuestas .....................................................................................191
➢ Ejercicios resueltos en vídeo ......................................................................................................192
Anexo: Problemas de razonamiento cuantitativo ...................................................................... 194
➢ Definición ....................................................................................................................................195
➢ Dimensiones, nivel y temas del nivel .........................................................................................195
➢ Problemas resueltos ...................................................................................................................196
➢ Problemas propuestos ...............................................................................................................201
➢ Respuestas .................................................................................................................................202
➢ Rúbrica de razonamiento cuantitativo .......................................................................................203
Profesores MA420
viii
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Introducción:
Este texto, al cual llamaremos libro digital, está diseñado para utilizarse en el curso de Matemática
Básica para ingeniería (MA420), curso que se dicta en la Universidad Peruana de Ciencias Aplicadas
(UPC).
El contenido obedece a un objetivo fundamental: preparar adecuadamente a los alumnos para llevar
con éxito los cursos siguientes en cada una de sus carreras y por lo tanto contiene temas que servirán
de base a los mismos, además que la metodología usada obedece a un aprestamiento que el alumno
adquirirá para lograr su adaptación al proceso universitario.
El presente libro está pensado para que el docente, en cada sesión dedique un tiempo a:
✓ repasar lo más importante de los temas que se trabajaron en las sesiones anteriores.
✓ motivar el tema que corresponde a la sesión, ya sea presencial o virtual.
✓ que el alumno resuelva personalmente, en grupo o con las diferentes dinámicas que se puedan
emplear, los ejercicios y problemas planteados en cada sesión, a estos espacios de aprendizaje
los hemos llamado practiquemos en clase.
Después de cada sesión de clase el alumno tiene como reto seguir aprendiendo, para ello este libro
proporciona una lista de ejercicios propuestos a los que hemos llamado practiquemos más en casa y
a la vez una lista de ejercicios resueltos en vídeo, los cuales ayudarán al estudiante reforzar lo
aprendido en clase.
El libro también proporciona al estudiante todas las respuestas de los ejercicios y problemas
propuestos con la finalidad de que el estudiante pueda comprobar su autoaprendizaje y de ser
necesario revisarlas con el profesor Asistente de Aprendizaje a Distancia (AAD).
El éxito del curso no radica únicamente en el esfuerzo hecho para ofrecer este libro o en las clases
prácticas e integrales que trabajamos en este curso previo a las evaluaciones. Tampoco estará
centrado en el Profesor o en el asistente (AAD), sino fundamentalmente está dado por el esfuerzo y la
dedicación del alumno para lograr su propio aprendizaje. Los espacios para procurar aprendizaje están
propuestos, el aprovecharlos es lo que permitirá alcanzar el éxito deseado. En este aspecto hay una
frase de una canción que resume todo lo que se quiere indicar aquí: “…tienes que amar el tiempo de
los intentos…”, el procurarse un horario fijo de estudio y llevarlo a cabo, el participar constantemente
en clase, el preguntar, el trabajar correctamente en grupo, el investigar, el leer, el adelantar…, son los
tiempos de los intentos que se deben apreciar, si se logra esto, el éxito vendrá por añadidura.
Finalmente, en cada uno de los temas hacemos referencia al libro de James Stewart, séptima edición,
libro que nos sirvió como referencia básica para diseñar este texto y que sirve para que el estudiante
siga complementando sus aprendizajes dentro y fuera del salón de clase.
Mg. Alejandro Serquén Pisfil
Coordinador del equipo de autores
UPC, 2021
Profesores MA420
ix
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Plano cartesiano - distancia y punto
medio-pendiente de una recta-rectas
paralelas y perpendiculares
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante analiza y aplica los conceptos de distancia
entre dos puntos, punto medio y ecuaciones de una recta en la resolución de ejercicios, demostrando
responsabilidad y capacidad de aprender por su propia cuenta.
CONTENIDOS
MOTIVACIÓN
1.1. Distancia y punto medio.
• Definiciones y notaciones
• Ejemplos
1.2. Ecuación de la recta
• Pendiente de un segmento
• Definición de pendiente
• Ecuación de la recta punto pendiente
• Rectas verticales y horizontales
• Rectas paralelas y perpendiculares
1.3. Practiquemos en clase
• Ejercicios
1.4. Practiquemos más en casa
• Ejercicios
Profesores MA420
1
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Motivación
Las siguientes figuras muestran situaciones en las que la pendiente es importante. Por ejemplo, los carpinteros
usan el término inclinación para la pendiente de un techo o una escalera; el término pendiente se usa también
para la pendiente de una carretera.
Una recta se usa para modelar la relación entre dos cantidades (o variables) que se relacionan linealmente, la
pendiente de la recta en muchas aplicaciones es la rapidez de cambio de una cantidad con respecto a la otra. Por
ejemplo: la figura adjunta muestra la cantidad de gas en un tanque que se está llenando, la pendiente entre los
puntos indicados es:
6 galones
𝑚=
= 2 gal/min
3 minutos
La pendiente es la rapidez a la que se está llenando el tanque, es decir 2 galones por minuto.
Profesores MA420
2
UPC – Departamento de Ciencias - Matemática Básica (MA420)
El plano coordenado es el vínculo entre el álgebra y la geometría. En el plano coordenado podemos trazar gráficas
de ecuaciones algebraicas. Las gráficas, a su vez, nos permiten “ver” la relación entre las variables de la ecuación.
En esta sección estudiamos la distancia entre dos puntos del plano cartesiano, punto medio de un segmento,
pendiente de un segmento y finalmente las diferentes formas de escribir la ecuación de la recta.
1.1 DISTANCIA Y PUNTO MEDIO ENTRE DOS PUNTOS
Si se conocen las coordenadas de dos puntos del plano, se puede hallar la
𝑦
distancia que los separa. Para ello se deduce una sencilla fórmula que es
consecuencia directa del teorema de Pitágoras. Consideremos que los
puntos 𝑃(𝑥1 ; 𝑦1 ) y 𝑄(𝑥2 ; 𝑦2 ) son conocidos y se quiere hallar la distancia
R
entre 𝑃 y 𝑄. En la Figura 1 los puntos 𝑃 y 𝑄 se han representado en el
plano y se muestra el segmento 𝑃𝑄 cuya longitud se desea hallar. El
segmento 𝑃𝑄 es la hipotenusa del triángulo rectángulo 𝑃𝑅𝑄. Los catetos
de este triángulo miden respectivamente |𝑥2 − 𝑥1 | y |𝑦2 − 𝑦1 |. Al aplicar
el teorema de Pitágoras al triángulo rectángulo 𝑃𝑅𝑄 se obtiene la fórmula
𝑥
para la distancia entre 𝑃 y 𝑄, la cual escribimos como sigue:
Figura 1: Distancia entre dos puntos
𝑑(𝑃; 𝑄) = √(𝑥2 − 𝑥1 )2 + (𝑦2 − 𝑦1 )2
𝑦
𝑦2
Siendo 𝑃(𝑥1 ; 𝑦1 ) y 𝑄(𝑥2 ; 𝑦2 ) los extremos de un segmento, llamemos a
𝑀(𝑥; 𝑦) punto medio (ver figura 2), que es el punto que divide al
segmento 𝑃𝑄 en dos partes iguales.
El punto medio de un segmento es único y equidista de los extremos del
segmento.
Q(x2 ;y2 )
M(x; y )
P(x1 ;y1 )
En resumen: las coordenadas del punto medio del segmento 𝑃𝑄 son:
x1
𝑦1
x
x2 𝑥
Figura 2: Punto medio entre dos puntos
𝑀(𝑥; 𝑦) = (
𝑥1 + 𝑥2 𝑦1 + 𝑦2
;
)
2
2
1.2 ECUACIÓN DE LA RECTA
• Pendiente de un segmento de recta
𝑦
Consideremos un segmento de recta determinado por dos puntos del
plano 𝑃1 (𝑥1 ; 𝑦1 ) y 𝑃2 (𝑥2 ; 𝑦2 ). La pendiente de este segmento es un
número real que mide la inclinación del segmento con respecto a la
horizontal.
𝑥
Figura 3: Segmento P1P2
Profesores MA420
3
UPC – Departamento de Ciencias - Matemática Básica (MA420)
•
Definición de Pendiente
La pendiente 𝑚 del segmento no vertical determinado por los puntos 𝑃1 (𝑥1 ; 𝑦1 ) y 𝑃2 (𝑥2 ; 𝑦2 ) es el número:
𝑚=
𝑦2 − 𝑦1
𝑥2 − 𝑥1
𝑦
(a;y1 )
¿Un segmento vertical tendrá pendiente?, explique su respuesta:
Si observamos en la figura adjunta, los puntos de un segmento vertical son tal que la
abscisa siempre es el mismo valor, entonces para el par de puntos (𝑎; 𝑦1 ) y (𝑎; 𝑦2 ) la
𝑦2 −𝑦1
𝑦 −𝑦
posible pendiente sería 𝑚 = 𝑎−𝑎
= 2 0 1 de donde observamos que no existe un
valor posible para 𝑚. Así los segmentos verticales no tienen pendiente.
(a;y2 )
a
𝑥
Figura 4: Recta vertical
Observación: del signo de la pendiente dependerá si el segmento (o recta) es creciente, decreciente o constante.
Es decir:
Si 𝑚 > 0, el segmento (o recta) es creciente.
Si 𝑚 < 0, el segmento (o recta) es decreciente.
Si 𝑚 = 0, el segmento (o recta) es constante.
•
Ecuación de la Recta: Forma Punto – Pendiente de la Recta
De la Figura 5, se tiene la pendiente:
L
𝑚=
𝑦 − 𝑦0
𝑥 − 𝑥0
P
y
𝑃 = (𝑥; 𝑦) Punto arbitrario en la recta.
𝑃0 = (𝑥0 ; 𝑦0 ) Punto conocido (punto de paso).
Despejando se tiene la siguiente ecuación:
𝐿: 𝑦 − 𝑦0 = 𝑚(𝑥 − 𝑥0 ) … … … (∗)
y0
P0
x0
x
𝑥
Figura 5: Forma punto - pendiente
La cual representa a la recta en su forma punto – pendiente.
Profesores MA420
4
UPC – Departamento de Ciencias - Matemática Básica (MA420)
•
Ecuación de la Recta: Forma Pendiente – Intersección con el eje 𝒚
De la Figura 6, se tiene que la recta pasa por el punto (0; 𝑏)
remplazamos en la ecuación dada en (*) obtenemos:
𝐿: 𝑦 − 𝑏 = 𝑚(𝑥 − 0)
𝑦
y si
b
Luego al despejar, se obtiene:
𝐿: 𝑦 = 𝑚𝑥 + 𝑏 … … . . (∗∗)
L
m : pendiente
𝑥
Figura 6: Forma pendiente – intersección
La cual representa a la recta en su forma pendiente intersección al eje 𝑦.
•
Ecuación General de la Recta
La ecuación general de una recta es la expresión de la forma:
𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0
Dónde: 𝑎 y 𝑏 no son ceros al mismo tiempo.
Si 𝑏 ≠ 0, entonces la ecuación general se puede escribir de la siguiente forma:
𝑎
𝑐
𝑦 = − 𝑥 + (− )
𝑏
𝑏
•
Recta Vertical y Horizontal
En el caso de los segmentos y las rectas verticales el concepto de pendiente
no se define.
Establezca una característica para las rectas verticales, ayudándose de la
recta que pasa por 𝑥 = 2, como se muestra en la Figura 7.
Por lo tanto, las rectas verticales poseen ecuaciones del tipo:
Figura 7: Recta vertical
𝑥 = 𝑥0 ; 𝑥0 ∈ ℝ
El caso de las rectas horizontales es más sencillo porque ellas sí poseen
pendiente. Su pendiente es cero entonces haciendo 𝑚 = 0 en cualquiera de
las ecuaciones vistas anteriormente se aprecia que la ecuación de las rectas
horizontales tiene la forma:
y0
𝑦 = 𝑦0 ; 𝑦0 ∈ ℝ
Figura 8: Recta horizontal
Profesores MA420
5
UPC – Departamento de Ciencias - Matemática Básica (MA420)
•
Rectas Paralelas y Perpendiculares
Cuando se conocen las ecuaciones de dos rectas 𝐿1 y 𝐿2 con pendientes 𝑚1 y 𝑚2
respectivamente, es muy simple determinar cuándo se trata de rectas paralelas, en
este caso sus pendientes son iguales, es decir:
𝑦
L1
L2
𝑚1 = 𝑚2
𝑥
Figura 9: Rectas paralelas
La perpendicularidad entre rectas requiere que las pendientes satisfagan la
condición:
𝑚1 ∙ 𝑚2 = −1
𝑦
L1
L2
𝑥
Figura 10: Rectas perpendiculares
1.3 PRACTIQUEMOS EN CLASE
EJERCICIOS
1. Sean 𝐴(1; 1), 𝐵(−3; 4) 𝑦 𝐶(4; 5) los vértices de un triángulo. Determine la longitud del segmento que une
el vértice 𝐴 y el punto medio del lado 𝐵𝐶.
2. Determine la ecuación punto pendiente de la recta que pasa por el punto (6; −2) y su pendiente es −1/2.
3. Determine la ecuación de una recta que pasa por los puntos (−3; 4) 𝑦 (4; 5). Escriba la ecuación de la recta
en las 3 formas estudiadas y trace su gráfica indicando los puntos de corte con los ejes coordenados.
4. Determine la ecuación de la recta que pasa por el punto (2; 5) y es paralela a la recta 8𝑥 − 4𝑦 = −12. Trace
su gráfica indicando los puntos de corte con los ejes coordenados.
5. Sean las rectas 𝐿1 : 10𝑥 − 4𝑦 = 10 y 𝐿2 : 6𝑥 + 9𝑦 = 18. Determine la ecuación de una recta que pasa por
el punto de intersección de las rectas 𝐿1 y 𝐿2 , y es perpendicular a la recta 𝐿1 .
6. Determine una ecuación de la recta cuya gráfica se muestra a
continuación. Además, determine las coordenadas de los
puntos de corte con los ejes.
Profesores MA420
6
UPC – Departamento de Ciencias - Matemática Básica (MA420)
RESPUESTAS DE PRACTIQUEMOS EN CLASE
1. 3,54 u
1
2. 𝑦 + 2 = − 2 (𝑥 − 6)
3. Los tres tipos de ecuaciones son:
1
Forma Punto – Pendiente de la Recta: 𝑦 − 5 = 7 (𝑥 − 4)
𝑥
Forma Pendiente – Intersección con el eje y: 𝑦 = 7 +
31
7
Ecuación General de la Recta: 𝑥 − 7𝑦 + 31 = 0
Para graficar cada recta, halle los puntos de corte con los ejes.
4. 𝑦 − 5 = 2(𝑥 − 2), para graficar halle los puntos de corte con los ejes.
20
2
27
5. 𝑦 − 19 = − 5 (𝑥 − 19)
2
6. 𝑦 − 3 = − 3 (𝑥 + 1)
1.4 PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1. Los puntos 𝐴(0; 0), 𝐵(5; 2) y 𝐶(−1; −2) son los vértices de un triángulo. Determine la longitud del
segmento que une el vértice 𝐴 y el punto medio del lado BC.
2. Dados los puntos: 𝐴 (−7; 4), 𝐵 (2; 8) y 𝐶(0; −2)
a. Determine la distancia y el punto medio entre los puntos 𝐴 y 𝐶 .
b. Determine la ecuación general de la recta que pasa por los puntos 𝐵 y 𝐶.
3. Dadas las rectas 𝐿1 : 8𝑥 − 6𝑦 = 24 y 𝐿2 : 9𝑥 − 6𝑦 = −18 , determine la ecuación de la recta que pasa
por el punto de intersección de las rectas 𝐿1 y 𝐿2 , y es perpendicular a la recta 𝐿2 .
4. Si la recta 𝐿1 pasa por los puntos (1; −1) y (6; 14) y la recta 𝐿2 pasa por los puntos (9; 3) y (−6; 8).
¿Las rectas 𝐿1 y 𝐿2 son paralelas, perpendiculares o ninguna de ellas?
5. Determine la ecuación de la recta que pasa por el punto medio del segmento 𝐴𝐵, con 𝐴(−1; 4) y
𝐵(3; 2), y es perpendicular a la recta cuya ecuación es 3𝑦 + 2𝑥 = 3. Trace su gráfica indicando los
puntos de corte con los ejes coordenados.
6. Determine la ecuación de la recta que pasa por el punto (2; 5) y es paralela a la recta cuya ecuación es
−4𝑥 + 6𝑦 = 24. Trace su gráfica indicando los puntos de corte con los ejes coordenados.
7. Determine la ecuación de la recta formada por los puntos que equidistan de los puntos (1; 6) y de (5; 2).
Profesores MA420
7
UPC – Departamento de Ciencias - Matemática Básica (MA420)
RESPUESTAS PRACTIQUEMOS MÁS EN CASA
1. 2u
7
2. a. 𝑑(𝐴; 𝐶) = √85 𝑢 = 9,22 𝑢. Punto medio de 𝐴 y 𝐶 es: 𝑀 (− 2 ; 1)
b. 𝐿: 5𝑥 − 𝑦 − 2 = 0
2
−3𝑥
3. 𝑦 =
− 88
4. Las rectas 𝐿1 y 𝐿2 son perpendiculares.
3
5. 𝐿: 𝑦 − 3 = (𝑥 − 1). Para graficar, halle los puntos de corte con los ejes.
2
𝑥
3
2
11
6. 𝐿: 𝑦 =
+ . Para graficar, halle los puntos de corte con los ejes.
3
7. 𝐿: −𝑥 + 𝑦 − 1 = 0
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Enlace
Determinar la ecuación de la recta
en sus tres formas.
https://tinyurl.com/y2pn9vbv
Determinar la ecuación de la recta
y graficarla en el plano cartesiano.
https://tinyurl.com/y2s2kyd2
Código QR
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
RECTAS: Revisar páginas desde 106 hasta 116.
Profesores MA420
8
UPC – Departamento de Ciencias - Matemática Básica (MA420)
La circunferencia
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante analiza y aplica el concepto de
circunferencia en la soluciona ejercicios, demostrando responsabilidad y capacidad de aprender por su propia
cuenta.
CONTENIDOS
MOTIVACIÓN
1.1. La circunferencia
• Ecuación de la circunferencia
• Ejemplos
1.2. Practiquemos en clase
• Ejercicios
1.3. Practiquemos más en casa
• Ejercicios
Profesores MA420
9
UPC – Departamento de Ciencias - Matemática Básica (MA420)
MOTIVACIÓN
La Rueda
Una rueda es un objeto mecánico que tiene forma de un disco y que se
instala en un eje para que gire a su alrededor, las ruedas son una pieza
más dentro de una máquina más compleja.
Las ruedas primitivas estaban hechas con madera y presentaban un
orificio en su centro, que permitía que sean insertadas en un eje. Un paso
decisivo para el desarrollo de la rueda fue la inclusión de radios o rayos,
que son las barras que unen, de manera rígida, el centro de la rueda con
su región perimetral. Los radios ayudaron a la construcción de vehículos
más ligeros y, por lo tanto, más veloces.
Un radio o rayo de una rueda es cada una de las barras que une rígidamente la zona
central con la perimetral (contorno de la rueda).
Rayo
Contorno
Profesores MA420
10
UPC – Departamento de Ciencias - Matemática Básica (MA420)
•
ECUACIÓN DE LA CIRCUNFERENCIA
Después de los puntos, los objetos matemáticos más simples son las curvas (suponiendo que una recta es un tipo
especial de curva). Sin embargo, una curva, por más sencilla que pueda parecer, está formada por infinitos
puntos. Por suerte, muchas curvas tienen la característica de que todos sus puntos cumplen una cierta condición;
si esta condición la podemos representar mediante una ecuación, entonces decimos que dicha ecuación es “la
ecuación de la curva” y también que “la curva es la gráfica de la ecuación”.
En esta sección se abordará una de las curvas más importantes, por su simplicidad geométrica y por su utilidad:
la circunferencia.
Definición:
Se llama circunferencia al conjunto de puntos 𝑃(𝑥; 𝑦) del plano cartesiano que equidistan de un punto fijo
𝐶(ℎ; 𝑘) llamado centro. La distancia 𝑟 de cualquier punto sobre la circunferencia al centro se le llama radio.
Para determinar la ecuación de la circunferencia necesitamos expresar la definición anterior mediante una
ecuación, para ello, veamos los elementos de la definición anterior en un plano cartesiano, tal como aparece en
la Figura 2.
𝑦
De la Figura 2, se tiene que el valor del radio es la distancia entre los
puntos 𝐶 y 𝑃, es decir:
𝑑(𝐶; 𝑃) = √(𝑥 − ℎ)2 + (𝑦 − 𝑘)2 = 𝑟
De donde se deduce la ecuación de la circunferencia:
(𝑥 − ℎ)2 + (𝑦 − 𝑘)2 = 𝑟 2
Figura 2: La circunferencia
𝑥
EJEMPLOS
Ejemplo 1. Determine la ecuación de la circunferencia con centro en (3; 2) y radio 4. Además, trace su gráfica
indicando las coordenadas de los puntos de corte con los ejes.
Solución
Hallamos los elementos de la circunferencia:
Centro: 𝐶 = (ℎ; 𝑘) = (3; 2)
Radio: 𝑟 = 4
Entonces la ecuación de la circunferencia es:
(𝑥 − 3)2 + (𝑦 − 2)2 = 42 = 16 … (∗)
Profesores MA420
11
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Calculamos los puntos de corte con los ejes:
• Corte con eje 𝑥: se hace 𝑦 = 0 y se reemplaza en la ecuación (*):
•
(𝑥 − 3)2 + (−2)2 = 16 ⇒ 𝑥 = 3 ± 2√3
Luego los puntos de corte son: 𝑃1 = (3 − 2√3; 0) y 𝑃2 = (3 + 2√3; 0) o de forma aproximada:
(−0,46; 0) y (6,46; 0).
Corte con eje 𝑦: se hace 𝑥 = 0 y se reemplaza en la ecuación (*):
(−3)2 + (𝑦 − 2)2 = 16 ⇒ 𝑦 = 2 ± √7
Luego los puntos de corte son 𝑃3 = (0; 2 − √7 ) y 𝑃4 = (0; 2 + √7) o de forma aproximada:
(0; −0,65) y (0; 4,65).
Trazamos la gráfica: Para hacer una buena gráfica se recomienda
usar compás, se debe ubicar las coordenadas del centro y trazar
la circunferencia de tal manera que pase por los puntos indicados
y cortes hallados (no olvidar que la distancia entre los puntos de
la circunferencia y el centro es igual al valor del radio).
NOTA: Se debe notar que la circunferencia pasa por los puntos
IZQUIERDA, DERECHA, ABAJO y ARRIBA del centro, además de los
puntos de corte, tal como se muestra en la figura.
Ejemplo 2. Dada la circunferencia de ecuación 𝑥 2 + 2𝑥 + 𝑦 2 − 6𝑦 + 6 = 0, calcule las coordenadas del centro,
el valor de su radio y trace su gráfica.
Solución:
Completando cuadrados se tiene:
(𝑥 2 + 2𝑥 + 1) + (𝑦 2 − 6𝑦 + 9) = −6 + 1 + 9
(𝑥 + 1)2 + (𝑦 − 3)2 = 4
Observamos que se trata de una circunferencia de centro 𝐶 = (−1; 3) y radio 𝑟 = 2.
Calculamos los puntos de corte:
Corte con eje 𝑥: se hace 𝑦 = 0
(𝑥 + 1)2 + (−3)2 = 4 ⇒ (𝑥 + 1)2 = −5 < 0 (Por lo cual, no existe corte con eje 𝑥.)
Corte con eje 𝑦: se hace 𝑥 = 0
(1)2 + (𝑦 − 3)2 = 4 ⇒ 𝑦 = 3 ± √3
Luego los puntos de corte son 𝑃1 = (0; 3 − √3) y 𝑃2 = (0; 3 + √3) o de forma aproximada: (0; 1,27) y
(0; 4,73)
Trazamos la gráfica:
Profesores MA420
12
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Ejemplo 3. Determine la ecuación de la circunferencia sabiendo que uno de sus diámetros tiene como puntos
extremos a: (1; 3) y (5; 7).
Solución:
De la figura adjunta, podemos deducir que el centro de la circunferencia es el punto medio del segmento
𝐴𝐵. AB.
1+5 3+7
𝐶 = (ℎ; 𝑘) = (
;
) = (3; 5)
2
2
Su radio puede ser encontrado hasta de tres formas distintas, una de ella es:
2𝑟 = 𝑑(𝐴; 𝐵) = √(5 − 1)2 + (7 − 3)2 = 4√2 ⇒ 𝑟 = 2√2,
Luego se tiene 𝑟 2 = 8.
Finalmente, la ecuación de la circunferencia es:
(𝑥 − 3)2 + (𝑦 − 5)2 = 8
PRACTIQUEMOS EN CLASE
1. Determine la ecuación estándar de la circunferencia. Si los puntos 𝐴(−3; −3) y 𝐵(5; 3) son los extremos de
uno de sus diámetros.
2. Dada la ecuación general de la circunferencia 𝐶: 𝑥 2 + 𝑦 2 + 6𝑥 – 4𝑦 – 3 = 0. Determine su ecuación
estándar, las coordenadas del centro y el valor de su radio.
3. Determine las coordenadas del centro, radio, corte con los ejes coordenadas y trace la gráfica de la
circunferencia de ecuación (𝑥 − 2)2 + (𝑦 + 1)2 = 16.
4. La figura muestra la gráfica de una circunferencia, donde los puntos 𝐴 y 𝐵 son extremos de uno de sus
diámetros. Determine su ecuación y las coordenadas de los puntos de corte con el eje Y (aproxime a dos
cifras decimales).
𝐴
𝐵
Profesores MA420
13
UPC – Departamento de Ciencias - Matemática Básica (MA420)
RESPUESTAS DE LOS EJERCICIOS PRACTIQUEMOS EN CLASE
1.
2.
3.
4.
(𝑥 − 1)2 + (𝑦 − 0)2 = 25
(𝑥 + 3)2 + (𝑦 − 2)2 = 16, 𝐶 = (−3; 2) y 𝑟 = 4
𝐶 = (2; −1) y 𝑟 = 4
(𝑥 + 1,5)2 + (𝑦 − 2)2 = 9
PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1. Determine la ecuación de la circunferencia con centro en el origen y que pasa por el punto (−5; 4).
2. Determine la ecuación de la circunferencia, si los puntos extremos de uno de los diámetros son 𝐴(3; 4) y
𝐵(−5; −2). Trace su gráfica indicando los puntos de corte con los ejes coordenados.
3. Determine la ecuación canónica o estándar de la circunferencia 𝑥 2 + 𝑦 2 − 6𝑥 − 10𝑦 + 33 = 0 y trace su
gráfica indicando los puntos de corte con los ejes coordenados.
4. Determine la ecuación de la circunferencia cuyo centro es 𝐶(0; 0) y cuyo radio es igual a la distancia entre
el origen de coordenadas y la recta 6𝑥 − 8𝑦 − 12 = 0.
Nota: La distancia entre un punto 𝑃(𝑥0 ; 𝑦0 ) y una recta 𝐿: 𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0 es: 𝑑(𝑃; 𝐿) =
|𝑎𝑥0 +𝑏𝑦0 +𝑐|
√𝑎 2 +𝑏2
RESPUESTAS DE LOS EJERCICIOS PRACTIQUEMOS MÁS EN CASA
1. 𝑥 2 + 𝑦 2 = 41
2. (𝑥 + 1)2 + (𝑦 − 1)2 = 25.
3. (𝑥 − 3)2 + (𝑦 − 5)2 = 1.
36
4. 𝑥 2 + 𝑦 2 = 25
Profesores MA420
14
UPC – Departamento de Ciencias - Matemática Básica (MA420)
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Enlace
Determinar la ecuación de una
circunferencia.
https://tinyurl.com/y6k9x8dc
Trazar la gráfica
circunferencia.
de
una
Código QR
https://tinyurl.com/y2yn375r
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
CIRCUNFERENCIA: Revisar páginas desde 88 hasta 90. Y los ejercicios de la página
94, desde el ejercicio 87 hasta el 108.
Profesores MA420
15
UPC – Departamento de Ciencias - Matemática Básica (MA420)
La parábola con eje focal paralelo al eje 𝑥
y al eje 𝑦
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante analiza y aplica el concepto de parábola
en la resolución de ejercicios, demostrando responsabilidad y capacidad de aprender por su propia cuenta.
CONTENIDOS
MOTIVACIÓN
1.1. Definición geométrica de la parábola
1.2. Ecuaciones y gráficas de parábolas
• Parábola con eje focal vertical y vértice en el origen de coordenadas
• Parábolas trasladadas con eje focal paralelo al eje 𝑦
• Parábola con eje focal horizontal y vértice en el origen de coordenadas
• Parábolas trasladadas con eje focal paralelo al eje 𝑥
1.3. Practiquemos en clase
• Ejercicios
1.4. Practiquemos más en casa
• Ejercicios
Profesores MA420
16
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Motivación
Las principales aplicaciones de las parábolas comprenden su uso
como reflectores del sonido, la luz, las ondas de radio y otras ondas
electromagnéticas. Si se rota una parábola en un espacio
tridimensional con respecto a su eje, la parábola genera un
paraboloide de revolución. Si se coloca una fuente de señales en el
foco de un paraboloide reflectora, la señal se refleja fuera de la
superficie en forma de líneas paralelas al eje de simetría, como se
muestra en la Figura 1. Esta propiedad se utiliza en las luces de las
linternas, los faros, reflectores, repetidoras de microondas y
receptores satelitales.
Figura 1. Paraboloide reflector
El principio también funciona para señales que viajan en sentido
contrario; las señales paralelas que llegan al eje del reflector
parabólico se dirigen hacia el foco del reflector. Esta propiedad se
utiliza para intensificar las señales que se reciben de los
radiotelescopios y las antenas de televisión satelital, para
concentrar calor en hornos solares y para magnificar el sonido de
los micrófonos de la línea de banda. Ver Figura 2.
Figura 2. Reflector parabólico
La gráfica de la parábola podría ser representada con la siguiente ecuación:
𝑦 = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐
Es una curva de la forma de U llamada parábola que abre ya sea hacia arriba o hacia abajo, dependiendo de si el
signo del coeficiente principal “𝑎” es positivo o negativo.
En esta sección estudiaremos parábolas desde un punto de vista geométrico más que algebraico. Empezaremos
con la definición geométrica de una parábola y mostraremos cómo esto nos lleva a la fórmula algebraica con la
que ya estamos familiarizados.
Profesores MA420
17
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1.1. DEFINICIÓN GEOMÉTRICA DE UNA PARÁBOLA
Desde el punto de vista geométrico una parábola es la curva de intersección entre un
plano y un cono, de tal manera que el plano sea paralelo a una generatriz del cono
(ver figura)
Definición: Una parábola es el conjunto de puntos 𝑃(𝑥; 𝑦) del plano que equidistan
de un punto fijo 𝐹 (llamado foco) y de una recta fija 𝐿 (llamada directriz), es decir:
𝑑(𝑃; 𝐹) = 𝑑(𝑃; 𝐿)
Esta definición está ilustrada en la Figura 3. El vértice de la parábola se encuentra a la mitad entre el foco y la
directriz, y el eje de simetría es la recta que pasa por el foco perpendicular a la directriz.
Figura 3. Elementos de la parábola1
Para comenzar pongamos nuestra atención a parábolas que están situadas con el vértice en el origen de
coordenadas, del plano cartesiano XY, y que tienen un eje de simetría vertical u horizontal. Si el foco de dicha
parábola es el punto 𝐹(0; 𝑝), entonces el eje de simetría debe ser vertical y la directriz tiene la ecuación 𝑦 = −𝑝.
La Figura 4 ilustra el caso 𝑝 > 0.
Figura 4. Parábola con vértice en el origen y 𝒑 > 𝟎
2
1
2
Fuente: http://190.90.112.209/precalculo_-_matematicas_para_el_calculo-1.pdf
Fuente: http://190.90.112.209/precalculo_-_matematicas_para_el_calculo-1.pdf
Profesores MA420
18
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Si 𝑃(𝑥; 𝑦) es cualquier punto en la parábola, entonces la distancia de 𝑃 al foco 𝐹(0; 𝑝) (usando la fórmula de
distancia) es:
𝑑(𝑃; 𝐹) = √𝑥 2 + (𝑦 − 𝑝)2
La distancia de 𝑃 a la directriz 𝐿 es:
𝑑(𝑃; 𝐿) = |𝑦 − (−𝑝)| = |𝑦 + 𝑝|
Por la definición de una parábola estas dos distancias deben ser iguales:
√𝑥 2 + (𝑦 − 𝑝)2 = |𝑦 + 𝑝|
𝑥 2 + (𝑦 − 𝑝)2 = |𝑦 + 𝑝|2 = (𝑦 + 𝑝)2
𝑥 2 + 𝑦 2 − 2𝑝𝑦 + 𝑝2 = 𝑦 2 + 2𝑝𝑦 + 𝑝2
𝑥 2 − 2𝑝𝑦 = 2𝑝𝑦
𝑥 2 = 4𝑝𝑦
Si 𝑝 > 0, entonces la parábola abre hacia arriba, si 𝑝 < 0 hacia abajo. La gráfica es simétrica con respecto al eje
𝑌.
Podemos usar las coordenadas del foco para estimar el “ancho” de una parábola cuando tracemos su gráfica. El
segmento de recta que pasa por el foco y es perpendicular al eje, con puntos extremos en la parábola, se llama
lado recto, y su longitud es el diámetro focal (o ancho focal) de la parábola. De la Figura 5 podemos ver que la
distancia de un punto extremo Q del lado recto a la directriz también es 2p (por la definición de una parábola),
de modo que el diámetro focal es 4 p .
Figura 5. Lado recto de una parábola3
3
Fuente: http://190.90.112.209/precalculo_-_matematicas_para_el_calculo-1.pdf
Profesores MA420
19
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1.2. ECUACIONES Y GRÁFICAS DE PARÁBOLAS
A continuación, analizaremos la ecuación y sus características de una parábola.
•
Parábola con eje focal vertical y vértice en el origen de coordenadas
Gráfica de la parábola
𝑝 < 0
La parábola se abre hacia arriba si 𝑝 > 0 o hacia abajo si 𝑝 < 0.
Ecuación canónica de la parábola es:
𝑥 2 = 4𝑝𝑦
Propiedades:
❖
❖
❖
❖
❖
•
Vértice: 𝑉(0; 0)
Foco: 𝐹(0; 𝑝)
Ecuación del eje focal: 𝑥 = 0
Ecuación de la directriz: 𝑦 = −𝑝
Longitud del ancho focal o lado recto: 𝑑(𝐿; 𝑅) = |4𝑝|
Parábolas trasladadas con eje focal paralelo al eje 𝒚
Gráfica de la parábola
La parábola se abre hacia arriba si 𝑝 > 0 o hacia abajo si 𝑝 < 0.
Ecuación estándar de la parábola es:
(𝑥 − ℎ)2 = 4𝑝(𝑦 − 𝑘)
Profesores MA420
20
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Propiedades:
❖
❖
❖
❖
❖
Vértice: 𝑉(ℎ; 𝑘)
Foco: 𝐹(ℎ; 𝑘 + 𝑝)
Ecuación del eje focal: 𝑥 = ℎ
Ecuación de la directriz: 𝑦 = 𝑘 − 𝑝
Longitud del ancho focal o lado recto: 𝑑(𝐿; 𝑅) = |4𝑝|
Si reflejamos la gráfica de la Figura 4 con respecto a la recta 𝑦 = 𝑥, se tiene que intercambiar las variables
𝑥 por 𝑦. Esto resulta una parábola con eje focal horizontal.
•
Parábola con eje focal horizontal y vértice en el origen de coordenadas
Gráfica de la parábola
La parábola se abre hacia la derecha si 𝑝 > 0 o se abre hacia izquierda si 𝑝 < 0.
Ecuación canónica de la parábola es:
𝑦 2 = 4𝑝𝑥
Propiedades:
❖
❖
❖
❖
❖
Vértice: 𝑉(0; 0)
Foco: 𝐹(𝑝; 0)
Ecuación del eje focal: 𝑦 = 0
Ecuación de la directriz: 𝑥 = −𝑝
Longitud del ancho focal o lado recto: 𝑑(𝐿; 𝑅) = |4𝑝|
Profesores MA420
21
UPC – Departamento de Ciencias - Matemática Básica (MA420)
•
Parábolas trasladadas con eje focal paralelo al eje 𝒙
Gráfica de la parábola
La parábola se abre hacia la derecha si 𝑝 > 0 o hacia izquierda si 𝑝 < 0.
Ecuación estándar de la parábola es:
❖
❖
❖
❖
❖
(𝑦 − 𝑘)2 = 4𝑝(𝑥 − ℎ)
Vértice: 𝑉(ℎ; 𝑘)
Foco: 𝐹(ℎ + 𝑝; 𝑘)
Ecuación del eje focal: 𝑦 = 𝑘
Ecuación de la directriz: 𝑥 = ℎ − 𝑝
Longitud del ancho focal o lado recto: 𝑑(𝐿; 𝑅) = |4𝑝|
1.3. PRACTIQUEMOS EN CLASE
1. En cada caso determine la ecuación estándar de la parábola que satisface las condiciones dadas:
a. Vértice(4; 3), se abre hacia arriba y la longitud del lado recto es 8 unidades.
b. Foco (2; −1) y la ecuación de la directriz es 𝑥 = 6.
2. A partir de la gráfica, determine la ecuación de la parábola.
a.
Profesores MA420
b.
22
UPC – Departamento de Ciencias - Matemática Básica (MA420)
3. Determine las coordenadas del vértice, foco, ecuación del eje focal y de la directriz, longitud del lado y trace
la gráfica de la siguiente cónica (𝑦 + 2)2 = 8𝑥. Además, determine los puntos de corte con los ejes
coordenados.
4. Determine las coordenadas del vértice, foco, ecuación del eje focal y de la directriz, longitud del lado recto y
trace la gráfica de la siguiente cónica 𝑥 2 + 2𝑥 + 4𝑦 − 11 = 0. Además, determine los puntos de corte con
los ejes coordenados.
RESPUESTAS DE PRACTIQUEMOS EN CLASE
1. 𝐚. (𝑥 − 4)2 = 8(𝑦 − 3);
2. 𝐚. (𝑦 + 2)2 = 4(𝑥 − 1) ;
𝐛. (𝑦 + 1)2 = −8(𝑥 − 4)
𝐛. (𝑥 + 1)2 = −8(𝑦 − 3)
1
2
3. V(0; −2), F(2; −2), 𝐿𝑓 : 𝑦 = −2, 𝐿𝑑 : 𝑥 = −2, |4𝑝| = 8, puntos de corte ( ; 0) y (0; −2).
4. 𝑉(−1; 3), 𝐹(−1; 2) , 𝐿𝑓 : 𝑥 = −1, 𝐿𝑑 : 𝑦 = 4, |4𝑝| = 4, puntos de corte (−2√3 − 1; 0), (2√3 − 1; 0)
y (0;
11
).
4
Nota: 𝐿𝑓 : Eje focal, 𝐿𝑑 : Directriz, |4𝑝| = Longitud del lado recto (diámetro focal)
1.4. PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1. En cada caso determine la ecuación de una parábola que satisface las condiciones dadas:
a. Foco (– 4; 2), directriz 𝑥 = 4.
b. Vértice (2; −3), se abre a la izquierda y ancho focal 8.
c. Vértice (3; 4) y foco (5; 4).
2. A partir de la gráfica, determine la ecuación de la parábola.
a.
b.
3. En cada caso determine las coordenadas del vértice, foco, ecuación del eje focal y de la directriz, longitud del
lado recto y trace la gráfica. Además, determine los puntos de corte con los ejes coordenados.
a. (𝑦 − 1)2 = −4(𝑥 + 2)
b. (𝑥 + 2)2 = 6(𝑦 + 3)
Profesores MA420
23
UPC – Departamento de Ciencias - Matemática Básica (MA420)
c. 𝑥 2 + 4𝑥 − 6𝑦 + 7 = 0
d. 𝑦 2 − 8𝑦 + 4𝑥 = 0
RESPUESTAS DE PRACTIQUEMOS MÁS EN CASA
1. 𝐚. (𝑦 − 2)2 = −16(𝑥) ;
𝐛. (𝑦 + 3)2 = −8(𝑥 − 2);
𝐜. (𝑦 − 4)2 = 8(𝑥 − 3)
2
2
2. 𝐚. (𝑥 − 3) = 8(𝑦 + 1) ;
𝐛. (𝑦 − 1) = −2(𝑥 − 3)
3.
a.
b.
c.
d.
1
• V(-2;1)
• V(-2;-3),
• 𝑉(4; 4)
• V(−2; 2)
3
• 𝐹(3; 4)
• F(-3;1)
• F(−2; − 2)
• 𝐹(−2; 2)
• 𝐿𝑓 : 𝑦 = 4
• 𝐿𝑓 : y = 1
• 𝐿𝑓 : 𝑥 = −2
• 𝐿𝑓 : 𝑥 = −2
• 𝐿𝑑 : 𝑥 = 5
• 𝐿𝑑 : 𝑥 = −1
9
• 𝐿𝑑 : 𝑦 = −1
• 𝐿𝑑 : 𝑦 = − 2
• |4𝑝| = 4
• |4𝑝| = 4
• |4𝑝| = 6
|4𝑝|
•
=
6
• Puntos de corte:
• Punto de corte:
• Puntos de corte:
9
• Puntos de corte:
(0; 0),(0; 0) 𝑦
(− 4 ; 0)
7
(−3√2 − 2; 0),
(0; )
(0; 8)
6
(3√2 − 2; 0) y
7
(0; − )
3
Observación: La gráfica de una parábola debe pasar por el vértice, los extremos del lado recto y por los
puntos de corte con los ejes si es que los tiene.
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Enlace
Determinar la ecuación de una parábola
a partir de su gráfica.
https://tinyurl.com/y6bmjmkx
Determinar la ecuación de una parábola
a partir de condiciones dadas.
https://tinyurl.com/yxf366oe
Determinar los elementos de una
parábola a partir de su ecuación
estándar.
https://tinyurl.com/y3dces7n
Profesores MA420
Código QR
24
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Habilidad
Graficar una parábola a partir de
condiciones dadas.
Enlace
Código QR
https://tinyurl.com/yxbot7gd
Graficar una parábola a partir de su
https://tinyurl.com/y52k6lom
ecuación estándar.
Graficar una parábola a partir de
https://tinyurl.com/y2tz2adq
condiciones dadas.
Determinar la ecuación de una parábola
https://tinyurl.com/y3ws4ods
a partir de su gráfica.
Completar cuadrados para determinar
los elementos y la gráfica de una https://tinyurl.com/y56ehg64
parábola.
Profesores MA420
25
UPC – Departamento de Ciencias - Matemática Básica (MA420)
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
LA PARÁBOLA: Revisar páginas desde 782 hasta 790. Pág. 810.
Pág. 813 – 815, ejercicios 2, 13 al 20, 30, 34, 39, 40, 45, 46, 47, 50, 54, 66.
Profesores MA420
26
UPC – Departamento de Ciencias - Matemática Básica (MA420)
La elipse con eje focal paralelo al eje 𝑥 y
al eje 𝑦
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante analiza y aplica el concepto de elipse en
la resolución de ejercicios, demostrando responsabilidad y capacidad de aprender por su propia cuenta.
CONTENIDO
MOTIVACIÓN
1.1. Definición y elementos.
• Definiciones
• Excentricidad
1.2. Elipse con centro 𝐶(ℎ; 𝑘) y eje focal paralelo al eje 𝑥
1.3. Elipse con centro 𝐶(ℎ; 𝑘) y eje focal paralelo al eje 𝑦
1.4. Practiquemos en clase
• Ejercicios
1.5. Practiquemos más en casa
• Ejercicios
Profesores MA420
27
UPC – Departamento de Ciencias - Matemática Básica (MA420)
MOTIVACIÓN
Aplicación 1: Orbita de un satélite artificial
La idea de poner objetos en el espacio en órbitas alrededor de la tierra ocurrió después de finalizar la Segunda
Guerra Mundial. En 1945 un oficial de radar de la RAF (Real Fuerza Aérea), llamado Arthur C. Clarke, escribió un
artículo en la revista Wirelees World que hablaba de colocar tres repetidores separados 120° entre sí, a una
distancia de 36 000 km de la Tierra (Peredo, 2004).
La figura 1 muestra las posiciones de varios cientos de satélites en
órbita alrededor de la Tierra. Cada punto representa la posición de
un satélite en la tarde del 23 de junio de 2004. En órbitas bajas,
solo a unos cuantos cientos de kilómetros sobre el nivel del mar,
se encuentran satélites de comunicación para sistemas de
telefonía, la Estación Espacial Internacional, el telescopio espacial
Hubble y otras aplicaciones (puntos amarillos). El círculo perfecto
de satélites a una distancia de aproximadamente 5,6 radios
terrestres sobre la superficie (puntos verdes) está compuesto por
los satélites geoestacionarios, los cuales orbitan a la misma
velocidad angular que la Tierra y así permanecen sobre el mismo
punto en el suelo. Los satélites entre la órbita geoestacionaria y la
órbita baja (puntos rojos) son sobre todo aquellos usados para el
Sistema de Posicionamiento Global, pero también se incluyen
algunos que llevan instrumentos de investigación (Bauer, 2011)
Figura 1: Las posiciones de algunos satélites
alrededor de la Tierra el 23 de junio de 2004
(Bauer, 2011)
Aplicación 2: La litotricia
En Medicina, la litotricia es un procedimiento médico que utiliza ondas de choque para romper cálculos en el
riñón, la vejiga o el uréter (el conducto que lleva la orina de los riñones a la vejiga) y después del procedimiento,
los diminutos pedazos de los cálculos salen del cuerpo a través de la orina. El aparato utilizado para este
procedimiento es llamado litotriptor el cual tiene la forma de un elipsoide (ver figuras).
Profesores MA420
28
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1.1. DEFINICIÓN GEOMÉTRICA DE UNA ELIPSE
Desde el punto de vista geométrico una elipse es la curva de intersección
entre un plano y un cono, de tal manera que el plano corte a todas las
generatrices del cono. (El plano no debe de pasar por el vértice del cono).
(ver figura)
Definición: Una elipse es un conjunto de puntos
𝑃(𝑥; 𝑦) del plano XY tal que la suma de sus distancias
a dos puntos fijos 𝐹1 y 𝐹2 , llamados focos, es una
constante, es decir:
𝑑(𝐹1 ; 𝑃) + 𝑑(𝑃; 𝐹2 ) = cte = 2𝑎
De la figura, definimos:
Centro: 𝐶(0; 0)
Vértices: 𝑉1 𝑦 𝑉2
Focos: 𝐹1 y 𝐹2
Eje focal: Eje que contiene a los focos y a los vértices
de la elipse.
❖ 𝑎 = 𝑑(𝑉1 ; 𝐶) = 𝑑(𝐶; 𝑉2 )
❖
❖
❖
❖
𝑏 = 𝑑(𝐴; 𝐶) = 𝑑(𝐶; 𝐵)
𝑐 = 𝑑(𝐹1 ; 𝐶) = 𝑑(𝐶; 𝐹2 )
Observe que 𝑎 es mayor que 𝑏, 𝑐. Además, 𝑎, 𝑏 𝑦 𝑐 son números positivos
❖ El segmento 𝑉1 𝑉2 es llamado “eje mayor” y su longitud es 2𝑎.
❖ El segmento 𝐴𝐵 es llamado “eje menor” y su longitud es 2𝑏.
❖ Relación Pitagórica: En la figura, si ubicamos el punto 𝑃 junto al punto 𝐵 , es fácil observar que el
triángulo𝐹1 𝑃𝐹2 es isósceles y que el triángulo 𝑃𝐶𝐹2 es rectángulo, recto en 𝐶, es decir se cumple la relación.
𝑎2 = 𝑏 2 + 𝑐 2
❖ Excentricidad: Denotada por la letra “𝑒” y se calcula mediante la fórmula:
𝑐
𝑒=𝑎=
√𝑎 2 −𝑏2
𝑎
La excentricidad es un número entre 0 y 1 (0 < 𝑒 < 1) y nos indica la forma de una elipse; una elipse será más
redondeada (semejante a una circunferencia) si el número 𝑒 se aproxima al valor de cero. Por ejemplo, la
excentricidad de la órbita de la tierra es muy pequeña, de manera que la órbita es casi circular ya que su
excentricidad es menor a 0,2.
Profesores MA420
29
UPC – Departamento de Ciencias - Matemática Básica (MA420)
e = 0,1
e = 0,68
e = 0,5
e = 0,86
En nuestro curso estudiaremos elipses con eje focal paralelo al eje 𝑋 y al eje 𝑌. A continuación, presentamos
ambos casos:
1.2. ELIPSE CON CENTRO 𝐶(ℎ; 𝑘) Y EJE FOCAL PARALELO AL EJE 𝒙
Gráfica de la elipse
En este caso, la ecuación estándar que representa a la elipse es:
(𝑥 − ℎ)2 (𝑦 − 𝑘)2
+
=1
𝑎2
𝑏2
;𝑎 > 𝑏
Propiedades:
❖
❖
❖
❖
❖
❖
Centro: 𝐶(ℎ; 𝑘)
Vértices: 𝑉1 (ℎ − 𝑎; 𝑘) y 𝑉2 (ℎ + 𝑎; 𝑘)
Focos: 𝐹1 (ℎ − 𝑐; 𝑘) y 𝐹2 (ℎ + 𝑐; 𝑘)
El segmento 𝑉1 𝑉2 es llamado “eje mayor” y su longitud es 𝟐𝒂
El segmento 𝐴𝐵 es llamado “eje menor” y su longitud es 𝟐𝒃
En este caso la ecuación del eje focal es: 𝒚 = 𝒌
Si el centro de la elipse está en 𝐶(0; 0) en este caso, la ecuación se denomina canónica:
𝑥2
𝑎2
Profesores MA420
𝑦2
+ 𝑏2 = 1
;𝑎 > 𝑏
30
UPC – Departamento de Ciencias - Matemática Básica (MA420)
ELIPSE CON CENTRO 𝐶(ℎ; 𝑘) Y EJE FOCAL PARALELO AL EJE 𝒚
Gráfica de la elipse
En este caso, la ecuación estándar que representa a la elipse es:
(𝑥 − ℎ)2 (𝑦 − 𝑘)2
+
=1 ; 𝑎>𝑏
𝑏2
𝑎2
Propiedades:
❖
❖
❖
❖
❖
❖
Centro: 𝐶(ℎ; 𝑘)
Vértices: 𝑉1 (ℎ; 𝑘 − 𝑎) y 𝑉2 (ℎ; 𝑘 + 𝑎)
Focos: 𝐹1 (ℎ; 𝑘 − 𝑐) y 𝐹2 (ℎ; 𝑘 + 𝑐)
El segmento𝑉1 𝑉2 es llamado “eje mayor” y su longitud es: 𝟐𝒂
El segmento 𝐴𝐵 es llamado “eje menor” y su longitud es: 𝟐𝒃
En este caso la ecuación del eje focal es: 𝒙 = 𝒉
Si el centro de la elipse está en 𝐶(0; 0) en este caso, la ecuación se denomina canónica:
𝑥2 𝑦2
+
=1
𝑏 2 𝑎2
Profesores MA420
;𝑎 > 𝑏
31
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1.3. PRACTIQUEMOS EN CLASE
1. Determine la ecuación estándar o canónica de la elipse, si se sabe que el eje mayor tiene sus puntos
extremos en (−2; −1) y (8; −1), y el valor de su excentricidad es 0,4.
2. Determine la ecuación estándar o canónica de la elipse, donde los focos están en (3; −2) y (3; 2). Además,
la longitud del eje mayor es 8 unidades.
3. A partir de la gráfica, determine la ecuación de la elipse:
a.
b.
4. Dada la ecuación de la elipse
(𝑥+2)2
9
+
(𝑦−1)2
16
= 1, describa sus elementos y trace su gráfica. Además,
determine los puntos de corte con los ejes coordenados.
5. Dada la ecuación de la elipse 4𝑥 2 + 9𝑦 2 − 16𝑥 + 18𝑦 − 11 = 0, describa sus elementos y trace su gráfica.
Además, determine los puntos de corte con los ejes coordenados.
RESPUESTA DE PRACTIQUEMOS EN CLASE
1.
(𝑥−3)2
25
2.
𝑦2
16
3. 𝐚.
+
+
(𝑦+1)2
21
(𝑥−3)2
12
(𝑦−1)2
9
+
= 1.
= 1.
(𝑥+2)2
4
= 1; 𝐛.
(𝑥−1)2
25
+
(𝑦+2)2
9
= 1.
4. C(−2; 1), 𝐹1 : (−2; 1 − √7), 𝐹2 : (−2; 1 + √7), 𝑉1 : (−2; −3), 𝑉2 : (−2; 5), 𝐿𝑓 : 𝑥 = −2. puntos de corte
−3√15
−
4
(
5.
3√15
−
4
2; 0), (
2; 0), (0;
−4√5
+
3
1) y (0;
4√5
+
3
1).
C(2; −1); 𝐹1 : (2 − √5; −1), 𝐹2 : (2 + √5; −1), 𝑉1 : (−1; −1), 𝑉2 : (5; −1), 𝐿𝑓 : 𝑦 = −1. puntos de corte
−3√3
+
2
(
3√3
+
2
2; 0), (
Profesores MA420
2; 0), (0;
−2√5
−
3
1) y (0;
2√5
−
3
1).
32
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1.4. PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1. Determine la ecuación estándar de la elipse con centro en (−1; 3), uno de sus focos se ubica en el punto
(−1; 0) y con uno de sus vértices en el punto (−1; 7). Además, determine los puntos de corte con los ejes
y grafique.
2. Dada la ecuación de la elipse
(𝑥−3)2
25
+
(𝑦+2)2
9
= 1, describa sus elementos y trace su gráfica. Además,
determine los puntos de corte con los ejes coordenados.
3. Dada la ecuación de la elipse 25𝑥 2 + 36𝑦 2 + 100𝑥 + 72𝑦 − 764 = 0, describa sus elementos y trace su
gráfica. Además, determine los puntos de corte con los ejes coordenados.
4. A partir de la gráfica, determine la ecuación de la elipse:
RESPUESTA DE PRACTIQUEMOS MÁS EN CASA
1.
(𝑦−3)2
16
+
(𝑥+1)2
7
= 1, puntos de corte (−
11
; 0),
4
3
(4 ; 0), (0;
−4√42
+
7
3) y (0;
4√42
+
7
3).
−5√5
+
3
2. 𝐶(3; −2), 𝐹1 : (−1; −2), 𝐹2 : (7; −2), 𝑉1 : (−2; −2), 𝑉2 : (8; −2), 𝐿𝑓 : 𝑦 = −2, puntos de corte (
5√5
3
3; 0), (
+ 3; 0), (0;
−22
)
5
2
y (0; 5).
3. 𝐶(−2; −1), 𝐹1 : (−2 − √11; −1), 𝐹2 : (−2 + √11; −1), 𝑉1 : (−8; −1), 𝑉2 : (4; −1), 𝐿𝑓 : 𝑦 = −1, puntos
−12√6
−
5
de corte (
4.
(𝑦−2)2
25
+
Profesores MA420
(𝑥+3)2
16
12√6
−
5
2; 0), (
2; 0), (0;
−10√2
−
3
1) y (0;
10√2
−
3
1).
=1
33
UPC – Departamento de Ciencias - Matemática Básica (MA420)
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Enlace
Código QR
Determinar la ecuación estándar
de una elipse a partir de https://tinyurl.com/yxvx89xk
condiciones dadas.
Determinar los elementos y trazar
la gráfica de una elipse a partir de https://tinyurl.com/yyl95hye
su ecuación estándar.
Determinar la ecuación estándar
de una elipse a partir de https://tinyurl.com/yykr9vko
condiciones dadas.
Determinar los elementos y trazar
la gráfica de una elipse a partir de https://tinyurl.com/y3stlxjx
su ecuación estándar.
Completar
cuadrados
para
determinar la ecuación estándar
https://tinyurl.com/y3ppsyqo
de una elipse y trazar su gráfica
(eje vertical).
Identificar los elementos y graficar
una elipse a partir de su ecuación https://tinyurl.com/y4v8wggp
estándar (eje horizontal).
Profesores MA420
34
UPC – Departamento de Ciencias - Matemática Básica (MA420)
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
LA ELIPSE: Revisar páginas desde 790 hasta 799. Pág. 808 y 809
Pág. 814 – 816, ejercicios 3, 5 - 12, 31, 32, 35, 36, 43, 44, 48, 51, 52, 97
Profesores MA420
35
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Resolución de problemas con cónicas
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante resuelve problemas de modelación con
cónicas (la parábola y la elipse), demostrando responsabilidad y capacidad de aprender por su propia cuenta.
1.1. Practiquemos en clase
• Problemas
1.2. Practiquemos más en casa
• Problemas
PRACTIQUEMOS EN CLASE
1. La figura muestra la imagen de un arco parabólico que tiene 20 m de
altura y 30 m de ancho. Si la parte superior del arco es el vértice de la
parábola.
a. Considere un sistema de referencia adecuado y encuentre la
ecuación del arco parabólico mostrado en la figura.
b. ¿A qué altura sobre la base tiene la parábola un ancho de 18
metros?
2. La figura muestra una lámpara con un reflector parabólico. La bombilla
eléctrica está colocada en el foco y el diámetro focal es 16 centímetros.
a. Considere un sistema de referencia adecuado y determine la
ecuación del arco parabólico mostrado en la figura.
b. ¿Cuál es la longitud del ancho de abertura 𝐶𝐷 del reflector
parabólico?
3. Muchas veces las operaciones mineras se despliegan sobre áreas
irregulares, con equipo y materia prima en diferentes arreglos. Cubrir
pilas de almacenamiento bajo estas condiciones es un desafío para la
Ingeniería. La tecnología Freedome permite construir domos en una
variedad de dimensiones y formas: irregulares, circulares,
paraboloides, elípticas o longitudinales.
El Domo San Cristóbal (Bolivia) es de tipo paraboloide, su base tiene
140 m de diámetro y su altura es de 59_m.
a. Considere un sistema de referencia adecuado y determine la
ecuación del arco parabólico1 descrito por el Domo de San
Cristóbal (Ver figuras).
1
La sección transversal es una vista al interior cortando a través del mismo. Recuperado: shorturl.at/lDF35
Profesores MA420
36
UPC – Departamento de Ciencias - Matemática Básica (MA420)
b.
Determine la altura “𝑟” (desde el punto 𝑄 hasta la base del domo), si la distancia del punto 𝑄 al eje
focal es 28 m.
4. Se desea conocer el área de la cancha del estadio Elías Aguirre de
Chiclayo, si se sabe que la cancha está inscrita en una elipse cuyo
eje mayor mide 120 metros, el eje menor mide 80 metros y los
centros de los arcos están ubicados en los focos de la elipse tal
como se muestra en la figura.
a. Determine la ecuación de la elipse.
b. Determine el área de la cancha de fútbol.
RESPUESTAS DE PRACTIQUEMOS EN CLASE
1.
45
a. Eligiendo como (0; 0) el centro de la base del arco parabólico se tiene 𝑥 2 = − (𝑦 − 20). Defina las
4
variables y restricciones. Nota: puede elegir el (0; 0) en otro punto del arco parabólico y obtendrá otra
ecuación valida.
b. A 12,8m de altura sobre la base la parábola tiene un ancho de 18 m.
2.
a. Eligiendo como (0; 0) el punto O del arco parabólico se tiene 𝑦 2 = 16𝑥. Defina las variables y
restricciones. Nota: puede elegir el (0; 0) en otro punto del arco parabólico y obtendrá otra ecuación
valida.
b. La longitud del del segmento CD es 43,82 cm. aproximadamente.
3.
4900
a. Eligiendo como (0; 0) el centro de la base del arco parabólico se tiene 𝑥 2 = −
(𝑦 − 59). Defina las
59
variables y restricciones. Nota: puede elegir el (0; 0) en otro punto del arco parabólico y obtendrá otra
ecuación valida.
b. La altura ℎ mide 49,56 m aproximadamente.
4.
𝑥2
𝑦2
a. Considere un sistema Eligiendo como (0; 0) el centro de la cancha del estadio se tiene 3600 + 1600 = 1.
Defina las variables y restricciones. Nota: puede elegir el (0; 0) en otro punto del arco parabólico y
obtendrá otra ecuación valida.
b. El área del estadio Elías Aguirre de Chiclayo es de 4770,28 metros cuadrados aprox.
Profesores MA420
37
UPC – Departamento de Ciencias - Matemática Básica (MA420)
PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1. En la imagen, se muestra un arco parabólico que tiene 25m de altura
y 30 de ancho. Si en la parte superior del arco se ubica el vértice de la
parábola.
a. Considere un sistema de referencia adecuado y determine la
ecuación del arco parabólico.
b. ¿A qué altura sobre la base tiene la parábola un ancho de 14m?
2. Un puente colgante es un puente cuyo tablero, en vez de estar apoyado sobre pilas o arcos se sujeta
mediante cables o piezas atirantadas desde una estructura a la que van sujetas. Desde la antigüedad este
tipo de puentes han sido utilizados por la humanidad para salvar obstáculos. Con el paso de los siglos, la
introducción y mejora de distintos materiales de construcción, ha permitido que este tipo de puentes sean
capaces de soportar el tráfico rodado o líneas de ferrocarril. En el puente colgante de la figura adjunta, los
cables de suspensión de acero tienen forma parabólica. La distancia entre los pilones (torres de apoyo), es
de 60 metros, el punto más bajo de los cables está a 15 metros por debajo del extremo superior de los pilones
y a 6 metros de AB.
a. Considere un sistema de referencia adecuado y determine la ecuación del arco parabólico mostrado en
la figura.
b. ¿Cuál es la longitud de los postes MN y PQ sabiendo que se encuentran a 5 metros de cada pilón?
3. Los pobladores del puerto de Pacasmayo desean promover
el turismo de su pueblo, para lo cual han decidido construir
una entrada que tenga la forma de un arco semielíptico,
con un aviso de entrada al puerto que mida 18 m de largo
y esté sostenido por cables a ambos lados (ver figura
adjunta).
a. Determine la ecuación del arco semielíptico.
b. ¿A qué altura sobre la carretera tendrán que colocar
el aviso?
Profesores MA420
38
UPC – Departamento de Ciencias - Matemática Básica (MA420)
4. El arco de un puente es semielíptico, con eje mayor horizontal. La longitud de la base del puente es de 30
metros y la parte más alta del puente está a 10 metros sobre el pavimento, como se muestra la figura.
a. Considere un sistema de referencia adecuado y
determine la ecuación del arco semielíptico.
b. Analice la ecuación hallada en la parte (a) y
determine la altura desde el pavimento al arco
del puente que se encuentra a 6 metros del
centro de la base del pavimento.
RESPUESTAS DE PRACTIQUEMOS MÁS EN CASA
1.
2.
a. Eligiendo como (0; 0) el centro de la base del arco parabólico se tiene 𝑥 2 = −9(𝑦 − 25). Defina las
variables y restricciones. Nota: puede elegir el (0; 0) en otro punto del arco parabólico y obtendrá otra
ecuación valida.
b. A una altura 19,56 m aproximadamente el arco parabólico tiene un ancho de 14 m.
a. Eligiendo como (0; 0) el centro del tramo AB del arco parabólico se tiene 𝑥 2 = 60(𝑦 − 6). Defina las
variables y restricciones. Nota: puede elegir el (0; 0) en otro punto del arco parabólico y obtendrá otra
ecuación valida.
b. La medida de la altura de los postes MN y PQ es de 16,42m aproximadamente.
3.
𝑥2
𝑦2
a. Considere Eligiendo como (0; 0) el centro de la base del arco semielítico se tiene 225 + 400 = 1. Defina
las variables y restricciones. Nota: puede elegir el (0; 0) en otro punto del arco parabólico y obtendrá
otra ecuación valida.
b. El aviso se colocará a16 m sobre la carretera aproximadamente.
4.
𝑥2
𝑦2
a. Eligiendo como (0; 0) el centro de la base del arco semielíptico se tiene 225 + 100 = 1. Defina las
variables y restricciones. Nota: puede elegir el (0; 0) en otro punto del arco parabólico y obtendrá otra
ecuación valida.
b. La altura desde el pavimento al arco del puente que se encuentra a 6 metros del centro de la base del
pavimento es 9,17 metros aproximadamente.
Profesores MA420
39
UPC – Departamento de Ciencias - Matemática Básica (MA420)
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Determinar la ecuación de un
problema de modelación con
parábola.
Determinar la ecuación de un
problema de modelación con
parábola.
Determinar la ecuación de un
problema de modelación con
parábola.
Enlace
Código QR
https://bit.ly/3sRm16S
https://bit.ly/39W4amI
https://bit.ly/3668xu0
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
PROBLEMAS CON CÓNICAS: Revisar las páginas 789- 790 y página 799.
Profesores MA420
40
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Matrices y determinantes
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante analiza y aplica el concepto de matrices,
operaciones con matrices y determinantes en la resolución de ejercicios, mostrando responsabilidad y
capacidad de aprender por su propia cuenta.
CONTENIDOS
MOTIVACIÓN
1.
Matrices
• Definición
• Orden de una matriz
• Matriz por extensión
• Tipos de matrices
• Traspuesta de una matriz
2.
Operaciones con matrices
• Suma de matrices
• Multiplicación de una matriz por un escalar
• Multiplicación de matrices
3.
Determinantes
• Definición
• Determinante de orden 2 × 2 y 3 × 3
4.
Practiquemos en clase
• Ejercicios
5.
Practiquemos más en casa
• Ejercicios
6.
Respuestas
Profesores MA420
41
UPC – Departamento de Ciencias - Matemática Básica (MA420)
MOTIVACIÓN
Una matriz es simplemente un conjunto rectangular de números. Las matrices se usan para organizar
información en categorías que corresponden a las filas y columnas de la matriz. Por ejemplo, un científico podría
organizar información sobre una población de ballenas en peligro como sigue:
Ésta es una forma compacta de decir que hay 12 machos inmaduros, 15 hembras inmaduras, 18 machos adultos,
etc.
En general las matrices son de suma importancia en las ciencias, como la ingeniería, la economía y otras ciencias
aplicadas. Son útiles para representar datos en forma ordenada, para modelar problemas y resolver sistemas de
ecuaciones lineales, para indicar las interrelaciones que existen en los diferentes sectores de la economía (Matriz
Insumo – Producto), entre otras aplicaciones.
1. MATRICES
Definición: Una matriz es un arreglo rectangular de números reales, ordenados en filas y columnas.
𝑛 columnas
𝑚 filas
𝒂𝟏𝟏 𝒂𝟏𝟐
𝒂𝟐𝟏 𝒂𝟐𝟐
[ ⋮
⋮
𝒂𝒎𝟏 𝒂𝒎𝟐
⋯ 𝒂𝟏𝒏
⋯ 𝒂𝟐𝒏
⋮
⋮ ]
⋯ 𝒂𝒎𝒏
Orden 𝑚 × 𝑛
❖ Generalmente las matrices se escriben de la forma: 𝐴 = [𝑎𝑖𝑗 ]𝑚×𝑛
Donde: 𝑎𝑖𝑗 indica la posición 𝑖- ésima fila con la 𝑗- ésima columna de sus elementos, por ejemplo: 𝑎21 nos
indica la posición fila 2- columna 1.
𝑚 × 𝑛: Nos indica el orden de la matriz, es decir, 𝑚 filas y 𝑛 columnas (manteniendo el orden “primero las
filas y luego las columnas”)
❖ Las matrices se denotan con letras mayúsculas, por ejemplo, 𝐴, 𝐵, etc.
❖ Si el número de filas es igual al número de columnas, es decir 𝑚 = 𝑛, las matrices reciben el nombre de
matrices cuadradas.
•
Orden de una Matriz
El orden de una matriz es el número de filas por el número de columnas que tiene dicha matriz, y se representa
por 𝑚 × 𝑛.
1 5 2
] es de orden 2 × 3 porque hay 2 filas y 3 columnas. Además, por ejemplo,
2 −1 4
el valor en la posición 𝑎12 es 5.
Ejemplo 1: La matriz 𝐴 = [
Profesores MA420
42
UPC – Departamento de Ciencias - Matemática Básica (MA420)
•
Matriz por extensión
Dada la matriz 𝐴 = [𝑎𝑖𝑗 ]𝑚×𝑛 donde 𝑎𝑖𝑗 define los elementos de la matriz entonces podremos determinar dichos
elementos.
Ejemplo 2: Dada la matriz 𝐴 = [𝑎𝑖𝑗 ]2×3 donde 𝑎𝑖𝑗 = 2𝑖 − 𝑗 entonces halle la matriz 𝐴 por extensión.
Primero debemos observar que la matriz tiene dos filas y tres columnas, es decir, es de la forma:
𝑎11 𝑎12 𝑎13
𝐴 = [𝑎
]
21 𝑎22 𝑎23
Luego usamos la condición dada para hallar el valor de cada elemento, es decir:
𝑎11 = 2(1) − 1 = 1 ; 𝑎12 = 2(1) − 2 = 0 ; 𝑎13 = 2(1) − 3 = −1
𝑎21 = 2(2) − 1 = 3 ; 𝑎22 = 2(2) − 2 = 2 ; 𝑎23 = 2(2) − 3 = 1
1 0 −1
Finalmente, la matriz por extensión es: 𝐴 = [
]
3 2 1
•
Tipos de Matrices
Matriz Nula: Es aquella matriz donde todos sus elementos son ceros y se representa por 𝑶, es decir.
0 0 ⋯ 0
0 0 ⋯ 0
𝑶=[
]
⋮ ⋮
⋮
0 0 ⋯ 0 𝑚×𝑛
Las siguientes matrices son ejemplos de matrices nulas: 𝐴 = [
0 0
0 0 0
y𝐵 =[
]
]
0 0 2×2
0 0 0 2×3
Matriz Identidad: Es una matriz cuadrada cuyos elementos en la diagonal principal son todos unos, mientras que
en los demás son todos ceros. Se denota con la letra 𝐼.
1 0 ⋯ 0
0 1 ⋯ 0
𝐼=[
]
⋮ ⋮
⋮
0 0 ⋯ 1
Diagonal principal
Son ejemplos de matriz identidad:
1 0
𝐼2 = [
],
0 1
1 0
𝐼3 = [0 1
0 0
1
0
0
0 ] , 𝐼4 = [
0
1
0
0
1
0
0
0
0
1
0
0
0
]...
0
1
Matriz Traspuesta: Dada la matriz 𝐴 = [𝑎𝑖𝑗 ] de orden 𝑚 × 𝑛, se llama matriz traspuesta de 𝐴 y se representa
por 𝐴𝑇 a la matriz que se obtiene cambiando las filas por las columnas (o viceversa) en la matriz. Es decir.
𝑎11
𝑎
𝐴 = [ 21
⋮
𝑎𝑚1
Profesores MA420
𝑎12
𝑎22
⋮
𝑎𝑚2
⋯ 𝑎1𝑛
𝑎11
⋯ 𝑎2𝑛
𝑎
] ⇒ 𝐴𝑇 = [ 12
⋮
⋮
⋱
𝑎1𝑛
⋯ 𝑎𝑚𝑛
𝑎21
𝑎22
⋮
𝑎2𝑛
⋯ 𝑎𝑚1
⋯ 𝑎𝑚2
]
⋮
⋱
⋯ 𝑎𝑚𝑛
43
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Ejemplo 3: Sea la matriz 𝐴 = [
1 5
1 3 2
] entonces 𝐴𝑇 = [3 4]
5 4 7
2 7
Igualdad de matrices: Las matrices 𝐴 = [𝑎𝑖𝑗 ] y 𝐵 = [𝑏𝑖𝑗 ] son iguales si y solo si tienen el mismo orden 𝑚 × 𝑛 y
𝑎𝑖𝑗 = 𝑏𝑖𝑗 para 𝑖 = 1, 2, ⋯ , 𝑚 y 𝑗 = 1, 2, ⋯ , 𝑛
2
Ejemplo 4: Las matrices [
𝑎
−5
2 𝑏
]=[
] son iguales si 𝑎 = 3 y 𝑏 = −5.
1
3 1
2. OPERACIONES CON MATRICES
•
Suma de matrices
Sean las matrices 𝐴 = [𝑎𝑖𝑗 ] y 𝐵 = [𝑏𝑖𝑗 ] de orden 𝑚 × 𝑛, la suma de la matriz 𝐴 y 𝐵 es otra matriz 𝐶 = 𝐴 + 𝐵 de
orden 𝑚 × 𝑛, definida por 𝐶 = [𝑐𝑖𝑗 ] , donde 𝐶 = 𝐴 + 𝐵 = [𝑎𝑖𝑗 + 𝑏𝑖𝑗 ]. Esto es:
𝑎11 +𝑏11 𝑎12 + 𝑏12 𝑎1𝑛 + 𝑏1𝑛
𝑎21 +𝑏21 𝑎22 + 𝑏22 𝑎2𝑛 + 𝑏2𝑛
𝐴 + 𝐵 = [𝑎𝑖𝑗 + 𝑏𝑖𝑗 ] = [
]
⋮
⋮
⋮
𝑎𝑚1 + 𝑏𝑚1 𝑎𝑚2 +𝑏𝑚2 𝑎𝑚𝑛 +𝑏𝑚𝑛
Observación: Solo se suman matrices del mismo orden.
Ejemplo 4: Sean las matrices 𝐴 = [
1 3
5 4
2
−8 −3 2
] y 𝐵=[
] calcule 𝐴 + 𝐵
7
−15 42 17
Solución:
Como en orden de las matrices son iguales entonces podemos sumar o restar.
1 3 2
−8 −3 2
−7
0
4
𝐴+𝐵 =[
]+[
]=[
]
5 4 7
−15 42 17
−10 46 24
•
Multiplicación de una matriz por un escalar.
Sea la matriz 𝐴 = [𝑎𝑖𝑗 ] de orden 𝑚 × 𝑛 y sea 𝑘 un número real. El producto del número 𝑘 por la matriz 𝐴 es otra
matriz de orden 𝑚 × 𝑛 y se denota por 𝑘𝐴 = [𝑘𝑎𝑖𝑗 ]
Para multiplicar un número real por una matriz, se multiplica el número 𝑘 por cada uno de los elementos de la
matriz 𝐴.
𝑘𝑎11 𝑘𝑎12 ⋯ 𝑘𝑎1𝑛
𝑘𝑎
𝑘𝑎22 ⋯ 𝑘𝑎2𝑛
𝑘𝐴 = 𝑘[𝑎𝑖𝑗 ] = [ 21
] = [𝑘𝑎𝑖𝑗 ]
⋮
⋮
⋮
⋮
𝑘𝑎𝑚1 𝑘𝑎𝑚2 ⋯ 𝑘𝑎𝑚𝑛
Ejemplo 5: Sea la matriz 𝐴 = [
1
Solución: 𝟑𝐴 = 3 [
5
Profesores MA420
1 3 2
] calcule 3𝐴
5 4 −7
3 2
3
9
6
]=[
]
4 −7
15 12 −21
44
UPC – Departamento de Ciencias - Matemática Básica (MA420)
•
Multiplicación de matrices
Sea la matriz 𝐴 = [𝑎𝑖𝑗 ] de orden 𝑚 × 𝑟 y la matriz 𝐵 = [𝑏𝑖𝑗 ] de orden 𝑟 × 𝑛. Entonces el producto de 𝐴 y 𝐵, es
la matriz 𝐶 = [𝑐𝑖𝑗 ] de orden 𝑚 × 𝑛, tal que:
𝑎11
𝑎21
𝐴𝐵 = [𝑎𝑖𝑗 ][𝑏𝑖𝑗 ] = [ ⋮
𝑎𝑚1
𝑎12
𝑎22
⋮
𝑎𝑚2
⋯ 𝑎1𝑟 𝑏11 𝑏12 ⋯ 𝑏1𝑛
⋯ 𝑎2𝑟 𝑏21 𝑏22 ⋯ 𝑏2𝑛
]
⋮
⋮ ][ ⋮
⋮
⋮
⋮
⋯ 𝑎𝑚𝑟 𝑏𝑟1 𝑏𝑟2 ⋯ 𝑏𝑟𝑛
El producto 𝑨𝑩 = [𝒄𝒊𝒋 ] es la matriz de orden 𝒎 × 𝒏, donde cada 𝒄𝒊𝒋 es el resultado de multiplicar la 𝒊-ésima
fila de la primera matriz con la 𝒋-ésima columna de la segunda matriz.
Observación
Dos matrices 𝐴𝑛×𝑟 y 𝐵𝑟×𝑚 se pueden multiplicar si y sólo si el número de columnas de la matriz 𝐴 es igual al
número de filas de la matriz 𝐵 y el resultado es una matriz 𝐶𝑛×𝑚 .
𝐴𝑛×𝑟 × 𝐵𝑟×𝑚 = 𝐶𝑛×𝑚
En general, 𝐴𝐵 ≠ 𝐵𝐴 (respetar el orden de las matrices).
2
5
1 3 2
Ejemplo 6: Dadas las matrices 𝐴 = [
] y 𝐵 = [−1 −2] entonces:
5 7 6
3
1
2
5
1 3 2
5
1
𝐴𝐵 = [
] [−1 −2] = [
]
5 7 6
21 17
3
1
Recuerde que para hallar cada elemento de la matriz producto, se multiplica las filas por las columnas, es decir:
𝐶11 = (1)(2) + (3)(−1) + (2)(3) = 5
𝐶12 = (1)(5) + (3)(−2) + (2)(1) = 1
𝐶21 = (5)(2) + (7)(−1) + (6)(3) = 21
𝐶22 = (5)(5) + (7)(−2) + (6)(1) = 17
5
2𝑗 − 3; 𝑖 < 𝑗
−5 −2
y 𝑅 = [2
], 𝑁 = [𝑛𝑖𝑗 ]3×2 con 𝑛𝑖𝑗 = {
4 + 2𝑖; 𝑖 ≥ 𝑗
2 −3
7
a. Determine por extensión la matriz N .
b. Calcule 𝑁 𝑇 − 2𝑀 y 𝐼3 − 4𝑅 si existe, donde 𝐼3 es una matriz identidad de orden 3x3.
c. Calcule 𝑀𝑁 si existe.
3
Ejemplo 7: Sean las matrices 𝑀 = [
5
Solución:
a. Como la matriz 𝑁 está dada por: 𝑁 = [𝑛𝑖𝑗 ]3×2 , entonces
𝑛11
𝑛
𝑁 = [ 21
𝑛31
b. La traspuesta de 𝑁 está dado por:
Profesores MA420
𝑛12
4 + 2(1) 2(2) − 3
6
1
𝑛22 ] = [4 + 2(2) 4 + 2(2)] = [ 8
8]
𝑛32
4 + 2(3) 4 + 2(3)
10 10
6
𝑁𝑇 = [
1
8 10
]
8 10
45
2 3
−4 4]
−7 3
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Como las matrices 𝑁 𝑇 y 𝑀 son del mismo orden 3 × 2 entonces existe la matriz 𝑁 𝑇 − 2𝑀.
Además
6 −10 −4
3 −5 −2
2𝑀 = 2 [
]=[
]
10
4
−6
5 2 −3
entonces
6 8 10
6 −10 −4
0 18 14
∴ 𝑁 𝑇 − 2𝑀 = [
]−[
]=[
]
1 8 10
10
4
−6
−9 4 16
1 0 0
1
5 2 3
∴ 𝐼3 − 4𝑅 = [0 1 0] − 4 [2 −4 4] = [0
0 0 1
0
7 −7 3
0 0
20
8
12
−19 −8 −12
1 0] − [ 8 −16 16] = [ −8 17 −16]
0 1
28 −28 12
−28 28 −11
6
1
−5 −2
] es de orden 2 × 3 y 𝑁 = [ 8
8 ] es de orden3 × 2, entonces si existe 𝑀𝑁
2 −3
10 10
y es de orden 2 × 2, luego
3
c. La matriz 𝑀 = [
5
6
1
𝑐11
3 −5 −2
𝑀𝑁 = [
].[ 8
8 ] = 𝐶 = [𝑐
5 2 −3
21
10 10
𝑐12
𝑐22 ]
Donde
𝑐11 = 3(6) + (−5)(8) + (−2)(10) = −42
𝑐12 = 3(1) + (−5)(8) + (−2)(10) = −57
𝑐21 = 5(6) + (2)(8) + (−3)(10) = 16
𝑐22 = 5(1) + (2)(8) + (−3)(10) = −9
Por lo tanto, obtenemos el producto de matrices.
−42 −57
∴ 𝑀𝑁 = [
]
16
−9
1
Ejemplo 8: Sean las matrices 𝐴 = [ 3
−3
a. Calcule la matriz 𝐴𝐵 si existe.
b. Calcule 𝐴𝑇 − 3𝐵 si existe.
2
5 −1
1 0 ] y 𝐵=[ 4
−3
5 3
Solución:
3 −1
0 2]
1 2
1
2
5 −1
a. La matriz 𝐴 = [ 3
1 0 ] es de orden 3 × 3 y 𝐵 = [ 4
−3
−3
5 3
existe 𝐴𝐵 = 𝐶 y es de orden 3 × 3, luego
1
𝐴𝐵 = [ 3
−3
2
5 −1
1 0 ].[ 4
−3
5 3
Donde
𝑐11 = (1)(2) + (5)(4) + (−1)(−3) = 25
𝑐12 = (1)(3) + (5)(0) + (−1)(1) = 2
𝑐13 = (1)(−1) + (5)(2) + (−1)(2) = 7
𝑐21 = (3)(2) + (1)(4) + (0)(−3) = 10
𝑐22 = (3)(3) + (1)(0) + (0)(1) = 9
𝑐23 = (3)(−1) + (1)(2) + (0)(2) = −1
Profesores MA420
3 −1
0 2 ] es de orden3 × 3, entonces si
1 2
𝑐11
3 −1
0 2 ] = 𝐶 = [𝑐21
𝑐31
1 2
𝑐12 𝑐13
𝑐22 𝑐23 ]
𝑐32 𝑐33
46
UPC – Departamento de Ciencias - Matemática Básica (MA420)
𝑐31 = (−3)(2) + (5)(4) + (3)(−3) = 5
𝑐32 = (−3)(3) + (5)(0) + (3)(1) = −6
𝑐33 = (−3)(−1) + (5)(2) + 2(3) = 19
1
𝐴𝐵 = [ 3
−3
2
5 −1
1 0 ].[ 4
−3
5 3
3 −1
25
0 2 ] = [10
1 2
5
2 7
9 −1]
−6 19
Por lo tanto, obtenemos el producto de matrices
2 7
9 −1]
−6 19
25
𝐴𝐵 = [10
5
b. La traspuesta de 𝐴 está dado por:
1
3 −3
𝐴𝑇 = [ 5
1 5]
−1
0 3
Como las matrices 𝐴𝑇 y 𝐵 son del mismo orden 3 × 3 entonces existe la matriz 𝐴𝑇 − 3𝐵.
Además
2
3𝐵 = 3 [ 4
−3
3 −1
6
0 2 ] = [ 12
1 2
−9
9 −3
0 6 ],
3 6
Por lo tanto, obtenemos 𝐴𝑇 − 3𝐵.
1
𝐴𝑇 − 3𝐵 = [ 5
−1
3 −3
6
1 5 ] − [ 12
0 3
−9
9 −3
−5
0 6 ] = [−7
3 6
8
−6 0
1 −1]
−3 −3
𝑎−𝑏
Ejemplo 9: Dada las matrices 𝐴 = [𝑎𝑖𝑗 ]2×2 con 𝑎𝑖𝑗 = 2𝑖 − (−1)𝑗 y la matriz 𝐵 = [
3𝑎 − 𝑏
cumple que 𝐴 = 𝐵.
Solución:
La matriz 𝐴, está dada por: 𝐴 = [𝑎𝑖𝑗 ]
𝑎11
𝐴 = [𝑎
21
2×2
entonces
𝑎12
21 − (−1)1
=
[
]
𝑎22
22 − (−1)1
Obtenemos la matriz 𝐴
Como 𝐴 = 𝐵, se tiene que:
Entonces:
1
] calcule 𝑎 y 𝑏, si se
3
3
𝐴=[
5
3
[
5
21 − (−1)2
]
22 − (−1)2
1
]
3
1
𝑎−𝑏
]=[
3
3𝑎 − 𝑏
1
]
3
𝑎−𝑏 =3
3𝑎 − 𝑏 = 5
Por lo tanto, resolviendo el sistema, se tiene que 𝑎 = 1 y 𝑏 = −2.
Profesores MA420
47
UPC – Departamento de Ciencias - Matemática Básica (MA420)
3. DETERMINANTES
Definición:
Si 𝐴 es una matriz de orden 𝑛 × 𝑛 entonces la función determinante asocia con 𝐴 exactamente un número
real llamado determinante de 𝐴. Se denota el determinante con |𝐴| o det 𝐴.
•
•
Si 𝐴 = [𝑎11 ] es una matriz de orden 1 × 1 entonces |𝐴| = 𝑎11 .
Por ejemplo:
✓ |2| = 2
✓ |−5| = −5
𝑎11
Si 𝐴 = [𝑎
21
𝑎12
𝑎22 ] es una matriz de orden 2 × 2 entonces |𝐴| = 𝑎11 𝑎22 − 𝑎12 𝑎21 .
Por ejemplo:
2 5
✓ |
| = (2)(3) − (−1)(3) = 6 + 3 = 9
−1 3
−3 −4
✓ |
| = (−3)(1) − (2)(−4) = −3 + 8 = 5
2
1
•
Para calcular el determinante de una matriz de orden 3 × 3 o más, usaremos el método de menores y
cofactores.
Definición:
Sea 𝐴 una matriz de orden 𝑛 × 𝑛 (𝑛 > 2). El determinante de 𝐴, expresado como |𝐴| o det 𝐴 es la suma
de las entradas de cualquier fila o cualquier columna multiplicada por sus respectivos cofactores 𝐴𝑖𝑗 , es
decir:
𝑎11 𝑎12 ⋯ 𝑎1𝑛
𝑎
𝑎22 ⋯ 𝑎2𝑛
|𝐴| = 𝑎𝑖1 𝐴𝑖1 + 𝑎𝑖2 𝐴𝑖2 + ⋯ + 𝑎𝑖𝑛 𝐴𝑖𝑛
Si 𝐴 = [𝑎𝑖𝑗 ] = [ 21
⋮
⋮
⋮ ] entonces 𝑑𝑒𝑡(𝐴) =
⋱
𝑎𝑛1 𝑎𝑚2 ⋯ 𝑎𝑛𝑛
Donde:
❖ El cofactor 𝐴𝑖𝑗 se define como 𝐴𝑖𝑗 = (−1)𝑖+𝑗 𝑀𝑖𝑗 .
❖ El menor 𝑀𝑖𝑗 se define como el determinante de los números que quedan al eliminar la 𝑖 ésima
fila con la 𝑗 ésima columna.
Por ejemplo:
1 2 −2
✓ |−3 5 −1| = (1)𝐴11 + (2)𝐴12 + (−2)𝐴13
2 4 1
= (1)(−1)1+1 𝑀11 + (2)(−1)1+2 𝑀12 + (−2)(−1)1+3 𝑀13
−3 −1
5 −1
−3 5
=|
|− 2|
|− 2|
|
2
1
4 1
2 4
= (5 + 4) − 2(−3 + 2) − 2(−12 − 10)
= 55
Nota: En este ejemplo se eligió la fila 1, usted puede elegir otra fila o columna.
Profesores MA420
48
UPC – Departamento de Ciencias - Matemática Básica (MA420)
4. PRACTIQUEMOS EN CLASE
−1 4
1. Dadas las matrices 𝐴 = [
2 5
−2
5
]y𝐵 =[ 5
−6
3
−3
8 ]
−4
a. Calcule la matriz 2𝐵 − 𝐴𝑇 .
b. Calcule la matriz 𝐴𝐵.
c. Calcule el determinante de la matriz 𝐴𝐵.
3
6
−2𝑖 + 𝑗 si 𝑖 = 𝑗
2. Dadas las matrices 𝐴 = [−2
5 ] y 𝐵 = [𝑏𝑖𝑗 ]3×2 con 𝑏𝑖𝑗 = { 2
𝑖 − 1 si 𝑖 ≠ 𝑗
−4 −4
a. Determine por extensión la matriz 𝐵.
b. Calcule la matriz 2𝐴 − 𝐵 si existe.
c. Calcule la matriz 𝐴 𝐵𝑇 si existe.
max{𝑖; 2𝑗} si 𝑖 > 𝑗
2
3 −2
si 𝑖 = 𝑗
3. Dadas las matrices 𝑀 = [ 4
2 −4 ] y 𝐵 = [𝑏𝑖𝑗 ]3×3 con 𝑏𝑖𝑗 = { 𝑖 + 𝑗
2
−5 −4 −7
−𝑖 + 𝑗
si 𝑖 < 𝑗
a. Determine por extensión la matriz 𝐵.
b. Calcule el det 𝑀.
c. Calcule la matriz 𝑀𝑇 − 3𝐼 si existe, donde 𝐼 es matriz identidad.
RESPUESTAS DE PRACTIQUEMOS EN CLASE
1.
2.
3.
−3 −8
a. [ 6 11 ]
1 −2
−1
0
a. [
3
− 2]
8
8
2
3 8
a. [ 2
4 7]
3
4 6
b. [
37 15
]
3 58
7
12
b. [ −7
12 ]
−16 −16
b. det(𝑀) = 96
c. |𝐴𝐵| = 2101
−3
c. [ 2
4
−1
c. [ 3
−2
−3
−16
−4
4
−1
−4
72
24 ]
−64
−5
−4 ]
−10
5. PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1. Dadas las matrices 𝐴 = [𝑎𝑖𝑗 ]
2×2
con 𝑎𝑖𝑗 = máx (𝑖; 𝑗) y la matriz 𝐵 = [𝑏𝑖𝑗 ]
2×3
𝑖 + 𝑗 si 𝑖 ≥ 𝑗
con 𝑏𝑖𝑗 = { 2
,
𝑖 − 1 si 𝑖 < 𝑗
determine:
a. Por extensión las matrices 𝐴 y 𝐵.
b. El valor del determinante de la matriz 𝐴2 − 3𝐼2
c. La matriz 𝐵𝑇 𝐴.
Profesores MA420
49
UPC – Departamento de Ciencias - Matemática Básica (MA420)
2𝑗 − 3; 𝑖 < 𝑗
3 −5 −2
2. Sean las matrices 𝐴 = [
.
], 𝐵 = [𝑏𝑖𝑗 ]3×2 con 𝑏𝑖𝑗 = {
4
+ 2𝑖; 𝑖 ≥ 𝑗
5 2 −3
a. Determine por extensión la matriz 𝐵.
b. Calcule 𝐵𝑇 − 3𝐴
c. Calcule 𝐴𝐵 si existe.
1
3 −1
2
3 −1
3. Sean las matrices 𝐴 = [ 7
4 0 ] y 𝐵=[ 4
0 2]
−3
5 2
−3
1 5
a. Calcule el valor del determinante de la matriz 𝐴𝐵.
b. Calcule 𝐵𝑇 + 3𝐴 si existe.
RESPUESTAS DE PRACTIQUEMOS MÁS EN CASA
1
1. Parte (a): 𝐴 = [
2
2
2 0
] y 𝐵=[
2
3 4
2
Parte (b): 𝐴2 − 3𝐼2 = [
6
8
Parte (c): 𝐵𝑇 𝐴 = [8
6
0
]
3
6
] ; det(𝐴2 − 3𝐼2 ) = − 26
5
10
8]
6
6
1
2. Parte (a): 𝐵 = [ 8
8]
10 10
Parte (b): 𝐵𝑇 − 3𝐴 = [
−3 23 16
]
−14 2 19
−42 −57
Parte (c): 𝐴𝐵 = [
]
16
−9
17
3. Parte (a): 𝐴𝐵 = [30
8
2
0
21 1 ] ; det(𝐴𝐵) = 6966
−7 23
5
Parte (b): 𝐵𝑇 + 3𝐴 = [ 24
−10
Profesores MA420
13 −6
12 1 ]
17 11
50
UPC – Departamento de Ciencias - Matemática Básica (MA420)
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Enlace
Determinar los elementos de una
matriz por extensión.
https://bit.ly/3pemH43
Determinar suma, transpuesta y
producto de matrices.
https://bit.ly/39bKn3x
Código QR
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
MATRICES: Revisar páginas desde 712 hasta 721.
Profesores MA420
51
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Vectores en 2D
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante aplica el concepto de vectores en 2D y de
sus propiedades en la resolución de ejercicios, demostrando responsabilidad y capacidad de aprender por su
propia cuenta.
CONTENIDOS
MOTIVACIÓN
1.
Vectores en 2D
• Magnitud o longitud de un vector
• Operaciones algebraicas sobre vectores
• Dirección de un vector
• Vector en términos de su componente horizontal y vertical
• Vector unitario en la dirección de un vector
• Producto punto
• Ángulo entre dos vectores
• Vectores ortogonales y paralelos
• La proyección de un vector sobre otro vector
• Propiedades de vectores
2.
Practiquemos en clase
3.
Practiquemos más en casa
Profesores MA420
52
UPC – Departamento de Ciencias - Matemática Básica (MA420)
MOTIVACIÓN
Un vector en matemática y en física sirve para determinar, representar y calcular las magnitudes
vectoriales como el desplazamiento de un cuerpo en movimiento, su velocidad, aceleración, fuerza, etc.
Por ejemplo, con un vector podemos indicar la velocidad,
dirección y sentido que lleva un avión en vuelo.
Con la ayuda de los vectores podemos verificar las leyes de la física y determinar los esfuerzos a los que
están sometidos las cuerdas y cables.
La importancia de los vectores se da en la ciencia, como la ingeniería, la medicina y otras ciencias
aplicadas. En ingeniería, cuando se aplican fuerzas constantes y momentos, en los diseños de estructuras
que forman el esqueleto metálico, se aplican fuerzas para conocer el desplazamiento de dichas
estructuras, y así evitar que estas se rompan, así mismo en hidráulica, en cuanto al diseño y colocación
de las tuberías para aguas potables, deben mantener un sentido y dirección para mantener un flujo
constante, igualmente se refleja en las tuberías de aguas residuales, deben mantener su sentido y
dirección para lograr el adecuado movimiento desde el punto de partida al punto de llegada o encuentro,
de allí la importancia de la magnitud vectorial.
Profesores MA420
53
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1. VECTORES EN 2D
Magnitud Escalar
Es cualquier magnitud matemática o física que se pueda representar solamente por un número real.
Ejemplos: longitud (m), área (m2), volumen (m3), temperatura en grados kelvin (°K), etc.
Magnitud Vectorial
Son aquellas magnitudes en las que además del número que las determina, se requiere conocer la
dirección.
Ejemplos: desplazamiento (m), fuerza (N), aceleración (m/s2), etc.
El ente matemático que representa a estas magnitudes se llama vector.
Un vector en el plano es un segmento de recta con una dirección asignada.
Tracemos un vector como se ve en la figura con una flecha para especificar la
dirección. Denotamos este vector con ⃗⃗⃗⃗⃗
𝐴𝐵. El punto A es llamado punto inicial y B
es llamado punto terminal del vector ⃗⃗⃗⃗⃗
𝐴𝐵. La longitud del segmento de recta 𝐴𝐵
|𝐴𝐵| =
recibe el nombre de magnitud o longitud del vector y está denotado por ⃗⃗⃗⃗⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗
‖𝐴𝐵‖. Usamos letras negritas para denotar vectores. Entonces, escribimos 𝐮 =
⃗⃗⃗⃗⃗
𝐴𝐵.
El vector 𝐯 está representado por su componente horizontal v𝑥 y
componente vertical v𝑦 donde:
𝐯 = ⟨v𝑥 ; v𝑦 ⟩ = ⟨𝑎; 𝑏 ⟩
•
Magnitud o longitud de un vector
𝐯
𝑣𝑦
=𝑏
𝜽
𝑣𝑥 = 𝑎
|𝐯| = ‖𝐯‖ = √𝑎2 + 𝑏 2
•
Operaciones algebraicas sobre vectores
Si 𝐮 = ⟨u1 ; u2 ⟩ y 𝐯 = ⟨v1 ; v2 ⟩, entonces:
✓ 𝐮 + 𝐯 = ⟨u1 ; u2 ⟩ + ⟨v1 ; v2 ⟩ = ⟨u1 + v1 ; u2 + v2 ⟩
✓ 𝐮 − 𝐯 = ⟨u1 ; u2 ⟩ − ⟨v1 ; v2 ⟩ = ⟨u1 − v1 ; u2 − v2 ⟩
✓ c𝐮 = c⟨u1 ; u2 ⟩ = ⟨cu1 ; 𝑐u2 ⟩; c ∈ ℝ
Profesores MA420
54
UPC – Departamento de Ciencias - Matemática Básica (MA420)
•
Dirección de un vector
La dirección 𝜽 del vector 𝐯, es el ángulo positivo en posición
normal formado por el eje 𝒙 positivo y el vector 𝐯 (ver figura).
Por ejemplo, si el vector se ubica en el primer cuadrante
hallaremos la dirección del vector usando la siguiente expresión.
v
v
𝑏
tan(𝜽) = v𝑦 ⇒ 𝜽 = tan−𝟏 (v𝑦 ) = tan−𝟏 (𝑎)
𝑥
𝑥
Nota: La expresión 𝐭𝐚𝐧−𝟏, llamada tangente inverso se calculará haciendo uso de la calculadora,
debemos asegurarnos de que este programada para obtener el resultado en grados sexagesimales, modo
D en nuestras calculadoras.
Cuando el vector se ubica en el segundo, tercero o cuarto cuadrante,
hallaremos la dirección del vector usando la expresión anterior (haciendo
la reducción al primer cuadrante) y alguna de las relaciones de sus ángulos.
Por ejemplo:
1. Si el ángulo de dirección está en el segundo cuadrante y en sentido
𝑏
antihorario, usaremos la relación: 𝜃 = 180° − tan−1 (|𝑎|)
2. Si el ángulo de dirección está en el tercer cuadrante y en sentido
𝑏
antihorario, usaremos la relación: 𝜃 = 180° + tan−1 (| |)
𝑎
3. Si el ángulo de dirección está en el cuarto cuadrante y en sentido antihorario, usaremos la relación:
𝑏
𝜃 = 360° − tan−1 (| |)
𝑎
•
Vector en términos de su componente
horizontal y vertical
Sea 𝐯 un vector con magnitud ‖𝐯‖ y dirección 𝜽.
Donde v𝑥 = ‖𝐯‖ cos(𝜽) y v𝑦 = ‖𝐯‖ sen(𝜽). El vector
𝐯 se expresa como.
‖𝐯‖
𝑣𝑦 = ‖𝐯‖ sen(𝜽)
𝜽
𝐯 = ⟨v𝑥 ; v𝑦 ⟩ = ⟨‖𝐯‖cos(𝜽); ‖𝐯‖sen(𝜽)⟩
= ‖𝐯‖ ⟨ cos(𝜽); sen(𝜽) ⟩
Profesores MA420
𝑣𝑥 =‖𝐯‖ cos(𝜽)
55
UPC – Departamento de Ciencias - Matemática Básica (MA420)
•
Vector unitario en la dirección de un vector
𝐯
𝑎
𝑏
⟩
𝐮𝐯 =
=⟨
;
‖𝐯‖
√𝑎2 + 𝑏 2 √𝑎2 + 𝑏 2
OBS: Un vector de magnitud 1 se llama vector unitario, es decir
‖𝐮𝐯 ‖ = 1.
𝐮𝐯
VECTORES EN TÉRMINOS DE 𝐢 Y 𝐣
Los vectores unitarios 𝐢 y 𝐣, denominados vectores canónicos
están definidos por:
𝐢 = ⟨1; 0⟩
𝐣 = ⟨0; 1⟩
OBS: El vector 𝐯 = ⟨𝑎; 𝑏⟩ puede ser expresado en términos de
𝐢 y 𝐣 por:
𝐯 = ⟨𝑎; 𝑏⟩ = 𝑎𝐢 + 𝑏𝐣
𝐯
𝐯
= ⟨𝒂; 𝒃⟩
𝐣
𝐢
FORMA COMPONENTE DE UN VECTOR
Si un vector 𝐯 está representado en el plano con punto
inicial 𝐴(𝑥1 ; 𝑦1 ) y punto terminal 𝐵(𝑥2 ; 𝑦2 ), entonces sus
componentes son: v𝑥 = 𝑥2 − 𝑥1 y v𝑦 = 𝑦2 − 𝑦1 .
𝐯 = ⃗⃗⃗⃗⃗
𝐴𝐵 = ⟨𝑥2 − 𝑥1 ; 𝑦2 − 𝑦1 ⟩ = ⟨v𝑥 ; v𝑦 ⟩
𝐯
𝑣𝑦
𝑣𝑥
• Producto punto
Dado los vectores 𝐯 = ⟨𝑣1 ; 𝑣2 ⟩ y 𝐮 = ⟨𝑢1 ; 𝑢2 ⟩, su producto punto o producto escalar, denotado por 𝐯 ∙
𝐮 está definido por:
𝐯 ∙ 𝐮 = 𝑣1 𝑢1 + 𝑣2 𝑢2
•
Ángulo entre dos vectores
𝐯
El ángulo 𝛼 determinado por los vectores 𝐮 y 𝐯 se define por:
𝐮 ∙ 𝐯 = |𝐮||𝐯| cos 𝛼 ; 0 ≤ 𝛼 ≤ 𝜋 o (0 ≤ 𝛼 ≤ 180° )
𝐮∙𝐯
cos 𝛼 = |𝐮||𝐯|
𝐮
𝛼
Entonces
𝐮∙𝐯
𝛼 = cos −1 (|𝐮||𝐯|)
Profesores MA420
56
UPC – Departamento de Ciencias - Matemática Básica (MA420)
•
Vectores ortogonales y paralelos
VECTORES ORTOGONALES
VECTORES PARALELOS
Los vectores 𝐮 y 𝐯 son ortogonales sí y solo si:
Los vectores 𝐮 y 𝐯 son paralelos sí y solo si
existe un único 𝑡 ∈ 𝐑 tal que 𝐮 = 𝑡 𝐯
𝐮∙𝐯=0
u
v
•
Proyección de un vector sobre otro vector
La proyección del vector 𝐮 sobre 𝐯, denotada por proy𝐯 𝐮, es un vector paralelo a 𝐯.
proy𝐯 𝐮 = (
•
𝐮∙𝐯
)𝐯
‖𝐯‖𝟐
Propiedades de vectores
Sean los vectores 𝐮, 𝐯 y 𝐰, y sea c un número escalar.
❖ 𝐮∙𝐯=𝐯∙𝐮
❖ 𝐮 ∙ 𝐮 = |𝐮|2
❖ 𝟎∙𝐯=0
❖ 𝐮 ∙ (𝐯 + 𝐰) = 𝐮 ∙ 𝐯 + 𝐮 ∙ 𝐰
❖ (𝐮 + 𝐯) ∙ 𝐰 = 𝐮 ∙ 𝐰 + 𝐯 ∙ 𝐰
❖ (c𝐮) ∙ 𝐯 = c(𝐮 ∙ 𝐯
2. PRÁCTIQUEMOS EN CLASE
EJERCICIOS
1. Dado los vectores 𝐚 = ⟨−2; 4⟩, 𝐛 = ⟨3; 5⟩ y 𝐜 = −3𝐢 + 𝐣, y los puntos 𝑃(2; −1) y 𝑄(0; −4).
Determine:
a. el vector 𝐰 = 𝐚 − 2𝐜 y expréselo como combinación lineal de los vectores canónicos 𝐢 y 𝐣.
b. la magnitud del vector 𝐫 = 𝐛 + 𝟒𝐚.
c. el vector unitario en la dirección del vector ⃗⃗⃗⃗⃗
𝑃𝑄 .
2. Dado los vectores 𝐮 = ⟨−7; −2⟩, 𝐯 = ⟨−3; 6⟩ y 𝐰 = 𝐢 − 𝟐𝐣, y los puntos A(−2; 8) y B(7; −3).
Determine:
a. la dirección del vector 𝐰.
⃗⃗⃗⃗⃗ .
b. el ángulo entre los vectores 𝐮 y 𝐵𝐴
Profesores MA420
57
UPC – Departamento de Ciencias - Matemática Básica (MA420)
c. el vector proyección del vector 𝐮 sobre el vector 𝐰.
3. Determine si los vectores 𝐮 y 𝐯 son ortogonales o paralelos.
a. 𝐮 = ⟨5; −6⟩ y 𝐯 = ⟨−12; −10⟩
b. 𝐮 = 2𝐢 − 7𝐣 y 𝐯 = −4𝐢 + 14𝐣
RESPUESTAS DE PRACTIQUEMOS EN CLASE
−2
−3
⟩
;
√13 √13
1. a. 4𝐢 + 2𝐣
b. √466 u
c. ⟨
2. a. θ = 296.57°
b. θ = 66,66°
c. ⟨ 5 ; 5⟩
−3
6
3. a. Los vectores 𝐮 y 𝐯 son ortogonales.
b. Los vectores 𝐮 y 𝐯 son paralelos.
3. PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD
para asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1. Dado los vectores 𝐮 = ⟨−1; 2⟩, 𝐯 = ⟨−2; 5⟩ y 𝐰 = 𝐢 − 4j, y los puntos A(−2; 1) y B(−3; 4).
Determine:
a. el vector 𝐫 = 𝐮 − 2𝐯 y expréselo como combinación lineal de los vectores canónicos 𝐢 y 𝐣.
b. la magnitud del vector 𝐚 = 𝟒𝐰 + 𝟐𝐮
⃗⃗⃗⃗⃗
c. el ángulo entre los vectores 𝐮 y 𝐴𝐵
d. dirección del vector 𝐯
e. un vector paralelo al vector 𝐰
f. un vector ortogonal al vector 𝐰
⃗⃗⃗⃗⃗ sobre 𝐯
g. proyección del vector 𝐴𝐵
2. Sean los vectores 𝐮 = ⟨−2; n − 4⟩, 𝐯 = ⟨2; −2⟩ y 𝐰 = 3𝐢 + (4m)𝐣. Determine:
a. el valor de n de manera que el vector 𝐮 sea ortogonal al vector 𝐯 .
b. el valor de m de manera que el vector 𝐯 sea paralelo al vector 𝐰.
c. el valor de n, de modo que |𝐮| = 5.
RESPUESTAS DE PRACTIQUEMOS MÁS EN CASA
1. a. 3𝐢 − 8𝐣
b. 12,17 𝑢
c. 𝜃 = 8,13°
d. 𝜃 = 111,8°
e. ⟨2; −8⟩ (puede haber más de una respuesta correcta)
f. ⟨4; 1⟩ (puede haber más de una respuesta correcta)
−34 85
g. ⟨
; ⟩
29
29
Profesores MA420
58
UPC – Departamento de Ciencias - Matemática Básica (MA420)
2. a. 𝑛 = 2
b. 𝑚 = −0,75
c. 𝑛 = 4 ± √21
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Enlace
Determinar la dirección y
ángulo entre dos vectores
https://bit.ly/2MgwWWQ
Determinar la dirección,
ángulo y proyección de
vectores.
Código QR
https://bit.ly/3oeMJml
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.:
Cengage Learning. (515 STEW/P 2017)
VECTORES EN 2D: Revisar páginas desde 630 hasta 646.
Profesores MA420
59
UPC – Departamento de Ciencias - Matemática Básica (MA420
Espacio tridimensional y Vectores en 3D
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante aplica el concepto de vectores en 3D
y la de sus propiedades en la resolución de ejercicios, demostrando responsabilidad y capacidad de
aprender por su propia cuenta.
CONTENIDO
INTRODUCCIÓN
1.1.
Sistema tridimensional de coordenadas cartesianas
• Planos coordenados
• Distancia entre dos puntos
• Punto medio de un segmento
1.2.
Vectores en 3D
• Magnitud o módulo de un vector
• Vector unitario
• Vector unitario en la dirección de un vector
• Vectores unitarios canónicos
• Propiedades
• Ángulo entre vectores
• Producto vectorial
• Propiedades
1.3.
Respuestas de ejercicios propuestos
Profesores MA420
60
UPC – Departamento de Ciencias - Matemática Básica (MA420
INTRODUCCIÓN
Para localizar un punto en un plano, son necesarios dos puntos. Sabemos que cualquier punto en el plano
cartesiano puede estar representado como un par ordenado (𝑎; 𝑏) de números reales, donde 𝑎 es la
coordenada 𝑥 y 𝑏 es la coordenada 𝑦. En el espacio tridimensional se agrega una tercera dimensión, de modo
que cualquier punto en el espacio está representado por una terna ordenada (𝑎; 𝑏; 𝑐) de números reales.
1.1. SISTEMA TRIDIMENSIONAL DE COORDENADAS CARTESIANAS
Consta de un punto fijo u origen de coordenadas 𝑂, y tres rectas o ejes coordenados 𝒙, 𝒚 y 𝒛 que pasan por
𝑂 y son perpendiculares entre sí; los semiejes positivos se orientan de acuerdo con la regla de la mano
derecha.
Este sistema divide al plano en ocho partes denominados octantes.
Un punto en el espacio se denota por 𝑷(𝒙; 𝒚; 𝒛) o simplemente por
la terna ordenada (𝑥; 𝑦; 𝑧), donde los números reales 𝑥, 𝑦 y 𝑧 se
llaman coordenadas cartesianas del punto 𝑃.
En la figura adjunta tenemos un punto 𝑃 que pertenece al primer
octante y cuyas coordenadas son (2; 2; 3). Observa que en el primer
octante todas las coordenadas de un punto son todas positivas.
¿Cuál o cuáles de los siguientes puntos pertenecen al primer octante?
𝐴(4; 2; 9) , 𝐵(3; – 2; 6), 𝐶(4; 8; 0), 𝐷(5; 1; 7), 𝐸(0; 3; 9)
Respuesta: Solo los puntos 𝐴 y 𝐷 pertenecen al primer octante.
Profesores MA420
61
UPC – Departamento de Ciencias - Matemática Básica (MA420
PLANOS COORDENADOS
Los ejes coordenados forman planos denominados:
Plano 𝒙𝒚 formado por los ejes 𝑥 e 𝑦, todos los puntos de este plano
tienen 𝑧 = 0, por ejemplo: 𝐴(3; 4; 0) y 𝐵(3; – 5; 0)
Plano 𝒙𝒛 formado por los ejes 𝑥 y 𝑧, todos los puntos de este plano
tienen 𝑦 = 0, por ejemplo: 𝑃(5; 0; 6) y 𝑄(– 3; 0; 4)
Plano 𝒚𝒛 formado por los ejes 𝑦 y 𝑧, todos los puntos de este plano
tienen 𝑥 = 0, por ejemplo: 𝑀(0; 7; 6) y 𝑁(0; 2; 5)
DISTANCIA ENTRE DOS PUNTOS EN 𝑹𝟑
La
distancia
entre
dos
puntos
cualesquiera
𝑃(𝑥1 ; 𝑦1 ; 𝑧1 ) y 𝑄(𝑥2 ; 𝑦2 ; 𝑧2 ) se determina por:
𝑑(𝑃; 𝑄) = √(𝑥2 − 𝑥1 )2 + (𝑦2 − 𝑦1 )2 + (𝑧2 − 𝑧1 )2
Ejemplo:
Dados los puntos 𝑃 y 𝑄 con coordenadas (2; − 5; 3) y
(−2; 5; 4) respectivamente. ¿Cuál es la distancia
entre los puntos P y Q?
Solución:
2
𝑑(𝑃; 𝑄) = √(−2 − 2)2 + (5 − (−5)) + (4 − 3)2 → 𝑑(𝑃; 𝑄) = √117 ≈ 10,82
La distancia entre los puntos 𝑃 y 𝑄 es 10,82 unidades aproximadamente.
PUNTO MEDIO DE UN SEGMENTO EN 3D
Dado un segmento cuyos extremos son 𝑃(𝑥1 ; 𝑦1 ; 𝑧1 ) y
𝑄(𝑥2 ; 𝑦2 ; 𝑧2 ), el punto medio 𝑀 de dicho segmento cuyas
coordenadas son (𝑥𝑚 ; 𝑦𝑚 ; 𝑧𝑚 ) se calcula de la siguiente manera:
𝑥𝑚 =
𝑥1 + 𝑥2
𝑦1 + 𝑦2
𝑧1 + 𝑧2
, 𝑦𝑚 =
, 𝑧𝑚 =
2
2
2
Ejemplo:
En la figura adjunta las coordenadas de los extremos del segmento 𝑃𝑄 son 𝑃(3; 3; −2) y 𝑄(−2; 5; 4).
Halle las coordenadas de 𝑀 sabiendo que es punto medio de 𝑃𝑄.
Profesores MA420
62
UPC – Departamento de Ciencias - Matemática Básica (MA420
Solución:
Los extremos del segmento 𝑃𝑄 son 𝑃(3; 3; −2) y 𝑄(−2; 5; 4), entonces las coordenadas del punto medio
𝑀 son: 𝑥𝑚 =
3+(−2)
2
1
2
= , 𝑦𝑚 =
3+5
2
= 4, 𝑧𝑚 =
−2+4
2
=1
1
Respuesta: Las coordenadas del punto medio 𝑀 del segmento 𝑃𝑄 son (2 ; 4; 1).
Ejercicio 1
Las coordenadas de los vértices de un triángulo son 𝐴(6; – 2; 4), 𝐵(3; 5; 6) y 𝐶(2; 4; 8)
a) Halle el perímetro del triángulo.
b) Halle la distancia del vértice 𝐵 al punto medio del lado 𝐴𝐶.
1.2. VECTORES EN 3D
El concepto de vector en el plano se puede extender de
manera natural, con ligeros cambios, en el espacio.
Los vectores tienen tres componentes en lugar de dos y al
igual que en el plano, el conjunto de segmentos dirigidos de
rectas (o flechas) son vectores.
Todo vector tiene un punto de origen y un punto final, en la
figura adjunta se puede observar que el punto de inicio es el
origen de coordenada y el punto final es 𝑃 cuyas
coordenadas son (𝑥1 ; 𝑦1 ; 𝑧1 ), a este tipo de vectores les
llamamos vectores posición.
La flecha que va desde 𝑂 hasta 𝑃 representa al vector v.
El vector se representa por 𝐯 = ⟨𝑥1 ; 𝑦1 ; 𝑧1 ⟩ a diferencia de un punto que se representa con paréntesis.
Donde: 𝑥1 es la componente en el eje 𝑥, 𝑦1 es la componente en el eje 𝑦 y 𝑧1 es la componente en el eje 𝑧.
Cuando el punto de inicio de un vector es 𝑃(𝑥1 ; 𝑦1 ; 𝑧1 )
y su punto final es 𝑄(𝑥2 ; 𝑦2 ; 𝑧2 ) como se observa en la
→
figura adjunta, en estos casos el vector PQ se llama
vector desplazado y sus coordenadas de calculan de la
→
siguiente manera: PQ = ⟨𝑥2 − 𝑥1 ; 𝑦2 − 𝑦1 ; 𝑧2 − 𝑧1 ⟩
Ejemplo:
En la figura adjunta las coordenadas de los puntos 𝑃 y
→
𝑄 son (2; −5; 3) y (−2; 5; 4) respectivamente. Determine las coordenadas del vector PQ.
Profesores MA420
63
UPC – Departamento de Ciencias - Matemática Básica (MA420
Solución:
→
Por teoría se sabe que: PQ = ⟨𝑥2 − 𝑥1 ; 𝑦2 − 𝑦1 ; 𝑧2 − 𝑧1 ⟩
→
En este caso el vector es: PQ = ⟨−2 − 2; 5 − (−5); 4 − 3⟩ = ⟨−4; 10; 1⟩
Ejercicio 2
Las coordenadas de los vértices de un triángulo son 𝐴(6; – 2; 4), 𝐵(3; 5; 6) y 𝐶(2; 4; 8). Determine las
→
→
→
coordenadas de los vectores AB, BC y CA.
MAGNITUD O MÓDULO DE UN VECTOR EN 3D
Se denomina magnitud o módulo de un vector a la medida
de la longitud del vector.
Definición: Dado un vector 𝐯 = ⃗⃗⃗⃗⃗
𝑃𝑄 = ⟨𝑎; 𝑏; 𝑐 ⟩ =
⟨𝑥2 − 𝑥1 ; 𝑦2 − 𝑦1 ; 𝑧2 − 𝑧1 ⟩ entonces el módulo se
representa mediante la notación |𝐯| o ‖𝐯‖ y se calcula de
la siguiente manera:
|𝐯| = ‖𝐯‖ = √𝑎2 + 𝑏 2 + 𝑐 2
Ejemplo:
Los puntos extremos de un vector son 𝑃(1; 2; 3) y 𝑄(4; 6; 15), calcule la magnitud del vector ⃗⃗⃗⃗⃗
𝑃𝑄 .
Solución:
→
Primero se halla las coordenadas del vector: PQ = ⟨4 − 1; 6 − 2; 15 − 3⟩ = ⟨3; 4; 12⟩
→
Luego se la magnitud es: |PQ| = √32 + 42 + 122 = 13
⃗⃗⃗⃗⃗ es 13 unidades.
Respuesta: La magnitud del vector 𝑃𝑄
Ejercicio 3
Dados los vectores 𝐚 = ⟨−4; 5; 3⟩ y 𝐛 = ⟨8; 2; −2⟩, calcule: |𝐚| + |𝐛|
VECTOR UNITARIO
Se denomina vector unitario a todo vector cuyo módulo es igual a 1, es
decir si 𝐯 = ⟨𝑣𝑥 ; 𝑣𝑦 ; 𝑣𝑧 ⟩ y se cumple que |𝐯| = 1entonces 𝐯 es un vector
unitario.
¿El vector 𝐚 = ⟨1; 1; 1 ⟩ es unitario?
Para responder se halla la magnitud del vector 𝐚, de donde 𝐚 = √12 + 12 + 12 = √3 ≠ 1
Como se puede observar el resultado no es uno por lo tanto se puede afirmar que 𝐚 no es un vector
unitario.
3
4
¿El vector 𝐛 = ⟨5 ; 0; 5⟩ es unitario?
Profesores MA420
64
UPC – Departamento de Ciencias - Matemática Básica (MA420
3 2
4 2
Para responder se halla la magnitud del vector 𝐛, de donde |𝐛| = √(5) + 02 + (5) = 1
Como se puede observar el resultado es uno por lo tanto se puede afirmar que 𝐛 es un vector unitario.
VECTOR UNITARIO EN LA DIRECCIÓN DE UN VECTOR
El vector unitario en la dirección de un vector 𝐯 se representa por: 𝐮𝐯
𝐯
𝑣
𝑣
𝑣
Se calcula de la siguiente manera: 𝐮𝐯 = |𝐯| = ⟨|𝐯|𝑥 ; |𝐯|𝑦 ; |𝐯|𝑧 ⟩
Ejemplo:
Dados los vectores 𝐚 = ⟨−3; 12; 4⟩ y 𝐛 = ⟨3; 0; 1⟩, calcule el vector unitario en la dirección de cada uno de
los vectores dados.
Solución:
⟨−3;12;4⟩
𝐚
Vector unitario en la dirección de 𝐚: 𝐮𝐚 = |𝐚| =
⟨3;0;1⟩
𝐛
Vector unitario en la dirección de 𝐛: 𝐮𝐛 = |𝐛| =
=
√(−3)2 +122 +4 2
√32 +02 +12
=
⟨−3;12;4⟩
⟨3;0;1⟩
√10
13
−3 12
4
= ⟨ 13 ; 13 ; 13⟩
3
0
1
;
; ⟩
√10 √10 √10
=⟨
Ejercicio 4
Dados los vectores 𝐚 = ⟨−3; 12; 4⟩ y 𝐛 = ⟨3; 0; 1⟩, calcule el vector unitario en la dirección de 𝐚 + 𝐛.
VECTORES UNITARIOS CANÓNICOS
Son aquellos vectores unitarios que se encuentran en la dirección
positiva de los ejes coordenados, se representan por las letras 𝐢, 𝐣, 𝐤.
El vector 𝐢 está en la dirección positiva del eje 𝑥 : 𝐢 = ⟨1; 0; 0⟩
El vector 𝐣 está en la dirección positiva del eje 𝑦 : 𝐣 = ⟨0; 1; 0⟩
El vector 𝐤 está en la dirección positiva del eje 𝑧: 𝐤 = ⟨0; 0; 1⟩
La importancia de los vectores canónicos es que todo vector se puede
expresar en términos de 𝐢, 𝐣, 𝐤.
Si 𝐯 = ⟨𝑣𝑥 ; 𝑣𝑦 ; 𝑣𝑧 ⟩entonces 𝐯 = 𝑣𝑥 𝐢 + 𝑣𝑦 𝐣 + 𝑣𝑧 𝐤
Ejemplos:
𝐚 = ⟨−3; 12; 4⟩ = – 3𝐢 + 12𝐣 + 4𝐤
𝐛 = ⟨3; 0; 1⟩= 3 𝐢 + 0 𝐣 + 𝐤 =3 𝐢 + 𝐤
𝐜 = 5 𝐢 + 4 𝐣 – 2 𝐤 =⟨5; 4; −2⟩
𝐝 = –7 𝐢 – 3 𝐣 + 8 𝐤 = ⟨−7; 3; 8⟩
IGUALDAD DE VECTORES: Dos vectores 𝐚 = ⟨𝑎𝑥 ; 𝑎𝑦 ; 𝑎𝑧 ⟩ y 𝐛 = ⟨𝑏𝑥 ; 𝑏𝑦 ; 𝑏𝑧 ⟩ son iguales si y solo si sus
componentes son respectivamente iguales, es decir: 𝑎𝑥 = 𝑏𝑥 , 𝑎𝑦 = 𝑏𝑦 , 𝑎𝑧 = 𝑏𝑧
Profesores MA420
65
UPC – Departamento de Ciencias - Matemática Básica (MA420
OPERACIONES CON VECTORES EN 3D
ADICIÓN – SUSTRACCIÓN: Dados los vectores 𝐚 = ⟨𝑎𝑥 ; 𝑎𝑦 ; 𝑎𝑧 ⟩ y 𝐛 = ⟨𝑏𝑥 ; 𝑏𝑦 ; 𝑏𝑧 ⟩
𝐚 + 𝐛 = ⟨𝑎𝑥 ; 𝑎𝑦 ; 𝑎𝑧 ⟩+⟨𝑏𝑥 ; 𝑏𝑦 ; 𝑏𝑧 ⟩=⟨𝑎𝑥 + 𝑏𝑥 ; 𝑎𝑦 + 𝑏𝑦 ; 𝑎𝑧 + 𝑏𝑧 ⟩
𝐚 − 𝐛 = ⟨𝑎𝑥 ; 𝑎𝑦 ; 𝑎𝑧 ⟩–⟨𝑏𝑥 ; 𝑏𝑦 ; 𝑏𝑧 ⟩=⟨𝑎𝑥 − 𝑏𝑥 ; 𝑎𝑦 − 𝑏𝑦 ; 𝑎𝑧 − 𝑏𝑧 ⟩
Ejemplo:
Dados los vectores 𝐚 = ⟨6; −5; 4⟩ y 𝐛 = ⟨−1; 3; −2⟩
𝐚 + 𝐛 = ⟨6; −5; 4⟩ + ⟨−1; 3; −2⟩ = ⟨6 − 1; −5 + 3; 4 − 2⟩ = ⟨5; −2; 2⟩
𝐚 − 𝐛 = ⟨6; −5; 4⟩ − ⟨−1; 3; −2⟩ = ⟨6 + 1; −5 − 3; 4 + 2⟩ = ⟨7; −8; 6⟩
PRODUCTO DE UN ESCALAR POR UN VECTOR: Dados un vector 𝐚 = ⟨𝑎𝑥 ; 𝑎𝑦 ; 𝑎𝑧 ⟩ y 𝑘 un número real,
entonces: 𝑘𝐚 = 𝑘⟨𝑎𝑥 ; 𝑎𝑦 ; 𝑎𝑧 ⟩ = ⟨𝑘𝑎𝑥 ; 𝑘𝑎𝑦 ; 𝑘𝑎𝑧 ⟩
Ejemplo:
Si 𝐚 = ⟨6; −5; 4⟩ entonces 7𝐚 =7⟨6; −5; 4⟩=⟨42; −35; 28⟩
PRODUCTO ESCALAR O PUNTO: Dados los vectores 𝐚 = ⟨𝑎𝑥 ; 𝑎𝑦 ; 𝑎𝑧 ⟩ y 𝐛 = ⟨𝑏𝑥 ; 𝑏𝑦 ; 𝑏𝑧 ⟩
𝐚 ∙ 𝐛 = ⟨𝑎𝑥 ; 𝑎𝑦 ; 𝑎𝑧 ⟩.⟨𝑏𝑥 ; 𝑏𝑦 ; 𝑏𝑧 ⟩=𝑎𝑥 𝑏𝑥 + 𝑎𝑦 𝑏𝑦 + 𝑎𝑧 𝑏𝑧
Ejemplo:
Si 𝐚 = ⟨6; −5; 4⟩ y 𝐛 = ⟨−1; 3; −2⟩
𝐚 ∙ 𝐛 = ⟨6; −5; 4⟩.⟨−1; 3; −2⟩=(6)(−1) + (−5)(3) + (4)(−2) = −29
Ejercicio 5
Dados los vectores 𝐚 = ⟨−1; 3; 1⟩ y 𝐛 = ⟨−2; 1; 4⟩, halle: (2𝐚 + 𝐛) ⋅ (𝐚 − 2𝐛)
ÁNGULO ENTRE VECTORES
Dados los vectores 𝐚 y 𝐛 el ángulo que forman dichos vectores se halla
𝐚⋅𝐛
aplicando la siguiente fórmula: 𝜃 = cos−1 (|𝐚||𝐛|)
Ejemplo:
Calcule el ángulo formado por los vectores 𝐚 = ⟨6; −5; 4⟩ y 𝐛 = ⟨−1; 3; −2⟩
Solución:
Sea 𝜃 el ángulo formado por los vectores 𝐚 y 𝐛, para aplicar la fórmula dada, primero hacemos los cálculos
que se van a utilizar y luego se reemplaza en la fórmula.
𝐚 ∙ 𝐛 = ⟨6; −5; 4⟩.⟨−1; 3; −2⟩=(6)(−1) + (−5)(3) + (4)(−2) = −29
|𝐚| = √62 + (−5)2 + 42 = √77 y |𝐛| = √(−1)2 + 32 + (−2)2 = √14
𝐚⋅𝐛
−29
)
√77√14
Se reemplaza en la fórmula: 𝜃 = cos −1 (|𝐚||𝐛|) = cos−1 (
= 152,04° (No olvidar de que la
calculadora debe estar en modo D, grados sexagesimales)
Profesores MA420
66
UPC – Departamento de Ciencias - Matemática Básica (MA420
Por lo tanto, el ángulo formado por los vectores 𝐚 y 𝐛 mide 152,04° aproximadamente.
Ejercicio 6
Dados los vectores 𝐚 = ⟨4; 1; −3⟩ y 𝐛 = ⟨−2; −1; 3⟩, calcule el ángulo formado por los vectores 𝐚 y 𝐛.
PRODUCTO VECTORIAL
El producto vectorial entre dos vectores 𝐚 y 𝐛 de 3D, distintos del vector nulo, se representa como 𝐚 × 𝐛.
Como se puede observar el resultado del producto vectorial es otro vector, la
dirección del vector 𝐚 × 𝐛 es perpendicular a la dirección del vector 𝐚 y la
dirección del vector 𝐛. Por lo tanto, 𝐚 × 𝐛 es perpendicular al plano que
determinan 𝐚 y 𝐛.
Para calcular el producto vectorial entre dos vectores 𝐚 y 𝐛 de 3D definidos
como 𝐚 = ⟨𝑎𝑥 ; 𝑎𝑦 ; 𝑎𝑧 ⟩y 𝐚 = ⟨𝑏𝑥 ; 𝑏𝑦 ; 𝑏𝑧 ⟩ primero se arma un determinante de tercer orden y se desarrolla
en tres determinantes de orden dos, tal como se muestra a continuación:
𝐢
𝑎
𝐚×𝐛=| 𝑥
𝑏𝑥
𝐣
𝑎𝑦
𝑏𝑦
𝐤
𝑎
𝑎𝑧 | = | 𝑦
𝑏𝑦
𝑏𝑧
𝑎𝑧
𝑎𝑥
𝐢
−
|
|
𝑏𝑧
𝑏𝑥
𝑎𝑥
𝑎𝑧
𝐣
+
|
|
𝑏𝑧
𝑏𝑥
𝑎𝑦
𝑏𝑦 | 𝐤
Luego, al calcular cada determinante de orden dos, se obtiene las componentes del vector que resulta del
producto vectorial, esto es:
𝐚 × 𝐛 = (𝑎𝑦 𝑏𝑧 − 𝑏𝑦 𝑎𝑧 )𝐢 − (𝑎𝑥 𝑏𝑧 − 𝑏𝑥 𝑎𝑧 )𝐣 + (𝑎𝑥 𝑏𝑦 − 𝑏𝑥 𝑎𝑦 )𝐤
Nota: Para calcular un determinante de cualquier orden se recomienda utilizar la regla de Laplace o de
menores y cofactores. Para mayor detalle revise las páginas 734 – 735 del libro de Stewart.
Ejemplo:
Dados los vectores 𝐚 = ⟨6; −5; 4⟩ y 𝐛 = ⟨−1; 3; −2⟩, calcule 𝐚 × 𝐛
𝐢
𝐣
𝐤
Paso (1) se arma el determinante de orden 3: 𝐚 × 𝐛 = | 6 −5 4 |
−1 3 −2
6
4
−5 4
6 −5
Paso (2) se descompone en determinantes de orden 2: 𝐚 × 𝐛 = |
|𝐢 − |
|𝐣 + |
|𝐤
−1 −2
3 −2
−1 3
Paso (3) se calcula cada determinante: 𝐚 × 𝐛 = (10 − 12)𝐢 − (−12 + 4)𝐣 + (18 − 5)𝐤 = −2𝐢 + 8𝐣 + 13𝐤
Finalmente, el resultado es: 𝐚 × 𝐛 = −2𝐢 + 8𝐣 + 13𝐤 o 𝐚 × 𝐛 = ⟨−2; 8; 13⟩
Ejemplo: Dado los vectores 𝐮 = ⟨6; −5; 4⟩ y 𝐯 = −𝐢 + 3𝐣 − 2𝐤. Determine:
a) 𝐮 × 𝐯
b) 𝐯 × 𝐮
Profesores MA420
67
UPC – Departamento de Ciencias - Matemática Básica (MA420
Solución: Para ver la solución revise el siguiente video:
Solución del ejemplo
Link:
Código QR:
https://www.youtube.com/watch?v=ZJJiD_XLYc
PROPIEDADES DEL PRODUCTO VECTORIAL
(I) El sentido del vector 𝐚 × 𝐛 se puede determinar mediante la regla de la mano
derecha.
(II) Producto vectorial de los vectores canónicos i, j, k.
𝐢×𝐣 =𝐤
𝐣×𝐤=𝐢
𝐤×𝐢=𝐣
Ejercicio 7
Dados los vectores 𝐚 = ⟨6; −5; 4⟩ y 𝐛 = ⟨−1; 3; −2⟩, calcule (𝐚 + 𝐛) × (𝐚 − 𝐛)
1.3. RESPUESTAS DE EJERCICIOS PROPUESTOS
Número
Ejercicio 1
Ejercicio 2
Ejercicio 3
Tema
Respuestas
Distancia entre dos puntos
a) Perímetro=√62 + 2√17 + √6 ≈ 18,57u.
Punto medio de un segmento
b) Distancia √17 ≈ 4,12u.
Vectores en R3
Magnitud o módulo de un
→
→
→
AB = ⟨−3; 7; 2⟩, BC = ⟨−1; −1; 2⟩, CA = ⟨4; −6; −4⟩
|𝐚| + |𝐛| = 5√2 + 6√2 = 11√2
vector
Ejercicio 4
Vector unitario
Ejercicio 5
Propiedades de vectores
Ejercicio 6
Ángulo entre vectores
Ejercicio 7
Producto vectorial
𝐮𝐚+𝐛 =
⟨0; 12; 5⟩
12 5
= ⟨0; ; ⟩
13
13 13
(𝟐𝐚 + 𝐛) ⋅ (𝐚 − 𝟐𝐛)=⟨−4; 7; 6⟩ ⋅ ⟨3; 1; −7⟩ = −47
𝜃 = cos−1 (
−18
√26√14
) ≈ 160,64°
(𝐚 + 𝐛) × (𝐚 − 𝐛) = ⟨5; −2; 2⟩ × ⟨7; −8; 6⟩
Profesores MA420
= ⟨−4; −16; −26⟩
68
UPC – Departamento de Ciencias - Matemática Básica (MA420
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
VECTORES EN 3D: Revisar páginas desde 653 hasta 666.
Profesores MA420
69
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Sistemas de ecuaciones lineales (SEL)
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante resuelve un sistema de ecuaciones lineales
escalonando su matriz ampliada mediante operaciones por filas y las clasifica según su solución, demostrando
responsabilidad y capacidad de aprender por su propia cuenta.
CONTENIDOS
MOTIVACIÓN
1.
Sistemas de ecuaciones lineales
• Clasificación
• Método de solución: Forma escalonada por filas
2.
Practiquemos en clase
• Ejercicios y problemas
3.
Practiquemos más en casa
• Ejercicios y problemas
Profesores MA420
70
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Motivación
Los sistemas de ecuaciones lineales son de suma importancia en las ciencias, como la ingeniería, la economía y
otras ciencias aplicadas. Algunas de las utilidades se muestran en la representación mediante sistemas de
ecuaciones lineales el flujo de tránsito en un determinado ovalo, una resistencia equivalente a partir de ciertas
resistencias conocidas, entre otras aplicaciones.
Aplicación 1: Flujo de tráfico
Cuando analizamos el flujo del tráfico en un ovalo en donde
cruzan varias avenidas, podemos modelar el flujo mediante
un sistema de ecuaciones lineales, y podríamos usar el
método de Gauss para resolver el sistema.
Aplicación 2: Circuito eléctrico
Si dos resistencias 𝑅1 y 𝑅2 de un circuito eléctrico están conectadas en paralelo, se encuentra la resistencia total
𝑅 con la fórmula:
1
1
1
=
+
𝑅 𝑅1 𝑅2
Ejemplo:
Dada tres resistencias 𝐴, 𝐵 y 𝐶, se conoce que la resistencia total de 𝐴 y 𝐵 conectadas en paralelo es de 48 ohms.
La resistencia total de 𝐵 y 𝐶, conectadas en paralelo es de 80 ohms y la de 𝐴 y 𝐶 (también conectadas en paralelo)
es de 60 ohms. Para calcular el valor de cada resistencia A, B y C se resuelve mediante un sistema de ecuaciones
lineales.
1.
SISTEMAS DE ECUACIONES LINEALES (SEL)
Definición: Un sistema de ecuaciones lineales (SEL), es un sistema de ecuaciones en el cual cada ecuación es
lineal. Resolver un sistema consiste encontrar los valores de las variables que satisfacen cada una de las
ecuaciones.
𝑎11 𝑥1 + 𝑎12 𝑥2 + ⋯ + 𝑎1𝑛 𝑥𝑛 = 𝑏1
𝑎21 𝑥1 + 𝑎22 𝑥2 + ⋯ + 𝑎2𝑛 𝑥𝑛 = 𝑏2
{
⋮
𝑎𝑚1 𝑥1 + 𝑎𝑚2 𝑥2 + ⋯ + 𝑎𝑚𝑛 𝑥𝑛 = 𝑏𝑚
(1)
Donde 𝑎11 ; 𝑎12 ; … ; 𝑎𝑚𝑛 y 𝑏1 ; 𝑏2 ; … ; 𝑏𝑚 son números reales, y 𝑥1 ; 𝑥2 ; … ; 𝑥𝑛 son las variables.
Profesores MA420
71
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Existen varios métodos para resolver un SEL, en este curso usaremos el método de escalonamiento de la matriz
ampliada a través de operaciones elementales de filas, por tal razón dado un SEL se deben reconocer las
siguientes matrices:
𝑎11 𝑎12 𝑎13 𝑎14 … 𝑎1𝑛
𝑎21 𝑎22 𝑎23 𝑎24 … 𝑎2𝑛
❖ La matriz de coeficientes es: 𝐴 = [
]
⋮
⋮
⋮
⋮
⋱
⋮
𝑎𝑚1 𝑎𝑚2 𝑎𝑚3 𝑎𝑚4 … 𝑎𝑚𝑛
𝑥1
𝑥2
❖ La matriz de variables es: 𝑋 = [ ⋮ ]
𝑥𝑛
𝑏1
𝑏2
❖ La matriz de término independiente es: 𝐵 = [ ]
⋮
𝑏𝑚
❖ La matriz ampliada o aumentada se forma a partir de las matrices A y B, es decir:
𝑎11
𝑎
[A⃓B] = [ 21
⋮
𝑎𝑚1
•
𝑎1𝑛
𝑎12
𝑎13 …
𝑎21
𝑎21 …
𝑎21
⋮
⋮
⋱
⋮
𝑎𝑚2 𝑎𝑚3 𝑎𝑚4 𝑎𝑚𝑛
𝑏1
𝑏2
]
⋮
𝑏𝑚
Clasificación del sistema de ecuaciones lineales
Por lo estudiado en las primeras semanas se sabe que la ecuación de la forma 𝑎𝑥 + 𝑏𝑦 = 𝑐, geométricamente
hablando es una recta, entonces los SEL de orden 2 × 2 nos permiten recordar de manera fácil como se puede
clasificar un SEL según su conjunto solución, es decir:
Primer caso: Si las rectas se cruzan en un solo punto, el sistema tiene una única
solución, por ejemplo:
2𝑥 + 3𝑦 = 5
El SEL {
tiene una única solución, es decir 𝐶𝑆 = {(−2; 3)} y por
−3𝑥 + 5𝑦 = 21
lo tanto se clasifica como:
Sistema compatible determinado
Segundo caso: Si las rectas coinciden y son paralelas, el sistema tiene infinitas
soluciones, por ejemplo:
4𝑥 − 5𝑦 = 2
2+5𝑡
; CS = {(
; 𝑡) / 𝑡 ∈ ℝ}
{
4
−12𝑥 + 15𝑦 = −6
Y se clasifica como sistema compatible indeterminado
Profesores MA420
72
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Tercer caso: Si las rectas son paralelas y no se cruzan, el sistema no tiene
solución, por ejemplo:
𝑥 − 3𝑦 = −2
; CS = { }
{
2𝑥 − 6𝑦 = 4
Y se clasifica como sistema incompatible
NOTA: En forma general, todo SEL de cualquier orden se clasifica según su solución de la siguiente manera (ver
el esquema):
• Operaciones elementales de filas (renglones)
Una combinación de las operaciones siguientes transformará una matriz en la forma escalonada por filas.
1. Intercambia de posición a cualquiera de las dos filas.
2. Multiplica todos los elementos de una fila por un número real distinto de cero.
3. Suma un múltiplo de una fila a otra fila.
Usaremos las siguientes notaciones para describir las operaciones elementales de filas (renglones)
𝑘𝐹𝑖 : Indica la multiplicación de la fila 𝑖 por 𝑘 (𝑘 es escalar).
𝑘𝐹𝑗 + 𝐹𝑖 → 𝐹𝑖 : Indica la multiplicación de la fila 𝑗 por 𝑘 luego se suma a la fija 𝑖.
𝐹𝑗 ↔ 𝐹𝑖 : Indica el intercambio de la fila 𝑗 y la fila 𝑖.
• Forma escalonada por filas de una matriz
Una matriz está en la forma escalonada por filas si satisface las siguientes condiciones.
•
•
•
Las filas que consisten únicamente en ceros (si los hay) aparecen en la parte inferior de la matriz.
En una fila que no consiste sólo de ceros, la primera entrada diferente de cero es 1.
El subíndice de la columna con el 1 de más a la derecha aumenta conforme el subíndice de la fila aumenta.
1 7
1 − 2
0 1 − 2 − 7
0 0 0 3
Profesores MA420
73
UPC – Departamento de Ciencias - Matemática Básica (MA420)
A continuación, veremos una forma sistemática de poner una matriz en forma escalonada por filas usando
operaciones elementales de filas:
Se sugiere que el primer elemento de la primera fila sea 1, luego obtenga ceros debajo del 1, para ello sume
múltiplos de la primera fila a las filas que están debajo de ella.
A continuación, se sugiere obtener 1 como primer elemento no nulo en la segunda fila, enseguida obtenga ceros
debajo de ese 1.
Continúe con este proceso hasta que llegue a una matriz en forma escalonada por filas.
Una vez que una matriz aumentada esté en forma escalonada por filas, podemos resolver el sistema de
ecuaciones lineales usando sustitución. Esta técnica se llama eliminación gaussiana, en honor a su inventor, el
matemático alemán C. F. Gauss.
2.
PRACTIQUEMOS EN CLASE
1.
Determine el conjunto solución del sistema de ecuaciones lineales, escalonando su matriz ampliada y
clasifíquelo según su solución:
a.
2.
𝑥 − 2𝑦 + 𝑧 = 7
{ 3𝑥 − 5𝑦 + 𝑧 = 14
2𝑥 − 2𝑦 − 𝑧 = 3
𝑥 − 2𝑦 + 𝑧 = 1
b. { 𝑥 − 3𝑦 + 2𝑧 = 3
3𝑥 − 6𝑦 + 3𝑧 = 5
𝑥 + 2𝑦 − 3𝑧 = −1
c. {2𝑥 + 3𝑦 − 4𝑧 + 𝑤 = −1
3𝑥 + 5𝑦 − 6𝑧 + 𝑤 = −2
Una bióloga ha colocado tres cepas bacterianas (denotadas como I, II y III) en un tubo de ensayo, donde
serán alimentadas con tres distintas fuentes alimenticias (A, B y C). Cada día 2300 unidades de A, 800
de B y 1500 de C se colocan en el tubo de ensayo, y cada bacteria consume cierto número de unidades
de cada alimento por día, como se muestra en la tabla. ¿Cuántas bacterias de cada cepa pueden
coexistir en el tubo de ensayo y consumir todo el alimento?
Cepa
Bacteriana I
Cepa
Bacteriana II
2
1
1
2
2
3
Alimento A
Alimento B
Alimento C
Cepa
Bacteriana
III
4
0
1
RESPUESTAS DE PRACTIQUEMOS EN CLASE
1. a. CS = {(2; −1; 3)}
b. CS = { }
c. CS = {( −1 − 2t; t; 0; 1 + t)/t ∈ R} u otra
solución equivalente
Nota: Clasifique su respuesta de acuerdo con la solución obtenida como sistema compatible
determinado, indeterminado o incompatible.
Profesores MA420
74
UPC – Departamento de Ciencias - Matemática Básica (MA420)
2. 100; 350 y 350. Nota: Defina las variables, plantee un sistema de ecuaciones lineales (SEL), determina las
restricciones y redacte su respuesta.
3.
PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1.
Determine el conjunto solución de los siguientes sistemas de ecuaciones lineales (SEL) escalonando su
matriz ampliada y clasifíquelos según su solución.
𝑥 + 3𝑦 − 𝑧 = −3
a. { 3𝑥 − 𝑦 + 2𝑧 = 1
2𝑥 − 𝑦 + 𝑧 = −1
𝑥 + 2𝑦
=4
𝑦
+
2𝑧
=3
b.{
𝑥 + 3𝑦 + 2𝑧 = 7
c.{
𝑥 + 𝑦 − 𝑧 = −20
2𝑥 − 𝑦 + 𝑧 = 11
2.
Una fábrica de muebles, manufactura mesas, sillas y armarios. Cada pieza requiere tres operaciones:
corte de la madera, ensamble y acabado. Cada proceso requiere la cantidad de horas (h) que se da en
la tabla adjunta. Los trabajadores de la fábrica pueden proporcionar 480 h de corte, 760 h de ensamble
y 855 h de acabado por semana. ¿Cuántas mesas, sillas y armarios se deben producir de modo que
todas las horas de mano de obra se utilicen?
Mesa
Silla
Armario
Corte (h)
½
1
1
Ensamble
½
1½
2½
(h)
Acabado(h)
1
1 ½
3
3.
En una construcción podemos hacer columnas, calzaduras y vigas. Para cada columna necesitamos 4
1
varillas de acero de 2 pulgada; 0,2 m3 de concreto y 8 horas hombre, para cada calzadura necesitamos
1 m3 de concreto y 12 horas hombre y para cada viga 6 varillas de acero de
1
1
2
pulgada; 0,4 m3 de
concreto y 10 horas hombre. Si disponemos de 58 varillas de acero de 2 pulgada; 15,4 m3 de concreto
y 250 horas hombre. ¿cuántas columnas, calzaduras y vigas podemos realizar optimizando los recursos?
RESPUESTAS DE PRACTIQUEMOS MÁS EN CASA
3
t
1. a. CS = {(−2; 1; 4)}
b. CS = {( 4 − 2t; t; 2 − 2)/t ∈ R} u otra solución equivalente
𝐜. CS = {(−3; t − 17; t)/t ∈ R } u otra solución equivalente
Nota: Clasifique su respuesta de acuerdo con la solución obtenida como sistema compatible
determinado, indeterminado o incompatible.
2. 120; 350 y 70.
Nota: Defina las variables, plantee un sistema de ecuaciones lineales (SEL), determina las restricciones y
redacte su respuesta.
3. 7; 12 y 5.
Nota: Defina las variables, plantee un sistema de ecuaciones lineales (SEL), determina las restricciones y
redacte su respuesta.
Profesores MA420
75
UPC – Departamento de Ciencias - Matemática Básica (MA420)
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Enlace
Código QR
Determinar el conjunto solución
de un sistema de ecuaciones
https://tinyurl.com/y569d3wx
lineales compatible determinado.
Determinar el conjunto solución
de un sistema de ecuaciones https://tinyurl.com/y4m73qdp
lineales compatible determinado.
Determinar el conjunto solución
de un sistema de ecuaciones
https://tinyurl.com/y4gb7zvd
lineales incompatible.
Determinar el conjunto solución
de un sistema de ecuaciones
https://tinyurl.com/y36wat4g
lineales
compatible
indeterminado.
Resolver un problema de
modelación que involucra un https://tinyurl.com/y4ufcdrv
sistema de ecuaciones lineales.
Profesores MA420
76
UPC – Departamento de Ciencias - Matemática Básica (MA420)
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
SISTEMA DE ECUACIONES LINEALES (SEL): Revisar páginas desde 679 hasta 711.
Profesores MA420
77
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Funciones: Dominio y rango
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante interpreta de forma gráfica y algebraica el
concepto de función y determina su dominio y rango. Demostrando responsabilidad y capacidad de aprender
por su propia cuenta.
CONTENIDOS
MOTIVACIÓN
1. Función
• Definición
• Notaciones
• Gráfica de una función
• Criterio de la recta vertical
• Dominio y rango de forma geométrica
• Dominio de forma algebraica.
2. Practiquemos en clase
• Ejercicios
3. Practiquemos más en casa
• Ejercicios
Profesores MA420
78
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Motivación
¿Y si tuviéramos 2 respuestas?
Los ingenieros trabajan basados en normas y reglamentos que garantizan calidad, seguridad y homogeneidad
ante las diferentes situaciones que debemos afrontar.
Por ejemplo, un ingeniero civil, diseña elementos estructurales. ¿Cómo sabe cuántas varillas de acero debe
usar en una viga determinada de una edificación?, seguramente para resolver esto y tomar una decisión
correcta tendrá una norma que se indicará mediante una ecuación, el número que estamos buscando.
¿Y qué pasaría si dicha ecuación nos diera dos
respuestas?, por ejemplo: puedo usar 4 varillas
de acero de ½” o 8 varillas de acero de ½”. Si
escojo usar 4 varillas tal vez no está muy seguro
que la estructura sea adecuada para resistir
todos los casos a los que se someterá, en cambio,
si usa 8 varillas no está optimizando y está yendo
en contra de la parte económica, esto
obviamente no se debería dar y mi pregunta
sería: ¿de dónde parte este problema?
Seguramente ya captaste lo que queremos dar a entender: necesitamos reglas que transformen datos y nos
dé una única respuesta para cada caso, estas reglas que dan respuesta única ante diferentes posibilidades,
se les llama funciones.
Para determinar un único número de varillas de acero de ½” que se necesitan ante ciertos requerimientos
estructurales de una viga, necesitamos saber claramente varias cosas, entre ellas: que luz tiene la viga
(distancia entre las columnas en las que se apoya), que pesos resiste, cuáles son sus dimensiones y otras cosas
más. Es decir, para determinar el número único de varillas de ½” que necesita una viga necesitamos los valores
de varias variables, en nuestro curso no estudiaremos aún estos casos, sino que estudiaremos funciones que
tengan una sola variable.
Profesores MA420
79
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1.
DEFINICIÓN DE FUNCIÓN
Una función es una regla que asigna a cada elemento de un conjunto 𝐷 (llamado dominio) un único elemento
en un conjunto 𝑅 (llamado rango).
D
D
R
1
2
1
a
b
3
4
b
3
c
4
d
Este gráfico nos representa una
función debido a que cada
elemento del dominio 𝐷 solo
tiene un elemento en el rango 𝑅.
Notaciones:
a
2
c
5
R
5
d
e
Este gráfico NO representa una
función debido a que el elemento
“1” que pertenece a 𝐷 tiene 2
elementos asignados en el
conjunto 𝑅 (recuerda la lectura de
la página anterior).
❖ La regla de correspondencia de una función será denotada por la ecuación:
𝑦 = 𝑓(𝑥)
Donde:
• “𝑥” es la variable independiente y los valores que tome (sobre los reales) deben pertenecer al dominio
de la función, los cuales ubicaremos en el eje 𝑥 del plano cartesiano 𝑥𝑦.
• “𝑦” es la variable dependiente y los valores 𝑓(𝑥) deben pertenecer al rango de la función, los cuales
ubicaremos en el eje 𝑦 del plano cartesiano 𝑥𝑦.
❖ El dominio de una función será denotado por el conjunto:
Dom(𝑓) = {𝑥 ∈ ℝ/restricció𝑛}
❖ El rango de una función será denotado por el conjunto:
Ran(𝑓) = {𝑓(𝑥)/𝑥 ∈ Dom(𝑓)}
Profesores MA420
80
UPC – Departamento de Ciencias - Matemática Básica (MA420)
GRÁFICA DE UNA FUNCIÓN
Si f es una función con dominio 𝐷 entonces la gráfica de 𝑓 es el conjunto de puntos:
{(𝑥; 𝑓(𝑥)) ∈ 𝑅 2 /𝑥 ∈ Dom(𝑓)}
y
(x; f (x))
f (x)
x
x
CRITERIO DE LA RECTA VERTICAL
Suponga que 𝐶 es una curva en el plano 𝑥𝑦 . La curva 𝐶 será la gráfica de una función 𝑓 con regla de
correspondencia 𝑦 = 𝑓(𝑥) si toda recta vertical que la corta lo hace en un solo punto.
Ejemplo: De las cuatro gráficas que se muestran, ¿cuáles no corresponden a la gráfica de una función?
Gráfica 2
y
x
x
x
Gráfica 1
y
y
y
Gráfica 3
x
Gráfica 4
y
Solución:
❖ Trazando una recta vertical en la gráfica 1, observamos que esta toca en
dos puntos a la curva dada, es decir no cumple con el criterio de la recta
vertical. Por lo tanto, la curva dada no es una gráfica de una función.
x
y
❖ Trazando rectas verticales en la gráfica 2, observamos que estas tocan en un único
punto a la curva dada. Por lo tanto, la curva corresponde a la gráfica de una
función.
x
y
❖ En la gráfica 3, la curva corresponde a la gráfica de una función.
Profesores MA420
x
81
UPC – Departamento de Ciencias - Matemática Básica (MA420)
y
❖ En la gráfica 4, observamos que la recta vertical trazada toca en tres puntos
a la curva dada. Por lo tanto, la curva no es la gráfica de una función.
x
Respuesta: La gráfica 1 y 4 no corresponden a la gráfica de una función.
DOMINIO Y RANGO DE FORMA GEOMÉTRICA
Una primera habilidad a desarrollar es determinar el dominio y el rango de una función a partir de su gráfica
(forma geométrica).
Ejemplo 1:
La figura muestra la gráfica de la función f, interprétela y determine el dominio y el rango.
Solución:
• Para determinar el dominio a partir de la gráfica debemos
proyectar todos los puntos de la gráfica sobre el eje 𝑥, luego
observemos desde donde varía la proyección en el eje 𝑥, lo
cual es el dominio:
Dom(𝑓) = ]−4; −1] ∪ ]0; 2[
• Para el rango debemos proyecta todos los puntos sobre el
eje 𝑦, luego observamos desde donde varía la proyección en
el eje 𝑦, lo cual es el rango:
Ran(𝑓) = ]−4; 2[
DOMINIO DE FORMA ALGEBRAICA
La segunda habilidad a desarrollar es determinar el dominio de una función a partir de su regla de
correspondencia (forma algebraica).
√4−𝑥 2
Ejemplo 3: Determine el dominio de la función 𝑓 con regla de correspondencia: 𝑓(𝑥) = |𝑥−1|−2
Solución:
Dom(𝑓) = {𝑥 ∈ 𝑅 / 4 − 𝑥 2 ≥ 0
•
∧ | 𝑥 − 1| − 2 ≠ 0}
Para 4 − 𝑥 2 ≥ 0
(2 − 𝑥)(2 + 𝑥) ≥ 0
Números de referencia: 2 y -2:
𝑥𝜖[−2; 2]
Profesores MA420
82
UPC – Departamento de Ciencias - Matemática Básica (MA420)
•
Para | 𝑥 − 1| − 2 ≠ 0
𝑥−1≠2 → 𝑥 ≠3
| 𝑥 − 1| ≠ 2 ⇒ {
𝑥 − 1 ≠ −2 → 𝑥 ≠ −1
Por lo tanto, el dominio es:
Dom(𝑓) = [−2; 2] − {−1}
2.
PRACTIQUEMOS EN CLASE
EJERCICIOS
1. La figura muestra la gráfica de la función 𝑓 y 𝑔, respectivamente.
Determine:
a. El dominio y el rango de ambas funciones.
b. El valor de 𝑓(2) + 𝑔(0) − 𝑔(1).
2.
Determine el dominio de las siguientes funciones con regla de correspondencia:
√3−𝑥
a.
𝑓(𝑥) = 𝑥 2 −6𝑥+8
b.
𝑔(𝑥) = √9𝑥 − 𝑥 3
c.
ℎ(𝑥) = |𝑥+2|−5
d.
𝑓(𝑥) =
4
3
√𝑥+5
𝑥 2 −9
√2𝑥−5
RESPUESTA DE LOS EJERCICIOS PRACTIQUEMOS EN CLASE
1. a. Dom(𝑓) = [−2 ; 4[ ; Ran(𝑓) = ]−1 ; 3] ; Dom(𝑔) = [−4 ; ∞[ ; Ran(𝑔) = ]−∞ ; 2]
b. 4
2. a. Dom(𝑓) =] − ∞; 3] − {2} b. Dom(𝑔) =] − ∞; −3] ∪ [0; 3]
c.Dom(ℎ) = ℝ − {−7; 3}
Profesores MA420
5
d. Dom(𝑓) =] 2 ; ∞[
83
UPC – Departamento de Ciencias - Matemática Básica (MA420)
3.
PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1.
A partir de la gráfica de la función 𝑓, determine el dominio y el rango.
2.
A partir de la gráfica de la función 𝑓, determine el dominio y el rango.
3.
Dada la función 𝑓 con regla de correspondencia 𝑓(𝑥) =
4.
Dada la función 𝑓 con regla de correspondencia 𝑓(𝑥) =
√1−𝑥
, determine su dominio.
𝑥 2 −𝑥−6
(𝑥−5)
, determine su dominio.
(𝑥−1)√𝑥+3
RESPUESTAS DE LOS EJERCICIOS PRACTIQUEMOS MÁS EN CASA
1. Para determinar el dominio y rango a partir de la gráfica de funciones revise los ejemplos 1 y 2 del libro
digital. Pág. 73.
2. Para determinar el dominio y rango a partir de la gráfica de funciones revise los ejemplos 1 y 2 del libro
digital. Pág. 74
3. Dom(𝑓) = ]−∞; 1] − {−2}
4. Dom(𝑓) = ]−3; ∞[ − {1}
Profesores MA420
84
UPC – Departamento de Ciencias - Matemática Básica (MA420)
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Enlace
Calcular el dominio y rango de una
función f, a partir del gráfico.
https://goo.gl/azR5EU
Calcular el dominio y rango de una
función f, a partir de su regla de
correspondencia.
Código QR
https://goo.gl/0DdD7H
Calcular el dominio y rango de una
función f, a partir del gráfico.
https://tinyurl.com/y5t7cyrj
Calcular el dominio de una función
a partir de su regla de
correspondencia.
https://tinyurl.com/y6d6gur2
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
FUNCIONES DOMINIO Y RANGO: Revisar páginas desde 147 hasta 159, 164, 170 a
171.
Profesores MA420
85
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Propiedades de funciones
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante interpreta de forma gráfica y algebraica el
concepto de función y sus propiedades, y los aplica en la solución de ejercicios, demostrando responsabilidad
y capacidad de aprender por su propia cuenta.
CONTENIDOS
MOTIVACIÓN
1.1.
1.2.
Propiedades de funciones
•
Ceros de una función
•
Intervalos donde una función es positiva o negativa
•
Continuidad de una función
•
Intervalos de monotonía de una función
•
Extremos de una función
Practiquemos en clase
•
1.3.
Ejercicios
Practiquemos más en casa
•
Ejercicios
Profesores MA420
86
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Motivación
Las funciones tienen una representación gráfica; en las gráficas se puede observar algunas características de las
funciones: creciente, decreciente, constante, positiva, negativa, etc. Un ejemplo de la importancia de saber
interpretar las gráficas se hizo evidente desde las primeras semanas de la pandemia por el Covid 19, para poder
entender la evolución del número de contagios, decesos; que debería de servir para que la población y las
autoridades puedan planificar las acciones a tomar para controlar la pandemia.
1.1. PROPIEDADES DE FUNCIONES
CEROS DE UNA FUNCIÓN
Un número 𝑐 del dominio de la función 𝑓 es un cero de la función, si y solo si 𝑓(𝑐) = 0.
OBS: Para calcular los ceros de una función, es equivalente a calcular los puntos de intersección con el eje
𝑥 de la gráfica de 𝑦 = 𝑓(𝑥), o calcular la solución de la ecuación 𝑓(𝑥) = 0.
Forma gráfica
Forma analítica
Si 𝑓(𝑥) =
Haciendo la interpretación del gráfico de izquierda a
derecha, los siguientes puntos de la gráfica intersecta
al eje 𝑥: 1 y 3, luego la respuesta es:
Los ceros de la función 𝑓 están en 1 y 3.
Profesores MA420
𝑥√25−𝑥
𝑥+2
Para calcular los ceros de la función 𝑓 se
debe hallar el dominio y resolver la
ecuación:
𝑥√25−𝑥
𝑥+2
= 0.
87
UPC – Departamento de Ciencias - Matemática Básica (MA420)
INTERVALOS DONDE UNA FUNCIÓN ES POSITIVA O NEGATIVA
Para calcular los intervalos donde una función es positiva o negativa, es equivalente a calcular los valores
en el eje 𝑥 tal que 𝑓(𝑥) > 0 o 𝑓(𝑥) < 0, respectivamente.
Haciendo la interpretación del gráfico
de izquierda a derecha, la función es
positiva cuando la gráfica está sobre el
eje 𝑥, en este caso observamos que:
Haciendo la interpretación del gráfico de
izquierda a derecha, la función es
negativa cuando la gráfica está debajo
del eje x, en este caso observamos que:
La función 𝑓 es positiva en el intervalo
La función 𝑓 es negativa en el intervalo
]−2; 1].
]−2; 1].
CONTINUIDAD DE UNA FUNCIÓN
Una de las propiedades de la mayoría de las funciones que modelan un comportamiento del mundo real, es
que sean continuas. Desde el punto de vista gráfico, una función es continua en un punto si la gráfica no se
separa en ese punto. Podemos ilustrar el concepto con las siguientes gráficas.
Veamos cada uno de estos casos individualmente.
Figura 1. a. Una función es continua en todas partes cuando su gráfica puede dibujarse de un solo trazo, es
decir, se puede dibujar sin levantar el lápiz de la hoja de papel.
Dom(𝑓) = [0; +∞[
Dom(𝑓) = ℝ
y
x
Continua en todos los reales
Figura 1.a.
Profesores MA420
Ejemplo 1. a.
La función f es continua en
todo su dominio.
88
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Figura 1. b. Esta gráfica es continua en todas partes, excepto en el “agujero” en a. La función presenta una
discontinuidad removible en 𝑎 porque se puede redefinir el valor de f (a) de modo que desaparezca el
agujero, es decir, definir el valor de f (a) igual a b.
y
f (a)
b
x
a
Discontinuidad removible o evitable en a.
Ejemplo 1. b.
La función f tiene una
discontinuidad removible en 1.
Figura 1.b.
Figura 1. c. Esta gráfica también tiene una discontinuidad removible en 𝑎. La función presenta una
discontinuidad removible en 𝑎 porque se puede definir el valor de 𝑓 (𝑎) de modo que desaparezca el
agujero, es decir, definir el valor de 𝑓 (𝑎) igual a 𝑏.
y
b
a
x
Figura 1.c.
Ejemplo 1. c.
Discontinuidad removible o evitable en a.
La función f tiene una discontinuidad
de tipo removible en -1.
Figura 1. d. Aquí está una discontinuidad que no es removible. Es una discontinuidad de salto en a, porque
es más que un agujero en 𝑎; hay un salto en los valores de la función que forma un espacio imposible de
llenar.
y
y
a
x
a
x
Discontinuidad de salto en a.
Figura 1. d.
Profesores MA420
89
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Ejemplo 1.d.
Ejemplo 1.e.
La función 𝑓 tiene una discontinuidad
de tipo salto en 0.
La función 𝑔 tiene una discontinuidad
de tipo salto en 1.
Figura 1. e. Esta gráfica tiene una discontinuidad en 𝑎 que no se clasifica como una discontinuidad del tipo
salto, se dice que la función presenta una discontinuidad infinita en a, porque no es posible realizar un salto
desde un punto hacia el infinito o viceversa.
y
y
a
x
y
a
x
a
x
Discontinuidad infinita en a.
Figura 1.e.
OBS: Si hay una discontinuidad infinita en a entonces hay una recta vertical llamada asíntota y se representa
mediante la ecuación 𝑥 = 𝑎.
Ejemplo 1.f.
La función f tiene una
discontinuidad infinita en −1
y la ecuación de la asíntota
vertical es: 𝑥 = −1
Profesores MA420
La función f tiene una
discontinuidad infinita en 1 y
la ecuación de la asíntota
vertical es: 𝑥 = 1
La función f tiene una
discontinuidad infinita en −1 y
la ecuación de la asíntota
vertical es: 𝑥 = −1
90
UPC – Departamento de Ciencias - Matemática Básica (MA420)
INTERVALOS DE MONOTONÍA DE UNA FUNCIÓN
Otra característica de las funciones que es fácil de comprender de manera gráfica es la de ser creciente o
decreciente en un intervalo. Interpretemos las siguientes gráficas (Figura 2).
Figura 2. a. Una función 𝑓 es creciente en un intervalo si 𝑓( 𝑥1 ) < 𝑓( 𝑥2 ) siempre que 𝑥1 < 𝑥2 en 𝐼.
IMPORTANTE: Se dice que una función es
creciente cuando su gráfica sube a medida que
avanzamos de izquierda a derecha en el eje X.
Figura 2.a. Función creciente
Figura 2. b. Una función f es decreciente en un intervalo si 𝑓( 𝑥1 ) > 𝑓( 𝑥2 ) siempre que 𝑥1 < 𝑥2 en 𝐼.
IMPORTANTE: Se dice que una función es decreciente
cuando su gráfica baja a medida que avanzamos de
izquierda a derecha en el eje X.
Figura 2. b. Función decreciente
EXTREMOS DE UNA FUNCIÓN
a. Máximo absoluto de una función
Sea 𝐷 el dominio de 𝑓, se dice que en 𝑐𝐷 ocurre máximo absoluto de 𝑓 si:
𝑓(𝑥) ≤ 𝑓(𝑐) Para todo 𝑥 en 𝐷
El número 𝑓(𝑐) se llama valor máximo absoluto de 𝑓 en 𝐷 (el valor del máximo absoluto es 𝑓(𝑐) y
ocurre en 𝑐).
Profesores MA420
91
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Figura 3. a. Máximo absoluto de la función f .
b. Mínimo absoluto de una función
Sea 𝐷 el dominio de 𝑓, se dice que en 𝑐𝐷 ocurre mínimo absoluto de 𝑓 si:
𝑓(𝑐) ≤ 𝑓(𝑥) para todo 𝑥 en 𝐷
El número 𝑓(𝑐) se llama valor mínimo absoluto de 𝑓 en 𝐷 (el valor del mínimo absoluto es 𝑓(𝑐) y
ocurre en 𝑐).
Figura 3. b. Mínimo absoluto de la función f.
c. Máximo relativo o local de una función
Sea 𝐷 el dominio de 𝑓, se dice que en 𝑐 ∈ 𝐷 ocurre un máximo relativo o local de 𝑓 si:
𝑓(𝑥) ≤ 𝑓(𝑐) cuando 𝑥 es cercano a 𝑐
(Esto significa que 𝑓(𝑥) ≤ 𝑓(𝑐) para toda 𝑥 en algún intervalo abierto que contenga a 𝑐).
El número 𝑓(𝑐) se llama valor máximo relativo o local (el valor del máximo relativo es 𝑓(𝑐) y ocurre
en 𝑐).
Profesores MA420
92
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Figura 3. c. Máximo local de la función f.
d. Mínimo relativo o local de una función
Sea 𝐷 el dominio de 𝑓, se dice que en 𝑐 ∈ 𝐷 ocurre un mínimo relativo o local de 𝑓 si:
𝑓(𝑐) ≤ 𝑓(𝑥) cuando 𝑥 es cercano a 𝑐
(Esto significa que 𝑓(𝑐) ≤ 𝑓(𝑥) para toda 𝑥 en algún intervalo abierto que contenga a c).
El número 𝑓(𝑐) se llama valor de mínimo relativo o local (el valor del mínimo relativo es 𝑓(𝑐) y ocurre
en 𝑐).
Figura 3. d. Mínimo local de la función f.
Profesores MA420
93
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1.2.
PRACTIQUEMOS EN CLASE
1. La figura muestra la gráfica de la función f.
Interprete y determine lo siguiente:
a. dominio y rango
b. los ceros de la función
c. los intervalos donde la función
es positiva y negativa
d. los puntos de discontinuidad, si
existen, luego clasifíquelos.
e. los intervalos de monotonía.
f. los valores extremos absolutos y
relativos.
2. Determine el dominio y los ceros, de las siguientes funciones con regla de correspondencia:
a.
𝑓(𝑥) =
𝑥 3 −16𝑥
√𝑥+3
b. 𝑔(𝑥) =
(𝑥 2 −8𝑥+7)√5−𝑥
𝑥−2
3. Determine el dominio y los intervalos donde la función es positiva y negativa, de las siguientes funciones
con regla de correspondencia:
a. 𝑓(𝑥) = −2𝑥 3 + 6𝑥 2 + 8𝑥
b. 𝑔(𝑥) = −𝑥 4 + 4𝑥 2
RESPUESTAS DE PRACTIQUEMOS EN CLASE
1.
Para obtener las respuestas de esta pregunta revise la teoría y los ejemplos resueltos de este libro.
2.
a. Dom(𝑓) = ]−3; ∞[
Los ceros de la función están en 0 y 4.
b. Dom(𝑓) = ]−∞; 5] − {2}
Los ceros de la función están en 1 y 5.
3.
a. Dom(𝑓) = ℝ
La función es positiva en los intervalos: ]−∞; −1[ y ]0; 4[
La función es negativa en los intervalos: ]−1; 0[ y ]4; ∞[
b. Dom(𝑓) = ℝ
La función es positiva en los intervalos: ]−2; 0[ y ]0; 2[
La función es negativa en los intervalos: ]−∞; −2[ y ]2; ∞[
Profesores MA420
94
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1.3. PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1. La figura muestra la gráfica de la función f.
Interprete y determine lo siguiente:
a. Dominio y rango
b. Los ceros de la función
c. Los intervalos donde la función es positiva y negativa.
d. Los puntos de discontinuidad, si existen, luego clasifíquelos.
e. Los intervalos de monotonía.
f. Los valores extremos absolutos.
2. La figura muestra la gráfica de la función f. Interprete y determine lo siguiente:
a. Dominio y rango
b. Los ceros de la función
c. Los intervalos donde la función
es positiva y negativa.
d. Las ecuaciones de las asíntotas
e. Los puntos de discontinuidad, si
existen, luego clasifíquelos.
f. Los intervalos de monotonía
g. Los valores extremos absolutos y
relativos (locales).
3. Determine el dominio y los ceros, de las siguientes funciones con regla de correspondencia:
a.
𝑓(𝑥) =
(3−𝑥) (𝑥 2 +8𝑥)
√𝑥+7
√𝑥 2 −9
b. 𝑔(𝑥) = 𝑥 2 +5𝑥
4. Determine el dominio y los intervalos donde la función es positiva y negativa, de las siguientes funciones
con regla de correspondencia:
a. 𝑓(𝑥) = 4𝑥 3 − 6𝑥 2 + 2𝑥
b. 𝑔(𝑥) = 𝑥 4 − 4𝑥 2
Profesores MA420
95
UPC – Departamento de Ciencias - Matemática Básica (MA420)
RESPUESTAS PRACTIQUEMOS MÁS EN CASA
1.
Para obtener las respuestas de esta pregunta revise la teoría y los ejemplos resueltos de este libro.
2.
Para obtener las respuestas de esta pregunta revise la teoría y los ejemplos resueltos de este libro.
3.
a. Dom(𝑓) = ]−7; ∞[
Los ceros de la función están en 0 y 3.
b. Dom(𝑓) = ]−∞; −3] ∪ [3; ∞[ − {−5}
Los cerros de la función están en -3 y 3.
4.
a. Dom(𝑓) = ℝ
La función es positiva en los intervalos: ]0; 0,5[ y ]1; ∞[
La función es negativa en los intervalos: ]−∞; 0[ y ]0,5; 1[
b. Dom(𝑓) = ℝ
La función es positiva en los intervalos: ]−∞; −2[ y ]2; ∞[
La función es negativa en los intervalos: ]−2; 0[ y ]0; 2[
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Enlace
Código QR
Interpretar la gráfica descrita por https://tinyurl.com/y6jy8jxf
el recorrido de un ciclista.
Calcular los ceros y los intervalos
donde la función f es negativa a https://tinyurl.com/y6d3kttx
partir
de
su
regla
de
correspondencia.
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
PROPIEDADES DE FUNCIONES: Revisar páginas desde 173 hasta 182.
Profesores MA420
96
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Funciones básicas, seccionadas y
técnicas de graficación
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante analiza el comportamiento algebraico y
gráfico de funciones seccionadas, cuyos tramos son funciones básicas y/o sus transformaciones (técnicas de
graficación), demostrando responsabilidad y capacidad de aprender por su propia cuenta.
CONTENIDO
MOTIVACIÓN
1.1 Funciones básicas
• Definiciones
1.2 Funciones seccionadas
• Definición
1.3 Técnicas de graficación
• Traslación horizontal
• Traslación Vertical
1.4. Practiquemos en clase
• Ejercicios
1.5. Practiquemos más en casa
• Ejercicios
Profesores MA420
97
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Motivación
Existen diversos métodos para graficar funciones, como el método simple de tabulación (no siempre
adecuado) y otros más avanzados y precisos que utilizan conceptos de cálculo diferencial. También, a
partir de la gráfica de una función y transformaciones como la traslación, reflexión, alargamiento o
compresión de la gráfica es posible tener la gráfica de una nueva función de forma precisa y sobre todo
simple.
1.1. FUNCIONES BÁSICAS
En esta sección trazaremos la gráfica de 6 funciones básicas y analizaremos la gráfica de cada una de las
funciones para representar sus propiedades tales como dominio, rango, ceros, continuidad, extremos
globales y locales, monotonía, asíntotas, intervalos en donde la función es positiva y negativa.
Función constante
Una función cuyo rango consta de un único número se llama función constante y su grafica es una recta
horizontal que corta al eje 𝑦 en un punto.
Regla de correspondencia de la función constante es: 𝑓(𝑥) = 𝑘
Interpretando la gráfica de izquierda a derecha y
proyectando sobre el eje 𝑥, y de abajo hacia arriba y
proyectando sobre el eje 𝑦, observamos que el dominio
y rango de la función queda representado por:
Dom(𝑓) = ℝ
Ran(𝑓) = {𝑘}
Profesores MA420
98
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Función identidad
La función identidad está definida para todos los números reales y su regla de correspondencia es:
𝑓(𝑥) = 𝑥
Observación: Cuando trace la gráfica una función debe
mostrar por lo menos tres o más puntos de referencia por
donde pasa la gráfica y debe usar una escala adecuada.
Interpretando la gráfica de izquierda a derecha,
representemos algunas de las propiedades de la
función identidad.
Dom(𝑓) = ℝ
Ran(𝑓) = ℝ
Función cuadrática
La función cuadrática está definida para todos los números reales, y su gráfica de esta función es una
parábola que se usa en la fabricación de faros, discos de satélites, y su regla de correspondencia es:
𝑓(𝑥) = 𝑥 2
Interpretando la gráfica de izquierda a derecha,
representemos algunas de las propiedades.
a. La función f es positiva en ]−∞; 0[ y ]0; +∞[
b. El cero de la función f está en 0
c. La función f es creciente en [0; +∞[
d. El valor del mínimo absoluto de la función f es 0
Función raíz cuadrada
La función raíz cuadrada está definida para todos los números positivos y cero, y su regla de
correspondencia es: 𝑓(𝑥) = √𝑥
Profesores MA420
99
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Interpretando la gráfica de izquierda a derecha, representemos
algunas de las propiedades.
a. La función f es positiva en ]0; +∞[
b. El cero de la función f está en 0
c. Rango de la función f es: Ran(𝑓) = [0; +∞[
Función valor absoluto
La función valor absoluto está definida para todos los números reales, y la gráfica de esta función tiene
un cambio abrupto en el origen, y su regla de correspondencia es: 𝑓(𝑥) = |𝑥|
Interpretando la gráfica de izquierda a derecha
representemos algunas de las propiedades.
a. La función f es positiva en ]−∞; 0[ y ]0; +∞[
b. El cero de la función f está en 0
c. Rango de la función f es Ran(𝑓) = [0; +∞[
Función recíproca
La función recíproca está definida para todos los números reales excepto el número cero, y es la primera
función asintótica (presenta asíntota horizontal y vertical) y su regla de correspondencia es:
1
𝑓(𝑥) = 𝑥
Interpretando la gráfica de izquierda a derecha,
representemos algunas de las propiedades.
a. La función f es positiva en ]0; +∞[
b. Rango de la función f es Ran(𝑓) = ℝ − {0}
c. Ecuación de la asíntota vertical es: 𝑥 = 0
d. La función f tiene una discontinuidad de tipo infinita en
0. (Ya que existe una asíntota vertical de ecuación 𝑥 = 0)
Profesores MA420
100
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1.2 FUNCIONES SECCIONADAS
En algunos casos, una única regla de correspondencia no define con claridad una función, en este caso es
conveniente utilizar una función seccionada, para describir la situación, y cuya definición presentamos a
continuación.
Definición de función seccionada
En una función seccionada para relacionar las variables x con y, requiere de varias reglas de
correspondencia, cada una de estas reglas de correspondencia tiene su propio dominio, es decir, tiene la
forma.
𝑓1(𝑥);
𝑓2(𝑥);
𝑓(𝑥) =
{𝑓𝑛(𝑥);
𝑠𝑖 𝑥∈𝐷1
𝑠𝑖 𝑥∈𝐷2
.
.
.
𝑠𝑖 𝑥∈𝐷𝑛
El dominio de la función f se representa como la unión de los dominios de cada función seccionada.
Dom(𝑓) = 𝐷1 ∪ 𝐷2 ⋯ 𝐷𝑛
El rango de la función f se representa como la unión de rango de cada función restringida a su dominio.
Ran(𝑓) = Ran(𝑓1 ) ∪ Ran(𝑓2 ) ⋯ Ran(𝑓𝑛 )
Cuando tracemos la gráfica de una función seccionada, debemos trazar cada uno de los tramos en su
dominio restringido y recuerde que debe mostrar por lo menos tres o más puntos de referencia por donde
pasa la gráfica de cada tramo y use una escala adecuada.
1.3 TÉCNICAS DE GRAFICACIÓN
Traslación Horizontal
Una traslación horizontal es un desplazamiento hacia la izquierda o hacia la derecha de la gráfica de
ecuación 𝑦 = 𝑓(𝑥)
Es decir, si 𝑐 > 0 la gráfica de la ecuación 𝑦 = 𝑓(𝑥 − 𝑐) es una traslación horizontal de 𝑐 unidades hacia
la derecha; mientras que la de 𝑦 = 𝑓(𝑥 + 𝑐), es una traslación horizontal de 𝑐 unidades hacia la
izquierda.
Profesores MA420
101
UPC – Departamento de Ciencias - Matemática Básica (MA420)
y = f (x)
y = f (x - c)
Es una traslación horizontal de 𝑐
unidades hacia la derecha.
y = f (x + c)
y = f (x)
Es una traslación horizontal de 𝑐
unidades hacia la izquierda.
Traslación Vertical
Una traslación vertical es un desplazamiento hacia arriba o hacia abajo de la gráfica con ecuación 𝑦 =
𝑓(𝑥).
Es decir, si 𝑐 > 0 la gráfica de 𝑦 = 𝑓(𝑥) + 𝑐 es una traslación vertical de 𝑐 unidades hacia arriba; mientras
que de 𝑦 = 𝑓(𝑥) − 𝑐, es una traslación vertical de 𝑐 unidades hacia abajo.
y = f (x) + c
y = f (x)
y = f (x)
y = f (x) - c
Es una traslación vertical de c
unidades hacia arriba.
Profesores MA420
Es una traslación vertical de c
unidades hacia abajo.
102
UPC – Departamento de Ciencias - Matemática Básica (MA420)
EN RESUMEN
Traslaciones
Sea 𝑐 un número real positivo. Entonces las transformaciones siguientes resultan de las traslaciones
de la gráfica de 𝑦 = 𝑓(𝑥)
Traslaciones horizontales
𝑦 = 𝑓(𝑥 − 𝑐): significa una traslación horizontal de 𝑐 unidades hacia la derecha
𝑦 = 𝑓(𝑥 + 𝑐) : significa una traslación horizontal de 𝑐 unidades hacia la izquierda
Traslaciones verticales
𝑦 = 𝑓(𝑥) + 𝑐 : significa una traslación vertical de 𝑐 unidades hacia arriba
𝑦 = 𝑓(𝑥) − 𝑐 : significa una traslación vertical de 𝑐 unidades hacia abajo
1.4 PRACTIQUEMOS EN CLASE
1. Dadas las funciones 𝑓 y 𝑔 con reglas de correspondencia:
3 ; 𝑥 < −1
2
𝑥
i.
ii. 𝑔(𝑥) = { ; −1 ≤ 𝑥 < 2
1
; 𝑥≥2
𝑥
Trace su gráfica e Interprete y determine lo siguiente:
a. Dominio y rango
b. ¿Cuáles son los intervalos donde la función es creciente y decreciente?
|𝑥| ; 𝑥 < 1
𝑓(𝑥) = {
√𝑥 ; 𝑥 ≥ 1
2. Dada la gráfica de una función 𝑓
con 𝑦 = 𝑓(𝑥), analice cada
tramo y escriba una regla de
correspondencia de la función
como una función seccionada de
funciones básicas, además
indique el dominio restringido
de cada tramo.
Profesores MA420
103
UPC – Departamento de Ciencias - Matemática Básica (MA420)
3. Describa con sus palabras los pasos a seguir para que a partir de la gráfica de 𝑦 = 𝑥 2 se grafique la
función 𝑦 = (𝑥 + 3)2 − 2.
|𝑥| + 2
; 𝑥 < −2
2
(𝑥
; −2 ≤ 𝑥 < 1. Trace su
4. Dada la función ℎ con regla de correspondencia ℎ(𝑥) = { + 1)
−
1
−
2;
𝑥≥1
√𝑥
gráfica calculando e indicando los puntos de corte con los ejes coordenados.
RESPUESTAS DE PRACTIQUEMOS EN CLASE
1. Para i:
a. Dom(𝑓) = ]−∞; ∞[, Ran(𝑓) = [0; ∞[.
b. La función f es creciente en [0; +∞[ y decreciente en ]−∞, 0] .
Para ii:
a. Dom(𝑔) = ]−∞; ∞[ y Ran(𝑔) = [0; 4[
b. La función g es creciente en [0; 2[ y decreciente en [−1; 0], ]2; +∞[
2. Debe de usar las funciones básicas en cada tramo de la gráfica y se obtiene la regla de
correspondencia de la función 𝑓.
−2 , −5 < 𝑥 < −2
𝑓(𝑥) = { 𝑥 2 , −2 < 𝑥 < 1
𝑥, 2 ≤ 𝑥 ≤ 4
3. Paso 1: Función básica 𝑦 = 𝑥 2
Paso 2: Traslación de 3 unidades hacia la izquierda 𝑦 = (𝑥 + 3)2
Paso 3: Traslación de 2 unidades hacia abajo 𝑦 = (𝑥 + 3)2 − 2
4. Para graficar use técnicas de graficación, además los puntos de corte con el eje 𝑥 son
(-1;0) y (5;0); corte con el eje 𝑦 es (0;1).
1.5 PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
|𝑥| ; 𝑥 < 0
1. Dada la función 𝑓 con regla de correspondencia 𝑓(𝑥) = {
. Trace su gráfica e
√𝑥 ; 0 ≤ 𝑥 < 9
Interprete y determine lo siguiente:
a. Dominio y rango
b. ¿Dónde están los ceros de la función?
c. ¿Cuáles son los intervalos donde la función es positiva y negativa?
𝑥 + 5 ; 𝑥 < −1
2
2. Dada la función h con regla de correspondencia ℎ(𝑥) = { 𝑥 ; −1 ≤ 𝑥 < 2 . Trace su gráfica e
1
;2 ≤ 𝑥
𝑥
Interprete y determine lo siguiente:
Profesores MA420
104
UPC – Departamento de Ciencias - Matemática Básica (MA420)
a.
b.
c.
d.
Dominio y rango
¿Dónde están los ceros de la función?
¿Cuáles son los intervalos donde la función es positiva y negativa?
¿Cuáles son los valores 𝑥 de tal qué ℎ(𝑥) = 3,5?
3. Utilice las técnicas de graficación para graficar paso a paso la siguiente función con regla de
correspondencia 𝑓(𝑥) = (𝑥 − 2)2 − 2.
1
4. Describa con sus palabras los pasos a seguir para que a partir de la gráfica de 𝑦 = x se grafique la
1
función 𝑦 = −3 + 𝑥+4.
RESPUESTAS PRACTIQUEMOS MÁS EN CASA
1. a. Dom(𝑓) = ]−∞; 9[ y Ran(𝑓) = [0; ∞[
b. El cero de la función es 0.
c. La función es positiva: ]−∞; 0[ y ]0; 9[
La función es negativa: no existe
2. a. Dom(𝑓) = ]−∞; ∞[ y Ran(𝑓) = ]−∞; 4[
b. Los ceros de la función son: −5 y 0
c. La función es positiva: ]−5; −1[ , [−1; 0[, ]0; 2[ y [2; ∞[
La función es negativa: ]−∞; −5[
d. Los valores de 𝑥 que hacen que la función ℎ(𝑥) = 3,5 son: −1,5 y √3,5
3. Paso 1: Función básica 𝑦 = 𝑥 2
Paso 2: Traslación de 2 unidades hacia la derecha 𝑦 = (𝑥 − 2)2
Paso 3: Traslación de dos unidades hacia abajo 𝑦 = (𝑥 − 2)2 − 2
1
4. Paso 1: Función básica 𝑦 = 𝑥
1
Paso 2: Traslación de 4 unidades hacia la izquierda 𝑦 = 𝑥+4
1
Paso 3: Traslación de 3 unidades hacia abajo 𝑦 = 𝑥+4 − 3
Profesores MA420
105
UPC – Departamento de Ciencias - Matemática Básica (MA420)
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Enlace
Determinar
la
regla
de
correspondencia de una función
seccionada a partir de su gráfica.
https://tinyurl.com/yxebovc8
Graficar una función seccionada
conociendo
su
regla
de
correspondencia.
https://tinyurl.com/y2ctul42
Construir una función seccionada.
https://tinyurl.com/y488926v
Construir una función seccionada
que modela la velocidad de un
móvil en función del tiempo.
https://tinyurl.com/y27lddwc
Código QR
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.:
Cengage Learning. (515 STEW/P 2017)
FUNCIONES BÁSICAS, SECCIONADAS Y TECNICAS DE GRAFICACIÓN: Revisar
páginas desde 159 hasta 162, 166-167 ejercicios 4, 5-11, 19, 20, 22, 24, 33-55.
Profesores MA420
106
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Técnicas de graficación
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante traza la gráfica de funciones
(incluyendo las seccionadas) utilizando las técnicas de graficación, demostrando responsabilidad y
capacidad de aprender por su propia cuenta.
CONTENIDO
MOTIVACIÓN
1.1.
Técnicas de graficación
• Reflexión con respecto al eje 𝑥
• Reflexión con respecto al eje 𝑦
• Alargamientos y compresiones verticales
1.2.
Practiquemos en clase
• Ejercicios
1.3.
Practiquemos más en casa
• Ejercicios
Profesores MA420
107
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Motivación
Existen diversos métodos para graficar funciones, como el método simple de tabulación (no siempre
adecuado) y otros más avanzados y precisos que utilizan conceptos de cálculo diferencial. También, a
partir de la gráfica de una función y transformaciones como la traslación, reflexión, alargamiento o
compresión de la gráfica es posible tener la gráfica de una nueva función de forma precisa y sobre todo
simple.
TÉCNICAS DE GRAFICACIÓN
Reflexión respecto al eje 𝒙
La gráfica con ecuación 𝑦 = −𝑓(𝑥) es el reflejo (como un espejo) de la gráfica de la ecuación 𝑦 = 𝑓(𝑥)
con respecto al eje 𝑥.
y = f (x)
y = - f (x)
Ejemplo: Usando las técnicas de graficación trace la gráfica de la función con regla de correspondencia:
𝑓(𝑥) = −|𝑥|
Solución:
Profesores MA420
108
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Paso 1: Función básica: 𝑓(𝑥) = |𝑥|
Paso 2: Reflexión respecto al eje 𝑥: 𝑓(𝑥) = −|𝑥|
Reflexión respecto al eje 𝒚
La gráfica con ecuación 𝑦 = 𝑓(−𝑥) es el reflejo (como un espejo) de la gráfica de la ecuación 𝑦 =
𝑓(𝑥) con respecto al eje 𝑦.
y = f (-x)
y = f (x)
Ejemplo: Usando las técnicas de graficación trace la gráfica de la función con regla de correspondencia:
𝑓(𝑥) = √−𝑥
Solución:
En este caso tenemos una reflexión con el eje 𝑦. Para obtener la gráfica de y = − x a partir de la
gráfica de 𝑦 = √𝑥 fijamos (por ejemplo) los valores 0 , − 1 y − 4 del eje 𝑥 y evaluamos de la siguiente
manera:
𝑥
0
𝑦 = √𝑥
𝑦 = √0 = 0
𝑦 = √−𝑥
𝑦 = √−0 = 0, así tenemos (0; 0)
1
𝑦 = √1 = 1
𝑦 = √−(−1) = 1, así tenemos (−1; 1)
4
𝑦 = √4 = 2
𝑦 = √−(−4) = 2, así tenemos (− 4; 2)
Este proceso lo podemos hacer mental. Pero es importante que conozcamos tres o más puntos por
donde pasa la función básica 𝑦 = √𝑥. Observe los puntos fijados en la gráfica siguiente:
Profesores MA420
109
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Alargamientos y compresiones verticales
✓ Si 𝑐 > 1, la gráfica de la ecuación 𝑦 = 𝑐 . 𝑓(𝑥) es un alargamiento vertical en un factor de c respecto
a la gráfica de 𝑦 = 𝑓(𝑥).
✓ Si 0 < 𝑐 < 1, la gráfica de la ecuación 𝑦 = 𝑐. 𝑓(𝑥) es una compresión vertical en un factor de c
respecto a la gráfica de 𝑦 = 𝑓(𝑥).
Ejemplo: Trace la gráfica de la función con regla de correspondencia: 𝑓(𝑥) = 2√𝑥
Solución:
En este caso tenemos un alargamiento vertical. Para obtener la gráfica de 𝑦 = 2√𝑥 a partir de la
gráfica de 𝑦 = √𝑥 fijamos (por ejemplo) los valores 0 , 1 y 4 del eje 𝑥 y evaluamos de la siguiente
manera:
𝑥
0
𝑦 = √𝑥
𝑦 = √0 = 0
1
𝑦 = √1 = 1
4
𝑦 = √4 = 2
𝑦 = 2√𝑥
𝑦 = 2√0 = 0, así tenemos (0; 0)
𝑦 = 2√1 = 2(1) = 2, así tenemos (1; 2)
𝑦 = 2√4 = 2(2) = 4, así tenemos (4; 4)
Este proceso lo podemos hacer mental. Pero es importante que conozcamos tres o más puntos por
donde pasa la función básica 𝑦 = √𝑥. Observe los puntos fijados en la gráfica siguiente:
Profesores MA420
110
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Ejemplo: Usando las técnicas de graficación trace la gráfica de la función con regla de correspondencia:
𝑓(𝑥) = −2(𝑥 + 1)2 + 5
Solución: Mostrar tres o más puntos de referencia para trazar la gráfica.
Paso 1: Función básica: 𝑦 = 𝑥 2
Paso 3: Alargamiento vertical de un factor 2:
𝑦 = 2(𝑥 + 1)2
Paso 2: Traslación horizontal de 1 unidades
hacia la izquierda: 𝑦 = (𝑥 + 1)2
Paso 4: Reflexión respecto al eje 𝑥:
𝑦 = −2(𝑥 + 1)2
Paso 5: Traslación vertical de 5 unidades hacia arriba: 𝑓(𝑥) =
−2(𝑥 + 1)2 + 5
En la última gráfica debemos hallar corte con los ejes coordenados
Corte con el eje 𝒙: (𝑦 = 0)
−2(𝑥 + 1)2 + 5 = 0
(𝑥 + 1)2 = 5/2 = 2,5
𝑥 + 1 = ±√2,5 ⇒ 𝑥1 = −1 − √2,5 ; 𝑥2 = −1 + √2,5
Por lo tanto, los puntos de corte con el eje 𝑥 son: (−1 − √2,5; 0) y
(−1 + √2,5; 0).
Corte con el eje 𝒚: (𝑥 = 0)
𝑦 = −2(0 + 1)2 + 5 = 3
Por lo tanto, los puntos de corte con el eje 𝑦 es: (0; 3)
Profesores MA420
111
UPC – Departamento de Ciencias - Matemática Básica (MA420)
PRACTIQUEMOS EN CLASE
1. Dadas las funciones con reglas de correspondencia:
1
a. 𝑓(𝑥) = 5 − (𝑥 + 4)2
b. 𝑔(𝑥) = 2√−𝑥
c. ℎ(𝑥) = − 𝑥+2 − 4
En cada una de ellas, describa los pasos que se deben seguir para graficar las funciones usando las
técnicas de graficación.
Nota:
✓ Comience identificando la función básica.
✓ En este ejercicio no debe graficar, solo debe describir cada uno de los pasos.
2. Usando las técnicas de graficación trace la gráfica de las siguientes funciones con reglas de
correspondencia:
a. 𝑓(𝑥) = 3 − |𝑥 + 2|
b. 𝑔(𝑥) = 2(𝑥 − 3)2 − 1
c. ℎ(𝑥) = 1 + √−𝑥
En la gráfica final calcule e indique los puntos de corte con los ejes coordenados.
3. Trace la gráfica de la función con regla de correspondencia: 𝑓(𝑥) = {
3 − |𝑥| si 𝑥 ≤ 1
2
𝑥−1
si 𝑥 > 1
En la gráfica final calcule e indique los puntos de corte con los ejes coordenados.
RESPUESTAS DE PRACTIQUEMOS EN CLASE
1. a. Paso 1: Función básica 𝑦 = 𝑥 2
Paso 2: Traslación de 4 unidades hacia la izquierda 𝑦 = (𝑥 + 4)2
Paso 3: Reflexión respecto al eje x 𝑦 = −(𝑥 + 4)2
Paso 4: Traslación de 5 unidades hacia arriba 𝑦 = 5 − (𝑥 + 4)2
b. Paso 1: Función básica 𝑦 = √𝑥
Paso 2: Reflexión al eje y 𝑦 = √−𝑥
Paso 3: Alargamiento vertical en un factor de 2 unidades 𝑦 = 2√−𝑥
1
c. Paso 1: Función básica 𝑦 = 𝑥
Paso 2: Traslación de 2 unidades hacia la izquierda 𝑦 =
1
Paso 3: Reflexión respecto al eje x 𝑦 = − 𝑥+2
1
𝑥+2
1
Paso 4: Traslación de 4 unidades hacia abajo 𝑦 = − 𝑥+2 − 4
2.
a. Para graficar use técnicas de graficación, además los puntos de corte con el eje 𝑥 son (-5;0) y
(0;1); el punto de corte con el eje 𝑦 es (0;1).
b. Para graficar use técnicas de graficación, además los puntos de corte con el eje 𝑥 son (2,29;0) y
(3,71;0); el punto de corte con el eje 𝑦 es (0;17).
c. Para graficar use técnicas de graficación, además el punto de corte con el eje 𝑦 es (0;1).
Profesores MA420
112
UPC – Departamento de Ciencias - Matemática Básica (MA420)
3. Para graficar use técnicas de graficación, además el punto de corte con el eje 𝑥 es (-3;0) y el punto
de corte con el eje 𝑦 es (0;3).
PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD
para asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1. Dadas las funciones con reglas de correspondencia:
a. 𝑓(𝑥) = 3(𝑥 − 2)2 − 1
b. 𝑔(𝑥) =
1
√−𝑥
2
+1
c. ℎ(𝑥) = −|𝑥 + 2| − 3
En cada una de ellas, describa los pasos que se deben seguir para graficar las funciones usando las
técnicas de graficación.
Nota:
✓ Comience identificando la función básica.
✓ En este ejercicio no debe graficar, solo debe describir cada uno de los pasos.
2. Usando las técnicas de graficación trace la gráfica de las siguientes funciones con reglas de
correspondencia:
b.
1
𝑓(𝑥) = 4 − 𝑥+2
b. 𝑔(𝑥) = 1 − 2(𝑥 + 1)2
c. ℎ(𝑥) = 2 − √−𝑥
En la gráfica final calcule e indique los puntos de corte con los ejes coordenados.
−(𝑥 + 3)2 ; 𝑥 < 1
3. Trace la gráfica de la función con regla de correspondencia: ℎ(𝑥) = {
−√𝑥 + 3 ; 1 ≤ 𝑥
En la gráfica final calcule e indique los puntos de corte con los ejes coordenados.
RESPUESTAS PRACTIQUEMOS MÁS EN CASA
1. a. Paso 1: Función básica 𝑦 = 𝑥 2
Paso 2: Traslación de 2 unidades hacia la derecha 𝑦 = (𝑥 − 2)2
Paso 3: Alargamiento vertical en un factor de 3 unidades 𝑦 = 3(𝑥 − 2)2
Paso 4: Traslación de 1 unidad hacia abajo 𝑦 = 3(𝑥 − 2)2 − 1
b. Paso 1: Función básica 𝑦 = √𝑥
Paso 2: Reflexión al eje y 𝑦 = √−𝑥
Paso 3: Traslación de 1 unidad a la derecha 𝑦 = √−𝑥 + 1
1
Paso 4: Compresión vertical en un factor de 1/2 unidades 𝑦 = √−𝑥 + 1
2
c. Paso 1: Función básica 𝑦 = |𝑥|
Paso 2: Traslación de 2 unidades hacia la izquierda 𝑦 = |𝑥 + 2|
Paso 3: Reflexión respecto al eje x 𝑦 = −|𝑥 + 2|
Paso 4: Traslación de 3 unidades hacia abajo 𝑦 = −|𝑥 + 2| − 3
2.
a. Para graficar use técnicas de graficación, además el punto de corte con el eje 𝑥 es (-1,75;0) y el
punto de corte con el eje 𝑦 es (0;3,5).
Profesores MA420
113
UPC – Departamento de Ciencias - Matemática Básica (MA420)
b. Para graficar use técnicas de graficación, además los puntos de corte con el eje 𝑥 son (-1,71;0)
y (-0,29;0); el punto de corte con el eje 𝑦 es (0; -1).
c. Para graficar use técnicas de graficación, el punto de corte con el eje 𝑥 es (-4;0) y el punto de
corte con el eje 𝑦 es (0;2)
3. Para graficar use técnicas de graficación, además los puntos de corte con el eje 𝑥 son (-3;0) y (9;0);
el punto de corte con el eje 𝑦 es (0; -9).
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Enlace
Trazar la gráfica de una función
usando las técnicas de
graficación.
https://tinyurl.com/y3dxw9xb
Describir los pasos que
permiten graficar una función
mediante las técnicas de
graficación.
https://tinyurl.com/y2gssphg
Graficar
una
función
seccionada usando técnicas de
graficación.
https://tinyurl.com/y4tstkbb
Graficar una función usando
técnicas de graficación.
https://tinyurl.com/y67hf53f
Profesores MA420
Código QR
114
UPC – Departamento de Ciencias - Matemática Básica (MA420)
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.:
Cengage Learning. (515 STEW/P 2017)
TÉCNICAS DE GRAFICACIÓN: Revisar páginas desde 198 hasta 203, Pág.
206 ejercicios: 1-16,19-28, Además, desde 207 hasta 209.
Profesores MA420
115
UPC - Área de Ciencias - Matemática Básica – Blended (MA420)
Función inyectiva e inversa - Operaciones con
funciones
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante aplica los conceptos sobre función
inyectiva, inversa y operaciones con funciones para solucionar ejercicios, demostrando responsabilidad y
capacidad de aprender por su propia cuenta.
CONTENIDO
MOTIVACIÓN
1.1. Función Inyectiva o uno a uno
• Criterios de la recta horizontal
• Ejemplos
1.2. Función Inversa
• Definición
• Principio de reflexión
• Regla de correspondencia de la función inversa
• Ejemplos
1.3. Operaciones con funciones
• Definición
• Ejemplos
1.4. Practiquemos en clase
• Ejercicios
1.5. Practiquemos más en casa
• Ejercicios
Profesores MA420
116
UPC - Área de Ciencias - Matemática Básica – Blended (MA420)
Motivación
En funciones, si tenemos dos variables A y B, y
determinamos que una es la variable independiente y la
otra es la variable dependiente se termina definiendo A
como una función de B o al revés, B como una función
de A. Por ejemplo, si las variables de un proceso son solo
cantidad producida de un bien (q), y el precio unitario
de venta de dicho bien (p), se puede definir p como una
función de q o al revés, q como una función de p. Esto,
bajo ciertas condiciones, determina dos funciones
denominadas inversas.
1.1.
FUNCIÓN INYECTIVA O UNO A UNO
• Criterio de la recta horizontal (CRH)
Una función f es inyectiva o uno a uno si y sólo si toda recta horizontal corta a su gráfica en a lo más un punto.
Figura 1
Observamos que cualquier recta horizontal, por donde
la tracemos, siempre va a intersectar en un solo punto
a la gráfica de la función. Por lo tanto, decimos, por el
criterio de la recta horizontal, 𝑓 es inyectiva.
Profesores MA420
Figura 2
Observamos que la recta horizontal trazada
intersecta en 2 puntos a la gráfica de la función.
Entonces, por el criterio de la recta horizontal, g
no es inyectiva.
117
UPC - Área de Ciencias - Matemática Básica – Blended (MA420)
1.2.
FUNCIÓN INVERSA
• Definición
Si 𝑓 es una función inyectiva (o uno a uno) con dominio 𝐷 y rango 𝑅 entonces la función inversa de 𝑓, denotada
por 𝑓 −1, es la función con dominio 𝑅 y rango 𝐷, definida mediante 𝑓 −1 (𝑏) = 𝑎 ⇔ 𝑓(𝑎) = 𝑏
NOTA:
De la definición, podemos concluir que: Dom(𝑓 −1 ) = Ran(𝑓); Ran(𝑓 −1 ) = Dom(𝑓)
• Principio de Reflexión
Los puntos (𝑎; 𝑏) y (𝑏; 𝑎) en el plano cartesiano satisfacen el principio de reflexión si son simétricos respecto a
la recta 𝑦 = 𝑥. En otras palabras, los puntos (𝑎; 𝑏) y (𝑏; 𝑎) se pueden ver como una reflexión uno del otro
respecto a la recta 𝑦 = 𝑥.
𝒴
y=x
(a; b)
(b; a)
𝒳
Figura 3: Reflexión de un punto
✓ El principio de reflexión proporciona un método para obtener la gráfica de 𝑓 −1 a partir de la gráfica de
𝑓. Es decir:
✓ El punto (𝑎; 𝑏) está sobre la gráfica de 𝑓 si y solo si el punto (𝑏; 𝑎) está sobre la gráfica de 𝑓 −1
✓ La gráfica de 𝑓 −1 se obtiene al reflejar la gráfica de 𝑓 respecto a la recta 𝑦 = 𝑥
Profesores MA420
118
UPC - Área de Ciencias - Matemática Básica – Blended (MA420)
𝒴
y=x
y = f (x)
y = f -1(x)
𝒳
Figura 4: Reflexión de la gráfica de una función
• Regla de correspondencia de la función inversa
Dada la función 𝑦 = 𝑓(𝑥), para determinar la regla de correspondencia para 𝑓 −1. Se debe seguir los siguientes
pasos:
Paso 1: Verifique que 𝑓 es inyectiva o uno a uno, para garantizar la existencia de 𝑓 −1 .
Paso 2: Escriba 𝑦 = 𝑓(𝑥). Luego despeje la variable 𝑥 en función de variable 𝑦.
Paso 3: Ahora escriba 𝑓 −1 (𝑥) en lugar de la variable 𝑥 y en lugar de la variable 𝑦, escriba 𝑥.
Paso 4: Determine el dominio para 𝑓 −1.
1.3.
OPERACIONES CON FUNCIONES
Es importante saber cómo una función se combina con otra función, pues es el primer paso para aplicar las
herramientas de cálculo. Dado que las funciones tienen su propia álgebra con base en las mismas operaciones
que se aplica a los números reales (suma, resta, multiplicación y división); entonces una forma de construir
nuevas funciones es aplicar estas operaciones utilizando las siguientes definiciones:
• Definición
Dadas las funciones 𝑓 y 𝑔 con dominios Dom(𝑓) y Dom(𝑔) respectivamente, talque Dom(𝑓) ∩ Dom(𝑔) ≠ ∅ y
con reglas de correspondencia 𝑓(𝑥) y 𝑔(𝑥) respectivamente, entonces las operaciones algebraicas de 𝑓 y 𝑔
están definidas mediante las siguientes reglas de correspondencia:
a. Suma:
▪
Regla de correspondencia: (𝑓 + 𝑔)(𝑥) = 𝑓(𝑥) + 𝑔(𝑥)
▪
Dominio: Dom(𝑓 + 𝑔) = Dom(𝑓) ∩ Dom(𝑔)
Profesores MA420
119
UPC - Área de Ciencias - Matemática Básica – Blended (MA420)
b. Resta:
▪
Regla de correspondencia: (𝑓 − 𝑔)(𝑥) = 𝑓(𝑥) − 𝑔(𝑥)
▪
Dominio: Dom(𝑓 − 𝑔) = Dom(𝑓) ∩ Dom(𝑔)
c. Producto:
▪
Regla de correspondencia: (𝑓. 𝑔)(𝑥) = 𝑓(𝑥). 𝑔(𝑥)
▪
Dominio: Dom(𝑓 ⋅ 𝑔) = Dom(𝑓) ∩ Dom(𝑔)
d. Cociente:
𝑓
𝑓(𝑥)
▪
Regla de correspondencia: (𝑔) (𝑥) = 𝑔(𝑥)
▪
Dominio: Dom ( ) = (Dom(𝑓) ∩ Dom(𝑔)) − {𝑥 ∈ 𝑅 ⁄𝑔(𝑥) = 0}
𝑓
𝑔
Nota 1: En todos los casos, el dominio de la nueva función consiste en la intersección del dominio de la función
𝑓 y el dominio de la función 𝑔; salvo el dominio de la función cociente que excluye los ceros del denominador.
1.4.
PRACTIQUEMOS EN CLASE
1. Demuestre gráficamente si las siguientes funciones son uno a uno.
a. 𝑓(𝑥) = |𝑥 + 2| − 3 con 𝑥 ∈ ]−∞; 2]
b. 𝑓(𝑥) = (𝑥 − 4)2 + 1 con 𝑥 ∈ ]−∞; 4[
2. Dada la gráfica de la función 𝑓, trace la gráfica de 𝑓 −1 en el mismo plano cartesiano. Además, calcule el valor
de 𝑓(1) y 𝑓 −1 (0) si existe en cada gráfica.
a.
b.
3. Dadas las funciones 𝑓 y 𝑔 con reglas de correspondencia:
▪ 𝑓(𝑥) = 4 − (𝑥 − 2)2 , definida en 𝑥 ∈ ]−∞; 2]
1
▪ 𝑔(𝑥) = 𝑥+2 − 3
Profesores MA420
120
UPC - Área de Ciencias - Matemática Básica – Blended (MA420)
En cada una:
a. Demuestre gráficamente que existe su función inversa.
b. Determine la regla de correspondencia de su función inversa y su dominio.
4. Dadas las funciones 𝑓 y 𝑔 con regla de correspondencia 𝑓(𝑥) = √𝑥 − 3 y 𝑔(𝑥) = 4 − 𝑥 2 con 𝑥 ∈ ]−1; 8[.
Determine el dominio y la regla de correspondencia: 𝑓 + 𝑔 y 𝑓. 𝑔. Además, calcule (𝑓 + 𝑔)(7).
5. Dadas las funciones 𝑓 y 𝑔 con regla de correspondencia 𝑓(𝑥) = √5 − 𝑥 y 𝑔(𝑥) = 𝑥 2 − 16
𝑔
𝑓
]−2; 8]. Determine el dominio y la regla de correspondencia:
y
𝑓
𝑔
con 𝑥 ∈
.
RESPUESTAS DE PRACTIQUEMOS EN CLASE
1. En cada una de las gráficas debe mostrar al menos tres puntos de referencia por donde pasa la gráfica.
a. De acuerdo con el criterio de la recta horizontal, la función 𝑓 no es inyectiva.
b. De acuerdo con el criterio de la recta horizontal, la función 𝑓 es inyectiva.
2.
a.
b.
3.
a. Por el criterio de la recta horizontal puede demostrar que f y 𝑔 son funciones inyectivas
entonces existe 𝑓 −1 y 𝑔−1 .
b.
𝑓 −1 (𝑥) = 2 − √4 − 𝑥 ,
Dom (𝑓 −1 ) = ]−∞, 4]
1
𝑔−1 (𝑥) = 𝑥+3 − 2
Dom(𝑔−1 ) = ℝ − {3}
4. (𝑓 + 𝑔)(𝑥) = √𝑥 − 3 + 4 − 𝑥 2 , Dom (𝑓 + 𝑔) = [3; 8[ , (𝑓 + 𝑔)(7) = −43
(𝑓. 𝑔)(𝑥) = (4 − 𝑥 2 )√𝑥 − 3 , Dom (𝑓. 𝑔) = [3; 8[
Profesores MA420
121
UPC - Área de Ciencias - Matemática Básica – Blended (MA420)
5.
𝑔
𝑥 2 −16
, Dom
√5−𝑥
(𝑓 ) = ]−2, 5[
𝑓
𝑔
√5−𝑥
, Dom
𝑥 2 −16
( ) = ]−2, 5] − {4}
(𝑓 ) (𝑥) =
( ) (𝑥) =
1.5.
𝑔
𝑓
𝑔
PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1. Dada la función inyectiva 𝑔 con regla de correspondencia: 𝑔(𝑥) = 3 − √𝑥 + 2
a. Determine la regla de correspondencia de 𝑔−1 e indique su dominio y su rango.
b. Determine el valor de: 𝑔(2) + 𝑔−1 (−1).
2. La figura muestra la gráfica de una función 𝑦 = 𝑓(𝑥):
Encuentre la gráfica de la inversa de la función. (Sugerencia: use el principio de reflexión)
3. Dada la función 𝑓 con regla de correspondencia 𝑓(𝑥) = −3 + √𝑥 + 2.
a. Demuestre que existe 𝑓 −1 .
b. Determine la regla de correspondencia de 𝑓 −1 , su dominio y rango.
c. Trace la gráfica de 𝑓 y 𝑓 −1 en un mismo plano.
4. Dada la función 𝑓 con regla de correspondencia 𝑓(𝑥) = (𝑥 − 1)2 + 1, definida en 𝑥 ∈ ]−∞; 1]
a. Demuestre que existe 𝑓 −1 .
b. Determine la regla de correspondencia de 𝑓 −1 , su dominio y rango.
c. Trace la gráfica de 𝑓 y 𝑓 −1 en un mismo plano, además calcule el valor de 𝑓 −1 (10) + 𝑓(−1).
5. Dadas las funciones 𝑓 y 𝑔 con regla de correspondencia 𝑓(𝑥) = √4 − 𝑥 2
y
𝑔(𝑥) = 2 − 3𝑥 + 𝑥 2.
𝑓
Determine el dominio y la regla de correspondencia: 𝑓 + 𝑔, 𝑓 − 𝑔, 𝑓. 𝑔 y 𝑔.
6. Dadas las funciones 𝑓 y 𝑔 con regla de correspondencia 𝑓(𝑥) = 𝑥 2 − 9𝑥 y 𝑔(𝑥) = √1 − 𝑥 2 . Determine el
𝑔
dominio y la regla de correspondencia 𝑓 .
Profesores MA420
122
UPC - Área de Ciencias - Matemática Básica – Blended (MA420)
RESPUESTAS DE PRACTIQUEMOS MÁS EN CASA
1.
a. 𝑔−1 (𝑥) = (𝑥 − 3)2 − 2, Dom (𝑔−1 ) = ]−∞; 3] 𝑦 Ran(𝑔−1 ) = [−2; +∞[
b. 15
2.
c.
3. a.
Por el criterio de la recta horizontal,
f es inyectiva entonces existe 𝑓 −1 .
𝐛.
𝑓 −1 (𝑥) = (𝑥 + 3)2 − 2
Dom (𝑓 −1 ) = [−3, +∞[
Ran(𝑓 −1 ) = [−2, +∞[
4.
a.
La función f es uno a uno, por el criterio de la recta horizontal. Por lo tanto, existe la función inversa.
Profesores MA420
123
UPC - Área de Ciencias - Matemática Básica – Blended (MA420)
b. 𝑓 −1 (𝑥) = 1 − √𝑥 − 1 , Dom (𝑓 −1 ) = [1; +∞[ 𝑦 Ran (𝑓 −1 ) = ]−∞; 1]
c.
5.
(𝑓 + 𝑔)(𝑥) = √4 − 𝑥 2 + 2 − 3𝑥 + 𝑥 2
(𝑓 − 𝑔)(𝑥) = √4 − 𝑥 2 − 2 + 3𝑥 − 𝑥 2
(𝑓. 𝑔)(𝑥) = (√4 − 𝑥 2 )(2 − 3𝑥 + 𝑥 2 )
Dom(𝑓 + 𝑔) = Dom(𝑓 − 𝑔) = Dom(𝑓. 𝑔) = [−2; 2]
𝑓
√4−𝑥 2
𝑓
, Dom (𝑔)
2−3𝑥+𝑥 2
𝑔
𝑓
√1−𝑥 2
𝑔
, Dom ( )
𝑥 2 −9𝑥
𝑓
(𝑔) (𝑥) =
= [−2; 2[−{1}
6.
( ) (𝑥) =
Profesores MA420
= [−1; 1] − {0}
124
UPC - Área de Ciencias - Matemática Básica – Blended (MA420)
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Dada la regla de correspondencia
de una función 𝑓, determinar la
regla de correspondencia y el
dominio de la función inversa 𝑓 −1.
Dada la regla de correspondencia
de una función 𝑓, determinar la
regla de correspondencia y el
dominio de la función inversa 𝑓 −1.
Determinar
la
regla
de
correspondencia y el dominio de
una suma, resta y multiplicación de
funciones.
Enlace
Código QR
https://bit.ly/3sOJYeV
https://cutt.ly/UjBmIvO
https://bit.ly/2Y7HKsX
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
FUNCIÓN INYECTIVA Y FUNCIÓN INVERSA: Revisar páginas desde 219 hasta 227
OPERACIONES CON FUNCIONES: Revisar páginas, desde 210 al 212, y de la página
216 a 217.
Profesores MA420
125
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Composición de funciones
LOGRO DE LA SESIÓN DE CLA
SE: Al finalizar la sesión, el estudiante analiza el concepto de composición de funciones y los aplica en la
resolución de ejercicios, demostrando responsabilidad y capacidad de aprender por su propia cuenta.
CONTENIDO
MOTIVACIÓN
1.1. Función composición
• Definición
1.2. Practiquemos en clase
• Ejercicios
1.3. Practiquemos más en casa
• Ejercicios
Profesores MA420
126
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Motivación
De dos funciones a una sola
Tenemos un problema: necesitamos comprar equipos especializado en hacer vibrar el concreto para que no deje
vacíos al vaciarlo en un encofrado, pero esos equipos sólo lo venden en dólares, ¿cómo resolveríamos ese
problema?, pues al parecer es un problema de solución sencilla:
1. Compramos dólares
2. Con esos dólares, compramos los equipos
Cada uno de estos pasos se puede modelar con una función, la función 𝑓 podría ser la compra de los dólares
tomando en cuenta el valor de la compra del dólar y la segunda función podríamos modelarla con la función 𝑔
que sería el costo con los impuestos que tendríamos que pagar. ¿Se podrá hacer esta operación con una sola
función equivalente, pero con su equivalente en soles?
En esta sección se estudia una forma muy importante de combinar dos funciones para obtener una nueva
función.
1.1.
COMPOSICIÓN DE FUNCIONES
Ahora consideremos una forma muy importante de combinar dos funciones para obtener una nueva función.
Suponga que 𝑓(𝑥) = √𝑥 y 𝑔(𝑥) = 𝑥 2 + 1. Podemos definir una nueva función ℎ como.
ℎ(𝑥) = 𝑓(𝑔(𝑥)) = 𝑓(𝑥 2 + 1) = √𝑥 2 + 1
La función ℎ está formada por las funciones 𝑓 y 𝑔 en una forma interesante: dado un número 𝑥, primero le
aplicamos la función 𝑔 y luego aplicamos 𝑓 al resultado. En otras palabras, obtenemos la regla ℎ al aplicar la
regla 𝑔 y luego la regla 𝑓. La figura 1 muestra un diagrama de máquina para ℎ.
x
entrada
g
x2 + 1
f
x2 +1
salida
Figura 1. La máquina ℎ está compuesta de la máquina 𝑔 y luego por la máquina 𝑓.
Profesores MA420
127
UPC – Departamento de Ciencias - Matemática Básica (MA420)
•
Definición
Dadas las funciones𝑓 y 𝑔, tal que Dom(𝑓) ∩ Ran(𝑔) ≠ ∅. La composición 𝑓 de 𝑔, denotada 𝑓 ∘ 𝑔 se define
mediante la siguiente regla de correspondencia:
(𝑓 ∘ 𝑔)(𝑥) = 𝑓(𝑔(𝑥))
Donde: Dom(𝑓 ∘ 𝑔) = {𝑥 ∈ 𝑅 ⁄𝑥 ∈ Dom(𝑔) ∧ 𝑔(𝑥) ∈ Dom(𝑓)}
La definición anterior se puede representar gráficamente de la siguiente forma:
Figura 2. Esquema gráfico de la composición de funciones
De la figura 2, se puede interpretar que la composición de funciones 𝑓 ∘ 𝑔 es un camino inmediato que lleva los
valores del dominio de 𝑔 al rango de 𝑓. Para que esto suceda, 𝑥 debe estar en el dominio de 𝑔 y a su vez 𝑔(𝑥)
debe estar en el dominio de 𝑓.
Observación 1:
✓ La composición 𝑔 de 𝑓, denotada 𝑔 ∘ 𝑓, se define de manera similar.
✓ En la mayoría de los casos 𝑓 ∘ 𝑔 y 𝑔 ∘ 𝑓 son funciones distintas.
1.2.
PRACTIQUEMOS EN CLASE
1. Dadas las funciones 𝑓 y 𝑔 con regla de correspondencia 𝑓(𝑥) = 𝑥 + 7 con 𝑥 ∈ ]−4; 9] y 𝑔(𝑥) = −𝑥 +
1 con 𝑥 ∈ ]−7; 7]. Determine el dominio y la regla de correspondencia de 𝑓 ∘ 𝑔 y 𝑔 ∘ 𝑓.
2. Dadas las funciones 𝑔 y ℎ con regla de correspondencia 𝑔(𝑥) = 𝑥 2 − 7 con 𝑥 ∈ ]1; 5] y ℎ(𝑥) = √𝑥 − 2.
Determine el dominio y la regla de correspondencia de 𝑔 ∘ ℎ y ℎ ∘ 𝑔.
3. Dadas las funciones 𝑓 y 𝑔 con regla de correspondencia 𝑓(𝑥) = √25 − 𝑥 2 y 𝑔(𝑥) = 4 + 𝑥 con 𝑥 ∈
[−2: +∞[. Determine la regla de correspondencia y dominio de 𝑓 ∘ 𝑔. Además, calcule (𝑓 ∘ 𝑔)(2) sí
existe.
Profesores MA420
128
UPC – Departamento de Ciencias - Matemática Básica (MA420)
4. Dadas las funciones 𝑓 y 𝑔 con regla de correspondencia 𝑓(𝑥) = 𝑥 2 − 9 con 𝑥 ∈ ]0; 3] y 𝑔(𝑥) = √𝑥 + 5.
Determine la regla de correspondencia y dominio de: 𝑓 ∘ 𝑔 y 𝑔 ∘ 𝑓. Además, calcule (𝑓 ∘ 𝑔)(−5) y
(𝑔 ∘ 𝑓)(2,5) sí existen.
RESPUESTAS DE PRACTIQUEMOS EN CLASE
1.
Dom(𝑓 ∘ 𝑔) =] − 7; 5[ ; (𝑓 ∘ 𝑔)(𝑥) = −𝑥 + 8
Dom(𝑔 ∘ 𝑓) = ]−4; 0] ; (𝑔 ∘ 𝑓)(𝑥) = −𝑥 − 6
2.
(𝑔 ∘ ℎ)(𝑥) = 𝑥 − 9 ; Dom(𝑔 ∘ ℎ) =]3; 27]
(ℎ ∘ 𝑔)(𝑥) = √𝑥 2 − 9 ; Dom(ℎ ∘ 𝑔) = [3; 5]
3.
(𝑓 ∘ 𝑔)(𝑥) = √9 − 8𝑥 − 𝑥 2 ; Dom(𝑓 ∘ 𝑔) = [−2; 1]
(𝑓 ∘ 𝑔)(2) no existe, pues 2 ∉ Dom(𝑓 ∘ 𝑔)
4.
(𝑓 ∘ 𝑔)(𝑥) = 𝑥 − 4 ; Dom(𝑔 ∘ 𝑓) = ]−5; 4]
(𝑔 ∘ 𝑓)(𝑥) = √𝑥 2 − 4 ; Dom(𝑔 ∘ 𝑓) = [2; 3]
(𝑓 ∘ 𝑔)(−5) no existe, pues −5 ∉ Dom(𝑓 ∘ 𝑔)
(𝑔 ∘ 𝑓)(2,5) = 1,5 sí existe, pues 2,5 ∈ Dom(𝑔 ∘ 𝑓)
1.3.
PRACTIQUEMOS MAS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1.
Dadas las funciones 𝑓 y 𝑔 con regla de correspondencia 𝑓(𝑥) = 2 − 𝑥 2 con Dom(𝑓) =] − 3; 2[ y
𝑔(𝑥) = √1 − 𝑥. Determine el dominio y la regla de correspondencia de la función 𝑔 ∘ 𝑓. Además,
calcule (𝑔 ∘ 𝑓)(0) sí existe.
2.
Dadas las funciones 𝑔 y ℎ con regla de correspondencia 𝑔(𝑥) = 2𝑥 2 − 7 y ℎ(𝑥) = √𝑥 − 1. Determine
la regla de correspondencia y dominio de: ℎ ∘ 𝑔 y 𝑔 ∘ ℎ.
3.
Dadas las funciones 𝑓 y 𝑔 con regla de correspondencia 𝑓(𝑥) = 2 − 𝑥 y 𝑔(𝑥) = 𝑥 2 − 2. Determine
el valor de 𝑏 si se cumple que: ( 𝑔 ∘ 𝑓)(𝑏) + (𝑓 ∘ 𝑔)(𝑏) = −2
RESPUESTAS DE PRACTIQUEMOS MÁS EN CASA
1.
(𝑔 ∘ 𝑓)(𝑥) = √𝑥 2 − 1 ; Dom(𝑔 ∘ 𝑓) = ]−3; −1] ∪ [1; 2[
(𝑔 ∘ 𝑓)(0) no existe, pues 0 ∉ Dom(𝑔 ∘ 𝑓)
Profesores MA420
129
UPC – Departamento de Ciencias - Matemática Básica (MA420)
2.
Dom(ℎ ∘ 𝑔) = ]−∞; −2] ∪ [2; +∞[; (ℎ ∘ 𝑔)(𝑥) = √2𝑥 2 − 8
Dom(𝑔 ∘ ℎ) = [1; +∞[ ; (𝑔 ∘ ℎ)(𝑥) = 2𝑥 − 9
3.
𝑏=2
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Determinar
la
regla
de
correspondencia y el dominio de la
composición
de
funciones
(método práctico).
Determinar
la
regla
de
correspondencia y el dominio de
composición de funciones (usando
la definición).
Enlace
Código QR
https://cutt.ly/ejBQKI4
https://cutt.ly/hjB4PmC
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
COMPOSICIÓN DE FUNCIONES: Revisar páginas, desde 212 al 217.
Profesores MA420
130
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Función cuadrática y problemas de
optimización
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante analiza el concepto de función cuadrática
y lo aplica en la resolución de ejercicios y problemas de optimización, demostrando responsabilidad y
capacidad de aprender por su propia cuenta.
CONTENIDO
MOTIVACIÓN
1.1. Motivación
1.2. Función cuadrática
• Definición
• Valor máximo o mínimo absoluto
1.3. Practiquemos en clase
• Ejercicios
• Problemas
1.4. Practiquemos más en casa
• Ejercicios
• Problemas
Profesores MA420
131
UPC – Departamento de Ciencias - Matemática Básica (MA420)
MOVIMIENTO VERTICAL, EN CAÍDA LIBRE
1.1.
Motivación
Desde la época de Galileo Galilei (1564-1642) y de Isaac Newton (1642-1727), se había entendido bien el
movimiento vertical de un cuerpo en caída libre. La velocidad vertical y la posición vertical (altura) de un cuerpo
en caída libre (como función del tiempo) son aplicaciones clásicas de funciones lineales y cuadráticas.
La altura ℎ y la velocidad vertical 𝑣 de un objeto en caída
libre están dadas por
1
ℎ(𝑡) = − 𝑔𝑡 2 + 𝑣0 𝑡 + ℎ0 ,
2
donde t es el tiempo (en segundos), 𝑔 ≈ 32 pies/s2 ≈
9,8 m/s2 es la aceleración debida a la gravedad, 𝑣0 es la
velocidad vertical inicial del objeto y ℎ0 es su altura inicial.
Esta fórmula no toma en cuenta la resistencia del aire y
los dos valores dados para 𝑔 son válidos al nivel del mar.
1.2.
FUNCIÓN CUADRÁTICA
Una función cuadrática es una función 𝑓 con regla de correspondencia 𝑓(𝑥) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 , donde 𝑎; 𝑏 𝑦 𝑐
son constantes y 𝑎 ≠ 0.
Cualquier función cuadrática de la forma 𝑓(𝑥) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐, con 𝑎 ≠ 0, puede escribirse en la forma
normal.
𝑓(𝑥) = 𝑎(𝑥 − ℎ)2 + 𝑘
−𝑏
La gráfica de una función cuadrática f es una parábola de vértice (ℎ; 𝑘), donde ℎ = 2𝑎 y 𝑘 = 𝑓(ℎ).
Profesores MA420
132
UPC – Departamento de Ciencias - Matemática Básica (MA420)
❖ Se abre hacia arriba si a > 0.
El valor del mínimo
absoluto
❖ Se abre hacia abajo si a < 0.
El valor del máximo
absoluto
Valor del máximo o mínimo absoluto de una función cuadrática
Sea 𝑓 una función cuadrática con forma normal 𝑓(𝑥) = 𝑎(𝑥 − ℎ)2 + 𝑘. El valor máximo o mínimo de 𝑓 ocurre
en 𝑥 = ℎ.
❖ Si 𝑎 > 0, entonces el valor mínimo absoluto de 𝑓 es 𝑓(ℎ) = 𝑘 y ocurre en ℎ.
❖ Si 𝑎 < 0, entonces el valor máximo absoluto de 𝑓 es 𝑓(ℎ) = 𝑘 y ocurre en ℎ.
Nota: Los ceros de la función cuadrática 𝑓, existen si
∆= 𝑏 2 − 4𝑎𝑐 ≥ 0, y ocurren en: 𝑥 =
−𝑏 ± √𝑏2 − 4𝑎𝑐
2𝑎
Donde:
𝑥1 =
−𝑏−√𝑏2 −4𝑎𝑐
2𝑎
Profesores MA420
; 𝑥2 =
−𝑏+√𝑏2 −4𝑎𝑐
2𝑎
133
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Observación: El eje simetría de la parábola es la recta vertical de ecuación 𝑥 = ℎ.
1.3.
PRACTIQUEMOS EN CLASE
1. Dada las siguientes funciones con regla de correspondencia:
a. 𝑓(𝑥) = 2𝑥 2 − 8𝑥 + 1
b. 𝑡(𝑥) = −0,5𝑥 2 + 5𝑥 − 5
En cada una de ellas, determine máximo o mínimo absoluto y exprese en su forma normal. Luego, trace su
gráfica calculando e indicando los puntos de corte con los ejes coordenados.
2. La figura muestra la gráfica de una función cuadrática 𝑓 , a partir de
ella determine:
a. Las coordenadas del vértice.
b. Si 𝑓(−5) = 3, determine la regla de correspondencia de la
función 𝑓, su dominio restringido y rango.
c. El valor de 𝑓(−3,5) y el valor de 𝑥 tal que 𝑓(𝑥) = 2.
3. La utilidad 𝑈 en dólares que se genera al vender 𝑥 mesas de dibujo está dado por la función con regla de
correspondencia 𝑈(𝑥) = −9900 + 50𝑥 − 0,0025𝑥 2 ; 𝑥 ∈ ]200; 19800[.
¿Cuál es la utilidad máxima y cuántas mesas de dibujo se deben vender para generar esta ganancia?
4. Una empresa que se dedica a la fabricación de puertas de 620 cm
de perímetro; utiliza un tablón rectangular para el panel central y
tres listones para el marco de una puerta de 10cm de ancho (lados
laterales) y 15 cm (lado superior), como se muestra en la figura.
a. Determine una función que permita expresar el área del panel
central de la puerta, en función de 𝑥 y su dominio restringido.
b. Determine las dimensiones del panel central de la puerta de
área máxima y el área máxima.
Profesores MA420
134
UPC – Departamento de Ciencias - Matemática Básica (MA420)
RESPUESTAS DE PRACTIQUEMOS EN CLASE
1.
𝐚. V = (2; −7); 𝑓(𝑥) = 2(𝑥 − 2)2 − 7 tiene mínimo absoluto en -7.
𝐛. V = (5; 7,5); 𝑓(𝑥) = −0,5(𝑥 − 5)2 + 7,5 tiene máximo absoluto en 7,5.
2.
3.
4.
a. 𝑉 = (−2; 5)
2
b. 𝑓(𝑥) = − 9 (𝑥 + 2)2 + 5; 𝐷𝑜𝑚(𝑓) = [−6,743 … ; 0]; 𝑅𝑎𝑛(𝑓) = [0; 5]
c. 𝑓(−3,5) = 4,5 y para que 𝑓(𝑥) = 2,5 : 𝑥 = −5,574 …
La ganancia máxima es 240 100 dólares y se logra al vender 10 000 mesas de dibujo.
𝐚. 𝑓(𝑥) = −𝑥 2 + 275𝑥; Dom(𝑓) = ]0; 275[
b. El ancho y largo del panel central de área máxima es 137,5 𝑐𝑚 respectivamente; y el área máxima
es 18906,25 𝑐𝑚2 .
PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1. Dada las siguientes funciones con regla de correspondencia:
a. 𝑓(𝑥) = 3𝑥 2 + 12𝑥 − 3
c. 𝑓(𝑥) = −0,6𝑥 2 + 3𝑥 + 5
b. 𝑓(𝑥) = −𝑥 2 + 2𝑥 + 5
Profesores MA420
d. 𝑓(𝑥) = 0,2𝑥 2 + 2𝑥 + 15
135
UPC – Departamento de Ciencias - Matemática Básica (MA420)
En cada una de ellas, determine las coordenadas del vértice, el extremo absoluto y además exprese la función
en su forma normal. Luego, trace su grafica calculando e indicando los puntos de corte con los ejes
coordenados.
1
2. Dada la función 𝑓 con regla de correspondencia 𝑓(𝑥) = − 4 (𝑥 − 4)2 + 8. Trace la gráfica de 𝑓 en el primer
cuadrante (incluye los ejes coordenados) y determine extremo absoluto si existe.
3. Un agricultor tiene 1500 metros de material para construir una cerca. Quiere cercar un terreno rectangular
que colinda con un río a lo largo del cual no se requiere cercar. Sea x el lado del terreno, paralelo al río.
a. Determine una función A que permita expresar el área del terreno rectangular, en términos de x.
b. Calcula las dimensiones del terreno para que su área sea máxima y cuánto mide el área máxima.
4. Un Ingeniero dispone de 3600 metros de cerca para la construcción de un supermercado que se dividirá en
tres zonas según la clasificación de la mercadería a vender, como se muestra en la figura.
Las zonas de abarrotes y ropa son cuadradas y de igual longitud, y la zona de artefactos es rectangular.
a. Halle una función que permita determinar el área de la zona de artefactos, en función de uno de sus
lados.
b. Determine las dimensiones de la zona de artefactos para que el área sea máxima y el área máxima
respectiva.
RESPUESTAS PRACTIQUEMOS MÁS EN CASA
1.
𝐚. V = (−2; −15); 𝑓(𝑥) = 3(𝑥 + 2)2 − 15 el mínimo absoluto es -15.
𝐛. V = (1; 6); 𝑓(𝑥) = −(𝑥 − 1)2 + 6 el máximo absoluto es 6.
𝐜. V = (2,5; 8,75); 𝑓(𝑥) = −0,6(𝑥 − 2,5)2 + 8,75 el máximo absoluto es 8,75.
𝐝. V = (−5; 10); 𝑓(𝑥) = −0,2(𝑥 + 5)2 + 10 , el mínimo absoluto es 10.
2.
El máximo absoluto es: 8.
3.
𝐚. 𝐴(𝑥) = −0,5𝑥 2 + 750𝑥; Dom(𝑓) =]0; 1 500[
𝐛. El área máxima del terreno es 281 250 𝑚2 y su ancho mide 375 𝑚 y su largo 750 𝑚.
Profesores MA420
136
UPC – Departamento de Ciencias - Matemática Básica (MA420)
4.
𝐚. 𝐴(𝑥) = −4𝑥 2 + 1800𝑥; Dom(𝐴) = ]0; 450 [
𝐛. Las dimensiones del área de artefactos son 225 metros de ancho y 900 metros de largo y el área
máxima es 202 500 m2 .
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Determinar la función cuadrática
que permite calcular el área de un
compartimiento en función de uno
de sus lados, las dimensiones de un
compartimiento y el área máxima.
Calcular
la
altura máxima
alcanzada por la pelota y en qué
tiempo ocurre.
Determinar la función cuadrática
que permite calcular el área del
terreno en función de uno de sus
lados, las dimensiones y el área
máxima.
Enlace
Código QR
https://tinyurl.com/y2o99wwo
https://tinyurl.com/y366s25z
https://tinyurl.com/y4pse4dc
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
FUNCIÓN CUADRÁTICA Y PROBLEMAS DE OPTIMIZACIÓN: Revisar páginas desde
246 hasta Página 253.
Pág. 251 – 253, ejercicios 9 al 24, 51 al 65.
Profesores MA420
137
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Ecuación exponencial y logarítmica
Función exponencial
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante interpreta de forma gráfica y algebraica el
concepto de función exponencial y resuelve ecuaciones exponenciales y logarítmicas, demostrando
responsabilidad y capacidad de aprender por su propia cuenta.
CONTENIDO
1.1. Ecuación exponencial y logarítmica
Propiedades
MOTIVACIÓN
1.2. Función exponencial
• Definición de función exponencial
• Gráfica de funciones exponenciales
• Definición de la función exponencial natural
1.3. Practiquemos en clase
• Ejercicios
1.4. Practiquemos más en casa
• Ejercicios
Profesores MA420
138
UPC – Departamento de Ciencias - Matemática Básica (MA420)
ECUACIÓN EXPONENCIAL Y LOGARÍTMICA
En la ecuación 3 = 2𝑥+1 , intente despejar la variable 𝑥. Queda claro que tenemos la necesidad de conocer el
siguiente concepto.
Definición: Un logaritmo es el exponente al que está elevado un número positivo 𝑏 llamado base, donde
0 < 𝑏 ≠ 1.
Ejemplo 1:
➢ 30 = 7𝑥 : significa que 𝑥 es el logaritmo en base 7 de 30, sin embargo, en este caso necesitamos usar una
calculadora para poder saber el valor de 𝑥.
Lo dicho anteriormente, se puede escribir de la siguiente manera:
➢ 30 = 7𝑥 ⇔ 𝑥 = log 7 ( 30) = 1,747 ⋯ Valor encontrado con una calculadora.
Actualmente, todas las calculadoras científicas tienen a los logaritmos dentro de sus opciones de cálculo.
Conclusión: Hay una relación de ida y vuelta entre los logaritmos y las exponenciales vistas anteriormente, la
cual formulamos de la siguiente manera:
𝒚 = 𝐥𝐨𝐠 𝒃(𝒙) ⇔ 𝒙 = 𝒃𝒚 --- (I)
Donde:
➢ 𝑏: se llama base y es 0 < 𝑏 ≠ 1
➢ 𝑥: es un número real positivo, es decir 𝑥 > 0
LEYES DE LOS LOGARTIMOS:
✓
✓
✓
✓
✓
Si 𝑏 = 10, denotaremos el logaritmo de la siguiente manera: 𝑦 = 𝑙𝑜𝑔( 𝑥)
Si 𝑏 = 𝑒, denotaremos el logaritmo como: 𝑦 = ln( 𝑥) y lo llamaremos logaritmo natural.
log 𝑏 ( 1) = 0 Por ejemplo: log 3 ( 1) = log( 1) = ln( 1) = 0 (compruebe con su calculadora)
log 𝑏 ( 𝑏) = 1 Por ejemplo: log 5( 5) = log( 10) = ln( 𝑒) = 1 (compruebe con su calculadora)
log 𝑏 ( 𝑏 𝑥 ) = 𝑏 log𝑏(𝑥) = 𝑥
Profesores MA420
139
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Para las siguientes propiedades consideremos 𝐴, 𝐵, 𝑐 números reales con 𝐴 > 0 y 𝐵 > 0
✓ Regla del producto: log 𝑏 ( 𝐴 ⋅ 𝐵) = log 𝑏 ( 𝐴) + log 𝑏 ( 𝐵)
𝐴
𝐵
✓ Regla del cociente: log 𝑏 ( ) = log 𝑏 ( 𝐴) − log 𝑏 ( 𝐵)
✓ Regla de la potencia: log 𝑏 ( 𝐴𝑐 ) = 𝑐 ⋅ log 𝑏 ( 𝐴)
ECUACIÓN LOGARÍTMICA
Una ecuación logarítmica es aquella en la cual la variable está en el argumento del logaritmo (este argumento
debe ser siempre positivo). Por ejemplo,
log 3 (𝑥 − 2) + 5 = 6
Para resolver una ecuación logarítmica, se recomienda tener en cuenta los siguientes pasos.
✓ Determine el CVA de la ecuación.
CVA = {𝑥 ∈ ℝ/ 𝑥 − 2 > 0} = ]2; +∞[
✓ Aísle las expresiones con logaritmos en un lado de la ecuación, podría ser necesario combinar primero
los términos de logaritmo usando algunas propiedades.
log 3 (𝑥 − 2) = 1
La variable 𝑥 presenta una dificultad porque está en el argumento. Para resolver esta dificultad, aplicamos
la propiedad (I) de los logaritmos:
✓ Aplicando la propiedad (I) de Logaritmo,
𝑥 − 2 = 31
✓ Despeje la variable.
𝑥 =2+3=5
✓ Verifique que los valores obtenidos pertenezcan al conjunto de valores admisibles.
𝑥 = 5 ∈ CVA
CS = {5}
Ejemplo: Determine el conjunto de valores admisibles (CVA) y conjunto de solución (CS) de las siguientes
ecuaciones:
a. ln(𝑥) + ln(𝑥 + 3) = 2 ln(𝑥 + 1)
b. log 9(𝑥 + 1) + log 9 9(𝑥 + 1) = 2
a. ln(𝑥) + ln(𝑥 + 3) = 2 ln(𝑥 + 1)
Solución:
CVA = {𝑥 ∈ ℝ/𝑥 > 0 ∧ 𝑥 + 3 > 0 ∧ 𝑥 + 1 > 0}
CVA = {𝑥 ∈ ℝ/𝑥 > 0 ∧ 𝑥 > −3 ∧ 𝑥 > −1}
CVA = ]0; +∞[
Resolviendo la ecuación
ln(𝑥) + ln(𝑥 + 3) = 2 ln(𝑥 + 1)
ln[(𝑥)(𝑥 + 3)] = ln(𝑥 + 1)2
⇒ 𝑥 2 + 3𝑥 = 𝑥 2 + 2𝑥 + 1 ⇒ 𝑥 = 1 ∈ CVA
Por lo tanto CS = {1}
Profesores MA420
140
UPC – Departamento de Ciencias - Matemática Básica (MA420)
𝐛. log 9 (𝑥 + 1) + log 9 9(𝑥 + 1) = 2
Solución:
CVA = {𝑥 ∈ ℝ/𝑥 + 1 > 0 ∧ 9(𝑥 + 1) > 0}
CVA = {𝑥 ∈ ℝ/𝑥 > −1}
CVA = ]−1; +∞[
Resolviendo la ecuación
log 9 (𝑥 + 1) + log 9 9(𝑥 + 1) = 2
log 9 [(𝑥 + 1)9(𝑥 + 1)] = 2
(𝑥 + 1)2 9 = 92 ⇒ (𝑥 + 1)2 = 9
⇒ 𝑥 + 1 = 3 ˅ 𝑥 + 1 = −3 ⇒ 𝑥 = 2 ∈ 𝐶𝑉𝐴 ˅ 𝑥 = −4 ∉ CVA
Por lo tanto CS = {2}
ECUACIÓN EXPONENCIAL
Recuerde la propiedad 0 < 𝑏 ≠ 1, 𝑏 𝑥 > 0, es decir, siempre es positiva y nunca se anula.
Una ecuación exponencial es aquella en la que la variable está en el exponente. Por ejemplo:
3𝑥 + 5 = 9
✓ Traslade el término exponencial a un lado de la ecuación.
3𝑥 = 4
La variable x presenta una dificultad porque está en el exponente. Para resolver esta dificultad, aplicamos la
propiedad (I) de los logaritmos:
✓ Tomamos el logaritmo de cada lado y luego usamos la propiedad (IV) de Logaritmos para “bajar x” del
exponente.
𝑥 = log 3 4
✓ Finalmente: CS = {1,26 … } (compruebe con su calculadora)
Ejemplo: Determine el conjunto de valores admisibles (CVA) y conjunto de solución (CS) de las siguientes
ecuaciones:
a.
3𝑥𝑒 𝑥 + 𝑥 2 𝑒 𝑥 = 0
b.
6𝑥 − 61−𝑥 = 8
a. 3𝑥𝑒 𝑥 + 𝑥 2 𝑒 𝑥 = 0
Solución:
𝐶𝑉𝐴 = ℝ
Factorizando
3𝑥𝑒 𝑥 + 𝑥 2 𝑒 𝑥 = 0
𝑥(𝑥 + 3)𝑒 𝑥 = 0 ⇒ 𝑥 = 0
⇒ 𝑥 = 0 ∨ 𝑥 = −3
Por lo tanto, CS = {−3; 0}
Si: a b = 0 a = 0 b = 0
∨
𝐛. 6𝑥 − 61−𝑥 = 8
Solución: CVA = ℝ
6
Descomponemos: 6𝑥 − 6𝑥 = 8
𝑥+3=0
∨
𝑒 𝑥 = 0(No existe solución porque:𝑒 𝑥 > 0, ∀𝑥 ∈ ℝ)
6
Haciendo: 𝑎 = 6𝑥 obtenemos: 𝑎 − 𝑎 = 8
𝑎 = −0,69041 … → 6𝑥 = −0,69041 → 6𝑥 > 0(No existe solución)
→ 𝑎2 − 8𝑎 − 6 = 0 → {
𝑎 = 8,69042 … . → 6𝑥 = 8,69042 → 𝑥 = 1,206 …
Por lo tanto, CS = {1,206 … }
Profesores MA420
141
UPC – Departamento de Ciencias - Matemática Básica (MA420)
PROCESO DE FABRICACIÓN DEL ACERO Y LAMINACIÓN EN CALIENTE
MOTIVACIÓN
El acero1 es la columna vertebral de la industria gracias a su
legendaria fortaleza, desde rascacielos a puentes, de
artefactos eléctricos a automóviles, hidroeléctrica, torres
de electricidad y todo lo que se encuentra en medio.
SiderPerú es una empresa Siderúrgica del Perú que tiene
plantas en Lima, y Chimbote, ella comercializa y fabrica
acero para el consumo de la construcción de viviendas,
industria y la minería.
En el proceso de producción del acero2 se dan diversas
etapas como Cargas metálicas, Proceso de reducción
directa, Proceso de fragmentación del acero, Acería y
Proceso de laminación3.
Proceso de laminación en caliente
Fuente: SIDERPERU
Modelación de función exponencial: Ley de enfriamiento de Newton
En SIDERPERU el proceso de laminación en caliente se inicia en el horno de precalentamiento en donde las
palanquillas de acero son llevadas a una cámara que opera a cierta temperatura para la elaboración de sus
productos terminados de perfiles de acero y varillas de construcción. Además, si la temperatura de las
palanquillas está modelada por la función 𝑇 (ley de enfriamiento de Newton):
𝑇(𝑡) = 𝑇𝑚 + 𝐶𝑒 𝑘𝑡 ,
𝑡≥0
¿Cuál es el
Dónde:
comportamiento de
𝑇(𝑡): Es la temperatura (en °C) del material en el tiempo 𝑡.
esta función?
𝑇𝑚 : Es la temperatura (en °C) del medio ambiente.
𝑡: Es el tiempo transcurrido (en minutos) en el proceso de enfriamiento.
𝐶: Es la constante del proceso. (en °C)
𝑘: Constante que define el ritmo de enfriamiento. (en min-1)
En esta sección estudiaremos una nueva clase de funciones llamadas funciones exponenciales, estudiaremos su
comportamiento algebraico y gráfico.
1.1. FUNCIÓN EXPONENCIAL
Definición de función exponencial
La función exponencial 𝑓 definida con regla de correspondencia:
𝑓(𝑥) = 𝑎 ⋅ 𝑏 𝑥 ; Dom(𝑓) = ℝ
Donde 𝑎 ≠ 0, 𝑏 > 0, 𝑏 ≠ 1, se llama función exponencial con base 𝑏 y valor inicial 𝑓(0) = 𝑎.
El acero es Aleación de hierro y carbono, en la que este entra en una proporción entre el 0,02 y el 2 %, y que, según su tratamiento, adquiere
especial elasticidad, dureza o resistencia. Recuperado http://dle.rae.es/?id=0OElb4b .
2
Proceso de producción del acero (19 de marzo 2018, Recuperado de: http://www.sider.com.pe/contenidos/detalle/108/video
3
Laminación en Caliente https://image.slidesharecdn.com/ope-ii-final-1234642912038194-1/95/impactos-ambientales-generados-por-la-produccin-delacero-6-728.jpg?cb=1242559116
1
Profesores MA420
142
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Ejemplo 1: En la función 𝑔 con regla de correspondencia 𝑔(𝑥) = −2 ∙ 4𝑥 ; observamos que 𝑎 = −2, 𝑏 =
4, y el exponente 𝑥 puede tomar cualquier número real.
GRÁFICA DE FUNCIONES EXPONENCIALES
A continuación, estudiaremos la gráfica de la función 𝑓 definida con regla de correspondencia:
𝒇(𝒙) = 𝒃𝒙
Caso I: si 𝑏 > 1, por ejemplo, vamos a graficar 𝑓(𝑥) = 2𝑥
Hacemos una tabulación para analizar el comportamiento gráfico de esta función.
𝑥
⋮
−1
0
1
⋮
𝑓(𝑥) = 2𝑥
𝑓(−1) = 2−1
1
=
2
𝑓(0) = 1
𝑓(1) = 2
1/2
AH: 𝑦 = 0
Observe que cuando x tiende al infinito los valores de la función tiende al infinito (crece rápidamente) y cuando
x tiene al menos infinito los valores de la función tiende a cero. Por esta razón, en las gráficas de estas funciones,
existe una recta horizontal y = 0, llamada asíntota.
1 𝑥
Caso II: Si 0 < 𝑏 < 1, por ejemplo, vamos a graficar 𝑓(𝑥) = (2)
De manera análoga, hacemos una tabulación para analizar el comportamiento gráfico de esta función.
𝑥
⋮
−1
0
1
⋮
1 𝑥
𝑓(𝑥) = ( )
2
1 −1
𝑓(−1) = ( )
2
=2
𝑓(0) = 1
1
𝑓(1) =
2
1/2
y=0
En este caso, observe que cuando 𝑥 tiende al menos infinito los valores de la función tiende al más infinito
(decrece rápidamente) y cuando 𝑥 tiene al infinito los valores de la función tiende a cero, es decir se mantiene
la asíntota horizontal 𝑦 = 0, pero esta vez por la derecha del eje X.
DEFINICIÓN DE FUNCIÓN EXPONENCIAL NATURAL
Cualquier número positivo diferente de uno puede ser tomado como base para una función exponencial, pero
algunas bases se usan con más frecuencia que otras, la base más importante es el número denotado por la letra
𝑒.
Profesores MA420
143
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1 𝑛
El número 𝑒se define como el valor al que se aproxima (1 + 𝑛) cuando 𝑛se vuelve grande. El cálculo de esta
idea se hace más preciso por el concepto de límite. Se define:
𝑒 = 2,71828182845904523536. ..
NOTA: Observe que este número se encuentra en todas las calculadoras y lo usaremos en adelante.
Definición: La función 𝑓 definida con regla de correspondencia𝑓(𝑥) = 𝑒 𝑥 ; 𝑥 ∈ 𝑅, con base 𝑒 es llamada
función exponencial natural.
Ejemplo: Trace la gráfica de las siguientes funciones exponenciales calculando e indicando los puntos de corte
con los ejes coordenados. Además, escriba la ecuación de la asíntota, indicando si es vertical u horizontal.
a. 𝑓(𝑥) = 𝑒 𝑥 − 2
b. ℎ(𝑥) = −4𝑥 + 3
Solución:
𝐚. 𝑓(𝑥) = 𝑒 𝑥 − 2
Dom(𝑓) = ℝ
Para graficar esta función se recomienda identificar la
función básica, y tabular 3 puntos como mínimo. En
nuestro caso la función básica es 𝑒 𝑥 con un
desplazamiento vertical de 2 unidades hacia abajo.
Entonces, la asíntota horizontal: y = -2
Corte con el eje Y, se halla haciendo x = 0
Evaluando en la función 𝑓(0) = −1; obtenemos: 𝐴 =
(0; −1)
Corte con el eje X, se halla haciendo y = 0
0 = 𝑒 𝑥 − 2 ⇒ 𝑒 𝑥 = 2 ⇒ 𝑥 = ln(2) ⇒ 𝑥 = 0,69 …
Obtenemos: 𝐵 = (0,69. . ; 0)
Ahora tabulamos para obtener un tercer punto, por ejemplo
Para 𝑥 = −1 obtenemos 𝐶 = (−1; −1,63 … )
𝐛. ℎ(𝑥) = −4𝑥 + 3
Solución:
Dom(𝑓) = ℝ
Para graficar esta función se recomienda identificar la función básica, y tabular 3 puntos como mínimo. En
nuestro caso la función básica es −4𝑥 , con un desplazamiento vertical de 3 unidades hacia arriba.
Profesores MA420
144
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Entonces, la asíntota horizontal: y = 3
Corte con el eje Y, se halla haciendo x = 0
Evaluando en la función 𝑓(0) = 2; obtenemos: 𝐴 = (0; 2)
Corte con el eje X, se halla haciendo y = 0
0 = −4𝑥 + 3
ln (3)
⇒ 4𝑥 = 3 ⇒ 𝑥 = ln (4) ⇒ 𝑥 = 0,79 …
Obtenemos: 𝐵 = (0,79. . ; 0)
Ahora tabulamos para obtener un tercer punto, por ejemplo,
para 𝑥 = −2 obtenemos 𝐶 = (−2; 2,93 … )
PRACTIQUEMOS EN CLASE:
1. Determine el conjunto de valores admisibles y el conjunto solución de las siguientes ecuaciones:
a. 32𝑥−1 − 2𝑥 = 0
b. 3𝑥 + 6(3−𝑥 ) = 5
c. log 5 (4𝑥 − 1) − log 5 (−𝑥 + 13) = −log 5 (12 + 𝑥)
2. Trace la gráfica de las siguientes funciones exponenciales calculando e indicando los puntos de corte con los
ejes coordenados. Además, escriba la ecuación de la asíntota, indicando si es vertical u horizontal.
b. 𝑓(𝑥) = 𝑒 𝑥 − 2
b. ℎ(𝑥) = 3 − 2𝑥+1
−2 + 3𝑥 ; 𝑥 ≤ 1
. Trace su gráfica y determine
−√𝑥 − 1 ; 1 < 𝑥
analíticamente los puntos de corte con los ejes coordenados e indíquelos como pares ordenados en su
gráfica. Además, escriba la ecuación de la asíntota, indicando si esta es vertical u horizontal.
Nota: La gráfica se considera correcta, si pasa por lo menos por tres puntos de referencia.
3. Dada la función 𝑓 con regla de correspondencia 𝑓(𝑥) = {
RESPUESTAS DE LOS EJERCICIOS PRACTIQUEMOS EN CLASE
1
1
1. a. CVA = ℝ; CS = {0,7304 ⋯ } b. CVA = ℝ CS = {1; 0,6309 ⋯ };
b. CVA = ]4 ; 13[; CS = {2}
2. Puntos de corte con los ejes coordenados: (0; −1) y (0,6931 … ; 0). AH: 𝑦 = −2
Puntos de corte con los ejes coordenados: (0; 1) y (0,5849 … ; 0). AH: 𝑦 = 3
3. Puntos de corte con los ejes coordenados: (0; −1) y (0,6309 … ; 0). AH: 𝑦 = −2
PRACTIQUEMOS MÁS EN CASA:
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1. Determine el conjunto de valores admisibles (CVA) y conjunto de solución (CS) de las siguientes
ecuaciones:
a. 4𝑥+2 − 7𝑥−1 = 0
c. 6𝑥 − 61−𝑥 = 1
b. 𝑒 2𝑥 + 4𝑒 𝑥 − 21 = 0
d. 𝑒 2𝑥 − 2𝑒 𝑥 − 15 = 0
2. Determine el conjunto de valores admisibles (CVA) y conjunto solución (CS) de las siguientes ecuaciones.
Profesores MA420
145
UPC – Departamento de Ciencias - Matemática Básica (MA420)
a. log 3 2𝑥 − 2 log 3 𝑥 = 15
b. log 9 (𝑥 − 5) + log 9 (𝑥 + 3) = 1
𝐜. ln(𝑥 + 1) − ln(𝑥) + ln 2 = ln(𝑥 + 3)
d. ln(𝑥) − ln(6 − 𝑥) = ln(7 − 𝑥)
3. Trace la gráfica de las siguientes funciones exponenciales calculando e indicando los puntos de corte con
los ejes coordenados. Además, escriba la ecuación de la asíntota, indicando si es vertical u horizontal.
c. 𝑓(𝑥) = 𝑒 𝑥 − 4
b. ℎ(𝑥) = 4 − 2𝑥
𝑒 𝑥+1 − 2, si 𝑥 < 0
. Trace su gráfica, calcule e
|𝑥 − 3| − 1, si 𝑥 ≥ 0
indique las coordenadas de los puntos de corte con los ejes. Además, escriba la ecuación de la asíntota,
indicando si es vertical u horizontal.
𝑒 𝑥+1 − 3
;
𝑥 < −1
5. Dada la función 𝑟 con regla de correspondencia 𝑟(𝑥) = {−2𝑥−2 + 1
; −1 ≤ 𝑥 < 3 . Trace su gráfica,
2
𝑥>3
(𝑥 − 3) − 4 ;
calcule e indique las coordenadas de los puntos de corte con los ejes. Además, escriba la ecuación de la
asíntota, indicando si es vertical u horizontal.
4. Dada la función 𝑓 con regla de correspondencia 𝑓(𝑥) = {
RESPUESTAS DE LOS EJERCICIOS PRACTIQUEMOS MÁS EN CASA:
Pregunta 1. El conjunto de valores admisibles (CVA) en esta pregunta es todos los números reales.
a. CS = {8,43 … }
b. CS = {1,09 … }
c. CS = {0,61 … }
d. CS = {1,61 … }
Pregunta 2.
2
a. CVA = ]0; +∞[ y CS = {315 }
d. CVA = ]0; 6[ y CS = {4,35 … }
b. CVA = [5; +∞[ y CS = {6}
c. CVA = ]0; +∞[ y CS = {1}
Pregunta 3.
a.
Profesores MA420
b.
146
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Pregunta 4.
Pregunta 5.
AH: 𝑦 = −2
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Enlace
Código QR
Determinar el CVA y el CS de una https://tinyurl.com/yymgeynn
ecuación logarítmica.
Determinar el CVA y el CS de una
ecuación logarítmica.
Trazar la gráfica de la función
exponencial usando las técnicas de
graficación.
Profesores MA420
https://tinyurl.com/y3socztz
https://tinyurl.com/yxt2by9g
147
UPC – Departamento de Ciencias - Matemática Básica (MA420)
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
FUNCIÓN EXPONENCIAL, ECUACIONES EXPONENCIALES Y LOGARÍTMICAS: Revisar
páginas desde 330 hasta 346. Pág. 330 a 369.
Pág. 368 – 369, ejercicios 11-38, 39-44
Pág. 368 – 369, ejercicios 55-68, 69-76
Profesores MA420
148
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Función logaritmo
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante interpreta de forma gráfica y algebraica el
concepto de función logaritmo y los aplica en la resolución de ejercicios, demostrando responsabilidad y
capacidad de aprender por su propia cuenta.
CONTENIDO
MOTIVACIÓN
1.
Función logaritmo
2.
Practiquemos en clase
3.
Practiquemos más en casa
Profesores MA420
149
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Motivación
Weber estableció su ley de la sensación (o Ley de Weber) en la que formulaba la relación matemática que
existía entre la intensidad de un estímulo y la sensación producida por este.
𝐼
𝑆 = 𝐾 log
𝐼0
La respuesta sensorial 𝑆 es una función logarítmica de la intensidad 𝐼 del estímulo.
En esta sección estudiamos las inversas de funciones exponenciales.
1. FUNCIÓN LOGARITMO
LOGARITMOS Y SUS PROPIEDADES
En la ecuación 3 = 2𝑥+1 , intente despejar la variable 𝑥. Queda claro que tenemos la necesidad de conocer el
siguiente concepto.
Definición: Un logaritmo es el exponente al que está elevado un número positivo 𝑏 llamado base, donde 0 <
𝑏 ≠ 1.
Ejemplo 1:
✓ 30 = 7𝑥 : significa que 𝑥 es el logaritmo en base 7 de 30, sin embargo, en este caso necesitamos usar una
calculadora para poder saber el valor de 𝑥.
Lo dicho anteriormente, se puede escribir de la siguiente manera:
✓ 30 = 7𝑥 ⇔ 𝑥 = log 7 ( 30) = 1,747 ⋯ Valor encontrado con una calculadora.
Profesores MA420
150
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Actualmente, todas las calculadoras tienen a los logaritmos dentro de sus
opciones de cálculo.
Conclusión: Hay una relación de ida y vuelta entre los logaritmos y las exponenciales
vistas anteriormente, la cual formulamos de la siguiente manera:
𝒚 = 𝐥𝐨𝐠 𝒃(𝒙) ⇔ 𝒙 = 𝒃𝒚
donde:
✓ 𝑏: se llama base y es 0 < 𝑏 ≠ 1
✓ 𝑥: es un número real positivo, es decir 𝑥 > 0
PROPIEDADES:
LEYES DE LOS LOGARTIMOS:
✓ Si 𝑏 = 10, denotaremos el logaritmo de la siguiente manera: 𝑦 = log( 𝑥)
✓ Si 𝑏 = 𝑒, denotaremos el logaritmo como: 𝑦 = ln( 𝑥) y lo llamaremos logaritmo natural.
✓ log 𝑏 ( 1) = 0 Por ejemplo: log 3 ( 1) = log( 1) = ln( 1) = 0 (compruebe con su calculadora)
✓ log 𝑏 ( 𝑏) = 1 Por ejemplo: log 5( 5) = log( 10) = ln( 𝑒) = 1 (compruebe con su calculadora)
✓ log 𝑏 ( 𝑏 𝑥 ) = 𝑏 log𝑏(𝑥) = 𝑥
Para las siguientes propiedades consideremos 𝐴, 𝐵, 𝑐 números reales con 𝐴 > 0 y 𝐵 > 0
✓ Regla del producto: log 𝑏 ( 𝐴 ⋅ 𝐵) = log 𝑏 ( 𝐴) + log 𝑏 ( 𝐵)
𝐴
✓ Regla del cociente: log 𝑏 ( 𝐵) = log 𝑏 ( 𝐴) − log 𝑏 ( 𝐵)
✓ Regla de la potencia: log 𝑏 ( 𝐴𝑐 ) = 𝑐 ⋅ log 𝑏 ( 𝐴)
DEFINICIÓN DE FUNCIÓN LOGARITMO
Sea b un número positivo y diferente de uno (0 < 𝑏 ≠ 1). La función logarítmica con base b, denotada por
log 𝑏 , se define como:
𝑓(𝑥) = log 𝑏 (𝑥); Dom(𝑓) = {𝑥 ∈ R/ 𝑥 > 0} = ]0; +∞[
Por lo tanto, log 𝑏 (𝑥) es el exponente al cual la base b debe ser elevado para obtener 𝑥. Es decir:
log 𝑏 (𝑥) = 𝑓(𝑥) = 𝑦 ⟺ 𝑏 𝑦 = 𝑏 log𝑏 (𝑥) = 𝑥
Profesores MA420
151
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Función logaritmo natural
El logaritmo con base e se denomina función logaritmo natural y se define como:
𝑓(𝑥) = ln(𝑥) = log 𝑒 (𝑥); Dom(𝑓) = {𝑥 ∈ R / 𝑥 > 0} = ]0; +∞[
GRÁFICAS DE FUNCIONES LOGARITMO
A continuación, estudiaremos la gráfica de la función 𝑓 definida con regla de correspondencia:
𝑓(𝑥) = log 𝑏 𝑥
Caso I: si 𝑏 > 1, por ejemplo, vamos a graficar 𝑓(𝑥) = log 2 𝑥
Para graficar estas funciones se recomienda observar el valor de la base, y tabular 3 puntos como mínimo (ver
tabla). En este caso 𝑏 = 2 y sabemos qué Dom(𝑓) = ]0; +∞[ .
𝑥
0
1
= 2−1
2
1
2
⋮
𝑓(𝑥) = log 2 𝑥
Para valores cercanos a CERO,
tenemos una asíntota vertical
porque la función tiende al menos
infinito.
1
2
𝑓(2−1 ) = log 2 ( 2−1 ) = −1
𝑓(1) = log 2 ( 1) = 0
𝑓(1) = log 2 ( 2) = 1
Para valores mayores a 2, la
función crece
Dom(𝑓) = ]0; +∞[ ; Ran(𝑓) = ℝ y ecuación de la asíntota vertical: 𝑥 = 0
Caso II: si 0 < 𝑏 < 1, por ejemplo, vamos a graficar 𝑓(𝑥) = log 1 𝑥
2
Para graficar estas funciones se recomienda observar el valor de la base, y tabular 3 puntos como mínimo (ver
tabla). En este caso 𝑏 = 2 y sabemos qué Dom(𝑓) = ]0; +∞[ .
Profesores MA420
152
UPC – Departamento de Ciencias - Matemática Básica (MA420)
𝑓(𝑥) = log 1 𝑥
𝑥
0
1
= 2−1
2
1
2
⋮
2
Para valores cercanos a CERO, tenemos
una asíntota vertical porque la función
tiende al más infinito.
𝑓(2−1 ) = log 1 ( 2−1 ) = 1
2
𝑓(1) = log 1 ( 1) = 0
2
𝑓(1) = log 1 ( 2) = −1
2
1
Para valores mayores a 2, la función
1
2
decrece
Dom(𝑓) = ]0; +∞[ ; Ran(𝑓) = ℝ y ecuación de la asíntota vertical: 𝑥 = 0
2. PRACTIQUEMOS EN CLASE
1.
Determine el dominio de las siguientes funciones con regla de correspondencia:
a. 𝑓(𝑥) = log(−2𝑥 + 8) + log(1 + 𝑥)
b. 𝑔(𝑥) = log 5 (𝑥 − 2) + ln(9 − 𝑥 2 )
2.
Trace la gráfica de las siguientes funciones con regla de correspondencia:
1 − |𝑥 + 2| ; 𝑥 ≤ 2
a. 𝑓(𝑥) = log 3( 𝑥 + 5) − 2
b. 𝑓(𝑥) = {
ln(𝑥 − 2) ; 𝑥 > 2
Determine analíticamente los puntos de corte con los ejes coordenados e indíquelos como pares
ordenados en su gráfica. Además, determine la ecuación de sus asíntotas y diga si son verticales u
horizontales.
Nota: La gráfica de cada tramo se considera correcta si queda claro los extremos más algún otro punto
de paso.
3.
Dada la función inyectiva 𝑓 con regla de correspondencia 𝑓(𝑥) = log 2 (3 − 𝑥) + 1. Determine la regla
de correspondencia de 𝑓 −1 y su dominio.
4.
Dabas las funciones f y g cuyas reglas de correspondencias son: 𝑓(𝑥) = ln (𝑥 − 1) y 𝑔(𝑥) = 𝑥 2 − 2
con 𝑥 ∈ [1; 10[. Determine el dominio y la regla de correspondencia de 𝑓o𝑔.
RESPUESTAS DE PRACTIQUEMOS EN CLASE
1.
a. Dom(𝑓) = ]−1; 4[
2.
a. Dom(𝑓) = ]−5; +∞[
Ecuación de la asíntota vertical: 𝑥 = −5
Puntos de corte con los ejes coordenado
Eje 𝑥: (4; 0)
Eje 𝑦: (0; −0,53 … )
Profesores MA420
b. Dom(𝑔) = ]2; 3[
b. Dom(𝑓) = ℝ − {2}
Ecuación de la asíntota vertical: 𝑥 = 2
Puntos de corte con los ejes coordenado
Eje 𝑥: (3; 0) y (1; 0)
Eje 𝑦: (0; 0,69 … )
153
UPC – Departamento de Ciencias - Matemática Básica (MA420)
3.
4.
𝑓 −1 (𝑥) = 3 − 2𝑥−1 ; Dom(𝑓 −1 ) = ℝ
(𝑓𝑜𝑔)(𝑥) = ln(𝑥 2 − 3); Dom(𝑓𝑜𝑔) = ]√3; 10[
3. PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1.
Determine el dominio de las siguientes funciones con regla de correspondencia:
a. 𝑔(𝑥) = log(𝑥 2 − 4𝑥)
b. 𝑓(𝑥) = log 3 (3𝑥 − 7) − ln(𝑥 + 4) + √5
2.
Trace la gráfica de las siguientes funciones con regla de correspondencia:
log (1 − 𝑥) ; 𝑥 < 1
c. 𝑓(𝑥) = { 2
−ln(𝑥 − 1) ; 1 < 𝑥
Determine analíticamente los puntos de corte con los ejes coordenados e indíquelos como pares
ordenados en su gráfica. Además, determine la ecuación de sus asíntotas y diga si son verticales u
horizontales.
Nota: La gráfica de cada tramo se considera correcta si queda claro los extremos más algún otro punto
de paso.
a.
𝑓(𝑥) = − log 3 ( 𝑥 + 2) + 1
b. 𝑓(𝑥) = ln( 4 − 𝑥) + 2
3.
Dada la función inyectiva 𝑓 con regla de correspondencia 𝑓(𝑥) = 𝑒 3−2𝑥 − 5. Determine la regla de
correspondencia de 𝑓 −1 y su dominio.
4.
Dadas las funciones 𝑓 y 𝑔 con regla de correspondencia 𝑓(𝑥) = log 8 (3 − 𝑥) y 𝑔(𝑥) = 4 − 𝑥 2 con 𝑥 ∈
[−6; 7[. Determine el dominio y la regla de correspondencia de 𝑓 ∘ 𝑔. Además, calcule (𝑓 ∘ 𝑔)(−4) sí
existe.
RESPUESTAS DE PRACTIQUEMOS MAS EN CASA
1.
a. Dom(𝑔) = ]−∞; 0[ ∪ ]4; +∞[
2.
a. Dom(𝑓) = ]−2; +∞[
Ecuación de la asíntota vertical: 𝑥 = −2
Puntos de corte con los ejes coordenado
Eje 𝑥: (1; 0)
Eje 𝑦: (0; 0,36 … )
b. Dom(𝑓) = ]−∞; 4[
Ecuación de la asíntota vertical: 𝑥 = 4
Puntos de corte con los ejes coordenado
3.
4.
3
7
b. Dom(𝑓) = ]3 ; +∞[
Eje 𝑥: (3,86 … ; 0)
Eje 𝑦: (0; 3,38 … )
c. Dom(𝑓) = ℝ − {1}
Ecuación de la asíntota vertical: 𝑥 = 1
Puntos de corte con los ejes coordenado
Eje 𝑥: (0; 0), (2; 0)
Eje 𝑦: (0; 0)
1
𝑓 −1 (𝑥) = 2 − 2 ln(𝑥 + 5); Dom(𝑓 −1 ) =] − 5; ∞[
(𝑓 ∘ 𝑔)(𝑥) = log 8(𝑥 2 − 1) ; Dom(𝑓 ∘ 𝑔) = [−6; −1[ ∪ ]1; 7 [; (𝑓 ∘ 𝑔)(−4) = log 8 (15)
Profesores MA420
154
UPC – Departamento de Ciencias - Matemática Básica (MA420)
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Determinar los ceros de una
función
cuya
regla
de
correspondencia
involucra
funciones
exponenciales
y
logaritmo.
Trazar la gráfica de una función
logaritmo usando las técnicas de
graficación.
Trazar la gráfica de la función
seccionada
cuya
regla
de
correspondencia
involucra
funciones
exponenciales
y
logarítmicas.
Determinar
la
regla
de
correspondencia y el dominio de la
composición de funciones que
involucra a una función logaritmo.
Profesores MA420
Enlace
Código QR
https://tinyurl.com/yxv9enda
https://tinyurl.com/y2khhewu
https://tinyurl.com/y55jcs5q
https://bit.ly/3sQS6M0
155
UPC – Departamento de Ciencias - Matemática Básica (MA420)
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
FUNCIONES LOGARÍTMICAS: Revisar páginas desde 344 hasta 360. Pág.
Pág. 352 – 353, ejercicios 61 al 72, 73 al 78.
Profesores MA420
156
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Problemas con funciones exponenciales y
logarítmicas
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante resuelve problemas de modelación
que involucran a función exponencial y logarítmica, demostrando responsabilidad y capacidad de
aprender por su propia cuenta.
1. Practiquemos en clase
• Problemas
2. Practiquemos más en casa
• Problemas
Un gran número de procesos que se presentan en la naturaleza, por ejemplo, el crecimiento poblacional, la
desintegración radiactiva, la difusión de calor y otros muchos, se pueden modelar usando funciones
exponenciales. Se usan funciones logarítmicas en modelos para la intensidad de sonidos, la intensidad de
terremotos y otros numerosos fenómenos. En esta sección estudiamos modelos exponenciales y
logarítmicos.
PRACTIQUEMOS EN CLASE
1.
Una enfermedad infecciosa empieza a propagarse en una pequeña ciudad de 10000 habitantes.
Después de 𝑡 días, el número de personas que han sucumbido al virus está modelado por la función
10000
𝑣(𝑡) =
5 + 1245𝑒 −0,97𝑡
a. ¿Cuántas personas infectadas hay inicialmente y cuántas después de cinco días?
b. ¿Después de cuántos días hay 1563 infectados?
c. Trace la gráfica de 𝑣, escriba la ecuación de la asíntota y diga que representa a largo plazo.
2.
En una olla a presión se hierve agua y se empieza a enfriar de acuerdo con la Ley
de enfriamiento de Newton, de modo que la temperatura en el tiempo 𝑡 está dada
por: 𝑇(𝑡) = 30 + 60 𝑒 −0,0673𝑡 donde t se mide en minutos y T se mide en °C.
a. ¿Cuál es la temperatura inicial del agua y a los 22 minutos?
b. ¿Después de cuánto tiempo la temperatura del agua será de 40 °C?
c. Trace la gráfica de 𝑇, escriba la ecuación de la asíntota y diga qué representa a largo plazo.
3.
Se sabe que el monto acumulado 𝐴 de invertir un capital 𝑃 a una tasa de interés anual
𝑟, capitalizable 𝑘 veces por año y durante un periodo de 𝑡 años. Se calcula mediante:
𝑟 𝑘𝑡
𝐴(𝑡) = 𝑃 (1 + )
𝑘
a. Si el Sr. Jhonny invierte $ 1000 a una tasa de interés anual de 6 %. ¿Cuál es el saldo que obtiene
después de 10 años si el interés se capitaliza trimestralmente?
b. Si el Sr. José recibió $ 1849,39 después de 𝑡 años de haber invertido $1500 a una tasa de interés
anual del 7 %, capitalizable mensualmente. ¿En cuántos años obtuvo dicho monto?
Nota: Si la capitalización es mensual 𝑘 = 12, bimestral 𝑘 = 6, trimestral 𝑘 = 4, semestral 𝑘 = 2,…
Profesores MA420
157
UPC – Departamento de Ciencias - Matemática Básica (MA420)
4.
La longitud 𝑓 (en centímetros) de las truchas de 𝑡 meses de edad en la “etapa
juvenil” se puede aproximar mediante una función de crecimiento de la forma:
𝑓(𝑡) = 90(1 − 0,956𝑒 −0,15𝑡 )
a. Estime la longitud de la trucha al momento de iniciar esta esta etapa.
b. En el mercado internacional la trucha se compra cuando tiene una longitud mínima de 42,7cm,
estime cuanto tiempo debe pasar para poder ofertar un lote en el mercado internacional.
c. Trace la gráfica de 𝑓, escriba la ecuación de la asíntota y diga que representa a largo plazo.
5.
La percepción de la intensidad 𝐵 (en decibeles, dB) de un sonido con intensidad física 𝐼 (en watts por
metro cuadrado, W/m2 ) está dada por:
𝐼
𝐵 = 10 log ( )
𝐼0
donde 𝐼0 es la intensidad física de un sonido apenas audible. Encuentre el nivel de decibeles
(intensidad) de un sonido cuya intensidad física 𝐼 es 100 veces la de 𝐼0 .
EJERCICIO ADICIONAL
6.
Dadas las funciones 𝑓 y 𝑔 con reglas de correspondencia:
−2𝑥+1 + 3
;𝑥 ≤ 1
a. 𝑓(𝑥) = −log 2 (𝑥 + 2) − 3
b. 𝑔(𝑥) = {
ln(𝑥 − 1) + 4 ; 𝑥 > 1
Trace su gráfica y determine analíticamente los puntos de corte con los ejes coordenados e indíquelos
como pares ordenados en su gráfica. Además, escriba la ecuación de la asíntota, indicando si esta es
vertical u horizontal.
RESPUESTAS DE PRACTIQUEMOS EN CLASE
1.
a. 8 y 678 aproximadamente
b. 7 aproximadamente
c. A largo plazo, la máxima cantidad de infectados será de 2000 personas.
2.
a. 𝑇(0) = 90 °C, la temperatura inicial del agua es 90 °C
𝑇(22) = 43,65 °C, después de 22 minutos la temperatura del agua es 43,65 C° aprox.
b. La temperatura del agua será 40°C, después de 26,62 min aprox.
c. A largo plazo, la temperatura del agua cuando se enfría tiende a ser la temperatura ambiente 30 °C.
3.
a. El saldo después de 10 años es $ 1 814,02 aprox.
b. Dicho monto lo obtuvo en 3 años.
4.
a. Al nacer la trucha mide 3,96 cm
b. Para ofertar un lote, deben pasar 4 meses aprox.
c. A largo plazo, la longitud de las truchas tiende a ser 90 cm.
5.
La intensidad del sonido es de 20 dB.
6.
a. Dom (ℎ) = ]−2 ; +∞ [
Puntos de corte con los ejes coordenados:
Eje 𝑥: (-1,875; 0)
Eje 𝑦: (0; -4)
Asíntota Vertical: 𝑥 = - 2
Profesores MA420
158
UPC – Departamento de Ciencias - Matemática Básica (MA420)
b. Puntos de corte con los ejes coordenados:
Eje 𝑥: (0,585…; 0) ; (1,018… ; 0)
Eje 𝑦: (0; 1)
Asíntota Vertical: 𝑥 = 1
Asíntota Horizontal: 𝑦 = 3
PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1. Dadas las funciones 𝑓 y 𝑔 con reglas de correspondencia:
−𝑒 𝑥−1 + 1
;𝑥 ≤ 2
a. 𝑓(𝑥) = ln(𝑥 + 1) − 2
b. 𝑔(𝑥) = {
log 2 (𝑥 − 2) + 1 ; 𝑥 > 2
Trace su gráfica y determine analíticamente los puntos de corte con los ejes coordenados e indíquelos
como pares ordenados en su gráfica. Además, escriba la ecuación de la asíntota, indicando si esta es
vertical u horizontal.
PROBLEMAS DE MODELACIÓN
2. Si en el proceso de desintegración de cierta sustancia radiactiva, se sabe que la masa restante 𝑄 (en
gramos) después de 𝑡 minutos esta modelada mediante la siguiente función: 𝑄(𝑡) = 6,6𝑒
a. ¿Cuál fue la cantidad inicial de sustancia radiactiva?
b. ¿Al cabo de qué tiempo quedará 2,5 gramos de sustancia?
− 𝑙𝑛 2
𝑡
14
3. La población 𝑃 de avestruces después de 𝑡 años en el criadero de Pimentel, está
1001
modelada mediante la función: 𝑃(𝑡) = 1+90𝑒 −0,2𝑡
a. ¿Cuál fue la población inicial de avestruces?
b. ¿Al cabo de qué tiempo el número de avestruces será de 76?
4. Los biólogos han determinado que cuando se dispone de suficiente espacio
y nutrientes, el número de bacterias 𝑁 de un cultivo crece
exponencialmente después de 𝑡 minutos, mediante la función:
ln (3)
𝑁(𝑡) = 2000 𝑒 20 𝑡
a. ¿Cuántas bacterias detectaron los biólogos inicialmente? y ¿Cuántas
bacterias habrá al cabo de una hora?
b. ¿Al cabo de qué tiempo el número de bacterias será de 486 000?
5. La rapidez a la que se carga una batería es torna más lenta cuanto la batería está más cerca de su carga
máxima 𝐶0 . El tiempo 𝑡 (en horas) necesario para cargar una batería que está completamente descargada
a una carga 𝐶 está dado por:
𝐶
𝑡 = −𝑘 ln (1 − )
𝐶0
donde 𝑘 es una constante positiva que depende de la batería. Para cierta batería el valor de 𝑘 es 0,25, Si
esta batería está completamente descargada, ¿cuánto tomará cargarla al 90 % de su carga máxima 𝐶0 ?
6. Se sabe que el monto acumulado 𝐴 de invertir un capital 𝑃 a una tasa de interés anual 𝑟, capitalizable 𝑘
𝑟 𝑘𝑡
veces por año y durante un periodo de 𝑡 años. Se calcula mediante: 𝐴(𝑡) = 𝑃 (1 + 𝑘)
¿En cuánto tiempo una inversión de $ 2000 crecerá hasta $ 5000, si se invierte a una tasa anual de 8 %,
capitalizable semestralmente?
Profesores MA420
159
UPC – Departamento de Ciencias - Matemática Básica (MA420)
7. Un pollo a la brasa se saca del horno cuando su temperatura es de 185 °F y se coloca en una mesa en una
habitación donde la temperatura es de 75 °F.
a. Si la temperatura del pollo es de 150 °F después de media hora, ¿cuál es su temperatura después de
45 minutos? (utilice el modelo 𝑇(𝑡) = 𝑇𝑚 + (𝑇𝑜 − 𝑇𝑚 )𝑒 −𝑘∙𝑡 , donde 𝑇(𝑡) es la temperatura en °F
luego de un tiempo t (en minutos), 𝑇𝑚 es la temperatura del ambiente, 𝑇𝑜 es la temperatura inicial en
°F y k es una constante positiva que depende del tipo de cuerpo.
b. ¿Después de cuánto tiempo el pollo se enfría a 110 °F?
c. Trace la gráfica de T, escriba la ecuación de la asíntota y diga que representa a largo plazo.
8. Una población de ardillas grises fue introducida en cierto condado de la Gran Bretaña hace 30 años. Los
biólogos observaron que la población se duplica cada 6 años y ahora la población es de 100 000.
a. ¿Cuál es el tamaño inicial de la población de ardillas?
b. Trace una gráfica de la población de ardillas
Nota: utilice el modelo 𝑛(𝑡) = 𝑛𝑜 2𝑡/𝑎 , donde 𝑎 y 𝑡 se miden en las mismas unidades de tiempo,
𝑛𝑜 es la población inicial y 𝑛(𝑡) es la población en un tiempo 𝑡
9. Se sabe que el monto acumulado 𝐴 de invertir un capital 𝑃, a una tasa de interés1 anual 𝑟, capitalizable2
continuamente (en cada instante de tiempo) y durante un periodo de 𝑡 años.
Se calcula mediante: 𝐴(𝑡) = P𝑒 𝑟𝑡
a. Si el Sr. Dennis invierte $ 2000 a una tasa de interés anual de 4 %. ¿Cuál es el saldo que obtiene a
los 12 años de inversión, si el interés se capitaliza continuamente?
b. Si la Sra. María invirtió $ 2500 y después de 𝑡 años recibió el monto de $ 3574,38. Y se sabe que la
inversión se hizo a una tasa de interés anual del 6,5 %, capitalizable continuamente. ¿En cuántos
años obtuvo dicho monto?
10. La masa 𝑊(𝑡) (en gramos) que queda de una pastilla luego de 𝑡 segundos de haber ingerido para calmar
el dolor de garganta, está dada por 𝑊(𝑡) = 0,24(10−0,02𝑡 ).
a. Determine la masa inicial de la pastilla.
b. Calcule la masa luego de 1 minuto de haber ingerido la pastilla.
c. ¿Después de cuánto tiempo la masa se habrá reducido a 0,1 gramos?
RESPUESTAS DE PRACTIQUEMOS MÁS EN CASA
1. a. Dom(𝑓) = ]−1 ; +∞ [
Puntos de corte con los ejes coordenados:
Eje 𝑥: (6,389…; 0)
Eje 𝑦: (0; -2)
Asíntota Vertical: 𝑥 = - 1
b. Puntos de corte con los ejes coordenados:
Eje 𝑥: (1; 0); (2,5; 0)
Eje 𝑦: (0; 0,632…)
Asíntota Vertical: 𝑥 = 2
Asíntota Horizontal: 𝑦 = 1
2.
a. La cantidad inicial de la sustancia radiactiva fue 6,6 gramos.
b. Quedará 2,5 gramos de sustancia radiactiva al cabo de 19,6 minutos aprox.
La tasa de interés o tipo de interés, en economía, es la cantidad que se abona en una unidad de tiempo por cada unidad de capital invertido. También puede
decirse que es el interés de una unidad de moneda en una unidad de tiempo o el rendimiento de la unidad de capital en la unidad de tiempo.
2 Definición de capitalización. Se denomina capitalización al acto y la consecuencia de capitalizar: aprovechar algo en beneficio propio. En el contexto
específico de la economía, capitalizar supone transformar algo en capital o aportar capital a una compañía.
1
Profesores MA420
160
UPC – Departamento de Ciencias - Matemática Básica (MA420)
3.
a. La población inicial de avestruces fue 11.
b. El número de avestruces será 76 al cabo de 10 años aprox.
4.
a. Inicialmente los biólogos detectaron 2 000 bacterias y al de una hora 54 000 bacterias.
b. El número de bacterias será de 486 000 al cabo de 100 minutos aprox.
5. 0,58 minutos
6. El tiempo de la inversión fue 11,7 años aprox.
7.
a. Después de 45 minutos la temperatura es 136,93 °F
b. Se enfría a 110° F después de 89,7 minutos aprox.
c. A largo plazo, la temperatura del pollo a la brasa tiende a ser la temperatura ambiente 75 °F.
8.
a. La población inicial fue 3125 ardillas.
9.
a. El saldo después de 12 años es $ 3232,15 aprox.
b. La Sra. María obtuvo dicho monto en 5,5 años.
10. a. La masa inicial de la pastilla es 0,24 gramos.
b. Luego de 1 min. La masa de la pastilla es 0,0151 gramos.
c. La masa de la pastilla se habrá reducido a 0,1 gr. luego de 19 segundos aprox.
Profesores MA420
161
UPC – Departamento de Ciencias - Matemática Básica (MA420)
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Resolver problemas de modelación que
involucran a funciones exponenciales
(Interés compuesto).
Resolver problemas de modelación que
involucran a funciones exponenciales
(Ley de enfriamiento de Newton).
Enlace
Código QR
https://bit.ly/3ocb787
https://bit.ly/3c7XhBa
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
MODELACIÓN CON FUNCIONES EXPONENCIALES: Revisar las páginas, desde
340 al 353.
Profesores MA420
162
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Modelo educativo UPC
Funciones trigonométricas
seno, coseno y sus inversas
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante analiza el concepto de las funciones
trigonométricas seno y coseno, así como de sus inversas, y las interpreta gráficamente, demostrando
responsabilidad y capacidad de aprender por su propia cuenta.
CONTENIDOS
MOTIVACIÓN
1.1 Funciones trigonométricas seno, coseno y sus inversas
• Circunferencia unitaria
• Definiciones y notaciones
• Ejemplos
1.2 Practiquemos en clase
• Ejercicios
1.3 Practiquemos más en casa
• Ejercicios
Profesores MA420
163
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Modelo educativo UPC
Motivación
El ángulo óptimo de ramificación vascular
El sistema circulatorio es tal que la circulación de la sangre
(del corazón a los órganos y viceversa) se realice con el gasto
mínimo de energía. Así es razonable suponer que, cuando
una arteria se ramifica, el ángulo entre la arteria “madre” y
la “hija” debe hacer mínima la resistencia al flujo de sangre.
La figura muestra una arteria pequeña de radio 𝑟 que es una
ramificación de una mayor, de radio 𝑅. La sangre fluye en
dirección de las flechas, desde el punto 𝐴 al punto 𝐵 de
ramificación, y luego hasta 𝐶 y 𝐷. Queremos hallar el ángulo
𝜃 de ramificación que hace mínima la resistencia total del
flujo de sangre cuando va de 𝐴 a 𝐵 y luego hasta el punto 𝐶,
que está a una distancia ℎ (en perpendicular de la recta 𝐴𝐷).
𝑟4
𝑅
Se demuestra que se cumple 𝜃 = cos−1 ( 4 ), donde cos −1 hace referencia a la función trigonométrica
arcocoseno.
1.
FUNCIONES TRIGONOMÉTRICAS SENO, COSENO Y SUS INVERSAS
CIRCUNFERENCIA UNITARIA
La circunferencia unitaria es una circunferencia cuyo radio mide 1 y cuyo centro está en el origen de coordenadas.
Sea t cualquier número real y 𝑃(𝑥; 𝑦) el punto correspondiente a t situado en la circunferencia. Entonces:
1
−1
1
−1
NOTA:
El punto 𝑃(𝑥; 𝑦) = (cos t ; sen 𝑡) es llamado punto terminal, donde 𝑡 es la longitud de arco S = 𝑡. 1 = 𝑡 donde
𝑡 se mide en radianes. El punto (1; 0) se considera como el punto de partida para las medidas, es decir, la
longitud de arco en este punto es cero.
Si la medida se hace en sentido antihorario (contrario al movimiento de las agujas del reloj), hasta en el punto
(0; 1) el ángulo trigonométrico es
𝜋
2
= 1,57 …, pero si la medida se hace en sentido horario (en la misma
𝜋
dirección de las agujas del reloj) hasta en el punto (0; -1) ángulo trigonométrico es − 2 = −1,57 …
Profesores MA420
164
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Modelo educativo UPC
Esta manera de representar los puntos sobre la circunferencia unitaria nos permite representarlos de infinitas
formas en términos de la longitud de arco.
FUNCIÓN PERIÓDICA
Una función 𝑓, con regla de correspondencia 𝑦 = 𝑓(𝑥) se dice que es periódica si hay un número positivo c
tal que:
𝑓(𝑥 + 𝑐) = 𝑓(𝑥)
Para todos los valores de 𝑥 en el dominio de 𝑓. Al más pequeño de tales números c se le conoce como periodo
de la función.
La circunferencia unitaria de 16 puntos (x; y) = (cos t; sen t)
FUNCIÓN SENO
Definición: Es aquella cuya regla de correspondencia es:
𝑓(𝑥) = sen 𝑥
Donde 𝑥 es la longitud de arco en la circunferencia unitaria medida en radianes, es decir Dom(𝑓) = ℝ
La gráfica de la función Seno son los valores de las segundas componentes de la circunferencia unitaria, por
𝜋
6
1
2
ejemplo: si la longitud de arco es observamos en la circunferencia de 16 puntos que el valor del seno es ,
𝜋
1
es decir sen ( 6 ) = 2; si la longitud de arco es
𝜋
2
𝜋
entonces el valor del seno es 1, es decir sen ( 2 ) = 1, y así
sucesivamente, luego ubicamos estos puntos en el plano cartesiano, donde el eje x representa la longitud de
arco medida en radianes. De la circunferencia unitaria de 16 puntos, podemos observar que en cada vuelta
completa los valores del seno se repiten, esto quiere decir que el periodo de es esta función es 2𝜋.
Profesores MA420
165
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Modelo educativo UPC
La función seno en todo su dominio.
CARACTERÍSTICAS DE LA FUNCIÓN SENO
❖ La gráfica de la función seno es simétrica con respecto al origen (es función impar: sen(−𝑥) =
−sen(𝑥)).
❖ Sus ceros tienen la forma de {k𝜋 / 𝑘 𝜖 ℤ}.
❖ Su período es 2𝜋 (cada 2𝜋 se repite el mismo bloque)
❖ Dominio: Dom( 𝑓) = ℝ
❖ Rango: Ran( 𝑓) = [−1; 1]
FUNCIÓN INVERSA DEL SENO O FUNCIÓN ARCOSENO
La gráfica de la función seno con regla de correspondencia 𝑓(𝑥) = sen 𝑥, por el criterio de la recta horizontal
(CRH) observamos que 𝑓 no es inyectiva y por lo tanto no tiene función inversa1.
Sin embargo, hay muchas maneras de restringir el dominio de cualquier función de tal manera que podamos
hablar de su inversa en un dominio restringido. Por conveniencia vamos a restringir el dominio de la función seno
de modo que sea inyectiva.
1
Puede recordar el concepto de función inversa a través de los videos: https://youtu.be/cQU0SaPvjh4 y https://youtu.be/d8TkntRumJU
Profesores MA420
166
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Modelo educativo UPC
𝜋 𝜋
La función seno con regla de correspondencia 𝑓(𝑥) = sen 𝑥 es uno a uno (inyectiva) en [− 2 ; 2 ], por lo
tanto, existe la función inversa, es decir, su gráfica sería:
¿Cuál es la regla de correspondencia de la función inversa de la función seno? ¿Cómo podemos despejar la
variable 𝑥 de 𝑦 = sen 𝑥? Para ello veamos la siguiente definición
Definición:
𝜋 𝜋
Sea 𝑓(𝑥) = sen 𝑥 con 𝑥 ∈ [− 2 ; 2 ] entonces definimos la función arcoseno o seno inverso mediante la regla
de correspondencia 𝑔(𝑥) = arcsen 𝑥 = sen−1 𝑥 = 𝑓 −1 (𝑥)
Además, es fácil comprobar que:
Dom(𝑓 −1 ) = Ran(𝑓) = [−1; 1]
𝜋 𝜋
Ran(𝑓 −1 ) = Dom(𝑓) = [− ; ]
2 2
Aplicando el principio de reflexión en la figura 3 se obtiene la
gráfica de la función arcoseno (ver figura 4)
Composición de la función seno con su inversa
sen(sen−1 𝑥) = 𝑥
sen−1(sen 𝑥) = 𝑥
Profesores MA420
para
para
𝑥 ∈ [−1; 1]
𝜋 𝜋
𝑥 ∈ [− ; ]
2 2
167
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Modelo educativo UPC
FUNCIÓN COSENO
Definición: Es aquella cuya regla de correspondencia es:
𝑓(𝑥) = cos 𝑥
Donde 𝑥 es la longitud de arco en la circunferencia unitaria medida en radianes, es decir Dom(𝑓) = ℝ
La gráfica de la función coseno se forma por las primeras componentes de la circunferencia unitaria, por
ejemplo: si la longitud de arco es
coseno es
𝜋
√3
, es decir cos ( 6 )
2
=
𝜋
6
observamos en la circunferencia de 16 puntos (página 3) que el valor del
𝜋
𝜋
√3
; si la longitud de arco es 2 entonces el valor del coseno es 0, es decir cos ( 2 )
2
=
0, y así sucesivamente, luego ubicamos estos puntos en el plano cartesiano, donde el eje 𝑥 representa la longitud
de arco medida en radianes. De la circunferencia unitaria de 16 puntos, podemos observar que en cada vuelta
completa los valores del coseno se repiten, esto quiere decir que el periodo de esta función también es 2𝜋.
La función coseno en todo su dominio.
Características de la función Coseno
❖ La gráfica de la función coseno es simétrica con respecto al eje 𝑦 (es función par: cos( − 𝑥) = cos( 𝑥)
𝜋
❖ Sus ceros tienen la forma de { 2 + k𝜋 / 𝑘 𝜖 ℤ}, porque se repiten cada 𝜋 unidades.
❖ De período 2𝜋 (cada 2𝜋 se repite el mismo bloque)
❖ Dominio: Dom( 𝑓) = ℝ
❖ Rango: Ran( 𝑓) = [−1; 1]
Profesores MA420
168
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Modelo educativo UPC
Función inversa del coseno o función arcocoseno
La gráfica de la función coseno con regla de correspondencia𝑓(𝑥) = cos 𝑥, por el criterio de la recta horizontal
(CRH) observamos que no es inyectiva y que por lo tanto no tiene función inversa.
Sin embargo, hay muchas maneras de restringir el dominio de cualquier función de tal manera que podamos
hablar de su inversa en un dominio restringido. Por conveniencia vamos a restringir el dominio de la función seno
de modo que sea inyectiva.
La función coseno con regla de correspondencia 𝑓(𝑥) = cos 𝑥 es uno a uno (inyectiva) en [0; 𝜋], por lo tanto,
existe la función inversa, es decir, su gráfica sería:
¿Cuál es la regla de correspondencia de la función inversa de la función seno? ¿Cómo podemos despejar la
variable 𝑥 de 𝑦 = sen 𝑥? Para ello veamos la siguiente definición:
Definición:
Sea 𝑓(𝑥) = cos 𝑥 con 𝑥 ∈ [0; 𝜋] entonces definimos la función arcocoseno o coseno inverso mediante la
regla de correspondencia 𝑔(𝑥) = arccos 𝑥 = cos−1 𝑥 = 𝑓 −1 (𝑥)
Además, es fácil comprobar que:
Ran(𝑓
−1 )
Dom(𝑓 −1 ) = Ran(𝑓) = [−1; 1]
= Dom(𝑓) = [0; 𝜋]
Aplicando el principio de reflexión en la figura anterior se obtiene la
gráfica de la función arcocoseno.
Profesores MA420
169
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Modelo educativo UPC
Composición de la función coseno con su inversa
cos(cos−1 𝑥) = 𝑥
cos−1 (cos 𝑥) = 𝑥
𝑥 ∈ [−1; 1]
𝑥 ∈ [0; 𝜋]
para
para
2.
PRACTIQUEMOS EN CLASE
1.
Usando su calculadora en modo R (Radianes), calcule los valores de:
𝜋
a. cos ( 4 )
b. sen(3𝜋)
c. cos−1 (−
√2
)
2
1
d. sen−1 (3)
e. cos−1(√2)
f. sen−1 (−1,5)
Nota: En caso no existe el valor, diga porqué.
2.
Dadas las funciones 𝑓 y 𝑔 con reglas de correspondencia:
a. 𝑓(𝑥) = cos(𝑥), 𝑥 ∈ ]−𝜋;
3𝜋
]
2
b. 𝑔(𝑥) = sen(𝑥), 𝑥 ∈ ]−𝜋; 𝜋]
Trace su gráfica, determine los ceros y el rango.
3.
Determine el dominio, rango, periodo y trace su grafique en su periodo principal de las siguientes
funciones.
a. 𝑓(𝑥) = 4 sen 𝑥 − 2
b. 𝑓(𝑥) = − 3sen 𝑥 + 1
c. 𝑔(𝑥) = −2 cos 𝑥 + 3
RESPUESTAS DE PRACTIQUEMOS EN CLASE
Ejercicio 1
√2
a.
b. 0
c.
2
f. No existe (−1,5∉ [−1; 1])
3𝜋
4
d. 0,3398
Ejercicio 2: Trace la gráfica en el dominio dado.
a.
𝑓(𝑥) = cos(𝑥), 𝑥 ∈
𝜋 𝜋 3𝜋
3𝜋
]−𝜋; 2 ]
Ceros: − 2 ; 2 ; 2
Ran(𝑓) = [−1; 1]
e. No existe (√2 ∉ [−1; 1])
b.
𝑔(𝑥) = sen(𝑥), 𝑥 ∈ ]−𝜋; 𝜋]
Ceros: 0; 𝜋
Ran(𝑔) = [−1; 1]
Ejercicio 3: Trace la gráfica en el dominio dado.
a.
𝑓(𝑥) = 4 sen 𝑥 − 2
Dom(𝑓) = ℝ
Ran(𝑓) = [−6; 2]
Periodo: 𝑇 = 2𝜋
Profesores MA420
b.
𝑓(𝑥) = − 3sen 𝑥 + 1
Dom(𝑓) = ℝ
Ran(𝑓) = [−2; 4]
Periodo: 𝑇 = 2𝜋
c.
𝑔(𝑥) = −2 cos 𝑥 + 3
Dom(𝑓) = ℝ
Ran(𝑓) = [1; 5]
Periodo: 𝑇 = 2𝜋
170
UPC – Departamento de Ciencias - Matemática Básica (MA420)
3.
Modelo educativo UPC
PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1.
Dadas las funciones 𝑓 y 𝑔 con reglas de correspondencia:
a.
𝑓(𝑥) = cos(𝑥) , 𝑥 ∈ ]−
3𝜋 𝜋
; ]
2 2
b. 𝑔(𝑥) = sen(𝑥), 𝑥 ∈ ]−𝜋;
3𝜋
]
2
Trace su gráfica, determine los ceros y el rango.
2.
Grafique en su periodo principal las siguientes funciones con reglas de correspondencia. Luego determine
el dominio, el rango y el periodo.
a. 𝑓(𝑥) = −2,5 sen 𝑥 + 0,5
b. 𝑓(𝑥) = 3 cos 𝑥 − 1
c. 𝑔(𝑥) = 2 sen 𝑥 − 3
3.
Determine el valor de las siguientes expresiones:
a. tan−1 (50)
4
b. cos −1 (5)
√3
c. tan (sen−1 ( 2 ))
1
d. sen (cos −1 (2))
RESPUESTAS DE PRACTIQUEMOS MÁS EN CASA
Ejercicio 1
a.
b.
Profesores MA420
171
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Ejercicio 2
a.
b.
𝑓(𝑥) = −2,5 sen 𝑥 + 0,5
Dom(𝑓) = ℝ
Ran (𝑓) = [−2; 3]
Periodo: 𝑇 = 2𝜋
𝑓(𝑥) = 3 cos 𝑥 − 1
Dom(𝑓) = ℝ
Ran (𝑓) = [−4; 2]
Periodo: 𝑇 = 2𝜋
c.
𝑔(𝑥) = 2 sen 𝑥 − 3
Dom (𝑔) = ℝ
Ran (𝑔) = [−5; −1]
Periodo: 𝑇 = 2𝜋
Ejercicio 3
a. tan−1 (50) = 1,551
4
5
b. cos−1 ( ) = 0,6435
√3
1
c. tan (sen−1 ( 2 )) = √3
d. sen (cos −1 (2)) =
√3
2
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Trazar la gráfica de una función
trigonométrica usando técnicas
de graficación
Profesores MA420
Enlace
Código QR
https://tinyurl.com/y6m6afer
172
UPC – Departamento de Ciencias - Matemática Básica (MA420)
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
FUNCIONES TRIGONOMÉTRICAS Y SUS INVERSAS: Revisar páginas desde 419
hasta 430, 439 a 442.
Profesores MA420
173
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Resolución de triángulos
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante analiza los conceptos de ley de senos y
cosenos y los aplica en la resolución de problemas, demostrando responsabilidad y capacidad de aprender
por su propia cuenta.
CONTENIDO
MOTIVACIÓN
1.1.
Ángulo de elevación y ángulo depresión
• ¿Qué es un ángulo de elevación?
• ¿Qué es un ángulo de depresión?
• Resolución de problemas usando trigonometría
1.2.
Ley de Senos y Ley de Cosenos
• Ley de Senos
• Ley de Cosenos
• Resolución de problemas usando trigonometría
Profesores MA420
174
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Motivación
Los egipcios y los babilonios 1000 años a.c. Utilizaron los ángulos de un triángulo y las razones entre dos de
los lados de un triángulo en la agricultura, para construir pirámides luego en la astronomía para encontrar
distancia entre cuerpos celestes, en la navegación y otros.
1.1. ÁNGULO DE ELEVACIÓN Y ÁNGULO DE DEPRESIÓN
•
¿Qué es un ángulo de elevación?
Es el ángulo 𝛼 formado entre la línea de visión y la horizontal, donde el ojo del observador se mueve hacia
arriba desde la horizontal para observar algún objeto que se encuentra en lo alto.
Horizontal
•
¿Qué es un ángulo de depresión?
Es el ángulo 𝛽 formado entre la línea de visión y la horizontal, donde el ojo del observador se mueve hacia
abajo desde la horizontal para observar algún objeto que se encuentra por debajo.
Profesores MA420
175
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Horizontal
•
Resolución de problemas usando trigonometría
Ejercicio 1: Desde la parte superior de un edificio que mide 100 pies de altura, un hombre observa un
automóvil que se desplaza frente al edificio. Si el ángulo de depresión del automóvil cambia de 22° a 46°
durante el periodo de observación, ¿cuánto recorre horizontalmente el automóvil?
46
22
100 pies
Solución:
El problema está modelado en la figura. Obsérvese que se han señalado los ángulos agudos en las dos
posiciones de 22° y 46°, esto porque el ángulo de elevación desde el automóvil es igual al ángulo de
depresión desde el edificio, (ángulos entre paralelas).
Aplicando los pasos, tenemos:
Paso 1: Definición de variables
𝑥: La distancia (en pies) que el automóvil recorre horizontalmente
𝑑: La distancia (en pies) en la segunda observación
Paso 2: Planteamiento, en este caso haremos uso de las razones trigonométricas
100 pies
22
x
Profesores MA420
46
d
176
UPC – Departamento de Ciencias - Matemática Básica (MA420)
❖ Del triángulo pequeño
tan 46° =
100
100
⇒𝑑=
⋯ (∗)
𝑑
tan 46°
tan 22° =
100
𝑥+𝑑
❖ Del triángulo grande
⇒𝑥+𝑑 =
100
⋯ (∗∗)
tan 22°
Paso 3: Resolver
Como lo que se quiere es hallar 𝑥 entonces de (**) se tiene:
100
𝑥=
−𝑑
tan 22°
Pero de (*): 𝑑 =
100
100
𝑡𝑎𝑛 46°
el cual reemplazamos, obteniendo
100
𝑥 = tan 22° − tan 46°
Asegúrese de que la
calculadora está
programada con el
sistema sexagesimal
(comando “D” en la parte
superior de la pantalla de
su calculadora).
Hacemos uso de la calculadora y obtenemos: 𝑥 = 150,9398. ..
Paso 4: Respuesta:
Durante el periodo de observación el automóvil recorre aproximadamente 150,94 pies.
Ejercicio 2: El ángulo de depresión desde la parte alta de un faro con respecto a una boya es de 12°. Si el
faro está a 134 pies sobre la superficie del agua (ver figura), ¿qué tan lejos está la boya del faro?
12
134 pies
Solución:
De la figura, obsérvese que se ha señalado el ángulo de depresión con 12°, y esto es igual al ángulo de
elevación desde la boya al faro.
Aplicando los pasos, tenemos:
Paso 1: Definición de variables
𝑑: La distancia en pies de la boya al faro.
Paso 2: Planteamiento, en este caso haremos uso de las razones trigonométricas
Profesores MA420
177
UPC – Departamento de Ciencias - Matemática Básica (MA420)
𝟏𝟐°
134 pies
𝟏𝟐°
12
Asegúrese de que la calculadora
está programada con el sistema
sexagesimal (comando “D” en la
parte inferior de la pantalla de su
calculadora).
d
❖ Del triángulo
tan 12° =
134
𝑑
134
⇒ 𝑑 = tan 12° = 630,420...
Hacemos uso de la calculadora y obtenemos: 𝑑 = 630,420...
Paso 3: Respuesta
La boya está a una distancia de 630,42 pies aproximadamente del faro.
Ejercicio 3: Dos observadores, separados 155 metros, ven un globo aerostático directamente entre ellos,
pero con los ángulos de elevación que se muestran en la figura. Determine a qué altura se encuentra el
globo con respecto al suelo.
27
38
A
B
155 m
Solución:
En la figura, trazamos la altura.
Aplicando los pasos, tenemos:
Paso 1: Definición de variables
ℎ: Altura a que se encuentra el globo con respecto al suelo en metros
Paso 2: Planteamiento, en este caso haremos uso de las razones trigonométricas
C
h
38
27
A
Profesores MA420
x
M
155 m
y
B
178
UPC – Departamento de Ciencias - Matemática Básica (MA420)
❖ Del triángulo 𝐴𝐶𝑀
tan 27° =
ℎ
𝑥
⇒𝑥=
ℎ
. . . (∗)
tan 27°
Asegúrese de que la
calculadora está programada
con el sistema sexagesimal
(comando “D” en la parte
superior de la pantalla de su
calculadora).
❖ Del triángulo 𝐵𝐶𝑀
ℎ
ℎ
tan 38° = 𝑦 ⇒ 𝑦 = tan 38° . . . (∗∗)
Sumando (∗)y (∗∗)se obtiene
𝑥+𝑦 =
ℎ
ℎ
+
𝑡𝑎𝑛 27°
𝑡𝑎𝑛 38°
⇒ 155 =
ℎ
ℎ
+
𝑡𝑎𝑛 27°
𝑡𝑎𝑛 38°
Despejando ℎ y haciendo uso de la calculadora se obtiene: ℎ = 47,8018...
Paso 3: Respuesta: El globo aerostático se encuentra aproximadamente a una altura de 47,80 metros
con respecto al suelo.
LEY DE SENOS Y LEY DE COSENOS
• Ley de senos
La ley de los senos establece que la razón del seno de un ángulo a la longitud de su lado opuesto es la misma
para los tres ángulos de cualquier triángulo, es decir:
En cualquier triángulo 𝛥𝐴𝐵𝐶, con ángulos 𝐴, 𝐵 y 𝐶 y lados opuestos 𝑎, 𝑏 y 𝑐, respectivamente. La ecuación
siguiente es verdadera:
sen𝐴
𝑎
=
sen𝐵
𝑏
=
sen𝐶
𝑐
C
C
b
h
A
c
a
b
a
B
A
c
h
B
• Ley de cosenos
La ley de cosenos con frecuencia se denomina “teorema de Pitágoras generalizado”, ya que tiene como caso
especial a ese teorema clásico.
La ley de cosenos nos permite conocer el tercer lado desconocido cuando se conocen dos lados consecutivos
y el ángulo entre ellos.
Profesores MA420
179
UPC – Departamento de Ciencias - Matemática Básica (MA420)
En cualquier triángulo 𝛥𝐴𝐵𝐶, con ángulos 𝐴, 𝐵 y 𝐶 y lados opuestos 𝑎, 𝑏 y 𝑐, respectivamente. Se cumple:
B
a
c
C
A
•
𝑎2 = 𝑏 2 + 𝑐 2 − 2𝑏𝑐 ∙ cos 𝐴
𝑏 2 = 𝑎2 + 𝑐 2 − 2𝑎𝑐 ∙ cos 𝐵
𝑐 2 = 𝑎2 + 𝑏 2 − 2𝑎𝑏 ∙ cos 𝐶
b
Resolución de problemas usando trigonometría.
Ejercicio 4: Tony debe determinar la distancia entre dos puntos, 𝐴 y 𝐵, en lados opuestos de un lago, selecciona
un punto 𝐶 que está a 860 pies de 𝐴 y 225 pies de 𝐵, como se muestra en la figura. Si la medida del ángulo 𝐶 es
78°, determine la distancia entre 𝐴 y 𝐵.
B
225 pies
78
A
860 pies
C
Solución:
Sea 𝑥: la distancia entre los puntos 𝐴 y 𝐵. Si analizamos la figura observamos que conocemos las medidas
de dos lados consecutivos y la medida del ángulo formado entre ellos, es decir tenemos la forma (LAL),
por lo cual vamos a usar la ley de cosenos para hallar la distancia 𝑥.
𝑥 2 = 8602 + 2252 − 2(860)(225) 𝑐𝑜𝑠 7 8°
𝑥 = √8602 + 2252 − 2(860)(225) 𝑐𝑜𝑠 7 8°
𝑥 = 842,474. ..
Nuevamente, les recuerdo que el problema
exige que su calculadora deba estar
programada en el sistema sexagesimal.
Respuesta: La distancia entre los puntos 𝐴 y 𝐵 (lados opuestos del lago) es de aproximadamente
842,47 pies.
Ejercicio 5: Dos marcas, 𝐴y 𝐵, están separadas 80 pies del mismo lado del borde de un cañón como se muestra
en la figura. Un excursionista está ubicado del otro lado del cañón en el punto 𝐶. Un agrimensor determina que
el ∠𝐵𝐴𝐶 = 70° y ∠𝐴𝐵𝐶 = 65°. ¿Cuál es la distancia del excursionista al punto A?
Profesores MA420
180
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Solución:
Sea 𝑥: la distancia entre el excursionista y el punto 𝐴. Si analizamos la figura observamos que conocemos las
medidas de dos ángulos consecutivos y la medida de un lado, es decir tenemos la forma (ALA), por lo cual
vamos a usar la ley de senos para hallar la distancia 𝑥.
sen45°
80
=
sen65°
𝑥
⇒ 𝑥 = 80
sen65°
sen45°
= 102,5370211 ⋯
Respuesta: La distancia del excursionista al punto A es 102,54 pies
aproximadamente.
Ejercicio 6: En un instante dado, desde lo alto de una montaña, una persona observa un avión que se encuentra
a 420 metros de distancia con un ángulo de elevación de 28°. Al mismo tiempo y en el mismo plano vertical, esta
persona observa un bote que se encuentra a 720 metros con un ángulo de depresión de 22°.
a.
b.
¿Cuál es la distancia que hay entre el avión y el bote, en ese instante?
¿Con qué ángulo se observa el avión desde el bote?
Solución:
En este problema, no se ha proporcionado una figura que lo describa, por ello debemos leer con mayor
concentración y definir de manera geométrica las variables que permitan resolverlo.
A
𝑂: Observador
𝐴: Avión
420
O
𝐵: Bote
28
Horizontal
22
x
720
22
𝑥: Distancia entre el avión y el bote en metros
B
a. De la figura, observamos que tenemos la forma (LAL) y que aplicando la ley de cosenos podemos
encontrar la medida de 𝑥, es decir:
𝑥 2 = 4202 + 7202 − 2(420)(720) 𝑐𝑜𝑠 5 0
𝑥 = √4202 + 7202 − 2(420)(720) 𝑐𝑜𝑠 5 0
𝑥 = 553,2106. ..
Respuesta: La distancia entre el avión y el bote es de aproximadamente 553,21 metros.
Profesores MA420
181
UPC – Departamento de Ciencias - Matemática Básica (MA420)
b. En esta parte nos piden el ángulo de elevación 22° + 𝛼. De la figura, observamos que basta aplicar
la ley de senos para encontrar la medida del ángulo 𝛼, es decir:
sen𝛼
420
⇒
sen50°
420sen50°
=
⇒ 𝛼 = sen−1 (
)
𝑥
𝑥
420 sen(50°)
𝛼 = 𝑠𝑒𝑛−1 ( 553,2106 ) = 35,56205 ⋯
Se debe tener mucho cuidado cuando se use la
función arco seno, pues no siempre nos dará la
respuesta de manera directa, en este caso lo
aplicamos sin temor ya que se sabe que es un
ángulo agudo (ver figura).
Respuesta: El avión es observado desde el bote con un ángulo de elevación de 57,56°
aproximadamente.
PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1. Un cable conecta la parte superior de una torre con un punto al nivel del
piso, el cual está a 5 metros del centro de la base de la torre (ver figura).
Si el ángulo de elevación formado por este cable es de 78°, ¿cuál es la
longitud del cable y la altura de la torre?
78ο
2. En el siguiente mapa se muestran las estaciones Angamos,
Ayacucho y San Juan de la línea del metro de Lima. La distancia
entre la estación Angamos (A) y la estación Ayacucho (B) es 2,74
km, además mediante un aplicativo se determinó que la medida
del ángulo en la posición Angamos es 29° y en la posición San Juan
es 18°.
a. ¿Cuál es la distancia entre la Estación Angamos y la Estación San
Juan?
b. Si Carlos vive en el punto P y su casa está a 1,5 km de la estación
Angamos, determine la distancia entre su casa y la estación
Ayacucho.
3. Dos observadores están separados 60 metros y están en lados opuestos de un árbol. Los ángulos de elevación
de los observadores a la parte más alta del árbol son de 32° y 64° respectivamente. Determine la altura del
árbol.
4. En un instante dado, desde lo alto de una montaña, una persona observa un avión que se encuentra a 420
metros de distancia con un ángulo de elevación de 28º. Al mismo tiempo y en el mismo plano vertical, esta
persona observa un bote que se encuentra a 720 metros con un ángulo de depresión de 22º.
a. ¿Cuál es la distancia que hay entre el avión y el bote en ese instante?
b. ¿Con qué ángulo se observa el avión desde el bote?
Profesores MA420
182
UPC – Departamento de Ciencias - Matemática Básica (MA420)
5. Una embarcación parte desde un faro que tiene una altura de 50 m. Cuando se encuentra a 2 Km del faro
sufre fallas en sus equipos de comunicación y envía una señal mediante un reflector. ¿Cuál debe ser el
ángulo de elevación de la señal desde la embarcación hacia la parte más alta del faro?
6. Una persona se encuentra en la ventana de su departamento que está situada a 18 m del piso y observa el
edificio de enfrente. La parte superior con un ángulo de elevación de 35º y la parte inferior con un ángulo de
depresión de 41º. Determine la altura del edificio observado.
RESPUESTAS DE LOS EJERCICIOS ADICIONALES
1. La longitud del cable es de 24,05 metros aproximadamente y la altura de la torre es 23,52 metros
aproximadamente.
2. Respuestas:
a. La distancia entre las estaciones Angamos y San Juan es de 6,48 km aproximadamente.
b. La distancia entre la casa de Carlos y la estación Ayacucho es de 1,60 km aproximadamente.
3. La altura del árbol es de 28,73 metros aproximadamente.
4. Respuestas:
a. La distancia entre el avión y el bote es de 553,21 m aproximadamente.
b. Desde el bote el avión se observa con un ángulo de elevación 57,56° aproximadamente.
5. El ángulo de elevación debe ser de 1, 43° aproximadamente.
6. La altura del edificio es de 32,50 m aproximadamente.
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
RESOLUCIÓN DE TRIÁNGULOS: Revisar páginas desde 501 hasta 523
Profesores MA420
183
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Funciones sinusoidales y ecuaciones
trigonométricas
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante analiza el comportamiento algebraico y
gráfico de las funciones sinusoidales y los aplica en la resolución de ecuaciones trigonométricas, demostrando
responsabilidad y capacidad de aprender por su propia cuenta.
CONTENIDO
MOTIVACIÓN
1.1
FUNCIONES SINUSOIDALES
• Definiciones y notaciones
• Ejemplo
1.2
ECUACIONES TRIGONOMÉTRICAS
• Definiciones y notaciones
• Ejemplo
1.3
Practiquemos en clase
• Ejercicios
1.4
Practiquemos más en casa
• Ejercicios
Profesores MA420
184
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Motivación
Energía eléctrica doméstica
En la actualidad, la mayoría de las actividades
humanas están regidas por el uso de algún artefacto
eléctrico o electrónico que nos ayuda en el
desarrollo de nuestras actividades diarias. Un
computador para consultar alguna información en
internet, un televisor para ver las noticias o alguna
película, el horno microondas para calentar la
comida, la lavadora para el lavado de la ropa, el
refrigerador para conservar los alimentos, etc.
El funcionamiento de estos artefactos es gracias a la
energía eléctrica que llega a nuestros hogares, en
Figura 1. Artefactos eléctricos domésticos
forma de voltaje, por medio de las redes de
distribución de las empresas eléctricas del país.
La toma de corriente doméstica normal proporciona un
voltaje de CA1 sinusoidal, la cual tiene la forma de una onda
seno o sinusoidal a una frecuencia de operación de 60 Hz (60
ciclos por segundo). La figura 2 muestra la representación
gráfica de una onda de voltaje sinusoidal de amplitud 𝐴 y
𝐼
periodo 𝑇 = 𝑓 (𝑓 frecuencia de operación).
Figura 2. Onda de voltaje
1
Corriente alterna
Profesores MA420
185
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1.1. FUNCIONES SINUSOIDALES
Definición: Una función f es llamada sinusoidal si su regla de correspondencia es de la forma:
𝑓(𝑥) = 𝑎 sen(𝑏(𝑥 − 𝜙)) + 𝑘
𝑓(𝑥) = 𝑎 cos(𝑏(𝑥 − 𝜙)) + 𝑘
o
Donde: 𝑎 ≠ 0, 𝑏 ≠ 0 y 𝑘 son constantes reales.
Para graficar una función sinusoidal se debe seguir los siguientes pasos (teniendo en cuenta las técnicas de
graficación vistas anteriormente):
❖ Determine el valor de la amplitud, cuyo valor es |𝑎| (valor absoluto de 𝑎)
2𝜋
❖ Determine el valor del periodo de la función, cuyo valor se obtiene mediante:|𝑏|𝑇 =
2𝜋
|𝑏|
❖ Determine el valor del desplazamiento horizontal (𝜙).
❖ Determine el valor del desplazamiento vertical (𝑘).
❖ Finalmente, basta graficar para un periodo que inicia en 𝜙 y finaliza en 𝜙 + 𝑇, este intervalo se debe
dividir en cuatro partes iguales:
P2
P1
+T
P3
Donde:
•
•
•
Recuerde: El valor medio entre los valores 𝑎 y
𝑏 es igual a la semisuma, es decir
𝑎+𝑏
2
𝑃1 es el valor medio entre 𝜙 y 𝜙 + 𝑇.
𝑃2 es el valor medio entre 𝜙 y 𝑃1
𝑃3 es el valor medio entre 𝑃1 y 𝜙 + 𝑇
Ejemplo
𝜋
Dada la función 𝑓 con regla de correspondencia 𝑓(𝑥) = sen[2 (𝑥 + 2 )]. Determine el dominio, la amplitud, el
periodo, la traslación horizontal, el desplazamiento vertical, el rango y trace la gráfica en su periodo principal.
Solución:
• Paso 1:
Dominio:
Amplitud:
Periodo:
Dom(𝑓) = ℝ
𝐴 = |1| = 1
2𝜋
𝑇 = |2| = 𝜋
−𝜋
∅= 2
𝑘 = 0 (Eje de simetría)
Traslación horizontal:
Desplazamiento vertical:
•
Paso 2: Periodo principal
−𝜋/2
•
−𝜋/4
0
𝜋/4
𝜋/2
Paso 3: Representación gráfica en su periodo principal.
Profesores MA420
186
UPC – Departamento de Ciencias - Matemática Básica (MA420)
•
Paso 4: Rango: Ran(𝑓) = [−1; 1]
1.2. ECUACIONES TRIGONOMÉTRICAS
Definición:
Una ecuación trigonométrica es una igualdad donde la variable debe estar afectada necesariamente por una
función trigonométrica. Por ejemplo:
•
•
sen(4𝑥) + cos(4𝑥) = 1
tan2 𝑥 − tan 𝑥 − 6 = 0
Resolveremos ecuaciones trigonométricas para obtener soluciones generales y particulares, los pasos a seguir
son explicados en el siguiente ejemplo:
Ejemplo
Soluciones generales:
a. Determine el conjunto solución (CS) de la ecuación: 2 cos 𝑥 − √3 = 0
Solución: Despejando se obtiene: cos 𝑥 =
√3
2
En un mismo plano cartesiano, graficamos 𝑦 = cos 𝑥 en su periodo principal y también la función
√3
constante 𝑦 = . Las soluciones de la ecuación trigonométrica, en el periodo principal, estarán en los
2
puntos donde ambas gráficas se intersecten (ver figura).
Profesores MA420
187
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Luego, despejamos la variable 𝑥 y usamos la calculadora en radianes para hallar la solución 𝑥1 , es decir:
√3
√3
𝜋
cos 𝑥 = 2 ⇒ 𝑥 = cos −1 ( 2 ) ⇒ 𝑥 = 6 = 𝑥1 (Ver gráfica)
Para hallar la segunda solución, usamos la simetria mostrada en la gráfica, obteniendo:
𝜋 11𝜋
𝑥2 = 2𝜋 − 𝑥1 = 2𝜋 − =
6
6
Para obtener las soluciones generales, a cada solución se debe sumar el periodo de la función 𝑦 = cos 𝑥,
que en este caso es 𝑇 = 2π, y se multiplica por la constante 𝑘 ∈ ℤ, es decir:
𝜋
𝜋
𝑥1 = 6 + 𝑇𝑘 = 6 + 2𝜋𝑘
; 𝑘∈ℤ
{
11𝜋
11𝜋
𝑥2 =
+ 𝑇𝑘 =
+ 2𝜋𝑘
6
6
𝜋
Por lo tanto, obtenemos la solución general: CS = { 6 + 2𝜋𝑘;
11𝜋
6
+ 2𝜋𝑘} ; 𝑘 ∈ ℤ
Soluciones particulares:
𝜋
b. Determine el conjunto solución (CS) de la ecuación √2 sen(4𝑥) − 1 = 0, 𝑥 ∈ [0 ; 2 ]
Solución: Despejando se tiene: sen(4𝑥) =
1
√2
En un mismo plano cartesiano, graficamos 𝑦 = sen(4𝑥) en su periodo principal y también la función
1
constante 𝑦 = 2. Las soluciones de la ecuación trigonométrica, en el periodo principal, estarán en los
√
puntos donde ambas gráficas se intersecten (ver figura).
Luego, despejamos la variable 𝑥 y usamos la calculadora en radianes para hallar la solución 𝑥1 , es decir:
sen(4𝑥) =
1
√2
1
√2
⇒ 4𝑥 = sen−1 (
)=
𝜋
4
𝜋
⇒ 𝑥 = 16 = 𝑥1 (Ver gráfica)
Para hallar la segunda solución, usamos la simetria mostrada en la gráfica, obteniendo:
Profesores MA420
188
UPC – Departamento de Ciencias - Matemática Básica (MA420)
𝑥2 =
𝜋
𝜋
𝜋
3𝜋
− 𝑥1 = −
=
4
4 16 16
𝜋
𝜋
Como ambas soluciones pertenecen al intervalo [0 ; 2 ] entonces la solución particular es: CS = {16 ;
3𝜋
}
16
Nota: Para hallar las soluciones particulares, siempre debemos tomar en cuenta en intervalo donde nos
solicitan las soluciones.
1.3. PRACTIQUEMOS EN CLASE
1.
Dadas las funciones con reglas de correspondencia:
𝜋
𝜋
a. 𝑓(𝑥) = 3sen (𝑥 − ) − 2
b. 𝑓(𝑥) = −4cos (3𝑥 + ) + 2
3
4
En cada una de ellas, determine: el dominio, la amplitud, el periodo, la traslación horizontal, la
traslación vertical, el rango y trace su gráfica en su periodo principal.
2.
Determine el conjunto solución (CS) de las siguientes ecuaciones trigonométricas.
a. 4sen(𝑥) − 2 = 0, 𝑥 ∈ [0; 2𝜋[
b. 2cos(𝑥) + √3 = 0, 𝑥 ∈ [0;
3𝜋
]
2
3.
Determine y el conjunto solución (CS) de las siguientes ecuaciones trigonométricas.
a. 2sen(𝑥) + √3 = 0
b. 2cos(3𝑥) − 1 = 0
4.
La figura muestra la gráfica de función 𝑓 con regla de correspondencia 𝑓(𝑥) = −4 sen(6𝜋𝑥) para
𝑥 ∈ [0;
1
]
3
A partir de la gráfica, determine:
a. Los ceros de la función.
b. El intervalo donde la función es creciente.
c. El intervalo donde la función es negativa.
d. Los valores de "𝑥" tal que 𝑓(𝑥) = −3 (muestre el proceso).
Profesores MA420
189
UPC – Departamento de Ciencias - Matemática Básica (MA420)
RESPUESTAS DE PRACTIQUEMOS EN CLASE
PREGUNTA 1:
a.
𝜋
𝑓(𝑥) = 3sen (𝑥 − ) − 2
3
Dom(𝑓) = ℝ
Amplitud: A = 3
Periodo: 𝑇 = 2𝜋
𝜋
TH: ϕ =
3
Traslación Vértical: k = −1
Ran(𝑓) = [−5; 1]
La gráfica debe mostrarse en el periodo principal, en este periodo muestre los 5 puntos de paso explicados en
este libro e indique que la curva continúa su recorrido pues su dominio es todos los reales.
b.
𝜋
𝑓(𝑥) = −4cos (3𝑥 + ) + 2
4
Dom(𝑓) = ℝ
Amplitud: A = 4
2𝜋
Periodo: 𝑇 =
3
𝜋
TH: ϕ = −
12
Traslación Vértical: k = 2
Ran(𝑓) = [−2; 6]
La gráfica debe mostrarse en el periodo principal, en este periodo muestre los 5 puntos de paso explicados en
este libro e indique que la curva continúa su recorrido pues su dominio es todos los reales.
PREGUNTA 2: Trace la gráfica en el dominio dado.
𝜋 5𝜋
}
6 6
a. CS = { ;
PREGUNTA 3
4𝜋
a. CS = { 3 + 2𝑘𝜋;
b. CS = {
5𝜋
3
𝜋
+ 2𝑘𝜋}; 𝑘 ∈ 𝑍
PREGUNTA 4
1
a. Los ceros de la función son: 0; 6 ;
1
5𝜋 7𝜋
; }
6
6
b. CS = { 9 +
2𝜋𝑘 5𝜋
; 9
3
+
2𝜋𝑘
};
3
𝑘∈𝑍
1
3
1
b. 𝑓 es creciente en: ]12 ; 4[
1
c. 𝑓 es negativa en: ]0; 6[
d. 𝑥 ≈ 0,0450 ∧ 𝑥 ≈ 0,1217
Profesores MA420
190
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1.4. PRACTIQUEMOS MÁS EN CASA
Resuelve los siguientes ejercicios y si tienes dudas aprovecha la asesoría virtual con tu profesor AAD para
asegurar que tus soluciones son correctas y retroalimentar tu aprendizaje.
1.
Dadas las funciones con reglas de correspondencia:
𝜋
a. 𝑓(𝑥) = 4 cos (2𝑥 − ) − 1
3
b. 𝑔(𝑥) = −2sen(4𝜋𝑥) + 1
𝜋𝑥
c. 𝑓(𝑥) = −3 sen ( ) + 2
8
d. 𝑓(𝑥) = 4cos(3𝑥 + 𝜋) − 1
En cada una de ellas, determine: el dominio, la amplitud, el periodo, la traslación horizontal, la
traslación vertical, el rango y trace su gráfica en su periodo principal.
2.
Determine el conjunto solución (CS) de las siguientes ecuaciones trigonométricas.
𝜋
a. 2cos(𝑥) + 1 = 0, 𝑥 ∈ [0; 2𝜋 [
c. √2sen(𝑥) − 1 = 0, 𝑥 ∈ [0; ]
b. √2cos(𝑥) − 1 = 0, 𝑥 ∈ [0; 𝜋]
2
d. 4sen(𝑥) + 1 = 0, 𝑥 ∈ [0; 2𝜋]
3.
Determine el conjunto solución (CS) de las siguientes ecuaciones trigonométricas.
a. (sen(𝑥) + 1)(cos(𝑥) − 2) = 0
b. (2 cos(2𝑥) + 3)(cos(𝑥) − 1) = 0
c. 3 cos(2𝑥) + √2 = 0
d. 2 sen(4𝑥) − 1 = 0
4.
Grafique la función ℎ con regla de correspondencia ℎ(𝑡) = −6 sen (4𝜋𝑡) − 2 para 𝑡 ∈ [0; 2]. Luego
determine:
a. Los ceros de la función.
b. El intervalo donde la función es creciente.
c. Los intervalos donde la función es negativa.
d. Los valores de “𝑡” tal que ℎ(𝑡) = 1 (muestre el proceso).
1
RESPUESTAS DE PRACTIQUEMOS MÁS EN CASA
Pregunta 1
a.
Dom(𝑓) = ℝ
Amplitud: A = 4
Periodo: 𝑇 = 𝜋
𝜋
TH: ϕ =
6
Traslación Vértical: k = −1
Ran(𝑓) = [−5; 3]
La gráfica debe mostrarse en el periodo principal, en
este periodo muestre los 5 puntos de paso
explicados en este libro e indique que la curva
continúa su recorrido pues su dominio es todos los
reales.
Profesores MA420
c.
Dom(𝑓) = ℝ
Amplitud: 𝐴 = 3
Periodo: 𝑇 = 16
TH: ϕ = 0
Traslación Vértical: k = 2
Ran(𝑓) = [−1; 5]
La gráfica debe mostrarse en el periodo principal, en
este periodo muestre los 5 puntos de paso explicados en
este libro e indique que la curva continúa su recorrido
pues su dominio es todos los reales.
191
UPC – Departamento de Ciencias - Matemática Básica (MA420)
b.
Dom(𝑓) = ℝ
Amplitud: 𝐴 = 2
1
Periodo: T =
2
TH: ϕ = 0
Traslación Vértical: 𝑘 = 1
Ran(𝑓) = [−1; 3]
La gráfica debe mostrarse en el periodo principal, en
este periodo muestre los 5 puntos de paso
explicados en este libro e indique que la curva
continúa su recorrido pues su dominio es todos los
reales.
d.
Dom(𝑓) = ℝ
Amplitud: 𝐴 = 4
2𝜋
Periodo: 𝑇 =
3
𝜋
TH: ϕ = −
3
Traslación Vértical: k = −1
Ran(𝑓) = [−5; 3]
La gráfica debe mostrarse en el periodo principal, en
este periodo muestre los 5 puntos de paso explicados en
este libro e indique que la curva continúa su recorrido
pues su dominio es todos los reales.
Pregunta 2
2𝜋 4𝜋
}
3
𝜋
{ }
4
𝜋
{ }
4
a. CS = { 3 ;
b. CS =
c. CS =
d. CS = {3,394 ⋯ ; 6,03 ⋯ }
Pregunta 3
𝜋
2
a. CS = {− + 2𝜋𝑘}; , 𝑘 ∈ 𝑍
b. CS = {2𝜋𝑘}; 𝑘 ∈ 𝑍
c. CS = {1,0308 … + 𝜋𝑘; 2,1107 … + 𝜋𝑘}; 𝑘 ∈ 𝑍
d. CS = {0,1308 … +
𝜋𝑘
𝜋𝑘
; 0,6544 … + 2
2
}; 𝑘 ∈ 𝑍
Pregunta 4
a. Los ceros de la función son: 𝑡 ≈ 0,28 ∧ 𝑡 ≈ 0,47
1 3
b. 𝑓 es creciente en: ]8 ; 8[
c. 𝑓 es negativa en: [0; 0,28[
d. 𝑡 ≈ 0,29 ∧ 𝑡 ≈ 0,46.
EJERCICIOS RESUELTOS EN VIDEO
Habilidad
Trazar la gráfica de una función
sinusoidal y determinar sus
elementos.
Profesores MA420
Enlace
Código QR
https://bit.ly/367rcFY
192
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Trazar la gráfica de una función
sinusoidal y determinar sus
elementos.
Determinar el conjunto solución
de una ecuación trigonométrica.
https://bit.ly/3iNgUjp
https://bit.ly/36758et
Determinar el conjunto solución
de una ecuación trigonométrica.
https://tinyurl.com/y4l3mcw6
Determinar el conjunto solución
de una ecuación trigonométrica.
https://tinyurl.com/y5hmluod
MÁS EJERCICIOS RESUELTOS Y PROPUESTOS EN:
Bibliografía Básica:
STEWART James, Redlin, Lothar; WATSON, Saleem y ROMO MUÑOZ, Jorge
Humberto (2017) Precálculo: matemáticas para el cálculo. México, D.F.: Cengage
Learning. (515 STEW/P 2017)
FUNCIONES SINUSIODALES: Revisar páginas desde 424 hasta 425
ECUACIONES TRIGONOMÉTRICAS: Revisar páginas desde 564 hasta 575
Profesores MA420
193
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Anexo: Problemas de la vida real
LOGRO DE LA SESIÓN DE CLASE: Al finalizar la sesión, el estudiante resuelve problemas de contexto real y
explica la solución detallando las dimensiones de la competencia de razonamiento cuantitativo, demostrando
responsabilidad y capacidad de aprender por su propia cuenta.
CONTENIDO
COMPETENCIA: RAZONAMIENTO CUANTITATIVO
1.1
RAZONAMIENTO CUANTITATIVO
• Definiciones
• Problemas resueltos
• Problemas propuestos
1.2
RÚBRICA DE RAZONAMIENTO CUANTITATIVO
Profesores MA420
194
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1.1
RAZONAMIENTO CUANTITATIVO
Definición: Se define como la capacidad para interpretar, representar, comunicar y utilizar información
cuantitativa diversa en situaciones de contexto real. Incluye calcular, razonar, emitir juicios y tomar
decisiones con base en esta información cuantitativa.
Dimensiones:
1. Interpretación: Capacidad para dar significado a información cuantitativa presentada en diversos
formatos.
2. Representación: Capacidad para expresar mediante objetos matemáticos (matematizar) situaciones
cuantitativas de contexto real.
Matematiza: Habilidad para expresar una situación o problema mediante objetos matemáticos.
3. Cálculo: Capacidad para utilizar algoritmos y procedimientos estándar de la matemática y estadística
en situaciones de contexto real
4. Análisis: Capacidad para estudiar una situación real mediante la aplicación de métodos matemáticos y
estadísticos adecuados con el fin de llegar a conclusiones objetivas.
5. Comunicación/argumentación: Capacidad para formular ideas, y emitir juicios con base en
información cuantitativa.
Nivel: En este curso trabajaremos el nivel 1 (primeros ciclos).
Temas del nivel 1: Los contenidos teóricos que el estudiante debe manejar para responder la
problemática son:
‐
‐
‐
‐
‐
Operaciones combinadas
Intervalos y desigualdades
Razones y proporciones
Regla de tres
Porcentajes y variaciones porcentuales
Profesores MA420
195
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Problemas resueltos
Problema 1: Se debe pintar 520 m2 de pared y para ello se ofrecen dos tipos de pintura con las siguientes
características:
Rosita
S/52,00
Rendimiento
(cantidad de
m2 que cubre
o que se
puede pintar
por cada
galón)
34
UV-extra
S/45,00
28
Nombre
de la
pintura
Precio
de lista
(por
galón)
Descuento que se ofrece por la compra
Por cada tres galones se ofrece un descuento del 12% por
galón, dicho descuento solo se aplica por paquetes de 3
unidades, no por compras de galones individuales
Se ofrece un descuento de 10% por el total de la compra
Tomando en cuenta solo la parte económica, ¿cuál de las dos pinturas conviene comprar, ¿cuántos galones y
cuál será el presupuesto en pintura?
Solución
Rosita:
520
Número de galones:
= 15,29 …, entonces deben comprarse 16 galones
34
Costo: 15*52*0,88+1*52 =738,4
UV-extra:
520
Número de galones: 28 = 18,57 …, entonces deben comprarse 19 galones
Costo: 19*45*0,9=769,5
Conviene comprar la pintura Rosita puesto que cuesta S/738,4 contra la otra pintura que cuesta S/769,5.
Problema 2: La tabla 1 muestra la cantidad de postulantes, entre varones y mujeres, hacia las áreas A y B que
ofreció una universidad privada de Lima – Perú, para el primer ciclo de un determinado año.
Total de varones
Total de mujeres
Área “A”
Área “B”
Área “A”
Área “B”
Total
de
postulantes
1426
720
701
1023
3870
Año | Ciclo
2019 01
Tabla 1: Elaboración propia
Profesores MA420
196
UPC – Departamento de Ciencias - Matemática Básica (MA420)
La tabla 2 muestra la escala de pagos por crédito que paga cada alumno en dicho año.
Grado de escala
Valor del crédito en S/. (Sin IGV)
5
1008,20
4
928,20
3
832,90
2
729,20
1
623,20
Tabla 2: Elaboración propia
a. Determine la razón geométrica entre el número total de postulantes mujeres y el número total de
postulantes varones, que postularon al área A.
Solución
La razón geométrica entre el número total de postulantes mujeres y el número total de postulantes varones,
que postularon al área A es
𝑟=
701
1426
b. Si se sabe que entre las áreas A y B ingresaron un total de 3096 estudiantes, que todos son matriculados
en 18 créditos y que la tercera parte de los estudiantes que ingresaron se clasificó en una escala
intermedia (Escala 3). A cuánto asciende el monto que obtendrá esta universidad por los pagos que
realicen los estudiantes en esta escala, sabiendo que el monto que paga cada alumno es igual al valor del
crédito más el IGV, multiplicado por el total de créditos.
Nota: IGV = 18% del valor del crédito.
❖
❖
❖
Solución
Número de estudiantes que fueron clasificados en la escala 3 es:
1
(3096) = 1032 estudiantes
3
El monto de pago de cada estudiante en la escala 3 es: 832,90 × 1.18 × 18 =17 690,796 soles
El monto que obtendrá la universidad por el pago de los estudiantes que se encuentran en la escala
3 es: 17 690,796 × 1032 = 18 256 901,47 soles
Problema 3: Carlos desea renovar el piso de su dormitorio, averiguando los tipos de porcelanato y sus precios,
él decide comprar el porcelanato de la marca A, que es de su preferencia y que cuesta S/ 26,90 el metro
cuadrado, si comprara esta marca le ofrecen un descuento del 12%. Si se sabe que el dormitorio tiene una
Profesores MA420
197
UPC – Departamento de Ciencias - Matemática Básica (MA420)
longitud de 4,2 m × 6 m y que cada porcelanato mide 60 cm × 60 cm. Determine, justificando sus respuestas
las siguientes preguntas:
a. La cantidad de porcelanatos que se necesita para colocar en el dormitorio de Carlos.
b. Si Carlos cuenta con S/ 840,00 para renovar el piso de su dormitorio y la instalación de cada m2 o fracción
de m2 le cuesta S/ 10,00. ¿Le alcanza el dinero a Carlos para renovar el piso de su dormitorio (instalación
y costo del porcelanato)?
Nota: Asuma que no existe perdida en la instalación de los porcelanatos y que la venta de los mismos es
por metro cuadrado.
a. Para sacar el número de porcelanatos:
4,20
0,60
Solución:
6,00
= 7 𝑦 0,60 = 10
Por lo tanto, se necesitarán 7×10= 70 porcelanatos
b. Área a recubrir con porcelanatos: 4,2×6,0=25,20 m2
Costo del porcelanato:
Se deberán comprar 26 m2 de porcelanato
26(26,90)(0,88)=S/615,472
Costo de instalación
26(10)=S/260,00
Costo total:
S/ 615,472 +S/260,00 = S/ 875,472
A Carlos no le alcanza el dinero para cubrir su dormitorio con el porcelanato, le falta S/35,472
Problema 4: Ejecución de una obra civil: Para que un contratista realice la obra civil DR-01-2019, debe contratar
maestros, oficiales y peones, cuyas responsabilidades se describen a continuación:
Maestro: Es el responsable de la ejecución de la obra y recibe instrucciones del ingeniero residente de la obra.
Oficial: Realiza trabajos especializados relacionados con la obra civil como albañilería, carpintería, electricidad,
etc.
Peón: Apoya en diferentes labores cuando el volumen de trabajo lo requiere y no necesariamente participa
durante todo el proceso de la obra.
Tabla 1.
Información del pago diario al personal de la obra DR- 01- 2019.
Categoría
Pago diario (Soles)
Maestro
85,00
Oficial
75,00
Peón
60,00
Nota: Tabla de elaboración propia.
Profesores MA420
198
UPC – Departamento de Ciencias - Matemática Básica (MA420)
La Nueva Ley de Contrataciones del Estado y su Reglamento Aplicado a Obras, establece que, si el contratista
incurre en retraso injustificado en la ejecución de la obra, la penalidad se calculará mediante la siguiente
fórmula:
𝟎, 𝟐𝟓 × 𝐌𝐨𝐧𝐭𝐨
𝐏𝐝 =
𝐏𝐥𝐚𝐳𝐨 𝐞𝐧 𝐝í𝐚𝐬
Donde:
𝐏𝐝: Penalidad diaria, en soles.
Monto: valor presupuestado para realizar la obra en un plazo dado, en soles.
PREGUNTA N°1: Indique dos factores que debe tener en cuenta un contratista para hacer la obra DR-012019.
Solución
▪ Debe tomar en cuenta el plazo en que se ejecutará la obra para evitar pago por el retraso.
▪ Para realizar la obra, debe tomar en cuenta cuantos maestros, oficiales y peones debe contratar.
PREGUNTA N°2: Considerando la tabla 1, determine el pago total P (en soles) que debe hacer el contratista al
contratar a un maestro y a un oficial que trabajan juntos 𝑥 días.
Solución
▪
▪
▪
𝑃 = 85𝑥 + 75𝑥 = 160𝑥
𝑥: cantidad de días que trabajan el maestro y oficial
𝑃: Pago en soles por contratista al maestro y oficial por trabajar 𝑥 días
PREGUNTA N°3: El contratista debió entregar la obra DR-01-2019 en 20 días para evitar pagar una penalidad
de acuerdo a ley. Si se sabe que el presupuesto para la obra es de S/. 30000,00 y la obra se entregó con un
atraso de 4 días. ¿Cuánto de penalidad pagó el contratista por los 4 días?
Solución
𝟎,𝟐𝟓×𝐌𝐨𝐧𝐭𝐨
𝐏𝐥𝐚𝐳𝐨 𝐞𝐧 𝐝í𝐚𝐬
=
𝟎,𝟐𝟓×30000
20
▪
𝐏𝐝 =
= 375
▪
▪
Penalidad por 4 días 375*4=1500
El contratista debe pagar 1500 soles de penalidad por el retraso de 4 días
PREGUNTA N°4: El contratista debería cobrar por la obra S/. 30000,00 pero se retrasa 4 días y por cada día de
retraso tiene que pagar
(0,25)(30000)
soles.
20
¿El contratista logrará obtener exactamente S/. 28000,00?
Solución
𝟎,𝟐𝟓×𝐌𝐨𝐧𝐭𝐨
𝐏𝐥𝐚𝐳𝐨 𝐞𝐧 𝐝í𝐚𝐬
=
𝟎,𝟐𝟓×30000
20
▪
𝐏𝐝 =
= 375 y penalidad por 4 días 375*4=S/.1500
▪
▪
30000-1500 = S/. 28500
Es falso ya que el contratista logrará obtener S/.28500 por la ejecución de la obra.
PREGUNTA N°5: En caso de que el contratista pueda asignar la obra DR-01-2019 a:
• un maestro, dos oficiales y cuatro peones, o
Profesores MA420
199
UPC – Departamento de Ciencias - Matemática Básica (MA420)
• un maestro, tres oficiales y dos peones.
Si en ambos casos el contratista termina la obra sin retrasos, desde el punto de vista económico cuál de las
alternativas de personal le conviene contratar.
Solución
▪
Categoría
Pago diario (Soles)
Monto (S/.)
1 maestro
85,00
85
2 oficiales
75,00
150
4 peones
60,00
240
Monto a pagar por un día de trabajo
475
▪
▪
Categoría
Pago diario (Soles)
Monto (S/.)
1 maestro
85,00
85
3 oficiales
75,00
225
2 peones
60,00
120
Monto a pagar por un día de trabajo
430
Conviene la segunda alternativa ya que pagaría S/430 cada día de trabajado, así estaría ahorrando
S/. 45 por día
Profesores MA420
200
UPC – Departamento de Ciencias - Matemática Básica (MA420)
Problemas propuestos
Problema 1: Luis tiene un auto que usa gasolina de “97 octanos”, él actualmente se encuentra en un centro
comercial y está analizando los precios por galón de diferentes establecimientos de un distrito cercano al centro
comercial para ir y abastecer de gasolina su auto, buscando por internet obtiene la siguiente tabla:
Establecimientos
A
B
C
Precio de venta por Distancia desde el centro
galón
comercial a los
establecimientos según Google
maps
S/ 12,99
2,66 km
S/ 13,86
1,83 km
S/ 14,99
1,69 km
Recuperado de: http://www.facilito.gob.pe/facilito
Considere que un galón equivale a 3,78 litros y además que el auto de Luis recorre 20 km por litro de
combustible. A continuación, responda las siguientes preguntas:
a. Calcule la cantidad de combustible (en galones) que consumiría el auto de Luis si elige ir desde el centro
comercial hasta el establecimiento A.
b. Sí Luis decidió comprar la gasolina en el establecimiento C y sabe que desde dicho lugar hasta su casa gasta
0,595 galones, ¿Cuántos kilómetros hay desde el establecimiento C a la casa de Luis? ¿Cuánto dinero gasto
en combustible por dicho recorrido?
c. Luis en una semana recorre 557,1 km y sabe que cada galón tiene un rendimiento de 75,6 km. Además, él
eligió comprar el combustible en el establecimiento B, pues cuenta con la siguiente oferta: que por cada
tres galones obtiene un descuento del 11% (dicho descuento solo se realizaría por paquetes de 3 galones,
no por compras de galones individuales). ¿Cuánto gastó en combustible?
Problema 2: Marco apertura su negocio y compró los siguientes artefactos entre televisores y refrigeradoras
cuyas cantidades y precios de costo por unidad se muestran en la Tabla 1.
Tabla 1.
Cantidad de artefactos y precio de costo por unidad en soles
Artefactos
Cantidad
Precio de costo por unidad (S/)
Televisor LED 50 pulgadas
18
1 800.00
Refrigeradora 1.8 m3
Profesores MA420
15
Fuente: Elaboración propia
1 200.00
201
UPC – Departamento de Ciencias - Matemática Básica (MA420)
ELECTRODOMÉSTICOS
Figura 1 Electrodomésticos. Fuente:
https://www.creditoseconomicos.com/audio-y-video/tv-y-
En la primera semana Marco:
•
•
Vende la mitad de los televisores ganando por cada uno el 30%
Vende la quinta parte de las refrigeradoras perdiendo por cada uno el 10%
En la segunda semana:
•
•
Vende la tercera parte de los televisores que quedaba perdiendo por cada uno el 25%
Vende la cuarta parte de las refrigeradoras que quedaban ganando por cada uno el 20%
En la tercera semana se da cuenta que tiene algunos electrodomésticos dañados que no sirven para la venta ni
devolución, siendo la relación entre televisores dañados y refrigeradoras dañadas de 2 a 5.
Si Marco por emergencia debe viajar al extranjero y decide rematar todos los televisores y refrigeradoras
restantes vendiéndolos cada uno con una pérdida del 10%. ¿Marco recuperó su inversión?
(No considerar en los cálculos, gastos de instalación, gastos operativos, ni IGV, estos ya están incluidos en la
venta)
Respuestas:
Problema 1:
a. La cantidad de combustible a usar será 0,352 de galón.
b. Por dicho recorrido gastará S/. 8,92.
c. El presupuesto por combustible será de 101,73 soles.
Problema 2:
Inversión: 50400 soles
Ventas: 43470 soles
Marco no llegó a recuperar su inversión, perdió S/ 6 930,00.
Profesores MA420
202
UPC – Departamento de Ciencias - Matemática Básica (MA420)
1.2
RÚBRICA DE RAZONAMIENTO CUANTITATIVO
Criterios
INTERPRETACIÓN
REPRESENTACIÓN
CÁLCULO
ANÁLISIS
COMUNICACIÓN/
ARGUMENTACIÓN
Profesores MA420
En proceso
Explica parcialmente la
información dada en
situaciones de contexto
real, presentada en
diferentes formatos, no
establece relaciones o
establece relaciones
parcialmente.
Matematiza parcialmente
la información dada
presentada en diferentes
formatos. Solo establece
la ley del modelo.
Efectúa procedimientos
matemáticos parcial o
incorrectamente,
utilizando algoritmos
convencionales para la
situación dada
Examina en forma
incompleta los resultados
obtenidos, aplicando
métodos matemáticos,
llegando a conclusiones
imprecisas.
Explica con argumentos
imprecisos, las
conclusiones de su
razonamiento.
Nivel
Nivel mínimo de logro
Explica
completamente la
información dada en
situaciones de
contexto real,
presentada en
diferentes formatos,
pero no define
claramente el camino
para resolver el
problema.
Matematiza la
información dada
presentada en
diferentes formatos,
define variables y ley
que modela, mediante
un proceso simple.
Efectúa
procedimientos
matemáticos
correctamente,
utilizando algoritmos
convencionales para la
situación dada.
Examina
completamente los
resultados obtenidos,
llegando a
conclusiones
evidentes.
Explica con
argumentos sencillos y
evidentes, las
conclusiones de su
razonamiento
haciendo uso de un
lenguaje adecuado.
Sobresaliente
Explica completamente
la información dada en
situaciones de contexto
real, presentada en
diferentes formatos, y
establece relaciones.
Matematiza la
información dada
presentada en diferentes
formatos, considerando
la definición de variables,
sus restricciones y la ley
que define el modelo.
Efectúa procedimientos
matemáticos
correctamente,
utilizando algoritmos
convencionales para la
situación dada, y termina
con una respuesta
completa.
Examina completamente
los resultados obtenidos,
llegando a conclusiones
evidentes y consistentes.
Explica y argumenta, de
forma ordenada y
coherente, las
conclusiones de su
razonamiento haciendo
uso de un lenguaje
adecuado.
203



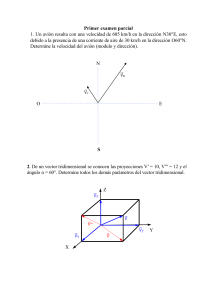

![Prueba Segundos2[1]](http://s2.studylib.es/store/data/003397536_1-3ac4e8618b6474fb10e9bb3037bc9dd2-300x300.png)