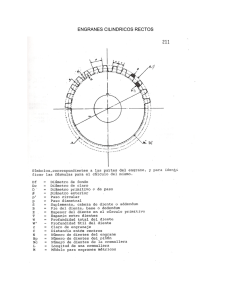
TEORIA DE ENGRANES OBJETIVOS: Al terminar el estudio de esta unidad, se podrá: 1. Identificar y decir cuál es el propósito de los seis tipos de engranes utilizados en la industria 2. Aplicar diversas fórmulas para calcular las dimensiones de los dientes de los engranes 3. Determinar el procedimiento de corte de los engranes. Cuando se requiere transmitir un movimiento giratorio de un eje a otro, pueden utilizarse varios métodos como bandas, poleas y engranes. Si los ejes son paralelos entre sí y están separados a una distancia suficiente, se puede utilizar una banda plana y poleas grandes para impulsar el segundo eje, cuya velocidad puede ser controlada por el tamaño de las poleas. Cuando los ejes están cerca entre sí, como en el caso de un taladro, puede utilizarse una banda en V, que tiende a reducir el deslizamiento excesivo de una banda plana. Aquí, la velocidad del eje impulsado puede controlarse mediante poleas en escalón o de velocidad variable. Cuando los ejes están cerca uno de: otro y paralelos, se puede transmitir algo de potencia mediante dos rodillos en contacto, con un rodillo montado en cada uno de los ejes. El problema principia aquí es el deslizamiento, no siendo posible mantener la velocidad deseada del eje impulsado. Los métodos que se delinean en esta unidad son medios mediante los cuales se puede transmitir potencia de un eje a otro, pero la velocidad del eje impulsado pudiera no ser precisa en todos los casos, debido a deslizamiento entre los miembros impulsor e impulsado (bandas, poleas o rodillos). A fin de eliminar el deslizamiento y producir una impulsión positiva, se utilizan los engranes. ENGRANES Y ENGRANAJES Los engranes se utilizan para transmitir potencia positivamente de un eje a otro, mediante dientes que se van acoplando de manera sucesiva (en dos engranes). Se utilizan en lugar de las transmisiones por banda y de otras formas de transmisión por fricción, cuando debe mantenerse una relación exacta de velocidad y de transmisión de potencia. Los engranes también pueden ser utilizados para incrementar o reducir la velocidad del eje impulsado, reduciendo o incrementando así el par de torsión del miembro impulsado. Los ejes en una transmisión o tren de engranes son por lo general paralelos. Pueden, sin embargo, mediante engranes adecuadamente diseñados, ser impulsados en cualquier ángulo. TIPOS DE ENGRANES Los engranes rectos (Figura 69-1) se utilizan generalmente transmitir potencia entre dos ejes paralelos. Los dientes de engranes son rectos y paralelos a los ejes a los cuales están Cuando dos engranes de tamaño diferente están acoplados. El más grande se conoce como engrane, en tanto que el más pequeño se conoce como piñón. Los engranes rectos se utilizan se requiere impulsión a velocidad lenta a moderada. Los engranes internos (Figura 69-2) se utilizan donde ejes son paralelos y los centros deben estar más cerca entre lo que podría lograrse utilizando engranes rectos o helicoidales. Esta disposición proporciona una impulsión más resistente, que existe un área mayor de contacto que con la impulsión engrane convencional. También proporciona reducciones de velocidad con un requerimiento mínimo de espacio. Los engranes internos se utilizan en tractores de servicio pesado donde se re- quiere un gran par de torsión. Figura 69-1 Un engrane y un piñón rectos se utilizan para Velocidades más bajas. Figura 69-2 Los engranes internos proporcionan reducciones de velocidad con un requerimiento mínimo de espacio. Figura 69-3 Engranes helicoidales (a) para transmisiones paralelas entre sí, (b) para transmisiones en ángulo recto. Los engranes helicoidales (Figura 69-3) pueden utilizarse para conectar ejes paralelos o ejes en ángulo. Debido a la acción progresiva, más bien que intermitente, de los dientes, los engranes helicoidales operan más suave y silenciosamente que los engranes rectos. En vista de que en todo momento hay más de un diente en acoplamiento, los engranes helicoidales son más resistentes que los engranes rectos de un mismo tamaño y paso. Sin embargo, para superar el empuje axial producido por estos engranes al girar, se requiere a menudo en los ejes de rodamientos especiales (rodamientos de empuje). En la mayor parte de las instalaciones donde es necesario eliminar el empuje axial, se utilizan engranes espina de pescado (Figura 69-4). Este tipo de engrane se parece a dos engranes helicoidales colocados uno aliado del otro, una mitad de hélice izquierda y la otra de hélice derecha. Estos engranes tienen una acción suave y continua, y eliminan la necesidad de rodamientos de empuje. a) Figura 69-4 Los engranes espina de pescado eliminan el empuje axial sobre los ejes. d) b) Figura 69-5 (a) Los engranes cónicos transmiten potencia a 90°, (b) los engranes cónicos impulsor e impulsado son del mismo tamaño, (e) los engranes cónicos en ángulo se utilizan para ejes que no están en ángulo recto, (d) los engranes hipoides se utilizan en transmisiones de automóvil. Cuando dos ejes están localizados en ángulo, con sus líneas axiales cruzándose a 90°, la potencia se transmite generalmente utilizando engranes cónicos (Figura 69-5a). Cuando los ejes están en ángulo recto y los engranes son del mismo tamaño, se conocen como engranes a inglete (Figura 69-5b). Sin embargo, no es necesario que los ejes estén en ángulo recto para transmitir potencia. Si la dirección de los ejes se cruza en cualquier otro ángulo distinto a 90°, los engranes se conocen como engranes cónicos en ángulo (Figura 69-5c). Los engranes cónicos tienen dientes rectos, muy similares a los engranes rectos. Los engranes cónicos modificados con dientes helicoidales se conocen como engranes hipoides (Figura 69-5d). Los ejes de estos engranes, aunque estén en ángulo recto, no están en un mismo plano y por lo tanto, no se cruzan. Los engranes hipoides se utilizan en las transmisiones automotrices. Cuando los ejes están en ángulo recto y se requiere una considerable reducción de velocidad, se pueden utilizar engranes de tornillo sinfín y rueda dentada (Figura 69-6). El tornillo sinfín, que se acopla con la rueda dentada, puede tener una rosca de uno o de múltiples inicios. Un tomillo sinfín con una rosca de doble inicio puede hacer girar a la rueda dentada del tornillo sinfín dos veces más rápido que un tornillo sinfín con una rosca de una sola entrada y del mismo paso. Cuando es necesario convertir un movimiento giratorio en movimiento lineal, se puede utilizar una cremallera y piñón (Fi- gura 69-7). La cremallera, que es realmente un engrane recto o plano, puede tener dientes rectos para acoplarse con un engrane recto, o dientes en ángulo, para acoplarse con un engrane helicoidal. TERMINOLOGIA DE ENGRANES Es deseable un conocimiento de los términos más comunes de los engranes para comprenderlos y para efectuar los cálculos necesarios para cortar un engrane (Figura 698). La mayor parte de estos términos son aplicables a cualesquiera de los engranes en pulgadas o métricos, aunque puede diferir el método de calcular las dimensiones. Estos métodos, aplicables al corte de engranes en pulgadas y métricos, se explican más adelante. Figura 69-6 Para reducción Figura 69-7 Un piñón y una cremallera convierten un de velocidad se utiliza un movimiento giratorio en movimiento lineal. engrane tornillo sinfín y una rueda dentada. Visita: http://www.eurogear.cl/caja-de-engranajes.html http://www.engranesdemexico.com.mx/reparacion-fabricacion-de-engranes/ http://www.engranor.com/ http://www.hmcgears.com/es/job-shop.php Tabla 69.1 reglas y fórmulas para engranes rectos Para obtener Si se conoce Regla Adéndum (A) Paso circular Distancia entre centros (CD) Paso diametral Adéndum cordal (corregido)( CA) Espesor cordal (CT) Paso circular (CP) Multiplique el paso circular por 𝐴 = 𝐶𝑃 × 0.3183 0.3183. 1 Divida 1 entre el paso 𝐴 = 𝐷𝑃 diametral. Paso circular Paso diametral Diámetro paso, adéndum número de dientes de Diámetro paso y número dientes de Distancia centro a centro de y de Multiplique el número de dientes de ambos engranes por el paso circular, y divida el producto entre 6.2832. Divida el número total de dientes de ambos engranes por dos veces el paso diametral. Reste de 1 el coseno del resultado de 90° dividido entre el número de dientes. Multiplique este resultado por la mitad del diámetro de paso. A este producto, súmele el adéndum. Divida 90 por el número de dientes; encuentre el seno de este resultado y multiplique por el diámetro de paso Multiplique la distancia de centro a centro por 6.2832, y divida el producto entre el número total de dientes de ambos engranes. 𝐶𝐷 = (𝑁 + 𝑛) × 𝐶𝑃 6.2832 𝐶𝐷 = 𝑁+𝑛 2 × 𝐷𝑃 90 𝑃𝐷 ) ] 𝑁 2 +𝐴 𝐶𝐴 = [(1 − 𝐶𝑜𝑠 𝐶𝑇 = 𝑆𝑒𝑛 𝐶𝑃 = 90 × 𝑃𝐷 𝑁 𝐶𝐷 × 6.2832 𝑁+𝑛 Paso diametral 3.1416 Divida 3.1416 entre el paso 𝐶𝑃 = diametral. 𝐷𝑃 Diámetro de paso y número de dientes Multiplique el diámetro de paso 𝑃𝐷 × 3.1416 por 3.1416 y divida entre el 𝐶𝑃 = 𝑁 número de dientes. Paso circular Divida el paso circular entre 20. 𝐶𝐿 = Claro (CL) Paso diametral Dedéndum (D) Formula Paso circular 𝐶𝑃 20 0.157 Divida 0.157 entre el paso 𝐶𝐿 = diametral. 𝐷𝑃 Multiplique el paso circular por 𝐷 = 𝐶𝑃 × 0.3683 0.3683. Paso diametral Paso circular Número dientes diámetro exterior Número dientes diámetro paso Paso diametral (DP) de y de y de 1.157 Divida 1.157 entre el paso 𝐷 = diametral. 𝐷𝑃 3.1416 Divida 3.1416 entre el paso 𝐷𝑃 = circular. 𝐶𝑃 Sume 2 al número de dientes y 𝑁+2 divida la suma entre el diámetro 𝐷𝑃 = exterior. 𝑂𝐷 Divida el número de dientes entre el diámetro de paso. DP = 𝑁 𝐷𝑃 *Existen tres formas de diente de engrane de uso común, que tienen ángulos de presión de 14 ½º, 20º y 25º. Las formas de dientes de 20º y de 25º están ahora reemplazando la de 14 ½º porque la base de diente es más ancha y más resistente. Para la fórmula relacionada con la forma de dientes de 20º y de 25º vea los manuales Machinery's o American Machinist's. Para obtener Número de dientes (N) Si se conoce Diámetro exterior y paso diametral Regla Fórmula Multiplique el diámetro exterior por 𝑁 = 𝑂𝐷 × 𝐷𝑃 − 2 el paso diametral y reste 2. Diámetro de paso y paso circular Multiplique el diámetro de paso por 3.1416 y divida entre el paso circular. Multiplique el diámetro de paso por el paso diametral. Agregue 2 al número de dientes y multiplique la suma por el paso circular. Divida este producto entre 3.1416. Sume dos al número de dientes y divida la suma entre el paso diametral. Al diámetro de paso súmele 2 y divida entre el paso diametral. Diámetro de paso y paso diametral Número de dientes y paso circular Diámetro exterior (OD) Número de dientes Y paso diametral Diámetro de paso y paso diametral Diámetro paso (PD) de Número de dientes y paso circular Número de dientes y paso 𝑁 = 𝑃𝐷 × 3.1416 𝐶𝑃 𝑁 = 𝑃𝐷 × 𝐷𝑃 𝑂𝐷 (𝑁 + 2) × 𝐶𝑃 = 3.1416 𝑂𝐷 = 𝑁+2 𝐷𝑃 𝑂𝐷 = 𝑃𝐷 + 2 𝐷𝑃 𝑁 × 𝐶𝑃 Multiplique el número de dientes 𝑃𝐷 = 3.1416 por el paso circular y divida entre 3.1416. 𝑁 Divida el número de dientes entre 𝑃𝐷 = 𝐷𝑃 el paso diametral. diametral Diámetro exterior y número de dientes Espesor del diente (T) Profundidad total (WD) • • • • • • • • • • Paso circular Multiplique el número de dientes por el diámetro exterior y divida el 𝑃𝐷 = 𝑁 × 𝑂𝐷 𝑁+2 producto por el número de dientes más 2. 𝐶𝑃 Divida el paso circular entre 2. 𝑇= 2 Paso circular Multiplique el paso circular por 0.5. 𝑇 = 𝐶𝑃 × 0.5 Paso diametral 1.5708 Divida l.5708 entre el paso 𝑇= diametral. 𝐷𝑃 Multiplique el paso circular por 𝑊𝐷 = 𝐶𝑃 × 0.6866 0.6866. 2.157 Divida 2.157 entre el paso 𝑊𝐷 = diametral. 𝐷𝑃 Paso circular Paso diametral La altura de la cabeza o adéndum es la distancia radial entre el círculo de paso y el diámetro exterior, o la altura del diente por encima del círculo de paso. La distancia entre centros es la distancia más corta entre los dos ejes de los engranes acoplados, o la distancia igual a la mitad de la suma de los diámetros de paso. La altura o adéndum cordal es la distancia radial, medida desde la parte superior del diente a un punto donde el espesor cordal y el círculo de paso se cruzan en el borde del diente. El claro es la distancia radial entre la parte superior de un diente y la parte inferior del espacio del diente acoplado correspondiente. La raíz o dedéndum es la distancia radial desde el círculo de paso al fondo del espacio del diente. El dedéndum es igual al adéndum más el claro. El paso diametral (engranes en pulgadas) es la relación del número de dientes por cada pulgada de diámetro de paso del engrane. Por ejemplo, un engrane de un paso diametral 10 y de un diámetro de paso 3 pulgadas tendría 10 X 3, es decir, 30 dientes. (Siempre que sea aplicable, utilice las fórmulas que involucran al paso diametral, y no al paso circular). La involuta o envolvente es la línea curva producida por un punto de un cordel estirado cuando es desenrollado de un cilindro dado (Figura 69-9). El paso lineal es la distancia de un punto en un diente a un punto similar en el diente siguiente de una cremallera. Módulo (engranes métricos) es el diámetro de paso de un engrane dividido por el número de dientes. Se trata de una dimensión real, a diferencia del paso diametral, que es una relación del número de dientes al diámetro de paso. El diámetro exterior es el diámetro general del engrane, que es el círculo de paso • • • • • • • • • • • • más dos adéndums. Círculo de paso es un círculo que tiene el radio de la mitad del diámetro de paso con su centro en el eje del engrane. Circunferencia de paso es la circunferencia del círculo de paso. Diámetro de paso es el diámetro del círculo de paso que es igual al diámetro exterior menos dos adéndums. Ángulo de presión es el ángulo formado por una línea a través del punto de contacto de dos dientes en contacto o acoplados y tangente a los dos círculos de base y a una línea a ángulos rectos con la línea central de los engranes. Círculo de raíz es el círculo formado por los fondos de los espacios de los dientes. El espesor cordal es el espesor del diente, medido en el círculo de paso por la longitud de cuerda que subtiende el arco del círculo de paso. El paso circular es la distancia de un punto en un diente al punto correspondiente en el diente siguiente, medido sobre el círculo de paso. El espesor circular es el espesor del diente, medido sobre el círculo de paso; también conocido como espesor de arco. Diámetro de raíz es el diámetro del círculo de raíz. Espesor del diente es el espesor del diente medido en el círculo de paso. Profundidad total es la profundidad completa del diente o la distancia igual al adéndum más el dedéndum. Profundidad de trabajo es la distancia que se extiende el diente de un engrane dentro del espacio de un diente del engrane acoplado, que es igual a dos adéndums. Figura 69-8 Partes de un engrane Figura 69-9 Generación de una involuta Ejercicios: Calcula el diámetro de paso, el diámetro exterior y profundidad total del diente, para los engranes siguientes: 8DP – 36 dientes, 12DP – 81 dientes, 16DP – 100 dientes, 6DP – 23 dientes y 6DP – 54 dientes CORTE DE ENGRANES OBJETIVOS Al terminar el estudio de esta está unidad, se podrá: 1. Seleccionar la fresa apropiada para cortar cualquier engrane. 2. Calcular las dimensiones de los dientes de un engrane, para engranes en pulgadas. 3. Poner a punto y cortar un engrane recto. La mayor parte de los engranes que se cortan en una fresadora generalmente se utilizan para reparar o reemplazar un engrane que se ha roto o se ha perdido y que ya no se tiene en inventario. La industria generalmente produce en masa los engranes en máquinas especiales diseñadas para este fin. Los tipos más comunes de máquinas generadoras de engranes máquinas formadoras de engranes y las máquinas generadoras de engranes. Es Generalmente más económico adquirir engranes de una empresa que se especializa en la manufactura de engranes, a menos que sea importante que la máquina esté otra vez en operación pronto. Es bastante posible que se le pida a un mecánico que corte un engrane, a fin de reparar rápidamente la máquina, y volverla a poner en producción. Fresas para engranes de involuta Las fresas para engrane son un ejemplo de fresas perfiladoras. Este tipo de fresa es afilada en la cara y asegura una duplicación exacta de la forma del diente, independientemente de cómo se ha afilado la cara del diente. Figura 70-1 tamaños comparativos de los dientes de engrane: 4 a 16. Las fresas para engranes están disponibles en muchos tamaños, que van desde un paso diametral de 1 hasta 48 (DP). Las fresas para dientes más pequeños que a 48 DP están disponibles como fresas especiales. En la Figura 70-1 se muestran los tamaños comparativos de los dientes que van desde 4 hasta 16 DP. Cuando se cortan los dientes en cualquier engrane, se debe seleccionar una fresa que cumpla con el DP y con el número de dientes (N). El espacio entre dientes para un piñón pequeño no puede tener la misma forma que el espacio del diente para un engrane acoplado grande. Los dientes de los engranes más pequeños deben ser más "curvos" para impedir que se traben los dientes del engrane acoplado. Por lo tanto, se fabrican conjuntos de fresas para engranes en una serie de formas ligeramente diferentes, para permitir el corte en un engrane de cualquier número deseado de dientes, con la seguridad de que los dientes se acoplarán correctamente con los del otro engrane que tenga el mismo DP. Figura 70-2 Perfiles de involuta para un juego de fresas para engrane. Estas fresas se fabrican generalmente en juegos de 8 y se numeran del 1 al 8 (Figura 10-2). Note el cambio gradual en la forma desde la fresa número 1, que tiene costados prácticamente rectos, a los costados mucho más curvos de la fresa número 8. Como se puede observar en la tabla 70-1, la fresa número 1 se utiliza para cortar cualquier número de dientes en un engrane desde 135 dientes hasta una cremallera, en tanto que la fresa número 8 sólo cortará 12 y 13 dientes. Debe hacerse notar que para que se acoplen los engranes, deben tener el mismo DP; el número de la fresa permite únicamente un acoplamiento más preciso de los dientes. Figura 70-3 Cómo verificar la alineación de los centros de índice con un indicador de carátula. (Kelmar Associates) Figura 70-4 Cómo centrar una fresa para engranes y la pieza de trabajo. (Kelmar Associates) Algunos fabricantes de fresas para engrane han aumentado el juego de 8 fresas con siete fresas adicionales en medios tamaños, haciendo un total de 15 fresas por juego, numeradas 1, 1 ½, 2,1/2, etc. En la serie de medias, una fresa del número 1 ½ se utilizaría para cortar de 80 a 134 dientes, pero una fresa de 7 ½ cortaría sólo 13 dientes (Tabla 70-1). EJEMPLO Un engrane y piñón de 10 DP acoplados tienen 100 dientes y 24 dientes respectivamente. ¿Qué fresas se utilizarían para cortar estos engranes? Selección de fresa Puesto que los engranes están acoplados, ambos deben ser cortados con una fresa de 10 DP. Deberá utilizarse una fresa número 2 para cortar los dientes del engrane, ya que corta de 55 a 134 dientes. Se utilizaría una fresa número 5 para cortar el piñón, ya que ésta corta de 21 a 25 dientes. CÓMO CORTAR UN ENGRANE RECTO El procedimiento para maquinar un engrane recto aparece en el ejemplo siguiente. EJEMPLO Se requiere de un engrane de 52 dientes con un 8 DP. Procedimiento 1. Calcule todos los datos necesarios del engrane (Tabla 70-1). a) Diámetro exterior: 𝑂𝐷 = 𝑁+2 𝐷𝑃 = 54 8 b) Profundidad total del diente: WD = = 6.750 𝑝𝑢𝑙𝑔. 2.157 DP = 2.157 8 = 0.2697 pulg. c) Numero de fresa = 3 (35 a 54 dientes) d) Indización (usando plato estándar Cincinnati) 40/N = 40/50 = 10/13 x 3/3 = 30 perforaciones en un círculo de 39 perforaciones. 2. Tornee la pieza en bruto del engrane al diámetro exterior adecuado (6.750 pulg.) 3. Sujete firmemente la pieza en bruto del engrane en el mandril. Nota: Si la pieza en bruto fue torneada en un árbol, asegúrese que está apretada, porque el calor generado por el torneado pudiera ligeramente haberla dilatado. 4. Monte el cabezal divisor y el contrapunto y verifique la alineación de los centros de indización (Figura 70-3). 5. Ajuste el cabezal divisor, de manera que el perno indicador entre en una perforación en el círculo de 39 perforaciones y los brazos de sector estén colocados a 30 perforaciones. Nota: No cuente la perforación en la cual está colocado el perno. 6. Monte el árbol (y pieza de trabajo) con el extremo grande hacia el cabezal divisor, entre los centros de indización. Nota: a. La punta del contrapunto debe ajustarse firmemente sobre el árbol y bloquearse en posición. b. El perno debe ser apretado adecuadamente sobre el árbol y la cola del perro no debe atorarse en la ranura. c. La cola del perro debe entonces bloquearse en la horquilla impulsora del cabezal divisor mediante los prisioneros. Esto asegurará que no habrá juego entre cabezal divisor y árbol. d. El perro debe estar lo suficientemente lejos de la pieza en bruto para asegurar que la fresa no golpeará al perro al ser cortado el engrane. 7. Mueva la mesa cerca de la columna y mantenga todo el arreglo tan rígido como sea posible. 8. Monte una fresa 8 DP número 3 sobre el árbol de la máquina fresadora en el centro aproximado del engrane. Asegúrese que la fresa gira en dirección al cabezal divisor. 9. Centre la pieza en bruto con la fresa siguiendo cualquiera de los métodos siguientes: a. Coloque una escuadra contra el diámetro exterior del engrane (Figura 70-4). Con un par de compases de puntas para interiores o una regla, verifique la distancia entre la escuadra y el costado de la fresa. Ajuste la mesa hasta que sean iguales las distancias desde ambos lados de la pieza en bruto a los lados de la fresa. b. Un método más preciso de centrar la fresa es utilizando bloques patrón en vez de compases de punta o una regla. 10. BLOQUEE EL AVANCE TRANSVERSAL. 11. Encienda la fresadora y pase la pieza por debajo de la misma fresa. 12. Eleve la mesa hasta que la fresa justo toque la pieza. Esto se puede hacer utilizando una marca de gis sobre la pieza en bruto o un pedazo de papel entre la pieza en bruto y la fresa, para indicar cuando la fresa está apenas tocando la pieza (Figura 70-5). 13. Coloque el anillo de avance graduado del avance vertical en cero (0). 14. Mediante la manivela de avance longitudinal mueva la pieza, librándola de la fresa, y eleve la mesa aproximadamente dos terceras partes de la profundidad del diente (0.180 pulg.); entonces bloquee la abrazadera de la rodilla. Nota: A veces se utiliza una fresa de desbastar especial para desbastar los dientes. 15. Haga una pequeña muesca de todos los dientes del engrane en el extremo de la pieza, para verificar la indización correcta (Figura 70-6). 16. Desbaste el primer diente y ajuste el perro de disparo del avance automático, después que la fresa haya salido de la pieza. 17. Regrese la mesa a la posición de inicio. Nota: Libre el extremo de la pieza con la fresa. 18. Corte los dientes restantes y regrese la mesa a la posición inicial. 19. Afloje la abrazadera de la rodilla, eleve la mesa a la profundidad total de 0.270 pulg, y bloquee la abrazadera de la rodilla. Nota: Es aconsejable retirar la manivela del eje elevadora de rodilla, a fin de que no sea movida accidentalmente y cambie el ajuste. 20. Haga el corte de acabado en todos los dientes. Nota: Una vez que cada uno de los dientes haya sido cortado, la fresa debe ser detenida, antes que la mesa sea regresada, para impedir marcar el acabado de los dientes del engrane. Y A LIMPIAR LA MAQUINA…………… Figura 70-5 Cómo ajustar una fresa para Figura 70-6 Al hacer muescas en todos engranes al diámetro de la pieza de trabajo. (Kelmar Associates) los dientes de los engranes se eliminan errores. (Kelmar Associates) FRESADO HELICOIDAL OBJETIVOS Al terminar el estudio de esta unidad, se podrá: 1. Calcular el avance y el ángulo de la hélice de un engrane helicoidal 2. Ajustar una máquina fresadora para maquinar una hélice 3. Efectuar los cálculos y la puesta a punto para el fresado de un engrane helicoidal El proceso de fresar ranuras helicoidales como las ranuras de un taladro, los dientes de engranes helicoidales o la rosca helicoidal en un eje, se conoce como fresado helicoidal. Se lleva a cabo sobre la máquina fresadora universal al engranar el cabezal divisor a través del eje del tornillo sinfín con el tornillo de avance. Términos helicoidales El término espiral se utiliza a menudo de manera incorrecta en lugar de hélice. • Una hélice es una línea o trayectoria teórica generada sobre una superficie cilíndrica por una herramienta de corte que avanza longitudinalmente a una velocidad uniforme, en tanto que el cilindro también gira a una velocidad uniforme (Figura 711). Las ranuras de una broca o la rosca de un perno son ejemplos de hélices. • Una espiral es la trayectoria generada por un punto que se mueve a una velocidad de avance fija a lo largo de una superficie de un cono O plano giratorio (Figura 712). La rosca de un tomillo de madera y la rosca para tubería son ejemplos de espirales cónicas. Los resortes para reloj y la rosca en caracol de un mandril universal para tomo son ejemplos de espirales planas. Figura 71-1 Una hélice será generada si la pieza Figura 71-2 Un espiral se es girada conforme la herramienta se mueve con uniformidad a produce en una superficie cónica. a) Figura 71-3 Relación del avance de la circunferencia al ángulo de la hélice b) Figura 71-4 (a) Cuando la mesa es girada en el ángulo de la hélice, se generará el perfil exacto de la fresa, (b) un ángulo incorrecto producirá un perfil incorrecto. A fin de cortar ya sea una hélice en pulgadas o métrica, de- ben conocerse dos datos cualesquiera de los siguientes: 1. El avance de la hélice, que es la distancia longitudinal que avanza axialmente la hélice, en una revolución completa de la pieza. 2. El ángulo de la hélice, que se forma en la intersección de la hélice con el eje de la pieza de trabajo. 3. El diámetro (y circunferencia) de la pieza de trabajo. Al comparar dos hélices diferentes, se observará que mientras mayor sea el ángulo con la línea central, más corto será el avance. Sin embargo, si el diámetro se incrementa, pero el ángulo de la hélice se conserva igual, más grande será el avance. Por lo que es evidente que el avance de una hélice varía con: 1. El diámetro de la pieza. 2. El ángulo de la hélice. La relación entre el diámetro (y la circunferencia), el ángulo de la hélice y el avance aparecen en la Figura 71-3. Note que si la superficie del cilindro se pudiera desenrollar, para producir una superficie plana, la hélice formaría la hipotenusa de un triángulo rectángulo, formando la circunferencia el lado opuesto, y el avance el lado o cateto adyacente. Cómo cortar una hélice Para cortar una hélice en un cilindro, son necesarios los pasos siguientes: 1. Haga girar la mesa en la dirección apropiada al ángulo de la hélice, para asegurar que será producida una ranura con el mismo contorno que la fresa. 2. La pieza debe girar una vuelta al mismo tiempo que la mesa recorre longitudinalmente la distancia igual al avance. Esto se consigue instalando los apropiados engranes de cambio entre el tornillo sinfín del cabezal divisor y el tornillo de avance de la fresadora. Determinación del ángulo de la hélice Para asegurar que se produce una ranura del mismo contorno que la fresa, la mesa debe ser girada al ángulo de la hélice (Figura 7l-4a). La importancia de lo anterior aparece en la figura 7l-4b. Note que cuando la mesa no es girada (Figura 7l-4b) se generará una hélice que tiene el avance apropiado, pero un contorno incorrecto. Haciendo referencia a la figura 71-3, se puede observar fácilmente que el ángulo se puede calcular como sigue: Tangente del ángulo de la hélice = circunferencia de la pieza avance de la helice = 3.1416×diametro (D) avance de la helice EJEMPLO (PULGADAS) ¿A qué ángulo debe girarse la mesa de la fresadora para cortar una hélice que tiene un avance de 10.882 pulgadas. En una pieza de trabajo de 2 pulgadas de diámetro? Tangente del ángulo de la hélice = 3.1416×2) 10.882 6.2832 = 10.882 = 0.57739 Angulo de la hélice 30º Una vez calculado el ángulo de la hélice, es necesario de-terminar la dirección en la cual se debe girar la mesa para producir la rosca de hélice correcta (esto es, giro derecho o giro izquierdo). Fresado de levas, cremalleras, tornillos sinfín y embragues OBJETIVOS Al terminar el estudio de esta unidad, se podrá. 1. 2. 3. 4. Calcular y cortar una leva de movimiento uniforme Poner a punto la máquina y cortar una cremallera Comprender cómo se corta un tornillo sinfín Ajustar la máquina y cortar un embrague La diversidad de dispositivos disponibles hacen de la fresadora una máquinaherramienta versátil. Además de las operaciones estándar que por lo general se llevan a cabo en una fresadora, con los ajustes y aditamentos adecuados es posible cortar levas, cremalleras, tornillos sinfín y embragues. Aunque quizá no se le pida a un mecánico que las ejecute con frecuencia, resulta prudente estar familiarizado con estas operaciones, de manera que usted pueda cortar la forma requerida. Una leva es un dispositivo generalmente aplicado a una máquina para cambiar un movimiento giratorio en un movimiento lineal o reciprocante, y para transmitir este movimiento a otras partes de la máquina a través de un seguidor. El árbol de levas de un motor de automóvil incorpora varias levas, que controlan la abertura y cierre de las válvulas de admisión y de escape. Muchas operaciones de máquina, especialmente de máquinas automáticas, están controladas por levas, que transmiten el movimiento deseado a la herramienta de corte a través de un seguidor, y algún tipo de varilla de empuje. Las levas también se utilizan para transformar un movimiento lineal en un movimiento reciprocante del seguidor. Las levas de este tipo se conocen como levas de placa o de barra, y se conocen también como plantillas. Las plantillas se utilizan con frecuencia en máquinas fresadoras y tomos de tipo pantógrafo donde deben producirse partes según el perfil de la plantilla. Las levas también se pueden utilizar como dispositivos de cierre. Se encuentran muchas aplicaciones de las levas en el diseño de dispositivos y aditamentos, así como en abrazaderas de cierre rápido. LEVAS UTILIZADAS PARA IMPARTIR MOVIMIENTO Las levas utilizadas para impartir movimiento generalmente se encuentran en máquinas y pueden ser de dos tipos: la positiva y la no positiva. Las levas de tipo positivo, como la cilíndrica y la de placa ranurada (Figura 72-1), controlan en todo momento al seguidor; esto es, el seguidor se mantiene acoplado en la ranura en la cara de la periferia de la leva, y no se utiliza ningún otro medio para mantener este acoplamiento. Ejemplos de levas de tipo no positivo son las de placa, dedo y barredor, y de corona (Figura 72-2). En los tipos no positivos, la leva empuja el seguidor en una dirección dada y depende de alguna fuerza externa, como la gravedad o resortes, para mantener al seguidor apoyado contra la superficie de la leva. b) a) Figura 72-1 (a) Leva cilíndrica o de tambor con seguidor de rodillo cónico, (b) leva de placa ranurada con seguidor de rodillo. Los seguidores pueden ser de varios tipos: • El de tipo cuchilla o puntiagudo (figura 72-3a) se utiliza en levas más complejas, porque permite seguir con mayor facilidad contornos muy precisos que al utilizar una leva de rodillos. • El tipo plano o de embolo (figura 72-3b) se utiliza para transmitir grandes fuerzas y requiere lubricación. • El de tipo de rodillos (Figura 72-3c) es el que tiene la menor fricción de arrastre, y requiere poca o ninguna lubricación. • El tipo de rodillos cónico (Figura 72-3d) se utiliza con levas de placa ranurada o cilíndricas. Figura 72-2 (a) leva de placa con seguidor de cuchilla, (b) leva de dedo y barredor, (c) leva de corona Figura 72-3 Tipos de seguidor: a) de cuña, b) de cara plana, c) de rodillo y d) de zapata. MOVIMIENTO DE LAS LEVAS Existen tres tipos estándar de movimientos impartidos por las levas a los seguidores y a las partes de las máquinas: 1. Movimiento uniforme. 2. Movimiento armónico. 3. Movimiento uniformemente acelerado y desacelerado. La leva de movimiento uniforme mueve al seguidor a la misma velocidad desde el principio hasta el fin de la carrera. Dado que el movimiento va de cero a plena velocidad de manera instantánea y termina de la misma forma abrupta, existe un choque claro al principio y al final de la carrera. Las máquinas que utilizan este tipo de leva deben ser rígidas y suficientemente fuertes para soportar este choque constante. TERMINOLOGIA DE LA LEVA RADIAL Un lóbulo es una parte que se proyecta de la leva y que imparte un movimiento reciprocante al seguidor. Las levas pueden tener uno o varios lóbulos (Figuras 72-4 y 725), dependiendo de la aplicación a la máquina. La elevación es la distancia en que un lóbulo elevará o bajará al seguidor, al dar vuelta a la leva. El avance es el recorrido total que se le impartiría al seguidor en una revolución de una leva de elevación uniforme, con un solo lóbulo en 360°. En la Figura 72-5, el avance para una leva de doble lóbulo es dos veces el avance de una leva de un lóbulo sencillo de la misma elevación. Es el avance de la leva y no la elevación la que controla la selección de los engranes en el fresado de las levas. La elevación uniforme es la elevación generada en una leva que se mueve hacia adentro a una velocidad uniforme alrededor de la leva, asumiendo la forma de un espiral de Arquímedes. Esta elevación es causada por una alimentación y rotación uniforme de la pieza al maquinar la leva. Fresado de cremalleras Una cremallera, en conjunción con un engrane (piñón), se utiliza para convertir un movimiento giratorio en un movimiento longitudinal. Las cremalleras se encuentran en tomos, taladros y muchas otras máquinas en un taller. Una cremallera se puede considerar como un engrane recto, que ha sido enderezado, de manera que todos los dientes están en un solo plano. La circunferencia del círculo de paso de este engrane se convierte ahora en una línea recta, que apenas tocaría el círculo de paso del engrane que se acopla con la cremallera. Por lo que la línea de paso de una cremallera es la distancia de un adéndum (1/DP) por debajo de la parte superior del diente. El paso de una cremallera se mide en paso lineal (circular) que se obtiene al dividir 3.1416 entre el paso diametral; esto es: 𝑃𝑎𝑠𝑜 𝑑𝑒 𝑙𝑎 𝑐𝑟𝑒𝑚𝑎𝑙𝑙𝑒𝑟𝑎 = 3.1416 𝐷𝑃 El método utilizado para cortar una cremallera dependerá en general de la longitud de la misma. Si la cremallera es razonablemente corta [10 pulg (250 milímetros)] o menos, se puede sujetar en la prensa de la máquina fresadora en una posición paralela al árbol de la fresa. En cremalleras cortas, los dientes pueden cortarse moviendo con precisión el avance transversal de la máquina una cantidad igual al paso circular del engrane y entonces moviendo la mesa longitudinalmente para cortar cada uno de los dientes. Si la cremallera es más larga que el recorrido transversal de la mesa de la fresadora, debe ser colocada longitudinalmente sobre la mesa, y por lo general sujeta con un aditamento especial. La fresa se sujeta en un aditamento de fresado de cremalleras (Figura 72-11). Cuando se cortan dientes rectos, la fresadora se sujeta a 90° en relación con la posición utilizada al cortar un engrane recto. Es posible montar fresas de ranurar o de fresado lateral en el aditamento de fresado de cremalleras para operaciones de fresado que pueden manejarse con mayor facilidad utilizando el avance transversal de la máquina. ADITAMENTO DE INDIZACION DE CERMALLERAS Cuando se corta una cremallera utilizando un aditamento de fresado de cremalleras, a menudo la mesa se mueve (indiza) para cada diente mediante el aditamento de indización de cremallera (Figura 72-11). Éste está formado por un plato perforado con dos muescas diametralmente opuestas y un perno de fijación. Dos engranes de cambio seleccionados de un juego de 14 se montan según se puede observar en la Figura 7211. Diferentes combinaciones de engranes de cambio permiten que la mesa pueda ser movida con precisión en incrementos correspondientes al paso lineal (circular) de la cremallera, efectuando ya sea una media vuelta o una vuelta completa de la placa. Para indizaciones que requieran de una sola vuelta únicamente, se tiene previsto el poder cerrar una de las ranuras, evitando así cualquier error de indización. Figura 72-11 Corte de los dientes de una cremallera helicoidal utilizando los aditamentos de fresado e indización de cremalleras. (Cincinnati Milacron, Inc.) Este aditamento permite la indización de todos los pasos diametrales desde 4 hasta 32, así como todos los pasos circulares desde 1/8 de pulg hasta ¾ de pulg, variando en dieciseisavos. También se pueden producir los siguientes movimientos de la mesa: 1/7, 1/6, 1/5, 2/7, 1/3 y 2/5 de pulg. Tornillos sinfín y ruedas dentadas para tornillos sinfín Los tornillos sinfín y las ruedas dentadas para tornillos sinfín se utilizan cuando se requiere una gran reducción de relación entre el eje impulsor e impulsado. Un tomillo sinfín es un cilindro, en el cual se ha cortado una rosca de tipo Acme de uno o de múltiples inicios. El ángulo de esta rosca va de 14.5º a 30° de ángulo de presión. Conforme se incrementa el ángulo de avance del tornillo sinfín, más grande deberá ser el ángulo de presión del lado de la rosca. Los dientes de un engrane sinfín se maquinan en una ranura periférica, que tiene un radio igual a la mitad del diámetro de la raíz del sinfín. La relación de impulsión entre un ensamble de engranes de tomillos sinfín y rueda dentada depende del número de dientes de la rueda dentada y de si el tomillo sinfín tiene una rosca de uno o de doble inicio. Por lo que si una rueda dentada tiene 50 dientes, la relación sería de 50:1, siempre y cuando el tornillo sinfín tenga una rosca de un solo inicio. Si tuviera una rosca de doble inicio, la relación sería de 50:2, es decir, 25:1.