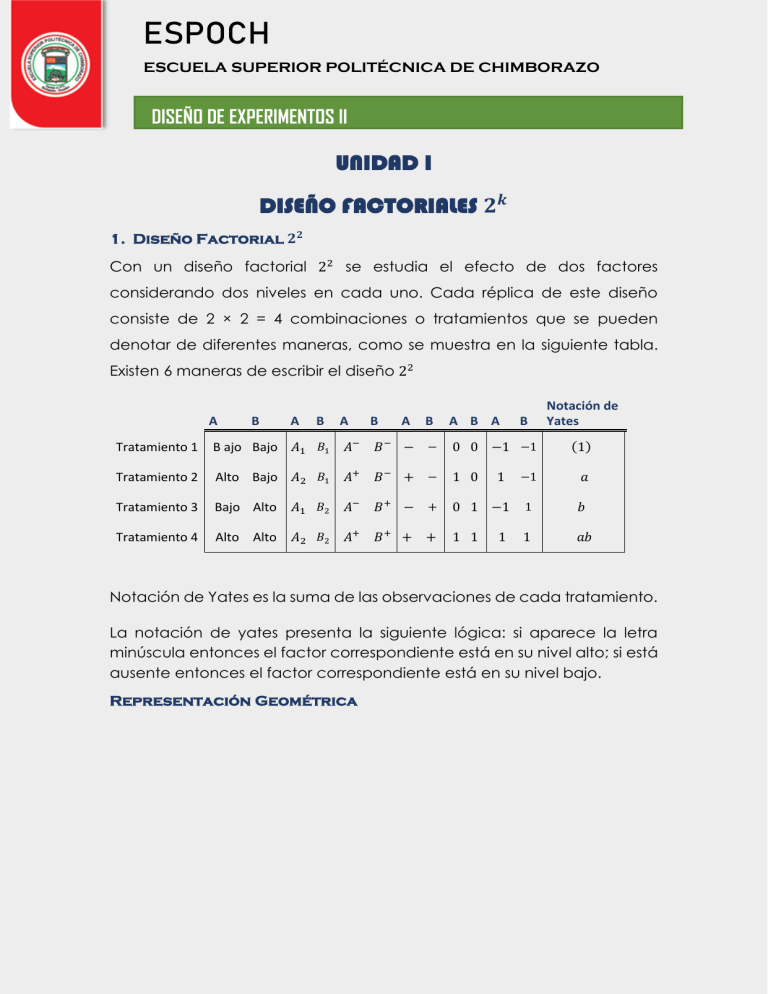
ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II UNIDAD I DISEÑO FACTORIALES 𝟐𝒌 1. Diseño Factorial 𝟐𝟐 Con un diseño factorial 22 se estudia el efecto de dos factores considerando dos niveles en cada uno. Cada réplica de este diseño consiste de 2 × 2 = 4 combinaciones o tratamientos que se pueden denotar de diferentes maneras, como se muestra en la siguiente tabla. Existen 6 maneras de escribir el diseño 22 A B A B A B A B A B A B Tratamiento 1 B ajo Bajo 𝐴1 𝐵1 𝐴− 𝐵− − − 0 0 −1 −1 Tratamiento 2 Alto Bajo 𝐴2 𝐵1 𝐴+ 𝐵− + − 1 0 Tratamiento 3 Bajo Alto 𝐴1 𝐵2 𝐴− 𝐵+ − + Tratamiento 4 Alto Alto 𝐴2 𝐵2 𝐴+ 𝐵+ + + Notación de Yates (1) −1 𝑎 0 1 −1 1 𝑏 1 1 1 𝑎𝑏 1 1 Notación de Yates es la suma de las observaciones de cada tratamiento. La notación de yates presenta la siguiente lógica: si aparece la letra minúscula entonces el factor correspondiente está en su nivel alto; si está ausente entonces el factor correspondiente está en su nivel bajo. Representación Geométrica ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II Cada vértice del cuadrado representa un tratamiento El área limitada por el cuadrado se conoce como Región Experimental Las conclusiones que se obtengan del experimento sólo tienen validez dentro de la región. Cálculo de los efectos Tenemos 3 efectos de interés: Efectos principales (𝐴 𝑌 𝐵) y el efecto de interacción (𝐴𝐵). Con el uso de la notación de Yates podemos ver que si cada tratamiento tiene n replicas, la media de 𝑌 en el nivel alto del factor A es: (𝑎 + 𝑎𝑏) 2𝑛 En el nivel bajo la media de 𝑌es: (𝑏 + (1)) 2𝑛 El efecto de 𝐴 se calcula de la siguiente forma: 𝐸𝑓𝑒𝑐𝑡𝑜 𝐴 = 1 𝑎 + 𝑎𝑏 𝑏 + (1) [𝑎 + 𝑎𝑏 − 𝑏 − (1)] = − 2𝑛 2𝑛 2𝑛 la media de 𝑌en el nivel alto del factor B es: (𝑏 + 𝑎𝑏) 2𝑛 En el nivel bajo la media de 𝑌es: ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II (𝑎 + (1)) 2𝑛 El efecto de 𝐵 se calcula de la siguiente forma: 𝐸𝑓𝑒𝑐𝑡𝑜 𝐵 = 1 𝑏 + 𝑎𝑏 𝑎 + (1) [𝑏 + 𝑎𝑏 − 𝑎 − (1)] = − 2𝑛 2𝑛 2𝑛 El efecto de interacción entre los factores 𝐴 𝑦 𝐵 está dado la diferencia entre el efecto de A en el nivel alto de B y el efecto de A en el nivel bajo de 𝐵 donde: 𝐸𝑓𝑒𝑐𝑡𝑜 𝐴𝐵 = 1 𝑎𝑏 − 𝑏 𝑎 − (1) 𝑎𝑏 + (1) 𝑎 + 𝑏 [𝑎𝑏 + (1) − 𝑎 − 𝑏] = − = − 2𝑛 2𝑛 2𝑛 2𝑛 2𝑛 Ejemplo A: Tiempo B: Velocidad 𝐸𝑓𝑒𝑐𝑡𝑜 𝐴 = Aditivo Tratamiento 1 𝐵𝑎𝑗𝑜 = 3 𝐵𝑎𝑗𝑜 = 600 17.10 (1) Tratamiento 2 𝐴𝑙𝑡𝑜 = 6 𝐵𝑎𝑗𝑜 = 600 16.26 𝑎 Tratamiento 3 𝐵𝑎𝑗𝑜 = 3 𝐴𝑙𝑡𝑜 = 1000 18.76 𝑏 Tratamiento 4 𝐴𝑙𝑡𝑜 = 6 𝐴𝑙𝑡𝑜 = 1000 18.16 𝑎𝑏 1 1 [𝑎 + 𝑎𝑏 − 𝑏 − (1)] = (16.26 + 18.16 − 18.76 − 17.10) = −0.72 2𝑛 2 𝐸𝑓𝑒𝑐𝑡𝑜 𝐵 = 1 1 [𝑏 + 𝑎𝑏 − 𝑎 − (1)] = (18.76 + 18.16 − 16.26 − 17.10) = 1.78 2𝑛 2 𝐸𝑓𝑒𝑐𝑡𝑜 𝐴𝐵 = 1 1 [𝑎𝑏 + (1) − 𝑎 − 𝑏] = (18.16 + 17.10 − 16.26 − 18.76) = 0.12 2𝑛 2 Análisis de Varianza Definición de contraste Es la combinación lineal de la forma: 2𝑘 𝐶 = ∑ 𝑐𝑖 𝑌𝑖 𝑐𝑜𝑛 ∑ 𝑐𝑖 = 0 𝑖=1 ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II Se llama contraste. Donde 𝑌𝑖 : términos de la notación de Yates, con la condición de que la suma de los coeficientes sea igual a cero. La suma de los cuadrados para cualquier contraste 𝐶 esta dado por: 2 𝑘 𝑆𝐶𝑐 = (∑2𝑖=1 𝑐𝑖 𝑌𝑖 ) 𝑘 𝑛 ∑2𝑖=1 𝑐𝑖 2 Que contiene un grado de libertad. Note que cada termino 𝑌𝑖 representa un término de la notación de Yates. Los contrastes correspondientes a los tres efectos 𝐴, 𝐵 𝑦 𝐴𝐵 en el diseño factorial 22 están definidos por: 𝐶𝑜𝑛𝑡𝑟𝑎𝑠𝑡𝑒 𝐴 = [𝑎 + 𝑎𝑏 − 𝑏 − (1)] 𝐶𝑜𝑛𝑡𝑟𝑎𝑠𝑡𝑒 𝐵 = [𝑏 + 𝑎𝑏 − 𝑎 − (1)] 𝐶𝑜𝑛𝑡𝑟𝑎𝑠𝑡𝑒 𝐴𝐵 = [𝑎𝑏 + (1) − 𝑎 − 𝑏] En el diseño factorial 2𝑘 con 𝑛 replicas los contrastes se dividen por 𝑛2(𝑘−1) para estimar los efectos. En el diseño 22 con 𝑛 replicas los contrastes se dividen por 𝑛2(2−1) = 2𝑛 Métodos para calcular contrastes Una manera practica de calcular los contrastes de cualquier efecto sea principal o de interacción en el diseño factorial 2𝑘 es mediante el auxilio de una tabla de signos. La tabla de signos se construye a partir de la matriz de diseño, multiplicando las columnas que intervienen en la interacción calculada. A B AB Yates + - + (1) - + - 𝑎 𝑏 + + + 𝑎𝑏 Pasos para llegar al ANOVA ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II Contrastes Efectos Suma de cuadrados ANOVA Para investigar cuáles de los 3 efectos son significativos se procede aprobar la hipótesis dada: 𝐻0 : 𝐸𝑓𝑒𝑐𝑡𝑜 𝐴 = 0 𝐻1 : 𝐸𝑓𝑒𝑐𝑡𝑜 𝐴 ≠ 0 𝐻0 : 𝐸𝑓𝑒𝑐𝑡𝑜 𝐵 = 0 𝐻1 : 𝐸𝑓𝑒𝑐𝑡𝑜 𝐵 ≠ 0 𝐻0 : 𝐸𝑓𝑒𝑐𝑡𝑜 𝐴𝐵 = 0 𝐻1 : 𝐸𝑓𝑒𝑐𝑡𝑜 𝐴𝐵 ≠ 0 Estas hipótesis se prueban con el análisis de varianza, para lo cual es necesario calcular la suma de cuadrados que corresponden a los efectos 𝐴, 𝐵 𝑦 𝐴𝐵. [𝑎 + 𝑎𝑏 − 𝑏 − (1)]2 𝑆𝐶𝐴 = 𝑛22 𝑆𝐶𝐵 = 𝑆𝐶𝐴𝐵 [𝑏 + 𝑎𝑏 − 𝑎 − (1)]2 𝑛22 [𝑎𝑏 + (1) − 𝑎 − 𝑏]2 = 𝑛22 𝑇𝑜𝑡𝑎𝑙 𝑑𝑒 𝑙𝑎𝑠 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑐𝑖𝑜𝑛𝑒𝑠 = 𝑛2𝑘 ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II 𝑀𝑒𝑑𝑖𝑎 𝑑𝑒 𝑙𝑜𝑠 𝑑𝑎𝑡𝑜𝑠 = 𝑛2𝑘−1 Cada una de estas sumas de cuadrados tiene solo 1 grado de libertad debido a que cada factor tiene únicamente dos niveles. La suma de cuadrados totales se calcula con la expresión: 2 2 𝑛 2 𝑆𝐶𝑇 = ∑ ∑ ∑ 𝑌𝑖𝑗𝑙 − 𝑖=1 𝑗=1 𝑙=1 𝑌…2 𝑛22 Y tiene 𝑛22−1 grados de libertad. Suma de cuadrados del error: 𝑆𝐶𝐸 = 𝑆𝐶𝑇 − 𝑆𝐶𝐴 − 𝑆𝐶𝐵 − 𝑆𝐶𝐴𝐵 Y tiene (𝑛22−1 ) − 3 = 4(𝑛 − 1) grados de libertad. Tabla de ANOVA Fuente de Variación Suma de Cuadrados Grados de libertad Cuadrado Medio A 𝑆𝐶𝐴 1 𝐶𝑀𝐴 B 𝑆𝐶𝐵 1 𝐶𝑀𝐵 AB ERROR TOTAL 𝑆𝐶𝐴𝐵 𝑆𝐶𝐸 𝑆𝐶𝑇 1 4(𝑛 − 1) 𝐶𝑀𝐴𝐵 𝐶𝑀𝐸 (𝑛22 ) − 1 𝑭𝟎 Valor p 𝐶𝑀𝐴 ⁄𝐶𝑀 𝑃(𝐹 > 𝐹0 ) 𝐸 𝐶𝑀𝐵 ⁄𝐶𝑀 𝑃(𝐹 > 𝐹0 ) 𝐸 𝐶𝑀𝐴𝐵 ⁄𝐶𝑀 𝑃(𝐹 > 𝐹 ) 0 𝐸 Ejemplo 1 A una compañía le interesa estudiar el efecto del tamaño de broca (factor A) y de la velocidad (factor B) sobre la vibración de la ranuradora (respuesta Y). Para ello, se decide utilizar un diseño factorial 22 con cuatro réplicas, lo cual da un total de 4 × 22 = 16 corridas del proceso, que se realizan en orden aleatorio. El tamaño de la broca se prueba en 1/16 y en 1/8 de pulgada y la velocidad en 40 y 90 revoluciones por segundo, según se describe en la siguiente tabla: FACTOR A B Datos para ranuradora NIVELES 1/16 40 UNIDAD 1/8 pulg. 90 rps. ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II A: Broca 𝟏/𝟏𝟔 𝟏/𝟖 𝟏/𝟏𝟔 𝟏/𝟖 B: Velocidad 40 40 90 90 A + + B + + 𝒙𝟏 -1 1 -1 1 𝒙𝟐 -1 -1 1 1 18,2 27,2 15,9 41 Vibración 18,9 12,9 24 22,4 14,5 15,1 43,9 36,3 14,4 22,5 14,2 39,9 Desarrollo Objetivo: Minimizar la vibración de la ranuradora Factor A: Tamaño de la broca Factor B: Velocidad Factor de Interacción: Interacción entre la broca y la velocidad sobre la vibración de la ranuradora Variable respuesta: vibración de la ranuradora Unidad experimental: Ranuradora 1. Planteamiento de la hipótesis Efecto A 𝐻0 : 𝐸𝑓𝑒𝑐𝑡𝑜 𝐴 = 0 𝐻1 : 𝐸𝑓𝑒𝑐𝑡𝑜 𝐴 ≠ 0 Efecto B 𝐻0 : 𝐸𝑓𝑒𝑐𝑡𝑜 𝐵 = 0 𝐻1 : 𝐸𝑓𝑒𝑐𝑡𝑜 𝐵 ≠ 0 Efecto AB 𝐻0 : 𝐸𝑓𝑒𝑐𝑡𝑜 𝐴𝐵 = 0 𝐻1 : 𝐸𝑓𝑒𝑐𝑡𝑜 𝐴𝐵 ≠ 0 2. Nivel de significancia 𝛼 = 0.05 3. Estadístico de prueba Fuente de Variación Suma de Cuadrados Grados de libertad Cuadrado Medio A B AB ERROR TOTAL 1107,22563 227,255625 303,630625 71,7225 1709,83438 1 1 1 12 15 1107,22563 227,255625 303,630625 5,976875 4. Región de Rechazo 𝑣𝑎𝑙𝑜 𝑝 > 𝛼 No se rechaza la hipótesis nula 5. Decisión Fo Valor p 185,251595 1,17467E-08 38,0224825 4,82629E-05 50,8008993 1,20108E-05 ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II En el análisis de varianza se evidenció un valor p de 𝟎 para los tres factores, por lo tanto: El efecto del tamaño de la broca influye significativamente en la vibración de la ranuradora El efecto de la velocidad influye significativamente en la vibración de la ranuradora El tamaño de la broca y la velocidad influye significativamente en la vibración de la ranuradora Graficas de interacción Velocidad=alto Velocidad=bajo Velocidad=bajo Velocidad=alto Interpretación Cuando la broca se encuentra en su nivel bajo, la velocidad no afecta de manera significativa la vibración, por el contrario, cuando la broca se encuentra en su nivel alto la velocidad tiene un efecto considerable sobre la vibración. ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II Broca=alto Broca=alto Broca=bajo Broca=bajo Interpretación Cuando la velocidad se encuentra en su nivel bajo, la broca no afecta de manera significativa la vibración, por el contrario, cuando la velocidad se encuentra en su nivel alto la broca tiene un efecto considerable sobre la vibración. Interpretación Cuando la broca cambia del nivel bajo (1/16 pulg.) al nivel alto (1/8) existe una diferencia significativa en la vibración. ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II EFECTO PRINCIPAL DE B 30 V ibración 25 20 15 10 5 0 Bajo Alto Velocidad Interpretación Cuando la velocidad cambia del nivel bajo (40 rps.) al nivel alto (90 rps.) existe una diferencia significativa en la vibración. Conclusión Se debe mantener la velocidad y el tamaño de la broca en niveles bajos si se quiere minimizar la vibración de la ranuradora. Comparación de medias Método LSD 𝟐𝑪𝑴𝑬 𝒏 √ 𝟐;𝑵−𝑲 𝒕𝜶⁄ Planteamiento de hipótesis 𝐻0 : 𝜇1 = 𝜇2 𝐻1 : 𝜇1 ≠ 𝜇2 𝐻0 : 𝜇1 = 𝜇3 𝐻1 : 𝜇1 ≠ 𝜇3 𝐻0 : 𝜇1 = 𝜇4 𝐻1 : 𝜇1 ≠ 𝜇4 𝐻0 : 𝜇2 = 𝜇3 𝐻1 : 𝜇2 ≠ 𝜇3 𝐻0 : 𝜇2 = 𝜇4 𝐻1 : 𝜇2 ≠ 𝜇4 𝐻0 : 𝜇3 = 𝜇4 𝐻1 : 𝜇3 ≠ 𝜇4 ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II MODELO DE REGRESIÓN Es útil ajustar un modelo de regresión a los datos experimentales con la finalidad de predecir el valor de 𝑌 es decir el valor esperado de las características de interés sobre valores de los factores estudiados. Modelo de efectos fijos 𝒀𝒊𝒋𝒌 = 𝝁 + 𝜶𝒊 + 𝜷𝒋 + (𝜶𝜷)𝒊𝒋 + 𝜺𝒊𝒋𝒌 ; 𝒊 = 𝟏, … , 𝒂; 𝒋 = 𝟏, … , 𝒃; 𝒌 = 𝟏, … , 𝒏 Modelo de regresión teórico 𝒀𝒊𝒋𝒌 = 𝜷𝟎 + 𝜷𝟏 𝒙𝟏 + 𝜷𝟐 𝒙𝟐 + 𝜷𝟏𝟐 𝒙𝟏 𝒙𝟐 + 𝜺𝒊𝒋𝒌 Modelo de regresión ajustado ̂𝟎 + 𝜷 ̂ 𝟏 𝒙𝟏 + 𝜷 ̂ 𝟐 𝒙𝟐 + 𝜷 ̂ 𝟏𝟐 𝒙𝟏 𝒙𝟐 ̂=𝜷 𝒀 ❖ Formas para calcular el modelo 1. Consideremos el mejor predictor lineal de 𝒀 a partir de las variables explicativas. Este predictor tendrá la forma: Ecuación de regresión múltiple ̂𝟎 + 𝜷 ̂ 𝟏 𝒙𝟏 + 𝜷 ̂ 𝟐 𝒙𝟐 + 𝜷 ̂ 𝟏𝟐 𝒙𝟏 𝒙𝟐 ̂ 𝒊𝒋𝒌 = 𝜷 𝒀 ̂ = 𝑺−𝟏 𝜷 𝒑−𝟏 𝑺𝒙𝒚 Donde: −1 𝑆𝑝−1 es la inversa de la matriz de varianzas y covarianzas de los 𝑝 − 1 variables explicativas 𝑆𝑥𝑦 la columna de la matriz de covarianzas correspondiente a las varianzas de las variables 𝑌 con el resto. 2. Determinación del modelo mediante los efectos ̂ 𝟎 = ̅̅̅ 𝜷 𝑌… media de las observaciones 𝑒𝑓𝑒𝑐𝑡𝑜 𝐴 ̂𝟏 = 𝜷 2 𝑒𝑓𝑒𝑐𝑡𝑜 𝐵 ̂𝟐 = 𝜷 2 𝑒𝑓𝑒𝑐𝑡𝑜 𝐴𝐵 ̂ 𝟏𝟐 = 𝜷 2 Coeficiente de Determinación Dos de los estadísticos más útiles para medir la calidad del modelo de regresión múltiple es el coeficiente de determinación (𝑅 2 ) y el coeficiente ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II 2 de determinación ajustado (𝑅𝑎𝑗 ) que están definidos de la siguiente manera: 𝑅2 = 𝑆𝐶𝑇 − 𝑆𝐶𝐸 𝑆𝐶𝑀𝑜𝑑𝑒𝑙𝑜 ∗ 100 = ∗ 100 𝑆𝐶𝑇 𝑆𝐶𝑇 2 𝑅𝑎𝑗 = 𝐶𝑀𝑇 − 𝐶𝑀𝐸 ∗ 100 𝐶𝑀𝑇 Estos coeficientes cuantifican el porcentaje de variabilidad presente en los datos que explica el modelo; por ello, son deseables valores próximos a 100. En general, para fines de predicción se recomienda un coeficiente de determinación ajustado de al menos 70%. Cuando hay muchos 2 factores se prefiere el estadístico 𝑅𝑎𝑗 en lugar del 𝑅 2 . 2 Si 𝑅𝑎𝑗 es al menos el 70%, significa que los factores estudiados son responsables o explican un alto porcentaje de la variabilidad observada en la variable de respuesta, por lo tanto, el efecto atribuible a factores no estudiados, ya sea que se hayan mantenido en un nivel fijo o que hayan tenido pequeñas variaciones, más el efecto de errores experimentales, fueron pequeños en comparación con el efecto de los factores estudiados. 2 En caso de que 𝑅𝑎𝑗 o 𝑅 2 hayan sido pequeños, esto indicaría que el efecto o variabilidad atribuible a los factores estudiados es pequeña en comparación con el resto de la variación observada en el experimento. Un 𝑅 2 bajo puede deberse a una o varias de las siguientes razones: Los factores estudiados, por sí solos no tienen la suficiente influencia para explicar las variaciones observadas en la variable de respuesta. Los niveles de los factores estudiados son demasiado estrechos, por lo que el efecto sobre la variable de respuesta al cambiar de un nivel a otro es demasiado pequeño. Otros factores no estudiados en el experimento no se mantuvieron suficientemente fijos, por lo que al tener variaciones durante el experimento causaron mucha variación experimental. Los errores experimentales y los errores de medición fueron altos. Se debe tener la precaución de analizar cuáles de las razones anteriores influyeron para tener coeficientes de determinación bajos; es decir, no se debe caer en el error de desechar el experimento y creer que “no sirvió”. ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II En general, los experimentos generan información que debe utilizarse para plantear conjeturas y estudios experimentales nuevos. Gráficos de superficie Es la superficie que resulta de representar gráficamente el modelo ajustado, y describe el comportamiento de la respuesta promedio en cada punto de la región experimental. ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II Gráfica de superficie de VIBRACION vs. VELOCIDAD; BROCA 40 VIBRACION 30 1 20 0 10 -1 0 BROCA Gráfica de contorno 1 -1 VELOCIDAD ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II Gráfica de contorno de VIBRACION vs. VELOCIDAD; BROCA 1,0 VIBRACION < 15 15 – 20 20 – 25 25 – 30 30 – 35 35 – 40 > 40 VELOCIDAD 0,5 0,0 -0,5 -1,0 -1,0 -0,5 0,0 0,5 1,0 BROCA Análisis de Residuos ̂ 𝒊𝒋𝒌 𝒆𝒊𝒋𝒍 = 𝒐𝒃𝒔𝒆𝒓𝒗𝒂𝒅𝒐 − 𝒑𝒓𝒆𝒅𝒊𝒄𝒉𝒐 = 𝒀𝒊𝒋𝒌 − 𝒀 Prueba estadística para probar la hipótesis de igualdad de varianzas ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II 2 2 𝐻0 : 𝜎𝑖,𝑗 = 𝜎𝑖,𝑗 2 2 𝐻1 : 𝜎𝑖,𝑗 ≠ 𝜎𝑖,𝑗 𝑺𝟐𝒊,𝒋 𝒁∗𝟎 = 𝐥𝐧 [ 𝟐 ] 𝑺𝒊,𝒋 Se rechaza 𝐻0 si |𝒁∗𝟎 | es mayor que 𝑍𝛼/2 Verificación de supuestos Los supuestos del modelo de análisis de varianza deben Verificarse antes de dar por válidas las conclusiones de la etapa de interpretación, la tabla de ANOVA supone que los residuos se distribuyen normales, independientes y con varianza constante. SPSS ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II Verificación de supuestos ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II ANALISIS EN RSTUDIO setwd("D:/1. ABRIL - SEPTIEMBRE 2021/3. DESEÑO DE EXPERIMENTOS II/PRIMER PARCIAL/RESOLUCIÓN DE EJERCICIOS") ejemplo<-read.csv("Ejemplo.csv", header = TRUE, sep = ";",dec = ",", fill = TRUE, comment.char = "", encoding = "unknown") View(ejemplo) attach(ejemplo) names(ejemplo) str(ejemplo) # Creación del diseño install.packages(FrF2) library(FrF2) experimento<- FrF2(nruns = 4, nfactors = 2, factor.names = list(Broca=c(-1,1), Velocidad=c(-1,1)), replications = 4, randomize = F) experimento ESPOCH ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO DISEÑO DE EXPERIMENTOS II ## Se agrega la respuesta experimento_r<- add.response(design = experimento, response =Vibracion) experimento_r ## Análisis de la tabla ANOVA Broca<- factor(Broca) Velocidad<- factor(Velocidad) Modelo <- lm(Vibracion~(Broca+Velocidad)^2) ANOVA <- aov(Modelo) summary(ANOVA) summary(Modelo) ## Gráficas de efectos principales MEPlot(experimento_r) ## Gráficas de Interacciones IAPlot(experimento_r, lwd = 2) ###PRUEBA DE NORMALIDAD shapiro.test(rstandard(Modelo))









