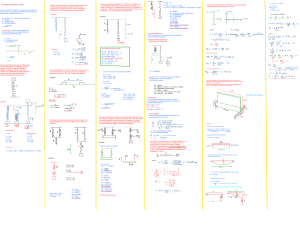
Xt = X1 + X2 F = KX F = mg = 42.5*9.81 = 416.93N Xt = F1/K1 + F2/K2 = 416.93/4000 + 416.93/5000 = 18.76cm Se tiene 2 resortes de constante K1 = 50N/cm, k2 = 60N/cm, se han acoplado en serie tal que el extremo libre del resorte 1, se sujeta a un techo y en el extremo libre del resorte 2, se instala una carga de P = 250N, Determine las deformaciones de cada uno de los resortes, asi como el perido de las oscilaciones. Solucion V=w A - X dF = dm*X Vibraciones Mecanicas Es el movimiento de una particula que oscila alrededor de una posicion de equilibrio. F = KX K = constante elastica x = deformacion Vibraciones libres de particulas - Movimiento armonico simple Se tiene un edificio en donde el peso vibra con una amplitud de 0.004cm, y con una frecuencia de 10 rad/seg, se desea aislar un instrumento sencible por medio de 4 resortes iguales. La maxima amplitud de vibracion permisible para el instrumento es de 0.004cm. Determine la constante necesaria para cada resorte, el instrumento pesa 220kg, considere el sistema sin amortiguamiento b = 0 MA = 0 T=2 10000/8000000 = 0.222seg Si se trata de resorte en serie: Fy = 0 F=P KX = mg X/g = m/K Xt = X1 + X2 +X3 +........Xn Ft = F1 = F2 = F3 = F4 = .......Fn 1/Ke = 1/K1 + 1/K2 + 1/K3 ..... Ke = K1*K2/(K1+K2) Si se trata de resorte en paralelo: Xt = X1 = X2 =X3 = ....Xn Ft = F1 + F2 + F3 + F4 .... Ke = k1+K2+K3+..... m/k f = 1/T * Para el primer tramo: Solucion *Para el segundo tramo Una particula realiza un movimiento armonico simple en torno a un punto de modo que a 2cm, de ese punto su velocidad y aceleracion son 6cm/s y 12cm/s2, Determine la amplitud Como los resortes se encuentran en SERIE F1 = F2 =Ft K1X1 = K2X2 = 250 50X1 = 60X2 = 250 Solucion W=K estatico Se sabe F = ma, recordando que a es la segunda derivada de x , de x con respecto a t. por lo tanto se escribe. X1 = 5cm X2 = 4.17cm X=2 V = 6cm/s a = 12cm/s2 T =2 m/k ; M =masa (kg) K = Constante (N/m) F = mg 250 = m(9.81) m = 25.48kg V= w A - X 1/Ke = 1/K1 + 1/K2 1/Ke = 1/50 + 1/60 Ke = 27.27N/cm Ke = 2727N/m a= wx Solucion: Por semejanza de triangulos Solucion: Ley de Hooke.- En todo cuerpo elastico las fuerzas deformadoras son proporcionales a sus respectivas deformaciones Se tiene dos bloques de masa de 10kg, y estan firmemente unidos a un muelle de constante elastica 120N/m, los que se muestran en equilibrio en la figura. Determine la altura maxima, que puede hacer descender al bloque superior de modo que el bloque inferior no llegue a saltar durante las oscilaciones. dF = dm*X Pero : W = mg m = W/g dm = dw/g = wdx /g Wn = K/m Ke = 4*5/(4+5) = 2.222 = 2222.22N/m Wn = 2222.22/42.5 Wn = 7.23rad/seg T = 2 /Wn T = 2 /7.23 T = 0.87seg. Vm = Xm*Wn Vm = 0.1876* 7.23 = 1.37m/s am = Xm*Wn am = 0.1876*7.23 = 9.81m/s2 Solucion: X = A sen(wt + ) ; ecuacion del movimiento A = Amplitud = angulo de fase w = velocidad angular T= 2 F = ma, pero : a = dx /dt Describa el desplazamiento del sistema y determine el periodo de la siguiente figura mostrada. g = 10m/s2 12 = W (2) W = 2.45rad/s 6 = 2.45 A - 2 2.449 = A - 4 A = 3.16cm En la figura mostrada el sistema se estira 25cm, debido a un bloque que pesa 15N, Cual es la longitud que se estira en el resorte X. T=2 mx + kx = 0 Wn = K/m; K = (N/m), m = kg, Wn = rad/seg Wn = frecuencia circular natural T = 2 /Wn , T =(seg) Vm = Xm*Wn, Xm = (metros), Vm =(m/s) am = Xm*Wn ,am =(m/s2) Una viga de rigidez infinita soporta el peso de un muro de ladrillo. Esta viga se apoya sobre otro flexible de 25x50cm2, y sobre un dado de concreto en el otro extremo. Determine el periodo de vibracion de la viga infinitamente rigida cuya seccion es de 15x80m2, considere E = 210Tn/cm2. Para la figua mostrada determine la frecuencia y el perido que tiene una carga de 140kg, aplicado al extremo atravez de un resorte K2, la viga tiene un espesor de t = 0.5cm, y un ancho b = 5cm, su modulo de elasticidad es E = 2.1x10 kg/cm2, la longitud de la viga es de L = 55cm, la constante del resorte es K2 = 2kg/cm2. Peso especifico del muro = 1800kg/m3 Peso especifico del concreto = 2400kg/m3 Vibracion libre En el caso de vibracion libre el sistema no tiene amortiguamiento ni fuerza exitadora de modo que su ecuacion viene dado por: 25.48/2727 X + W X =0 T = 0.61seg viga rigid a Se sabe: a = dx /dt = X Se tiene un bloque de 42.5kg, se mueve entre guias verticales como se muestra en la figura, el bloque es empujado 5cm hacia abajo (para el resorte en paralelo) desde su posicion de equilibrio y se suelta. Para cada arreglo de resorte determine el periodo de la vibracion, la maxima velocidad del bloque y sus maxima aceleracion. fle xib le Es todo movimiento rectilineo y vibratorio que se repite del mismo modo y que presenta una aceleracion directamente proporcional a la posicion del movil. Se tiene un bloque de masa y un resorte desconocido, pero se sabe que al suspender el bloque del resorte, este experimenta una deformacion de x = 25cm, Determine el periodo de las oscilaciones del sistema bloque-resorte. Transmisibilidad El caso de mayor interes desde el punto de vista estructural es el de los sismos Solucion: vig a MOVIMIENTO ARMONICO SIMPLE El extremo de la viga produce un desplazamiento debio a la carga de 140kg. Solucion: Peso de muro mas peso de la viga: Para el caso 2 p = mg Fo = KXo P = Fo mg = KXo Xo = mg/K - Peso de muro : 4.2*2.4*0.15*1800 = 2721.6 - Peso de la viga: 4.2*0.8*0.15*2400 = 1209.6 Peso total (w) = 3931.2kg Yo = Es la amplitud de la exitacion A/Yo = Es la transmisibilidad Para el caso 3 F = KX p = mg F=p KX = mg X = mg/K O = arco para un tiempo t Solucion * Para los resorte en paralelo A = Xo + X A = mg/K + mg/K = 2mg/K = 2(10)(9.81)/120 = 1.635m La carga distribuida sobre la viga sera: Ke = K1*K2/(K1+K2) w = 3931.2/4.2 = 936kg/m = desplazamiento Q = cargas Una masa m, es frenada por un resorte de constante K, se encuentra inicialmente en reposo, en el tiempo t=0, se encuentra bajo la accion de una fuerza exitadora. F = Fo coswt, suponiendo que no haya amortiguamiento y dado que w/2 = 8ciclos/segundo, m= 8.584kg, k = 3kg/ m, Fo = 46kg, Determine la amplitud de las vibraciones, considere g = 10m/s2. K1 = 3x2.1x10 x 5x0.5 /(12 x 55 ) = 1.97kg/cm Ke = 1.97*2/(1.97+2) = 0.992kg/cm Ke = 0.992x9.81x100 = 973.152N/m La reaccion del punto B, de 1965.6kg, deflexiona a la viga flexible generando un Solucion: 973.152/140 Solucion: Ft = F1 = F2 15 = F1 = F2 Ke = K1+K2 Ke = 4 + 5 = 9KN/m Wn = K/m Wn = 9000/42.5 Wn = 14.55 rad/s F = KX 15 = KX Para una viga simplemente apoyada. ( carga puntual) = PL/ (48EI) Xt = x1 + x2 25 = x1 + X2 T = 2 /Wn T = 2 /14.55 T = 0.43seg La rigidez lateral se expresa: K = P/ = 48EI /L 1/Ke = 1/K1 + 1/K2 1/Ke = 1/K +1/2K ke = 2K/3 Ft = Ke Xt 15 = 2K/3(25) K = 0.9N/cm en la ecuacion 1: 15 = 0.9X1 X1 = 16.67cm Vm = Xm*Wn Vm = 0.05*14.55 Vm = 0.73m/s am = Xm*Wn am = 0.05*14.55 am = 10.59m/s2. Para los resortes en serie: = 48*210* 25*50 /[12 * 320 ] = 80.109tn/cm Para el calculo del periodo de vibracion de la viga AB, lo tomamos como articulado en A. El extremo B, lo colocamos como resorte debido a que en este tramo existe un A = 46/3 / (1- -0.021m = 2.636rad/seg