Solucionario Examen Investigación de Operaciones 1 (IN172)
Anuncio
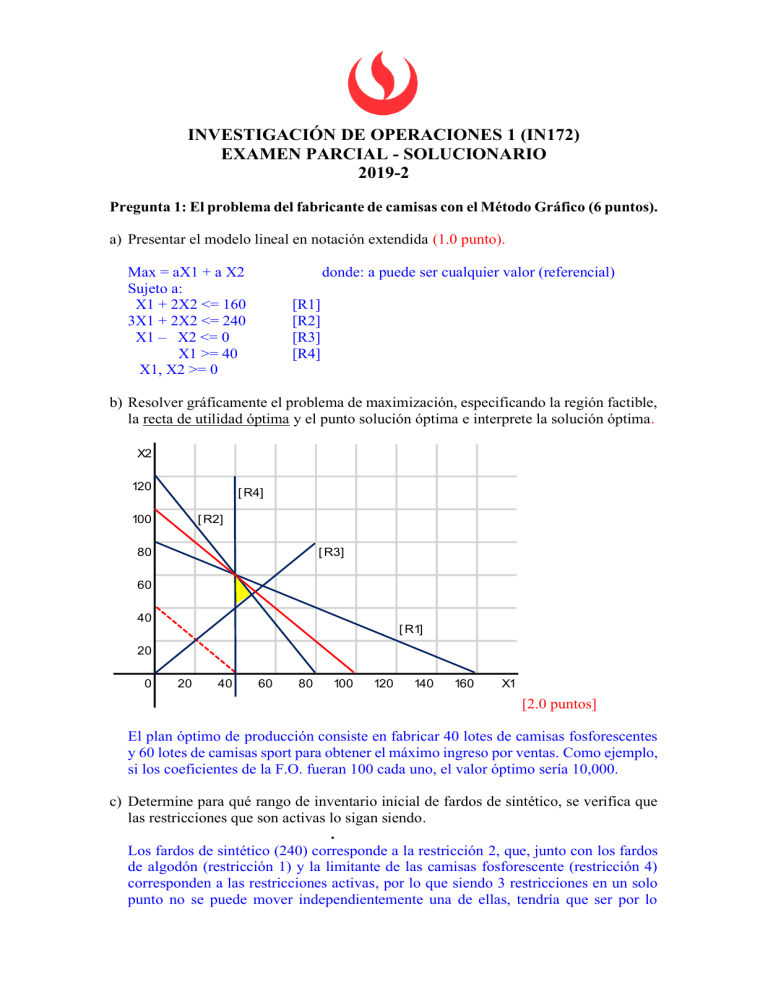
INVESTIGACIÓN DE OPERACIONES 1 (IN172) EXAMEN PARCIAL - SOLUCIONARIO 2019-2 Pregunta 1: El problema del fabricante de camisas con el Método Gráfico (6 puntos). a) Presentar el modelo lineal en notación extendida (1.0 punto). Max = aX1 + a X2 Sujeto a: X1 + 2X2 <= 160 3X1 + 2X2 <= 240 X1 – X2 <= 0 X1 >= 40 X1, X2 >= 0 donde: a puede ser cualquier valor (referencial) [R1] [R2] [R3] [R4] b) Resolver gráficamente el problema de maximización, especificando la región factible, la recta de utilidad óptima y el punto solución óptima e interprete la solución óptima. X2 120 [ R4] 100 [ R2] 80 [ R3] 60 40 [ R1] 20 0 20 40 60 80 100 120 140 160 X1 [2.0 puntos] El plan óptimo de producción consiste en fabricar 40 lotes de camisas fosforescentes y 60 lotes de camisas sport para obtener el máximo ingreso por ventas. Como ejemplo, si los coeficientes de la F.O. fueran 100 cada uno, el valor óptimo sería 10,000. c) Determine para qué rango de inventario inicial de fardos de sintético, se verifica que las restricciones que son activas lo sigan siendo. . Los fardos de sintético (240) corresponde a la restricción 2, que, junto con los fardos de algodón (restricción 1) y la limitante de las camisas fosforescente (restricción 4) corresponden a las restricciones activas, por lo que siendo 3 restricciones en un solo punto no se puede mover independientemente una de ellas, tendría que ser por lo menos 2 y no es el caso, por tanto para que sigan siendo activas las 3 restricciones, se debe mantener sin variación el inventario inicial de fardos sintéticos (1.0 puntos). d) Si el precio de venta de cada lote de camisas fuera de 200 soles, determine cuánto es lo máximo que puede disminuir el precio del lote de las camisas sport para que el plan de producción no varíe. Sea c2 el precio de las camisas sport. Para que no cambie la solución óptima, geométricamente si c2 disminuye, la pendiente de la recta de la función objetivo podrá cambiar hasta igualar a la pendiente de la restricción 2, es decir: -200/c2 debe ser igual a -3/2. Entonces el mínimo valor del c2 será 400/3. Como el precio actual es 200 soles, lo máximo que puede disminuir es [200-400/3] soles (1 punto). e) Considere ahora que las restricciones iniciales no han cambiado, pero el precio de venta de un lote de camisas fosforescentes es 80 soles y el precio de un lote de camisas sport es 200 soles. Bajo esas nuevas condiciones de precios, determine e interprete los costos reducidos para la producción de camisas fosforescente y para camisas sport (1.0 punto). X2 120 [ R4] 100 [ R2] 80 [ R3] 60 40 [ R1] 20 0 20 40 60 80 100 120 140 160 X1 Con los nuevos precios, la solución óptima no ha variado esto es X1 = 40 y X2 = 60 por lo que no existe costo reducido para ambos productos (1.0 punto) Pregunta 2: Modelamiento de un PL con notación compacta para una refinería petrolera (7 puntos). a) Las variables de decisión e índices que el modelo empleará (1.5 puntos). 𝑋𝑖 ∶ 𝐶𝑎𝑛𝑡𝑖𝑑𝑎𝑑 (𝑏𝑎𝑟𝑟𝑖𝑙𝑒𝑠) 𝑑𝑒 𝑐𝑟𝑢𝑑𝑜 𝑖 𝑎 𝑐𝑜𝑚𝑝𝑟𝑎𝑟 𝑌𝑗𝑘 ∶ 𝐶𝑎𝑛𝑡𝑖𝑑𝑎𝑑 (𝑏𝑎𝑟𝑟𝑖𝑙𝑒𝑠) 𝑑𝑒 𝑔𝑎𝑠𝑜𝑙𝑖𝑛𝑎 𝑗 𝑎 𝑣𝑒𝑛𝑑𝑒𝑟 𝑒𝑛 𝑒𝑙 𝑚𝑒𝑟𝑐𝑎𝑑𝑜 𝑘 Donde: 𝑖: 𝐶𝑟𝑢𝑑𝑜𝑠 (1, … 4) 𝑗: 𝐺𝑎𝑠𝑜𝑙𝑖𝑛𝑎𝑠 (1,2,3) 𝑘: 𝑀𝑒𝑟𝑐𝑎𝑑𝑜𝑠 (1,2,3) b) Las estructuras de datos que el modelo empleará (1.0 punto). 𝐷𝑖𝑠𝑝𝑜𝑖 = (1000 1500 2000 1000) 𝐶𝑜𝑠𝑡𝑜𝑖 = (58 60 59 57) 𝐹𝑟𝑎𝑐𝑐𝑖𝑜𝑛𝑖𝑗 = [0.20 0.30 0.20 0.20 0.35 0.25 0.25 0.25 0.25 𝑀𝑎𝑥𝑖𝑚𝑜𝑗𝑘 = [500 600 700 400 300 600 500 500 500] 𝑃𝑟𝑒𝑐𝑖𝑜𝑗𝑘 = [ 4.7 4.8 5.0 4.1 4.0 4.5 3.5 3.4 3.3] 0.15 0.30 0.30] c) El modelo de programación lineal de notación compacta que permita a la refinería maximizar su utilidad total (1.5 puntos por la función objetivo y 3.0 puntos por el total de las restricciones) [(no se calificará la notación extendida]. 3 3 4 𝑀𝑎𝑥 𝑍 = ∑ ∑ 42 ∗ 𝑃𝑟𝑒𝑐𝑖𝑜𝑗𝑘 ∗ 𝑌𝑗𝑘 − ∑ 𝐶𝑜𝑠𝑡𝑜𝑖 ∗ 𝑋𝑖 𝑗=1 𝑘=1 𝑖=1 [1.5 puntos] 𝑆𝑢𝑗𝑒𝑡𝑜 𝑎: 𝑋𝑖 ≤ 𝐷𝑖𝑠𝑝𝑜𝑖 𝑌𝑗𝑘 ≥ 100 𝑌𝑗𝑘 ≤ 𝑀𝑎𝑥𝑖𝑚𝑜𝑗𝑘 4 ∀𝑖 = 1, … ,4 ∀𝑗 = 1,2,3 ∀𝑘 = 1,2,3 ∀𝑗 = 1,2,3 ∀𝑘 = 1,2,3 3 ∑ 𝑋𝑖 ∗ 𝐹𝑟𝑎𝑐𝑐𝑖𝑜𝑛𝑖𝑗 = ∑ 𝑌𝑗𝑘 𝑖=1 [0.5 puntos] [0.5 puntos] [0.5 puntos] ∀𝑗 = 1,2,3 𝑘=1 [1.0 punto] 𝑋𝑖 ≥ 0 𝑌𝑗𝑘 ≥ 0 ∀𝑖 = 1, … ,4 ∀𝑗 = 1,2,3 ∀𝑘 = 1,2,3 [0.5 puntos] Problema 3: El problema de la venta de tamales, interpretación y análisis de sensibilidad en Lingo (7 puntos) a) Identifique las variables de decisión y su significado (1.0 punto) X(i,j) = Tamales a producir en planta i y a enviar al centro de distribución j. Y(j) = Tamales a vender en el centro de distribución j. W(j,k) = Tamales a enviar desde el centro de distribución j para venderlos en el punto de venta k. Donde: i = 1, 2 ; j = 1,…,7 ; k = 1,2,3 b) Presente el reporte administrativo con precisión de la distribución a realizar y el objetivo económico (1.0 punto). Utilidad óptima: $ 1689 . Planta Chorrillos San Miguel Punto de venta San Isidro Surco Magdalena Envíos ( tamales ) Barranco Miraflores 450 50 400 0 Producción de las plantas (tamales) 500 400 Venta (en tamales) 250 160 415 c) ¿El modelo tiene soluciones óptimas alternativas? Sustente (1.0 punto). Si, el modelo tiene soluciones óptimas alternativas ya que la cantidad de tamal a enviar de san miguel a Miraflores es “0” y su costo reducido, también es “0”. d) Si la empresa de transportes ha considerado ya no cobrar por el envío de Chorrillos a Barranco, es decir, si su costo de envío inicial era de S/0.10 por tamal, ahora será S/0.00/tamal ¿Afecta la distribución propuesta? Sustente. ¿Cómo queda y cuál sería el valor óptimo? (1.0 punto). El costo de producción en Chorrillos es 3.0 soles/tamal y el costo de envío (o de transportes) de Chorrillos a Barranco es de 0.10 soles/tamal, el costo total sería de 3.10 soles/tamal, si se reduce el costo total en 0.10 soles/tamal quedaría en 3.0, la distribución propuesta afecta la solución toda vez que este valor como costo (-3.0) está fuera de los límites para el rango valor incremental o decremental aceptable [3.1+0; -3.2-0.2] ó [-3.1,-3.4]. En consecuencia, para obtener el nuevo valor de Z se tendría que correr el nuevo modelo. e) ¿Hasta cuánto puede incrementarse la venta mínima de tamales en Magdalena para que la distribución de envíos propuesta no cambie? (Sustente) (1.0 punto). La venta mínima actual a Magdalena es de 250 [Row10] y su exceso es de 165 con un precio dual de 0.00; en consecuencia, la solución y el valor óptimo no cambia; además el valor incremental aceptable para que la solución no cambie es de 165. f) Tamalitos Nancy desea incrementar sus ingresos a partir de la reducción en las restricciones activas, ¿En cuál de ellas cambiaría? (identifíquelo) y ¿Cuánto sería el nuevo ingreso óptimo? Para que la solución se mantenga sin modificar sus variables duales (2.0 puntos). Las restricciones activas, sus variables duales, los valores de los parámetros y los nuevos valores de la solución óptima después de la reducción están en el cuadro siguiente: Allowable Parámetro Nuevo valor Row activa Dual Price Parámetro Valor Z* Decrease residual Z* 2 1.90 500 950.00 165 335 1,375.50 3 2.30 400 920.00 165 235 1,309.50 4 -1.00 25 -25.00 25 0 1,714.00 5 -1.30 50 -65.00 50 0 1,754.00 8 -0.30 250 -75.00 250 0 1,764.00 9 -0.10 160 -16.00 160 0 1,705.00 11 -5.00 0 0.00 inf 0 --12 -5.10 0 0.00 50 0 --1,689.00 La restricción activa 8 es el envío a San Isidro, esto es, reducir la exigencia de la venta mínima semanal a San Isidro a cero. El nuevo ingreso óptimo sería 1,764 soles.