OBJETIVOS

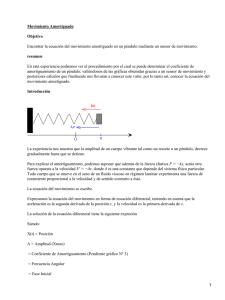
OBJETIVOS
Se pretende determinar experimentalmente un conjunto de magnitudes de interés
en el movimiento vibratorio armónico simple, amortiguado y forzado en un
péndulo giratorio (péndulo de Pohl).
FUNDAMENTO TEORICO
A. Movimiento vibratorio armónico simple
La Fig. 1 muestra un esquema del dispositivo a utilizar. La presencia de un
muelle espiral hace que sobre el sólido rígido actúe un momento M = -K  2
cuando el sólido se desplaza un ángulo  3 respecto a su posición de equilibrio.
La ecuación de movimiento del sólido vendrá dada por:
M = I
siendo I el momento de inercia del sólido respecto al eje de rotación. La ecuación
 +  o2  = 0
diferencial (1) puede también escribirse:
siendo  o = (K/I )1/2 5 la frecuencia natural de oscilación del péndulo. La solución,
bien conocida, de la ecuación (2) es:
 =  o sen(  o t +  )
B. Movimiento amortiguado
Supóngase ahora que el momento resultante de las fuerzas que actúan
sobre el volante puede desdoblarse en el momento recuperador del muelle y un
momento resistente o de frenado, de acuerdo con la ecuación:
M = M
rec
+M
res
= -K  - b 
1
con lo que la ecuación de movimiento será:
I + b  + K  = 0
que puede igualmente escribirse:
 + 2  +  o2  = 0
siendo  = b/2I 10 el llamado parámetro de amortiguamiento.
La solución general de esta ecuación para  o2 >  2 11 (movimiento oscilatorio
amortiguado) es:
siendo  1 = (  o2 -  2 )1/2 13 la frecuencia angular del oscilador amortiguado.
 =  o exp (-  t) cos (  1 t -  )
Recuérdese que cuando  o2 =  2 14 (movimiento CRITICO) o  o2 <  2 15
(movimiento SUPERCRITICO) el movimiento es aperiódico.
C. Movimiento forzado
C.1 Sin amortiguamiento
Se supondrá en cualquier caso que el extremo libre del muelle realiza
oscilaciones armónicas de frecuencia  16. La ecuación de movimiento será:
 +  o2  = B cos  t
cuya solución, con las condiciones  = 0,  = 0 en t = 0 18 es:
 = C( cos  t - cos  o t)
De acuerdo con la ecuación (9), las oscilaciones serán en forma de
pulsaciones o latidos de frecuencia entre la frecuencia natural y la impulsora. No
se podrá alcanzar entonces un estado estacionario de amplitud constante.
C.2 Con amortiguamiento
2
La ecuación diferencial del movimiento es:
 + 2  +  o2  = B cos  t
cuya solución estacionaria (despreciando los términos transitorios) viene dada
por:
 (t) =
B cos (  t -  )
[(  o2 -  2 ) + 4  2  ]
2
2
1/2
con
 = arctan
2
o -
2
2
Nótese que la magnitud  23 representa la diferencia de fase entre la fuerza
impulsora externa y el movimiento resultante. Para  o 24 dado,  25 varía entre
0 (   0) 26 y  (    ) 27 .
Puede demostrarse que a la frecuencia
 =  R = (  o2 - 2  )
2
1/2
la amplitud de  (t) 29 es máxima. Se produce entonces la resonancia en la
amplitud. A  R 30 se le llama frecuencia de resonancia.
METODOLOGIA
El péndulo de Pohl mostrado esquemáticamente en la Fig. 1 es un sistema
cuya oscilación propia está provocada por un muelle espiral. El amortiguamiento
(variable) se debe a las corrientes de Foucault que aparecen en el péndulo al
moverse el disco metálico en el seno de un campo magnético. Finalmente, un
motor de corriente continua de velocidad variable provoca oscilaciones en el
extremo más externo del muelle, dando así lugar al movimiento forzado.
3
Con objeto de lograr la mayor estabilidad en el giro del motor, se
alimentará directamente con UNA TENSION MAXIMA, V ex 31 , de 15 V, en las
bornas 10 de la Fig. 1. La velocidad, y por tanto la frecuencia impulsora  32 se
puede variar modificando la tensión de alimentación aplicada en 10.
La segunda fuente de alimentación se utiliza para aplicar una tensión
continua a las bobinas, usando las bornas 14 de la Fig. 2. Es MUY IMPORTANTE
que la corriente que pase por las bobinas no sea nunca mayor de 2 A, y sólo
debe circular durante 2 o 3 minutos como máximo si 1A < I < 2A. 33.
RESULTADOS
1.- CALIBRADO DE LA TENSION DE EXCITACION.
Determinamos las veces que sean necesarias, la frecuencia de giro de la rueda
11 en función de Vex.
TABLA I
Error! Bookmark not
defined. Vex (mV)( 0.1)
T (s) ( 0.01)
 ( s -1 ) 34
2.69
5.17
5.10
5.40
1.203 0.002
3.47
3.50
3.70
3.83
1.708 0.005
4.09
2.80
2.85
2.90
2.205 0.008
4.79
2.47
2.32
2.25
2.677 0.011
5.43
2.09
2.10
1.99
3.050 0.015
7.05
1.52
1.53
1.60
4.05 0.03
8.11
1.34
1.37
1.40
4.59 0.03
1.24
4
8.45
1.31
1.32
4.87 0.04
9.01
1.24
1.27
1.30
4.95 0.04
10.37
1.02
0.99
1.07
6.10 0.06
13.20
0.70
0.76
0.85
8.16 0.11
15.01
0.65
0.59
0.59
10.47 0.16
Para determinar el número de medidas que teníamos que realizar obtuvimos 3,
y calculamos la dispersión. Como en todos los casos obteniamos una dispersión
menor del 2% nos quedamos con las tres medidas y calculamos la frecuencia en
cada caso con el valor medio de las tres.
Representamos gráficamente  35 frente a Vex, y ajustamos los datos
resultantes mediante mínimos cuadrados.
Los parametros de ajuste de la gráfica I son:
a = ( 0.70 0.06) mV-1 s-1
b = (- 0.9 0.5) s-1
r = 0.98424852
2.- PENDULO NO AMORTIGUADO. FRECUENCIA NATURAL.
Partiendo de la posición de equilibrio y procurando que sea el cero de la escal
determinamos la frecuencia natural de las oscilaciones. Tendremos que
demostrar si la frecucia natural de las oscilaciones depende o nó de la amplitud.
Consideramos las oscilaciones desde amplitudes distintas y medimos el periodo
tres veces para cada amplitud.
5
TABLA II
PERIODO (seg) ( 0.01)
Error! Bookmark not defined.
AMPLITUD ( 0.2 unid.)
5.0
1.72
1.74
1.75
10.0
1.77
1.78
1.76
15.0
1.74
1.75
1.76
En los tres casos el tanto por ciento de
dispersión es menor del 2 % por lo que podemos tomar
el valor medio de las tres medidas como periodo para
cada amplitud. En los tres periodos obtenidos la
dispersión vuelve a ser menor del 2 % por lo que
podemos tomar como periodo natural de las
oscilaciones el valor medio.
=
2
T
=
2
= 3.59
1.75
 = (3.59 + _ 0.02) s - 1
La frecuencia natural no depende de la amplitud.
3.- MOVIMIENTO AMORTIGUADO.
6
Para dos valores diferentes de la corriente suministrada a las bobinas de
frenado determinamos:
i) A partir de la elongación máxima posible, la elongaciónes máximas sucesivas
a un mismo lado:
A la izquierda, para una intensidad de corriente en las bobinas de (0.45 0.01)
A:
TABLA III
Error!
Book
mark
not
define
d.18.0
13.0
9.6
7.0
Error!
Book
mark
not
define
d.0.8
0.6
0.4
0.2
5.0
3.6
2.6
1.8
1.2
Error : 0.2 unidades.
Para una intensidad de corriente en las bobinas de (0.70 0.01) A:
TABLA IV
Error!
Book
mark
not
define
d.13.4
5.4
2.0
0.4
0.2
Error : ( 0.2) unidades.
ii) Partiendo de la misma elongación anterior las elongaciones máximas
sucesivas al lado opuesto.
A la derecha, para una intensidad de corriente en las bobinas de (0.45 0.01) A:
TABLA V
Error!
Book
mark
not
define
d.20.0
14.6
10.8
7.8
5.6
Error!
0.8
0.6
0.4
0.2
4.2
3.0
2.2
1.6
7
Book
mark
not
define
d.1.2
Error : 0.2 unidades.
Para una intensidad de corriente en las bobinas de (0.70 0.01) A:
TABLA VI
Error!
Book
mark
not
define
d.20.0
8.1
3.4
1.4
0.4
0.2
Error: ( 0.2) unidades.
iii) Periodo T de las oscilaciones.
Realizamos tres medidas del periodo.
T1 = 1.80
T2 = 1.81
T3 = 1.82
Representamos gráficamente estos resultados:
4.- EL MOVIMIENTO FORZADO Y AMORTIGUADO.
El motor de c.c. es el encardo de provocar las oscilaciones forzadas
aumentanto y disminuyendo sinousidalmente (mediate el sistema de biela) la
tensión en el muelle elicoidal. Una vez puesto en marcha el motor y transcurrido
el tiempo necesario para la desaparición de los transitorios (caracterizados en
muchas ocasiones por la presencia de pulsaciones entre la frecuencia natural y la
externa), se llegará a un movimiento estacionario. En estas condiciones
determinamos, para distintos valores de la corriente de amortiguamiento (máximo
1 A), la amplitud A0 de la respuesta del oscilador para todo el intervalo de
frecuencias impulsoras  37.
TABLA VII
Para una corriente de amortiguamiento de (0.23 0.01)A
Error! Bookmark not defined.
Vex (mV) ( 0.01)
A0 (unidades) ( 0.2)
2.22
0.8
3.57
1.0
4.41
1.2
5.15
2.4
5.91
4.4
8
7.15
1.8
8.50
0.2
11.00
0.0
11.50
0.0
TABLA VIII
Para una corriente de amortiguamiento de (0.66 0.01)A
Error! Bookmark not defined.
Vex (mV) ( 0.01)
A0 (unidades) ( 0.2)
2.22
0.6
3.57
0.8
4.41
1.0
5.15
1.4
5.91
2.2
7.15
1.0
8.50
0.4
11.00
0.2
11.50
0.1
TABLA IX
Para una corriente de amortiguamiento de (0.75 0.01)A
Error! Bookmark not defined.
Vex (mV) ( 0.01)
A0 (unidades) ( 0.2)
2.22
0.8
3.57
1.0
4.41
1.2
5.15
1.6
5.91
1.8
9
7.15
1.6
8.50
1.0
11.00
0.4
11.50
0.2
TABLA X
Para una corriente de amortiguamiento de (0.98 0.01)A
Error! Bookmark not defined.
Vex (mV) ( 0.01)
A0 (unidades) ( 0.2)
2.22
0.6
3.57
0.8
4.41
1.0
5.15
1.2
5.91
1.0
7.15
1.0
8.50
0.6
11.00
0.4
11.50
0.2
Finalmente representamos los valores obtenidos en una gráfica de A0 en
función de  /  0 38, siendo  39 la frecuencia del oscilador forzado y
amortiguado y  0 40 la frecuencia natural del oscilador. Para ello sustituímos los
valores del voltaje en la ecuación de la recta ajustada en la gráfica I para obtener
las frecuencias del oscilador amortiguado y forzado; y después dividimos cada
una por la frecuencia natural de oscilación. De este modo obtenemos la siguiente
tabla de valores.
Error! Bookmark
not defined.  41 (s1)
 /  0 42
0.704 0.001
0.194 0.003
1.651 0.002
0.460 0.005
2.239 0.008
0.624 0.006
2.758 0.011
0.768 0.007
2.291 0.015
0.917 0.007
10
4.16 0.03
1.159 0.008
5.11 0.04
1.422 0.010
6.86 0.08
1.910 0.012
7.2 0.1
2.008 0.013
CUESTIONES
1.- Razone que el movimiento generado por el motor sobre el péndulo
corresponde efectivamente a un movimiento forzado sinousoidalmente (o,
de otra manera, que el extremo de la barra 12 se mueve sinuosidalmente).
El extremo fijado al motor realiza un movimiento circular. Cuando el extremo se
encuentra en el punto A, el otro extremo se encuentra en el punto cero que
consideramos como origen. Cuando la rueda gira  /2 43 radianes en el sentido de
las agujas del reloj, el extremo se muve a una distancia igual al radio, siendo ese
su máximo desplazamiento en dicho sentido. Cuando se vuelve a girar  /2 44
radianes vuelve al punto cero y si giramos otros  /2 45 radianes alcanza ahora
su máximo desplazamiento en sentido contrario.
Si ahora consideramos un pequeño desplazamiento del punto A,
desplazamiento que sufrirá la barra será  x = Rsen  46. Por tanto
desplazamiento se puede representar en función del angulo, de forma que
movimiento que realiza se puede describir con una función sinuosidal como
anterior.
el
el
el
la
2.- Demuestre que el frenado provocado por las bobinas es proporcional a
la velocidad, como se supone en la ecuación.
Las corrientes inducidas tienden siempre a oponerse a las variación de flujo
que la originan. por ello si un cuerpo solido metálico se mueve en un campo
magnetico, se engendrarán en su interior corrientes en torbellino, llamadas de
Foucault, que reaccionando con el campo que las indcen tenderán a opnerse a la
variación del flujo en el interior del metal. Habrá que tener en cuenta que aunque
11
las f.e.m. inducidas son pequeñas, las corrientes turbillonarias pueden ser muy
intensa, porque la resistencia ohmica del metal es muy pequeña o casi nula.
Supongamos por ejemplo un disco que gira en un campo magnetico
perpendicular a su plano, pero en el que el flujo queda limitado a una porción de
éste. La corriente inducida en dicho disco se opondrá a la variación de flujo que
tiene lugar durante el giro de la superficie metálica, y por esta causa se
engendrarán corrientes turbillonarias que en la zona A darán lugar a un flujo
saliente (torbellinos en sentido contrario a las agujas del reloj, caras norte) para
compensar el aumento de flujo que experimenta esta zona en su giro hacia C,
mientras que desde C a B los torbellinos girarán sentido contrario para provocar
un efecto opuesto, ya que el disco en esa zona va perdiendo flujo magnético.
Debido a ello, parte de la energía cinética del disco se utiliza en engendrar dichas
corrientes, y aquel disminuye su velocidad de rotación. De aquí que cualquier
masa metálica que oscila en el campo de un elctroimán es frenada rápidamente
en cuanto se excita la corriente en dicho electroimán, y que el frenado provocado
es directamente proporcional a la velocisdad, debido a esa disminución de la
energía cinética que hemos señalado.
3.- Comente los aspectos más notables de las curvas obtenidas en los
apartados (3) y (4) de los resultados.
En las curvas de apartado podemos destacar, entre otras cosas, como las
oscilaciones permanecen invariables en las proximidades del equilibrio, de modo
que tiende a una recta paralela al eje, independiente de la resistencia. También
podría permanecer invariable con la resistencia el periodo de oscilacion, que
implicaria que fuera el mismo en ambos casos.
En las curvas del apartado 4 podríamos destacar el aumento de la amplitud de
las oscilaciones cuando se dan las condiciones de resonancia.
4.-Comente cómo será el desfase en cada uno de los casos considerados
en el apartado 4.
La ecuacion del desfase viene dada por:
 = arctg
2
0 -
2
2
siendo  48 la resistencia para cada intensidad.
De esta forma para las diferentes amplitudes obtenidas obtendríamos:
* (0.23 0.01) A
 = arctg
21  1
0 -1
2
2
* (0.66 0.01) A
12
 = arctg
2 2  2
0 -2
2
2
* (0.75 0.01) A
 = arctg
2 3  3
0 -3
2
2
* (0.98 0.01) A
 = arctg
2 4  4
0 -4
2
2
5.- Estime el valor de la frecuencia de resonancia en la amplitud en el
movimiento forzado a partir de las gráficas obtenidas en el apartado 4.
Comente estos resultados.
La frecuencia de resonancia en la amplitud es aquella para la cual el cociente
entre esta y la frecuencia natural del oscilador es igual a 1, y tal que hace máxima
la amplitud.
Por tanto interpolando en la Tabla XI obtenemos una frecuencia de resonancia
de (2.93 0.06) s-1.
BIBLIOGRAFIA
-Catalá, Física, Ed. Saber, Madrid 1977.
- Marion, Dinamica Clásica de las partículas y los sistemas, Ed. Reverté,
Barcelona 1984.
- Tipler, Fisica, Ed reverté, Barcelona 1993.
13