formulario

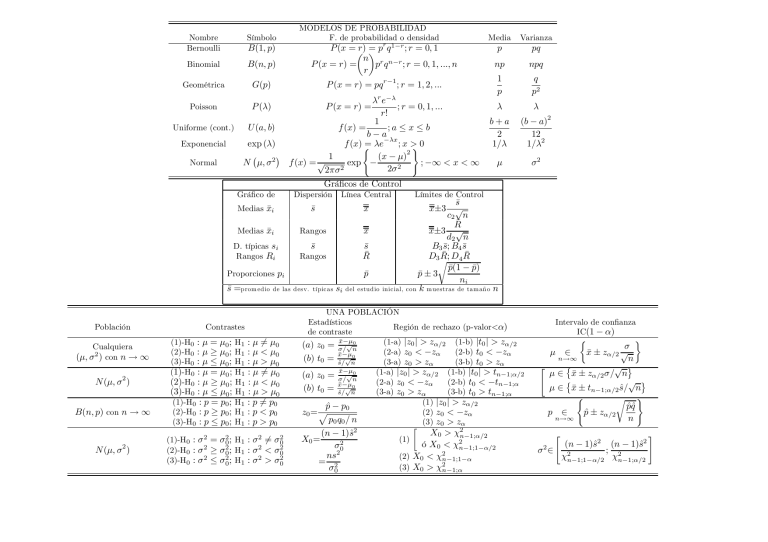
Nombre
Bernoulli
Símbolo
Binomial
B(n, p)
Geométrica
G(p)
B(1, p)
MODELOS DE PROBABILIDAD
F. de probabilidad o densidad
r 1−r
P (x = µ
r) =
¶ p q ; r = 0, 1
n r n−r
P (x = r) =
p q
; r = 0, 1, ..., n
r
Varianza
p
pq
np
npq
1
p
q
p2
λ
λ
b+a
2
1/λ
(b − a)
12
1/λ2
µ
σ2
P (x = r) = pq r−1 ; r = 1, 2, ...
λr e−λ
; r = 0, 1, ...
r!
1
;a ≤ x ≤ b
Uniforme (cont.)
U (a, b)
f (x) =
b−a
−λx
Exponencial
exp (λ)
f (x) (
= λe
;x >
)0
2
¢
¡
1
(x
−
µ)
Normal
N µ, σ2 f (x) = √
exp −
; −∞ < x < ∞
2σ 2
2πσ2
P (λ)
Poisson
Media
P (x = r) =
2
Gráficos de Control
Gráfico de
Dispersión
Línea Central
Medias x̄i
s̄
x
Medias x̄i
Rangos
x
D. típicas si
Rangos Ri
s̄
Rangos
s̄
R̄
Proporciones pi
s̄ =p rom ed io
Población
Cualquiera
(µ, σ2 ) con n → ∞
N (µ, σ2 )
B(n, p) con n → ∞
2
2
N (µ, σ )
de las d esv. típicas
Contrastes
(1)-H0 : µ = µ0 ; H1
(2)-H0 : µ ≥ µ0 ; H1
(3)-H0 : µ ≤ µ0 ; H1
(1)-H0 : µ = µ0 ; H1
(2)-H0 : µ ≥ µ0 ; H1
(3)-H0 : µ ≤ µ0 ; H1
(1)-H0 : p = p0 ; H1
(2)-H0 : p ≥ p0 ; H1
(3)-H0 : p ≤ p0 ; H1
(1)-H0 : σ =
(2)-H0 : σ 2 ≥
(3)-H0 : σ 2 ≤
σ20 ;
σ20 ;
σ20 ;
: µ 6= µ0
: µ < µ0
: µ > µ0
: µ 6= µ0
: µ < µ0
: µ > µ0
: p 6= p0
: p < p0
: p > p0
2
H1 : σ 6=
H1 : σ 2 <
H1 : σ 2 >
p̄
σ20
σ20
σ20
si
d el estud io
Límites de Control
s̄
x±3 √
c2 n
R̄
x±3 √
d2 n
B3 s̄; B4 s̄
D3r
R̄; D4 R̄
p̄(1 − p̄)
p̄ ± 3
ni
inicial, con k muestras de tamañ o n
UNA POBLACIÓN
Estadísticos
Región de rechazo (p-valor<α)
de contraste
x̄−µ0
(1-a) |z0 | > zα/2 (1-b) |t0 | > zα/2
√
(a) z0 = σ/
n
(2-a) z0 < −zα
(2-b) t0 < −zα
x̄−µ0
(b) t0 = ŝ/√n
(3-a) z0 > zα
(3-b) t0 > zα
x̄−µ0
(1-a) |z0 | > zα/2 (1-b) |t0 | > tn−1;α/2
√
(a) z0 = σ/
n
(2-a) z0 < −zα
(2-b) t0 < −tn−1;α
√0
(b) t0 = x̄−µ
ŝ/ n
(3-a) z0 > zα
(3-b) t0 > tn−1;α
(1)
|z
|
> zα/2
0
p̂ − p0
(2) z0 < −zα
z0 = p
p0 q0 / n
(3) z0 > zα
(n − 1)ŝ2
X0 =
σ20
ns2
= 2
σ0
·
X0 > χ2n−1;α/2
ó X0 < χ2n−1;1−α/2
(2) X0 < χ2n−1;1−α
(3) X0 > χ2n−1;α
(1)
Intervalo de confianza
IC(1 − α)
½
¾
σ
µ ∈
x̄ ± zα/2 √
n→∞
n
©
√ ª
"
µ ∈ x̄ ± zα/2 σ/ n
©
√ ª
µ ∈ x̄ ± tn−1;α/2 ŝ/ n
(
r )
p̂q̂
p ∈
p̂ ± zα/2
n→∞
n
"
(n − 1)ŝ2 (n − 1)ŝ2
σ ∈ 2
;
χn−1;1−α/2 χ2n−1;α/2
2
#
Dos poblaciones x1 , x2
Cualesquiera con
E(x1 ) = µ1 ; var(x1 ) = σ21
E(x2 ) = µ2 ; var(x2 ) = σ22
Datos apareados
d = x1 −x2
x̄1 − x̄2
(a) z0 = q 2
σ1
σ 22
n1 + n2
(1)-H0 : µ1 = µ1 ; H1 : µ1 =
6 µ2
(2)-H0 : µ1 ≥ µ2 ; H1 : µ1 < µ2
(3)-H0 : µ1 ≤ µ2 ; H1 : µ1 > µ2
(1)-H0 : µd = 0; H1 : µd =
6 0
(2)-H0 : µd ≥ 0; H1 : µd < 0
(3)-H0 : µd ≤ 0; H1 : µd > 0
Cualesquiera con
E(x1 ) = µ1 ; var(x1 ) = σ2
E(x2 ) = µ2 ; var(x2 ) = σ2
(1)-H0 : µ1 = µ2 ; H1 : µ1 =
6 µ2
(2)-H0 : µ1 ≥ µ2 ; H1 : µ1 < µ2
(3)-H0 : µ1 ≤ µ2 ; H1 : µ1 > µ2
Binomiales
x1 ∼ B(n1 , p1 )
x2 ∼ B(n2 , p2 )
(1)-H0 : p1 = p2 ; H1 : p1 6= p2
(2)-H0 : p1 ≥ p2 ; H1 : p1 < p2
(3)-H0 : p1 ≤ p2 ;H1 : p1 > p2
Normales
¡
(1)-H0 : σ 21 = σ21 ; H1 : σ21 =
6 σ22
2
2
2
(2)-H0 : σ 1 ≥ σ2 ; H1 : σ1 < σ22
(3)-H0 : σ 21 ≤ σ22 ; H1 : σ21 > σ22
¢
x1 ∼ N ¡µ1 , σ 21 ¢
x2 ∼ N µ2 , σ 22
CONTRASTES- DOS POBLACIONES
Estadísticos de contraste
Contrastes
Dos poblaciones x1 , x2
Cualesquiera con
E(x1 ) = µ1 ; var(x1 ) = σ 21
E(x2 ) = µ2 ; var(x2 ) = σ 22
Región de rechazo (p-valor<α)
x̄1 − x̄2
(b) t0 = q 2
ŝ1
ŝ22
n1 + n2
(1-a) |z0 | > zα/2
(2-a) z0 < −zα
(3-a) z0 > zα
(1) |t0 | > zα/2
(2) t0 < −zα
(3) t0 > zα
d¯
√
t0 =
ŝd / n
si
x̄1 − x̄2
(a) z0 = q
σ n11 + n12
x̄1 − x̄2
(b) t0 = q
ŝT n11 + n12
2
2
1
n1
(1) |z0 | > zα/2
2
Cualesquiera con
E(x1 ) = µ1 ; var(x1 ) = σ 2
E(x2 ) = µ2 ; var(x2 ) = σ 2
µ1 − µ2
Normales con
E(x1 ) = µ1 ; var(x1 ) = σ 21
E(x2 ) = µ2 ; var(x2 ) = σ 22
σ21
σ22
Binomiales con
x1 ∼ B(n1 , p1 ); x2 ∼ B(n2 , p2 )
p1 − p2
(2) z0 < −zα
Siempre que
(3) z0 > zα
n1 , n2 → ∞
F0 > Fn1 −1;n2 −1;α/2 ó F0 < ±Fn1 −1;n2 −1;1−α/2
donde Fn1 −1;n2 −1;1−α/2 = 1 Fn2 −1;n1 −1;α/2
(2) F0 < Fn1 −1;n2 −1;1−α (3) F0 > Fn1 −1;n2 −1;α
(1)
ESTIMADORES-DOS POBLACIONES
Parámetro
Intervalo de confianza, IC(
s1 − α)
(
µ1 − µ2
(1-b)|t0 | > tn1 +n2 −2;α/2
(2-b) t0 < −tn1 +n2 −2;α
(3-b)t0 > tn1 +n2 −2;α
Sólo si hay n orm alidad
+ n1
n1 p̂1 + n2 p̂2
con p̂0 =
n1 + n2
ŝ2
F0 = 12
ŝ2
(1) |t0 | > tn−1;α/2
(2) t0 < −tn−1;α
(3) t0 > tn−1;α
S ólo si hay normalidad
(1) |z0 |, |t0 | > zα/2
(2) z0 , t0 < −zα
(3) z0 , t0 > zα
1 +(n2 −1)ŝ2
con ŝ2T = (n1 −1)ŝ
n1 +n2 −2
z0 = r (p̂1³−p̂2 ) ´
p̂0 q̂0
n→∞
(1-b) |t0 | > zα/2
(2-b) t0 < −zα
(3-b) t0 > zα
)
σ 21 σ22
µ1 − µ2 ∈ x̄1 − x̄2 ± zα/2
+
n1
n2
Si no hay normalidad, sólo si n1 , n2 → ∞
s
(
)
ŝ22
ŝ21
µ1 − µ2 ∈ x̄1 − x̄2 ± zα/2
+
n1
n2
r2 → ∞ ¾
½ Siem pre qu e n1 , n
1
1
µ1 − µ2 ∈ x̄1 − x̄2 ± zα/2 σ
+
n1 n2
Si no hay normalidad, sólo si n1 , n2 → ∞
r
½
¾
1
1
µ1 − µ2 ∈ x̄1 − x̄2 ± zα/2 ŝT
+
n1 n2
Siem pre qu e n1 , n2 → ∞
r
½
¾
1
1
µ1 − µ2 ∈ x̄1 − x̄2 ± tn1 +n2 −2;α/2 ŝT
+
n1 n2
Sólo si hay norm alidad
· 2
¸
ŝ1
ŝ21
σ21
∈
F
;
F
σ22
ŝ22 n2 −1;n1 −1;1−α/2 ŝ±22 n2 −1;n1 −1;α/2
donde Fn2 −1;n1 −1;1−α/2 = 1 Fnr
1 −1;n2 −1;α/2
½
¾
p̂1 q̂1 p̂2 q̂2
p1 − p2
∈
+
p̂1 − p̂2 ± zα/2
n1 ,n2 →∞
n1
n2