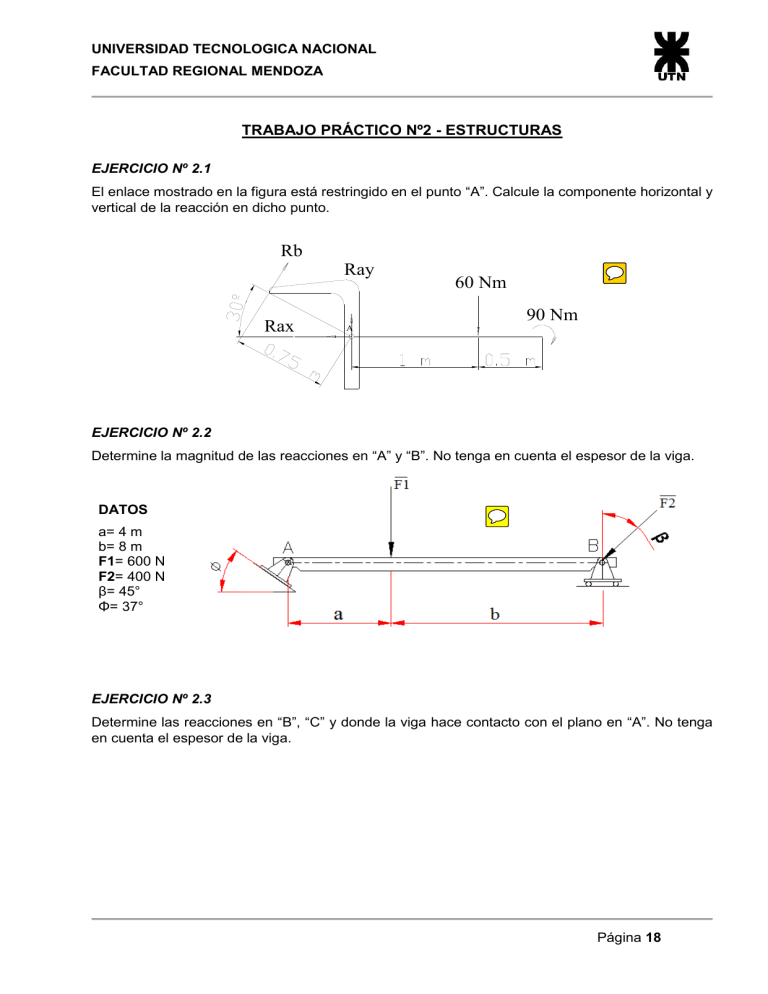
UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA TRABAJO PRÁCTICO Nº2 - ESTRUCTURAS EJERCICIO Nº 2.1 El enlace mostrado en la figura está restringido en el punto “A”. Calcule la componente horizontal y vertical de la reacción en dicho punto. Rb Ray Rax 60 Nm 90 Nm A EJERCICIO Nº 2.2 Determine la magnitud de las reacciones en “A” y “B”. No tenga en cuenta el espesor de la viga. DATOS a= 4 m b= 8 m F1= 600 N F2= 400 N β= 45° Φ= 37° EJERCICIO Nº 2.3 Determine las reacciones en “B”, “C” y donde la viga hace contacto con el plano en “A”. No tenga en cuenta el espesor de la viga. Página 18 UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA DATOS a= 4 m b= 2 m c= 6 m F1= 500 N F2= 800 N β= 60° α= 37° EJERCICIO Nº 2.4 Determine las componentes de reacción horizontal y vertical para la viga cargada como se muestra en la figura. Desprecie el peso de la viga en los cálculos. DATOS a= 2 m b= 3 m c= 2 m d= 0,2 m F1= 600 N F2= 200 N F1= 100 N EJERCICIO Nº 2.5 Determine las reacciones en los soportes de la viga de la figura. DATOS a= 8 m b= 4 m c= 5 m F= 500 N M= 800 Nm Página 19 UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA EJERCICIO Nº 2.6 Una fuerza “F” actúa sobre el extremo de la viga. Determine la magnitud y dirección de la reacción en el perno “A” y la tensión del cable “BC”. DATOS a= 6” b= 8” c= 3” d= 1,5” F= 150 lb EJERCICIO Nº 2.7 Dibuje el diagrama de cuerpo libre de la pieza mostrada en la figura y determine las reacciones. DATOS a= 0,25 m F= 50 kg β= 45° EJERCICIO Nº 2.8 El malacate mostrado en la figura está soportado por un cojinete de empuje en “A” (empuje axial y radial) y un cojinete en “B” (radial), los cuales están adecuadamente alineados sobre el eje. Determine la magnitud de la fuerza vertical “P” que debe aplicarse al mango para mantener el equilibrio de la carga “F”. También calcule las reacciones en los cojinetes. Página 20 UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA DATOS a= 0,26 m b= 0,5 m c= 0,15 m d= 0,3 m e= 0,2 m f= 0,1 m F= 981 N Φ= 20° EJERCICIO Nº 2.9 Suponiendo que el máximo valor admisible para cada una de las reacciones es de 150 Kg, y que la reacción en “A” debe estar dirigida hacia arriba, determinar el intervalo de valores de “F3” dentro del cual la viga mostrada no ofrece peligro. DATOS a= 1,5 m b= 3 m c= 1 m d= 1 m F1= 30 kg F2= 30 kg EJERCICIO Nº 2.10 Una viga en voladizo está cargada como se indica en la figura, empotrada en el extremo izquierdo y libre en el derecho. Determine las reacciones en “A”. Página 21 UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA DATOS a= 1,5 m b= 2,5 m c= 2 m F1= 200 kg F2= 400 kg F3= 800 kg EJERCICIO Nº 2.11 Una grúa fija de una tonelada de peso se emplea para levantar una carga “W”. La grúa es sostenida por medio de un pasador fijo en “B” y un apoyo deslizante en “A”. El centro de gravedad está localizado en “G”. Determinar las componentes de las reacciones en “A” y “B”. DATOS a= 2 m b= 4 m c= 1,5 m W= 2,4 t Página 22 UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA EJERCICIO Nº 2.12 Determine los esfuerzos que actúan en todas las barras de la estructura mostrada. DATO S a= 5 m F= 500 kN α= 20° β= 65° A continuación se explicará el procedimiento para resolver ejercicios de cálculo de esfuerzos en elementos de estructuras, por el método de los nodos y el método de las secciones. A- MÉTODO DE LOS NODOS “Este método se basa en el hecho de que toda la armadura está en equilibrio y por lo tanto todos los nodos también lo están. Trazando el diagrama de cuerpo libre de cada nodo, se pueden emplear las ecuaciones de equilibrio para obtener las fuerzas que actúan en los elementos de la armadura”. Inicialmente debemos representar la armadura mediante un diagrama de cuerpo libre consignando todas las fuerzas activas y reactivas que actúan en ella para obtener las reacciones en los vínculos “A” y “C”. Planteando ecuaciones de equilibrio estático en el plano: ∑ Fx = 0 = 500 kN − RCx → 𝐑𝐂𝐱 = 𝟓𝟎𝟎 𝐤𝐍 ∑ Fy = 0 = −RAy + RCy → 𝐑𝐂𝐲 = 𝐑𝐀𝐲 = 𝟏𝟏𝟔, 𝟓 𝐤 𝐍 ∑ MA = 0 = −500 kN ∗ 2,33 m + RCy ∗ 10 m → RCy = 116,5 kN Una vez obtenidas las reacciones vamos a dibujar el diagrama de cuerpo libre de un nodo que tenga al menos una fuerza conocida y como mucho dos fuerzas desconocidas. De este modo, la aplicación de ΣFx= 0 y ΣFy= 0 resulta en dos ecuaciones algebraicas de las cuales se pueden despejar las dos incógnitas. Página 23 UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA Suponga siempre que las fuerzas desconocidas en los elementos que actúan en el diagrama de cuerpo libre del nodo se alejan del mismo como “jalándolo” (las suponemos de tensión). Si se procede así, entonces la solución numérica de las ecuaciones de equilibrio darán escalares positivos para elementos en tensión y escalares negativos para elementos en compresión. Nodo A. El diagrama de cuerpo libre del nodo se muestra a continuación. Al aplicar las ecuaciones de equilibrio en el mismo, tenemos: ∑ Fx = 0 = FAB ∗ cos 25° + FAD ∗ cos 20° ∑ Fy = 0 = −116,5 kN + FAB ∗ sen 25° + FAD ∗ sen 20° Resolviendo el sistema de ecuaciones: 𝐅𝐀𝐁 = 𝟏𝟐𝟓𝟔 𝐤𝐍 (T) 𝐅𝐀𝐃 = −𝟏𝟐𝟏𝟏 𝐤𝐍 (C) Podemos ver que la barra AB se encuentra traccionada mientras que AD se encuentra comprimida. Una vez que se conocen estas tensiones vemos claramente que podemos proceder a calcular las tensiones en las barras restantes aplicando las ecuaciones de equilibrio en los otros nodos. Nodo C. A partir del diagrama de cuerpo libre del nodo, establecemos: ∑ Fx = 0 = −500 kN − FCB ∗ cos 25° − FCD ∗ cos 20° ∑ Fy = 0 = 116,5 kN + FCB ∗ sen 25° + FCD ∗ sen 20° Luego, las tensiones en las barras son: 𝐅𝐂𝐁 = 𝟕𝟎𝟔 𝐤𝐍 (T) 𝐅𝐂𝐃 = −𝟏𝟐𝟏𝟑 𝐤𝐍 (C) Observamos que, para el sentido de las fuerzas convenido, la barra CB se encuentra traccionada a la vez que CD se encuentra trabajando a la compresión. Finalmente podemos calcular la fuerza en la barra BD, a partir de los nodos B o D, ya que conocemos las fuerzas en el resto de los elementos de la armadura. Nodo B. Para este nodo las ecuaciones de equilibrio quedan: ∑ Fx = 0 = 500 kN − FAB ∗ cos 25° + FCB ∗ cos 25° ∑ Fy = 0 = −FBD − FAB ∗ sen 25° − FCB ∗ sen 25° Reemplazando los valores de FAB y FCB, y resolviendo el sistema tenemos: Página 24 UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA 𝐅𝐁𝐃 = −𝟖𝟐𝟗 𝐤𝐍 (C) De este modo quedan calculadas todas las fuerzas en los elementos de la armadura. Otro procedimiento utilizado para determinar las fuerzas en una armadura es el método de las secciones que detallamos a continuación. B- MÉTODO DE LAS SECCIONES “El presente se basa en el hecho de que si la armadura está en equilibrio, entonces cualquier elemento de la misma también lo estará”. Para resolver un problema por el método enunciado debemos trazar en el diagrama de cuerpo libre de la armadura una sección imaginaria que pase por no más de 3 elementos desconocidos, ya que solo podemos aplicar 3 ecuaciones de equilibrio independientes en el plano (ΣFx= 0; ΣFy= 0; ΣM= 0). En caso de que se corten más elementos, nos tendremos que valer de más secciones para resolver el problema. En el diagrama de cuerpo libre de arriba hemos marcado dos posibles secciones. Seleccionamos arbitrariamente la sección a-a. A continuación debemos utilizar el diagrama de cuerpo libre de la armadura a la izquierda o a la derecha de la sección a-a. Nos inclinaremos por la parte izquierda debido a que posee una menor cantidad de fuerzas: Página 25 UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA Hemos adoptado la misma forma de proceder que en el método anterior en cuanto al sentido de las fuerzas. Las consideramos a todas de tracción (como “jalando al eslabón”), y, por lo tanto, un signo negativo nos va a indicar que la fuerza posee el sentido contrario y actúa comprimiendo la barra. Si planteamos el equilibrio de fuerzas para la parte izquierda de la armadura, tenemos: ∑ Fx = 0 = FAB ∗ cos 25° + FCD ∗ cos 20° ∑ Fy = 0 = −RAy + FBD + FAB ∗ sen 25° − FCD ∗ sen 20° ∑ MD = 0 = RAy ∗ 5 m − FAB ∗ d Siendo “d” la distancia perpendicular desde el nodo “D” a la recta de acción de FAB. Las reacciones en los vínculos fueron calculadas anteriormente y sus valores resultaron: 𝐑𝐂𝐱 = 𝟓𝟎𝟎 𝐤𝐍 𝐑𝐂𝐲 = 𝐑𝐀𝐲 = 𝟏𝟏𝟔, 𝟓 𝐤𝐍 Por lo tanto reemplazando estos valores y resolviendo el sistema de 3 ecuaciones con 3 incógnitas, tenemos: FAB = 1256 kN (T) FCD = −1213 kN (C) FBD = −829 kN (C) Finalmente el valor de las fuerzas en las barras CB y AD se puede obtener aplicando el método de los nodos ya visto, o nuevamente aplicando el procedimiento de las secciones. En la imagen que sigue podemos observar el cálculo aproximado de la armadura realizado mediante el software Mdsolids. Aclaramos que es aproximado debido a que el programa posee escalas determinadas por lo que no se han podido introducir las medidas exactas de la armadura: Página 26 UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA Como conclusión podemos decir que la selección del método a emplear para el cálculo de fuerzas en armaduras va a depender del caso que se nos presente y de las herramientas conceptuales que haya adquirido el alumno mediante la ejercitación, que le permitirán decidir por la metodología más eficiente para la resolución del problema. EJERCICIO Nº 2.13 La estructura utilizada para soportar un balcón se encuentra sujeta a la carga mostrada. Aproxime cada unión como un perno y determine la fuerza en cada miembro, estableciendo si los miembros se encuentran sometidos a tracción o compresión. Página 27 UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA DATOS a= 1 m b= 1 m c= 1 m F1= 6 kN F1= 4 kN α= 45° β= 45° EJERCICIO Nº 2.14 Determine la fuerza en cada miembro de la estructura y establezca si los miembros se encuentran a tracción o compresión. Página 28 UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA DATOS a= 2 m b= 2 m c= 1,5 m F1= 8 kN F2= 4 kN F3= 10 kN EJERCICIO Nº 2.15 Determine la fuerza en cada miembro de la estructura y establezca si los miembros se encuentran a tracción o compresión. DATOS a= 10 ft b= 10 ft c= 10 ft d= 10 ft F1= 100 lb F2= 200 lb F3= 300 lb α= 30° Página 29 UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA EJERCICIO Nº 2.16 La armadura Howe para puente está sometida a las cargas que se muestran. Determine la fuerza en los elementos “HI”, “HB” y “BC”, y establezca si los elementos están en tracción o compresión. DATOS a= 4 m F1= 20 kg F2= 20 kg F3= 40 kg Página 30 UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA EJERCICIO Nº 2.17 Determine la fuerza en los miembros “CD”, “CJ”, “KJ”, Y “DJ” de la armadura que sirve para soportar la estructura de un puente. Establezca si se encuentran en tracción o en compresión. DATOS a= 9” b= 9” c= 9” d= 9” e= 9” f= 9” g= 12” F1= 4000 lb F2= 8000 lb F3= 5000 lb EJERCICIO Nº 2.18 Determine la fuerza en el miembro “EB” de la estructura de techo mostrada en la figura. Indique si tal miembro se encuentra en tracción o en compresión. DATOS a= 2 m b= 2 m c= 2 m d= 2 m F1= 1000 N F2= 3000 N F3= 1000 N F4= 1000 N α= 30° EJERCICIO Nº 2.19 Determine la fuerza en cada barra de la estructura y establezca si las mismas se encuentran traccionadas o comprimidas. Página 31 UNIVERSIDAD TECNOLOGICA NACIONAL FACULTAD REGIONAL MENDOZA DATOS a= 2 m b= 4 m c= 2 m d= 4 m F1= 400 kg F2= 100 kg EJERCICIO Nº 2.20 Determine la fuerza en cada barra de la estructura mostrada, indique si se encuentran en tracción o compresión. DATOS a= 5 m b= 5 m c= 6 m F1= 700 kg F1= 600 kg EJERCICIO Nº 2.21 Determine la fuerza en cada barra de la estructura mostrada. Indique si se encuentran en tracción o compresión. DATOS a= 3 m b= 3 m F1= 8 kN F1= 600 kN Página 32